Trajectory Segmentation and Clustering in Terminal Airspace Using Transformer–VAE and Density-Aware Optimization
Abstract
1. Introduction
1.1. Literature Review
1.2. Our Contributions
- (1)
- We develop a dynamic-featured segmentation algorithm (DFE-MDL) that incorporates speed variation and heading rate into the description length criterion, thereby improving robustness under irregular sampling and maneuvering noise while preserving critical trajectory structures.
- (2)
- We design a Transformer–VAE model for representation learning and couple the encoder with clustering assignments through a joint optimization procedure, enabling the generation of compact and separable latent embeddings that enhance clustering consistency.
- (3)
- We validate the proposed framework using large-scale ADS-B data collected from a busy terminal area, and the results demonstrate notable improvements in clustering quality, trajectory discrimination, and computational efficiency, confirming its operational relevance in complex terminal environments.
1.3. Organization of This Paper
2. Methodology
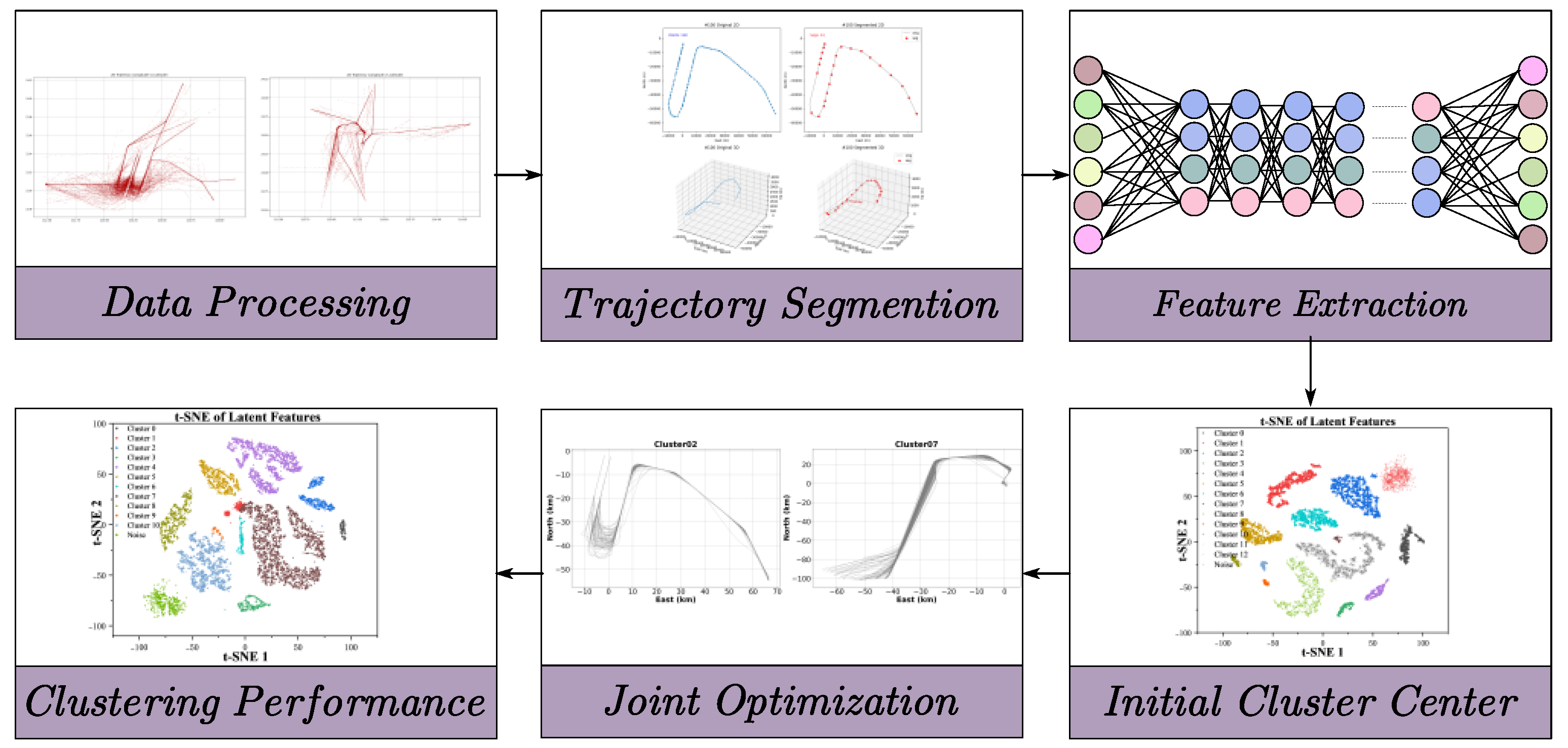
2.1. Overview of the Proposed Method
2.2. Data Preprocessing
- WGS−84 to Earth-Centered Earth-Fixed (ECEF):
- 2.
- Convert ECEF to ENU using a reference point:
- To enrich the motion description, several dynamic features are derived. Specifically:
- Speed change rate:
- Heading angle change rate:
- Linear acceleration:
2.3. Trajectory Segmentation
2.4. Derivation of Dynamic and Geometric Features
2.5. Cluster Initialization and Joint Optimization
- Initial Cluster Assignment via HDBSCAN
- 2.
- Soft Assignment and Target Distribution
- 3.
- Optimization Objective and Training Procedure
- Encode all trajectories using the Transformer–VAE to obtain ;
- Apply HDBSCAN to obtain initial cluster centers ;
- Compute soft assignments and target distribution ;
- Update encoder parameters and cluster centers by minimizing ;
- Repeat steps 3–4 until convergence criteria are met, such as stabilization of cluster assignments or reduction in KL divergence.
3. Experimental Results
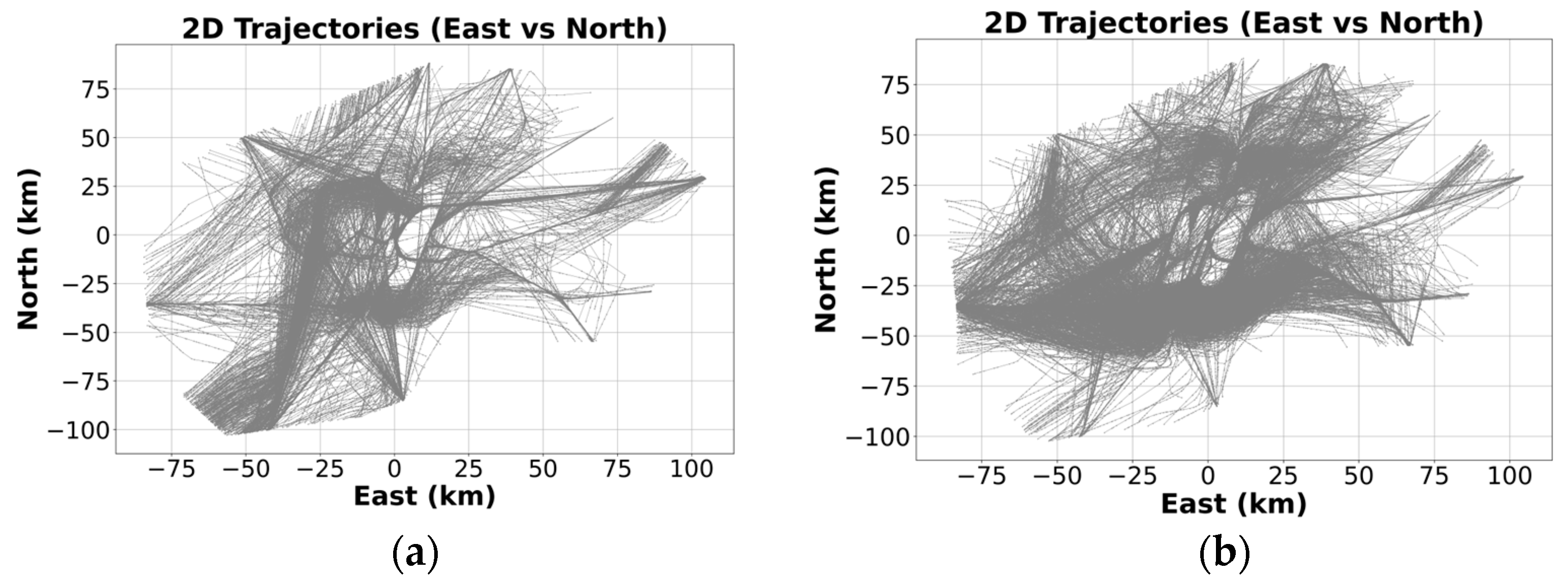
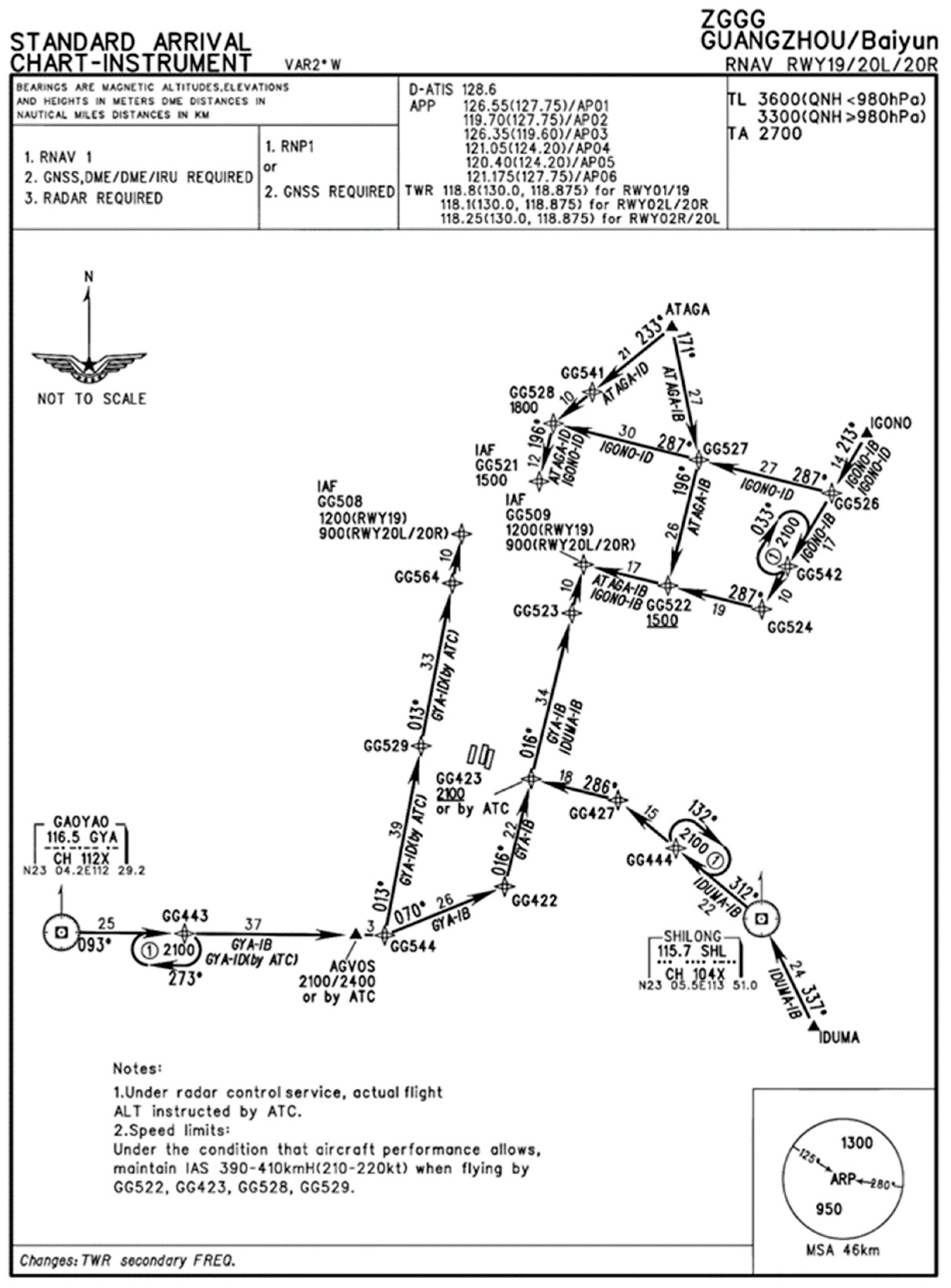
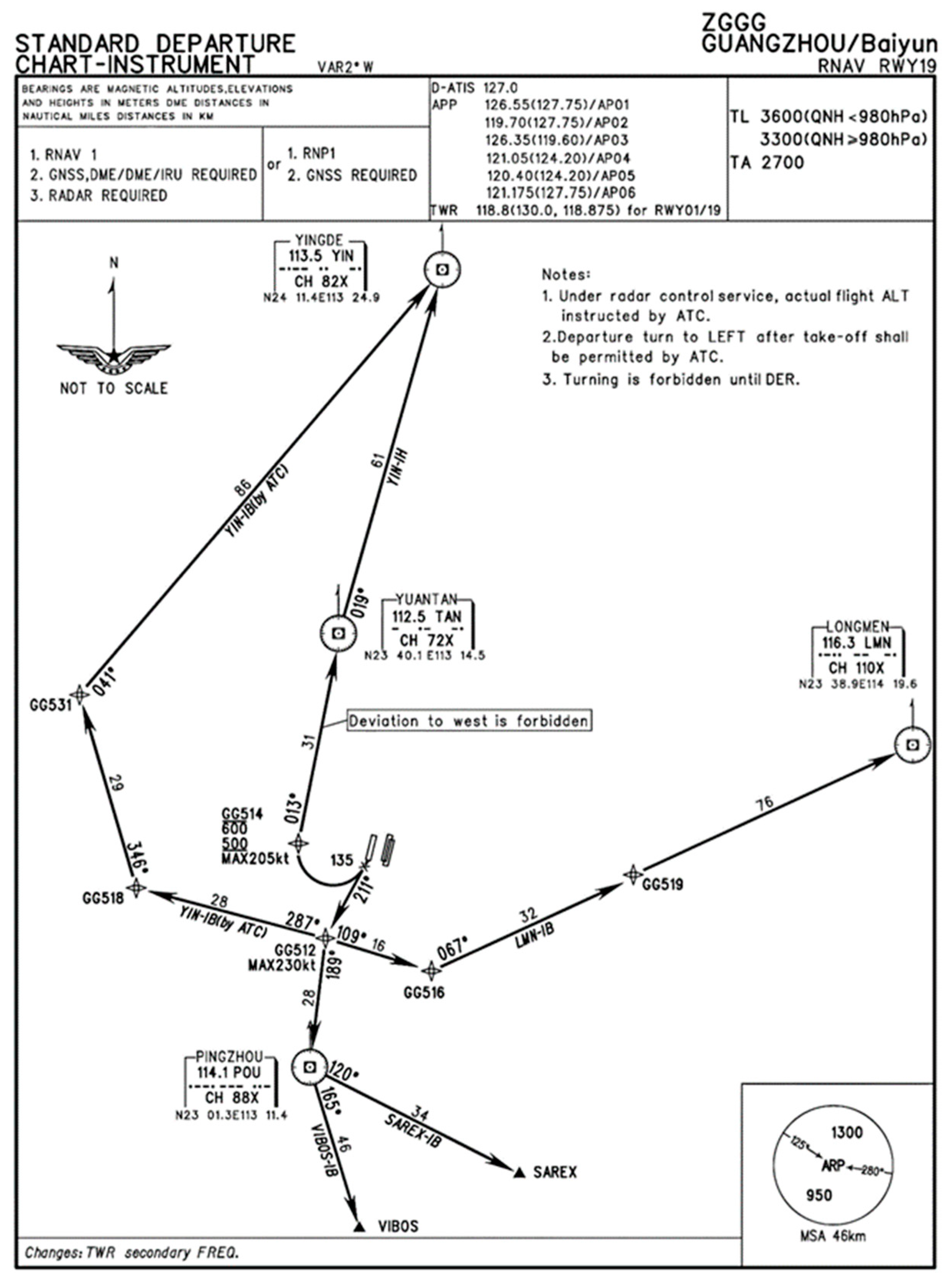
3.1. Dataset
3.2. Experimental Setup
3.3. Evaluation Metrics and Visualization
- Clustering Evaluation Metrics
- 2.
- Latent Space Visualization
- 3.
- Optimization Convergence Monitoring
3.4. Verification of the Segmentation Algorithm
3.5. Feature Extraction
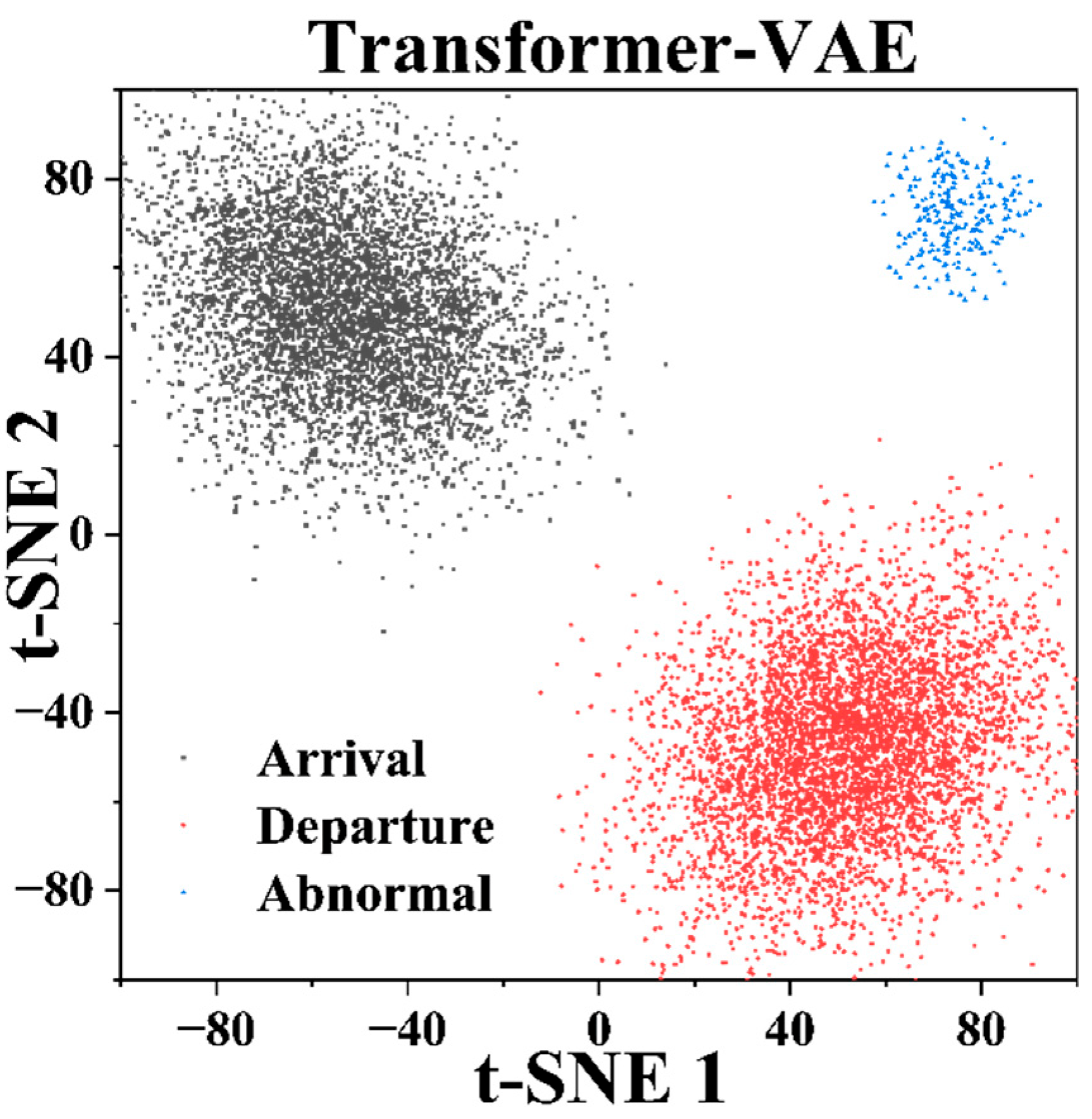
3.5.1. Latent Space Visualization and Discrimination Analysis
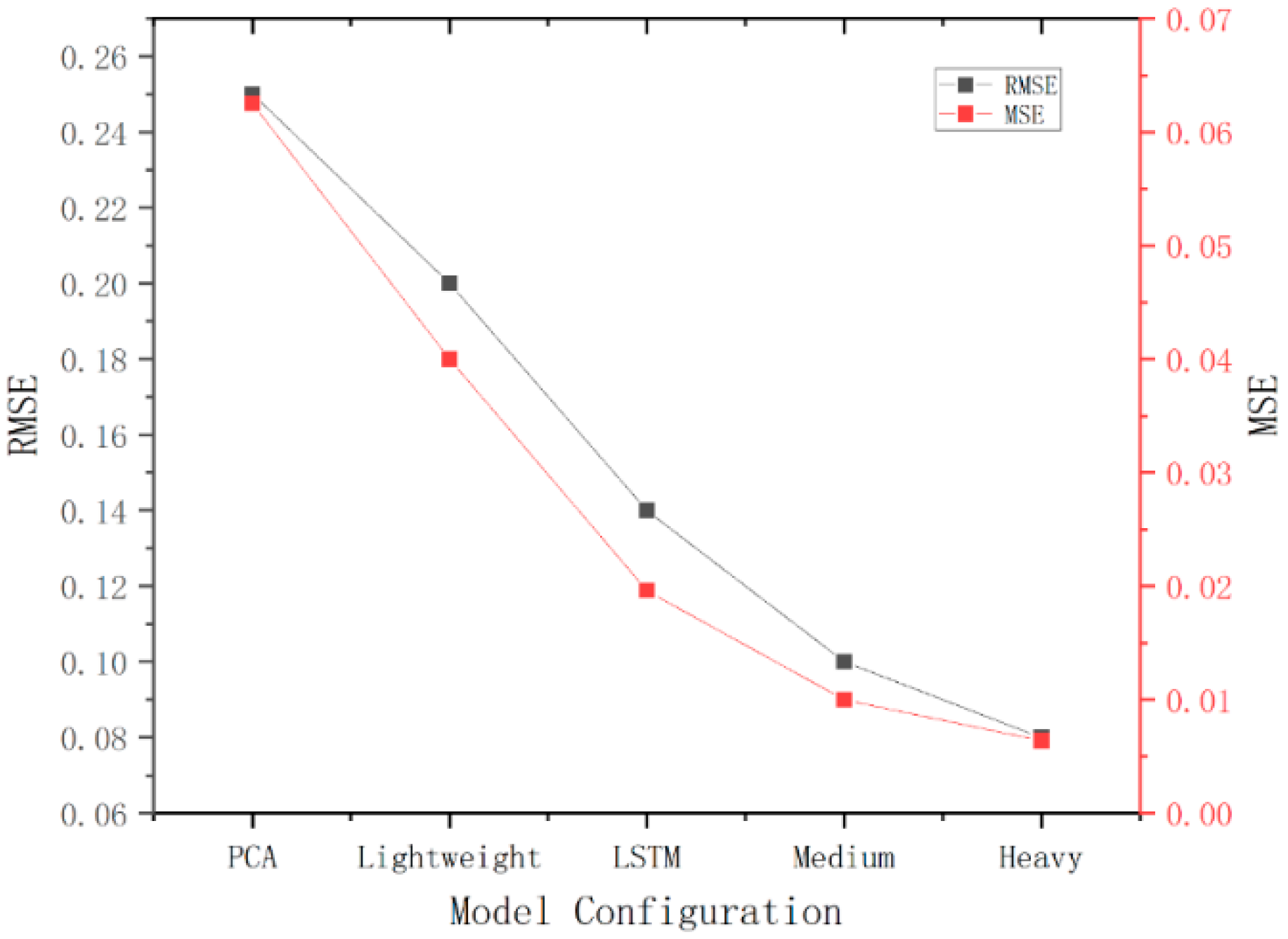
3.5.2. Comparison with Other Feature Extraction Models
3.6. Initial Cluster Center Extraction
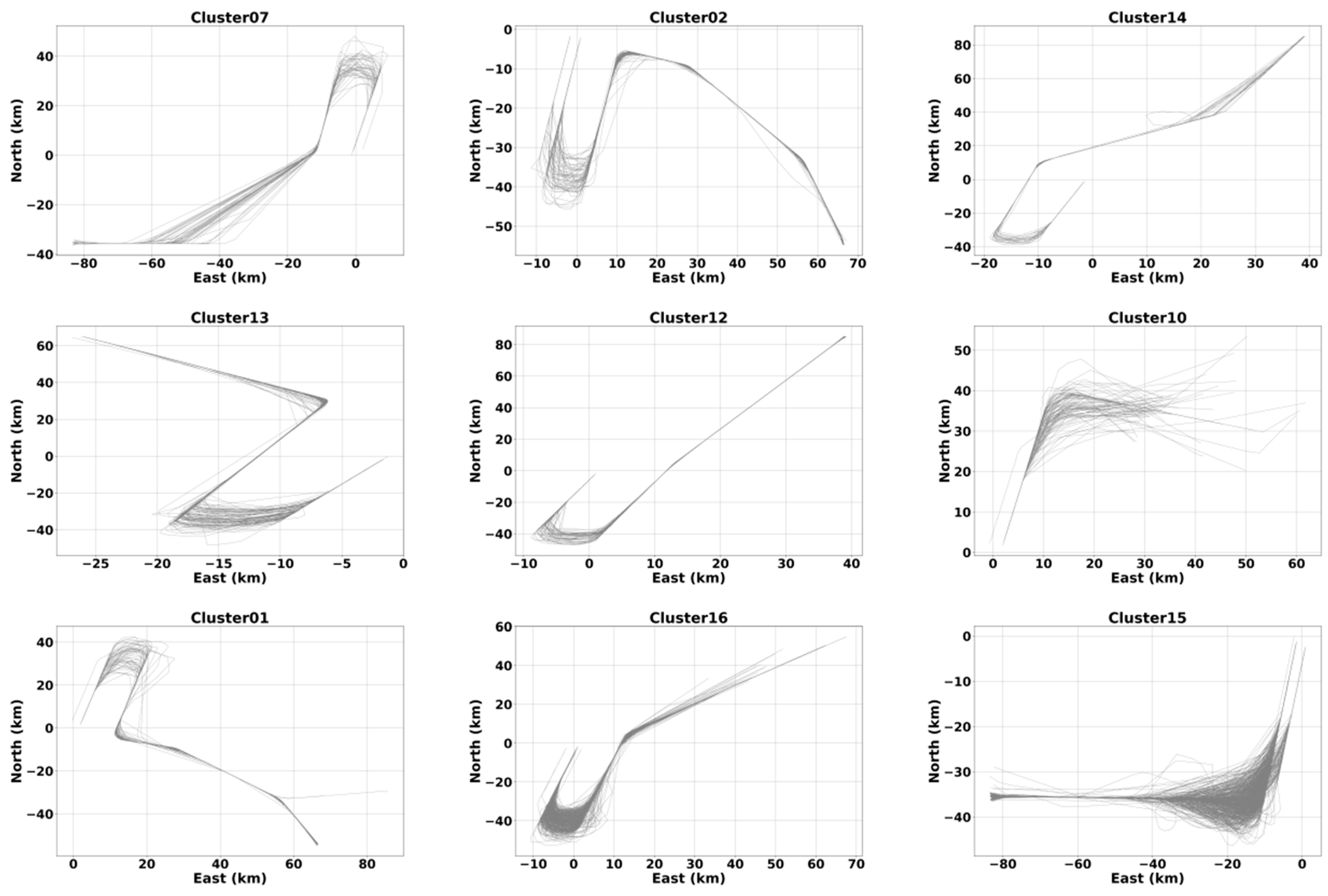
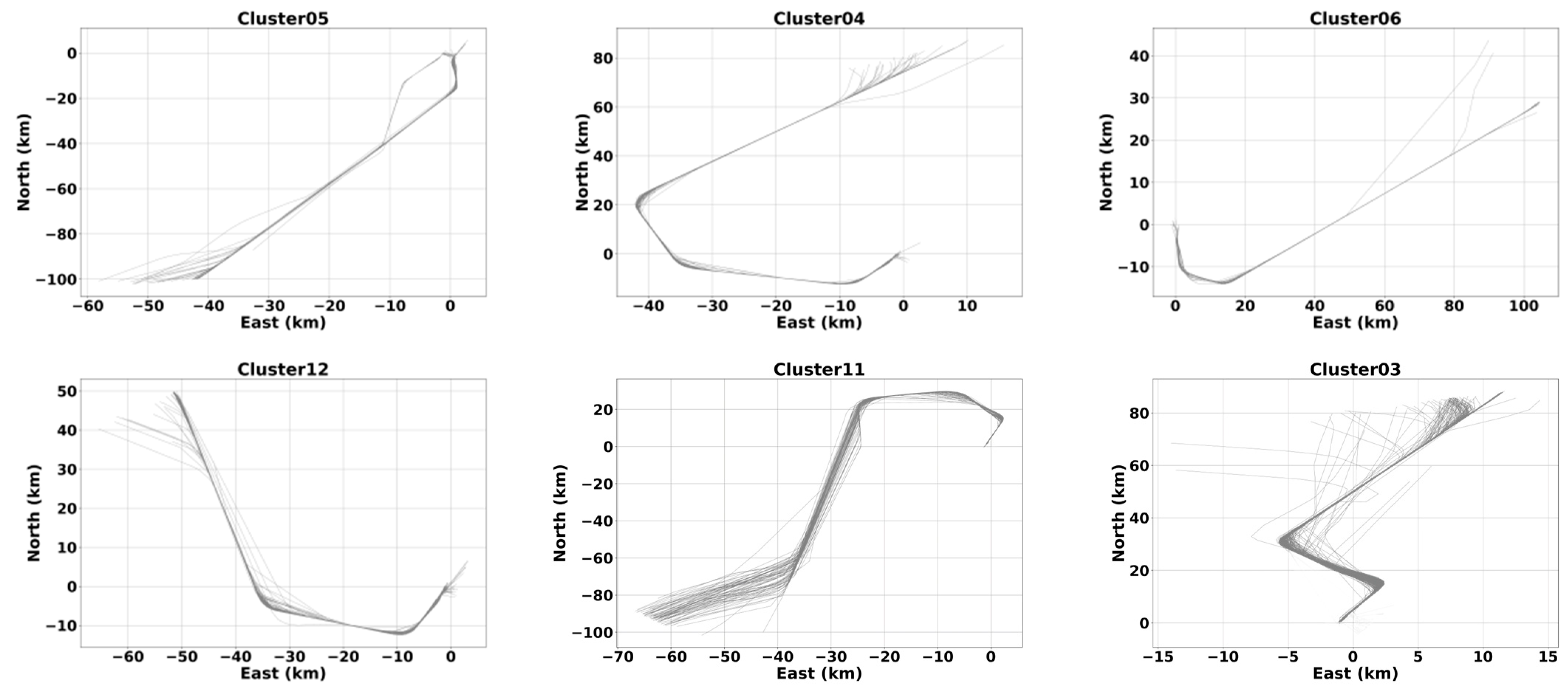
3.7. Trajectory Clustering Results and Visualization
3.7.1. Clustering Results for Arrival Trajectories
3.7.2. Clustering Results for Departure Trajectories
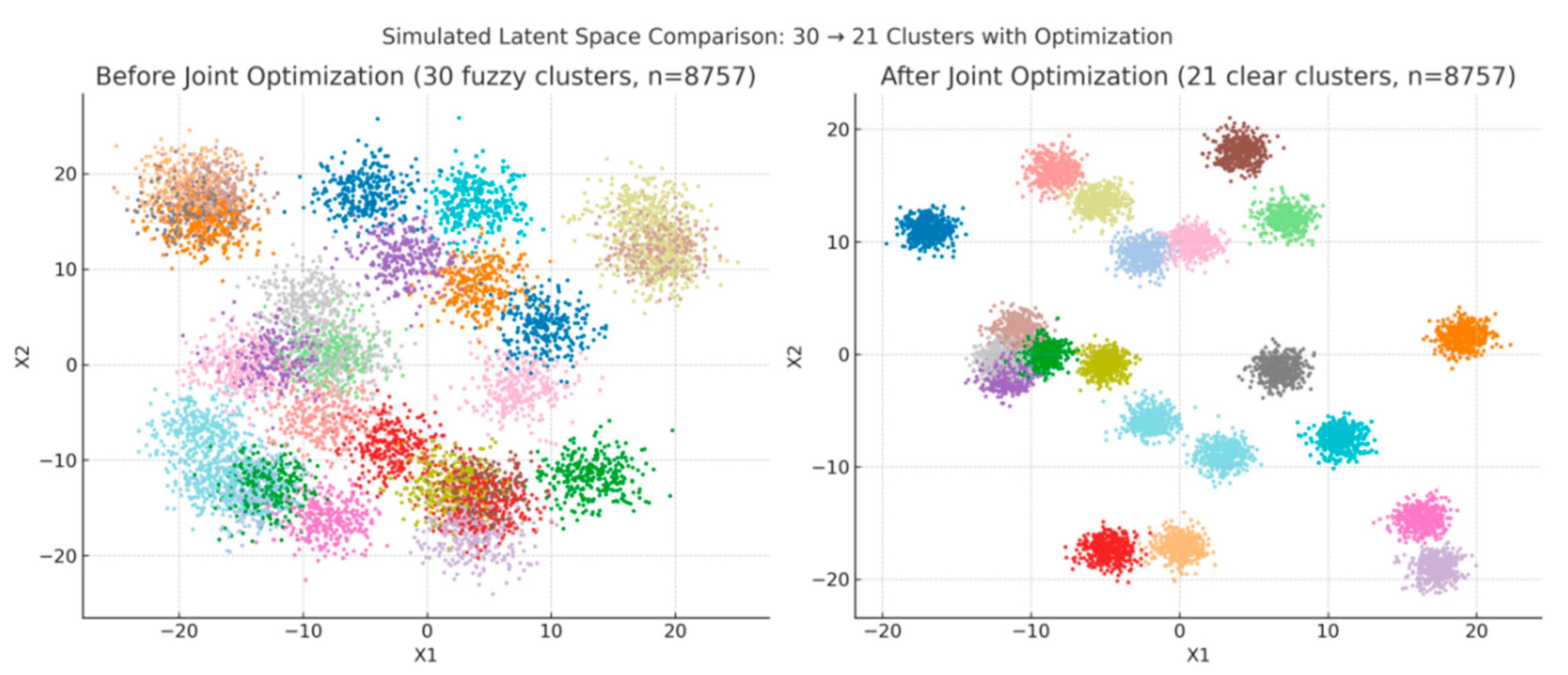
3.8. Effectiveness of Joint Optimization
3.9. Computational Efficiency and Large-Scale Evaluation
4. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TMAs | Terminal Maneuvering Areas |
| ATM | Air Traffic Management |
| TBO | Trajectory Based Operations |
| ATOP | Aircraft Trajectory Optimization Problem |
| t-SNE | t-Distributed Stochastic Neighbor Embedding |
| HDBSCAN | Hierarchical Density-based Spatial Clustering of Applications with Noise |
| VAE | Variational Autoencoder |
References
- ICAO. Annual Safety Report 2023; ICAO: Montreal, QC, Canada, 2023. [Google Scholar]
- Eurocontrol. Challenges of Growth 2018—Summary Report; Eurocontrol: Brussels, Belgium, 2018. [Google Scholar]
- SESAR Joint Undertaking. European ATM Master Plan—Digitalising Europe’s Aviation Infrastructure; SESAR JU: Brussels, Belgium, 2020. [Google Scholar]
- ICAO. Global Air Navigation Plan 2022–2038; ICAO: Montreal, QC, Canada, 2022. [Google Scholar]
- Olive, X.; Basora, L.; Delahaye, D. Deep learning for aircraft trajectory clustering: An enabler for traffic complexity analysis. Transp. Res. Part C Emerg. Technol. 2023, 147, 103956. [Google Scholar] [CrossRef]
- Wang, S.; Wu, Y.; Wang, Y. Deep spatiotemporal trajectory representation learning for clustering. IEEE Trans. Intell. Transp. Syst. 2024, 25, 7687–7700. [Google Scholar] [CrossRef]
- Lee, J.G.; Han, J.; Whang, K.Y. Trajectory clustering: A partition-and-group framework. In Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data, Beijing, China, 11–14 June 2007; pp. 593–604. [Google Scholar] [CrossRef]
- Li, Z.; Ding, B.; Han, J.; Kays, R.; Nye, P. Mining periodic behaviors for moving objects. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–28 July 2010; pp. 1099–1108. [Google Scholar] [CrossRef]
- Mahboubi, H.; Miller, N.; Kamgarpour, M. Trajectory Clustering with Application to Air Traffic. In AIAA Scitech 2021 Forum; AIAA: Reston, VA, USA, 2021. [Google Scholar] [CrossRef]
- Bolić, T.; Pantazis, A.; Reyes, L. Trajectory clustering for air traffic categorisation. Aerospace 2022, 9, 227. [Google Scholar] [CrossRef]
- Hao, J.-Y.; Xu, C.; Fan, R.; Li, S.; Zhang, T. Trajectory clustering based on length-scale directive Hausdorff. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, The Netherlands, 6–9 October 2013; pp. 1300–1305. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational Bayes. arXiv 2014. [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Zhang, W.; Hu, M.; Du, J. An end-to-end framework for flight trajectory data analysis based on deep autoencoder network. Aerosp. Sci. Technol. 2022, 123, 107726. [Google Scholar] [CrossRef]
- Liu, Y.; Ng, K.H.; Chu, N.; Hon, K.K.; Zhang, X. Spatiotemporal image-based flight trajectory clustering model with deep convolutional autoencoder network. J. Aerosp. Inf. Syst. 2023, 20, 234–247. [Google Scholar] [CrossRef]
- Postnikov, A.; Gamayunov, A.; Ferrer, G. Transformer-based trajectory prediction. arXiv 2021, arXiv:2112.04350. [Google Scholar] [CrossRef]
- Nogueira, T.P.; Braga, R.B.; Oliveira, C.T.; Martin, H. FrameSTEP: A framework for annotating semantic trajectories based on episodes. Expert Syst. Appl. 2018, 92, 533–545. [Google Scholar] [CrossRef]
- Cao, H.; Mamoulis, N.; Cheung, D.W. Discovery of periodic patterns in spatiotemporal sequences. IEEE Trans. Knowl. Data Eng. 2007, 19, 453–467. [Google Scholar] [CrossRef]
- Hu, D.; Chen, L.; Fang, H.; Fang, Z.; Li, T.; Gao, Y. Spatio-temporal trajectory similarity measures: A comprehensive survey and quantitative study. IEEE Trans. Knowl. Data Eng. 2024, 36, 2191–2212. [Google Scholar] [CrossRef]
- Fang, Z.; Du, Y.; Zhu, X.; Hu, D.; Chen, L.; Gao, Y.; Jensen, C.S. Spatio-temporal trajectory similarity learning in road networks. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 347– 356. [Google Scholar] [CrossRef]
- Li, L.; Si, J.; Lv, J.; Lu, J.; Zhang, J.; Dai, S. MSST: Multi-scale spatial-temporal representation learning for trajectory similarity computation. IEEE Trans. Big Data 2025, 11, 2657–2668. [Google Scholar] [CrossRef]
- Su, H.; Liu, S.; Zheng, B.; Zhou, X.; Zheng, K. A survey of trajectory distance measures and performance evaluation. VLDB J. 2020, 29, 3–32. [Google Scholar] [CrossRef]
- Liang, A.; Yao, B.; Wang, B.; Liu, Y.; Chen, Z.; Xie, J.; Li, F. Sub-trajectory clustering with deep reinforcement learning. VLDB J. 2024, Online First. [Google Scholar] [CrossRef]
- Zeng, W.; Guo, X.; Chen, W.; Zhang, R.; Liu, P. Aircraft trajectory clustering in terminal airspace based on deep autoencoder and Gaussian mixture model. Aerosp. Sci. Technol. 2022, 122, 107674. [Google Scholar] [CrossRef]
- Barratt, S.T.; Kochenderfer, M.J.; Boyd, S.P. Learning probabilistic trajectory models of aircraft in terminal airspace from position data. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3536–3545. [Google Scholar] [CrossRef]
- Bombelli, A.; Soler, L.; Trumbauer, E.; Mease, K.D. Strategic air traffic planning with Fréchet distance aggregation and rerouting. J. Guid. Control Dyn. 2017, 40, 700–711. [Google Scholar] [CrossRef]
- Zhang, W.; Payan, A.; Mavris, D.N. Air traffic flow identification and recognition in terminal airspace through machine learning approaches. In Proceedings of the AIAA Scitech 2024 Forum, Orlando, FL, USA, 8–12 January 2024. Paper AIAA 2024-0536. [Google Scholar] [CrossRef]
- Paradis, C.; Davies, M.D. Visualizing corridors in terminal airspace using trajectory clustering. In Proceedings of the IEEE/AIAA 41st Digital Avionics Systems Conference (DASC), Portsmouth, VA, USA, 18–22 September 2022. [Google Scholar] [CrossRef]








| Method | RMSE | APD |
|---|---|---|
| Uniform Sampling | 0.0571 | 0.0312 |
| Douglas–Peucker | 0.0465 | 0.0251 |
| Visvalingam–Whyatt | 0.0423 | 0.0215 |
| DFE-MDL (proposed) | 0.0294 | 0.0187 |
| Dimensions | RMSE | MAE |
|---|---|---|
| East (km) | 0.0018 | 0.0014 |
| North (km) | 0.0015 | 0.0012 |
| Altitude (m) | 22.6 | 18.2 |
| Speed (kt) | 5.2 | 4.1 |
| Heading angle (°) | 7.1 | 5.6 |
| Model Parameters | Light | Medium |
|---|---|---|
| Hidden Dimensions | 128 | 256 |
| Number of Encoder and Decoder Layers | 2 | 4 |
| Feedforward Network Dimension | 512 | 1204 |
| Initialization Strategy | SSE | Silhouette Coefficient | Calinski-Harabasz | Davies-Bouldin |
|---|---|---|---|---|
| Random | 520.4 | 0.5 | 300.2 | 0.9 |
| K-means++ | 480.1 | 0.58 | 350.7 | 0.72 |
| HDBSCAN | 430.7 | 0.65 | 410.9 | 0.55 |
| Metric | Before Optimization | After Optimization |
|---|---|---|
| SSE | 124,500 | 83,200 |
| Silhouette Coefficient | 0.31 | 0.48 |
| Calinski–Harabasz | 4300 | 7950 |
| Davies–Bouldin | 1.87 | 1.12 |
| Module Stage | Processing Time (per Trajectory) | Before Optimization (Full Trajectory) | After Optimization (Segmented + Filtered) |
|---|---|---|---|
| Trajectory Preprocessing | ~5 ms | ~5 ms | Constant |
| Segmentation Computation | Avg. 42 ms | ~95 ms | Reduced to 28 ms |
| Feature Extraction (VAE) | ~22 ms | — | Constant |
| Clustering Initialization (HDBSCAN) | ~1.3 min (overall) | — | Constant |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Le, M. Trajectory Segmentation and Clustering in Terminal Airspace Using Transformer–VAE and Density-Aware Optimization. Aerospace 2025, 12, 969. https://doi.org/10.3390/aerospace12110969
Chen Q, Le M. Trajectory Segmentation and Clustering in Terminal Airspace Using Transformer–VAE and Density-Aware Optimization. Aerospace. 2025; 12(11):969. https://doi.org/10.3390/aerospace12110969
Chicago/Turabian StyleChen, Quanquan, and Meilong Le. 2025. "Trajectory Segmentation and Clustering in Terminal Airspace Using Transformer–VAE and Density-Aware Optimization" Aerospace 12, no. 11: 969. https://doi.org/10.3390/aerospace12110969
APA StyleChen, Q., & Le, M. (2025). Trajectory Segmentation and Clustering in Terminal Airspace Using Transformer–VAE and Density-Aware Optimization. Aerospace, 12(11), 969. https://doi.org/10.3390/aerospace12110969





