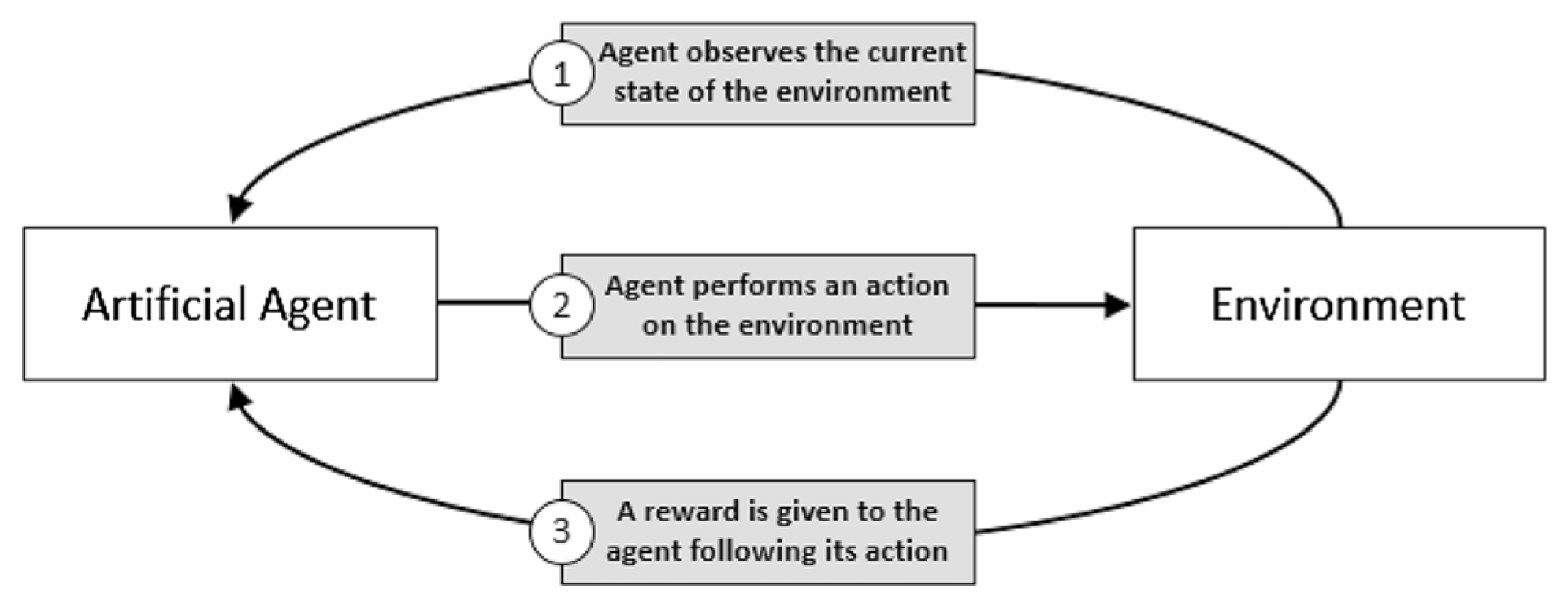
Figure 1.
Structure of a Reinforcement Learning algorithm [
6].
Figure 1.
Structure of a Reinforcement Learning algorithm [
6].
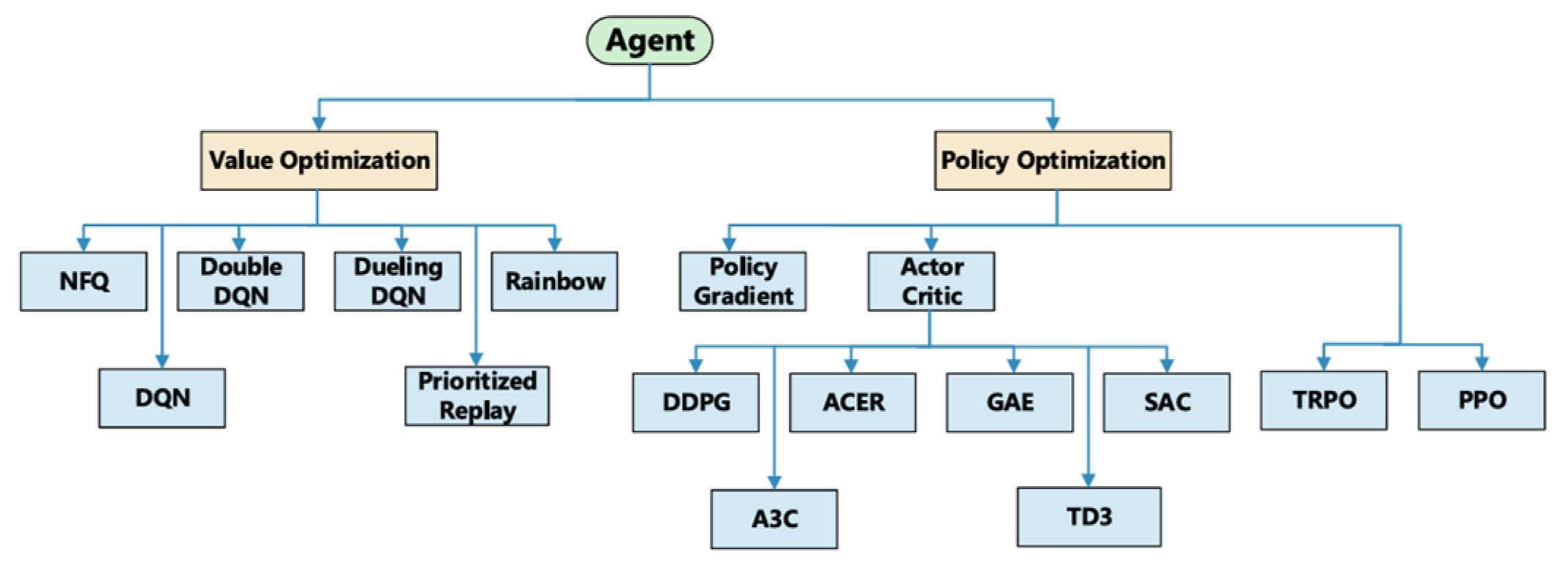
Figure 2.
Scheme of deep reinforcement learning agents [
11].
Figure 2.
Scheme of deep reinforcement learning agents [
11].
Figure 3.
Comparison of analyses obtained with NeuralFoil and XFOIL models [
15].
Figure 3.
Comparison of analyses obtained with NeuralFoil and XFOIL models [
15].
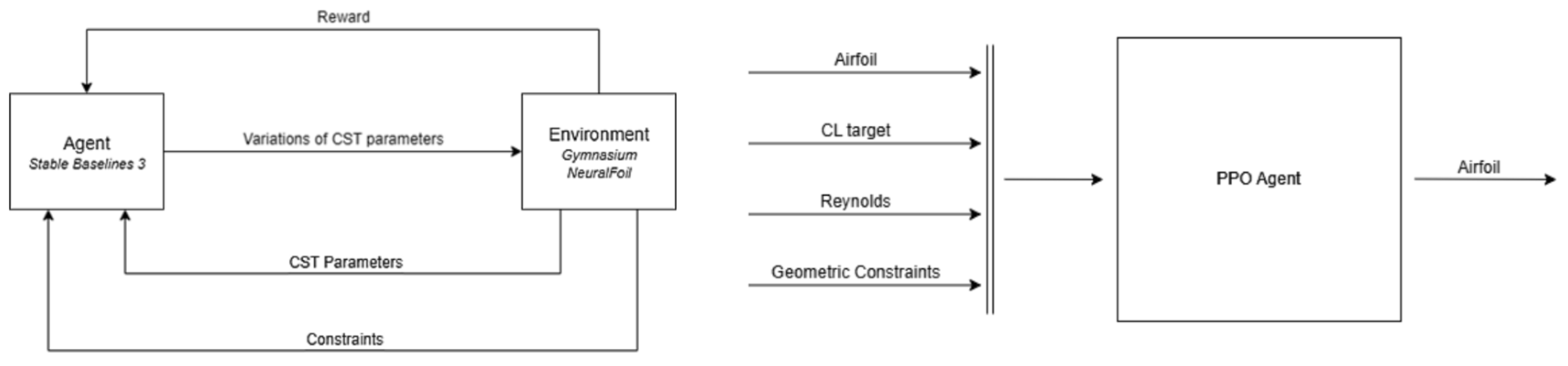
Figure 4.
Flow chart of the optimisation process.
Figure 4.
Flow chart of the optimisation process.
Figure 5.
Block diagram of the inference process.
Figure 5.
Block diagram of the inference process.
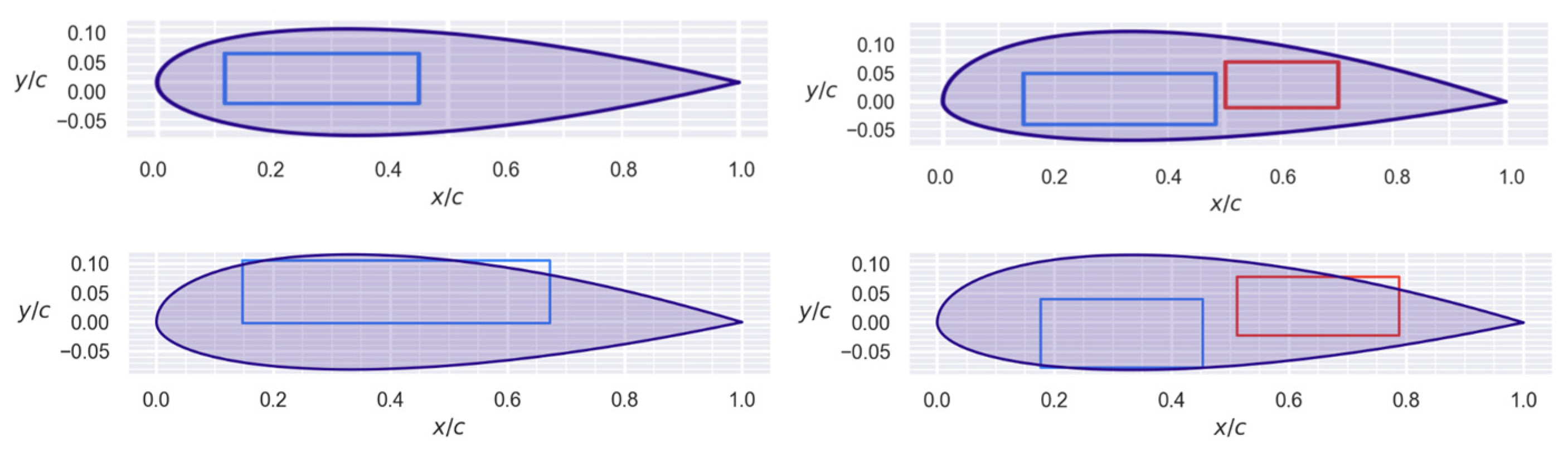
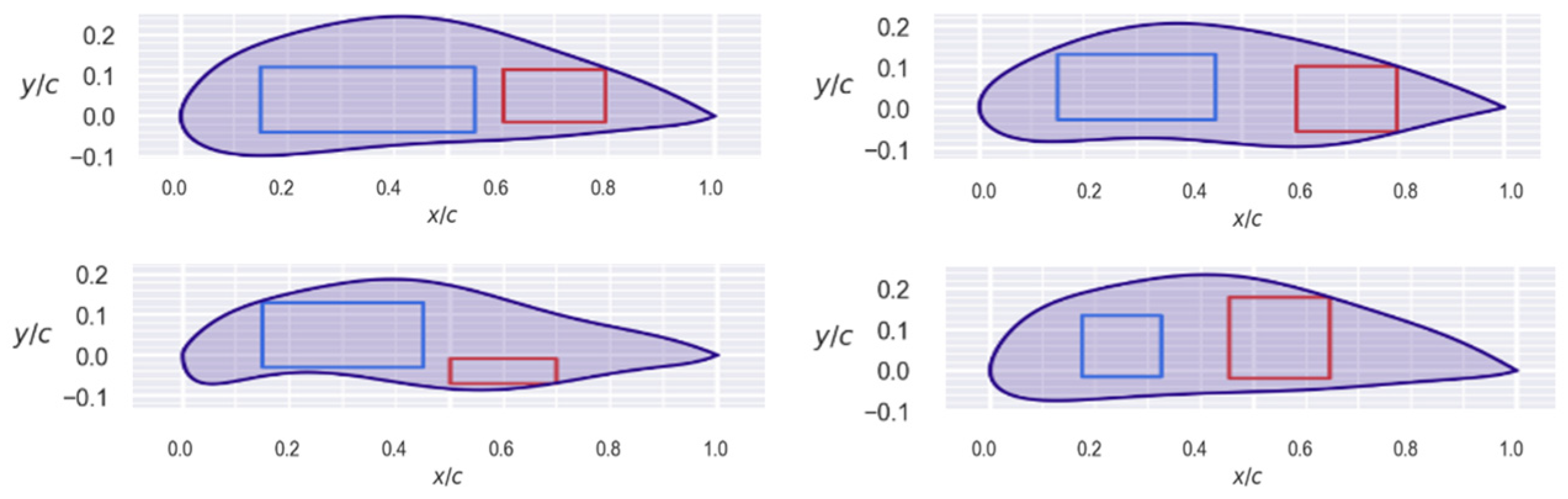
Figure 6.
Examples of restriction boxes (blue and red rectangles). At the top are valid profiles, while at the bottom are invalid profiles.
Figure 6.
Examples of restriction boxes (blue and red rectangles). At the top are valid profiles, while at the bottom are invalid profiles.
Figure 7.
Diagram of the DRLFoil PPO network.
Figure 7.
Diagram of the DRLFoil PPO network.
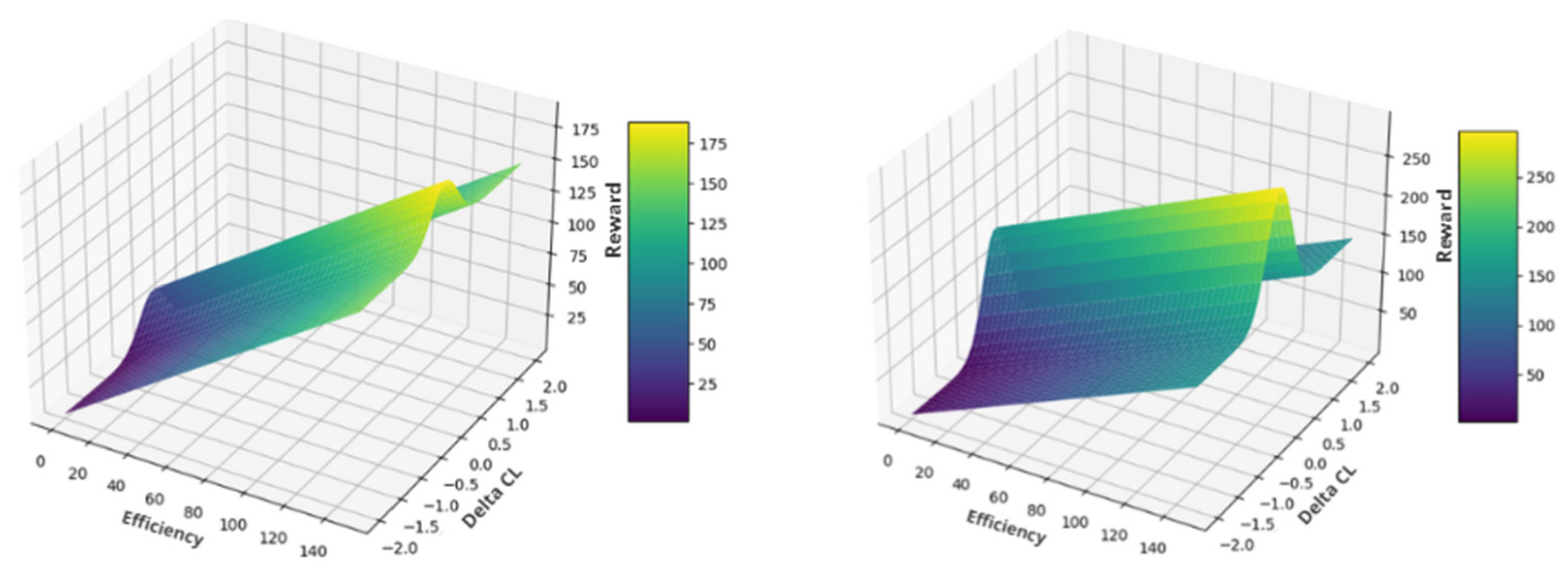
Figure 8.
Representation of the linear-Gaussian function of the reward, with value. (Left), and ; (right), and .
Figure 8.
Representation of the linear-Gaussian function of the reward, with value. (Left), and ; (right), and .
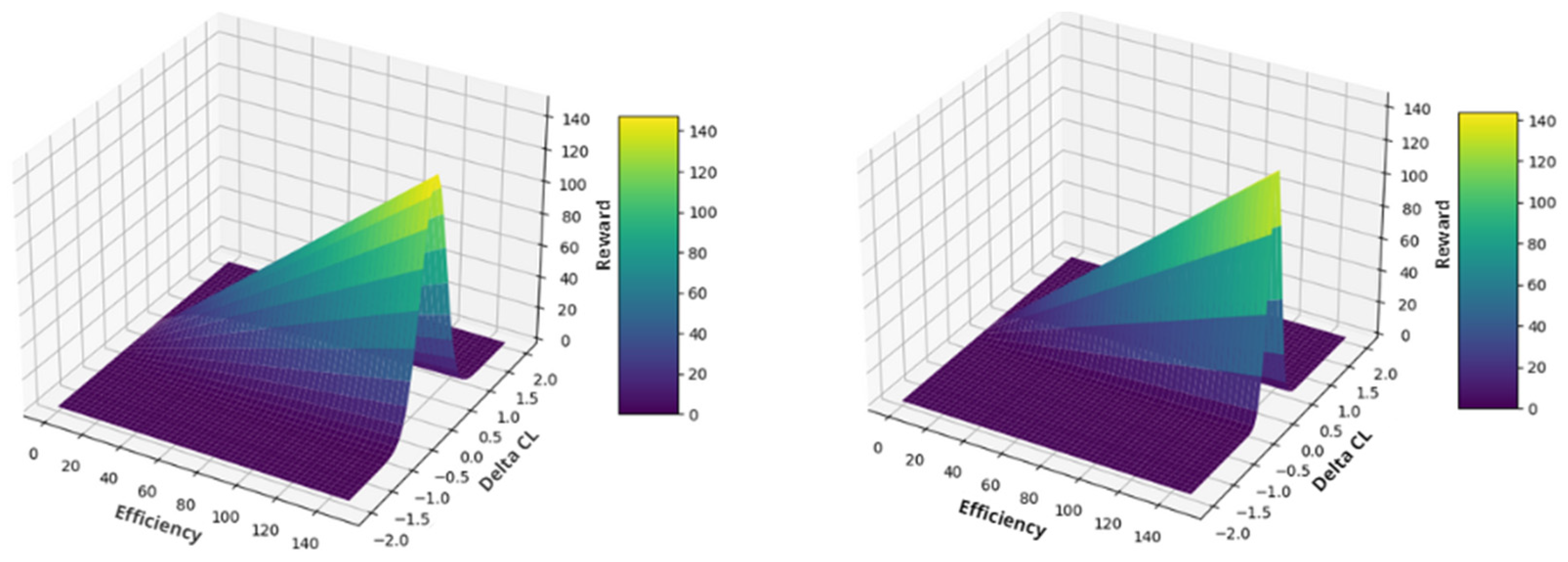
Figure 9.
Representation of the Gaussian function of the reward, with value . (Left), ; (right), .
Figure 9.
Representation of the Gaussian function of the reward, with value . (Left), ; (right), .
Figure 10.
Generation of peaks in the profiles.
Figure 10.
Generation of peaks in the profiles.
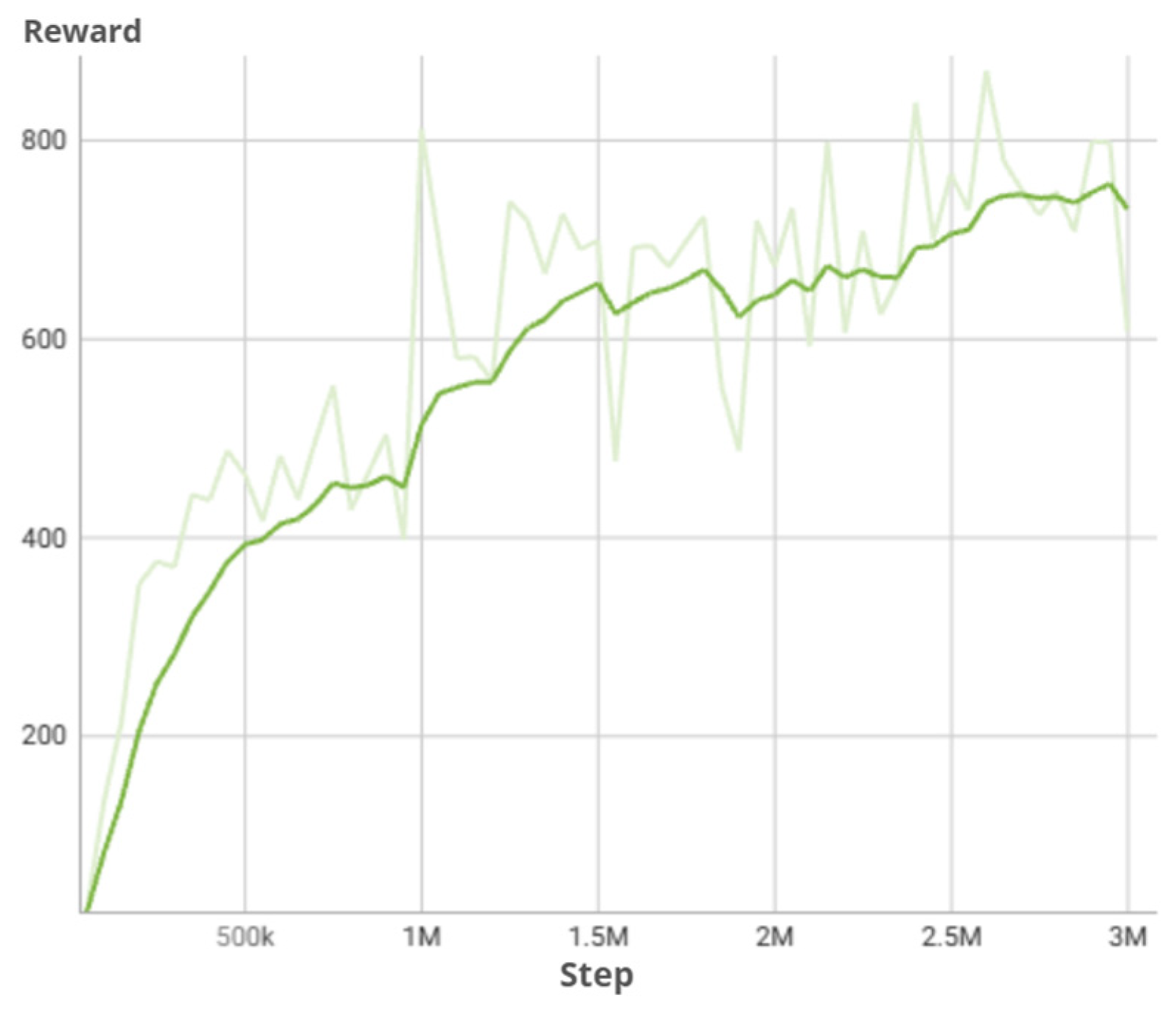
Figure 11.
Plot of average rewards as a function of pace obtained in each model.
Figure 11.
Plot of average rewards as a function of pace obtained in each model.
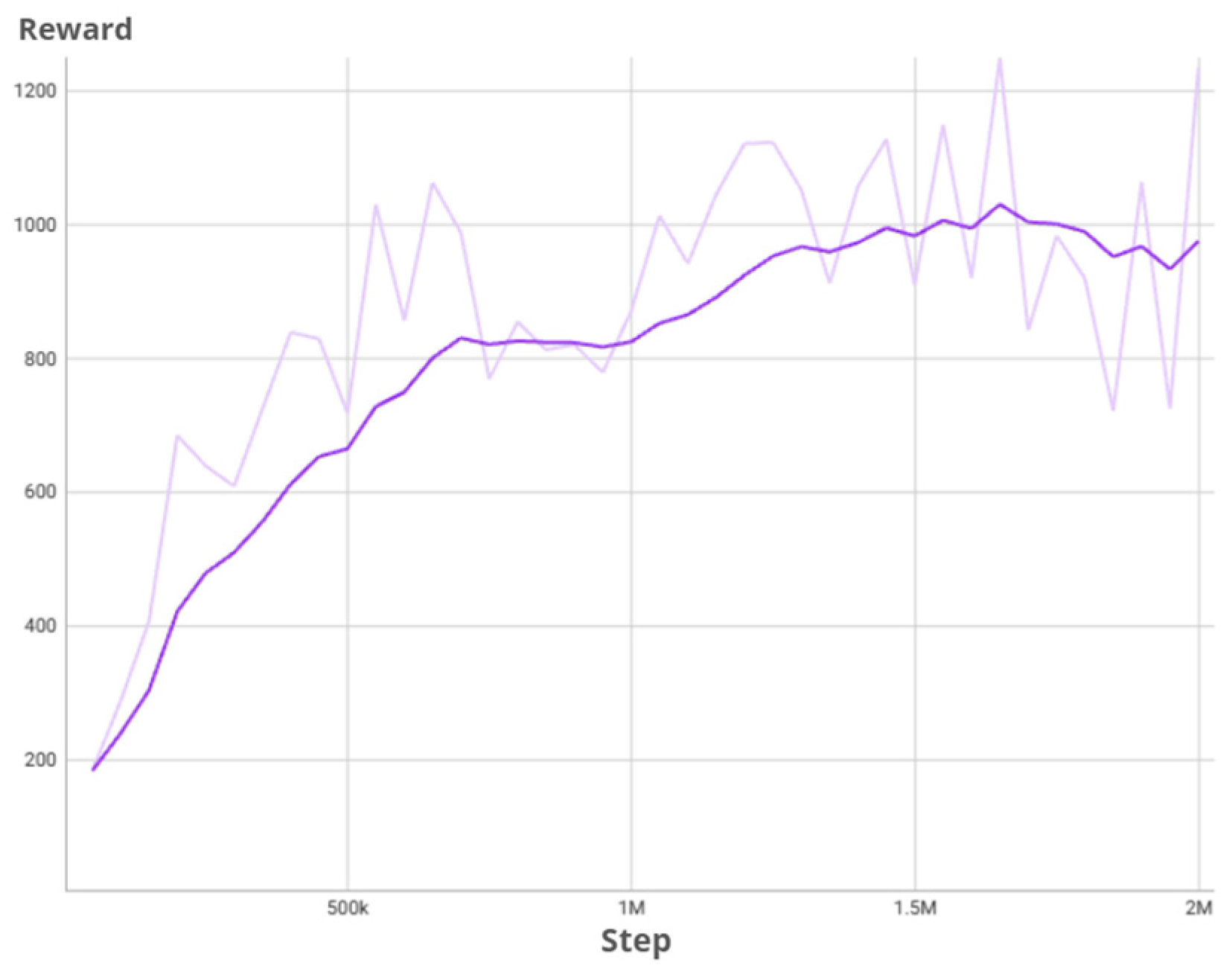
Figure 12.
Graph of average rewards for the model without boxes.
Figure 12.
Graph of average rewards for the model without boxes.
Figure 13.
Profiles obtained for different CL targets: (above left), 0.4; (above right), 0.7; (bottom left), 1; (bottom right), 1.3.
Figure 13.
Profiles obtained for different CL targets: (above left), 0.4; (above right), 0.7; (bottom left), 1; (bottom right), 1.3.
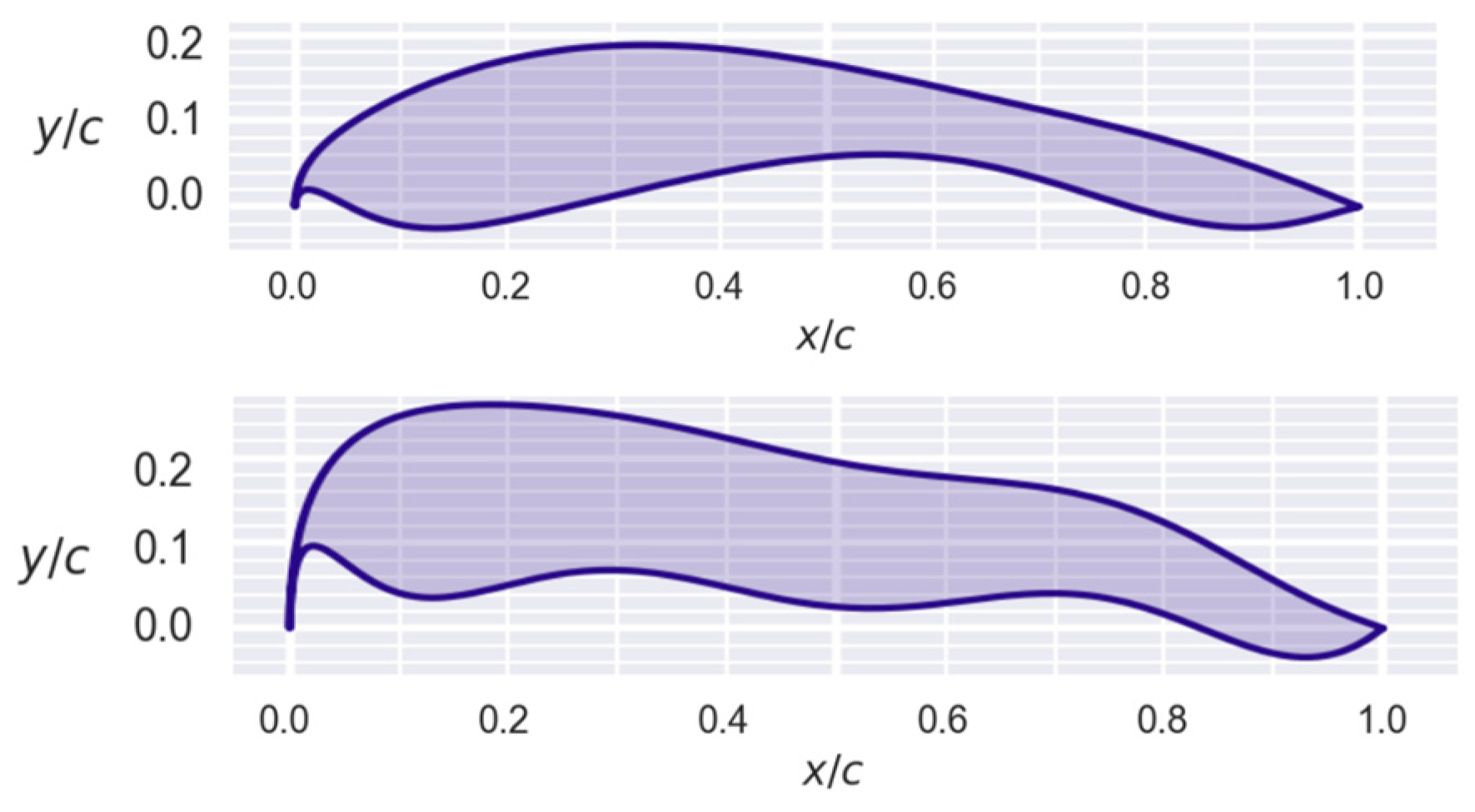
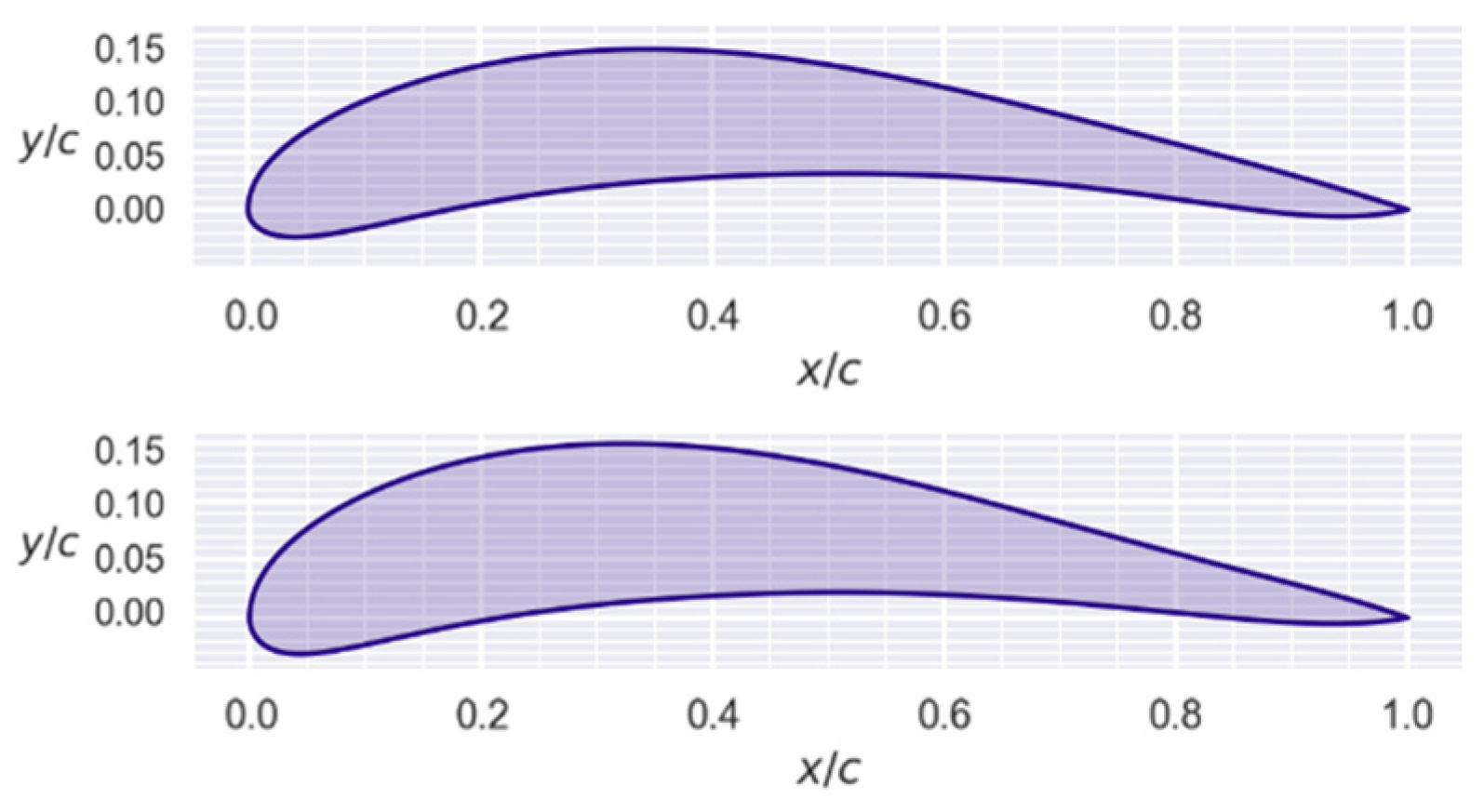
Figure 14.
Comparison of two profiles at different Reynolds: (top), 100,000; (bottom), forty million.
Figure 14.
Comparison of two profiles at different Reynolds: (top), 100,000; (bottom), forty million.
Figure 15.
Graph of average rewards for the one-box model.
Figure 15.
Graph of average rewards for the one-box model.
Figure 16.
Profiles generated with a CL target of 0.4 and Reynolds number of 10,000,000.
Figure 16.
Profiles generated with a CL target of 0.4 and Reynolds number of 10,000,000.
Figure 17.
Profiles generated with a CL target of 0.9 and Reynolds number 10,000,000.
Figure 17.
Profiles generated with a CL target of 0.9 and Reynolds number 10,000,000.
Figure 18.
Comparison of two profiles with the same constraint box and Reynolds number 10,000,000. (left), CL target of 0.3; (right), 1.3.
Figure 18.
Comparison of two profiles with the same constraint box and Reynolds number 10,000,000. (left), CL target of 0.3; (right), 1.3.
Figure 19.
Average reward graph of the two-box model.
Figure 19.
Average reward graph of the two-box model.
Figure 20.
Airfoils generated with a CL target of 0.4 and Reynolds number of 10,000,000.
Figure 20.
Airfoils generated with a CL target of 0.4 and Reynolds number of 10,000,000.
Table 1.
Action spaces and multithreading support for some of the SB3 algorithms [
12].
Table 1.
Action spaces and multithreading support for some of the SB3 algorithms [
12].
| Name | Box | Discrete | MultiDiscrete | MultiBinary | Multiprocessing |
|---|
| PPO | Yes | Yes | Yes | Yes | Yes |
| DDPG | Yes | No | No | No | Yes |
| DQN | No | Yes | No | No | Yes |
| RecurrentPPO | Yes | Yes | Yes | Yes | Yes |
Table 2.
Comparison of different model sizes of NeuralFoil with XFOIL [
15].
Table 2.
Comparison of different model sizes of NeuralFoil with XFOIL [
15].
| Model | CL MAE | CD MAE | CM MAE | Time (1 Execution) |
|---|
| NF “medium” | 0.02 | 0.039 | 0.003 | 5 ms |
| NF “large” | 0.016 | 0.03 | 0.003 | 8 ms |
| NF “xlarge” | 0.013 | 0.024 | 0.002 | 13 ms |
| NF “xxlarge” | 0.012 | 0.022 | 0.002 | 16 ms |
| NF “xxxlarge” | 0.012 | 0.02 | 0.002 | 56 ms |
| XFOIL | 0 | 0 | 0 | 73 ms |
Table 3.
Hyperparameters to be set in the PPO algorithm [
12].
Table 3.
Hyperparameters to be set in the PPO algorithm [
12].
| Hyperparameter | Value | Hyperparameter | Value |
|---|
| learning_rate | 0.0003 | clip_range_vf | None |
| n_steps | 2048 | ent_coef | 0.0 |
| batch_size | 64 | vf_coef | 0.5 |
| n_epochs | 10 | max_grad_norm | 0.5 |
| gamma | 0.99 | target_kl | None |
| gae_lambda | 0.95 | net_arch | 128, 128 |
| clip_range | 0.2 | Activation_fn | Tanh |
Table 4.
Comparison of CL target with the CL obtained using the reward function 9. The parameters of the equation are α = 1, β = 80 and γ = 15. The results of the highest rewards are shown for each case.
Table 4.
Comparison of CL target with the CL obtained using the reward function 9. The parameters of the equation are α = 1, β = 80 and γ = 15. The results of the highest rewards are shown for each case.
| CL Target | 0.30 | CL Target | 0.40 | CL Target | 0.60 |
|---|
| Efficiency | 77.87 | Efficiency | 82.74 | Efficiency | 78.60 |
| CL | 0.74 | CL | 0.81 | CL | 0.69 |
| CL Error | 0.44 | CL Error | 0.41 | CL Error | 0.09 |
Table 5.
Comparison of CL target with CL obtained using the reward function 10. The parameters of the equation are α = 1, = 20. The results of the highest rewards are shown for each case.
Table 5.
Comparison of CL target with CL obtained using the reward function 10. The parameters of the equation are α = 1, = 20. The results of the highest rewards are shown for each case.
| CL Target | 0.30 | CL Target | 0.40 | CL Target | 0.60 |
|---|
| Efficiency | 50.61 | Efficiency | 54.89 | Efficiency | 76.22 |
| CL | 0.40 | CL | 0.43 | CL | 0.69 |
| CL Error | 0.10 | CL Error | 0.03 | CL Error | 0.09 |
Table 6.
Specifications of the computer used for the development of DRLFoil.
Table 6.
Specifications of the computer used for the development of DRLFoil.
| Element | Specification |
|---|
| CPU | Intel Core i7-14700K |
| GPU | NVIDIA GeForce RTX 4060 Ti 16 GB |
| RAM | 32 GB (2×16 GB) DDR5 6000 MHz CL36 |
| Storage | 2 TB SSD M.2 Gen4 |
| Operative System | Windows 11 Pro |
| CUDA | 12.1 |
| Python | 3.10.11 |
| PyTorch | 2.3.0 |
Table 7.
Description of the parameters of the environment.
Table 7.
Description of the parameters of the environment.
| Parameter | Description |
|---|
| max_steps | Number of steps per episode |
| n_params | Number of weights per skin |
| scale_actions | Maximum variation of weights per step |
| airfoil_seed | Initial profile seed |
| cl_reward | Enable or disable the CL target |
| efficiency_param | Slope of reward growth |
| cl_wide | Width of the Gaussian bell curve |
| delta_reward | Difference between the current and previous step rewards. When enabled, the agent receives the relative change in performance instead of the absolute reward. |
| n_boxes | Number of constraint boxes |
Table 8.
Environment parameters used in hyperparameter optimisation.
Table 8.
Environment parameters used in hyperparameter optimisation.
| Parameter | Values |
|---|
| max_steps | 10 |
| n_params | 10 |
| scale_actions | 0.15 |
| airfoil_seed | Upper surface: [0.1, …, 0.1]
Lower surface: [0.1, …, 0.1]
Leading edge: [0.0] |
| cl_reward | True |
| efficiency_param | 1 |
| cl_wide | 20 |
| delta_reward | False |
| n_boxes | 1 |
Table 9.
Comparison of the rewards obtained after 600,000 steps. The six best resulting models are shown, as well as the unoptimized model used so far.
Table 9.
Comparison of the rewards obtained after 600,000 steps. The six best resulting models are shown, as well as the unoptimized model used so far.
| Model | Mean Reward |
|---|
| 1 | 311 |
| 2 | 31 |
| 3 | 20 |
| 4 | 5 |
| 5 | 1 |
| 6 | −3 |
| Not Optimised | −100 |
Table 10.
Hyperparameters selected as a basis after optimisation, making use of one constraint box.
Table 10.
Hyperparameters selected as a basis after optimisation, making use of one constraint box.
| Hyperparameter | Value | Hyperparameter | Value |
|---|
| learning_rate | 0.000268 | clip_range_vf | None |
| n_steps | 32 | ent_coef | 0.001 |
| batch_size | 512 | vf_coef | 0.754843 |
| n_epochs | 20 | max_grad_norm | 5 |
| gamma | 0.995 | target_kl | None |
| gae_lambda | 0.98 | net_arch | 64, 64 |
| clip_range | 0.3 | Activation_fn | Tanh |
Table 11.
Environment parameters used by the final models.
Table 11.
Environment parameters used by the final models.
| Parameter | Value |
|---|
| max_steps | 10 |
| n_params | 8 |
| scale_actions | 0.3 |
| airfoil_seed | Upper surface: [0.3, …, 0.3]
Lower surface: [0.3, …, 0.3]
Leading edge: [0.0] |
| efficiency_param | 1 |
| cl_wide | 20 |
Table 12.
Operating ranges of target lift coefficient and Reynolds number.
Table 12.
Operating ranges of target lift coefficient and Reynolds number.
| Parameter | Minimum | Maximum |
|---|
| CL target | 0.1 | 1.6 |
| Reynolds | 100,000 | 50,000,000 |
Table 13.
Rewards obtained in the evaluation of the agent in thirty random scenarios.
Table 13.
Rewards obtained in the evaluation of the agent in thirty random scenarios.
| Evaluation | Mean | Standard Deviation |
|---|
| General | 1036.06 | 382.31 |
| CL target = 0.3 | 586.77 | 101.37 |
| CL target = 0.6 | 991.91 | 233.73 |
| CL target = 0.9 | 1352.89 | 231.55 |
| CL target = 1.2 | 1395.8 | 140.71 |
| CL target = 1.5 | 1238.75 | 340.43 |
Table 14.
Results obtained for a fixed Reynolds value of 1,000,000.
Table 14.
Results obtained for a fixed Reynolds value of 1,000,000.
| CL Target | CL Obtained | Difference | CD Obtained | Efficiency |
|---|
| 0.1 | 0.225 | 0.125 | 0.007 | 33.195 |
| 0.3 | 0.36 | 0.06 | 0.008 | 43.704 |
| 0.5 | 0.531 | 0.031 | 0.008 | 68.981 |
| 0.7 | 0.746 | 0.046 | 0.01 | 77.644 |
| 0.9 | 0.959 | 0.059 | 0.011 | 90.067 |
| 1.1 | 1.113 | 0.013 | 0.014 | 80.394 |
| 1.3 | 1.225 | −0.075 | 0.014 | 87.353 |
| 1.5 | 1.313 | −0.187 | 0.017 | 77.894 |
Table 15.
Results obtained for a fixed value of CL target of 0.6.
Table 15.
Results obtained for a fixed value of CL target of 0.6.
| Reynolds | CL Obtained | Difference | CD Obtained | Efficiency |
|---|
| 100,000 | 0.583 | −0.017 | 0.032 | 17.958 |
| 300,000 | 0.623 | 0.023 | 0.014 | 45.441 |
| 500,000 | 0.622 | 0.022 | 0.011 | 55.501 |
| 1,000,000 | 0.627 | 0.027 | 0.08 | 74.043 |
| 3,000,000 | 0.611 | 0.011 | 0.07 | 90.149 |
| 5,000,000 | 0.609 | 0.009 | 0.06 | 100.311 |
| 10,000,000 | 0.616 | 0.016 | 0.05 | 113.093 |
| 40,000,000 | 0.607 | 0.007 | 0.05 | 128.499 |
Table 16.
Rewards earned in the agent’s evaluation with a box in thirty random scenarios.
Table 16.
Rewards earned in the agent’s evaluation with a box in thirty random scenarios.
| Evaluation | Mean | Standard Deviation |
|---|
| General | 712.25 | 262.26 |
| CL target = 0.3 | 483.72 | 78.62 |
| CL target = 0.6 | 782.38 | 158.52 |
| CL target = 0.9 | 925.88 | 97.28 |
| CL target = 1.2 | 842.97 | 293.73 |
| CL target = 1.5 | 646.77 | 11.12 |
Table 17.
Results obtained for a fixed constraint box and Reynolds value of 10,000,000.
Table 17.
Results obtained for a fixed constraint box and Reynolds value of 10,000,000.
| CL Target | CL Obtained | Difference | CD Obtained | Efficiency |
|---|
| 0.1 | - | - | - | - |
| 0.3 | 0.347 | 0.047 | 0.006 | 57.921 |
| 0.5 | 0.511 | 0.011 | 0.006 | 85.713 |
| 0.7 | 0.709 | 0.009 | 0.008 | 91.408 |
| 0.9 | 0.901 | 0.001 | 0.009 | 101.138 |
| 1.1 | 1.082 | −0.018 | 0.010 | 106.099 |
| 1.3 | 1.223 | −0.077 | 0.013 | 94.055 |
| 1.5 | 1.324 | −0.176 | 0.017 | 80.092 |
Table 18.
Rewards earned in the two-box agent evaluation in thirty random scenarios.
Table 18.
Rewards earned in the two-box agent evaluation in thirty random scenarios.
| Evaluation | Mean | Standard Deviation |
|---|
| General | 611.71 | 160.58 |
| CL target = 0.3 | 402.82 | 147.22 |
| CL target = 0.6 | 589.92 | 216.12 |
| CL target = 0.9 | 669.64 | 166.91 |
| CL target = 1.2 | 639.83 | 179.71 |
| CL target = 1.5 | 459.33 | 118.32 |