TBC-IG Random Variable-Dimension Algorithm for Aero-Engine Gas Path Sensor Optimization

Abstract

The complex configuration of the internal flow field in aero-engines leads to limitations on sensor installation positions, and how to accurately identify the disturbances of the installation influence parameters under this constraint has long been a significant challenge. To address this issue, this study proposes an optimization algorithm to identify the optimal sensor layout. This is achieved by employing mutually distinct integer encoding, which ensures the uniqueness of each sensor position and prevents duplication. More importantly, an objective evaluation system incorporating tracking error, sensor comprehensiveness, and spatial coverage is integrated into the fitness function design, thereby overcoming the one-sidedness and limitations of single-indicator evaluation. Building upon this foundation, a sensor optimization scheme is proposed for identifying installation influence parameters. This scheme integrates the rapid search capability of the Tabu Bee Colony Random Variation Dimension Algorithm with the global optimization capability of an Improved Genetic Random Variation Dimension Algorithm, resulting in a Tabu Bee Colony–Improved Genetic Random Variation Dimension Optimization Algorithm (TBC-IG-RVDOA). For each installation influence parameter, different perturbation conditions were established, and the selected optimal sensor combination was then validated using the Extended Kalman Filter (EKF). Experimental studies show that, under all perturbation scenarios, the TBC-IG-RVDOA demonstrates strong convergence, high computational efficiency, and fitness function values consistently exceeding 0.92, thereby accurately capturing the changes in each installation influence parameter.

1. Introduction

The health status of aero-engines is critical to flight safety. The performance calculation model of aero-engines can characterize the performance variation patterns of the engine under different operating conditions and is an effective tool for evaluating engine performance [1]. Compared with ground rig tests, under installed engine conditions, parameters such as the Reynolds Number Index (RNI), atmospheric humidity (d), bleed air (δ_q,hpc), and power extraction (ΔH_pext,lpt) alter the engine’s aerothermodynamic performance and component matching characteristics, consequently affecting overall engine performance. Therefore, during the model validation and optimization process, by introducing effective control of disturbances in the installation influence parameters, a systematic analysis of their sensitivity to engine performance can be conducted, thereby providing data support for the modification and optimization of the model.

Perturbations in installation parameters lead to varying degrees of change in the thermodynamic parameters of any engine air path component. These different perturbations can then be identified using correlation-based diagnostic methods. Currently, two main approaches exist: methods based on mathematical–physical models [2,3] and methods based on experimental data [4,5,6,7]. Model-based diagnostic results depend on modeling accuracy [8,9,10,11], while data-driven diagnostic methods heavily rely on measurement data obtained during engine tests [12]. Both approaches necessitate comprehensive parameter information. Given the complexity of the engine’s internal air path system and the multitude of components requiring monitoring, ensuring the comprehensiveness and effectiveness of the acquired air path information could theoretically be achieved by installing additional sensors. However, the engine gas path’s harsh operating environment severely limits the available installation locations for compatible sensors [13]. Furthermore, installing an excessive number of sensors not only significantly increases the system’s maintenance costs but also reduces its overall reliability due to sensor failures or interference. The performance and distribution of sensors within the system directly affect the integrity and accuracy of monitoring data, which in turn dictates its ultimate accuracy and reliability. Therefore, the judicious selection, layout, and optimized configuration of sensors are critical for enhancing the robustness and timeliness of engine condition monitoring [14].

Currently, numerous scholars internationally are focusing on the health monitoring of hydraulic facilities, high-rise complex buildings, or truss structure models [15,16,17]. They have conducted relevant research on the optimal configuration of sensors, mainly concentrating on utilizing well-established multi-objective optimization algorithms such as Particle Swarm Optimization and Bee Colony Algorithm to solve single-objective optimization problems in continuous space. These studies provide optimized ideas for sensor placement under engine installation conditions.

Rabelo applied a genetic algorithm with adaptive operators to optimize the layout of fuel volume measurement sensors [18]. However, the scope of the study was relatively narrow and did not cover the sensor layout of other important components of aero-engines. Simon combined sensor combinations with model calibration coefficient selection [19,20], added extra sensors on the basis of benchmark sensor combinations, and used an exhaustive method to obtain the optimal sensor configuration. This approach provided accurate status information for aero-engine fault diagnosis but had high computational costs and low efficiency. More efficient algorithms could be explored to replace the exhaustive method to improve the efficiency of obtaining the optimal sensor configuration. Bhushan conducted in-depth discussions on sensor configuration problems under two assumptions: single fault source and multiple fault sources [21,22]. Krysander improved the sensor layout in industrial valves based on the limitations of fault detection rate and identification accuracy [23], effectively enhancing identification accuracy. Lu integrated the state estimation capability of the Extended Kalman Filter (EKF) with the optimization characteristics of the adaptive genetic algorithm [24], achieving dual functions of engine performance degradation estimation and sensor fault detection. This effectively improved the accuracy and robustness of the diagnostic system. Yang proposed a sensor layout optimization method based on cutting sensor installation lines and accompanying set partitioning and merging strategies [25], but there were still deficiencies in solving efficiency. On this basis, Zheng proposed a multi-objective sensor layout optimization method based on the Differential Evolution Algorithm [26], which had significant advantages in improving fuel measurement accuracy and optimizing computational speed. Yuan optimized the layout of fuel measurement sensors using the Particle Swarm Optimization algorithm, improving the continuity and measurable range of fuel measurement [27]. In response to the situation where single-domain features do not provide comprehensive information for aero-engine fault diagnosis, Li used optimized multi-domain features as indicators to assess sensor health status, obtaining better diagnostic accuracy and computational efficiency [28].

Shi improved the genetic algorithm and fixed the sensor cardinality to realize optimal allocation of aero-engine gas-path sensors, successfully acquiring state parameters at critical cross-sections and completing gas-path data collection [29]. However, each iteration of the algorithm is time-consuming, which degrades optimization efficiency. Building on this work, Hu combined the fast-convergence characteristic of the artificial bee colony algorithm with the tabu mechanism of tabu search and further integrated the global-search superiority of an improved genetic algorithm [30], proposing the Tabu Search–Artificial Bee Colony–Improved Genetic Algorithm (TS-BC-IGA) to optimize aero-engine gas-path sensor placement and achieve rapid tracking of gas-path faults. Nevertheless, the method still has an important limitation: the number of sensors is preset as a fixed value throughout the optimization process, without considering that in practical applications, some sensors may contribute very little to the system output. Retaining these sensors not only increases computational complexity but may also introduce unnecessary noise interference. Moreover, since the operating conditions of aero-engines are dynamically changing, the optimal number of sensors required may vary under different conditions. A fixed-length sensor configuration strategy is difficult to adapt to such needs, thus limiting its robustness and practicality in multi-condition, multi-task scenarios. Therefore, how to develop an optimization method that can adaptively determine the number of sensors and dynamically adjust the configuration while ensuring diagnostic accuracy has become a key issue that needs to be urgently addressed in current air-path sensor layout research.

Although previous research has laid the foundation for sensor layout optimization, it often fails to fully consider the complexity of installation influence parameters. For example, d and the RNI can be obtained via external sensors or the flight status of an aircraft, but the δ_q,hpc and ΔH_pext,lpt cannot be monitored using external sensors. However, all four parameters are installation influence parameters that must be taken into account under normal flight conditions. When they are disturbed, they will trigger changes in the thermodynamic parameters at various sections of the air-path components, which will ultimately be reflected as deviations in the overall performance of the engine.

To achieve high-precision engine performance assessment, it is necessary to effectively capture the impact of installation influence parameters on engine performance. Therefore, this paper proposes a Tabu Bee Colony–Improved Genetic Random Variable-Dimension Optimization Algorithm (TBC-IG-RVDOA) that allows the algorithm to autonomously explore the optimal sensor quantity during optimization, eliminating the fixed-dimension constraint and enabling adaptive selection of set lengths under varying scenarios. The objective is to achieve “better and faster” optimization. To validate algorithmic efficacy, a nonlinear aero-engine system model is employed to replicate realistic operating conditions. Installation-influenced engine parameters are estimated and extracted via the Extended Kalman Filter (EKF). The TBC-IG-RVDOA is then applied to optimize the allocation of aero-engine gas-path sensors. The resulting optimal sensor set is reintroduced into the EKF framework for verification, thereby providing validation of the sensor configuration and realizing an efficient, precise, and adaptive optimization of the gas-path sensor layout. By constructing a dataset of air-path parameters under disturbance scenarios of installation influence parameters and training the sensor system to identify these, we provide effective data support for engine performance assessment.

The rest of this paper is organized as follows: Section 2 introduces the engine model applied in this study and alternative sensor locations; Section 3 proposes the TBC-IG-RVDOA algorithm and details its specific procedure and the design of the fitness function; Section 4 applies the TBC-IG-RVDOA algorithm to determine sensor layouts under various disturbance scenarios and validates these layouts within each respective scenario; finally, Section 5 concludes this study.

2. Model of Aero-Engine and Alternative Sensor Locations

The perturbation-identification approach for aero-engine installation influence parameters comprises two primary constituents: a nonlinear component-level model that replicates the installation influence parameters under true engine operating conditions, and a Kalman filter designed to track and estimate these installation influence parameters in real time.

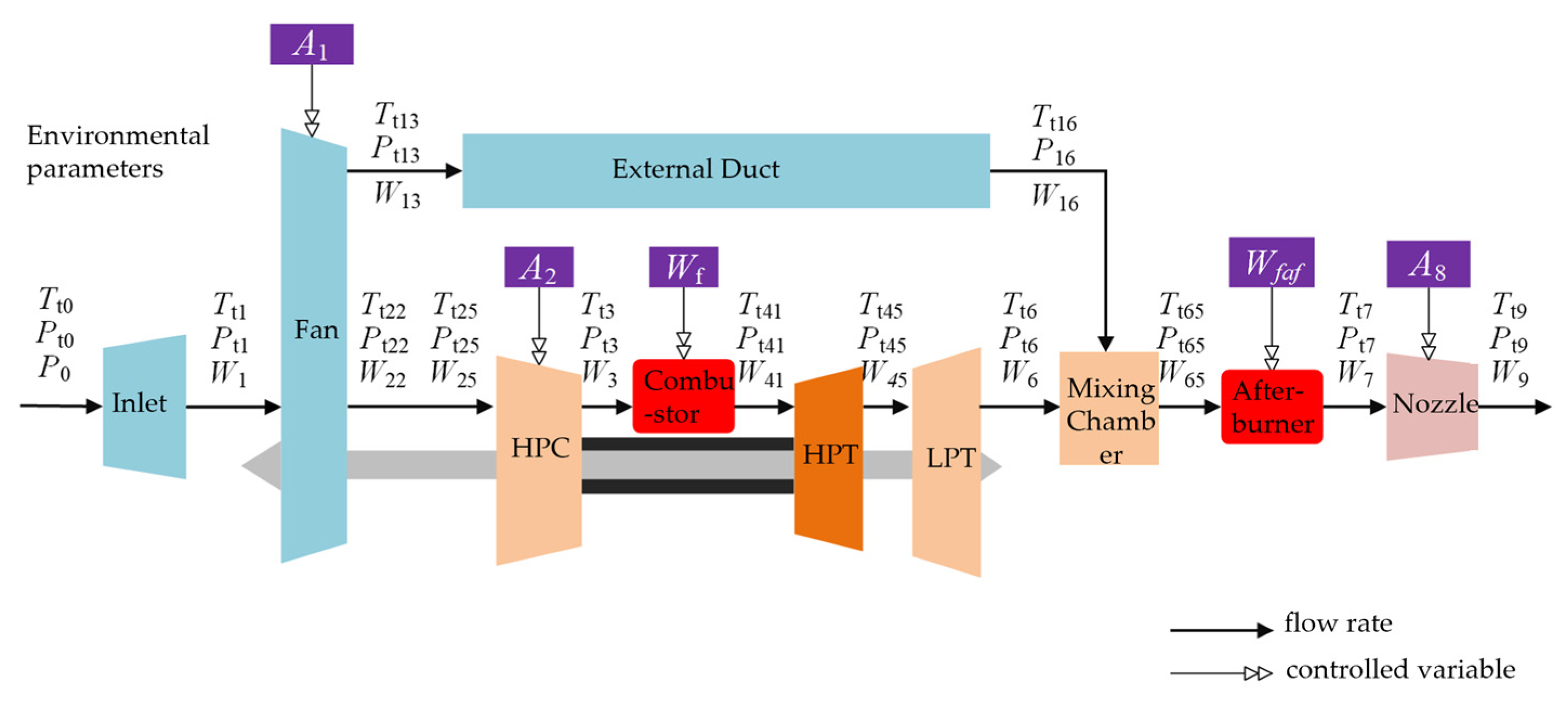
A twin-spool mixed-exhaust turbofan aero-engine is selected as the research platform; its architecture and characteristic parameters at each cross-section are illustrated in Figure 1.

Note that HPC, HPT, and LPT, as presented in Figure 1, respectively, denote the High-Pressure Compressor, High-Pressure Turbine, and Low-Pressure Turbine; T_ti, P_ti, W_i, and A_i represent the temperature, pressure, flow rate, and area at the inlet and outlet of the corresponding component cross-section, respectively; W_f and W_faf represent the fuel flow rate in the combustion chamber and afterburner, respectively.

Under the perturbation of installation influence parameters, the signals relied upon for engine tracking and diagnosis primarily originate from the existing sensor configuration of the control system. Given the large number of air-path components that need to be monitored, ensuring timely and accurate capture of dynamic changes in installation influence parameters is essential. This provides a data foundation for validating engine performance under real-world installation conditions. The following alternative sensor installation schemes are determined in consideration of the engine’s working environment characteristics and cross-sectional division as shown in Figure 1, as well as the changes in thermodynamic parameters at each cross-section under the perturbation of installation influence parameters. The specific installation details are presented in

Table 1. Alternative Sensor Installation Details.

Number	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Sensor	Nl	Nh	Pt22	Tt22	Pt13	Tt13	Pt3	Tt3	Pt45	Tt45	Pt6	Tt6	Pt65	Tt65	Pt9	Tt9

Note: Pti and Tti denote the pressure sensor and temperature sensor at the corresponding cross-section, respectively; N_l and N_h denote the low-pressure rotor speed sensor and high-pressure rotor speed sensor, respectively.

.

2.1. Nonlinear Component-Level Model of Aero-Engine

Aerothermodynamic calculations are performed independently for each component of the aero-engine to obtain the corresponding component characteristic calculation models, and further determine the characteristic parameters and state parameters at each section. Based on the balance relationships of mass flow rate, power, and other key parameters among the aero-engine components, a common working equation set is established, thereby deriving the nonlinear component-level performance calculation model of the aero-engine. On this basis, installation influence parameters are treated as state variables to construct a nonlinear aero-engine system considering installation influence parameters, and its mathematical model can be expressed as follows:

$$\left\{\begin{array}{l}\dot{\mathit{x}}=f(\mathit{x},\mathit{u},\mathit{z})+\mathit{p}\\ \mathit{y}=g(\mathit{x},\mathit{u},\mathit{z})+\mathit{q}\end{array}\right.$$

(1)

where $f(\cdot )$ and $g(\cdot )$ are nonlinear functions of the aero-engine operating process; $\mathit{y}\in R^m$ is the output measurement vector; $\mathit{x}\in R^n$ denotes the aero-engine state vector; $\mathit{u}\in R^l$ is the input control vector; $\mathit{z}=\left[RNI,RH,{\delta }_{q,hpc},\Delta H_{pext,lpt}\right]$ represents installation influence parameters, which are the Reynolds index, relative humidity, compressor bleed air volume, and low-pressure turbine power extraction, respectively; $\mathit{p}$ and $\mathit{q}$ are the process noise and measurement noise, respectively, and both are uncorrelated white noise signals. All measurement parameters are converted to the standard ground state based on similarity theory and normalized.

2.2. Gas-Path Monitoring Based on Extended Kalman Filter

The nonlinear component-level model of an aero-engine integrates the aerothermodynamic calculations of each core component and accurately represents their mutual coupling, thereby achieving a high degree of modeling fidelity. Nevertheless, the iterative solution of this model is characterized by high computational complexity and significant runtime, rendering it incompatible with the stringent real-time demands of engine control. As a recursive optimal state estimation technique, the EKF has demonstrated superior capabilities in tracking the states of dynamic systems [31]. To overcome the difficulties of initial-value selection and the risk of local optima inherent in traditional modeling approaches, an optimized fitting method was developed that synergistically combines the advantages of derivative-based and fitting-based techniques, effectively resolving the aforementioned limitations [12].

To mitigate the excessive computational burden of the nonlinear component-level model, the present study adopts the optimized fitting method to construct a linearized aero-engine model. Parameters that characterize installation influence parameters are designated as control variables u, and small simultaneous perturbations are applied to both these control variables u and the x themselves. The resulting step-response data of the state and output variables are then supplied as the input–output pairs for the iterative optimized fitting process, yielding an optimal linearized model that explicitly incorporates installation influence parameters. Subsequently, the installation influence parameters are augmented into the state vector, transforming the original state-variable model into an augmented state-variable model.

$$\left\{\begin{array}{l}\Delta \dot{\mathit{x}}=\mathit{A}\mathit{I}\Delta \mathit{x}+\mathit{B}\mathit{I}\Delta \mathit{u}+\mathit{p}\\ \Delta \mathit{y}=\mathit{C}\mathit{I}\Delta \mathit{x}+\mathit{D}\mathit{I}\Delta \mathit{u}+\mathit{q}\end{array}\right.$$

(2)

At this stage, the established state-variable model is continuous; however, the Kalman filtering procedure is inherently discrete. Consequently, the continuous system must be discretised to yield the discrete augmented state-variable model.

$$\left\{\begin{array}{l}\Delta {\dot{\mathit{x}}}_{k+1}=\mathit{G}\Delta {\mathit{x}}_k+\mathit{I}\Delta {\mathit{u}}_k+{\mathit{p}}_k\\ \Delta {\mathit{y}}_k=\mathit{H}\Delta {\mathit{x}}_k+\mathit{J}\Delta {\mathit{u}}_k+{\mathit{q}}_k\end{array}\right.$$

(3)

where G, I, H and J denote the coefficient matrices obtained from the discrete-time calculation, and p_k and q_k represent the process and measurement noise, respectively. By embedding the discretised augmented state-variable model within the Extended Kalman Filter (EKF) framework, the measurable gas-path output residuals Δy of the aero-engine are employed as feedback to recursively estimate the perturbations in installation influence parameters Δz for each gas-path component. The resulting perturbation estimates enable reliable detection of whether installation influence parameters have deviated from their nominal values.

3. Algorithm Optimization Based on TBCA and IGA

In the field of optimization, meta-heuristic algorithms play a crucial role in optimizing sensor combination schemes, providing an efficient and feasible method for determining the optimal sensor configuration. In view of this, this study integrates three different meta-heuristic algorithms and makes corresponding improvements in terms of adaptability, aiming to further enhance the optimization effect.

3.1. Meta-Heuristic Global Optimization Algorithms

The Tabu Search Algorithm (TSA) is a metaheuristic random search algorithm based on neighborhood search, introduced by Glover in 1986 [32]. It employs a tabu list to record previously explored local optimal solutions, thereby avoiding redundant searches and enabling the algorithm to escape from local optima. This effectively prevents premature convergence and accelerates the search for the global optimal solution. During the implementation of the Tabu Search Algorithm, when a solution is selected as the new current solution, certain attributes or moves associated with that solution are recorded in the tabu list, along with a specified tabu tenure. If the length of the tabu list exceeds a predefined value, the earliest entries are removed. This iterative search process is continuously repeated until a stopping criterion is met. This allows the algorithm to re-explore these solutions or moves in subsequent searches, aiding in the global search for the optimal solution.

The Artificial Bee Colony (ABC) algorithm, proposed by Turkish scholar Karaboga in 2005, is a swarm intelligence optimization algorithm that simulates the foraging behavior of honeybee colonies [33,34]. It classifies the honeybee colony into three types: Employed Bees, Onlooker Bees, and Scout Bees. Its core idea stems from the observation and abstraction of the foraging behavior of honeybee colonies. Taking the efficient collaboration and information-sharing mechanism of honeybee colonies as a blueprint, the algorithm solves complex optimization problems by simulating the behavioral patterns of honeybees in the process of searching for nectar.

In traditional bee colony algorithms, the length of the bee population, which corresponds to the number of sensors selected, is fixed. However, some sensors have minimal impact on the results—retaining them will only increase computational load or interfere with optimization. Meanwhile, the optimal combination length may vary across different scenarios. Therefore, the core objective of the optimized algorithm is to enable the algorithm to autonomously explore the optimal number of sensors while identifying the best combination for that number, thereby enhancing optimization flexibility and result rationality. Within the range of the maximum installable number of sensors, l_current is generated randomly first, followed by the generation of non-repetitive sensor indices corresponding to this length. An excessively small sensor combination length tends to cause insufficient information and poor performance; conversely, the length cannot exceed the total number of available sensors l_max, as this would prevent the algorithm from wasting computing power on meaningless lengths. To address this, a length penalty term l_p introduced during the algorithm optimization process. This penalty term is imposed on sensor schemes with excessively long lengths, avoiding the algorithm’s tendency to select solutions with longer lengths that do not necessarily yield better performance.

$$l_p=1-0.2{\displaystyle \frac{l_{current}-l_{min}}{l_{max}-l_{min}}}$$

(4)

where l_max and l_min are set to 16 and 6, respectively, based on multiple experiments.

The Genetic Algorithm (GA) is a typical global optimization search method inspired by the process of natural selection and the evolutionary process of genetic operators. It has been widely applied to solve practical problems across various fields [35,36]. In the GA, a set of chromosomes is defined as a population, where each chromosome represents a solution to the problem, and each gene on the chromosome corresponds to a parameter to be optimized. This characteristic enables the GA to search for the optimal solution throughout the entire solution space, endowing it with strong global optimization capabilities. However, in practical optimization processes, the algorithm is prone to falling into local optimal solutions. To overcome this limitation, this study introduces the optimal preservation strategy operator and the new population creation operator. Moreover, in response to the actual needs of gas-path system sensor combination optimization, a random chromosome length generation mechanism is proposed: that is, the number of genes in each chromosome is randomly generated in each iteration, showing dynamic changes. This not only meets the uncertainty of sensor combination scale in practical scenarios but also increases population diversity. As a result, the Improved Genetic Random Variable-Dimension Optimization Algorithm (IG-RVDOA) can explore better sensor combination schemes in solution spaces of different scales.

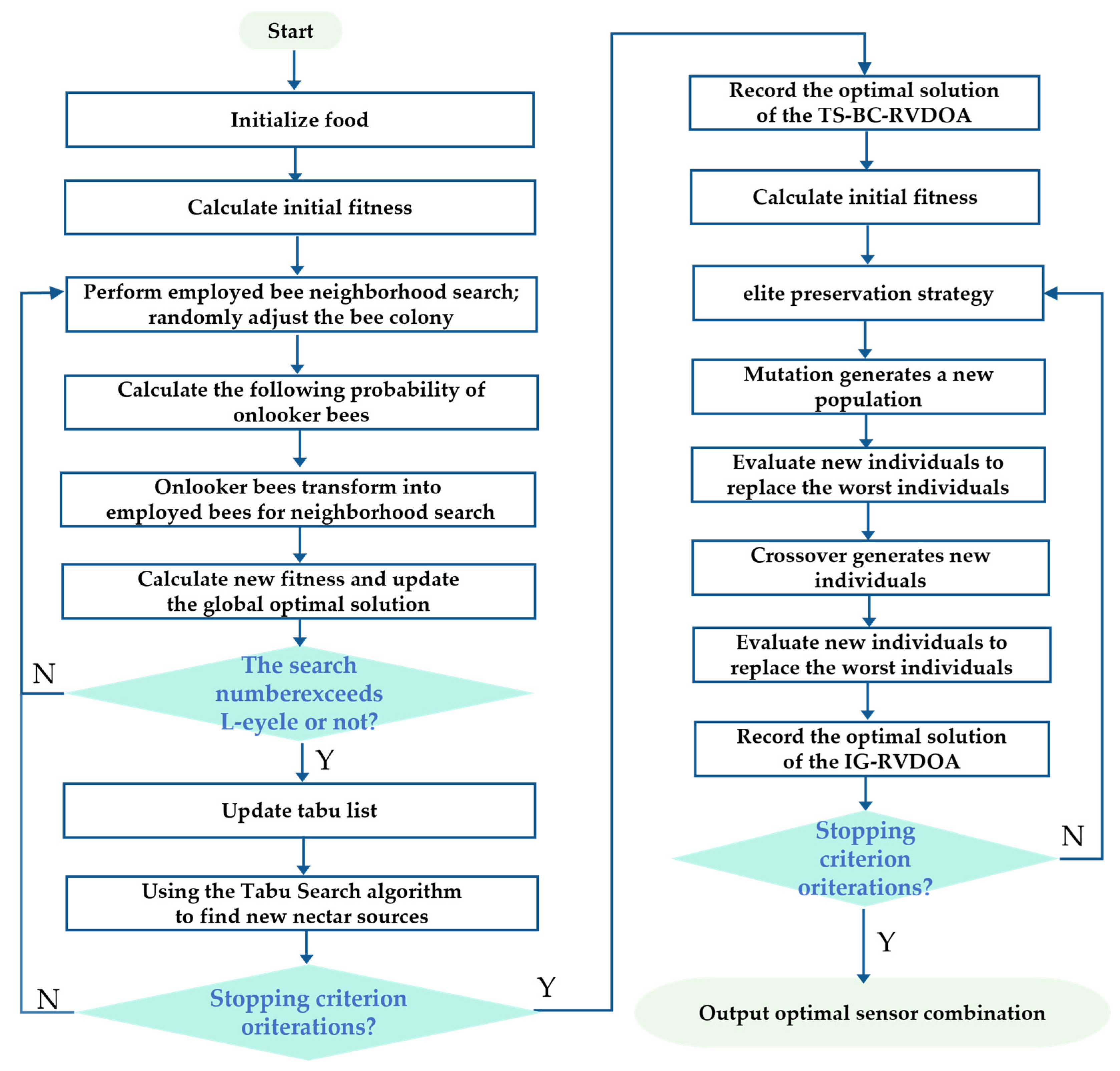
3.2. Tabu Search–Bee Colony Random Variable-Dimension Optimization Algorithm for Gas Path Sensors Optimization

To achieve efficient optimization of the globally optimal sensor combination, this study proposes the Tabu Search–Bee Colony Random Variable-Dimension Optimization Algorithm (TS-BC-RVDOA) based on the Bee Colony Algorithm. This algorithm integrates the constraint effect of the length penalty term l_p on solution length and the ability of Tabu Search to avoid local optimal solutions. Initially, 100 iterations are performed to obtain the corresponding local optimal points. This operation not only effectively avoids the trap of local optimal solutions and prevents the algorithm from stagnating in the optimization process but also narrows down the search range for the global optimal solution, thereby accelerating the exploration process for the global optimum. Building on this foundation, to further enhance the precision and efficiency of optimization, this paper introduces the Improved Genetic Algorithm (IG-RVDOA) and constructs the TBC-IG-RVDOA. The local optima obtained by TS-BC-RVDOA are used as the initial population for IGA, fully leveraging the high-quality characteristics of the initial solution set and combining the advantages of IG-RVDOA in global search. Through multiple rounds of genetic iterations, the algorithm deeply explores the potential optimal solutions, ultimately obtaining the global optimum. The overall process of TBC-IG-RVDOA is shown in Figure 2.

The main parameters of the TBC-IG-RVDOA are defined as follows: the total population size is set to 80; the upper limit of the number of sensors l_max = 16, the lower limit l_min = 6, and the length of an individual is randomly generated within the range of sensors; the maximum search times limit is set to 100, used to control the maximum number of search attempts for a single food source. The minimum and maximum crossover probabilities of the IG-RVDOA algorithm are set to 0.1 and 0.8, respectively. Similarly, the minimum and maximum mutation probabilities are also set to 0.1 and 0.8, respectively. Both the TS-BC-RVDOA and the IG-RVDOA algorithm have 100 iterations, and the number of runs is 10 to obtain more robust results.

The main steps are listed as follows:

A. TS-BC-RVDOA Phase

(1) Encoding. In the early stage, we noticed that the input order of sensor information would have a significant impact on the tracking results. Therefore, we clearly regard the sensor combination as a permutation problem, rather than a simple combination problem. This means that although different permutations may point to the same sensor combination in physical sense, they are regarded as different solutions in the algorithm’s search process. Meanwhile, considering that only one sensor can be installed at each cross-sectional location, we adopt the mutually exclusive integer encoding scheme to ensure that each individual contains no more than 16 different integers. For example:

$$unit=\left[6,5,1,3,0,9,11,12,7\right]$$

(5)

(2) Fitness Calculation. In the design of the fitness function, the TS-BC-RVDOA algorithm constructs an optimization objective based on multi-indicator weighting system that includes tracking accuracy, sensor comprehensiveness, and spatial coverage.

The Root Mean Square Error (RMSE) is employed as a metric for assessing the performance of prediction models. It not only ensures that the magnitude of the error is consistent with the original data, facilitating direct comparisons across different models or datasets, but also, due to its sensitivity to large errors, effectively reveals the prediction deviations of the model under specific conditions. This is instrumental in guiding the adjustment of algorithm parameters to minimize prediction errors. To this end, all error judgment conditions in this paper are based on the RMSE calculated between the implanted installation influence parameters perturbations and the estimated perturbations, thereby quantifying the performance of the EKF algorithm in the tracking estimation process and comprehensively evaluating the tracking accuracy of installation influence parameters perturbations by the sensor configuration schemes.

$$E_{sr}=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{\left({\overline{\Delta z}}_i-\Delta z_i\right)}^2}}$$

(6)

$$Accuarcy={\displaystyle \frac{10}{10+{\displaystyle \sum E_{sr}}}}$$

(7)

where ${\overline{\Delta z}}_i$ the ith estimated installation influence parameter of gas path faults, hi is the $\Delta z_i$ predefined installation influence parameter of the corresponding faults.

The 16 sensors are divided into eight independent location groups according to their physical deployment positions, which is consistent with the practical engineering application of sensor configuration. By partitioning into basic units, the quantification evaluation process of coverage is effectively simplified, making the calculation of coverage more intuitive and accurate. This systematically assesses the spatial coverage performance of the sensor configuration schemes.

$$Coverag\mathrm{e}={\displaystyle \frac{{\displaystyle \sum _{j=1}^8\mathrm{positions}}(j)}{8}}$$

(8)

The concept of “comprehensiveness” of sensor configuration is introduced to measure the balance and completeness of sensor coverage across different types of sensors. When the distribution of sensor types is more balanced, the smaller the standard deviation, the higher the comprehensiveness score, indicating that the sensor configuration is more balanced and comprehensive in covering different types of sensors. This effectively evaluates the performance of sensor configuration in terms of type diversity.

$$r_t={\displaystyle \frac{{\mathrm{T}}_{tcount}}{7}}$$

(9)

$$r_p={\displaystyle \frac{{\mathrm{P}}_{tcount}}{7}}$$

(10)

$$r_s={\displaystyle \frac{N_{count}}{2}}$$

(11)

$$\overline{r}={\displaystyle \frac{r_t+r_p+r_s}{3}}$$

(12)

$${\mathrm{D}}_{\mathrm{Score}}=1-\sqrt{{\displaystyle \frac{1}{2}}\left[{\left(r_t-\overline{r}\right)}^2+{\left(r_p-\overline{r}\right)}^2+{\left(r_s-\overline{r}\right)}^2\right]}$$

(13)

where T_tcount, P_tcount, and N_count represent the number of temperature sensors, pressure sensors, and velocity sensors, respectively; r_t, r_p, and r_s denote the proportions of temperature sensors, pressure sensors, and velocity sensors, respectively.

After numerous trials and computations, the fitness function for the TS-BC-RVDOA algorithm is ultimately determined as follows:

$$Fitness=(0.8Accuarcy+0.1D_{Score}+0.1Coverage)\cdot l_p$$

(14)

(3) Employed Bee Phase. During the employed bee phase, known food sources are searched and evaluated. Employed bees conduct a neighborhood search strategy to randomly explore around the current food source to find better positions. If the new food source is of higher quality, the original food source is abandoned, and the information is updated, thereby quickly discovering local optimal solutions. After the introduction of the tabu list, if an employed bee fails to find a better food source after Limit consecutive cycles, the corresponding solution is added to the tabu list to avoid redundant exploration of known local optimal solutions in subsequent searches.

(4) Onlooker Bee Phase. In the onlooker bee phase, onlooker bees select food sources for search based on the information provided by employed bees. The higher the quality of the food source, the greater the probability that it will be chosen by onlooker bees.

$$prob={\displaystyle \frac{0.9\ast Fitness}{Fitnes{s}_{\max }}}+0.1$$

(15)

(5) Scout Bee Phase. When a food source remains unimproved after multiple searches or its quality falls below a certain threshold L, the employed bee transforms into a scout bee. The scout bee explores the solution space by randomly generating new feasible solutions. To ensure that the newly generated solution is not within the scope of the tabu list, the Euclidean distance between the new solution and the solutions stored in the tabu list is calculated. If the Euclidean distance E_m between the new solution and any solution in the tabu list is less than the minimum Euclidean distance among the current solutions, the new solution is considered still within the scope of the tabu list and needs to be regenerated until a solution that breaks out of the tabu list’s range is produced.

$$E_m=\min \left(\sqrt{{\displaystyle \sum _i{\left(y_{new}-y_{habu}\right)}^2}}\right)$$

(16)

B. IG-RVDOA Phase

(6) Encoding. The coding pattern for each individual remains consistent with that in Equation (5). Detailed specifications are provided in (1).

(7) Fitness Calculation. To ensure the continuity of the algorithm, the fitness function value also uses Equation (14).

(8) Evolutionary operations. In the evolutionary operations of the GA, the optimal preservation strategy can effectively retain high-quality individuals from the early stages. However, it also makes these individuals difficult to be disrupted or replaced in subsequent crossover and mutation operations. This leads to the persistence of locally optimal individuals, ultimately restricting the algorithm’s global search capability. To counteract this phenomenon, the new population creation operator is introduced before the termination condition judgment. It randomly generates a new population using mutually exclusive integer encoding and evaluates it with the fitness function. If an individual’s fitness value is below the average, the mutation and crossover probabilities are increased to prevent the algorithm from falling into local optima; conversely, these probabilities are decreased. Moreover, if the fitness value of the best individual in the current population is higher than that of the worst individual, the best individual from the new population replaces the worst individual in the current population. This ensures the vitality and diversity of individuals within the population, thereby effectively enhancing the algorithm’s global search capability.

$$\left\{\begin{array}{l}{P}_c=\left\{\begin{array}{ll}{P}_{cmax}-{\displaystyle \frac{(P_{cmax}-P_{cmin})(F_{fitness,i}-F_{fitness,ave})}{(F_{fitness,max}-F_{fitness,ave})}},\hfill & F_{fitness,i}\ge F_{fitness,ave}\hfill \\ P_{cmax},\hfill & F_{fitness,i}<F_{fitness,ave}\hfill \end{array}\right.\hfill \\ P_m=\left\{\begin{array}{ll}{P}_{mmax}-{\displaystyle \frac{(P_{mmax}-P_{mmin})(F_{fitness,i}-F_{fitness,ave})}{(F_{fitness,max}-F_{fitness,ave})}},\hfill & F_{fitness,i}\ge F_{fitness,ave}\hfill \\ P_{mmax},\hfill & F_{fitness,i}<F_{fitness,ave}\hfill \end{array}\right.\hfill \end{array}\right.$$

(17)

where P_c is the cross probability, P_m is the mutation probability, P_cmax and P_cmin denote the set maximum and minimum cross probabilities, P_mmax and P_mmin denote the set maximum and minimum mutation probabilities, and F_fitness,i and F_fitness,ave denote the ith individual fitness value and the average.

4. Optimization for Gas Path Sensors Combination Based on TBC-IG-RVDOA

Perturbations of installation influence parameters in aero-engines are generally categorized into two types: gradual perturbations and abrupt perturbations. The former represents a slow variation process, while the latter denotes a sudden change occurring within a short period. Focusing on the four primary installation influence parameters of the turbofan aero-engine, namely the Reynolds index, relative humidity, compressor bleed flow, and low-pressure turbine power extraction, one installation influence is perturbed at a time during each test. Tests are performed by introducing perturbations at t = 2.00 s, and sensor optimization is carried out accordingly. Specific fault values are detailed in

Table 2. Perturbation Data of Installation Influence Parameters.

Installation Influence Parameters	Perturbation Data (%)
RNI	−0.0483
d	−0.0385
δq,hpc	−0.0281
ΔHpext,lpt	−0.0471

.

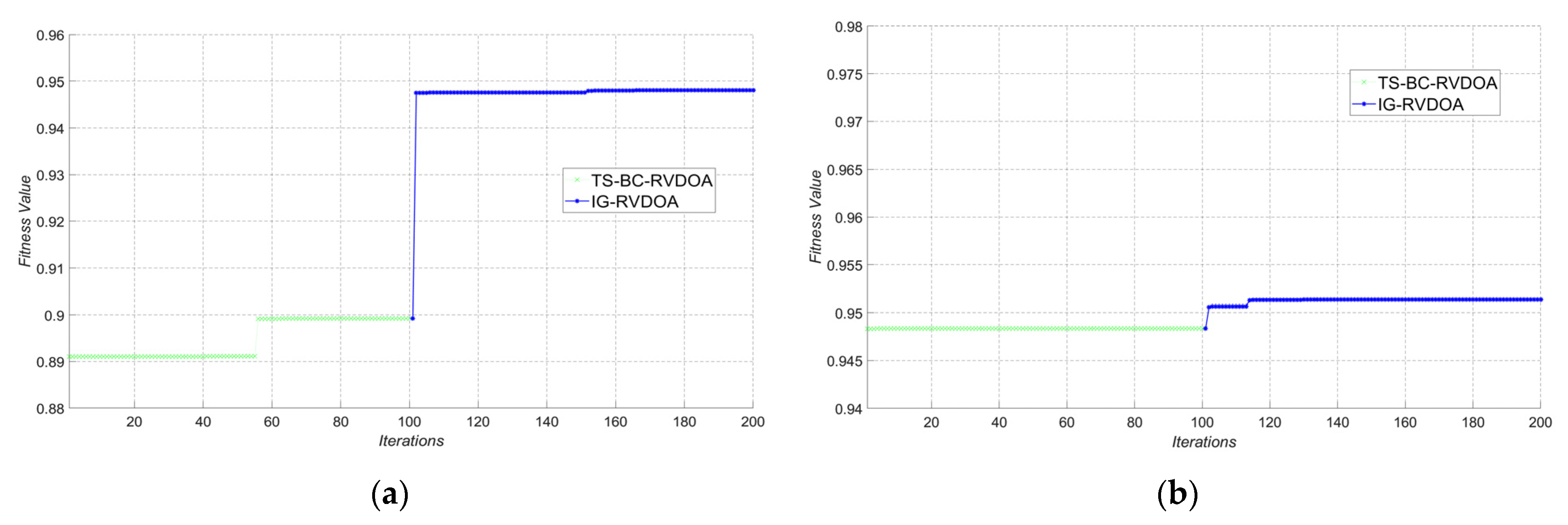
The optimization of gas-path sensors is conducted at the ground test condition corresponding to the steady-state point of the turbofan aero-engine with altitude H = 0, Mach number Ma = 0.6, and fan speed N_l = 100%N_l,design. To facilitate comparative analysis, the best sensor combinations were searched using both IG-RVDOA and TBC-IG-RVDOA. The fitness curve variations are shown in Figure 3 and Figure 4, respectively. The specific fitness function values, the optimal air-path sensor combinations, and the single-iteration time consumption are shown in

Table 3. Sensor Combination Optimization Results with IG-RVDOA.

	Sensor Combination	Fitness Function Value	Single-Iteration Time (s)
RNI	[1, 7, 13, 4, 8, 9, 5, 15, 4, 16]	0.9271	12.5678
d	[2, 7, 3, 12, 13, 9, 5, 15, 4, 16]	0.9065	13.2468
δq,hpc	[1, 7, 3, 12, 9, 13, 5, 15, 4, 16]	0.9718	11.9012
ΔHpext,lpt	[1, 7, 3, 12, 13, 9, 5, 15, 4, 16]	0.9716	12.5309

and

Table 4. Sensor Combination Optimization Results with TBC-IG-RVDOA.

	Sensor Combination	Fitness Function Value	Single-Iteration Time (s)
RNI	[1, 4, 5, 7, 8, 12, 13, 14,15]	0.9481	9.5678
d	[1, 3, 4, 5, 7, 10, 12, 13, 15]	0.9513	9.2914
δq,hpc	[1, 4, 5, 7, 10, 12, 13, 15, 16]	0.9709	9.8135
ΔHpext,lpt	[1, 4, 5, 7, 10, 12, 13, 15, 16]	0.9766	9.6789

, respectively.

By comparing Figure 3 and Figure 4, it can be observed that the integration of TS-BC with IGA provides a high-quality initial population for IGA by quickly searching for n local optima through TS-BC. This allows the optimization to start from a point closer to the global optimum, thereby accelerating the convergence speed and resulting in an improved fitness value compared to that obtained by IGRVDOA. Further examination of Figure 4 reveals that all fitness values of IGRVDOA are relatively ideal. Specifically, the fitness function value for ΔH_pext,lpt can reach 0.9766, while even the worst-case scenario for d can achieve a fitness function value of 0.9513. In addition, the single-iteration speed of the algorithm has also been enhanced. After hovering around the local optimum for each installation influence parameter disturbance, the global optimum can be obtained more quickly.

It can be seen from Table 3 and Table 4 that there are many identical sensor locations in the sensor combinations obtained by the algorithm. To determine which set can promptly detect all disturbances, the sensor combinations optimized by IG-RVDOA and TBC-IG-RVDOA were successively applied to the EKF to track the changes in installation influence parameters, thereby verifying the identification effectiveness of the sensors. 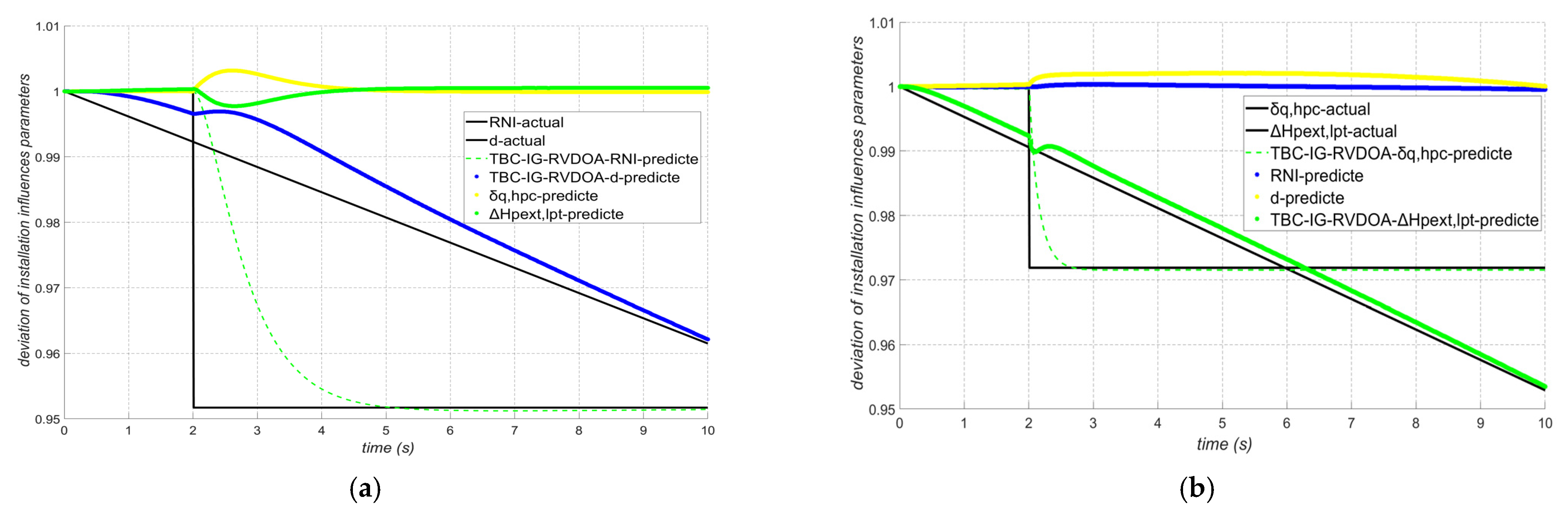The tracking effects of single abrupt disturbances of each installation influence parameter are shown in Figure 5 and Figure 6, respectively. The sensor combinations obtained from both algorithms can clearly identify the type of disturbance that occurs. However, by comparing Figure 5 and Figure 6, it can be seen that the sensor combination optimized by TBC-IG-RVDOA has higher recognition accuracy for disturbances of installation influence parameters. Through multiple experiments, it is calculated that the sensor combination [1, 4, 5, 7, 10, 12, 13, 15, 16] has a good diagnostic effect on different types of perturbations.

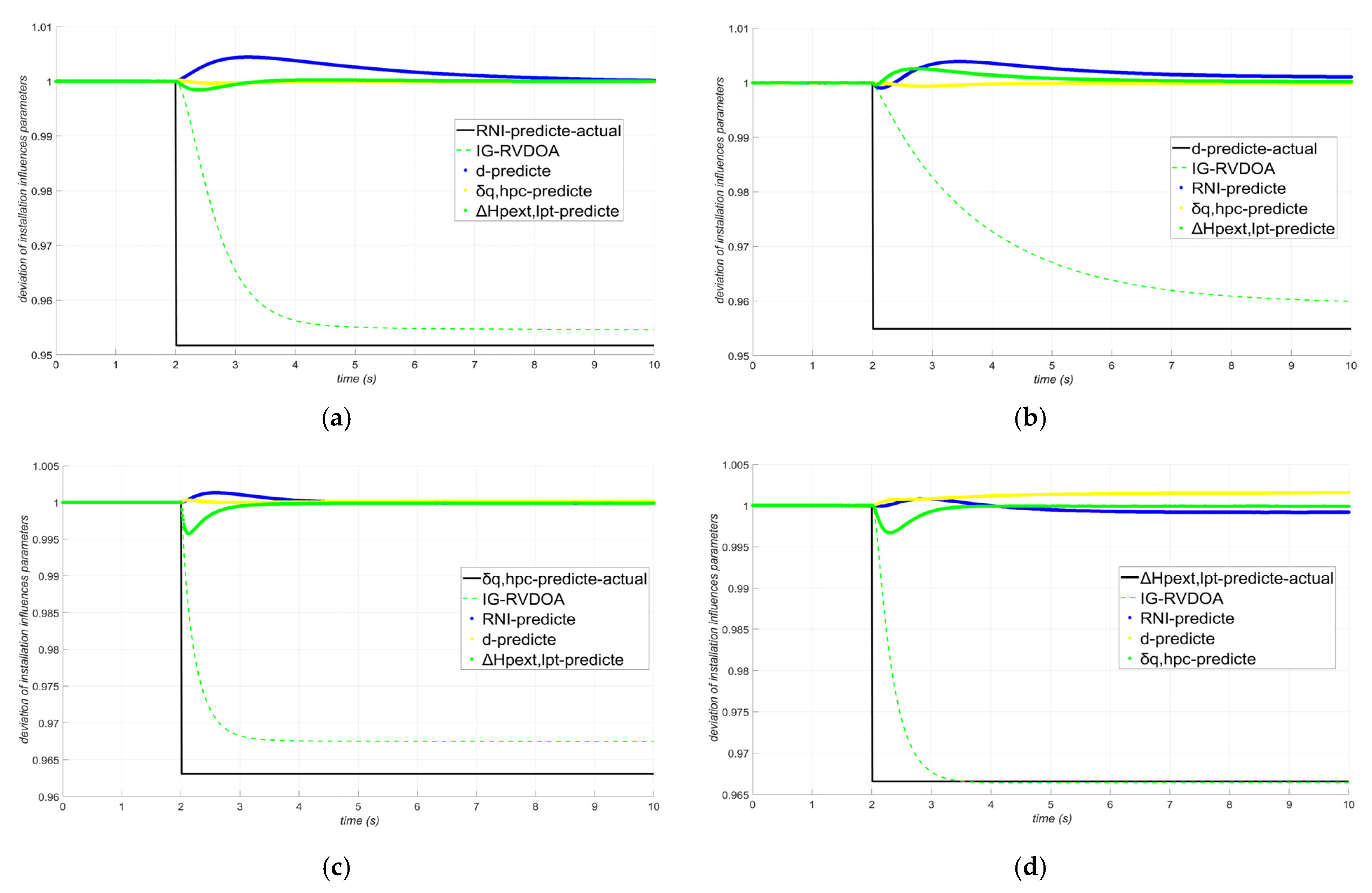
To further verify the effectiveness of the sensor combination in identifying disturbances, gradual changes in d and abrupt perturbations in RNI are simultaneously implanted. Data information is collected using this sensor combination, and the tracking effect is shown in Figure 7a. Similarly, the same sensor combination is used to identify the gradual changes in δ_q,hpc and the abrupt perturbations in ΔH_pext,lpt listed in Table 2, and the tracking results are shown in Figure 7b.

As can be clearly seen from Figure 6 and Figure 7, the sensor combination optimized by the TBC-IG-RVDOA can achieve ideal identification effects under different installation influence parameters perturbations. While accurately identifying the changing parameters, the other parameters only have minor fluctuations at t = 2 s when the perturbation is implanted, but then they can quickly stabilize at 1. It can be seen that the sensor combination [1, 4, 5, 7, 10, 12, 13, 15, 16] has a high identification accuracy for the perturbations of installation influence parameters of aero-engines. To explore the diagnostic accuracy rate of this sensor combination, five random numbers within the range of [0.01, 0.05] are selected for each installation influence parameter, and multiple simulation experiments are carried out. The perturbation values and corresponding fitness values are shown in

Table 5. Fitness Values for Different Perturbations of Installation Influence Parameters.

Mode	Perturbation	Fitness Value	Perturbation	Fitness Value	Perturbation	Fitness Value	Perturbation	Fitness Value	Perturbation	Fitness Value
RNI	−0.2980	0.9234	−0.4510	0.9423	−0.1930	0.9324	−0.3470	0.9389	−0.2260	0.9489
d	−0.0325	0.9378	−0.0142	0.9245	−0.0463	0.9278	−0.0218	0.9456	−0.0369	0.9213
δq,hpc	−0.0198	0.9521	−0.0405	0.9567	−0.0334	0.9683	−0.0268	0.9624	−0.0471	0.9601
ΔHpext,lpt	−0.0249	0.9745	−0.0391	0.9778	−0.0182	0.9659	−0.0445	0.9578	−0.0276	0.9675

.

It can be observed from Table 4 that this sensor achieves a high fitness value of over 0.92 for disturbances of different installation influence parameters, which can meet the requirements for effective identification of disturbances of installation influence parameters of the aero-engine.

5. Conclusions

Based on the improved genetic random variable-dimension algorithm and the tabu search bee colony random variable-dimension algorithm, this study proposes a hybrid algorithm known as the Tabu Bee Colony–Improved Genetic Random Variable-Dimension Optimization Algorithm (TBC-IG-RVDOA). This algorithm aims to achieve a faster convergence rate and better optimal sensor combination performance. Initially, the numerical sensitivity of sensors under different installation influence parameters perturbations is analyzed, which provides the basis and foundation for sensor optimization. Subsequently, considering the actual situation of sensor installation under installation influence parameters perturbation conditions, a length penalty term lp is introduced. Meanwhile, in the calculation of the fitness function, prediction accuracy, sensor diversity, and coverage degree are comprehensively taken into account to obtain the optimal sensor layout scheme for the aero-engine. During the optimization process of the TBC-IG-RVDOA, the initial population is rapidly searched through TS-BC-RVDOA, while the global optimal sensor combination is realized by IG-RVDOA, which has strong convergence ability. Through simulation analysis, it is verified that the TBC-IG-RVDOA has strong search ability, has a short single-iteration time, and can quickly converge to the required sensor combination. Finally, the sensor combinations obtained by the search are used to track and compare the perturbations of various installation influence parameters of the aero-engine, realizing accurate identification of the perturbations.

Due to the fact that the degradation of health parameters and the disturbance of installation parameters can both lead to the same changes in thermodynamic parameters, there is a risk of fault confusion and misjudgment. Therefore, we will focus our subsequent research on developing a sensor combination that can precisely identify both external installation effects and internal component degradation at the same time. We plan to explore how to use the optimized sensor configuration to identify changes in health parameters and achieve accurate diagnosis of abrupt air-path faults. At the same time, we will further investigate the adaptive capabilities of the TBC-IG-RVDOA, allowing it to automatically adjust parameters based on varying installation conditions and disturbance types, to enhance the algorithm’s versatility and robustness. We hope that through these efforts, we can further enhance the practicality and accuracy of the internal sensor combination, providing more robust technical support for the maintenance and operation of aero-engines.