Construction of Sampling Disturbance Model of Lunar Surface
Abstract
1. Introduction
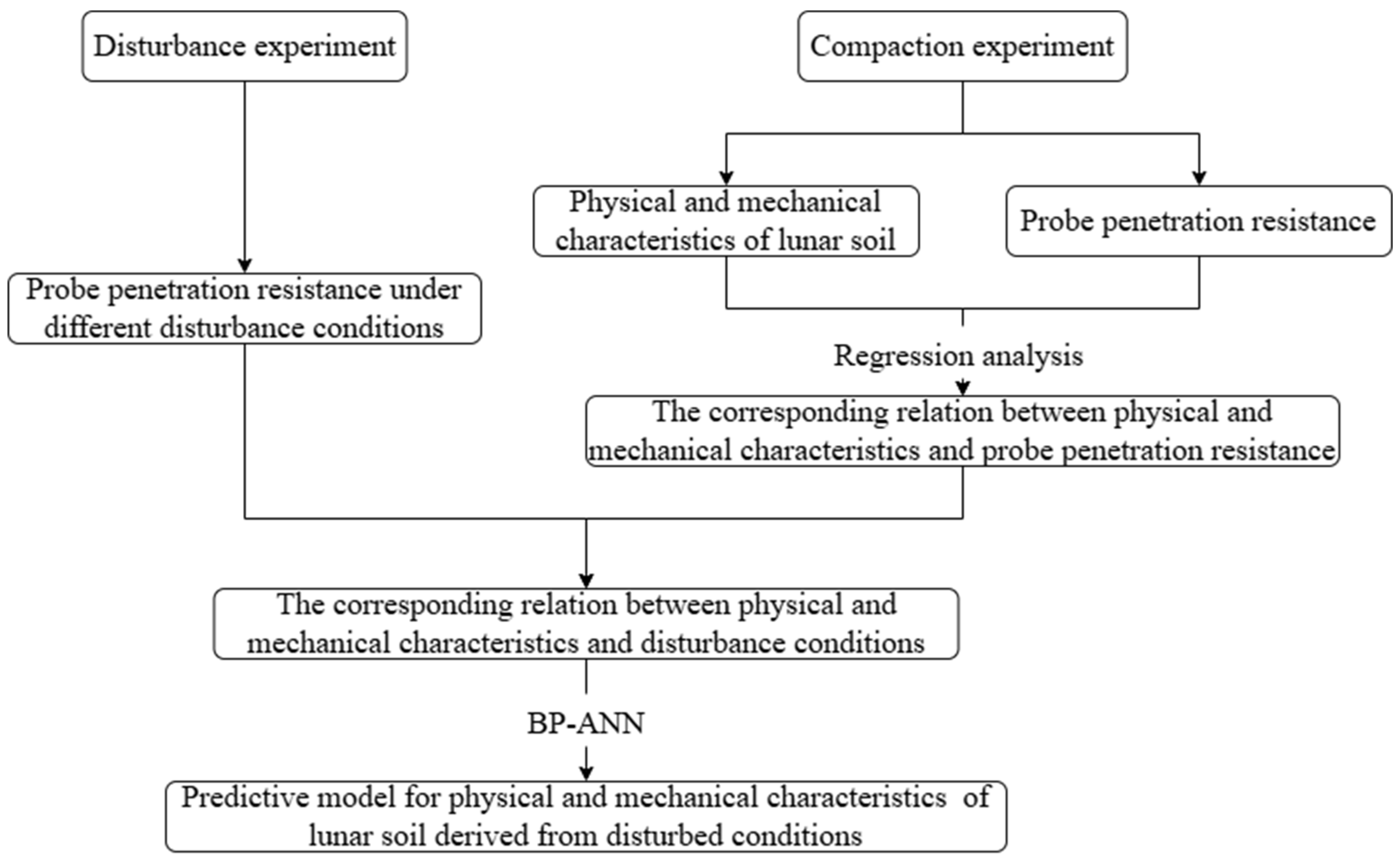
2. Experimental Procedure
3. Physical Experiments
3.1. Selection of Characteristic Parameters
- (1)
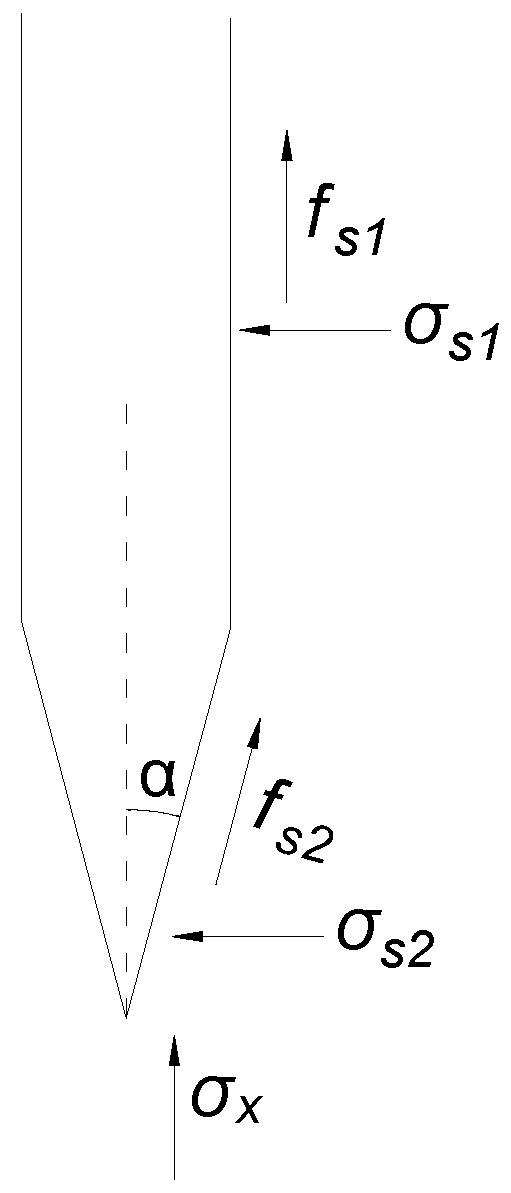
- Stress analysis of the lateral surface
- (2)
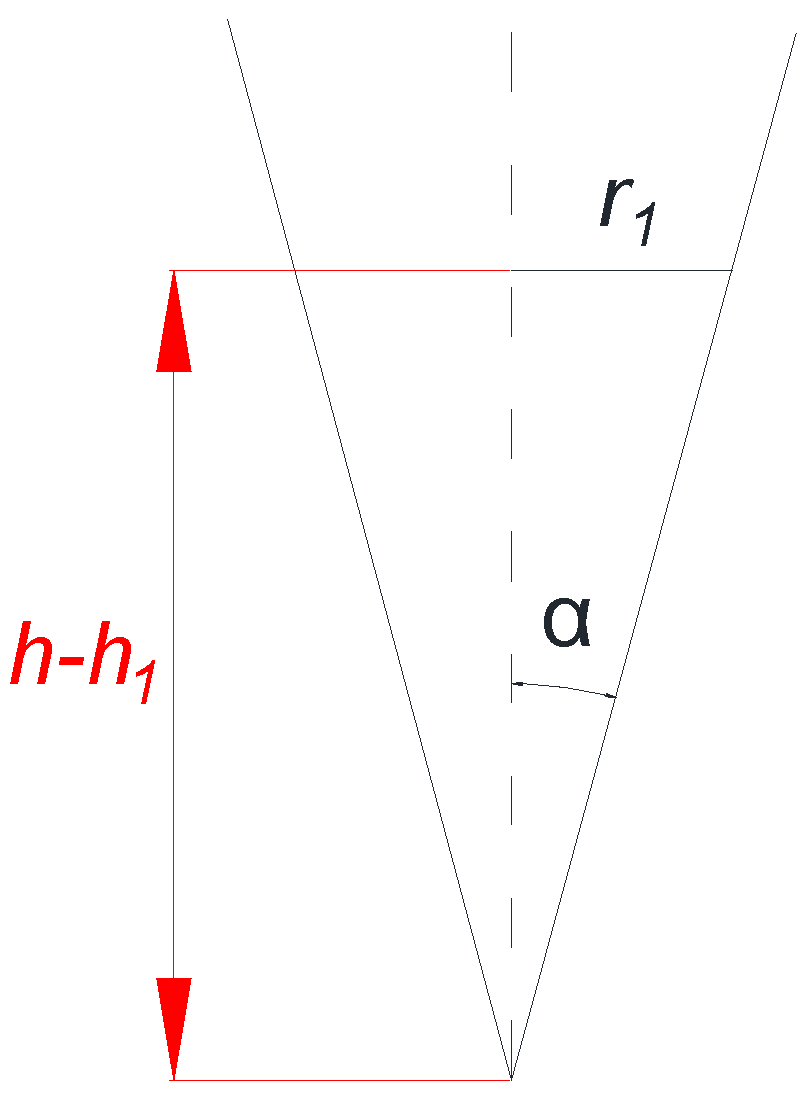
- Stress analysis of the conical surface
- (3)
- Force analysis of the lateral surface
- (4)
- Force analysis of the conical surface
- (5)
- Penetration Resistance Analysis of the Probe
3.2. Lunar Soil Simulant for Experiments
3.3. Experimental Testbed
3.3.1. Compaction Experiment
3.3.2. Disturbance Experiment


3.4. Analysis of Experimental Results
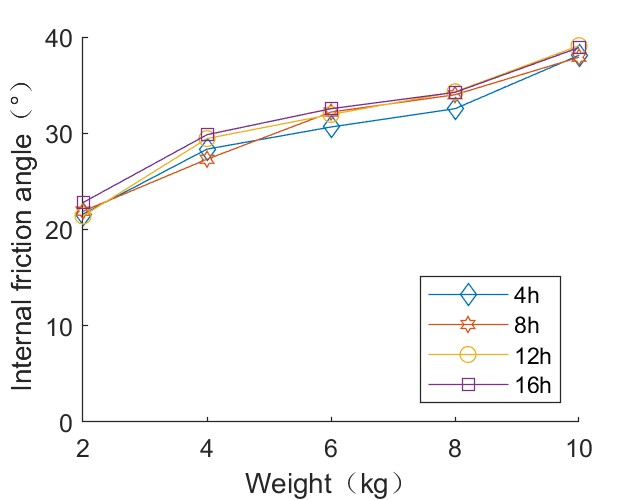
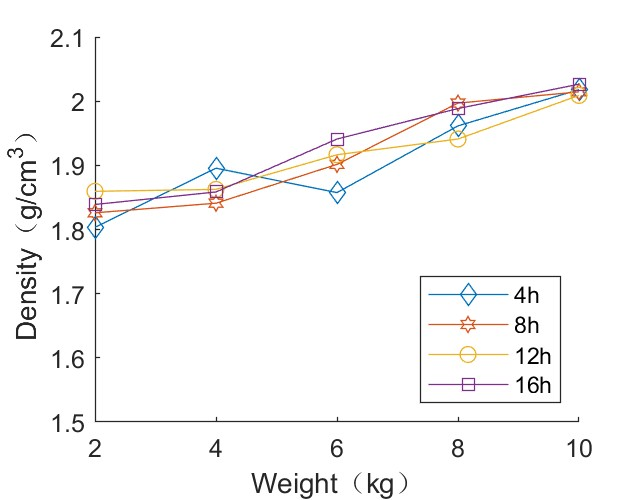
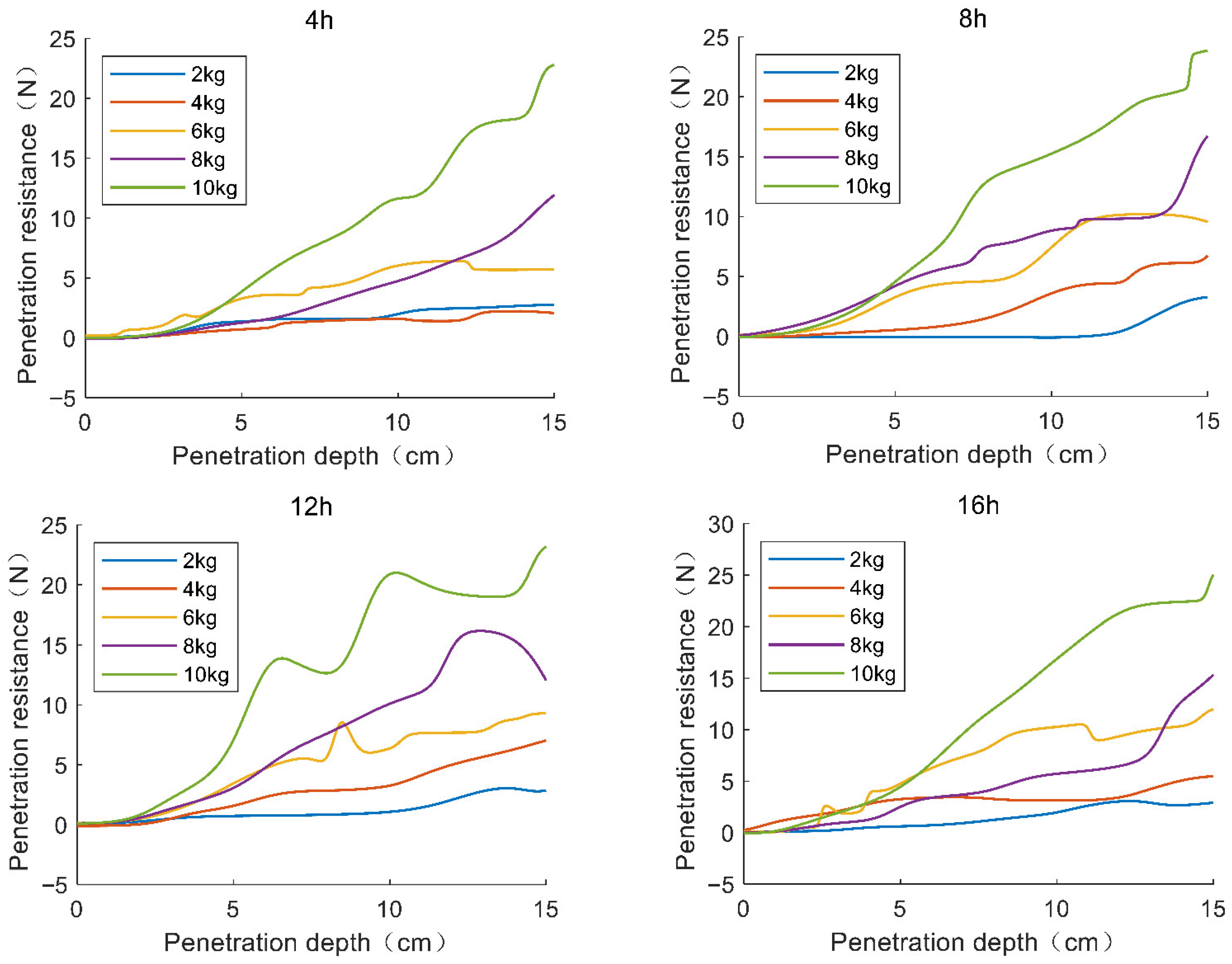
3.4.1. Compaction Experiment Results
3.4.2. Disturbance Experimental Results
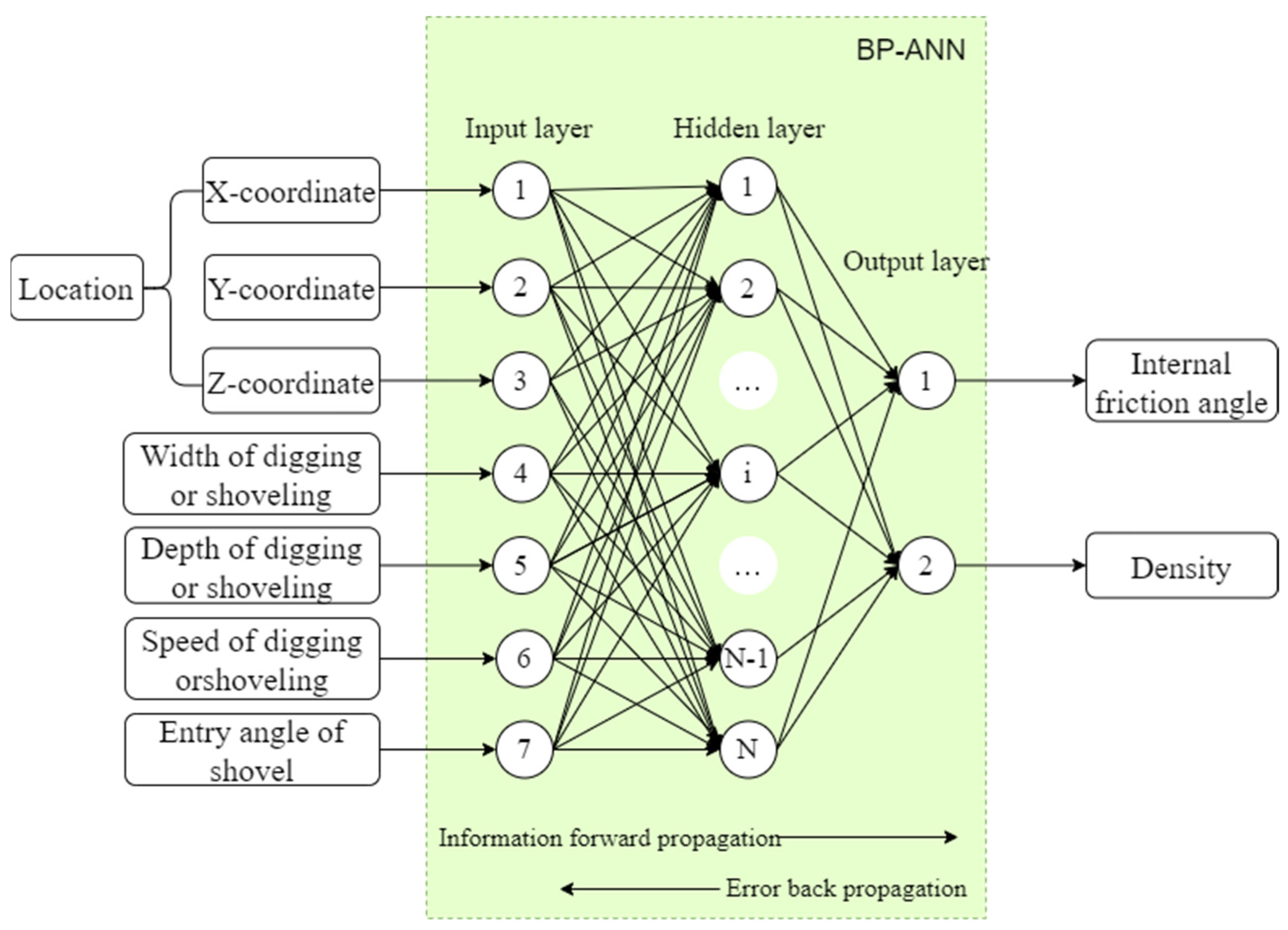
4. Disturbance Model Building
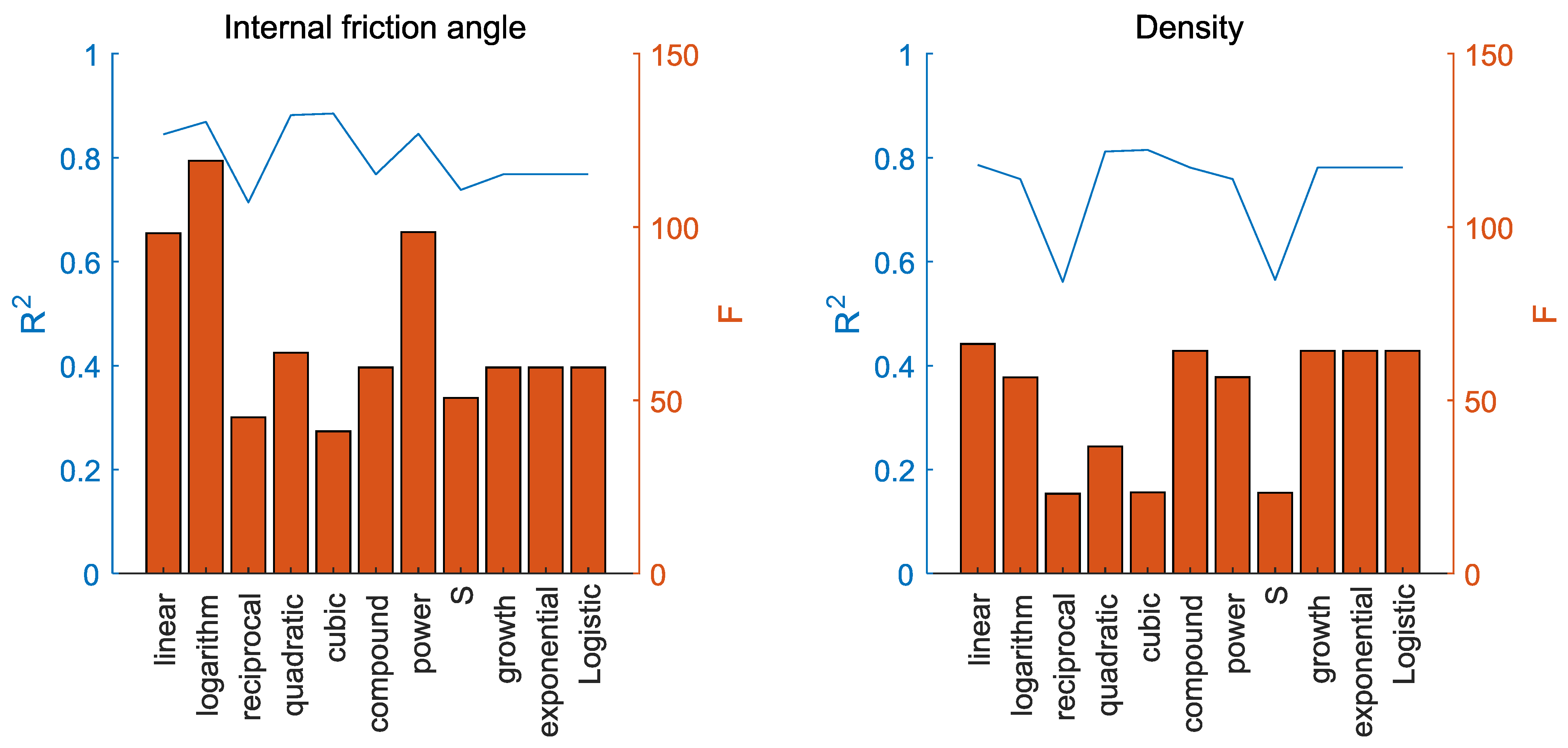
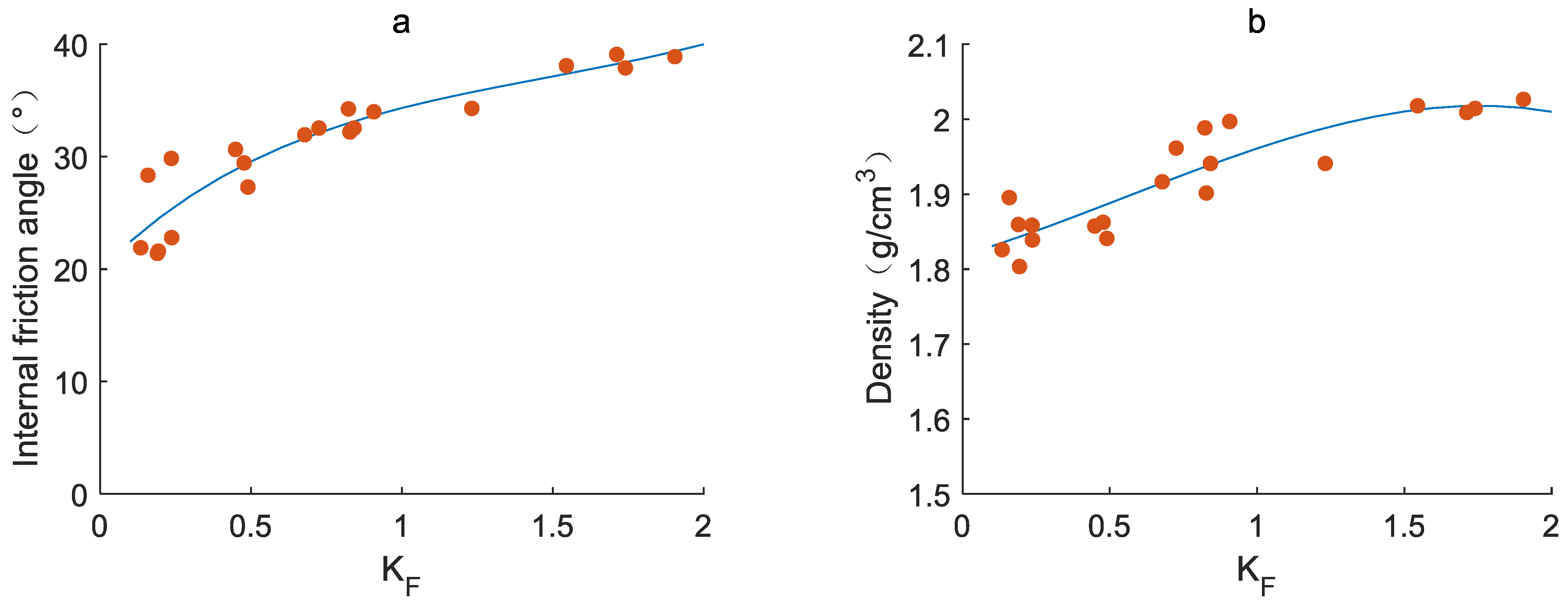
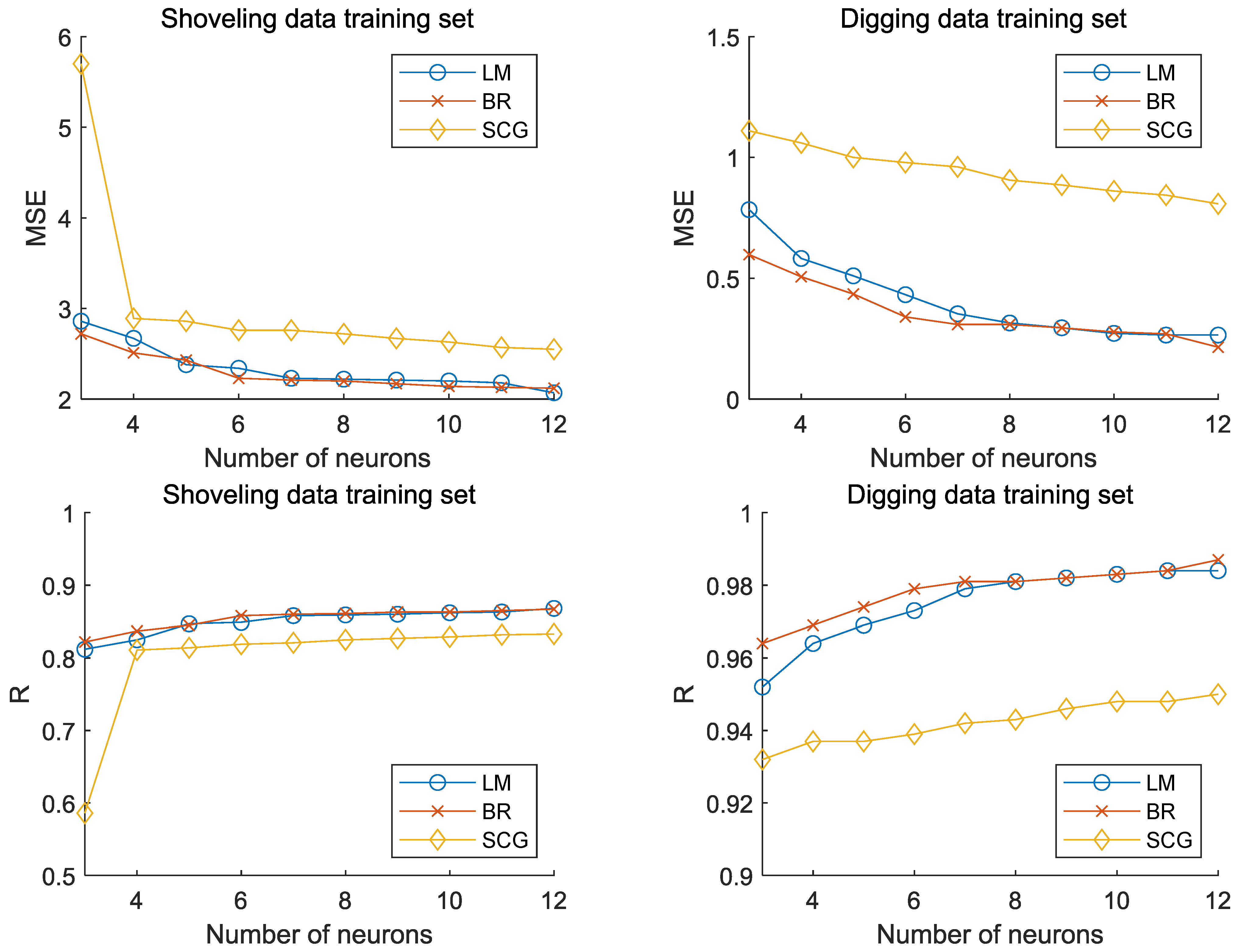
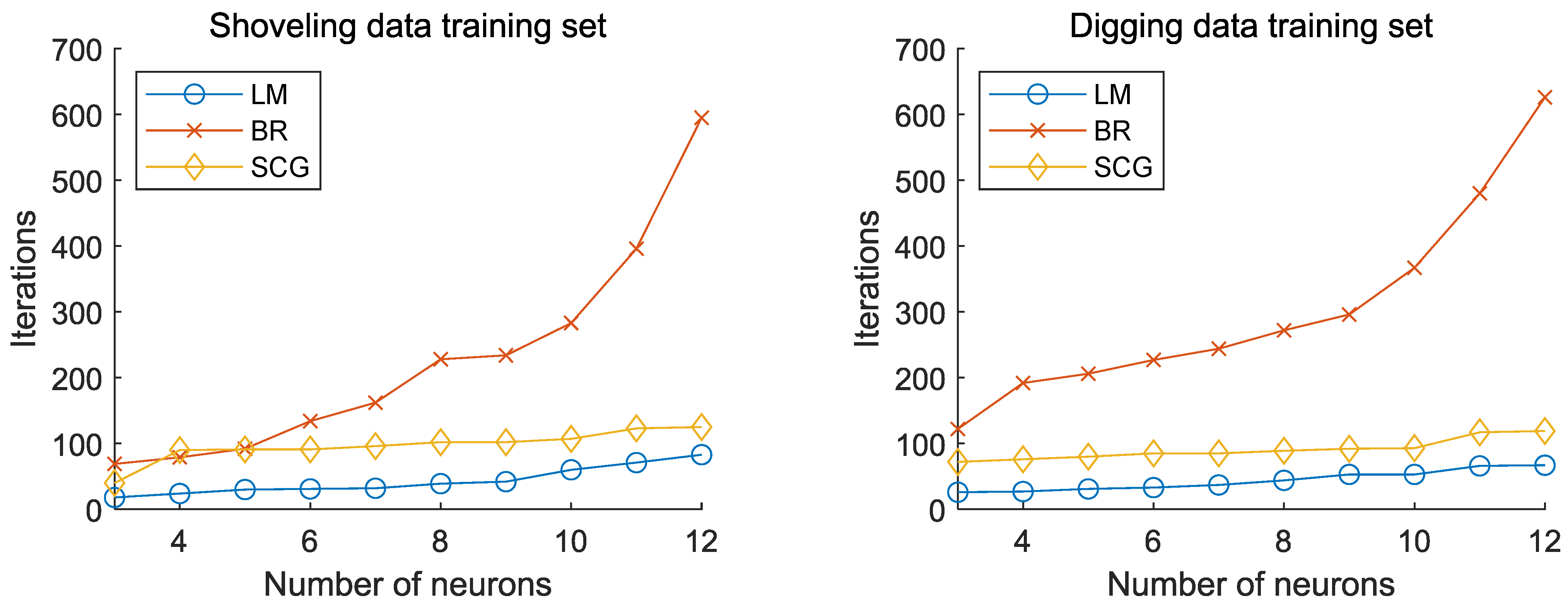
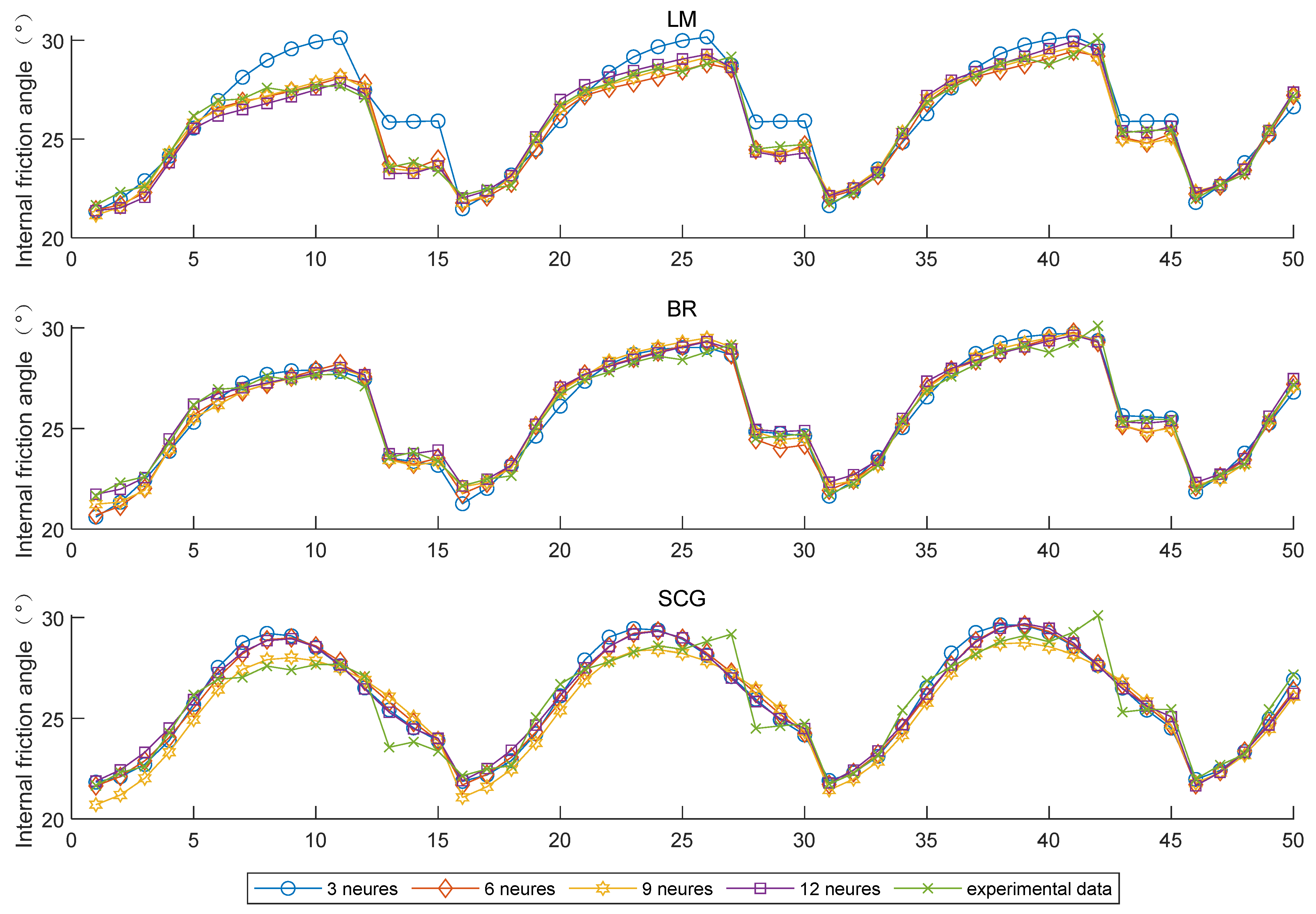
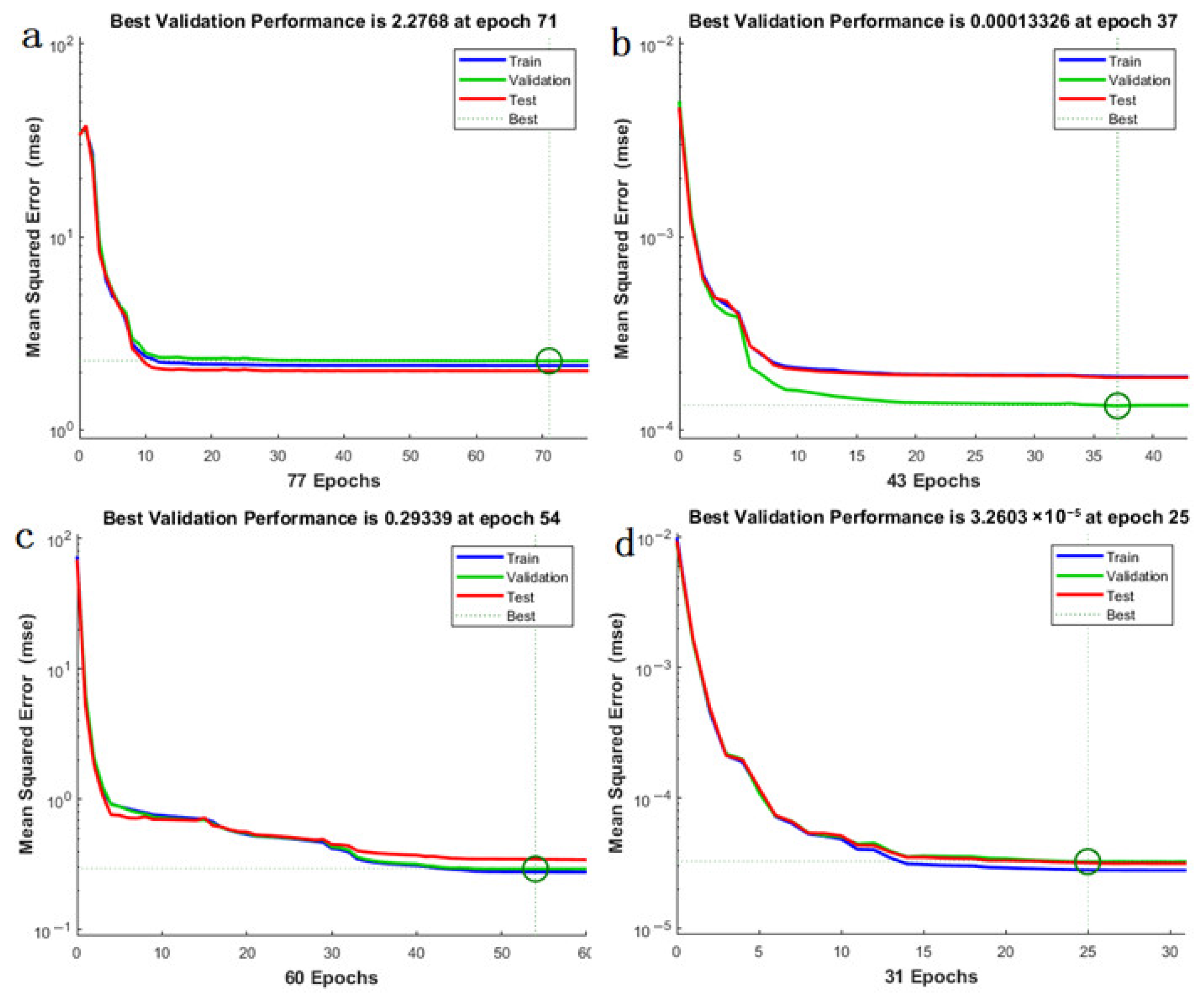
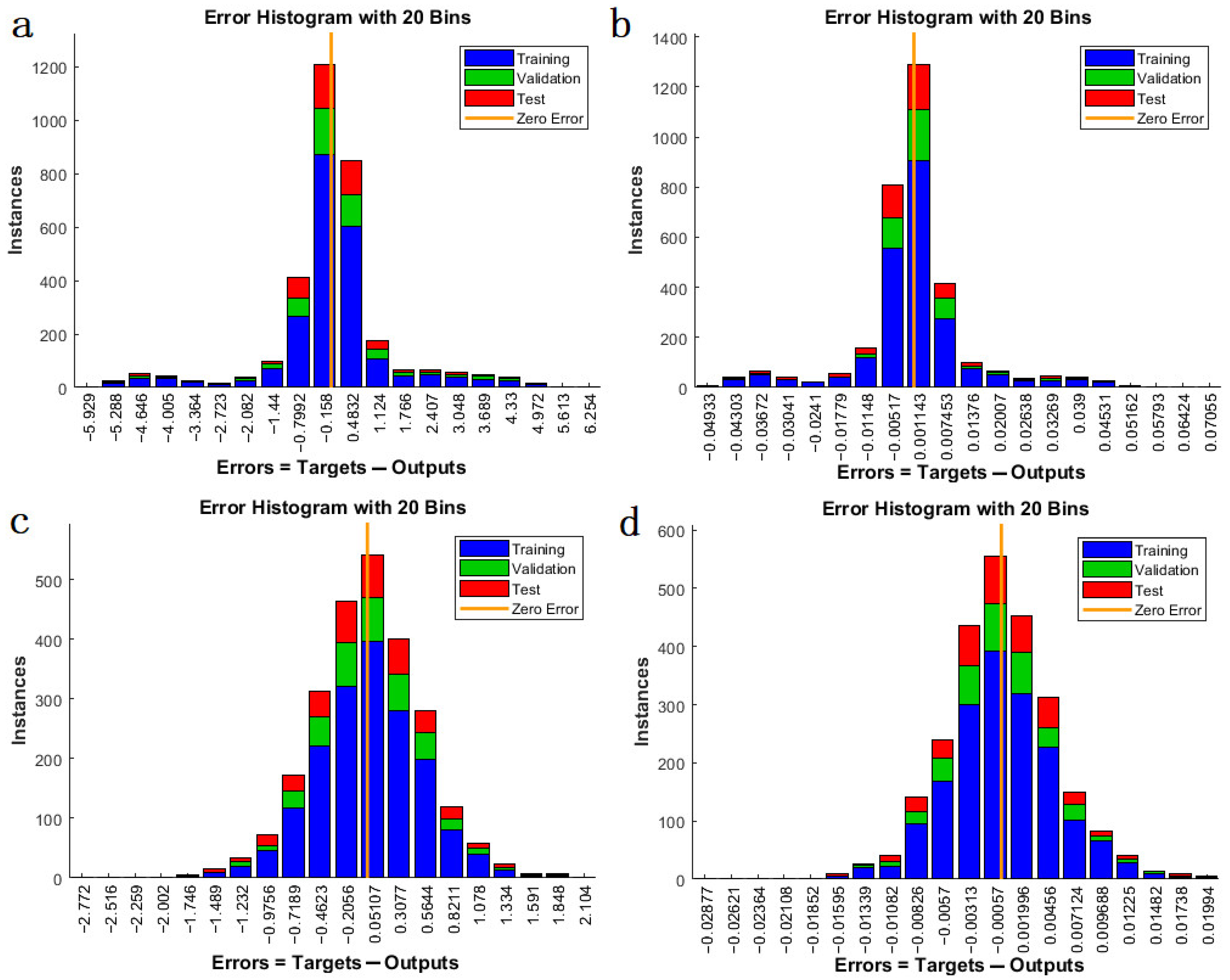
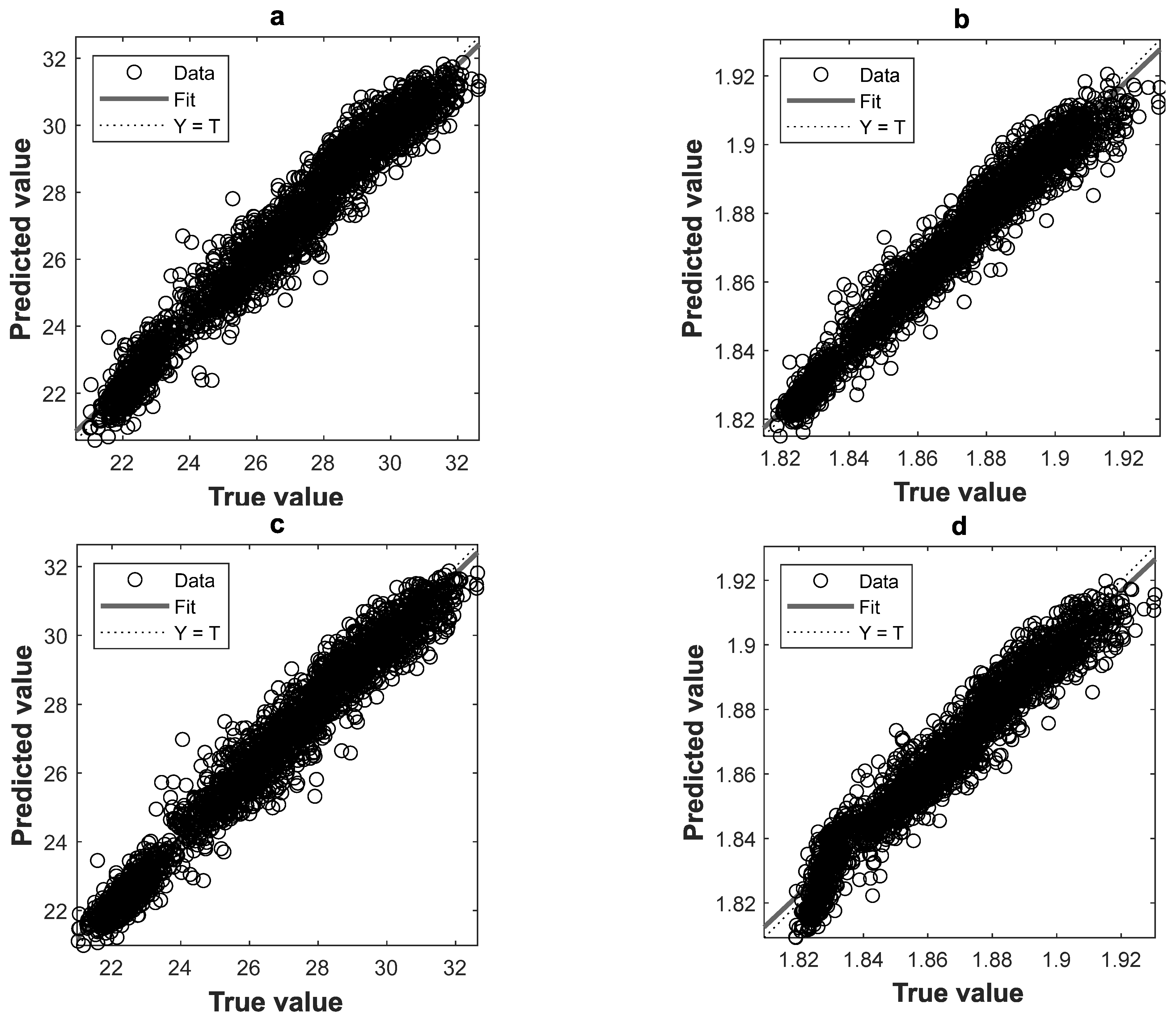
4.1. Algorithm Comparison
4.2. Prediction Results of BP-ANN
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Q.; Gao, H.; Xie, L.L.; Tan, S.C.; Duan, L.C. Review of research about lunar drilling technology. Explor. Eng. 2021, 48, 15–34. (In Chinese) [Google Scholar]
- Zheng, Y.H.; Deng, X.J.; Gu, Z.; Jin, S.Y.; Li, Q. Lunar surface sampling point selection of Chang’E 5. Opt. Precis. Eng. 2021, 29, 2935–2943. (In Chinese) [Google Scholar] [CrossRef]
- Yang, P.; Huang, Y.; Li, P.; Liu, S.; Shan, Q.; Zheng, W. Trajectory Determination of Chang’E-5 during Landing and Ascending. Remote Sens. 2021, 13, 4837. (In Chinese) [Google Scholar] [CrossRef]
- Gu, Y.; Sun, J.Y.; Xiao, Q.; Li, Y.H.; Wang, X.Y.; Cao, K.N. Morphology of Lunar Soil Returned by Chang’E-5 Mission and Implications for Space Weathering. Editor. Comm. Earth Sci. -J. China Univ. Geosci. 2022, 47, 4145–4160. (In Chinese) [Google Scholar]
- Zhang, T.; Ding, X. Drilling forces model for lunar regolith exploration and experimental validation. Acta Astronaut. 2017, 131, 190–203. [Google Scholar] [CrossRef]
- Yao, Y.; Xiao, C.; Wang, P.; Li, C.; Zhou, Q. Instrumental Neutron Activation Analysis of Chang’E-5 Lunar Regolith Samples. J. Am. Chem. Soc. 2022, 144, 5478–5484. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.; Wei, K.; Guo, Z.; Yu, H.; Chen, X.; Li, X.; Ma, W.; Liu, J. Study on surface characteristics of Chang’E-5 fine grained lunar soil. Sci. Phys. Mech. Astron. 2023, 53, 31–39. (In Chinese) [Google Scholar]
- Liu, C.; Li, J.; Zhang, T. Key technologies in the teleoperation of the Chang’e-5 lunar sampling. Sci. Sin. Technol. 2022, 52, 473–488. (In Chinese) [Google Scholar]
- Li, C.; Hu, H.; Yang, M.F.; Liu, J.; Zhou, Q.; Ren, X.; Liu, B.; Liu, D.; Zeng, X.; Zuo, W.; et al. Nature of the lunar far-side samples returned by the Chang’E-6 mission. Natl. Sci. Rev. 2024, 11, nwae328. [Google Scholar] [CrossRef]
- Tsuchiyama, A.; Sakurama, T.; Nakano, T.; Kentaro, U.; Makiko, O.; Takashi, M.; Kazuo, T.; Erik, M.G. Three-dimensional shape distribution of lunar regolith particles collected by the Apollo and Luna programs. Earth Planets Space 2022, 74, 172. [Google Scholar]
- Xu, L.; Qiao, L.; Xie, M.; Wang, Y.; Zhu, M.H.; Yan, J. Chronology, Local Stratigraphy, and Foreign Ejecta Materials at the Chang’e-6 Landing Site: Constraints on the Provenance of Samples Returned From the Moon’s Farside. Geophys. Res. Lett. 2024, 51, 13. [Google Scholar] [CrossRef]
- Wu, F.Y.; Li, Q.L.; Chen, Y.; Hu, S.; Yue, Z.Y.; Zhou, Q.; Wang, H.; Yang, W.; Tian, H.C.; Zhang, C.; et al. Lunar Evolution in Light of the Chang’e-5 Returned Samples. Annu. Rev. Earth Planet. Sci. 2024, 52, 159–194. [Google Scholar] [CrossRef]
- Long, T.; Qian, Y.; Norman, M.D.; Miljkovic, K.; Crow, C.; Head, J.W.; Che, X.; Tartèse, R.; Zellner, N.; Yu, X.; et al. Constraining the formation and transport of lunar impact glasses using the ages and chemical compositions of Chang’e-5 glass beads. Sci. Adv. 2022, 8, eabq2542. [Google Scholar] [CrossRef] [PubMed]
- Agui, J.H.; Bucek, M.; DeGennaro, A.; Wilkinson, R.A.; Zeng, X. Lunar Excavation Experiments in Simulant Soil Test Beds: Revisiting the Surveyor Geotechnical Data. J. Aerosp. Eng. 2013, 26, 117–133. [Google Scholar] [CrossRef]
- Hvorslev, M. (Ed.) Subsurface Exploration and Sampling of Soils for Civil Engineering Purposes; Waterways Experiment Station: Vicksburg, MI, USA, 1949.
- Desai, C.S.; Toth, J. Disturbed state constitutive modeling based on stress-strain and nondestructive behavior. Int. J. Solids Struct. 1996, 33, 1619–1650. [Google Scholar] [CrossRef]
- Hu, Q.; Xu, S.F.; Chen, R.P.; Ran, L. Influence of soil disturbance on metro tunnel in soft clay due to excavation of deep foundation pit. Int. J. Solids Struct. 2013, 35 (Suppl. S2), 537–541. (In Chinese) [Google Scholar]
- Yongfu, X. Quantitative identification of disturbance degree of soils influenced by construction. Dam Monit. Geotech. Test. 2000, 24, 8–10. (In Chinese) [Google Scholar]
- Spohn, T.; Knollenberg, J.; Ball, A.J.; Banaszkiewicz, M.; Benkhoff, J.; Grott, M.; Grygorczuk, J.; Hüttig, C.; Hagermann, A.; Kargl, G.; et al. COMETARY SCIENCE. Thermal and mechanical properties of the near-surface layers of comet 67P/Churyumov-Gerasimenko. Science 2015, 349, aab0464. [Google Scholar] [CrossRef]
- Seweryn, K.; Skocki, K.; Banaszkiewicz, M.; Grygorczuk, J.; Kolano, M.; Kuciński, T.; Mazurek, J.; Morawski, M.; Białek, A.; Rickman, H.; et al. Determining the geotechnical properties of planetary regolith using Low Velocity Penetrometers. Planet. Space Sci. 2014, 99, 70–83. [Google Scholar] [CrossRef]
- Apollo 15: Preliminary Science Report; Scientific and Technical Information Office: Washington, DC, USA, 1972; Volume 289.
- Zheng, Y.; Zhang, G.; Deng, X.; Zhang, W.; Jin, S.; Jia, X.; Zhang, N.; Jiang, S.; Li, H.; Yao, M. Design and implementation of the Chang’e-6 sampling and encapsulation system for the far side moon mission. Sci. Sin. Technol. 2025, 55, 1182–1193. (In Chinese) [Google Scholar] [CrossRef]
- Nie, J.; Cui, Y.; Senetakis, K.; Guo, D.; Wang, Y.; Wang, G.; Feng, P.; He, H.; Zhang, X.; Zhang, X.; et al. Predicting residual friction angle of lunar regolith based on Chang’e-5 lunar samples. Sci. Bull. 2023, 68, 730–739. [Google Scholar] [CrossRef] [PubMed]
- He, X.X.; Xiao, L.; Huang, J.; Wan, C.H.; Wu, T.; Gao, R.; Yan, S.W.; He, Q. Lunar Soil Simulant Development and Lunar Soil Simulant CUG-1A. Geol. Sci. Technol. Inf. 2011, 30, 137–142. (In Chinese) [Google Scholar]
- Zhang, H.; Gui, L.; Wang, T.; Yang, S. Prediction of Quaternary Cover Thickness and 3D Geological Modeling Based on BP Neural Network. Editor. Comm. Earth Sci. -J. China Univ. Geosci. 2024, 49, 550–559. (In Chinese) [Google Scholar]
- Yang, L.; Chen, Y.; Gao, X. Spatial Spillover Effect of Digital-Finance-Driven Technology Innovation Level Based on BP Neural Network. Sustainability 2023, 15, 1052. [Google Scholar] [CrossRef]
- Huizhen, H.; Qing, G.; Xiumian, H. Research Advances and Prospective in Mineral Intelligent Identification Based on Machine Learning. Editor. Comm. Earth Sci. -J. China Univ. Geosci. 2021, 46, 3091–3106. (In Chinese) [Google Scholar]
- Zhou, Z.; Li, H.; Wen, S.; Zhang, C. Prediction Model for the DC Flashover Voltage of a Composite Insulator Based on a BP Neural Network. Energies 2023, 16, 984. [Google Scholar] [CrossRef]
- Li, Q.; Jia, W. Phase Selection and Location Method of Generator Stator Winding Ground Fault Based on BP Neural Network. Energies 2023, 16, 1503. [Google Scholar] [CrossRef]


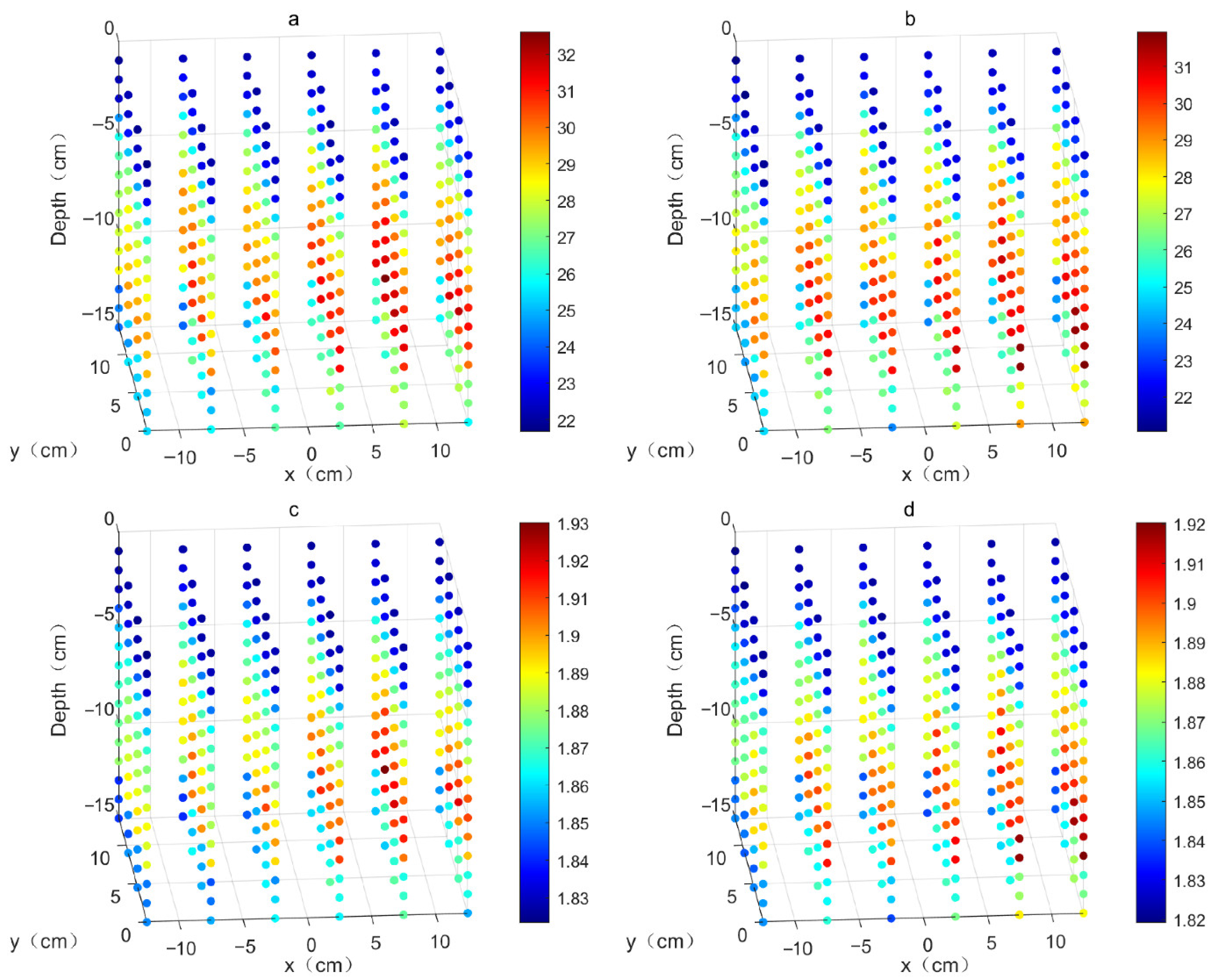
| Item | Value | Item | Value |
|---|---|---|---|
| Moisture content (%) | 0.240 | Porosity (%) | 36 |
| Moisture density (g/cm3) | 1.700 | Compressibility (MPa−1) | 0.09 |
| Dry density (g/cm3) | 1.696 | Compression modulus (MPa) | 17.43 |
| Bulk density (g/cm3) | 1.400 | Cohesion (kPa) | 1.36 |
| Relative density (%) | 261.1 | Internal friction angle (°) | 24.36 |
| Void ratio | 0.569 |
| Factor | Depth (cm) | Speed (mm/s) | Width (cm) | Entry Angle (°) | |
|---|---|---|---|---|---|
| Level | |||||
| 1 | 2 | 20 | 3 | 30 | |
| 2 | 3.5 | 35 | 4 | 45 | |
| 3 | 5 | 50 | 5 | 60 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, L.; Li, Q.; Hu, D.; Lv, J.; Zheng, H. Construction of Sampling Disturbance Model of Lunar Surface. Aerospace 2025, 12, 1011. https://doi.org/10.3390/aerospace12111011
Xie L, Li Q, Hu D, Lv J, Zheng H. Construction of Sampling Disturbance Model of Lunar Surface. Aerospace. 2025; 12(11):1011. https://doi.org/10.3390/aerospace12111011
Chicago/Turabian StyleXie, Lanlan, Qian Li, Dingkun Hu, Jiahang Lv, and Haijun Zheng. 2025. "Construction of Sampling Disturbance Model of Lunar Surface" Aerospace 12, no. 11: 1011. https://doi.org/10.3390/aerospace12111011
APA StyleXie, L., Li, Q., Hu, D., Lv, J., & Zheng, H. (2025). Construction of Sampling Disturbance Model of Lunar Surface. Aerospace, 12(11), 1011. https://doi.org/10.3390/aerospace12111011






