Stubborn Composite Disturbance Observer-Based MPC for Spacecraft Systems: An Event-Triggered Approach

Abstract

This paper studies spacecraft control under communication congestion, multi-source uncertainties, and input constraints. To reduce communication load, a static event-triggered mechanism is used so that transmissions occur only when necessary. Unknown nonlinearities are estimated online by a radial basis function neural network (RBFNN). To address sensor outliers and external disturbances, an event-triggered stubborn composite disturbance observer (ESCDO) is proposed, and sufficient conditions are derived to ensure its globally uniformly bounded stability. Based on this, an MPC-based composite anti-disturbance controller is designed to satisfy input constraints, and conditions are provided to guarantee the uniform bounded stability of the closed loop. Numerical simulations are conducted to demonstrate the effectiveness of the proposed approach.

1. Introduction

On-orbit servicing of spacecraft has attracted significant research attention in recent years, with applications including in-orbit fuel replenishment [1,2], space debris removal [3,4,5,6], and spacecraft maintenance [7,8,9]. The successful realization of these technologies depends on the precise control of spacecraft systems. Typically, spacecraft transmit measurement data to information-processing terminals, including space stations and ground stations [10], via wireless communication links, after which they receive and execute the corresponding control commands. However, during on-orbit servicing operations [11], the limited capacity of on-board communication equipment, together with the inherent multiple-input multiple-output (MIMO) characteristics of spacecraft, places a considerable burden on the already limited communication bandwidth when large volumes of measurement data must be transmitted [12,13,14]. This frequently results in packet loss [15] and transmission delays [16]. In addition, signal transmissions in the space environment are particularly vulnerable to electromagnetic interference and other disturbances [17], which can lead to anomalies in the measurement data. Such anomalous data points, which deviate from the expected measurement trends, are classified as outliers [18] and present substantial challenges for control system reliability. To alleviate communication bandwidth constraints, time-triggered [19] or event-triggered [20] mechanisms have been employed to reduce the data transmission volume. Although these methods effectively reduce the communication burden, they introduce undesirable artifacts such as chattering in the system state, making them unsuitable for high-precision spacecraft relative motion control tasks. Furthermore, to address the outlier problem, state observers incorporating limiting functions have been proposed [21].

In addition, spacecraft operating in the complex space environment is subject to multi-source uncertainties [22,23]. These uncertainties can be categorized into internal uncertainties and external uncertainties. The former include elastic disturbances generated by flexible devices such as antennas and solar panels [24], and actuator noise [25]; the latter arise from environmental disturbances encompassing gravity gradient torque, solar radiation, and geomagnetic torque [26]. From a modeling perspective, these disturbances can be classified into modelable disturbances [27] and unmodeled dynamics [28]. To mitigate the adverse effects of these disturbances, disturbance observers have been developed and extensively implemented in control systems for disturbance estimation [27]. For modelable disturbances that can be described by an exogenous system (model disturbance), a disturbance observer (DO) can utilize information from the exogenous system to render the error dynamics of the observer system asymptotically stable [29]. Conversely, when confronted with slowly time-varying disturbances that defy precise mathematical modeling but exhibit bounded derivatives, researchers have developed an extended state observer (ESO) [30,31]. Furthermore, for unknown nonlinear terms in the system, radial basis function neural networks (RBFNNs) are employed for estimation [32]. Moreover, a number of studies have investigated disturbance observation in the presence of measurement outliers. In [33], a discrete-time outlier-resistant ESO is designed for a discrete-time Nash equilibrium seeking problem. In [34], a stubborn ESO under the impact of outliers is designed for an event-triggered $ϵ$-Nash equilibrium seeking problem to estimate external disturbances. Despite these advances, existing composite DOs (CDOs) designed for multi-source uncertainties utilize the actual system output as the observer input, failing to account for the impact of sensor outliers on estimation performance. This critical oversight fails to leverage real measurement data for real-time and accurate estimation of unknown states and uncertainty terms. Specifically, when using high-gain observers, outliers can be amplified, substantially reducing estimation accuracy and even leading to disruptions in the closed-loop system. Consequently, the design of a composite disturbance observer to estimate multi-source uncertainties with measurement outliers is the motivation for this study.

Input constraints, arising from the inherent physical limitations of spacecraft actuators [28,35], present significant challenges for precise control performance. To address these constraints, researchers have introduced model predictive control (MPC) methods to obtain control inputs that satisfy the input constraints [36]. MPC is a receding-horizon strategy that optimizes a finite-horizon cost subject to system dynamics and constraints, applies only the first control action, and repeats the procedure at subsequent update instants. MPC is widely used when constraints are explicit design requirements and when trade-offs among tracking accuracy, control effort, and constraint satisfaction must be balanced [37]. Stability and feasibility are typically ensured through suitable terminal ingredients and/or robust design, while practical implementations often incorporate disturbance estimates to improve prediction fidelity [38]. When controlled systems are subject to disturbances, robust MPC [39] and tube-based MPC [40] have been developed to attenuate the adverse effects of perturbations. However, there has been insufficient research on MPC methods that account for both communication effects and multi-source uncertainties. Consequently, the development of an MPC method that addresses systems affected simultaneously by communication effects and multi-source uncertainties constitutes another motivation for this study.

In this paper, we design a composite anti-disturbance control strategy based on tube-based MPC for spacecraft systems that simultaneously experience communication congestion, sensor outliers, multi-source uncertainties, and input constraints. The major contributions of this paper are as follows:

(1)

An event-triggered stubborn composite disturbance observer (ESCDO) is proposed to estimate the system state and multi-source disturbances in the presence of outliers.

(2)

A composite anti-disturbance controller based on a tube-based MPC scheme is introduced to accommodate input constraints and suppress the effects of multi-source uncertainties.

(3)

Easy-to-check conditions are established to guarantee uniform bounded stability for both the ESCDO and the closed-loop system.

To ground the study, we consider spacecraft operating over bandwidth-limited links and subject to sporadic measurement outliers, multi-source disturbances, and actuator constraints—conditions under which periodic communication and classical observers either waste bandwidth or become brittle, and where constraint handling is often decoupled from disturbance rejection, risking infeasibility and loss of stability. Motivated by these coupled challenges, Section 2 formulates the control problem and modeling assumptions, including an outlier-corrupted measurement model, a multi-source disturbance channel, and input/communication constraints. Section 3 develops an ESCDO robust to outliers, and establishes convergence of the disturbance-estimation error while excluding Zeno behavior. Section 4 proposes an MPC-based composite anti-disturbance controller that enforces input constraints, with sufficient conditions ensuring feasibility of the optimization and uniform bounded stability of the closed loop. Section 5 presents a numerical case study validating the approach, and Section 6 concludes with limitations and directions for future research. The narrative structure of the paper is shown in Figure 1.

Figure 1. The narrative structure of this paper.

2. Problem Formulation and Preliminaries

System Model

In this paper, the Clohessy-Wiltshire equation [41] has been employed, and the ideal dynamic of the spacecraft is assumed to be

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)& =\overline{A}x\left(t\right)+\overline{B}(u\left(t\right)+f\left(x\left(t\right)\right))\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill y\left(t\right)& =\overline{C}x\left(t\right)\hfill \end{array}$$

(2)

where $x\left(t\right)=\left[x_1^T\left(t\right)x_2^T\left(t\right)\right]\in {\mathbb{R}}^6$ is the spacecraft system state with $x_1\left(t\right)={\left[\tilde{x}\left(t\right)\tilde{y}\left(t\right)\tilde{z}\left(t\right)\right]}^T$ and $x_2\left(t\right)={\left[\dot{\tilde{x}}\left(t\right)\dot{\tilde{y}}\left(t\right)\dot{\tilde{z}}\left(t\right)\right]}^T$ being the relative position and velocity components on three coordinate axes, respectively; $u\left(t\right)\in {\mathbb{R}}^3$ the system control input constrained by $u\left(t\right)\in \mathcal{U}\subseteq {\mathbb{R}}^3$ with $\mathbf{0}\in \mathcal{U}$; $f\left(x\left(t\right)\right)\in {\mathbb{R}}^3$ the unknown continuous nonlinear function related to the system state; $y\left(t\right)\in {\mathbb{R}}^3$ the output of the spacecraft system; $\overline{A}\in {\mathbb{R}}^{6\times 6}$, $\overline{B}\in {\mathbb{R}}^{6\times 3}$ and $C\in {\mathbb{R}}^{3\times 6}$ are system matrices with appropriate dimensions.

Given the significant distance between ground stations, tracking spacecraft, and target nodes, as well as the high volume of telemetry data, transmitting all measurements through satellite ground links poses a substantial risk of congestion-related delays and data loss.

To mitigate data congestion, we adopt an event-triggered mechanism, in which telemetry data are transmitted only when predefined conditions are satisfied, substantially reducing the data volume compared to conventional time-triggered approaches. In addition, telemetry data transmission is highly susceptible to interference from cosmic rays and atmospheric electromagnetic signals, resulting in measurement fluctuations (outliers). Taking this phenomenon and the event-triggered mechanism into account, the spacecraft relative motion model system (1) and (2) can be rewritten as a hybrid system

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)& =\overline{A}x\left(t\right)+\overline{B}u\left(t\right)+\overline{B}(f\left(x\left(t\right)\right)+d\left(t\right)+d_o\left(t\right))\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill y\left(t_k\right)& =x_1\left(t_k\right)+\beta \left(t_k\right)v\left(t_k\right)\hfill \end{array}$$

(4)

where $t_k$ is the event-triggering moment; $y\left(t_k\right)$ the wireless telemetry data transmitted at the event-triggering moment; $v\left(t_k\right)$ the outlier in wireless transmission; $\beta \left(t_k\right)$ indicates the presence of outliers. $\beta \left(t_k\right)=1$ indicates the presence of outliers, while $\beta \left(t_k\right)=0$ denotes the absence of outliers. Furthermore, $\beta \left(t_k\right)$ satisfies the Bernoulli distribution $\mathrm{Prob}\{\beta \left(t_k\right)=0\}=1-\beta$ and $\mathrm{Prob}\{\beta \left(t_k\right)=1\}=\beta$ for a constant $\beta \in [0,1)$. $d\left(t\right)\in {\mathbb{R}}^3$ is the external disturbance satisfying $\Vert \dot{d}\left(t\right)\Vert \le d_d$ with $d_d>0$ being a known constant. $d_o\left(t\right)\in {\mathbb{R}}^3$ is generated by the following exogenous system

$$\begin{array}{c}\hfill \dot{w}\left(t\right)=Ww\left(t\right),d_o\left(t\right)=Vw\left(t\right);\end{array}$$

(5)

where $w\left(t\right)\in {\mathbb{R}}^6$ is the state of disturbance $d_o\left(t\right)$; $W\in {\mathbb{R}}^{6\times 6}$ and $V\in {\mathbb{R}}^{3\times 6}$ are known matrices.

Remark 1. 

The assumptions on uncertainties and disturbances in this study are adopted from [32]. Reference [32] investigates the control of a tethered spacecraft under multi-source uncertainties and provides clear descriptions and models of the relevant uncertainty and disturbance sources. These effects are representative of the perturbations encountered by spacecraft during on-orbit operations. Accordingly, the uncertainty and disturbance assumptions used here are consistent with practical on-orbit conditions.

Remark 2. 

This work employs a relative-motion model of the spacecraft. However, the classical form of this model holds only under idealized assumptions that neglect perturbations such as the $J_2$ effect and atmospheric drag. In contrast, the present study does not assume an ideal environment: the relative motion is modeled under external disturbances—e.g., gravity-gradient torque, solar radiation pressure, and geomagnetic torque—as discussed in the introduction. These effects act on the spacecraft as exogenous torques (and associated forces); therefore, the model adopted here explicitly incorporates such disturbances rather than relying on the idealized relative-motion equations.

3. The Estimation of System State and Multi-Uncertainties

In this part, we design an RBFNN to estimate the unknown continuous nonlinear function $f\left(x\right(t\left)\right)$ in system (3). Furthermore, an ESCDO is proposed to estimate the system state $x\left(t\right)$, multi-source disturbances $d\left(t\right)$ and $d_o\left(t\right)$ in the presence of outliers.

3.1. Design of the RBFNNs

As stated in [42], a continuous nonlinear function $f\left(x\left(t\right)\right):{\mathbb{R}}^l\to {\mathbb{R}}^3$ defined on a compact set $\mathcal{F}$ can be approximated by the following RBFNN

$$\begin{array}{c}\hfill f\left(x\left(t\right)\right)={\theta }^{*T}\eta \left(x\left(t\right)\right)+\pi \left(t\right),\end{array}$$

(6)

where ${\theta }^{*}\in {\mathbb{R}}^{l\times 3}$, $\eta \left(x\left(t\right)\right)\in {\mathbb{R}}^{l\times 1}$ and $\pi \left(t\right)\in {\mathbb{R}}^{3\times 1}$ are the ideal weight vector, the vector-valued function, and the networked reconstruction error, respectively. Furthermore, $\eta \left(x\right(t\left)\right)$ is norm-bounded satisfying $\sqrt{\xi }\le \parallel \eta \left(x\left(t\right)\right)\parallel \le \sqrt{\varsigma }$ with $\xi >0$ and $\varsigma >0$ being known constants. Note that $\pi \left(t\right)$ is also continuously differentiable with $\parallel \pi \left(t\right)\parallel \le {\pi }_m$ and $\parallel \dot{\pi }\left(t\right)\parallel \le {\pi }_d$. Then, system (3) can be rewritten as

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)& =\overline{A}x\left(t\right)+\overline{B}u\left(t\right)+\overline{B}({\theta }^T\left(t\right)\eta \left(x\left(t\right)\right)+{\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)+d_f\left(t\right)+d_o\left(t\right))\hfill \end{array}$$

(7)

$$\begin{array}{cc}y\left(t_k\right)\hfill & =x_1\left(t_k\right)+\beta \left(t_k\right)v\left(t_k\right)\hfill \end{array}$$

(8)

where $d_f\left(t\right)\triangleq \pi \left(t\right)+d\left(t\right)$ and $\tilde{\theta }\left(t\right)\triangleq {\theta }^{*}-\theta \left(t\right)$ with $\theta \left(t\right)$ being the estimation of ${\theta }^{*}$. Then, systems (7) and (8) can be rewritten as

$$\begin{array}{cc}\hfill \dot{X}\left(t\right)& =AX\left(t\right)+Bu\left(t\right)+B{\theta }^T\left(t\right)\eta \left(x\left(t\right)\right)+B{\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)+Dh\left(t\right)\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill y\left(t_k\right)& =x_1\left(t_k\right)+\beta \left(t_k\right)v\left(t_k\right)\hfill \end{array}$$

(10)

where $X\left(t\right)\triangleq {\left[x^T\left(t\right)w^T\left(t\right)d_f^T\left(t\right)\right]}^T={\left[x_1^T\left(t\right)x_2^T\left(t\right)w^T\left(t\right)d_f^T\left(t\right)\right]}^T$, $h\left(t\right)\triangleq {\dot{d}}_f\left(t\right)$,

$$\begin{array}{c}\hfill A\triangleq \left[\begin{array}{ccc}\overline{A}& \overline{B}V& \overline{B}\\ \mathbf{0}& W& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}\end{array}\right],B\triangleq \left[\begin{array}{c}\overline{B}\\ \mathbf{0}\end{array}\right],D\triangleq \left[\begin{array}{c}\mathbf{0}\\ I\end{array}\right]\end{array}$$

3.2. ESCDO Design

In this part, an ESCDO is designed as

$$\begin{array}{cc}\hfill \dot{Z}\left(t\right)& =AZ\left(t\right)+Bu\left(t\right)+B{\theta }^T\left(t\right)\eta \left(x\left(t\right)\right)+L{\mathrm{sat}}_{\chi }(\rho \left(t\right)-z_1\left(t\right))\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \dot{\chi }\left(t\right)& =-{\alpha }_1\chi \left(t\right)+{\alpha }_2{\parallel \rho \left(t\right)-z_1\left(t\right)\parallel }^2\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \rho \left(t\right)& =\left\{\begin{array}{c}{\int }_{t_k}^t{z}_2\left(t\right)\mathrm{d}s+y\left(t_k\right),t\in [t_k,t_{k+1}),ifE\left(t\right)=0\\ x_1\left(t_k\right)+\beta \left(t_k\right)v\left(t_k\right),ifE\left(t\right)=1\end{array}\right.\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill \dot{\theta }\left(t\right)& =-3{\gamma }_3^{-1}\eta \left(x\left(t\right)\right){\eta }^T\left(x\left(t\right)\right)\theta \left(t\right)\hfill \end{array}$$

(14)

where $Z\left(t\right)={[z^T\left(t\right){\widehat{w}}^T\left(t\right){\widehat{d}}_f^T\left(t\right)]}^T$ is the estimation of $X\left(t\right)$ with $z\left(t\right)\triangleq {[z_1^T\left(t\right)z_2^T\left(t\right)]}^T$; L is the ESCDO gain matrix satisfying $L={\left[L_1{L}_2{L}_3\right]}^T$ with $L_1$, $L_2$ and $L_3$ as given parameters; $\rho \left(t\right)$ is the variable based on the inter-sample prediction term ${\int }_{t_k}^t{z}_2\left(t\right)\mathrm{d}s+y\left(t_k\right)$; ${\alpha }_1>0$, ${\alpha }_2>0$, ${\gamma }_3>0$ are adjustable parameters without direct physical meaning. Their purpose is to ensure convergence of the observer’s estimation error in the designed ESCDO. $E\left(t\right)$ is the event-triggered mechanism condition designed as

$$\begin{array}{c}\hfill E\left(t\right)=\left\{\begin{array}{cc}0,& e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)\le {\alpha }_e(e_1^T\left(t\right)e_1\left(t\right)+\chi \left(t\right)+{ϵ}_0)\\ 1,& e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)>{\alpha }_e(e_1^T\left(t\right)e_1\left(t\right)+\chi \left(t\right)+{ϵ}_0)\end{array}\right.\end{array}$$

(15)

where

$$\begin{array}{cc}\hfill e_{\rho }\left(t\right)& \triangleq \rho \left(t\right)-x_1\left(t\right),e_1\left(t\right)\triangleq CX\left(t\right)-z_1\left(t\right)=x_1\left(t\right)-z_1\left(t\right),C=\left[I\mathbf{0}\mathbf{0}\mathbf{0}\right]\hfill \end{array}$$

with ${\alpha }_e>0$ and ${ϵ}_0>0$ being two adjustable positive parameters. $E\left(t\right)=1$ and $E\left(t\right)=0$ represent the event triggered and the event not triggered, respectively. ${\mathrm{sat}}_{\chi }(·)$ is the saturation function with a non-negative dynamic variable $\chi \left(t\right)$ as its upper limit. The specific expression of ${\mathrm{sat}}_{\chi }(\rho \left(t\right)-z_1\left(t\right))$ is

$$\begin{array}{c}\hfill {\mathrm{sat}}_{\chi }(\rho \left(t\right)-z_1\left(t\right))={[{\mathrm{sat}}_{\chi }({\rho }_1\left(t\right)-z_{11}\left(t\right)),{\mathrm{sat}}_{\chi }({\rho }_2\left(t\right)-z_{12}\left(t\right)),{\mathrm{sat}}_{\chi }({\rho }_3\left(t\right)-z_{13}\left(t\right))]}^T\end{array}$$

where ${\mathrm{sat}}_{\chi }({\rho }_i\left(t\right)-z_{1i}\left(t\right))=max\{-\chi \left(t\right),min\{\chi \left(t\right),{\rho }_i\left(t\right)-z_{1i}\left(t\right)\}\}$, $i=1,2,3$.

Denote $e\left(t\right)\triangleq X\left(t\right)-Z\left(t\right)$ such that the dynamics of the estimation error can be obtained by (7)–(12) as

$$\begin{array}{cc}\hfill \dot{e}\left(t\right)& =Ae\left(t\right)+B{\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)-L{\mathrm{sat}}_{\chi }(e_1\left(t\right)+e_{\rho }\left(t\right))+Dh\left(t\right)\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill \dot{\chi }\left(t\right)& =-{\alpha }_1\chi \left(t\right)+{\alpha }_2{\parallel e_1\left(t\right)+e_{\rho }\left(t\right)\parallel }^2\hfill \end{array}$$

(17)

The control structure diagram of the spacecraft system under communication congestion, multi-source uncertainties, and the input constraint is given in Figure 2.

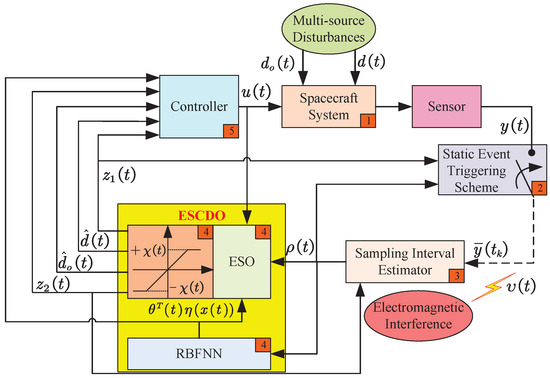
Figure 2. The control structure diagram of the spacecraft system.

Lemma 1. 

For the nonlinear function $q\left(t\right)=Ce\left(t\right)-{\mathrm{sat}}_{\chi }\left(Ce\left(t\right)\right)$, if $Ce\left(t\right)$ and $He\left(t\right)$ are elements in the polyhedron

$$\begin{array}{c}\hfill \Omega =\{e\left(t\right);\parallel (C_{\left(i\right)}-H_{\left(i\right)})e\left(t\right)\parallel \le {\chi }^2\left(t\right)\},\end{array}$$

(18)

where $C_{\left(i\right)}$ and $H_{\left(i\right)}$ represent the i-th line of matrices C and H, respectively, then the following inequality

$$\begin{array}{c}\hfill q^T\left(t\right)\mathsf{{\rm Y}}(He\left(t\right)-q\left(t\right))\ge 0\end{array}$$

(19)

holds for any positive definite diagonal matrix Υ.

Lemma 2. 

For a given symmetric matrix

$$\begin{array}{c}\hfill S=\left[\begin{array}{cc}{S}_{11}& S_{12}\\ S_{21}& S_{22}\end{array}\right]\end{array}$$

where $S_{11}\in {\mathbb{R}}^{a\times a}$, the following three conditions are equivalent

• (1) $S<0$;
• (2) $S_{11}<0,S_{22}-S_{12}^T{S}_{11}^{-1}{S}_{12}<0$;
• (3) $S_{22}<0,S_{11}-S_{12}{S}_{22}^{-1}{S}_{12}^T<0$.

Definition 1 

([43]). For a set Θ, the positive definite function $V_e\left(t\right)$ satisfies the inequality ${\dot{V}}_e\left(t\right)\le {\varpi }^T\left(t\right)\mathsf{\Psi }\varpi \left(t\right)+\Delta$ for any initial state $e\left(0\right)\in \mathsf{\Theta }$, where Δ is a bounded positive real number; $\varpi \left(t\right)$ is a vector and $\mathsf{\Psi }<0$. Then, the set is called the attraction domain of the estimation error system (16).

Definition 2 

([44]). For estimation error system (16), if there exists a positive definite function $V_e\left(t\right)$ satisfies

$$\begin{array}{c}\hfill {\dot{V}}_e\left(t\right)\le {\varpi }^T\left(t\right)\mathsf{\Psi }\varpi \left(t\right)+\Delta ,t\in [0,+\infty )\end{array}$$

where $\varpi \left(t\right)$ is a vector and $\mathsf{\Psi }<0$, then the estimation error system (16) is uniformly bounded stable.

Definition 3 

([45]). System (3) is said to be uniformly bounded if, for all ${\Xi }_1>0$, there exists a constant ${\Xi }_2\left({\Xi }_1\right)$ such that

$$\begin{array}{c}\hfill \parallel x\left(0\right)\parallel \le {\Xi }_1\Rightarrow \parallel x\left(t\right)\parallel \le {\Xi }_2\left({\Xi }_1\right)\end{array}$$

holds for all $x\left(0\right)\in {\mathbb{R}}^6$ and $t\in [0,+\infty )$.

Remark 3. 

For the inter-sample predictor, it is easy to obtain that the prediction estimation error is $e_{\rho }=\rho \left(t\right)-x_1\left(t\right)$ which has been given in the paper. When the static event-triggered mechanism is not triggered, we have $E\left(t\right)=0$. Then, there exists $\rho \left(t\right)={\int }_{t_k}^t{z}_2\left(t\right)\mathrm{d}s+y\left(t_k\right)$ for $t\in [t_k,t_{k+1})$ if $E\left(t\right)=0$, which is the output of the inter-sample estimator. From the static event-triggering condition (15), it follows that during intervals in which no event is triggered, inequality $e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)\le {\alpha }_e(e_1^T\left(t\right)e_1\left(t\right)+\chi \left(t\right)+{ϵ}_0)$ holds. This inequality characterizes the relationship between the estimator’s prediction accuracy between sampling instants and the static event-triggering parameters ${\alpha }_e>0$ and $ϵ>0$. For the same $e_1\left(t\right)$ and $\chi \left(t\right)$, large values of ${\alpha }_e$ and ϵ make it less likely to trigger data transmission, i.e., they correspond to a higher tolerance to the estimator’s prediction error. By appropriately selecting ${\alpha }_e$ and ϵ, it is possible to maintain a suitable event-triggering frequency while ensuring high prediction accuracy of the inter-sample predictor.

3.3. Convergence Analysis of the ESCDO

To verify the effectiveness of the proposed ESCDO, we analyze the convergence of observation errors and present sufficient conditions for achieving uniformly bounded stability of (16) and (17).

Theorem 1. 

If there exist positive definite symmetric matrix $P_V$, positive diagonal matrix Υ, matrix O, positive constants ${\alpha }_1$ and ${\alpha }_2$ such that the following linear matrix inequality (LMI)

$$\begin{array}{c}\hfill \left[\begin{array}{ccccccc}{R}_V& {\displaystyle \frac{1}{2}}{C}^T\mathsf{{\rm Y}}+O& 0& 0& O& P_{V}D& P_{V}B\\ \ast & -\mathsf{{\rm Y}}& 0& 0& 0& 0& 0\\ \ast & \ast & {\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2)-\mu {\alpha }_1& 0& 0& 0& 0\\ \ast & \ast & \ast & -{\displaystyle \frac{1}{{\gamma }_3}}I& 0& 0& 0\\ \ast & \ast & \ast & \ast & -{\displaystyle \frac{1}{{\gamma }_1}}I& 0& 0\\ \ast & \ast & \ast & \ast & \ast & -{\displaystyle \frac{1}{{\gamma }_2}}I& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & -{\displaystyle \frac{1}{{\gamma }_3}}I\end{array}\right]<0\end{array}$$

(20)

holds, where $R_V=P_{V}A+A^T{P}_V-OC-C^{T}O+((1+{\gamma }_4)\mu {\alpha }_2+{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2))C^{T}C$ and ${\gamma }_1,{\gamma }_2,{\gamma }_3,{\gamma }_4,\mu >0$ are given positive constants, then $L=P_V^{-1}O$ and estimation error system (16) is uniformly bounded stable with

$$\begin{array}{c}\hfill V_e\left(t\right)\le \left(V_e\left(0\right)+{\displaystyle \frac{\Delta }{{ϵ}_V}}\right)e^{{ϵ}_{V}t}-{\displaystyle \frac{\Delta }{{ϵ}_V}}\end{array}$$

(21)

where

$$\begin{array}{cc}\hfill \Delta \triangleq & {\gamma }_2^{-1}{d}_d^2+{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2){ϵ}_0+{\displaystyle \frac{9{\gamma }_3^{-1}}{4}}\varsigma {\parallel {\theta }^{\ast }\parallel }^2,{ϵ}_V\triangleq {\displaystyle \frac{\overline{\lambda }\left(\mathsf{\Psi }\right)}{\mathsf{\Pi }}}<0,\hfill \\ \hfill \mathsf{\Pi }\triangleq & \overline{\lambda }\left(P_V\right)+\mu +{\displaystyle \frac{1}{2\xi }}\hfill \\ \hfill \mathsf{\Psi }\triangleq & \left[\begin{array}{cccc}M& {\displaystyle \frac{1}{2}}{C}^T{W}^T+P_{V}L& 0& 0\\ \ast & -W& 0& 0\\ \ast & \ast & {\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2)-\mu {\alpha }_1& 0\\ \ast & \ast & \ast & -{\gamma }_3^{-1}\end{array}\right]<0\hfill \\ \hfill M\triangleq & P_V(A-LC)+{(A-LC)}^T{P}_V+{\gamma }_1{P}_{V}L{L}^T{P}_V+{\gamma }_2{P}_{V}D{D}^T{P}_V\hfill \\ \hfill & +{\gamma }_3{P}_{V}B{B}^T{P}_V+((1+{\gamma }_4)\mu {\alpha }_2+{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2))C^{T}C\hfill \end{array}$$

(22)

Proof. 

For estimation error system (16), the Lyapunov candidate function is chosen as

$$\begin{array}{c}\hfill V_e\left(t\right)=e^T\left(t\right)P_{V}e\left(t\right)+\mu \chi \left(t\right)+{\displaystyle \frac{1}{2}}\mathrm{tr}\left({\tilde{\theta }}^T\left(t\right)\tilde{\theta }\left(t\right)\right)\end{array}$$

where $P_V$ is a symmetric positive definite matrix and $\mu >0$ is a given positive constant. Then, the derivative of $V_e\left(t\right)$ can be obtained as

$$\begin{array}{cc}\hfill {\dot{V}}_e\left(t\right)=& e^T\left(t\right)P_V\dot{e}\left(t\right)+\mu \dot{\chi }\left(t\right)-\mathrm{tr}\left({\tilde{\theta }}^T\left(t\right)\dot{\theta }\left(t\right)\right)\hfill \\ \hfill =& 2e^T\left(t\right)P_V\left(Ae\left(t\right)+B{\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)-L{\mathrm{sat}}_{\chi }(e_1\left(t\right)+e_{\rho }\left(t\right))+Dh\left(t\right)\right)\hfill \\ \hfill & -\mu {\alpha }_1\chi \left(t\right)+\mu {\alpha }_2{\parallel e_1\left(t\right)+e_{\rho }\left(t\right)\parallel }^2-\mathrm{tr}\left({\tilde{\theta }}^T\left(t\right)\dot{\theta }\left(t\right)\right)\hfill \\ \hfill =& e^T\left(t\right)(P_V(A-LC)+{(A-LC)}^T{P}_V)e\left(t\right)+2e^T\left(t\right)P_{V}Lq\left(t\right)+2e^T\left(t\right)P_{V}Lg\left(t\right)\hfill \\ \hfill & +2e^T\left(t\right)P_{V}Dh\left(t\right)+2e^T\left(t\right)P_{V}B{\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)-\mathrm{tr}\left({\tilde{\theta }}^T\left(t\right)\dot{\theta }\left(t\right)\right)\hfill \\ \hfill & -\mu {\alpha }_1\chi \left(t\right)+\mu {\alpha }_2{\parallel e_1\left(t\right)+e_{\rho }\left(t\right)\parallel }^2\hfill \end{array}$$

(23)

where $q\left(t\right)\triangleq Ce\left(t\right)-{\mathrm{sat}}_{\chi }\left(Ce\left(t\right)\right)$ and $g\left(t\right)\triangleq {\mathrm{sat}}_{\chi }\left(Ce\left(t\right)\right)-{\mathrm{sat}}_{\chi }(e_{\rho }\left(t\right)+e_1\left(t\right))$ with $\parallel g\left(t\right)\parallel \le \parallel e_{\rho }\left(t\right)\parallel$.

Then, it follows

$$\begin{array}{cc}\hfill {\dot{V}}_e\left(t\right)=& e^T\left(t\right)(P_V(A-LC)+{(A-LC)}^T{P}_V)e\left(t\right)+2e^T\left(t\right)P_{V}Lq\left(t\right)+2e^T\left(t\right)P_{V}Lg\left(t\right)\hfill \\ \hfill & +2e^T\left(t\right)P_{V}Dh\left(t\right)+2e^T\left(t\right)P_{V}B{\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)-\mathrm{tr}\left({\tilde{\theta }}^T\left(t\right)\dot{\theta }\left(t\right)\right)-\mu {\alpha }_1\chi \left(t\right)\hfill \\ \hfill & +\mu {\alpha }_2{e}^T\left(t\right)C^{T}Ce\left(t\right)+\mu {\alpha }_2{e}_{\rho }^T\left(t\right)e_{\rho }\left(t\right)+2\mu {\alpha }_2{e}^T\left(t\right)C^T{e}_{\rho }\left(t\right)\hfill \end{array}$$

(24)

By Young’s inequality and ${\gamma }_3^{-1}$ given in (14), there exist positive real numbers ${\gamma }_1>0$, ${\gamma }_2>0$ and ${\gamma }_4>0$ such that

$$\begin{array}{cc}\hfill 2e^T\left(t\right)P_{V}Lg\left(t\right)& \le {\gamma }_1{e}^T\left(t\right)P_{V}L{L}^T{P}_{V}e\left(t\right)+{\gamma }_1^{-1}{g}^T\left(t\right)g\left(t\right)\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill 2e^T\left(t\right)P_{V}Dh\left(t\right)& \le {\gamma }_2{e}^T\left(t\right)P_{V}D{D}^T{P}_{V}e\left(t\right)+{\gamma }_2^{-1}{h}^T\left(t\right)h\left(t\right)\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill 2e^T\left(t\right)P_{V}B{\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)& \le {\gamma }_3{e}^T\left(t\right)P_{V}B{B}^T{P}_{V}e\left(t\right)+{\gamma }_3^{-1}{\eta }^T\left(x\left(t\right)\right)\tilde{\theta }\left(t\right){\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill 2e^T\left(t\right)C^T{e}_{\rho }\left(t\right)& \le {\gamma }_4{e}^T\left(t\right)C^{T}Ce\left(t\right)+{\gamma }_4^{-1}{e}_{\rho }^T\left(t\right)e_{\rho }\left(t\right)\hfill \end{array}$$

(28)

hold. Substituting (25)–(28) into (24), it follows

$$\begin{array}{cc}\hfill {\dot{V}}_e\left(t\right)\le & e^T\left(t\right)\left(P_V(A-LC)+{(A-LC)}^T{P}_V+{\gamma }_1{P}_{V}L{L}^T{P}_V+{\gamma }_2{P}_{V}D{D}^T{P}_V\right.\hfill \\ \hfill & \left.+{\gamma }_3{P}_{V}B{B}^T{P}_V+(1+{\gamma }_4)\mu {\alpha }_2{C}^{T}C\right)e\left(t\right)\hfill \\ \hfill & +2e^T\left(t\right)P_{V}Lq\left(t\right)+{\gamma }_2^{-1}{h}^T\left(t\right)h\left(t\right)+{\gamma }_3^{-1}{\eta }^T\left(x\left(t\right)\right)\tilde{\theta }\left(t\right){\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)\hfill \\ \hfill & -\mathrm{tr}\left({\tilde{\theta }}^T\left(t\right)\dot{\theta }\left(t\right)\right)-\mu {\alpha }_1\chi \left(t\right)+({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2)e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)\hfill \\ \hfill \le & e^T\left(t\right)\left(P_V(A-LC)+{(A-LC)}^T{P}_V+{\gamma }_1{P}_{V}L{L}^T{P}_V+{\gamma }_2{P}_{V}D{D}^T{P}_V\right.\hfill \\ \hfill & \left.+{\gamma }_3{P}_{V}B{B}^T{P}_V+((1+{\gamma }_4)\mu {\alpha }_2+{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2))C^{T}C\right)e\left(t\right)\hfill \\ \hfill & +2e^T\left(t\right)P_{V}Lq\left(t\right)+{\gamma }_2^{-1}{h}^T\left(t\right)h\left(t\right)+{\gamma }_3^{-1}{\eta }^T\left(x\left(t\right)\right)\tilde{\theta }\left(t\right){\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)-\mathrm{tr}\left({\tilde{\theta }}^T\left(t\right)\dot{\theta }\left(t\right)\right)\hfill \\ \hfill & -(\mu {\alpha }_1-{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2))\chi \left(t\right)+{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2){ϵ}_0\hfill \end{array}$$

(29)

Substituting (14) into (29), it gives

$$\begin{array}{cc}\hfill {\dot{V}}_e\left(t\right)\le & e^T\left(t\right)\left(P_V(A-LC)+{(A-LC)}^T{P}_V+{\gamma }_1{P}_{V}L{L}^T{P}_V+{\gamma }_2{P}_{V}D{D}^T{P}_V\right.\hfill \\ \hfill & \left.+{\gamma }_3{P}_{V}B{B}^T{P}_V+((1+{\gamma }_4)\mu {\alpha }_2+{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2))C^{T}C\right)e\left(t\right)\hfill \\ \hfill & +2e^T\left(t\right)P_{V}Lq\left(t\right)+{\gamma }_2^{-1}{h}^T\left(t\right)h\left(t\right)+{\gamma }_3^{-1}{\eta }^T\left(x\left(t\right)\right)\tilde{\theta }\left(t\right){\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)\hfill \\ \hfill & +3{\gamma }_3^{-1}{\eta }^T\left(x\left(t\right)\right)\theta \left(t\right){\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)-(\mu {\alpha }_1-{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2))\chi \left(t\right)\hfill \\ \hfill & +{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2){ϵ}_0\hfill \\ \hfill \le & e^T\left(t\right)\left(P_V(A-LC)+{(A-LC)}^T{P}_V+{\gamma }_1{P}_{V}L{L}^T{P}_V+{\gamma }_2{P}_{V}D{D}^T{P}_V\right.\hfill \\ \hfill & \left.+{\gamma }_3{P}_{V}B{B}^T{P}_V+((1+{\gamma }_4)\mu {\alpha }_2+{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2))C^{T}C\right)e\left(t\right)\hfill \\ \hfill & +{\gamma }_2^{-1}{h}^T\left(t\right)h\left(t\right)-{\gamma }_3^{-1}{\eta }^T\left(x\left(t\right)\right)\tilde{\theta }\left(t\right){\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)+{\displaystyle \frac{9{\gamma }_3^{-1}}{4}}{\eta }^T\left(x\left(t\right)\right){\theta }^{*}{\theta }^{*T}\eta \left(x\left(t\right)\right)\hfill \\ \hfill & +2e^T\left(t\right)P_{V}Lq\left(t\right)-(\mu {\alpha }_1-{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2))\chi \left(t\right)\hfill \\ \hfill & +{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2){ϵ}_0\hfill \end{array}$$

(30)

Choose $H=C$ such that (18) and (19) hold for any $e\left(t\right)$. Combining (19) and (30), it follows

$$\begin{array}{cc}\hfill {\dot{V}}_e\left(t\right)\le & e^T\left(t\right)\left(P_V(A-LC)+{(A-LC)}^T{P}_V+{\gamma }_1{P}_{V}L{L}^T{P}_V+{\gamma }_2{P}_{V}D{D}^T{P}_V\right.\hfill \\ \hfill & \left.+{\gamma }_3{P}_{V}B{B}^T{P}_V+((1+{\gamma }_4)\mu {\alpha }_2+{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2))C^{T}C\right)e\left(t\right)+{\gamma }_2^{-1}{d}_d^2\hfill \\ \hfill & +2e^T\left(t\right)P_{V}Lq\left(t\right)+q^T\left(t\right)\mathsf{{\rm Y}}Ce\left(t\right)-q^T\left(t\right)\mathsf{{\rm Y}}q\left(t\right)-{\gamma }_3^{-1}{\eta }^T\left(x\left(t\right)\right)\tilde{\theta }\left(t\right){\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)\hfill \\ \hfill & -(\mu {\alpha }_1-{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2))\chi \left(t\right)+{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2){ϵ}_0+{\displaystyle \frac{9{\gamma }_3^{-1}}{4}}\varsigma {\parallel {\theta }^{*}\parallel }^2\hfill \end{array}$$

(31)

Denote $\varpi \left(t\right)={\left[\begin{array}{cccc}{e}^T\left(t\right)& q^T\left(t\right)& \sqrt{\chi \left(t\right)}& {\eta }^T\left(x\left(t\right)\right)\tilde{\theta }\left(t\right)\end{array}\right]}^T$. Thus, inequality (31) can be rewritten as

$$\begin{array}{cc}\hfill {\dot{V}}_e\left(t\right)\le & {\varpi }^T\left(t\right)\mathsf{\Psi }\varpi \left(t\right)+\Delta \hfill \\ \hfill \le & \overline{\lambda }\left(\mathsf{\Psi }\right)\left(e^T\left(t\right)e\left(t\right)+\chi \left(t\right)+{\eta }^T\left(x\left(t\right)\right)\eta \left(x\left(t\right)\right)\mathrm{tr}\left\{{\tilde{\theta }}^T\left(t\right)\tilde{\theta }\left(t\right)\right\}\right)+\Delta \hfill \\ \hfill \le & {ϵ}_V{V}_e\left(t\right)+\Delta \hfill \end{array}$$

(32)

where $\mathsf{\Psi }$ is given in (22) and

$$\begin{array}{cc}\hfill \Delta \triangleq & {\gamma }_2^{-1}{d}_d^2+{\alpha }_e({\gamma }_1^{-1}+(1+{\gamma }_4^{-1})\mu {\alpha }_2){ϵ}_0+{\displaystyle \frac{9{\gamma }_3^{-1}}{4}}\varsigma {\parallel {\theta }^{*}\parallel }^2,\hfill \\ \hfill {ϵ}_V\triangleq & {\displaystyle \frac{\overline{\lambda }\left(\mathsf{\Psi }\right)}{\mathsf{\Pi }}}<0,\mathsf{\Pi }\triangleq \overline{\lambda }\left(P_V\right)+\mu +{\displaystyle \frac{1}{2\xi }}\hfill \end{array}$$

Integrating (32) in the interval $[0,t]$ for all $t\in [0,+\infty )$, (21) is obtained. This implies that $V_e\left(t\right)$ exponentially converge to a bounded constant $-\Delta {ϵ}_V^{-1}>0$. By selecting $O=P_{V}L$, inequality (22) can be converted to the LMI (20) according to the Schur’s supplementary in Lemma 2. Furthermore, (18) and (19) hold for any $e\left(t\right)$. Therefore, estimation error system (16) is uniformly bounded stable. This completes the proof. □

3.4. Analysis of Zeno Behavior

To ensure the event-triggered mechanism (15) avoids Zeno behavior, this subsection analyzes the minimum triggering interval of the mechanism (15), thereby proving the absence of Zeno behavior. To obtain the minimum triggering time interval, the following lemma is given first.

Lemma 3. 

If there exist positive constants $a_1$, $a_2$ and $a_3$ that can make the continuous differentiable nonnegative function $F\left(t\right)$, $t\in [t_k,+\infty )$ satisfy

$$\begin{array}{c}\hfill {\displaystyle \frac{\mathrm{d}F\left(t\right)}{\mathrm{d}t}}\le a_1(F^2\left(t\right)+a_{2}F\left(t\right)+a_3)\end{array}$$

then there is a time interval $t_d>0$ and a positive integer r that makes

$$\begin{array}{c}\hfill F\left(t\right)\le {\displaystyle \frac{a_2}{2}}\left({\displaystyle \frac{rtan\left(\frac{r{a}_1{a}_2}{2}(t-t_k)\right)+1}{1-\frac{1}{r}tan\left(\frac{r{a}_1{a}_2}{2}(t-t_k)\right)}}-1\right),t-t_k\le t_d\end{array}$$

hold.

Proof. 

Choose a positive constant r which gives rise to $(r^2+1){\displaystyle \frac{a_2^2}{4}}\ge a_3$. Denote $(r^2+1){\displaystyle \frac{a_2^2}{4}}\ge {\tilde{a}}_3$ and

$$\begin{array}{c}\hfill {\displaystyle \frac{\mathrm{d}\tilde{F}\left(t\right)}{\mathrm{d}t}}\le a_1({\tilde{F}}^2\left(t\right)+a_2\tilde{F}\left(t\right)+{\tilde{a}}_3)\end{array}$$

(33)

where $\tilde{F}\left(t_k\right)=0$ and $\tilde{F}\left(t\right)\ge 0$ for $t\in (t_k,\infty )$. Therefore, it is easy to obtain that $\tilde{F}\left(t\right)\ge F\left(t\right)$ holds for all $t\ge t_k$.

Based on (33), it follows

$$\begin{array}{c}\hfill {\int }_0^{\tilde{F}\left(t\right)}{\displaystyle \frac{\mathrm{d}\tilde{F}\left(t\right)}{{\tilde{F}}^2\left(t\right)+a_2\tilde{F}\left(t\right)+{\tilde{a}}_3}}={\int }_{t_k}^t{a}_1\mathrm{d}s\end{array}$$

which indicates

$$\begin{array}{c}\hfill {\int }_0^{\tilde{F}\left(t\right)}{\displaystyle \frac{\mathrm{d}\tilde{F}\left(t\right)}{{\left(\tilde{F}\left(t\right)+\frac{a_2}{2}\right)}^2+\left({\tilde{a}}_3-\frac{a_2^2}{4}\right)}}=a_1(t-t_k)\end{array}$$

(34)

By integrating both sides of (34), we have

$$\begin{array}{c}\hfill {\displaystyle \frac{2}{r{a}_2}}arctan\left({\displaystyle \frac{2}{r{a}_2}}\left(\tilde{F}\left(t\right)+{\displaystyle \frac{a_2}{2}}\right)\right)-{\displaystyle \frac{2}{r{a}_2}}arctan\left({\displaystyle \frac{1}{r}}\right)=a_1(t-t_k)\end{array}$$

(35)

From (35), the expression of $\tilde{F}\left(t\right)$ can be obtained as

$$\begin{array}{c}\hfill \tilde{F}\left(t\right)={\displaystyle \frac{a_2}{2}}\left({\displaystyle \frac{rtan\left(\frac{r{a}_1{a}_2}{2}(t-t_k)\right)+1}{1-\frac{1}{r}tan\left(\frac{r{a}_1{a}_2}{2}(t-t_k)\right)}}-1\right)\end{array}$$

To ensure $\tilde{F}\left(t\right)\ge 0$ hold for $\forall t\in [t_k,\infty )$, the following inequality must hold

$$\begin{array}{c}\hfill {\displaystyle \frac{tan\left(\frac{r{a}_1{a}_2}{2}(t-t_k)\right)}{r}}<1\end{array}$$

which yields $t-t_k<{\displaystyle \frac{2arctan\left(r\right)}{r{a}_1{a}_2}}$. Therefore, by letting $t_d={\displaystyle \frac{2arctan\left(r\right)}{r{a}_1{a}_2}}$ and $F\left(t\right)\le \tilde{F}\left(t\right)$, it gives

$$\begin{array}{c}\hfill F\left(t\right)\le {\displaystyle \frac{a_2}{2}}\left({\displaystyle \frac{rtan\left(\frac{r{a}_1{a}_2}{2}(t-t_k)\right)+1}{1-\frac{1}{r}tan\left(\frac{r{a}_1{a}_2}{2}(t-t_k)\right)}}-1\right),t-t_k\le t_d\end{array}$$

This completes the proof. □

Next, a lemma is used to prove that Zeno behavior will be absent and the minimum interval between two trigger times is given.

Lemma 4. 

For estimation error system (16), the trigger interval $t_{k+1}-t_k$ of event-triggered mechanism (15) satisfying

$$\begin{array}{c}\hfill t_{k+1}-t_k>{\displaystyle \frac{2}{r(1+{\alpha }_1+E_{max}{ϵ}_0^{-1})}}arctan{\displaystyle \frac{{\alpha }_{e}r}{r^2+{\alpha }_e+1}}>0\end{array}$$

where $E_{max}={\left(\mathbb{E}\left\{e^T\left(t\right)e\left(t\right)\right\}\right)}_{max}$ and r is a positive parameter satisfying

$$\begin{array}{c}\hfill r>\sqrt{{\displaystyle \frac{4E_{max}{\alpha }_2{ϵ}_0}{{[(1+{\alpha }_1){ϵ}_0+E_{max}]}^2}}-1}.\end{array}$$

Proof. 

Considering ${\dot{e}}_{\rho }\left(t\right)=z_2\left(t\right)-x_2\left(t\right)\triangleq e_2\left(t\right)$, it is easy to obtain

$$\begin{array}{c}\hfill {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\mathbb{E}\left\{e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)\right\}=\mathbb{E}\left\{2e_{\rho }^T\left(t\right){\dot{e}}_{\rho }\left(t\right)\right\}=\mathbb{E}\left\{2e_{\rho }^T\left(t\right)e_2\left(t\right)\right\}\le \mathbb{E}\left\{e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)\right\}+\mathbb{E}\left\{e^T\left(t\right)e\left(t\right)\right\}\end{array}$$

(36)

Besides, we have

$$\begin{array}{c}\hfill {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\mathbb{E}\left\{e_1^T\left(t\right)e_1\left(t\right)\right\}=\mathbb{E}\left\{2e_1^T\left(t\right){\dot{e}}_1\left(t\right)\right\}\le (1+{\alpha }_1)\mathbb{E}\left\{e_1^T\left(t\right)e_1\left(t\right)\right\}+\mathbb{E}\left\{e_2^T\left(t\right)e_2\left(t\right)\right\}+{\alpha }_1{ϵ}_0\end{array}$$

(37)

From (36) and (37), we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{\displaystyle \frac{\mathbb{E}\left\{e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)\right\}}{\mathbb{E}\left\{e_1^T\left(t\right)e_1\left(t\right)\right\}+\mathbb{E}\left\{\chi \left(t\right)\right\}+{ϵ}_0}}\hfill \\ \hfill \le & {\displaystyle \frac{\mathbb{E}\left\{e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)\right\}+\mathbb{E}\left\{e^T\left(t\right)e\left(t\right)\right\}}{\mathbb{E}\left\{e_1^T\left(t\right)e_1\left(t\right)\right\}+\mathbb{E}\left\{\chi \left(t\right)\right\}+{ϵ}_0}}\hfill \\ \hfill & -{\displaystyle \frac{\mathbb{E}\left\{e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)\right\}((1+{\alpha }_1)\mathbb{E}\left\{e_1^T\left(t\right)e_1\left(t\right)\right\}+\mathbb{E}\left\{e_2^T\left(t\right)e_2\left(t\right)\right\}+{\alpha }_1{ϵ}_0)}{{(\mathbb{E}\left\{e_1^T\left(t\right)e_1\left(t\right)\right\}+\mathbb{E}\left\{\chi \left(t\right)\right\}+{ϵ}_0)}^2}}\hfill \\ \hfill & +{\displaystyle \frac{\mathbb{E}\left\{e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)\right\}({\alpha }_1\mathbb{E}\left\{\chi \left(t\right)\right\}-{\alpha }_2\mathbb{E}\{\parallel e_1\left(t\right)+e_{\rho }{\left(t\right)\parallel }^2\left\}\right)}{{(\mathbb{E}\left\{e_1^T\left(t\right)e_1\left(t\right)\right\}+\mathbb{E}\left\{\chi \left(t\right)\right\}+{ϵ}_0)}^2}}\hfill \\ \hfill \le & {\displaystyle \frac{\mathbb{E}\left\{e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)\right\}}{\mathbb{E}\left\{e_1^T\left(t\right)e_1\left(t\right)\right\}+\mathbb{E}\left\{\chi \left(t\right)\right\}+{ϵ}_0}}\left({\alpha }_2{\displaystyle \frac{\mathbb{E}\left\{e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)\right\}}{\mathbb{E}\left\{e_1^T\left(t\right)e_1\left(t\right)\right\}+\mathbb{E}\left\{\chi \left(t\right)\right\}+{ϵ}_0}}+\left(1+{\alpha }_1+{\displaystyle \frac{E_{max}}{{ϵ}_0}}\right)\right)\hfill \\ \hfill & +{\displaystyle \frac{E_{max}}{{ϵ}_0}}\hfill \end{array}$$

(38)

where $E_{max}={\left(\mathbb{E}\left\{e^T\left(t\right)e\left(t\right)\right\}\right)}_{max}$.

Denote

$$\begin{array}{c}\hfill a_1\triangleq {\alpha }_2,a_2\triangleq {\displaystyle \frac{(1+{\alpha }_1){ϵ}_0+E_{max}}{{\alpha }_2{ϵ}_0}},a_3\triangleq {\displaystyle \frac{E_{max}}{{\alpha }_2{ϵ}_0}},F\left(t\right)\triangleq {\displaystyle \frac{\mathbb{E}\left\{e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)\right\}}{\mathbb{E}\left\{e_1^T\left(t\right)e_1\left(t\right)\right\}+\mathbb{E}\left\{\chi \left(t\right)\right\}+{ϵ}_0}},\end{array}$$

Then, (38) can be rewritten as ${\displaystyle \frac{\mathrm{d}F\left(t\right)}{\mathrm{d}t}}\le a_1(F^2\left(t\right)+a_{2}F\left(t\right)+a_3)$. Choose a positive constant r satisfying

$$\begin{array}{c}\hfill {\displaystyle \frac{r^2+1}{4}}{\left({\displaystyle \frac{(1+{\alpha }_1){ϵ}_0+E_{max}}{{\alpha }_2{ϵ}_0}}\right)}^2>{\displaystyle \frac{E_{max}}{{\alpha }_2{ϵ}_0}}\end{array}$$

By Lemma 3, there exists an interval $t_d={\displaystyle \frac{2arctan\left(r\right)}{r{a}_1{a}_2}}$ such that for any $t-t_k<t_d$ the following inequality

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathbb{E}\left\{e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)\right\}}{\mathbb{E}\left\{e_1^T\left(t\right)e_1\left(t\right)\right\}+\mathbb{E}\left\{\chi \left(t\right)\right\}+{ϵ}_0}}\hfill \\ \hfill \le & {\displaystyle \frac{(1+{\alpha }_1){ϵ}_0+E_{max}}{2{\alpha }_2{ϵ}_0}}\left({\displaystyle \frac{rtan\left(\frac{r(1+{\alpha }_1+E_{max}{ϵ}_0^{-1})}{2}(t-t_k)\right)+1}{1-\frac{1}{r}tan\left(\frac{r(1+{\alpha }_1+E_{max}{ϵ}_0^{-1})}{2}(t-t_k)\right)}}-1\right)\hfill \end{array}$$

(39)

According to (15), the next event will not be triggered when $e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)>{\alpha }_e(e_1^T\left(t\right)e_1\left(t\right)+\chi \left(t\right)+{ϵ}_0)$ holds. That is, $\mathbb{E}\left\{e_{\rho }^T\left(t\right)e_{\rho }\left(t\right)\right\}>{\alpha }_e(\mathbb{E}\left\{e_1^T\left(t\right)e_1\left(t\right)\right\}+\mathbb{E}\left\{\chi \left(t\right)\right\}+{ϵ}_0)$ also holds. Based on (39), there exists

$$\begin{array}{c}\hfill {\alpha }_e<{\displaystyle \frac{(1+{\alpha }_1){ϵ}_0+E_{max}}{2{\alpha }_2{ϵ}_0}}\left({\displaystyle \frac{rtan\left(\frac{r(1+{\alpha }_1+E_{max}{ϵ}_0^{-1})}{2}(t_{k+1}-t_k)\right)+1}{1-\frac{1}{r}tan\left(\frac{r(1+{\alpha }_1+E_{max}{ϵ}_0^{-1})}{2}(t_{k+1}-t_k)\right)}}-1\right)\end{array}$$

which indicates

$$\begin{array}{c}\hfill t_{k+1}-t_k>{\displaystyle \frac{2}{r(1+{\alpha }_1+E_{max}{ϵ}_0^{-1})}}arctan{\displaystyle \frac{{\alpha }_{e}r}{r^2+{\alpha }_e+1}}>0\end{array}$$

Therefore, the proposed event-triggered mechanism (15) will not lead to Zeno behavior. This completes the proof. □

4. Design of the Composite Anti-Disturbance Controller

In this section, we design a composite anti-disturbance controller for the spacecraft system by integrating the disturbance estimations obtained from the ESCDO and the MPC. First, we formulate the MPC optimization problem subject to robust state constraints. Then, we establish sufficient conditions to guarantee the recursive feasibility of the optimization scheme. Finally, we prove the uniform bounded stability of the closed-loop system under the proposed composite anti-disturbance controller.

4.1. The MPC Scheme

The nominal system of (7) is denoted as

$$\begin{array}{cc}\hfill \dot{\overline{x}}\left(t\right)& =\overline{A}\overline{x}\left(t\right)+\overline{B}\overline{u}\left(t\right)\hfill \end{array}$$

(40)

where $\overline{x}\left(t\right)$ is the nominal state; $\overline{u}\left(t\right)\triangleq u_{\mathrm{MPC}}^{*}\left(t\right)$ is the nominal control input with $u_{\mathrm{MPC}}^{*}\left(t\right)$ being the optimal control signal generated by the MPC scheme designed subsequently. Then, we design the composite anti-disturbance controller of the spacecraft system as

$$\begin{array}{c}\hfill u\left(t\right)=u_{\mathrm{MPC}}^{*}\left(t\right)+K(z\left(t\right)-\overline{x}\left(t\right))-{\widehat{d}}_o\left(t\right)-{\widehat{d}}_f\left(t\right)-{\theta }^T\left(t\right)\eta \left(x\left(t\right)\right)\end{array}$$

(41)

where $u_{\mathrm{MPC}}^{*}\left(t\right)$ is the optimal control signal generated by the MPC scheme designed subsequently; $z\left(t\right)\triangleq {\left[z_1^T\left(t\right)z_2^T\left(t\right)\right]}^T$ is the estimation of $x\left(t\right)$; $\overline{x}\left(t\right)$ is the nominal state of system (7); K is the feedback gain such that $\overline{A}+\overline{B}K$ is stable; ${\widehat{d}}_o\left(t\right)=V\widehat{w}\left(t\right)$ is the estimation of $d_o\left(t\right)$.

To obtain $u_{\mathrm{MPC}}^{*}\left(t\right)$, a new constrained optimization problem is constructed for the spacecraft system as

Prob 1:

$$\begin{array}{c}\hfill {\widehat{u}}_{\mathrm{MPC}}^{*}\left(s\right|t_k)=\arg \min J(\widehat{x}\left(s\right|t_k),{\widehat{u}}_{\mathrm{MPC}}\left(s\right|t_k))\end{array}$$

subject to

$$\begin{array}{cc}\hfill \dot{\widehat{x}}\left(s\right|t_k)& =\overline{A}\widehat{x}\left(s\right|t_k)+\overline{B}{\widehat{u}}_{\mathrm{MPC}}\left(s\right|t_k)\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill {\widehat{u}}_{\mathrm{MPC}}\left(s\right|t_k)& \in U_{\mathrm{MPC}},s\in [t_k,t_k+T]\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill \parallel \widehat{x}\left(s\right|t_k){\parallel }_P& \le {\displaystyle \frac{\psi \sigma }{s-t_k}}T,s\in [t_k+\delta ,t_k+T]\hfill \end{array}$$

(44)

Denote

$$\begin{array}{cc}\hfill & J(\widehat{x}\left(s\right|t_k),{\widehat{u}}_{\mathrm{MPC}}\left(s\right|t_k))\triangleq {\int }_{t_k}^{t_k+T}\left(\parallel \widehat{x}\left(s\right|t_k){\parallel }_Q^2+{\parallel {\widehat{u}}_{\mathrm{MPC}}\left(s\right|t_k)\parallel }_R^2\right)\mathrm{d}s+{\parallel \widehat{x}(t_k+T|t_k)\parallel }_P^2\hfill \end{array}$$

(45)

where $\widehat{x}\left(s\right|t_k)$ denotes the prediction of the state from time $t_k$ to time s; ${\widehat{u}}_{\mathrm{MPC}}\left(s\right|t_k)$ denotes the prediction of the MPC input signal from time instant $t_k$ to time instant s; $\delta$ is the sampling period with $\delta =t_{k+1}-t_k$; T is the prediction horizon satisfying $T\ge 2\delta$; $\sigma >0$ is a given constant; $Q>0$ and $R>0$ are symmetric matrices representing the weight matrix of appropriate dimensions; $P>0$ is a symmetric matrix denoting the terminal penalty matrix to be designed; $\widehat{x}\left(t_k\right|t_k)=x\left(t_k\right)$; $U_{\mathrm{MPC}}\triangleq \mathcal{U}\ominus U_{\mathrm{MPC}}^{-}$ where $U_{\mathrm{MPC}}^{-}\subseteq {\mathbb{R}}^3$ obtained by

$$\begin{array}{cc}\hfill u_f\left(t\right)& \in U_{\mathrm{MPC}}^{-},u_f\left(t\right)\triangleq K(z\left(t\right)-\overline{x}\left(t\right))-{\widehat{d}}_o\left(t\right)-{\widehat{d}}_f\left(t\right)-{\theta }^T\left(t\right)\eta \left(x\left(t\right)\right)\hfill \end{array}$$

Lemma 5 

([39]). For system (40), there exists a constant $\sigma >0$ such that: (1) The set $\Xi \left(\sigma \right)\triangleq \{\overline{x}\left(t\right):\parallel \overline{x}\left(t\right){\parallel }_P^2\le {\sigma }^2\}$ is a control invariant set with the control input $\overline{u}\left(t\right)=K\overline{x}\left(t\right)$, i.e., $\forall \overline{x}\left(0\right)\in \Xi \left(\sigma \right)$ means $\overline{x}\left(t\right)\in \Xi \left(\sigma \right)$, and $\overline{u}\left(t\right)=K\overline{x}\left(t\right)\in U_{\mathrm{MPC}}$, $\forall t\ge 0$; (2) for any $\overline{x}\left(t\right)\in \Xi \left(\sigma \right)$, the inequality ${\displaystyle \frac{\mathrm{d}\parallel \overline{x}{\left(t\right)\parallel }_P^2}{\mathrm{d}t}}\le -{\parallel \overline{x}\left(t\right)\parallel }_{Q^{*}}^2$ holds with $Q^{*}=Q+K^{T}RK$.

Remark 4. 

In this work, the MPC scheme is responsible for generating the optimal control input. By incorporating the disturbance compensation term provided by the ESCDO into the system dynamics, we derive the state constraints that the system must satisfy, as expressed in (44). In addition, the formulated MPC optimization problem explicitly handles the input constraint (43) acting on the system. Finally, the proposed MPC framework simultaneously enforces both input and state constraints while producing an optimal control action that drives the system state to converge to a neighborhood of the equilibrium point.

Remark 5. 

Due to the fact that MPC is an online optimization method, its computational complexity is an important indicator for determining the amount of computing resources occupied by the algorithm. Next, a simple analysis will be provided to examine the computational complexity of the model predictive control method proposed in this article. We discretize the continuous-time problem with sampling period h and prediction horizon T, giving $N=\lfloor T/h\rfloor$ steps and the linear dynamics $\widehat{x}(k+s+1|k)=\overline{A}\widehat{x}(k+s|k)+\overline{B}{\widehat{u}}_{\mathrm{MPC}}(k+s|k)$ for $s\in \mathbb{Z}[0,N-1]$ where $\mathbb{Z}[0,N-1]$ represents the integer interval from 0 to $N-1$. Let n and m be the state and input dimensions, and let p denote the number of per-step inequality constraints. Stacking variables as $z\triangleq {\left[\begin{array}{cccccc}{\widehat{x}}^T\left(k\right|k),& \cdots & {\widehat{x}}^T(k+N|k),& {\widehat{u}}_{\mathrm{MPC}}^T\left(k\right|k),& \cdots & {\widehat{u}}_{\mathrm{MPC}}^T(k+N-1|k)\end{array}\right]}^T$, the stage cost as ${\sum }_{s=0}^{N-1}\left\{\parallel \widehat{x}{(k+s|k)\parallel }_Q^2+{\parallel {\widehat{u}}_{\mathrm{MPC}}(k+s|k)\parallel }_R^2\right\}+{\parallel \widehat{x}(k+T|k)\parallel }_P^2$ yields a sparse quadratic program

$$\begin{array}{c}\hfill \underset{z}{min}{\displaystyle \frac{1}{2}}{z}^{T}Hz+f^{T}z,\mathrm{s}.\mathrm{t}.Ez=b,Gz\le g\end{array}$$

where H, f, E, b, G and g are parameters obtained from the Prob 1. In a primal–dual interior-point method, each Newton iteration solves a Karush-Kuhn-Tucker (KKT) condition linear system whose coefficient matrix inherits a block-tridiagonal sparsity pattern along the horizon. The local (per-stage) block that couples $(\widehat{x},{\widehat{u}}_{\mathrm{MPC}})$ with the active constraints has dimension approximately $(n+m+p)$. Factorizing such a block via Riccati recursion requires $\mathcal{O}\left({(n+m+p)}^3\right)$ flops. Due to that the blocks are processed sequentially across the N states, one Newton step costs $\mathcal{O}\left(N{(n+m+p)}^3\right)$. In this paper, we have $n=6$, $m=3$ and $p=3$ such that the computational complexity of the proposed MPC is $\mathcal{O}\left({12}^{3}N\right)=\mathcal{O}\left(1728N\right)$.

4.2. Recursive Feasibility

System (7) can be rewritten as

$$\begin{array}{cc}\hfill x\left(t\right)& =\overline{x}\left(t\right)+{\tilde{e}}_x\left(t\right)\hfill \end{array}$$

(46)

where ${\tilde{e}}_x\left(t\right)=e_{xz}\left(t\right)+e_{z\overline{x}}\left(t\right)$; $e_{xz}\left(t\right)\triangleq x\left(t\right)-z\left(t\right)$ and $e_{z\overline{x}}\left(t\right)\triangleq z\left(t\right)-\overline{x}\left(t\right)$. From Theorem 1, it is easy to obtain that ${lim}_{t\to +\infty }\parallel e_{xz}\left(t\right)\parallel =-{\displaystyle \frac{\Delta }{{ϵ}_V}}$ and $\parallel e_{xz}\left(t\right)\parallel \le V_e^{0.5}\left(0\right){\left(\underline{\lambda }\left(P_V\right)\right)}^{-0.5}$. Furthermore, there exists

$$\begin{array}{c}\hfill {\dot{e}}_{z\overline{x}}\left(t\right)=(\overline{A}+\overline{B}K)e_{z\overline{x}}\left(t\right)+L_1{\mathrm{sat}}_{\chi }(\rho \left(t\right)-z_1\left(t\right))\end{array}$$

(47)

which yields

$$\begin{array}{c}\hfill e_{z\overline{x}}\left(t\right)=e^{(\overline{A}+\overline{B}K)t}{e}_{z\overline{x}}\left(0\right)+{\int }_0^t{e}^{(\overline{A}+\overline{B}K)(t-\tau )}{L}_1{\mathrm{sat}}_{\chi }(\rho \left(\tau \right)-z_1\left(\tau \right))\mathrm{d}\tau ,t\in [0,+\infty )\end{array}$$

(48)

with $e_{z\overline{x}}\left(0\right)=\mathbf{0}$. Considering term $L_1{\mathrm{sat}}_{\chi }(\rho \left(t\right)-z_1\left(t\right))$, it is easy to obtain that $\parallel L_1{\mathrm{sat}}_{\chi }(\rho \left(t\right)-z_1\left(t\right))\parallel \le \parallel L_1\parallel \chi \left(t\right)\le \parallel L_1\parallel {\mu }^{-1}{V}_e\left(0\right)$ by Theorem 1 and the definition of ${\mathrm{sat}}_{\chi }(\rho \left(t\right)-z_1\left(t\right))$.

Subsequently, it can be obtained from (48) that

$$\begin{array}{cc}\hfill \parallel e_{z\overline{x}}\left(t\right)\parallel =& ∥{\int }_0^t{e}^{(\overline{A}+\overline{B}K)(t-\tau )}{L}_1{\mathrm{sat}}_{\chi }(\rho \left(\tau \right)-z_1\left(\tau \right))\mathrm{d}\tau ∥\hfill \\ \hfill \le & \parallel L_1\parallel {\mu }^{-1}{V}_e\left(0\right)∥{(\overline{A}+\overline{B}K)}^{-1}\left(e^{(\overline{A}+\overline{B}K)t}-1\right)∥\hfill \end{array}$$

(49)

holds for $t\in [0,+\infty )$. $\overline{A}+\overline{B}K$ is stable, which means that the eigenvalues of $\overline{A}+\overline{B}K$ are negative. Therefore, it gives from (49) that ${lim}_{t\to +\infty }\parallel e_{z\overline{x}}\left(t\right)\parallel =0$ and $\parallel e_{z\overline{x}}\left(t\right)\parallel \le {\overline{e}}_{z\overline{x}}$ hold with

$$\begin{array}{cc}\hfill {\overline{e}}_{z\overline{x}}\triangleq & {\mu }^{-1}{V}_e\left(0\right)\parallel L_1\parallel ∥{(\overline{A}+\overline{B}K)}^{-1}∥\hfill \end{array}$$

Thus, we have

$$\begin{array}{cc}\hfill \parallel {\tilde{e}}_x\left(t\right)\parallel =& \parallel e_{xz}\left(t\right)+e_{z\overline{x}}\left(t\right)\parallel \le \parallel e_{xz}\left(t\right)\parallel +\parallel e_{z\overline{x}}\left(t\right)\parallel \le \varrho ,\underset{t\to +\infty }{lim}\parallel {\tilde{e}}_x\left(t\right)\parallel =-{\displaystyle \frac{\Delta }{{ϵ}_V}}\hfill \end{array}$$

with $\varrho \triangleq V_e^{0.5}\left(0\right){\left(\underline{\lambda }\left(P_V\right)\right)}^{-0.5}+{\mu }^{-1}{V}_e\left(0\right)\parallel L_1\parallel ∥{(\overline{A}+\overline{B}K)}^{-1}∥$.

Lemma 6. 

If Prob 1 is feasible at time $t_k$, then it is feasible at time $t_{k+1}$ under the sampling period satisfying

$$\begin{array}{c}\hfill -{\displaystyle \frac{2\overline{\lambda }\left(P\right)}{\underline{\lambda }\left(Q^{*}\right)}}ln\psi \le \delta \le {\displaystyle \frac{(1-\psi )\sigma }{\overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel T}}}\end{array}$$

(50)

where $\overline{\omega }\triangleq {\mu }^{-1}{V}_e\left(0\right)\parallel \overline{B}K\parallel \parallel L_1\parallel ∥{(\overline{A}+\overline{B}K)}^{-1}∥+V_e^{0.5}\left(0\right)\parallel \overline{B}\parallel ({\left(\underline{\lambda }\left(P_V\right)\right)}^{-0.5}+\sqrt{2}\varsigma )$ and $0.5\le \psi \le 1$.

Proof. 

Consider a possible solution at time $t_{k+1}$ for Prob 1 as

$$\begin{array}{c}\hfill \tilde{u}\left(s\right|t_{k+1})=\left\{\begin{array}{cc}{\widehat{u}}_{\mathrm{MPC}}^{*}\left(s\right|t_k),& s\in [t_{k+1},t_k+T]\\ K\tilde{x}\left(s\right|t_{k+1}),& s\in (t_k+T,t_{k+1}+T]\end{array}\right.\end{array}$$

where $\tilde{u}\left(s\right|t_{k+1})$ is a feasible solution of Prob 1 at time $t_{k+1}$; ${\widehat{u}}_{\mathrm{MPC}}^{*}\left(s\right|t_k)$ is the optimal control input obtained at time $t_k$; and $\tilde{x}\left(s\right|t_{k+1})$ is a feasible state of Prob 1 at time $t_{k+1}$.

Firstly, the feasibility of (43) is shown. By (7), (46) and (41), it gives

$$\begin{array}{c}\hfill \dot{x}\left(t\right)-\dot{\overline{x}}\left(t\right)=\overline{A}(x\left(t\right)-\overline{x}\left(t\right))+\omega \left(t\right)\end{array}$$

(51)

where

$$\begin{array}{cc}\hfill \omega \left(t\right)& \triangleq \overline{B}K{e}_{z\overline{x}}\left(t\right)+\overline{B}({\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)+e_f\left(t\right)+e_o\left(t\right)),\hfill \\ \hfill e_f\left(t\right)& \triangleq d_f\left(t\right)-{\widehat{d}}_f\left(t\right),e_o\left(t\right)\triangleq d_o\left(t\right)-{\widehat{d}}_o\left(t\right)\hfill \end{array}$$

Rewrite $\omega \left(t\right)$ as

$$\begin{array}{c}\hfill \omega \left(t\right)=\overline{B}K{e}_{z\overline{x}}\left(t\right)+\overline{B}{\tilde{\theta }}^T\left(t\right)\eta \left(x\left(t\right)\right)+\tilde{B}e\left(t\right)\end{array}$$

with $\tilde{B}\triangleq \left[\mathbf{0}\overline{B}V\overline{B}\right]$. Thus, we have

$$\begin{array}{cc}\hfill \parallel \omega \left(t\right)\parallel \le & \parallel \overline{B}K\parallel \parallel e_{z\overline{x}}\left(t\right)\parallel +\parallel \tilde{B}\parallel \parallel e\left(t\right)\parallel +\parallel \overline{B}\parallel \sqrt{\parallel {\eta }^T\left(x\left(t\right)\right)\tilde{\theta }{\left(t\right)\parallel }^2}\hfill \\ \hfill \le & {\mu }^{-1}{V}_e\left(0\right)\parallel \overline{B}K\parallel \parallel L_1\parallel ∥{(\overline{A}+\overline{B}K)}^{-1}∥+V_e^{0.5}\left(0\right)\parallel \overline{B}\parallel ({\left(\underline{\lambda }\left(P_V\right)\right)}^{-0.5}+\sqrt{2}\varsigma )\hfill \\ \hfill \triangleq & \overline{\omega }\hfill \end{array}$$

From (51), there also exists

$$\begin{array}{c}\hfill \dot{x}\left(s\right|t_k)-{\dot{\widehat{x}}}^{*}\left(t_k\right|s)=\overline{A}(x\left(s\right|t_k)-{\widehat{x}}^{*}\left(t_k\right|t_k))+\omega \left(s\right|t_k),s\in [t_k,t_k+T]\end{array}$$

(52)

with $\parallel \omega \left(s\right|t_k)\parallel \le \overline{\omega }$ at time $t_k$.

Using the triangle inequality, the following inequality can be obtained by (52)

$$\begin{array}{cc}\hfill & \parallel x\left(s\right|t_k)-{\widehat{x}}^{*}\left(s\right|t_k){\parallel }_P\hfill \\ \hfill \le & {\int }_{t_k}^s\parallel \omega \left(\tau \right|t_k){\parallel }_P\mathrm{d}\tau +\parallel \overline{A}\parallel {\int }_{t_k}^s{\parallel x\left(\tau \right|t_k)-{\widehat{x}}^{*}\left(\tau \right|t_k)\parallel }_P\mathrm{d}\tau \hfill \\ \hfill \le & (s-t_k)\overline{\lambda }\left(P^{0.5}\right)\overline{\omega }+\parallel \overline{A}\parallel {\int }_{t_k}^s{\parallel x\left(\tau \right|t_k)-{\widehat{x}}^{*}\left(\tau \right|t_k)\parallel }_P\mathrm{d}\tau ,s\in [t_k,t_k+T]\hfill \end{array}$$

Using Gronwall–Bellman inequality, we have

$$\begin{array}{cc}\hfill \parallel x\left(s\right|t_k)-{\widehat{x}}^{*}\left(s\right|t_k){\parallel }_P& \le (s-t_k)\overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel (s-t_k)},s\in [t_k,t_k+T]\hfill \end{array}$$

(53)

For time $t_{k+1}$, the dynamics of the feasible state is obtained as

$$\begin{array}{c}\hfill \dot{\tilde{x}}\left(s\right|t_{k+1})=A\tilde{x}\left(s\right|t_{k+1})+B\tilde{u}\left(s\right|t_{k+1}),s\in [t_{k+1},t_{k+1}+T]\end{array}$$

(54)

Combining (53), (54) and ${\widehat{x}}^{*}\left(s\right|t_k)$ for $s\in [t_{k+1},t_k+T]$, it can be obtained that

$$\begin{array}{cc}\hfill & \parallel \tilde{x}\left(s\right|t_{k+1})-{\widehat{x}}^{*}\left(s\right|t_k){\parallel }_P\hfill \\ \hfill \le & \parallel x\left(t_{k+1}\right)-{\widehat{x}}^{*}\left(t_{k+1}\right|t_k){\parallel }_P+\parallel \overline{A}\parallel {\int }_{t_{k+1}}^{t_k+T}{\parallel \tilde{x}\left(\tau \right|t_{k+1})-{\widehat{x}}^{*}\left(\tau \right|t_k)\parallel }_P\mathrm{d}\tau \hfill \\ \hfill \le & \delta \overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel \delta }+\parallel \overline{A}\parallel {\int }_{t_{k+1}}^s{\parallel \tilde{x}\left(\tau \right|t_{k+1})-{\widehat{x}}^{*}\left(\tau \right|t_k)\parallel }_P\mathrm{d}\tau \hfill \end{array}$$

(55)

Using Gronwall–Bellman inequality, (55) can be further obtained as

$$\begin{array}{cc}\hfill \parallel \tilde{x}\left(s\right|t_{k+1})-{\widehat{x}}^{*}\left(s\right|t_k){\parallel }_P& \le \delta \overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel (\delta +s-t_{k+1})}\hfill \end{array}$$

(56)

for $s\in [t_{k+1},t_k+T]$.

From (55), it is easy to obtain

$$\begin{array}{cc}\hfill \parallel \tilde{x}(t_k+T|t_{k+1}){\parallel }_P& \le \delta \overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel T}+{\parallel {\widehat{x}}^{*}(t_k+T|t_k)\parallel }_P\le \delta \overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel T}+\psi \sigma \hfill \end{array}$$

As Prob 1 is feasible at time $t_k$, there exists $\Vert {\widehat{x}}^{*}(t_k+T|t_k){\Vert }_P\le \psi \sigma$. Since $\delta \le {\displaystyle \frac{(1-\psi )\sigma }{\overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\Vert \overline{A}\Vert T}}}$, we have $\Vert \tilde{x}(t_k+T|t_{k+1}){\Vert }_P\le \sigma$. Based on Lemma 5, we have $\tilde{u}\left(s\right|t_{k+1})=K\tilde{x}\left(s\right|t_{k+1})\in U_{\mathrm{MPC}}$ for $s\in (t_k+T,t_{k+1}+T]$. Furthermore, there exists $\tilde{u}\left(s\right|t_{k+1})={\widehat{u}}^{*}\left(s\right|t_k)$ for $s\in [t_{k+1},t_k+T]$. Therefore, $\tilde{u}\left(s\right|t_{k+1})\in U_{\mathrm{MPC}}$ for $s\in [t_{k+1},t_{k+1}+T]$, which means that (43) holds at time $t_{k+1}$. Furthermore, it is easy to obtain from Lemma 5 that

$$\begin{array}{c}\hfill {\displaystyle \frac{\mathrm{d}\parallel \tilde{x}\left(s\right|t_{k+1}){\parallel }_P^2}{\mathrm{d}s}}\le -{\displaystyle \frac{\underline{\lambda }\left(Q^{*}\right)}{\overline{\lambda }\left(P\right)}}{\parallel \tilde{x}\left(s\right|t_{k+1})\parallel }_P^2,s\in [t_k+T,t_{k+1}+T]\end{array}$$

which yields

$$\begin{array}{c}\hfill \parallel \tilde{x}\left(s\right|t_{k+1}){\parallel }_P^2\le {\parallel \tilde{x}(t_k+T|t_{k+1})\parallel }_P^2{e}^{-{\displaystyle \frac{\underline{\lambda }\left(Q^{*}\right)}{\overline{\lambda }\left(P\right)}}(s-t_k-T)}\le {\sigma }^2{e}^{-{\displaystyle \frac{\underline{\lambda }\left(Q^{*}\right)}{\overline{\lambda }\left(P\right)}}(s-t_k-T)}\end{array}$$

(57)

As $\delta \ge -{\displaystyle \frac{2\overline{\lambda }\left(P\right)}{\underline{\lambda }\left(Q^{*}\right)}}ln\psi$, we have $\parallel \tilde{x}(t_{k+1}+T|t_{k+1}){\parallel }_P\le \psi \sigma$.

Secondly, the feasibility of (44) is shown. From (56), we have

$$\begin{array}{cc}\hfill \parallel \tilde{x}\left(s\right|t_{k+1}){\parallel }_P& \le \parallel {\widehat{x}}^{*}\left(s\right|t_k){\parallel }_P+\delta \overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel (\delta +s-t_{k+1})}\hfill \\ \hfill & \le {\displaystyle \frac{\psi \sigma }{s-t_k}}T+\delta \overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel (\delta +s-t_{k+1})}\hfill \end{array}$$

for $s\in [t_{k+1}+\delta ,t_k+T]$. Considering ${\displaystyle \frac{1}{2}}\le \psi <1$, $\delta \le {\displaystyle \frac{T}{2}}$ and $\delta \overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel (\delta +s-t_{k+1})}\le (1-\psi )\sigma$, we have

$$\begin{array}{c}\hfill {\displaystyle \frac{\psi \sigma }{s-t_k}}T+\delta \overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel (\delta +s-t_{k+1})}\le {\displaystyle \frac{\psi \sigma }{s-t_{k+1}}}T\end{array}$$

For $s\in [t_k+T,t_{k+1}+T]$, the feasibility of (44) is given as follows. Construct a function as

$$\begin{array}{c}\hfill M\left(s\right)=\sigma (s-t_{k+1})e^{-{\displaystyle \frac{\underline{\lambda }\left(Q^{*}\right)}{2\overline{\lambda }\left(P\right)}}(s-t_k-T)}-T\psi \sigma \end{array}$$

(58)

It is easy to obtain $M\left(s\right)\le 0$ for $s\in [t_k+T,t_{k+1}+T]$. Based on (57) and $M\left(s\right)\le 0$ for $s\in [t_k+T,t_{k+1}+T]$, we obtain

$$\begin{array}{c}\hfill \parallel \tilde{x}\left(s\right|t_{k+1}){\parallel }_P\le \sigma e^{-{\displaystyle \frac{\underline{\lambda }\left(Q^{*}\right)}{2\overline{\lambda }\left(P\right)}}(s-t_k-T)}\le {\displaystyle \frac{T\psi \sigma }{s-t_{k+1}}}\le 0\end{array}$$

Therefore, (44) holds for $s\in [t_{k+1}+\delta ,t_{k+1}+T]$. This completes the proof. □

4.3. Stability Analysis of the Closed-Loop System

In this subsection, we establish uniform bounded stability of the closed-loop system under the proposed controller (41) using easy-to-check sufficient conditions.

Theorem 2. 

If the sampling period δ satisfying (50) and the following inequality exists

$$\begin{array}{c}\hfill {\left({\displaystyle \frac{\overline{\lambda }\left(Q\right)}{\underline{\lambda }\left(P\right)}}\right)}^2{(1-\psi )}^2\left[(T-\delta )+2Tln{\displaystyle \frac{T}{\delta }}\right]+(1-{\psi }^2)-{\displaystyle \frac{\underline{\lambda }\left(Q\right)}{\overline{\lambda }\left(P\right)}}\delta {\psi }^2<0\end{array}$$

(59)

then system (3) is uniformly bounded stable under (41) and the state of system (3) converges to the set $\mathbb{S}\triangleq \{x\left(t\right):{lim}_{t\to +\infty }\parallel x\left(t\right)\parallel \le -{\displaystyle \frac{\Delta }{{ϵ}_V}}\}$.

Proof. 

According to Lemma 6, if Prob 1 is feasible at time $t_k$, it is also feasible at time $t_{k+1}$ under the given condition. Denote $J(\tilde{x}\left(s\right|t_{k+1}),\tilde{u}\left(s\right|t_{k+1}))$ as the feasible cost of Prob 1 at time $t_{k+1}$ with $\tilde{x}\left(s\right|t_{k+1})$ and $\tilde{u}\left(s\right|t_{k+1})$ given in Lemma 6. The optimal cost at time $t_k$ is denoted as $J({\widehat{x}}^{*}\left(s\right|t_k),{\widehat{u}}_{\mathrm{MPC}}^{*}\left(s\right|t_k))$. Define

$$\begin{array}{c}\hfill J_e\triangleq J(\tilde{x}\left(s\right|t_{k+1}),\tilde{u}\left(s\right|t_{k+1}))-J({\widehat{x}}^{*}\left(s\right|t_k),{\widehat{u}}_{\mathrm{MPC}}^{*}\left(s\right|t_k))\end{array}$$

Based on (45), $J_e$ is split as $J_e=J_{e,1}+J_{e,2}+J_{e,3}$, where

$$\begin{array}{cc}\hfill J_{e,1}& \triangleq {\int }_{t_{k+1}}^{t_k+T}\left(\parallel \tilde{x}\left(s\right|t_{k+1}){\parallel }_Q^2+\parallel \tilde{u}\left(s\right|t_{k+1}){\parallel }_R^2-\parallel {\widehat{x}}^{*}\left(s\right|t_k){\parallel }_Q^2-{\parallel {\widehat{u}}_{\mathrm{MPC}}^{*}\left(s\right|t_k)\parallel }_R^2\right)\mathrm{d}s\hfill \\ \hfill J_{e,2}& \triangleq {\int }_{t_k+T}^{t_{k+1}+T}\left(\parallel \tilde{x}\left(s\right|t_{k+1}){\parallel }_Q^2+{\parallel \tilde{u}\left(s\right|t_{k+1})\parallel }_R^2\right)\mathrm{d}s+\parallel \tilde{x}(t_{k+1}+T|t_{k+1}){\parallel }_P^2-{\parallel \widehat{x}(t_k+T|t_k)\parallel }_P^2\hfill \\ \hfill J_{e,3}& \triangleq -{\int }_{t_k}^{t_{k+1}}\left(\parallel \widehat{x}\left(s\right|t_k){\parallel }_Q^2+{\parallel \widehat{u}\left(s\right|t_k)\parallel }_R^2\right)\mathrm{d}s\hfill \end{array}$$

Considering $J_{e,1}$ with $\tilde{u}\left(s\right|t_{k+1})={\widehat{u}}_{\mathrm{MPC}}^{*}\left(s\right|t_k)$ for $s\in [t_{k+1},t_k+T]$, we have

$$\begin{array}{cc}\hfill J_{e,1}& \le {\int }_{t_{k+1}}^{t_k+T}\left(\parallel \tilde{x}\left(s\right|t_{k+1}){\parallel }_Q+{\parallel {\widehat{x}}^{*}\left(s\right|t_k)\parallel }_Q\right)\left(\parallel \tilde{x}\left(s\right|t_{k+1})-{\parallel {\widehat{x}}^{*}\left(s\right|t_k)\parallel }_Q\right)\mathrm{d}s\hfill \\ \hfill & \le {\int }_{t_{k+1}}^{t_k+T}{\left({\displaystyle \frac{\overline{\lambda }\left(Q\right)}{\underline{\lambda }\left(P\right)}}\right)}^2\left[{\left(\delta \overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel T}\right)}^2+{\displaystyle \frac{2\psi \sigma T\delta \overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel T}}{s-t_k}}\right]\mathrm{d}s\hfill \end{array}$$

(60)

With $\delta \overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel T}\le (1-\psi )\sigma$ obtained from Lemma 6, (60) can be further converted as

$$\begin{array}{cc}\hfill J_{e,1}& \le {\int }_{t_{k+1}}^{t_k+T}{\left({\displaystyle \frac{\overline{\lambda }\left(Q\right)}{\underline{\lambda }\left(P\right)}}\right)}^2\left[{(1-\psi )}^2{\sigma }^2+{\displaystyle \frac{2\psi {\sigma }^{2}T-2{\psi }^2{\sigma }^{2}T}{s-t_k}}\right]\mathrm{d}s\hfill \\ \hfill & \le {\left({\displaystyle \frac{\overline{\lambda }\left(Q\right)}{\underline{\lambda }\left(P\right)}}\right)}^2{\sigma }^2(1-\psi )\left[(T-\delta )(1-\psi )+(2T-2\psi T)ln{\displaystyle \frac{T}{\delta }}\right]\hfill \end{array}$$

For $J_{e,2}$, we have $\tilde{u}\left(s\right|t_{k+1})=K\tilde{x}\left(s\right|t_{k+1})$ for $s\in [t_k+T,t_{k+1}+T]$ such that

$$\begin{array}{cc}\hfill J_{e,2}=& {\int }_{t_k+T}^{t_{k+1}+T}\parallel \tilde{x}\left(s\right|t_{k+1}){\parallel }_{Q^{*}}^2\mathrm{d}s+\parallel \tilde{x}(t_{k+1}+T|t_{k+1}){\parallel }_P^2-{\parallel {\widehat{x}}^{*}(t_k+T|t_k)\parallel }_P^2\hfill \\ \hfill \le & {\int }_{t_k+T}^{t_{k+1}+T}\left[{\tilde{x}}^T\left(s\right|t_{k+1})({(\overline{A}+\overline{B}K)}^{T}P+P(\overline{A}+\overline{B}K))\tilde{x}\left(s\right|t_{k+1})\right]\overline{d}s\hfill \\ \hfill & +\parallel \tilde{x}(t_{k+1}+T|t_{k+1}){\parallel }_P^2-{\parallel {\widehat{x}}^{*}(t_k+T|t_k)\parallel }_P^2\hfill \\ \hfill \le & (\sigma +\psi \sigma )(\sigma -\psi \sigma )\hfill \\ \hfill =& {\sigma }^2(1-{\psi }^2)\hfill \end{array}$$

Using (53) and $x\left(s\right|t_k)\notin \Xi \left(\sigma \right)$, we have $\parallel {\widehat{x}}^{*}\left(s\right|t_k){\parallel }_P>\sigma -(s-t_k)\overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel (s-t_k)}$ for $s\in [t_k,t_k+T]$ such that

$$\begin{array}{c}\hfill -\parallel {\widehat{x}}^{*}\left(s\right|t_k){\parallel }_Q^2<-{\displaystyle \frac{\underline{\lambda }\left(Q\right)}{\overline{\lambda }\left(P\right)}}{\left(\sigma -(s-t_k)\overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel (s-t_k)}\right)}^2\end{array}$$

Then, $J_{e,3}$ is obtained as

$$\begin{array}{cc}\hfill J_{e,3}<& {\int }_{t_k}^{t_{k+1}}\left(-{\displaystyle \frac{\underline{\lambda }\left(Q\right)}{\overline{\lambda }\left(P\right)}}{\left(\sigma -(s-t_k)\overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel (s-t_k)}\right)}^2\right)\mathrm{d}s\hfill \\ \hfill <& -\delta {\displaystyle \frac{\underline{\lambda }\left(Q\right)}{\overline{\lambda }\left(P\right)}}{\left(\sigma -\delta \overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel \delta }\right)}^2\hfill \end{array}$$

Considering $-{\displaystyle \frac{2\overline{\lambda }\left(P\right)}{\underline{\lambda }\left(Q^{*}\right)}}ln\psi \le \delta \le {\displaystyle \frac{(1-\psi )\sigma }{\overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel T}}}$, we have

$$\begin{array}{c}\hfill -{\displaystyle \frac{2\overline{\lambda }\left(P\right)}{\underline{\lambda }\left(Q^{*}\right)}}\overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel \delta }ln\psi -\sigma \le \delta \overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel \delta }-\sigma \le {\displaystyle \frac{(1-\psi )\sigma }{e^{\parallel \overline{A}\parallel (T-\delta )}}}-\sigma <0\end{array}$$

Therefore, there exists

$$\begin{array}{c}\hfill {\left({\displaystyle \frac{(1-\psi )\sigma }{e^{\parallel \overline{A}\parallel (T-\delta )}}}-\sigma \right)}^2\le {\left(\delta \overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel \delta }-\sigma \right)}^2\le {\left({\displaystyle \frac{2\overline{\lambda }\left(P\right)}{\underline{\lambda }\left(Q^{*}\right)}}\overline{\lambda }\left(P^{0.5}\right)\overline{\omega }{e}^{\parallel \overline{A}\parallel \delta }ln\psi -\sigma \right)}^2\end{array}$$

which yields

$$\begin{array}{cc}\hfill J_{e,3}<& -\delta {\displaystyle \frac{\underline{\lambda }\left(Q\right)}{\overline{\lambda }\left(P\right)}}{\left({\displaystyle \frac{(1-\psi )\sigma }{e^{\parallel \overline{A}\parallel (T-\delta )}}}-\sigma \right)}^2<-\delta {\displaystyle \frac{\underline{\lambda }\left(Q\right)}{\overline{\lambda }\left(P\right)}}{\psi }^2{\sigma }^2\hfill \end{array}$$

Combining $J_{e,1}$, $J_{e,2}$ and $J_{e,3}$, it follows

$$\begin{array}{c}\hfill J_e\le {\left({\displaystyle \frac{\overline{\lambda }\left(Q\right)}{\underline{\lambda }\left(P\right)}}\right)}^2{\sigma }^2(1-\psi )\left[(T-\delta )(1-\psi )+(2T-2\psi T)ln{\displaystyle \frac{T}{\delta }}\right]+{\sigma }^2(1-{\psi }^2)-\delta {\displaystyle \frac{\underline{\lambda }\left(Q\right)}{\overline{\lambda }\left(P\right)}}{\psi }^2{\sigma }^2\end{array}$$

Let the sampling period $\delta$ satisfy

$$\begin{array}{c}\hfill {\left({\displaystyle \frac{\overline{\lambda }\left(Q\right)}{\underline{\lambda }\left(P\right)}}\right)}^2{(1-\psi )}^2\left[(T-\delta )+2Tln{\displaystyle \frac{T}{\delta }}\right]+(1-{\psi }^2)-\delta {\displaystyle \frac{\underline{\lambda }\left(Q\right)}{\overline{\lambda }\left(P\right)}}{\psi }^2<0\end{array}$$

Then, $J_e<0$ holds. As $J(\tilde{x}\left(s\right|t_{k+1}),\tilde{u}\left(s\right|t_{k+1}))$ is a feasible cost at time $t_{k+1}$, we can conclude that the optimal cost $J({\widehat{x}}^{*}\left(s\right|t_{k+1}),{\widehat{u}}_{\mathrm{MPC}}^{*}\left(s\right|t_{k+1}))$ at time $t_{k+1}$ is not greater that $J(\tilde{x}\left(s\right|t_{k+1}),\tilde{u}\left(s\right|t_{k+1}))$, i.e., $J({\widehat{x}}^{*}\left(s\right|t_{k+1}),{\widehat{u}}_{\mathrm{MPC}}^{*}\left(s\right|t_{k+1}))\le J(\tilde{x}\left(s\right|t_{k+1}),\tilde{u}\left(s\right|t_{k+1}))$. This indicates

$$\begin{array}{c}\hfill J({\widehat{x}}^{*}\left(s\right|t_{k+1}),{\widehat{u}}_{\mathrm{MPC}}^{*}\left(s\right|t_{k+1}))-J({\widehat{x}}^{*}\left(s\right|t_k),{\widehat{u}}_{\mathrm{MPC}}^{*}\left(s\right|t_k))\le J_e<0\end{array}$$

That is, the state ${\widehat{x}}^{*}\left(t_k\right|t_k)=\overline{x}\left(t_k\right)$ is asymptotically stable, i.e., ${lim}_{t\to +\infty }\parallel \overline{x}\left(t\right)\parallel =0$. From (46), it can be obtained that

$$\begin{array}{cc}\hfill \underset{t\to +\infty }{lim}\parallel x\left(t\right)\parallel & =\underset{t\to +\infty }{lim}\parallel \overline{x}\left(t\right)+{\tilde{e}}_x\left(t\right)\parallel \le \underset{t\to +\infty }{lim}(\parallel \overline{x}\left(t\right)\parallel +\parallel {\tilde{e}}_x\left(t\right)\parallel )\le \underset{t\to +\infty }{lim}\parallel {\tilde{e}}_x\left(t\right)\parallel =-{\displaystyle \frac{\Delta }{{ϵ}_V}}\hfill \end{array}$$

Therefore, system (7) is uniform bounded stable, indicating (3) is also uniform bounded stable. This completes the proof. □

Remark 6. 

This paper addresses the spacecraft control problem under the influence of multi-source disturbances, outliers, and constraints. To specifically handle these factors, we have designed an ESCDO based on a static event-triggered mechanism, and a composite disturbance-rejection controller based on MPC using the disturbance estimates. Due to the complexity of the factors involved, it is challenging to address the problem using a single approach. Therefore, this paper designs targeted solutions for each factor based on its characteristics, ultimately leading to the proposed results.

5. Results and Discussions

This study employs a spacecraft relative motion model to validate the effectiveness of the proposed method. The parameters of system (3) and (4) are as follows [41]

$$\begin{array}{c}\overline{A}=\left[\begin{array}{cccccc}0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& -2\tilde{\omega }& 0\\ 0& 0& 0& 2\tilde{\omega }& 3\tilde{\omega }& 0\\ 0& 0& -{\tilde{\omega }}^2& 0& 0& 0\end{array}\right],\overline{B}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right],\beta =0.6\end{array}$$

with $\tilde{\omega }=7.2722\times {10}^{-5}$. The constraint of control input is $u\left(t\right)\in \mathcal{U}\triangleq \{u\left(t\right):|u_i\left(t\right)|\le 500\}$ for $i=1,2,3$. The parameters of $d_o\left(t\right)$ in (5) are given as

$$\begin{array}{c}\hfill W=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 0.2\\ 0& 0& 0& 0& -0.2& 0\\ 0& 0& 0& 0.2& 0& 0\\ 0& 0& -0.2& 0& 0& 0\\ 0& 0.2& 0& 0& 0& 0\\ -0.2& 0& 0& 0& 0& 0\end{array}\right],V={\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]}^T\end{array}$$

The disturbance $d\left(t\right)$ and the nonlinear term $f\left(x\right(t\left)\right)$ are considered as

$$\begin{array}{c}\hfill d\left(t\right)=\left[\begin{array}{c}5+exp(-0.2t)arctan\left(t\right)\times 0.3\\ 5+exp(-0.2t)arctan\left(t\right)\times 0.4\\ 5+exp(-0.2t)arctan\left(t\right)\times 0.5\end{array}\right],f\left(x\left(t\right)\right)=\left[\begin{array}{c}0.1\times x_2\left(t\right)\times sin\left(x_1\left(t\right)\right)\\ 0.2\times x_3\left(t\right)\times sin\left(x_2\left(t\right)\right)\\ 0.3\times x_1\left(t\right)\times sin\left(x_3\left(t\right)\right)\end{array}\right]\end{array}$$

respectively.

Furthermore, the parameters of the ESCDO in (11)–(13) are given as

$$\begin{array}{c}\hfill {\alpha }_1=15,{\alpha }_2=0.01,{\alpha }_e=0.4,{ϵ}_0=10,L_1=\left[\begin{array}{c}200I_{3\times 3}\\ 200I_{3\times 3}\end{array}\right],L_2=\left[\begin{array}{c}10I_{3\times 3}\\ 10I_{3\times 3}\end{array}\right],L_3=10I_{3\times 3}\end{array}$$

For LMI (20), the parameters are chosen as

$$\begin{array}{c}\hfill {\gamma }_1=5.5972\times {10}^{11},{\gamma }_2=1.3991\times {10}^{-9},{\gamma }_3=10,{\gamma }_4=0.01,\mu ={10}^{-12}\\ \hfill \mathsf{{\rm Y}}={10}^{-12}\left[\begin{array}{ccc}2.5031& -2.0739\times {10}^{-3}& 1.1117\\ -2.0739\times {10}^{-3}& 1.3134& -2.1718\times {10}^{-3}\\ 1.1117& -2.1718\times {10}^{-3}& 2.3775\end{array}\right]\end{array}$$

The parameters of the MPC scheme are given as

$$\begin{array}{cc}\hfill Q& =10I_{6\times 6},R=I_{3\times 3},\delta =0.03\mathrm{s},T=0.3\mathrm{s},\psi =0.98,\sigma =5\times {10}^6\hfill \\ \hfill K& =\left[\begin{array}{cc}3.1623I_{3\times 3}& 4.0404I_{3\times 3}\end{array}\right],P=\left[\begin{array}{cc}{P}_{11}& P_{12}\\ P_{21}& P_{22}\end{array}\right],P_{21}=P_{12}^T,\hfill \\ \hfill P_{11}& =\left[\begin{array}{ccc}12.7768& 9.0333\times {10}^{-13}& 0\\ 9.0333\times {10}^{-13}& 12.7768& 0\\ 0& 0& 12.7768\end{array}\right],\hfill \\ \hfill P_{12}& =\left[\begin{array}{ccc}3.1623& -1.1383\times {10}^{-4}& 0\\ 1.1383\times {10}^{-4}& 3.1623& 0\\ 0& 0& 3.1623\end{array}\right],\hfill \\ \hfill P_{22}& =\left[\begin{array}{ccc}4.0404& 2.8440\times {10}^{-13}& 0\\ 2.8440\times {10}^{-13}& 4.0404& 0\\ 0& 0& 4.0404\end{array}\right].\hfill \end{array}$$

Furthermore, $\delta =0.03\mathrm{s}$ makes (50) and (59) hold. The initial state of the spacecraft system is given as

$$\begin{array}{c}\hfill x\left(0\right)={\left[\begin{array}{cccccc}60& 80& -140& 8& 13& -8\end{array}\right]}^T.\end{array}$$

Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 gives the simulation results of the spacecraft system under the above parameters. For the convenience of result display, the variable with subscript i represents the i-th element of this variable. Figure 3 shows the curves of the spacecraft system state under the proposed controller and the ESCDO. Figure 4 shows the curves of the control input of the system. Figure 5, Figure 6 and Figure 7 detail the estimation error $e_{xz}\left(t\right)$, $e_o\left(t\right)$ and $e_d\left(t\right)$ by using the proposed ESCDO, respectively. Figure 8 shows the first element of estimation error $\tilde{\theta }\left(t\right)\eta \left(x\left(t\right)\right)$ of the RBFNNs. Figure 9 indicates the upper limit $\chi \left(t\right)$ of the saturation function ${\mathrm{sat}}_{\chi }(\rho \left(t\right)-z_1\left(t\right))$. Figure 10 shows the first element ${\rho }_1\left(t\right)$ of $\rho \left(t\right)$. Figure 11 shows the inter sample estimation term ${\int }_{t_k}^t{z}_2\left(t\right)\mathrm{d}s$ between two event-triggered instant. Figure 12 shows the triggering status of the event triggering mechanism throughout the entire simulation time. The entire simulation duration is $300\mathrm{s}$, and the sampling period is $0.03\mathrm{s}$, indicating 10,000 samples are taken during the simulation. Out of 10,000 samples, the number of times $E\left(t\right)=1$ is 1665, which means that only $16.65\%$ of the time needs to send the output $y\left(t\right)$, saving $83.35\%$ of communication resources.

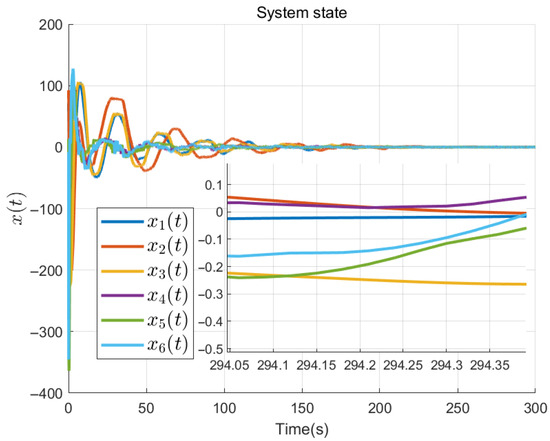
Figure 3. The state $x\left(t\right)$ of the spacecraft system.

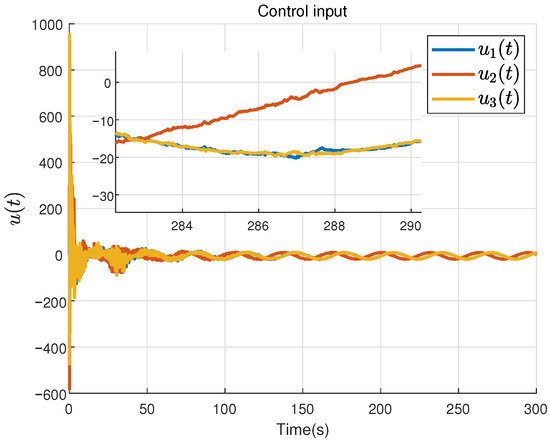
Figure 4. The control input $u\left(t\right)$ of the spacecraft system.

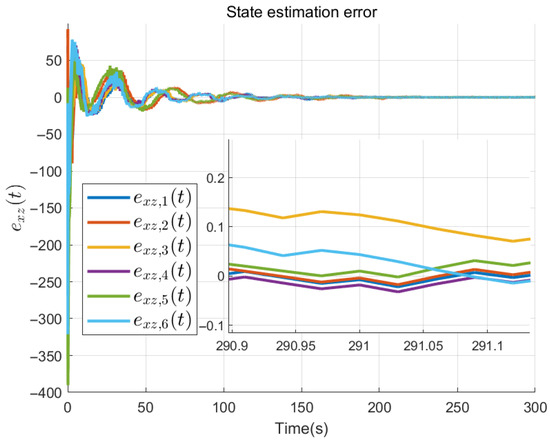
Figure 5. The estimation error $e_{xz}\left(t\right)$ of the system state $x\left(t\right)$.

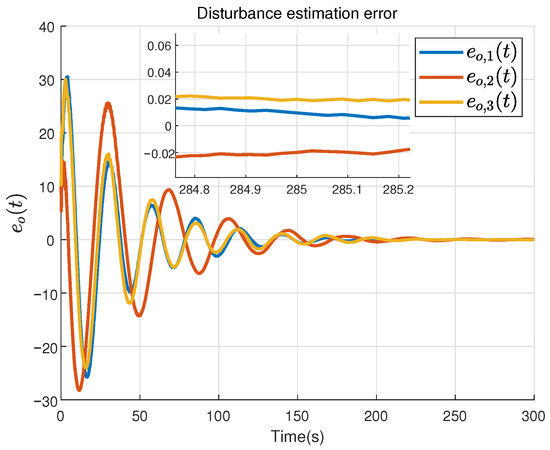
Figure 6. The estimation error $e_o\left(t\right)$ of disturbance $d_o\left(t\right)$.

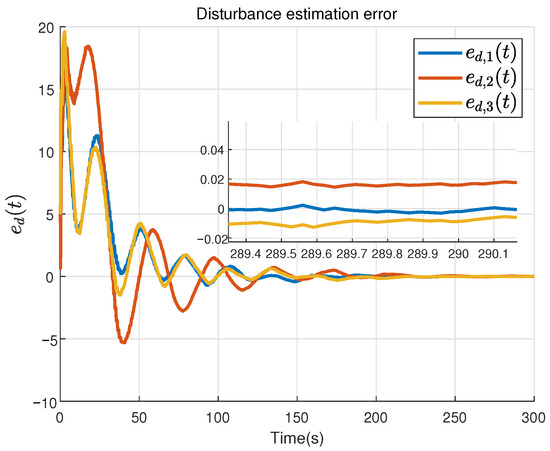
Figure 7. The estimation error $e_d\left(t\right)$ of disturbance $d\left(t\right)$.

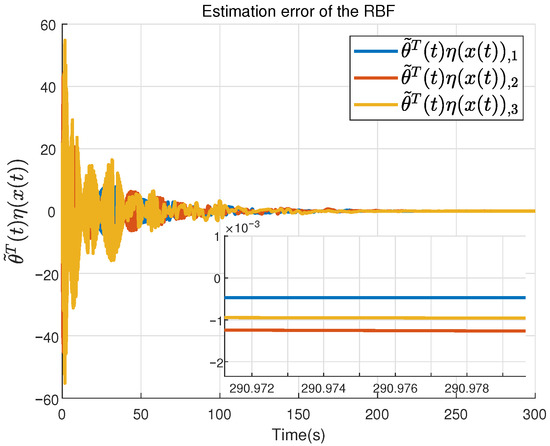
Figure 8. The estimation error $\tilde{\theta }\left(t\right)\eta \left(x\left(t\right)\right)$ of the RBFNNs.

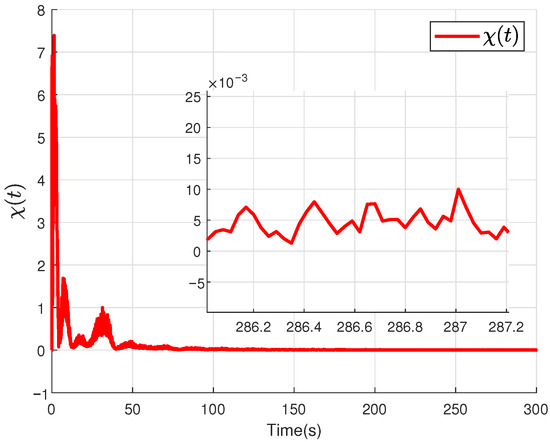
Figure 9. The upper limit $\chi \left(t\right)$ of the saturation function ${\mathrm{sat}}_{\chi }(\rho \left(t\right)-z_1\left(t\right))$.

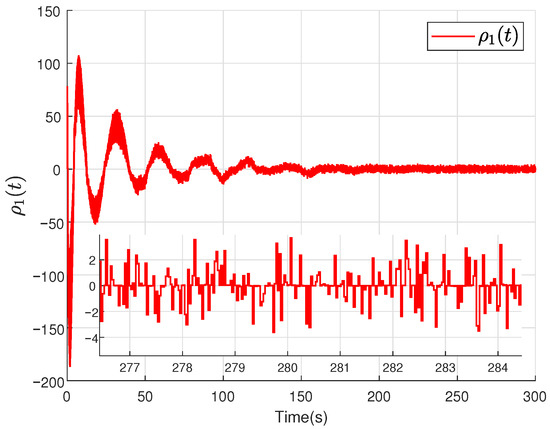
Figure 10. The first element of the $\rho \left(t\right)$.

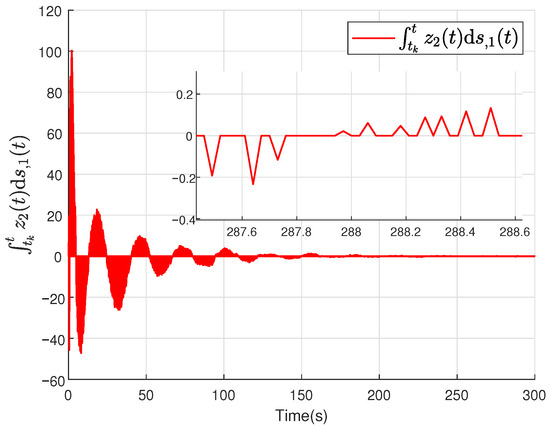
Figure 11. The first element of the term ${\int }_{t_k}^t{z}_2\left(t\right)\mathrm{d}s$.

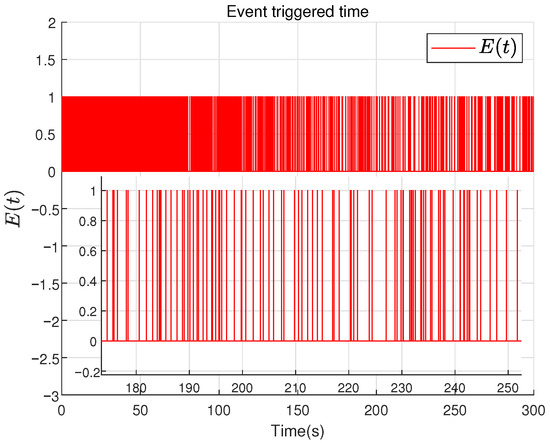
Figure 12. The event-triggered variable $E\left(t\right)$.

To more clearly demonstrate the effectiveness of the proposed ESCDO, the conventional CDO in [22] and ESO in [34] are used as baselines for comparison. The comparison focuses primarily on the estimation accuracy of the lumped disturbance (overall disturbance estimation error) and the root-mean-square error (RMSE). The parameters used for ESCDO, CDO, and ESO in the comparative simulations are listed in Table 1. Since the quantity that ultimately affects the closed-loop system is the estimation error $e_o\left(t\right)+e_d\left(t\right)$, $e_o\left(t\right)+e_d\left(t\right)$ is adopted as the comparison criterion. The results are shown in Figure 13, Figure 14 and Figure 15. In Figure 13, Figure 14 and Figure 15, $e_{o,i}\left(t\right)$ and $e_{d,i}\left(t\right)$ ($i=1,2,3$) represent the i-the element of $e_o\left(t\right)$ and $e_d\left(t\right)$, respectively. Superscripts ESCDO, CDO and ESO denote the errors obtained under observers ESCDO, CDO and ESO, respectively. In addition, we analyze the estimation error $e_o\left(t\right)+e_d\left(t\right)$ under the RMSE metric, yielding the results in Figure 16, Figure 17 and Figure 18. Accordingly, the RMSE of $e_o\left(t\right)+e_d\left(t\right)$ at the end of the simulation under ESCDO, CDO and ESO is given in Table 2, respectively.

Table 1. Parameters used in ESCDO, CDO and ESO, respectively.

Parameters of the ESCDO	${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2$	${\mathit{\alpha }}_{\mathit{e}}$	${\mathit{ϵ}}_0$	${\mathit{L}}_1$	${\mathit{L}}_2$	${\mathit{L}}_3$
Value	15	$0.01$	$0.4$	10	$\left[\begin{array}{c}200I\\ 200I\end{array}\right]$	$\left[\begin{array}{c}10I\\ 10I\end{array}\right]$	$10I$
Parameters of the CDO					$L_1$	$L_2$	$L_3$
Value					$\left[\begin{array}{c}20I\\ 10I\end{array}\right]$	$\left[\begin{array}{c}I\\ 0.1I\end{array}\right]$	$4I$
Parameters of the ESO					$L_1$		$L_3$
Value					$\left[\begin{array}{c}20I\\ 10I\end{array}\right]$		$9I$

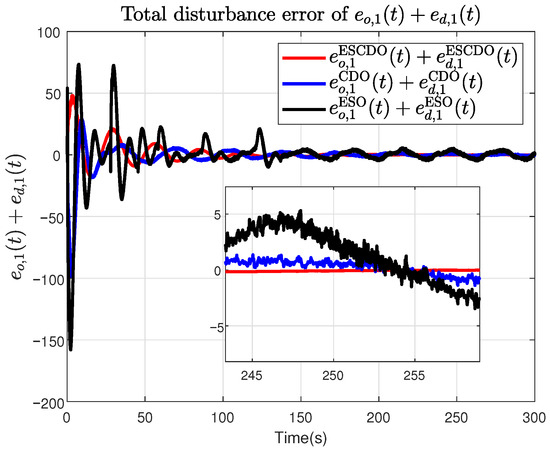
Figure 13. The total estimation error $e_{o,1}\left(t\right)+e_{d,1}\left(t\right)$ under ESCDO, CDO and ESO, respectively.

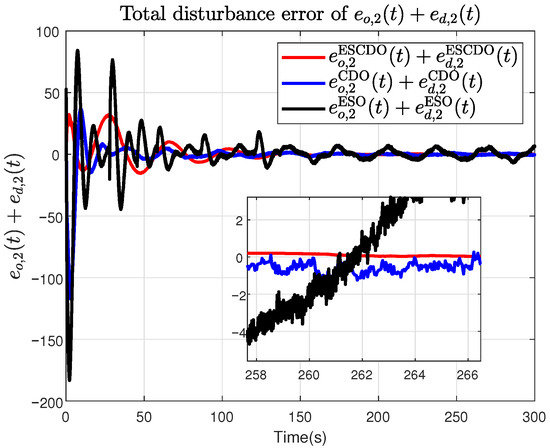
Figure 14. The total estimation error $e_{o,2}\left(t\right)+e_{d,2}\left(t\right)$ under ESCDO, CDO and ESO, respectively.

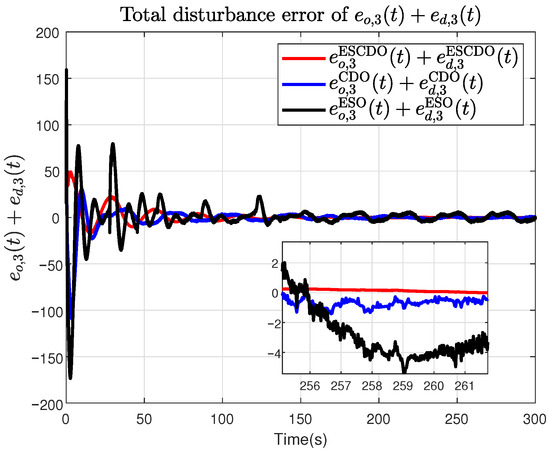
Figure 15. The total estimation error $e_{o,3}\left(t\right)+e_{d,3}\left(t\right)$ under ESCDO, CDO and ESO, respectively.

Figure 16. The RMSE of the total estimation error $e_{o,1}\left(t\right)+e_{d,1}\left(t\right)$ under ESCDO, CDO and ESO, respectively.

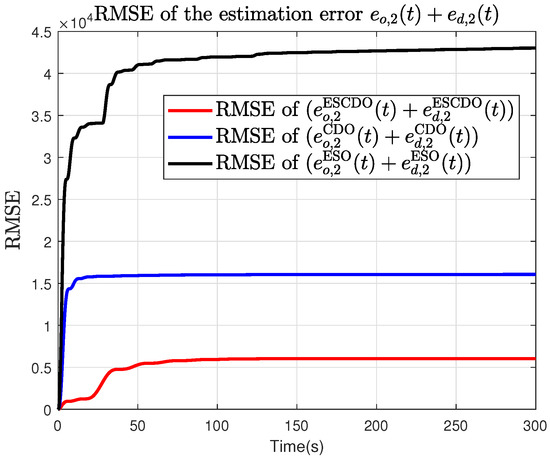
Figure 17. The RMSE of the total estimation error $e_{o,2}\left(t\right)+e_{d,2}\left(t\right)$ under ESCDO, CDO and ESO, respectively.

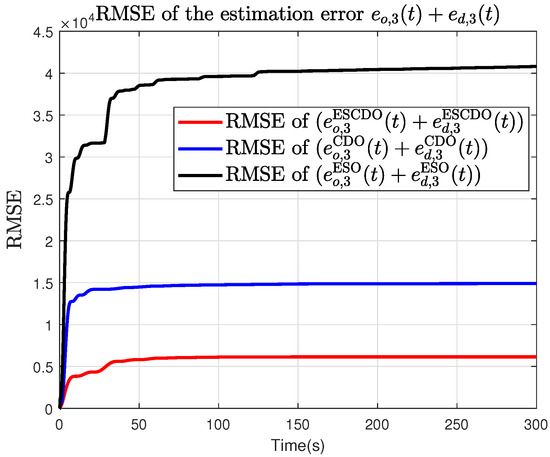
Figure 18. The RMSE of the total estimation error $e_{o,3}\left(t\right)+e_{d,3}\left(t\right)$ under ESCDO, CDO and ESO, respectively.

Table 2. RMSE of $e_o\left(t\right)+e_d\left(t\right)$ at the end of the simulation under ESCDO, CDO and ESO.

	ESCDO	CDO	ESO
RMSE of $e_{o,1}\left(t\right)+e_{d,1}\left(t\right)$	$5.8354\times {10}^3$	$1.1711\times {10}^4$	$3.2934\times {10}^4$
RMSE of $e_{o,2}\left(t\right)+e_{d,2}\left(t\right)$	$6.0348\times {10}^3$	$1.6067\times {10}^4$	$4.3040\times {10}^4$
RMSE of $e_{o,3}\left(t\right)+e_{d,3}\left(t\right)$	$6.1456\times {10}^3$	$1.4890\times {10}^4$	$4.0799\times {10}^4$

From Figure 13, Figure 14 and Figure 15, it can be seen that the proposed ESCDO yields the smallest disturbance estimation error $e_o\left(t\right)+e_d\left(t\right)$, whereas the ESO-alone scheme performs the worst. Moreover, Figure 16, Figure 17 and Figure 18 show that the proposed ESCDO achieves the smallest RMSE, whereas the ESO method yields the largest RMSE. This indicates that, over the entire simulation horizon, the estimation accuracy of our approach surpasses that of both CDO and ESO, thereby further validating the effectiveness of the proposed method.

The simulation results demonstrate the effectiveness of the proposed method. The method not only accurately estimates unknown nonlinear terms and multi-source disturbances in the spacecraft system but also, through an event-triggered mechanism, greatly reduces communications frequency. This ensures system state convergence while conserving communication resources.

The open-source simulation code with license CC-BY 4.0 in the paper and provided the corresponding link https://github.com/2018100049/Paper-Simulation/tree/main (accessed on 1 October 2025).

6. Conclusions

This paper investigates control of spacecraft systems under communication congestion, multi-source uncertainties, and input constraints. To reduce data transmissions and mitigate congestion risk, a static event-triggered scheme is proposed; between successive triggering instants, an inter-sample predictor is introduced to preserve output continuity. Furthermore, an ESCDO is constructed to simultaneously estimate system states and multi-source disturbances in the presence of outliers, wherein a saturation function is embedded to attenuate outliers induced by electromagnetic interference and related factors. Building on this observer, a composite anti-disturbance controller based on tube-MPC is designed to suppress multi-source uncertainties and ensure convergence of the system states. Easily verifiable sufficient conditions are established to guarantee the uniform bounded stability of both the ESCDO and the closed-loop system. Numerical simulations demonstrate the effectiveness of the proposed approach.

Although the proposed control framework achieves satisfactory robustness against communication congestion, multi-source disturbances, and input constraints, several factors may lead to performance degradation in practical implementations. First, the static event-triggered mechanism reduces communication load but may cause delayed control updates when the system dynamics vary rapidly, resulting in larger transient tracking errors. The inclusion of a non-zero triggering threshold to avoid Zeno behavior further introduces conservatism, which can reduce control precision during fast disturbances. Second, the RBFNN only provides an approximate estimation of unknown nonlinearities within its activation domain; limited basis coverage or improper adaptation rates may lead to residual estimation errors that deteriorate closed-loop performance. Third, the ESCDO mitigates the impact of sensor outliers, but its “stubborn” property may introduce estimation lag when external disturbances change abruptly. Additionally, the asynchronous triggering between the controller and observer can temporarily freeze the disturbance estimation, reducing compensation accuracy. Finally, the MPC-based controller is affected by model mismatch and input saturation: when control inputs reach their limits, the system cannot apply the optimal action, leading to slower convergence and increased steady-state error. Overall, these factors jointly constrain the achievable tracking accuracy and anti-disturbance capability, implying an inherent trade-off between communication efficiency, computational feasibility, and control performance.

To further enhance closed-loop performance, several potential improvements can be considered in the future study. First, introducing an adaptive or dynamic event-triggering mechanism could adjust the triggering threshold according to system states or disturbance intensity, thereby reducing unnecessary transmissions while preserving timely control updates. Second, integrating adaptive learning rates or forgetting factors into the RBFNN structure would allow faster convergence under time-varying nonlinearities. Third, a joint design of the ESCDO and MPC layers could be explored to synchronize the observer and controller updates, minimizing estimation delays during rapid disturbance variations. Finally, developing robust MPC formulations that explicitly account for model mismatch and input saturation may further improve performance and extend the applicability of the proposed method to real spacecraft systems.