A Fast Heuristic for Aircraft Landing Scheduling with Time Windows: Application to Guarulhos Airport

Abstract

This paper focuses on the aircraft landing problem with time windows (ALP-TW), which consists of determining a landing schedule for each aircraft within a specified time window and determining the minimum required separation interval between successive operations. This NP-hard state-dependent scheduling problem plays a key role in the operational efficiency of busy airports. We propose a fast and efficient heuristic, called the CAS-TW (Closest Aircraft Sequence with Time Windows), to generate landing sequences that minimize total delay while respecting operational constraints. The method combines a greedy algorithm with a discretization strategy to explore feasible landing intervals. We validate the approach using real data from São Paulo/Guarulhos International Airport (GRU), comparing the CAS-TW to traditional scheduling strategies and optimal solutions obtained via a commercial solver. Computational experiments show reductions in makespan up to 21% in theoretical datasets and 5% in real-world datasets. The CAS-TW solved instances with 50 aircraft in less than 1 s of computation time. The results showed that our algorithm was quickly implemented, equitable, easy to use, and obtained good solutions. These results translated into an increase in airport capacity.

1. Introduction

Reducing airport congestion has become a fundamental challenge in air traffic management (ATM) [1]. Several techniques have been developed to mitigate its congestion and address demand–capacity imbalances. At the operational level, these techniques involve operational changes to air traffic flows to match capacity. Adjustments in the existing methodology for setting airport arrival rates can significantly improve arrival times in terminal maneuvering areas (TMAs) [2]. From the standpoint of air traffic, accurate aircraft scheduling selections may eliminate bottlenecks in airport operations [3]. Exploiting operational efficiency measures provides a quickly implementable solution to this capacity problem. Among the simplest techniques employed by air traffic control (ATC) is the first come, first served (FCFS) sequence, where an air traffic controller sets a time slot for each aircraft as it arrives. This procedure neglects important aspects, including delay costs of individual flights [4].

A cost-efficient way to increase the utilization of an existing runway system is to improve its take-off and landing schedules [5]. The aircraft sequencing problem (ASP) is a class of problems that seek to optimally sequence aircraft operating on a runway, subject to a range of operational constraints [6]. ASP is classified into two distinct categories: the aircraft landing problem (ALP) and aircraft take-off problem (ATP). In the ALP, each arriving aircraft is allocated a specific arrival window. Based on the aircraft involved, a minimum time interval is required between successive landings [7]. Solving the ALP is important because small increases in capacity (even as low as 5%) can improve safety and reduce fuel consumption during times of congestion [8].

Recent research has explored other techniques to solve the ALP. Pang et al. [9] propose a machine learning-enhanced TSP framework method with the objective of reducing the total landing time when compared to FCFS. Their results showed a reduction of 17% when compared to the benchmark method. Shone et al. [10] present a simheuristic approach for the ALP under uncertainty. The method was validated using Heathrow Airport data. Maru [11] developed a graph-based reinforcement learning method, capable of generating aircraft landing sequences with increased runway capacity when compared to the standard FCFS approach.

The ALP is a non-deterministic polynomial-time hardness (NP-hard) problem, and exact methods can only solve small instances. Consequently, heuristics can be used to find proper solutions [3,12,13,14,15,16]. In this paper, we apply an adapted greedy heuristic which we have named the Closest Aircraft Sequence with Time Window constraint (CAS-TW) to find an aircraft set that minimizes the landing time of the last airplane, thereby improving runway throughput. Our proposed greedy algorithm draws from heuristic approaches to the travelling salesman problem (TSP) and combines a tour constructive heuristic and an insertion heuristic. Both heuristics are adapted with hard constraints (inviolable) of time windows and safety separations. Another aspect of our proposed algorithm adjustment is that the FCFS sequence is respected: the earliest aircraft in the initial FCFS order is selected when multiple candidate solutions (within the same allowed time window) possess identical pairwise distance.

Some key desired properties for the solution to this capacity problem are short execution time and equity. A quick solution is needed because a schedule must be made in a very short timeframe so that each aircraft receives its assigned slot by the controller in a timely fashion. In practice, it is typically required that a schedule should be settled in one radar duration, which corresponds to a very short period of time [17]. Equity is modelled in the CAS-TW by limiting the deviation from a nominal order or by minimizing variance in delay as a function of the maximum constrained position shifting (CPS) [18]. We considered the time-window restriction influenced by the CPS. In our model, there is complete knowledge of the set of aircraft that will arrive (static case). We model the problem as an open asymmetric travelling salesman problem (OATSP). To maintain safety and avoid collisions, we consider wake vortex separation for every sequencing. The Airland test case from the O-R Library benchmark problems and real data from the Sao Paulo-Guarulhos International Airport were used in our study to validate the effectiveness and efficiency of our proposed algorithm. We compared our results with FCFS and a commercial mixed-integer programming (MIP) solver (CPLEX).

This article contributes to the ALP literature by providing a new heuristic model for airport runway operations with general assumptions—equity and time window. It focuses on achieving a solution that is easily applied and provides faster results. Unlike traditional MIP models or metaheuristics that often require high computational resources and are very time consuming, our proposed approach is based on a straightforward method that produces competitive solutions in a small amount of time. The method combines a time-window-based greedy algorithm with a domain-specific local search that respects feasibility constraints while it converges to close to optimum solutions, making it an interesting solution for airports with high demand and capacity constraints where fast-decision making is desirable.

The article is structured as follows: in Section 2, the materials are described, a mixed-integer programming formulation is developed for the problem, and our proposed algorithm is designed for the ALP. Section 3 presents the numerical results obtained from both experimental testbeds and the actual environment of Sao Paulo-Guarulhos International Airport. Section 4 discusses the obtained results. Last, a short summary is presented in Section 5.

2. Materials and Methods

2.1. Materials

In this subsection, we present the material of the MIP formulation discussed in Section 2.2, and the CAS-TW heuristic introduced in Section 2.2.1. These methods were used for all problems analyzed in this study. We used 8 instances, Airland1 to Airland8, available from the OR-library, comprising 10 to 50 aircraft per batch. We also evaluated actual data from Sao Paulo-Guarulhos International airport, sequencing up to 32 aircraft. The CPS has a direct impact on the capacity gain. Therefore, we simulated 3 scenarios featuring varying maximum early (m_ne) and late (m_nl) CPS values derived from the original FCFS sequence. The conservative scenario was with an m_ne and m_nl equal to 1. The normal scenario had an m_ne equal to 3 and m_nl equal to 5. The permissive scenario had an m_ne equal to 5 and m_nl equal to 10.

IBM ILOG CPLEX Optimization software, version 12.9.0, ref. [19] was used to achieve an optimal landing schedule in the solution space. Since the search space was too large, it failed to present an optimal solution in a very short timeframe. We set the maximum execution time for the CPLEX sequence to 600 s. The proposed method was implemented in the Python programming language, version 3.13, and all computations were executed on an Intel (R) Core (TM) i7- 5500UCPU (Intel Corporation, Santa Clara, CA, USA) with 2.4 GHz, 8GB RAM, and the Windows 10 operating system. The MILP model was solved with CPLEX 12.9.0 using default parameter settings. To align with performance metrics previously adopted in the ALP literature, the evaluation approach proposed by Rodríguez-Díaz et al. [18] was followed, measuring the percentage improvement in the cost function value of minimizing the time of landing of the last aircraft in the sequence, thereby increasing air capacity, as shown in Equation (1):

$$\% \mathrm{i}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}={\displaystyle \frac{\left(C_{Solution}-C_{CAS-TW}\right)}{C_{Solution}}}$$

(1)

where C_solution is the cost function of the compared solution (FCFS and CPLEX), and C_CAS-TW is the cost function of the CAS-TW algorithm.

We conducted experiments on OR-Library benchmark problems. From this library, we used the Airland database. In the literature, the OR-library benchmark has been adopted in several related works [3,7,17,20,21,22,23,24,25,26,27,28,29]. We chose a maximum of 50 aircraft to sequence. Some studies scheduled up to 200 aircraft by assigning all elements through a unified procedure. Many researchers criticized this approach as it was ineffective to consider that many aircraft simultaneously due to the extensive search space and the operational dynamic environment, where unexpected disturbances may occur, such as delays, flight cancellations, and emergency landings [30,31,32]. Consequently, we did not use Airland9 to Airland13 because our study concentrates on a single airport where up to 35 aircraft can be handled per hour, a scenario that takes place daily at the airport under study.

We executed the following modification steps from the original database to adapt it to our reality:

• From the OR-library scenarios, we used the target landing time (TLT) and the minimum safe separation matrix with different values from

  Table 1. Minimum safe separation (in seconds) for different pairs of aircraft types operating on the same runway.

  		Trailing Aircraft
  		Heavy	Medium	Light
  Leading Aircraft	Heavy	94	114	167
  	Medium	74	74	138
  	Light	74	74	98

  ;
• TLT was used to create the FCFS sequence;
• Once the sequential order of arrival was obtained, TLT was abandoned. The time window for each aircraft was created using the time-window module in the CAS-TW procedure, and the aircraft were sequenced using the separation matrix;
• The cost function for the FCFS (CFCFS) was the scheduled landing time of the last aircraft to land.

Bennell et al. [33] mention that many of the algorithms for solving the ALP have not been tested using real data. We chose to use actual data from Sao Paulo-Guarulhos International airport, the largest Brazilian airport for commercial traffic. We considered a single runway for landing, and it operates independently. The instances were extracted from a year-long analysis. We adopted the top two busiest schedule times in the year period. We chose the 7 a.m. and 7 p.m. schedules. The 7 a.m. schedule contained 30 aircraft with an aircraft mix of 25% heavy and 75% medium, and the 7 p.m. schedule had 32 scheduled arrivals with an aircraft mix of 15% heavy and 85% medium. Following the methodology adopted in similar real-data studies [34,35], we implemented a schedule generator that uses Monte Carlo simulation to generate a realistic instance from operational flight schedules. For each schedule, we generated five testbeds that maintained the aircraft mix but rearranged the arrival sequence.

2.2. Methods

2.2.1. Model Formulation

We formulated the ALP as an open asymmetric TSP with time windows (OATSP-TW), drawing on the graph-theoretic foundations described in [36] and the asymmetry principles outlined in [37]. As shown in Table 1, there is asymmetry in the minimum safe separations for different pairs of aircraft types. For example, the separation between a heavy aircraft and a light aircraft is 167 s, and the separation between a light aircraft and a heavy one is 74 s. The presence of asymmetry is directly linked to the aircraft mix in a given optimized set and varies during the day. In our model, we considered the time-window restriction as a function of the maximum CPS in a timely form as suggested by Bennell et al. [6]. Our mixed-integer programming problem (MIP) formulation adapts the formulation originally proposed by Da Silva and Urrutia [38].

Consider a Hamiltonian tour starting from the first aircraft that agreed with all the time windows to minimize the makespan and to increase airport capacity. The tour can be formulated on graph G = (N, A), where $\mathrm{N}=\left\{1,2,\dots ,\mathrm{n}\right\}$ is the set of aircraft waiting to land on a single runway for a determined airport, 0 represents the first aircraft in the sequence, and $\mathrm{A}=\left\{\left(i,j\right):i,j \in N \cup \left\{0\right\}, i\ne j\right\}$ is the set of arcs between aircraft.

• Notations:
• Sets:
• N = the number of aircraft
• 0 = the first aircraft in the sequence
• Parameters:
• $e_i$ = the earliest landing time for aircraft i (i, …, N)
• $l_i$ = the latest landing time for aircraft i (i, …, N)
• $\left[e_i,l_i\right]$ = time window
• $s_{ij}$ = the separation time between two aircraft i and j when landing
• M = big constant
• Decision variables:

$$x_{ij}= \left\{\begin{array}{c}1, if leading aircraft i is followed by trailing aircraft j\hfill \\ 0, otherwise\hfill \end{array}\right\}$$

• ${\beta }_i$ = the time that aircraft i land on the runway

$$Minimize {\displaystyle \sum }_{i \in N \cup \left\{0\right\}}{\displaystyle \sum }_{j \in N \cup \left\{0\right\}}{s}_{ij}{x}_{ij}$$

(2)

Subject to:

$$\sum _{i\in N\cup \left\{0\right\}, i\ne j }{x}_{ij}=1 \forall j \in N \cup \left\{0\right\}$$

(3)

$$\sum _{j\in N\cup \left\{0\right\}, i\ne j }{x}_{ij}=1 \forall i \in N \cup \left\{0\right\}$$

(4)

$${\beta }_j\ge {\beta }_i+c_{ij}-M\left(1-x_{ij}\right) \forall i,j \in N \cup \left\{0\right\}, j \ne 0$$

(5)

$$e_i\le {\beta }_i\le l_i$$

(6)

$$x_{i0}=0 \forall i \in N$$

(7)

$$x_{ij} \in \left\{0, 1\right\} \forall i, j \in N \cup \left\{0\right\}$$

(8)

$${\beta }_i\in R_{\ge 0} \forall i \in N U \left\{0\right\}$$

(9)

$$e_i, l_i\in R_{\ge 0} \forall i \in N U \left\{0\right\}$$

(10)

The main differences between our approach and the modelling proposed by Da Silva and Urrutia [38] is that we substitute the cost of travelling from i to j (cij) for the wake vortex separation (sij). We substitute 0 (the depot) for the first aircraft in the original FCFS sequence. We also add Constraint (7) because there is no need to connect the last landed aircraft to the first aircraft in the sequence (depot in [38]).

The objective function (2) minimizes the total minimum time separation and completes all runway operations in the shortest possible time. It aims to minimize the last operation that is scheduled for a determined set of runways. Constraints (3) and (4) state that every aircraft must land only once and establish the aircraft sequencing. Constraint (5) ensures that the arrival time of a given aircraft cannot be smaller than the arrival time of a previously landed aircraft plus the pairwise (wake vortex) separation between aircraft i and j. Since all separations are positive, Constraint (5) avoids the formation of sub-cycles. Constraint (6) is the time window hard constraint that ensures equity. Constraint (7) removes the obligation that the last aircraft is linked to the first one, which makes the problem an open version of the problem. Constraint (8) sets the decision variable as a binary value. Constraint (9) states that aircraft i must land within a positive time value. Constraint (10) ensures that the time windows are not negative.

2.2.2. Closest Aircraft Sequence with Time Window (CAS-TW) Heuristic for the Aircraft Landing Problem

• Notations:
• Sets:
• N = the number of aircraft in the sequence
• N_FCFS = the final set of aircraft in the FCFS algorithm
• $N_{{FCFS}_p}$ = the set of aircraft landing in position p with the FCFS algorithm
• ${\mathrm{N}}_{{\mathrm{F}\mathrm{C}\mathrm{F}\mathrm{S}}_{\mathrm{T}\mathrm{W}}}$ = the set of aircraft in FCFS with a time window for each aircraft
• N_CAS-TW = the final set of aircraft on the landing sequence after the CAS-TW algorithm
• $N_{{CAS-TW}_p}$ = the set of aircraft landing in position p with the CAS-TW algorithm
• Csol_p = the set of candidate solutions for position p in the landing sequence
• $N_{{CAS-TW}_{p-selected}}$ = the aircraft selected in $N_{{CAS-TW}_p}$
• N_op = the set of aircraft that were not initially chosen in the CAS-TW algorithm
• $N_{{op}_i}$ = the aircraft in position i from N_op
• Index:
• p = position of the aircraft in the sequence, $\mathrm{p}=\left\{1,\dots ,\mathrm{N}\right\}$
• i, j = indices representing aircraft
• Parameters:
• n_MECPS = the maximum number of earliest CPS
• n_MLCPS = the maximum number of latest CPS
• d_lpd = the largest pairwise distance in the set
• e_i = earliest landing time for aircraft i
• l_i = latest landing time for aircraft i
• p_lt = present landing time
• t_i = FCFS time for aircraft i. It is the landing time that the aircraft i is scheduled to land after wake vortex separation.
• $s_{ij}$ = the separation time between two aircraft i and j when landing

We propose a systematic way to create a better landing sequence compared to the FCFS sequence. Our algorithm is divided into three modules. First, it generates all the time windows for each aircraft in the set. Second, it uses a constructive heuristic based on the nearest neighbour algorithm to determine the aircraft sequence. Finally, if the algorithm fails to provide a final landing sequence, an insertion heuristic based on the cheapest insertion algorithm inserts an aircraft, orphan point, between a pair, already included, respecting all time windows. A pseudocode for the main procedures is shown in Algorithm 1.

Algorithm 1 Pseudocode for the CAS-TW main procedures
Initialization
Input: NFCFS
Output: NCAS-TW
1.	CAS-TW.TIME-WINDOWS module
2.	while NFCFS ≠ Ø
3.	CAS-TW.CONSTRUCTION module
4.	if NFCFS > 0 and the search stopped
5.	CAS-TW.INSERTION module
6.	else
	end while
7.	end while
8.	End

Time-Window Module in the CAS-TW Procedure

The time-window module aims to calculate the time window constraint for each aircraft in the set. The time-window calculation follows the equity-based approach proposed by Bennell et al. [6], which defines fairness using time shifting rather than position shifting constraints.

Constrained position shifting (CPS) restricts how far an aircraft can be moved within the FCFS landing sequence, preventing the indefinite delay of any aircraft. Aligned with previous studies [8,12,13,39,40], CPS was adopted as a key sequencing constraint that limits the extent of scheduling revisions. It may incorporate the following parameters for the determination of the landing sequence: aircraft order—from one up to three [8] or from one up to nine [40]—or a defined time window, bounded by the earliest and latest time. The earliest time represents the earliest an aircraft is able to land if it flies at its maximum airspeed. The latest time represents the latest an aircraft can land if it flies at its most fuel-efficient airspeed while also holding (circling) for the maximum allowable time. Some studies establish the maximum landing time according to fuel requirements and assume that this maximum duration is sufficiently long so as to have no consequences [39]. Bennell et al. [6] suggested a preferable alternative to CPS that adopts the maximum time shifting, where an aircraft’s landing time cannot deviate by more than a given amount of time from its unconstrained landing time. Because the frequency of air traffic changes during the day, applying restraints on time shifts avoids the volatility in a flight’s delay that can occur when applying constraints on position shifts. In our study, we have used Bennell’s alternative.

Algorithm 2 shows the pseudocode for the time-window module.

Algorithm 2 Pseudocode for the time-window module in the CAS-TW heuristic
Initialization
Input: NFCFS
Output: ${\mathrm{N}}_{{\mathrm{F}\mathrm{C}\mathrm{F}\mathrm{S}}_{\mathrm{T}\mathrm{W}}}$
1.	Set nMECPS, nMLCPS, dlpd
2.	Set plt = 0, p = 1
3.	Calculate ei
4.	if ei < 0:
5.	Set ei = 0
	end if
6.	Else
7.	Maintain ei
8.	end else
9.	Calculate li

This module takes the FCFS sequence as input. One contribution of our proposed method is the definition of the time windows for each aircraft using the original (FCFS) sequence. The output of this module is the FCFS arrangement along with the earliest and latest allowed landing time. This is treated as a hard constraint in our algorithm. If a proposed solution violates this hard constraint, the result is considered infeasible. We use the largest pairwise distance in the set (d_lpd) in all calculations, and this distance depends on the greatest wake vortex separation across all sets.

Equation (11) is adopted to calculate the earliest landing time of aircraft i (e_i) as a function of the FCFS time for aircraft i (t_i), the maximum number of earliest CPS (n_MECPS), and the largest pairwise distance in the set (d_lpd). The term e_i may take on negative values, especially for the first elements in the set. In this case, e_i is set to zero.

$${\mathrm{e}}_{\mathrm{i}}={\mathrm{t}}_{\mathrm{i}}-\left({\mathrm{n}}_{\mathrm{M}\mathrm{E}\mathrm{C}\mathrm{P}\mathrm{S} }\mathrm{x}{ \mathrm{d}}_{\mathrm{l}\mathrm{p}\mathrm{d}}\right)$$

(11)

Equation 12 shows the steps to calculate the latest landing time (l_i) for aircraft i. It uses the same parameters as the e_i calculation.

$${\mathrm{l}}_{\mathrm{i}}={\mathrm{t}}_{\mathrm{i}}+\left({\mathrm{n}}_{\mathrm{M}\mathrm{L}\mathrm{C}\mathrm{P}\mathrm{S} }\mathrm{x}{ \mathrm{d}}_{\mathrm{l}\mathrm{p}\mathrm{d}}\right)$$

(12)

The next step in our algorithm is the construction module.

Construction Module in the CAS-TW Procedure

Algorithm 3 shows the pseudocode for the construction module in the CAS-TW.

Algorithm 3 Pseudocode for the construction module in the CAS-TW heuristic
Input:${ \mathrm{N}}_{{\mathrm{F}\mathrm{C}\mathrm{F}\mathrm{S}}_{\mathrm{T}\mathrm{W}}}$
Output: NCAS-TW
1.	Set plt = 0, p = 1
2.	$\mathrm{S}\mathrm{e}\mathrm{t} N_{{NNA-TW}_1}= N_{{FCFS}_1}$, remove $N_{{FCFS}_1}$ from NFCFS, p += 1
3.	while NFCFS ≠ Ø
4.	if ei ≥ plt and li ≤ plt
5.	Add aircraft i to Csolp
	end if
6.	Else
7.	Disregard aircraft i
8.	end else
9.	Set $N_{{CAS-TW}_{p-selected}}$
10.	Remove$N_{{CAS-TW}_{p-selected}}$ from NFCFS, p += 1
11.	if NFCFS > 0 and the search stopped
12.	CAS-TW.INSERTION module
13.	else
14.	end while
15.	end while

The construction module relies on the Nearest Neighbour (NN) algorithm. The CAS-TW uses a combination of constructive and insertion heuristics. The NN heuristic [41] enables the fast generation of initial sequences by minimizing local separation times, while the cheapest insertion heuristic [42,43] ensures that orphan aircraft are reintroduced into the sequence without violating time-window constraints.

NN is a tour constructive heuristic, which picks an arbitrary city from a collection of cities and later incrementally constructs a feasible TSP tour by including new cities that are elected following a specific heuristic procedure. To construct our algorithm, we used a concept from NN: in the search process for the next aircraft spot in the landing sequence, we chose from the available candidates the one that had the lowest pairwise separation from the preceding aircraft in the landing sequence. In the primary NN algorithm, the initial starting point is an arbitrary node. In our proposed method, the first aircraft is selected in advance. We select the first aircraft in the FCFS sequence to be the starting point in our sequence. The starting input in the NN is a two-dimensional distance matrix, and in the CAS-TW, is a two-dimensional wake vortex separation matrix and a one-dimensional earliest and latest time matrix. In the search process for the next point, the NN algorithm uses the shortest distance between the last node and the next node as the specific parameter. In the CAS-TW, choosing the next point is a direct function of the shortest distance, but it is constrained by the time window.

For each aircraft position in the CAS-TW algorithm ($N_{{CAS-TW}_p}$), all aircraft that are inside the time window are combined with the candidate solution set (Csolp). The selected aircraft ($N_{{CAS-TW}_p}$) is the one with the smallest value in the wake vortex separation time (sij), where i is the $N_{{NNA-TW}_{p-1}}$ aircraft, and j is an aircraft in Csolp. The selected aircraft is then removed from the FCFS set (N_FCFS), and the algorithm searches for the next aircraft in the sequence until the FCFS set is empty. Construction heuristics visit most points, but some points may be left out, especially the ones that cross the TSP path, because the distances to proceed to another neighbourhood of the problem or to go to left-over positions are generally much longer than the distances inside a neighbourhood [42]. The insertion module is implemented when there are aircraft that are not sequenced for landing.

Insertion Module in the CAS-TW Procedure

Algorithm 4 presents the pseudocode for the insertion module in the CAS-TW heuristic.

Algorithm 4 Pseudocode for the insertion module in the CAS-TW heuristic
Input: NFCFS
Output: NCAS-TW
1.	if NFCFS > 0 and the search stopped
	Set Nop, Set NCAS-TW
2.	while Nop ≠ Ø
3.	For $N_{{op}_i}$ and each pair of aircraft (i-j) in NCAS-TW at the same time window
4.	$\underset{S_{{\mathit{op}}_i}}{\min }\left\{\underset{\mathit{ij}}{\min }{\delta }_{N_{{op}_i}ij}=s_{i{N}_{{op}_i}}+s_{N_{{op}_i}j}-s_{ij} \right\}$
5.	Add $\underset{N_{{op}_i}}{\mathrm{m}\mathrm{i}\mathrm{n}}$ to NCAS-TW
6.	end while

The main problem of construction heuristics is when the algorithm fails to visit some nodes on the route (orphan points). To overcome this problem, we opted to implement the cheapest insertion heuristic. This heuristic first rules that, for every remaining free or unvisited point, there is an optimal link that introduces this point. The algorithm chooses the position that has the minimum associated insertion penalty to introduce the point. The insertion cost is the sum of the distance to the free point, minus the distance of the link that will be cut out. This refers to the minimization in Equation (13), where k is the orphan point, i-j are the links of the tour, and c is the cost of the tour [42]. Insertion heuristics can be adapted to address specific constraints in real-world TSP variants, such as time windows, asymmetric costs, and precedence constraints [43].

$$\underset{k}{\min }\left\{\underset{\mathit{ij}}{\min }\left\{{\delta }_{kij}=c_{ik}+c_{kj}-c_{ij}\right\}\right\}$$

(13)

In the original cheapest insertion heuristic, the only criterion of choice is to establish the minimum cost of the inserted point. In the CAS-TW, another factor is that the inserted point must respect the allowed time window.

Our proposed solution maintains the greedy behaviour of both the NN and the cheapest insertion heuristics. Greedy algorithms exclusively focus on the next step (local optimum) and do not change prior decisions, are effective in real-time scenarios like ATM. Even in classic optimization problems such as the TSP, heuristic strategies like Dijkstra’s algorithm have proven useful [42]. This reinforces that even complex scheduling problems benefit from heuristic strategies, especially when real-time applicability is the main issue.

To illustrate in a practical way how the CAS-TW works under operational restrictions, an example with four aircraft has been included. This example highlights the logic behind the aircraft prioritization, focusing on viable sequences that respect the assigned time window for each aircraft in the sequence.

Consider four aircraft (A1, A2, A3, and A4) with an arriving sequence based on the FCFS algorithm. Each aircraft belongs to the following wake vortex category:

• A1: Heavy;
• A2: Medium;
• A3: Light; and
• A4: Medium.

The minimum separation among aircraft pairs, according to each aircraft category, is presented in

Table 2. Minimum safe separation times (in seconds) among aircraft pairs operating on the same runway.

		Trailing Aircraft
		A2 (Medium)	A3 (Light)	A4 (Medium)
Leading Aircraft	A1 (Heavy)	114	167	114
	A2 (Medium)	-	138	74
	A3 (Light)	74	-	74

.

Let us suppose that the FCFS sequence estimates the following landing times for each aircraft, resulting in a final makespan (landing time) of 300 s:

• A1: 0 s;
• A2: 120 s;
• A3: 210 s; and
• A4: 300 s.

Considering nMECPS = 1, nMLCPS = 1, and dlpd = 167 s (the greatest separation time among the aircraft in the sequence), each aircraft has the following time window:

• A1: [0, 167] s;
• A2: [0, 287] s;
• A3: [43, 377] s; and
• A4: [133, 467] s.

With this information, there are 24 possible aircraft landing sequences. For simplicity, we analyze three of them to illustrate the concepts previously presented:

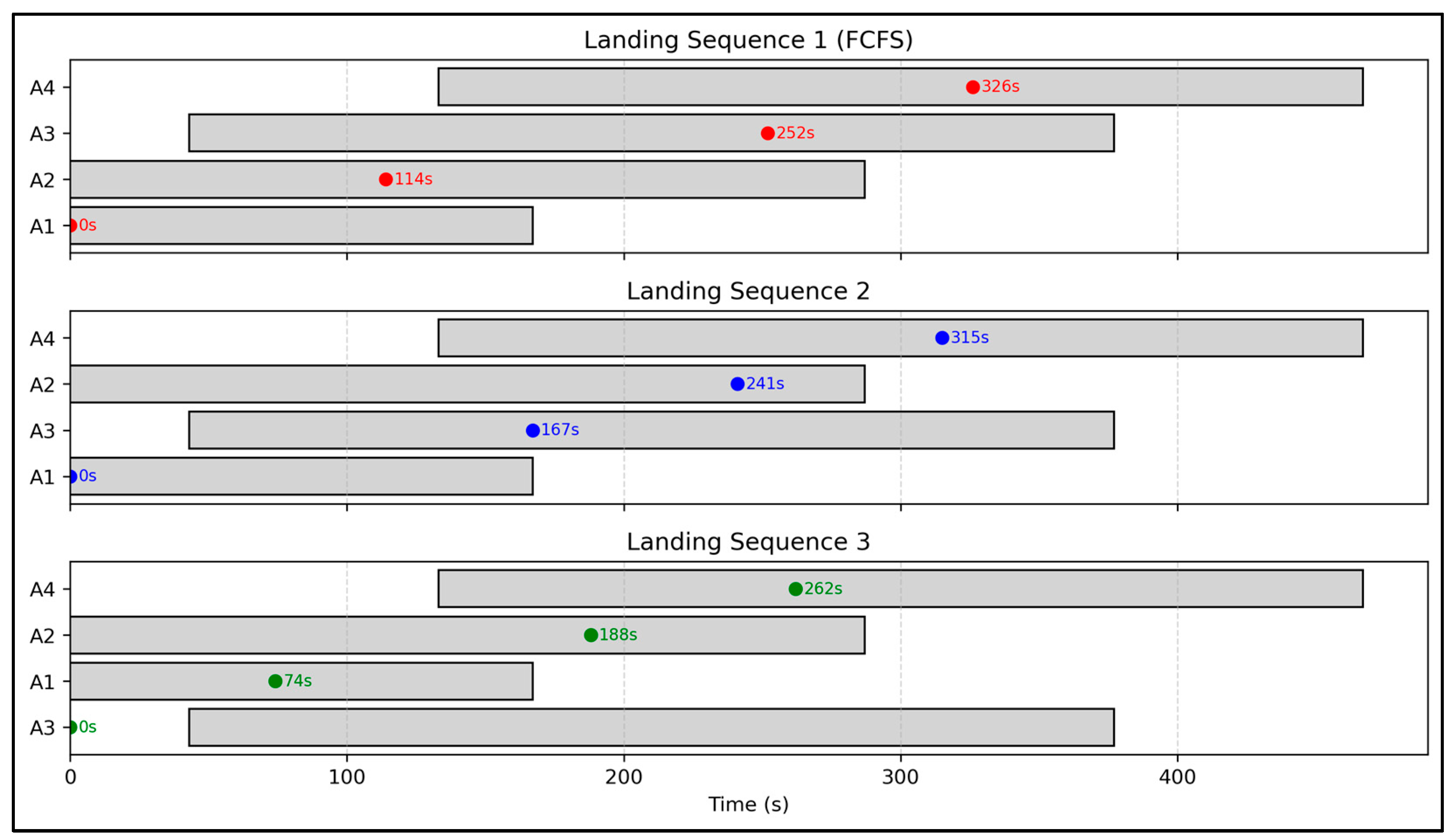
(a) Landing Sequence 1 (FCFS): A1; A2; A3; A4;

• Landing time: [0, 114, 252, 326] s;
• Makespan: 326 s; and
• Viable sequence: all time windows are respected.

(b) Landing Sequence 2: A1; A3; A2; A4;

• Landing time: [0, 167; 241; 315] s;
• Makespan: 315 s;
• Viable sequence: all time windows are respected; and
• Better sequence than Landing Sequence 1.

(c) Landing Sequence 3: A3; A1; A2; A4;

• Landing time: [0; 74; 188; 262] s;
• Makespan: 262 s; and
• Unviable sequence: violates A3′s time window [43, 377] seconds.

Table 3. Scheduled landing times (in seconds) for the examples above.

Aircraft	Time Window (s)	Sequence 1 (FCFS)	Sequence 2	Sequence 3
A1	[0, 167]	0	0	74
A2	[0, 287]	114	241	188
A3	[43, 377]	252	167	0
A4	[133, 467]	326	315	262

shows the scheduled landing times for the three landing sequences analyzed above.

To better illustrate the above example, Figure 1 shows a Gantt chart comparing the landing sequences, including the standard FCFS (Landing Sequence 1) and two alternative sequences. Landing Sequence 2 is a viable option, while Landing Sequence 3 violates one time-window constraint (unviable sequence).

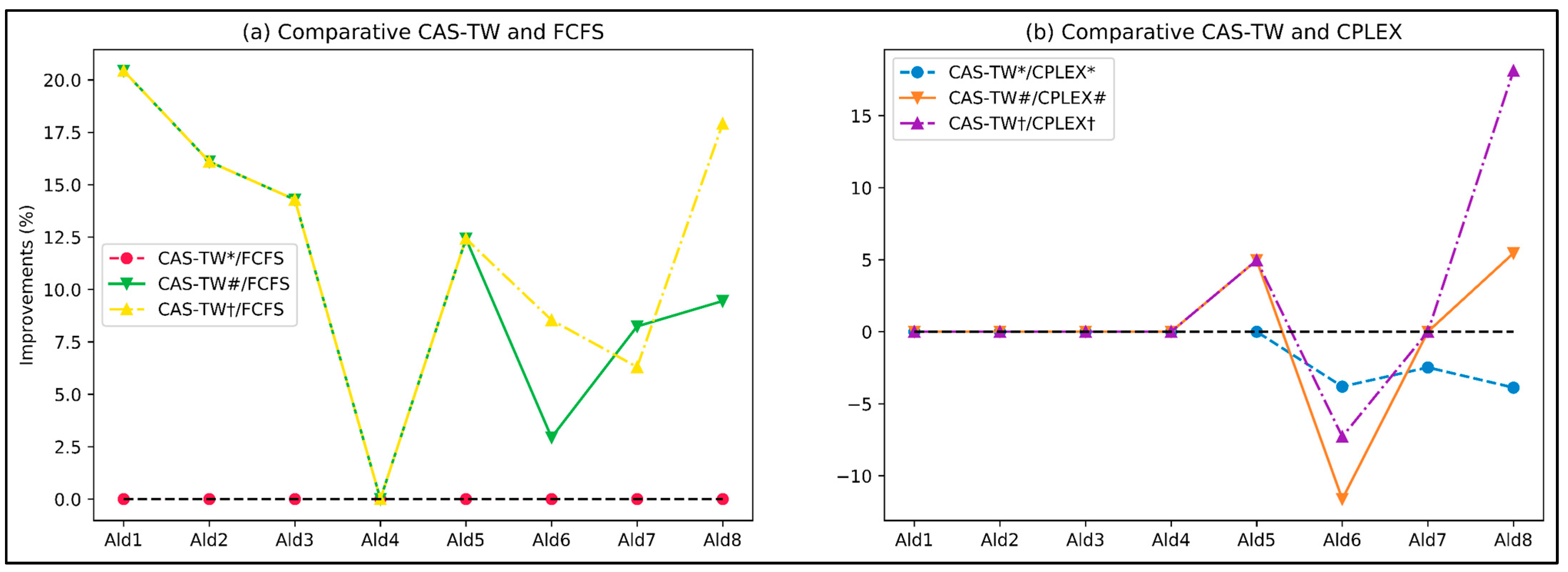
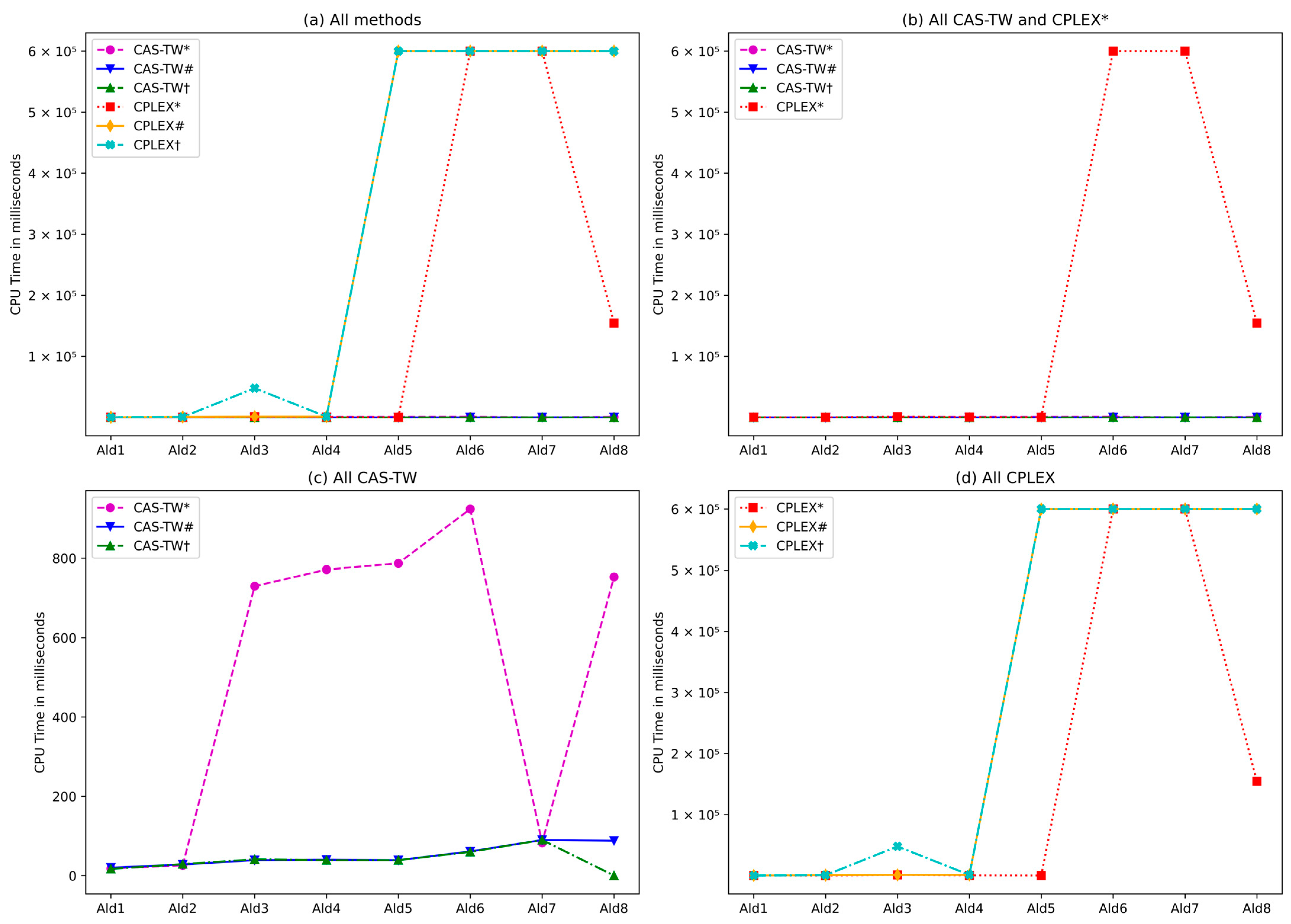
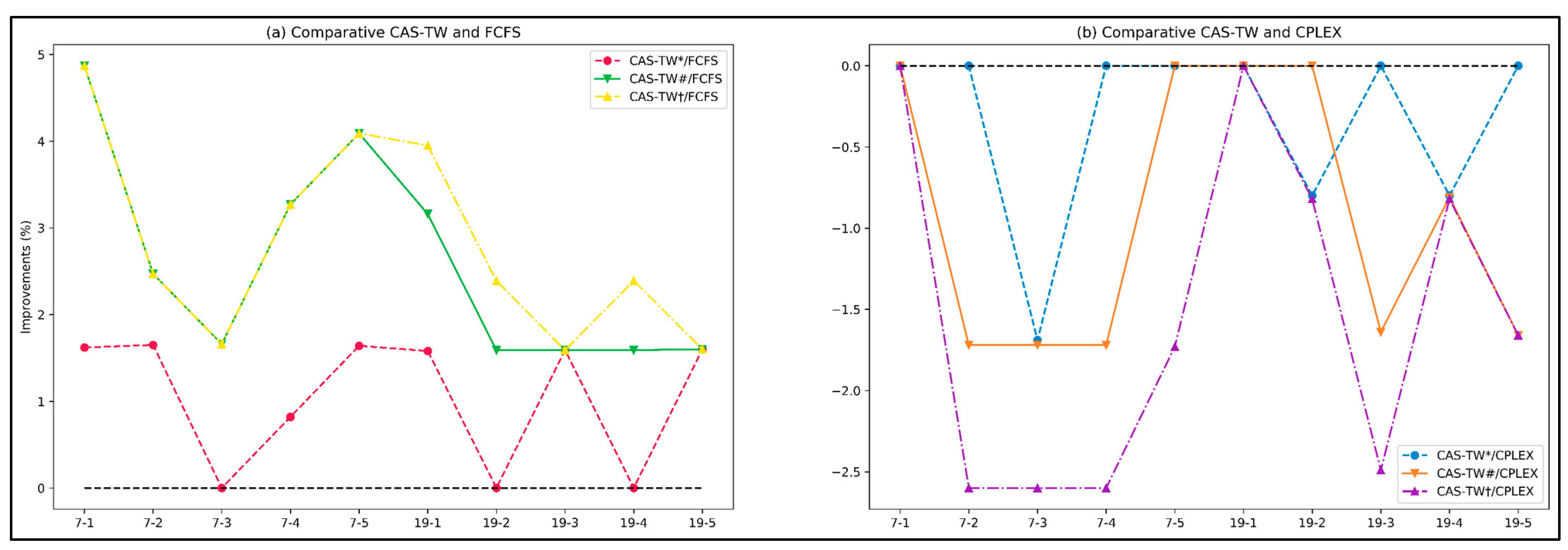
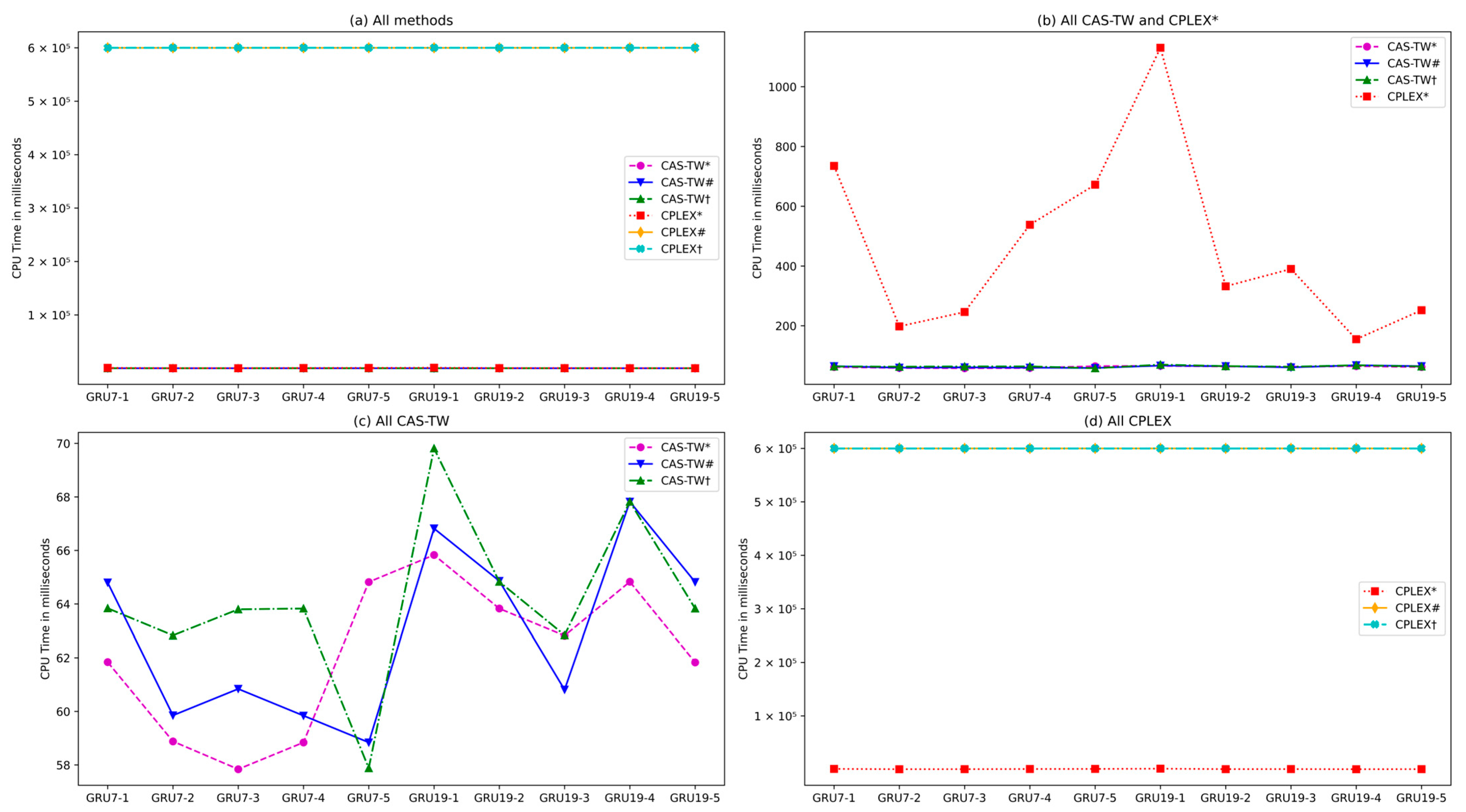
Even with a better makespan, unviable sequences are not used. This example considers only a sequence with four aircraft. In real-world problems, however, aircraft sequences may involve more than 30 aircraft, which exponentially increases the computational time required to solve the problem (NP-Hard). To avoid solving this problem by brute force, the CAS-TW algorithm selects only candidate aircraft with feasible times for each available time window, as previously described in the Section Insertion Module in the CAS-TW Procedure.

2.3. Justification and Generalization of the Proposed Heuristic

The CAS-TW was developed due to its viability, interpretability and computational efficiency. The method incorporates key features of the ALPTW and the ATC operations, particularly the concepts of time-window operations and wake turbulence separation.

A greedy algorithm based on the NN was chosen due to its proven ability to provide feasible solutions to the OTSP-TW in a short computational time. That is one of the key characteristics that was looked for while researching for solving this type of problem. ATC and ATFM environments, due to their nature, require fast and feasible solutions, which demand fast and feasible sequencing strategies that increase runway capacity while minimizing the total operation time of the last aircraft.

The problem was modelled as an OTSP-TW due to its compatibility with the operational characteristics of runway scheduling. It also encompasses the asymmetrical separation among aircraft due to its nature, and it does not require the return to the starting point. Although several algorithms have been developed for the TSP, they are not directly applicable to the ALPTW due to the time-window constraints and dynamic pairwise separation, which limit the use of traditional TSP heuristics.

The benchmark data used in this study were also restricted to better reflect actual airport operations. In practice, most commercial airports, including São Paulo-Guarulhos International Airport, conduct all landing operations on a single runway, managing arrival sequences of 30 to 35 aircraft per hour. For this reason, we did not include the Airland9 to Airland 13 datasets, with up to 200 aircraft, a scenario not consistent with the studied airport.

Although the main objective of the present study is the ALPTW, future research may explore the inclusion of take-offs or other sequencing problems with asymmetrical costs and flexible time constraints, such as the job-shop scheduling problem, or even strategic scheduling environments [44].

3. Results

3.1. OR-Library Instances

Table 4. Cost function value results (in seconds) for the OR-library.

Airland	#	FCFS	CPLEX *	CPLEX #	CPLEX †	CAS-TW *	CAS-TW #	CAS-TW †
1	10	93	93	74	74	93	74	74
2	15	118	118	99	99	118	99	99
3	20	133	133	114	114	133	114	114
4	20	134	134	134	134	134	134	134
5	20	153	146	134	134	153	134	134
6	30	3266	3146	2840	2840	3170	2996	2987
7	44	4952	4832	4544	4544	4832	4640	4640
8	50	402	387	364	330	387	364	330

Stands for: * conservative, # normal, and † permissive scenarios.

presents the computational results for the OR-Library. The first column is the test problem from the Airland database. The second column is the number of aircraft that are sequenced. The remaining columns are the cost function value results for each method, in the CPS scenario.

For the sake of clarity, all figures in this section are presented in Appendix A. Figure A1 shows the percentage capacity improvement, calculated using Equation (1). Figure A2 presents the computational times for the OR-Library.

3.2. Application to São Paulo-Guarulhos International Airport

Table 5. Cost function value results (in seconds) for the Sao Paulo-Guarulhos International airport.

GRU	#	FCFS	CPLEX *	CPLEX #	CPLEX †	CAS-TW *	CAS-TW #	CAS-TW †
7-1	30	2466	2426	2346	2346	2426	2346	2346
7-2	30	2426	2386	2326	2306	2386	2366	2366
7-3	30	2406	2366	2326	2306	2406	2366	2366
7-4	30	2446	2426	2326	2306	2426	2366	2366
7-5	30	2446	2406	2346	2306	2406	2346	2346
19-1	32	2534	2494	2454	2434	2494	2454	2434
19-2	32	2514	2494	2474	2434	2514	2474	2454
19-3	32	2514	2474	2434	2414	2474	2474	2474
19-4	32	2514	2494	2454	2434	2514	2474	2454
19-5	32	2494	2454	2414	2414	2454	2454	2454

Stands for: * conservative, # normal, and † permissive scenarios.

presents the results for the São Paulo-Guarulhos International Airport instances.

Figure A3 presents the comparative improvement. Figure A4 presents the computational time for the GRU test problem.

4. Discussion

4.1. OR-Library Instances

When analyzing the theoretical instances (OR-Library), as shown in Table 4 and Figure A1, for the conservative scenario, where the maximum number of early and late CPS, based on the original FCFS sequence, equalled one, there were no capacity gains in any of the instances. In contrast, for the normal and permissive scenarios, except for Airland4, there was a capacity gain ranging from 2.94% to 20.43% compared with the FCFS sequence. Figure A3b compares the CAS-TW and the CPLEX. Negative values occurred where the CPLEX gave a smaller cost function value compared to the value given by the CAS-TW. Positive values work in the opposite direction. In most cases, our proposed algorithm gave the same solution as the CPLEX. For five cases, the CPLEX was up to 12% better, and in four cases, the CAS-TW produced better solutions than a commercial MIP solver, achieving, in one instance, a 19% improvement. Airland4 is an interesting case. It illustrates that, depending on the aircraft sequence in a determined set, there is no gain in runway capacity because ALP modelling is based on Equation (1), minimizing the total sum of the wake vortex. Certain configurations, even in the permissive scenario, do not produce effective rearrangements in the aircraft sequence.

For the computational times, Figure A2 highlights that the CPLEX took longer to execute solutions. Sets with less complexity, fewer than 20 instances, and in the conservative scenario were the fastest. In Airland5 to Airland8, except for the conservative scenario, all results were achieved within the time stop criteria of 600 s (10 min), and the CPLEX did not deliver an optimal solution. For the CAS-TW, higher values occurred in the conservative scenario, and when the insertion module had to be used. This measure increased the execution time by 10, but it still produced an execution time response of less than 1 s.

4.2. Application to São Paulo-Guarulhos International Airport

As presented in Table 5, the CAS-TW also increased airport capacity when using real data. It maintained a more practical capacity increase compared to the theoretical data, since it only had two wake vortex categories to reschedule.

The capacity improvements in the real instances were lower than those obtained using the theoretical data. One reason for this result is the different number of wake vortex categories for aircraft separation. Airland consists of four categories, while practical data is classified into three categories. However, Guarulhos operates under two aircraft categories (medium and heavy), because it is the main Brazilian international airport and small aircraft are not allowed most of the time.

Comparing the CAS-TW and FCFS in the conservative scenario (GR7-3, GR19-2, and GR19-4), our proposed method was not able to produce a better aircraft sequence. The normal scenario produced, on average, slightly worse results compared to the permissive scenario (0.24%). Regarding airline preferences, it would be interesting to use the normal scenario, with fewer cost impacts, increased fuel consumption, and increased comfort for passengers. The CAS-TW was not able to produce better solutions than the CPLEX, but 40% of the outcomes generated by our algorithm were equal to the solutions of the CPLEX, and our algorithm produced the solutions faster (0.02% of CPLEX computational time). On average, the CAS-TW produced solutions 2.6% worse than the CPLEX, showing the quality of our algorithm.

The CPLEX was not able to produce an optimal solution in the normal and permissive scenarios. All answers were derived within the time stop criteria. In the worst case, the CAS-TW took 0.01% of CPLEX computational time to produce a solution that was 2.49% worse. On average, it took 0.02% of CPLEX time to produce a solution that was 0.93% worse.

5. Conclusions

Aviation has become increasingly popular in the last few decades. It provides shorter travel times and a global reach to all destinations served by an airport. The air transport industry provides a service to every country in the world and plays a key role in creating a universal economy. As the demand for air transportation continues to grow, some aircraft cannot land at their preferred landing times due to the high volume of arriving flights approaching runway capacity. The resulting landing delays lead to increased fuel use and greater aircraft emissions. Delays may also yield extra costs for both passengers and airline companies. Increasing the handling efficiency of congested airports is a crucial management issue. Building new runways at existing airports is often not feasible due to environmental, financial, and geographical constraints.

The aircraft landing problem (ALP) establishes the aircraft sequence operating on a runway and optimizes the expressed objectives, subject to a range of operational constraints. In this study, an efficient, adapted heuristic called the Closest Aircraft Sequence with Time Windows (CAS-TW) is proposed to solve the ALP for a single runway that works independently. The results showed that the CAS-TW produced near or equal solutions compared to a commercial MIP solver (CPLEX) in a fraction of CPU time, especially when the number of landing aircraft increased. The algorithm produced good solutions using both theoretical and real databases. Up to 20% capacity gains for theoretical databases and 5% for real databases highlight the importance of this type of research, especially for congested airports. Another significant result of this study is that capacity increase is not just a function of rescheduling the landing sequence, but is also correlated with the maximum CPS allowed during the setup. Although the proposed method yields good results, the addition of other techniques could increase its performance. Future studies can incorporate our heuristic to construct an initial viable solution within local search methods and metaheuristics for addressing the aircraft landing problem.