Convex Optimization for Spacecraft Attitude Alignment of Laser Link Acquisition Under Uncertainties
Abstract
1. Introduction
- (1)
- Existing spacecraft attitude dynamics models predominantly rely on deterministic frameworks. In contrast, the proposed stochastic attitude dynamics model explicitly incorporates random disturbances prevalent in space gravitational wave detection missions. This approach more fully reflects real-world environmental uncertainties and better approximates the operational conditions of laser link acquisition.
- (2)
- Building upon existing work that solely considers deterministic hard constraints, this paper’s strategy combines stochastic constraints with covariance control. This integration enables explicit quantification of the impact of random perturbations, ensuring probabilistic satisfaction of key performance indicators. This approach avoids the overly conservative or infeasible outcomes associated with deterministic constraint methods alone.
- (3)
- Compared with traditional convexification methods for chance constraints, this paper proposes a hierarchical convexification approach that integrates the Schur complement theorem, second-order cone relaxation, and Taylor expansion. This method not only effectively handles the non-convex terms in chance constraints but also ensures the losslessness of relaxation. Consequently, it renders the optimization problem computationally tractable without compromising solution accuracy.
2. Problem Formulation
2.1. Stochastic System Dynamics
2.2. Constraints
2.3. Original Problem
3. Convexification
3.1. Relaxation of Covariance Dynamics
3.2. Chance Constrain Convexity Strategy
3.3. Convex Optimization Problem
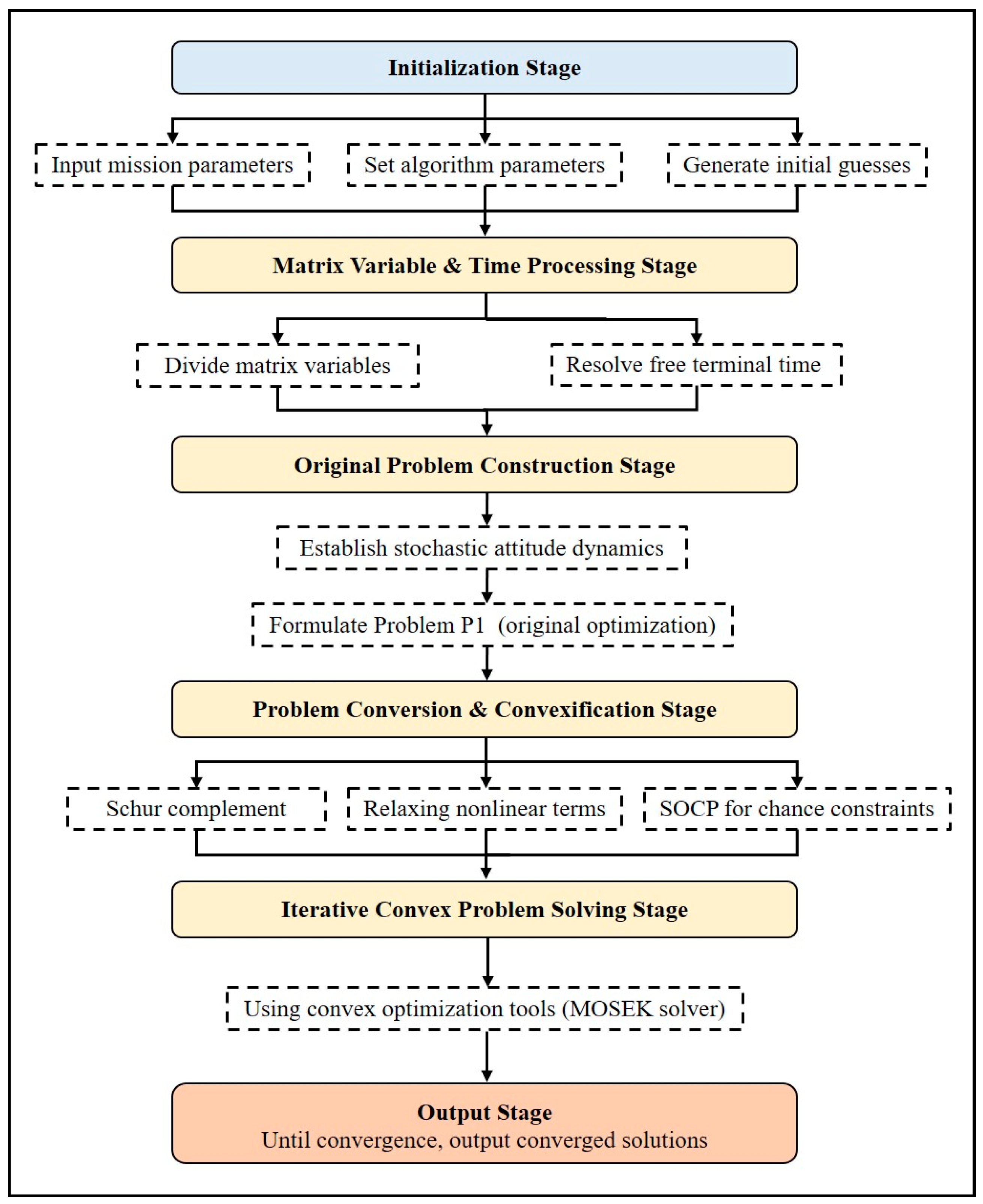
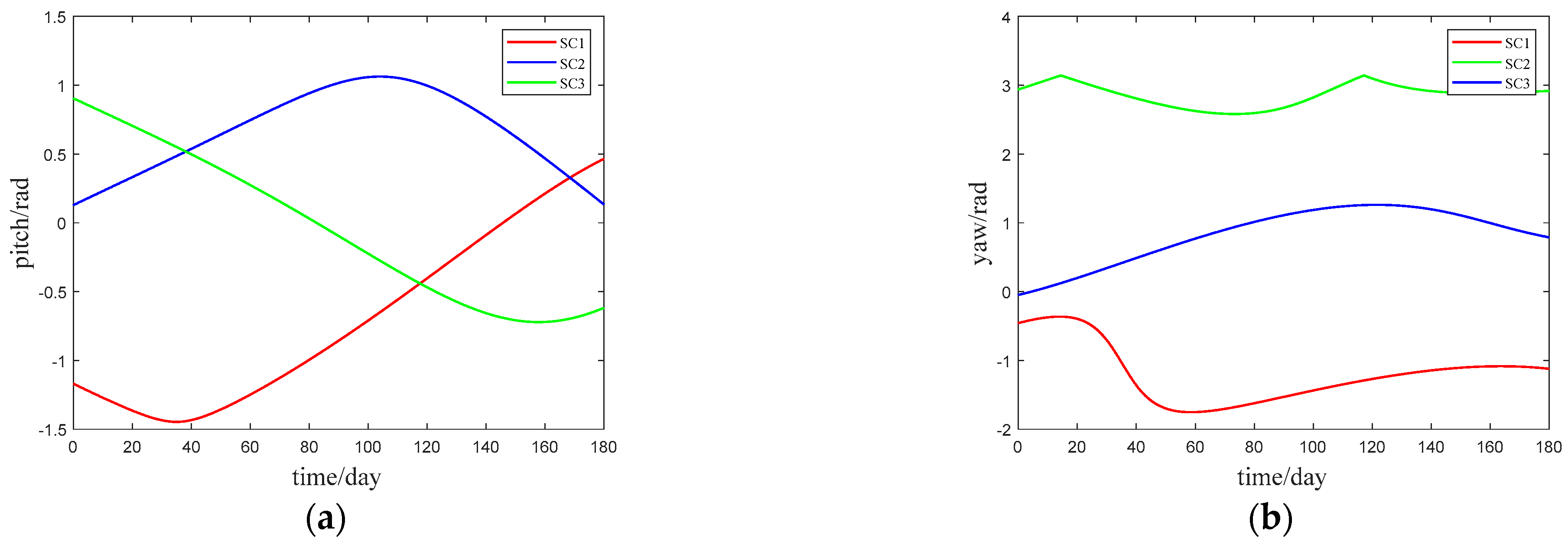
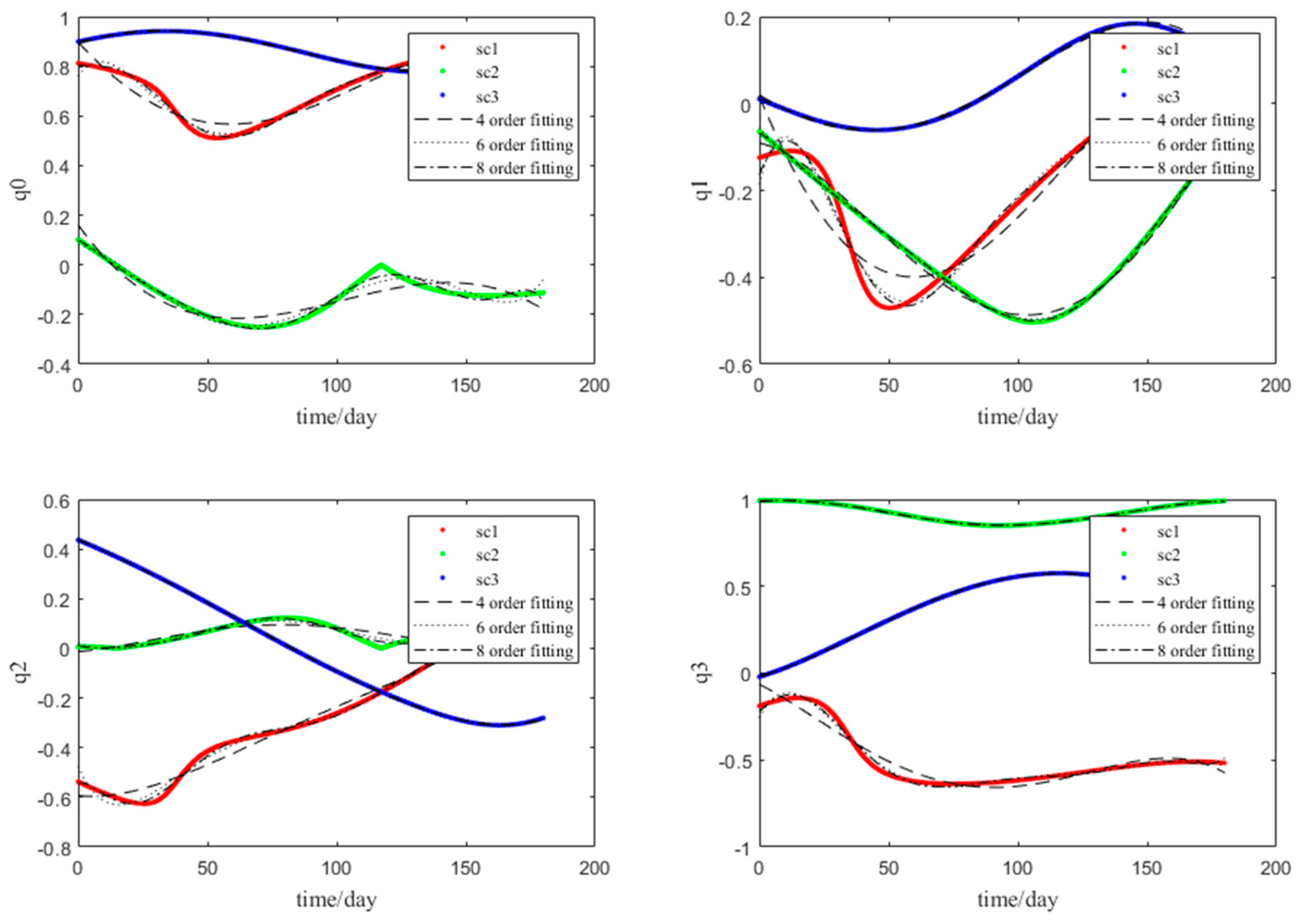
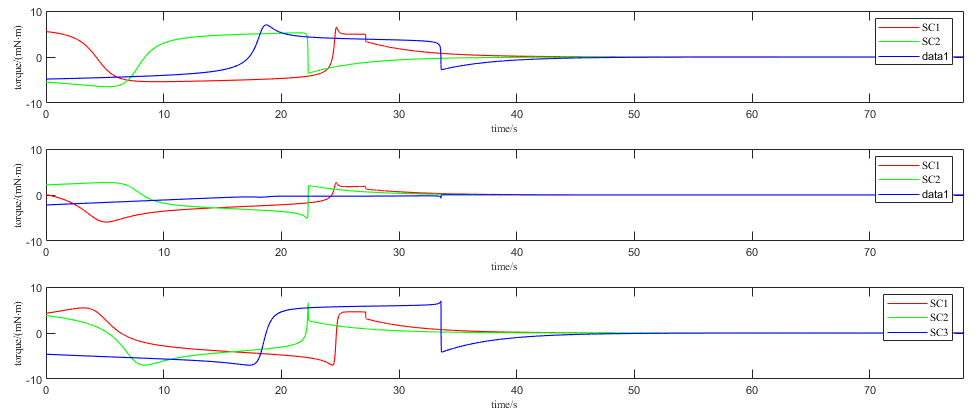
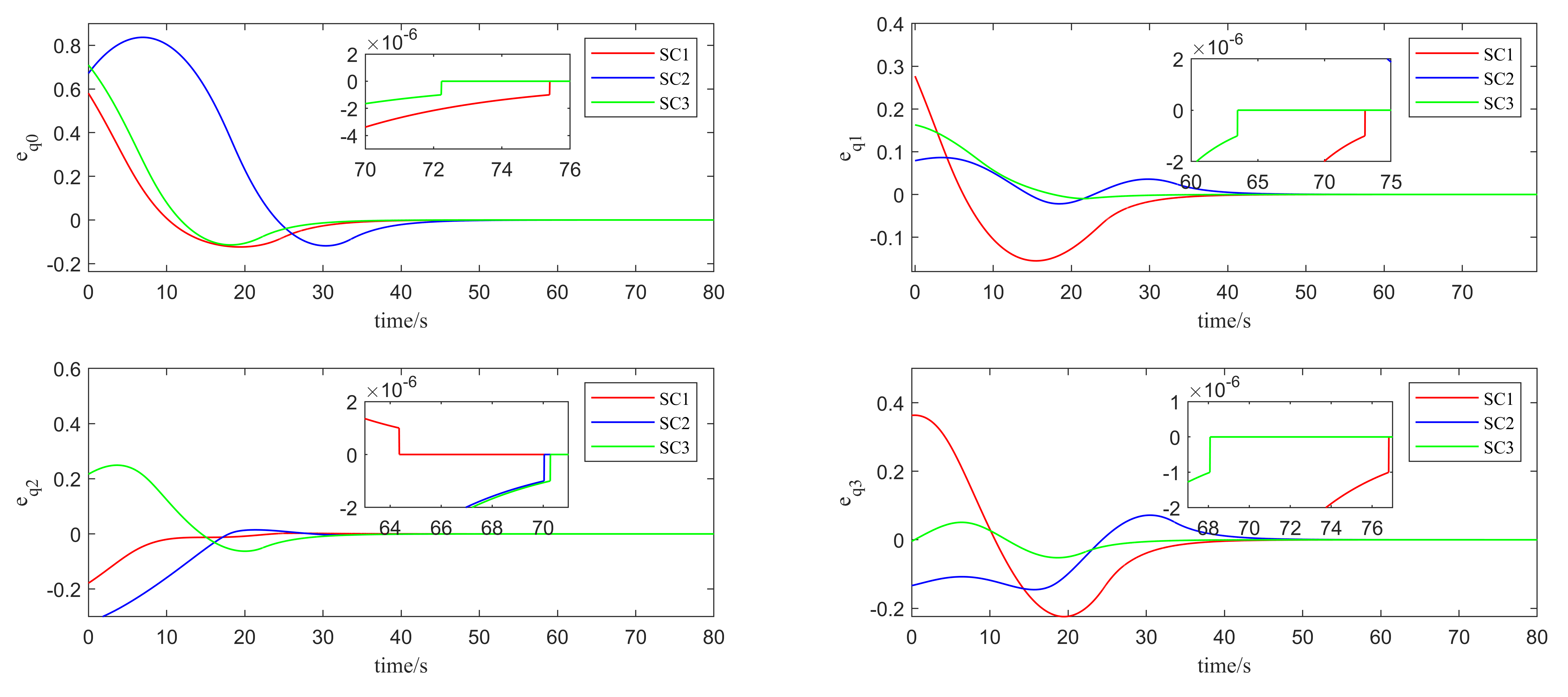
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SCP | Sequential convex programming |
| CC-SCP | Chance-constrained sequential convex programming |
| SOCP | Second-order cone programming |
| IPM | Interior point method |
| ZOH | Zero-order hold |
| LMIs | Linear matrix inequalities |
| SOC | Second-order cone constraint |
| STR | Star tracker |
| MSFA | Memorizable Smoothed Functional Algorithm |
| SED | Safe Experimentation Dynamics Algorithm |
| SPSA | Simultaneous Perturbation Stochastic Approximation |
| CVX | Convex Optimization Toolbox |
| MOSEK | Mosek Optimization Tools |
| DWS | Differential wave-front sensing |
References
- Cirillo, F.; Gath, P.F. Control system design for the constellation acquisition phase of the LISA mission. J. Phys. Conf. Ser. 2009, 154, 012014. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, P.; Lian, X.; Lu, L.; Liu, W. A predefined-time control for the laser acquisition in space gravitational wave detection mission. Sensors 2022, 22, 7021. [Google Scholar] [CrossRef]
- Zhang, J.; Biggs, J.D.; Ye, D.; Sun, Z. Finite-time attitude set-point tracking for thrust-vectoring spacecraft rendezvous. Aerosp. Sci. Technol. 2020, 96, 105588. [Google Scholar] [CrossRef]
- Hao, L.; Zhang, Y. Design and analysis of the integrated drag-free and attitude control system for TianQin mission: A preliminary result. Aerospace 2024, 11, 416. [Google Scholar] [CrossRef]
- Cirillo, F. Controller Design for the Acquisition Phase of the LISA Mission Using a Kalman Filter. University of Pisa, Pisa, Italy, 2007. [Google Scholar]
- Ales, F.; Gath, P.F.; Johann, U.; Braxmaier, C. Modeling and simulation of a laser ranging interferometer acquisition and guidance algorithm. J. Spacecr. Rocket. 2014, 51, 226–238. [Google Scholar] [CrossRef]
- Virdis, M.; Vidano, S.; Pagone, M.; Ruggiero, D.; Novara, C. The LISA DFACS: Effects of micrometeoroid impacts in the drag-free mode. In Proceedings of the International Astronautical Congress 2021 on Space Science, Dubai, United Arab Emirates, 25–29 October 2021. [Google Scholar]
- Liu, Z.; Yang, H.; Chen, T. Low-thrust formation keeping for heliocentric space-based gravitational wave detection mission. Adv. Space Res. 2025, 76, 1713–1728. [Google Scholar] [CrossRef]
- Song, Y.; Gong, S. Solar-sail deep space trajectory optimization using successive convex programming. Astrophys. Space Sci. 2019, 364, 106. [Google Scholar] [CrossRef]
- Scheinfeld, M.; Kopeika, N.; Melamed, R. Acquisition system for microsatellites laser communication in space. In Proceedings of the Free-Space Laser Communication Technologies XII, San Jose, CA, USA, 24–28 January 2000; Volume 3932, pp. 166–175. [Google Scholar]
- Celani, F.; Lucarelli, D. Spacecraft attitude motion planning using gradient-based optimization. J. Guid. Control. Dyn. 2020, 43, 140–145. [Google Scholar] [CrossRef]
- Nakajima, K.; Yoshimura, Y.; Chen, H.; Hanada, T. How are multiple satellites seen from the ground? Relative apparent motion and formation stabilization. Astrodynamics 2024, 8, 121–134. [Google Scholar] [CrossRef]
- Madonna, A.; Napolano, G.; Nocerino, A.; Opromolla, R.; Fasano, G.; Grassi, M. Guidance and control architecture for rendezvous and approach to a non-cooperative tumbling target. Aerospace 2025, 12, 708. [Google Scholar] [CrossRef]
- Mühlich, N.S.; Gerger, J.; Seifert, B.; Aumayr, F. Performance improvements of IFM Nano Thruster with highly focused ion beam generated with a compact electrostatic lens module. Acta Astronaut. 2022, 201, 464–471. [Google Scholar] [CrossRef]
- Hechenblaikner, G.; Delchambre, S.; Ziegler, T. Optical link acquisition for the LISA mission with in-field pointing architecture. Opt. Laser Technol. 2023, 161, 109213. [Google Scholar] [CrossRef]
- Mühlich, N.S.; Gerger, J.; Seifert, B.; Aumayr, F. Simultaneously measured direct and indirect thrust of a FEEP thruster using novel thrust balance and beam diagnostics. Acta Astronaut. 2022, 197, 107–114. [Google Scholar] [CrossRef]
- Lin, M.; Zhang, J.; He, Y. Minimum-time control for the test mass release phase of drag-free spacecraft. Space: Sci. Technol. 2024, 4, 0151. [Google Scholar] [CrossRef]
- Sun, Z.; Simo, J.; Gong, S. Satellite attitude identification and prediction based on neural network compensation. Space Sci. Technol. 2023, 3, 0009. [Google Scholar] [CrossRef]
- Mok, R.H.; Ahmad, M.A. Fast and optimal tuning of fractional order PID controller for AVR system based on memorizable-smoothed functional algorithm. Eng. Sci. Technol. Int. J. 2022, 35, 101264. [Google Scholar] [CrossRef]
- Ahmad, M.A.; Yoganathan, G.; Rashid, M.I.M.; Hao, M.R.; Suid, M.H.; Tumari, M.Z.M. Improved smoothed functional algorithms-optimized PID controller for efficient speed regulation of wind turbines. IEEE Trans. Ind. Appl. 2025, 61, 7546–7560. [Google Scholar] [CrossRef]
- Ghazali, M.R.; Ahmad, M.A.; Raja Ismail, R.M.T. Adaptive safe experimentation dynamics for data-driven neuroendocrine-PID control of MIMO systems. IETE J. Res. 2022, 68, 1611–1624. [Google Scholar] [CrossRef]
- Saat, S.; Ahmad, M.A.; Ghazali, M.R. Data-driven brain emotional learning-based intelligent controller-PID control of MIMO systems based on a modified safe experimentation dynamics algorithm. Int. J. Cogn. Comput. Eng. 2025, 6, 74–99. [Google Scholar] [CrossRef]
- Ahmad, M.A.; Azuma, S.; Sugie, T. Identification of continuous-time Hammerstein systems by simultaneous perturbation stochastic approximation. Expert Syst. Appl. 2016, 43, 51–58. [Google Scholar] [CrossRef]
- Ahmad, M.A.; Azuma, S.; Sugie, T. A model-free approach for maximizing power production of wind farm using multi-resolution simultaneous perturbation stochastic approximation. Energies 2014, 7, 5624–5646. [Google Scholar] [CrossRef]
- Zhao, Z.; Shang, H.; Gao, A.; Xu, R. Autonomous laser-link reacquisition for gravitational wave detection using multistage convex optimization. J. Guid. Control. Dyn. 2023, 46, 1348–1364. [Google Scholar] [CrossRef]
- Zhao, Z.; Shang, H.; Dong, Y. Autonomous attitude planning for gravity wave detection using hybrid convex optimization. Aerosp. Sci. Technol. 2022, 130, 107923. [Google Scholar] [CrossRef]
- Sagliano, M. Pseudospectral convex optimization for powered descent and landing. J. Guid. Control. Dyn. 2018, 41, 320–334. [Google Scholar] [CrossRef]
- Jansson, O.; Harris, M.W. Convex optimization-based techniques for trajectory design and control of nonlinear systems with polytopic range. Aerospace 2023, 10, 71. [Google Scholar] [CrossRef]
- Liu, X.; Lu, P. Solving Nonconvex optimal control problems by convex optimization. J. Guid. Control. Dyn. 2014, 37, 750–765. [Google Scholar] [CrossRef]
- Huang, J.; Zeng, Y. An hp-legendre pseudospectral convex method for 6-degree-of-freedom powered landing problem. Aerospace 2023, 10, 849. [Google Scholar] [CrossRef]
- Mu, R.; Deng, Y.; Wu, P. Adaptive convex optimization guidance for lunar landing. Aerospace 2023, 10, 634. [Google Scholar] [CrossRef]
- Kubo, Y.; Chujo, T. Optimization of body configuration and joint-driven attitude stabilization for transformable spacecraft under solar radiation pressure. Astrodynamics 2024, 8, 47–60. [Google Scholar] [CrossRef]
- Lew, T.; Bonalli, R.; Pavone, M. Chance-constrained sequential convex programming for robust trajectory optimization. In Proceedings of the 2020 European Control Conference (ECC), Saint Petersburg, Russia, 12–15 May 2020; pp. 1871–1878. [Google Scholar]
- Song, Y.; Miao, X.; Gong, S. Adaptive powered descent guidance based on multi-phase pseudospectral convex optimization. Acta Astronaut. 2021, 180, 386–397. [Google Scholar] [CrossRef]
- Zhang, P.; Wu, D.; Gong, S. Trajectory optimization for aerodynamically controlled missiles by chance-constrained sequential convex programming. Aerosp. Sci. Technol. 2024, 153, 109464. [Google Scholar] [CrossRef]
- Okamoto, K.; Tsiotras, P. Optimal stochastic vehicle path planning using covariance steering. IEEE Robot. Autom. Lett. 2019, 4, 2276–2281. [Google Scholar] [CrossRef]
- Okamoto, K.; Goldshtein, M.; Tsiotras, P. Optimal covariance control for stochastic systems under chance constraints. IEEE Control. Syst. Lett. 2018, 2, 266–271. [Google Scholar] [CrossRef]
- Qiao, D.; Zhou, X.; Li, X. Analytical configuration uncertainty propagation of geocentric interferometric detection constellation. Astrodynamics 2023, 7, 271–284. [Google Scholar] [CrossRef]
- Oguri, K.; McMahon, J.W. Robust Spacecraft guidance around small bodies under uncertainty: Stochastic optimal control approach. J. Guid. Control. Dyn. 2021, 44, 1295–1313. [Google Scholar] [CrossRef]
- Mesbah, A. Stochastic model predictive control: An overview and perspectives for future research. IEEE Control. Syst. Mag. 2016, 36, 30–44. [Google Scholar]
- Gui, H.; Vukovich, G. Finite-time angular velocity observers for rigid-body attitude tracking with bounded inputs. Int. J. Robust Nonlinear Control. 2017, 27, 15–38. [Google Scholar] [CrossRef]
- Nemirovski, A.; Shapiro, A. Convex approximations of chance constrained programs. SIAM J. Optim. 2006, 17, 969–996. [Google Scholar] [CrossRef]
- Liu, C.; Yang, H.; Li, S.; Li, J. Convex optimization of stochastic path-constrained trajectories near asteroids. Aerosp. Sci. Technol. 2024, 153, 109463. [Google Scholar] [CrossRef]
- Kim, Y.; Mesbahi, M.; Singh, G.; Hadaegh, F.Y. On the convex parameterization of constrained spacecraft reorientation. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1097–1109. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, H.; Li, S.; Zhou, Y. On-board modeling of gravity fields of elongated asteroids using Hopfield neural networks. Astrodynamics 2023, 7, 101–114. [Google Scholar] [CrossRef]
- Szmuk, M.; Acikmese, B.; Berning, A.W. Successive convexification for fuel-optimal powered landing with aerodynamic drag and non-convex constraints. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San Diego, CA, USA, 4–8 January 2016; p. 378. [Google Scholar]
- Bernardini, N.; Baresi, N.; Armellin, R. State-dependent trust region for successive convex programming for autonomous spacecraft. Astrodynamics 2024, 8, 553–575. [Google Scholar] [CrossRef]
- Ridderhof, J.; Pilipovsky, J.; Tsiotras, P. Chance-constrained covariance control for low-thrust minimum-fuel trajectory optimization. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Big Sky, MT, USA, 9–11 August 2021; pp. 9–13. [Google Scholar]
- Chujo, T.; Watanabe, K.; Takao, Y. Integrated attitude-orbit control of solar sail with single-axis gimbal mechanism. Astrodynamics 2021, 8, 483–506. [Google Scholar] [CrossRef]
- Sapunkov, Y.G.; Molodenkov, A.V. Quasioptimal spacecraft attitude control constructed according to the poinsot concept. Aerospace 2023, 10, 402. [Google Scholar] [CrossRef]


| Item | Symbol | Value |
|---|---|---|
| arm-length of constellation | km | 2.5 × 106 |
| changing of internal angle | degree | ±1 |
| changing rate of internal angle | nrad/s | <5 |
| Parameters | Unit | Value |
|---|---|---|
| P0 | [/, /, /, /, (rad/s)2, (rad/s)2, (rad/s)2] | diag(10−9, 10−9, 10−9, 10−9, 10−10, 10−10, 10−10) |
| Pf | [/, /, /, /, (rad/s)2, (rad/s)2, (rad/s)2] | diag(10−9, 10−9, 10−9, 10−9, 10−10, 10−10, 10−10) |
| g | Nm/μN | 10−6 |
| p | 0.95 | |
| nu | 3 | |
| nx | 7 | |
| αy, αH, ατ | 104 | |
| Δt | s | 0.12 |
| τk | Nm | 0.01 |
| ε | 10−6 |
| Spacecraft | Constraint Name | Constraint Parameter |
|---|---|---|
| all | initial time | 0 s |
| translational inertial | diag(551.25, 450.83, 450.83) kg∙m2 | |
| forbidden cone 1 axis | [0.5000, −0.8660, 0]T | |
| forbidden cone 2 axis | [0.2432, 0.9077, −0.3420]T | |
| forbidden cone 3 axis | [0.4924, 0.0868, −0.8660]T | |
| forbidden cone 1 half angle | 30 deg | |
| forbidden cone 2 half angle | 30 deg | |
| forbidden cone 3 half angle | 30 deg | |
| maximum value of control | 7 × 10−3 Nm | |
| spacecraft 1 | initial quaternion | [−0.73224, 0.07897, 0.42632, 0.52521]T |
| initial angle velocity | [0.08606, 0.10219, 0.06650] rad/s | |
| mandatory cone axis | [−0.7660, 0.6428, 0]T | |
| mandatory cone half angle | 60 deg | |
| spacecraft 2 | initial quaternion | [−0.73224, 0.07897, 0.42632, 0.52521]T |
| initial angle velocity | [0.08606, 0.10219, 0.06650] rad/s | |
| mandatory cone axis | [−0.7660, 0.6428, 0]T | |
| mandatory cone half angle | 60 deg | |
| spacecraft 3 | initial quaternion | [−0.73224, 0.07897, 0.42632, 0.52521]T |
| initial angle velocity | [0.08606, 0.10219, 0.06650] rad/s | |
| mandatory cone axis | [−0.7660, 0.6428, 0]T | |
| mandatory cone half angle | 60 deg |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, M.; Huang, P.; Yang, H. Convex Optimization for Spacecraft Attitude Alignment of Laser Link Acquisition Under Uncertainties. Aerospace 2025, 12, 939. https://doi.org/10.3390/aerospace12100939
Guo M, Huang P, Yang H. Convex Optimization for Spacecraft Attitude Alignment of Laser Link Acquisition Under Uncertainties. Aerospace. 2025; 12(10):939. https://doi.org/10.3390/aerospace12100939
Chicago/Turabian StyleGuo, Mengyi, Peng Huang, and Hongwei Yang. 2025. "Convex Optimization for Spacecraft Attitude Alignment of Laser Link Acquisition Under Uncertainties" Aerospace 12, no. 10: 939. https://doi.org/10.3390/aerospace12100939
APA StyleGuo, M., Huang, P., & Yang, H. (2025). Convex Optimization for Spacecraft Attitude Alignment of Laser Link Acquisition Under Uncertainties. Aerospace, 12(10), 939. https://doi.org/10.3390/aerospace12100939






