The Operational Safety Evaluation of UAVs Based on Improved Support Vector Machines
Abstract
1. Introduction
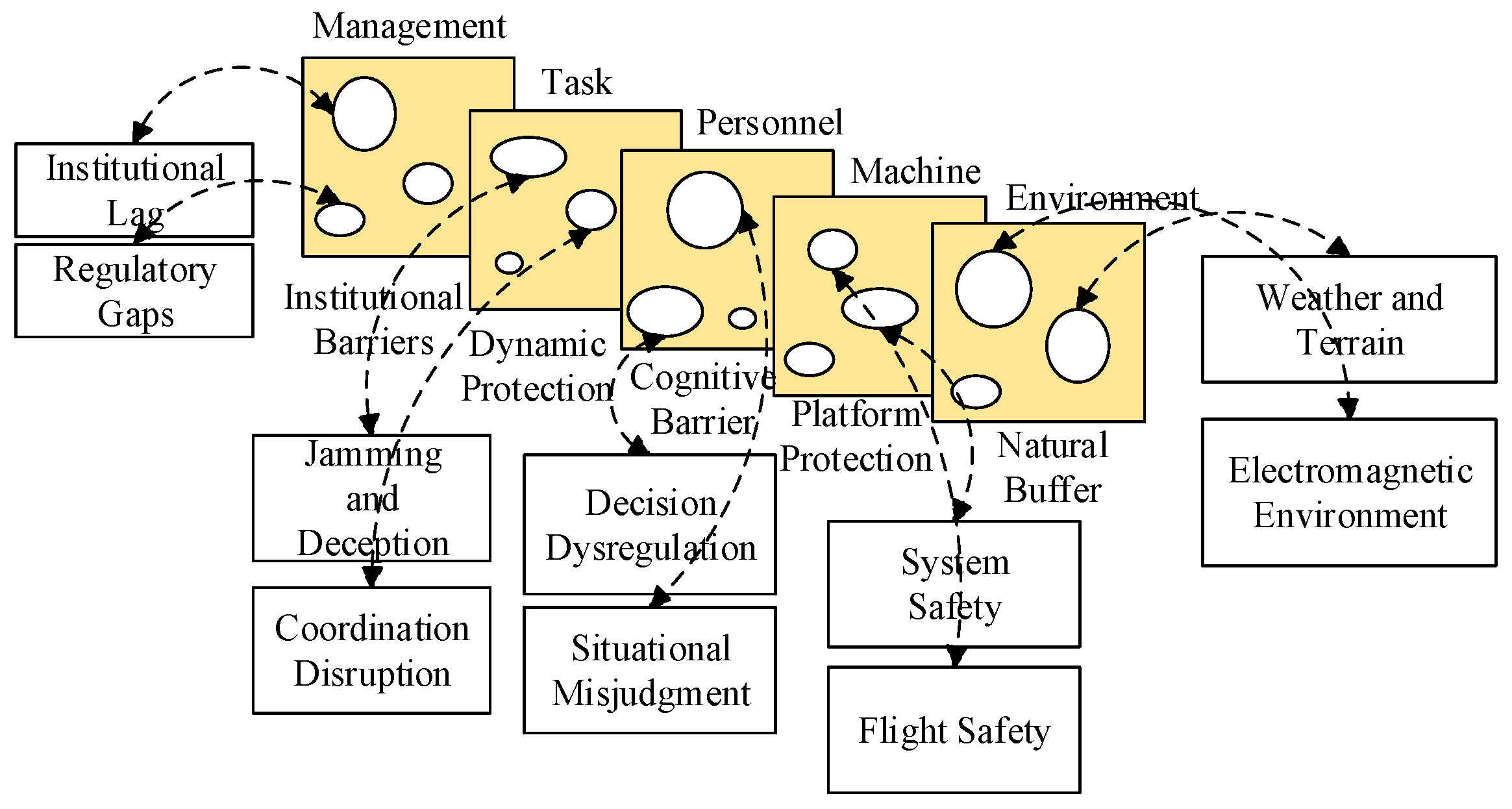
2. Construction of Index System Framework for Operational Safety
2.1. Construction of the Operational Safety Assessment Index System
2.2. Analysis of Index System for Operational Safety
2.3. Quantitative Data Acquisition of Indicators
3. Operational Safety Level Classification
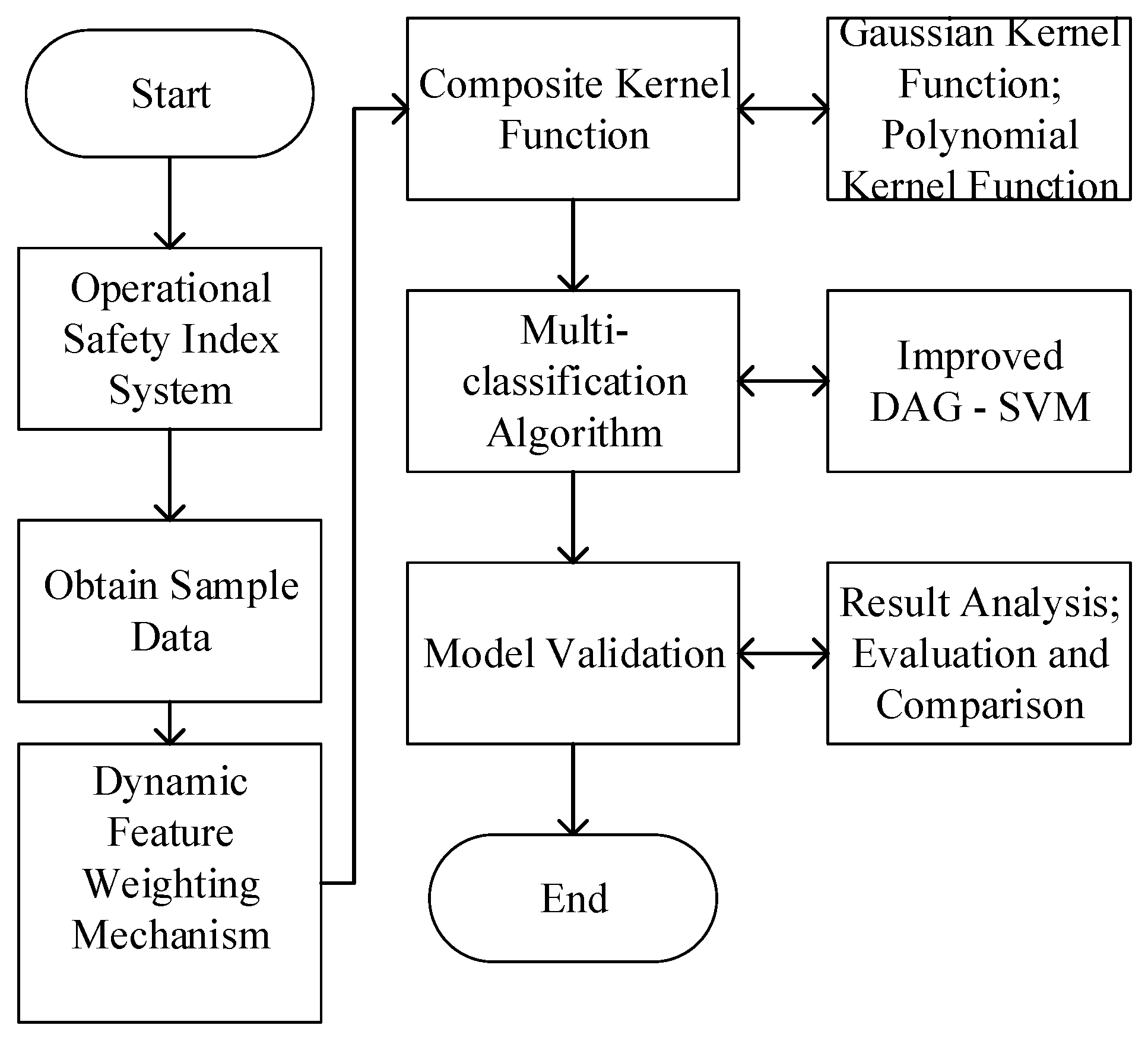
4. Research on Improved SVM Evaluation Model
4.1. Improved Dynamic Feature Weighting Mechanism Based on Information Entropy
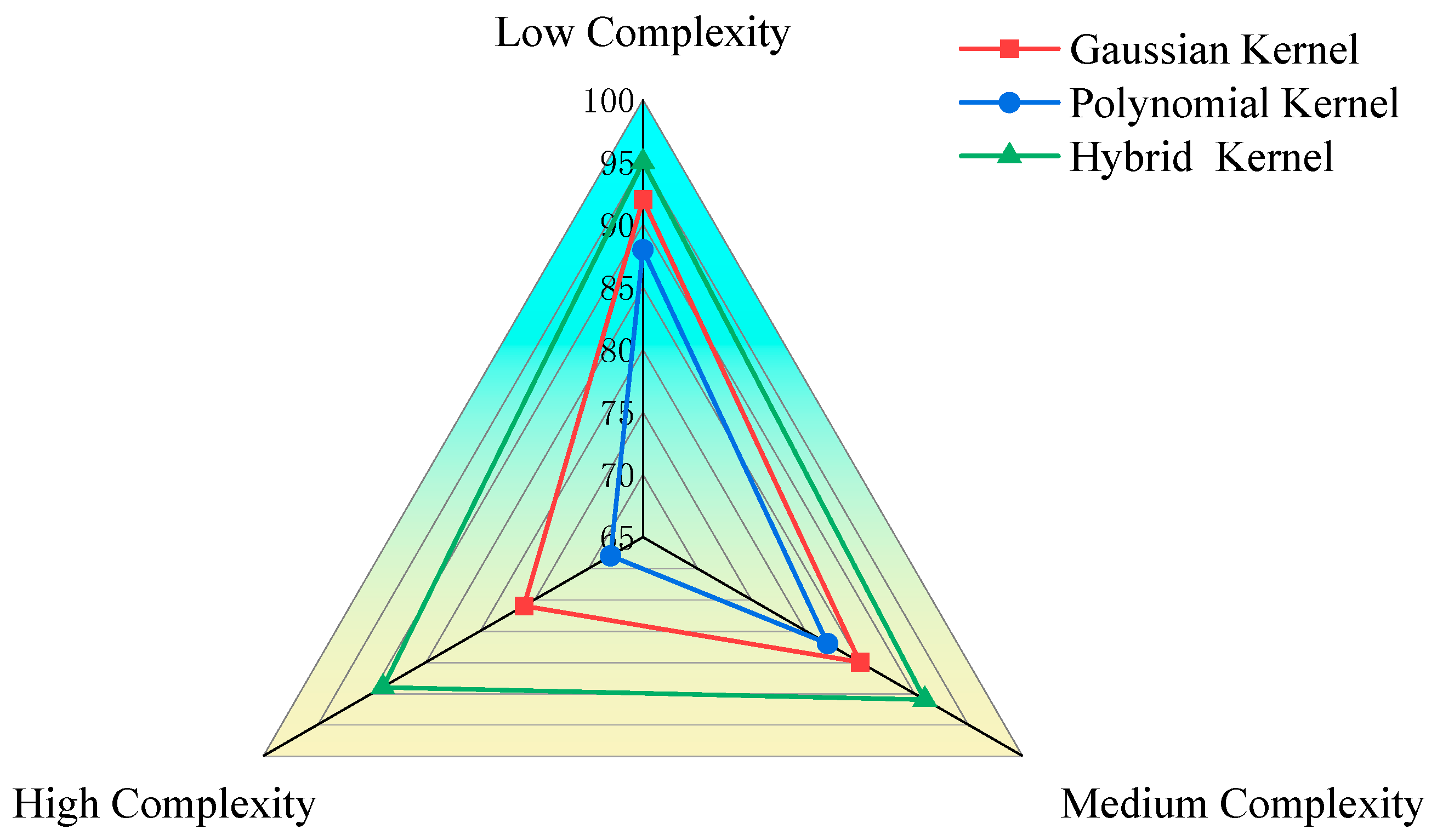
4.2. Ensemble Kernel SVM Model
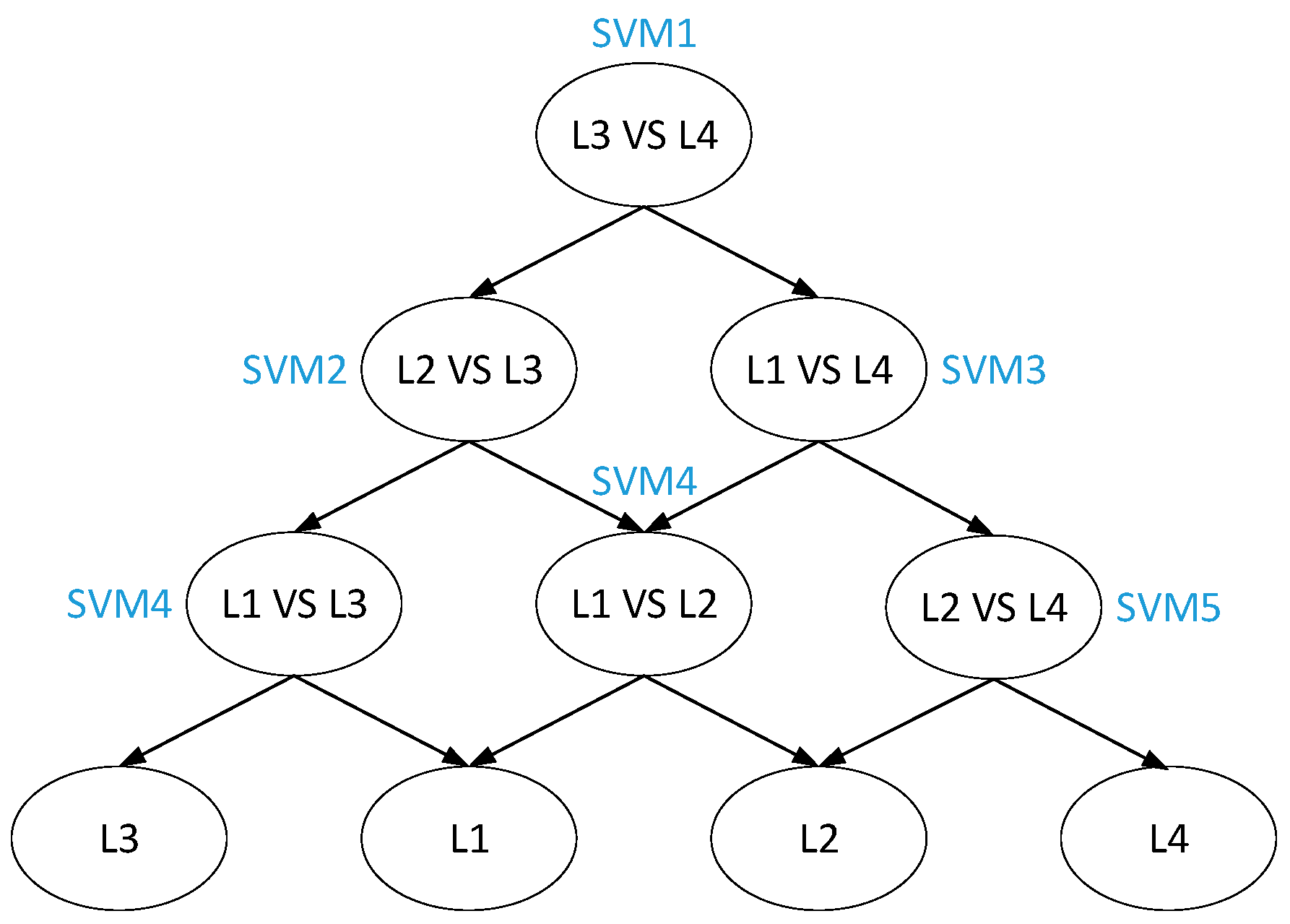
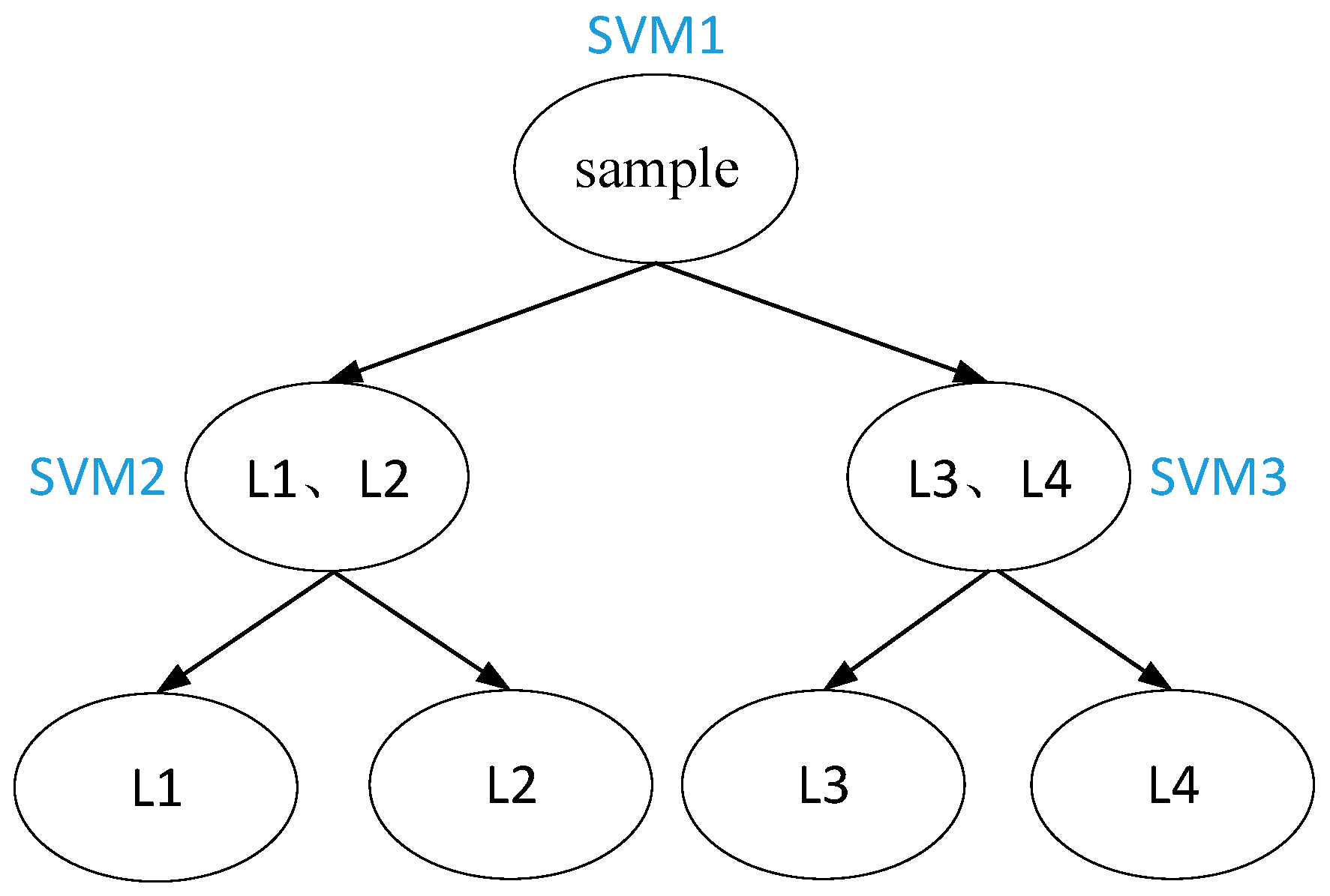
4.3. Improve Multi Classification Algorithm
5. Combat Simulation and Evaluation Verification Analysis
5.1. Operational Planning
5.1.1. Force Deployment
5.1.2. Combat Process
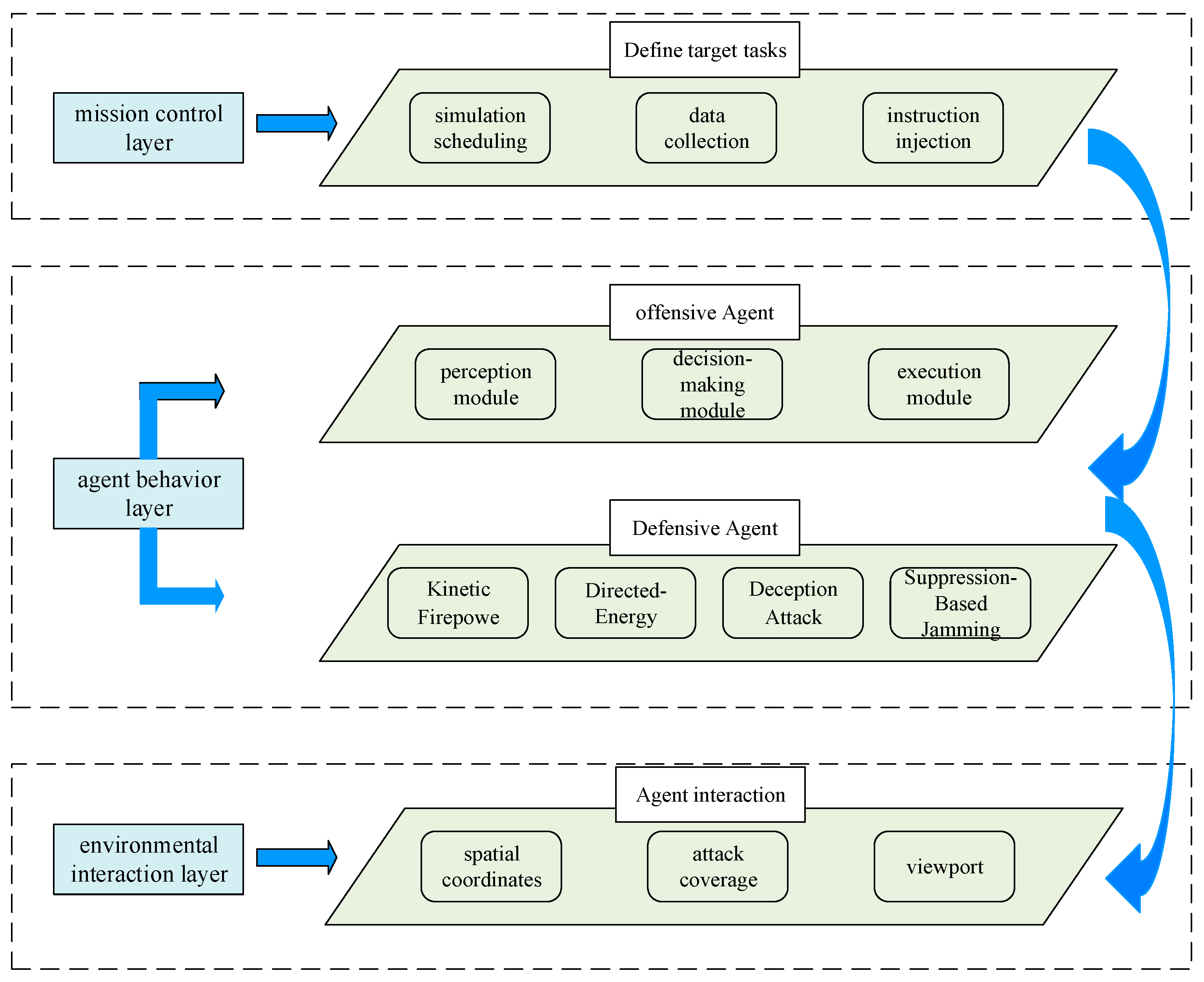
5.2. Simulation of Offensive–Defensive Confrontation Based on ABMS
5.2.1. The Offensive Agent
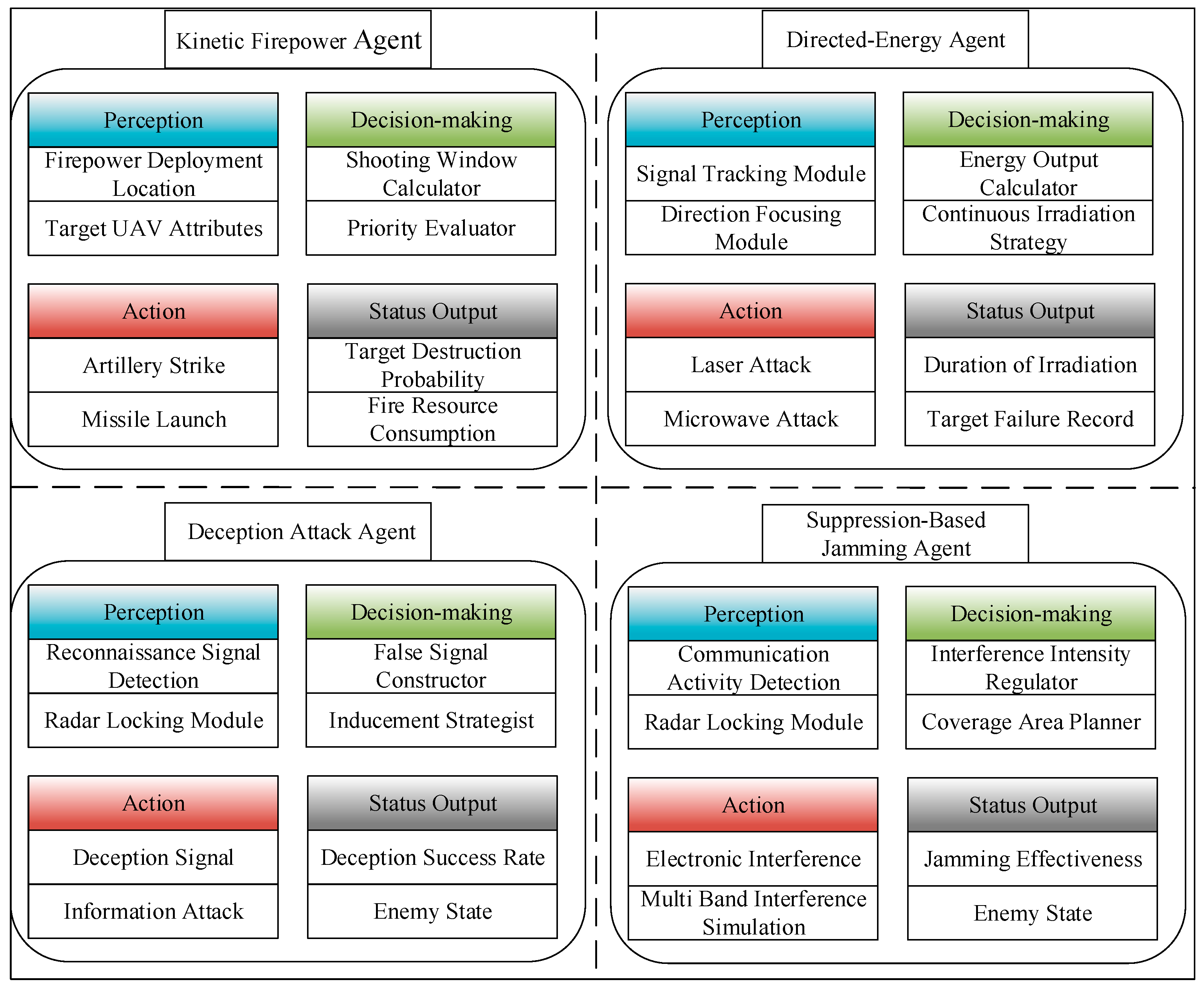
5.2.2. The Defensive Agent
5.3. Validation of the Evaluation Model
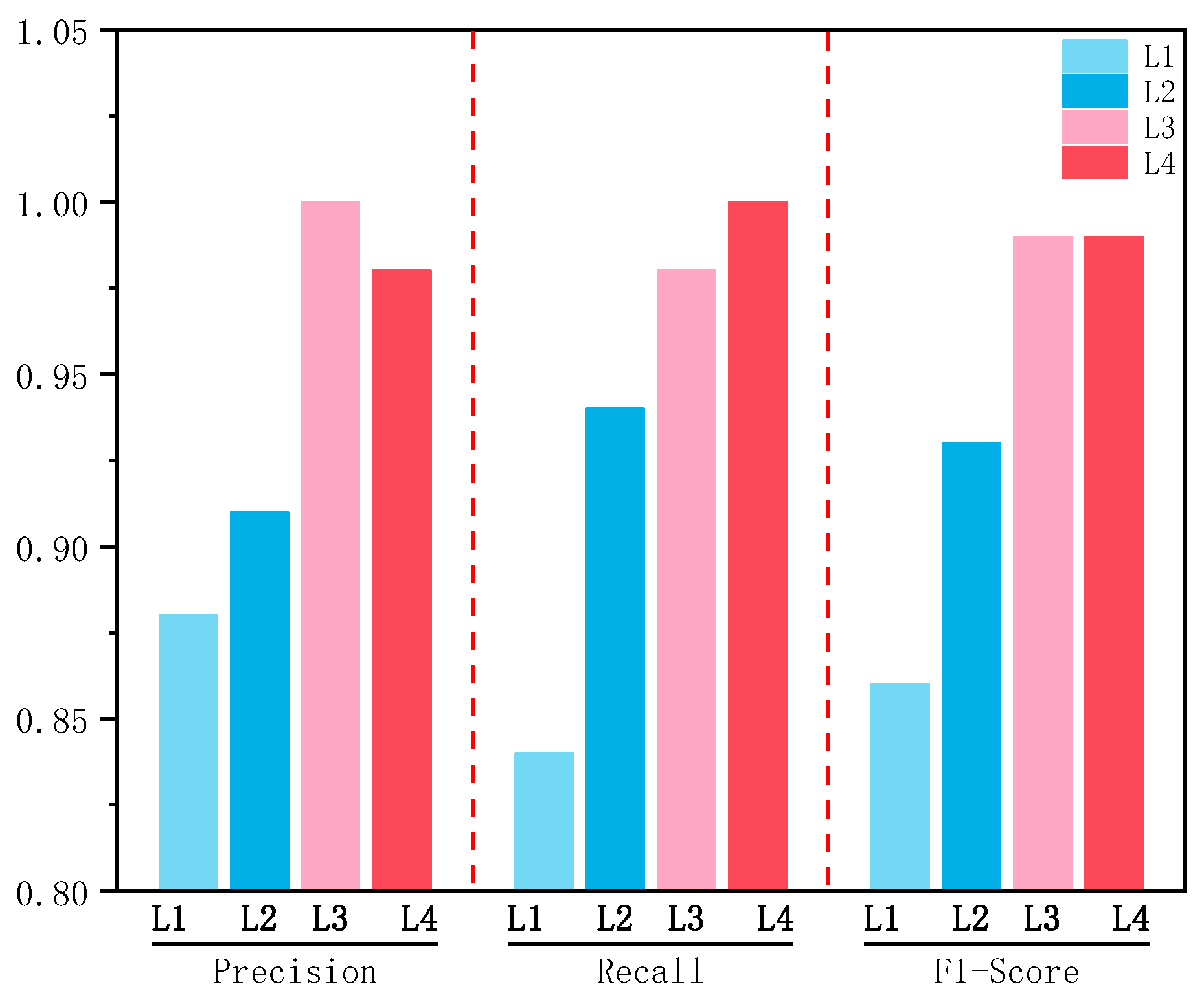
5.4. Analysis of the Evaluation Results
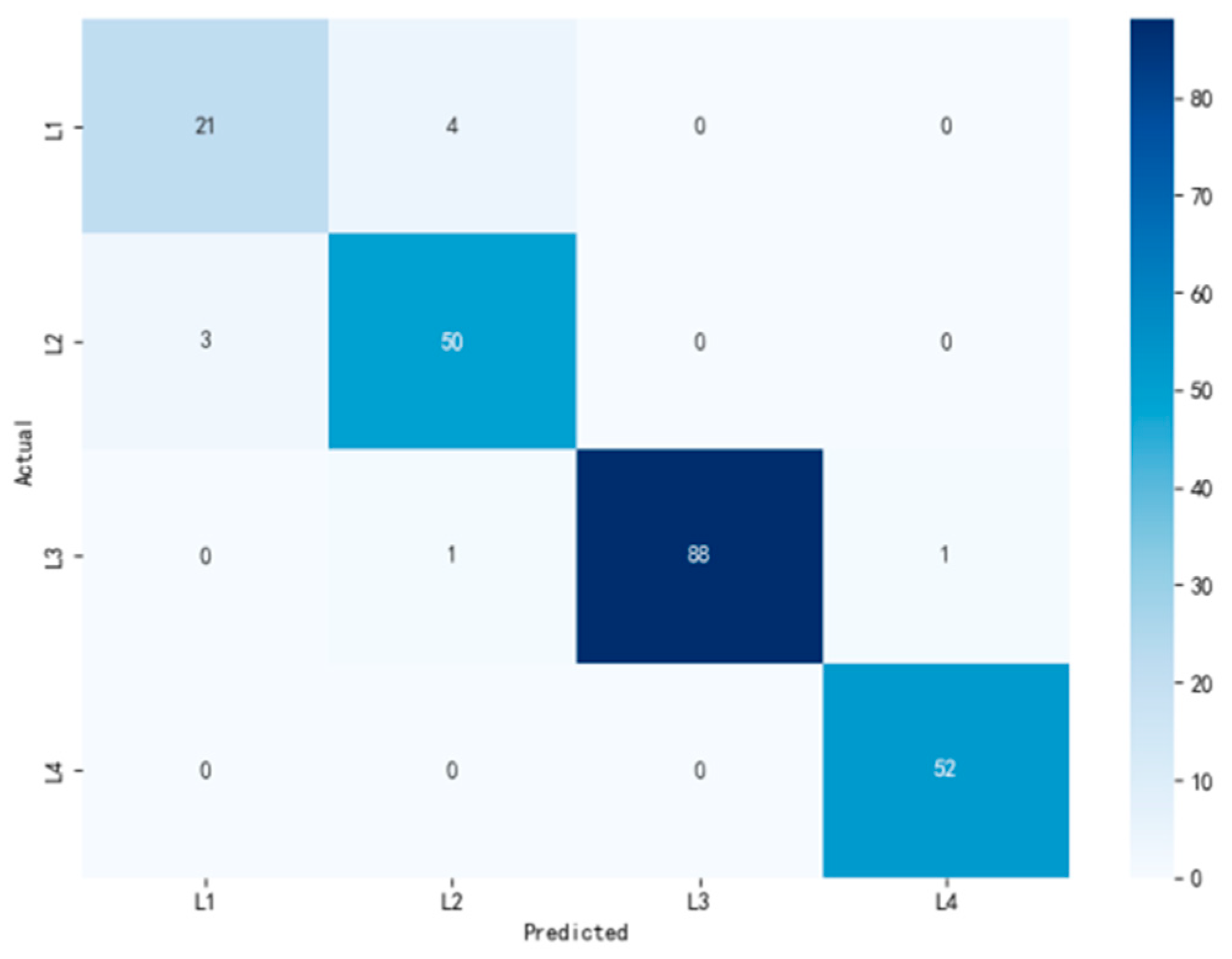
5.4.1. Result Analysis
5.4.2. Comparison of Evaluation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, Y.; Liu, S.; Wang, K. An Assessment on Use and Safety of Reconnaissance-Strike UAV Based on Improved Bayesian Network. J. Air Force Eng. Univ. 2025, 26, 86–95. (In Chinese) [Google Scholar]
- Gholami, M.; Sanjari, M.J.; Safari, M.; Akbari, M.; Kamali, M.R. Static Security Assessment of Power Systems: A Review. Int. Trans. Electr. Energy Syst. 2020, 30, e12432. [Google Scholar] [CrossRef]
- Shen, Z.; Pan, P.; Zhang, D.; Huang, S. Rapid Structural Safety Assessment Using a Deep Neural Network. J. Earthq. Eng. 2020, 26, 2625–2641. [Google Scholar] [CrossRef]
- Basak, S.; Lu, L. Safety Assessment of Passive Safety Systems in Nuclear Reactors Using Artificial Neural Networks. Reliab. Eng. Syst. Saf. 2025, 264, 111355. [Google Scholar] [CrossRef]
- Xiong, L.; Li, Z.; Zhong, D.; Xu, P.; Tang, C. Rule-Guidance Reinforcement Learning for Lane Change Decision-Making: A Risk Assessment Approach. Chin. J. Mech. Eng. 2025, 38, 30. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, L.; Wang, X.; Zheng, H.; Gu, M.; Li, S.; Fang, X. Risk Assessment of Deep Coal and Gas Outbursts Based on IQPSO-SVM. Int. J. Environ. Res. Public Health 2022, 19, 12869. [Google Scholar] [CrossRef]
- Zheng, K.; Chen, Y.; Jiang, Y.; Qiao, S. A SVM-Based Ship Collision Risk Assessment Algorithm. Ocean Eng. 2020, 202, 107062. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, A.; Chen, P.; Li, H.; Zeng, X.; Chen, S.; Dong, T.; Shi, P.; Lang, Y.; Zhou, Q. Application of Artificial Intelligence Hybrid Models in Safety Assessment of Submarine Pipelines: Principles and Methods. Ocean Eng. 2024, 312, 119203. [Google Scholar] [CrossRef]
- Li, F.; Wang, W.; Xu, J.; Yi, J.; Wang, Q. Comparative Study on Vulnerability Assessment for Urban Buried Gas Pipeline Network Based on SVM and ANN Methods. Process Saf. Environ. Prot. 2019, 122, 23–32. [Google Scholar] [CrossRef]
- He, L.; Li, Z.; Yang, X.; Zhou, Y.; Qu, Z.; Ren, Z. Research on Quantitative Safety Risk Assessment Methods at Vehicle Controllability Level. IEEE Access 2025, 13, 82527–82539. [Google Scholar] [CrossRef]
- Tan, Y.; Zheng, Y.; Yi, W.; Li, S.; Chen, P.; Cai, R.; Song, D. Intelligent Inspection of Building Exterior Walls Using UAV and Mixed Reality Based on Man-Machine-Environment System Engineering. Autom. Constr. 2025, 177, 106344. [Google Scholar] [CrossRef]
- Bonsu, J.; van Dyk, W.; Franzidis, J.-P.; Petersen, F.; Isafiade, A. A Systems Approach to Mining Safety: An Application of the Swiss Cheese Model. J. S. Afr. Inst. Min. Metall. 2016, 116, 776–784. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Zhang, Y.; Guan, X.; Delahaye, D.; Tang, L. Safety Assessment and Risk Estimation for Unmanned Aerial Vehicles Operating in National Airspace System. J. Adv. Transp. 2018, 2018, 731585. [Google Scholar] [CrossRef]
- Kobaszyńska-Twardowska, A.; Łukasiewicz, J.; Sielicki, P.W. Risk Management Model for Unmanned Aerial Vehicles during Flight Operations. Materials 2022, 15, 2448. [Google Scholar] [CrossRef]
- Wen, Z.; Fan, Z.; Su, H. An APPSO–SVM Approach Building the Monitoring Model of Dam Safety. Soft Comput. 2022, 26, 11451–11459. [Google Scholar] [CrossRef]
- Huang, Q.; Sun, H.; Wei, Y.; Zhang, J.; Jin, X. Comprehensive Assessment of Mental Workload of Armored Vehicle Operators Based on SVM and DS Evidence Theory. Cogn. Technol. Work 2025, 27, 137–157. [Google Scholar] [CrossRef]
- Li, S.; Chen, G.; Men, J.; Li, X.; Zhao, Y.; Xu, Q.; Zhao, J. A Novel Dynamic Risk Assessment Method for Hazardous Chemical Warehouses Based on Improved SVM and Mathematical Methodologies. J. Loss Prev. Process Ind. 2024, 89, 105302. [Google Scholar] [CrossRef]
- Pawara, P.; Okafor, E.; Groefsema, M.; He, S.; Schomaker, L.R.B.; Wiering, M.A. One-vs-One Classification for Deep Neural Networks. Pattern Recognit. 2020, 108, 107528. [Google Scholar] [CrossRef]
- Xu, X.; Li, Y.; Yuan, C. Conditional Image Generation with One-Vs-All Classifier. Neurocomputing 2021, 434, 261–267. [Google Scholar] [CrossRef]
- Lee, C.-P.; Lin, C.-J. A Study on L2-Loss (Squared Hinge-Loss) Multiclass SVM. Neural Comput. 2013, 25, 1302–1323. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Wang, Y.; Huang, L.; Jiang, B.; Wang, X. Fast CU Partition Decision for H.266/VVC Based on the Improved DAG-SVM Classifier Model. Multimed. Syst. 2021, 27, 1–14. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Z.; Zhang, Q. FSVM- and DAG-SVM-Based Fast CU-Partitioning Algorithm for VVC Intra-Coding. Symmetry 2023, 15, 1078. [Google Scholar] [CrossRef]
- Bodine, E.N.; Panoff, R.M.; Voit, E.O.; Weisstein, A.E. Agent-Based Modeling and Simulation in Mathematics and Biology Education. Bull. Math. Biol. 2020, 82, 101. [Google Scholar] [CrossRef] [PubMed]
- Stieler, D.; Schwinn, T.; Leder, S.; Maierhofer, M.; Kannenberg, F.; Menges, A. Agent-Based Modeling and Simulation in Architecture. Autom. Constr. 2022, 141, 104426. [Google Scholar] [CrossRef]
- Chechkin, A.; Pleshakova, E.; Gataullin, S. A Hybrid KAN-BiLSTM Transformer with Multi-Domain Dynamic Attention Model for Cybersecurity. Technologies 2025, 13, 223. [Google Scholar] [CrossRef]
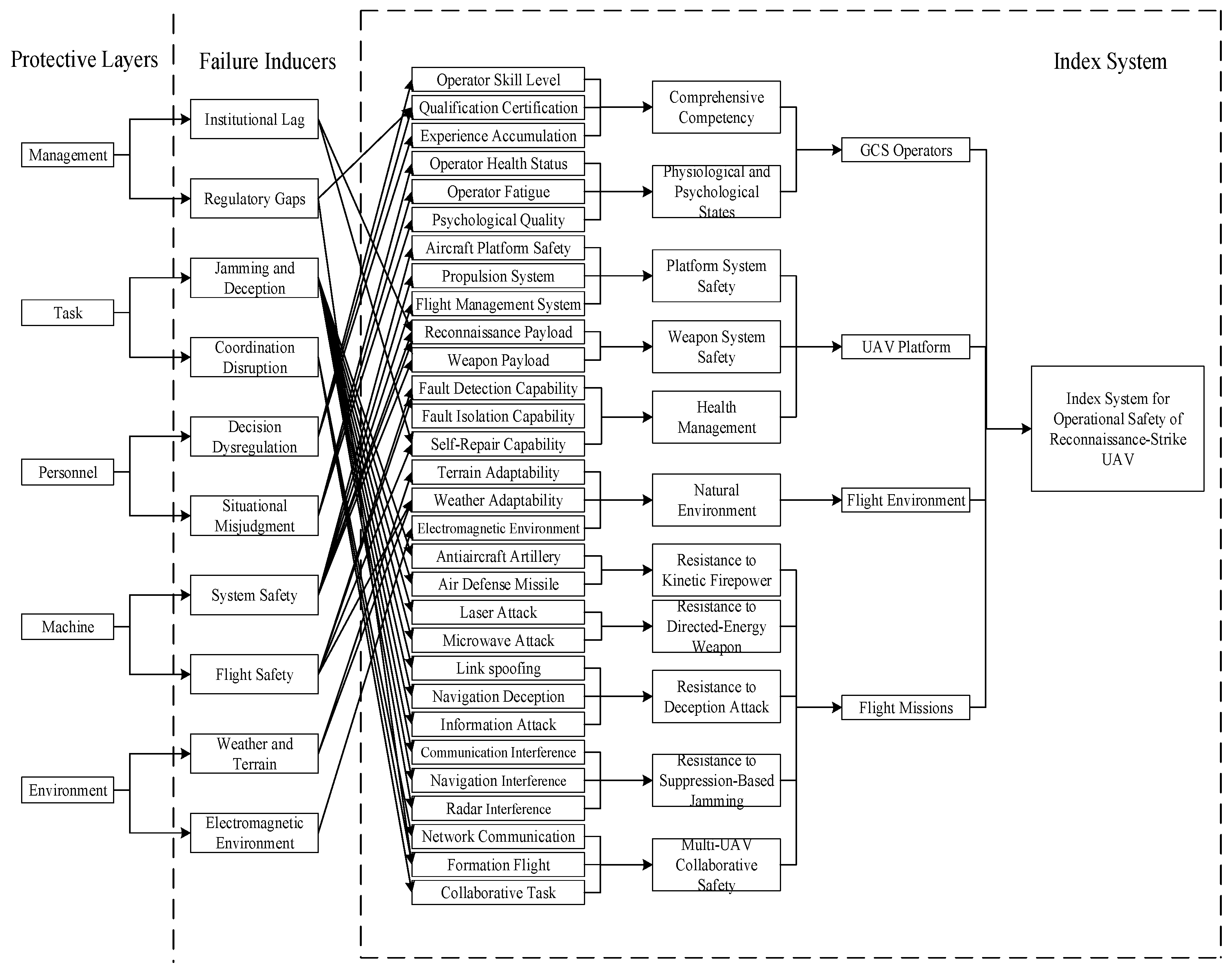





| Target Layer | Criterion Layer | Element Layer | Indicator Layer |
|---|---|---|---|
| Evaluation Index System (A) | GCS Operators (B1) | Comprehensive Competency (C1) | Operator Skill Level (D1) |
| Qualification Certification (D2) | |||
| Experience Accumulation (D3) | |||
| Physiological and Psychological States (C2) | Operator Health Status (D4) | ||
| Operator Fatigue (D5) | |||
| Psychological Quality (D6) | |||
| UAV Platform (B2) | Platform System Safety (C3) | Aircraft Platform Safety (D7) | |
| Propulsion System (D8) | |||
| Flight Management System (D9) | |||
| Weapon System Safety (C4) | Reconnaissance Payload (D10) | ||
| Weapon Payload (D11) | |||
| Health Management (C5) | Fault Detection Capability (D12) | ||
| Fault Isolation Capability (D13) | |||
| Self-Repair Capability (D14) | |||
| Flight Environment (B3) | Natural Environment (C6) | Terrain Adaptability (D15) | |
| Weather Adaptability (D16) | |||
| Electromagnetic (D17) | |||
| Flight Missions (B4) | Resistance to Kinetic Firepower (C7) | Antiaircraft Artillery (D18) | |
| Air Defense Missile (D19) | |||
| Resistance to Directed-Energy (C8) | Laser Attack (D20) | ||
| Microwave Attack (D21) | |||
| Resistance to Deception Attack (C9) | Link spoofing (D22) | ||
| Navigation Deception (D23) | |||
| Information Attack (D24) | |||
| Resistance to Suppression-Based Jamming (C10) | Communication Interference (D25) | ||
| Navigation Interference (D26) | |||
| Radar Interference (D27) | |||
| Multi-UAV Collaborative Safety (C11) | Network Communication (D28) | ||
| Formation Flight (D29) | |||
| Collaborative Task (D30) |
| Method | Acquisition Method |
|---|---|
| Historical task record data | This involves retrieving historical logs from the UAV, including flight records, sensor data, and environmental records. |
| Simulation data | Using a flight simulation platform to create typical mission scenarios, this method simulates flight data and unexpected events. |
| Field test sampling data | Experimental tasks are designed with embedded sensors and recording modules to collect flight status data during real-world tests. |
| Delphi method | A systematic expert knowledge collection method that allows professionals to assess and score mission risks. |
| Model parameter calculation | By establishing mathematical, physical, engineering, or statistical models, the parameters of the system are calculated. |
| Method Threat Type | Hazard Level | Core Impact |
|---|---|---|
| Loss of control | High (Level II) | Mission chain disruption |
| Forced landing | Low (Level IV) | Difficulty in equipment recovery |
| Crash | Medium (Level III) | Induction of secondary hazards |
| Deception | Extreme (Level I) | Leakage of classified information |
| Safety Level | Threat Scope Coverage | Typical Application Scenarios |
|---|---|---|
| L1 (Extreme Protection) | Addressing ≥3 types of Level I threats | Strategic operations, penetration of nuclear facilities |
| L2 (High Protection) | Combination of Level I + Level II threats | High-value target reconnaissance and strikes |
| L3 (Standard Protection) | Addressing a single Level I or Level II threat | Routine battlefield patrols, border surveillance |
| L4 (Basic Protection) | Addressing Level III or lower threats | Low-intensity area reconnaissance, training missions |
| Algorithm | Training Complexity | Prediction Speed | Applicability |
|---|---|---|---|
| OvO | High | Slow | Nonlinear, small-sample scenarios |
| OvA | Low | Medium | Fast training, balanced data distribution |
| CS | Medium | Fast | Linear data, high real-time requirements |
| DS | High | Fast | Embedded deployment, nonlinear scenarios |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | L |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.388 | 0.271 | 0.828 | 0.356 | 0.542 | 0.140 | 0.802 | 0.074 | 0.986 | 0.772 | 0.198 | L3 |
| 0.005 | 0.815 | 0.706 | 0.729 | 0.074 | 0.358 | 0.115 | 0.863 | 0.623 | 0.330 | 0.063 | L3 |
| 0.310 | 0.325 | 0.729 | 0.637 | 0.472 | 0.119 | 0.713 | 0.760 | 0.561 | 0.770 | 0.493 | L1 |
| 0.522 | 0.427 | 0.025 | 0.107 | 0.636 | 0.314 | 0.508 | 0.907 | 0.249 | 0.410 | 0.755 | L4 |
| 0.228 | 0.076 | 0.289 | 0.161 | 0.808 | 0.633 | 0.871 | 0.803 | 0.186 | 0.892 | 0.539 | L1 |
| 0.806 | 0.785 | 0.801 | 0.800 | 0.468 | 0.576 | 0.552 | 0.728 | 0.764 | 0.645 | 0.577 | L2 |
| 0.807 | 0.896 | 0.318 | 0.110 | 0.427 | 0.818 | 0.860 | 0.006 | 0.510 | 0.417 | 0.222 | L3 |
| 0.563 | 0.474 | 0.691 | 0.525 | 0.273 | 0.361 | 0.446 | 0.591 | 0.459 | 0.361 | 0.351 | L3 |
| 0.717 | 0.609 | 0.787 | 0.722 | 0.505 | 0.669 | 0.481 | 0.556 | 0.755 | 0.680 | 0.559 | L2 |
| 0.796 | 0.881 | 0.767 | 0.713 | 0.467 | 0.552 | 0.424 | 0.678 | 0.624 | 0.632 | 0.735 | L2 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | L |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.009 | 0.029 | 0.062 | 0.013 | 0.042 | 0.015 | 0.052 | 0.012 | 0.088 | 0.090 | 0.008 | L3 |
| 0.001 | 0.076 | 0.022 | 0.011 | 0.009 | 0.034 | 0.009 | 0.161 | 0.022 | 0.031 | 0.005 | L3 |
| 0.033 | 0.035 | 0.002 | 0.011 | 0.035 | 0.017 | 0.041 | 0.124 | 0.024 | 0.083 | 0.038 | L1 |
| 0.051 | 0.024 | 0.002 | 0.006 | 0.044 | 0.021 | 0.029 | 0.120 | 0.016 | 0.038 | 0.073 | L4 |
| 0.025 | 0.007 | 0.031 | 0.015 | 0.055 | 0.049 | 0.052 | 0.055 | 0.013 | 0.026 | 0.052 | L1 |
| 0.063 | 0.051 | 0.025 | 0.030 | 0.047 | 0.084 | 0.046 | 0.090 | 0.048 | 0.076 | 0.021 | L2 |
| 0.106 | 0.077 | 0.034 | 0.014 | 0.028 | 0.054 | 0.048 | 0.001 | 0.019 | 0.013 | 0.018 | L3 |
| 0.046 | 0.039 | 0.057 | 0.043 | 0.022 | 0.030 | 0.037 | 0.049 | 0.038 | 0.030 | 0.029 | L3 |
| 0.058 | 0.050 | 0.064 | 0.059 | 0.043 | 0.057 | 0.039 | 0.045 | 0.063 | 0.058 | 0.046 | L2 |
| 0.065 | 0.075 | 0.061 | 0.058 | 0.039 | 0.047 | 0.034 | 0.054 | 0.052 | 0.054 | 0.063 | L2 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.72 | 0.68 | 0.85 | 0.82 | 0.78 | 0.65 | 0.70 | 0.62 | 0.55 | 0.60 | 0.80 |
| 0.73 | 0.69 | 0.84 | 0.81 | 0.77 | 0.66 | 0.71 | 0.63 | 0.56 | 0.61 | 0.79 |
| 0.71 | 0.67 | 0.83 | 0.80 | 0.76 | 0.64 | 0.69 | 0.61 | 0.54 | 0.59 | 0.81 |
| 0.70 | 0.66 | 0.82 | 0.79 | 0.75 | 0.63 | 0.68 | 0.60 | 0.53 | 0.58 | 0.82 |
| 0.74 | 0.70 | 0.86 | 0.83 | 0.79 | 0.67 | 0.72 | 0.64 | 0.57 | 0.62 | 0.78 |
| 0.69 | 0.65 | 0.81 | 0.78 | 0.74 | 0.62 | 0.67 | 0.59 | 0.52 | 0.57 | 0.83 |
| 0.72 | 0.68 | 0.80 | 0.77 | 0.76 | 0.65 | 0.70 | 0.62 | 0.55 | 0.60 | 0.79 |
| 0.046 | 0.039 | 0.057 | 0.043 | 0.022 | 0.030 | 0.037 | 0.049 | 0.038 | 0.030 | 0.029 |
| 0.058 | 0.050 | 0.064 | 0.059 | 0.043 | 0.057 | 0.039 | 0.045 | 0.063 | 0.058 | 0.046 |
| 0.065 | 0.075 | 0.061 | 0.058 | 0.039 | 0.047 | 0.034 | 0.054 | 0.052 | 0.054 | 0.063 |
| Model Variant | Accuracy | F1-Score |
|---|---|---|
| Baseline SVM | 0.87 | 0.86 |
| +Entropy weighting | 0.90 | 0.90 |
| +Hybrid kernel | 0.93 | 0.92 |
| +Improved DAG-SVM | 0.94 | 0.93 |
| Full Model (ours) | 0.96 | 0.94 |
| Algorithm | Accuracy | Macro F1 | L1 Recall Rate |
|---|---|---|---|
| Logistic Regression | 0.72 | 0.68 | 0.58 |
| Random Forest | 0.86 | 0.83 | 0.77 |
| Convolutional Neural Network | 0.88 | 0.85 | 0.79 |
| Long Short-Term Memory Network | 0.90 | 0.88 | 0.82 |
| Improved SVM | 0.96 | 0.94 | 0.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Liu, S. The Operational Safety Evaluation of UAVs Based on Improved Support Vector Machines. Aerospace 2025, 12, 932. https://doi.org/10.3390/aerospace12100932
Zhou Y, Liu S. The Operational Safety Evaluation of UAVs Based on Improved Support Vector Machines. Aerospace. 2025; 12(10):932. https://doi.org/10.3390/aerospace12100932
Chicago/Turabian StyleZhou, Yulin, and Shuguang Liu. 2025. "The Operational Safety Evaluation of UAVs Based on Improved Support Vector Machines" Aerospace 12, no. 10: 932. https://doi.org/10.3390/aerospace12100932
APA StyleZhou, Y., & Liu, S. (2025). The Operational Safety Evaluation of UAVs Based on Improved Support Vector Machines. Aerospace, 12(10), 932. https://doi.org/10.3390/aerospace12100932





