A Fair and Congestion-Aware Flight Authorization Framework for Unmanned Traffic Management

Abstract

With the expected increase in drone operations, inter-operator fairness issues and congestion problems are expected to arise due to the strategic authorization approach mandated in European regulation. As an alternative, the proposed authorization method is based on a deferred authorization decision with multiple-priority classes that are gate-kept by a series of scarce flight tokens. In it, operators can guide the aerial traffic deconfliction process by indicating the criticality of each operation (i.e., selected priority class) based on their business logic and the available flight tokens. Scarce token distribution is performed by a centralized service following a fairness- or congestion-management policy defined by authorities. Also, geographical and temporal incentives can be considered using a 4D-dependent temporal airspace cost to compute the required number of tokens per flight. Results based on several simulation scenarios demonstrate the validity of the approach and its capability in prioritizing different operators’ behaviors (fairness management) or avoiding flight hotspots (congestion management). Overall, it is concluded that the proposed method is an efficient, fair, simple and scalable novel authorization process that can be integrated into the U-space ecosystem.

1. Introduction

Unmanned Aircraft Systems (UAS) are already enabling novel and efficient applications including infrastructure surveys, law-enforcement surveillance, parcel delivery, or people mobility. As the drone ecosystem continues to mature, a significant increase on unmanned operations is foreseen in the coming years. Particularly, traffic will concentrate in urban environments where 70,000 delivery drones are expected to deliver parcels across Europe by 2035 [1]. In fact, according to [2], UAS traffic density in metropolitan areas will represent a six-fold increase from current worldwide commercial traffic.

To enable this prospective scenario, regulation and technological advancements are required to ensure the safe operation of drones, considering both air-to-air and air-to-ground risks. In this regard, unmanned traffic management (UTM) systems are being developed to enforce and monitor UAS separation prior to (i.e., flight authorization or strategic phase) and during (i.e., tactical phase) flights [3] so that a target safety level can be met (e.g., an air collision probability or a ground fatality risk). To do so, UTM systems rely on the prior declaration of flight operation intents that must be authorized before flight to avoid that two drones operate closer than a distance required to meet the safety target level. Operational intents can also be referred to as flight authorization requests, flight plan or U-plan and consists of a definition of the airspace to be used in an aerial operation, usually described as a series of 4D volumes (i.e., portions of 3D airspace occupied during a given time). Thereby, a priori separation between operations can be enforced and conformance with the expected operation can also be monitored in real time. In the future, advanced tactical separation loss detection and resolution services are envisioned to also manage separation at the tactical phase.

Specifically, in the European landscape (readers are advised that this article focuses on the European regulatory context, concepts and terminology), the U-space concept has been proposed in [4] as an ecosystem “relying on digital services and automation of functions designed to support safe, secure and efficient access to airspace for a large number of UAS”. At the moment, preliminary implementations of U-space services are being deployed [5] to support simple UAS operations in environments with low traffic density and low ground risk. Services to UAS operators (e.g., UAS flight authorization, traffic information, conformance monitoring services…) are provided by decentralized, autonomous entities known as U-space Service Providers (USSPs), which are equivalent to UAS Service Suppliers (USS) in FAA terminology. These entities may be coordinated by a Common Information Service Provider (CISP) providing relevant common information to all USSPs. An extension of the CISP role (namely, Centralized Platform or Exchange Services) is being considered in some countries to enable data exchange between USSP and provide additional functionalities. Similarly, a centralized Flight Information Management System (FIMS) exists in the USA concept, which is complemented by direct inter-USS information exchange [6].

In Europe, strategic separation enforcing currently implies that a 4D airspace volume cannot be simultaneously used by two UAS operations. Therefore, from the operators’ point of view, airspace is a contested resource of which access is necessary to achieve their business plan. Additionally, European regulations also stipulate that available capacity must be allocated to operators on a First Come–First Served (FC-FS) basis [4,7]. This term implies that those operators who request the usage of a given airspace volume (through the submission of a U-plan) in the first place, are those who are authorized to fly. While this flight authorization approach may be valid for the time being when airspace is uncongested, it might generate problems in the future when operators start to compete to access congested airspace. It is therefore necessary to analyze the fairness implications of this approach and propose suitable alternatives.

1.1. Motivation

Operators’ needs can be very different depending on the characteristics of their unmanned aerial operations [8]. In this sense, some operators can schedule their operations in advance (e.g., agricultural inspection) while others cannot do so until almost the moment of take-off (e.g., urban delivery operations). As a result, with an FC-FS authorization process, the former operators could monopolize airspace usage over the later operators. Additionally, each operation yields a benefit/has a value for the operator depending on its criticality for its objectives or business logic (e.g., a monetary value). Accordingly, some operations can be subject to changes (i.e., route changes, delays) at little cost to the operator (e.g., parcel delivery) while others have strong restrictions on when and where they must be performed (e.g., a photoshoot of a relevant event). These operators’ needs are also not considered in the regulation-mandated FC-FS approach and can generate inequalities in airspace access.

One of the objectives to be considered in the design of U-space systems is to ensure that access to airspace is “equitable and fair” for all operators irrespective of their different needs [9]. In this sense, fairness in U-space can be understood as the virtuous state in which the welfare of each operator is maximized, subject to capacity constraints and the needs and limitations of the other operators [10]. From all the above, it is evident that the current logic of airspace access (i.e., FC-FS), where the first operator to report the operation is the one who gains access to the airspace, does not meet this fairness criterion. This means that operators can take advantage of the FC-FS logic to authorize a greater number of operations or being subjected to fewer deconfliction changes, such as delays. In fact, simulated studies [11] show that when operators with different behaviors (e.g., different flight submission times) are introduced into the existing U-space systems, the achieved fairness is reduced.

Authors in [8] also argue that the existing authorization mechanism is not appropriate. As a solution, they discuss a series of requirements that should be considered in an alternative protocol: efficiency (airspace should be used efficiently to avoid congestion), fairness (for which different notions of what is fair can be selected by the regulator), simplicity (operators should easily report their preferences, hiding the complexity of the underlying fairness optimization logic), incentives (operators should be encouraged to truthfully communicate their preferences.) and scalability (the mechanism must support the expected high number of operations).

From a practical point of view, fairness issues in airspace access will appear hand in hand with airspace congestion. Demand and capacity management protocols are expected to set congestion thresholds and propose measures that homogenize geographical and time distribution of traffic to avoid hotspots [12]. Also, politically imposed constraints related to social (e.g., privacy) or ecological aspects (e.g., noise pollution) are to be expected. Ideally, an alternative authorization mechanism should also be able to deal with these aspects in conjunction with fairness considerations.

Overall, it seems reasonable to conclude that a new airspace access control mechanism is needed to address the challenges of the future drone ecosystem (i.e., fairness, capacity management, regulatory constraints) while ensuring elements such as efficiency, scalability and simplicity.

1.2. Contributions and Outline

In view of the above, Section 2 reviews existing fairness management proposals and concludes the following: a) there does not exist a single notion of fairness; b) there does not exist a comprehensive authorization framework that considers fairness and is easily adapted to European regulations. Therefore, the objective of the article is to propose an enabling mechanism that supports advanced authorization schemes and paves the way to solve the previously identified challenges; that is, the manuscript aims to provide U-space stakeholders (i.e., national regulators, USSPs and operators) with an easily implementable and transparent framework that allows the implementation of a broad set of protocols to jointly optimize different notions of fairness, congestion management or social restrictions. To achieve this objective, the article relies on the following methods and contributions:

• Definition of an alternative strategic flight authorization/deconfliction workflow that is based on the current European regulations and proposes a gradual evolution by implementing a deferred and multi-priority authorization scheme.
• Definition of a token-based framework that guides the authorization process enabling operators to state the expected value of each operation (i.e., operation preferences in a privacy-aware way) while authorities/U-space services can establish temporal, geographical and operator-linked incentives to implement different notions of fairness, congestion or other constraints. On the former topic, it is not the focus of the article to decide what that fairness notion (and its associated incentives/implementation) should be, and several alternatives are discussed.

To explore these contributions, the article provides further details as follows. Previous work on this topic is addressed in Section 2. The proposed authorization workflow and token-based framework are described in Section 3. Then, Section 4 discusses how the proposed protocol can be used to implement a variety of fairness and congestion management policies. Finally, Section 5 and Section 6 explore an experimental setup to assess the proposed contributions and describe the obtained results with comparisons with the current FC-FS mandated approach.

2. Related Work

The flight authorization process in UTM systems (also known as strategic deconfliction) can be considered as a resource allocation problem in which 4D airspace volumes are reserved to authorized operations. In this sense, fair resource assignment has been previously studied in domains such as communication networks [13], cloud computing [14] or even healthcare [15]. When addressing fairness in such systems, two topics should be contemplated: measuring fairness (i.e., what is considered fair) and algorithms/protocols to implement fair resource allocation.

On the first topic, different notions of fairness are possible such as min–max or proportional fairness [16]. In the first case, an allocation is fair as long as an increase in resources for one participant does not result in a decrease for another participant with a smaller resource share; that is, the utility of the worst user is to be maximized. On the contrary, in proportional fairness, assignments are made to ensure that each individual receives a proportional share of their total possible allocations. This way, a compromise is reached between system efficiency and egalitarian fairness (i.e., max–min fairness). To measure if these fairness notions (or others) are met, fairness metrics must analyze the variability in the distributed resources among the set of demands [17]. In this sense, given a magnitude that measures how many resources have been allocated to each individual, simple statistical measures over that magnitude such as the standard deviation can be used to represent resource distribution (i.e., the higher the standard deviation, the less fair the allocation has been). More complex metrics can also be derived to obtain a normalized figure of merit such as the ratio of the geometric and arithmetic mean [18] or the Gini coefficient.

Focusing on measuring fairness in UTM systems, a thorough discussion can be found in [10] which warns that defining a single airspace usage fairness notion is difficult due to different benefit perceptions across stakeholders (mainly operators). For instance, in [19], if an FC-FS allocation is assumed to be fair (which is debatable, as it has been previously discussed), the number of arrival reversals (i.e., the deviation in the arrival order vs. FC-FS) can be considered as a fairness metric. In [20,21], fairness is studied in a Urban Air Mobility setting where operations are delayed (either in ground or in air) to maintain separation. As a result, the incurred time delays are used as a metric to compare how different operations are treated. The literature also discusses how fairness can be measured at an operator level by measuring the overall delay across all operations such as in [22].

As for the second topic (i.e., ensuring fairness), fair resource allocation usually consists in solving an optimization problem (e.g., mixed-integer linear programming) to which fairness constraints are added, as in the case of [23]. However, in systems with scalability or real-time requirements (e.g., communication networks or job allocation on computers), the resolution of these problems is intractable, and one has to resort to approximate models and heuristics. Thus, techniques such as round-robin scheduling in processors might be used and result in max–min fairness under certain conditions [24]. Also, techniques such as fair queuing or token buckets are used in networks to provide differentiated traffic allocation for different groups (even achieving different qualities of service) [25]. Focusing on UTM systems, the existing literature on fairness management is scarce and can be grouped in three different approaches: market-based, based on optimization techniques and distributed mechanisms.

Authors in [26] perform an economic study on the possible adoption on a money-based market that is similar to road pricing but managing airspace usage. They argue that a pay-per-usage (i.e., operators pay a fee depending on the airspace occupation of each flight) scheme is equitable and efficient and should be adopted. Continuing with proposals based on a market supported by money, the author of [27] concludes that portions of airspace should be delimited and allocated exclusively to some operators based on an auction process. Thereby, operators would not pay per flight, but for the right of unlimited and unique usage of some air corridors. A technical implementation of an airspace auction is also proposed in [28]. Authors articulate pre-departure strategic deconfliction through bids on the set of airspace cells required for a flight plan. Within the framework, airspace price and bids are shared between operators through a common centralized price heatmap. In [8], authors conceptually discuss the possibility of introducing a market with an artificial currency (or token) that would be distributed to operators based on how their behavior aligns with the regulator’s notion of fairness. Such point-based system is also proposed in [12] to decide which flight plans are subjected to changes in a congestion management protocol. However, no comprehensive proposal in terms of the strategic flight authorization (i.e., considering flight plan authorization timing, services interactions…) was discussed in any of the previous cases. Similarly, no discussion was made regarding how such a scheme could be technically implemented and whether it is possible to distribute such schemes within the U-space ecosystem.

In addition to the above examples that articulate airspace access as a market, there exists another set of authors that propose introducing optimization techniques within the authorization loop to simultaneously solve congestion and fairness issues. In this lane, authors of [29] propose the usage of an adapted version of ATFM (Air Traffic Flow Management, a congestion management algorithm envisioned for conventional aviation) which consists in formulating a mixed-integer programming problem to assign delays to UAS aircraft in order to ensure separation between them. The proposed algorithm simultaneously handles a batch of operations and tries to ensure their separation while maximizing different fairness metrics. This work is further refined in [19] by introducing operator preferences (e.g., delay sensitivity) into the ATFM formulation. A rolling horizon implementation is also proposed to allow real-time flight submission. In both cases, the optimization process is performed in a centralized way, which might not be consistent with current U-space trends where decisions are taken in a decentralized manner by different USSPs. Similarly, authors in [21,30] also address the problem of fairly and efficiently assigning delays to balance demand and capacity. In this case, both centralized and decentralized processing are explored. However, as in the case of network resource allocation, scalability concerns are cited as a limiting factor of optimization-based techniques.

Another set of deconfliction and capacity management strategies are explored in [20,22], which constitute the most exhaustive proposal found in the literature. In this case, the operation deconfliction problem is projected onto a grid and reduced to deconflicting aircraft movements between adjacent cells. To this end, they establish a priority queuing system that regulates access to each cell and a distributed algorithm that defines which aircraft can switch cells. The mechanism is privacy-aware, decentralized and studies different prioritization mechanisms (e.g., random, delay-based, auctions-based where operators can define their priority). While it is shown that fairness is achieved (in terms of delays induced in each operation), the proposed mechanism is oriented to short term deconfliction (almost tactical) as it does not allow deconfliction of a complete route (strategic deconfliction). Thus, it does not seem suitable for the current European regulatory paradigm where flights must be fully authorized before take-off. Another distributed approach is presented in our previous work in [31], which proposes a new authorization workflow (aligned with European regulations) to enable fairness management in a multi-USSP environment. However, this proposal lacks thorough discussion on fairness strategies and how operator preferences can be considered.

Finally, regarding congestion management techniques in UTM, the available literature is scarce. Some of the already cited proposals attempt to solve this problem by means of optimization mechanisms [21,30]. Also, in the DACUS project [12] a new central entity (Dynamic Capacity Management service) has been proposed to jointly analyze the full flight picture and change U-plans specification to avoid the formation of hotspots.

From the review on fairness metrics, it can be concluded that there are several notions of fairness in UTM systems (e.g., price-based, FC-FS, delay-based…). In this sense, the authorization framework that will be proposed in the next section is not limited to a given notion but rather allows the implementation of different fairness policies (as will be discussed in Section 4). In addition, all the fairness metrics proposals discussed above are derived from Urban Air Mobility applications where operations are dynamic and can be subject to small delays at low cost to the operator. However, as explained in Section 1.1, in the U-space ecosystem there are a wide variety of operators’ needs, with some operations that cannot be subjected to delays. Therefore, the previous metrics might not be directly applicable to the considered use case. As a result, as will be elaborated in Section 5 and Section 6, the flight authorization rate will be used instead as a fairness metric for the purpose of validating the proposed framework.

As for fairness-enabling authorization frameworks in UTM, there does not exist a comprehensive proposal jointly covering all the following requirements:

• It enables the management of fairness (i.e., surpasses current regulation-mandated FC-FS approach) and congestion issues.
• It is scalable (in terms of the number of managed aircraft). Thus, optimization-based alternatives should be avoided.
• It is distributable between different entities to comply with the CISP-USSP functionality distribution mandated in European regulations. Thus, alternatives operated by a central entity should be avoided.
• It can be adapted to the European regulation-mandated authorization workflow in which flight plans are submitted over time and require full authorization before flying.
• It is flexible in order to allow the implementation of different fairness notions.
• It enables operators to state their operation preferences.

In this sense, this article surpasses the existing literature (including our previous work) by proposing a comprehensive authorization framework based on a non-monetary market that is well-defined and integrated within an extension of the European regulation-mandated authorization workflow. Moreover, it enables implementing different fairness policies (including some of the mentioned ones in the existing state-of-the-art) and jointly considering fairness and congestion management. Furthermore, the framework is scalable, and authorization decisions can be taken in a decentralized manner by USSPs, also considering operator preferences.

3. Token-Based Authorization Framework

3.1. Deferred and Multiple-Priority Authorization Workflow

While the mandated FC-FS authorization scheme facilitates the implementation of the deconfliction workflow, it prevents the adoption of other protocols (e.g., authorizing operations from different operators with different priorities…), addressing the previously identified fairness and congestion challenges. It can be argued that these protocols can be applied once an authorization has been provided to the operator. However, this would imply making changes to already approved operations in a way that is not transparent nor predictable from the operator’s point of view. The inherent fairness problems in the FC-FS approach should also be addressed.

As an alternative, this article embraces the proposal in [9] that delays the definitive flight authorization until sufficient information is available to apply those protocols. This proposal would require regulatory changes but does not imply a total paradigm shift as other proposals in the literature would entail (e.g., flights are still authorized in advance; authorization responsibility remains with the USSPs…). In this case, when an operator submits a flight authorization request, the flight plan is only registered into the U-space system and considered as part of the expected traffic. Thus, authorization is not issued immediately as mandated by the regulation. Alternatively, the operator could be provided with an authorization probability estimate that considers both existing information and an estimation of future traffic patterns and expected measures/changes to instill some certainty and transparency into the process.

Later on, when most flight plans that could possibly be conflicting have already been submitted, it is feasible to simultaneously perform strategic deconfliction (i.e., to select which U-plan should access the contested airspace) between them, irrespective of when they were submitted and considering additional deconfliction protocols. This situation occurs at an agreed decision time relative to each flight plan take-off time, denoted RTTA (Reasonable Time To Act). After t_{take off}—RTTA, the flight plan is either approved or rejected and is not subject to any modifications except in the case of abrupt changes in airspace conditions (e.g., new geofences/no-fly zones) or special operations (as required by regulations [7]).

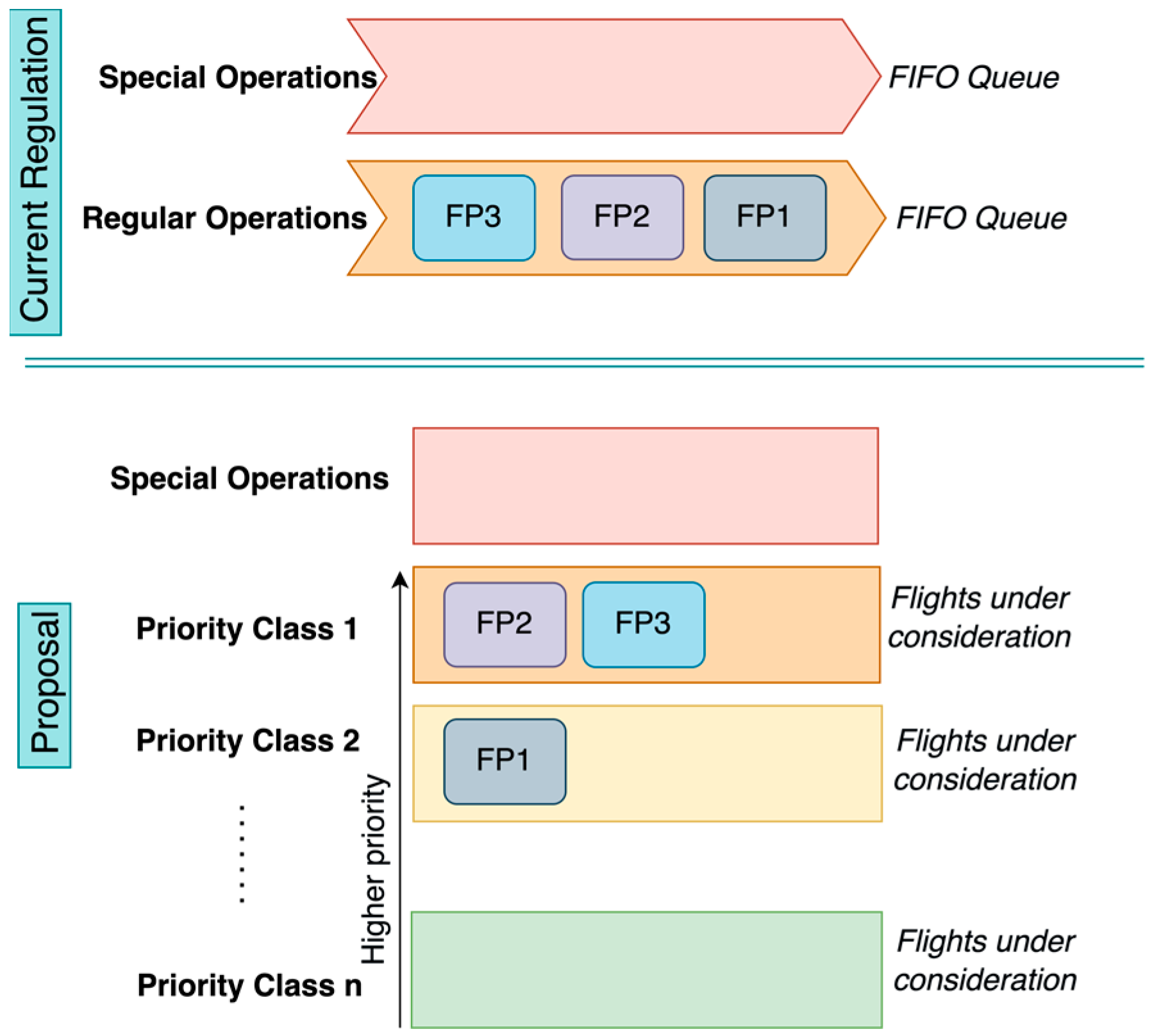
The difference between the adopted approach and regulation is depicted in an example scenario in Figure 1. It compares the authorization process for three submitted operations that are competing to operate in the same 4D volume but are submitted at different times. In the FC-FS approach, the operation that is submitted first (i.e., FP1) is approved immediately and the rest of operations are denied. Conversely, in the deferred approach, the authorization decision is made later in time and can yield different results due to the application of a given prioritization protocol. In the deferred example, FP2 is approved instead.

Besides breaking the implicit unfairness of the FC-FS approach, the deferred authorization scheme also enables the adoption of other deconfliction protocols. In this regard, we propose a multi-priority system for the authorization process through a set of priority classes. Again, the proposal is inspired by the current European regulation, extending the authorization priorities currently in place (i.e., a nominal priority and a higher priority for special operations as defined in [32], e.g., medical flights, law-enforcement flights). Here, instead of treating all non-special operations (i.e., the proposal would not apply to special operations) equally, each flight is assigned to a priority class by the operator. For the former, through the proposed prioritization framework, the operator can easily inform the U-space system of the criticality or perceived value of each operation so that this information can be implicitly considered within the deconfliction process.

In this prioritization system, a U-space operator (denoted $o{p}_p$ where OP is the set of all U-space operators) defined as

$$o{p}_p\in OP \stackrel{\scriptscriptstyle\mathrm{def}}{=} \{o{p}_1, .o{p}_p, .o{p}_P\}$$

(1)

must submit flight plans together with their selected priority class (denoted $p{c}_i$). Multiple priority classes can be considered:

$$p{c}_i\in PC \stackrel{\scriptscriptstyle\mathrm{def}}{=} \left\{p{c}_1, p{c}_2, \dots ,p{c}_i, \dots , p{c}_N\right\}$$

(2)

where $PC$ is the set of all considered priority classes (N classes). Hence, the approach is being referred to as the multi-priority authorization framework. Within the set, each class has less priority than the previous one:

$$\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{y}\left\{p{c}_i\right\}>\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{y}\left\{p{c}_{i+1}\right\}$$

(3)

This means that, when checking for conflicts (i.e., detecting contested 4D volumes), only those flights in the same class or classes with higher priority than the target flight will be considered as possible conflicting flights. This can be understood in terms of flight plans being entered into a pool of “virtual priority sets”, only conflicting with those in sets of higher or equal priority. Figure 2 depicts the proposed multiple priority authorization process showing those virtual priority sets in which U-plans can be entered. It also compares this approach with the regulated one where all U-plans are considered jointly (except for special operations). Referring to the example in Figure 1, FP2 and FP3 have been submitted in priority class $p{c}_1$ while FP1 has been submitted in $p{c}_2$. The prioritization system explains why FP1 has been denied even if considered earlier for authorization.

Within the same priority class, an additional prioritization strategy is required. Multiple strategies could be followed: a random selection based on an identifier, an FC-FS prioritization based on the submission time, an FC-FS prioritization based on the take-off time… In keeping with the spirit of deferred authorization (i.e., irrespective of the submission time), the later strategy is adopted for in-class deconfliction. Also, take-off time is constrained by mission requirements (e.g., when the customer wants to operate) and thus is somewhat immune to possible abuses by the operators. Following this approach, in the example, FP2 is authorized over FP3 as it has an earlier take-off time. However, authors recognize that it could also be argued that a FC-FS based on submission time would be advisable to incentivize operators to submit operations as soon as possible. This approach would enable U-space to perform reactive congestion management by promptly issuing dynamic capacity balancing measures (as proposed in the DACUS project [12]) but would retain a fairness bias.

3.2. Basic Token Authorization (BTA) Workflow: Token-Controlled Access to Priority Classes

In the previous proposal, if operators were to act fairly and not by self-interest, those operations with the highest perceived value (i.e., those that have been entered in the first priority classes) would be mostly authorized. However, nothing prevents operators from acting selfishly and declaring all operations as having high value (high priority class). This case generates a “tragedy of the commons” situation in which the proposed mechanism loses its raison d’être (it degenerates into an unprioritized access to airspace). Therefore, it seems necessary to establish a gatekeeper mechanism to limit access to each of the priority classes. This mechanism would apply to all priority classes except for special operations that should be managed separately.

In this sense, we propose the concept of scarce “flight tokens” that are distributed between operators and used to access a given priority class. The underlying philosophy is to transfer the scarcity of limited airspace into the access mechanism of the prioritization classes so that abusive behavior is avoided. As tokens are limited, operators must manage them according to their business logic in order to properly transmit the criticality of their operations to the U-space system. In essence, tokens and their associated priorities involve a preference sharing system that maintains the privacy of the operators’ business logic.

Further elaborating on this idea, each flight token (which may be individually denoted as $tk$) can be considered as a tuple with the following properties: an identifier (denoted $t{k}_{\mathrm{i}\mathrm{d}}$), an assigned priority class ($t{k}_{\mathrm{p}\mathrm{c}})$, a value ($t{k}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}$), a pledge state ($t{k}_{\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d}}$), an expiration date ($t{k}_{\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{i}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}$) and an assigned operator ($t{k}_{\mathrm{o}\mathrm{p}}$):

$$tk=(t{k}_{\mathrm{i}\mathrm{d}}, t{k}_{\mathrm{p}\mathrm{c}}, t{k}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}},t{k}_{\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d}},t{k}_{\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{i}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}},t{k}_{\mathrm{o}\mathrm{p}})$$

(4)

Flight tokens have the following characteristics:

• They are atomic and unique. A token cannot be subdivided to optimize its usage, and two tokens cannot have the same identifying index ($t{k}_{\mathrm{i}\mathrm{d}}\in \mathbb{N}$).
• They are scarce to effectively restrict access to the priority classes:

$$t{k}_{\mathrm{i}\mathrm{d}}<{\mathrm{N}}_{\mathrm{m}\mathrm{a}\mathrm{x} \mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}\mathrm{s}}$$

(5)

where ${\mathrm{N}}_{\mathrm{m}\mathrm{a}\mathrm{x} \mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}\mathrm{s}}$ is the maximum number of tokens that can be issued. This restriction can be relaxed for comparison purposes, allowing infinite tokens so that the mechanism degenerates into a non-scarce token assignment problem.

• They are linked to a priority class for which they can grant access, represented as

$$t{k}_{\mathrm{p}\mathrm{c}}=p{c}_i; p{c}_i\in PC$$

(6)

which denotes that token $tk$ is only assigned to priority class $p{c}_i$.

• They have an intrinsic, limited value in terms of the amount of airspace occupation (i.e., 3D volume for a certain amount of time) they can insert into a priority class. This value, denoted TK_value, is constant and equal for all tokens and must be decided before implementing the proposed authorization scheme.

$${t{k}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}=\mathrm{T}\mathrm{K}}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}} {\in {\mathbb{R}}^{+}[\mathrm{m}}^3·\mathrm{s}/\mathrm{p}\mathrm{e}\mathrm{r} \mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}]$$

(7)

It signifies that ${\mathrm{T}\mathrm{K}}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}$ tokens are required to access 1 ${\mathrm{m}}^3·\mathrm{s}$ of airspace.

• They are single use: they can only be pledged once to access a priority class. This is defined by the following token property:

$$t{k}_{\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d}}=\left\{0, 1\right\} \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\left\{\begin{array}{c}0;\mathrm{i}\mathrm{f} \mathrm{u}\mathrm{n}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d}\\ 1; \mathrm{i}\mathrm{f} \mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d}\end{array}\right.$$

(8)

• They expire at a given date, $t{k}_{\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{i}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}$, to avoid token harvesting by operators.
• They are uniquely assigned to an operator ($o{p}_p$):

  $$t{k}_{\mathrm{o}\mathrm{p}}=o{p}_p; o{p}_p\in OP$$

  (9)

  which denotes that token $tk$ is assigned to operator $o{p}_p$. In principle, tokens are non-transferrable, but exchange mechanisms between operators could be ideated in the future.

Periodically, each operator ($o{p}_p$) is assigned a set of individual tokens (denoted $T_{o{p}_p}$) distributed among the different priority classes:

$$T_{o{p}_p}=T_{o{p}_p}^{p{c}_1}\cup T_{o{p}_p}^{p{c}_2}\cup T_{o{p}_p}^{p{c}_i}\dots \cup T_{o{p}_p}^{p{c}_N}$$

(10)

$$T_{o{p}_p}^{p{c}_i}=\left\{tk | t{k}_{\mathrm{o}\mathrm{p}}=o{p}_p \wedge t{k}_{\mathrm{p}\mathrm{c}}=p{c}_i\right\}$$

(11)

where $T_{o{p}_p}^{p{c}_i}$ represents the set of tokens assigned to operator $o{p}_p$ for priority class $p{c}_i$. The total number of tokens assigned per operator (i.e., the cardinality of the $T_{o{p}_p}$ set: $\left|T_{o{p}_p}\right|$) and the distribution of tokens per priority class (i.e., the cardinality of the $T_{o{p}_p}^{p{c}_i}$ set: $\left|T_{o{p}_p}^{p{c}_i}\right|$) can be decided by policymakers and regulators based on different policies that will be described in Section 4 These policies can enforce different fairness notions by adequately distributing tokens between operators in a non-uniform manner. This way, some operators may be incentivized over others depending on their characteristics.

When an operator $o{p}_p$ wants to submit a flight plan (denoted fp) for authorization in a priority class $p{c}_i$, it must also pledge a set of previously unpledged tokens, denoted $T_{\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d} \mathrm{f}\mathrm{o}\mathrm{r} fp}$, to cover that flight. Using the token notation, this set can be defined as

$$T_{\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d} \mathrm{f}\mathrm{o}\mathrm{r} fp}=\left\{tk\right| tk\in T_{o{p}_p}^{p{c}_i} \wedge t{k}_{\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d}}=0\}$$

(12)

The number of required tokens to submit a given flight (fp) is denoted as the flight Token Cost (TC_fp). It is related to the occupation of the flight plan and the fixed token value. As previously stated, all authorized flight plans require the reservation of a set of 4D boxes around their expected trajectory to ensure their separation in case of navigation errors, piloting errors… The sum of the temporal–spatial volume (i.e., 3D volume multiplied by the time occupation) occupied by each 4D box constitutes the airspace occupation of that flight, denoted: $o_{fp}$. From it, and given the airspace occupation right granted by a single token (defined by the ${\mathrm{T}\mathrm{K}}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}$), the token cost of a flight can be computed as

$$T{C}_{fp}=⌈{\displaystyle \frac{o_{fp}}{{\mathrm{T}\mathrm{K}}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}}} ⌉ \in \mathbb{N}\left[\mathrm{n}º \mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}\mathrm{s}\right]$$

(13)

Thus, at submission, the U-space system must ensure that the operator has enough tokens remaining (i.e., not-pledged tokens) to generate the $T_{\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d} \mathrm{f}\mathrm{o}\mathrm{r} fp}$ set; that is, the cardinality of the pledged tokens set ($\left|T_{\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d} \mathrm{f}\mathrm{o}\mathrm{r} fp}\right|$) must be equal to the token cost of the flight ($T{C}_{fp}).$ As a result, the flight will enter the desired priority class and be subjected to the authorization process. Additionally, the subset of submitted tokens will become pledged and cannot be used again:

$$\left|T_{\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d} \mathrm{f}\mathrm{o}\mathrm{r} fp}\right|=T{C}_{fp}$$

(14)

$$t{k}_{\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d}}=1, \forall tk\in T_{\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d} \mathrm{f}\mathrm{o}\mathrm{r} fp}$$

(15)

Overall, and as depicted in summary in Figure 3, the mechanism discussed so far introduces a gate at each priority class that can be surpassed using a virtual currency: flight tokens. As tokens are limited, it prevents an operator from monopolizing the use of airspace. Moreover, as the consumption of tokens is linked to the flight plan occupation, it also incentivizes an efficient use of airspace. This token-based mechanism will be referred to as the Basic Token Authorization (BTA) workflow. Conceptually, the proposed mechanism is analogous to priority queues and the token bucket algorithm commonly used in computer science and networking to allocate tasks or traffic and to prevent resource abuse.

3.3. Geographically Aware Token Authorization (GTA) Workflow: Introducing Temporal and Geographical Incentives

The previous BTA protocol contemplated a flight token cost that was geographically and time-independent. This implies that the location and take-off time of a flight plan do not affect the number of tokens required to fly, only the required airspace occupation. However, airspace capacity is not uniform as it is affected by UAS zones restrictions (i.e., geofences/geocages) or CNS (i.e., Communications, Navigation and Surveillance) capabilities. Similarly, traffic demand also follows geographical and temporal patterns that should be considered. In this sense, it is possible to extend the token cost computation to consider this heterogeneity by implementing geographical and temporal incentives. This extension will result in a new authorization protocol named Geographically aware Token Authorization (GTA) workflow.

To do so, a new element is introduced: the airspace cost (AC). This parameter consists of a three-dimensional grid that evolves over time and can be operator-dependent. It can be interpreted as a matrix of weights/multipliers affecting the flight token cost computation. Through these multipliers, different portions of the airspace will have a different cost in terms of the number of tokens required to occupy that airspace portion. Mathematically, the AC matrix can be defined as follows:

$$\begin{gathered} \mathit{A}\mathit{C}\left(t, o{p}_p\right)={\left[ac{\left(t, o{p}_p, fp\right) }_{x,y,z}\right]}_{0\le x\le {<x}_{max}, 0\le y<y_{max}, 0\le z<z_{max}} \\ ac{\left(t, o{p}_p,fp\right) }_{x,y,z}\in \left[0, \infty \right); \\ x, y, z\in \mathbb{N}; \\ 0\le t<t_{max}, t\in \mathbb{N} \end{gathered}$$

(16)

where x, y, z are the indexes of the matrix (grid) representing the coordinates of a discretized 3D space where each index represents longitude, latitude and height axes, respectively. Then, each matrix element, $ac{\left(t, o{p}_p,fp\right) }_{x,y,z}$, represents the cost multiplier at time t (also in a discretized axis), for operator $o{p}_p$, in the grid coordinates (x, y, z). High values of this cost multiplier will require a greater number of tokens, creating a disincentive to fly at these 4D volumes. Conversely, low values will reduce the cost of flying in those areas, incentivizing its use. Finally, each matrix element can also be dependent on the type of mission (represented by the dependence on the flight plan, fp). This would allow for the incentivization of certain types of missions (lower airspace cost) over others (higher airspace cost) based on spatiotemporal logic. As with token allocation in the BTA mechanism, the airspace cost is a parameter that can be adjusted according to different policies, which will be explored in Section 4.

So far, the airspace occupation of a flight plan has been considered as a single aggregated value (denoted o_fp). However, to calculate the number of tokens required considering the 4D-dependent airspace, the flight plan occupancy needs to be projected into the same temporal–spatial grid, obtaining a finer view on which areas of airspace are used and when. Thus, we define a new version of this variable, denoted geographic occupation ${\mathit{O}}_{\mathit{f}\mathit{p}}$ of flight plan fp:

$$\begin{gathered} {\mathit{O}}_{\mathit{f}\mathit{p}}\left(t\right)={\left[o_{fp}{\left(t\right) }_{x,y,z}\right]}_{0\le x\le {<}_{max}, 0\le y<y_{max}, 0\le z<z_{max}} \\ {o}_{fp}{\left(t\right) }_{x,y,z}\in {\mathbb{R}}^{+} \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} \mathrm{u}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{s} \mathrm{o}\mathrm{f} \left[{\mathrm{m}}^3\mathrm{s}\right] \\ x, y, z\in \mathbb{N}; \\ 0\le t<t_{max}, t\in \mathbb{N} \end{gathered}$$

(17)

where x, y, z are the indexes of the matrix (spatial grid). Each element of the matrix, denoted $o_{fp}{\left(t\right) }_{x,y,z}$, indicates how much airspace (in ${\mathrm{m}}^3\mathrm{s}$) the flight plan fp is occupying in the (x, y, z) cell of the grid within the t time interval. Alternatively, and provided that a small enough cell size is selected in the grid, each element within the matrix could be converted into a binary value (0, 1) depending on whether the flight plan passes through the cell or not (as exemplified in Figure 4). In this way, the computational load of calculating the flight plan geographic occupation could be reduced.

Now, if both matrices are multiplied in an element-wise manner and added across all dimensions, it is possible to obtain a weighted version of the previous token cost ($\mathrm{T}{\mathrm{C}}_{\mathrm{f}\mathrm{p}}^{\mathrm{w}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}\mathrm{e}\mathrm{d}}$). This new figure considers that, depending on the area or time instant, more tokens will be required to occupy the same volume of airspace, as a function of the incentives defined in the airspace cost. It can be computed as

$$T{C}_{fp}^{\mathrm{w}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}\mathrm{e}\mathrm{d}}=⌈{\displaystyle \frac{{\sum }_{t=0}^{t_{max}}{\sum }_{\forall x,y,z}\mathit{A}\mathit{C}\left(t, op\right)\circ {\mathit{O}}_{\mathit{f}\mathit{p}}\left(t\right)}{{\mathrm{T}\mathrm{K}}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}}} ⌉ \left[\mathrm{n}º \mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}\mathrm{s}\right]$$

(18)

where $\circ$ represents the element-wise multiplication across dimensions x, y, z of the AC and O_fp matrices, so that each occupation element/cell is weighted by the corresponding airspace cost. From the aggregated weighted occupation figure obtained (numerator in (18)), the token cost can be derived from the token value: ${\mathrm{T}\mathrm{K}}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}$. The computation of this geographical, temporal and operator-aware token cost is represented in Figure 4. In the previous equation, rounding to the nearest whole number may introduce a slight bias against operators who receive fewer tokens depending on the selected policy. However, given the high total number of tokens to be distributed, the overall impact is expected to be negligible.

Once the required number of tokens has been obtained, considering both the geographical occupation and the geographical incentives, the gated access to the priority queues would work as already explained above for the BTA workflow. That is, the number of pledged tokens (cardinality of $T_{\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d} \mathrm{f}\mathrm{o}\mathrm{r} fp}$) must be equal to the weighted token cost of the flight:

$$\left|T_{\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{d} \mathrm{f}\mathrm{o}\mathrm{r} fp}\right|= T{C}_{fp}^{\mathrm{w}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}\mathrm{e}\mathrm{d}}$$

(19)

3.4. Integration on UTM/Architectures

So far, the proposed authorization workflow and its two versions (i.e., BTA and GTA) have been described without referring to its implementation within the U-space ecosystem. As mentioned, the proposed mechanism goes beyond the current European regulation. Therefore, its implementation would require some regulatory changes but not a paradigm shift. This section explores how the proposal could be implemented and distributed between the two main U-space systems: the Common Information Service Provider (or a central platform that extends such a role), CISP, and U-space Service Providers, USSPs [33].

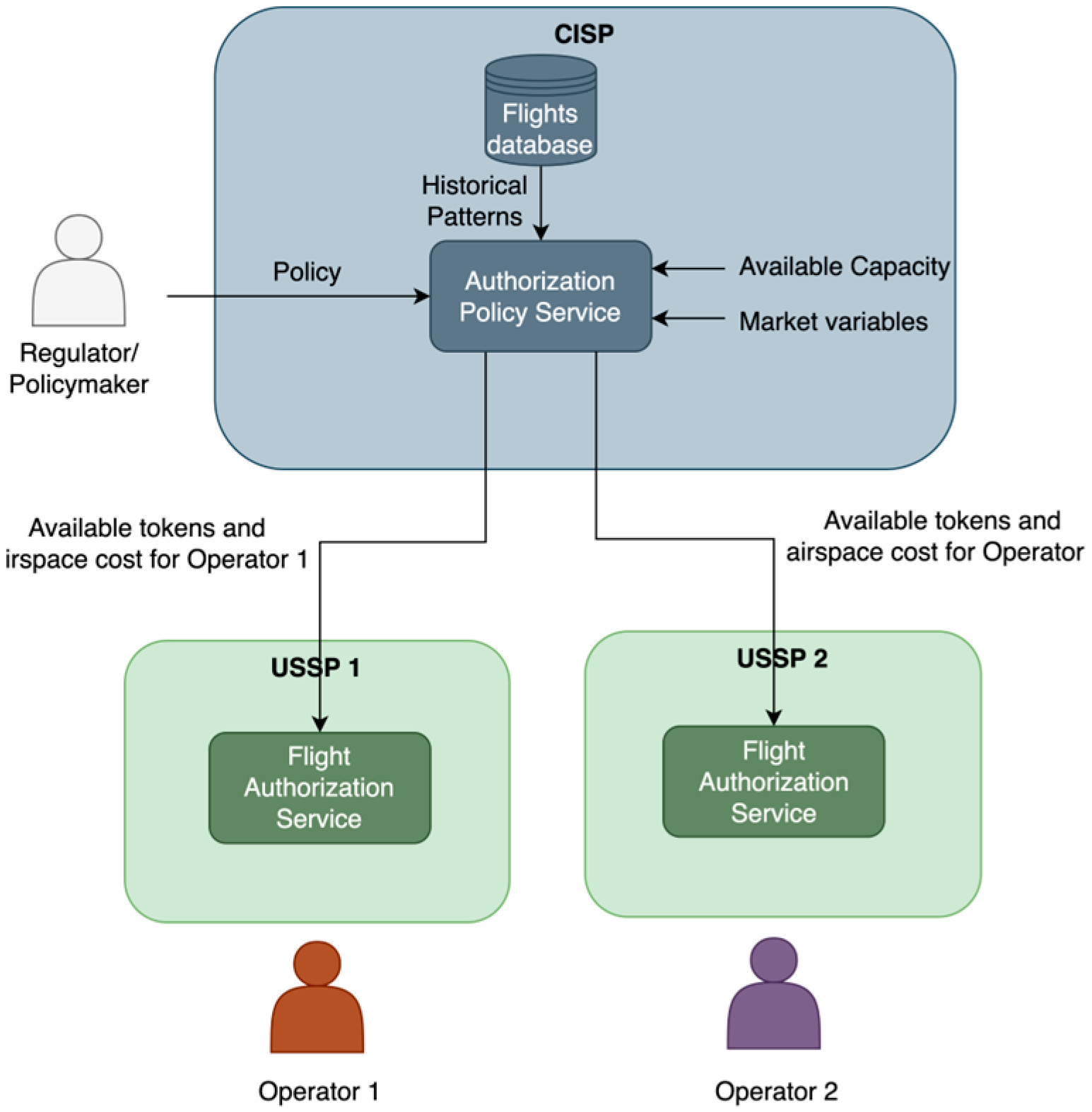
In this regard, we propose the creation of a new centrally deployed service, extending the CISP core functionalities: the Authorization Policy Service (APS). This service is depicted in the U-space architecture in Figure 5 together with its more relevant interactions and dependent services. The APS would be responsible for implementing a given fairness policy by setting the airspace cost and distributing tokens among the operators of each USSP. This process can be based on optimization techniques or heuristics, grounded on relevant information coming from different sources: historical flight data, capacity and demand estimates, possible markets established for token management… The APS operates periodically (i.e., daily) and far in advance so that it is decoupled from the dynamic nature of the flight authorization process. The centralization of this service is justified since it is linked to the authorities/policymakers activities, allowing them to introduce incentives to govern the U-space authorization process.

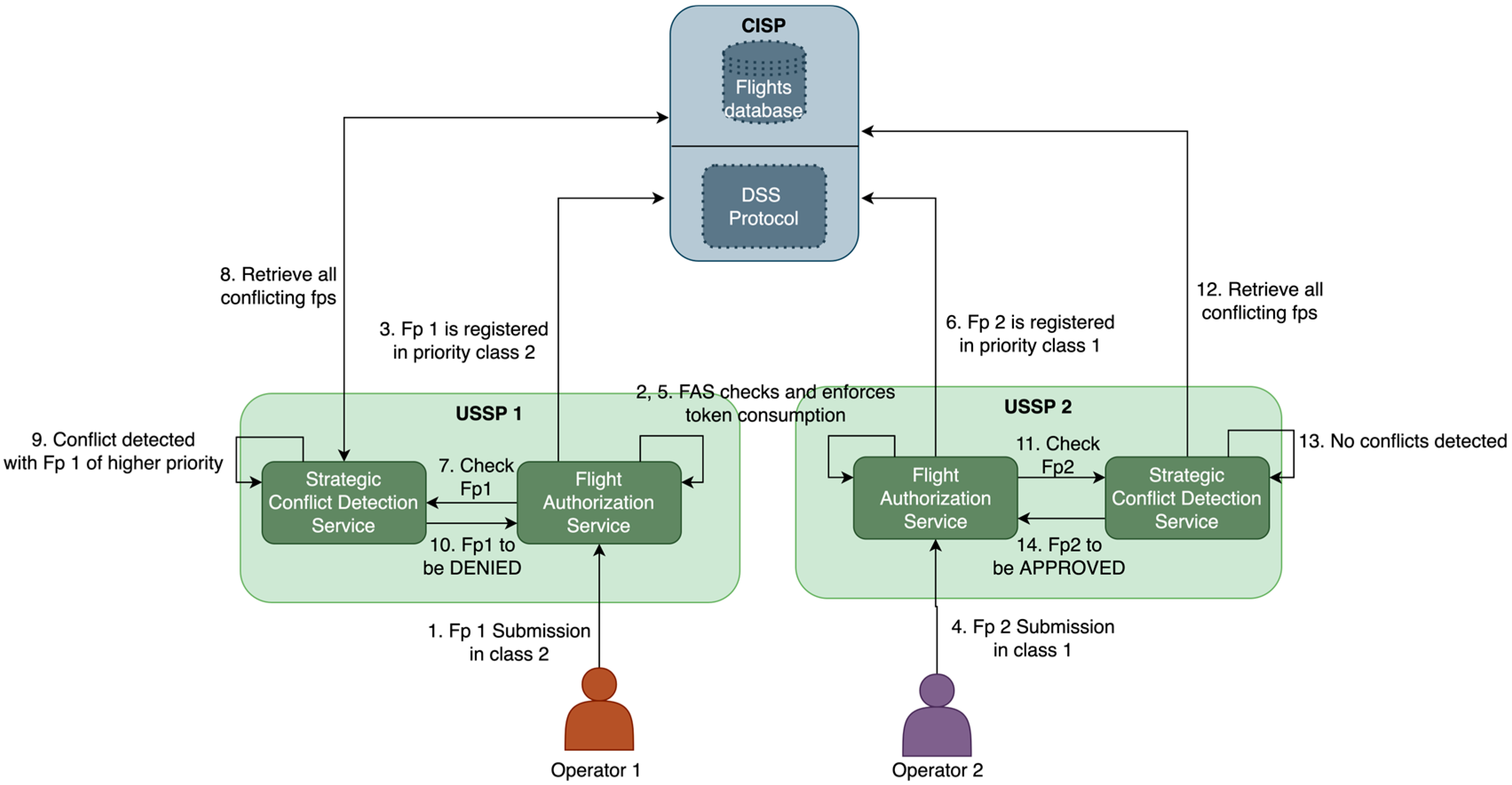
Once the tokens have been distributed a priori (i.e., before flights are submitted), USSPs can operate in a distributed way, without intervention from the APS. This is demonstrated in Figure 6 which shows the sequence of interactions (i.e., the numbered steps) through this process in a scenario where two operators submit a flight plan in different priority classes across different USSPs. When a flight is submitted (interaction 1), the operator would express the criticality of its operation through the selection of the desired priority class, subject to token scarcity. Optionally, the functionality of the USSP’s U-plan preparation service (i.e., as defined in [9], to assist operators in defining a U-plan for their operations) could be extended to include the calculation of the number of tokens required for an operation so that operators can make informed decisions. Then, within each USSP, the Flight Authorization Service (FAS) would be in charge of managing operators’ tokens (already distributed by the APS), ensuring that enough tokens are pledged to access the desired priority class (interaction 2).

Next (interaction 3), the submitted flight plan could be registered in a common centralized Flights Database (FD), together with its associated priority class. Alternatively, a decentralized flight information exchange protocol could also be used to directly exchange flight information between USSPs assisted by a Discovery and Synchronization Service (DSS, as proposed in [34]). An adapted, extended version of existing protocols (mainly, ASTM F3548-21 [35]) would be needed to contemplate priority classes and additional flight plans states. Even if all U-plans are to be registered and shared across USSPs, this information must not be shared with operators for privacy reasons and to avoid abuses of the proposed authorization system.

At t_{take off}—RTTA, the Strategic Conflict Detection Service (SCD) would retrieve (interaction 8) all possible conflicting flight plans (i.e., already approved flights and flights under consideration in higher priority classes) so that conflicts can be checked (interaction 9) and a final authorization decision can be individually made by each USSP (interaction 10).

In conclusion, both BTA and GTA workflows can be performed without resorting to direct intermediation between USSPs to deconflict flights while considering fairness and/or capacity issues. The APS encapsulates all policy management complexity avoiding in-the-loop optimizations for each authorization request. In this sense, tokens serve as a pre-emptive gatekeeper that can be managed individually by each USSPs once tokens are distributed. Then, as prioritization information is registered in a centralized DB or exchanged with a distributed protocol, each USSP can also autonomously take authorization decisions. Overall, the discussed integration details show that the proposed authorization approach is viable and easy to implement into the real U-space ecosystem while providing high scalability (due to its distribution between different systems).

4. Policies for Token Distribution and Airspace Cost Setting

In the previous section, a flexible strategic authorization framework has been proposed based on priority classes, scarce flight tokens to control the access to those classes and a variable airspace cost to introduce geographical incentives into the authorization process. The proposal makes it possible to incorporate into the same framework the operators’ preferences (communicated through the selection of a priority class), flexible fairness enforcement (with the choice of policy by regulators, that will be described in this section) and even congestion management. This framework is policy-agnostic in the sense that it allows enforcing multiple fairness notions, congestion management and, in general, prioritization strategies which would be configured in the APS. Two variables are key in implementing these policies: the token distribution between operators (($|T_{o{p}_p}^{p{c}_i}|$), both in BTA and GTA) and the airspace cost ($\mathit{A}\mathit{C}\left(t, o{p}_p\right),$in GTA). The former incentivizes certain operators by assigning them more tokens or using a different distribution of tokens between priority classes. In turn, the latter creates geographical and temporal incentives, as already explained. Figure 7 exemplifies how the policy objectives (operator-level or geographical incentives, on the left) can be implemented through token distribution and airspace cost (on the right). Note how operators to be incentivized (in green) are assigned more tokens and how areas to be disincentivized (in red) have a higher airspace cost.

Although it is out of the scope of this paper to determine an optimal fairness notion or congestion management-enabling policy, some policies will be explored to prove the usefulness and flexibility of the approach. Those policies are (A) unlimited token distribution, (B) scarce, uniform token distribution, (C) scarce, non-uniform token distribution (D) pay-per-token distribution, (E) pay-per-airspace distribution, (F) congestion management and other space-based incentives. A straight-forward, non-optimal version of each policy will be implemented in Section 5 and Section 6 for validation purposes. For simplicity and ease of understanding, these preliminary implementations of each general policy are constrained to three priority classes ($p{c}_i$ with $i\in \left\{1,2,3\right\},$ which will be denoted HIGH, MEDIUM and LOW, respectively) and will also be described in the following subsections. Again, the proposed implementations are not intended to provide an optimal and complete solution to the fairness problem but rather explore the possibilities of the enabling mechanism discussed in the previous section.

4.1. Unlimited Token Distribution Policy

As a starting point for the implementation of the proposal, a trivial policy would consist in not constraining access to the priority classes. Thus, relying on the operator’s good faith in declaring each operation’s value (i.e., selecting the appropriate priority class). To do so, an unlimited number of tokens of all types could be distributed to all operators while keeping the airspace cost uniform (i.e., using the BTA version of the proposal):

$$\mathrm{BTA} \mathrm{workflow} \mathrm{with} \left|T_{o{p}_p}^{p{c}_i}\right|=\infty , \forall p{c}_i\in PC, o{p}_p\in OP$$

(20)

where the previously established notation is followed in which $T_{o{p}_p}^{p{c}_i}$ represents the set of tokens for priority class $p{c}_i$ assigned to operator $o{p}_p$, $\left|T_{o{p}_p}^{p{c}_i}\right|$ being the number of tokens in such set. In the simplified implementation for validation, this means that all operators receive an unlimited number of tokens for LOW, MEDIUM and HIGH priority classes:

$$\left|T_{o{p}_p}^{p{c}_{LOW}}\right|=\left|T_{o{p}_p}^{p{c}_{MEDIUM}}\right|=\left|T_{o{p}_p}^{p{c}_{HIGH}}\right|=\infty$$

(21)

Tokens in this case would serve to inform the system of operators’ benefit/expected criticality of each operation but would not limit the number of flights each operator can submit. For instance, let us assume two operators: one with 100 flights and one with 10 flights, for whom, according to their business logic, 50% of the total operations are critical and the remaining can be labeled as having low value. Following this unlimited distribution of tokens, the first operator could submit 50 operations in the high priority class ($p{c}_{HIGH}$), informing the U-space of their high value. Similarly, the second operator would only submit five high priority operations. These operations would have a high probability of being authorized over the rest of operations submitted to $p{c}_{LOW}$ priority class.

With this approach, the intrinsic unfairness of the FC-FS approach would be solved but operators with dissimilar characteristics could yield to an unfair distribution of flights. As the previous example exposes, operators submitting a higher number of U-plans would receive a higher number of authorizations than low-traffic operators. More importantly, as already discussed, greedy operators (i.e., those who do not declare operation preferences faithfully) could take advantage of the policy by submitting all flights to the higher priority classes, monopolizing airspace access (i.e., the aforementioned tragedy of the commons).

4.2. Scarce, Uniform Token Distribution Policy

To avoid a tragedy of the commons, scarce token distribution policies can be implemented. In this case, a limited number of tokens of each priority class is distributed to each operator. In principle, the number of tokens assigned to high priority classes should be lower than the number assigned to low priority classes. By doing so, token scarcity is used as a signal to inform operators of the relative value (i.e., higher authorization rates) of each priority class. Thus, the operator is forced to analyze comparatively the utility of each operation and decide which ones to prioritize. It would be expected that those operations with higher utility should be assigned a higher priority class, subject to token scarcity. Mathematically,

$$\mathrm{BTA} \mathrm{workflow} \mathrm{with} \left|T_{o{p}_p}^{p{c}_i}\right|<\left|T_{o{p}_p}^{p{c}_{i+1}}\right|, \forall p{c}_i\in PC$$

(22)

A possible token distribution that meets this condition is one in which, in each priority class, all operators obtain the same number of tokens:

$$\left|T_{o{p}_p}^{p{c}_i}\right|=\left|T_{o{p}_{p+1}}^{p{c}_i}\right|=k_{p{c}_i}, \forall o{p}_p\in OP$$

(23)

The number of tokens for a priority class (i.e., $k_{p{c}_i}$) should be related to the maximum available airspace capacity and the relative advantage that the priority class gives for airspace access (i.e., how likely it is that a flight plan will be authorized in that priority class). These values could be obtained with an optimization by simulation process or based on historical statistics. Moreover, if the opportunity to access the airspace is to be guaranteed at all times (albeit entirely unprioritized), the number of assigned tokens in the lowest priority class (i.e., $p{c}_N$) should be unlimited:

$$\left|T_{o{p}_p}^{p{c}_N}\right|=\infty ,\forall o{p}_p\in OP$$

(24)

Following the example in Section 4.1, let us now assume that each operator receives five tokens for the high priority class ($k_{p{c}_{HIGH}}=5)$, five for the medium priority class ($k_{p{c}_{MEDIUM;}}=5)$ and an unlimited number in the low priority class ${(k}_{p{c}_{LOW}}=\infty )$. Also, for simplicity, let us assume that each flight requires just one token for its submission. With this distribution, the operator with 100 flights would have to use its business logic (expected value of each operation) to distribute its 50 critical flights among the three priority classes, as it does not have a sufficient number of tokens. This way, monopolization of the airspace would be prevented. On the contrary, the second operator would be able to submit all of its critical flights in the high priority class. Indeed, with this uniform distribution policy, small operators can benefit over large operators (i.e., those with a high number of submitted flights). The former can enter a higher proportion of flights in the higher priority classes and therefore secure a higher authorization rate.

In particular, this policy has been implemented with the following assumptions. First, the number of tokens to be distributed in total (${\mathrm{N}}_{\max \mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}\mathrm{s}}$) is defined as the number of tokens required to authorize the maximum number of concurrent flights in an airspace (i.e., $f{p}_{max}$, the airspace capacity). To compute it, the average number of tokens required per flight (i.e., $\overline{T{C}_{fp}}$) is estimated from historical data, obtaining

$${\mathrm{N}}_{\max \mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}\mathrm{s}}=\overline{T{C}_{fp}}·f{p}_{max}$$

(25)

These tokens are equally divided by the number of operators (i.e., |OP|). Additionally, it has been assumed that the high priority class gives a 50% higher chance of authorizing a flight. And thus, the number of tokens for each class must be inversely proportional to this advantage. Therefore, the implemented policy is

$$k_{p{c}_i}=\left\{\begin{array}{cc}{\displaystyle \frac{1}{3}}· {\displaystyle \frac{\overline{T{C}_{fp}}·f{p}_{max}}{\left|OP\right|}},& if p{c}_i=HIGH\\ {\displaystyle \frac{2}{3}}· {\displaystyle \frac{\overline{T{C}_{fp}}·f{p}_{max}}{\left|OP\right|}}, & if p{c}_i=MEDIUM\\ \infty , & if p{c}_i=LOW\end{array}\right.$$

(26)

4.3. Scarce, Non-Uniform Token Distribution Policy

Alternatively, to uniform token distribution, tokens can be allocated non-uniformly based on an operator’s past behavior. A possibility would be to establish a virtue-points system (such as the one proposed in [12]) in which those operators whose behavior has been reliable, safe, efficient… are rewarded with more tokens over non-conforming operators. Another viable approach would consist of allocating tokens based on an operator’s traffic share. This way, large operators could have a higher proportion of tokens assigned to support their historical traffic so that their authorization probability can be similar to those of small operators.

Assuming the existence of an allocation function (denoted f) that depends on an operator’s historical behavior and condenses the non-uniform distribution logic for each priority class ($p{c}_i$), this policy can be formalized as

$$\begin{gathered} \mathrm{BTA} \mathrm{workflow} \mathrm{with} \\ \left|T_{o{p}_p}^{p{c}_i}\right|\ne \left|T_{o{p}_{p+1}}^{p{c}_i}\right|=\mathrm{f}\left(o{p}_{p+1} past behavior, p{c}_i\right), p{c}_i\in PC, o{p}_p\in OP \end{gathered}$$

(27)

In the validation implementation, the later allocation function is implemented by distributing tokens proportionally to the flight share of an operator (i.e., historical number of flights relative to total number of flights, denoted $shar{e}_{o{p}_p}$). Moreover, the distribution of tokens per priority class and the total number of allotted tokens is consistent with the previous policy defined in Equation (25). Therefore, the implemented function is as follows:

$$\mathrm{f}\left(o{p}_p, p{c}_i\right)= \left\{\begin{array}{cc}{\displaystyle \frac{1}{3}}·{\mathrm{N}}_{\max \mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}\mathrm{s}}·shar{e}_{o{p}_p},& if p{c}_i=HIGH\\ {\displaystyle \frac{2}{3}}· {\mathrm{N}}_{\max \mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}\mathrm{s}}·shar{e}_{o{p}_p}, & if p{c}_i=MEDIUM\\ \infty , & if p{c}_i=LOW\end{array}\right.$$

(28)

where non-integer token values should be rounded to the nearest integer. Following the previous example, let us assume that the number of tokens to be distributed is 20 (N_{max tokens} = 20). If the large operator submits 100 operations and the small operator submits 10, their historical number of flights would be approximately $shar{e}_{o{p}_{large}}=0.91, shar{e}_{o{p}_{small}}=0.09$. As a result, the small operator would receive just one token for both HIGH and MEDIUM priority classes, whereas the large operator would receive 6 for the HIGH priority class and 12 for the MEDIUM priority class. This way, both operators would be able to submit a similar proportion of their critical flights in the higher priority classes (i.e., 2 flights over 5 critical and 20 flights over 50 critical) and have similar authorization rates irrespective of their size.

4.4. Pay-per-Token Distribution Policy

Following on with policies based on token distribution (based on the BTA alternative), a pay-per-use approach such as the one mentioned in [26] can also be implemented with the proposed framework. This would require assigning a monetary value to the flight tokens of each of the priority classes (denoted $t{k}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{e}}\left(p{c}_i\right)$). Thus, the number of tokens in each class ($\left|T^{p{c}_i}\right|)$ could be unlimited as the scarcity notion is already included in the token price. Additionally, to signal the different values of each priority class, those classes of higher priority should have a higher economic cost:

$$\begin{gathered} \mathrm{BTA} \mathrm{workflow} \mathrm{with} \\ \left|T^{p{c}_i}\right|=\infty , \forall p{c}_i\in PC \\ t{k}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{e}}\left(p{c}_i\right) [€] | t{k}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{e}}\left(p{c}_i\right)>t{k}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{e}}(p{c}_{i+1}), \forall p{c}_i\in PC \end{gathered}$$

(29)

Setting the token price for each priority class would be the responsibility of the regulators that need to consider the available airspace capacity and the profitability of drone operations so that airspace is economically accessible. They would also need to consider that this policy can create inequalities if operators’ marginal income (revenue per flight) is diverse, as those operators with lower operating costs and more expensive operations would be incentivized. On the positive side, since the cost in number of tokens is related to airspace usage, less efficient operators would be disincentivized as they would need to spend a higher amount of money.

From the operators’ point of view, instead of allocating the tokens in advance, they would have to pay to obtain the desired number of tokens to submit their operations. Depending on the revenue and cost per operation, operators may pay (represented as function h) for one priority class or another according to their business logic, while also avoiding economic losses. This operator’s behavior will be further explained in Section 5.2.

$$\left|T_{o{p}_p}^{p{c}_i}\right|=\mathrm{h}\left(o{p}_p \mathrm{b}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s} \mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{c}\right)$$

(30)

A more sophisticated version of this policy could also incorporate the GTA workflow and the dependency of the airspace cost on the mission type. This way, it would be possible to differentiate between operations with varying operational costs. For instance, to avoid penalizing mission types with high operation costs, the airspace cost could be lower for such missions, thus reducing the number of tokens required and the total monetary cost.

4.5. Pay-per-Airspace Distribution Policy

Moving on to geographic incentives (i.e., GTA workflow), the proposed framework can also implement a fairness policy such as the one described in [27] that grants exclusive (or preferrable) flying access into some corridors/airspace areas to bid-winning operators (pay-per-airspace). To model this, an operator-dependent airspace cost (previously denoted as $ac{\left(t, o{p}_p\right)}_{x,y,z}$) would be used.

Operators who have paid to use certain area (e.g., $o{p}_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}$ in Equation (31)) would have a null airspace cost within the reserved grid cells (a set denoted as $A_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}}=\{\left(x,y,z\right)\dots \}$). Conversely, the rest of the operators would be assigned an infinite cost (or a high cost if flight is non-exclusive but disincentivized) in the same areas. Non reserved cells would have a cost of 1, allowing for their contested access by all operators:

$$\begin{gathered} \mathrm{GTA} \mathrm{workflow} \mathrm{with} \\ ac{\left(t, o{p}_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}},fp\right)}_{x,y,z}=\left\{\begin{array}{c}0, if (x,y,z)\in A_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}}\\ 1, \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right. \end{gathered}$$

(31)

$$ac{\left(t, o{p}_p,fp\right)}_{x,y,z}=\left\{\begin{array}{c}\infty , if \left(x,y,z\right)\in A_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}}\\ 1, \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right.; o{p}_p\ne o{p}_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}$$

(32)

Thereby, the former operators could fly without limits (without spending tokens) in their reserved area, while the latter would have to dedicate a very high number of tokens to do the same (or even be impeded to fly). The proposed framework allows more flexibility than the literature proposal, as it would allow a hybrid approach considering both a mix of reserved and free-flight zones or even allowing access to reserved cells to other operators but at a very high cost. Token allocation for this policy can be performed with any of the previous policies (Section 4.1, Section 4.2, Section 4.3 and Section 4.4). Particularly, in the implemented proof-of-concept, a scarce uniform token distribution has been used.

4.6. Congestion Management Policy

Finally, the spatiotemporal airspace cost (GTA workflow) can also be used as a congestion management protocol. Historical data allows us to estimate which airspace areas are more congested, modeling it as a congestion grid. From the detailed grid-discretized version of a flight plan occupation (${\mathit{O}}_{\mathit{f}\mathit{p}}\left(t\right)$, defined in Equation (17)), the congestion in a grid cell can be measured as the sum of the occupation in that cell for all approved flight plans:

$$\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(x,y,z\right)= \sum _{\begin{array}{c}\forall authorized fp, \\ \forall t\end{array}}{o}_{fp}{\left(t\right) }_{x,y,z}$$

(33)

Thus, cells that are occupied by many flights will have a high congestion value. Then, this value can be translated into an airspace cost matrix that deters operators from accessing congested areas. In this sense, a function c could assign low airspace cost to areas with low congestion, whereas congested areas would have a higher cost:

$$\begin{gathered} \mathrm{GTA} \mathrm{workflow} \mathrm{with} \\ ac{\left(t, o{p}_p,fp\right)}_{x,y,z} =c \left(x,y,z\right) \\ \mathrm{F}\mathrm{u}\mathrm{n}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{c} \mathrm{i}\mathrm{s} \mathrm{s}.\mathrm{t}.:\mathrm{i}\mathrm{f} \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(x_1,y_1,z_1\right)> \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(x_2,y_2,z_2\right) ⟹ \\ ac{\left(t, o{p}_p,fp\right)}_{x_1,y_1,z_1}> ac{\left(t, o{p}_p,fp\right)}_{x_2,y_2,z_2} \end{gathered}$$

(34)

As an example of such a function, in the test implementation, the relationship between the congestion of a cell and its corresponding airspace value is as follows:

$$\mathrm{c}\left(x,y,z\right)=\left\{\begin{array}{c}\begin{array}{cc}5 & \mathrm{i}\mathrm{f} \mathrm{R}\mathrm{C}(x,y,z)\ge 0.8\end{array}\\ \begin{array}{cc}4& \mathrm{i}\mathrm{f} 0.6>\mathrm{R}\mathrm{C}(x,y,z)>0.8\end{array}\\ \begin{array}{c}\begin{array}{cc}3& \mathrm{i}\mathrm{f} 0.4>\mathrm{R}\mathrm{C}(x,y,z)>0.6\end{array}\\ \begin{array}{cc}1& otherwise\end{array}\end{array}\end{array}\right.$$

(35)

where $\mathrm{R}\mathrm{C}\left(x,y,z\right)$ is the relative congestion of a cell related to the maximum congestion of all cells (i.e., ${\displaystyle \frac{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(x,y,z\right)}{\max \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(x,y,z)}})$. This way, operators wanting to operate in congested areas would require a higher number of tokens (again, distributed following any of the previous token-distribution policies described for the BTA workflow in Section 4.1, Section 4.2, Section 4.3 and Section 4.4), being compelled to avoid such areas (if possible). Overall, this policy would pre-emptively prevent congestion by incentivizing the use of low-traffic areas and disincentivizing the use of high-traffic areas, all while avoiding tight restrictions.

A similar approach can be followed to manage other U-space aspects with a geographical component such as noise limits, social impacts… For example, the air cost dependency on the operation (fp) could be employed to discourage aerial photography operations within urban areas (due to privacy concerns) by assigning this mission type a higher airspace cost. Similarly, recreational drone flights could be disincentivized during nighttime hours in order to reduce noise-related disturbances. In fact, the framework could also be used to code the constraints of geofences by assigning those areas an infinite cost.

5. Materials and Methods: Experimental Setup

The U-space ecosystem is being deployed across Europe slowly. For this reason, it is not possible to conduct validation tests in a large-scale operational environment, nor is it feasible to obtain datasets to replicate actual drone flight patterns. Instead, the previous literature (e.g., [21,22]) has demonstrated the usage of simple simulation scenarios (i.e., randomly distributed linear flights) to validate novel methods in unmanned traffic management. 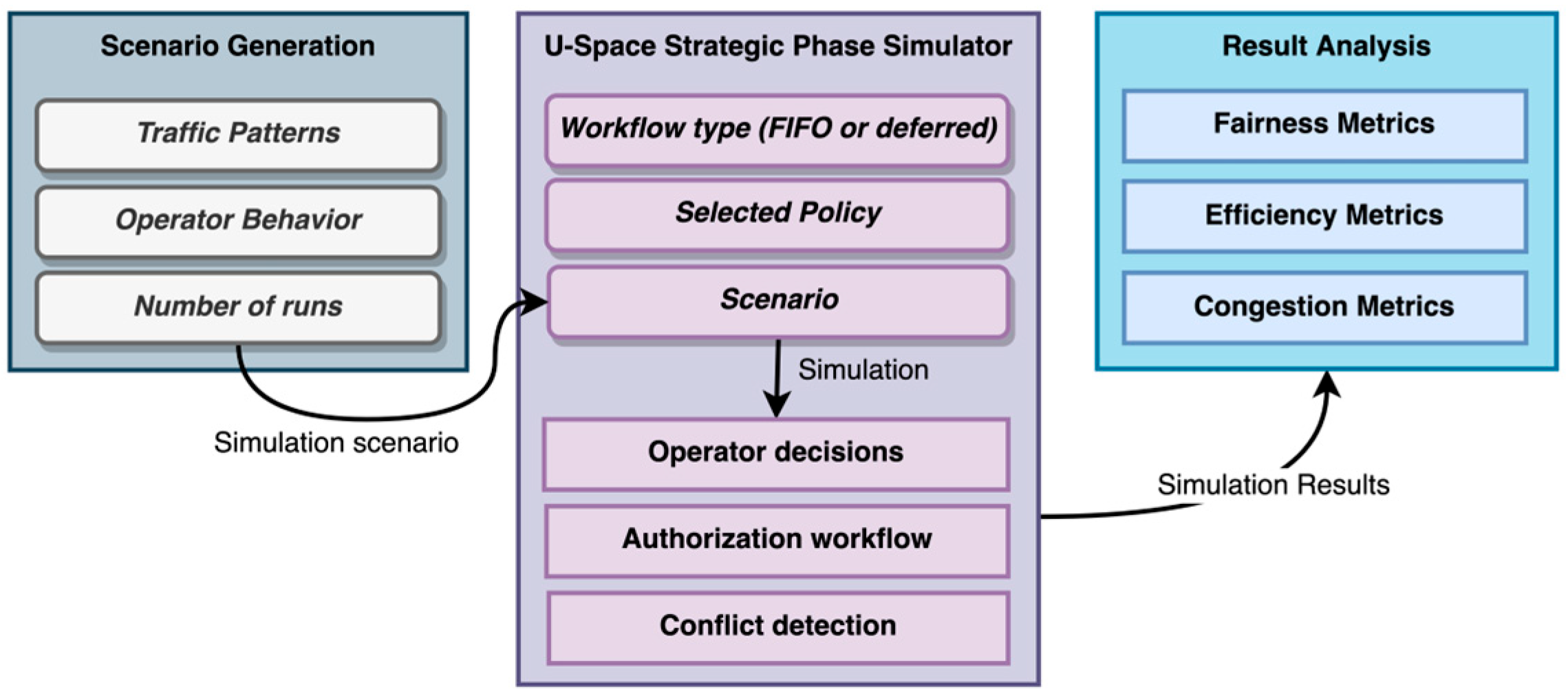Based on this approach, the experimental setup shown in Figure 8 relies on simulation to assess the validity of the proposed framework and to demonstrate its capability to successfully implement different authorization management policies within the strategic deconfliction phase.

First, a series of simulation scenarios are randomly generated to perform Montecarlo simulation. Then, the scenarios are simulated using a U-space strategic phase simulator where the proposed authorization framework has been implemented and integrated into pre-existing, regulation-mandated services. This simulator mimics the interactions and structure of the real U-space ecosystem, serving as preliminary evidence that the proposed framework could be implemented in a real U-space. Finally, the results are analyzed using a set of common metrics.

5.1. Scenario Generation

Each scenario consists of a series of runs (i.e., different random realizations of the scenario generation process for the same input parameters) to perform Montecarlo simulation. Within each run, operators with different behaviors are considered. This allows the comparison of the policies’ effect on different types of operators. As summarized in Figure 9, a combination of the following behaviors is possible:

• Operators that concentrate their operations in an area/corridors or operators with sparse operations. Areas, in which operations are generated, are randomly selected ensuring that there are no overlaps between operators.
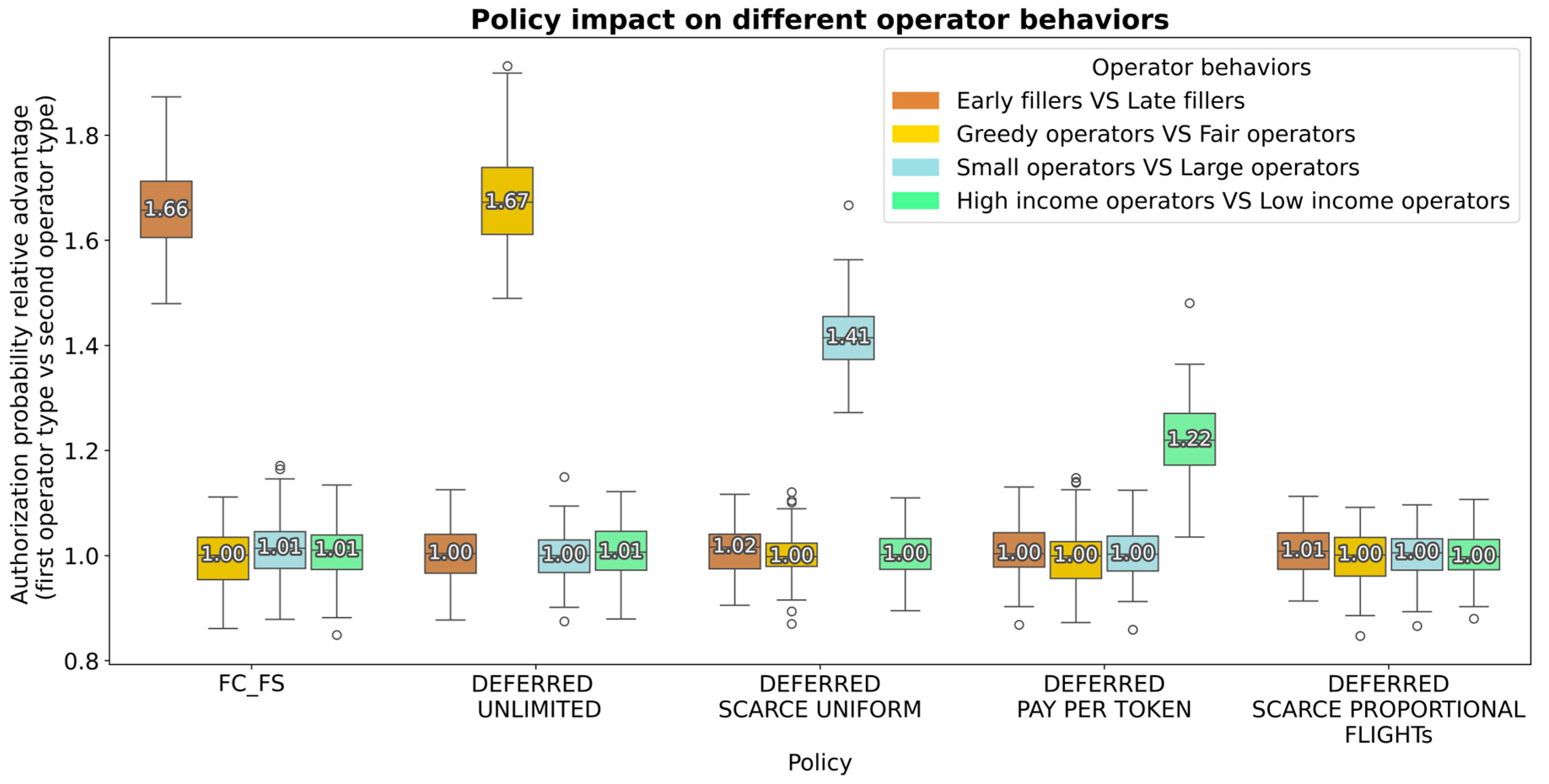
• Operators with different levels of traffic: large operators (each submitting 100 or 150 flights) or small operators (each submitting 50 flights).
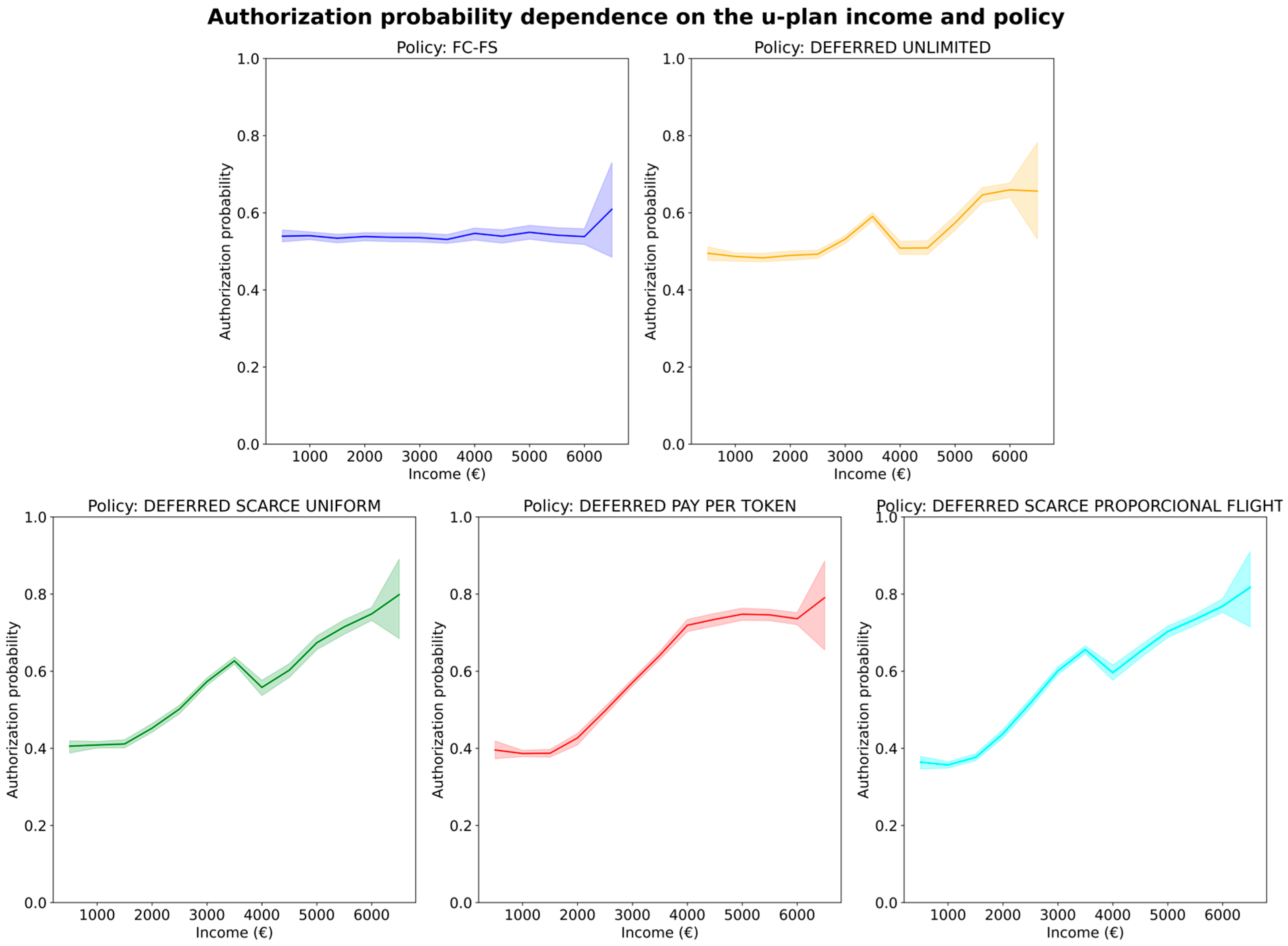
• Operators with different levels of income per flight: high income (randomly selected between 1500 and 10,000 € per flight) or low income (from 100 to 6000 €/flight).
• Operators that act fairly or that are self-interested (i.e., do not faithfully report operation preferences if not conveyed to do so).
• Operators that submit their operations early (far from the take-off time, randomly selected for each flight from 3 to 6 h before) or operators that submit them late (close to the take-off time, half an hour to 4 h before).

Drone traffic is generated in a non-restricted airspace (i.e., UAS zones, geofences or no-fly areas are not considered). This allows us to find a bound for the operation of the proposed framework since the inclusion of UAS zones would reduce the available airspace, increasing congestion and fairness problems. For each operator, traffic (i.e., the set of flight plans that will be submitted to the U-space) is generated considering a selection of the previous behaviors. This will determine the number of submitted flights, their geographical flight distribution… Individual flight geometries are generated using the authors’ previous work in [36]. Particularly, and although other types of operations could be considered, all operators perform linear flights at constant height, between two waypoints. As the base, flights are generated with a uniform distribution (random origins and destinations) within an area. This generates a scenario where congestion and conflicts are uniformly distributed. Additionally, it is also possible to stochastically generate them around hotspots to simulate airspace congestion (e.g., around vertiports or in cities). Then, to generate the required 4D volumes, flight heights and a lateral buffer of 10 m along the rectilinear trajectory are used together with a drone cinematic model to compute time constraints. 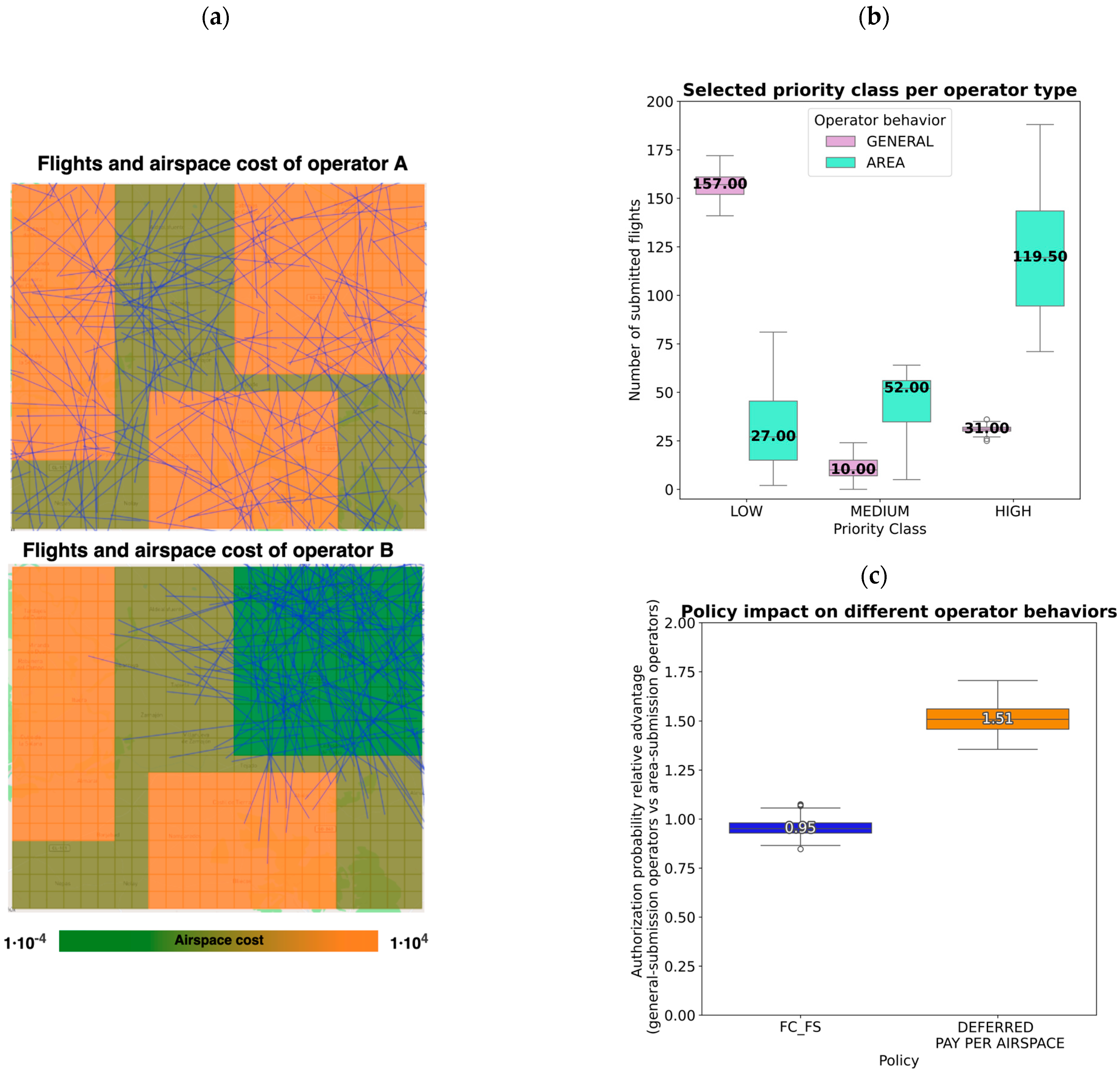An example of generated flights is shown in Figure 10 which depicts the linear flights generated for two operators’ behaviors: general distribution operators (e.g., flights in yellow) and area distribution operators (e.g., flights in brown).

In this step, two relevant properties are also stochastically assigned (from a statistical model) to each flight plan: the take-off time and the submission time (i.e., how far in advance, before take-off, the flight is submitted). Flight take-off times are uniformly distributed throughout the scenario duration. Related to this, a common RTTA value of 20 min is assumed for all operators. Finally, the value or benefit of performing each flight (i.e., having airspace allocated) for the operator is modeled in economic terms. This way, each U-plan is assigned an income value that is only obtained if the U-plan is authorized (denoted $in{c}_{fp}$, income of a given fp).

5.2. U-Space Strategic Simulator

In order to execute each of the Montecarlo runs within a scenario, a time-accelerated, parallelizable agent-based simulator of the U-space ecosystem has been used. It models all the interactions in the strategic phase in a multi-USSP deployment. To do so, the simulator consists of three different types of agents: operators, USSP and CISP agents, which will be described hereafter. This simulator has been used in the context of the SESAR SPATIO project [37], which reaches a TRL7 technological maturity level, thus ensuring that the results obtained through it are scalable and adjusted to realistic environments.

5.2.1. Operator Agents

Operator agents submit flight plans ($f{p}_f\in F{P}_{o{p}_p}=\{\mathrm{s}\mathrm{e}\mathrm{t} \mathrm{o}\mathrm{f} \mathrm{f}\mathrm{p}\mathrm{s} \mathrm{o}\mathrm{f} \mathrm{o}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{o}\mathrm{r} o{p}_p\}$) according to the defined scenario and set submission times. To do so, they autonomously assign a priority class to each flight, considering the authorization framework restrictions (i.e., available tokens and airspace cost) and their business logic. After each U-plan submission, Operator agents wait for an authorization result at t_takeoff-RTTA. In case the USSP agent detects a conflict, no deconfliction action (e.g., submission of an alternative operation) is taken by the agent and the operation is set as rejected (i.e., it cannot be flown).

As previously discussed, operator preferences (i.e., the perceived value or welfare of having each operation authorized) are understood in economic terms. Therefore, operators seek to have as many operations authorized as follows. To this end, operators must be efficient in flight token consumption and operations may be rerouted in some cases (e.g., congestion policy) to avoid high airspace cost areas. This is possible by converting the flight rerouting problem into a path search problem in which the weight of each node is related to the airspace cost. The A* algorithm is used to search for optimal paths (that minimize the token cost), subjected to the original flight plan origin and destination.

Once operations are rerouted, flight tokens are assigned to each operation. As the operator value/welfare function is related to economic benefit, operators assign priority classes to each flight plan so that their total benefit is maximized. In those cases where the number of tokens is scarce (e.g., pay-per-token policy), this is done by formulating and solving a mixed-integer linear optimization (MILP) where the objective is to maximize the overall benefit, considering an income expectation for each operation depending on its assigned priority class (which determines if that income is finally realized, i.e., if the operation is flown). In this sense, it is assumed that if operations within a certain priority class ($p{c}_i$) are approved with probability $aut{h}_{rate}^{p{c}_i}$, the total expected revenue from those operations will be the cumulative income multiplied by that probability. The defined MILP problem, detailed in the next subsection, seeks to maximize this expected benefit, subject to policy constraints (e.g., available tokens, prices…). In general, this results in operations which yield higher incomes at a lower token cost to be given higher priority classes.

Operator Business Logic Modeling

Particularly, the following MILP is used to decide which tokens to buy for each operation within the pay-per-token policy (thus implementing previous g function). In this formulation, the decision variable is denoted as $d_{f{p}_f}$ which encodes the decision taken for $f{p}_f$. At the same time, each variable consists of four possible values ($d_{f{p}_f}^{p{c}_{HIGH}}, d_{f{p}_f}^{p{c}_{MEDIUM}}, d_{f{p}_f}^{p{c}_{LOW}},d_{f{p}_f}^{NO FLIGHT}$) that can only take {0, 1} values. Respectively, they represent whether a HIGH, MEDIUM, LOW priority class should be selected or if the flight should be avoided. Also, according to previous nomenclature, the token cost of a flight is denoted as $T{C}_{f{p}_f}$, and the price of a token in each of the classes is expressed as $t{k}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{e}}\left(p{c}_{HIGH}\right), t{k}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{e}}\left(p{c}_{MEDIUM}\right), t{k}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{e}}\left(p{c}_{LOW}\right)$. From these variables, the expected revenue of a flight can be defined as

$$expected incom{e}_{f{p}_f}=in{c}_{f{p}_f} \left(aut{h}_{rate}^{p{c}_{HIGH}}·d_{f{p}_f}^{p{c}_{HIGH}}+aut{h}_{rate}^{p{c}_{MEDIUM}}·d_{f{p}_f}^{p{c}_{MEDIUM}}+aut{h}_{rate}^{p{c}_{LOW}}·d_{f{p}_f}^{p{c}_{LOW}}+0·d_{f{p}_p}^{NO FLIGHT}\right)$$

(36)

$$cos{t}_{f{p}_f}=T{C}_{f{p}_f}·\left(t{k}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{e}}\left(p{c}_{HIGH}\right)·d_{f{p}_f}^{p{c}_{HIGH}}+k_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{e}}\left(p{c}_{MEDIUM}\right)·d_{f{p}_f}^{p{c}_{MEDIUM}}+t{k}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{e}}\left(p{c}_{LOW}\right)·d_{f{p}_f}^{p{c}_{LOW}}+0·d_{f{p}_f}^{NO FLIGHT}\right)$$

(37)

$$expected revenu{e}_{f{p}_f}=expected incom{e}_{f{p}_f}-cos{t}_{f{p}_f}$$

(38)

where Equation (36) defines the expected income as a function of the selected priority class, Equation (37) defines the expected economic cost of purchasing the required tokens depending on the priority class and Equation (38) computes the difference to obtain the expected revenue. Finally, the MILP is defined as

$$\max \sum _{\forall f{p}_f \in F{P}_{o{p}_f}}expected revenu{e}_{f{p}_f}$$

(39)

$$\mathrm{subject} \mathrm{to} d_{f{p}_f}^{p{c}_{HIGH}}+d_{f{p}_f}^{p{c}_{MEDIUM}}+d_{f{p}_f}^{p{c}_{LOW}}+d_{f{p}_f}^{NO FLIGHT}=1; \forall f{p}_f\in F{P}_{o{p}_p}$$

(40)

$$expected revenu{e}_{f{p}_f}\ge 0; \forall f{p}_f\in F{P}_{o{p}_p}$$

(41)

where Equation (39) formulates the objective function (i.e., maximization of the total revenue), the restriction in (40) guarantees that only one decision is taken and the one in (41) ensures that the operator does not incur losses.

5.2.2. USSP Agents

USSP (U-space Service Provider) agents manage the authorization workflow, detect conflicts between submitted operations and take a final authorization decision. The Flight Authorization Service (FAS) cited in Section 3.4 is simulated within this agent and implements two authorization workflows:

• the regulation-mandated FC-FS (which will serve as a baseline),
• and the proposed workflows (i.e., BTA and GTA) with deferred authorization and multiple priority queues (N = 3, denoted LOW, MEDIUM and HIGH priorities for better legibility).

The existence of special operations is not considered. The Strategic Conflict Detection (SCD) service is also implemented within the USSP agent. It detects conflicts by checking for 4D volume intersections between the flight plan under analysis and other possible conflicting flight plans (considering the different priority classes if needed). In the absence of conflicts, a flight plan is approved. A known limitation of the simulation platform is that a Strategic Conflict Resolution service is not available within the USSPs. Thus, conflicting U-plans are automatically rejected without considering the effect of a possible operation replanning to avoid conflicts (i.e., strategic deconfliction, either by the USSP or by the operator). From the results point of view, this implies that the obtained authorization data will correspond to the worst-case scenario and that better authorization rates may be obtained as a result of operation changes due to the deconfliction process.

5.2.3. CISP Agent

Finally, the CISP (Common Information Service Provider) agent simulates a centralized entity extending the role of the CISP by including data exchange and fairness management features. Thus, this agent includes a centralized Flight Database (FD) and the Authorization Policy Service (APS) functionality. USSPs register in the CISP agent all submitted flight plans and update them accordingly once a final authorization decision is taken. Token distribution and airspace cost setting (using a 1 km x 1 km cell size) is performed here.

To demonstrate the flexibility of the proposed framework, the six policies detailed in Section 4 have been implemented within the agent:

• the unlimited tokens distribution policy (hereby denoted UNLIMITED, and described in Section 4.1),
• the scarce tokens policy with uniform distribution among operators (i.e., SCARCE_UNIFORM, explained in Section 4.2),
• the scarce tokens policy with non-uniform distribution based on a proportional assignment based on historical flight patterns (i.e., SCARCE_PROPORTIONAL_FLIGHTS, depicted in Section 4.3)
• the pay-per-token policy (i.e., PAY_PER_TOKEN, laid out in Section 4.4),
• a pay-per-airspace policy based on the GTA workflow with a scarce, uniform number of tokens per operator (i.e., PAY_PER_AIRSPACE, proposed in Section 4.5),
• a congestion management policy also based on the GTA workflow with a scarce, uniform number of tokens per operator (i.e., CONGESTION, presented in Section 4.6).

Implementation details for each policy have already been commented on in the referenced subsections. Moreover, the CISP agent is also able to work with an FC-FS authorization workflow (as detailed in Section 1) for comparison purposes.

5.2.4. Simulation Workflow Summary

In summary, Figure 11 shows the different interactions and processes carried out by the agents described in this section throughout the simulation process. First, the simulation scenario is generated (interactions 1 to 4) by defining the flight plans associated with each operator (including flight submission times and associated economic benefit). Then, at the beginning of the simulation, the CISP agent performs token distribution and airspace cost setting according to the simulated policy (interactions 5 to 9). As a result, the operators’ token allocation decision-making process is simulated by means of an MILP that assigns tokens to each operation. Then, each operation is sent to the USSP at its associated submission time. The USSP agent checks that the number of tokens pledged for the operation are sufficient and registers the operation in the CISP (interactions 10 to 14). At this time, no authorization decision is returned. Finally, at the t_takeoff-RTTA of each operation (interactions 15 to 17), the USSP checks for conflicts with other operations taking into account priority classes. Depending on this, the operation is authorized or rejected. In the latter case, a possible replanning is not considered.

5.3. Evaluation Metrics

Once results are obtained (in terms of which priority classes have been assigned to each flight, which flights are finally authorized…) several metrics may be used for their analysis from both the fairness, congestion and efficiency points of views.

5.3.1. Fairness Metric

As previously discussed in Section 2, several metrics exist to assess fairness in UAM use cases (e.g., number of reversals from FC-FS, air or ground delays). However, it can be argued that those are not applicable to the U-space ecosystem and to this validation setup in particular, since operations are not rerouted/delayed but either authorized/rejected. Furthermore, an adequate definition of such a metric is a challenging endeavor since its suitability would depend on the notion of fairness selected by U-space authorities (from those explored in Section 4), which lies outside of this article’s scope.

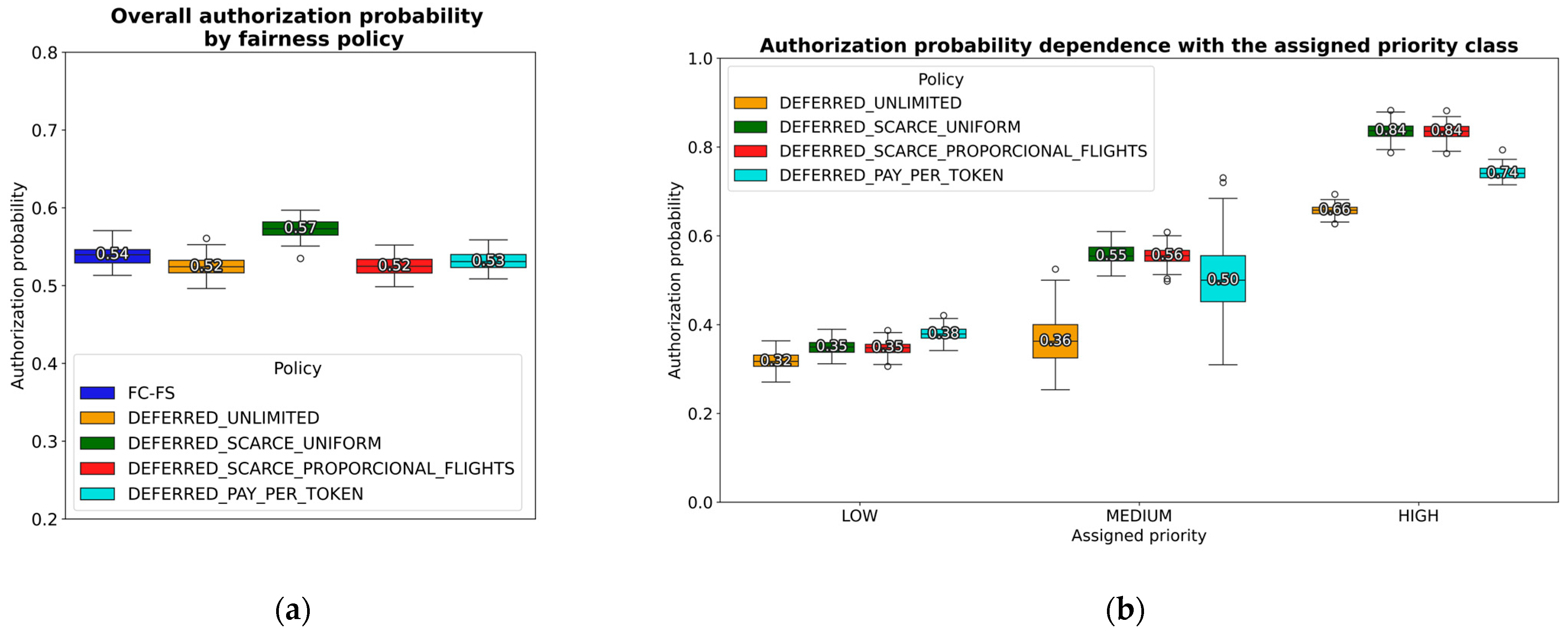
Accordingly, and just for the purpose of evaluating whether the proposed framework effectively induces incentives or disincentives across different categories of operators, it is possible to compare the proportion of flights that each operator has successfully authorized. This metric is named the flight authorization rate (or authorization probability) and measures the number of authorized flights ($N_{\mathrm{a}\mathrm{u}\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{z}\mathrm{e}\mathrm{d}})$ over the total number of submitted flights ($N_{\mathrm{s}\mathrm{u}\mathrm{b}\mathrm{m}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{d}}):$

$$aut{h}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}}={\displaystyle \frac{N_{\mathrm{a}\mathrm{u}\mathrm{t}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{z}\mathrm{e}\mathrm{d}}}{N_{\mathrm{s}\mathrm{u}\mathrm{b}\mathrm{m}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{d}}}} \in [0, 1]$$

(42)

If this figure is computed for groups of operators exhibiting similar behavior (e.g., small operators) and compared against the metric obtained for other operators with complementary behaviors (e.g., large operators), it is possible to analyze whether the framework and selected policy treats them equally (thus reaching a given notion of fairness) or whether it effectively incentivizes one behavior over the other. Alternatively, if the metric is computed based on submission time, it can be analyzed whether the framework mitigates the FC-FS bias in current regulation. Additionally, this figure may also be computed, filtering by priority class to analyze if the operator preferences (expressed through the priority class selection) are respected in the final authorization result.

An economic perspective may be alternatively adopted by comparing the rate of benefits accrued by each operator with the total potential benefits had all operations been approved. However, since the economic value of each operation is used as a signal of its perceived value (see Section 5.2.1), the results are expected to align with those obtained using the previous metric. Also, future research could explore a comparative analysis of results expressed in absolute terms (i.e., number of authorized flights) versus relative terms (i.e., authorized flights) in order to contrast an egalitarian approach with a min–max fairness strategy.

5.3.2. Congestion Metrics

Congestion management requires different metrics from fairness management, even if both can be addressed jointly with the proposed framework. In this sense, airspace congestion has already been defined in Equation (33) as the sum of the airspace–time occupied by all authorized operations in a given 4D volume. This way, it is possible to compute the value for a set of cells within a grid to detect congestion hotspots and analyze if they are removed by the policy proposed in Section 4.6.

5.3.3. Efficiency Metrics

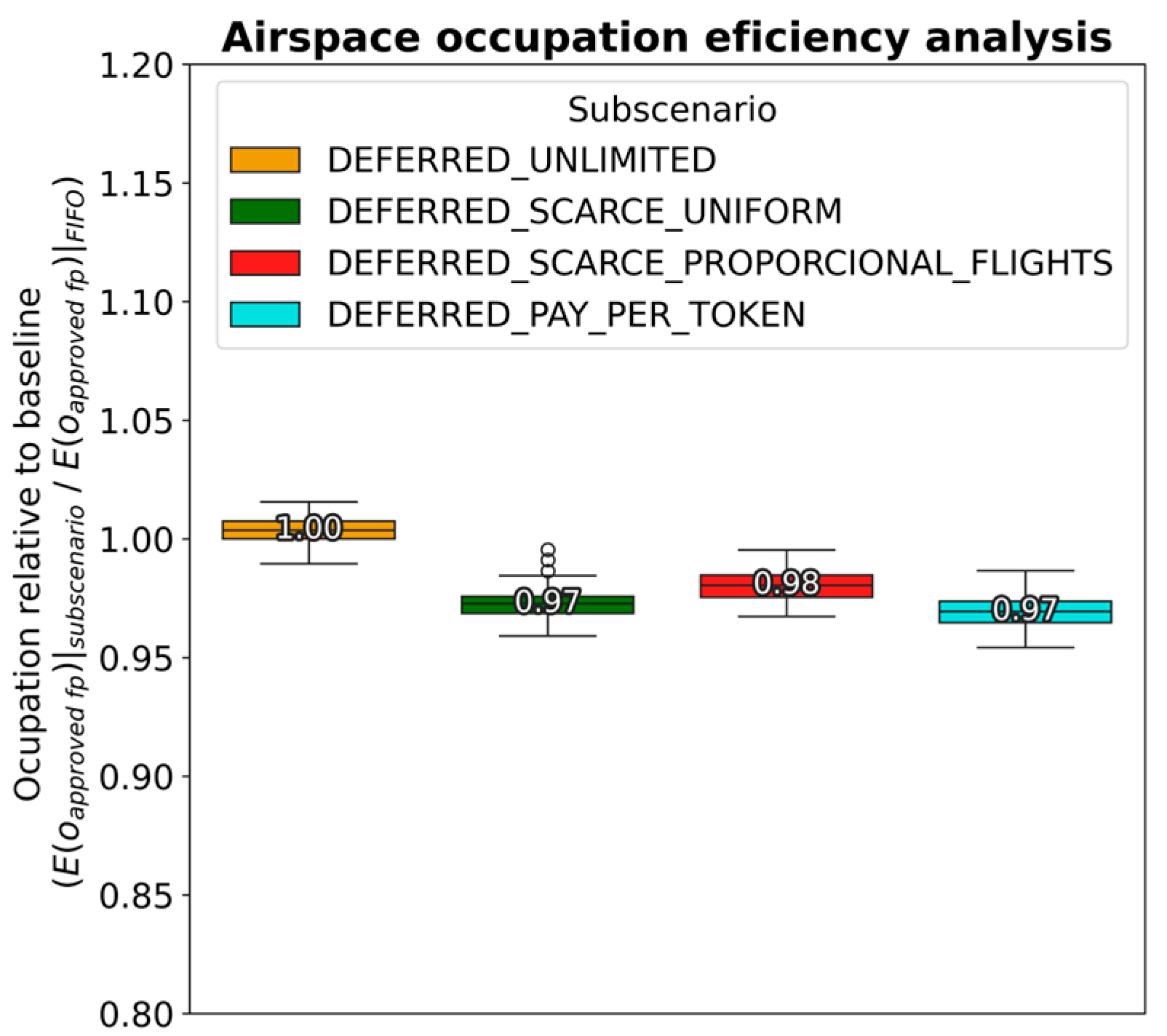
Finally, in order to assess if the proposed framework manages to promote efficiency, the overall number of authorized operations can be used as a metric. If a policy increases the number of approved operations compared to a baseline with the same available 4D airspace, it improves airspace usage efficiency. That is, the more missions that can be flown, the more efficient the use of airspace. In parallel, airspace use efficiency can be measured from the average airspace occupation of approved flight plans (i.e., $\mathrm{E}\left(o_{fp}\right){\mathbf{|}}_{fp \mathrm{i}\mathrm{s} \mathrm{a}\mathrm{p}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{d}}$). In this case, the more efficient use of airspace will result in a lower occupation per flight plan.

6. Results and Discussion

Using the previous experimental setup, three different scenarios have been simulated. Scenarios are described in

Table 1. Scenario description.

Scenario	Tested Operator Behaviors	Tested Workflow and Policies
1	A combination of fair/greedy, early filler/late filler, low flights/high flights, low-income/high-income operators	FC-FS, UNLIMITED, SCARCE_UNIFORM, SCARCE_PROPORTIONAL_FLIGHTS, PAY_PER_TOKEN
2	Local (area-based) operators vs. general operators	FC-FS, PAY_PER_AIRSPACE
3	Not Applicable	FC-FS, CONGESTION

. In each one, the FC-FS workflow is used as a baseline to compare it against the proposed workflow and policies, showing how they allow the implementation of different notions of fairness. The first scenario (Section 6.1) demonstrates how the proposed deferred authorization workflow manages to break the FC-FS bias when authorizing flights; it also showcases how the BTA workflow can be used to implement different fairness policies that benefit certain operator behaviors and how operators can inform their preferences through an appropriate selection of priority classes (in order to optimize their benefit). In turn, the second scenario (Section 6.2) explores the GTA workflow and proves how geographical incentives can be used to benefit local operators. Finally, the third scenario (Section 6.3), presents how the proposed framework enables the joint management of fairness and congestion, allowing for pre-emptive demand and capacity balancing.

Each scenario consists of 100 Montecarlo runs to ensure statistical soundness of the results. Within each run, 16 operators are simulated with a total of 1600 flights over 24 h, in an area of around 500 km². Different operator behaviors are considered in each case to analyze how they are treated by the selected policy. A dataset containing each scenario and the simulated results is available as Supplementary Material of this paper.

6.1. Scenario 1

This validation scenario aims to demonstrate the implementation of different fairness policies by exclusively using the token distribution logic (BTA workflow). For this purpose, the same scenario has been run for baseline (FC-FS) operation and for five different policies (as shown in Table 1).

A first element to verify is whether the proposed mechanism reduces or eliminates the dependence between the probability of authorization and the flight plan submission time. This is explored in Figure 12 which depicts the authorization rate for flights submitted at different times before take-off. It can be seen how in the FC-FS case (or FC-FS, in dark blue) the authorization probability strongly declines as flights are submitted closer to the take-off time (i.e., with less time in advance). Conversely, and as desired, in the rest of the simulated cases (which implement the proposed deferred authorization workflow) this dependency is almost eliminated, as demonstrated by the horizontal lines. In non-FC-FS cases, a slight authorization drop off can be observed when the submission time is very small. This behavior is related to the RTTA value: if a U-plan is submitted very close to its t_takeoff-RTTA, there is a chance that other operations may have been assessed for authorization without considering it. This may happen if their take-off time is slightly earlier than the one of the last submitted operation t_takeoff (i.e., their RTTA is reached before the last operation arrives). As a result, the operations that are sent close to their RTTA may have a slight disadvantage with respect to the rest, and the visualized border effect appears.

This improvement in fairness is achieved without significantly impacting the overall authorization rate. This can be seen in Figure 13a where the average authorization probability remains almost constant regardless of the chosen workflow and policy. Another advantage of the proposed authorization mechanism is that operators can inform the U-space system of their flight priorities, and these preferences can be considered in the authorization process. In this sense, Figure 13b shows how operations submitted to different priority classes are treated differently in terms of authorization success. It can be seen that if an operator informs the system of the criticality of an operation by assigning a high priority class to it, significantly higher approval probabilities are obtained. Conversely, low priority operations obtain lower authorization probabilities. This behavior is consistent notwithstanding the selected token distribution policy. In addition, since the utility of each operation has been aligned with its economic value, it would be expected that those operations with a higher income would more likely be approved. To this end, the income and authorization probability dependency has been depicted in Figure 14. Indeed, it is shown that contrary to the FC-FS approach where it is not possible to encode each operation value (i.e., as demonstrated by the obtained horizonal line), those flights which yield higher incomes are authorized more (as evidenced by the increasing trends for the rest of the policies).

So far it has been demonstrated that the proposed authorization mechanism breaks the FC-FS dependency, allows operators to express their preferences and does so without affecting the overall authorization rate. The following figure (Figure 15) allows the analysis of the impact on efficiency. To do so, for each of the tested policies within the proposed framework, the average airspace occupation per authorized operation compared against the occupation in the FC-FS workflow is depicted. It can be seen that the proposed mechanism together with an appropriate policy can also slightly increase the efficiency of the U-space systems (i.e., relative values are below 1). This happens for token distribution policies that limit the number of tokens (i.e., SCARCE_UNIFORM, SCARCE_PROPORTIONAL_FLIGHTS, and indirectly for the PAY_PER_TOKEN case). In those cases, operators try to maximize their profit by prioritizing those flights that yield a higher revenue with a lower consumption of tokens. Thus, they are implicitly selecting the most efficient operations. Efficiency improvements are small since the duration of operations is similar. However, if operators with different levels of efficiency were introduced, it would be expected that more efficient operators would be able to authorize a greater number of operations.

Finally, Figure 16 showcases the flexibility of the proposed authorization workflow in implementing different fairness notions. In it, the relative authorization advantage obtained by operators with different behaviors (color legend) is shown for different workflows (FC-FS) and token distribution policies. For example, in the regulation-mandated FC-FS case, operators who send flight plans early achieve an authorization rate that is on median 1.66 times of those who send operations later. As previously demonstrated and also shown in this graph, this advantage is eliminated if the proposed framework is implemented regardless of the fairness policy. Nevertheless, the choice of policy by regulators is crucial; depending on the choice, either some behaviors are incentivized over others, or fairness is obtained. For instance, if the number of available tokens is not limited (i.e., UNLIMITED), those operators who do not faithfully report the criticality of their trades benefit. However, even if tokens are limited to avoid the latter, other dependencies with the number of flights (if tokens are evenly distributed, i.e., SCARCE_UNIFORM) or with operators’ revenues (if a price per token is introduced, i.e., PAY_PER_TOKEN) may be introduced. In the former case, small operators can take advantage of having a larger number of tokens per submitted flight to enter flights into higher priority classes. In the latter, operators with higher incomes can pay for more tokens than low-income operators. Overall, a scarce token distribution based on the historical flight patterns of operators (i.e., SCARCE_PROPORTIONAL_FLIGHTS) seems to eliminate these biases and achieve fairness. This statement assumes fairness to mean obtaining a similar authorization rate for all operator cohorts. However, other notions of fairness could also be considered and analyzed.

In sum, scenario results show that the proposed framework meets its expectations in terms of FC-FS bias reduction, preference sharing and flexibility. Also, by implementing different fairness policies through the distribution of tokens (BTA workflow), it is possible to incentivize different behaviors or types of operators over others. Therefore, it can be concluded that the proposed mechanism allows an increase in the fairness of the system, given an appropriate choice of policy. Moreover, it does so without compromising safety, since the conflict detection process ensures that authorized operations are free of 4D intersection, as does the FC-FS mandated authorization process.

6.2. Scenario 2

The second scenario (results shown in Figure 17) is aimed at showing the implementation of incentives per operator based on the cost of airspace (GTA workflow). In this case, two types of operators are simulated: some that fly mainly in limited geographical areas (area operator) and others that operate throughout the entire area under study (general operator) are simulated. Following the airspace reservation policy (i.e., PAY_PER_AIRSPACE), the former type of operators is able to reserve their area of operation.

As detailed in Section 4.5, airspace reservation is encoded through an operator-dependent airspace cost. This cost is shown as a 2D heatmap in Figure 17a. It depicts how operator B, of the “area” type, has a very low airspace cost (green grid cells) in the reserved area that concentrates its flights. The remaining areas have nominal (gold cells) or high costs (orange cells) depending on whether the area is reserved by other operators. On the other hand, operator A, of the “general” type, can only operate at normal cost in a reduced set of zones because they have been reserved by other operators, and is disincentivized to operate in those zones.

The implementation of these geographical incentives has an impact on the selection of priority classes per operator that is shown in Figure 17b. It can be seen how area-type operators can send most of their operations with high priorities (as they have a very low airspace cost in the areas where they operate). On the contrary, general operators have to limit themselves to low priority classes as they do not have reserved portions of airspace. As a result of this operator-dependent priority class distribution, different authorization priorities are obtained for each operator type. Figure 17c depicts the relative authorization rate of area operators over general operators for the baseline (i.e., FC-FS) and PAY_PER_AIRSPACE policies. It can be seen how geographical-based incentives manage to prioritize area-based operators over general operators. The former manages to authorize a median of 51% more flights than the general operators.

6.3. Scenario 3

Finally, the third scenario (whose results are depicted in Figure 18) shows how the proposed framework enables us to simultaneously enforce fairness and perform demand–capacity balancing. Indeed, thanks to the use of geographic incentives (i.e., GTA workflow with CONGESTION policy), it is possible to pre-emptively avoid congestion. To implement this policy, the aggregate demand of all flight plans considered in a simulation run is used to estimate congestion in different cells of a geographical grid. In this sense, Figure 18a showcases the congestion estimates as a heatmap and reveals the existence of several flight hotspots (orange-colored areas). This estimate is used to set high airspace costs in those cells that are congested (as detailed in Section 4.6).

Consequently, operators are compelled to avoid those zones by rerouting (as explained in Section 5.2.1) if it is compatible with their business logic (i.e., if they are able to reroute their operations). As a result, drone occupation density is dispersed throughout the whole area. This is supported by Figure 18b which depicts the resulting occupation heatmap after applying the congestion management policy. It clearly shows that the previous orange hotspots have been dissolved. Statistically, Figure 18c estimates a probability density function for the airspace occupation metric. In it, the reference distribution (i.e., FC-FS, in blue) presents a tail with high occupation values (corresponding to the cells with hotspots) while the distribution with the proposed protocol (in red) concentrates the occurrences in lower occupation values.

However, this reduction in airspace occupation per cell could be due to a significantly lower flight authorization rate. For this purpose, Figure 18d compares the authorization probability in the FC-FS case with the proposed mechanism. Although there has been a reduction in the authorization rate when applying the congestion management mechanism, this change is small and could be explained by the increase in total occupation shown in Figure 18e. Indeed, by having to reroute operations to avoid congested areas, operations are longer and new conflicts may arise, which explains the change.

In conclusion, these last two scenarios demonstrate the power of the proposed GTA workflow in jointly managing fairness issues and other relevant aspects such as congestion.

7. Conclusions

As the number of drone operations increases, it is expected that issues related to inter-operator fairness and congestion management, among others, will arise. However, the strategic flight plan authorization process currently set out in the European regulation is not adequate to deal with these issues. The existing literature only deals with this problem broadly, without proposing a feasible comprehensive technical framework that is somehow compatible with European regulations. Also, scalability issues are overlooked in some cases. As an alternative, this article has proposed an efficient, fair, simple and scalable alternative authorization workflow to address this problem.

The proposed alternative is articulated around a deferred authorization phase based on the determination of a time (RTTA) in which all operations in potential conflict are evaluated simultaneously. In addition, it introduces different priority classes so that operators may guide the U-space system by indicating their preference in each operation according to their business logic. Access to each priority class is controlled by a set of scarce tokens that are distributed among operators. Each operation sent to the U-space system must be accompanied by a sufficient number of tokens related to airspace occupancy in a way that promotes efficiency and a correct declaration of priorities. Furthermore, the number of tokens also depends on the occupied area and when it is occupied, so that temporal and geographical incentives can be established.

This comprehensive logic allows for the joint implementation of a broad set of fairness and capacity management policies (e.g., uniform or operator-dependent distribution of tokens, assigning an economic value to tokens or to airspace, and congestion disincentivization). Its technical feasibility has been demonstrated by discussing the integration of the Authorization Policy Service into the U-space ecosystem. Further supporting its viability, the proposal has been implemented into a simulated U-space ecosystem that has served as a test bed to compare the previous policies with the regulation-mandated FC-FS approach. Furthermore, it allows its integration in distributed U-space systems as it decouples authorization decisions from each of the USSPs, making it a scalable system as well. Finally, the proposed mechanism is simple and transparent from the operator’s point of view, abstracting the operator from the underlying logic of fairness management through the use of tokens. In short, the proposed framework meets the desiderata previously described in [8] for an alternative authorization system.

The results, based on simulations, quantitatively demonstrate how the proposed framework eliminates the FC-FS dependency imposed by the regulation-mandated framework. In this sense, when comparing the regulation framework with the proposed one, the relative advantage of early-filling operators over late-filling operators decreases from a median value of 1.66 to around 1.00 (i.e., no advantage). Furthermore, the findings (in Scenario 1) show that operators are able to prioritize their operations according to an economic benefit logic, such that missions with higher value are more likely to be authorized. Similarly, the comparison across different simulation scenarios confirms that the framework can be used to incentivize or disincentivize groups of operators with distinct behavior patterns, in alignment with a fairness criterion defined by the authorities. Finally, as seen in Scenario 3, the framework is proven to be effective in reducing the occurrence of demand hotspots, thereby contributing to congestion management. Therefore, the proposed alternative goes beyond the existing literature by introducing a novel framework that is compatible with European regulation while surpassing the FC-FS model and managing congestion. As an added advantage, it also embraces some pre-existing proposals (i.e., pay-per-fly, reserved air corridors) unifying their implementation into a single framework.

As for the limitations, the validity of the proposed framework has only been explored from a formal and technical point of view. The opinions of the regulators and the operators themselves on its possible practical implementation have not been gathered. On the other hand, the article has identified different fairness policies that have been proven to be implementable in the proposed framework. However, it has not carried out an exhaustive comparison of them nor has it selected an optimal policy that would be desirable to implement in real U-space systems. Future work could consist in implementing a token allocation policy based on a mixed-integer lineal programming optimization model, assisted by simulation results to estimate the authorization rates obtained in each priority class. Also, Reinforcement Learning models trained within the simulated U-space environment could yield optimal token allocation policies. Even if not mandated by regulation, another limitation of the study is that Strategic Conflict Resolution services have not been considered. Future studies should analyze how it interacts with the proposed token-based authorization framework, possibly requiring limitations on what changes are allowed on deconflicted operations. Finally, the robustness and fault tolerance of the framework in the face U-space communication failures or attempts by operators to abuse it should be analyzed. The study of these gaps as future work will bring the proposal closer to its possible implementation in U-space systems.