Research of Hierarchical Vertiport Location Based on Lagrange Relaxation
Abstract
1. Introduction
2. Problem Description and Modeling
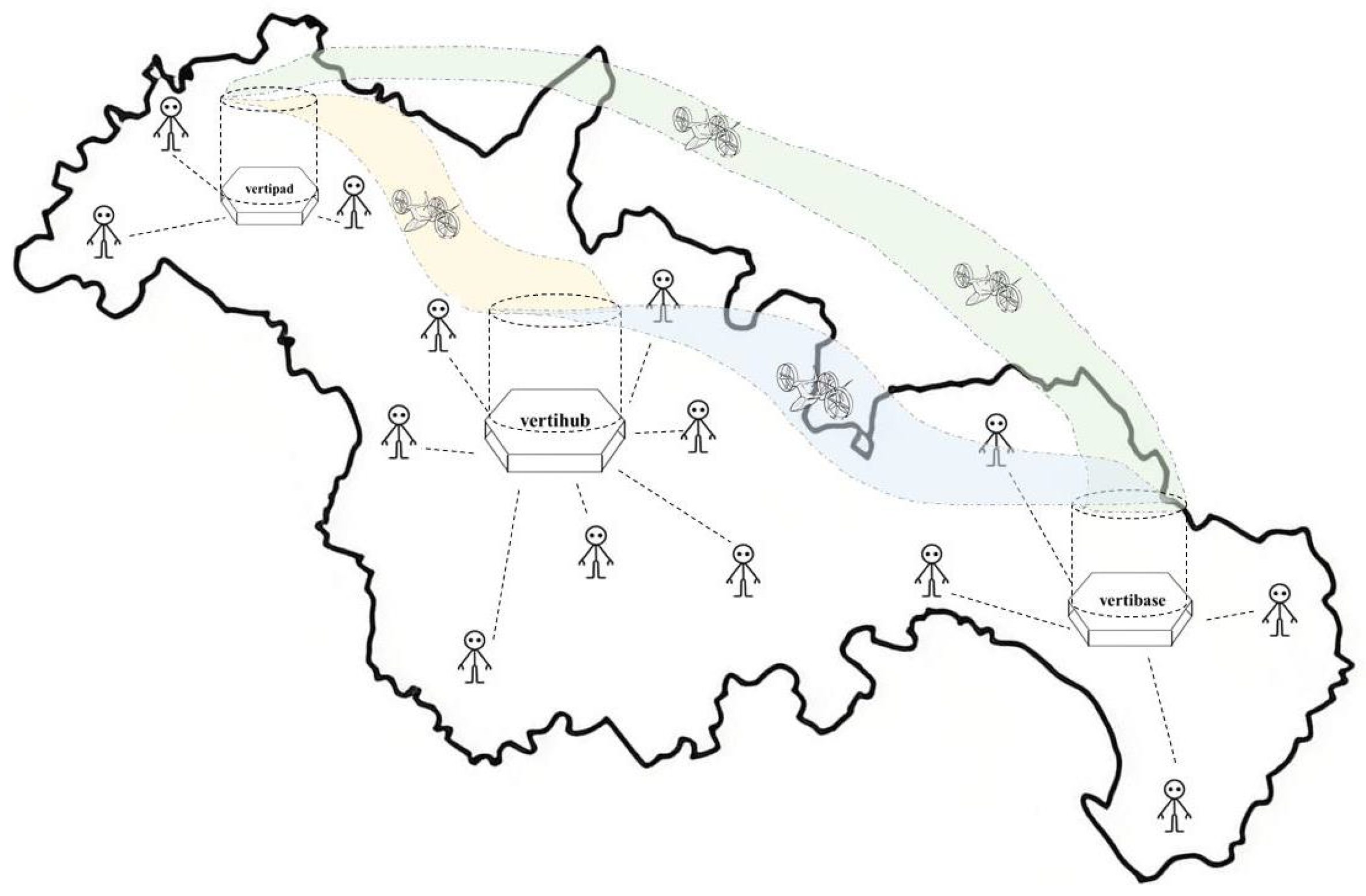
2.1. Problem Description
2.2. Model Formulation
2.3. Model Reformulation
3. Optimization Algorithm
3.1. Lagrange Relaxation
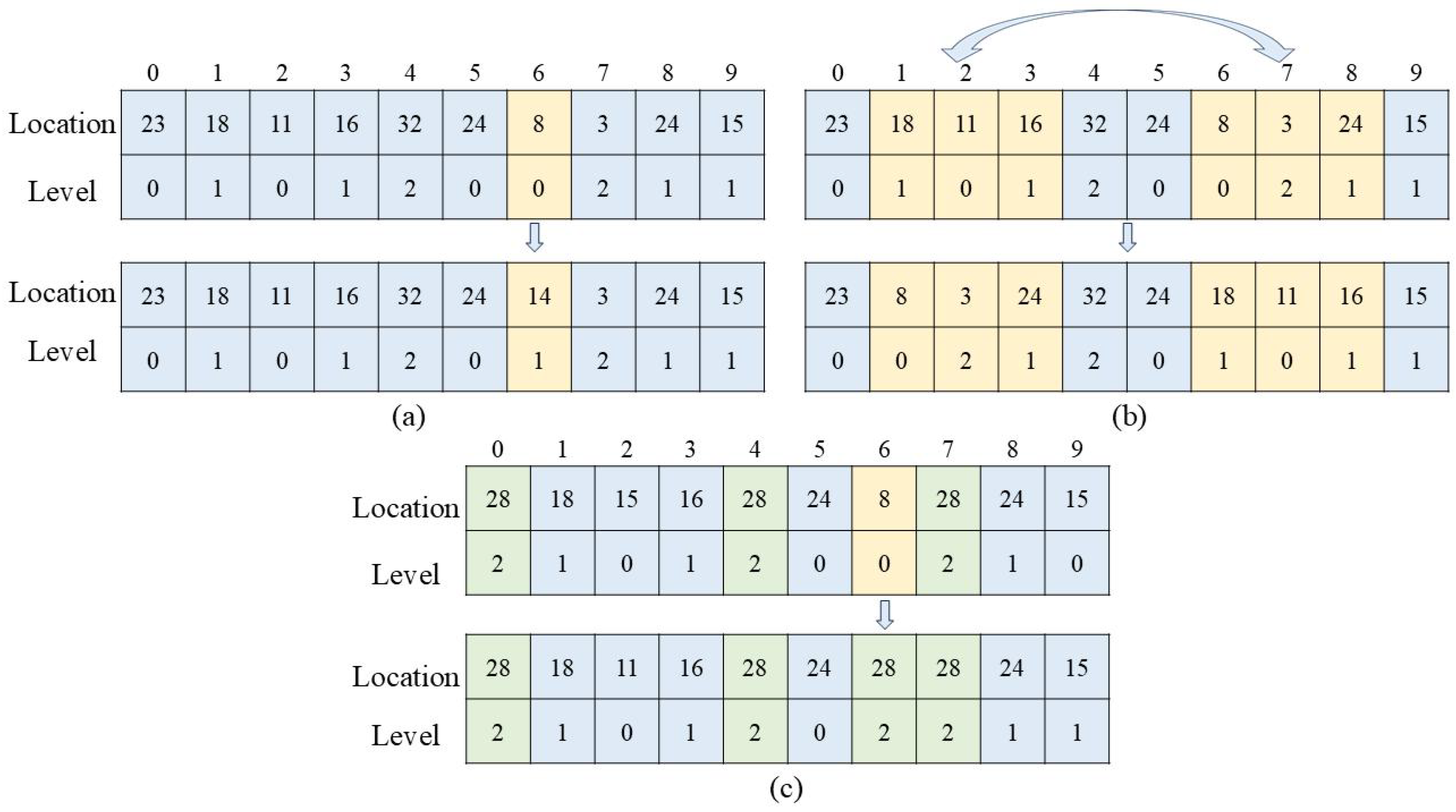
3.2. Variable Neighborhood Search
4. Experimental Design and Result Analysis
4.1. Experimental Design
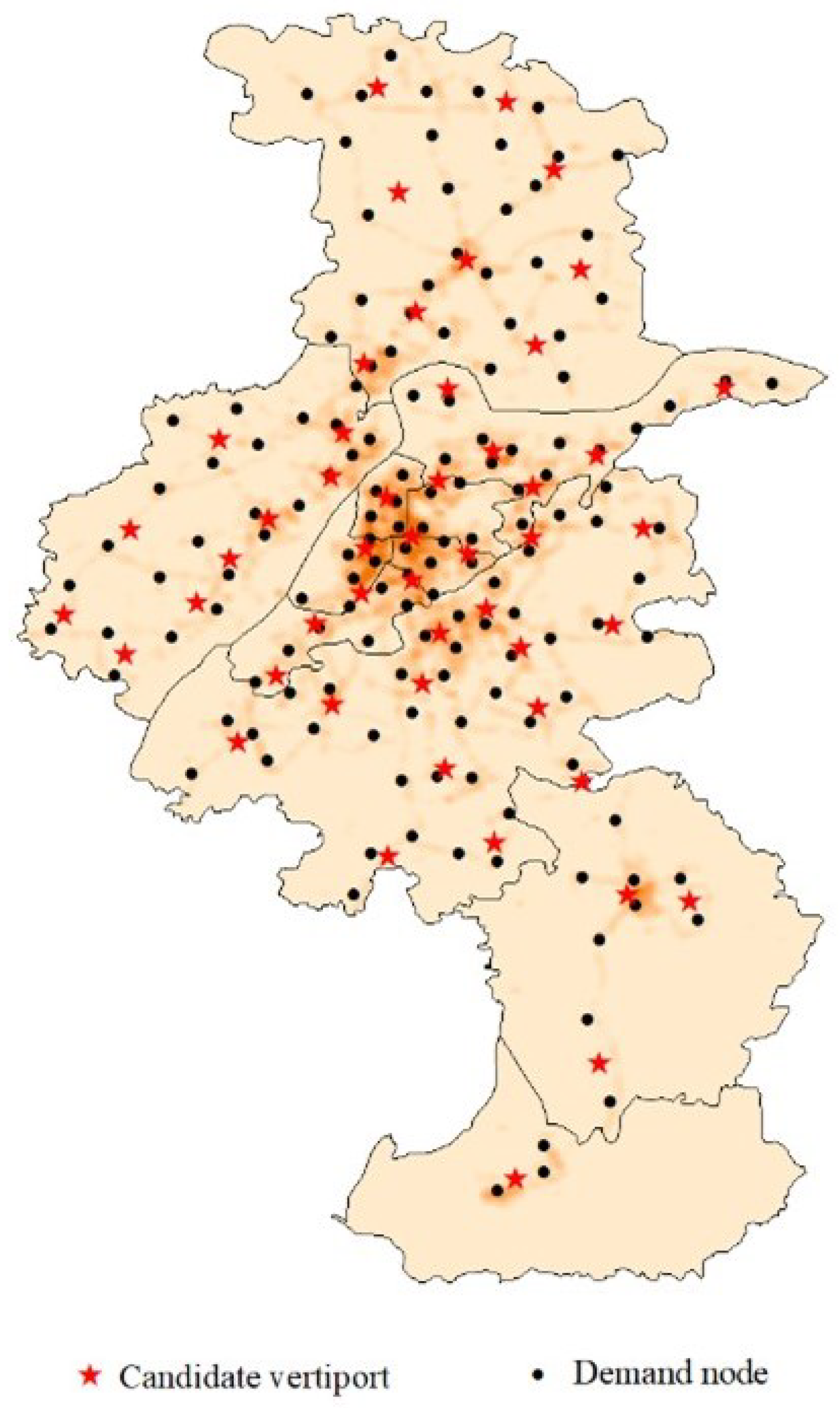
4.1.1. Selection of Candidate Vertiports and Demand Points
4.1.2. Demand Quantity Setting
4.1.3. Parameter Setting
4.2. Experimental Result and Analysis
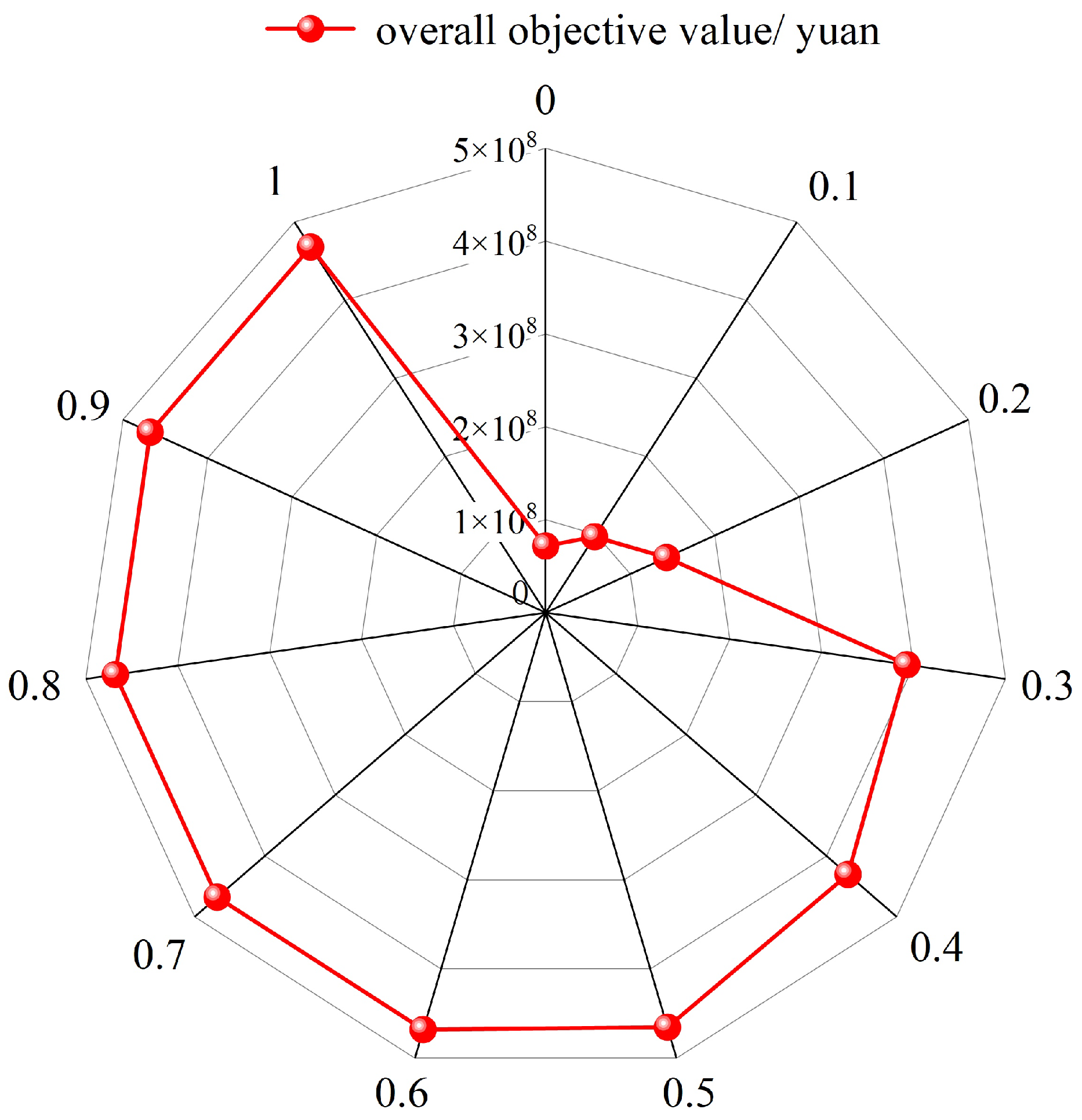
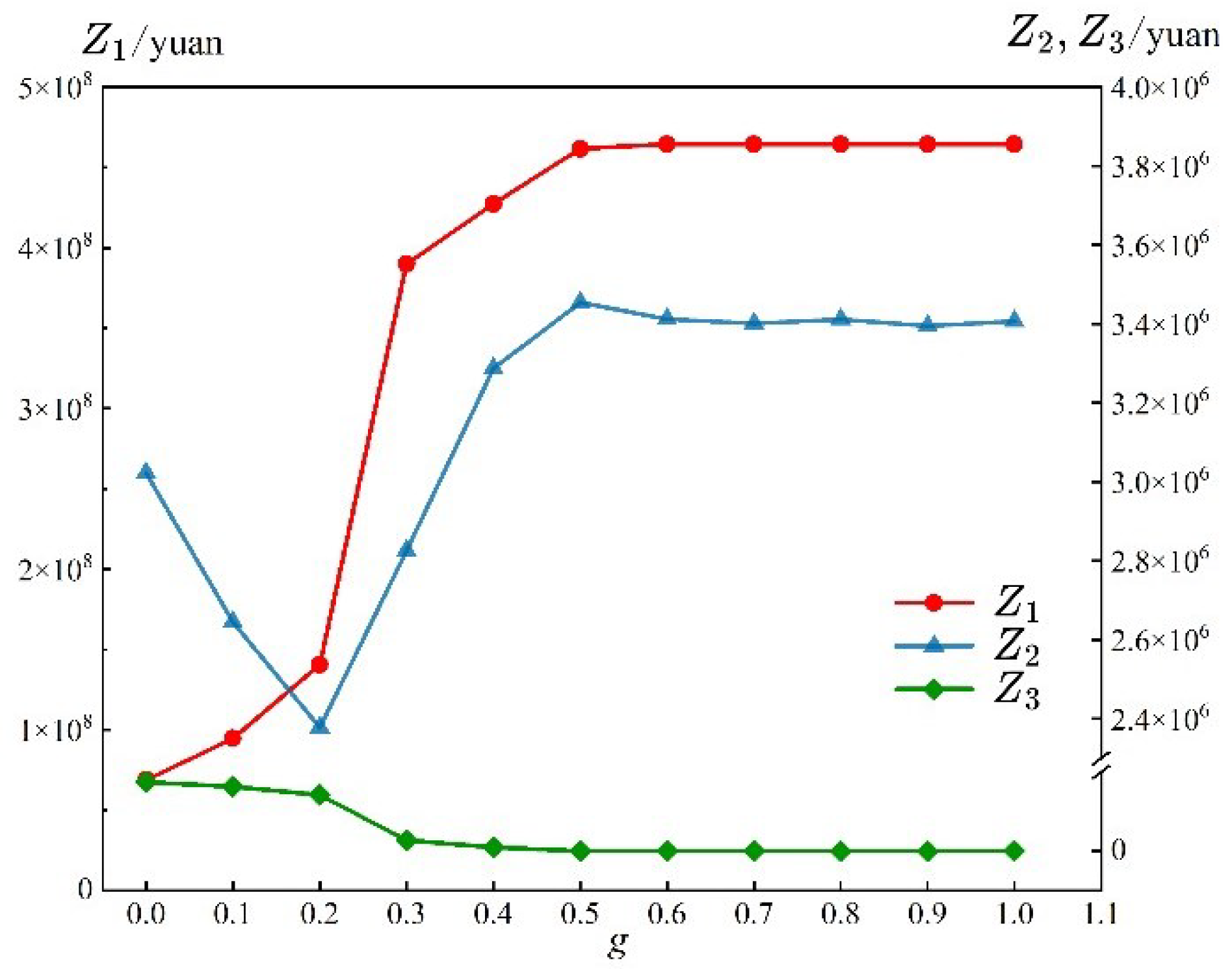
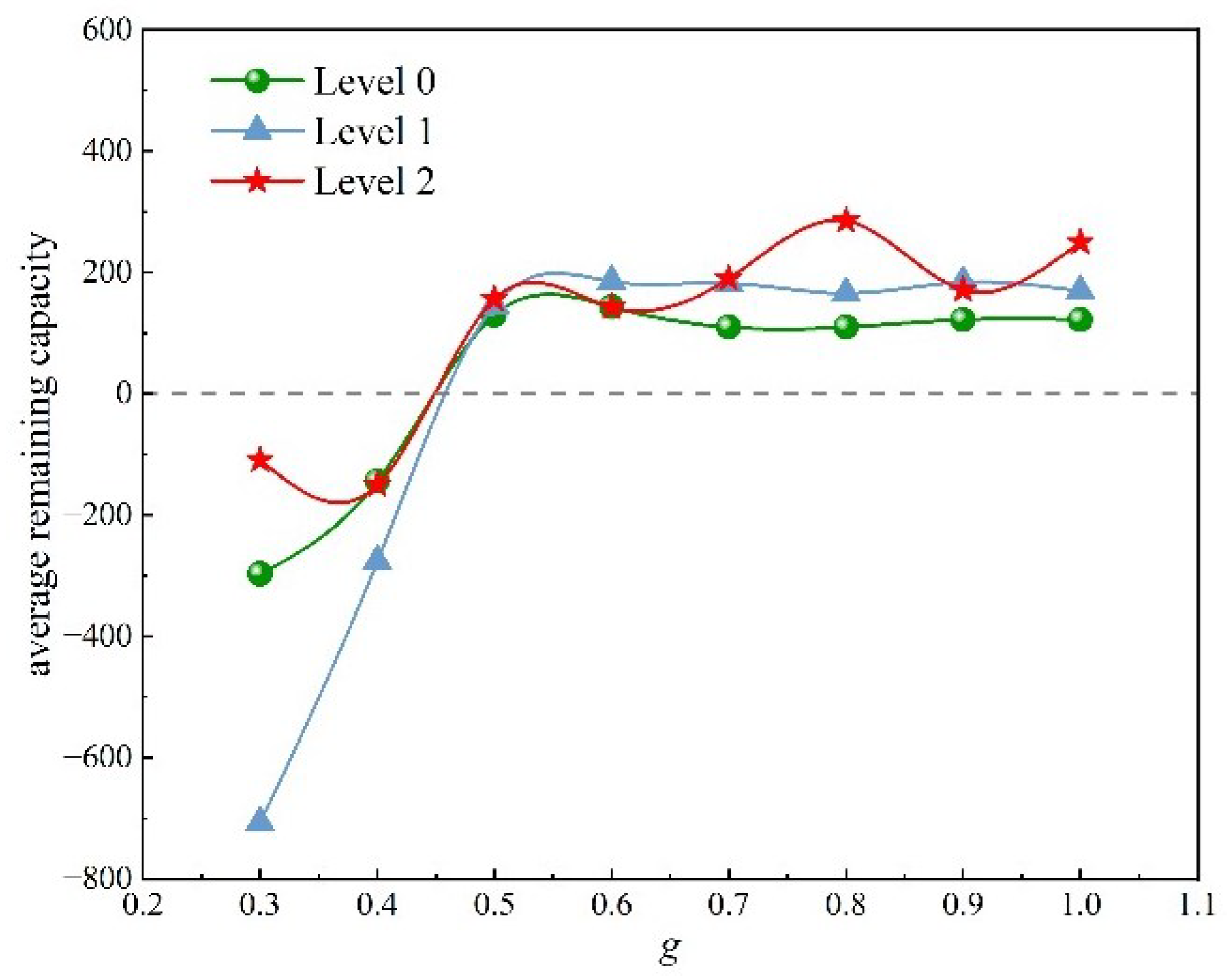
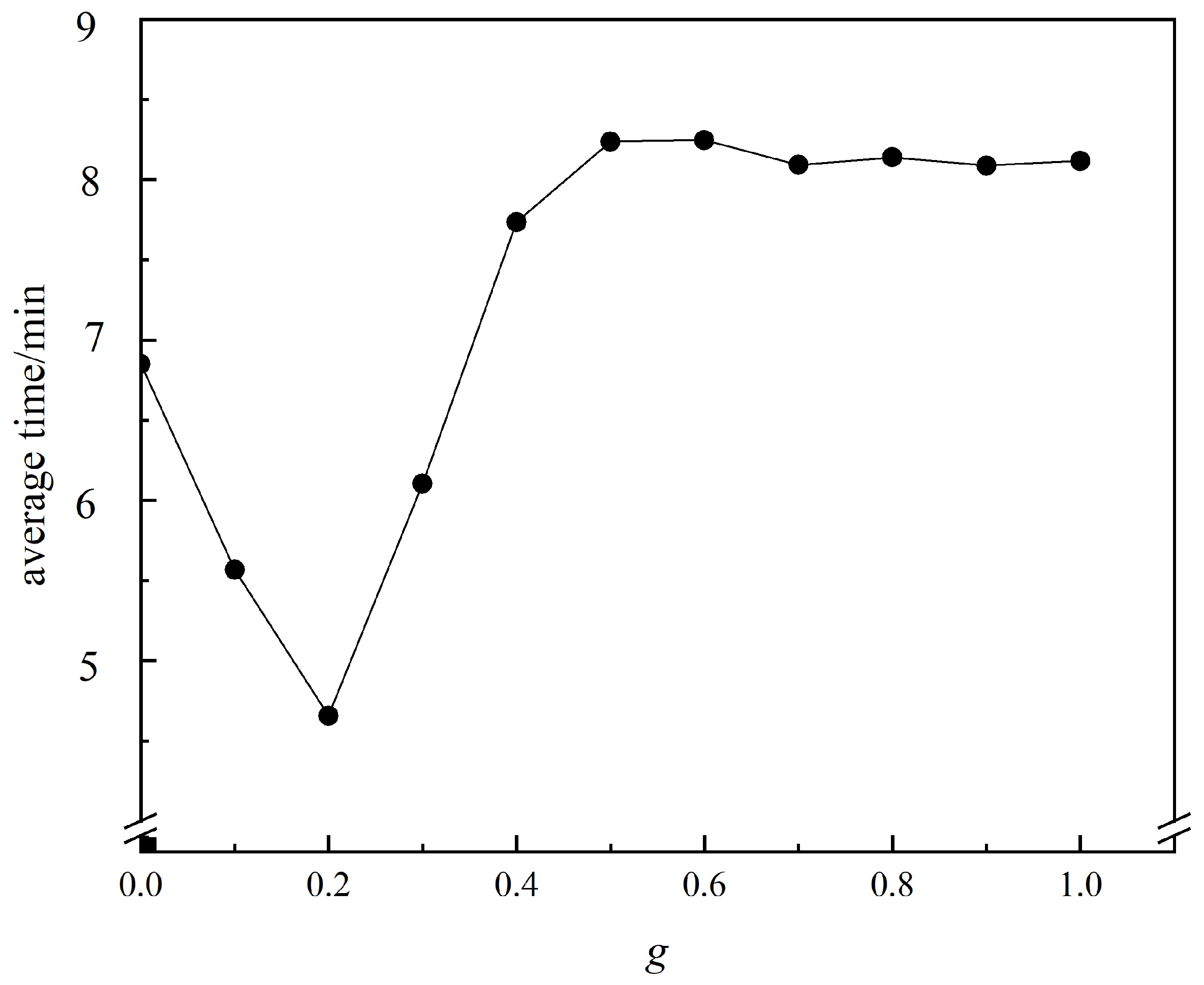
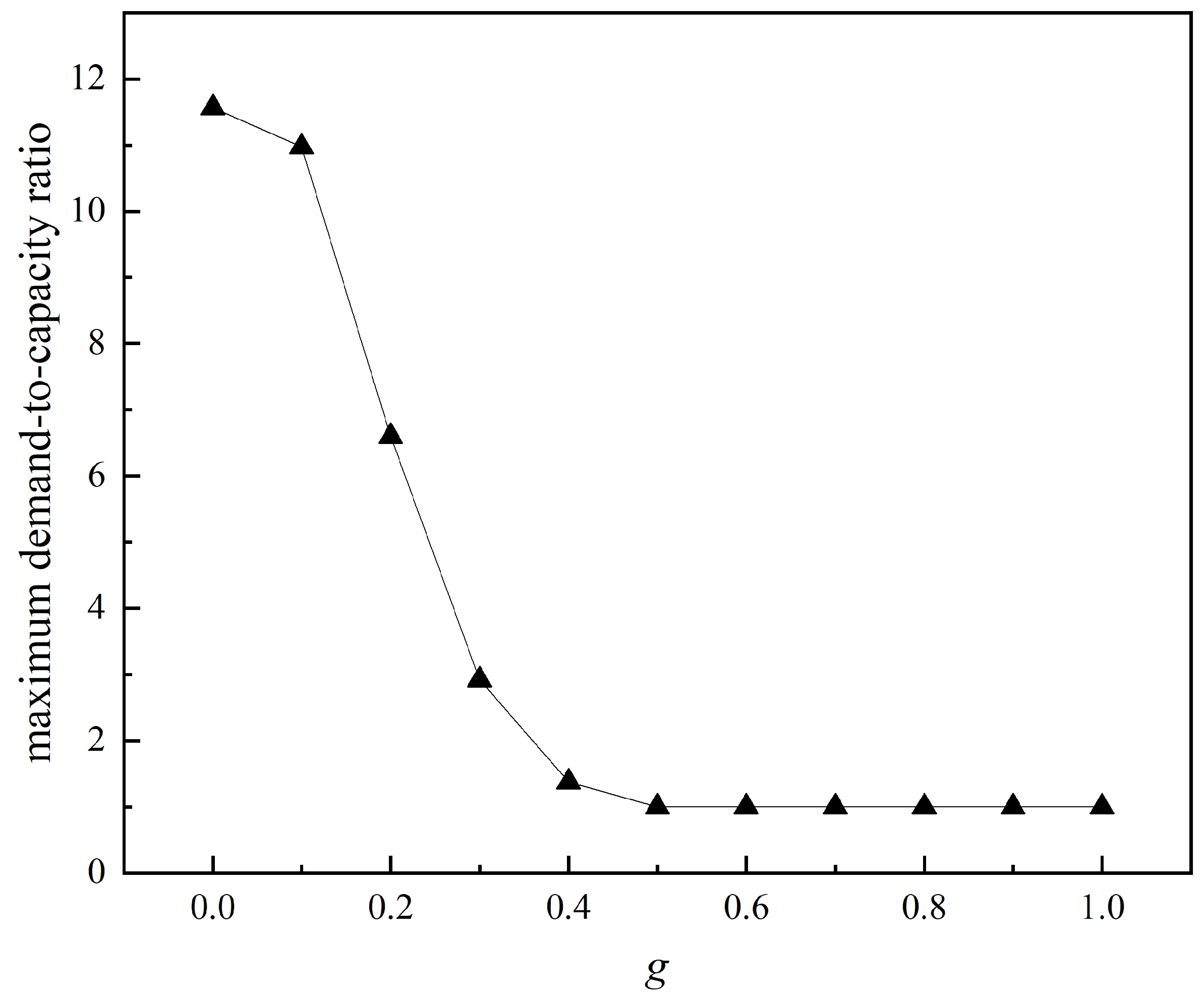
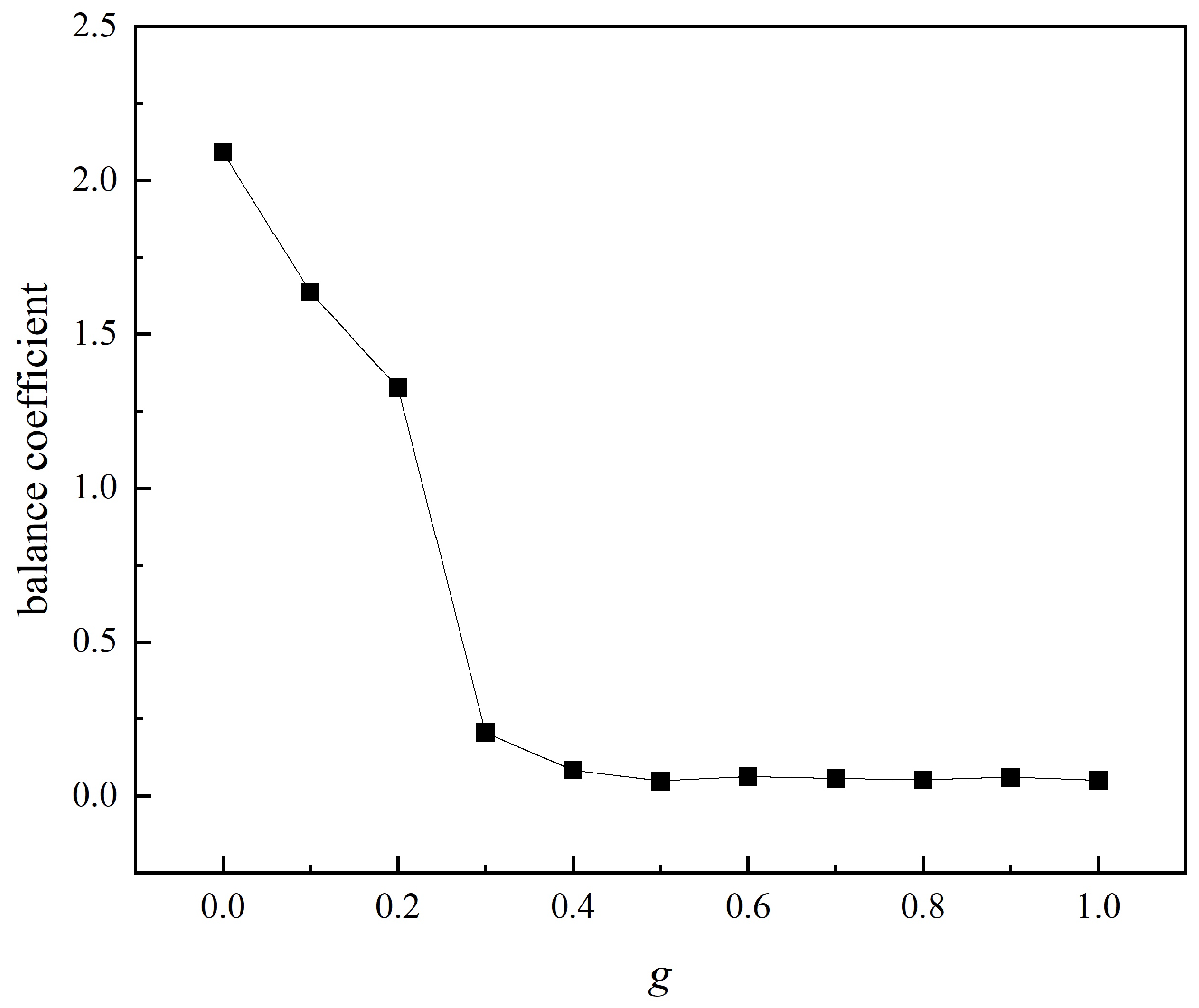
4.2.1. Analysis of the g-Value
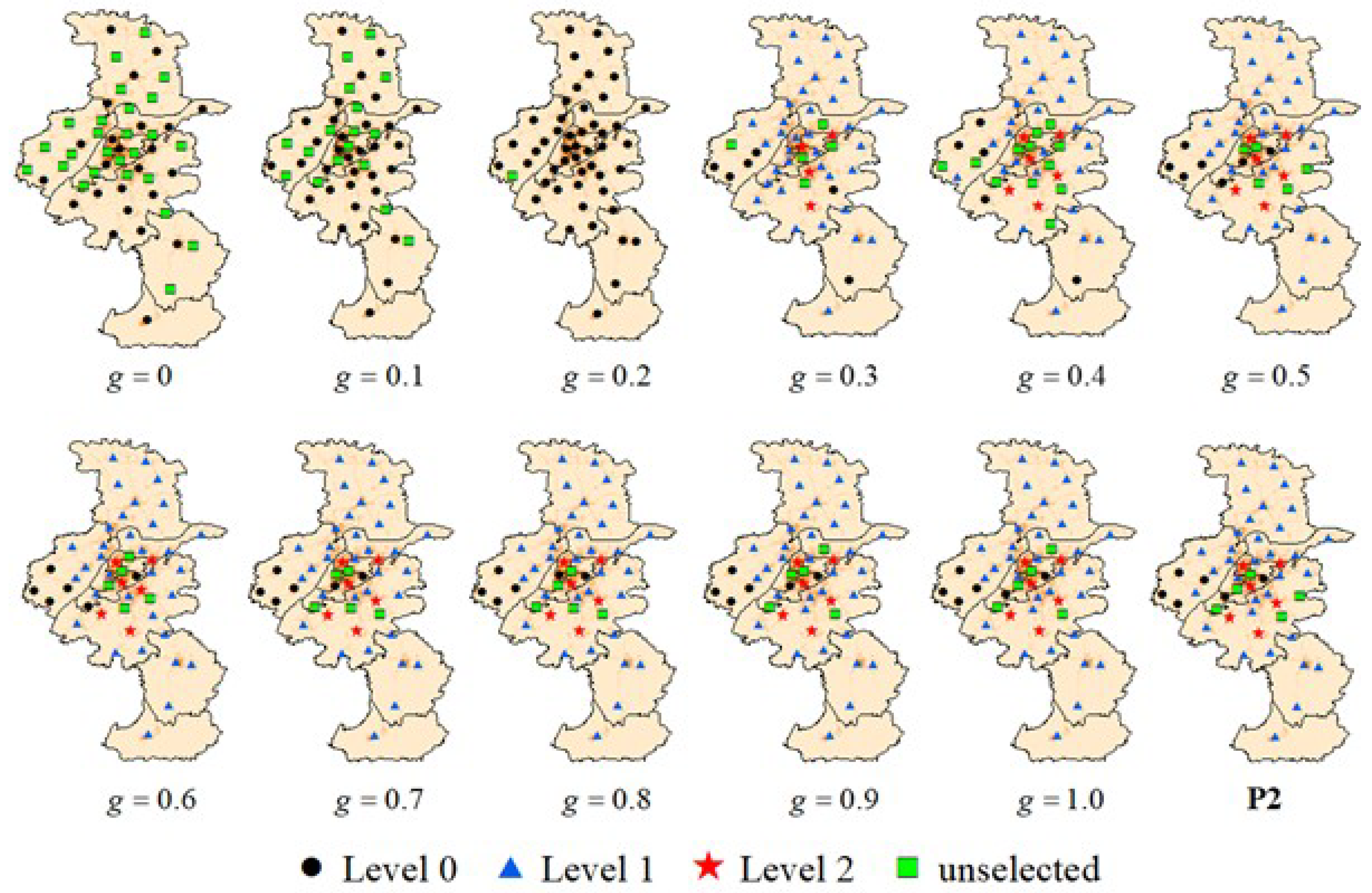
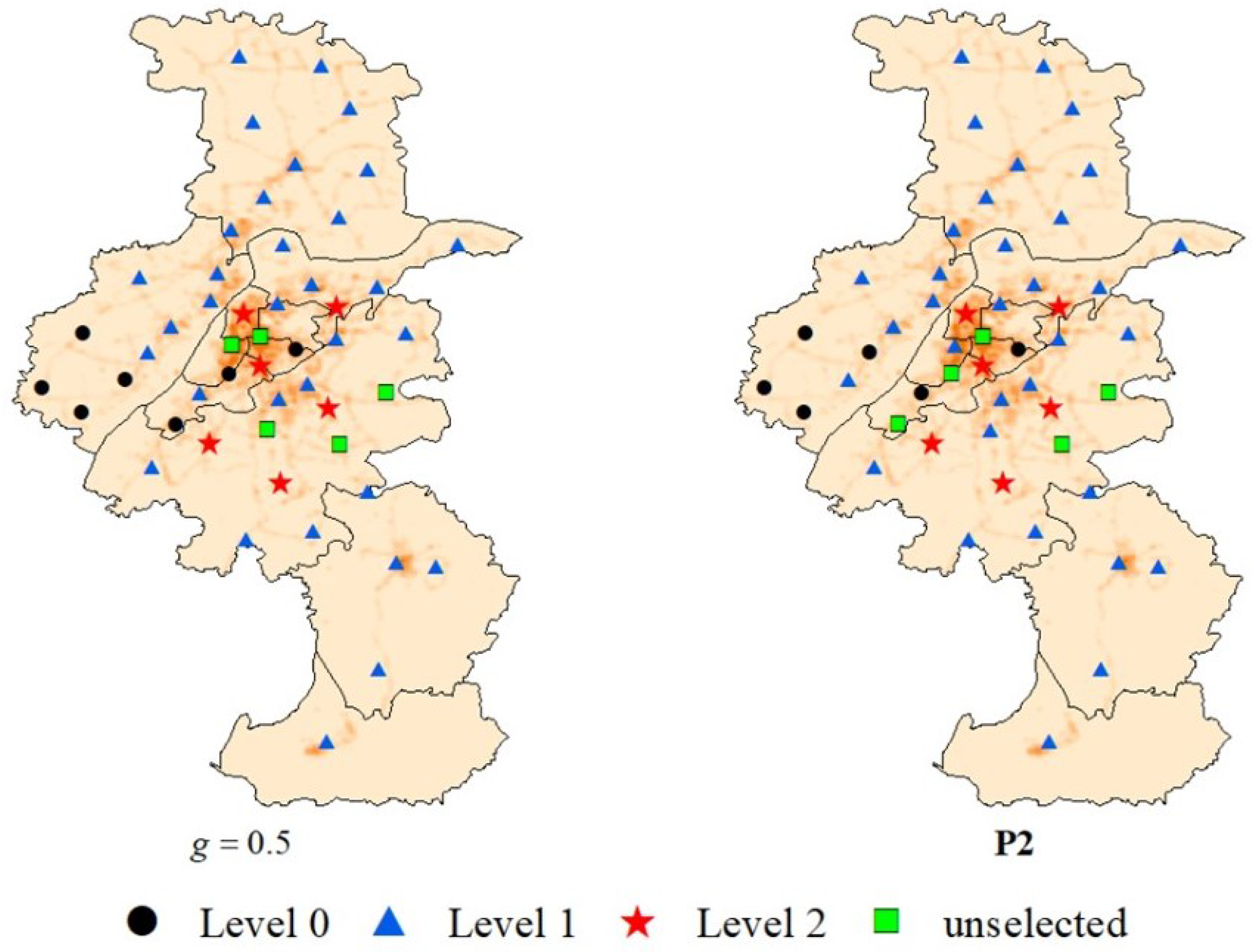
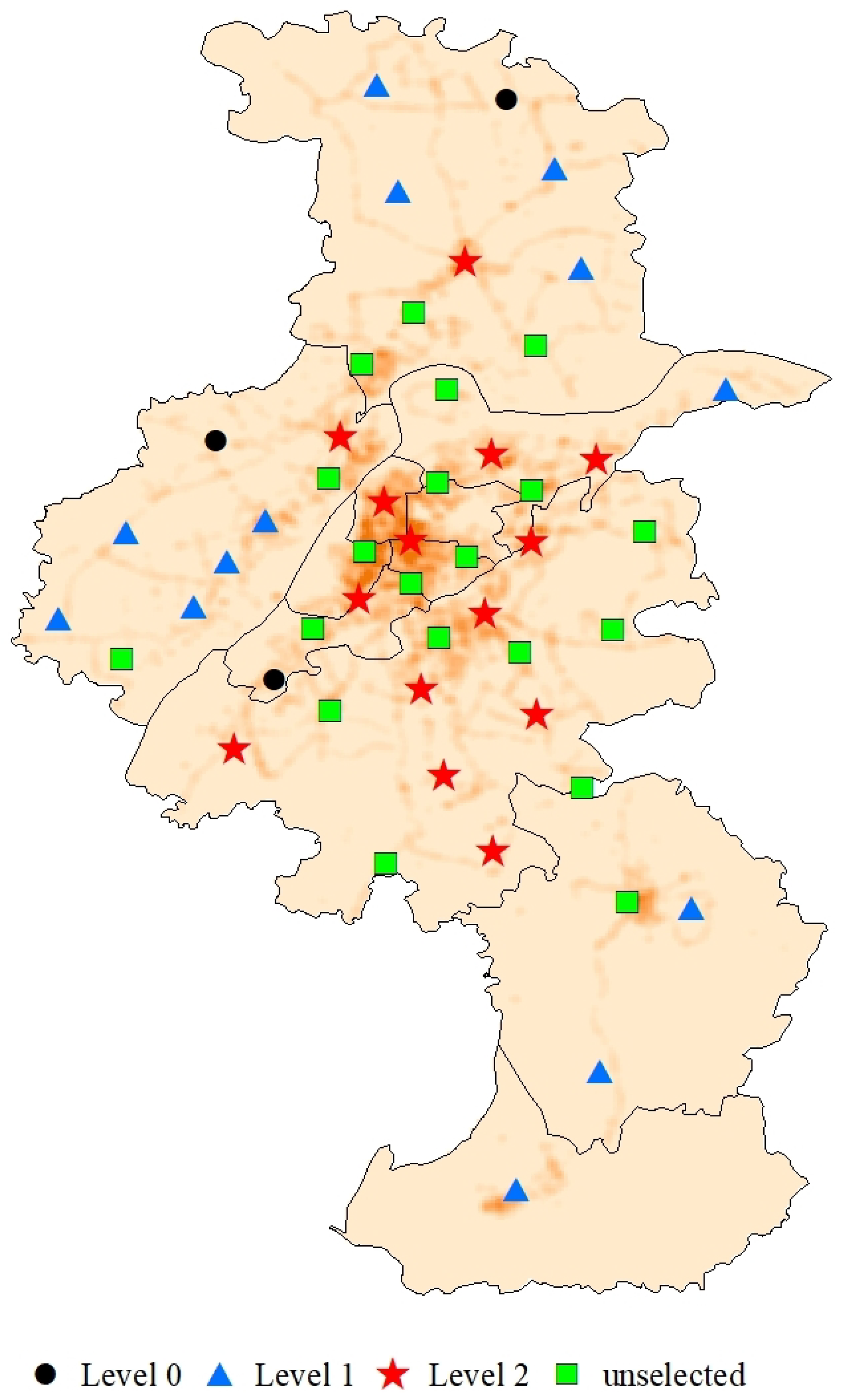
4.2.2. Location Visualization
4.2.3. Model Comparison
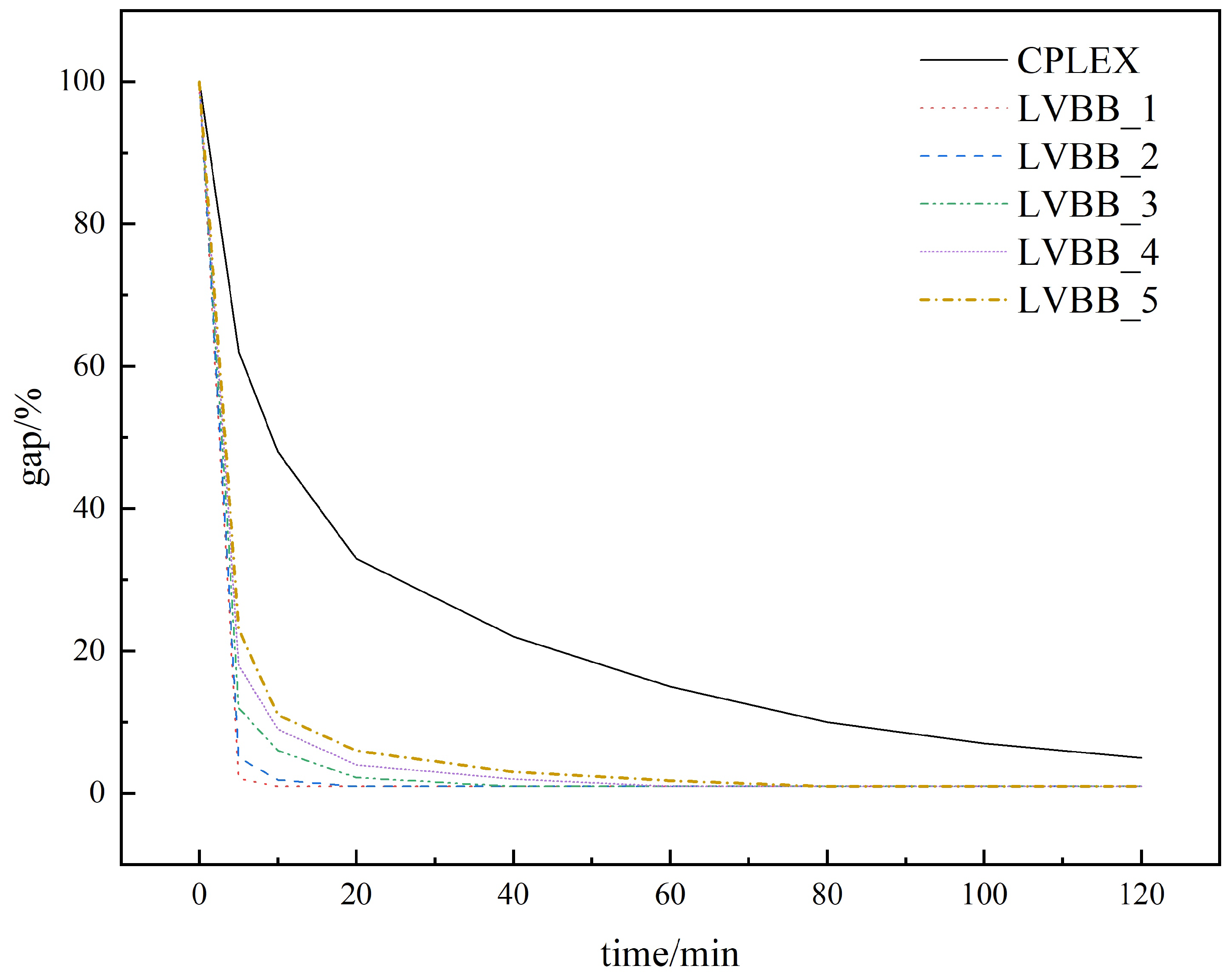
4.2.4. Computational Efficiency Analysis
4.2.5. Utility Analysis of Air and Ground Transportation
4.2.6. Stochastic Analysis Under Uncertain Demand
5. Conclusions
5.1. Contributions
- (1)
- The first hierarchical vertiport framework is introduced to address the gap in existing single-level, facility-focused literature.
- (2)
- A penalty mechanism is proposed to dynamically balance capacity overload and construction costs, with experimental results showing an optimal equilibrium at .
- (3)
- To handle the nonlinear terms in the objective function, the Big-M method is applied for linearization. For the reformulated optimization model, an improved branch-and-bound algorithm (LVBB) is developed. It achieves faster computation effectiveness than CPLEX.
- (4)
- For numerical experiments, first, the K-means clustering algorithm is employed to determine the geographical locations of demand points and candidate vertiports. Then, a comprehensive evaluation method is used to estimate the demand quantity. Finally, numerical experiments are carried out using the LVBB algorithm on the reformulated model. The results show that the proposed location plan balances construction and commuting costs, improves vertiport utilization, and meets capacity requirements.
- (5)
- Robustness was verified via chance-constrained programming. Under demand fluctuations, the number of high-capacity vertihubs increased from 6 to 14, offering actionable insights for resilient infrastructure design.
5.2. Discussion
5.3. Limitations and Future Research
- (1)
- The demand estimation was based on entropy weighting without validation from real-world UAM travel data. Future research should incorporate multi-source data (e.g., mobile signaling records, ride-hailing platform data) to enhance the accuracy of demand forecasting.
- (2)
- Although the LVBB algorithm outperforms CPLEX, systematic comparisons with state-of-the-art heuristics such as NSGA-III and Tabu Search are still needed to fully evaluate its solution quality and computational efficiency.
- (3)
- Stochastic construction cost, distance cost, and flight time were not considered. Robust optimization or stochastic programming should be incorporated to enhance model resilience.
- (4)
- Future studies should jointly optimize ground-air connectivity (e.g., metro/bus interchange) for integrated urban mobility.
- (5)
- Static demand allocation assumptions overlook real-time fluctuations and disruptions (e.g., weather-related route adjustments). Online optimization strategies are recommended for practical deployment.
- (6)
- Future research could introduce multi-objective Pareto optimization to simultaneously balance construction cost, passenger commute time, and capacity utilization, generating diversified location schemes for enhanced decision support.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAM | Urban Air Mobility |
| eVTOL | electric vertical takeoff and landing |
| LVBB | Lagrange relaxation-Variable neighborhood Branch-and-Bound |
| VNS | Variable Neighborhood Search |
| VND | Variable Neighborhood Descent |
References
- Qin, R.; Li, W.; Jin, J. Low altitude economy based on resource-based view. J. Civ. Aviat. Univ. China 2011, 29, 56–60. [Google Scholar]
- The Central People’s Government of the People’s Republic of China. The State Council of the Central Committee of the Communist Party of China issued the Outline of the National Comprehensive Stereoscopic Transportation Network Plan. 2021. Available online: https://www.gov.cn/zhengce/2021-02/24/content_5588654.htm (accessed on 9 October 2024).
- The Central People’s Government of the People’s Republic of China. Report on the Work of the Government. 2024. Available online: https://www.gov.cn/gongbao/2024/issue_11246/202403/content_6941846.html (accessed on 9 October 2024).
- Cohen, A.P.; Shaheen, S.A.; Farrar, E.M. Urban Air Mobility: History, Ecosystem, Market Potential, and Challenges. IEEE Trans. Intell. Transp. Syst. 2021, 22, 6074–6087. [Google Scholar] [CrossRef]
- Thipphavong, D.P.; Apaza, R.; Barmore, B. Urban air mobility airspace integration concepts and considerations. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018; p. 3676. [Google Scholar]
- Wei, Q.; Gao, Z.; Clarke, J. Risk-aware urban air mobility network design with overflow redundancy. Transp. Res. Part B Methodol. 2024, 185, 102967. [Google Scholar] [CrossRef]
- Zheng, X.; Li, Z. Research progress and trends of urban air mobility. Flight Dyn. 2025, 43, 10–18. [Google Scholar]
- Brunelli, M.; Ditta, C.; Postorino, M. New infrastructures for Urban Air Mobility systems: A systematic review on vertiport location and capacity. J. Air Transp. Manag. 2023, 112, 102460. [Google Scholar] [CrossRef]
- Charnsethikul, C.; Silva, J.; Verhagen, W. Urban Air Mobility Aircraft Operations in Urban Environments: A Review of Potential Safety Risks. Aerospace 2025, 12, 306. [Google Scholar] [CrossRef]
- Yunus, F.; Casalino, D.; Avallone, F. Efficient prediction of urban air mobility noise in a vertiport environment. Aerosp. Sci. Technol. 2025, 139, 108410. [Google Scholar] [CrossRef]
- Kierzkowski, A.; Dziewoński, B.; Kaliszuk, K. Evaluation of Light Electric Flying-Wing Unmanned Aerial System Energy Consumption During Holding Maneuver. Energies 2025, 18, 1300. [Google Scholar] [CrossRef]
- Meng, L.; Wu, M.; Wen, X. Optimization of Flight Scheduling in Urban Air Mobility Considering Spatiotemporal Uncertainties. Aerospace 2025, 12, 413. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Yuan, Y. Joint Optimization of Cost and Scheduling for Urban Air Mobility Operation Based on Safety Concerns and Time-Varying Demand. Aerospace 2024, 11, 861. [Google Scholar] [CrossRef]
- Cunningham, E.; Healy, J.; Cuffe, P. An Analysis of the Feasibility of Providing On-demand Ground Level Illumination from a Loitering Unmanned Aerial Vehicle. In Proceedings of the 2024 IEEE International Workshop on Technologies for Defense and Security (TechDefense), Naples, Italy, 11–13 November 2024; pp. 86–91. [Google Scholar]
- Shao, Q.; Shao, M.; Lu, Y. Terminal area control rules and eVTOL adaptive scheduling model for multi-vertiport system in urban air Mobility. Transp. Res. Part C Emerg. Technol. 2021, 132, 103385. [Google Scholar] [CrossRef]
- Jin, Z.; Ng, K.; Zhang, C. Robust optimisation for vertiport location problem considering travel mode choice behaviour in urban air mobility systems. J. Air Transp. Res. Soc. 2024, 2, 100006. [Google Scholar] [CrossRef]
- Jeong, J.; So, M.; Hwang, H. Selection of vertiports using k-means algorithm and noise analyses for urban air mobility (UAM) in the seoul metropolitan area. Appl. Sci. 2021, 11, 5729. [Google Scholar] [CrossRef]
- Sinha, A.; Rajendran, S. A novel two-phase location analytics model for determining operating station locations of emerging air taxi services. Decis. Anal. J. 2022, 2, 100013. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y. Integrated network design and demand forecast for on-demand urban air mobility. Engineering 2021, 7, 473–487. [Google Scholar] [CrossRef]
- Shin, H.; Lee, T.; Lee, H. Skyport location problem for urban air mobility system. Comput. Oper. Res. 2022, 138, 105611. [Google Scholar] [CrossRef]
- Chen, L.; Wandelt, S.; Dai, W. Scalable vertiport hub location selection for air taxi operations in a met-ropolitan region. INFORMS J. Comput. 2022, 34, 834–856. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, Z.; Wang, Y. Vertiport location for eVTOL considering multidimensional demand of urban air mobility: An application in Beijing. Transp. Res. Part Policy Pract. 2025, 192, 104353. [Google Scholar] [CrossRef]
- Petit, V.; Ribeiro, M. Multi-objective vertiport location optimization for a middle-mile package delivery framework: Case study in the South Holland Region. J. Air Transp. Manag. 2024, 125, 102757. [Google Scholar] [CrossRef]
- Willey, L.; Salmon, J. A method for urban air mobility network design using hub location and subgraph isomorphism. Transp. Res. Part C Emerg. Technol. 2021, 125, 102997. [Google Scholar] [CrossRef]
- Kai, W.; Jacquillat, A.; Vaze, V. Vertiport planning for urban aerial mobility: An adaptive discretization approach. Manuf. Serv. Oper. Manag. 2022, 24, 3215–3235. [Google Scholar] [CrossRef]
- Johnston, T.; Riedel, R.; Sahdev, S. To Take off, Flying Vehicles First Need Places to Land. New York. 2020. Available online: https://www.mckinsey.com/industries/automotive-and-assembly/our-insights/to-take-off-flying-vehicles-first-need-places-to-land (accessed on 23 December 2024).
- Nanjing Municipal People’s Government. Notice of the General Office of the Municipal Government on the Issuance of the Implementation Plan for Promoting the High-Quality Development of Low Altitude Economy in Nanjing (2024–2026). 2024; [EB/OL]. Available online: https://www.nanjing.gov.cn/zzb/zfxxgk/fdzdgknr/szfjbgtwj/202405/t20240514_4666425.html (accessed on 26 August 2024).
- Preis, L. Quick sizing, throughput estimating and layout planning for VTOL aerodromes–a methodology for vertiport design. In Proceedings of the AIAA Aviation 2021 Forum, Virtual, 2–6 August 2021; p. 2372. [Google Scholar]



| Author | Object | Constraint | Solution Method |
|---|---|---|---|
| Wu, et al. [19] | minimize the monetized time value and travel cost | vertiport count, mode exclusivity, economic feasibility | Gurobi |
| Shin, et al. [20] | minimize the travel cost, facility cost, and collision risk cost | the nearest skyport, collision feasibility | Genetic Algorithm |
| Chen, et al. [21] | minimize total travel cost | single allocation, flow balance | Grid-VNS |
| Jiang, et al. [22] | maximize the coverage of on-demand mobility demand, regular shuttle demand, and congestion alleviation, minimize the redundant coverage of regular shuttle | facility capacity, socioeconomic limitation, minimum spacing | NSGA-III |
| Petit, et al. [23] | minimize the fraction of demand not served, minimize the sum of safety scores, minimize the sum of noise scores | vertiport count, coverage capability, capacity, safety distance, airspace restriction | multi-objective Tabu Search |
| Willey, et al. [24] | maximize the reduction in passenger travel time compared to ground transportation | hub count, closest hub allocation, connectivity, time savings requirement, subgraph structure | five heuristic algorithms |
| Kai, et al. [25] | maximize total profit | demand matching, queuing network | adaptive discretization algorithm |
| Vertiport Level | Description |
|---|---|
| vertihub (high-level) | Vertihub is established mainly in areas with high traffic flow (e.g., city center) and has about 10 take-off and landing platforms and 20 parking or maintenance platforms, as well as shopping and other services for passengers. |
| vertibase (medium-level) | Vertibase is primarily established in areas with moderate traffic flow (e.g., office building, supermarket) and has about three take-off and landing platforms and six parking or maintenance platforms. |
| vertipad (low-level) | Vertipad is established mainly in areas with low traffic flow (e.g., suburban area) and has approximately one take-off and landing platform and two parking or maintenance platforms. |
| No. | Latitude & Longitude | Geographical Location | No. | Latitude & Longitude | Geographical Location |
|---|---|---|---|---|---|
| 0 | (118.751003° N, 32.076942° E) | Nanjing Ding Shan Garden Hotel | 25 | (118.753051° N, 31.690457° E) | Qixian Mountain Rose Garden |
| 1 | (119.010477° N, 31.469133° E) | Menghuayuan Scenic Area | 26 | (118.903008° N, 31.911857° E) | Ledongli Jiangning Digital Sports Center |
| 2 | (118.734453° N, 32.528839° E) | Phoenix Reservoir | 27 | (118.539931° N, 31.965801° E) | Qionghua Lake Park |
| 3 | (118.780373° N, 31.880843° E) | Shuichang Street Vehicle Base | 28 | (118.85328° N, 32.063511° E) | Zhongshan Scenic Area |
| 4 | (119.025304° N, 32.051312° E) | Tangshan Happy Water World | 29 | (119.013071° N, 31.648975° E) | Shitang Reservoir |
| 5 | (119.075445° N, 31.636296° E) | Zhongshan Reservoir | 30 | (118.997365° N, 31.942594° E) | Nanjing Chaopeng Logistics Co., Ltd. |
| 6 | (118.838561° N, 32.336404° E) | Wanda Plaza (Luhe Store) Phase I | 31 | (118.725989° N, 31.976911° E) | Tongyue Valley Family Park |
| 7 | (118.421888° N, 31.943368° E) | Wancheng Ecological Park | 32 | (118.85547° N, 32.52002° E) | Zhaoqiao Reservoir |
| 8 | (118.820442° N, 31.923056° E) | Jiangning Golden Eagle | 33 | (118.834481° N, 32.006183° E) | Qiqiao Weng Ecological Wetland Park |
| 9 | (118.589911° N, 31.825354° E) | Binjiang New Town Park | 34 | (118.627258° N, 31.89677° E) | Nanjing Meishan Hospital |
| 10 | (118.724075° N, 32.246659° E) | Duwei Wetland Park | 35 | (118.779359° N, 32.004173° E) | Yuhuatai Scenic Area |
| 11 | (118.579119° N, 32.005996° E) | Nanjing LinDa Ecological Park | 36 | (118.921453° N, 32.25601° E) | Hongshanyao Scenic Area |
| 12 | (118.875531° N, 31.731864° E) | Nanjing Lukou Airport | 37 | (118.814199° N, 32.006282° E) | Nanjing Airport Logistics Center |
| 13 | (118.806841° N, 32.092823° E) | Cross-shaped Cypress Forest Park | 38 | (118.465652° N, 31.936634° E) | Lingquan Fugui Scenic Area |
| 14 | (118.939031° N, 32.428805° E) | Jinniu Lake Hospital | 39 | (118.661313° N, 32.108797° E) | Buddha Hand Lake Country Park |
| 15 | (118.899471° N, 32.034937° E) | Nanwan Ying Park | 40 | (118.701338° N, 32.376512° E) | Chisong Lake National Wetland Park |
| 16 | (118.897912° N, 31.337092° E) | Wujiazu Legal Culture Park | 41 | (119.121375° N, 32.15936° E) | Shui Yifang Ecological Leisure Tourism Area |
| 17 | (118.911981° N, 31.850795° E) | Longdu Town Fenqian Primary School | 42 | (118.781183° N, 32.286663° E) | Jinshan Building Materials and Furniture City |
| 18 | (118.728521° N, 32.177187° E) | Datang Jin Fragrant Grass Valley | 43 | (118.893572° N, 32.092955° E) | Nanjing Jiangning Hospital |
| 19 | (118.784352° N, 32.178177° E) | Nanjing First Hospital | 44 | (118.873448° N, 32.129654° E) | Taiping Mountain Park |
| 20 | (118.703775° N, 32.151846° E) | Southeast University Chengxian College | 45 | (118.616187° N, 32.057481° E) | Qiuyushan Cultural Park |
| 21 | (118.990617° N, 32.306321° E) | Fangshan | 46 | (118.666341° N, 31.938391° E) | Redsun Home Expo Center |
| 22 | (118.776935° N, 32.040071° E) | Tongyu Garden | 47 | (118.998881° N, 31.758726° E) | Daren Mountain Life Park |
| 23 | (118.986025° N, 32.126679° E) | Nanjing Xianlin Lake Park | 48 | (118.480984° N, 32.052933° E) | Chuyun Flower Fragrance Scenic Area |
| 24 | (118.562459° N, 32.134747° E) | Houchong Scenic Area | 49 | (118.831043° N, 32.207572° E) | Mosanghua Du Scenic Area |
| No. | Demand | No. | Demand | No. | Demand | No. | Demand | No. | Demand | No. | Demand |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2403 | 25 | 1173 | 50 | 1513 | 75 | 1911 | 100 | 1788 | 125 | 864 |
| 1 | 1579 | 26 | 533 | 51 | 641 | 76 | 726 | 101 | 641 | 126 | 2234 |
| 2 | 1064 | 27 | 2010 | 52 | 1742 | 77 | 2065 | 102 | 1943 | 127 | 972 |
| 3 | 2495 | 28 | 1959 | 53 | 1988 | 78 | 2987 | 103 | 2019 | 128 | 2711 |
| 4 | 2142 | 29 | 994 | 54 | 680 | 79 | 618 | 104 | 1855 | 129 | 1210 |
| 5 | 757 | 30 | 1196 | 55 | 618 | 80 | 733 | 105 | 533 | 130 | 1819 |
| 6 | 795 | 31 | 1056 | 56 | 1389 | 81 | 726 | 106 | 1357 | 131 | 1250 |
| 7 | 672 | 32 | 2480 | 57 | 2726 | 82 | 641 | 107 | 717 | 132 | 1865 |
| 8 | 603 | 33 | 733 | 58 | 1589 | 83 | 625 | 108 | 818 | 133 | 634 |
| 9 | 789 | 34 | 2019 | 59 | 1988 | 84 | 1240 | 109 | 741 | 134 | 1025 |
| 10 | 2049 | 35 | 834 | 60 | 1896 | 85 | 549 | 110 | 1548 | 135 | 533 |
| 11 | 1240 | 36 | 2465 | 61 | 1403 | 86 | 1880 | 111 | 882 | 136 | 1779 |
| 12 | 841 | 37 | 502 | 62 | 1456 | 87 | 2189 | 112 | 634 | 137 | 1942 |
| 13 | 557 | 38 | 941 | 63 | 895 | 88 | 1127 | 113 | 687 | 138 | 1926 |
| 14 | 1742 | 39 | 702 | 64 | 880 | 99 | 1517 | 114 | 1071 | 139 | 2034 |
| 15 | 2034 | 40 | 2049 | 65 | 2049 | 90 | 748 | 115 | 726 | 140 | 1511 |
| 16 | 757 | 41 | 2588 | 66 | 2465 | 91 | 634 | 116 | 1526 | 141 | 680 |
| 17 | 1471 | 42 | 1788 | 67 | 849 | 92 | 1071 | 117 | 518 | 142 | 1372 |
| 18 | 1419 | 43 | 1341 | 68 | 1056 | 93 | 1957 | 118 | 2087 | 143 | 1788 |
| 19 | 1164 | 44 | 818 | 69 | 941 | 94 | 1788 | 119 | 1733 | 144 | 1757 |
| 20 | 772 | 45 | 1886 | 70 | 2126 | 95 | 1763 | 120 | 774 | 145 | 1609 |
| 21 | 1271 | 46 | 1725 | 71 | 818 | 96 | 1102 | 121 | 456 | 146 | 541 |
| 22 | 2265 | 47 | 687 | 72 | 2563 | 97 | 1440 | 122 | 1471 | 147 | 1880 |
| 23 | 1680 | 48 | 1819 | 73 | 764 | 98 | 603 | 123 | 2210 | 148 | 1726 |
| 24 | 1858 | 49 | 1225 | 74 | 1811 | 99 | 2203 | 124 | 718 | 149 | 1040 |
| Level | Vertipad () | Vertibase () | Vertihub () |
|---|---|---|---|
| Construction Cost (yuan) | |||
| Capacity (flights/day) | 1300 | 2600 | 20,000 |
| P1 () | P2 | ||
|---|---|---|---|
| No. vertiport | Level 0 | 7,27,31,33,34,38,48 | 7,11,33,38,46,48 |
| Level 1 | 1,2,4,5,6,8,9,10,11,12,13,14,15,16,20,21,23, 24,25,29,32,36,39,40,41,42,43,44,45,46,47,49 | 1,2,3,4,5,6,8,9,10,12,13,14,15,16,19,20,21,23, 24,25,27,29,32,36,39,40,41,42,43,44,45,47,49 | |
| Level 2 | 0,18,26,28,35,37 | 0,18,26,28,35,37 | |
| Number of Vertiports | Level 0 | 7 | 6 |
| Level 1 | 32 | 33 | |
| Level 2 | 6 | 6 | |
| Total | 45 | 45 | |
| Cost (yuan) | Construction Cost | ||
| Distance Cost | |||
| Penalty Cost | 0 | / | |
| Total | |||
| Average Remaining Capacity | Level 0 | 130 | 170 |
| Level 1 | 146 | 154 | |
| Level 2 | 156 | 285 | |
| Avg. | 145 | 174 | |
| Average Time (min) | / | 8.34 | 8.13 |
| Maximum Demand-to-capacity ratio | / | 0.99 | 0.99 |
| Balance Coefficient | / | 0.048 | 0.052 |
| Algorithm | Time/s |
|---|---|
| CPLEX | 7200+ |
| LVBB_1 | 343.38 |
| LVBB_2 | 569.73 |
| LVBB_3 | 2390.45 |
| LVBB_4 | 3678.32 |
| LVBB_5 | 4323.39 |
| LVBB_avg | 2261.05 |
| O | D | Dis/km | PT/min | PC/yuan | TT/min | TC/yuan | AT/min | AC/yuan | Time Saved | Cost Multiple | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Public | Taxi | Public | Taxi | |||||||||
| DGF a (18) | QWE b (33) | 33 | 122 | 6 | 34 | 65 | 10 | 198 | 92% | 71% | 33.00 | 3.04 |
| DGF a (18) | HSA c (36) | 69 | 218 | 15 | 57 | 140 | 21 | 414 | 91% | 64% | 27.60 | 2.96 |
| DGF a (18) | SR d (29) | 43 | 147 | 12 | 41 | 88 | 13 | 258 | 91% | 69% | 21.50 | 2.93 |
| DGF a (18) | QCP e (45) | 41 | 143 | 11 | 44 | 97 | 12 | 164 | 91% | 72% | 14.91 | 1.69 |
| QWE b (33) | HSA c (36) | 43 | 155 | 12 | 41 | 91 | 13 | 172 | 92% | 69% | 14.33 | 1.89 |
| QWE b (33) | SR d (29) | 49 | 181 | 13 | 43 | 96 | 15 | 294 | 92% | 66% | 22.60 | 3.06 |
| QWE b (33) | QCP e (45) | 25 | 104 | 8 | 33 | 49 | 8 | 150 | 93% | 77% | 18.75 | 3.06 |
| HSA c (36) | SR d (29) | 84 | 245 | 28 | 70 | 181 | 25 | 504 | 90% | 64% | 18.00 | 2.78 |
| HSA c (36) | QCP e (45) | 53 | 167 | 12 | 56 | 125 | 16 | 318 | 90% | 72% | 26.50 | 2.54 |
| SR d (29) | QCP e (45) | 71 | 184 | 12 | 62 | 137 | 21 | 426 | 88% | 66% | 35.50 | 3.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Yao, J.; Jiang, J.; Qiao, D. Research of Hierarchical Vertiport Location Based on Lagrange Relaxation. Aerospace 2025, 12, 672. https://doi.org/10.3390/aerospace12080672
Guo Y, Yao J, Jiang J, Qiao D. Research of Hierarchical Vertiport Location Based on Lagrange Relaxation. Aerospace. 2025; 12(8):672. https://doi.org/10.3390/aerospace12080672
Chicago/Turabian StyleGuo, Yuzhen, Junjie Yao, Jing Jiang, and Dongxiao Qiao. 2025. "Research of Hierarchical Vertiport Location Based on Lagrange Relaxation" Aerospace 12, no. 8: 672. https://doi.org/10.3390/aerospace12080672
APA StyleGuo, Y., Yao, J., Jiang, J., & Qiao, D. (2025). Research of Hierarchical Vertiport Location Based on Lagrange Relaxation. Aerospace, 12(8), 672. https://doi.org/10.3390/aerospace12080672





