1. Introduction
The CoAX 600 rotorcraft, developed by edm aerotec GmbH [
1] in Geisleden, Germany, was converted to a remotely piloted drone via a robotic actuator system. The CoAX 600 is a coaxial helicopter with a maximum take-off weight (MTOW) of 600 kg. It has been designed according to the German ultralight (UL) rotorcraft standards [
2] and has a UL-type certificate from the German ultralight association (DULV). It is a two-seater rotorcraft, fitted with mechanical controls. The conversion of this rotorcraft to an unmanned aerial vehicle (UAV) was accomplished by designing a minimally invasive robotic flight control unit, which was installed on the copilot seat. The system directly actuates the pilot inceptors and allows for the conversion of the manned rotorcraft to a UAV in limited time. Furthermore, the conversion can be reversed, since the original mechanical flight controls remain untouched. To the best knowledge of the authors, this paper (initially published at SciTech 2024 [
3]) marks the first occasion that the details of such a modular flight control system, applied to a full-size rotorcraft in free flight, have been published. This approach is beneficial not only for the quick and reversible conversion of existing rotorcraft to UAVs, but also leverages the existing (already certified and tested) mechanical controls, which can be beneficial for acquiring a permit-to-fly from the aviation authority.
The advantages and use-cases of unmanned aerial vehicles of different weight classes and configurations in the civil and military contexts have become more evident in the recent years. Besides the low-cost, mostly multi-rotor drones, widely available to the public for photo- and videography, aerospace manufacturers have developed multiple UAVs with vertical take-off and landing capabilities for different applications. The Kaman Corporation was recently awarded for the development of a cargo UAV quadcopter [
4]. The KARGO UAV is capable of transporting a payload of up to 800 lbs over 500 NM. Other manufacturers such as the Israel Aerospace Industry [
5] headquartered in Lod, Israel have developed rotorcraft UAVs using the main and tail rotor configuration, capable of lifting up to a 180 kg payload with a top speed of 150
. The K-Max helicopter with intermeshing rotors can be mentioned as a pioneer of unmanned helicopters designed for (external) cargo transport [
6,
7]. The intermeshing double rotor design is known to be more efficient than conventional main and tail rotor configuration when flight operations mostly consist of hovering and slow flight. In a more recent project, a Black Hawk helicopter was transformed into an optionally piloted vehicle (OPV) by Sikorsky Aircraft [
8], headquartered in Stratford, CT, USA. Another example of recent rotorcraft UAV projects is the VSR700 by Airbus Helicopters [
9], which is a 700 kg tactical UAV developed for the French Navy, also capable of ship-borne operations. The A160 Hummingbird [
10], developed by Frontier Systems and, later, Boeing, is another pioneer of rotorcraft unmanned aerial systems (UASs), which broke the endurance (more than 20 h) and altitude records (30,000 ft) at the time of its introduction. The project was abandoned by the US Army in 2012. Frontier Systems, a company based in Irvine, CA, USA, which was later acquired by Boeing, initiated the development of the A160 Hummingbird and also designed the Maverick VTOL UAS [
11]. The Maverick VTOL UAS was developed based on a Robinson R22 and was later used as a test-bed for the development of the A160 Hummingbird at Boeing.
Other relevant work includes the conversion of manned aircraft with mechanical flight controls to optionally piloted vehicles (OPVs). Reference [
12] compares the characteristics of avionic systems for manned and unmanned aircrafts, and uses the optionally piloted DA42 [
13] and the Sagitta fixed-wing UAV [
14] research platforms to elaborate on the differences of flight control systems for the two categories.
In all of the projects mentioned above, the actuators are deeply integrated in the rotorcraft mechanical control system. The rotorcraft are either designed as unmanned systems from the beginning or the manned–unmanned conversion is a long process and not easily reversible. The idea of retrofitting a robotic flight control system with integrated avionics has been investigated before. In the ROBOPilot project [
15], such a system was designed for and tested on a Cessna 172 aircraft. The system successfully demonstrated automatic flight. In another study, a robotic actuator system was mounted into an SVH-4 rotorcraft and was tested in a hovering platform [
16]. No free flight of the helicopter was reported in this project. The control mechanism in the cockpit consisted of a multi-arm robot and additional mechanisms for controlling the pedals and the collective lever. This concept is similar to an Aurora Flight Sciences study [
17], in which a multi-arm multi-purpose robot was retrofitted into a Cessna Caravan copilot seat and could successfully fly the aircraft.
Some of the UAVs mentioned above, such as the VSR700 [
9] and Kaman Kargo [
4], were conceived as products. However, the majority of the projects, such as the DA 42 OPV [
13] and the Sagitta fixed-wing UAV [
14] research platforms, were developed as research platforms to test new flight control systems and functions. The DA 42 OPV was used in Ref. [
18] to test vision-augmented navigation systems for automatic landings. The AirSTAR program at NASA is another example of a UAV, developed as a test-bed for testing new flight control laws and avionic systems [
19,
20], mostly focused on the goals of NASA’s Aviation Safety Program. The CoAX 600 UAV (also referred to as CoAX 600 UAS) falls into this category as well. The full-size rotorcraft is a valuable asset suitable for testing novel rotorcraft flight control laws and modern avionics.
This paper details the engineering challenges that were faced during the conversion of the CoAX 600 to an unmanned system and their solutions, focusing on the following:
Mechanical design of the robotic actuator system;
Modeling and simulation of the robotic system and the development of an in-flight feed-forward inverse-kinematics robot control software;
The system architecture of the onboard avionics systems;
Testing and evaluation of the systems and functions, involving flight testing in a hover frame and free flights.
The robotic actuator system was developed in CATIA, and a multi-body model of the robotic actuator system, consisting of multiple actuators and nonlinear kinematics, was developed in Simulink, using the Simscape toolbox. The CATIA–MATLAB interface of Ref. [
21] was used for this purpose. The multi-body simulation model was coupled with physics-based models of the actuators. The simulation model was utilized to develop an onboard robot control software to cancel the nonlinear kinematics of the control mechanism. The onboard robot control software needed to be simple, robust, and avoid complex or non-determinstic simulation software (such as multi-body simulations). Furthermore, linear low-order systems of the actuators were also estimated from the test data captured during flights on a hover frame. A system architecture consisting of aerospace-grade components was developed, which facilitates the unmanned operation of the rotorcraft in compliance with the relevant aviation regulations. It also enabled recording the flight parameters from a wide array of sensors installed on the rotorcraft.
The paper starts with the details of the mechanical design of the control rods and the choice of the actuators in
Section 2 and continues with the development of multi-body simulations and the robot control software in
Section 2.1 and
Section 2.2. Furthermore, the architecture of the flight control system (FCS) is discussed in
Section 3.
Section 4 focuses on the conducted tests, in the lab, on the rotorcraft in a hover frame, and in free flight.
Section 5.1 describes the identification of linear low-order systems of the actuators using hover-frame flight data.
Section 5.2 discusses the dynamics of the gimbal-mounted rotorcraft in the hover frame. Finally, the conclusion section focuses on the valuable lessons learned from the process of converting the CoAX 600 to a UAV.
Each of the sections includes a discussion of the applied methods and their effectiveness in achieving the goal of the project, which is the reversible conversion of the manned coaxial rotorcraft to a UAS in limited time. The UAS is intended to be used as a test-bed for the development of flight control systems and functions and advancing rotorcraft technology.
2. The Control Mechanism—Hardware and Software
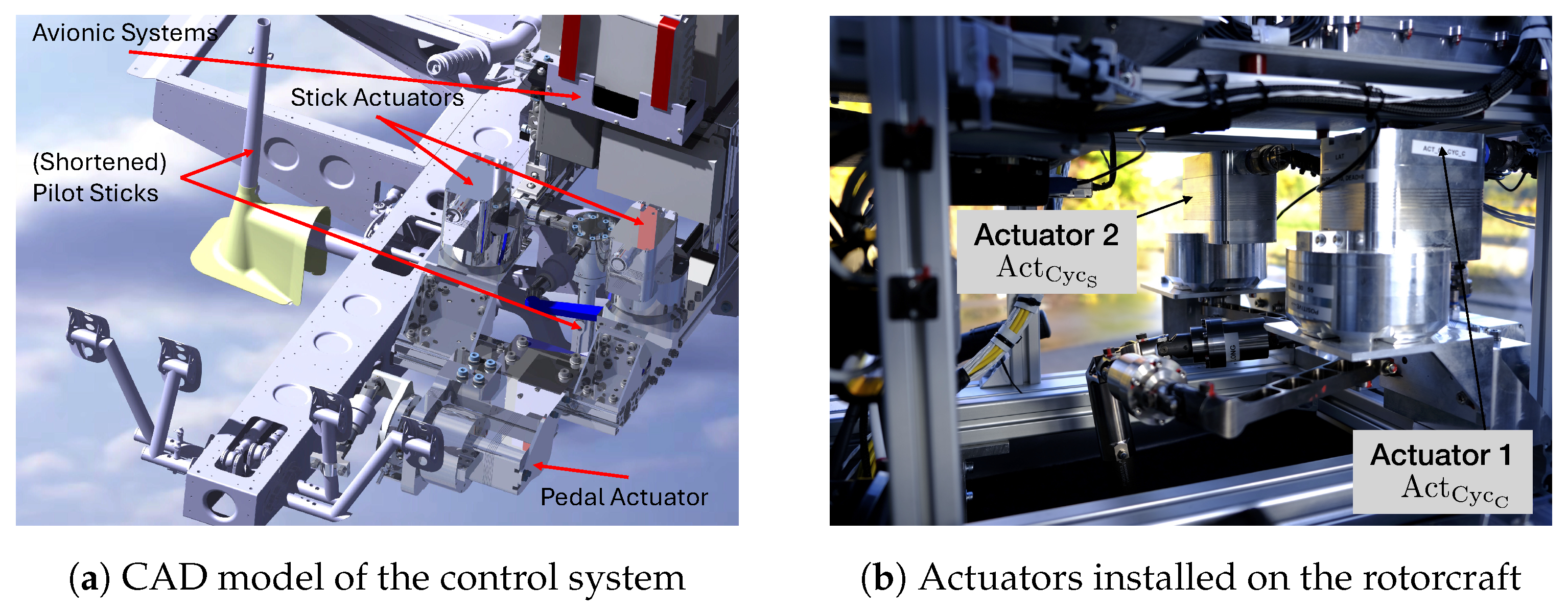
The robotic system consists of three separate mechanisms, which control the stick, collective lever, and the pedals. The stick motion is controlled by two servos sitting on top of the shortened stick in the orientation depicted in
Figure 1. Simultaneous actuation by both servos is required for a linear motion of the stick in any direction, commanded by the flight control laws. This combined actuation is realized by the robot control software, which cancels the nonlinear kinematics of the mechanism.
The development of the mechanical control hardware and software was supported by a multi-body, multi-domain simulation model of the robotic flight control system, implemented in Simulink, based on the developed CAD models of the robot integrated in the rotorcraft. The robot control software generates commands for each actuator to realize the commanded flight controls. The actuator commands are computed using the inverse kinematics of the robotic system, which is integrated in the robot control software as multi-dimensional look-up tables (LuTs). The robot control software is described in
Section 2.2 in detail. The LuTs, determined from the multi-body simulation model, were corrected with limited measurements on the integrated robot in the helicopter copilot seat.
The pedal and the collective lever are also each controlled by a servo, as depicted in
Figure 2a,b. The nonlinear control kinematics in this case is also canceled with inverse-kinematics LuTs embedded into the robot control software. However, the LuTs are one-dimensional for the collective lever and the pedal and can be easily determined based on a multi-body simulation model and corrected using measurements on the real system.
The overall weight of the system (including the electronics and power systems) was comparable to an average human pilot. All of the four servos on the rotorcraft are of the type DA70, developed by VOLZ Servos GmbH. The mechanical levers were manufactured from aerospace-grade aluminum and stainless steel. High precision machining was utilized for in the manufacturing process, such that no backlash could be noticed in the robot joints. The dual-motor servos also include an anti-backlash function, which uses force-fighting between two motors to significantly reduce any backlash in the actuators to 0.1 deg or less. This section provides more details about the model-based development process of the robotic system, and its feed-forward controller. The electronic flight control system of
Section 3 was used to control the rotorcraft via the robotic actuator system.
2.1. Design of the Robotic Control System and the Multi-Body Simulation
The robotic flight control system was developed in the CAD software CATIA V5 R20. The design needed to satisfy the following requirements:
Covering the complete motion space of the cockpit inceptors;
Avoiding singularities in the motion space;
Meeting the actuation rate requirements;
Satisfying the required forces needed for the control of the cockpit inceptors;
The safe operation of the system, including the custom-designed parts as well as the selected norm parts;
A compact and light-weight design that would fit into the limited space of the CoAX 600 cockpit.
A multi-body simulation model was developed based on the CAD models already in the early stages of the design and development process to ensure that the designed kinematics overall and each individual part fulfilled the requirements mentioned above. Furthermore, by augmenting the multi-body simulation model of the control kinematics with physics-based models for the actuators, the development of the actuators could be supported by providing requirements such as the expected torque, or deflection rates.
The toolbox ProSys (ProSys is not publicly released. The Institute of Flight Dynamics of TU Munich can be contacted for inquiries about using the software package) [
21], developed at the institute of Flight System Dynamics of TU Munich, was utilized to set up the multi-body simulation model. ProSys can automatically import the system dynamic and kinematic information of a mechanism from CATIA into Matlab and set up a Simulink–Simscape model, if certain guidelines are followed in the development of the CATIA model, such as the mechanism being modeled as a DMU kinematics module. The imported data include the information about the system mechanical joints (type, position, and degree of freedom), as well as the mass, center of gravity position, and the moments of inertia of each part. The automatically generated multi-body simulation model does not have any actuation and is, by default, simulated only under the influence of gravity.
Simscape allows for each joint available in the multi-body model to be actuated. This function was used to actuate the mechanism using the joints that represent the connection of an arm to a servo. If the rotational motion is commanded at a rotational joint, the required torque to realize the commanded motion can be measured at the same joint. This interface was also utilized to couple the Simscape multi-body model with physics-based models of the actuators in Simulink.
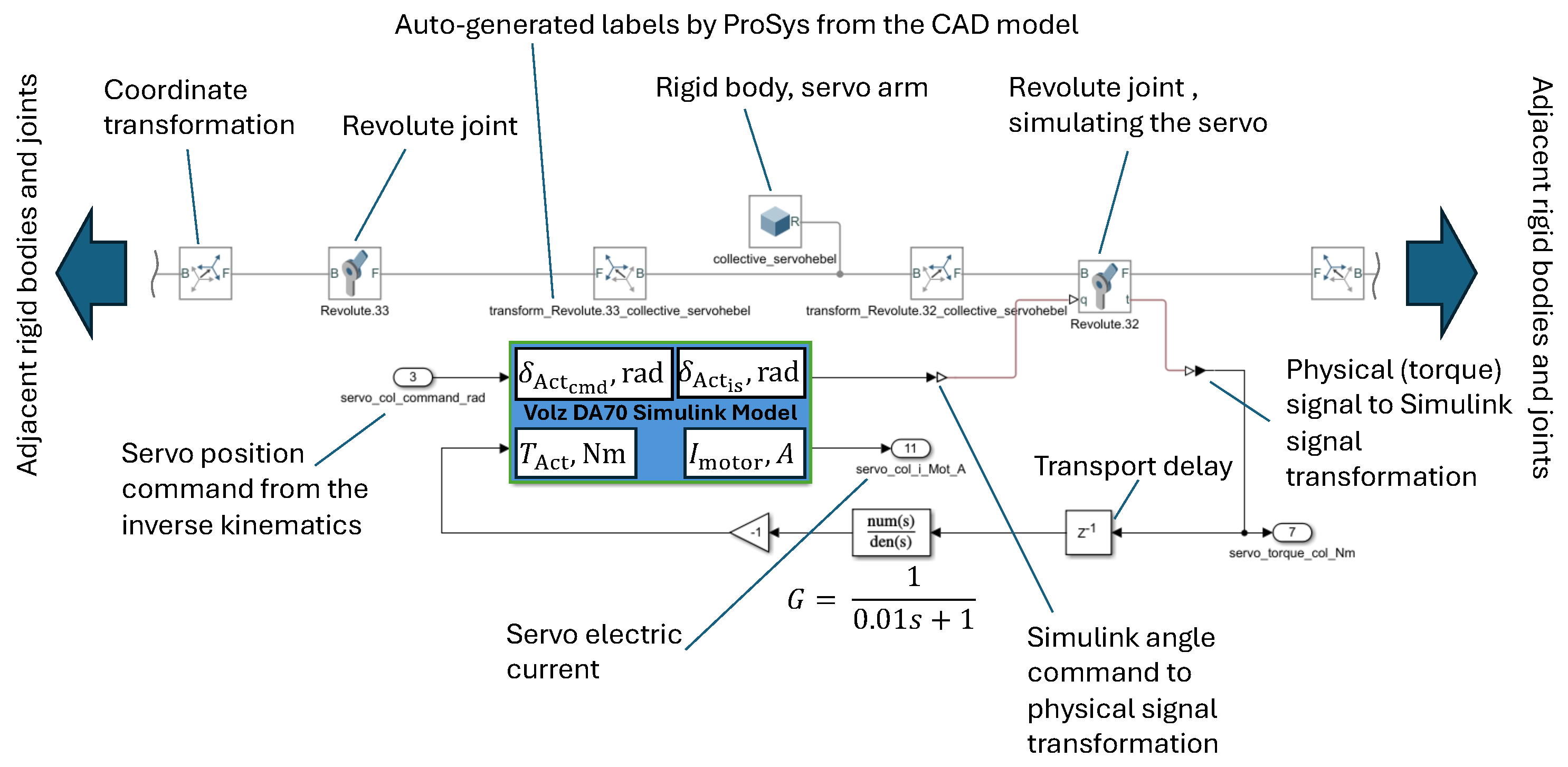
Figure 3 shows the coupling of the servo Simulink model with the revolute joint, modeling the connection of the collective servo arm with the servo shaft, as an example. As seen in
Figure 3, the servo position commands generated by the inverse-kinematics software are fed to the actuator model. The “is” position of the actuator (
in
Figure 3) is used to simulate the motion of the joint. The moment at the joint due to this motion is measured and fed back to the actuator with a transport delay to avoid an algebraic loop. The hinge moment is computed by the multi-body simulation mainly based on the aerodynamic forces and moments, which are modeled as torsion spring and damping coefficients at the pilot inceptors. The Simscape multi-body simulation propagates these moments through the nonlinear kinematics of the system to compute the moments at the servo shaft. In addition to the aerodynamic moments, the inertia of the system parts also contribute to the total moment at the servos, due to their acceleration. The actuator Simulink models consist of its subsystems models, i.e., the electric DC motors (developed as described in Ref. [
22]), the gearbox, the proportional–differential motor controller, and the electronics. The actuator models were parametrized based on the initial selection of the components during the design process. The multi-body simulation model, coupled with the actuators, conclude the simulation model for the forward kinematics of the robot.
The same auto-generated non-actuated model was used to develop a model for the inverse kinematics of the robot. In the inverse-kinematics subsystem, the joints representing the position of the cockpit inceptors (cyclic stick, collective lever, and the pedal) were used for the actuation of the multi-body simulation model. The revolute joints at the respective servo shafts rotate according to the commanded cockpit inceptor position such that the boundary conditions of the kinematics are fulfilled. The motion of the revolute joints at the servo shafts was tapped and used as input for the servo models of the forward kinematics in the simulation.
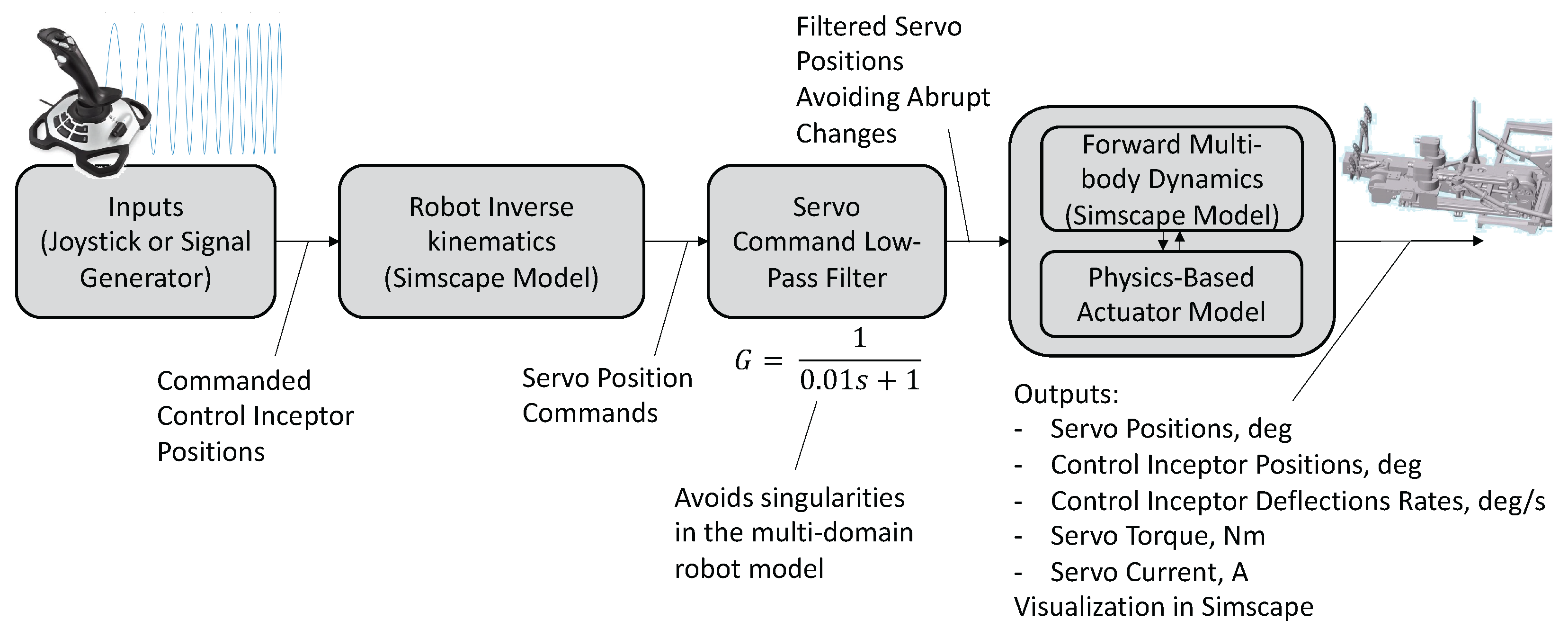
Figure 4 provides an overview of the overall simulation setup. It shows how the same auto-generated multi-body model was utilized to create the inverse- and forward-dynamics/kinematics models. The servo position commands going to the forward dynamics model, which also includes the actuator dynamics, were low-pass filtered, since jumps in the commands drive the linear algebraic system to a singularity.
The overall multi-body simulation model required a low integration time-step of 0.005 s to remain numerically stable. The model was integrated over time using the MATLAB ODE15 solver [
23], which is suitable for stiff differential equations. The actual position of the cockpit inceptor joints, achieved with the actuation of the servos under load, as well as the moments acting on the servos, and the servo power usage, are provided as the outputs of the overall simulation model.
2.2. Robot Control Software
Each servo has its own position controller designed by the manufacturer VOLZ Servos GmbH, a company based in Offenbach, Germany. However, a feed-forward inverse-kinematics controller was needed to generate position commands for the servos, which would result in a specific position of a cockpit inceptor matching a blade pitch angle command generated by the flight control law. The simulation setup, presented in
Section 2.1, already included the inverse kinematics of the robot. The complex Simscape model was, however, not suitable for deployment on a flight control computer. The simulation of such multi-body models in real time requires computational resources that exceed those of a typical flight control computer. Furthermore, solving such linear algebraic equations is not deterministic and the execution time is difficult to predict. Therefore, the inverse kinematics of the robot was integrated in the robot control software as one-dimensional lookup tables (LuTs) for the pedal and the collective lever, and two-dimensional LuTs for the control stick.
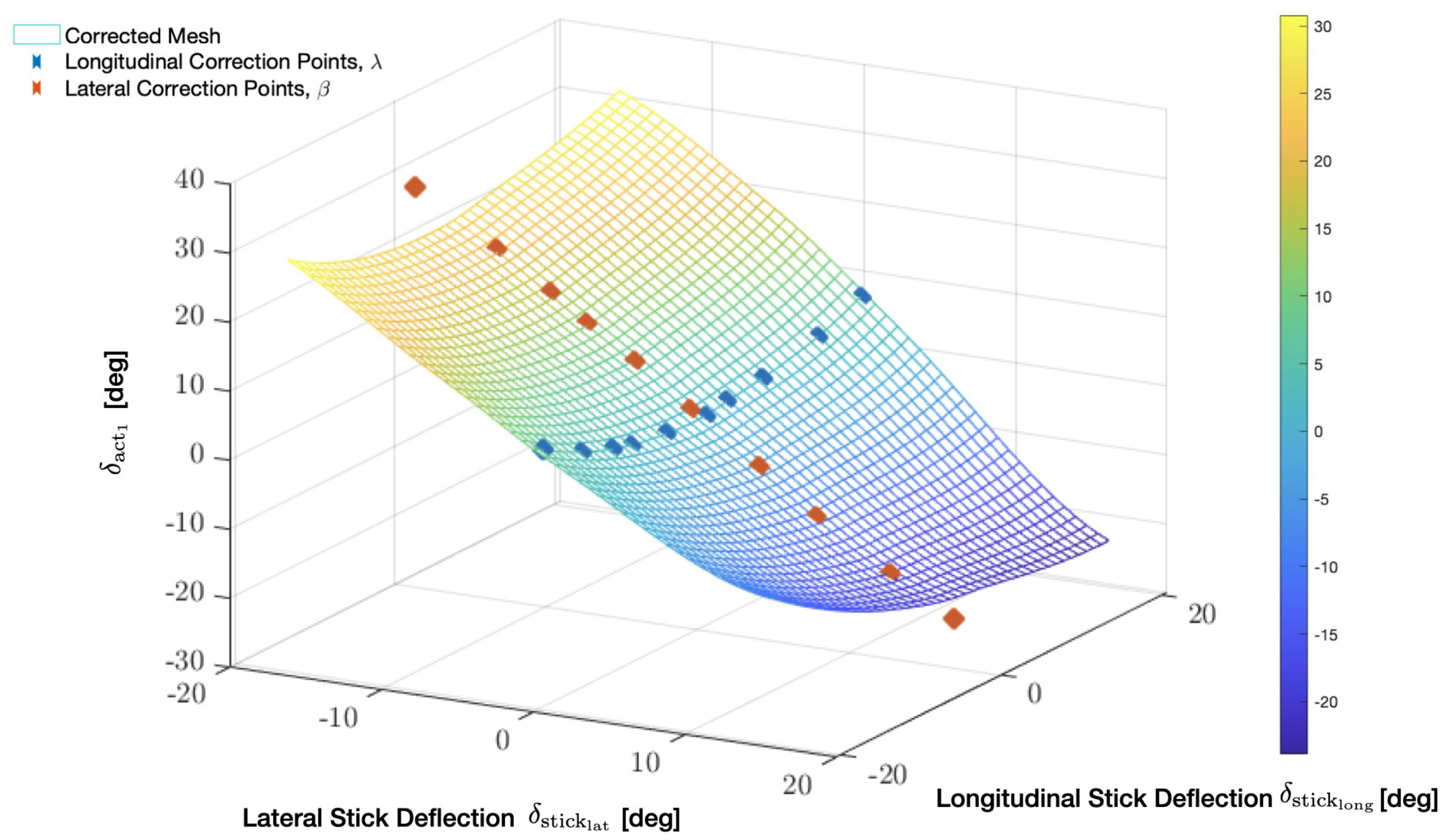
The stick LuTs were determined by simulating the inverse-kinematics multi-body simulation for a 45 × 45 uniform grid of the cyclic stick in equidistant longitudinal and lateral positions. The corresponding positions of the servos
(actuator 1) and
(actuator 2) were recorded during 2025 simulation runs of the multi-body simulation model at the 45 × 45 cyclic stick positions. Limited adjustment of the LuTs based on measurements on the real system were necessary due to the manufacturing tolerances and further inaccuracies in the assembly of the robot in the helicopter. The servo internal position measurements using a hall sensor and the angles of the control stick, measured by inclinometers, were used for the calibration of the LuTs. The selected longitudinal and lateral calibration points, as well as the full inverse-kinematics LuTs, are visualized in
Figure 5 and
Figure 6. The correction points were chosen arbitrarily along the lateral and longitudinal stick deflection directions, while attempting to achieve a uniform distribution of points in both directions.
A linear interpolation scheme was applied to the points of the 45 × 45 grid
for each actuator (
), denoted by
, which can be evaluated at any stick position query point
to determine the output shaft position of each of the actuators (
) required to achieve a desired stick position. The grid for each actuator consists of the vectors of the longitudinal and lateral stick positions at which the virtual measurements took place (
and
), and the corresponding position of the servo output shaft
:
The initial simulation-based uncorrected grid was evaluated at the measured stick positions to compute the error between the simulation-based grid and the longitudinal measurement points (the blue points in
Figure 5 and
Figure 6), denoted as
:
where
is the measured position of the stick actuators 1 and 2.
and
are the longitudinal and lateral deflections of the stick at which the actuator position was sampled on the real system. The chosen longitudinal positions of the stick were commanded via the initial simulation-based inverse-kinematics grid as pure longitudinal commands. Therefore, any measured nonzero
is a result of the error in the inverse-kinematics grid. We can form a longitudinal error grid for each actuator with
, and the sampling points
:
In a similar way, the grid error for the lateral measurement points
(the red points in
Figure 5 and
Figure 6) is computed after the application of the longitudinal correction, using the above error grid
of the longitudinal measurement points and the two-dimensional linear interpolation operator
:
The lateral measurement points can be collected together with their associated error to form the grid
for the correction of the inverse-kinematics grids with respect to the stick lateral deflection measurement points. The feed-forward control law for each actuator becomes
and is visualized in
Figure 5 and
Figure 6 for the actuators 1 and 2.
The one-dimensional LuTs for the pedal and collective lever were developed only based on the direct measurements on the system, as enough points in the motion space could be measured in the one-dimensional case.
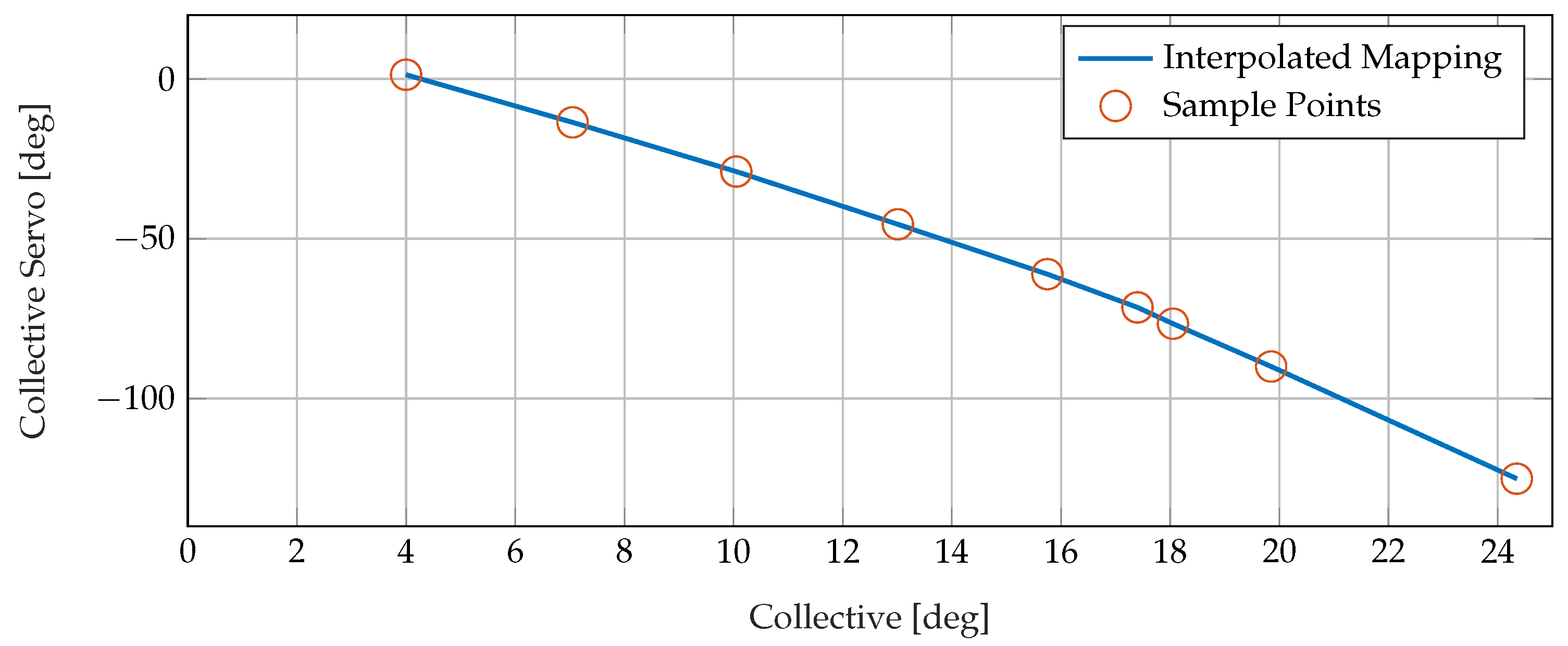
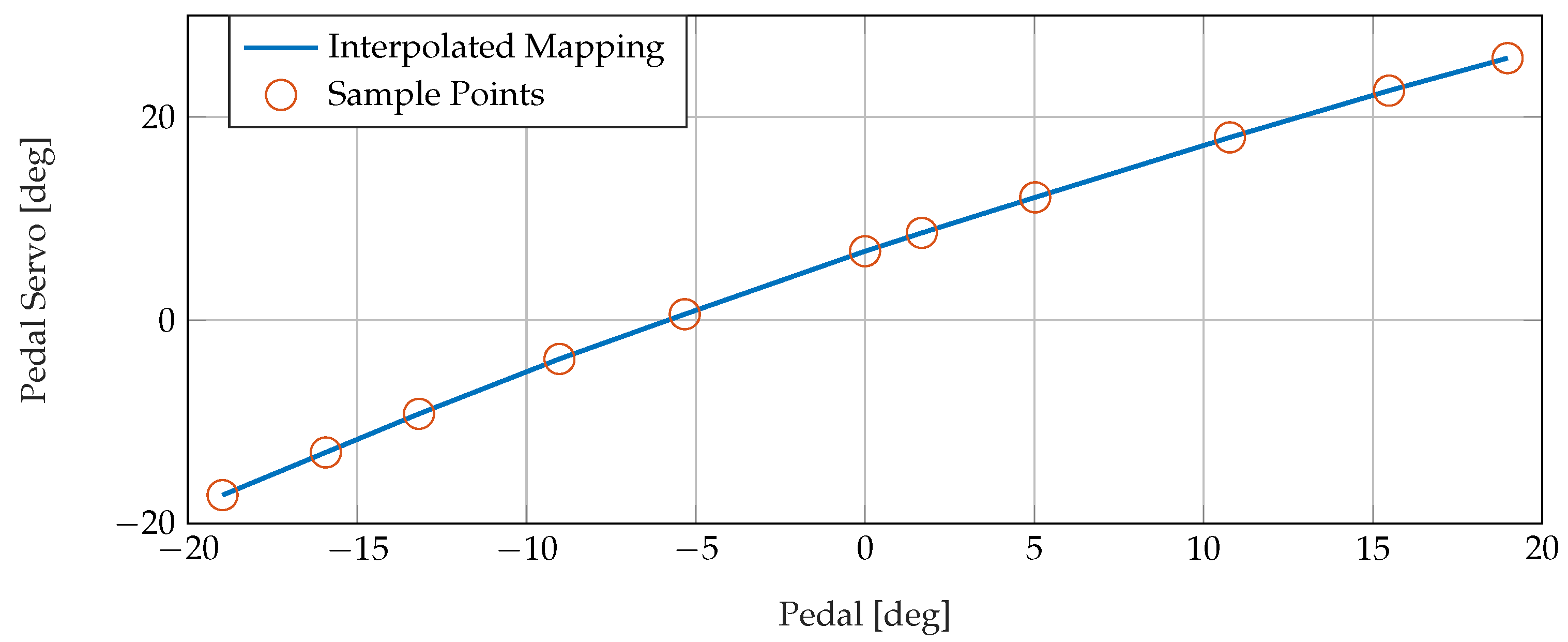
Figure 7 and
Figure 8 show the mapping between the collective and pedal positions and their respective actuators. Nonlinearities are evident in all of the one- and two-dimensional mappings.
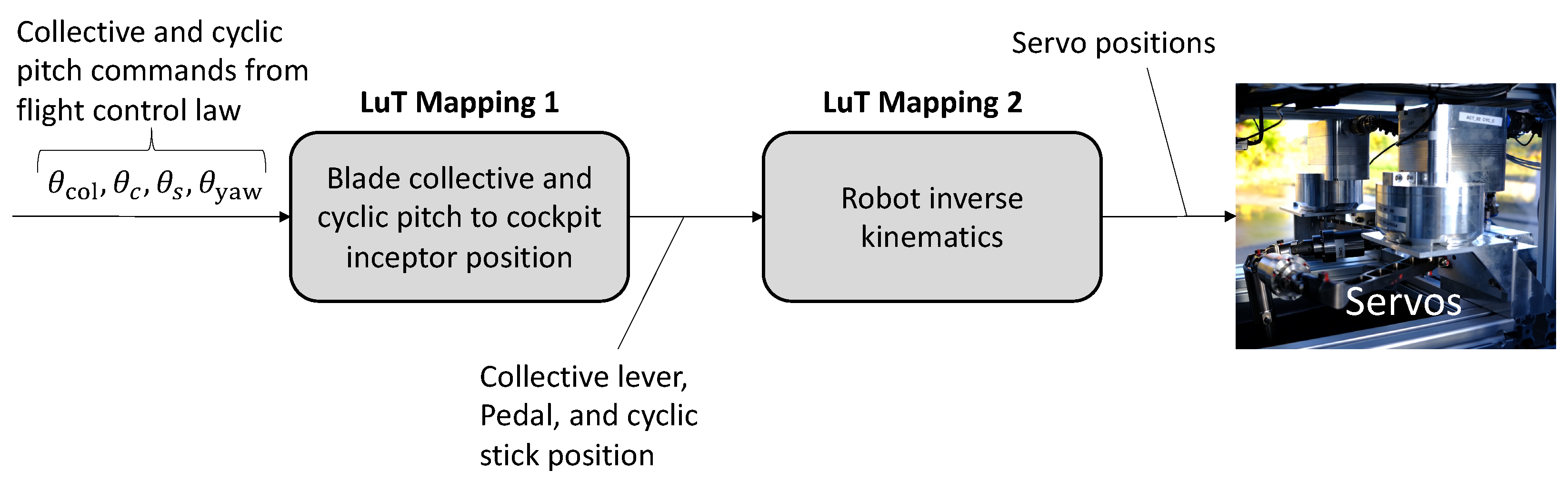
The structure of the robot control software is provided in
Figure 9. The collective and cyclic commands, computed by the flight control law are converted to cockpit inceptor positions by a first set of linear one-dimensional LuTs. The LuTs of
Figure 5,
Figure 6,
Figure 7 and
Figure 8 are applied to the cockpit inceptor positions to compute the corresponding servo positions. The kinematics of the control system, specifically in case of the stick with two actuators, was successfully canceled via the approach described here, such that the lateral or longitudinal commands from the flight controller were executed as such on the pilot stick without any cross-axis coupling.
3. Flight Control System
This section describes the onboard flight control system (FCS). It starts with the operational concept and the requirements of the FCS, and continues with a description of the system architecture, and the remote crew interface. The section concludes with an overview of the validation steps taken for the FCS.
3.1. Operational Concept and Requirements
The concept for the FCS was driven by the intended application as an unmanned technology demonstrator for the robotic actuation system. The main required functions of the system are as follows:
Manual remote control: during the system definition, it was decided to implement only manual control (feedback-augmented, and attitude law) in a first step in order to reduce the complexity for the demonstration flights. The manual remote control system also serves as a basis for a potential later extension with automatic flight control functions. In this case, fallback to manual control would provide an emergency procedure to mitigate malfunctions of the automatic flight control system.
Telemetry data indication: the system must provide the capability for the remote crew to monitor critical system parameters in real time on the ground during operations.
Remote flight termination: the possibility to remotely shut down the engine is required as a safety measure to ensure containment of the UAV within a predefined geographical volume, thereby reducing the risk to other airspace participants or third parties on the ground in the event of a control loss.
Measurement data collection for post-flight processing: a wide array of sensors has been mounted on the rotorcraft, including two inertial measurement units at different positions, two GPS receivers, an angular acceleration sensor, and potentiometers and strain gauges at different positions along the control rods.
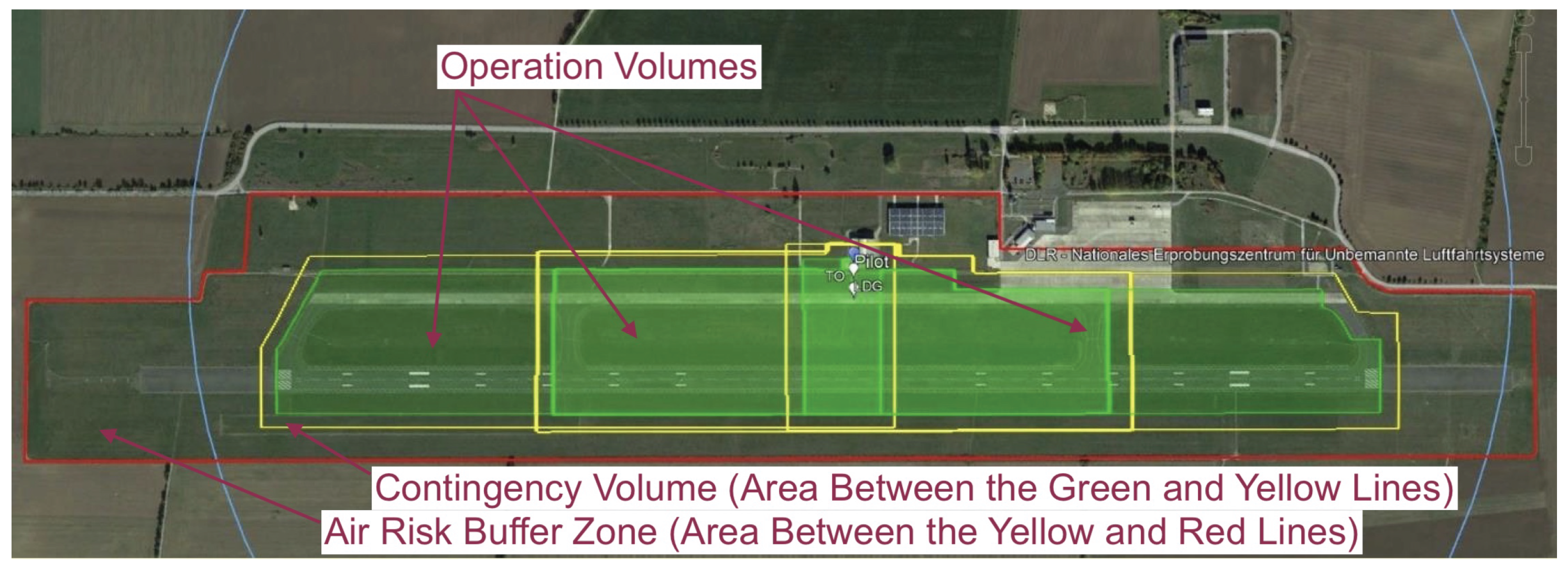
Additional safety objectives resulted from the application of the SORA (specific operations risk assessment, see Ref. [
24], Article 11) process, which was required for the operational authorization of the rotorcraft as an unmanned aircraft system (UAS) by the German authorities. Following this process, objectives were defined based on a specific assurance and integrity level (SAIL). The SAIL is a qualitative measure that drives the objectives to be fulfilled by an applicant. It is defined based on an assessment of the risk of the UAS operation on the ground and in the air (for details refer to Ref. [
24], AMC 1 to Article 11). As we chose to operate the rotorcraft over a so-called “controlled ground area” where access was restricted to members of the remote crew, operate only within visual line of sight (VLOS), and reduce the risk of encountering another aircraft by operating in an active aerodrome traffic zone (ATZ), which was exclusively used by the UAS, the operation was classified as SAIL II. In this context, two fundamental safety requirements are given by Ref. [
24]:
Containment: “No probable failure of the UAS or any external system supporting the operation should lead to operation outside the operational volume.” [
24], p. 61;
Safety and reliability: “The resulting hazards are minimized in the event of a probable malfunction or failure of the UAS.” [
24], p. 109.
The first objective requires to contain the operations to a predefined, approved geographic volume and addresses the risk resulting from exceeding this operating volume as a result of a loss of control over the UAS. It should be noted that compliance with the second requirement is optional for SAIL II operations, but it was decided to use this as a governing principle for the system architecture design as far as practicable. As a basic design principle, fault tolerance against any single failure, unless it can be reasonably assumed to be improbable, was required for the presented system architecture as a result of this objective.
3.2. System Architecture
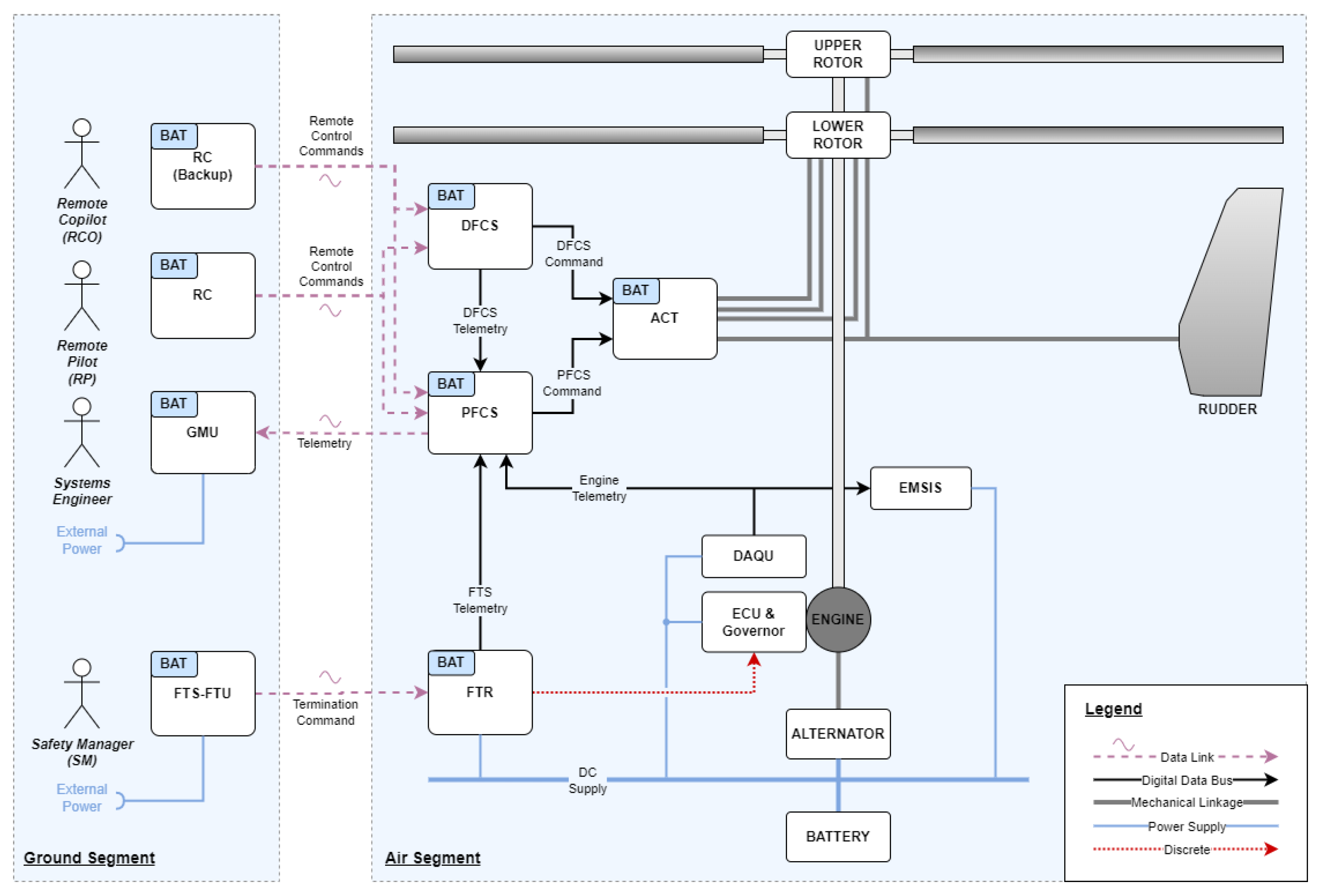
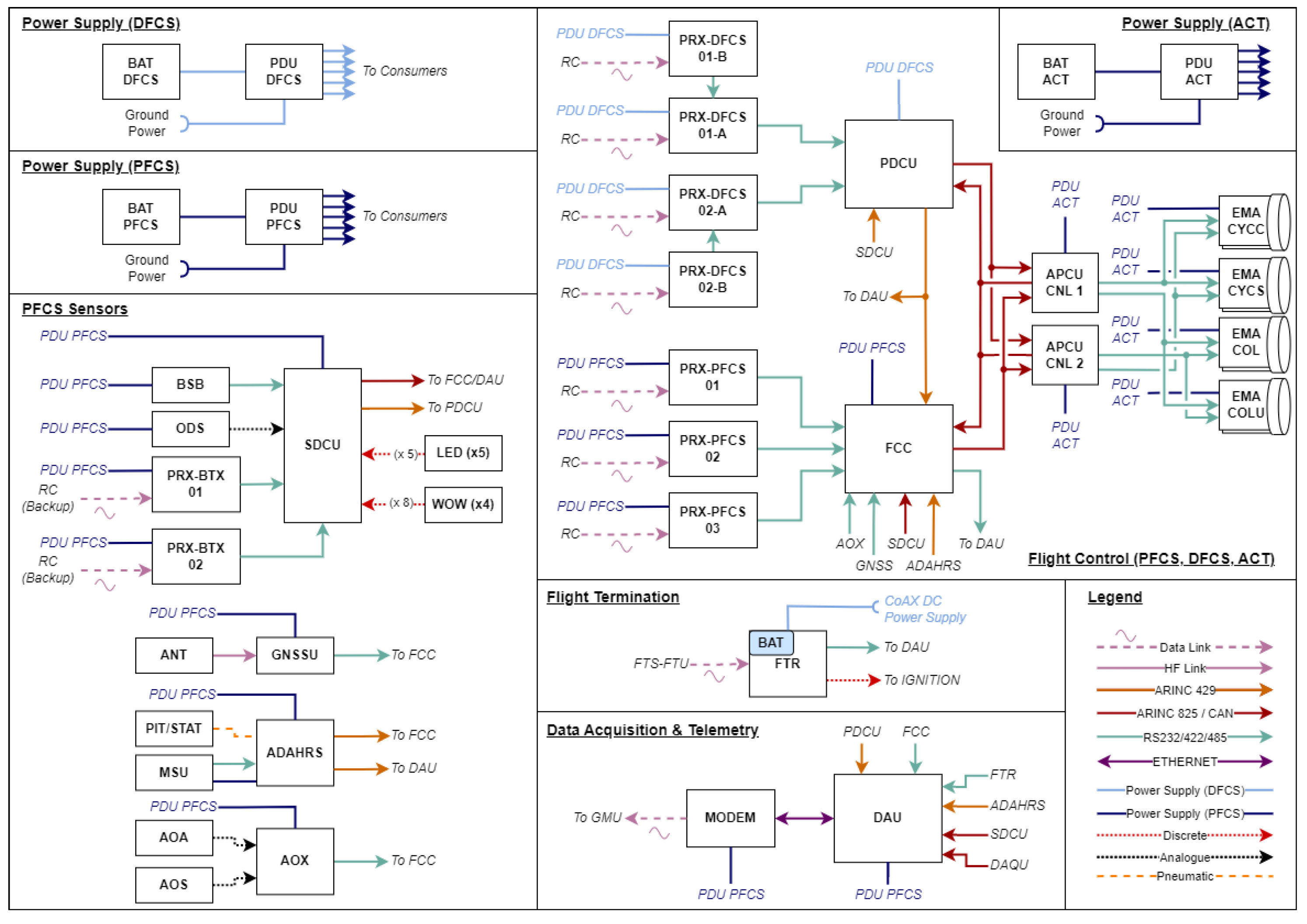
A schematic overview of the flight control system is shown in
Figure 10. The aircraft is always—in all operating modes—controlled remotely by the remote pilot, using a hand-held remote control (RC). Furthermore, a second remote pilot can take over control using a backup RC. A ground monitoring unit (GMU) provides live indication of telemetry data. Onboard the air vehicle, two separate flight control channels process the commands received from the remote pilot: A primary flight control system (PFCS) provides active closed-loop control of the rotorcraft and additionally contains the equipment required for measurement data acquisition and the telemetry data link. The direct flight control system (DFCS) acts as a backup system and provides a direct control mode in which the commanded blade pitch angles of the lower and upper rotor and the rudder deflection are directly proportional to the control stick deflections on the remote control, without any artificial feedback loops. Each flight control channel has its own, independent power supply as well as its own set of receiver units to process radio control (RC) signals. Most of the main components of the system ran with a sampling rate of 50 Hz. The flight data recorder could log signals with a sampling rate of up to 1 kHz.
A separate dual-channel control unit (APCU) executes the robot control software and translates the flight control commands into direct servo deflection orders. The electromechanical servos feature a duplex design, where the output shaft is driven by two electric motors that are combined using a torque summing gearbox. Each electric motor is driven by its own motor control unit, which is connected to one of the two APCU channels.
The detailed electronic architecture is shown in
Figure 11. The remote-control functions are executed on two control units: The flight control computer (FCC) provides closed-loop attitude and angular rate control. The inertial measurements for these control functions are captured by an air data attitude heading reference (ADAHRS) unit. It should be noted that no air data measurements are used for closed-loop control. The backup direct mode control is executed by the so-called “Pilot-DCU” (PDCU). Each control unit receives command signals from the RC through multiple receiver units (called PRX in
Figure 11). The receiver units are placed on different locations outside the helicopter fuselage to ensure stable reception on multiple units in any orientation of the helicopter. A cross-talk interface between the PDCU and FCC additionally forwards the control commands received by the PDCU to the FCC such that the augmented control through the FCC remains available even if reception is lost on all of the directly connected receiver units.
The fallback to the DFCS is implemented by a simple priority selection logic on the actuator control unit: In normal operating conditions, the PDCU is passive and the FCC is in command. Whenever the PDCU is transmitting commands, the PDCU commands are selected by the APCU channels. The PDCU can be activated either manually (using dedicated switches on the RC) or automatically, when a loss of commands from the FCC is detected. For this purpose, the actuator control unit monitors the periodic reception of control commands from the FCC and forwards the reception status to the PDCU.
Additional sensors are included for data recording and telemetry: A GPS receiver (GNSSU) provides the 3D position for monitoring the containment of the UAV with respect to the boundaries of the operating volume on the ground. An additional inertial measurement unit (BSB) with an integrated GPS receiver provides rate and acceleration data and a second GPS position for post-flight processing. The omega-dot sensor (ODS) measures angular accelerations. A data concentrator unit (SDCU) forwards these measurements on a common digital data bus. The SDCU also acquires discrete signals that drive the warning LEDs that are normally used to indicate engine warnings in the manned version of the helicopter. The AOX unit acquires the analog signals from a cardan-mounted combined angle of attack/angle of sideslip probe that is located on a boom.
A central data acquisition unit (DAU) captures and records measurement data from all connected devices and forwards telemetry data to the modem for transmission to the ground station. It is also connected to the helicopter’s engine instrumentation; another data acquisition unit (DAQU) provides measurements of rotor and motor RPM, oil pressure and temperature, and other engine parameters. In the manned version of the helicopter, these parameters are provided to the pilot on a display unit (EMSIS) in the cockpit. For the unmanned version, the same parameters are forwarded to the ground, where an identical display unit is mounted in the ground monitoring unit (cf.
Section 3.3).
The containment requirement is addressed by a separate flight termination system, which, completely independent from the FCS, allows to remotely shut down the rotorcraft combustion engine by interrupting the power supply to its ignition circuits. The system uses a separate data link for the transmission of the termination trigger from a ground unit (FTS-FTU) to the airborne receiver (FTR). It is developed to the RCC-319 standard [
25], which is based on a robust analogue tone-based modulation of the transmitted command signal. In order to avoid disturbances from interfering with RF signals, the data link uses a restricted frequency band that requires authorization by the German telecommunications authority.
3.3. Remote Crew Interface
The remote crew interfaces are shown in
Figure 12. Two identical commercial hand-held remote-control transmitters are used for the manual control of the rotorcraft by the remote pilot (cf.
Figure 12a). This RC system was selected due to its redundant data link (each transmitter provides two 2.4 GHz modules and a backup 900 MHz module) and its wide application in the RC model community. In addition to the four main control channels for roll, pitch, yaw, and collective control, buttons on the RC are used to select the operating mode of the onboard flight control system. The two centrally located “TAKE OVER” buttons allow to take over the control through the backup RC in case of a control malfunction.
A ground monitoring unit (cf.
Figure 12b) provides real-time indication of flight critical system parameters such as the voltage levels of the FCS batteries and the signal strength of the different data links on a main indications panel. This panel also includes an indication of the position of the UAV over a synthetic map view, together with the boundaries of the operating volume. The engine warning LEDs that are installed in the manned version of the helicopter are replicated by software lamps. The panel also includes synoptics sections showing the current operating mode of the flight control system, which are used mainly to provide feedback to the remote pilot during operations and for troubleshooting. Engine parameters and the current fuel level are indicated on a separate display unit (EMSIS), which is identical to the indication unit normally installed in the cockpit of the manned version of the helicopter. Therefore, all indications and warnings according to the aircraft flight manual of the manned variant are also provided in the unmanned version.
3.4. Validation
The system architecture design and functions were validated in an integrated system simulation environment that included the design models for the FCC, PDCU and APCU control software, the GMU display software, sensor models, emulators for the two RCs, and the complete digital communication architecture. This integrated system model was developed from a centralized description of the logical transport layer and physical interfaces of the system architecture and stored in a machine-readable database format, as described in Ref. [
26].
Due to the time and budget constraints of the project, an exhaustive requirements-based testing of the FCS equipment and the integrated system was not performed. Instead, test cases were derived based on operational sequences that describe the intended system behavior under nominal conditions as well as in failure conditions. This principle is further described in Ref. [
27]. Those sequences were used to define test cases that test the system behavior in the integrated simulation environment, as well as in hardware-in-the-loop (HIL) tests and ground tests of the integrated system.
Additionally, dedicated ground tests have been performed with the fully integrated system in order to verify the effective range of the data links for remote control, telemetry data transmission, and remote flight termination. An overview of the HIL tests as well as system tests in a hover frame are provided in the following section.
6. Conclusions
A 600 kg coaxial rotorcraft was converted to a UAV. A robotic actuator system was developed and retrofitted into the cockpit to enable unmanned flight. The robotic actuator system is directly connected to the cockpit inceptors and does not require a modification of the rotorcraft’s mechanical control system. This minimally invasive approach makes the reversible conversion of a new CoAx 600 rotorcraft to a UAV possible with limited effort and in limited time. This is, to the best knowledge of the authors, the first time a robotic control system has been used for the unmanned flight of a full-size rotorcraft, and it demonstrates the feasibility of this approach.
The nonlinear kinematics of the robotic system are canceled by the onboard feed-forward robot control software, which was developed using a Simscape multi-body simulation model and numerically adjusted based on limited manual measurements on the helicopter. The applied numerical grid adjustment method was described. The following lessons were deduced from the development process:
The operation of the pilot stick using two actuators working together to execute commands in the lateral or longitudinal directions was effective in both theory and practice.
The multi-body simulation model, coupled with the actuator models, was an indispensable tool in designing the robotic actuator system. It was used for verifying the kinematics, the selection of the actuator components, and the system dynamic and power requirements.
The Simscape multi-body model can be used to derive inverse-kinematics look-up tables for the onboard feed-forward robot control software to cancel the nonlinear (multi-dimensional) kinematics of the control rods. However, due to manufacturing tolerances, the simulation-based two-dimensional look-up tables needed to be corrected using measurements on the actual system. The methods of
Section 2.2 were developed for this purpose.
An electronic flight control system, consisting of primary and emergency flight control paths, was designed and developed, allowing the pilots to control the aircraft using RC transmitters. The onboard system also sent the flight parameters to a ground station via a telemetry link to monitor the flight tests. It was demonstrated that the described flight control system satisfies the requirements of the UAV operation according to SAIL II in the context of SORA.
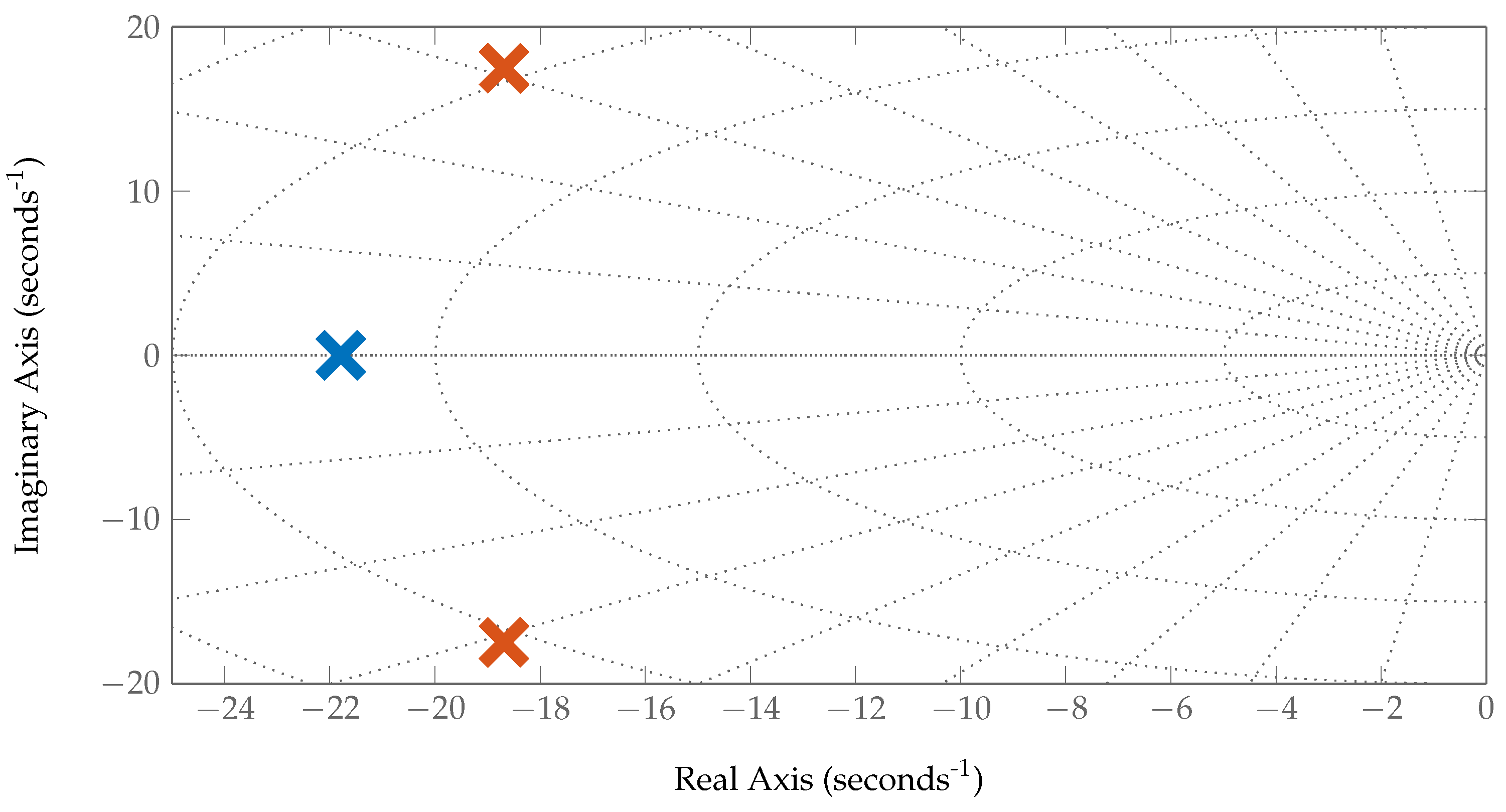
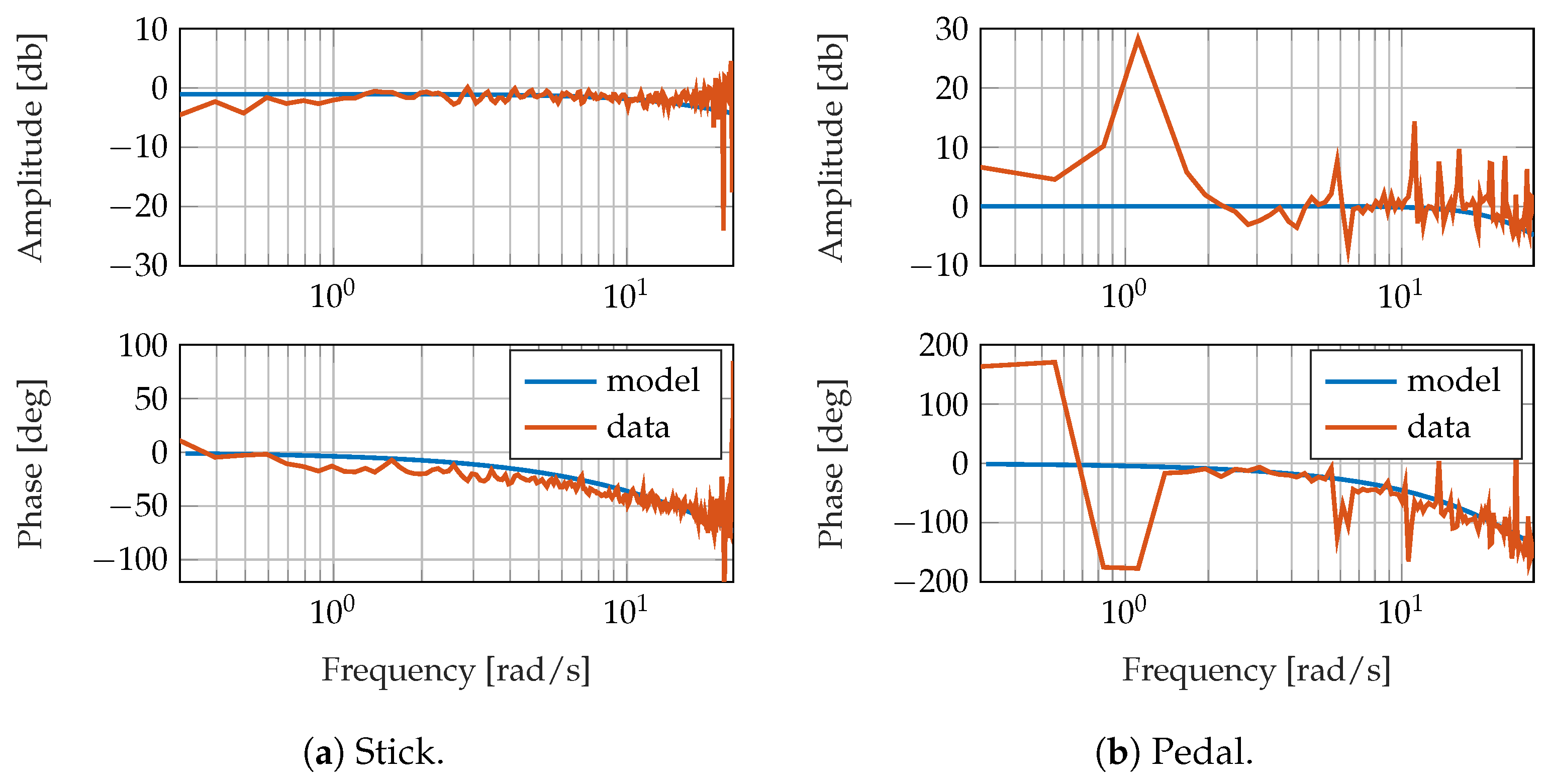
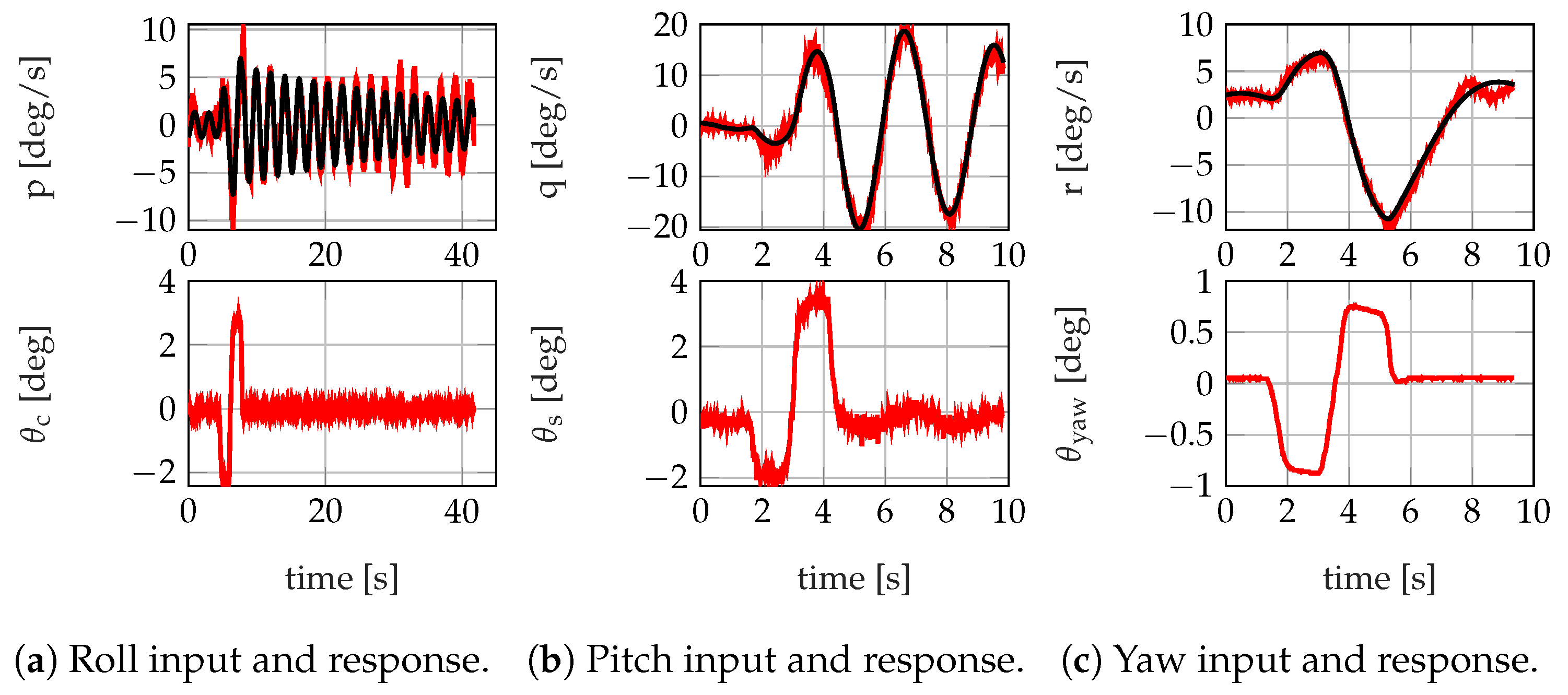
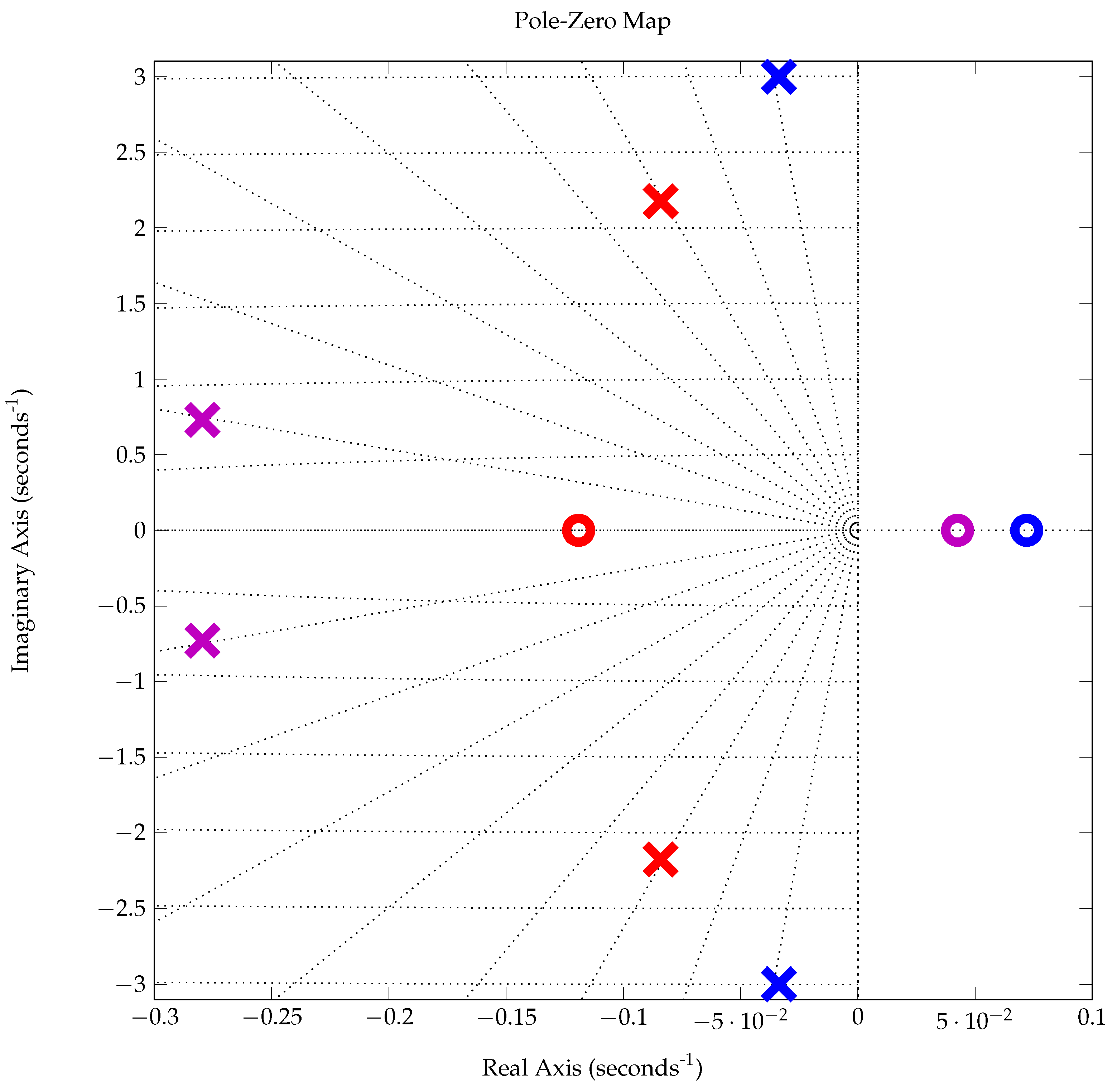
The flight control systems and functions were tested in a HIL setup and later in a hover frame, before commencing the free-flight test campaign. The data captured on the hover frame were used to estimate linear low-order system models of the actuator dynamics, as well as the rotational dynamics of the helicopter while flying in the hover frame. It was demonstrated that, although the hover frame is a valuable tool for testing the systems and crew training, it is not a suitable means for testing flight control functions due to differences of the rotorcraft flight dynamics between the hover frame and free flight, as demonstrated in
Section 5.2. The differences are mainly the result of the offset of the mounting position of the rotorcraft on the hover frame from its center of gravity. These considerations are important due to the increased use of such hover frames in urban and advanced air mobility research and development. With regards to the system, avionics, and the HIL tests, the following conclusions were drawn:
The overall resulting actuator dynamics from flight control law commands to the actual deflections at the swashplate were estimated in
Section 5.1. Due to aerodynamic loads on the full-size rotorcraft, the actuator dynamics were slower than those of smaller UAVs. Such in-flight actuator tests were, therefore, essential to identify the correct actuator dynamics to be used in flight control law design.
The HIL tests revealed that the remote pilots could not effectively operate the unmanned rotorcraft in open loop, due to the actuator dynamics and system time delays. This information was further motivation for designing closed-loop flight control laws and keeping them active at all times during the unmanned flight tests.
The flight tests took place in the attitude mode flight control law at the national test center for unmanned aircraft at the Magdeburg–Cochstedt airport (EDBC) in Germany. The remote operation of the rotorcraft was possible with limited pilot workload, despite windy days with significant gusts. The rotorcraft with the closed-loop flight controller showed excellent flying qualities. However, it was observed that only a limited section of the operating volume could be used for the flight tests, since the pilots could not safely identify the orientation of the rotorcraft at higher distances. Therefore, a velocity controller is required for more complex maneuvers.