Adaptive Attitude Roll Control of Guided Projectile Based on a Novel Unidirectional Global Sliding Mode Algorithm
Abstract
1. Introduction
2. System Modeling of a Conventional Guided Projectile
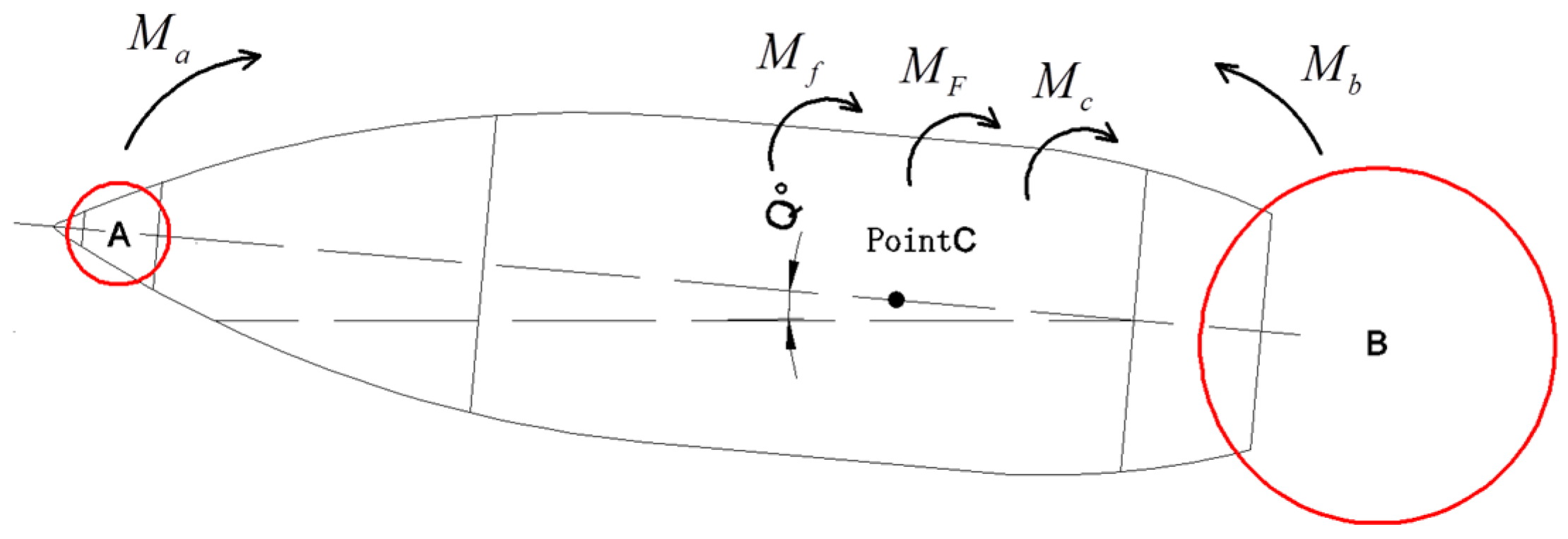
2.1. The Dynamics Model of Projectile
2.2. The Frictional Torque Model
2.3. The State Space of Whole System
3. The Design of Robust Roll Control System Based on Dynamics Model
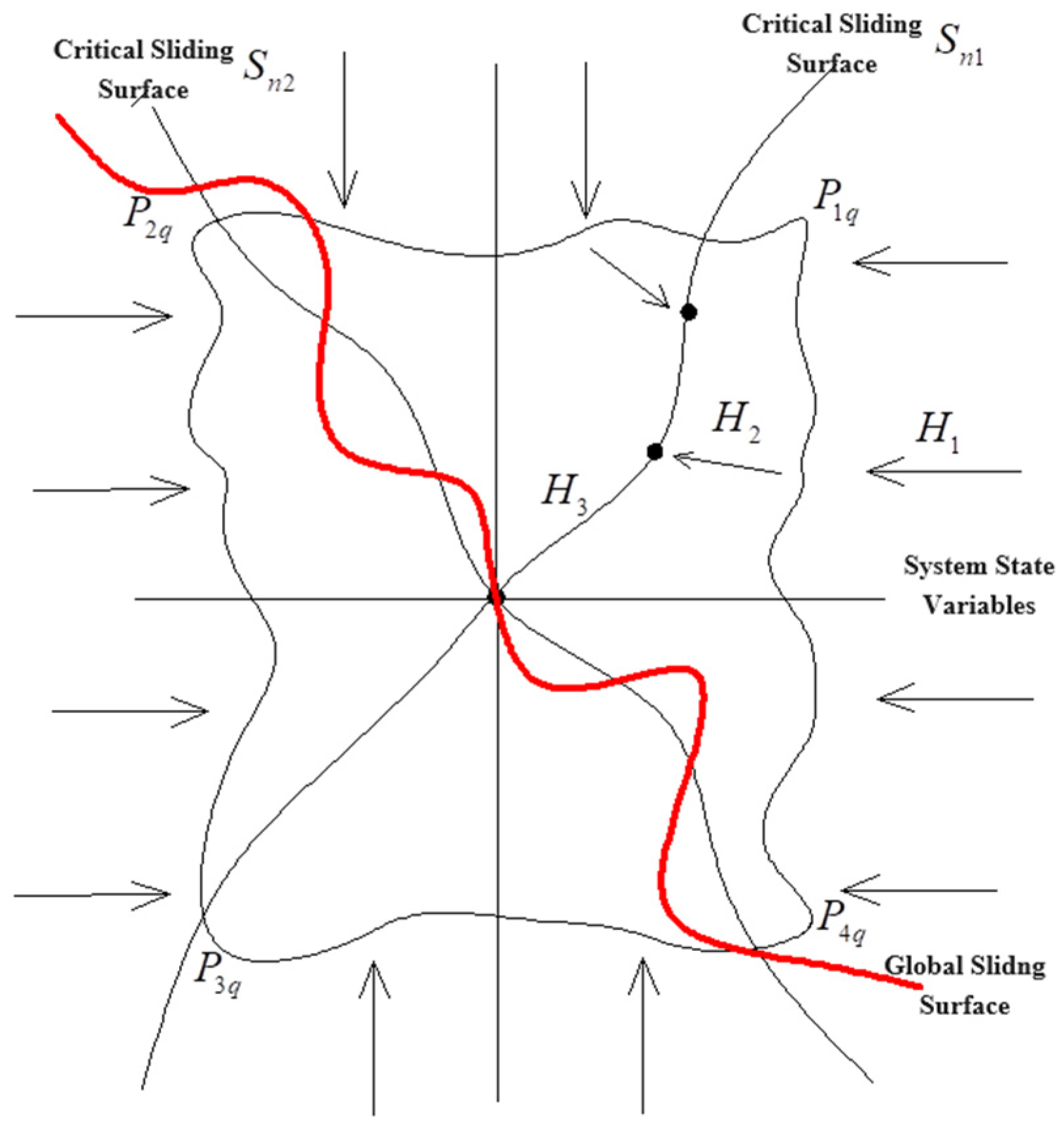
3.1. The Relevant Lemmas
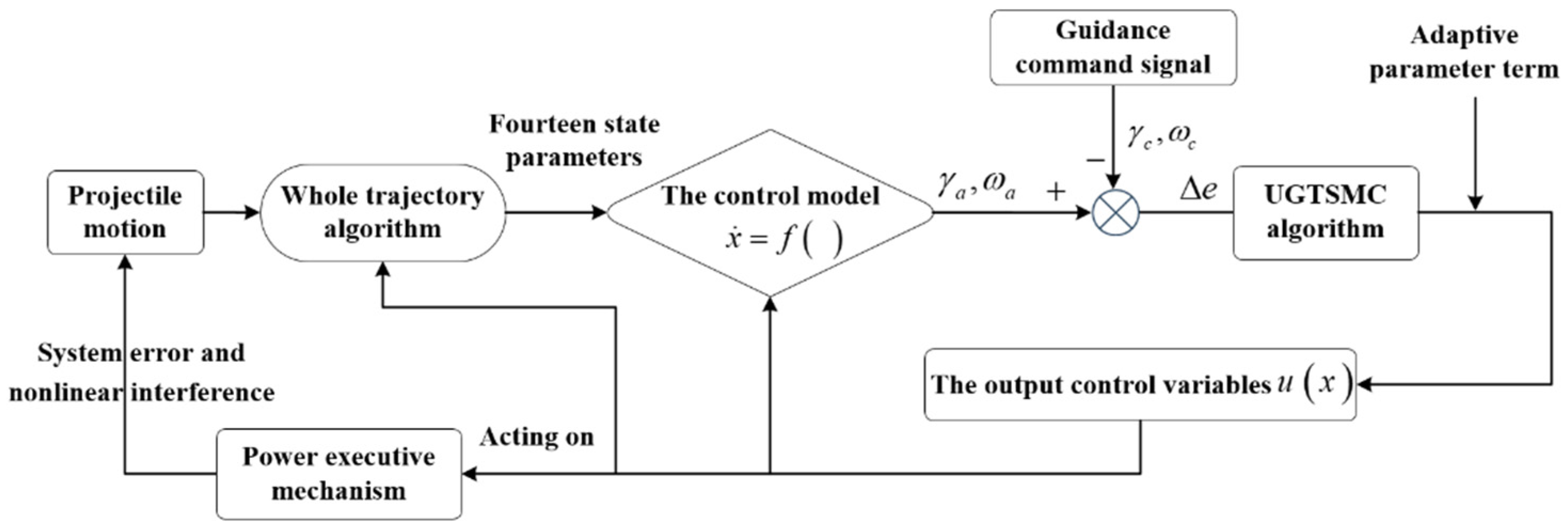
3.2. The Design of the Upper Control Algorithm
3.3. The Lower-Layer Control Command
3.4. The Designed Robust Autopilot Based on the Control Algorithm
4. The Simulation Verification
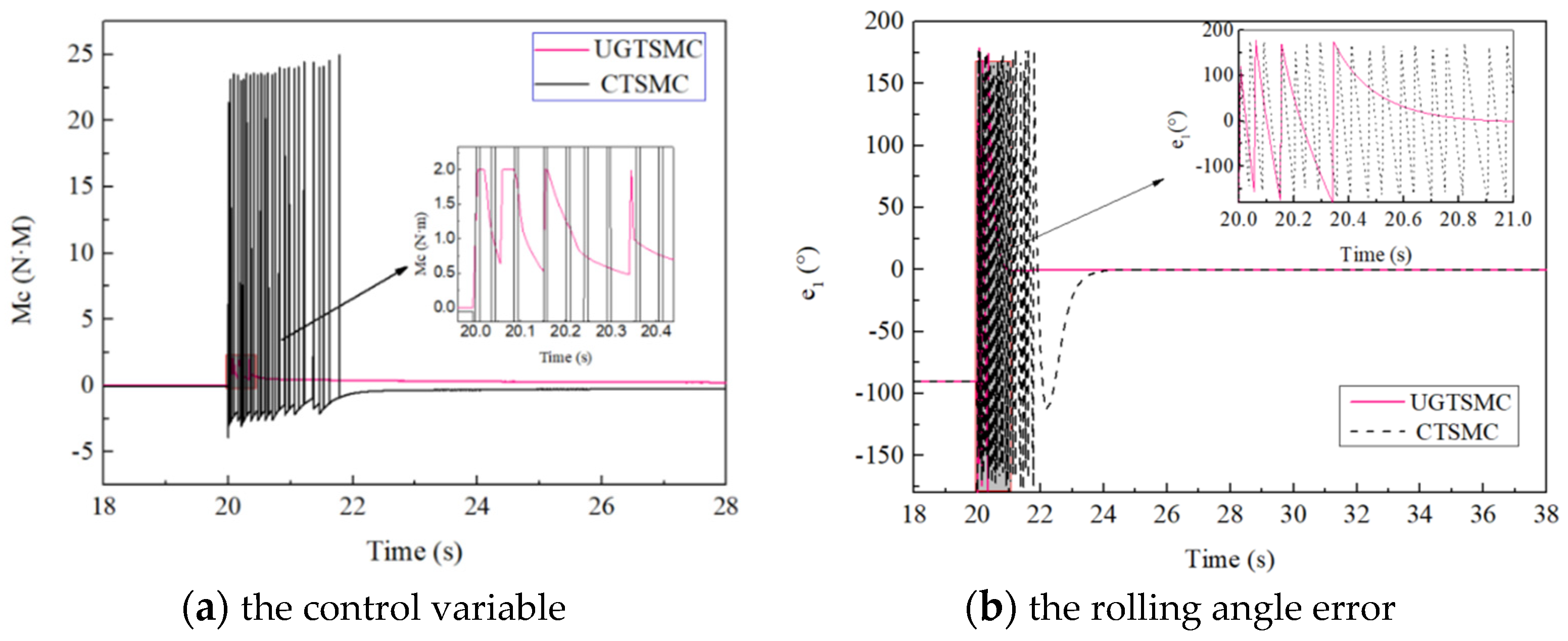
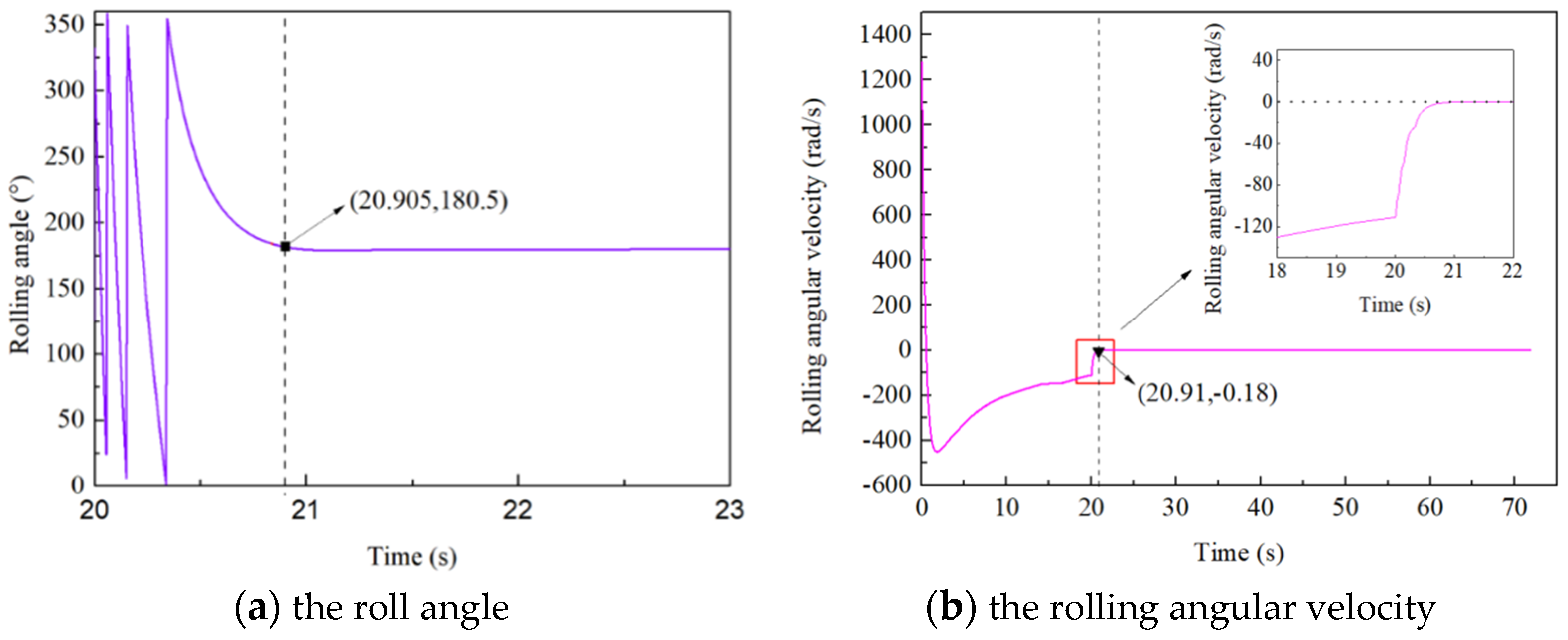
4.1. The Control Effects of the Roll Channel
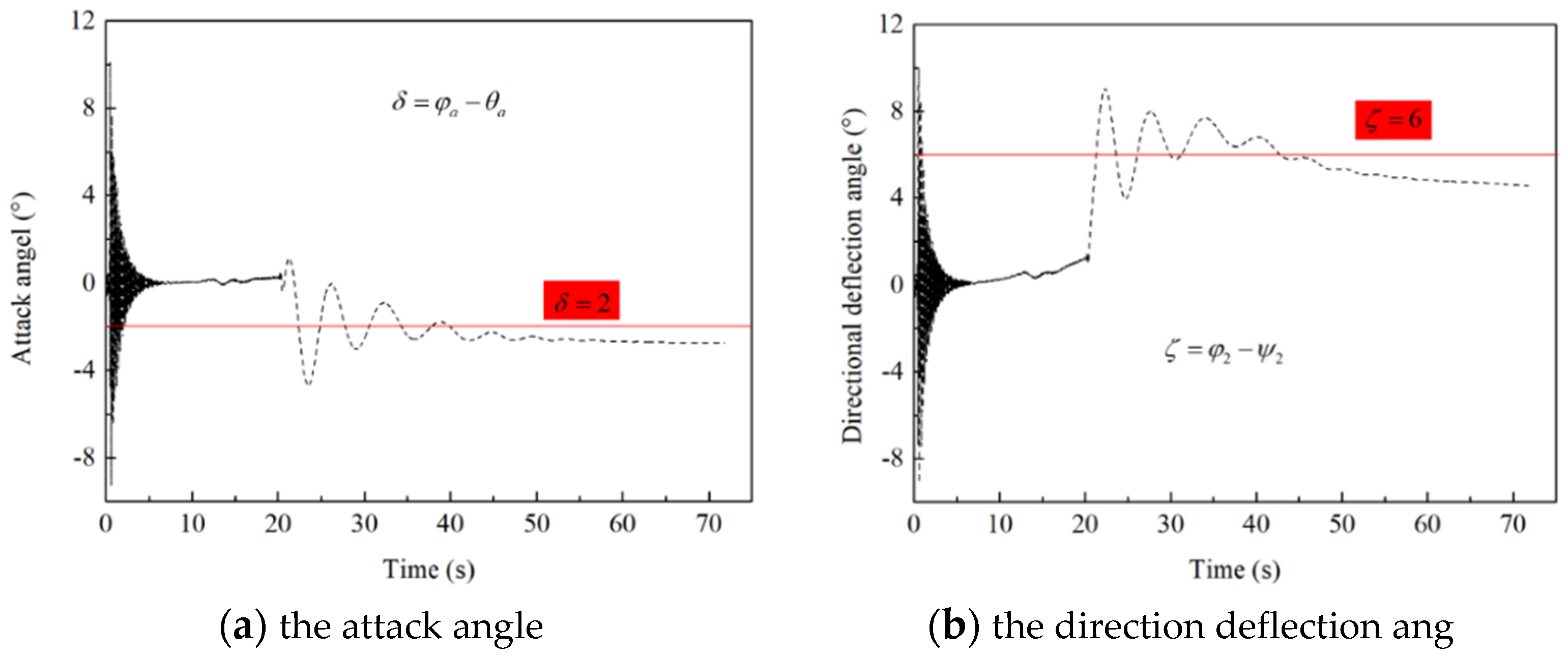
4.2. The Control Effect Analysis of the Motion Attitude
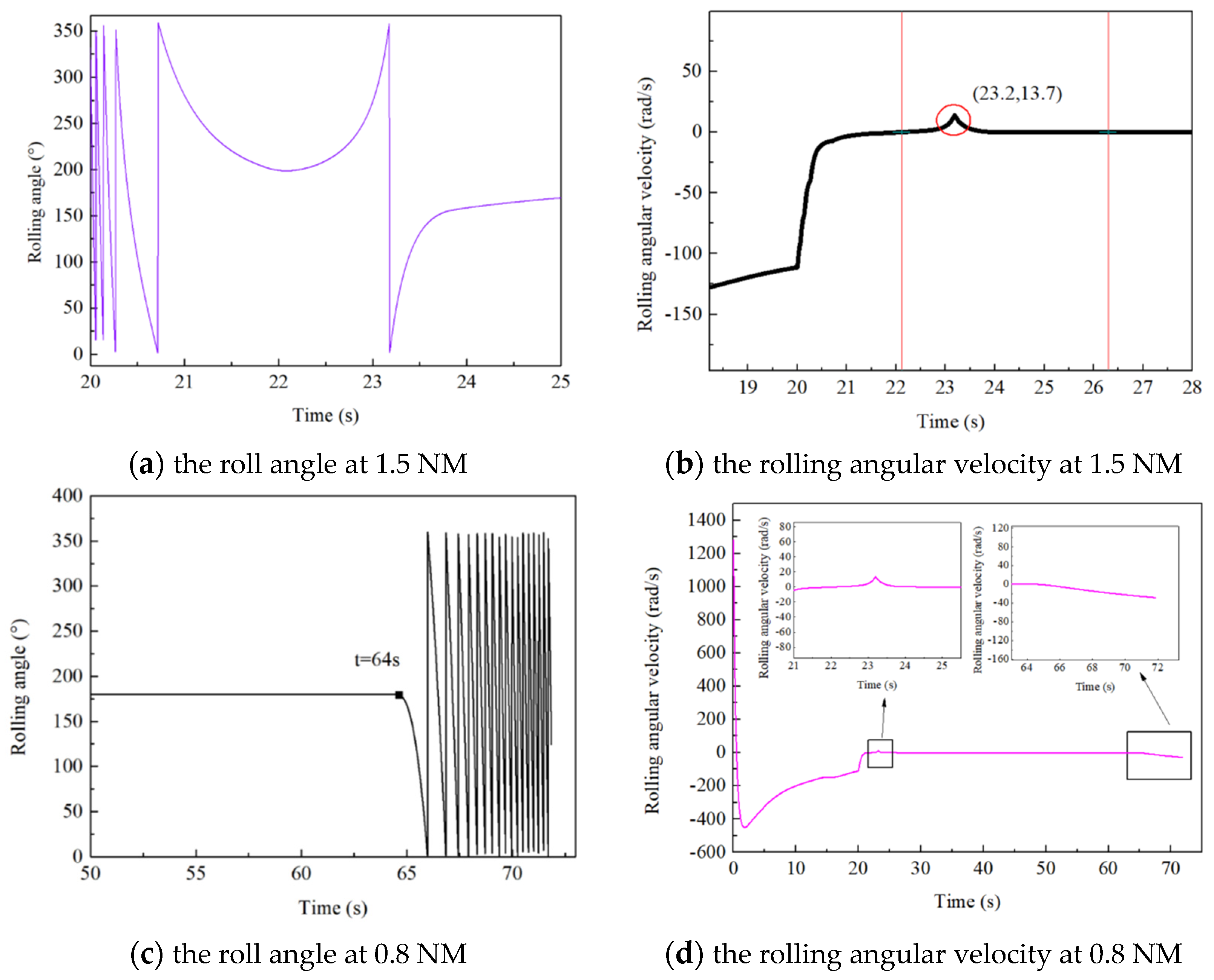
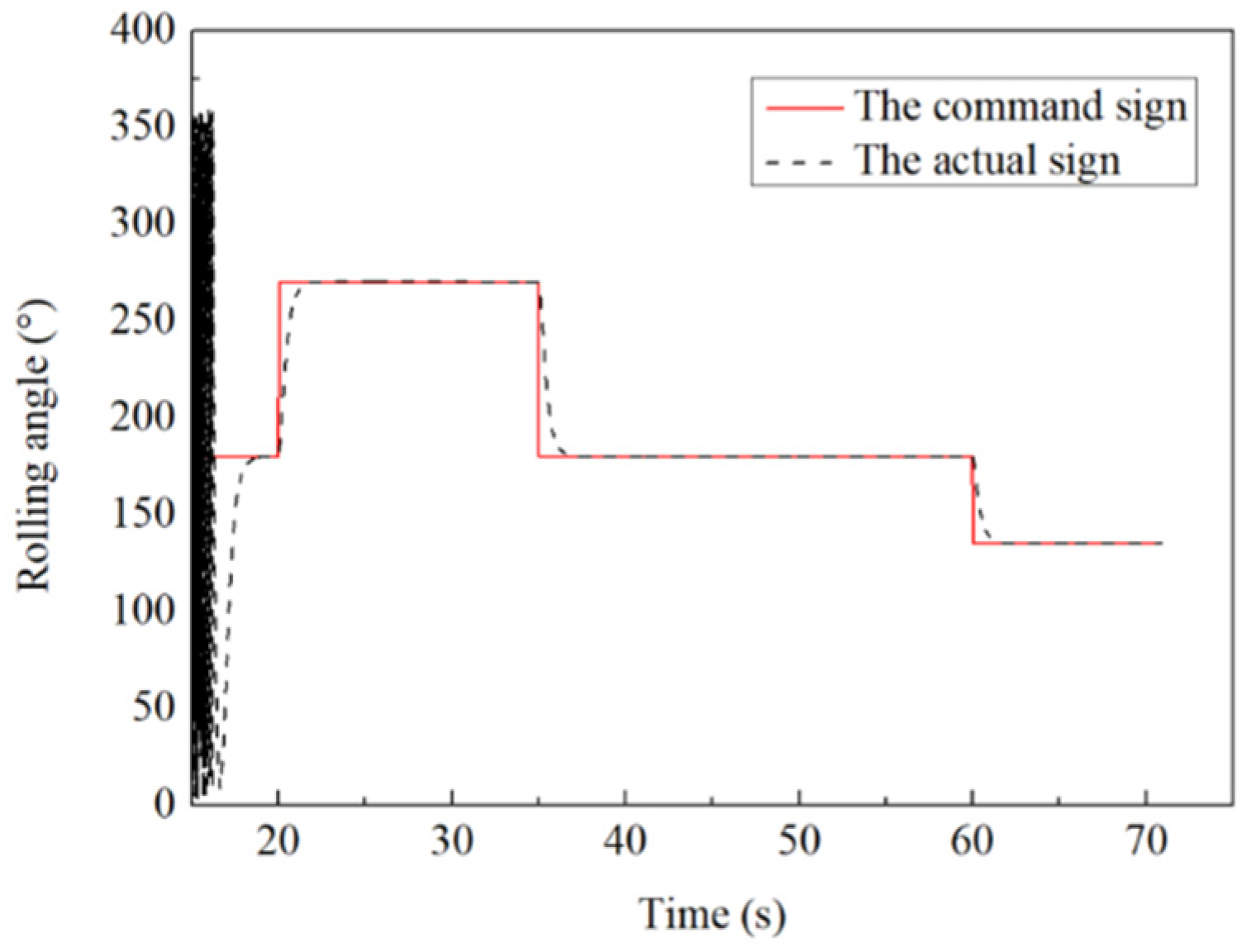
4.3. The Simulation Calculations under Different Control Parameter and Guidance Strategies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ground coordinate system | |
| ballistic coordinate system | |
| projectile axis coordinate system | |
| projectile body coordinate system | |
| second axis coordinate system | |
| , | the corresponding acting moments by the airflow |
| the rolling angular velocity of the projectile’s main body around the x-axis | |
| the rolling angular velocity of the control-flaps around the x-axis | |
| , | the rolling angular velocities of the projectile around the y-axis and z-axis |
| the polar damping moment of the projectile around the x-axis | |
| the polar damping moment of the control-flaps component around the x-axis | |
| , | the components of the aerodynamic moment of the projectile’s main body and the control moment in the y-axis and z-axis directions |
| the frictional resistance moment | |
| the gyroscopic moment of the control-flaps | |
| the control moment acting on the rudder | |
| the equatorial moment of inertia | |
| the polar moments of inertia of the projectile’s main body | |
| the azimuth angle of the projectile’s axis | |
| the roll angle of the main body component | |
| the roll angle of the control-flaps | |
| , | the air density and the velocity of the projectile relative to the air |
| , | the cross-sectional area and the length of the projectile |
| , | the diameter of the projectile and the deflection angle of the control-flaps |
| , | the coefficients for gyroscopic moment of the control-flaps and polar damping of the main body |
| , | the coefficients of frictional resistance and relative motion resistance |
| the total amount of aerodynamic drag | |
| the total amount of aerodynamic lift | |
| the total amount of self-gravity | |
| ,, | the components of the wind speed in the velocity coordinate system around x, y, and z axis |
| , | the unknown comprehensive disturbances; |
| , | the parameter uncertainties in the model |
| , | the equivalent disturbances |
| , | the flight-path inclination angle and flight-path azimuth angle |
| the lift coefficient | |
| ,,, | the suitable points on the critical sliding surface |
| , | the coefficient of the critical sliding mode surface |
| the region of the positive invariant | |
| , | the critical sliding surface |
| the adaptive parameter terms for the global terminal sliding mode dynamics. | |
| eight basic parameter terms on the four subdivided subspaces | |
| the convergence time of the error | |
| the initial error term | |
| , | the dual coefficient setting of the sliding surface |
| the relative distance between the projectile and the target | |
| the current velocity of the projectile. | |
| the motion time | |
| the output instruction when it is uncontrolled | |
| , | the time points of starting controlling and ending control state in the whole control process |
| the end control time points in different control stages | |
| the control command output in different control stages | |
| the commanded roll angle of the control-flaps | |
| the commanded rolling angular velocity | |
| the tracking error of the roll angle | |
| the drag coefficient | |
| the zero-lift drag coefficient | |
| the lift coefficient |
References
- Wang, Z.Y.; Shi, J.G.; Chang, S.J.; Li, Y.; Chen, Q.; Yi, W.; Wang, X. Review on development of technology of trajectory correction projectile. J. Ballist. 2021, 33, 1–12. [Google Scholar]
- Li, S.H.; Wang, X.Y.; Ding, S.Y. Research on the Theory and Application of Sliding Mode Control; Science Press: Beijing, China, 2022; pp. 28–55. [Google Scholar]
- Pang, B.C.; Jiang, S.J.; Zhao, C. Research on dynamic aerodynamic characteristics of spin tail canard layout projectiles and arrows based on numerical virtual flight. J. Proj. Arrows Guid. 2021, 41, 101–110. [Google Scholar]
- Zhong, Y.; Wang, L.M.; Li, Y. Calculation model of normal force of canard on spin stabilized two-dimensional trajectory correction projectile. J. Ballist. 2019, 31, 48–54. [Google Scholar]
- Ma, G.L. Control effect analysis of dual-spin projectile based on modified mass point trajectory model. Trans. Beijing Inst. Technol. 2019, 39, 777–783. [Google Scholar]
- Zhao, X.X.; Shi, J.G.; Wang, Z.Y. Study on angular motion characteristics and control stability with the fixed canard dual spin projectile. J. Harbin Inst. Technol. 2022, 54, 123–131. [Google Scholar]
- Fang, X.; Yang, W.J.; Fan, Z.; Zhang, K. Multi-Power Sliding-Mode Control for Hypersonic Vehicles. Solid Rocket Technol. 2018, 41, 258–264. [Google Scholar]
- Wang, C.; Wang, X.G. Terminal slip mode control of hypersonic guided projectiles. Syst. Eng. Electron. 2020, 42, 2859–2866. [Google Scholar]
- Wang, C.; Ma, J.J.; Zhang, X.L.; Wang, X.G.; Wu, Y.F. Backstepping sliding mode control of hypersonic guided projectiles based on disturbance compensation. J. Artill. Firing Control 2023, 12, 12–21. [Google Scholar]
- Jiang, S.; Tian, F.Q.; Sun, S.Y. Integrated design of spatial multi-constraint guidance and control for rolling naval gun guided projectiles. J. Aeronaut. 2019, 40, 32–41. [Google Scholar]
- Han, J.X.; Ma, F.Y.; Dian, S.Y. Terminal sliding mode control for uncertain systems based on nonlinear disturbance observers. Electro-Opt. Control 2020, 27, 29–34. [Google Scholar]
- Yin, T.T.; Jia, F.X.; Yu, J.Y.; Wang, X.O. Robust adaptive control of roll position of fixed rudder for dual-spin projectile with improved LuGre friction model. Acta Armamentarii 2019, 40, 2425–2432. [Google Scholar]
- Zhao, Z.H.; Cao, D.; Yang, J.; Wang, H. High-order sliding mode observer-based trajectory tracking control for a quadrotor UAV with uncertain dynamics. Nonlinear Dyn. 2020, 102, 2583–2596. [Google Scholar] [CrossRef]
- Xing, B.N.; Du, Z.H.; Du, C.X. Review of two-dimensional ballistic modified projectiles and their guidance control technology. J. Natl. Univ. Def. Technol. 2021, 43, 53–68. [Google Scholar]
- Zhang, X.; Yao, X.X. Research on roll control of fixed-wing dual-rotor correction components. Trans. Beijing Inst. Technol. 2020, 40, 386–395. [Google Scholar]
- Sherstinsky, A. Fundamentals of recurrent neural network and long short-term memory network. Nonlinear Phenom. 2020, 4, 132–142. [Google Scholar] [CrossRef]
- Lewis, F.W.; Jagannatan, S.; Yesildirak, A. Neural Network Control of Robot Manipulators and Non-Linear Systems; CRC Press: Boca Raton, FL, USA, 2020; pp. 1–12. [Google Scholar]
- Han, Z.P. Exterior Ballistics of Projectiles and Rockets; Beijing Institute of Technology Press: Beijing, China, 2008; pp. 25–39. [Google Scholar]
- Yin, T.T. Research on the Rolling Control System of Fixed Canard Rudder with a Spaced Duck Rudder Ballistic Correction Projectile; Nanjing University of Science and Technology: Nanjing, China, 2020; pp. 65–89. [Google Scholar]
- Yang, Z.W.; Wang, L.M. Movement characteristics of a dual-spin guided projectile subjected to a lateral impulse. Aerospace 2021, 8, 309. [Google Scholar] [CrossRef]
- Wang, Y. Analysis of Guidance and Corrective Strategy for a Spin-Stabilized Projectile Equipped with Fixed Canards; Nanjing University of Science and Technology: Nanjing, China, 2019; pp. 22–33. [Google Scholar]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 22.15 | 0.0034 | ||
| 0.668 | 0.041 | ||
| 0.122 | 0.5069 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| 2 | 5 | 9 | |||
| 1 | 3 | 7 | |||
| 7 | 2 | 1 | |||
| 5 | 1 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Wang, L.; Fu, J. Adaptive Attitude Roll Control of Guided Projectile Based on a Novel Unidirectional Global Sliding Mode Algorithm. Aerospace 2024, 11, 683. https://doi.org/10.3390/aerospace11080683
Guo S, Wang L, Fu J. Adaptive Attitude Roll Control of Guided Projectile Based on a Novel Unidirectional Global Sliding Mode Algorithm. Aerospace. 2024; 11(8):683. https://doi.org/10.3390/aerospace11080683
Chicago/Turabian StyleGuo, Shouyi, Liangming Wang, and Jian Fu. 2024. "Adaptive Attitude Roll Control of Guided Projectile Based on a Novel Unidirectional Global Sliding Mode Algorithm" Aerospace 11, no. 8: 683. https://doi.org/10.3390/aerospace11080683
APA StyleGuo, S., Wang, L., & Fu, J. (2024). Adaptive Attitude Roll Control of Guided Projectile Based on a Novel Unidirectional Global Sliding Mode Algorithm. Aerospace, 11(8), 683. https://doi.org/10.3390/aerospace11080683






