Abstract
The minimum ignition equivalence ratio of the strut stabilizer is an important parameter in the design of integrated afterburners. The ignition location significantly affects the ignition equivalence ratio and flame propagation, and therefore, it should be deeply studied. The ignition equivalence ratio and flame propagation at different axial ignition locations downstream of the strut stabilizer are studied in this paper. When the ignition distance is approximately the bluff body trailing edge width, a lower ignition equivalence ratio is required for ignition, and the flame propagates faster through the entire combustion chamber. For different ignition locations, the generated flame kernel at different locations all first propagates to the shear layer. Subsequently, the unilateral flame rapidly extends, ultimately igniting the entire combustion chamber. The flame propagation trajectory depends on the ignition location controlled by the non-reacting flow field and the distribution of kerosene concentration. The flame propagation trajectory mainly includes three paths: (1) the flame kernel is directly downstream the shear layer when the ignition location is close to the tail edge of the stabilizer, (2) the flame propagates upstream into the shear layer in a U-shape when the ignition location is far from the stabilizer but still in the recirculation zone, and (3) the flame propagates upstream into the recirculation zone and shear layer in a U-shape when the ignition location is outside the recirculation zone. In addition, the time for flame propagation to the shear layer is directly related to the ignition performance when the ignition location is within the recirculation zone. If the flame reaches the shear layer in a longer time, there will be more energy loss during the flame propagation process, and the ignition performance will deteriorate. The speed of the flame-trailing edge extension is directly related to the ignition fuel-air ratio, and the downstream extension of the flame is mainly affected by the turbulence velocity in the shear layer.
1. Introduction
Bluff body stabilizers are used in various applications to stabilize flames, including scramjet engines, ramjet engines, and gas turbines. Gas turbine augmentors employ bluff-body flame-holding devices to stabilize the flame. The bluff body provides a hot recirculation zone, allowing the thermal combustion products to interact with the fresh mixture and maintain combustion. Past augmentors utilized spray rods and V-gutter flameholders due to their light weight, low cost, and simplicity [1]. However, traditional flame stabilizers, due to their obstruction of the flow channel, cause substantial pressure losses, particularly in non-afterburner conditions, which have become one of the key factors limiting the further enhancement of the engine’s thrust-to-weight ratio. Modern augmentors have transitioned to employing close-coupled fuel injector/flameholder designs, which integrate fuel bars and flame stabilizers [2]. The evolution in augmentor design reflects advancements aimed at enhancing combustion efficiency and stability. The strut stabilizer has the functions of load bearing, flame stabilization, and fuel supply, which is consistent with the development of integrated afterburners [3,4]. It is also crucial for the flame stabilization of ramjet engines and gas turbines. The actual combustion and ignition process are complex due to the interaction between the reaction zone and the vortex structure. These structures range from the small-scale turbulence to the Kelvin-Helmholtz shear layer instabilities and large coherent Bemard/von-Karman vortex streets [5]. Due to the fact that the fuel enters from the strut stabilizer, the short mixing distance makes it difficult to form a uniformly distributed fuel concentration behind the stabilizer, which poses a greater challenge to the ignition problem of the strut stabilizer. The transient ignition process of flame stabilizers involves complex phenomena, which are of great significance for the design and stable operation of afterburners and ramjet engines. The spark ignition was widely applied in afterburners and ramjet engines due to its simple structure and lightweight ignition device [6,7,8,9,10]. The recirculation zone behind the stabilizer had strong heat and mass transfer processes [11]. Successful ignition was affected by the flow field and fuel concentration distribution in the recirculation zone, and it also required that the spark of the high-energy spark plug be greater than a critical value in order to successfully ignite the fuel-air mixture. The critical energy of the spark was related to many parameters such as the airflow temperature, pressure, speed, and fuel-air ratio [12,13]. However, the reliability of the direct ignition of the high-energy spark plug decreased under high temperature, and the spark plug itself required protection by cooling gas [14]. Due to the requirements of advanced power, the inlet temperature of the afterburner reached 1300 K, which also led to certain challenges for the structural design of high-energy spark plugs [15].
Laser ignition, which is as a high-temperature ignition source, had been widely applied in engines [16,17,18,19]. Non-resonant breakdown was the most commonly used ignition mode due to its free choice of laser wavelength and power. Laser ignition had great advantages in gas turbine ignition applications due to the fact that it provided remote and multi-point ignition, which avoided the heat loss of the plug and reduced the ignition response time. However, the reliability, vibration, and soot formation of the laser ignition system in a real engine remain challenging [20,21]. A compact diode-pumped high-energy neodymium doped yttrium aluminium garnet (Nd: YAG) laser was designed in [22]. It successfully operated on an internal combustion engine at high temperature and vibration levels. Its passive Q-switch generated 25 mJ at 3 ns, and its repetition rate reached 150 Hz. Sreenath [23] applied the laser igniters in a 350 kW, six-cylinder, stationary natural gas reciprocating engine, which extended the operational envelope and improved by an order of 2.6 points. The optical transmissivity exceeded 98% due to the fouling mitigation strategies under the engine operation. Masaki [24] developed a compact (electric spark-plug sized), diode-pumped, passively Q-switched Nd: YAG/Cr 4+: YAG microlaser for engines. The enhanced combustion of this microlaser ignition was successfully demonstrated in a constant-volume chamber at room temperature and atmospheric pressure. This laser ignition system generated flame kernel at almost any location in the combustion chamber, and the laser outperformed the traditional spark plug at some axial distances [25]. In addition, the active species induced by the laser can shorten the ignition delay time and improve the laminar flame speed [26]. If the laser ignition was successful, the ignition kernel was denoted by the flame kernel. The minimum reliable ignition energy increased with the bulk velocity but decreased with the increasing equivalence ration and initial pressure [27,28,29]. In addition, the multi-point laser ignition can improve the ignition performance [30,31,32].
The ignition location and duration significantly affected the ignition probability in the combustion chamber. The processes of turbulent flame propagation, non-uniformly dispersed droplet atomization field, and flame stability in the recirculation zone were necessary for the spray combustion [33,34]. Moreover, it was assumed that the propagation of flame edges were a combination of axial/azimuthal velocity and turbulent flame speed [35]. The ignition location inside the region of negative velocity, relatively small droplet Sauter mean diameter, and mean equivalence ratio was more likely to result in successful flame establishment [36]. The ignition position of the laser ignition system was not limited by space, and the ignition position in the combustion chamber should be further considered to ensure successful reignition and shorter time after shutdown. Wang [37] conducted an experimental study on the ignition performance of different radial ignition positions in gas turbines. Their results show that flames at different ignition positions eventually propagate to the same position, and the ignition performance is the highest when the ignition position is close to that position. Roberto [38,39,40] studied the flame expansion process during the transient ignition in a fully premixed swirled bluff-body-stabilized annular combustor. The ignition location was varied longitudinally, located inside and downstream of the recirculation zone. The flame propagation trajectory depended on the initial flame kernel location. Moreover, the low velocity and turbulent intensity were beneficial for the flame propagation upstream and azimuthally when the ignition location was far downstream in the annular combustor. Lin [41] studied the ignition of kerosene spray in a simplified combustor and compared the ignition performance and flame behavior in four locations. The ignition location at the maximum width of the recirculation zone was more likely to result in full flame.
It can be deduced from this literature review that there are few studies on the impact of the ignition location on the ignition limit from the perspective of flame propagation. Therefore, this paper studies the impact of different ignition locations on the ignition performance of the strut stabilizer by analyzing the flow field, fuel concentration distribution, and flame propagation trajectory. The ignition limits were first obtained after successfully igniting at different ignition locations, and each ignition test was repeated three times. In addition, the formation of the flame kernel and flame propagation processes was recorded using a high-speed camera. Numerical simulation methods were then used to obtain the non-reacting flow field of the strut stabilizer in order to evaluate the flame extension. Afterwards, the kerosene concentration distribution behind the stabilizer was studied using the kerosene Planar laser induced fluorescence (PLIF), and the propagation of flames in the horizontal direction was explained. Finally, the influence of different ignition locations on the flame propagation mechanism and ignition limit was detailed.
2. Materials and Methods
2.1. Experimental Methods
The entire experimental system consists of an air supply system, a fuel supply system, an optical testing system, a strut stabilizer combustion chamber, and a plasma-laser-induced ignition system. The air is supplied by the compressor and dried through an adsorption dryer. It enters the combustion chamber through an air surge tank. The fuel type is Chinese aviation kerosene RP-3. Its physical and chemical properties are similar to jet-A [42]. The fuel is filtered before entering the strut stabilizer. The mass flow rate of the fuel is measured using a Coriolis mass flow meter having an uncertainty of ±0.1%. The inlet temperature of the combustion chamber is measured using a two-point K-type thermocouple having an uncertainty of 1%. The air flow rate is measured using a vortex flowmeter having an uncertainty of 1.5%. The rig schematic of the ignition test system is shown in Figure 1a. The ignition test is conducted under the following constant operating conditions: test rig inlet mass flow rate of 0.39 kg/s, inlet airflow heated to 573 K, and atmospheric pressure in the combustion chamber. The ignition test starts with a high equivalence ratio. After establishing the incoming air at the predetermined conditions, open the kerosene circuit valve and adjust the kerosene flow to the target value. Activate the laser and perform repeated ignition attempts for 5 s. Upon successful ignition, cease kerosene injection and purge the test section for 3–5 min to prevent residual kerosene from affecting the ignition test. Decrease the kerosene flow rate and initiate the next ignition test until ignition fails. Record the minimum ignition equivalence ratio achieved for that location, which is the fuel flow rate divided by the air flow rate and then divided by the stoichiometric fuel-to-air ratio. Within 5 s after the ignition starts, the flame can be stabilized and not extinguished, which indicates a successful ignition. The number of ignition attempts within 5 s is sufficient to effectively illustrate the impact of the ignition randomness. Before each ignition test, air should be supplied for at least 5 min to cool the combustion chamber and avoid the interference between the two ignition tests. The ignition test is repeated three times for each ignition position.
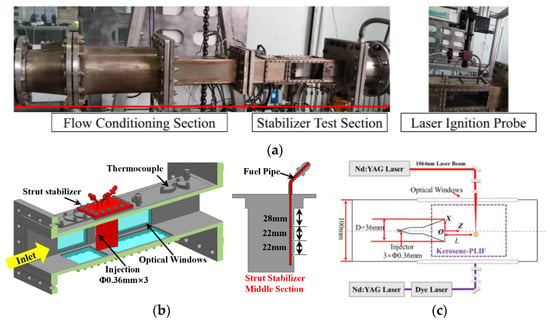
Figure 1.
(a) Schematic of the rig of the ignition test system; (b) Isometric diagram of the test section; (c) Kerosene-PLIF and plasma-laser-induced ignition setup.
The combustion chamber of the strut stabilizer is a 100 mm × 100 mm rectangular channel. The strut stabilizer has a width (D) of 36 mm. There are three circular holes on the front edge of the strut stabilizer, having a diameter of 0.35 mm and a spacing of 25 mm. They are used to inject aviation kerosene. The combustion chamber is designed with detachable optical glass windows for capturing flames, and JGS1 is used as glass material. The structure of the combustion chamber is shown in Figure 1b.
The Kerosene-PLIF and plasma-laser-induced ignition setup is shown in Figure 1c. The Planar Laser Induced Fluorescence (PLIF) measurement system used in the experiment consists of the Nd: YAG laser (Harbin Institute of Technology, Harbin, China), dye laser (Sirah Credo, Kaarst, Germany), sheet shaping system, detection system, and sequence control system. The working frequency of the Nd: YAG laser is 1 kHz, the pulse width is 7 ns, and the single pulse energy is 25 mJ@532 nm. The laser operates in an external trigger mode and serves as the pump source for the dye laser. The pulsed laser of Nd: YAG generates a 283.553 nm ultraviolet light through a Sirah tunable dye laser, which excites the kerosene fluorescence signal. The detection system uses an ICMOS camera (Excelitas, Pittsburgh, PA, USA) paired with a WG320 (Semrock, New York, NY, USA) -UG11 (Schott, Mainz, Germany) -R532 bandpass filter, in order to capture kerosene fluorescence signals in the area covered by the sheet light. To ensure that the fluorescence signal excited by the laser can be captured by the ICMOS camera, the DG645 digital delay/pulse generator (Stanford Research Systems, Sunnyvale, CA, USA) is used as the synchronizer of the PLIF system. The sheet shaping system consists of a beam expander, a collimator, and a focusing mirror. The ultraviolet laser output from the dye laser is formed by the sheet shaping system, which results in a sheet length of 100 mm and a thickness of 0.3 mm.
The Dawa 200 Nd: YAG laser having a repetition rate of 20 Hz is used in the plasma-laser-induced ignition. It has a pulse width of 9 ns and a pulse energy of 200 mJ for a wavelength of 1064 nm. The diameter of the laser spot is approximately 8 mm. After the laser is introduced from the optical window and focused behind the strut stabilizer, the vertical and horizontal positions of the focusing lens can be controlled by moving two vertical platforms, which allows adjustment of its ignition position. In this study, plasma is generated by focusing laser pulses to form an initial flame kernel, which propagates and ultimately forms a stable flame.
The flame luminosity is observed through a JGS1 optical window, captured by a Nikon 85 mm f/1.8 lens (PCO) high-speed camera having a frame rate of 5000 frames per second (fps) and a resolution of 1000 × 1000 pixels. The spatial resolution of this high-speed camera is approximately 0.14 mm/pixel. Stanford Research Systems DG645 and 9524 triggers (Quantum Composers Inc., Bozeman, MT, USA) are used for the synchronization and triggering of the lasers and cameras in order to collect the formation and development of flame kernel. DG645 sends a trigger signal to the laser in order to operate according to the given frequency and timing, which ensures the synchronization between the laser ignition and high-speed camera. After receiving the trigger signal of DG645, the 9524 trigger outputs two trigger signals, one for the CLK In of the laser and the other for its Q In.
2.2. Numerical Simulation Methods
2.2.1. Computational Setup and Flow Conditions
In this study, the large eddy simulation (LES) turbulence model in the commercial software Ansys Fluent 2021 is used to simulate the non-reacting flow field of the strut stabilizer. The characteristic of turbulence is that vortices have a wide range of length and time scales. In LES, large eddies are resolved directly, while small eddies are modeled using a subgrid scale model. The governing equations for an incompressible flow form of the continuity and the Reynolds Averaged Navier-Stokes equations are specified as follows [43]
where is the filtered velocity component along the Cartesian coordinates, , is the density of fluid, is the pressure, and is the subgrid-scale stresses term.
The subgrid-scale stresses resulting from filtering operation are modeled by the Boussinesq hypothesis in Ansys Fluent, computing subgrid-scale turbulent stresses from
where is the subgrid-scale turbulent viscosity, is the isotropic part of the subgrid-scale stresses, and is the rate-of-strain tensor for the resolved scale.
Wall-Adapting Local Eddy-Viscosity (WALE) Model is designed to return the correct wall asymptotic behavior for wall bounded flows, which is therefore preferable compared to the Smagorinsky-Lilly model. In the WALE model, the eddy viscosity is modeled by [44]
where and in the WALE model are defined, respectively, as
where is the von Kármán constant, is the distance to the closest wall, is the WALE constant, and V is the volume of the computational cell.
In this study, the LES model is adopted with WALE model. Semi-implicit method for pressure-linked equations (SIMPLE) pressure-based solver is assigned to the simulation. A second-order temporal discretization scheme was used to get a stable solution. The bounded central differencing scheme was employed for spatial discretization in the momentum equations, whereas transient formulation was performed using bounded second-order implicit. The case was started with steady-state flow using the SST model, and after the simulation had converged, the instantaneous field of the steady-state RANS simulation was used as an initial field for LES run. For the transient simulation, the constant time step was specified, meeting the requirement of CFL number less than 1.
The grid used to calculate the non-reacting flow field contains 8 million elements, refined near the wall of the strut stabilizer and the non-slip wall. The height of the first boundary layer of the grid is 0.02 mm, which ensures that y+ is less than 1. The strut stabilizer has a width (D) of 36 mm and a spanwise length of 100 mm. The coordinate system is defined as Z in the axial direction, X in the vertical direction, and Y in the spanwise direction, and the origin is on the centerline of the stabilizer trailing edge. The width of the experimental section is 100 mm, and the blockage rate is 0.3. The computational domain ignores the 3 mm deep pits on the flow channel caused by optical window slices. The inflow boundary conditions are consistent with the experiment. The inlet velocity (u0) and inlet temperature (T) are equal to 65 m/s and 573 K, respectively. Partially non-reflective inflow and outflow boundary conditions are adopted. The outlet pressure is set to one atmospheric pressure. On all solid walls, the no-slip boundary conditions were set.
Compared with the Smagorinsky model, the WALE model improves the accuracy of solving near wall turbulence, and the subgrid viscosity can be restored to zero under laminar shear flow conditions. Figure 2 shows the mesh schematic of the computational domain and the power spectral density of the static pressure fluctuation in the shear layer at Z/D = 1 for non-reacting LES. In Figure 2b, the turbulence energy spectrum with a −5/3rd power scaling rate is also shown. By comparing the attenuation law of the obtained energy spectrum in the high frequency range, it is verified that the calculation method in this paper meets the accuracy requirements of turbulence flow analysis. It can be seen that the grid resolution is acceptable by reasonably restoring the inertial range. The Strouhal number defined by St = fD/u0 is typically between 0.2 and 0.29 for the flow around a circular cylinder, where f is the vortex shedding frequency. The non-reacting simulation result provides f = 529 Hz or St = 0.29.
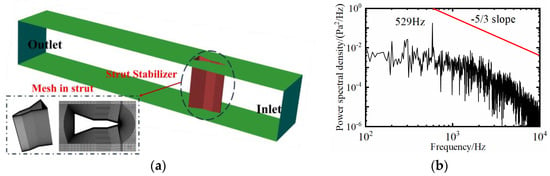
Figure 2.
(a) Mesh schematic of the computational domain; (b) Power spectral density of the static pressure fluctuation in the shear layer at Z/D = 1 for non-reacting LES.
2.2.2. Validation of the Numerical Simulation Methods
Sjunnesson [45] used the PIV and CARS techniques to conduct detailed measurements of the velocity temperature fields downstream of the triangular stabilizer. The obtained results are used in this paper to validate the proposed numerical model. Figure 3a shows a schematic diagram of the calculation domain of the triangular stabilizer. The computational domain consists of a rectangular channel with a size of 1000 mm × 120 mm × 48 mm and a triangular stabilizer with a side length of 40 mm. The triangular stabilizer is placed at the center of the rectangular channel. The inlet velocity (U∞) and temperature are equal to 17.6 m/s and 288 K, respectively. The outlet is at atmospheric pressure. The normalized mean axial velocity along the centerline is shown in Figure 3b. The recirculation zone length is predicted by LES capturing a profile that is almost similar to that measured in the experiment. Figure 3c shows the normalized mean axial velocity profiles at four different axial locations. It can be seen that the LES results are consistent with the experimental results. The calculated average error of the axial velocity distribution between the experiment and simulation is 6.3%. The numerical simulation methods have a certain degree of reliability, and they can be used to analyze the non-reacting flow-field distribution behind the strut stabilizer.
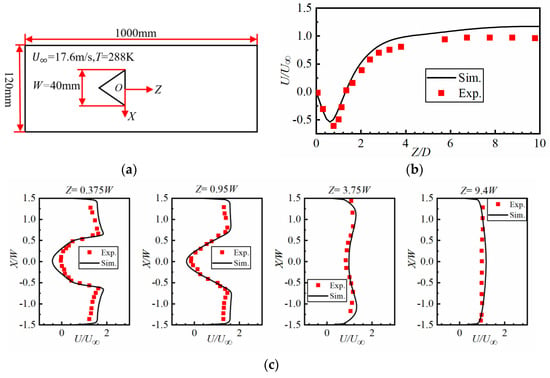
Figure 3.
(a) Computational domain for stabilizer configuration; (b) Normalized mean axial velocity along the centerline; (c) Normalized mean axial velocity profiles at four different axial locations.
3. Results and Discussion
3.1. Ignition Performance and Processes at Different Locations
Figure 4 shows the minimum ignition equivalence ratio at different axial ignition locations, which is the fuel flow rate divided by the air flow rate and then divided by the stoichiometric fuel−to−air ratio. The lean blowout equivalent ratio is 0.08 under this operating condition. When the ignition location is close to the tail edge of the stabilizer, the ignition limit at this location is close to the blowout equivalent ratio. As the ignition position moves downstream of the stabilizer, the equivalence ratio of ignition rapidly increases. After reaching its maximum value at 15 mm downstream, the ignition equivalence ratio starts to decrease. For ignition distances (L) of 30 mm and 40 mm, there is little change in the ignition equivalence ratio. For L = 65 mm, the ignition position is outside the recirculation zone, and the ignition equivalence ratio reaches its highest value. The ignition performance is related to the non-reacting flow field and fuel distribution. The differences in flame propagation trajectories at different ignition locations can also affect the ignition performance.
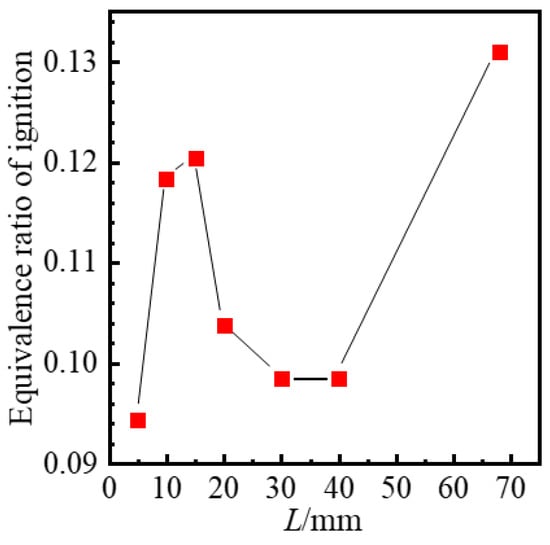
Figure 4.
The minimum ignition equivalence ratio at different axial ignition locations.
Each ignition test was repeated three times, and the ignition processes were recorded using the high-speed camera. Due to the high temperature and high heat release rate, flames with high luminous intensity can be observed in the experiment. The luminous intensity of the flame can accurately reflect its propagation process. Therefore, in this paper, the gray value of the two-dimensional digital image was used to represent the combustion intensity. The magnitude of the flame intensity can be reflected by the integral value of the flame image:
where φ(i, j) is the gray value at point (i, j) in the flame image.
The min-max normalization was used to perform dimensionless processing on the integral value of the flame image, where the maximum normalized value is the average integral intensity during a stable flame combustion. After determining the threshold of the image using the Otsu method [46], the regions of flames at different times are extracted. Due to the fact that the spatial resolution of the image is 0.14 mm/pixel, the total number of pixels in the flame area is consistent with its actual area. Similarly, the min-max normalization is used to obtain the normalized flame area (S). The maximum normalized value is the total number of pixels in the flame area during the stable combustion of the flame. The average flame intensity ( is equal to
Figure 5 shows the evolution of the normalized flame area, flame intensity, and average flame intensity. According to the variation of the average flame intensity, the ignition process can be divided into five stages: (1) G0: kernel generation; (2) G1: kernel attenuation and propagation; (3) G2: unilateral flame enhancement; (4) G3: global flame enhancement; and (5) G4: stable combustion. When the laser is focused at a certain position, the energy density is high enough to break through the air and produce a high-temperature, high-pressure plasma, which triggers a chain reaction of combustion.
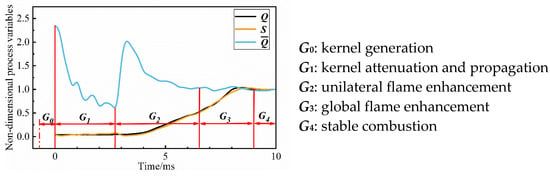
Figure 5.
Evolution of the normalized flame area, flame intensity, and average flame intensity.
The flame propagation process of different ignition locations is shown in Figure 6. The equivalence ratio for each subfigure is the lean ignition limit. All the flame propagation processes at different locations consist of the above 5 stages. t = 0 ms represents the time when the initial flame kernel is formed. The flame kernel area is almost circular. Due to the short duration of the laser and plasma formation times, the G0 stage was not recorded by the highspeed cameras. The G1 stage is the process of flame kernel attenuation and propagation. At the beginning of this stage, the average intensity of the flame is relatively high. Due to the effect of turbulence, there are obvious wrinkles on the surface of the flame while it propagates. Although the flame area increases, the average flame intensity significantly decreases, and the flames are unstable. If the average flame intensity decreases to a certain level, it may lead to ignition failure. G2 is the stage of unilateral combustion enhancement. In the experiment, due to the fact that the ignition center is located 5 mm below the centerline, even if some flames propagate to the upper side during the diffusion process of the flame kernel, the propagation of the flames is still enhanced by combustion on one side and then propagates to the other side. During this stage, the flame propagates to the shear layer where its intensity and average intensity rapidly increase. Using this location as the source of flame, the latter rapidly propagates downstream on one side. The average flame intensity during this stage is similar to that during the stable combustion, and it remains stable, which indicates that the single side flame reached a stable combustion state during the G2 stage. G3 is the global flame enhancement stage. During this stage, the flame propagates towards the other side, and its total intensity and area gradually increase. However, its average intensity slowly decreases. This is due to the fact that during the flame propagation towards the other side, the flame intensity between the shear layers is relatively low. Finally, G4 is the stable combustion stage, where the flame intensity has a certain fluctuation. All the flame kernels will propagate to the shear layer for different locations. However, the specific flame propagation trajectories are different.


Figure 6.
The flame propagation process of different ignition locations. From (a–g), L = 5, 10, 15, 20, 30, 40, 50, and 65 mm.
3.2. Non-Reacting Flow Field
The distribution of the flow field plays a crucial role in the flame propagation and stable combustion, which indicate that the ignition locations may be selected based on the non-reacting flow field of the combustor. Therefore, the LES method is applied on the non-reacting flow of the strut stabilizer, the axial velocity (u) is analyzed, and the turbulent kinetic energy (k) is evaluated at different locations behind the stabilizer. The propagation speed and the trajectory of the flames are both related to the velocity distribution of air, and the turbulent kinetic energy can be used to analyze the dissipation of flames. Figure 7 shows the numerical simulation results of the distribution of the mean axial velocity (upper part) and turbulent kinetic energy (lower part) in a non-reacting flow field. A recirculation zone is formed downstream of the stabilizer, which plays an important role in the flame stability. The purple contour line represents a contour line with a null axial velocity, and it can be used to indicate the position and size of the recirculation zone. The simulation results show that the length of the recirculation zone is approximately 1.4 times the width of D.
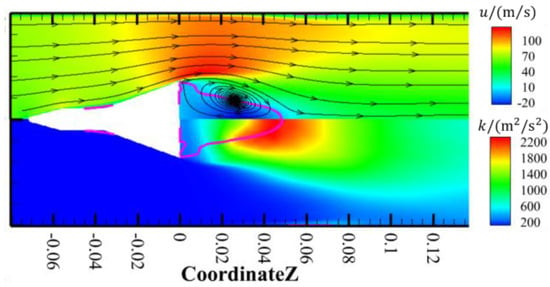
Figure 7.
The distribution of the mean axial velocity (upper part) and turbulent kinetic energy (lower part) in a non-reacting flow field. The purple line represents the contour where the axial velocity is 0.
Figure 8 shows the mean axial velocity distributions at different locations on the middle plane. The flow field has a lower axial velocity, while X/D is less than 0.5. The distribution of the turbulent kinetic energy in Figure 7 shows that it is lower in the range of 0.3–0.5 for X/D. In general, the velocity and turbulent kinetic energy are lower in the range of 0.3–0.4 for X/D, which is beneficial for the stability of the flame during propagation.
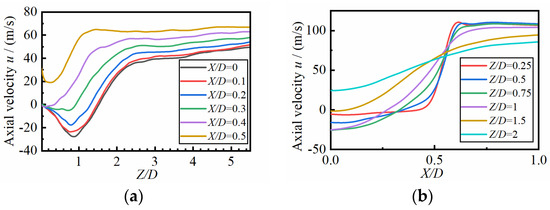
Figure 8.
Distributions of the mean axial velocity at different (a) vertical and (b) horizontal locations on the middle plane.
Figure 9 shows the instantaneous axial velocity variation at points within 20 ms at different positions on X/D = 0. The non-dimension distances Z/D from points 1 to 6 to the trailing edge of the stabilizer are 0.25, 0.5, 0.75, 1, 1.5, and 2, respectively. η is the probability that the axial velocity is less than 0. When Z/D increases, the probability of axial velocity less than 0 first increases and then decreases. For Z/D = 2, there is still a certain probability that the instantaneous axial velocity is negative, which indicates that the velocity direction points towards the recirculation zone. That is, even when the ignition position is outside the recirculation zone, the flame may still propagate towards it. However, due to the lower probability of axial velocity pointing towards the recirculation zone, the flame may be more difficult to propagate into it.
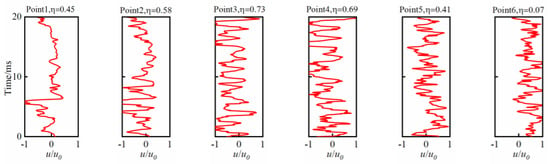
Figure 9.
Variation of the instantaneous axial velocity at points within 20 ms and at different locations on X/D = 0.
3.3. Kerosene Distribution Characteristics
The kerosene distribution has a significant impact on the ignition characteristics of the strut stabilizer. During the flame propagation process of the strut stabilizer, the kerosene distribution significantly affects the initial flame kernel generation and flame propagation trajectory. The fluorescence intensity under different locations is mapped to the interval [0,1] through min–max normalization. The non-dimension fluorescence intensity ( of kerosene can qualitatively reflect its concentration at this location. The equivalence ratio is defined as the ratio of the actual fuel-to-air ratio to the stoichiometric fuel-to-air ratio. In this study, the actual fuel-to-air ratio is determined by the ratio of the kerosene flow rate to the air flow rate. Figure 10a shows the time-averaged distribution (of 2000 instantaneous distributions) of the non-dimension kerosene fluorescence intensity at = 0.09. Due to the short mixing distance, the distribution uniformity of kerosene is low. The kerosene concentration is higher in the shear layer than in the recirculation zone. Figure 10b shows the non-dimension kerosene concentration on the centerline X/D = 0 under different equivalence ratios. For Z/D < 1 (i.e., in the recirculation zone), the kerosene concentration first increases and then decreases, and it reaches its highest value for Z/D = 0.5. For 1 < Z/D < 1.4, due to the high turbulence intensity in the region, kerosene and air are well mixed, and the concentration of kerosene remains almost unchanged. A uniform mixture of fuel and air is beneficial for the formation and propagation of flame kernel. Due to the relatively high concentration of kerosene for 0 < Z/D < 1.4, flame propagation along the horizontal direction often occurs in this area. For Z/D > 1.4, due to the mixing effect of the wake, the concentration of kerosene further decreases, and if the ignition position is after this, it may lead to a higher ignition fuel-air ratio.
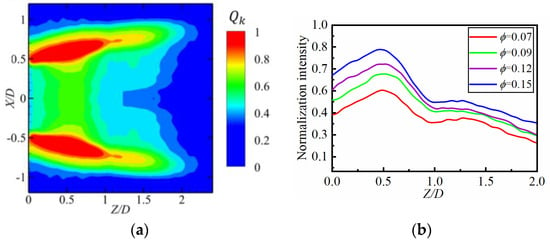
Figure 10.
(a) Time-averaged distribution of the non-dimension kerosene fluorescence intensity at ; (b) Non-dimension kerosene concentration on the centerline X/D = 0 under different equivalence ratios.
3.4. Flame Propagation Trajectory
The propagation processes of flame kernel were captured by a high-speed camera. For different ignition locations, there are significant differences in the flame morphology and propagation trajectory. In order to further study the impact of the ignition locations on the ignition performance, a method was developed to analyze the ignition process of the strut stabilizer. The flame propagation trajectory of the centroid and the features of the flame edge are received by extracting the flame area from the flame image. Based on the experiment results without ignition, the background is first subtracted from the original 16-bit monochromatic image. 5 × 5 Weiner and Gaussian filtering are then performed to reduce the image noise. Afterwards, the Otsu method is used to binarize the image and extract the edges and regions of the flame [46]. Finally, based on the flame region, the relative positions of the flame centroid are calculated, which is defined as the weighted center of the pixel values inside the flame object. The latter is denoted by , where i and j respectively denote the numbers of the row and column in the flame area; and are respectively the total pixel values of the rows and columns.
The average flame intensity greatly varies during the flame propagation process, and the flame luminescence is inhomogeneous at different stages, as shown in Figure 5. Therefore, in this paper, the flame centroid is selected to calculate the flame propagation trajectory. Figure 11 shows the flame centroid and flame edge propagation trajectories at different ignition locations. The flame centroids are connected and colored in chronological order to reflect the propagation trajectory of the flame. Moreover, the flame edges at certain times are displayed in the image to characterize the transient flame structure. It can be seen that the flame propagation exhibits diversity in flame structure and trajectory at different ignition positions. In addition, the flame propagation trajectory is determined by the flow field characteristics and kerosene concentration distribution behind the strut stabilizer.
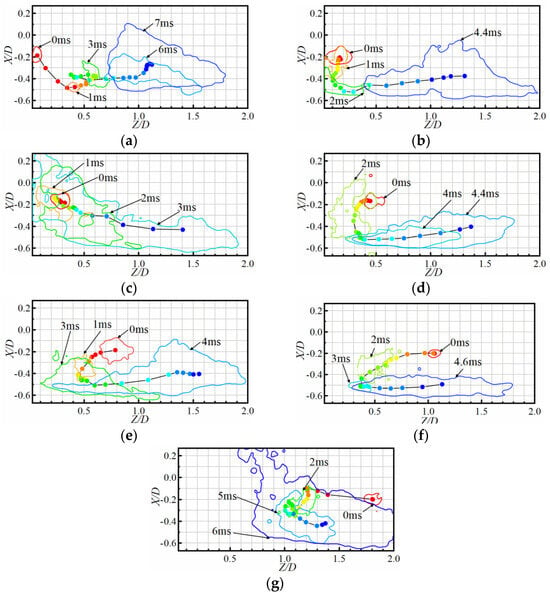
Figure 11.
Flame centroid and flame edge propagation trajectories at different ignition locations. From (a–g), L = 5, 10, 15, 20, 30, 40, 50, and 65 mm.
The schematic diagram of the flame propagation is shown in Figure 12. The successful ignition modes at different locations can be divided into three types. The first type is where the ignition location is located in the upper part of the flow direction of the recirculation zone (i.e., L = 5, 10, and 15 mm). When the initial flame kernel is at these locations, the turbulent kinetic energy of the flow field is relatively small and the airflow velocity is low, but the concentration of kerosene is relatively low. After the formation of the flame kernel, it is difficult to stably burn at these locations. Under the influence of turbulence, the flame kernel spreads and propagates unilaterally along the X direction. When the flame propagates to the vicinity of X/D = −0.4, it rapidly propagates downstream, and its intensity rapidly increases. In general, the flame kernel directly propagates into the shear layer. A stable combustion occurs in the shear layer for Z/D between 0.3 and 0.6. Afterwards, the flame starts to propagate to the other side and eventually the combustion is stabilized, with the flame roots fixed at the tail edge of the stabilizer. The second mode is where the ignition locations are in the flow direction of the recirculation zone towards the rear half (i.e., L = 20, 30, and 40 mm). When the initial flame kernel is at these locations, the concentration of kerosene is higher and the axial velocity is lower. However, in the recirculation zone with Z/D greater than 0.5, the turbulent kinetic energy is higher, and the flame kernel undergoes higher stretching at this point. It can also be seen from the flame edge that there are more folds and local blowout at the flame edge during the flame propagation process. Under the influence of the flow field, the flame first propagates upstream in the recirculation zone and also propagates in the shear layer direction (i.e., the X direction). After the flame propagates into the shear layer, the flame centroid propagates downstream. This is because the axial velocity inside the shear layer is positive, and the instantaneous velocity is also very unlikely to be lower than 0. This indicates that the axial velocity inside the shear layer is along the flow direction, which makes it difficult for the flame centroid to propagate upstream under the influence of the flow field. This leads to a U-shaped structure in the overall propagation trajectory. The flame is stabilized within the shear layer, with a strip-shaped shape. Afterwards, it starts to further propagate downstream, gradually increasing its area, and also spreading to the other side, which allows the ultimate stabilization of the combustion.
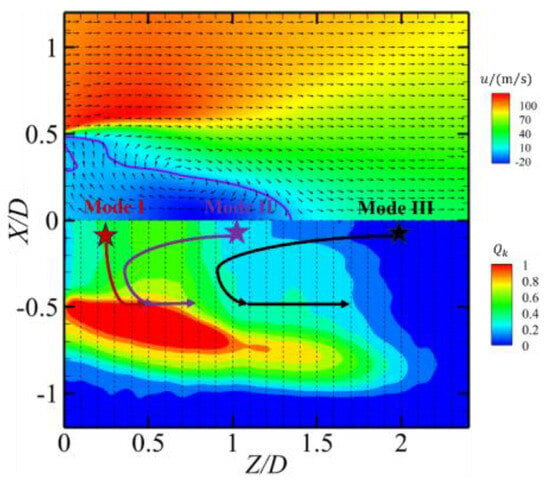
Figure 12.
Schematic diagram of the flame propagation.
The third mode is where the ignition location is outside the recirculation zone (i.e., L = 65 mm). At this point, the initial fire kernel is located outside the recirculation zone, where the turbulent kinetic energy and flow velocity are relatively high. This indicates that the initial fire kernel loses more heat during propagation, and the kerosene concentration is lower due to the mixing and diffusion effect compared with the inside of the recirculation zone, which results in lower ignition performance at this location. After the formation of the initial flame kernel, it quickly propagates upstream and enters the recirculation zone. During the upstream propagation process, due to the high turbulence level, there are obvious wrinkles and local quenching on the flame surface, as shown in the flame edges of 2 ms and 5 ms in Figure 11g. Similar to the second propagation mode, the flame propagation trajectory also presents a U-shaped structure, and the flame propagates into the recirculation zone before continuing to propagate into the shear layer. Compared with the other ignition positions, it is difficult for the initial flame kernel to reach the vicinity of Z/D = 0.5, due to the high turbulent kinetic energy after Z/D = 0.75. Even if the flame, after the initial flame kernel falls off, continues to propagate upstream, it will quickly extinguish. Therefore, after propagating upstream to a certain position, the flame propagates in the X direction under the influence of the flow field. When the flame propagates into the shear layer, it is successfully stabilized in the shear layer, and then starts to extend and propagate towards the other side.
As previously mentioned, at different ignition locations, the fire kernel will propagate to the shear layer through the recirculation zone after generation, enhance the combustion, and propagate to the other side. The energy loss during the flame propagation process determines whether the combustion chamber is successfully ignited. Therefore, it is believed that the time and distance of the flame centroid reaching the shear layer are directly related to the ignition performance. The area of the shear layer in the X−Z central plane is determined based on the time-averaged distribution of the previous large eddy simulation. By determining the position of the flame centroid, the time when the flame centroid reaches the shear layer and the path length during flame propagation, are obtained. In addition, the path length is determined by summing the distances between the flame centroids at adjacent times:
where n represents the number of flame centroids located within the shear layer and is the linear distance between the centroids of adjacent flames.
Figure 13 shows the propagation time and path length at different ignition locations. When the ignition location is within the recirculation zone, as the ignition position gradually moves away from the tail edge of the stabilizer, the flame propagation time first increases and then decreases. The time required for flame propagation to the shear layer is correlated with the minimum ignition equivalence ratio. In this scenario, the flame propagates to the shear layer and stabilizes near the bluff body’s trailing edge, creating a stable heat source. The longer it takes for the flame kernel to reach the shear layer, the more heat will be dissipated during propagation, necessitating a stronger initial flame kernel. The equivalence ratio directly influences the size and temperature of the initial flame during its formation. When the ignition position is outside the recirculation zone, as shown in Figure 11, the flame does not reach the vicinity of the bluff body’s trailing edge upon reaching the shear layer. This differs from the previously observed stability mechanism, rendering the aforementioned correlation inapplicable. In addition, the length of the flame propagation path first decreases and then increases, which is directly related to the flame propagation mode. It is difficult to determine the ignition performance based on the length of the path. The flames propagate from the recirculation zone to the shear layer. However, in the initial stage, it is difficult for the flame to be fixed at the tail edge of the stabilizer. Instead, it is stabilized within the shear layer in the Z/D range of 0.3–0.6. Therefore, for L = 10 mm and 15 mm, they have smaller propagation path lengths. When L increases, the distance between the flame stabilization area and the tail edge of the stabilizer increases, and the flame propagation path length also increases. When the ignition position is outside the recirculation zone, the ignition equivalence ratio is relatively high, but the propagation time is still relatively short. This is mainly due to the fact that when the ignition position is outside the recirculation zone, although the flame first propagates to the recirculation zone and then to the shear layer, the tail of the recirculation zone is relatively narrow, and the flame quickly spreads to the shear layer after propagating to the recirculation zone. There is a higher turbulence intensity behind the recirculation zone, which also makes it easier for the flame to extinguish over long distances. According to the flame propagation spectrum at L = 65 mm, the flame centroid is always located after Z/D = 1, which is significantly different from the flame propagation mode in the recirculation zone where the ignition position is located. This also makes it difficult for the flame propagation time to reflect the ignition performance of the ignition position outside the recirculation zone.
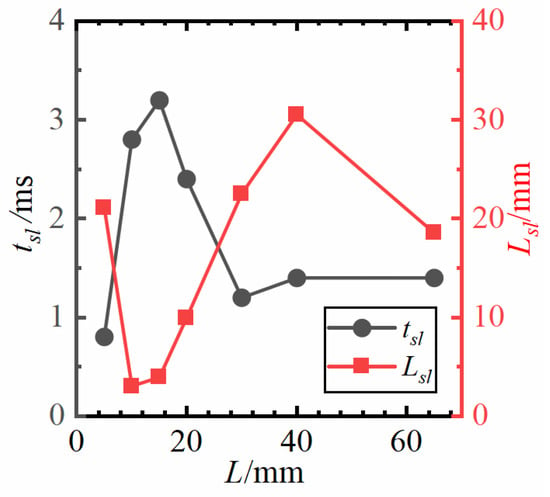
Figure 13.
Propagation time and path length at different ignition locations.
For different ignition locations, after the flame propagates to the shear layer, it starts to rapidly extend and propagate to the other side, enhances the global combustion, and ultimately stabilizes the combustion. The variation pattern of the flame edge can better reflect the global combustion enhancement process. The edges of the flame region in four directions are extracted to obtain time maps of each direction of the flame leading edge. Figure 14 shows the variation pattern of the flame edge propagation location along the X-axis direction. The red line is the extremum of the flame edge in positive X directions at various times (i.e., flame upper edge); and the green line is the extremum of the flame edge in negative X directions at various times (i.e., flame under edge). For different ignition locations, the variation of the flame propagation along the negative X direction is relatively gentle. When the ignition position is within the recirculation zone, the flames slowly propagate in the negative X direction, exhibiting good monotonicity. However, when the ignition location is outside the recirculation zone (i.e., L = 68 mm), the flame edge propagates faster to the vicinity of X/D = −1. In addition, it can be observed from the flame image that the flame has many holes and wrinkles. This is because the ignition position is too far back, and during the forward propagation of the flame, under the influence of turbulence, its kernel attenuates, and its area increases. This can be proven by the distance between the edges on the two sides shown in Figure 14g. However, at this time, the average flame intensity is low, which makes it difficult to be stabilized, leading to the propagation of the flame back to the area with low velocity. For different ignition positions, the propagation of the flame along the positive X direction first slowly changes or remains almost stable. This may be due to the fact that the flame on this side is always in an area with low turbulence and velocity, which results in less energy loss and easier flame stability. After a certain moment, the flame rapidly propagates along the positive X direction, accompanied by significant flame expansion in the negative X direction. At this stage, the flame intensity also rapidly increases, and the combustion chamber successfully ignites.
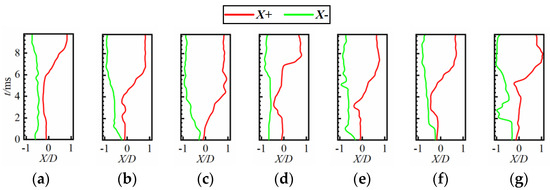
Figure 14.
Variation of the flame edge propagation location along the X-axis direction. From (a–g), L = 5, 10, 15, 20, 30, 40, 50, and 65 mm. The red line is the extremum of the flame edge in positive X directions at various times (i.e., flame upper edge); and the green line is the extremum of the flame edge in negative X directions at various times (i.e., flame under edge).
Figure 15 shows the variation of the flame edge propagation location along the Z-axis direction. The blue line is the extremum of the flame edge in positive Z directions at various times, i.e., flame trailing edge; and the purple line is the extremum of the flame edge in negative Z directions at various times (i.e., flame leading edge). When the ignition locations are within the recirculation zone, the flame leading edge is mainly stabilized within the range of 0–20 mm, where the velocity is low, and the flame is prone to stable combustion. After the generation of ignition kernel, the flame front edge first propagates upstream. However, due to the weaker flame intensity at this point and the greater shear force borne by the flame at this location, it is difficult for the flame to stabilize at the tail edge of the stabilizer, and thus it continues to propagate downstream. When the ignition position is outside the recirculation zone, the flame front edge rapidly propagates upstream. Under the influence of strong turbulence intensity and high velocity in the propagation trajectory, the flame kernel breaks into many small flame clusters, and some of them propagate to the tail edge of the stabilizer. However, due to the lack of a certain degree of flame formation downstream of the stabilizer, the temperature in the recirculation zone is relatively low, which makes it impossible to heat the fresh mixture in the shear layer. When the flame trailing edge propagates to the rear of the recirculation zone (i.e., Z/D > 1.4), it rapidly propagates downstream. During this process, the leading edge of the flame starts to propagate upstream and eventually becomes fixed at the trailing edge of the stabilizer.
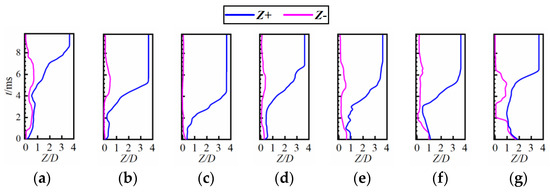
Figure 15.
Variation of the flame edge propagation location along the Z-axis direction. From (a–g), L = 5, 10, 15, 20, 30, 40, 50, and 65 mm. The blue line is the extremum of the flame edge in positive Z directions at various times, i.e., flame trailing edge; and the purple line is the extremum of the flame edge in negative Z directions at various times, i.e., flame leading edge.
The average velocity at which the flame edge propagates in all the directions after the flame trailing edge reaches Z/D = 1.4 is defined as the flame extended speed (. This speed can reflect the process of global flame enhancement. Figure 16 shows in various directions at different ignition locations. The relationship between along the positive Z-axis direction and the ignition location is consistent with the variation law of the ignition fuel-air ratio at different ignition locations. When the fuel-air ratio is higher, the expansion angle of the flame is larger. For the shear layer, a position farther away from the centerline leads to a greater axial velocity. The downstream extended speed of the flame is consistent with the axial velocity of the shear layer. This indicates that the extension of the flame downstream is mainly affected by the turbulent flow velocity in the shear layer. The flame extended speed along the negative direction of the Z-axis has little change, ranging between 5 m/s and 11 m/s. It can be seen from the image of the flame edge that, when the flame rapidly propagates downstream, the position of its leading edge is distributed within the shear layer, and the axial velocity within the latter is positive. This study assumes that the upstream propagation of the flame edges is mainly affected by the flame propagation speed and turbulent diffusion. The propagation speed of the flame edge along the X-axis direction is not affected by the ignition location and the fuel-air ratio. When the flames propagate in the positive X direction, they pass through an area with high turbulence intensity. Under the influence of turbulent diffusion, the flame extended speed in the positive X direction is greater.
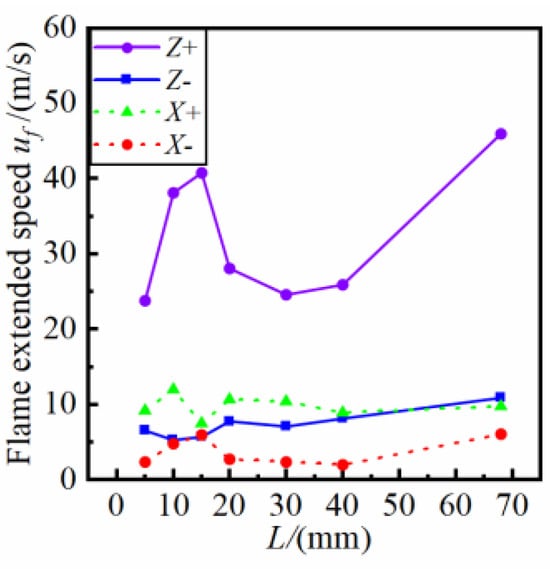
Figure 16.
Flame extended speed in various directions at different ignition locations.
4. Conclusions
In this paper, the influence of the plasma-laser-induced ignition location on the ignition characteristic of the strut stabilizer was studied through experimental and numerical methods. For the strut stabilizer, the non-reacting flow-field characteristics of the ignition condition were obtained through LES. The distribution of kerosene under different equivalence ratios were analyzed through kerosene-PLIF. The formation of flame kernel and the flame propagation was obtained using high-speed cameras. The ignition characteristics and flame propagation trajectory at different axial distances from the tail edge of the stabilizer were then compared. Afterwards, the ignition performance and flame propagation at different ignition locations were analyzed by correlating the flame propagation trajectory, local flow characteristics, and kerosene concentration field. The main conclusions can be summarized as follows:
- (1)
- The ignition test results show that when the ignition distance increases, the equivalence ratio of ignition first decreases (L = 5–15 mm) and then increases (L = 20–40 mm). When the ignition location is outside the recirculation zone (L = 65 mm), the ignition equivalence ratio reaches its highest value.
- (2)
- For different ignition locations, after the formation of the flame kernel, it propagates to the shear layer, the flame then rapidly expands, and the entire combustion chamber steadily burns. The flame propagation trajectory is related to the ignition location. When the ignition position is close to the tail edge of the stabilizer, the flame propagates directly downstream to the shear layer. When the ignition position is far from the stabilizer but still within the recirculation zone, the flame propagates upstream into the shear layer in a U-shaped pattern. When the ignition location is outside the recirculation zone, the flame also propagates in a U-shaped pattern, first into the recirculation zone and then into the shear layer.
- (3)
- When the ignition position is within the recirculation zone, the time for the flame to propagate to the shear layer is directly related to the ignition performance. If the flame stays in the shear layer for a longer time, there will be more energy loss during the flame propagation process, and the ignition performance deteriorates. Due to the different propagation modes at different ignition positions, it is difficult to determine the ignition performance based on the length of the flame propagation path. When the ignition position is outside the recirculation zone, the flame propagation distance upstream is shorter. Although the ignition equivalence ratio is relatively high, the time for the flame to propagate to the shear layer is shorter.
- (4)
- The downstream extension speed of the flame after propagating to the shear layer is directly related to the ignition fuel-air ratio. When the latter is higher, the expansion angle of the flame is greater. However, for the shear layer, a position farther away from the centerline leads to a greater axial velocity. The downstream extension speed of the flame is consistent with the axial velocity of the shear layer. The expansion of flames downstream is mainly affected by the turbulent velocity within the shear layer. The speed of flame propagation upstream is in the range of 5–11 m/s, independent of the equivalence ratio and ignition oil gas ratio, and mainly driven by the turbulent flame speed and flame dilatation.
In this present study, only the impact of different axial ignition locations on ignition performance was investigated. However, we noticed that the offset along the horizontal direction is significant. As one moves away from the center along the horizontal direction, the equivalence ratio of the mixture gradually increases, favoring ignition. However, , the airflow speed also increases concurrently, which is detrimental to ignition. Thus, there may be a point along the direction where the minimum ignition equivalence ratio is at its minimum. Future experiments will be conducted to investigate them.
Author Contributions
Conceptualization, X.J.; methodology, X.J. and B.H.; software, X.J.; validation, X.J. and B.H.; formal analysis, W.Z. (Wei Zhao); investigation, X.J.; resources, W.Z. (Wen Zeng) and J.P.; data curation, X.J. and B.H.; writing—original draft preparation, X.J.; writing—review and editing, W.Z. (Wei Zhao); visualization, J.P.; supervision, B.H. and Q.Z.; project administration, W.Z. (Wen Zeng); funding acquisition, Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant number 62175053, and the APC was funded by the Institute of Engineering Thermophysics, Chinese Academy of Sciences.
Data Availability Statement
The research data are unavailable due to privacy or ethical restrictions.
Acknowledgments
We acknowledge the technical support from the school of astronautics HIT.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Inamura, T.; Takahashi, M.; Kumakawa, A. Combustion characteristics of a liquid-fueled ramjet combustor. J. Propuls. Power 2001, 17, 860–868. [Google Scholar] [CrossRef]
- Wadia, A.R.; James, F.D. F110-GE-132: Enhanced Power Through Low-Risk Derivative Technology. J. Turbomach. 2001, 123, 544–551. [Google Scholar] [CrossRef]
- Li, W.; Tan, X.; Huang, X.; Wei, Y.; Deng, Y. Application of double-wall cooling structure in the integrated strut flame stabilizer. Therm. Sci. Eng. Prog. 2022, 36, 101526. [Google Scholar] [CrossRef]
- Ebrahimi, H. Overview of gas turbine augmentor design, operation, and combustion oscillation. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006. [Google Scholar]
- Dagaut, P.; Cathonnet, M. The ignition, oxidation, and combustion of kerosene: A review of experimental and kinetic modeling. Prog. Energy Combust. Sci. 2006, 32, 48–92. [Google Scholar] [CrossRef]
- Clenci, A.; Berquez, J.; Stoica, R.; Niculescu, R.; Cioc, B.; Zaharia, C.; Iorga-Simăn, V. Experimental investigation of the effect of an afterburner on the light-off performance of an exhaust after-treatment system. Energy Rep. 2022, 8, 406–418. [Google Scholar] [CrossRef]
- Huang, Y.; He, X.; Jin, Y.; Zhu, H.; Zhu, Z. Effect of non-uniform inlet profile on the combustion performance of an afterburner with bluff body. Energy 2021, 216, 119142. [Google Scholar] [CrossRef]
- Tonarely, M.E.; Fortin, M.K.; Genova, T.; Morales, A.; Stiehl, B.; Ahmed, K.A. C2*/CH* Intensity Ratios of Bluff Body Stabilized Flames Approaching Lean Blowout at Elevated Pressures. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Ivanov, V.S.; Frolov, S.M.; Zangiev, A.E.; Zvegintsev, V.I.; Shamshin, I.O. Hydrogen fueled detonation ramjet: Conceptual design and test fires at Mach 1.5 and 2.0. Aerosp. Sci. Technol. 2021, 109, 106459. [Google Scholar] [CrossRef]
- Tsuboi, S.; Miyokawa, S.; Matsuda, M.; Yokomori, T.; Iida, N. Influence of spark discharge characteristics on ignition and combustion process and the lean operation limit in a spark ignition engine. Appl. Energy 2019, 250, 617–632. [Google Scholar] [CrossRef]
- Morales, A.J.; Lasky, I.M.; Geikie, M.K.; Engelmann, C.A.; Ahmed, K.A. Mechanisms of flame extinction and lean blowout of bluff body stabilized flames. Combust. Flame 2019, 203, 31–45. [Google Scholar] [CrossRef]
- Badawy, T.; Bao, X.C.; Xu, H. Impact of spark plug gap on flame kernel propagation and engine performance. Appl. Energy 2017, 191, 311–327. [Google Scholar] [CrossRef]
- Tilz, A.; Kiesling, C.; Meyer, G.; Nickl, A.; Pirker, G.; Wimmer, A. Experimental investigation of the influence of ignition system parameters on combustion behavior in large lean burn spark ignited gas engines. Exp. Therm. Fluid Sci. 2020, 119, 110176. [Google Scholar] [CrossRef]
- Zhu, S.; Akehurst, S.; Lewis, A.; Yuan, H. A review of the pre-chamber ignition system applied on future low-carbon spark ignition engines. Renew. Sustain. Energy Rev. 2022, 154, 111872. [Google Scholar] [CrossRef]
- Lovett, J.; Brogan, T.; Philippona, D.; Kiel, B.; Thompson, T. Development needs for advanced afterburner designs. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, FL, USA, 11–14 July 2004; p. 4192. [Google Scholar]
- Morsy, M.H. Review and recent developments of laser ignition for internal combustion engines applications. Renew. Sustain. Energy Rev. 2012, 16, 4849–4875. [Google Scholar] [CrossRef]
- Patane, P.; Nandgaonkar, M. Multipoint laser ignition system and its applications to IC engines. Opt. Laser Technol. 2020, 130, 106305. [Google Scholar] [CrossRef]
- O’Briant, S.A.; Gupta, S.B.; Vasu, S.S. Laser ignition for aerospace propulsion. Propuls. Power Res. 2016, 5, 1–21. [Google Scholar] [CrossRef]
- Pavel, N.; Bärwinkel, M.; Heinz, P.; Brüggemann, D.; Dearden, G.; Croitoru, G.; Grigore, O.V. Laser ignition-Spark plug development and application in reciprocating engines. Prog. Quantum Electron. 2018, 58, 1–32. [Google Scholar] [CrossRef]
- Ju, Y.; Sun, W. Plasma assisted combustion: Dynamics and chemistry. Prog. Energy Combust. Sci. 2015, 48, 21–83. [Google Scholar] [CrossRef]
- Andrey, S.; Nickolay, A. Plasma-assisted ignition and combustion. Prog. Energy Combust. Sci. 2013, 39, 61–110. [Google Scholar]
- Gerhard, K.; Georg, F.; Ernst, W. Novel miniaturized high-energy Nd-YAG laser for spark ignition in internal combustion engines. Optical. Eng. 2009, 48, 014202. [Google Scholar]
- Gupta, S.B. Fouling Mitigation for Laser Igniters in Natural Gas Engines. ASME J. Eng. Gas Turbines Power 2022, 144, 041020. [Google Scholar] [CrossRef]
- Tsunekane, M.; Inohara, T.; Ando, A.; Kido, N.; Kanehara, K.; Taira, T. High peak power, passively q-switched microlaser for ignition of engines. IEEE J. Quantum Electron. 2010, 46, 277–284. [Google Scholar] [CrossRef]
- Moesl, K.G.; Vollmer, K.G.; Sattelmayer, T.; Eckstein, J.; Kopecek, H. Experimental study on laser-induced ignition of swirl-stabilized kerosene flames. J. Eng. Foe Gas Turbines Power 2009, 131, 021501. [Google Scholar] [CrossRef]
- You, B.; Liu, X.; Kong, L.; Yang, J.; Chen, M.; Zheng, H.; Li, S. Experimental study on direct ignition of blast furnace gas by plasma igniter in a gas turbine combustor. Part C J. Mech. Eng. Sci. 2022, 236, 9306–9315. [Google Scholar] [CrossRef]
- Kopecek, H.; Maier, H.; Reider, G.; Winter, F.; Wintner, E. Laser ignition of methane–air mixtures at high pressures. Exp. Therm. Fluid Sci. 2003, 27, 499–503. [Google Scholar] [CrossRef]
- Seunghyun, J.; Jay, P. Laser ignition energy for turbulent premixed hydrogen air jets. Combust. Flame 2022, 236, 111767. [Google Scholar]
- Weinrotter, M.; Kopecek, H.; Wintner, E.; Lackner, M.; Winter, F. Application of laser ignition to hydrogen–air mixtures at high pressures. Int. J. Hydrog. Energy 2005, 30, 319–326. [Google Scholar] [CrossRef]
- Weinrotter, M.; Kopecek, H.; Tesch, M.; Wintner, E.; Lackner, M.; Winter, F. Laser ignition of ultra-lean methane/hydrogen/air mixtures at high temperature and pressure. Exp. Therm. Fluid Sci. 2005, 29, 569–577. [Google Scholar] [CrossRef]
- An, B.; Wang, Z.; Yang, L.; Li, X.; Liu, C. The ignition characteristics of the close dual-point laser ignition in a cavity based scramjet combustor. Exp. Therm. Fluid Sci. 2019, 101, 136–140. [Google Scholar] [CrossRef]
- Lyon, E.; Kuang, Z.; Cheng, H.; Page, V.; Shenton, T.; Dearden, G. Multi-point laser spark generation for internal combustion engines using a spatial light modulator. J. Phys. D Appl. Phys. 2014, 47, 475501. [Google Scholar] [CrossRef]
- Mastorakos, E. Ignition of turbulent non-premixed flames. Prog. Energy Combust. Sci. 2009, 35, 57–97. [Google Scholar] [CrossRef]
- Sitte, M.P.; Bach, E.; Kariuki, J.; Bauer, H.J.; Mastorakos, E. Simulations and experiments on the ignition probability in turbulent premixed bluff-body flames. Combust. Theory Model. 2016, 20, 548–565. [Google Scholar] [CrossRef]
- Bourgouin, J.F.; Durox, D.; Schuller, T.; Beaunier, J.; Candel, S. Ignition dynamics of an annular combustor equipped with multiple swirling injectors. Combust. Flame 2013, 160, 1398–1413. [Google Scholar] [CrossRef]
- Marchione, T.; Ahmed, S.F.; Mastorakos, E. Ignition of turbulent swirling n-heptane spray flames using single and multiple sparks. Combust. Flame 2009, 156, 166–180. [Google Scholar] [CrossRef]
- Wang, X.; Huang, Y.; Liu, Y.; Sun, L. Effect of the ignition location on lean light-off limits for a gas turbine combustor. Combust. Flame 2022, 245, 112295. [Google Scholar] [CrossRef]
- Ciardiello, R.; de Oliveira, P.M.; Skiba, A.W.; Mastorakos, E.; Allison, P.M. Effect of spark location and laminar flame speed on the ignition transient of a premixed annular combustor. Combust. Flame 2020, 221, 296–310. [Google Scholar] [CrossRef]
- Ciardiello, R.; Pathania, R.S.; Allison, P.M.; de Oliveira, P.M.; Mastorakos, E. Ignition probability and lean ignition behavior of a swirled premixed bluff body stabilized annular combustor. J. Eng. Gas Turbines Power 2021, 143, 041024. [Google Scholar] [CrossRef]
- Ciardiello, R. Transient phenomena in annular combustors. Doctoral Dissertation, University of Cambridge, Cambridge, UK, 2021. [Google Scholar]
- Lin, B.X.; Wu, Y.; Xu, M.X.; Chen, Z.G. Experimental investigation on spark ignition and flame propagation of swirling kerosene spray flames. Fuel 2021, 303, 121254. [Google Scholar] [CrossRef]
- Mao, Y.; Yu, L.; Wu, Z.; Tao, W.; Wang, S.; Ruan, C.; Zhu, L.; Lu, X. Experimental and kinetic modeling study of ignition characteristics of RP-3 kerosene over low-to-high temperature ranges in a heated rapid compression machine and a heated shock tube. Combust. Flame 2019, 203, 157–169. [Google Scholar] [CrossRef]
- Hinze, J.O. Experimental investigation on secondary currents in the turbulent flow through a straight conduit. Appl. Sci. Res. 1973, 28, 453–465. [Google Scholar] [CrossRef]
- Ducros, F.; Nicoud, F.; Poinsot, T. Wall-adapting local eddy-viscosity models for simulations in complex geometries. Numer. Methods Fluid Dyn. VI 1998, 6, 293–299. [Google Scholar]
- Sjunnesson, A.; Henriksson, R.; Löfström, C. CARS measurements and visualization of reacting flows in bluffbody stabilized flame. In Proceedings of the 28th Joint Propulsion Conference and Exhibit, Nashville, TN, USA, 6–8 July 1992. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).