Abstract
Aviation networks exhibit multi-layer characteristics and heterogeneity of nodes and edges. Identifying key nodes in a multi-layer heterogeneous aviation network (MHAN) and elucidating its cascading failure process are of great practical significance for enhancing the ability to resist failure and strengthening network resilience. Therefore, this paper first establishes the basic model of MHAN and then designs an intra-layer node importance evaluation method based on the improved TOPSIS-grey correlation analysis (ITG) method and an inter-layer influence weight quantification method based on the gravity model. By integrating the information transmission characteristics between network nodes, a key node identification method in MHAN through aggregating multi-source information is proposed. Finally, based on the actual overload operation of aviation networks, the initial load adjustment coefficient, capacity limit, and overload coefficient are introduced based on the traditional capacity–load model, a cascading failure model of MHAN considering overload condition and failure probability is constructed, and a node influence index based on this model is defined to verify the accuracy of the key node identification results. The instance analysis conducted on the aviation network in western China demonstrates that the intra-layer node importance evaluation method based on ITG yields results with better distinguishability and higher accuracy. The key nodes are predominantly hub en-route nodes and sector nodes. In the cascading failure model, increasing the overload coefficient and capacity limit within a specific range while reducing the initial load adjustment coefficient helps reduce the network failure scale. The key nodes identified by the node influence index are consistent with those identified by the method proposed in this paper, validating the accuracy and effectiveness of the key node identification method in MHAN through aggregating multi-source information herein.
1. Introduction
The aviation network comprises multiple sub-networks such as airports, en-routes, and sectors [1]. It has numerous layers, with nodes being homogeneous within each sub-network but heterogeneous across different sub-networks. Moreover, the interaction relationships among the nodes are intricate and diverse. Therefore, the aviation network is a multi-layer heterogeneous network. In recent years, the expansion of airport networks, optimization of en-route networks, and adjustment of sector networks have been carried out due to the continuous growth of air transportation demand. This expansion has led to the aviation network’s increasing density and complexity. However, the aviation network can experience disruptions during operation due to severe weather, air traffic control issues, and equipment failures [2]. These disruptions, when accumulated, can diminish or impair the operational capacity of nodes, affecting adjacent nodes and potentially leading to a significant number of node failures or even network collapse. As a result, flight safety and operational efficiency in air transportation are severely impacted. Furthermore, the intensity and scope of the impact on the aviation network vary when nodes operate abnormally due to the various attributes of nodes in the aviation network. Nodes with a greater and more profound influence on the aviation network are considered key nodes. Therefore, identifying key nodes in the aviation network and implementing targeted protection measures, clarifying the cascade propagation mechanism of node failures, and formulating corresponding emergency strategies are not only crucial for ensuring the safety and efficiency of aviation network operations but also serve as a guide for optimizing the structure and enhancing the resilience of the aviation network.
Identifying key nodes is one of the hot issues in complex network analysis [3]. In aviation, existing work on key node identification mainly focuses on three aspects. First, by quantifying the centrality of nodes [4,5], the identification of key nodes is completed. Second, the importance of nodes is determined by measuring the degree of decline in network performance after deleting nodes [6,7]. Third, various indices are selected to construct an evaluation index system of node importance, and an appropriate evaluation method is used to assess the importance of nodes, ultimately identifying the key nodes in the network [8,9]. The results above have been carried out on a single-layer network structure. However, the aviation network is an open and complex system with sub-networks such as airport networks, en-route networks, and sector networks. There are more complex interactions between these sub-networks, which adds to the complexity of the overall aviation network. Consequently, using a single-layer network topology, it is impossible to adequately describe the interdependent and connected links between various entities in the aviation network. The key node identification methods discussed above will not work well for identifying key nodes in aviation networks.
Cascading failure refers to the dynamic process where the failure of some nodes in a network triggers the redistribution of network traffic or load, subsequently causing other nodes to fail due to the excessive burden [10]. In the realm of aviation, there have been studies analyzing and researching the cascade failure propagation mechanisms of airport networks [11], en-route networks [12], and sector networks [13]. Additionally, relevant research has been conducted on the cascade failure principles of military aviation communication networks [14]. The studies mentioned above all focus on single-layer networks. However, the aviation network is a multi-layer heterogeneous network where each layer has different structures and functions, and failures occur in different ways. Additionally, the close coupling between various layers in the aviation network leads to the mutual influence of node failures between different layers. Simply analyzing the cascade failure mechanism of isolated layer networks cannot effectively reflect the cascade failure phenomenon of the aviation network. A smaller portion of studies have constructed multi-layer aviation network models and analyzed their cascading failures [15,16,17]. However, most of these studies assume deterministic node failures, meaning that once a node’s load exceeds its maximum capacity, it fails immediately. In contrast, due to the unique characteristics of aviation networks, nodes often have redundant capacity and do not fail immediately when overloaded. Instead, they reduce their efficiency in handling traffic loads and possess a particular ability to manage excess loads. Consequently, the existing cascading failure models do not adapt well to aviation networks.
This paper introduces a method for identifying key nodes in a multi-layer heterogeneous aviation network (MHAN) and constructs a cascading failure model of MHAN tailored to reflect operational realities. Empirical research is then conducted using the aviation network in western China as a case study. This research has profound implications for the following reasons:
- It introduces a novel node importance evaluation method based on ITG for single-layer networks, expanding the methods available for assessing node importance in such networks.
- A node importance identification method in MHAN through aggregating multi-source information is proposed. Enhancing the protection of key nodes and preventing key node collapses provide a reference for improving aviation network resilience.
- A cascading failure model of MHAN is developed, which fully considers the super-capacity operation of the aviation network, thus enhancing the applicability of cascading failure studies to real-world aviation networks. It guides the structural optimization and invulnerability improvement of aviation networks.
- The node influence index defined based on the cascading failure model provides a new method and idea for identifying important nodes in multi-layer networks.
The rest of this paper is organized as follows. Section 2 reviews relevant literature on key node identification and cascading failure. Section 3 shows the methodological framework of this paper. Section 4 introduces the MHAN model. Section 5 proposes a method for identifying key nodes in MHAN through aggregating multi-source information. Section 6 outlines a cascading failure model of MHAN. In Section 7, taking the aviation network in western China as a case study, the network construction, key node identification, and cascading failure process analysis are completed, and the accuracy of the key node identification results is verified based on the node influence index. Finally, Section 8 offers conclusions and suggests future research directions.
2. Literature Review
2.1. Key Nodes Identification
Key nodes, as fundamental components of complex networks, significantly influence the configuration and functionality of networks and have been extensively researched and utilized [18,19]. Currently, methods for identifying key nodes in complex networks can be classified into three categories. The first category involves utilizing classical algorithms such as degree centrality, betweenness centrality, K-shell, PageRank, or optimizing classical algorithms to identify key nodes accurately [20,21,22,23]. The second type is to determine the importance of nodes by assessing the extent of network performance decline following node deletion [24,25]. The last category involves selecting a variety of algorithms for fusion to complete the identification of key nodes [8,26]. Significant advancements have been made in detecting key nodes in complex aviation networks. Zhou et al. [4] proposed a new metric based on efficiency and robustness to identify key airports in weighted air transport networks. Li et al. [6] identified the most critical backbone network in the aviation network based on the minimum connected dominating set. Zhang et al. [7] employed the weighted node shrinkage method to determine the critical nodes inside the global aviation network. In addition to building an airport network with gravity correlation and establishing a system of node importance evaluation indicators, Zhang et al. [9] also employed an improved TOPSIS method to calculate the comprehensive importance of nodes in the airport network. Wang et al. [5] took into account the intrinsic characteristic between aircraft, created a weighted temporal network based on the supra-adjacency matrix, and identified crucial aircraft nodes using eigenvector centrality. The studies mentioned above are all concentrated on single-layer networks (SLNs), where the identification of key nodes is based on the interaction patterns between nodes of the same type. They consider the neighborhood characteristics of nodes in a single interaction relationship and the positional information of nodes under a single topological pattern.
Multi-layer complex networks are composed of two or more single-layer networks [27]. According to whether there is a connection between different network layers, they can be divided into multi-dimensional multi-layer networks (MMNs) and interdependent multi-layer networks (IMNs) [28]. The characteristic of multi-dimensional multi-layer networks is that the number of nodes in each layer is the same, but the edges in each layer are heterogeneous, and there is no connection between layers. Some existing research has extended the classical algorithms of identifying key nodes from single-layer networks to multi-dimensional multi-layer networks. To complete the important computation of nodes in multiplex networks, Chakraborty et al. [29] suggested cross-layer betweenness centrality, which modified the importance of intra-layer and inter-layer edges by parameters. Maulana et al. [30] designed a multiplex network eigenvector centrality identification method based on a multi-objective optimization method and obtained the key node set of the multiplex network. In light of the differences in layer importance in multi-layer networks, Rahmede et al. [31] proposed a method for calculating layer centrality and developed a MultiRank algorithm based on the PageRank algorithm. This method correctly determined the key nodes of the large multiplex networks after considering the layer centrality and node centrality. Ding et al. [32] introduced a topologically biased multiplex PageRank technique and determined the centrality ranking of nodes in multiplex networks via the impact of topology on random walks. Furthermore, another research approach for recognizing important nodes in multi-dimensional multi-layer networks is based on aggregating multi-dimensional data or the networks’ propagation angle. A node importance measurement index was established by Luo et al. [33] using a mathematical framework of multi-layer social networks based on tensor algebra. The index was then improved using the Dempster–Shafer evidence theory by integrating the centrality, prestige, and transitivity of nodes. Feng et al. [34] built the evaluation index system of node importance, measured the node importance evaluation value in the single-layer network through the improved TOPSIS method, and fused the node importance evaluation values from the various network layers employing the grey correlation method to calculate the overall node importance in the China railway express transportation network. Based on the important characteristics that define propagation performance, Zhou et al. [35] developed a layer-weighting method and determined the multiplex network’s key nodes. Relying on the PageRank centrality of nodes, the significance of the community in which the nodes are placed, and the nodes’ influence, Lv et al. [36] assessed the nodes’ importance within the layer network and presented a layer centrality calculation method. Nodes in multi-layer networks can have their importance defined as a weighted fusion of layer centrality and the importance of nodes in all layer networks.
In the interdependent multi-layer network, the layers may have different numbers of nodes, and there are inter-layer connections that influence the overall network. Each node has a distinct importance due to its heterogeneity [37]. Limited studies have been conducted on interdependent multi-layer networks thus far, with the majority of related studies taking place in the biological sciences. Novoa-del-Toro et al. [38] introduced a multi-objective genetic algorithm to find important active modules in gene–protein multi-layer biological networks. Wu et al. [39] constructed a multi-layer RNA network to find putative essential genes connected to clear cell renal cell carcinoma based on node degree, closeness centrality, and betweenness centrality. In other fields, Fan [40] established a multi-layer interdependent network of complex electronic information systems and proposed a key node identification algorithm based on the importance of layers and interlayers. To identify significant nodes in multi-layer heterogeneous citation networks, Wan et al. [3] first quantified the intra-layer centrality of nodes, then computed the inter-layer weights based on network connections, and lastly, fused the centrality of heterogeneous nodes under multi-connected relationships. The aforementioned studies serve as a guide for identifying key nodes in aviation networks.
Several representative key node identification methods in complex networks are summarized in Table 1, and the relevant explanations for Table 1 are given as follows:

Table 1.
Various methods for key node identification in complex networks.
- (1)
- Network structure: The network structure includes the single-layer network (SLN), multi-layer network (MMN), and interdependent multi-layer network (IMN). It should be noted that the SLN does not have intra-layer nodes or layers.
- (2)
- Method: In the process of identifying key nodes, it is generally necessary to calculate the intra-layer node importance (INI), the layer importance (LI), and the final node importance (NI) based on certain methods. These methods include classical algorithms or optimizing classical algorithms (CAs), the comprehensive evaluation method (CEM), results fusion (RF), and the aggregation of multi-source information (AMS). Among them, RF focuses on combining processing results from different sources using, for example, weighted summation or weighted averaging, and AMS focuses on the use of algorithms to integrate data or features from multiple sources of information [3].
- (3)
- Symbol descriptions: Checkmarks (√) mean that the network structure is used in the study. N/A means that the network does not have the corresponding structure. Circles (o) mean that it is not considered in this study.
In summary, the multi-layer heterogeneous aviation network constructed in this paper belongs to the IMN category. Currently, there are very few studies on identifying key nodes in IMNs. Most existing methods for INI are based on CA, which provides a single perspective and cannot accurately reflect all the attributes of nodes. The calculation of LI is either not considered or only calculated using a certain CA, which does not adequately capture the significance of layers in the network. When determining the final NI based on the quantified INI and LI, the CA or RF fails to represent the complex and interdependent relationships between the nodes in the network.
2.2. Cascading Failure
Presently, professionals and academics conducting related research both domestically and internationally primarily use the load–capacity model [10], coupled map lattice model [41], or percolation theory [42] to study the cascading failure of complex networks. In the realm of air traffic, there have been studies analyzing and researching the cascade failure propagation mechanisms of airport networks [11], en-route networks [12], and sector networks [13]. Additionally, relevant research has been conducted on the cascade failure principles of military aviation communication networks [14]. The above-mentioned studies all focus on single-layer networks.
With the continuous development of the economy and advancements in science and technology, the coupling and interdependence among various system networks have become increasingly intense, forming interdependent multi-layer networks [43]. The mechanism of cascading failure propagation in these networks during destructive events has gradually become an important research direction. Currently, research on cascading failures in multi-layer interdependent networks is still in its infancy, with most results based on load–capacity models, coupled map lattice models, or percolation theory. The focus of the study has shifted to multi-layer network cascading failure. Buldyrev et al. [28] were among the first to study the robustness of interdependent networks subject to cascading failures. Taking the underload failure of the real supply chain networks into account, Li et al. [44] established a multi-layer supply chain network mixed failure model considering both overload cascading failure and underload failure. Li et al. [45] constructed a cyber-physical power interdependent network model and then developed a dynamic model based on the load–capacity model to analyze the cascading failure. Wang et al. [46] created a cascade failure model based on coupled map lattice by introducing the resistance characteristic parameter of nodes in the heterogeneous multi-layer transportation network. Zhang et al. [47] designed a load delay judgment mechanism and a load distribution strategy and then constructed a cascading failure model with tunable parameters for multi-layer directed dependent networks. Jia et al. [48] paid attention to the robustness and cascading dynamics of multi-layer networks based on percolation theory. Few studies have been performed on the cascading failure of multi-layer networks in the context of air traffic. Chen et al. [15] constructed an air transportation interdependent network and proposed a capacity–load-based interdependent network cascading failure model. Wang et al. [16] built an air traffic interdependent network model and examined its structural vulnerability and functional vulnerability by analyzing the cascading failure process. Later, they coupled the physical network with the information network to construct the air traffic cyber–physical system network and explored the cascading failure process [17].
Several representative studies related to cascading failure in complex networks are summarized in Table 2, and the relevant explanations for Table 2 are given as follows:

Table 2.
Various methods for cascading failure in complex networks.
- (1)
- Network structure: The network structure includes SLN and IMN.
- (2)
- Load redistribution: The load redistribution encompasses the redistribution strategies of loads for both overloaded and failed nodes. Typically, these strategies involve distributing loads based on one of the following criteria: the number of neighboring nodes (NNs), the load proportion of neighboring nodes (LPN), or the real-time residual capacity of neighboring nodes (RRCN).
- (3)
- Symbol descriptions: Checkmarks (√) mean that the study uses the network structure. Bold checkmarks (✔) and squares (☐) mean that the study does and does not consider the element, respectively.
The study of cascading failures in interdependent multi-layer networks is still in its early stages. Most existing research assumes deterministic node failures, meaning that once a node’s load exceeds its maximum capacity, the node fails immediately. These models overlook the redundancy capacity of nodes in aviation networks resulting from their actual overcapacity operation. Only a few studies have considered the overload condition of nodes, but they do not differentiate between load redistribution strategies for overloaded nodes and failed nodes.
3. Methodological Framework
This paper comprehensively considers the multi-layer nature and the node heterogeneity of aviation networks, integrates the interdependencies between units in the aviation network to establish a multi-layer heterogeneous aviation network (MHAN) model, and employs mathematical notation to delineate the detailed information and the correspondence between different layers of the MHAN. Aiming to address the problem of key node identification in aviation networks, this paper presents a node importance identification method in MHAN by aggregating multi-source information. Initially, an evaluation index system of the intra-layer node importance is devised from the perspectives of network structural characteristics, network vulnerability, and traffic flow characteristics. The importance of each node is then assessed using the improved TOPSIS-grey relational analysis (ITG) method. Subsequently, considering the influence of inter-layer interaction patterns on the importance of each node in MHAN, an inter-layer influence weight quantization method based on the gravity model is designed. Finally, by aggregating multi-source information based on the attribute features and transmission characteristics of nodes, the ranking of the node importance for MHAN is determined. This paper addresses the issue of cascading failure in aviation networks by delving into the cascading propagation process and designing a cascading failure model that better fits the reality: combining the realities of aviation networks operating beyond capacity, it enhances the traditional load–capacity model by incorporating the overload condition and failure probability and employs different load redistribution strategies for overloaded nodes and failed nodes. Utilizing this cascading failure model, the paper introduces a node influence index that accounts for the network failure scale and the average load change in their neighboring nodes resulting from failed nodes. This index serves to validate the effectiveness and feasibility of the key node identification result. This paper’s main contributions include the construction of the MHAN model, the identification of key nodes, the design of the cascading failure model, and the significant findings obtained through empirical research on the aviation network in western China. The content and logical flow of this paper are shown in Figure 1.
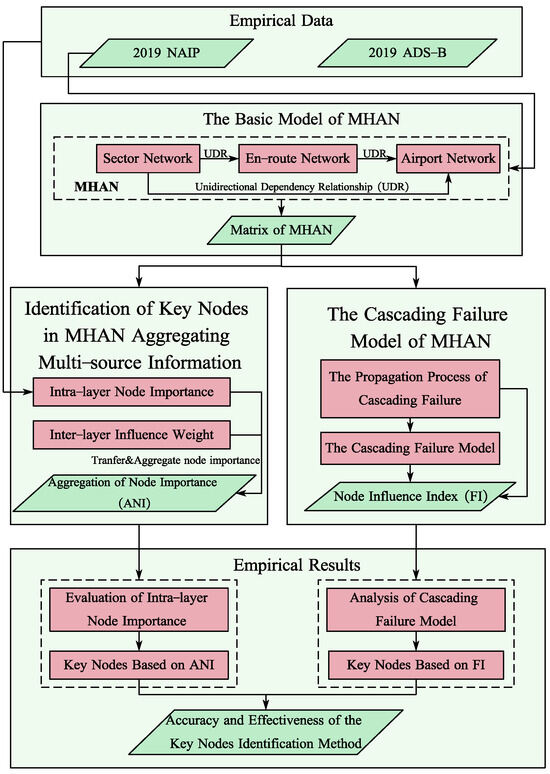
Figure 1.
The structure of the proposed framework.
4. The Basic Model of Multi-Layer Heterogeneous Aviation Network
The MHAN constructed in this paper integrates an airport network (AN), an en-route network (EN), and a sector network (SN), incorporating various types of nodes and edges, including intra-layer edges and inter-layer edges.
4.1. Construction Description and Assumptions
In this paper, the following description and assumptions are made to construct MHAN.
- Nodes. In this MHAN framework, airports are represented as nodes in the AN, while the EN employs ground navigation facilities like omnidirectional beacon stations, distance-finding stations, or non-directional beacon stations as nodes. Additionally, the SN merges high sectors into corresponding low sectors, disregarding temporarily open sectors, with sectors serving as nodes. Thus, the MHAN comprises three distinct types of heterogeneous nodes.
- Edges. The MHAN comprises both intra-layer and inter-layer edges. Intra-layer edges are defined as follows: within the AN, edges form between any two airports if there are flights between them; within the EN, edges represent the routes between ground navigation facilities; within the SN, edges correspond to the handover relationships of inter-sector flights. Inter-layer edges are delineated as follows: based on air traffic management rules [49], inter-layer edges between AN and EN represent the connections between airport nodes and corresponding en-route nodes, indicating the connection relationship of aircraft entering en-routes from airports or landing at airports from en-routes. The inter-layer edge between the AN and SN represents the connection between airport nodes and corresponding sector nodes, depicting control sectors’ authority over aircraft takeoff and landing at the respective airports. Lastly, the inter-layer edge between the EN and SN denotes the links between nodes of en-route points and corresponding sector nodes, illustrating the sectors’ management of traffic flow along en-routes. Consequently, the MHAN encompasses six types of heterogeneous edges.
- The MHAN is directed. During aircraft operation, aircraft can take off or land from airports, pass en-route points, and enter or exit sectors. Therefore, it is assumed that the AN, EN, and SN are all undirected. However, there exists a unidirectional dependency relationship [16] between the networks: the airport node facilitates flight takeoff and landing under the normal operation of the corresponding en-route node and sector node, and the en-route node executes flight transportation functions when the associated sector node operates effectively. Hence, the inter-layer edges are directed. Consequently, the MHAN is an intra-layer undirected inter-layer directed network.
4.2. The Construction of Multi-Layer Heterogeneous Aviation Network
Based on Section 4.1, the MHAN can be represented by a binary group , where denotes the set of nodes containing types in . In this paper, the node types comprise airport nodes, en-route nodes, and sector nodes. With regard to the homogeneity characteristics of nodes within the layer network of the MHAN, also denotes the number of MHAN layers, while N represents the total number of nodes in . represents the set of edges in , where signifies the set of edges of l-th class of relations, and indicates there are sets of edges in . For MHAN, it can be hierarchically represented in two parts: intra-layer networks and inter-layer networks, with each layer corresponding to a type of relationship.
Definition 1.
The k-th intra-layer network corresponding to the k-th class of relations in is denoted by , where , is the number of nodes in . The set of connected edges within can be written as:
Definition 2.
The intra-layer connections of can be represented by an adjacency matrix, denoted as , and
Definition 3.
is used to represent the directed inter-layer network of layer k and layer h in , where , is the number of nodes in , the set of directed edges of the inter-layer network can be written as:
Definition 4.
The inter-layer connections corresponding to can also be represented by an adjacency matrix, denoted as , and
According to Definitions 2 and 4, the basic model of MHAN can be represented by a matrix as:
5. Identification of Key Nodes in Multi-Layer Heterogeneous Aviation Network through Aggregating Multi-Source Information
The characteristics of MHAN lie in its multiple hierarchical levels, where nodes within each layer share the same type, but nodes across different layers are heterogeneous. Moreover, intricate and diverse interaction relationships exist among nodes. Therefore, this paper proposes a method for identifying key nodes in MHAN through aggregating multi-source information, with the aim of uncovering key nodes in MHAN influenced by multiple relationships. First, concentrating on the layer networks, based on the homogeneity of nodes within them, this study formulates an index system to assess the importance of intra-layer nodes from three angles: network structural characteristics (NSCs), network vulnerability (NV), and traffic flow characteristics (TFCs). A comprehensive evaluation model of intra-layer node importance is devised using the improved TOPSIS-grey relational analysis (ITG) method. Consequently, the intra-layer importance of each node in MHAN is determined. Next, considering the impact intensity of inter-layer interaction patterns on node importance in MHAN, and amalgamating the connection relationships between heterogeneous nodes in different layer networks with the intra-layer node importance, a model for computing inter-layer influence weights is formulated using the gravity model. Finally, by aggregating multi-source information based on the attribute features and transmission characteristics of nodes, the node importance through aggregating multi-source information, abbreviated as the aggregation of node importance (ANI), is obtained, and then the identification of key nodes in MHAN is completed. This method not only considers the unique attribute characteristics of nodes themselves but also focuses on the MHAN’s topological structure. It also emphasizes the mutual attraction degree and influence contribution value of neighboring heterogeneous nodes. The overall architecture of the method for identifying key nodes in MHAN by aggregating multi-source information is illustrated in Figure 2.
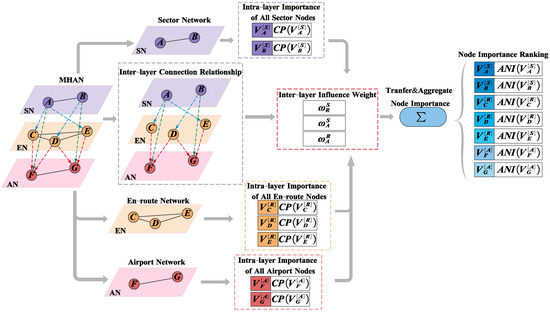
Figure 2.
The overall architecture of the method for identifying key nodes in MHAN by aggregating multi-source information.
In Figure 2, the MHAN model includes three layer networks: AN, EN, and SN. A and B in SN represent sector nodes, C, D, and E in EN represent en-route nodes, and F and G in AN represent airport nodes. Dashed lines of different colors indicate the unidirectional dependency relationships between nodes: blue indicates en-route nodes depending on sector nodes, green indicates airport nodes depending on sector nodes, and red indicates airport nodes depending on en-route nodes. At first, the importance of nodes in each layer is analyzed layer by layer, and the intra-layer node importance of each node is obtained based on the ITG algorithm. Secondly, based on the inter-layer connection relationships, the inter-layer influence weights are calculated using the gravity model in conjunction with . Then, each node in the MHAN is taken as a target node in turn, and based on the transmission characteristics of nodes, the importance of the target node’s neighboring nodes in other layers is transmitted along the inter-layer connections and aggregated with the of the target node, which leads to the aggregation of node importance . Finally, the key nodes in MHAN are identified based on the ranking.
5.1. Evaluation of Intra-Layer Node Importance
Focusing on the layer networks within MHAN, the intra-layer node importance is evaluated. Due to the abundance of attribute information associated with nodes in layer networks, using a single index makes it challenging to assess the importance of nodes exactly [36]. To accurately and reasonably evaluate the intra-layer importance of each node in MHAN, laying the foundation for the subsequent identification of key nodes, this paper has comprehensively established an index system for evaluating intra-layer node importance from three perspectives: network structural characteristics, network vulnerability, and traffic flow characteristics. Based on this index system, the ITG method is proposed as a comprehensive evaluation model, which systematically assesses the intra-layer importance of each node in MHAN.
5.1.1. The Index System for Evaluating Intra-Layer Node Importance
- 1.
- Network Structural Characteristics (NSC)
(1) Degree centrality (DC)
The DC of a node is determined by the number of edges between the node and its neighboring nodes, known as the node’s degree [18], which is utilized to gauge the node’s importance. A higher degree indicates relatively more significant importance. DC reflects the extent to which a node is central in its local network. For the k-th layer network in MHAN , the equation for calculating the DC of node is:
where is the DC of node ; represents the edge between and , when they are connected, ; otherwise, .
(2) Betweenness centrality (BC)
BC refers to the ratio of the number of shortest paths passing through a node to the total number of shortest paths in the network. The larger the ratio, the relatively more important the node. BC is a global index reflecting the importance of nodes. In , the equation for calculating the BC of node is:
where is the BC of node ; represents the number of shortest paths between any two nodes and ; represents the number of shortest paths passing through node between any two nodes and in .
(3) Clustering coefficient (CC)
The CC of a node refers to the ratio of the actual number of edges existing among the neighboring nodes of the node in the network to the maximum possible number of edges among its neighboring nodes [50]. The CC measures the closeness of connections between a node and its neighboring nodes. It is not only used to describe the degree of clustering of nodes in the network but also to explain the community structure and clustering phenomena in the network. In , the CC of node is calculated by Equation (10):
where is the CC of node ; represents the total number of neighboring nodes of ; and stands for the actual number of edges existing among the neighboring nodes of .
(4) Improved K-shell (IK)
The central idea of the K-shell method is to recursively peel off nodes with degrees less than k (k = 1, 2, …) and their edges from a complex network, ensuring that the remaining nodes in the network have degrees greater than or equal to k [21]. While the K-shell method characterizes global topological information, it has drawbacks such as overly coarse identification precision and limited algorithm applicability. Therefore, the node information entropy is introduced to improve the K-shell method [51]: iterations are conducted in the order of decreasing K-shell layers, and in each layer of unselected nodes, the node with the highest node information entropy is selected until all nodes in the network are chosen. In , the node information entropy of is defined as:
where is defined as the node information entropy of ; is the node importance of based on DC; and represents the set of same-layer neighboring nodes of .
- 2.
- Network Vulnerability (NV)
(1) Network efficiency decrease rate (DE)
Network efficiency (NE) is used to measure the impact of changes in network structure on the shortest distance. In , the equation for calculating NE is as follows:
where represents the length of the shortest path between and .
For , after node is removed, the traffic capacity and connectivity of decrease, leading to a reduction in NE. Therefore, the decrease in NE caused by removing node is calculated as:
In Equation (14), stands for the network efficiency decrease rate corresponding to node ; is the new NE after removing node and its edges. A larger indicates a more significant decrease in network efficiency, implying that the removed node is more important.
(2) Network connectivity coefficient decrease rate (DN)
If is not connected or if important nodes are deleted, forming subnetworks, the network connectivity coefficient (NCC) [52] is commonly used to measure network topological performance. The equation for calculating the NCC is:
where is the number of connected components of ; is the number of nodes in the i-th connected component; is the average shortest path of the i-th connected component, represents the number of shortest paths in the i-th connected component, and is the length of the shortest path between and in the i-th connected component. The fewer the number of connected components and the smaller the average shortest path of each component, the better the network connectivity, and the larger the NCC.
When node is deleted from , the network may be divided into multiple connected components, resulting in a significant decrease in network connectivity. Therefore, the network connectivity coefficient decrease rate is used to measure the importance of nodes. It is expressed as:
where is the network connectivity coefficient decrease rate corresponding to node ; is the new NCC after removing node and its edges. The more pronounced the decrease in network connectivity, the more important the removed node.
- 3.
- Traffic Flow Characteristics (TFC)
As the aviation network serves as the foundation for aircraft operations, the operational characteristics of aircraft also reflect the importance of aviation network nodes. Therefore, this paper selects indices such as hourly average flow (HAF) and peak hour flow (PHF) to reflect the importance of nodes in the aviation network from the perspective of traffic flow.
(1) Hourly average flow (HAF)
In an aviation network, HAF is calculated using Equation (18):
where represents the number of statistical slots. varies depending on the different layers of MHAN: when k represents the AN, is the number of flights taking off and landing at the airport during slot t; when k represents the EN, is the number of aircraft passing through the en-route point during slot t; when k represents the SN, is the number of aircraft handed over by air traffic control during slot t.
(2) Peak hour flow (PHF)
In different slots, the traffic flow of each node varies. Therefore, the highest hourly flow of each node is taken as the peak hour flow, that is:
5.1.2. Evaluation of Intra-Layer Node Importance Based on Improved TOPSIS-Grey Relational Analysis
The TOPSIS method is a comprehensive and efficient evaluation approach, widely applied in various evaluation problems. However, the traditional TOPSIS algorithm based on Euclidean distance cannot adequately represent the correlation between indices for evaluating the importance of intra-layer nodes and the impact of the overlap of information contained in the indices on the decision-making process. Additionally, its simple linear summation method makes it difficult to accurately reflect the functional relationship between evaluation indices and evaluation results. The Mahalanobis distance has the characteristics of eliminating the correlation between indices and being unaffected by dimensional influences. Therefore, it can eliminate the influence of index correlation on evaluation results in the traditional TOPSIS method. The grey relational analysis reflects the degree of closeness between various indices from the perspective of curve shape similarity, which can compensate for the shortcomings of only calculating relative distances and ignoring the inability to accurately reflect the actual situation caused by the trend of curves. As a result, this paper replaces the Euclidean distance with the Mahalanobis distance and introduces grey relational analysis into the TOPSIS method, establishing an evaluation model based on the improved TOPSIS-grey relational analysis (ITG). Additionally, from both subjective and objective perspectives, this paper utilizes the AHP-CRITIC [53] method to calculate the weights of the indices. The complete process of evaluating the intra-layer node importance based on ITG is shown in Algorithm 1.
| Algorithm 1. Evaluation of intra-layer node importance based on ITG |
| ; |
| 1. do |
| 2. ; |
| 3. ; |
| 4. ; |
| 5. ; |
| 6. by |
| ; |
| 7. do |
| 8. by |
| is |
| ; |
| 9. do |
| 10. by |
| ; |
| 11. end for |
| 12. ; |
| 13. ; |
| 14. ; |
| 15. end for |
| 16. end for |
| 17. |
5.1.3. Evaluation Criterion of Intra-Layer Node Importance
To validate the accuracy of the proposed method for evaluating the intra-layer node importance based on ITG, this study adopts the monotonicity index [54], SIR model [55], and Kendall’s Tau coefficient [56] as evaluation criteria.
- (1)
- The Monotonicity Index
This paper employs the monotonicity index to quantify the resolution of different evaluation methods. In the k-th layer network, the calculation equation of is:
represents the intra-layer node importance ranking vector of the k-th layer network and represents the number of nodes with the same intra-layer importance. The value of is between 0 and 1. If , indicating that the ranking vector is completely monotonic, and the method can fully distinguish the importance of all nodes in the layer network. If , indicating that all nodes in the layer network have the same importance.
- (2)
- SIR Model
Propagation dynamics models are frequently employed to validate the effectiveness of key node assessment results. In this paper, the SIR model is adopted. In the SIR model, each node in the k-th layer network can be in one of three states: susceptible (S), infected (I), or removed (R). In the initial stage of propagation, infected node in the network acts as the source of infection, denoted as state I, while the rest of the nodes are in state S. During the propagation process, at each time step, nodes in state I attempt to infect their neighboring nodes in state S with a transmission rate , while there is also a certain probability for nodes to recover to state R, where they are no longer infected. Once a node in state S is infected, it transitions back to state I. The propagation process ends when there are no more nodes in state I in the network. After the entire SIR propagation process concludes, the number of nodes in state R in the k-th layer network can be regarded as the spreading capability of node . The greater the spreading capability, the more important the node. Sorting the propagation capabilities in descending order yields the spreading capability ranking vector .
In the SIR model, the most critical parameter is the transmission rate . If is inappropriate, it may hinder the propagation process, making it difficult to accurately assess the spreading capability of each node. Therefore, this paper sets the transmission rate threshold as:
is the second-order neighbor average degree of the network. In order to ensure normal propagation, the transmission rate in this paper is valued near , and .
- (3)
- Kendall’s Tau Coefficient
To measure the accuracy of the intra-layer node importance evaluation method, this paper utilizes Kendall’s Tau coefficient to assess the correlation between the intra-layer node importance ranking vector and the node-spreading capability ranking vector of the k-th layer network.
Kendall’s Tau coefficient, denoted as , is used to measure the correlation between two sequences. For the k-th layer network, the , and with the number of nodes , a new sequence is constructed by pairing each element of with its corresponding element in . For any pair of elements and in the sequence , if and , or and , then the pair of elements is considered concordant; if and , or and , then the pair of elements is considered discordant; if and , this pair of elements is neither concordant nor discordant. The calculation equation for is:
where and represent the number of concordant pairs and discordant pairs in , respectively. The value of lies between −1 and 1. When , it indicates a completely positive correlation between the two sequences, meaning that the closer is to 1, the higher the accuracy. Conversely, if approaches −1, it signifies a completely negative correlation.
5.2. Quantification of Inter-Layer Influence Weight
In MHAN, intra-layer node importance reflects the interaction between nodes within the same layer network. However, it is also necessary to consider the interaction between different layers of heterogeneous nodes. MHAN focuses on the interaction patterns between different layer networks, where inter-layer connections between adjacent heterogeneous nodes will affect the node’s importance. This plays a crucial role in assessing the importance of nodes in the MHAN. Hence, the concept of inter-layer influence weight is introduced, fully considering the contribution of inter-layer interaction patterns to the multi-source information of nodes. It integrates node attributes with network layer information, quantifying layer importance based on the node’s intra-layer importance and inter-layer connectivity relationships.
Two layer networks in MHAN form inter-layer connectivity between heterogeneous nodes through some associations. The more associations there are, the stronger the mutual influence between the two layer networks. Moreover, a significant characteristic of MHAN is the differences in the attributes and numbers of nodes in different layer networks, resulting in varying attributes of inter-layer connections. Additionally, the intra-layer node importance significantly influences the quantification of the inter-layer influence. The gravity model [57] can be utilized to quantify the correlation and interaction strength between heterogeneous adjacent nodes across layers. As a result, building upon the gravity model, this paper extends it and integrates the intra-layer node importance calculated in Section 5.1, proposing a model for calculating inter-layer influence weight, defined as follows:
where represents the inter-layer influence weight between the h-th layer and the k-th layer networks in MHAN; G is a gravitational constant, in this paper, ; and represent the intra-layer importance of node in the k-th layer network and node in the h-th layer network, respectively; is the shortest path length between nodes and . The larger , the stronger the mutual influence between the h-th and the k-th layer networks.
5.3. Calculation of Node Importance through Aggregating Multi-Source Information
In MHAN, node importance should consider not only its importance within the layer network but also the contribution of inter-layer interaction patterns to the node importance. Thus, based on the intra-layer node importance obtained from Section 5.1 and the inter-layer influence weight from Section 5.2, according to the information transmission characteristics of the network, the weighted node importance is propagated along inter-layer connections and aggregated with the intra-layer importance of the goal nodes. This process allows for the determination of the importance of each node in MHAN, thereby identifying key nodes.
Section 4.1 mentions the existence of the unidirectional dependency relationship among the AN, the EN, and the SN in MHAN. For that reason, in the process of aggregating node importance, the importance of airport nodes only needs to be determined based on their intra-layer importance without aggregating information from other layer heterogeneous neighbor nodes. En-route nodes not only need to consider their intra-layer importance but also need to aggregate information from neighboring airport nodes. Sector nodes, on the basis of their intra-layer importance, also need to aggregate multi-source information from neighboring airport nodes and en-route nodes. The equation for calculating the node importance through the aggregation of multi-source information (ANI) is shown in Equation (24), and Figure 3 illustrates the process of aggregating node importance in MHAN.
where is the node importance of through aggregating multi-source information; , , and represent the inter-layer influence weights between EN and AN, SN and AN, SN and EN, respectively; is the set of cross-layer neighbor nodes of node .
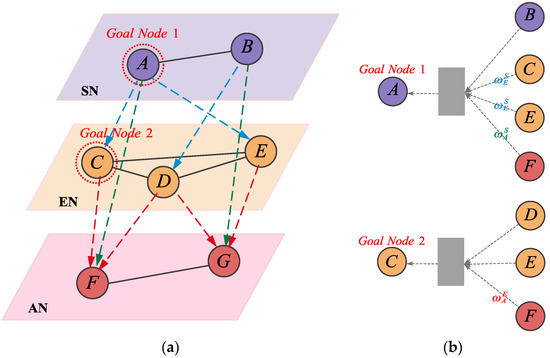
Figure 3.
The process of aggregating node importance in MHAN. (a) The schematic diagram of MHAN. (b) The process of aggregating node importance.
Algorithm 2 provides the algorithmic description of ANI. The higher the ANI, the more critical the corresponding node is in MHAN.
| Algorithm 2. Calculation of ANI |
| ; |
| the adjacency matrix of MHAN |
| 1. do |
| 2. do |
| 3. using Algorithm 1; 4. end for |
| 5. end for |
| 6. do |
| 7. using Equation (23); |
| 8. end for |
| 9. do |
| 10. do |
| 11. using Equation (24); |
| 12. end for |
| 13. end for |
| 14. |
6. The Cascading Failure Model of Multi-Layer Heterogeneous Aviation Network
In order to explore the propagation process of cascading failure in MHAN and verify the accuracy of the identification results of key nodes based on ANI, a cascading failure model of MHAN is established. Firstly, the propagation process of cascading failure in MHAN is analyzed. Then, in combination with the actual situation of the aviation network’s super-capacity operation, considering the redundant capacity characteristic of MHAN nodes, we introduce the overload condition and failure probability to describe this characteristic, and different load redistribution strategies are adopted for failed nodes and overloaded nodes. Thus, a cascading failure model considering the overload condition and failure probability of MHAN is proposed. Finally, the node influence index is put forward to confirm the accuracy of the key node identification results based on ANI.
6.1. The Propagation Process of Cascading Failure in Multi-Layer Heterogeneous Aviation Network
Considering that various types of nodes in MHAN all have overload disposal capacity, when the load of a node exceeds its capacity, the node will not immediately fail but instead enters an overload condition, and the efficiency of traffic load disposal of the node decreases. As the traffic load of the node continues to increase, its failure probability gradually increases until it eventually fails. Based on this, regarding the failure of nodes in MHAN, the cascading propagation process in both the current layer network and other layer networks is analyzed.
- Airport Node Failure
Stage 1: When an airport node fails, the edges departing from and arriving at that airport immediately fail as well. The load of the failed airport node is then redistributed to its neighboring airport nodes.
Stage 2: Some airport nodes fail as their load exceeds the permissible range of their maximum capacity, allocating the load to their neighboring nodes. Meanwhile, partial airport nodes operate in an overload condition without exceeding the permissible range of their maximum capacity, redistributing the excess load to the remaining nodes through scheduling, thus avoiding failure.
Stage 3: The en-route nodes and sector nodes connected to the failed airport nodes continue operating normally.
- En-route Node Failure
Stage 1: When an en-route node fails, the en-route edges connected to it become invalid, and the load of the failed en-route node is redistributed to its neighboring en-route nodes.
Stage 2: Some en-route nodes fail due to their load exceeding the permissible range of their maximum capacity, and the load is allocated to their neighboring en-route nodes. The load of some en-route nodes does not exceed the permissible range of their maximum capacity and is in an overload condition, the excess load is distributed to the remaining en-route nodes, and these nodes do not fail.
Stage 3: If the failed en-route node is the only connecting en-route node for a particular airport node, then the airport node fails, and the load distribution is performed according to the airport node failure previously proposed. However, if there are other en-route nodes connected to the airport node apart from the failed en-route node, then the airport node continues to operate normally.
Stage 4: The sector nodes connected to the failed en-route nodes remain in normal operation.
- Sector Node Failure
Stage 1: The failure of a sector node will cause its connection edge to fail, and the load of the sector node is redistributed to its neighboring sector nodes.
Stage 2: Some sector nodes fail because their load exceeds the permissible range of their maximum capacity, and their load is redistributed to neighboring sector nodes. Partial sector nodes may not exceed the permissible range of their maximum capacity but are in an overload condition. In such cases, the excess load is distributed to other remaining sector nodes, preventing node failures.
Stage 3: Since en-route points are commanded by the sector they belong to, all en-route nodes connected to the failed sector node also fail, and the load distribution of the failed en-route nodes follows the previously mentioned process for en-route node failure.
Stage 4: If the failed sector node is the only connected sector to a certain airport node, then the airport node fails, and the procedure for airport node failure mentioned earlier is followed.
Combining the above, the cascading failure process of MHAN can be divided into the following four phases:
- Initial normal operation phase. Initialize the load and capacity of each node in MHAN, where the load of each node does not exceed its capacity and air traffic operates normally.
- Node failure phase under attack. When a node within MHAN is subjected to a random or deliberate attack, it immediately fails, triggering the redistribution of its load to neighboring nodes within the same layer. This redistribution follows a predefined load redistribution strategy.
- Cascade failure propagation phase. Firstly, assess whether the neighbor nodes of other layers connected to the failure nodes are restricted by them. If restricted, these neighboring nodes fail, and the load is allocated to the neighbor nodes of the same layer according to the redistribution strategy. Secondly, after the load of the failed nodes is allocated to the neighbor nodes, some of them have loads exceeding the maximum capacity permissible range and fail, and the load is redistributed to their neighbor nodes in the same layer. Additionally, nodes that do not exceed their maximum capacity permissible range but operate in an overload condition will redistribute excess load to the remaining neighbor nodes of the same layer. The above two steps are cycled sequentially to store the propagation process of cascade failure.
- Termination phase of failure. The cascading failure process concludes when no new nodes fail in MHAN and all nodes stabilize.
6.2. The Cascading Failure Model of Multi-Layer Heterogeneous Aviation Network
6.2.1. Initial Load
The load characteristics play a crucial role in influencing the cascading failure of complex networks. In this paper, we extend the concept of node load as defined in [10] by considering the influence of neighboring nodes. Specifically, we define the initial load of a node as the product of its degree and the degrees of its neighboring nodes. Taking into account that the load redistribution occurs only within the same-layer network of MHAN following node failure, we define the initial load of node as follows:
where is the initial load of node ; represents the degree of in the k-th layer network; is the initial load adjustment coefficient, controlling the intensity of initial load. A higher value of indicates a larger disparity in the initial load between nodes.
6.2.2. Critical Capacity
The critical capacity refers to the maximum load that a node can sustain. Greater critical capacity implies a reduced risk of failure due to overload, enhancing the networks’ resilience against cascading failures. Nevertheless, practical limitations prevent critical capacity from increasing infinitely. In this paper, the critical capacity is defined to be proportional to the initial load. Therefore, the critical capacity of each node is defined as:
where is the critical capacity of node ; represents the capacity limit, which controls the capacity threshold for the node. A larger value signifies a higher critical capacity, enhancing its resilience against cascading failure.
6.2.3. Overload Coefficient and Failure Probability
All the nodes within MHAN possess redundant capacity. When nodes are in overloaded operation, they do not immediately turn to the failure condition, i.e., the nodes have a certain scheduling ability for the overload. Hence, this paper introduces the concept of failure probability to elucidate the failure rules of overloaded nodes, enhancing the model’s alignment with the cascading failure process of MHAN.
For node , a critical capacity is established. When the load of reaches or surpasses the permissible limit value , node becomes overloaded and fails. Here, represents the limit capacity coefficient, indicating the maximum extent by which the overloaded node is permitted to exceed its critical capacity. If the load of is more than but less than , the node enters an overload condition and fails with a certain probability. When the load of the node is less than , it remains in a normal state and does not fail. Therefore, the failure probability of the node is given by:
where represents the failure probability of node and represents the actual load of node at time step s, ; is the redundant capacity of .
In the actual operation of MHAN, there are differences in the workload of each node. The busier the node, the higher its failure probability, so it needs to be equipped with more redundant capacity. Conversely, less busy nodes are unlikely to experience overload, so they do not need to add excessive redundant capacity. Therefore, this paper sets the redundant capacity to be proportional to the initial load of the node. The formula for calculating is:
where is the overload coefficient; and characterizes the relative size of the initial load of node in the k-th layer network. At this point, the redundant capacity of node is not only related to its initial load but also to the overload coefficient . Adjusting can adapt the ability of MHAN to cope with cascading failure according to actual conditions.
6.2.4. Load Redistribution Strategy
When nodes in MHAN fail, distributing these nodes’ load to their neighboring nodes becomes essential. This paper categorizes load redistribution into two main types: one involves the load redistribution of the failed nodes, while the other addresses the redistribution of excess load from nodes in an overload condition. Load redistribution from failed nodes primarily relies on the proportion of load among its neighboring nodes. When node fails, the additional load allocated to its neighboring node is determined by:
where and are the actual loads of nodes and at time step s, respectively; S represents the total number of time steps from the initial state to the end of the cascading failure.
For the redistribution of excess load from nodes in an overload condition, a distribution strategy based on the real-time residual capacity of neighboring nodes is employed. The allocation ratio from the overloaded node to its neighboring node is given by:
where is the same-layer neighboring node of . Then, the excess load allocated from node to node is given by:
6.3. Node Influence Index
To comprehensively evaluate the overall impact of node failure on MHAN, this study adopts a dual perspective. It considers the average load change in neighboring nodes of the failed nodes from a local standpoint, while also incorporating the influence range of node failures on the entire network from a global viewpoint, thereby establishing the node influence index. A higher node influence index signifies a greater impact of node failure on the overall network, indicating the node’s increased importance.
6.3.1. The Network Failure Scale
The network failure scale in the overall network serves as a metric for understanding the extent of cascading failure propagation. The failure of node in MHAN can lead to cascading failure propagation throughout the network. Once cascading failures subside, the total count of failed nodes and edges provides insight into the breadth of the impact, revealing the scope of influence on the whole network. A higher count indicates a more substantial impact stemming from the failure of node , underscoring its importance within the network. Therefore, we define the network failure scale of node from a global perspective, which is calculated by Equation (32):
where and represent the total number of failed nodes and edges in MHAN after the network-wide cascade failure caused by the failure of node , respectively; N and M represent the total number of nodes and edges, respectively. Consequently, the higher the value of , the more important the node .
6.3.2. The Average Load Change in Neighboring Nodes
Based on the load redistribution strategy outlined in Section 6.2.4, it becomes apparent that by following the failure of node , its load gets distributed to its same-layer neighboring nodes. In the event that node carries a substantial load, the redistributed load received by its neighboring nodes will also be significant, leading to a reduction in the redundant capacity of these neighboring nodes. As a result, they become more susceptible to failure, diminishing the overall network’s resilience to disturbances. Hence, by computing the average load change in same-layer neighboring nodes, we can gauge the influence of node failure on its immediate surroundings. The index of node is defined from a local perspective to characterize the average load change in neighboring nodes, and the calculation equation is as follows:
where represents the number of same-layer neighboring nodes of node ; represents the load of node after the cascade failure concludes. As becomes smaller, it indicates that the loads of neighboring nodes are closer to their capacities, making these nodes more prone to failure. Therefore, the smaller the , the greater the impact on the network, indicating the higher importance of the node .
6.3.3. Node Influence Index
It can be observed that the cascading failure propagation caused by the failure of node in MHAN will simultaneously lead to changes in and . represents the influence range of node ’s failure on the entire network, while depicts the degree of influence of node ’s failure on neighboring nodes. Based on this, the influence index of node is defined as follows:
7. Empirical Results: Case Study of the Aviation Network in Western China
7.1. Multi-Layer Heterogeneous Aviation Network in Western China
This study focuses on the aviation network in western China. Based on the 2019 National Aeronautical Information Publication (NAIP) of China, the AN, EN, and SN of western China are constructed, respectively, as illustrated in Figure 4. The statistical characteristics of each layer network are shown in Table 3. Here, and represents the total number of nodes and edges in the k-th layer network, respectively, denotes the average degree, represents the average shortest path length, stands for the clustering coefficient, denotes the transmission rate threshold in the SIR model, and represents the actual transmission rate value. From Table 3, it is evident that the AN and the SN share similar structures: both networks exhibit a relatively high average degree, with values of 4.3256 and 4, respectively, suggesting robust connectivity within the networks. Moreover, the is also relatively high, with values of 0.5063 and 0.5833, respectively, indicating a notable degree of clustering in these networks. Additionally, the small average shortest path lengths, with values of 2.2625 and 2.7095, respectively, reflect the small-world characteristics inherent in these networks. Although the EN has a significant number of nodes and edges, it demonstrates a lower average degree of 2.4679, a clustering coefficient of 0.0293, and a higher average shortest path length of 13.1761. These characteristics indicate a comparatively lower level of network connectivity. However, this also implies a structured distribution of en-route points along designated en-routes established by air traffic control units. This structure suggests a regulated system where flights are constrained to navigate between specific en-route points rather than having free navigation between any two en-route points.
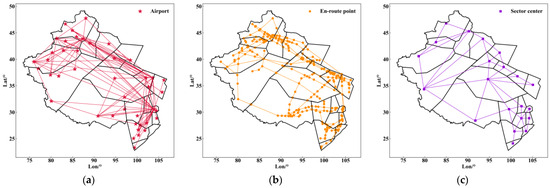
Figure 4.
Layer network diagram of the aviation network in western China. (a) AN. (b) EN. (c) SN.

Table 3.
Statistical characteristics of each layer network.
Based on air traffic management rules, inter-layer edges are established, and their statistics are presented in Table 4, where A-E, A-S, and E-S represent the inter-layer edges between the AN and EN, between the AN and SN, and between the EN and SN, respectively. Analyzing Table 4 reveals that the AN exhibits the highest count of inter-layer edges with the EN, while it has the fewest inter-layer edges with the SN.

Table 4.
Statistics of inter-layer edges.
The layer networks and inter-layer edges are integrated to form the MHAN in Western China. Subsequently, the data are imported into Gephi 0.10 software for topological visualization processing, yielding the result depicted in Figure 5. This figure is color-coded according to node types, where the nodes and edges of AN, EN, and SN are highlighted in red, orange, and purple, respectively. Additionally, the inter-layer edges of A-E, A-S, and E-S are represented in grey, black, and green, respectively. This visualization succinctly captures the multi-layered structure of the aviation network and effectively illustrates the heterogeneity of nodes and edges.
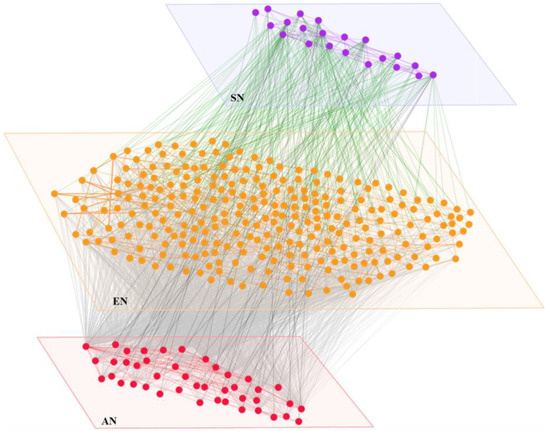
Figure 5.
The topological structure of MHAN in western China.
7.2. Evaluation of Intra-Layer Node Importance
7.2.1. Calculation of Evaluation Index Weight
The quantification of intra-layer node importance evaluation indices in each layer network of MHAN in western China is carried out by combining the node importance evaluation indices constructed in Section 5.1.1 with the ADS-B data for November 2019 and 2019 NAIP data using Python 3.7.16 software. Subsequently, the evaluation index weights of each layer network were calculated based on the AHP-CRITIC method. The weight calculation results are presented in Table 5, while Figure 6a illustrates the distribution differences of evaluation index weights in each layer network. In the three layer networks, the index with the highest weight is IK, underscoring the significant influence of node core level on the intra-layer node importance. Conversely, in the AN and SN, the weight of the DN is the smallest, implying that changes in network connectivity have a relatively minor impact on intra-layer node importance. In contrast, in the EN, the Peak hour flow of nodes has the least impact on node importance.

Table 5.
Weight calculation results of each layer network.
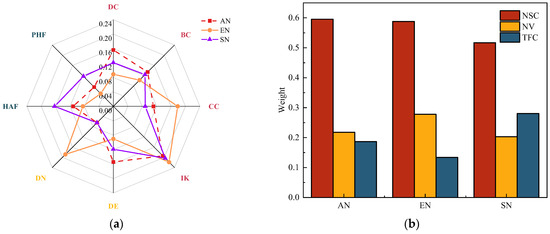
Figure 6.
The weight distribution of evaluation indices in each layer network. (a) Distribution of index weights in each layer network. (b) Distribution of weights for NSC, NV, and TFC in each layer network.
Figure 6b depicts the total weight distribution of indices for NSC, NV, and TFC in each layer network. From this figure, it can be observed that the total weight of NSC is the largest in each layer network, and all weights are greater than 0.5. This suggests that, based solely on the data, the network structural characteristics take precedence, while the other two characteristics act as supplementary factors in evaluating the intra-layer node importance. Furthermore, according to reference [58] and the actual network operating conditions, it can be inferred that the primary factor influencing node characteristics resides within the network itself. Consequently, the indices related to network structural characteristics hold greater significance. This observation aligns with the findings of this study, underscoring the efficacy of the AHP-CRITIC method employed for weight calculation.
7.2.2. Evaluation Results of Intra-Layer Node Importance
Based on the weights of evaluation indices for each layer network, Algorithm 1 is utilized to calculate the intra-layer node importance expressed by CP, as illustrated in Figure 7. In the AN, the value of CP is relatively concentrated, primarily around 0.35, with three nodes having a CP value greater than 0.5. In the EN, a significant proportion of nodes with a CP value less than 0.3, and seven have a CP value greater than 0.5. In the SN, the CP value is mostly concentrated around 0.45, with one node having a CP value greater than 0.5. It is apparent that in each layer network, the importance of most nodes is relatively low, with only a few nodes being highly important. These nodes play crucial roles in the overall network structure, network performance, and traffic flow.
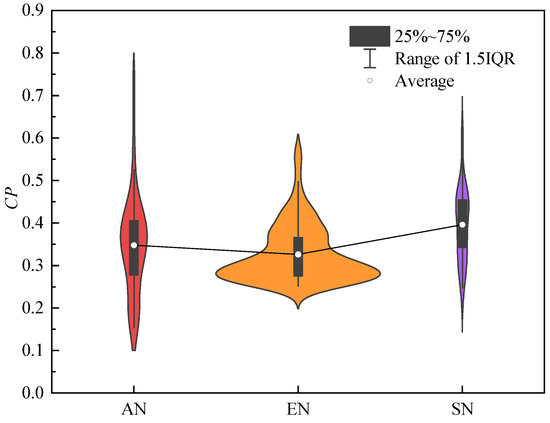
Figure 7.
The evaluation results distribution of intra-layer node importance in each layer network.
Table 6 displays the top 15 nodes ranked by their intra-layer node importance within each layer network. Nodes with a CP value greater than 0.5 are key nodes. In the AN, the most critical nodes are ZUUU (Chengdu Shuangliu International Airport), ZWWW (Urumqi Diwopu International Airport), and ZLLL (Lanzhou Zhongchuan International Airport). These airports are located in Chengdu, Urumqi, Leshan, and other regions, which hold significant locational advantages and strategic geographic positions within the domestic aviation network. They not only serve the transportation needs of local passengers but also connect to other major cities domestically and internationally, functioning as crucial hubs in the aviation transport network. SADAN, AKS, LESVI, PAMLI, KANPI, OMBON, and XKC are key nodes in the EN. These en-route nodes are typically connected to major aviation hubs or multiple domestic and international airports. They often support a high frequency of flight operations and offer diverse route selections. Additionally, they are mostly located in densely populated areas of the route network layout. Similarly, in the SN, the most critical node is ZLLLAR04, which is situated in the central area of the western airspace. It has control transfer relationships with multiple sectors and manages a significant volume of aircraft during control transfers. Under the influence of external interference, the above key nodes will lead to a decline in their operational capacity, resulting in a large number of flight delays or flight cancellations and a large number of passengers being stranded, which will also have a potential impact on aviation safety. These findings align well with operational realities. Thus, the evaluation results of the intra-layer node importance within each layer network appear reasonable and effective.

Table 6.
The ranking of intra-layer node importance in each layer network (Top 15).
7.2.3. Evaluation Results Validity Analysis of Intra-Layer Node Importance
In order to better analyze the advantages and disadvantages of the ITG method proposed in this paper, DC, BC, CC, IK, and the classical TOPSIS (CT) method were selected as comparative methods. The resolutions of the five comparative methods and the ITG method are examined using , which reflects the distinguishability of intra-layer node importance. Table 7 records the resolution of different evaluation methods in each layer network. It is evident that the ITG method performs remarkably well in all three layer networks. Compared to other methods, M(ITG) is close to 1 in all three networks. Therefore, the ITG method proposed in this paper is better at distinguishing the intra-layer node importance. Additionally, the method of IK and CT also exhibits good distinguishability.

Table 7.
Monotonicity index of different evaluation methods in each layer network.
Next, the spreading capability ranking vector in each layer network is obtained using the SIR model, and Kendall’s Tau coefficient of different evaluation methods is calculated. A higher indicates a more accurate evaluation of intra-layer node importance. Since the iteration process of the SIR model is stochastic, this paper repeats the simulation process for each node and then takes the average. The simulation will follow these rules: when , the simulation will iterate 104 times, and when , the simulation will iterate 103 times. This paper sets the recovery rate , and the transmission rate is shown in Table 3. Table 8 shows Kendall’s Tau coefficients for the layer networks at certain transmission rates. From Table 8, it can be seen that the values of the ITG method are all greater than 0.9, indicating that the correlation of the ITG method is the most significant among the three layer networks compared with other methods. Therefore, the accuracy of the ITG method has been preliminarily validated.

Table 8.
Kendall’s Tau coefficient between SIR and evaluation methods under a certain transmission rate.
In the SIR model, the transmission rate significantly influences the propagation capability of nodes. Inappropriate values of can disrupt the propagation process, impacting the accurate assessment of node propagation capability. To further validate the accuracy and reliability of the proposed method, Kendall’s Tau coefficients between the evaluation methods and the SIR model ranking results under different transmission rates are compared, as depicted in Figure 8. It is evident that when approaches the transmission threshold , the values of the ITG method surpass those of other methods in all three layer networks, indicating a significant correlation with the node propagation capability derived from the SIR model. When significantly deviates from , the IK and CT methods also demonstrate notable correlations. However, in the AN and SN, the CC method exhibits the weakest correlation performance, while in the EN, the BC method fares the poorest. Overall, the proposed ITG method in this paper more accurately evaluates the importance of nodes.
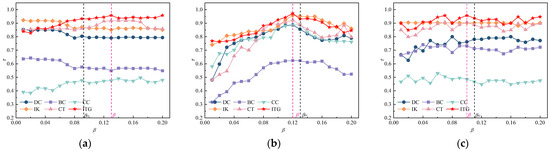
Figure 8.
Kendall’s Tau coefficient between SIR and the evaluation methods under different transmission rates. (a) AN. (b) EN. (c) SN.
7.3. Calculation of Node Importance in Multi-Layer Heterogeneous Aviation Network through Aggregating Multi-Source Information
Section 7.2 computed the intra-layer importance of each node and validated the accuracy of the results. Therefore, leveraging the research from Section 5.2, in conjunction with the model of MHAN and the intra-layer node importance, the quantification of inter-layer influence weights is completed, as illustrated in Table 9. It is evident that the inter-layer influence weights vary among different layer networks. The inter-layer influence weight between the AN and the EN is the highest, indicating a strong relationship between AN and EN. Conversely, the inter-layer influence weight between EN and the SN is the lowest, indicating a weaker relationship between EN and SN. It can be seen that the inter-layer influence weight can aptly reflect the information transmission intensity and connection strength between the layer networks, which plays an important role in determining the importance of nodes in the entire network.

Table 9.
Inter-layer influence weight quantification results.
Based on the calculation results presented in Table 9, Algorithm 2 is applied to compute the ANI of each node in MHAN. The importance of a node in MHAN corresponds directly to its ANI value, where a higher ANI value signifies greater importance. Table 10 lists the top 15 nodes ranked by ANI value in MHAN, representing key nodes within the network. Among the top 5 key nodes, including ZWWWAR02, ZWWWAR06, ALLLAR04, OMBON, and ZPXX01, four are sector nodes while one is an en-route node.

Table 10.
The ranking of node importance in MHAN (Top 15).
Due to dependencies and inter-layer influence weights, when a node has high intra-layer node importance, it may not necessarily be more critical in the overall MHAN. Notably, key nodes in MHAN are predominantly sector nodes and en-route nodes. Among them, the sector node of ZWWWAR02 has an ANI value of 1.7092, ranking first, and it is adjacent to 2 sectors and controls 10 airports and 25 en-route points, including the key airport node ZWWW in AN. ZWWWAR06 has an ANI value of 1.6843, and it is adjacent to 3 sectors and provides command and control services to 5 airports and 20 en-route points, including the key en-route nodes SADAN, AKS, LESVI, PAMLI, and KANPI in EN. ZLLLAR04 has an ANI value of 1.5550 and is adjacent to 8 sectors, and it provides command and control services to 2 airports and 22 en-route points. OMBON has an ANI value of 1.5547 and is connected to 5 en-route points and 16 airports. ZPXX01 has an ANI value of 1.5133 and is adjacent to 3 sectors, and it commands 26 en-route points and 3 airports. It can be seen that the above key nodes hold central positions in MHAN, which command and control a large number of airport nodes and en-route nodes. Once the key nodes fail, it will directly cause the failure of a large range of airport and en-route nodes in the MHAN, and the network will easily fall into paralysis.
7.4. The Cascade Failure of Multi-Layer Heterogeneous Aviation Network
Utilizing the cascading failure model outlined in Section 6, we elucidate the mechanism behind cascading failure propagation within the MHAN. Through this analysis, we validate the accuracy of identifying key nodes within the MHAN.
7.4.1. Analysis of Cascading Failure in Multi-Layer Heterogeneous Aviation Network under Different Attack Modes
To clarify the cascading effects in MHAN, this study employs two attack modes. Firstly, the random attack randomly selects nodes in MHAN for disabling, mimicking unpredictable failures in the network. Secondly, the deliberate attack prioritizes node failure based on their ANI values. The overload coefficient , initial load adjustment coefficient , and capacity limit are selected, and the variation of the network failure scale CF of MHAN under the two attacks is shown in Figure 9.
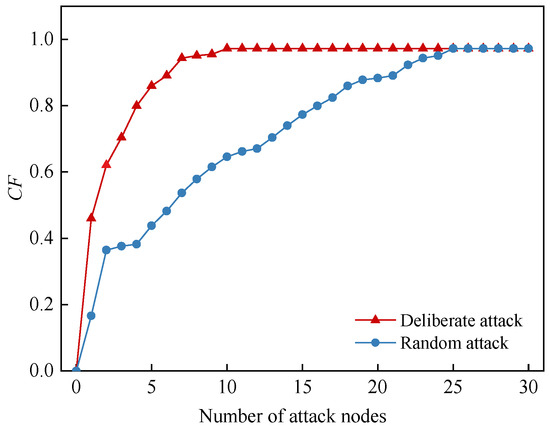
Figure 9.
The network failure scale CF of MHAN under the two attack modes.
Figure 9 illustrates the impact of increasing the number of attacked nodes on the network failure scale CF. Notably, the curve corresponding to deliberate attack consistently exceeds that of random attack. This trend arises because deliberate attacks prioritize the failure of key nodes, leading to more extensive failure and severe cascade effects, and when the number of attacked nodes reaches 10, the value of CF stabilizes, indicating complete network collapse. In contrast, random attacks involve randomly selecting nodes for failure, resulting in varying levels of cascade failures. However, as the number of attacked nodes continues to increase, the MHAN gradually tends to collapse, with complete collapse occurring when the number of attacked nodes reaches 25. Therefore, a deliberate attack on key nodes can trigger a widespread node failure and quickly crash the MHAN.
7.4.2. The Correlation between Network Failure Scale and Parameters of Cascade Failure Model
As the parameters in the cascading failure model are closely related to the overall network failure scale, adopting a deliberate attack strategy based on ANI, the correlation between the network failure scale CF and the overload coefficient , the initial load adjustment coefficient , and the capacity limit are extracted. This relationship is depicted in Figure 10.
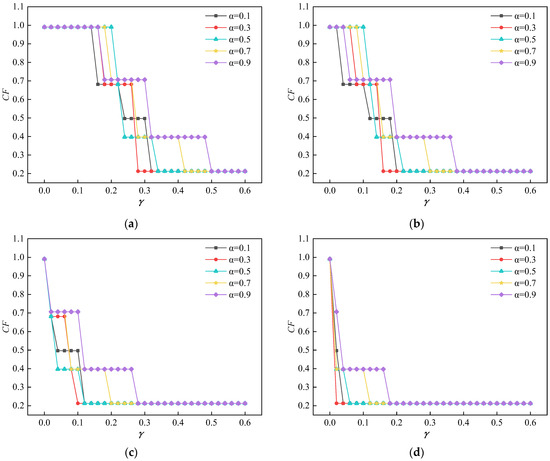
Figure 10.
The change curve of network failure scale under different parameter controls. (a) , (b) , (c) , (d) .
From the trend of the curves in Figure 10, it can be observed that as the capacity limit increases, the value of CF decreases. This trend is attributed to the role of in adjusting node capacities.
In the provided scenario involving and , as increases, the network failure scale of MHAN also rises. This is because primarily controls the intensity of the initial load on nodes. With a larger , discrepancies in initial loads among nodes become more pronounced, consequently leading to greater variations in node capacities. During deliberate attacks based on ANI, priority is assigned to disabling nodes with the highest importance. These highly important nodes often carry heavier initial loads, which are then redistributed to their neighboring nodes with smaller capacities. This additional load easily overwhelms these neighboring nodes with limited capacities, thereby amplifying the cascading failure scale.
Comparing Figure 10a–d, it is evident that as the overload coefficient increases, the curves shift to the left. When , it implies no consideration for redundant capacity and failure probability. At this point, MHAN experiences a significant failure scale. However, with the increase in , the network’s failure scale dramatically decreases, indicating that the introduction of the overload coefficient enhances the ability of MHAN to resist cascading failures. When the initial load adjustment coefficient is fixed, the required for MHAN to avoid cascading failures continues to decrease. This is because as the increases, the critical capacity of nodes in MHAN increases, leading to a reduction in the network failure scale.
7.5. Node Importance Verification Analysis Based on Node Influence Index
Utilizing the node influence index outlined in Section 6.3, with an overload coefficient , initial load adjustment coefficient , and capacity limit , each node within MHAN is sequentially chosen as the initial failed node. Subsequently, the network failure scale CF and average load change in neighboring nodes CL resulting from these failures are computed. Using Equation (34), the node influence FI is determined. Based on FI, the 329 nodes in MHAN are ranked. Table 11 presents the top 15 nodes ranked by FI, comparing them with the top 15 nodes ranked by ANI.

Table 11.
Comparison of node influence and node importance.
According to Table 11, based on the validation of the cascade failure model, the failure of nodes ZWWWAR06, ZWWWAR02, ZLLLAR04, OMBON, and ZPXX01 can indeed cause significant degradation of the network performance, which has a huge impact on MHAN. This again demonstrates the criticality of the above nodes in the MHAN. The key nodes identified based on FI are generally similar to those identified based on ANI. Among the top 15 key nodes, 8 nodes have exactly the same ranking based on both FI and ANI. Although there are differences in the rankings of ZWWWAR06 and ZWWWAR02, they both rank in the top 2 based on both FI and ANI, and their FI values are very close. Similarly, while there are differences in the rankings of ZLXYAR09, URC, DNC, BESMI, and VIKUP between the two methods, ZLXYAR09 and URC have FI values of 0.8126, and BESMI and VIKUP have FI values of 0.8118. Additionally, the differences in FI values among these 5 nodes are not significant, and they all rank in the top 10. Kendall’s Tau coefficient calculated between the ANI ranking and FI ranking of the 329 nodes in MHAN in western China is found to be 0.7254, which is close to 1. This indicates a high correlation between the FI and ANI. Therefore, by using the node influence index based on cascade failure, the effectiveness of the proposed method for identifying key nodes in MHAN through aggregating multi-source information has been validated.
It is evident that key nodes in the MHAN can also be identified based on node influence. However, this method relies heavily on accurate modeling of the network structure and failure propagation process. If the assumptions or parameter settings of the cascading failure model are inaccurate, the FI values of nodes may be erroneous, thus affecting the reliability of the assessment. Additionally, this method may be limited to specific types of networks or failure propagation assumptions, restricting their generalizability.
The method for identifying key nodes in MHAN through aggregating multi-source information is comprehensive and integrative. By aggregating multi-source information, it enhances the robustness of the evaluation results. Even if a particular data source is abnormal or noisy, information from other sources can provide supplementation or correction, thereby reducing the risk of misjudgment caused by a single data source. Furthermore, this method is suitable for various types of networks and application scenarios, demonstrating good versatility.
8. Conclusions
This study advances the understanding of the MHAN by constructing a comprehensive network model that incorporates diverse node and edge types, facilitating an investigation into the intricate relationships between network nodes and the overarching network topology. Leveraging insights into intra-layer node importance and inter-layer influence weight, the study proposes a method for identifying key nodes in MHAN by aggregating multi-source information. Additionally, it introduces a cascading failure model explicitly tailored for MHAN, which considers the overload condition and failure probability. Furthermore, the study defines a node influence index that considers both the global network failure scale and local load margin change, verifying the effectiveness of the key node identification method.
Systematic analyses are conducted based on the proposed method for identifying key nodes and the cascading failure model using a case study of the aviation network in western China, and the primary conclusions drawn from the research are outlined below:
- For each layer network of MHAN, network structural characteristics emerge as the most crucial indices. Moreover, the intra-layer node importance evaluation method based on the improved TOPSIS-grey Relational Analysis demonstrates superior capability in distinguishing the intra-layer node importance, yielding more accurate assessment outcomes.
- When the intra-layer importance of a node is large, it may not necessarily be a key node in the overall MHAN; the more critical nodes in MHAN are sector nodes and pivotal en-route nodes situated at hubs.
- As the cascading failure model is influenced by the overload coefficient , initial load adjustment coefficient , and capacity limit , variations in these parameters directly impact the failure scale of MHAN. As increases, there is a notable decrease in the network’s failure scale; when and are fixed, a higher results in a larger cascading failure scale. With increasing within a certain range, the failure scale of MHAN significantly decreases. Thus, judiciously setting these parameters can effectively govern the extent of cascading failures in MHAN.
- Based on the node influence index, it is verified that the key node identification method of MHAN by aggregating multi-source information proposed in this paper is accurate and effective.
- Compared with the key node identification method by aggregating multi-source information, the key node identification method based on node influence relies heavily on accurate modeling of the network structure and failure propagation process and is limited to specific types of networks or specific failure propagation assumptions, which restricts its generalization ability. The key node identification method through aggregating multi-source information is comprehensive and robust, and it is suitable for various types of networks and application scenarios.
The key node identification method of MHAN through aggregating multi-source information proposed in this paper represents a preliminary exploration into identifying key nodes in such networks. This method focuses on intra-layer undirected inter-layer directed networks without considering network weights. Future research should extend this approach to encompass multi-layer heterogeneous directed networks and multi-layer heterogeneous weighted directed networks. At the same time, this method has high computational complexity, making it difficult to respond promptly to highly dynamic networks. Future research should extend this method to dynamic network scenarios. Building on identifying node importance in static multi-layer heterogeneous networks, it should aim to determine important nodes at new time points as the network evolves dynamically. The paper solely examined the interplay among various parameters and the network failure scale. In future research work, there is a need to optimize the cascading failure model to bolster the invulnerability of aviation networks. Validating the effectiveness of the key node identification method for multi-layer heterogeneous networks by aggregating multi-source information using real failure scenarios in interdependent multi-layer networks is also a direction for future research. It will help ensure the proposed method is robust and applicable to real-world situations. Since the paper has already pinpointed the key nodes in the aviation network, it underscores the importance of proactively implementing control measures to avert potential failures triggered by emergencies. By taking preemptive action to safeguard these key nodes, the risk of aviation network collapse can be mitigated effectively.
Author Contributions
Conceptualization, Q.G.; Methodology, Q.G. and L.Y.; Software, Q.G. and Z.Z.; Validation, Q.G.; Formal analysis, Q.G.; Investigation, Q.G. and Z.Z.; Resources, Q.G.; Data curation, Q.G.; Writing—original draft, M.H. and L.Y.; Writing—review & editing, M.H. and L.Y.; Visualization, Q.G.; Supervision, M.H. and L.Y.; Project administration, M.H., L.Y. and Z.Z.; Funding acquisition, L.Y. and Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 61903187), the Natural Science Foundation of Jiangsu Province (BK20231447), the National Key R&D Program of China (No. 2022YFB4300905) and the China-Europe Aviation Science and Technology Cooperation Project of Ministry of Industry and Information Technology (MJ-2020-S-03).
Data Availability Statement
The data used in this paper involves China’s airspace structure and is confidential and sensitive. So the data presented in this paper are available on request from the corresponding authors.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Abbreviation | Full Name |
| MHAN | Multi-layer Heterogeneous Aviation Network |
| SLN | Single-layer Network |
| MMN | Multi-dimensional Multi-layer Network |
| IMN | Interdependent Multi-layer Network |
| INI | Intra-layer Node Importance |
| LI | Layer Importance |
| NI | Node Importance |
| CA | Classical Algorithms or Optimizing Classical Algorithms |
| CEM | Comprehensive Evaluation Method |
| RF | Results Fusion |
| AMS | Aggregation of Multi-source Information |
| NN | Number of Neighboring Nodes |
| LPN | Load Proportion of Neighboring Nodes |
| RRCN | Real-time Residual Capacity of Neighboring Nodes |
| ITG | Improved TOPSIS-grey Relational Analysis |
| AN | Airport Network |
| EN | En-route Network |
| SN | Sector Network |
| NSC | Network Structural Characteristics |
| NV | Network Vulnerability |
| TFC | Traffic Flow Characteristics |
| ANI | Node Importance through Aggregating Multi-source Information |
| DC | Degree Centrality |
| BC | Betweenness Centrality |
| CC | Clustering Coefficient |
| IK | Improved K-shell |
| DE | Network Efficiency Decrease Rate |
| NE | Network Efficiency |
| DN | Network Connectivity Coefficient Decrease Rate |
| NCC | Network Connectivity Coefficient |
| HAF | Hourly Average Flow |
| PHF | Peak Hour Flow |
| S | Susceptible |
| I | Infected |
| R | Removed |
| CT | Classical TOPSIS |
| Parameter | Implication |
| Set of nodes and edges in MHAN | |
| Set of all nodes in MHAN | |
| Set of all edges in MHAN | |
| Nodes of type m, | |
| Number of node types | |
| N | Total number of nodes in MHAN |
| Edges of type l, | |
| Number of edge types | |
| The k-th intra-layer network | |
| / | Number of nodes in or |
| Adjacency matrix of , | |
| A | Set of intra-layer adjacency matrices |
| The directed inter-layer network of layer k and layer h | |
| Set of directed edges of | |
| Adjacency matrix of , | |
| B | Set of inter-layer adjacency matrices |
| The matrix of MHAN | |
| DC of node | |
| Edge between and | |
| the BC of node | |
| Number of shortest paths between any two nodes and | |
| Number of shortest paths passing through node between any two nodes and | |
| CC of node | |
| Total number of neighboring nodes of | |
| Actual number of edges existing among the neighboring nodes of | |
| Node information entropy of | |
| Node importance of based on DC | |
| Set of same-layer neighboring nodes of | |
| Length of the shortest path between and | |
| Network efficiency decrease rate corresponding to node | |
| New NE after removing node and its edges | |
| Number of connected components of | |
| Number of nodes in the i-th connected component | |
| Average shortest path of the i-th connected component | |
| Number of shortest paths in the i-th connected component | |
| Length of the shortest path between and in the i-th connected component | |
| Network connectivity coefficient decrease rate corresponding to node | |
| New NCC after removing node and its edges | |
| Hourly average flow of | |
| Number of statistical slots | |
| Number of flights during slot t | |
| Peak hour flow of | |
| Evaluation index vector of , | |
| Intra-layer importance of | |
| Initial decision matrix of , | |
| Standardized initial decision matrix of | |
| Weight vector of , | |
| Weighted decision matrix of , | |
| Positive ideal solution of | |
| Negative ideal solution of | |
| , | Weighted Mahalanobis distance of |
| Covariance matrix of | |
| Diagonal matrix of , | |
| , | Grey correlation coefficients of |
| Resolution-function ratio | |
| , | Grey correlation degree of |
| , | Proximity of |
| , | Preference coefficients of position and shape, respectively |
| Inter-layer influence weight between the h-th layer and the k-th layer networks in MHAN | |
| G | Gravitational constant |
| Set of cross-layer neighbor nodes of node | |
| , , | Inter-layer influence weights between EN and AN, SN and AN, SN and EN, respectively |
| Initial load of node | |
| Degree of | |
| Initial load adjustment coefficient | |
| Critical capacity of node | |
| Capacity limit | |
| Limit capacity coefficient | |
| Failure probability of the node | |
| Actual load of node at time step s | |
| Overload coefficient | |
| Additional load allocated from the failed node to its neighboring node | |
| S | Total number of time steps from the initial state to the end of the cascading failure |
| Allocation ratio from the overloaded node to its neighboring node | |
| Excess load allocated from the overloaded node to node | |
| Network failure scale of node | |
| Number of failed nodes in MHAN | |
| Number of failed edges in MHAN | |
| M | Number of edges in MHAN |
| Average load change in neighboring nodes of node | |
| Number of same-layer neighboring nodes of node | |
| Load of node after the cascade failure concludes | |
| Node influence index of | |
| Average degree | |
| Average shortest path length | |
| Clustering coefficient | |
| Transmission rate threshold in the SIR model | |
| Transmission rate | |
| Monotonicity index | |
| Intra-layer node importance ranking vector of the k-th layer network | |
| Number of nodes with the same intra-layer importance | |
| Recovery rate | |
| Spreading capability ranking vector of the k-th layer network | |
| Second-order neighbor average degree | |
| Kendall’s Tau coefficient | |
| Combination sequence based on and , | |
| Number of concordant pairs in | |
| Number of discordant pairs in |
References
- Wang, X.; Pan, W.; Zhao, M. Analysis of both robustness and congestion of aeronautical interdependent network. China Saf. Sci. J. 2018, 28, 110–115. [Google Scholar]
- Xu, Z.; Zeng, W.; Chu, X.; Cao, P. Multi-aircraft trajectory collaborative prediction based on social long short-term memory network. Aerospace 2021, 8, 115. [Google Scholar] [CrossRef]
- Wan, L.; Zhang, M.; Li, X.; Sun, L.; Wang, X.; Liu, K. Identification of important nodes in multilayer heterogeneous networks incorporating multirelational information. IEEE Trans. Comput. Soc. Syst. 2022, 9, 1715–1724. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, J.; Huang, G. Efficiency and robustness of weighted air transport networks. Transp. Res. Part E Logist. Transp. Rev. 2019, 122, 14–26. [Google Scholar] [CrossRef]
- Wang, H.; Ma, L.; Xu, P. Research on identification method of key aircraft based on temporal network. J. Beijing Univ. Aeronaut. Astronaut. 2023, 5, 1–17. [Google Scholar]
- Li, J.; Wen, X.; Wu, M.; Liu, F.; Li, S. Identification of key nodes and vital edges in aviation network based on minimum connected dominating set. Phys. A Stat. Mech. Its Appl. 2020, 541, 123340. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, J.; Wang, J.; Zhu, P. An optimization method for critical node identification in aviation network. Front. Phys. 2022, 10, 944136. [Google Scholar] [CrossRef]
- Tian, W.; Fang, Q.; Zhou, X.; Song, J. Research on identification method of key nodes in en-route network. J. Southwest Jiaotong Univ. 2022, 7, 1–10. [Google Scholar]
- Zhang, Z.; Qu, C. Node importance analysis of airport network considering gravitational correlation. J. Saf. Environ. 2022, 22, 3269–3279. [Google Scholar]
- Motter, A.E.; Lai, Y.C. Cascade-based attacks on complex networks. Phys. Rev. E 2002, 66, 065102. [Google Scholar] [CrossRef]
- Fan, C.; Wang, B.; Tian, J. Cascading failure model in aviation network considering overload condition and failure probability. J. Comput. Appl. 2022, 42, 502–509. [Google Scholar]
- Tian, W.; Zhou, X.; Fang, Q.; Song, J. Vulnerability analysis of en-route network based on cascading failure. J. Southwest Jiaotong Univ. 2023, 11, 1–17. [Google Scholar]
- Kong, J.; Lu, J.; Liang, H. Air traffic control sector network resilience evaluation based on cascading failures model. J. Saf. Environ. 2023, 23, 3978–3984. [Google Scholar]
- Zhang, C.; Zhang, F.; Wang, Y.; Wu, H. Method to analyse the robustness of aviation communication network based on complex networks. Syst. Eng. Electron. 2015, 37, 180–184. [Google Scholar]
- Chen, S. Research on Resilience of Air Transportation Interdependent Network. Master Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2019. [Google Scholar]
- Wang, X.; Pan, W.; Zhao, M. Vulnerability of air traffic interdependent network. Acta Aeronaut. Astronaut. Sin. 2018, 39, 275–284. [Google Scholar]
- Wang, X.; Wei, Y.; He, M. Air traffic CPS structural characteristics and resilience evaluation. J. Beijing Univ. Aeronaut. Astronaut. 2022, 50, 1–16. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Bonacich, P. Factoring and weighting approaches to status scores and clique identification. J. Math. Sociol. 1972, 2, 113–120. [Google Scholar] [CrossRef]
- Kitsak, M.; Gallos, L.K.; Havlin, S.; Liljeros, F.; Muchnik, L.; Stanley, H.E.; Makse, H.A. Identification of influential spreaders in complex networks. Nat. Phys. 2010, 6, 888–893. [Google Scholar] [CrossRef]
- Tang, X.; Wang, J.; Zhong, J.; Pan, Y. Predicting essential proteins based on weighted degree centrality. IEEE/ACM Trans. Comput. Biol. Bioinform. 2013, 11, 407–418. [Google Scholar] [CrossRef] [PubMed]
- Prountzos, D.; Pingali, K. Betweenness centrality: Algorithms and implementations. In Proceedings of the 18th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, Shenzhen, China, 23–27 February 2013; pp. 35–46. [Google Scholar]
- Li, P.; Ren, Y.; Xi, Y. An importance measure of actors (set) within a network. Syst. Eng. 2004, 4, 13–20. [Google Scholar]
- Cheng, G.; Lu, Y.; Zhang, M.; Huang, J. Node importance evaluation and network vulnerability analysis on complex network. J. Natl. Univ. Def. Technol. 2017, 39, 120–127. [Google Scholar]
- Bian, T.; Hu, J.; Deng, Y. Identifying influential nodes in complex networks based on AHP. Phys. A Stat. Mech. Its Appl. 2017, 479, 422–436. [Google Scholar] [CrossRef]
- Yang, S.; Jiang, Y.; Tong, T.; Yan, Y.; Gan, G. A method of evaluating importance of nodes in complex network based on Tsallis entropy. Acta Phys. Sin. 2021, 70, 273–284. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, T.; Narayanam, R. Cross-layer betweenness centrality in multiplex networks with applications. In Proceedings of the 2016 IEEE 32nd International Conference on Data Engineering (ICDE), Helsinki, Finland, 16–20 May 2016; pp. 397–408. [Google Scholar]
- Maulana, A.; Emmerich, M.T. Towards many-objective optimization of eigenvector centrality in multiplex networks. In Proceedings of the 2017 4th International Conference on Control, Decision and Information Technologies (CoDIT), Barcelona, Spain, 5–7 April 2017; pp. 0729–0734. [Google Scholar]
- Rahmede, C.; Iacovacci, J.; Arenas, A.; Bianconi, G. Centralities of nodes and influences of layers in large multiplex networks. J. Complex Netw. 2018, 6, 733–752. [Google Scholar] [CrossRef]
- Ding, C.; Li, K. Centrality ranking in multiplex networks using topologically biased random walks. Neurocomputing 2018, 312, 263–275. [Google Scholar] [CrossRef]
- Luo, H.; Yan, G.; Zhang, M.; Bao, J.; Li, J.; Liu, T.; Yang, B.; Wei, J. Research on node importance fused multi-information for multi-relational social networks. J. Comput. Res. Dev. 2020, 57, 954–970. [Google Scholar]
- Feng, F.; Cai, M.; Jia, J. Key node identification of China railway express transportation network based on multi-layer complex network. J. Transp. Syst. Eng. Inf. Technol. 2022, 22, 191–200. [Google Scholar]
- Zhou, X.; Bouyer, A.; Maleki, M.; Mohammadi, M.; Arasteh, B. Identifying top influential spreaders based on the influence weight of layers in multiplex networks. Chaos Solitons Fractals 2023, 173, 113769. [Google Scholar] [CrossRef]
- Lv, L.; Hu, P.; Zheng, Z.; Bardou, D.; Zhang, T.; Wu, H.; Niu, S.; Yu, G. A community-based centrality measure for identifying key nodes in multilayer networks. IEEE Trans. Comput. Soc. Syst. 2023, 2, 2448–2463. [Google Scholar] [CrossRef]
- Wang, D.; Wang, H.; Zou, X. Identifying key nodes in multilayer networks based on tensor decomposition. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Novoa-del-Toro, E.M.; Mezura-Montes, E.; Vignes, M.; Térézol, M.; Magdinier, F.; Tichit, L.; Baudot, A. A multi-objective genetic algorithm to find active modules in multiplex biological networks. PLoS Comput. Biol. 2021, 17, e1009263. [Google Scholar] [CrossRef]
- Wu, Y.; Ding, Y.; Wang, J.; Wang, X. Determination of the key ccRCC-related molecules from monolayer network to three-layer network. Cancer Genet. 2021, 256, 40–47. [Google Scholar] [CrossRef]
- Fan, L. Research and Application of Key Node Identification and Reliability of Multi-layer Complex Network. Master Thesis, Xidian University, Xi’an, China, 2022. [Google Scholar]
- Wang, X.; Xu, J. Cascading failures in coupled map lattices. Phys. Rev. E 2004, 70, 056113. [Google Scholar] [CrossRef]
- Dorogovtsev, S.N.; Mendes, J.F.F.; Samukhin, A.N. Giant strongly connected component of directed networks. Phys. Rev. E 2001, 64, 025101. [Google Scholar] [CrossRef]
- Li, C.; Li, W.; Cao, C.; Wang, Y. Robustness analysis of interdependent networks for cascading failure. J. Syst. Simul. 2019, 31, 538–548. [Google Scholar]
- Li, S.; Yang, H.; Song, B. Study on co-evolution of underload failure and overload cascading failure in multi-layer supply chain network. Comput. Sci. 2021, 48, 351–358. [Google Scholar]
- Li, Y.; Wang, B.; Wang, H.; Ma, F.; Zhang, J.; Ma, H.; Zhang, Y.; Mohamed, M.A. Importance assessment of communication equipment in cyber-physical coupled distribution networks based on dynamic node failure mechanism. Front. Energy Res. 2022, 10, 911985. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, Z.; Chen, H.; Sun, J.; Guan, W.; RIVERA-DURóN, R.R. Node resistance characteristic of heterogeneous multi-layer transportation networks under cascading failure based on coupled map lattice. China J. Highw. Transp. 2022, 35, 263–274. [Google Scholar]
- Zhang, J.; Huang, J.; Zhang, Z. Analysis of the effect of node attack method on cascading failures in multi-layer directed networks. Chaos Solitons Fractals 2023, 168, 113156. [Google Scholar] [CrossRef]
- Jia, C.; Li, M.; Liu, R. Percolation and cascading dynamics on multilayer complex networks. J. Univ. Electron. Sci. Technol. China 2022, 51, 148–160. [Google Scholar]
- CCAR-93-R5; Civil Aviation Air Traffic Management Rules. Ministry of Transport of the People’s Republic of China: Beijing, China, 2017.
- Kenett, D.Y.; Perc, M.; Boccaletti, S. Networks of networks–an introduction. Chaos Solitons Fractals 2015, 80, 1–6. [Google Scholar] [CrossRef]
- Wang, M.; Li, W.; Guo, Y.; Peng, X.; Li, Y. Identifying influential spreaders in complex networks based on improved k-shell method. Phys. A Stat. Mech. Its Appl. 2020, 554, 124229. [Google Scholar] [CrossRef]
- Wu, J.; Tan, Y. Study on measure of complex network invulnerability. J. Syst. Eng. 2005, 20, 128–131. [Google Scholar]
- Zheng, M.; Yang, J. Construction method evaluation of roadbed underpass high-speed railway bridge based on AHP-CRITIC method and TOPSIS method. J. Saf. Environ. 2023, 23, 2563–2571. [Google Scholar]
- Zeng, A.; Zhang, C. Ranking spreaders by decomposing complex networks. Phys. Lett. A 2013, 377, 1031–1035. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 2001, 86, 3200. [Google Scholar] [CrossRef]
- Knight, W.R. A computer method for calculating Kendall’s tau with ungrouped data. J. Am. Stat. Assoc. 1966, 61, 436–439. [Google Scholar] [CrossRef]
- Ma, L.; Ma, C.; Zhang, H.; Wang, B. Identifying influential spreaders in complex networks based on gravity formula. Phys. A Stat. Mech. Its Appl. 2016, 451, 205–212. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Liu, G.; Wang, L. Evaluation method of importance for nodes in complex networks based on importance contribution. Complex Syst. Complex. Sci. 2014, 11, 26–32+49. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).