Influence of Double-Ducted Serpentine Nozzle Configurations on the Interaction Characteristics between the External and Nozzle Flow of Aircraft

Abstract

To clarify the influence of the serpentine nozzle configurations on the flow characteristics and aerodynamic performance of aircraft, the flow features and aerodynamic performances of the double-ducted serpentine nozzles with different aspect ratios (AR), length–diameter ratios (LDR) and shielding ratios (SR) are numerically investigated. The results show that the asymmetric nozzle flow occurs due to the curved profile of serpentine nozzles, and a local accelerating effect exists at the S-bend, causing the increase in wall shear stress. The unilateral unsymmetrical expansion of the tail jet in the upward direction interacts with the separated external flow of the afterbody, forming an obvious cross-shock wave and shear layer structure. The surface pressure of the afterbody increases along the external flow direction, and decreases sharply in the separation point of the boundary layer. With the increase in AR and LDR, the local accelerating effect of the nozzle flow weakens, while with the increase in SR, the accelerating effect increases. The total pressure recovery coefficient, flow coefficient and axial thrust coefficient all decrease with the increase in AR, LDR, and SR. The thrust vector angle decreases with the increase in AR but is less affected by LDR and SR.

1. Introduction

As the main source of infrared radiation signature (IRS), radar cross-section (RCS) reflection, noise and aircraft wake, a low detectable exhaust system is the key to improve the viability of the aircraft in the future [1,2,3]. To this end, the serpentine nozzle with the characteristics of large curvature, multi-bend, a two-dimensional outlet and unilateral expansion was proposed [4,5,6]. The serpentine nozzle with the two-dimensional outlet could not only weaken IRS by completely shielding the high temperature sections of the turbofan and enhancing the external and nozzle flow mixing [7,8], but also cause the radar waves to refract repeatedly and eventually dissipate [9,10]. Consequently, serpentine nozzle technology is regarded as the key technology for 21st century fighter aircraft [11], and widely applied in stealth bombers and unmanned aerial vehicles, such as X-47B [12], B-21 [13], and Eikon [6].

The complex geometrical configuration of the serpentine nozzle has a significant impact on the aerodynamic performance of the exhaust system, involving many geometrical parameters and external conditions. For instance, Crowe et al. [14] analyzed the internal flow and aerodynamic performance of serpentine nozzles with different aspect ratios (AR) and length–diameter ratios (LDR). A local accelerating zone appears at the corner of S-bend, and the variations in AR and LDR would induce the streamwise vorticity. The small LDR causes internal flow separation, tending to reduce hot flow impingement at the nozzle outlet. The authors of [15] pointed out that the high-temperature core plumes shorten significantly with the increase in AR, while a high AR could induce a relatively higher IRS level on the on the left and right sides and below the nozzle. Markus [16] analyzed the tail jet characteristics of single-/double-ducted serpentine nozzles with different AR. The results show that the double-ducted serpentine nozzle with small AR can enhance the mixing of the inner/outer ducted flow and effectively shorten the length of the tail jet core area. Sun et al. propose a design method of a serpentine nozzle based on coupled parameters [17], and systematically investigate the influence of serval key design parameters and inlet configurations on nozzle flow characteristics via experiments and computations. The centerline distributions of the serpentine nozzle have a significant effect on nozzle flow acceleration, and a large curvature of the centerline would result in high friction loss and secondary loss at the S-bend; hence, the centerline with a gentle curve is recommended for a maximum aerodynamic performance [18]. Friction loss increases with the increasing of AR due to the increment of a wetted perimeter, while a small AR leads to a large secondary flow loss. The small area of the serpentine duct and LDR induce large friction loss and local loss, respectively [19]. Moreover, the natural vortices at the corners of the nozzle are independent of the existence of the bypass, the tail cone, and the struts. The performance and high-temperature region of serpentine nozzle decrease as the inlet swirl angle and the setting angle of the struts increase [20]. As for the influence of the shielding ratio (SR), Cheng et al. [21,22,23] reported that a large SR and AR have an obvious suppressing effect on the IRS of the tail jet, while the centerline variation has a slight effect on it. The main impact of IRS is the SR of the serpentine nozzle, and the vertical IRS level is greater than that in the horizontal plane, but this work does not focus on the effect of SR on the flow characteristics and aerodynamic performance of the serpentine nozzle. Recently, Hui et al. [24] reported that the configurations of the serpentine nozzle, especially LDR, affect the flow coefficient and thrust coefficient. Both the flow coefficient and thrust coefficient decrease as the pressure difference between the core flow and bypass flow increases.

As mentioned above, the current published works mainly focus on the influence of key design parameters (AR, LDR, SR, etc.) on the nozzle flow characteristics and IRS of a single serpentine nozzle, but seldom involve the effect of them on the interaction characteristics between the external and nozzle flow and the performance of an aircraft afterbody equipped with the serpentine nozzle. As far as is known, Rao et al. [25] carried out a experimental study on the external and internal flow properties of a circular nozzle, a 2D nozzle and a single serpentine nozzle at a nozzle pressure ratio (NPR) of 1.6. The curvature of the serpentine nozzle induces diffusion in the flow at certain locations and the generation of secondary nozzle flows, making the nozzle flow asymmetric. Such an asymmetric nozzle flow also vectors the external jet toward the lower wall, and a different flow expansion on the upper and lower walls appears due to the secondary flow. Sun et al. [26] also investigated the nozzle flow and external flow characteristics of the serpentine nozzle with different AR, and found the opposite lateral flow appears inside the nozzle and the length of the potential core decreases with the increase in AR. Such works only investigate the internal and external flow characteristics of a single serpentine nozzle and the influence of AR, but the effect of the key design parameters on the performance of the aircraft afterbody equipped with the serpentine nozzle is still a question that remains unanswered. The interactions between the external flow and high-speed nozzle flow make it more difficult to accurately predict the aerodynamic performance of an aircraft. It will be a challenge to improve the aerodynamic performance of an aircraft through the integrated design of a serpentine nozzle and afterbody. To this end, the numerical simulation of the coupling characteristics between the internal and external flow of an aircraft under cruising conditions is carried out in this paper. The interaction characteristics between the internal and external flow and the aerodynamic performance of afterbody equipped with the serpentine nozzle are analyzed carefully, and the influence of key design parameters (AR, LDR, SR) on them are obtained.

2. Geometric Model and Numerical Methodology

2.1. Geometric Model

Figure 1 shows a whole geometric model for the blended wing body aircraft equipped with a double-ducted serpentine nozzle, which can be mainly divided into a blended wing basic body and an afterbody located at the exhaust system area. The shape of the aircraft is similar to the Northrop Grumman X-47B (Northrop Grumman, Augustine, FL, USA), with a blended wing body. The length, wingspan, and altitude of the aircraft are 11,678 mm, 18,863 mm, and 1838 mm, respectively. The nozzle is a double serpentine and double-ducted configuration, and its key designed geometric parameters are shown in Figure 2, and the corresponding values are shown in

Table 1. The key designed geometric parameters of serpentine nozzle.

Non-Dimensional Parameters	Designed Values
AR (We/He)	3	4	5	6	7
LDR (L/D)	2.2	2.4	2.6	2.8	3.0
SR	0	0.25	0.5	0.75	1.0
D/L1 = 1.43, D/D1 = 1.93, D/D2 = 1.13

.

During the process of creating the nozzle/afterbody integrated design, the designed profile of the double serpentine nozzle is determined based on the alterable section method with diverse coupled parameters [17], which consisted of a centerline and a series of alterable cross-sections along its axis, including a double serpentine convergence part and an equal straight part. Unless otherwise stated, in the present work, nozzles adopt the common tangent rule to completely shade the high-temperature turbine at the entrance, to consider the infrared suppression of the double serpentine nozzle [22]. For different design schemes, the nozzle and afterbody are combined by intersecting and cutting, and then the transition modification treatment is carried out at the cutting position to form an integrated design scheme. In addition, the geometric model intercepted a section of the inlet, which is not the focus in the present work, to simulate the external flow around the inlet and to better reconstruct the external flow field around the afterbody.

2.2. Numerical Simulation Methodology

The evolution characteristics of the interaction between the external and nozzle flow of the double-ducted serpentine nozzle with different geometric parameters are numerically calculated by the finite volume method. The second-order upwind scheme is used to discretize the computational domain, and the three-dimensional compressible RANS equation is solved based on a density coupling solver. The mass, momentum and energy conservation of the RANS equations can be given as:

$${\displaystyle \frac{\partial \rho }{\partial t}}+{\displaystyle \frac{\partial \left(\rho U_i\right)}{\partial x_i}}=0$$

(1)

$${\displaystyle \frac{\partial \rho U_i}{\partial t}}+{\displaystyle \frac{\partial \left(\rho U_i{U}_j+P{\delta }_{ij}\right)}{\partial x_j}}={\displaystyle \frac{\partial \left({\tau }_{ij}-\rho \overline{U_i{U}_j}\right)}{\partial x_j}}$$

(2)

$${\displaystyle \frac{\partial \left(\rho E\right)}{\partial t}}+{\displaystyle \frac{\partial \left[\left(\rho E+P\right)U_i\right]}{\partial x_i}}=-{\displaystyle \frac{\partial \left({\tau }_{ij}-\rho \overline{U_i{U}_j}\right)U_j}{\partial x_i}}-{\displaystyle \frac{\partial \left(q_i+C_p\rho \overline{U_i\theta }\right)}{\partial x_i}}+{\displaystyle \frac{\partial }{\partial x_i}}\left[\rho \left(\mu +{\displaystyle \frac{{\mu }_t}{\overline{{\sigma }_k}}}{\displaystyle \frac{\partial k}{\partial x_i}}\right)\right]$$

(3)

where ρ, U_i, x_i, are the density, velocity and coordinates, respectively. P is the pressure, E the total energy, q_i the heat flux, τ_ij the shear stress, C_p the specific heat at constant pressure, and k the turbulent kinetic energy. σ_k, μ, and μ_t are the closure constants, the laminar viscosity coefficient, and the turbulent viscosity coefficient, respectively.

To guarantee a more accurate calculation, the k-ω SST turbulence model is chosen to predict the interaction between external and nozzle flow [19]. The k-ω shear stress transport (SST) turbulence model combines the advantages of the k-ε model away from the wall and the k-ω model near the wall, and is widely adopted in turbulence flow simulation for its accuracy and efficiency. The governing equation of the SST model can be written as:

$${\displaystyle \frac{\partial \left(\rho k\right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho U_{i}k\right)}{\partial x_i}}={\tilde{P}}_k-{\beta }^{\ast }\rho k\omega +{\displaystyle \frac{\partial }{\partial x_i}}\left[\left(\mu +{\sigma }_k{\mu }_t\right){\displaystyle \frac{\partial k}{\partial x_i}}\right]$$

(4)

$${\displaystyle \frac{\partial \left(\rho \omega \right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho U_i\omega \right)}{\partial x_i}}={\displaystyle \frac{\gamma }{{\mu }_t}}{P}_k-\beta \rho {\omega }^2+{\displaystyle \frac{\partial }{\partial x_i}}\left[\left(\mu +{\sigma }_{\omega }{\mu }_t\right){\displaystyle \frac{\partial \omega }{\partial x_i}}\right]+2\left(1-F_1\right)\rho {\sigma }_{\omega 2}{\displaystyle \frac{1}{\omega }}{\displaystyle \frac{\partial k}{\partial x_i}}{\displaystyle \frac{\partial \omega }{\partial x_i}}$$

(5)

$${\mu }_t={\displaystyle \frac{\rho a_{1}k}{max\left(a_1\omega ,F_{2}S\right)}}$$

(6)

where ω and S are the dissipation rate and strain rate constant, respectively. β*, β, γ, σ_ω and a₁ are closure constants. The production term P_k is defined as:

$$P_k=\left[{\mu }_t\left({\displaystyle \frac{\partial U_i}{\partial x_j}}+{\displaystyle \frac{\partial U_j}{\partial x_i}}+{\displaystyle \frac{2}{3}}{\displaystyle \frac{\partial U_k}{\partial x_k}}{\delta }_{ij}\right)-{\displaystyle \frac{2}{3}}\rho k{\delta }_{ij}\right]{\displaystyle \frac{\partial U_i}{\partial x_j}}$$

(7)

The term was limited as:

$${\tilde{P}}_K=min\left(P_k,10\rho {\beta }^{\ast }k\omega \right)$$

(8)

F₁ and F₂ are the bending functions to adjust the closure constants in different flow regions, which can be written as:

$$F_1=tanh\left\{{\left[min\left(max\left({\displaystyle \frac{\sqrt{k}}{{\beta }^{\ast }\omega d}},{\displaystyle \frac{500\mu }{d^2\omega \rho }}\right),{\displaystyle \frac{4{\sigma }_{\omega 2}\rho k}{C{D}_{k\omega }{d}^2}}\right)\right]}^4\right\}$$

(9)

$$C{D}_{k\omega }=max\left(2\rho {\sigma }_{\omega 2}{\displaystyle \frac{1}{\omega }}{\displaystyle \frac{\partial k}{\partial x_i}}{\displaystyle \frac{\partial \omega }{\partial x_i}},{10}^{-10}\right)$$

(10)

$$F_2=tanh\left\{{\left[max\left({\displaystyle \frac{2\sqrt{k}}{{\beta }^{\ast }\omega d}},{\displaystyle \frac{500\mu }{d^2\omega \rho }}\right)\right]}^2\right\}$$

(11)

where d is the distance to the wall, and a₁ = 0.31, β = 0.075, β* = 0.09, σ_ω = 0.5, σ_ω2 = 0.856, σ_k = 0.85, γ = 0.553.

The mesh system of the whole geometric model adopts the structured grids, and the computational domain size is 30L_a × 10L_a × 10L_a (L_a is the length of aircraft). The three-dimensional structured grid model and boundary conditions are shown in Figure 3. The mesh near the wall is encrypted locally, and the thickness of the first layer mesh is 0.01 mm, to ensure that the mesh height near the wall is y⁺ < 1.0. The inlet of the serpentine nozzle is divided into inner and outer inlets (Figure 2), adopting a pressure inlet boundary. The total pressure and total temperature of the inner inlet are $P_{inner}^{\ast }=89,550 \mathrm{Pa}$ and $T_{inner}^{\ast }=340 \mathrm{K}$, respectively, while $P_{outer}^{\ast }=85,140 \mathrm{Pa}$ and $T_{outer}^{\ast }=822 \mathrm{K}$ are the values for the outer inlet. The computational domain boundary is set as the far-field boundary without pressure reflection, the incoming flow Mach number is Ma_ꝏ = 0.8, and the far-field static pressure and static temperature are $P_a=85,140 \mathrm{Pa}$ and $T_a=216.7 \mathrm{K}$, respectively. The angle of attack (AoA) of the aircraft is zero for all cases. Non-slip and non-permeable adiabatic wall boundary conditions are adopted for the serpentine nozzle and blended wing body walls.

Four aerodynamic performance parameters (total pressure recovery coefficient σ_e, flow coefficient C_D, axial thrust coefficient C_fg and thrust vector angle γ_c) are chosen to evaluate the aerodynamic performance of the integrated design of the serpentine nozzle and afterbody. σ_e is defined as the ratio of the nozzle outlet average total pressure P_ex* to the inlet average total pressure P_in*, the flow coefficient C_D is the ratio of the nozzle actual mass flux m to the ideal mass flux m_i, and the axial thrust coefficient C_fg is the ratio of the actual axial thrust F_s to the ideal isentropic thrust F_i. The thrust vector angle γ_c is given as:

$${\gamma }_c=\arctan {\displaystyle \frac{F_y}{F_x}}$$

(12)

where F_x and F_y represent the axial thrust of the nozzle (the component of the nozzle thrust in the x direction) and the normal thrust of the nozzle (the component of the nozzle thrust in the y direction), respectively, and they can be written as:

$$F_x={\displaystyle \underset{A_{ex}}{\int }(\rho U_x{U}_x+}(P_{ex}-P_a))d{A}_{ex}, F_y={\displaystyle \underset{A_{ex}}{\int }(\rho U_x{U}_y}+(P_{ex}-P_a))d{A}_{ex}$$

(13)

Here, A_ex is the nozzle outlet area. The ideal mass flux m_i and the ideal isentropic thrust F_i can be obtained as:

For P_in*/P_a < 1.893

$$m_i=\sqrt{{\displaystyle \frac{K}{R}}{({\displaystyle \frac{2}{K+1}})}^{{\displaystyle \frac{K+1}{K-1}}}}{\displaystyle \frac{{P_{in}}^{\ast }}{\sqrt{{T_{in}}^{\ast }}}}{A}_{ex}q(Ma)$$

(14)

$$F_i=m\sqrt{2{\displaystyle \frac{K}{K-1}}R{T_{in}}^{\ast }[1-{({\displaystyle \frac{P_a}{P_{in}^{\ast }}})}^{{\displaystyle \frac{K-1}{K}}}]}$$

(15)

For P_in*/P_a ≥ 1.893

$$m_i=\sqrt{{\displaystyle \frac{K}{R}}{({\displaystyle \frac{2}{K+1}})}^{{\displaystyle \frac{K+1}{K-1}}}}{\displaystyle \frac{{P_{in}}^{\ast }}{\sqrt{{T_{in}}^{\ast }}}}{A}_{ex}$$

(16)

$$F_i=m\sqrt{2{\displaystyle \frac{K}{K-1}}R{T}^{\ast }}+(0.528P_{ex}^{\ast }-P_a)A_{ex}$$

(17)

where T_in* is the average total temperature of nozzle inlet, R the gas constant, K the ratio of specific heat, and q(Ma) the stream function.

To verify the rationality of the grid scale, grid independence verification is conducted. Under the condition of the same mesh topology and height of the first layer near the wall, the serpentine nozzle is selected as the main verification object, and the whole mesh is changed adaptively. Five mesh systems with different spatial resolutions are constructed. The nozzle mesh quantities are 6.0 × 10⁵, 9.0 × 10⁵, 1.2 × 10⁶, 1.8 × 10⁶ and 2.4 × 10⁶, respectively, and the corresponding whole mesh quantities are 2.9 × 10⁶, 3.8 × 10⁶, 4.9 × 10⁶, 6.8 × 10⁶ and 9.3 × 10⁶, respectively. The results of the grid independence verification are given in

Table 2. Influence of grid size on aerodynamics performance.

Grid Number of Nozzles	σe	CD	Cfg	γc (°)
6.0 × 105	0.964	0.983	0.974	4.188
9.0 × 105	0.965	0.983	0.974	4.180
1.2 × 106	0.965	0.983	0.974	4.151
1.8 × 106	0.965	0.983	0.974	4.186
2.4 × 106	0.965	0.982	0.975	4.095

. σ_e, C_D and C_fg are almost unchanged with the increase in mesh quantity, and the maximum relative error from the results of the finest mesh is only 0.1%. The thrust vector angle γ_c fluctuates slightly, but the maximum relative error is less than 2.3%, which indicates that the grid discretization error meets the requirement when the nozzle grid quantity reaches 9.0 × 10⁵. Considering the accuracy and economy, the mesh system of 9.0 × 10⁵ for the nozzle is adopted in the present work.

To verify the reliability of the numerical method, a serpentine nozzle with the same geometric parameters as Ref. [19] is constructed, which involves an integrated design with an aircraft afterbody, and the nozzle flow characteristic under the same working conditions is numerically simulated. Figure 4 shows that the static pressure distribution on the upper wall of the serpentine nozzle is consistent with the experimental data in Ref. [19]. The maximum relative error is less than 2%, which demonstrates that the numerical method implemented in this work is capable of accurately predicting the flow characteristics.

3. Results and Discussions

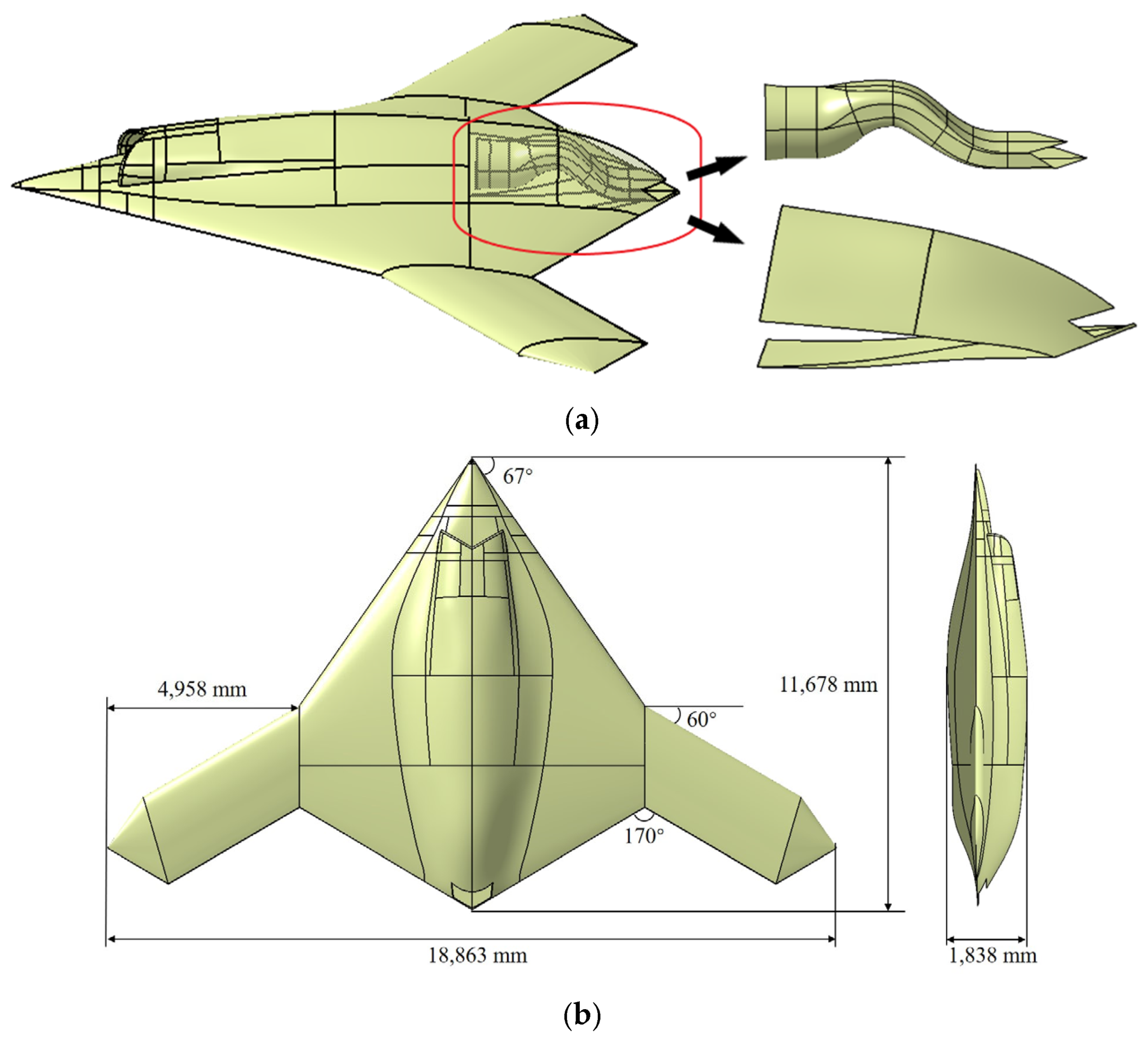
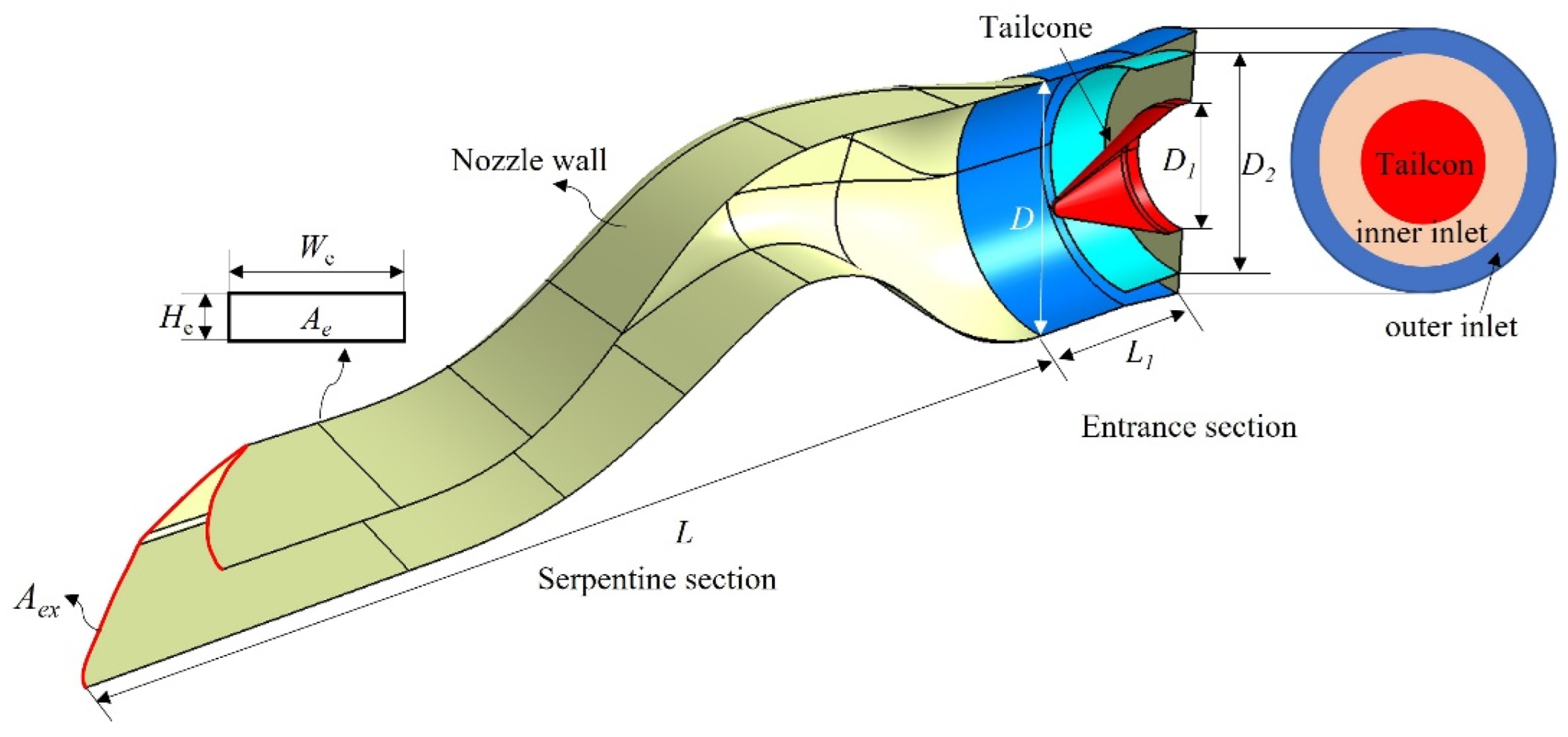
3.1. Effect of AR on the Interaction between the Nozzle Flow and External Flow

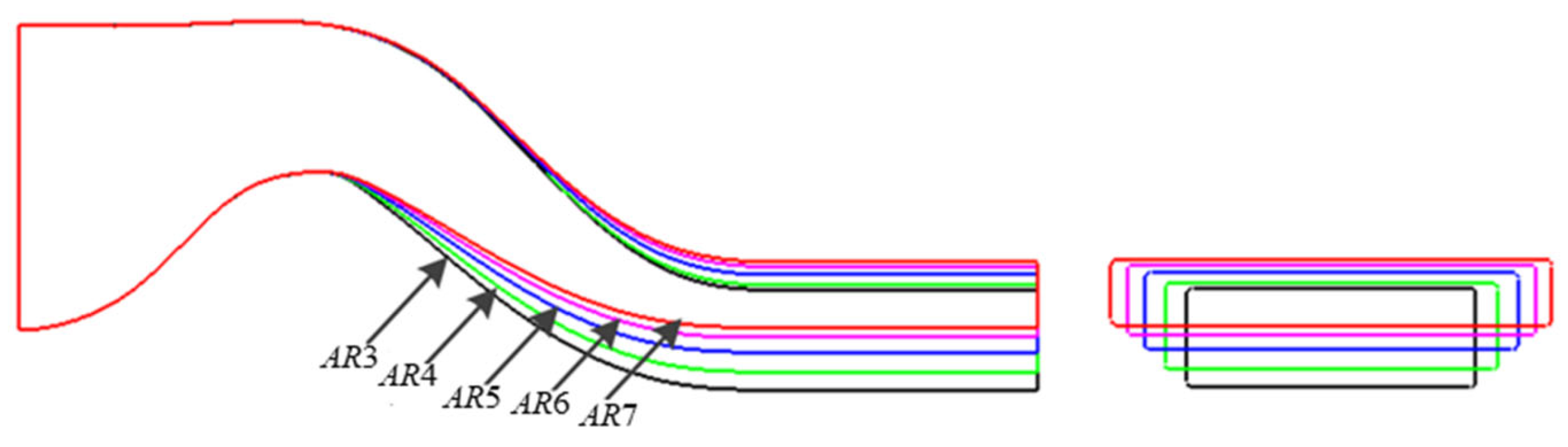
Figure 5 shows the symmetrical cross-section and outlet profile of the serpentine nozzle with different aspect ratios under the design criteria of the equal-area nozzle outlet (LDR = 2.6, SR = 1.0). The longitudinal deflection of the second bend decreases with increasing AR, while the transverse expansion of the nozzle profile increases, resulting in a gradual decrease in the longitudinal curvature of the nozzle profile. Thus, the transverse curvature of nozzle profile increases, as well as the wetted circumference of the nozzle flow.

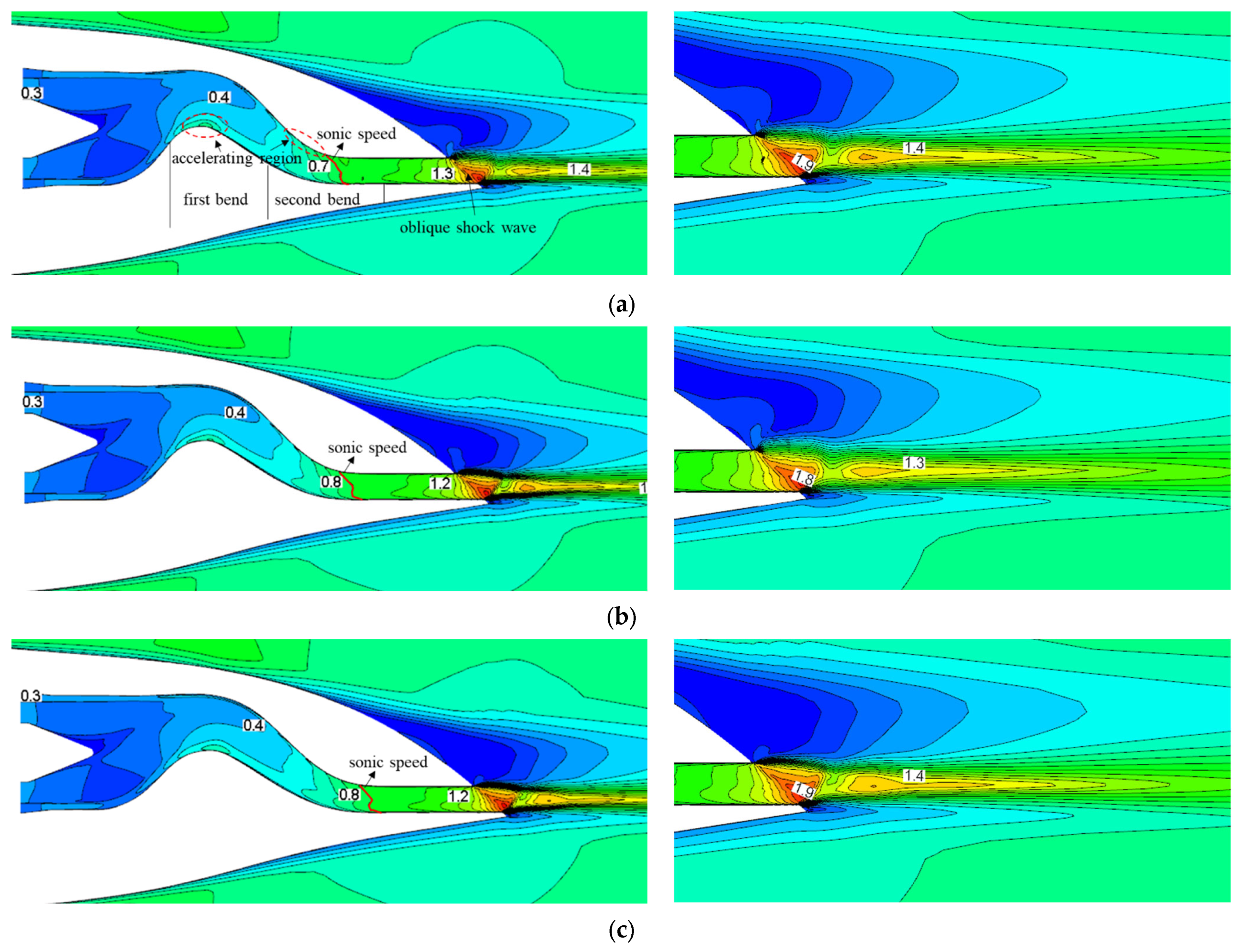
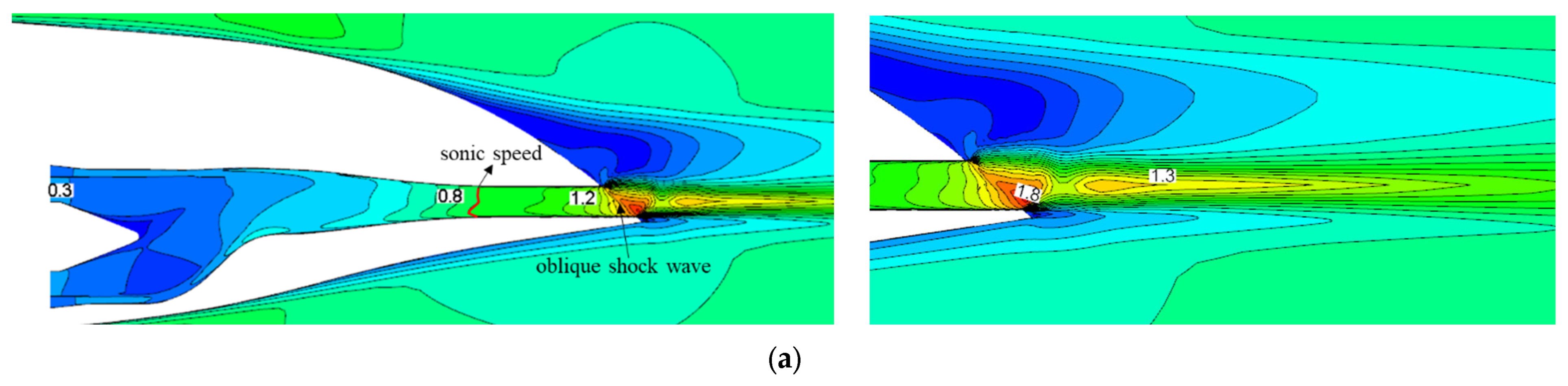
Figure 6 shows the Ma distribution on the symmetrically cut plane of the whole aircraft assembled with serpentine nozzles of different outlet aspect ratios. For the serpentine configuration, the flow field inside the nozzle is asymmetric. There is a local accelerating region near the lower wall of the first bend and the upper wall of the second bend (indicated by the red dashed box). The internal flow first accelerates to supersonic speed at the upper wall of the second bend, forming a locally inclined and curved sonic speed surface (indicated by the red curve), and eventually reaches the maximum velocity and generates an oblique shock wave at the nozzle outlet. Due to the integrated conformal design of the nozzle and the aircraft, the length of the upper wall at the nozzle outlet is shorter than that of the lower wall, which corresponds to the existence of a baffle (indicated by the thick red line). Such a lower baffle causes the tail jet to only expand unilaterally upward, resulting in the thrust of the nozzle deflecting upwards. The interaction between the high-speed tail jet and the separated flow of the afterbody induces a distinct shear layer structure. The velocity of the tail jet exhibits the intermittent Mach wave, characteristic of “high-low-high” speed. Due to the complete expansion of the outlet flow, the detached tail jet no longer expands, and continues to mix with the afterbody external flow, resulting in a gradual decrease in the velocity of the tail jet. Since the differences in the profiles between the serpentine nozzles with different aspect ratios are mainly located at the second S-bend runner (Figure 5), the variation in AR has less influence on internal flow at the first S-bend runner and its upstream area, and thus the corresponding distribution of Ma is basically the same. Once the flow enters the second S-bend runner, the difference in the internal flow field caused by the increase in AR gradually amplifies, e.g., the degree of the bending and inclination of the sonic speed surface reduces. As AR increases, the longitudinal offset of the nozzle profile decreases while the transverse expansion increases, resulting in a decrease in the longitudinal curvature and an increase in the transverse curvature at the second bend runner. This, in turn, slows down the internal flow acceleration near the upper wall of the second bend and shrinks the accelerating region. The increase in the wetted circumference causes a larger shear area between the high-speed tail jet and the external flow, leading to an increase in the mixing loss as well as the energy loss of the tail jet. The length of the tail jet is shortened, and the intensity of the shock wave is weakened. In addition, with the increase in AR, the outlet height decreases, and the length difference between the upper and lower wall of the nozzle outlet decreases. Therefore, the degree of upward unilateral expansion of the tail jet is weakened. The region of the afterbody separating flow gradually increases, while the external flow has no significant effect on the tail jet.

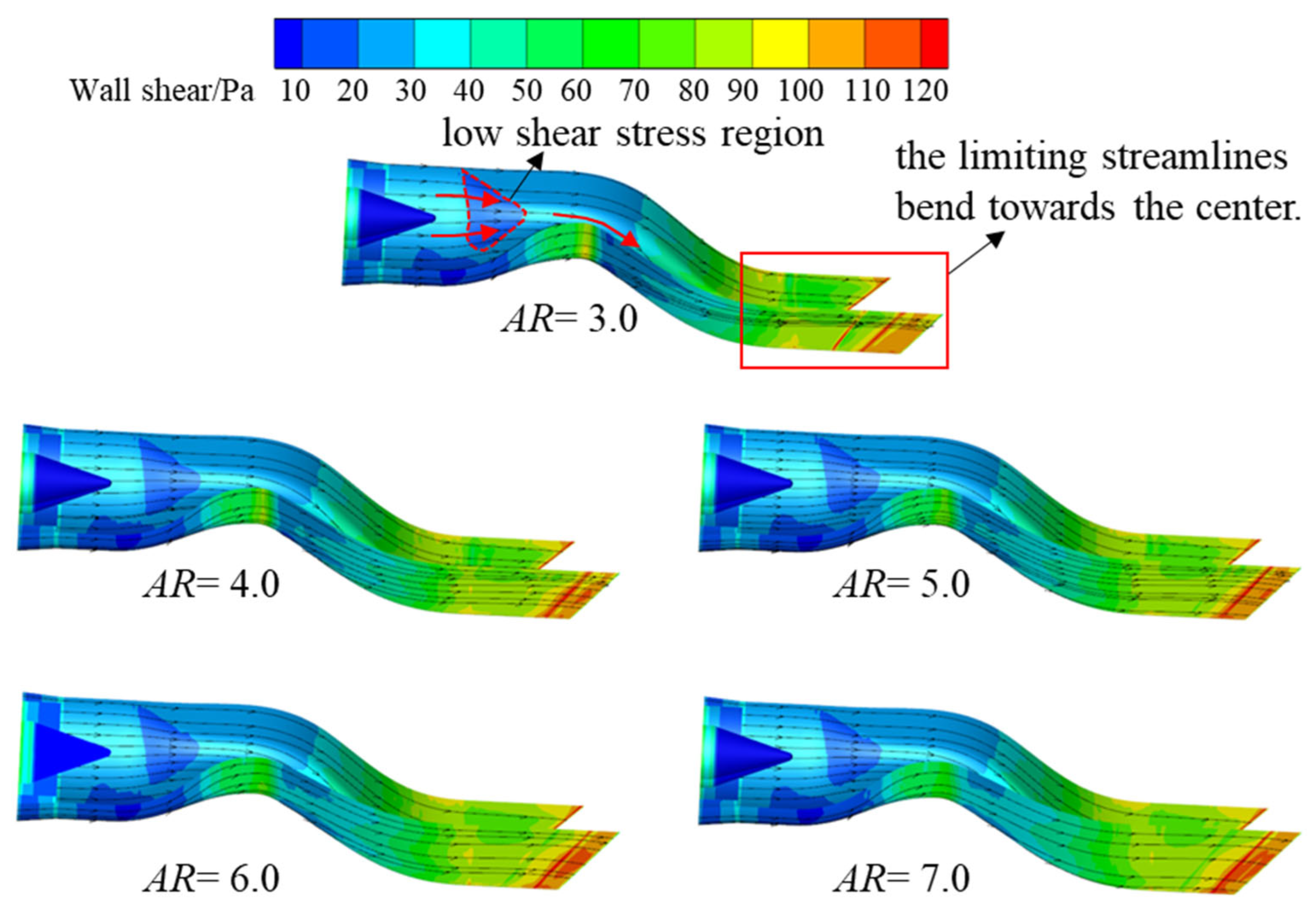
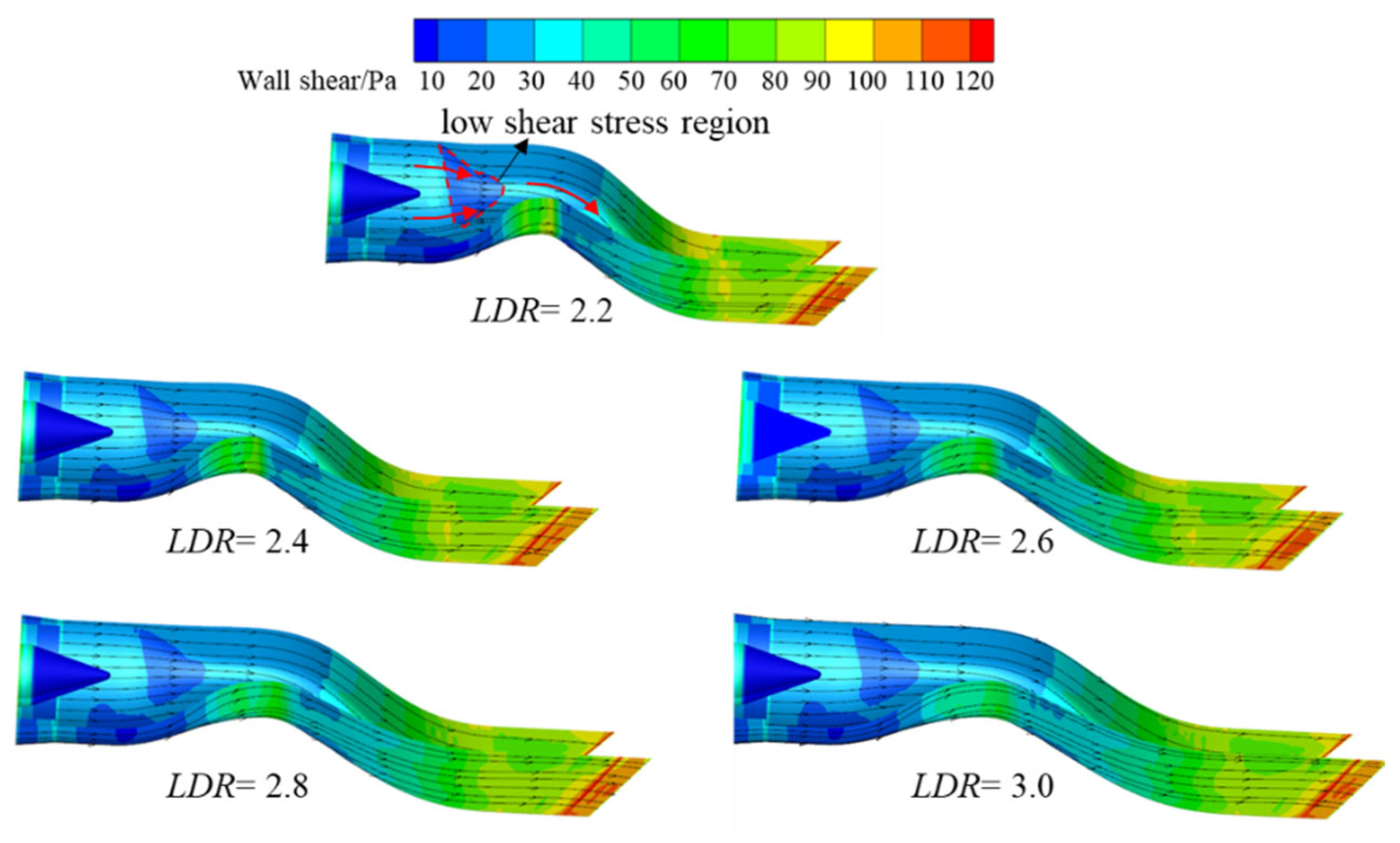
The distribution of limiting streamlines and wall shear stresses on the surface of the nozzle with different AR is shown in Figure 7. With the transition of the runner cross-section from circular to square, a low wall shear stress region exists in the center region of the square runner (indicated by the red dashed area), where the central shear stress is smaller than that of surrounding area, causing the limiting streamlines to bend towards the center. At the second S-bend runner, the wall shear stress on the upper and lower wall outside is larger than that of the center, leading to the convergence of the limiting streamlines on the upper and lower walls at the straight section towards the center. The longitudinal deflection characteristic of the nozzle causes the limiting streamlines on the side wall to bend accordingly, leading to a sharp increase in wall shear stress on the inner wall located at the bend region. Therefore, the limiting streamlines on the side wall of the equal straight section deflect downwards. As AR increases, the transverse expansion of the nozzle profile increases while the longitudinal deflection decreases. The wall shear stresses gradually become uniform. Thus, the transverse deflection of the limiting streamlines of the upper and lower wall surfaces increases, but the longitudinal bending decreases. Moreover, the reduction in longitudinal deflection weakens the internal flow accelerating effect near the lower wall of the first bend and the upper wall of the second bend, and reduces the corresponding wall shear stress.

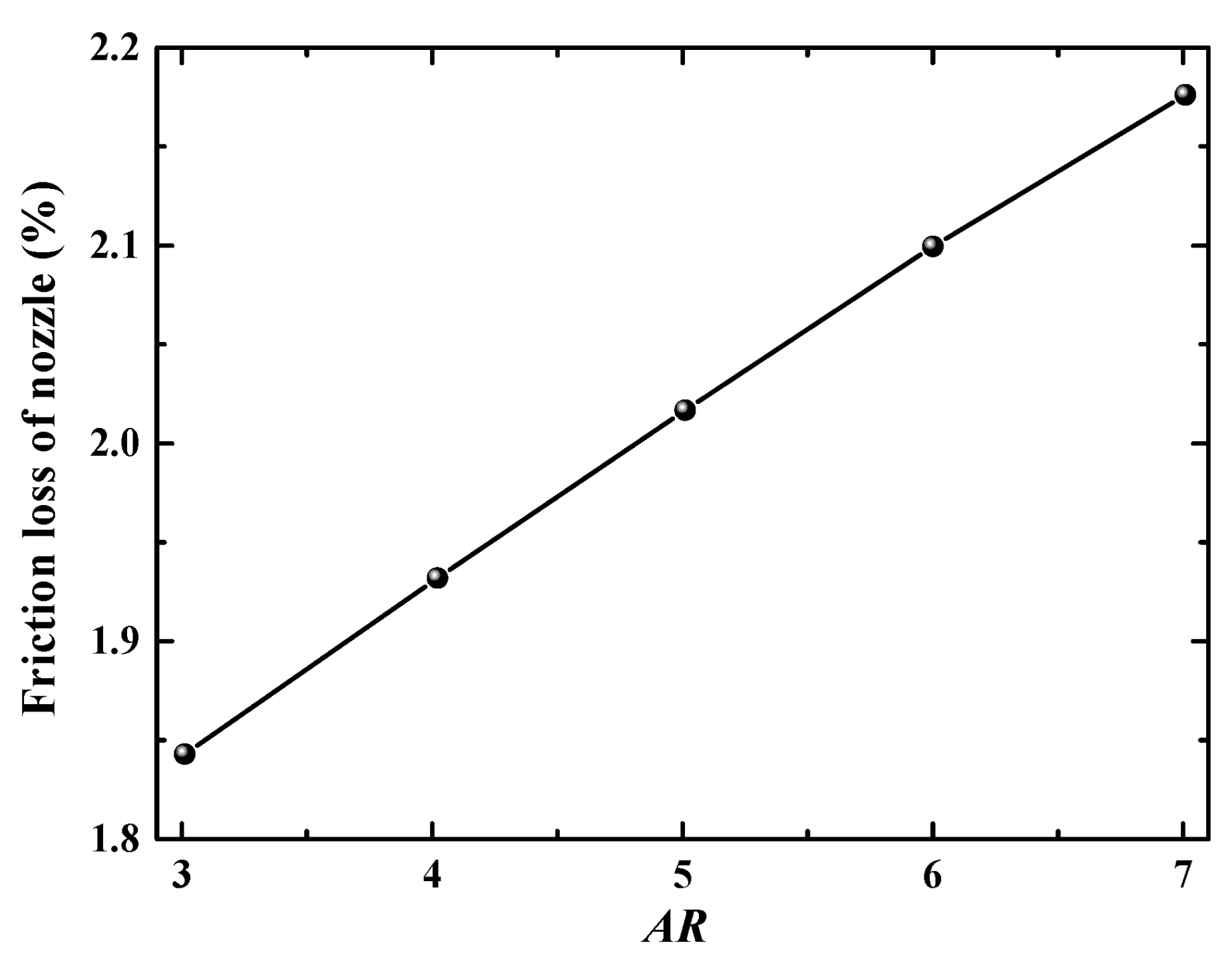
The increase in AR weakens the accelerating effect of the internal flow, resulting in a decrease in the longitudinal deflection of the internal flow. The wall shear stress on the lower wall of the first bend and the upper wall of the second bend gradually decreases, thereby reducing the friction loss, local acceleration loss, and collision loss in the corresponding areas. However, the larger the AR, the larger the wetted area of the internal flow runner, and the stronger the transverse expansion of the internal flow, resulting in greater friction losses. Therefore, the friction loss of the nozzle needs to comprehensively consider the above two factors. Figure 8 shows the effect of AR on the friction loss of the nozzle. As AR increases, the friction loss increases linearly, indicating that the increase in the AR weakens the aerodynamic performance of the serpentine nozzle.

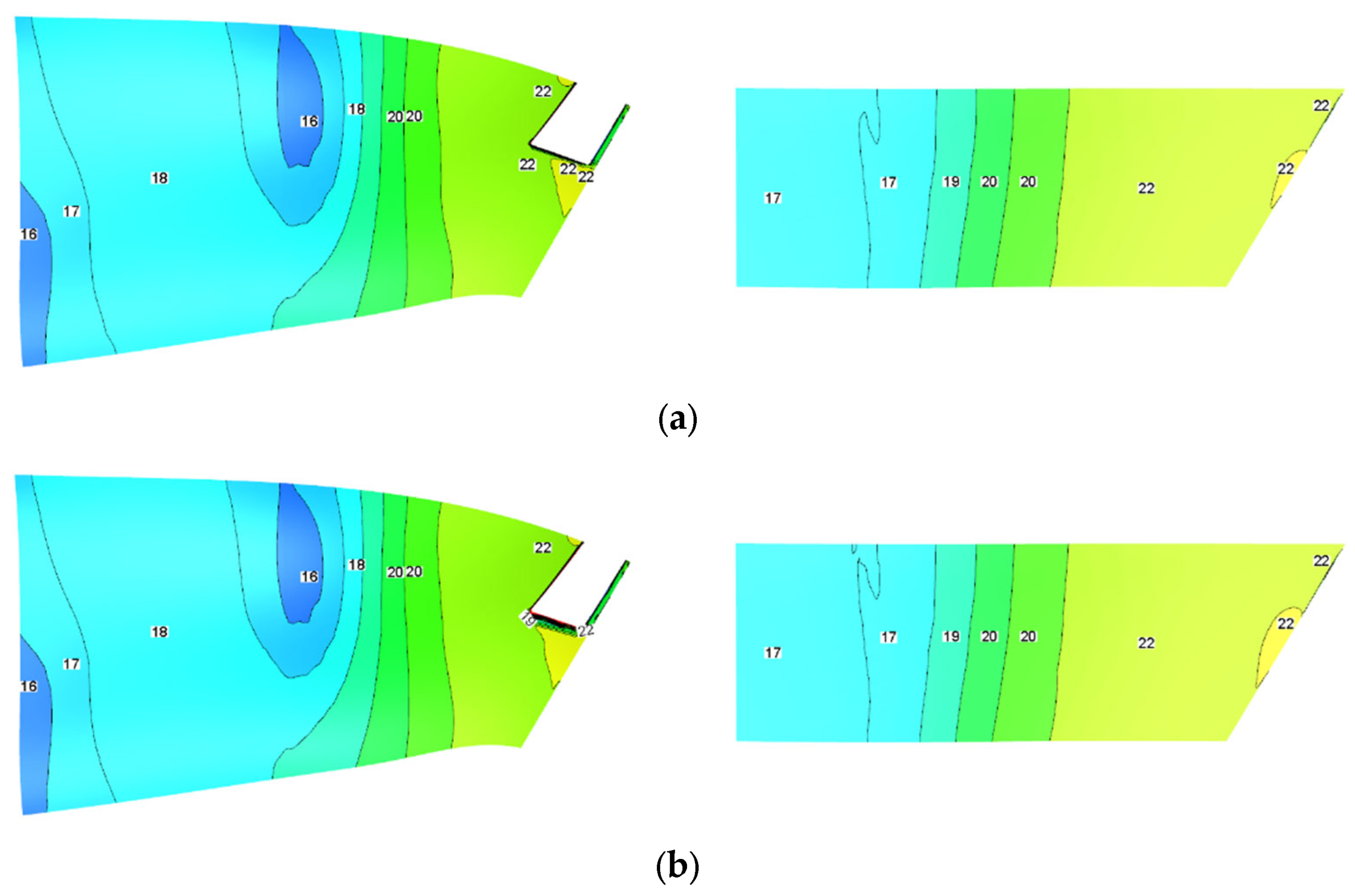
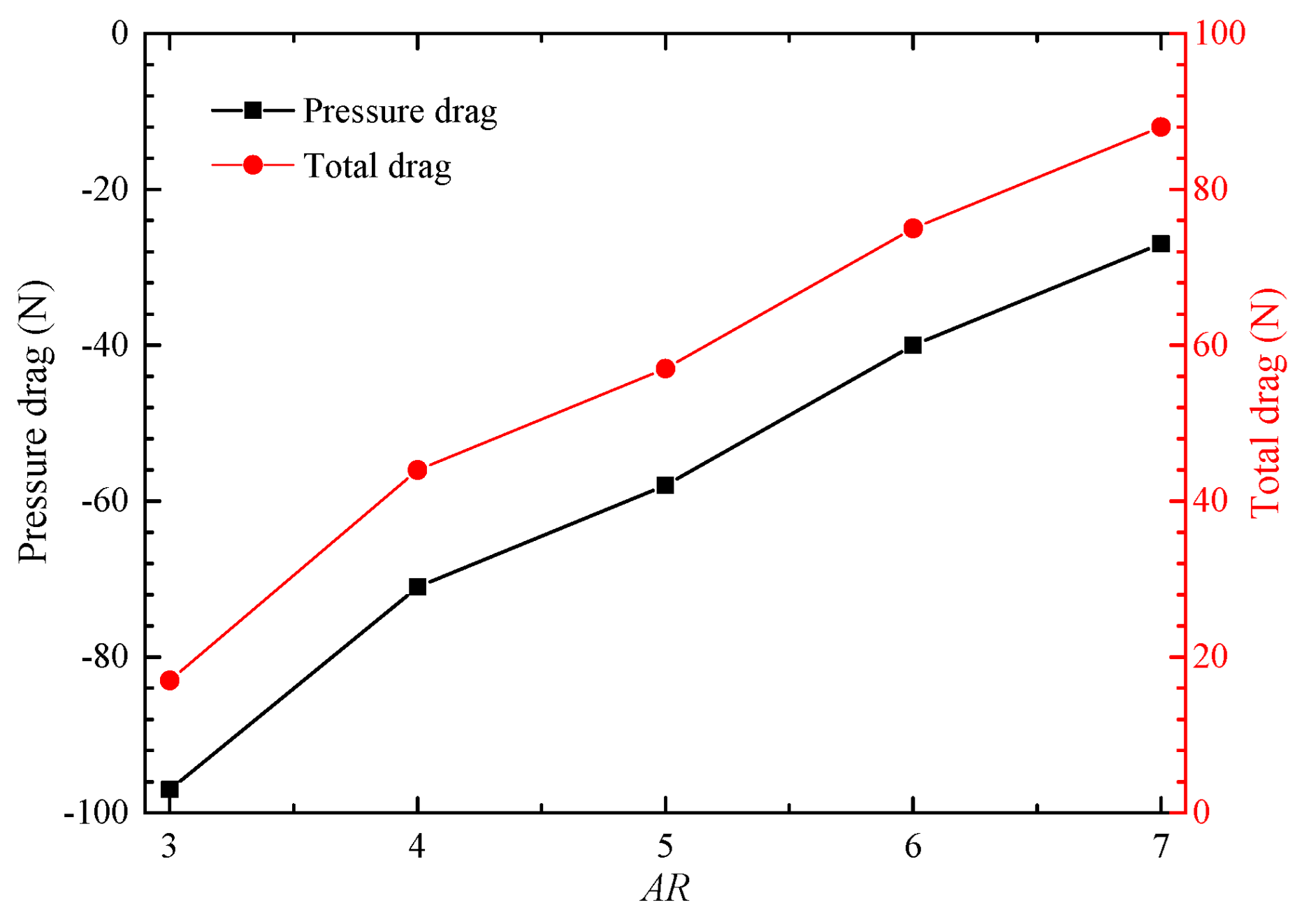
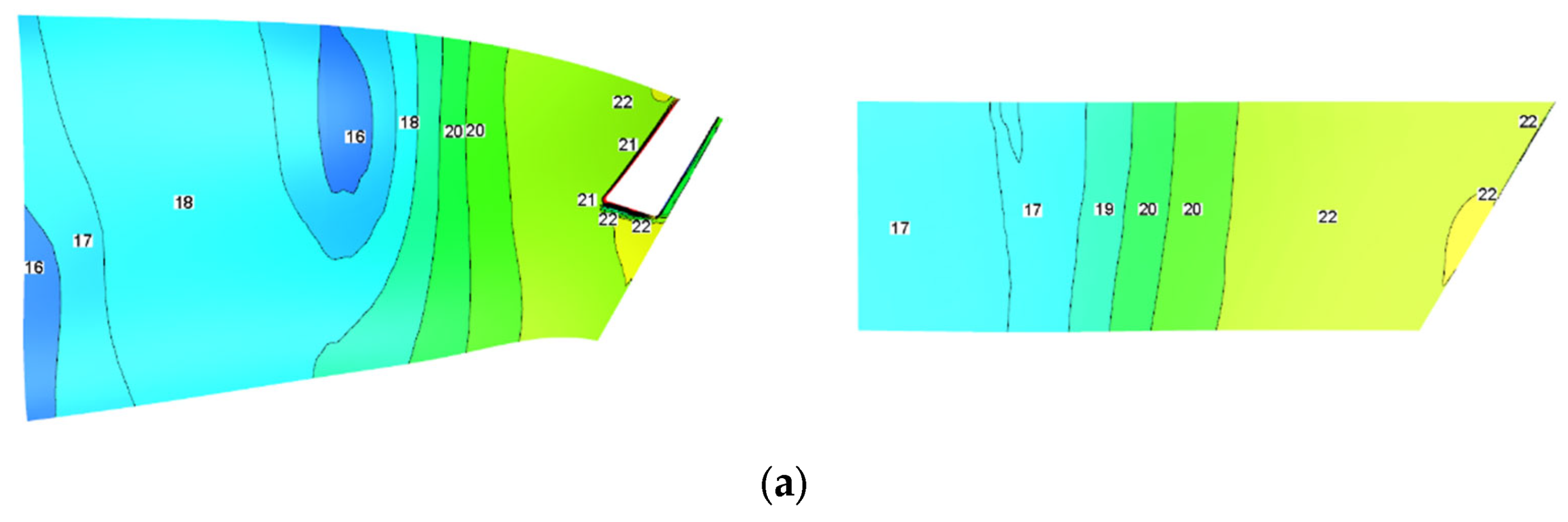
To further explore the impact of internal and external flow coupling on the aircraft afterbody, the pressure distribution on the upper and lower surfaces of the afterbody under different AR is shown in Figure 9. The upper surface pressure increases gradually along the flow, then drops sharply at the boundary layer separation point, but finally increases continuously. This is because the afterbody surface converges rapidly after the separation point, and the sudden expansion of the subsonic external flow runner causes the external flow to slow down, thereby causing the surface pressure to increase along the way. However, in the region near the nozzle outlet, a low-pressure region is formed due to the unilateral expansion of the internal flow. The lower surface pressure of the afterbody increases uniformly along the way, and is less affected by the internal flow of the nozzle. The variation in AR only affects the pressure distribution near the nozzle outlet of afterbody. With the increase in AR, the wetted circumference of the internal flow runner becomes longer, and the low-pressure region near the nozzle outlet expands, which increases the pressure difference drag of the afterbody. As a result, the total drag of the afterbody increases, and thus the aerodynamic performance of the aircraft is reduced, as shown in Figure 10.

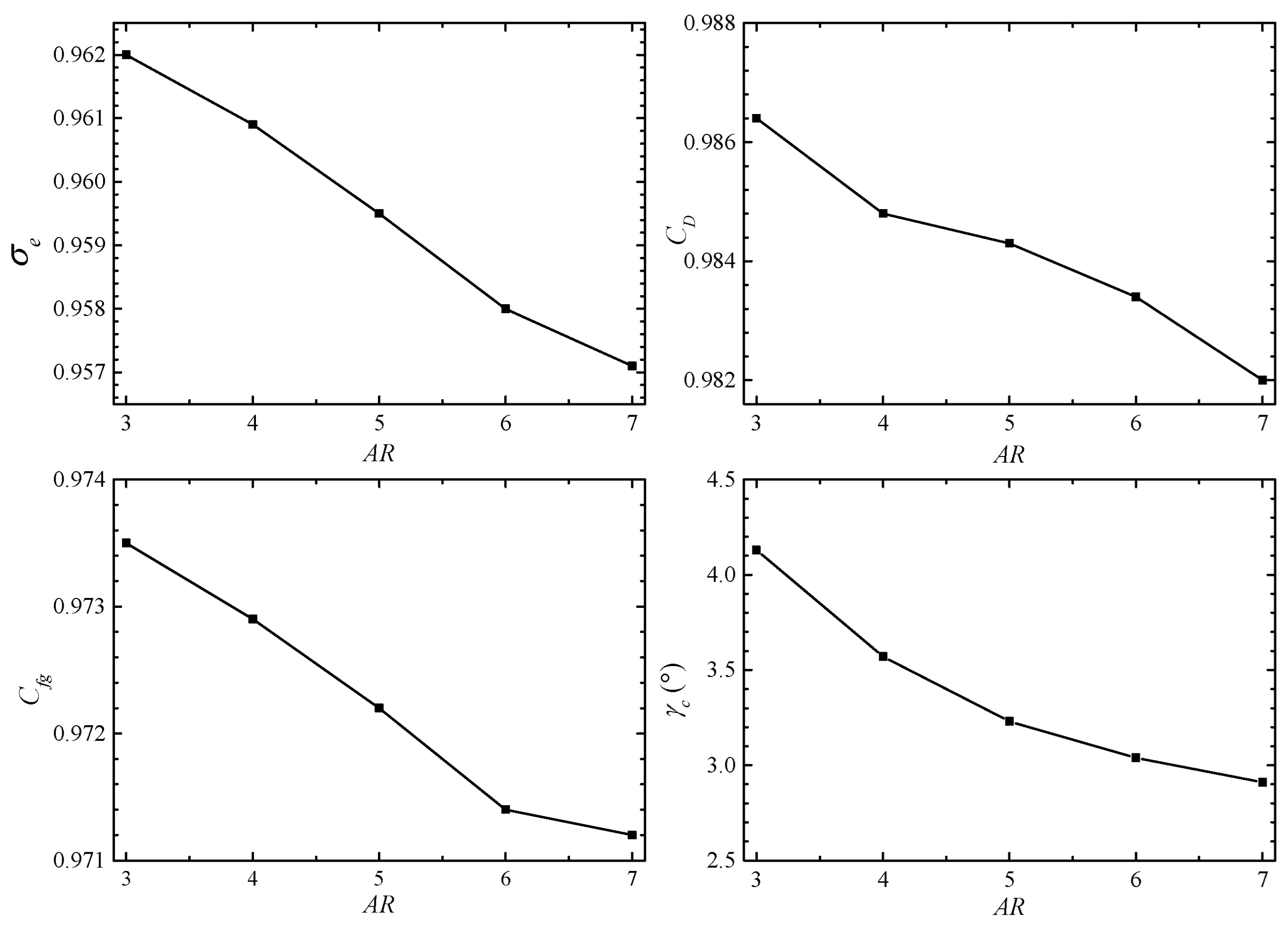
Figure 11 analyzes the influence of AR on the aerodynamic performance of the serpentine nozzle. The total pressure recovery coefficient, flow coefficient, axial thrust coefficient and thrust vectoring angle all decrease with the increase in AR. The increase in AR increases the wetted area of the internal flow runner, which increases the friction loss, thereby reducing the aerodynamic performance of the nozzle. However, the increase in AR weakens the accelerating effect of internal flow, reducing the wall shear stress at the bend area. The friction loss, local acceleration loss, and collision loss in the corresponding region decrease, and thus enhance the aerodynamic performance of the nozzle. These two have opposite effects on the aerodynamic performance of the nozzle, and the degree of weakening is stronger (Figure 8). It ultimately induces a reduction in the total pressure recovery coefficient, flow coefficient, and axial thrust coefficient. Compared with AR = 3, the total pressure recovery coefficient, flow coefficient and axial thrust coefficient of the AR = 7 nozzle decreased by 0.51%, 0.45% and 0.24%, respectively. The thrust vector angle of the nozzle is mainly determined by the degree of the uneven longitudinal expansion of the tail jet. The length of the lower baffle at the nozzle outlet shortens as AR increases, which reduces the upward unilateral expansion nonuniformity of the tail jet (Figure 6), resulting in a decrease in the thrust vector angle.

3.2. Effect of LDR on the Interaction between the Nozzle Flow and External Flow

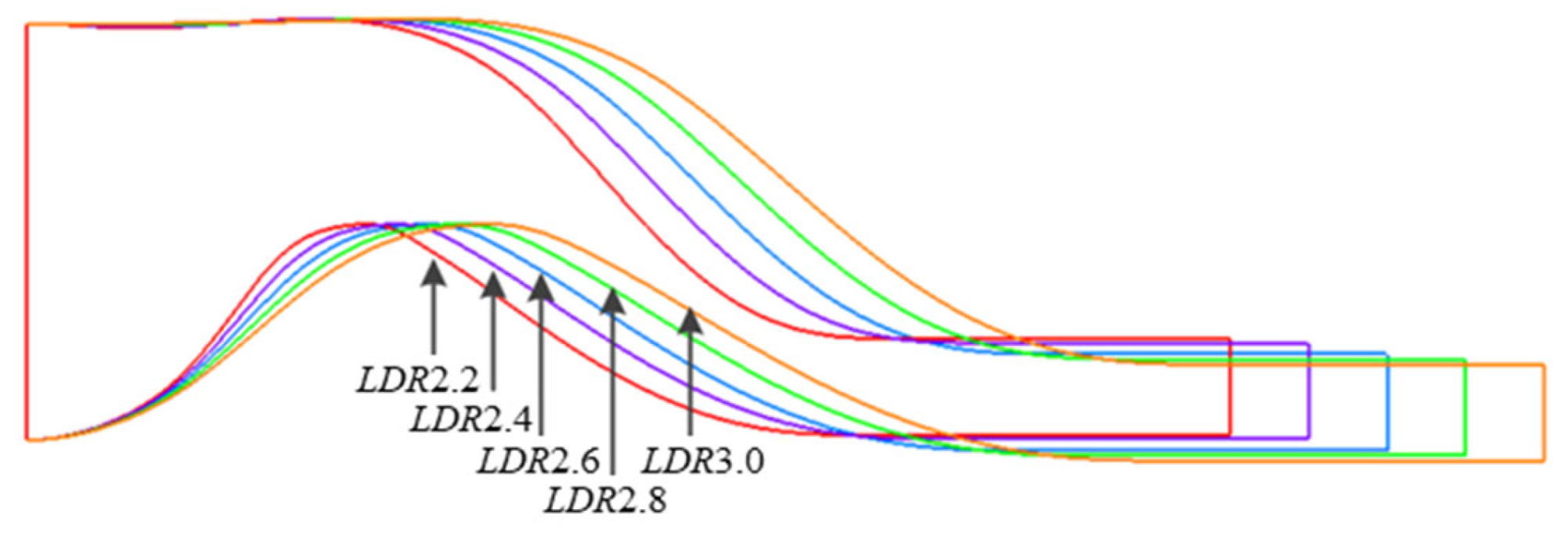
The LDR of the serpentine nozzle directly affects the longitudinal turning and lateral expansion of the internal flow runner, which changes the flow characteristics of the nozzle flow, and in turn affects its aerodynamic performance. To this end, under the constraints of equal inlet and outlet areas and complete shielding (SR = 1) design criteria, five different serpentine nozzles with different LDR (=2.2, 2.4, 2.6, 2.8, 3.0, AR = 6.0) are constructed, as shown in Figure 12. As LDR increases, the length of the nozzle increases, and the curvature at the first and second bends decreases, resulting in a slower longitudinal deflection and lateral expansion of the internal flow runner, but the longitudinal offset of the nozzle outlet slightly increases.

Figure 13 illustrates the Mach number distribution on the symmetric cut plane of the aircraft equipped with nozzles of different LDR. The flow field inside the nozzle exhibits an asymmetric configuration, wherein the internal flow accelerates continuously along the convergent runner. The flow reaches the sonic speed near the second S-bend, forming a left-inclined sonic speed surface, and finally accelerates to the maximum velocity at the nozzle outlet. As LDR increases, the curvature of the internal flow runner slows down, resulting in a decrease in the local accelerating effect of the flow at the bends, as well as a decrease in the accelerating region and flow velocity within the accelerating region. However, the Mach number distribution at the nozzle outlet remains unaffected by the variation in LDR. Notably, the nozzle outlet profile and assembly position remain unchanged, thereby having no significant impact on the interaction between the nozzle flow and external flow.

Figure 14 shows that the wall shear stress along the runner shows an increasing trend, and reaches a maximum value at the nozzle outlet. Meanwhile, the variation in the internal flow direction caused the local wall shear stress near the lower wall of the first bend and the upper wall of the second bend to increase significantly. The increase in LDR induces the longitudinal deflection and lateral expansion of the internal flow runner to slow down, resulting in the weakening of the local accelerating effect at the two bends and a reduction in the local acceleration loss. Furthermore, as LDR increases, the shear stress at the lower wall of the first bend and the upper wall of the second bend gradually decreases, which reduces the friction loss and collision loss in the corresponding areas. However, the longer the length of the serpentine nozzle, the larger the wetted area of the internal flow, which leads to the increase in friction loss along the runner. The combined effect of these causes the internal flow friction loss to increase with the increase in LDR, as shown in Figure 15.

Figure 16 displays the surface pressure distribution on the afterbody of aircraft equipped with serpentine nozzles with different LDR. The upper surface pressure increases gradually along the external flow direction, and then rises rapidly after a sudden drop near the separation point, reaching the maximum near the nozzle outlet, while the lower surface pressure increases continuously along the external flow direction. Since the nozzle outlet profile and assembly position are independent of LDR, the Mach number distribution of the nozzle tail jet under different LDR is also similar (Figure 13), and the difference in LDR has no significant effect on the surface pressure distribution on the afterbody of the aircraft. Therefore, the pressure drag and total drag of the afterbody are slightly changed with the increase in LDR, as shown in Figure 17.

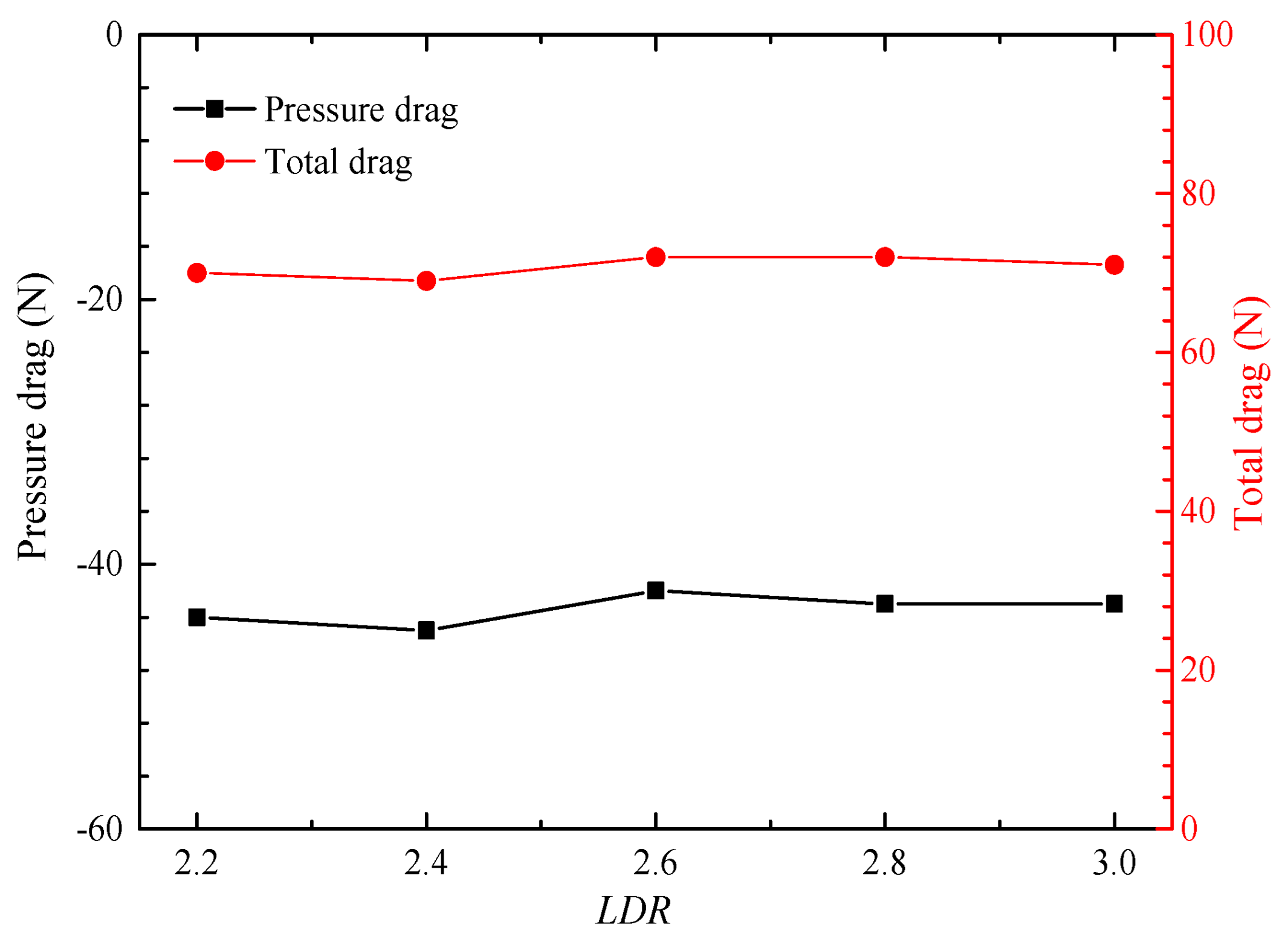
The increase in LDR leads to an increase in internal flow friction loss (Figure 15), and the increase in longitudinal offset will cause an increase in nozzle flow resistance. Although the longitudinal deflection and lateral expansion of the internal flow runner become slower, reducing the impact loss and acceleration loss at the bends, the degree of flow deterioration is stronger, resulting in a decline in the aerodynamic performance of the nozzle, as shown in Figure 18. With the increase in LDR, the total pressure recovery coefficient, flow coefficient and axial thrust coefficient all decrease slightly, while the thrust vector angle remains constant. Compared with LDR = 2.2, the total pressure recovery coefficient, flow coefficient and axial thrust coefficient of the LDR = 3.0 configuration are reduced by 0.21%, 0.41% and 0.13%, respectively, indicating that the variation in LDR has little effect on the aerodynamic performance of the serpentine nozzle.

3.3. Effect of SR on the Interaction between the Nozzle Flow and External Flow

The shielding rate of the serpentine nozzle determines the degree of exposure of the high-temperature components of the aircraft, and has an important impact on the infrared radiation intensity of the high-temperature wall and the aircraft tail jet. 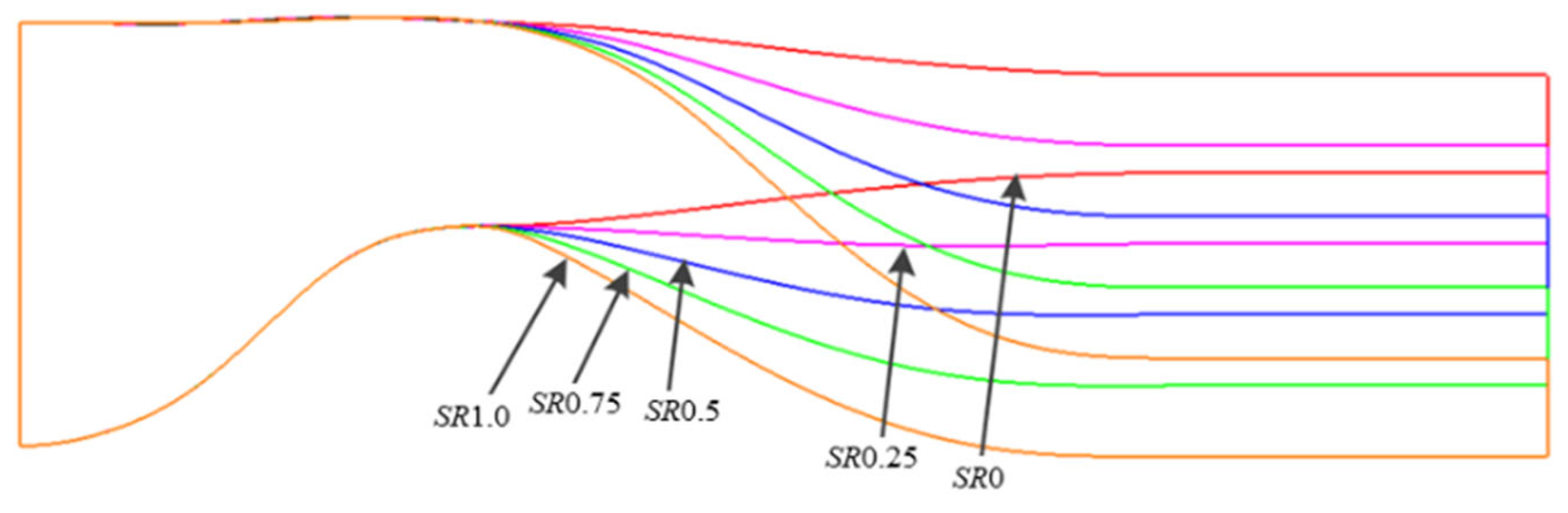To explore the influence of SR on the interaction between the nozzle flow and external flow, five nozzles with different SR (=0, 0.25, 0.5, 0.75, 1.0, AR = 6.0, LDR = 2.6) are adopted, as shown in Figure 19. The change in SR is mainly realized by modifying the profile of the second S-bend runner. The higher the SR, the greater the offset of the nozzle outlet, and the greater the longitudinal curvature of the second S-bend.

Figure 20 depicts the Mach number distribution on the symmetry cut plane of the aircraft under different SR. For SR = 0, the runner behind the first S-bend is a rectangular convergent nozzle, and the internal flow continues to accelerate until the velocity in the straight section reaches the sonic speed. The Mach number contour at the second S-bend shows a rightward inclination trend, with the degree of leftward inclination decreasing as it approaches the nozzle outlet, and eventually an oblique shock wave is formed at the outlet. The tail jet expands unilaterally upward because of the lower baffle at the outlet, and mixes with the separated external flow around the afterbody, producing significant interference shock waves and shear layer structures. As SR increases, the curvature of the second S-bend increases gradually, as well as the accelerating effect near the upper surface of the second S-bend. The accelerating region also expands gradually, inducing the gradual leftward inclination of the Mach number contour at the nozzle outlet. However, due to the consistent geometric characteristics of the nozzle outlet, the Mach number distribution tends to be similar within the straight section, and the corresponding flow characteristics of the tail jet are also similar.

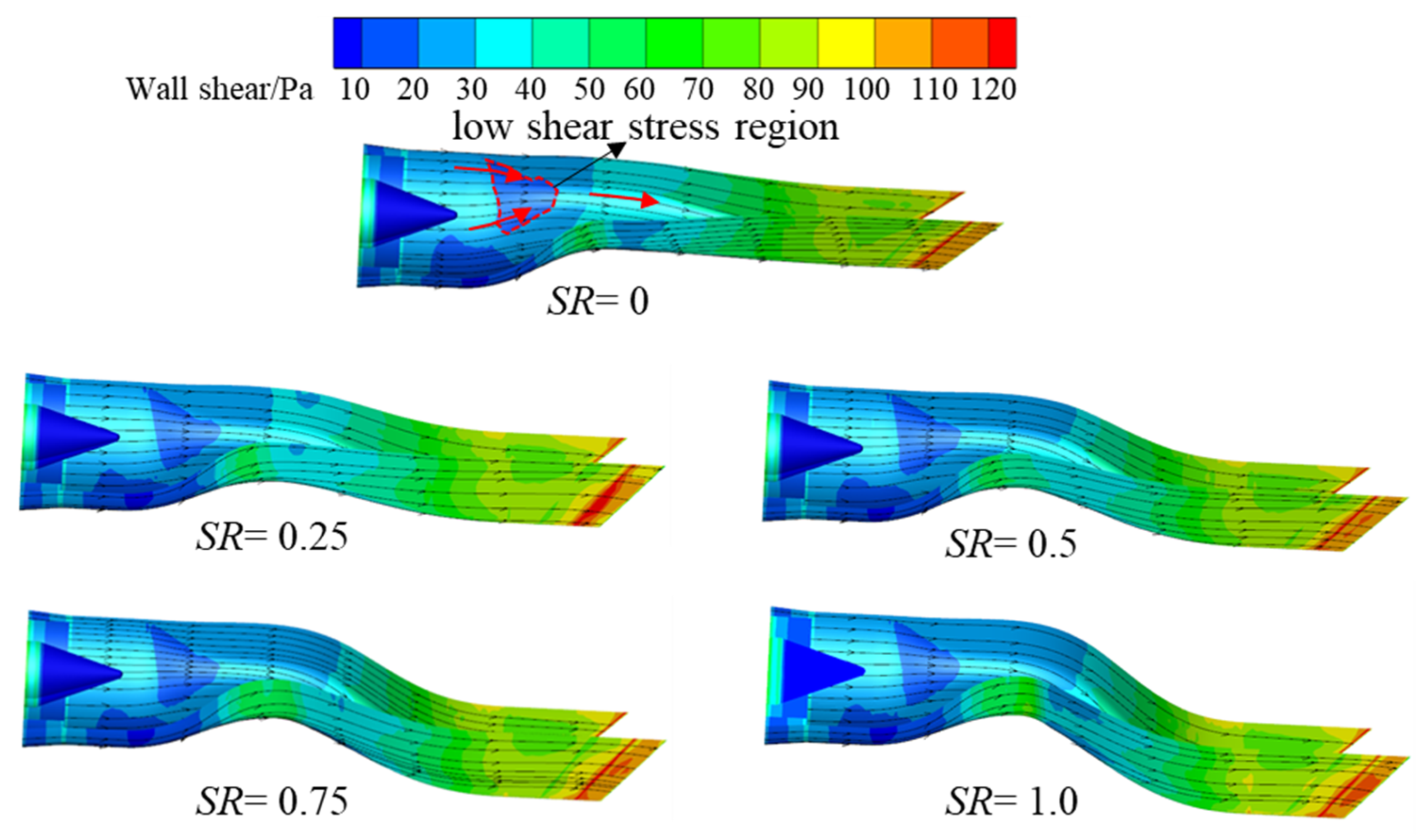
Figure 21 shows the distribution of wall shear stress and the limiting streamline on the nozzle wall under different SR. For SR = 0, the wall shear stress tends to increase along the nozzle flow, but a local high wall shear stress zone appears near the lower wall of the first S-bend. With the increase in the second S-bend curvature, the longitudinal bending degree of the limiting streamline increases, and the limiting streamline at the equal straight section gradually closes inward. With the increase in shielding ratio, the wall shear stress located at the lower wall of the first S-bend and the upper wall of the second S-bend gradually increases, which leads to the increase in the local friction loss. 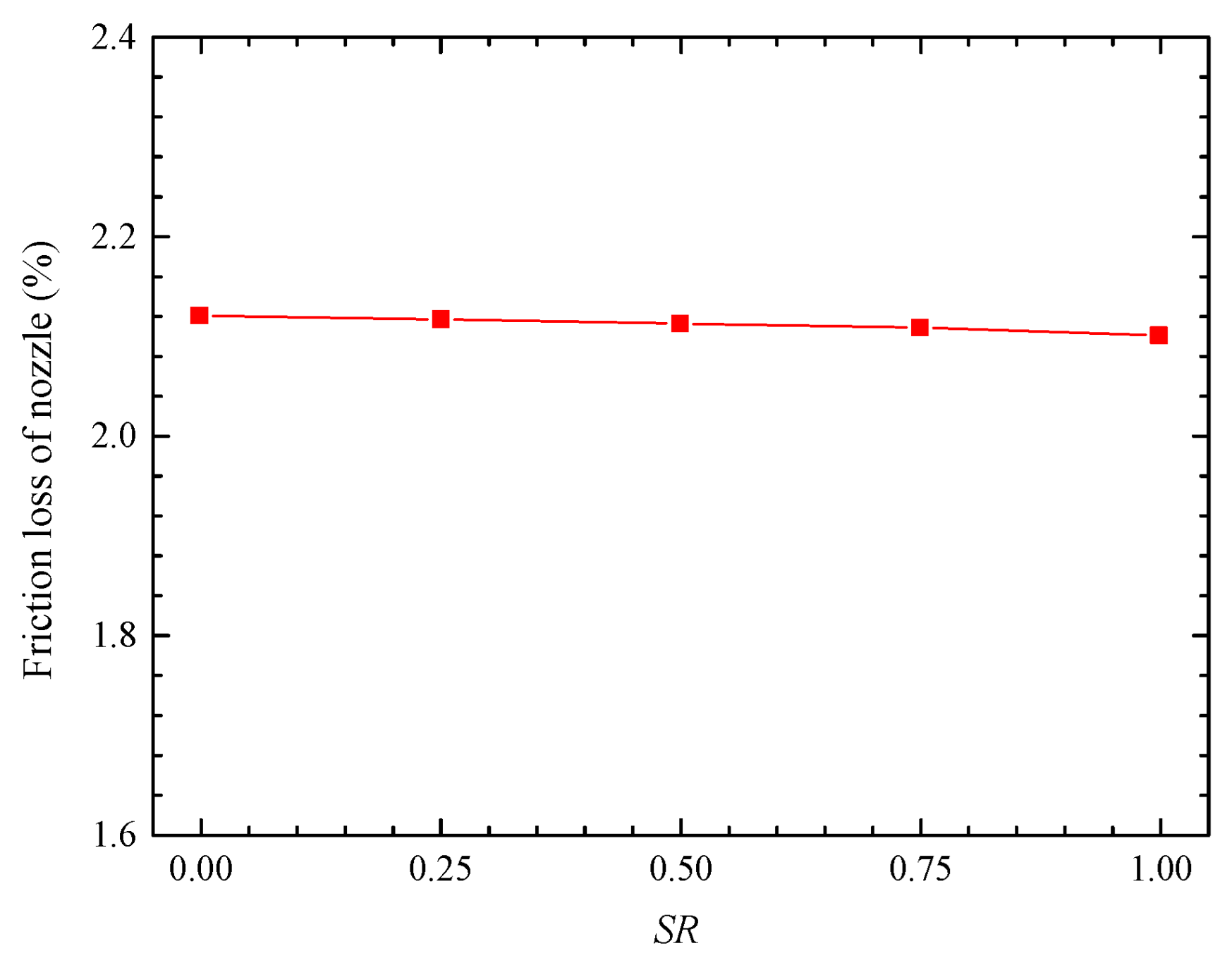Furthermore, although the LDR of nozzles with different SR is equal, the length of the nozzle flow runner becomes slightly longer as the SR increases, which causes the wetted circumference area to increase, leading to the increase in friction loss. However, the wall shear stress on upper wall of the second S runner generally decreases, which reduces the friction loss in this area. These two factors have opposite effects on nozzle friction loss, and the influence degree is similar, which eventually leads to a slight change in nozzle flow friction loss, as shown in Figure 22.

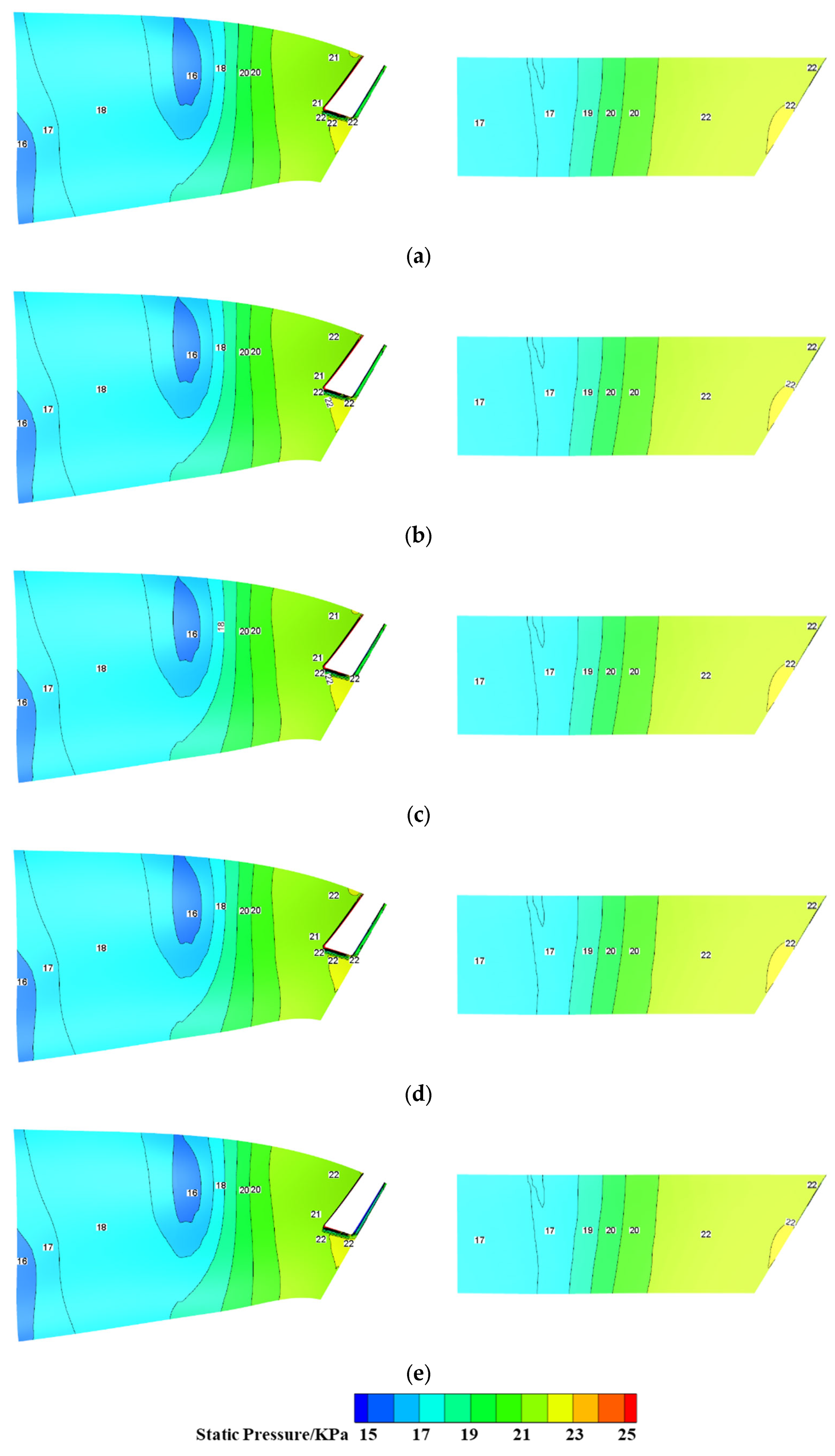
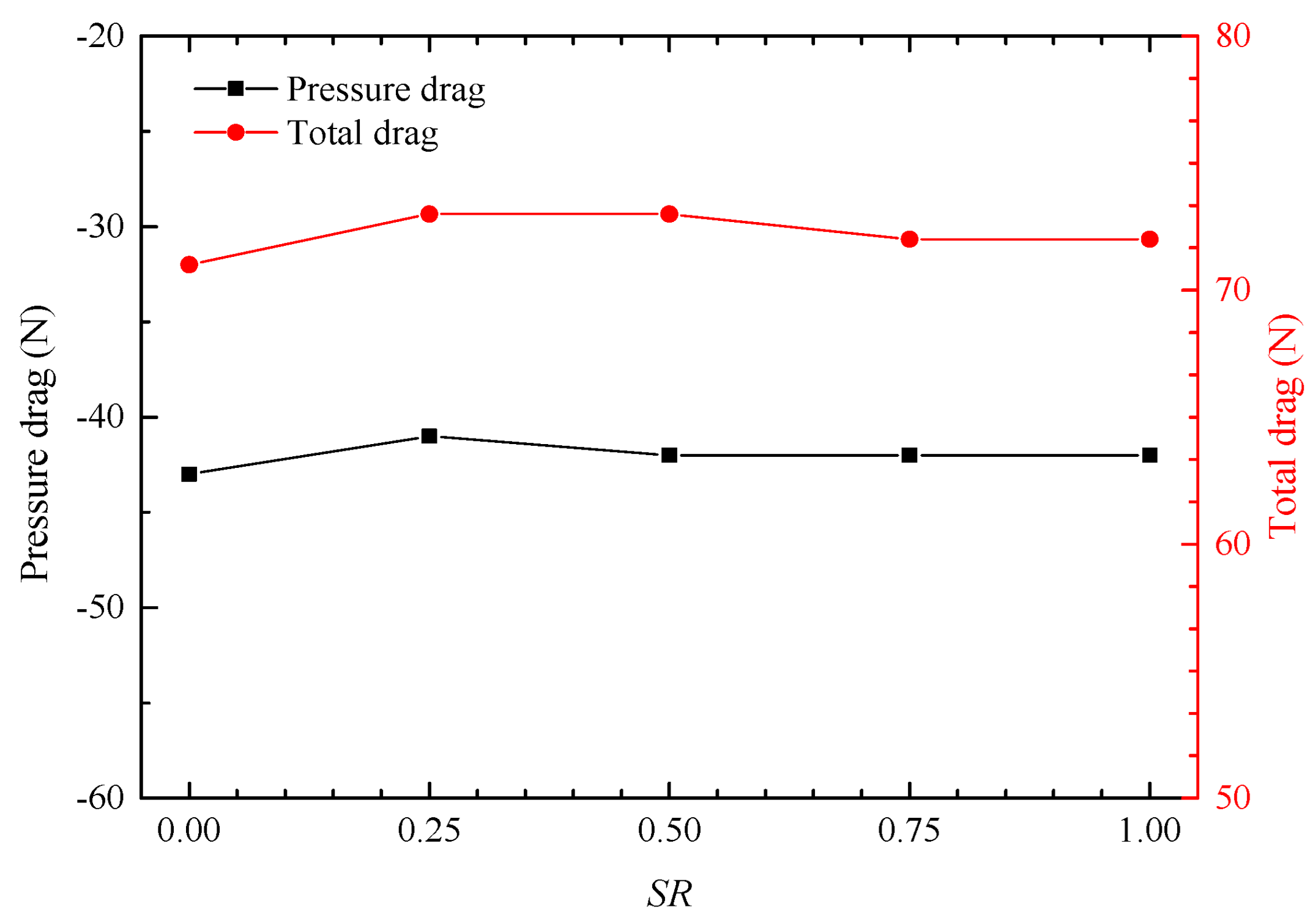
Figure 23 depicts the influence of SR on the surface pressure distribution of the afterbody. Due to the similarity in the flow characteristics of tail jets (Figure 20), the surface pressure distribution of the afterbody is basically the same under different SR, so the pressure drag and total drag of the afterbody change slightly (Figure 24), indicating that the variation in SR has slight influence on the aerodynamic characteristics of the afterbody.

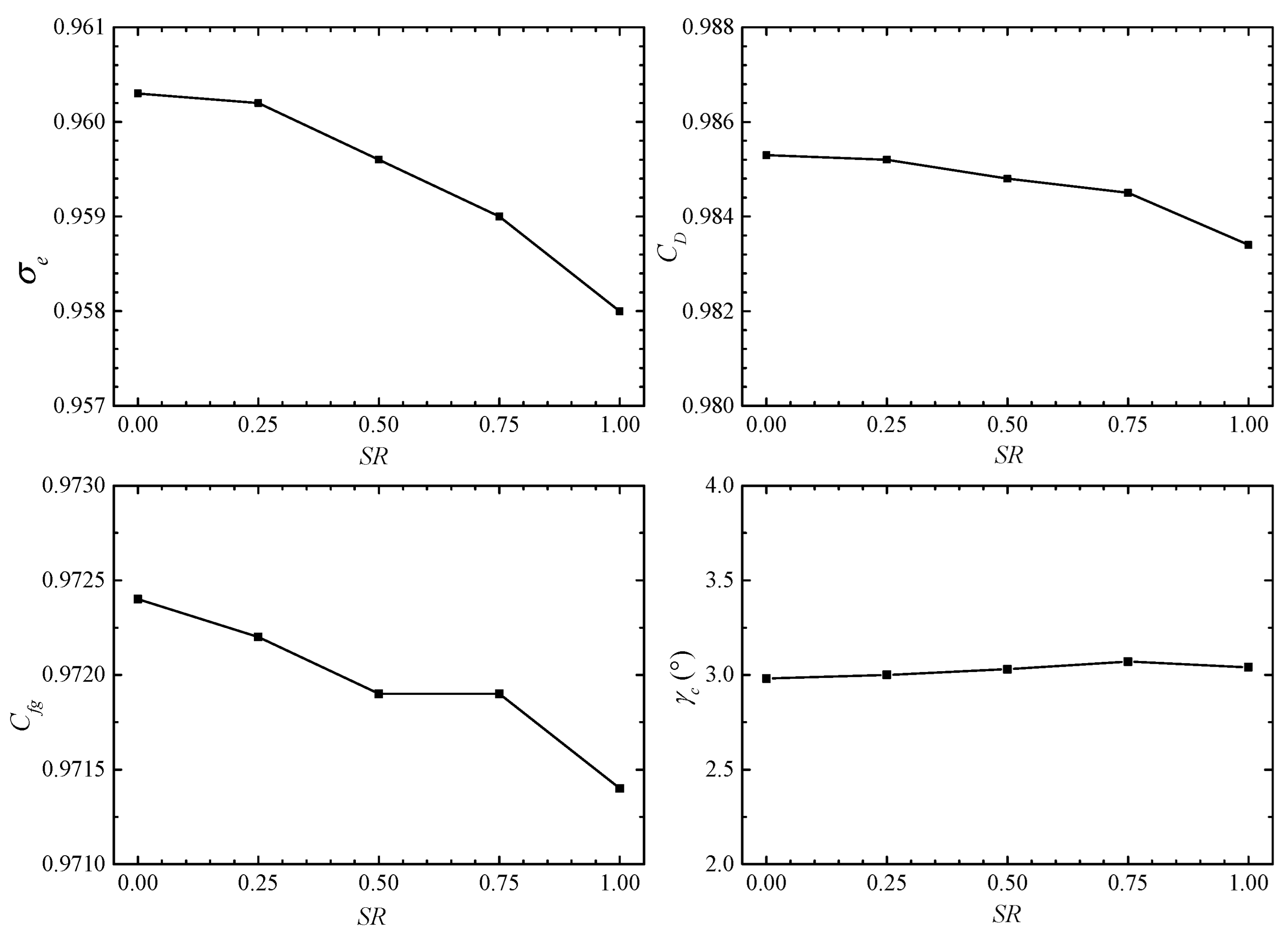
As the SR increases, the curvature of the second S-bend increases, which leads to the strengthening of the flow accelerating effect at the bend and the expansion of the accelerating region. Meanwhile, the local collision loss and acceleration loss increase, while the friction loss along the route is almost unchanged (Figure 22). Therefore, the aerodynamic performance decreases. The total pressure recovery coefficient, flow coefficient and axial thrust coefficient all decrease with the increase in SR, as shown in Figure 25. Compared with the non-shielded nozzle (SR = 0), the total pressure recovery coefficient, flow coefficient and axial thrust coefficient of the fully shielded nozzle (SR = 1) decreased by 0.24%, 0.19%, and 0.10%, respectively. However, the thrust vector angle is almost constant, which is independent of SR.

4. Conclusions

This study examines the influence of the serpentine nozzle configurations on the flow characteristics and aerodynamic performance of aircraft that have a double-ducted serpentine nozzle under cruising conditions. It discusses the effects of AR, LDR, and SR on the aerodynamic characteristics of the afterbody and nozzle performances using numerical investigation.

The distribution of Mach number in the nozzle flow at the symmetrical plane is asymmetrical. Near the S-bend, there is a local accelerating effect that causes the wall shear stress to be higher than that of the surrounding wall. The interaction between the high-speed nozzle flow and the separated flow outside the afterbody produces a visible cross-shockwave and shear layer structure. With the increases in AR and LDR, the local accelerating effect of nozzle flow weakens, and the corresponding wall shear stress reduces; hence, the friction loss of nozzle flow increases linearly. Conversely, an increase in SR enhances the local accelerating effect and expands the corresponding accelerating region, causing an increase in the wall shear stress. An increase in AR promotes the mixing of nozzle flow and external flow, shortening the core area of the tail jet and weakening the shockwave intensity. However, the interaction characteristics between the nozzle flow and external flow, as well as the surface pressure distribution of the afterbody, are less affected by the variation in LDR and SR, so the friction drag and total drag of the afterbody change only slightly. The total pressure recovery coefficient, flow coefficient, and axial thrust coefficient all decrease with an increase in AR, LDR, and SR. The thrust vector angle is only dependent on AR, and the larger the AR, the smaller the thrust vector angle. These findings provide valuable insights into the complex interaction between the external and nozzle flow of aircraft equipped with a double-ducted serpentine nozzle, which can aid designers in optimizing their designs for improved aerodynamic performance.