Abstract
Gamma-ray bursts (GRBs) are intense and short-lived cosmic explosions. Miniaturised CubeSat-compatible instruments for the study of GRBs are being developed to help bridge the gap in large missions and assist in achieving full sky coverage. CubeSats are small, compact satellites conforming to a design standard and have transformed the space industry. They are relatively low-cost and are developed on fast timescales, which has provided unparalleled access to space. This paper focuses on GMOD, the gamma-ray module, onboard the 2U CubeSat EIRSAT-1, launched on December 1st 2023. GMOD is a scintillation-based instrument with a cerium bromide crystal coupled to an array of sixteen silicon photomultipliers, designed for the detection of GRBs. The characterisation of GMOD in the spacecraft, along with the validation of an updated spacecraft MEGAlib model is presented and this approach can be followed by other CubeSats with similar science goals. The energy resolution of the flight model is 7.07% at 662 keV and the effective area peaks in the tens to hundreds of keV, making it a suitable instrument for the detection of GRBs. An investigation into the instrument’s angular response is also detailed. The results from this characterisation campaign are a benchmark for the instrument’s performance pre-launch and will be used to compare with the detector’s performance in orbit.
1. Introduction
Gamma-ray bursts (GRBs) are violent, bright and brief explosions in the universe resulting from the death of a massive star or the collision of two compact objects, such as neutron star–neutron star or neutron star–black hole mergers [,]. The breakthrough coincident detection of electromagnetic signals (from radio to gamma rays) and gravitational waves in 2017 facilitated a new way to probe these complex events [,]. A major challenge to the future of gamma-ray astronomy and the progression of GRB science is the lack of new missions. The legacy and current gamma-ray missions have excelled in advancing the understanding of these objects but the majority are operating beyond their nominal lifetimes [,,,]. Additionally, current gamma-ray observatories cannot provide full-sky coverage in a single observation for these brief isotropic explosions, which is critical for future coincident detections. Obtaining a population of GRB/gravitational wave joint detections will be important in determining the characteristics of the different types of GRBs, confirming other theorised progenitors and the extracted properties can be used to search archival data (e.g., []) for similar candidates. Furthermore, increasing the number of joint detections could constrain the neutron star equation of state, advance the understanding of the origin of the heaviest elements in the universe and provide new insights into fundamental physics such as investigating the difference between the speed of gravity and the speed of light [,].
CubeSats are small-scale satellites, usually conforming to a design standardisation, defined by Cal Poly specifications []. CubeSats have grown in popularity in recent years due to their science and technology demonstration capabilities [,,,]. CubeSats were originally developed as an educational tool [,], resulting in the production of commercial-off-the-shelf (COTS) components. COTS components can be used for the fundamental subsystems of the satellite, e.g., power, communications and onboard computer (OBC), allowing for more resources to be applied to the science objectives of the mission []. CubeSats are relatively low-cost and have short launch timescales [], making them ideal candidates to bridge the gap in gamma-ray missions during the multi-messenger era []. In addition to the current large-scale gamma-ray missions, a fleet of GRB-detecting CubeSats could allow for the adequate detection and localization of GRBs, and increased sky coverage. SmallSats with GRB detection and localisation capabilities are in development, e.g., BurstCube [,], MoonBEAM [], HERMES [], GRBAlpha [] and CAMELOT [].
The Educational Irish Research Satellite (EIRSAT-1) is a 2U CubeSat with a primary payload, the gamma-ray module, GMOD, developed for the detection of GRBs [,] at energies 60 keV to ≈2 MeV, as presented in Figure 1. GMOD is a <1 U scintillation-based detector and consists of two main components: the detector assembly and the GMOD Motherboard (MB) [,,]. The detector assembly holds the CeBr3 scintillation crystal (25 mm × 25 mm × 40 mm), which interacts with gamma-ray photons from GRBs to produce optical photons, which are collected by a tiled array of 16 silicon photomultipliers (SiPMs). The outputs from the SiPMs are read out and digitised by an application-specific integrated circuit (ASIC), produced by Integrated Detector Electronics AS (IDEAS), Oslo, Norway called SIPHRA (Silicon Photomultiplier Readout ASIC) []. The GMOD motherboard was developed in-house [,] and supports the electronics for power and the readout of the detector assembly. The GMOD MB converts the channel data into time-tagged events (TTEs). TTEs are generated for the 16 individual channels of SIPHRA and for the sum channel (sum of 16 channels). Both sum and 16 channel TTEs are sent in pages to OBC. GMOD is based on in-house instrument heritage and will be used to scale up to a 6U mission with detection and localisation capabilities, called Gamma-ray Investigation of the Full Transient Sky (GIFTS) [,,,,].

Figure 1.
The flight model of EIRSAT-1 including the location of major subsystems and the GMOD detector assembly and motherboard. The coordinate system of the spacecraft is also detailed.
The characterisation of an instrument in the spacecraft is necessary to investigate its performance and ensure that it is capable of achieving the mission’s science goals []. Instrument characterisation as presented in this paper provides an in-depth understanding of the behaviour of the instrument that could not be achieved via functional testing. Performing the characterisation of the flight model of GMOD in EIRSAT-1 is essential for interpreting the downlinked science data throughout the mission and identifying intrinsic features in the data products. This characterisation campaign also provides a benchmark of the experiment’s performance pre-launch. The results from this campaign can be used to compare with the detector’s performance in-orbit, during commissioning and nominal operations.
Initially, the ground-based energy calibration of GMOD was performed to map the analog-to-digital (ADC) values to energy. Once the data were in energy space, the properties of the detector could be investigated, including the instrument’s resolution. A calibration of the instrument will be performed post-launch using the signature of galactic positron annihilation at 511 keV to determine the shift in the energy spectrum []. Additionally, lines from solar activity, e.g., the 2.2 MeV line from neutron capture on hydrogen [], can be used for in-orbit calibration. In addition to the ground characterisation, in-orbit cross-calibration will be performed when GRBs are detected in coincidence with other missions (e.g., Ref. []).
The aim of these tests was, first, to evaluate the effective area of the GMOD detector as a function of energy and source incident angle to correctly generate the detector response files []. This gave an understanding of the response of the detector and allowed an interpretation of the mission’s science data when analysing potential GRB triggers from different sky positions (on- and off-axis). Some triggers were also simulated by bringing a source close to the spacecraft for a short period of time. The aim of these tests was to further validate the correct operation of the trigger algorithm and data processing and protection in the onboard software (OBSW) v18.3; see Refs. [,] for more details. Simulations were performed in MEGAlib, a collection of programs to simulate gamma-ray instrumentation [], to correlate with measurements in the lab and validate a Geomega EIRSAT-1 model, with the original model detailed in Ref. [].
Section 2 presents the experimental set-up in the cleanroom, including the angular measurements on a motorised turntable, where all the characterisation tests were performed with the EIRSAT-1 flight model (FM). The methods for producing the calibration and energy resolution are outlined in Section 3 and Section 4. The effective area of GMOD as a function of energy and the angular response of GMOD are presented in Section 5. The trigger data analysis is presented in Section 6. The simulations performed in MEGALib are discussed in Section 7 and compared to the experimental data to assess the accuracy of the model.
2. Characterisation Test Set-Up
2.1. Energy Calibration Hardware Set-Up
Initially, the measurements to determine the channel–energy relation of GMOD were performed. The main goal of these measurements was to maximise the number of counts during the integration interval. The spacecraft was secured in a vertical support stand for the energy calibration source measurements. The EIRSAT-1 FM was connected to the power and data acquisition ground-support equipment (GSE) via the Umbilical Interface Unit (UIU), as labelled in Figure 2 (Panel B). The UIU interfaced with a bench power supply unit (PSU) to provide a battery voltage of 8.35 V for the spacecraft. The UIU also provided an interface between the spacecraft and the laptop used to command the satellite via the MCS v21.2 and Python v3.7 scripts and retrieve the experimental data stored on the OBC. On the laptop, a terminal was used to monitor the debug log from the spacecraft throughout the test activities.
In the first test, different radiative sources (enumerated 1–6, see Table 1) were placed close to GMOD. As in Figure 2, sources 1–5 were positioned on the cross-hairs, which identified the centre of GMOD’s CeBr3 crystal, on a cap on the +Z face of the spacecraft (Panels A and C of Figure 2). The distance from the end cap to the centre of the crystal (CoC) is 49.6 mm. The position of source 6 is centred on the X face of the crystal, 222 mm from the +Y face and 119 mm from the −Z face (see Panel D of Figure 2). It was found that, with some of the sources in this position, the OBC could not manage the rate at which GMOD was generating data for long durations. To determine the GMOD data rate that the OBC could successfully handle, the sources were placed at different distances from the CoC.

Table 1.
Radioactive sources used for GMOD characterisation. The peak energies and transition probabilities for sources marked with an * are from [] and those marked with † are from []. The source activity for sources 1, 2, 3 and 6 are in Ci and quoted as of 12:00 GMT on 1 December 1979. The activity of source 5 is quoted as of 15 May 2013.
For each source position, the GMOD data production rate, in pages/min, was monitored via the MCS. The address of the GMOD sum page received by the OBC was determined at the same time as the address of the most recent page of generated summed data multiple times over a few minutes. If the difference between these was increasing as time progressed, the rate at which GMOD was producing data was greater than the rate at which the OBC was reading data. The source was moved until the difference between these two parameters remained the same over time, indicating that the OBC could manage the data rate produced by GMOD. This was found to be ∼250 pages/min. Each page contains 31 TTEs, so the TTE rate that the OBC can keep up with for long-duration experiments (∼hours) is ∼130 TTEs/s or 130 counts/s. As GRBs are on much shorter timescales, this issue will not affect GMOD’s ability to detect these events. Table 2 contains the exact sources used for the energy calibration measurements, their location with respect to the CoC in GMOD and the integration times.

Table 2.
Energy calibration source positions and the duration of spectral integrations. Sources 1–5 were placed above the +Z endcap of the spacecraft at various distances from the centre of the GMOD crystal (CoC). Source 6 was aligned with the CoC in X, placed 222 mm from the +Y face and 119 mm from the −Z face on the table.

Figure 2.
(A) EIRSAT-1, including co-ordinate system, on vertical integration stand for energy calibration measurements with a source positioned on the +Z endcap. (B) GSE for measurements; on the left is the FM, in the centre is the UIU and on the right is the PSU powering the spacecraft. (C) Source positioned on the +Z endcap on cross-hairs marking the centre of the CeBr3 crystal. (D) Position of source 6 in Table 2, the source is centred on X of the crystal, 222 mm from the +Y face and 119 mm from the −Z face.
2.2. Angular Measurements Hardware Set-Up
For the determination of the angular response of the FM, two sources with known activities, 241Am and 137Cs, were used. Due to the limited time with the FM, integrations with these sources at various angles were performed at the same time, with the two sources taped together. They were selected as the gamma-ray peaks from each were at sufficiently different energies so as to not interfere with each other. Figure 3 presents the hardware set-up used, where the spacecraft was mounted on a turntable with an attached moveable appendage. The turntable had a slip ring and interface printed circuit boards (PCBs), which facilitated powering and commanding the spacecraft via the UIU. The UIU provided an interface with a bench PSU to provide power for the spacecraft. It also provided the connection to the MCS on the laptop, which facilitated setting up the experiment and downlinking the data. This hardware was designed for attitude control and mission testing and utilised for GMOD characterisation.

Figure 3.
The test set-up for the measurements made to determine the angular response of GMOD. The FM was secured on a motorised turntable and the source was mounted on a moveable appendage, to vary the polar and azimuthal angles, respectively.
The sources were placed at a variety of different positions relative to the spacecraft, with some example orientations displayed in Figure 4. This was achieved by varying the polar and azimuthal angles. The polar angle was varied by mounting the source on a movable arm that could be rotated about an axis that went through the centre of the detector. The azimuthal angle was varied by securing the spacecraft on the controllable turntable, and moving it to the required positions. The turntable was also controlled via the Python test scripts, and a separate script was written for these measurements containing the set-up commands for GMOD and the commands for the turntable to move the spacecraft to a specified range of angles.

Figure 4.
(A) EIRSAT-1 FM on vertical integration stand mounted to the turntable for polar 0° measurement, i.e., the sources, circled in orange, mounted at the crystal centre in X, Y and 22.5 cm above the +Z face of the spacecraft. (B) FM on turntable with the sources, circled in orange, positioned at the polar 60°, azimuthal 270° measurements. (C) FM on turntable with the sources, circled in orange, positioned at the polar 90°, azimuthal 0° measurements. (D) Source positions (blue points) for all off-axis measurements. The red point marks the centre of the scintillator (40 mm in length along Y and 25 mm along X and Z). The orange point marks the centre of the spacecraft.
Table 3 shows the locations tested, in both polar and azimuthal angles with respect to the crystal centre and in Cartesian coordinates with respect to the centre of the spacecraft. These Cartesian coordinates are included, as they were required for the MEGAlib simulations discussed in Section 7. The final column of Table 3 shows the integration time (in seconds). During the test runs, all the scripts were run for 3.5 h; however, for locations where GMOD was most sensitive (e.g., +Y face, polar 90°, Az 270°) the number of TTEs downlinked from the OBC was not representative of the number of TTEs generated by GMOD. This issue was due to the OBC being unable to manage the rate at which GMOD was producing data; this was accounted for in the data analysis. The analysis and results of these off-axis measurements are presented in Section 5.

Table 3.
Positions at which the source was placed for the angular response investigation for GMOD FM. These positions are provided in polar and azimuthal angles with respect to the crystal centre and in Cartesian coordinates with respect to the centre of the spacecraft. The integration time for each measurement is provided in the final column.
2.3. Data Acquisition and Scripting
Due to time constraints on the availability of the EIRSAT-1 FM, the ability to execute tests overnight and without an operator always present was paramount. Python scripts were composed to configure the ∼40 parameters to set up GMOD and then allow for the specified amount of time for spectral integration. The scripts interfaced with the mission control software (MCS v21.2) and commanded the experiment as if it were in flight. The main interface with the spacecraft was via Bright Ascension’s MCS []. The Python scripts performed the following tasks: turning on GMOD and experiment configuration including firmware version and operational mode. The script then synchronised the time on GMOD’s microcontroller to the OBC time, and initiated GMOD generating data and streaming it to the OBC. The script recorded the storage location of each run on the OBC and, once a number of integrations had been completed, a second script could be used to downlink the data. The data were downlinked through the satellite telemetry interface using the MCS connected to the OBSW. This campaign provided the opportunity to test the robustness of the chain of data acquisition that will be followed during the actual mission.
3. Energy Calibration
3.1. Single-Source Spectra
The FM of GMOD was configured to take a 12 h measurement for each of the sources from 1 to 6 in Table 2. The summed channel TTEs stored on the OBC corresponding to each measurement were downlinked and analysed in Python. A 24 h background integration was also performed and downlinked. All of the data sets were divided by their respective integration times, and the background spectrum was subtracted from the raw source spectra. Figure 5 presents the raw spectrum (purple), background spectrum (grey) and background-subtracted spectrum (teal) for each source.
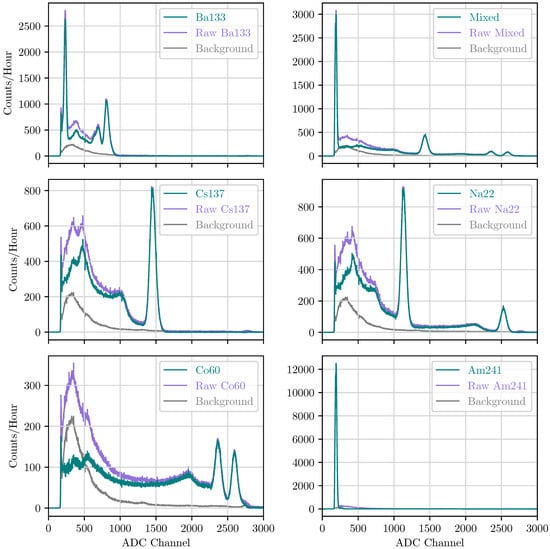
Figure 5.
GMOD FM background-subtracted spectra (teal) in counts/hour for the six sources in Table 2. In each panel, the background spectrum (grey) and the raw source spectrum (purple) are presented.
3.2. Channel–Energy Relation
All the source spectra produced with GMOD followed a primarily Gaussian shape, which varied depending on the underlying interaction with the CeBr3 crystal. The photopeaks all fit with the following Gaussian function:
where N is the height of the peak, is the standard deviation and is the position of the centre of the peak []. In order to translate the ADC channels to energy values, a channel–energy relationship was first determined. Each photopeak from the sources listed in Table 2 was fitted with a Gaussian function, and the channel number for the centre of the photopeak, , was extracted. Figure 6 presents four examples of the functions fitted to energy peaks in the spectra to determine the channel number of the peak centre.
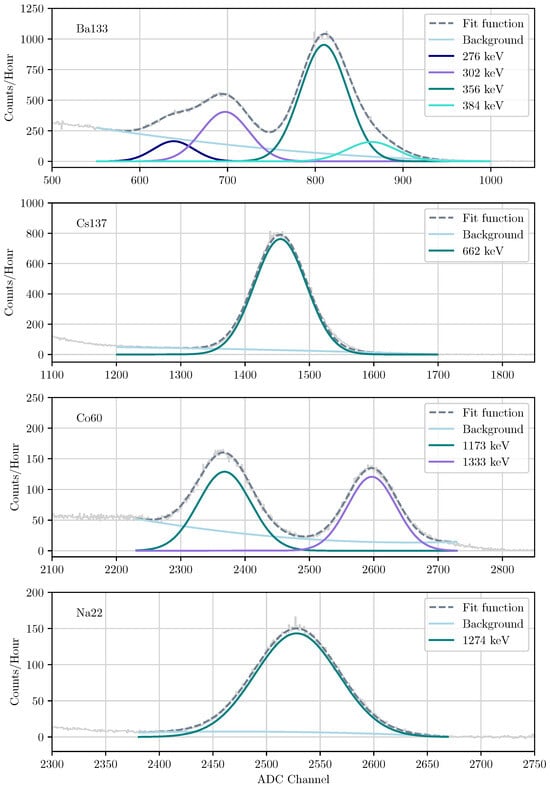
Figure 6.
A sample of four fits to GMOD spectra in terms of ADC channel number. Each panel shows the fit (dashed grey line) to the background-subtracted spectrum. The composite functions of the fit are plotted as solid lines.
In the analysis, the gamma-ray photopeaks could not be fitted with a simple Gaussian, as there are other contributions in the photopeak such as from back-scattering off of nearby structures, background contributions and Compton distributions (as seen in the spectra in Figure 5). In general, the peaks were fitted with a combination of a Gaussian function and a polynomial function to account for other contributions to the photopeak. The final fit is plotted as a dashed line and the composite functions are plotted separately as solid lines in Figure 6.
The ADC channel numbers associated with each peak centre, , were then plotted against the known energy of the photopeaks, as listed in Table 1, to map the channel numbers to energy. Figure 7 presents the channel–energy relation for GMOD FM. The relationship between the ADC channel number and energy, E, was best fitted with a quadratic of the form
where a, b and c are the fit coefficients. The coefficients of the fit to the GMOD channel energy relation are a = 3.56 × 10−5, b = 0.42 and c = .
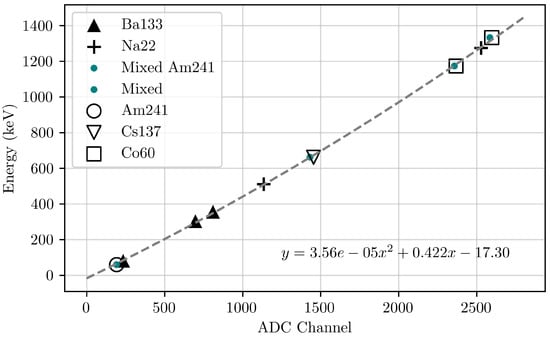
Figure 7.
Energy–channel calibration relation for GMOD FM. The relationship was fit with a quadratic (dashed line) with the coefficients a = 3.56 × 10−5, b = 0.42 and c = . The teal points representing the mixed source were not used in the final fit due to the lab temperature being different for these measurements. Measurement errors for gamma-ray line centres are on the order of 0.3 ADC channel.
4. Energy Resolution
The energy resolution represents the broadening of a gamma-ray line due to photoelectron statistics and detector effects, it quantifies how well the detector can define a gamma-ray line for a specific energy.
The energy resolution, R, of a detector is defined as
where the full-width at half-maximum (FWHM) of the energy pulse is divided by the location of the peak’s centre, []. The FWHM is calculated using the standard deviation, , of the Gaussian fit function, as follows:
There are a number of contributing factors resulting in the increase of a detector’s energy resolution such as the aforementioned photoelectron statistics, changes to the configuration of GMOD and non-uniformity of the scintillator’s response or the SiPMs’ performance. The sources used in this testing were only a sample of the full range of energies that could be emitted by astrophysical sources. The resolution of the detector for this larger energy range can be extrapolated by fitting the following function to the physical measurements []:
The constant, a, is negligible because SiPMs are high-gain devices and the noise is not an issue for the measurement of gamma rays above 50 keV. The term accounts for the fluctuations in the number of scintillated photons and photoelectrons produced by the SiPMs. The final term, , is attributed to the non-ideal transfer of the scintillated photon energy from their creation locations to the SiPMs.
The energy calibration was first applied to the spectra produced by GMOD for the sources listed in Table 2, such that the spectral counts/keV/hour were plotted against energy in keV, rather than channel number, as in Figure 8.
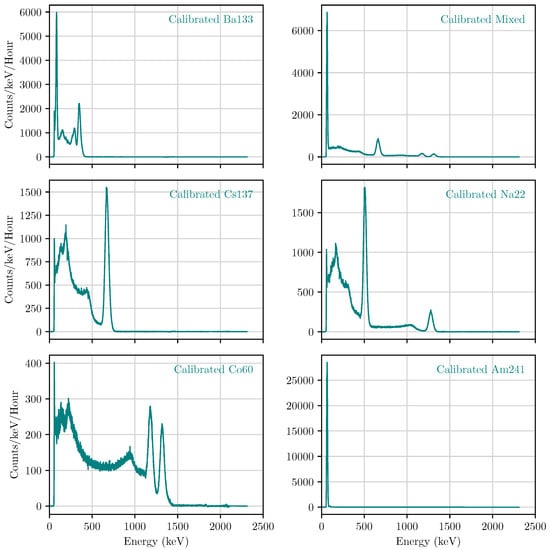
Figure 8.
GMOD FM-calibrated spectra (teal) in counts/keV/hour for the six sources in Table 2.
The photopeaks were then re-fitted with a combination of a Gaussian(s) and a polynomial function to account for other contributions to the photopeak to determine and, using Equation (4), the FWHM in terms of energy. Figure 9 presents four examples of fitting the photopeaks of the sources in energy space. Figure 10 presents the values for the photopeaks as a function of energy. Equation (5) was then fitted to these points with coefficients b = 0.6761 and c = 8.9754 × 10−3.
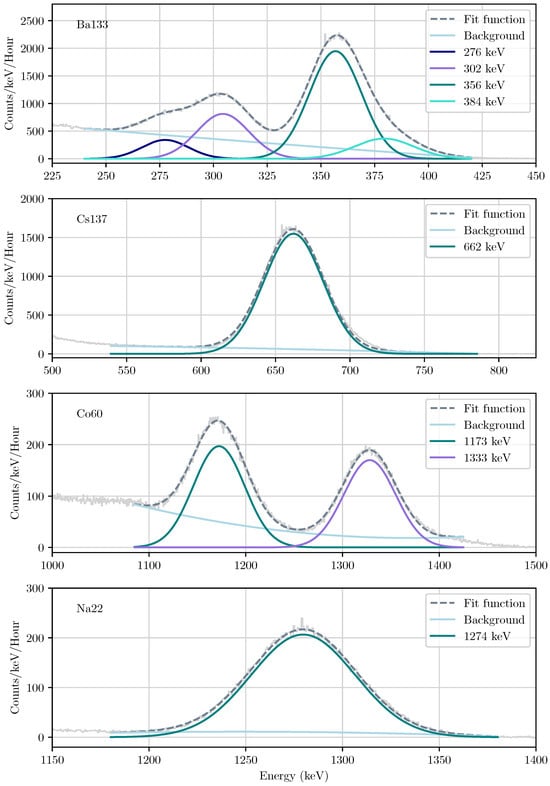
Figure 9.
A sample of four fits to GMOD spectra in terms of energy (keV). Each panel shows the fit (dashed grey line) to the energy-calibrated spectrum. The composite functions of the fit are plotted as solid lines.
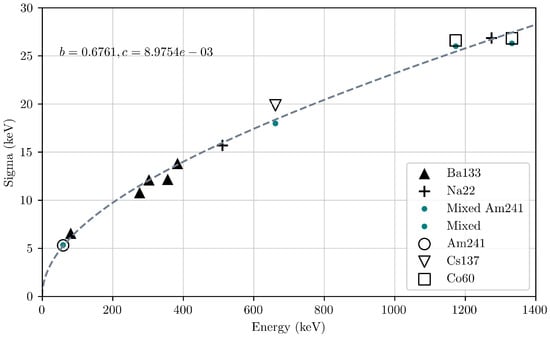
Figure 10.
GMOD FM as a function of energy, fit (dashed line) with Equation (3) and coefficients a = 0, b = 0.6761 and c = 8.9754 × 10−3. Relative statistical errors in the sigma values are under 4%.
The energy resolution of the photopeaks were determined using Equation (3). This energy resolution was plotted as a function of energy, as in Figure 11. Equation (5) can be expressed in terms of the FWHM (%), as follows:
and can be fitted to the data in Figure 11 to determine the resolution of the GMOD FM over a wide range of energies. The obtained coefficients of the fit are b = 0.6294 and c = 6.8994 × 10−3. The energy resolution of GMOD FM improves for incoming photons with higher energies and was found to be 7.07% at 662 keV.
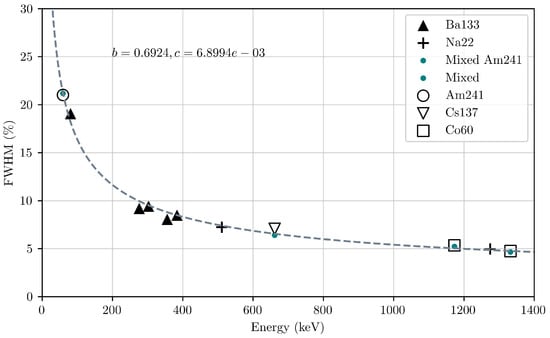
Figure 11.
Energy resolution in terms of FWHM (%) fit with Equation (6) and coefficients a = 0, b = 0.6294 and c = 6.8994 × 10−3. Relative statistical errors in the resolution values are under 4%.
5. Effective Area
The effective area of a gamma-ray detector accounts for the detection efficiency of the instrument and the observable area. The full-energy peak effective area, (cm2), for a detector is determined as []
where C is the number of counts in the photopeak, i.e., the area under the Gaussian, is the transition probability, s is the distance (cm) between the source and the detector and is the activity of the radioactive source (1/s). The activity is given by
where is the activity of the source (s−1) at a specified time, t is the time (s) between the determination of the activity and the performance of the test campaign and is the half-life of the source (s).
As the source is emitting gamma rays in all directions but only a fraction is observable to the detector, the term accounts for the fraction of photons emitted by the source that will actually come in contact with the detector.
Figure 12 presents the effective area of the flight model of GMOD as a function of energy, where all the sources were positioned above the +Z face of the spacecraft at the CoC. The source activity must be known for the determination of an absolute effective area, which limited the sources in Table 1 that could be used to determine GMOD’s effective area. Sources 1–3, 5 and 6 were used to determine the effective area of GMOD as a function of energy. Table 2 provides the position of these sources relative to the crystal centre, the s term in Equation (7). In Figure 12, the previously simulated effective area (blue) from [] is in good agreement with the physical measurements (see Section 7.2 for the updates made to the model to represent the FM including the addition of the GMOD top reinforcement bracket (GTRB), the structural bracket the detector assembly is mounted on). The instrument’s sensitivity appears to peak in the range of tens to a few hundred keV, as is desired for the detection of the prompt emission of GRBs. The effective area is lower for smaller energies as a result of gamma-ray absorption by the detector housing and spacecraft.
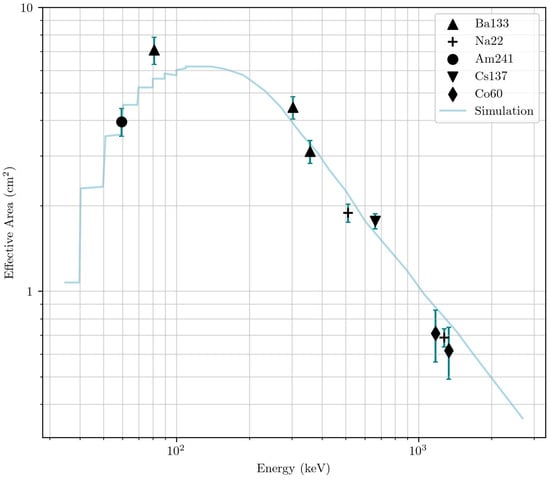
Figure 12.
GMOD FM effective area as a function of energy, where all the sources were positioned above the +Z face of the spacecraft at the CoC. Simulated photopeak effective area from [] plotted in teal for comparison to physical measurements.
The effective area of FM GMOD as a function of source incident angle was also investigated. As described in Section 2.2, due to time constraints, two sources, 137Cs and 241Am, were used together for the angular measurements. The effective area of GMOD was determined at 34 different incident angles, as listed in Table 3. Figure 13 presents the angular response of GMOD at 662 keV and Figure 14 at 59.4 keV. The angular response of GMOD at both these energies follows similar profiles. As shown in Figure 13 and Figure 14, the calculated values of the effective area have an uncertainty of 6–7%, which is due to an uncertainty of the source activity (5% for the 241Am source and 3.5% for the 137Cs source) and errors in the source-to-crystal distance (about 5 mm).
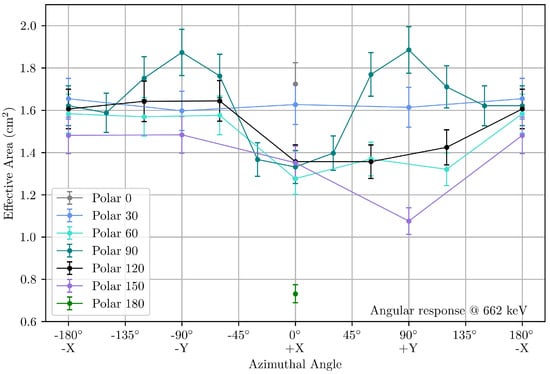
Figure 13.
Angular effective area of GMOD FM at 662 keV.
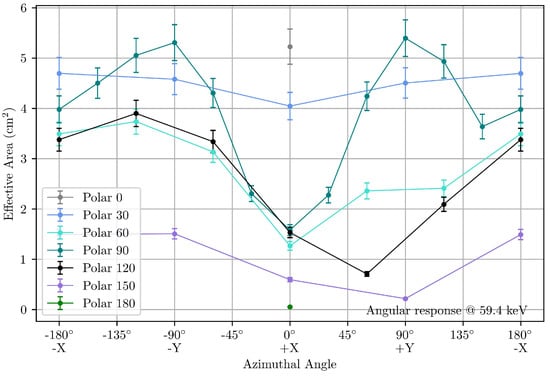
Figure 14.
Angular effective area of GMOD FM at 59.4 keV.
The measurements at polar angle 90° show the most diversity and the impact of the crystal geometry on the detector’s performance. The area of the Y and Z faces of the GMOD crystal is 10 cm2, and the X faces are 6.25 cm2. The effective area of GMOD peaks at the −Y and +Y faces, which correspond to the longer faces of the crystal. The only obstacle between the source and crystal at these faces are the spacecraft panels with mounted solar arrays. At the −X face, the effective area drops by ∼0.2 cm2, as this face of the crystal is smaller. The effective area is at a minimum at the +X face as the gamma-ray photons are attenuated by the PCBs (SIPHRA and adapter boards) before reaching the crystal. For the other polar angles, the effective area tends to be at a minimum at azimuthal angle 0° (+X face). The effect of the spacecraft is also evident by the difference in effective area between polar angles 0° and 180°. At 59.4 keV, the effective area at polar angle 0° (+Z face) is similar to the −Y and +Y faces at > 5 cm2. The spacecraft components beneath GMOD attenuate the incoming photons as, at polar angle 180°, the effective area is ∼0.05 cm2. As expected, at higher energies (662 keV), the photons are capable of reaching the crystal through the spacecraft and there is a smaller difference in the effective area between the −Z and +Z of ∼1 cm2.
6. Trigger Algorithm Testing
Additionally, the correct operation of the OBC-triggering algorithm and the processing and protection of the TTEs around the time of the trigger were tested during the characterisation campaign. GMOD was configured for experiment-running and the OBC’s triggering algorithm was enabled. During these tests, the source was brought close to each face of the spacecraft (without touching the satellite) for a fixed amount of time, i.e., 10 s. GMOD triggered on the source at multiple positions, and it was confirmed that the trigger time and duration were correct, contributing to the verification of the functionality of the onboard triggering algorithm. The trigger data processing and protection in the OBSW around the time of the trigger were also validated as the data analysed from these triggers were downlinked from the protected trigger data storage channels on the OBC. The OBC successfully recorded 21 triggers. Figure 15 presents six triggers, where each trigger had the source located at a different face of the spacecraft (+X, −X, +Y, −Y, +Z, −Z) for ten seconds. Panel A of Figure 2 presents the EIRSAT-1 coordinate system.
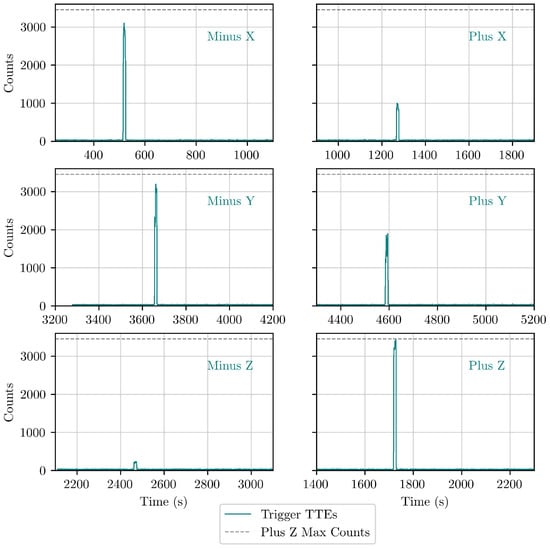
Figure 15.
Each panel shows the counts recorded in a GMOD trigger as a function of time. A 137Cs source was used to trigger GMOD; the source was briefly positioned at each face of the spacecraft for ∼10 s. The protected trigger data was plotted. The maximum counts were recorded when the source was at the +Z face; each panel shows this max count value as a dashed green line to facilitate trigger comparison.
In Figure 15, the sources were approximately the same distance from each face of the spacecraft for the same duration, so the intensity of the triggers reflects the impact of the crystal geometry and surrounding spacecraft on the performance of GMOD. The highest number of counts in a trigger (∼3500) was when the source was at the +Z face of the spacecraft; the only components between the source and GMOD are EMOD and the GTRB. As expected, the counts in the trigger are at a minimum when the source is at the −Z face of the spacecraft. The trigger only creates ∼230 counts, as the CubeSat stack of PCBs attenuates the gamma-ray photons before they arrive at the GMOD detector. Similarly, the +X trigger has relatively low counts, as the gamma-ray photons need to pass through the components in the detector assembly (SIPHRA, Interface PCB) before reaching the scintillator. The +Y trigger has ∼2000 counts, as the source is further away from the GMOD detector. The −Y and −X triggers have a similar number of ∼3000 counts in the trigger, as there was only a solar panel between them and the source.
7. Characterisation Simulations
In order to understand and predict the performance of GMOD as a GRB detector and ensure that the correct response is used if the event location is known, it is important to have an accurate spacecraft and detector model. The engineering qualification model (EQM) of EIRSAT-1, developed using MEGAlib, is described in []. This model needed to be updated to reflect the changes to the configuration of GMOD in the flight model. The first hardware design change was in the mounting of GMOD in EIRSAT-1. In the EQM, GMOD was mounted to the GMOD motherboard. In the FM, GMOD is suspended above the motherboard, and mounted in the PCB stack via, on a structural bracket, the GTRB. The second hardware change was that ceramic capacitors were used on the GMOD EQM MB. The GMOD FM motherboard has metal framed capacitors, as these are more robust against PCB flexure. Simulations were then performed with this updated model to correlate with measurements in the lab and validate the updated EIRSAT-1 model.
Section 7.1 provides an overview of the MEGAlib software v4.0 used to update the model and run the simulations. Section 7.2 outlines the updates made to the spacecraft geometry model. Section 7.3 presents the results of the simulations with a comparison to the physical measurements to confirm that the model was representative of the performance of the physical spacecraft.
7.1. MEGALib
The Medium-Energy Gamma-ray Astronomy library (MEGALib) v4.0 is a collection of programs for simulating gamma-ray instrumentation []). The software library was initially developed for the telescope MEGA []), which combined Compton scattering and pair production instrumentation; therefore, the higher-level data analysis tools concentrate on Compton telescope processes. However, the flexible design of the tools makes it applicable to many detector types, including scintillation-based instruments like GMOD on EIRSAT-1.
The simulations performed with MEGALib for EIRSAT-1 used the following three MEGAlib packages []:
- Geometry for MEGAlib (Geomega);
- A Cosmic Simulator for MEGAlib (Cosima);
- Real Event Analyser (Revan).
The geometry of the detector and the satellite were first defined using Geomega, as seen in Figure 16; then, the gamma-ray source(s) were defined and, using Cosima and Revan tools, the response of GMOD in EIRSAT-1 to the sources was simulated.
Figure 16.
Updated EIRSAT-1 MEGAlib mass model including the GTRB with one solar panel cut out to view the internal components.
The main input file of Geomega includes the list of materials, the volumes of all the components of the spacecraft, the characteristics of the detector and any trigger criteria. In MEGAlib, the lengths of all objects are defined in half lengths and, throughout the programme, all the units are in cm, keV, g and deg. The materials that comprise the different components of the detector and the satellite, their densities and chemical compositions are defined in a separate file in Geomega and included in the main input file. The volumes can be a variety of different shapes including boxes, spheres, tubes and trapezoids.
The gamma-ray detector also needs to be defined in the geometry file in MEGAlib. Various properties of the detector are defined in the geometry file including trigger thresholds, noise thresholds and energy resolution in the case of scintillation-based detectors. The definition of the detector identifies which volume(s) in the model in which the positions and energies of interactions should be recorded.
The second tool used in MEGAlib is Cosima. Cosima is a Geant-4-based [] simulator of the detection of gamma rays in the keV to a few hundreds of GeV range via photo-electric absorption, Compton scattering and pair production by gamma-ray telescopes. The Cosima simulation is directed by an input “source” file. The first input into the source file is the Geomega geometry definition of the satellite and the detector, as shown in the sample code below. The second section of the source file describes the electromagnetic interactions package that will be used to describe the interactions in the simulation. The Livermore low-energy EM package describes gamma-ray interactions in the 250 eV to 100 GeV range []. The output format of the simulated data is then defined (e.g., storage of simulation history and ionisation information) and the final section describes a simulated run. One source file can define multiple simulation runs that will be performed in succession. Each run must have a defined output file name, stop criterion (time), definition of the radioactive source including the particle type, beam type and position, source spectrum and the average total flux integrated over beam and spectrum. The flux (particles/s) is calculated by multiplying the activity of the source (Bq) by the transition probability.
The output of the Cosima simulation contains the interaction history of all the primary and secondary particles and all of the hits in the detector. Along with each hit, the associated position in world coordinates and energy are recorded. Revan is the final MEGAlib package used in this chapter, to combine the Cosima simulation results and the Geomega geometry together to generate a simulated detector response. Revan is used to generate the spectrum recorded by the simulated detector of the gamma-ray source. This spectrum can then be analysed and compared to the physical measurements to confirm that the simulated model of the spacecraft is in close agreement.
7.2. EIRSAT-1 MEGAlib Model
In order to determine the performance of GMOD in orbit, it is important to consider the impact of the remainder of the spacecraft on its ability to detect incoming gamma rays. The initial geometry of EIRSAT-1 in MEGAlib is described in detail in []; however, due to design changes, the model required an update. The major addition to the model was the creation and inclusion of the GMOD GTRB.
In Geomega, to create the GTRB, a plate of aluminium was defined. The structure of the GTRB was then modelled by making vacuum cut-outs in the shapes of cuboids and trapezoids. Figure 17 shows the GTRB model in Geomega, the shapes highlighted in green are all vacuum cut-outs. The GTRB is 5 mm thick at the edge and then there is a 1 mm indent, as shown by the dark blue sections which are large vacuum cut-outs.
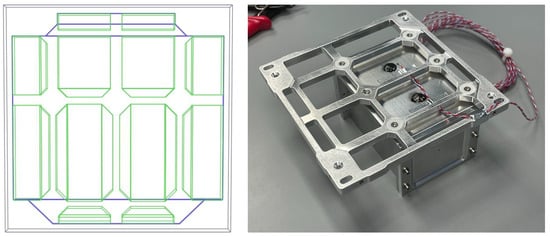
Figure 17.
The left panel presents GMOD GTRB modelled in MEGAlib Geomega. The shapes highlighted in green are all vacuum cut-outs. The GTRB is 5 mm thick at the edge and then there is a 1 mm indent, as shown by the dark blue sections, which are large vacuum cut-outs. The right panel is the physical GMOD GTRB attached to the GMOD detector assembly.
The GTRB was inserted above the GMOD detector assembly, as shown in the left panel of Figure 18, and the right panel shows the new GMOD assembly included in the full spacecraft.
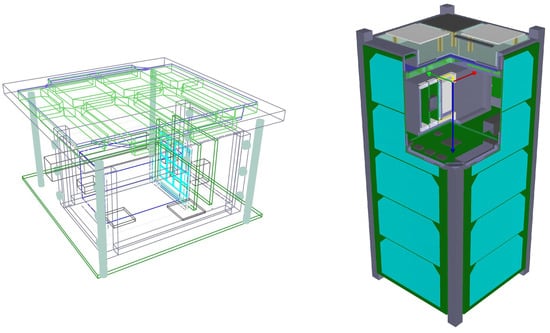
Figure 18.
The GMOD GTRB modelled in MEGAlib Geomega included above the detector assembly (LHS) and then within the full spacecraft model (RHS) where the position of the detector assembly has also been updated to reflect the flight model.
The position of the detector assembly also required modification as, in the FM, the aluminium housing was inverted and secured to the GTRB (in the EQM, the aluminium housing was mounted to the GMOD MB below).
7.3. Simulations and Comparison with Physical Measurements
Two groups of simulations were performed to compare with the GMOD FM physical measurements and investigate the accuracy of the EIRSAT-1 MEGAlib model. Initially, the 12 h integrations were simulated using MEGAlib. The activity of the source is required as a simulation input; therefore, the response of GMOD to the five sources with known activities from Table 1 were simulated, i.e., 241Am, 137Cs, 133Ba, 60Co and 22Na. The measurement duration, source activity and position relative to the centre of the spacecraft were input into the Cosima source file. Cosima was run to generate all the particle interactions. Revan was then used to process the Cosima output file, along with the spacecraft and instrument geometry, to produce a spectrum recorded by the simulated detector. Figure 19 presents a comparison of the simulated spectra (teal) and the spectra produced by the physical FM (grey) for each source. Both spectra are displayed in counts/keV/hour. As expected, the number of counts in the simulated photopeaks does not exactly match that of the physical measurements; these differences can be accounted for with uncertainties in the activities and positions of the sources.
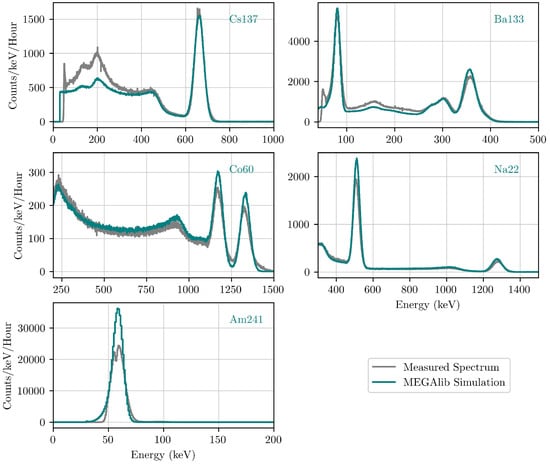
Figure 19.
Spectra (counts/keV/hour) produced by the simulated MEGAlib GMOD detector (teal) for the five sources with known activities in Table 1. In each panel, the spectra produced by the physical GMOD FM are plotted for comparison.
As most evident in the 137Cs spectrum, the additional low energy counts in the region of ∼50 keV to 250 keV in the physical measurements can be attributed to scattering from the surrounding environment. The MEGAlib simulation assumes that the spacecraft is in a vacuum, so there are no testing mounts or walls to scatter the gamma rays.
The photopeak of the gamma-ray line at 59.4 keV in the measured 241Am spectrum (grey spectrum in the last panel of Figure 19) has an unusual profile, as this peak is at the energy threshold of the physical flight model of GMOD. Prior to FM vibration, GMOD was capable of detecting the full peak at 59.4 keV. After FM vibration testing, a shift in energies down in the channel number was observed in the GMOD spectra due to a lower current being produced by the SiPMs. A lower current could be caused by a lower light collection or an electronic issue with the SiPM bias voltage. As the bias voltage has been measured and confirmed to be configured correctly, the issue is attributed to the lower light collection. An optical coupling issue would cause lower light collection, e.g., trapped air between the scintillator and SiPMs. However, as the spacecraft had been qualified after the FM environmental testing, it could not be disassembled to confirm this possible cause or rectify it.
The peaks of the simulated spectra were fitted using the same method as followed for the measured spectra to determine the relationship between and energy, as shown in Figure 20. The relationship described by Equation (5) was fitted to the simulated data points (teal) with the fit coefficients b = 0.6810 and c = 9.6791 × 10−3. The model is in good agreement with the relationship fit to the measured spectra (grey solid line).
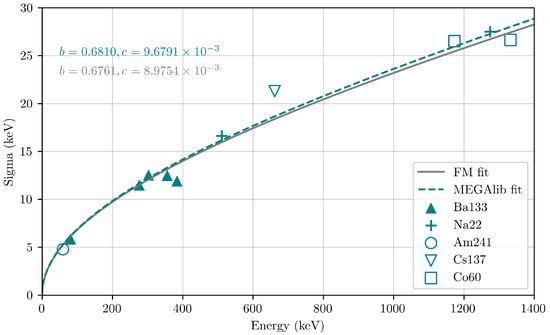
Figure 20.
GMOD simulated as a function of energy, fitted with Equation (5) and coefficients a = 0, b = 0.6810 and c = 9.6791 × 10−3. The model is in good agreement with the relationship fit to the measured spectra (grey solid line). Relative statistical errors in the sigma values are under 4%.
The energy resolution, in terms of FWHM (%), of the simulated detector was then determined using these values and Equation (3). The energy resolutions of the simulated spectra were fitted with the relationship described by Equation (6) and fit coefficients b = 0.6274 and c = 1.3940 × 10−2, as in Figure 21. The MEGAlib model results (teal) reflect the measured energy resolution of GMOD FM (grey solid line).
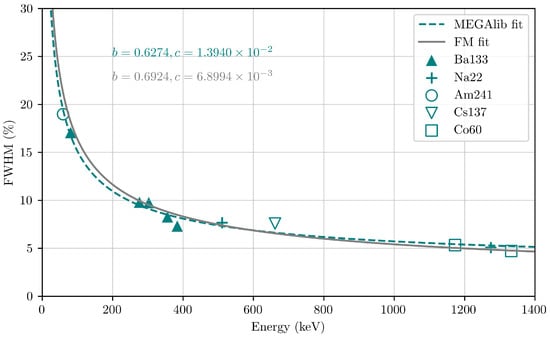
Figure 21.
Simulated energy resolution in terms of FWHM (%) fit with Equation (6) and coefficients a = 0, b = 0.6274 and c = 1.3940 × 10−2. The model is in good agreement with the relationship fit to the measured spectra (grey solid line). Relative statistical errors in the resolution values are under 4%.
The effective area as a function of energy of the simulated detector was determined, as seen in Figure 22. As expected, the effective area of the model is slightly higher across all energies, with the average difference between the measured and simulated energies being 0.5 cm2. This is due to the previously explained difference in photopeak counts of the simulated spectra in comparison to the measured spectra.
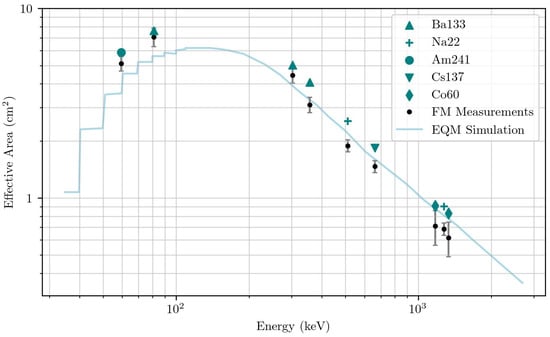
Figure 22.
GMOD FM simulated effective area as a function of energy, where all the simulated source positions were above the +Z face of the spacecraft at the CoC.
The second set of simulations performed was to investigate the accuracy of the MEGAlib GMOD model’s angular effective area. Source files for the measurements at the 34 angles were run with Cosima. The spectra were processed using Revan and analysed to calculate the effective areas. Table 4 compares the calculated effective areas at polar angle 0° and polar angle 180°, which correspond to the source being 22.5 cm from the +Z and of the spacecraft, respectively. Figure 23 and Figure 24 compare the measured (grey) and simulated (teal) angular response of GMOD FM at 662 keV and 59.4 keV, respectively. The updated FM model produces the expected angular response from GMOD in agreement with the measured results. Across all angles, the simulated effective area is higher due to there being more counts in the simulated photopeaks. There is also a larger difference in values for the 59.4 keV peak due to the physical FM not fully detecting this peak in 241Am.

Table 4.
Comparison of effective area for measured and simulated GMOD FM at 662 keV and 59.4 keV at +Z (polar angle 0°) and (polar angle 180°).
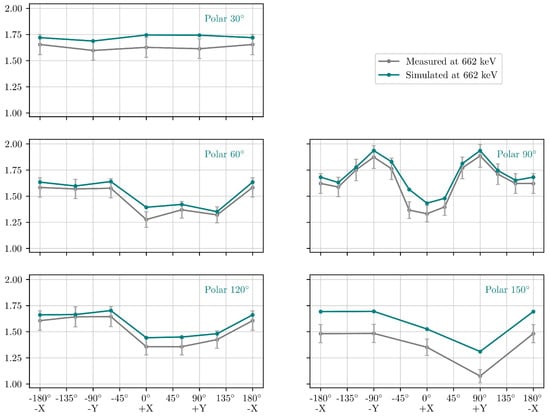
Figure 23.
GMOD FM simulated angular response compared with the measured FM response at 662 keV. Errors in measured values are mainly due to systematic uncertainties. Errors for simulated values are purely statistical and under 1%.
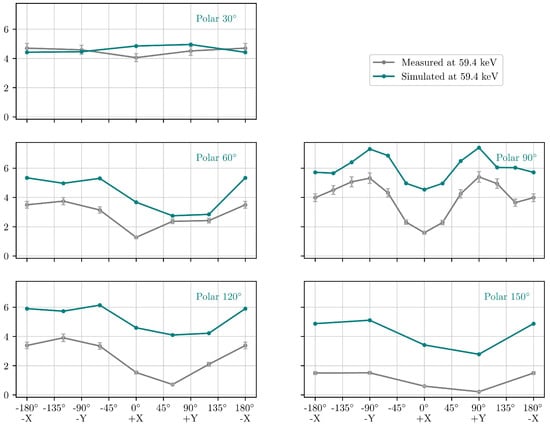
Figure 24.
GMOD FM simulated angular response compared with the measured FM response at 59.4 keV. Errors in measured values are mainly due to systematic uncertainties. Errors for simulated values are purely statistical and under 1%.
8. Conclusions
The characterisation of the flight model instrument provides a comprehensive understanding of the instrument’s behaviour pre-launch. Initially, an energy calibration was performed on GMOD to map the ADC channel values to energy. Then, the properties of the detector were determined, with the FM having an energy resolution of 7.07% at 662 keV. The effective area as a function of energy and incident angle was investigated, which is important for interpreting the downlinked science data during the mission. The effective area of GMOD peaks in the energy range of tens to a few hundred keV, as is required by the specifications of our scientific case for GRB detection. As expected, the detector is most sensitive on the faces with minimal obstruction and the least sensitive faces are those where gamma-ray photons must first pass through the CubeSat stack or the PCBs in the detector assembly. In addition to these measurements with the physical flight model, the EIRSAT-1 MEGAlib model was updated to reflect the new configuration of GMOD in the flight model. This updated model was validated by simulating the measurements made in the lab and confirming consistency between the simulated and physical results. This approach to characterising an instrument for GRB science can be followed by other CubeSats with similar science goals. The results from this characterisation campaign can be used for comparison with the detector’s performance in orbit. In reference [], simulations performed with the original MEGAlib model predicted that GMOD will detect 11–14 GRBs at a significance greater than 10 during a nominal one-year mission. Future work would include performing these simulations with the updated MEGAlib model presented in this paper and producing the response files for spectral fitting.
Author Contributions
Conceptualization, D.M. (David Murphy), A.U., J.M., M.D., B.S. and S.M.; Methodology, R.D. and J.T.; Software, M.D.; Validation, A.U.; Formal analysis, R.D.; Investigation, R.D. and D.M. (David Murphy); Resources, J.M. and J.T.; Writing—original draft, R.D.; Writing—review & editing, R.D., A.U., J.M., M.D., J.T., C.d.B., L.H., D.M. (David McKeown), B.S. and S.M.; Supervision, D.M. (David Murphy), A.U., L.H. and S.M.; Project administration, L.H., D.M. (David McKeown) and S.M.; Funding acquisition, L.H., D.M. (David McKeown) and S.M. All authors have read and agreed to the published version of the manuscript.
Funding
The EIRSAT-1 project is carried out with the support of ESA’s Education Office under the Fly Your Satellite! 2 programme. The authors acknowledge the guidance from Jean-Philippe Halain of the ESA PRODEX Office. The authors acknowledge all students who have contributed to EIRSAT-1 and support from Parameter Space Ltd. R.D., M.D., D.M. and J.T. acknowledge support from the Irish Research Council (IRC) under grants GOIPG/2019/2033, GOIP/2018/2564, GOIPG/2014/453 and GOIPG/2014/684, respectively. S.M.B., D.M., A.U. and J.M. acknowledge support from Science Foundation Ireland under grant 17/CDA/4723. S.M.B. and C.D.B. acknowledge support of Science Foundation Ireland grant 21/FFP-A/9043. L.H. acknowledges support from SFI under grant 19/FFP/6777 and support from the EU H2020 AHEAD2020 project (grant agreement 871158). This study was supported by the European Space Agency’s Science Programme under contract 4000104771/11/NL/CBi and by the European Space Agency’s PRODEX Programme under contract number C 4000124425.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author. The datasets presented in this article are not readily available because the data are part of an ongoing study. Requests to access the datasets should be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Vedrenne, G.; Atteia, J.L. Gamma-ray Bursts: The Brightest Explosions in the Universe. Phys. Today 2010, 63, 56–57. [Google Scholar] [CrossRef]
- Luongo, O.; Muccino, M. A Roadmap to Gamma-ray Bursts: New Developments and Applications to Cosmology. Galaxies 2021, 9, 77. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Cahillane, C.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. 2017, 848, L13. [Google Scholar] [CrossRef]
- Meegan, C.; Lichti, G.; Bhat, P.N.; Bissaldi, E.; Briggs, M.S.; Connaughton, V.; Diehl, R.; Fishman, G.; Greiner, J.; Hoover, A.S.; et al. The Fermi Gamma-ray Burst Monitor. Astrophys. J. 2009, 702, 791–804. [Google Scholar] [CrossRef]
- Atwood, W.B.; Abdo, A.A.; Ackermann, M.; Althouse, W.; Anderson, B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. The Large Area Telescope on the Fermi Gamma-ray Space Telescope Mission. Astrophys. J. 2009, 697, 1071–1102. [Google Scholar] [CrossRef]
- Gehrels, N.; Chincarini, G.; Giommi, P.; Mason, K.O.; Nousek, J.A.; Wells, A.A.; White, N.E.; Barthelmy, S.D.; Burrows, D.N.; Cominsky, L.R.; et al. The Swift Gamma-ray Burst Mission. Astrophys. J. 2004, 611, 1005–1020. [Google Scholar] [CrossRef]
- Winkler, C.; Courvoisier, T.J.-L.; Di Cocco, G.; Gehrels, N.; Giménez, A.; Grebenev, S.; Hermsen, W.; Mas-Hesse, J.M.; Lebrun, F.; Lund, N.; et al. The INTEGRAL mission. Astron. Astrophys. 2003, 411, L1–L6. [Google Scholar] [CrossRef]
- von Kienlin, A.; Meegan, C.A.; Paciesas, W.S.; Bhat, P.N.; Bissaldi, E.; Briggs, M.S.; Burns, E.; Cleveland, W.H.; Gibby, M.H.; Giles, M.M.; et al. The Fourth Fermi-GBM Gamma-ray Burst Catalog: A Decade of Data. Astrophys. J. 2020, 893, 46. [Google Scholar] [CrossRef]
- Bailes, M.; Berger, B.K.; Brady, P.R.; Branchesi, M.; Danzmann, K.; Evans, M.; Holley-Bockelmann, K.; Iyer, B.R.; Kajita, T.; Katsa-nevas, S.; et al. Gravitational-wave physics and astronomy in the 2020s and 2030s. Nat. Rev. Phys. 3 2021, 3, 344–366. [Google Scholar] [CrossRef]
- The CubeSat Program. CubeSat Design Specification Rev. 14. California Polytechnic State University. In Technical Report CP-CDS-R14; California Polytechnic State University (Cal Poly): San Luis Obispo, CA, USA, 2020. [Google Scholar]
- Bloser, P.; Murphy, D.; Fiore, F.; Perkins, J. CubeSats for Gamma-ray Astronomy. In Handbook of X-ray and Gamma-ray Astrophysics; Springer Nature: Singapore, 2022; pp. 1–33. [Google Scholar] [CrossRef]
- Serjeant, S.; Elvis, M.; Tinetti, G. The future of astronomy with small satellites. Nat. Astron. 2020, 4, 1031–1038. [Google Scholar] [CrossRef]
- Mero, B.; Quillien, K.; McRobb, M.; Chesi, S.; Marshall, R.; Gow, A.; Clark, C.; Anciaux, M.; Cardoen, P.; Keyser, J.D.; et al. PICASSO: A State of the Art CubeSat. In Proceedings of the 29th Annual AIAA/USU Small Satellite Conference, Logan, UT, USA, 8–13 August 2015. Technical Session III: Next on the Pad: SSC15-III-2. [Google Scholar]
- Liddle, J.D.; Holt, A.P.; Jason, S.J.; O’Donnell, K.A.; Stevens, E.J. Space science with CubeSats and nanosatellites. Nat. Astron. 2020, 4, 1026–1030. [Google Scholar] [CrossRef]
- Nieto-Peroy, C.; Emami, M.R. CubeSat Mission: From Design to Operation. Appl. Sci. 2019, 9, 3110. [Google Scholar] [CrossRef]
- Twiggs, R. Origin of CubeSat. In Small Satellite: Past, Present and Future; Helvajian, H., Janson, S.W., Eds.; The Aerospace Press: El Segundo, CA, USA, 2008; Chapter 5; pp. 151–173. [Google Scholar]
- Straub, J.; Villela, T.; Costa, C.A.; Brandão, A.M.; Bueno, F.T.; Leonardi, R. Towards the Thousandth CubeSat: A Statistical Overview. Int. J. Aerosp. Eng. 2019, 2019, 5063145. [Google Scholar] [CrossRef]
- Shkolnik, E.L. On the Verge of an Astronomy CubeSat Revolution. Nat. Astron. 2018, 2, 374–378. [Google Scholar] [CrossRef]
- Engel, K.; Lewis, T.; Stein, M.; Venters, T.; Ahlers, M.; Albert, A.; Allen, A.; Solares, H.; Anandagoda, S.; Andersen, T.; et al. Advancing the Landscape of Multimessenger Science in the Next Decade. arXiv 2022, arXiv:2203.10074. [Google Scholar] [CrossRef]
- Racusin, J.; Perkins, J.S.; Briggs, M.S.; de Nolfo, G.; Krizmanic, J.; Caputo, R.; McEnery, J.E.; Shawhan, P.; Morris, D.; Connaughton, V.; et al. BurstCube: A CubeSat for Gravitational Wave Counterparts. arXiv 2017, arXiv:1708.09292. [Google Scholar] [CrossRef]
- Joens, A.; Brewer, I.; Briggs, M.; Bruno, A.; Burns, E.; Caputo, R.; Cenko, B.; de Nolfo, G.; Goldstein, A.; Griffin, S.; et al. BurstCube: A CubeSat for gravitational wave counterparts. In Proceedings of the Space Telescopes and Instrumentation 2022: Ultraviolet to Gamma Ray, Montréal, QC, Canada, 17–22 July 2022; Volume 12181, p. 121811N. [Google Scholar]
- Hui, C.M.; Briggs, M.S.; Goldstein, A.; Jenke, P.; Kocevski, D.; Wilson-Hodge, C.A. MoonBEAM: A Beyond-LEO Gamma-ray Burst Detector for Gravitational-Wave Astronomy. Deep Space Gatew. Concept Sci. Workshop 2018, 2063, 3060. [Google Scholar]
- Fuschino, F.; Campana, R.; Labanti, C.; Evangelista, Y.; Feroci, M.; Burderi, L.; Fiore, F.; Ambrosino, F.; Baldazzi, G.; Bellutti, P.; et al. HERMES: An ultra-wide band X and gamma-ray transient monitor on board a nano-satellite constellation. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2019, 936, 199–203. [Google Scholar] [CrossRef]
- Pál, A.; Ohno, M.; Mészáros, L.; Werner, N.; Ripa, J.; Frajt, M.; Hirade, N.; Hudec, J. GRBAlpha: A 1U CubeSat mission for validating timing-based gamma-ray burst localization. In Proceedings of the Space Telescopes and Instrumentation 2020: Ultraviolet to Gamma Ray, Online, 14–18 December 2020; Volume 11444, pp. 825–833. [Google Scholar] [CrossRef]
- Werner, N.; Řípa, J.; Pál, A.; Ohno, M.; Tarcai, N.; Torigoe, K.; Tanaka, K.; Uchida, N.; Mészáros, L.; Galgóczi, G.; et al. CAMELOT: Cubesats Applied for MEasuring and LOcalising Transients mission overview. In Proceedings of the Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray, Austin, TX, USA, 10–15 June 2018; Volume 10699, pp. 672–686. [Google Scholar] [CrossRef]
- David, M.; Flanagan, J.; Joseph, W.T.; Maeve, D.; Jessica, E.; Andrew, G.; Conor, O.; Lana, S.; Daire, S.; Sarah, W.; et al. EIRSAT-1—The Educational Irish Research Satellite. In Proceedings of the 2nd Symposium on Space Educational Activities, Barcelona, Spain, 27–28 April 2018; pp. 201–205. [Google Scholar]
- Maeve, D.; David, M.; Jack, R.; Joseph, T.; Sarah, W.; Reddy, A.S.K.; Rachel, D.; Jessica, E.; Gabriel, F.; Joseph, M.; et al. Update on the status of the Educational Irish Research Satellite (EIRSAT-1). In Proceedings of the 4th Symposium on Space Educational Activities, Barcelona, Spain, 27–29 April 2022; pp. 294–299. [Google Scholar] [CrossRef]
- Murphy, D.; Ulyanov, A.; McBreen, S.; Doyle, M.; Dunwoody, R.; Mangan, J.; Thompson, J.; Shortt, B.; Martin-Carrillo, A.; Hanlon, L. A compact instrument for gamma-ray burst detection on a Cubesat platform I: Design drivers and expected performance. Exp. Astron. 2021, 52, 59–84. [Google Scholar] [CrossRef]
- Murphy, D.; Ulyanov, A.; McBreen, S.; Mangan, J.; Dunwoody, R.; Doyle, M.; O’Toole, C.; Thompson, J.; Reilly, J.; Walsh, S.; et al. A compact instrument for gamma-ray burst detection on a CubeSat platform II. Exp. Astron. 2022, 53, 961–990. [Google Scholar] [CrossRef] [PubMed]
- Dunwoody, R.; Doyle, M.; Murphy, D.; Finneran, G.; O’Callaghan, D.; Reilly, J.; Thompson, J.; Akarapu, S.K.R.; de Barra, C.; Cotter, L.; et al. Development, description, and validation of the operations manual for EIRSAT-1, a 2U CubeSat with a gamma-ray burst detector. J. Astron. Telesc. Instruments Syst. 2023, 9, 037001. [Google Scholar] [CrossRef]
- Dirk, M.; Jörg, A.; Alf, O.; Hans, K.; Hans, B.; Amir, H.; Akif, A.; Suleyman, A.; Bahram, N.; Jahanzad, T.; et al. SIPHRA 16-Channel Silicon Photomultiplier Readout ASIC. In Proceedings of the 6th International Workshop on Analogue and Mixed-Signal Integrated Circuits for Space Applications, Gothenburg, Sweden, 12–16 June 2016. [Google Scholar] [CrossRef]
- Mangan, J.; Murphy, D.; Dunwoody, R.; Doyle, M.; Ulyanov, A.; Hanlon, L.; Shortt, B.; McBreen, S. Embedded Firmware Development for a Novel CubeSat Gamma-ray Detector. In Proceedings of the 2021 IEEE 8th International Conference on Space Mission Challenges for Information Technology (SMC-IT), Pasadena, CA, USA, 26–30 July 2021; pp. 14–22. [Google Scholar] [CrossRef]
- Joseph, M.; David, M.; Rachel, D.; Maeve, D.; Alexey, U.; Mike, H.; Reddy, A.S.K.; Jessica, E.; Gabriel, F.; Fergal, M.; et al. Experiences in firmware development for a CubeSat instrument payload. In Proceedings of the 4th Symposium on Space Educational Activities 2022, Barcelona, Spain, 27–29 April 2022. [Google Scholar] [CrossRef]
- Ulyanov, A.; Morris, O.; Hanlon, L.; McBreen, S.; Foley, S.; Roberts, O.J.; Tobin, I.; Murphy, D.; Wade, C.; Nelms, N.; et al. Performance of a monolithic LaBr3:Ce crystal coupled to an array of silicon photomultipliers. Nucl. Instruments Methods Phys. Res. A 2016, 810, 107–119. [Google Scholar] [CrossRef]
- Ulyanov, A.; Morris, O.; Roberts, O.J.; Tobin, I.; Hanlon, L.; McBreen, S.; Murphy, D.; Nelms, N.; Shortt, B. Localisation of gamma-ray interaction points in thick monolithic CeBr3 and LaBr3:Ce scintillators. Nucl. Instruments Methods Phys. Res. A 2017, 844, 81–89. [Google Scholar] [CrossRef]
- Murphy, D.; Mangan, J.; Ulyanov, A.; Walsh, S.; Dunwoody, R.; Hanlon, L.; Shortt, B.; McBreen, S. Balloon flight test of a CeBr3 detector with silicon photomultiplier readout. Exp. Astron. 2021, 52, 1–34. [Google Scholar] [CrossRef] [PubMed]
- Bissaldi, E.; von Kienlin, A.; Lichti, G.; Steinle, H.; Bhat, P.N.; Briggs, M.S.; Fishman, G.J.; Hoover, A.S.; Kippen, R.M.; Krumrey, M.; et al. Ground-based calibration and characterization of the Fermi gamma-ray burst monitor detectors. Exp. Astron. 2009, 24, 47–88. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.M.; Silk, J.; Taylor, J.E.; Maccarone, T.J. On the origin of the 511-keV emission in the Galactic Centre. Mon. Not. R. Astron. Soc. 2009, 392, 1115–1123. [Google Scholar] [CrossRef]
- Ramaty, R.; Lingenfelter, R.E. Gamma-ray Lines from Solar Flares. In Solar Gamma-, X-, and EUV Radiation; Kane, S.R., Ed.; Springer: Amsterdam, The Netherlands, 1975; Volume 68, p. 363. [Google Scholar]
- Tierney, D.; McBreen, S.; Hanlon, L.; Foley, S.; Martin-Carrillo, A.; Topinka, M.; Meehan, S. Spectral Cross-Calibration of Fermi-GBM and INTEGRAL-ISGRI using Gamma-ray Bursts. In Proceedings of the Gamma Ray Bursts 2010, Annapolis, MD, USA, 1–4 November 2010; Volume 1358, pp. 397–400. [Google Scholar] [CrossRef]
- Doyle, M.; Gloster, A.; Griffin, M.; Hibbett, M.; Kyle, J.; O’Toole, C.; Mangan, J.; Murphy, D.; Wong, N.L.; Akarapu, S.K.R.; et al. Design, development, and testing of flight software for EIRSAT-1: A university-class CubeSat enabling astronomical research. In Proceedings of the Software and Cyberinfrastructure for Astronomy VII, Montreal, QC, Canada, 17–23 July 2022; Volume 12189, p. 1218915. [Google Scholar] [CrossRef]
- Zoglauer, A.; Andritschke, R.; Schopper, F. MEGAlib – The Medium Energy Gamma-ray Astronomy Library. New Astron. Rev. 2006, 50, 629–632. [Google Scholar] [CrossRef]
- Be, M.-M.; Chiste, V.; Dulieu, C.; Kellett, M.A.; Mougeot, X.; Arinc, A.; Chechev, V.P.; Kuzmenko, N.K.; Kibedi, T.; Luca, A.; et al. LNE-LNHB/CEA Table de Radionucleides. 2016. Bureau International des Poids et Mesures, Pavillon de Breteuil, F-92310 Sevres, France. Available online: http://www.bipm.org/utils/common/pdf/monographieRI/Monographie_BIPM-5_Tables_Vol8.pdf (accessed on 9 July 2024).
- Bright Ascension Ltd. User Manual—COAST MCS, BAL-COAST-MCS-UM-21.2. 2021. Available online: https://brightascension.com/portal/knowledge-base/mcs-user-manual/ (accessed on 23 June 2023).
- Knoll, G. Radiation Detection and Measurement; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Andritschke, R.; Zoglauer, A.; Kanbach, G.; Bloser, P.F.; Schopper, F. The Compton and pair creation telescope MEGA. Exp. Astron. 2005, 20, 395–403. [Google Scholar] [CrossRef]
- Zoglauer, A.; Weidenspointner, G.; Galloway, M.; Boggs, S.E.; Wunderer Cosima, C.B. The cosmic simulator of MEGAlib. In Proceedings of the 2009 IEEE Nuclear Science Symposium Conference Record (NSS/MIC), Orlando, FL, USA, 24 October–1 November 2009; pp. 2053–2059. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. GEANT4—A simulation toolkit. Nucl. Instrum. Meth. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Livermore Low-Energy Package (2023). Available online: https://twiki.cern.ch/twiki/bin/view/Geant4/LoweMigratedLivermore (accessed on 20 June 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).