Experimental Determination of Pitch Damping Coefficient Using Free Oscillation Method

Abstract

This paper outlines an experimental investigation conducted at the INCAS trisonic wind tunnel, focusing on the determination of pitch damping coefficient. The model used for this investigation is the Basic Finner Model, a standard model for dynamic tests which consists in a cone-cylinder body with four rectangular fins. The study aims to evaluate the influence of various parameters—including the Mach number, angle of attack, reduced frequency, center of rotation, and roll angle—on pitch damping coefficient. The employed method for determining these coefficients is the free oscillation method which consists in measuring the model oscillation in free stream after an initial perturbation. In order to perform these dynamic tests in the wind tunnel, a dedicated rig was developed to initiate the model’s oscillation using a linear servo-actuator and to record its oscillation using a strain gauge. The results obtained from the experiments illustrate how each parameter impacts the pitch damping coefficient, highlighting the precision of the measurements. The paper’s conclusion presents that the developed rig and the method used provide accurate results, and the variation in different parameters can change the damping coefficient.

1. Introduction

The aerodynamic damping coefficients are of major importance for the stability evaluation and control system design of aerospace vehicles. Focusing on the longitudinal trajectory, the most representative damping coefficient is the pitch damping coefficient $C_{mq}+C_{m\dot{\alpha }}$. This coefficient represents the sum of the pitch moment derivative with pitch rate q and the pitch moment derivative with an angle of attack changing rate $\dot{\alpha }$.

The identification of the pitch damping coefficient can be obtained using a numerical or experimental approach. The numerical methods consist in analytical and CFD models which require appropriate settings for accurate results, as shown in [1,2]. The analytical models are based on semi-empiric relations as shown in [3,4], and can provide results with good accuracy for simple geometries using reduced requirements. The CFD models are based on governing equations of fluid dynamics or simplified models and can be used for complex geometries providing high accuracy, but these models require high computational resources.

The experimental methods consist of wind tunnel and ballistic experiments which require dedicated installations for pitch damping coefficient determination. The ballistic experiments related to pitch damping determination [5,6,7,8] show a high scattering of results, especially near the transonic regime. The wind tunnel experiments presented in [9,10,11,12,13] show good accuracy in results, but the interference between the model and its support can alter the results, especially near the transonic regime.

This study continues the previous work, presented in [14,15,16], related to the development and validation of damping rigs for wind tunnel dynamic measurement. This paper aims to present the experimental wind tunnel campaign performed at National Institute for Aerospace Research “Elie Carafoli” and the rig developed for pitch damping coefficient determination that uses the free oscillation technique. The aim of the experimental campaign was to evaluate the influence of different parameters on the pitch damping coefficient such as the Mach number, angle of attack, center of rotation, oscillation frequency, or roll angle of the model.

The main objective of this paper is to extend the current aerodynamic data-base of the Basic Finner Model with wind tunnel results and also to analyze how the pitch damping coefficient varies with different parameters.

The Basic Finner Model represents a standard model for dynamic measurements in a wind tunnel which is used as a calibration model. Many international wind tunnel facilities used the Basic Finner Model to validate their pitch damping mechanism. Among the most representative wind tunnels that perform aerodynamic tests using the Basic Finner Model are the following: U.S. Naval Ordnance Laboratory [9], Arnold Engineering Development Center [10], von Karman Institute for Fluid Dynamics [12], and French-German Research Institute of Saint-Louis [13]. These tests are performed using the free oscillation method. The results presented in [9] are obtained only for supersonic Mach numbers (from 1.58 to 3.24) at AoA = 0° and a 45° roll angle for two centers of rotations and different oscillation amplitudes. The paper [10] presents results obtained only for Mach 1.96 at angles of attack between −12° and 86° for two Reynolds numbers, a 45° roll angle, and a center of rotation at 6.1 D. The results presented in [12] are obtained for three Mach numbers (0.7, 0.8, and 0.9), two angles of attack (0° and 3°), and a 45° roll angle. The paper [13] presents results obtained at different Mach numbers (from 0.6 to 2.0), AoA = 0°, a center of rotation at 6 D, a 45° roll angle and different oscillation frequencies.

Besides wind tunnel experiments, two papers are also considered where the results are obtained from ballistics tests. These papers present results from Ballistic Research Laboratories [5,17] and from the French-German Research Institute of Saint-Louis [8].

The precursor of this work is presented in [18] where a free-to-tumble rig was developed and used to evaluate the pitch damping coefficient for an inter-stage model.

The pitch damping rig used to perform this study presents a low aerodynamic interaction with the model because the pitch damping mechanism is connected through the back of the model in contrast to other pitch damping mechanisms which present a lateral connection [9,10,12,13]. The lateral connection between the pitch damping mechanism and the model causes high aerodynamic interference due to the wake of the support which interacts with the fins of the model, while the aft connection presents a small aerodynamic interference only in subsonic regimes. While the lateral connection enables large oscillations, this feature is not crucial for measuring pitch damping. Reference [9] indicates that the pitch damping coefficient remains relatively constant across different oscillation amplitudes. Considering these, it is more important to minimize the aerodynamic interference than to perform tests at a large oscillation amplitude.

An aft connection pitch damping mechanism is presented in [11], but this mechanism utilizes the forced oscillations method in contrast with the one presented in this paper which utilizes the free oscillations method. The mechanism from [11] has a maximum oscillation amplitude equal to 1.5°, while the mechanism presented in this paper has a maximum oscillation amplitude equal to 2.38°.

Considering the free oscillation method and wind tunnel testing for pitch damping coefficient determination, the scientific literature presents many methods for designing the oscillating system, the most relevant being as follows: flexors [10,19,20], wires [12,13], bearings [21,22], springs [9,21], and knife-edge pivots [22].

The oscillating system of the pitch damping rig uses three flexors and two adapters for sting and model. The flexors used are fixed with M3 screws on adapters. This feature allows the changing of the flexors to be very fast and easy in order to obtain the necessary stiffness and oscillation frequency.

The actuation of the model is realized with an electromagnetic servo-actuator. This actuator is linked with a slider-crank system that positions the model at a desired incidence. When the actuator is retracting, the slider-crank system releases the model to oscillate. This mechanical solution presents a better solution than the pneumatic one regarding the response of the model at actuation, as presented in [19]. Furthermore, an electromagnetic servo-actuator represents a simpler solution than a hydraulic servo-actuator which requires electric pump, valves, hydraulic cylinder, pipes, and hydraulic tanks.

2. Experimental Setup

2.1. Test Facility

The experimental campaign was performed at the trisonic wind tunnel of the National Institute for Aerospace Research “Elie Carafoli” [23]. This wind tunnel is a blow-down type capable of achieving Mach numbers between 0.4 and 3.5 at different static pressures. The cross section of the test chamber is rectangular with dimensions of 1.2 m × 1.2 m and it is equipped with perforated walls for subsonic and transonic regimes. This experimental facility is presented in Figure 1.

2.2. Pitch Damping Rig

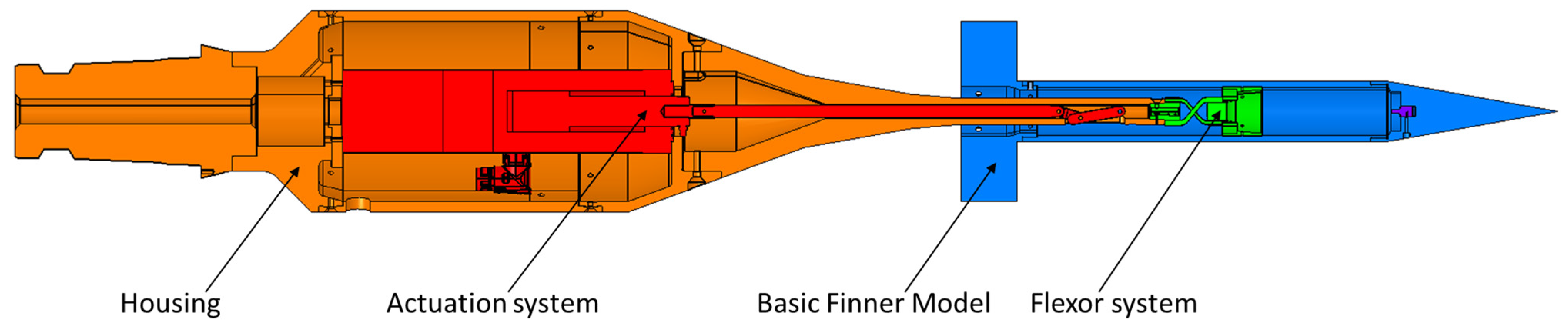
The pitch damping rig (PDR) represents the installation specially developed for the trisonic wind tunnel to determine the pitch damping coefficient using the free oscillation method. This rig comprises the housing, the actuation system, the flexors system, and the model, as shown in Figure 2.

The pitch damping tig, shown in Figure 3a, uses a servo-actuator and a slider-crank system to deflect the model at the desired angle of attack. The model’s oscillation is possible due to the flexors placed in cross position as shown in Figure 3b. In order to control the frequency of oscillation, flexors with different thicknesses have been used in the flexor system.

The pitch damping rig is positioned in the center of the test chamber of the wind tunnel, on the strut (pitch mechanism) as shown in Figure 3a. The aerodynamic interaction between the rig and the model is minimal due to the aft positioning of the support. Minimal aerodynamic interaction is present only in subsonic regimes, while in transonic and supersonic regimes the aerodynamic influence of the rig on the model does not exist because in these regimes the information does not transfer upstream.

The flexors system comprises two adapters (for the rig and for the model), three flexors (two lateral flexors and one central flexor), two lateral pawls, and a spacer that keeps the pawls distanced. A strain gauge is connected on the central flexor in order to measure the oscillations produced by the model. The lateral pawls are designed to limit the angular amplitude of the model at 3°. A three-wire, quarter-bridge strain gauge circuit is employed to assess the superficial tension in the central flexor. This design specifically addresses the issue of cable length by incorporating compensation techniques.

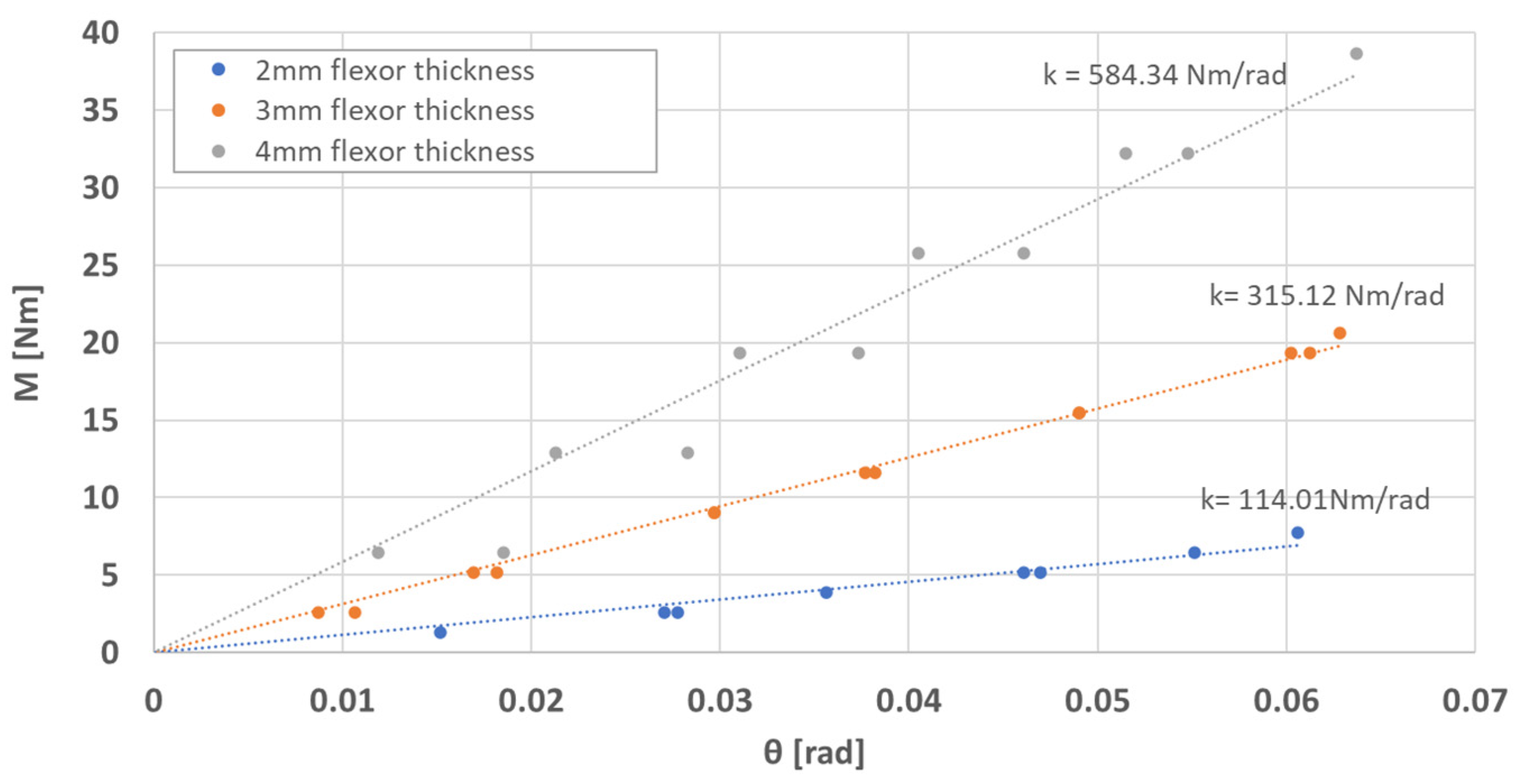
To evaluate the effect of frequency oscillation on the pitch damping coefficient it is necessary to use several flexors with different thickness (2 mm, 3 mm and 4 mm). For these flexors, the stiffness is experimentally determined. Figure 4 presents the variation between the pitch moment and the pitch angle for the flexors systems. The 2 mm thickness flexors system has a stiffness k = 114.01 Nm/rad and an eigen frequency around 34 Hz, the 3 mm thickness flexors system has a stiffness k = 315.12 Nm/rad and an eigen frequency around 56 Hz, and the 4 mm thickness flexors system has a stiffness k = 584.34 Nm/rad and an eigen frequency around 76 Hz.

Figure 4 was obtained by loading the model with calibrated weights and reading the pitch angles of the model with an inclinometer which has the maximum error allowed under 0.033°. Also, the stiffness values of the flexor system were estimated in an FEA (finite element analysis) and the difference between the FEA estimation and the measured values of stiffness was below 1%.

A typical actuation is carried out as follows: the servo-actuator pushes the slider-crank mechanism which deflects the model at a specific pitch angle, then the servo-actuator retracts rapidly, releasing the model to oscillate freely due to the flexors system. The wind tunnel tests as well as the tare tests present four actuations.

2.3. Model Used

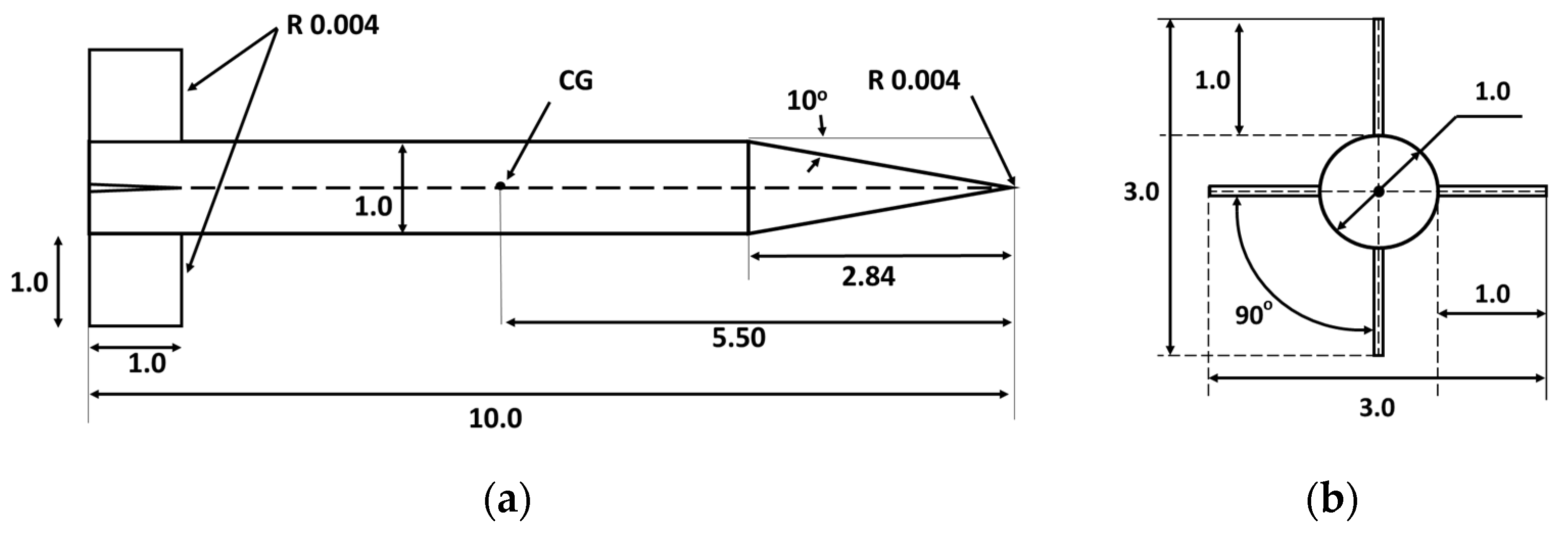
In order to validate the pitch damping rig, the Basic Finner Model was utilized to perform the aerodynamic experiments. This model is also known as Army Navy Finner and it is a standard model for dynamic tests proposed by the STAI (Supersonic Tunnel Association, International) and AGARD (Advisory Group for Aerospace Research and Development), as shown in [17]. The Basic Finner Model consists in a cone-cylinder body with four rectangular fins as presented in Figure 5a,b.

The reference length of the model is the diameter (60 mm) and the reference area of the model is the cross-section area (11309.73 mm²).

The model utilized in the experimental campaign has a 60 mm diameter and the overall length is 600 mm. The centers of rotation considered in the experiments are at 5.5 D (330 mm) and 6.1 D (366 mm) with respect to the model’s nose. The moments of inertia on the pitch axis with respect to the centers of rotation are 0.100 kg·m², and 0.102 kg·m². The model is tested in two positions: the ‘+’ position at a 0° roll angle and the ‘×’ position at a 45° roll angle.

The model dimensions and moments of inertia are considered from the CAD (Computer-Aided Design) model and are verified physically; the difference between the CAD estimation and the physical values is smaller than 1%.

2.4. Identification Technique

The dynamic stability of the pitch axis of an aerospace vehicle can be determined considering a mass-spring-damper system with one degree of freedom as shown in the second order differential equation that describes the pitch motion (1) [24].

$$I_{yy}·\ddot{\theta }+c·\dot{\theta }+k·\theta =\sum M_y ,$$

(1)

where $I_{yy}$ represents the moment of inertia on pitch axis, $c$ represents the damping factor, $k$ represents the stiffness factor, $\theta$ represents the pitch angle, and $M_y$ represents the moments that act around pitch axis, e.g., an oscillatory mechanism.

The utilization of a flexors system for the pitch damping coefficient determination implies that the damping and stiffness factors have an aerodynamic part as well as a structural part as presented in (2), where the subscripts A and S represent the aerodynamic and structural terms.

$$I_{yy}·\ddot{\theta }+\left(c_A+c_S\right)·\dot{\theta }+\left(k_A+k_S\right)·\theta =\sum M_y ,$$

(2)

$$I_{yy}·\ddot{\theta }+\left[q_{\infty }SD\left(C_{mq}+C_{m\dot{\alpha }}\right)\frac{D}{2U_{\infty }}+c_S\right]·\dot{\theta }+\left(q_{\infty }SD{C}_{m\alpha }+k_S\right)·\theta =\sum M_y .$$

(3)

Equation (3) presents the extended form of the aerodynamic factors where $q_{\infty }$ represents the free-stream dynamic pressure, $U_{\infty }$ represents the free-stream velocity, $S$ represents the reference area (the cross-section area of the model), $D$ represents the reference length (the diameter of the model), $C_{mq}+C_{m\dot{\alpha }}$ represents the pitch damping coefficient and $C_{m\alpha }$ represents the pitch moment coefficient. The structural terms may be eliminated for performing tare measurements in no-flow conditions or preferably in a vacuum chamber as presented in [22].

The terms that describe the pitch damping coefficient ($C_{mq}+C_{m\dot{\alpha }}$) represent the derivatives of the pitch moment coefficient with the pitch rate ($q$), $C_{mq}$, with the angle of attack rate ($\dot{\alpha }$), $C_{m\dot{\alpha }}$. In wind tunnel measurements, the pitch angle and the angle of attack are equal, resulting in the two coefficients ($C_{mq}$ and $C_{m\dot{\alpha }}$) being equal. Considering the longitudinal stability, the knowledge of this sum is sufficient [22].

The most common method for determination of the pitch damping coefficient is the free oscillation method which is used for both ballistics tests and wind tunnel tests. This method involves deflecting the model to an initial pitch angle then releasing it to oscillate. The model restrained by the flexor system will start to oscillate due to its inertia and flexor elasticity. The time variation of the model pitch angle is recorded and analyzed, resulting in the damping coefficient [22].

Considering the hypothesis of the free oscillation method, the equation of motion (3) presents null external pitch moments meaning that the right-hand side of the equation becomes zero. The solution for this homogeneous second-order differential equation is presented in [22], and the damping factor is given by the following:

$$c=-2I_{yy}\frac{\ln \frac{{\theta }_2}{{\theta }_1}}{t_2-t_1} .$$

(4)

The damping factor obtained represents the sum of the aerodynamic and structural damping. The tare correction should be applied using the following relation:

$$c_A=-2I_{yy}\left[{\left(\frac{\ln \frac{{\theta }_2}{{\theta }_1}}{t_2-t_1}\right)}_{WT}-{\left(\frac{\ln \frac{{\theta }_2}{{\theta }_1}}{t_2-t_1}\right)}_{VC}\frac{f_{VC}}{f_{WT}}\right] ,$$

(5)

where the subscripts WT and VC represent the quantity measured in the wind tunnel condition and in the vacuum chamber condition respectively. The terms ${\theta }_2$ and ${\theta }_1$ represent the pitch angle of the model at $t_2$ and $t_1$ times, and f represents the oscillation frequency.

After the tare correction of the damping factor, the pitch damping coefficient results from damping factor nondimensionalization:

$$C_{mq}+C_{m\dot{\alpha }}=c_A·\frac{2V_{\infty }}{q_{\infty }S{D}^2} .$$

(6)

2.5. Experimental Investigation

The experimental investigation consists in 19 tests at different parameters as shown in

Table 1. Experimental matrix.

No.	Mach No. [−]	Re [106]	AoA [deg]	C.R. (*D)	Roll Angle [deg]	f0 [Hz]
1	0.4	0.81	0	5.5	0	34
2	0.4	0.804	0	5.5	0	56
3	0.4	0.798	5	5.5	0	56
4	0.4	0.774	0	5.5	45	56
5	0.8	1.284	0	5.5	0	56
6	0.95	1.374	0	5.5	0	56
7	1.6	1.356	0	5.5	0	56
8	1.6	1.356	3	5.5	0	56
9	1.6	1.362	0	5.5	45	56
10	1.6	1.368	0	6.1	0	56
11	2	1.332	0	6.1	0	56
12	2	1.332	0	5.5	0	56
13	2	1.326	3	5.5	0	56
14	2	1.326	0	5.5	45	56
15	2.5	1.452	0	5.5	45	56
16	2.5	1.446	0	5.5	0	56
17	3	2.238	0	5.5	0	56
18	3.5	2.064	0	5.5	0	56
19	1.2	1.446	0	5.5	0	56

. These tests are performed to evaluate the influence of the Mach number, angle of attack, center of rotation, roll angle, and oscillation frequency. The Mach number varies from subsonic regime at Mach 0.4 to supersonic regime at Mach 3.5. The angle of attack is predominantly 0°, the center of rotation is predominantly 5.5*D with respect to the model’s nose, the roll angle is predominantly 0°, and the flexor thickness is predominantly 3 mm.

The f₀ represents the eigen frequency of the model in the no-flow condition. This frequency increases in the flow condition due to the aerodynamic pitch moment which increases the stiffness. To evaluate the effect of oscillation frequency on pitch damping coefficients, one test is realized with 2 mm flexors (34 Hz) while the other tests are realized with 3 mm flexors (56 Hz).

It is observed that the Reynolds number is not constant with the same Mach number. This is happening due to the total pressure of the blow-down which presents slightly different values for distinct experiments.

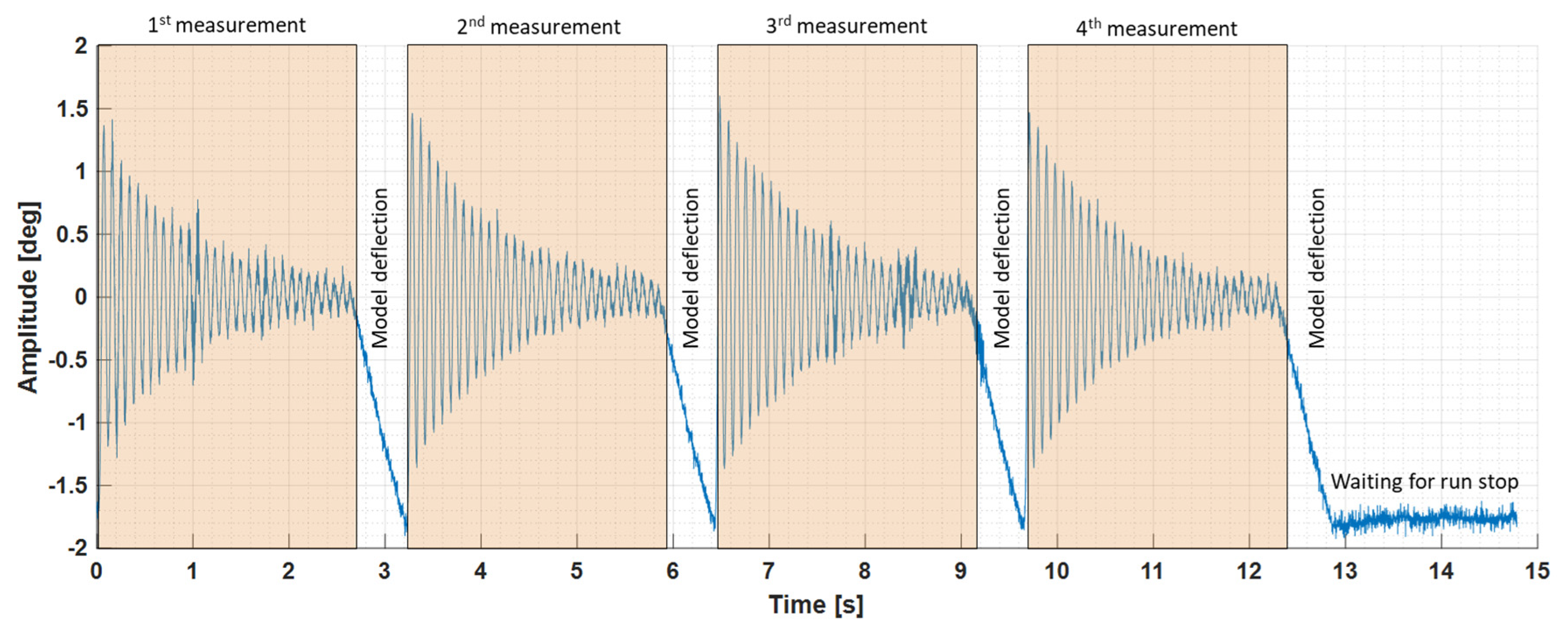
Each test lasts approximatively 13 s and consists in four model actuations as shown in Figure 6.

The test starts with the model locked at the maximum pitch angle to avoid the oscillations induced by the start-up loads. When the total pressure of the flow is established, the rod of the actuation system is retracted, releasing the model to oscillate in flow conditions. After approximatively 2.5 s, the rod is pushed by the rig’s actuator, deflecting the model at the maximum pitch angle; then it is rapidly retracted, releasing the model to oscillate in flow conditions. This action is performed four times, then the model is deflected at the maximum pitch angle while waiting for the run to stop.

If the model is stable on the longitudinal axis, the amplitude of the oscillation decreases, and if the model is unstable on the longitudinal axis, the amplitude of the oscillation increases.

After each wind tunnel test (under flow conditions), a tare test (no flow conditions) is performed to evaluate the structural contribution in damping and stiffness.

2.6. Data Processing

To determine the pitch damping coefficient using the time history of the model’s oscillation it is necessary to perform several steps. The first step is to identify the oscillation time-frames representative for analysis. The second step is to fit the raw data with the regression function (7):

$$\theta \left(t\right)=e^{at}\sin (ft+b)+c.$$

(7)

The $\theta \left(t\right)$ represents the regression function of the pitch angle in time where the regression coefficients $a$, $b$, and $c$, represent the damping exponent, the oscillation phase, and the offset of pitch angle. The frequency $f$ is obtained by Fourier analysis, while the regression coefficients are obtained by the least squares method.

This processing procedure is applied for both types of tests: under flow conditions (WT) and no-flow conditions (VC).

The aerodynamic damping coefficient can be determined from the wind tunnel damping coefficient and the tare damping coefficient by applying the relation (5). Then using the relation (6), the pitch damping coefficient can be obtained for each measurement performed. The pitch damping coefficient is obtained as an average between the four values of each measurement.

The uncertainties are estimated based on the values obtained from the four actuations. These values are used to calculate the standard deviation and the mean value of the pitch damping coefficient.

3. Results

3.1. Pitch Damping Coefficient Variation with Mach number, Roll Angle, and Oscillation Frequency

The results are presented in comparison with reference data to validate the developed pitch damping rig. First, the effect of Mach number, roll angle, and oscillation frequency on the pitch damping coefficient is analyzed. The reference data used are obtained in ballistics tests [6,7,8] and in wind tunnel tests [9,13] using the free oscillation method.

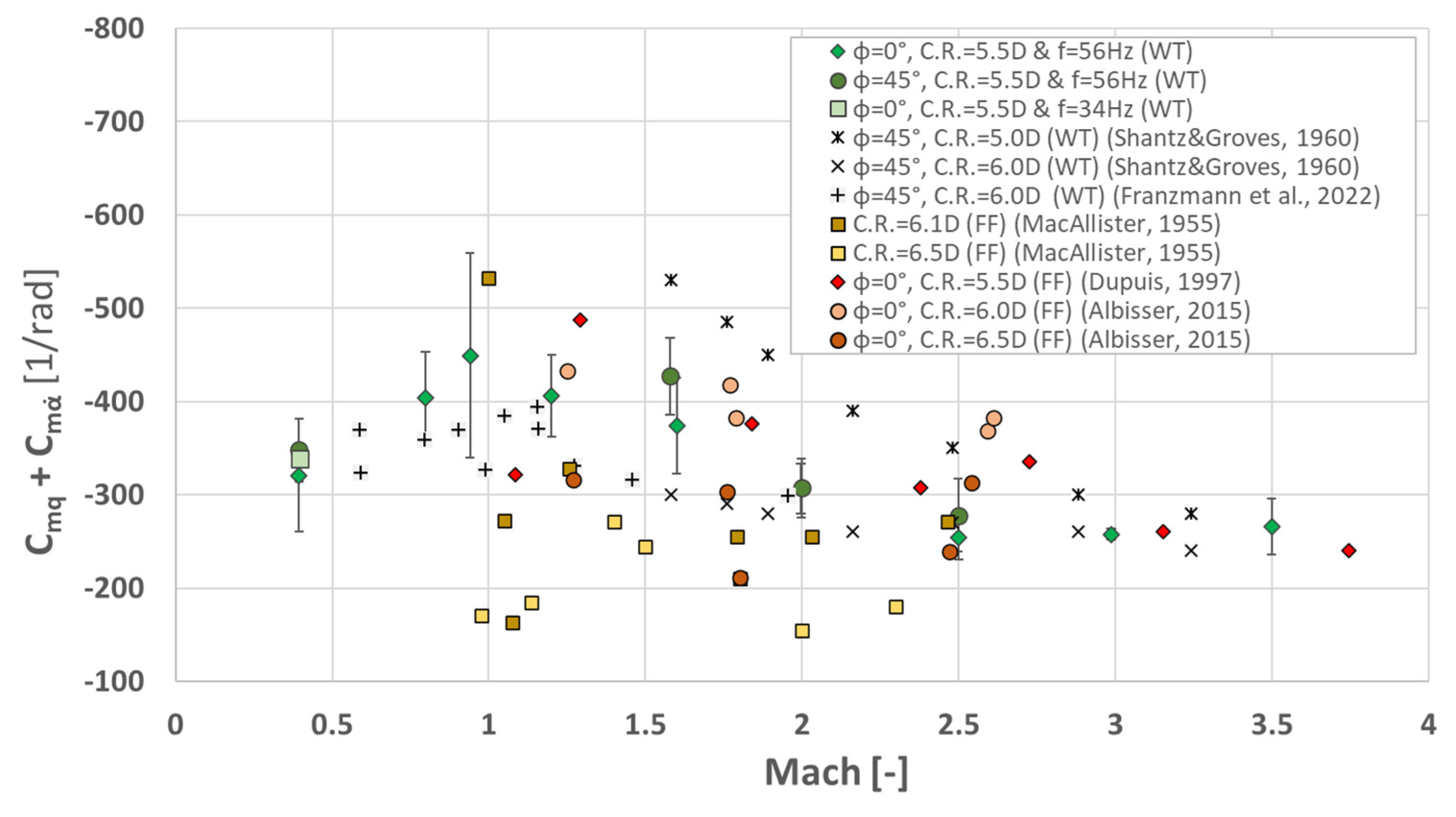
Figure 7 presents the obtained results in comparison to the reference results. It can be seen that the reference data present a high scattering especially in transonic and low supersonic regimes, while the subsonic and high-supersonic regimes present data with low scattering.

The standard test configuration of the model is AoA = 0°, C.R. = 5.5 D, ϕ = 0°, and f = 56 Hz. This test configuration shows that the pitch damping coefficient presents negative values which indicate longitudinal stability. The obtained values decrease in the transonic regime where the present maximum value is around −450 per rad, then increase asymptotically in the supersonic regime to a value around −250 per rad. This behavior of variation is similar to roll damping coefficient variation with Mach number [14].

The resulting data fit to the reference data within the specified error intervals. It is important to mention that aerodynamic experiments were not performed respecting all similitude parameters such as Reynolds number or reduced frequency due to limits of the testing facility and the pitch damping rig.

It is observed that the free-flight results (FF) present a higher scattering than the wind tunnel results (WT). Although the reference results do not have the same testing conditions as the performed tests, the results seem to be very close, which means that the effect of testing parameters is small compared to the damping effect.

The effect of roll angle on the pitch damping coefficient was studied for only three Mach numbers (0.4, 1.6, and 2.5). Each test shows that the model at a 45° roll angle presents higher values of pitch damping coefficient than the model at a 0° roll angle. The reason for this effect is that the fins area that contributes to pitch damping is 42% higher when the model is positioned at 45° than when the model positioned at a 0° roll angle.

The effect of oscillation frequency was studied only with the 2 mm thickness flexors at Mach 0.4 due to the large start-up forces that appear at higher regimes that overcome the safety limits. It is observed that the value of the pitch damping coefficient obtained with 2 mm thickness flexors is higher than the value obtained using the 3 mm thickness flexors. This is happening because the wings start to lose efficiency when the model oscillate with high frequency. This phenomenon is also present in the paper [12] when the results obtained for different flow conditions are compared.

3.2. Pitch Damping Coefficient Variation with Angle of Attack

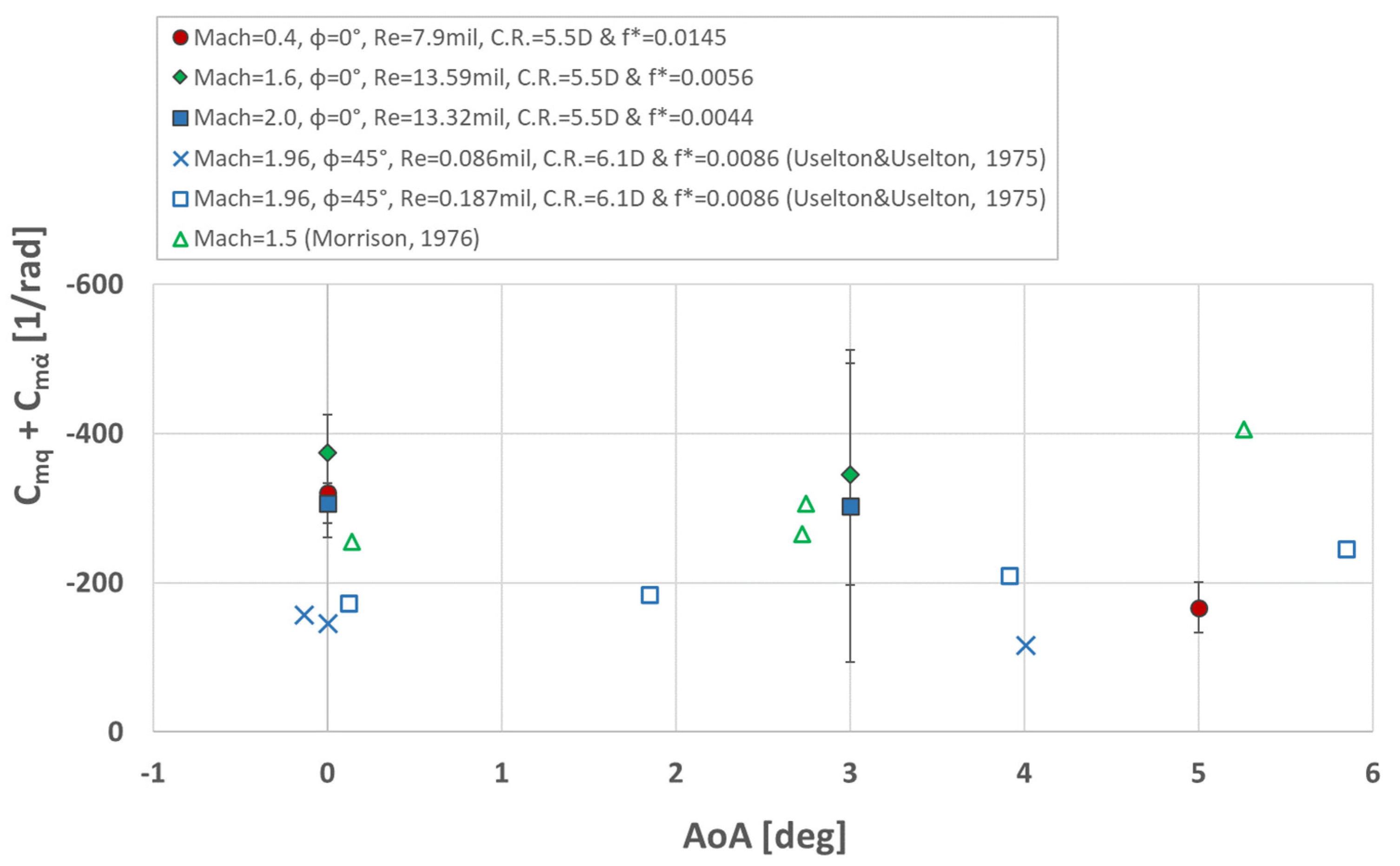
The variation in the pitch damping coefficient with the angle of attack is also very important and very difficult to obtain because the model’s pitching moment at a specific angle of attack can overcome the flexors stiffness. Due to this reason, the current study was performed only for a small angle of attack, where the model’s pitching moment was small enough to allow the model to oscillate. For the subsonic Mach regime, the model was tested at 5° AoA, but for the supersonic regimes the model was tested at 3° AoA due to the high pitch moment.

To obtain the pitch damping coefficient at an angle of attack where the pitching moment coefficient is different from zero, the aerodynamic stiffness must be subtracted from the aerodynamic pitch damping as presented in relation (3).

Figure 8 presents the variation in the pitch damping coefficient with the angle of attack for different Mach numbers.

The reference data considered for comparison belong to the papers [10,25], and are available only for two supersonic regimes, Mach = 1.5 and Mach = 2. In order to analyze the effect of the angle of attack on the pitch damping coefficient, three regimes were performed: Mach = 0.4, Mach = 1.6, and Mach = 2.0.

It can be seen that the obtained results present small differences with respect to the reference results. These differences appear due to the testing parameters, which are also different. The Reynolds number of the reference data is very small compared to the performed tests; the roll angle and the center of rotation also differ. However, the obtained data are in good agreement with the reference data in terms of the variation trend and being in their proximity.

The variation in the pitch damping coefficient with the angle of attack is quasi-linear and almost constant for all three analyzed cases considering the small interval of AoA. As stated in [10], the variation in the pitch damping coefficient with the angle of attack becomes nonlinear at higher incidences due to the vortex structures and to the interaction between them and the wings of the model. At Mach = 0.4 and Mach = 1.6, a small increase in the pitch damping coefficient with the angle of attack is observed, while at Mach = 2.0, the value of the pitch damping coefficient is similar for both angles of attack.

3.3. Pitch Damping Coefficient Variation with the Center of Rotation

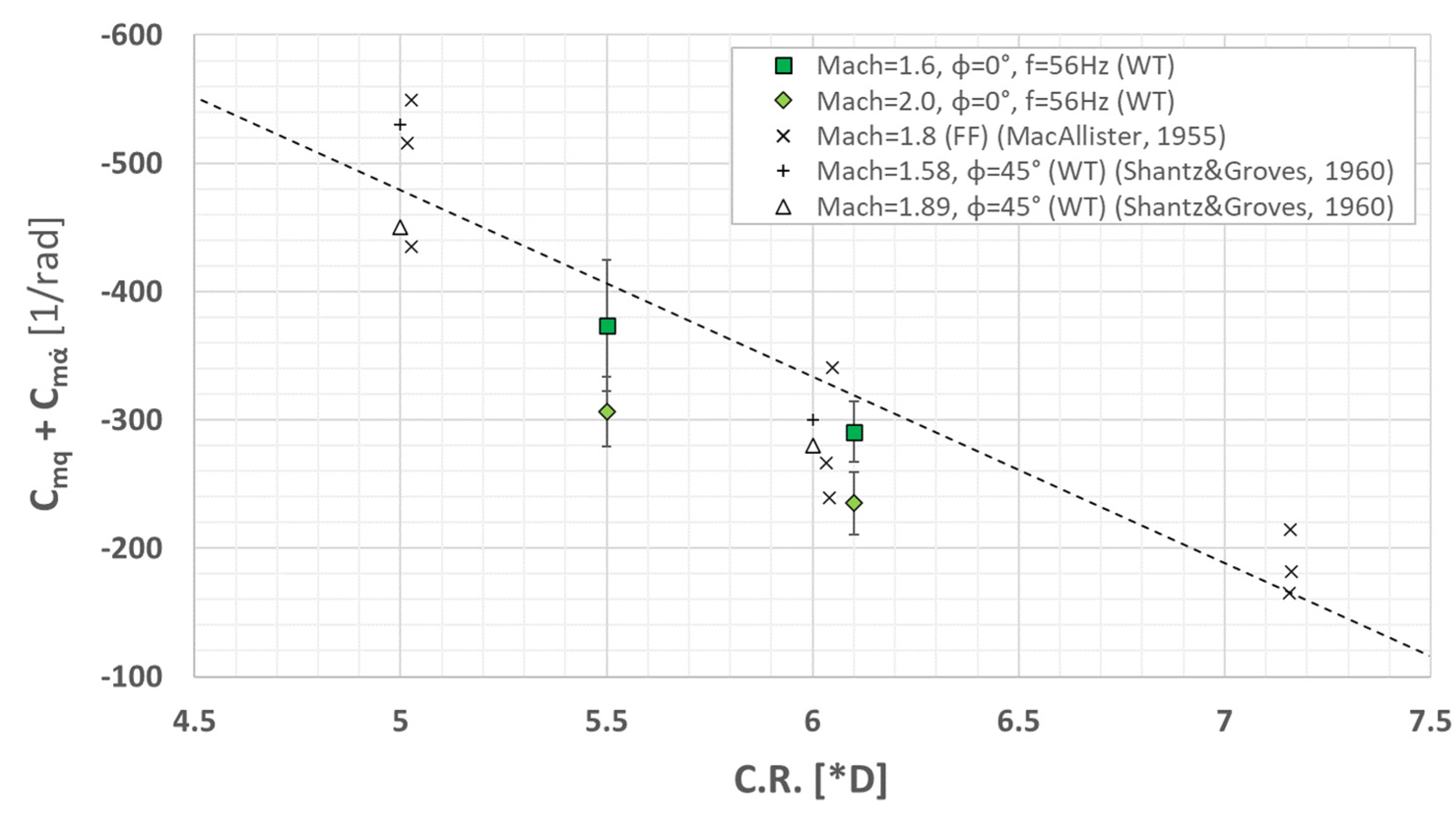
Figure 9 presents the variation in the pitch damping coefficient with the center of rotation, comparing the obtained results with reference results from ballistics tests [6] and wind tunnel tests [9]. In order to evaluate the effect of the center of rotation (C.R.) on the pitch damping coefficient, two regimes were considered (Mach = 1.6 and Mach = 2.0). The reference data are obtained for Mach = 1.58 and Mach = 1.89 in wind tunnel testing [9], and for Mach = 1.8 in ballistic testing [6]. The testing parameters of the reference data are not fully known and it can be observed that the roll angle of the model tested in [9] differs from the roll angle of the model used in this study.

The center of rotation (C.R.) represents the pitch axis and corresponds to the center of mass. The C.R. is defined with respect to the nose of the model and it is given in multiples of diameters. According to scientific literature, the most common centers of rotations for the Basic Finner Model are between 5 D and 7.5 D. In this study, only two centers of rotation have been used, C.R. = 5.5 D and C.R. = 6.1 D.

Although the testing parameters are not similar between the performed tests and the reference tests, the results obtained are in good agreement with the reference data. The results obtained in [6] present a high scattering even if the results are obtained in the same conditions. Results from [9] together with the results obtained in this study show that the pitch damping coefficient increases with Mach number at any C.R. and the difference between two values at different Mach numbers decreases when the C.R. increases, as presented in Figure 9.

Also, it is observed that the variation in the pitch damping coefficient with C.R. location (Figure 9) is quasi-linear with a positive slope. This is happening due to the distance between the C.R. and the fins aerodynamic center where the normal force is acting. By decreasing this distance, a smaller pitch damping moment for the same aerodynamic force developed on the fins is obtained.

4. Conclusions

This paper presents a rig for the experimental determination of the pitch damping coefficient using the free oscillation method. The pitch damping rig uses a three-wire, quarter-bridge strain gauge to measure the oscillation decay of the model. An accelerometer could have been used as redundancy for oscillation measuring, but due to the high electromagnetic interference produced by the actuator it was unused.

This rig is validated using reference data obtained in ballistics tests [6,7,8] and in wind tunnel tests [9,10,13]. A standard model has been used to perform the study. This model is a slender body which consists of a cone-cylinder fuselage with four rectangular fins, used for dynamic tests by several research aerodynamic facilities.

The study comprises 19 wind tunnel tests with different testing parameters as follows: nine Mach numbers (0.4, 0.8, 0.95, 1.2, 1.6, 2.0, 2.5, 3.0, and 3.5), three incidences (0°, 3°, and 5°), two roll angles (0° and 45°), two centers of rotations (5.5 D and 6.1 D) and two oscillation frequencies (34 Hz and 56 Hz). The parameters considered for each test are presented in Table 1. The different testing conditions are necessary to evaluate the effect of each parameter on the pitch damping coefficient and to compare them with reference data in order to validate the installation and the processing algorithm. The results obtained show a good agreement with reference data and validate the pitch damping rig.

The study focuses on the variations in the pitch damping coefficient with the Mach number, angle of attack, roll angle, center of rotation, and oscillation frequency. The results obtained fit the reference data with reasonable precision. Also, the variation in the pitch damping coefficient with the studied parameters respects the variation tendency observed in reference data.

The variation in the pitch damping coefficient with Mach number (Figure 7) shows the obtained results for nine distinct Mach numbers between 0.4 and 3.5 in comparison with the reference data obtained in wind tunnel tests and in ballistics tests. The obtained results present a good accuracy, being very close to the reference data, although the similitude parameters are not fully respected due technical limits. It is observed that the pitch damping coefficient decreases powerfully from −350 per rad (at Mach = 0.4) to −450 per rad (at Mach = 0.95), then increases asymptotically to −250 per rad (at Mach = 3.5). This variation tendency is also observed for the roll damping coefficient. The model used presents only negative values for the pitch damping coefficient in the studied range, which indicates a good stability on the pitch axis. The stability on the pitch axis is given by the aft mounted fins which tend to stabilize the model when perturbations appear.

The variation in the pitch damping coefficient with the angle of attack (Figure 8) is performed only for small incidences (up to 5°) because at higher incidences the pitching moment became so large that the model was deflected on maximum position without oscillating. To evaluate the pitch damping coefficient at higher incidences, flexors with higher stiffness are necessary. The 5° AoA was tested only in the subsonic regime, where the pitching moment is significantly lower compared to the supersonic regime, where the angle of attack was limited to 3°. Even if this analysis does not present many tests, the performed ones were enough to validate the rig and to identify the pitch damping coefficient at non-zero incidences. The obtained results showed small differences with respect to the reference data due to the different testing parameters such as the Reynolds number, roll angle, and center of rotation. However, the obtained results respect the variation tendency and indicate values in good agreement with the reference data.

The third study deals with the variation in the pitch damping coefficient with the center of rotation (Figure 9). It was observed that the pitch damping coefficient increases quasi-linearly with the center of rotation. This is due to the decreasing moment arm between the fins and the center of rotation, generating smaller pitch damping moment for the same aerodynamic forces developed by the fins. Moreover, the movement of the center of rotation generates changes in the flow around the model due to the different effective incidences of the fins at the same AoA with different C.R. location. The results obtained indicate a good accuracy with respect to the reference data obtained in wind tunnel [9] and in ballistics tests [6].

5. Patents

The presented mechanism for pitch damping determination is under evaluation for patenting at the State Office for Inventions and Trademarks from Romania.