Abstract
The high cost and low emission frequency of microparticle launchers have resulted in a long lead time for the development of detectors for micro-debris in space. In this paper, two low-cost, high-emission-frequency, small-size, millimeter-sized particle launchers are designed using the principles of gas expansion and surge propulsion by a high-speed air stream. Electrostatic detection is utilized to determine the emission velocity of the microbeads and their deviation from a specific position on the flight trajectory. The emission rate and accuracy of both methods were experimentally evaluated, along with the deviation of the detection system. Both devices emitted microbeads to simulate micro-debris, providing experimental data for the development of a space debris detector and establishing research conditions for studying the impact of micro-debris.
1. Introduction
With the development of human spaceflight activities, space debris, the vast majority of which is small, is contributing to environmental degradation. Currently, space debris is managed by reducing its generation (e.g., equipping spacecraft with de-orbiting equipment [1,2,3]) and improving its detection (e.g., investing in new space debris-detecting radars [4], and deducing the target’s attitude through optical observations [5]). Presently, there are approximately 130 million micro-debris pieces ranging in size between 1 mm and 1 cm [6]. While micro debris does not cause catastrophic damage to spacecraft, millimeter-sized debris may lead to perforations on spacecraft surfaces, damage to battery arrays, deformation of antennas, leakage of pressure vessels or sealed compartments, and other failures and mission failures. The cumulative impact of micron-sized space debris can result in abrasive etching of spacecraft surfaces, degradation of the functionality of devices such as photosensitive or thermosensitive devices, or even their failure [7]. Millimeter-sized and smaller debris and micrometeoroids are typically detected in situ to obtain their statistical parameters.
Debris simulation is essential in the design and manufacture of in-situ detectors to aid in their development. In Low Earth Orbit (LEO), space debris collides with spacecraft at velocities typically in the thousands of meters per second. A common method to accelerate an object to such high velocities is by using a two-stage light gas gun. Two-stage light gas guns can launch various projectiles, including millimeter-sized projectiles, using sabots [8]. However, they have a large footprint and are extremely expensive to manufacture and operate. Moreover, the long lead time for launching a two-stage light gas gun does not allow for many experiments to be conducted in a short period of time, thus delaying the detector development cycle. Laser-driven particle launchers, on the other hand, are only suitable for micrometer-sized particles [9]. To conduct experiments on space debris detectors and study debris impact effects, there is a necessity to develop a low-cost, small-size system to launch particles and simulate small debris. This paper is motivated by the need to design such a particle launching system.
The cost of explosive accelerators is relatively low. Usherenko can achieve particle flow speeds of 1000–3000 m/s using explosives less than 0.3 kg, and Aleksenseva’s method can generate particle flow speeds of 950–1200 m/s [10]. These emission methods use particle flow as the emitter, which is more suitable for studying the interaction between high-speed particles and materials. Space debris detectors mainly detect individual particles, and particle flow is not suitable for simulating the impact signal of small debris.
2. Analysis and Design
The composition of the particle launching system is shown in Figure 1, which includes a launching device, a motion measuring device, a vacuum pumping device, and a control system. The schematic structure of the device is illustrated in Figure 2. The system utilizes two different principles of launching devices to launch silica microbeads, which can be adjusted based on the requirements. The motion measurement device of the system is designed to measure targets with small volume, light weight, and high speed, which are challenging to measure using traditional detection methods. This device employs an electrostatic detection method that facilitates the detection of deviations between the speed and flight trajectory of high-speed flying objects to measure the motion of microbeads. Due to the light weight and high speed of the microbeads, the gas friction after launching significantly affects the speed of the microbeads. To enhance the end speed of the microbeads, prior to the experiment, a vacuum device was used to evacuate the flight area of the microbeads, reducing gas friction. The control system ensures that the systems operate normally according to the required time sequence.
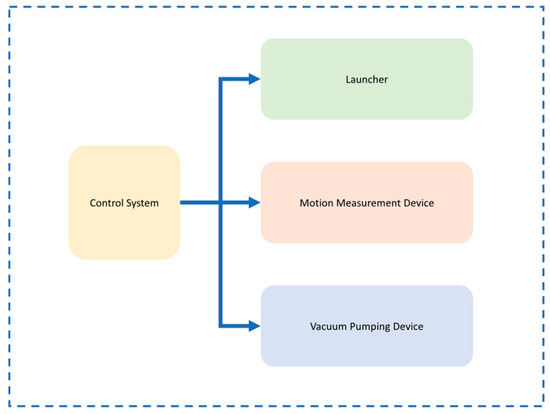
Figure 1.
System Components.
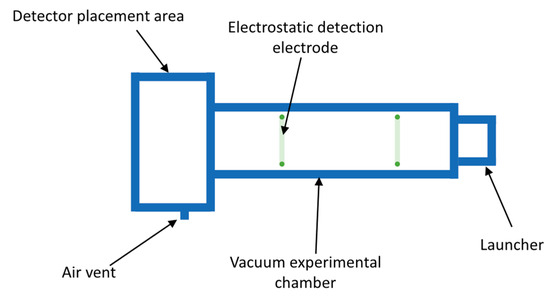
Figure 2.
Schematic diagram of device structure.
2.1. Launcher Analysis and Design
Launchers use 0.5 mm to 1 mm silica microbeads as emitters and high-velocity gas as a power source to accelerate the microbeads along the pipeline towards the detector under test. Launchers are categorized into high-pressure gas cylinder-driven and gas explosion-generated high-temperature and high-pressure gas-driven types based on the method of gas power generation. The microbeads are exceptionally lightweight and have ample time to accelerate within the launcher, with the launch rate being dependent on the gas velocity at the launcher’s exit.
There are two types of power sources for the launcher: high-pressure gas stored in gas cylinders and high-temperature, high-pressure gas from a flammable gas explosion. The gas in cylinders has a greater amount of gas substance and a more stable gas stream, but the gas is at a lower temperature. On the other hand, the gas produced by the explosion is at a higher temperature, but the amount of gas substance is limited, the gas stream is of short duration, and the gas stream is unstable.
There are two ways to accelerate the microbeads to high speeds using gases: one is by utilizing the shockwave generated by the high-speed gas flow, and the other is through gas expansion. The first method involves leveraging the velocity difference between the high-speed gas stream and the microbeads to create a surge pressure that propels the microbeads. The second method involves using high-pressure gas expansion to accelerate the microbeads.
The first method requires stabilizing gas flow. The launch consumes a significant amount of gas, making it suitable for gas cylinder drives. However, it is limited by the gas temperature in the cylinder. The second method allows the gas to fully do its work, accelerating the microbeads with a small amount of gas. This method is suitable for explosion-generated gas drives. Due to the machining tolerances of the microbeads, they need to be screened to prevent pipeline clogging. This paper introduces two principles of microbead launching devices: a shockwave-accelerated particle device driven by a high-pressure gas source (SAPD-P) and a gas expansion acceleration particle device driven by explosion (GEAPD-E).
2.1.1. SAPD-P Analysis and Design
Based on the principle of high-speed surge acceleration, the launch device SAPD-P is designed to launch microbeads using high-pressure gas. When the velocity difference between the microbeads in the launch line and the launch gas stream is greater than Mach 1, a surge is generated on the windward side of the microbeads, which results in the forward thrust of the microbeads achieving surge acceleration. The surge acceleration method can eliminate the screening process of the microbeads, and with the loading mechanism, it can achieve high launching efficiency.
The internal structure of SAPD-P is illustrated in Figure 3, primarily consisting of a launch pipeline with a throat and a loading mechanism. The throat in the launch pipeline can accelerate the airflow to a Mach number greater than 1. The loading mechanism comprises a loading port, a stepper motor, a loading wheel, and a loading needle. The entire loading mechanism is linked to the launch pipeline and operates in a vacuum. Its side view is depicted in Figure 4. The slot size of the filling mechanism beneath this structure varies based on the emitted microbeads. The loading wheel features grooves matching the microbead sizes and is driven by a stepper motor to rotate. Each rotation at a specific angle aligns a microbead groove with the pipeline, enabling the microbeads to enter and be launched. Simultaneously, an empty groove faces the loading port. The pressure needle guides the microbeads into the loading wheel through gravity. To prevent structural damage from the pressure needle falling into the loading teeth and jamming the wheel after all microbeads are loaded, the loading needle is connected to the sealing plug of the loading port via a wire rope of a specific length for positioning. The loading mechanism enables the launch device to perform multiple launches after a single loading.
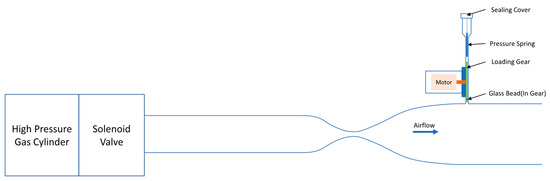
Figure 3.
SAPD-P structure.
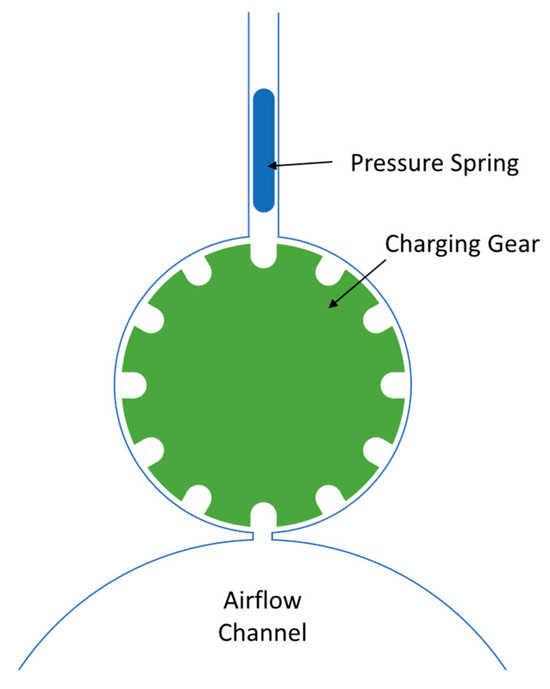
Figure 4.
SAPD-P loading mechanism structure.
According to the equation for isentropic flow, the Mach number of the launch tube is related to the upstream and downstream pressure ratios:
where is the outlet pressure, is the inlet pressure, is the Mach number, and is the specific heat ratio. To ensure that the microbeads are not affected by oblique shock waves and decelerate at the outlet, the airflow should flow smoothly into the environment or maintain an under-expansion state at the outlet, that is:
represents the back pressure at the nozzle exit. The higher the Mach number of the airflow, the greater the velocity at which the microbeads can be propelled by the airflow shockwave. Since the velocity of the microbeads cannot exceed the airflow velocity, the maximum velocity of the microbeads must be increased to match the maximum airflow velocity. The airflow within the nozzle can be considered an isentropic flow, and its temperature relationship is as follows:
where is the temperature inside the flow tube and is the inlet temperature. The local speed of sound of the gas is:
is the Boltzmann constant. It is obtained from Equations (3) and (4):
where is the speed of sound at the entrance. To achieve the surge thrust, microbeads need a speed and an air velocity difference of more than Mach 1, according to the definition of Mach number. Microbeads can achieve the maximum speed of the shockwave thrust by:
On the right side of Equation (6) is the subtraction function of . Combined with Equations (3) and (4), it can be concluded that the larger the Mach number, the larger the . According to Equations (1) and (2), increasing the Mach number of the airflow requires increasing the gas source pressure and reducing the environmental backpressure below the outlet pressure. Based on the Mach area relationship, it can be concluded that [11]:
where is the area of the pipe cross-section and is the area of the throat. To increase the Mach number, increase the ratio of the area of the pipe cross-section to the throat.
Since air is used as the working gas stream, the static temperature inside the nozzle should not be less than 75 K to prevent the gas from condensing and disrupting the gas flow due to the low static temperature of the gas. The thermostat on the high-pressure gas tank can maintain the tank at a maximum of more than 130 °C. is taken to be 400 K, is taken to be 1.4. From Equation (5), the maximum Mach number of the nozzle is 4.65, and the design Mach number of the nozzle is 4.5. From Equations (4) and (5), the speed of sound is 174.88 m/s, and from Equation (6), the velocity of the gas stream is 786.97 m/s, which is obtained by the maximum velocity of the surge thrust at 612.09 m/s. From Equation (7), the maximum nozzle area ratio is 16.56. From Equation (1), the downstream and upstream pressure ratios of the nozzle are 3.455 × 10−3. The maximum flow rate of the nozzle is:
The suction device can reduce the experimental pressure, which is the back pressure of the nozzle, to 2 Pa. When calculating, the experimental section downstream of the nozzle is considered a vacuum. Due to the upper limit of the nozzle flow rate, when calculating the maximum operating time, it can be assumed that the nozzle will continue to operate at the maximum flow rate after startup until the pressure reaches the nozzle outlet pressure. This period is used as the nozzle’s operating time. At the end of the nozzle’s operating time, the gas mass downstream of the nozzle is:
The pressure in the high-pressure gas tank decreases with the operation of the nozzle. By substituting Equations (1) and (3) into Equation (9), it can be concluded that:
Among them, is the pressure of the high-pressure gas tank at the end of the nozzle operation time. The conservation of gas mass at the beginning and end of the nozzle operation time can be obtained from Equation (9):
is the maximum gas mass of the high-pressure gas tank upstream of the nozzle, and is the gas mass of the high-pressure gas tank at the end of the nozzle operating time. From Equations (10) and (11), it can be concluded that:
is the initial pressure of the high-pressure gas tank. From Equation (12), it can be concluded that:
The nozzle operating time can be obtained from Equations (8), (12), and (13) as follows:
The volume of the high-pressure gas tank is 6 L, the pressure is 30 MPa, and the volume of the experimental section is 0.069 L. According to Equation (14), the working time of the launch nozzle must be greater than needs to be greater than 200 ms, and the throat radius should be less than 7.0667 mm. The designed throat section radius is 7 mm, the launch nozzle section radius is 28.5 mm, and the maximum valve opening time is 200 ms.
The pipeline inlet is connected to the high-pressure solenoid valve and high-pressure gas cylinder. During the launch process, the solenoid valve must be opened for a specific period of time. There are three purposes for doing this: first, to ensure that there is enough gas to accelerate the microbeads; second, to prevent signal interference caused by high airflow affecting detectors and microbead motion measurement equipment; and third, to minimize gas entry into the vacuum laboratory to reduce the necessary pumping time between two launches. Before launch, microbeads can be loaded through the filling port. Once the filling port is sealed, the experimental area can be evacuated. Each launch of the microbeads requires pumping of the experimental area to ensure that the downstream pressure of the launch nozzle meets the specified standards.
This launching device can control the speed of the microbeads by adjusting the opening time of the solenoid valve. The device can be reloaded without breaking the negative pressure condition. Air must be pumped between two launches until the pressure in the test vacuum chamber meets the launch condition. The pumping time between launches is notably shorter than the pumping time required before the initial launch, which can enhance the launch frequency. The maximum speed for launching microbeads can reach 697 m/s. The SAPD-P is illustrated in Figure 5.

Figure 5.
SAPD-P Structure.
2.1.2. GEAPD-E Analysis and Design
Based on the principle of work completed by gas expansion, launching device GEAPD-E is designed to use high-temperature and high-pressure gas expansion to push the microbeads. The principle of the gas expansion accelerated launching device is to fill the explosive chamber with flammable gas and oxygen and then detonate the gas using the spark plug. The reaction heat released by the explosion will increase the gas temperature and pressure, break the diaphragm of the enclosed gas, and propel the microbeads along the pipeline to fly out. Its structure and principle are relatively simple, as shown in Figure 6, including the launch pipeline, gas diaphragm, combustion chamber, upper/lower vent, and spark plug. The diaphragm is set on the housing and is pressed by the gas from the combustion chamber on the ring seal after evacuation. The vent seal plugs, and spark plugs are sealed to the housing. When venting gas into the combustion chamber, sufficient oxygen is first introduced through the upper vent, air is expelled, and then, depending on the relative size of the combustible gas to be filled and the density of oxygen, either the upper or lower vent is opened, and a fixed amount of combustible gas is filled. The combustion chamber of the GEAPD-E consists of left and right sections connected by a seal. Before launching, it is necessary to open the launching device, load the microbeads from the back of the piping section, install the gas diaphragm, seal the combustion chamber, and then complete the filling process. The microbeads can be fired after inflation.
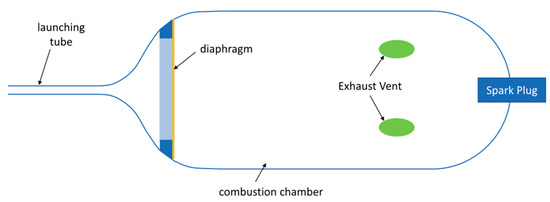
Figure 6.
Schematic structure of GEAPD-E.
In the calculation of the gas state, when disregarding the gas explosion and combustion time, the gas is assumed to break through the diaphragm at the same temperature as the moment of explosion, disregarding the pressure changes in the diaphragm due to volume deformation. To facilitate the mixing of combustible gases and oxygen, ensuring that the volume of gas after the reaction is greater than before, ethane is used as the combustible gas and pure oxygen for the reaction. Once filled, the combustion chamber is sealed and heated to 400 K. Finally, the gas is detonated by the spark plugs arc.
The gas state process inside the launch device is as follows: 1. A mixture of oxygen and ethane with = 300 K, = 1 atm, and , where represents the gas temperature, denotes the gas pressure, and is the amount of gas substance. 2. A mixture of oxygen and ethane with = 400 K and . 3. After the explosion, a mixture of CO2 and H2O with is produced. The entire explosion process is adiabatic. The explosion process is divided into two steps to calculate the gas state: 1. The enthalpy of the mixture of oxygen and ethane changes to a mixture of CO2 and H2O before the reaction. 2. The mixed gas after the reaction absorbs the reaction heat and heats up. The relationship between the heat generated during the reaction process and the temperature rise of the mixed gas after the reaction is:
Among them, is the enthalpy change of the gas, and is the heat released from the reaction. The relationship between the enthalpy of a gas and its internal energy , pressure , and volume is:
By substituting the ideal gas state equation and the relationship between gas internal energy, gas degrees of freedom and temperature into Equation (16), we can obtain:
where is the gas constant. Taking the differentiation of Equation (17) yields:
Introduce CO2 and H2O gases into Equation (18) and calculate their respective sums. Substitute the molar quantities of CO2 and H2O, and , into the equation with respect to , to obtain:
and represent the degrees of freedom of CO2 and H2O, respectively. Integrating Equation (19) and substituting it into Equation (15) yields:
The relationship between the degrees of freedom of a gas and its molar constant pressure and heat capacity is:
Among them, is the molar constant pressure heat capacity of the gas. The molar constant pressure heat capacity of CO2 can be expressed as a fitting formula [12]:
The fitting range is 50 K < < 5000 K. The molar constant pressure heat capacity of H2O can be expressed using a fitting formula [13]:
The suitable range is 175 K < < 6000 K. The heat generated by the reaction is:
is the heat released by the reaction of 1 mol of ethane with oxygen. By substituting Equations (24) and (21) into Equation (20), we can obtain:
By substituting Equations (22) and (23) into Equation (25), is calculated to be 5264.48 K, which exceeds the range of the fitted formula for the molar constant pressure heat capacity of CO2. Given that the characteristic temperatures of the four stretching vibrational modes of CO2 are 961.2 K, 961.2 K, 1999.8 K, and 3384.0 K [14], respectively, the molecules’ vibrational degrees of freedom are fully activated at temperatures exceeding 5000 K, with approaching 7.5R. Assuming the degree of freedom of CO2 is 13 for > 5000 K, then becomes:
Change Equation (20) to:
Substitute Equation (26) into Equation (27) and correct to obtain = 5234.36 K. The airflow in the flow tube reaches its maximum velocity at the inlet point, where Mach 1 is achieved. According to (3), its temperature is 4859.4 K. According to (4), the local sound speed is 1280.93 m/s, which is the theoretical upper limit of the emission speed.
GEAPD-E can accelerate the microbeads to higher velocities, up to 1150 m/s. However, compared with SAPD-P, its launch velocity is less controllable. Each launch requires breaking the sealing condition for loading and re-pumping, and the time between launches is mainly the time spent pumping, resulting in a lower launch frequency. GEAPD-E can still be launched when the backpressure of the experimental vacuum cavity is higher, and it can also be used at atmospheric pressure, thereby increasing the launch frequency. GEAPD-E is illustrated in Figure 7.

Figure 7.
GEAPD-E Structure.
2.2. Principles of a Microbead Motion Measuring Device
The microbead motion device utilizes electrostatic detection to measure the velocity of the microbeads and the deviation of their trajectory from the point of intersection with the Circular Surface Enclosed by Ring Electrodes (CSERE).
The principle of electrostatic detection utilizes the phenomenon of electrostatic induction of conductors. When a charged object approaches or passes through the electrostatic detector, the electrode surface inside the detector rapidly senses a change in charge distribution. If the electrode is grounded and a current detection circuit is added between the electrode and ground, the process of electrostatic induction in the induced charge will pass through the current detection circuit and generate the induced current signal. Since the process of electrostatic induction to reach equilibrium is extremely rapid, it can be considered that the electrodes of the detector and the associated circuitry are maintained in a dynamic electrostatic equilibrium at any instant. Due to the smaller size of the microbeads, they do not carry a large charge by themselves due to their limited capacitance. However, when the microbeads traverse the detection area, the relative speed of movement between them and the electrodes is high, and the spacing between them is small, so the movement of the microbeads leads to significant changes in the electric field near the electrodes. According to Gauss’s theorem for electrostatic fields, the strength of the electric field at the surface of an electrode is directly related to the charge distribution on its surface. Therefore, an increase in the rate of change of the electric field means that the rate of change of the charge on the surface of the electrode also increases, resulting in a larger current in the circuit.
Since the emitter is a conductor and the wall of the experimental vacuum chamber is an insulator, a negative voltage can be applied to the emitter to cause the microbeads to fly out of the emitter with a charge and be detected by the velocimetry device. The electrode distribution is shown in Figure 8, where two circular electrodes are arranged at a certain distance apart in the path that the microbeads fly through. Due to the large velocity/mass ratio of the microbeads, the effect of gravity can be ignored for a short distance after launching. The microbeads can be theoretically regarded as flying along the axis of the device and passing through the center of the electrodes when other factors are not considered. The whole structure and physical process are symmetric with respect to the device axis, and its symmetric cross-section model is shown in Figure 9. A coordinate system is established in the cross-section, with the direction of the flight of the microbeads as the x-axis and the direction of the radius of the annular electrode as the y-axis. The response of the electrode is first discussed in the two-dimensional case when the charged body moves along the x-axis.

Figure 8.
Schematic diagram of the electrode arrangement of the microbead motion measurement device.
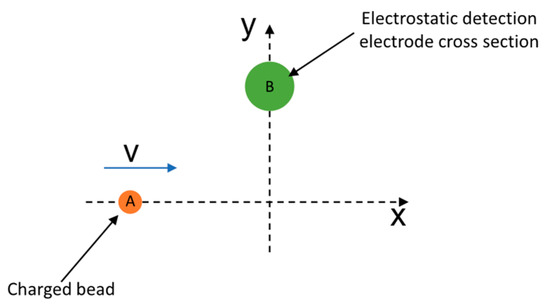
Figure 9.
Symmetric cross-section model of electrostatic detection electrodes.
Due to the extremely small volume of microspheres, a point charge model is used to describe the charged microspheres and their cross-sections. Mark the cross-section of the charged microbeads as C and the circular cross-section of the electrodes as B. The total charge of charged microbeads is denoted as , the relationship between the charge of microbead cross-section C and is:
The induced charge density of B, according to the electrostatic mirror image method [15,16], is:
Let represent the radius of the electrode cross-section B, and denote the distance from C to the center of circle B. If we denote the velocity of C as , the distance from B to the origin as , and the moment when C crosses the origin as moment 0, we can derive the following:
This can be obtained by substituting (30) into (29) and deriving it for :
This expression can be derived by substituting Equation (30) into Equation (29) and then differentiating with respect to . The resulting expression is
where is the induced current of B. Integrating over gives the induced current of the circular electrode as:
From Equation (32), it can be concluded that in order to generate stronger induction signals for circular electrodes, the following three directions of optimization are needed: 1. reduce the diameter of the circular ring; 2. increase the cross-sectional diameter of the ring; 3. increase the charge of microspheres by raising the potential of the emitting device.
From Equation (32), it can be inferred that the current at zero crossing time = 0, and from Equation (30), it can be inferred that the charged target is passing through the central torus of the electrode at this time. The typical signal when a charged target horizontally flies over the detection electrode is shown in Figure 10, and the signal feature points include two poles and a zero crossing point. Due to the known distance between the two electrodes, the velocity of the microbeads can be obtained by analyzing the time difference between the zero crossing points of the detection signals from the two electrodes. To avoid vibration and electromagnetic interference caused by the operation of the pumping device on the detection electrode of the speed measuring device, the pumping device needs to be turned off during emission.
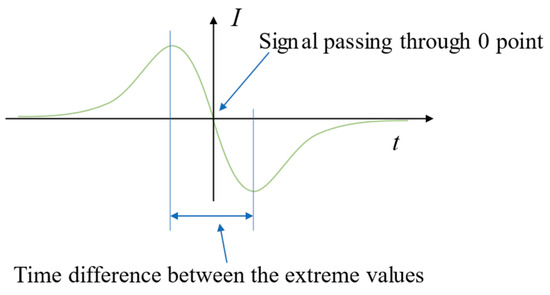
Figure 10.
Typical signals from charged target fly-by electrodes.
In theory, the micro ball should undergo projectile motion with air resistance in the initial velocity direction of the device’s symmetrical axis after being accelerated by the launching device. However, the micro ball velocity is very fast, and the experimental area is in a vacuum state. The influence of gravity and air resistance can be ignored, and the trajectory of the micro ball can be seen as a straight line. However, in practical situations, under the influence of geometric shape errors of microspheres and asymmetric friction between microspheres and the launching device, the initial velocity of microsphere emission will vary in magnitude and deviate from the symmetry axis of the device, making it impossible for microspheres to pass through the electrode from the center of the circular electrode during the experiment. The angle between the microsphere trajectory and the central axis will affect the error of the velocity measurement system. COMSOL simulation is used to verify the velocity measurement error caused by the deviation of the charged microsphere trajectory. The simulation model is shown in Figure 11. The schematic diagram of microbead trajectory deviation is shown in Figure 12. Due to the circular electrode shape, the maximum-angle trajectory is shown by the black dashed line. The theoretical maximum angle of microbead trajectory that the velocity measurement system composed of two electrodes can pass through is shown by the red dashed line. If the distance between the intersection point of the trajectory and the circular electrode plane and the center of the electrode is set as the deviation difference between the landing point and the radius, and the ratio of the deviation distance to the radius is set as the landing point deviation rate , then the angle between the trajectory and the central axis can be described using the deviation rate. The measurement error of the axial component of velocity caused by the different deviation rates between the trajectory of the microbeads and the intersection of the two electrode surfaces is shown in Figure 13. It can be seen that the theoretical maximum error of this electrode structure is less than 1.25%. Due to the limitation of the launch port on the trajectory of the microbeads, the maximum deviation rate of the intersection point between the microbeads and the first electrode is only 0.81, so the maximum possible deviation is shown in the dashed box in Figure 13.
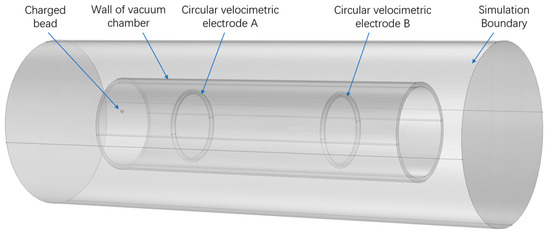
Figure 11.
COMSOL simulation modeling of microbead fly-by electrodes.
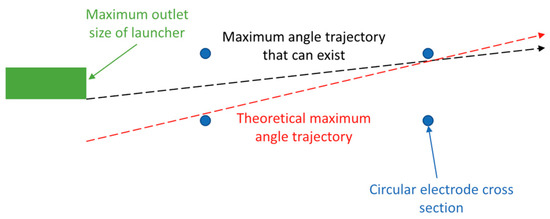
Figure 12.
Schematic diagram of microbead trajectory deviation.
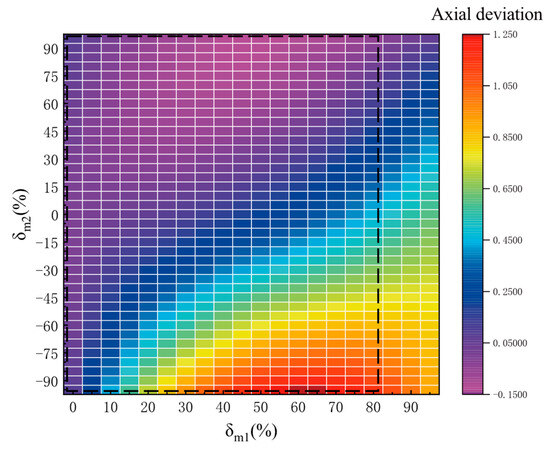
Figure 13.
Position detection deviation.
The time difference between the extreme values of the detection electrode signal (as shown in Figure 10) is related to the axial velocity of the microbeads and the deviation rate when flying over the electrode. The axial velocity of the microbeads is directly proportional to the time difference between the amplitudes of the two electrode signals and the intersection point of 0. Therefore, the time difference between the maximum and minimum values of a single signal divided by the time difference between the amplitudes of the two electrode signals and the intersection point of 0 forms a dimensionless quantity , which can reflect the deviation rate when the microbeads fly over the electrode. The relationship between and delta is shown in Figure 14, and it can be concluded that and have a monotonic relationship.
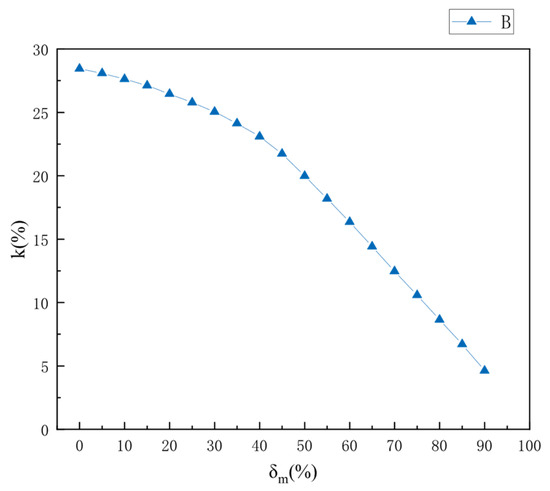
Figure 14.
Relationship between k-value and deviation rate.
After processing the electrostatic detection signal and with a known electrode spacing, the speed of the microbeads can be calculated by determining the time difference between the signals of the two electrodes crossing the zero point. The speed can be calculated as:
The distance between the two electrodes is denoted as , while and represent the instances when the signals from electrodes A and B intersect the zero point, respectively. The parameter , indicative of the characteristics of the two electrode plates, is given by:
where and represent the times corresponding to the extreme value point and the extreme value point of the electrode signal, respectively. The deviation rate at the time of the flyby electrode can be determined through a curve fitting calculation applied to Figure 14 as follows:
2.3. System Structure
The system structure is illustrated in Figure 15. To minimize the resistance of the microbeads during flight and to meet the requirements of the nozzle operation, the experimental area, which is the flight path of the microbeads, needs to be evacuated. The electrostatic probe electrodes are fixed in the vacuum cavity. The left section serves as the detection area of the test detector, where the space debris detector is positioned to detect the microbeads, and the pumping unit’s pumping holes are arranged in this section. The central part is the flight section, where the microbeads are launched from the launcher and pass through the area, and where the motion measurement device is located to determine the speed and trajectory deviation of the microbeads. The rightmost part is the replaceable microbead launcher. The vacuum chamber is constructed from transparent material to allow easy observation of the experimental status. The pumping system comprises a check valve, a solenoid valve, and an air pump. The solenoid valve opens only when the air pump is activated under normal circumstances, and both the solenoid valve and the air pump close after the pumping process to maintain an airtight experimental environment. The check valve opens when the air pressure inside the experimental area exceeds atmospheric pressure, facilitating the microbead launching experiment when the back pressure of the experimental vacuum cavity is at atmospheric pressure.

Figure 15.
System structure. (a) SAPD-P launcher structure diagram; (b) GEAPD-E launcher structure diagram.
3. System Testing and Discussion
Performance testing of the system involved assessing errors in the microbead kinematic measurement system and evaluating the performance of the two launching devices. Errors in the microbead motion measurement device included inaccuracies in the microbeads’ velocity and deviations in trajectory measurement from the intersection point of the CSERE. The performance of the launch device primarily involves the launch speed of the microbeads and the degree of deviation from the landing point. Various parameters of the launch device will result in different values for the two launch performance indicators. Testing the performance of the launch device aims to investigate the correlation between its parameters and performance indicators. Aluminum foil target paper was positioned 400 mm from the launching port in the test area. Upon impact with the target paper, the launched microbeads would either penetrate it or create craters, allowing for the determination of the microbeads’ drop point. The launching process was recorded using a high-speed camera, and the microbeads’ velocity was subsequently calculated.
3.1. Microbead Motion Measurement System Error
The microbead motion measurement system analyzes two main components: the measurement error of microbead velocity and the error in measuring the deviation of the trajectory from the intersection point of the CSERE. Gravity was not taken into account when calculating the deviation rate of the microbeads based on their drop point. The trajectory was assumed to be a straight line connecting the launching port and the drop point. The GEAPD-E, with a small diameter at the launching port, was utilized as the launching device to enhance measurement accuracy.
The photographs taken by the high-speed camera are shown in Figure 16. The velocity of the microbeads was calculated as , ignoring the optical aberration of the device housing. The relationship between the microbead velocimetry error , the axial velocity , and the microbead velocity obtained by the microbead velocimetry system is as follows:
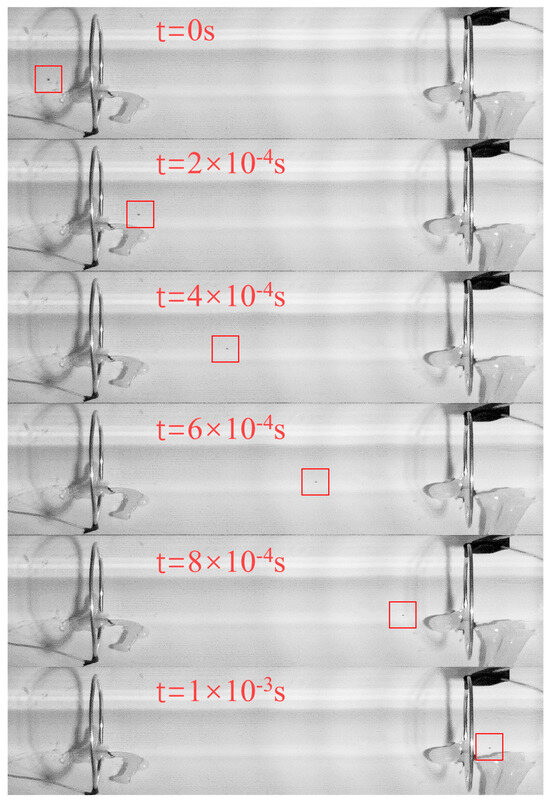
Figure 16.
Photographs taken by a high-speed camera. The black point in the red box is a microbead.
The value of the experiment is shown in Figure 17.
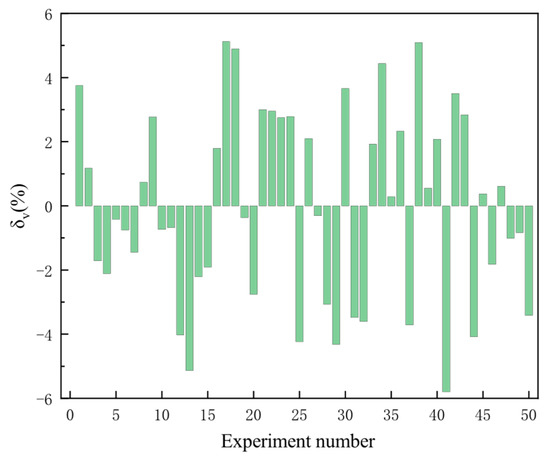
Figure 17.
Microbead velocity measurement error.
The measurement of the axial velocity of the microbeads will have a maximum error of about 6%, mainly due to the accuracy of the time coordinates of the characteristic points of the signals, which is affected by the sampling rate limitation of the velocimetry system as well as the interference signals generated by the airflow.
The relationship between the measurement error of the microbead deviation of electrodes A and B and the position of the microbead drop point is:
where and represent the measurement errors of the deviation of the microbead trajectories of the two electrodes from the position of the intersection of the two CSERE, respectively. and denote the microbead deviation rates measured by the signals of the two electrodes, stands for the radius of the line connecting the centers of circular electrode cross sections, and is the distance of the drop point of the microbead from the center point. The experimental values of and are illustrated in Figure 18.
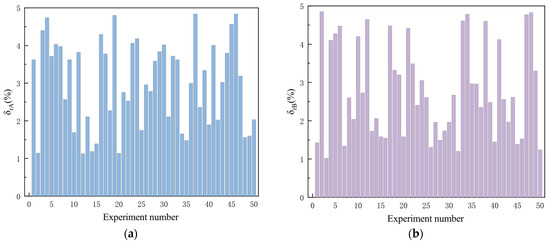
Figure 18.
Measurement error of the positional deviation. (a) For electrode A; (b) For electrode B.
Also, subject to airflow signal interference and sampling rate limitations of the test system, the rate of deviation of the two electrodes from the microbeads in repeated experiments results in a maximum error of approximately 5%.
3.2. SAPD-P Launch Performance Testing
The launch performance of the SAPD-P is affected by three parameters: solenoid opening time, microbead release time, solenoid opening interval, and microbead size. The SAPD-P uses the same launch line for different microbeads; only the loading system is different. The effect on launch speed and accuracy was tested by varying the solenoid valve opening time and the microbead release time under the condition of determining the microbead diameter. Since it takes about 20 ms for the solenoid valve to turn on and off, the moments of the solenoid valve, turning on and off under the condition of ignoring the response time of the circuit are calculated starting from the moment when the control circuit sends an action command to the solenoid valve. The moment of solenoid valve opening is defined as the 0 moment, the moment of microbead release is , and the moment of valve closing is .
The SAPD-P testing scenario is depicted in Figure 19. The relationship between the axial velocity () of microspheres and the emission time parameters ( and ) is illustrated in Figure 20. When falls within the 0–30 ms range, the axial velocity gradually increases. However, due to the time required for the solenoid valve to open, the velocity of the microbeads deviates significantly from the theoretical value. When the difference between and is 10 ms, and the solenoid valve is closed, the microbeads fail to launch from the device, thereby affecting the axial velocity. Once exceeds 30 ms, the velocity of the microbeads stabilizes. Nevertheless, the injection of airflow into the vacuum experimental chamber before microbead launch and the resulting turbulence formation inside increase the flight resistance of the microbeads. Consequently, the velocity of the microbeads decreases as increases.

Figure 19.
SAPD-P test experiment scenario.
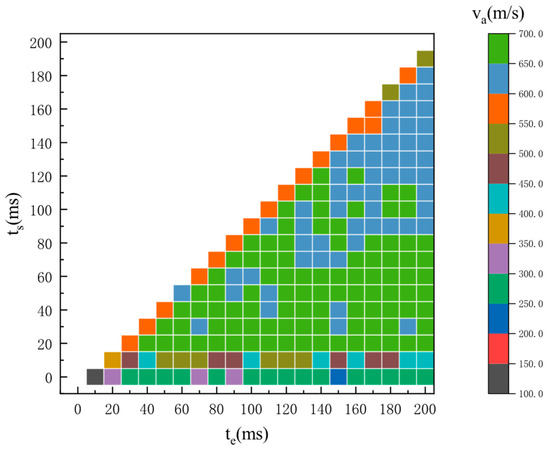
Figure 20.
Relationship of to and for SAPD-P.
The relationship between the launch accuracy and the launch time parameters and is illustrated in Figure 21. Similar to the axial velocity trend of microbeads, the deviation of the micro-beads landing point is significant when is very small, and even the microspheres collide with the annular velocity measuring electrode at = 0. Once exceeds 30 ms, the error of the microbeads stabilizes, ranging between 16 and 35 mm.
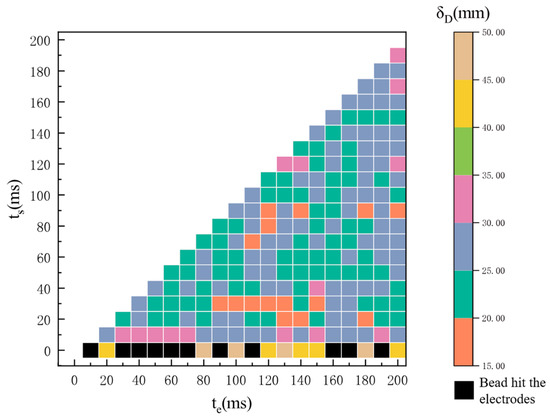
Figure 21.
to and for SAPD-P devices.
Considering the results of the deviation of the emission velocity of the microbeads from the drop point and the need to minimize the pumping time between the two experiments, values of 30 ms and 40 ms for and , respectively, are optimal.
3.3. GEAPD-E Launch Performance Testing
The GEAPD-E test scenario is shown in Figure 22. The operational performance of the device is affected by the size of the beads, and since the firing rate is strongly influenced by the tolerance of the bead size and the blast effect, a large number of repetitive experiments are required to make a fundamental assessment of the performance of the launcher.

Figure 22.
GEAPD-E test experiment scenario.
The data from the repeated experiments of microbead axial velocities with different sizes of microbeads are shown in Figure 23. The intervals of the speeds in the repeated experiments varied widely, ranging from 750 m/s to 1150 m/s, and the highest speeds of the three sizes of microbeads were all greater than 1000 m/s.
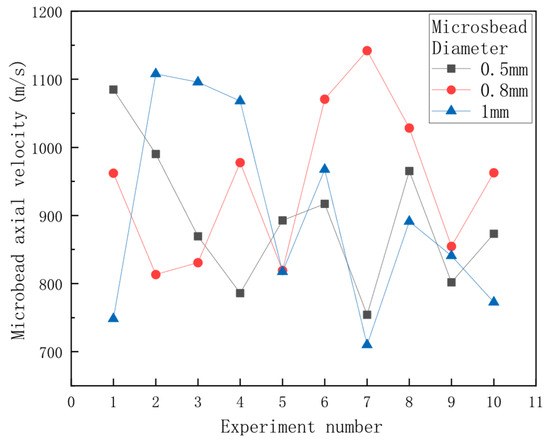
Figure 23.
GEAPD-E replicates experiments of .
The volumetric energy density of combustible gas combustion is limited. If the gas is changed to a solid explosive, the combustion product can achieve a higher temperature and a faster firing rate due to the microbead velocity.
The launching accuracy of with different sizes of microbeads in repeated experimental data is illustrated in Figure 24. Irrespective of the microbeads’ diameter, the accuracy of this launching method varies significantly across repeated experiments, ranging from a minimum error of only 5.3 mm to a maximum of 48.1 mm.
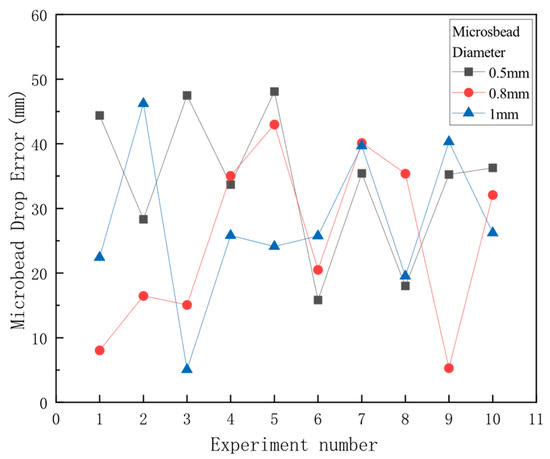
Figure 24.
of GEAPD-E replicate experiments.
4. Summary
In this paper, two low-cost simulation devices for launching micro-debris are designed to meet practical needs and support the development of space micro-debris detectors. Two different devices were designed to launch glass microbeads less than 1 mm in diameter. One device uses tank-stored high-pressure gas, while the other uses mixed-combustible gas to propel the microbeads. The first device, SAPD-P, achieves a maximum launch speed of 697 m/s with a launch accuracy ranging from 16 mm to 35 mm. The second device, GEAPD-E, achieves a maximum launch speed of 1150 m/s with a launch accuracy between 5.1 mm and 48.1 mm. These devices can be selected based on experimental requirements. The velocity of the emitted microbeads and the positional deviation of the trajectory’s intersection point with the CSERE were measured using electrostatic induction. The velocity measurement deviation was less than ±6%, and the positional deviation was less than 5%.
Author Contributions
Conceptualization, R.Y. and K.T.; methodology, R.Y. and K.T.; software, X.L.; validation, C.H., Y.L. (Yu Liu) and Y.L. (Yue Liu); formal analysis, R.Y.; investigation, R.Y.; resources, X.L. and Y.L. (Yue Liu); data curation, C.H.; writing—original draft preparation, R.Y.; writing—review and editing, K.T.; visualization, Y.L. (Yue Liu); supervision, K.T.; project administration, Y.L. (Yu Liu); funding acquisition, K.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 51707008 and the Research Improvement Fund Project of BISTU—Electrostatic Detection of Space Micro Debris, grant number 5212410945.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy reasons.
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Chen, J.; Chen, S.; Qin, Y.; Zhu, Z.; Zhang, J. Aerodynamic Analysis of Deorbit Drag Sail for CubeSat Using DSMC Method. Aerospace 2024, 11, 315. [Google Scholar] [CrossRef]
- Niccolai, L.; Bassetto, M.; Quarta, A.A.; Mengali, G. Trajectory approximation of a Coulomb drag-based deorbiting. Aerospace 2022, 9, 680. [Google Scholar] [CrossRef]
- Bassetto, M.; Niccolai, L.; Quarta, A.A.; Mengali, G. Rapid evaluation of the decay time of a plasma brake-based CubeSat. Aerospace 2022, 9, 636. [Google Scholar] [CrossRef]
- Pisanu, T.; Muntoni, G.; Schirru, L.; Ortu, P.; Urru, E.; Montisci, G. Recent advances of the BIRALET system about space debris detection. Aerospace 2021, 8, 86. [Google Scholar] [CrossRef]
- Piergentili, F.; Zarcone, G.; Parisi, L.; Mariani, L.; Hossein, S.H.; Santoni, F. LEO object’s light-curve acquisition system and their inversion for attitude reconstruction. Aerospace 2020, 8, 4. [Google Scholar] [CrossRef]
- Space Environment Statistics. Available online: https://sdup.esoc.esa.int/discosweb/statistics/ (accessed on 11 June 2024).
- Tao, J.; Cao, Y.; Ding, M. Progress of space debris detection technology. Laser Optoelectron. Prog. 2022, 59, 126–136. [Google Scholar]
- Kawai, N.; Tsurui, K.; Hasegawa, S.; Sato, E. Single microparticle launching method using two-stage light-gas gun for simulating hypervelocity impacts of micrometeoroids and space debris. Rev. Sci. Instrum. 2010, 81, 115105. [Google Scholar] [CrossRef]
- Veysset, D.; Sun, Y.; Kooi, S.E.; Lem, J.; Nelson, K.A. Laser-driven high-velocity microparticle launcher in atmosphere and under vacuum. Int. J. Impact Eng. 2020, 137, 103465. [Google Scholar] [CrossRef]
- Usherenko, Y.; Mironovs, V.; Lapkovskis, V.; Usherenko, S.; Gluschenkov, V. Powder particle flow acceleration methods for simulation of interaction with materials used in spacecrafts. Agron. Res. 2019, 17, 2445–2454. [Google Scholar]
- Matsunaga, M.; Fujio, C.; Ogawa, H.; Higa, Y.; Handa, T. Nozzle design optimization for supersonic wind tunnel by using surrogate-assisted evolutionary algorithms. Aerosp. Sci. Technol. 2022, 130, 107879. [Google Scholar] [CrossRef]
- Carl, L.Y. Matheson Gas Data Book, 7th ed.; Matheson Company: Irving, TX, USA, 2001; pp. 880–894. [Google Scholar]
- The Engineering ToolBox. Available online: https://www.engineeringtoolbox.com/water-vapor-d_979.html (accessed on 13 June 2024).
- Xue, W.; Zhu, Z.; Zou, L.; Zhang, G. Theoretic calculation on the thermodynamic character for carbon dioxide. J. At. Mol. Phys. 2002, 19, 24–26+30. [Google Scholar]
- Cai, S.; Wang, L. On Electrostatic Problem Electrical Image Method and Direct Method Research of Grounding Conductor Ball and a Uniformly Charged Ring. J. Leshan Norm. Univ. 2014, 29, 17. [Google Scholar]
- Feynman, R.P. The Feynman Lectures on Physics; Addison-Wesley Publishing Co.: Reading, MA, USA, 1966; pp. 53–58. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).