Data-Driven-Method-Based Guidance Law for Impact Time and Angle Constraints
Abstract
1. Introduction
- By drawing on a large number of related studies, such as the effective use of PNG [19,20,22,23,44,45,46,47,56,64,65], PNG is applied to data-driven ITACG design. Compared with other literature, it not only retains the advantages of PNG but also has a simple structure, does not require small angle assumption, and does not need the remaining flight time information.
- A new paradigm is developed for the data-driven method, and a new time-independent ITACG law is designed. Compared with the existing literature [28], the guidance law has less overload in the guidance process, less control energy consumption, strong adaptability, and high precision.
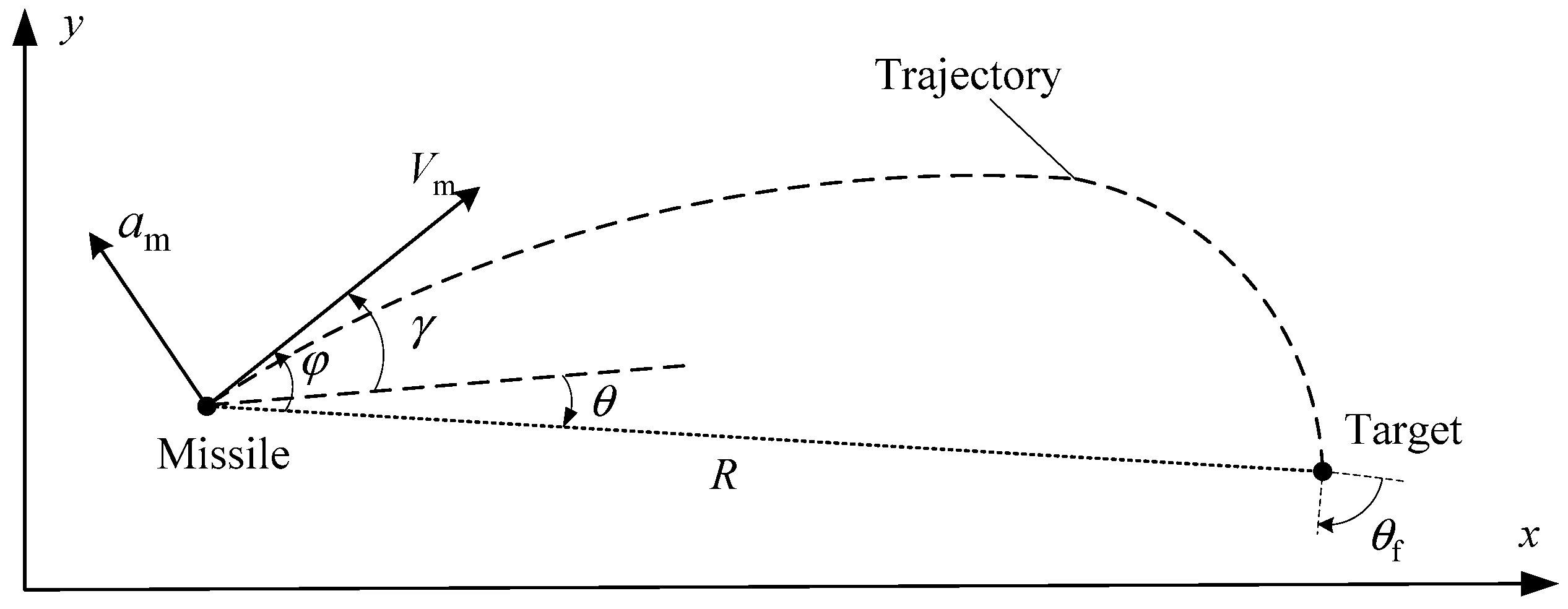
2. Problem Description and General Scheme
2.1. Equations of Motion for Engagement
- The flight vehicle is considered a point mass.
- Only the normal acceleration perpendicular to the velocity vector of the flight vehicle is considered.
- The autopilot lag is neglected.
2.2. General Scheme for ITACG Design
3. Predesign: A Pure Impact Angle Control Guidance Law
3.1. Theoretical Analysis
3.2. Guidance Command for Impact Angle Control
3.3. Stability and Convergence Analysis
4. Design of the Impact Time and Angle Control Guidance Law
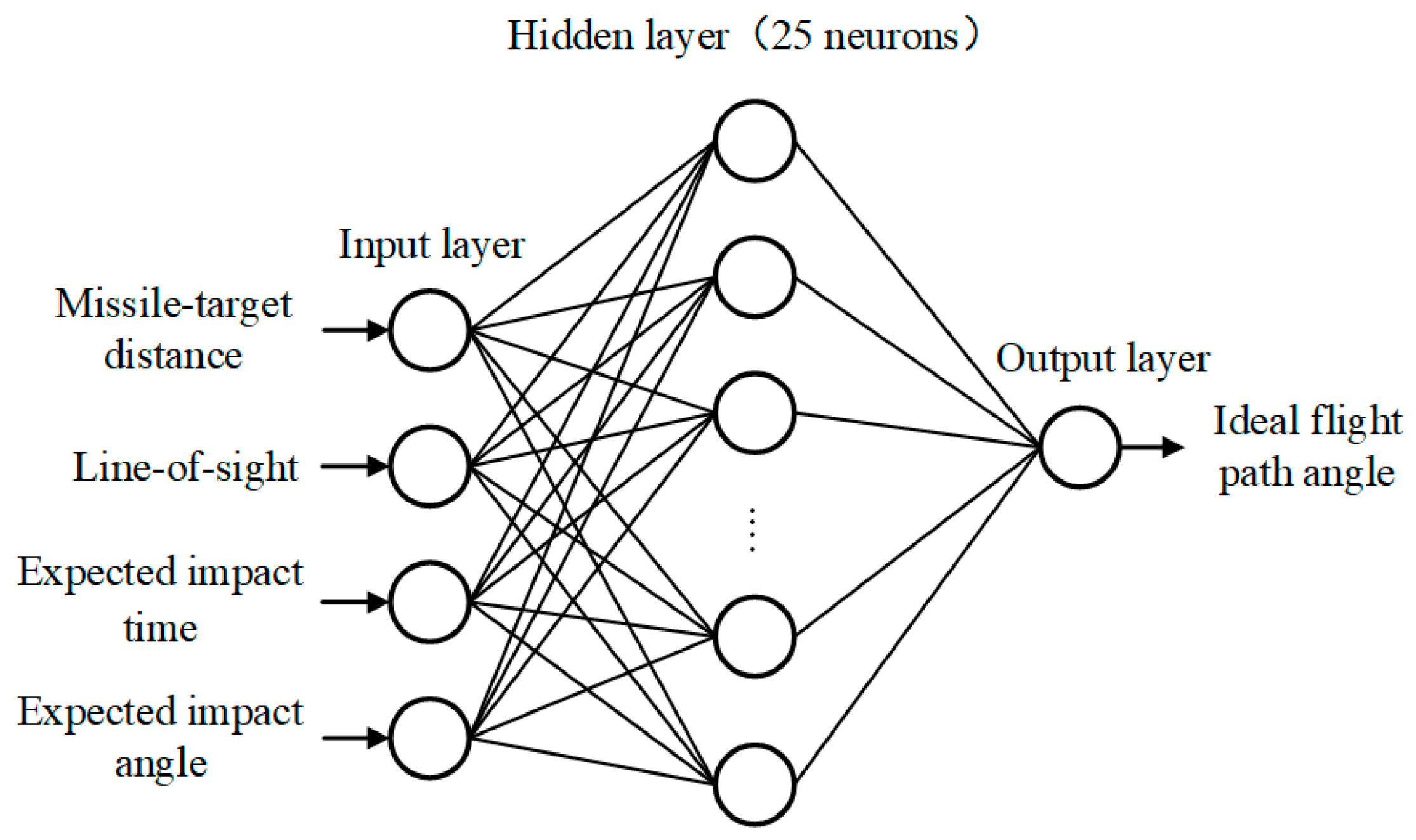
4.1. Application Paradigm of an ANN
4.2. Guidance Command for Impact Time and Angle Control
5. Simulation Results
5.1. Simulation Results of Pure Impact Angle Control
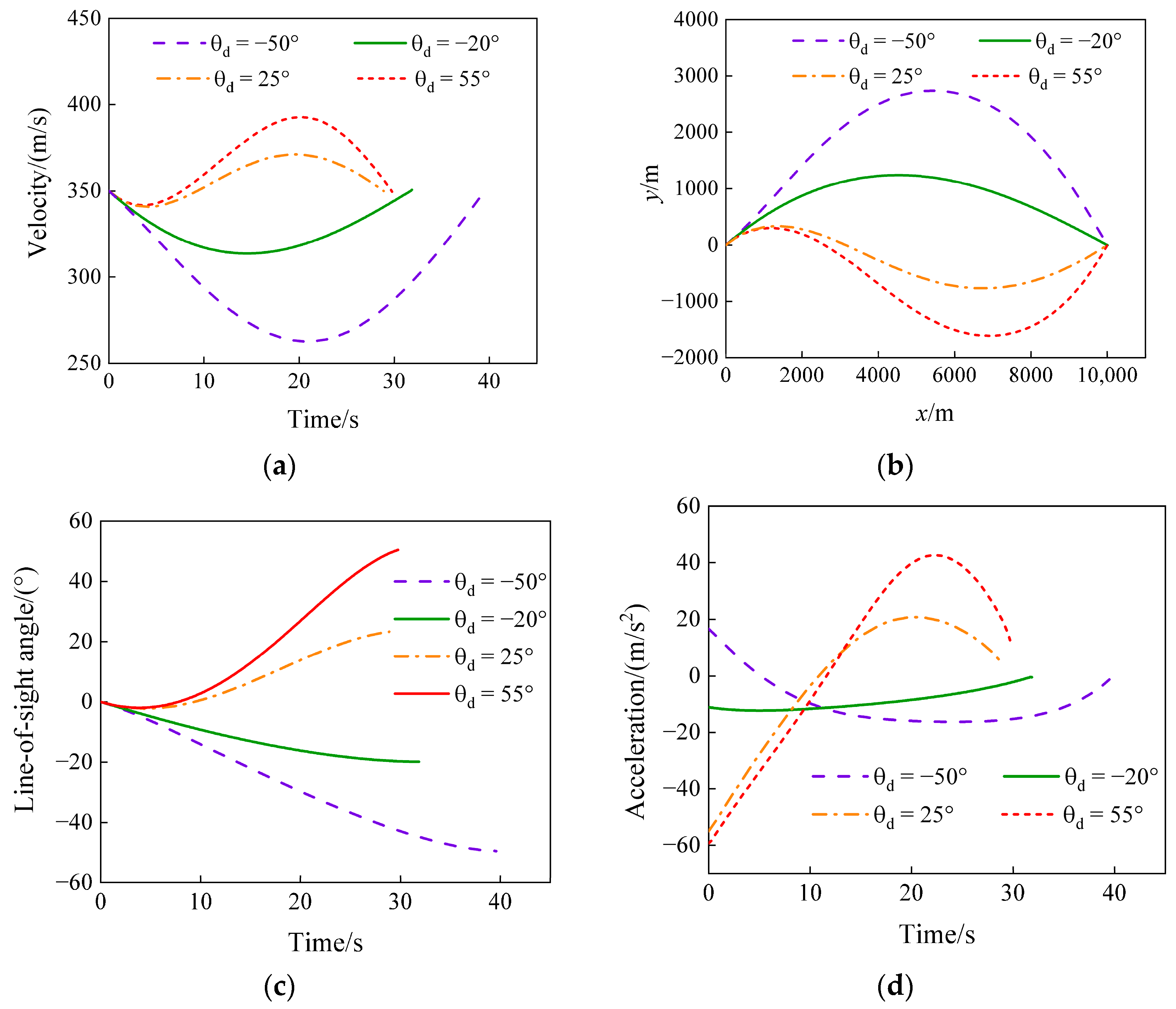
5.1.1. For Various Expected Impact Angles
5.1.2. For Various Initial Conditions
5.1.3. Considering the Velocity Variation
5.2. Simulation Results of Impact Time and Angle Control
5.2.1. Building a Specific Mapping Network
- (a)
- The values of the flight state variables are chosen as , , , and . For each expected impact angle in the set, taking values with the respective range of flight states results in a total of 155,160 sets of initial simulation conditions.
- (b)
- By performing the simulation of impact angle control under each set of initial conditions, the datasets and containing 155,160 sets of data are obtained. These data can be used to train the neural network, after which, the mapping network of the ideal flight path angle is established.
5.2.2. For Various Expected Impact Times with Constant Impact Angle
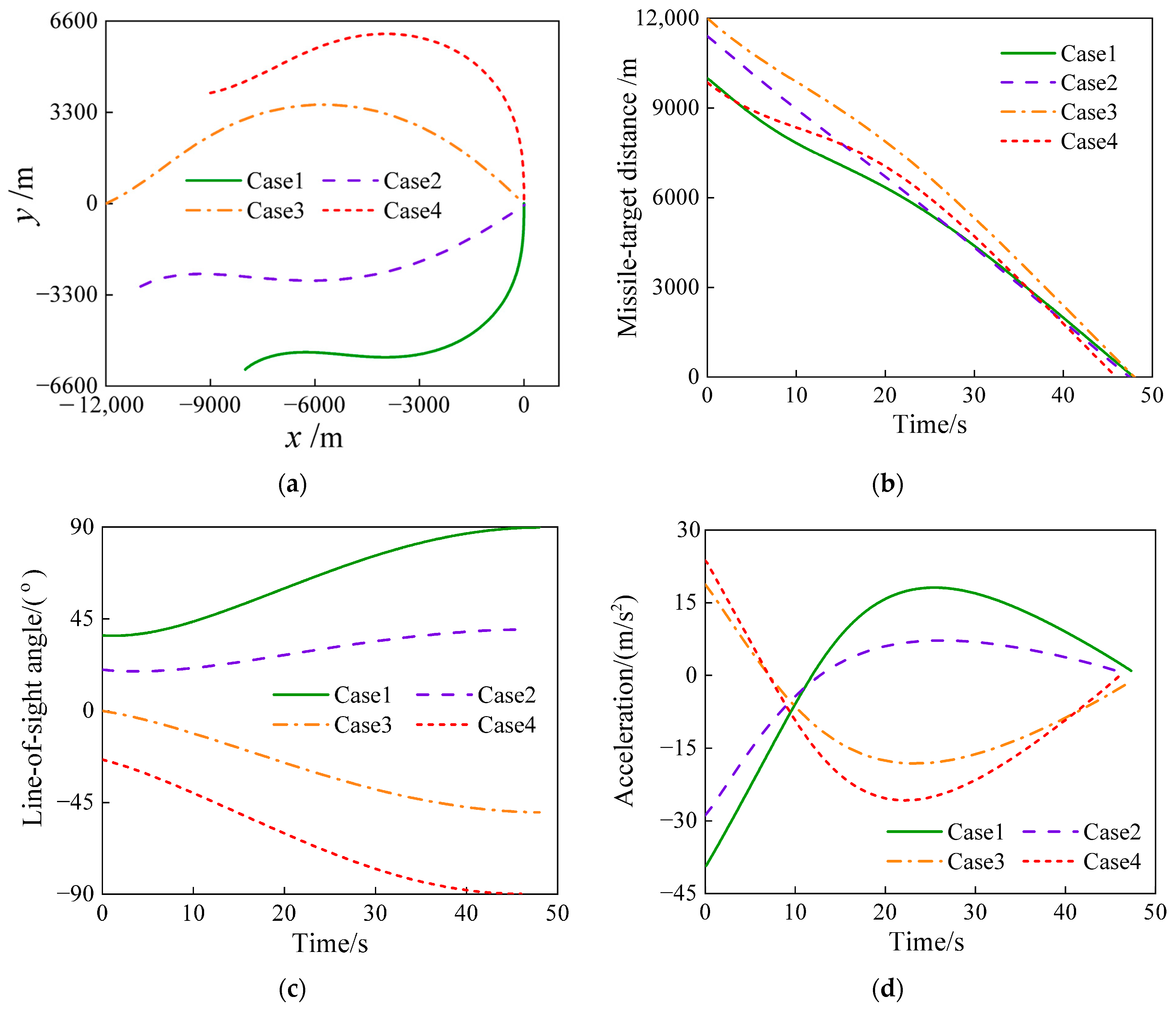
5.2.3. Comparative Simulation
5.2.4. Simulation of Cooperative Attack
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, M.; Grider, K.V. Terminal Guidance for Impact Attitude Angle Constrained Flight Trajectories. IEEE Trans. Aerosp. Electron. Syst. 1973, AES-9, 852–859. [Google Scholar]
- Ryoo, C.; Cho, H.; Tahk, M. Optimal Guidance Laws with Terminal Impact Angle Constraint. J. Guid. Control Dyn. 2005, 28, 724–732. [Google Scholar] [CrossRef]
- Jeon, I.; Lee, J.; Tahk, M. Impact-Time-Control Guidance Law for Anti-Ship Flight Vehicles. IEEE Trans. Control Syst. Technol. 2006, 14, 260–266. [Google Scholar] [CrossRef]
- Lee, J.; Jeon, I.; Tahk, M. Guidance Law to Control Impact Time and Angle. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 301–310. [Google Scholar]
- Lee, C.; Seo, M. New Insights into Guidance Laws with Terminal Angle Constraints. J. Guid. Control Dyn. 2018, 41, 1828–1833. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; He, S.; Lee, C. Nonlinear Optimal Impact-Angle-Constrained Guidance with Large Initial Heading Error. J. Guid. Control Dyn. 2021, 44, 1663–1676. [Google Scholar] [CrossRef]
- Lin, L.; Xin, M. Impact Angle Guidance Using State-Dependent (Differential) Riccati Equation: Unified Applicability Analysis. J. Guid. Control Dyn. 2020, 43, 2175–2182. [Google Scholar] [CrossRef]
- Li, B.; Tang, P.; Xu, H.; Zheng, D. Terminal Impact Angle Control Guidance Law Considering Target Observability. Aerospace 2022, 9, 193. [Google Scholar] [CrossRef]
- Wang, J.; Tao, X.; Dong, W.; Wang, C. Three-Dimensional Predefined-Time Impact Angle Control Guidance Law with Field-of-View Limit. J. Frankl. Inst. 2023, 360, 7621–7644. [Google Scholar] [CrossRef]
- Cho, D.; Kim, H.J.; Tahk, M. Nonsingular Sliding Mode Guidance for Impact Time Control. J. Guid. Control Dyn. 2016, 39, 61–68. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J. Nonsingular Sliding-Mode Control for Field-of-View Constrained Impact Time Guidance. J. Guid. Control Dyn. 2018, 41, 1210–1218. [Google Scholar] [CrossRef]
- Hu, Q.; Han, T.; Xin, M. Sliding-Mode Impact Time Guidance Law Design for Various Target Motions. J. Guid. Control Dyn. 2019, 42, 136–148. [Google Scholar] [CrossRef]
- Tekin, R.; Erer, K.; Holzapfel, F. Quartic Range Shaping for Impact Time Control. In Proceedings of the 25th Mediterranean Conference on Control and Automation (MED), Valletta, Malta, 3–6 July 2017; pp. 1213–1218. [Google Scholar]
- Tekin, R.; Erer, K.; Holzapfel, F. Impact Time Control with Generalized-Polynomial Range Formulation. J. Guid. Control Dyn. 2018, 41, 1188–1193. [Google Scholar] [CrossRef]
- Tekin, R.; Erer, K.; Holzapfel, F. Polynomial Shaping of the Look Angle for Impact Time Control. J. Guid. Control Dyn. 2017, 40, 2666–2671. [Google Scholar] [CrossRef]
- Tekin, R.; Erer, K.; Holzapfel, F. Adaptive Impact Time Control via Look-Angle Shaping Under Varying Velocity. J. Guid. Control Dyn. 2017, 40, 3247–3255. [Google Scholar] [CrossRef]
- Tsalik, R.; Shima, T. Circular Impact-Time Guidance. J. Guid. Control Dyn. 2019, 42, 1836–1847. [Google Scholar] [CrossRef]
- Tekin, R.; Erer, K.; Holzapfel, F. Control of Impact Time with Increased Robustness via Feedback Linearization. J. Guid. Control Dyn. 2016, 39, 1678–1685. [Google Scholar] [CrossRef]
- Ma, S.; Wang, Z.; Wang, X.; Chen, Q. Three-Dimensional Impact Time Control Guidance Considering Field-of-View Constraint and Velocity Variation. Aerospace 2022, 9, 202. [Google Scholar] [CrossRef]
- Chang, S.; Chen, S. Nonsingular PNG-Based Impact Time Control Guidance with Lower Dependence on Time to go Estimate. Int. J. Aerosp. Eng. 2019, 2019, 5031245. [Google Scholar] [CrossRef]
- Wang, P.; Guo, Y.; Ma, G.; Wie, B. New Differential Geometric Guidance Strategies for Impact-Time Control Problem. J. Guid. Control Dyn. 2019, 42, 1982–1992. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, G.; Liu, A. Guidance Law with Impact Time and Impact Angle Constraints. Chin. J. Aeronaut. 2013, 26, 960–966. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Ma, G. Impact time control guidance law with large impact angle constraint. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 2119–2131. [Google Scholar] [CrossRef]
- Harl, N.; Balakrishnan, S.N. Impact Time and Angle Guidance with Sliding Mode Control. IEEE Trans. Control Syst. Technol. 2012, 20, 1436–1449. [Google Scholar] [CrossRef]
- Kumar, S.R.; Ghose, D. Impact Time and Angle Control Guidance. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, AIAA Paper 2015-0616, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Zhao, Y.; Sheng, Y.; Liu, X. Analytical Impact Time and Angle Guidance via Time-Varying Sliding Mode Technique. ISA Trans. 2016, 62, 164–176. [Google Scholar] [CrossRef] [PubMed]
- Hou, Z.; Yang, Y.; Liu, L.; Wang, Y. Terminal Sliding Mode Control Based Impact Time and Angle Constrained Guidance. Aerosp. Sci. Technol. 2019, 93, 105142. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J. Sliding-Mode Guidance for Simultaneous Control of Impact Time and Angle. J. Guid. Control Dyn. 2019, 42, 394–401. [Google Scholar] [CrossRef]
- Liu, X.; Li, G. Adaptive Sliding Mode Guidance with Impact Time and Angle Constraints. IEEE Access 2020, 8, 26926–26932. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, W.; Liu, X.; Cheng, J. Three-Dimensional Fixed-Time Robust Cooperative Guidance Law for Simultaneous Attack with Impact Angle Constraint. Aerosp. Sci. Technol. 2021, 110, 106523. [Google Scholar] [CrossRef]
- Yu, H.; Dai, K.; Li, H.; Zou, Y.; Ma, X.; Ma, S.; Zhang, H. Three-Dimensional Adaptive Fixed-Time Cooperative Guidance Law with Impact Time and Angle Constraints. Aerosp. Sci. Technol. 2022, 123, 107450. [Google Scholar] [CrossRef]
- You, H.; Chang, X.; Zhao, J.; Wang, S.; Zhang, Y. Three-Dimensional Impact-Angle-Constrained Fixed-Time Cooperative Guidance Algorithm with Adjustable Impact Time. Aerosp. Sci. Technol. 2023, 141, 108574. [Google Scholar] [CrossRef]
- Kim, T.; Lee, C.; Jeon, I. Augmented Polynomial Guidance with Impact Time and Angle Constraints. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 2806–2817. [Google Scholar] [CrossRef]
- Zhao, Y.; Sheng, Y.; Liu, X. Trajectory Reshaping Based Guidance with Impact Time and Angle Constraints. Chin. J. Aeronaut. 2016, 29, 984–994. [Google Scholar] [CrossRef][Green Version]
- Kang, S.; Tekin, R.; Holzapfel, F. Generalized Impact Time and Angle Control via Look-Angle Shaping. J. Guid. Control Dyn. 2019, 42, 695–702. [Google Scholar] [CrossRef]
- Tekin, R.; Erer, K. Impact Time and Angle Control Against Moving Targets with Look Angle Shaping. J. Guid. Control Dyn. 2020, 43, 1020–1025. [Google Scholar] [CrossRef]
- Wang, P.; Guo, Y.; Ma, G.; Lee, C.; Wie, B. New Look-Angle Tracking Guidance Strategy for Impact Time and Angle Control. J. Guid. Control Dyn. 2022, 45, 545–557. [Google Scholar] [CrossRef]
- Catak, A.; Emre, K. Dynamic Line of Sight Shaping for Impact Time and Angle Control Guidance. IFAC Pap. Line 2023, 56, 4514–4519. [Google Scholar] [CrossRef]
- Erer, K.S.; Tekin, R. Impact Time and Angle Control Based on Constrained Optimal Solutions. J. Guid. Control Dyn. 2016, 39, 2445–2451. [Google Scholar] [CrossRef]
- Lee, J.; Kim, H.J. Impact Time and Angle Control Guidance with Rendezvous Concept. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, AIAA Paper 2018-1322, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Chen, X.; Wang, J. Optimal Control Based Guidance Law to Control Both Impact Time and Impact Angle. Aerosp. Sci. Technol. 2019, 84, 454–463. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, W.; Li, J.; Yu, W. Guidance Algorithm for Impact Time, Angle, and Acceleration Control Under Varying Velocity Condition. Aerosp. Sci. Technol. 2022, 123, 107462. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, S.; Wang, X. Impact Time and Angle Control Optimal Guidance with Field-of-View Constraint. J. Guid. Control Dyn. 2022, 45, 2369–2378. [Google Scholar] [CrossRef]
- Hu, Q.; Han, T.; Xin, M. New Impact Time and Angle Guidance Strategy via Virtual Target Approach. J. Guid. Control Dyn. 2018, 41, 1755–1765. [Google Scholar] [CrossRef]
- Wang, C.; Yu, H.; Dong, W.; Wang, J. Three-Dimensional Impact Angle and Time Control Guidance Law Based on Two-Stage Strategy. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5361–5372. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, K.; Zhang, G.; Yan, L. Virtual Target Approach-Based Optimal Guidance Law with Both Impact Time and Terminal Angle Constraints. Nonlinear Dyn. 2022, 107, 3521–3541. [Google Scholar] [CrossRef]
- Zhu, J.; Su, D.; Xie, Y.; Sun, H. Impact Time and Angle Control Guidance Independent of Time-to-go Prediction. Aerosp. Sci. Technol. 2019, 86, 818–825. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J. Two-stage Guidance Law with Impact Time and Angle Constraints. Nonlinear Dyn. 2019, 95, 2575–2590. [Google Scholar] [CrossRef]
- Kim, H.; Lee, J.; Kim, H.J.; Kwon, H.; Park, J. Look-Angle-Shaping Guidance Law for Impact Angle and Time Control with Field-of-View Constraint. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1602–1612. [Google Scholar] [CrossRef]
- Yan, X.; Zhu, J.; Kuang, M.; Yuan, X. A Computational-Geometry-Based 3-Dimensional Guidance Law to Control Impact Time and Angle. Aerosp. Sci. Technol. 2020, 98, 105672. [Google Scholar] [CrossRef]
- Hou, L.; Luo, H.; He, S.; Shi, H.; Shin, H. An Optimal Geometrical Guidance Law for Impact Time and Angle Control. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 9821–9830. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, Q.; Han, T.; Xin, M. Two-Stage Guidance Law with Constrained Impact via Circle Involute. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1301–1316. [Google Scholar] [CrossRef]
- Shima, T.; Livermore, R. Deviated Pure-Pursuit-Based Optimal Guidance Law for Imposing Intercept Time and Angle. J. Guid. Control Dyn. 2018, 41, 1805–1812. [Google Scholar]
- Manchester, I.R.; Savkin, A.V.; Faruqi, F.A. Method for Optical-Flow-Based Precision Missile Guidance. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 836–842. [Google Scholar] [CrossRef]
- Dong, W.; Wang, C.; Liu, J.; Wang, J.; Xin, M. Three-Dimensional Vector Guidance Law with Impact Time and Angle Constraints. J. Frankl. Inst. 2023, 360, 693–718. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J.; Shan, J. Cooperative guidance for multiple powered Flight Vehicles with constrained impact and bounded speed. J. Guid. Control Dyn. 2021, 44, 825–840. [Google Scholar] [CrossRef]
- Brunton, S.L.; Kutz, J.N.; Manohar, K.; Aravkin, A.Y.; Morgansen, K. Data-Driven Aerospace Engineering: Reframing the Industry with Machine Learning. AIAA J. 2021, 59, 2820–2847. [Google Scholar] [CrossRef]
- Yan, L.; Chang, X.; Wang, N.; Zhang, L.; Liu, W.; Deng, X. Aerodynamic Identification and Control Law Design of a Flight Vehicle Using Machine Learning. AIAA J. 2023, 61, 2998–3018. [Google Scholar] [CrossRef]
- He, S.; Shin, H.S.; Tsourdos, A. Computational Flight Vehicle Guidance: A Deep Reinforcement Learning Approach. J. Aerosp. Inf. Syst. 2021, 18, 571–582. [Google Scholar]
- Cheng, L.; Jiang, F.; Wang, Z. Multiconstrained Real-Time Entry Guidance Using Deep Neural Networks. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 325–340. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, M.; Skelton, R.E. A Markov data-based approach to system identification and output error covariance analysis for tensegrity structures. Nonlinear Dyn. 2024, 112, 7215–7231. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, M.; Skelton, R.E. Q-Markov Covariance equivalent realizations for unstable and marginally stable systems. Mech. Syst. Signal Process. 2023, 196, 110343. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, W.; Han, G.; Zhang, Y. Finite Time Convergent Wavelet Neural Network Sliding Mode Control Guidance Law with Impact Angle Constraint. Int. J. Autom. Comput. 2015, 12, 588–599. [Google Scholar] [CrossRef][Green Version]
- Guo, Y.; Li, X.; Zhang, H.; Cai, M.; He, F. Data-Driven Method for Impact Time Control Based on Proportional Navigation Guidance. J. Guid. Control Dyn. 2020, 43, 955–966. [Google Scholar] [CrossRef]
- Huang, J.; Chang, S. Data-Driven Method Based Impact Time and Impact Angle Control Guidance Law. Syst. Eng. Electron. 2022, 44, 3213–3220. (In Chinese) [Google Scholar]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; Jesús, O.D. Neural Network Design, 2nd ed.; eBook; PWS Publishing Co.: Pacific Grove, CA, USA, 2017. [Google Scholar]

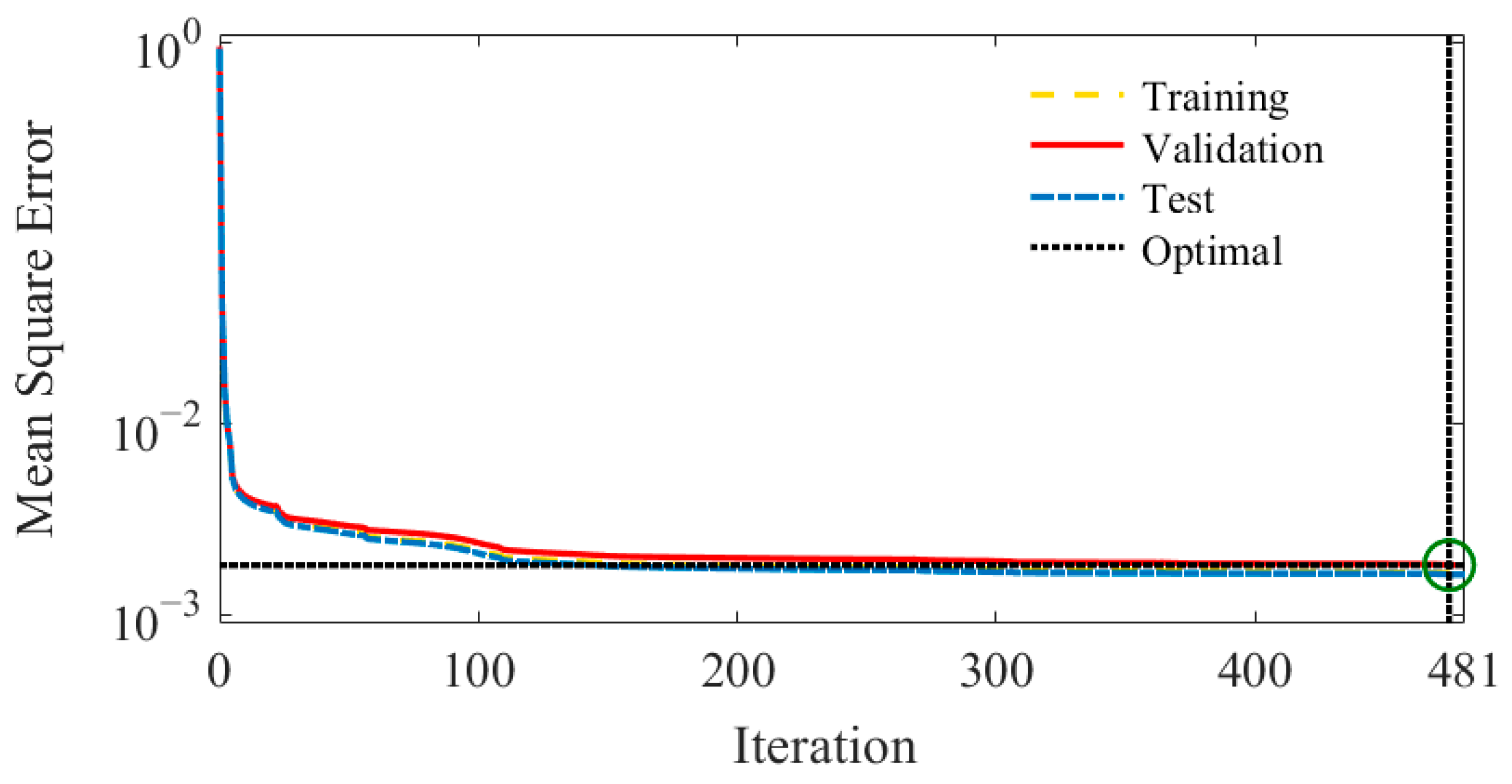
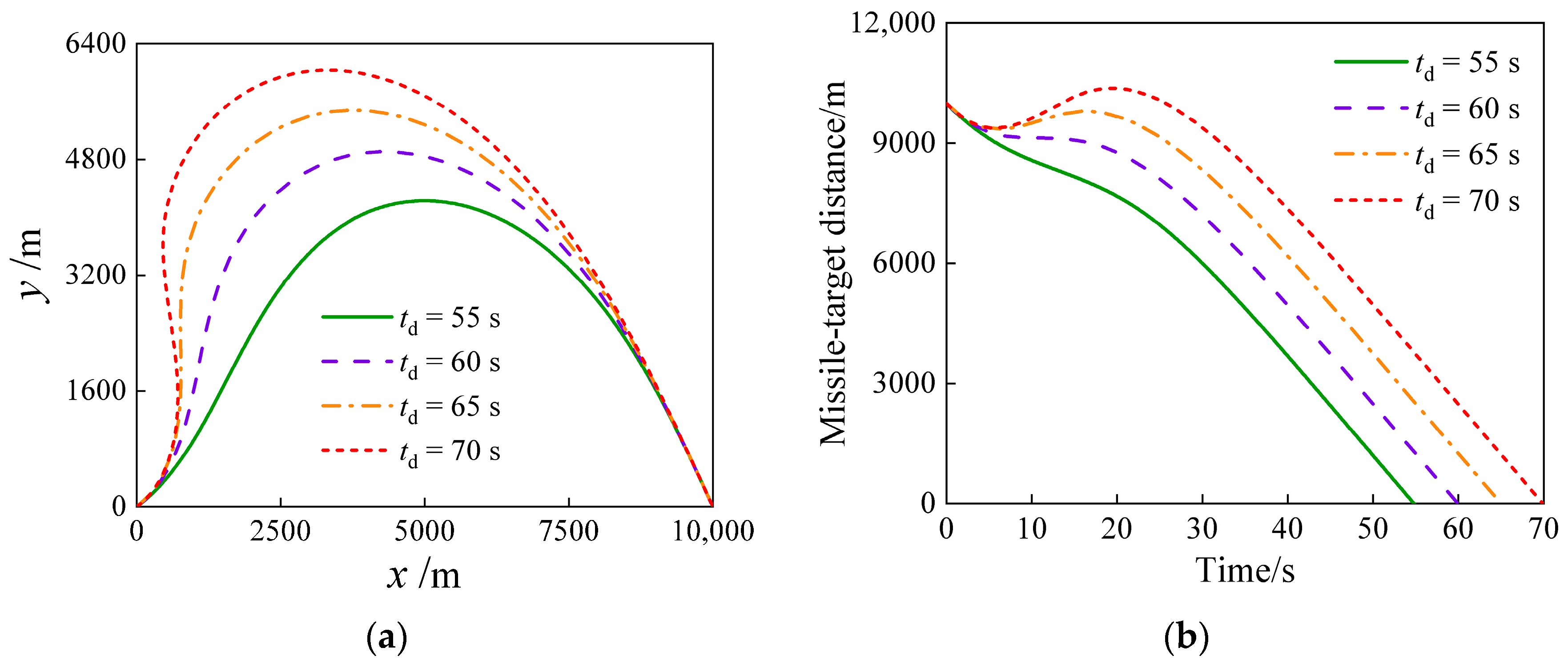
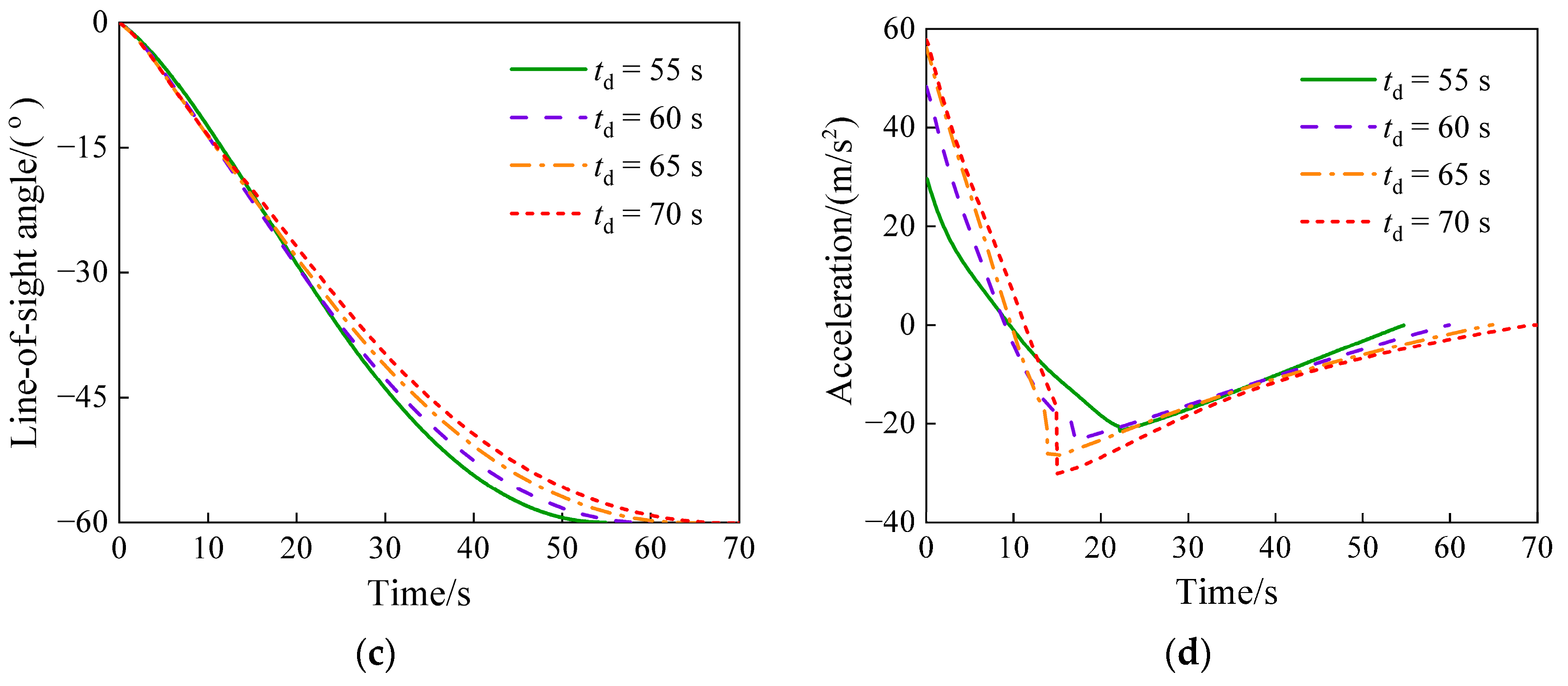

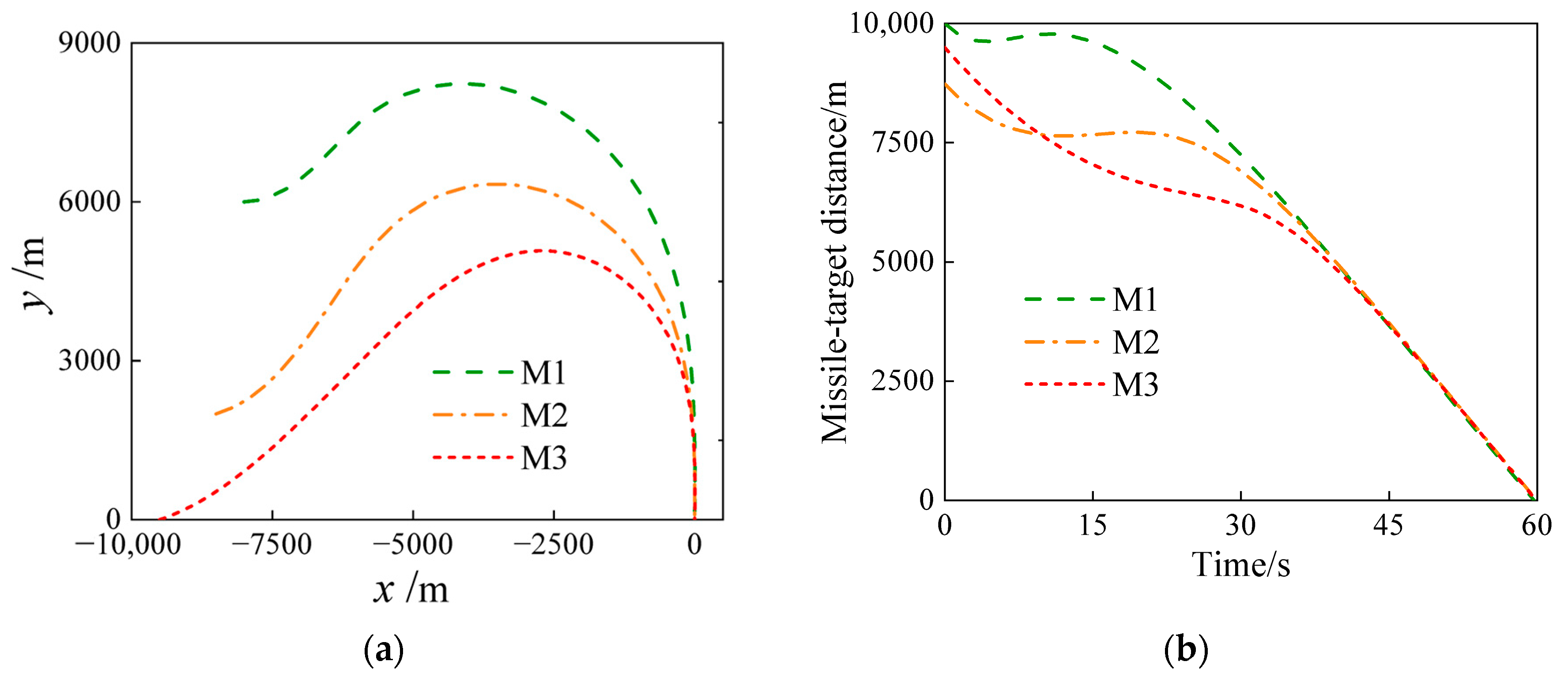
| Case No | Initial Position (m) | Flight Vehicle-Target Distance (m) | Velocity (m/s2) | Initial Heading Error (°) | Desired Impact Angle (°) |
|---|---|---|---|---|---|
| 1 | (−8000, −6000) | 10,000 | 250 | 10 | 90 |
| 2 | (−11,000, −3000) | 11,402 | 250 | 20 | 40 |
| 3 | (−12,000, 0) | 12,000 | 300 | 30 | −50 |
| 4 | (−9000, 4000) | 9849 | 300 | 40 | −90 |
| Case No | Expected Impact Time (s) | Impact Time Error (s) | Impact Angle Error (o) |
|---|---|---|---|
| 1 | 55 | 0.177 | 0.014 |
| 2 | 60 | 0.017 | 0.021 |
| 3 | 65 | 0.050 | 0.037 |
| 4 | 70 | 0.030 | 0.083 |
| Case No. | Guidance Law | Impact Time (s) | ) |
|---|---|---|---|
| 1 | Proposed | 55 | |
| 2 | Ref. [28] | 55 | |
| 3 | Proposed | 60 | |
| 4 | Ref. [28] | 60 |
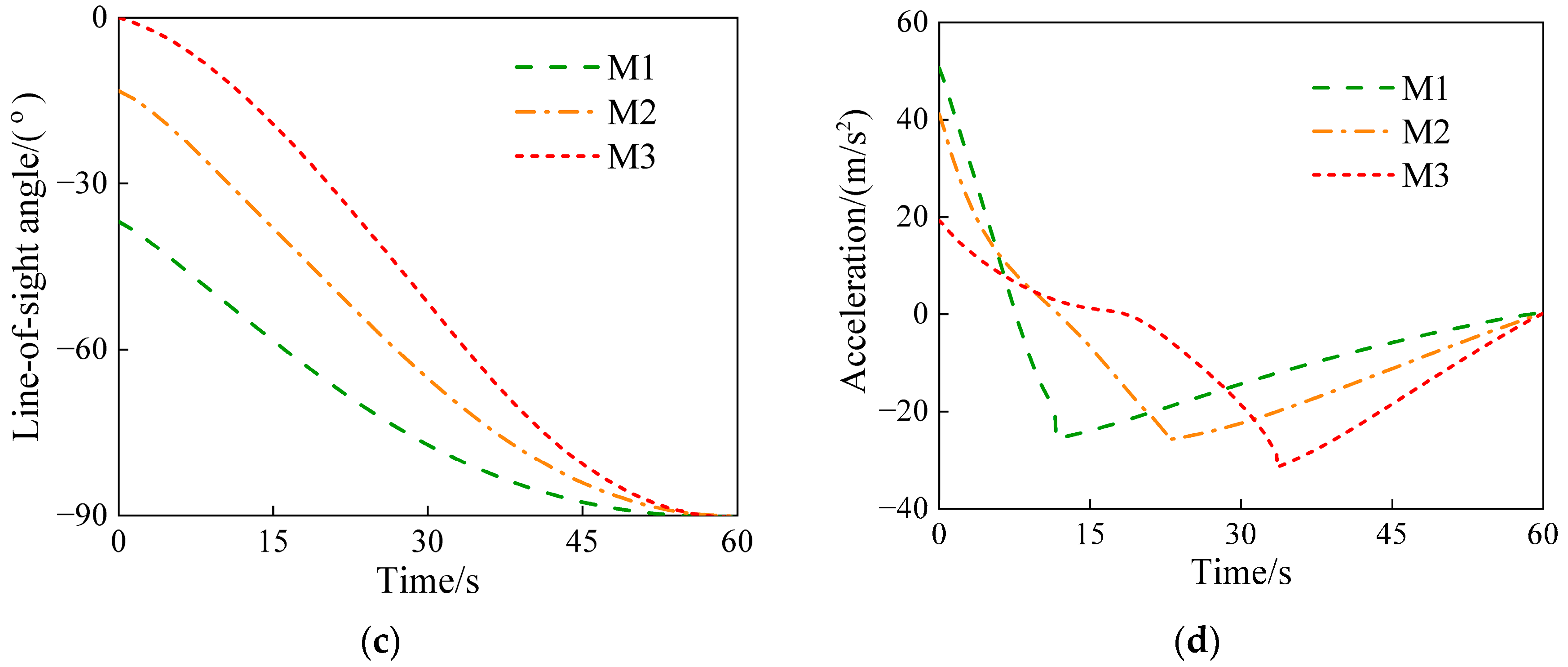
| Object | Initial Position (m) | Distance between Flight Vehicle and Target (m) | Initial Heading Error (°) |
|---|---|---|---|
| M1 | (−8000, 6000) | 10,000 | 40 |
| M2 | (−8500, 2000) | 8732 | 30 |
| M3 | (−9500, 0) | 9500 | 20 |
| Target | (0, 0) | N/A 1 | N/A 1 |
| Object | Error of Impact Time (s) | Error of Impact Angle (°) |
|---|---|---|
| M1 | 0.032 | 0.13 |
| M2 | 0.015 | 0.04 |
| M3 | 0.033 | 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, W.; Huang, J.; Chang, S. Data-Driven-Method-Based Guidance Law for Impact Time and Angle Constraints. Aerospace 2024, 11, 540. https://doi.org/10.3390/aerospace11070540
Cao W, Huang J, Chang S. Data-Driven-Method-Based Guidance Law for Impact Time and Angle Constraints. Aerospace. 2024; 11(7):540. https://doi.org/10.3390/aerospace11070540
Chicago/Turabian StyleCao, Wenjie, Jia Huang, and Sijiang Chang. 2024. "Data-Driven-Method-Based Guidance Law for Impact Time and Angle Constraints" Aerospace 11, no. 7: 540. https://doi.org/10.3390/aerospace11070540
APA StyleCao, W., Huang, J., & Chang, S. (2024). Data-Driven-Method-Based Guidance Law for Impact Time and Angle Constraints. Aerospace, 11(7), 540. https://doi.org/10.3390/aerospace11070540





