Abstract
To enhance the performance of rigid coaxial rotors across both hovering and high-speed cruising conditions, this study develops a novel aerodynamic optimization method that differentiates between the upper and lower rotors. Utilizing the lifting line and reformulated viscous vortex particle method (rVPM), this approach models the complex wake fields of coaxial rotors and accurately assesses the aerodynamic loads on the blades. The optimization of geometric properties such as planform configuration and nonlinear twist is conducted through an innovative solver that integrates simulated annealing with the Nelder–Mead algorithm, ensuring both rapid and comprehensive optimization results. Comparative analyses demonstrate that these tailored geometric adjustments significantly enhance efficiency in both operational states, surpassing traditional methods. This research provides a strategic framework for addressing the varied aerodynamic challenges presented by different flight states in coaxial rotor design.
1. Introduction
Next-generation rotorcraft are expected to excel in both hovering and high-speed cruising capabilities. The design of rigid coaxial rotors has emerged as a promising solution to meet these requirements [1]. This design features two sets of coaxial counter-rotating rigid rotors, bypassing the flight speed limits imposed by retreating blade stall in traditional helicopters through a concept that balances the lift on the advancing sides of both rotors. In contrast with conventional rotors, rigid coaxial rotors need to address complex operational conditions, encompassing both hovering and high advance ratios in high-speed forward flight [2,3]. During hovering, intense mutual interference occurs between the coaxial rotors, particularly as the lower rotor operates under the strong downwash of the upper rotor [4], creating significantly different aerodynamic environments for each. Adopting distinct aerodynamic shapes and twist distributions for the upper and lower rotors seems advantageous for improving hovering efficiency. In high advance ratio conditions, where upper and lower rotor interference diminishes, the rotor blades encounter high subsonic speeds. As such, an effective aerodynamic design of these blades is crucial to enhance the performance during forward flight.
In aerodynamic optimization of coaxial rigid rotor blades, traditional approaches have often involved the use of approximate theories or analytical models to analyze rotor aerodynamics. These methods offer high computational efficiency but depend on empirical parameters for accuracy. Recently, computational fluid dynamics (CFD) and discrete vortex methods have evolved rapidly, becoming key methodologies in the design of blade aerodynamics. CFD’s precision hinges on extensive, high-resolution grid divisions, theoretically enabling very high confidence levels [5], albeit with reduced computational efficiency. Discrete vortex methods, conversely, manage to balance between achieving medium-to-high confidence and maintaining computational efficiency.
A number of experts have focused on optimizing the aerodynamic configuration of coaxial rotors. Leishman and colleagues [6] optimized the aerodynamic performance of coaxial rotors using the free wake method. Researchers such as Jun [7], Rand [8], and Giovanetti [2] have optimized the aerodynamic shape of coaxial rotor blades based on momentum blade element theory, with a focus on hovering performance. Giovanetti and team [3] further advanced this by targeting the forward flight performance of coaxial rotors, leading to an aerodynamic shape distinct from that in hovering conditions. Syal and others [9] integrated the free wake method into an optimization strategy for independently designing the blades of the upper and lower rotors of a coaxial system, with an emphasis on hovering performance. Their findings indicate that utilizing different blade shapes for the upper and lower rotors is key to achieving the best performance in coaxial rotors. Moreover, the complexity of optimizing different aspects of coaxial rotors raises the bar for designing effective optimization strategies. Wang and his team [10] developed a surrogate model using the CFD solver CLORNS, which they integrated with genetic algorithms. This was aimed at optimizing the high-speed flight performance of rigid coaxial rotors, resulting in an elliptical blade shape featuring a swept-back taper and a non-linear chord distribution.
In the aforementioned design of coaxial rotors, the momentum blade element method offers the highest computational efficiency but fails to account for the interference characteristics of the coaxial rotors. The free wake method has moderate computational efficiency, yet its calculation precision depends on the selection of empirical parameters. The computational fluid dynamics (CFD) method boasts the highest accuracy but suffers from lower computational efficiency, necessitating the use of surrogate models to enhance optimization efficiency, inevitably leading to a loss in method precision.
Within the realm of discrete vortex methods, the viscous vortex particle method (VPM) has recently gained popularity [11]. This method, compared with the free wake method, offers finer granularity and avoids issues such as blade penetration through line vortices found in the line vortex model. By incorporating a reconstructed equation for adjusting vortex particle size, the numerical stability of the classical vortex particle method can be enhanced, making it more suitable for simulating the complex wake of rigid coaxial rotors [12]. The combination of lifting line and viscous vortex particle methods effectively leverages the computational precision of the latter and the efficiency of the former, thus allowing for direct integration into the optimization framework without the need for additional surrogate models.
In aerodynamic optimization of coaxial rigid rotor blades, the complexity of the design challenges conventional optimization methods, often requiring a more sophisticated approach to effectively navigate the highly non-linear and non-convex problem spaces involved. To address these challenges, this research adopts a hybrid optimization strategy combining simulated annealing (SA) and the Nelder–Mead (NM) algorithms, a method proven to balance global search capabilities and rapid local convergence effectively. Simulated annealing is renowned for its ability to escape local optima through a probabilistic acceptance of worse solutions, particularly effective in the expansive search required at the initial stages of optimization [13]. On the other hand, the Nelder–Mead algorithm excels in fine-tuning solutions within a local search area, rapidly converging to an optimum without the need for derivative information [14].
The integration of these methods into a single hybrid strategy allows for an expansive yet precise exploration of the design space. The effectiveness of such a hybrid approach, particularly the simulated Nelder–Mead algorithm with random variables updating (SNMRVU), has been demonstrated in solving large-scale global optimization problems, offering high-quality solutions with lower computational costs compared with other algorithms [15]. This previous success underlines the potential of the SA-NM hybrid method to optimize the geometric properties of coaxial rotor blades effectively, thereby enhancing both hover and forward flight efficiencies. Through this strategic hybridization, the current study aims to leverage the global optimization properties of SA with the precise, rapid search capabilities of NM, thus maximizing the optimization process while ensuring robust solutions across diverse aerodynamic environments.
Empirical studies have demonstrated that hybrid approaches, which integrate global and local optimization techniques, can significantly outperform single-method strategies in complex engineering applications, offering better robustness against local optima and improved convergence speeds. Therefore, the choice of the SA-NM hybrid method provides a balanced, efficient, and effective tool for the aerodynamic optimization of coaxial rotor blades, specifically tailored to overcome the unique challenges posed by their design.
Taking everything into consideration, this paper, drawing on the advanced design experiences of current coaxial rigid rotor aerodynamics, presents a concept for the optimized differential blade shape design of rigid coaxial rotors. A combined optimization method was established by integrating the lifting line/reformulated viscous vortex particle method with a mixed optimization strategy of simulated annealing/Nelder–Mead algorithms. Based on this method, which offers medium-to-high confidence, acceptable computational efficiency, and global search capabilities, an independent aerodynamic layout optimization design for the upper and lower rotors of a coaxial rigid rotor was carried out. This resulted in an optimized coaxial rigid rotor blade aerodynamic layout design that balances both hovering and cruising performance.
2. Numerical Method
In recent years, the classical viscous vortex particle method has been progressively applied to the aerodynamic modeling of coaxial rotors [16], achieving satisfactory results. However, due to the small spacing between the upper and lower rotors of rigid coaxial rotors and severe rotor wake interference, forming complex and unstable wake vortex structures, the classical viscous vortex particle method tends to encounter numerical instabilities in such scenarios, affecting computational convergence and accuracy. To address this issue, this research, based on the concept of the rVPM method [12], improves the classical viscous vortex particle method through the approach of large eddy simulation. This improved method is then combined with the lifting line model and applied to the aerodynamic modeling of rigid coaxial rotors. While maintaining computational efficiency similar to the classic VPM method, this approach results in a coaxial rigid rotor aerodynamic analysis model with better numerical stability and accuracy.
2.1. Reformulated Viscous Vortex Particle Model
In the classical viscous vortex particle method, the rotor wake is discretized into a vortex blob model, which is a particle model with a finite vortex core size [17]. The essence of the viscous vortex particle method is to solve the vorticity form of the Navier–Stokes equations within a Lagrangian framework:
In this equation, represents the flow velocity, is the air viscosity, is the vorticity field, denotes the material derivative, and is the Laplace operator. The discretized vorticity field can be expressed as:
Here, represents the spatial position of the particle, the subscript p denotes the vortex particle, is the total number of vortex particles in the flow field, is the vorticity strength of the pth vortex particle, and is the smoothing kernel function [18], where is the vortex blob radius of the particle.
In this equation, is a cutoff function, and several options for cutoff functions are provided in the literature [19]. This study has chosen the Gaussian function, given by the following equation:
For the aforementioned viscous vortex particle method, the governing equations for the changes in vortex particle strength and spatial position are given by the following set of equations.
In the equation, the local velocity of the vortex particle, , is composed of the free-stream velocity, , and the vorticity field-induced velocity, . The induced velocity component can be solved using the Biot–Savart law.
As the flow transitions into turbulent regions, classical vortex particle methods (VPMs) often exhibit numerical instabilities that restrict their applicability. These instabilities primarily arise from Lagrangian deformation and the disruption of vorticity field incompressibility. To address these limitations, this paper introduces the reformulated viscous vortex particle method (rVPM), which significantly enhances the conservation of local mass and angular momentum. This is achieved by dynamically adjusting particle sizes, thus improving numerical stability in simulations characterized by complex, interacting wake structures.
The rVPM method refines the conventional mechanisms of vortex stretching and tilting, ensuring better conservation of mass and momentum at high rotational speeds and amidst intricate blade–vortex interactions, typical in coaxial rotor configurations. These critical modifications not only maintain the integrity of the vorticity field—thereby preventing numerical diffusion—but also result in more accurate simulations of aerodynamic loads and rotor performance metrics. Accordingly, the governing equations have been adapted to accommodate the evolution of vortex particle sizes, optimizing the method’s efficacy in predicting and analyzing complex aerodynamic phenomena.
In the above equation, governs the evolution of vortex particle size, is the control equation for the vortex stretching term, and is the filtered vorticity strength of the particle. The coefficients and , as defined in Equation (7), modulate the strength of these interactions based on the conservation parameters and , set to ensure angular momentum and mass conservation within the vortex blobs. The convection control equation for vortex particles remains unchanged, and the viscous diffusion term is solved using the particle strength exchange (PSE) method [20]. To improve computational efficiency, the fast multipole method (FMM) [21] is used to accelerate the N-body problem solving involved in the computation.
The incorporation of large eddy simulation (LES) principles within the rVPM framework significantly enhances the method’s stability and accuracy, particularly in the simulation of turbulent flows. LES explicitly models the effects of smaller, unresolved scales through the introduction of the subfilter-scale (SFS) stress tensor, . This tensor captures the critical interactions between the resolved large-scale dynamics and the unresolved subfilter-scale dynamics. The LES-filtered Navier–Stokes equations, expressed in vorticity form as:
where represents the SFS vorticity advection and represents the SFS vortex stretching, serve as the foundation for the enhanced rVPM formulation. This approach ensures the accurate resolution of essential flow structures while avoiding the computational burden of a fine mesh required for resolving all scales of turbulence.
Incorporating LES within the rVPM introduces a new set of governing equations, meticulously derived from the LES-filtered Navier–Stokes equations. These equations reinforce the conservation of mass and angular momentum by dynamically reshaping the vortex elements in response to vortex stretching. This key modification significantly improves the numerical stability of the rVPM, especially for complex flows with interacting wake structures, such as those encountered in coaxial rotor configurations. Furthermore, the rVPM, when coupled with a novel subfilter-scale model of vortex stretching, constitutes a meshless and numerically stable LES scheme. This scheme efficiently preserves vortical structures, eliminates the complexities of mesh generation, and is free from the numerical dissipation typically associated with mesh-based CFD methods. Moreover, it does not suffer from the restrictions imposed by the conventional Courant–Friedrichs–Lewy (CFL) condition, thereby enabling larger time steps and faster simulations. For a more detailed mathematical derivation of this method, please refer to [22].
By addressing the instabilities of classical VPM through improved particle size evolution and vorticity management, rVPM significantly expands the applicability of vortex particle methods to more complex rotorcraft configurations. These improvements in the rVPM are vital for simulations involving coaxial rotors, where traditional methods struggle to maintain accuracy and computational efficiency. The computational efficiency of the coaxial rotor aerodynamic analysis method developed in this paper is enhanced by 1 to 3 orders of magnitude compared with traditional methods such as Reynolds-averaged Navier–Stokes (RANS), lattice Boltzmann method (LBM), and detached eddy simulation (DES) [23].
2.2. Rigid Coaxial Rotor Model
The motion of coaxial rigid rotor blades includes pitching, flapping, and lead-lag. The pitching control logic is designed following the approach in the literature [24], and, based on the principles of equivalent flapping offset and flapping spring from sources such as [25,26], the modeling of rigid rotor flapping motion has been conducted. Due to the significantly higher rotor flapping stiffness of X2TD-like aircraft compared with conventional rotors, the Coriolis force resulting from flapping motion is relatively low, and the amplitude of lead-lag motion is very small, having limited impact on overall aerodynamic performance. To focus on more critical issues and enhance computational efficiency, this study omits the model of lead-lag motion. According to the equivalent flapping rules, the flapping motion is given by the following equation.
In the equation, is the flapping angle, represents the non-dimensional equivalent flapping offset, and is the equivalent flapping spring stiffness. Here, is the non-dimensional flapping frequency, R is the rotor radius, is the blade mass static moment, is the blade moment of inertia, and represents the sum of aerodynamic forces, inertial forces, gravitational forces, and Coriolis moment.
To ensure optimization efficiency, this study employs a lifting line model to calculate the aerodynamic loads of the rotor blades and integrates the motion model of rigid coaxial rotors with the viscous vortex particle wake model. In this research, the lifting line is positioned at the 1/4 chord length on the mean camber line of the blade and is divided radially into a certain number of lifting line segments. The lift, drag, and moment coefficients, , of each segment are functions of the local angle of attack, , Reynolds number, , and Mach number, , where:
Based on the Kutta–Joukowski theorem, the bound circulation, , of the lifting line segment, as a solution to the non-linear problem [27], is linked to the aerodynamic coefficients. Each lifting line segment with bound circulation, , forms a closed vortex lattice with the corresponding trailed and shed vorticities. This vortex lattice has a length equal to the lifting line segment and a width equal to the blade chord, thus extending 1/4 chord length beyond the blade trailing edge. The strength of the vortex lattice, , matches the scalar value of the bound circulation, . As time steps forward, the vortex lattices are released from the blade trailing edge and are subsequently converted into newly formed vortex particles according to rules [28,29], moving with the local flow velocity. In this way, the lifting line model is coupled with the reformulated vortex particle model. As shown in Figure 1, the schematic of vortex particle generation illustrates the process in rigid coaxial rotors.
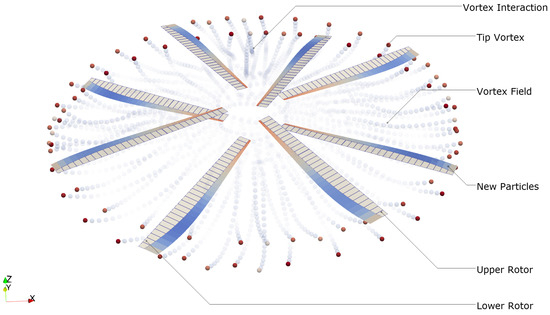
Figure 1.
Schematic of vortex particle generation in coaxial rotors.
2.3. Method Verification
Figure 2 displays a comparison between the computational results of the developed aerodynamic model and experimental data, where the experimental data are derived from wind tunnel tests of a scaled model based on the X2TD coaxial rigid rotor [30]. The model rotor parameters are summarized in Table 1. Figure 2a shows the comparison of the coaxial rigid rotor’s hovering efficiency between test data and computational results, with the horizontal axis representing the blade loading coefficient, obtained by varying the collective pitch of the upper and lower rotors. As shown in the figure, the rVPM model predictions fall within the error bars of the experimental data, while the VPM model slightly underestimates the results but still agrees well with the experimental trends. A similar trend for VPM underestimation of coaxial rotor hover figure of merit was also observed in the study [31]. Figure 2b presents the comparison of the coaxial rigid rotor’s forward flight performance between test data and computational results, where the horizontal axis is the rotor’s advance ratio, , and the vertical axis is the equivalent lift-to-drag ratio, , in forward flight. The graph shows the equivalent lift-to-drag ratios at different collective pitches. A comparison reveals that both the rVPM and VPM results fall within the error bars of the experimental data and exhibit consistent trends. Quantitatively, the rVPM model demonstrates a mean absolute error (MAE) of 0.252 and a mean squared error (MSE) of 0.081, while the VPM model yields an MAE of 0.267 and an MSE of 0.103. The lower MAE and MSE values of the rVPM model indicate its overall closer agreement with the experimental data. A comparison of the experimental data, classical VPM results, and rVPM results reveals that the rVPM model exhibits higher accuracy in predicting hover performance, where flow field interference is significant. This improvement is likely attributed to the enhanced numerical stability of the rVPM algorithm. In forward flight, where the rotor wake is quickly convected away from the rotor disk due to the freestream velocity, resulting in reduced interference, the accuracy of both methods becomes more comparable.
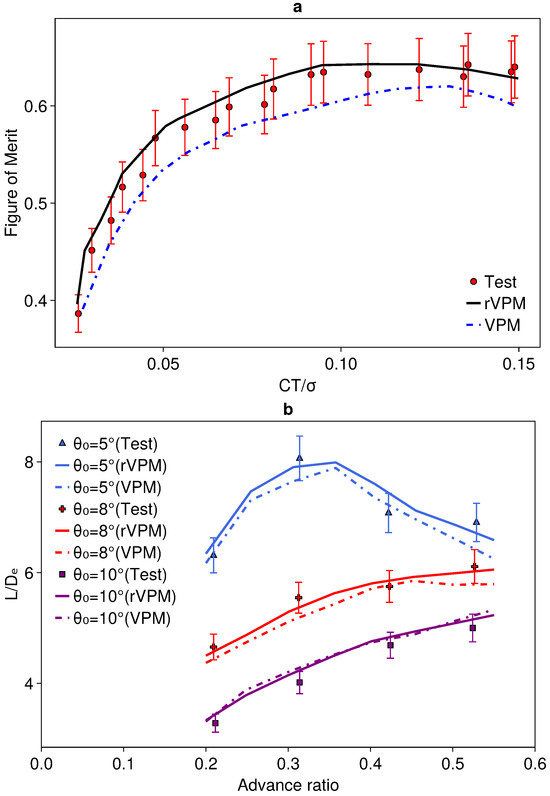
Figure 2.
Comparison of a scaled X2TD-like rotor performance in hover and forward flight: (a) the figure of merit of hover at different blade loadings, and (b) the equivalent rotor lift-to-drag ratio at different advance ratios.

Table 1.
Summary of model rotor properties.
The equivalent lift-to-drag ratio, given by the equation
is a critical performance metric in rotorcraft aerodynamics, providing a measure of the rotor’s efficiency in forward flight. In this equation, denotes the thrust coefficient, representing the dimensionless thrust generated by the rotor. is the torque coefficient, indicative of the dimensionless torque required to overcome the aerodynamic drag of the rotor. is a coefficient accounting for additional drag forces parallel to the rotor disk.
Following the simplified modeling approach proposed by Hersey et al. [32], simplified models of the fuselage, tail, and propeller were integrated with the rotor aerodynamic model developed in this study. The fuselage was treated as a rigid body, with its aerodynamic characteristics derived from wind tunnel test data. Rotor–fuselage interference was accounted for using empirical coefficients. The pusher propeller, mounted parallel to the aircraft’s x-axis, was modeled to generate thrust solely along its axis, neglecting the moment contribution from the reaction torque. At the target forward flight condition of , the propeller’s aerodynamic efficiency was assumed constant (0.85) and independent of thrust. The aircraft’s trim state was determined by solving a system of nonlinear algebraic equations that enforced equilibrium in lift and weight, torque balance between the two rotors, and a match between the calculated rolling moment and the lift offset value obtained from flight tests [33]. This iterative solution process also included the calculation of the rotor wake geometry. Using these models, the required power for the X2TD-like aircraft was calculated across various flight speeds and compared with flight test data. As shown in Figure 3, the numerical results demonstrate good agreement with the flight test data, validating the effectiveness of the developed method in predicting the performance of X2TD-like rigid coaxial rotors. It is important to note that the experimental results exhibit a significant degree of scatter, which is typical in such complex aerodynamic measurements. Despite this inherent variability, the numerical model accurately captures the overall trends and key performance metrics, indicating its robustness and reliability.
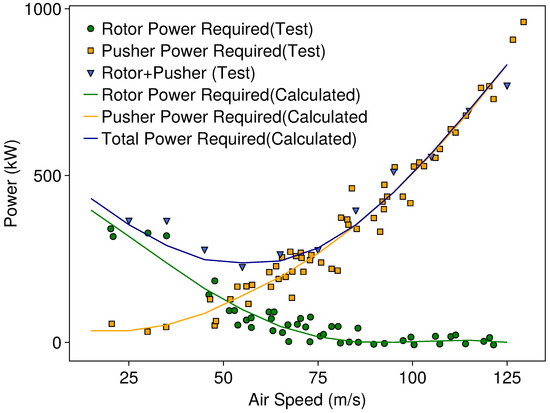
Figure 3.
Validation of the required power of X2TD.
3. Optimization
3.1. Design Parameters
The optimization design is based on a rotor similar to the Sikorsky X2TD, consisting of two sets of coaxial counter-rotating rigid rotors, each with four blades of identical shape. The blade root starts at 0.16 R, where R = 4.023 m is the rotor radius. The upper rotor is set to rotate counterclockwise and the lower rotor is set to rotate clockwise. As shown in Table 2, the X2TD blade utilizes a specific airfoil distribution across different radial stations [1]. The inner segment employs the DBLN-526 double-blunted airfoil, the middle segment the SC1210-R8 airfoil, and the outer segment the SSCA09 airfoil [34]. The aerodynamic coefficients of the airfoil are pre-calculated using a hardware-accelerated LBM method [35] and formed into C81 tables, integrated into the coaxial rigid rotor aerodynamic model described earlier. The specific distribution of airfoils is shown in Table 1.

Table 2.
X2TD blade airfoil distribution.
Two design objectives are selected: the hovering figure of merit, , and the equivalent lift-to-drag ratio, , at a cruise speed of = 0.6. Based on the X2TD flight test data, the blade tip Mach number is set to 0.55 during hover, corresponding to a maximum tip speed of 187 m/s; at = 0.6, the blade tip Mach number is 0.80, with a maximum tip speed of 270 m/s. To ensure consistency in performance calculations, the hover state uses rotor force balance as the trim condition. The trim condition for forward flight is slightly different; in addition to force balance, the rotor roll moment, , needs to match the set lift offset value, , calculated as = . In the calculations of this paper, the net rotor thrust, T, is equal to the total weight of the X2TD aircraft at 2040 kg, and the lift offset is fitted according to X2TD’s test flight data [33], taking 0 during hover and 0.2 in cruising flight. The design variables and objective functions are specified as per the optimization strategy section.
The chord length and twist angle distribution of the coaxial rigid rotor blades are expressed using B-spline curves. A B-spline is a linear combination of B-spline basis curves. An order B-spline curve (corresponding to a spline curve degree of m = n + 1) can be expressed as a linear combination of order B-spline basis curves:
In Equation (12), are the control points, N is the number of internal knot vectors of the B-spline curve, are the B-spline basis curves, x represents the sampling point position, and denotes the ordered division of the sampling point domain. The overall design variables are , where represents the control point coefficients of the spline basis curve corresponding to B-splines, with the subscripts and denoting chord length and twist, and u and l indicating the upper and lower rotors, respectively. In this study, each set of chord control point coefficients consists of five points, and each set of twist control point coefficients has three points, totaling 16 variables. As shown in Figure 4, the fitting curve of rotor blade chord distribution for the X2TD is based on the B-spline method.
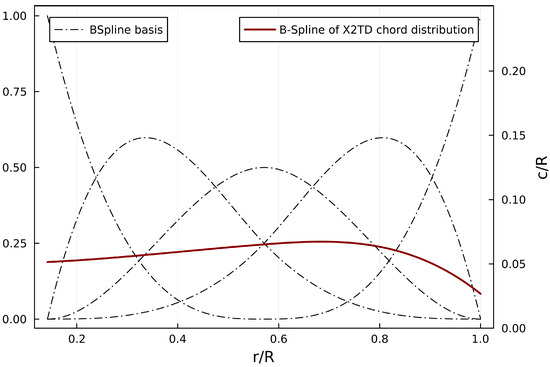
Figure 4.
Fitting curve of rotor blade chord distribution of X2TD based on B-spline method.
In the context of this study, design variable exploration is intentionally constrained within 20% of the baseline aerodynamic shape. This restriction aims to significantly reduce the potential impact on rotor dynamic characteristics, a consideration reserved for more comprehensive analysis in future multidisciplinary investigations. The 20% boundary provides a safeguard, allowing for significant aerodynamic advancements while precluding changes that could potentially perturb the rotor dynamic equilibrium. This measured approach aligns with the research’s objective to incrementally refine rotor design within a controlled and aerodynamically focused parameter space.
Additionally, the B-spline method is employed to parameterize the blade chord distribution, offering a flexible and efficient way to represent complex geometric shapes. The number of base functions used in the B-spline representation is intentionally limited to mitigate the risk of overfitting and to maintain computational efficiency during the optimization process. However, the choice of the number and type of base functions could potentially influence the optimization results. To address this, future work will investigate the impact of using a higher number of base functions, as well as alternative types such as non-uniform rational B-splines (NURBS). This approach will help assess the sensitivity of the optimized designs to the discretization scheme and ensure the robustness of the proposed methodology.
3.2. Optimization Objective
In this study, the primary optimization objectives for the coaxial rotor system include maximizing the hovering figure of merit, , and optimizing the forward flight lift-to-drag ratio, . These objectives are critical for enhancing the overall aerodynamic efficiency and performance of coaxial rotors in diverse operating conditions.
The figure of merit, a key performance indicator in rotorcraft aerodynamics, quantifies the efficiency of a helicopter rotor in hover and is calculated using the formula derived from the induced power required relative to the ideal power condition. Optimizing this metric directly correlates to improved energy efficiency and reduced operational costs during hover, which is vital for vertical takeoff and landing (VTOL) aircraft.
Similarly, the lift-to-drag ratio during forward flight is essential for operational efficiency at high speeds, impacting the aircraft’s range and fuel consumption. Enhancing this ratio through optimized rotor blade geometry ensures better performance across the aircraft’s operational envelope, particularly at cruise conditions.
Initially, a weighted single-objective approach combines these metrics into one objective function to streamline the broad search across the design space, as shown in the following equation:
Here, = 0.4 and = 0.6 are the weights derived from prior optimization studies [36] and the specific requirements of high-speed flight, helping to balance the focus on hover and cruise efficiencies.
To fully explore the inherent trade-offs between these objectives, a Pareto frontier analysis is employed in the subsequent stages. This multi-objective approach allows for the selection of optimal designs from a Pareto-effective set, providing a clear visual representation of the trade-offs involved. This supports nuanced decision-making tailored to the specific performance priorities of the rotor system, ensuring that all aspects of performance are optimally addressed.
In this study, the primary focus was to enhance the aerodynamic efficiency of coaxial rotor blades through shape optimization. However, we acknowledge that changes in blade shape could potentially affect rotorcraft controllability. While traditional constraints like solidity, power, and maximum thrust were incorporated to ensure basic aerodynamic performance, a comprehensive evaluation of control moments and forces was not included in the current model. Future work will address this by incorporating control-specific parameters, such as blade pitch limits and dynamic response characteristics, into the optimization constraints. This will ensure that the optimized blades not only offer enhanced aerodynamic efficiency but also meet the necessary control authority requirements for practical rotorcraft operation. Furthermore, future research will consider environmental factors and operational constraints. Variations in temperature and air density can significantly impact rotor performance and will be integrated into the optimization process. Operational constraints like vibration limits are also crucial for safety and reliability and will be included in the expanded objective function and constraints. This comprehensive approach, encompassing both aerodynamic and operational considerations, will yield more robust and adaptable rotor blade designs, better suited for real-world applications.
3.3. Optimization Strategy
Differential optimization of the upper and lower rotors in a coaxial rotor system is considered reasonable, as these rotors consistently operate in distinct aerodynamic environments, particularly under varying operational conditions such as hovering and high-speed cruising. Since this optimization problem involves the differential design of upper and lower rotors, with a large number of design variables and a large computational scale, it falls under the category of complex nonlinear, non-convex problems and may encounter local optima. Traditional deterministic optimization methods are prone to becoming trapped in local extrema, while random algorithms are computationally expensive and have long optimization cycles. To address this, this paper develops a hybrid optimization strategy, SANM, combining simulated annealing (SA) and Nelder–Mead (NM) algorithms. In this strategy, the NM method, also known as the downhill simplex method, is a direct search method based on function comparison, requiring relatively small computational effort per iteration [37]. However, its convergence is highly influenced by the initial simplex. With poor initial values, the NM method is more likely to become stuck, leading to a high number of total iterations and possibly falling into local optima. SA is a random distribution-based algorithm that includes both uphill and downhill steps in the optimization process, effectively avoiding becoming trapped in local extrema and ultimately tending towards the global optimum [38]. SA is clearly more robust than NM, but this robustness comes at the cost of longer run times. This paper combines both to form a hybrid optimization strategy that reduces sensitivity to initial values, improves globality, and ensures computational costs are not excessively high.
Figure 5 illustrates the flowchart of the SANM hybrid optimization strategy, integrating simulated annealing (SA) and the Nelder–Mead (NM) algorithms. The process begins with an initial random population, optimized first by NM to refine local minima. SA then takes over to explore global solutions, ensuring escape from local optima and enhancing the search for a global optimum. The flowchart highlights key transition points between algorithms, illustrating how the hybrid approach balances detailed local searches with broader global explorations to optimize performance efficiently.
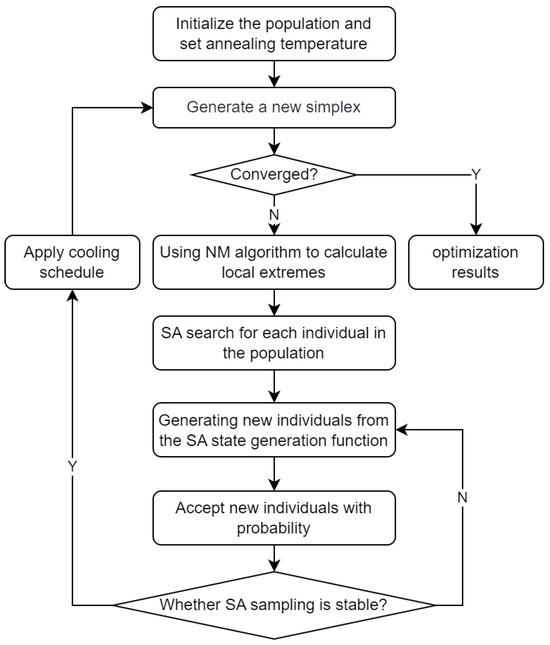
Figure 5.
Optimization process of SANM hybrid strategy.
4. Result and Analyses
4.1. Optimization Process
The optimization process begins by determining the initial values for the B-spline curve coefficients of the blade chord length and twist distribution, based on fitting the X2TD rotor shape B-spline curves. To explore the design space, 50 random sample points are generated within a ±20% range of each variable. Initial calculations of hovering efficiency and the lift-to-drag ratio at a cruising flight advance ratio of = 0.6 illustrate the significant impact of blade twist and planform shape on aerodynamic performance.
This study employs a dual-stage optimization strategy, starting with a weighted single-objective approach to simplify the vast design space. This initial phase aggregates the primary objectives—hovering figure of merit and forward flight lift-to-drag ratio—into a single objective function, as detailed in Equation (13). It quickly filters out less promising configurations, focusing analysis on the most viable candidates.
The first generation of optimization rapidly identifies local optima using the Nelder–Mead (NM) method. To escape these local optima and pursue a global optimum, the simulated annealing (SA) method introduces probabilistic jumps, as demonstrated in Figure 6. This figure shows how objective function values evolve, indicating a convergence of optimization efforts by the third generation.
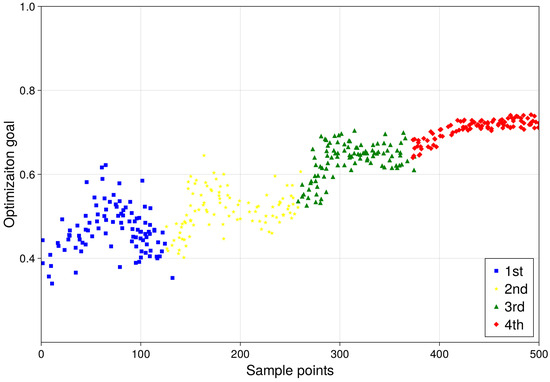
Figure 6.
Objective function value comparison during optimization process.
Table 3 details changes in objective function values across the generations, highlighting improvements in mean, maximum, and standard deviation values, which underscore the increasing efficiency of the optimization process.

Table 3.
Objective function value change analyses.
Subsequently, the process transitions to a multi-objective framework using Pareto frontier analysis to explore trade-offs between hovering efficiency and the forward flight lift-to-drag ratio. This approach identifies designs where improvements in one objective do not excessively compromise the other, ensuring a balanced optimization of performance metrics.
This dual-stage strategy not only streamlines the design process but also enhances the thoroughness and reliability of the final design choices. Each candidate from the initial weighted optimization is compared on the Pareto frontier, facilitating a comprehensive evaluation based on the rotor system’s performance priorities and ensuring robustness across varied operational parameters.
Figure 7 shows the vortex particle wake field distribution of the X2TD-like rotor established in this paper during the optimization initialization stage. Calculations were performed for both hovering and = 0.6 forward flight states. It can be observed that, in the hovering state, the lower rotor is immersed in the wake field of the upper rotor, experiencing severe interference. At the high-speed forward flight state of = 0.6, due to the small spacing between the upper and lower rotors of the coaxial rigid rotor, there is still some interference in the wake field, but the degree of mutual interference is much less than in the hovering state. Additionally, due to the high forward flight speed, the wake is rapidly blown towards the rear of the rotors, and thus the wake’s induced effect on the rotor plane is much weaker compared with the hovering state.
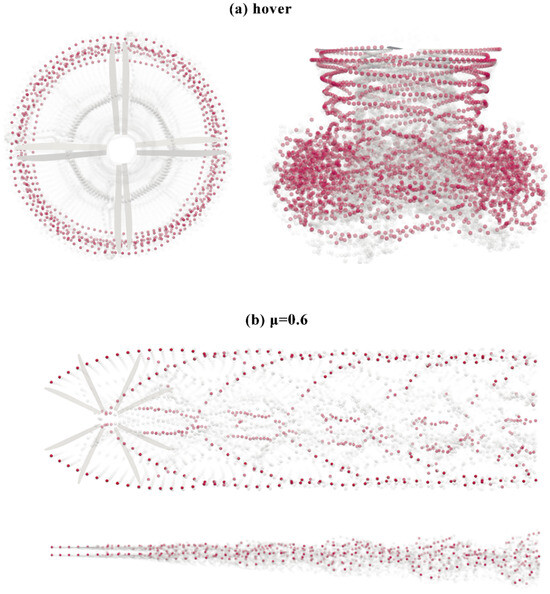
Figure 7.
Vorticity wake of rigid coaxial rotor in (a) hover and (b) = 0.6 cruise states.
4.2. Optimization Results
The computational results indicate that adopting differential aerodynamic shape designs for the upper and lower rotor blades of the coaxial rigid rotor significantly enhances the overall aerodynamic performance, including hovering efficiency and forward flight equivalent lift-to-drag ratio. In the hovering state, the wake of the upper rotor causes strong interference with the lower rotor. Reducing the twist angle and size of the outer segment of the upper rotor mitigates this by weakening the bound circulation near the blade tips, thus reducing the strength of the tip vortices and minimizing their interference impact on the lower rotor. This adjustment leads to an improved induced velocity distribution across the lower rotor disc, thereby enhancing overall performance. In high advance ratio ( = 0.6) forward flight conditions, where blade tips operate at higher Mach numbers (approximately 0.8), aerodynamic compressibility effects become significant. Reducing the chord length at the blade tips notably decreases drag, thereby improving the equivalent lift-to-drag ratio in cruise flight and enhancing forward flight performance.
Table 4 presents a comparative analysis of the figure of merit and lift-to-drag ratios for different rotor blade configurations against the baseline X2TD design. As detailed in the table, both the general optim and differential optim configurations surpass the baseline X2TD’s performance. The differential optim configuration, which utilizes distinct geometric designs for the upper and lower rotors, shows a more significant improvement in optimizing hovering efficiency compared with the general optim. This configuration also achieves competitive results in forward flight performance, demonstrating that targeted optimizations for different flight conditions can yield more optimal outcomes. It is important to note that, while some feasible solutions within the general optim and differential optim sets may excel in one objective, they might underperform in the other. Such solutions are considered less competitive in the context of this research, as the aim is to achieve a balanced improvement across both hovering and forward flight performance.

Table 4.
Comparison of optimization results for coaxial rotor configurations.
The Pareto frontier, illustrated in Figure 8, visually supports these findings by highlighting the superior performance envelope achieved through these optimizations. The graph clearly shows that both customized configurations not only improve upon the baseline but also provide a range of feasible solutions with enhanced performance metrics, validating the effectiveness of the differential design approach in complex aerodynamic environments.
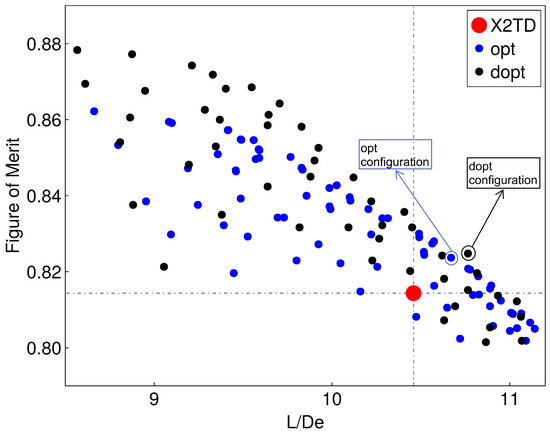
Figure 8.
Schematic diagram of Pareto front solution set.
The selection of the ‘opt’ and ‘dopt’ configurations from the Pareto front was a critical step in the optimization process. Initially, configurations surpassing the baseline X2TD design in both the hovering and the forward flight were identified. These promising configurations, located in the upper-right region of Figure 8, indicated potential for enhancing both key performance metrics. To select the final configurations, these candidates were evaluated using the weighted objective function defined in Equation (13). This function integrates and , with weights derived from previous research and tailored to prioritize high-speed flight performance, a key focus of this study. The ‘opt’ and ‘dopt’ configurations, boasting the highest weighted objective function values, were ultimately chosen. This selection represents a strategic balance between maximizing hover performance and optimizing cruise efficiency. While the ‘opt max’ and ‘dopt max’ configurations represent the theoretical maxima of the combined objective function, they were not selected due to potential drawbacks. Their extreme nature could introduce undesirable trade-offs in other performance aspects or pose practical limitations in real-world applications. The chosen ‘opt’ and ‘dopt’ configurations, while not maximizing any single metric, offer a more balanced and pragmatic approach to performance enhancement, aligning with the broader goals of this research.
Figure 9 presents a comparison of the planform shapes of the blades corresponding to the opt configuration and dopt configuration with X2TD, while Figure 10 shows the optimized blades’ spanwise chord length and twist distribution. It can be observed from the figures that the optimized blade shapes retain the elliptical planform shape and nonlinear twist distribution of the original X2TD blades. The dopt configuration exhibits significant differences in the planform shape of the upper and lower rotors beyond 0.6 R; the upper rotor has a greater taper ratio, while the lower rotor’s shape is closer to X2TD. In contrast, the planform shape of the blades in the opt configuration is similar to X2TD, but the chord length between 0.3 R and 0.9 R is smaller than in X2TD. Regarding the twist angle, the upper rotors of both the opt configuration and dopt configuration have similar values, with a greater range of twist changes compared with the lower rotor of the dopt configuration and the X2TD.
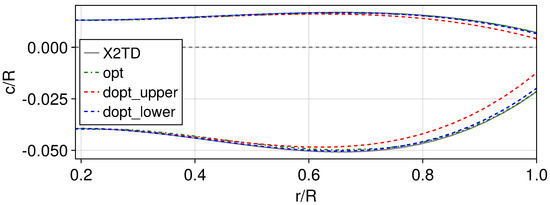
Figure 9.
Planform of optimized blade and X2TD blade.
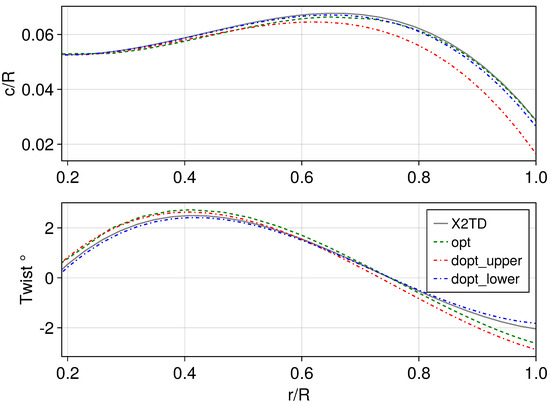
Figure 10.
Distributionof chord and twist of optimized blade and XT2D blade.
4.3. Hover Analyses
Figure 11 illustrates that the optimization result with identical blade designs for both rotors achieves better hovering efficiency around the target blade loading coefficient compared with the X2TD baseline. However, in the lower thrust coefficient region, the performance of the opt configuration is relatively average. In contrast, the dopt configuration, with different blade designs for the upper and lower rotors, shows better performance across the entire thrust coefficient range. This improvement is likely due to the differential design mitigating the aerodynamic interference of the upper rotor on the lower rotor, thereby effectively enhancing the coaxial rotor’s hovering performance.
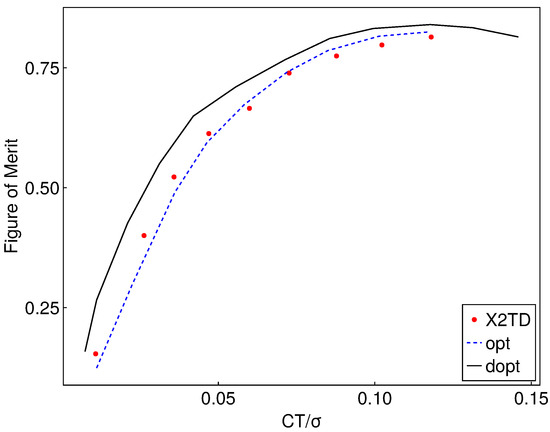
Figure 11.
Hover performance changes with thrust coefficient.
As shown in Figure 12, the dopt configuration improves the spanwise distribution of thrust coefficients for both rotors, leading to a more uniform distribution of the overall thrust across the middle section of the blades, thereby enhancing hovering efficiency. In the opt configuration, where both rotors must maintain the same blade design, only more moderate results can be achieved. While the opt configuration significantly improves the spanwise distribution of thrust coefficients for the upper rotor, the improvements for the lower rotor are quite limited. This demonstrates that differential blade design for upper and lower rotors can significantly enhance the coaxial rotor’s hovering efficiency.
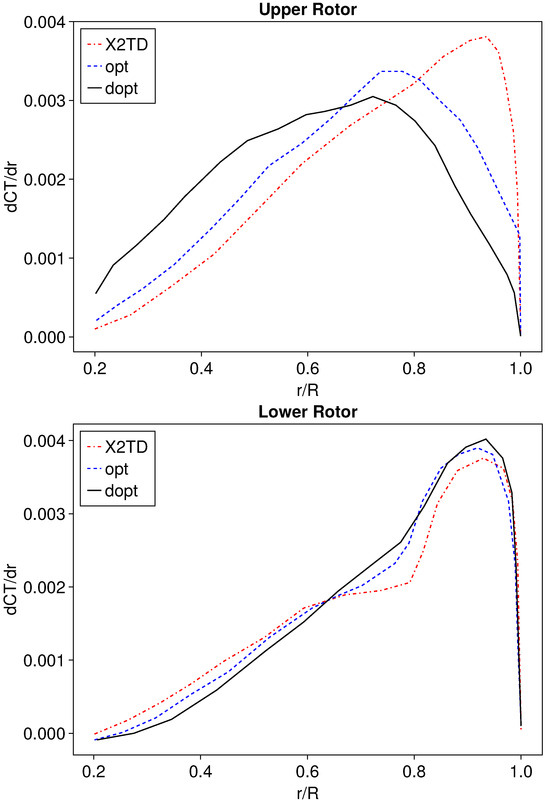
Figure 12.
Thrust coefficient distribution spanwise.
Figure 13 shows the radial distribution of the blade aerodynamic angle of attack for the X2TD baseline, opt, and dopt configurations in hover. For the upper rotor, the dopt configuration exhibits the smoothest angle of attack distribution, consistently maintaining a higher angle of attack than the other two configurations. The opt configuration has a relatively steeper angle of attack distribution in the inner region, but, in the outer region, where most of the lift is generated, its angle of attack is smoother and higher than the X2TD baseline. Considering that the X2TD baseline configuration has a wider chord length in the outer blade section, this result is consistent with the spanwise distribution of the blade thrust coefficient. For the lower rotor, a noticeable fluctuation in the angle of attack is observed near 0.8R, attributed to the significant interference from the upper rotor, which is also reflected in the fluctuation of the thrust coefficient at a similar location in Figure 12. Moreover, the lower rotor of the dopt configuration still maintains a smoother angle of attack distribution, but near the blade tip its distribution is closer to that of the opt configuration. This is likely because the chord length distribution of the lower rotor is more similar to the opt configuration.
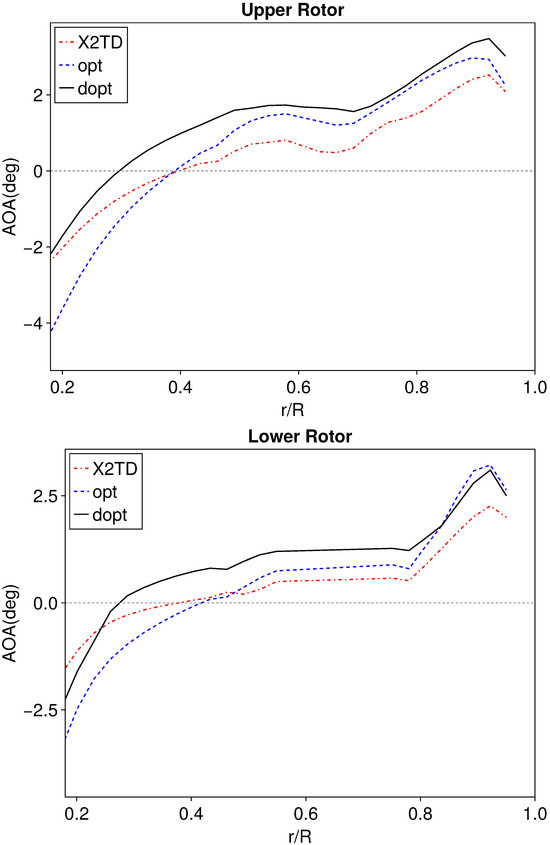
Figure 13.
Angle of attack distribution spanwise.
Combining the blade geometry, thrust coefficient, and angle of attack distributions, it can be concluded that both the dopt and opt configurations have better angle of attack distributions in the outer blade sections, where most of the lift is generated. However, the dopt configuration has a smoother overall angle of attack distribution, and the differentiated aerodynamic shapes of the upper and lower rotors reduce the interference effect of the upper rotor on the lower rotor, thereby improving the overall hover aerodynamic efficiency. This demonstrates the significance of differentiated optimization of the upper and lower rotors in hover conditions where aerodynamic interference effects are substantial.
4.4. Cruise Analyses
Figure 14 shows that, before the advance ratio reaches 0.3, the interference between the upper and lower rotors is relatively significant. In this phase, the dopt configuration, due to its differential blade design, exhibits slightly superior forward flight performance compared with the X2TD and opt configurations. As the advance ratio increases (between 0.3 and 0.5), the interference between the rotors diminishes, and the lift-to-drag ratios of X2TD and opt configurations gradually rise, slightly surpassing the dopt configuration. Beyond an advance ratio of 0.5, the lift-to-drag ratio performance of X2TD blades evidently lags behind the opt and dopt configurations, possibly due to the X2TD blades being designed with a focus on performance at a specific speed (such as = 0.5), while this study emphasizes performance at = 0.6.
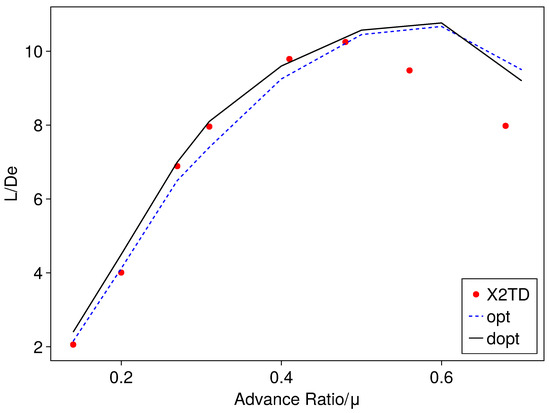
Figure 14.
Cruise performance comparison of optimized and X2TD blade.
Figure 15 shows that, at an advance ratio of 0.35, the peak value of the thrust coefficient for the upper rotor of the X2TD is more biased towards the outer side and more evenly distributed compared with the opt and dopt configurations, with smaller differences observed among the lower rotors of the three configurations, resulting in a slightly better lift-to-drag ratio for the X2TD configuration.
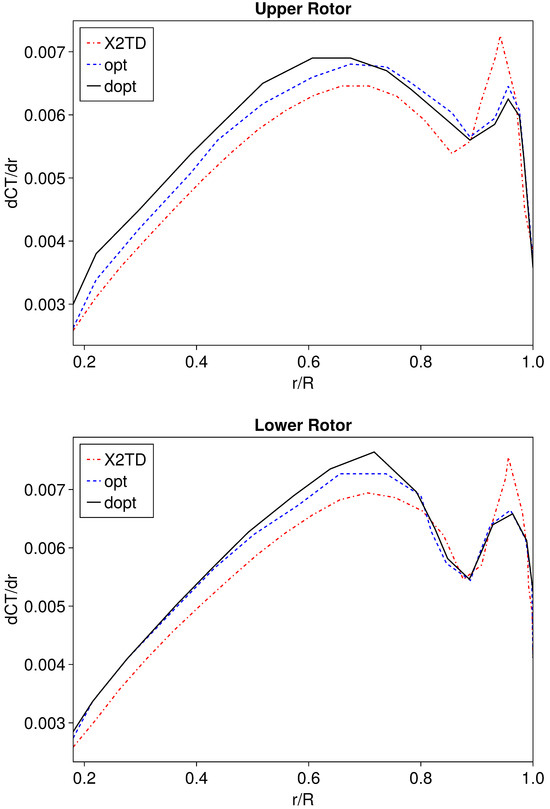
Figure 15.
Thrust coefficient distribution spanwise of upper rotor ( = 90°, = 0.35).
Figure 16 indicates that, at an advance ratio of 0.5, the lowest values of the troughs in the outer segment of both the upper and lower rotors of X2TD are greater than those of the opt and dopt configurations. This is due to both opt and dopt configurations optimizing the chord length distribution in the outer segment of the blades, improving the strength of the tip vortices, and thereby reducing the vortex interference on the blades.
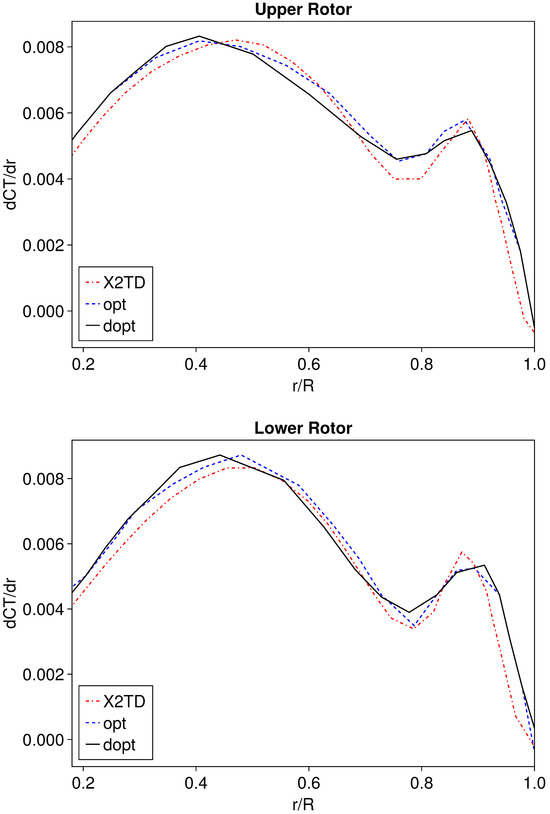
Figure 16.
Thrust coefficient distribution spanwise of upper rotor ( = 90°, = 0.5).
Figure 17 shows that, at an advance ratio of 0.65, the difference between the lowest values of the troughs in the outer segment of the upper and lower rotors of the X2TD and the opt and dopt configurations further widens. In the dopt configuration, the thrust distribution of the blade loading coefficients is more evenly distributed along the middle section of the blades. This can, to some extent, offload the load from the blade tip segment, thereby enhancing rotor efficiency in high-speed forward flight conditions. Thus, this configuration has a better lift-to-drag ratio at high advance ratios compared with the other two.
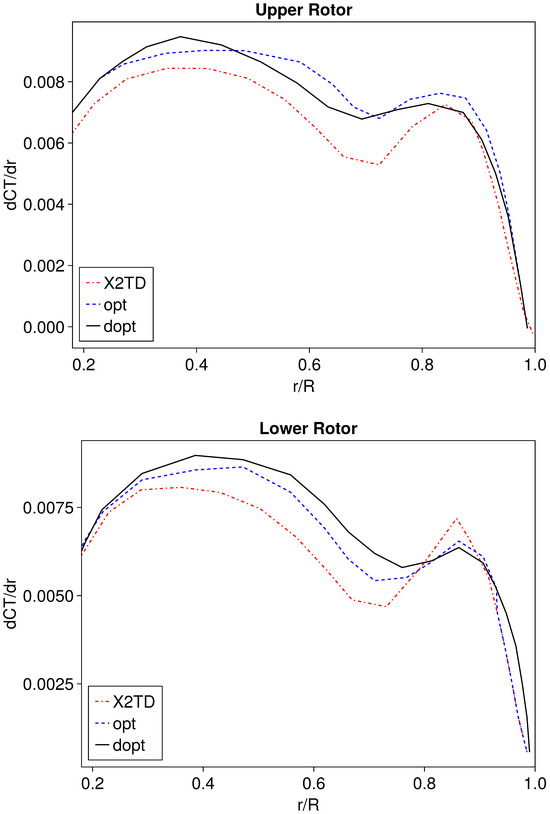
Figure 17.
Thrust coefficient distribution spanwise of upper rotor ( = 90°, = 0.6).
Combining Figure 15, Figure 16 and Figure 17, it is evident that both the upper and lower rotors exhibit a trough in the outer segment of their blade loading coefficients. At an advance ratio of 0.35, the difference between the lowest values of the troughs of the lower and upper rotors is significant, but as the advance ratio increases the gap narrows, becoming almost identical at an advance ratio of 0.6. This is because, with the increase in the advance ratio, the angle between the rotor tip vortex wake and the rotor disc plane gradually decreases, reducing the impact of the upper rotor’s wake on the lower rotor. Hence, the phenomena between the upper and lower rotors become more consistent.
Figure 18 shows the overhead view of the wake structure of the upper rotor tip vortexes of the X2TD at different advance ratios. As seen in the figure, with increasing forward flight speed, the tip vortex wake of the rotor rapidly moves rearward under the influence of the forward inflow, causing the tip vortex of one blade to significantly interfere with the outer segment of the subsequent blade. The higher the advance ratio is, the more the area of interference contracts inward, corroborating the trough phenomenon in the blade-loading coefficients observed in Figure 15, Figure 16 and Figure 17.
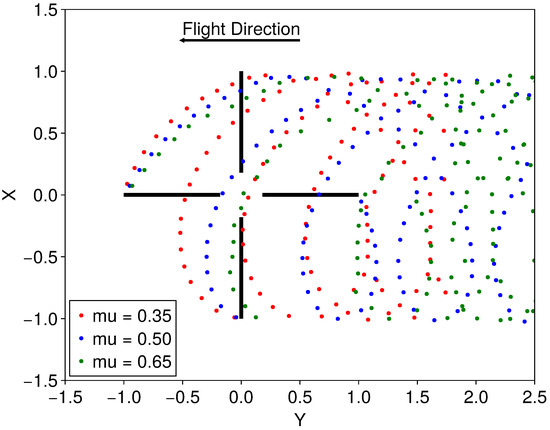
Figure 18.
Tip vortex structure of upper rotor at different advance ratios.
Figure 19 shows the distribution of the blade angle of attack with respect to radius and azimuth at an advance ratio of . It can be observed that the angle of attack distributions of the upper and lower rotors are generally similar at high advance ratios, as the freestream flow quickly convects the rotor wake downstream, significantly reducing the interference between the two rotors. A noticeable change in the angle of attack can be seen on the advancing side of the blade near 0.6–0.7 R, similar to the phenomenon observed in the thrust coefficient distribution at ψ = 90°, which is likely caused by tip vortex interference. The angle of attack distribution reveals that the dopt configuration has the smoothest distribution, followed by the opt configuration, while the X2TD baseline configuration has relatively more significant variations. Moreover, the former two configurations have smaller angles of attack near the tip region on the advancing side. In high-speed flight, a smaller angle of attack in the outer blade region, especially near the tip, is crucial for reducing forward flight drag. Additionally, the angle of attack distribution shows that the dopt configuration has a smaller retreating side stall region compared with the other two configurations, and the opt configuration also has a significantly smaller retreating side stall region than the baseline configuration.
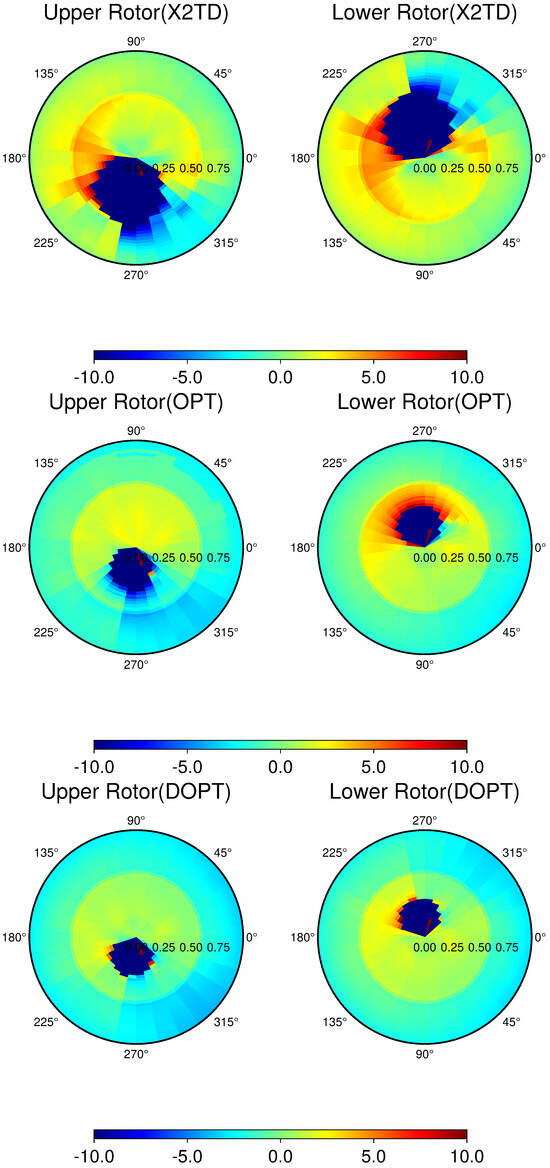
Figure 19.
Angle of attack distribution on the rotor disk ( = 0.6).
In summary, differential optimization of the upper and lower rotor blades shows significant effects in improving rotor hovering efficiency, and also achieves results in improving the rotor forward flight lift-to-drag ratio, although the degree of improvement is lower compared with the hovering state. This might be due to the weaker interference between the coaxial rotors at high advance ratios and high-speed flight conditions, making the effects of differential optimization less pronounced than in hovering and low-speed conditions.
5. Conclusions
This study, based on the coaxial rigid rotor lifting line/viscous vortex particle method performance model and the SANM hybrid optimization strategy for rotor blade aerodynamic shape, has designed a differentially shaped set of coaxial rigid rotor blades that balance the objectives of hovering and cruising performance. The following conclusions can be drawn:
- The coaxial rigid rotor aerodynamic analysis model established in this paper, based on the rVPM method and lifting line model, aligns well with experimental data in terms of rotor aerodynamic load calculation and performance simulation.
- The performance model of the coaxial rigid rotor combined with the SANM hybrid optimization strategy developed in this paper can efficiently optimize the aerodynamic shape of the coaxial rigid rotor.
- The optimized differential coaxial rigid rotor blades show a significant improvement in hovering efficiency compared with the baseline non-differential upper and lower rotors, and, while the improvement in forward flight efficiency is relatively lower, it still represents an enhancement. This proves that a combination of differential nonlinear chord length and twist distribution for the upper and lower rotors is beneficial for optimizing overall performance in both hovering and forward flight, with a greater increase in hovering efficiency compared with the equivalent lift-to-drag ratio in forward flight.
- The performance improvements brought by the optimized shape are primarily due to, in hovering and low-speed states, the different twist and chord length distribution designs for the upper and lower rotor blades, which are in different flow environments, and result in a more rational overall lift distribution, fully exploiting the lift potential of both rotors. In high-speed flight states, the smaller tip area of the upper rotor blades weakens the intensity of the strong tip vortices, reducing their interference and impact, thereby improving the blade thrust distribution. Additionally, the larger tip taper ratio reduces the relative airspeed perpendicular to the tip leading edge, helping to mitigate the strong compressibility effects of the high Mach number inflow at the tip, collectively enhancing the forward flight lift-to-drag ratio.
This study has developed a medium-to-high fidelity aerodynamic model specifically tailored for analyzing the aerodynamic performance of rigid coaxial rotors. The research successfully optimized the rotor blade planform and twist distribution, validating the effectiveness of differential optimization strategies for the upper and lower rotors.
While this study has yielded promising results, it is crucial to acknowledge that the aerodynamic model, though rigorously validated against existing experimental data, would benefit from further empirical testing. Future research should prioritize conducting comprehensive experimental investigations, potentially in collaboration with specialized aerodynamic testing facilities. These experiments would focus on validating the numerical findings of this study across a wider range of operating conditions and rotor configurations, thereby solidifying the practical applicability of the proposed optimization methodology.
Furthermore, future work will focus on two primary objectives. First, the aerodynamic model will be refined by integrating more sophisticated blade models, potentially replacing the existing lifting line/surface models. Second, the impact of additional differential design variables on rigid coaxial rotor performance will be investigated. This includes exploring varied combinations and distributions of airfoils, designing three-dimensional tip shapes, and incorporating other disciplines such as blade dynamics to enhance the research’s comprehensiveness.
The methodological framework established by this study provides a robust foundation for these future endeavors, ensuring that subsequent investigations are built on a solid scientific base.
Author Contributions
Conceptualization, Z.D. and C.Z.; methodology, Z.D.; validation, Z.D. and D.D.; investigation, Z.D.; resources, Z.D.; data curation, C.Z.; writing—original draft preparation, Z.D.; writing—review and editing, D.D. and J.L.; visualization, Z.D.; supervision, J.L.; project administration, J.L.; funding acquisition, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This project was funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bagai, A. Aerodynamic Design of the X2 Technology™ Demonstrator Main Rotor Blade; Sikorsky Aircraft Corp.: Stratford, CT, USA, 2008; pp. 211–242. [Google Scholar]
- Giovanetti, E.B.; Hall, K.C. Minimum loss load, twist, and chord distributions for coaxial helicopters in hover. J. Am. Helicopter Soc. 2017, 62, 1–9. [Google Scholar] [CrossRef]
- Giovanetti, E.; Hall, K. A Variational Approach to Multipoint Aerodynamic Optimization of Conventional and Coaxial Helicopter Rotors. In Proceedings of the American Helicopter Society 71st Annual Forum, Virginia Beach, VA, USA, 5–7 May 2015; Volume 71, pp. 1–13. [Google Scholar]
- Wang, C.; Huang, M.; Peng, X.; Zhang, G.; Tang, M.; Wang, H. Wind Tunnel Studies on Hover and Forward Flight Performances of a Coaxial Rigid Rotor. Aerospace 2021, 8, 205. [Google Scholar] [CrossRef]
- Li, L.; Zhou, C.; Chen, M.; Wang, F.; Xu, A. The Influence of Rotor Overlapping Azimuth on Compound Coaxial Helicopter Performance Based on Unsteady CFD Simulation. Appl. Sci. 2023, 13, 820. [Google Scholar] [CrossRef]
- Leishman, J.G.; Ananthan, S. Aerodynamic optimization of a coaxial proprotor. In Proceedings of the 62nd Annual Forum of the American Helicopter Society, Phoenix, AZ, USA, 9 May 2006; pp. 64–85. [Google Scholar]
- Jun, S.; Yee, K.; Lee, J.; Lee, D.H. Robust design optimization of unmanned aerial vehicle coaxial rotor considering operational uncertainty. J. Aircr. 2011, 48, 353–367. [Google Scholar] [CrossRef]
- Rand, O.; Khromov, V. Aerodynamic optimization of coaxial rotor in hover and axial flight. In Proceedings of the 27th International Congress of the Aeronautical Sciences, Nice, France, 19–24 September 2010; pp. 1–13. [Google Scholar]
- Syal, M.; Leishman, J.G. Aerodynamic Optimization Study of a Coaxial Rotor in Hovering Flight. J. Am. Helicopter Soc. 2012, 57, 1–15. [Google Scholar] [CrossRef]
- Wang, B.; Yuan, X.; Zhao, Q.; Zhu, Z. Geometry Design of Coaxial Rigid Rotor in High-Speed Forward Flight. Int. J. Aerosp. Eng. 2020, 2020, 6650375. [Google Scholar] [CrossRef]
- Granata, D.; Savino, A.; Zanotti, A. Numerical Evaluation of Aircraft Aerodynamic Static and Dynamic Stability Derivatives by a Mid-Fidelity Approach. Aerospace 2024, 11, 213. [Google Scholar] [CrossRef]
- Alvarez, E.; Ning, A. High-Fidelity Modeling of Multirotor Aerodynamic Interactions for Aircraft Design. AIAA J. 2020, 58, 1–16. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Ali, A.F. Hybrid simulated annealing and Nelder-Mead algorithm for solving large-scale global optimization problems. Int. J. Res. Comput. Sci. 2014, 4, 1. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, G.; Shi, Y.; Hu, Z. Analysis of the Aeroacoustic Characteristics of a Rigid Coaxial Rotor in Forward Flight Based on the CFD/VVPM Hybrid Method. Aerospace 2024, 11, 21. [Google Scholar] [CrossRef]
- Cottet, G.H.; Koumoutsakos, P.D. Vortex Methods: Theory and Practice; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Speck, R. Generalized Algebraic Kernels and Multipole Expansions for Massively Parallel Vortex Particle Methods; Forschungszentrum Jülich: Jülich, Germany, 2011. [Google Scholar]
- Winckelmans, G.S.; Leonard, A. Contributions to Vortex Particle Methods for the Computation of Three-Dimensional Incompressible Unsteady Flows. J. Comput. Phys. 1993, 109, 247–273. [Google Scholar] [CrossRef]
- Gallic, S.M. Deterministic Particle Method: Diffusion and Boundary Conditions. In Vortex Dynamics and Vortex Methods; AMS Lectures in Applied Mathematics; American Mathematical Society: Providence, RI, USA, 1991; Volume 28, pp. 433–480. [Google Scholar]
- Cheng, H.; Greengard, L.; Rokhlin, L. A Fast Adaptive Multipole Algorithm in Three Dimensions. J. Comput. Phys. 1999, 155, 468–498. [Google Scholar] [CrossRef]
- Alvarez, E. Reformulated Vortex Particle Method and Meshless Large Eddy Simulation of Multirotor Aircraft. Ph.D. Thesis, Brigham Young University, Provo, UT, USA, 2022. [Google Scholar]
- Alvarez, E.J.; Ning, A. Stable Vortex Particle Method Formulation for Meshless Large-Eddy Simulation. AIAA J. 2024, 62, 637–656. [Google Scholar] [CrossRef]
- Yuan, Y.; Chen, R.; Li, P. Trim investigation for coaxial rigid rotor helicopters using an improved aerodynamic interference model. Aerosp. Sci. Technol. 2019, 85, 293–304. [Google Scholar] [CrossRef]
- Padfield, G.D. Helicopter Flight Dynamics: Including a Treatment of Tiltrotor Aircraft; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Leishman, G.J. Principles of Helicopter Aerodynamics with CD Extra; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Gallay, S.; Laurendeau, E. Nonlinear Generalized Lifting-Line Coupling Algorithms for Pre/Poststall Flows. AIAA J. 2015, 53, 1–9. [Google Scholar] [CrossRef]
- Lewis, R.I. Vortex Element Methods for Fluid Dynamic Analysis of Engineering Systems; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar] [CrossRef]
- Tugnoli, M.; Montagnani, D.; Syal, M.; Droandi, G.; Zanotti, A. Mid-fidelity approach to aerodynamic simulations of unconventional VTOL aircraft configurations. Aerosp. Sci. Technol. 2021, 115, 106804. [Google Scholar] [CrossRef]
- Cameron, C.G.; Sirohi, J. Performance and Loads of a Lift Offset Rotor Hover and Wind Tunnel Testing. J. Am. Helicopter Soc. 2019, 64, 1–12. [Google Scholar] [CrossRef]
- Zhao, J.; He, C. Real-Time Simulation of Coaxial Rotor Configurations with Combined Finite State Dynamic Wake and VPM. In Proceedings of the American Helicopter Society 70th Annual Forum, Montreal, QC, Canada, 20 May 2014; p. 12. [Google Scholar]
- Hersey, S.; Sridharan, A.; Celi, R. Multiobjective Performance optimization of a Coaxial Compound Rotorcraft Configuration. J. Aircr. 2017, 54, 1498–1507. [Google Scholar] [CrossRef]
- Walsh, D.; Weiner, S.; Arifian, K.; Lawrence, T.; Wilson, M.; Millott, T.; Blackwell, R. High Airspeed Testing of the Sikorsky X2 Technology™ Demonstrator. In Proceedings of the Annual Forum Proceedings—AHS International, Virginia Beach, VA, USA, 3–5 May 2011; pp. 2999–3010. [Google Scholar]
- Passe, B.J.; Sridharan, A.; Baeder, J.D. Computational Investigation of Coaxial Rotor Interactional Aerodynamics in Steady Forward Flight. In Proceedings of the 33rd AIAA Applied Aerodynamics Conference; American Institute of Aeronautics and Astronautics, Dallas, TX, USA, 19 June 2015. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Q.; Yu, H.; Duan, D.; Ding, Z.; Li, J. Trimming Analysis Method of Quad Tilt Rotor Based on Aerodynamic Interference Model. J. Aircr. 2020, 58, 253–265. [Google Scholar] [CrossRef]
- Johnson, W.; Moodie, A.M.; Yeo, H. Design and Performance of Lift-Offset Rotorcraft for Short-Haul Missions. In Proceedings of the AHS Future Vertical Lift Aircraft Design Conference, San Francisco, CA, USA, 18–20 January 2012. [Google Scholar]
- Gao, F.; Han, L. Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Comput. Optim. Appl. 2012, 51, 259–277. [Google Scholar] [CrossRef]
- Goffe, W.L. SIMANN: A global optimization algorithm using simulated annealing. Stud. Nonlinear Dyn. Econom. 1996, 1, 169–176. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).