Effects of Leading Edge Radius on Stall Characteristics of Rotor Airfoil
Abstract
:1. Introduction
2. Numerical Methods
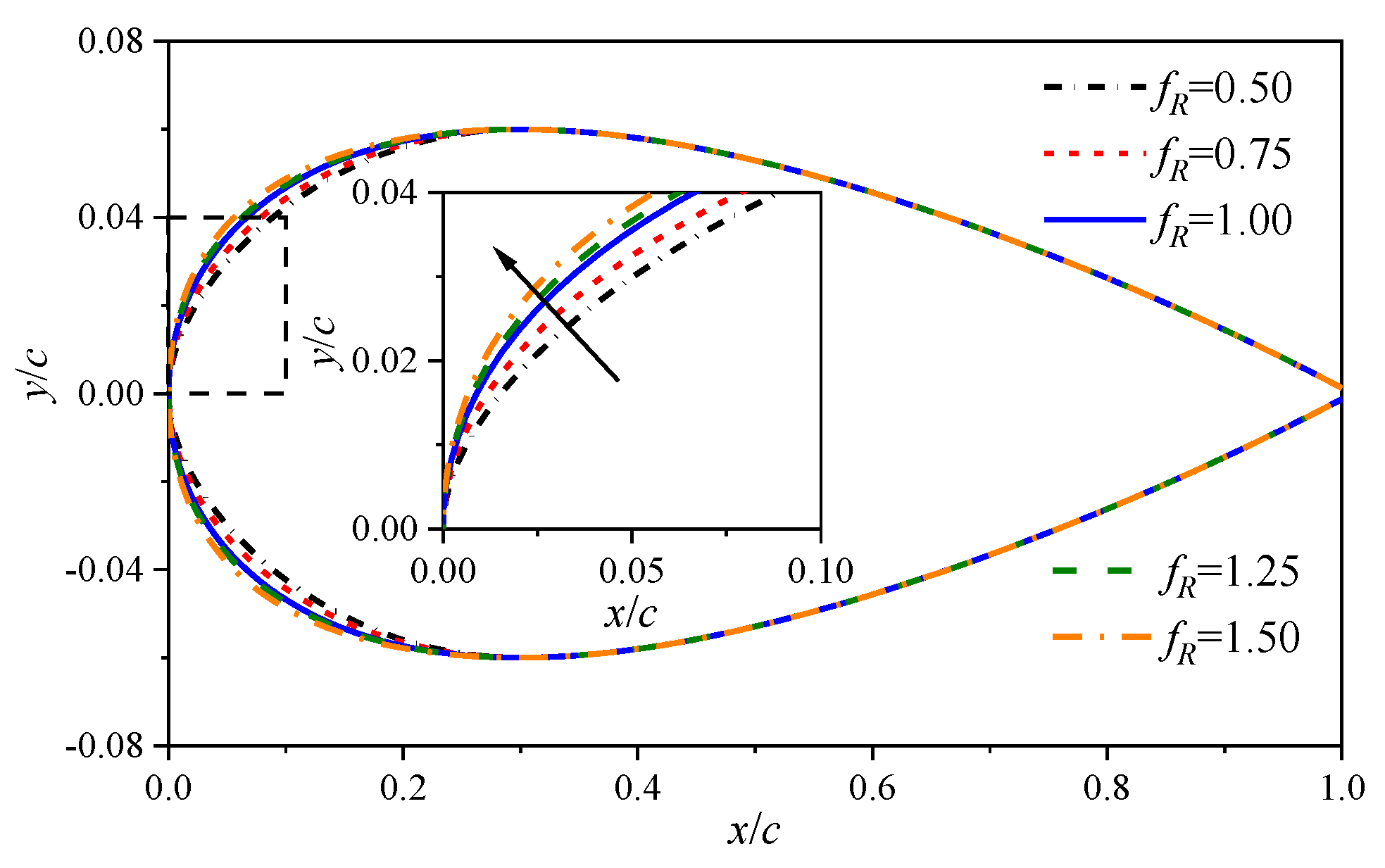
2.1. Airfoil Parametrization Method
2.2. CFD Method
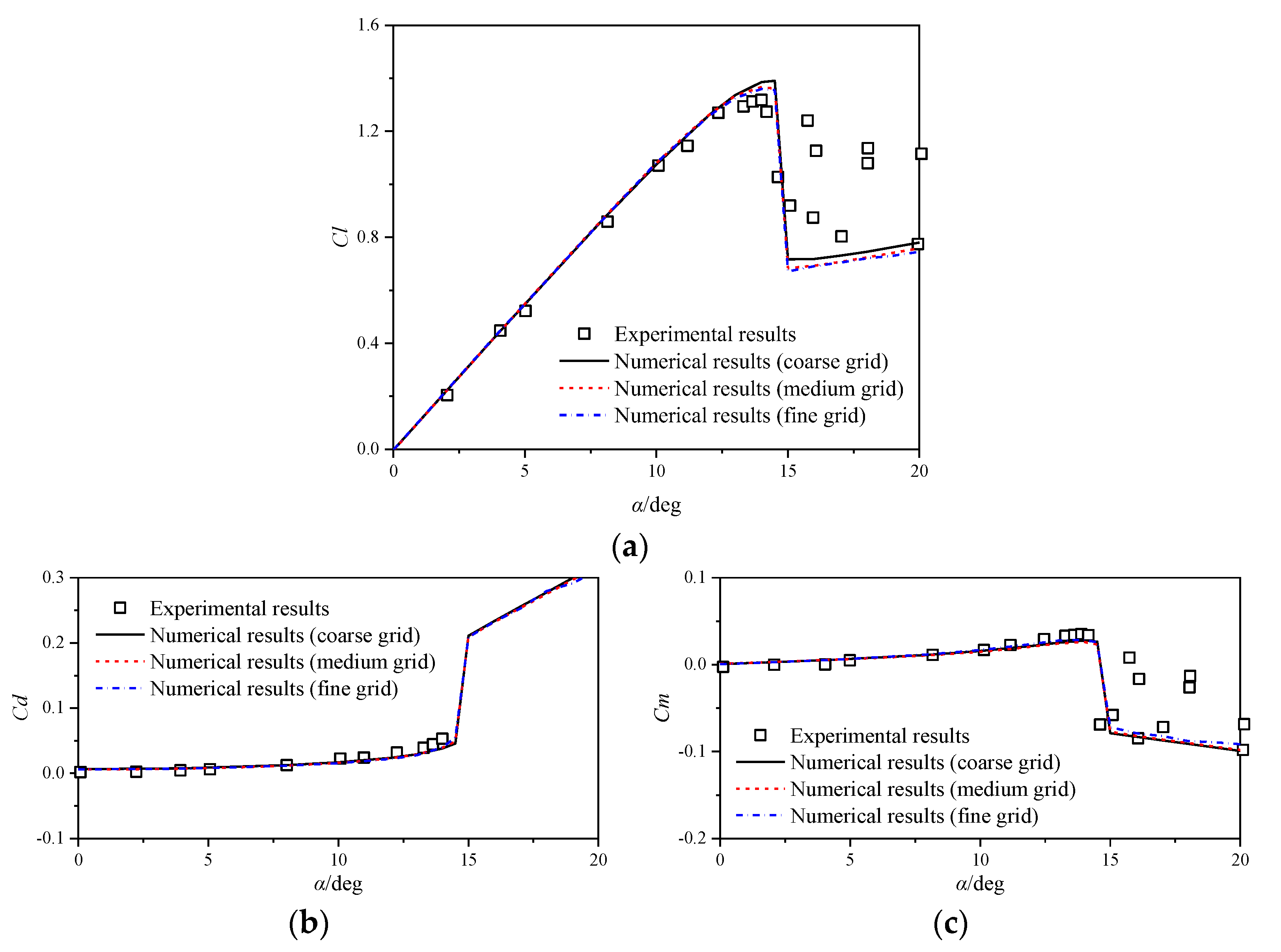
2.3. Validation for CFD Method
2.3.1. Static NACA 0012 Airfoil
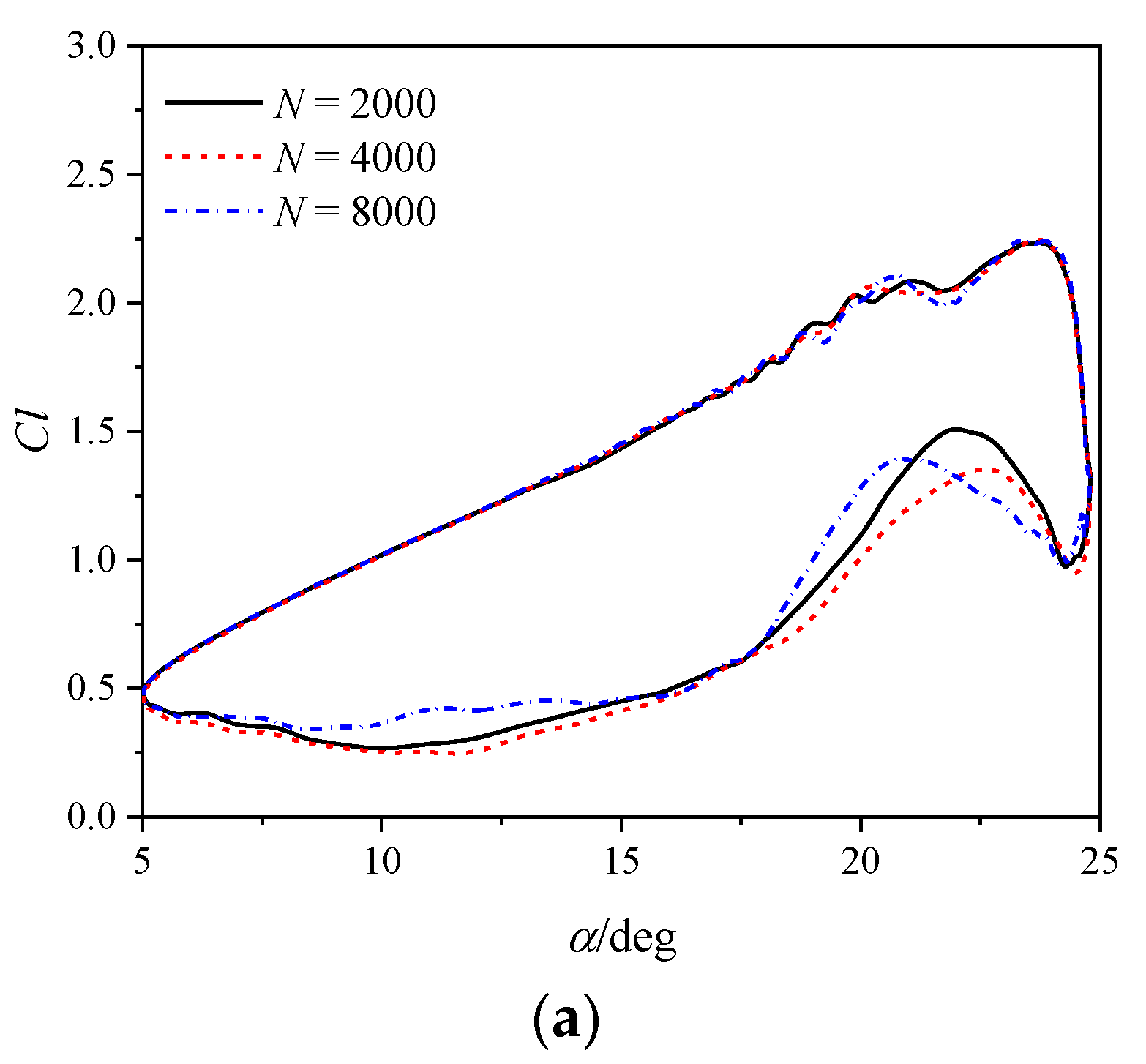
2.3.2. Pitching NACA 0012 Airfoil
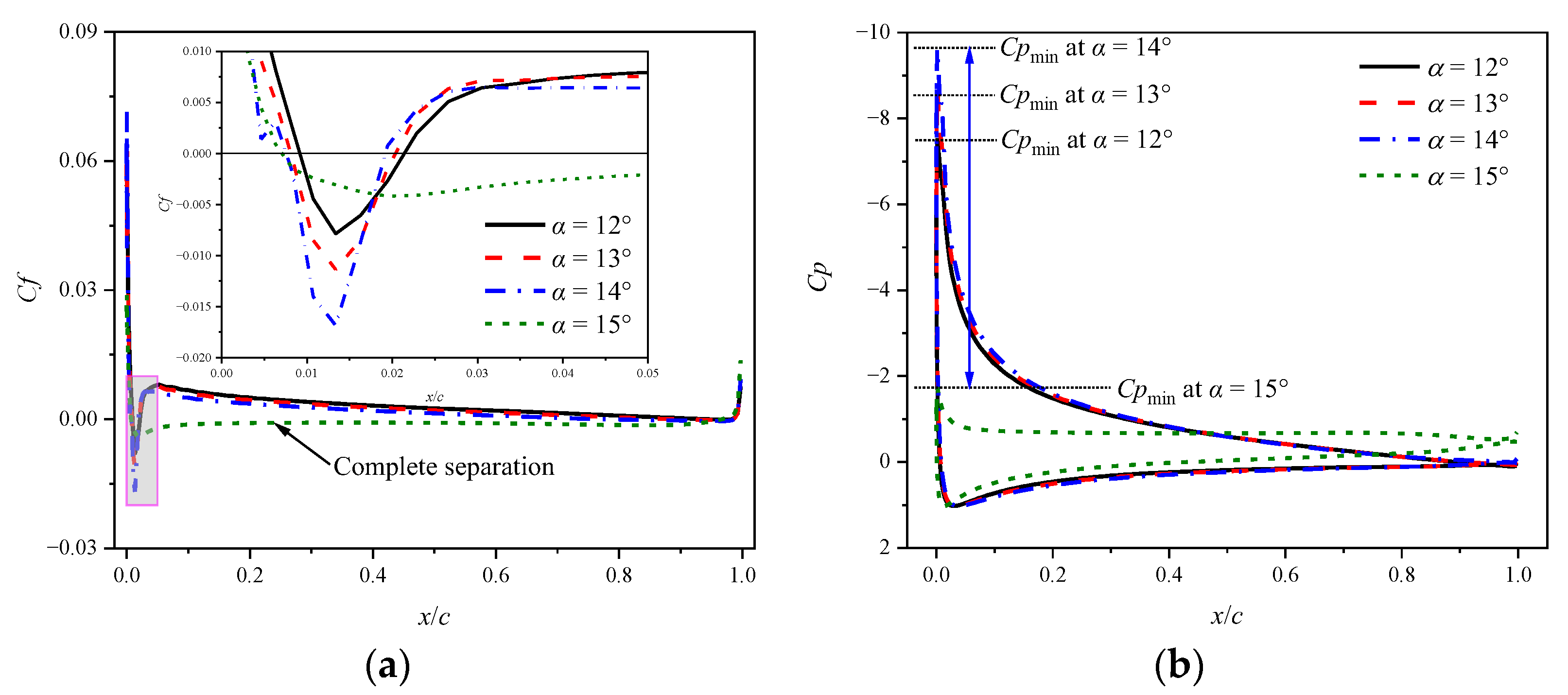
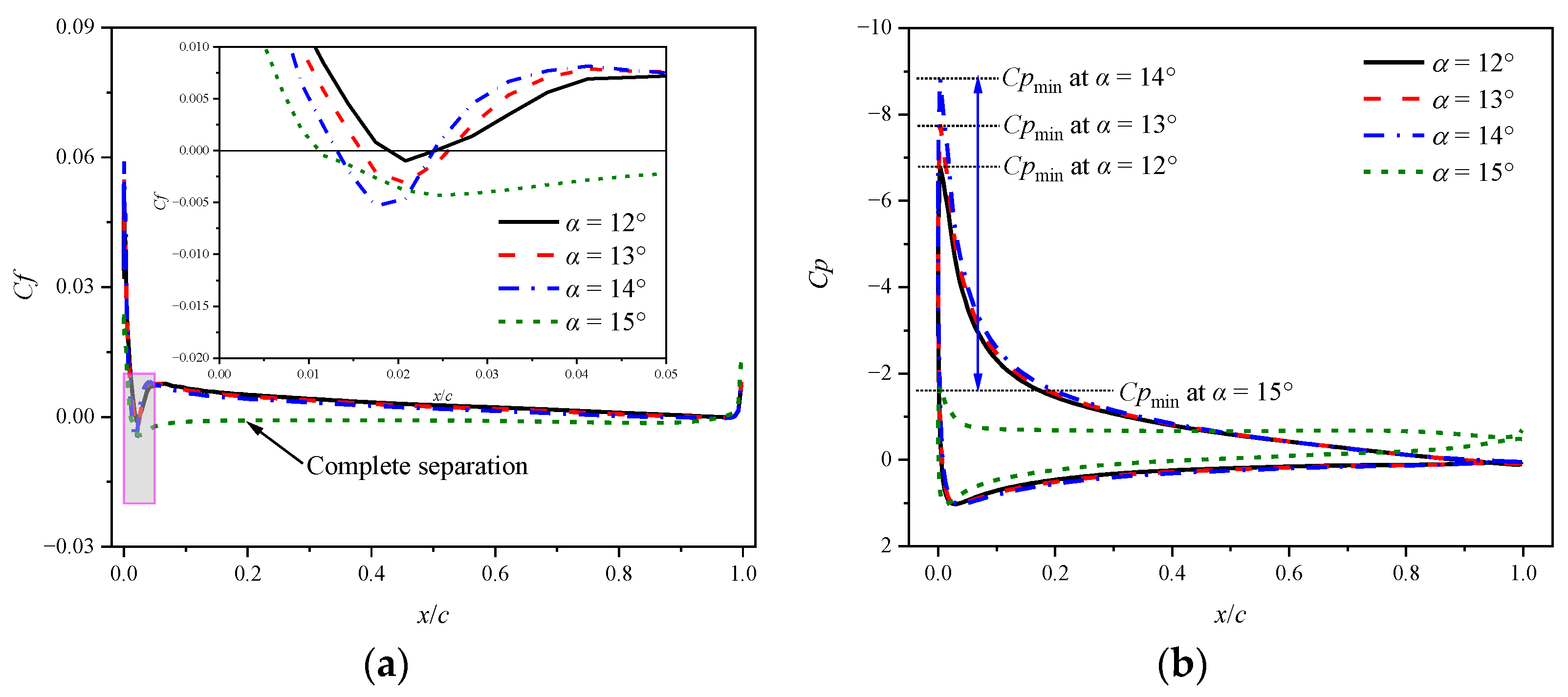
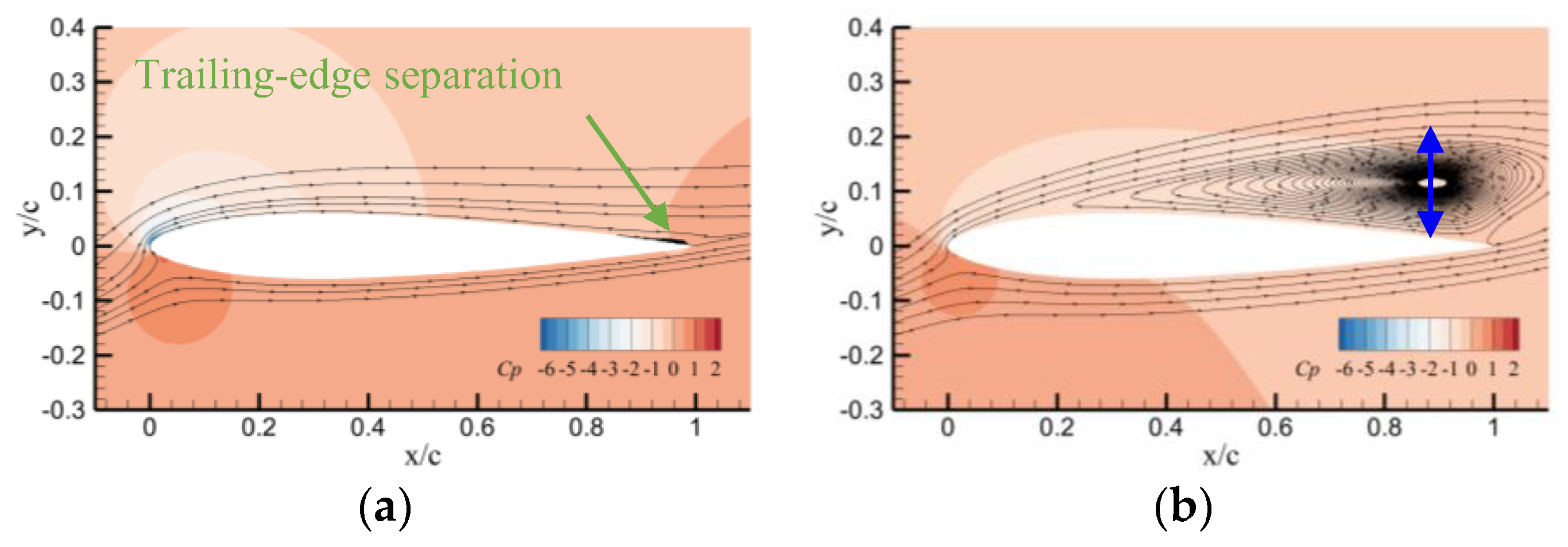
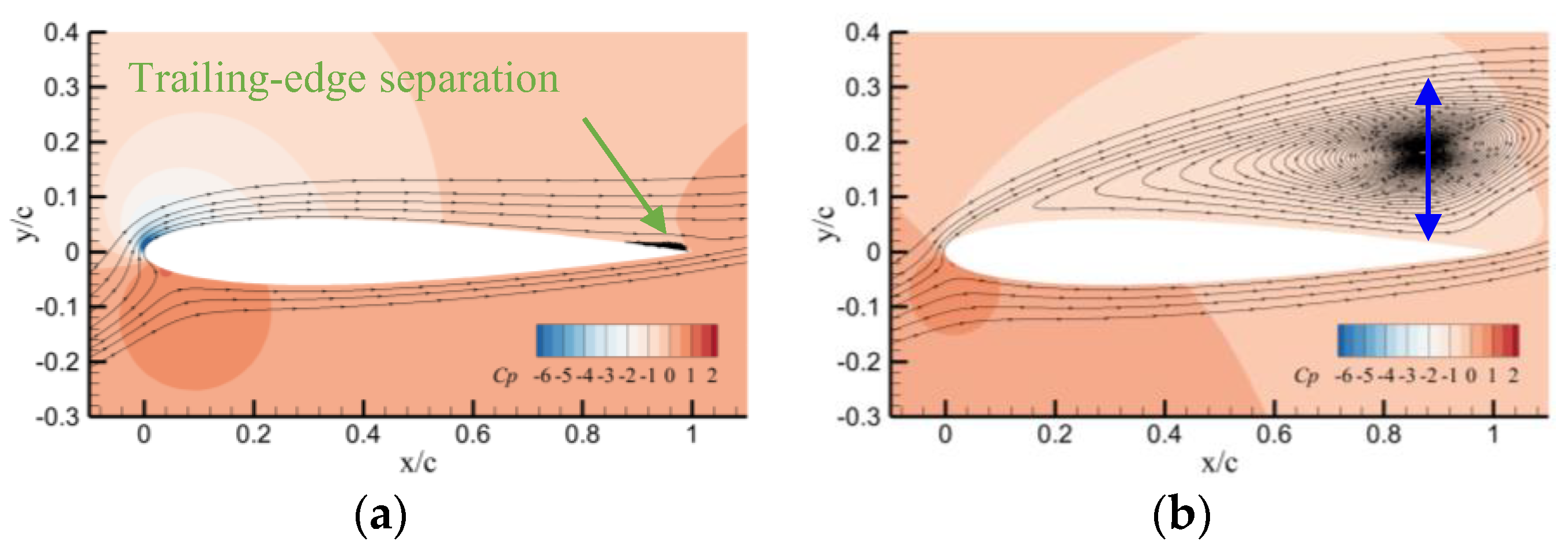
3. Results and Discussions
3.1. Impacts on Static Aerodynamic Characteristics
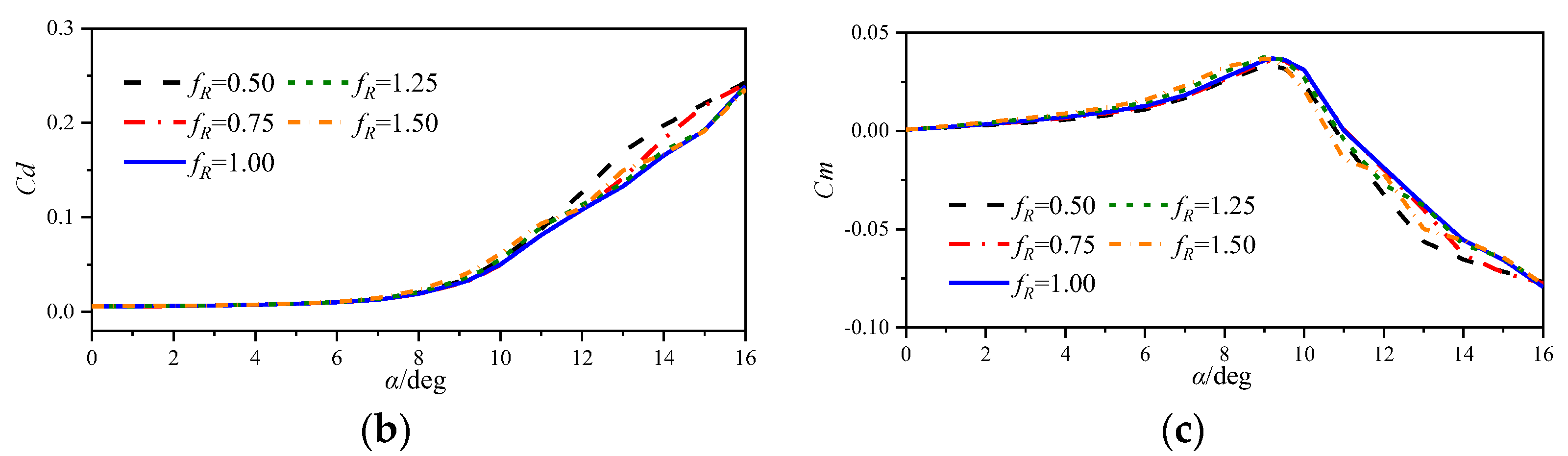
3.1.1. Static Cases at a Mach Number of 0.283
3.1.2. Static Cases at a Mach Number of 0.5
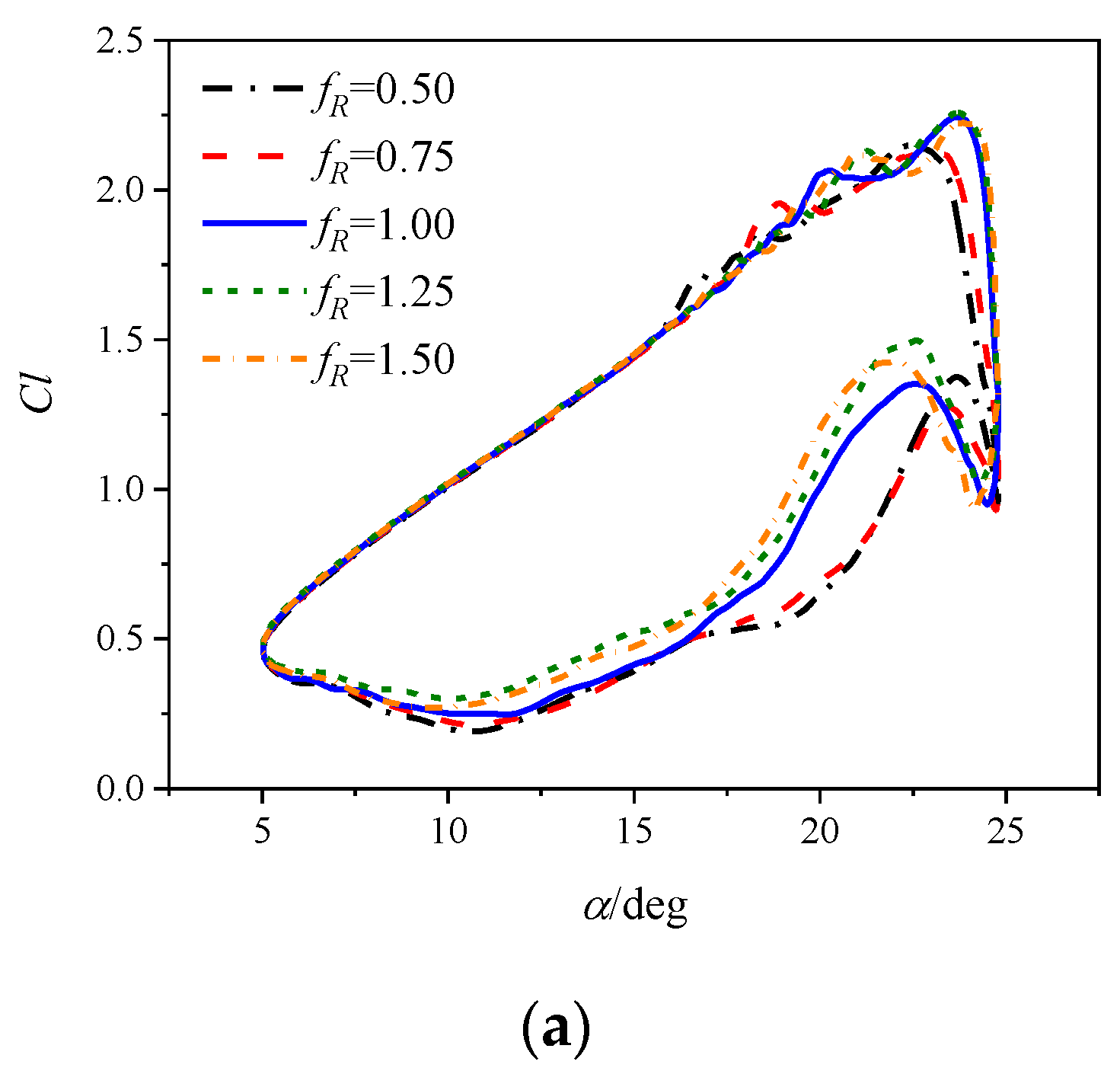
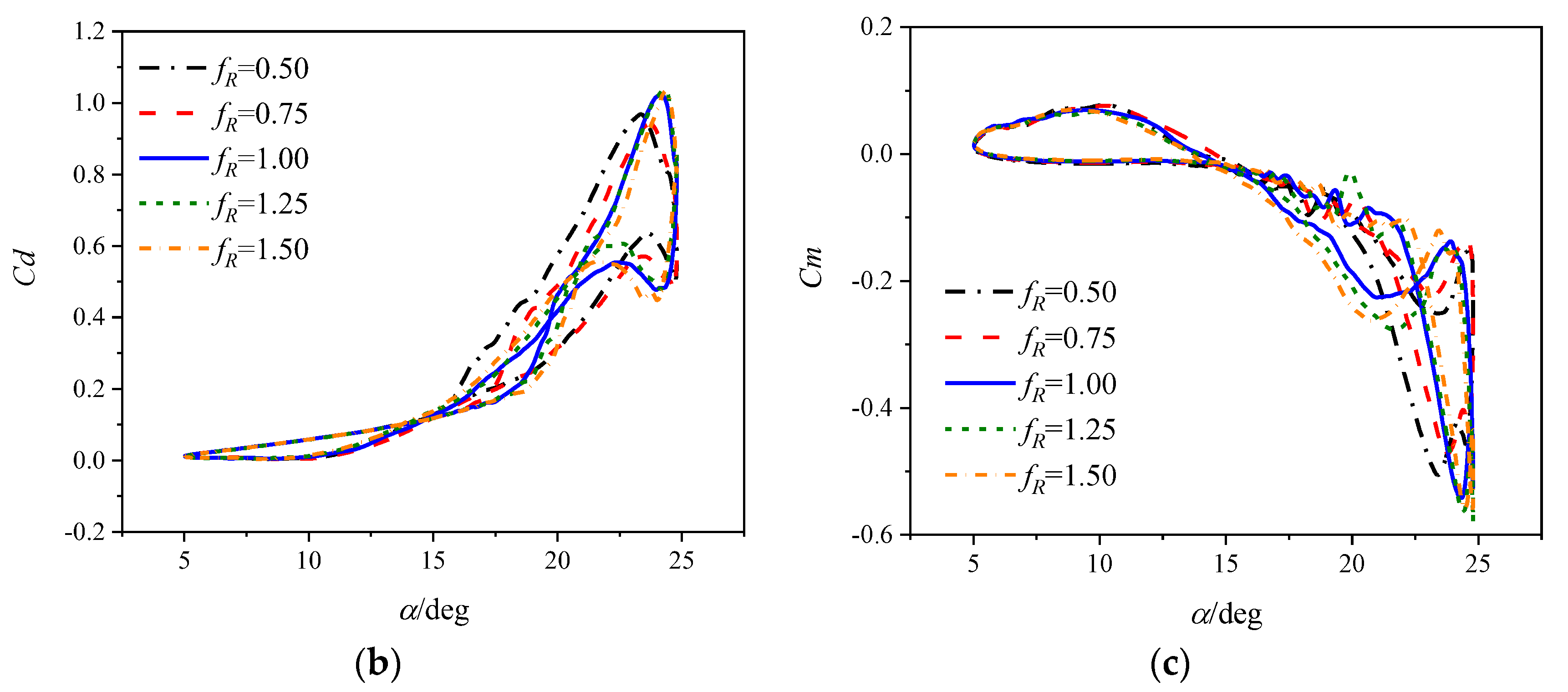
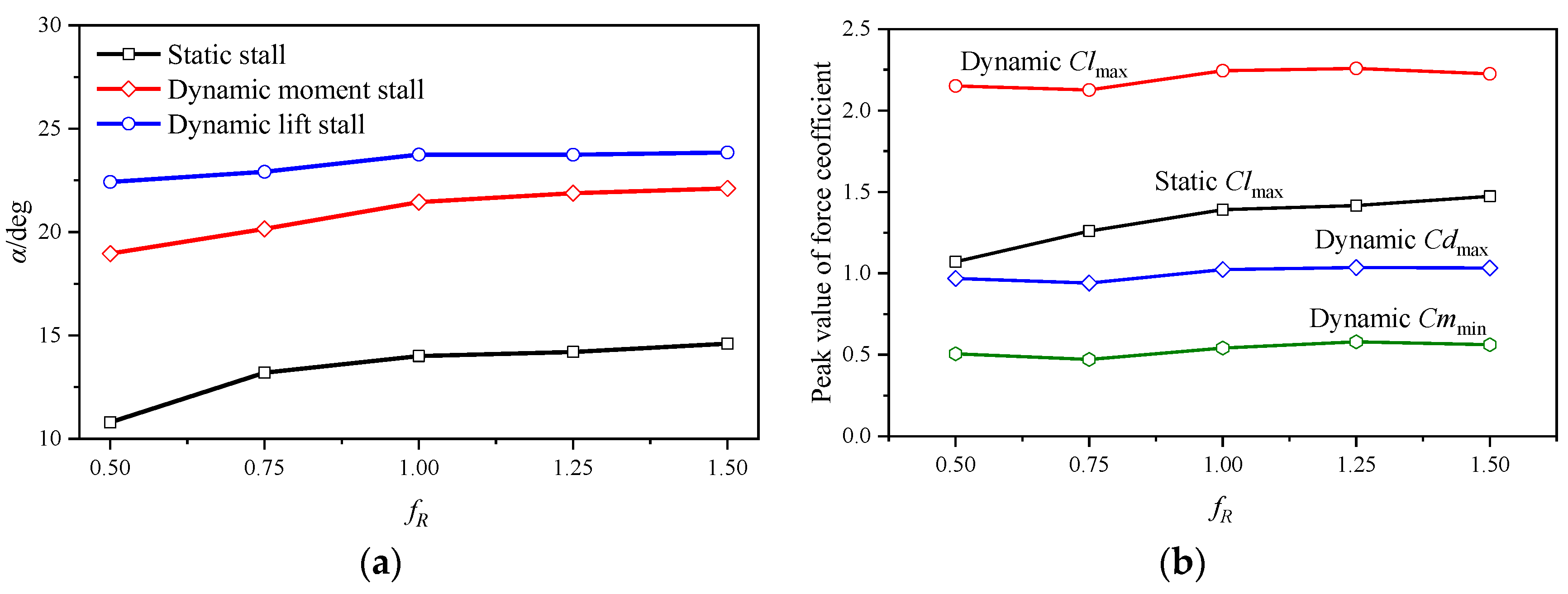
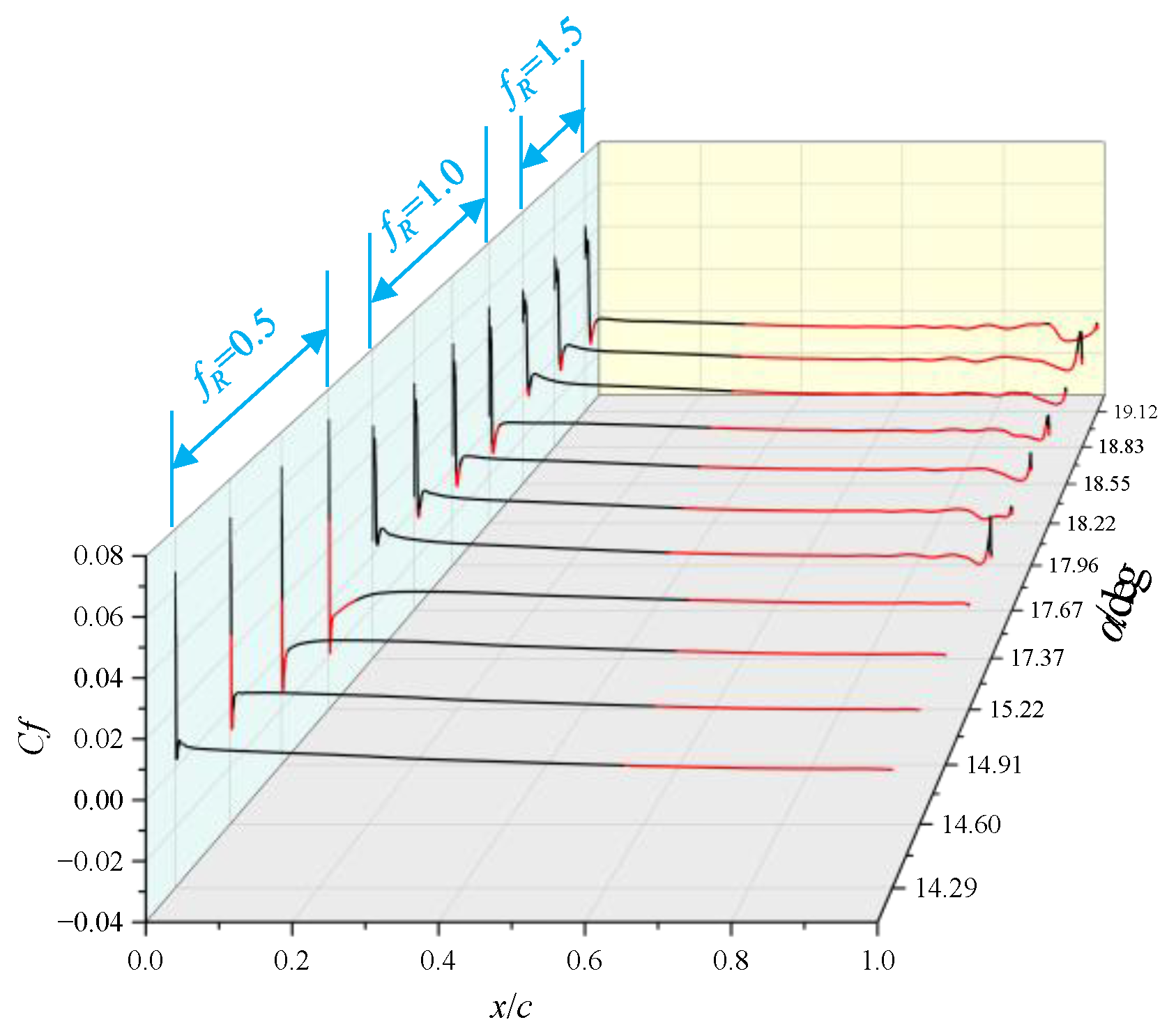
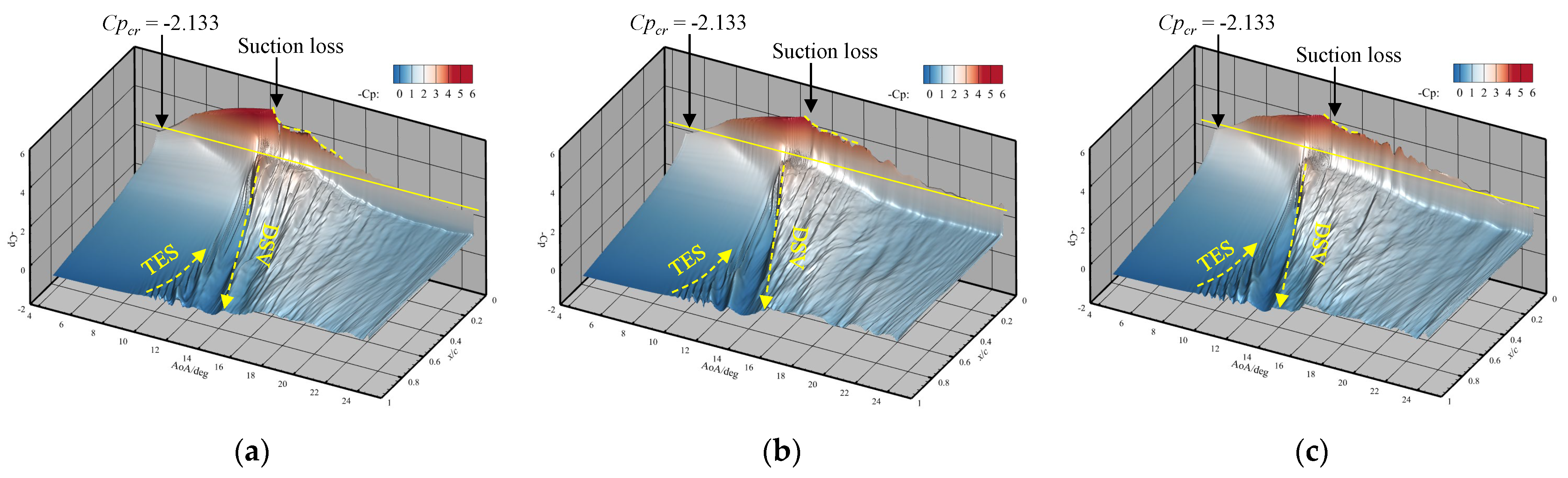
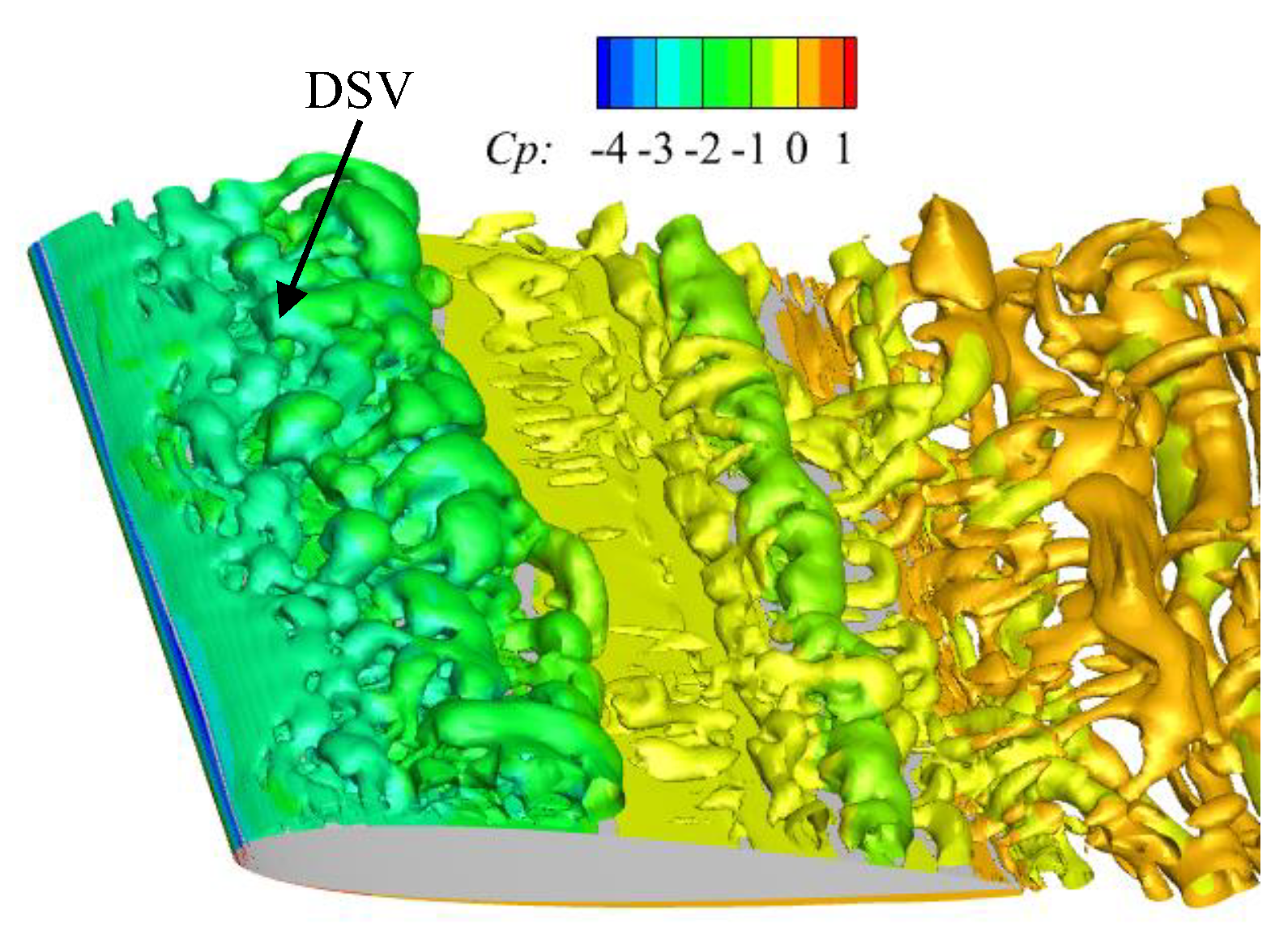
3.2. Impacts on Dynamic Stall Characteristics
3.2.1. Dynamic Cases at a Mach Number of 0.283
3.2.2. Dynamic Cases at a Mach Number of 0.5
4. Conclusions
- (1)
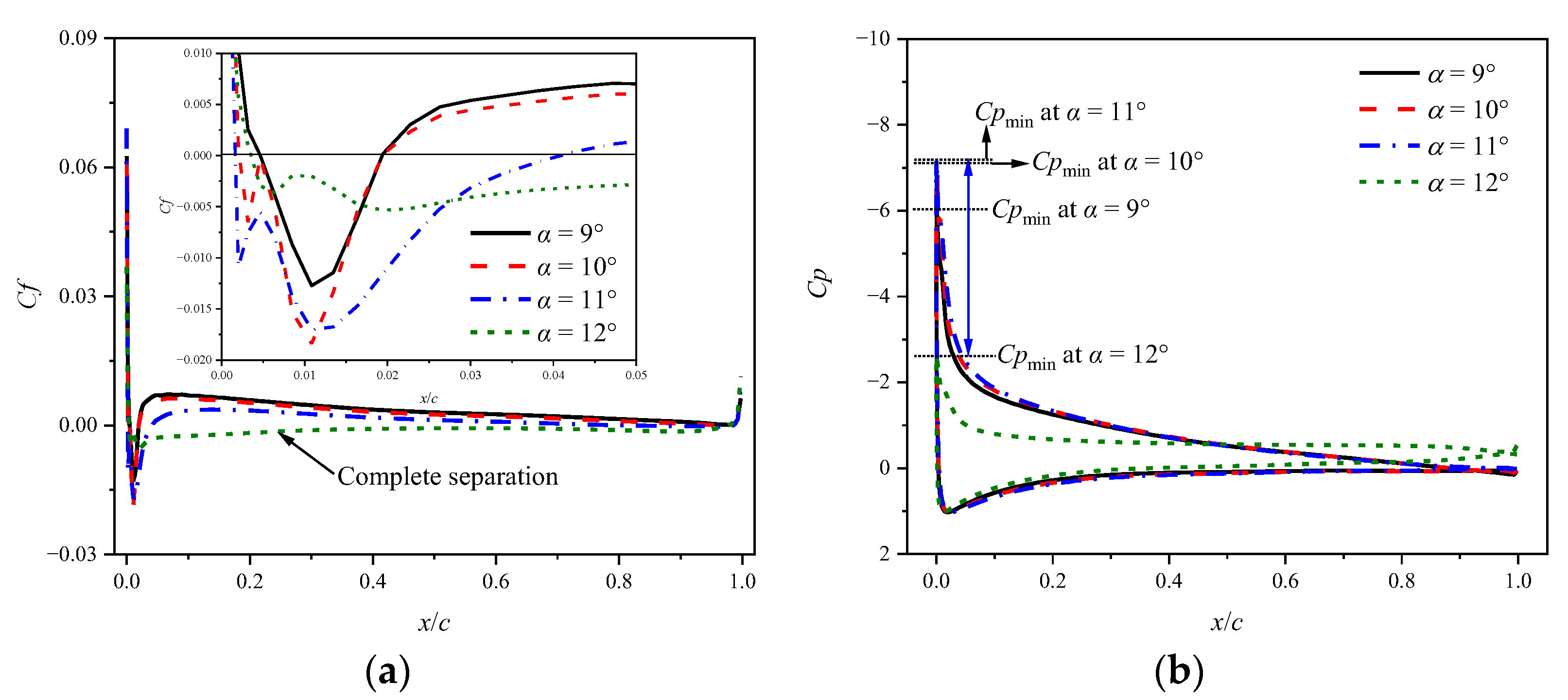
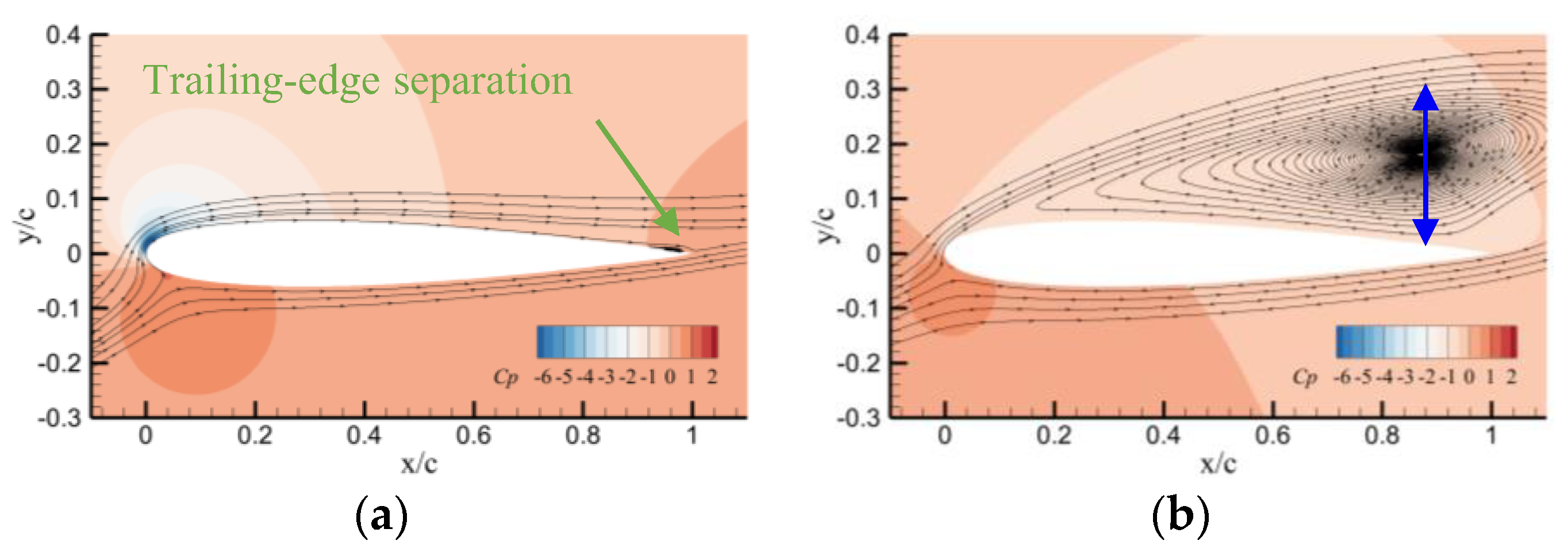
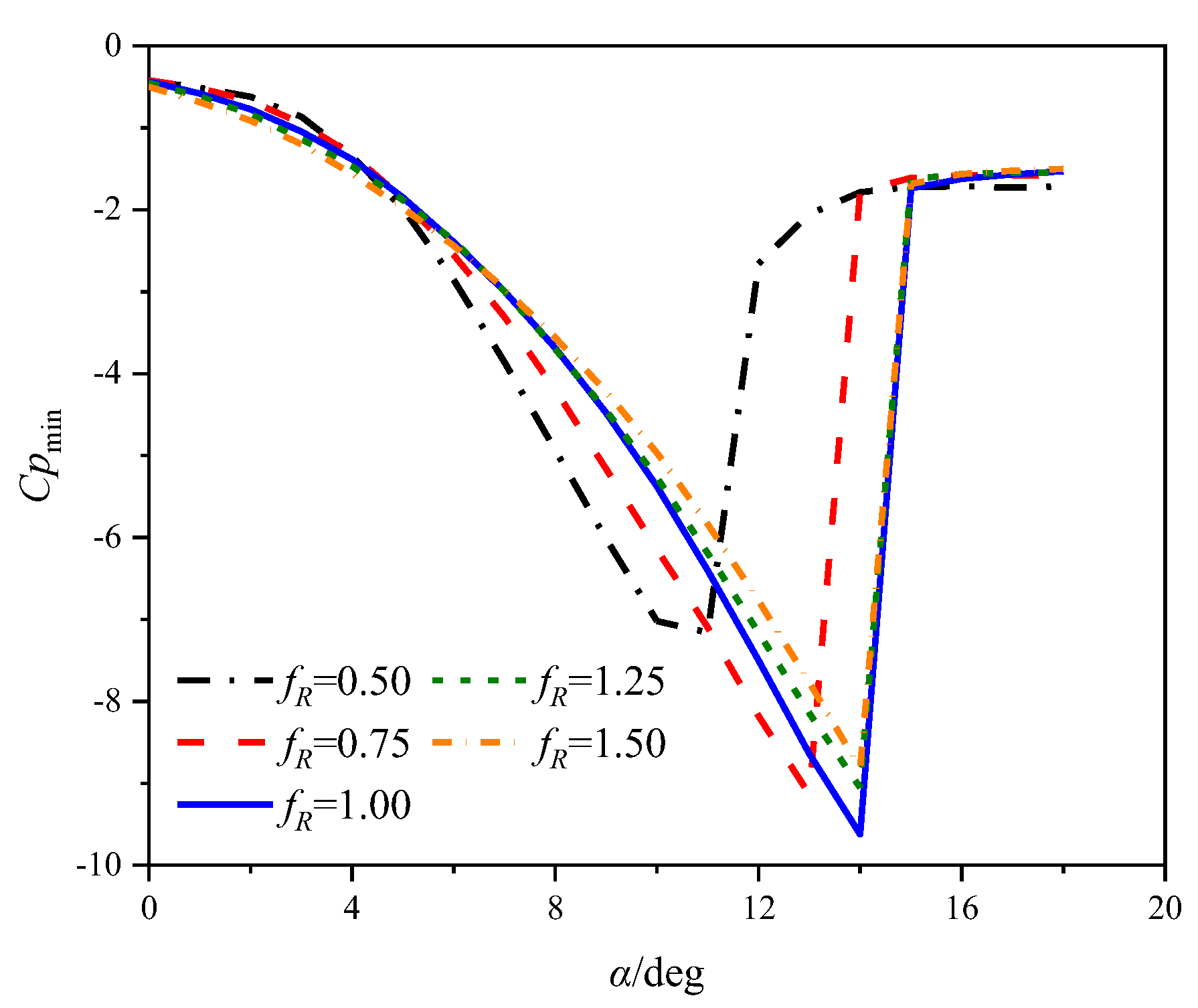
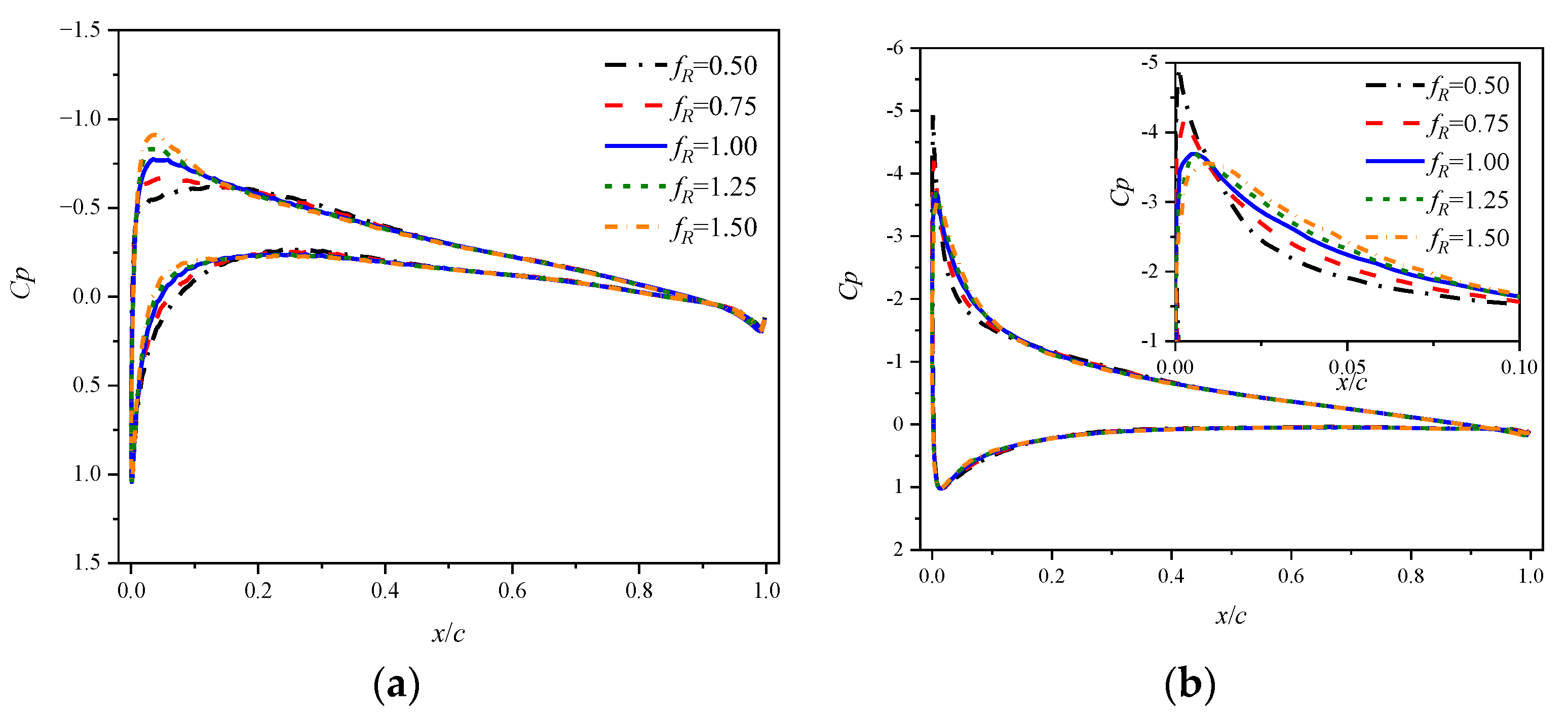
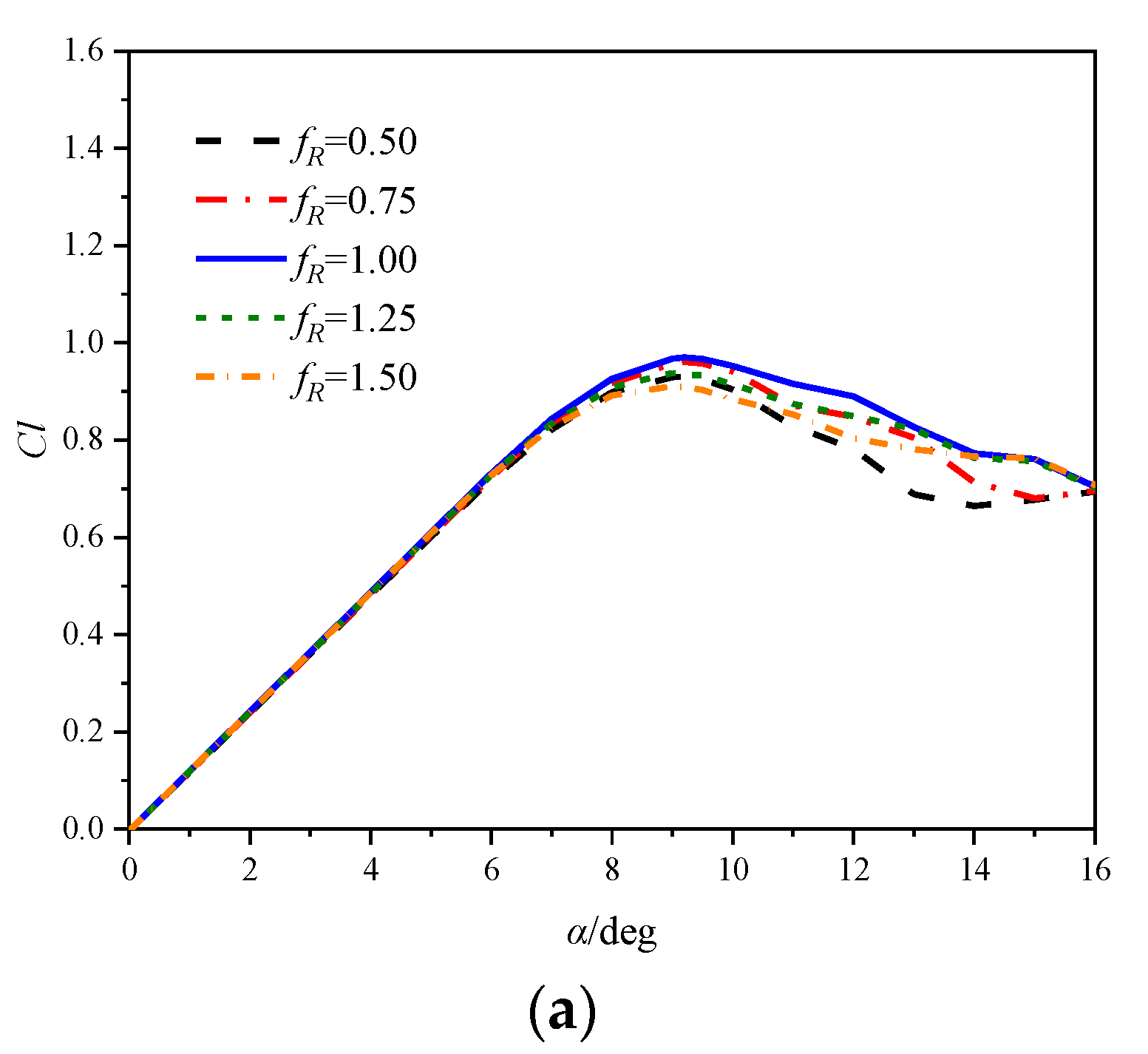
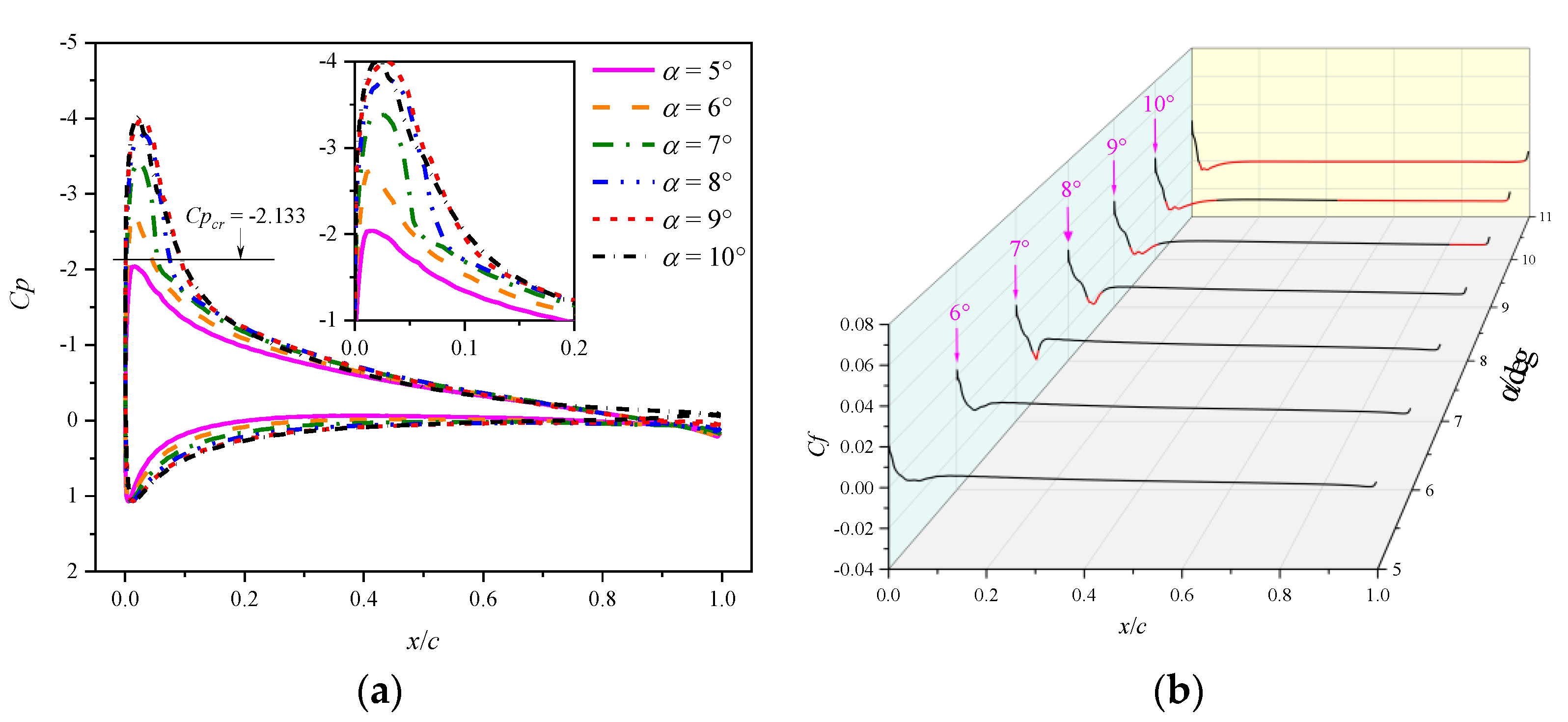
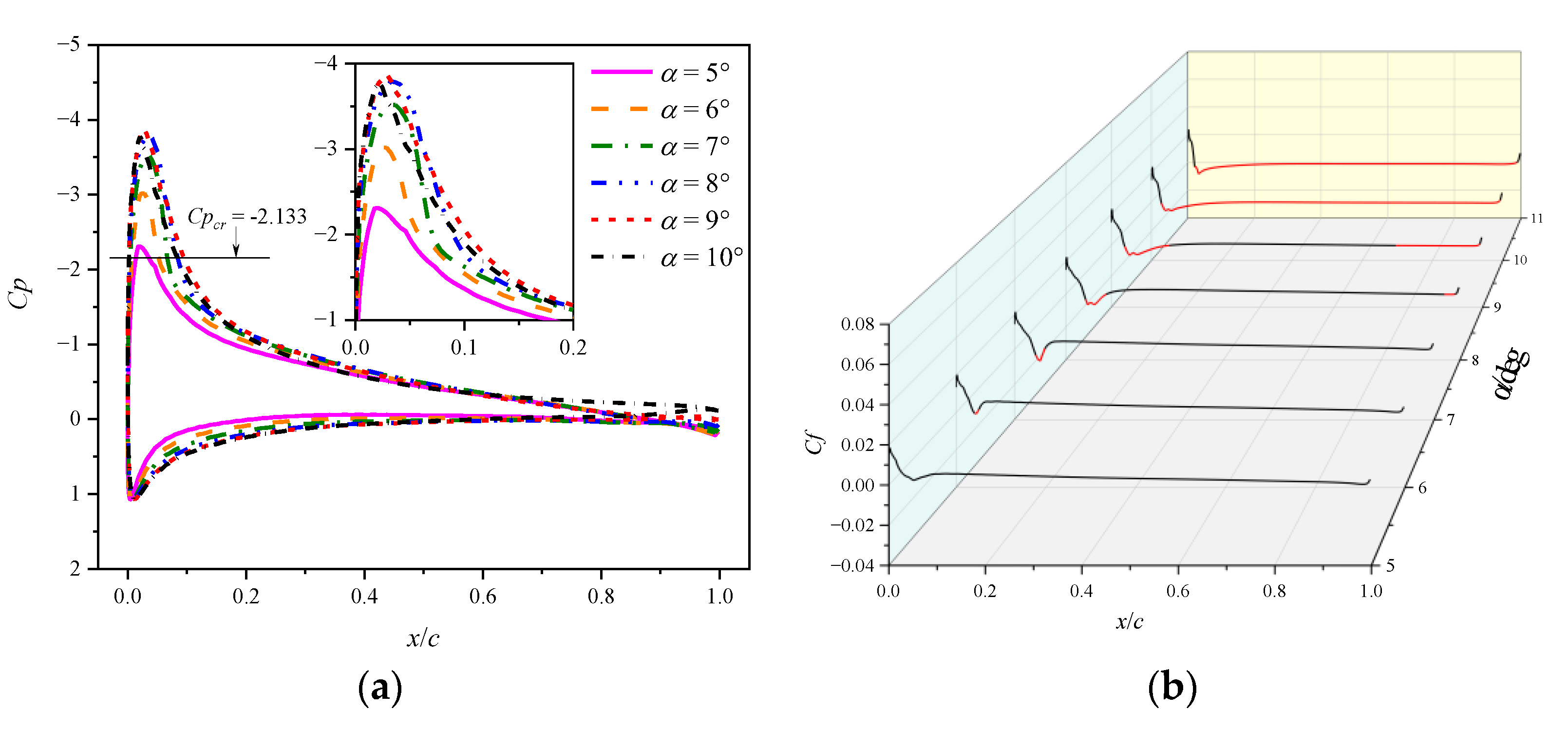
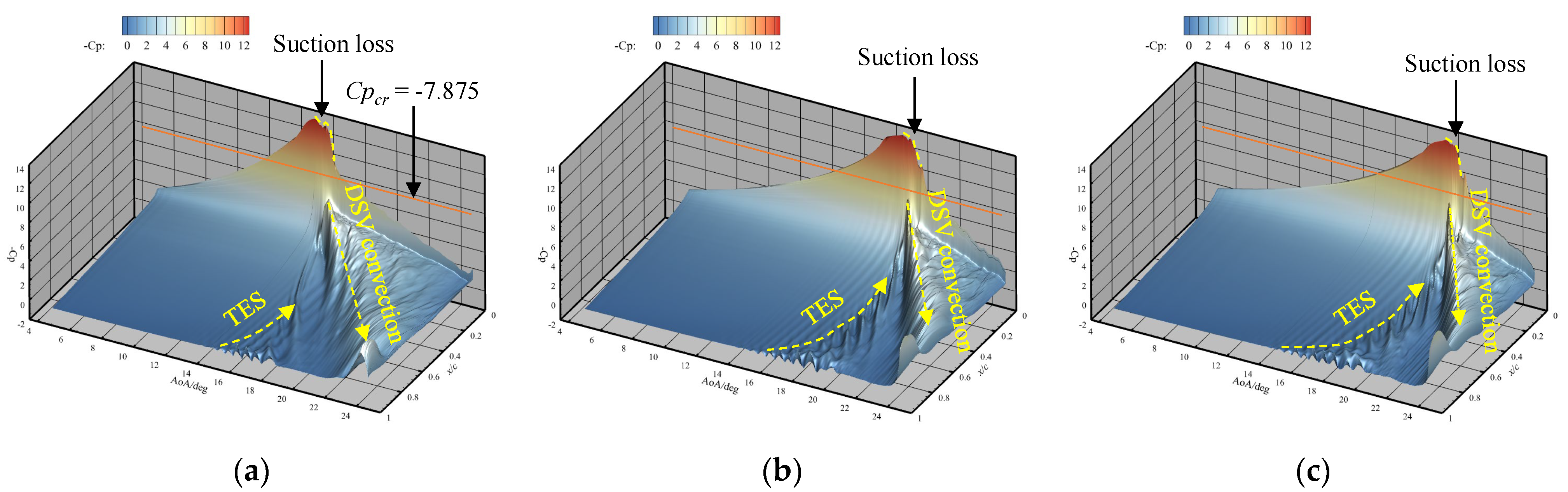
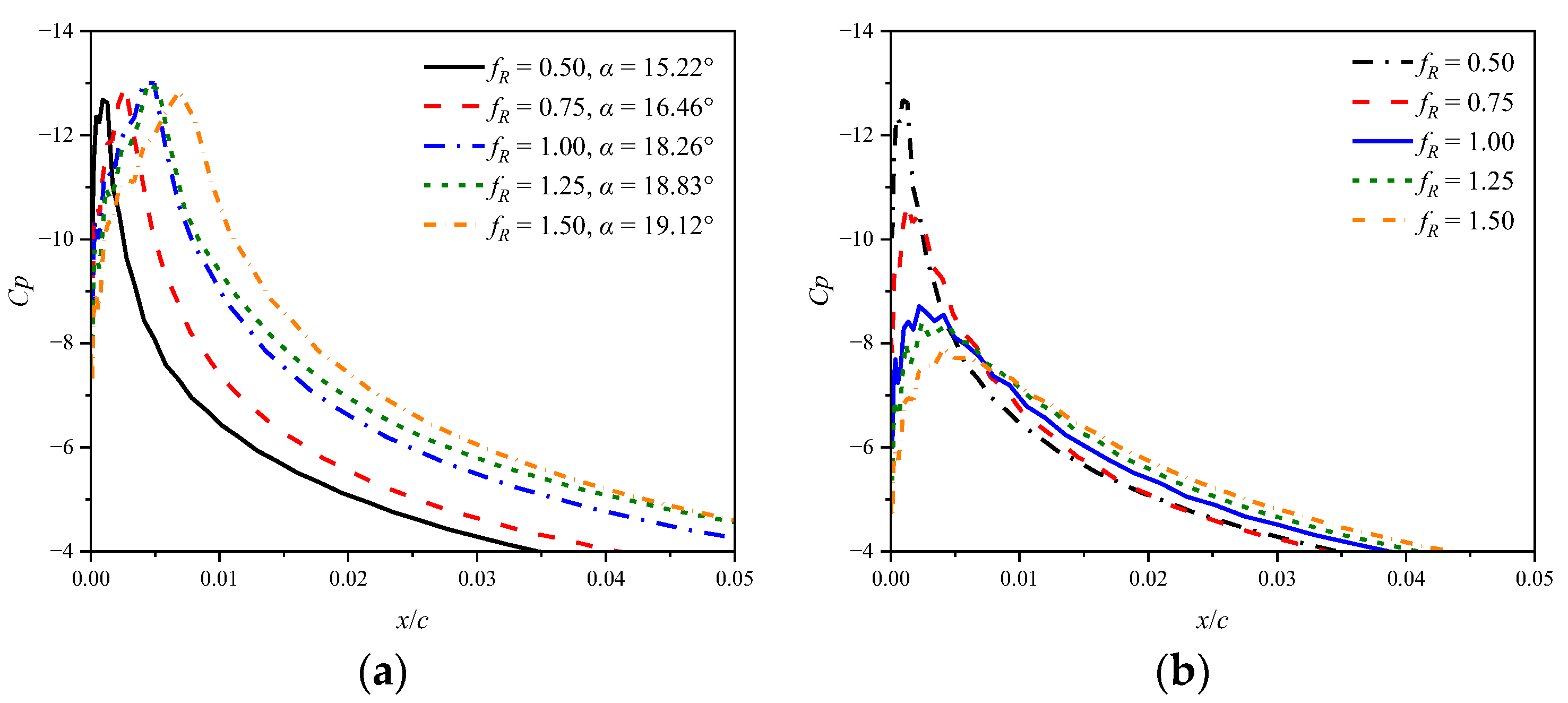
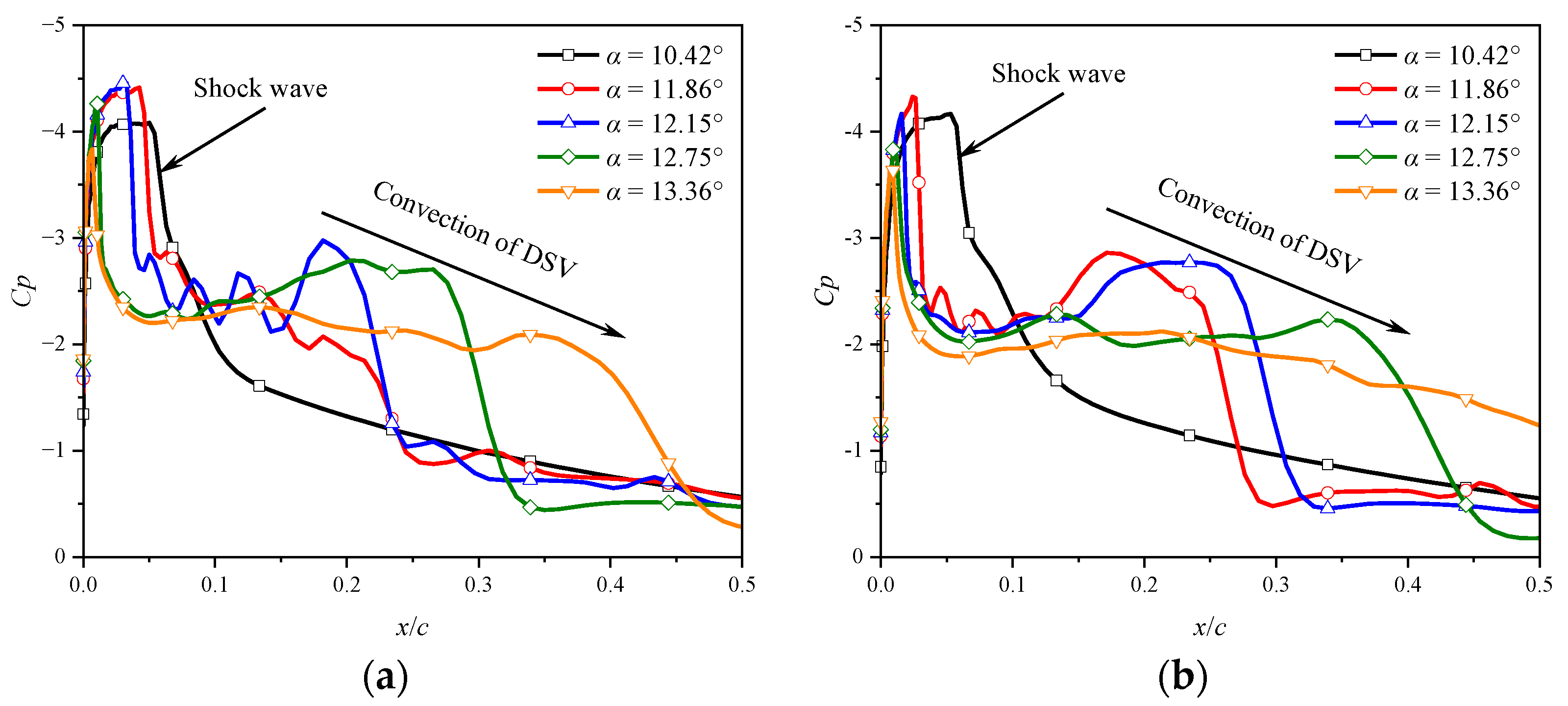
- At a low Mach number of 0.283, the airfoil experiences an abrupt leading edge stall in both static and dynamic cases. In the dynamic cases, unsteady motion delays the stall to a higher AoA compared to the static cases, and supercritical flow is observed on the airfoil. Despite the existing local supersonic flow near the leading edge, no visible shock wave is observed. The high adverse pressure gradient near the leading edge is the primary cause of both static and dynamic stall at the low Mach number. The stall regime remains unaffected by variations in the leading edge radius. However, increasing the leading edge radius reduces the suction pressure peak and adverse pressure gradients, hence delaying the leading edge separation and stall.
- (2)
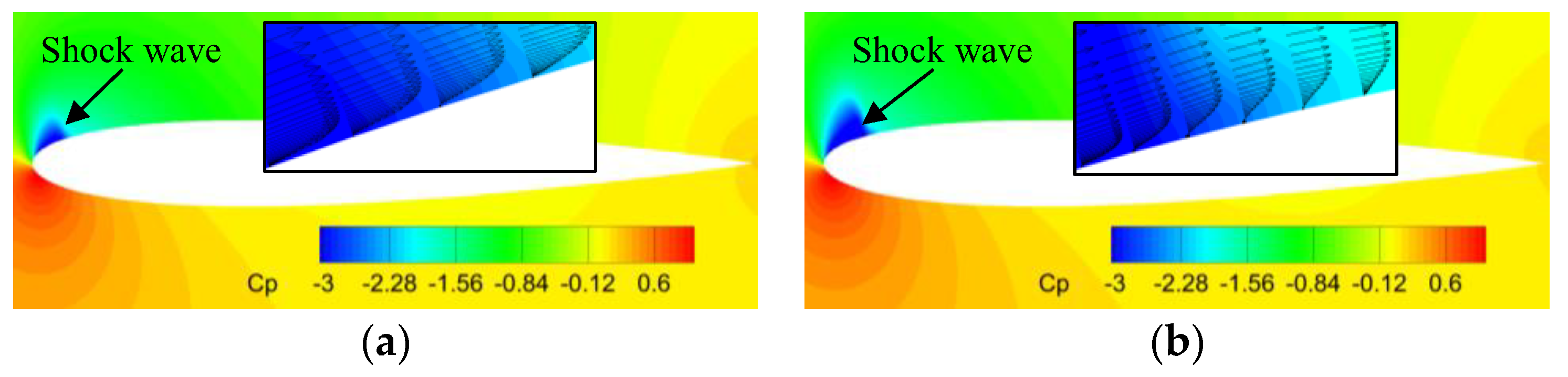
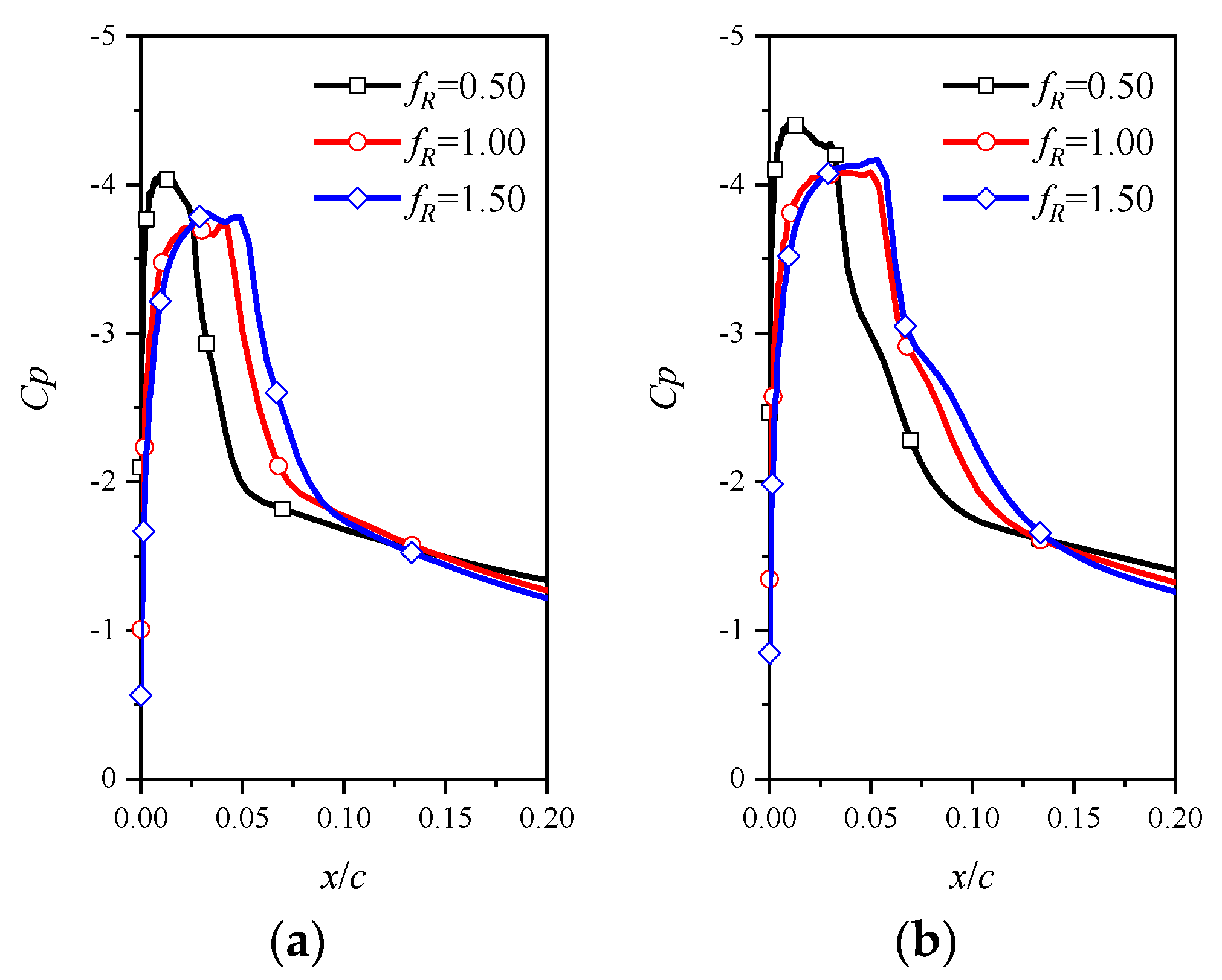
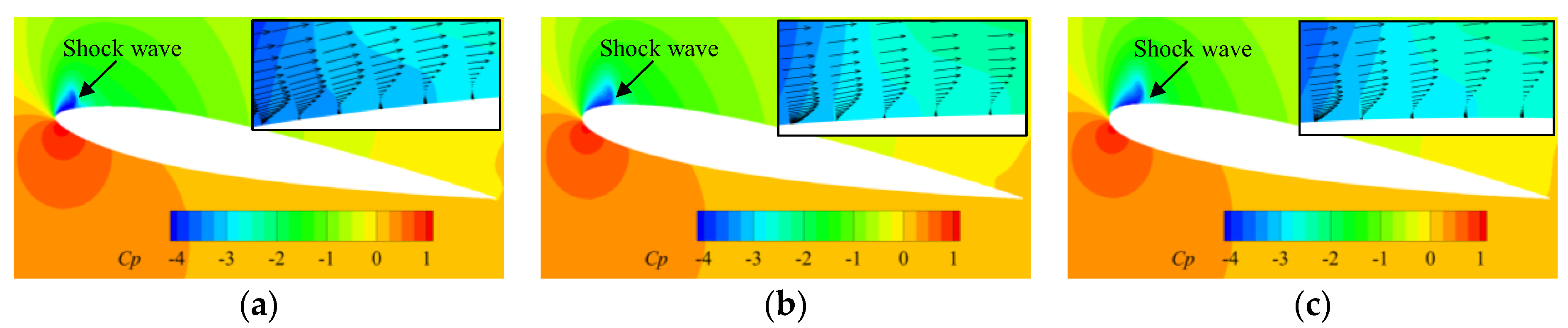
- At a high Mach number of 0.5, the airfoil encounters a moderate leading edge stall in both static and dynamic cases. Due to the significant compressibility effects, a shock wave forms near the leading edge and the high adverse pressure gradient near the shock wave induces flow separation. Instead of a collapse of the suction pressure peak, the shock-induced separation expands and causes a gradual decrease in the suction pressure peak, resulting in a smooth variation in aerodynamic loads. Increasing the leading edge radius reduces the compressibility effects, weakens the shock wave and shifts the shock wave aft on the chord, but has minimal effects on the adverse pressure gradient near the shock wave. Consequently, variations in the leading edge radius have minimal effects on the shock-induced stall characteristics.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Leishmann, J.G. Principles of Helicopter Aerodynamics; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- McCroskey, W.J.; Carr, L.W.; McAlister, K.W. Dynamic Stall Experiments on Oscillating Airfoils. AIAA J. 1976, 14, 57–63. [Google Scholar] [CrossRef]
- Carr, L.W.; McAlister, K.W.; McCroskey, W.J. Analysis of the Development of Dynamic Stall Based on Oscillating Airfoil Experiments. NASA TN D-8382, 1 January 1977. [Google Scholar]
- McCroskey, W.J.; McAlister, K.W.; Carr, L.W.; Pucci, S.L.; Lambert, O.; Indergrand, R.F. Dynamic Stall on Advanced Airfoil Sections. J. Am. Helicopter Soc. 1981, 26, 40–50. [Google Scholar] [CrossRef]
- Noonan, K.W.; Bingham, G.J. Aerodynamic Characteristics of Three Helicopter Rotor Airfoil Sections at Reynolds Number from Model Scale to Full Scale at Mach Numbers from 0.35 to 0.90. NASA-TP-1701, 1 September 1980. [Google Scholar]
- Benton, S.I.; Visbal, M.R. Effects of Compressibility on Dynamic-Stall Onset Using Large-Eddy Simulation. AIAA J. 2020, 58, 1194–1205. [Google Scholar] [CrossRef]
- Fung, K.Y.; Carr, L.W. Effects of Compressibility on Dynamic Stall. AIAA J. 1991, 29, 306–308. [Google Scholar] [CrossRef]
- Carr, L.W.; Chandrasekhara, M.S. Compressibility effects on dynamic stall. Prog. Aerosp. Sci. 1996, 32, 523–573. [Google Scholar] [CrossRef]
- Kim, T.; Kim, S.; Lim, J.; Jee, S. Numerical Investigation of Compressibility Effect on Dynamic Stall. Aerosp. Sci. Technol. 2020, 105, 105918. [Google Scholar] [CrossRef]
- Jacobs, E.N.; Sherman, A. Airfoil Section Characteristics as Affected by Variations of the Reynolds Number. NACA-TR-586, 1 January 1937. [Google Scholar]
- Kiefer, J.; Brunner, C.E.; Hansen, M.O.L.; Hultmark, M. Dynamic Stall at High Reynolds Numbers Induced by Ramp-Type Pitching Motions. J. Fluid Mech. 2022, 938, A10. [Google Scholar] [CrossRef]
- Zhu, W.; Bons, J.P.; Gregory, J.W. Reynolds Scaling Effects on Dynamic Stall of VR-7 and VR-12 Airfoils. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- McCroskey, W.J. The Phenomenon of Dynamic Stall. NASA TM-81264, 1 March 1981. [Google Scholar]
- Choudhuri, P.G.; Knight, D.D. Effects of compressibility, pitch rate, and Reynolds number on unsteady incipient leading-edge boundary layer separation over a pitching airfoil. J. Fluid Mech. 1996, 308, 195–217. [Google Scholar] [CrossRef]
- McCroskey, W.J.; McAlister, K.W.; Carr, L.W.; Pucci, S.L. An Experimental Study of Dynamic Stall on Advanced Airfoil Sections Volume 1. Summary of the Experiment. NASA-TM-84245, 1 July 1982. [Google Scholar]
- McAlister, K.W.; Pucci, S.L.; McCroskey, W.J.; Carr, L.W. An Experimental Study of Dynamic Stall on Advanced Airfoil Sections Volume 2. Pressure and Force Data. NASA-TM-84245, 1 September 1982. [Google Scholar]
- Carr, L.W.; McCroskey, W.J.; McAlister, K.W.; Pucci, S.L.; Lambert, O. An Experimental Study of Dynamic Stall on Advanced Airfoil Sections Volume 3. Hot-Wire and Hot-Film Measurements. NASA-TM-84245, 1 December 1982. [Google Scholar]
- Sharma, A.; Visbal, M. Numerical Investigation of the Effect of Airfoil Thickness on Onset of Dynamic Stall. J. Fluid Mech. 2019, 870, 870–900. [Google Scholar] [CrossRef]
- Shum, J.G.; Lee, S. Effect of Airfoil Design Parameters on Deep Dynamic Stall under Pitching Motion. In Proceedings of the AIAA SciTech 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]
- Ekaterinaris, J.A. Numerical investigations of dynamic stall active control for incompressible and compressible flows. J. Aircr. 2002, 39, 71–78. [Google Scholar] [CrossRef]
- Müller-Vahl, H.F.; Strangfeld, C.; Nayeri, C.N.; Paschereit, C.O.; Greenblatt, D. Control of Thick Airfoil, Deep Dynamic Stall Using Steady Blowing. Aiaa J. 2015, 53, 277–295. [Google Scholar] [CrossRef]
- Rehman, A.; Kontis, K. Synthetic Jet Control Effectiveness on Stationary and Pitching Airfoils. J. Aircr. 2006, 43, 1782–1789. [Google Scholar] [CrossRef]
- Martin, P.B.; McAlisterK, W.; Chandrasekhara, M.S.; Geissler, W. Dynamic stall measurements and computations for a VR-12 airfoil with a variable droop leading edge. In Proceedings of the AHS International Forum 59, Phoenix, AZ, USA, 6–8 May 2003.
- Chandrasekhara, M.S.; Martin, P.B.; Tung, C. compressible dynamic stall control using a variable droop leading edge airfoil. J. Aircr. 2012, 41, 862–869. [Google Scholar] [CrossRef]
- Hassan, A.A.; Straub, F.K.; Noonan, K.W. Experimental/Numerical Evaluation of Integral Trailing Edge Flaps for Helicopter Rotor Applications. J. Am. Helicopter Soc. 2005, 50, 3–17. [Google Scholar] [CrossRef]
- Tang, J.W.; Hu, Y.; Song, B.F.; Yang, H. Unsteady Aerodynamic Optimization of Airfoil for Cycloidal Propellers Based on Surrogate Model. J. Aircr. 2017, 54, 1241–1256. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, Q.J. Rotor Airfoil Profile Optimization for Alleviating Dynamic Stall Characteristics. Aerosp. Sci. Technol. 2018, 72, 502–515. [Google Scholar] [CrossRef]
- Jing, S.M.; Zhao, Q.J.; Zhao, G.Q.; Wang, Q. Multi-Objective Airfoil Optimization Under Unsteady-Freestream Dynamic Stall Conditions. J. Aircr. 2023, 60, 293–309. [Google Scholar] [CrossRef]
- Lim, J.W. Application of Parametric Airfoil Design for Rotor Performance Improvement. In Proceedings of the 44th European Rotrocraft Forum, Delft, The Netherlands, 18–21 September 2018. [Google Scholar]
- Zhao, Q.J.; Zhao, G.Q.; Wang, B.; Wang, Q.; Shi, Y.J.; Xu, G.H. Robust Navier-Stokes Method for Predicting Unsteady Flowfield and Aerodynamic Characteristics of Helicopter Rotor. Chin. J. Aeronaut. 2018, 31, 214–224. [Google Scholar] [CrossRef]
- Gritskevich, M.S.; Garbaruk, A.V.; Schutze, J.; Menter, F.R. Development of DDES and IDDES Formulations for the k-ω Shear Stress Transport Model. Flow Turbul. Combust. 2012, 88, 431–449. [Google Scholar] [CrossRef]
- Travin, A.; Shur, M.; Strelets, M.; Spalart, P. Detached-Eddy Simulations past a Circular Cylinder. Flow Turbul. Combust. 2000, 63, 293–313. [Google Scholar] [CrossRef]
- Khalifa, N.M.; Rezaei, A.; Taha, H.E. On Computational Simulations of Dynamic Stall and Its Three-Dimensional Nature. Phys. Fluids 2023, 35, 105143. [Google Scholar] [CrossRef]
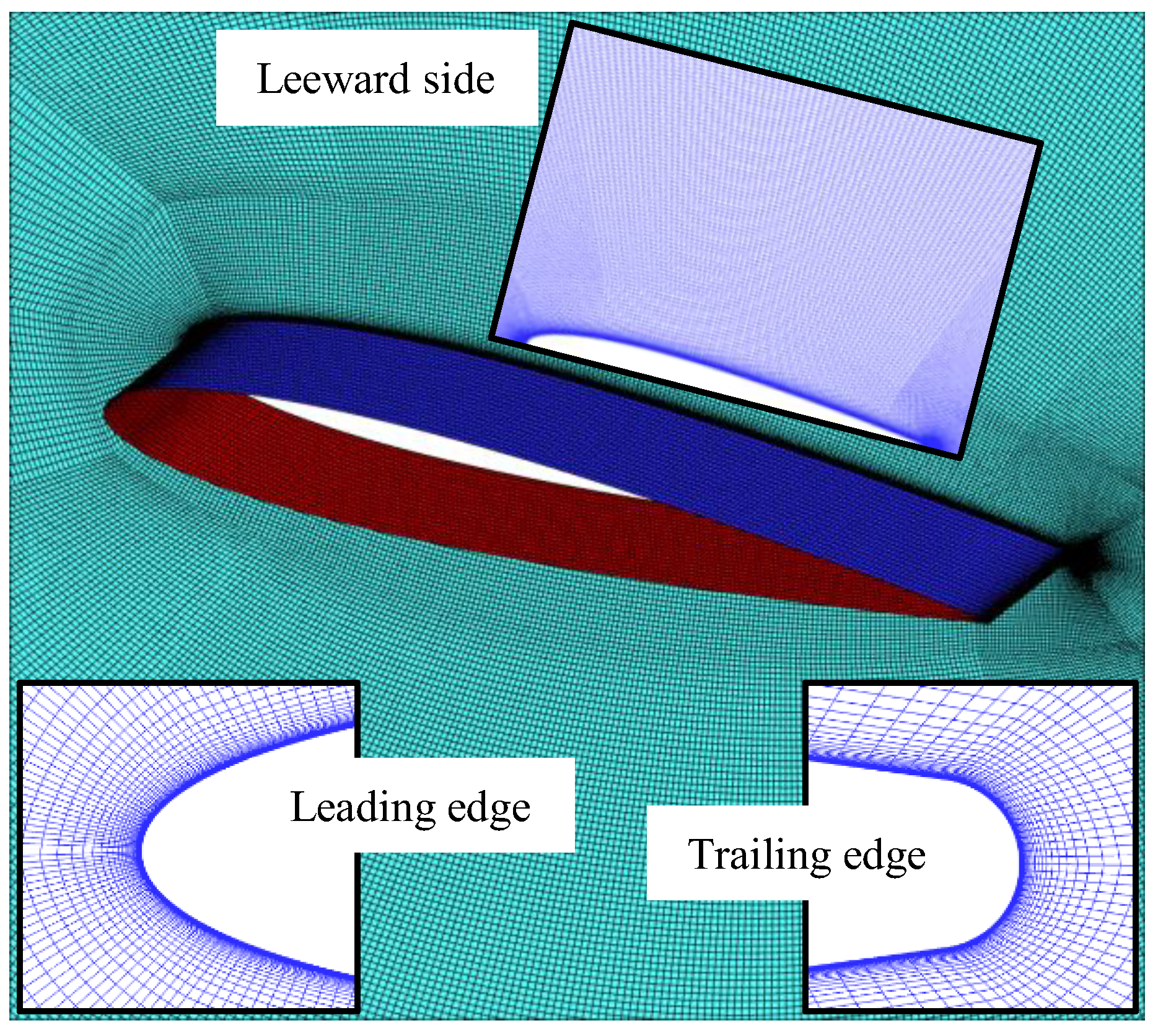
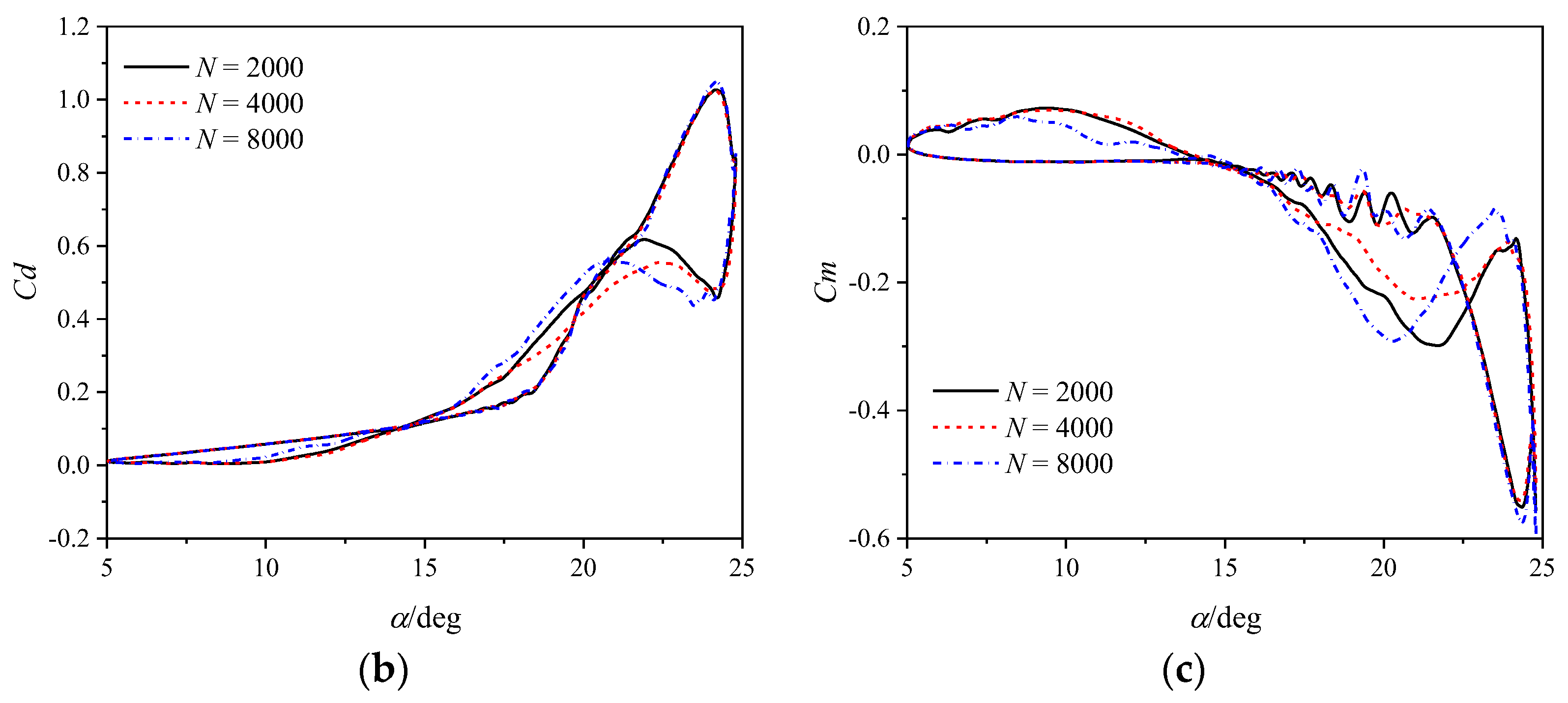
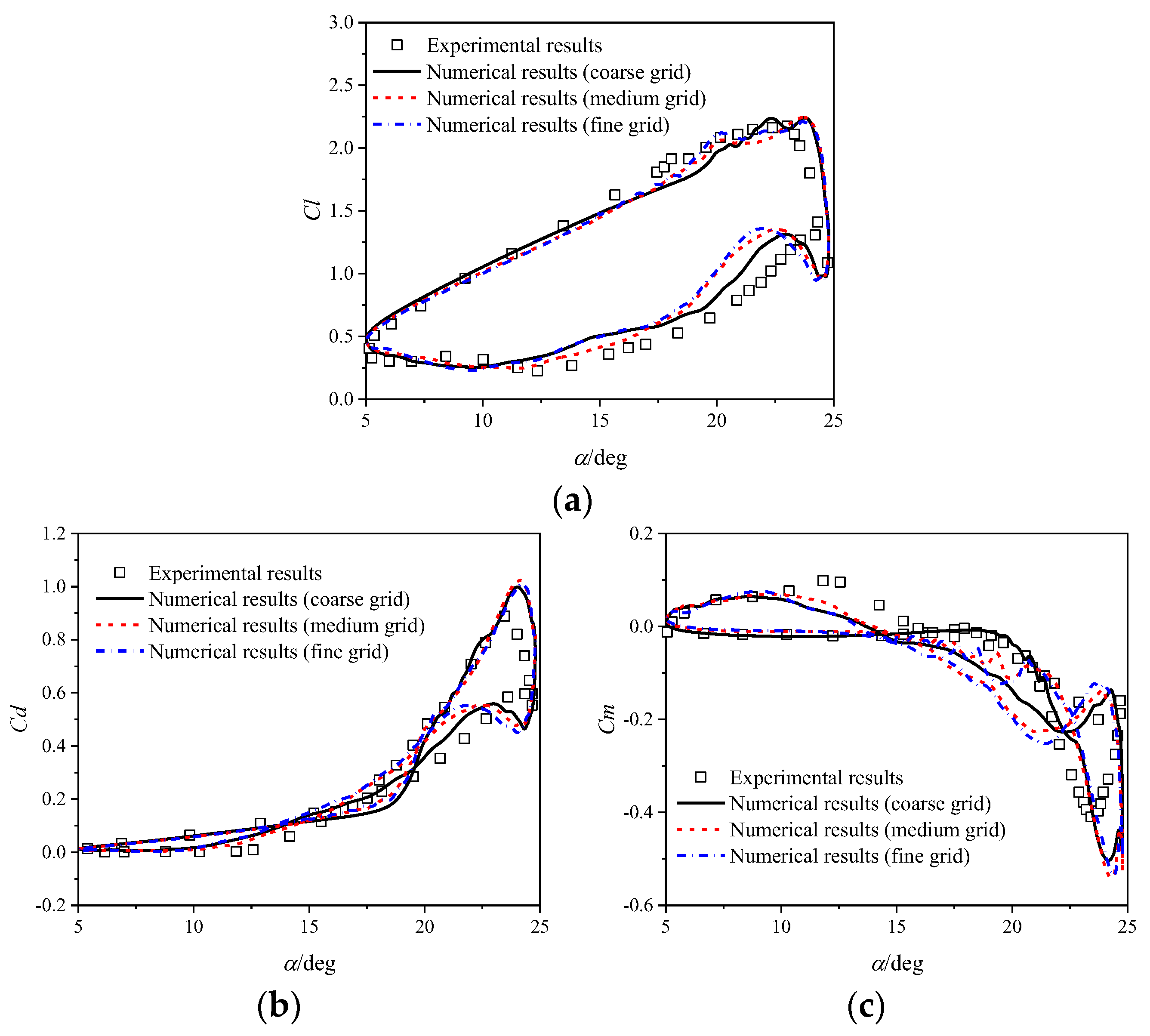
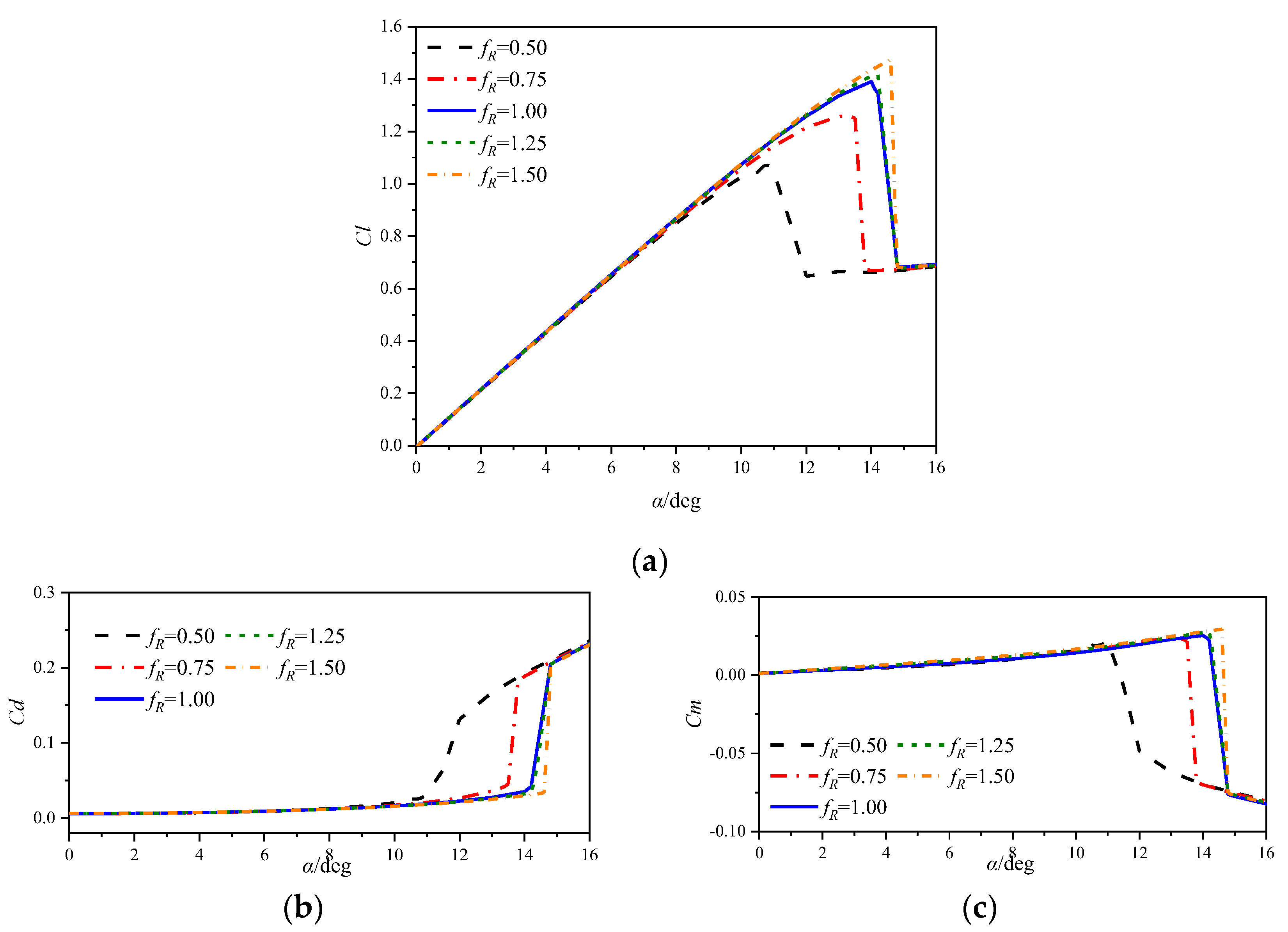



| Grid Resolution | Number of Grid Points |
|---|---|
| Coarse | 248 × 95 |
| Medium | 306 × 112 |
| Fine | 421 × 142 |
| Grid Resolution | Total Number of Grid Points | Cell Size in the LES Region |
|---|---|---|
| Coarse | 248 × 95 × 51 | 0.02c |
| Medium | 306 × 112 × 67 | 0.015c |
| Fine | 421 × 142 × 101 | 0.01c |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, S.; Zhao, G.; Gao, Y.; Zhao, Q. Effects of Leading Edge Radius on Stall Characteristics of Rotor Airfoil. Aerospace 2024, 11, 470. https://doi.org/10.3390/aerospace11060470
Jing S, Zhao G, Gao Y, Zhao Q. Effects of Leading Edge Radius on Stall Characteristics of Rotor Airfoil. Aerospace. 2024; 11(6):470. https://doi.org/10.3390/aerospace11060470
Chicago/Turabian StyleJing, Simeng, Guoqing Zhao, Yuan Gao, and Qijun Zhao. 2024. "Effects of Leading Edge Radius on Stall Characteristics of Rotor Airfoil" Aerospace 11, no. 6: 470. https://doi.org/10.3390/aerospace11060470
APA StyleJing, S., Zhao, G., Gao, Y., & Zhao, Q. (2024). Effects of Leading Edge Radius on Stall Characteristics of Rotor Airfoil. Aerospace, 11(6), 470. https://doi.org/10.3390/aerospace11060470






