The Modeling and Control of a Distributed-Vector-Propulsion UAV with Aero-Propulsion Coupling Effect
Abstract
1. Introduction
- An aero-propulsion coupling model (APCM) is developed to meet the requirements of flight dynamics and flight control. The proposed APCM is an analytical model and could balance computational accuracy and speed so that it has the capability to be directly applied to flight dynamics and control, which is the first attempt to the best of our knowledge.
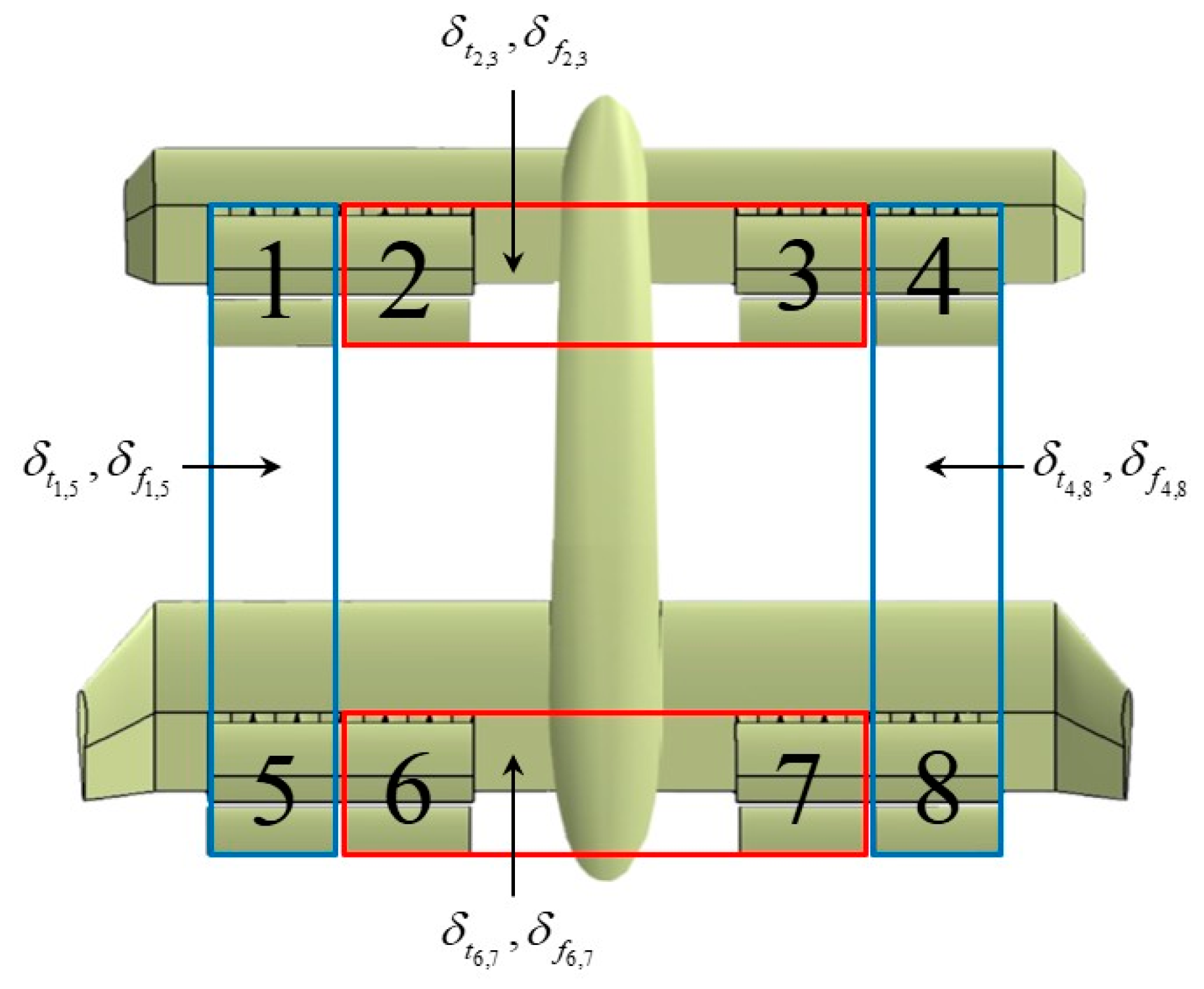
- A unique control framework is designed for the DVPUAV, a system with complex control coupling and so many inputs. Based on the logic of baseline inputs plus longitudinal differential inputs or lateral directional increment inputs, the decoupling of longitudinal and lateral directional control as well as the decoupling of roll and yaw control are realized. The number of inputs is greatly reduced from 32 to 8, which is beneficial to reducing the computational burden.
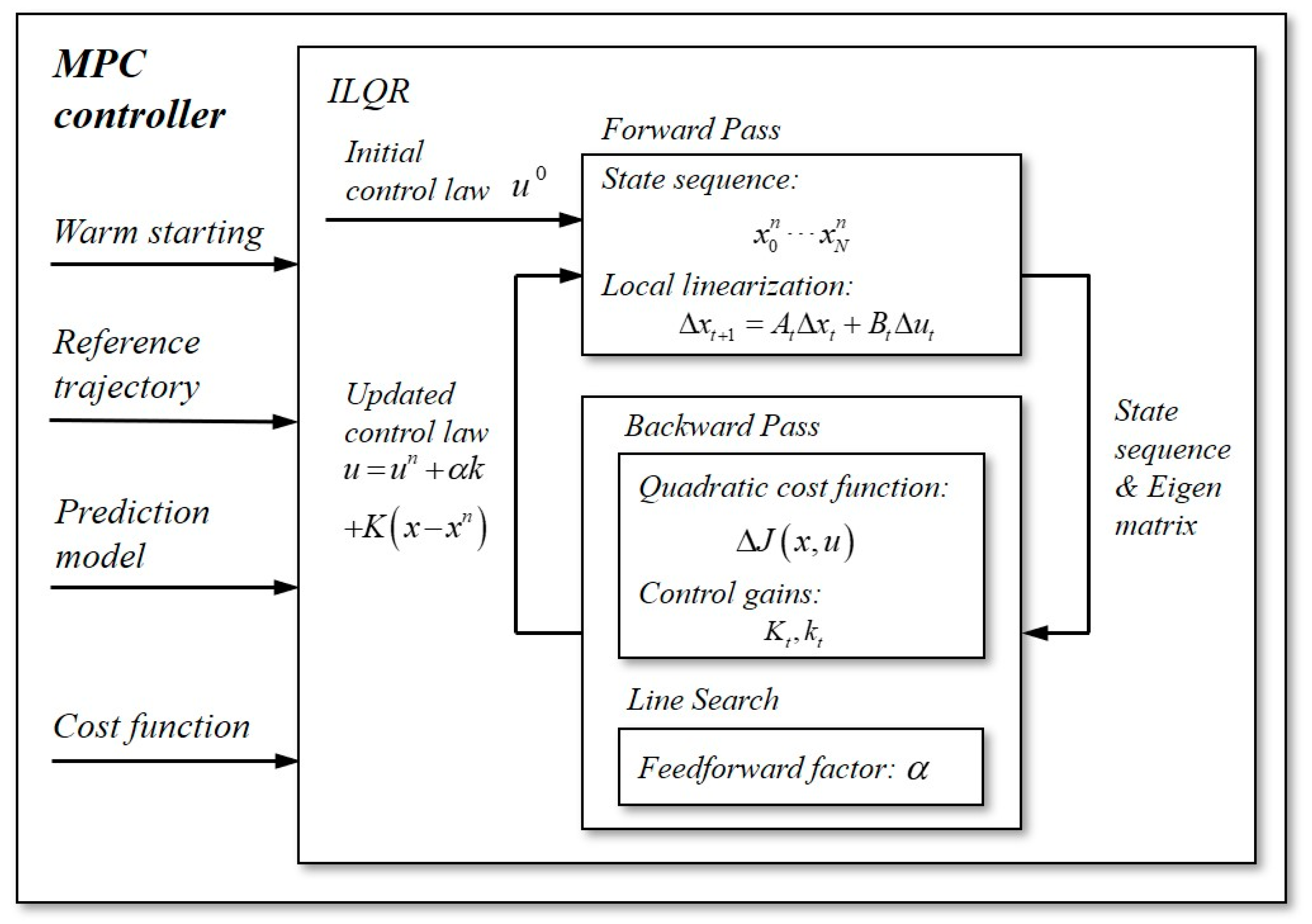
- An MPC controller is presented based on ILQR, which is capable of efficiently solving nonlinear control problems with linear complexity. Therefore, this controller is suitable for the DVPUAV with an aero-propulsion coupling effect, which is a novel application in the field of VTOL aircraft. Moreover, this controller is a unified one for the full flight envelope, which is fundamentally superior to the conventional VTOL controller.
2. Modeling of the DVPUAV
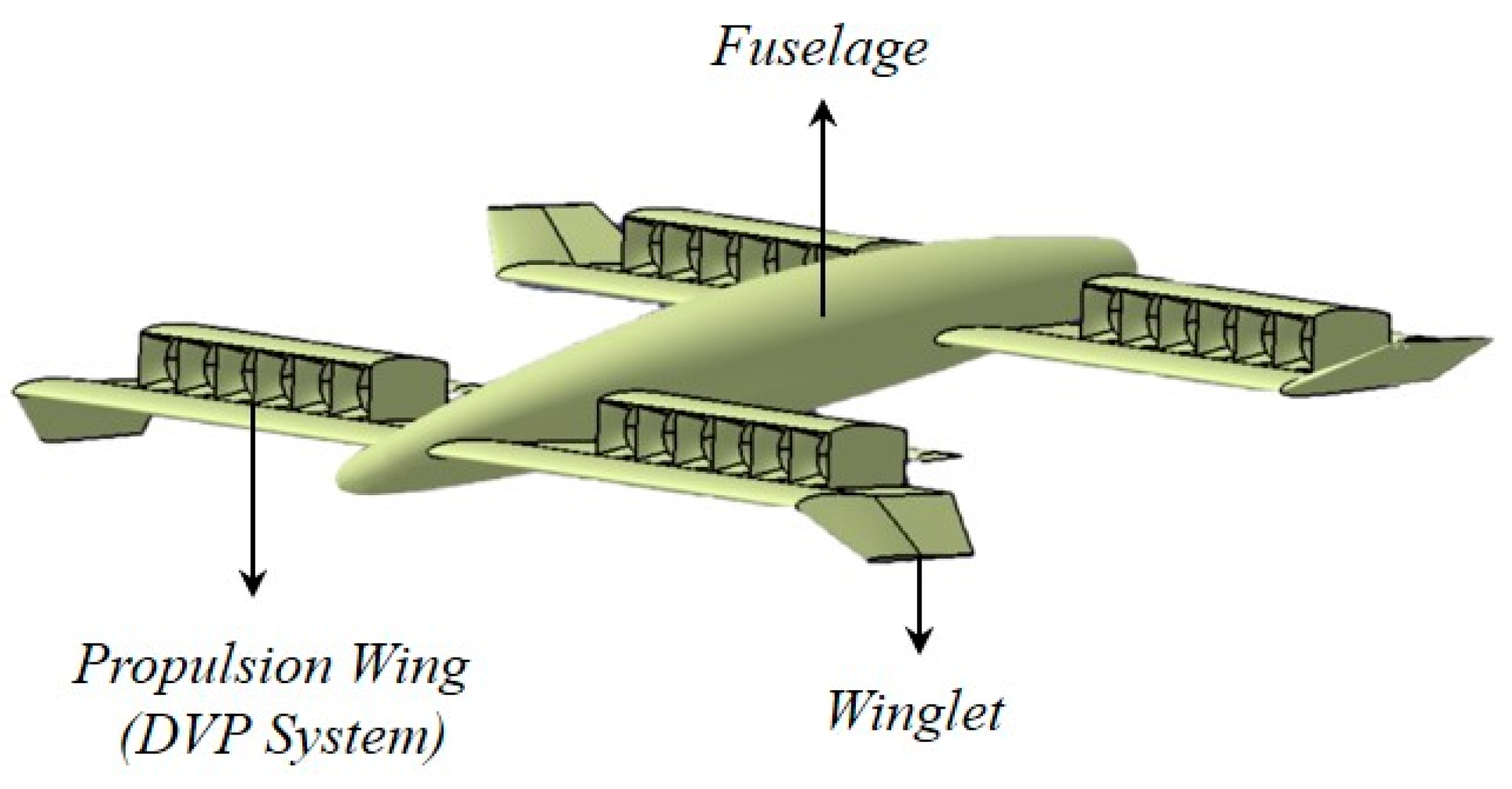
2.1. DVPUAV Conceptual Design
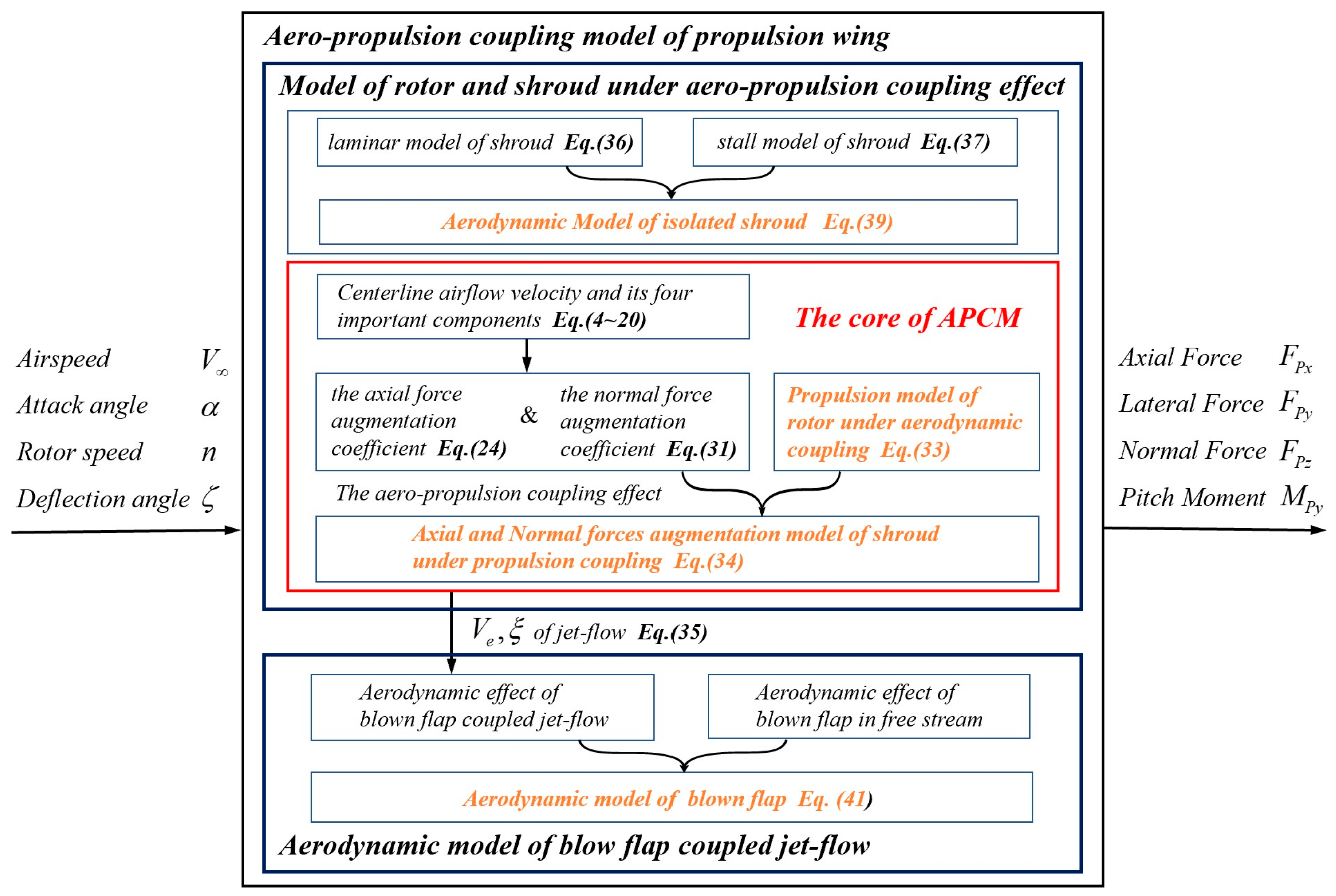
2.2. Aero-Propulsion Coupling Model of Propulsion Wing
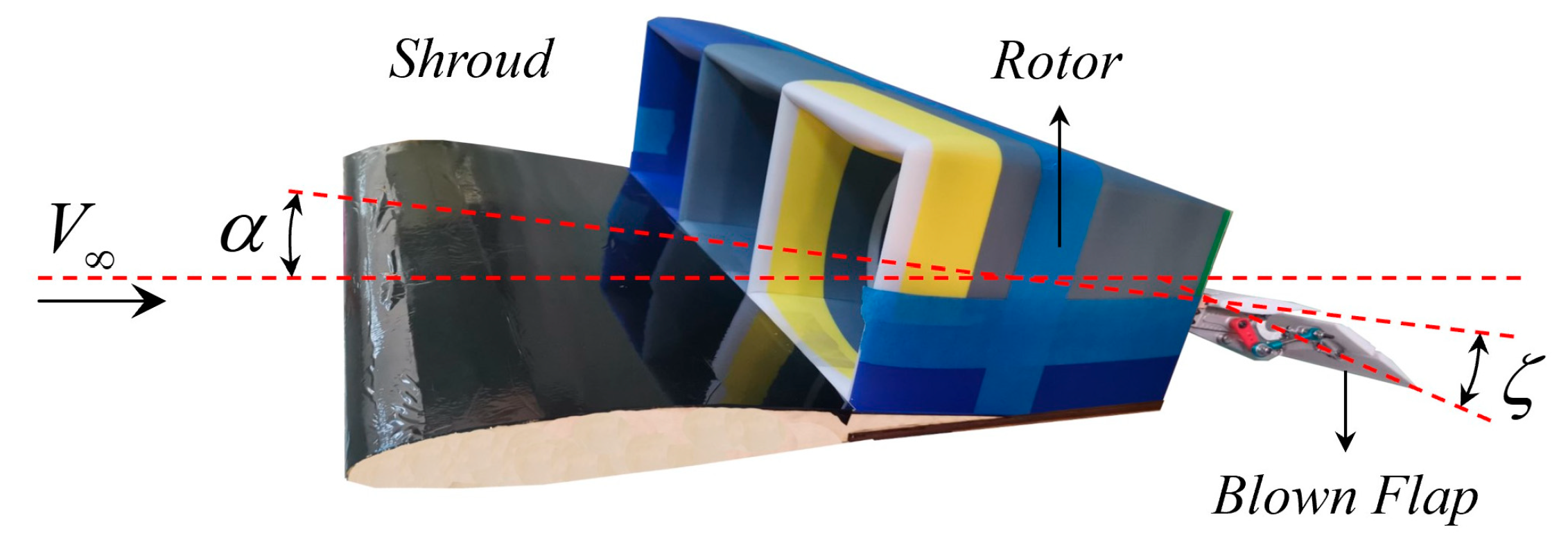
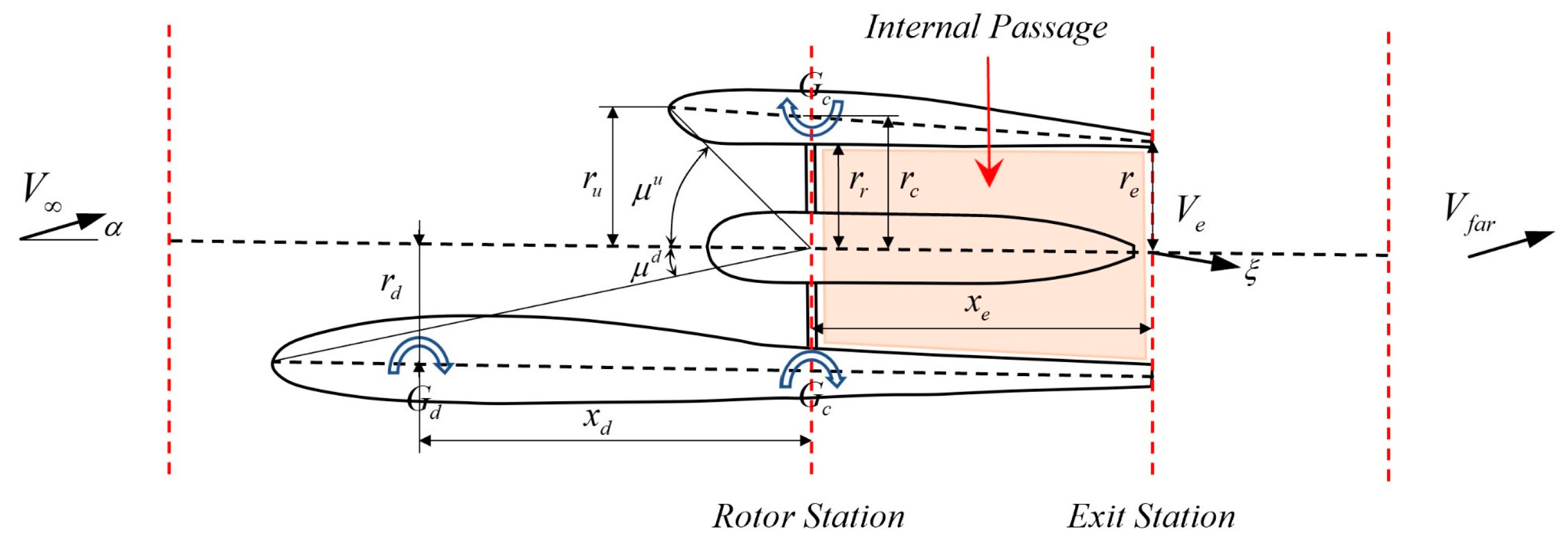
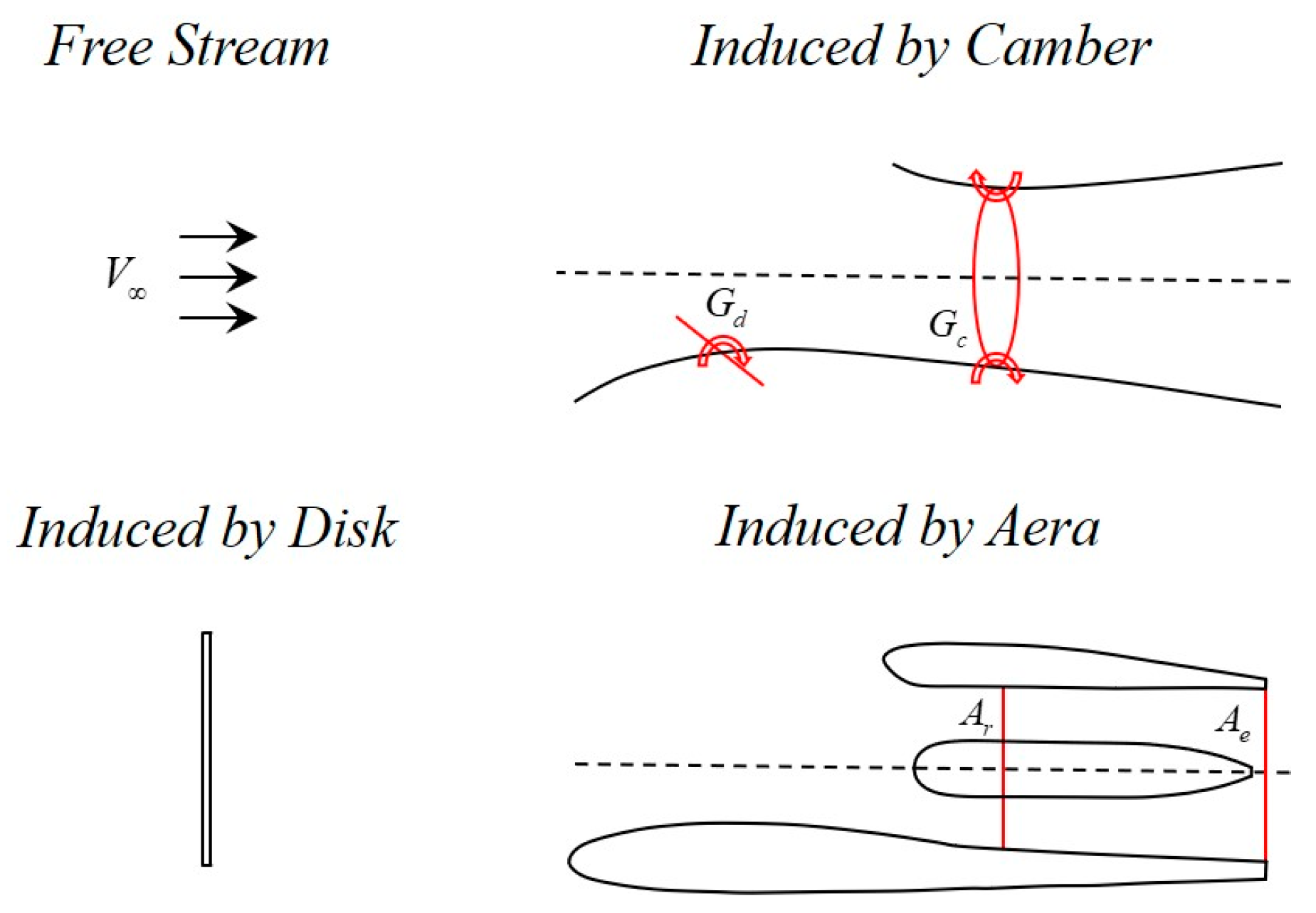
2.2.1. Model of Rotor and Shroud under Aero-Propulsion Coupling Effect
2.2.2. Aerodynamic Model of Blown Flap Coupled Jet-Flow
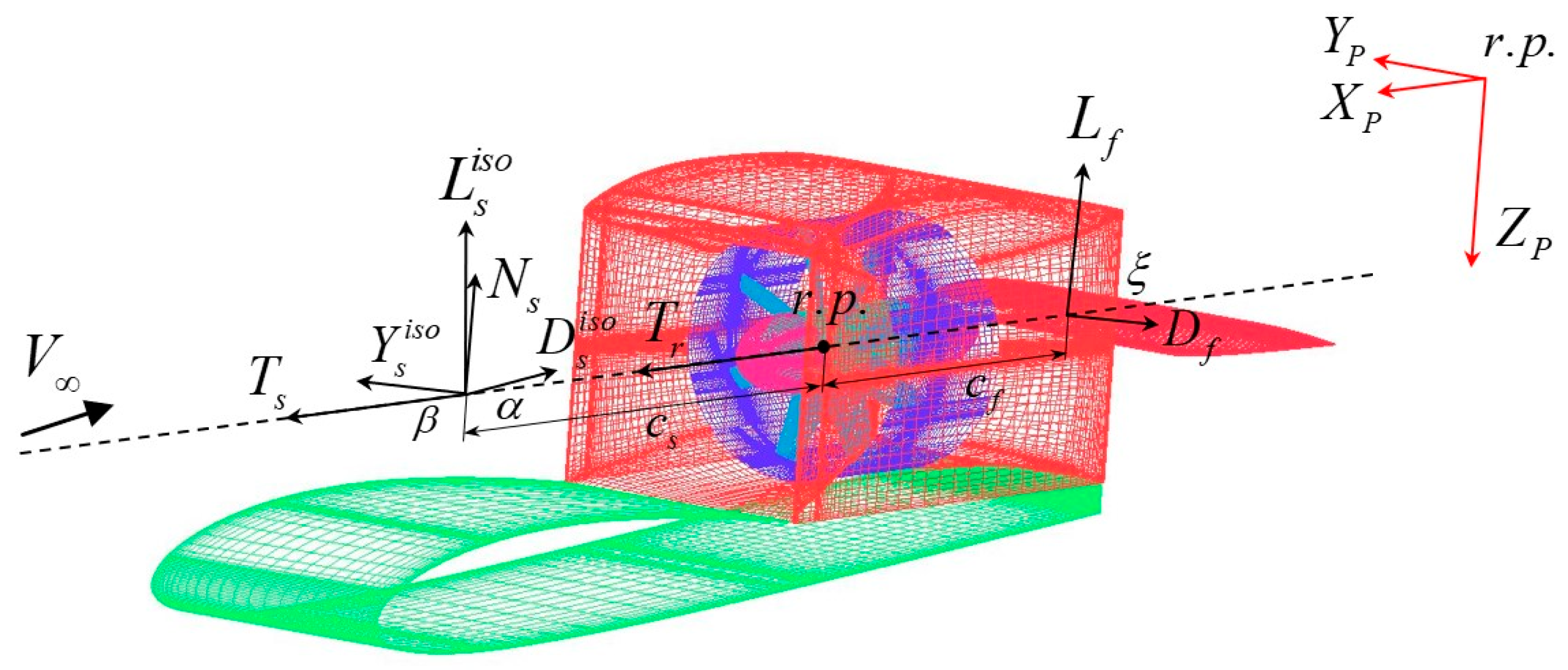
2.2.3. Forces and Moments of Propulsion Wing
2.3. Nonlinear Dynamics Model
3. Control Scheme Design
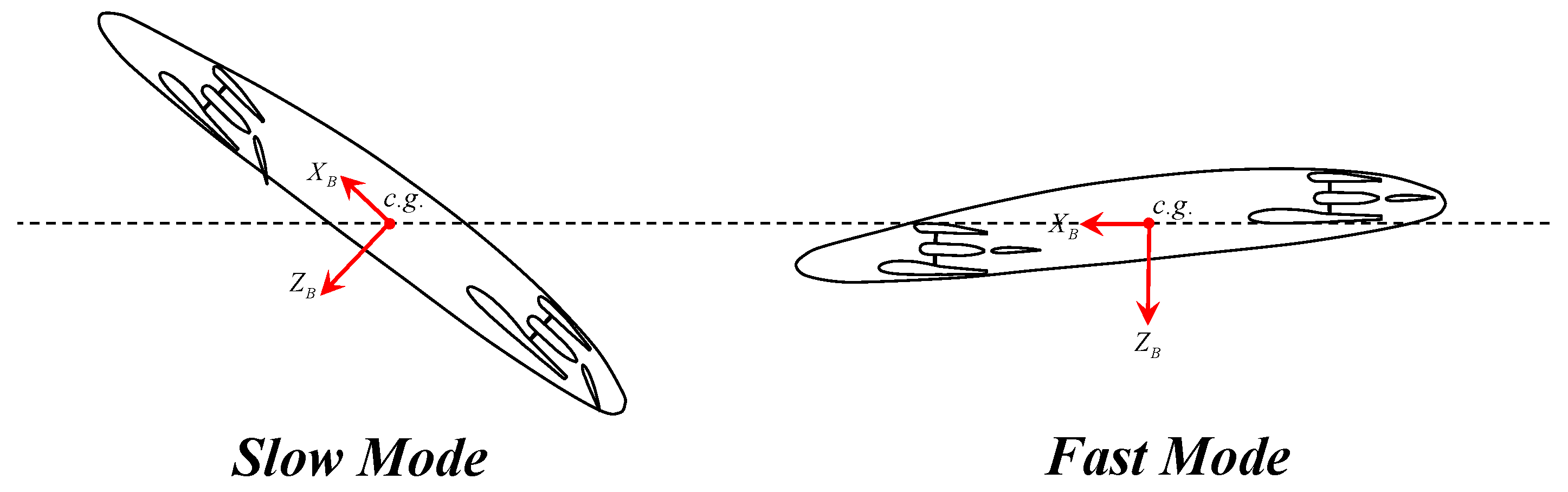
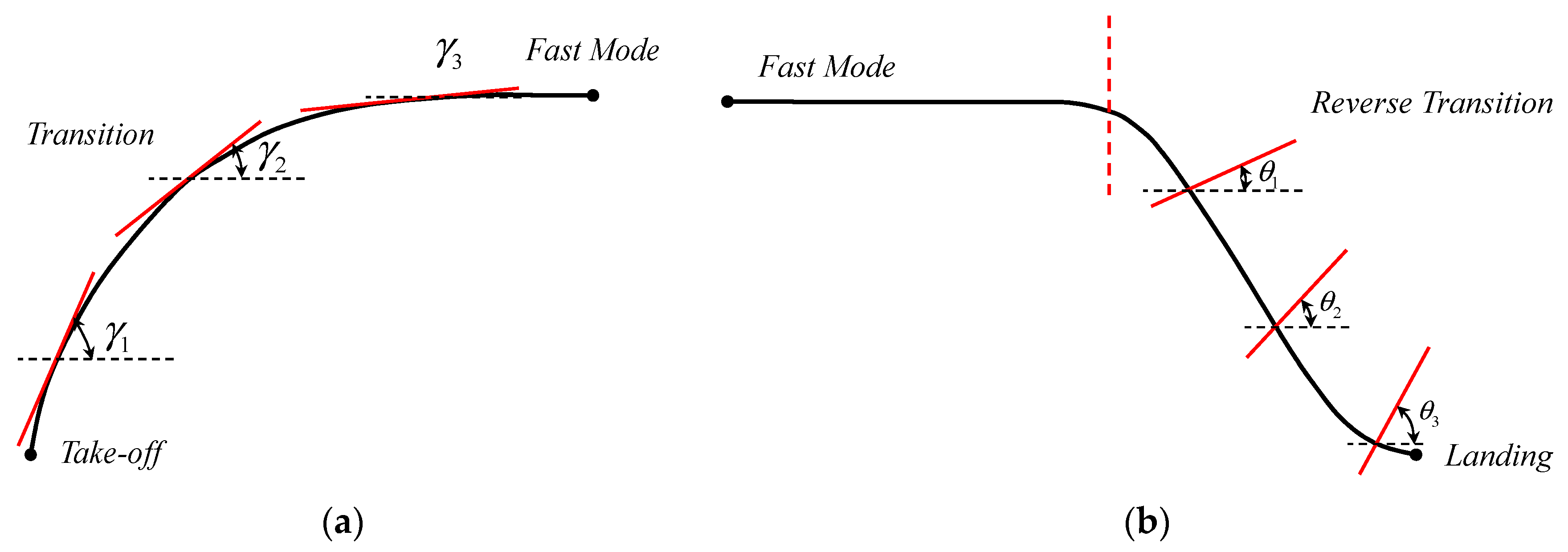
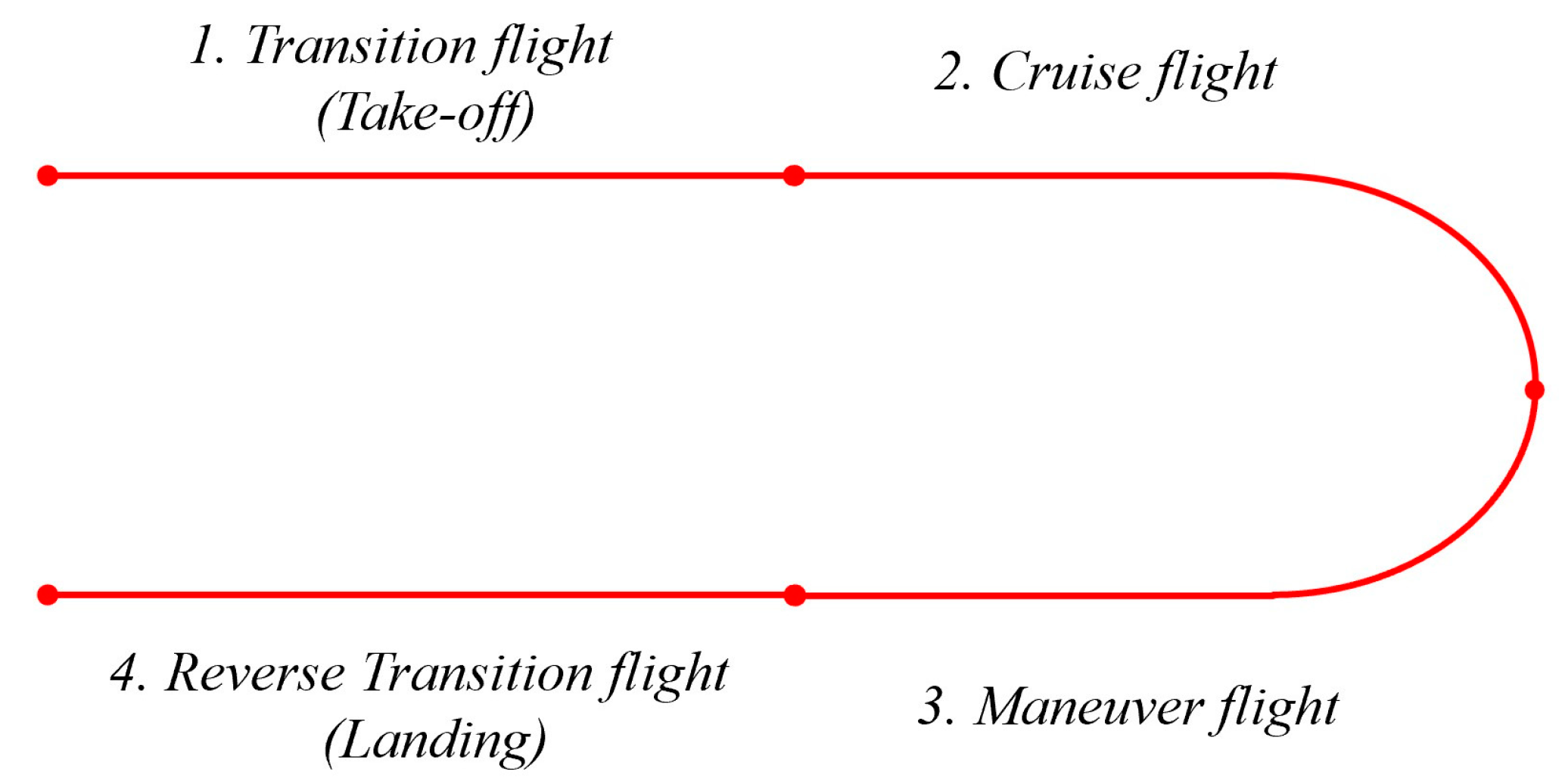
3.1. Flight Strategy
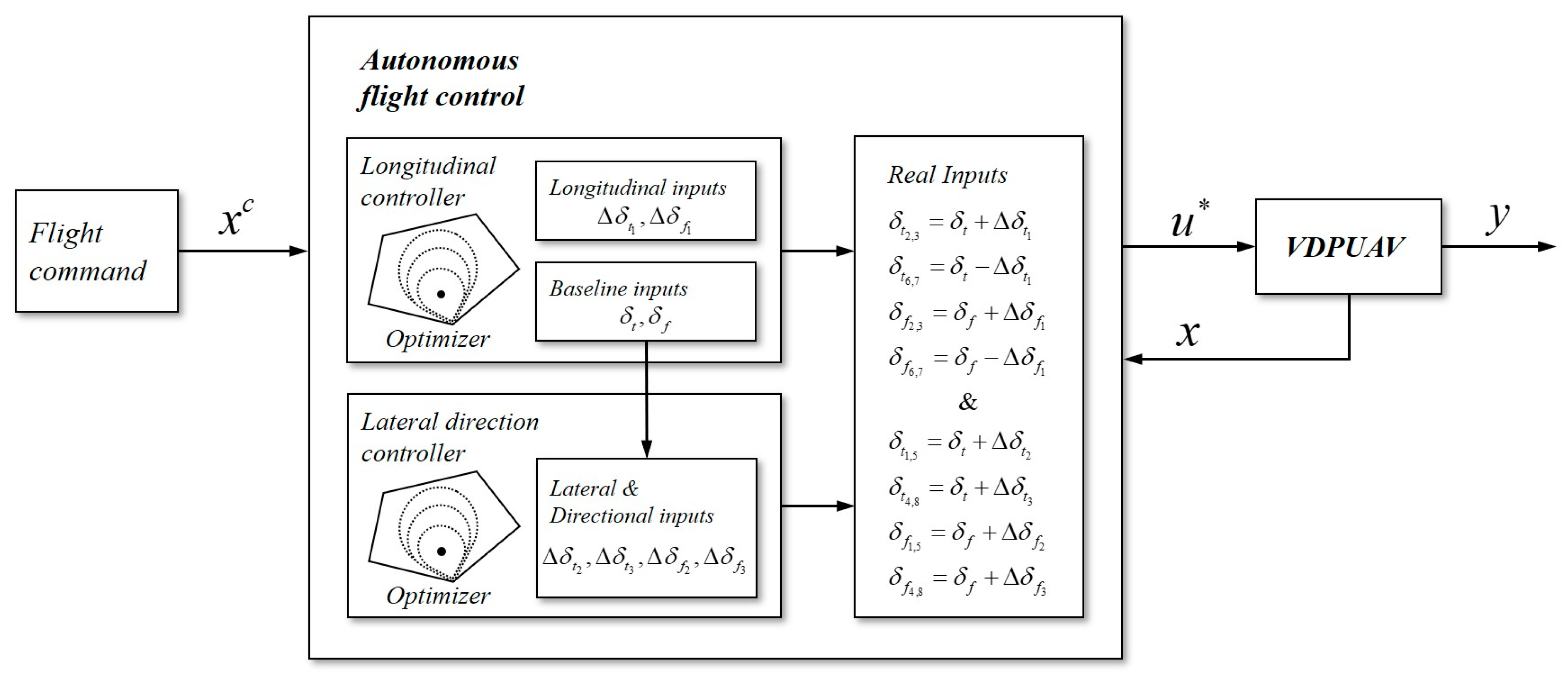
3.2. Control Framework
- First Step: Inputs Grouping
- Second Step: Decoupling 1 (Longitudinal and Lateral Directional Control Decoupling)
- Third Step: Decoupling 2 (Roll and Yaw Control Decoupling)
- Fourth Step: Virtual & Real Inputs
3.3. MPC Controller
3.3.1. ILQR Formulation
3.3.2. Controller Design
- (1)
- State variables and Inputs
- (2)
- Constraints
- (3)
- Warm starting
- (4)
- Reference trajectory
- (5)
- Prediction model
- (6)
- Cost function
| Algorithm 1 Finite horizon optimal control for the DVPUAV | |
| 1: | Input |
| 2: | Warm starting: |
| 3: | Reference trajectory: |
| 4: | Output |
| 5: | Optimal control: |
| 6: | From virtual inputs to real inputs: |
| 7: | Repeat |
| 8: | Longitudinal sub-controller |
| 9: | Warm starting: |
| 10: | Reference trajectory: |
| 11: | Prediction model: Discrete form of Equation (46) |
| 12: | Cost function: |
| 13: | Run ILQR Obtain |
| 14: | Lateral directional sub-controller |
| 15: | Warm starting: |
| 16: | Reference trajectory: |
| 17: | Prediction model: Discrete form of Equation (46) |
| 18: | Cost function: |
| 19: | Run ILQR Obtain |
| 20: | Inputs integration |
| 21: | |
| 22: | Until terminal time |
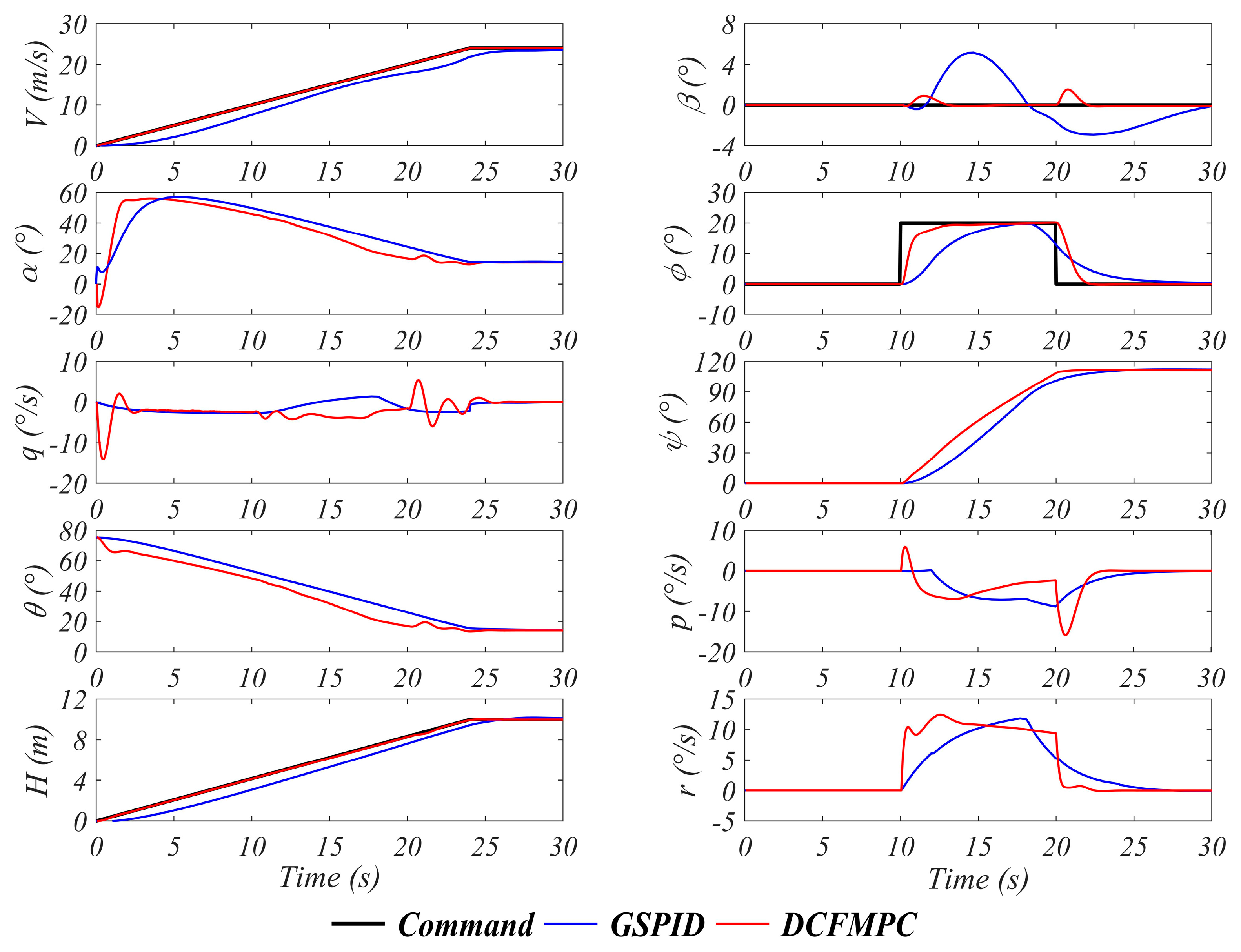
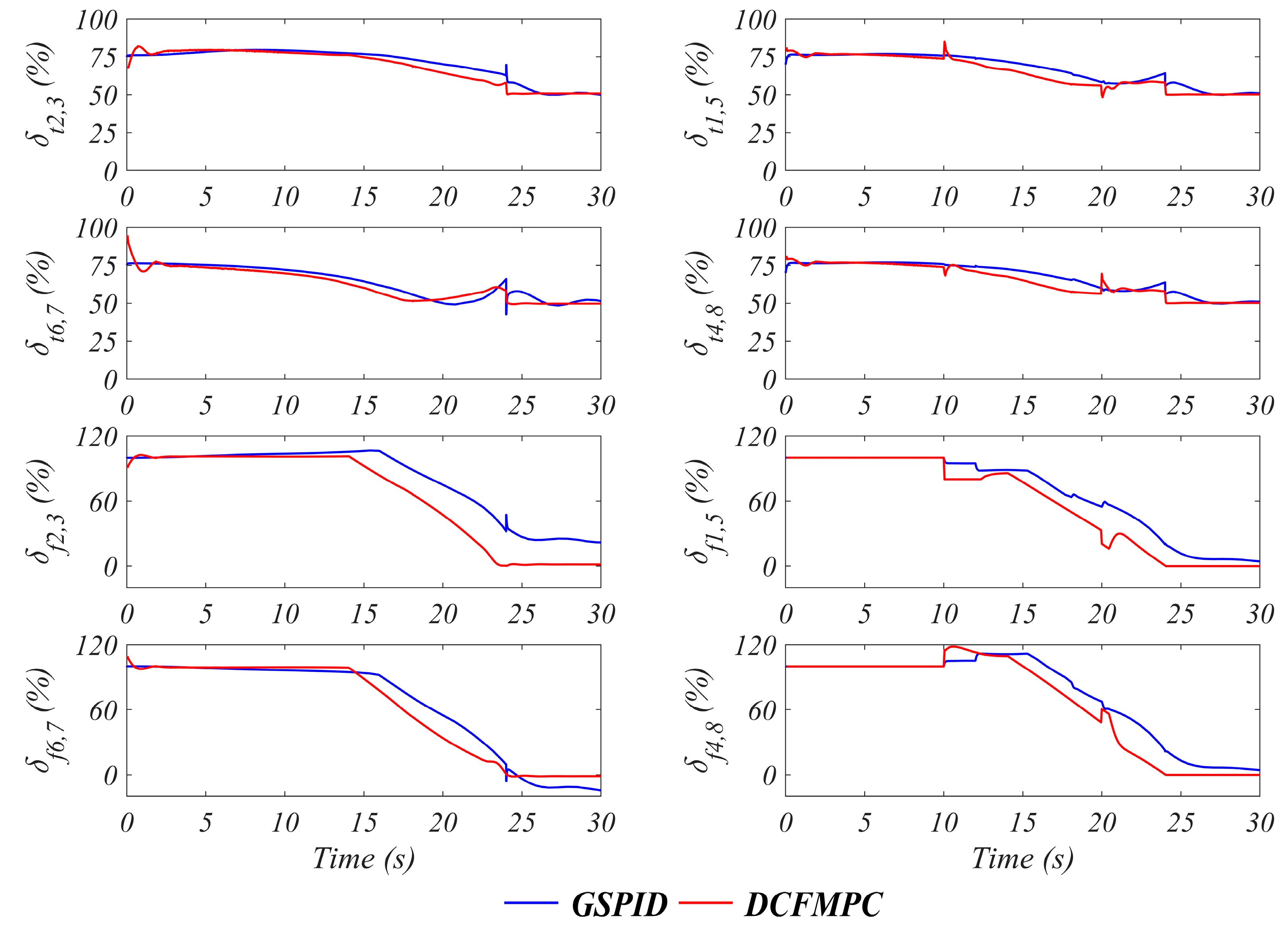
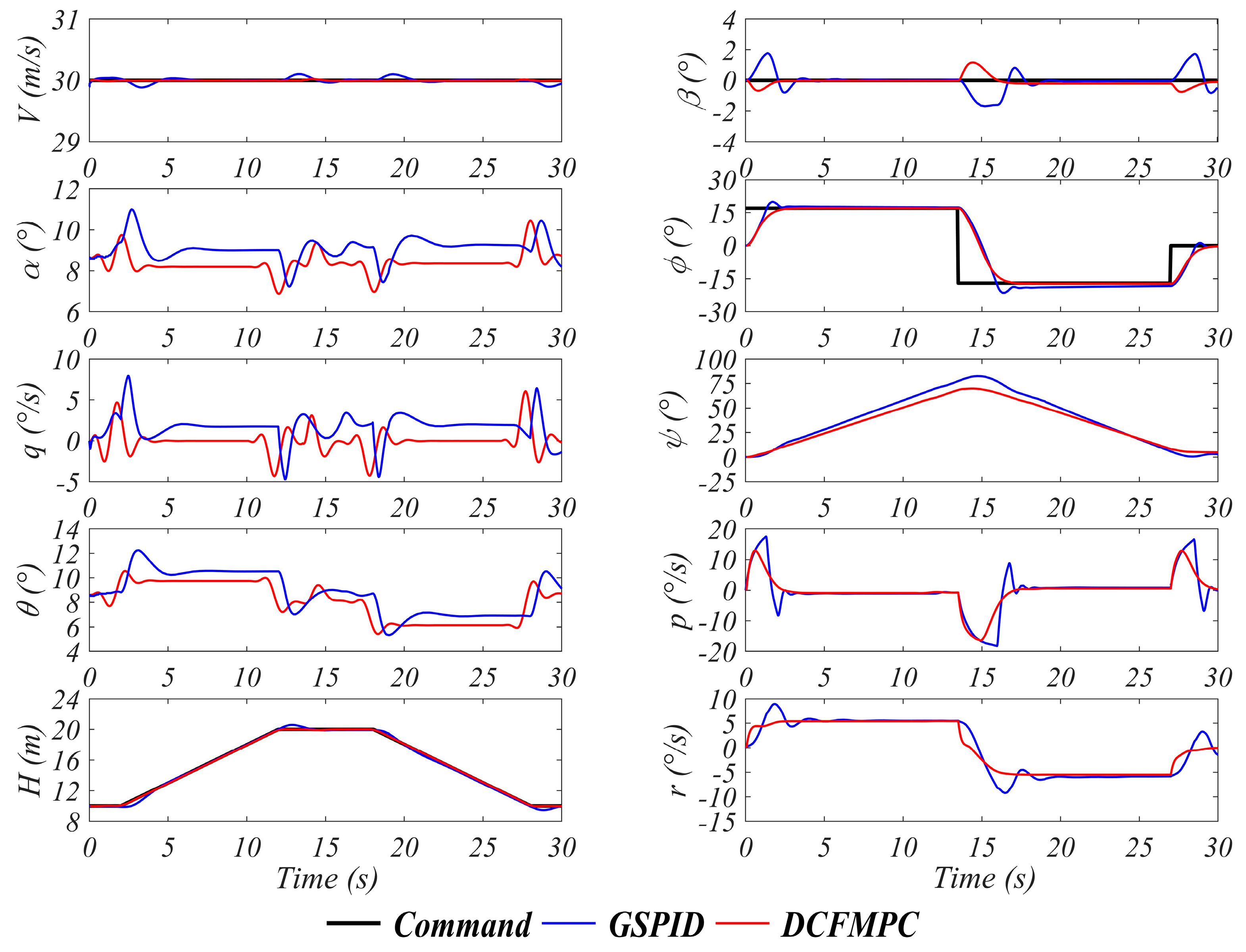
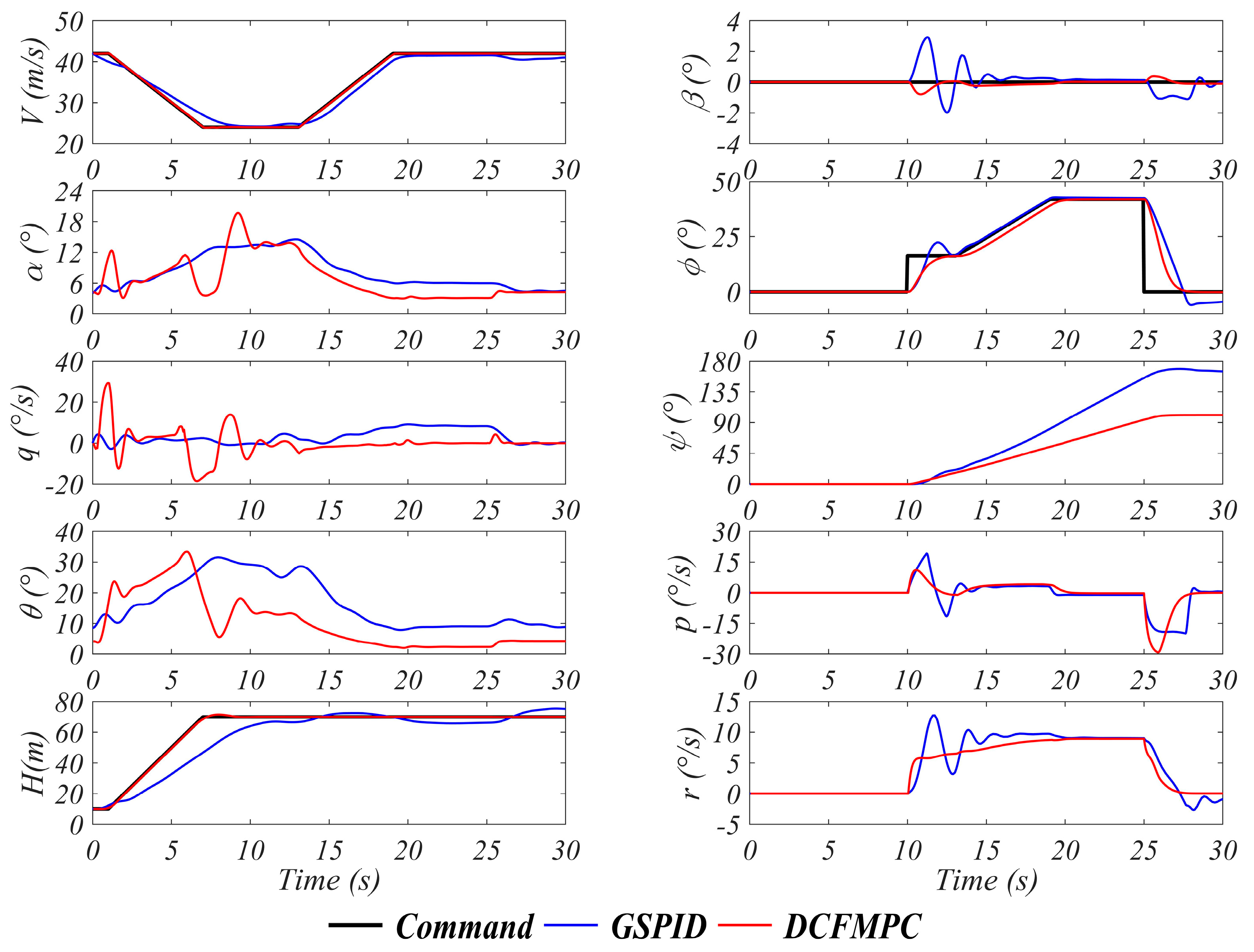
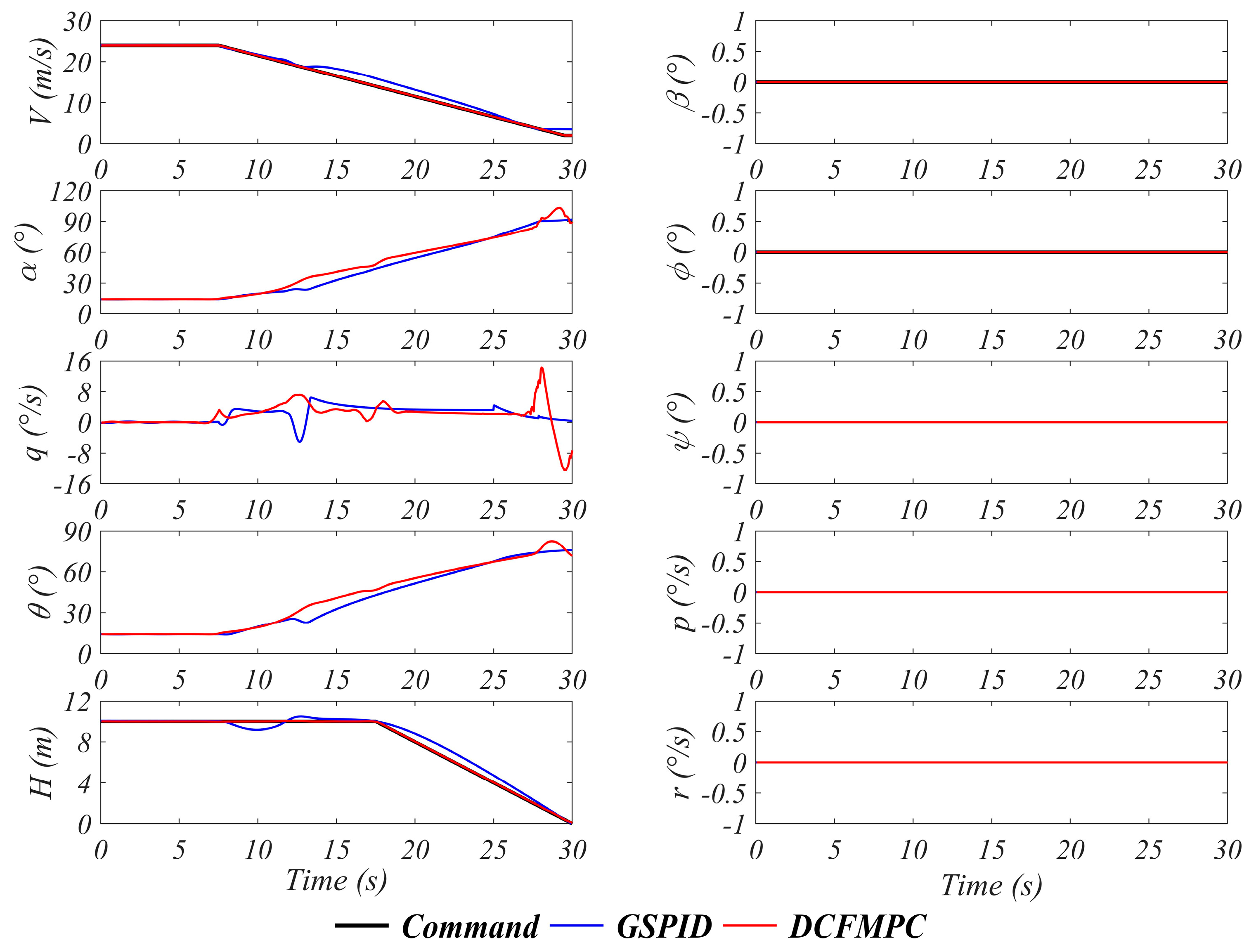
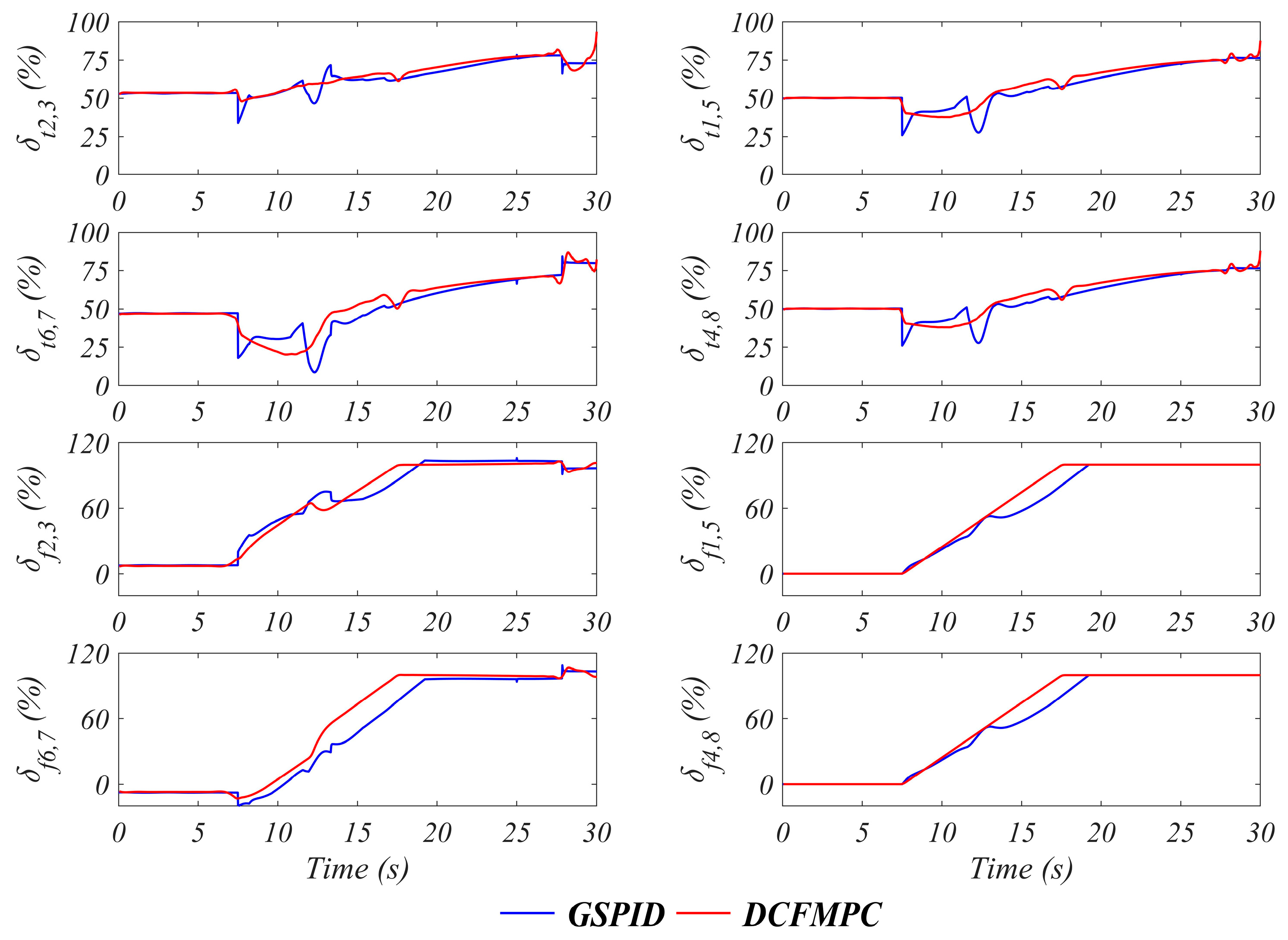
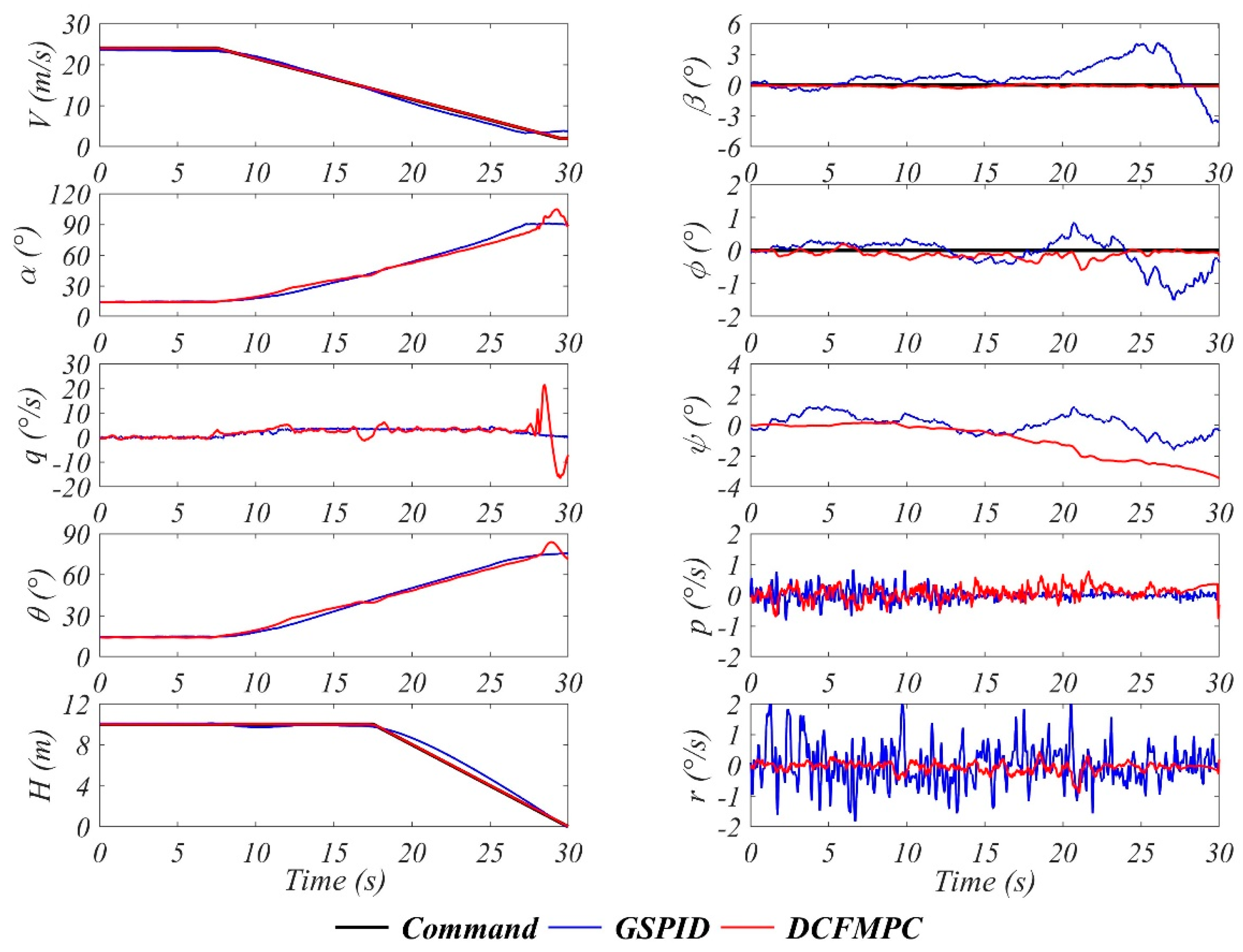
4. Discussion and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Velocity of free-stream | |
| Velocity of exit flow | |
| Velocity of far field flow | |
| Attack angle of propulsion wing | |
| Attack angle of blown flap | |
| Deflection angle of the blown flap | |
| Downwash angle of exit flow | |
| Span of propulsion wing unit | |
| Chord length of upper surface of shroud | |
| Chord length of lower surface of shroud | |
| Chord length of blown flap | |
| Equivalent angle of the upper lip of shroud | |
| Equivalent angle of the lower lip of shroud | |
| Axial distance from the lower lip to rotor disc | |
| Axial distance from exit station to rotor disc | |
| Radius of lower lip | |
| Radius of upper lip | |
| Radius of rotor | |
| Radius of rotor station (camber line) | |
| Radius of exit station | |
| Nondimensionalized parameter of | |
| Nondimensionalized parameter of | |
| Pressure before the rotor disc | |
| Pressure after the rotor disc | |
| Air Density | |
| Axial component of airspeed | |
| Axial velocities of rotor station | |
| Axial velocities of far field | |
| Thrust of rotor | |
| Thrust of shroud | |
| Total thrust of rotor and shroud system | |
| System thrust augmentation coefficient | |
| Axial force augmentation coefficient of shroud | |
| Normal force augmentation coefficient of shroud | |
| Dimensionless axial velocity on the centerline | |
| Dimensionless axial induced velocity by rotor disc | |
| Dimensionless axial induced velocities by airfoil camber of shroud (rotor station) | |
| Dimensionless axial induced velocities by airfoil camber of shroud (lower lip) | |
| Dimensionless axial induced velocity by area | |
| Dimensionless normal velocity | |
| Dimensionless normal velocity on the centerline | |
| Dimensionless normal induced velocity by free-stream | |
| Dimensionless normal induced velocity by airfoil camber of shroud (lower lip) | |
| Mutual repulsion effect of airflow | |
| Circulation term related to rotor disc | |
| circulation term related to vortexes of shroud (rotor station) | |
| circulation term related to vortexes of shroud (lower lip) | |
| Cross-sectional area of rotor station | |
| Cross-sectional area of exit station | |
| Normal force of shroud | |
| Axial velocity of exit flow | |
| Normal velocity of exit flow | |
| Lift coefficient at zero attack angle of isolated shroud | |
| Lift curve slope of isolated shroud | |
| Zero lift drag coefficient of isolated shroud | |
| Induced drag factor of isolated shroud | |
| Term related to maximum lift coefficient of isolated shroud stall model | |
| Term related to maximum drag coefficient of isolated shroud stall model | |
| Slew factor of laminal and stall models of isolated shroud | |
| Slew attack angle | |
| Slew rate | |
| Reference area of shroud | |
| Lift of isolated shroud | |
| Drag of isolated shroud | |
| Lateral force of isolated shroud | |
| Sideslip angle | |
| Deflection angle of wake | |
| Reaction force generated by jet deflection caused by the blown flap | |
| Blowing momentum coefficient | |
| Reference area of shroud | |
| Aerodynamic derivatives of blown flap related to free stream | |
| Induced drag factor of blown flap | |
| Lift of blown flap | |
| Drag of blown flap | |
| Propulsion wing unit coordinate system | |
| Coordinate system of the front propulsion wing | |
| Coordinate system of the rear propulsion wing | |
| Body coordinate system | |
| Inertial coordinate system | |
| Forces on the shroud in | |
| Forces on the blown flap in | |
| Forces of propulsion wing unit | |
| Pitch moment of propulsion wing unit | |
| Reference point of propulsion wing unit | |
| Distance between action position of to the | |
| Distance between action position of to the | |
| Rotation transformation matrix from to | |
| Rotation transformation matrix from to | |
| Relative angle between and | |
| Location throttle and deflection input of propulsion wing | |
| Front propulsion wing groups number | |
| Rear propulsion wing groups number | |
| Longitudinal distance parameters of DVPUAV | |
| Lateral distance parameters of DVPUAV | |
| Vertical distance parameters of DVPUAV | |
| Aerodynamic forces and moments of fuselage and winglets | |
| Gravity of DVPUAV | |
| Mass of DVPUAV | |
| Moment of inertia of DVPUAV | |
| Angular velocity vector | |
| Velocity vector | |
| Throttle inputs distribution on DVPUAV | |
| Deflection inputs distribution on DVPUAV | |
| Baseline inputs | |
| Longitudinal differential inputs | |
| Lateral directional increment inputs | |
| Flight state of UAV | |
| Flight command of UAV | |
| Control input | |
| System output | |
| State sequence | |
| Input sequence | |
| Number of knots | |
| Discrete moment | |
| State variables at moment | |
| Inputs at moment | |
| Gradient and Hessian matrices of the cost function | |
| First derivation of dynamics about state and input | |
| Reference state sequence | |
| Reference input sequence | |
| Constraint set of inputs | |
| State variables for longitudinal sub-controller | |
| Inputs for longitudinal sub-controller | |
| State variables for lateral sub-controller | |
| Inputs for lateral sub-controller | |
| Airspeed of DVPUAV | |
| Flight altitude | |
| Path angle | |
| Roll angle | |
| Pitch angle | |
| Yaw angle | |
| Roll rate | |
| Pitch rate | |
| Yaw rate | |
| Reference state at moment | |
| Deviation of a state from a desired one at moment | |
| Weight matrix of terminal cost | |
| Weight matrix of state cost | |
| Weight matrix of input cost | |
| Horizon of control and prediction | |
| Sample time |
References
- Pornet, C.; Isikveren, A.T. Conceptual design of hybrid-electric transport aircraft. Prog. Aerosp. Sci. 2015, 79, 114–135. [Google Scholar] [CrossRef]
- Baskaran, P.; Corte, B.D.; van Sluis, M.; Rao, A.G. Aeropropulsive Performance Analysis of Axisymmetric Fuselage Bodies for Boundary-Layer Ingestion Applications. AIAA J. 2022, 60, 1592–1611. [Google Scholar] [CrossRef]
- Kim, H.D.; Perry, A.T.; Ansell, P.J. A review of distributed electric propulsion concepts for air vehicle technology. In Proceedings of the 2018 AIAA/IEEE Electric Aircraft Technologies Symposium, Cincinnati, OH, USA, 12–14 July 2018; AIAA: Reston, VA, USA, 2018. [Google Scholar]
- Perry, A.T.; Timothy, B.; Phillip, J.A. Aeropropulsive Coupling Effects on a General-Aviation Aircraft with Distributed Electric Propulsion. J. Aircr. 2020, 58, 1351–1363. [Google Scholar] [CrossRef]
- Uranga, A.; Drela, M.; Greitzer, E.M.; Hall, D.K.; Titchener, N.A.; Lieu, M.K.; Siu, N.M.; Casses, C.; Huang, A.C.; Gatlin, G.M.; et al. Boundary Layer Ingestion Benefit of the D8 Transport Aircraft. AIAA J. 2017, 55, 3693–3708. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, Z.; Fan, Z.; Guo, J. Aerodynamic design of tractor propeller for high-performance distributed electric propulsion aircraft. Chin. J. Aeronaut. 2021, 35, 20–35. [Google Scholar] [CrossRef]
- Mohamed, A.; Eike, S. Aero-propulsive interaction model for conceptual distributed propulsion aircraft design. Aircr. Eng. Aerosp. Technol. 2022, 94, 948–964. [Google Scholar]
- Zhang, X.; Zhang, W.; Li, W.; Zhang, X.; Lei, T. Experimental research on aero-propulsion coupling characteristics of a distributed electric propulsion aircraft. Chin. J. Aeronaut. 2023, 36, 201–211. [Google Scholar] [CrossRef]
- Gohardani, A.S. A synergistic glance at the prospects of distributed propulsion technology and the electric aircraft concept for future unmanned air vehicles and commercial/military aviation. Prog. Aerosp. Sci. 2013, 57, 25–70. [Google Scholar] [CrossRef]
- Li, Z.Y.; Liu, Y.D.; Zhou, W.W. Lift augmentation potential of the circulation control wing driven by sweeping jets. AIAA J. 2022, 60, 1–22. [Google Scholar] [CrossRef]
- Ducard, G.J.J.; Allensoach, M. Review of designs and flight control techniques of hybrid and convertible VTOL UAVs. Aerosp. Sci. Technol. 2021, 118, 107035. [Google Scholar] [CrossRef]
- Ugwueze, O.; Statheros, T.; Horri, N.; Bromfield, M.A.; Simo, J. An Efficient and Robust Sizing Method for eVTOL Aircraft Configurations in Conceptual Design. Aerospace 2023, 10, 311. [Google Scholar] [CrossRef]
- Rostami, M.; Bardin, J.; Neufeld, D.; Chung, J. EVTOL Tilt-Wing Aircraft Design under Uncertainty Using a Multidisciplinary Possibilistic Approach. Aerospace 2023, 10, 718. [Google Scholar] [CrossRef]
- Rohr, D.; Studiger, M.; Stastny, T.; Lawrance, N.R.J.; Siegwart, R. Nonlinear model predictive velocity control of a VTOL tiltwing UAV. IEEE Robot. Autom. Lett. 2021, 6, 5776–5783. [Google Scholar] [CrossRef]
- Xia, J.Y.; Zhou, Z. Model Predictive Control Based on ILQR for Tilt-propulsion UAV. Aerospace 2022, 9, 688. [Google Scholar] [CrossRef]
- Liu, N.; Cai, Z.; Zhao, J.; Wang, Y. Predictor-based model reference adaptive roll and yaw control of a quad-tiltrotor UAV. Chin. J. Aeronaut. 2020, 33, 282–295. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Katupitiya, J. Modeling and control of a novel vectored-thrust quadcopter. J. Guid. Control Dyn. 2021, 44, 1399–1409. [Google Scholar] [CrossRef]
- Bauersfeld, L.; Spannagl, L.; Ducard, G.J.J.; Onder, C.H. MPC Flight Control for a Tilt-rotor VTOL Aircraft. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2395–2409. [Google Scholar] [CrossRef]
- Mike, A.; Guillaume, J.J.D. Nonlinear model predictive control and guidance for a propeller-tilting hybrid unmanned air vehicle. Automatica 2021, 132, 109790. [Google Scholar]
- Bauersfeld, L.; Ducard, G. Fused-PID Control for Tilt-Rotor VTOL Aircraft. In Proceedings of the 2020 28th Mediterranean Conference on Control and Automation (MED), Saint-Raphaël, France, 15–18 September 2020. [Google Scholar]
- Rostami, M.; Chung, J.; Park, H.U. Design optimization of multi-objective proportional-integral-derivative controllers for enhanced handling quality of a twin-engine, propeller-driven airplane. Adv. Mech. Eng. 2020, 12, 1687814020923178. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O.M. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Budhiraja, R.; Carpentier, J.; Mastalli, C.; Mansard, N. DDP for multi-phase rigid contact dynamics. In Proceedings of the IEEE-RAS 18th International Conference on Humanoid Robots (Humanoids), Beijing, China, 6–9 November 2018. [Google Scholar]
- Bellman, R.R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef]
- Tassa, Y.; Mansard, N.; Todorov, E. Control-Limited Differential Dynamic Programming. In Proceedings of the IEEE International Conference on Robotics & Automation (ICRA), Hong Kong, China, 29 September 2014. [Google Scholar]
- Grandia, R.; Farshidian, F.; Ranftl, R.; Hutter, M. Feedback MPC for Torque-Controlled Legged Robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019. [Google Scholar]
- Liu, Z.; Yang, T.; Li, Z.; Li, Z. Automatic landing trajectory control of aircraft based on Iterative-LQR algorithm. In Proceedings of the 2022 9th International Forum on Electrical Engineering and Automation (IFEEA), Zhuhai, China, 4–6 November 2022. [Google Scholar]
- Sgueglia, A.; Schmollgruber, P.; Bartoli, N.; Atinault, O.; Benard, E.; Morlier, J. Exploration and sizing of a large passenger aircraft with distributed ducted electric fans. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; AIAA: Reston, VA, USA, 2018; p. 1745. [Google Scholar]
- Beckers, M.F.; Schollenberger, M.; Lutz, T.; Bongen, D.; Radespiel, R.; Florenciano, J.L.; Funes-Sebastian, D.E. Numerical Investigation of High-Lift Propeller Positions for a Distributed Propulsion System. J. Aircr. 2023, 60, 995–1006. [Google Scholar] [CrossRef]
- Werle, M.J. Analytical model for ring-wing propulsor thrust augmentation. J. Aircr. 2020, 57, 901–913. [Google Scholar] [CrossRef]
- McCormick, B.W. Aerodynamics of V/STOL Flight; Courier Corporation: North Chelmsford, MA, USA, 1999. [Google Scholar]
- Werle, M.J. Aerodynamic Loads and Moments on Axisymmetric Ring-Wing Ducts. AIAA J. 2014, 52, 2359–2364. [Google Scholar] [CrossRef]
- Werle, M.J. Analytical Model for Ring-Wing Propulsors at Angle of Attack. J. Aircr. 2022, 59, 1351–1362. [Google Scholar] [CrossRef]
- ESDU. Aircraft Forces due to Interference between a Jet Efflux and a Slotted Flap; ESDU: Reston, VA, USA, 1982. [Google Scholar]
- Jakobsson, B. Definition and Measurement of Jet Engine Thrust. J. R. Aeronaut. Soc. 1951, 55, 226–243. [Google Scholar] [CrossRef]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Zhong, J.Y.; Wang, C. Transition characteristics for a small tail-sitter unmanned aerial vehicle. Chin. J. Aeronaut. 2021, 34, 220–236. [Google Scholar] [CrossRef]
- Liu, N.; Cai, Z.; Wang, Y.; Zhao, J. Fast level-flight to hover mode transition and altitude control in tiltrotor’s landing operation. Chin. J. Aeronaut. 2021, 34, 181–193. [Google Scholar] [CrossRef]
- Ullah, S.; Mehmood, A.; Khan, Q.; Rehman, S.; Iqbal, J. Robust Integral Sliding Mode Control Design for Stability Enhancement of Under-actuated Quadcopter. Int. J. Control Autom. Syst. 2020, 18, 1671–1678. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, Q.; Zaidi, M.M.; Hua, L.-G. Neuro-adaptive non-singular terminal sliding mode control for distributed fixed-time synchronization of higher-order uncertain multi-agent nonlinear systems. Inf. Sci. 2024, 659, 120087. [Google Scholar] [CrossRef]





| 100 | 0 | 0 | 0 | 100 | 100 | 100 | 500 | 100 | |
| 100 | 100 | 0 | 0 | 0 | 500 | 500 | 100 | 100 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, J.; Zhou, Z. The Modeling and Control of a Distributed-Vector-Propulsion UAV with Aero-Propulsion Coupling Effect. Aerospace 2024, 11, 284. https://doi.org/10.3390/aerospace11040284
Xia J, Zhou Z. The Modeling and Control of a Distributed-Vector-Propulsion UAV with Aero-Propulsion Coupling Effect. Aerospace. 2024; 11(4):284. https://doi.org/10.3390/aerospace11040284
Chicago/Turabian StyleXia, Jiyu, and Zhou Zhou. 2024. "The Modeling and Control of a Distributed-Vector-Propulsion UAV with Aero-Propulsion Coupling Effect" Aerospace 11, no. 4: 284. https://doi.org/10.3390/aerospace11040284
APA StyleXia, J., & Zhou, Z. (2024). The Modeling and Control of a Distributed-Vector-Propulsion UAV with Aero-Propulsion Coupling Effect. Aerospace, 11(4), 284. https://doi.org/10.3390/aerospace11040284






