Abstract
The rotor–stator interaction noise is a major source of fan noise. Especially for low-speed fan stages, the tonal component is typically a dominant noise source. A challenge is to reduce this tonal noise, as it is typically perceived as unpleasant. Therefore, in this paper, we analytically, numerically and experimentally investigate an acoustic effect to lower the tonal noise excitation. Our study on an existing low-speed fan indicates a reduction in tonal interaction noise of more than 9 dB at the source if the excited acoustic modes propagate parallel to the stator leading edge angle. Moreover, a design-to-low-noise approach is demonstrated in order to apply this effect to two new fan stages with fewer stator than rotor blades. The acoustic design of both fans is determined by an appropriate choice of the rotor and stator blade numbers in order to align the modal propagation angle with the stator stagger angle. The blade geometries are obtained from aerodynamic optimization. Both fans provide similar aerodynamic but opposing acoustic radiation characteristics compared to the baseline fan and a significant tonal noise reduction resulting from the impact of the modal propagation angle on noise excitation. To ensure that this effect can also be applied to other low-speed fans, a design rule is derived and validated.
1. Introduction
Recently, new electrified propulsion systems, for example, with distributed, low-speed fan stages or distributed propellers, are under development to power the next generation of urban and regional aircrafts. The noise emitted, especially that from the engines, is a crucial sound source that can be unpleasant to hear. Therefore, acoustic effects that enable a low-noise design of the propulsion system need to be investigated and understood [1]. In particular, reduction mechanisms should be evaluated that allow for the reduction in noise directly at its source.
In general, the noise emission of fan stages is composed of several sources that can radiate noise at discrete frequencies (tonal noise) and throughout a wide frequency range (broadband noise). Typically, for low-speed fan stages, the rotor–stator interaction noise represents the dominant source [2]. An important challenge is to reduce the tonal component, as it is often perceived as unpleasant [3,4]. Consequently, there is a need to assess noise reduction methods, particularly those that minimize the tonal component of this noise source.
Analytical and numerical studies on low-speed fan stages indicate that the excitation of tonal rotor–stator interaction noise is significantly affected by the propagation angles of the acoustic modes relative to the stator leading edge angle [2,5,6]. In [6], an analytical and numerical acoustic investigation of fan stages with fewer stator than rotor blades is performed. These designs are called low-count outer guide vane (OGV) fans [2,6]. It is shown that, for certain blade count numbers, a tonal advantage is achieved if the propagation angles of the dominantly excited modes are nearly parallel to the stator leading edge angle [2,6]. In recent measurements on a low-speed fan stage, the effect was also confirmed experimentally in design operating conditions [7]. Regarding the transmission of sound through rotor or stator blade rows, a similar effect is known as the “modal condition” [8,9].
The described effect can be achieved if the modal propagation angle is aligned with the stator stagger angle. Thus, the rotor and stator blade numbers need to be chosen appropriately. The reason for this is that the choice of blade numbers determines the excited Tyler and Sofrin mode orders, and the azimuthal mode orders define the modal propagation angles for the respective flow conditions. Consequently, an acoustic advantage is achieved by iterating the blade numbers until the exact acoustic modes that preferably propagate parallel to the stator leading edge angle become dominant. In this paper, it is verified that, depending on the fan design, the effect can reduce the excitation of tonal interaction noise upstream or downstream. The effect is particularly suitable for low-speed fan stages, as only a few acoustic modes are excited.
In the first part of this paper, we verify and validate the impact of the modal propagation angle on tonal noise excitation for a wider range of operating points, including off-design conditions, using analytical, numerical and experimental data. The studies are performed on a low-speed shrouded fan, which is representative of aircraft engines for urban and regional air mobility. The experimental measurements are conducted in DLR’s fan test facility, Co-/Contra Rotating Acoustic Fan Test rig (CRAFT) [10].
In the second part of this paper, the noise reduction potential of the described effect is demonstrated on two new low-count OGV fan stages. Reducing the tonal interaction noise is particularly relevant for low-count OGV fans, as these designs may have a tonal disadvantage. Contrary to conventional fan designs, the usually dominant blade-passing frequency tone may no longer be cut off, since fewer stator than rotor blades are used [6]. Due to the described effect, for both low-count OGV fans, the tonal disadvantage is eliminated, as the results indicate a significant tonal noise reduction compared to the baseline fan. However, contrary to the baseline fan, due to an appropriate choice of blade numbers, the tonal noise is not reduced upstream but downstream. Consequently, an opposing noise radiation characteristic is achieved. Thus, this effect not only reduces tonal noise but also specifically influences the radiation direction. Taking into account liners and shielding effects, this can be used to improve certification levels and the psychoacoustic noise impact.
The rotor and stator geometries of both low-count OGV fan stages are designed in a multi-objective aerodynamic optimization. The optimization ensures that all considered fan stages provide similar aerodynamic characteristics. However, opposing acoustic characteristics are achieved due to the modal propagation angles. Therefore, all fans are well suited for acoustic and psychoacoustic investigations.
2. Rotor–Stator Interaction Noise
The rotor–stator interaction (RSI) noise source consists of a broadband and a tonal component. This source results from the aerodynamic flow around the rotor blade and its interaction with the stator leading edge. Particularly, the velocity boundary layers on the suction and pressure sides of the rotor blades lead both to an inhomogeneous velocity distribution (rotor wake) and to an increased turbulence intensity behind the rotor [2]. These flow disturbances interact with the downstream stator vanes and generate the interaction noise.
The broadband component of the RSI noise source occurs due to turbulent fluctuations that interact with the stator leading edge. The tonal component results from the rotor wakes, which periodically impinge on the stator leading edge. Therefore, it can be classified as unsteady lift-generated noise. The tonal noise occurs at discrete blade passing frequencies (BPFs), which are calculated as multiples of the number of rotor blades and the rotational speed.
As visualized in Figure 1, the periodic impingement of rotor wakes on the stator leading edge results in a dipole noise source with its main radiation axis perpendicular to the leading edge angle. The excited azimuthal mode orders m can be determined from formulated by Tyler and Sofrin [11]. In this relation, represents the harmonics of the rotor blade number B, and describes the scattering at the stator vanes V.
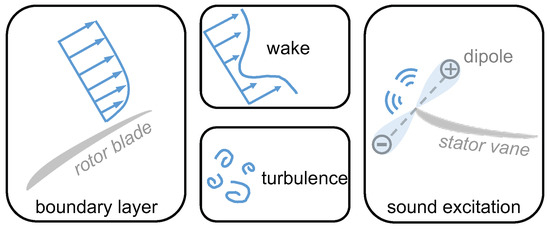
Figure 1.
Excitation mechanism of the RSI noise source.
The Impact of the Modal Propagation Angle on Noise Excitation
The propagation directions of acoustic modes with azimuthal order m and radial order n can be described with the modal propagation angle [12,13].
The formulation in Equation (1) is obtained from Moreau [13] and is equivalent to Equation (27) from Rice [12]. In Equation (1), the upstream propagating modes are indicated by (−) and the downstream propagating modes by (+). The axial Mach number is , and is the cut-on factor. As specified in [13], under consideration of a solid body swirl, the cut-on factor is calculated as
In Equation (2), is the zero of the first derivative of the radial eigenfunction at the walls, k is the acoustic wave number and is the swirl Mach number.
The modal propagation angle has a direct impact on the modal sound pressure amplitude , since depends on the source term , which is a function of the wave number normal to the profile chord , which, in turn, is a function of the modal propagation angle. The expressions used to calculate these quantities are provided in Equations (3)–(5).
As derived in [13],
describes the modal sound pressure amplitude within the duct, where r is the hub radius, R is the tip radius, is the axial wave number and and define the leading edge (LE) position. The definition of the induct Green’s function can be obtained from [13,14].
The source term is composed of different terms for the respective noise-generation mechanisms, where
is the source term for the lift-generated component (e.g., tonal RSI noise) [13]. In Equation (4), specifies the chordwise distribution of lift, is the chordwise wave number and l defines the chordwise position of the noise source on the blade. The lift-generated tonal noise component depends on the normal wave number
which depends on the modal propagation angle and the stator leading edge angle .
As indicated in Equations (3)–(5), an acoustic mode () will not be excited if the modal propagation angle is exactly parallel to the stator leading edge angle (). In contrast, the strongest sound excitation occurs if the modal propagation angle is exactly perpendicular to the stator leading edge angle (). The reason for this is that the modal propagation angle is in line with the dipole radiation axis in this case.
In order to simplify the subsequent analysis, the difference between the modal propagation angle and the stator leading edge angle is scaled to the range [0, 90 deg] and specified as
Figure 2 schematically illustrates a dipole noise source at the stator leading edge and visualizes the relation between , and . In order to illustrate the modal propagation angle, the propagation direction of a negative acoustic mode , which propagates upstream (−) and downstream (+), is exemplarily shown. In the sketched example, the modal propagation angle is nearly parallel to the stator leading edge angle upstream (see ), whereas downstream, the modal propagation angle is nearly perpendicular to the leading edge angle (see ). Thus, in this case, a lower noise excitation would be expected upstream.
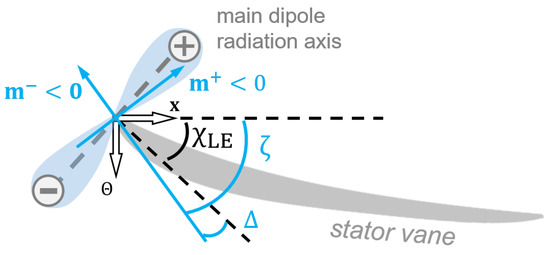
Figure 2.
Illustration of a dipole noise source at the stator LE and exemplary visualization of the propagation directions of an acoustic mode .
3. The Baseline Fan Stage
The baseline rotor–stator fan stage is equipped with rotor blades and stator vanes. For this blade count combination, the acoustic modes at the first blade passing frequency (BPF1) are cut-on. The fan has a diameter of m and is shown in Figure 3a. The stator leading edge angle is .
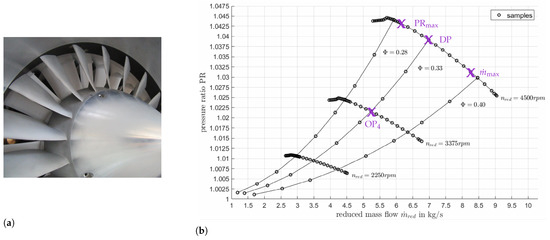
Figure 3.
Baseline fan stage. (a) Baseline fan geometry [10]; (b) performance map [15].
Table 1 outlines the four considered operating points for the studies in this paper. These operating conditions are also highlighted in the performance map in Figure 3b. At the design point (DP), the rotor–stator stage is operated at kg/s with a rotational speed of 4500 . The resulting pressure ratio is and the rotor tip Mach number is . In addition to the design point, three additional operating points are considered for the acoustic analysis: PRmax and are located on the 4500 rpm speed line and define the points at maximum pressure ratio and maximum mass flow, respectively. OP4 is the operating point at zero incidence on the 3375 rpm speed line.

Table 1.
Operating conditions for the CRAFT rotor–stator stage. Pressure ratios and Mach numbers are determined from RANS simulations. Mach numbers are flux-averaged values calculated upstream of the stator leading edge.
4. Methods
The subsequent investigation of the tonal noise excitation on low-speed fan stages is based on analytical, numerical and experimental data. The methods used to determine the noise levels are described in Section 4.1, Section 4.2 and Section 4.3. In Section 4.4, the aerodynamic optimization procedure is described.
4.1. Analytical Noise Prediction
The analytical fan noise prediction is performed with the in-house tool PropNoise (PN) [2,13]. PropNoise can be used with different operating methods. One option to operate PropNoise is the so-called stand-alone method. This method provides an aerodynamic pre-design of the fan stage and a fully analytical noise prediction following the process visualized in Figure 4.
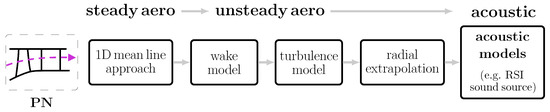
Figure 4.
Process chain used for the analytical noise prediction.
The stand-alone method uses a meanline approach to calculate the steady and unsteady aerodynamic quantities. The representative streamline for the meanline calculations is at radial blade height. Afterwards, the aerodynamic quantities are extrapolated radially. The radial distributions serve as input for a radial strip approach in order to determine the acoustic source terms. This implies that the response of the blade to an aerodynamic excitation is calculated on each radial strip as if the problem were two-dimensional. Finally, the source term is integrated radially to obtain the induct modal sound pressure amplitude (see Equation (3)). A detailed description of the stand-alone module is outlined in [13].
4.2. Numerical Noise Prediction
For the numerical fan noise prediction, two methods are used: (1) a RANS-based analytical noise prediction and (2) a fully numerical prediction of fan tonal noise using harmonic balance (HB) simulations. The RANS and HB simulations are processed on a structured grid with O-C-H topology around the blades using the in-house Navier–Stokes solver TRACE [16,17]. The numerical grid is generated with the in-house software PyMesh [18]. On the rotor and stator blade surfaces, the first grid cell is placed in the laminar sublayer of the velocity boundary layer (). In the spanwise direction, the grid consists of 131 cells, of which 15 cells are placed in the rotor tip clearance. Overall, the grid consists of more than cells. The outlet is located five axial stator chord lengths downstream of the stator trailing edge, and the inlet is located five axial rotor chord lengths upstream of the rotor leading edge. A single rotor–stator flow passage is modeled, and the closure of the equation system is achieved with the Menter SST k- turbulence model. The domain for the numerical simulations is shown in Figure A1, and the grid around the rotor and stator blade is exemplarily visualized in Figure A2.
In addition to the stand-alone method of PropNoise, another method is the RANS-based analytical prediction of fan noise sources [2]. For the RANS-informed noise prediction, the radial distributions of all necessary aerodynamic quantities are extracted from 3D steady-state RANS simulations (see Figure 5). The RANS-based prediction with PropNoise uses the same acoustic models as the fully analytical prediction with the stand-alone method. A detailed description of the RANS-based noise prediction is given in [2].
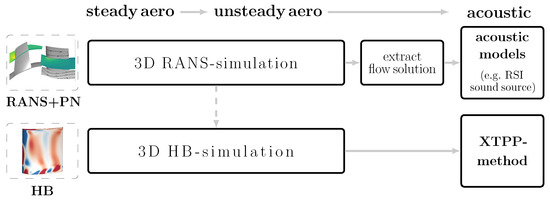
Figure 5.
Process chain used for the numerical noise prediction.
The fully numerical calculation of tonal RSI noise relies on unsteady HB simulations. The HB simulations are based on a Fourier transformation of the RANS equations. Selected frequencies, which are non-linearly coupled, are solved in the frequency domain [19,20,21]. An XTPP method (extended triple plane pressure mode matching method) is used to separate the convective and acoustic flow disturbances and to perform a radial mode analysis [22,23,24]. With this approach, the tonal sound power levels are extracted from the flow solution.
4.3. Experimental Noise Measurement
The experimental noise measurements are conducted at the CRAFT test facility of the DLR Department of Engine Acoustics [10]. In Figure 6, a lateral sketch of the experimental setup is shown, where (1) is the inflow control device, (2) is a honeycomb grid, (3a) and (3b) are the upstream and downstream microphone arrays, (4) is the rotor, (5) is the stator and (6) is the nozzle.
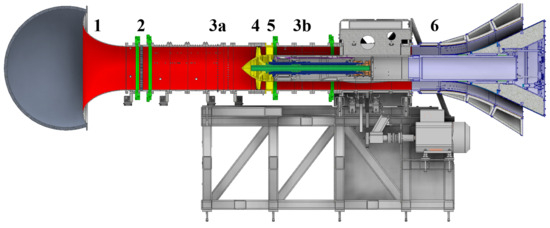
Figure 6.
CRAFT test facility.
The test facility is equipped with a two-shaft system to operate either rotor–stator fan stages, counter-rotating rotor–rotor configurations or an isolated rotor [10]. For the studies presented in this paper, the CRAFT test facility is equipped with the baseline rotor–stator fan stage described in Section 3. The operating point is adjusted using a variable nozzle. The hub radius is m and the tip radius is m. Along the test section, the radii are constant in order to minimize the impact on the propagation of the acoustic modes.
To ensure comparability between the noise prediction and different measurements, the rotational speed and mass flow are normalized to ISA standard conditions (, 101,325 Pa). The upstream and downstream microphone arrays consist of 30 and 22 G.R.A.S. microphones type 40BP with a pre-amplifier type 26AR, respectively. The microphones are wall-mounted at a distance of 24 mm. To enable a full radial mode analysis, the microphones are mounted in a rotating array, which is rotated to 59 evenly distributed circumferential positions. With this setup, measurements of 10 s are performed. The microphone pattern allows radial mode analyses up to 6 kHz, which includes the first four BPFs at maximum speed. With a synchronously recorded shaft trigger, phase-locked averaging is applied. The resulting spectrum contains only rotor coherent sound field components. The mid-frequencies of this spectrum are integer multiples of 1/8 of the rotation frequency. The results of the radial mode analysis are the modal sound pressure amplitudes at the first four BPFs [25]. The sound power of every mode is calculated with the formulation given by Morfey [26]. In addition, the inflow control device ensures low turbulent inflow conditions and prevents undesired noise sources, for example, due to vortex structures sucked in from the laboratory. This experimental setup is well suited for comparisons with analytical and numerical predictions as the inflow is almost free from undesired disturbances.
4.4. Aerodynamic Optimization Procedure
Two new, low-count OGV fan stages are designed for the CRAFT test facility with identical operating conditions as the baseline fan. The rotor and stator geometries of the two low-count OGV fan stages are obtained from a multi-objective aerodynamic optimization procedure. The optimization is performed with the in-house software AutoOpti developed in DLR’s Fan and Compressor Department [27,28,29]. As the acoustic design is determined by an appropriate choice of the blade numbers, the optimization should ensure that the aerodynamic characteristics are as similar as possible to the baseline fan. Therefore, aerodynamic efficiency and pressure ratio are the primary criteria for evaluating the optimization results. Similar aerodynamic characteristics ensure the comparability of all three fans for aeroacoustic studies.
The blade numbers of both new fan stages are chosen to reduce the excitation of tonal RSI noise due to the effects resulting from the modal propagation angle. Thus, the blade numbers are determined prior to the optimization process and do not represent a degree of freedom of the optimization. Instead, the 3D geometry of the fan blades is being optimized. Thus, the following parameters defining the shape of the airfoil geometry are chosen as degrees of freedom:
- Metal angles at the leading edge and trailing edge.
- Leading edge and trailing edge radii.
- Shape of the profile at the leading edge.
- Axial airfoil length.
- Profile contours of the pressure and suction side.
- Thickness of the profile.
In order to avoid intersections between the suction side and pressure side, the profile control points of the pressure side are defined at a relative distance to the suction side. This procedure is schematically illustrated in Figure 7.
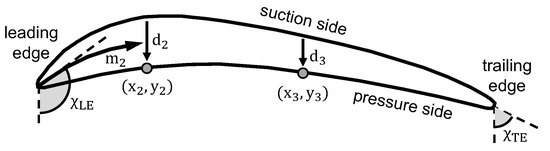
Figure 7.
Construction of pressure side with thickness of distributed control points.
The optimization of the above parameters is performed on three radial sections, which are located at , and blade height. In total, 42 degrees of freedom are specified, 14 on each radial section. In addition, the optimization is performed using two operating points. These are the design point and the point on the same speed line at the maximum pressure ratio. The latter is used to ensure a sufficient stability margin.
Table 2 summarizes the objectives and constraints. The optimization is carried out with two objectives: that the efficiency and pressure ratio under the design operating conditions are maximized. Moreover, three constraints are specified. These constraints ensure (1) a wide operating range on the design speed line (), (2) a minimum remaining swirl in the flow downstream of the stator () and (3) that the rotor does not impinge on the tip lining ().

Table 2.
Objectives and constraints for aerodynamic optimization.
As sketched in Figure 8, initially, the optimization process generates randomly distributed configurations within the parameter space, which are subsequently passed through the process chain and evaluated with regard to the objectives and constraints. Based on this evaluation, a Pareto rank is determined for all configurations that successfully pass the process. Afterwards, the configurations are stored in the database according to the Pareto rank.
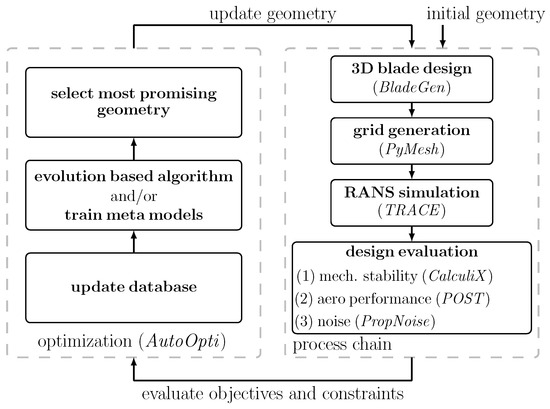
Figure 8.
Process chain used for multidisciplinary optimization. Figure adapted from [2].
To generate new configurations, a surrogate model is trained with the updated database. Based on the surrogate model, sub-optimizations are performed using evolution-based algorithms. In the sub-optimizations, new configurations are selected using the volume gain criterion [28]. This criterion ensures that new configurations provide an increase in volume compared to the existing Pareto front [28]. The gradient-enhanced Kriging meta-model, which is explained in detail in [30], is applied as a surrogate model. The Kriging model is used as it offers reliable extrapolation capabilities [30]. This allows us to keep the number of initial configurations small and still make meaningful predictions in those parts of the parameter space for which no configurations have been evaluated yet.
The physical process chain consists of six steps: (1) 3D blade design, (2) grid generation with PyMesh [18], (3) RANS simulation with TRACE [16,17], (4) evaluation of the mechanical stability with CalculiX [31], (5) evaluation of the aerodynamic performance with POST [32] and (6) noise source prediction with PropNoise [2,13]. The grid generation and set-up for the numerical simulations are performed according to the specifications in Section 4.2.
5. Results
In this section, the impact of the modal propagation angle on the excitation of tonal RSI noise is analyzed. First, in Section 5.1, this is investigated analytically and numerically and validated experimentally using the baseline fan stage. Secondly, in Section 5.2, the noise reduction potential resulting from the modal propagation angle is demonstrated on two new fan stages, a low-tone fan and a low-broadband fan. For both fans, the rotor and stator blades are designed for aerodynamic optimization. In Section 5.2.2 and Section 5.2.3, the optimization results are outlined and the acoustic noise emission is examined.
5.1. Acoustic Validation Using the Baseline Fan
The current CRAFT baseline fan stage is equipped with an 18-blade rotor and a 21-vane stator. For the subsequent comparison of the RSI noise levels between measurements and prediction, the axial distance between the rotor trailing edge and stator leading edge is 63 mm, measured at the casing. The comparison is performed at the three operating points DP, and (see Table 1). A detailed description of the pure experimental data can additionally be found in [33].
In Figure 9, the tonal RSI sound power levels are compared between measurements (M), a fully analytical prediction (PN) and a fully numerical prediction (HB). Note that the arrows correspond to the experimental results and indicate the differences between upstream and downstream noise radiation. Figure 9a shows the sound power levels of the dominantly excited BPF1 azimuthal mode , and Figure 9b shows the sound power levels of the dominantly excited BPF2 azimuthal mode . Note that for both and , only one radial mode, , is excited.
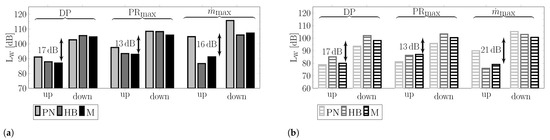
Figure 9.
Analytical (PN), numerical (HB) and experimental (M) predictions of tonal RSI noise for the baseline fan, determined for three operating conditions. (a) BPF1, ; (b) BPF2, .
For all considered operating points, the tonal noise emission of the CRAFT baseline fan stage is mainly dominated by BPF1 and BPF2. Moreover, the experimental results indicate a significant difference between the upstream and downstream radiated tonal BPF1 and BPF2 noise levels. Overall, the numerical simulation and analytical noise prediction both accurately reproduce this level difference and provide good agreement with the experimental results. However, for operating conditions, the fully analytical prediction provides higher absolute values.
For all operating conditions, the upstream noise radiation of the dominantly excited BPF1 mode () is more than 13 dB lower than that of the downstream. The BPF2 shows an identical radiation characteristic. The noise levels of the dominantly excited mode () are also more than 13 dB lower upstream. The reason for the significantly different noise radiation upstream and downstream can be found in the excitation of the fan tones. For the excitation of modes () and () at the stator leading edge, the scenario schematically illustrated in Figure 2 applies. Upstream, the modal propagation angles are almost parallel to the stator leading edge angle. As a result, the acoustic modes are excited weakly upstream. By contrast, downstream, a stronger noise excitation of the modes () and () occurs, as the propagation angles downstream are almost perpendicular to the stator leading edge angle. This is shown in Table 3, which depicts the difference between the stator leading edge angle and the modal propagation angle obtained from HB simulations for the dominantly excited BPF1 and BPF2 modes at design, and PR max operating conditions. For all considered operating points and all acoustic modes, upstream, the modal propagation angle is nearly parallel to the stator LE angle (), and downstream, it is nearly perpendicular (). Thus, the upstream noise excitation of the baseline fan stage shows a strong dependence on the modal propagation angle over a wide operating range. This leads to significantly lower sound power levels upstream compared to downstream. Similar values for are obtained from fully analytical predictions and measurements. These values are listed in Table A1 in Appendix B.

Table 3.
Difference between stator LE angle and modal propagation angle as well as for BPF1 and BPF2 modes obtained from HB simulations.
Figure 10a shows the tonal RSI noise obtained from an HB simulation in design operating conditions. The sound power levels are plotted along the axial position within the flow channel, where location 3a from Figure 6 is at position m and locations 4 and 5 are at position m and m, respectively. The numerical simulation confirms that the difference between the upstream and downstream tonal RSI levels arises from the noise excitation. A difference of more than 10 dB is predicted between upstream and downstream noise levels under design conditions. The numerical data indicate that the transmission of sound through the rotor blade row does not dominantly contribute to the level difference between upstream and downstream. The BPF1 and BPF2 noise levels are reduced by approximately 2 dB due to transmission through the rotor blade row. Figure 10b,c show that these findings are also valid for the two other operating points.
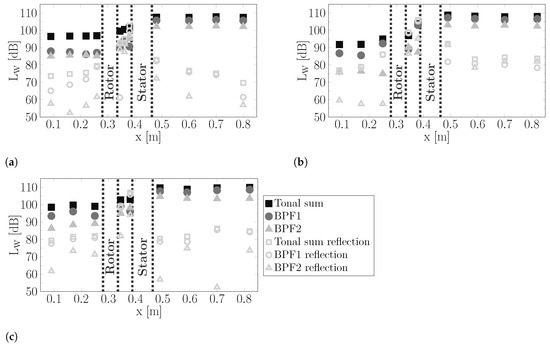
Figure 10.
Tonal RSI noise levels for the baseline fan obtained from HB simulations and plotted along the axial position. (a) Design operating point; (b) operating point; (c) operating point.
In order to further quantify the impact of the modal propagation angle on tonal noise excitation, a trend study is shown in Figure 11. The results are calculated fully analytically using PropNoise. For the trend study, the propagation angles of all cut-on BPF1 modes are intentionally manipulated in PropNoise code. The modal propagation angles are continuously varied between and . For , the modal propagation angles are parallel to the stator LE angle, and for the latter case, the modal propagation angles are perpendicular to the LE angle. In Figure 11, the resulting BPF1 sound power levels are plotted over the difference .
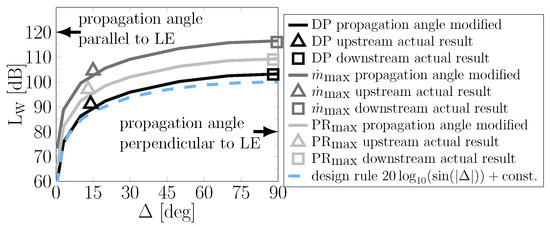
Figure 11.
Variation in : BPF1 sound power levels analytically predicted with PN.
The triangle and square markers indicate the actual upstream and downstream BPF1 sound power levels of the CRAFT baseline fan without any manipulation. The three curves for the three operating points are vertically shifted and are at a constant offset to each other. The results illustrate that the modal propagation angle strongly influences tonal noise excitation. The difference in sound power level between and is approximately 40 dB, according to the analytical prediction.
Based on the results obtained from the analysis of the modal propagation angle, a design rule for future acoustic designs of low-speed fan stages could be derived. Using Equation (5), it can be deduced that the expected noise level reduction compared to the case can be estimated with the factor
Equation (7) shows the correlation between the estimated noise level reduction and the difference between the stator leading edge angle and modal propagation angle. In practice, this means that once the rotor and stator blade numbers and the stagger angles are known, the expected reduction in noise level compared to can be calculated using Equation (7). In Figure 11, this design rule is visualized by the dashed line and plotted for .
As an intermediate conclusion, the analytical, numerical and experimental data illustrate that the modal propagation angle significantly impacts the excitation of tonal RSI noise for all considered operating points. Also, in off-design conditions, for the baseline fan, the tonal RSI noise is reduced by more than 10 dB upstream compared to downstream, as the modal propagation angle upstream is nearly parallel to the stator leading edge angle. Thus, a tonal advantage is achieved upstream due to the impact of the modal propagation angle on noise excitation.
The experimental data obtained from the CRAFT test facility and the baseline fan provide, first, a validation of the analytical and numerical results, and second, experimental evidence that the modal propagation angles strongly influence the excitation of tonal RSI noise. Especially for low-speed fan stages, where only a few azimuthal modes are cut-on, tonal RSI noise can be significantly reduced using the described effect. The acoustic benefits can be achieved with an appropriate choice of the rotor and stator blade numbers, since the blade numbers determine the excited Tyler and Sofrin mode orders, and with the azimuthal mode orders, the modal propagation angles are defined, as indicated in Equation (1). In a fan pre-design process, the stator leading edge angle is typically known at an early stage, as it directly results from rotational speed and fan pressure ratio. Consequently, the blade numbers should be iterated until the propagation angles of the dominantly excited modes are preferably parallel to the stator leading edge angle. To demonstrate the impact of the modal propagation angle on noise generation, this design-to-noise process is subsequently applied to select blade numbers for two new, low-count OGV fan stages, which are intended to be operated in the CRAFT test facility.
5.2. Low-Count OGV Fan Stages
The analyzed noise reduction potential of the effect resulting from the modal propagation angle is demonstrated on two low-noise fan stages with fewer stator than rotor blades. Both new, low-count OGV fans are designed according to the design-to-noise process outlined at the end of Section 5.1. Consequently, in order to apply the described effect to low-count OGV fan stages and to achieve acoustic benefit, the rotor and stator blade numbers have to be chosen appropriately. The blade numbers of both new fans are chosen to achieve a weak tonal noise excitation due to the impact of the modal propagation angle. Thus, the blade numbers should be selected in such a way that the dominant excited modes propagate parallel to the stator leading edge angle. Due to the given flow conditions in the CRAFT test rig, the rotor and stator stagger angles are predefined. Thus, the rotor and stator blade numbers are varied in order to find suitable blade count combinations for which exactly those modes are dominantly excited with the modal propagation angle approximately parallel to the stator stagger angle ().
Achieving an acoustic benefit based on the effect resulting from the modal propagation angle is the primary acoustic design criterion for both new low-count OGV fan stages. In addition to that, additional design criteria are defined that set further requirements regarding the acoustic behavior of the fan stages. This is important as the fans are intended to be used in a process consisting of measurements, virtual flyover simulations, auralizations and listening tests in the future. In order to achieve fundamentally different perceived noise characteristics with the same aerodynamic performance, the fan stages should also differ with regard to the following aspects:
- (a)
- Different dominant noise radiation direction.
- (b)
- Different ratio between tonal and broadband noise levels.
- (c)
- Different base frequency.
5.2.1. Blade Count Selection
In order to assess which blade count combinations satisfy the defined requirements, analytical blade count variations are performed using RANS-based noise prediction with PropNoise (see Figure 12). The baseline fan stage with 18 rotor blades and 21 stator vanes is selected as the initial configuration for the blade count variation. This configuration is framed in purple in Figure 12. The blade count pairing of the baseline fan is chosen such that the acoustic BPF1 modes are cut-on, which results in very high sound power levels and a tonally dominant sound radiation.

Figure 12.
Overall sound power levels for different rotor and stator blade counts calculated with RANS-based noise prediction. For each blade count paring, the overall sound power level is summed over three operating points (DP, PRmax and OP4).
Using the baseline fan, a RANS simulation is performed for the three operating points, DP, and OP 4 (see Table 1). The aerodynamic flow field is extracted from each RANS simulation and used as input for PropNoise in order to analytically predict the noise levels, following the process visualized in Figure 5. Based on this initial prediction, the blade numbers are subsequently varied using PropNoise, and the noise levels are calculated for the new configurations for each operating point. For the blade count variation, the following assumptions are made:
- All aerodynamic flow parameters and streamlines remain unchanged. Therefore, RANS simulations are performed only for the initial configuration.
- The blade’s solidity is constant. Thus, the chord length changes between the configurations (e.g., the lower the blade count, the longer the blade chord).
A detailed description of the procedure applied to the RANS-based noise prediction and blade count variation with PropNoise is given in [2,6].
Figure 12 shows the overall sound power levels of the RSI noise source summed over the three operating points as a function of the rotor and stator blade numbers. In [6], a similar blade count variation is performed, and several acoustically promising areas are introduced. These areas are marked in green and blue in Figure 12. For all blade count pairings within the green area, two acoustic effects ensure that lower sound power levels occur. Firstly, the BPF1 tone is inversely cut off. Secondly, an acoustic benefit is achieved due to the effect resulting from the modal propagation angle. Due to these acoustic advantages, the first blade count combination for one of the new fan stages is selected from the green area. This fan stage consists of a 31-blade rotor combined with a 21-vane stator. As the 21-vane stator already exists (stator of the baseline fan), this blade count combination is also a good choice to keep the manufacturing costs low. The B31V21 low-count OGV fan is subsequently named the low-tone fan, and the aeroacoustic results are shown in Section 5.2.2.
For all blade count pairings within the blue area, two acoustic effects also ensure that lower sound power levels occur. Similar to the green area, the impact of the modal propagation angle on noise excitation leads to an acoustic benefit. In addition to that, as the number of stator vanes is reduced compared to configurations in the green area, a reduction in broadband noise is obtained. Due to these acoustic benefits, the second blade count combination for one of the new fan stages is selected from the blue area. This low-count OGV fan also uses the 31-blade rotor, which is combined with a 10-vane stator. The B31V10 fan is subsequently named the low-broadband fan, and the aeroacoustic results are shown in Section 5.2.3.
5.2.2. Low-Tone Fan: Aerodynamic Optimization and Acoustic Evaluation
The low-tone fan is equipped with a new 31-blade rotor and the 21-vane baseline stator. Since the 21-vane stator geometry already exists, only the rotor geometry is optimized using the multi-objective optimization process described in Section 4.4.
Figure 13a shows the generated members of the optimization and the Pareto front between the efficiency and pressure ratio for design operating conditions. The baseline fan stage is marked in purple, and the selected member for the 31-blade rotor is marked in green. The reason for choosing this particular member is that the fan stages should be similar to each other regarding their aerodynamic characteristics. The final geometry of the 31-blade rotor is shown on the left in Figure 13b, and the combination of this rotor with the baseline 21-vane stator is shown on the right.
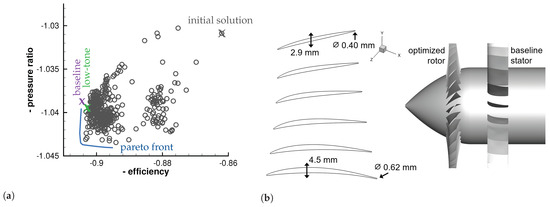
Figure 13.
Results of the optimization for the 31-blade rotor. (a) Pareto front; (b) geometry of the 31-blade rotor.
This B31V21 low-count OGV fan stage is named the low-tone fan since two acoustic effects are used to efficiently reduce the tonal noise component. Firstly, the rotor–stator blade counts are chosen such that the acoustic BPF1 modes are inversely cut off. The inverse cut-off is achieved due to the low rotor tip Mach number, . Conventionally, a cut-off design is realized with stator vane counts larger than the rotor blade count. However, in [6], it is verified that a cut-off design can also be achieved with fewer stator than rotor blades on condition that the rotor tip Mach number is low enough. This is called an inverse cut-off. As a design rule to achieve an inverse cut-off, the Mach number should be lower than a critical Mach number [6]. This critical Mach number is defined as . For the low-tone fan is approximately . Consequently, the inverse cut-off of the BPF1 tone is possible, since .
Secondly, in addition to the inverse cut-off of the BPF1 tone, the blade numbers of this fan stage are chosen such that the excited BPF2 modes benefit from the impact of the propagation angle upstream. For the BPF2 tone, the acoustic mode () is dominantly excited. As shown in Table 4, the propagation angle of this mode upstream is nearly parallel to the stator leading edge angle, and downstream it is nearly perpendicular. Therefore, the mode is excited more weakly upstream, leading to lower sound power levels.

Table 4.
Difference between stator LE angle and modal propagation angle as well as for the BPF1 and BPF2 modes under design conditions for the low-tone fan stage.
This is confirmed by the results from the HB simulation, which are shown in Figure 14. The HB simulation is performed under design operating conditions. The results indicate a difference of 5 dB between the upstream and downstream noise excitations, leading to significantly lower noise radiation upstream. In addition to the effect resulting from the propagation angle, the upstream noise radiation also benefits from the transmission of the mode through the rotor blade row. The reason for this is that the mode rotates against the rotor’s rotation direction. According to Philpot [34], modes rotating against the rotor’s rotation are attenuated more efficiently when propagating through a rotor blade row compared to modes rotating in the same direction. In the present case, the HB simulation shows that, due to the transmission through the rotor, the noise levels are attenuated by 3 dB. Adding the 5dB from the noise excitation results in a total difference of 8dB between the upstream and downstream noise radiation.
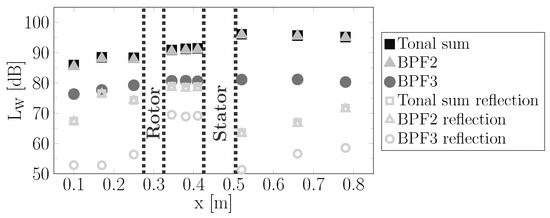
Figure 14.
Tonal RSI noise levels under design conditions obtained from an HB simulation and plotted along the axial position for the low-tone fan stage.
Compared to the numerical results of the baseline fan stage presented in Figure 10a, this fan shows lower sound power levels of more than 10 dB in both upstream and downstream directions. Nevertheless, the general tonal noise radiation characteristic is similar to that of the baseline fan: lower tonal sound power levels occur upstream, whereas higher levels are observed downstream.
Figure 15 shows the noise directivity of the low-tone fan at design operating conditions. The noise directivity indicates that, over all radiation angles, the tonal component of the RSI noise has similar levels compared to the broadband component. For radiation angles between and , the tonal noise levels are even lower than the broadband levels, such that the broadband component is the dominant sound source over a wide range of radiation angles. Consequently, the noise impression of this low-speed fan is mainly characterized by broadband noise, whose energy is spread over a wide range of frequencies, and less by discrete frequencies that create tonal noise. This is particularly interesting for future listening tests, since broadband sounds are often perceived as less annoying.
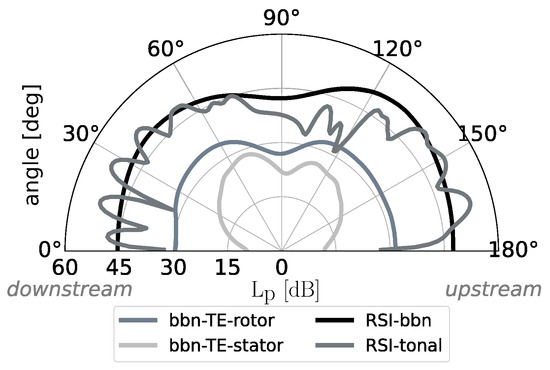
Figure 15.
Noise directivity at design operating conditions for the low-tone fan stage obtained from RANS-based noise prediction.
As an intermediate summary, the noise emission of the low-tone fan is characterized by the following features:
- The BPF1 tone is inversely cut off.
- Upstream, the tonal noise excitation at the second BPF benefits from a modal propagation angle that is relatively parallel to the stator LE angle.
- The dominant tonal noise radiation direction is downstream.
- The tonal RSI noise is lower than the broadband component over a wide range of radiation angles.
For a possible application of this fan design in an urban air mobility airplane (e.g., a small airtaxi with a distributed propulsion system), it should be noted that this fan is equipped with a large amount of rotor and stator blades, which might increase production as well as maintenance costs. Therefore, an additional fan design with a significantly lower stator vane count is investigated in the following subsection.
5.2.3. Low-Broadband Fan: Aerodynamic Optimization and Acoustic Evaluation
The low-broadband fan is equipped with the 31-blade rotor from Section 5.2.2 and a new 10-vane stator. Similar to the 31-blade rotor, the new stator geometry is optimized using the multi-objective optimization process described in Section 4.4.
The generated members of the optimization and the Pareto front between the efficiency and pressure ratio for design operating conditions are shown in Figure 16a. Again, the baseline fan is marked in purple and the low-tone fan in green. The selected member from the optimization for the 10-vane stator is marked in blue. It becomes evident that all three fan stages provide similar efficiencies and pressure ratios for design operating conditions. Thus, the aerodynamic and acoustic comparability of all three fan stages is ensured. In Figure 16b, the geometry of the 21-vane stator is shown in detail, and its combination with the 31-blade rotor is illustrated.
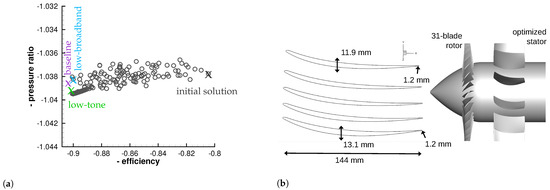
Figure 16.
Results of the optimization for the 10-vane stator. (a) Generated members. (b) Geometry of the 10-vane stator.
Compared to the baseline fan and the low-tone fan, which both have 21 stator vanes, the number of stator vanes is approximately halved for the low-broadband fan. Due to the reduced number of stator vanes, the broadband noise is reduced significantly, as this noise source scales with the number of stator vanes [2]. As a rule of thumb, the broadband noise is reduced by 3 dB if the number of stator vanes is halved. This is the reason why the B31V10 fan stage is named the low-broadband fan.
In order to reduce not only the broadband noise component but also the tonal component, the rotor–stator blade count of this fan stage is chosen such that the excitation of BPF1 benefits downstream from the impact of the modal propagation angle (see Table 5). Downstream, the propagation angle of the dominantly excited mode () is relatively parallel to the stator leading edge angle, resulting in lower noise levels. This is confirmed by the HB simulation performed under design operating conditions and plotted in Figure 17. The numerical results indicate a difference of 7 dB between the inter-stage and the downstream BPF1 noise levels. Consequently, the dominant noise radiation direction is upstream. Compared to the low-tone fan, which primarily emits tonal noise downstream, the low-broadband fan provides an opposing tonal radiation characteristic (see Figure 14 and Figure 17). Thus, both fan stages are well suited to investigate the impact of the dominant noise radiation direction on noise perception in future psychoacoustic assessments.

Table 5.
Difference between stator LE angle and modal propagation angle as well as for the BPF1 and BPF2 modes under design conditions for the low-broadband fan stage.
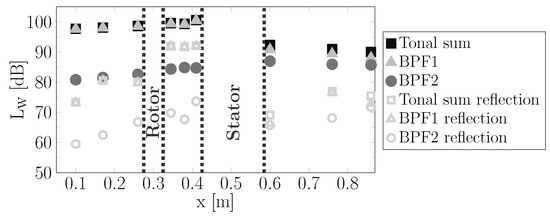
Figure 17.
Tonal RSI noise levels under design conditions obtained from an HB simulation and plotted along the axial position for the low-broadband fan stage.
In line with our expectations, for the transmission through the rotor blade row, the HB simulation predicts only slight attenuation of the dominantly excited mode (see gray triangles). This is because the mode rotates in the rotor rotation direction. As outlined in Section 5.2.2, for the low-tone fan, the mode is dominantly excited, so opposing transmission behavior is expected. Therefore, both fan stages are well suited to investigate the transmission through the rotor blade row, as rotates against the rotor rotation direction and rotates with the rotor rotation.
Figure 18 shows the noise directivity of the low-broadband fan at design operating conditions. The radiation characteristic of the tonal RSI noise clearly reflects the impact of the modal propagation angle. Downstream, the tonal noise levels are reduced due to the modal propagation angle, and thus, similar noise levels are observed for the tonal and broadband noise components for radiation angles between and . Upstream, the tonal noise levels are higher compared to the broadband levels (see radiation angles between and ). Thus, for the low-broadband fan, tonal RSI noise is the dominant noise source over a wide range of radiation angles. In contrast, for the low-tone fan, it is observed that the broadband component is the dominant source over a wide range of radiation angles. Therefore, due to this opposing noise emission characteristic, both fan stages are well suited to investigate the impact of differences between tonal and broadband noise levels on noise perception.
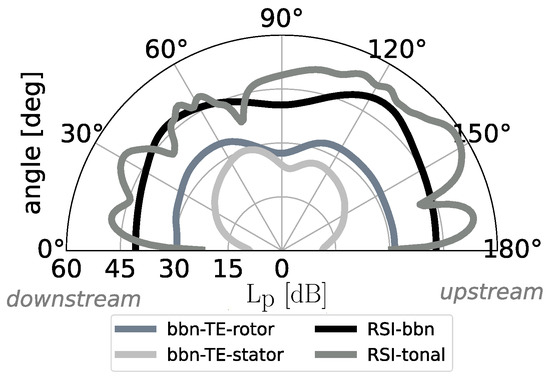
Figure 18.
Noise directivity at design operating conditions for the low-broadband fan stage obtained from RANS-based noise prediction.
As an intermediate summary, the noise emission of the low-broadband fan is characterized by the following features:
- The BPF1 tone is cut-on.
- Downstream, the tonal noise excitation at the first BPF benefits from a modal propagation angle that is relatively parallel to the stator LE angle.
- The dominant tonal noise radiation direction is upstream.
- Upstream, the tonal RSI noise is higher than the broadband component, and downstream, similar levels are predicted.
In total, as summarized in Table 6, the baseline, low-tone and low-broadband fan stages are very similar regarding their aerodynamic characteristics. However, as illustrated in Section 5.1, Section 5.2.2 and Section 5.2.3 and as summarized in Table 7, all three fans provide opposing acoustic characteristics. In particular, the fan stages differ with regard to the dominant noise radiation direction and with regard to the ratio between tonal and broadband noise levels.

Table 6.
Pressure ratio and efficiency for all three fan stages in design as well as conditions.

Table 7.
Summary of the acoustic characteristics of all three fan stages.
Additionally, compared to the baseline fan, for both new low-count OGV fans, the rotor blade count changes from to blades. Thus, as shown in Table 7, the base frequency of the fan tones increases from 1350 Hz to 2325 Hz for the low-broadband fan and to 4650 Hz for the low-tone fan. Despite the same number of rotor blades, the low-tone fan has a higher base frequency than the low-broadband fan, as the first blade passing the frequency tone is inversely cut off. This allows us to investigate the impact of a frequency change on humans’ noise perception. Moreover, due to atmospheric absorption, higher frequencies are significantly attenuated during propagation from the noise source to an observer on the ground. This provides an additional advantage for the low-tone fan, as the higher-frequency tonal components are further attenuated while propagating through the atmosphere. All in all, as summarized in Table 7, the fan stages are well suited to assess the acoustic criteria (a)–(c) defined in Section 5.2.
6. Discussion and Conclusions
Using the CRAFT baseline fan stage, an acoustic effect resulting from the modal propagation angle is experimentally confirmed. This effect has already been investigated analytically as well as numerically, and it is now experimentally verified on the CRAFT baseline fan for a wide range of operating conditions. In good agreement, the experimental data provide validation of the analytical and numerical studies.
The experimental data confirm that the modal propagation angle significantly impacts the excitation of tonal rotor–stator interaction noise at the stator leading edge. In particular, if the propagation direction of the dominantly excited mode is nearly parallel to the stator leading edge angle, an acoustic benefit is achieved. In this case, the acoustic mode is only weakly excited. The experimental data for different operating conditions confirm that the acoustic benefit can be more than 13 dB for individual modes, even in off-design conditions. As a rule of thumb, the expected noise level reduction can be estimated with , where is the difference between the stator stagger angle and the modal propagation angle. Particularly for low-speed ducted fan stages or ventilators, where only a few azimuthal modes are excited, this effect may efficiently reduce tonal rotor–stator interaction noise. Depending on the design, the effect can be used to reduce the tonal noise component upstream or downstream. Thus, in addition to noise reduction, this also allows us to specifically control the fan’s radiation direction, which in turn can be used to improve certification levels and psychoacoustic characteristics, taking into account liners, shielding and flight trajectories.
In a fan pre-design process, acoustic benefits can be achieved with a suitable choice of rotor and stator blade numbers, since the blade numbers define the excited acoustic interaction modes, and with the interaction modes, the propagation angles are defined. In particular, the modes should be excited whose propagation angles are parallel to the stator leading edge angle. Typically, the leading edge angle is known at an early stage in a pre-design process as it directly results from rotational speed and pressure ratio. Therefore, through a smart blade count selection, the excited mode orders can be adjusted in such a way that the resulting modal propagation angle is aligned with the stator stagger angle.
This design-to-noise process is demonstrated at two low-speed fan stages with fewer stator than rotor blades, which are representative of ducted fans in urban air mobility aircraft. The blade numbers are chosen such that for the first fan stage, the dominant modes are excited weakly upstream due to the impact of the modal propagation angle. Thus, the upstream noise levels are reduced. For the second fan stage, the blade numbers are chosen to provide an opposing radiation characteristic. Consequently, the modal propagation angle downstream is nearly parallel to the stator leading edge angle in order to reduce the downstream noise excitation. In total, for both fan stages, the radiated noise levels are approximately 10 dB lower than the baseline fan. The geometry of all rotor and stator blades is obtained from an aerodynamic optimization process.
As these fan stages provide opposing acoustic characteristics, these fans will be used in a future process consisting of measurements at the CRAFT test facility, virtual flyover simulations, auralizations and listing tests in order to evaluate the noise perception.
Author Contributions
Conceptualization, S.S. and R.J.; writing—original draft preparation, S.S.; writing—review and editing, S.S., R.J. and A.M.; writing—experimental noise measurement section, L.K.; experimental data, L.K.; visualization, S.S.; data curation, S.S.; formal analysis, S.S.; supervision, R.J. and A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following symbols and abbreviations are used in this manuscript:
| Symbols | ||
| axial Mach number | ||
| tip Mach number | ||
| swirl Mach number | ||
| m | azimuthal mode order | |
| n | radial mode order | |
| h | harmonics of rotor blade number | |
| k | scattering index | |
| modal propagation angle | rad | |
| cut-on factor | ||
| derivative of radial eigenfunction | ||
| R | tip radius | m |
| r | hub radius | m |
| modal sound pressure amplitude | Pa | |
| induct Green’s function | ||
| axial wave number | ||
| normal wave number | ||
| chordwise wave number | ||
| x-coordinate of LE | m | |
| circumferential LE coordinate | rad | |
| acoustic source term | ||
| acoustic source term lift-noise | ||
| chordwise distribution of lift | ||
| l | chordwise position | m |
| leading edge angle | rad | |
| trailing edge angle | rad | |
| difference between and | rad | |
| isentropic efficiency | ||
| mass flow | kg/s | |
| D | rotor radial displacement | m |
| stator outflow angle | rad | |
| Lw | sound power level | dB |
| Lp | sound pressure level | dB |
| Abbreviations | ||
| CRAFT | Co/Counter Rotating Acoustic Fan Test rig | |
| OGV | outer guide vane | |
| LE | leading edge | |
| RSI | rotor–stator interaction | |
| BPF | blade passing frequency | |
| B | number of rotor blades | |
| V | number of stator vanes | |
| OP | operating point | |
| DP | design point | |
| operating point at maximum pressure ratio | ||
| operating point at maximum mass flow | ||
| RANS | Reynolds-averaged Navier–Stokes | |
| HB | harmonic balance | |
| PR | pressure ratio | |
| PN | PropNoise | |
| XTPP | extended triple plane pressure | |
| M | measurement | |
| up | upstream | |
| down | downstream | |
| N | rotational speed | |
| bbn | broadband noise | |
| TE | trailing edge |
Appendix A
In this section, two additional plots are shown, one illustrating the domain for the numerical simulations (Figure A1) and one depicting an example of the mesh around the rotor and stator blades (Figure A2).
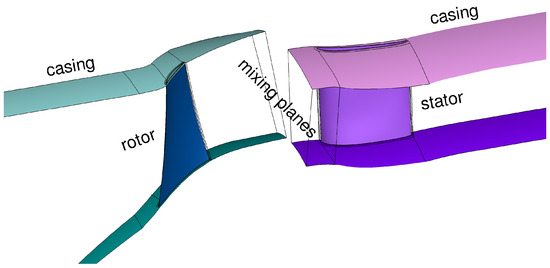
Figure A1.
Domain for numerical simulations.

Figure A2.
Numerical grid around the rotor (left) and stator (right).
Appendix B
Table A1 compares the difference between measurements and fully analytical predictions. Since the upstream measurement position is located upstream of the spinner (position 3a in Figure 6), and could not be experimentally determined in the inter-stage area. Therefore, “—” is entered in Table A1 in the corresponding cells.

Table A1.
Difference between stator LE angle and modal propagation angle as well as for BPF1 and BPF2 modes obtained from analytical predictions and experiments.
Table A1.
Difference between stator LE angle and modal propagation angle as well as for BPF1 and BPF2 modes obtained from analytical predictions and experiments.
| Upstream | Downstream | |||||
|---|---|---|---|---|---|---|
| Operating Point | Mode | Method | [deg] | [deg] | ||
| DP | PN | 0.795 | 13.4 | 0.795 | 88.8 | |
| M | — | — | 0.760 | 86.9 | ||
| PN | 0.805 | 14.3 | 0.805 | 87.7 | ||
| M | — | — | 0.772 | 88.1 | ||
| PN | 0.795 | 14.4 | 0.795 | 89.8 | ||
| M | — | — | 0.764 | 88.3 | ||
| PN | 0.805 | 15.3 | 0.805 | 89.1 | ||
| M | — | — | 0.776 | 89.5 | ||
| PRmax | PN | 0.796 | 12.8 | 0.796 | 87.8 | |
| M | — | — | 0.758 | 87.8 | ||
| PN | 0.806 | 13.6 | 0.806 | 86.8 | ||
| M | — | — | 0.770 | 89.0 | ||
References
- Rizzi, S.A.; Huff, D.L.; Boyd, D.D.; Bent, P.; Henderson, B.S.; Pascioni, K.A.; Sargent, D.C.; Josephson, D.L.; Marsan, M.; He, H.; et al. Urban Air Mobility Noise: Current Practice, Gaps, and Recommendations; NASA/TP-2020-5007433; NASA: Langley Research Center: Hampton, VA, USA, 2020. [Google Scholar]
- Jaron, R. Aeroakustische Auslegung von Triebwerksfans mittels multidisziplinärer Optimierungen. Ph.D. Dissertation, German Aerospace Center, Institute of Propulsion Technology, Berlin, Germany, 2018. [Google Scholar] [CrossRef]
- Töpken, S.; Verhey, J.L.; Weber, R. Perceptual space, pleasantness and periodicity of multi-tone sounds. J. Acoust. Soc. Am. 2015, 138, 288–298. [Google Scholar] [CrossRef] [PubMed]
- More, S.; Davies, P. Human responses to the tonalness of aircraft noise. Noise Control Eng. J. 2010, 58, 420–440. [Google Scholar] [CrossRef]
- Duncan, P.; Dawson, B. Reduction of interaction tones from axial flow fans by suitable design of rotor configuration. J. Sound Vib. 1974, 33, 143–154. [Google Scholar] [CrossRef]
- Schade, S.; Jaron, R.; Moreau, A.; Guérin, S. Mechanisms to reduce the blade passing frequency tone for subsonic low-count OGV fans. Aerosp. Sci. Technol. 2022, 125, 107083. [Google Scholar] [CrossRef]
- Schade, S.; Klähn, L.; Jaron, R. Analytische, numerische und experimentelle Untersuchung des tonalen Rotor–Stator Interaktionsschalls in einer langsam drehenden, ummantelten Fanstufe. In DAGA 2023—49. Jahrestagung für Akustik; Conference Proceedings; DAGA: Hamburg, Germany, 2023; pp. 526–529. [Google Scholar]
- Hanson, D. Acoustic reflection and transmission of rotors and stators including mode and frequency scattering. In Proceedings of the 3rd AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 12–14 May 1997. [Google Scholar] [CrossRef]
- Behn, M.; Tapken, U.; Puttkammer, P.; Hagmeijer, R.; Thouault, N. Comparative study of different analytical approaches for modelling the transmission of sound waves through turbomachinery stators. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016. [Google Scholar] [CrossRef]
- Tapken, U.; Caldas, L.; Meyer, R.; Behn, M.; Klähn, L.; Jaron, R.; Rudolphi, A. Fan test rig for detailed investigation of noise generation mechanisms due to inflow disturbances. In Proceedings of the AIAA Aviation 2021 Forum, Virtual Event, 2–6 August 2021. [Google Scholar] [CrossRef]
- Tyler, J.M.; Sofrin, T.G. Axial Flow Compressor Noise Studies; SAE Technical Papers; SAE International: Warrendale, PA, USA, 1962. [Google Scholar] [CrossRef]
- Rice, E.; Heidmann, M.; Sofrin, T. Modal propagation angles in a cylindrical duct with flow and their relation to sound radiation. In Proceedings of the 17th Aerospace Sciences Meeting, New Orleans, LA, USA, 15–17 January 1979. [Google Scholar] [CrossRef]
- Moreau, A. A Unified Analytical Approach for the Acoustic Conceptual Design of Fans for Modern Aero-Engines. Ph.D. Dissertation, German Aerospace Center, Institute of Propulsion Technology, Berlin, Germany, 2017. [Google Scholar] [CrossRef]
- Rienstra, S.; Tester, B. An Analytic Green’s Function for a Lined Circular Duct Containing Uniform Mean Flow. In Proceedings of the 11th AIAA/CEAS Aeroacoustics Conference, Monterey, CA, USA, 23–25 May 2005. [Google Scholar] [CrossRef]
- Mosch, B.J. Erweiterung der Steuerung eines Fan-Prüfstands um die Regelung aerodynamischer Betriebsgrößen zur Realisierung dynamischer Fuhrungsgrößenverläufe. Master’s Thesis, Technische Universität Berlin, Berlin, Germany, 2023. [Google Scholar]
- Nürnberger, D.; Eulitz, F.; Schmitt, S.; Zachcial, A. Recent Progress in the Numerical Simulation of Unsteady Viscous Multistage Turbomachinery Flow. In Proceedings of the ISOABE 2001–1081, Bangalore, India, September 2001. [Google Scholar]
- Yang, H.; Nürnberger, D.; Kersken, H.P. Towards Excellence in Turbomachinery Computational Fluid Dynamics: A Hybrid Structured-Unstructured Reynolds-Averaged Navier-Stokes Solver. J. Turbomach. 2006, 128, 390–402. [Google Scholar] [CrossRef]
- Weber, A. G3DHexa-3D Structured Grids for Multistage/Multipassage Turbomachines and Linear Cascades; DLR Internal Report DLR-IB-325-03-14; Version 2.0; German Aerospace Center (DLR): Cologne, Germany, 2014. [Google Scholar]
- Frey, C.; Ashcroft, G.; Kersken, H.; Voigt, C. A harmonic balance technique for multistage turbomachinery applications. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar] [CrossRef]
- Hall, K.C.; Ekici, K.; Thomas, J.P.; Dowell, E.H. Harmonic balance methods applied to computational fluid dynamics problems. Int. J. Comput. Fluid Dyn. 2013, 27, 52–67. [Google Scholar] [CrossRef]
- Wang, D.; Huang, X. A complete rotor–stator coupling method for frequency domain analysis of turbomachinery unsteady flow. Aerosp. Sci. Technol. 2017, 70, 367–377. [Google Scholar] [CrossRef]
- Ovenden, N.C.; Rienstra, S.W. Mode-matching strategies in slowly varying engine ducts. AIAA J. 2016, 42, 1832–1840. [Google Scholar] [CrossRef]
- Wohlbrandt, A.; Weckmüller, C.; Guérin, S. A robust extension to the triple plane pressure mode matching method by filtering convective perturbations. Int. J. Aeroacoustics 2016, 15, 41–58. [Google Scholar] [CrossRef]
- Guérin, S. Improvement of the triple-plane pressure mode matching technique and application to harmonic balance simulations. In Proceedings of the 16th International Symposium on Unsteady Aerodynamics Aeroacoustics and Aeroelasticity of Turbomachines ISUAAAT16, Toledo, Spain, 19–23 September 2022. [Google Scholar]
- Behn, M.; Pardowitz, B.; Tapken, U. Separation of tonal and broadband noise components by cyclostationary analysis of the modal sound field in a low-speed fan test rig. In Proceedings of the International Conference of Fan Noise, Aerodynamics, Applications and Systems, Darmstadt, Germany, 18–20 April 2018. [Google Scholar]
- Morfey, C. Sound transmission and generation in ducts with flow. J. Sound Vib. 1971, 14, 37–55. [Google Scholar] [CrossRef]
- Voß, C.; Aulich, M.; Kaplan, B.; Nicke, E. Automated Multiobjective Optimisation in Axial Compressor Blade Design. Volume 6: Turbomachinery, Parts A and B. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; pp. 1289–1297. [Google Scholar] [CrossRef]
- Voß, C.; Aulich, M.; Raitor, T. Metamodel Assisted Aeromechanical Optimization of a Transonic Centrifugal Compressor. In Proceedings of the 15th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, HI, USA, 24–28 February 2014. [Google Scholar]
- Aulich, M.; Voß, C.; Raitor, T. Optimization Strategies demonstrated on a Transonic Centrifugal Compressor. In Proceedings of the 15th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, HI, USA, 24–28 February 2014. [Google Scholar]
- Schmitz, A. Entwicklung eines objektorientierten und parallelisierten Gradient Enhanced Kriging Ersatzmodells. Ph.D. Dissertation, Fernuniversität Hagen, Hagen, Germany, 2013. [Google Scholar]
- Dhondt, G. The Finite Element Method for Three-Dimensional Thermomechanical Applications; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Frey, C.; Ashcroft, G.; Müller, M.; Wellner, J. Analysis of Turbomachinery Averaging Techniques. Volume 10C: Turbomachinery—Design Methods and CFD Modeling for Turbomachinery; Ducts, Noise, and Component Interactions. In Proceedings of the ASME Turbo Expo 2022: Turbomachinery Technical Conference and Exposition, Rotterdam, The Netherlands, 13–17 June 2022. [Google Scholar] [CrossRef]
- Klähn, L.; Caldas, L.; Meyer, R.; Moreau, A.; Tapken, U. Experimental Investigation of Inflow-Distortion-Induced Tonal Noise in a Sub-Sonic Fan Test Rig. In Proceedings of the 29th International Congress on Sound and Vibration, Prague, Czech Republic, 9–13 July 2023. [Google Scholar]
- Philpot, M.G. The role of rotor blade blockage in the propagation of fan noise interaction tones. In Proceedings of the AIAA 2nd Aeroacoustics Conference, Hampton, VA, USA, 24–26 March 1975. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).