A Python Toolbox for Data-Driven Aerodynamic Modeling Using Sparse Gaussian Processes
Abstract
1. Introduction
2. Sparse Gaussian Processes
2.1. Gaussian Processes Regression
2.2. Covariance Parameter Estimation
2.3. Sparse Approximations of Gaussian Processes
2.3.1. Fully Independent Training Conditional (FITC)
2.3.2. Variational Free Energy (VFE)
2.3.3. Comparison and Contrast of the Two Methods
3. Surrogate Modeling Toolbox (SMT)
4. Numerical Illustrations
4.1. Analytical Example Database
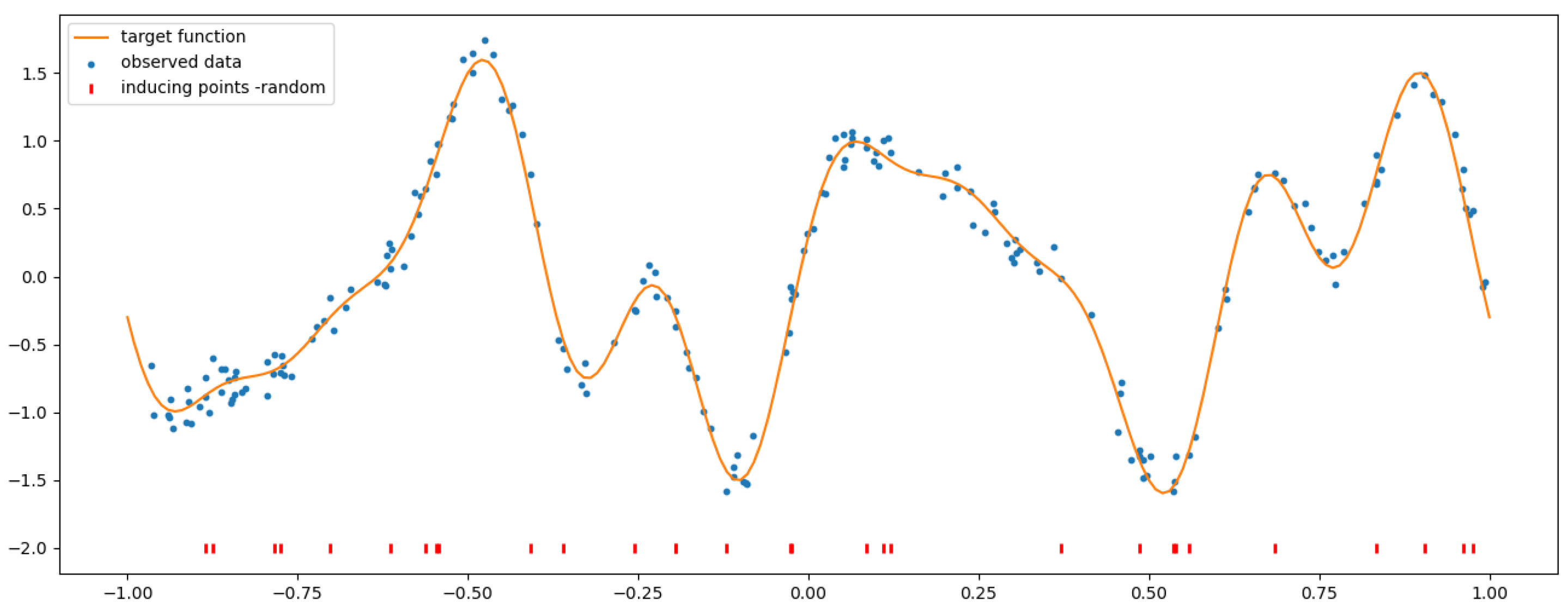
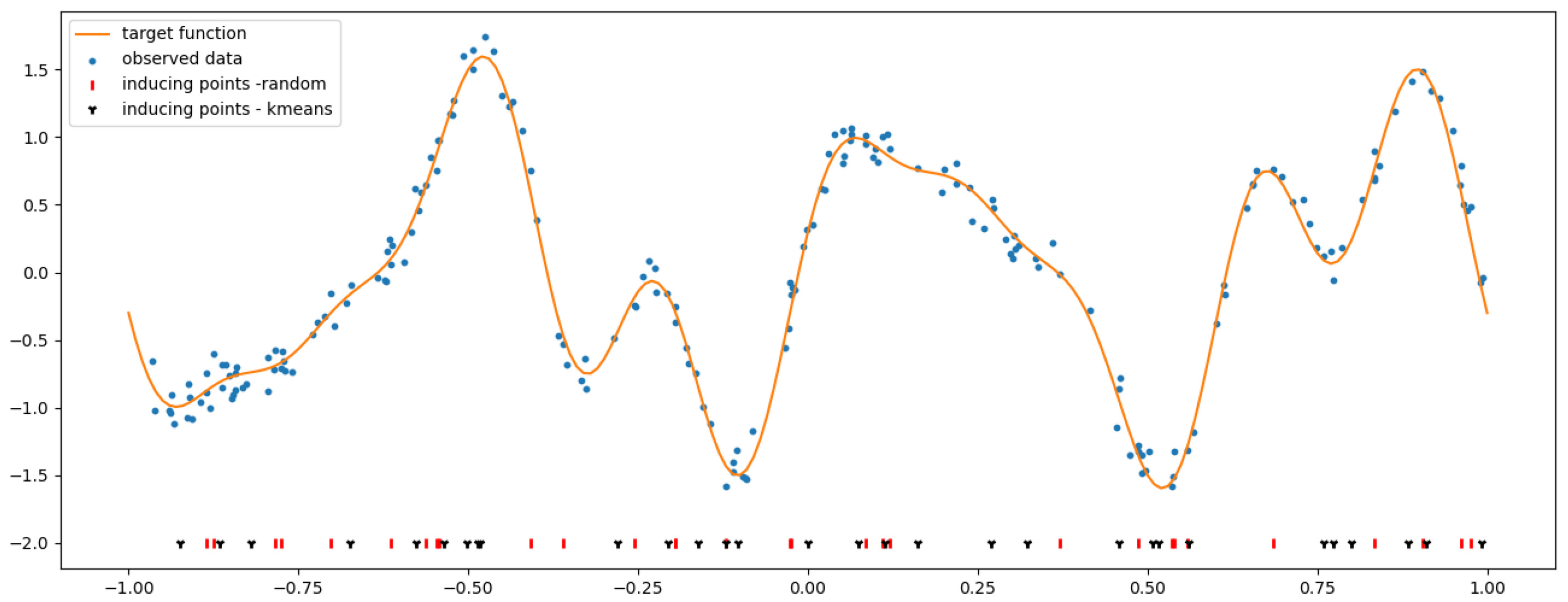
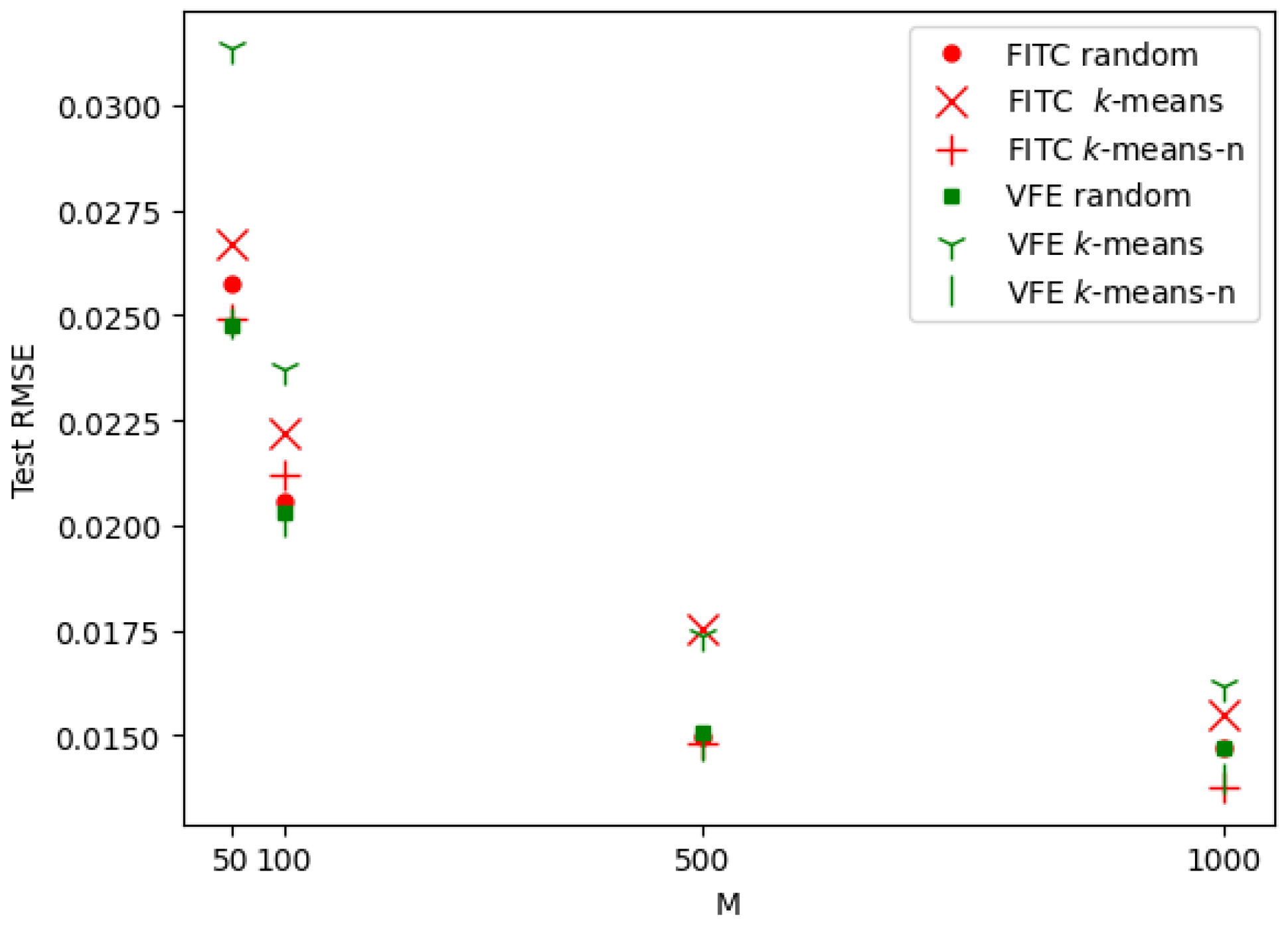
4.2. SGP Using a Random Selection of Inducing Inputs
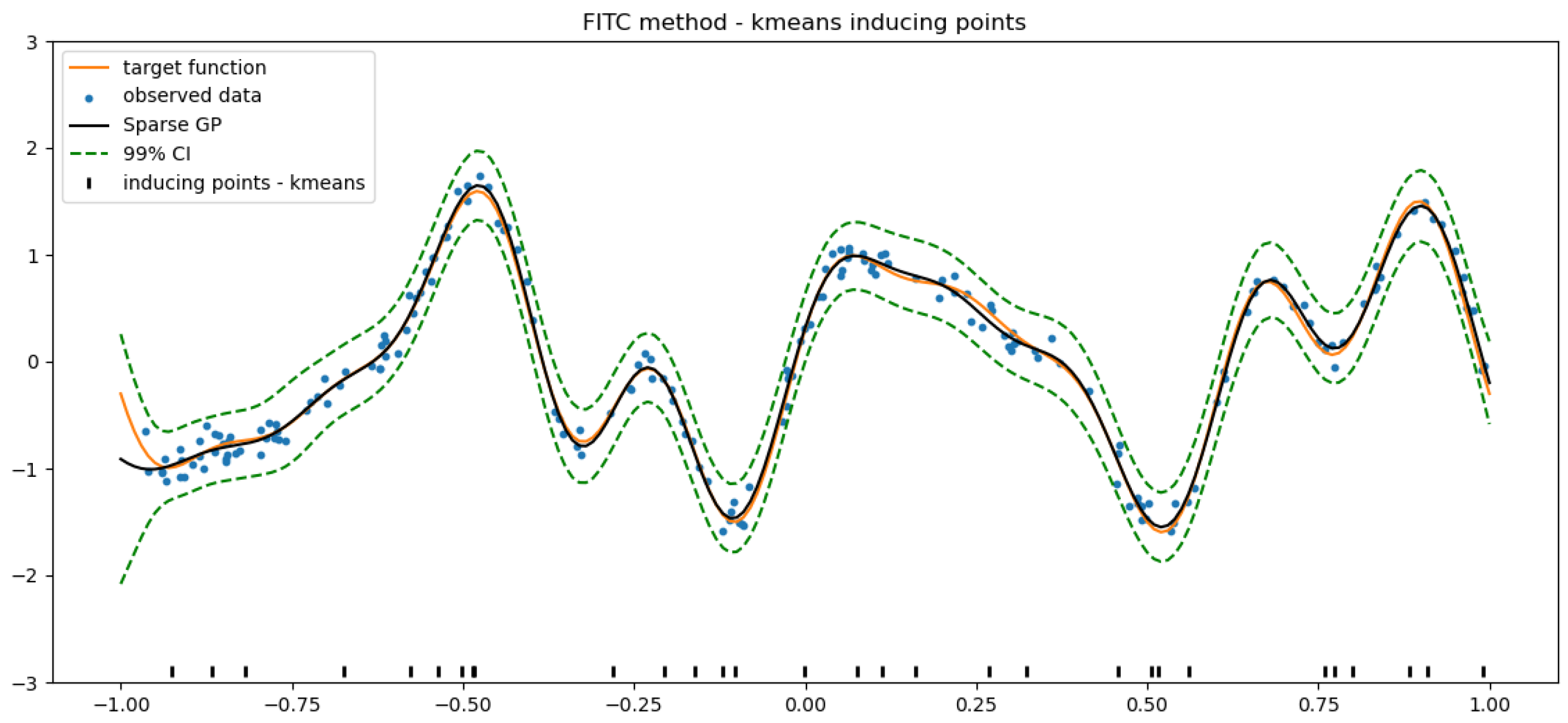
4.3. k-Means Clustering for the Selection of Inducing Inputs
- Perform k-means clustering on all input–output pairs of the observations to partition the training set into M clusters , each one being characterized by its centroid .
- Define the inducing inputs as the x-component of the centroids , i.e., .
5. Wind Tunnel Application
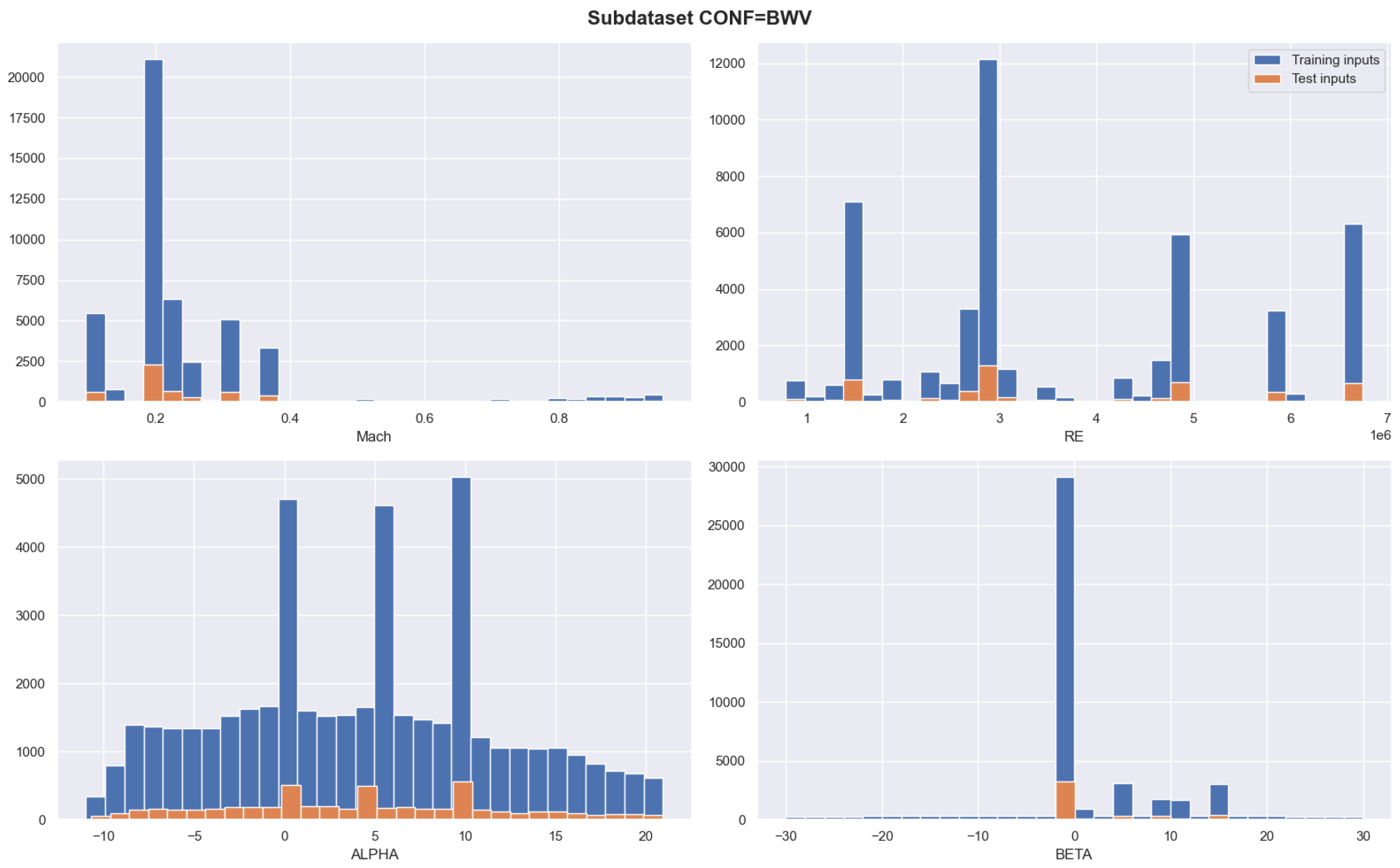
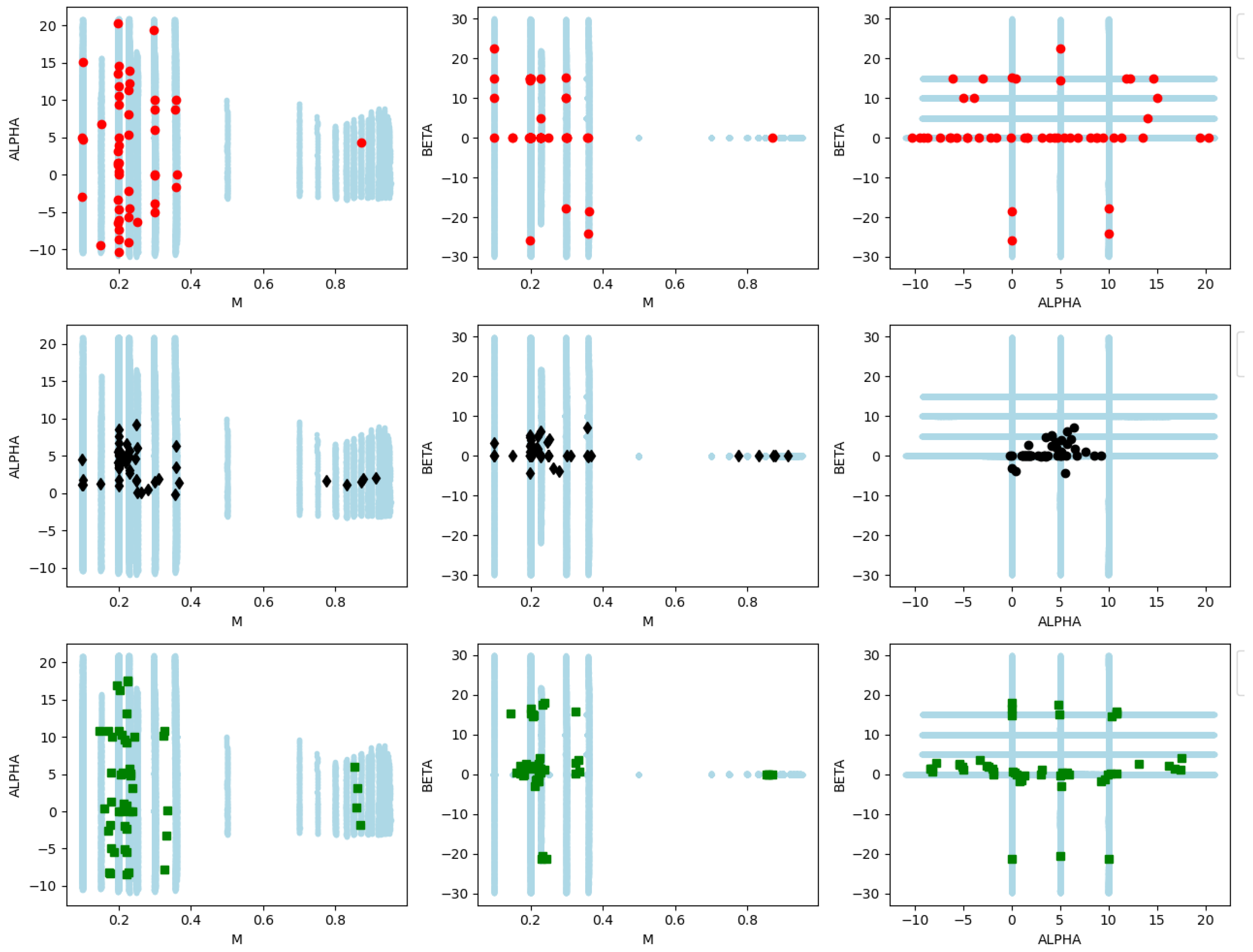
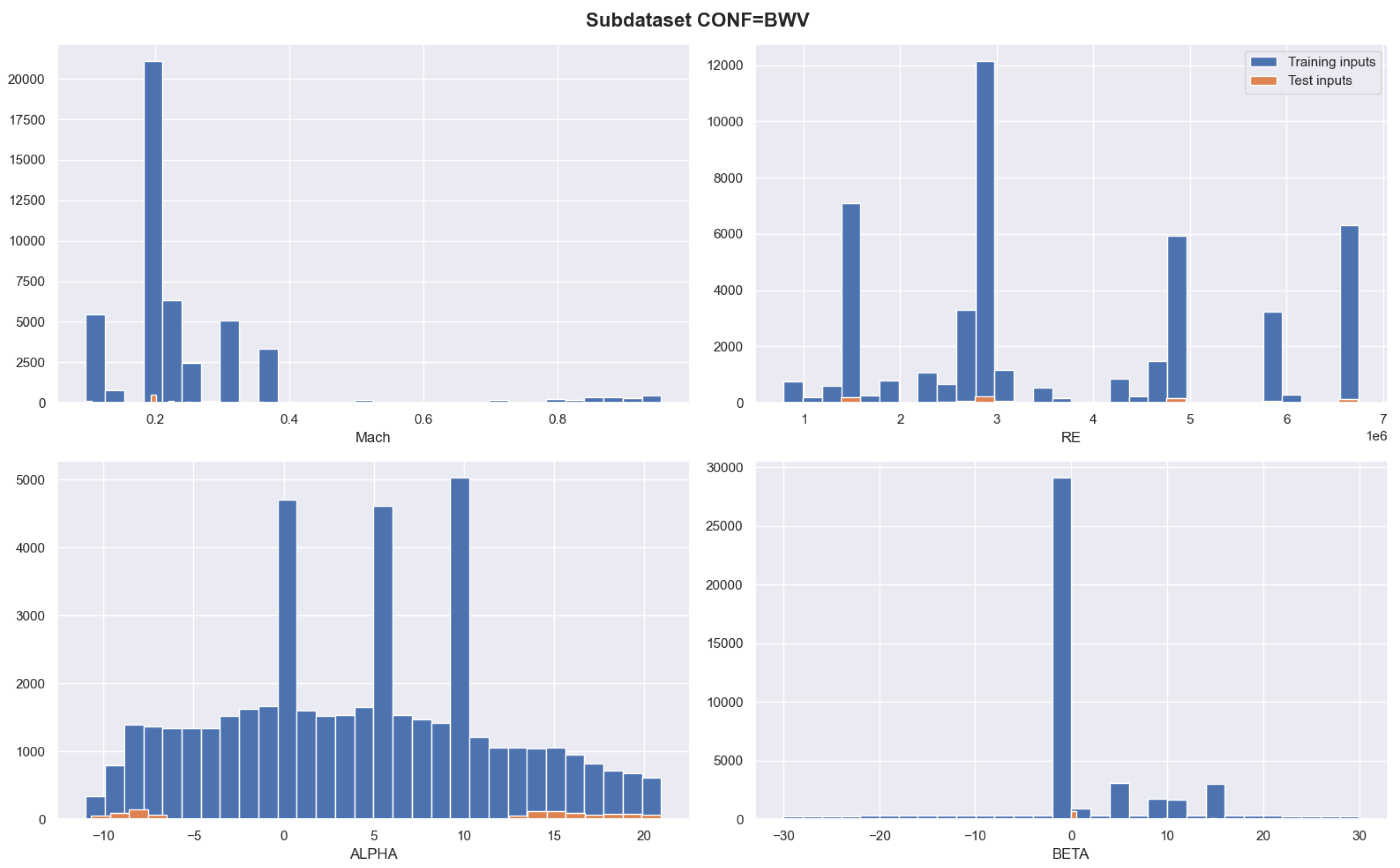
5.1. Database Description
- Four inputs corresponding to the Mach number (), the Reynolds number (), the angle of attack ( [deg]), and the sideslip angle ( [deg]). Pairwise histograms for those input parameters can be found in [7].
- Three outputs describing the drag coefficient (), the lift coefficient (), and the pitch moment coefficient ().
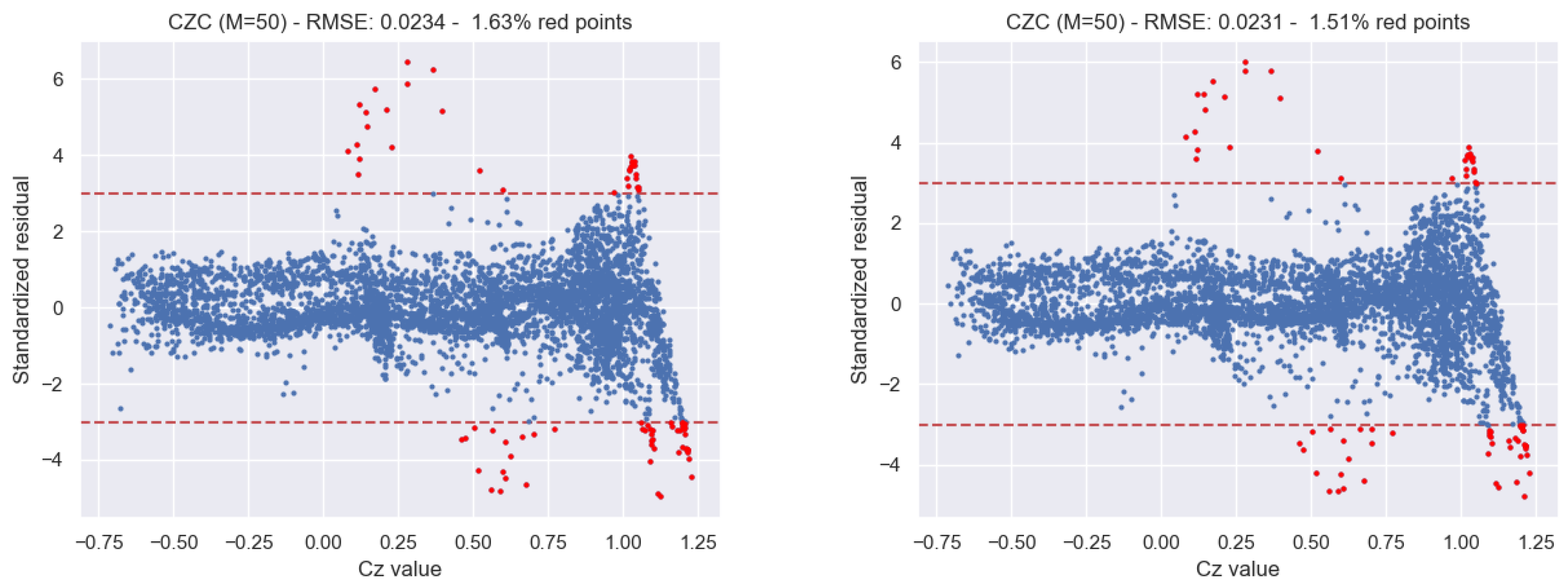
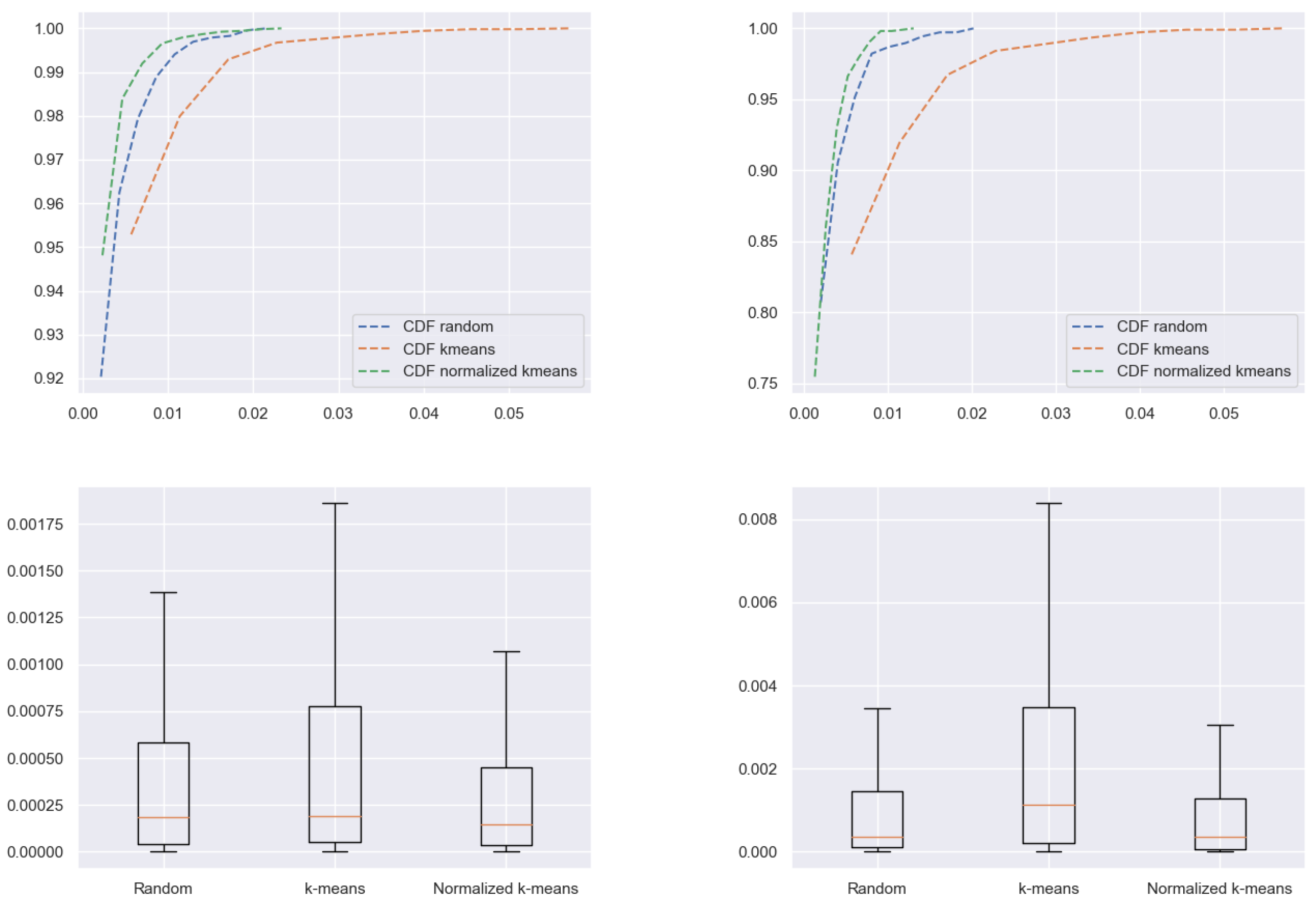
5.2. Results Analysis
5.3. Results on a Testing Subset
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HPC | High-Performance Computing |
| GP | Gaussian Process |
| SGP | Sparse Gaussian Process |
| NMLL | Negative Marginal Log-Likelihood |
| FITC | Fully Independent Training Conditional |
| VFE | Variational Free Energy |
| KL | Kullback–Leibler |
| ELBO | Evidence Lower Bound |
| SMT | Surrogate Modeling Toolbox |
| DoE | Design of Experiments |
| RMSE | Root Mean Square Error |
| WT | Wind Tunnel |
| CRM | Common Reference Model |
| CFD | Computational Fluid Dynamics |
Appendix A
Appendix A.1. Implementations of the FITC and VFE Methods in SMT
- The log-determinant term can be rewritten as:where is a diagonal matrix whithatch refers to either or . Applying the matrix determinant lemma, we then have:Hence, using the Cholesky decomposition , it can be shown that the log-determinant term can also be expressed as:where is the vector containing the diagonal terms of , whose computations are straightforward but slightly different between the FITC and VFE methods given their respective definitions.
- The quadratic term, also referred to as the “Mahalanobis” term, is computed using the Woodbury matrix identity to obtain the inverse of :Thus, as is a diagonal matrix, we can simply replace it with the inverse of the vector computed beforehand. By relying again on the factorization of matrix , we can still gain in efficiency by noticing the following:Hence, the computation is straightforward, as we only need to compute the inverse of vector and of triangular factor .
- The trace term (only appearing in the VFE method) does not present any particular difficulty; relying on the Cholesky decomposition of , we obtain the following:
Appendix A.2. Complementary Results
Appendix A.2.1. Analytic Example
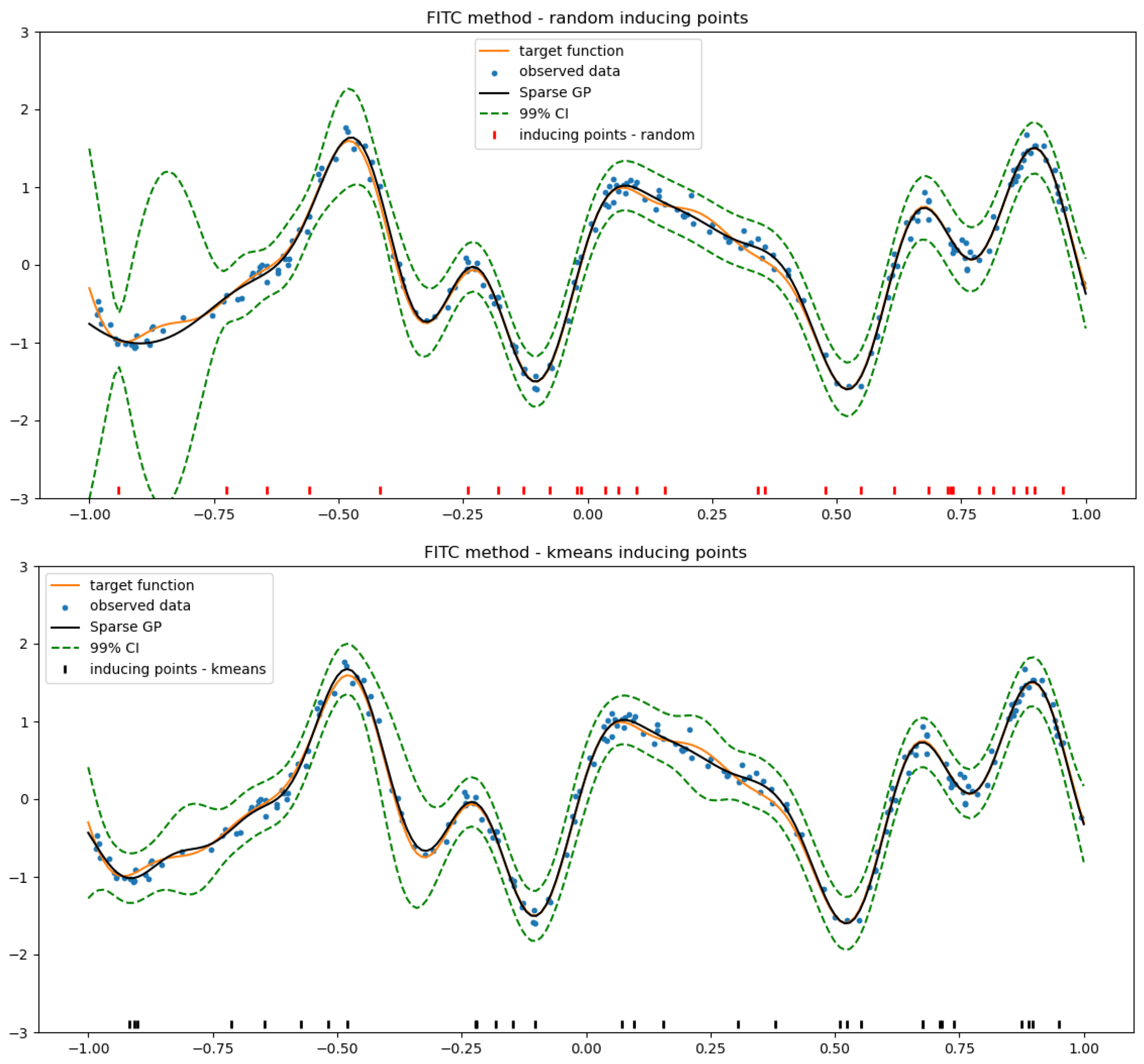
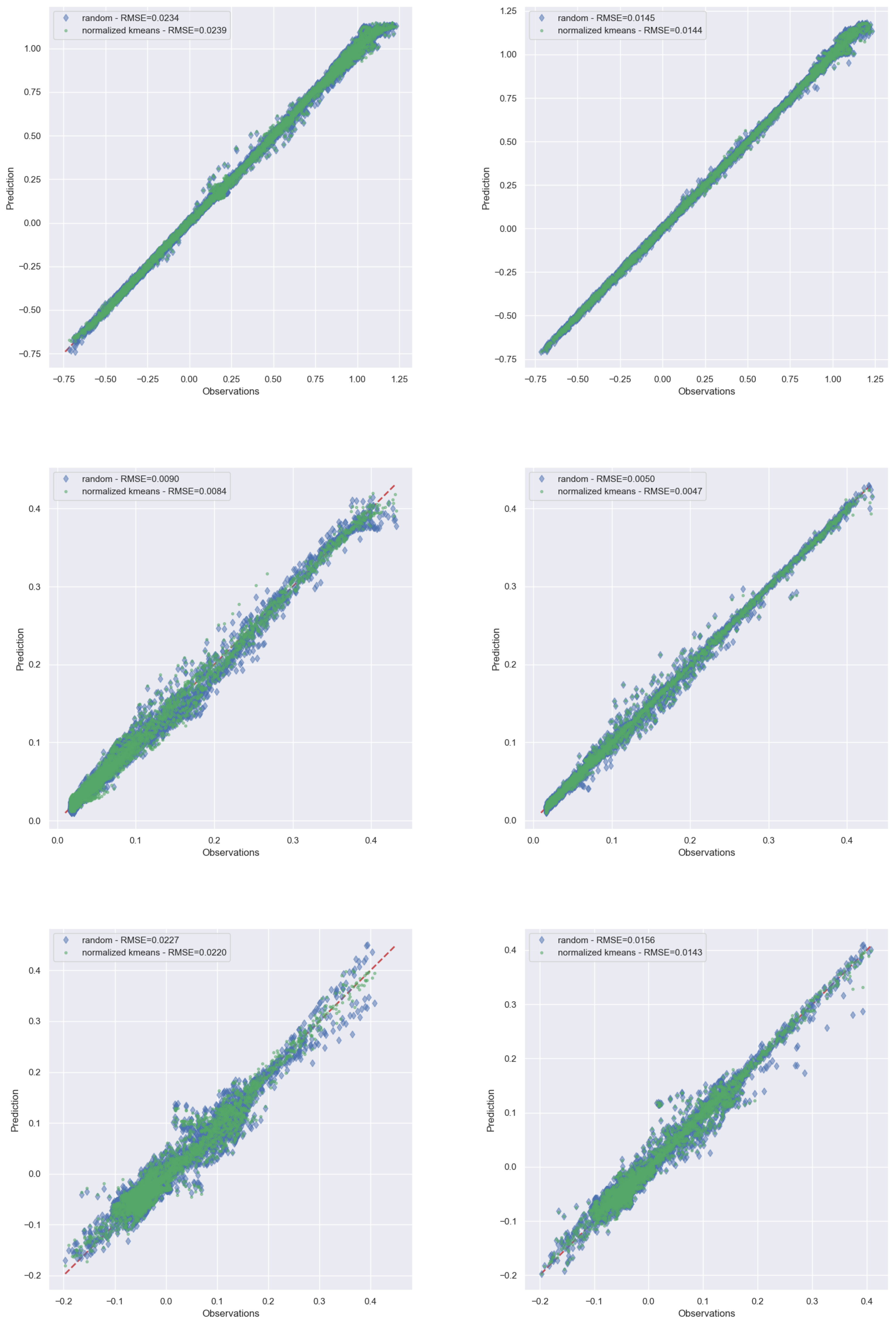
Appendix A.2.2. WT Application
References
- Svendsen, D.H.; Martino, L.; Camps-Valls, G. Active Emulation of Computer Codes with Gaussian Processes— Application to Remote Sensing. Pattern Recognit. 2020, 100, 107103. [Google Scholar] [CrossRef]
- Slotnick, J.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavripilis, D. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences. In NASA Technical Report; NASA/CR-2014-218178; NASA: Washington, DC, USA, 2014; pp. 1–51. [Google Scholar]
- Malik, M.; Bushnell, D. Role of Computational Fluid Dynamics andWind Tunnels in Aeronautics R and D. In NASA Technical Report; NASA/TP–2012-217602; NASA: Washington, DC, USA, 2012; pp. 1–63. [Google Scholar]
- Yondo, R.; Bobrowski, K.; Andres, E.; Valero, E. A Review of Surrogate Modeling Techniques for Aerodynamic Analysis and Optimization: Current Limitations and Future Challenges in Industry. In Advances in Evolutionary and Deterministic Methods for Design, Optimization and Control in Engineering and Sciences; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 19–33. [Google Scholar]
- Andrés-Pérez, E.; Paulete-Periáñez, C. On the Application of Surrogate Regression Models for Aerodynamic Coefficient Prediction. Complex Intell. Syst. 2021, 7, 1991–2021. [Google Scholar] [CrossRef]
- Giangaspero, G.; MacManus, D.; Goulos, I. Surrogate Models for the Prediction of the Aerodynamic Performance of Exhaust Systems. Aerosp. Sci. Technol. 2019, 92, 77–90. [Google Scholar] [CrossRef]
- Arenzana, R.C.; López-lopera, A.F.; Mouton, S.; Bartoli, N.; Lefebvre, T. Multi-Fidelity Gaussian Process Model for CFD and Wind Tunnel Data Fusion. In Proceedings of the Aerobest (An ECCOMAS Conference on Multidisciplinary Design Optimization of Aerospace Systems), Lisbon, Portugal (online conference), 21–23 July 2021; pp. 98–119. [Google Scholar]
- López-Lopera, A.F.; Idier, D.; Rohmer, J.; Bachoc, F. Multioutput Gaussian Processes with Functional Data: A Study on Coastal Flood Hazard Assessment. Reliab. Eng. Syst. Saf. 2022, 218, 108139. [Google Scholar] [CrossRef]
- Forrester, A.; Sobester, A.; Keane, A. Multi-Fidelity Optimization via Surrogate Modelling. Proc. R. Soc. A 2007, 463, 3251–3269. [Google Scholar] [CrossRef]
- Fu, W.; Chen, Z.; Luo, J. Aerodynamic Uncertainty Quantification of a Low-Pressure Turbine Cascade by an Adaptive Gaussian Process. Aerospace 2023, 10, 1022. [Google Scholar] [CrossRef]
- Pham, V.; Tyan, M.; Nguyen, T.A.; Lee, J.W. Extended Hierarchical Kriging Method for Aerodynamic Model Generation Incorporating Multiple Low-Fidelity Datasets. Aerospace 2024, 11, 6. [Google Scholar] [CrossRef]
- Meliani, M.; Bartoli, N.; Lefebvre, T.; Bouhlel, M.; Martins, J.; Morlier, J. Multi-Fidelity Efficient Global Optimization: Methodology and Application to Airfoil Shape Design. In Proceedings of the AIAA Aviation Forum, Dallas, TX, USA, 17–21 June 2019; pp. 1–18. [Google Scholar]
- Rasmussen, C.; Williams, C. Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning); The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Quiñonero Candela, J.; Rasmussen, C. A Unifying View of Sparse Approximate Gaussian Process Regression. J. Mach. Learn. Res. 2005, 6, 1939–1959. [Google Scholar]
- Snelson, E.; Ghahramani, Z. Sparse Gaussian Processes using Pseudo-inputs. Adv. Neural Inf. Process. Syst. 2005, 18, 1257–1264. [Google Scholar]
- Titsias, M.K. Variational Learning of Inducing Variables in Sparse Gaussian Processes. J. Mach. Learn. Res. Proc. Track 2009, 5, 567–574. [Google Scholar]
- Van Der Wilk, M. Sparse Gaussian Process Approximations and Applications. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2019. [Google Scholar]
- Liu, H.; Ong, Y.S.; Shen, X.; Cai, J. When Gaussian Process Meets Big Data: A Review of Scalable GPs. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4405–4423. [Google Scholar] [CrossRef] [PubMed]
- Bouhlel, M.A.; Hwang, J.T.; Bartoli, N.; Lafage, R.; Morlier, J.; Martins, J.R. A Python Surrogate Modeling Framework with Derivatives. Adv. Eng. Softw. 2019, 135, 102662. [Google Scholar] [CrossRef]
- Titsias, M.K. Variational Model Selection for Sparse Gaussian Process Regression; Technical report; University of Manchester, School of Computer Science: Manchester, UK, 2009. [Google Scholar]
- Bauer, M.; van der Wilk, M.; Rasmussen, C.E. Understanding Probabilistic Sparse Gaussian Process Approximations. In Advances in Neural Information Processing Systems; Lee, D., Sugiyama, M., Luxburg, U., Guyon, I., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, New York, USA, 2016; Volume 29. [Google Scholar]
- Saves, P.; Lafage, R.; Bartoli, N.; Diouane, Y.; Bussemaker, J.; Lefebvre, T.; Hwang, J.T.; Morlier, J.; Martins, J.R. SMT 2.0: A Surrogate Modeling Toolbox with a Focus on Hierarchical and Mixed Variables Gaussian Processes. Adv. Eng. Softw. 2024, 188, 103571. [Google Scholar] [CrossRef]
- GPy: A Gaussian Process Framework in Python. 2012. Available online: https://gpy.readthedocs.io/en/deploy/ (accessed on 10 January 2024).
- Matthews, A.G.d.G.; van der Wilk, M.; Nickson, T.; Fujii, K.; Boukouvalas, A.; León-Villagrá, P.; Ghahramani, Z.; Hensman, J. GPflow: A Gaussian Process Library using TensorFlow. J. Mach. Learn. Res. 2017, 18, 1–6. [Google Scholar]
- Hensman, J.; Fusi, N.; Lawrence, N.D. Gaussian Processes for Big Data. In Proceedings of the Twenty-Ninth Conference on Uncertainty in Artificial Intelligence, Arlington, VA, USA, 11–15 July 2013; pp. 282–290. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; AAAI Press: Washington, DC, USA, 1996. KDD’96. pp. 226–231. [Google Scholar]
- Vassberg, J.; Dehaan, M.; Rivers, M.; Wahls, R. Development of a Common Research Model for Applied CFD Validation Studies. In Proceedings of the 26th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 18–21 August 2008; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2008; pp. 1–22. [Google Scholar]
- Carrara, J.; Masson, A. Three Years of Operation of the ONERA Pressurized Subsonic Wind Tunnel. In Proceedings of the 12th Congress of the International Council of the Aeronautical Sciences, Munich, Germany, 12–17 October 1980; pp. 778–792. [Google Scholar]
- Cartieri, A.; Hue, D.; Chanzy, A.; Atinault, O. Experimental Investigations on Common Research Model at ONERA-S1MA–Drag Prediction Workshop Numerical Results. J. Aircr. 2017, 55, 1491–1508. [Google Scholar] [CrossRef]
- Rivers, M.; Dittberner, A. Experimental Investigation of the NASA Common Research Model. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June–1 July 2010; pp. 1–29. [Google Scholar]
- Rivers, M.; Quest, J.; Rudnik, R. Comparison of the NASA Common Research Model European Transonic Wind Tunnel Test Data to NASA National Transonic Facility Test Data. Ceas Aeronaut. J. 2018, 9, 307–317. [Google Scholar] [CrossRef]
- Hantrais-Gervois, J.; Piat, J. A Methodology to Derive Wind Tunnel Wall Corrections from RANS Simulations. In Proceedings of the Advanced Wind Tunnel Boundary Simulation, ST0/NATO, Torino, Italy, 16–18 April 2018; pp. 1–24. [Google Scholar]
- Cartieri, A.; Hue, D. Using RANS Computations to Calculate Support Interference Effects on the Common Research Model. In Proceedings of the Advanced Wind Tunnel Boundary Simulation, ST0/NATO, Torino, Italy, 16–18 April 2018; pp. 1–18. [Google Scholar]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Bertram, A.; Zimmermann, R. Theoretical Investigations of the New CoKriging Method for Variable-Fidelity Surrogate Modeling: Well-Posedness and Maximum Likelihood Training. Adv. Comput. Math. 2018, 44, 1693–1716. [Google Scholar] [CrossRef]
- Stradtner, M.; Liersch, C.; Bekemeyer, P. An Aerodynamic Variable-Fidelity Modelling Framework for a Low-Observable UCAV. Aerosp. Sci. Technol. 2020, 107, 106232. [Google Scholar] [CrossRef]
- Bekemeyer, P.; Bertram, A.; Hines Chaves, D.A.; Dias Ribeiro, M.; Garbo, A.; Kiener, A.; Sabater, C.; Stradtner, M.; Wassing, S.; Widhalm, M.; et al. Data-driven aerodynamic modeling using the DLR SMARTy toolbox. In Proceedings of the AIAA Aviation 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022; p. 3899. [Google Scholar]

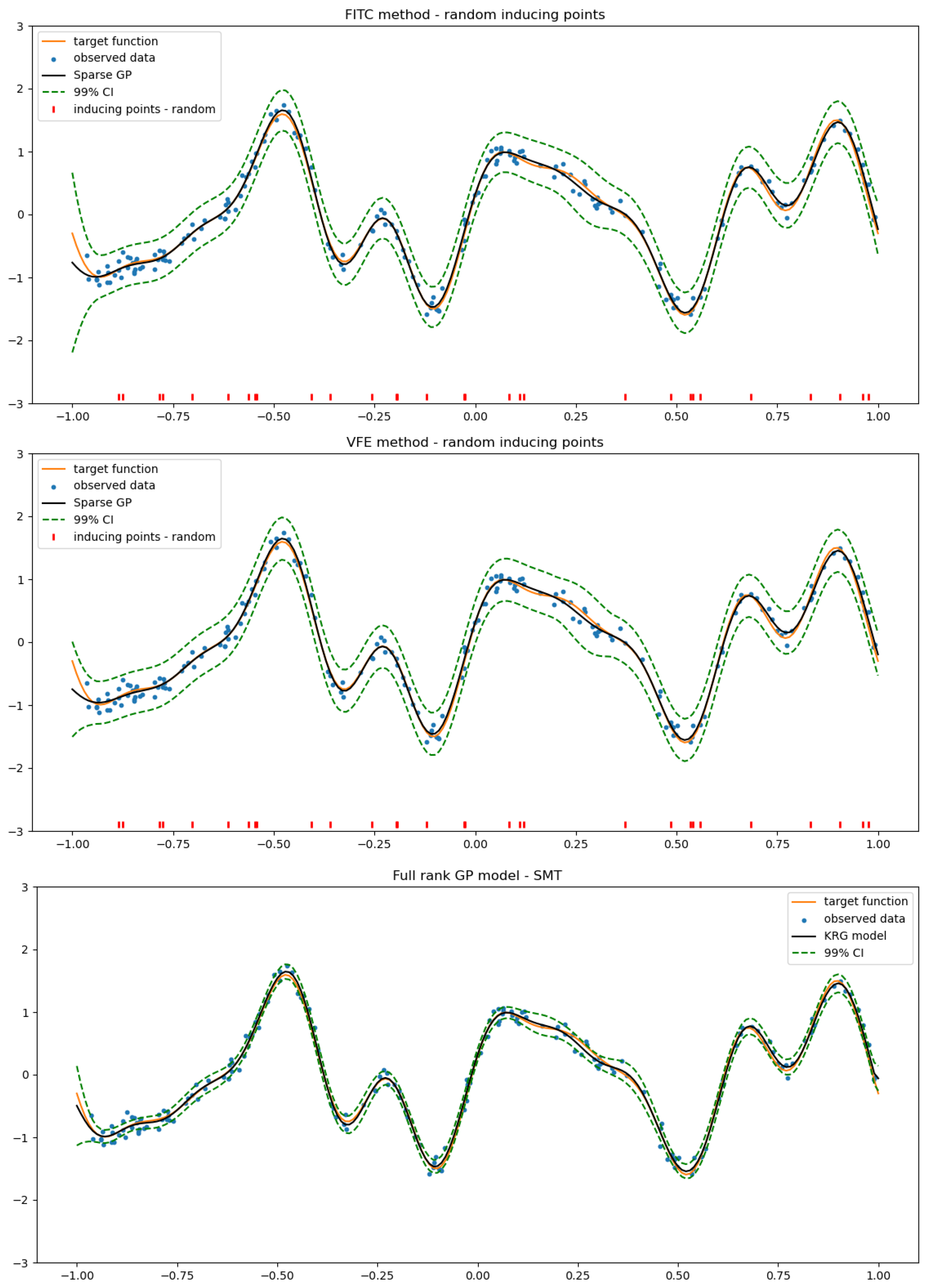

| SGP-FITC | SGP-VFE | Exact GP | |
|---|---|---|---|
| Optimal | 4.78 | 0.81 | 0.88 |
| Optimal | 37.04 | 44.80 | 20.96 |
| Optimal (noise) | 0.010 | 0.012 | 0.011 |
| Training time [s] | 0.19 | 0.18 | 0.42 |
| Optimal likelihood | 280.11 | 266.99 | 303.90 |
| RMSE-training data | 0.0962 | 0.0969 | 0.0945 |
| RMSE-test data | 0.1105 | 0.1092 | 0.1050 |
| SGP-FITC | SGP-VFE | Exact GP | |
|---|---|---|---|
| Optimal | 0.70 | 0.80 | 0.88 |
| Optimal | 56.84 | 54.42 | 20.96 |
| Optimal (noise) | 0.010 | 0.013 | 0.011 |
| Training time [s] | 0.19 | 0.18 | 0.42 |
| Optimal likelihood | 282.99 | 276.63 | 303.90 |
| RMSE-training data | 0.0966 | 0.0964 | 0.0945 |
| RMSE-test data | 0.1153 | 0.1115 | 0.1050 |
| SGP-FITC | SGP-VFE | |||||
| Random | k-Means | k-Means-n | Random | k-Means | k-Means-n | |
| Likelihood | 150,709 | 147,636 | 150,614 | 147,646 | 137,891 | 147,919 |
| RMSE-training data | 0.0257 | 0.0262 | 0.0246 | 0.0248 | 0.0314 | 0.0251 |
| RMSE-test data | 0.0267 | 0.0267 | 0.0249 | 0.0247 | 0.0314 | 0.0248 |
| Inducing time | ≈0 | 5 | 10 | ≈0 | 7 | 9 |
| Training time | 19 | 19 | 20 | 19 | 19 | 19 |
| Prediction time | 0.02 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 |
| Likelihood (🡹) | 161,201 | 155,554 | 157,966 | 156,422 | 148,673 | 158,380 |
| RMSE-training data (🡻) | 0.0205 | 0.0227 | 0.0209 | 0.0205 | 0.0240 | 0.0202 |
| RMSE-test data (🡻) | 0.0206 | 0.0222 | 0.0212 | 0.0203 | 0.0237 | 0.0201 |
| Inducing time (🡹) | ≈0 | 24 | 18 | ≈0 | 33 | 19 |
| Training time (🡹) | 40 | 40 | 42 | 56 | 40 | 38 |
| Prediction time (🡹) | 0.03 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 |
| Likelihood (🡹) | 172,894 | 171,246 | 173,187 | 171,502 | 161,872 | 172,228 |
| RMSE-training data (🡻) | 0.0145 | 0.0179 | 0.0148 | 0.0147 | 0.0177 | 0.0145 |
| RMSE-test data (🡻) | 0.0150 | 0.0175 | 0.0148 | 0.0151 | 0.0174 | 0.0148 |
| Inducing time (🡹) | ≈0 | 333 | 90 | ≈0 | 326 | 89 |
| Training time (🡹) | 218 | 219 | 219 | 213 | 213 | 213 |
| Prediction time (🡹) | 0.17 | 0.17 | 0.17 | 0.17 | 0.17 | 0.17 |
| Likelihood (🡹) | 172,704 | 173,003 | 175,620 | 172,884 | 165,026 | 175,077 |
| RMSE-training data (🡻) | 0.0144 | 0.0157 | 0.0134 | 0.0143 | 0.0165 | 0.0136 |
| RMSE-test data (🡻) | 0.0147 | 0.0155 | 0.0138 | 0.0147 | 0.0162 | 0.0140 |
| Inducing time (🡹) | ≈0 | 319 | 127 | ≈0 | 296 | 125 |
| Training time (🡹) | 471 | 472 | 475 | 464 | 471 | 461 |
| Prediction time (🡹) | 0.34 | 0.34 | 0.34 | 0.34 | 0.36 | 0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valayer, H.; Bartoli, N.; Castaño-Aguirre, M.; Lafage, R.; Lefebvre, T.; López-Lopera, A.F.; Mouton, S. A Python Toolbox for Data-Driven Aerodynamic Modeling Using Sparse Gaussian Processes. Aerospace 2024, 11, 260. https://doi.org/10.3390/aerospace11040260
Valayer H, Bartoli N, Castaño-Aguirre M, Lafage R, Lefebvre T, López-Lopera AF, Mouton S. A Python Toolbox for Data-Driven Aerodynamic Modeling Using Sparse Gaussian Processes. Aerospace. 2024; 11(4):260. https://doi.org/10.3390/aerospace11040260
Chicago/Turabian StyleValayer, Hugo, Nathalie Bartoli, Mauricio Castaño-Aguirre, Rémi Lafage, Thierry Lefebvre, Andrés F. López-Lopera, and Sylvain Mouton. 2024. "A Python Toolbox for Data-Driven Aerodynamic Modeling Using Sparse Gaussian Processes" Aerospace 11, no. 4: 260. https://doi.org/10.3390/aerospace11040260
APA StyleValayer, H., Bartoli, N., Castaño-Aguirre, M., Lafage, R., Lefebvre, T., López-Lopera, A. F., & Mouton, S. (2024). A Python Toolbox for Data-Driven Aerodynamic Modeling Using Sparse Gaussian Processes. Aerospace, 11(4), 260. https://doi.org/10.3390/aerospace11040260







