Installed Fan Noise Simulation of a Supersonic Business Aircraft
Abstract
:1. Introduction
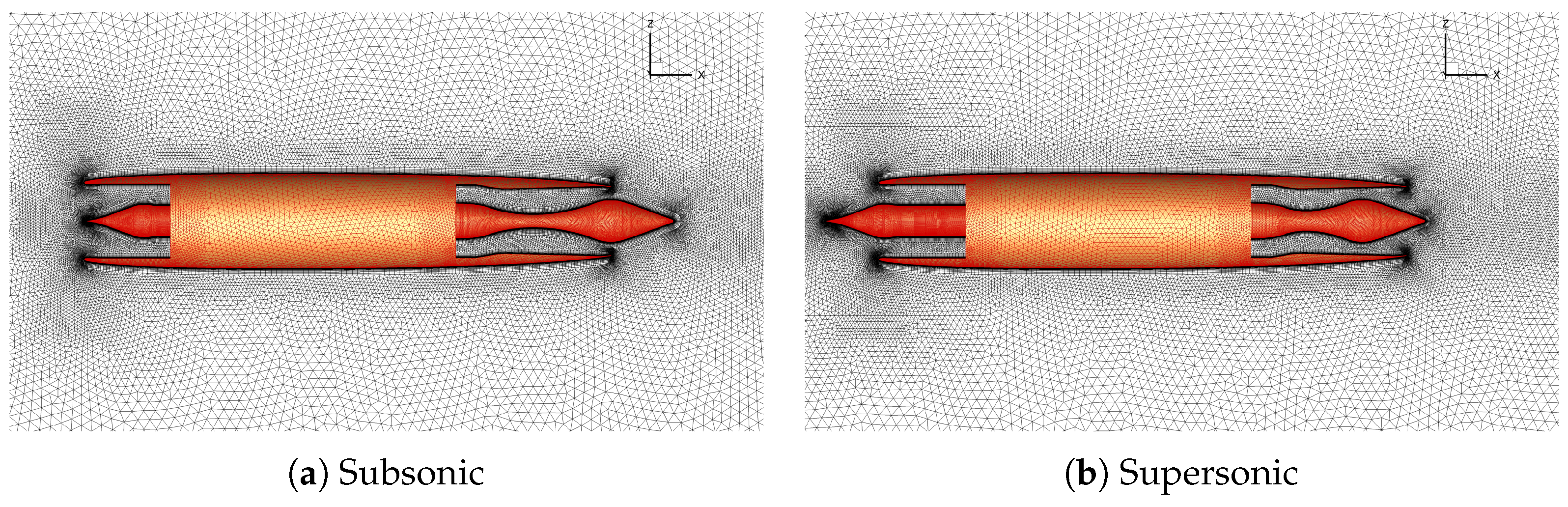
2. Geometry and Flow Simulations
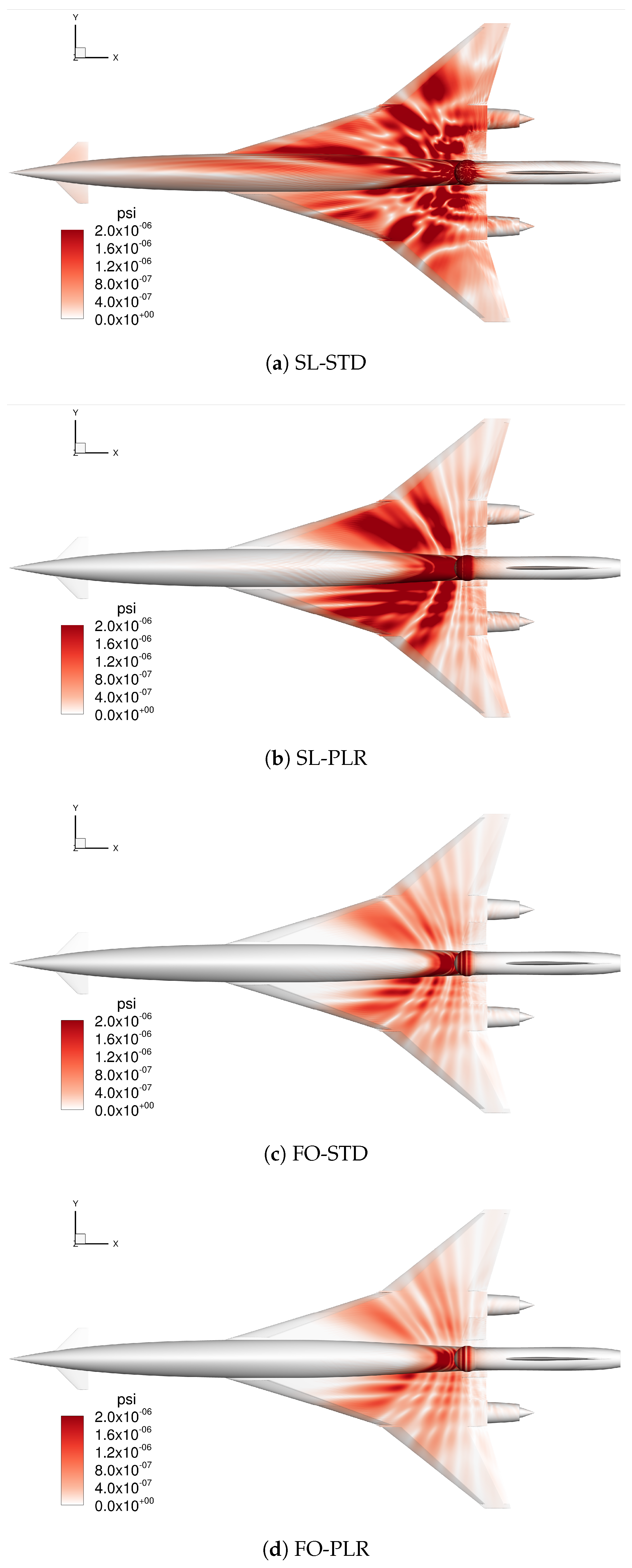
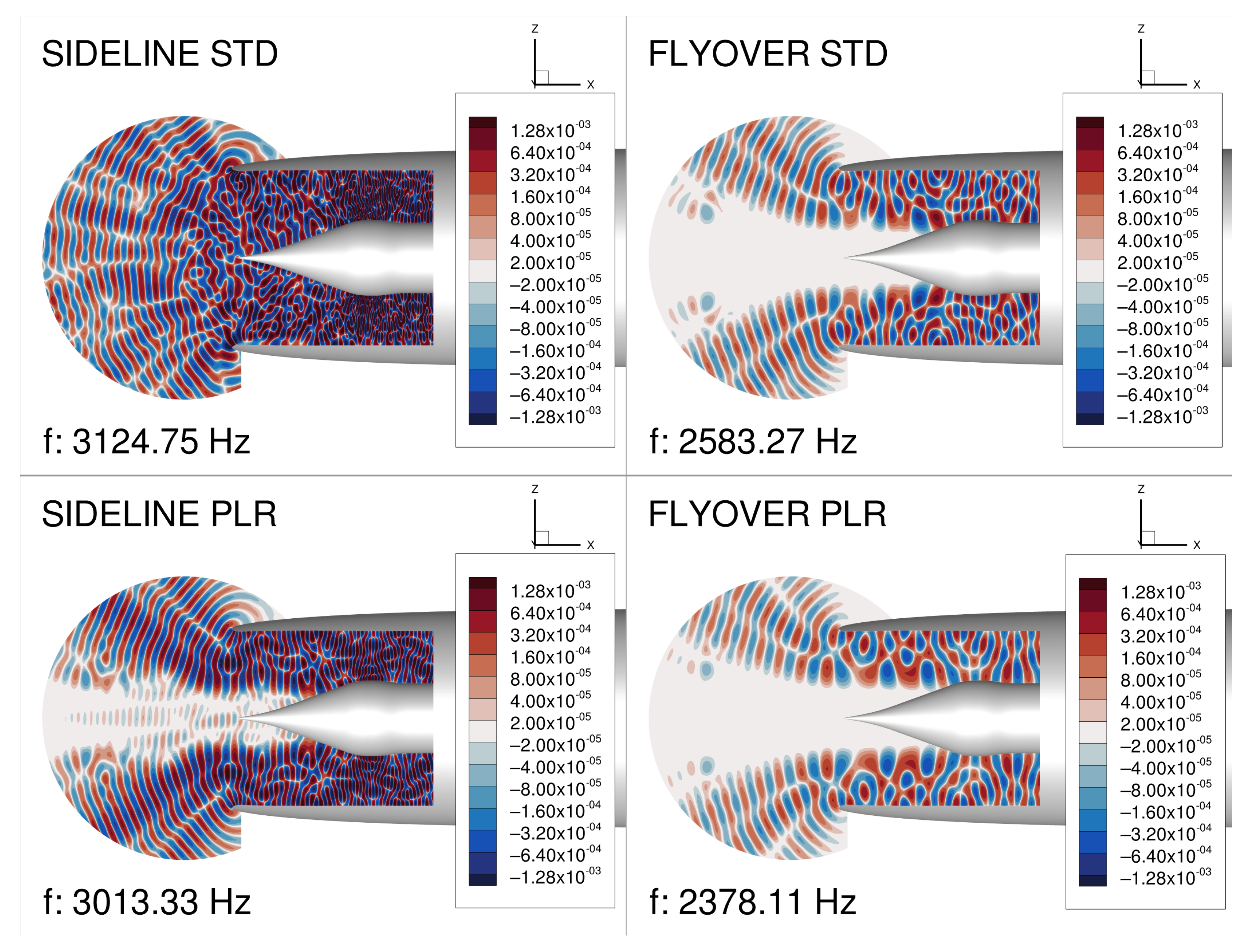
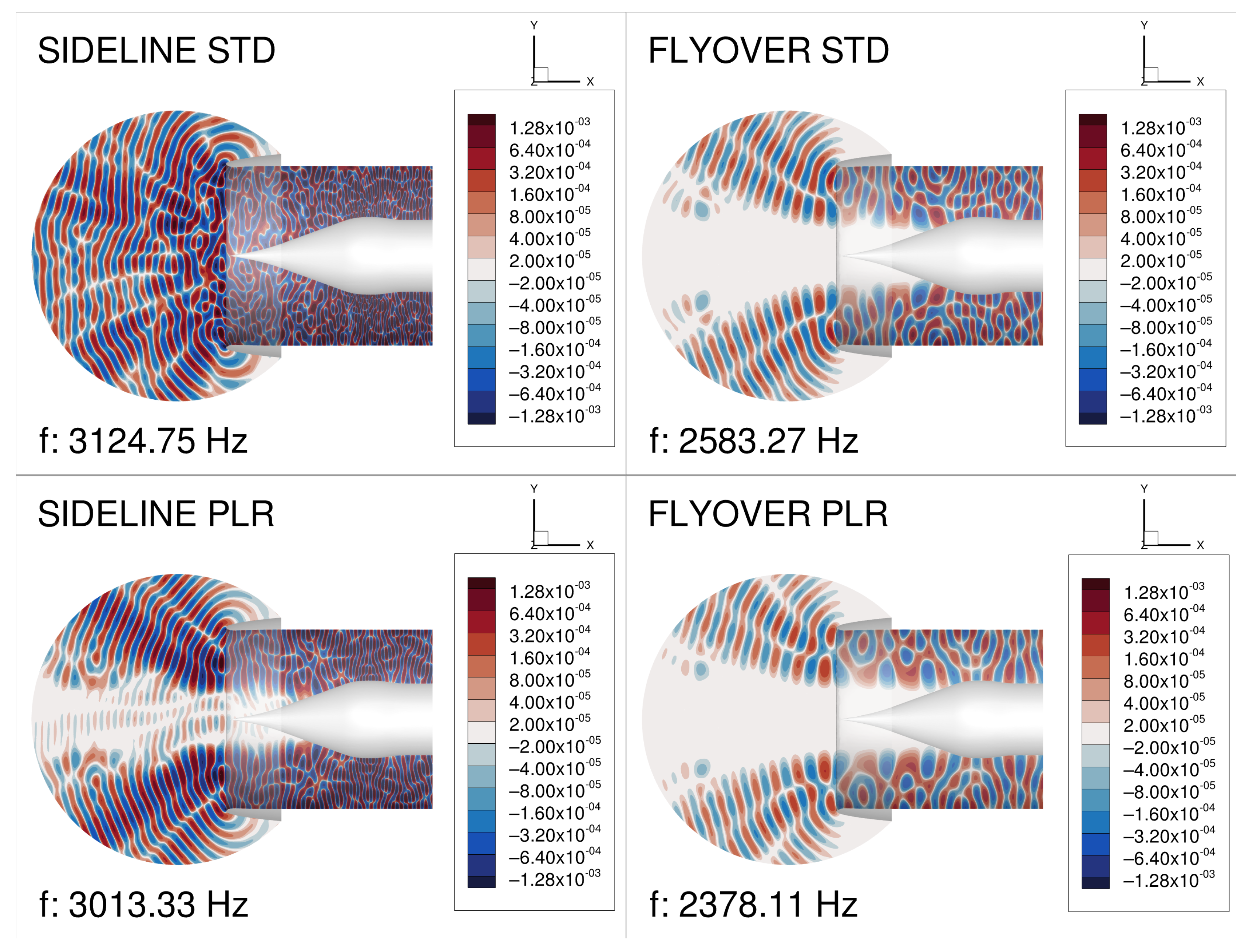
3. Volume-Resolving CAA
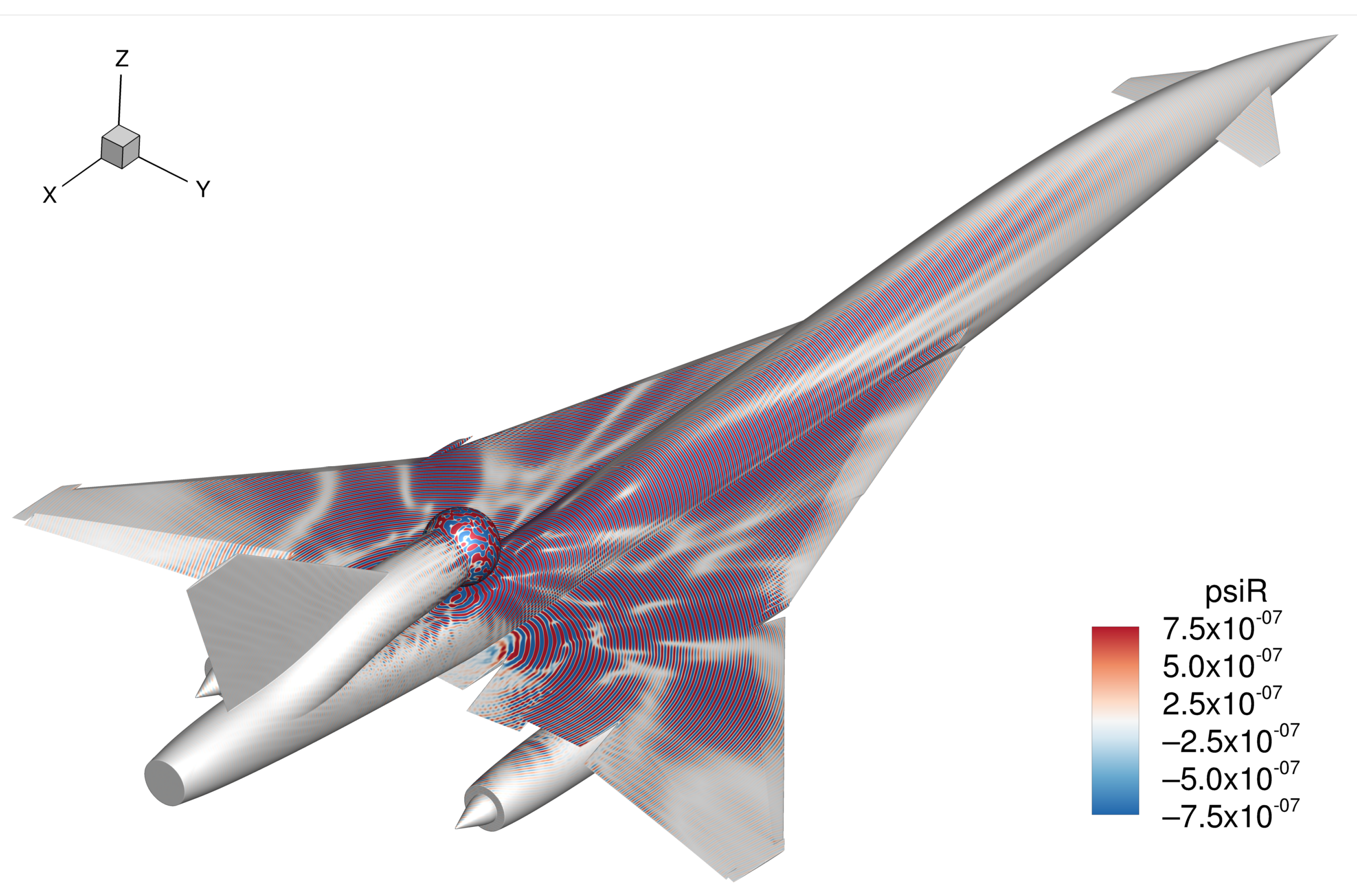
4. Coupled Solutions and Acoustic Scattering
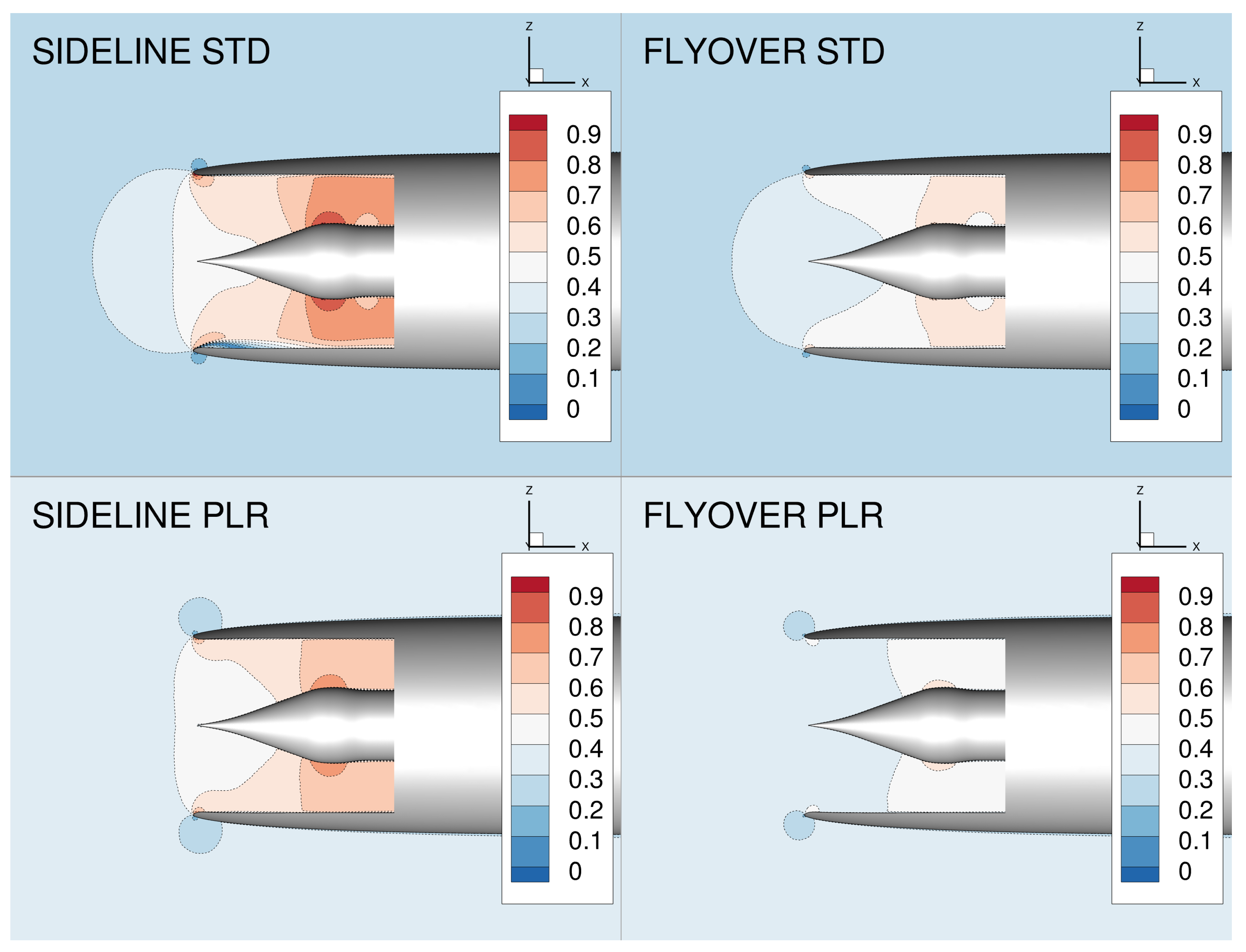
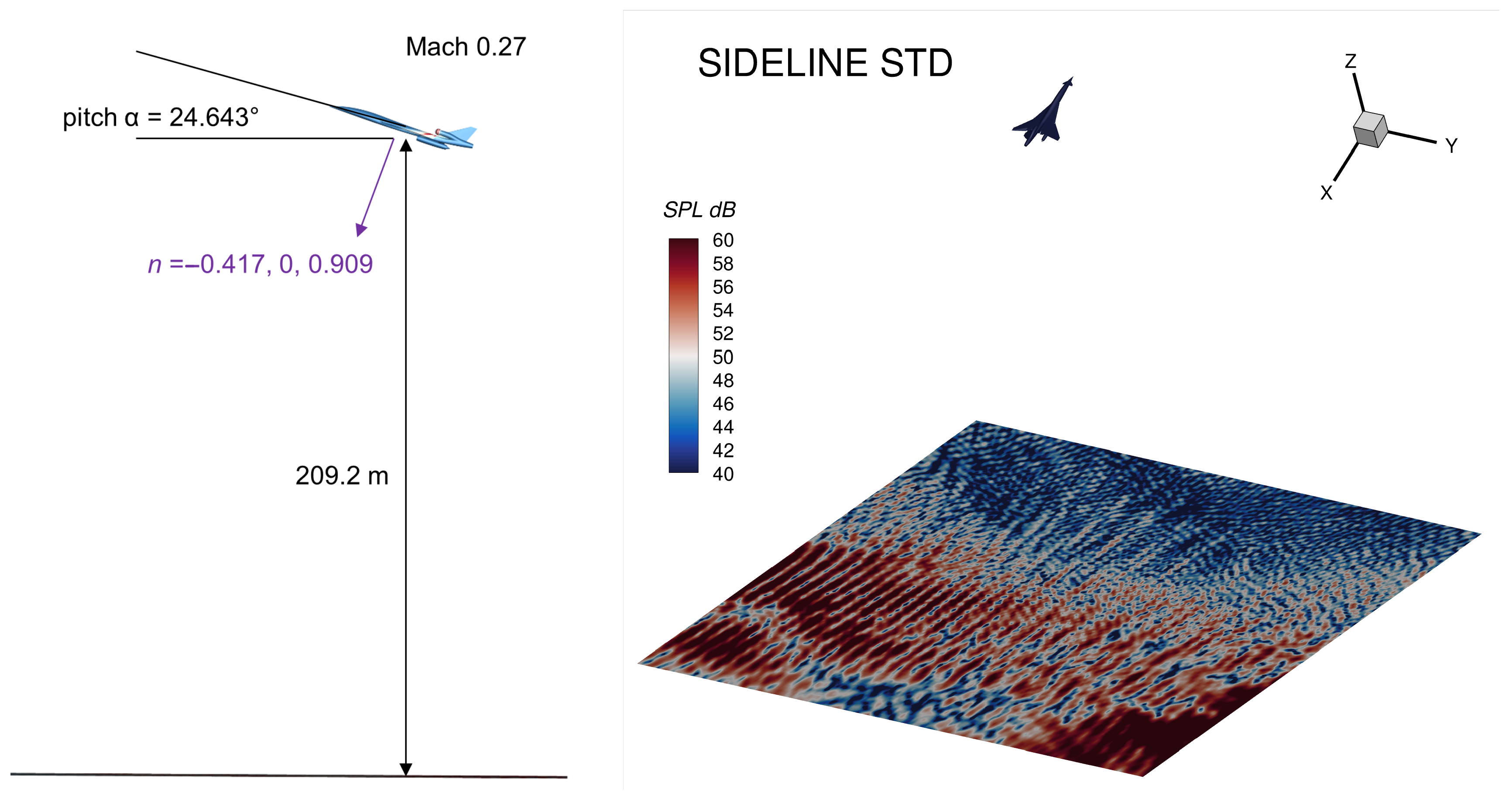
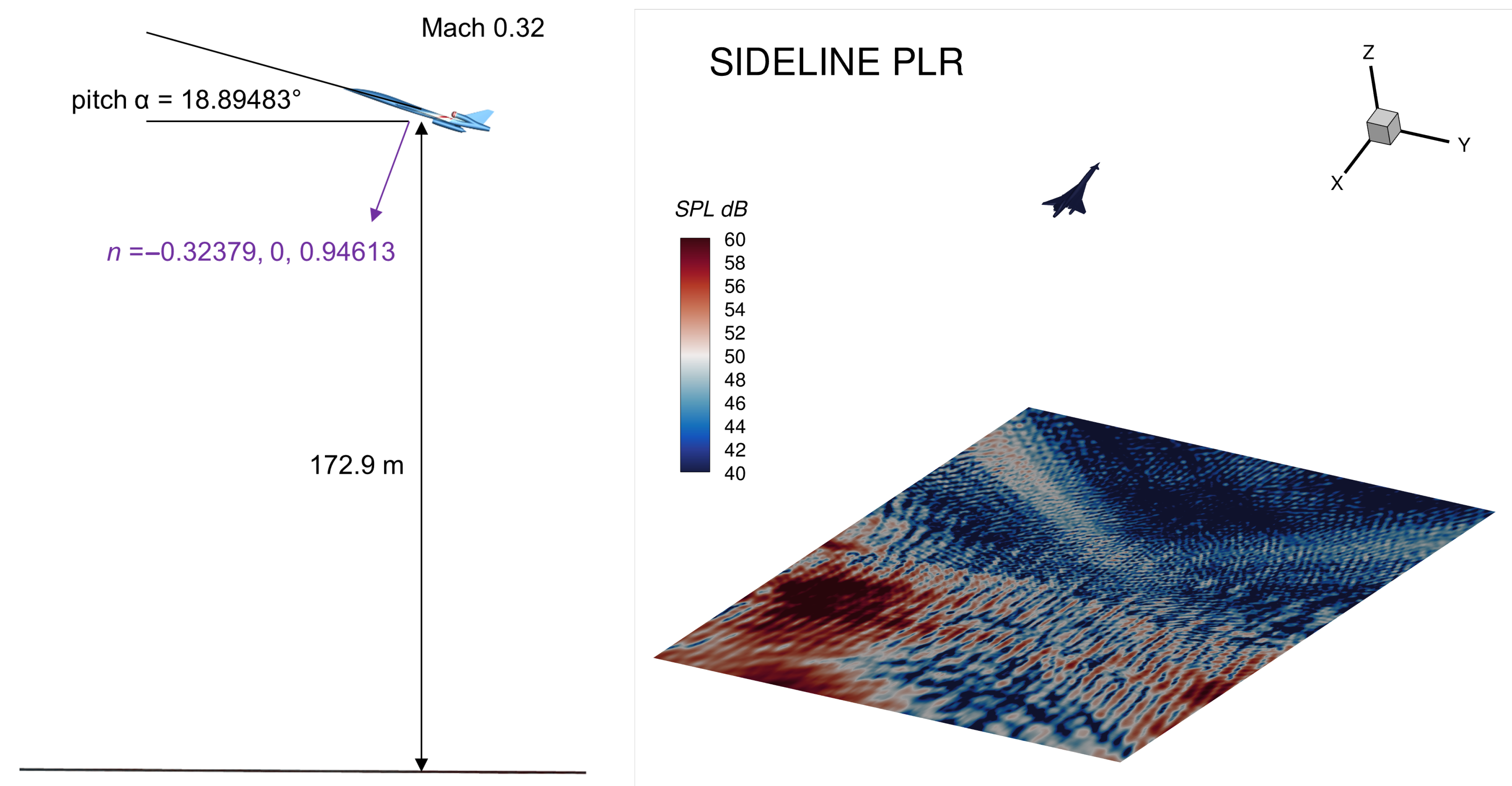
5. Far-Field Signature
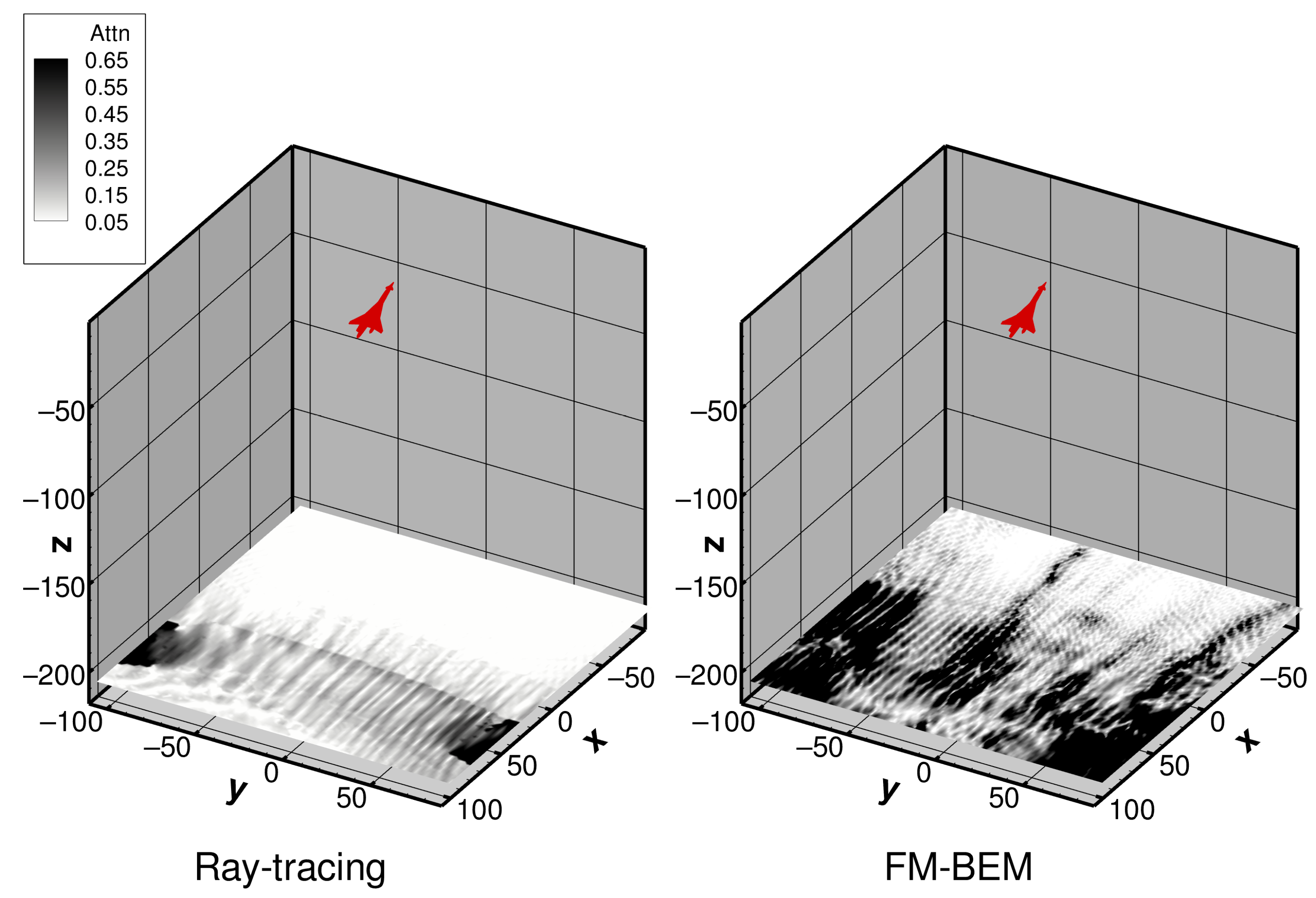
Ray-Tracing
6. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AIAA | American Institute of Aeronautics and Astronautics |
| APE | Acoustic perturbation equations |
| BMVI | German Federal Ministry of Transport and Digital Infrastructure |
| CAA | Computational aeroacoustics |
| CAD | Computer-aided design |
| CFD | Computational fluid dynamics |
| DG | Discontinuous Galerkin (method) |
| DISCO++ | Discontinuous Galerkin code on C++ |
| DLR | German Aerospace Center |
| EASA | European Aviation Safety Agency |
| ELTON | Estimation of landing and take-off noise |
| f | Frequency, Hz |
| FM-BEM | Fast multipole boundary element method |
| FMCAS | Fast multipole code for acoustic shielding |
| FMM | Fast multipole method |
| FO-STD | Standard flyover (test point) |
| GTlab | Gas turbine laboratory (software) |
| ICAO | International Civil Aviation Organization |
| JAXA | Japan Aerospace Exploration Agency |
| LTO | Landing and take-off |
| MDPI | Multidisciplinary Digital Publishing Institute |
| NASA | National Aeronautics and Space Administration |
| p | Pressure, Pa |
| PANAM | Parametric aircraft noise analysis module |
| PLR | Programmed lapse rate |
| ppw | Points per wavelength |
| PrADO | Preliminary aircraft design and optimization program |
| psi | Acoustic potential |
| psiR | Real part of acoustic potential |
| RANS | Reynolds-averaged Navier–Stokes |
| SL-STD | Standard sideline (test point) |
| SPL | Sound pressure level, dB |
| SST | Supersonic transport |
| STCA | Supersonic Technology Concept Aeroplane |
| TAU | DLR CFD software package |
Appendix A

References
- Berton, J.J.; Huff, D.L.; Geiselhart, K.; Seidel, J. Supersonic Technology Concept Aeroplanes for Environmental Studies. In Proceedings of the AIAA Scitech Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Akatsuka, J.; Ishii, T. System Noise Assessment of NASA Supersonic Technology Concept Aeroplane Using JAXA’s Noise Prediction Tool. In Proceedings of the AIAA Scitech Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Nöding, M.; Schuermann, M.; Bertsch, L.; Koch, M.; Plohr, M.; Jaron, R.; Berton, J.J. Simulation of Landing and Take-Off Noise for Supersonic Transport Aircraft at a Conceptual Design Fidelity Level. Aerospace 2022, 9, 9. [Google Scholar] [CrossRef]
- Bertsch, L. Noise Prediction within Conceptual Aircraft Design; Technical Report DLR-FB-2013-20; Deutsches Zentrum für Luft- und Raumfahrt (DLR): Göttingen, Germany, 2013. [Google Scholar]
- Moreau, A. A Unified Analytical Approach for the Acoustic Conceptual Design of Fans of Modern Aero-Engines. Ph.D. Thesis, Technical University-Berlin, Berlin, Germany, 2017. [Google Scholar]
- Ewert, R.; Schröder, W. Acoustic Perturbation Equations Based on Flow Decomposition via Source Filtering. J. Comput. Phys. 2003, 257, 627–644. [Google Scholar] [CrossRef]
- Mößner, M.; Delfs, J.; Kissner, C.; Enghardt, L. Computational chain for virtual fly-over simulations applied to fan noise. In Proceedings of the 24th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Lummer, M. Aircraft noise generation and assessment. Installation: Numerical investigation. CEAS Aeronaut. J. 2019, 10, 159–178. [Google Scholar] [CrossRef]
- Proskurov, S.; Ewert, R.; Lummer, M.; Mößner, M.; Delfs, J.W. Sound Shielding Simulation by Coupled Discontinuous Galerkin and Fast Boundary Element Methods. Eng. Appl. Comput. Fluid Mech. 2022, 16, 1690–1705. [Google Scholar] [CrossRef]
- Nöding, M.; Bertsch, L.; Kirz, J.; Ewert, R.; Berton, J.J. Application and comparison of proposed SST noise certification regulations to a conceptual business aircraft. In Proceedings of the AIAA Aviation Forum, San Diego, CA, USA, 12–16 June 2023. [Google Scholar]
- Schwamborn, D.; Gerhold, T.; Heinrich, R. The DLR TAU-Code: Recent Applications in Research and Industry. In Proceedings of the European Conference on Computational Fluid Dynamics, Egmond aan Zee, The Netherlands, 5–8 September 2006. [Google Scholar]
- Lummer, M. Maggi-Rubinowicz Diffraction Correction for Ray-Tracing Calculations of Engine Noise Shielding. In Proceedings of the 14th AIAA/CEAS Aeroacoustics Conference, Vancouver, BC, Canada, 5–7 May 2008. [Google Scholar]
- Taylor, K. A transformation of the acoustic equation with implications for wind-tunnel and low-speed flight tests. Proc. R. Soc. Lond. 1978, 363, 271–281. [Google Scholar]
- Liu, X.; Wu, H.; Jiang, W.; Sun, R. A fast multipole boundary element method for three-dimensional acoustic problems in a subsonic uniform flow. Int. J. Numer. Meth. Fluids 2021, 93, 1669–1689. [Google Scholar] [CrossRef]



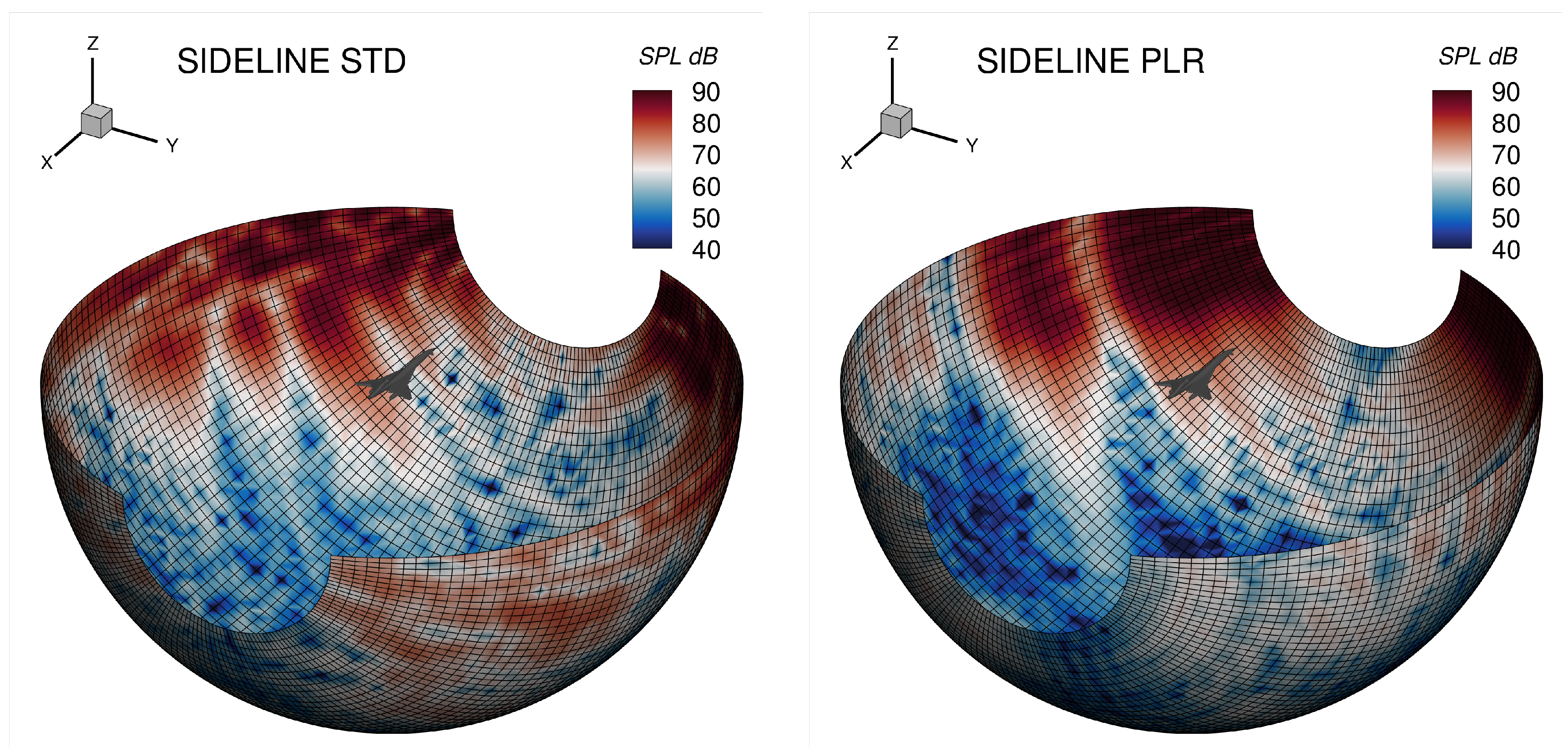

| Flight Point | Type | Centre | Normal | Longitudinal 1 | Transverse 1 |
|---|---|---|---|---|---|
| Sideline STD | Plane | 17.5, 0, −209.2 | −0.417, 0, 0.909 | 200 | 200 |
| Sideline STD | Hemisphere | 25, 0, 0 | r = 100 | ||
| Sideline PLR | Plane | 17.5, 0, −172.9 | −0.32379, 0, 0.94613 | 250 | 200 |
| Sideline PLR | Hemisphere | 25, 0, 0 | r = 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Proskurov, S.; Lummer, M.; Delfs, J.W.; Ewert, R.; Kirz, J.; Plohr, M.; Jaron, R. Installed Fan Noise Simulation of a Supersonic Business Aircraft. Aerospace 2023, 10, 773. https://doi.org/10.3390/aerospace10090773
Proskurov S, Lummer M, Delfs JW, Ewert R, Kirz J, Plohr M, Jaron R. Installed Fan Noise Simulation of a Supersonic Business Aircraft. Aerospace. 2023; 10(9):773. https://doi.org/10.3390/aerospace10090773
Chicago/Turabian StyleProskurov, Stan, Markus Lummer, Jan Werner Delfs, Roland Ewert, Jochen Kirz, Martin Plohr, and Robert Jaron. 2023. "Installed Fan Noise Simulation of a Supersonic Business Aircraft" Aerospace 10, no. 9: 773. https://doi.org/10.3390/aerospace10090773
APA StyleProskurov, S., Lummer, M., Delfs, J. W., Ewert, R., Kirz, J., Plohr, M., & Jaron, R. (2023). Installed Fan Noise Simulation of a Supersonic Business Aircraft. Aerospace, 10(9), 773. https://doi.org/10.3390/aerospace10090773







