Parametric Design Method and Lift/Drag Characteristics Analysis for a Wide-Range, Wing-Morphing Glide Vehicle
Abstract
1. Introduction
2. Design and Optimization of the Vehicle Shape
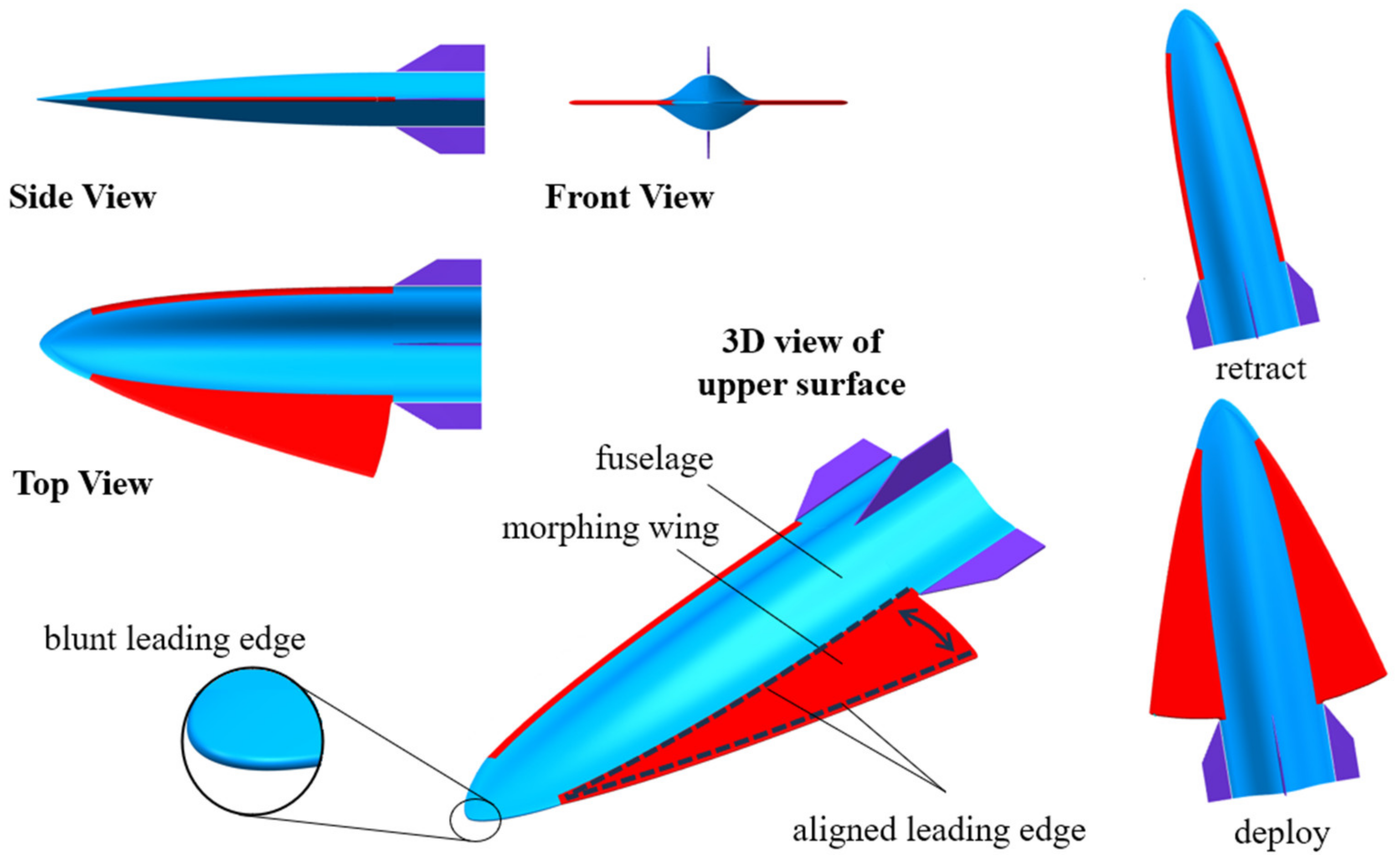
2.1. Aerodynamic Configuration
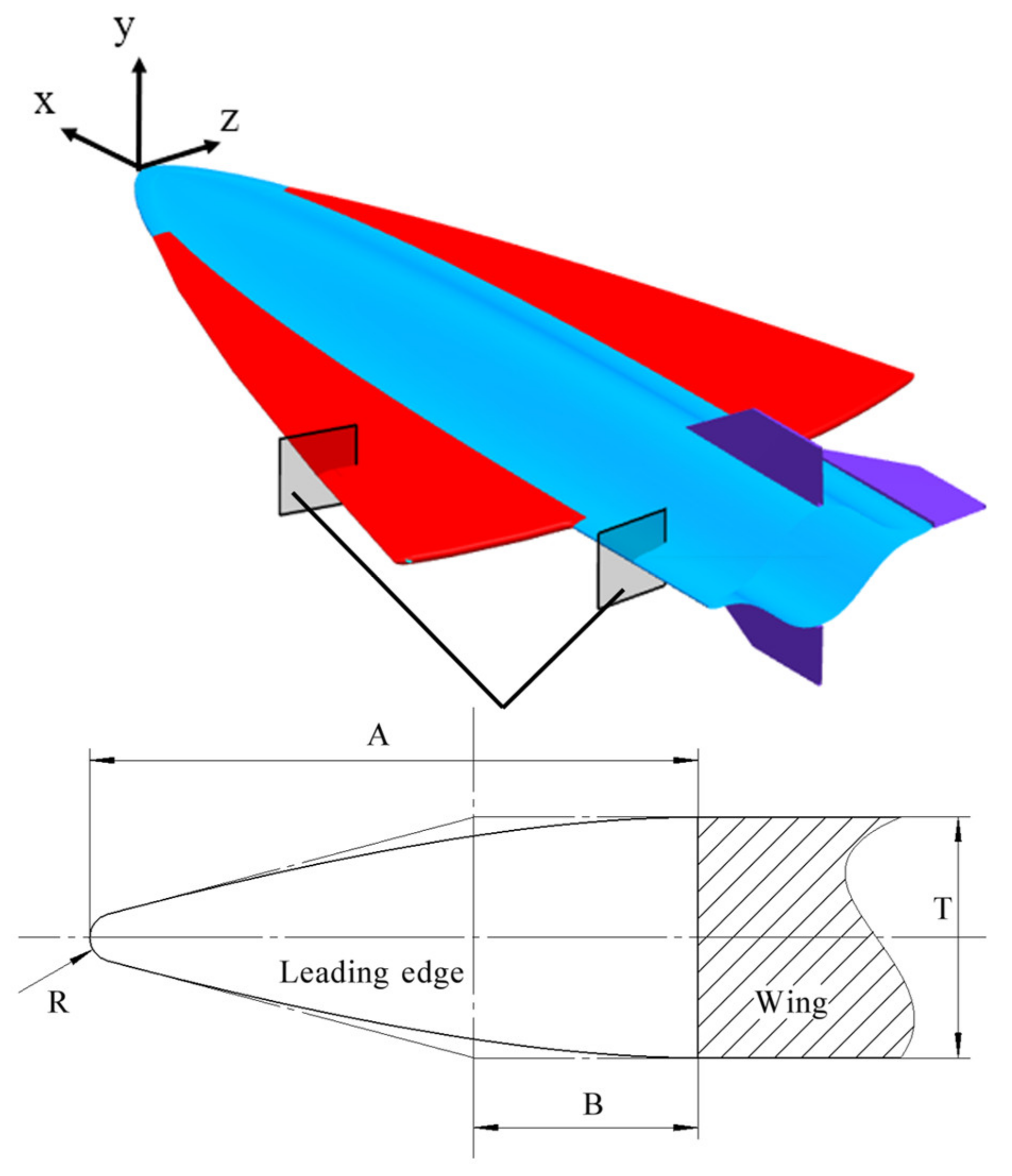
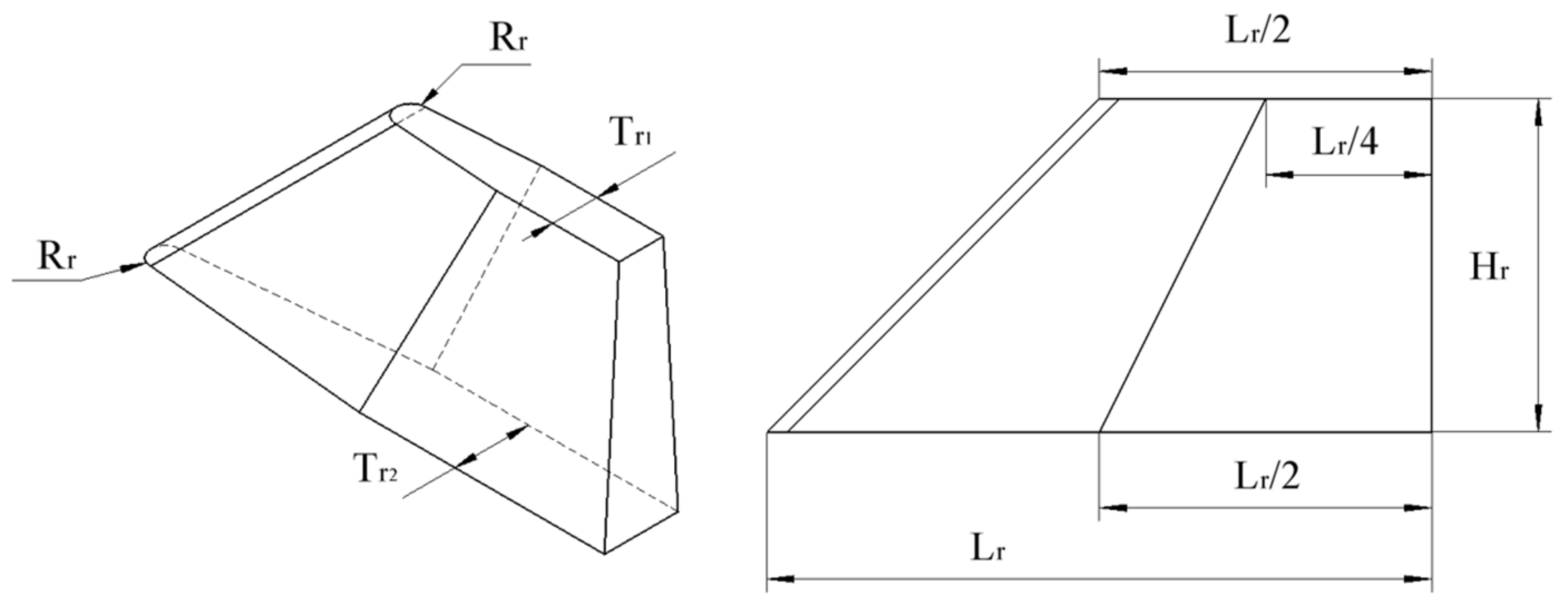
2.2. Parameterization Method of Vehicle
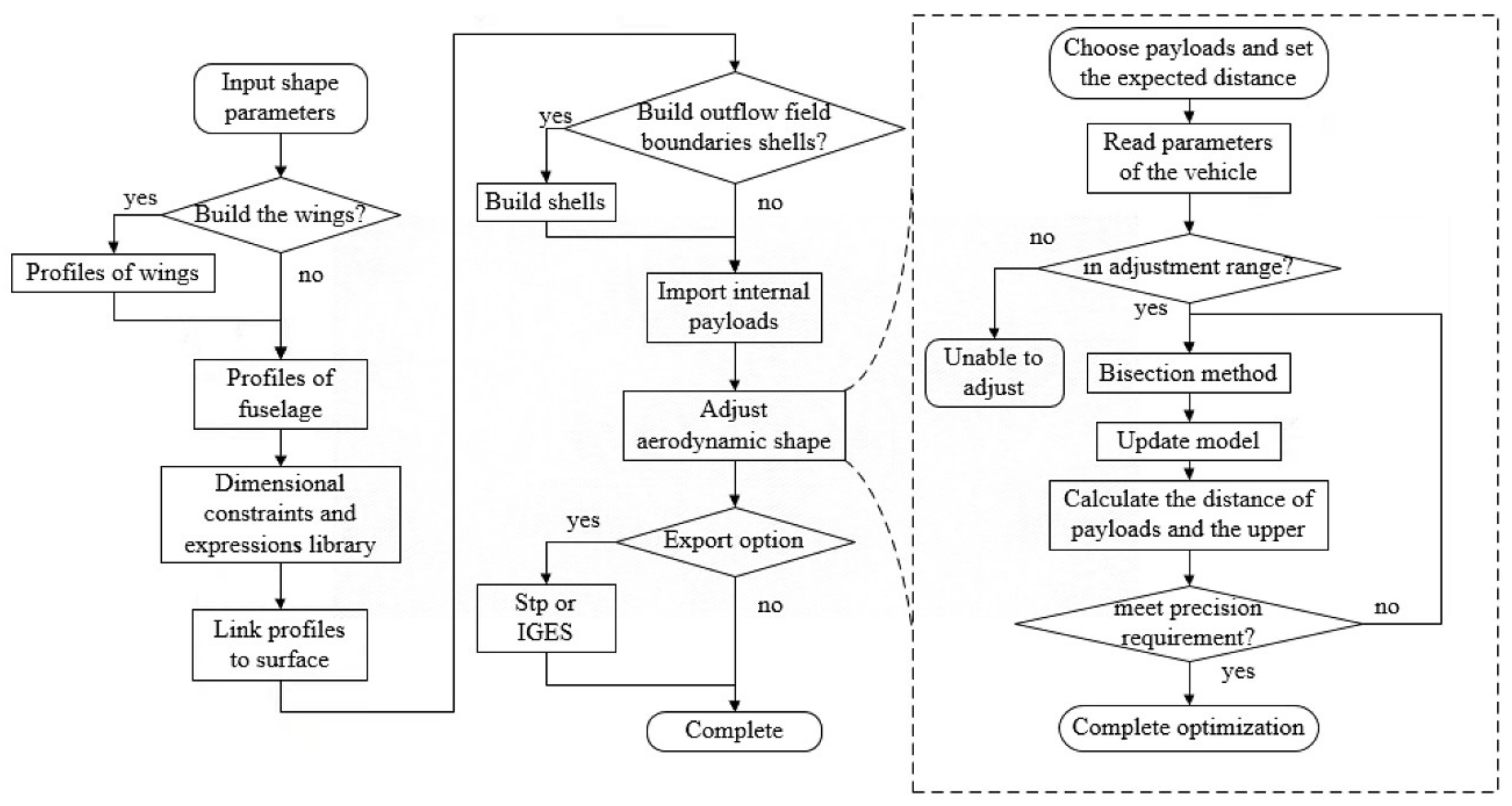
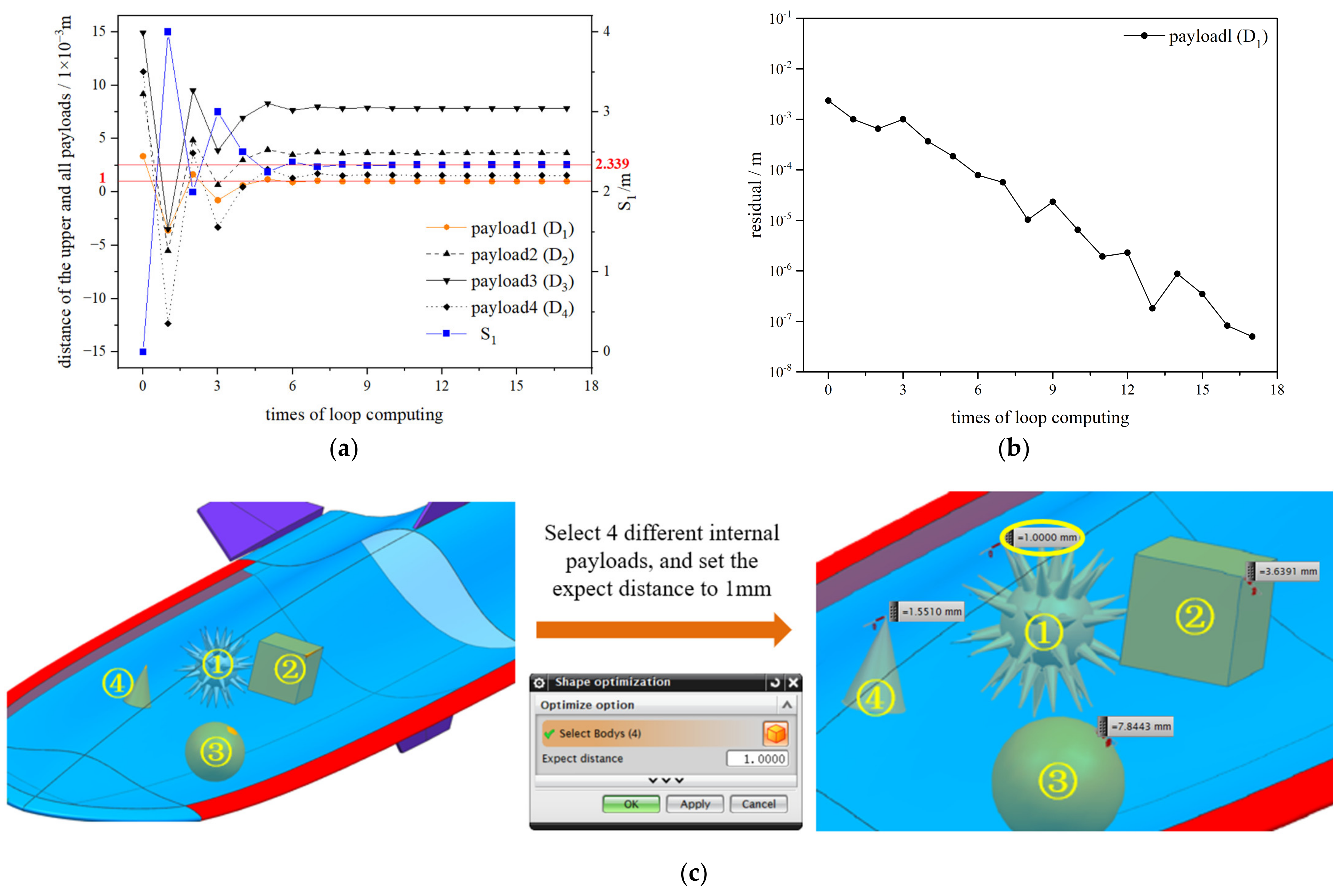
2.3. Shape Optimization
3. Numerical Simulation
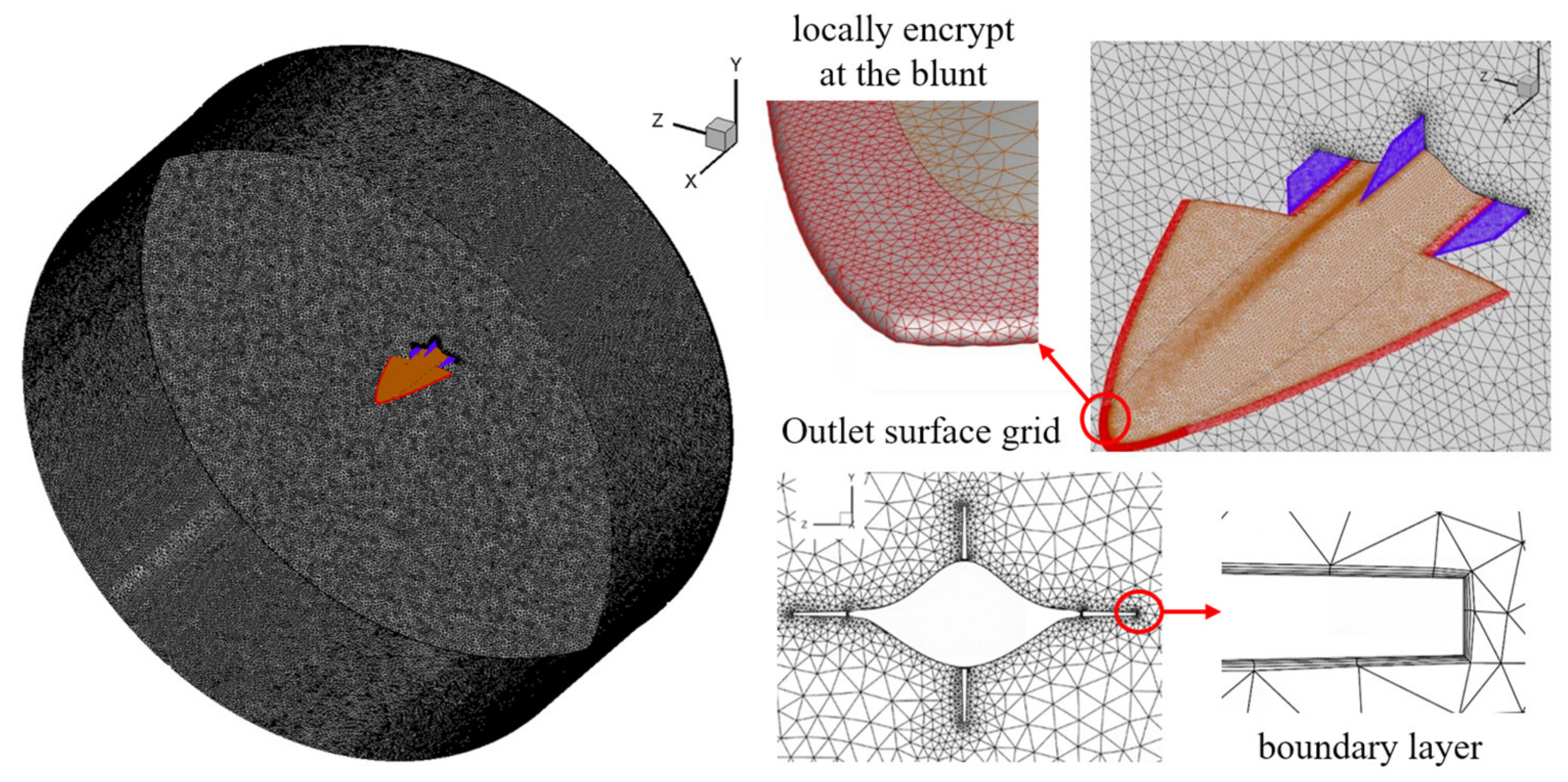
3.1. Settings
3.2. Simulation Result and Discussion
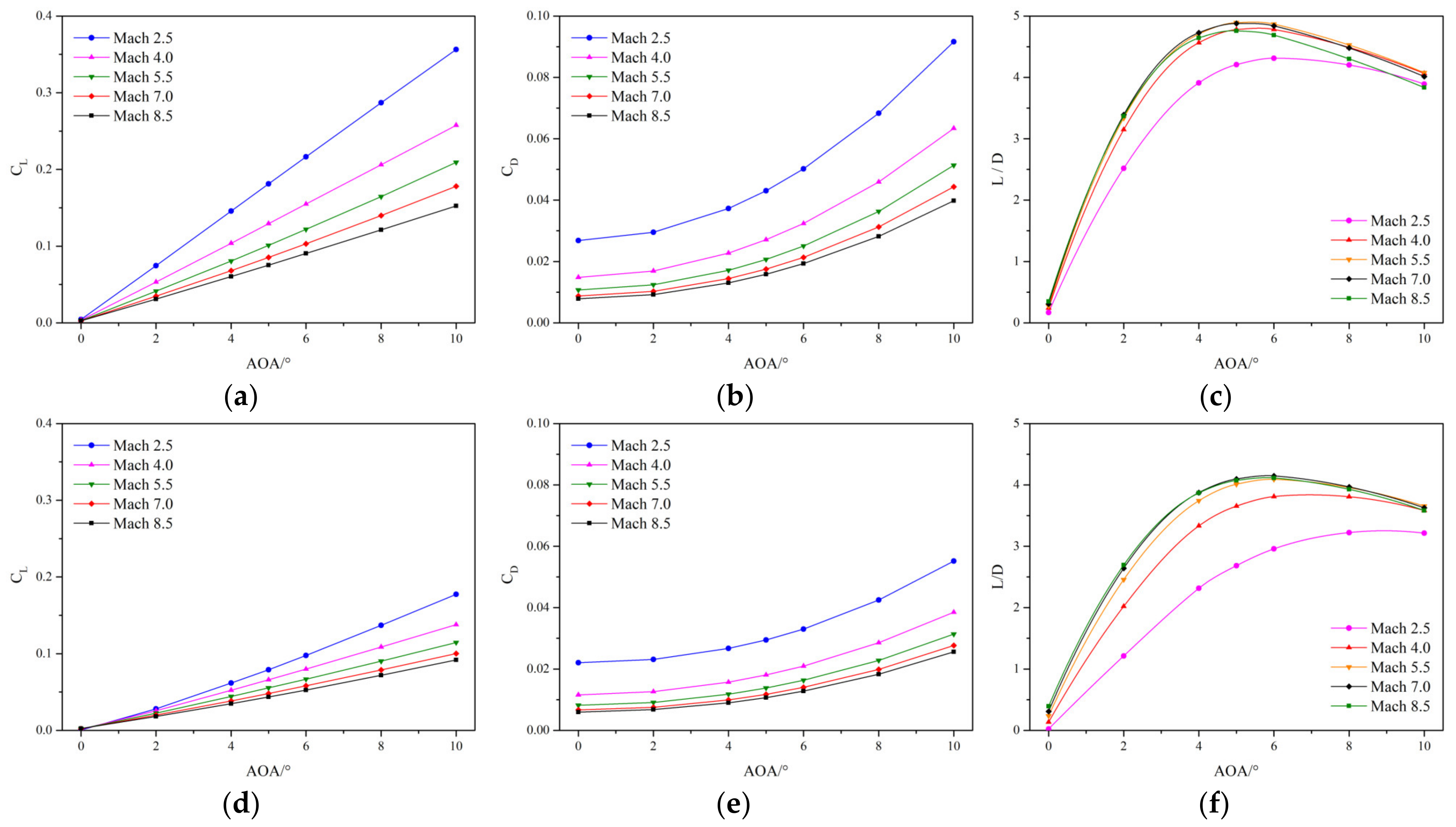
3.2.1. Lift/Drag Characteristics
- The lift coefficient, as illustrated in Figure 11a,d, displays a linear increasing trend with the AOA under various flight conditions and with the wings deployed or retracted. Additionally, it was observed that the lift coefficient increases as the inflow Mach number and flight altitude decrease. At AOA 0°, the lift coefficients of both the deployed and the retracted configurations are essentially the same; at AOA 5°, for Mach 2.5, the values are 0.181 and 0.079, respectively, indicating that deploying the wings increases the lift by 129% compared to when the wings are retracted; at 10°, the values are 0.356 and 0.177, respectively, representing a 101% increase in lift. This suggests that at Mach 2.5, as the angle of attack increases, the proportion of lift contributed by the wings exhibits a decreasing trend. At Mach 4.0, the lift increases, provided by the wings at AOA 5° and 10° are 96% and 87%, respectively, while at Mach 5.5 and Mach 7.0, these increases stabilize at 82% and 77%. However, at Mach 8.5, the increases drop to 73% and 66%, indicating a declining trend. This illustrates that, as the inflow Mach number and flight altitude increase, the effectiveness of the wings in providing lift gradually decreases.
- As depicted in Figure 11b,e, the drag coefficient increases in a quadratic trend with the AOA and rises as the inflow Mach number and flight altitude decrease. At AOA 0°, the additional drag when the wings are deployed compared to when the wings are retracted is between 20 and 30%, with the drag coefficient slowly increasing as the inflow Mach number and altitude increase, although its impact is significantly less than that of the lift coefficient. As AOA increases, the drag experienced by the wings also increases; the drag coefficient with deployed wings increases by about 46% at AOA 5° and between 55 and 65% at AOA 10°, but as the inflow Mach number and altitude increase, the drag coefficients for both the deployed and retracted wings show a slow declining trend.
- The L/D, as depicted in Figure 11c,f, reaches its maximum at AOA 5–6° under different inflow conditions when the wings are deployed, with the maximum L/D between Mach 4.0 and Mach 8.5 consistently at 4.7 and peaking at 4.9 at Mach 5.5. With the wings retracted, the maximum L/D in the high hypersonic range is consistently above 4, showing suboptimal performance in the supersonic range. However, with the assistance of the wings, the L/D at Mach 4.0 can still reach 4.7, although there is a significant decrease in performance at Mach 2.5.
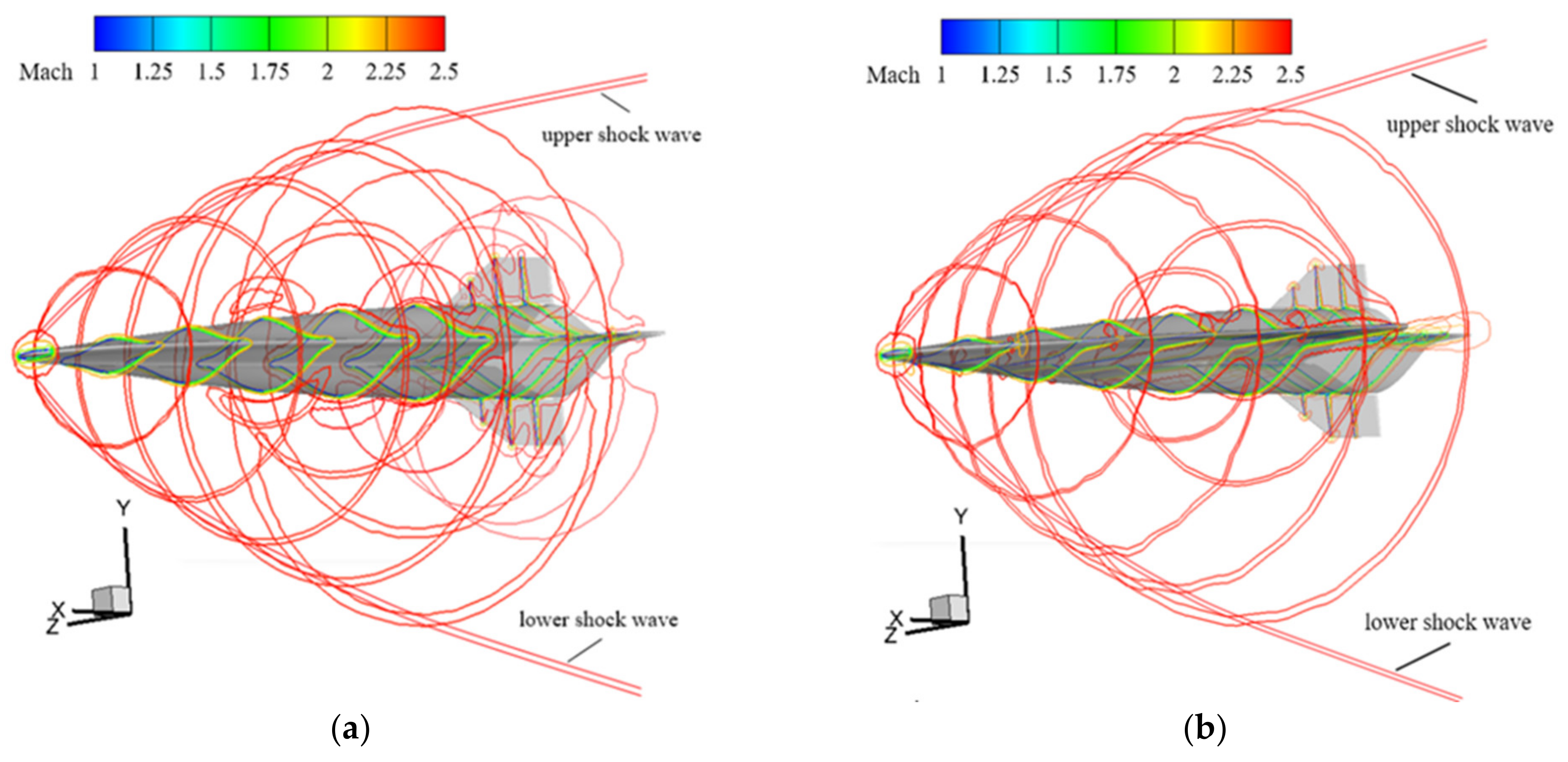
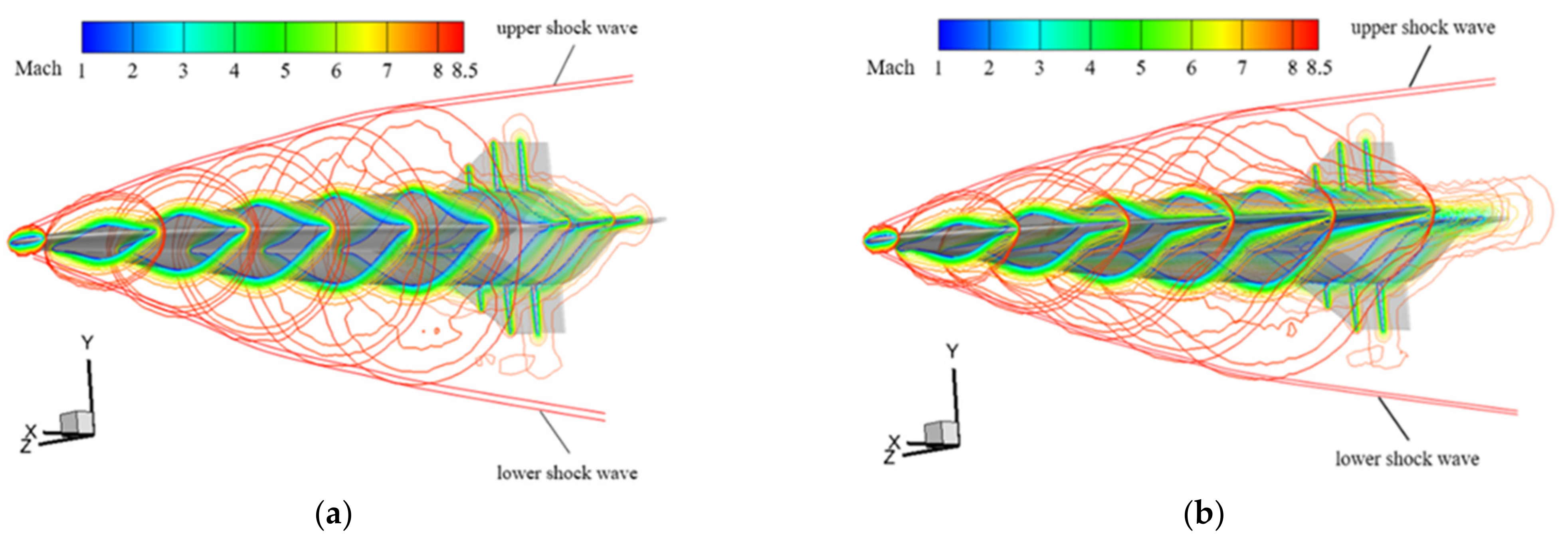
3.2.2. Flow Field Analysis (Mach)
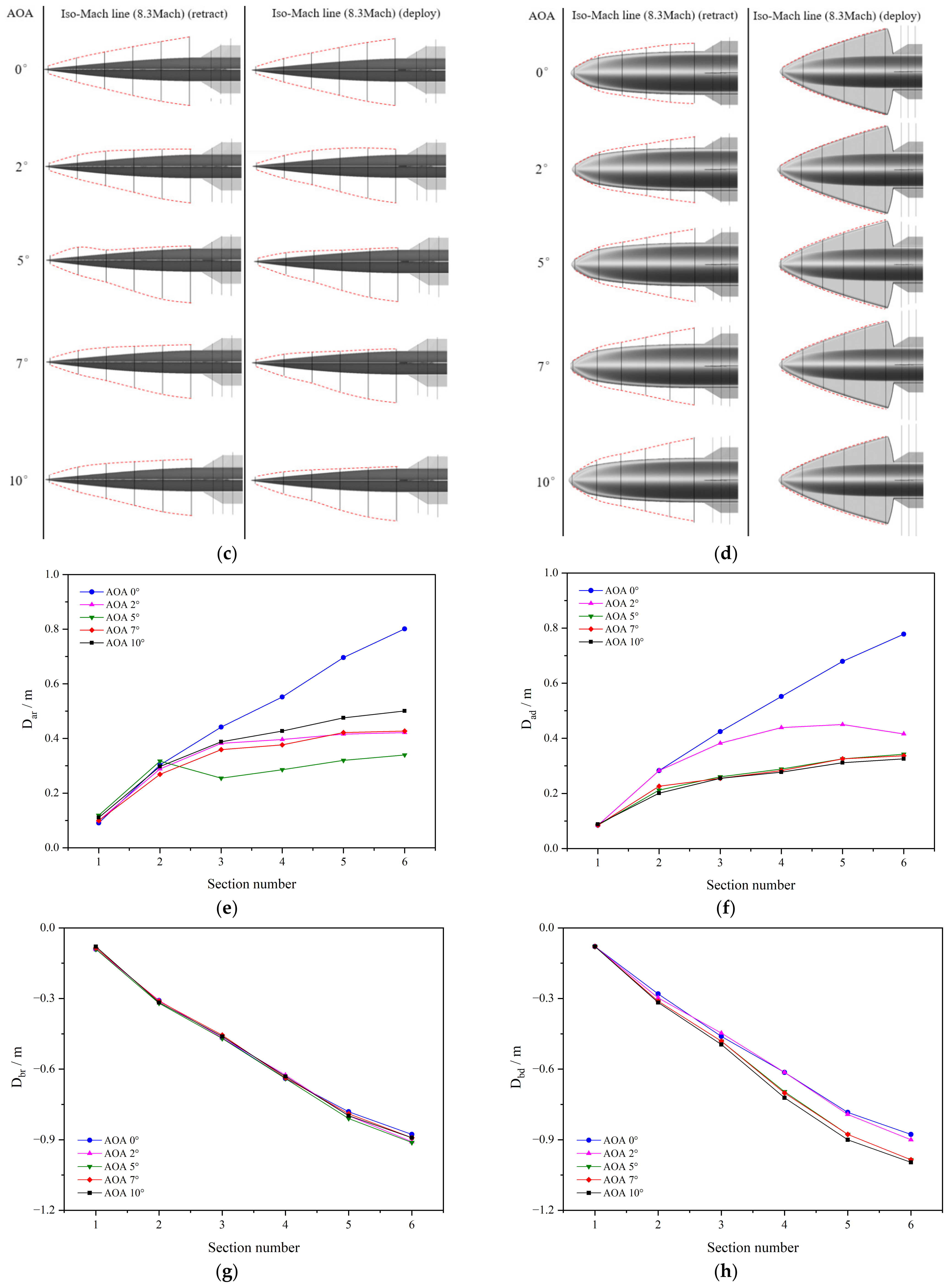
- Figure 12c describes the changes in iso-Mach lines above and below the fuselage with wing mode, and Figure 12e–h provides detailed information on the positions of the intersections between the iso-Mach lines and the six cross-sections. These images collectively reveal that the iso-Mach lines are further from the fuselage at various attack angles when the wings are deployed.
- The iso-Mach line above the fuselage at AOA 5° is the lowest for both wing modes, and as seen in Figure 11, this condition yields the maximum L/D for the vehicle; at AOA 2° and 5°, a turning appears on the upper surface iso-Mach lines due to the upper surface gradually transitioning from the windward to the leeward side, with gas decelerating through the shock wave, then accelerating over the surface through the expansion wave; with the increasing attack angle, the expansion waves gradually move forward. Subsequently, at AOA 7° and 10°, the iso-Mach lines gradually rise due to an increased overflow with the rising attack angle, causing increased air pressure above the fuselage and, by the principle of the conservation of mechanical energy, an increase in pressure of the potential energy means a certain decrease in the velocity of the potential energy; hence, the iso-Mach line moves up, enlarging the low-speed area.
- In Figure 12g,h, a downward turn is observed in the iso-Mach lines at the third and fourth cross-sections with the wings deployed, compared to when the wings are retracted. This indicates that deploying the wings increases the pressure on the lower side of the vehicle, which is the same as the aforementioned principle of the conservation of mechanical energy, resulting in an expansion of the low-speed area below.
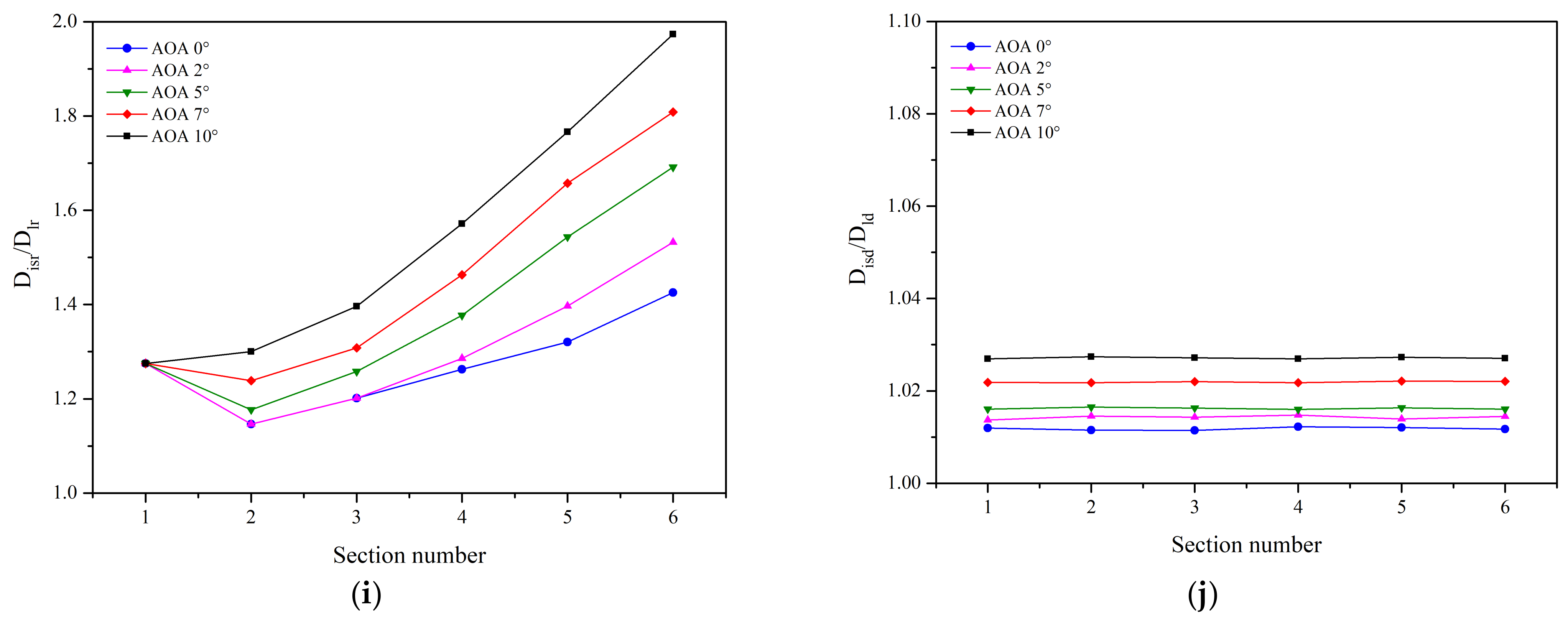
- Upon examining Figure 12d,i,j, it becomes evident that at Mach 2.5, the angle at which the wings are deployed is less than that of the shock wave angle, resulting in an overflow at the leading edges of the wings. Consequently, at Mach 2.5, the vehicle lacks the capability for the waverider effect, leading to a maximum L/D that is inferior to that observed at other Mach numbers. Moreover, Figure 12i,j demonstrates that, with an increase in the attack angle, the iso-Mach lines progressively distance themselves from the leading edge of the vehicle, illustrating an augmentation in the overflow on both sides of the vehicle as the attack angle increases.
- As shown in Figure 13c,e,f,g,h, the iso-Mach lines above the fuselage at AOA 5°, which are consistent with those of Mach 2.5, are the lowest with both wing modes; a turn also appears in the upper surface iso-Mach lines at AOA 2° and 5°. Subsequently, at AOA 7° and 10°, the iso-Mach lines with the wings retracted begin to rise again, but the rise is considerably less significant with the wings deployed due to the shock waves being closer to the wing-leading edges, suppressing the overflow from the lower to the upper surface, which confirms the occurrence of the waverider effect.
- In Figure 13g,h, compared to when the wings are retracted, the iso-Mach lines under the lower side of the vehicle with the wings deployed show a slight downward shift overall. This shift can be attributed to the generation of the waverider effect at Mach 5.5, which results in a higher airflow pressure below and leads to an expansion of the low-speed area; this is consistent with the aforementioned principle of the conservation of mechanical energy.
- It can be seen in Figure 13d,i,j, at Mach 5.5 with the wings deployed, that the iso-Mach lines are very close to the wing-leading edges, confirming the occurrence of the waverider effect, with the maximum L/D under this inflow condition reaching the highest point compared to the other Mach inflow conditions.
- As depicted in Figure 13j, with an increase in the attack angle, the distance between the iso-Mach lines and the leading edges of the vehicle incrementally expand, which is consistent with the phenomenon observed at Mach 2.5. It also demonstrates that, under the Mach 5.5 inflow condition, the overflow on both sides of the vehicle amplifies as the attack angle ascends.
- As shown in Figure 14c,e,f,g,h, the iso-Mach line above the fuselage at AOA 5° is the lowest in both wing modes, which is consistent with Mach 2.5 and 5.5; a turn appears in the upper surface iso-Mach lines at AOA 2° and 5°. Subsequently, at AOA 7° and 10°, the iso-Mach lines above the fuselage with the wings retracted have a much larger rise than the fuselage with the wings deployed; this is consistent with Mach 5.5 and confirms the occurrence of the waverider effect at Mach 8.5.
- In Figure 14g,h, comparing wings deployed with wings retracted, there is no significant turn in the iso-Mach lines on the lower side of the vehicle, unlike at Mach 2.5 and 5.5. Although waverider effects are still generated, the faster inflow speed has a greater impact on the shock waves, making this phenomenon less pronounced.
- As can be seen in Figure 14d,i,j, at Mach 8.5 with wings deployed, the iso-Mach lines are closer to the wing-leading edges compared to Mach 5.5, confirming the occurrence of the waverider effect, but due to an increased wave drag, the highest L/D at Mach 8.5 is slightly lower than at Mach 5.5.
- From Figure 14j, as the attack angle increases, the distance from the iso-Mach lines to the leading edge of the vehicle slightly increases, but to a lesser extent than at Mach 5.5; combined with the conditions at Mach 2.5, this indicates that the closer the shock waves are to the leading edge of the vehicle, the smaller the overflow from the lower to the upper surface.
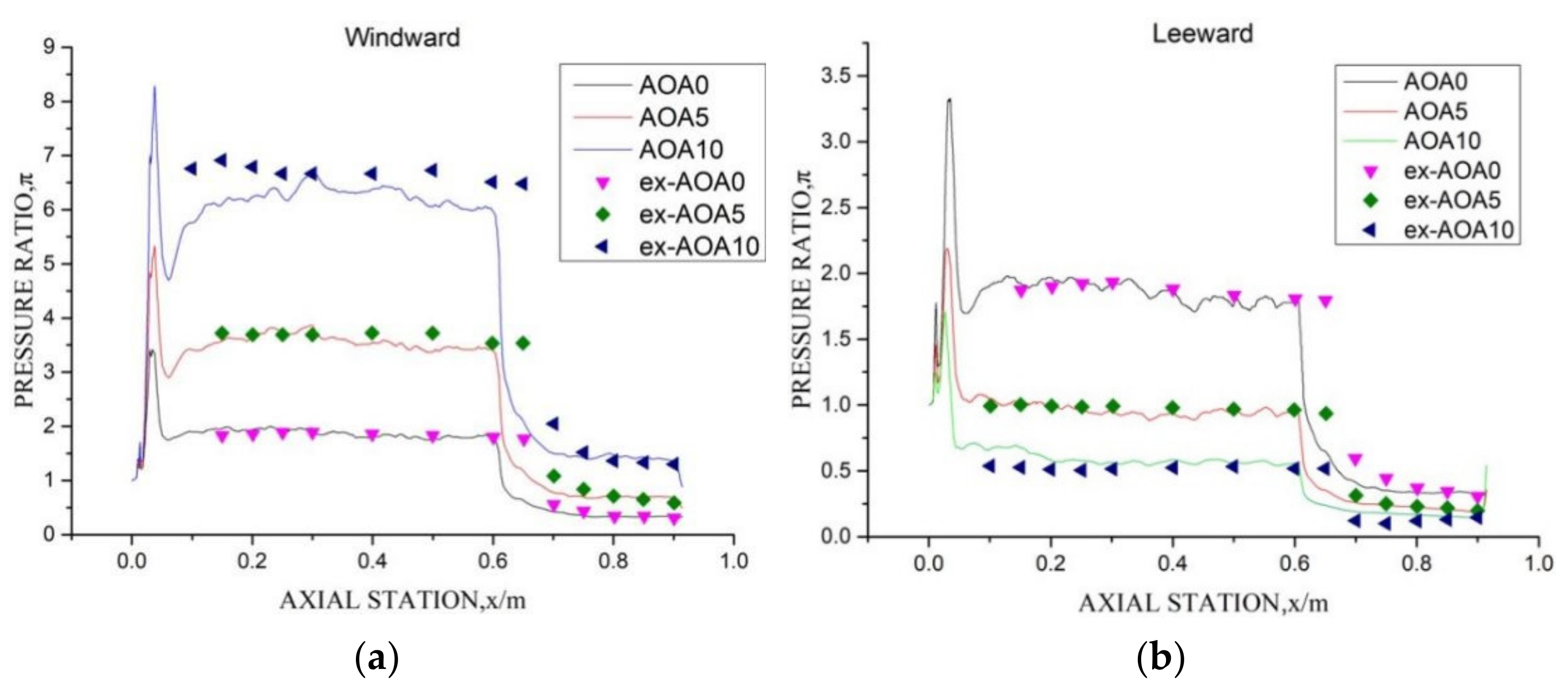
3.2.3. Flow Field Analysis (Pressure)
- As the inflow Mach number increases, the pressure ratio on the lower surface progressively strengthens, which also represents an increase in the intensity of the shock wave.
- At Mach 2.5, the inflow pressure at each cross-section is relatively low. Regardless of whether the wings are deployed or retracted, overflow from the lower to the upper surface occurs, indicating that the vehicle does not exhibit a high lift-to-drag performance under this inflow condition; as shown in Figure 11c, the maximum lift-to-drag ratio is 4.3, which is lower than that of the other inflow conditions.
- At Mach 4.0, the front of the vehicle (0.3 m) shows a certain waverider effect, enhancing the lift-to-drag performance. However, in subsequent parts of the vehicle, significant overflow is observed when the wings are retracted, while deploying the wings substantially suppresses overflow on the lower surface and significantly improves the lift-to-drag performance.
- At Mach 5.5, due to the reduction in the shock wave angle, a high-pressure zone begins to appear at the leading edge of the vehicle. As shown by the closed lift-to-drag ratio in Figure 11f, the waverider effect is noticeably enhanced. With the wings deployed, a high-pressure zone appears at the edges in all four sections, trapping high-pressure air beneath the lower surface and achieving the highest L/D of 4.9.
- At Mach 7.0 and Mach 8.5, with the wings retracted, the first three sections (0.3 m, 1.4 m, and 2.5 m) display the waverider effect, showing a higher L/D compared to the first three conditions (Mach 2.5, 4.0, and 5.5). When the wings are deployed, the high-pressure area at the wing edges gradually expands, resulting in a higher wave drag and thus slightly reducing the lift-to-drag performance when compared to Mach 5.5.
- As the AOA increases, the pressure on the lower surface gradually rises, and the flow lines disperse towards the sides; conversely, the pressure on the upper surface decreases, with the wall flow lines converging towards the centerline.
- At AOA 0°, the pressure is concentrated around the nose, the leading edge, and the central line on the fuselage. Due to the symmetrical blunt leading edge, the pressure distribution at the leading edge is almost identical on both the upper and lower surfaces. As shown in the sections (see the S1 sections in Figure 16), the lower surface of the fuselage exhibits more protrusion than the upper surface; hence, there is a higher pressure distribution.
- For the upper surface at a certain AOA during the flight, the airflow forms a small high-pressure area after passing the leading edge shockwave, then continuously expands and accelerates along the upper surface, resulting in an overall low-pressure area.
- Corresponding to the section at Ma 5.5 depicted in Figure 16, with the wings retracted, the angle between the leading edge tangent line of the fuselage and the direction of the incoming flow exceeds the shock wave angle. It happens in the area of approximately the first third of the lower surface. This causes the high-pressure airflow below to concentrate on the lower surface due to the combined effects of the shockwave and leading edge, thereby generating a certain waverider effect in this area, which led to high pressure, as the Figure 16 shows. However, beyond this area, the angle gradually reduces to less than the shock wave angle, and the gas under the lower surface overflows upwards at the middle of the fuselage, thus reducing pressure in this area and leading to some lift loss. At this juncture, deploying the wings in order to have the leading edge of the wings take over from the leading edge of the fuselage can re-establish the waverider effect. This adjustment not only elevates the pressure in the previously low-pressure area observed during wing retraction around the midsection of the fuselage but also, with the added lift provided by the wing’s lower surface, optimizes the L/D of the vehicle under this inflow condition.
4. Conclusions
- The parametric design method in this study, which was based on two-dimensional B-splines, employed 27 parameters to fully characterize the features of the entire vehicle. This study also presented a shape optimization method suitable for internal payloads of any number and shape. Both of the methods were implemented through UG secondary development, allowing for the rapid design and optimization of hypersonic vehicle aerodynamic shapes according to specified internal payloads in practical engineering applications, thereby enhancing design efficiency.
- The numerical simulations of the models generated using the above methods across a typical Mach number range (Mach 2.5–8.5) analyzed the lift/drag characteristics of the wings in various flight vectors. The results demonstrated that the highest L/D exceeded 4.7 under flow conditions from Mach 4 to Mach 8.5. With the wings retracted, the drag coefficient remained below 0.02 within AOA 5°, reducing drag by approximately 20–30% compared to the scenario with the wings deployed. Furthermore, a continuous and flexible adjustment of the L/D (0.3–4.7) within a 0–5° angle of attack was achievable, endowing the vehicle with a certain maneuverability and flexibility.
- Flow field analysis of the vehicle in various flight states showed that between Mach 2.5 and Mach 8.5 the vehicle can match the corresponding shockwave angles at different inflow velocities by adjusting the wing opening, thereby generating a certain waverider effect and minimizing overflow from the lower surface to the upper surface. Analysis of the pressure field indicated that wing deployment maintains a higher pressure difference between the lower and upper surfaces, effectively enhancing overall lift performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Simulation Results
| Mach | AOA/° | Fx/N | Fy/N | Lift Force/N | Drag Force/N | L/D | CL | CD |
|---|---|---|---|---|---|---|---|---|
| 8.5 | 0 | −4663.55 | 1828.79 | 1828.79 | 4663.55 | 0.392145 | 0.002334 | 0.005953 |
| 8.5 | 2 | −4790.66 | 14,427.50 | 14,251.52 | 5291.25 | 2.693411 | 0.018191 | 0.006754 |
| 8.5 | 4 | −5115.03 | 27,615.60 | 27,191.52 | 7028.94 | 3.868512 | 0.034708 | 0.008972 |
| 8.5 | 5 | −5356.08 | 34,609.50 | 34,010.99 | 8352.12 | 4.072141 | 0.043412 | 0.010661 |
| 8.5 | 6 | −5644.95 | 41,933.90 | 41,114.12 | 9997.31 | 4.112518 | 0.052479 | 0.012761 |
| 8.5 | 7 | −5976.00 | 49,695.90 | 48,597.18 | 11,987.86 | 4.053867 | 0.06203 | 0.015301 |
| 8.5 | 8 | −6355.64 | 57,731.10 | 56,284.73 | 14,328.40 | 3.928193 | 0.071843 | 0.018289 |
| 8.5 | 10 | −7274.43 | 74,260.21 | 71,868.84 | 20,059.07 | 3.582861 | 0.091735 | 0.025604 |
| 7 | 0 | −7678.78 | 2375.10 | 2375.10 | 7678.78 | 0.309307 | 0.002061 | 0.006663 |
| 7 | 2 | −7861.00 | 23,178.80 | 22,890.34 | 8665.14 | 2.641658 | 0.019863 | 0.007519 |
| 7 | 4 | −8316.83 | 44,992.10 | 44,302.35 | 11,435.06 | 3.874256 | 0.038443 | 0.009923 |
| 7 | 5 | −8652.98 | 56,409.50 | 55,440.69 | 13,536.46 | 4.095655 | 0.048108 | 0.011746 |
| 7 | 6 | −9053.81 | 68,234.30 | 66,914.12 | 16,136.64 | 4.14672 | 0.058064 | 0.014002 |
| 7 | 7 | −9513.92 | 80,532.86 | 78,773.12 | 19,257.49 | 4.090518 | 0.068355 | 0.01671 |
| 7 | 8 | −10,041.30 | 93,197.40 | 90,892.93 | 22,914.15 | 3.966673 | 0.078871 | 0.019884 |
| 7 | 10 | −11,313.89 | 119,262.35 | 115,485.85 | 31,851.69 | 3.625737 | 0.100212 | 0.027639 |
| 5.5 | 0 | −12,712.10 | 2991.54 | 2991.54 | 12,712.10 | 0.23533 | 0.00192 | 0.008157 |
| 5.5 | 2 | −12,951.10 | 35,294.00 | 34,820.51 | 14,174.95 | 2.456482 | 0.022344 | 0.009096 |
| 5.5 | 4 | −13,524.86 | 69,819.30 | 68,705.77 | 18,362.26 | 3.741683 | 0.044087 | 0.011783 |
| 5.5 | 5 | −13,920.40 | 87,867.80 | 86,320.19 | 21,525.61 | 4.010116 | 0.05539 | 0.013813 |
| 5.5 | 6 | −14,410.00 | 106,081.47 | 103,994.09 | 25,419.59 | 4.0911 | 0.066731 | 0.016311 |
| 5.5 | 7 | −14,971.63 | 124,917.71 | 122,162.01 | 30,083.68 | 4.060741 | 0.078389 | 0.019304 |
| 5.5 | 8 | −15,620.70 | 144,136.00 | 140,559.30 | 35,528.53 | 3.956237 | 0.090195 | 0.022798 |
| 5.5 | 10 | −17,122.80 | 184,323.00 | 178,549.38 | 48,870.02 | 3.653556 | 0.114572 | 0.031359 |
| 4 | 0 | −20,874.10 | 2798.47 | 2798.47 | 20,874.10 | 0.134064 | 0.001552 | 0.011574 |
| 4 | 2 | −21,126.30 | 46,696.70 | 45,930.96 | 22,743.12 | 2.019554 | 0.025468 | 0.012611 |
| 4 | 4 | −21,669.39 | 96,108.16 | 94,362.47 | 28,320.77 | 3.331917 | 0.052322 | 0.015703 |
| 4 | 5 | −22,054.80 | 121,316.00 | 118,932.15 | 32,544.26 | 3.654474 | 0.065945 | 0.018045 |
| 4 | 6 | −22,531.16 | 147,140.21 | 143,979.01 | 37,788.07 | 3.810171 | 0.079833 | 0.020953 |
| 4 | 7 | −23,078.51 | 173,671.93 | 169,564.84 | 44,071.77 | 3.84747 | 0.09402 | 0.024437 |
| 4 | 8 | −23,705.90 | 201,246.00 | 195,988.26 | 51,483.23 | 3.806837 | 0.108671 | 0.028546 |
| 4 | 10 | −25,184.00 | 256,857.00 | 248,581.61 | 69,404.15 | 3.581653 | 0.137833 | 0.038483 |
| 2.5 | 0 | −27,668.00 | 616.36 | 616.36 | 27,668.00 | 0.022277 | 0.000491 | 0.022041 |
| 2.5 | 2 | −27,790.90 | 36,206.80 | 35,214.86 | 29,037.57 | 1.212734 | 0.028054 | 0.023133 |
| 2.5 | 4 | −28,018.56 | 79,718.55 | 77,569.88 | 33,511.20 | 2.314745 | 0.061795 | 0.026696 |
| 2.5 | 5 | −28,189.40 | 102,092.00 | 99,246.64 | 36,980.03 | 2.68379 | 0.079064 | 0.02946 |
| 2.5 | 6 | −28,397.47 | 126,183.25 | 122,523.66 | 41,431.65 | 2.957248 | 0.097607 | 0.033006 |
| 2.5 | 7 | −28,638.75 | 151,036.89 | 146,420.90 | 46,832.05 | 3.126511 | 0.116645 | 0.037308 |
| 2.5 | 8 | −28,910.50 | 177,729.00 | 171,975.79 | 53,364.24 | 3.222678 | 0.137003 | 0.042512 |
| 2.5 | 10 | −29,575.00 | 231,178.00 | 222,530.24 | 69,269.33 | 3.212536 | 0.177277 | 0.055183 |
| Mach | AOA/° | Fx/N | Fy/N | Lift Force/N | Drag Force/N | L/D | CL | CD |
|---|---|---|---|---|---|---|---|---|
| 8.5 | 0 | −6127.12 | 2122.37 | 2122.37 | 6127.12 | 0.346389 | 0.002709 | 0.007821 |
| 8.5 | 2 | −6357.37 | 24,527.4 | 24,290.59 | 7209.491 | 3.369252 | 0.031005 | 0.009202 |
| 8.5 | 4 | −6854.7 | 47,826.71 | 47,232.05 | 10,174.22 | 4.642324 | 0.060288 | 0.012987 |
| 8.5 | 5 | −7203.52 | 59,811.72 | 58,956.29 | 12,389.04 | 4.758744 | 0.075253 | 0.015814 |
| 8.5 | 6 | −7619.11 | 72,020.3 | 70,829.35 | 15,105.54 | 4.688964 | 0.090408 | 0.019281 |
| 8.5 | 7 | −8101.47 | 84,452.45 | 82,835.63 | 18,333.25 | 4.518328 | 0.105733 | 0.023401 |
| 8.5 | 8 | −8650.6 | 97,108.17 | 94,959.19 | 22,081.26 | 4.300443 | 0.121207 | 0.028185 |
| 8.5 | 10 | −9949.17 | 123,090.3 | 119,492.6 | 31,172.43 | 3.83328 | 0.152522 | 0.039789 |
| 7 | 0 | −10,104.9 | 3115.41 | 3115.41 | 10,104.9 | 0.308307 | 0.002703 | 0.008768 |
| 7 | 2 | −10,431 | 40,526.8 | 40,138.08 | 11,839.01 | 3.390323 | 0.034829 | 0.010273 |
| 7 | 4 | −11,080 | 79,399 | 78,432.69 | 16,591.6 | 4.727252 | 0.068059 | 0.014397 |
| 7 | 5 | −11,510.2 | 99,706.7 | 98,324.11 | 20,156.41 | 4.878056 | 0.08532 | 0.017491 |
| 7 | 6 | −12,004.8 | 120,762 | 118,845.6 | 24,562.1 | 4.838576 | 0.103127 | 0.021314 |
| 7 | 7 | −12,572.22 | 142,549.5 | 139,954.8 | 29,850.93 | 4.688458 | 0.121444 | 0.025903 |
| 7 | 8 | −13,215.62 | 164,733 | 161,290.6 | 36,013.41 | 4.478626 | 0.139958 | 0.03125 |
| 7 | 10 | −14,720.04 | 210,813.6 | 205,054.8 | 51,103.81 | 4.012515 | 0.177934 | 0.044345 |
| 5.5 | 0 | −16,663.7 | 4554.85 | 4554.85 | 16,663.7 | 0.27334 | 0.002923 | 0.010693 |
| 5.5 | 2 | −17,059.4 | 65,103.4 | 64,468.38 | 19,321.08 | 3.336685 | 0.041368 | 0.012398 |
| 5.5 | 4 | −17,848.66 | 127,065.4 | 125,510.8 | 26,668.82 | 4.706277 | 0.080538 | 0.017113 |
| 5.5 | 5 | −18,358 | 159,793 | 157,584.9 | 32,215.02 | 4.89166 | 0.10112 | 0.020672 |
| 5.5 | 6 | −18,953.39 | 192,984.8 | 189,946.4 | 39,021.97 | 4.867679 | 0.121885 | 0.02504 |
| 5.5 | 7 | −19,632.22 | 227,165.4 | 223,079.6 | 47,170.38 | 4.72923 | 0.143146 | 0.030268 |
| 5.5 | 8 | −20,403.2 | 261,765 | 256,377.9 | 56,635.28 | 4.526824 | 0.164513 | 0.036342 |
| 5.5 | 10 | −22,163 | 335,045 | 326,106.3 | 80,006.25 | 4.076011 | 0.209257 | 0.051339 |
| 4 | 0 | −26,719.5 | 6428.71 | 6428.71 | 26,719.5 | 0.2406 | 0.003565 | 0.014815 |
| 4 | 2 | −27,113.8 | 96,994.5 | 95,989.16 | 30,482.34 | 3.149009 | 0.053224 | 0.016902 |
| 4 | 4 | −27,851.4 | 189,619.9 | 187,215.2 | 41,010.77 | 4.565025 | 0.103807 | 0.02274 |
| 4 | 5 | −28,312.9 | 236,749 | 233,380.5 | 48,839.2 | 4.778549 | 0.129404 | 0.02708 |
| 4 | 6 | −28,896.79 | 283,795.3 | 279,220.1 | 58,403.18 | 4.780906 | 0.154821 | 0.032383 |
| 4 | 7 | −29,538.23 | 331,522.4 | 325,451.4 | 69,720.47 | 4.667946 | 0.180456 | 0.038658 |
| 4 | 8 | −30,278.3 | 379,530 | 371,622.5 | 82,804 | 4.487978 | 0.206056 | 0.045913 |
| 4 | 10 | −31,918 | 477,415 | 464,619.5 | 114,335.3 | 4.063656 | 0.257621 | 0.063396 |
| 2.5 | 0 | −33,707.3 | 5621.76 | 5621.76 | 33,707.3 | 0.166782 | 0.004479 | 0.026853 |
| 2.5 | 2 | −33,794.5 | 94,627.4 | 93,390.34 | 37,076.36 | 2.518865 | 0.074399 | 0.029537 |
| 2.5 | 4 | −33,894.62 | 185,676 | 182,859.4 | 46,764.16 | 3.910246 | 0.145673 | 0.037254 |
| 2.5 | 5 | −34,028.7 | 231,213 | 227,367.4 | 54,050.75 | 4.206553 | 0.18113 | 0.043059 |
| 2.5 | 6 | −34,251.26 | 276,781.5 | 271,685 | 62,995.17 | 4.312791 | 0.216436 | 0.050185 |
| 2.5 | 7 | −34,499.9 | 322,564.6 | 315,955.8 | 73,553.48 | 4.295592 | 0.251704 | 0.058596 |
| 2.5 | 8 | −34,785.2 | 368,649 | 360,220.2 | 85,752.7 | 4.200686 | 0.286966 | 0.068314 |
| 2.5 | 10 | −35,543 | 460,633 | 447,463 | 11,4991.1 | 3.891283 | 0.356468 | 0.091607 |
Appendix B. Position Information of the Iso-Mach Lines in Figure 12, Figure 13 and Figure 14
| Name/Unit | Section Number | AOA 0° | AOA 2° | AOA 5° | AOA 7° | AOA 10° |
|---|---|---|---|---|---|---|
| Dar/m | 1 | 0.156 | 0.162 | 0.165 | 0.174 | 0.180 |
| 2 | 0.564 | 0.540 | 0.354 | 0.315 | 0.336 | |
| 3 | 0.894 | 0.726 | 0.324 | 0.336 | 0.408 | |
| 4 | 1.164 | 0.489 | 0.348 | 0.393 | 0.507 | |
| 5 | 1.404 | 0.435 | 0.366 | 0.462 | 0.627 | |
| 6 | 1.626 | 0.345 | 0.366 | 0.504 | 0.735 | |
| Dad/m | 1 | 0.150 | 0.156 | 0.162 | 0.174 | 0.186 |
| 2 | 0.633 | 0.606 | 0.510 | 0.447 | 0.420 | |
| 3 | 0.969 | 0.909 | 0.564 | 0.564 | 0.594 | |
| 4 | 1.254 | 1.065 | 0.630 | 0.639 | 0.744 | |
| 5 | 1.495 | 0.804 | 0.651 | 0.735 | 0.900 | |
| 6 | 1.701 | 0.690 | 0.699 | 0.795 | 1.026 | |
| Dbr/m | 1 | −0.153 | −0.153 | −0.153 | −0.150 | −0.150 |
| 2 | −0.630 | −0.648 | −0.663 | −0.660 | −0.693 | |
| 3 | −0.984 | −0.999 | −1.011 | −1.014 | −1.026 | |
| 4 | −1.266 | −1.281 | −1.290 | −1.269 | −1.284 | |
| 5 | −1.548 | −1.560 | −1.530 | −1.536 | −1.524 | |
| 6 | −1.806 | −1.830 | −1.806 | −1.788 | −1.710 | |
| Dbd/m | 1 | −0.156 | −0.156 | −0.153 | −0.153 | −0.153 |
| 2 | −0.672 | −0.708 | −0.714 | −0.738 | −0.744 | |
| 3 | −1.020 | −1.056 | −1.077 | −1.074 | −1.095 | |
| 4 | −1.431 | −1.539 | −1.584 | −1.611 | −1.629 | |
| 5 | −1.686 | −1.794 | −1.848 | −1.872 | −1.881 | |
| 6 | −1.920 | −2.058 | −2.115 | −2.130 | −2.130 | |
| Disr/Dlr ratio | 1 | 1.342 | 1.421 | 1.447 | 1.474 | 1.526 |
| 2 | 1.517 | 1.569 | 1.586 | 1.629 | 1.681 | |
| 3 | 1.764 | 1.793 | 1.914 | 1.950 | 2.036 | |
| 4 | 2.013 | 2.084 | 2.245 | 2.272 | 2.403 | |
| 5 | 2.294 | 2.362 | 2.519 | 2.619 | 2.756 | |
| 6 | 2.534 | 2.656 | 2.877 | 2.982 | 3.129 | |
| Disd/Dld ratio | 1 | 1.281 | 1.281 | 1.282 | 1.282 | 1.284 |
| 2 | 1.339 | 1.357 | 1.366 | 1.375 | 1.393 | |
| 3 | 1.326 | 1.343 | 1.384 | 1.407 | 1.459 | |
| 4 | 1.388 | 1.405 | 1.445 | 1.467 | 1.489 | |
| 5 | 1.381 | 1.419 | 1.474 | 1.526 | 1.585 | |
| 6 | 1.429 | 1.449 | 1.516 | 1.554 | 1.660 |
| Name/Unit | Section Number | AOA 0° | AOA 2° | AOA 5° | AOA 7° | AOA 10° |
|---|---|---|---|---|---|---|
| Dar/m | 1 | 0.105 | 0.105 | 0.123 | 0.138 | 0.135 |
| 2 | 0.375 | 0.354 | 0.330 | 0.309 | 0.309 | |
| 3 | 0.576 | 0.534 | 0.270 | 0.270 | 0.285 | |
| 4 | 0.780 | 0.654 | 0.288 | 0.354 | 0.368 | |
| 5 | 0.870 | 0.339 | 0.330 | 0.423 | 0.435 | |
| 6 | 0.999 | 0.339 | 0.348 | 0.483 | 0.498 | |
| Dad/m | 1 | 0.108 | 0.108 | 0.108 | 0.114 | 0.126 |
| 2 | 0.378 | 0.360 | 0.321 | 0.324 | 0.327 | |
| 3 | 0.561 | 0.537 | 0.342 | 0.352 | 0.361 | |
| 4 | 0.738 | 0.696 | 0.354 | 0.363 | 0.375 | |
| 5 | 0.897 | 0.411 | 0.363 | 0.375 | 0.386 | |
| 6 | 1.014 | 0.396 | 0.372 | 0.402 | 0.422 | |
| Dbr/m | 1 | −0.105 | −0.105 | −0.105 | −0.096 | −0.084 |
| 2 | −0.360 | −0.363 | −0.363 | −0.378 | −0.372 | |
| 3 | −0.555 | −0.573 | −0.561 | −0.564 | −0.540 | |
| 4 | −0.726 | −0.783 | −0.786 | −0.789 | −0.789 | |
| 5 | −0.969 | −0.981 | −0.981 | −0.981 | −1.017 | |
| 6 | −1.110 | −1.101 | −1.101 | −1.086 | −1.125 | |
| Dbd/m | 1 | −0.099 | −0.099 | −0.090 | −0.084 | −0.084 |
| 2 | −0.366 | −0.375 | −0.354 | −0.363 | −0.366 | |
| 3 | −0.585 | −0.576 | −0.558 | −0.558 | −0.546 | |
| 4 | −0.816 | −0.810 | −0.810 | −0.810 | −0.804 | |
| 5 | −1.026 | −1.044 | −1.035 | −1.050 | −1.020 | |
| 6 | −1.134 | −1.161 | −1.155 | −1.170 | −1.140 | |
| Disr/Dlr ratio | 1 | 1.332 | 1.335 | 1.343 | 1.349 | 1.356 |
| 2 | 1.221 | 1.221 | 1.261 | 1.285 | 1.310 | |
| 3 | 1.307 | 1.327 | 1.360 | 1.399 | 1.445 | |
| 4 | 1.420 | 1.450 | 1.540 | 1.599 | 1.659 | |
| 5 | 1.567 | 1.612 | 1.771 | 1.816 | 1.885 | |
| 6 | 1.689 | 1.778 | 1.956 | 2.028 | 2.122 | |
| Disd/Dld ratio | 1 | 1.015 | 1.019 | 1.026 | 1.027 | 1.035 |
| 2 | 1.011 | 1.018 | 1.025 | 1.026 | 1.033 | |
| 3 | 1.012 | 1.017 | 1.026 | 1.029 | 1.033 | |
| 4 | 1.011 | 1.020 | 1.022 | 1.030 | 1.035 | |
| 5 | 1.014 | 1.017 | 1.026 | 1.030 | 1.034 | |
| 6 | 1.013 | 1.017 | 1.026 | 1.027 | 1.032 |
| Name/Unit | Section Number | AOA 0° | AOA 2° | AOA 5° | AOA 7° | AOA 10° |
|---|---|---|---|---|---|---|
| Dar/m | 1 | 0.091 | 0.099 | 0.119 | 0.099 | 0.110 |
| 2 | 0.303 | 0.289 | 0.317 | 0.269 | 0.297 | |
| 3 | 0.442 | 0.382 | 0.255 | 0.359 | 0.388 | |
| 4 | 0.552 | 0.396 | 0.286 | 0.376 | 0.427 | |
| 5 | 0.696 | 0.416 | 0.320 | 0.422 | 0.475 | |
| 6 | 0.801 | 0.422 | 0.340 | 0.427 | 0.501 | |
| Dad/m | 1 | 0.085 | 0.085 | 0.085 | 0.085 | 0.088 |
| 2 | 0.283 | 0.283 | 0.212 | 0.226 | 0.201 | |
| 3 | 0.425 | 0.382 | 0.260 | 0.255 | 0.255 | |
| 4 | 0.552 | 0.439 | 0.289 | 0.283 | 0.277 | |
| 5 | 0.679 | 0.450 | 0.325 | 0.325 | 0.311 | |
| 6 | 0.778 | 0.416 | 0.342 | 0.337 | 0.325 | |
| Dbr/m | 1 | −0.091 | −0.091 | −0.091 | −0.085 | −0.079 |
| 2 | −0.308 | −0.308 | −0.320 | −0.311 | −0.317 | |
| 3 | −0.467 | −0.467 | −0.470 | −0.456 | −0.461 | |
| 4 | −0.640 | −0.625 | −0.640 | −0.637 | −0.631 | |
| 5 | −0.781 | −0.798 | −0.810 | −0.790 | −0.798 | |
| 6 | −0.877 | −0.908 | −0.912 | −0.892 | −0.892 | |
| Dbd/m | 1 | −0.079 | −0.079 | −0.079 | −0.079 | −0.079 |
| 2 | −0.280 | −0.297 | −0.311 | −0.311 | −0.317 | |
| 3 | −0.461 | −0.447 | −0.481 | −0.481 | −0.495 | |
| 4 | −0.614 | −0.614 | −0.696 | −0.702 | −0.722 | |
| 5 | −0.784 | −0.792 | −0.877 | −0.877 | −0.900 | |
| 6 | −0.877 | −0.900 | −0.985 | −0.985 | −0.996 | |
| Disr/Dlr ratio | 1 | 1.272 | 1.274 | 1.277 | 1.280 | 1.282 |
| 2 | 1.146 | 1.148 | 1.177 | 1.238 | 1.300 | |
| 3 | 1.201 | 1.203 | 1.258 | 1.308 | 1.396 | |
| 4 | 1.263 | 1.286 | 1.377 | 1.463 | 1.571 | |
| 5 | 1.321 | 1.397 | 1.543 | 1.658 | 1.766 | |
| 6 | 1.426 | 1.532 | 1.691 | 1.809 | 1.973 | |
| Disd/Dld ratio | 1 | 1.011 | 1.014 | 1.016 | 1.021 | 1.026 |
| 2 | 1.011 | 1.014 | 1.016 | 1.022 | 1.026 | |
| 3 | 1.011 | 1.014 | 1.017 | 1.022 | 1.026 | |
| 4 | 1.012 | 1.015 | 1.017 | 1.022 | 1.027 | |
| 5 | 1.012 | 1.015 | 1.017 | 1.022 | 1.027 | |
| 6 | 1.012 | 1.015 | 1.018 | 1.023 | 1.027 |
References
- Wang, J.F.; Wang, X.D.; Li, J.W.; Yang, T.P.; Li, L.F.; Cheng, K.M. Overview on aerodynamic design of cruising waverider configuration for hypersonic vehicles. Acta Aerodyn. Sin. 2018, 36, 705–728. [Google Scholar]
- Ajaj, R.M.; Beaverstock, C.S.; Friswell, M.I. Morphing aircraft: The need for a new design philosophy. Aerosp. Sci. Technol. 2016, 49, 154–166. [Google Scholar] [CrossRef]
- Xu, X.P.; Zhang, T.T.; Shen, Y. Parametric Modeling and Multi-Objective Design Optimization of Common Aero Vehicle. Aero Weapon. 2022, 29, 56–63. [Google Scholar]
- Yuan, Y.; Liu, J.; Yu, J.Q.; Zhang, C.; Ren, P.F. Research on aerodynamic layout optimization technology of high-speed folding vehicle. J. Beijing Univ. Aeronaut. Astronaut. 2023, 48, 1–11. [Google Scholar] [CrossRef]
- Gao, T.Y.; Cui, K.; Hu, S.C.; Wang, X.P. Multi-Objective Optimization and Aerodynamic Performance Analysis of the Upper Surface for Hypersonic Vehicles. Chin. J. Theor. Appl. Mech. 2013, 45, 193–201. [Google Scholar]
- Shuwei, M.; Du, B.; Wanchun, C. Collaborative optimization of hypersonic vehicle based on surrogate model. J. Beijing Univ. Aeronaut. Astronaut. 2013, 39, 1042–1047. [Google Scholar]
- Viviani, A.; Iuspa, L.; Aprovitola, A. Multi-objective optimization for re-entry spacecraft conceptual design using a free-form shape generator. Aerosp. Sci. Technol. 2017, 71, 312–324. [Google Scholar] [CrossRef]
- Coulter, B.G.; Huang, D.; Wang, Z. Geometric Design of Hypersonic Vehicles for Optimal Mission Performance with High-Fidelity Aerodynamic Models. J. Aircr. 2022, 60, 870–882. [Google Scholar] [CrossRef]
- Liu, J.M.; Hou, Z.Q.; Song, G.B.; Zhu, X.C. Optimization design and aerodynamic characteristic analysis of waverider based hypersonic cruise missile configuration. Acta Aerodyn. Sin. 2011, 29, 118–123. [Google Scholar]
- Peng, J.; Lu, Z.L.; Li, W.Z. Upper/Lower Surface of Waverider Integrated Optimization. J. Nanjing Univ. Aeronaut. Astronaut. 2007, 39, 307–311. [Google Scholar] [CrossRef]
- Ma, Y.; Yang, T.; Feng, Z.; Zhang, Q. Hypersonic lifting body aerodynamic shape optimization based on the multiobjective evolutionary algorithm based on decomposition. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 229, 1246–1266. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, C.; Wang, F.; Ye, Z. Design and Optimization Method for Hypersonic Quasi-Waverider. AIAA J. 2020, 58, 2132–2146. [Google Scholar] [CrossRef]
- Lobbia, M.; Suzuki, K. Design and analysis of payload-optimized waveriders. In Proceedings of the 10th AIAA/NAL-NASDA-ISAS International Space Planes and Hypersonic Systems and Technologies Conference, Kyoto, Japan, 24–27 April 2001; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2001. [Google Scholar] [CrossRef]
- Lobbia, M.A.; Suzuki, K. Experimental Investigation of a Mach 3.5 Waverider Designed Using Computational Fluid Dynamics. AIAA J. 2014, 53, 1590–1601. [Google Scholar] [CrossRef]
- Lobbia, M.A. Multidisciplinary Design Optimization of Waverider-Derived Crew Reentry Vehicles. J. Spacecr. Rocket. 2016, 54, 233–245. [Google Scholar] [CrossRef]
- Peng, W.; Feng, Z.; Yang, T. Rapid Aerodynamic Shape Optimization with Payload Size Constraints for Hypersonic Vehicle. IEEE Access 2019, 7, 84429–84447. [Google Scholar] [CrossRef]
- Zhang, B.; Feng, Z.; Xu, B.; Yang, T. Efficient Aerodynamic Shape Optimization of the Hypersonic Lifting Body Based on Free Form Deformation Technique. IEEE Access 2019, 7, 147991–148003. [Google Scholar] [CrossRef]
- Yao, M. Automation of Aircraft Layout and Mass Estimation Using CAD Model. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2008. [Google Scholar]
- Zhang, T.; Wang, Z.; Huang, W.; Yan, L. A review of parametric approaches specific to aerodynamic design process. Acta Astronaut. 2018, 145, 319–331. [Google Scholar] [CrossRef]
- Straathof, M.H.; van Tooren, M.J.L. Extension to the Class-Shape-Transformation Method Based on B-Splines. AIAA J. 2011, 49, 780–790. [Google Scholar] [CrossRef]
- Liu, C.; Peng, B.; Chen, B.; Ji, C. Rapid Design and Optimization of Waverider from 3D Flow. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016. [Google Scholar] [CrossRef]
- Sudasinghe, A.; Rajakareyar, P.; Matida, E.; Abo El Ella, H.; ElSayed, M.S.A. Aerodynamic Shape Optimization of an Aircraft Propulsor Air Intake with Boundary Layer Ingestion. Appl. Mech. 2022, 3, 1123–1144. [Google Scholar] [CrossRef]
- Farin, G. Chapter 7—Spline Curves in Bézier Form. In Curves and Surfaces for Computer-Aided Geometric Design, 3rd ed.; Farin, G., Ed.; Academic Press: Boston, MA, USA, 1993; pp. 101–120. [Google Scholar]
- Dakeev, U. Chapter 1—Introduction to Parametric Design. In Creo Parametric Modeling with Augmented Reality; Dakeev, U., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2023; pp. 1–10. [Google Scholar]
- Huang, Y. Examples of UG/Open API, MFC and COM Development; National Defense Industry Press: Beijing, China, 2009; pp. 46–58. [Google Scholar]
- Skarka, W.; Nalepa, R.; Musik, R. Integrated Aircraft Design System Based on Generative Modelling. Aerospace 2023, 10, 677. [Google Scholar] [CrossRef]
- Li, J. Research on Method of Missile Configuration Parametric Design Based On Secondary Development of UG. Master’s Thesis, Beijing Institute of Technology, Beijing, China, 2015. [Google Scholar]
- Chen, X.; Zheng, H.; Pan, G.; Jia, X. Parametarski sustav modeliranja komore izgaranja plinske turbine. Teh. Vjesn. 2014, 21, 1213–1219. [Google Scholar]
- Sziroczak, D.; Smith, H. A review of design issues specific to hypersonic flight vehicles. Prog. Aerosp. Sci. 2016, 84, 1–28. [Google Scholar] [CrossRef]
- ELLIOTT, G.A.; HANKEY, W.L. Hypersonic lifting body optimization. J. Spacecr. Rocket. 1968, 5, 1463–1467. [Google Scholar] [CrossRef]
- Golubkin, V.N.; Negoda, V.V. Optimum lifting body shapes in hypersonic flow at high angles of attack. Theor. Comp. Fluid Dyn. 1995, 7, 29–47. [Google Scholar] [CrossRef]
- Theisinger, J.E.; Braun, R.D. Multi-Objective Hypersonic Entry Aeroshell Shape Optimization. J. Spacecr. Rocket. 2009, 46, 957–966. [Google Scholar] [CrossRef]
- Siemens. NX 10 Programming Tools Help. Available online: https://docs.plm.automation.siemens.com/tdoc/nx/10/nx_api/#uid:index (accessed on 3 January 2024).
- Lockman, W.K.; Lawrence, S.L.; Cleary, J.W. Flow over an all-body hypersonic aircraft—Experiment and computation. J. Spacecr. Rocket. 1992, 29, 7–15. [Google Scholar] [CrossRef]
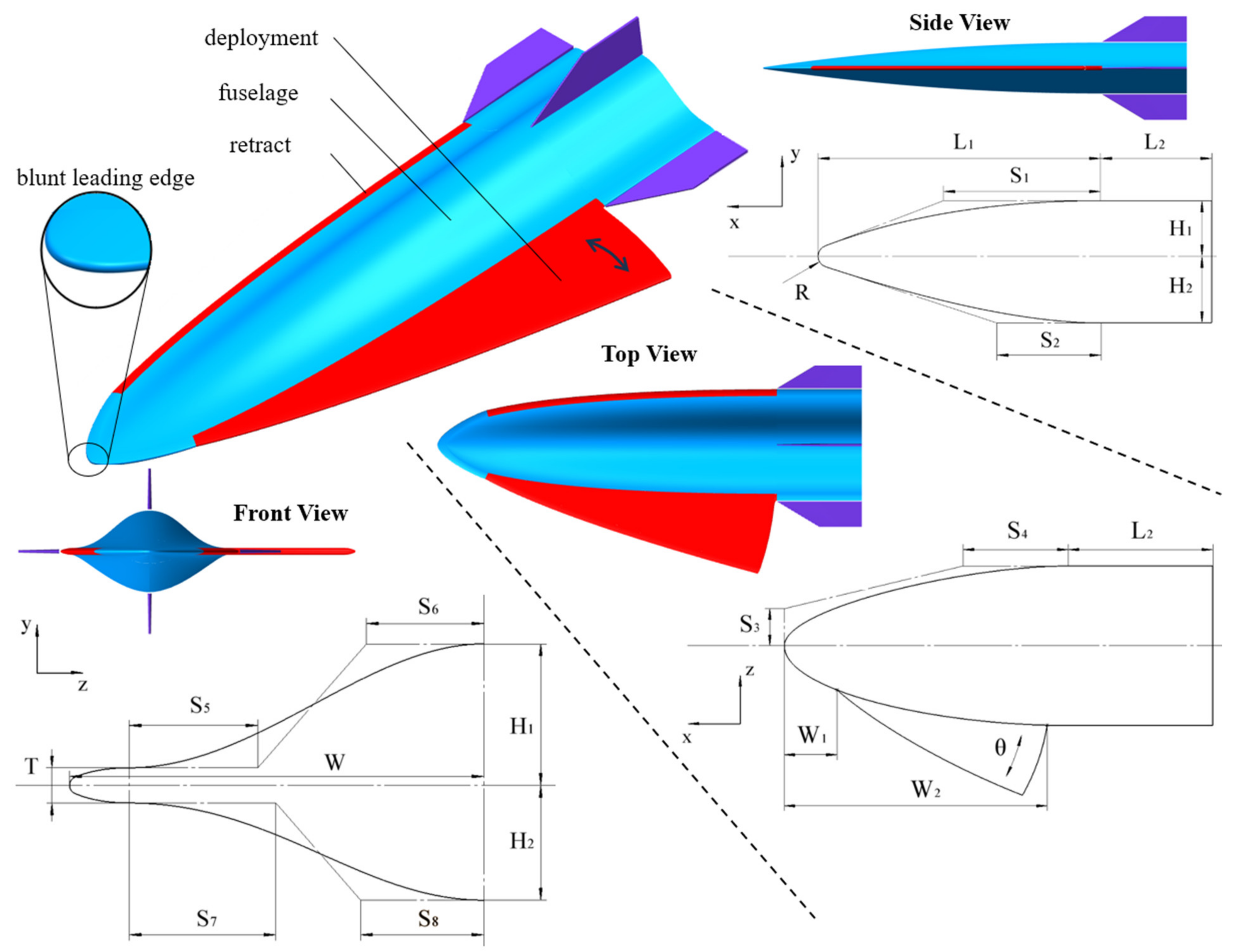
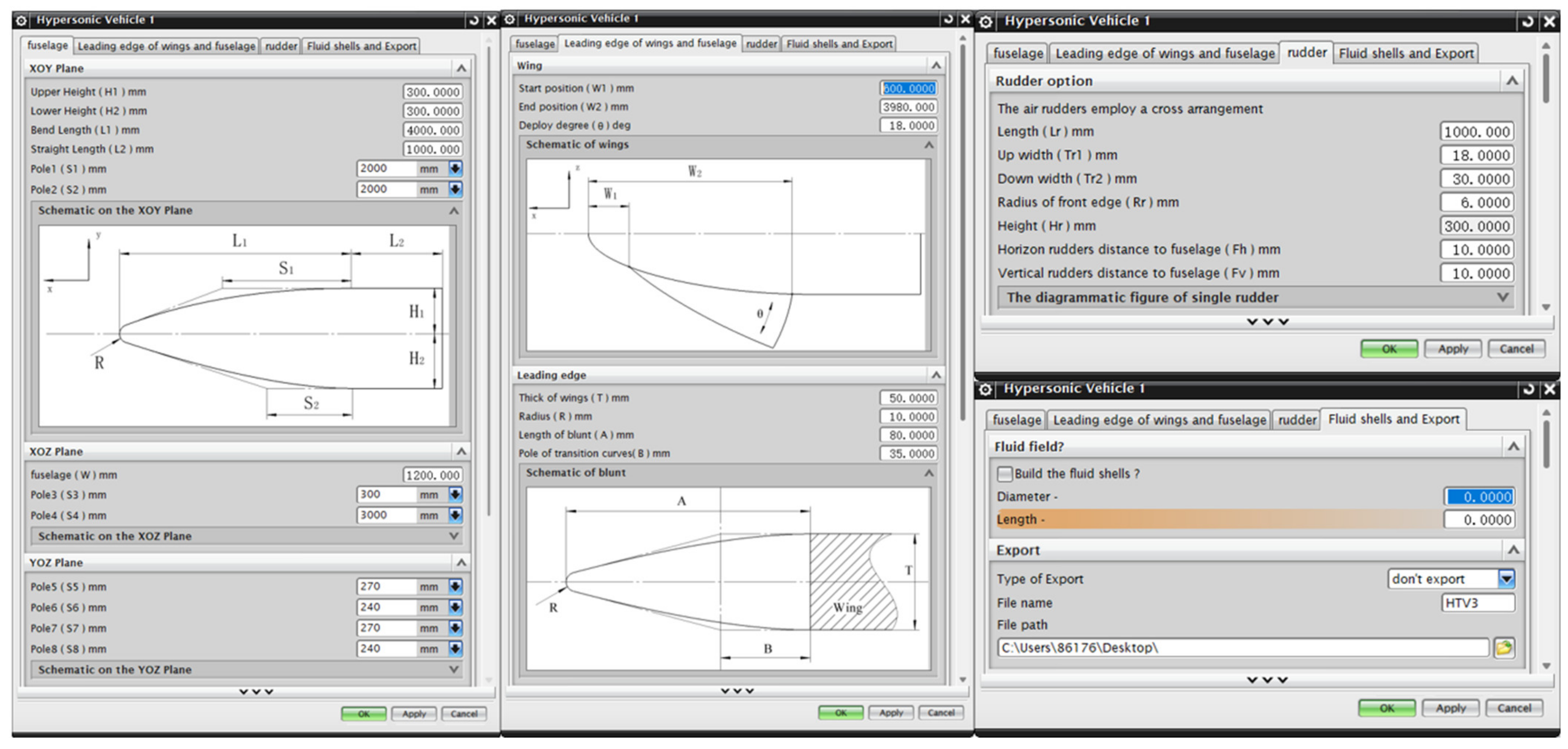




| Serial | Part | Description/Name | Initial Value |
|---|---|---|---|
| 1 | Fuselage | Upper height/H1 | 0.3 m |
| 2 | Lower height/H2 | 0.3 m | |
| 3 | Bend length/L1 | 4 m | |
| 4 | Stright length/L2 | 1 m | |
| 5 | Half width of the fuselage/W | 0.6 m | |
| 6 | Pole 1 of B-spline/S1 | 2 m | |
| 7 | Pole 2 of B-spline/S2 | 2 m | |
| 8 | Pole 3 of B-spline/S3 | 0.5 m | |
| 9 | Pole 4 of B-spline/S4 | 3 m | |
| 10 | Pole 5 of B-spline/S5 | 0.275 m | |
| 11 | Pole 6 of B-spline/S6 | 0.18 m | |
| 12 | Pole 7 of B-spline/S7 | 0.055 m | |
| 13 | Pole 8 of B-spline/S8 | 0.24 m | |
| 14 | Wing | Wing start point/W1 | 0.6 m |
| 15 | Wing end point/W2 | 3.98 m | |
| 16 | Wing angle/θ | 15° | |
| 17 | Wing thickness/T | 0.05 m | |
| 18 | Rudder | Radius of rudder front/Rr | 0.006 m |
| 19 | Up width of rudder/Tr1 | 0.018 m | |
| 20 | Down width of rudder/Tr2 | 0.03 m | |
| 21 | Rudder length/Lr | 1 m | |
| 22 | Rudder height/Hr | 0.3 m | |
| 23 | Distance between horizon rudders and fuselage/D1 | 0.01 m | |
| 24 | Distance between horizon rudders and fuselage/D2 | 0.01 m | |
| 25 | Leading edge | Radius of leading edge/R | 0.01 m |
| 26 | Length of blunt/A Control point of transition curve/B | 0.075 m | |
| 27 | 0.0375 m |
| Type | Mesh Number | Fx/kN | Fy/kN | Lift-to-Drag Ratio |
|---|---|---|---|---|
| Coarse grid | 5.3 million | −11.82 | 101.1 | 4.842 |
| Medium grid | 7.5 million | −11.51 | 99.7 | 4.878 |
| Fine grid | 9.6 million | −11.42 | 98.6 | 4.869 |
| Altitude/km | Temperature/K | Pressure/Pa | Mach |
|---|---|---|---|
| 6 | 249.19 | 47,217.5 | 2.5 |
| 10 | 223.25 | 26,499.76 | 4 |
| 15 | 216.65 | 12,111.4 | 5.5 |
| 20 | 216.65 | 5529.1 | 7 |
| 25 | 221.552 | 2549.15 | 8.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Z.; Yu, Z.; Meng, F.; Zhang, W.; Cui, J.; He, X.; Lei, Y.; Musa, O. Parametric Design Method and Lift/Drag Characteristics Analysis for a Wide-Range, Wing-Morphing Glide Vehicle. Aerospace 2024, 11, 257. https://doi.org/10.3390/aerospace11040257
Jin Z, Yu Z, Meng F, Zhang W, Cui J, He X, Lei Y, Musa O. Parametric Design Method and Lift/Drag Characteristics Analysis for a Wide-Range, Wing-Morphing Glide Vehicle. Aerospace. 2024; 11(4):257. https://doi.org/10.3390/aerospace11040257
Chicago/Turabian StyleJin, Zikang, Zonghan Yu, Fanshuo Meng, Wei Zhang, Jingzhi Cui, Xiaolong He, Yuedi Lei, and Omer Musa. 2024. "Parametric Design Method and Lift/Drag Characteristics Analysis for a Wide-Range, Wing-Morphing Glide Vehicle" Aerospace 11, no. 4: 257. https://doi.org/10.3390/aerospace11040257
APA StyleJin, Z., Yu, Z., Meng, F., Zhang, W., Cui, J., He, X., Lei, Y., & Musa, O. (2024). Parametric Design Method and Lift/Drag Characteristics Analysis for a Wide-Range, Wing-Morphing Glide Vehicle. Aerospace, 11(4), 257. https://doi.org/10.3390/aerospace11040257








