Abstract
In the framework of the “Multidisciplinary Optimization and Regulations for Low-boom and Environmentally Sustainable Supersonic aviation” project, pursued by a consortium of European government and academic institutions, coordinated by Politecnico di Torino under the European Commission Horizon 2020 financial support, the Italian Aerospace Research Centre is computationally investigating the high-pressure hydrogen/air kinetic combustion in the operative conditions typically encountered in supersonic aeronautic ramjet engines. This task is being carried out starting from the zero-dimensional and one-dimensional chemical kinetic assessment of the complex and strongly pressure-sensitive ignition behavior and flame propagation characteristics of hydrogen combustion through the validation against experimental shock tube and laminar flame speed measurements. The 0D results indicate that the kinetic mechanism by Politecnico di Milano and the scheme formulated by Kéromnès et al. provide the best matching with the experimental ignition delay time measurements carried out in high-pressure shock tube strongly argon-diluted reaction conditions. Otherwise, the best behavior in terms of laminar flame propagation is achieved by the Mueller scheme, while the other investigated kinetic mechanisms fail to predict the flame speeds at elevated pressures. This confirms the non-linear and intensive pressure-sensitive behavior of hydrogen combustion especially in the critical high-pressure and low-temperature region which is hard to be described by a single all-encompassing chemical model.
1. Introduction
The global energy shortage and the increasingly serious issues related to the Greenhouse Gas (GHG) emissions target, set by governments and institutions, pose hydrogen as an ideal candidate as an energy vector due to its high efficiency and zero carbon combustion characteristics. It is widely esteemed as a promising propellant for high-speed, air-breathing, trans-atmospheric, and long-term passenger transportation aircraft since it can be burned efficiently and reliably in supersonic combustion engines [1]. Moreover, among the various available fuels, it possesses the highest heat release with the shortest kinetic time, wide flammability limits (4–75% by volume in air), and excellent cooling properties [2].
Furthermore, H2 can be considered an ideal gas over an extensive temperature range and even at high pressures, and it is so strongly diffusive and highly buoyant that its mixing characteristic time can be neglected in several practical industrial applications.
Additionally, H2 is a clean fuel since the overall product of its complete oxy-combustion is only water, even if, when reacting with air, it also produces NOx, due to the very elevated flame temperatures reached during conventional combustion. In any case, the advantage of burning hydrogen from an environmental point of view is that it avoids the production of the greenhouse gas CO2, nor any of the several other pollutant species, i.e., CO, unburned hydrocarbons, Polycyclic Aromatic Hydrocarbons (PAHs), and soot.
For the above-mentioned reasons, hydrogen is esteemed as a fundamental energy vector toward the decarbonized economy.
Supersonic hydrogen/air combustion is a very challenging process, consisting of several critical phenomena, e.g., injection, compressible mixing, chemical kinetics, ignition, flame holding, vortices generation, flashbacks, combustion instability, turbulence combustion, interactions among shock waves, boundary layer, and heat release, etc. Moreover, ramjet engine operations are further complicated by the very short residence time (~10−3 s) of the flow inside the thrust chamber, which is of the same order of magnitude as the chemical kinetic ignition time of hydrogen/air mixtures at the typical conditions of ramjet operation. Since experimental investigations are often unfeasible due to several difficulties in measuring multispecies, reacting, high-speed, unsteady flow fields [1], the most convenient way to design and develop ramjet engine-propelled vehicles relies on CFD modelling and simulations.
In the framework of the MORE&LESS project, the high-pressure combustion hydrogen/air chemical kinetic assessment is presented in this work since it is an important, preliminary task for the development of physical–chemical combustion models to be implemented into CFD codes.
MORE&LESS is a research project pursued by a consortium of European government and academic institutions including CIRA, and it is coordinated by Politecnico di Torino under the EC Horizon 2020 financial support.
This project aims to address the challenges regarding the environmental impact of supersonic, air-breathing aviation implementing a holistic approach based on a synergic coupling between low and high-fidelity modelling of several processes, e.g., aerodynamics, jet-noise, sonic-boom, propulsion, and above all pollutant and climate-changing chemical emissions.
Advanced propulsion systems are essential enablers of supersonic aviation, and the proper understanding of their working principles is required to operate them efficiently and with low pollutant emissions, thus extending the design space and flight envelope. Modelling of propulsion systems of these aircraft, the optimization of their components, and properly estimating their performance are some of the main goals of the MORE&LESS project, together with the estimation of bio-fuel and hydrogen combustion with associated emissions. Consequently, solid strategies are developed to reduce pollutant emissions for future supersonic aircraft.
CIRA is in charge of the assessment of available hydrogen/air reaction mechanisms, in particular with (i) a thorough investigation of detailed and reduced kinetic mechanisms performed through a literature survey, (ii) theoretical investigations and identification of the most performing kinetic schemes for hydrogen/air combustion at selected operative flight conditions, and (iii) 0D/1D simulations of hydrogen/air combustion and comparison of ignition delay times and adiabatic flame temperatures against the available literature experimental data. The work described in the present paper emanates directly from what was recently accomplished in the previous H2020 STRATOFLY project [3,4,5,6] and the present task represents a continuation and extension of it to a wider range of operative conditions. The optimal scheme arises as a suitable trade-off between the accuracy, required for a truthful description of ignition and combustion phenomena, and the computational costs, associated with the available calculation speed and memory storage capacity. For this purpose, a preliminary 0D/1D kinetic analysis of hydrogen/air combustion at the most representative operative conditions for this application was performed using the kinetic and thermodynamic Cantera [7] open-source software through the calculation of induction times and laminar flame speeds.
Furthermore, since in aeronautic engines, the working pressure is often much more than the atmospheric level reaching values of up to 20 bars, to design hydrogen/air combustion chambers that are able to guarantee a minimum NOx release, the deepened understanding of the complex and nonlinear hydrogen/oxygen ignition kinetics at such an elevated pressure is of paramount importance.
This paper is conceived as a comprehensive overview of the chemical/kinetic models for high-pressure hydrogen ignition and combustion, intended to be a valuable support for the identification of the most suitable kinetic mechanism to be implemented within RANS and LES commercial and in-house CFD codes for the design and rebuilding of hydrogen combustion processes, especially in the framework of aeronautic engines.
The following sub-sections of the introduction briefly disclose the kinetic mechanisms for the high-pressure hydrogen combustion analyzed in this work. Section 2 describes the numerical methodology implemented for the kinetic assessment presented here, while Section 3 reports the computational 0D/1D results in terms of IDT (Ignition Delay Times) and LFS (Laminar Flame Speed) predicted using the different kinetic schemes and the comparison with the available measurements acquired at elevated pressures. An overall discussion regarding the behavior of the several investigated mechanisms for high-pressure hydrogen ignition and combustion completes Section 3, and finally, the general conclusions are drawn in Section 4.
1.1. Selection of the Kinetic Mechanisms
Based on the author’s experience [3,4] and the review of Hu and co-workers [5], only the following eleven available study schemes were considered as the most promising kinetic mechanisms since they were specifically designed and developed to describe not only the hydrogen/oxygen combustion at atmospheric conditions but also at intermediate to high pressures:
- Mueller—1999 [8].
- Li—2004 [9].
- Ó’Conaire—2004 [8,10,11,12].
- CRECK—2012 [13,14,15,16,17,18].
- Kéromnès—2013 [19].
- Z22—2018 [20,21,22].
- Z24—2022 [23].
- RAMEC [24].
- GRI-Mech 3.0 [25].
- USC-II [26].
- Aramco-II [27,28,29].
The last four schemes are large kinetic mechanisms dedicated not only to hydrogen oxidation but suitably formulated for the description of natural gas, i.e., GRI-Mech 3.0 [25] and USC-II [26], and high-molecular-weight-hydrocarbon combustion in petrochemical applications, i.e., Aramco-II [27,28,29]. In any case, they include the accurate H/O sub-mechanism, which is of paramount importance also in the combustion of every hydrocarbon, and they were used in the present work as fully detailed mechanisms for reference purposes.
Table 1 summarizes the main features of the considered kinetic mechanisms ordered with an increasing number of chemical species.

Table 1.
The number of chemical species and elementary reactions for the kinetic mechanisms numerically investigated in this work.
1.2. Mueller—1999
This kinetic mechanism was developed by Mueller and collaborators at Princeton University, NJ, USA. They employed a variable pressure flow reactor to investigate the explosion characteristics of mixtures involving H2/O2 combustion. The experiments demonstrated the significant involvement of HO2 and H2O2 in the initiation and combustion processes of pure hydrogen/oxygen systems, particularly under high pressure of approximately 16 atmospheres [8].
The rate at which the specified reactions occur underwent adjustments when compared to a prior kinetic mechanism presented by Yetter and colleagues [11]. These modifications were made through a refinement process that relied on the findings from high-pressure flow reactor experiments conducted by Kim and collaborators [12].
[RM9] H + O2 + (N2) = HO2 + (N2)
[RM13] HO2 + OH = H2O + O2
[RM14] HO2 + HO2 = H2O2 + O2
1.3. Li—2004
The Li mechanism [9] represents an enhanced and updated rendition of the previous Mueller scheme [4], originally devised for H2/O2. This revision was undertaken by incorporating novel kinetic and thermodynamic experimental data. The mechanism underwent rigorous testing and validation through experiments involving shock tubes, flow reactors, and laminar premixed flames.
The rate constants for steps [RL1] and [RL2], as well as the thermodynamic properties of OH, were refined using data from measurements conducted by Ruscic and colleagues [15]. A critical constraint on the interplay between reactions (RL1) and (RL2) is imposed by their ratio within the temperature range of 800 ÷ 900 K.
[RL1] H + O2 = O + OH
[RL2] O + H2 = H + OH
Above and below this temperature range, one or the other of these reactions becomes significantly less dominant, and the determination of their ratio becomes affected by uncertainties.
Analyses also show that Reaction RL3 is worth noting in the case of high-pressure flame propagation:
[RL3] H2 + OH = H2O + H
Moreover, Li and co-workers highlight that the irreversible termolecular, high-pressure sensitive step, i.e., the RL8 reaction plays a role of paramount importance:
[RL8] H + OH + M = H2O + M
1.4. O’Conaire—2004
The O’Conaire scheme is an elaborate kinetic mechanism designed for simulating the combustion of H2/O2 mixtures across a wide temperature range of 298 to 2700 K, pressures ranging from 0.05 to 87 atm, and equivalence ratios spanning from 0.2 to 6 [10]. This model serves as an updated version of the previous Mueller et al. scheme [8], which, in turn, originated from the CO/H2/O2 reaction mechanism by Yetter et al. [11] and was later refined by Kim et al. [12]. In the final iteration of the model, certain original Arrhenius parameters were adjusted to enhance the agreement with experimental data, encompassing not only flow reactors but also shock-tube and burner-stabilized flame speeds across a broader operational range. The revision process particularly focused on the crucial pressure-sensitive reaction.
[OR8] H + OH (+M) = H2O (+M)
This reversible step consists of the termolecular collision of the key radicals: Hꞏ, i.e., the primary product of the thermal decomposition of the stable hydrogen molecule, and the OH radical, i.e., the flame marker and the main radical involved in the chain branching process with a third body, i.e., (M), whose presence promotes the [OR8] reaction.
1.5. CRECK—2012
The CRECK Modelling Group at Politecnico di Milano developed a hierarchical mechanism designed as a foundational sub-mechanism for integration into heavier fuels, ranging from hydrocarbons to jet biodiesels. This kinetic mechanism underwent evaluation through 0D ignition delay times and 1D laminar flame speed calculations. Validation involved comparing the model against available experimental data, utilizing a specifically formulated in-house kinetic and thermodynamic tool, i.e., OpenSMOKE.
The mechanism experienced an improvement process, starting with a detailed kinetic H2/O2 combustion scheme. This upgrade incorporated new kinetic and thermodynamic measurements and was thoroughly validated across a broad spectrum of temperatures, pressures, and equivalence ratios [13,14,15,16,17,18]. Notably, its performance at high pressures was significantly enhanced, particularly by adjusting higher rate parameters for the specific thermo-molecular reaction.
[CR10] H + OH (+M) = H2O (+M)
The frequency factor for this step was increased twofold compared to the original mechanism [13,14]. Subsequent investigations revealed the significant importance of the [CR10] reaction in the propagation of laminar flame speed at high pressure, while its sensitivity under flow reactor and shock tube conditions was found to be less pronounced. Additionally, a slight modification was applied to the Chaperon efficiency of the bath gases to increase the agreement with the entire set of considered experimental measurements.
Furthermore, the mechanism now includes a high-pressure limit based on Troe’s parameters models, aimed at appropriately describing the fall-off behavior of the [CR10] reaction. This adjustment is crucial, especially for applications involving very elevated pressure.
All thermodynamic and transport properties of the CRECK 2012 mechanism were sourced from the CHEMKIN database, with a notable exception being the enthalpy of radicals OH and HO2 formation. This exception was revised in accordance with both theoretical and experimental recommendations arising from Ruscic et al. [15].
In a more recent development, the CRECK—2012 model underwent further improvements by integrating the H2/O2 with C1–C2 sub-mechanisms from [13], as revised in [14], and heavier fuels sub-mechanisms from Ranzi et al. [15]. This update allows for efficient utilization as a chemical kinetic mechanism for syngas combustion.
1.6. Kéromnès—2013
This detailed kinetic mechanism is specifically designed for examining the oxidation of a syngas mixture, encompassing H2/CO/O2/N2/Ar, under pressure levels ranging from 1 to 70 bar. The investigation spans a temperature spectrum from 900 to 2550 K, with equivalence ratios varying from 0.1 to 4 [19]. As indicated in Table 1, this kinetic scheme includes 10 chemical species, and among them, the excited radical OH* is engaged in interactions through 31 reversible reactions.
An extensive literature review has pinpointed several reactions deemed crucial for hydrogen oxidation. The reactivity of hydrogen is primarily governed by the competition among these reactions, notably emphasizing the chain-branching reaction
and the pressure-dependent chain-propagating reaction
[RK1] H + O2 ⇄ O + OH
[RK9] H + O2 (+M) ⇄ HO2 (+M)
For this reason, [RK1] and [RK9] reactions were extensively investigated, and it was noticed that, at high-pressure conditions, the thermal decomposition of hydrogen peroxide (H2O2) through the pressure-dependent reaction
becomes the dominant chain-branching step. Moreover, as for most fuels, at intermediate temperatures, the following reaction between the fuel, i.e., hydrogen, and the radical HO2 is important in the prediction of accurate ignition delay times:
[RK15] H2O2 (+M) ⇄ OH + OH (+M)
[RK17] H2 + HO2 ⇄ H + H2O2
At temperatures ranging from low to intermediate levels (<1000 K), commonly encountered in the Rapid Compression Machine (RCM), the primary influence on hydrogen oxidation is attributed to Reaction RK9. This reaction results in the formation of the hydroperoxyl radical (HO2) through subsequent interaction with molecular hydrogen, leading to the generation of H2O2 according to Reaction RK17. The oxygenated water then decomposes into two OH radicals, as specified by Reaction RK15.
Conversely, in the high temperatures experienced within shock tube equipment, the competition between Reactions RK1 and RK9 introduces pressure dependence in ignition delay times. Depending on the pressure, the oxidation process at elevated temperatures is predominantly regulated by Reaction RK1. The temperature range where the competition between kinetic steps of RK1 and RK9 occurs is contingent on the operational pressure due to the pressure dependence of Reaction RK9.
In their study [19], the authors explored the impact of the reaction rate constants on ignition delay times through a sensitivity analysis across a wide pressure range of 1 to 100 bars and temperatures ranging from 850 to 1200 K. Their conclusion was that at low temperatures (<1000 K) and relatively low pressure (1 bar), the reaction kinetics is mainly governed by the interplay between the chain-branching reaction RK1 and the chain-terminating reaction RK9. However, at higher temperatures (>1000 K), reactivity is solely dictated by the chain-branching reaction R1. Under high pressure and intermediate temperature conditions, the reaction kinetics follows the sequence identified by Pitz and Westbrook, involving steps RK15 and RK17, wherein H2 and the HO2 radical contribute to the production and consumption of H2O2, which subsequently decomposes to release two OH radicals, leading to the chain-branching reaction.
The Kéromnes 2013 mechanism incorporates the OH* sub-mechanism to enhance the accuracy of predicting the experimental ignition delay times observed in shock tube tests, capturing the onset, maximum rate of increase, or peak of the chemiluminescence emission of OH*.
1.7. Z22—2018
This detailed kinetic mechanism is specifically tailored for hydrogen/oxygen reactions, encompassing nine distinct species and 22 irreversible elementary reactions [20]. It derives its H2-O2 chemical structure from [21] and incorporates three supplementary fuel breakdown reactions from [22].
Zettervall and Fureby [20] underscore the significance of the competition between the chain-branching reaction ZR4, H + O2 → OH + O, and the chain-propagating reaction ZR12, H + O2 (+M) → HO2 (+M). The former establishes a pool of radical species, effectively reducing the ignition time, while the latter generates the hydroperoxyl radical, inhibiting the chain-branching combustion process and thereby extending the induction time.
The interplay between these reactions and the resulting distribution of fast O, H, and OH radicals, along with the slow radical HO2, exhibits a strong temperature dependence. Moreover, a region of rapid ignition, corresponding to the chain-branching explosion at high temperatures, and a region of slow ignition, associated with thermal explosion at low temperatures, are separated by a crossover region. This intermediate temperature zone is dominated by intricate chemical processes, and interestingly, it is precisely within this connecting and critical zone that numerous ramjets, scramjets, and dual-mode engines operate.
Z22 incorporates reactions crucial for the entire temperature spectrum, both below and above the crossover region. During mechanism development, considerable efforts were directed towards enhancing its capability to accurately replicate ignition experimental behavior, particularly in the intermediate connecting region. This focus is crucial for ensuring flame anchoring and stabilization within supersonic combustion engines [1].
At low temperatures, Reaction ZR12 prevails over Reaction ZR4, leading to an increase in HO2 concentration. New reaction paths gain prominence, such as ZR16, HO2 + HO2 → H2O2 + O2, and ZR20, H2O + HO2 → H2O2 + OH. These reactions elevate the concentration of H2O2, with its primary consumption occurring through Reaction ZR17: H2O2 (+M) → OH + OH (+M). This reaction produces two OH radicals, which, in turn, generate H radicals through ZR8: H2 + OH → H2O + H.
1.8. Z24—2022
This is a recent detailed reaction mechanism for hydrogen/air combustion essentially representing an updated version of the previous Z22 kinetic mechanism developed by Zettervall and Fureby [2] [AD1] to expand the operating pressure range above 8 atm.
It was formulated by the Swedish Research and Defence Agency (FOI), and it is openly available [23].
The improvement consists of the addition of the following two pressure-dependent irreversible reactions for the production of the fundamental OH radical:
[RZ23] H2O2 + N2 = > OH + OH + N2
[RZ24] H2O2 + O2 = > OH + OH + O2
1.9. Considered Detailed Kinetic Mechanisms
Thorough analysis of detailed mechanisms was conducted to enhance kinetic assessments and provide a more comprehensive chemical depiction of ignition and combustion processes. The examined full mechanisms include RAMEC [24], GRI-Mech 3.0 [25], USC-II [26], and Aramco-II [27,28,29].
RAMEC, known as the RAM accelerator Mechanism, is a kinetic scheme comprising 38 species and 190 reactions, initially designed for simulating methane–oxygen ignition and combustion under high pressures (40 ÷ 260 atm), intermediate temperatures (1040 ÷ 1500 K), low dilution levels (<70%), and equivalence ratios from 0.4 to 6 [24]. Originating from the Gas Research Institute’s GRI 1.2 scheme [30], it was developed by Petersen and co-workers, who incorporated specific radical species crucial for combustion in extreme conditions [24]. While primarily intended for C1 hydrocarbon combustion, RAMEC inherently includes a detailed H/O sub-mechanism, making it applicable to hydrogen/air combustion, especially for high-pressure spouting of hydrogen into the air [31]. Given the operating conditions of supersonic gas turbines, ramjet, and scramjet engines, which involve elevated pressures, fuel-lean conditions, and temperatures up to around 2800 K, RAMEC is considered for modelling the kinetics of hydrogen/air ignition and combustion.
GRI-Mech 3.0 is a widely recognized detailed scheme extensively optimized with robust sensitivity studies for modelling natural gas ignition and combustion, mainly methane, along with NO formation and reburn chemistry. Developed through computational and experimental research sponsored by the Gas Research Institute, it underwent collaborative efforts at The University of California Berkeley, Stanford University, The University of Texas at Austin, and SRI International [25].
USC-II, a detailed kinetic scheme created by the University of Southern California, aims to describe various combustion processes from C0 to C4. With 111 species and 784 reversible reactions, it underwent systematic optimization and validation against reliable H2–CO combustion data, covering a range from shock-tube ignition delays to detailed species profiles during H2 and CO oxidation in different experimental setups [26].
Aramco-II, developed by the National University of Ireland Galway, follows a hierarchical approach, starting with an H2/O2 sub-mechanism and expanding to include larger carbon species and oxygenated species. Validated against a wide array of experimental measurements, including shock tubes, rapid compression machines, flames, jet-stirred, and plug-flow reactors, Aramco-II provides a comprehensive and kinetically accurate model for various combustion scenarios [27,28,29].
2. Methodology
2.1. Mathematical Chemical Model
Zero-dimensional kinetic analysis of hydrogen/air combustion at the most representative operative conditions for the investigated applications was performed using the kinetic and thermodynamic Cantera open-source software [7] through calculation of induction times in a homogeneous, adiabatic, isochoric batch reactor using the eleven mechanisms listed in Table 1.
The mathematical–chemical model consists of the following mass and energy balance equations:
The initial temperature, pressure, and equivalence ratios for every run were selected according to the considered shock tube experiments.
The pressure of the reacting mixture was evaluated using the ideal gas law.
Laminar Flame Speeds (LFS) of planar, adiabatic, premixed hydrogen/air outwardly expanding flames were calculated using 1D time-dependent simulations with Cantera software under the Python interface [7].
Cantera comprises a set of models for representing steady-state, quasi-one-dimensional reacting flow, resembling common burning conditions including freely propagating premixed laminar flames with multicomponent transport properties. They are simulated as flames stabilized in an axisymmetric stagnation flow. The solution is computed along the stagnation streamline (r = 0) adopting a similarity approach to reduce the 3D governing equations to a single 1D mathematical model [16] described by the following fundamental equations:
Relationship (4) is the continuity equation, while (5) describes the radial momentum balance, (6) the energy transport law, and (7) the conservation of a single chemical species mass.
In this model, the tangential velocity w is completely ignored, and the fluid is assumed to behave as an ideal gas. Finally, to speed up the achievement of a numerical solution of the discretized version of the mathematical model, a differential equation for the scalar pressure eigenvalue Λ is conveniently added to the planar, adiabatic, one-dimensional premixed flame:
2.2. Comparison of Computational Ignition Delay Times against Shock Tube Measurements
The accuracy and reliability of detailed and reduced chemical mechanisms of fuel/oxidant combustion are generally assessed as the first fundamental step through the calculation of the ignition delay times using 0D kinetic time-dependent simulations.
Indeed, the computation of the induction times in perfectly stirred, adiabatic, isochoric batch reactors is exclusively determined by the following reaction pathways and the kinetic reversible interactions among the various chemical species involved in the combustion scheme. Moreover, the ignition delay times (IDTs) are combustion characteristics completely uncoupled from the turbulence and fluid dynamics variables, i.e., mixing, and therefore, it is totally associated with the chemical kinetic behavior.
In the literature, several diagnostic techniques were designed and used to effectively measure the ignition of the combustion process. In the work reported here, the chemical criterion was employed based on the definition of the induction time as the instant corresponding to the achievement of the maximum concentration of the OH radical or its excited state OH*.
The following three different experimental datasets were compared with the computational IDT, i.e.,
- (a)
- Herzler—2009 [32].
- (b)
- Petersen—2011 [33].
- (c)
- Hu—2016 [34].
In the experimental study and the related kinetic rebuilding carried out by Hu and coworkers [5], the ignition delay times were defined as time spacing between the arrival of the reflected shock waves at the end-wall of the used test rigs and the linear extrapolation of the steepest rise of OH* emission signal to zero level, which is slightly lower than the time corresponding to the maximum mass fraction of the radical OH or its excited version OH*.
3. Results and Discussion
In this section, the comparison between the numerical and the experimental ignition delay time values is presented, subdivided mainly according to the reacting mixture composition, i.e., the equivalence ratio, and then for increasing experimental pressures.
In order to estimate the deviation of the calculation from the experimental data, the degree of mismatching between the experimental measurements and the corresponding numerical predictions, computed at the same initial operative conditions and using the eleven investigated kinetic mechanisms, was defined as follows.
where Numi is the numerical prediction, respectively, of the ignition delay times or the laminar flame speeds, while Expi refers to the associated experimental measurement, and the subscript i denotes the specific operative condition reported in the considered dataset. Moreover, the average values ADM along the overall experimental dataset for every analyzed scheme were evaluated at each investigated combustion pressure and reported in the following figures. ADM values were computed according to Equation (10):
where n is the number of points of each experimental dataset.
3.1. Shock Tube Tests in Argon with Fuel-Lean Composition
In Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, the numerical IDT values were reported and compared for the experimental datasets in the fuel-lean composition and strong argon dilution.
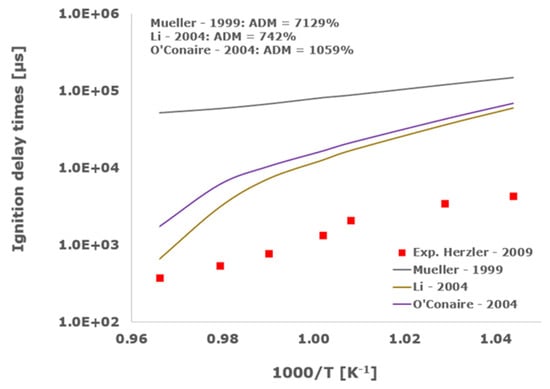
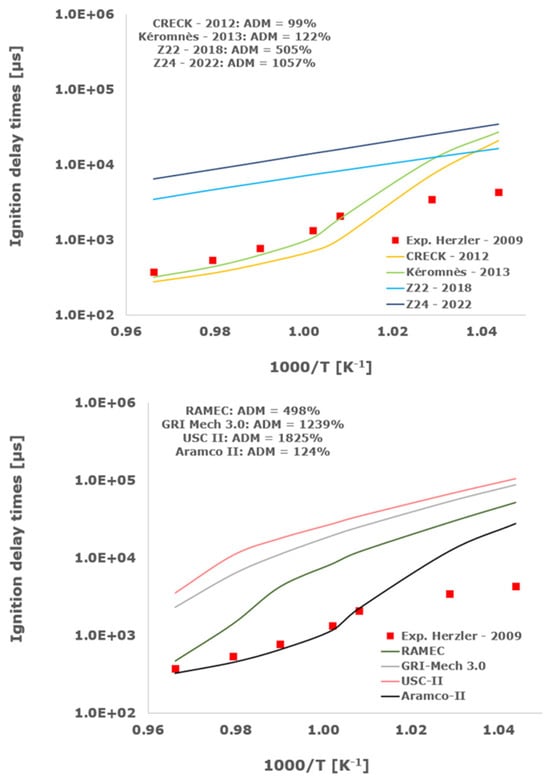
Figure 1.
Comparison of ignition delay times measured by Herzler et al. [32] in a shock tube at pressures between 3.78 and 4.09 bars with fuel lean composition (φ = 0.5) in strongly diluted argon conditions (XH2 = 0.03, XO2 = 0.03 and XAr = 0.94) and the eleven investigated kinetic schemes split in three separate plots including the average absolute degree of mismatching for every mechanism.
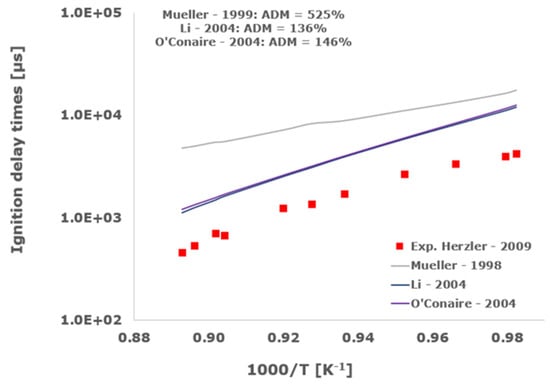
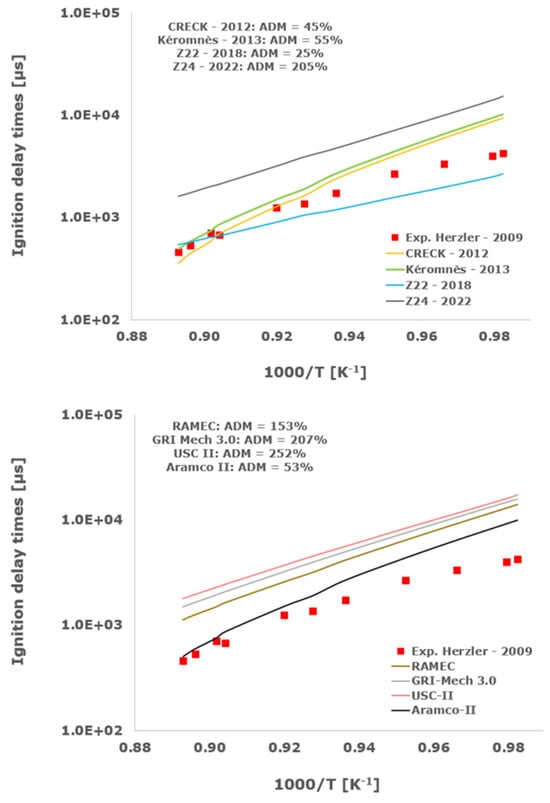
Figure 2.
Comparison of ignition delay times measured by Herzler et al. [32] in a shock tube at pressures between 15.13 and 16.37 bars with fuel lean composition (φ = 0.5) in strongly diluted argon conditions (XH2 = 0.03, XO2 = 0.03 and XAr = 0.93) and the eleven investigated kinetic schemes split in three separate plots including the average absolute degree of mismatching for every mechanism.
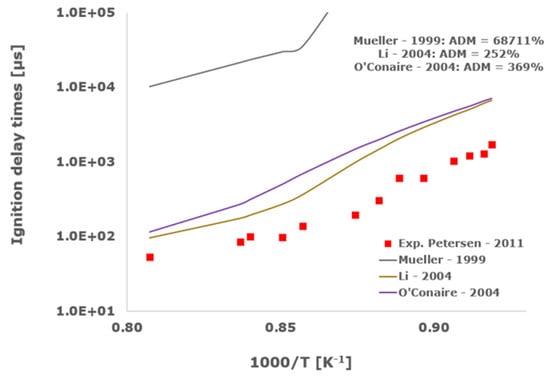
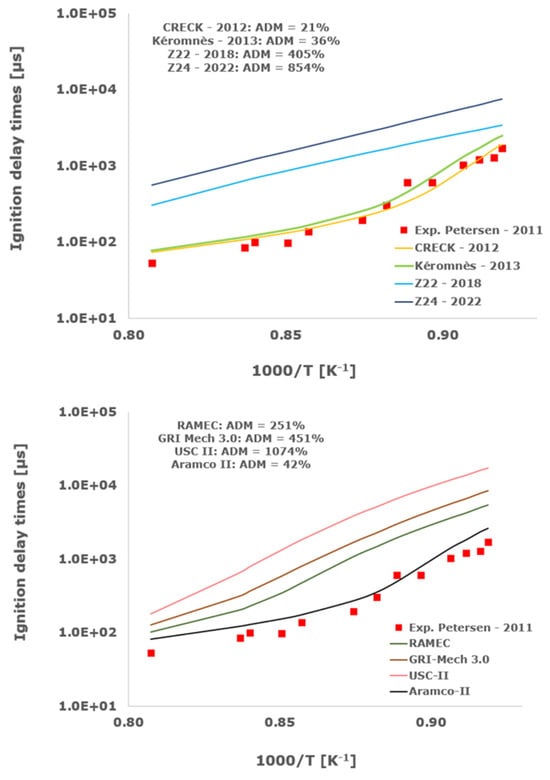
Figure 3.
Comparison of ignition delay times measured by Petersen et al. [33] in a shock tube at a pressure of 13.3 atm with fuel lean composition (φ = 0.5) in strongly diluted argon conditions (XH2 = 0.03, XO2 = 0.03 and XAr = 0.94) and the eleven investigated kinetic schemes split in three separate plots including the average absolute degree of mismatching for every mechanism.
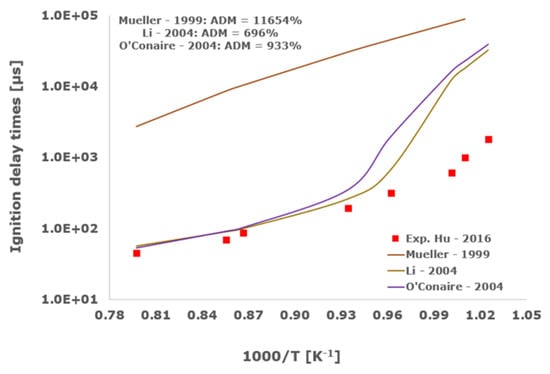
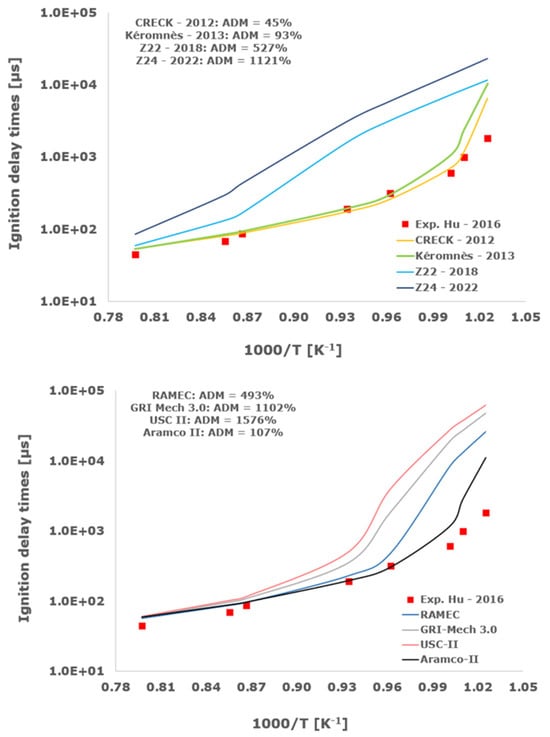
Figure 4.
Comparison of ignition delay times measured by Hu et al. [34] in a shock tube at a pressure of 4 atm with fuel lean composition (φ = 0.5) in strongly diluted argon conditions (XH2 = 0.03, XO2 = 0.03 and XAr = 0.94) and the eleven investigated kinetic schemes split in three separate plots including the average absolute degree of mismatching for every mechanism.
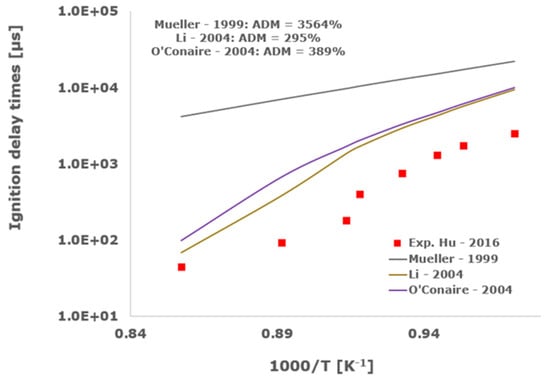
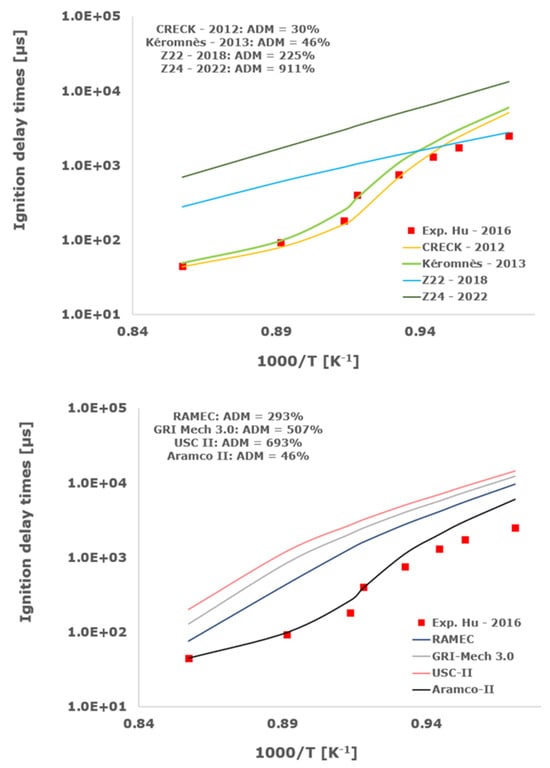
Figure 5.
Comparison of ignition delay times measured by Hu et al. [34] in a shock tube at a pressure of 10 atm with fuel lean composition (φ = 0.5) in strongly diluted argon conditions (XH2 = 0.03, XO2 = 0.03 and XAr = 0.94) and the eleven investigated kinetic schemes split in three separate plots including the average absolute degree of mismatching for every mechanism.
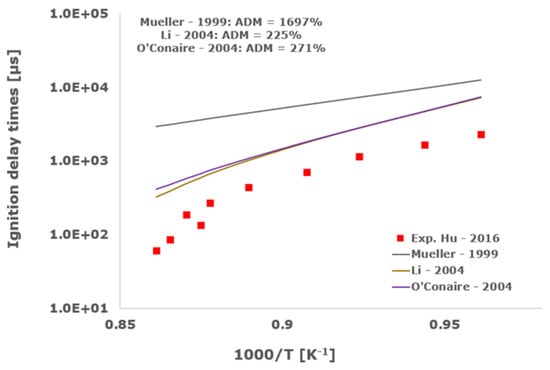
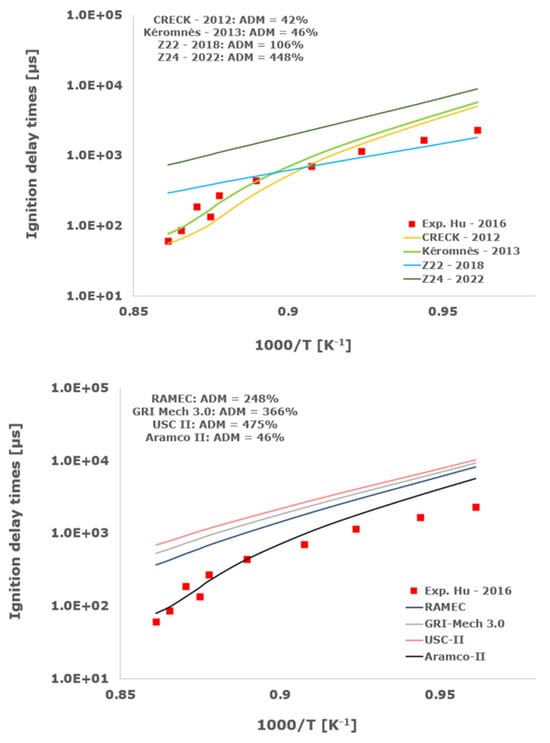
Figure 6.
Comparison of ignition delay times measured by Hu et al. [34] in a shock tube at a pressure of 16 atm with fuel lean composition (φ = 0.5) in strongly diluted argon conditions (XH2 = 0.03, XO2 = 0.03 and XAr = 0.94) and the eleven investigated kinetic schemes split in three separate plots including the average absolute degree of mismatching for every mechanism.
In the captions, ϕ denotes the equivalence ratio, defined as follows:
In Table 2, the average absolute degrees of mismatching for every analyzed kinetic mechanism and experimental dataset in fuel-lean conditions are listed.

Table 2.
Summary of the ADM computed for all the investigated IDT operative conditions and the analyzed kinetic mechanisms in fuel-lean conditions.
3.2. Shock Tube Tests in Argon with Stoichiometric Composition
In Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, the numerical IDT values were reported and compared for the experimental datasets in stoichiometric composition and strong argon dilution.
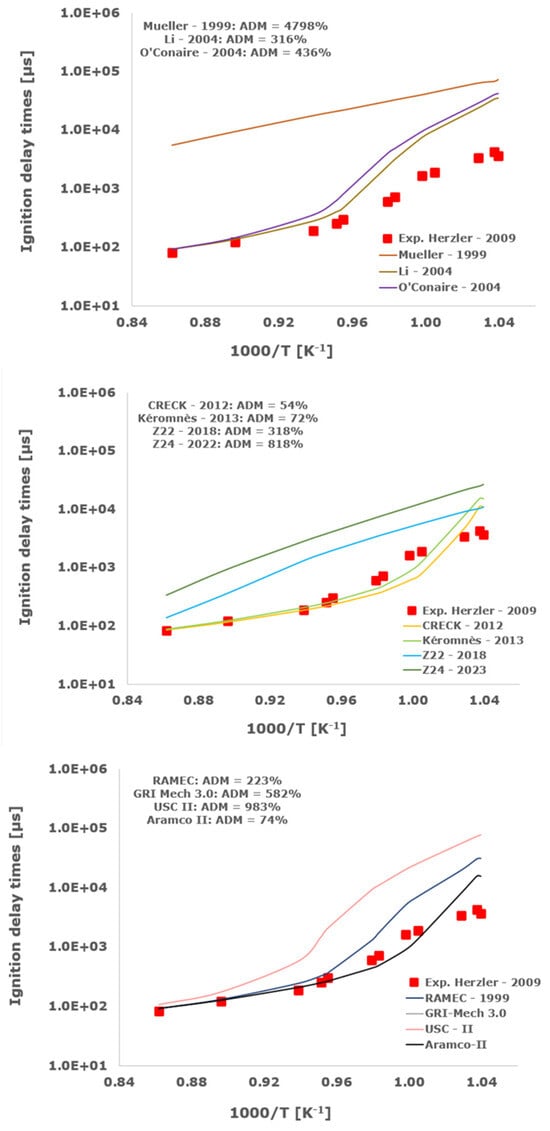
Figure 7.
Comparison of ignition delay times measured by Herzler et al. [32] in a shock tube at pressures between 3.89 and 4.15 bars with stoichiometric composition (φ = 1) in strongly diluted argon conditions (XH2 = 0.06, XO2 = 0.03 and XAr = 0.91) and the eleven investigated kinetic schemes split in three separate plots including the average absolute degree of mismatching for every mechanism.
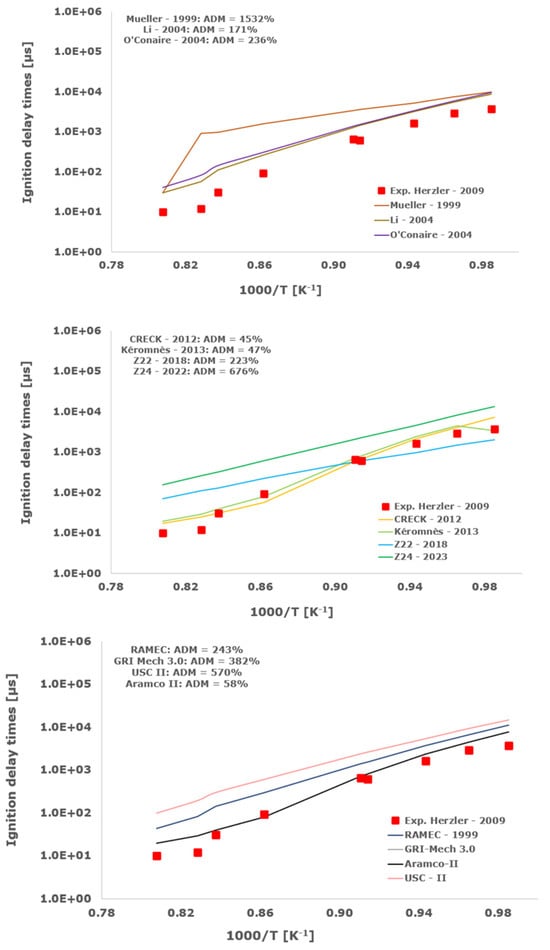
Figure 8.
Comparison of ignition delay times measured by Herzler et al. [32] in a shock tube at pressures between 15.10 and 19.27 bars with stoichiometric composition (φ = 1) in strongly diluted argon conditions (XH2 = 0.06, XO2 = 0.03 and XAr = 0.91) and the eleven investigated kinetic schemes split in three separate plots including the average absolute degree of mismatching for every mechanism.
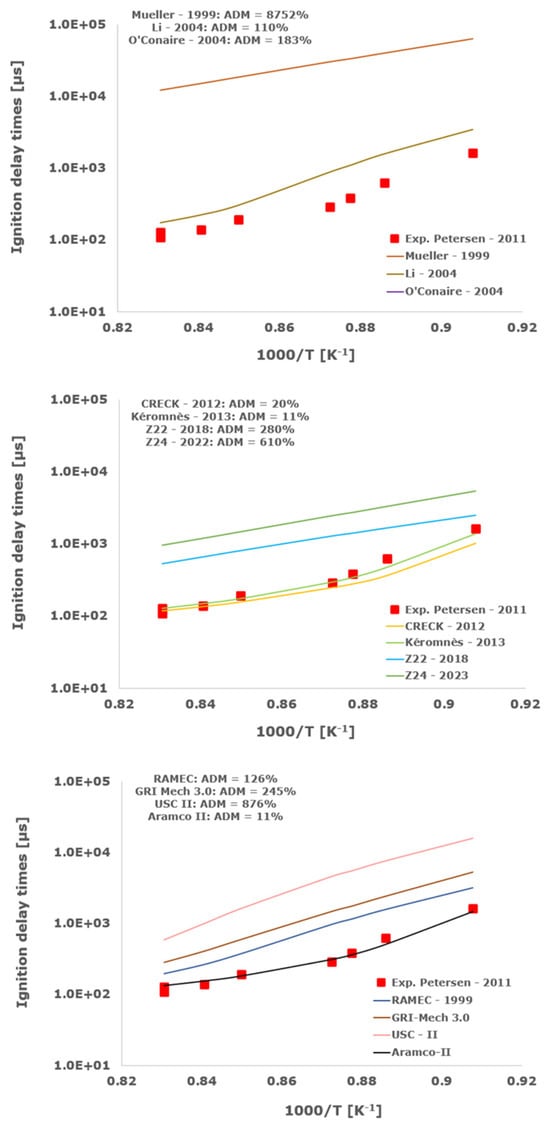
Figure 9.
Comparison of ignition delay times measured by Petersen et al. [33] in a shock tube at a pressure of 13.8 atm with stoichiometric composition (φ = 1) in strongly diluted argon conditions (XH2 = 0.013, XO2 = 0.007 and XAr = 0.98) and the eleven investigated kinetic schemes split in three separate plots including the average absolute degree of mismatching for every mechanism.
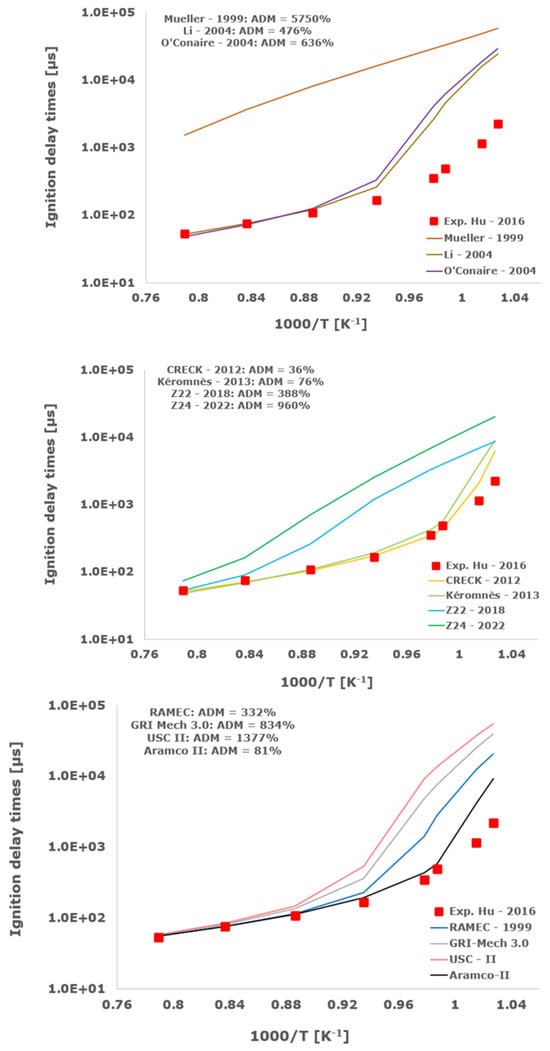
Figure 10.
Comparison of ignition delay times measured by Hu et al. [34] in a shock tube at a pressure of 4 atm with stoichiometric composition (φ = 1) in strongly diluted argon conditions (XH2 = 0.06, XO2 = 0.03 and XAr = 0.91) and the eleven investigated kinetic schemes split in three separate plots including the average absolute degree of mismatching for every mechanism.
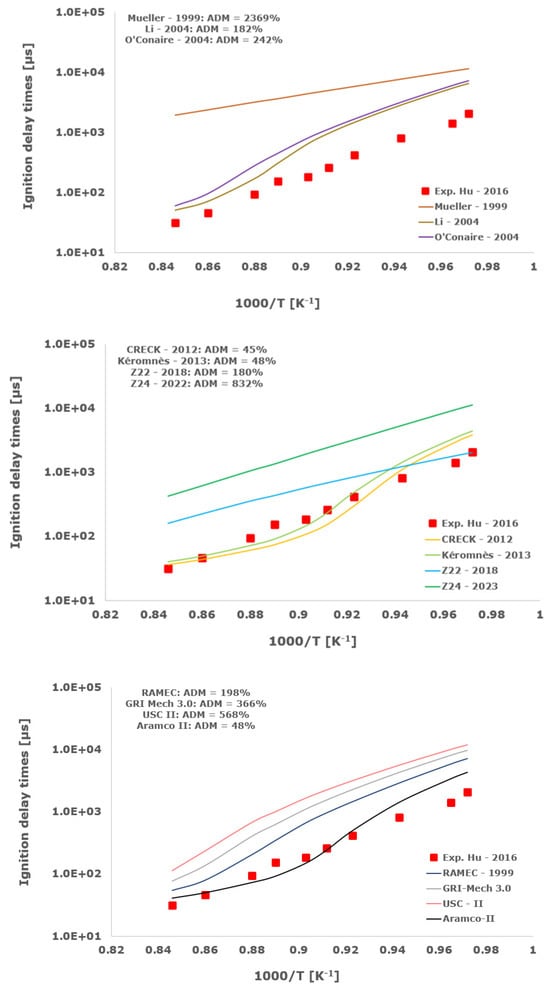
Figure 11.
Comparison of ignition delay times measured by Hu et al. [34] in a shock tube at a pressure of 10 atm with stoichiometric composition (φ = 1) in strongly diluted argon conditions (XH2 = 0.06, XO2 = 0.03 and XAr = 0.91) and the eleven investigated kinetic schemes split in three separate plots including the average absolute degree of mismatching for every mechanism.
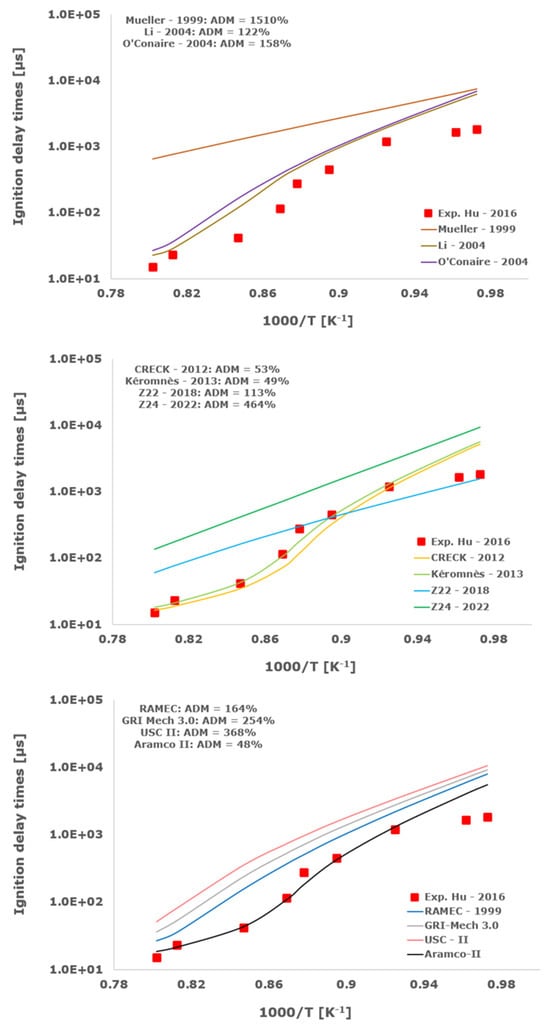
Figure 12.
Comparison of ignition delay times measured by Hu et al. [34] in a shock tube at a pressure of 16 atm with stoichiometric composition (φ = 1) in strongly diluted argon conditions (XH2 = 0.06, XO2 = 0.03 and XAr = 0.91) and the eleven investigated kinetic schemes split in three separate plots including the average absolute degree of mismatching for every mechanism.
In Table 3, the average absolute degrees of mismatching for every analyzed kinetic scheme and experimental dataset in stoichiometric composition are summarized.

Table 3.
Summary of the ADM computed for all the investigated IDT operative conditions and the analyzed kinetic mechanisms in the stoichiometric composition.
3.3. Shock Tube Tests in Argon with Fuel-Rich Composition
In Figure 13, Figure 14 and Figure 15, the numerical IDT values were reported and compared for the experimental datasets in fuel-rich composition and strong argon dilution.
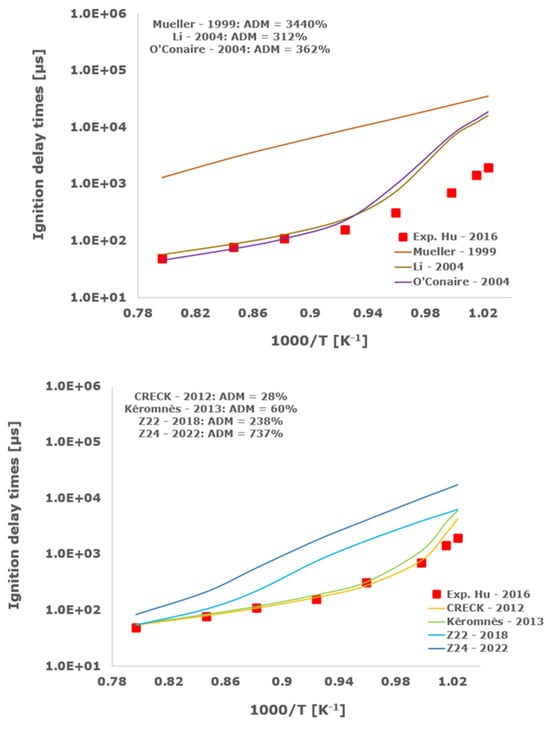
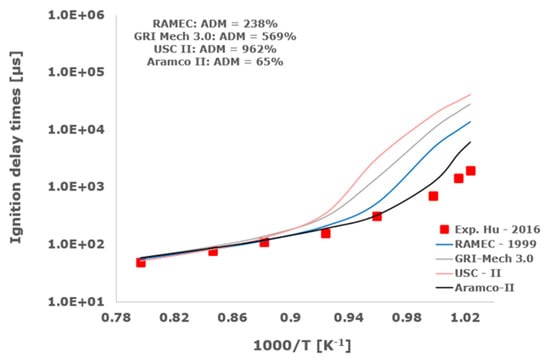
Figure 13.
Comparison of ignition delay times measured by Hu et al. [34] in a shock tube at a pressure of 4 atm with fuel-rich composition (φ = 2) in strongly diluted argon conditions (XH2 = 0.09, XO2 = 0.02 and XAr = 0.89) and the eleven investigated kinetic schemes split in three separate plots including the average absolute degree of mismatching for every mechanism.
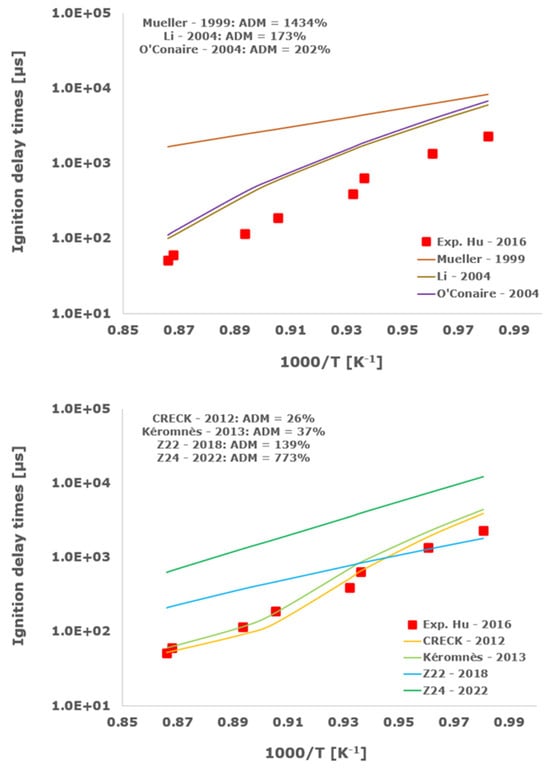
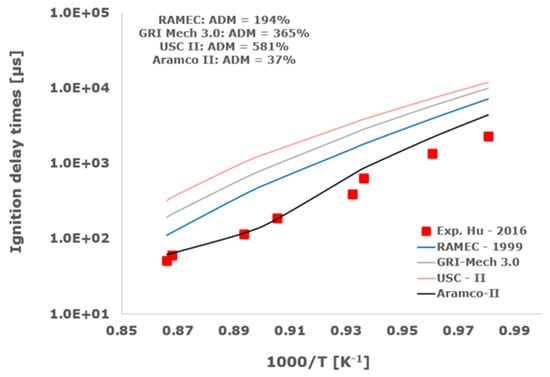
Figure 14.
Comparison of ignition delay times measured by Hu et al. [34] in a shock tube at a pressure of 10 atm with fuel-rich composition (φ = 2) in strongly diluted argon conditions (XH2 = 0.09, XO2 = 0.02 and XAr = 0.89) and the eleven investigated kinetic schemes split in three separate plots including the average absolute degree of mismatching for every mechanism.
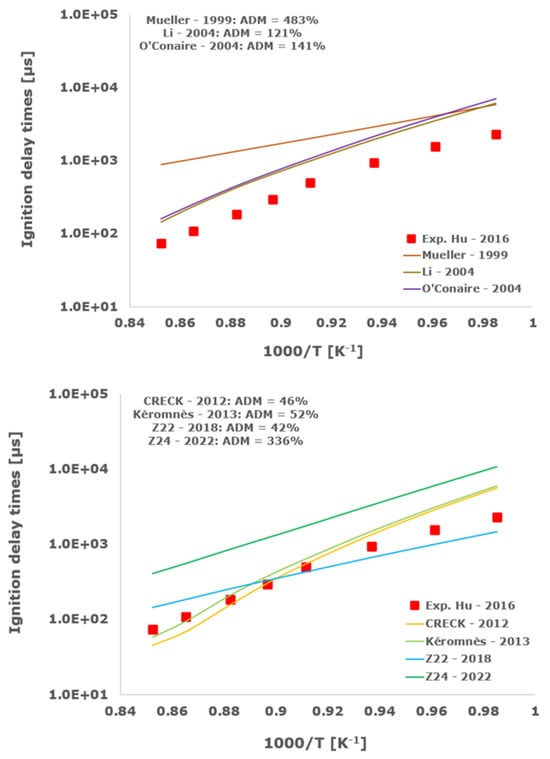
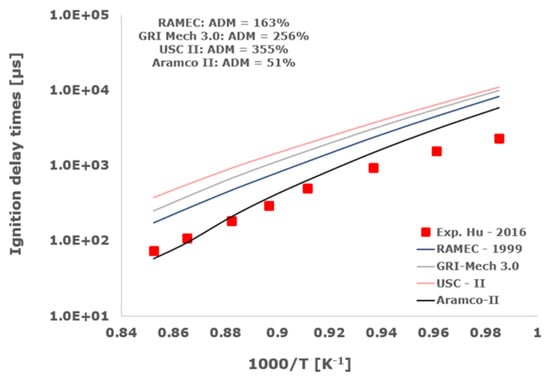
Figure 15.
Comparison of ignition delay times measured by Hu et al. [34] in a shock tube at a pressure of 16 atm with fuel-rich composition (φ = 2) in strongly diluted argon conditions (XH2 = 0.09, XO2 = 0.02 and XAr = 0.89) and the eleven investigated kinetic schemes split in three separate plots including the average absolute degree of mismatching for every mechanism.
In Table 4, the average absolute degrees of mismatching for every analyzed kinetic mechanism and experimental dataset in fuel-rich conditions are reported.

Table 4.
Summary of the ADM computed for all the investigated IDT operative conditions and the analyzed kinetic mechanisms in fuel-rich conditions.
Results indicate that the CRECK 2012 [13,14,15,16,17,18] and the Kéromnès [19] schemes almost straightforwardly intercept the experimental shock tube measurements in all of the investigated operative envelopes up to an engine pressure of about 20 bars and equivalence ratios ranging from fuel-lean up to stoichiometric and fuel-rich compositions, with ADM almost always being lower than 100%.
The Muller 1999 [8] kinetic scheme overestimates the ignition delay times, with ADM always being greater than 1000% in all of the examined conditions, while its improved version, i.e., Li 2004 [9], is slightly better than the older one with minimum ADM of the order of 100%. Analogously, the O’Conaire [10] model fails to predict the IDT experimental data with ADM not lower than 141%.
The Z22 2018 [20,21,22] chemical kinetic mechanism seems able to adequately reproduce the experimental ignition delay times in some cases for low-temperature conditions, confirming its ability to reasonably capture the non-linear hydrogen/oxygen ignition behavior, especially in the critical crossing-over region. At least in argon-diluted shock-tube experiments, Z24 2022 [23] does not represent an improvement of the previous more compact Z22 2018 scheme [20,21,22], with ADM always being higher than the corresponding average degree of mismatching for Z22 2018 [20,21,22].
Among the analyzed detailed kinetic schemes, only the Aramco-II [27,28,29] shows a satisfactory matching with the examined experimental data, with the ADM only in two cases being slightly higher than 100%, while RAMEC [24], GRI-Mech 3.0 [25], and USC-II [26] provide induction times close to the shock-tube measurements only at elevated temperatures. Otherwise, at temperatures below 1100 K, they give values significantly far from the experimental determinations with ADM values in some instances greater than 1000%. This behavior is emphasized at more elevated pressures and for equivalence ratios equal to 2.
3.4. Laminar Flame Speed Analysis
The Laminar Flame Speed (LFS) is one of the most essential and practically important thermochemical parameters for a premixed combustible mixture, arising from a combined effect of diffusivity, exothermicity, and reactivity [35].
Fundamentally, it indicates the rate at which the combustible mixture is consumed by propagating in a doubly infinite domain of a steady, one-dimensional, adiabatic, laminar, free flame, and it is frequently needed in the assessment of several combustion phenomena, e.g., ignition quenching, stabilization, and turbulent flame propagation [36]. It determines the burning rate and flame stabilization in engines. Moreover, LFS provides an estimation of the minimum reactivity limits since LSF decreases as a fuel diminishes its reactivity leading to destabilizing blowout phenomena [36].
LFS embodies the basic diffusive and reactive information about the fuel, and it is also an important target for validating chemical mechanisms. Therefore, in the literature, there are many studies [37] on the LFS. It is an important target for chemical mechanism validation and development, especially in fuel-lean and high-pressure conditions.
The difference between experimental and numerical results might be caused by the uncertainty in experimental measurement and/or the inaccuracy of chemical mechanisms. The uncertainties of experimental data may come from several sources [37] such as ignition, flame instability, radiation, and extrapolation.
LFS calculated using eight different kinetic mechanisms were compared with the experimental stretch-free data at elevated pressures of up to 20 bar of hydrogen/air spark-ignited, outwardly expanding spherical flames in an enclosed chamber measured by Tse and co-workers [36]. Among the several possible techniques developed to measure the laminar burning velocity, the experimental data acquired with the spherical method were selected in the present work since they are the most commonly used set-up for the determination of LFS at high pressures [35]. Tse et al. expended extensive efforts in the development of innovative diagnostics techniques for direct imaging of the flame in near-constant pressure propagation conditions. In this way, the flame morphology and shape, the stretch intensity, and possible distortion due to buoyancy were deeply analyzed. Particular emphasis was paid to avoiding or at least mitigating the hydrodynamic, diffusion-thermal, and cellular instabilities.
For the sake of completeness, the 1D LFS behavior of the several investigated kinetic schemes was also analyzed against the experimental data of Krejci et al. [38] and of Aung et al. [39] at atmospheric and low-medium pressures of up to 3 atm acquired using the spherical flame method.
For all calculations, the unburned mixture temperature of 298 K was selected.
The LFS results are reported in Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22 and Figure 23 and analogously to the comparison of the IDT, and in Table 5, a summary of all of the average absolute degrees of mismatching for every analyzed kinetic mechanism of the several investigated experimental conditions is reported.
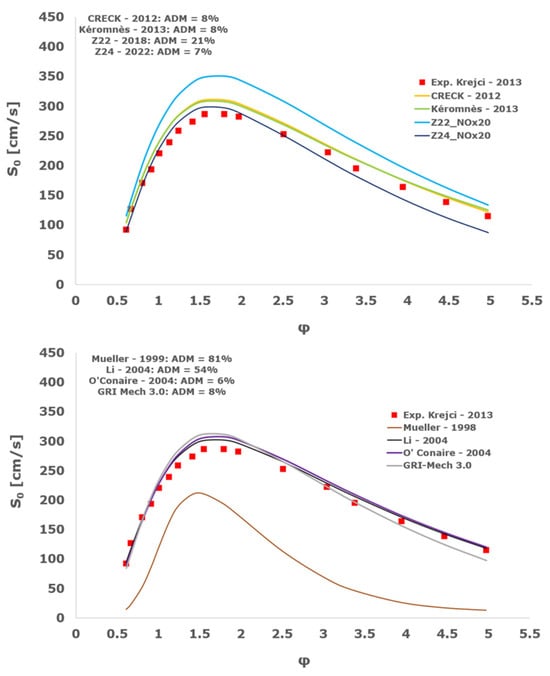
Figure 16.
Comparison of laminar flame speeds among the experimental measurements of Krejci 2013 in the air at 298 K and the eight investigated kinetic schemes for a pressure of 1 atm, split into two separate plots including the average absolute degree of mismatching for every mechanism.
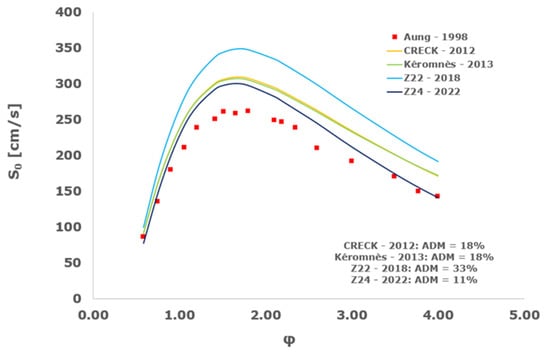
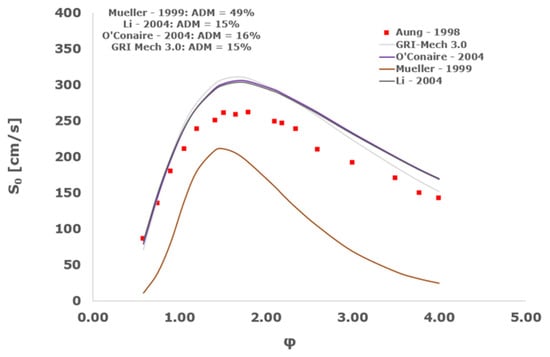
Figure 17.
Comparison of laminar flame speeds among the experimental measurements of Aung 1998 in the air at 298 K and the eight investigated kinetic schemes for a pressure of 1 atm, split into two separate plots including the average absolute degree of mismatching for every mechanism.
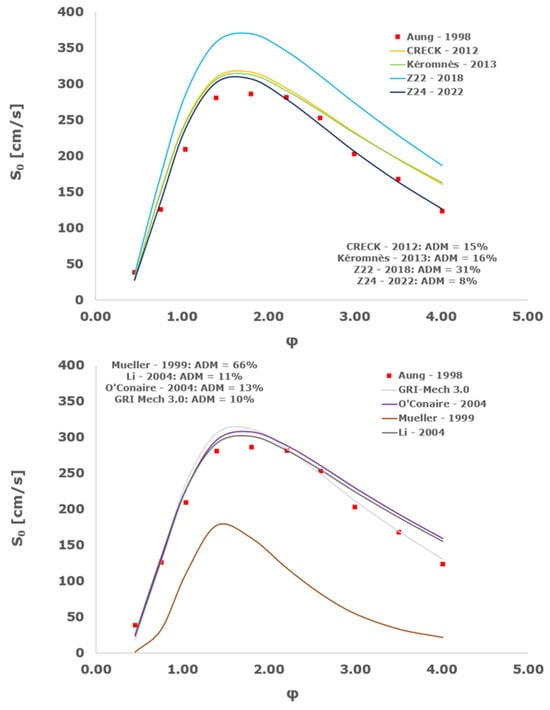
Figure 18.
Comparison of laminar flame speeds among the experimental measurements of Aung 1998 in the air at 298 K and the eight investigated kinetic schemes for a pressure of 2 atm, split into two separate plots including the average absolute degree of mismatching for every mechanism.
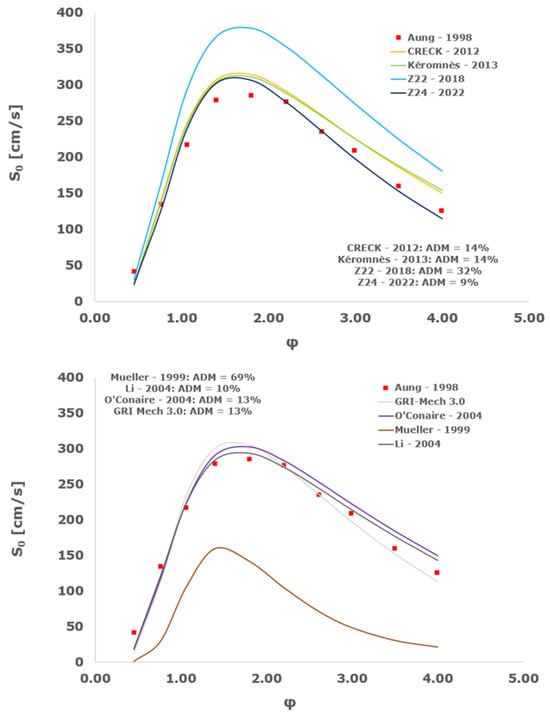
Figure 19.
Comparison of laminar flame speeds among the experimental measurements of Aung 1998 in the air at 298 K and the eight investigated kinetic schemes for a pressure of 3 atm, split into two separate plots including the average absolute degree of mismatching for every mechanism.
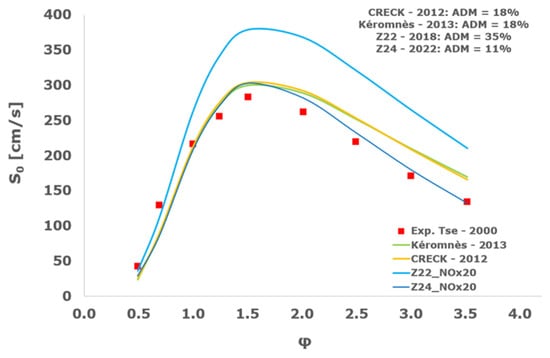
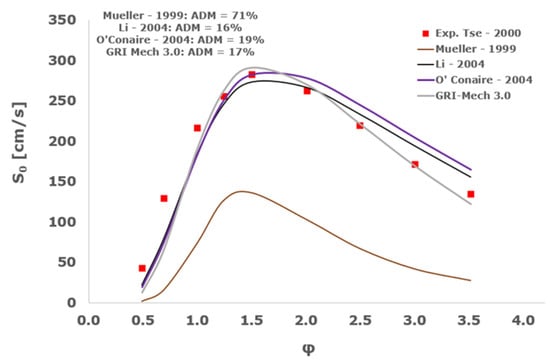
Figure 20.
Comparison of laminar flame speeds among the experimental measurements of Tse 2000 in the air at 298 K and the eight investigated kinetic schemes for a pressure of 5 atm, split into two separate plots including the average absolute degree of mismatching for every mechanism.
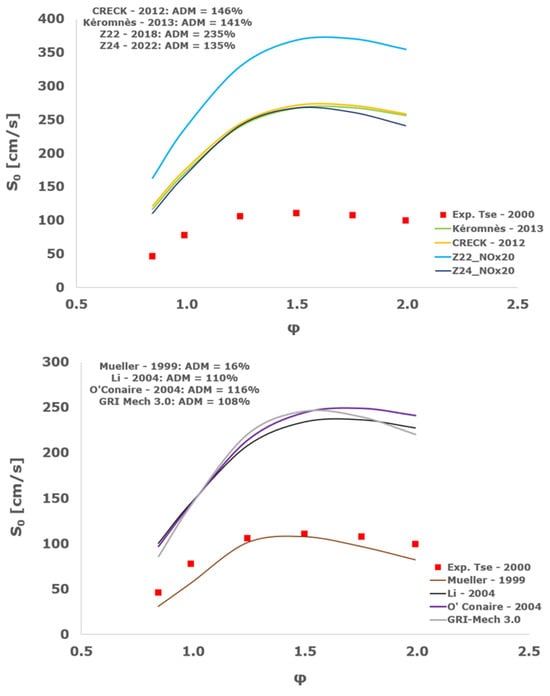
Figure 21.
Comparison of laminar flame speeds among the experimental measurements of Tse 2000 in the air at 298 K and the eight investigated kinetic schemes for a pressure of 10 atm, split into two separate plots including the average absolute degree of mismatching for every mechanism.
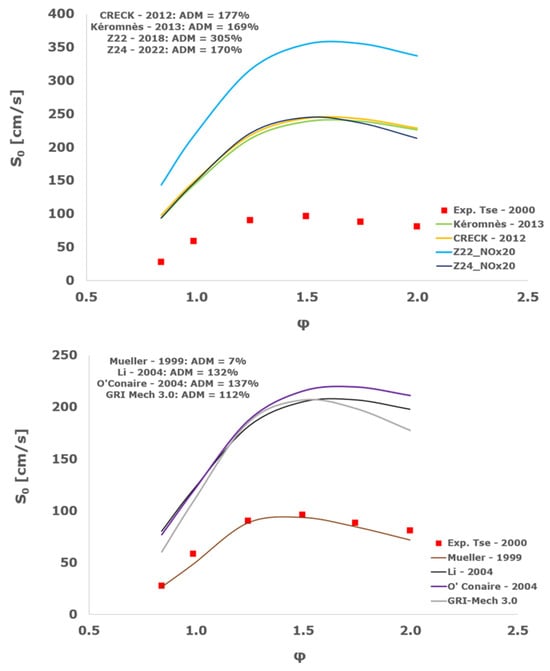
Figure 22.
Comparison of laminar flame speeds among the experimental measurements of Tse 2000 in the air at 298 K and the eight investigated kinetic schemes for a pressure of 15 atm, split into two separate plots including the average absolute degree of mismatching for every mechanism.
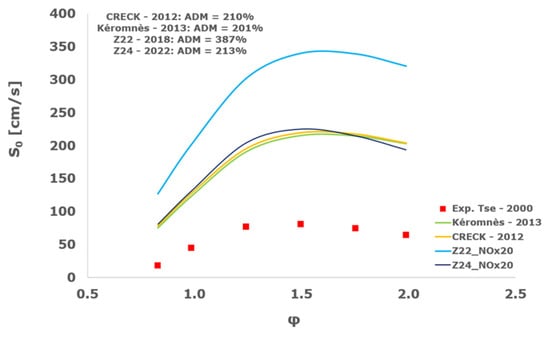
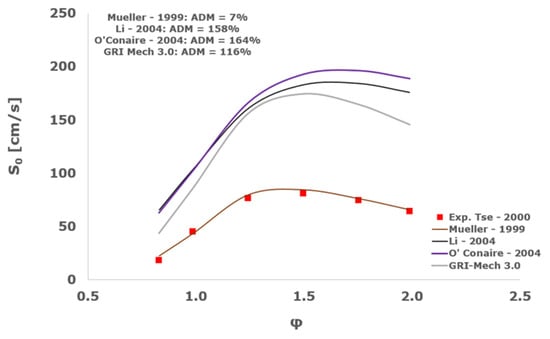
Figure 23.
Comparison of laminar flame speeds among the experimental measurements of Tse 2000 in the air at 298 K and the eight investigated kinetic schemes for a pressure of 20 atm, split into two separate plots including the average absolute degree of mismatching for every mechanism.

Table 5.
Summary of the ADM computed for all the investigated LFS operative conditions and the analyzed kinetic mechanisms.
At atmospheric pressure, almost all the investigated kinetic mechanisms exhibit satisfactory agreement with the laminar flame speed measurements of Krejci et al. [39] and Aung et al. [40], except for the scheme of Mueller and co-workers [8]. The best agreement was achieved by the chemical model Z24 [23] which reveals its superior performance for modelling combustion in air rather than in strongly diluted argon medium, which was the case for the IDT assessment.
Almost the same behavior is shown at 2 and 3 atm with the experimental dataset of Aung et al. [40] and at 5 atm with the measurements of Tse and collaborators [36], at which the Z24 scheme [23] is practically superimposed to the experimental values, with ADM not being higher than 11%, also the CRECK [13,14,15,16,17,18], Kéromnès [19], Li [9], and O’Conaire [10] mechanisms exhibit a satisfactory agreement, with ADM not being greater than 20%, while the Mueller scheme fails to predict the experimental measurements with ADM around 70%.
Interestingly, at the more elevated pressures of 10, 15, and 20 atm, an excellent matching is achieved only by the mechanism of Mueller and co-workers [8] with a maximum AMD equal to 16%, whereas all the other analyzed chemical models provide significant disagreement. This intriguing performance was observed also by Tse et al. [36].
It is worth noting that, based on this kinetic assessment, the Mueller et al. mechanism [8] provides outstanding results in terms of laminar flame speed numerical results for pressures between 10 and 20 atm, but in the same operative envelope, it completely fails to predict the ignition behavior with ADM as high as ~70,000%. This is probably ascribed to the prevailing importance of the HO2 and H2O2 reaction pathway in the Mueller scheme in comparison to the other chemical models, which is the dominant factor in the correct calculation of LFS, while leading to inadequate estimations of IDT, especially at the lower temperatures.
4. Conclusions
In this work, we presented a thorough kinetic assessment of the most suitable combustion mechanisms to accurately describe the ignition characteristics and flame propagation characteristics of hydrogen oxidation at intermediates/high pressures, and temperatures and compositions spanning from fuel-lean to stoichiometric and fuel-rich equivalence ratios are presented. This was accomplished through a comparison with the available high-pressure shock tube and laminar flame speeds experimental data.
Based on the published results on ignition delay times, the CRECK 2012 [13,14,15,16,17,18], immediately followed by the Kéromnès [19], shows a good agreement with IDT experimental data at almost all of the investigated conditions equating only to the Aramco-II mechanism, which is too numerically heavy to be implemented and successfully used in CFD (both RANS and LES) fully 3D simulations of the engine’s combustion chamber. Therefore, this kinetic model seems worthy to be further updated and improved with the suitable inclusion of the most relevant NOx generation reactions for an accurate and reliable chemical evaluation of hydrogen/air pollutant and greenhouse gas emissions released by high-pressure, supersonic, airbreathing hydrogen-fueled ramjet/scramjet engines.
However, the propagation flame phenomenon at medium–high pressures is well captured only by the Mueller et al. scheme [8], while the CRECK chemical model significantly overpredicts the LSF measurements.
These results uphold the non-linear and strongly pressure-dependent behavior of hydrogen combustion, which is a peculiar feature of this non-carbon, low molecular weight, highly diffusive, and powerfully exothermic fuel. The critical revision of the kinetic parameters of the separately most promising mechanisms, i.e., CRECK [13,14,15,16,17,18] for IDT and Mueller [8] for LFS, will be a matter of future work aimed at building a novel kinetic mechanism able to successfully join the advantageous capability of both of them.
Author Contributions
Conceptualization, G.S. and M.M.; methodology, G.S.; software, G.S.; validation, G.S. and M.M.; formal analysis, G.S.; investigation, G.S.; resources, G.S.; data curation, G.S.; writing—original draft preparation, G.S.; writing—review and editing, M.M.; visualization, G.S.; supervision, M.M.; project administration, M.M.; funding acquisition, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been carried out within the frame of “MDO and Regulations for Low boom and Environmentally Sustainable Supersonic aviation” (MORE&LESS) project. This project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 101006856.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
List of Variables
| ADM | Average absolute degree of mismatching [%] |
| ADMi | Absolute degree of mismatching for a single data point [%] |
| cp,mix | Reacting mixture specific heat at constant pressure [J/(kg K)] |
| cp,k | k-th component specific heat at constant pressure [J/(kg K)] |
| Expi | Single experimental measurement of IDT or LFS |
| hk | Specific enthalpy of the k-th component [J/kg] |
| i | Single data point for IDT or LFS |
| jk | Diffusive mass flux of the k-th component |
| Mw,k | Molecular weight of the k-th chemical component [kg/mol] |
| mtot | Total mixture mass [kg] |
| mk | Mass of the k-th chemical component [kg] |
| Numi | Single numerical prediction of IDT or LFS |
| N | Number of data points [/] |
| rk | Rate constant of the k-th component [mol/(m3 s)] |
| r | Radial coordinate [m] |
| t | Time [s] |
| T | Temperature [K] |
| U | Internal energy [J] |
| u | Axial velocity [m/s] |
| u | Axial velocity [m/s] |
| V | Reacting mixture volume [m3] |
| v | Radial velocity [m/s] |
| w | Tangential velocity [m/s] |
| Yk | Mass fraction of the k-th species [/] |
| z | Axial coordinate [m] |
| φ | Equivalence Ratio |
| Λ | Pressure eigenvalue |
| λ | Thermal conductivity [W/(mK)] |
| μ | Dynamic viscosity [Pa·s] |
| ρ | Density [kg/m3] |
| ν | Stoichiometric coefficient |
| τign | Ignition delay time [s] |
| Molar production rate of the k-th chemical species |
References
- Cecere, D.; Ingenito, A.; Giacomazzi, E.; Romagnosi, L.; Bruno, C. Hydrogen/air supersonic combustion for future hypersonic vehicles. Int. J. Hydrogen Energy 2011, 30, 11969–11984. [Google Scholar] [CrossRef]
- Tsujikawa, Y.; Northambi, G.B. Effects of hydrogen active cooling on scramjet engine performance. Int. J. Hydrogen Energy 1996, 21, 299–304. [Google Scholar] [CrossRef]
- Viola, N.; Fusaro, R.; Gori, O.; Marini, M.; Roncioni, P.; Saccone, G.; Saracoglu, B.H.; Ispir, A.C.; Fureby, C.; Nilsson, T.; et al. STRATOFLY MR3—How to reduce the environmental impact of high-speed transportation. In AIAA Scitech Forum Virtual Event; Aerospace Research Central: Reston, VA, USA, 2021. [Google Scholar] [CrossRef]
- Viola, N.; Fusaro, R.; Ferretto, D.; Gori, O.; Saracoglu, B.H.; Ispir, A.C.; Schram, C.; Grewe, V.; Plezer, J.F.; Martinez, J.; et al. H2020 STRATOFLY project: From Europe to Australi in less than 3 hours. In Proceedings of the CAS 2021 The 32nd Congress of the International Council of the Aeronautical Sciences, Shanghai, China, 6–10 September 2021. [Google Scholar]
- Saccone, G.; Natale, P.; Cutrone, L.; Marini, M. Hydrogen/Air Supersonic Combustion Modelling and Validation for Scramjet Applications. J. Fluid Flow Heat Mass Transf. 2022, 9, 136–147. [Google Scholar] [CrossRef]
- Saccone, G.; Ispir, A.C.; Saracoglu, B.H.; Cutrone, L.; Marini, M. Computational evaluations of emissions indexes released by the STRATOFLY air-breathing combined propulsive system. Aircr. Eng. Aerosp. Technol. 2022, 94, 1499–1507. [Google Scholar] [CrossRef]
- Goodwin, D.; Moffat, H.K.; Speth, R.L. Cantera: An Object-Oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes, (Version 2.6). 2023. Available online: http://www.cantera.org (accessed on 1 December 2023).
- Mueller, M.A.; Yetter, R.A.; Dryer, F.L. Flow reactor studies and kinetic modeling of the H2/O2 reaction. Int. J. Chem. Kinet. 1999, 31, 113–125. [Google Scholar] [CrossRef]
- Li, J.; Zhao, Z.; Kazanov, A.; Dryer, F.L. An Updated Comprehensive Kinetic Model of Hydrogen Combustion. Int. J. Chem. Kinet. 2004, 36, 566–575. [Google Scholar] [CrossRef]
- Conaire, M.Ó.; Curran, H.J.; Simmie, J.M.; Pitz, W.J.; Westbrook, C.K.A. Comprehensive Modeling Study of Hydrogen Oxidation. Int. J. Chem. Kinet. 2004, 36, 603–622. [Google Scholar] [CrossRef]
- Yetter, R.A.; Dryer, F.L.; Rabbitz, H. A Comprehensive Reaction Mechanism for Carbon Monoxide/Hydrogen/Oxygen Kinetics. Combust. Sci. Technol. 1991, 79, 97–128. [Google Scholar] [CrossRef]
- Kim, T.J.; Yetter, R.A.; Dryer, F.L. New results on moist CO oxidation: High pressure, high temperature experiments and comprehensive kinetic modelling. Proc. Combust. Inst. 1994, 25, 759–766. [Google Scholar] [CrossRef]
- Frassoldati, A.; Faravalli, T.; Ranzi, E. A wide range modeling study of NOx formation and nitrogen chemistry in hydrogen combustion. Int. J. Hydrogen Energy 2006, 31, 2310–2328. [Google Scholar] [CrossRef]
- Ranzi, E.; Frassoldati, A.; Granata, S.; Faravelli, T. Wide-Range Kinetic Modeling Study of the Pyrolysis, Partial Oxidation, and Combustion of Heavy n-Alkanes. Ind. Eng. Chem. Res. 2005, 44, 5170–5183. [Google Scholar] [CrossRef]
- Ruscic, B.; Wagner, A.F.; Harding, L.B.; Asher, R.L.; Feller, D.; Dixon, D.A.; Peterson, K.A.; Song, Y.; Qian, X.; Ng, C.Y.; et al. On the Enthalpy of Formation of Hydroxyl Radical and Gas-Phase Bond Dissociation Energies of Water and Hydroxyl. J. Phys. Chem. A 2002, 106, 2727–2747. [Google Scholar] [CrossRef]
- Metcalfe, W.K.; Burke, S.M.; Ahmed, S.S.; Curran, H.J. A hierarchical and comparative kinetic modeling study of C1−C2 hydrocarbon and oxygenated fuels. Int. J. Chem. Kinet. 2013, 45, 638–675. [Google Scholar] [CrossRef]
- Bagheri, G.; Ranzi, E.; Pelucchi, M.; Parente, A.; Frassoldati, A.; Faravelli, T. Comprehensive kinetic study of combustion technologies for low environmental impact: MILD and OXY-fuel combustion of methane. Combust. Flame 2020, 212, 142–155. [Google Scholar] [CrossRef]
- Ranzi, E.; Frassoldati, A.; Stagni, A.; Pelucchi, M.; Cuoci, A.; Faravelli, T. Reduced kinetic schemes of complex reaction systems: Fossil and biomass-derived transportation fuels. Int. J. Chem. Kinet. 2014, 46, 512–542. [Google Scholar] [CrossRef]
- Kéromnès, A.; Metcalfe, W.K.; Heufer, K.A.; Donohoe, N.; Das, A.K.; Sung, C.J.; Herzler, J.; Naumann, C.; Griebel, P.; Mathieu, O.; et al. An Experimental and Detailed Chemical Kinetic Modelling Study of Hydrogen and Syngas Mixtures at Elevated Pressures. Combust. Flame 2013, 160, 995–1011. [Google Scholar] [CrossRef]
- Zettervall, N.; Fureby, C. Computational Study of Ramjet, Scramjet and Dual Mode Ramjet/Scramjet Combustion in a Combustor with a Cavity Flameholder. In Proceedings of the AIAA Aerospace Science, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Larsson, A.; Zettervall, N.; Hurtig, T.; Nilsson, E.J.K.; Ehn, A.; Petersson, P.; Alden, M.; Larfeldt, J.; Fureby, C. Skeletal Methane-Air Reaction Mechanism for Large Eddy Simulation of Turbulent Microwave-Assisted Combustion. Energy Fuels 2017, 31, 1904. [Google Scholar] [CrossRef]
- Alekseev, V.A.; Christensen, M.; Konnov, A.A. The Effect of Temperature on the Adiabatic Burning Velocities of Diluted Hydrogen Flames: A Kinetic Study using an Updated Mechanism. Combust. Flame 2015, 162, 1884. [Google Scholar] [CrossRef]
- Zettervall, N. Reaction Mechanism for Hydrogen-Air Combustion, FOI-D-1153-SE. 2022. Available online: https://www.foi.se/en/foi.htm (accessed on 1 December 2021).
- Petersen, E.L.; Davidson, D.F.; Hanson, R.K. Kinetic Modelling of Shock-Induced Ignition in Low-Dilution CH4/O2 Mixtures at High Pressures and Intermediate Temperatures. Combust. Flame 1999, 11, 272–290. [Google Scholar] [CrossRef]
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, W.C.; et al. GRI-Mech 3.0. 1999. Available online: http://www.me.berkeley.edu/gri_mech/ (accessed on 1 December 2023).
- Wang, H.; You, X.; Joshi, A.V.; Davis, S.G.; Laskin, A.; Egolfopoulos, F.; Law, C.K. USC Mech Version II. High-Temperature Combustion Reaction Model of H2/CO/C1-C4 Compounds. 2007. Available online: https://ignis.usc.edu/USC_Mech_II.htm (accessed on 1 December 2023).
- Li, Y.; Zhou, C.W.; Somers, K.P.; Zhang, K.; Curran, H.J. The Oxidation of 2-Butene: A High Pressure Ignition Delay, Kinetic Modeling Study and Reactivity Comparison with Isobutene and 1-Butene. Proc. Combust. Inst. 2017, 36, 403–411. [Google Scholar] [CrossRef]
- Zhou, C.W.; Li, Y.; O’Connor, E.; Somers, K.P.; Thion, S.; Keesee, C.; Mathieu, O.; Petersen, E.L.; DeVerter, T.A.; Oehlschlaeger, M.A.; et al. A Comprehensive experimental and modeling study of isobutene oxidation. Combust. Flame 2016, 167, 353–379. [Google Scholar] [CrossRef]
- Burke, U.; Metcalfe, W.K.; Burke, S.M.; Heufer, K.A.; Dagaut, P.; Curran, H.J. A Detailed Chemical Kinetic Modeling, Ignition Delay time and Jet-Stirred Reactor Study of Methanol Oxidation. Combust. Flame 2016, 165, 125–136. [Google Scholar] [CrossRef]
- Frenklach, M.; Wang, H.; Goldenberg, M.; Smith, G.P.; Golden, D.M.; Bowman, C.T.; Hanson, R.K.; Gardiner, W.C.; Lissianski, V. GRI Topical Report No. GRI-95/0058. 1995. Available online: https://www.gti.energy/ (accessed on 1 December 2023).
- Yamada, E.; Kitabayashi, N.; Koichi Hayashi, A.; Tsuboi, N. Mechanism of high-pressure hydrogen auto-ignition when spouting into air. Int. J. Hydrogen Energy 2011, 36, 2560–2566. [Google Scholar] [CrossRef]
- Herzler, J.; Naumann, C. Shock-tube study of the ignition of methane/ethane/hydrogen mixtures with hydrogen contents from 0% to 100% at different pressures. Proc. Combust. Inst. 2009, 32, 213–220. [Google Scholar] [CrossRef]
- Petersen, E.L. Turbulent Flame Speeds and NOx Kinetics of HHC Fuels with Contaminants and High Dilution Levels; Topical Report 1; Texas Engineering Experiment Station: College Station, TX, USA, 2011. [Google Scholar]
- Hu, E.; Pan, L.; Gao, Z.; Lu, X.; Meng, X.; Huang, Z. Shock tube study on ignition delay of hydrogen and evaluation of various kinetic models. Int. J. Hydrogen Energy 2016, 41, 13261–13280. [Google Scholar] [CrossRef]
- Konnov, A.A.; Mohammad, A.; Kishore, V.R.; Kim, N.I.; Prathap, C.; Kumar, S. A comprehensive review of measurements and data analysis of laminar burning velocities for various fuel + air mixtures. Prog. Energy Combust. Sci. 2018, 68, 197–267. [Google Scholar] [CrossRef]
- Tse, S.D.; Zhu, D.L.; Law, C.K. Morphology and Burning Rates of Expanding Spherical Flames in H2/O2/Inert Mixtures up to 60 Atmospheres. Proc. Combust. Inst. 2000, 28, 1793–1800. [Google Scholar] [CrossRef]
- Zhang, W.; Gou, X.; Kong, W.; Chen, Z. Laminar flame speeds of lean high-hydrogen syngas at normal and elevated pressures. Fuel 2016, 181, 958–963. [Google Scholar] [CrossRef]
- Chaos, M.; Dryer, F.L. Chemical-Kinetic Modeling of Ignition Delay: Considerations in Interpreting Shock Tube Data. Int. J. Chem. Kinet. 2010, 42, 143–150. [Google Scholar] [CrossRef]
- Krejci, M.C.; Mathieu, O.; Vissotski, A.J.; Ravi, S.; Sikes, T.G.; Petersen, E.L.; Kéromnès, A.; Metcalfe, W.; Curran, H.J. Laminar Flame Speed and Ignition Delay Time Data for the Kinetic Modeling of Hydrogen and Syngas Fuel Blends. J. Eng. Gas Turbine Power 2013, 135, 021503. [Google Scholar] [CrossRef]
- Aung, K.T.; Hassan, M.I.; Faeth, G.M. Effects of pressure and nitrogen dilution on flame/stretch interactions of laminar premixed H2/O2/N2 flames. Combust. Flame 1998, 112, 1–15. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).