A Novel Optimal Sensor Placement Method for Optimizing the Diagnosability of Liquid Rocket Engine
Abstract
1. Introduction
- A two-stage diagnosis algorithm is proposed for constructing hierarchical diagnosability metrics achieving multi-scale optimization of diagnosability of the LRE online PHM system;
- A two-stage OSP method is proposed to solve the intelligent optimal decision-making problem in the Pareto Solutions (PSs);
- The proposed diagnosability metrics can be computed for different sensor placements without retraining the classifier model while optimizing, and the superiority of the proposed method is verified by retraining the classifier model based on the optimal sensor configuration selected from PSs;
- The proposed method in this paper implements system-level Optimal Sensor Placement for LRE fault diagnosis, and the effectiveness of the proposed method was verified by LRE system-level simulation and ground hot-fire test-run experiments. The results show the proposed method has the potential to be used for the developing of reusable LREs.
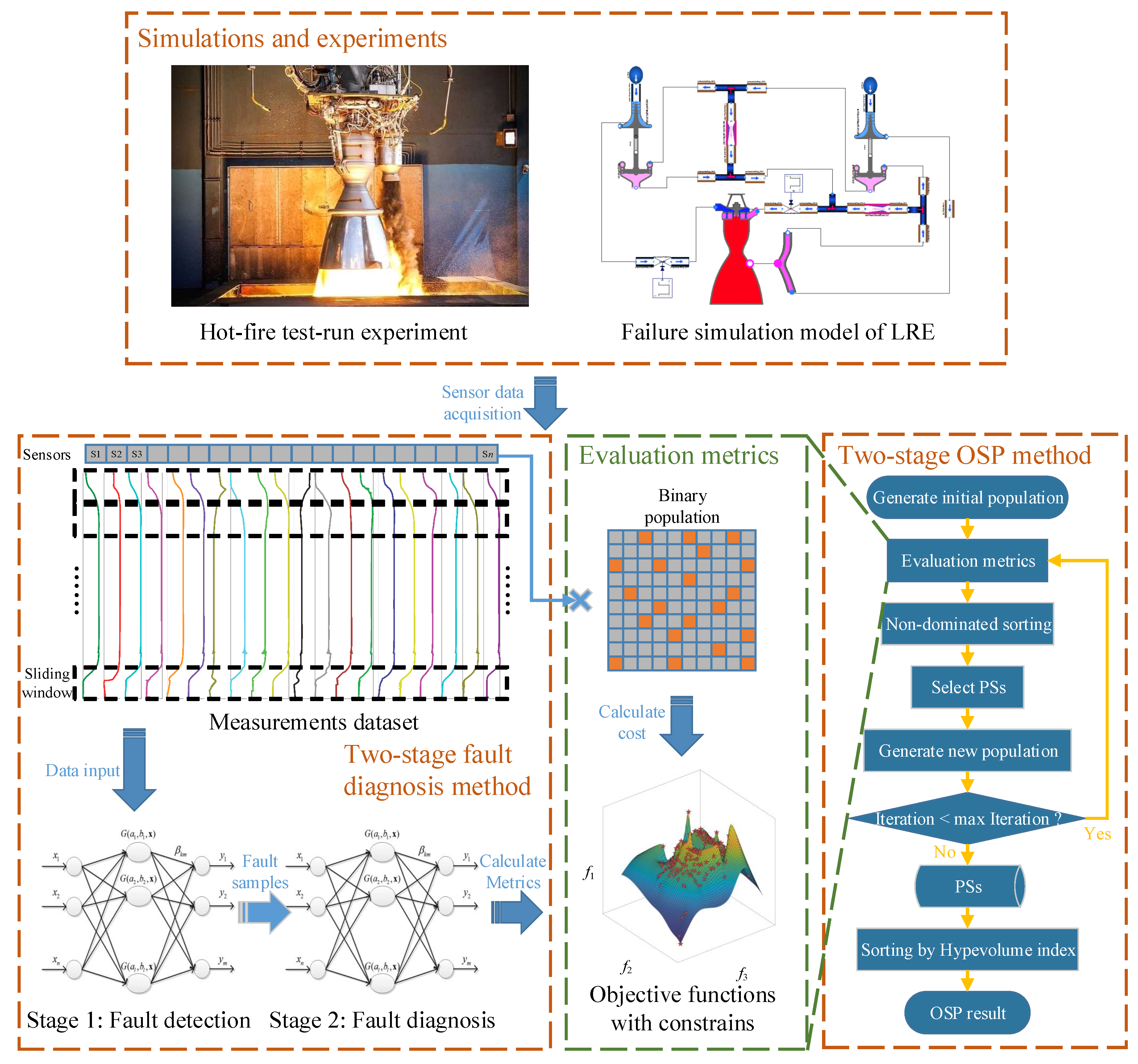
2. Methodology
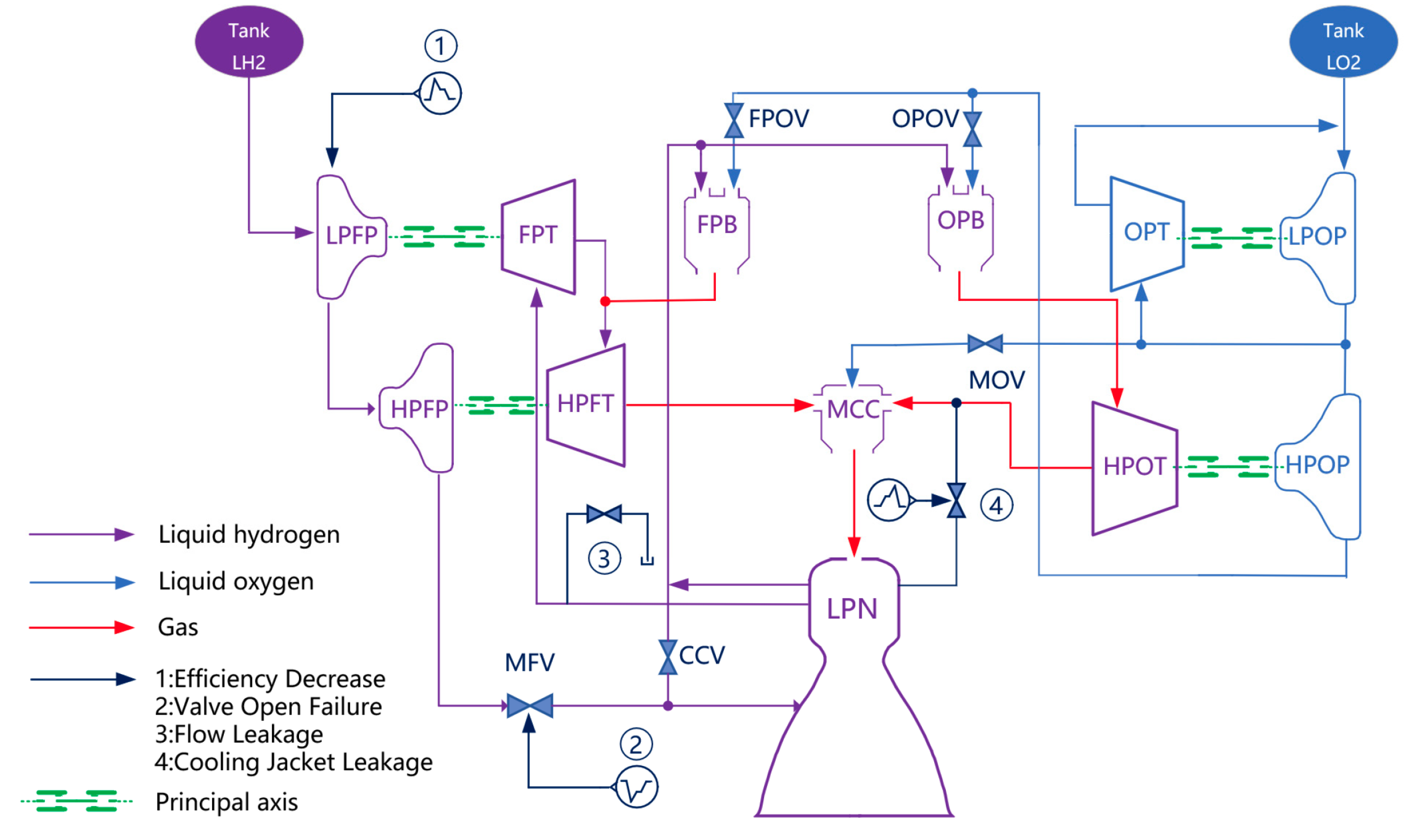
2.1. System-Level Failure Simulation Model of LRE
2.2. Diagnosability Modeling of LRE
2.3. OSP Problem Analysis
2.4. Two-Stage OSP Method
3. Simulations and Experiments
3.1. LRE Failure Simulations
3.2. Hot-Fire Test-Run Experiments
4. Results and Discussions
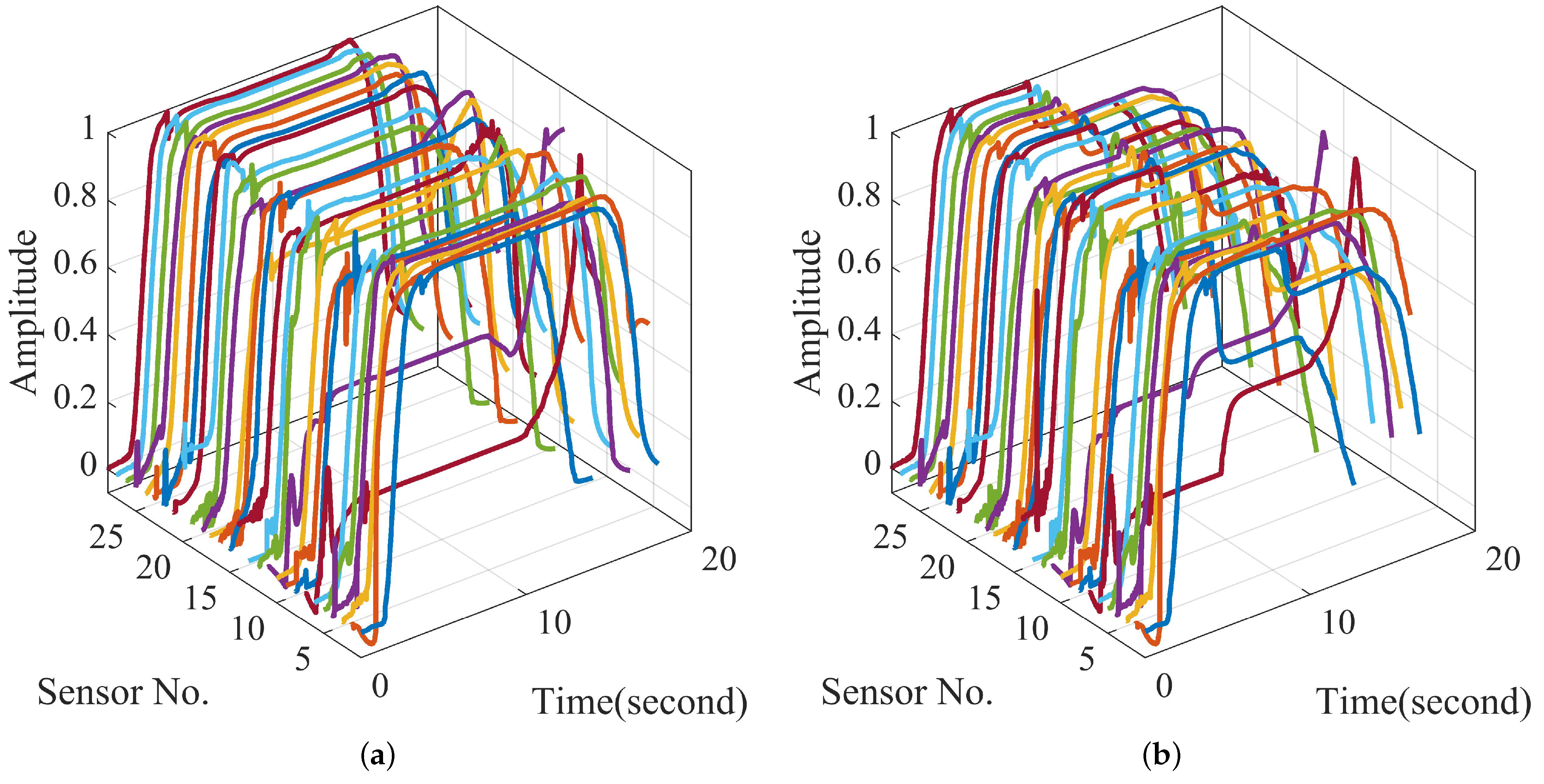
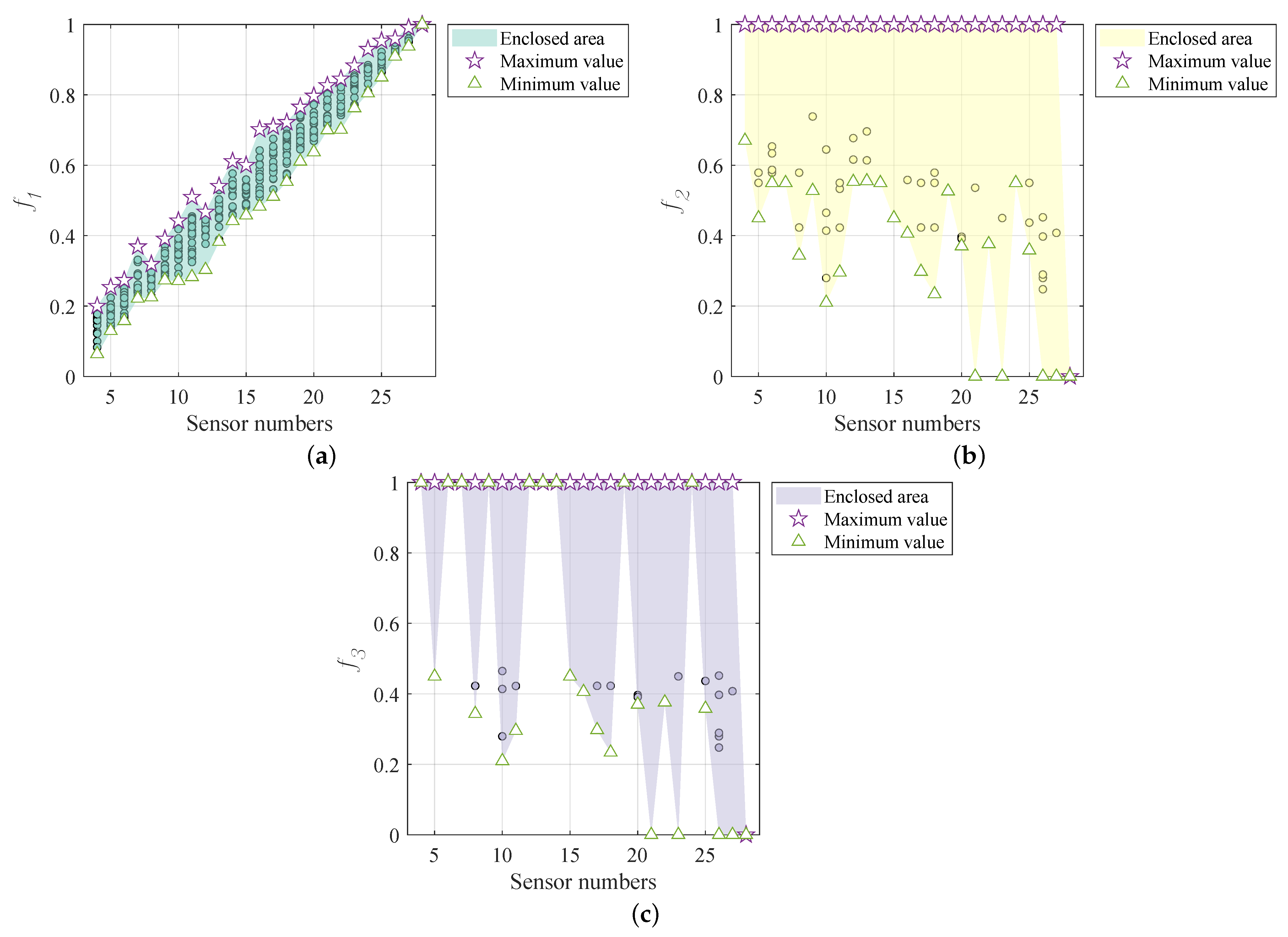
4.1. Results on the Simulated Datasets
4.2. Results on the Experimental Datasets
5. Conclusions Remarks and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LRE | Liquid Rocket Engine |
| PHM | Prognosis and Health Management |
| OSP | Optimal Sensor Placement |
| ATA | Adaptive Threshold Algorithm |
| DTW | Dynamic Time Warping |
| LSTM | Long Short-Term Memory |
| RUL | Remaining Useful Life |
| TDQN | transferable deep Q network |
| DRL | Deep Reinforcement Learning |
| TL | Transfer Learning |
| CAE | Convolutional Autoencoder |
| FIM | Fisher Information Matrix |
| GANs | Generative Adversarial Networks |
| 1D-CNN | one-dimension Convolutional Neural Network |
| KELM | Kernel Extreme Learning Machine |
| HREA | Hierarchy Ranking Evolutionary Algorithm |
| PSs | Pareto Solutions |
| SSME | Space Shuttle Main Engine |
| RBF | Radial Basis Function |
| BMOA | Binary Multi-objective Optimization Algorithm |
| PFs | Pareto Fronts |
| HV | Hypervolume |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm-II |
| AGE-MOEA-II | Adaptive Geometry Estimation based Multi-objective Evolutionary Algorithm-II |
| BCE-MOEA/D | Bi-criterion Evolution in MOEA based on Decomposition |
| CMMOPSO | Competitive Mechanism based Multi-objective Particle Swarm Optimizer |
| SNR | Signal-to-Noise Ratio |
References
- Lin, R.; Yang, J.; Huang, L.; Liu, Z.; Zhou, X.; Zhou, Z. Review of Launch Vehicle Engine PHM Technology and Analysis Methods Research. Aerospace 2023, 10, 517. [Google Scholar] [CrossRef]
- Pérez-Roca, S.; Marzat, J.; Piet-Lahanier, H.; Langlois, N.; Farago, F.; Galeotta, M.; Le Gonidec, S. A survey of automatic control methods for liquid-propellant rocket engines. Prog. Aerosp. Sci. 2019, 107, 63–84. [Google Scholar] [CrossRef]
- Maul, W.A.; Kopasakis, G.; Santi, L.M.; Sowers, T.S.; Chicatelli, A. Sensor selection and optimization for health assessment of aerospace systems. J. Aerosp. Comput. Inf. Commun. 2008, 5, 16–34. [Google Scholar] [CrossRef][Green Version]
- Deng, L.; Cheng, Y.; Yang, S.; Wu, J.; Shi, Y. Fault detection and diagnosis for liquid rocket engines with sample imbalance based on Wasserstein generative adversarial nets and multilayer perceptron. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 237, 1751–1763. [Google Scholar] [CrossRef]
- Ma, M.; Sun, C.; Chen, X. Deep coupling autoencoder for fault diagnosis with multimodal sensory data. IEEE Trans. Ind. Inform. 2018, 14, 1137–1145. [Google Scholar] [CrossRef]
- Ma, M.; Mao, Z. Deep-convolution-based LSTM network for remaining useful life prediction. IEEE Trans. Ind. Inform. 2020, 17, 1658–1667. [Google Scholar] [CrossRef]
- Chen, X.; Ma, M.; Zhao, Z.; Zhai, Z.; Mao, Z. Physics-informed deep neural network for bearing prognosis with multisensory signals. J. Dyn. Monit. Diagn. 2022, 1, 200–207. [Google Scholar] [CrossRef]
- Wang, H.; Xu, J.; Yan, R. Intelligent fault diagnosis for planetary gearbox using transferable deep q network under variable conditions with small training data. J. Dyn. Monit. Diagn. 2023, 2, 30–41. [Google Scholar]
- Lee, K.; Cha, J.; Ko, S.; Park, S.Y.; Jung, E. Fault detection and diagnosis algorithms for an open-cycle liquid propellant rocket engine using the Kalman filter and fault factor methods. Acta Astronaut. 2018, 150, 15–27. [Google Scholar] [CrossRef]
- Kawatsu, K. PHM by using multi-physics system-level modeling and simulation for EMAs of liquid rocket engine. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–10. [Google Scholar]
- Kawatsu, K.; Tsutsumi, S.; Hirabayashi, M.; Sato, D. Model-based fault diagnostics in an electromechanical actuator of reusable liquid rocket engine. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1624. [Google Scholar]
- Tsutsumi, S.; Hirabayashi, M.; Sato, D.; Kawatsu, K.; Sato, M.; Kimura, T.; Hashimoto, T.; Abe, M. Data-driven fault detection in a reusable rocket engine using bivariate time-series analysis. Acta Astronaut. 2021, 179, 685–694. [Google Scholar] [CrossRef]
- Deng, L.; Cheng, Y.; Shi, Y. Fault detection and diagnosis for liquid rocket engines based on long short-term memory and generative adversarial networks. Aerospace 2022, 9, 399. [Google Scholar] [CrossRef]
- Zhang, X.; Hua, X.; Zhu, J.; Ma, M. Intelligent Fault Diagnosis of Liquid Rocket Engine via Interpretable LSTM with Multisensory Data. Sensors 2023, 23, 5636. [Google Scholar] [CrossRef]
- Jana, D.; Patil, J.; Herkal, S.; Nagarajaiah, S.; Duenas-Osorio, L. CNN and Convolutional Autoencoder (CAE) based real-time sensor fault detection, localization, and correction. Mech. Syst. Signal Process. 2022, 169, 108723. [Google Scholar] [CrossRef]
- Park, S.Y.; Ahn, J. Deep neural network approach for fault detection and diagnosis during startup transient of liquid-propellant rocket engine. Acta Astronaut. 2020, 177, 714–730. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Zhao, Z.; Chen, X.; Hu, J. Dynamic model-assisted transferable network for liquid rocket engine fault diagnosis using limited fault samples. Reliab. Eng. Syst. Saf. 2024, 243, 109837. [Google Scholar] [CrossRef]
- Sun, H.; Cheng, Y.; Jiang, B.; Lu, F.; Wang, N. Anomaly Detection Method for Rocket Engines Based on Convex Optimized Information Fusion. Sensors 2024, 24, 415. [Google Scholar] [CrossRef] [PubMed]
- Mehrjoo, A.; Song, M.; Moaveni, B.; Papadimitriou, C.; Hines, E. Optimal sensor placement for parameter estimation and virtual sensing of strains on an offshore wind turbine considering sensor installation cost. Mech. Syst. Signal Process. 2022, 169, 108787. [Google Scholar] [CrossRef]
- Ercan, T.; Sedehi, O.; Katafygiotis, L.S.; Papadimitriou, C. Information theoretic-based optimal sensor placement for virtual sensing using augmented Kalman filtering. Mech. Syst. Signal Process. 2023, 188, 110031. [Google Scholar] [CrossRef]
- Wang, M.; Incecik, A.; Feng, S.; Gupta, M.; Królczyk, G.; Li, Z. Damage identification of offshore jacket platforms in a digital twin framework considering optimal sensor placement. Reliab. Eng. Syst. Saf. 2023, 237, 109336. [Google Scholar] [CrossRef]
- Kohtz, S.; Zhao, J.; Renteria, A.; Lalwani, A.; Xu, Y.; Zhang, X.; Haran, K.S.; Senesky, D.; Wang, P. Optimal sensor placement for permanent magnet synchronous motor condition monitoring using a digital twin-assisted fault diagnosis approach. Reliab. Eng. Syst. Saf. 2024, 242, 109714. [Google Scholar] [CrossRef]
- Wrobel, M.; Meurer, T. Optimal sensor placement and estimator-based temperature control for a deep drawing process. J. Process Control 2023, 124, 92–104. [Google Scholar] [CrossRef]
- Manohar, K.; Kutz, J.N.; Brunton, S.L. Optimal sensor and actuator selection using balanced model reduction. IEEE Trans. Autom. Control 2021, 67, 2108–2115. [Google Scholar] [CrossRef]
- Inoue, T.; Ikami, T.; Egami, Y.; Nagai, H.; Naganuma, Y.; Kimura, K.; Matsuda, Y. Data-driven optimal sensor placement for high-dimensional system using annealing machine. Mech. Syst. Signal Process. 2023, 188, 109957. [Google Scholar] [CrossRef]
- Yarinezhad, R.; Hashemi, S.N. A sensor deployment approach for target coverage problem in wireless sensor networks. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 5941–5956. [Google Scholar] [CrossRef]
- Taher, S.A.; Li, J.; Fang, H. Simultaneous seismic input and state estimation with optimal sensor placement for building structures using incomplete acceleration measurements. Mech. Syst. Signal Process. 2023, 188, 110047. [Google Scholar] [CrossRef]
- Kim, C.; Oh, H.; Chang Jung, B.; Moon, S.J. Optimal sensor placement to detect ruptures in pipeline systems subject to uncertainty using an Adam-mutated genetic algorithm. Struct. Health Monit. 2022, 21, 2354–2369. [Google Scholar] [CrossRef]
- Kong, X.; Cai, B.; Liu, Y.; Zhu, H.; Liu, Y.; Shao, H.; Yang, C.; Li, H.; Mo, T. Optimal sensor placement methodology of hydraulic control system for fault diagnosis. Mech. Syst. Signal Process. 2022, 174, 109069. [Google Scholar] [CrossRef]
- Karnik, N.; Abdo, M.G.; Perez, C.E.E.; Yoo, J.S.; Cogliati, J.J.; Skifton, R.S.; Calderoni, P.; Brunton, S.L.; Manohar, K. Optimal Sensor Placement with Adaptive Constraints for Nuclear Digital Twins. arXiv 2023, arXiv:2306.13637. [Google Scholar]
- Jiang, J.A.; Wang, J.C.; Wu, H.S.; Lee, C.H.; Chou, C.Y.; Wu, L.C.; Yang, Y.C. A novel sensor placement strategy for an IoT-based power grid monitoring system. IEEE Internet Things J. 2020, 7, 7773–7782. [Google Scholar] [CrossRef]
- Zhong, Z.; Jiang, H.; Zuo, H. An optimization method of electrostatic sensor array based on Kriging surrogate model and improved non-dominated sorting genetic algorithm with elite strategy algorithm. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 238, 198–210. [Google Scholar] [CrossRef]
- Papadimitriou, C. Optimal sensor placement methodology for parametric identification of structural systems. J. Sound Vib. 2004, 278, 923–947. [Google Scholar] [CrossRef]
- Udwadia, F.E. Methodology for optimum sensor locations for parameter identification in dynamic systems. J. Eng. Mech. 1994, 120, 368–390. [Google Scholar] [CrossRef]
- Jana, D.; Mukhopadhyay, S.; Ray-Chaudhuri, S. Fisher information-based optimal input locations for modal identification. J. Sound Vib. 2019, 459, 114833. [Google Scholar] [CrossRef]
- Omata, N.; Satoh, D.; Tsutsumi, S.; Kawatsu, K.; Abe, M. Model-based supervised sensor placement optimization to detect propellant leak in a liquid rocket engine. Acta Astronaut. 2022, 195, 234–242. [Google Scholar] [CrossRef]
- Yang, C.; Xia, Y. A novel two-step strategy of non-probabilistic multi-objective optimization for load-dependent sensor placement with interval uncertainties. Mech. Syst. Signal Process. 2022, 176, 109173. [Google Scholar] [CrossRef]
- Li, B.; Zhao, Y.P.; Wu, H.; Tan, H.J. Optimal sensor placement using data-driven sparse learning method with application to pattern classification of hypersonic inlet. Mech. Syst. Signal Process. 2021, 147, 107110. [Google Scholar] [CrossRef]
- Huang, G.B. An insight into extreme learning machines: Random neurons, random features and kernels. Cogn. Comput. 2014, 6, 376–390. [Google Scholar] [CrossRef]
- Li, W.; Yao, X.; Zhang, T.; Wang, R.; Wang, L. Hierarchy ranking method for multimodal multiobjective optimization with local Pareto fronts. IEEE Trans. Evol. Comput. 2022, 27, 98–110. [Google Scholar] [CrossRef]
- de la Fuente, D.; Vega-Rodríguez, M.A.; Pérez, C.J. Automatic selection of a single solution from the Pareto front to identify key players in social networks. Knowl. Based Syst. 2018, 160, 228–236. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Panichella, A. An improved Pareto front modeling algorithm for large-scale many-objective optimization. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO 2022), Boston, MA, USA, 9–13 July 2022; pp. 565–573. [Google Scholar]
- Li, M.; Yang, S.; Liu, X. Pareto or non-Pareto: Bi-criterion evolution in multiobjective optimization. IEEE Trans. Evol. Comput. 2015, 20, 645–665. [Google Scholar] [CrossRef]
- Gu, Q.; Liu, Y.; Chen, L.; Xiong, N. An improved competitive particle swarm optimization for many-objective optimization problems. Expert Syst. Appl. 2022, 189, 116118. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, X.; Cheng, R.; Qiu, J.; Jin, Y. A competitive mechanism based multi-objective particle swarm optimizer with fast convergence. Inf. Sci. 2018, 427, 63–76. [Google Scholar] [CrossRef]


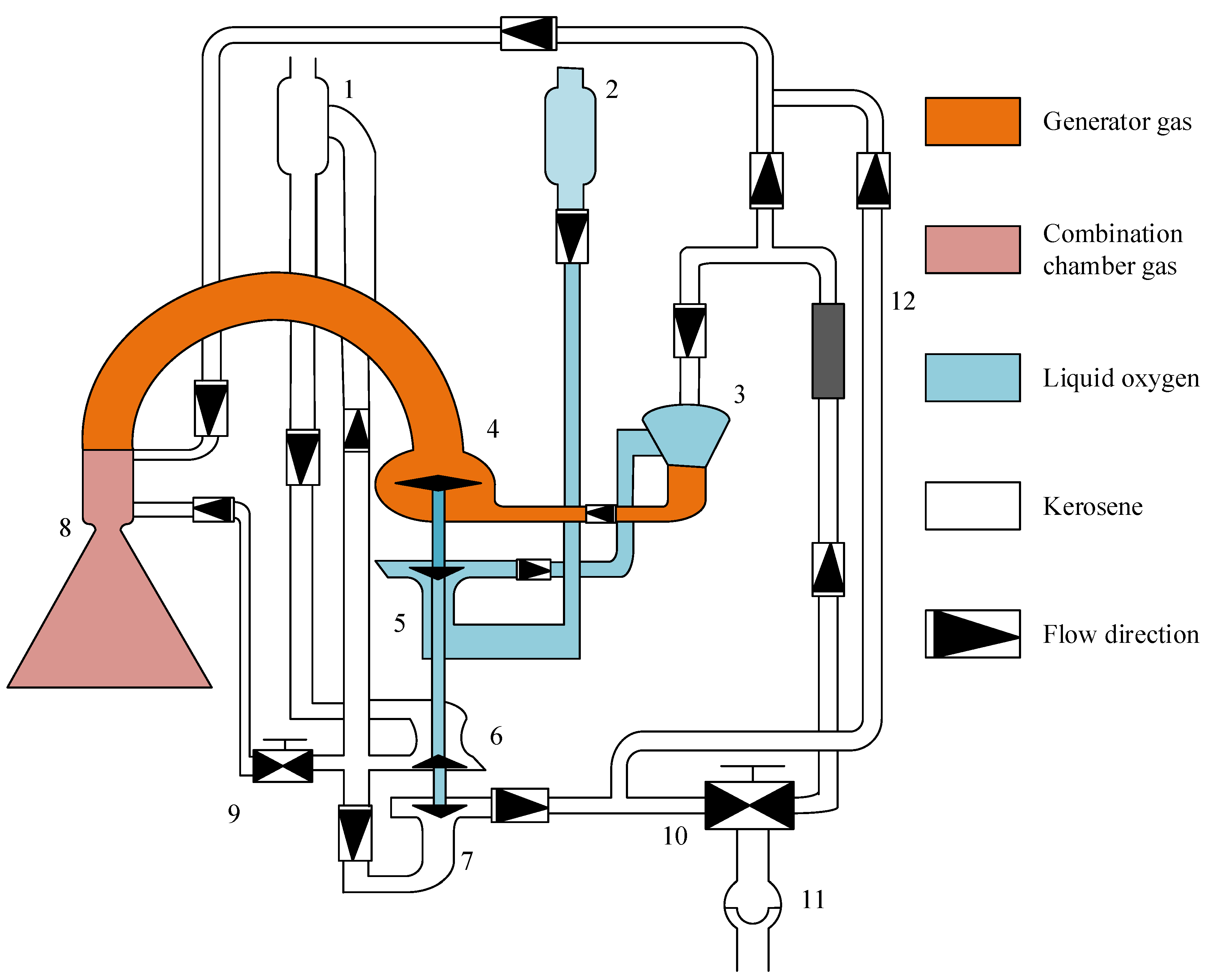
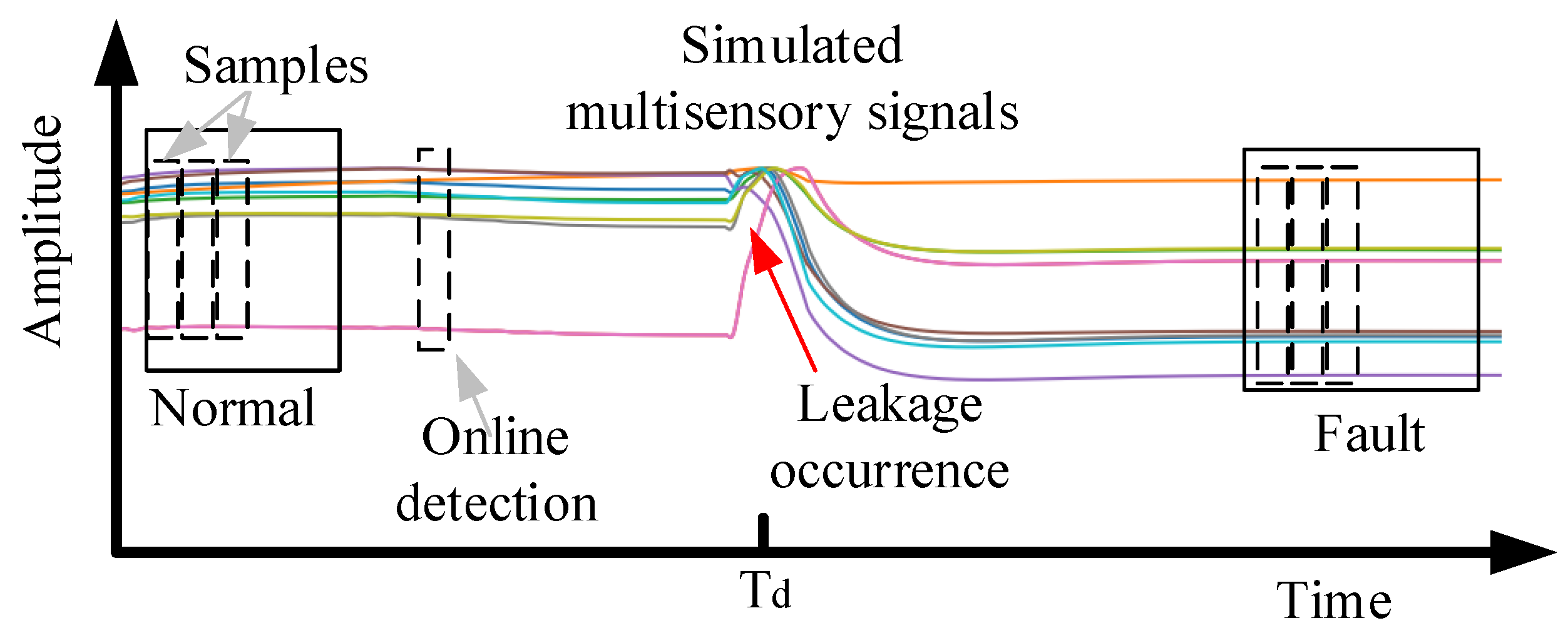
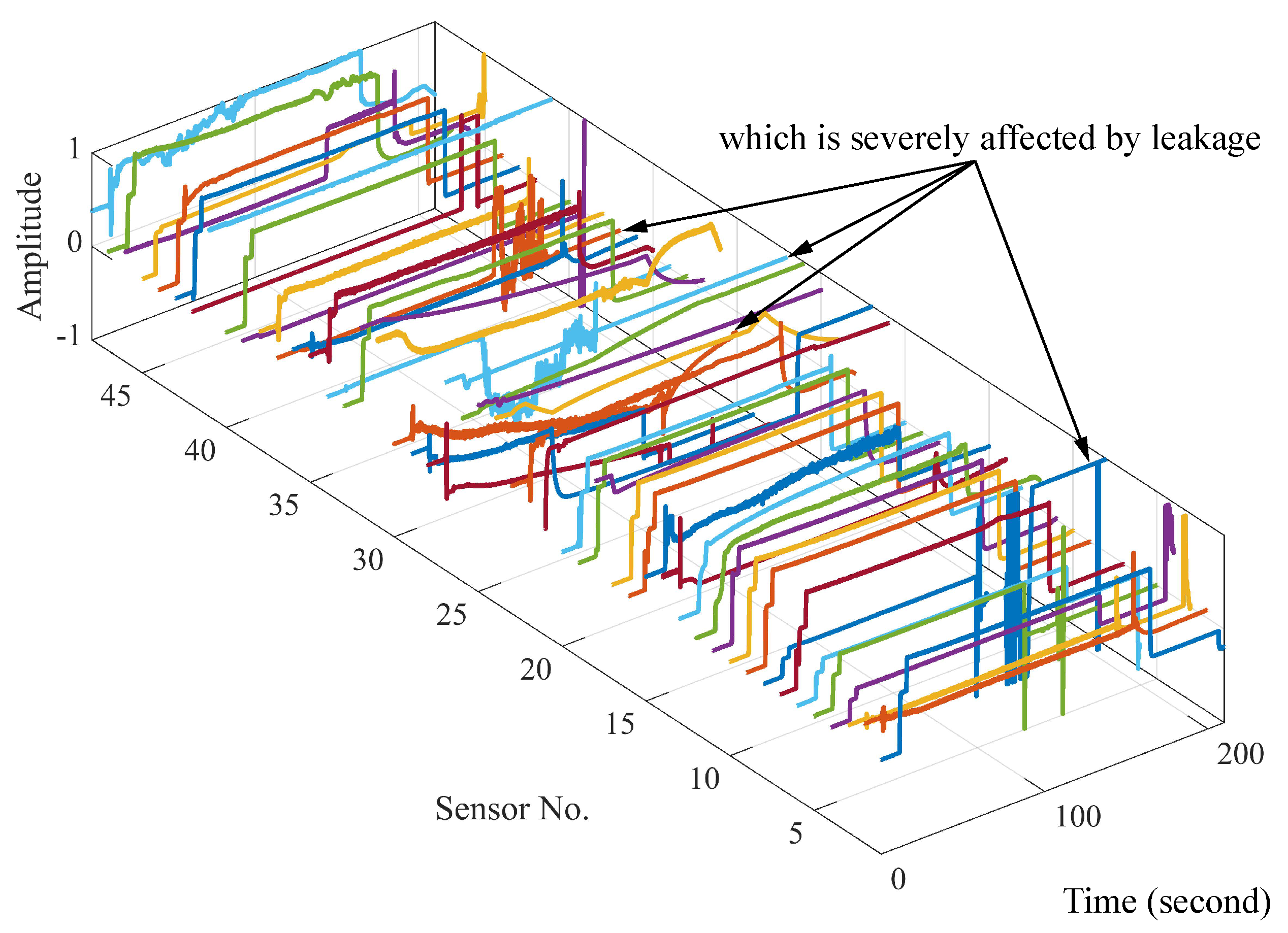
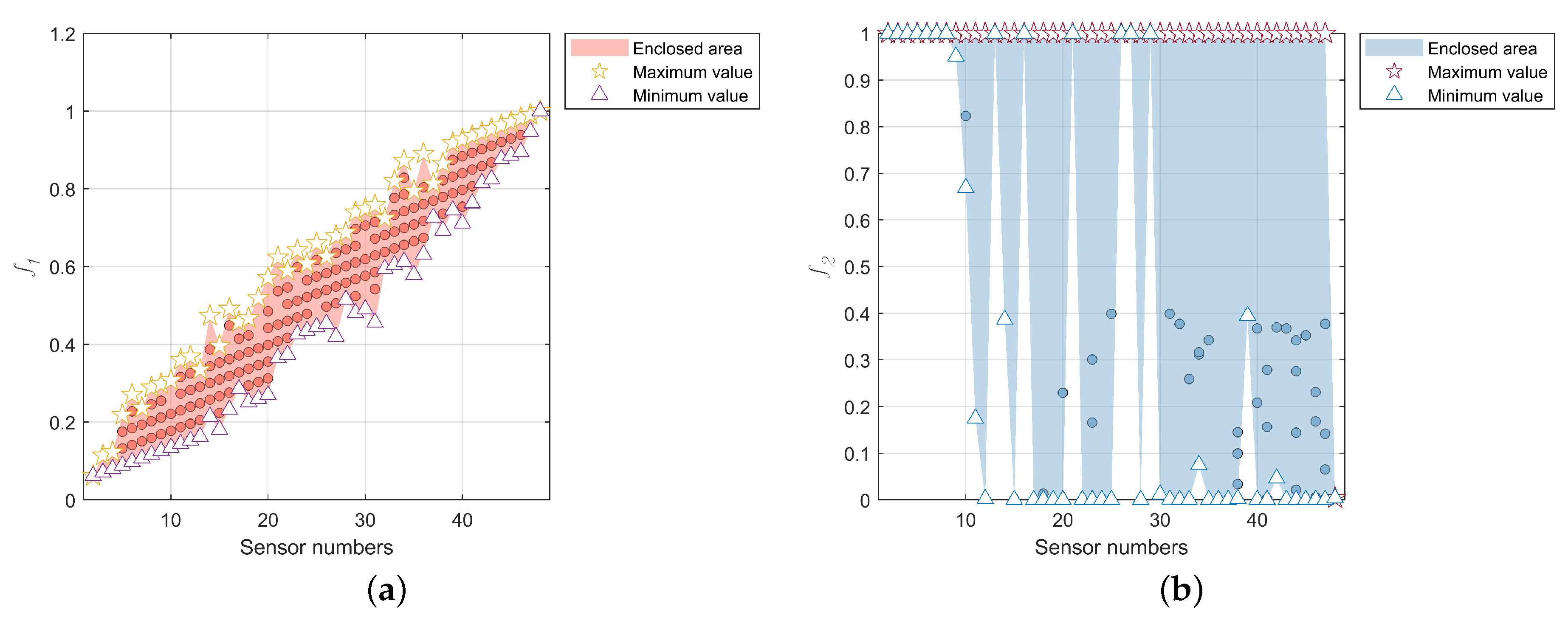
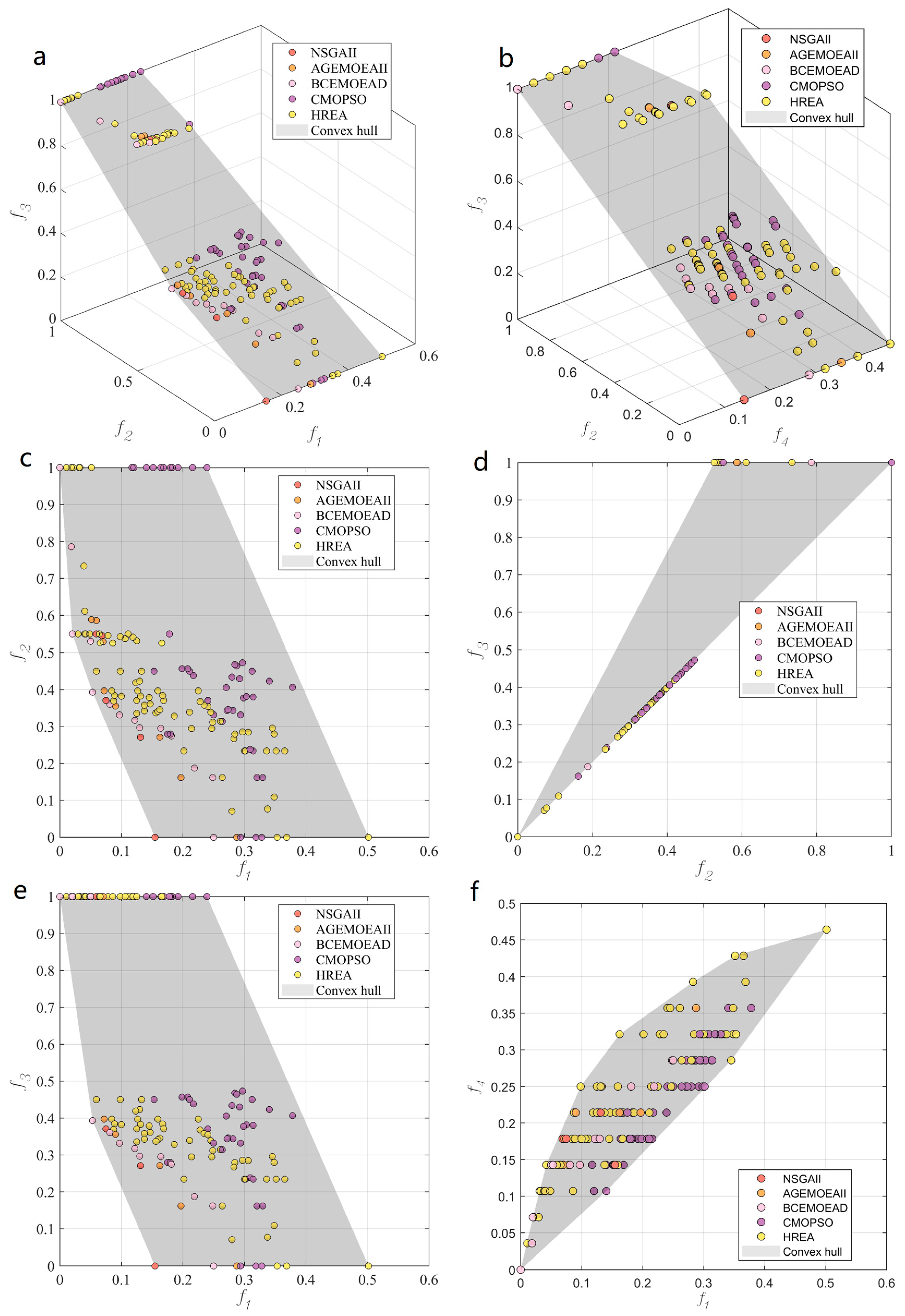
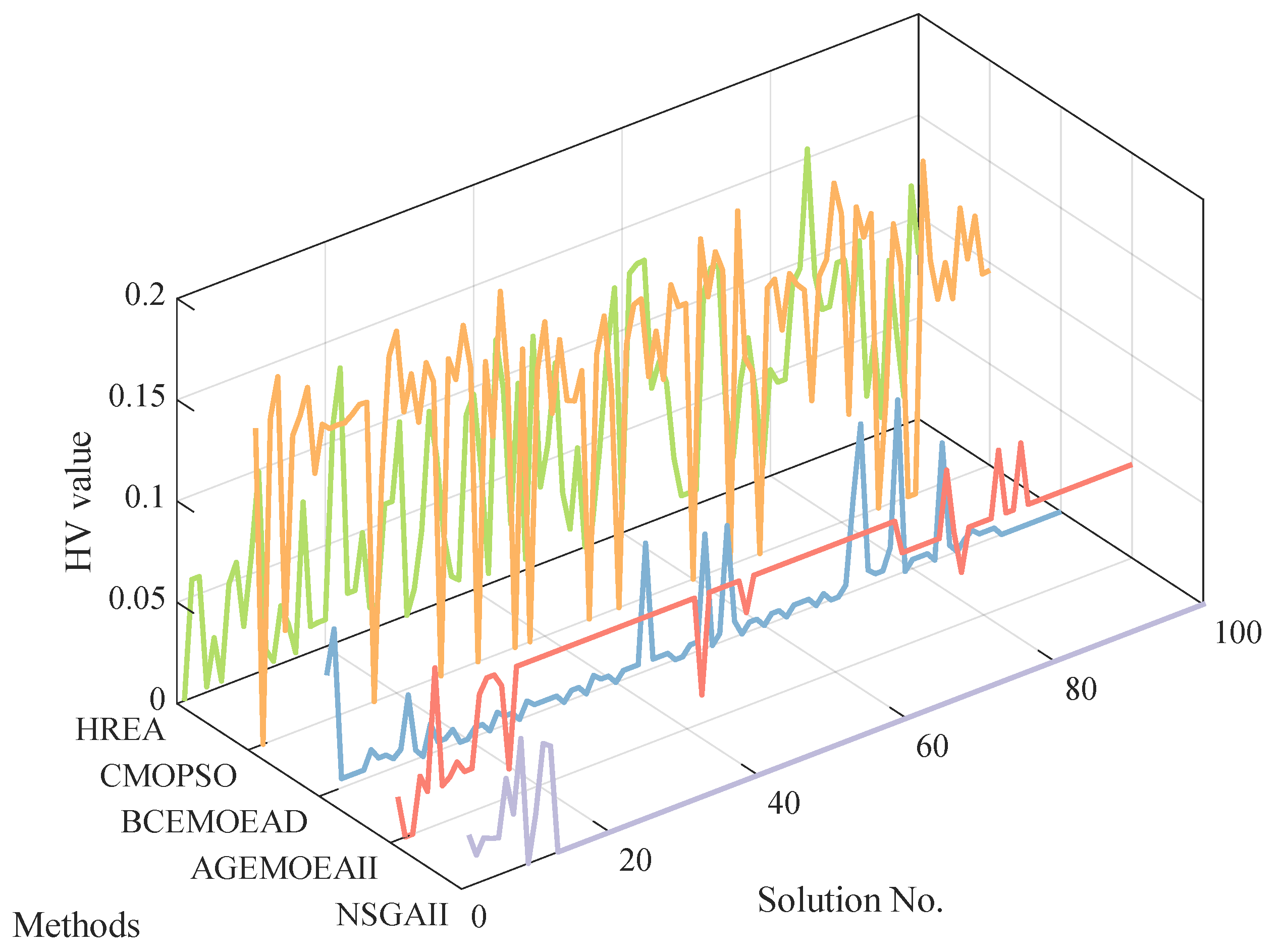
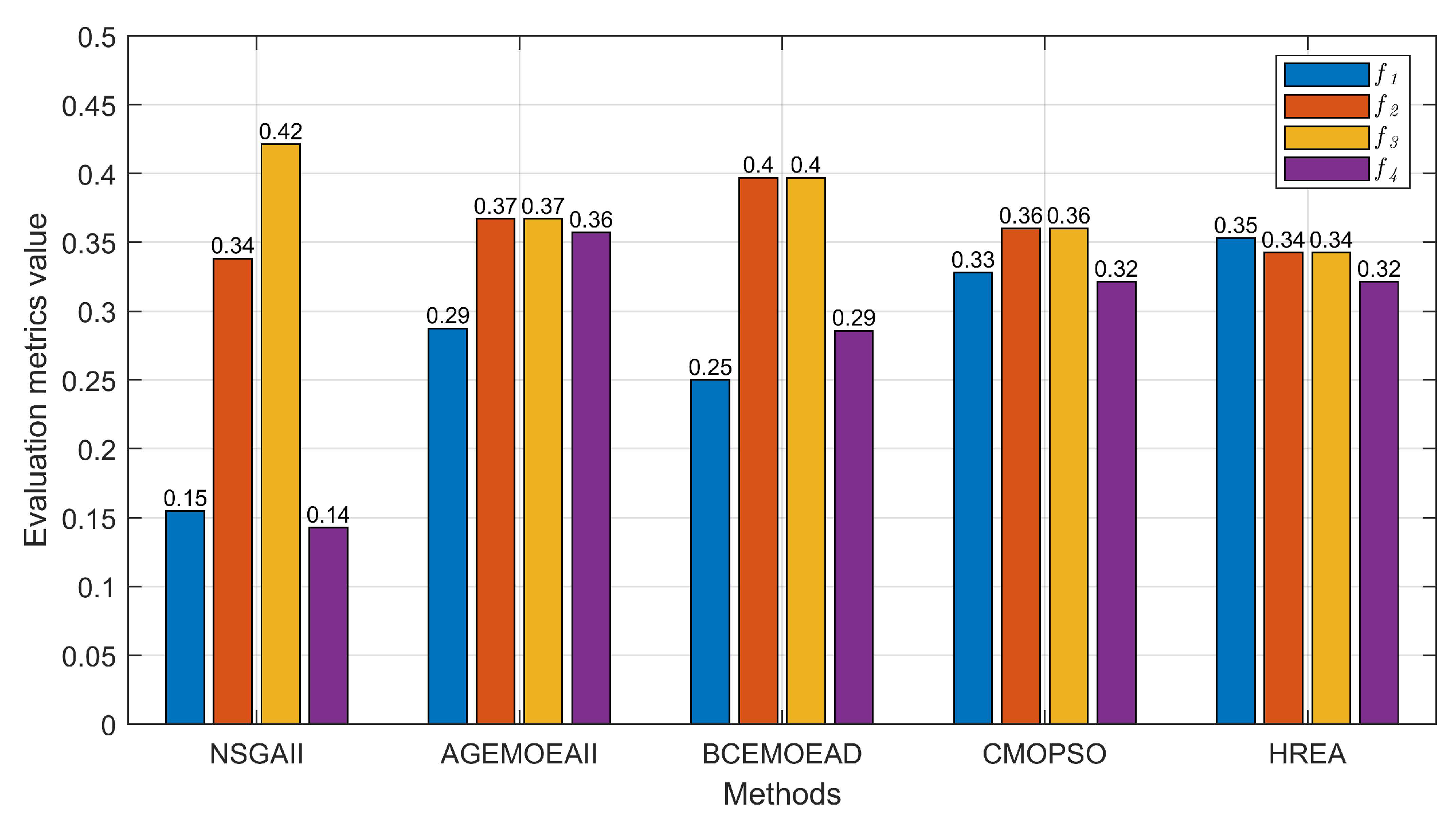




| Sensor No. | Sensor Label | Price Per Sensor (Chinese Yuan) | Description |
|---|---|---|---|
| 1 | Pc | 10,000 | Main combustion chamber pressure |
| 2 | Tc | 10,000 | Main combustion chamber temperature |
| 3 | Qhoc | 3750 | Main combustion chamber fuel/oxidizer mixture flow |
| 4 | Qfc | 6500 | Main combustion chamber fuel flow |
| 5 | Qoc | 7500 | Main combustion chamber oxidizer flow |
| 6 | fpbPc | 10,000 | Fuel preburner pressure |
| 7 | fpbTc | 3000 | Fuel preburner temperature |
| 8 | fpbQfc | 2000 | Fuel preburner chamber fuel flow |
| 9 | fpbQoc | 4000 | Fuel preburner chamber oxidizer flow |
| 10 | opbPc | 8000 | Oxidizer preburner pressure |
| 11 | opbTc | 7500 | Oxidizer preburner temperature |
| 12 | opbQfc | 7500 | Oxidizer preburner chamber fuel flow |
| 13 | opbQoc | 5000 | Oxidizer preburner chamber oxidizer flow |
| 14 | lpftpPo | 1750 | Low-pressure fuel turbopump outlet pressure |
| 15 | lpftpN | 1750 | Low-pressure fuel turbopump speed |
| 16 | lpftpQ | 6500 | Low-pressure fuel turbopump outlet flow |
| 17 | hpftpPo | 6500 | High-pressure fuel turbopump outlet pressure |
| 18 | hpftpN | 7500 | High-pressure fuel turbopump speed |
| 19 | hpftpQ | 5000 | High-pressure fuel turbopump outlet flow |
| 20 | lpotpPo | 1500 | Low-pressure oxidizer turbopump outlet pressure |
| 21 | lpotpN | 3000 | Low-pressure oxidizer turbopump speed |
| 22 | lpotpQ | 7000 | Low-pressure oxidizer turbopump outlet flow |
| 23 | hpotpPo | 7000 | High-pressure oxidizer turbopump outlet pressure |
| 24 | hpotpN | 6500 | High-pressure oxidizer turbopump speed |
| 25 | hpotpQ | 3000 | High-pressure oxidizer turbopump outlet flow |
| 26 | cjP | 1750 | Cooling jacket pressure |
| 27 | ncP | 10,000 | Main combustion cooling pressure |
| 28 | pfsP | 6500 | Preburner fuel supply pressure |
| Algorithms | Parameters |
|---|---|
| NSGA-II | Population size is 1000, maximum generations are 5600, crossover fraction is 0.5, migration fraction is 0.2 and Pareto fraction is 0.1. |
| AGE-MOEA-II | Population size is 1000, maximum generations are 5600, crossover fraction is 0.5 and uniform mutation fraction rate is 0.01. |
| BCE-MOEA/D | Population size is 1000, maximum generations are 5600, the size of neighborhood is 100, the probability of parent individuals selected from the neighborhood is 0.9 and the maximum number of replaced individuals is 10. |
| CMMOPSO | Population size is 1000, maximum generations are 5600 and parameter is 10. |
| Sensor No. | Sensor Label | Price Per Sensor (Chinese Yuan) | Description |
|---|---|---|---|
| 1 | P1 | 1750 | Unknown |
| 2 | P2 | 10,000 | Oxidizer inlet pressure |
| 3 | P3 | 1750 | Unknown |
| 4 | P4 | 10,000 | Fuel solenoid valve outlet pressure |
| 5 | P5 | 10,000 | Fuel pressure before generator injector |
| 6 | P6 | 1750 | Unknown |
| 7 | P7 | 1750 | Unknown |
| 8 | P8 | 1750 | Unknown |
| 9 | P9 | 10,000 | Fuel primary pump outlet pressure 2 |
| 10 | P10 | 1750 | Unknown |
| 11 | P11 | 10,000 | Fuel pressure before Main combustion chamber injector |
| 12 | P12 | 1750 | Unknown |
| 13 | P13 | 1750 | Unknown |
| 14 | P14 | 1750 | Unknown |
| 15 | P15 | 1750 | Unknown |
| 16 | P16 | 1750 | Unknown |
| 17 | P17 | 10,000 | Fuel primary pump outlet pressure 1 |
| 18 | P18 | 1750 | Unknown |
| 19 | P19 | 1750 | Unknown |
| 20 | P20 | 1750 | Unknown |
| 21 | P21 | 1750 | Unknown |
| 22 | P22 | 1750 | Unknown |
| 23 | P23 | 10,000 | Oxidizer pump inlet pressure |
| 24 | P24 | 1750 | Unknown |
| 25 | P25 | 1750 | Unknown |
| 26 | P26 | 1750 | Unknown |
| 27 | P27 | 1750 | Unknown |
| 28 | S1 | 1750 | Unknown |
| 29 | S2 | 1750 | Unknown |
| 30 | S3 | 1750 | Unknown |
| 31 | P28 | 10,000 | Oxidizer pre-compressed pump gas mixing chamber pressure 2 |
| 32 | P29 | 1750 | Unknown |
| 33 | P30 | 1750 | Unknown |
| 34 | P31 | 1750 | Unknown |
| 35 | P32 | 10,000 | Oxidizer pre-compressed pump oxygen mixing chamber pressure |
| 36 | P33 | 1750 | Unknown |
| 37 | P34 | 1750 | Unknown |
| 38 | P35 | 1750 | Unknown |
| 39 | P36 | 1750 | Unknown |
| 40 | P37 | 1750 | Unknown |
| 41 | P38 | 1750 | Unknown |
| 42 | P39 | 1750 | Unknown |
| 43 | P40 | 10,000 | Oxidizer pump outlet pressure |
| 44 | P41 | 1750 | Unknown |
| 45 | P42 | 1750 | Unknown |
| 46 | P43 | 10,000 | Oxidizer pre-compressed pump gas mixing chamber pressure 1 |
| 47 | P44 | 10,000 | Oxidizer pump cooling bearing reflux tube pressure |
| 48 | P45 | 10,000 | Oxidizer pump cooling bearing reflux tube pressure 1 |
| Methods | Sensors Number | Sensor Configuration |
|---|---|---|
| NSGA-II | 4 | 1, 2, 15, 25 |
| AGE-MOEA-II | 10 | 1, 2, 3, 8, 14, 15, 19, 21, 23, 26 |
| BCE-MOEA/D | 8 | 1, 2, 7, 9, 15, 21, 26, 28 |
| CMOPSO | 9 | 2, 5, 12, 15, 16, 18, 22, 25, 26 |
| HREA | 9 | 1, 2, 3, 9, 10, 15, 19, 22, 23 |
| Methods | Sensors Number | Sensor Configuration |
|---|---|---|
| NSGA-II | 2 | 31, 32 |
| AGE-MOEA-II | 2 | 5, 12 |
| BCE-MOEA/D | 3 | 10, 31, 32 |
| CMOPSO | 17 | 2, 3, 5, 7, 11, 12, 15, 17, 21, 22, 24, 38, 39, 42, 43, 47, 48 |
| HREA | 2 | 17, 33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, M.; Zhong, Z.; Zhai, Z.; Sun, R. A Novel Optimal Sensor Placement Method for Optimizing the Diagnosability of Liquid Rocket Engine. Aerospace 2024, 11, 239. https://doi.org/10.3390/aerospace11030239
Ma M, Zhong Z, Zhai Z, Sun R. A Novel Optimal Sensor Placement Method for Optimizing the Diagnosability of Liquid Rocket Engine. Aerospace. 2024; 11(3):239. https://doi.org/10.3390/aerospace11030239
Chicago/Turabian StyleMa, Meng, Zhirong Zhong, Zhi Zhai, and Ruobin Sun. 2024. "A Novel Optimal Sensor Placement Method for Optimizing the Diagnosability of Liquid Rocket Engine" Aerospace 11, no. 3: 239. https://doi.org/10.3390/aerospace11030239
APA StyleMa, M., Zhong, Z., Zhai, Z., & Sun, R. (2024). A Novel Optimal Sensor Placement Method for Optimizing the Diagnosability of Liquid Rocket Engine. Aerospace, 11(3), 239. https://doi.org/10.3390/aerospace11030239






