Forced Vibration Induced by Dynamic Response Under Different Inlet Distortion Intensities

Abstract

Boundary layer ingestion propulsion systems have attracted much attention due to their significant potential to reduce the fuel consumption of future commercial aircraft. However, the aeroelastic stability of the fan blade is affected by the continuous non-uniform incoming flow induced by the ingestion of the boundary layer. When the fan blades rotate in the junction area between the distorted area and the clean area, blade pressure fluctuations occur. This phenomenon triggers a dynamic response process in the blade. Previous numerical investigations explored the influence of the distorted inflow on the blade vibration amplitude, and found that there are two sources of low-order excitation to the blades: the distorted inflow and the dynamic response of the blade. The results show that the low-order excitation existing in the distorted inflow varies sinusoidally with the distortion extent. However, as a new source of excitation, the key influence mechanism of dynamic response is still unclear. To explore this issue, calculations and analyses were conducted for different distorted inflow intensities. The results show that the blade vibration amplitude increases with the rise in distortion intensity. The total pressure at the leading and trailing edge of the rotor blade was extracted for analysis. It was found that when the blade enters or leaves the distorted area, there is a consistent lag in the change in total pressure at the trailing edge compared to the leading edge. This lag leads to an abrupt variation in the total pressure ratio, which constitutes the dynamic response process of the rotor blade. This periodic change generates a second-order excitation that causes the blade to vibrate.

1. Introduction

Boundary layer ingestion (BLI) as a propulsion concept can reduce vehicle fuel consumption significantly, and the idea of applying the concept to aircraft was established in the late 1940s [1,2]. The principle is that part or all of the boundary layer is absorbed by the propulsion system, instead of entering the wake undisturbed [3]. Many studies have shown that BLI generates additional non-uniform flow distortion in circumferential directions [4,5]. Such distorted inflow can detrimentally affect the blades, potentially inducing forced vibrations that could result in blade failure [6,7,8,9]. Numerous studies have been conducted to investigate the relationship between distorted inflow and blade vibration with the objective of preventing blade failures caused by forced vibration [10,11,12]. The presence of distorted in-flow conditions leads to the creation of both distorted and clean areas in the circumferential direction. As the fan blades move between these distinct areas, a noticeable and irregular fluctuation in pressure occurs within the working environment [13,14]. This rapid pressure variation process is recognized as a dynamic response [15,16].

Previous studies have suggested that inlet distortion-induced low-order excitation is the sole source of excitation leading to aeroelastic problems. However, this is not accurate. The amplitude of inlet distortion excitation does not directly correspond to the amplitude of blade vibration, indicating that the dynamic response must be further analyzed as an excitation source. In cases of distorted inflow conditions, the pressure change during the dynamic response process is nonlinear and generates dynamic signals. Therefore, it is necessary to further explore the dynamic response. Peter et al. [17] delved into the investigation of internal losses in the turbine subjected to distorted inflow conditions, identifying a dynamic response phenomenon within the shear layer situated between the regions of distorted and clean inflow. Notably, this region exhibited significant energy fluctuations. Additionally, David [18] utilized two-dimensional CFD simulations to probe the transient flow dynamics in the engine, emphasizing the importance of considering pressure changes during periods of substantial fluid pressure discrepancies. Greitzer [19,20] employed a nonlinear model to predict the dynamic response characteristics of a disturbed compression system, observing that this process reveals non-linear oscillations with an amplitude attenuation trend leading to eventual stabilization. A critical parameter known as the time constant was derived to epitomize the timescale necessary for the system to attain a new equilibrium state following a disturbance.

The time constant can quantitatively represent the dynamic response process. When fluid flows into the blade channel, the blade requires a certain amount of time to adapt to the changes in flow conditions. This response time is commonly known as the time constant. Cousins [21,22] discovered through the study of axial flow compressors that abrupt alterations in inlet conditions cause flow separation on the blade surface. The time constant can quantify this response process. In investigations of rotating stall phenomena, Chen [23] observed distinct time constants governing blade stall and recovery dynamics. Fang [24] observed a gradual evolution of flow during turbomachinery’s rotating stall, indicating an asynchronous interaction between blades and the flow field, thus revealing a dynamic fluid response process described by the time constant. Our previous numerical simulation [25,26] employed the uncoupled FSI (fluid–structure interaction) method to examine the aeroelastic issues with NASA rotor 67 blades.

These analyses indicated a correlation between blade aeroelastic concerns and the transient response associated with variations in distortion areas. The time response constant was intricately linked to pressure disparities between distorted and clean areas. Hence, there is a need for quantitative exploration of blade forced vibrations arising from the transient response process under varying levels of inflow distortion. According to the description provided by William T. [22], it becomes crucial to first quantify the pressure variance between distorted and clean areas, with the distortion intensity coefficient reflecting the extent of this pressure discrepancy. To address these issues effectively, it is imperative to quantitatively establish the relationship between the distortion intensity coefficient and the amplitude of forced vibration generated by the dynamic response process through numerical computations.

This paper is organized as follows: Section 2 introduces the numerical method, including the research subject, numerical setting, validation, and the selection of distortion extent and coefficients. Then, in Section 3, the numerical results are introduced and analyzed, pointing out that the distortion intensity coefficient is related to the dynamic response and affects the amplitude of the low-order forced vibration. Finally, Section 4 gives the conclusions.

2. Methodology

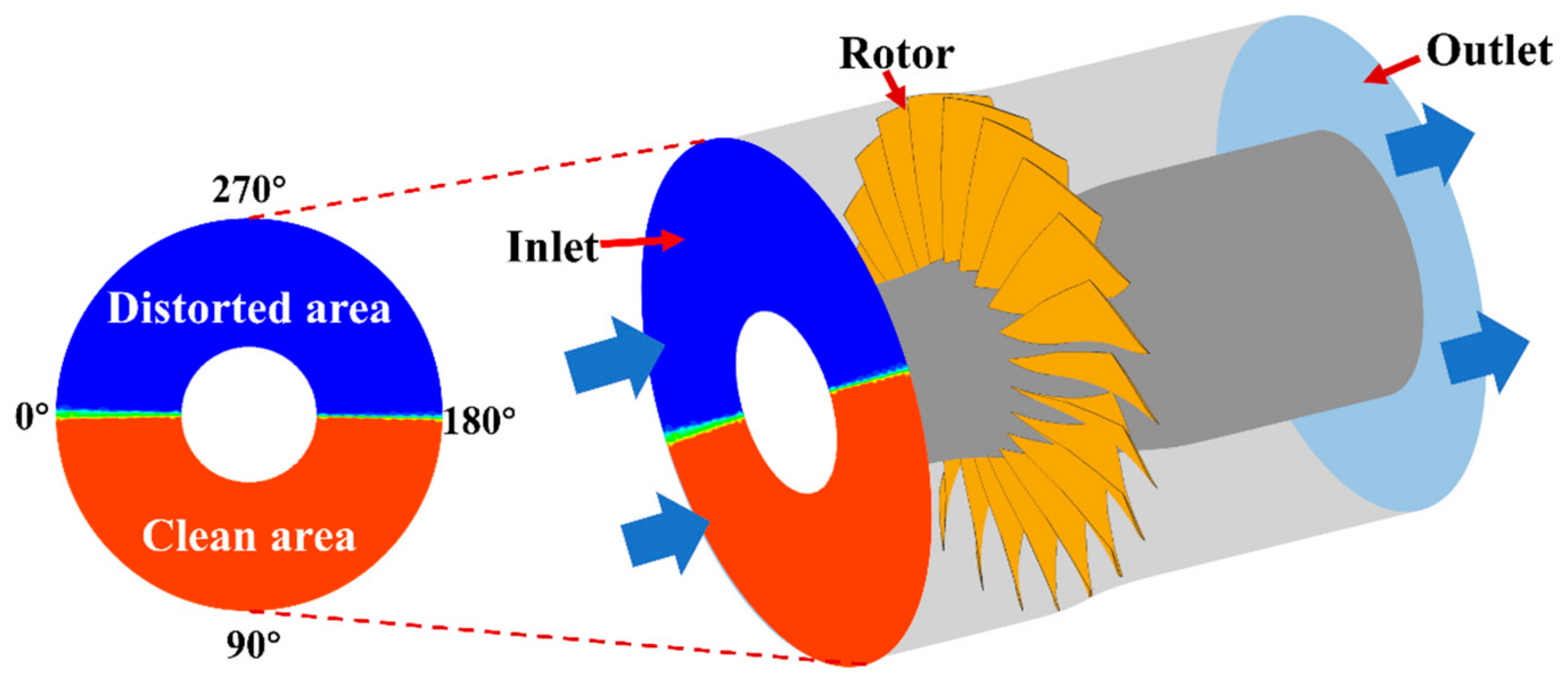
2.1. Research Subject

This article focuses on NASA rotor 67 as the research object. This compressor was developed by Strazisar et al. [27].

Table 1. Design parameters of NASA rotor 67.

Parameter	Numerical Value
Blade number	22
Design rotor rotate speed (rpm)	16,043
Design mass flow (kg/s)	33.25
Design total pressure ratio	1.63
Tip speed (m/s)	427
Aspect ratio	1.56
Hub/tip ratio (outlet)	0.395
Hub/tip ratio (inlet)	0.487

shows some design parameters of NASA rotor 67. Furthermore, the solid material properties of the rotor are shown in

Table 2. Material parameters of the rotor blade.

Young’s Modulus (E/Pa)	Density (ρ/kg·m−3)	Poisson Ratio
1.2 × 1011	4500	0.34

[28].

To mitigate potential interference from the compressor and facilitate the complete development of the fan outlet flow field, the inlet boundary is located one rotor diameter upstream from the leading edge (LE) of the rotor blade. Similarly, the outlet boundary is situated at a location 1.5 times the rotor diameter downstream of the rotor. The computational domain is visually represented in Figure 1. In the figure, red represents the clean area, blue represents the distorted area, and green represents the junction area.

Figure 2 provides the schematic diagram of the rotor simulation area and illustrates the location of measuring points. In the unsteady numerical simulation, transient interface connection is established between the rotating and the stationary domains. The pressure measuring points are evenly distributed along the span from hub to tip at positions ranging from 10% to 90%. These measuring points are situated at both the leading edge (LE) and trailing edge (TE) of the blade and follow the rotation of the blade within the rotational domain, as shown by red dots in Figure 2. The pressure parameters obtained at these locations form the basis for analysis in this paper, capturing the variations at the LE and TE of the blade during its rotation.

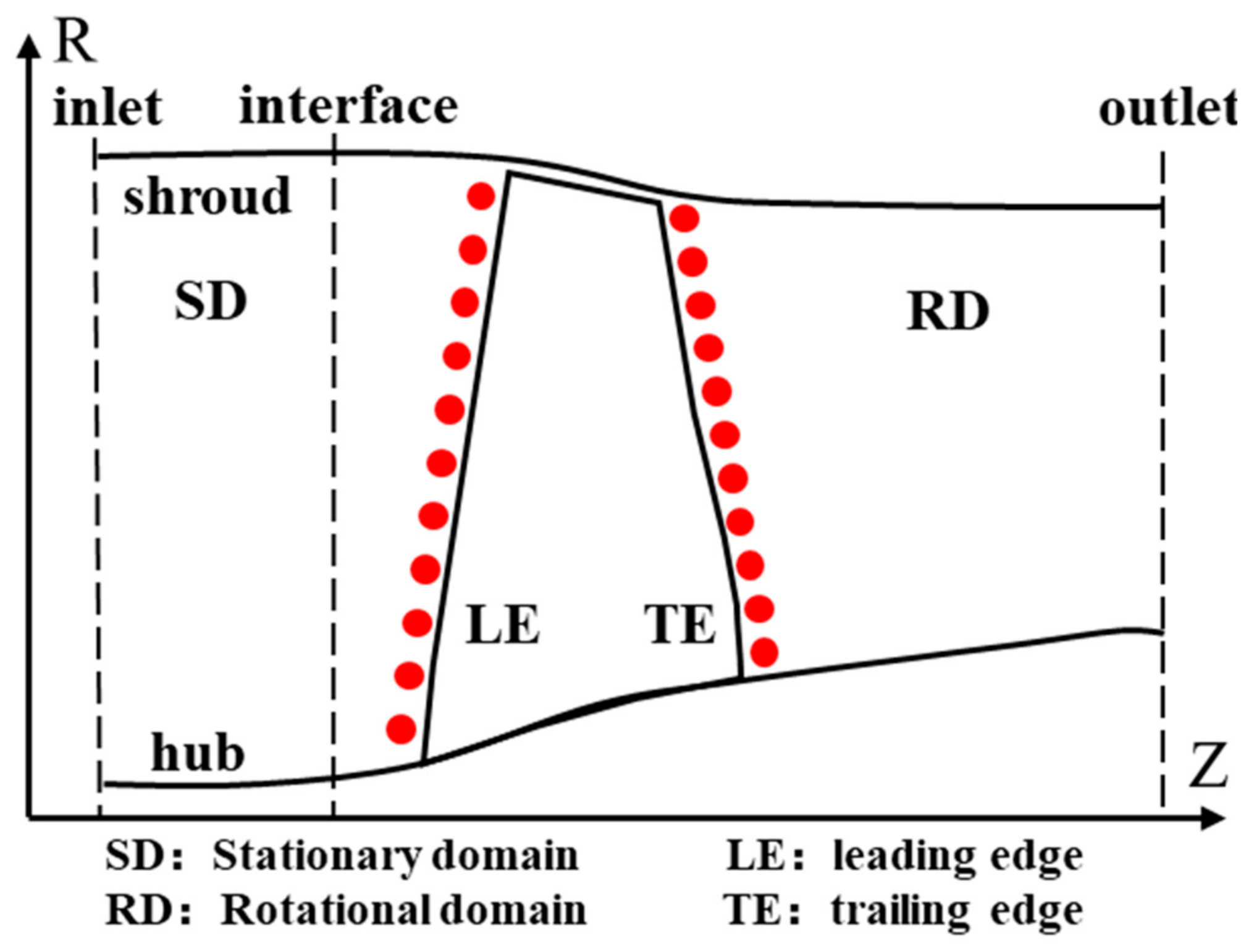
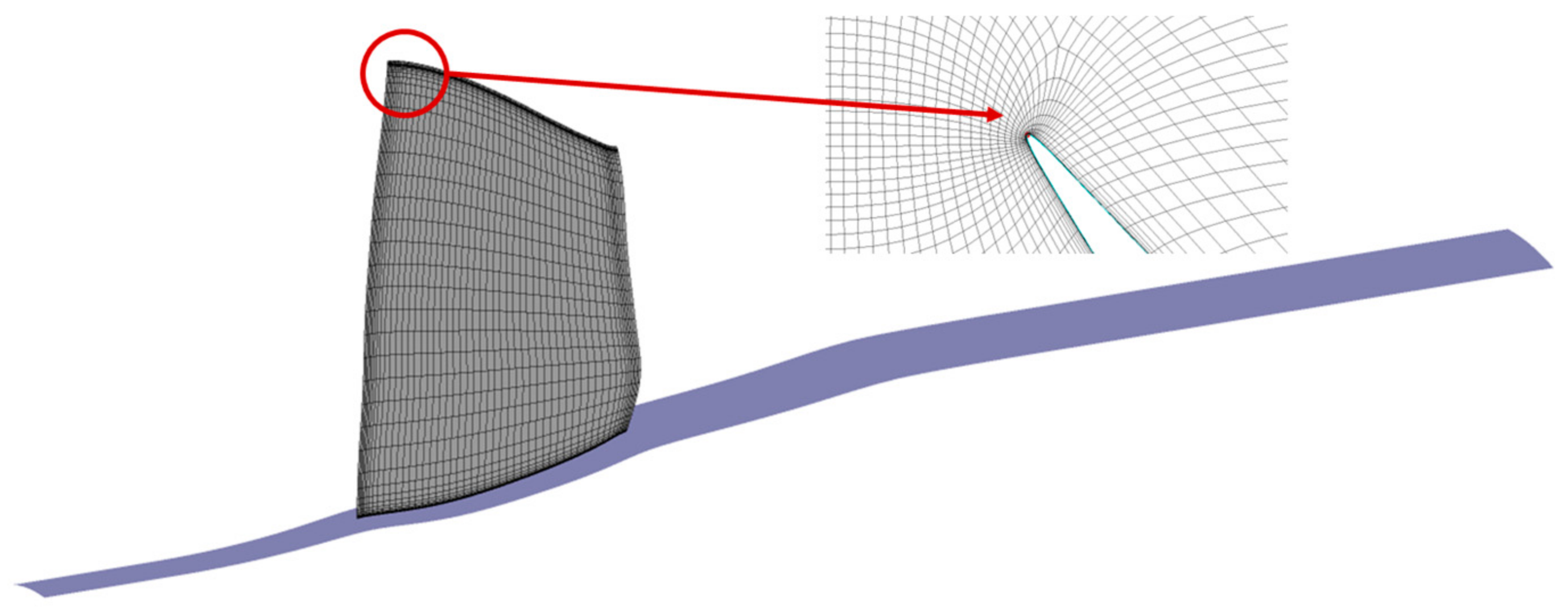
2.2. Numerical Setting

This article employs the ANSYS CFX solver to conduct numerical simulations of rotor 67 under varying distortion conditions. All solid surfaces within the computational domain are defined as adiabatic non-slip wall boundaries. The total temperature of the incoming flow is established at 288 K, and the air inlet mode is specified as the axial air inlet. Boundary conditions at the outlet enforce static pressure based on the radial equilibrium. Stable calculation results are obtained by adjusting the average outlet pressure to modify the compressor operating conditions. The steady computational results serve as the initial field for unsteady calculations. Following a comparative assessment of different turbulence models, the k-ε model structure was chosen for full-circumferential unsteady analysis, with the turbulence intensity set at 3%. The physical time step is designated as 1/30 of the time required for the rotor blade to pass through one blade passage, which is calculated to be 5.67 × 10⁻⁶ s. The internal virtual time steps iterated at least 6 times in each physical time step.

The mesh grid of the computational domain is generated by NUMECA, using the O4H structural grid. The blade is surrounded by the O-grid to form the boundary layer grid, while the remaining regions are populated with an H-grid. Figure 3 illustrates the grid configuration. To align with the k-ε turbulence model, the wall grid height is appropriately adjusted, ensuring the y+ value of approximately 10 adjacent to the solid surface.

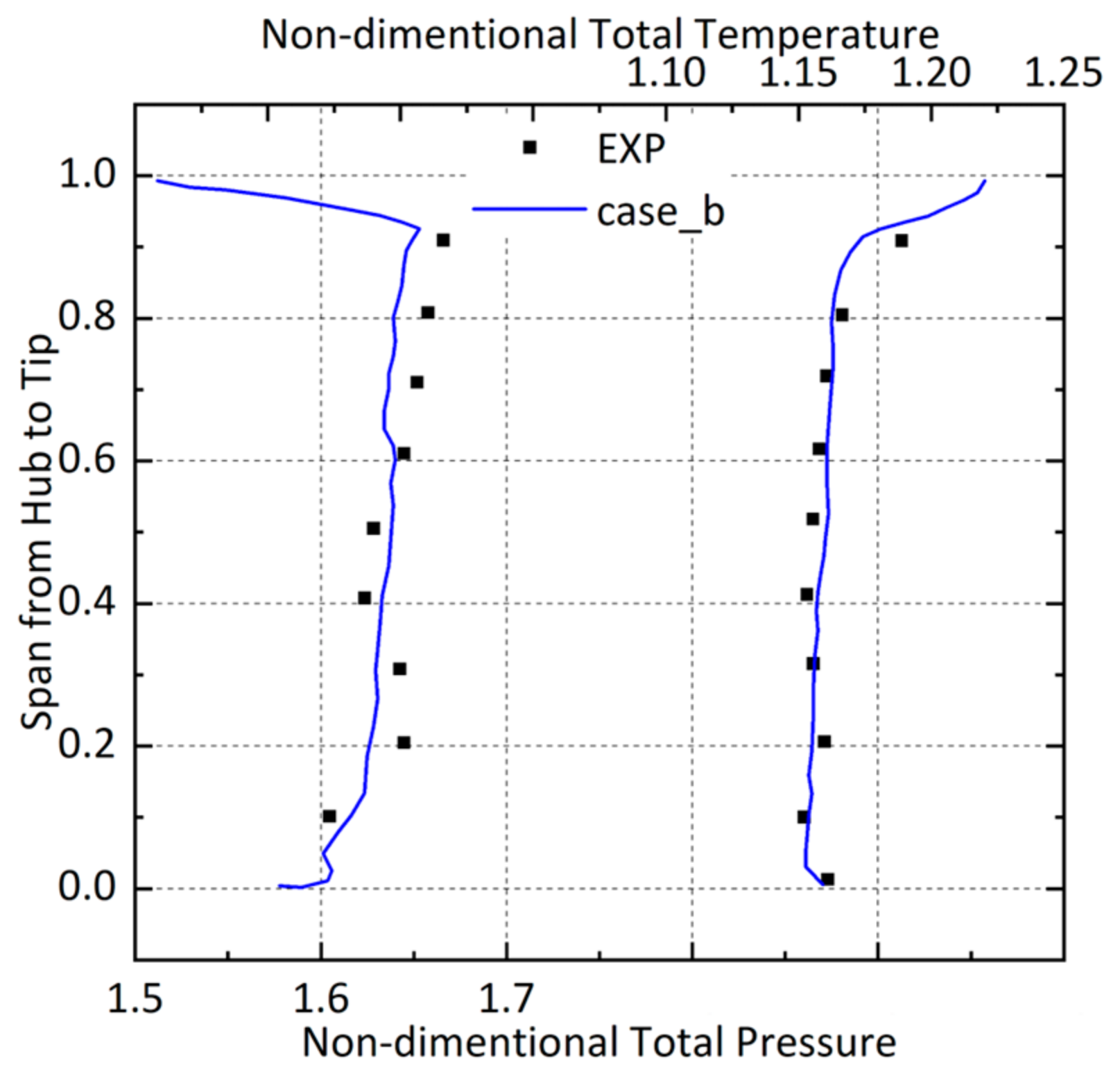
2.3. Validation

To ensure accuracy and to address potential computation errors stemming from varying grid densities, the grid independence of the rotor 67 alone was validated and compared with the experimental results. To conserve computational resources, calculations are performed on the single-channel grid with a uniform air inlet. Three distinct sets of grids were employed for the computations, featuring the following grid sizes: 900,000 cells (case-a), 350,000 cells (case-b), and 100,000 cells (case-c).

Figure 4 presents a comparison between the calculation results obtained with the three grid sets and the experimental results. The experimental data in comparison are obtained from reference [29]. It should be emphasized that the total pressure ratio characteristic lines of grids a and b closely coincide, indicating a higher level of agreement with the experimental results. Considering the computational efficiency for unsteady calculations, case-b with 350,000 cells is chosen for further calculations, resulting in a total grid count of approximately 7.7 million for the entire annulus.

In consideration of the forthcoming calculation focused on the peak efficiency point, a detailed investigation into the outlet distribution of total pressure and total temperature was carried out at this specific point. Figure 5 displays the comparative analysis of the overall distribution of total pressure and total temperature across the span using grid case-b, in contrast with the experimental results. The calculated distribution demonstrates a notable conformity with the experimental data. These results validate the accuracy of the computational approach and establish a robust groundwork for continued exploration in this domain.

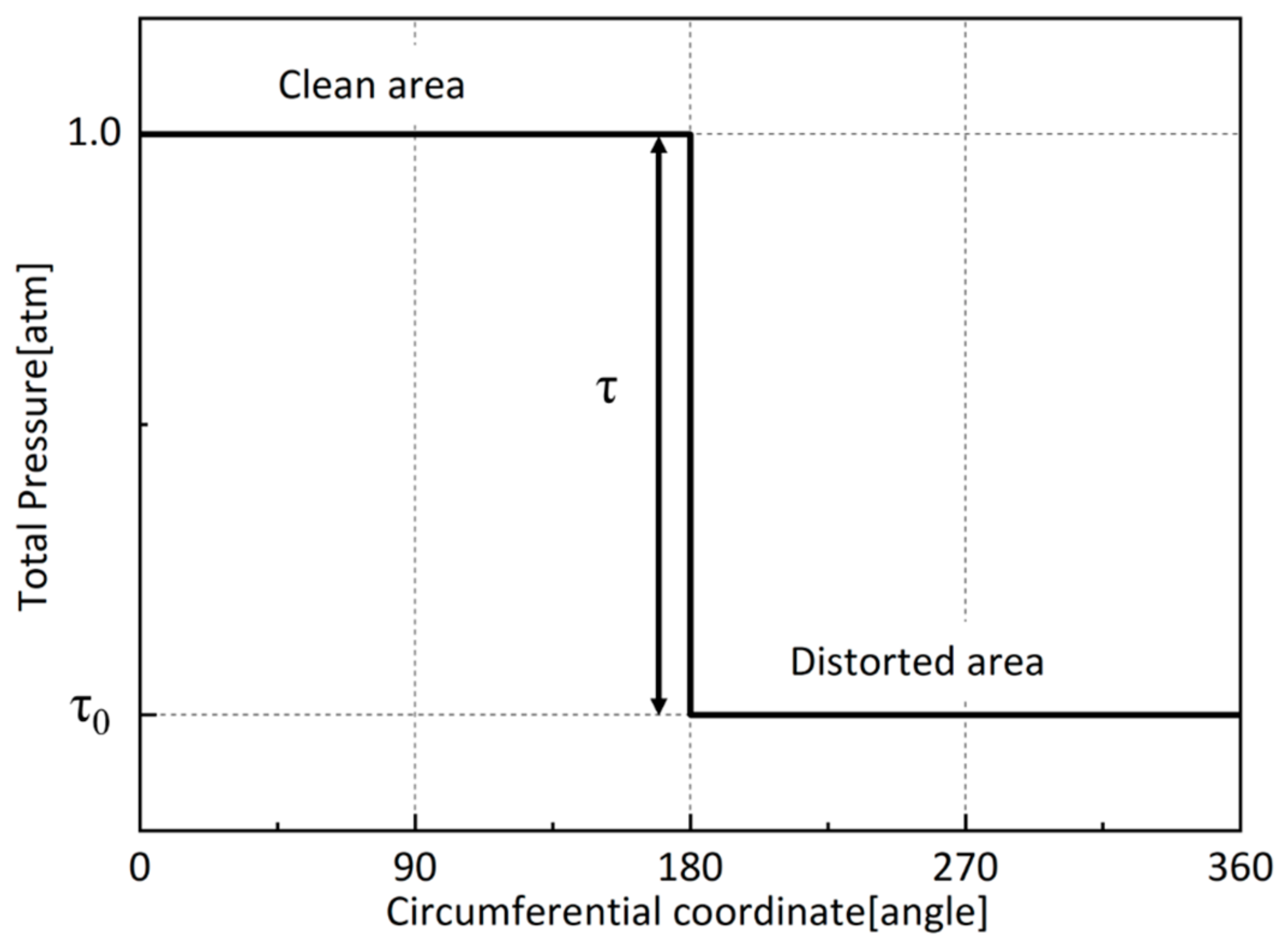
2.4. Distortion Extent and Coefficient Selection

In this paper, the boundary condition for total pressure distortion is imposed at the inlet of the computational domain. The definitions of distortion extent and distortion intensity used in this study are as follows:

Distortion extent (θ) is defined as the size of the sector angle of the distorted area. This can be visualized as the blue-colored distorted area shown in Figure 6.

Distortion intensity (DC) is quantified as the ratio of the total pressure difference between the clean area and the distorted area to the total pressure in the clean area. It can be represented by Equation (1), as shown below:

$$DC={\displaystyle \frac{T{P}_{clean\_area}-T{P}_{distorted\_area}}{T{P}_{clean\_area}}}={\displaystyle \frac{\tau }{T{P}_{clean\_area}}}$$

(1)

where TP_{clean_area} represents the total pressure of the clean area, TP_{distorted_area} represents the total pressure of the distorted area and τ represents the total pressure difference between the clean area and the distorted area.

Based on previous research [25,26], rotor 67 experiences forced vibrations due to incoming flow distortion. Notably, with the occurrence of the 1B (first-order bending) mode caused by the 2EO (second engine order) at the design rotor speed, a significant modal force will be generated. The amplitude of the 2EO is substantial and approaches resonance levels, necessitating careful consideration. Consequently, subsequent investigations are directed towards analyzing low-order vibrations typified by the 2EO. Additionally, it is important to recognize that the forced vibration of fan blades induced by distorted inflow is influenced not only by total pressure distortion but also by excitations arising during the dynamic response as the blades traverse the distortion area. To investigate the impact of excitation stemming from the inlet distortion itself, it becomes imperative to select an appropriate distortion extent for further analysis.

The total pressure distribution at the compressor inlet manifests as a square wave along the circumferential direction, exhibiting an even function, as depicted in Figure 7. The amplitude of second-order harmonics can be directly determined through Fourier transform analysis. The coefficients of sine and cosine components in the Fourier transform formula represent the excitation amplitudes of each harmonic. Equation (2) represents the expansion of the cosine component coefficient and the sine component coefficient bn, where n denotes the order. When the distortion extent is 180 degrees, the amplitude of the 2EO can be obtained by setting n = 2, as shown in Equation (3). The meaning of τ is consistent with Equation (1). It should be noted that due to the 180-degree distortion extent, a₂ is nearly zero and is only influenced by the circumferential total pressure difference.

$$\left\{\begin{array}{l}{a}_n={\displaystyle \frac{2}{T}}{\displaystyle {\int }_{-T/2}^{T/2}{f}_T(t)\cos n\omega t}dt(n=0,1,2,\dots )\\ b_n={\displaystyle \frac{2}{T}}{\displaystyle {\int }_{-T/2}^{T/2}{f}_T(t)\sin n\omega t}dt(n=1,2,\dots )\end{array}\right.$$

(2)

$$\left\{\begin{array}{l}{a}_2={\displaystyle \frac{1}{\pi }}{\displaystyle {\int }_{-\pi }^{\pi }{f}_T(t)\cos 2x}dx=\tau {\displaystyle \frac{2}{\pi }}\sin 2\theta (n=2)\\ b_2={\displaystyle \frac{1}{\pi }}{\displaystyle {\int }_{-\pi }^{\pi }{f}_T(t)\sin 2x}dx=0(n=2)\end{array}\right.$$

(3)

$$f_T(t)=\left\{\begin{array}{l}1,t=(-{\displaystyle \frac{\pi }{2}}+2n\pi ,{\displaystyle \frac{\pi }{2}}+2n\pi )\\ x,t=({\displaystyle \frac{\pi }{2}}+2n\pi ,{\displaystyle \frac{\pi }{2}}+2n\pi )\end{array}\right.$$

(4)

In order to validate the results obtained using Equation (3), the total pressure at the LE is extracted under the condition of 180-degree distortion with varying distortion intensities. Figure 8 shows the corresponding distribution. It should be noted that the flow field mixing in the transition area between the distorted and clean areas causes fluctuations in the total pressure as the rotor enters and exits the distorted area. Subsequently, Fourier transform analysis is performed on the total pressure signal at LE of the blade, and the relative magnitudes of the first ten modal amplitudes are isolated, as shown in Figure 9.

The results illustrate that when the distortion intensity is 0.05, the fluctuation of the total pressure is insignificant, and the amplitude of 2EO nearly approaches zero. However, as the distortion intensity escalates, the fluctuation of the total pressure in the transition region becomes more prominent, deviating from the square wave form, and the amplitude of 2EO correspondingly increases. Nevertheless, throughout the examined parameter ranges, the percentage contribution of the 2EO amplitude within the distorted inflow consistently remains below 2%. This marginal impact implies that it exerts minimal influence on the forced vibration of the blade.

According to Equation (2), when the inlet distortion extent is 180 degrees, the second-order excitation resulting from vibrations induced by the inlet distortion can be ignored. Consequently, the forced vibration arising from the distorted inlet flow is solely linked to the dynamic response process. To delve into the low-order excitations generated by this dynamic response process, this paper selects the distortion extent to be 180 degrees, as shown in Figure 6. To explore the effects of varying distortion intensities, this study simulated five cases based on previous studies [30,31], setting distortion intensity coefficients to 0.05, 0.10, 0.15, 0.20, and 0.25, respectively.

3. Results and Discussion

This paper calculates the flow field of rotor 67 under different distortion intensity coefficients (0.05, 0.10, 0.15, 0.20, 0.25) for the distortion extent of 180 degrees, obtains the corresponding blade vibration amplitudes and discusses the relationship between the 2EO generated by the dynamic responses and the distortion intensity.

This section contains three parts. The first part focuses on analyzing the variation law of the forced vibration amplitude under different distortion intensity coefficients based on the modal force analysis. The second part discusses the important factors affecting the change in the forced vibration amplitude under different distortion intensity coefficients by analyzing the dynamic response process in the distorted flow field. The third part quantifies the relationship between the 2EO amplitude and the distortion intensity generated by the dynamic response process.

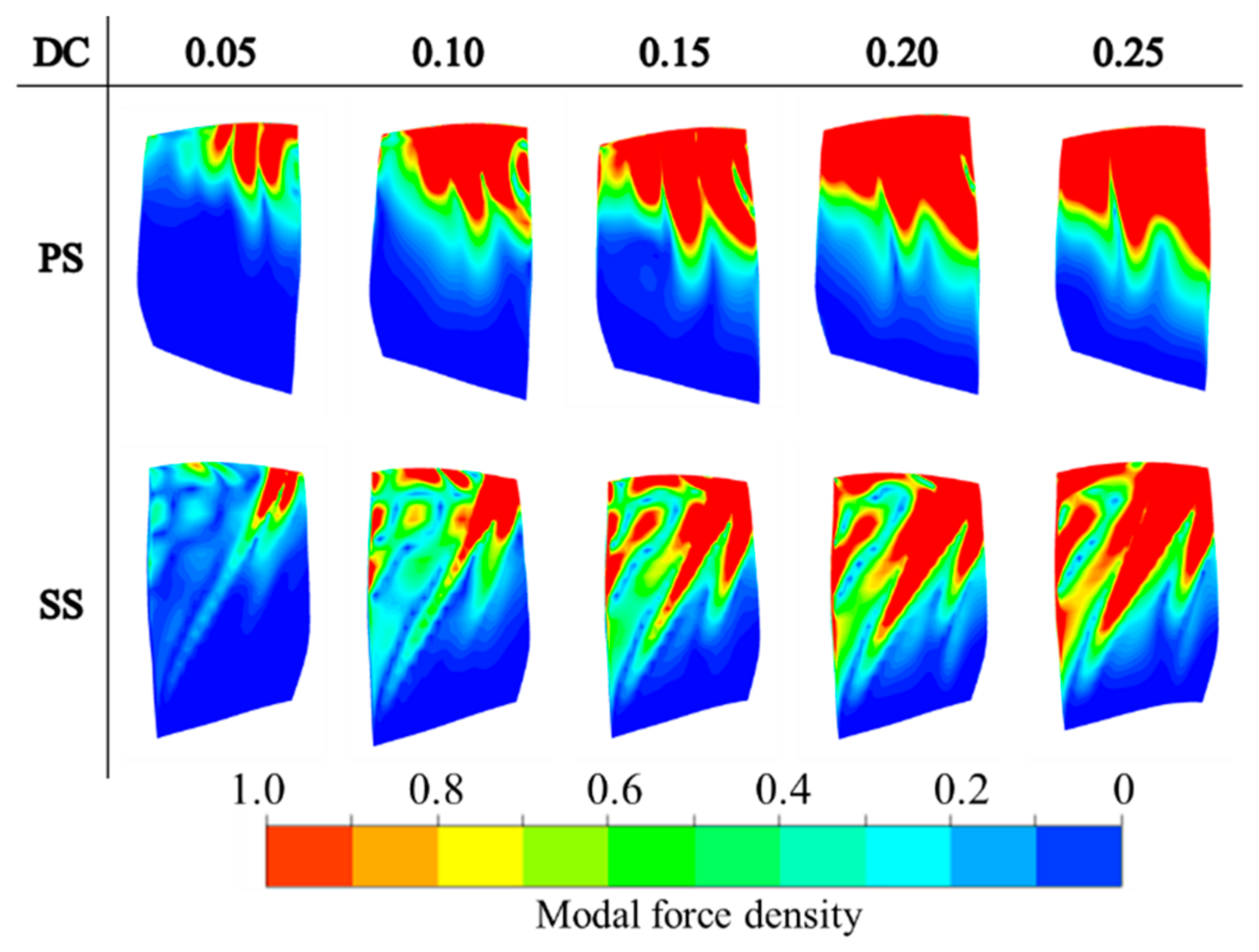
3.1. Modal Force Analysis Under Different Distortion Intensities

In this paper, the amplitude of blade vibration is evaluated using the modal force concept. The blade surface pressure is extracted from the unsteady simulations, and Fourier coefficients are determined through Fast Fourier Transform (FFT). By integrating the Fourier coefficients of the blade surface pressure and the vibration mode tied to the 2EO, the blade surface modal force density distribution is derived.

The distributions of modal force density on the blade surface with 180-degree distortion extent under different distortion intensities are shown in Figure 10. It can be noted that the modal force density increases gradually from the hub to the tip of the blade and concentrates above 60% of the span. Furthermore, there is a notable difference in amplitude between the pressure and suction surfaces, with the pressure surface exhibiting higher values.

By integrating the modal force density on the blade surface, the amplitude of the modal force can be obtained [25], as shown in Equation (5) below:

$$\tilde{Q}={\displaystyle \int \tilde{p}\overline{\varphi }·}\overline{n}dA={\displaystyle \int \tilde{p}(n_x{\varphi }_x+n_y{\varphi }_y+n_z{\varphi }_z)}dA$$

(5)

where $\tilde{p}$ is the Fourier coefficients of the second-order harmonic, ϕ is the distribution of the 1B mode shape obtained with the ANSYS 18.1 FEM software, and n is the unit normal vector of the blade surface. In order to render the modal force amplitude dimensionless, the second-order harmonic is normalized by the average total pressure at the inlet, and the integrated amplitude is then divided by the blade surface area.

The results of normalized modal force amplitudes are shown in Figure 11. It can be noted that within the research range, an escalation in distortion intensity correlates with a gradual increase in the modal force, indicative of a rise in blade vibration amplitude. However, the growth rate of the modal force gradually diminishes. Specifically, for distortion intensities ranging from 0.05 to 0.10, the modal force amplitude increases by approximately 1 unit. On the other hand, distortion intensities between 0.20 and 0.25 result in a smaller increment in the modal force amplitude, approximately around 0.2 units.

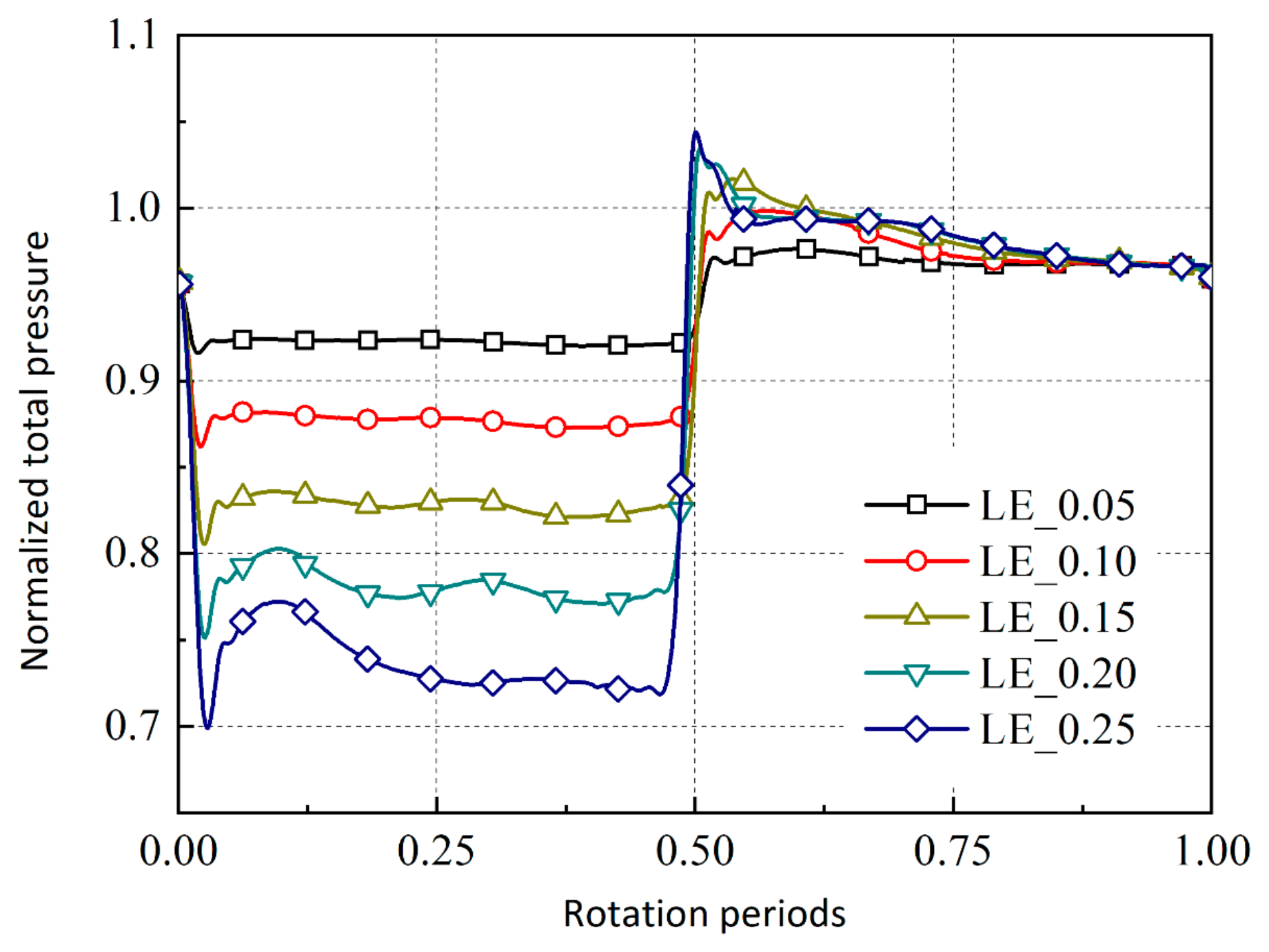
3.2. Excitation Variation During Dynamic Response Process

In this section, the trend in modal force variation and the excitation impacting forced vibration will be scrutinized. Specifically, the analysis will focus on examining the 2EO amplitude at the blade TE region and delving into its influence on dynamic responses.

3.2.1. Variation in 2EO at TE

Fourier transform is applied to the total pressure signal at the TE to isolate the 2EO amplitude. Since the profile of airfoil varies along the spanwise direction, the total pressure variation for different spans is extracted for further analysis. Figure 12 shows the 2EO amplitudes in the total pressure across various spans at the TE of the blade. The calculation results were obtained under a 180-degree distortion extent with a distortion intensity of 0.25.

The results indicate that the 2EO amplitude varies across different spans, with a more pronounced increase observed in the tip area. Comparing the 2EO amplitude at the TE with that at the LE, it is found that the increase is more gradual below the 0.6 span. Meanwhile, beyond the 0.7 span, there is a notable surge in the 2EO amplitude, peaking at the 0.9 span. This trend aligns with the distribution of modal force density, suggesting the presence of a 2EO excitation within the blade passage. It can be concluded that the 2EO amplitude primarily increases in the blade tip region.

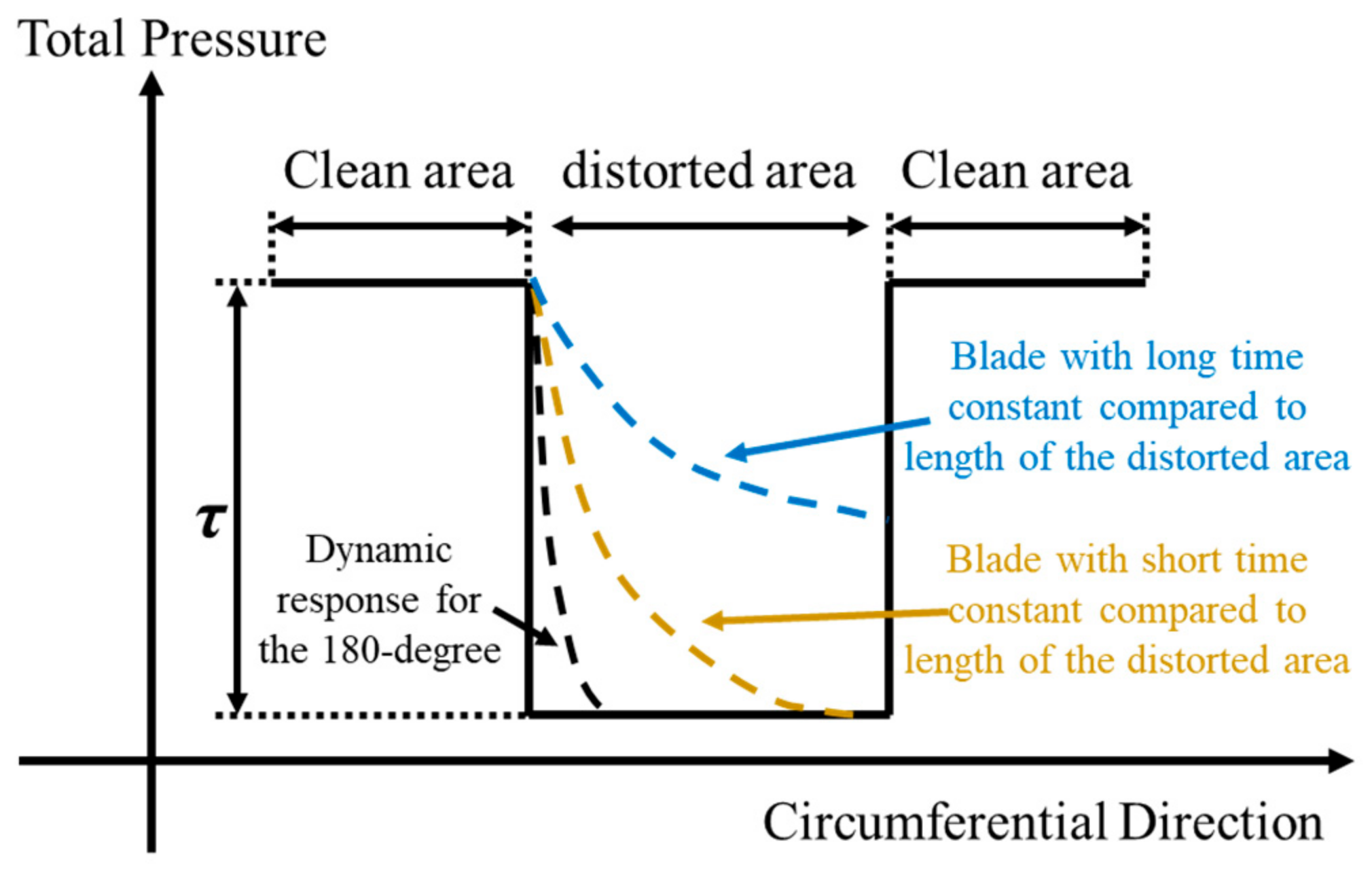
3.2.2. Dynamic Response Analysis

For the case where the blade traverses between the distorted and the clean areas, William [32] proposed that a sudden change in the incoming flow conditions can lead to disruption of fluid flow within the blade channel, resulting in flow separation, which can adversely affect the pressurization capability and lead to changes in blade loading. As the blade rotates through the distorted inflow, resembling a square wave signal, the response of the blade is maximized when the fluid takes less time to pass through the throat of the blade passage compared to the duration the blade spends in low-momentum fluid regions. This relationship is illustrated in Figure 13. The dynamic response time of the blade is positively correlated with k, which is defined as follows [33]:

$$k={\displaystyle \frac{b\times \omega }{V}}$$

(6)

where b represents the airfoil half-chord, ω represents the frequency of the disturbance in radians/second, and V is the relative flow velocity. The previous work [26] demonstrates that, for rotor 67 with a 180-degree extent of distorted inflow, the dynamic response time is shorter than the residence time of the blade in the distorted area. The black dashed line in Figure 13 shows the dynamic response process.

To investigate the dynamic response mechanism of the blade as it enters and exits the distorted area, the Mach number cloud map at 80% span was extracted for analysis. As indicated in Figure 14, it is evident that the tip region of the channel employs a supersonic primitive-level design, contributing to the generation of shock waves within the rotor channel. This design characteristic enhances the pressurization ability and elevates blade loads significantly in the tip region.

Considering the correlation between variations in blade load and the increase in 2EO, the total pressure contour at 80% span is extracted, as depicted in Figure 15. The figure demonstrates noticeable increases and decreases in the total pressure at the TE of the blade as it transitions into and out of the distorted area. Upon observation of the rotor blade in both the distorted and clean areas, it becomes evident that the LE and TE of the rotor manifest asynchronous responses to total pressure fluctuations. This asynchrony can have an impact on the blade load to a certain extent. Consequently, the total pressure and total pressure ratio at both the LE and TE were simultaneously derived for further analysis.

The total pressure and total pressure ratio at 80% span were extracted at both the LE and TE, as depicted in Figure 16. The parameters shown from bottom to top are the total pressure at the LE and TE of the rotor, and the total pressure ratio. It is evident that the total pressure at both the LE and TE of the blade experiences periodic fluctuations attributable to the distortion in the inlet flow. Therefore, the total pressure ratio exhibits significant fluctuations, characterized by distinct peaks and valleys.

Figure 17 shows the changes in total pressure and total pressure ratio as the rotor transitions before and after departing from the distorted area. It can be observed from the figure that as the rotor rotates to position A1, indicating its exit from the distorted area, the total pressure at the LE exhibits a prompt response, while the total pressure at the TE remains relatively stable. As the rotor continues to rotate to position B1, the total pressure at the LE stabilizes, whereas minimal change is noted at the TE. Consequently, during the period from A1 to B1, the total pressure at the LE continues to rise while the total pressure at the TE remains stable. This differential response causes a significant drop in the pressure ratio experienced by the blade, forming a trough at position B1.

As the rotor continues to rotate to position C1, there is a sudden response in the total pressure at the TE, while the total pressure at the LE remains relatively stable. As the rotor further progresses to position D1, the total pressure at the TE completes its response, and the total pressure at the LE stabilizes. During this period, the sudden increase in the total pressure at the TE leads to an increase in the total pressure ratio, forming a peak at position D1. Subsequently, the total pressure at the TE gradually decreases and stabilizes after position E1.

Similar observations can be made upon rotor entry into the distorted area, albeit in reverse. The non-synchronous behavior of total pressures at the LE and TE induces oscillations in the total pressure ratio, engendering both peaks and troughs.

The asynchronous reaction of LE and TE to abrupt total pressure changes induces substantial shifts in the total pressure ratio as the blade transitions in and out of the distorted area. This process gives rise to a wave-like pattern similar to a sine function. Different from the circumferential stationarity found in the total pressure ratio signal in ideal conditions, the sine-shaped total pressure ratio signal distinctly exhibits second-order excitation. Notably, this second-order excitation is distinguishable irrespective of whether the distorted inflow possesses an amplitude corresponding to the 2EO.

3.3. Relationship Between 2EO Produced by Dynamic Response and the Distortion Intensity

Based on the determination of the time response constant and the dynamic response process, Greitzer [19] further pointed out the load change in the dynamic response, which can be written as follows:

$$\tau \times {\displaystyle \frac{dC}{dt}}=C_{ss}-C$$

(7)

where C_ss represents the steady-state load on the rotor blade, C is the actual load on the rotor blade, and τ is the time response constant. It turns out that the blade load rate is determined by the difference between the actual blade load and the steady-state measured blade load. In Equation (7), the blade load is quantified using the total pressure ratio. According to the design parameter of rotor 67, the pressure ratio is 1.63, which represents the steady-state load of the blade, and the actual load is the change in the pressure ratio during the rotor rotation.

Figure 18 illustrates the variations in total pressure and total pressure ratio at the LE and TE through one revolution of the rotor under diverse distortion intensities. The solid lines of different colors correspond to distinct distortion intensities. The black dotted line represents the design pressure ratio, which serves as a reference for the steady-state load of the blade. The red dotted line represents the area where the total pressure ratio changes as the blade enters the distorted area. Similarly, the blue dotted line depicts the region where the total pressure at the trailing edge experiences variation upon entering the distorted area. It is noted that as the distortion intensity increases, the rate of decrease in total pressure at the TE within the blue dotted line area slows down. This indicates that the loss of total pressure at TE approaches a limit and decreases at a slower pace. Consequently, the loss of total pressure ratio within the red dotted line area also experiences a gradual slowdown and reaches a limit.

Conclusively, it can be deduced that as distortion intensity amplifies, the rise in total pressure loss of blades will gradationally diminish and converge towards a limiting value. This trend signifies that the discrepancy between the steady-state load of the blades and the actual load steadily expands with rising distortion intensity, ultimately stabilizing. Moreover, the dynamic response process decelerates with increasing distortion intensity. An enhanced distortion intensity leads to greater differences in dynamic response coefficients, resulting in larger magnitudes of second-order excitation. However, the growth rate gradually decelerates and approaches a limit, which is consistent with the result that the growth rate of modal forces decreases with increasing distortion intensity. When the blade passes through the transition area between the distorted and clean areas, blade dynamic response occurs. In this process, the lagging change in pressure at the TE results in the occurrence of 2EO during the total pressure variation. Furthermore, the fluctuation in the total pressure ratio of the transition area rises alongside an escalation in distortion intensity, yet it advances towards a stabilized state. The increase in the amplitude of 2EO also slows down to a limit, which is consistent with the variation in modal forces.

To quantify the excitation amplitude of the transition state process, the researchers [26] resolved the ordinary differential equation presented in Equation (8). When x equals −π/2, C equals C_initial (C_initial represents the total pressure before the inlet conditions change). When x is equal to (−π/2 + 2πk), C is equal to C_ss. Therefore, when x varies from −π to 0, the change in C can be expressed as follows:

$$\left\{\begin{array}{ll}{C}_{initial}& (-\pi <x<-{\displaystyle \frac{\pi }{2}})\\ {\displaystyle \frac{e(C_{initial}-C_{ss})}{e-1}}{e}^{-{\displaystyle \frac{x+\frac{\pi }{2}}{2\pi k}}}-{\displaystyle \frac{(C_{initial}-C_{ss})}{e-1}}+C_{ss}& (-{\displaystyle \frac{\pi }{2}}<x<-{\displaystyle \frac{\pi }{2}}+2\pi k)\\ C_{ss}& (-{\displaystyle \frac{\pi }{2}}+2\pi k<x<0)\end{array}\right.$$

(8)

In addition, the change in C when x changes from 0 to π can also be obtained. According to the Fourier series, the second-order Fourier coefficients can be expressed as follows:

$$\left\{\begin{array}{l}{a}_2={\displaystyle \frac{(C_{initial}-C_{ss})}{e-1}}·({\displaystyle \frac{1}{2}}(\sin (4\pi k_1)-\sin (4\pi k_2))-\\ ({\displaystyle \frac{2\pi k_1(\cos (4\pi k_1)-e)-8{(\pi k_1)}^2\sin (4\pi k_1)}{1+{(4\pi k_1)}^2}}-{\displaystyle \frac{2\pi k_2(\cos (4\pi k_2)-e)-8{(\pi k_2)}^2\sin (4\pi k_2)}{1+{(4\pi k_2)}^2}}))\\ b_2={\displaystyle \frac{(C_{initial}-C_{ss})}{e-1}}·({\displaystyle \frac{1}{2}}(\cos (4\pi k_2)-\cos (4\pi k_1))+\\ ({\displaystyle \frac{2\pi k_1\sin (4\pi k_1)+8{(\pi k_1)}^2(\cos (4\pi k_1)-e)}{1+{(4\pi k_1)}^2}}-{\displaystyle \frac{2\pi k_2\sin (4\pi k_2)+8{(\pi k_2)}^2(\cos (4\pi k_2)-e)}{1+{(4\pi k_2)}^2}}))\end{array}\right.$$

(9)

where k₁ and k₂ represent the time response constants when the blade enters the distorted area and leaves the distorted area, respectively. k₁ and k₂ are calculated according to Equation (6). The distance between the channel throat and the blade is 4.42 × 10⁻² m, and the relative speed is calculated from the rotor speed at 50% blade span. By analyzing the relative velocity under various distortion intensities, it has been observed that as the distortion intensity increases, the trend of velocity changes becomes smoother. This finding aligns with the actual flow conditions. The transition of the blade from the distorted to clean areas induces changes in velocity, but it has no effect on the airflow. There is a limit to the deflection effect, so the rate of speed change decreases. Utilizing these two outcomes, we have obtained the time response constants for blades entering and leaving the distorted area across various distortion intensities. By substituting the time response constants corresponding to the two dynamic response processes of the fan blade into Equation (10), the amplitude of 2EO(A_2EO) can be calculated as follows:

$$\sqrt{a_2^2+b_2^2}=(C_{initial}-C_{ss})A_{2EO}$$

(10)

The outcomes of the amplitude of 2EO under varying distortion intensities, determined using Equation (10), are illustrated in Figure 19. By comparing the modal force results in Figure 11, it can be concluded that the distribution of the 2EO amplitude generated by the dynamic response process with the distortion intensity is consistent with the distribution of the modal force. The amplitude of the 2EO gradually rises with an escalation in distortion intensity, though the rate of growth diminishes progressively. Specifically, as the distortion intensity elevates from 0.05 to 0.10, the amplitude of 2EO augments by approximately 0.4 units. On the contrary, when the distortion intensity escalates from 0.20 to 0.25, the amplitude of 2EO increases by about 0.15 units.

Based on the previous analysis, it can be concluded that the second-order excitation generated by the dynamic response process is independent of whether the non-uniform flow contains a second-order excitation signal. The amplitude of 2EO excitation generated by the dynamic response is consistent with the modal force amplitude trend of the blade, which proves that it directly affects the dynamic response process with the size of the distortion intensity coefficient, and then affects the amplitude of the blade forced vibration.

4. Conclusions

This paper focuses on the investigation of the influence mechanism of different distortion intensity coefficients on the forced vibration. The variation pattern of low-order forced vibration amplitudes is analyzed, and the source of low-order vibrations generated during the dynamic response process of the blade is discussed. Finally, the relationship between the low-order excitation and distortion intensity coefficients generated during the entire dynamic response process is quantified.

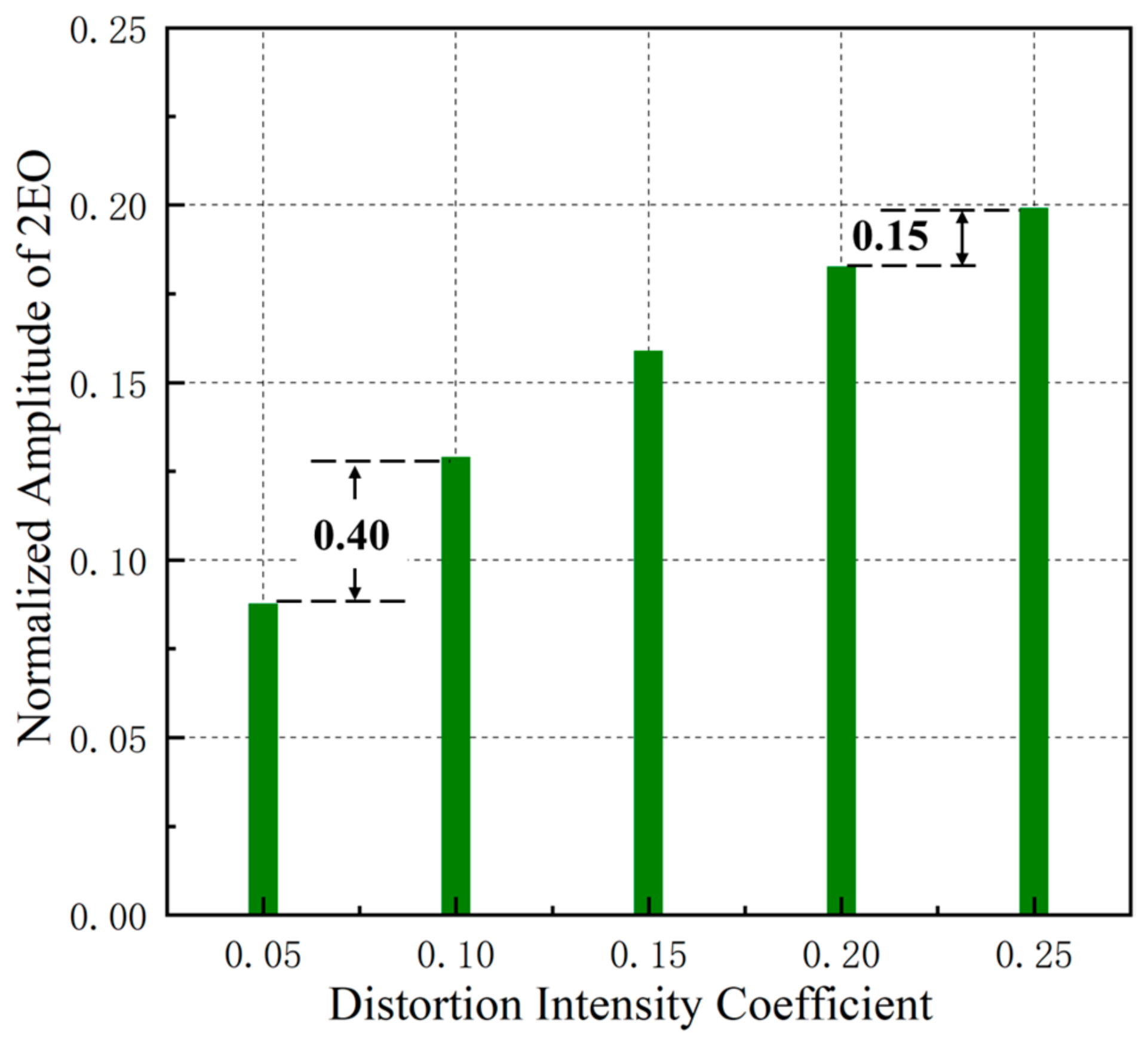
• In the context of this investigation, minimal 2EO is perceived at the LE in the distortion flow field spanning 180-degrees. However, as the fluid passes through the blade channel, the 2EO amplitude increases, especially in the blade tip area. This suggests the existence of excitation within the blade channel that contributes to the amplified 2EO amplitude. At the same time, the amplitude of the modal force increases as the distortion intensity increases. However, the rate of growth gradually decreases. For distortion intensities ranging from 0.05 to 0.10, the modal force amplitude increases by approximately 1 unit. On the other hand, the increase in modal force amplitude between 0.20 and 0.25 is only about 0.2 units.
• In the context of this investigation, minimal 2EO is perceived at the LE in the distortion flow field spanning 180 degrees. Nevertheless, as the fluid traverses the blade passage, the 2EO amplitude escalates notably, particularly in the blade tip vicinity. This indicates the presence of excitation within the blade channel that contributes to the enhanced 2EO amplitude. Simultaneously, the modal force amplitude rises with an increase in distortion intensity. However, the rate of growth progressively diminishes. For distortion intensities ranging from 0.05 to 0.10, the modal force amplitude elevates by approximately 1 unit. Conversely, distortion intensities between 0.20 and 0.25 result in a more modest rise in the modal force amplitude, approximately around 0.2 units.
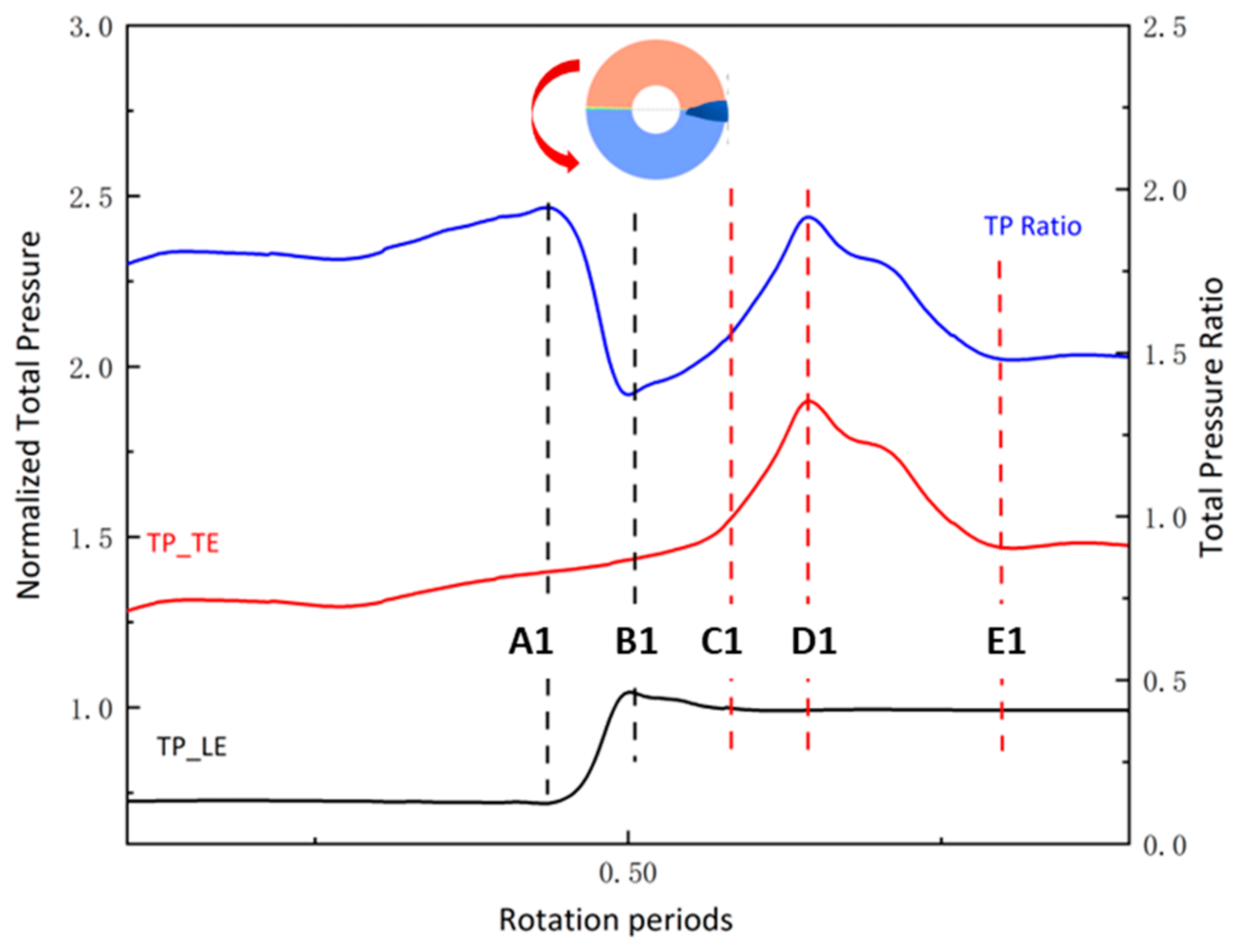
• During the dynamic response, the pressure at the LE and TE changes asynchronously, resulting in the abrupt change in the total pressure ratio, and thus the pressure difference change in the fluid in the flow channel produces 2EO. As the distortion intensity increases, the fluctuations in the total pressure ratio at the interface between the distorted area and clean area become more prominent but gradually approach a limit. Consequently, the amplification of the 2EO amplitude also progresses at a diminished rate, exhibiting consistency with the changes observed in the modal forces.
• The change in the second-order excitation amplitude of the dynamic response process is consistent with the change in the modal force, which strongly proves that the main excitation source within the 180-degree distortion extent is the 2EO generated in the blade channel. At the same time, the distortion intensity directly affects the dynamic response process and thus affects the amplitude of the blade forced vibration. Therefore, the aeroelasticity of fan blades caused by flow distortion is not only affected by the flow distortion, but also by the dynamic response in the blade channel. The low-order excitation amplitude generated by the dynamic response is related to the intensity of the flow distortion. This has important reference value for subsequent research on the suppression of the excitation source.

This paper investigates the aeroelasticity of rotor 67 under different distortion intensity coefficients, revealing the mechanisms and influencing factors behind the dynamic response. Building on these findings, the objective of future research is to reduce the excitation amplitude generated by the dynamic response, thereby mitigating aeroelasticity issues.