Optimizing Solid Rocket Missile Trajectories: A Hybrid Approach Using an Evolutionary Algorithm and Machine Learning
Abstract
1. Introduction
2. Materials and Methods
- A Simulink [24] model of the rocket: Engineered from experimental data obtained from the Icarus Team at Politecnico di Torino, this model aims to compute the trajectory of a maneuverable rocket. It provides validated data related to path dynamics.
- Optimization algorithm: built upon the Simulink model, the proposed genetic algorithm (GA) was designed to identify the optimal maneuver to achieve a target point with the desired accuracy.
- Artificial neural network: trained using data derived from the preceding GA simulations, this neural network (NN) improves decision-making and predictive capabilities in trajectory design, minimizing the computational cost to reach an optimum setup.
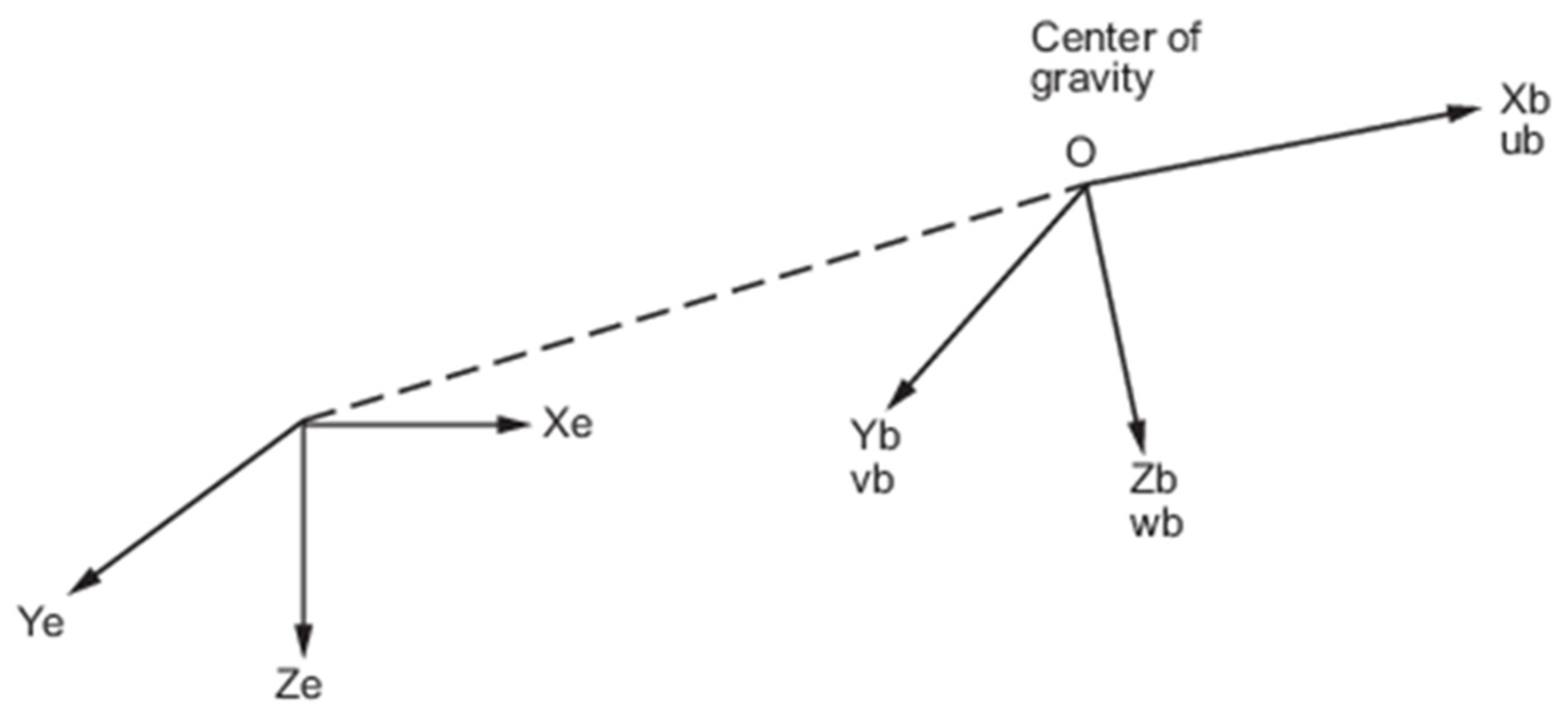
2.1. Simulink Model
- The atmosphere was modelled using the International Standard Atmosphere (ISA) model [25].
- The assumed rockets are non-spinning and stabilized with fixed wings.
- The flat earth reference frame is assumed to be inertial, which is acceptable for low-range rockets.
- Gravity is considered constant throughout the flight.
- The rocket operates under subsonic conditions, according to numerically and experimentally simulated design data.
- High-order aerodynamic effects, arising from unsteady aerodynamics, are considered negligible. While these reduce accuracy, particularly under conditions of high maneuvering angles, the resulting error from this assumption remains comparable in magnitude to other errors associated with other modeling assumptions and adopted simplifications.
- Erosive burning effects were not considered.
- The rocket was modelled as a rigid body.
2.2. Optimization Script
- The ramp zenith: This is defined as the angle between the earth’s vertical-to-surface axis and the ramp axis. This integer variable can adopt discrete values equal to 0°, 15°, 30°, or 45° sexagesimal degrees, representing a classified discrete ramp movement’s range.
- The thrust deflection angle: this represents the output of the thrust vector and is treated as a continuous variable bounded between 0° and 5°.
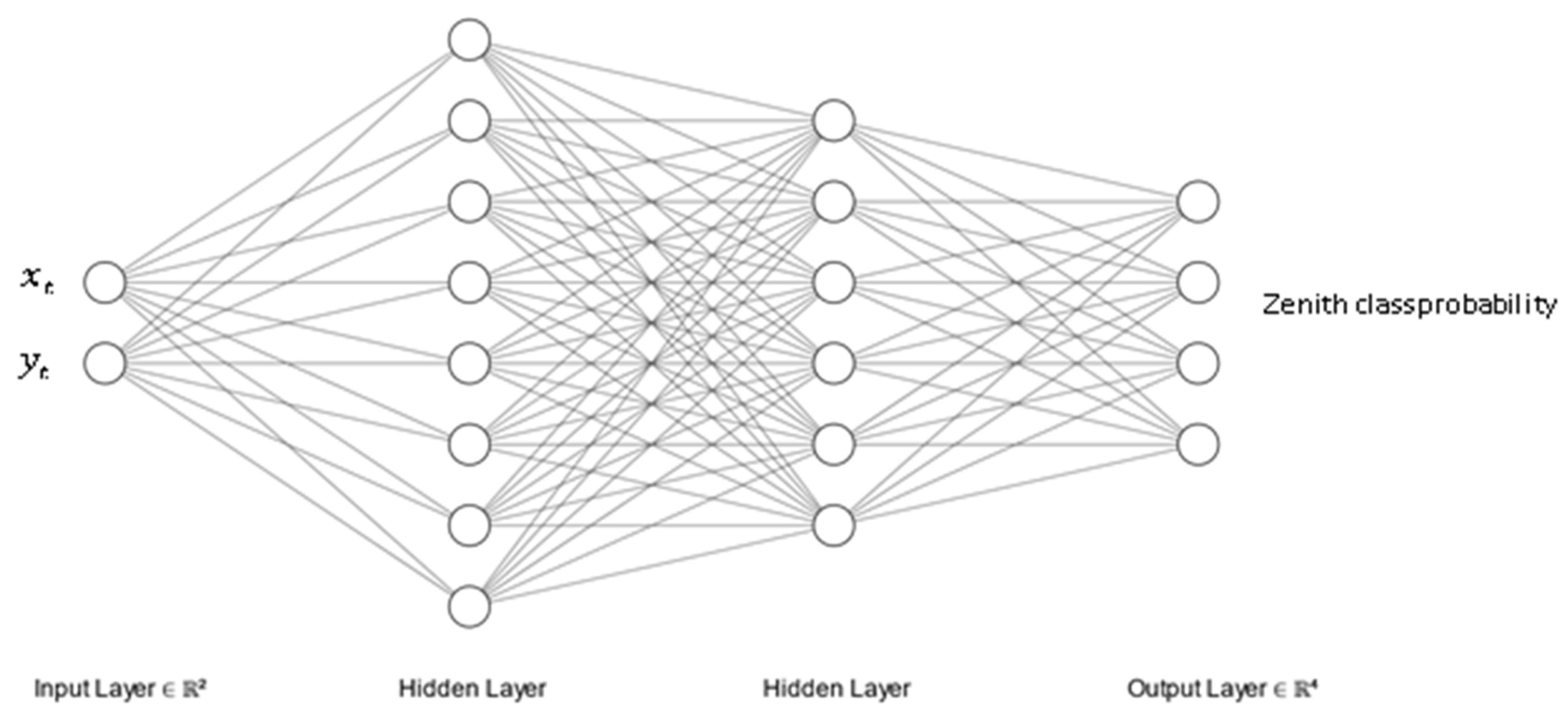
2.3. Neural Network
- Classification Algorithm: initially, the solution space is partitioned through a classification strategy, with the zenith angle serving as the clustering criterion.
- Regression: following the classification stage, a regression is adopted to forecast the continuous deflection angle based on the target coordinates, tailoring, for each cluster, the maneuverer’s deflection angle.
2.4. Workflow
3. Results
- The time elapsed until the target is reached.
- The zenith angle of the launch ramp.
- The deflection angle of the thrust required for implementing maneuvers.
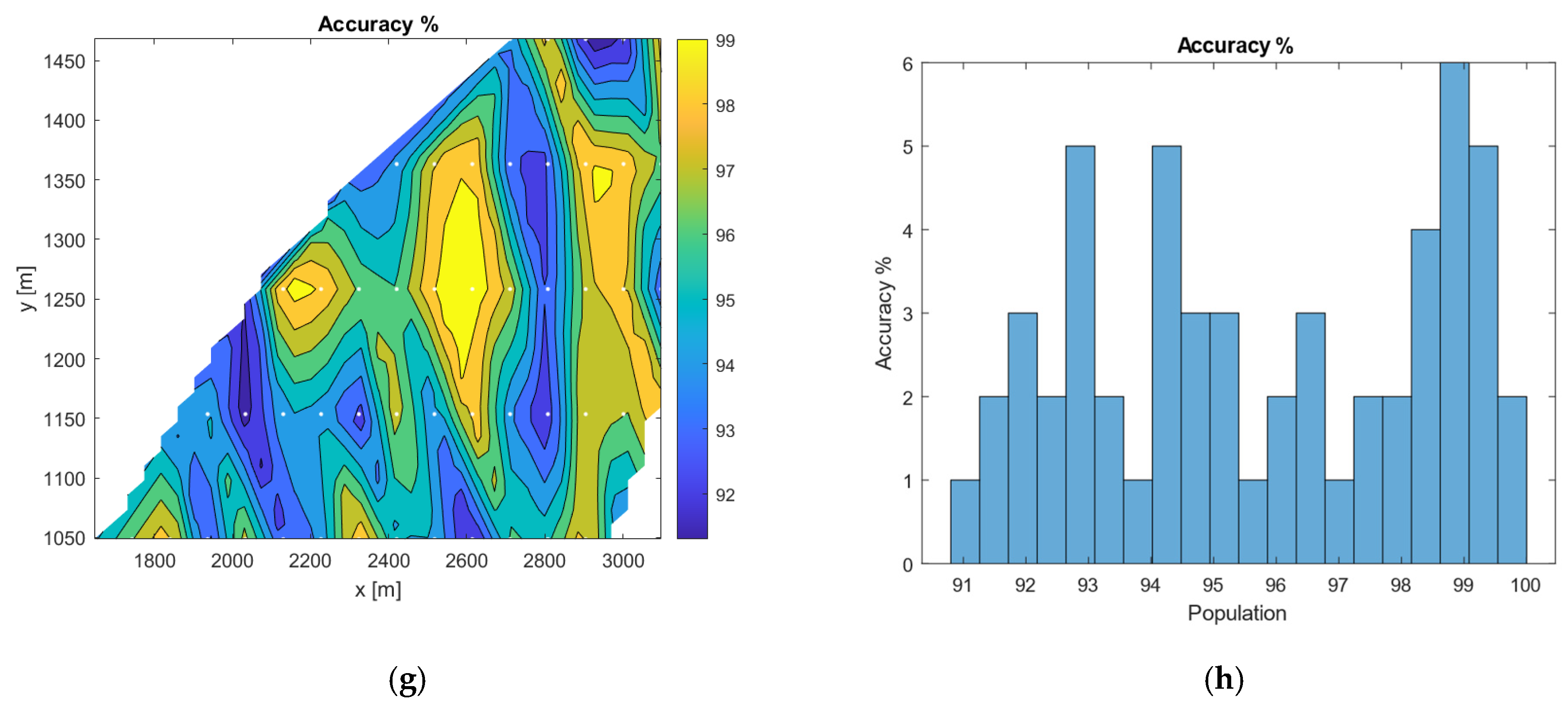
- Accuracy, quantified as a percentage, where 100% signifies exact alignment with the target’s center of gravity, and 0% indicates a failure to meet the target.
3.1. GA Results
3.2. Classification
3.3. Regression
3.4. Testing the Neural Network on a New Batch
3.5. Computational Cost Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Belkin, P.; Ek, C.; Mages, L.; Mix, D.E. NATO’S 60th Anniversary Summit. In European Economic and Political Developments; NATO: Washington, DC, USA, 2009; Available online: https://apps.dtic.mil/sti/pdfs/ADA496595.pdf (accessed on 1 November 2024).
- Chaurasiya, P.; Sawardekar, S.; Rautela, R. Enhancing Air and Missile Defense System with IoT Solution: A Conceptual Approach. Int. J. Res. Appl. Sci. Eng. Technol. 2023, 11, 1200–1207. [Google Scholar] [CrossRef]
- Dvorkin, V. Impact of missile defense systems on strategic stability and prospects for nuclear disarmament. World Econ. Int. Relat. 2019, 63, 5–12. [Google Scholar] [CrossRef]
- Klimov, V. The Missile Defense systems and concepts of limited nuclear war. World Econ. Int. Relat. 2022, 66, 16–24. [Google Scholar] [CrossRef]
- Khalil, M.; Ahmed, M.Y.M. Flight Performance and Dispersion Analysis for a Flexible Tactical Missile. J. Spacecr. Rocket. 2023, 60, 1297–1307. [Google Scholar] [CrossRef]
- Sahoo, S.; Dalei, R.K.; Rath, S.K.; Sahu, U.K. Selection of PSO parameters based on Taguchi design-ANOVA-ANN methodology for missile gliding trajectory optimization. Cogn. Robot. 2023, 3, 158–172. [Google Scholar] [CrossRef]
- Cai, Z. Missile trajectory defense planning and data simulation based on deep learning algorithm. Soft Comput. 2023, 1, 1–10. [Google Scholar] [CrossRef]
- Benton, N. The role of Russian air and missile defense systems. Comp. Strat. 2022, 47, 483–497. [Google Scholar] [CrossRef]
- Haggard, S.; Cheung, T.M. North Korea’s nuclear and missile programs: Foreign absorption and domestic innovation. J. Strat. Stud. 2021, 44, 802–829. [Google Scholar] [CrossRef]
- Khan, F.H. Strategic Risk Management in Southern Asia. J. Peace Nucl. Disarm. 2022, 5, 369–393. [Google Scholar] [CrossRef]
- Yingbo, H.; Yong, Q. THAAD-Like High Altitude Theater Missile Defense: Strategic Defense Capability and Certain Countermeasures Analysis. Sci. Glob. Secur. 2003, 11, 151–202. [Google Scholar] [CrossRef]
- Hussain, M.Z.; Ahmed, R.Q. Space Programs of India and Pakistan: Military and Strategic Installations in Outer Space and Precarious Regional Strategic Stability. Space Policy 2019, 47, 63–75. [Google Scholar] [CrossRef]
- Pirsalami, F.A.; Shirzadi, E. Regional deterrence, strategic challenges, and Saudi Arabia’s missile development program. Dig. Middle East Stud. 2023, 32, 281–299. [Google Scholar] [CrossRef]
- Zhang, L.; Gong, C.; Su, H.; Andrea, D.R. Design Methodology of a Mini-Missile Considering Flight Performance and Guidance Precision. J. Syst. Eng. Electron. 2024, 35, 195–210. [Google Scholar] [CrossRef]
- Li, J.; Jing, Z.; Zhang, X.; Zhang, J.; Li, J.; Gao, S.; Zheng, T. Optimization design method of a new stabilized platform based on missile-borne semi-strap-down inertial navigation system. Sensors 2018, 18, 4412. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lei, H.; Ye, J.; Bu, X. Backstepping sliding mode control for radar seeker servo system considering guidance and control system. Sensors 2018, 18, 2927. [Google Scholar] [CrossRef]
- Tuncer, O.; Cirpan, H.A. Adaptive fuzzy based threat evaluation method for air and missile defense systems. Inf. Sci. 2023, 643, 119191. [Google Scholar] [CrossRef]
- Multi-agent decision support system for missile defense based on improved PSO algorithm. J. Syst. Eng. Electron. 2017, 28, 514–525. [CrossRef]
- Das, A.K.; Acharyya, K.; Mankodi, T.K.; Saha, U.K. Fluidic Thrust Vector Control of Aerospace Vehicles: State-of-the-Art Review and Future Prospects. J. Fluids Eng. 2023, 145, 080801. [Google Scholar] [CrossRef]
- Afridi, S.; Khan, T.A.; Shah, S.I.A.; Shams, T.A.; Mohiuddin, K.; Kukulka, D.J. Techniques of Fluidic Thrust Vectoring in Jet Engine Nozzles: A Review. Energies 2023, 16, 5721. [Google Scholar] [CrossRef]
- Kim, K.U.; Kang, S.; Kim, H.J.; Lee, C.-H.; Tahk, M.-J. Realtime agile-turn guidance and control for an air-to-air missile. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar] [CrossRef]
- Jung, C.-G.; Kim, B.; Jung, K.-W.; Lee, C.-H. Thrust Integrated Trajectory Optimization for Multipulse Rocket Missiles Using Convex Programming. J. Spacecr. Rocket. 2023, 60, 957–971. [Google Scholar] [CrossRef]
- Biberstein, J.X.; Tal, E.; Karaman, S. Thrust Vectoring of Small-scale Solid Rocket Motors Using Additively Manufactured Jet Vanes. In Proceedings of the AIAA Propulsion and Energy 2021 Forum, Virtual, 9–11 August 2021. [Google Scholar]
- The MathWorks—MATLAB & SIMULINK. IEEE Circuits Syst. Mag. 2008, 6, 77. [CrossRef]
- Young, T.M. International Standard Atmosphere (ISA) Table. In Performance of the Jet Transport Airplane: Analysis Methods, Flight Operations and Regulations; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar] [CrossRef]
- Mikhailov, V.G. Data transmission with Simulink on 6-DoF platform on CAN BUS. System Anal. Appl. Inf. Sci. 2021, 1, 29–37. [Google Scholar] [CrossRef]
- Hajjem, M.; Victor, S.; Melchior, P.; Lanusse, P.; Thomas, L. Wind turbulence modeling for real-time simulation. Fract. Calc. Appl. Anal. 2023, 26, 1632–1662. [Google Scholar] [CrossRef]
- Oluleye, B.; Leisa, A.; Leng, J.; Dean, D. A Genetic Algorithm-Based Feature Selection. Int. J. Electron. Commun. Comput. Eng. 2014, 5, 899–905. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016. [Google Scholar]
- Gevorkyan, M.N.; Demidova, A.V.; Demidova, T.S.; Sobolev, A.A. Review and comparative analysis of machine learning libraries for machine learning. Discret. Contin. Model. Appl. Comput. Sci. 2019, 27, 305–315. [Google Scholar] [CrossRef]













| Description | Value |
|---|---|
| Population size | 50 |
| Maximum number of generations | 200 |
| Constraint tolerance | 1 × 10−3 |
| Creation function rate | 0.8 |
| Crossover function | Arithmetic crossover |
| Mutation function | Adaptive feasible mutation |
| Selection function | Roulette wheel selection |
| Distance measurement function | Crowding distance |
| Nonlinear constraint algorithm | Augmented Lagrangian |
| Elite count | 2 |
| Fitness limit | 1 |
| Fitness scaling function | Rank scaling |
| Function tolerance | 1 × 10−6 |
| Description | Value |
|---|---|
| Loss function | Categorical Crossentropy |
| Accuracy metric | Accuracy |
| Batch size | 512 |
| Hidden layers | 10, with a predetermined neuron distribution |
| Activation function | ReLU for hidden layers and Softmax for the output layer |
| Number of epochs | 10,000 |
| Description | Value |
|---|---|
| Loss function | Mean Square Error |
| Accuracy metric | Mean Absolute Error |
| Batch size | 512 |
| Hidden layers | 10, with a specific distribution of neurons per layer |
| Activation function | ReLU for hidden layers and linear for the output layer |
| Number of epochs | 10,000 |
| Zenith Angle [°] | Minimum Loss |
|---|---|
| 0° | 1.3869 × 10−6 |
| 15° | 3.0502 × 10−6 |
| 30° | 5.4031 × 10−6 |
| 45° | 1.8426 × 10−8 |
| Thrust Deflection [deg] | Zenith [deg] | Accuracy [%] | Elapsed Time [s] | |
|---|---|---|---|---|
| GA | 2.35 | 0 | 95% | 58.98 |
| NN | 2.29 | 0 | 89% | 1.05 |
| COMPARATION | 2.55% | 0% | −6.32% | 98.22% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferro, C.; Cafaro, M.; Maggiore, P. Optimizing Solid Rocket Missile Trajectories: A Hybrid Approach Using an Evolutionary Algorithm and Machine Learning. Aerospace 2024, 11, 912. https://doi.org/10.3390/aerospace11110912
Ferro C, Cafaro M, Maggiore P. Optimizing Solid Rocket Missile Trajectories: A Hybrid Approach Using an Evolutionary Algorithm and Machine Learning. Aerospace. 2024; 11(11):912. https://doi.org/10.3390/aerospace11110912
Chicago/Turabian StyleFerro, Carlo, Matteo Cafaro, and Paolo Maggiore. 2024. "Optimizing Solid Rocket Missile Trajectories: A Hybrid Approach Using an Evolutionary Algorithm and Machine Learning" Aerospace 11, no. 11: 912. https://doi.org/10.3390/aerospace11110912
APA StyleFerro, C., Cafaro, M., & Maggiore, P. (2024). Optimizing Solid Rocket Missile Trajectories: A Hybrid Approach Using an Evolutionary Algorithm and Machine Learning. Aerospace, 11(11), 912. https://doi.org/10.3390/aerospace11110912







