Nonlinear Extended State Observer and Prescribed Performance Fault-Tolerant Control of Quadrotor Unmanned Aerial Vehicles Against Compound Faults
Abstract
1. Introduction
- Innovative Improvements in the Dynamics Model: Systematic improvements have been made to the fault dynamics model of the quadrotor UAV. This scheme effectively calculates the UAV’s attitude and position, taking into account both composite body faults and environmental disturbances. Through this approach, all state variables rapidly and accurately reach the designed sliding mode surface, thus ensuring the system globally converges to a predetermined equilibrium state within a finite time.
- Design of a Non-Singular Terminal Sliding Mode Control Surface: We have designed a full-loop rapid non-singular terminal sliding mode control surface, overcoming the common singularity issues found in traditional sliding mode control. This design not only enhances the stability of the control system but also significantly accelerates its response speed, thereby optimizing system performance and achieving rapid convergence.
- Control Strategy Based on NLESO: To address potential unknown system faults encountered by the quadrotor UAV during complex task executions, we have developed a control strategy based on the NLESO. This control strategy, integrating prescribed performance control and a sliding mode controller, can rapidly and accurately estimate unknown states in the face of unknown composite faults and external disturbances. It effectively adjusts the system’s dynamic and steady-state performance as needed, ensuring the system can reliably return to its initial state.
2. System Model and Problem Formulation
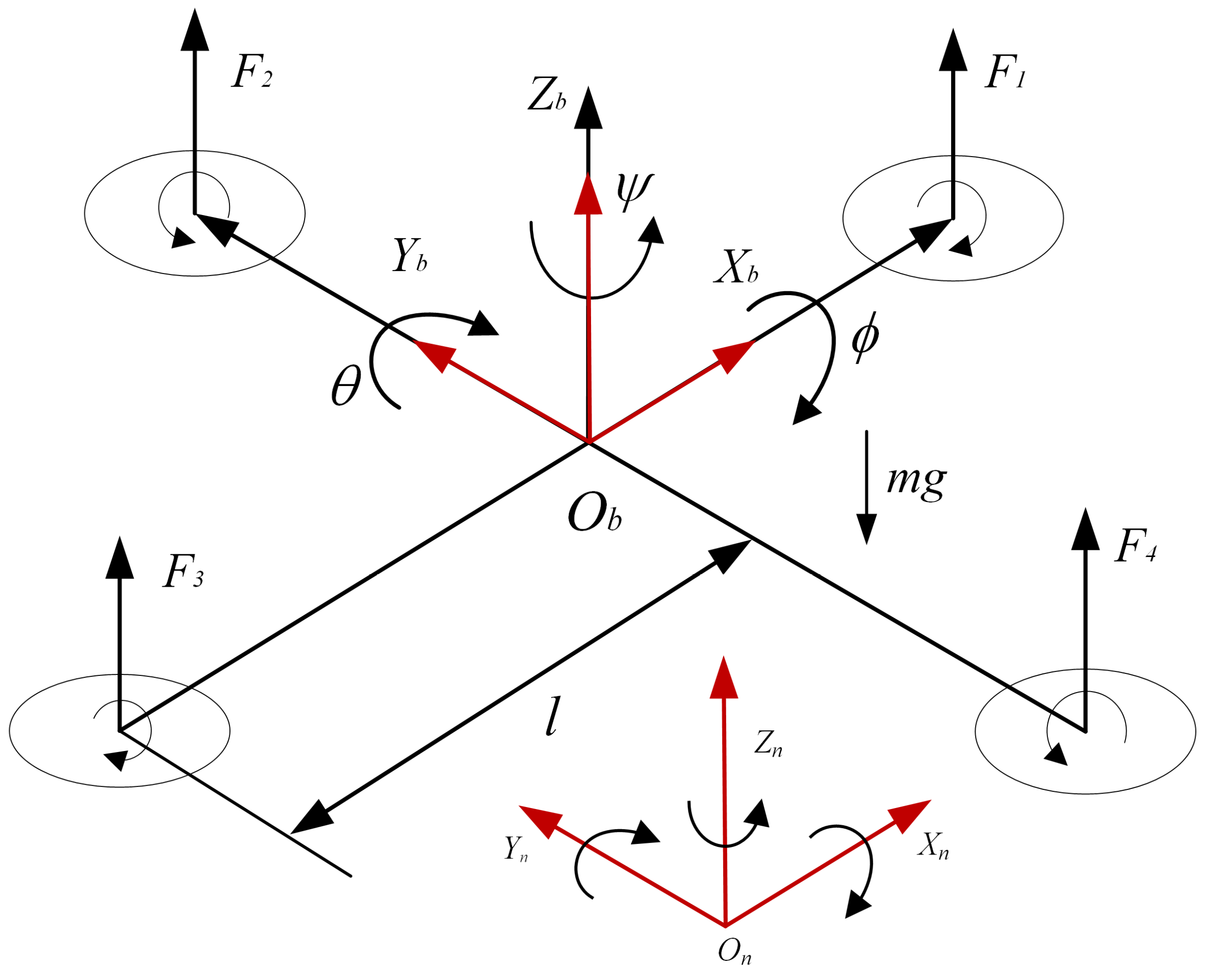
2.1. Modeling of a Quadrotor
2.2. Establishment of Fault Model for Quadrotor UAVs
2.3. Problem Formulation
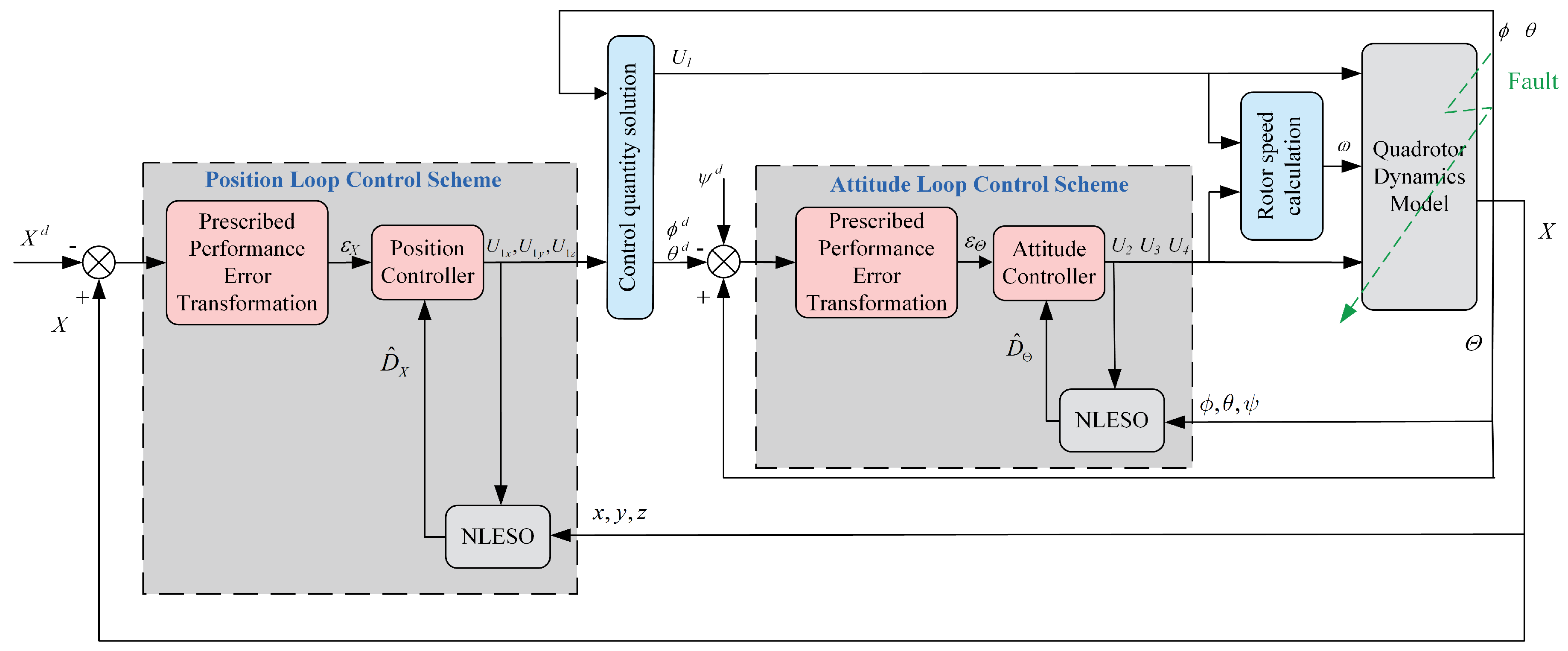
3. Prescribed Performance Controller Design
3.1. Prescribed Performance Control Concept
3.2. NLESO Design
- (1)
- Design of NLESO for position loop
- (2)
- Design of NLESO for attitude loop
3.3. Design of Position Fault-Tolerant Controller
3.4. Design of Attitude Fault-Tolerant Controller
4. Simulation
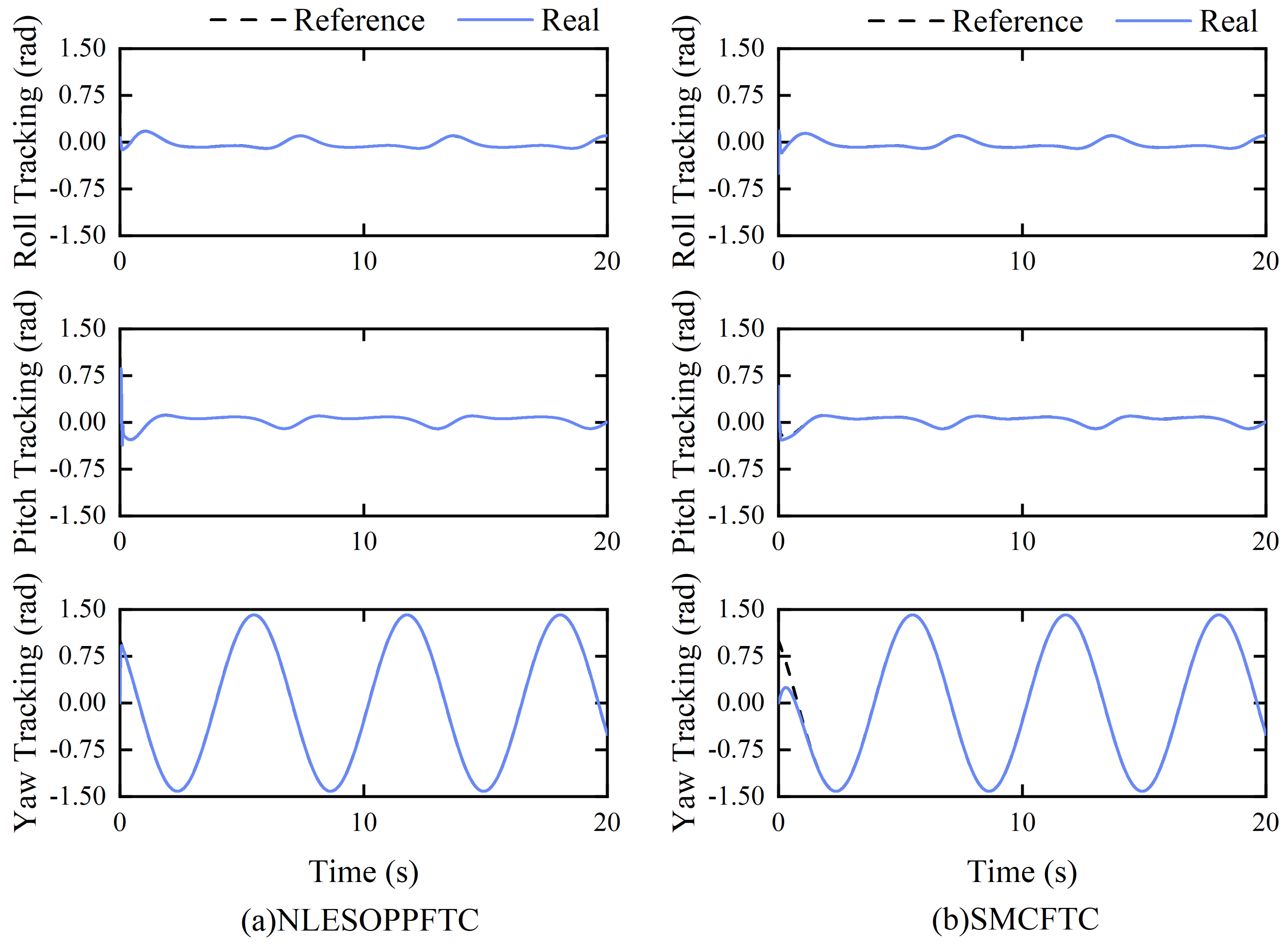
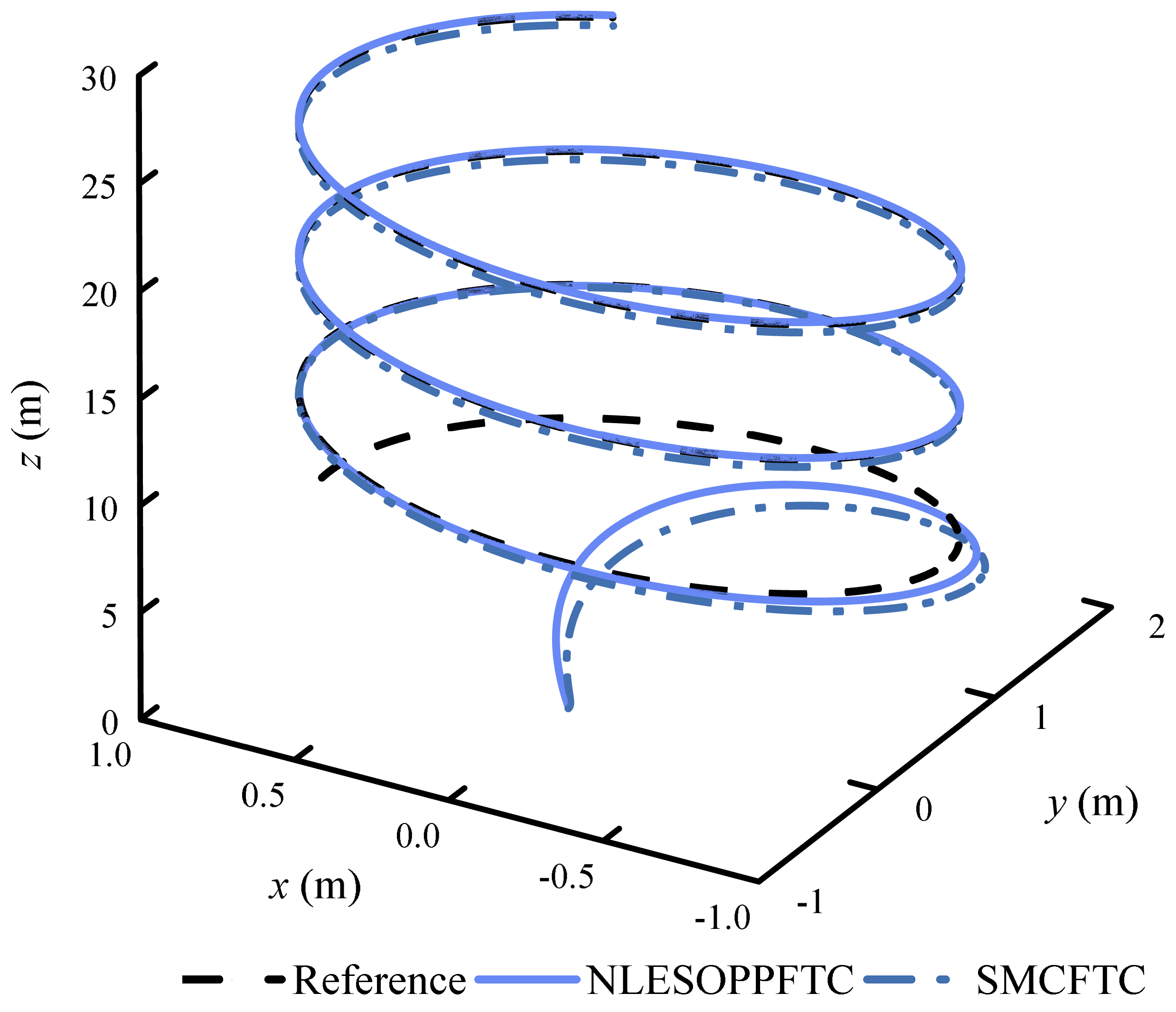
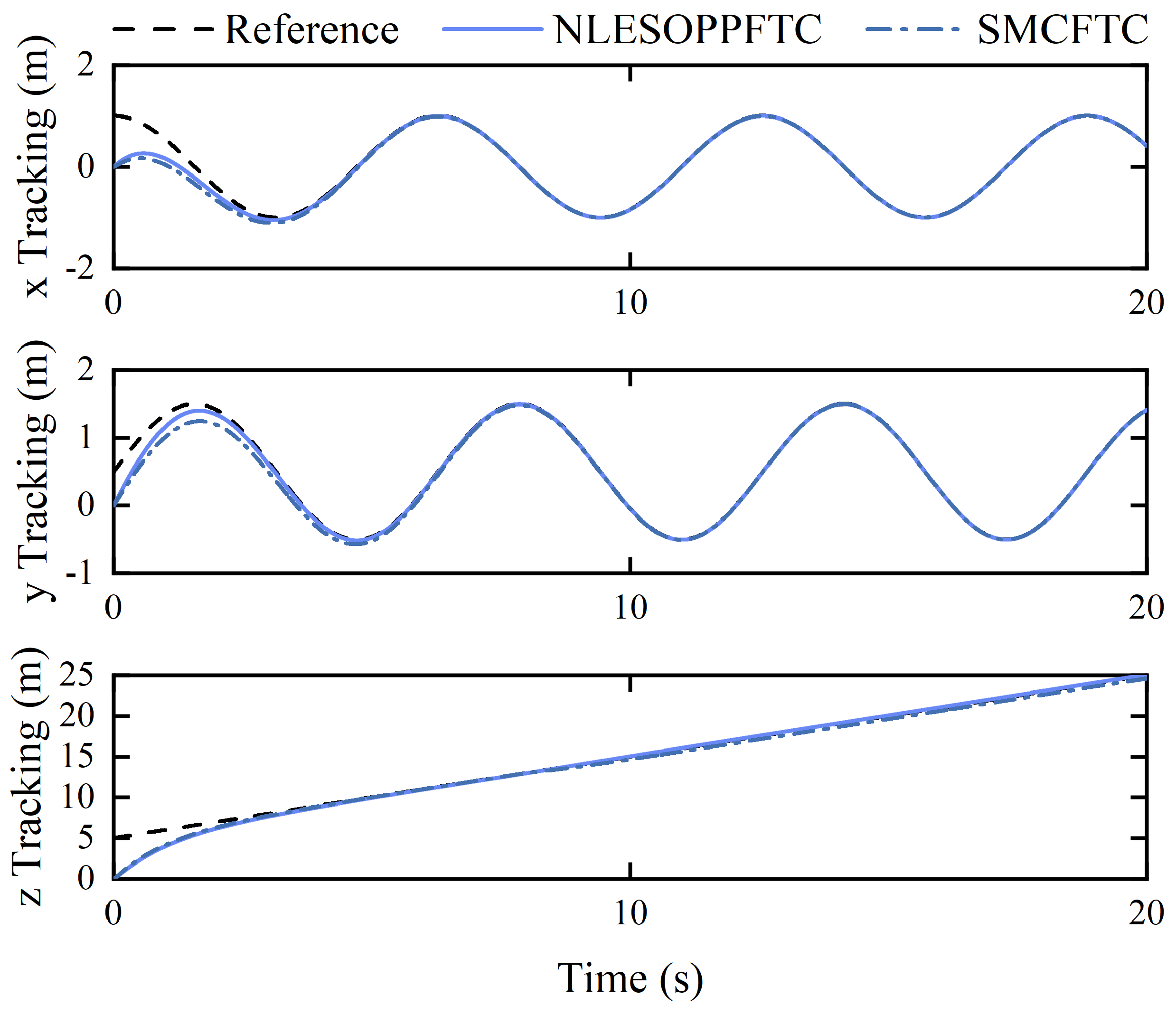
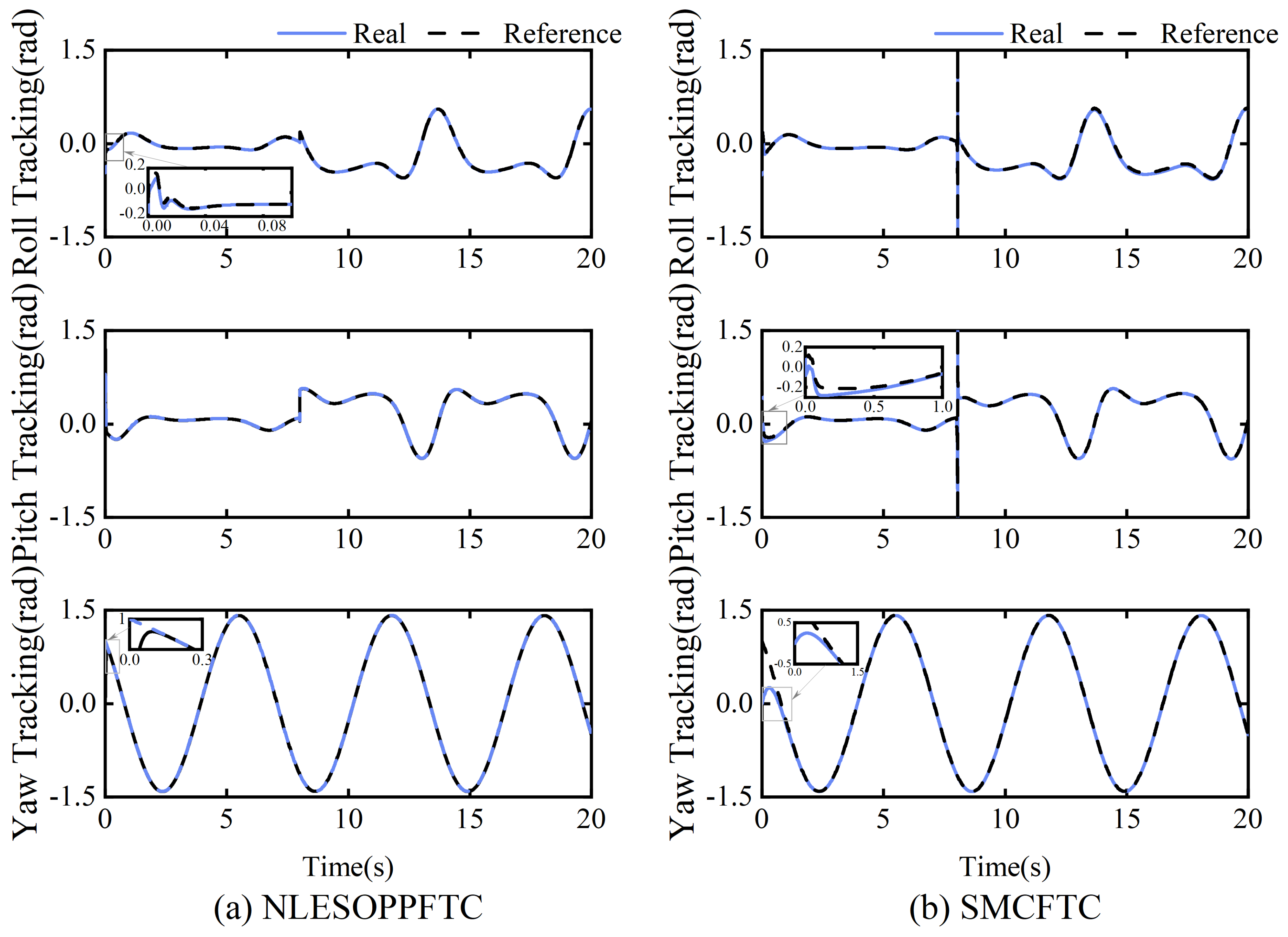
4.1. Case 1: Fault-Free and Disturbance-Free Tracking
4.2. Case 2: Constant Fault and Disturbance Tracking
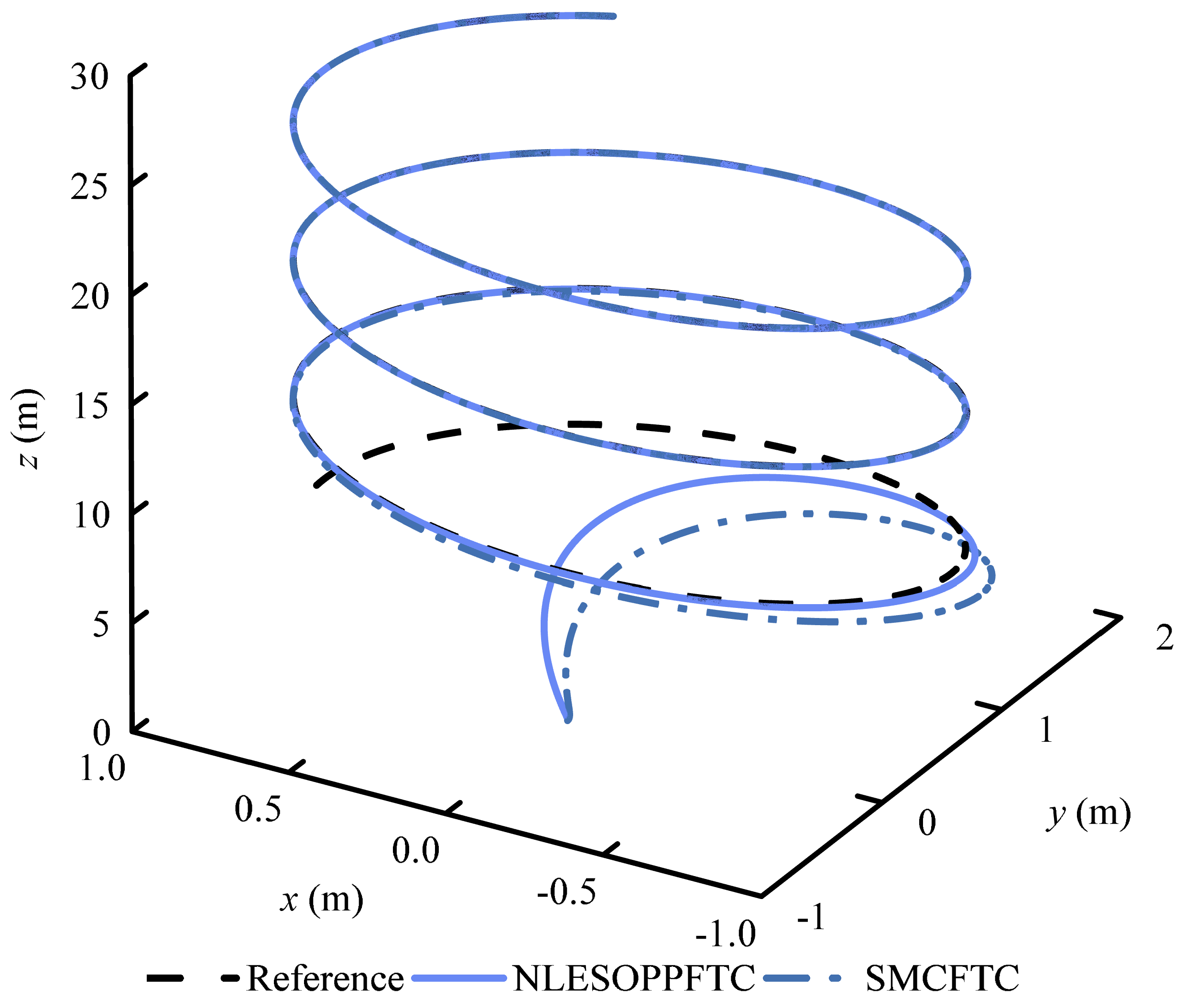
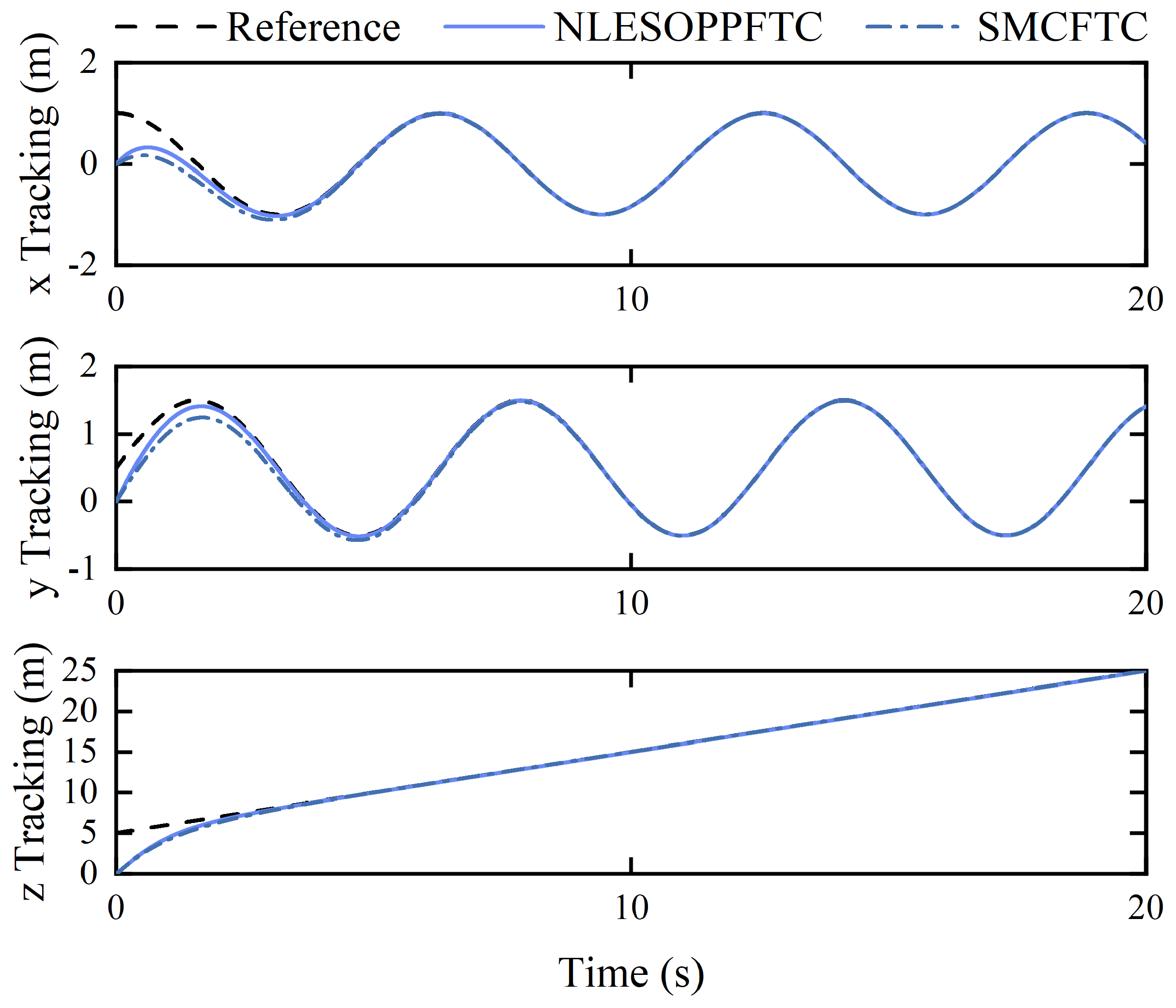
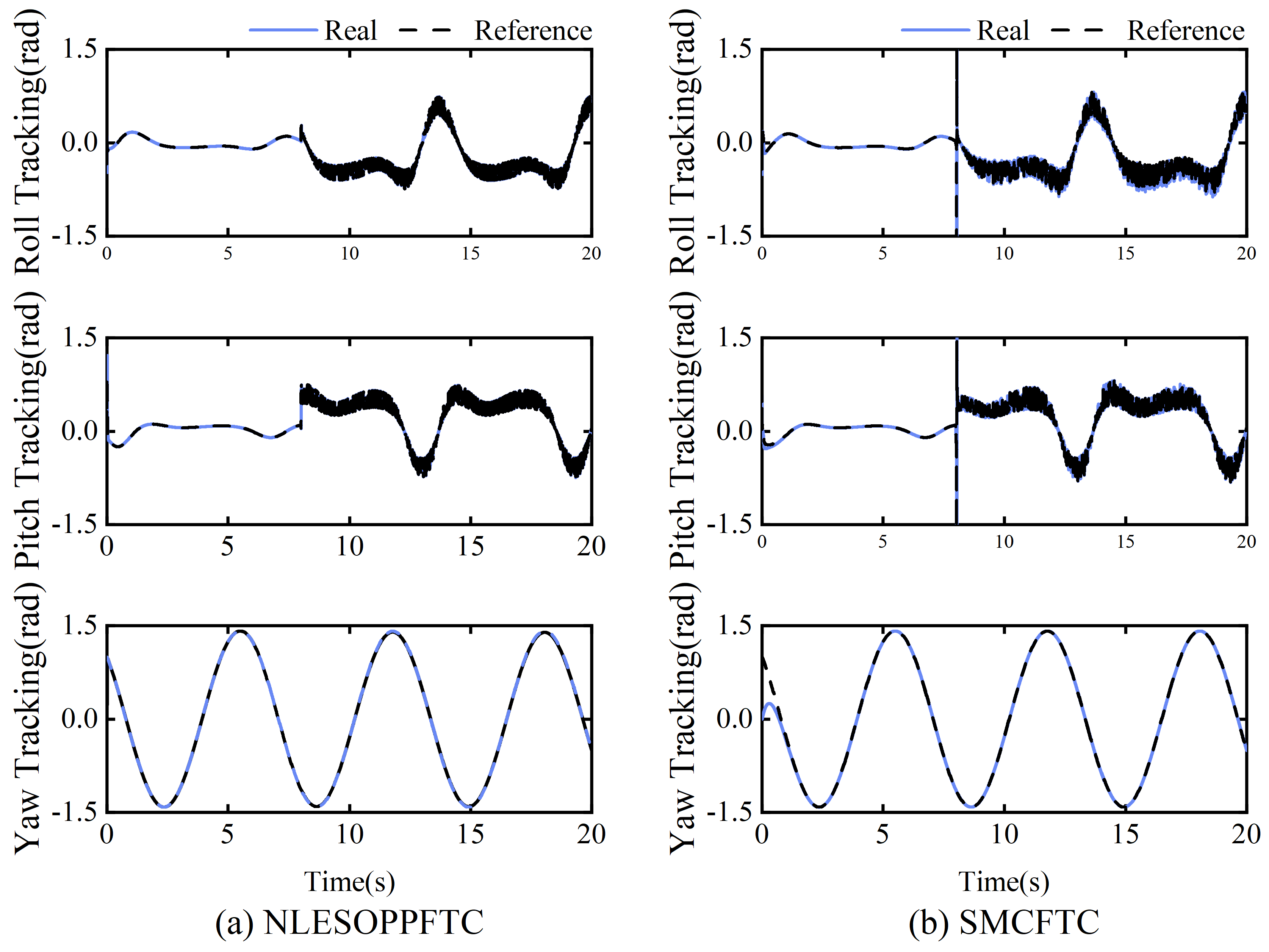
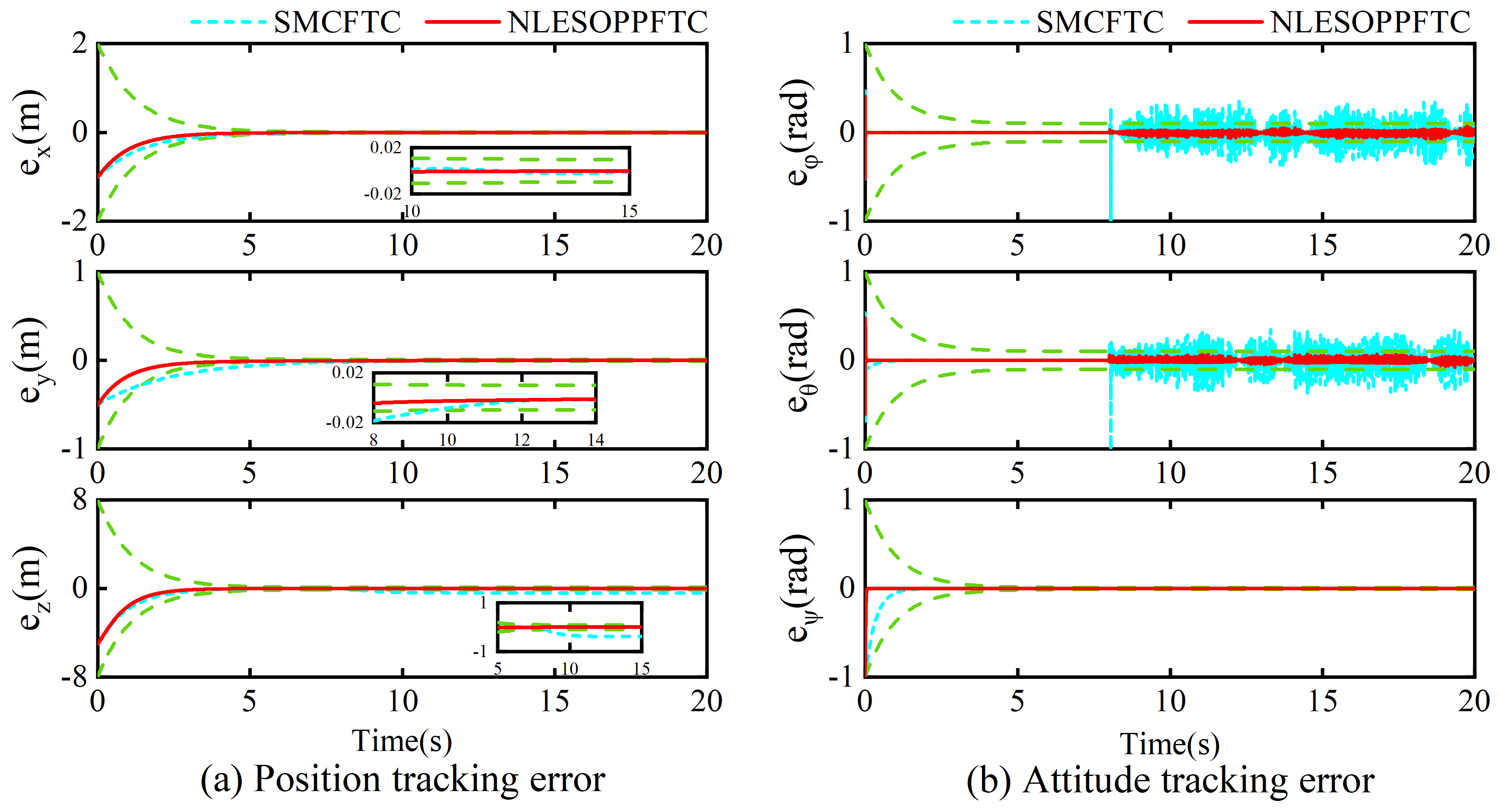
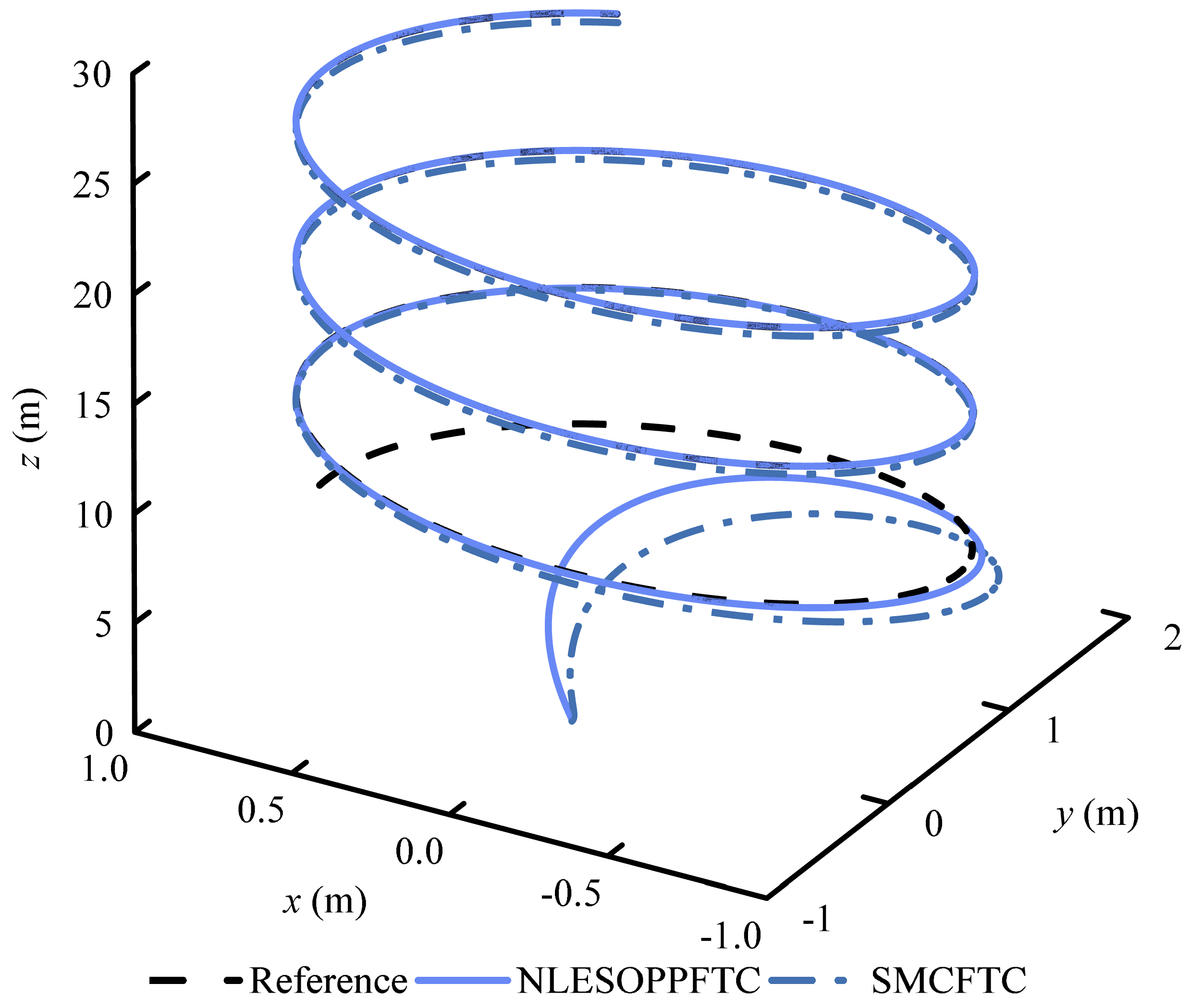
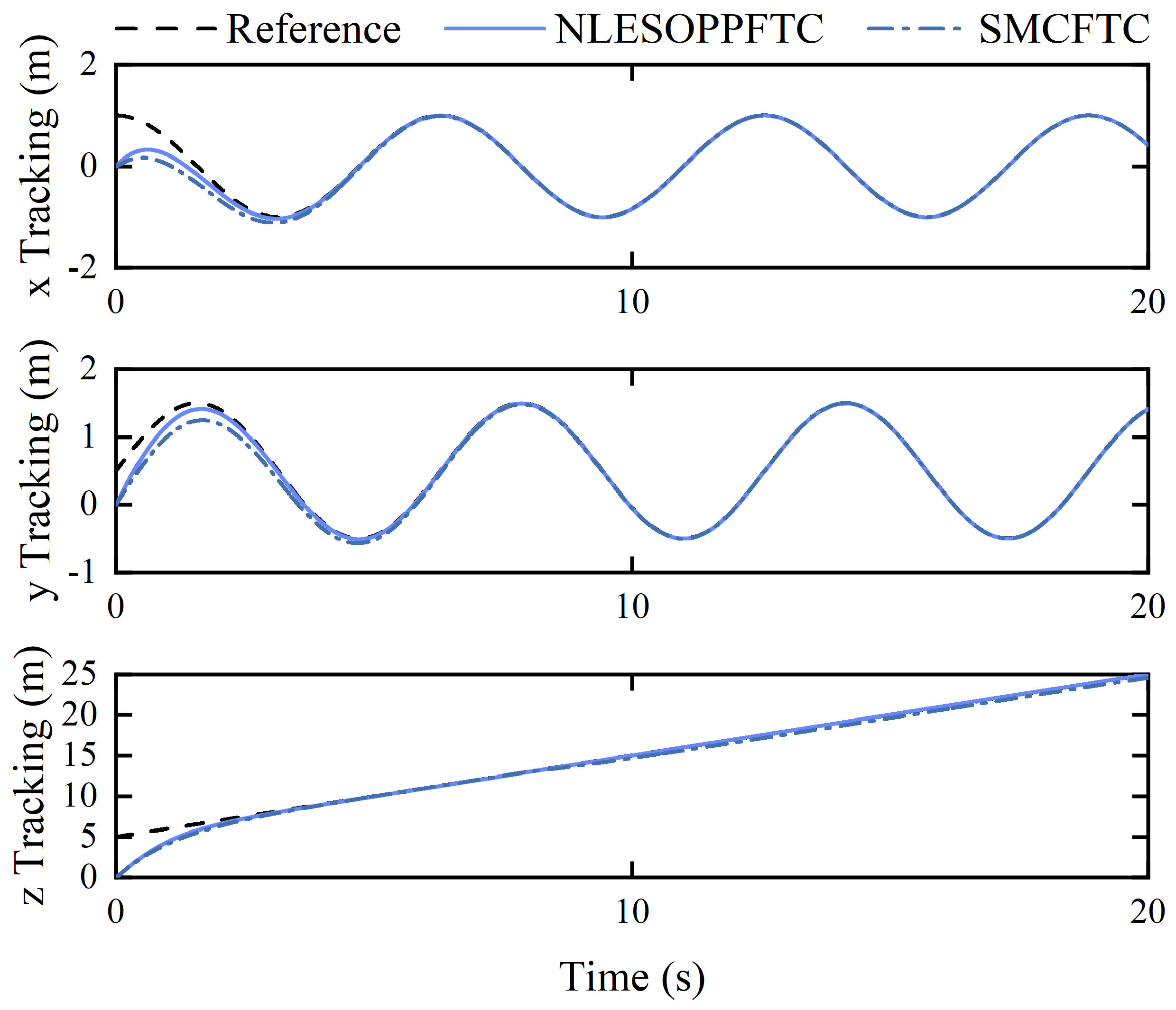
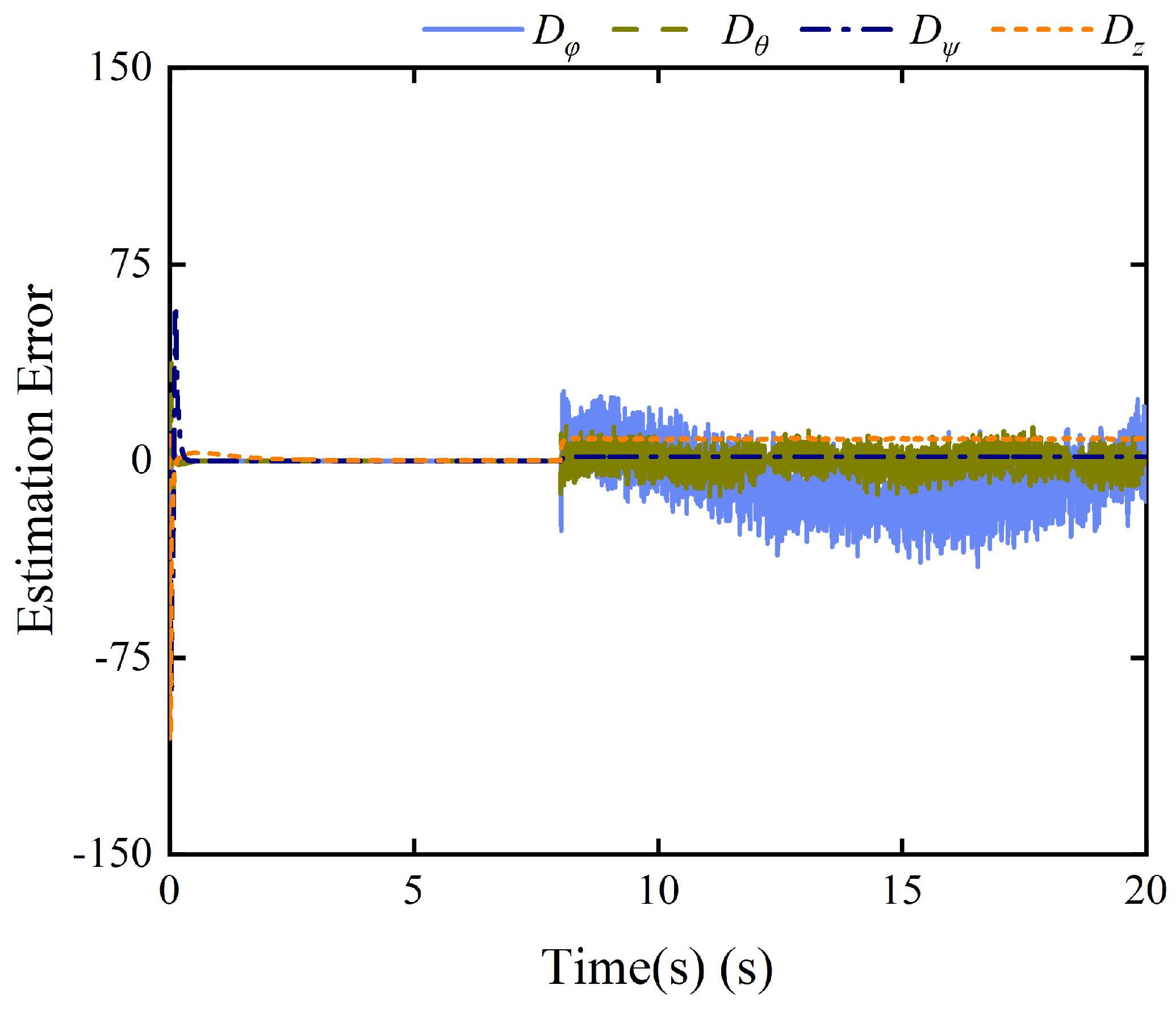
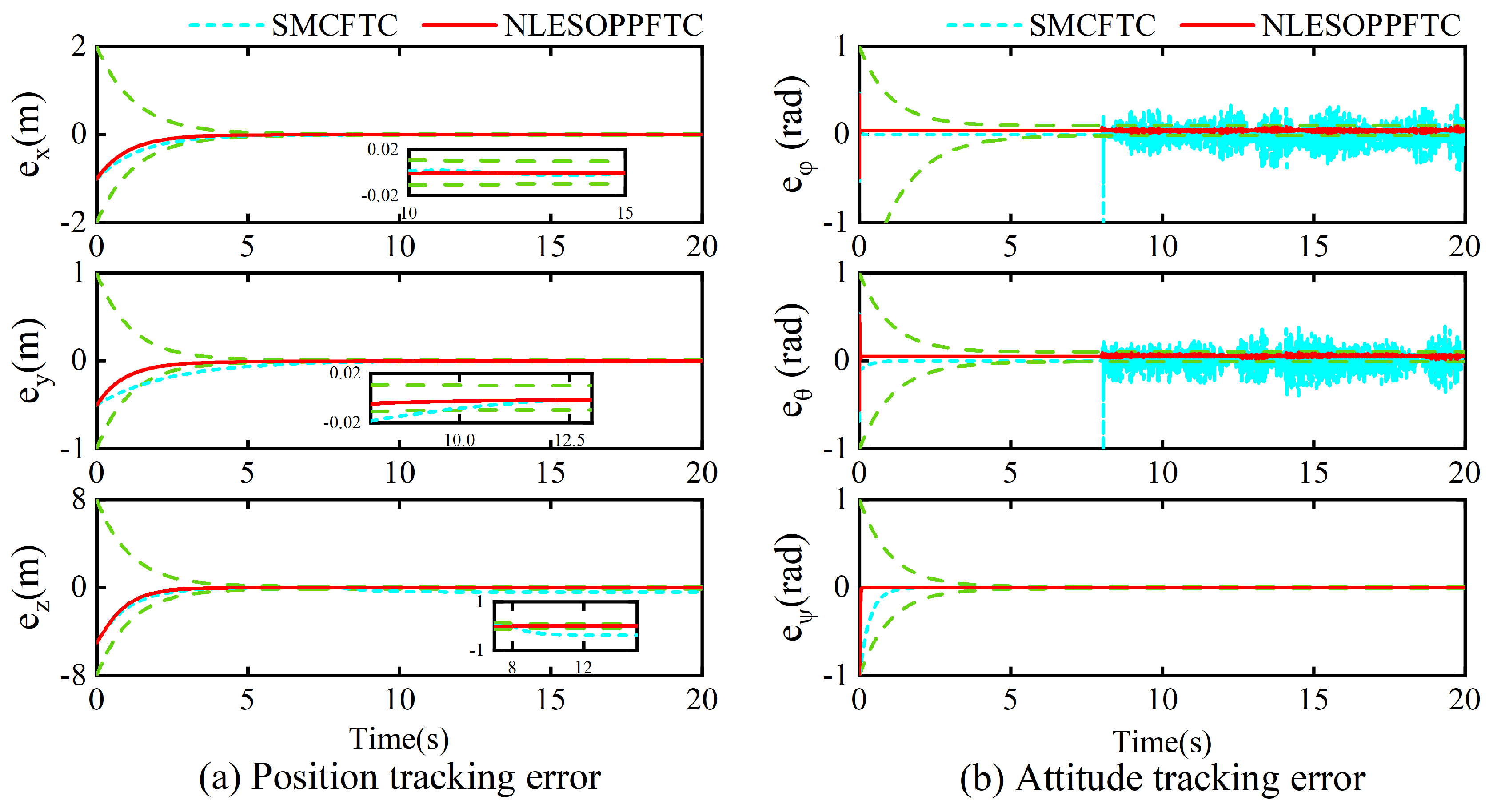
4.3. Case 3: Time-Varying Fault and Disturbance Tracking
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fan, B.; Li, Y.; Zhang, R.; Fu, Q. Review on the Technological Development and Application of UAV Systems. Chin. J. Electron. 2020, 29, 199–207. [Google Scholar] [CrossRef]
- Nawaz, H.; Ali, H.M.; Laghari, A.A. UAV communication networks issues: A review. Arch. Comput. Methods Eng. 2021, 28, 1349–1369. [Google Scholar] [CrossRef]
- Khattab, A.; Mizrak, I.; Alwi, H. Fault tolerant control of an octorotor UAV using sliding mode for applications in challenging environments. Annu. Rev. Control 2024, 57, 100952. [Google Scholar] [CrossRef]
- Zhao, Z.h.; Xiao, L.; Jiang, B.; Cao, D. Fast nonsingular terminal sliding mode trajectory tracking control of a quadrotor UAV based on extended state observers. Control Decis. 2022, 37, 2201–2210. [Google Scholar] [CrossRef]
- Hu, F.; Ma, T.; Su, X. Adaptive Fuzzy Sliding Mode Fixed-Time Control for Quadrotor Unmanned Aerial Vehicles with Prescribed Performance. IEEE Trans. Fuzzy Syst. 2024, 32, 4109–4120. [Google Scholar] [CrossRef]
- Wen, G.; Yu, D.; Zhao, Y. Optimized Fuzzy Attitude Control of Quadrotor Unmanned Aerial Vehicle Using Adaptive Reinforcement Learning Strategy. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 6075–6083. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, X.; Peng, X. Trajectory tracking control of four-rotor UAV based on nonlinear extended state observer and model predictive control in wind disturbance environment. J. Phys. Conf. Ser. 2024, 2764, 012075. [Google Scholar] [CrossRef]
- Derakhshan, R.E.; Danesh, M.; Moosavi, H. Disturbance observer-based model predictive control of a coaxial octorotor with variable centre of gravity. IET Control Theory Appl. 2024, 18, 764–783. [Google Scholar] [CrossRef]
- Chen, H.; Li, J.; Wang, A.; Zhang, Y.; Liang, H. Fault-tolerant control of quadrotor UAV attitude system with actuator failure. Flight Dyn. 2024, 42, 52–59. [Google Scholar]
- Wang, A.; Li, J.; Xia, G.; Chen, H. Quad-rotor Unmanned Helicopter Presets Performance Adaptive PID Control. Control Eng. China 2024, 31, 865–875. [Google Scholar]
- Jin, P.; Ma, Q.; Xu, S. Dynamic Event-Triggered Robust Optimal Attitude Control of QUAV Using Reinforcement Learning. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7798–7807. [Google Scholar] [CrossRef]
- Yan, K.; Zhang, J.R.; Ren, H.P. Interval Observer-based Robust Trajectory Tracking Control for Quadrotor Unmanned Aerial Vehicle. Int. J. Control. Autom. Syst. 2024, 22, 288–300. [Google Scholar] [CrossRef]
- Xu, S.; Huang, W.; Wang, H.; Zheng, W.; Wang, J.; Chai, Y.; Ma, M. A Simultaneous Diagnosis Method for Power Switch and Current Sensor Faults in Grid-Connected Three-Level NPC Inverters. IEEE Trans. Power Electron. 2023, 38, 1104–1118. [Google Scholar] [CrossRef]
- Xie, D.; Lin, C.; Deng, Q.; Lin, H.; Cai, C.; Basler, T.; Ge, X. Simple Vector Calculation and Constraint-Based Fault-Tolerant Control for a Single-Phase CHBMC. IEEE Trans. Power Electron. 2024, 1–14. [Google Scholar] [CrossRef]
- Abushafa, O.S.H.M.; Dahidah, M.S.A.; Gadoue, S.M.; Atkinson, D.J. Submodule Voltage Estimation Scheme in Modular Multilevel Converters with Reduced Voltage Sensors Based on Kalman Filter Approach. IEEE Trans. Ind. Electron. 2018, 65, 7025–7035. [Google Scholar] [CrossRef]
- Niederlinski, A. A heuristic approach to the design of linear multivariable interacting control systems. Automatica 1971, 7, 691–701. [Google Scholar] [CrossRef]
- Gong, W.; Li, B.; Yang, Y.; Ban, H.; Xiao, B. Fixed-time integral-type sliding mode control for the quadrotor UAV attitude stabilization under actuator failures. Aerosp. Sci. Technol. 2019, 95, 105444. [Google Scholar] [CrossRef]
- Abbaspour, A.; Mokhtari, S.; Sargolzaei, A.; Yen, K.K. A Survey on Active Fault-Tolerant Control Systems. Electronics 2020, 9, 1513. [Google Scholar] [CrossRef]
- Yang, S.; Zou, Z.; Li, Y.; Shi, H.; Fu, Q. Adaptive Fault-Tolerant Tracking Control of Quadrotor UAVs against Uncertainties of Inertial Matrices and State Constraints. Drones 2023, 7, 107. [Google Scholar] [CrossRef]
- Liu, H.; Tu, H.; Huang, S.; Zheng, X. Adaptive Predefined-Time Sliding Mode Control for QUADROTOR Formation with Obstacle and Inter-Quadrotor Avoidance. Sensors 2023, 23, 2392. [Google Scholar] [CrossRef]
- Jung, W.; Bang, H. Fault and Failure Tolerant Model Predictive Control of Quadrotor UAV. Int. J. Aeronaut. Space Sci. 2021, 22, 663–675. [Google Scholar] [CrossRef]
- Cui, G.; Yang, W.; Yu, J. Neural network-based finite-time adaptive tracking control of nonstrict-feedback nonlinear systems with actuator failures. Inf. Sci. 2021, 545, 298–311. [Google Scholar] [CrossRef]
- Brahim, K.S.; Hajjaji, A.E.; Terki, N.; Alabazares, D.L. Finite Time Adaptive SMC for UAV Trajectory Tracking Under Unknown Disturbances and Actuators Constraints. IEEE Access 2023, 11, 66177–66193. [Google Scholar] [CrossRef]
- Prochazka, K.F.; Stomberg, G. Integral Sliding Mode based Model Reference FTC of an Over-Actuated Hybrid UAV using Online Control Allocation. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 3858–3864. [Google Scholar] [CrossRef]
- Karahan, M.; Inal, M.; Kasnakoglu, C. Fault Tolerant Super Twisting Sliding Mode Control of a Quadrotor UAV Using Control Allocation. Int. J. Robot. Control Syst. 2023, 3, 270–285. [Google Scholar] [CrossRef]
- Nan, F.; Sun, S.; Foehn, P.; Scaramuzza, D. Nonlinear MPC for Quadrotor Fault-Tolerant Control. IEEE Robot. Autom. Lett. 2022, 7, 5047–5054. [Google Scholar] [CrossRef]
- Yang, P.; Wang, Z.; Zhang, Z.; Hu, X. Sliding Mode Fault Tolerant Control for a Quadrotor with Varying Load and Actuator Fault. Actuators 2021, 10, 323. [Google Scholar] [CrossRef]
- Dou, J.; Kong, X.; Wen, B. Backstepping Sliding Mode Active Disturbance Rejection Control of Quadrotor Attitude and Its Stability. J. Northeast. Univ. (Nat. Sci.) 2016, 37, 1415–1420. [Google Scholar] [CrossRef]
- He, D.; Wang, H.; Tian, Y. Model-Free Control Using Nonlinear Extended State Observer and Non-singular Fast Terminal Sliding Mode for Quadrotor Position and Attitude. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 1891–1896. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Robust Adaptive Control of Feedback Linearizable MIMO Nonlinear Systems with Prescribed Performance. IEEE Trans. Autom. Control 2008, 53, 2090–2099. [Google Scholar] [CrossRef]
- Pan, S.; Jiang, B.; Zhu, R.; Yin, X. Prescribed Performance Back-stepping Control of Fast Trajectory Tracking for Quad-rotor Aircraft. Control Eng. China 2021, 28, 2199–2208. [Google Scholar] [CrossRef]
- Gong, W.; Li, B.; Ahn, C.K.; Yang, Y. Prescribed-time extended state observer and prescribed performance control of quadrotor UAVs against actuator faults. Aerosp. Sci. Technol. 2023, 138, 108322. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, L.; Geng, B. Research Development of Prescribed Performance Control. J. Nav. Aeronaut. Astronaut. Univ. 2016, 31, 1–6. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, H.; Li, X. Active disturbance rejection preset finite-time control for a UAV with unknown initial tracking condition. J. Univ. Sci. Technol. Liaoning 2023, 46, 111–119. [Google Scholar]
- Zhu, W.; Wang, C.; Deng, W.; Liang, X.; Yao, J. Nonsingular Terminal Sliding Mode Based Prescribed Performance Control of Motor Servo Systems. J. Mech. Eng. 2023, 59, 359–366. [Google Scholar]
- Li, H.; Wei, J.; Fang, D.; Li, J. Prescribed performance control for hypersonic vehicle considering input constraint. J. Natl. Univ. Def. Technol. 2023, 45, 27–36. [Google Scholar] [CrossRef]
- Wang, L.; Pei, H.; Cheng, Z. Geometric Attitude Fault-Tolerant Control of Quadrotor Unmanned Aerial Vehicles with Adaptive Extended State Observers. Machines 2024, 12, 47. [Google Scholar] [CrossRef]
- Liu, J.; Tan, J.; Pu, M.; Zhang, G.; Dan, Z.; Guo, G. Novel third-order fixed-time convergent nonlinear extended state observer based on sliding mode control method. Control Decis. 2024. [Google Scholar] [CrossRef]
- Hasan, A.; Johansen, T.A. Model-based actuator fault diagnosis in multirotor UAVs. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 1017–1024. [Google Scholar]
- Zhang, S.; Wu, H.; Zheng, X. Finite-time fault tolerant control of quadrotor UAV with actuator faults. Control Theory Appl. 2023, 40, 1270–1276. [Google Scholar]
- Asadi, D. Model-based Fault Detection and Identification of a Quadrotor with Rotor Fault. Int. J. Aeronaut. Space Sci. 2022, 23, 916–928. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Yin, C.; Wang, S.; Gao, J. A unified design approach for control integrating processes with time delay. PLoS ONE 2024, 19, e0299893. [Google Scholar] [CrossRef]
- Shao, X.; Xu, L.; Zhang, W. Quantized Control Capable of Appointed-Time Performances for Quadrotor Attitude Tracking: Experimental Validation. IEEE Trans. Ind. Electron. 2022, 69, 5100–5110. [Google Scholar] [CrossRef]


| Description | Value | Unit |
|---|---|---|
| m | 1.2 | kg |
| g | 9.8 | m/s2 |
| 8.64 × 10−3 | kg·m2 | |
| 8.64 × 10−3 | kg·m2 | |
| 1.62 × 10−2 | kg·m2 | |
| L | 0.154 | m |
| 0.01 | N/(m/s)2 | |
| 3.14 × 10−6 | N/(rad/s)2 | |
| 1.58 × 10−8 | kg·m2 |
| Index | RMSE | |
|---|---|---|
| NLESOPPFTC | z | 0 |
| 5.11 × 10−2 | ||
| 5.31 × 10−2 | ||
| 1.83 × 10−9 | ||
| SMCFTC | z | 1.44 × 10−1 |
| 7.57 × 10−2 | ||
| 8.17 × 10−2 | ||
| 9.84 × 10−3 | ||
| Evaluation Indexes | NLESOPPFTC | SMCFTC | |
|---|---|---|---|
| ITAE a | x | 0.837 | 2.255 |
| y | 0.810 | 2.929 | |
| z | 5.873 | 65.690 | |
| 0.434 | 4.066 | ||
| 0.690 | 0.783 | ||
| 0.028 | 0.128 | ||
| Proposed control strategy b | 8.524 | 8.698 | |
| 1066 | 2.527 × 104 | ||
| 1156 | 2.264 × 104 | ||
| 0.488 | 0.507 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mai, G.; Wang, H.; Wang, Y.; Wu, X.; Jiang, P.; Feng, G. Nonlinear Extended State Observer and Prescribed Performance Fault-Tolerant Control of Quadrotor Unmanned Aerial Vehicles Against Compound Faults. Aerospace 2024, 11, 903. https://doi.org/10.3390/aerospace11110903
Mai G, Wang H, Wang Y, Wu X, Jiang P, Feng G. Nonlinear Extended State Observer and Prescribed Performance Fault-Tolerant Control of Quadrotor Unmanned Aerial Vehicles Against Compound Faults. Aerospace. 2024; 11(11):903. https://doi.org/10.3390/aerospace11110903
Chicago/Turabian StyleMai, Ge, Hongliang Wang, Yilin Wang, Xinghua Wu, Peiyao Jiang, and Genyuan Feng. 2024. "Nonlinear Extended State Observer and Prescribed Performance Fault-Tolerant Control of Quadrotor Unmanned Aerial Vehicles Against Compound Faults" Aerospace 11, no. 11: 903. https://doi.org/10.3390/aerospace11110903
APA StyleMai, G., Wang, H., Wang, Y., Wu, X., Jiang, P., & Feng, G. (2024). Nonlinear Extended State Observer and Prescribed Performance Fault-Tolerant Control of Quadrotor Unmanned Aerial Vehicles Against Compound Faults. Aerospace, 11(11), 903. https://doi.org/10.3390/aerospace11110903







