Disturbance Observer-Based Backstepping Terminal Sliding Mode Aeroelastic Control of Airfoils
Abstract
1. Introduction
2. Aeroelastic System Dynamic Model
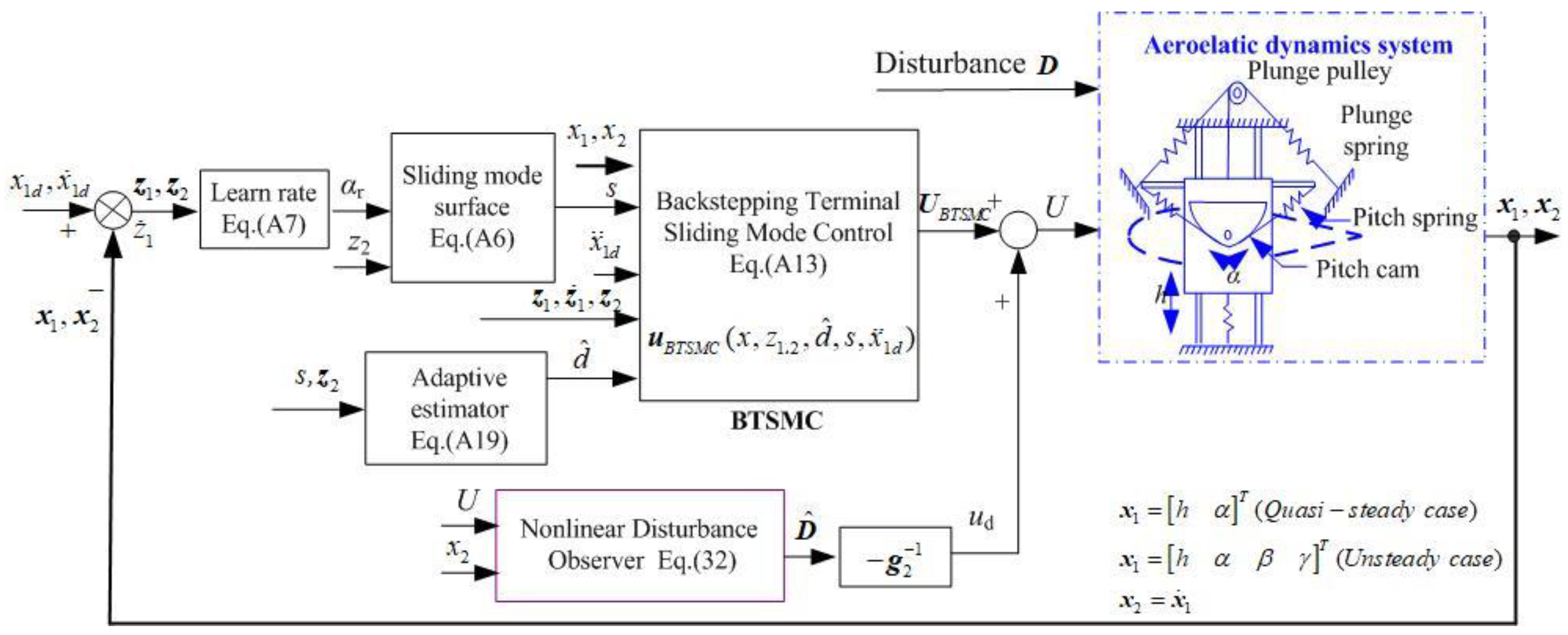
3. DO-BTSMC Aeroelastic Control Design
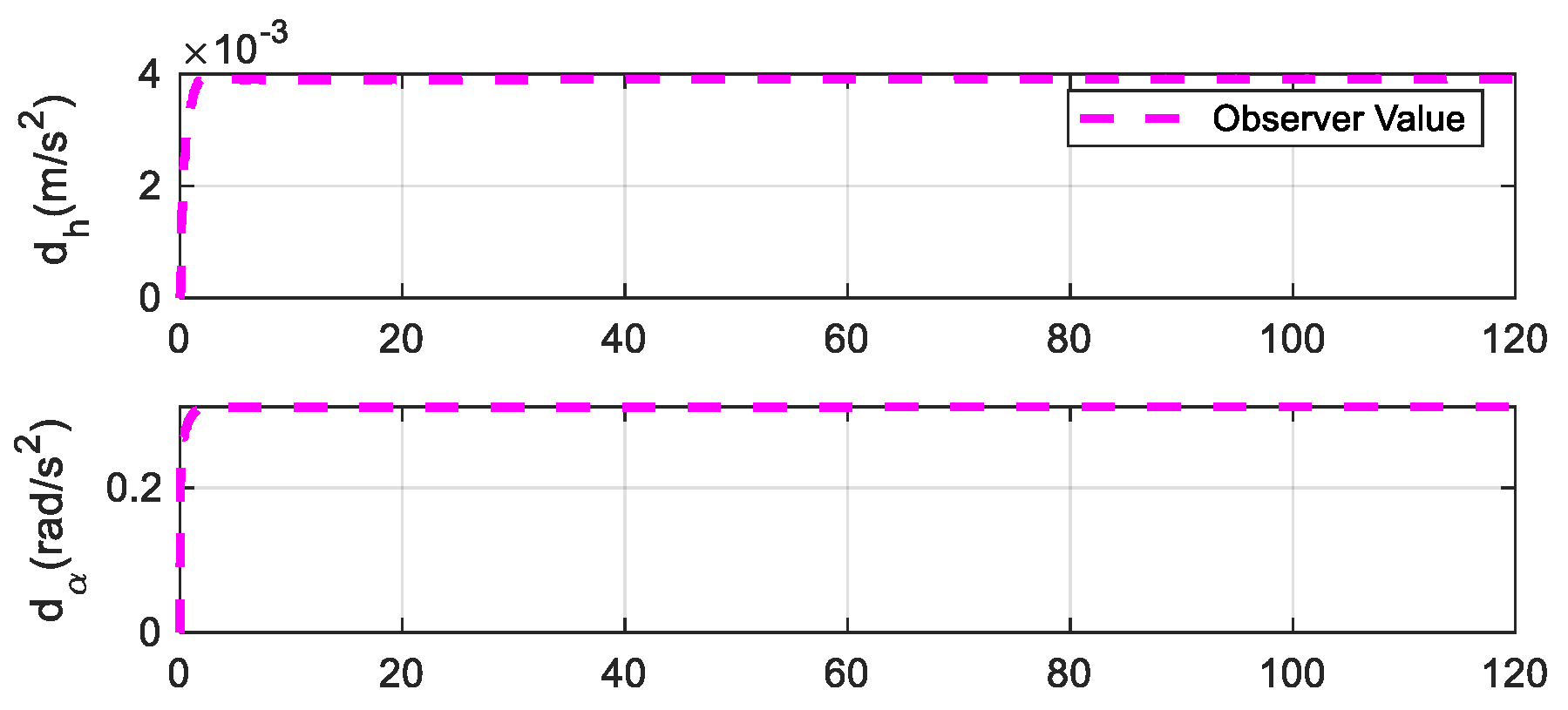
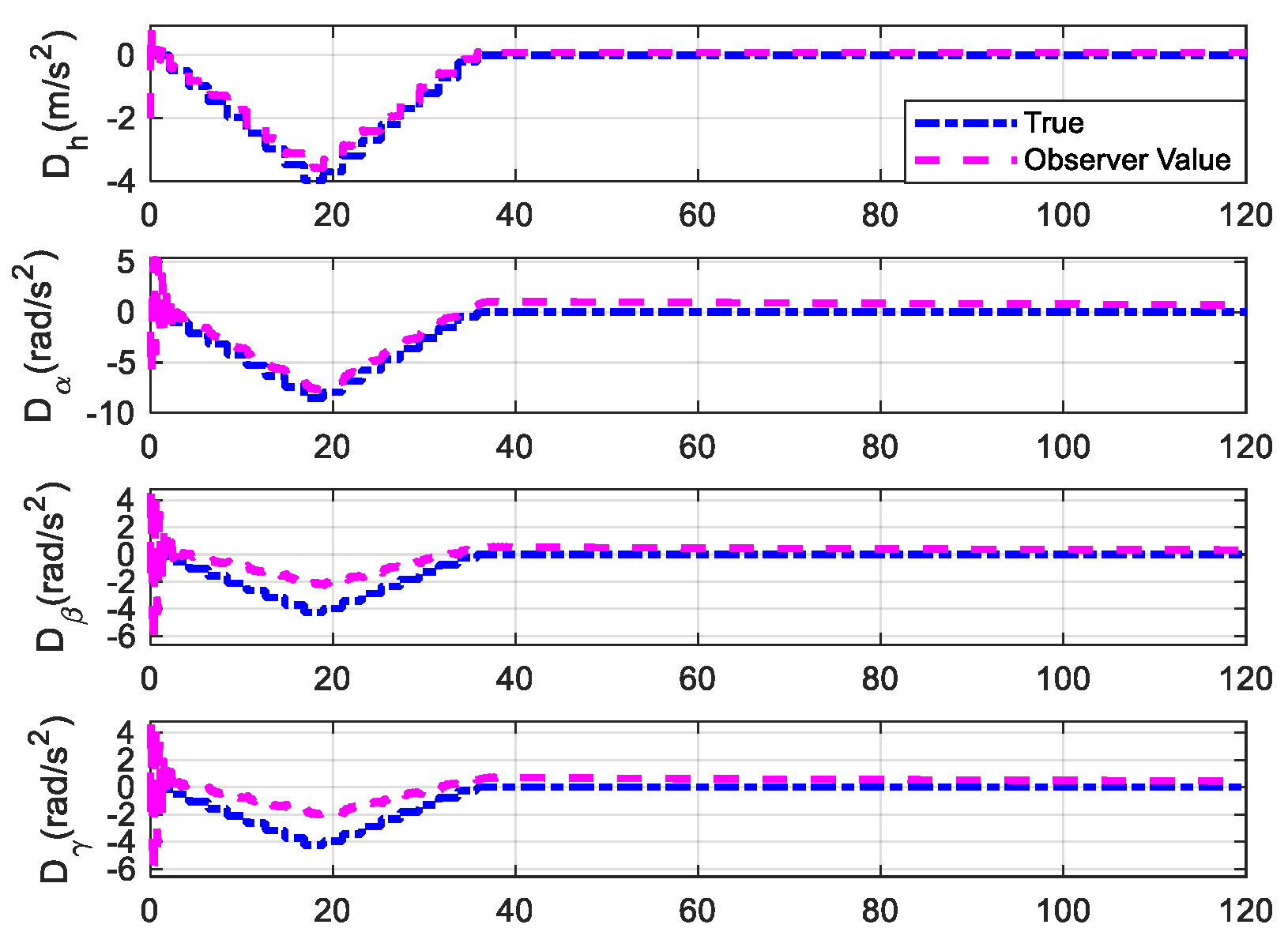
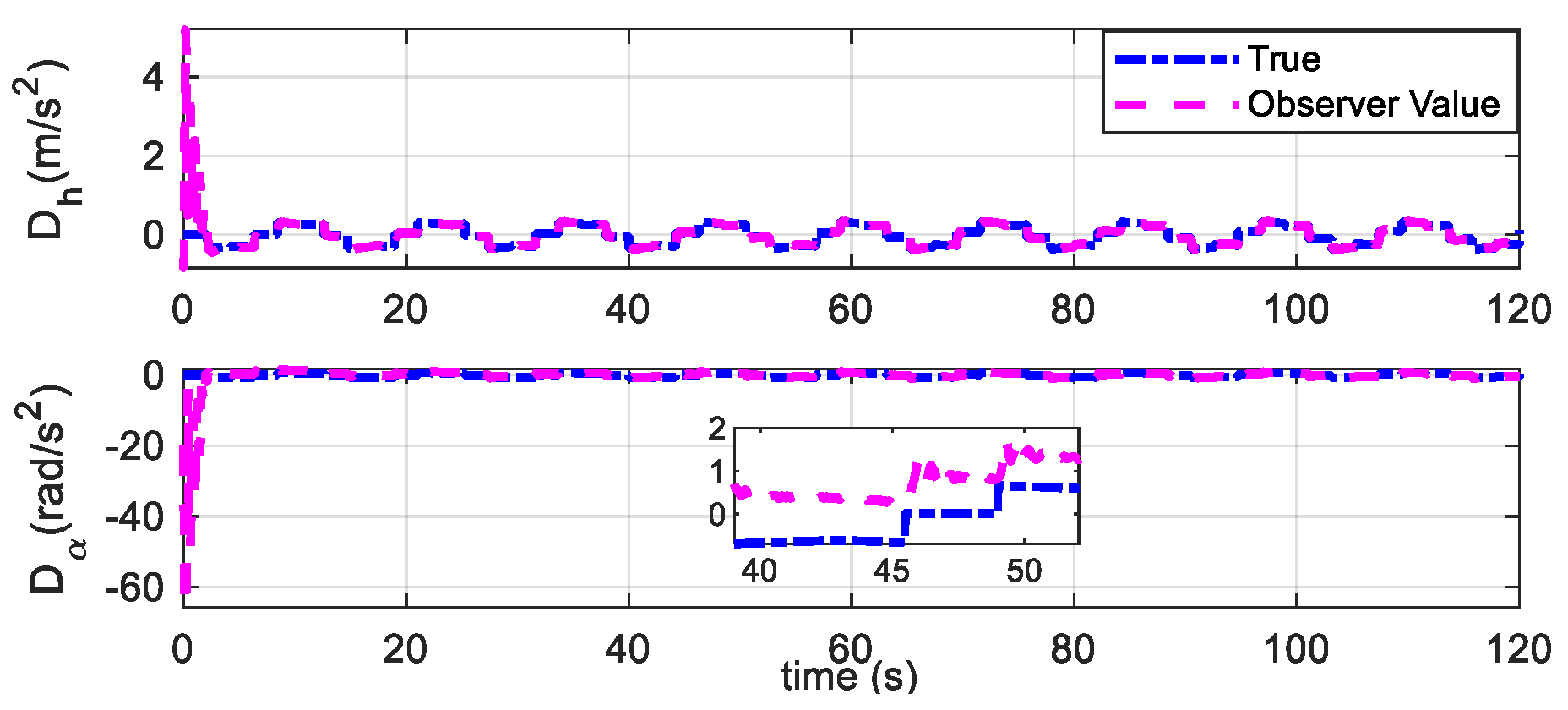
3.1. Nonlinear Disturbance Observer Design
3.2. DO-BTSMC-Based Aeroelastic Control Design
4. Discussion
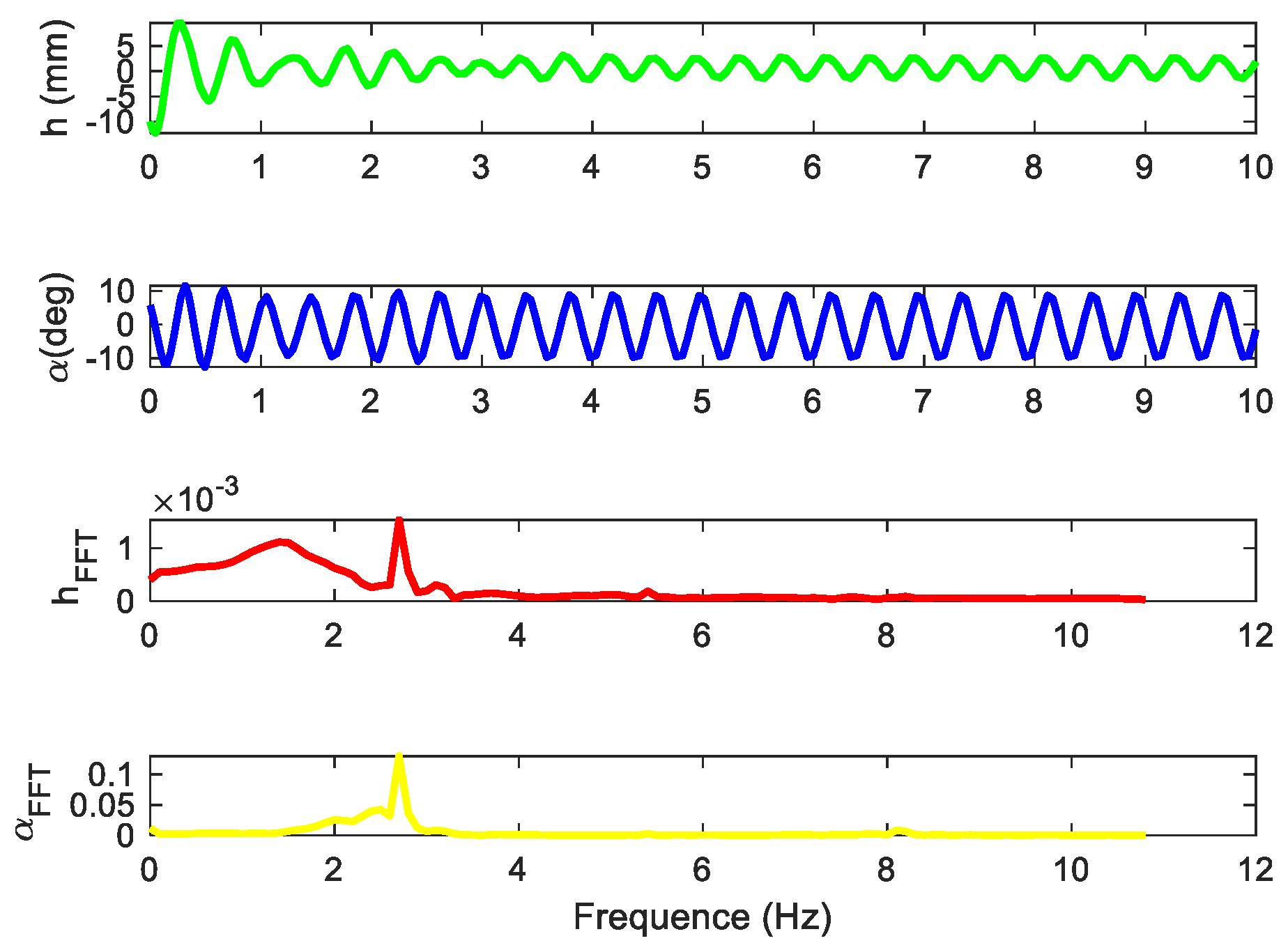
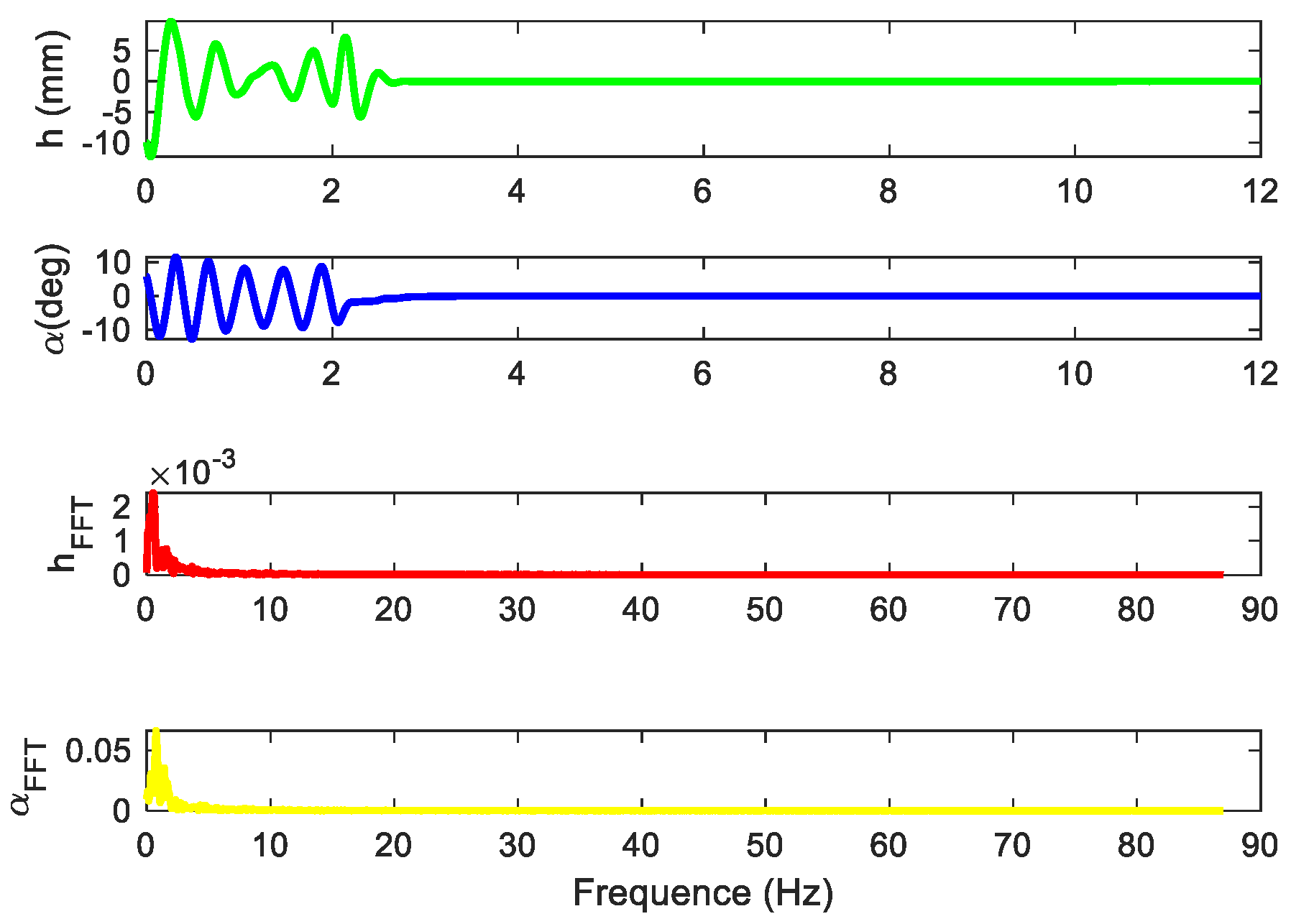
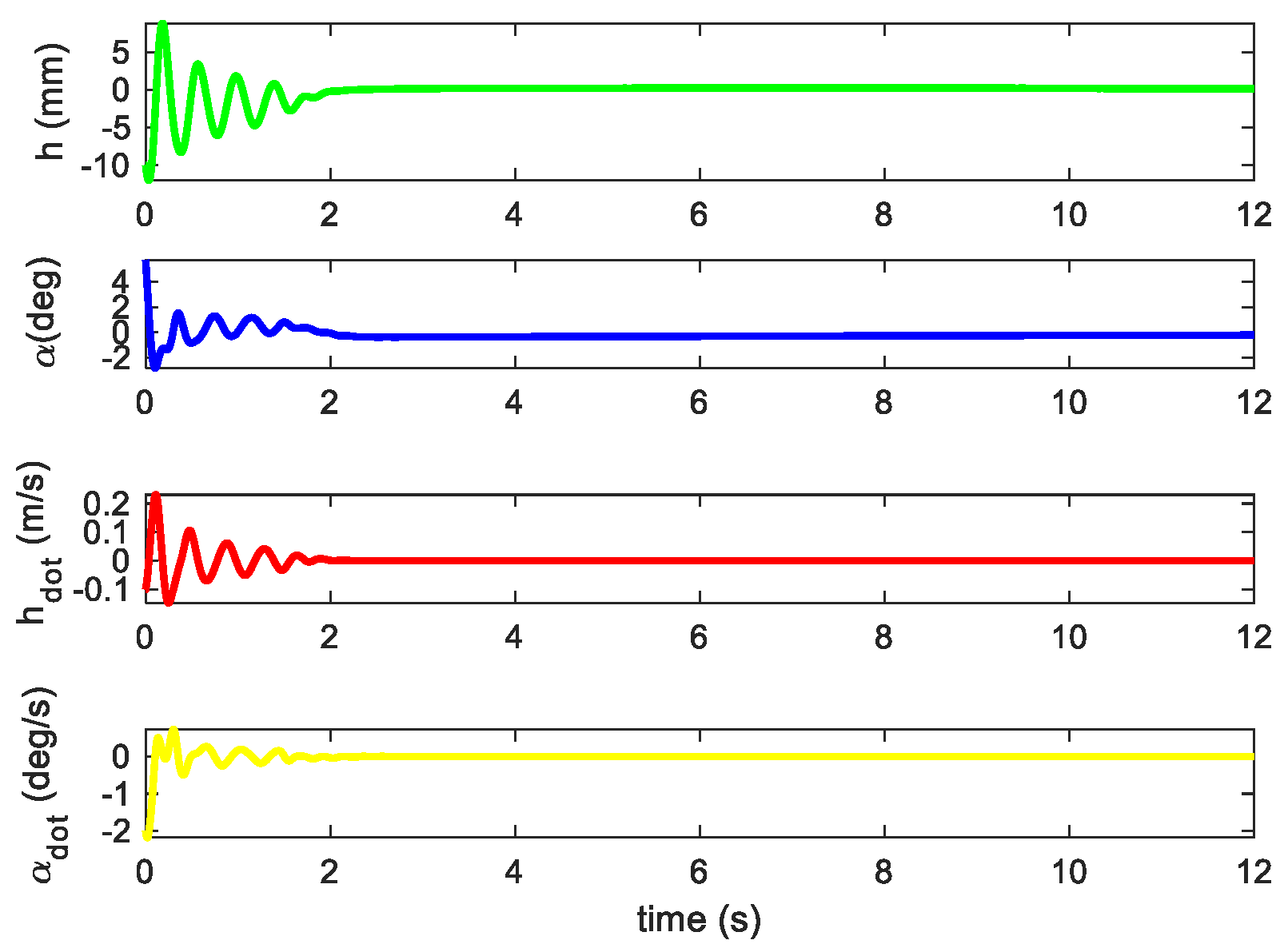
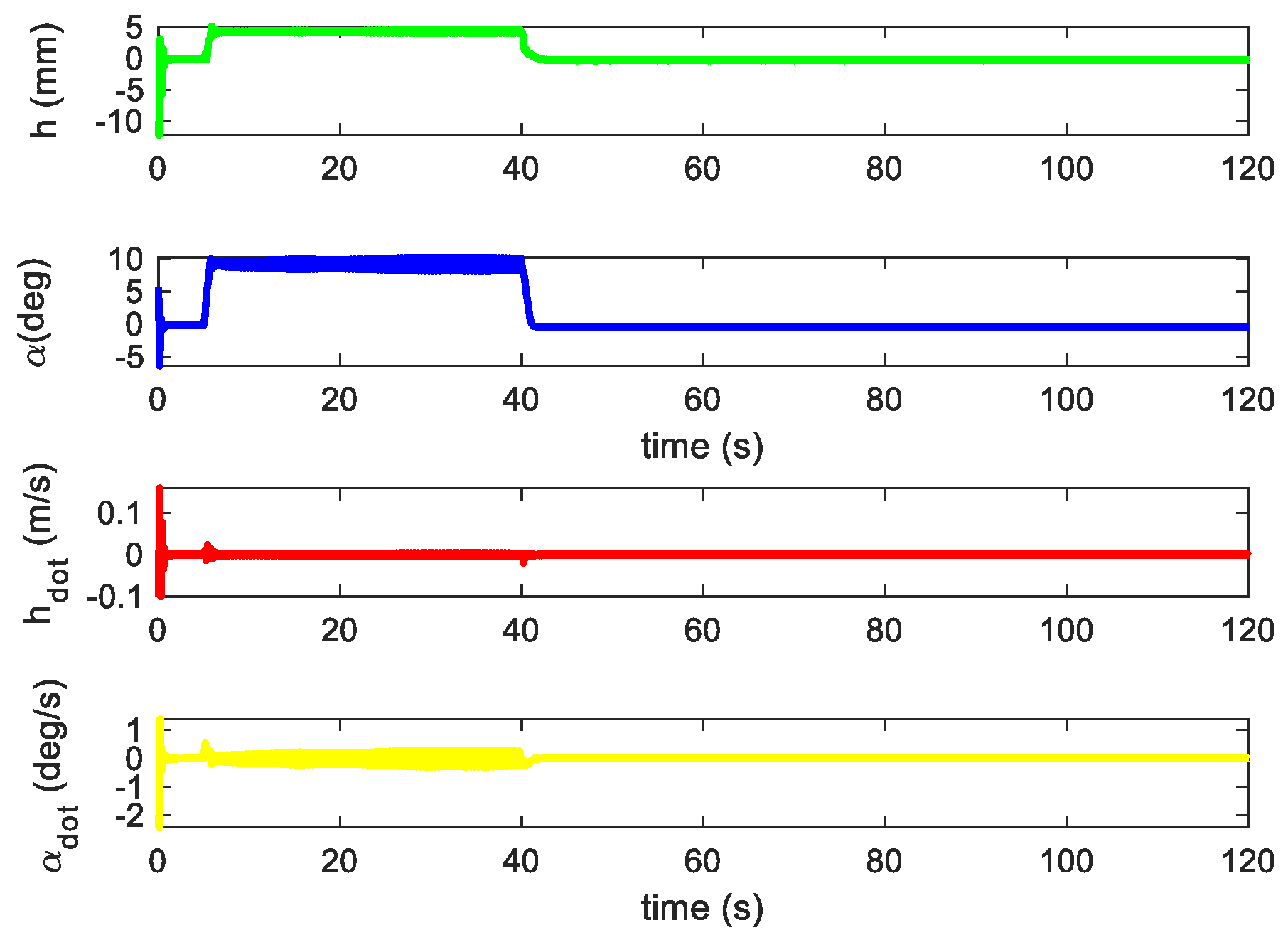
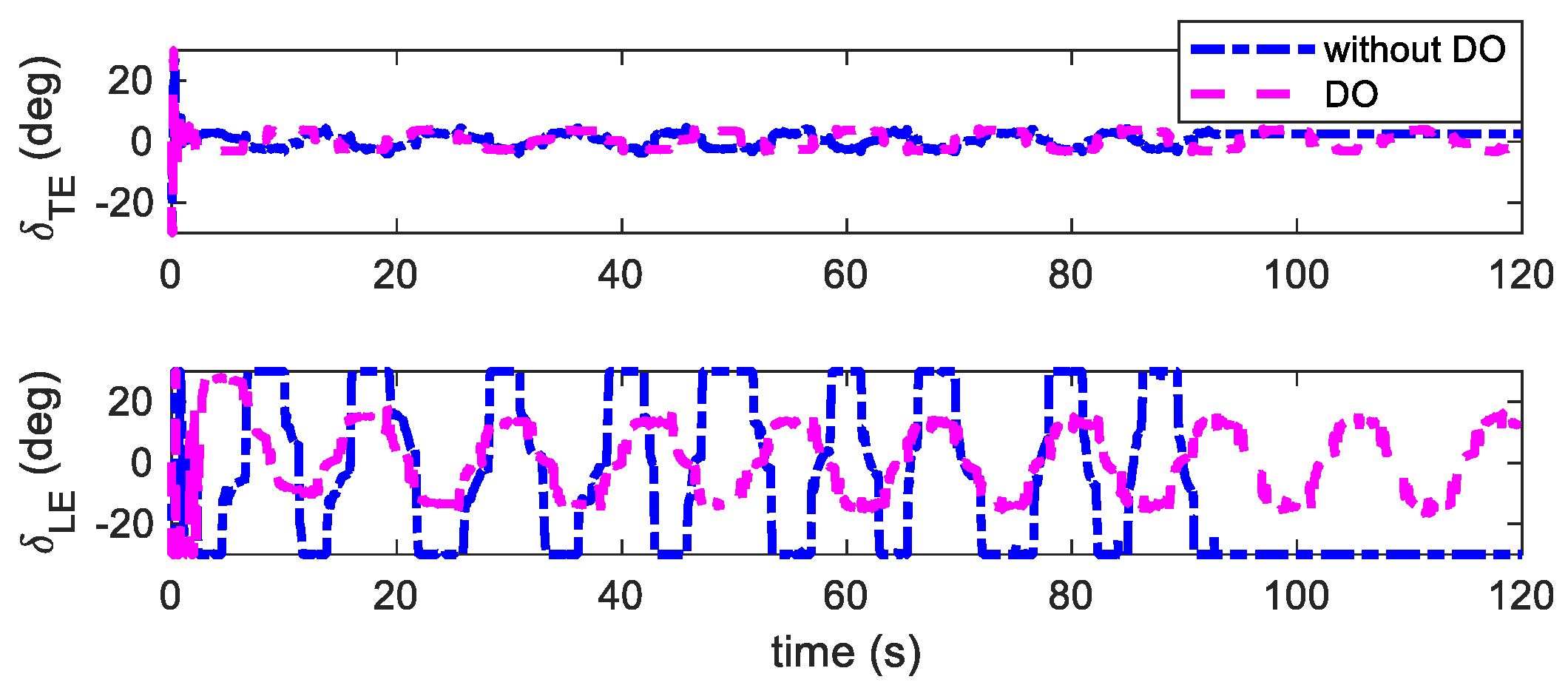
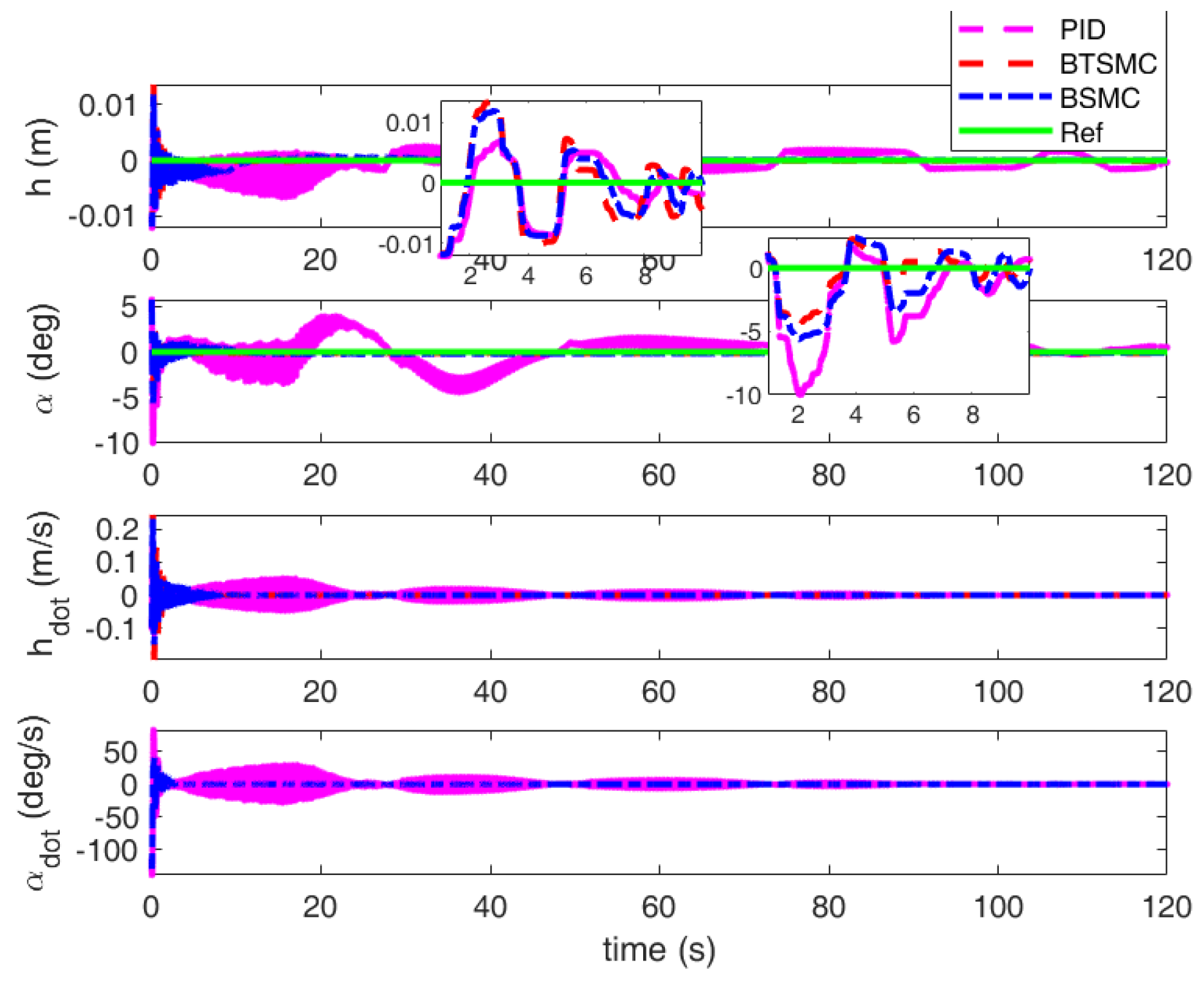
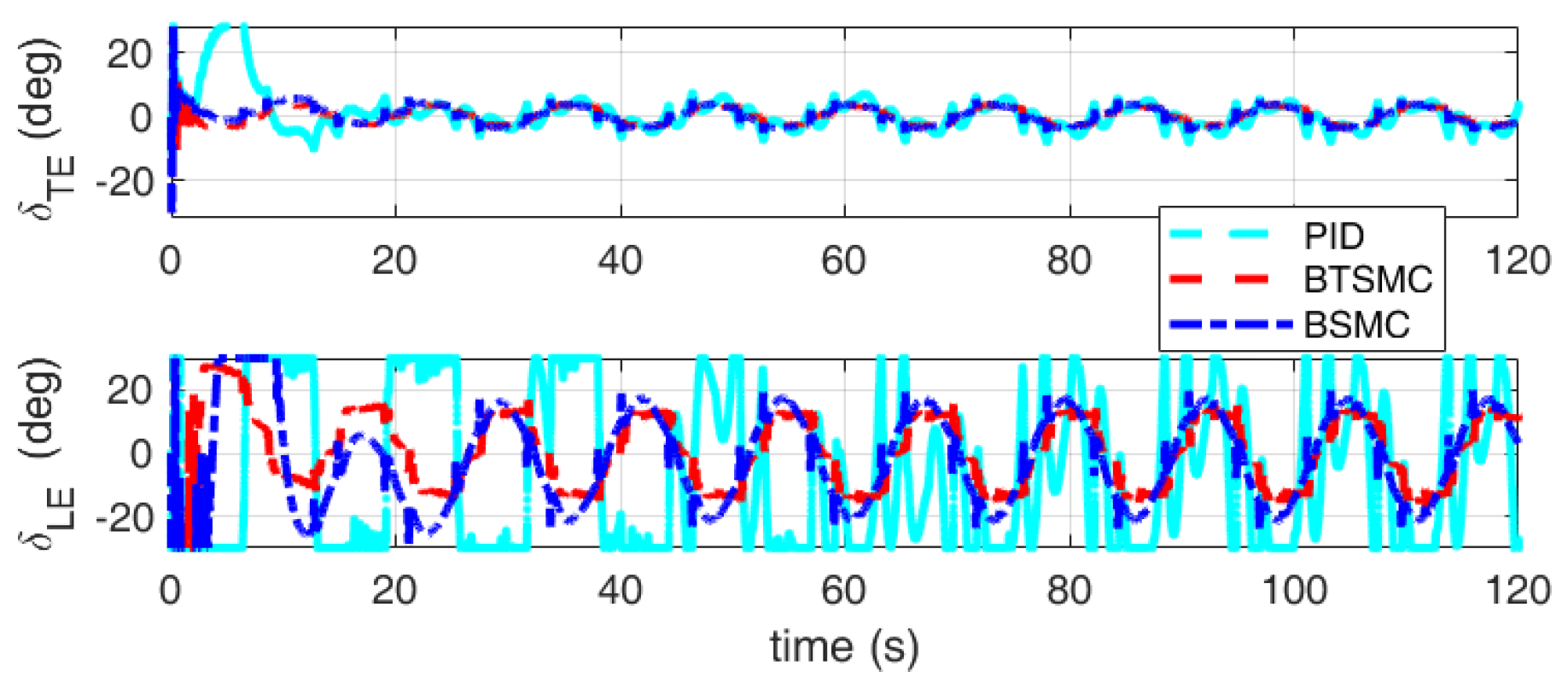
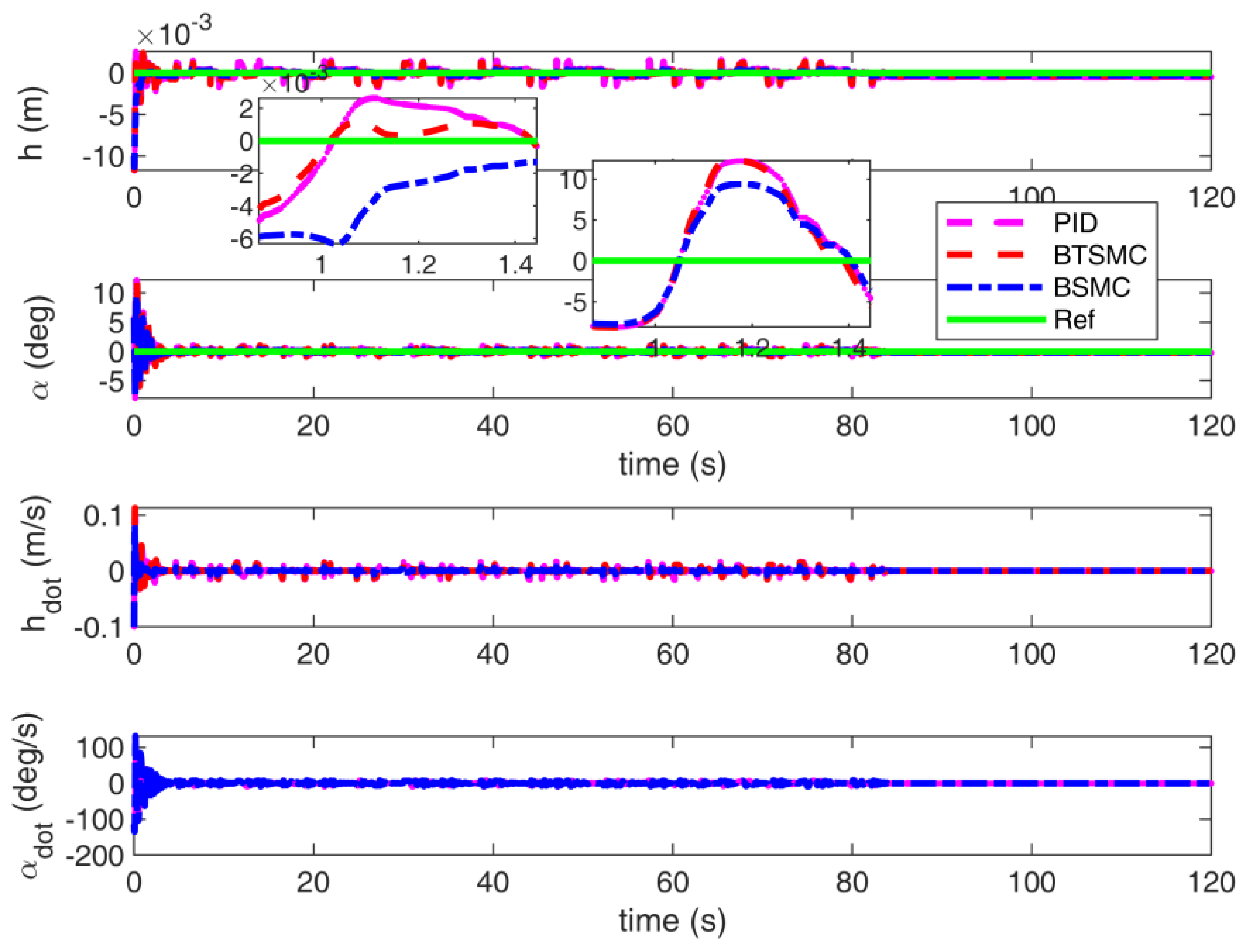
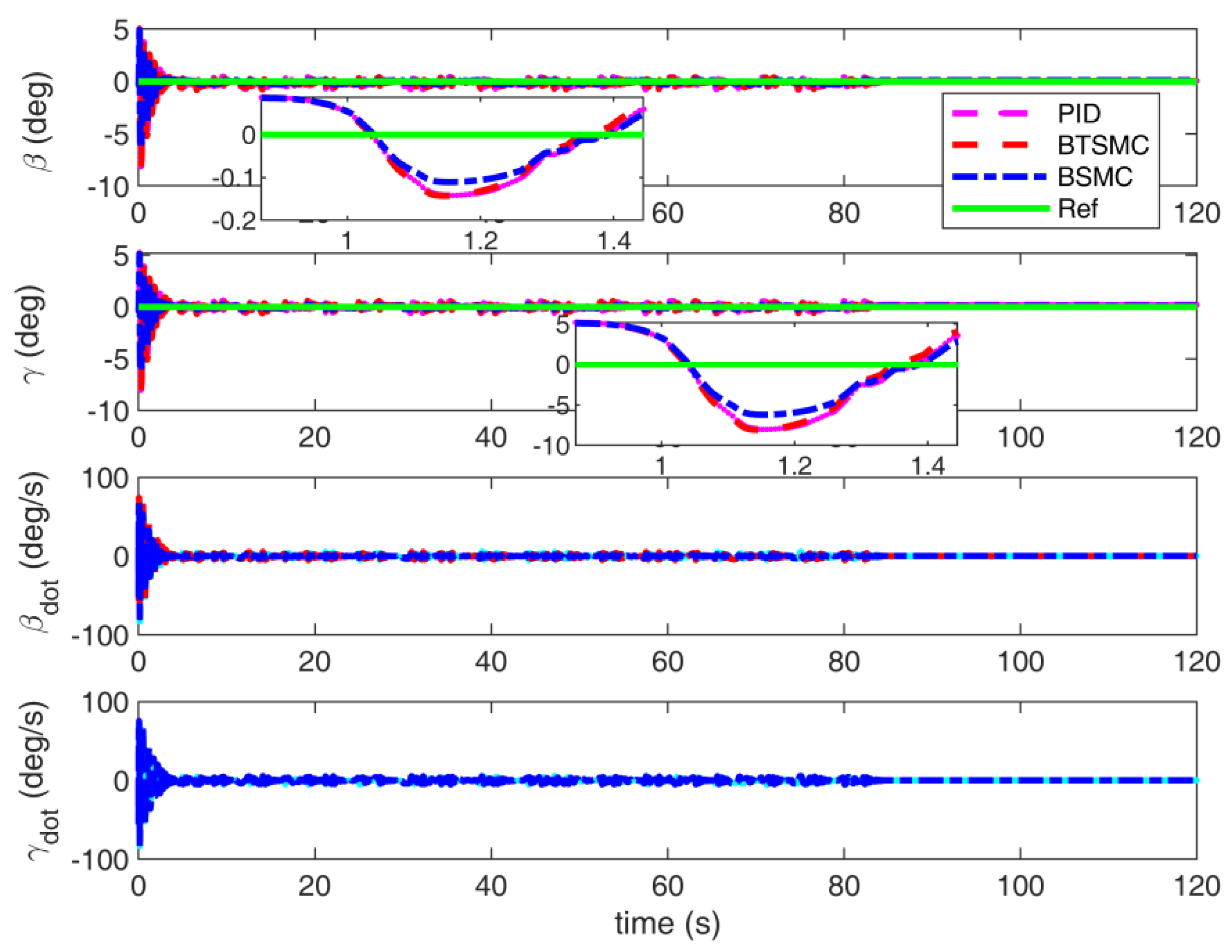
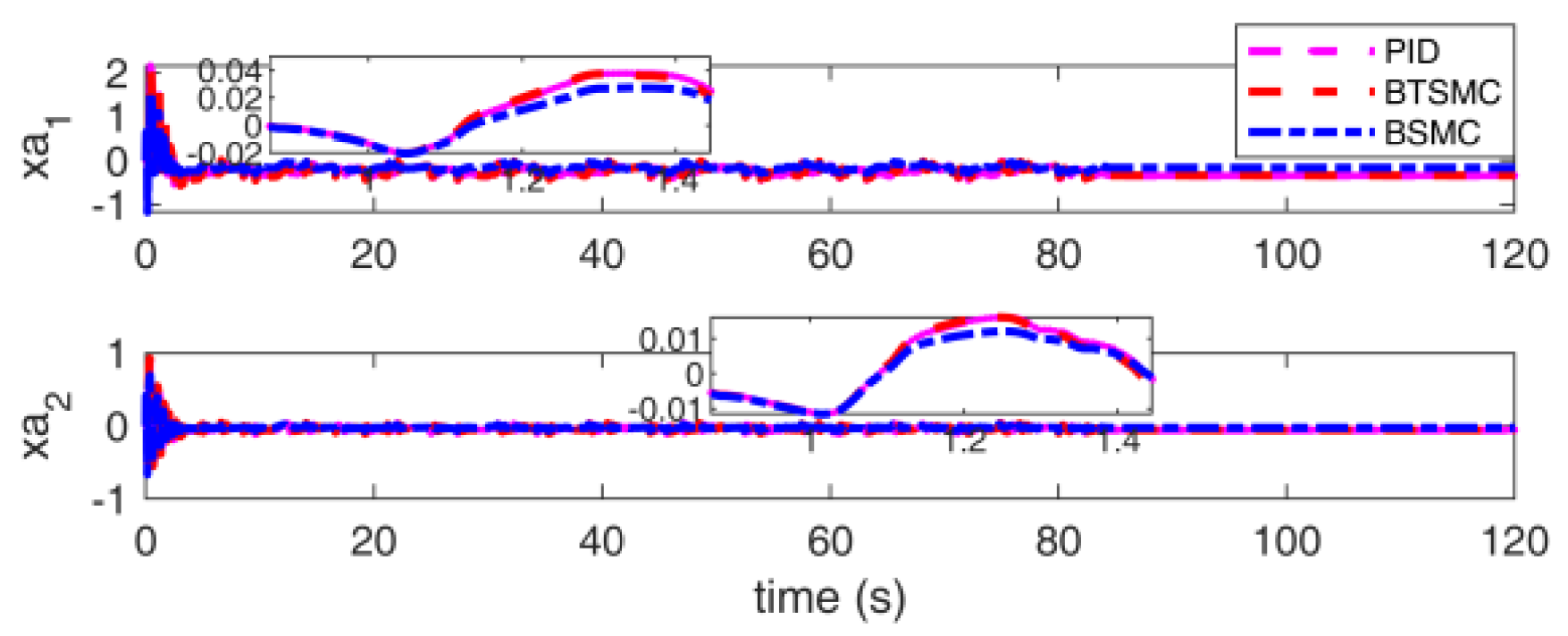
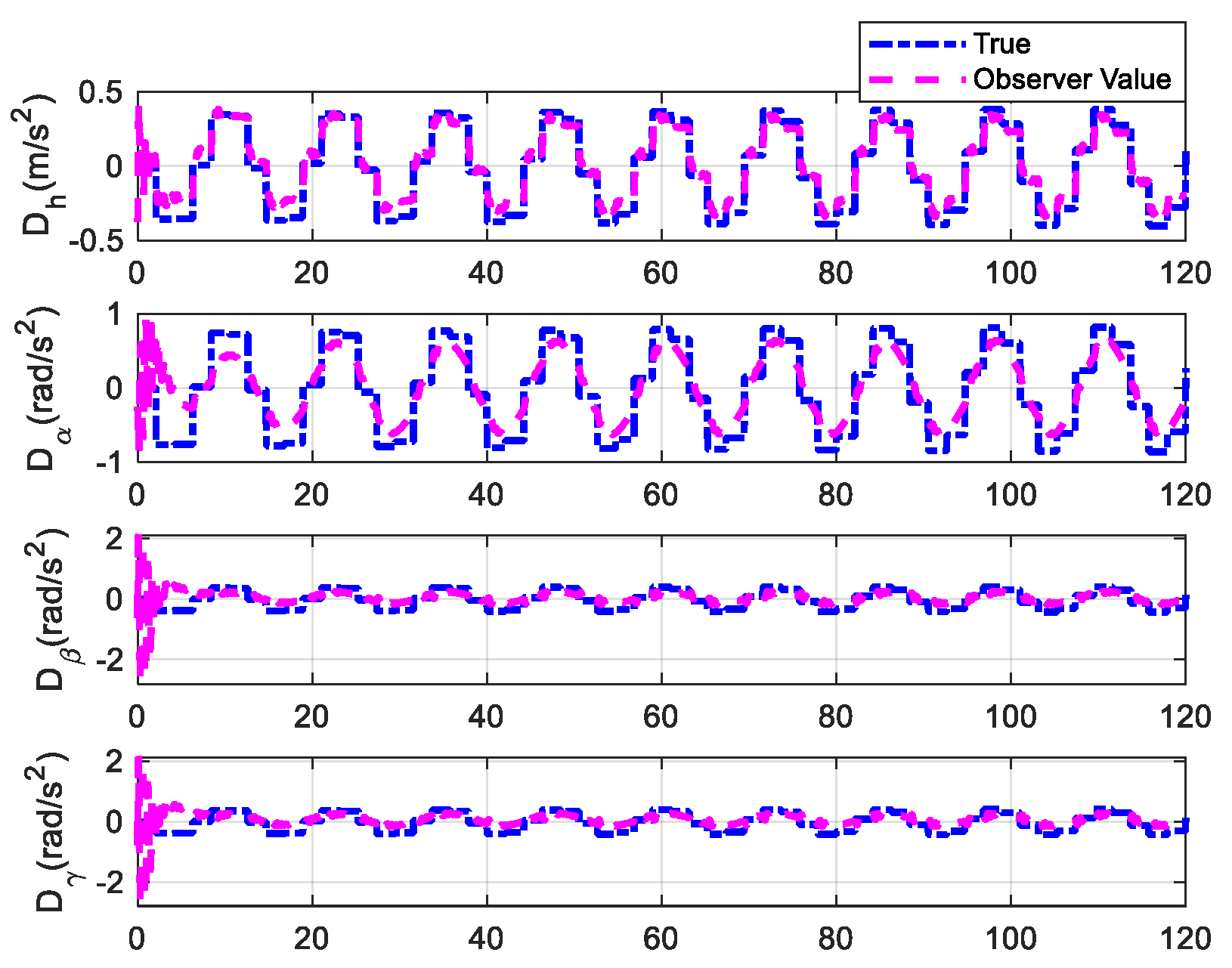
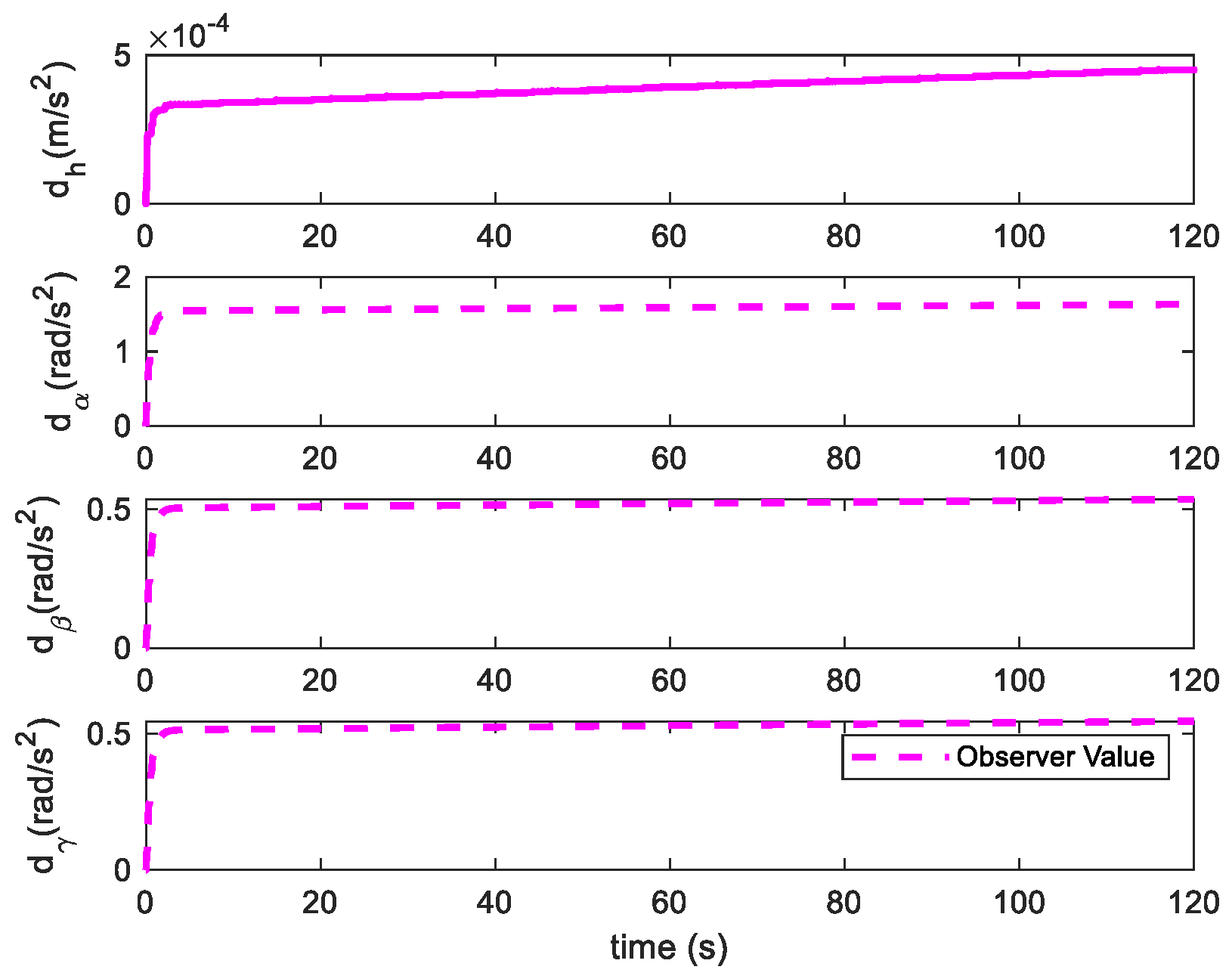
4.1. Flutter Suppression
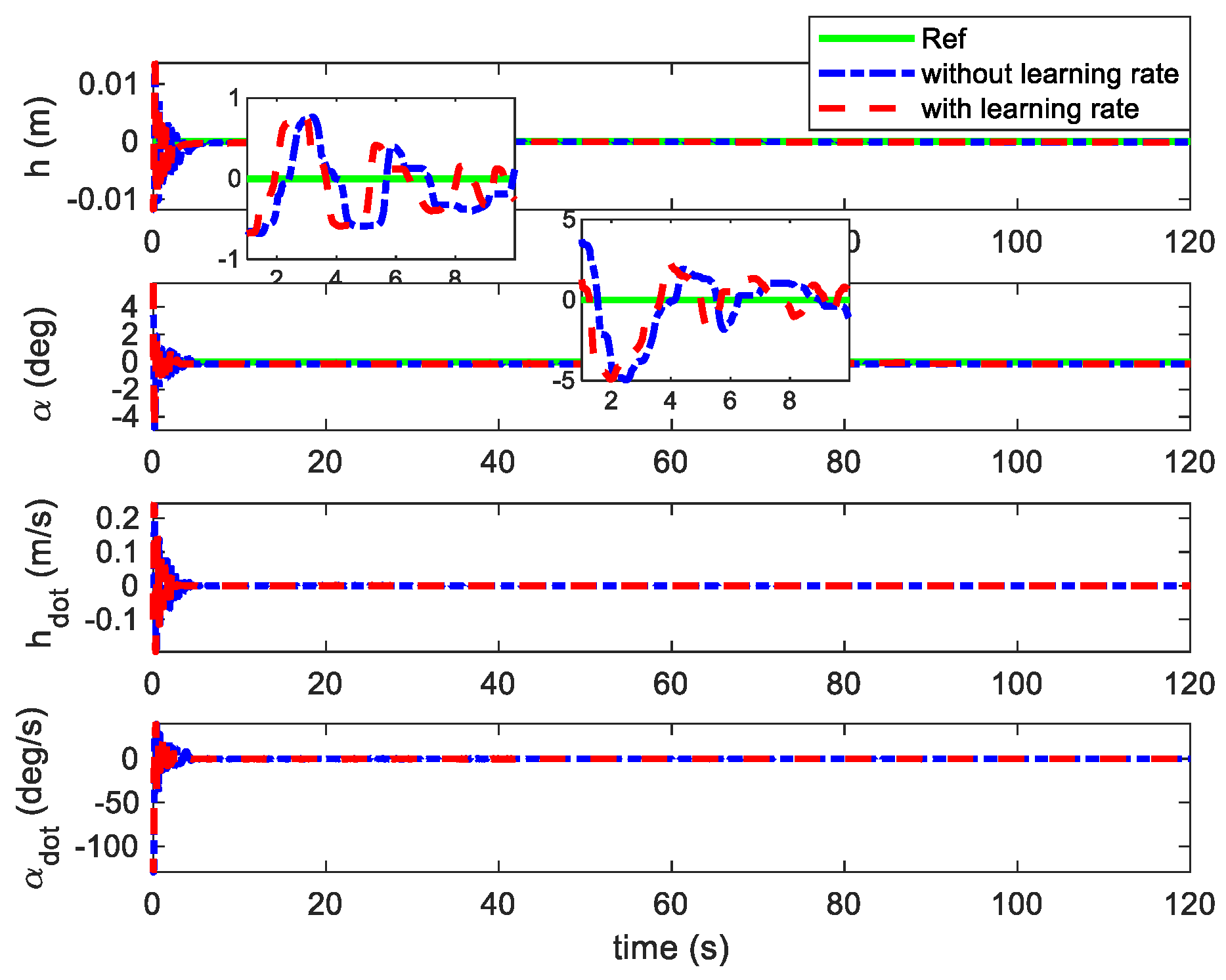
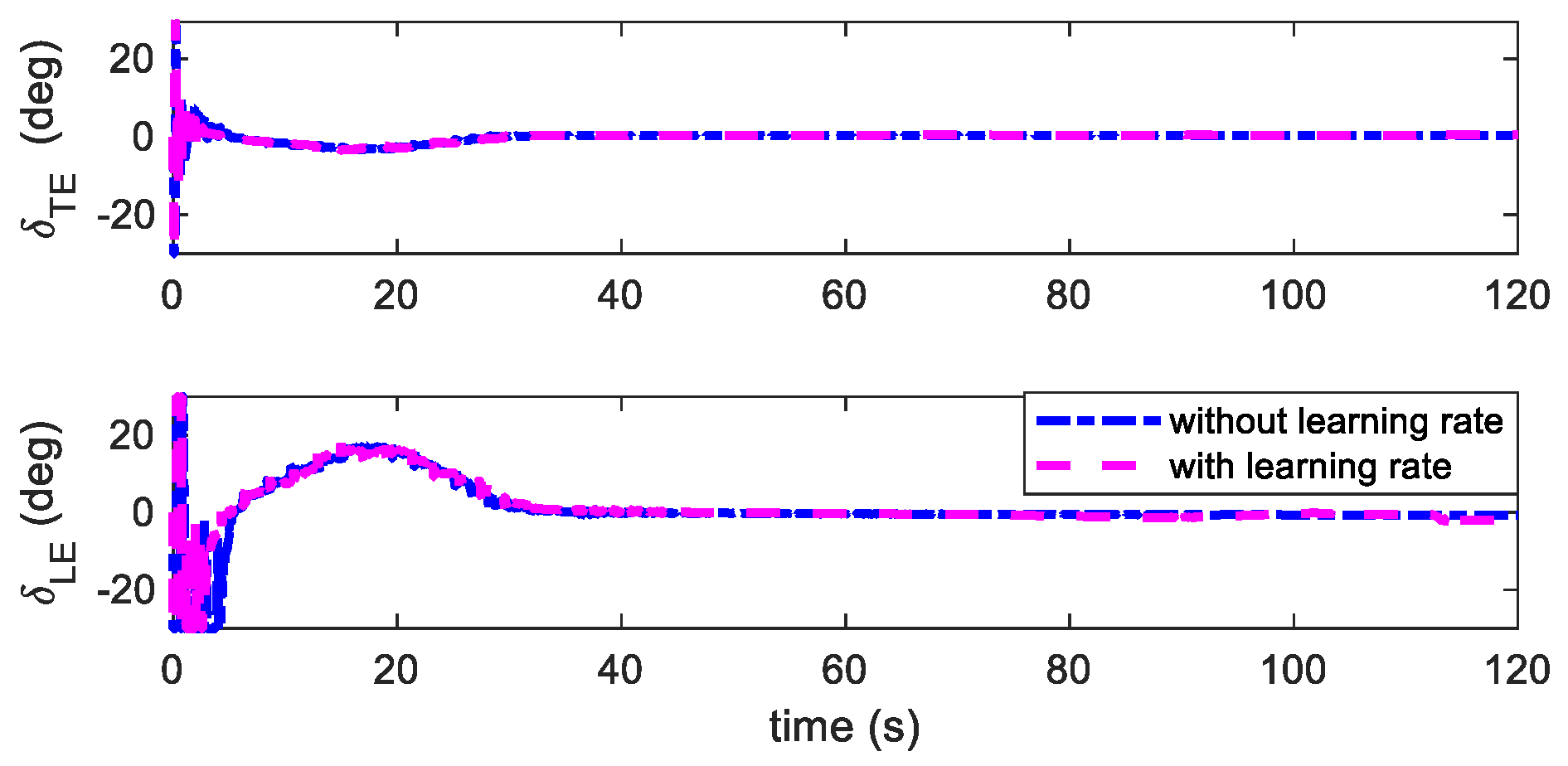
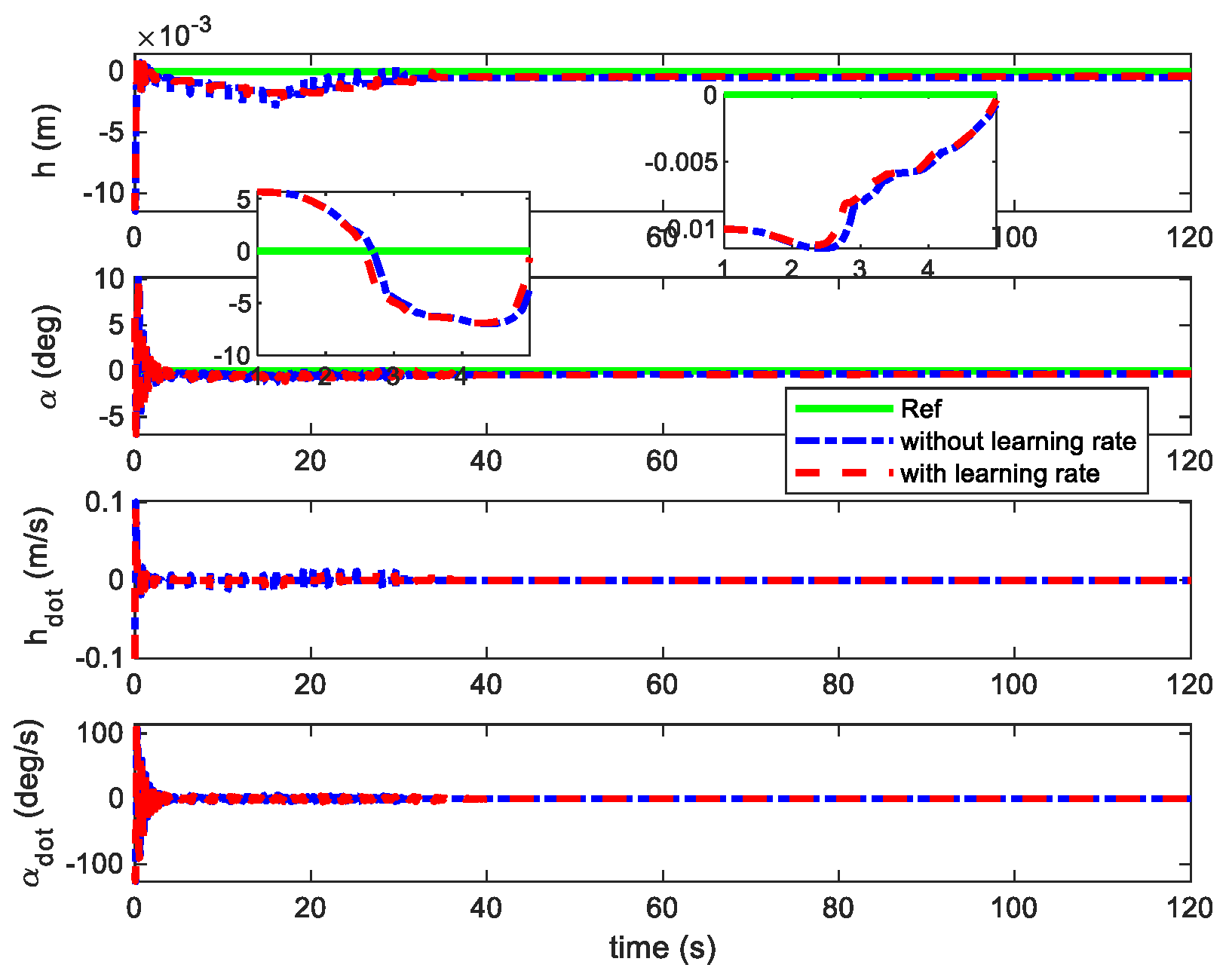
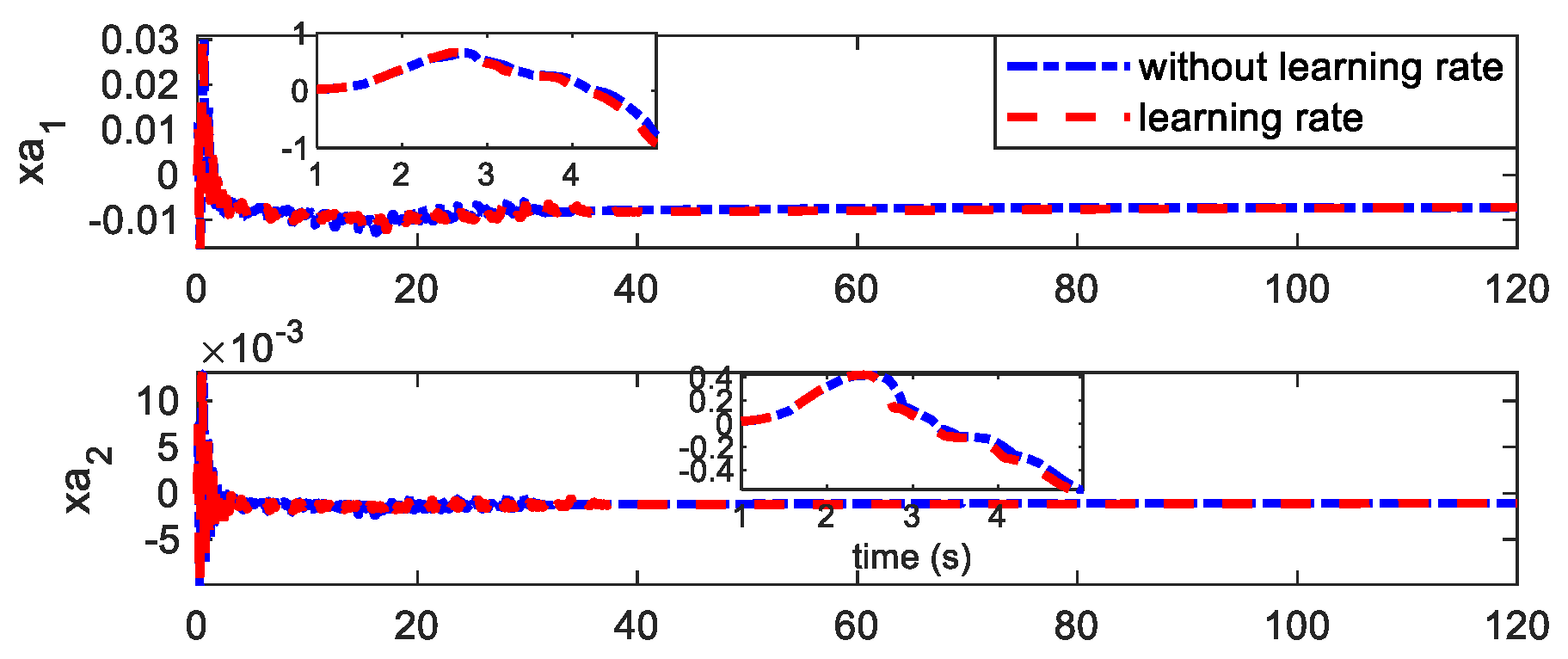
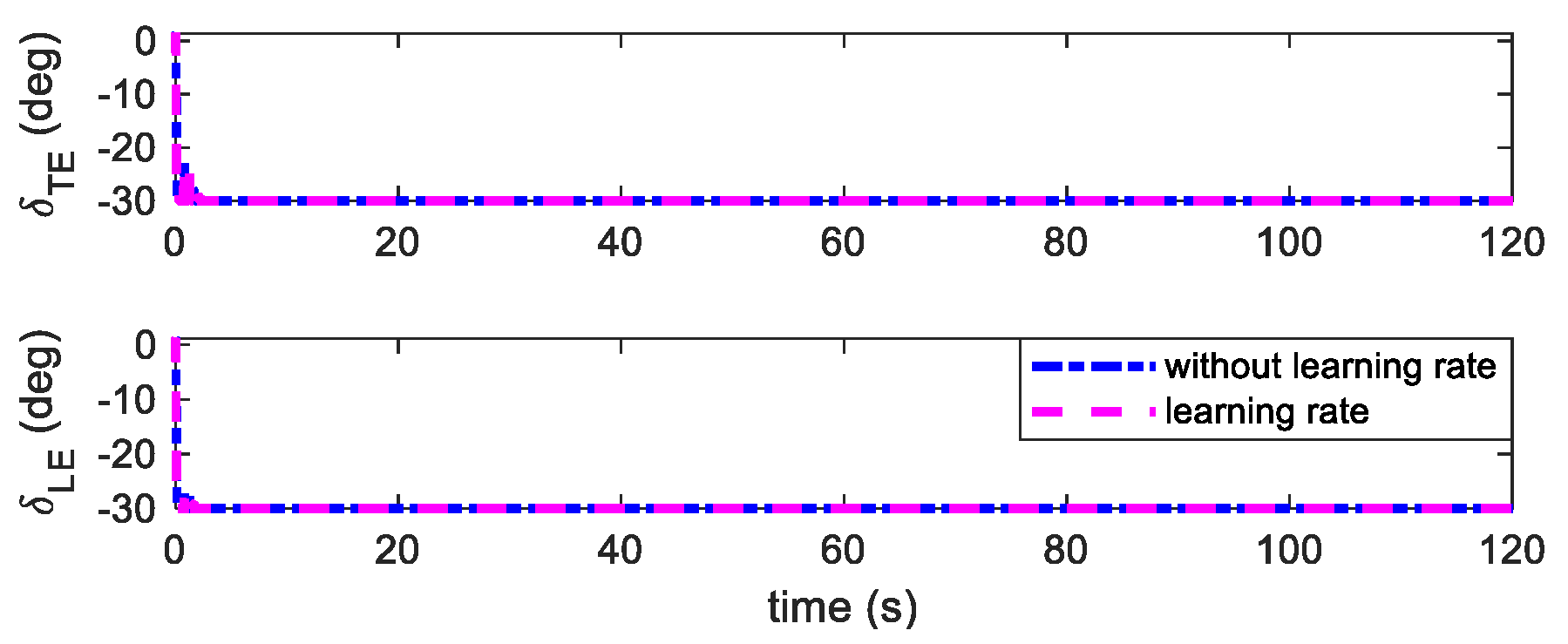
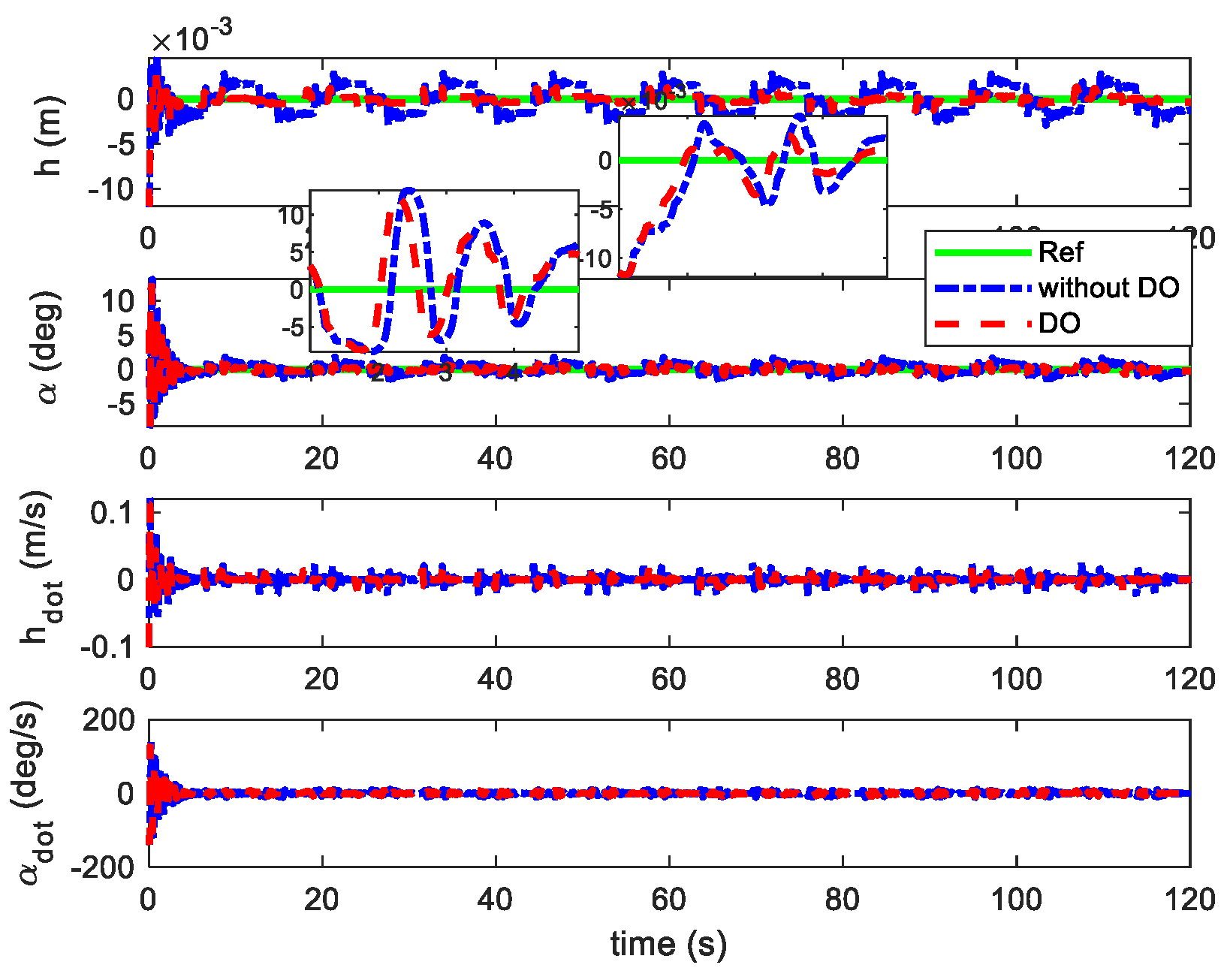
4.2. Flutter Suppression Under Unknown Wind Disturbances
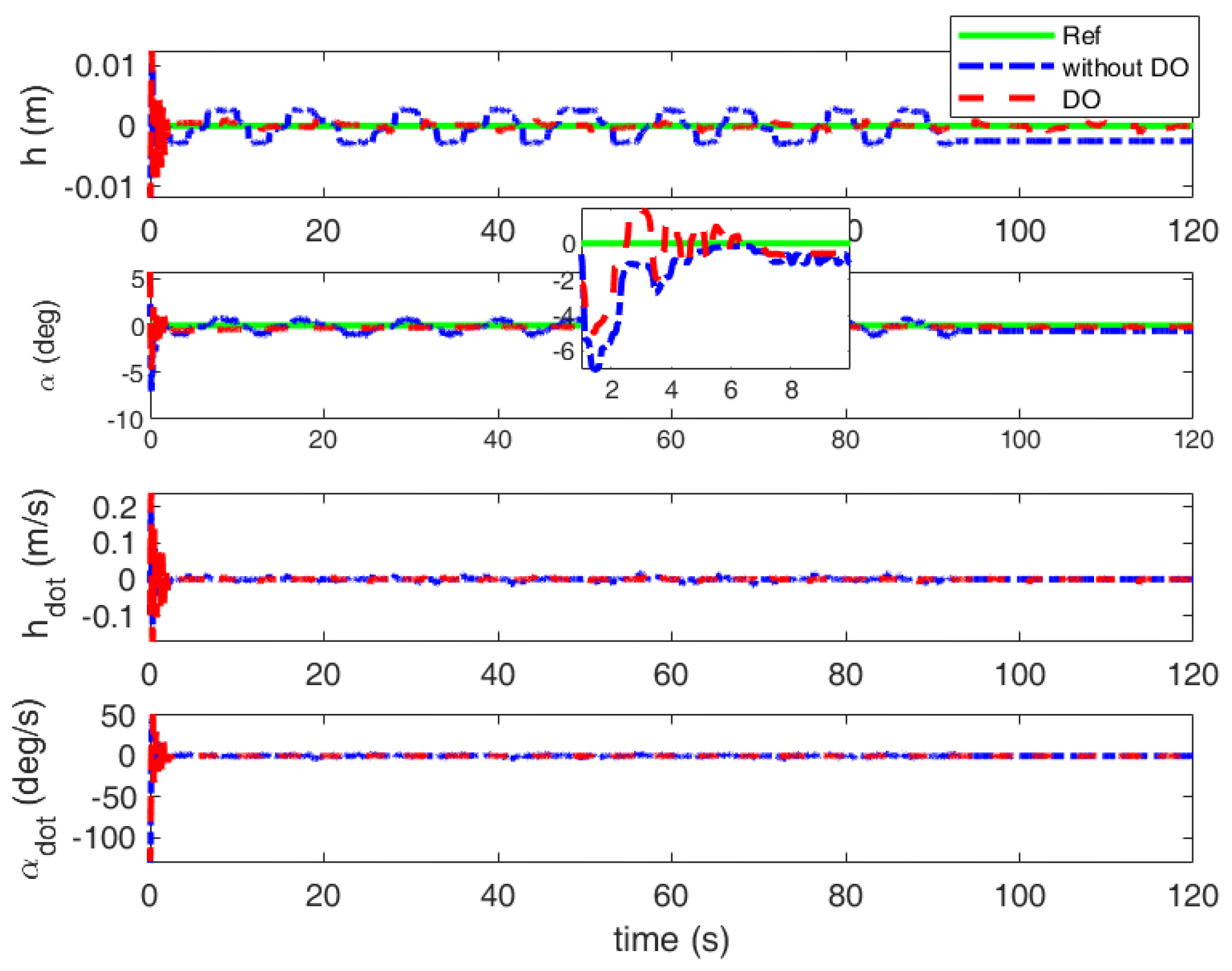
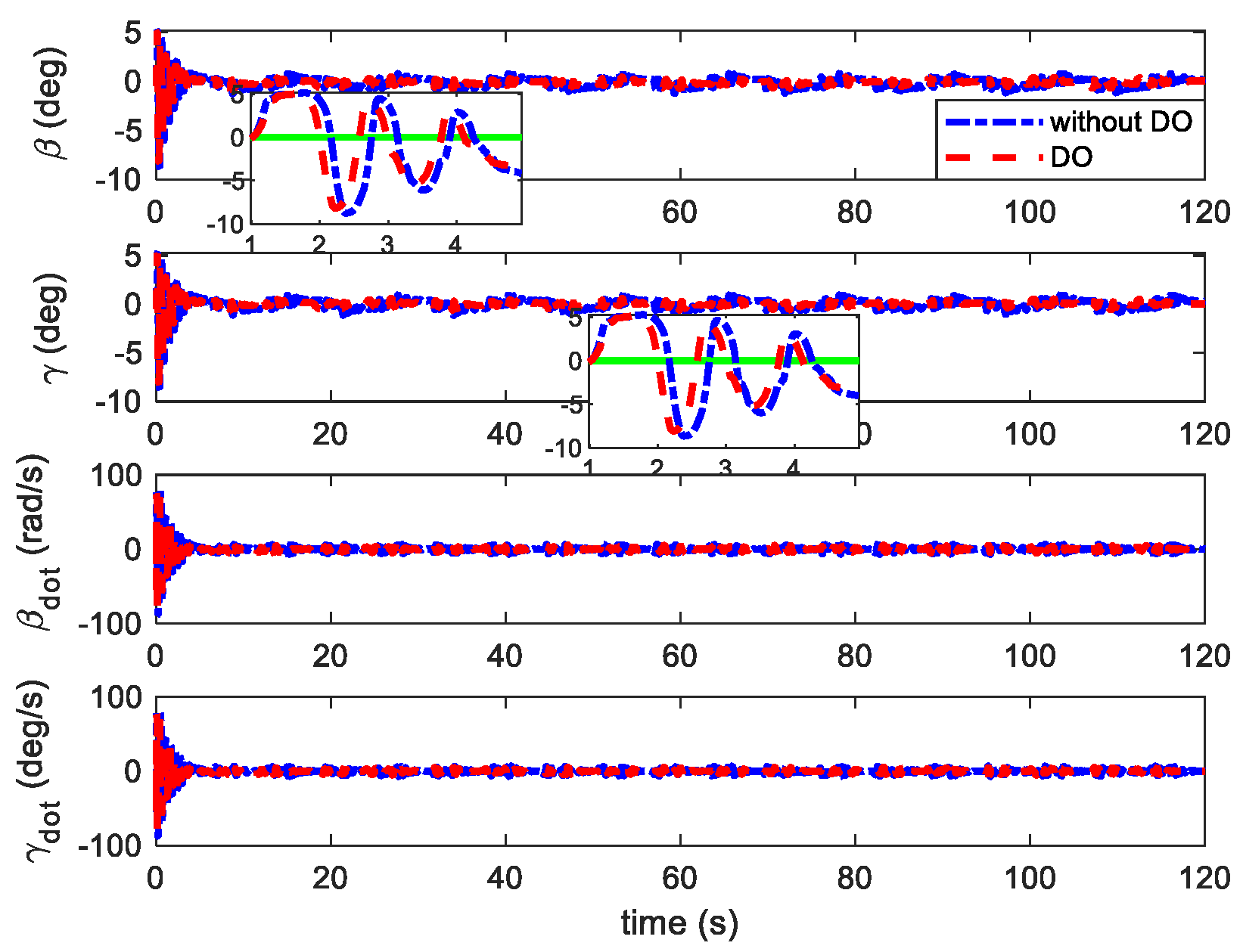
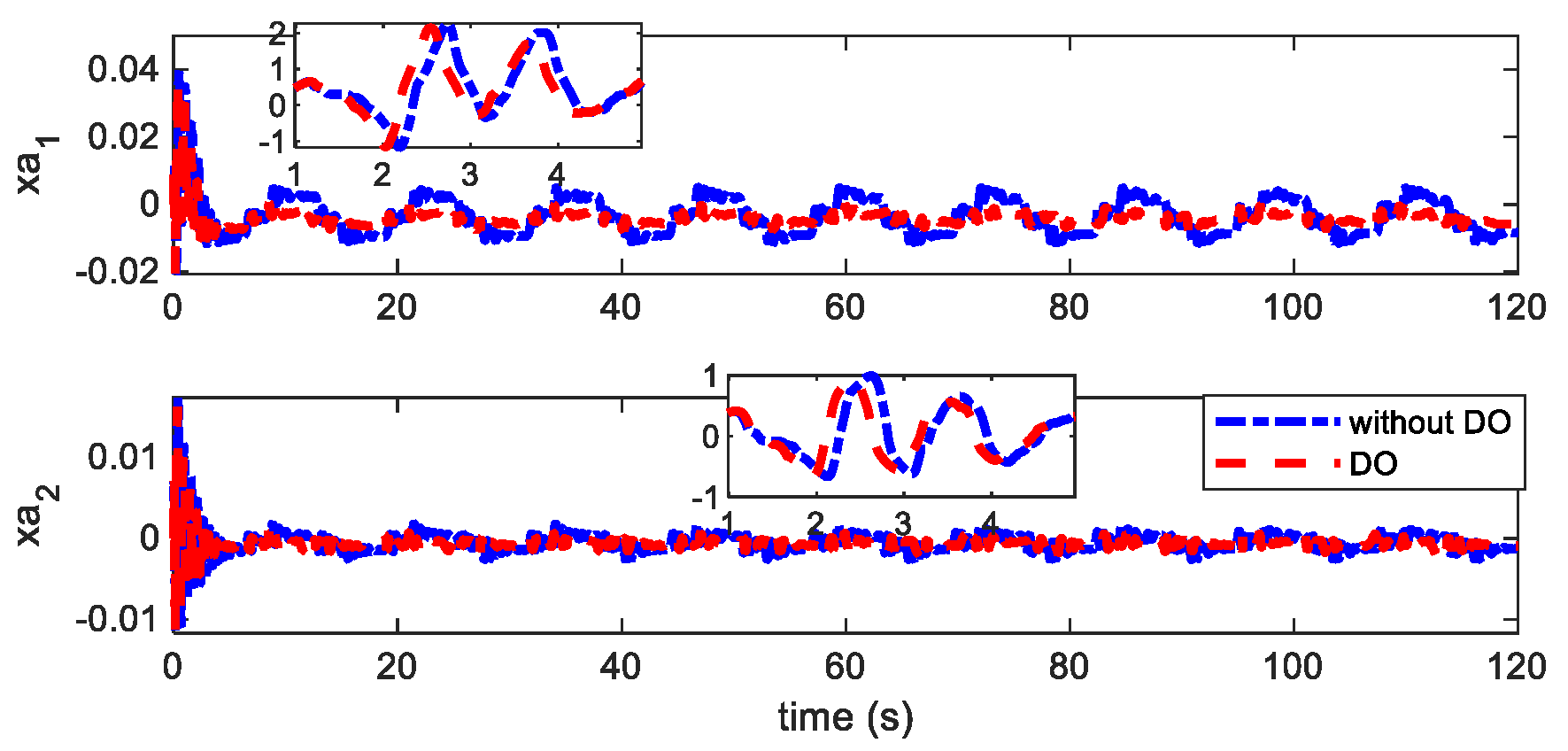
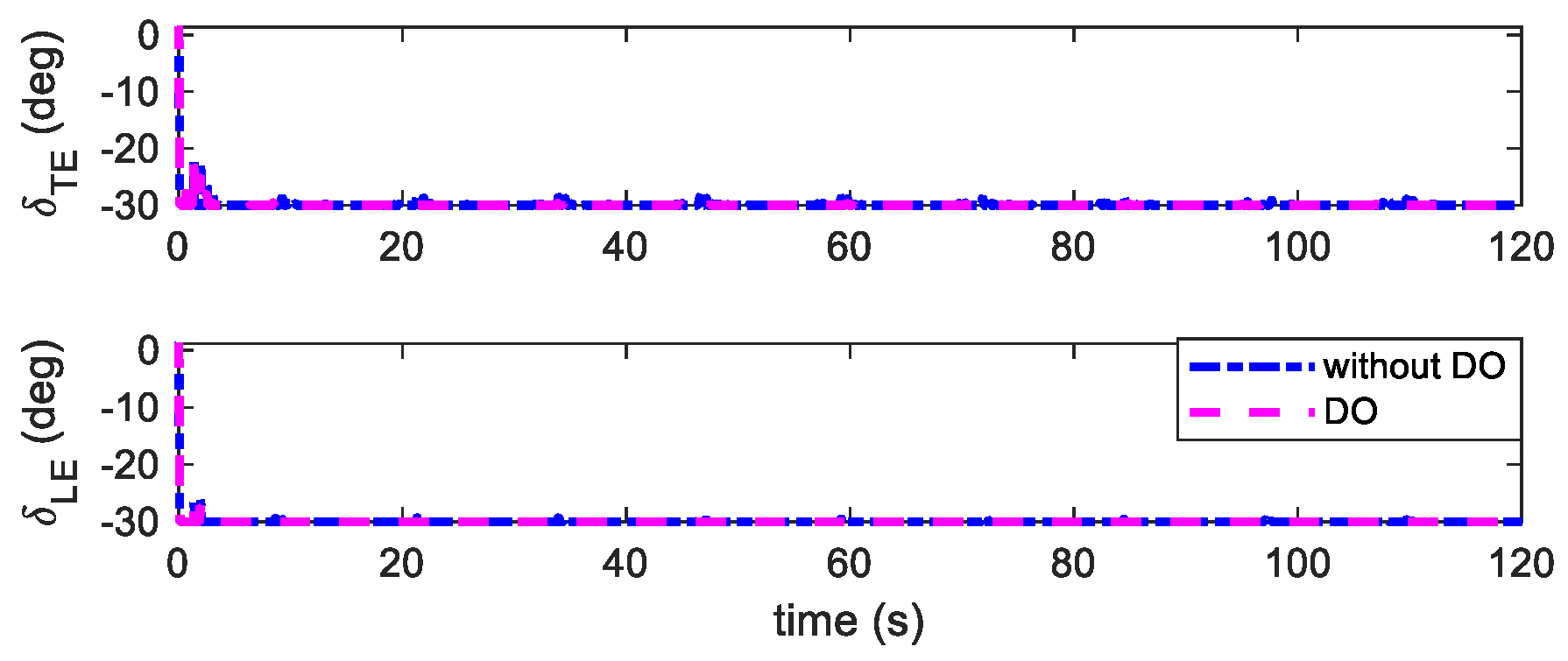
4.3. Robust Flutter Suppression with Parameter Uncertainties and Disturbances
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Aeroelastic Controller Design
Appendix B. Expression for the T Functions
References
- Dowell, E.H. A Modern Course in Aeroelasticity, 4th ed.; Kluwer Academic Publisher: Norwell, MA, USA, 2005. [Google Scholar]
- Gordon, J.T.; Meyer, E.E.; Minogue, R.L. Nonlinear stability analysis of control surface flutter with freeplay effects. J. Aircr. 2008, 45, 1904–1916. [Google Scholar] [CrossRef]
- Mukhopadhyay, V. Historical perspective on analysis and control of aeroelastic responses. J. Guid. Control Dyn. 2003, 26, 673–684. [Google Scholar] [CrossRef]
- Chai, Y.; Gao, W.; Ankay, B.; Li, F.; Zhang, C. Aeroelastic analysis and flutter control of wings and panels: A review. Int. J. Mech. Syst. Dyn. 2021, 1, 5–34. [Google Scholar] [CrossRef]
- Ouyang, Y.; Gu, Y.; Kou, X.; Yang, Z. Active flutter suppression of wing with morphing flap. Aerosp. Sci. Technol. 2021, 110, 106457. [Google Scholar] [CrossRef]
- Na, S.; Song, J.S.; Choo, J.H.; Qin, Z.M. Dynamic aeroelastic response and active control of composite thin-walled beam structures in compressible flow. J. Sound Vib. 2011, 330, 4998–5013. [Google Scholar] [CrossRef]
- O’Neil, T.; Strganac, T.W. Aeroelastic response of a rigid wing supported by nonlinear springs. J. Aircr. 1998, 35, 673–684. [Google Scholar] [CrossRef]
- Lee, H.K.; Jiang, L.Y.; Wong, Y.S. Flutter of an airfoil with a cubic nonlinear restoring force. J. Fluids Struct. 1999, 13, 75–101. [Google Scholar] [CrossRef]
- Singh, S.N.; Wang, L. Output feedback form and adaptive stabilization of a nonlinear aeroelastic system. J. Guid. Control Dyn. 2002, 25, 725–732. [Google Scholar] [CrossRef]
- Lin, C.M.; Chin, W.L. Adaptive decouple fuzzy sliding mode control of a nonlinear aeroelastic system. J. Guid. Control Dyn. 2006, 29, 206–209. [Google Scholar] [CrossRef]
- Chen, C.L.; Chang, C.W.; Yau, H.T. Terminal sliding mode control for aeroelastic systems. Nonlinear Dyn. 2012, 70, 2015–2026. [Google Scholar] [CrossRef]
- Bouma, A.; Basconcellos, R.; Abdelkefi, A. Nonlinear aeroelastic modeling and comparative studies of three degrees of freedom wing-based systems. Int. J. Non-Linear Mech. 2023, 149, 104326. [Google Scholar] [CrossRef]
- Vishal, S.; Ashwad, R.; Chandan, B.; Venkatramani, J. Routes to Synchronization in a pitch–plunge aeroelastic system with coupled structural and aerodynamic nonlinearities. Int. J. Non-Linear Mech. 2021, 135, 103766. [Google Scholar] [CrossRef]
- Livne, E. Active Flutter suppression state of the art and technology maturation needs. J. Aircr. 2018, 55, 410–450. [Google Scholar] [CrossRef]
- Zou, Q.T.; Huang, R.; Hu, H.Y. Body-freedom flutter suppression for a flexible flying-wing drone via time-delayed control. J. Guid. Control Dyn. 2022, 45, 28–38. [Google Scholar] [CrossRef]
- Trapani, M.; Guo, S. Design and analysis of a rudderless aeroelastic fin. Proc. IMechE Part G J. Aerosp. Eng. 2009, 223, 701–710. [Google Scholar] [CrossRef]
- Zhang, K.; Behal, A. Continuous robust control for aeroelastic vibration control of a 2-D airfoil under unsteady flow. J. Vib. Control 2016, 22, 2841–2860. [Google Scholar] [CrossRef]
- Lee, K.W.; Singh, S.N. L1 Adaptive control of an aeroelastic System with unsteady aerodynamics and gust Load. J. Vib. Control 2016, 24, 303–322. [Google Scholar] [CrossRef]
- Platanitis, G.; Strganac, T.W. Control of a nonlinear wing section using leading- and trailing-edge surfaces. J. Guid. Control Dyn. 2004, 27, 52–58. [Google Scholar] [CrossRef]
- Prime, Z.D. Robust Scheduling Control of Aeroelasticity. Ph.D. Thesis, University of Adelaide, Adelaide, Australia, 2010. [Google Scholar]
- Li, D.C.; Guo, S.J.; Xiang, J.W. Aeroelastic dynamic response and control of an airfoil section with control surface nonlinearities. J. Sound Vib. 2010, 329, 4756–4771. [Google Scholar] [CrossRef]
- Tang, L.D.; Chen, Z.; Tian, F.; Hu, E. A neural network approach for improving airfoil active flutter suppression under control input constraints. J. Vib. Control 2021, 27, 451–467. [Google Scholar] [CrossRef]
- Gao, M.Z.; Cai, G.P.; Nan, Y. Finite-time fault-tolerant control for flutter of wing. Control Eng. Pract. 2016, 51, 26–47. [Google Scholar]
- Chen, Z.; Shi, Z.W.; Chen, S.N.; Tong, S.X. Active flutter suppression for a flexible wing model with trailing-edge circulation control via reinforcement learning. AIP Adv. 2023, 13, 015317. [Google Scholar] [CrossRef]
- Pettit, C.L. Uncertainty quantification in aeroelasticity: Recent results and research challenges. J. Aircr. 2004, 41, 1217–1229. [Google Scholar] [CrossRef]
- Hao, Y.; Ma, C.; Hu, Y.D. Nonlinear stochastic flutter analysis of a three-degree-of-freedom wing in a two-dimensional flow field under stochastic perturbations. Aerosp. Sci. Technol. 2023, 138, 108323. [Google Scholar] [CrossRef]
- Lee, K.W.; Singh, S.N. Robust higher-order super-twisting control of aeroelastic system with unsteady aerodynamics. In Proceedings of the 2018 AIAA Guidance, Navigation, and Control Conference, AIAA SciTech Forum, Kissimmee, FL, USA, 8–12 January 2018; pp. 2018–2341. [Google Scholar]
- Prabhu, L.; Srinivas, J. Robust control of a three degrees of freedom aeroelastic model using an intelligent observer. In Proceedings of the 2015 International Conference on Robotics, Automation, Control and Embedded Systems (RACE), Chennai, India, 18–20 February 2015; pp. 1–5. [Google Scholar]
- Yuan, J.X.; Qi, N.; Qiu, Z.; Wang, F.X. Sliding Mode Observer Controller Design for a Two Dimensional Aeroelastic System with Gust Load. Asian J. Control 2019, 21, 130–142. [Google Scholar] [CrossRef]
- Xu, X.; Wu, W.; Zhang, W. Sliding mode control for a nonlinear aeroelastic system through backstepping. J. Aerosp. Eng. 2018, 31, 04017080. [Google Scholar] [CrossRef]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Liu, S.Q.; Whidborne, J.F. Neural network adaptive backstepping fault tolerant control for unmanned airships with multi-vectored thrusters. Proc. IMechE Part G J. Aerosp. Eng. 2021, 235, 1507–1520. [Google Scholar] [CrossRef]
- Thordorsen, T.; Garrice, I.E. Nonstatoinary Flow about a Wing Aileron Tab Combination Including Aerodynamic Balance; 19930091815, NACA Report No. 736; US Government Printing Office: Washington, DC, USA, 1942; pp. 129–138.
- Edwards, J.W. Unsteady Aerodynamic Modeling and Active Aeroelastic Control. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1977. [Google Scholar]
- Theodorsen, T. General Theory of Aerodynamic Instability and Mechanism of Flutter; NACA Report No. 496; US Government Printing Office: Washington, DC, USA, 1935; pp. 291–311.
- Marzocca, P.; Librescu, L.; Chiocchia, G. Aeroelastic response of 2-D lifting surfaces to gust and arbitrary explosive loading signatures. Int. J. Impact Eng. 2001, 25, 41–65. [Google Scholar] [CrossRef]
- Chen, W.H.; Ballance, D.J.; Gawthrop, P.J.; O’Reilly, J. A nonlinear disturbance roobserver for robotic manipulators. IEEE Trans. Ind. Electron. 2000, 47, 932–938. [Google Scholar] [CrossRef]
- Prime, Z.; Cazzolato, B.; Doolan, C.; Strganac, T. Linear-parameter-varying control of an improved three-degree-of-freedom aeroelastic model. J. Guid. Control Dyn. 2010, 33, 615–618. [Google Scholar] [CrossRef]
- Hassig, H. An approximate true damping solution of the flutter equation by determinant iteration. J. Aircr. 1971, 8, 885–889. [Google Scholar] [CrossRef]
- Liu, S.Q.; Whidborne, J.F.; He, L. Backstepping sliding-mode control of stratospheric airships using disturbance-observer. Adv. Space Res. 2021, 67, 1174–1187. [Google Scholar] [CrossRef]
- Van, M.; Mavrovouniotis, M.; Ge, S.S. An adaptive backstepping nonsingular fast terminal sliding mode control for robust fault tolerant control of robot manipulators. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2019, 49, 1448–1458. [Google Scholar] [CrossRef]







| Quasi-Steady Aerodynamic Model | Unsteady Aerodynamic Model | ||
|---|---|---|---|
| Parameter | Value | Parameter | Value |
| mwing | 4.34 kg | mh | 6.815 kg |
| mW(total) | 5.23 kg | mα | 5.715 kg |
| mT | 15.57 kg | mβ | 0.537 kg |
| sp | 0.5945 m | mγ | 0.5 kg |
| b | 0.1905 m | Iα | 0.119 kg·m2 |
| a | −0.6719 | Iβ | 1 × 10−5 kg·m2 |
| c | 0.381 m | Iγ | 1 × 10−5 kg·m2 |
| ICG.wing | 0.04342 kg·m2 | rα | 0.040 m |
| Icam | 0.04697 kg·m2 | rβ | 0 |
| ch | 27.43 kg/s | rγ | 0 |
| cα | 0.0360 kg·m2/s | rac | −0.033 m |
| ρ | 1.225 kg/m3 | r3/4c | 0.233 m |
| rcg | −b(0.0998+a) | Lβ | 0.233 m |
| CLα | 6.757 | Lγ | -0.01 m |
| CLβ | 3.774 | kβs | 766.08 Iβ |
| Cmα | 0 | cβs | 41.82 Iβ |
| Cmβ | −0.6719 | kγs | 530.24 Iγ |
| CLγ | −0.1566 | cγs | 44.27 Iγ |
| Cmγ | −0.1005 | cα | 0.205 Nm·s/rad |
| kh | 2844 N/m | ch | 27.43 Nm·s/rad |
| xα | rcg/b m | ωnβs | 27.68 rad/s |
| fLE | 0.15 | ζβs | 0.7555 |
| fTE | 0.2 | ωnγs | 23.03 rad/s |
| Iα | Icam + ICG.wing + mwing(rcg)2 kg⸱m2 | ζγs kh | 0.961 2844 N/m |
| kα | 12.77 + 53.47α + 1003α2Nm/rad | kα | 27.96 − 167.63α + 552.55α2 + 1589.3α3 − 3247.2α4 |
| Controller | Parameters | Value |
|---|---|---|
| PID | kp,z1, ki,z1, kp,z2, ki,z2 | diag(0.1,0.1), diag(0.1,0.1), diag(1,1), diag(0.4,0.4) |
| BTSMC | The same as Section 4.1 | |
| BSMC | K1, λ1 | diag(0.4,0.2), diag(0.5,0.5) |
| hs, ς | diag(0.5,0.5), diag(50, 30) | |
| φs, βs | 0.4, 1 |
| Gust Input | Controller | Data | Rising Time (s) | Over- Shoots | RMSE |
|---|---|---|---|---|---|
| Triangular gust (Case I, Example 1) | No LR (with DO) | h | 0.1770 | 0.0134 | 0.0023 |
| α | – | – | 0.0129 | ||
| LR (with DO) | h | 0.1187 | 0.0136 | 0.0022 | |
| α | – | – | 0.0120 | ||
| Sine gust (Case I, Example 2) | No DO (No LR) | h | 0.1084 | 0.0104 | 0.0027 |
| α | – | – | 0.0160 | ||
| DO (No LR) | h | 0.1205 | 0.0124 | 0.0018 | |
| α | – | – | 0.0110 |
| Controller | Variant | Rising Time (s) | Over- Shoots | RMSE |
|---|---|---|---|---|
| DO-PID | h | 0.1467 | 0.0067 | 0.0026 |
| α | - | - | 0.0345 | |
| DO- BTSMC | h | 0.1187 | 0.0136 | 0.0021 |
| α | - | - | 0.0120 | |
| DO- BSMC | h | 0.1215 | 0.0118 | 0.0022 |
| α | - | - | 0.0153 |
| Controller | Parameters | Value |
|---|---|---|
| PID | kp,z1, ki,z1, kp,z2, ki,z2 | diag(0.1,0.1,0.1,0.1), diag(0.1,0.1,0.1,0.1), diag(1,1,1,1), diag(0.4,0.4, 0.4, 0.4) |
| BTSMC | K1, λ1 | K1 = diag(0.2,0.1,0.1,0.1), λ = 1.8 × diag(1,1,1,1). |
| p, q | 5, 3 | |
| β, α0, β1 | β = diag(1,1,1,1), α0 = 10, β1 = 3, | |
| hs, ς | hs = diag(0.5,0.5,0.5,0.5), ς = diag(30,50, 30, 30), | |
| φs, βs | φs = 0.4, βs = 1 | |
| BSMC | K1, λ1 | diag(0.2,0.1,0.1,0.1), diag(0.5,0.5,0.5,0.5) |
| hs, ς | diag(0.5,0.5,0.5,0.5), diag(30,50, 30, 30) | |
| φs, βs | 0.4, 1 |
| Gust Input | Controller | Data | Rising Time (s) | Over- Shoots | RMSE |
|---|---|---|---|---|---|
| Triangular gust (Case II, Example 3) | No LR (with DO) | h | 0.2438 | 0.0010 | 0.0022 |
| α | - | 0.1758 | 0.0285 | ||
| LR (with DO) | h | 0.2278 | 0.0015 | 0.0020 | |
| α | - | 0.1782 | 0.0281 | ||
| Sine gust (Case II, Example 4) | No DO (No LR) | h | 0.1704 | 0.0045 | 0.0019 |
| α | - | 0.2312 | 0.0267 | ||
| DO (No LR) | h | 0.1447 | 0.0025 | 0.0013 | |
| α | - | 0.2144 | 0.0218 |
| Controller | Variant | Rising Time (s) | Over- Shoots | RMSE |
|---|---|---|---|---|
| DO-PID | h | 0.1481 | 0.0077 | 0.0025 |
| α | - | - | 0.0447 | |
| DO- BTSMC | h | 0.1205 | 0.0124 | 0.0018 |
| α | - | - | 0.0110 | |
| DO- BSMC | h | 0.1275 | 0.0045 | 0.0014 |
| α | - | - | 0.0173 |
| Controller | Variant | Rising Time (s) | Over- Shoots | RMSE |
|---|---|---|---|---|
| DO-PID | h | 0.1916 | 0.0024 | 0.0017 |
| α | - | 0.2137 | 0.0199 | |
| DO- BTSMC | h | 0.1415 | 0.0025 | 0.0010 |
| α | - | 0.2147 | 0.0183 | |
| DO- BSMC | h | 1.3885 | 0.0004 | 0.0010 |
| α | - | 0.1645 | 0.0151 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Yang, C.; Zhang, Q.; Whidborne, J.F. Disturbance Observer-Based Backstepping Terminal Sliding Mode Aeroelastic Control of Airfoils. Aerospace 2024, 11, 882. https://doi.org/10.3390/aerospace11110882
Liu S, Yang C, Zhang Q, Whidborne JF. Disturbance Observer-Based Backstepping Terminal Sliding Mode Aeroelastic Control of Airfoils. Aerospace. 2024; 11(11):882. https://doi.org/10.3390/aerospace11110882
Chicago/Turabian StyleLiu, Shiqian, Congjie Yang, Qian Zhang, and James F. Whidborne. 2024. "Disturbance Observer-Based Backstepping Terminal Sliding Mode Aeroelastic Control of Airfoils" Aerospace 11, no. 11: 882. https://doi.org/10.3390/aerospace11110882
APA StyleLiu, S., Yang, C., Zhang, Q., & Whidborne, J. F. (2024). Disturbance Observer-Based Backstepping Terminal Sliding Mode Aeroelastic Control of Airfoils. Aerospace, 11(11), 882. https://doi.org/10.3390/aerospace11110882







