A Physics- and Data-Driven Study on the Ground Effect on the Propulsive Performance of Tandem Flapping Wings
Abstract
1. Introduction
2. Materials and Methods
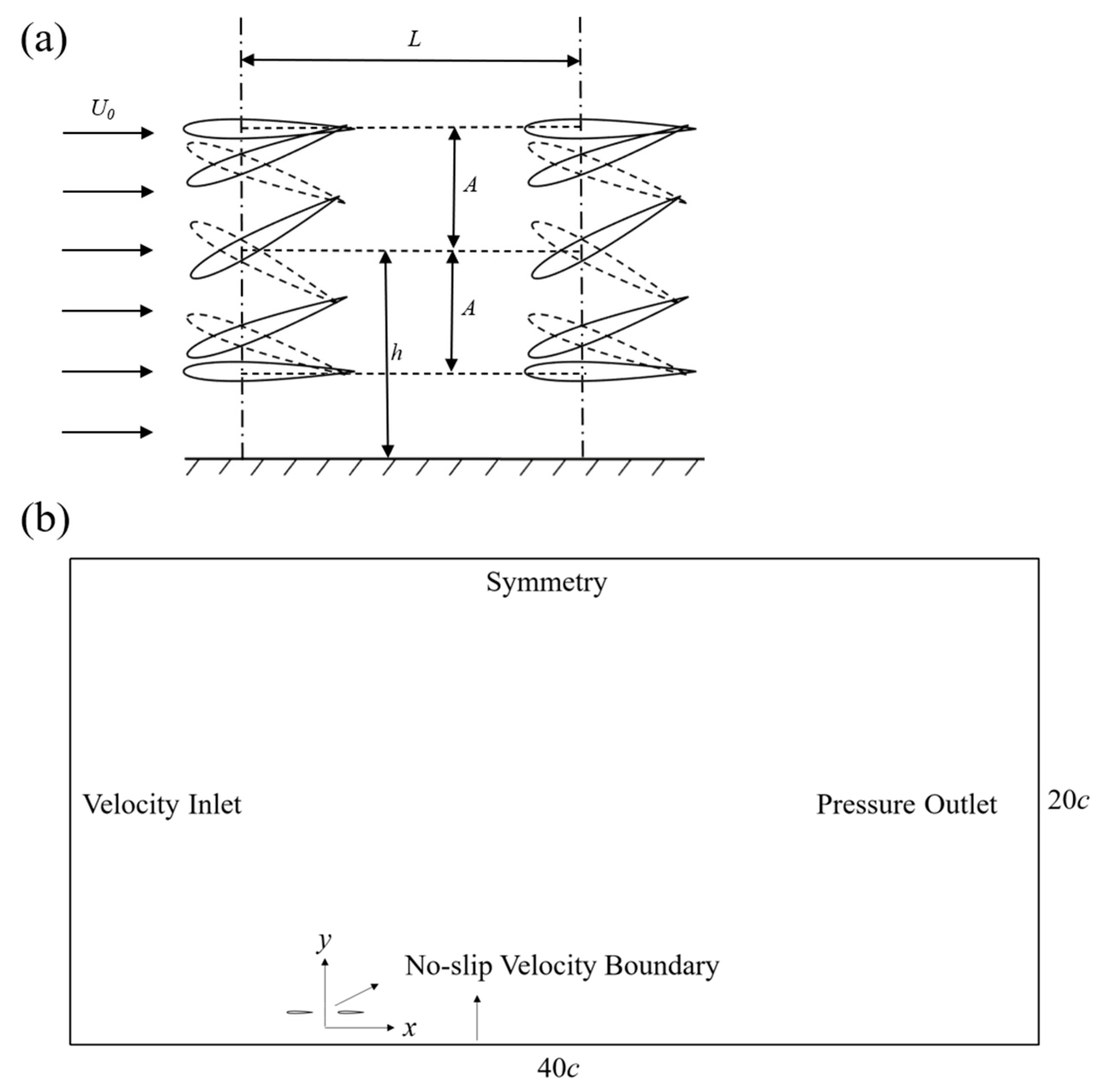
2.1. Physical Problem and Numerical Model
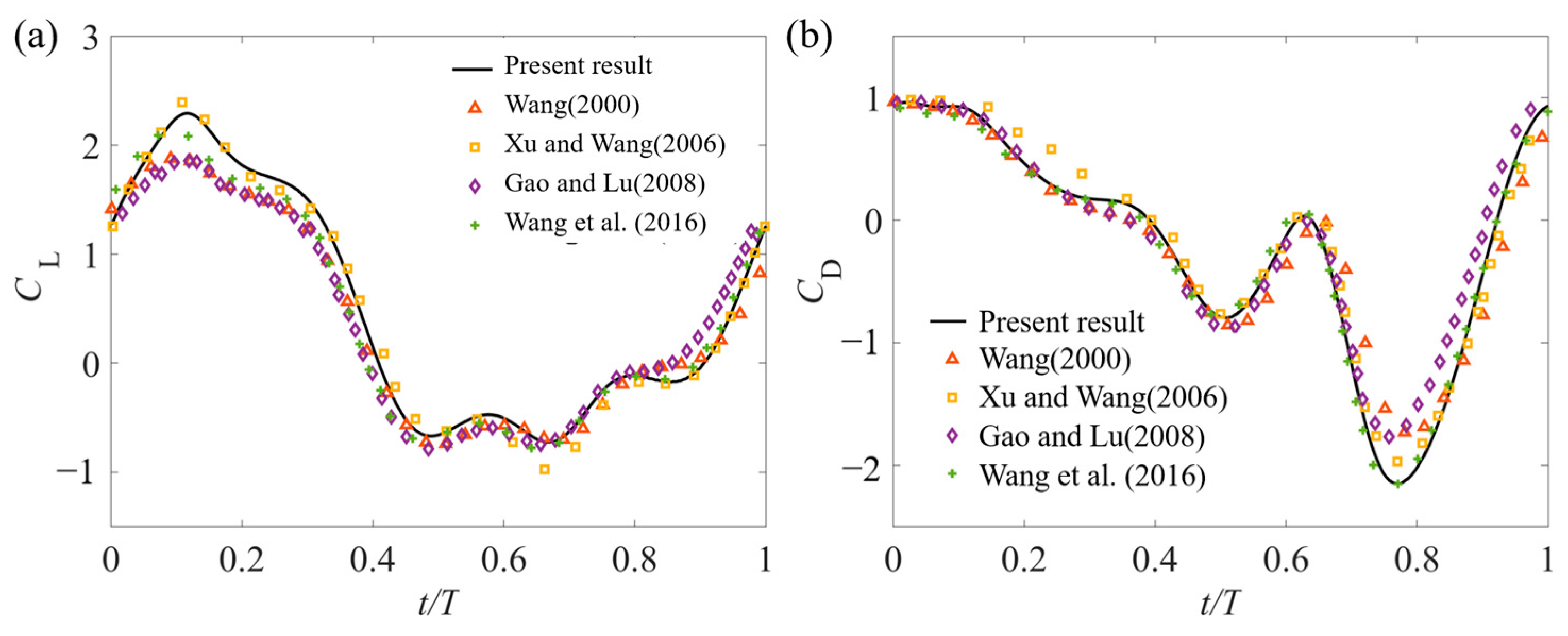
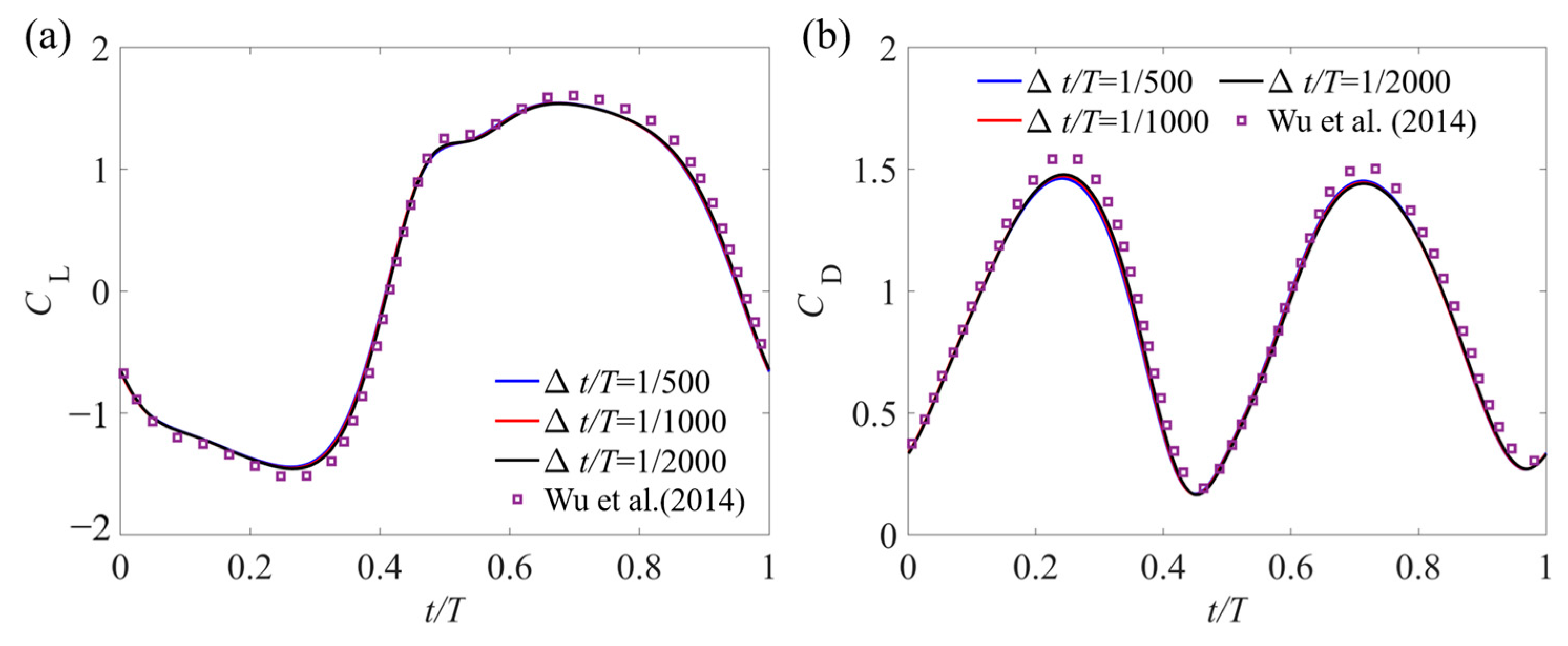
2.2. Validations of the Numerical Method
2.3. Neural Network Modeling of the Unsteady Aerodynamic Parameters
- Obtaining the input data. The original data are obtained by the verified numerical simulations, and the data are preprocessed to obtain the training set and the test set.
- Forward propagation. The input data are used to predict the aerodynamic coefficient or energy consumption coefficient predicted by the neural network under the current parameters.
- Calculating the loss. The mean square error loss between the current predicted values of the aerodynamic coefficient and energy consumption coefficient and the CFD results is calculated.
- Backward propagation and update of the model parameters. Backward propagation is performed, the gradient is calculated through the defined Adam optimizer, and the parameters of the neural network model are updated.
- The above steps are repeated until the mean square error loss is small enough.
3. Results and Discussion
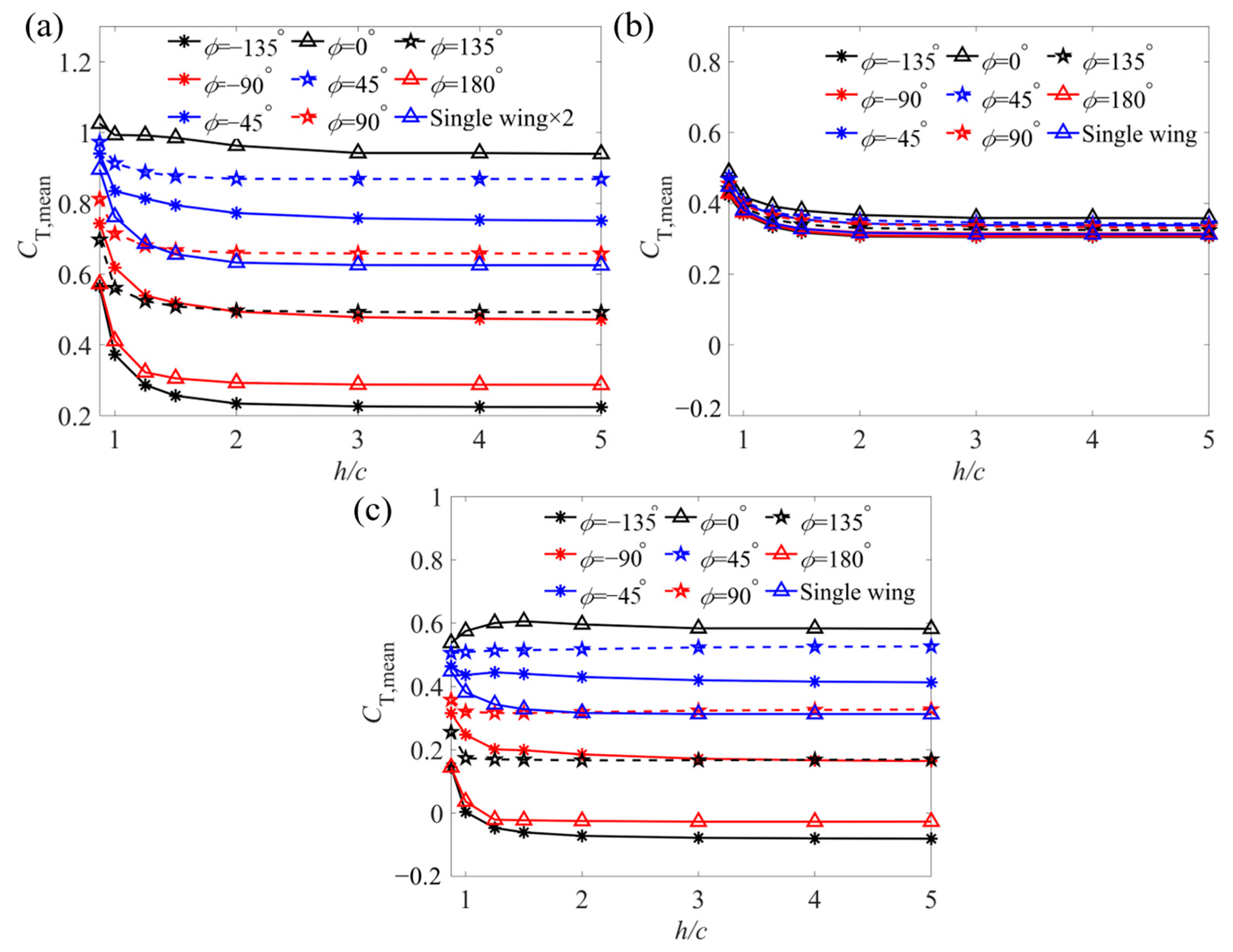
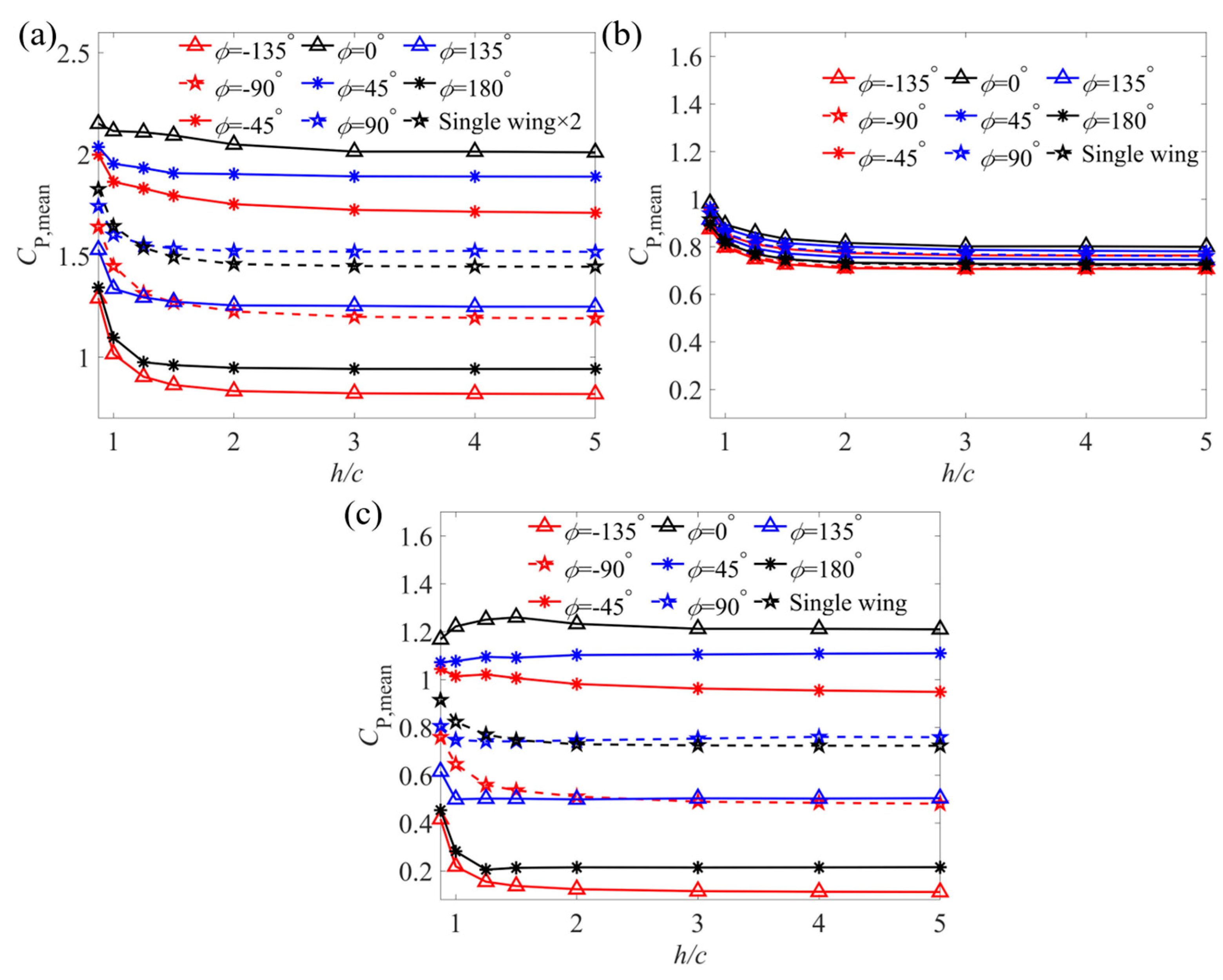
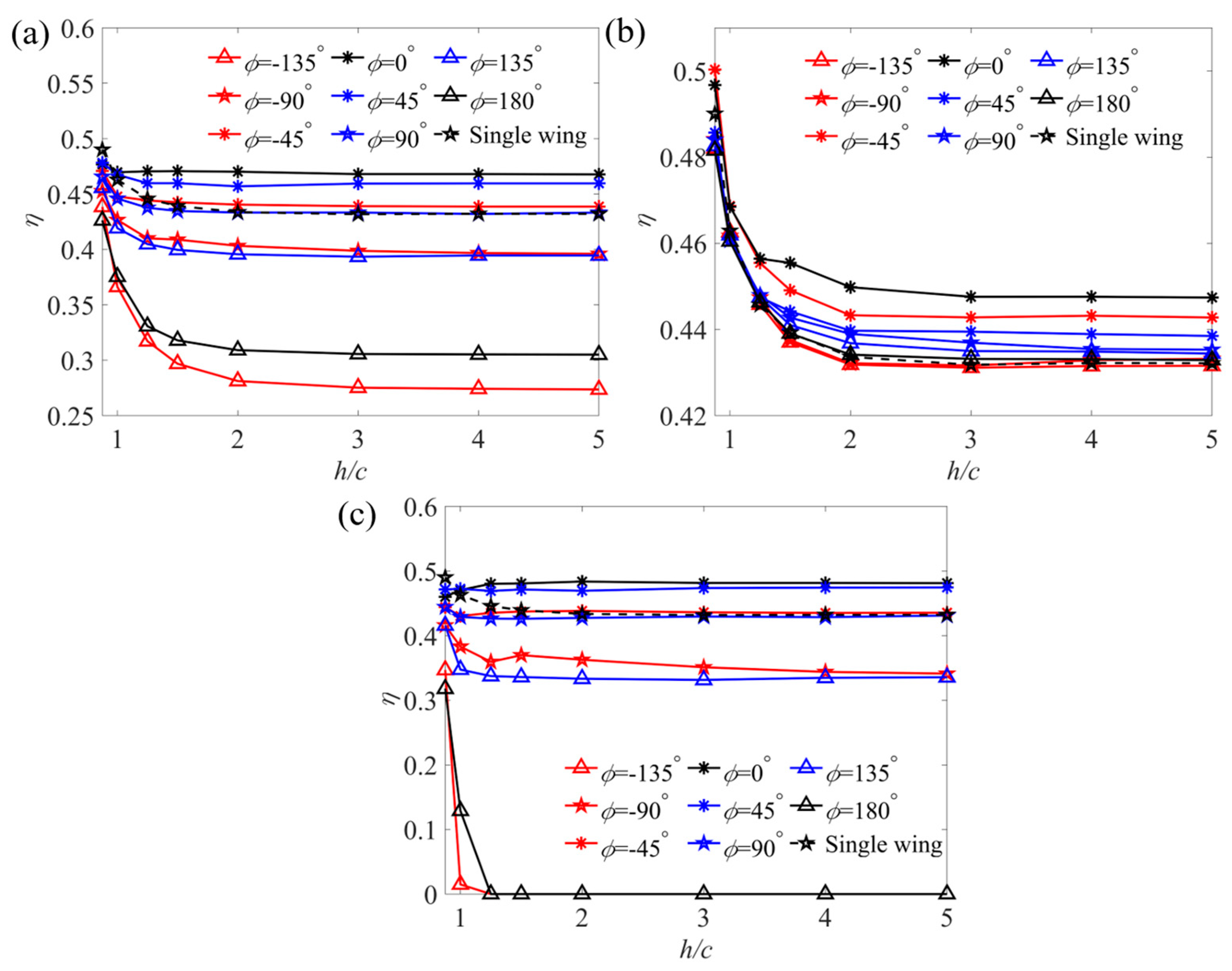
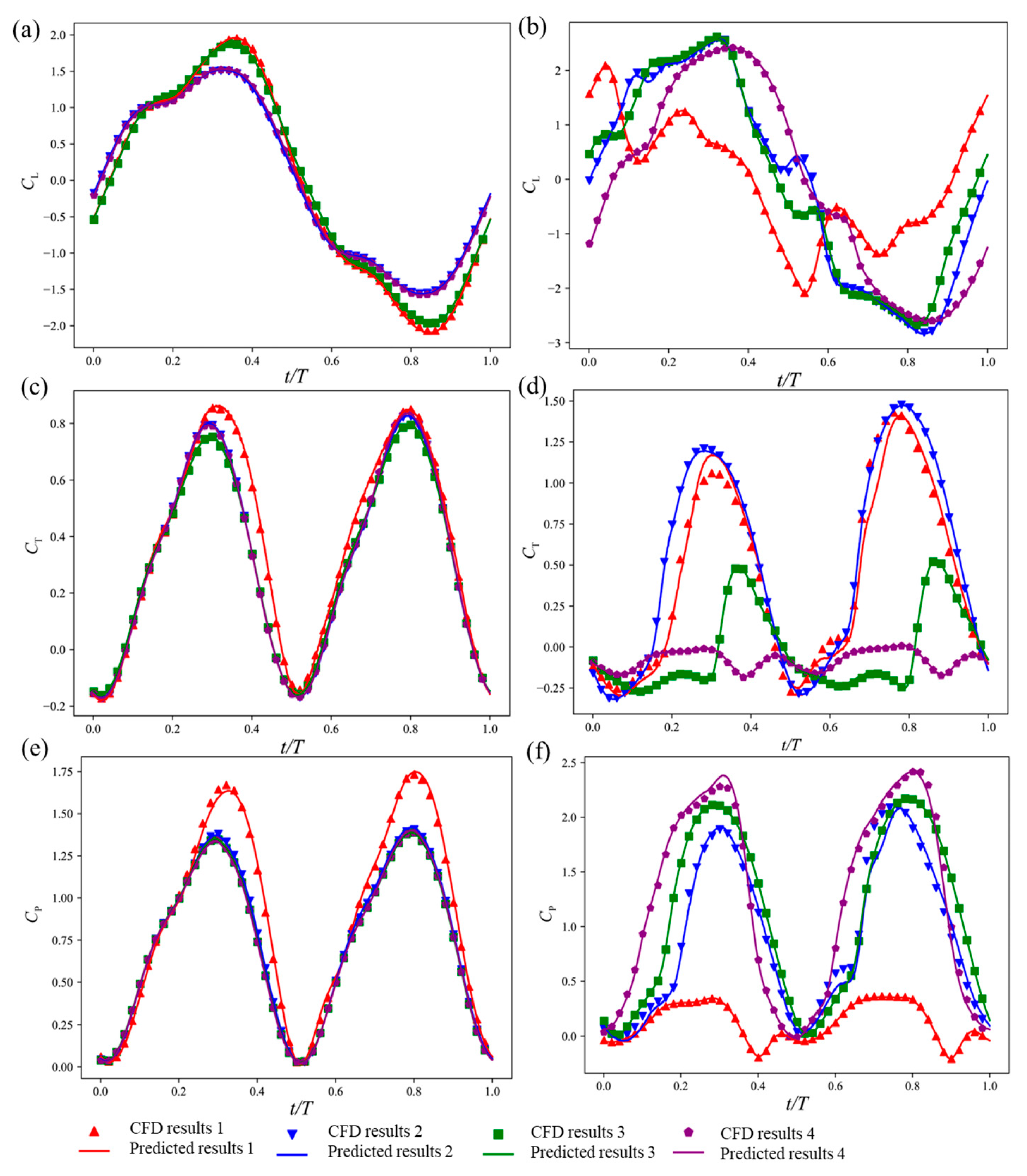
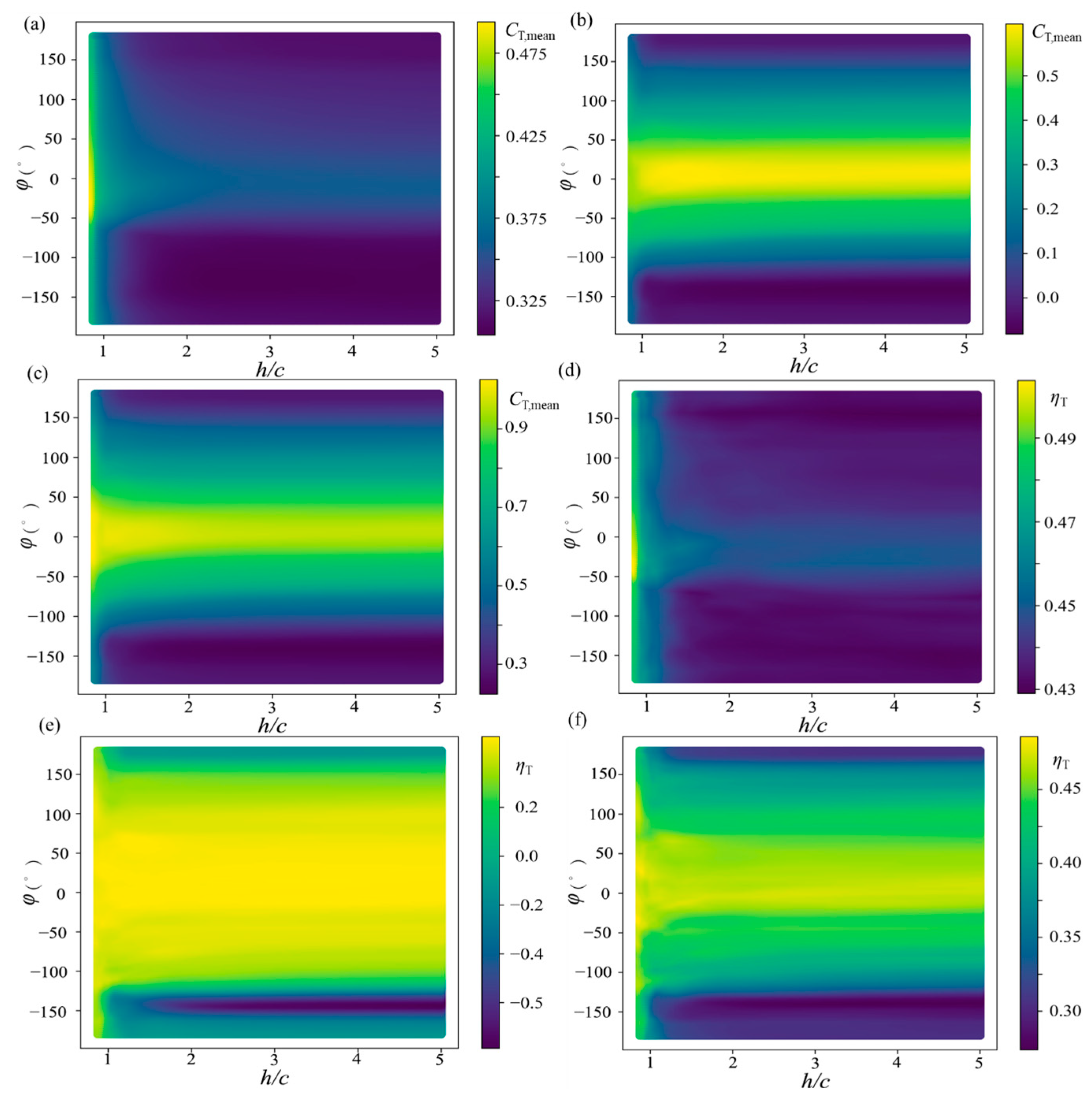
3.1. Effect of the Ground on the Aerodynamic Parameters
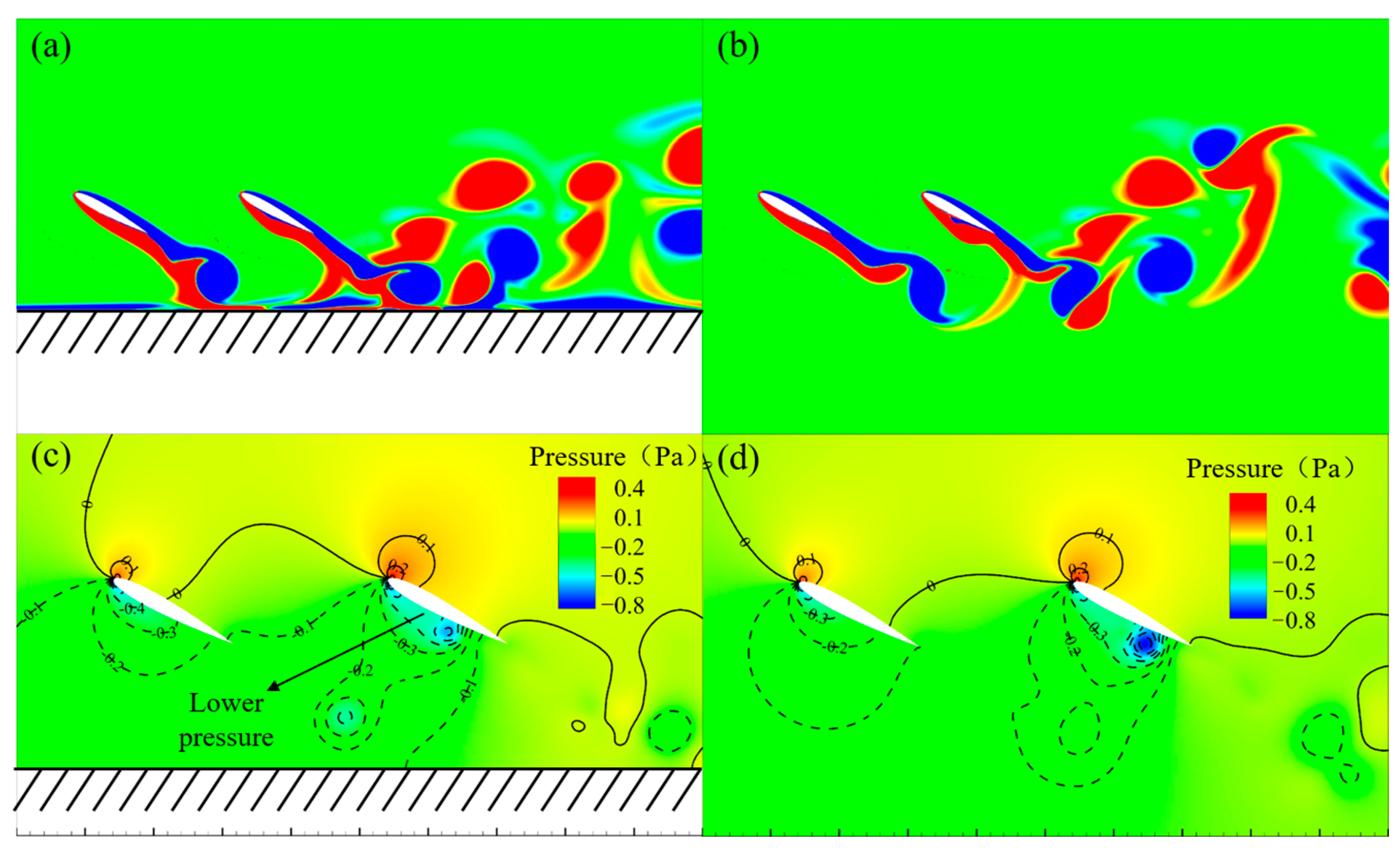
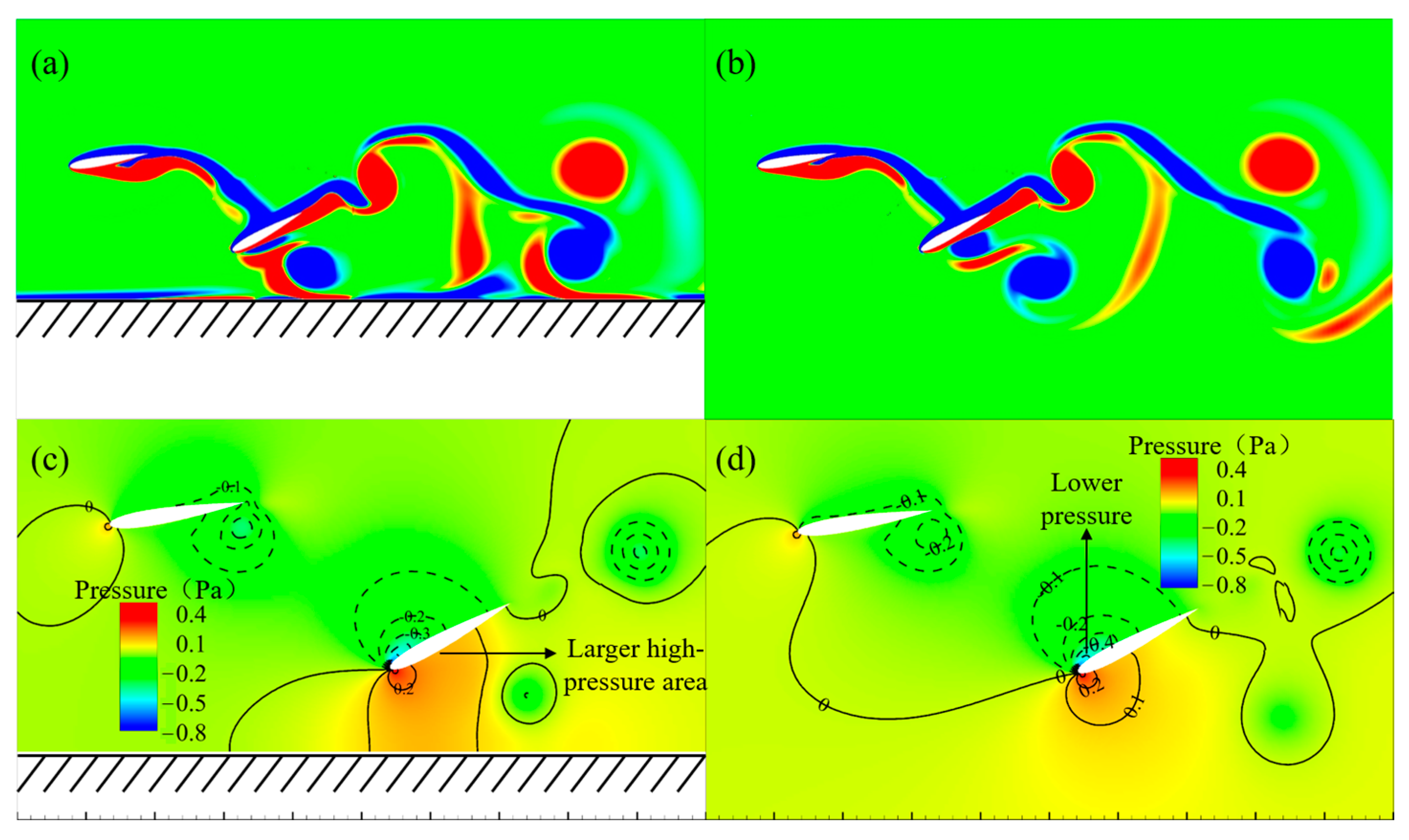
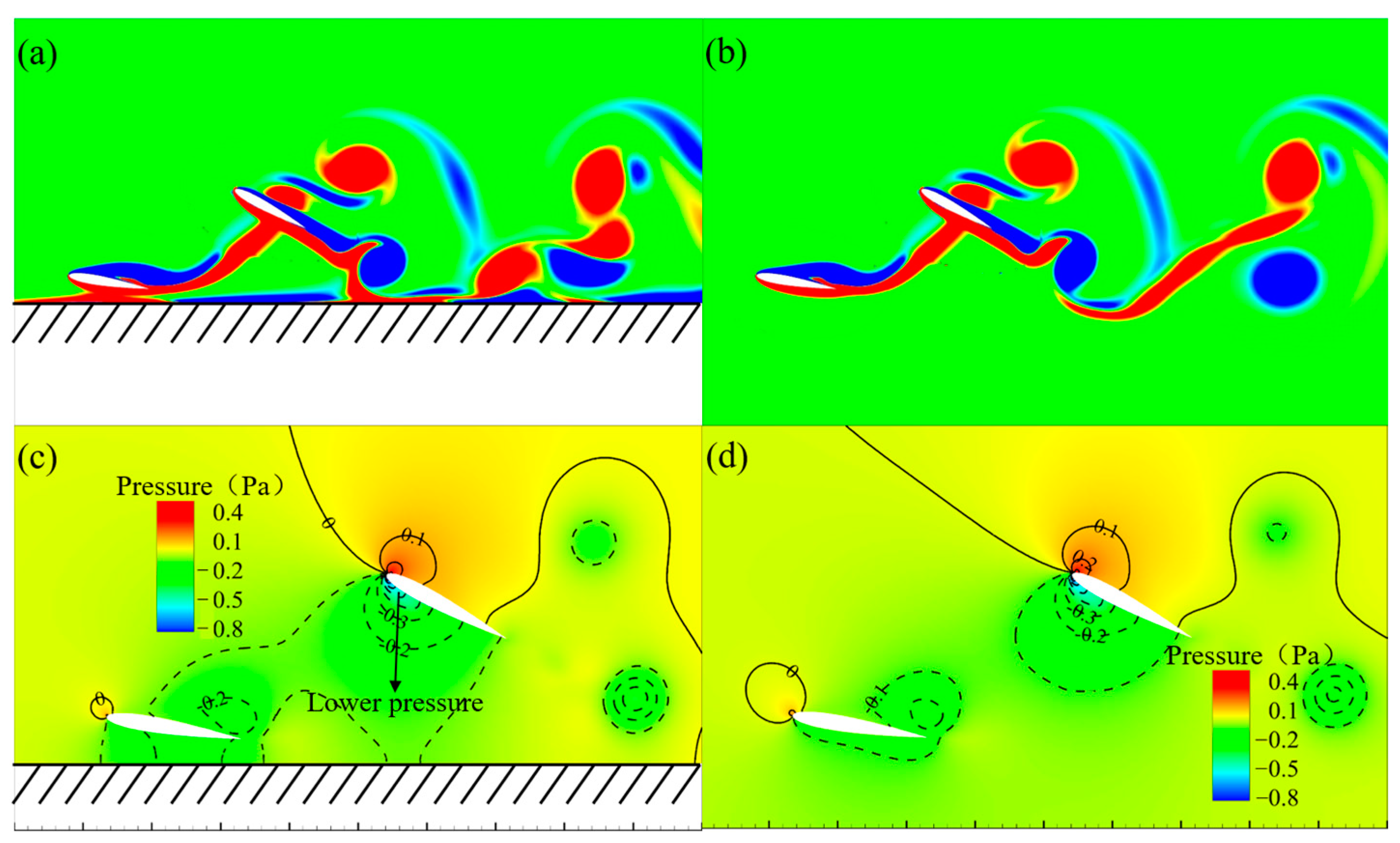
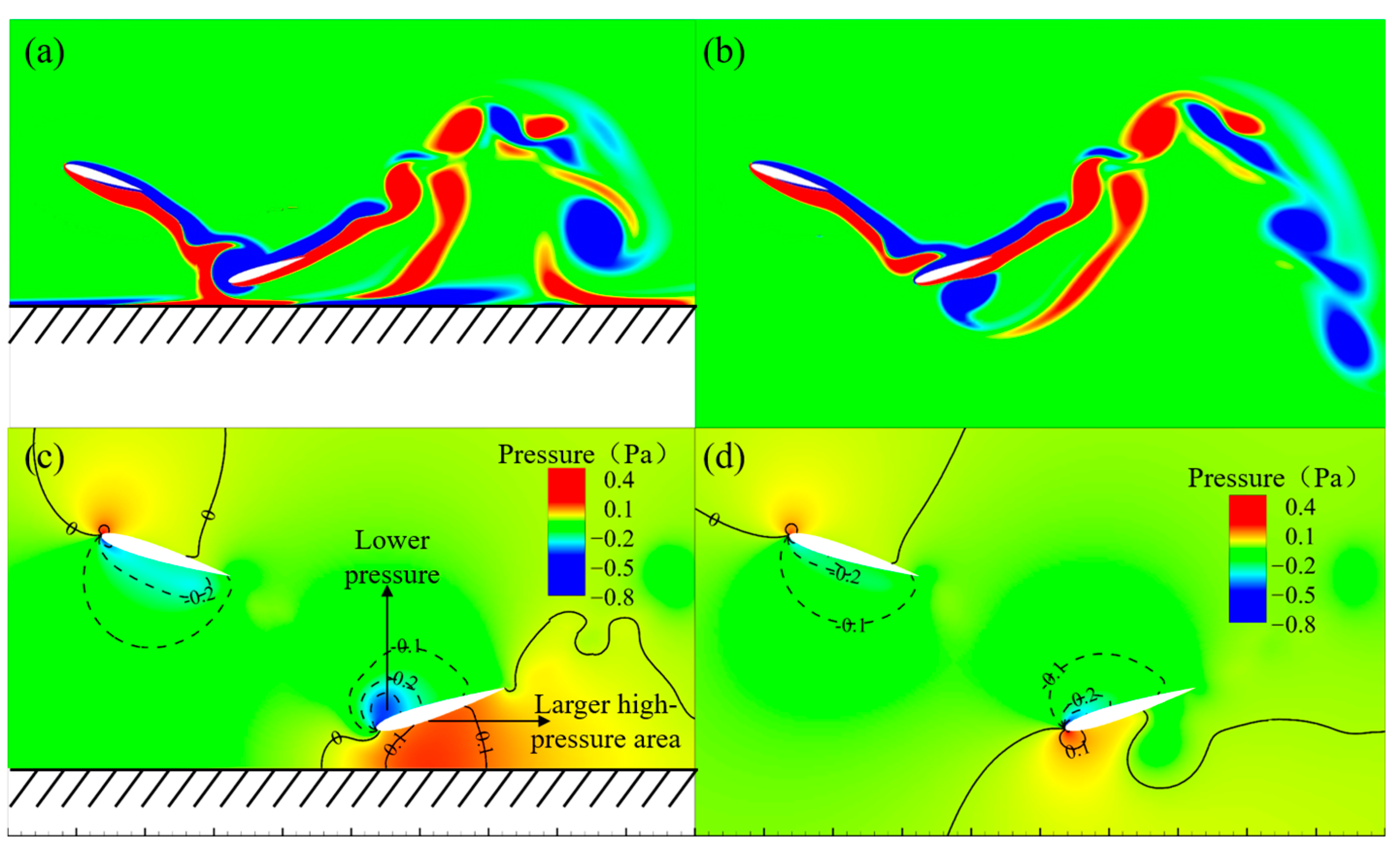
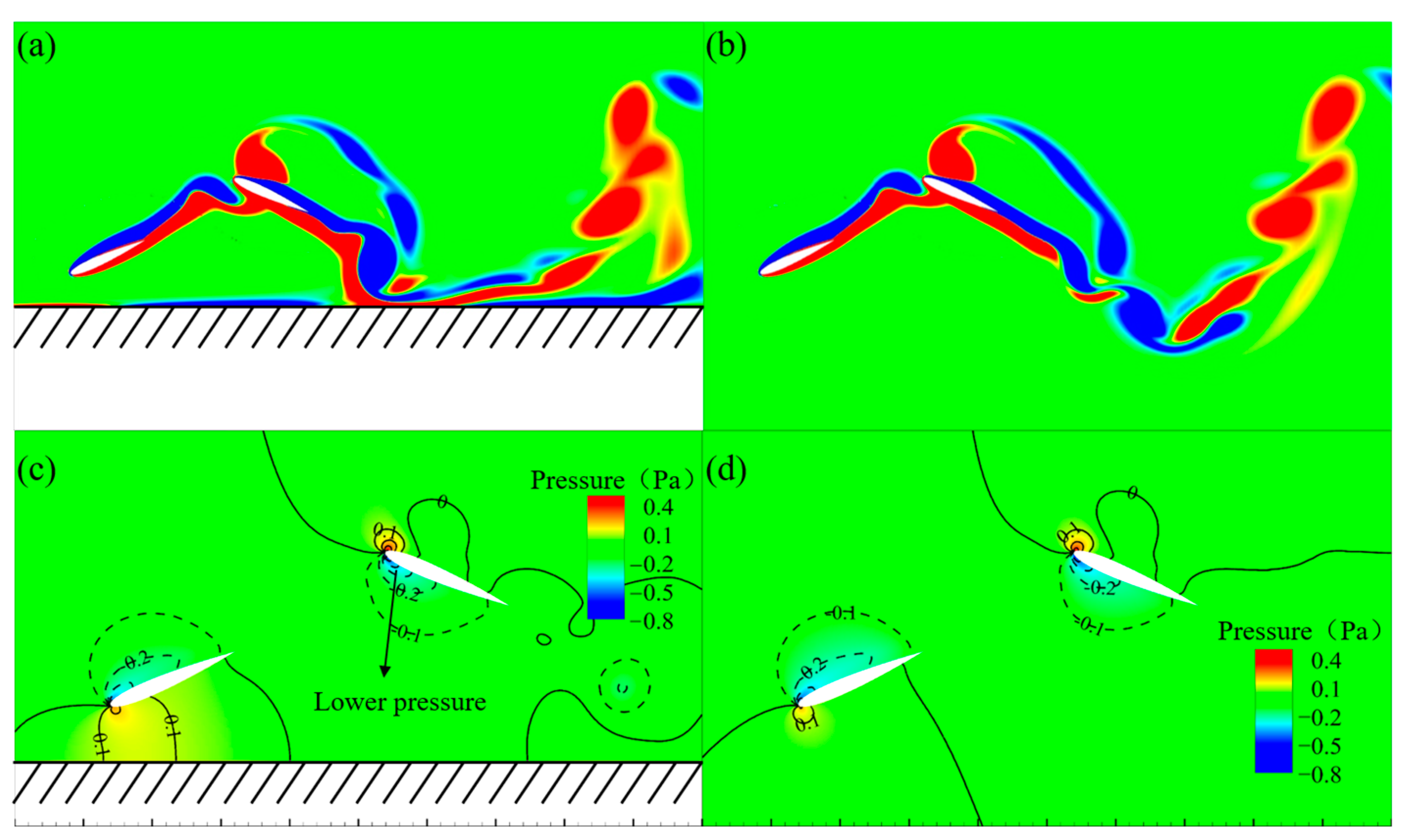
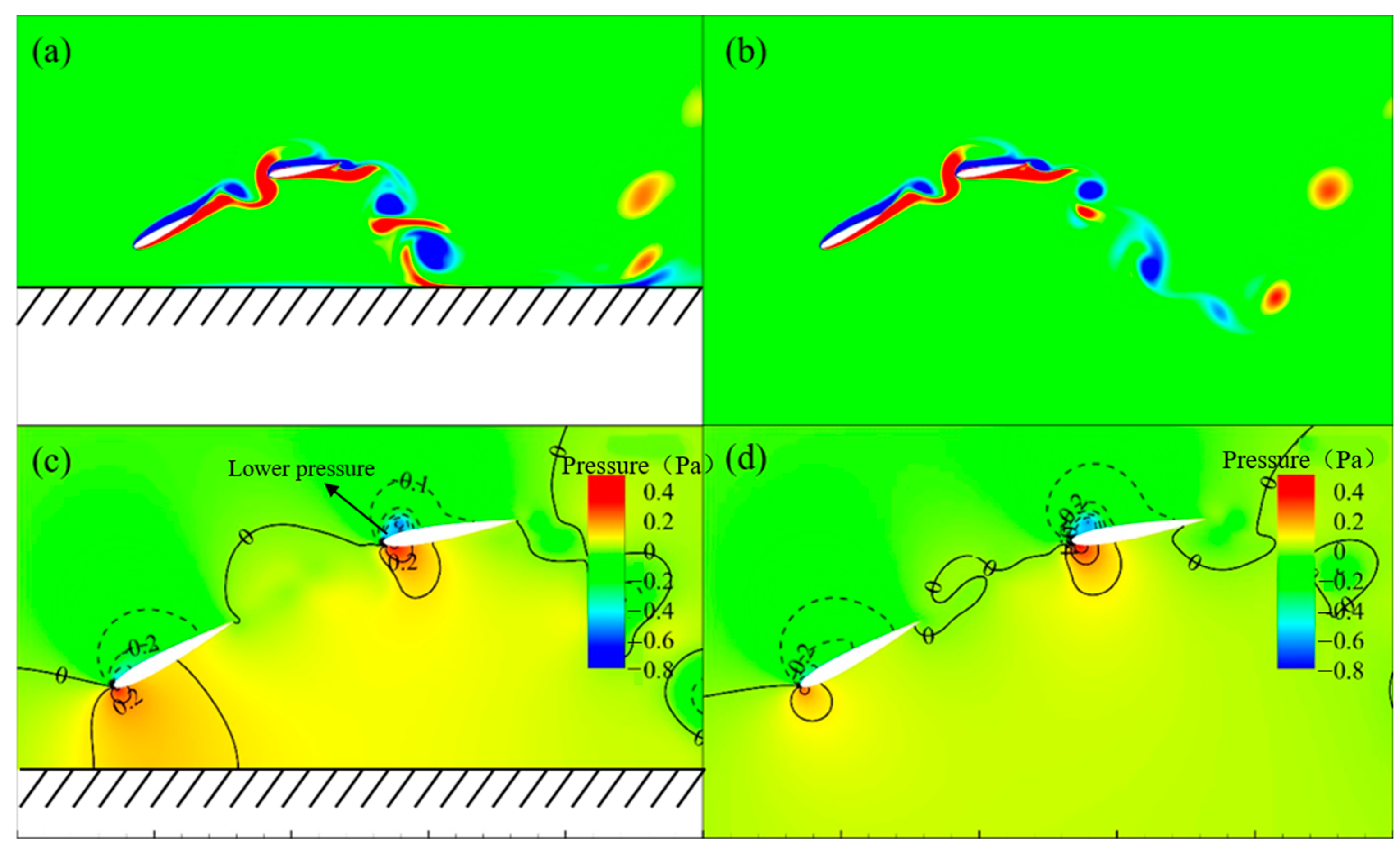
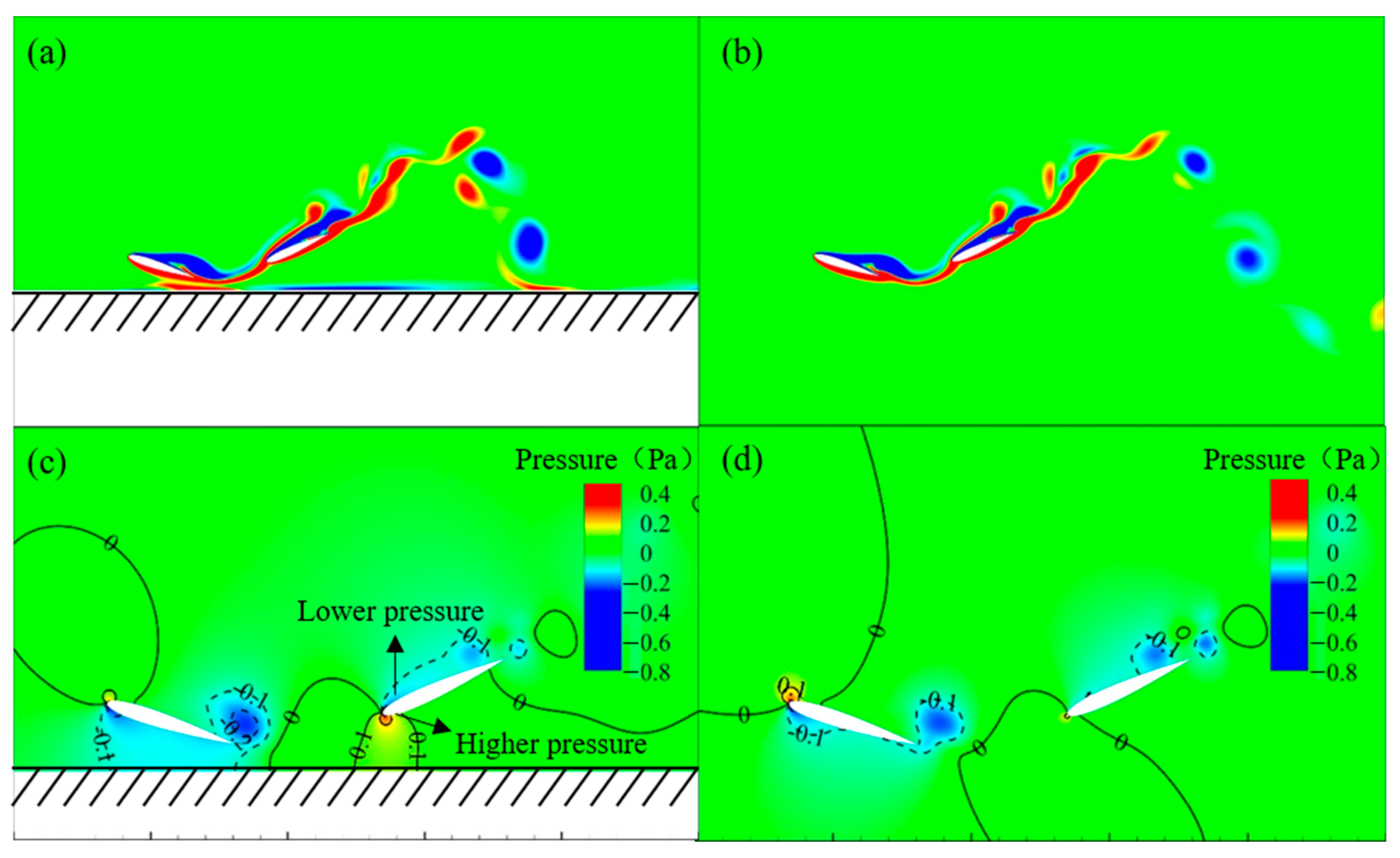
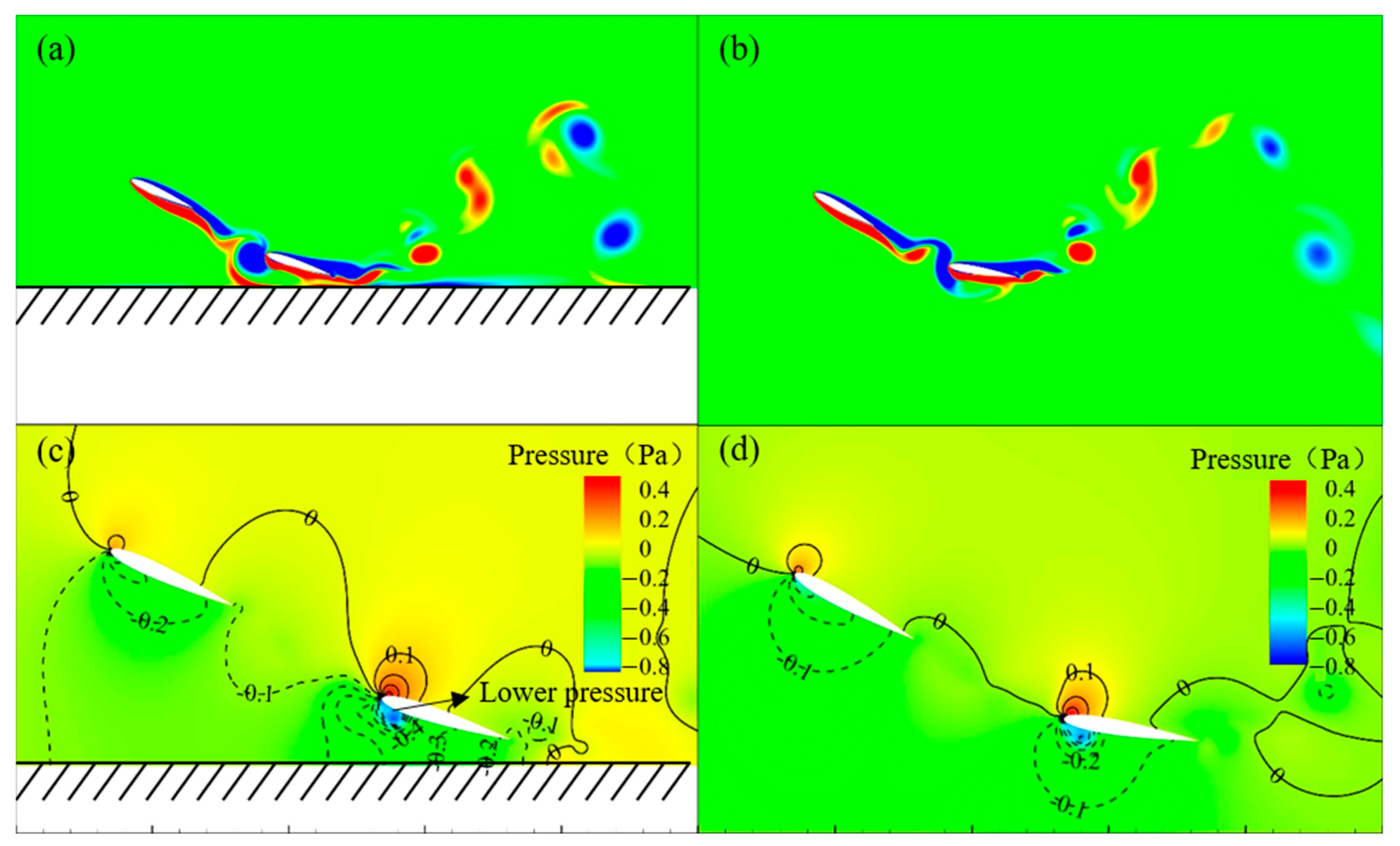
3.2. Effect of the Ground on Vortex Structure Evolution
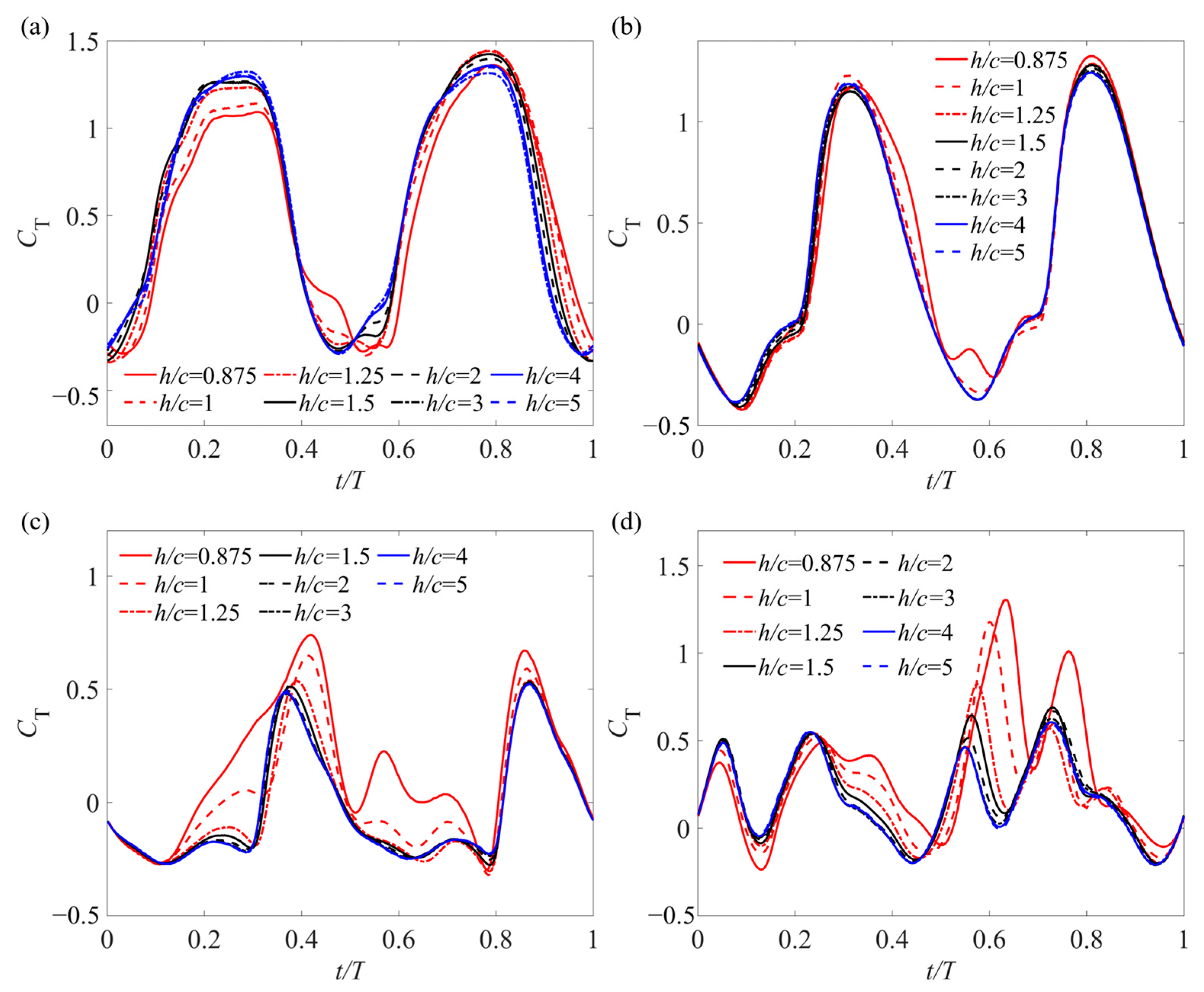
- For φ = 0° (in-phase flapping), the smaller h/c is, the smaller CT,mean is.
- For φ = 90° (the rear wing is ahead of the front wing), the smaller h/c is, the larger CT,mean is, but the increase is less than that of the ground effect on a single wing.
- For φ = −90° (the rear wing lags behind the front wing), the smaller h/c is, the larger CT,mean is, and the increase is greater than that of the ground effect on a single wing.
- For φ = 180° (anti-phase flapping), the smaller h/c is, the larger CT,mean is, and the increase is greater than that of the ground effect on a single wing.
3.3. Aerodynamic Performance Prediction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lian, Y.; Broering, T.; Hord, K.; Prater, R. The characterization of tandem and corrugated wings. Prog. Aerosp. Sci. 2014, 65, 41–69. [Google Scholar] [CrossRef]
- Chin, D.D.; Lentink, D. Flapping wing aerodynamics: From insects to vertebrates. J. Exp. Biol. 2016, 219, 920–932. [Google Scholar] [CrossRef] [PubMed]
- Haider, N.; Shahzad, A.; Mumtaz Qadri, M.N.; Ali Shah, S.I. Recent progress in flapping wings for micro aerial vehicle applications. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 245–264. [Google Scholar] [CrossRef]
- Han, J.-H.; Han, Y.-J.; Yang, H.-H.; Lee, S.-G.; Lee, E.-H. A Review of Flapping Mechanisms for Avian-Inspired Flapping-Wing Air Vehicles. Aerospace 2023, 10, 554. [Google Scholar] [CrossRef]
- De Manabendra, M.; Sudhakar, Y.; Gadde, S.; Shanmugam, D.; Vengadesan, S. Bio-inspired Flapping Wing Aerodynamics: A Review. J. Indian Inst. Sci. 2024, 104, 181–203. [Google Scholar] [CrossRef]
- Li, D.; Mu, Y.; Lau, G.-K.; Chin, Y.; Lu, Z. Numerical study on the aerodynamic performance of dragonfly (Anax parthenope julius) maneuvering flight during synchronized-stroking. Phys. Fluids 2024, 36, 091911. [Google Scholar] [CrossRef]
- Bomphrey, R.J.; Nakata, T.; Henningsson, P.; Lin, H.T. Flight of the dragonflies and damselflies. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2016, 371, 20150389. [Google Scholar] [CrossRef]
- Salami, E.; Montazer, E.; Ward, T.A.; Nik Ghazali, N.N.; Anjum Badruddin, I. Aerodynamic Performance of a Dragonfly-Inspired Tandem Wing System for a Biomimetic Micro Air Vehicle. Front. Bioeng. Biotechnol. 2022, 10, 787220. [Google Scholar] [CrossRef]
- Pinapatruni, G.V.R.; Duddupudi, M.B.; Dash, S.M.; Routray, A. On the investigation of the aerodynamics performance and associated flow physics of the optimized tubercle airfoil. Phys. Fluids 2024, 36, 051907. [Google Scholar] [CrossRef]
- Sinha, J.; Dash, S.M.; Lua, K.B. On the study of the pitch angular offset effects at various flapping frequencies for a two-dimensional asymmetric flapping airfoil in forward flight. Phys. Fluids 2024, 36, 041913. [Google Scholar] [CrossRef]
- Gao, T.; Lu, X.Y. Insect normal hovering flight in ground effect. Phys. Fluids 2008, 20, 087101. [Google Scholar] [CrossRef]
- Lu, H.; Lua, K.B.; Lim, T.T.; Yeo, K.S. Ground effect on the aerodynamics of a two-dimensional oscillating airfoil. Exp. Fluids 2014, 55, 1–15. [Google Scholar] [CrossRef]
- Maeda, M.; Liu, H. Ground Effect in Fruit Fly Hovering: A Three-Dimensional Computational Study. J. Biomech. Sci. Eng. 2013, 8, 344–355. [Google Scholar] [CrossRef]
- Umar, F.; Sun, M. Aerodynamic Force and Power for Flapping Wing at Low Reynolds Number in Ground Effect. In Proceedings of the International Bhurban Conference on Applied Sciences & Technology, Islamabad, Pakistan, 9–13 January 2018; pp. 553–558. [Google Scholar]
- Zheng, Y.; Qu, Q.; Liu, P.; Hu, T. Ground Effect of a Two-Dimensional Flapping Wing Hovering in Inclined Stroke Plane. J. Fluids Eng. 2022, 144, 111206. [Google Scholar] [CrossRef]
- Meng, X.; Zhang, Y.; Chen, G. Ceiling effects on the aerodynamics of a flapping wing with advance ratio. Phys. Fluids 2020, 32, 021904. [Google Scholar] [CrossRef]
- Meng, X.; Ghaffar, A.; Zhang, Y.; Deng, C. Very low Reynolds number causes a monotonic force enhancement trend for a three-dimensional hovering wing in ground effect. Bioinspir. Biomim. 2021, 16, 055006. [Google Scholar] [CrossRef]
- Meng, X.; Han, Y.; Chen, Z.; Ghaffar, A.; Chen, G. Aerodynamic Effects of Ceiling and Ground Vicinity on Flapping Wings. Appl. Sci. 2022, 12, 4012. [Google Scholar] [CrossRef]
- Wang, L.; Yeung, R.W. Investigation of full and partial ground effects on a flapping foil hovering above a finite-sized platform. Phys. Fluids 2016, 28, 071902. [Google Scholar] [CrossRef]
- Yin, B.; Yang, G.; Prapamonthon, P. Finite obstacle effect on the aerodynamic performance of a hovering wing. Phys. Fluids 2019, 31, 101902. [Google Scholar] [CrossRef]
- Wu, J.; Zhao, N. Ground Effect on Flapping Wing. Procedia Eng. 2013, 67, 295–302. [Google Scholar] [CrossRef]
- Wu, J.; Shu, C.; Zhao, N.; Yan, W. Fluid Dynamics of Flapping Insect Wing in Ground Effect. J. Bionic Eng. 2014, 11, 52–60. [Google Scholar] [CrossRef]
- Mivehchi, A.; Dahl, J.; Licht, S. Heaving and pitching oscillating foil propulsion in ground effect. J. Fluids Struct. 2016, 63, 174–187. [Google Scholar] [CrossRef]
- Lin, X.; Guo, S.; Wu, J.; Nan, J. Aerodynamic Performance of a Flapping Foil with Asymmetric Heaving Motion near a Wall. J. Bionic Eng. 2018, 15, 636–646. [Google Scholar] [CrossRef]
- Li, Y.; Pan, Z.; Zhang, N. Numerical analysis on the propulsive performance of oscillating wing in ground effect. Appl. Ocean Res. 2021, 114, 1–16. [Google Scholar] [CrossRef]
- Lin, C.; Jia, P.; Wang, C.; Zhong, Z. Fluid dynamics of a flapping wing interacting with the boundary layer at a flat wall. Phys. Fluids 2024, 36, 041917. [Google Scholar] [CrossRef]
- Sun, M.; Lan, S.L. A computational study of the aerodynamic forces and power requirements of dragonfly (Aeschna juncea) hovering. J. Exp. Biol. 2004, 207, 1887–1901. [Google Scholar] [CrossRef]
- Wang, Z.J.; Russell, D. Effect of Forewing and Hindwing Interactions on Aerodynamic Forces and Power in Hovering Dragonfly Flight. Phys. Rev. Lett. 2007, 99, 148101. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, X.-Y. Aerodynamic performance due to forewing and hindwing interaction in gliding dragonfly flight. Phys. Rev. E 2009, 80, 017302. [Google Scholar] [CrossRef]
- Lua, K.B.; Lu, H.; Zhang, X.H.; Lim, T.T.; Yeo, K.S. Aerodynamics of two-dimensional flapping wings in tandem configuration. Phys. Fluids 2016, 28, 121901. [Google Scholar] [CrossRef]
- Zheng, Y.; Wu, Y.; Tang, H. An experimental study on the forewing–hindwing interactions in hovering and forward flights. Int. J. Heat Fluid Flow 2016, 59, 62–73. [Google Scholar] [CrossRef]
- Nagai, H.; Fujita, K.; Murozono, M. Experimental Study on Forewing-Hindwing Phasing in Hovering and Forward Flapping Flight. AIAA J. 2019, 57, 3779–3790. [Google Scholar] [CrossRef]
- Sarbandi, A.; Naderi, A.; Parhizkar, H. The ground effect on flapping Bio and NACA 0015 airfoils in power extraction and propulsion regimes. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 287. [Google Scholar] [CrossRef]
- Cho, K.; Van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations Using RNN Encoder-Decoder for Statistical Machine Translation. In Proceedings of the EMNLP, Association for Computational Linguistics, Doha, Qatar, 25–29 October 2014. [Google Scholar]
- Taylor, G.K.; Nudds, R.L.; Thomas, A.L.R. Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 2003, 425, 707–711. [Google Scholar] [CrossRef]
- Younsi, A.; zamree bin abd Rahim, S.; Rezoug, T. Aerodynamic investigation of an airfoil under two hovering modes considering ground effect. J. Fluids Struct. 2019, 91, 102759. [Google Scholar] [CrossRef]
- Rezaei, A.S.; Taha, H. Circulation dynamics of small-amplitude pitching airfoil undergoing laminar-to-turbulent transition. J. Fluids Struct. 2021, 100, 103177. [Google Scholar] [CrossRef]
- Nawafleh, A.; Xing, T.; Durgesh, V.; Padilla, R. Fluid–structure interaction simulation of a flapping flag in a laminar jet. J. Fluids Struct. 2023, 119, 103869. [Google Scholar] [CrossRef]
- Mozafari, M.; Sadeghimalekabadi, M.; Fardi, A.; Bruecker, C.; Masdari, M. Aeroacoustic investigation of a ducted wind turbine employing bio-inspired airfoil profiles. Phys. Fluids 2024, 36, 041918. [Google Scholar] [CrossRef]
- Wang, Z.J. Two Dimensional Mechanism for Insect Hovering. Phys. Rev. Lett. 2000, 85, 2216–2219. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Z.J. An immersed interface method for simulating the interaction of a fluid with moving boundaries. J. Comput. Phys. 2006, 216, 454–493. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, C.; Xie, P. Numerical investigation on aerodynamic performance of a 2-D inclined hovering wing in asymmetric strokes. J. Mech. Sci. Technol. 2016, 30, 199–210. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, Z.; Gao, J.; Xu, C. Forecast Methods for Time Series Data: A Survey. IEEE Access 2021, 9, 91896–91912. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. CoRR arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical Evaluation of Rectified Activations in Convolutional Network. CoRR arXiv 2015, arXiv:1505.00853. [Google Scholar]





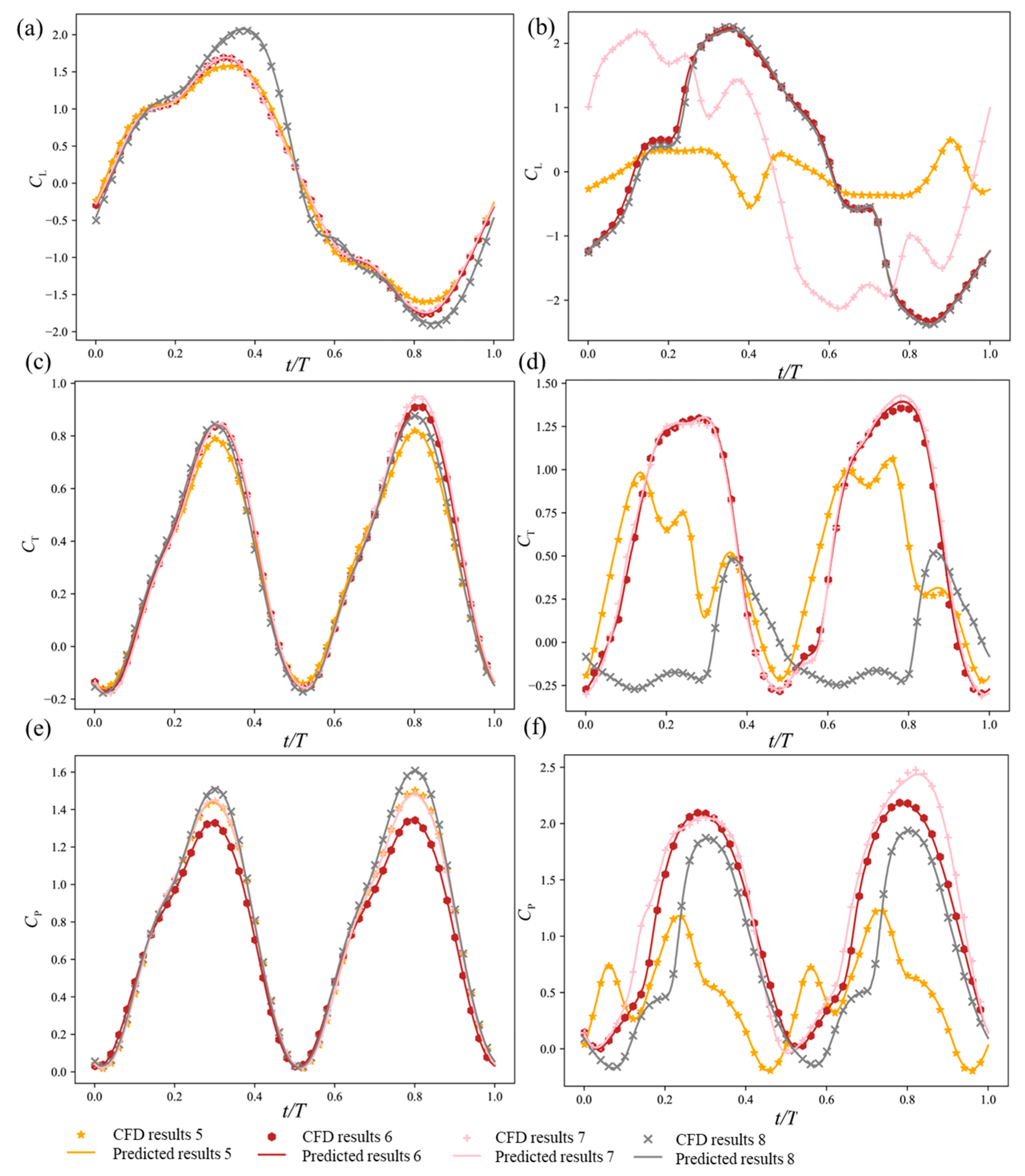
| Target | The Initial MSE | Iterations | Learning Rate * | The Final MSE |
|---|---|---|---|---|
| 3.32 | 30,000 | 0.01, 0.001, 0.0001 | ||
| 0.567 | 30,000 | 0.01, 0.001, 0.0001 | ||
| 1.93 | 30,000 | 0.01, 0.001, 0.0001 | ||
| 3.92 | 30,000 | 0.01, 0.001, 0.0001 | ||
| 0.681 | 30,000 | 0.01, 0.001, 0.0001 | ||
| 2.05 | 30,000 | 0.01, 0.001, 0.0001 |
| Training Objective | Percentage of Test Sets Total Samples | Average Relative Error | Relative Error with the Maximum Absolute Value | Average RMSE | Maximum RMSE |
|---|---|---|---|---|---|
| 10% | —— * | —— * | 0.01551 | 0.03021 | |
| 10% | —— * | —— * | 0.02330 | 0.05354 | |
| 10% | 0.3686% | 1.442% | 0.005820 | 0.01510 | |
| 10% | 1.165% | −3.506% | 0.02265 | 0.09046 | |
| 10% | 0.2518% | −0.6413% | 0.009269 | 0.02499 | |
| 10% | 0.7245% | −2.597% | 0.02912 | 0.09981 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, N.; Wang, C.; Zhou, J.; Jia, P.; Zhong, Z. A Physics- and Data-Driven Study on the Ground Effect on the Propulsive Performance of Tandem Flapping Wings. Aerospace 2024, 11, 904. https://doi.org/10.3390/aerospace11110904
Duan N, Wang C, Zhou J, Jia P, Zhong Z. A Physics- and Data-Driven Study on the Ground Effect on the Propulsive Performance of Tandem Flapping Wings. Aerospace. 2024; 11(11):904. https://doi.org/10.3390/aerospace11110904
Chicago/Turabian StyleDuan, Ningyu, Chao Wang, Jianyou Zhou, Pan Jia, and Zheng Zhong. 2024. "A Physics- and Data-Driven Study on the Ground Effect on the Propulsive Performance of Tandem Flapping Wings" Aerospace 11, no. 11: 904. https://doi.org/10.3390/aerospace11110904
APA StyleDuan, N., Wang, C., Zhou, J., Jia, P., & Zhong, Z. (2024). A Physics- and Data-Driven Study on the Ground Effect on the Propulsive Performance of Tandem Flapping Wings. Aerospace, 11(11), 904. https://doi.org/10.3390/aerospace11110904





