Effect of Bending Deformation on the Lateral Force of Spinning Projectiles with Large Aspect Ratio
Abstract
1. Introduction
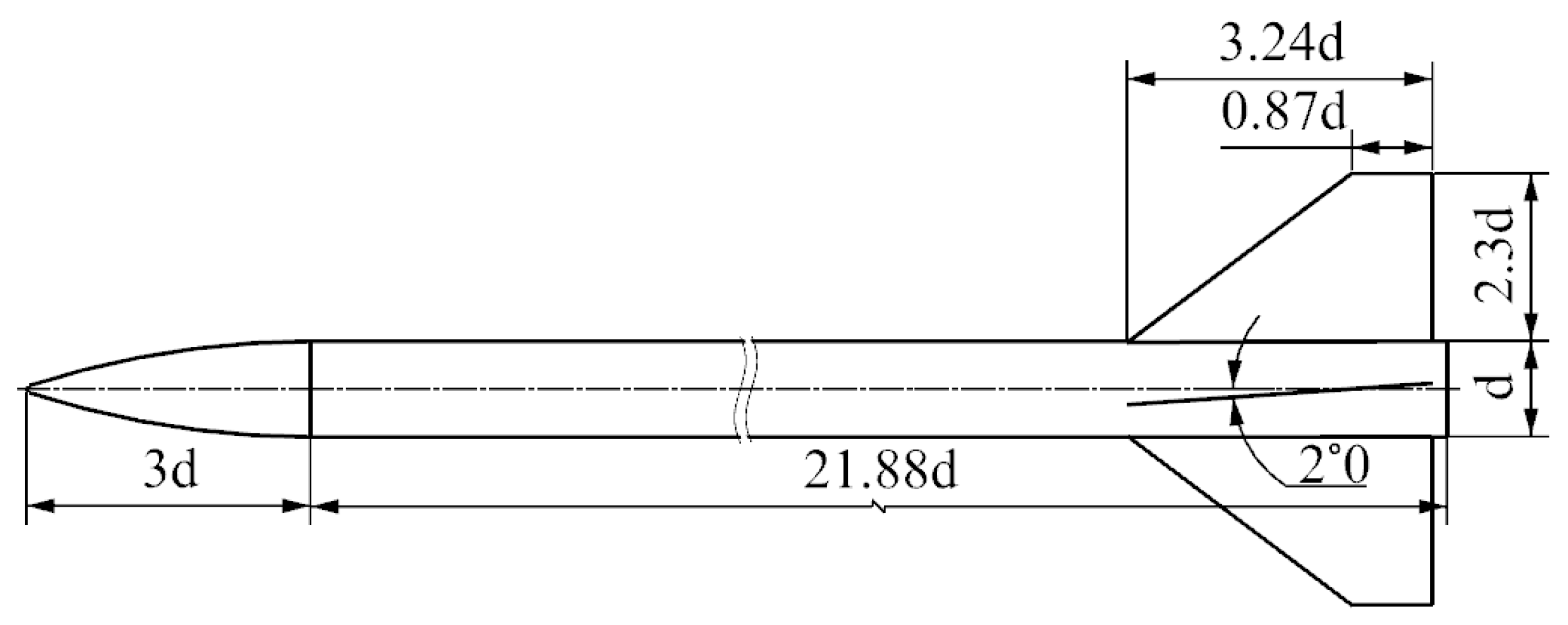
2. Computational Model and Grid
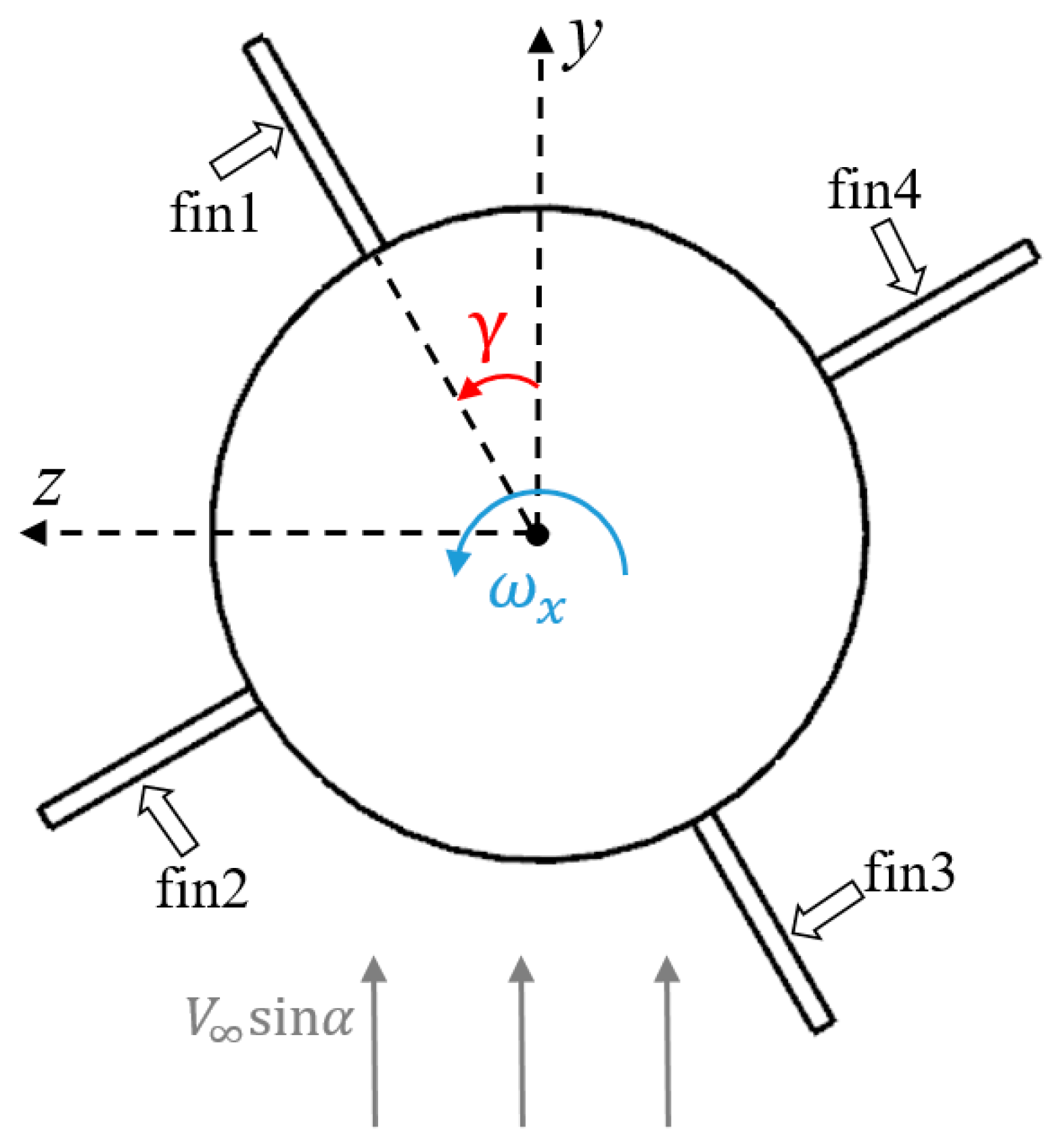
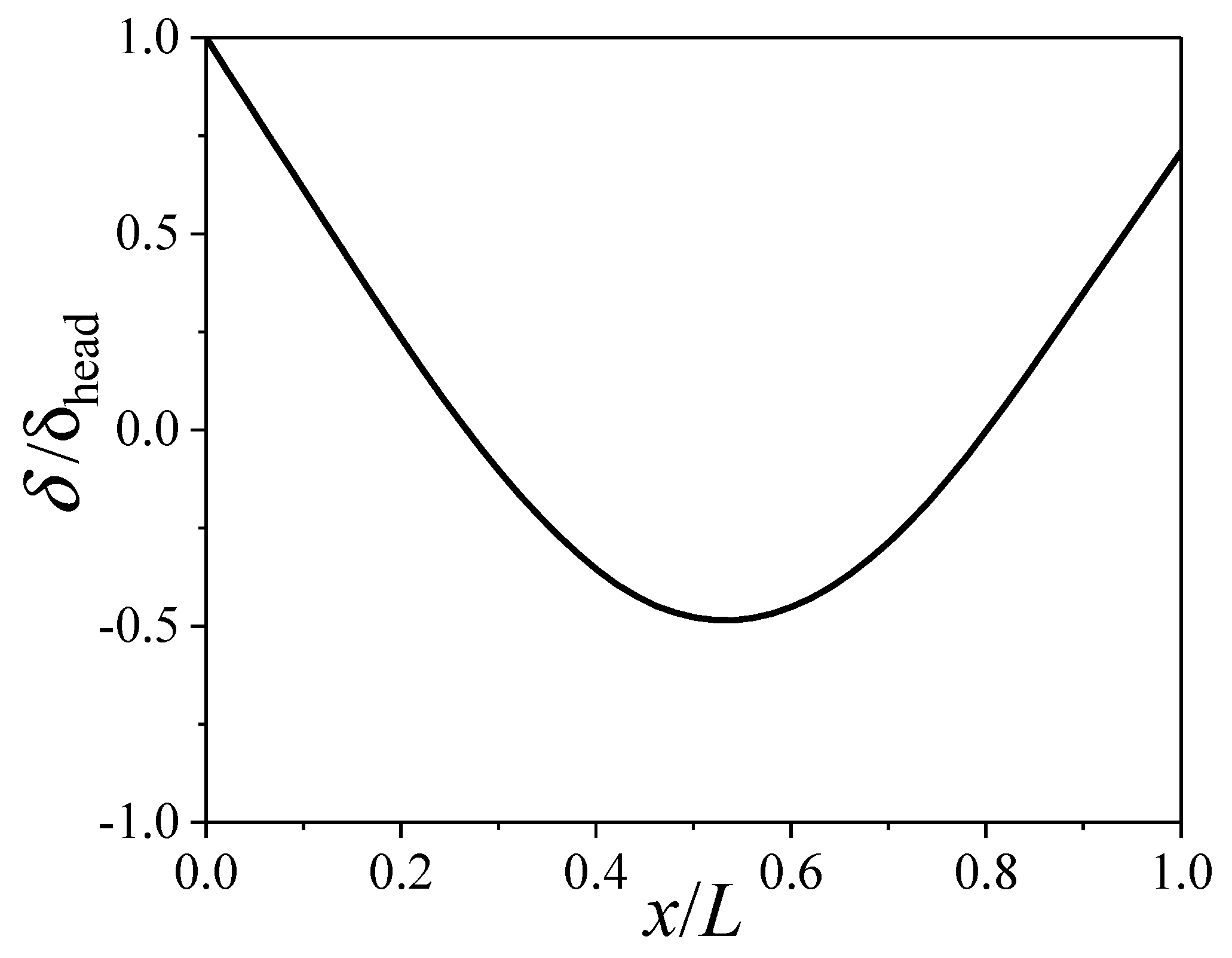
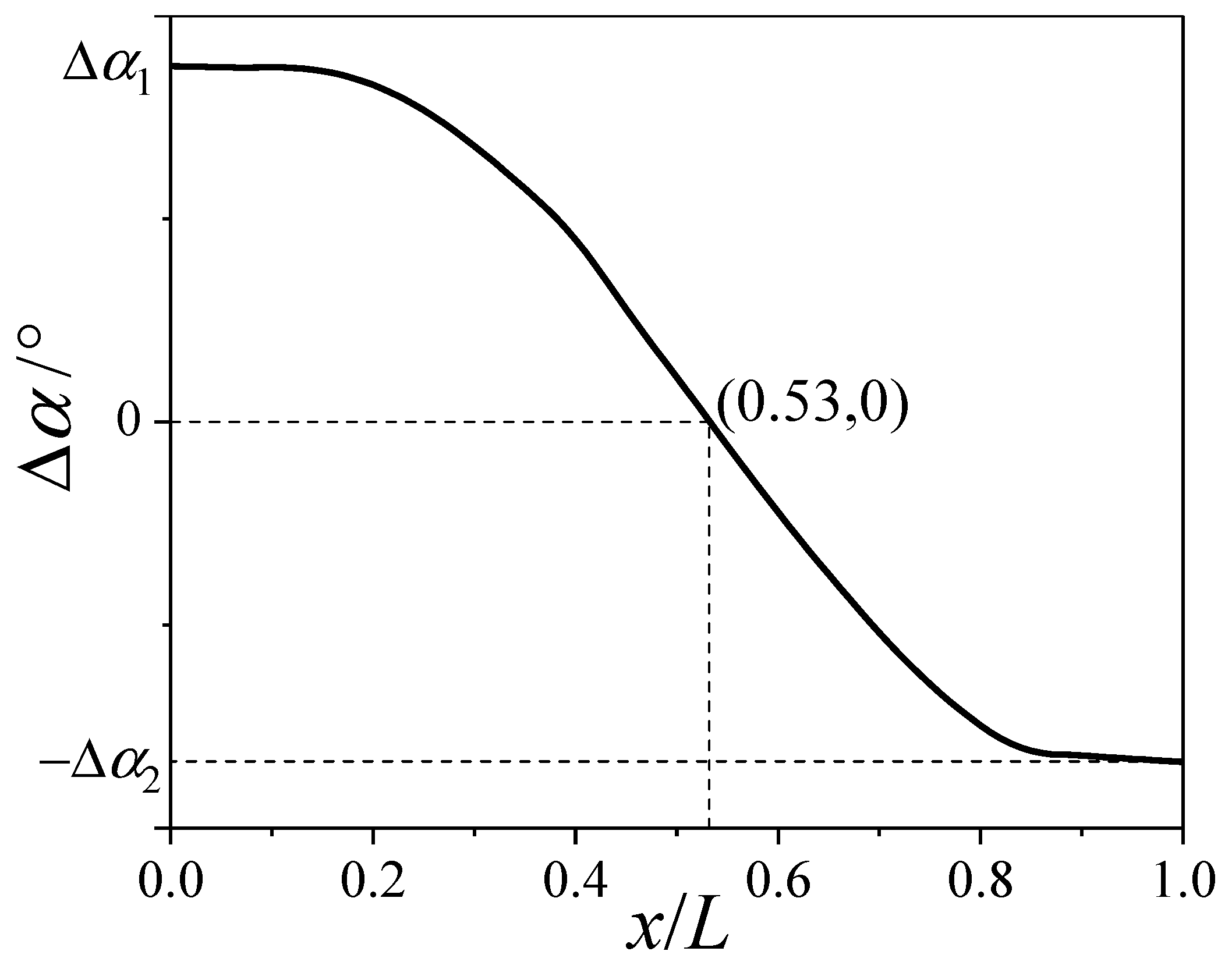
3. Spin−Deformation Coupling Motion
4. Numerical Method
4.1. Governing Equations and Turbulence Model
4.2. Dynamic Mesh Method
4.2.1. Rigid−Motion Mesh Method
4.2.2. RBF Mesh Deformation Method
4.3. Discretization Methods
5. Validation of Numerical Method
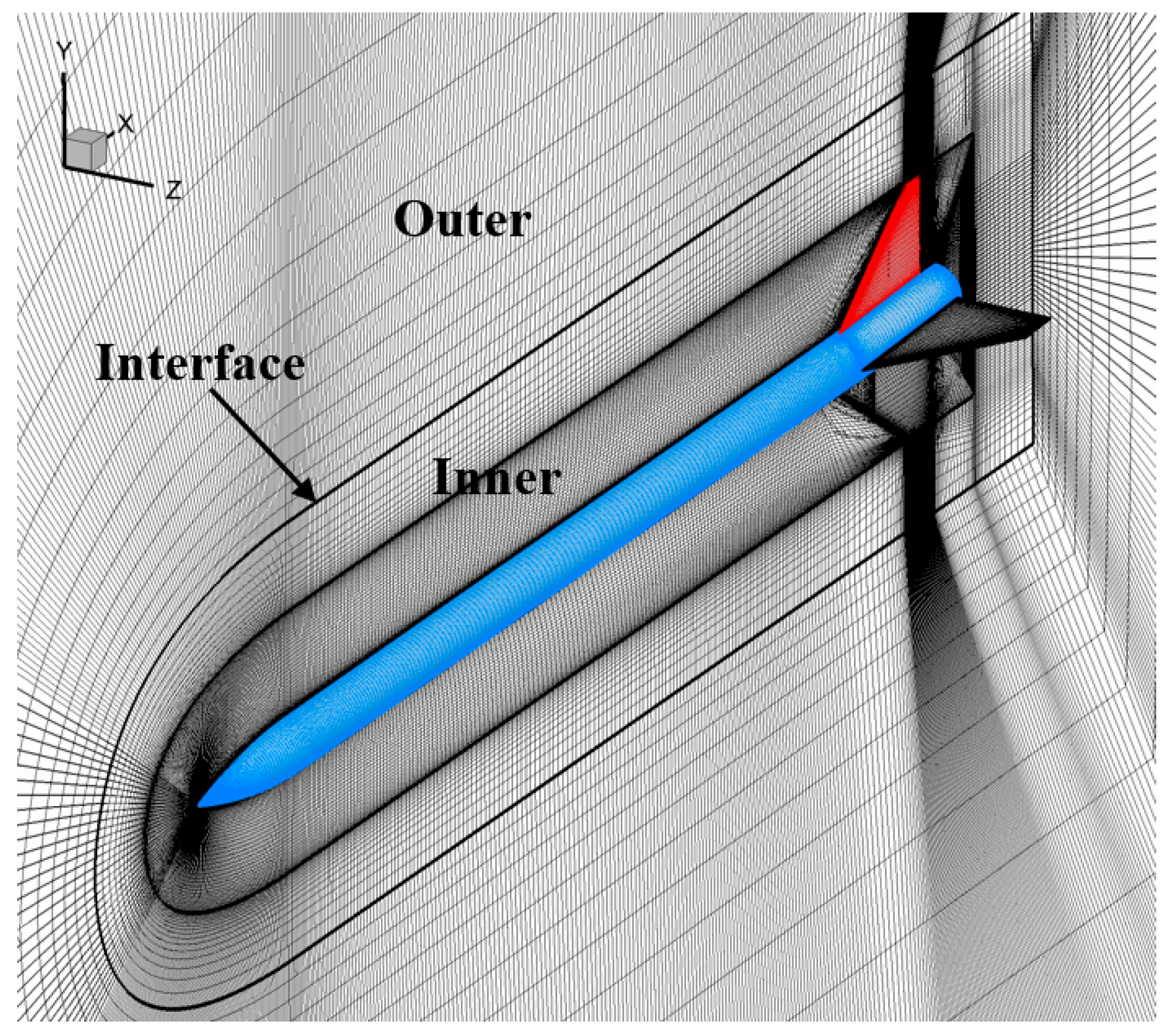
5.1. Grid Independence
5.2. Time Step Independence
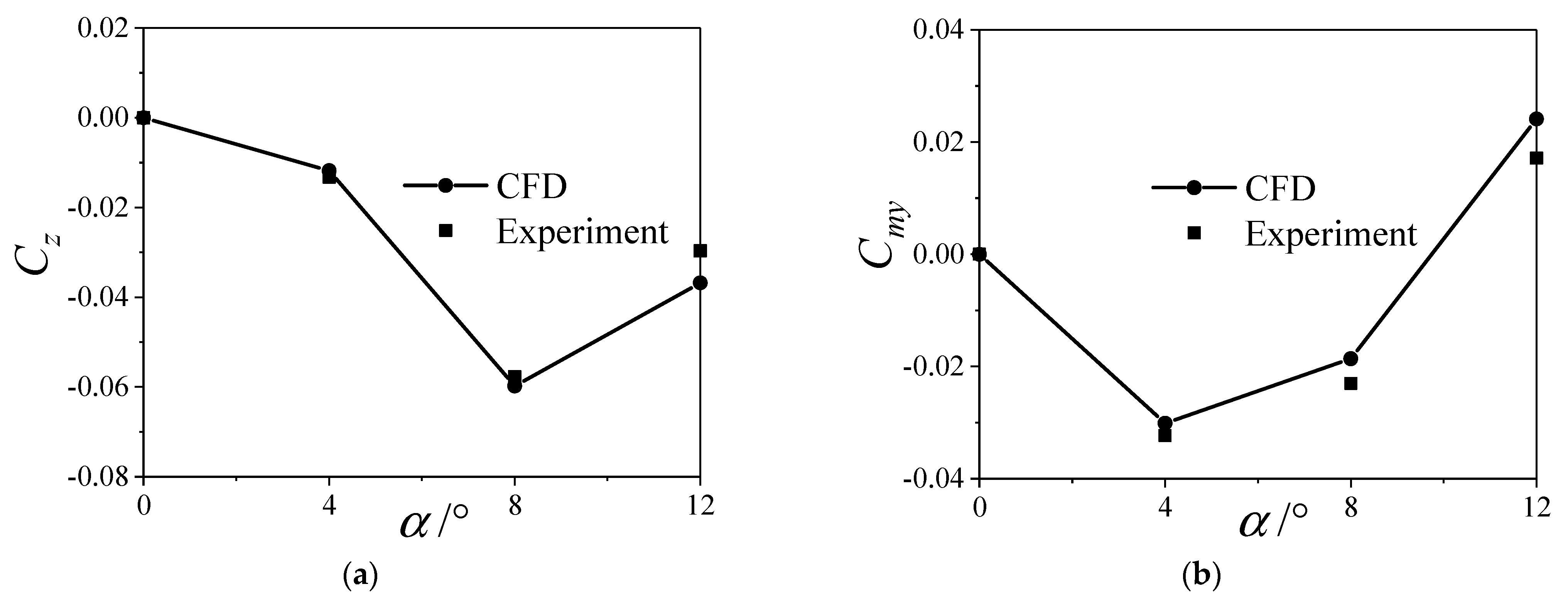
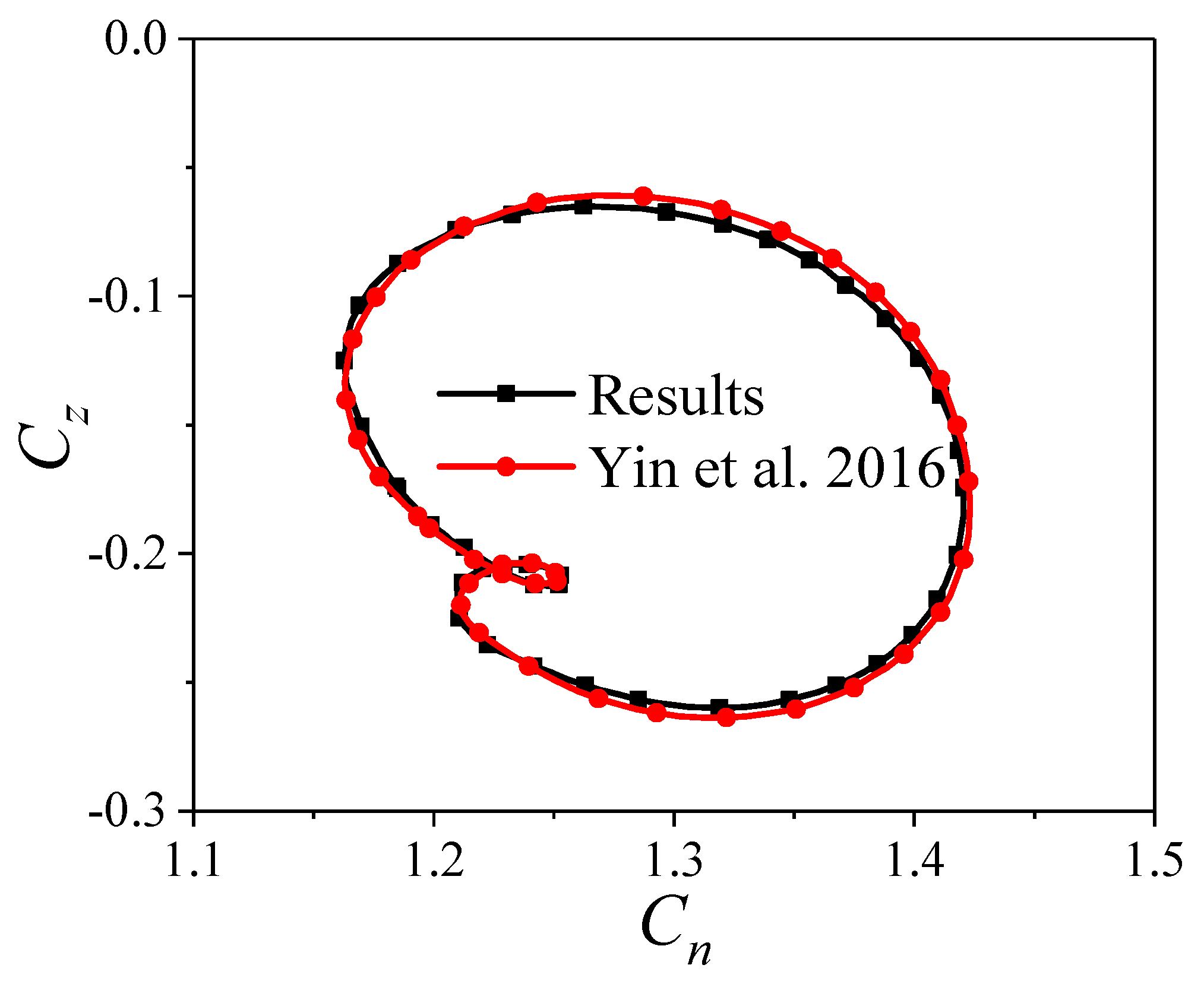
5.3. Comparison Validation
6. Effect of Deformation on Lateral Force
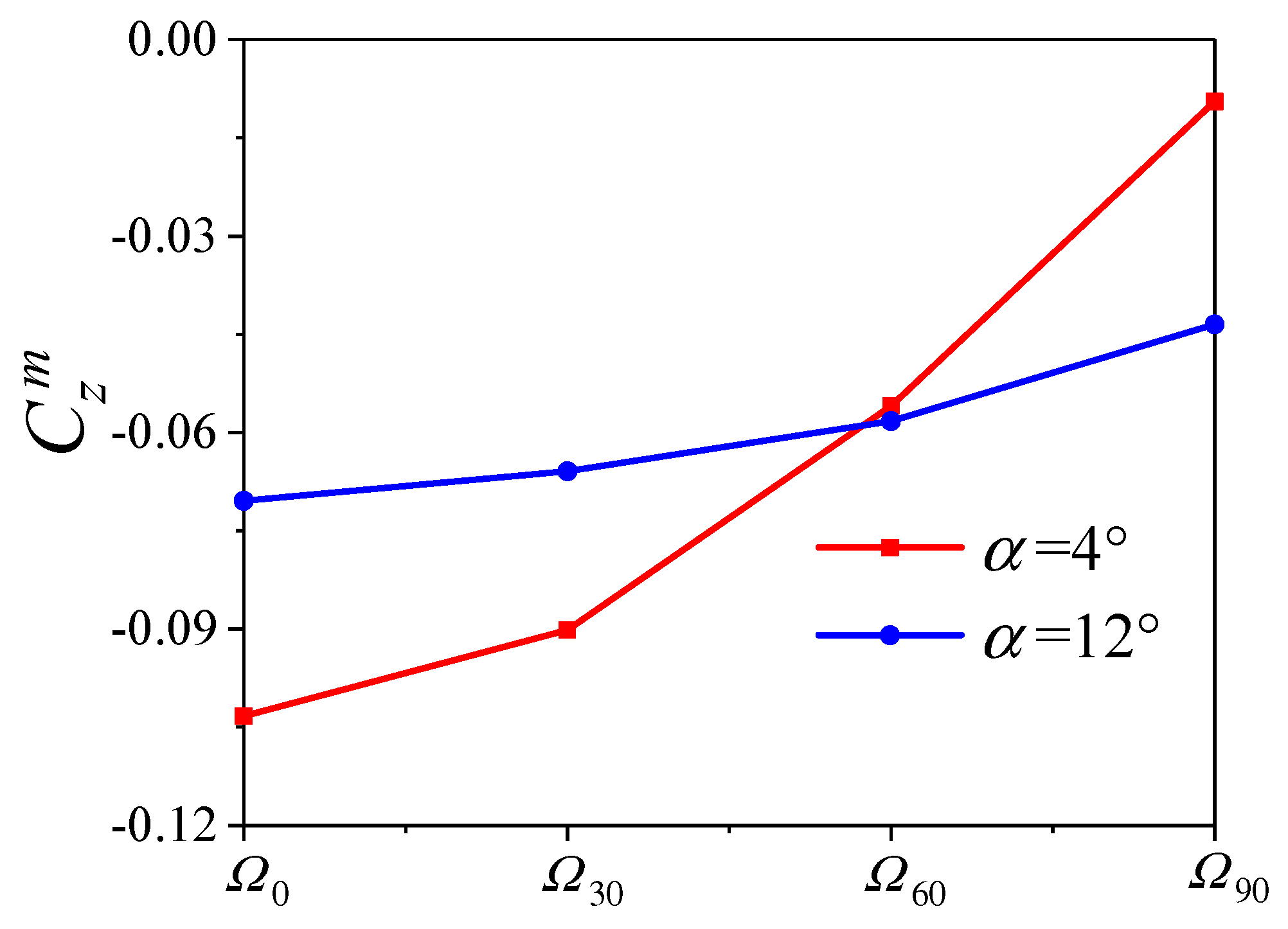
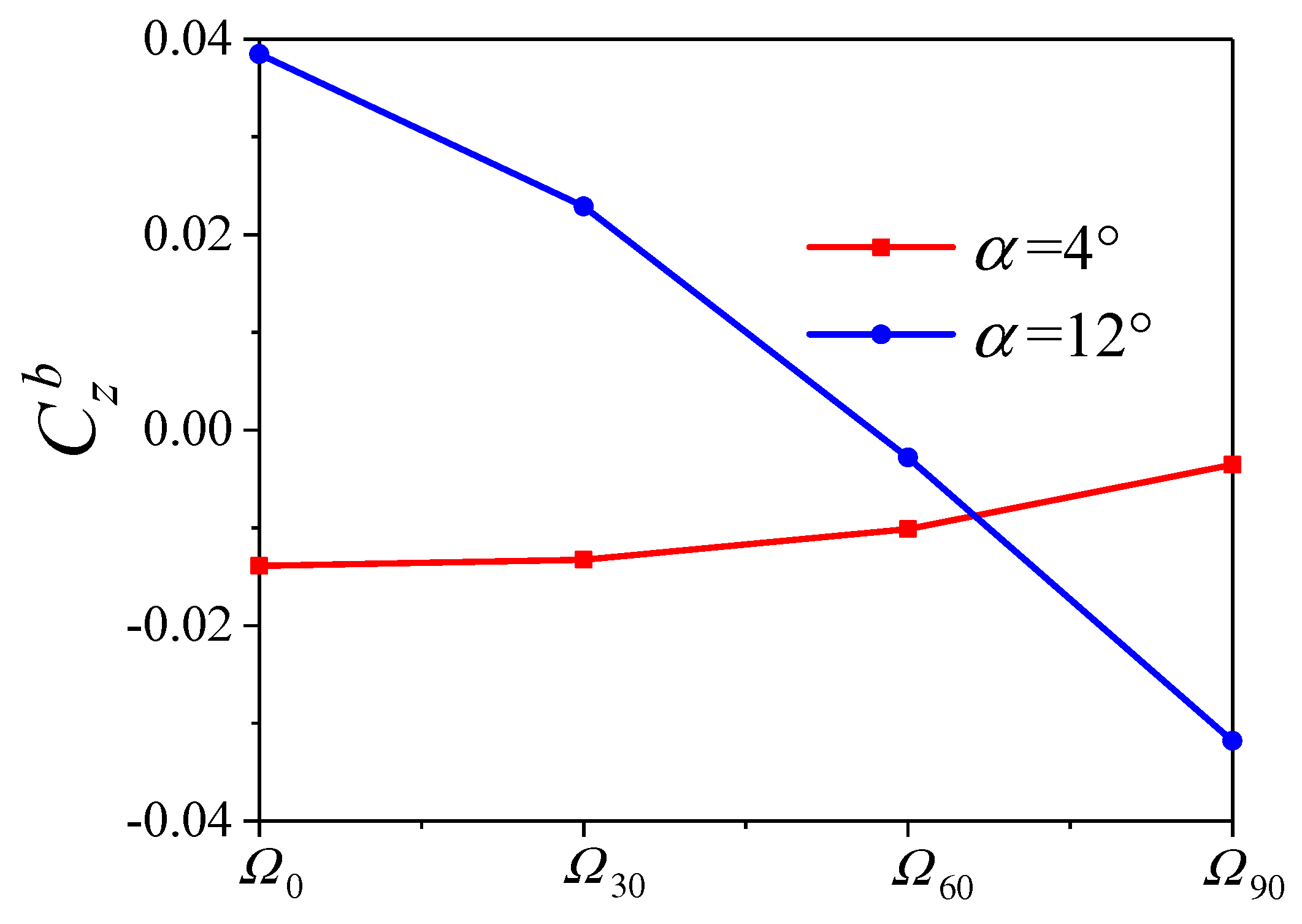
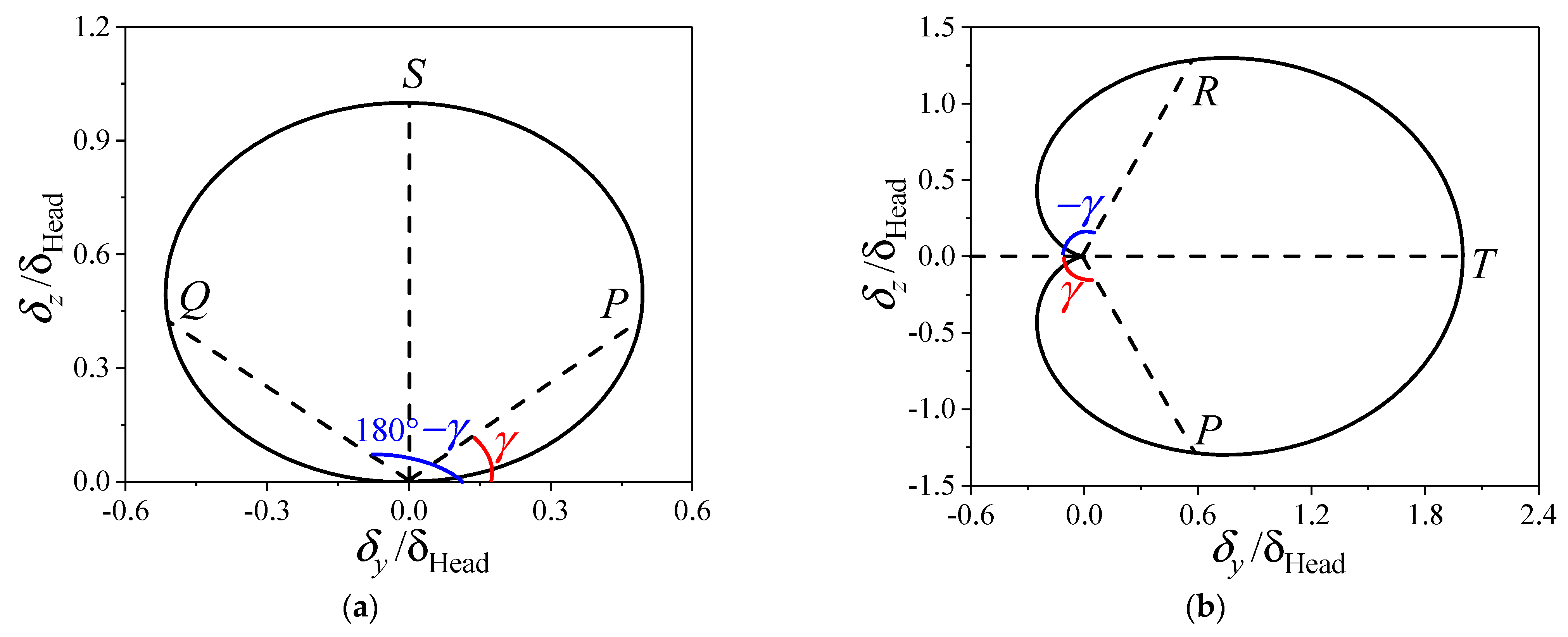
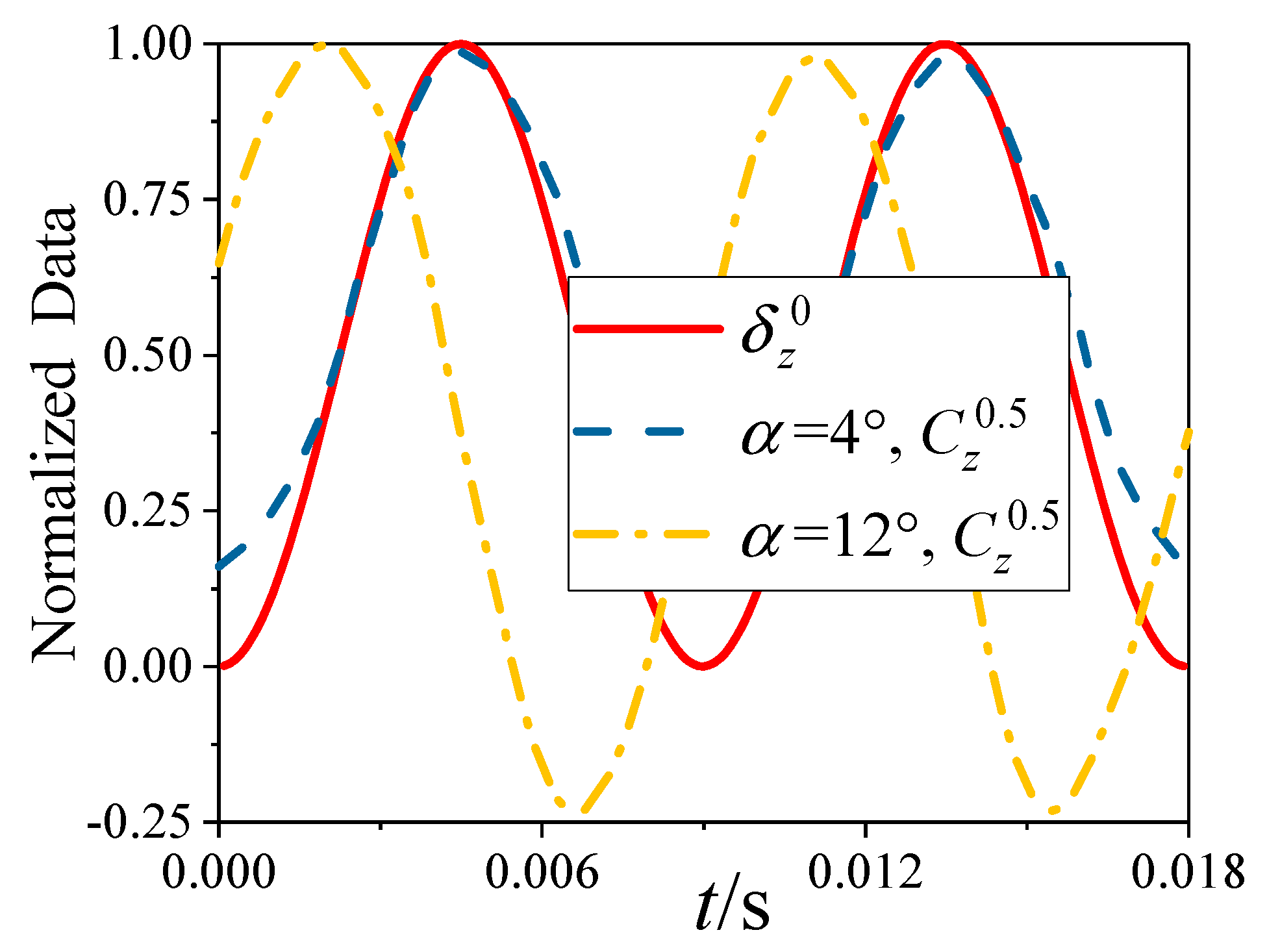
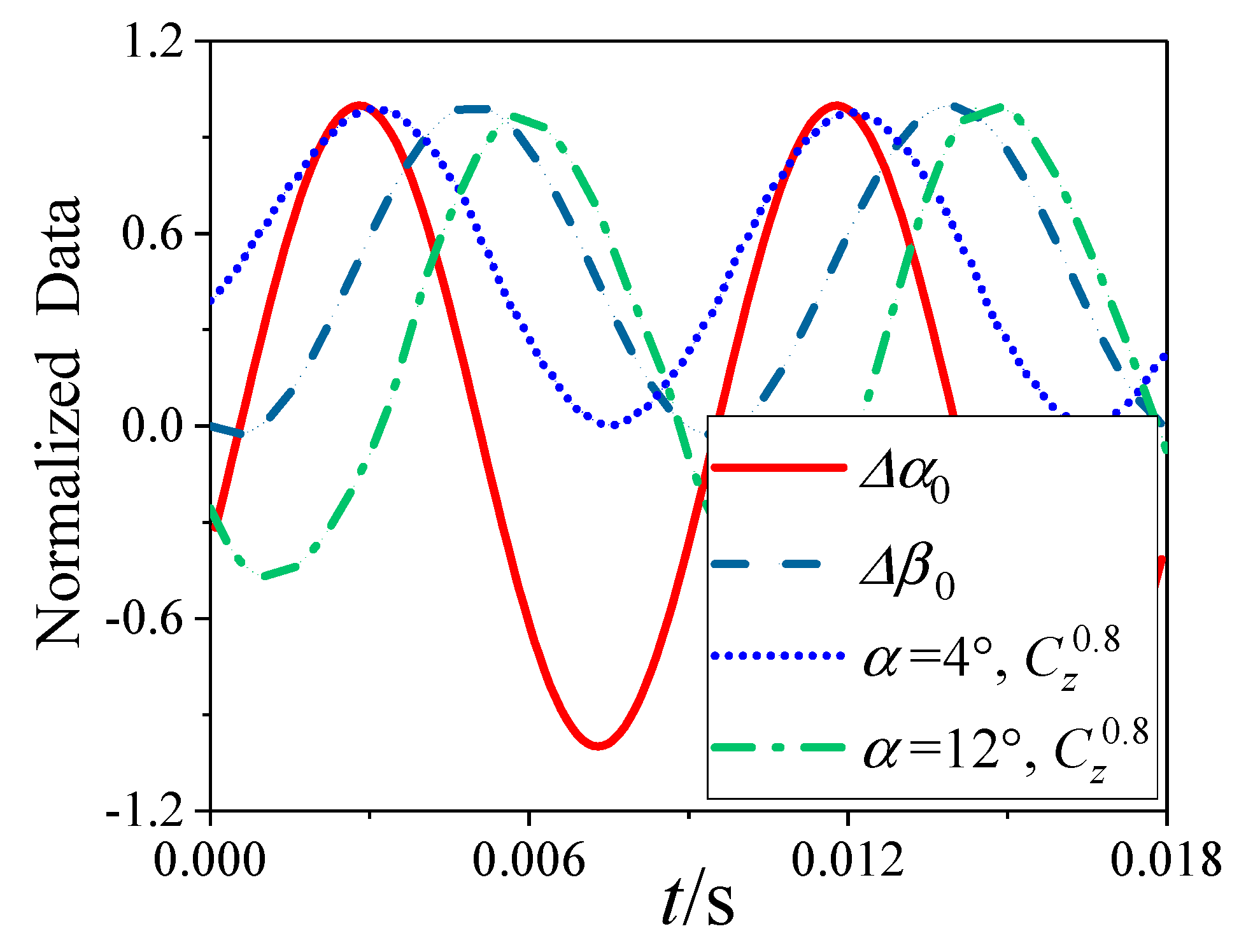
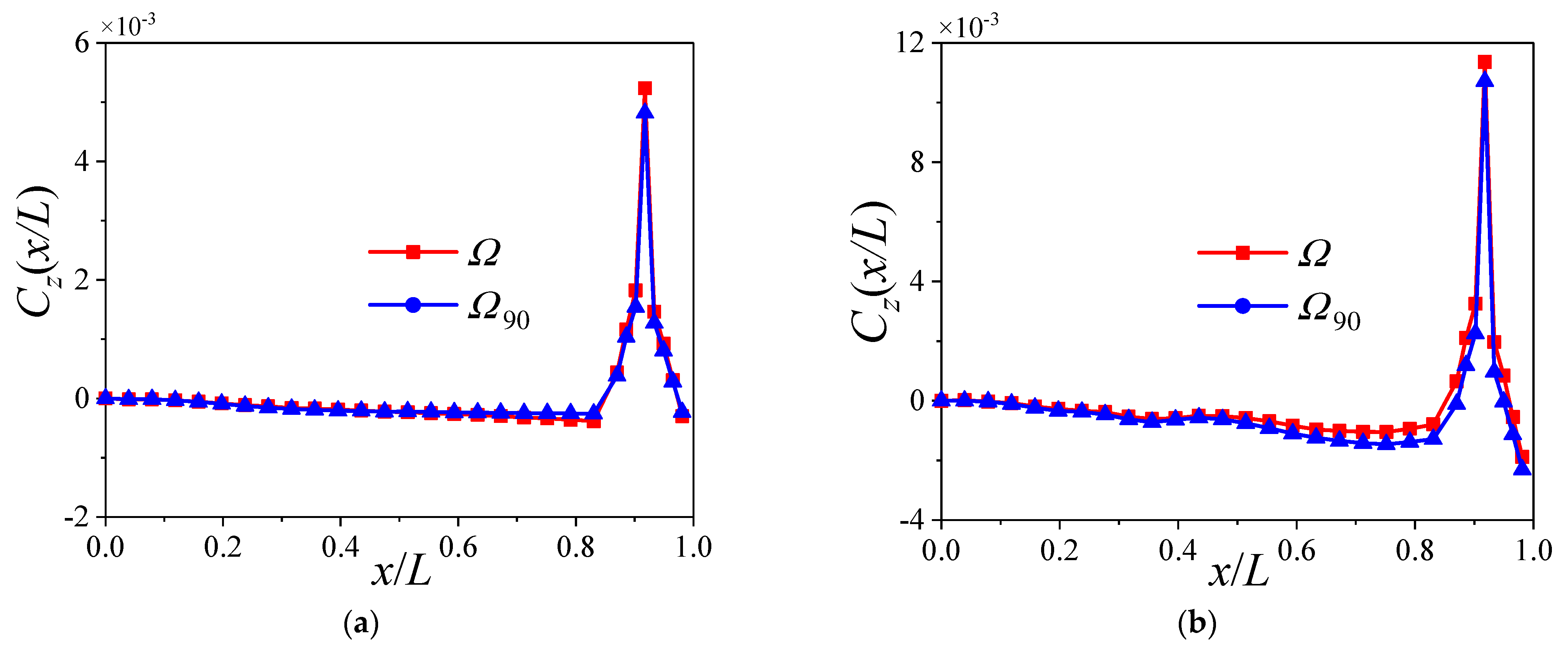
6.1. The Variation with Trajectory
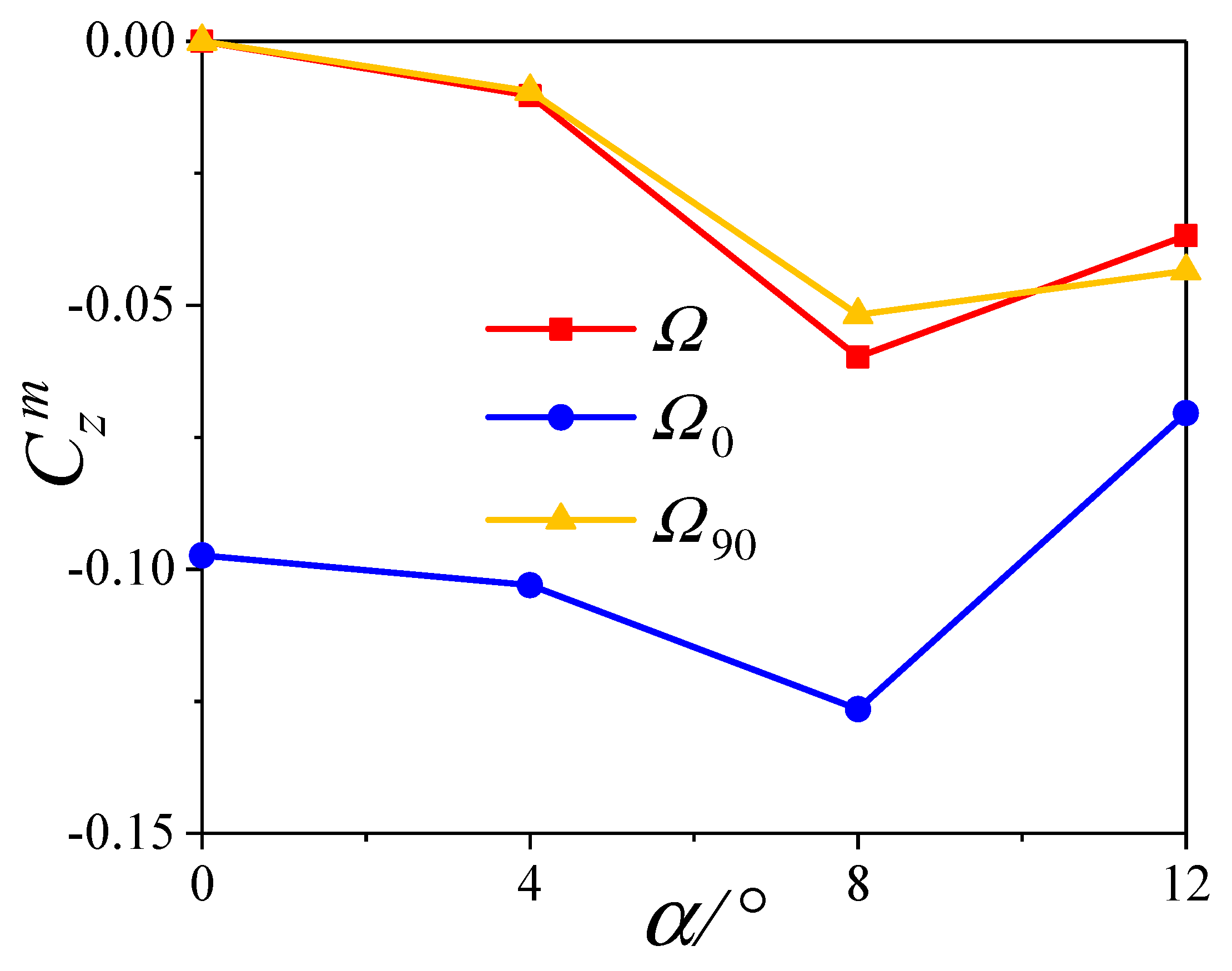
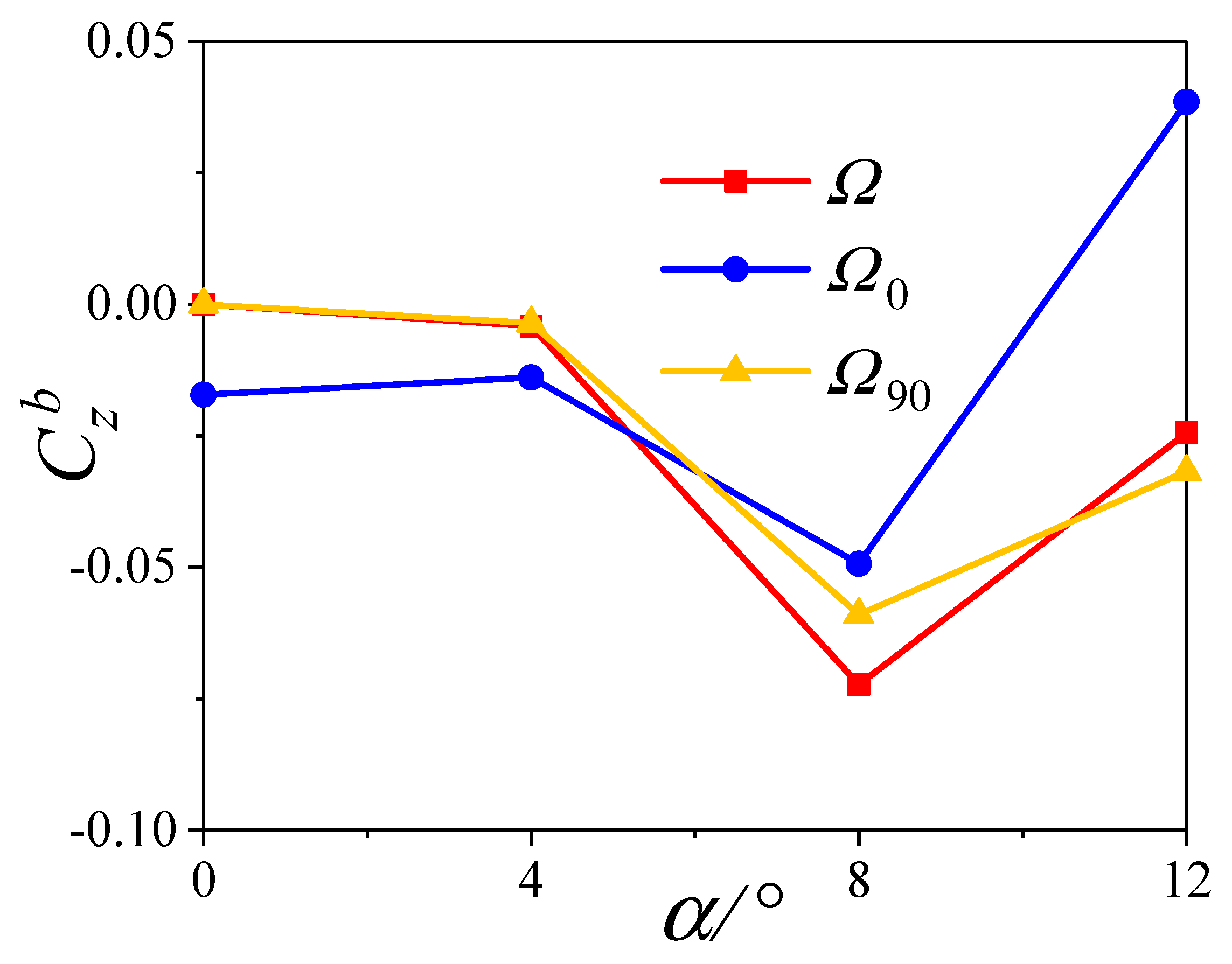
6.2. The Variation with Angles of Attack
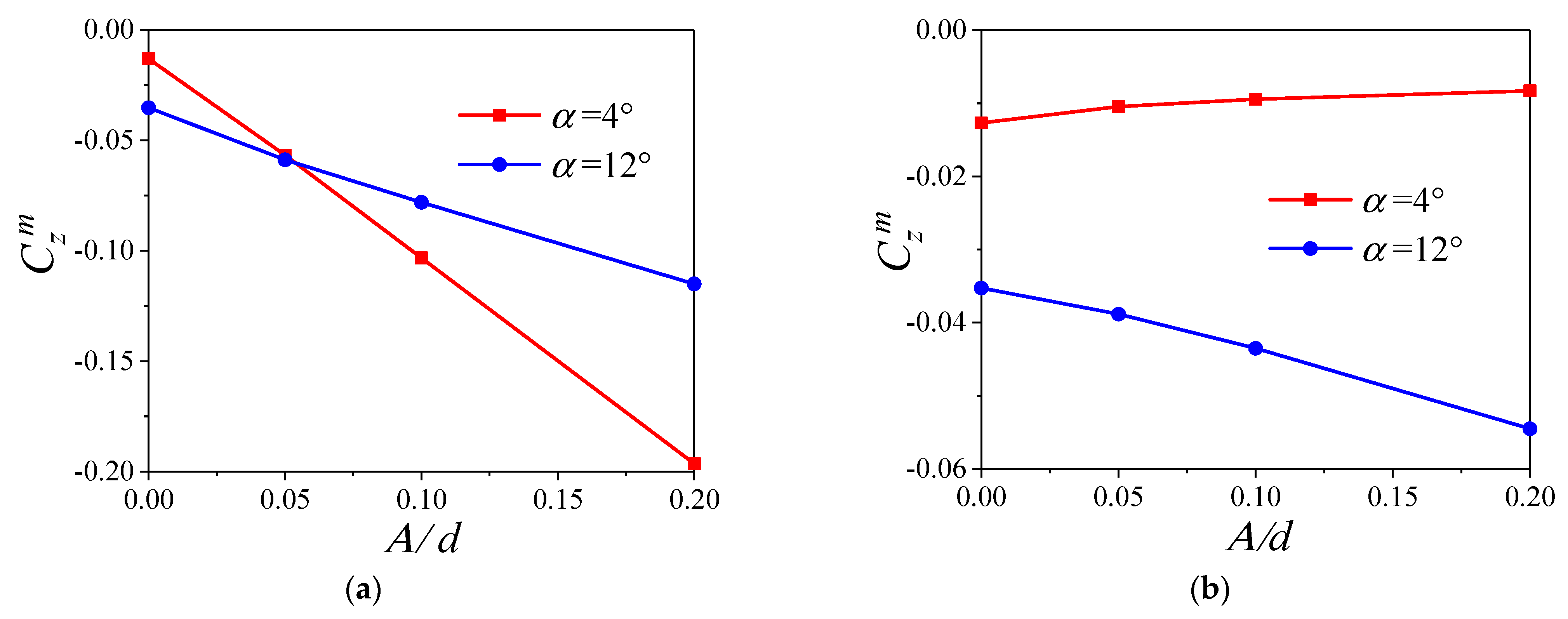
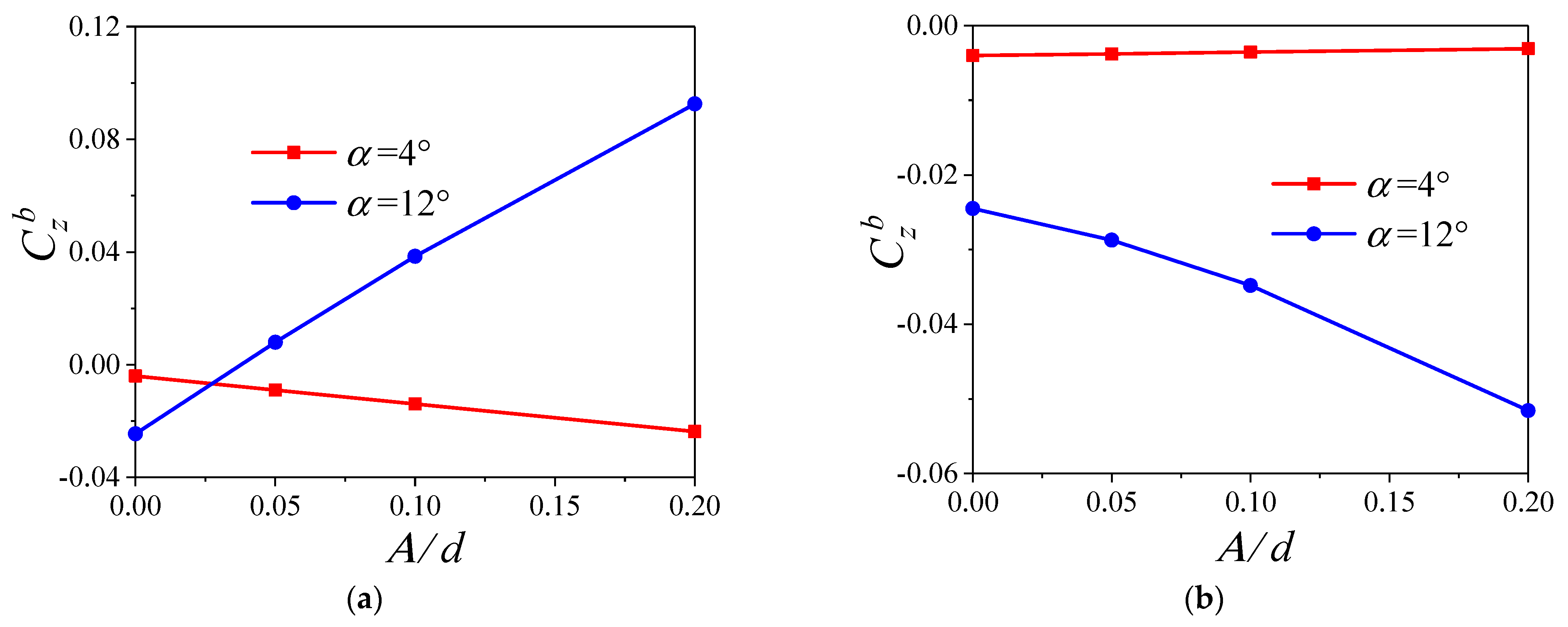
6.3. The Variation with Deformation Amplitude
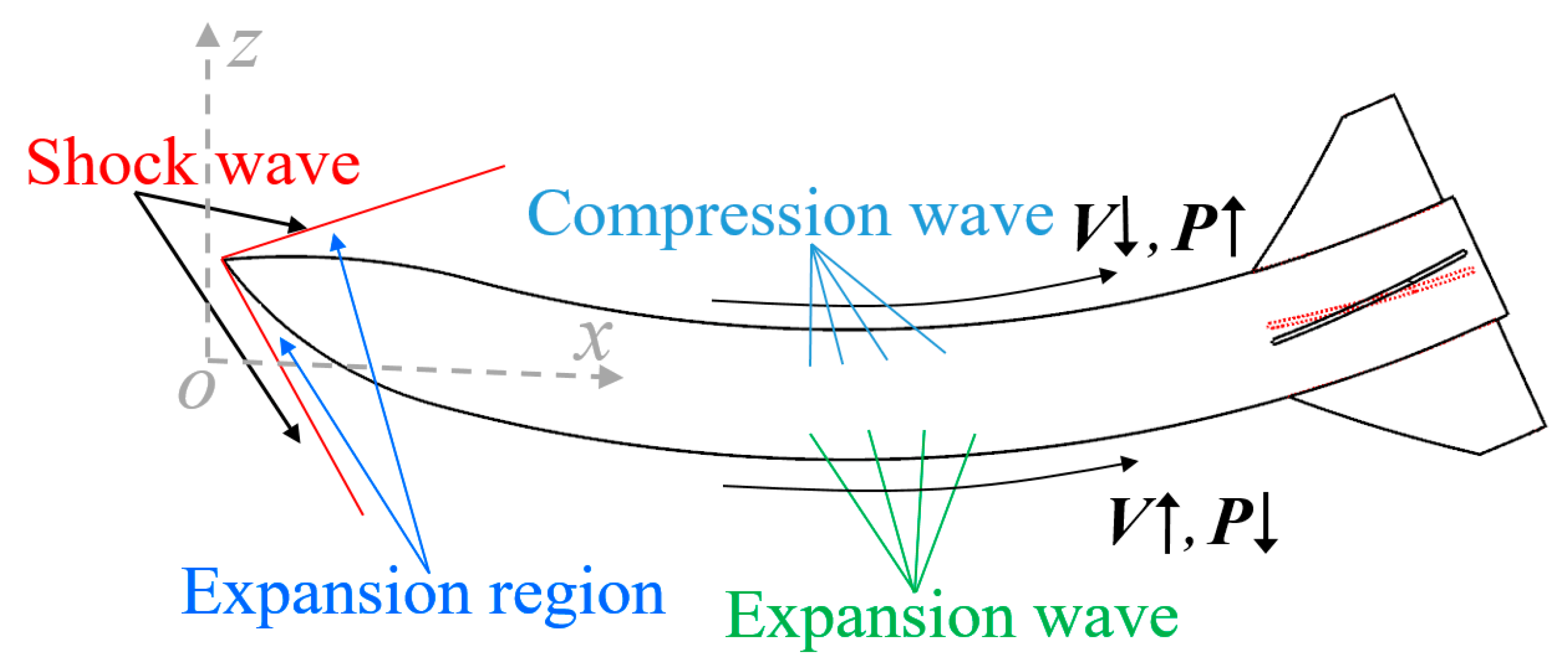
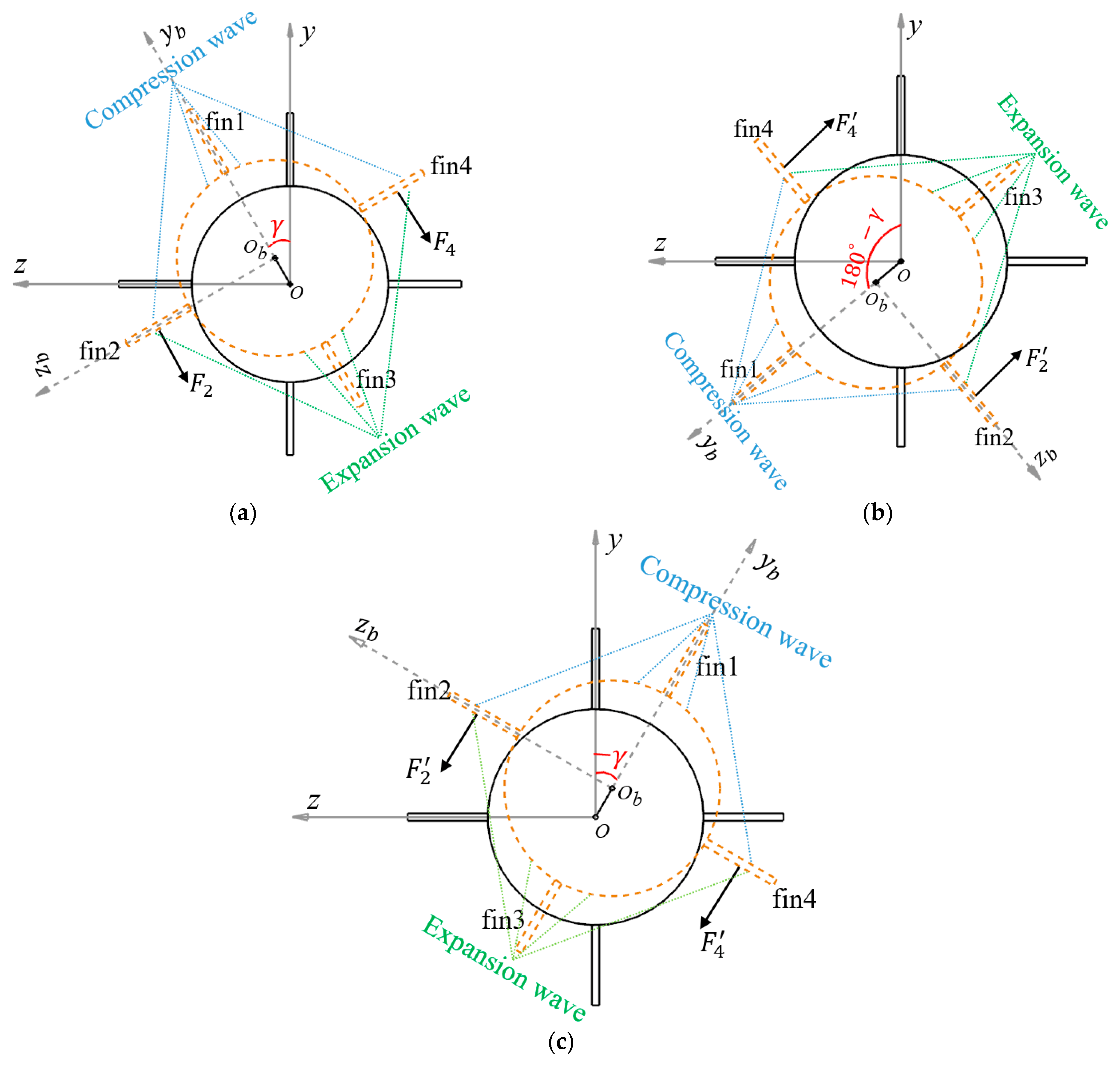
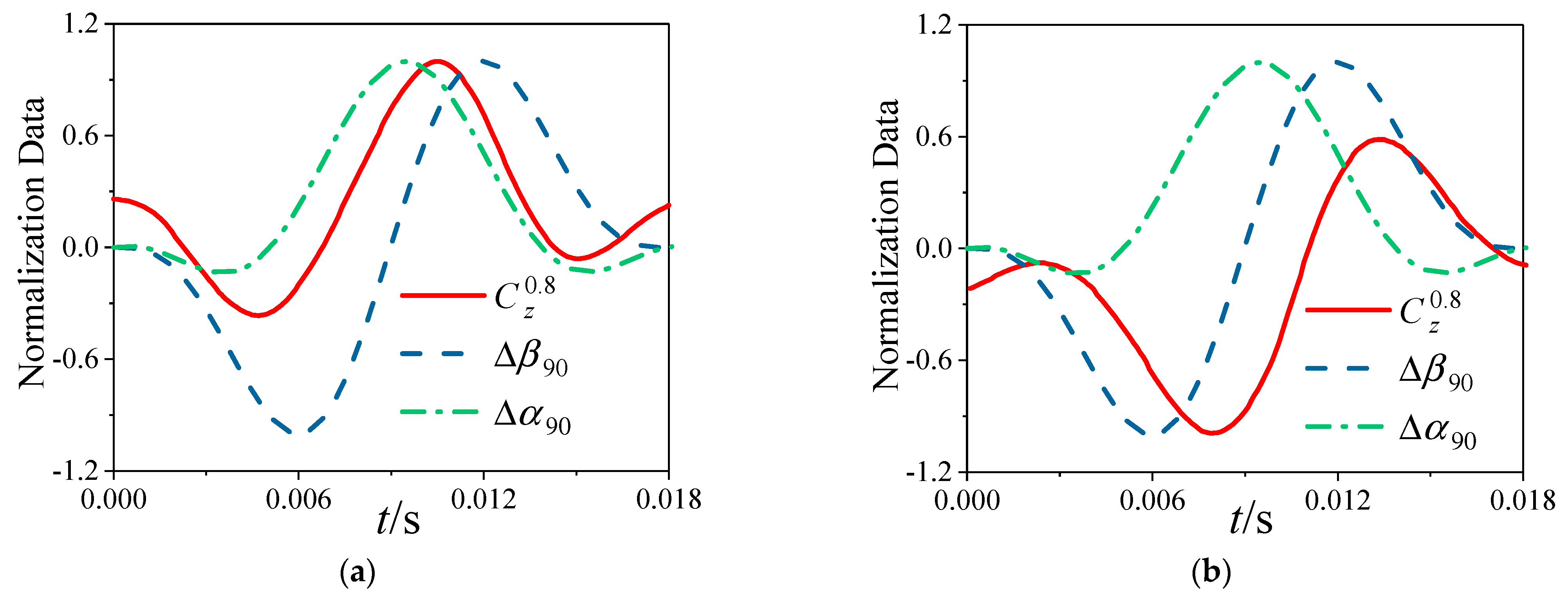
7. Mechanism on the Lateral Force Induced by Deformation
7.1. Compression and Expansion of the Fluid
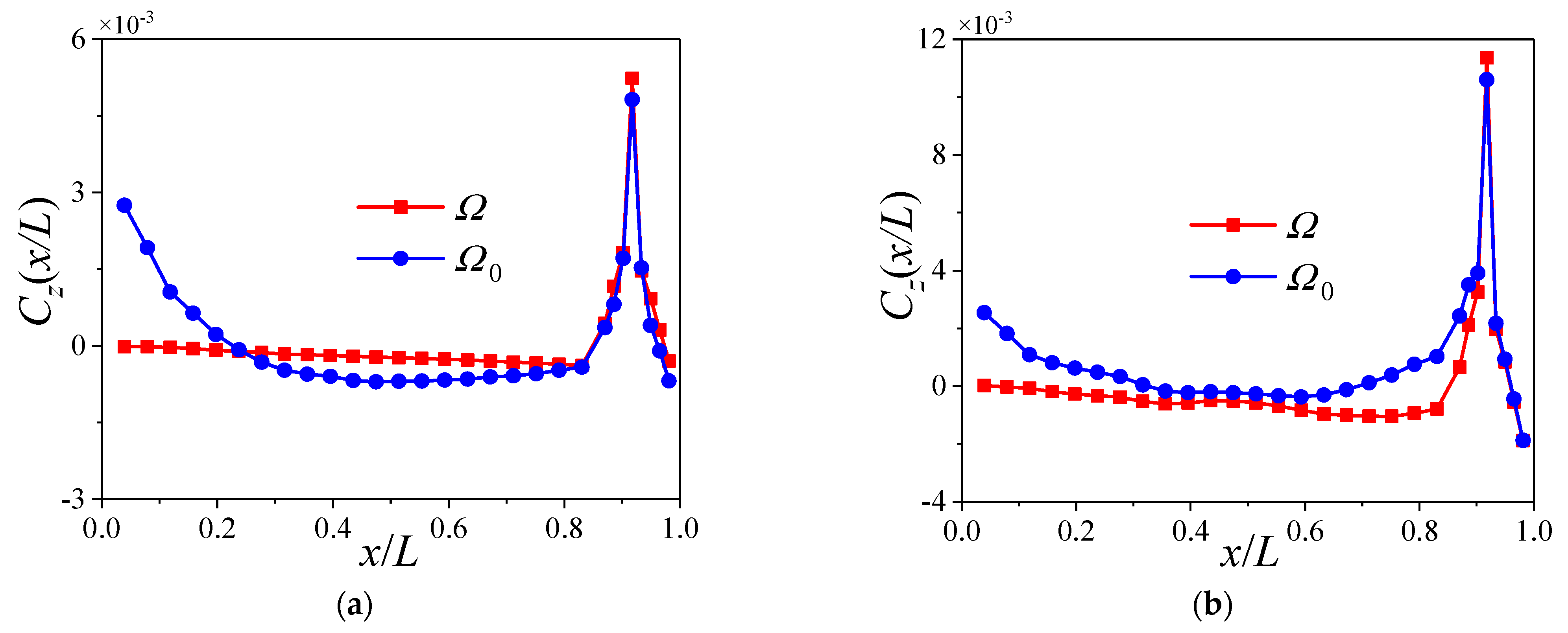
7.2. Change of Vortex and Pressure Distribution
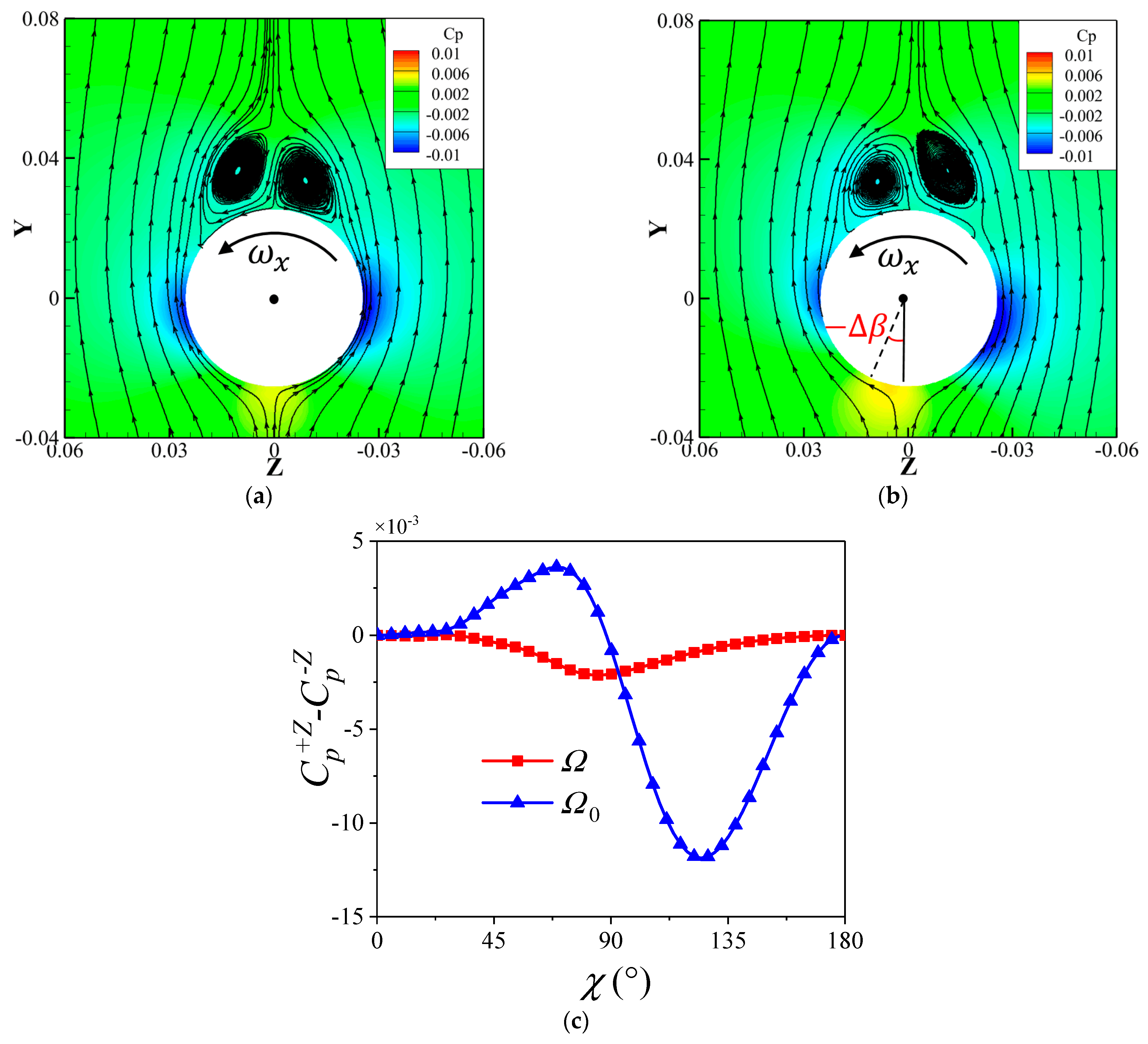
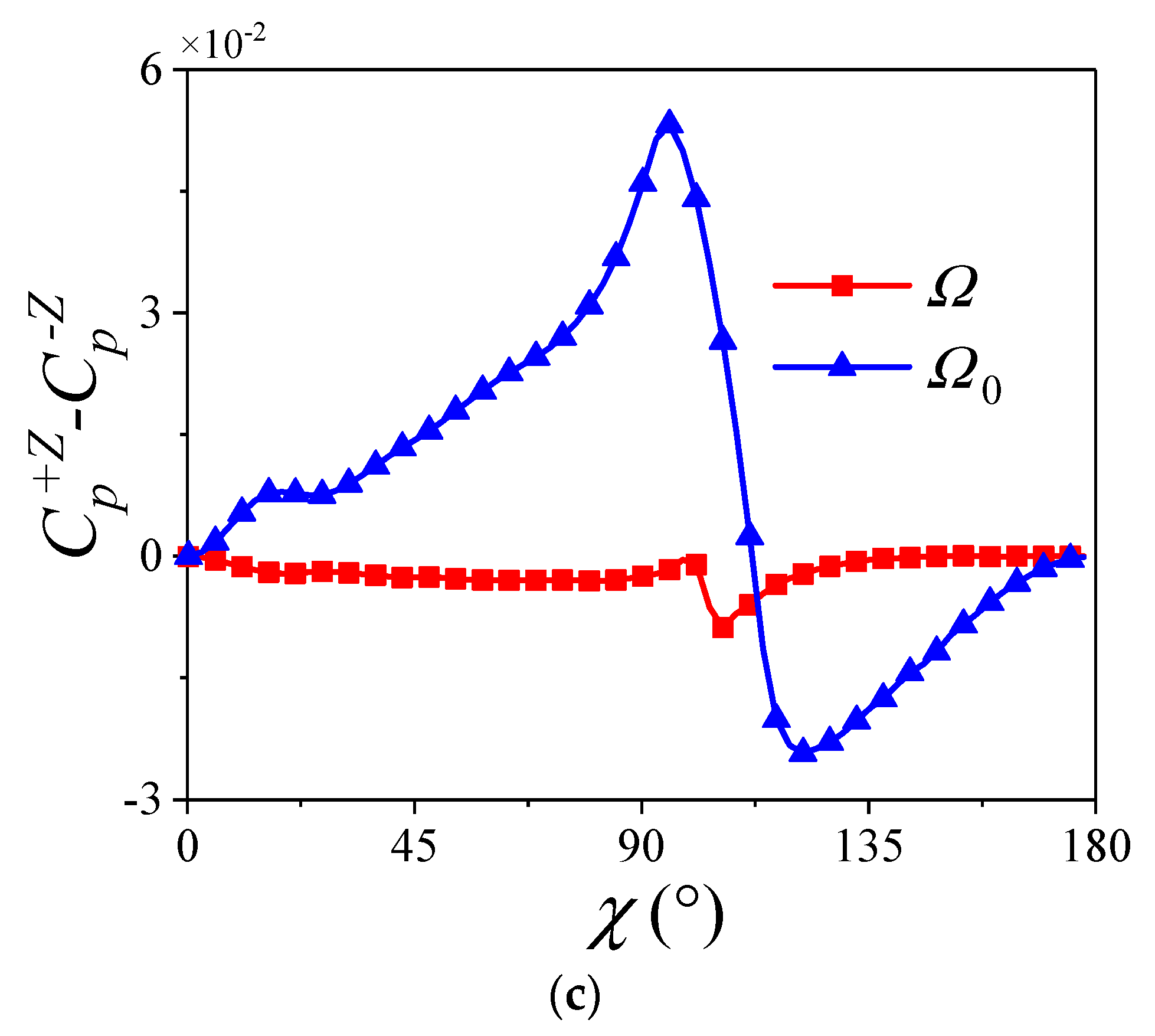
7.2.1. Effect of the Trajectory
7.2.2. Effect of the Trajectory
8. Conclusions
- The variation of the transient lateral force for the head of the projectile is consistent with that of the additional sideslip angle induced by the bending deformation, and it is almost independent of the angle of attack.
- The compression wave and expansion wave will increase the time−averaged lateral force for the middle of projectile at small angles of attack, while they have little effect on its value at large angles of attack.
- At small angles of attack, the coupling of the additional angle of attack and spinning motion is the main reason for the change of the transient lateral force for the tail of the projectile, while the additional sideslip angle will increase its time−averaged lateral force.
- At large angles of attack, the separation vortex will lead to a phase lag between the transient lateral force for the tail of the projectile and the additional sideslip angle, which will increase the time−averaged lateral force for the tail.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, C.; Liu, W.; Yang, G. Numerical studies of static aeroelastic effects on grid fin aerodynamic performances. Chin. J. Aeronaut. 2017, 30, 1300–1314. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, W.; Jiang, S.; Zhao, Z.; Zhu, H. Study of effect of elastic deformation on aerodynamic characteristics of a slender missile(rocket). J. Proj. Rocket. Missiles Guid. 2010, 30, 177–180. [Google Scholar]
- Yin, J.; Lei, J.; Wu, X.; Lu, T. Aerodynamic characteristics of a spinning projectile with elastic deformation. Aerosp. Sci. Technol. 2016, 51, 181–191. [Google Scholar] [CrossRef]
- Vaughn, H.R.; Reis, G.E. A magnus theory. AIAA J. 1973, 11, 1396–1403. [Google Scholar] [CrossRef]
- Jimenez−Varona, J. Numerical analysis of the Magnus effect on the forces past an axisymmetric body at high incidence. Aerospace 2023, 10, 163. [Google Scholar] [CrossRef]
- Sturek, W.B.; Kayser, L.D.; Nietubicz, C.J.; Reklis, R.P.; Opalka, K.O.; Dwyer, H.A. Computations of Magnus effects for a yawed, spinning body of revolution. AIAA J. 1978, 16, 687–692. [Google Scholar] [CrossRef]
- Cayzac, R.; Carette, E.; Denis, P.; Guillen, P. Magnus effect: Physical origins and numerical prediction. J. Appl. Mech. 2011, 78, 051005. [Google Scholar] [CrossRef]
- Martin, J.C. On Magnus effects caused by the boundary−layer displacement thickness on bodies of revolution at small angles of attack. J. Aeronaut. Sci. 1957, 24, 421–429. [Google Scholar] [CrossRef]
- Iversen, J.D. Correlation of Magnus force data for slender spinning cylinders. J. Spacecr. Rocket. 1973, 10, 268–272. [Google Scholar] [CrossRef]
- Morote, J.; Liaño, G. Prediction of nonlinear rolling and magnus coefficients of cruciform−finned missiles. J. Aircr. 2010, 47, 1413–1425. [Google Scholar] [CrossRef][Green Version]
- Simon, F.; Deck, S.; Guillen, P.; Merlen, A.; Cayzac, R. Numerical simulation of magnus force control for projectiles configurations. Comput. Fluids 2009, 38, 965–968. [Google Scholar] [CrossRef]
- Klatt, D.; Hruschka, R.; Leopold, F. Investigation of the Magnus effect of a generic projectile at Mach 3 up to 16 degrees angle of attack. J. Appl. Mech. 2013, 80, 031603. [Google Scholar] [CrossRef]
- Yin, J.; Wu, X.; Lei, J. Body−fin interference on the Magnus effect of spinning projectile in supersonic flows. Eng. Appl. Comput. Fluid Mech. 2017, 11, 496–512. [Google Scholar] [CrossRef]
- Yin, J.; Wu, X.; Lei, J.; Lu, T.; Liu, X. Canards interference on the Magnus effect of a fin−stabilized spinning missile. Adv. Mech. Eng. 2018, 10, 1–16. [Google Scholar] [CrossRef]
- Cayzac, R.; Carette, E.; Heddadj, S. Complex aerodynamics behavior of high spin APFSDS projectile. J. Appl. Mech. 2013, 80, 031601. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Yu, S.C.; Schlüter, J. Aerodynamic characteristics of a wrap−around fin rocket. Aircr. Eng. Aerosp. Technol. 2016, 88, 82–96. [Google Scholar] [CrossRef]
- Nygaard, T.A.; Meakin, R.L. Aerodynamic analysis of a spinning missile with dithering canards. J. Spacecr. Rocket. 2004, 41, 726–734. [Google Scholar] [CrossRef][Green Version]
- Blades, E.L.; Marcum, D.L. Numerical simulation of a spinning missile with dithering canards using unstructured grids. J. Spacecr. Rocket. 2004, 41, 248–256. [Google Scholar] [CrossRef]
- Murphy, C.H.; Mermagen Sr, W.H. Spin−yaw lockin of an elastic finned projectile. J. Guid. Control Dyn. 2005, 28, 121–130. [Google Scholar] [CrossRef][Green Version]
- Murphy, C.H.; Mermagen Sr, W.H. Flight motion of a continuously elastic finned missile. J. Guid. Control Dyn. 2003, 26, 89–98. [Google Scholar] [CrossRef][Green Version]
- Ehramianpour, M.; Haddadpour, H.; Ahmadian, M.T. Aeroelastic behavior of a slender body considering free fittings. J. Mech. Sci. Technol. 2010, 24, 1755–1762. [Google Scholar] [CrossRef]
- Ericsson, L.E.; Pavish, D. Aeroelastic vehicle dynamics of a proposed delta II 7920−10L launch vehicle. J. Spacecr. Rocket. 2000, 37, 28–38. [Google Scholar] [CrossRef]
- Dowell, E.; Edwards, J.; Strganac, T. Nonlinear aeroelasticity. J. Aircr. 2003, 40, 857–874. [Google Scholar] [CrossRef]
- Wu, X.; Lu, T.; Lei, J. Effects of head deformation on aerodynamic characteristics of spinning vehicle. Proc. Inst. Mech. Eng. G J. Aerosp. Eng. 2015, 229, 1975–1986. [Google Scholar] [CrossRef]
- Youn, E.B.; Silton, S.I. Numerical study on bending body projectile aerodynamics. In Proceedings of the 34th AIAA Applied Aerodynamics Conference, Washington, DC, USA, 14 June 2016; p. 4331. [Google Scholar]
- Paul, J.; Silton, S.I. Influence of bending locations and angles on the aerodynamic performance of a bent body projectile. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8 January 2018; p. 1269. [Google Scholar]
- Argyropoulos, C.D.; Markatos, N.C. Recent advances on the numerical modelling of turbulent flows. Appl. Math. Model. 2015, 39, 693–732. [Google Scholar] [CrossRef]
- Catalano, P.; Amato, M. An evaluation of RANS turbulence modelling for aerodynamic applications. Aerosp. Sci. Technol. 2003, 7, 493–509. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications; Butterworth−Heinemann: Oxford, UK, 2015. [Google Scholar]
- Ozcatalbas, M.; Acar, B.; Uslu, S. Effect of free−play and initial conditions on aeroelastic behavior of a missile canard in supersonic flow. In Proceedings of the AIAA AVIATION Forum, Virtual Event, 15−19 June 2020; p. 2663. [Google Scholar]
- De Boer, A.; Van der Schoot, M.S.; Bijl, H. Mesh deformation based on radial basis function interpolation. Comput. Struct. 2007, 85, 784–795. [Google Scholar] [CrossRef]
- Niu, J.; Lei, J.; He, J. Radial basis function mesh deformation based on dynamic control points. Aerosp. Sci. Technol. 2017, 64, 122–132. [Google Scholar] [CrossRef]
- Jameson, A. Time dependent calculations using multigrid, with applications to unsteady flows past airfoils and wings. In Proceedings of the 10th Computational Fluid Dynamics Conference, Honolulu, HI, USA, 24–26 June 1991; p. 1596. [Google Scholar]
- Pandya, S.A.; Venkateswaran, S.; Pulliam, T.H. Implementation of preconditioned dual−time procedures in overflow. In Proceedings of the 41st AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 23–26 June 2003; p. 72. [Google Scholar]
- Turkel, E.; Vatsa, V.N. Choice of variables and preconditioning for time dependent problems. In Proceedings of the 16th AIAA Computational Fluid Dynamics Conference, Orlando, FL, USA, 23–26 June 2003; p. 3692. [Google Scholar]
- Uselton, J.C.; Carman, J.B. A study of the Magnus effects on a sounding rocket at supersonic speeds. J. Spacecr. Rocket. 1971, 8, 28–34. [Google Scholar] [CrossRef]

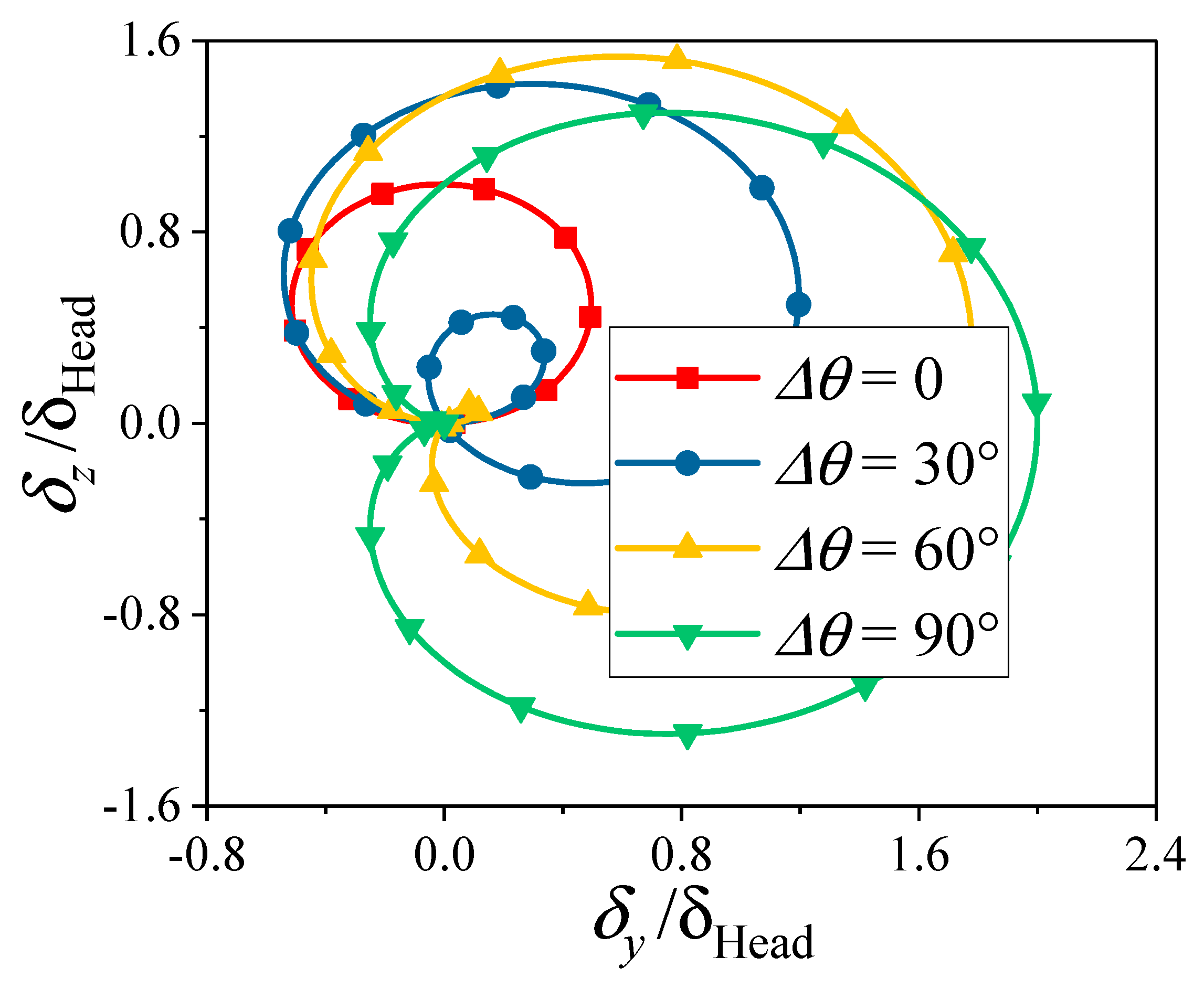
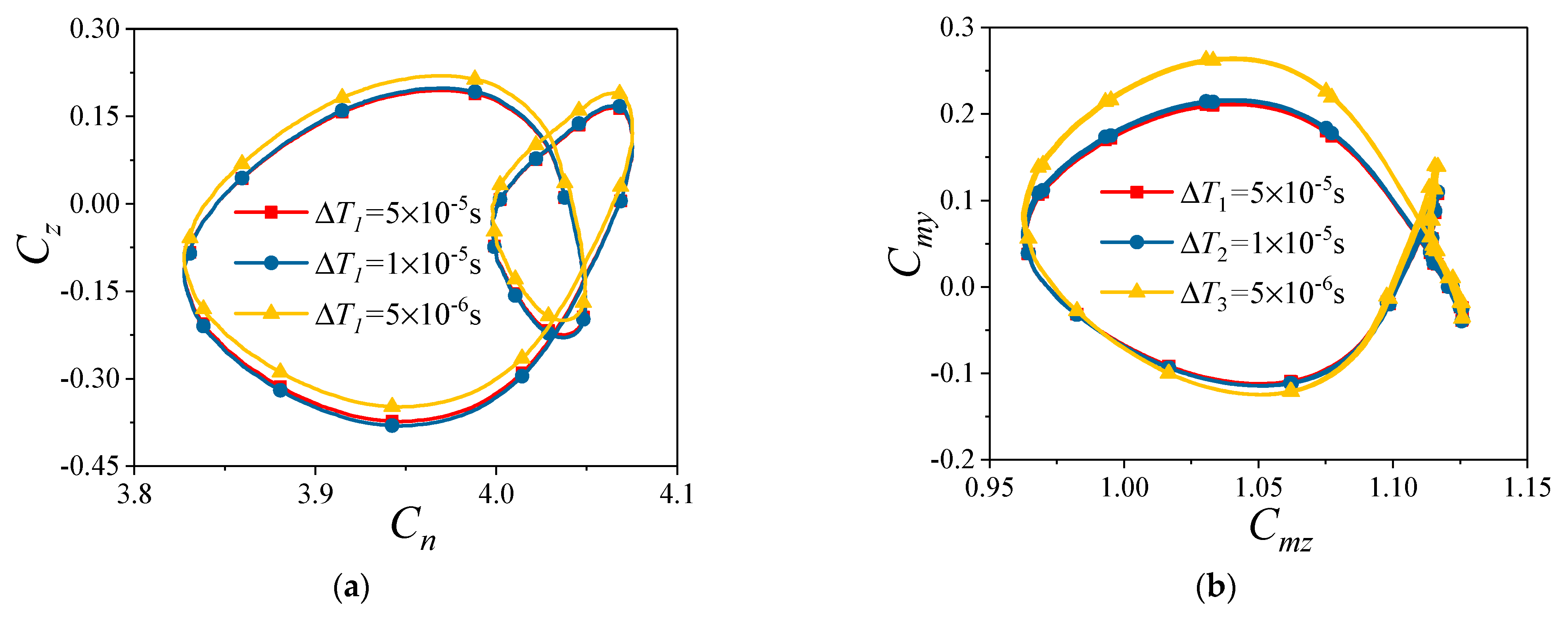
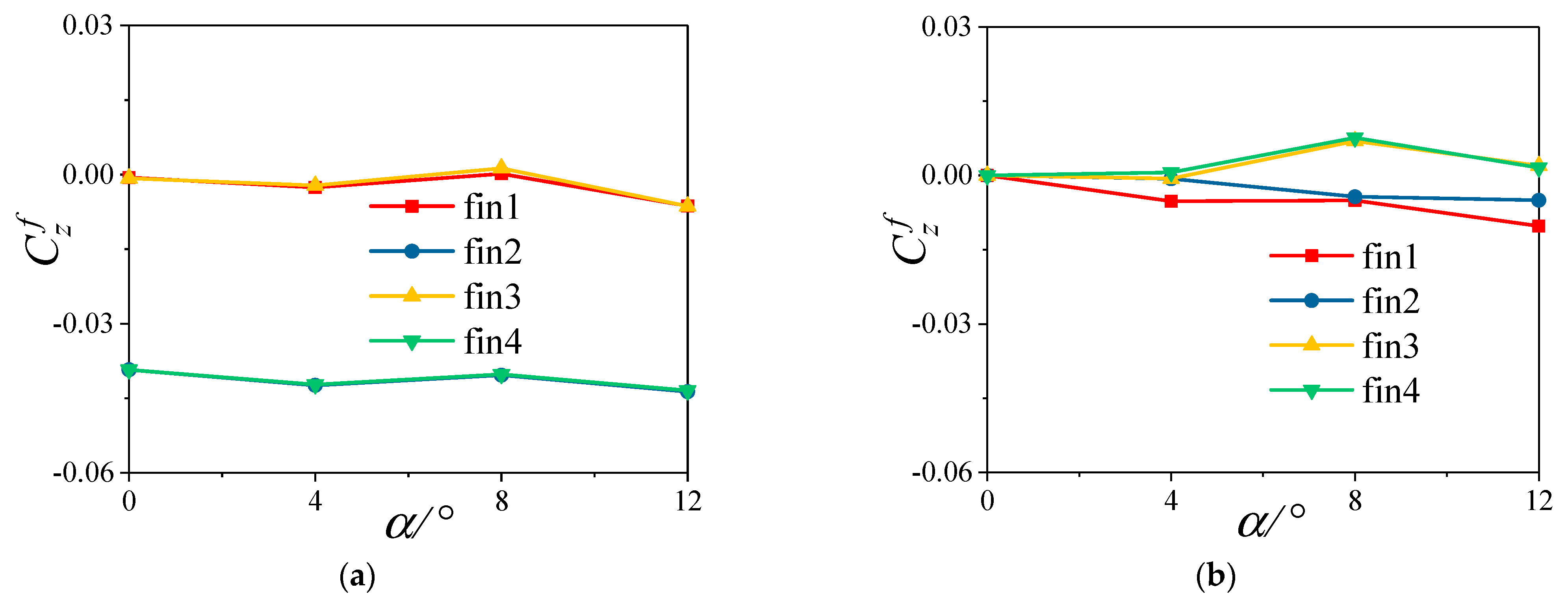



| Apache | Coarse | Fine |
|---|---|---|
| Axial | 345 | 505 |
| Spanwise | 71 | 91 |
| Circumferential | 140 | 180 |
| Total (Mil.) | 6.47 | 12.82 |
| Apache | ||||
|---|---|---|---|---|
| Coarse–Fine | −0.08 | −2.62 | −0.16 | 7.51 |
| Ma | A | ||||
|---|---|---|---|---|---|
| 1.54 × 107 | 3.0 | 0.011 | 0.44 | 0°~12° | 0~0.2d |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Lei, J.; Yu, Y.; Yin, J. Effect of Bending Deformation on the Lateral Force of Spinning Projectiles with Large Aspect Ratio. Aerospace 2023, 10, 810. https://doi.org/10.3390/aerospace10090810
Liu Q, Lei J, Yu Y, Yin J. Effect of Bending Deformation on the Lateral Force of Spinning Projectiles with Large Aspect Ratio. Aerospace. 2023; 10(9):810. https://doi.org/10.3390/aerospace10090810
Chicago/Turabian StyleLiu, Qi, Juanmian Lei, Yong Yu, and Jintao Yin. 2023. "Effect of Bending Deformation on the Lateral Force of Spinning Projectiles with Large Aspect Ratio" Aerospace 10, no. 9: 810. https://doi.org/10.3390/aerospace10090810
APA StyleLiu, Q., Lei, J., Yu, Y., & Yin, J. (2023). Effect of Bending Deformation on the Lateral Force of Spinning Projectiles with Large Aspect Ratio. Aerospace, 10(9), 810. https://doi.org/10.3390/aerospace10090810







