Aeroelasticity Model for Highly Flexible Aircraft Based on the Vortex Lattice Method

Abstract

With the increasing use of composite materials in aviation, structural aircraft design often becomes limited by stiffness, rather than strength. As a consequence, aeroelastic analysis becomes more important to optimize both aircraft structures and control algorithms. A low computational cost aeroelasticity model based on VLM and rigid-body dynamics is proposed in this work. UAV flight testing is performed to evaluate the accuracy of the proposed model. Two flight sections are chosen to be modeled based on recorded aerodynamic surface control data. The calculated accelerations are compared with recorded flight data. It is found that the proposed model adequately captures the general flight profile, with acceleration peak errors between −6.2% and +8.4%. The average relative error during the entire flight section is 39% to 44%, mainly caused by rebounds during the beginning and end of pull-up maneuvers. The model could provide useful results for the initial phases of aircraft control law design when comparing different control algorithms.

1. Introduction

With the increasing use of composite materials in aircraft structures [1], there is a general trend of decreasing structural stiffness. While modern composite materials have excellent strength-to-weight ratios, their stiffness-to-weight ratios are similar to or lower than traditional materials used in aviation construction [2]. If the structure of the aircraft is insufficiently stiff, aeroelastic effects can negatively impact its flight characteristics. Because of the reduced natural frequencies, the aircraft can become difficult or impossible to pilot manually [3]. Additionally, the maximum speed of the aircraft becomes limited by flutter. Because of these detrimental aeroelastic effects, stiffness, rather than strength, is often a limiting factor in composite aircraft design.

Many authors investigate ways to suppress these negative effects, in order to achieve good flight characteristics with a lighter structure [4,5,6,7,8,9]. Some authors focus on developing structural optimization methods, modifying the aircraft structure to have an acceptable aeroelastic response, while retaining a low weight [4,9]. Another proposed passive method of improving the aeroelastic response of the aircraft is to use optimized tuned mass dampers [5]. Most authors focus on active methods, using the control surfaces of the aircraft to suppress flutter and improve handling qualities [6,7,8].

These structural and control law optimizations are highly iterative processes, requiring either a lot of computing power or low-order computationally inexpensive aeroelasticity models. Some authors use aeroelasticity models based on computational fluid dynamics (CFD) [4,7]. Because of its accuracy and versatility, CFD is a commonly used tool in both aerospace and other disciplines [10,11,12,13,14]. However, because CFD is very computationally expensive, for aeroelastic analysis most authors use either an analytical aerodynamic model [8] or a vortex lattice method (VLM) or doublet lattice method (DLM)-based model [5]. VLM is more widely used for time-domain analysis, while DLM is most commonly used for frequency-domain analysis. Traditional VLM is a computationally efficient tool for both steady and unsteady aerodynamic calculations, providing good accuracy in subsonic regimes with attached flow, with some proposed VLM models suitable for modeling both transonic and detached flow [15,16].

These aerodynamic models are paired with a structural model to develop an aeroelasticity model. Traditionally, analytical structural models were used, today some authors choose this type of model when performing a fundamental analysis of a simple system. Currently, the most widely adopted approach is to use a finite element method (FEM) structural model [5,17,18]. FEM-based aeroelastic models are resource intensive, but provide accurate results and are relatively simple to set up.

Some authors are analyzing novel approaches to aeroelasticity modeling based on neural networks [19,20,21]. These models are based only on previously acquired aeroelasticity data and do not require any physics-based calculations once they are developed. This results in fast computational times well suited for real-time analysis, but with the downside of reduced accuracy. The large amount of available data required for the development of these models makes them difficult to develop.

In an attempt to develop a fast physics-based aeroelasticity model, this work proposes a model based on rigid-body dynamics, modeling the aircraft structure as a series of rigid bodies connected with elastic-damped joints. The proposed model would result in faster computational times compared to a FEM model, at the cost of a more complicated setup, requiring some preliminary structural analysis. When compared to a neural network-based model, the proposed model would be slower, but it could be set up without any additional data beyond the geometry and structure of the analyzed aircraft. Because the proposed structural model ignores longitudinal and shear deformations, the model is only suitable for analyzing bending and torsion-dominated aircraft structures. For the aerodynamic part of the aeroelasticity model, VLM was chosen for its relatively low computational cost when compared with CFD.

To evaluate the accuracy of the proposed model, flight testing was performed and the collected data was compared with modeling results. For comparison, a fully rigid version of the model was also analyzed, with infinitely stiff joints between bodies.

2. Aeroelasticity Model

2.1. Aerodynamic Model

A steady rigid-wake version of VLM was used to calculate aerodynamic forces and moments acting on the aircraft. The method was implemented as described by Katz and Plotkin [22]. Katz and Plotkin also provide an unsteady VLM formulation in the same book, but for this specific application, steady VLM was chosen to achieve faster computational times. The elements of the vortex lattice are shown in Figure 1. In general, when using VLM, the wing is divided into rectangular panels. The chord-wise length of the panels is $\Delta x$ and the span-wise length is $\Delta z$.

Each panel i has an attached vortex of strength ${\Gamma }_i$ and an integration point $p_i$. In this implementation, horseshoe-shaped vortices are used, with each vortex being composed of three straight vortex lines. One line is attached to the panel at the quarter-chord line, while the other two are shed into the wake, extending to infinity. The wake is shed parallel to the free-flow velocity. The integration point of each panel is usually located at the center of the three-quarter-chord line.

For each pair of panels i and j, some velocity $w_{ij}$ will be induced at integration point $p_i$ by the vortex ${\Gamma }_j$. This velocity depends on the strength of the vortex and on its position relative to the integration point [22]:

$$w_{ij}=A_{ij}{\Gamma }_j,$$

(1)

where $A_{ij}$ is a vortex influence coefficient calculated using the Biot-Savart law. By calculating $A_{ij}$ for each panel pair, Equation (1) can be rewritten in matrix form:

$$\overrightarrow{w}=\left[A\right]\overrightarrow{\Gamma }.$$

(2)

To satisfy the non-penetration condition at each integration point, the induced velocity must cancel out the free-flow velocity component normal to the panel. Based on this requirement, for each point, the required total induced velocity is equal to

$$w_i=-{\overrightarrow{V}}_{\infty }·{\overrightarrow{n}}_i,$$

(3)

where ${\overrightarrow{V}}_{\infty }$ is the free-flow velocity vector and ${\overrightarrow{n}}_i$ is the panel normal vector. Using Equation (3) the right-hand-side vector for Equation (2) can be calculated, which can then be solved for $\overrightarrow{\Gamma }$.

The lifting force for each panel can be calculated using the Kutta–Joukowski theorem:

$${\overrightarrow{L}}_i=2\rho {\Gamma }_i{\overrightarrow{V}}_{\infty }\times {\overrightarrow{k}}_i,$$

(4)

where $\rho$ is the air density and ${\overrightarrow{k}}_i$ is the quarter-chord line vector of the panel. The total force and moment acting on the aerodynamic surface can be calculated from the lifting force acting on each panel.

2.2. Unsteady Approximation Using Wagner’s Function

For comparison with the steady aerodynamic model, a version of the model was implemented using Wagner’s function for unsteady approximation. The use of Wagner’s function to approximate unsteady VLM is described by Kier [23]. Wagner’s function describes the change in the lift coefficient of an airfoil over time after it experiences a step change in the angle of attack. The function is commonly approximated:

$$\Phi \left(\tau \right)=1.0-0.165e^{-0.0455\tau }-0.335e^{-0.3\tau },$$

(5)

where $\tau$ is the reduced time after the step change.

This method approximates the delay in the change of aerodynamic forces caused by the wake vortex taking some time to achieve a steady state. Compared to a true unsteady VLM implementation, this method is faster computationally, but does not take into account the unsteady interactions between a downstream aerodynamic surface with the wake of an upstream aerodynamic surface (e.g., the interaction between the horizontal stabilizer and the wake of the main wing).

2.3. Structural Model

A rigid-body-based structural model was chosen due to relatively low computational demands when compared with finite-element-based models. The model consists of rigid elements, connected together with elastic-damped joints. Because the main deformation modes in a low-stiffness aircraft structure are bending and torsion, the joints are rigid in tension and shear directions, reducing the total number of unknowns that have to be solved for.

The bending-torsion stiffness and damping of each joint k is described using a stiffness matrix ${\left[K\right]}_k$ and a damping matrix ${\left[C\right]}_k$. For a joint k between bodies i and j, the stiffness and damping moments are calculated:

$${\overrightarrow{M}}_{K,k}=-{\left[K\right]}_k\Delta {\overrightarrow{\theta }}_{ij},$$

(6)

$${\overrightarrow{M}}_{C,k}=-{\left[C\right]}_k\Delta {\dot{\overrightarrow{\theta }}}_{ij},$$

(7)

where $\Delta {\overrightarrow{\theta }}_{ij}$ is the difference of angular position, and $\Delta {\dot{\overrightarrow{\theta }}}_{ij}$ is the difference of angular velocity between the bodies.

For comparison, a fully rigid version of the aircraft was also modeled, where all joints were rigid in both bending and torsion. The aerodynamic and mass properties of this rigid aircraft were the same as those of the elastic aircraft.

3. Experimental Setup

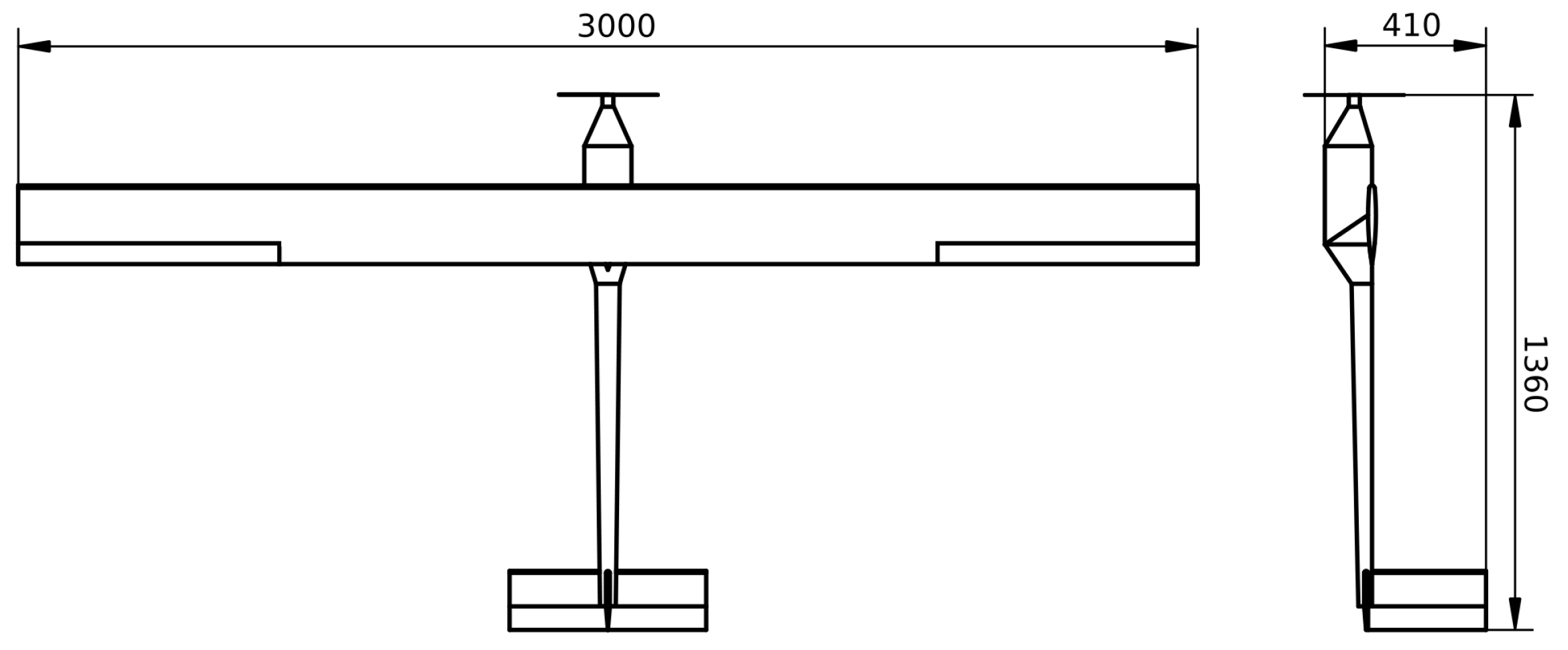
Flight testing was performed using a fixed-wing UAV. The main specifications of the UAV are provided in

Table 1. Main specifications of the UAV used for flight testing.

Specification	Value
Mass	$1.66 \mathrm{kg}$
Wing area	$0.60 {\mathrm{m}}^2$
Wing aspect ratio	15
Wing Airfoil	NACA 0010
Horizontal tail area	$0.075 {\mathrm{m}}^2$
Vertical tail area	$0.045 {\mathrm{m}}^2$
Tail surface airfoil	6.7% thickness flat plate

, and a general-view drawing is provided in Figure 2. The UAV was constructed out of extruded polystyrene foam, with a wooden spar in the wing.

The fuselage of the UAV was constructed out of 10 mm thick extruded polystyrene foam. The main part of the fuselage is a 0.25 × 0.12 × 0.12 m rectangular box which contains the battery and the electronics of the aircraft (except for the servo motors). In front of the box is a 0.08 m long taper toward the electric motor. At the rear end of the box, there is a 0.10 m long taper toward the tail part of the fuselage. The tail part is 0.82 m long, 0.07 m wide at the front and 0.05 m wide at the rear. The tail part is triangular in sections.

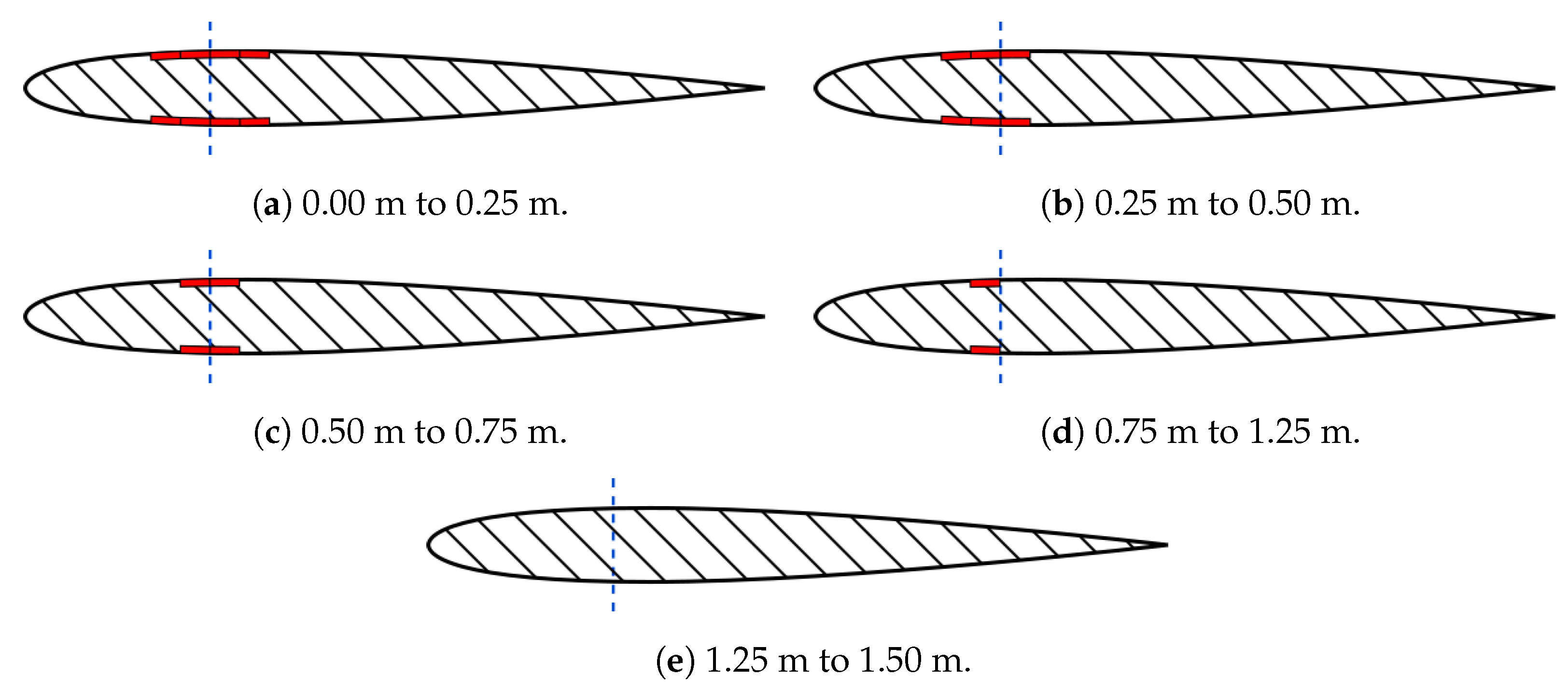
The main wing of the UAV has a rectangular planform. The wing has a wooden spar with flanges constructed out of 2 × 8 mm wooden strips. At the root of the wing, each flange is made out of 4 strips. The number of strips is reduced toward the wing tip, as seen in cross-sections at different span stations shown in Figure 3. The ailerons span the outer 0.75 m of each wing and take up 25% of the chord. The servo motors controlling the ailerons are mounted in the wing at the root end of the aileron.

The tail surfaces of the UAV were constructed out of 10 mm thick extruded polystyrene foam. Because both the horizontal and vertical stabilizers have a chord of 0.15 m, this gives an effective airfoil thickness of 6.7%. Both the elevator and the rudder take up 40% of the chord and the full span of the tail surfaces. The elevator and the rudder are controlled by servo motors mounted in the tail section of the fuselage, connected to the surfaces with 0.3 m long control rods.

The test flights were performed outside, during a day with no wind, at low altitudes. To achieve deformations of the aircraft structure, several dives were performed with a 3 g to 4 g pull-up at the end. To eliminate the influence of propeller wake, these maneuvers were performed at zero throttle.

During flight testing, the servo control signals, aircraft acceleration, and angular rate were recorded. The hardware used for measurements is described in

Table 2. Measurement hardware used for flight testing.

Measurement	Hardware	Discretization Rate	Measurement Limits	Error
Acceleration	Accelerometer- gyroscope LSM6DS3TR	$12 \mathrm{Hz}$	$\pm 16$ g	$\pm 0.040$ g
Angular rate		$12 \mathrm{Hz}$	$\pm 2000 {}^{\circ }/\mathrm{s}$	$\pm 10 {}^{\circ }/\mathrm{s}$
Servo control signal duration	Microcontroller Arduino Uno WiFi Rev.2	$12 \mathrm{Hz}$	0–$25 \mathrm{ms}$	–

. The block diagram of the electric system of the aircraft is presented in Figure 4. The power source is a 4S lithium-polymer battery, connected to the electronic speed controller (ESC) of the brushless electric motor. The built-in voltage converter of the ESC provides 5 V power to the low-voltage circuit of the aircraft, consisting of the RC receiver, the Arduino Uno WiFi Rev.2 microcontroller used for data logging and the control servo motors. The aircraft is controlled manually using an RC transmitter, which sends control signals to the onboard RC receiver. The receiver sends the control signals to the ESC and the four control servo motors (both aileron servo motors receive the same signal). All the signals sent from the receiver are also received by the Arduino microcontroller, which measures their duration and records it on an SD card. The Arduino microcontroller also contains a built-in LSM6DS3TR accelerometer-gyroscope unit, measuring in-flight acceleration and angular rates, and these data are also recorded on the SD card. Each data point is timestamped using the internal clock of the Arduino microcontroller, measuring the time passed since the microcontroller started receiving power.

The recorded servo control signals had to be converted to control surface deflection angles for flight modeling. To achieve this, a static test was performed, measuring the deflection of each control surface at a known control signal duration. Linear interpolation between the measured points was then used to calculate control surface deflection angles based on the duration of the servo motor control signal.

3.1. Structural Model of the UAV

A structural model of the UAV used for flight testing was created to be used for aeroelasticity modeling as described in Section 2.3. The aircraft was split into 9 rigid bodies connected by 13 joints as shown in Figure 5. Bodies 0 and 5 make up the fuselage, bodies 1–4 make up the wings, and bodies 6–8 make up the tail surfaces. The properties of each body are presented in

Table 3. Properties of the bodies of the structural model.

Nr.	Aircraft Part	m, g	${\mathit{x}}_{\mathit{m}}$, m	${\mathit{y}}_{\mathit{m}}$, m	${\mathit{z}}_{\mathit{m}}$, m	${\mathit{I}}_{\mathit{x}\mathit{x}}$, $\mathbf{g}·{\mathbf{m}}^2$	${\mathit{I}}_{\mathit{y}\mathit{y}}$, $\mathbf{g}·{\mathbf{m}}^2$	${\mathit{I}}_{\mathit{z}\mathit{z}}$, $\mathbf{g}·{\mathbf{m}}^2$	Aero. Surf.	Control Surface rel. Chord
0	Fuselage front	850	0.044	−0.050	0.000	1.6	1.8	1.8	No	–
1	Right wing root	160	0.090	0.000	−0.425	7.5	8.0	0.53	Yes	–
2	Right wing tip	115	0.090	0.000	−1.125	5.4	5.8	0.38	Yes	0.25
3	Left wing root	160	0.090	0.000	0.425	7.5	8.0	0.53	Yes	–
4	Left wing tip	115	0.090	0.000	1.125	5.4	5.8	0.38	Yes	0.25
5	Fuselage rear	180	0.450	0.000	0.000	0.30	0.38	0.38	No	–
6	Right hor. stab.	25	1.075	0.000	−0.125	0.13	0.18	0.047	Yes	0.4
7	Left hor. stab.	25	1.075	0.000	0.125	0.13	0.18	0.047	Yes	0.4
8	Vert. stab.	30	1.075	0.150	0.000	0.23	0.056	0.28	Yes	0.4

. m is the mass of each body, $x_m$, $y_m$ and $z_m$ is the position of the center of mass, $I_{xx}$, $I_{yy}$ and $I_{zz}$ are the rotational inertia moments.

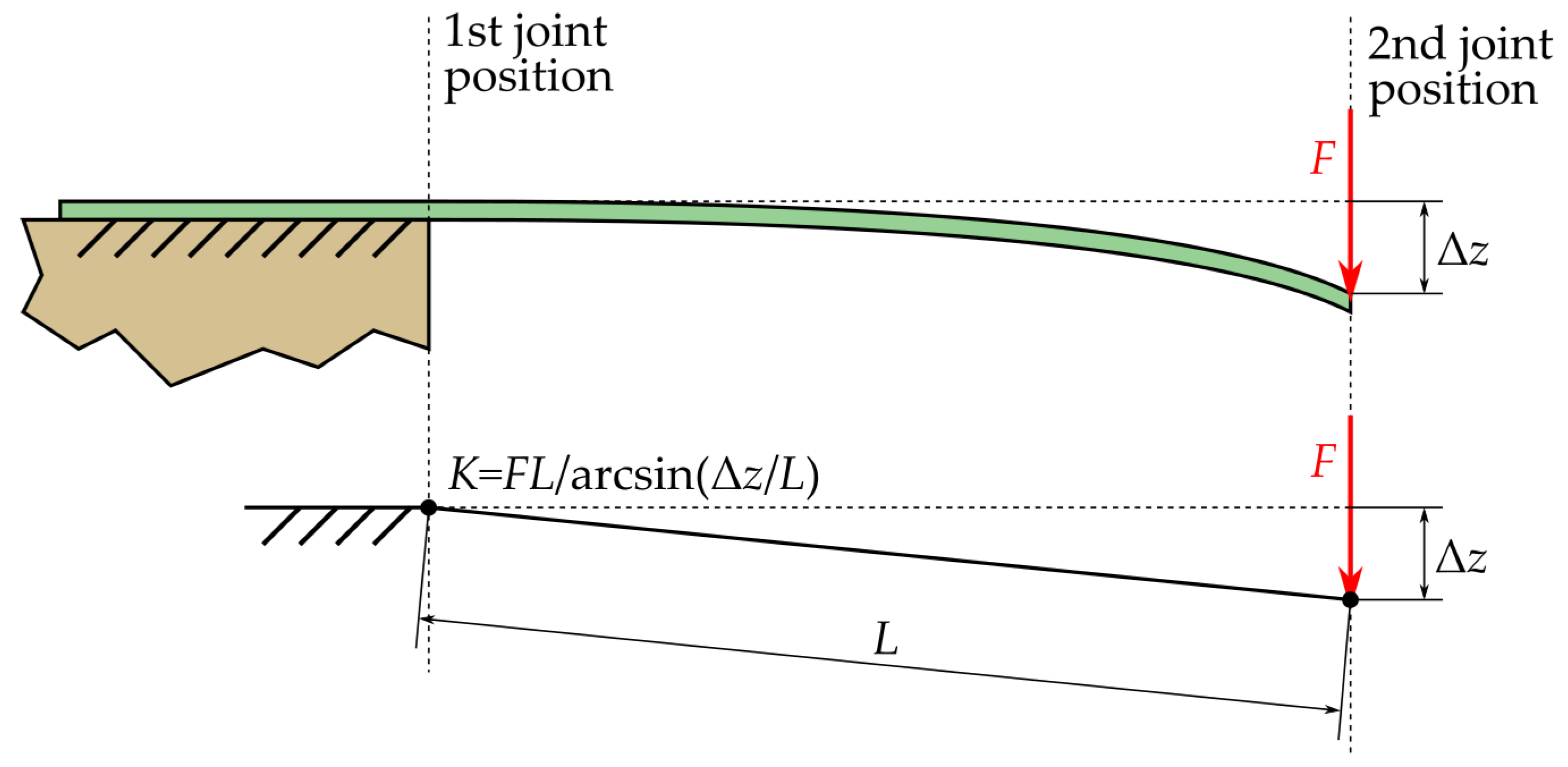
Out of the 13 joints making up the model, 8 are real joints, each connecting two bodies together, while the remaining 5 are connected only to a single body and are only for display purposes. The stiffness coefficients of the joints were determined by structural testing of the airframe as shown in Figure 6. The relevant part of the aircraft was fixed at the location of the joint for which the stiffness is being determined. The location of the next joint was loaded with a force F, equal to the expected loads at level flight for that part. The displacement at the second joint $\Delta z$ was measured, and the resulting angular stiffness of the first joint K was calculated using the formula:

$$K=\frac{FL}{arcsin(\Delta z/L)},$$

(8)

where L is the distance between the two joints. The damping coefficients were then determined by measuring the decay rate of manually induced airframe vibrations. The damping coefficients were tuned so that induced vibrations in the structural model were damped after the same number of cycles as vibrations in the real aircraft.

The properties of each joint are provided in

Table 4. Properties of the joints of the structural model.

Nr.	Connected Bodies	x, m	y, m	z, m	${\mathit{K}}_{\mathit{x}\mathit{x}}$, Nm/rad	${\mathit{K}}_{\mathit{y}\mathit{y}}$, Nm/rad	${\mathit{K}}_{\mathit{z}\mathit{z}}$, Nm/rad	${\mathit{C}}_{\mathit{x}\mathit{x}}$, Nm/rad/s	${\mathit{C}}_{\mathit{y}\mathit{y}}$, Nm/rad/s	${\mathit{C}}_{\mathit{z}\mathit{z}}$, Nm/rad/s
0	0.1	0.050	0.000	−0.100	165	660	25	8	32	0.5
1	1.2	0.050	0.000	−0.750	15.5	62	6.8	0.8	6.4	0.1
2	2	0.050	0.000	−1.500	–	–	–	–	–	–
3	0.3	0.050	0.000	0.100	165	660	25	8	32	0.5
4	3.4	0.050	0.000	0.750	15.5	62	6.8	0.8	6.4	0.1
5	4	0.050	0.000	1.500	–	–	–	–	–	–
6	0.5	0.200	0.000	0.000	16	32	32	3.2	6.4	6.4
7	5.6	1.075	0.000	−0.050	13	52	25	0.16	0.64	0.1
8	6	1.075	0.000	−0.250	–	–	–	–	–	–
9	5.7	1.075	0.000	0.050	13	52	25	0.16	0.64	0.1
10	7	1.075	0.000	0.250	–	–	–	–	–	–
11	5.8	1.075	0.050	0.000	13	25	52	0.16	0.1	0.64
12	8	1.075	0.300	0.000	–	–	–	–	–	–

. x, y and z is the global position of the joint, $K_{xx}$, $K_{yy}$ and $K_{zz}$ are the stiffness coefficients, $C_{xx}$, $C_{yy}$ and $C_{zz}$ are the damping coefficients.

3.2. Structural Validation

To test the validity of the used structural model, a ground vibration test of the main wing was performed and the measured frequency was compared with a modal analysis of the structural model of the wing. During vibration testing, the wing was fixed rigidly at the root. The vibrations were induced manually and the duration of 40 vibration cycles was measured. The measurement was performed three times for each wing. For the right wing the average duration of 40 cycles was 11.87 s, and for the left wing the average duration was 12.11 s, giving natural frequencies of 3.37 Hz and 3.30 Hz, respectively.

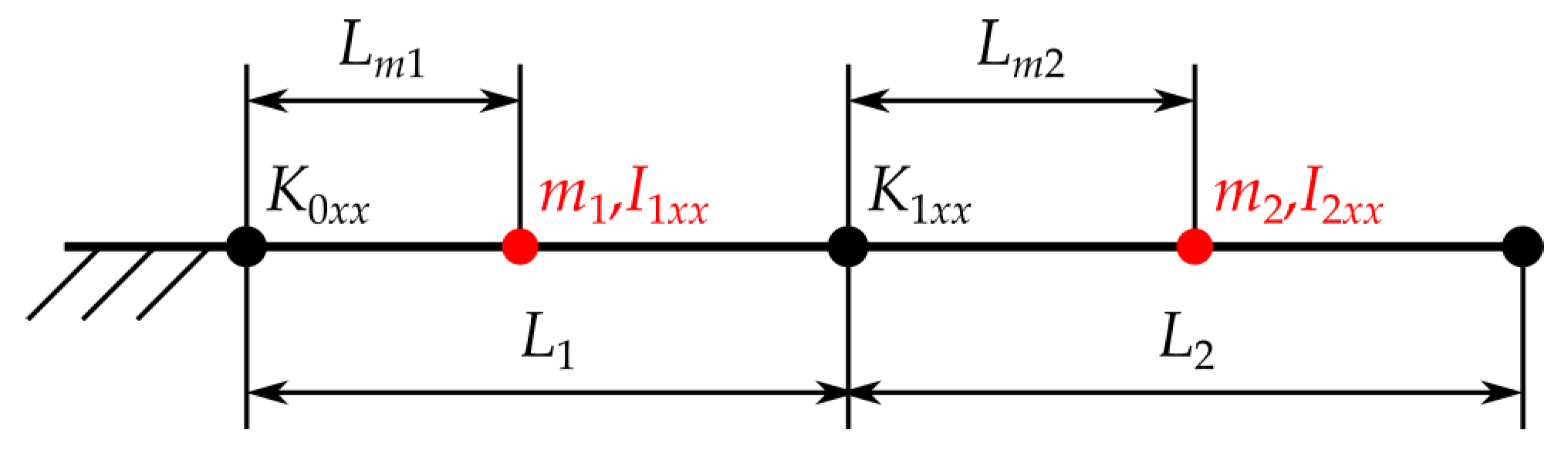
The diagram of the modal analysis is shown in Figure 7. The stiffness values $K_{0xx}$ and $K_{1xx}$ were taken from Table 4. The mass values $m_1$, $m_2$ and inertia values $I_{1xx}$, $I_{2xx}$ were taken from Table 3. The body lengths were calculated based on the relative positions of the joints, resulting in $L_1=0.65 \mathrm{m}$ and $L_2=0.75 \mathrm{m}$. The positions of the centers of mass were calculated relative to the joints and are $L_{m1}=0.325 \mathrm{m}$ and $L_{m2}=0.375 \mathrm{m}$. The system has two independent degrees of freedom, which were chosen to be the global angular positions of the bodies ${\varphi }_1$ and ${\varphi }_2$, giving the system position vector:

$$q^T=\left\{{\varphi }_1,{\varphi }_2\right\}.$$

(9)

The stiffness matrix of the system was then calculated to be

$$\left[K\right]=\left[\begin{array}{cc}{K}_{1xx}+K_{2xx}& -K_{2xx}\\ -K_{2xx}& K_{2xx}\end{array}\right],$$

(10)

and the mass matrix was calculated to be

$$\left[M\right]=\left[\begin{array}{cc}{I}_{1xx}+m_1{L}_{m1}^2+m_2{L}_1^2& m_2{L}_1{L}_{m2}\\ m_2{L}_1{L}_{m2}& I_{2xx}+m_2{L}_{m2}^2\end{array}\right].$$

(11)

The matrix $\left[K\right]{\left[M\right]}^{-1}$ has two eigenvalues, ${\lambda }_1=4.627 \times {10}^2$ and ${\lambda }_2=7.015 \times {10}^3$, corresponding to two vibration modes. The frequencies of these modes can be calculated using the formula:

$$f=\sqrt{\lambda }/2\pi ,$$

(12)

giving frequencies for the two modes equal to $f_1=3.42 \mathrm{Hz}$ and $f_2=13.33 \mathrm{Hz}$. In this case, the first mode is the relevant one. The vibration frequency of the first mode of the structural model has an error of +1.48% when compared to the actual vibration frequency of the right wing, and +3.64% when compared to the left wing. These errors are small enough to consider the used structural model valid.

4. Results

4.1. Flight Testing Data

In total, three successful flights were performed with the test UAV, with a total flight time of 122 s. Out of the data collected during flight testing, two flight sections were selected as suitable to be modeled. These sections were selected because during them the throttle was disabled for a sufficient amount of time (3.10 s and 2.67 s), and during that time the elevator was used for high-load maneuvers.

4.1.1. First Case

The first analyzed flight case consisted of the aircraft entering a dive, pulling up to level out, and then pulling up a second time to enter a climb. The elevator angle, throttle position, and total acceleration from this flight section are provided in Figure 8.

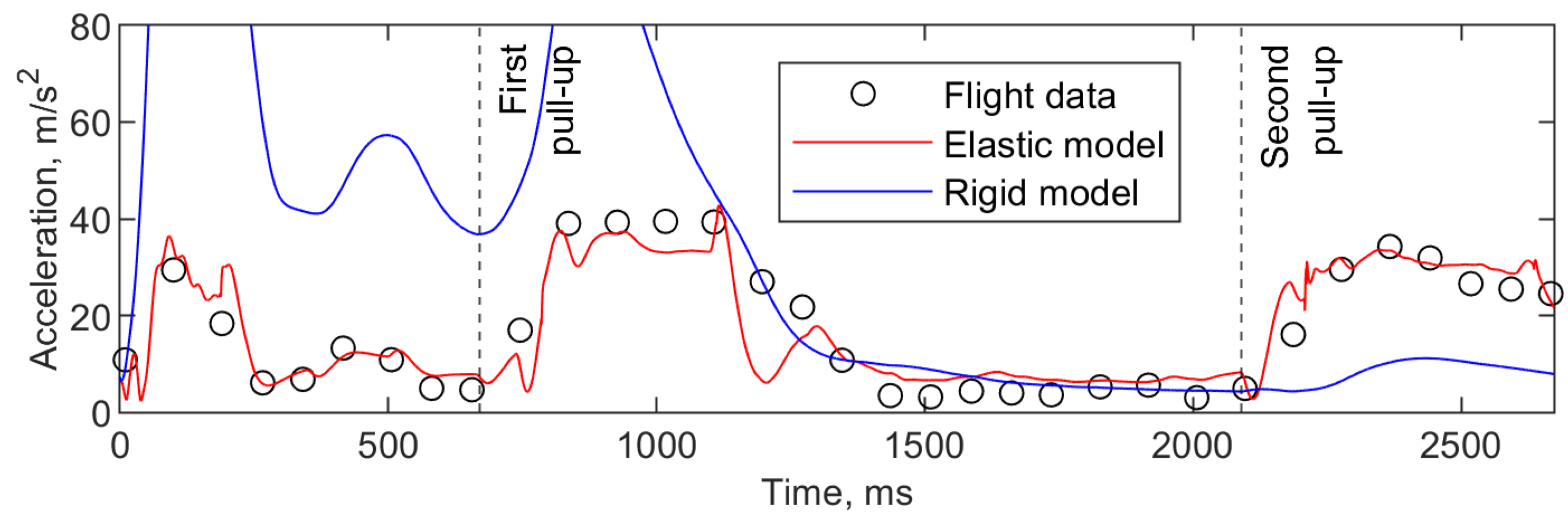
At the beginning of the section, until 632 ms, the elevator was deflected down, as the aircraft was entering a dive. At 902 ms to 1428 ms, a small mid-dive trajectory correction was performed. At 1502 ms, the elevator was sharply deflected upwards, and the aircraft pulled up, transitioning to level flight, this maneuver ended at 2194 ms. At 2523 ms, the elevator was again sharply deflected upwards, and the aircraft pulled up again, entering a climb. The throttle was enabled at 3100 ms, marking the end of the analyzed section before the second pull-up maneuver was completed.

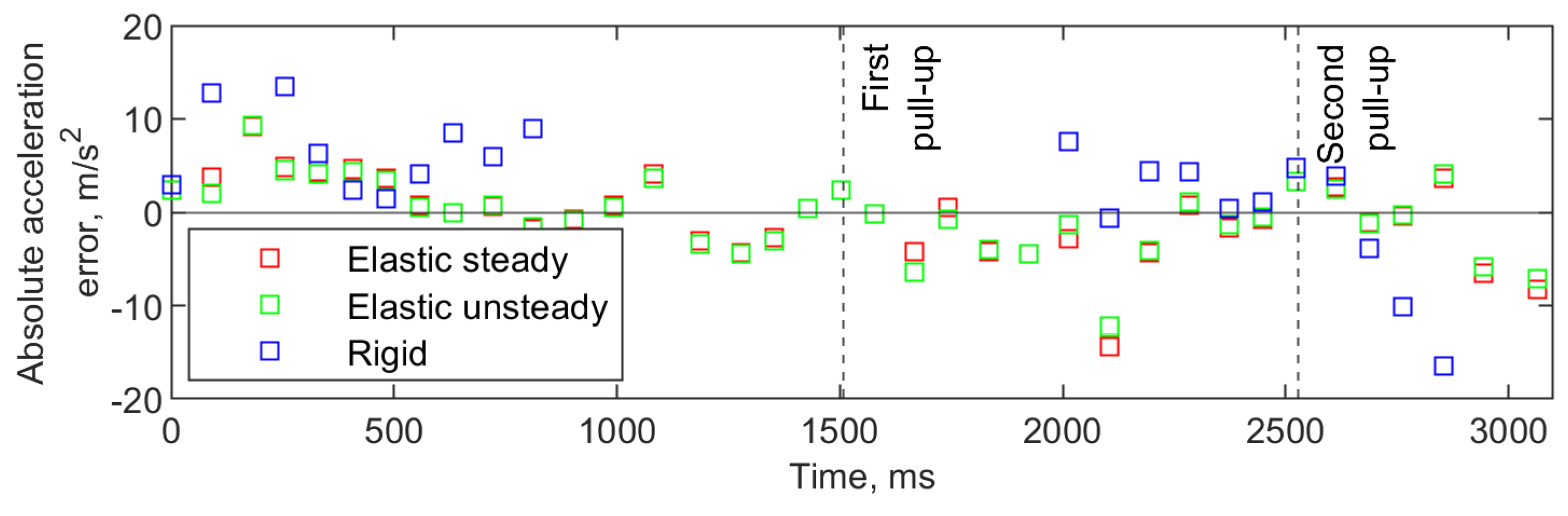
The mid-dive trajectory correction caused a small peak of acceleration at 1187 ms, reaching 13.1 m/s². The two main acceleration peaks caused by the pull-up maneuvers were at 1833 ms and 3064 ms, and reached 37.0 m/s² and 33.2 m/s², respectively.

4.1.2. Second Case

The second analyzed flight case began when the aircraft was in a dive. The aircraft pulled up to level out, slowly entered a shallow dive again, then pulled up a second time to enter a climb. The elevator angle, throttle position, and total acceleration from this flight section are provided in Figure 9.

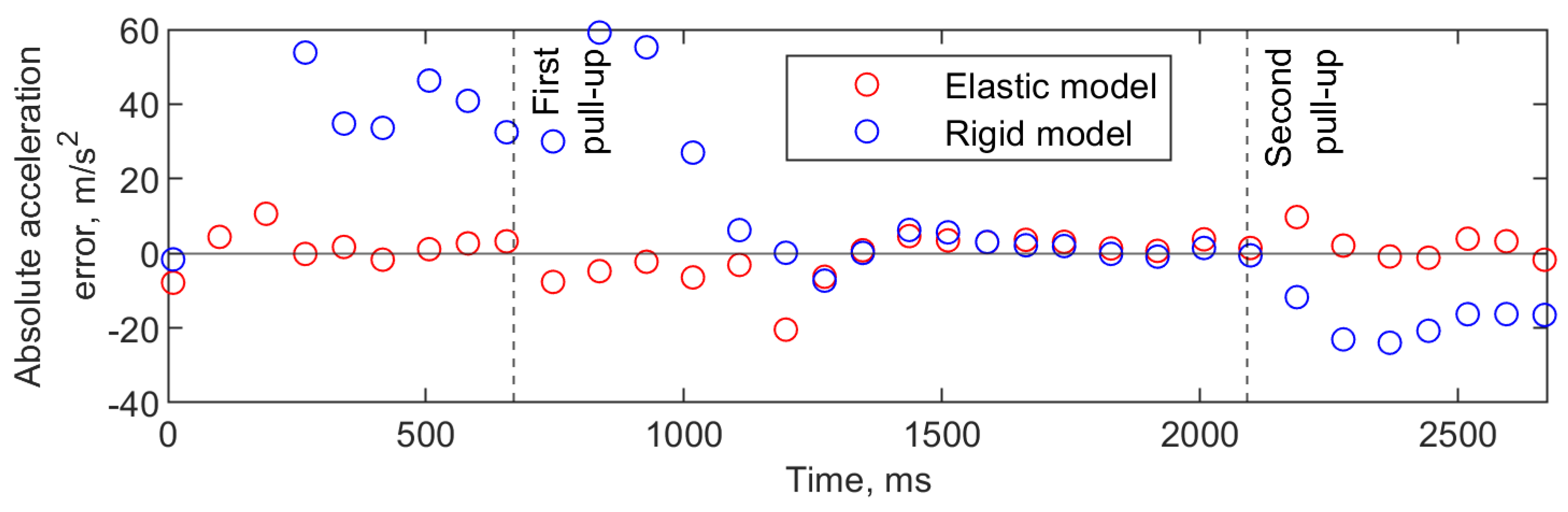
At the beginning of the section, the aircraft was already in a dive, with the elevator deflected at −30° for a mid-dive trajectory correction. At 190 ms, the elevator was returned to a −14° position, resulting in a decrease in acceleration. Another small deflection happened at 341 ms. At 656 ms, the aircraft pulled up sharply, exited the dive, and entered a shallow climb, finishing the maneuver at 1346 ms. After the maneuver the aircraft slowly transitioned from a shallow climb to a shallow dive, indicated by the <1 g acceleration section. At 2097 ms, the second pull-up was performed, entering a climb again. The analyzed section ended at 2670 ms as the throttle was enabled, before the second pull-up maneuver was complete.

The first trajectory correction caused an acceleration peak of 29.4 m/s² at 100 ms, and the second small correction had a peak of 13.3 m/s² at 416 ms. The main pull-ups caused acceleration peaks at 1017 ms and 2367 ms, reaching, respectively, 39.5 m/s² and 34.3 m/s².

4.2. Modeling Results

4.2.1. First Case

The first case was modeled using the elastic steady, the elastic unsteady, and the rigid models. The calculated acceleration graph for the first case is shown in Figure 10, and the error graph for all three models is shown in Figure 11. The absolute and relative errors for all three models are provided in

Table 5. Errors for first modeled case.

Model	Average abs. Error, m/s2	Maximum abs. Error, m/s2	Average rel. Error, %	Maximum rel. Error, %
Elastic steady	3.2	14.4	44	278
Elastic unsteady	3.0	12.2	42	284
Rigid	17.6	58.3	212	997

.

Both the elastic models began with a positive acceleration error but started coinciding well with flight data at around 550 ms. The modeled aircraft entered the mid-dive correction slower than was shown by experimental data. Entering the first pull-up, a rebound can be seen in the modeled acceleration, followed by a steep increase in acceleration, up to the first acceleration peak. After the peak, the acceleration decreased more steeply than shown by experimental data, and there was another rebound. As the aircraft entered the second pull-up, there was another rebound, and some numerical noise can be seen when the acceleration approached the peak.

The rigid model began with a higher positive acceleration error than the elastic model, and in general showed much higher accelerations during maneuvers than both the elastic model and experimental data, up to the first pull-up maneuver. During the second pull-up maneuver the rigid model showed very little increase in acceleration.

During the first pull-up, the maximum acceleration achieved by the steady elastic model was 34.7 m/s², by the unsteady elastic model 35.0 m/s², and by the rigid model 97.8 m/s². The relative error compared to flight data was, respectively, −6.2%, −5.3%, and +164.3%. During the second pull-up, the respective achieved accelerations were 36.0 m/s², 39.2 m/s² and 10.4 m/s², with relative errors equal to +8.4%, +18.2% and −68.7%.

4.2.2. Second Case

The second case was modeled using only the elastic steady and rigid models, because in the first case, the elastic unsteady model provided almost identical results but with more numerical instabilities (seen as extreme spikes in the acceleration plots). The calculated acceleration graph for the second case is shown in Figure 12, and the error graph for both models is shown in Figure 13. The absolute and relative errors for both models are provided in

Table 6. Errors for second modeled case.

Model	Average abs. Error, m/s2	Maximum abs. Error, m/s2	Average rel. Error, %	Maximum rel. Error, %
Elastic	4.0	20.5	39	134
Rigid	24.8	132.3	191	882

.

The elastic model tracked the experimental acceleration data throughout the duration of the second flight section, except for the rebounds when entering and exiting both the first and second pull-up maneuvers, similar to the first flight case. Also similar to the first flight case, the rigid model showed much higher accelerations than experimental data up to the first pull-up maneuver. During the second pull-up the rigid model again showed only a small increase in acceleration.

During the first pull-up, the maximum acceleration achieved by the elastic model was 42.7 m/s², and for the rigid model 103.4 m/s². The relative error compared to flight data was, respectively, +8.1% and +161.8%. During the second pull-up, the respective achieved accelerations were 33.6 m/s² and 11.2 m/s², with relative errors equal to −2.0% and −67.4%.

5. Discussion

Both modeled cases showed good qualitative agreement between experimental data and elastic modeling results. The general curve of acceleration was followed well, with coinciding peaks of similar size. Both the main pull-up peaks and the smaller trajectory correction peaks were replicated in the elastic model. The acceleration error of the peaks during pull-up varied between −6.2% and +8.4%. Although the general acceleration profile was similar to the experimental data, the average error over the flight sections was high, 3.2 m/s² for the first case and 4.0 m/s² for the second case.

From Figure 11 and Figure 13 it can be seen that for the elastic model, the highest momentary errors are associated with a rebound when either entering or exiting a pull-up. This was likely caused by insufficient damping in the structural model, causing the structure to oscillate. To avoid this in future modeling, a more advanced method of determining the damping qualities of the aircraft structure would have to be used.

There was little difference between elastic steady and unsteady modeling, with the unsteady model producing slightly better results with 3.0 m/s² average absolute error instead of 3.2 m/s², and 42% average relative error instead of 44%. However, the unsteady model generated more numerical instabilities, seen as sharp spikes in the acceleration plot.

It can be seen that the modeled aircraft tended to enter and exit pull-ups more suddenly than recorded in the flight data. In Figure 10 it is seen that this type of error was partially fixed by the unsteady model, with the acceleration gradient when entering a pull-up slightly lower than calculated by the steady model. However, the difference observed is minor. It is possible that a true unsteady VLM model would produce better results, because unsteady interaction between the wake of the main wing and the horizontal stabilizer would be taken into account. However, this approach would greatly increase the computational cost, because at each time step the shape of the wake would have to be recalculated. Alternatively, the unsteady interactions could possibly be emulated by a more advanced analytical method, taking into account the changing wake strength of other sections of the wing. This would have a lower accuracy when compared to true unsteady VLM, but could be computed much faster.

In both cases, rigid aircraft modeling achieved worse results, achieving very high accelerations at the beginning of both flight sections (with errors of +164.3% and +161.8% during the first pull-up), but low accelerations at the end (with errors of −68.7% and −67.4% during the second pull-up). The absence of tail twisting and fuselage bending greatly increased the effectiveness of the elevator, causing the aircraft to pull up very sharply at the first pull-up (and even during the mid-dive correction in the second case), which in turn caused the aircraft to lose a lot of speed, greatly reducing the effectiveness of the second pull-up. These results could possibly be improved by artificially reducing the effectiveness of the control surfaces based on their generated force.

Overall, the proposed model provided useful results with a very simple and computationally inexpensive structural model. Because the setup and modification of the structural model takes some effort (the stiffness and damping of each joint have to be determined), the proposed model is more suitable for control algorithm optimization, than it is for structural optimization. While the accuracy is insufficient to use for precise optimization, it could be used to rapidly iterate through the early stages of control law design, when comparing different control algorithms. The model could be further improved with either a more advanced aerodynamic model (such as unsteady VLM) or a more advanced artificial aerodynamic lag. The second option is viewed as more suitable by the authors, because of lower computational costs.