Abstract
Recent efforts in on-orbit servicing, manufacturing, and debris removal have accentuated some of the challenges related to close-proximity space manipulation. Orbital debris threatens future space endeavors driving active removal missions. Additionally, refueling missions have become increasingly viable to prolong satellite life and mitigate future debris generation. The ability to capture cooperative and non-cooperative spacecraft is an essential step for refueling or removal missions. In close-proximity capture, collision avoidance remains a challenge during trajectory planning for space manipulators. In this research, a deep reinforcement learning control approach is applied to a three-degrees-of-freedom manipulator to capture space objects and avoid collisions. This approach is investigated in both free-flying and free-floating scenarios, where the target object is either cooperative or non-cooperative. A deep reinforcement learning controller is trained for each scenario to effectively reach a target capture location on a simulated spacecraft model while avoiding collisions. Collisions between the base spacecraft and the target spacecraft are avoided in the planned manipulator trajectories. The trained model is tested for each scenario and the results for the manipulator and base motion are detailed and discussed.
1. Introduction
With an ever-increasing number of satellite operations in Earth’s orbit, the demand for space debris removal and on-orbit servicing (OOS) has become a necessity [1]. Space debris is a growing problem as it poses a serious threat to spacecraft that are leaving Earth’s atmosphere as well as currently orbiting spacecraft. As more space debris are added to orbit, it is increasingly difficult to avoid collisions with debris objects. Actively removing the debris in orbit will lower the risk of collisions with new and current spacecraft. On-orbit servicing provides an opportunity to extend mission life of damaged or fuel-depleted satellites as well as repair and correct any issues that need to be addressed physically. For example, refueling a satellite can prove to be much more cost effective, rather than terminating its use and launching an entirely new satellite [2]. The ability to refuel a depleted satellite would not only allow it to stay active for longer, but would reduce the amount of new debris created by abandoning it [2]. Space debris removal and on-orbit servicing are essential to the continuation of safe space exploration.
There has been extensive research in space debris removal and on-orbit servicing over the past couple of decades and the challenges associated with these tasks. For example, on the International Space Station (ISS) or the Hubble telescope, servicing often needs to be performed by astronauts in space. This requires a lot of equipment, such as life support equipment, compared to using robotic manipulators for precise and high-risk tasks [3]. Studies have been conducted to try to implement robotic manipulators for complex missions such as capturing a tumbling target. A significant challenge associated with capturing a tumbling target is avoiding undesirable contact or collisions when attempting grasp operations, particularly given the often complex geometry of target spacecraft [4]. Collision-free capture of non-cooperative, tumbling targets of complex geometry is a necessary first step towards advancing on-orbit capabilities in refueling, servicing, debris removal, and manufacturing. In all these operations, it is essential to avoid high-impact collisions that could cause significant damage to either of the bodies involved, possibly resulting in the generation of additional debris. The on-orbit capturing of non-cooperative targets is also particularly challenging due to a variety of other factors, such as imprecise estimation of the inertial and tumbling target parameters, imprecise knowledge of the capturing and target locations and trajectories, as well as irregular and complex target geometries (that also may be damaged). In [4], a detailed review is conducted on the major challenges and possible solutions related to obstacle avoidance in space robotics. For example, if a target is moving rapidly, this could be a potential challenge for capture due to the requirement to predict the motion of the target while approaching for capture. A predictive control method would thereby be ideal to make proper decisions for capture. Machine learning, more specifically deep reinforcement learning (DRL), has been applied to many different tasks that require a decision-making approach. It is used to make the best decisions regarding a process that uses sequential steps. This method is effective because it learns from interacting and existing in the environment with very little prior knowledge, making it appropriate for capturing targets that move irregularly [5]. This also allows DRL to be useful for a wide variety of capture missions.
In previous studies, reinforcement learning (RL) and deep reinforcement learning have been considered for the control of space manipulators [6,7,8,9]. In a recent paper [6], a new RL-based approach was proposed that leveraged the soft actor–critic (SAC) algorithm for robust motion planning and target tracking of a space manipulator. The study demonstrated efficient and robust motion tracking at different speeds for targets with known motion paths. Deep reinforcement learning approaches can be used to address uncertainty in the target’s movements, such as in [7], where a DRL-based approach was employed for a dual-arm free-floating robotic manipulator for trajectory planning. Further extensions on using DRL for space manipulators have been proposed in [8,9], wherein the space manipulator motion planning was constrained. These works both focused on using DRL for free-floating space manipulators trajectory planning, while considering self-collision avoidance and velocity constraints on the end-effector. The approach demonstrated effective trajectory planning for both motionless- and spinning-target scenarios.
In this paper, we develop a deep reinforcement learning method of trajectory planning and control for a small spacecraft-based space manipulator to avoid collisions with both itself and the target while constraining end-effector velocity for the capture of non-cooperative, tumbling targets. The kinematics and dynamics of the manipulator are outlined for both free-flying and free-floating scenarios. The deep deterministic policy gradient (DDPG) algorithm is adapted for velocity-based control of the space manipulator with reward functions created to ensure collision avoidance while approaching a pre-specified grasping location. The training environment models various cases of cooperative and non-cooperative targets in order to demonstrate the effectiveness of the developed approach for collision avoidance with tumbling targets. The effectiveness of this DRL approach is investigated through a series of simulations and the results are discussed in detail. In particular, this approach presents a novel intelligent model-free deep reinforcement learning method for trajectory planning and control that demonstrates the effectiveness of DRL for collision avoidance during the capture of non-cooperative tumbling targets with irregular geometry using a free-floating space manipulator.
This paper is structured as follows: Section 2 provides background information on space manipulator control, object capture, and the DDPG algorithm. Section 3 outlines the kinematics and dynamics of the small spacecraft-based manipulator. Section 4 details the deep reinforcement learning framework, including the DDPG algorithm, environment, and reward functions. Section 5 provides information on the simulation parameters for training and testing, with Section 6 presenting the results and discussion of the DRL-based controller. Finally, the paper is concluded in Section 7 and future work is discussed.
2. Background
Currently, there are many methods that are available to plan trajectories and control robotic manipulators. These methods range from simple human-input control to deep reinforcement learning algorithms. For space applications, manipulator control includes additional challenges due to the movement of the manipulator base. Depending on the actuation capabilities of the base or the desires of the operators, space-based manipulators are often considered as free-flying or free-floating.
For free-flying manipulators, the base spacecraft is capable of off-setting any forces or torques generated by the manipulator actuation. In contrast, in a free-floating system, the spacecraft is able to move freely in response to the robot arm movement [10]. This is often considered to conserve energy. The movement of the manipulator can cause position and attitude changes in the base spacecraft and make target capture more difficult. These changes can be detrimental to the safety of the manipulator or target object. A positional change is most likely to have a less severe consequence than an attitude change in the base. An attitude change could lead to a significant collision between the manipulator and another object in the active work space [11]. Path planning and control for free-floating manipulators have been approached using a variety of methods. For example, a nonlinear model predictive control was applied to a free-floating manipulator in [12]. This method was applied to capture a rotating target, but used an end-effector position error to calculate joint torques, therefore, neglecting the possibility of obstacles between the manipulator and target. A differential evolution algorithm was proposed in [13] for trajectory planning of a kinematically redundant free-floating space manipulator, which was able to overcome some singularity issues, but did not take into account collision detection or avoidance.
Capturing a tumbling target using a free-floating manipulator includes path planning and control, target grasping, and target detumbling strategies. Path planning and collision avoidance strategies have been proposed using many different techniques for space manipulators, such as nonlinear model predictive control or using dual manipulators to help compensate from the coupled dynamics of the spacecraft and manipulators when interacting with a target [4]. The task of collision avoidance has also been treated extensively for terrestrial applications. For example, in [14], an improved version of an exploring random tree algorithm was used to avoid obstacles when path planning. However, adapting these approaches to a small spacecraft-based space manipulator remains particularly challenging due to the dynamic coupling of the manipulator and base motion, tumbling and often uncertain dynamics of the target, and the typically redundant high-degrees-of-freedom systems required for performing capture maneuvers [4].
Target detumbling has often been introduced post-capture, e.g., [15,16], where the angular velocity of the capturing spacecraft and target object are reduced, and the combined orientation stabilized. However, in some studies the target detumbling is performed prior to capture and, as such, requires that the space manipulator follow multiple collision-free trajectories to iteratively contact the target to reduce its angular velocity prior to capture. For example, in [17], a single manipulator arm was used to make repeated intermittent contact with a tumbling body in order to detumble the target prior to grasping. Approaches that require iterative contact with the target object must also consider the contact dynamics and control approach. Impedance control is frequently used in manufacturing and relies on force feedback to determine proper contact [18]. Due to the success of impedance controllers for manufacturing processes and operations that include adaptation to force, impedance controllers have been applied to space operations. In [19], a disturbance-based impedance control approach was used to aid in a safe and secure capture. A force observer was used to measure the contact force between the manipulator and the target, which was then used to attain proper grasping. In [20], a position-based impedance control was proposed to recognize soft contact and remain in contact with the target. In contrast to impedance control, in [21], a nonlinear model predictive control was developed to allow the collision avoidance problem to be addressed as a constraint.
Machine-learning-based control methods have also been applied for manipulator control in dynamic environments. For example, in [22], the normalized advantage function (NAF) algorithm was used to control a robotic manipulator that operated in close proximity to humans. Specifically, this algorithm was used as an off-policy algorithm to avoid collisions in a human workspace. In [23], a deep deterministic policy gradient algorithm was used to control a soft continuum arm (SCA). The research trains a model-free control policy for path tracking of the SCA. Reinforcement learning and deep reinforcement learning approaches have also been applied to the task of free-floating space manipulator trajectory planning and control [6,7], including for cases of manipulator self-collision avoidance [8,9]; however, these works do not consider collision avoidance between the manipulator, the base spacecraft, and a tumbling target with velocity constraints during a grasping maneuver.
Deep Deterministic Policy Gradient
Deep deterministic policy gradient is a machine learning algorithm that combines aspects from deterministic policy gradient (DPG) and deep Q-network (DQN). Considered an off-policy algorithm, DDPG is especially useful for continuous action spaces. DDPG has been applied to many tasks that require a relatively robust decision-making model. This has caused it to become a dominant algorithm when considering a deep reinforcement learning framework for task completion even beyond robot arm control [24].
The DPG algorithm uses an actor and critic function for policy approximation. It can adapted to be an on-policy or off-policy algorithm [25]. The off-policy DPG is implemented by updating the weights and biases of the critic and actor functions in order to find the true action-value function [26]. To expand and improve the capabilities of DPG, neural networks were introduced to the algorithm. Based on the previous success of DQN, the critic and actor functions of DPG were replaced with critic and actor networks. This allowed better learning in large state and action spaces and became known as DDPG [27].
Since DDPG is off-policy, the updated policy is different than the used policy, which is the case with Q-learning in general [28]. DDPG is also considered to be a model-free deep reinforcement learning algorithm. This means that the agent relies on learning as the primary factor for performance rather than planning and having an expected outcome [28]. As an off-policy, model-free algorithm with a continuous action space, DDPG is ideal for collision avoidance of a space manipulator, which has many degrees of freedom and a large action space. It improves by making choices in the environment and directly receiving a reward value in the continuous action space.
3. Kinematics and Dynamics
This section details the design of the manipulator used in this research. First, a kinematic explanation is introduced in standard Denavit–Hartenberg conventions. The mass properties and employed dynamics equations are then discussed. A three-degrees-of-freedom manipulator (Figure 1) is considered for a small spacecraft and the Denavit–Hartenberg parameters for this manipulator are listed in Table 1.
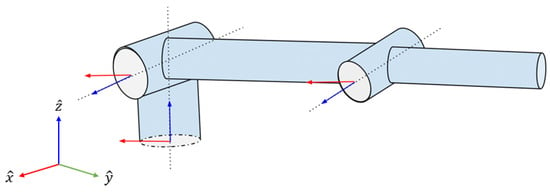
Figure 1.
3-DOF manipulator with shown rotation axes for each joint. Blue indicates the axis of rotation and red indicates the common normal.

Table 1.
Denavit–Hartenberg parameters for designed manipulator.
3.1. Kinematics
Robot kinematics can be separated into two distinct sections, forward and inverse kinematics. Forward kinematics is the use of specified joint positions in order to calculate an end-effector position using the characteristics of the robot. Inverse kinematics is the use of an end-effector position to calculate appropriate joint positions that correspond to that specific end-effector position.
The relationship between adjacent joints can be resolved using the Denavit–Hartenberg parameters according to the following formula [29].
In this formula, i is the specific joint, is the angle about the previous z-axis, a is the length of the common normal, d is the offset along the previous z-axis, is the angle about the common normal, with c and s representing the cosine and sine functions, respectively. By multiplying the transformation matrices of each consecutive joint, a formula for the end-effector position can be created based on the position of each joint:
where represents the relationship of the base frame to the end-effector frame when taking into consideration all other joint positions.
However, accounting for only the relationship of the end-effector to the base is insufficient for collision avoidance problems. There are often multiple solutions to the inverse kinematics problem for a given end-effector position. This can have a negative impact on performance when trying to avoid obstacles in the environment. This is because some joint configurations lead to collisions while others may avoid them entirely while reaching the same end-effector position. As a result, additional parameters and limits need to be employed to avoid collision within an environment.
3.2. Dynamics
The dynamics equations for a manipulator relate applied joint torques to joint accelerations, velocities, and positions. For simplicity, the joint positions (), velocities (), and accelerations () will be collectively referred to as joint states. Manipulator dynamics can be modeled using a plethora of different methods including the Newton–Euler [30] and Lagrangian methods [31]. In this research, the dynamics are modeled using the Newton–Euler method and the mass properties for the designed manipulator can be seen in Table 2, which assume a uniform mass distribution for cylindrical links. It should be noted that the center of mass parameters for each link are defined relative to the immediately preceding joint frame.

Table 2.
Mass and center of mass for each link.
When a free-flying or free-floating base is considered, the base can be considered another rigid body and the dynamics can be modeled in generalized coordinates. Additionally, the gravity term can be neglected due to the space environment. Taking into account external forces in the inertial frame, the dynamics equation becomes [13,32]:
where = , i.e., the translational acceleration and angular velocity of the base, is the Jacobian matrix of the base, is the Jacobian of the manipulator, is the inertia matrix of the base, is the inertia matrix of the manipulator, is the coupled inertia matrix, represents the angular acceleration of the base in the inertial frame expressed in the spacecraft frame, represents the joint accelerations of the manipulator, and and are the velocity-dependent nonlinear terms for the base and manipulator, respectively. The matrices and are the forces and moments on the base center of mass and the end-effector in the inertial frame, respectively. Since this paper only focuses on the approach of the end-effector for capture, no forces are considered to be acting on the end-effector, i.e., for both free-flying and free-floating scenarios. Further, it is assumed that no forces are acting on the base when it is considered to be free-floating (i.e., ), and, for the free-flying case, that the forces acting at the base are able to ideally compensate for any forces generated by the coupled base–manipulator system, such that the base position remains fixed. Now that the dynamics for a free-flying manipulator and a free-floating manipulator are defined, the DRL controller can be applied.
4. Deep Reinforcement Learning Model
In this section, an overview of the deep reinforcement learning algorithm, namely, DDPG, is presented, followed by a description of the learning environment and reward functions employed. The framework of the DDPG model can be seen in Figure 2. The framework for this model was constructed and trained using MATLAB’s reinforcement learning toolbox and deep learning toolbox [33,34].
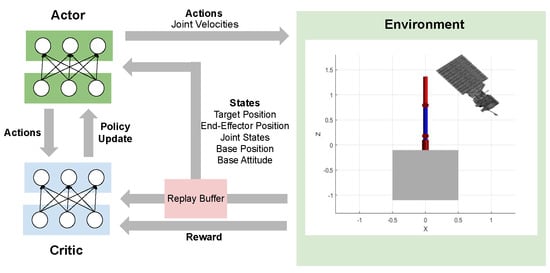
Figure 2.
Representation of DDPG algorithm framework. The distinct parts of this model are the actor, critic, environment, and replay buffer.
Reinforcement learning is a process in which an agent takes an action within a defined environment. This is completed through a specific amount of discrete timesteps. During each timestep, the agent is given an observation, decides an action, and then receives a reward. Agent behavior is determined based on a policy that correlates states to a probability distribution over the actions. The DDPG algorithm is a model-free deep reinforcement leaning method comprised of two neural networks to act as the agent. Specifically, there is an actor network and critic network that work in tandem to decide on the best action based on the reward values received. The environment is based on the Markov decision-making process, as such, there is a state space, and action space , as well as initial conditions, forward timestep dynamics, and a reward function [27].
4.1. Deep Deterministic Policy Gradient
In deterministic policy gradients, neural networks estimate Q-values which are then used to determine and update the policy. In the DDPG algorithm, this process is split between the actor and critic networks. The actor takes an action in the environment to optimize the current policy using the value function supplied by the critic. The critic then receives the reward from the action and then approximates the value function in order to optimize the policy that the actor uses. The critic is updated to minimize the loss function [35]:
where
In this equation, , , and represent the state, action, and reward at timestep i. represents the the Q-value function, and is the policy function. The weights and parameters of the actor network and actor target network are represented by and , respectively. For the critic network and critic target network, these values are represented by and , respectively, and the discount factor is denoted as [35]. The actor is updated according to the gradient described below.
The critic and actor are updated in an alternating pattern until the training converges.
The neural networks are made up of multiple layers and networks of perceptrons. The number of layers and size of the network is dependent on the task that is being performed as well as the environment that the agent is acting within. The governing equation for a perceptron h can be described as
where the output of a perceptron is denoted as , represents the jth element of the input vector, is the perceptron bias, is the associated perceptron weight for the jth element, and is the activation function [36].
The layers of both networks consist of 300 or 400 neurons. The actor network has an input layer, followed by a fully connected layer, and then a rectified linear unit (ReLU) layer. The next few layers are as follows: fully connected, ReLU, fully connected, and the output layer is a hyperbolic tangent layer. The critic is comprised of a state path and an action path to associate state–action pairs. The state and action path converges to the common path. The state path has the following layers: input, fully connected, ReLU, fully connected. The action path has only an input and fully connected layer. The paths are connected at the common path and the remaining layers are a ReLU layer and fully connected layer. The architecture for the actor and critic networks can be seen in Figure 3.
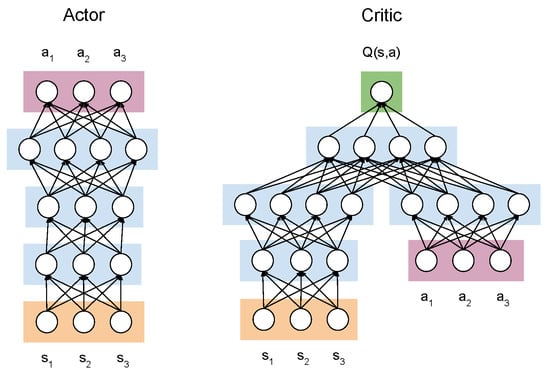
Figure 3.
An image representation of the neural network layers for both the actor and critic network.
As shown in the above figure, the actor network considers only the environment states as inputs. The states are then used to influence the next action that will be taken. The critic network accepts both states and actions as inputs and provides a Q-value indicating how useful the action was for that particular instance.
The DDPG algorithm in this research utilized Adam to optimize the neural networks with an actor and critic learn rate of [37]. The discount factor was 0.99, the experience buffer was , and the target smoothing factor was .
4.2. Environment
The 3-DOF manipulator dynamics have been defined previously based on the state-space equation and the applied joint velocities are considered to be the actions. The joint velocities are applied to the actuators and a new evaluation of the environment is supplied to the agent. In particular, the joint position and torque of each joint is numerically calculated using the equations presented in Section 3 and then used in the next iteration of the environment. The environment is modeled in a Cartesian coordinate system with the base frame of the manipulator centered at the origin. Therefore, the position of each object in the environment is determined by the -coordinates of the object center relative to the manipulator base.
The environment is constructed and trained using MATLAB. The manipulator model is comprised of three links with properties shown in Table 1 and Table 2. The target object is modeled after the Aqua Earth-observing satellite [38] and the base spacecraft is modeled as a rectangular prism. For convenience, the exact target grasp location is modeled as a small sphere. The exact target grasp location is restricted to a specific area near the Aqua satellite to illustrate a grasping zone.
All of the objects in the environment are modeled as convex geometries that can be used to determine if there is a collision. The manipulator collision geometry is comprised of multiple cylinders with radii of 4 cm. The target object and base spacecraft can be modeled similarly using the Aqua CAD model and a rectangular prism, respectively. Using the algorithm within MATLAB, which is based on [39], it can be determined whether two specified geometries are intersecting. A logic value of 1 is provided if there is an intersection and 0 if there is no collision.
States and Actions
The state space, , is defined as the target grasp location with respect to the manipulator base frame, the end-effector position with respect to the manipulator base frame, and the joint positions and velocities of the robot. The base position and orientation are also included as observations.
where
Vectors and are the Cartesian coordinates of the target grasp location and end-effector location, respectively, and represent the matrix of joint positions and velocities for each joint, and M represents the degrees of freedom of the manipulator and in this case . The position and orientation of the base spacecraft are represented by and , respectively.
The action space is defined as the manipulator joint velocities, and is represented as:
Specifying joint velocities allows full control of the manipulator’s motion and end-effector’s position relative to the manipulator’s base frame.
4.3. Reward Function
The reward function is the most important part of training and is responsible for improving and guiding the performance of an algorithm. This section aims to explain the design of the reward function used in each of the training cases. The reward function is comprised of continuous and sparse components. Considering the goal of this research, the reward function is based on the distance to the target grasp location, and interaction with collision objects as well as the joint velocities.
Each reward function is devised in such a way that the result is always negative. A negative reward function is advantageous, since it establishes a maximum value of zero and, as such, provides a clear convergence point for training. Another advantage to a negative reward function is that it encourages fast completion. In order for the episode to be complete, there is a specified termination condition in which the end-effector has to be within 0.05 m of the target grasp location. Fulfilling this condition in fewer steps means less cumulative negative reward and a higher reward overall.
The reward functions for the free-flying base and free-floating base scenarios are described in the following subsections. For both scenarios, the total reward for each episode is the summation of the reward values at each timestep, i.e., .
4.3.1. Free-Flying Base
The reward for the free-flying manipulator scenario at each timestep is based on the proximity of the end-effector to the target grasp location and is represented as:
where is the distance penalty associated with the distance between the end-effector and the target grasp location, and is a penalty associated with collision of the manipulator with itself or the target object. The term is a continuous reward and is modeled using a linear function. The distance from the end-effector to the target grasp location is determined using the Euclidean distance formula and is multiplied by a weight, , to obtain the proximity reward.
where and the constant is a negative value which causes a penalty that is proportional to the distance.
The term is a sparse penalty related to a collision with an obstacle. This penalty is only applied when any part of the manipulator is colliding with any of the collision objects in the environment. This is modeled using a piece-wise function in which the reward is zero when the manipulator is not colliding with any obstacles and a penalty is applied when a collision occurs. This function is described as follows:
where p represents the condition that any part of the manipulator is colliding with any of the collision objects in the environment; when there is a collision, p = 1 and when there is no collision, p = 0. The positive constant, , is a penalty that is subtracted from the reward at each timestep for each instance that the manipulator intersects one of the obstacles. It should be noted that the expanded reward function for the free-floating case was employed in the simulations presented in this paper, since it is sufficiently robust to handle both free-flying and free-floating scenarios. However, the free-flying reward function presented in this section has the advantage of fewer required observations; thus, reducing the computational requirements during training and implementation.
4.3.2. Free-Floating Base
With a free-floating base, movements by the manipulator can cause reactionary forces and torques on the base. Higher velocity actions have a greater impact on the overall system dynamics and the degrees of freedom of the system are increased. In order to compensate, a penalty term to reduce the amount of actions resulting in high velocities has been added to the reward function used for the free-flying base scenario, Equation (9). The reward function achieved by adding a velocity penalty, , is as follows:
Since the joints can move clockwise and counterclockwise, the velocity penalty is expressed as the sum of the absolute values of the joint velocities to account for any large velocities in the negative direction. The velocity penalty is computed using the following:
In this expression, M is the number of manipulator joints and is the jth component of the joint velocities . A positive constant, , is used to properly scale the penalty in comparison to the other components of the reward function.
5. Simulation Parameters for Training and Testing
In this work, training was performed for two separate scenarios, namely, a cooperative or a non-cooperative target satellite. For each of the two scenarios, the training was conducted for a free-floating spacecraft, but was tested for both free-floating and free-flying cases. Hence, the four test cases are as follows:
- Cooperative target, free-flying base spacecraft and manipulator
- Cooperative target, free-floating base spacecraft and manipulator
- Non-cooperative target, free-flying base spacecraft and manipulator
- Non-cooperative target, free-floating base spacecraft and manipulator
The training parameters and initial conditions for the test environments are described in this section. The hyperparameters for training can be seen in Table 3 and were determined through trial and error until satisfactory training results were achieved.

Table 3.
Hyperparameters for training all cases.
The observation frame is centered at the manipulator base frame and the primary axes align with the axes of the manipulator base. In the observation frame, the manipulator is centered at the origin and the top surface of the base spacecraft is translated just below the origin by 0.1 m. This is to avoid instant collision between the manipulator and the base and avoid unintended penalties. The initial characteristics for the base spacecraft include the physical dimensions and mass. These values are used in the parallel axis theorem referenced in Section 3.2 to calculate base movement as a result of manipulator motion. The manipulator starts in the vertical position with no initial joint velocities. The spacecraft characteristics and initial manipulator conditions for the simulation are shown in Table 4.

Table 4.
Initial conditions and base spacecraft parameters.
In training for the cooperative target cases, the target satellite has a fixed initial position and orientation relative to the capturing spacecraft. In training for the non-cooperative target cases, however, the target satellite has different initial positions, orientations, and motion paths to ensure the trained agent is capable of responding to a variety of capture scenarios. For both cases, the capturing satellite’s and manipulator’s initial orientations and poses remain fixed. These parameters and conditions are found in Table 5.

Table 5.
Initial conditions for the target satellite in the observation frame.
The target object is modeled using the CAD file for the Aqua satellite [38]. The original file was converted to an STL file so the vertices could be extracted and used to create the collision geometry. The original model was scaled down for the simulation so that the target satellite dimensions were on the same order of magnitude as the base spacecraft. The satellite has a main body and one solar array, where the target grasp location was set as a point on the main body of the satellite. In Figure 4, the collision geometry is shown superimposed over the target satellite to demonstrate that it effectively encompasses the satellite body while still allowing for close-proximity motion.
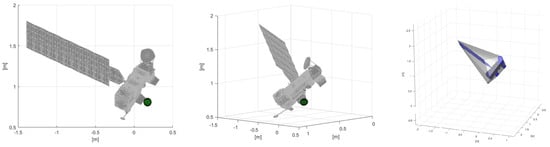
Figure 4.
Exact location for ideal grasping shown with a green sphere (left, middle) and the superimposed collision geometry for the satellite (right).
For the cooperative cases, the satellite is positioned in such a way that the grasping location is in a spot where the manipulator needs to avoid some parts of the satellite, as seen in Figure 5. In the non-cooperative cases, the target satellite is moving and rotating and the manipulator needs to avoid collisions with the moving target to reach the grasping location.
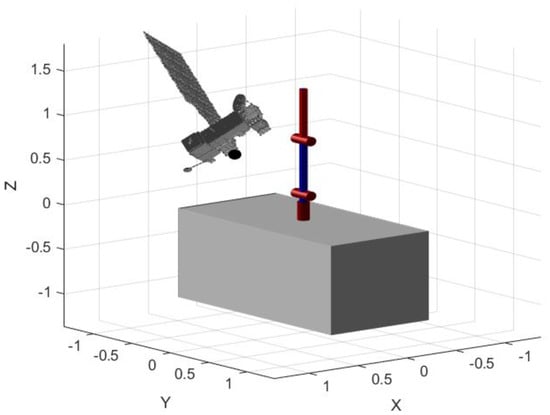
Figure 5.
Starting environment for the cooperative free-flying case.
6. Results and Discussion
This section provides the training results for each of the four cases as well as the resulting trajectories produced by each of the agents in testing. For the training results of both the cooperative and non-cooperative target satellite scenarios, the training graphs (see Figure 6 and Figure 7) are presented in the following sections. In both training graphs, the light blue points represent the reward at the current episode and the dark blue represents the average reward. The yellow points represent the current expected long-term reward, where it is ideal for the average reward to converge to the expected long-term reward.
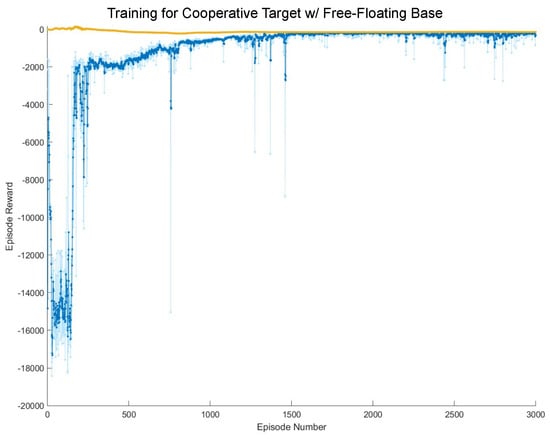
Figure 6.
Training results for the scenario with a cooperative target and free-floating base.
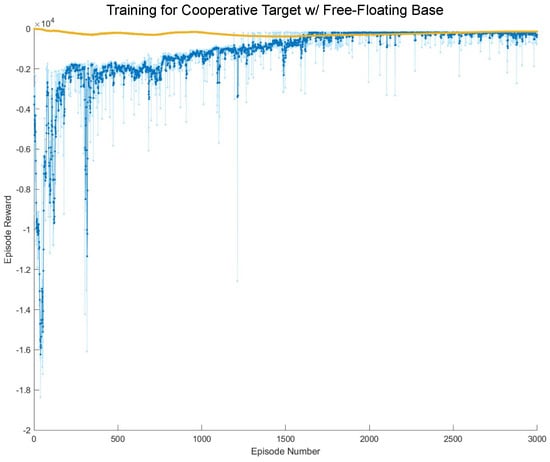
Figure 7.
Training results for the scenario with a non-cooperative target and free-floating base.
6.1. Cooperative Target
The agent for the cooperative target scenario was trained in an environment with a free-floating base and the results are shown in Figure 6. The training was performed over 3000 episodes.
As seen in Figure 6, the first few hundred episodes have very high variance and a relatively low average reward. At approximately episode 300, there was a significant decrease in variance, indicating that the agent is taking similar actions each episode. The training converges at an approximate reward value of −250 after about 2000 episodes.
The trained agent was first tested in an environment with a free-flying base. The resulting trajectory is shown in Figure 8 from multiple angles to demonstrate that the manipulator path avoided collision. The positions and velocities of the joints are graphically shown in Figure 9 along with the end-effector distance to the target grasp location and the magnitude of the end-effector velocity.

Figure 8.
Final trajectory for the free-flying cooperative target scenario shown from multiple angles. The front (left), top (middle), and angled views (right) are given.
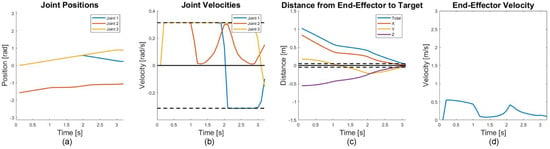
Figure 9.
Joint states and end-effector movement for the free-flying cooperative case. For (a,b), blue represents the base joint, red is the middle joint, and yellow is the last joint with the black dotted lines in (b) representing the velocity limits. In (c), the distance from each axis is shown with the black dotted lines representing a sufficient distance to the target. The magnitude of the end-effector velocity is shown in (d).
The environment is visualized in Figure 8 to show the trajectory produced by the agent’s actions. The satellite can be seen in an arbitrary position such that the manipulator has to actively avoid collisions when approaching the grasping location. The blue line is the end-effector path and clearly shows collision avoidance from multiple angles.
In Figure 9a,b, the joint positions and velocities are given in radians and radians per second, respectively. In Figure 9b, the joint velocity limits are represented as black dashed lines. As is evident from the figure, the manipulator moves at its maximum velocity for the first second and then slows as it nears the target grasp location. It should be noted that the velocity penalty in the reward function was not intended to necessarily ensure the velocity was small throughout the capture maneuver, as this would work contrary to both the time for capture and potentially restrict the possibility of capture in some scenarios. The velocity penalty becomes more important in cases where the manipulator is capable of moving at high speeds or where the base mass is small relative to the manipulator and coupled dynamics between the base and manipulator are more significant. The magnitude of the end-effector velocity is shown in Figure 9d. After two seconds, the base joint (joint 1) moved in the opposite direction to avoid a collision and then reached the grasping location. This is seen on the position graph where the base joint moved in the positive direction for two seconds and then moved in the negative direction. In Figure 9c, the total distance between the end-effector and target grasp location is given along with the distance in the x, y, and z-axes. The task is complete once the total distance is within five centimeters and this distance is represented on the distance graph by two black dashed lines.
The agent was then evaluated in a scenario with a free-floating base and the target satellite remained in the same position as the free-flying case. The results are given in Figure 10 and Figure 11 and the change in the base attitude and position are also shown.

Figure 10.
Final trajectory for the free-floating cooperative target scenario shown from multiple angles. The front (left), top (middle), and angled views (right) are given.
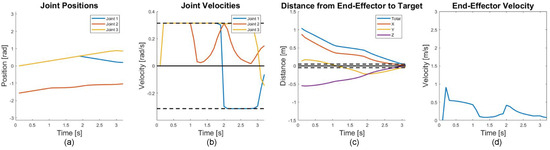
Figure 11.
Joint states and end-effector movement for the free-floating cooperative case. For (a,b), blue represents the base joint, red is the middle joint, and yellow is the last joint with the black dotted lines in (b) representing the velocity limits. In (c), the distance from each axis is shown with the black dotted lines representing a sufficient distance to the target. The magnitude of the end-effector velocity is shown in (d).
As shown in Figure 10, a similar path is taken for the free-floating case with a slight variation from the free-flying case as the base rotates and moves. The manipulator moves around the target to reach the grasping location without making contact with any other part of the satellite.
The joint states results (Figure 11) are very similar to the free-flying case. This is because a similar motion is required aside from very small variations due to the slight movement of the base. One of the more distinctive differences is the spike in the end-effector velocity (Figure 11d) which is not present in the free-flying case. The most likely reason for this spike is the effect of the added rotational velocity of the base caused by the initial movement of the manipulator, for which the trained agent was able to compensate. It is also important to note that the reward function did not explicitly penalize non-zero velocity at the point of capture. Hence, a small velocity is observed at the grasp point for each of the capture cases simulated. While the velocity is small, it is possible that a high-impact collision between the end-effector and grasp location could occur if the relative velocity is not reduced once in the grasping zone. To avoid this outcome, an additional term could be introduced in the reward function to penalize relative velocity at the capture point; however, by necessity, zero relative velocity can only be achieved within the capture zone specified and during the grasping task. In Figure 12, the base is shown at the beginning and end of the simulated results and compared to demonstrate that a shift occurred. The original base position is shown in orange and the resulting base position and orientation after movement is shown in green. It is important to note that minimization of the base motion was not a penalized or rewarded parameter in the reward function, e.g., large base rotations or angular velocities were not penalized. While there are advantages to minimizing the angular momentum of the base, depending on the relative masses of the spacecraft base and manipulator as well as the relative target motion, the amount of rotation permissible at the base can vary significantly. If minimization of the base motion is desired, this can be addressed through the addition of a term into the reward function (Equation (12)).
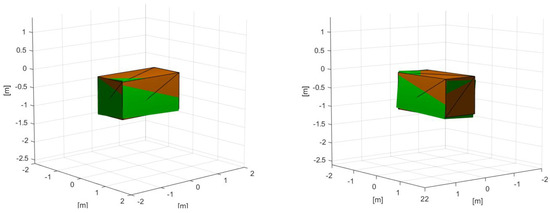
Figure 12.
Change in base orientation and position for the free-floating cases. The start is shown in orange and the end is shown in green.
6.2. Non-Cooperative Target
Similar to the cooperative target cases, a single agent was trained in an environment with a free-floating base and the results are shown in Figure 7. The training was completed over 3000 episodes.
The training for the non-cooperative target, as seen in Figure 7, had much more variance than in the cooperative case. This was as expected, since the target was non-cooperative, i.e., translating and rotating in an undesirable manner relative to the manipulator, and any collision was given a severe penalty. Therefore, if the target satellite collided with the manipulator due to the trajectory and motion of the target satellite, there was a large decrease in the reward. By approximately episode 1000, the variance was significantly lower and the reward was greatly improved. Around episode 2250, the training reaches its maximum value of approximately −500 with very little variance.
The trained agent was first tested in an environment where the base was free-flying and the target object was moving. The resulting trajectory is shown from multiple angles in Figure 13 to demonstrate collision avoidance. The velocities and positions of the joints are provided as well as the net end-effector velocity and distance to the target in Figure 14.
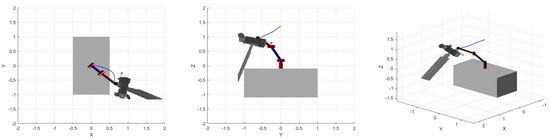
Figure 13.
Final trajectory for the free-flying non-cooperative target scenario shown from multiple angles. The front (left), top (middle), and angled views (right) are given. Target velocity = (0, 0.1, 0) m/s.
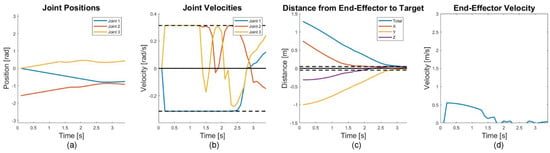
Figure 14.
Joint states and end-effector movement for the free-flying non-cooperative case. For (a,b), blue represents the base joint, red is the middle joint, and yellow is the last joint with the black dotted lines in (b) representing the velocity limits. In (c), the distance from each axis is shown with the black dotted lines representing a sufficient distance to the target. The magnitude of the end-effector velocity is shown in (d).
In Figure 13, the manipulator followed a path that reached the grasp location even when the target satellite was rotating and moving in an undesirable manner. As seen in the top view of the trajectory, the manipulator takes a rounded approach to reach the grasping location, rather than a linear approach. A linear approach towards the satellite was more likely to result in a collision between the target satellite and the manipulator due to the translational motion of the satellite. Instead, the manipulator moved along a path that allowed it to approach the satellite in almost the opposite direction of the satellite’s motion, thereby allowing for improved collision avoidance.
Since the target satellite was moving, the final position of the joints was different than in the cooperative cases. Similar to the cooperative scenarios, the manipulator moves at maximum velocity for the first second to minimize time (see Figure 14b). The base joint in this case moved in the negative direction (Figure 14a) because the manipulator reached the target grasp location relatively quickly. The end-effector velocity, seen in Figure 14d, started high and then decreased as it approached the target grasp location. The end-effector position was seen to follow the movement of the grasping location in Figure 14c before it reached a sufficient distance to the target grasp location to initiate grasping, and hence, end the simulation.
The agent was then evaluated in a scenario with a free-floating base. The target satellite had a similar motion path to the free-flying case (Figure 15). Similarly, the joint states and end-effector motions are presented in Figure 16, with the change in the base attitude and position shown in Figure 17.

Figure 15.
Final trajectory for the free-floating non-cooperative target scenario shown from multiple angles. The front (left), top (middle), and angled views (right) are given. Target velocity = (0, 0.1, 0) m/s.
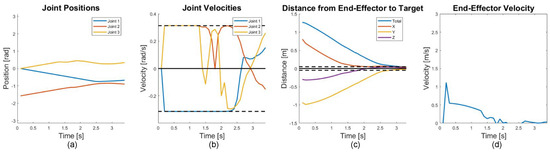
Figure 16.
Joint states and end-effector movement for the free-floating non-cooperative case. For (a,b), blue represents the base joint, red is the middle joint, and yellow is the last joint with the black dotted lines in (b) representing the velocity limits. In (c), the distance from each axis is shown with the black dotted lines representing a sufficient distance to the target. The magnitude of the end-effector velocity is shown in (d).
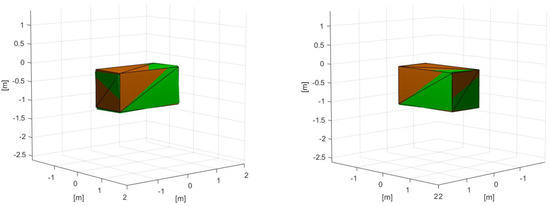
Figure 17.
Change in base orientation and position for the free-floating case with a cooperative target. The start is shown in orange and the end is shown in green.
The manipulator trajectory in the free-floating case (see Figure 15) was similar to the free-flying case. The resultant motion of the base can be clearly seen tilted towards the direction of the target satellite’s motion. As was seen in the cooperative case, a notable spike in the end-effector velocity was also observed in the non-cooperative free-floating case (Figure 16d). However, the manipulator still reaches the grasping location without resulting in collision with similar end-effector motion and joint states to the free-flying case.
7. Conclusions
This paper presented a DRL control approach for a free-floating space manipulator intended for non-cooperative target capture. The DDPG algorithm was employed to avoid collisions with a target satellite when approaching a grasping location. The approach was investigated by training agents for space manipulator control in two scenarios, namely, for cooperative and non-cooperative target satellites. The approach was applied to a 3-DOF space manipulator, where target collisions were introduced through convex meshes on the target satellite as well as on the manipulator and base spacecraft. The training results indicated that within a few thousand episodes the agents’ training had converged. The trained agents were then tested for four cases: free-flying manipulator with a cooperative target, free-floating manipulator with a cooperative target, free-flying manipulator with a non-cooperative target, and free-floating manipulator with a non-cooperative target. The resulting trajectories from each test case were shown in the environment following collision-free paths to the grasping locations on the target satellites. The trained agents effectively controlled the manipulator to avoid collisions when simulated with both stationary and moving target satellites. The joint states and the end-effector distance and velocities remained within acceptable bounds throughout the motion paths. The proposed method is off-policy and performs well in continuous action spaces making it particularly suited for this task as well as other space operations requiring capture maneuvers.
Author Contributions
Conceptualization, J.B. and M.C.F.B.; Methodology, J.B. and M.C.F.B.; Validation, J.B. and M.C.F.B.; Formal analysis, J.B. and M.C.F.B.; Investigation, J.B. and M.C.F.B.; Writing—Original Draft Preparation, J.B. and M.C.F.B.; Writing—Review and Editing, J.B. and M.C.F.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Ellery, A. Tutorial review on space manipulators for space debris mitigation. Robotics 2019, 8, 34. [Google Scholar] [CrossRef]
- Miller, D.; Magilton, E. On-Orbit Satellite Servicing Standards Are a Necessity for the Private Space Industry. Air Space Law 2018, 31, 4. [Google Scholar]
- Flores-Abad, A.; Ma, O.; Pham, K.; Ulrich, S. A review of space robotics technologies for on-orbit servicing. Prog. Aerosp. Sci. 2014, 68, 1–26. [Google Scholar]
- Rybus, T. Obstacle avoidance in space robotics: Review of major challenges and proposed solutions. Prog. Aerosp. Sci. 2018, 101, 31–48. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, X.Y.; Chen, P.; Cai, G. Hybrid control scheme for grasping a non-cooperative tumbling satellite. IEEE Access 2020, 8, 54963–54978. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, S.; Zheng, X.; Ma, W.; Xie, X.; Liu, L. Reinforcement learning with prior policy guidance for motion planning of dual-arm free-floating space robot. Aerosp. Sci. Technol. 2023, 136, 108098. [Google Scholar] [CrossRef]
- Wu, Y.H.; Yu, Z.C.; Li, C.Y.; He, M.J.; Hua, B.; Chen, Z.M. Reinforcement learning in dual-arm trajectory planning for a free-floating space robot. Aerosp. Sci. Technol. 2020, 98, 105657. [Google Scholar] [CrossRef]
- Li, Y.; Hao, X.; She, Y.; Li, S.; Yu, M. Constrained motion planning of free-float dual-arm space manipulator via deep reinforcement learning. Aerosp. Sci. Technol. 2021, 109, 106446. [Google Scholar] [CrossRef]
- Li, Y.; Li, D.; Zhu, W.; Sun, J.; Zhang, X.; Li, S. Constrained motion planning of 7-DOF space manipulator via deep reinforcement learning combined with artificial potential field. Aerospace 2022, 9, 163. [Google Scholar] [CrossRef]
- Papadopoulos, E.; Dubowsky, S. On the nature of control algorithms for free-floating space manipulators. IEEE Trans. Robot. Autom. 1991, 7, 750–758. [Google Scholar] [CrossRef]
- Huang, P.; Xu, Y.; Liang, B. Dynamic balance control of multi-arm free-floating space robots. Int. J. Adv. Robot. Syst. 2005, 2, 13. [Google Scholar] [CrossRef]
- Rybus, T.; Seweryn, K.; Sasiadek, J.Z. Control system for free-floating space manipulator based on nonlinear model predictive control (NMPC). J. Intell. Robot. Syst. 2017, 85, 491–509. [Google Scholar] [CrossRef]
- Wang, M.; Luo, J.; Fang, J.; Yuan, J. Optimal trajectory planning of free-floating space manipulator using differential evolution algorithm. Adv. Space Res. 2018, 61, 1525–1536. [Google Scholar] [CrossRef]
- Wang, X.; Luo, X.; Han, B.; Chen, Y.; Liang, G.; Zheng, K. Collision-free path planning method for robots based on an improved rapidly-exploring random tree algorithm. Appl. Sci. 2020, 10, 1381. [Google Scholar] [CrossRef]
- Nishida, S.; Yoshikawa, T. Space debris capture by a joint compliance controlled robot. In Proceedings of the Proceedings 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2003), Kobe, Japan, 20–24 July 2003; Volume 1, pp. 496–502. [Google Scholar]
- Hakima, H.; Bazzocchi, M.C. CubeSat with Dual Robotic Manipulators for Debris Mitigation and Remediation. In Proceedings of the 5th IAA Conference on University Satellite Missions and CubeSat Workshop, Rome, Italy, 28–31 January 2003. [Google Scholar]
- Liu, Y.Q.; Yu, Z.W.; Liu, X.F.; Cai, G.P. Active detumbling technology for high dynamic non-cooperative space targets. Multibody Syst. Dyn. 2019, 47, 21–41. [Google Scholar] [CrossRef]
- Lahr, G.J.; Soares, J.V.; Garcia, H.B.; Siqueira, A.A.; Caurin, G.A. Understanding the implementation of impedance control in industrial robots. In Proceedings of the 2016 XIII Latin American Robotics Symposium and IV Brazilian Robotics Symposium (LARS/SBR), Recife, Brazil, 8–12 October 2016; pp. 269–274. [Google Scholar]
- Gang, C.; Yuqi, W.; Yifan, W.; Liang, J.; Zhang, L.; Guangtang, P. Detumbling strategy based on friction control of dual-arm space robot for capturing tumbling target. Chin. J. Aeronaut. 2020, 33, 1093–1106. [Google Scholar]
- Flores-Abad, A.; Terán, M.A.G.; Ponce, I.U.; Nandayapa, M. Compliant Force Sensor-Less Capture of an Object in Orbit. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 497–505. [Google Scholar] [CrossRef]
- Liu, X.F.; Cai, G.P.; Wang, M.M.; Chen, W.J. Contact control for grasping a non-cooperative satellite by a space robot. Multibody Syst. Dyn. 2020, 50, 119–141. [Google Scholar] [CrossRef]
- Sangiovanni, B.; Rendiniello, A.; Incremona, G.P.; Ferrara, A.; Piastra, M. Deep reinforcement learning for collision avoidance of robotic manipulators. In Proceedings of the 2018 European Control Conference (ECC), Limassol, Cyprus, 12–15 June 2018; pp. 2063–2068. [Google Scholar]
- Satheeshbabu, S.; Uppalapati, N.K.; Fu, T.; Krishnan, G. Continuous control of a soft continuum arm using deep reinforcement learning. In Proceedings of the 2020 3rd IEEE International Conference on Soft Robotics (RoboSoft), New Haven, CT, USA, 15 May–15 July 2020; pp. 497–503. [Google Scholar]
- Rahimpour, Z.; Verbič, G.; Chapman, A.C. Actor-critic learning for optimal building energy management with phase change materials. Electr. Power Syst. Res. 2020, 188, 106543. [Google Scholar] [CrossRef]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the International Conference on Machine Learning, PMLR, Beijing, China, 21–26 June 2014; pp. 387–395. [Google Scholar]
- Wang, Y.; Sun, J.; He, H.; Sun, C. Deterministic policy gradient with integral compensator for robust quadrotor control. IEEE Trans. Syst. Man, Cybern. Syst. 2019, 50, 3713–3725. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Guoqing, M.; li, L.; Zhenglin, Y.; Guohua, C.; Yanbin, Z. Movement Characteristics Analysis and Dynamic Simulation of Collaborative Measuring Robot. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 187, p. 012043. [Google Scholar]
- Khalil, W. Dynamic modeling of robots using recursive newton-euler techniques. In Proceedings of the ICINCO2010, Madeira, Portugal, 15–18 June 2010. [Google Scholar]
- Zi, B.; Duan, B.; Du, J.; Bao, H. Dynamic modeling and active control of a cable-suspended parallel robot. Mechatronics 2008, 18, 1–12. [Google Scholar] [CrossRef]
- Zong, L.; Emami, M.R.; Luo, J. Reactionless control of free-floating space manipulators. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 1490–1503. [Google Scholar] [CrossRef]
- MATLAB Reinforcement Learning Toolbox; The MathWorks: Natick, MA, USA, 2022.
- MATLAB Deep Learning Toolbox; The MathWorks: Natick, MA, USA, 2022.
- Chu, C.; Takahashi, K.; Hashimoto, M. Comparison of Deep Reinforcement Learning Algorithms in a Robot Manipulator Control Application. In Proceedings of the 2020 International Symposium on Computer, Consumer and Control (IS3C), Taichung City, Taiwan, 13–16 November 2020; pp. 284–287. [Google Scholar]
- Malagon, M.; Ceberio, J. Evolving Neural Networks in Reinforcement Learning by means of UMDAc. arXiv 2019, arXiv:1904.10932. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Lane, K. NASA 3D Resources: Aqua; NASA: Washington, DC, USA, 2010. [Google Scholar]
- Gilbert, E.G.; Johnson, D.W.; Keerthi, S.S. A fast procedure for computing the distance between complex objects in three-dimensional space. IEEE J. Robot. Autom. 1988, 4, 193–203. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).