Study on the Forced Torsional Vibration Response of Multiple Rotating Blades with Underplatform Dampers
Abstract
:1. Introduction
2. Prediction of the Forced Torsional Vibration Response with Dampers
2.1. Modeling and Motion Equations
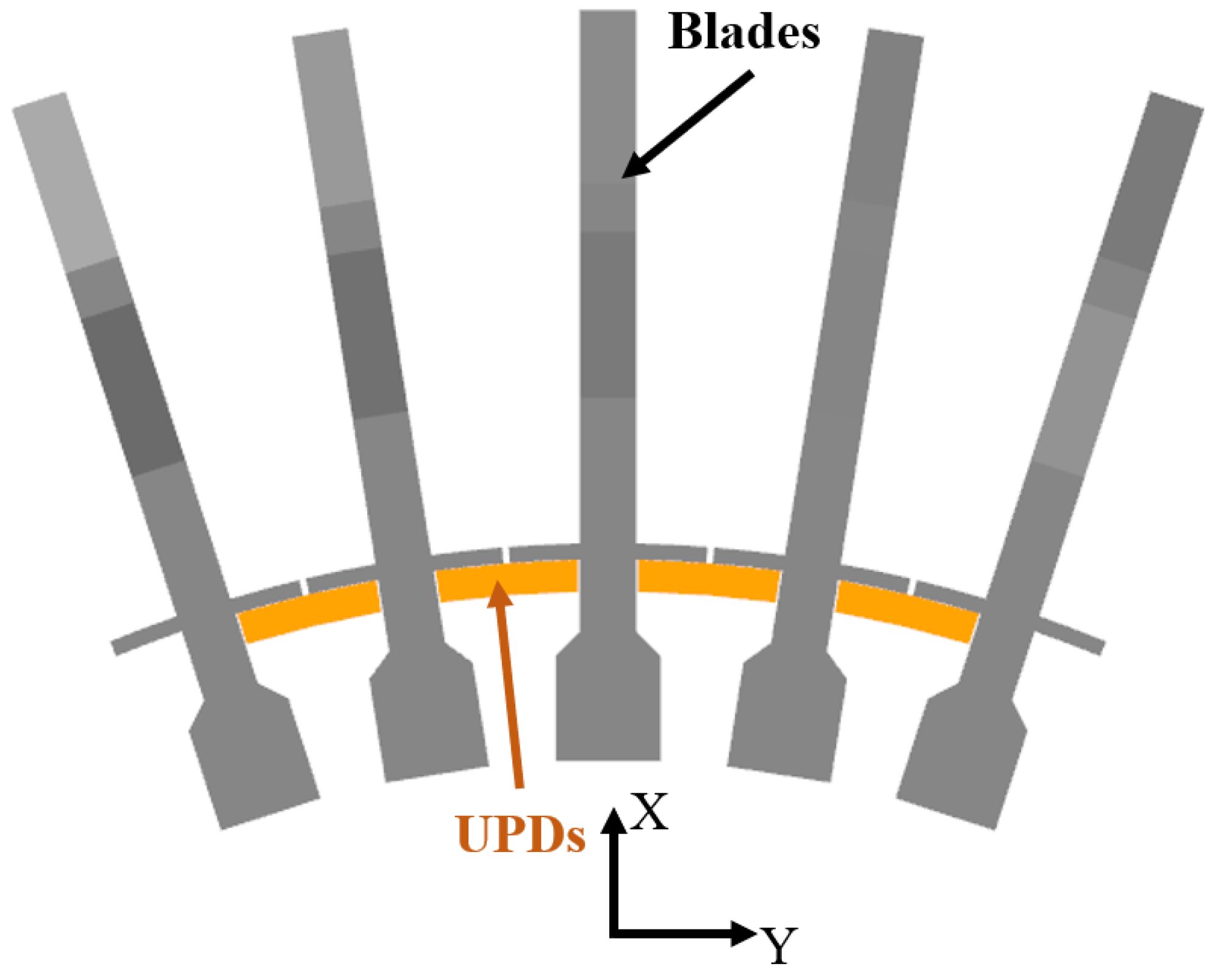
2.1.1. Modeling
2.1.2. Motion Equations
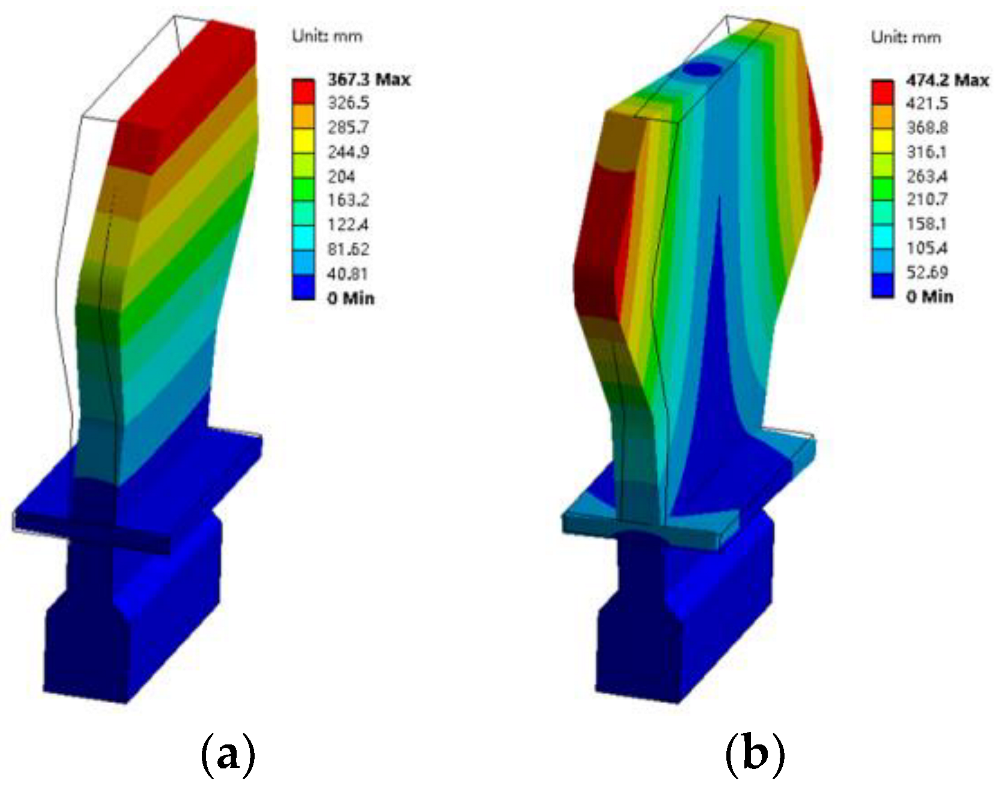
- Firstly, the model of a multi-blade system with UPDs was meshed with a solid hexahedral eight-node element, as shown in Figure 3.
- The influence of centrifugal load was taken into account in the static structural analysis. In the static structural calculation, the blade tenons were constrained in all directions and the contact parts of the UPDs and blades were treated as frictionless contacts. Only the influence of normal force was considered. The system had a constant rotational speed, which generated centrifugal force. The stress of the multi-blade system with UPDs under rotation and the contact state and normal stiffness between the blade and UPDs were obtained.
- Then, the modal analyses with pre-stress were performed. The results of the static structural analyses were used as the pre-stress for modal analyses so that the constant coefficient matrices of the multi-blade system with UPDs could be obtained.
2.2. Numerical Solution of the Nonlinear Motion Equations
2.2.1. The Harmonic Balance Method
2.2.2. The Newton Method
- Input the constants and matrices needed for the computation, such as the matrices obtained in Section 2.1, the mass of the UPDs, the rotational speed, excitation force, minimum calculation frequency f1, maximum calculation frequency f2, and node numbers for frictional force.
- Construct the excitation force vector fex, frictional force element fnl, and then the motion equation, as shown in Equation (1).
- Compute the blade’s vibration response without considering fnl.
- Construct the Fourier coefficient equations of the residual R in Equation (8) using the HBM and employ the ‘fsolve’ function to find an approximate solution at f1, which serves as the initial guess for the nonlinear equations.
- Employ the Newton method to solve the nonlinear Equation (10) within the frequency range of f1~f2. The convergence tolerance was set at 10−7. The computation adjusted the step size using the arc-length continuation method, increasing the step size at easily converging points to improve computational efficiency and decreasing the step size at difficult converging points to ensure converged solutions were obtained.
- Complete all the calculations within the frequency range and save the calculated data.
2.3. Numerical Results
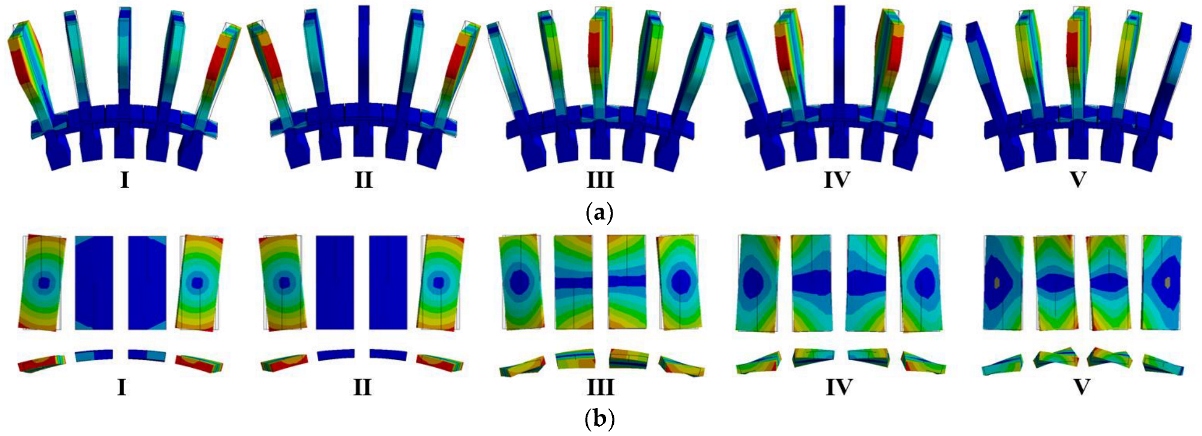
2.3.1. Modal Vibration of Multi-Blades System with Dampers
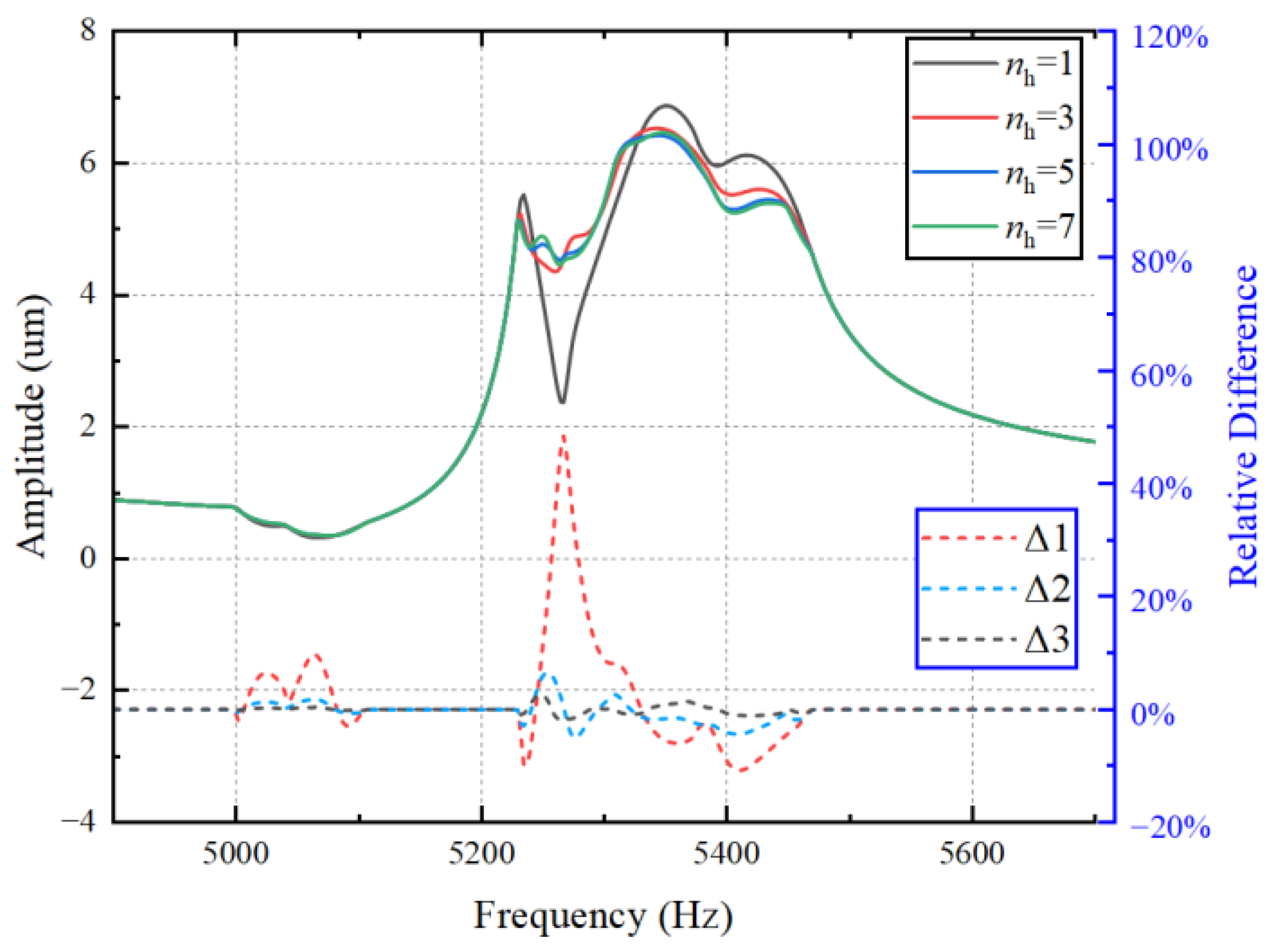
2.3.2. The Impact of Harmonic Truncation Order nh on the Solution of Nonlinear Vibrations
2.3.3. Effect of Normal Force Caused by UPDs
3. Excitation Experiments with a Spin Tester
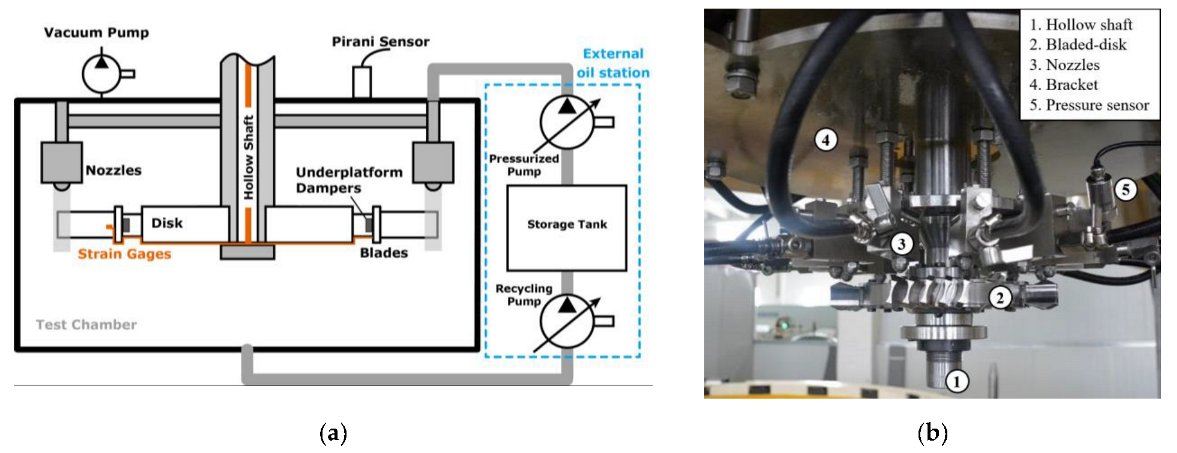
3.1. Description of the Test Equipment
- Vertical spin tester: The tester driven by the motor and pulley can perform controlled high-speed spin tests. During the test, the test chamber was kept in a vacuum state (pressure < 2 Torr) to avoid the influence of excessive airflow on the test results.
- External oil station: The supply and return oil of the spray excitation system are realized through an external oil station arranged outside the test chamber. Aviation lubricating oil is selected as the liquid for spraying, which can maintain a liquid state in an almost vacuum environment. The external oil station can pressurize and transport the oil outside the test chamber to the nozzle inside the test chamber. The supply pressure can be adjusted as required, and the maximum supply pressure is 1.0 MPa. The maximum pressure at the nozzle will have certain attenuation based on factors such as height, number of nozzles, and pipe length, generally ranging from 0.8 MPa to 0.85 MPa. In addition, components for oil recovery and filtration are installed in the test chamber to recycle and filter the liquid that has been sprayed out.
- Nozzles and bracket: The fuel injection nozzles were used in the experiment, which could produce a hollow conical shape under standard pressure. The flow rate Q of the nozzle is related to the pressure P at the nozzle and satisfies the equation:where Pst is the nominal standard pressure of the nozzle, and Qst is the flow rate of the nozzle corresponding to Pst pressure. The total number and installation position of the nozzles can be adjusted as needed. The number of nozzles is designed according to the size, speed, and vibration frequency of the test requirements. The installation height, radius, and angle of the nozzle can all be adjusted according to the test requirements.
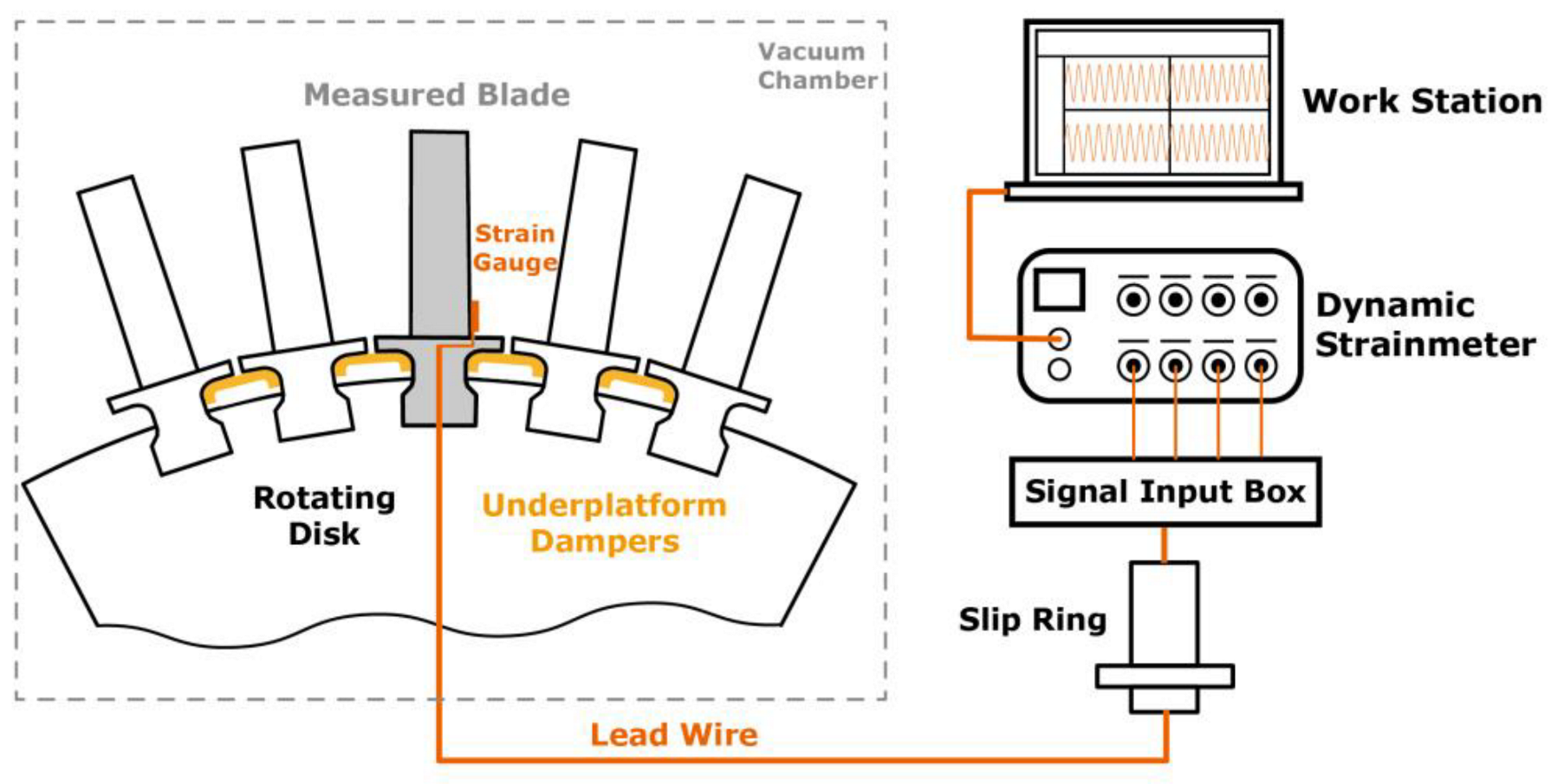
- Vibration signal acquisition system: The vibration information of the blades is obtained using strain gauges attached to the blade surface and transmitted to the top of the hollow shaft and high-speed slip ring through lead wires. The rotating signal is transmitted through the slip ring to the signal input box, which is connected to a dynamic strain meter. The vibration signals will be collected and stored in the dynamic strain meter. Finally, the dynamic strain meter is connected to a work station to achieve real-time display and analysis blade vibration signals, as shown in Figure 9. The strain gauges used were normal temperature single-axis strain gauges with the model number BE120-1AA, having a resistance of 120Ω and a grid length of 1 mm. The high-speed slip ring allowed a maximum rotational speed of 50,000 r/min, encompassing 16 channels. The rotating signals can be converted into non-rotating signals by the slip ring, facilitating the transmission of signals for data acquisition outside the test chamber. The dynamic strain meter comprised eight acquisition channels, with each individual channel’s sampling frequency set at 20,480 Hz.
3.2. Design of the Multi-Blade System with UPDs
- The test blade needs a platform that can install UPDs. The mortise and tenon joints were fir-tree-shaped to meet the strength requirements under high speeds. Additionally, it is crucial to ensure that there is enough normal pressure on the blade tenon contact surfaces in the vicinity of the test speed, with most of the contact surfaces in a stick state. In the stick state, the frictional force provided by the tenon joint contact surface is limited, which can reduce the impact of tenon joint friction on blade vibration.
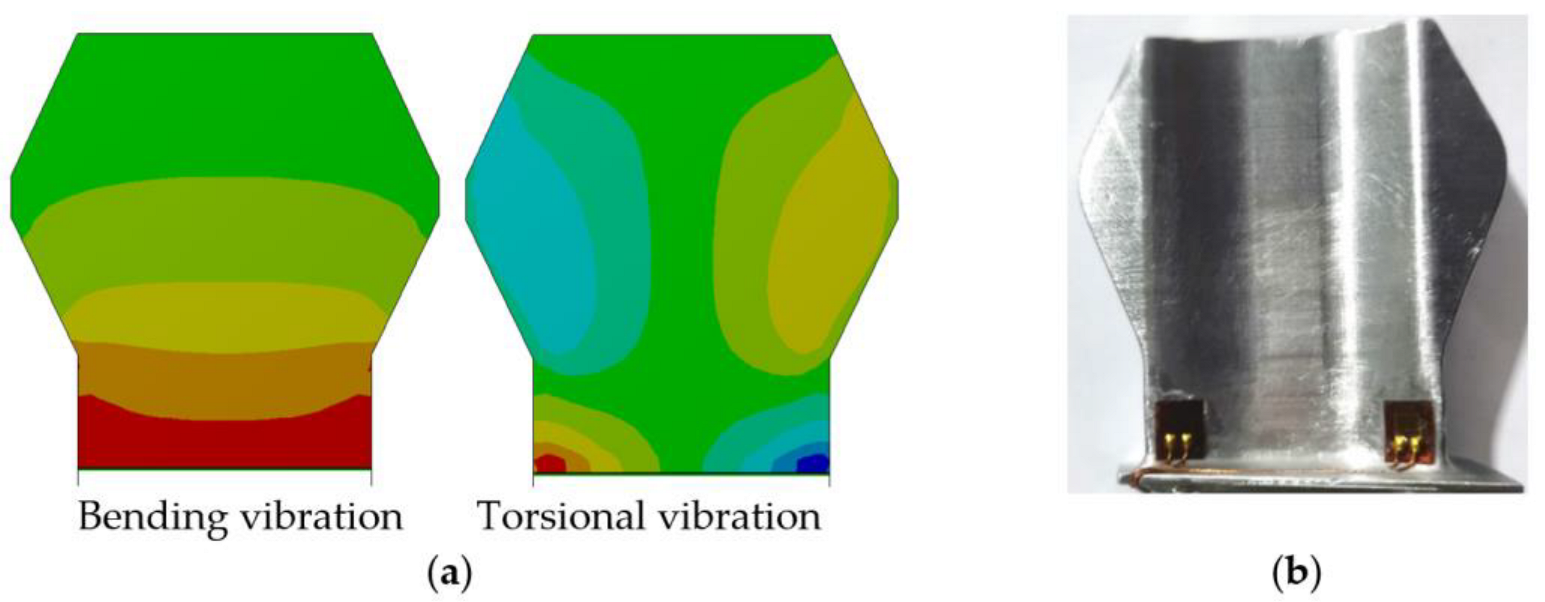
- The first-order bending and torsional vibration mode of the blade should be independent to each other, and the frequencies of the torsional vibration mode should be within the excitation range of the test equipment. According to the modal analysis results of the pre-stressed blade, the bending vibration frequency of the blade at a speed of 25,000 r/min is approximately 2350 Hz, and the torsional vibration frequency is approximately 5160 Hz. The two modal frequencies are significantly different, and there is no multiple relationship between them.
- The blade body has clear positions of torsional vibration stress concentration, which are relatively flat and easy to position strain gauges. The test blade shape is axially symmetrical, with almost identical vibrational strains at two locations where strain gauges can be attached to prevent signal loss due to gauge or wire breakage. The special blade shape design will not affect the vibration mode of the UPDs or the first-order bending and torsional vibration of the blade body. The radial vibration strain distributions of the blade body for first-order bending and torsional vibration obtained from the finite element modal analysis is shown in Figure 10a. The strain gauges were attached at locations with relatively large vibration strains, as in Figure 10b.
3.3. Number of Nozzles Determined
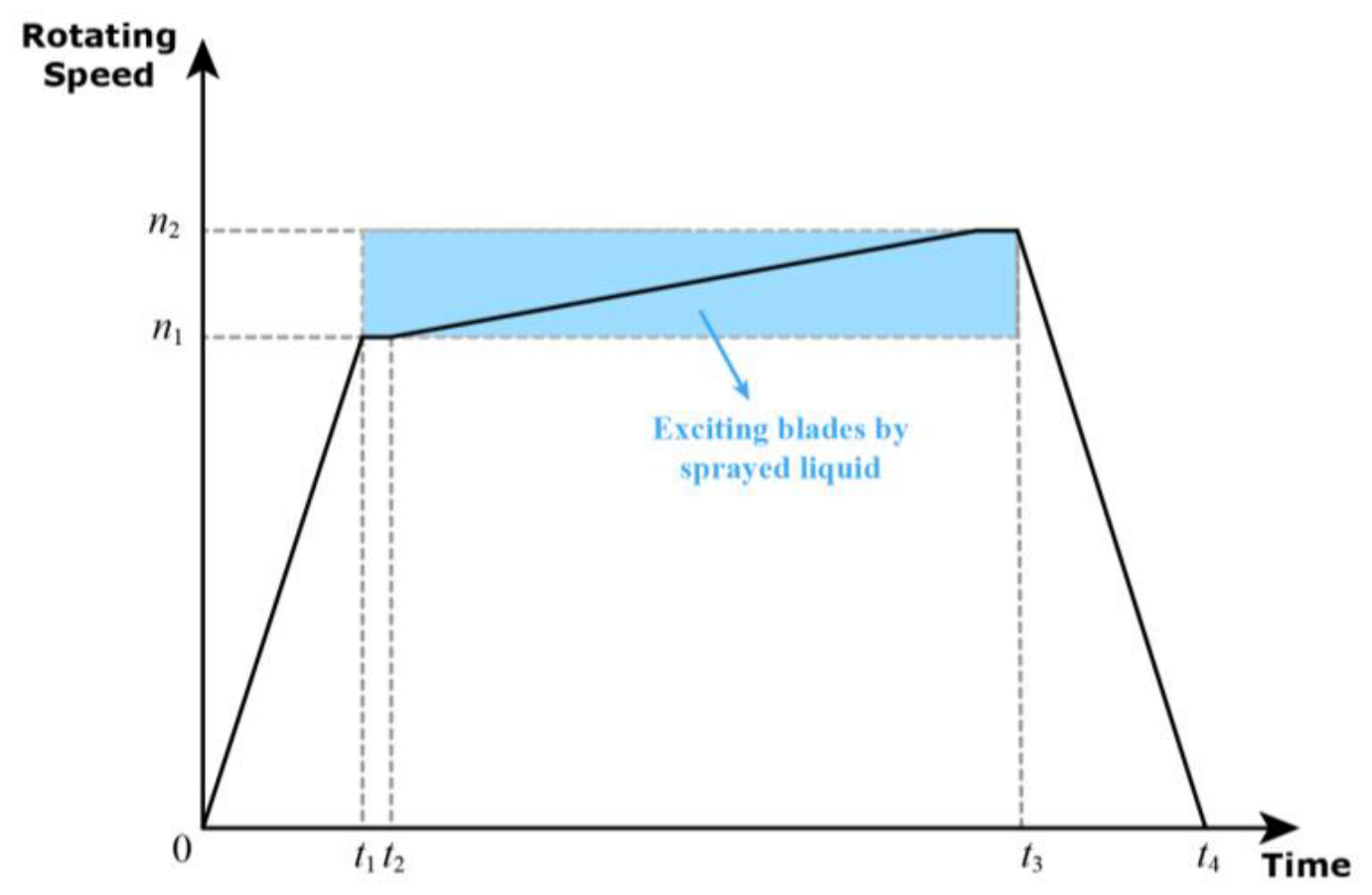
3.4. Brief Description of Experimental Steps
3.5. Experimental Results and Analysis
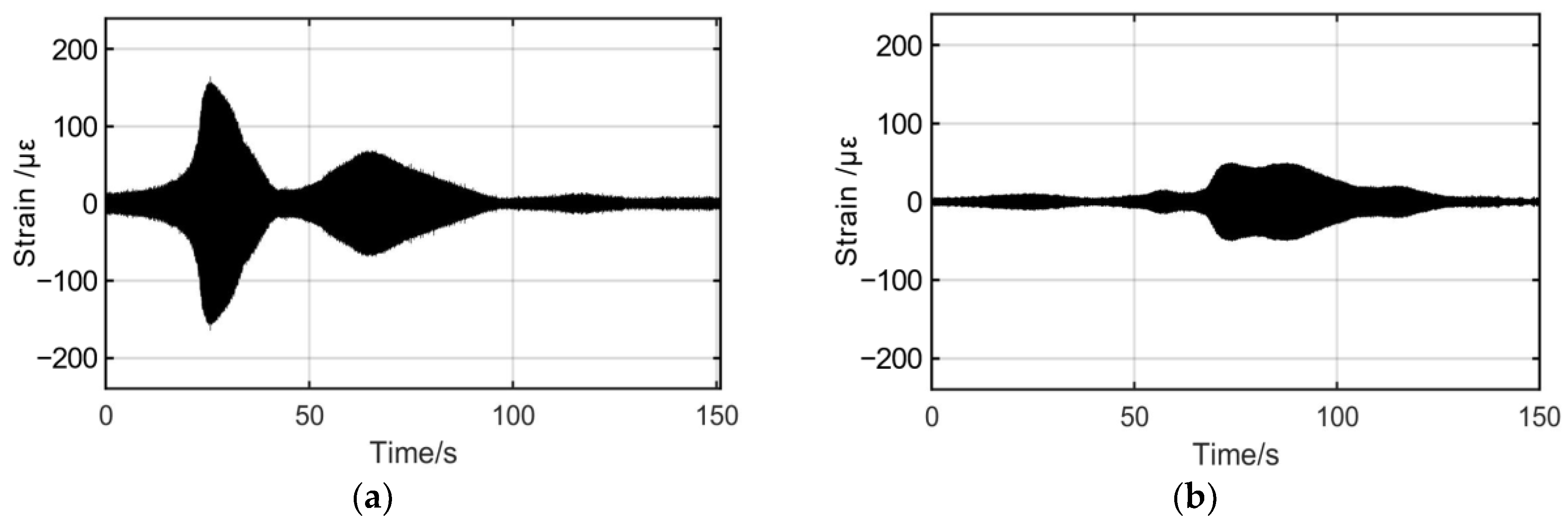
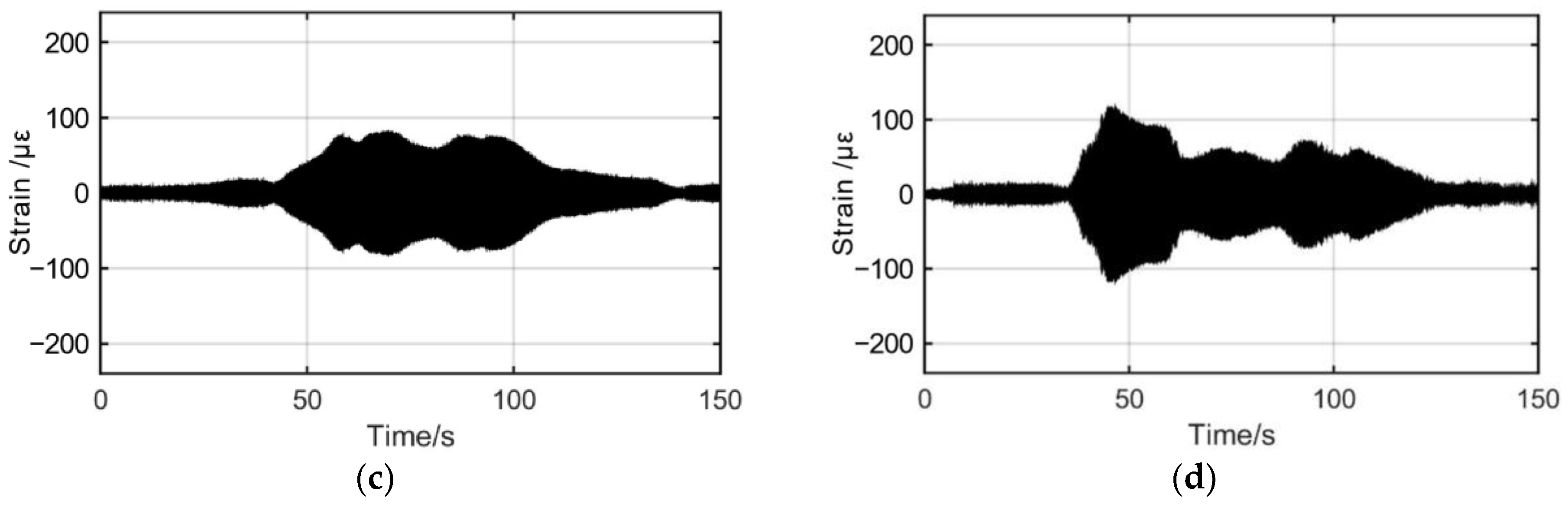
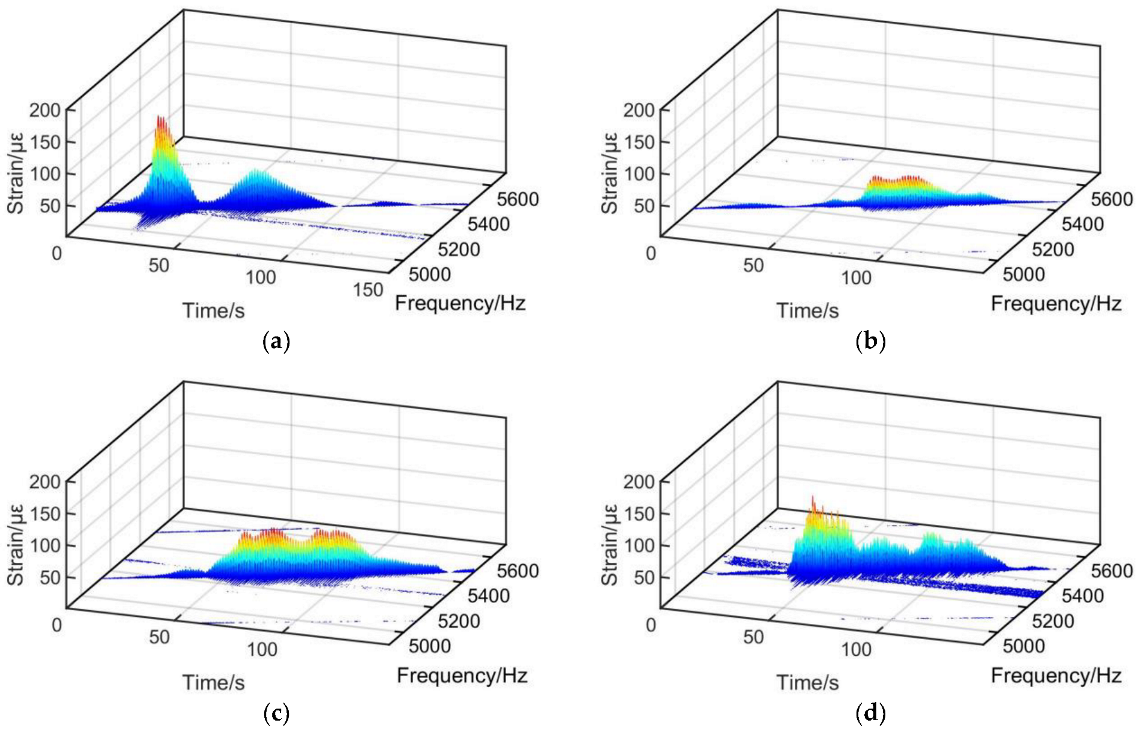
3.5.1. Liquid Spray Exciting Experimental Results
3.5.2. Comparison and Discussion between Experimental and Numerical Results
4. Conclusions
- The UPDs turned the multiple independently vibrating blades into a multi-blade system. In both the numerical and experimental results, blades with UPDs showed multiple peaks and higher resonance frequencies in their forced vibration response compared to those without dampers, and they were varied with the mass of UPDs.
- Properly selected masses of UPDs led to effective reduction of blade torsional vibration, with a 68.9% reduction in resonance amplitude achieved with 0.5 m0 UPDs. However, excessively high normal force or UPD mass could increase blade torsional vibration response and lead to multiple large peaks, emphasizing the importance of careful selection during the design phase.
- The numerical method used to predict forced torsional vibration response of rotating multi-blade systems with UPDs showed relatively close agreement with the experimental results, indicating its effectiveness in predicting the nonlinear response of multi-blade systems and providing a design reference for blades and UPDs.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ewins, D.J. Control of Vibration and Resonance in Aero Engines and Rotating Machinery—An Overview. Int. J. Press. Vessel. Pip. 2010, 87, 504–510. [Google Scholar] [CrossRef]
- Griffin, J.H. A Review of Friction Damping of Turbine Blade Vibration. Int. J. Turbo Jet Engines 1990, 7, 297–308. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, Y.; Qiao, B.; Fu, S.; Liu, M.; Luo, X.; Chen, X. Full-Field Dynamic Strain Reconstruction of Rotor Blades under Multi-Mode Vibration. Measurement 2022, 201, 111670. [Google Scholar] [CrossRef]
- Earles, S.W.E.; Williams, E.J. A Linearized Analysis for Frictionally Damped Systems. J. Sound Vib. 1972, 24, 445–458. [Google Scholar] [CrossRef]
- Griffin, J.H. Friction Damping of Resonant Stresses in Gas Turbine Engine Airfoils. J. Eng. Power 1980, 102, 329–333. [Google Scholar] [CrossRef]
- Cameron, T.M.; Griffin, J.H.; Kielb, R.E.; Hoosac, T.M. An Integrated Approach for Friction Damper Design. J. Vib. Acoust. 1990, 112, 175–182. [Google Scholar] [CrossRef]
- Panning, L.; Sextro, W.; Popp, K. Spatial Dynamics of Tuned and Mistuned Bladed Disks with Cylindrical and Wedge-Shaped Friction Dampers. Int. J. Rotat. Mach. 2003, 9, 219–228. [Google Scholar] [CrossRef]
- Cigeroglu, E.; An, N.; Menq, C.-H. A Microslip Friction Model with Normal Load Variation Induced by Normal Motion. Nonlin. Dyn. 2007, 50, 609–626. [Google Scholar] [CrossRef]
- Allara, M. A Model for the Characterization of Friction Contacts in Turbine Blades. J. Sound Vib. 2009, 320, 527–544. [Google Scholar] [CrossRef]
- Gastaldi, C.; Gola, M.M. On the Relevance of a Microslip Contact Model for Under-Platform Dampers. Int. J. Mech. Sci. 2016, 115, 145–156. [Google Scholar] [CrossRef]
- Yudi, C.; Yanrong, W. A Method for the Resonant Response Evaluation of Blades System with Underplatform Dampers. Vibroeng. Procedia 2014, 4, 164–169. [Google Scholar]
- Pesaresi, L.; Armand, J.; Schwingshackl, C.W.; Salles, L.; Wong, C. An Advanced Underplatform Damper Modelling Approach Based on a Microslip Contact Model. J. Sound Vib. 2018, 436, 327–340. [Google Scholar] [CrossRef]
- Li, D.; Botto, D.; Xu, C.; Liu, T.; Gola, M. A Micro-Slip Friction Modeling Approach and Its Application in Underplatform Damper Kinematics. Int. J. Mech. Sci. 2019, 161–162, 105029. [Google Scholar] [CrossRef]
- Krack, M.; Salles, L.; Thouverez, F. Vibration Prediction of Bladed Disks Coupled by Friction Joints. Arch. Comput. Methods Eng. 2017, 24, 589–636. [Google Scholar] [CrossRef]
- Phadke, R.; Berger, E.J. Friction damping analysis in turbine blades using a user-programmed function in Ansys; Paper ISROMAC12-2008-20176. In Proceedings of the 12th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, HI, USA, 17–22 February 2008. [Google Scholar]
- Urabe, M. Galerkin’s Procedure for Nonlinear Periodic Systems. Arch. Ration. Mech. Anal. 1965, 20, 120–152. [Google Scholar] [CrossRef]
- Zucca, S.; Firrone, C.M. Nonlinear Dynamics of Mechanical Systems with Friction Contacts: Coupled Static and Dynamic Multi-Harmonic Balance Method and Multiple Solutions. J. Sound Vib. 2014, 333, 916–926. [Google Scholar] [CrossRef]
- Gastaldi, C.; Berruti, T.M. A Method to Solve the Efficiency-Accuracy Trade-off of Multi-Harmonic Balance Calculation of Structures with Friction Contacts. Int. J. Non-Linear Mech. 2017, 92, 25–40. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, D.; Xie, Y. A Nonlinear Vibration Analysis of Forced Response for a Bladed-Disk with Dry Friction Dampers. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1522–1539. [Google Scholar] [CrossRef]
- Kwon, S.; Chung, J.; Yoo, H.H. Transient Vibration Characteristics of a Rotating Multi-Packet Blade System Excited by Multiple Nozzle Forces. Int. J. Mech. Sci. 2014, 83, 76–90. [Google Scholar] [CrossRef]
- Sever, I.A.; Petrov, E.P.; Ewins, D.J. Experimental and Numerical Investigation of Rotating Bladed Disk Forced Response Using Underplatform Friction Dampers. J. Eng. Gas Turbines Power 2008, 130, 042503. [Google Scholar] [CrossRef]
- Szwedowicz, J.; Gibert, C.; Sommer, T.P.; Kellerer, R. Numerical and Experimental Damping Assessment of a Thin-Walled Friction Damper in the Rotating Setup with High Pressure Turbine Blades. J. Eng. Gas Turbines Power Trans. ASME 2008, 130, 012502. [Google Scholar] [CrossRef]
- Armstrong, E.K. Recent Blade Vibration Techniques. J. Eng. Power 1967, 89, 437–444. [Google Scholar] [CrossRef]
- Peters, W.H.; Ranson, W.F. Digital Imaging Techniques in Experimental Stress Analysis. Opt. Eng. 1982, 21, 427–431. [Google Scholar] [CrossRef]
- Stanbridge, A.B.; Ewins, D.J. Modal Testing Using a Scanning Laser Doppler Vibrometer. Mech. Syst. Signal Process. 1999, 13, 255–270. [Google Scholar] [CrossRef]
- Zucca, S.; Di Maio, D.; Ewins, D.J. Measuring the Performance of Underplatform Dampers for Turbine Blades by Rotating Laser Doppler Vibrometer. Mech. Syst. Signal Process. 2012, 32, 269–281. [Google Scholar] [CrossRef]
- Kim, J.-H.; Park, Y.; Kim, Y.-Y.; Shrestha, P.; Kim, C.-G. Aircraft Health and Usage Monitoring System for In-Flight Strain Measurement of a Wing Structure. Smart Mater. Struct. 2015, 24, 105003. [Google Scholar] [CrossRef]
- Chen, Y.; Logan, P.; Avitabile, P.; Dodson, J. Non-Model Based Expansion from Limited Points to an Augmented Set of Points Using Chebyshev Polynomials. Exp. Tech. 2019, 43, 521–543. [Google Scholar] [CrossRef]
- Dimitriadis, G.; Carrington, I.B.; Wright, J.R.; Cooper, J.E. Blade-Tip Timing Measurement of Synchronous Vibrations of Rotating Bladed Assemblies. Mech. Syst. Signal Process. 2002, 16, 599–622. [Google Scholar] [CrossRef]
- Wu, S.; Russhard, P.; Yan, R.; Tian, S.; Wang, S.; Zhao, Z.; Chen, X. An Adaptive Online Blade Health Monitoring Method: From Raw Data to Parameters Identification. IEEE Trans. Instrum. Meas. 2020, 69, 2581–2592. [Google Scholar] [CrossRef]
- Botto, D.; Umer, M. A Novel Test Rig to Investigate Under-Platform Damper Dynamics. Mech. Syst. Signal Process. 2018, 100, 344–359. [Google Scholar] [CrossRef]
- Umer, M.; Botto, D. Measurement of Contact Parameters on Under-Platform Dampers Coupled with Blade Dynamics. Int. J. Mech. Sci. 2019, 159, 450–458. [Google Scholar] [CrossRef]
- Wu, Y.; Xuan, H.; Wu, C.; Mi, D. Effect of Under-Platform Dampers on the Forced Vibration of High-Speed Rotating Blades. J. Mech. Sci. Technol. 2022, 36, 3837–3850. [Google Scholar] [CrossRef]
- Hou, J.; Wicks, B.J.; Antoniou, R.A. An Investigation of Fatigue Failures of Turbine Blades in a Gas Turbine Engine by Mechanical Analysis. Eng. Fail. Anal. 2002, 9, 201–211. [Google Scholar] [CrossRef]
- Kim, H.-J. Fatigue Failure Analysis of Last Stage Blade in a Low Pressure Steam Turbine. Eng. Fail. Anal. 1999, 6, 93–100. [Google Scholar] [CrossRef]
- Castanier, M.P.; Pierre, C. Modeling and Analysis of Mistuned Bladed Disk Vibration: Current Status and Emerging Directions. J. Propuls. Power 2006, 22, 384–396. [Google Scholar] [CrossRef]
- Óttarsson, G.; Pierre, C. A Transfer Matrix Approach to Free Vibration Localization in Mistuned Blade Assemblies. J. Sound Vib. 1996, 197, 589–618. [Google Scholar] [CrossRef]
- Szwedowicz, J.; Kissel, M.; Ravindra, B.; Kellerer, R. Estimation of Contact Stiffness and Its Role in the Design of a Friction Damper. In Volume 4: Manufacturing Materials and Metallurgy; Ceramics; Structures and Dynamics; Controls, Diagnostics and Instrumentation; American Society of Mechanical Engineers: New Orleans, LA, USA, 2001; p. V004T03A049. [Google Scholar] [CrossRef]
- Smedowicz, J.; Secall-Wimmel, T.; Duenck-Kerst, P. Damping Performance of Axial Turbine Stages with Loosely Assembled Friction Bolts: The Nonlinear Dynamic Assessment. J. Eng. Gas Turbines Power Trans. ASME 2008, 130, 032505. [Google Scholar] [CrossRef]
- Krack, M.; Gross, J. Harmonic Balance for Nonlinear Vibration Problems; Springer International Publishing: Cham, Switzerland, 2019; ISBN 978-3-030-14022-9. [Google Scholar]
- Cameron, T.M.; Griffin, J.H. An Alternating Frequency/Time Domain Method for Calculating the Steady-State Response of Nonlinear Dynamic Systems. J. Appl. Mech. 1989, 56, 149–154. [Google Scholar] [CrossRef]
- Deuflhard, P. Newton Methods for Nonlinear Problems: Affine Invariance and Adaptive Algorithms; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 2011; Volume 35, ISBN 978-3-642-23898-7. [Google Scholar]





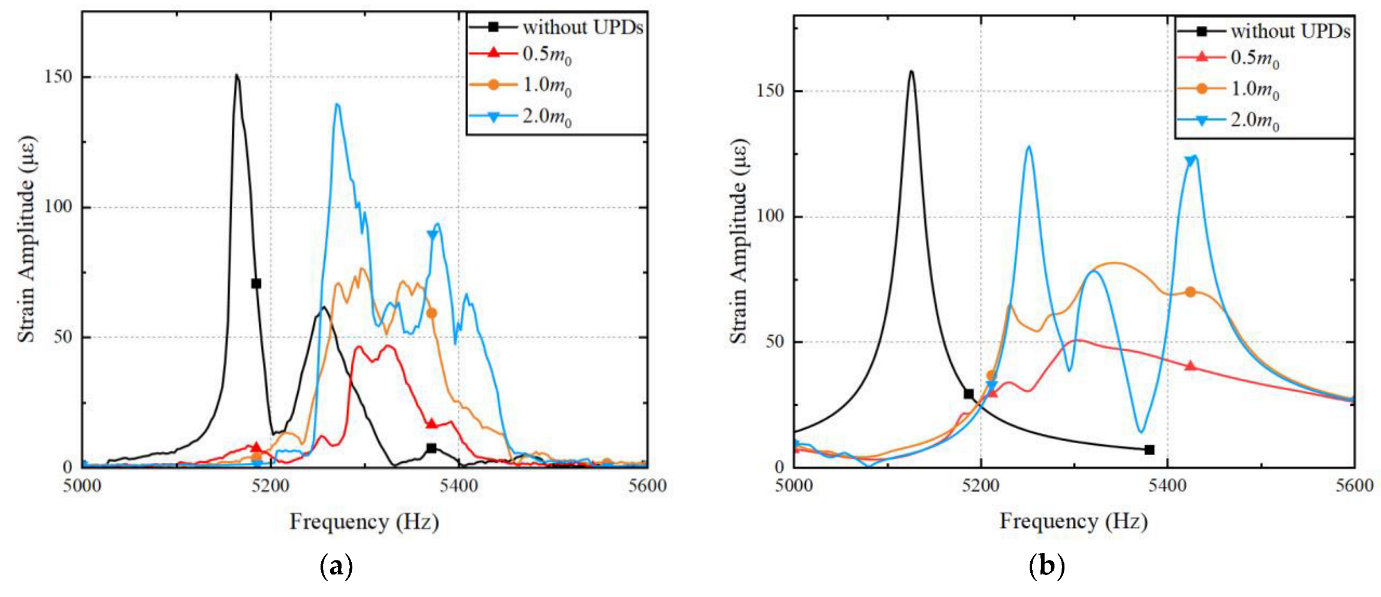
| Contrast Item | Without Dampers | With 0.5 m0 UPDs | With 1.0 m0 UPDs | With 2.0 m0 UPDs | |
|---|---|---|---|---|---|
| Numerical result | Frequency /Hz | 5124.7 | 5304.0 | 5341.5 | 5251.5 |
| increase ratio | - | 3.5% | 4.2% | 2.5% | |
| Experimental result | Frequency /Hz | 5164.0 | 5322.0 | 5296.0 | 5270.0 |
| increase ratio | - | 3.1% | 2.6% | 2.1% | |
| Contrast Item | Without Dampers | With 0.5 m0 UPDs | With 1.0 m0 UPDs | With 2.0 m0 UPDs | |
|---|---|---|---|---|---|
| Numerical result | Strain /με | 158.1 | 50.9 | 81.6 | 128.3 |
| reduction ratio | - | 67.8% | 48.3% | 18.9% | |
| Experimental result | Strain /με | 151.0 | 47.0 | 76.6 | 139.7 |
| reduction ratio | - | 68.9% | 49.2% | 7.5% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Xuan, H.; Wu, C.; Mi, D.; Qu, M.; Jin, T. Study on the Forced Torsional Vibration Response of Multiple Rotating Blades with Underplatform Dampers. Aerospace 2023, 10, 725. https://doi.org/10.3390/aerospace10080725
Wu Y, Xuan H, Wu C, Mi D, Qu M, Jin T. Study on the Forced Torsional Vibration Response of Multiple Rotating Blades with Underplatform Dampers. Aerospace. 2023; 10(8):725. https://doi.org/10.3390/aerospace10080725
Chicago/Turabian StyleWu, Yanan, Haijun Xuan, Changyao Wu, Dong Mi, Mingmin Qu, and Tao Jin. 2023. "Study on the Forced Torsional Vibration Response of Multiple Rotating Blades with Underplatform Dampers" Aerospace 10, no. 8: 725. https://doi.org/10.3390/aerospace10080725
APA StyleWu, Y., Xuan, H., Wu, C., Mi, D., Qu, M., & Jin, T. (2023). Study on the Forced Torsional Vibration Response of Multiple Rotating Blades with Underplatform Dampers. Aerospace, 10(8), 725. https://doi.org/10.3390/aerospace10080725






