Abstract
Multiple unmanned aerial vehicle (multi-UAV) cooperative air combat, which is an important form of future air combat, has high requirements for the autonomy and cooperation of unmanned aerial vehicles. Therefore, it is of great significance to study the decision-making method of multi-UAV cooperative air combat since the conventional methods are challenging to solve the high complexity and highly dynamic cooperative air combat problems. This paper proposes a multi-agent double-soft actor-critic (MADSAC) algorithm for solving the cooperative decision-making problem of multi-UAV. The MADSAC achieves multi-UAV cooperative air combat by treating the problem as a fully cooperative game using a decentralized partially observable Markov decision process and a centrally trained distributed execution framework. The use of maximum entropy theory in the update process makes the method more exploratory. Meanwhile, MADSAC uses double-centralized critics, target networks, and delayed policy updates to solve the overestimation and error accumulation problems effectively. In addition, the double-centralized critics based on the attention mechanism improve the scalability and learning efficiency of MADSAC. Finally, multi-UAV cooperative air combat experiments validate the effectiveness of MADSAC.
1. Introduction
Unmanned aerial vehicles (UAVs) have attracted significant attention as they effectively reduce mission costs and pilot casualties [1]. Due to recent advancements in electronics, computers, and communication technology, UAVs have become more autonomous and are now commonly used for missions that include reconnaissance, surveillance, and communications relay [2]. Nevertheless, current UAV autonomy is inadequate to meet the demands of highly complex and dynamic tasks. Multiple UAVs (multi-UAV) can execute tasks with more richness, efficiency, and task redundancy compared to a single UAV. Consequently, comprehensive research on methods for coordinated decision-making among multi-UAVs is necessary to enhance their autonomous cooperative abilities. Cooperative air combat, with its demanding and continuous complexity involving multi-UAVs, places significant emphasis on the decision-making capabilities of these UAVs. Hence, cooperative air combat constitutes an ideal situation where cooperative decision-making methods of multi-UAVs can be tested. Currently, research on automatic air combat decision-making can be categorized into two types, single-UAV air combat and multi-UAV cooperative air combat (MCAC).
Scholars have proposed multiple methods to address the issue of autonomous air combat in single UAVs by utilizing various theories, including game theory, expert systems, optimization algorithms, and machine learning. In air combat, game theory is used to address the optimal decision-making problem. In particular, Park designed automatic maneuver generation methods for air-to-air combat within the visual range of UAVs based on differential game theory [3]. The expert system has been explored by several researchers earlier. For example, Wang proposed an evolutionary expert system tree approach that integrates genetic algorithms and expert systems for solving decision problems in two-dimensional air combat [4]. Optimization algorithms formalize air combat decision problems as multi-objective optimization problems. Huang, for example, utilized Bayesian inference theory to develop an air situational model that adjusts the weights of maneuver decision-making factors based on situational evaluation results to create a more logical objective function [5]. Machine learning has shown its potential in single-UAV air combat. For instance, Fu employed a stacked sparse auto-encoder network and a Long short-term memory network as a maneuver decision-maker for supporting aircraft maneuver decisions [6]. Reinforcement learning methods, such as Q-Learning [7], Policy Gradient [8], and Deep Q-Network [9], were adopted to establish the maneuver decision model. They constructed value functions to evaluate the value of different actions in each state and made choices based on this or constructed strategy functions to build the mapping between different states and actions. Isci implemented air combat decisions based on the deep deterministic policy gradient (DDPG) algorithm and the proximal policy optimization algorithm in the air combat environment established in that literature by incorporating energy state rewards in the reward function [10]. Li applied the improved DDPG algorithm to autonomous maneuver decision-making of the UAVs [11]. Sun proposed a multi-agent hierarchical policy gradient algorithm for the air combat decision-making [12]. The complex hybrid action problem was solved using adversarial self-play learning, and the strategy performance was enhanced. Lockheed Martin proposed an approach that combines hierarchical structure with maximum entropy reinforcement learning to integrate expert knowledge through reward shaping and support the modularity of the policies [13].
MCAC is more challenging and involves higher model complexity than single-UAV air combat, as it requires consideration of not only the tactics of every UAV but also their tactical cooperation. To address the challenges of MCAC, researchers have suggested multiple methods. For example, Gao introduced a rough set theory into the tactical decision-making of cooperative air combat and proposed an attribute reduction algorithm to extract key data and tactical decision rules in the air combat [14]. Fu divided the MCAC decision process into four parts: situational assessment; attack arrangement; target assignment; and maneuver decision [15]. Furthermore, Zhang presented an evaluation method based on an improved group generalized intuitionistic fuzzy soft set. This method constructs a threat assessment system and indicators for air targets, introduces the generalized parameter matrix provided by multiple experts into the generalized intuitionistic fuzzy soft set, and uses subjective and objective weights to achieve more logical target threat assessment results [16]. Meng introduced an approach to identify the tactical intent of multi-UAV coordinated air combat by utilizing dynamic Bayesian networks, a threat assessment model, and a radar model to outline crucial features concerning maneuver occupancy. These features were utilized to teach support vector machines for the attack intent prediction [17]. Additionally, Ruan investigated the task assignment problem under time continuity constraints in cooperative air combat and developed a task assignment and integer planning model for cooperative air combat through time and continuity constraints [18]. Peng established an MCAC optimization model based on the destruction probability threshold and time-window constraints and then solved the target assignment problem by employing a hybrid multi-target discrete particle swarm optimization (DPSO) algorithm [19]. Lastly, Li created a multi-UAV cooperative occupation model by constructing an advantage function to evaluate the air combat situation. The model was resolved using an upgraded DPSO, resulting in a multi-UAV cooperative occupation scheme [20].
In recent years, multi-agent reinforcement learning (MARL) has made significant accomplishments. For instance, AlphaStar [21] and OpenAI Five [22] have achieved remarkable success in gaming. Multi-UAV systems, as a typical multi-agent system, have enormous potential applications when coupled with MARL. Li developed a MARL-based algorithm with a centralized critic, an actor using the gate recurrent unit model, and a dual experience playback mechanism for solving multi-UAV collaborative decision-making problems and evaluated it through simulations in a multi-UAV air combat environment [23]. In addition, Liu designed a missile attack zone model and combined it with the multi-agent proximal policy optimization (MAPPO) method to achieve beyond-visual-range air combat among multiple unmanned aerial vehicles [24]. The references [23,24] have investigated the MCAC decision-making problem concerning discrete action spaces. However, the MCAC decision-making problem in continuous action spaces is substantially more intricate and better suited to meet the decision-making requirements of unmanned aerial vehicles.
In the above research, game theory and expert systems are primarily employed in discrete environments, which lack learning capabilities and are unsuitable for changing scenarios. Optimization techniques may struggle to adapt to dynamic decision-making requirements as they require solving an optimization problem in real time. In contrast, machine learning methods, particularly reinforcement learning, offer considerable promise for multi-UAV cooperative decision-making due to their robust learning ability. However, overestimation bias and error accumulation can be problematic with many reinforcement learning algorithms with actor-critic framework and may lead to suboptimal strategies during the updating procedure [25]. Meanwhile, in the function approximation setting, estimation bias is inevitable due to the inaccuracy of the estimator. Furthermore, using temporal-difference (TD) learning exacerbates the problem of inaccurate estimation by updating the value function estimation based on subsequent states, leading to a build-up of errors [26]. This means that using inaccurate estimates in each update will lead to an accumulation of errors. Overestimation bias and error accumulation also exist in MARL algorithms that employ the actor-critic framework and TD learning, such as multi-actor-attention-critic (MAAC) [27], MAPPO [28], multi-agent soft actor-critic (MASAC) [29], and multi-agent deep deterministic policy gradient (MADDPG) [30].
Therefore, this paper proposes the multi-agent double-soft actor-critic (MADSAC) algorithm to solve the multi-UAV cooperative decision-making problem in three-dimensional continuous action space, as well as the overestimation bias and error accumulation problems in MARL. The contributions of this paper are threefold:
- (1)
- This paper proposes the MADSAC algorithm based on a decentralized partially observable Markov decision process (Dec-POMDP) using centralized training with decentralized execution (CTDE) framework. To solve the overestimation problem in MARL and to enhance the scalability of the algorithm, it uses the double-centralized critics based on an attention mechanism;
- (2)
- To reduce the impact of error accumulation on algorithm performance, this paper employs a delayed policy updates mechanism. This mechanism updates the policy network after the critic networks become stable to reduce policy scattering caused by the overestimation of the value network;
- (3)
- To address the challenge of sparse reward in the reward space during decision-making, this paper designs a segmented reward function, which accelerates algorithm convergence and obtains excellent strategies. Additionally, a new observation space is designed based on the air combat geometry model.
The rest of this paper is organized as follows. A multi-UAV cooperative simulation environment is established in Section 2. Section 3 introduces MARL knowledge, proposes the MADSAC algorithm, and a red-blue confrontation scenario. In Section 4, MADSAC and the comparison algorithm are trained, and the training results are compared and analyzed. Three sets of confrontation experiments between MADSAC and the comparison algorithm are also designed, and then the experimental results and the strategies obtained by MADSAC are analyzed. Finally, the conclusion of this paper and the outlook of the next work are given in Section 5.
2. Multi-UAV Cooperative Simulation Environment
To facilitate algorithm learning, this section establishes a multi-UAV cooperative simulation environment that supports enhanced learning interactions. In reality, communication among UAVs may face interference, causing delays in data transmission and reception, particularly during the broadcast mode, which can intensify communication stress. Therefore, communication between UAVs requires the use of information compression transmission technology [31] to reduce communication pressure. To simplify the communication model, this paper assumes smooth communication with minimal to no delay. The framework includes a UAV model, a sensor observation model, an aerial situation, an attack model, and a fixed strategy with a 0.1-s solution interval for all models.
2.1. UAV Model
The motion of the UAV is performed under the earth-fixed reference . Where denotes the north-east-down (NED) coordinate and its origin at , with as the horizontal coordinate pointing north, is the vertical coordinate pointing east, and is the vertical coordinate pointing to the ground. Similarly, the UAV’s body coordinate is represented by , and its origin is located at the center of mass of the UAV. , , and denote the x-axis, y-axis, and z-axis, respectively. The position relationship between the two coordinate systems is shown in Figure 1. The and in the figure indicate the pitch and yaw angles of the UAV, respectively.
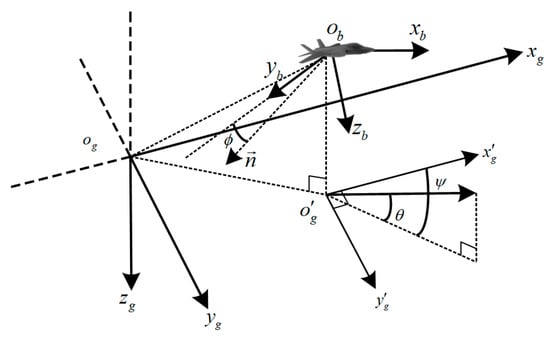
Figure 1.
Relationship between Earth-fixed reference and airframe reference.
The motion of the UAV is represented as the motion of a point of mass in the coordinate system with the center of mass located at the center of gravity, as shown in Equation (1):
where , , and denote the UAV’s velocity components on its corresponding axes, respectively. denotes the UAV’s speed.
Assuming that the engine thrust vector corresponds with the UAV’s x-axis and points to the positive direction of the x-axis, the UAV velocity direction is equal to the nose point, implying that the sideslip angle is zero. The effect of wind speed on the UAV is not considered. Equation (2) represents the UAV’s center-of-mass dynamics equation [23].
where and denote the tangential and normal accelerations of the UAV, which are generated by the tangential and normal components of the total force acting on the UAV, respectively. stands for gravitational acceleration, for the acceleration of the UAV, for pitch angle rate, and for yaw angle rate. The expectation of pitch angle, yaw angle, and speed of the UAV are denoted by , , and , respectively. is settled into the control quantity by the controller.
2.2. Sensor Observation Model of UAV
Given the errors inherent in sensor data during UAV flight, we develop an observation model to simulate sensor data acquisition. To simulate the data acquisition process, Gaussian noise is incorporated within the observed position, attitude, and velocity. Moreover, we assume that the data acquisition frequency of each sensor matches the operating frequency of the UAV system.
The position information of the UAV is obtained as shown in Equation (3):
where is the observed position of the UAV, which is obtained from the real position of the UAV adding Gaussian noise. The represents Gaussian noise, where is the scaling factor, and is a random number following the Gaussian distribution , taking values in the range ; that is .
Similar to acquiring position information, the attitude information of UAV is shown in Equation (4):
Moreover, adding Gaussian noise to the UAV’s real attitude information can obtain the observed attitude of the UAV. The represents Gaussian noise, where is the scaling factor, and is a random number following the Gaussian distribution, taking values in the range ; that is .
Finally, Gaussian noise is added to the real speed to obtain the observation speed of the UAV, as shown in Equation (5):
where is the scaling factor, and is the value range of Gaussian noise.
Simulating sensor noise can effectively enhance the robustness of the policy network in reinforcement learning. The noise, particularly with location, increases the variety of sampled data during the training, reducing the overfitting prospects.
2.3. Aerial Situation
Developing a UAV situational awareness process is critical in air combat because it is necessary to collect genuine air situational awareness in real time, which is the cornerstone for the timely decision-making of the UAVs. The situational information in the MCAC process includes information about both friendly and enemy UAVs. Information on friendly UAVs can be obtained using datalinks and radar, which covers position, speed, altitude, weaponry, and fuel levels. In addition, information can be learned about the courses of action taken by friendly UAVs in light of their present situation. Only radar and other sensing technologies can provide data on enemies, including their position and speed. As a result, the situational awareness module directly accesses information about other UAVs from the simulation environment as the UAV awareness information.
In air combat theory [32], the relative position of two UAVs flying at the same altitude is often described using the antenna train angle (ATA), aspect angle (AA), and horizontal crossing angle (HCA). When evaluating the complete position relationship in a three-dimensional space, the height line of sight angle (HA) is incorporated to depict the vertical position relationship. Together, these four angles comprehensively convey the positional relationship of two UAVs within three-dimensional space, as depicted in Figure 2, and can be calculated using Equation (6).
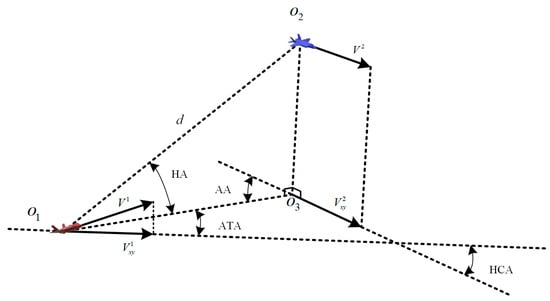
Figure 2.
The geometric relationship between the red and blue UAVs.
The radar scanning range is generally a sector area forward of the UAV nose. During air combat, the UAV can launch missiles after the UAV’s fire control radar has locked the target. Thus, it is extremely dangerous to be within the range of enemy radar. In Figure 3, the red UAV is in a dominant position relative to the blue UAV A, but it is easy to lose that target because A is at the edge of its radar detection, and the speed of A is perpendicular to its axis. It is at an absolute advantage relative to UAV B and a balanced relative to UAV C because it is locked on UAV C but is also locked on by UAV C. Therefore, the only way to ensure locking enemy UAVs while not being locked by them is to approach them from the rear or side, i.e., when the absolute values of both ATA and HA are less than 30 degrees, and the absolute value of AA is less than 90 degrees [13].
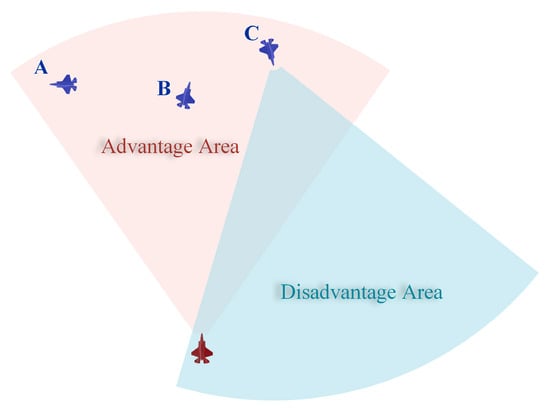
Figure 3.
The situation in air combat.
2.4. Attack Model
The weapon firing and hitting of the UAVs need to satisfy certain constraints. To simulate the weapon attack process of UAVs in air combat, a weapon launch model and a weapon hit model are set up in this section. In the real world, the UAV firing at the target needs to satisfy certain distance and angle constraints. According to these factors, the designed firing model is shown in Equation (7).
where and are attack angle constraints, which denote the maximum attack ATA and maximum attack HA, respectively. The attack distance constraints are and , which denote the minimum attack distance and the maximum attack distance, respectively.
The hit model of the weapon is a probabilistic model, and whether this attack hits or not is determined by three factors, d, ATA, and HA, as shown in Equation (8):
where is the Gaussian noise obeying the distribution . The and are the ATA and HA noise scaling factors, respectively. The is the effective hitting distance.
2.5. Fixed Strategy
This section presents a straightforward and efficient fixed strategy that focuses on attacking the nearest UAV during formation operations, thereby creating a local advantage, particularly when the opposing UAV is dispersed. In the initial phase, the blue UAV gathers positional data for all red UAVs in the space and selects the nearest red UAV as a pursuit target in each simulation step, switching to a new red UAV once the nearest one changes. The same pursuit strategy is also implemented during the attack phase. In real time, the attack model outlined in Section 2.4 is used to determine whether to fire a missile and whether to engage in destruction after firing.
Figure 4 illustrates the pursuit strategy for the blue UAV, in which condition 1 is: “Is the red UAV alive?”, Condition 2 is: “Is the target UAV alive?”, Condition 3 is: “Is a missile fired?”, and Condition 4 is: “Is the target UAV destroyed?”.
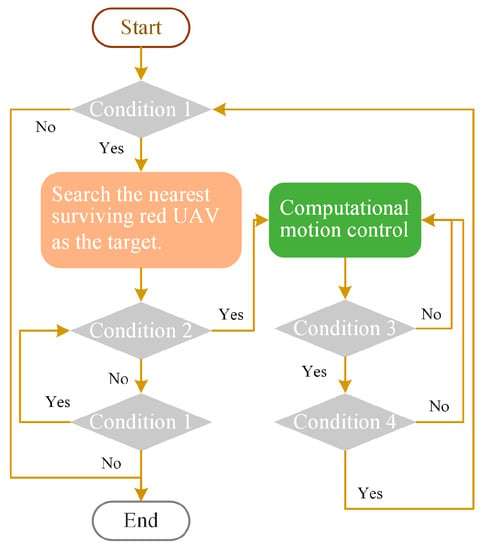
Figure 4.
Pursuit strategy of blue UAV.
3. Cooperative Air Combat Decision-Making Method
This section outlines the MARL approach for multi-UAV cooperative air combat decision-making, using a multi-UAV red-blue confrontation scenario to train and test the algorithm. Figure 5 depicts the MCAC decision-making architecture based on MARL, in which each UAV functions as an agent with its own strategy to interact with the environment. The UAV can perform a specific action that leads to receiving a reward from the environment. To accumulate more rewards, the UAVs continuously refine their strategies by interacting with the environment. This method uses the CTDE [33] approach to aid UAVs in converging strategies more quickly during centralized training while minimizing problems resulting from non-stationarity in multi-agent systems. During execution, the distributed method is utilized, with each UAV making decisions based on observation information.
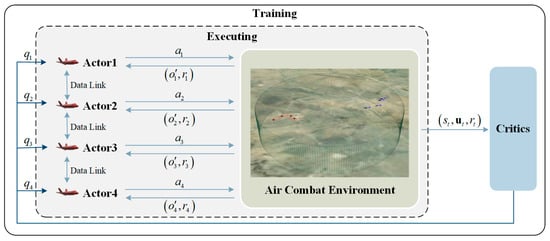
Figure 5.
Cooperative Air Combat Decision Method Framework Based on MARL.
3.1. Notation and Background
3.1.1. Markov Games
In the MCAC game, each UAV has the same goal, which is to achieve the final victory, so the problem is a fully cooperative game. This problem is formulated based on the Dec-POMDP [34], which is represented by the tuple . In this tuple, symbolizes the set of agents in the environment; denotes the state space; denotes the action space; denotes the reward function, and and denote the observation function and discount factor, respectively. is the observation of the agent under state . denotes the actions of the agent generated by the policy under its observation . denotes a joint action and . represents the transition function, that is, the probability of transition to the next state under state and joint action . In the above process, the environment will generate a return according to the return function , which is composed of . The action-value function is defined as , where is the discounted return. In the fully cooperative game, all agents use the same reward function, and they have the same purpose, which is to maximize the expected reward for the team, as shown in Equation (9).
3.1.2. Soft Actor-Critic
The soft actor-critic (SAC) algorithm is designed based on the maximum entropy RL framework, mainly to solve the problems of high sample complexity and hyperparameter crispness in deep reinforcement learning methods [35,36]. SAC alternates between optimizing both the soft Q-function and policy with stochastic gradient descent. The represents the policy’s network parameters, and represents the soft Q-function’s network parameters. The can be trained to minimize the soft Bellman residual, shown in Equation (10):
where the value function is implicitly parameterized by Equation (11) through soft Q-function parameters, which denotes the target soft Q-function parameters.
The Q-function is denoted by a differentiable neural so that the reparameterization trick can be easily applied to obtain lower variance estimates. For this purpose, SAC uses a neural network transformation reparameterization policy, shown as Equation (12):
where the input noise vector is sampled from a spherical Gaussian, and the objective function of the strategy is obtained by this operation, as in Equation (13):
where is defined implicitly in terms of . The policy parameters are updated by directly minimizing Equation (13).
3.1.3. Multi-Actor-Attention-Critic
MAAC is a MARL algorithm, which is designed based on SAC and introduces the attention mechanism [37] in CTDE. MAAC tries to teach agents to know which of the other agents is more important to their attention by using a centralized critic based on an attention mechanism. By adopting TD learning to minimize the joint regression loss function depicted in Equation (14), all critics in MAAC are updated.
where , , and represent the parameters of the critic, target critic, and target policy, respectively. The represents the temperature coefficient, which is used to regulate the ratio between maximized entropy and reward. is the action value function of the agent .
All policies in MAAC are updated by the descent of the gradient Equation (15).
where denotes the policy parameters of the agent . is used to compute the advantage function, in which denotes agents other than .
3.2. Multi-Agent Double-Soft Actor-Critic
To address the challenges of overestimation and error accumulation in MARL, the MADSAC algorithm is presented. Figure 6 portrays the algorithmic structure, which employs the CTDE framework with numerous actors sharing parameters and double-centralized critics based on the attention mechanism. All actors are updated through the guidance of double-centralized critics. During execution, UAV actions are generated via actor networks based on individual observations, while centralized training is implemented to enable double-centralized critics to obtain global information for updating actors. The double-centralized critics function to minimize both overestimation and estimation error effectively. During training, the attention-based double-centralized critics enhance the performance of the algorithm in complex interaction domains by dynamically focusing on agents [23]. Given that cooperative air combat with homogenous UAVs is the paper’s main focus, actor-network parameter sharing will quicken the training progress. MADSAC uses a maximum-entropy reinforcement learning framework and delayed policy updates, leading to better exploration and lower sample complexity. Meanwhile, the attention mechanism mitigates the challenge of high dimensionality from increased team membership, enhancing the algorithm’s scalability.
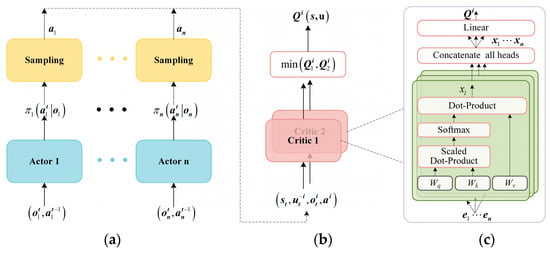
Figure 6.
The figure provides the structure of MADSAC, with (a) depicting the structure of actors, (b) illustrating the operating mode of double-centralized critics, and (c) demonstrating the network structure of critic based on self-attention mechanism.
3.2.1. Centralized Critic Based on the Attention Mechanism
This section introduces the network structure of the double-centralized critic. Figure 6b shows the structure of the double-centralized critic, which consists of two independent critics. The network structure of the critic is depicted in Figure 6c.
The critic receives the state and joint actions from all agents and computes Q-value for each agent. is the value function agent i’s action under observation , as well as other agents’ contributions, as shown in Equation (16):
where the function is an MLP of two-layer; and are embedding functions of two-layer MLP. The contribution from the agent , , is a weighted sum of each agent’s value. is an element-wise nonlinearity, such as leaky rectified linear activation (LReLU) function. The attention weight contrasts the embedding E with , using a bilinear mapping, and passes the similarity value between these two embeddings into the Softmax, as shown in Equation (17):
where and are used to convert into two matrices with matching dimensions, respectively, and then these two matrices are multiplied to obtain the attention weights. The structure of the critic is shown in Figure 6c.
3.2.2. Policy Evaluation: Train the Centralized Critic
Similarly to MADDPG, the framework of CTDE is used in MADSAC, where the actors use their local observations in the test, but the centralized critic allows the use of additional information to make the training more stable. However, when the number of agents is large, it may be difficult to learn the centralized critic based on the overall state and joint action [27]. Referring to MAAC, an attention mechanism is used for the centralized critic to address the linear growth of the input space with the number of agents. Due to the attention mechanism’s superior representational capability compared to MLP and the usage of a unique network structure created for multi-agent, the effect of increasing the number of agents on the critic network is lessened, enhancing the algorithm’s scalability. Specifically, MADSAC has two centralized critics that is called double-centralized critics, where is the parameters of joint Q-function. To solve the overestimation problem, the idea of underestimating rather than overestimating the action value is adopted here. Therefore, each update of the Q-function selects the one with the smallest Q value of the two critics. The centralized critics are trained by minimizing Equation (18):
where D is the replay buffer; is the parameters of the target policy, and the subscript represents the agent . The and denote the critic network parameters and target critic network parameters respectively, and represents the index of double independent soft Q-function parameters. The represents the temperature coefficient, which is used to regulate the ratio between maximized entropy and reward. Here, two separate soft Q-functions are maintained, and each soft Q-function is updated independently using Equation (19).
3.2.3. Policy Improvement: Train Actors
For the continuous policies, refer to the SAC to extend Equation (13) to the MARL field to obtain Equation (20). In the process of policy promotion, the double-soft Q-functions are used to take the minimum Q value as the updating direction of the policy gradient, to mitigate the positive deviation in the policy improvement steps. The double-soft Q-functions can reduce overestimation bias and significantly accelerate training, especially on more difficult tasks [36].
where is the coefficient of entropy; and are the network parameters of two soft Q-functions, respectively. The MADSAC also uses the reparameterization trick to represent by . It is because the Q-function is represented using a differentiable neural network, so the reparameterization trick is conveniently used to generate low-variance estimators. Then, the policy parameters are updated by Equation (21).
Equation (20) needs to be modified when solving the problem of discrete action space. The double-soft Q-functions are introduced in Equation (15) to obtain Equation (22), by which the discrete strategy is updated.
The complete algorithm is described in Algorithm 1.
| Algorithm 1: MADSAC |
| Initialize M parallel environments and replay buffer |
| Initialize double-centralized critics’ parameter vectors . |
| Initialize policy parameters vectors . |
| for episode = 1, N do |
| Reset all environments, obtain each agent’s initial . |
| for t = 1, L do |
| Select actions for each agent in M environments: . |
| All actions are sent to all environments; obtain each agent and next observation , and add the step to buffer . |
| If steps per update then |
| for each update step k = 1,..,n do |
| Sample minibatch B from . |
| end for |
| If t mod d, then |
| for each update step k = 1,..,n do |
| Sample minibatch B from . |
| end for |
| Update targets parameters: |
| end if |
| end if |
| end for |
| end for |
3.3. Testing Scenarios
3.3.1. Multi-UAV Confrontation Scenarios
An MCAC simulation scenario of red-blue confrontation is designed, which has an airspace with a diameter of 10 km. Four red UAVs form the red side, and four blue UAVs form the blue side, with both sides appearing randomly on both sides of the engagement area, as shown in Figure 7.
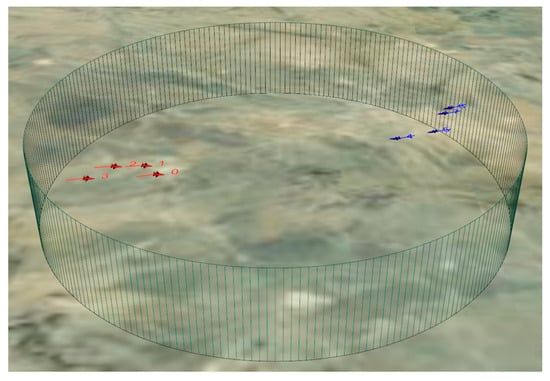
Figure 7.
The multi-UAV air combat simulation scenario of red-blue confrontation.
The red side’s combat objective is to destroy all enemies in the area and seize the air control in the area. The blue side’s combat objective is to prevent the red side from capturing the area. In both training and testing, the blue side’s strategy uses the strategy designed in Section 2. The condition for the red side to win is to destroy all Blue UAVs; otherwise, the mission is deemed to have failed, which means that the blue side wins since reinforcement learning training and testing are conducted in the same environment. To avoid the impact on the experiment due to the factor of random seeds, this paper opens a parallel training process with 24 different seeds in each algorithm training process while setting up a parallel testing environment with 20 different seeds that are completely different from the seeds used for training. The average of the 20 test results is taken as the test result of the evaluated strategy. In contrast to reference [23], a distinct initialization method is employed to improve the robustness of the learned strategy. At the beginning of each environment initialization, both sides are positioned at opposite ends of a randomly selected diameter within the area.
This can increase the algorithm’s exploration of the environment and avoid strategy divergence when the red-side UAVs are born in an untrained area. The parameters of the UAV in this scenario are shown in Table 1.

Table 1.
Environmental Parameters.
3.3.2. Continuous Action Space
For the MCAC problem, the complexity of the continuous action space is much higher than that of the discrete action space. In the field of UAVs, most of the flight control signals are continuous control quantities, while there are also discrete control signals containing radar switching, missile firing, landing gear retraction, etc. Therefore, the UAV’s action space is a mixed space. To simplify the problem, the firing decision of the UAV is controlled by the attack model designed in Section 2, and the flight decision is left to the algorithm. For this purpose, a continuous action space is designed as . The , , and are pitch angle increments, yaw angle increments, and velocity increments, respectively, as shown in Table 2.

Table 2.
Action Space Parameters.
The , , and are the outputs of the actors’ neural network. The expectation of , , and for the next moment is obtained by adding , , and with , , and of the UAV at the current moment, respectively. , , and are obtained through Equation (23).
3.3.3. Observation Space
In the red-blue confrontation scenario, the UAVs on either side can obtain the position and speed information of the other UAV through radar, as well as the position, speed, and action information of their teammates through communication links. Neural networks are usually used in deep reinforcement learning for fitting policies, called policy networks, which are updated by interacting with the environment. However, deep reinforcement learning consumes a large number of computational resources when training. In MARL, the method of compressing the policy space is usually used to speed up the convergence of the policy. Hence, this paper designs an observation function that preprocesses the state information to reduce the complexity of the policy space by introducing the air combat geometry model in Section 2. The definition of this observation function is shown in Equation (24):
Equation (24) denotes the observation function of the red UAV , where the first part represents the UAV’s position, velocity, and attitude. The second part gives information about the friendly UAV’s location, speed, and nose-pointing. The details on all the blue side UAVs are included in the third part. This information has been transformed into data under the body coordinate system of the UAV .
3.3.4. Reward Function
In the red-blue confrontation scenario designed in this paper, the red side’s combat objective is to destroy all enemy UAVs. In the MCAC based on the MARL method, each UAV wants to obtain more rewards from the environment, so the reward function can be designed to guide the UAV to gradually optimize the strategy to receive a higher reward. The reward function has the following principles:
- The reward function has a unique minimum value and maximum value in its definition domain to guarantee the consistency of the optimization direction of the guiding strategy;
- The reward function should be as continuous as possible, which means avoiding the appearance of sparse rewards;
- The reward function has to incorporate a punishment term so that the UAV can be appropriately penalized for performing improperly;
- The reward function should be kept as simple as possible based on satisfying the above conditions to avoid the agent getting lost in the complex reward function at the early stage of training.
In this paper, based on the above principles, a segmented reward function for MCAC is designed, as in Equation (25):
where the reward function is divided into four parts: is the main reward, which is to encourage the UAV to shoot down more blue UAVs; is to avoid the UAV’s escape strategy, thus causing the algorithm to fall into a local solution; is the guide reward, which is to encourage the UAV to move toward blue UAVs and also to avoid the problem of sparse reward; when the red UAV and blue UAV are close to a certain distance, encourages the red UAV to follow behind the blue UAV to find the opportunity to destroy it. denotes the distance from the blue UAV to the red UAV. The , , and between the blue UAV and the red UAV can be obtained by taking the blue UAV as the center.
4. Agent Training and Results Analysis
All algorithms, including MADSAC, MAAC, MAPPO, MADDPG, MASAC, and SAC, underwent training in the red-blue confrontation simulation scenario established in the previous section. The characteristics of all algorithms are shown in Table 3. Specifically, MAAC was modified to fit the continuous action space and incorporated into the shared parameter mechanism, still named MAAC henceforth. These algorithms functioned as the red side, employing a fixed strategy during the training process and confronting the blue side. Subsequently, the performance of MADSAC was compared to other algorithms, and the obtained strategies were discussed.

Table 3.
A comparison of algorithmic features of existing methods for MARL.
4.1. Agent Training
MADSAC employs two hidden layers of an MLP with 256 units per layer for all actors. For the critics, two attentional heads featuring two hidden layers of 256 units are implemented based on the attention mechanism. The Adam optimizer is used with a learning rate of 0.0001, a replay buffer size of 106, and a minibatch size of 1024 transitions for each update. The target networks are updated with a smoothing coefficient . The discount factor and temperature parameter are set to be 0.99 and 1/10, respectively. The experiments were carried out on a computer that was equipped with an NVIDIA RTX 2080s GPU and an AMD Ryzen 9 5950X CPU. The algorithm was tested once every two training cycles using a strategy simulated once in twenty environments infused with different seeds. The average score obtained from twenty rounds of simulations is recorded as the strategy’s average score. To achieve the win criterion, the red side must destroy all the blue UAVs, and the difference between the number of red wins in twenty simulations and 20 is counted as the strategy’s win rate. As shown in Figure 8, the learning curves of all algorithms represent the average return of five training processes with different seeds; the shadow represents the return fluctuation under a 95% confidence interval.
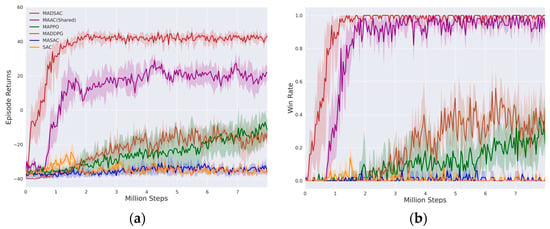
Figure 8.
This figure shows the curve of the agent training process, where (a) represents the average episode return change during the training process, and (b) represents the change in win rate during the training process.
During the entire training process, each algorithm sampled over eight million steps. MADSAC showed a rapid increase in average return in the first million steps, and after only 50,000 steps, the average return approached 0, with a winning rate close to 0.5. This indicated that the red UAV achieved combat effectiveness equivalent to the blue UAV. At around two million steps, MADSAC converged, maintaining an average return of about 41 and a win rate close to 100%. The average return of MAAC fluctuated around −35 for the first half-million steps but increased rapidly between 0.5 and 1.5 million steps. At around 1.2 million steps, the average return approached 0, with a winning rate close to 0.5. At 3.5 million steps, MAAC converged, demonstrating an average return of roughly 20 and a winning rate of roughly 95%. Although the baselines MAPPO and MADDPG showed slight improvements during training, their average return barely surpassed 0 for the entire process, and their winning rate was never superior to 50%. In contrast, SAC and MASAC barely learned effective strategies, maintaining a fluctuating learning curve around −35 with a win rate close to 0. However, MADSAC showed significant improvement in convergence performance and high sample efficiency.
In the red-blue confrontation scenario, MAAC outperformed DDPG, MAPPO, MASAC, and SAC regarding convergence speed, average return, and win rate. Combining the maximum entropy theory with an attention-based mechanism critic improved the convergence speed and sampling efficiency of MARL significantly. However, MADSAC’s convergence is quicker than MAAC’s, and its average return is roughly 20 points higher, with smaller fluctuations after convergence, indicating a lesser variance. As displayed in Figure 8 and Figure 9, MADSAC had an average loss of 0.6 UAVs per battle, whereas MAAC’s UAV losses averaged 2.5 and fluctuated more. Although MADSAC’s winning rate was only about 5% better than MAAC’s, it achieved these victories with less loss compared to MAAC, whose cost to win was roughly five times higher than MADSAC’s. Clearly, the double-soft critic and delayed policy update mechanisms effectively improved the algorithm’s performance.
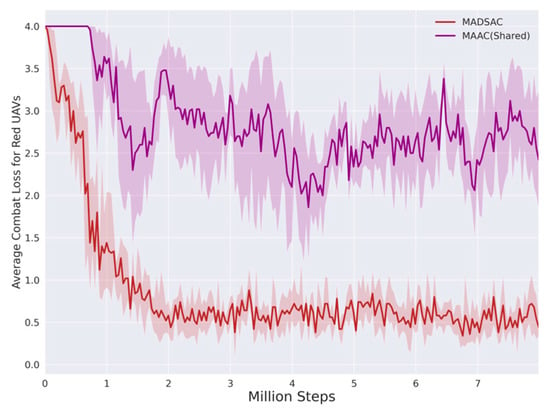
Figure 9.
Average combat loss curve of the red UAVs in each round of air combat during training.
4.2. Strategy Testing
Three experiments were conducted to demonstrate the performance of the strategies produced by MADSAC. In each experiment, the red side was represented by MASAC, while the blue side was represented by MADDPG, MAPPO, and MAAC, respectively. Since MASAC and SAC did not develop effective strategies, they were not included in the comparison. The results of the experiments are presented in Figure 10, and The experimental video is at https://bhpan.buaa.edu.cn:443/link/0B83BE79F08C104F9D935B0F251F9517 (accessed on 26 April 2023).
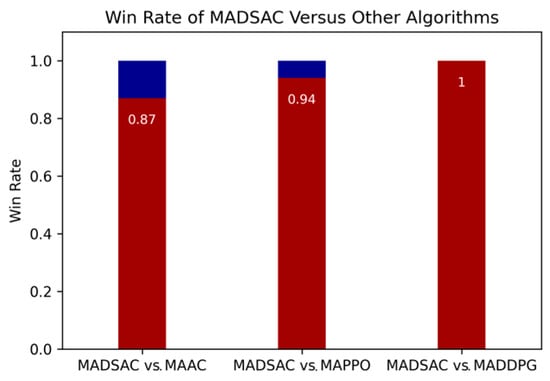
Figure 10.
The win rate of MADSAC versus other algorithms separately.
In Section 4.1, the algorithms were each trained five times. Strategies that produced a win rate of above 70% during training were saved in the pool, along with the most recent ones. As neither MADDPG nor MAPPO achieved a win rate above 70%, the latest strategies from the five training sessions for these algorithms were used as test strategies for the blue side. From the MADSAC strategies with a 100% win rate, thirty were randomly selected as red-side strategies. Each red strategy was then pitted separately against all blue side strategies, 100 times each, to calculate the win rate. The win rate of all red strategies was averaged to determine the red side’s win rate. Finally, MADSAC achieved a 100% win rate against MADDPG and a 94% win rate against MAPPO.
During testing, it was determined that the MADDPG strategy did not learn to fight in the designated area, resulting in the majority of the UAVs being judged dead when they left the engagement area, as shown in Figure 11. This phenomenon is mainly attributed to the algorithm’s insufficient exploration ability, resulting in local convergence. As the MADDPG strategy is trained against a fixed strategy that flies directly to the nearest target and attacks, it is unable to find an effective attack strategy, and no positive return can be obtained. In the reward function, the presence of a certain condition makes the negative reward for flying directly out of the engagement area smaller than the negative reward for being defeated by the blue UAV. As UAVs are always encouraged to obtain more rewards, they are more inclined to fly directly out of the engagement area. On the other hand, MAPPO showed signs of overfitting, with all five strategies hovering in place, as indicated in Figure 12. Although this strategy can withstand the fixed strategy to some extent, it performs poorly against MADSAC. However, it is worth noting that some of MADSAC’s strategies are still unable to achieve victory against this strategy.

Figure 11.
From (a–c) shows a confrontation process between MADSAC and MADDPG, where most of the blue UAVs using the MADDPG strategy fly directly outside the engagement area.

Figure 12.
From (a–c) a confrontation between MADSAC and MAPPO is shown, where the blue UAVs using the MAPPO strategy hover in place and are destroyed by the red UAVs using the MADSAC strategy.
For MADSAC and MAAC, thirty different strategies are randomly selected from the pool of strategies with a win rate of 100%, respectively. Each strategy of MADSAC is played 100 times against all MAAC strategies to obtain a win rate of 87%. Figure 13 shows one of the replays of MADSAC against MAAC, where MAAC demonstrates an effective offensive strategy and is able to cause the loss of the red UAV in most cases and even completely destroy them. However, overall, MADSAC still holds a significant advantage over MAAC.

Figure 13.
From (a–c), a confrontation between MADSAC and MAAC is shown. The blue UAVs using the MAAC strategy learn an effective attack strategy but still cannot win against the red UAVs using the MADSAC strategy.
Furthermore, the results of the win rates of all algorithms in adversarial testing are presented in Table 4. The first column of the table represents the blue strategy, with the first row representing the red strategy and the data indicating the red side’s win rate.

Table 4.
The adversarial testing success matrix for algorithms.
It is important to note that the success criterion for the scenario is the complete elimination of the blue drones, and a draw is considered a failure on the red side. Hence, in Table 4, when the same algorithm is pitted against itself, the win rate may be less than 50%. Additionally, within the same group of tests, the sum of the win rates of the red and blue sides may be less than one because of this criterion. The victory rate data of MAAC versus MAPPO and MAPPO self-confrontation are particularly interesting. The former highlights that the strategies obtained by MAAC perform poorly in response to MAPPO strategies. The latter is because the hovering strategy obtained by MAPPO does not actively attack, making it difficult to achieve victory in confrontation under existing winning standards.
Analysis of the experimental results in Section 4.1 and this section leads to the following conclusions: (1) MADSAC boasts faster convergence, higher average return, higher win rates, and smaller algorithm variance than other compared algorithms; (2) the improvements made in MADSAC for overestimation and error accumulation problems are effective; (3) maximizing entropy theory, double-centralized critics based on attention mechanisms, and delayed policy update techniques can effectively improve MARL’s performance in complex problems.
4.3. Strategy Analysis
Tests of the strategies obtained from MADSAC training show that the algorithm has learned several effective strategies, including the pincer movement, outflanking, and High-Yo-Yo strategies.
- Pincer movement strategy: the red UAVs split into two formations, using pincer movement to attack the blue UAVs. As shown in Figure 14, the red UAVs quickly split into two formations to approach the blue from both sides so that the blue UAVs lose their frontal advantage and are threatened on both sides simultaneously. In this case, the red UAVs can almost eliminate all the blue UAVs without loss;
- Outflanking strategy: some of the red UAVs attack the blue UAVs head-on while others flank them. As shown in Figure 15, a formation of the red UAVs engages the blue UAVs from the front to draw their fire, while the other formation speeds up from the flank to the rear of the blue UAVs to complete the outflank so that the blue UAVs are attacked front and rear and eliminated;
- High-Yo-Yo strategy: the red UAVs slow their approach rate by suddenly climbing, then making a quick turn and gaining a favorable position. As shown in Figure 16, the red UAVs induce the blue UAVs to approach, and then two of the red UAVs climb fast, completing a maneuver turn and circling the inside of the blue UAVs. In that way, the red UAVs occupy a favorable position and can eliminate all the blue UAVs.
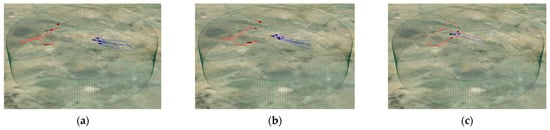
Figure 14.
Pincer movement strategy: from (a–c) shows the red UAVs split into two formations, using pincer movement to attack the blue UAVs.

Figure 15.
Flanking attack strategy: from (a–c) shows some of the red UAVs attacking the blue UAVs head-on while others flank them.

Figure 16.
High-Yo-Yo strategy: from (a–c) shows the red UAVs slowing their approach rate by suddenly climbing, then making a quick turn and gaining a favorable position.
Furthermore, the strategy model with a high success rate trained by MADSAC is allocated to both red and blue UAVs. During the air combat process, the two sides have a wonderful dogfight, as shown in Figure 17. According to the current situation, the two sides adjust their turning efficiency by the change in height and speed so that they can constantly make maneuvers to try to occupy a favorable position. Therefore, the two sides will appear in a spiral combat trajectory in the air combat process. From this point, it can be seen that the MADSAC algorithm has learned to flexibly maneuver and occupy a favorable position to attack based on the rapidly changing battlefield situation.

Figure 17.
MADSAC model is assigned to the red and blue UAVs at the same time. From (a–c) shows the two sides adjust their turning efficiency by the change in height and speed, appearing as a spiral combat trajectory in the air combat process.
5. Conclusions
This paper focuses on the cooperative air combat decision-making of multi-UAVs. At the starting point, a simulation environment for multi-UAV cooperative decision-making is created to support the design and training of the algorithm. Then, the MADSAC algorithm is proposed featuring multiple actors sharing network parameters and double-centralized critics based on the attention mechanism. The algorithm uses maximum entropy theory, target networks, and delayed policy update techniques to effectively avoid overestimation bias and error accumulation in MARL while improving algorithm stability and performance. Finally, the algorithm is evaluated by training MADSAC and comparison algorithms in an MCAC simulation scenario of red-blue confrontation. The experimental results illustrate that both MADSAC and MAAC exhibit satisfactory performance and outperform MASAC, SAC, MAPPO, and MADDPG. Specifically, MADSAC converges faster than the other five algorithms. Compared to MAAC, MADSAC shows better stability and convergence while achieving greater victories with fewer UAVs lost.
However, there are several limitations to this paper. Firstly, it only addresses the cooperative air combat decision-making process of isomorphic UAVs. In the future, it is necessary to explore the MAAC decision-making methods in heterogeneous UAVs. Secondly, the MADSAC algorithm requires UAVs to engage in real-time communication, which may result in significant communication pressure. Future research will focus on developing information compression mechanisms that reduce communication restrictions among UAVs and cooperative decision-making methods in situations where communication is limited.
Author Contributions
Conceptualization, S.L. and Y.W.; methodology, S.L.; software, S.L. and F.Y.; validation, S.L. and Y.W.; formal analysis, S.L. and Y.W.; investigation, H.S.; resources, Y.Z.; data curation, C.Z.; writing—original draft preparation, S.L. and H.S.; writing—review and editing, Y.J. and Y.Z.; visualization, H.S. and F.Y.; supervision, Y.J. and Y.Z.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 52272382, and the Aeronautical Science Foundation of China, grant number 20200017051001.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless Communications with Unmanned Aerial Vehicles: Opportunities and Challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Tsach, S.; Peled, A.; Penn, D.; Keshales, B.; Guedj, R. Development Trends for Next Generation of UAV Systems. In Proceedings of the AIAA Infotech@Aerospace 2007 Conference and Exhibit, Rohnert Park, CA, USA, 7–10 May 2007. [Google Scholar]
- Park, H.; Lee, B.-Y.; Tahk, M.-J.; Yoo, D.-W. Differential game based air combat maneuver generation using scoring function matrix. Int. J. Aeronaut. Space 2016, 17, 204–213. [Google Scholar] [CrossRef]
- Wang, X.; Wang, W.; Song, K.; Wang, M. UAV air combat decision based on evolutionary expert system tree. Ordnance Ind. Autom. 2019, 38, 42–47. [Google Scholar]
- Huang, C.Q.; Dong, K.S.; Huang, H.Q.; Tang, S.Q.; Zhang, Z.R. Autonomous air combat maneuver decision using Bayesian inference and moving horizon optimization. J. Syst. Eng. Electron. 2018, 29, 86–97. [Google Scholar] [CrossRef]
- Fu, L.; Wang, Q.; Xu, J.; Zhou, Y.D.; Zhu, K. Target Assignment and Sorting for Multi-target Attack in Multi-aircraft Coordinated Based on RBF. In Proceedings of the 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 1935–1938. [Google Scholar]
- Zhang, X.; Liu, G.; Yang, C.; Wu, J. Research on air confrontation maneuver decision-making method based on reinforcement learning. Electronics 2018, 7, 279. [Google Scholar] [CrossRef]
- Fang, J.; Zhang, L.; Fang, W.; Xu, T. Approximate dynamic programming for CGF air combat maneuvering decision. In Proceedings of the 2016 2nd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 14–17 October 2016; pp. 1386–1390. [Google Scholar]
- Yang, Q.; Zhang, J.; Shi, G.; Hu, J.; Wu, Y. Maneuver decision of UAV in short-range air combat based on deep reinforcement learning. IEEE Access 2019, 8, 363–378. [Google Scholar] [CrossRef]
- Isci, H.; Koyuncu, E. Reinforcement Learning Based Autonomous Air Combat with Energy Budgets. In Proceedings of the AIAA SCITECH 2022 Forum, Orlando, FL, USA, 8–12 January 2022; p. 0786. [Google Scholar]
- Li, Y.; Lyu, Y.; Shi, J.; Li, W. Autonomous Maneuver Decision of Air Combat Based on Simulated Operation Command and FRV-DDPG Algorithm. Aerospace 2022, 9, 658. [Google Scholar] [CrossRef]
- Sun, Z.X.; Piao, H.Y.; Yang, Z.; Zhao, Y.Y.; Zhan, G.; Zhou, D.Y.; Meng, G.L.; Chen, H.C.; Chen, X.; Qu, B.H.; et al. Multi-agent hierarchical policy gradient for Air Combat Tactics emergence via self-play. Eng. Appl. Artif. Intel. 2021, 98, 104112. [Google Scholar] [CrossRef]
- Pope, A.P.; Ide, J.S.; Mićović, D.; Diaz, H.; Rosenbluth, D.; Ritholtz, L.; Twedt, J.C.; Walker, T.T.; Alcedo, K.; Javorsek, D. Hierarchical reinforcement learning for air-to-air combat. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; pp. 275–284. [Google Scholar]
- Gao, J.; Tong, M.-a. Extracting Decision Rules for Cooperative Team Air Combat Based on Rough Set Theory. Chin. J. Aeronaut. 2003, 16, 223–228. [Google Scholar] [CrossRef]
- Fu, L.; Xie, F.H.; Wang, D.Z.; Meng, G.L. The Overview for UAV Air-combat Decision Method. In Proceedings of the 26th Chinese Control and Decision Conference (CCDC), Changsha, China, 31 May 31–2 June 2014; pp. 3380–3384. [Google Scholar]
- Zhang, Q.; Hu, J.H.; Feng, J.F.; Liu, A. Air multi-target threat assessment method based on improved GGIFSS. J. Intell. Fuzzy Syst. 2019, 36, 4127–4139. [Google Scholar] [CrossRef]
- Meng, G.L.; Zhao, R.N.; Wang, B.A.; Zhou, M.Z.; Wang, Y.; Liang, X. Target Tactical Intention Recognition in Multiaircraft Cooperative Air Combat. Int. J. Aerospace Eng. 2021, 2021, 18. [Google Scholar] [CrossRef]
- Ruan, C.W.; Zhou, Z.L.; Liu, H.Q.; Yang, H.Y. Task assignment under constraint of timing sequential for cooperative air combat. J. Syst. Eng. Electron. 2016, 27, 836–844. [Google Scholar] [CrossRef]
- Peng, G.; Fang, Y.; Chen, S.; Peng, W.; Yang, D. A Hybrid Multiobjective Discrete Particle Swarm Optimization Algorithm for Cooperative Air Combat DWTA. J. Optim. 2017, 2017, 8063767. [Google Scholar] [CrossRef]
- Li, W.H.; Shi, J.P.; Wu, Y.Y.; Wang, Y.P.; Lyu, Y.X. A Multi-UCAV cooperative occupation method based on weapon engagement zones for beyond-visual-range air combat. Def. Technol. 2022, 18, 1006–1022. [Google Scholar] [CrossRef]
- Vinyals, O.; Babuschkin, I.; Czarnecki, W.M.; Mathieu, M.; Dudzik, A.; Chung, J.; Choi, D.H.; Powell, R.; Ewalds, T.; Georgiev, P. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 2019, 575, 350–354. [Google Scholar] [CrossRef] [PubMed]
- Berner, C.; Brockman, G.; Chan, B.; Cheung, V.; Dębiak, P.; Dennison, C.; Farhi, D.; Fischer, Q.; Hashme, S.; Hesse, C. Dota 2 with large scale deep reinforcement learning. arXiv 2019, arXiv:1912.06680. [Google Scholar]
- Li, S.; Jia, Y.; Yang, F.; Qin, Q.; Gao, H.; Zhou, Y. Collaborative Decision-Making Method for Multi-UAV Based on Multiagent Reinforcement Learning. IEEE Access 2022, 10, 91385–91396. [Google Scholar] [CrossRef]
- Liu, X.; Yin, Y.; Su, Y.; Ming, R. A Multi-UCAV Cooperative Decision-Making Method Based on an MAPPO Algorithm for Beyond-Visual-Range Air Combat. Aerospace 2022, 9, 563. [Google Scholar] [CrossRef]
- Fujimoto, S.; van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. In Proceedings of the 35th International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Sutton, R.S. Learning to Predict by the Methods of Temporal Differences. Mach. Learn 1988, 3, 9–44. [Google Scholar] [CrossRef]
- Iqbal, S.; Sha, F. Actor-attention-critic for multi-agent reinforcement learning. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; pp. 2961–2970. [Google Scholar]
- Yu, C.; Velu, A.; Vinitsky, E.; Wang, Y.; Bayen, A.; Wu, Y. The surprising effectiveness of ppo in cooperative, multi-agent games. arXiv 2021, arXiv:2103.01955. [Google Scholar]
- Wu, T.; Wang, J.H.; Lu, X.N.; Du, Y.H. AC/DC hybrid distribution network reconfiguration with microgrid formation using multi-agent soft actor-critic. Appl. Energ. 2022, 307, 118189. [Google Scholar] [CrossRef]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv. Neural Inf. Process. Syst. 2017, 30, 1706. [Google Scholar]
- Li, J.; Ling, M.; Shui, J.; Huang, S.; Dan, J.; Gou, B.; Wu, Y. Smart Grazing in Tibetan Plateau: Development of a Ground-Air-Space Integrated Low-Cost Internet of Things System for Yak Monitoring. Wirel. Commun. Mob. Comput. 2022, 2022, 1870094. [Google Scholar] [CrossRef]
- Bonanni, P. The Art of the Kill; Spectrum HoloByte: Alameda, CA, USA, 1993. [Google Scholar]
- Foerster, J.; Assael, I.A.; De Freitas, N.; Whiteson, S. Learning to communicate with deep multi-agent reinforcement learning. Adv. Neural Inf. Process. Syst. 2016, 29, 2145–2153. [Google Scholar]
- Oliehoek, F.A.; Amato, C. A Concise Introduction to Decentralized POMDPs; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. In Proceedings of the 35th International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).