Adaptive PID Control via Sliding Mode for Position Tracking of Quadrotor MAV: Simulation and Real-Time Experiment Evaluation

Abstract

The lightweight nature of micro air vehicles (MAVs) makes them highly sensitive to perturbations, thus emphasizing the need for effective control strategies that can sustain attitude stability throughout translational movement. This study evaluates the performance of two controllers (Proportional-Integral-Derivative (PID) and Adaptive PID based on Sliding Mode Control (SMC)) on a MAV that is subjected to external disturbances. These controllers are initially simulated using MATLAB^®/Simulink™ and then implemented in real-time on the Parrot Mambo Minidrone. The observation on the waypoint follower and the orbit follower in both simulation and experiment showed that the Adaptive PID (APID) controller is more effective and robust than the PID controller against external disturbances such as wind gusts. The study provides evidence of the potential of the APID control scheme in enhancing the resilience and stability of MAVs, making them suitable for various applications including surveillance, search and rescue, and environmental monitoring.

1. Introduction

Micro air vehicles (MAVs) are gaining popularity in various applications, including surveillance, reconnaissance, and inspection. Accurate position control is essential for these tasks, and researchers have devoted significant effort to improving the position control of MAVs, particularly quadrotor MAVs. However, due to their small size, MAVs are highly vulnerable to disturbances such as wind gusts, which can make real-time implementation challenging. As a result, it is crucial to develop a reliable controller for the successful operation of MAVs, enabling researchers to evaluate and verify various approaches. To this end, a wide range of control strategies [1,2] have been explored, namely Proportional-Integral-Derivative (PID), Linear Quadratic Regulator (LQR), Backstepping, Feedback Linearization Control (FLC), Sliding Mode Control (SMC), Model Predictive Control (MPC), Neural Network, H-infinity, Fuzzy Logic, and Adaptive Control.

This research is focused on the Parrot Mambo Minidrone, which is a type of micro air vehicle (MAV) and one of several quadrotors designed for educational purposes that are available today. Weighing less than 1 kg, the Parrot Mambo Minidrone comes equipped with a range of sensors, including ultrasonic sensors, accelerometers, gyroscopes, air pressure sensors, and down-facing cameras (optical flow), allowing for six-degree-of-freedom control.

The Simulink Support Package for Parrot Minidrones (SSPPM) [3] provided by MATLAB is a valuable tool for researchers [4]. This package, which was developed by MIT and based on the Aerospace Blockset, enables researchers to enhance the tracking performance of the Parrot Mambo Minidrone by testing low-level control in a real-time platform. With SSPPM, researchers can create flight control algorithms using Simulink blocks, simulate systems to verify control laws and directly deploy control algorithms on the drone through a Bluetooth wireless network. Several studies were conducted on the topic of PID and LQR control techniques. For example, [5,6] have examined PID, while [7,8,9] have focused on LQR. In addition, fuzzy control was investigated by [10,11], INDI by [12], $H_{\infty }$ by [13], sliding mode control by [14,15,16,17,18,19] and adaptive control by [20,21,22].

In [7], it was concluded that LQI provides better flight than regular LQR due to its ability to reduce steady-state error, whereas [8] claims that LQR control yields better system tracking with minimum settling time. This optimal control can also be used instead of six PID controllers for the entire system, with one LQR controller being sufficient for multi-axis control of MAV [9], on the other hand, argues that MPC exceeds PID and LQR in confirming that the system is stable and robust, based on both simulation and experimental results. However, the authors detected that the performance of the sensor declines over a certain period of operation, and the controller is not efficient enough to demonstrate its full strength.

In [10], the pitch, roll, and vertical rate of the Parrot AR. Drones were controlled using three Fuzzy Logic Controllers (FLCs). Both the desired and real positions were used as inputs, while the FLCs generated pitch, roll, and vertical rate outputs. The input was represented using five triangular membership functions, and five singletons were used for the defuzzification process to speed up calculations. The study found that all three FLC schemes were effective in enabling the Parrot AR. Drone to reach the waypoint, but the approach that worked best involved flying straight towards the waypoint with FLCs functioning simultaneously. Meanwhile, ref. [11] reported on the use of the Fuzzy PI-PD controller to control the Parrot Mambo Minidrone quadrotor MAV. The controller utilized a 3 by 3 rule system for its FLC settings, with the input consisting of a triangle membership function and the output consisting of five singletons. To ensure robustness against nonlinearities, the center of sets was chosen as the defuzzification method. The author concluded that the Fuzzy PI-PD controller outperformed both the Parrot PD and PI-PD control systems.

One study presented in [12] investigated the effectiveness of the Incremental Nonlinear Dynamic Inversion (INDI) control strategy for the Parrot Mambo Minidrone. This strategy uses a cascade control structure with separate layers for attitude and position control. Through simulation as well as actual tests, the study evaluates the performance of the INDI controller, comparing it to the classical cascade PID control strategy. Results show that the INDI controller functions satisfactorily for the Mambo MAV, exhibiting admirable robustness against uncertainties and instrumentation models while effectively tracking trajectories. Thus, the paper suggests that the INDI controller is a suitable tool for educational purposes, particularly for teaching linearization of feedback and INDI control applications for in flight control.

Another study presented in [13] investigates the translational dynamics of Parrot Mambo Minidrones using data from real-time input-output obtained throughout experiments with four Mambo MAV platforms equipped with a motion capture system. The study selects a mathematical model consisting of integrator with first-order structure as well as dead-time delay and identifies $x$ and $y$ translational dynamics of each drone using an extended least-squares algorithm. Using a reduction technique, the study obtains new linear model collections minus the dead-time delay and designs a control approach that is based on a discrete-time linear system with parameter-variant. This method includes two robust control approaches: a robust controller for global stability and a robust nonlinear controller with disturbance estimation for effective reference tracking. The study conducts real-time flights to demonstrate the efficiency of the proposed method notwithstanding the existence of modelling perturbations, delays and other uncertainties.

Since sliding mode control has become popular for nonlinear control strategies, the integral terminal SMC approach has been utilized in adaptive saturated tracking control to achieve a fast convergence rate, eliminate input saturation, and suppress chattering, as reported in [14]. Subsequently, in [15], the same author applied a nonsingular fast fixed-time sliding mode surface for quadrotor attitude stabilization to achieve an even faster convergence rate. In the articles [16,17,18,19], the same author propose different control approaches for the position and attitude tracking problem of quadrotor systems, considering uncertainties, perturbations, and unknown dynamics. In [16], the author proposes a mix of Hierarchical Perturbation Compensator (HPC) and a Sliding Mode Controller (SMC) to compensate for perturbations in the system. Later on, in [17], the author improves upon the previous work by proposing a Three Loop Uncertainties Compensator (TLUC) and Exponential Reaching Law Sliding Mode Controller (ERSM) that can estimate and compensate for uncertainties and unknown time-varying disturbances in three loops to provide a greater level of support to the controller. In [18], the author studies the issue regarding the finite-time position and attitude trajectory of a modified second-order sliding mode algorithm based quadrotor UAV systems to ensure robustness against unknown dynamics and perturbations. In [19], the author suggests for an improved non-singular terminal super-twisting control for quadrotor UAVs position and attitude tracking affected by disturbances and uncertainties. The proposed control schemes in all references are tested through simulations and experiments on the Parrot-Rolling Spider quadrotor, and the acquired results indicate enhanced performance compared to other conventional methods, including improved tracking performance, and chattering reduction.

One proposed approach, as described in [20], for the Parrot Rolling Spider quadrotor MAV involves the use of an adaptive sliding mode controller. This controller is designed to reduce chattering and avoid perturbations by utilizing appropriate controls. Additionally, the same author discusses in [21], the development of a flight control for a quadrotor micro aerial vehicle which is robust towards the presence of external perturbations. The system mathematical model is represented by the spatial vectors convention and adaptive second order sliding mode technique is used to design the flight control. This controller is able to diminish matched and bounded perturbations with unidentified constraints, while also minimizing control effort and chattering effects through the use of adaptive gains. The performance of the planned adaptive flight control is compared to second order sliding mode method through simulation results, demonstrating the effectiveness and appeal of this strategy. Another technique, outlined in [22], utilizes a neural network (RBFNN) with radial basis function to approximate uncertainties and compensate for them, leading to accelerated error reduction. Consequently, fast error convergence in the closed loop control system is achievable.

Researchers successfully controlled a DC motor using FPGA technology by employing a sliding mode control approach with an adaptive mechanism, as reported in [23] while [24] has simulated it on UAV. This same approach was then applied to real-time control of the altitude of a Parrot Mambo Minidrone in a study comparing the performance of PID, adaptive PID as well as fuzzy compensator attached adaptive PID as described in [25]. The study found that the sliding mode control based adaptive PID was more robust than the PID controller, consuming 2% less power while maintaining the same level of hovering performance for the MAV.

This study compares the tracking performance of two controllers, namely; PID and APID, using a Parrot Mambo Minidrone as the platform. The key contribution of this research is the introduction of APID in the tracking the trajectory of the drone and assessing its performance in comparison to the PID controller. Furthermore, both simulation and real-time experiments are conducted to test the stability and robustness of the system against external disturbances such as wind gusts.

The organization of this manuscript is as follows. Section 2 describes the dynamics model of the parrot mambo MAV quadrotor. Section 3 shows the design of the APID for position control of the quadrotor. Section 4 presents the APID system’s simulation and experimental results, and Section 5 presents the conclusion of the research work.

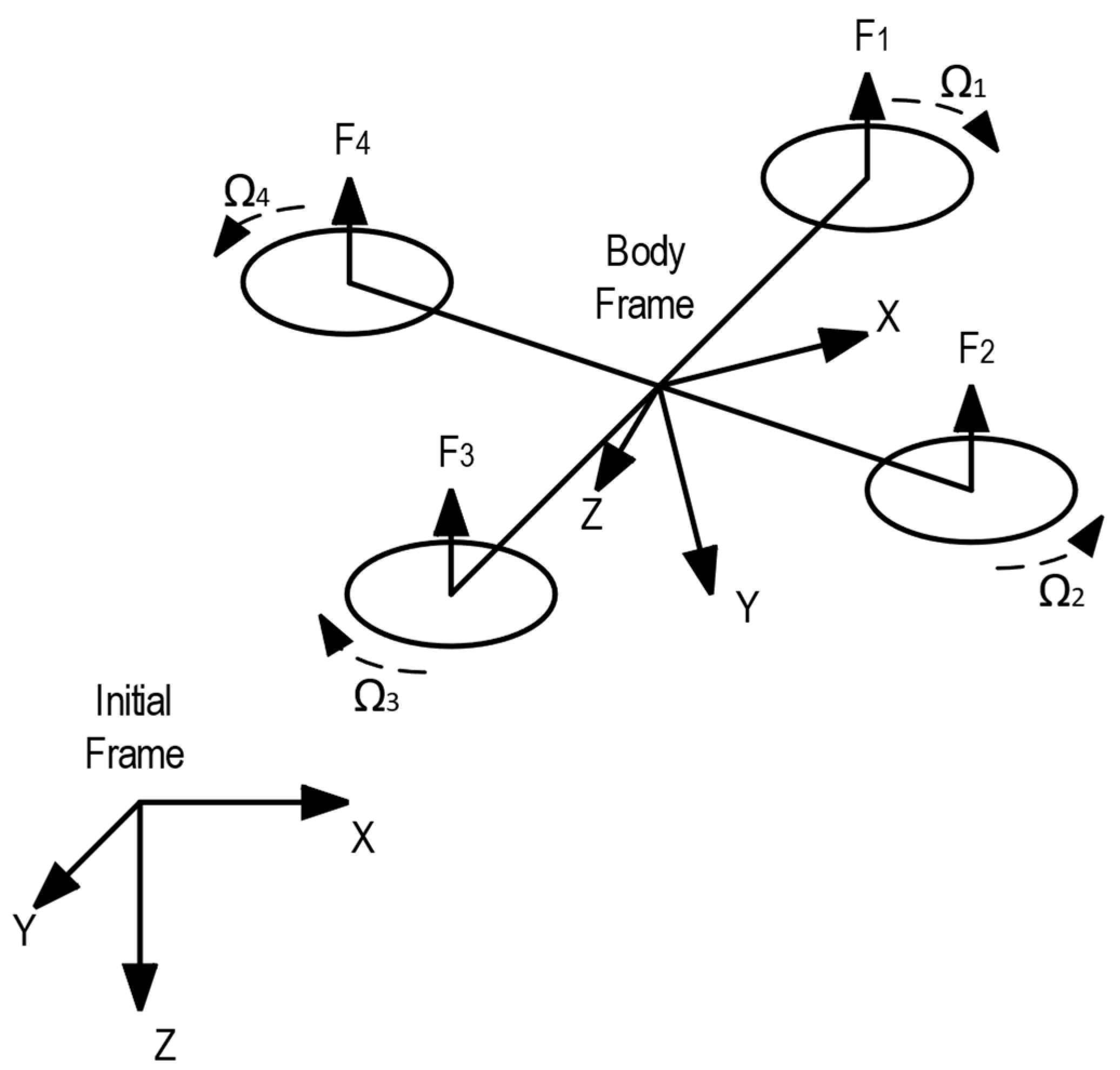
2. MAV Quadrotor Modeling

This section exhibits the quadrotor mathematical model. The quadrotor’s translations and orientations dynamics are described using a 6 degree-of-freedom (DOF) model, which is defined by two state vectors: $\xi ={\left[x,y,z\right]}^T$ and $\eta ={\left[\varphi ,\theta ,\psi \right]}^T$. To transform these vectors from the fixed frame body to the inertial frame (as shown in Figure 1), a rotation matrix $R$ is used, where $C$ represents cosine and $S$ represents sine.

$$R=\left[\begin{array}{ccc}C\theta C\psi & S\varphi S\theta C\psi -C\varphi S\psi & C\varphi S\theta C\psi +S\varphi S\psi \\ C\theta S\psi & S\varphi S\theta S\psi +C\varphi C\psi & C\varphi S\theta S\psi -S\varphi C\psi \\ -S\theta & S\varphi C\theta & C\varphi C\theta \end{array}\right]$$

(1)

As the thrust force is produced by rotor $i,i=1,2,3,4$ is $F_i=b.{\mathsf{\Omega }}_i^2$ where b is the factor of the thrust and ${\mathsf{\Omega }}_i$ is the rotor speed, we may acquire a first set of differential equations as described the quadrotor acceleration:

$$\ddot{\xi }=-g·\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)+R·\frac{b}{m}{\displaystyle \sum }_{i=1}^4{\mathsf{\Omega }}_i^2·\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$$

(2)

where, g is the gravitational coefficient, $m$ is quadrotor mass, and with the inertia matrix $I=diagonal{\left[I_{xx},I_{yy},I_{zz}\right]}^T$, the inertia of the rotor $J_r$ and the vector $\tau$ that expresses the torque, which is applied to the body frame, a second set of differential equations is obtained:

$$I\ddot{\eta }=-\dot{\eta }\times I\dot{\eta }-{\displaystyle \sum }_{i=1}^4{J}_r\left(\dot{\eta }\times \left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)\right){\mathsf{\Omega }}_i+\tau$$

(3)

The vector $\tau$ is termed as:

$$\tau =\left(\begin{array}{c}lb\left({\mathsf{\Omega }}_1^2-{\mathsf{\Omega }}_2^2-{\mathsf{\Omega }}_3^2+{\mathsf{\Omega }}_4^2\right)\\ lb\left({\mathsf{\Omega }}_1^2+{\mathsf{\Omega }}_2^2-{\mathsf{\Omega }}_3^2-{\mathsf{\Omega }}_4^2\right)\\ d\left(-{\mathsf{\Omega }}_1^2+{\mathsf{\Omega }}_2^2-{\mathsf{\Omega }}_3^2+{\mathsf{\Omega }}_4^2\right)\end{array}\right)$$

(4)

where $d$ is the drag factor and $l$ the length of the lever. The four rotational velocities ${\mathsf{\Omega }}_i$ of the rotors are the input variables of the real vehicle and the inputs transformation is suitable with regard to the attained model. Hence, the attained new artificial input variables are:

$$\begin{array}{c}{u}_1=b\left({\mathsf{\Omega }}_1^2+{\mathsf{\Omega }}_2^2+{\mathsf{\Omega }}_3^2+{\mathsf{\Omega }}_4^2\right)\hfill \\ u_2=b\left({\mathsf{\Omega }}_1^2-{\mathsf{\Omega }}_2^2-{\mathsf{\Omega }}_3^2+{\mathsf{\Omega }}_4^2\right)\hfill \\ u_3=b\left({\mathsf{\Omega }}_1^2+{\mathsf{\Omega }}_2^2-{\mathsf{\Omega }}_3^2-{\mathsf{\Omega }}_4^2\right)\hfill \\ u_4=d\left(-{\mathsf{\Omega }}_1^2+{\mathsf{\Omega }}_2^2-{\mathsf{\Omega }}_3^2+{\mathsf{\Omega }}_4^2\right)\hfill \end{array}$$

(5)

Nevertheless, an additional variable is obtained in the previous equations. The additional variable also depends on the rotational speeds of the rotors. Thus, it must be considered as the fifth artificial input:

$${\mathsf{\Omega }}_d=-{\mathsf{\Omega }}_1+{\mathsf{\Omega }}_2-{\mathsf{\Omega }}_3+{\mathsf{\Omega }}_4$$

(6)

Assessment of (2) and (3) produces an overall dynamic model which can be divided to two subsystems; underactuated system, corresponding to the $x$ and $y$ dynamics, and fully actuated system, which refers to the altitude $z$, and attitude $\varphi$, $\theta$, and $\psi$ dynamics:

$$underactuated \left\{\begin{array}{c}\ddot{x}=-\left(C\varphi S\theta C\psi +S\varphi S\psi \right)·\frac{u_1}{m}\\ \ddot{y}=-\left(C\varphi S\theta S\psi -S\theta C\psi \right)·\frac{u_1}{m}\end{array}\right.$$

(7)

$$fully actuated \left\{\begin{array}{c}\ddot{z}=-g+\left(C\varphi C\theta \right)·\frac{u_1}{m}\hfill \\ \ddot{\varphi }=\left(\frac{I_{yy}-I_{zz}}{I_{xx}}\right)\dot{\theta }\dot{\psi }-\frac{J_r{\mathsf{\Omega }}_d}{I_{xx}}\dot{\theta }+\frac{l}{I_{xx}}{u}_2\hfill \\ \ddot{\theta }=\left(\frac{I_{zz}-I_{xx}}{I_{yy}}\right)\dot{\varphi }\dot{\psi }+\frac{J_r{\mathsf{\Omega }}_d}{I_{yy}}\dot{\varphi }+\frac{l}{I_{yy}}{u}_3\hfill \\ \ddot{\psi }=\left(\frac{I_{xx}-I_{yy}}{I_{zz}}\right)\dot{\varphi }\dot{\theta }+\frac{1}{I_{zz}}{u}_4\hfill \end{array}\right.$$

(8)

The parameters for the Parrot Mambo Minidrone, which were provided by MATLAB in one of the project directory’s m-files, are listed in

Table 1. Parrot Mambo MAV Model Physical Parameters [24].

Specification	Parameter	Unit	Value
Quadrotor mass	$m$	$\mathrm{kg}$	$0.0630$
Lateral moment arm	$l$	$\mathrm{m}$	$0.0624$
Thrust coefficient	$b$	${\mathrm{Ns}}^2$	$0.0107$
Drag coefficient	$d$	${\mathrm{Nms}}^2$	$0.7826400\times {10}^{-3}$
Rolling moment of inertia	$I_{xx}$	${\mathrm{kgm}}^2$	$0.0582857\times {10}^{-3}$
Pitching moment of inertia	$I_{yy}$	${\mathrm{kgm}}^2$	$0.0716914\times {10}^{-3}$
Yawing moment of inertia	$I_{zz}$	${\mathrm{kgm}}^2$	$0.1000000\times {10}^{-3}$
Rotor moment of inertia	$J_r$	${\mathrm{kgm}}^2$	$0.1021\times {10}^{-6}$

.

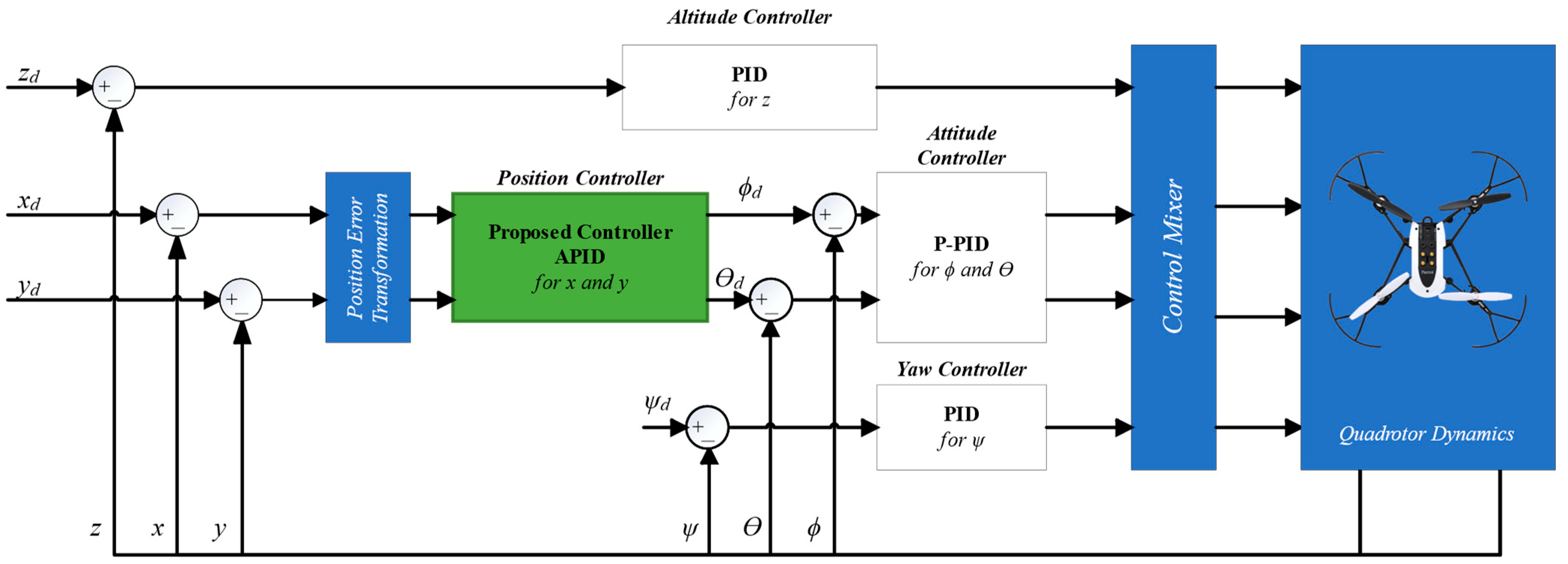
3. Flight Controller Design

The dynamics, which are both translational and rotational, as depicted in Equations (7) and (8), is represented by second-order state-space equations as

$$\ddot{x}=f\left(x\right)+g\left(x\right)u$$

(9)

In order to maintain simplicity in notation while creating a systematic control system design method, the state vector is expressed as:

$$x={\left[ x_1 x_2 x_3 x_4 x_5 x_6\right]}^T={\left[x y z \varphi \theta \psi \right]}^T$$

(10)

Defining the input vector as $u={\left[u_1 u_2 u_3 u_4\right]}^T$, the non-linear functions $f\left(x\right)$ and $g\left(x\right)$ can be reformulated as:

$$f\left(x\right)=\left[\begin{array}{c}{f}_1\left(x\right)\\ f_2\left(x\right)\\ f_3\left(x\right)\\ f_4\left(x\right)\\ f_5\left(x\right)\\ f_6\left(x\right)\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ g\\ a_1\dot{\psi }\dot{\theta }-a_2{\mathsf{\Omega }}_d\dot{\theta }\\ a_3\dot{\psi }\dot{\varphi }+a_4{\mathsf{\Omega }}_d\dot{\varphi }\\ a_5\dot{\theta }\dot{\varphi }\end{array}\right]$$

(11)

$$g\left(x\right)=\left[\begin{array}{cccc}{g}_1\left(x\right)& 0& 0& 0\\ g_2\left(x\right)& 0& 0& 0\\ g_3\left(x\right)& 0& 0& 0\\ 0& g_4\left(x\right)& 0& 0\\ 0& 0& g_5\left(x\right)& 0\\ 0& 0& 0& g_6\left(x\right)\end{array}\right]=\left[\begin{array}{cccc}-\frac{1}{m}{u}_x& 0& 0& 0\\ -\frac{1}{m}{u}_y& 0& 0& 0\\ -\frac{1}{m}{u}_z& 0& 0& 0\\ 0& b_1& 0& 0\\ 0& 0& b_2& 0\\ 0& 0& 0& b_3\end{array}\right]$$

(12)

where:

$$\begin{array}{c}{a}_1=\frac{I_{yy}-I_{zz}}{I_{xx}}, a_2=\frac{J_r}{I_{xx}}, a_3=\frac{I_{zz}-I_{xx}}{I_{yy}}\hfill \\ a_4=\frac{J_r}{I_{yy}}, a_5=\frac{I_{xx}-I_{yy}}{I_{zz}}, b_1=\frac{l}{I_{xx}}\hfill \\ b_2=\frac{l}{I_{yy}}, b_3=\frac{1}{I_{zz}}\hfill \end{array}$$

(13)

and:

$$\begin{array}{c}{u}_x=C\psi S\theta C\varphi +S\psi S\varphi \hfill \\ u_y=S\psi S\theta C\varphi -C\psi S\varphi \hfill \\ u_z=C\theta C\varphi \hfill \end{array}$$

(14)

Figure 2 displays the four controllers developed for the Parrot Mambo Minidrone. The controllers are attitude, yaw, position, and altitude controller. These controllers are designed to enable the drone’s orientation precise control, rotation, position and altitude. The upcoming section briefly outlines the design of the controller. Nonetheless, our emphasis in this work is on the position controller.

3.1. Fully Actuated System

In order to ensure stable and precise control of the MAV, three distinct controllers are developed. These controllers are designed to manage the attitude, yaw, and altitude of the MAV, respectively. The attitude controller governs the pitch and roll motion of the MAV, the yaw controller manages its heading, while the altitude controller regulates its vertical motion. Together, these controllers work seamlessly to enable smooth and accurate flight control of the MAV.

3.1.1. Attitude and Yaw Controller

The controller of the attitude is developed by PID control, which is cascaded. This is a widely used technique in control systems engineering. In this approach, the pitch and roll angle of the MAV are governed by the proportional loop. Meanwhile, its angular velocity is managed by the PID loop as:

$$U_i=k_P^i{e}_i+k_I^i\int e_i+k_D^i{\dot{e}}_i \left(i=\varphi ,\theta ,\psi \right)$$

(15)

Here, $e_i=i_d-i$ represents the unwanted deviation amid the coveted and received signals, while ${\dot{e}}_i={\dot{i}}_d-i$ is the derivative of that error. On the other hand, $k_P^i$, $k_I^i$, and $k_D^i$ are the parameters of the PID gains $\left(i=\varphi ,\theta ,\psi \right).$ In the meantime, the yaw controller uses classical PID control as expressed in (15).

3.1.2. Altitude Control Design

The altitude, z controller is created by the PID with gravity compensation controller, expressed as:

$$U_i=k_P^i{e}_i+k_I^i\int e_i+k_D^i{\dot{e}}_i \left(i=\varphi ,\theta ,\psi \right)+mg$$

(16)

3.2. Underactuated System

Figure 3 displays the adaptive PID scheme block diagram employed for the position control systems. The signals produced in this embedded system are relatively small, enabling them to function as the desired inputs of the attitude controller, ${\varphi }_d$ and ${\theta }_d$. Detailed information on the design procedure for this APID is elaborated on in the following sections.

The objective of the system is to decide on the control regulation that can make x to track $x_d$ as thoroughly as possible. The tracking error, e, is described as:

$$e=x_d-x$$

(17)

By assuming the optimal controller, $u^{\ast }$, is created once the entire related factors in (9) are recognized, this can then be stated as:

$$u^{\ast }=g^{-1}\left(-f+{\ddot{x}}_d+k_1\dot{e}+k_{2}e\right)$$

(18)

where $k_1$ and $k_2$ are selected as the non-zero positive coefficients to meet the Hurwitz condition, ensuring that $\underset{t\to \infty }{lim} e=0$ for any original starting states. Replacing (18) into (9) will then produces:

$$\ddot{e}+k_1\dot{e}+k_{2}e=0$$

(19)

In real-life implementation, the system dynamics are typically unidentified, and obtaining the optimal controller $u^{\ast }$ in (18) precisely is challenging. However, the sliding mode controller can be used in addressing this issue. Before the required controller is developed, the nominal model (9) needs to be reformulated as:

$$\ddot{x}=f_n\left(x\right)+g_n\left(x\right)u$$

(20)

where the nominal behavior of $f$ and $g$ is denoted as $f_n$ and $g_n$, respectively. To include uncertainties and external disturbances, (20) is further modified as:

$$\ddot{x}=\left(f_n+\mathsf{\Delta }f\right)+\left(g_n+\mathsf{\Delta }g\right)u+d=f_n+g_{n}u+w$$

(21)

where $d$ represents the external disturbance, such as wind, and $\mathsf{\Delta }f$ and $\mathsf{\Delta }g$ denote the system uncertainties. The lumped uncertainty w is defined as $w=\mathsf{\Delta }f+\mathsf{\Delta }gu+d$, assuming that $\left|w\right|\le W$, as $W$ is a constant that is positive.

In sliding mode control, the crucial requirement is to establish a sliding condition that ensures the existence of an environment where sliding action is possible. Therefore, a sliding facade can be expressed as:

$$s=\dot{e}+k_{1}e+k_2\int e dt$$

(22)

where $k_1$ and $k_2$ are two positive factors. Meanwhile, the rule for sliding-mode control can be specified as:

$$u_{sc}=u_{eq}+u_{ht}$$

(23)

where $u_{eq}$ is the comparative controller and it is stated as:

$$u_{eq}=g_n^{-1}\left(-f_n+\ddot{x}+k_1\dot{e}+k_{2}e\right)$$

(24)

whilst the hitting controller, $u_{ht}$ is crated to ensure the stability of the system and can be expressed as:

$$u_{ht}=\frac{W}{g_n}sgn\left(s\right)\& where sgn\left(s\right)\left\{\begin{array}{c}+1 if s<0\\ -1 if s>0\end{array}\right.$$

(25)

The derivative of (22) gives:

$$\dot{s}=\ddot{e}+k_1\dot{e}+k_{2}e$$

(26)

Inserting (23)–(25) into (21) yields:

$$\ddot{e}+k_1\dot{e}+k_{2}e=-w-Wsgn\left(s\right)=\dot{s}$$

(27)

Hence, the Lyapunov function is given as:

$$V_1=\frac{1}{2}{s}^2$$

(28)

Differentiating (28) in relation with time states that:

$$\dot{V_1}=s\dot{s}$$

(29)

To obtain stability, $\dot{\left(V_1\right)}\le 0$, replacing (27) into (29) produces:

$${\dot{V}}_1=-\left(W-\left|w\right|\right)\left|s\right|$$

(30)

In brief, the law of sliding mode control as ascertained corresponding to the Lyapunov theorem will warrant the system of its stability. Nevertheless, a greater control gain, W, will trigger a chattering impact. In addition, the switching function will not be as easily afforded due to the presence of restrictions experienced physically by the rotor, which the MAV used.

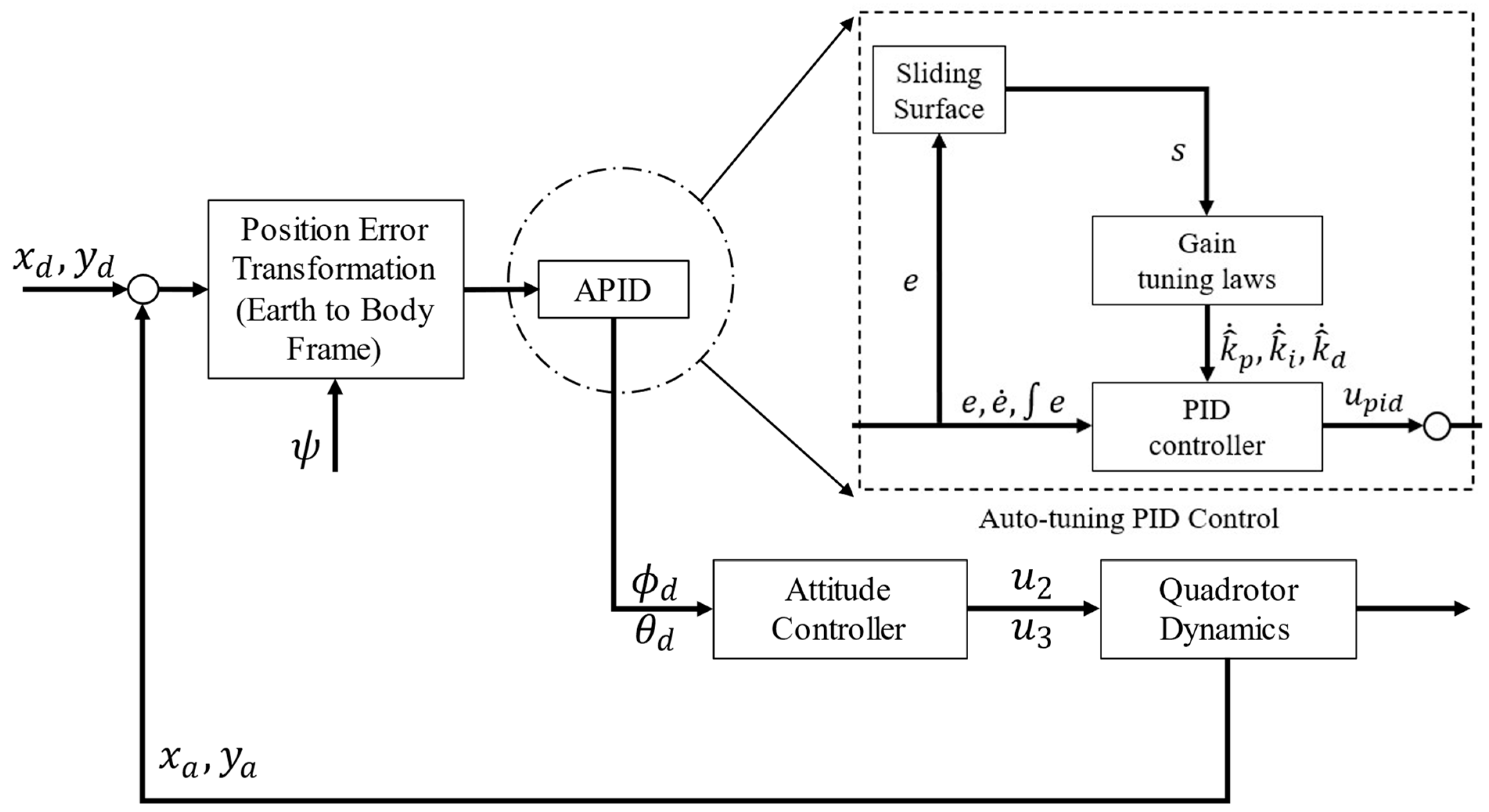
3.3. PID Controller Design

A standard PID controller can be specified as:

$$u_{pid}={\widehat{k}}_{p}e+{\widehat{k}}_i\int e dt+{\widehat{k}}_d\dot{e}$$

(31)

where ${\widehat{k}}_p$, ${\widehat{k}}_i$, and ${\widehat{k}}_d$ are the denomination of proportional gain, integral gain and derivative gain, correspondingly. To acquire stability, $\dot{s}=0$, and by combining (18) and (26), it can be observed that:

$$\dot{s}=\ddot{e}+k_1\dot{e}+k_{2}e=-f-gu+A_d$$

(32)

where $A_d={\ddot{x}}_d+k_1\dot{e}+k_{2}e$, substitute (31) into (32) and multiply by $s$,

$$s\dot{s}=-s\left[g\left(u_{pid}\right)+f-A_d\right]$$

(33)

Utilizing the approaches of gradient and the law of chain, ${\widehat{k}}_p$, ${\widehat{k}}_i$ and ${\widehat{k}}_d$ gains are modified by the rules as:

$$\begin{array}{c}{\dot{\widehat{k}}}_p=s{\beta }_{p}sgn\left(g\right)e={\beta }_{p}se\hfill \\ {\dot{\widehat{k}}}_i=s{\beta }_{i}sgn\left(g\right)\int edt= {\beta }_{i}s\int edt\hfill \\ {\dot{\widehat{k}}}_d=s{\beta }_{d}sgn\left(g\right)\dot{e}={\beta }_{d}s\dot{e}\hfill \end{array}$$

(34)

where ${\beta }_p$, ${\beta }_i$, and ${\beta }_d$ are the positive learning levels of ${\dot{\widehat{k}}}_p$, ${\dot{\widehat{k}}}_i$, and ${\dot{\widehat{k}}}_d$ correspondingly. Furthermore, the designed method dictates the usage of g value, that can be immediately achieved from the physical characteristics of the controlled system [25,26].

In short, if the ${\beta }_p$, ${\beta }_i$, and ${\beta }_d$ learning rate or the preliminary ${\widehat{k}}_p$, ${\widehat{k}}_i$, and ${\widehat{k}}_d$ of PID gains are not accurately selected, the condition of the system will differ. Therefore, the learning rate can be manually adjusted or optimized by applying the optimization technique. The algorithm to implement this control technique is as explained in [25,26]:

• APIDC system element preparation.
• Implementation of error tracking as in (17).
• Sliding surface, s, as described in (22).
• Application of the PID controller, u_pid, as revealed in (31).
• Manipulating the gains elements, ${\widehat{k}}_p$, ${\widehat{k}}_i$, and ${\widehat{k}}_d$ as reviewed in (34).

4. Results

This part provides a comprehensive overview of the results attained from these studies. We discuss the key findings, limitations, and implications of both simulation and experimental studies on Parrot Mambo Minidrones.

4.1. Simulation Results

Performing simulation is vital in this work in order to demonstrate the control scheme effectiveness before its real-time actual implementation. There are two trajectories path used in this simulation: Waypoint Follower and Orbit Follower. Both blocks are provided by MATLAB 2022b in Simulink in UAV Toolbox. These UAV Toolbox are used in the Simulink Support Package for Parrot Minidrones developed by MIT [4]. The simulation undergoes for $60$ s with set sampling time, $Ts=0.005$ s.

For the PID controller the parameters are remain unchanged since had well-tuned by MATLAB. However, for the Adaptive PID control scheme as proposed, the required parameters for sliding and learning rate are listed in

Table 2. System Parameters for controller $x$ and $y$.

	Dimension	$\mathit{X}$	$\mathit{Y}$
P-PI	$K_p$	0.7	0.7
	$K_p$	0.2	0.2
	$K_i$	0.1	0.1
APID	$K_1$	0.1	0.1
	$K_2$	0.01	0.02
	$B_p$	0.2	0.2
	$B_i$	0.7	0.8
	$B_d$	2	3

. The P-PI for controller x and y also stated in this table.

In this study, two cases were simulated to evaluate the proposed approach for controlling a drone quadrotor: one without wind disturbance and another with wind disturbance. The approach, similar to that presented in [27], combines momentum and blade element theory to determine the aerodynamic forces and moments, and then rewriting the model in state-space form with control inputs proportional to rotor angular velocities. The thrust is decomposed, and disturbances are considered as a function of wind signals, control, and system state. However, unlike previous studies, the wind disturbance in this study is modelled using a Dryden wind gust model [28,29], which effectively simulates forces of time-varying aerodynamic in the longitudinal and lateral directions which is due to the wind disturbances. Figure 4 displays the wind force disturbance in X and Y directions. These aerodynamics forces are injected into the system $15$ s after the flight.

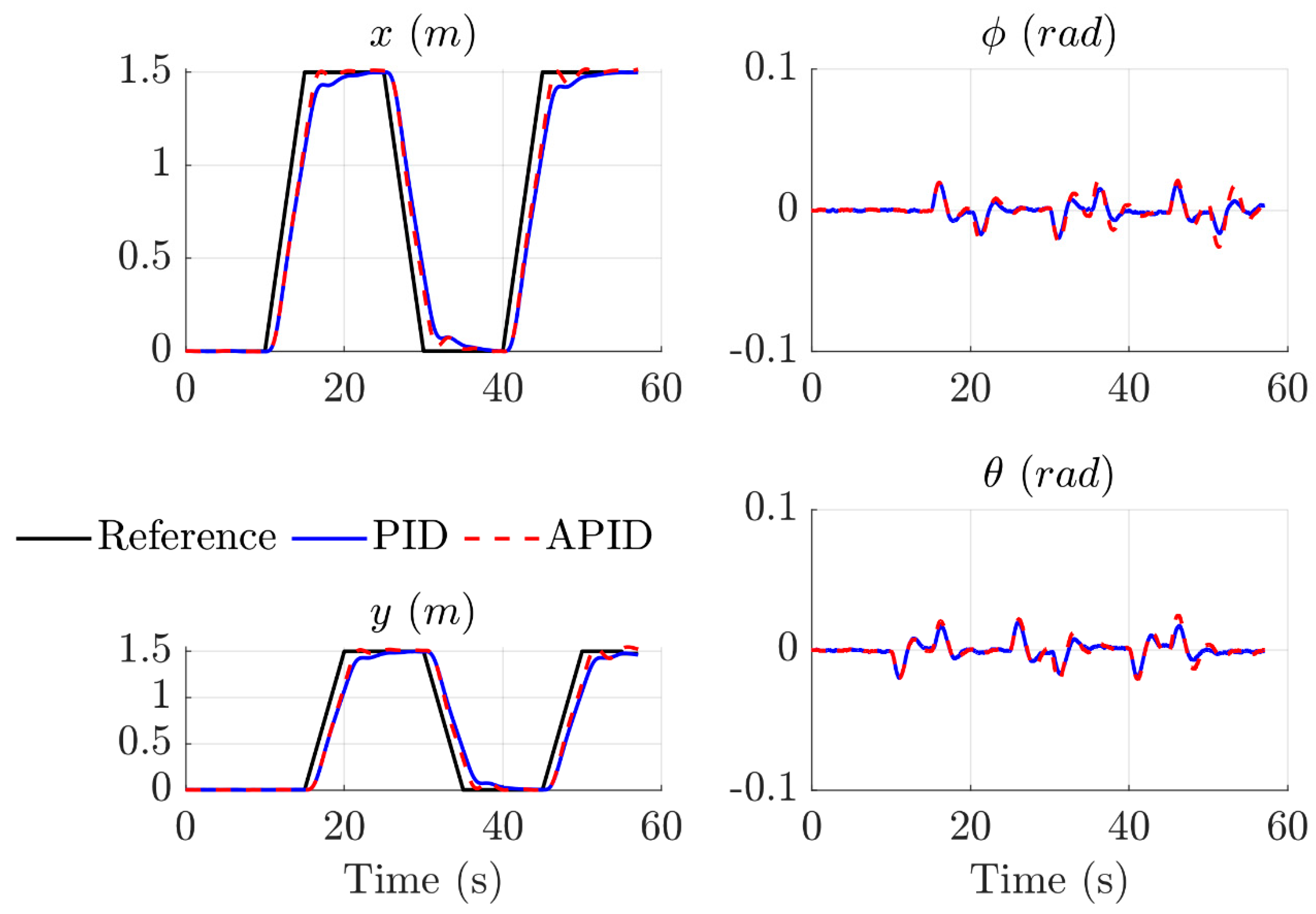
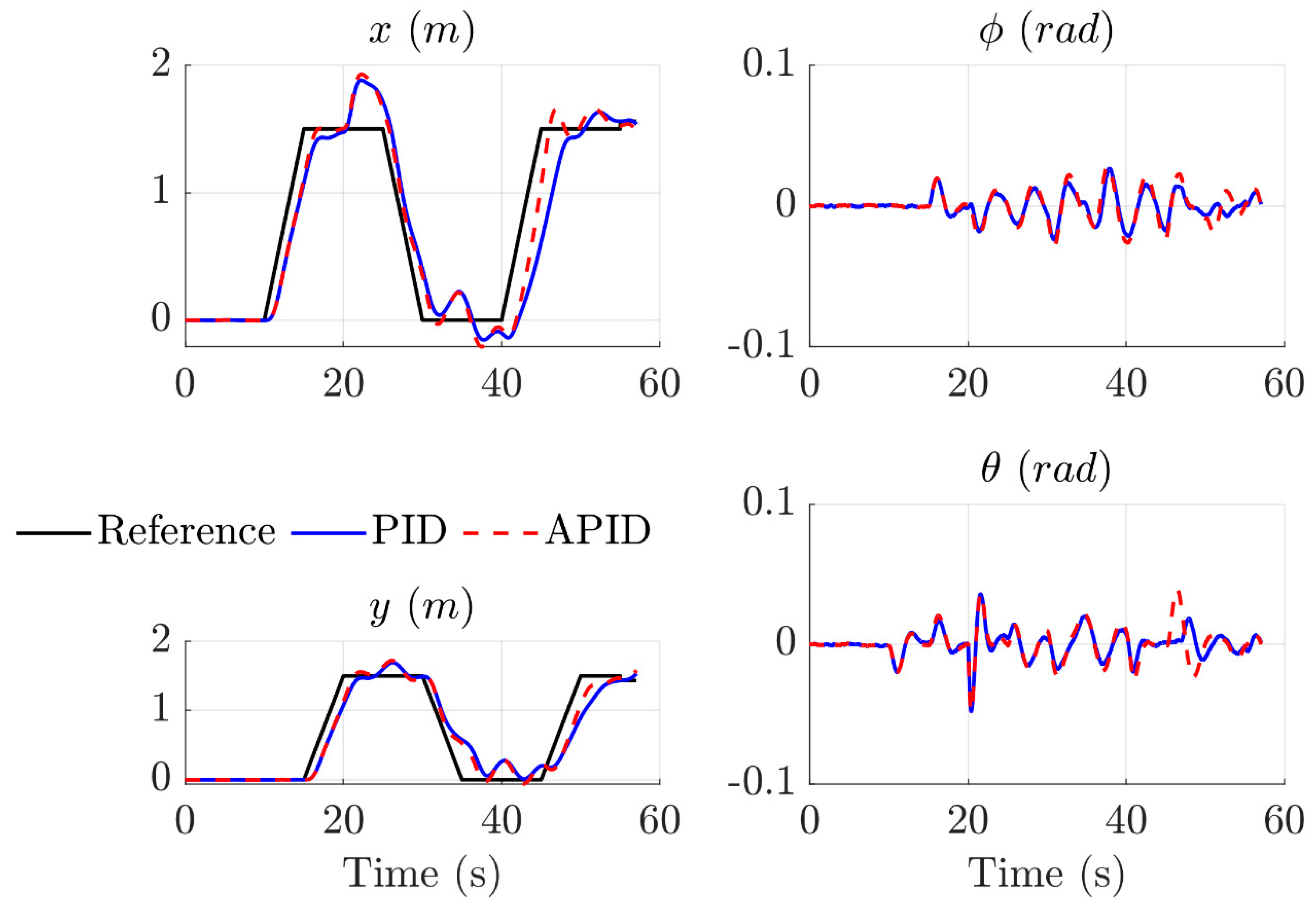
4.1.1. Waypoint Follower

The simulation begins by typing ‘parrotMinidroneWaypointFollowerStart’ in MATLAB command windows to open project model. For waypoint trajectory, the desired square shape of 1.5 m × 1.5 m was generated after the parrot mambo hover at 1.1 m. The yaw reference signal is held at zero, while the pitch and roll reference are produces by the virtual controller of x and y, respectively.

Figure 5 shows the performance of PID and APID controllers along the $x$, and $y$ axis, respectively. In this figure, the red dash line APID followed the desired reference black line closely, compared to the blue line PID for x and y, respectively. There are many ways to determine the performance of a system, as mentioned in [30]. However, in this case, we log the Integral Square Error (ISE) to measure the performance of the proposed control scheme, as shown in

Table 3. Waypoint Tracking error performance index using ISE.

	Dimension	PID	APID
Waypoint	$X$	1.9852	1.5537
	$Y$	2.0254	1.4851
Waypoint (Wind Gust)	$X$	4.8746	2.9054
	$Y$	3.0930	2.2544

. Without disturbance, the proposed APID controller scheme has improved over the PID controller by 21.7% and 24.5% for x and y, respectively. Figure 6 shows the trajectory in Cartesian coordinates for the examined controllers. Both PID and APID are able to maintain the aircraft on track, especially after performing take-off around starting point and landing nearly at the same position. However, it can be seen that APID closely to the reference projection and significantly 20% improve over the PID controller.

Figure 7 and Figure 8 show transient response along the x and y axes, and the trajectory in Cartesian coordinates when aerodynamics force injected into the system. Clearly shown in these figures, both PID and APID still able to keep the drone on track. However, the performance of each controller can determine by ISE on Table 3, where the error reduced from 4.8746 (PID) to 2.9054 (APID) on x axis, while 3.0930 (PID) to 2.2544 (APID) on y axis. Therefore, we can claim that the proposed APID controller scheme is more robust compared to PID controller against wind disturbance.

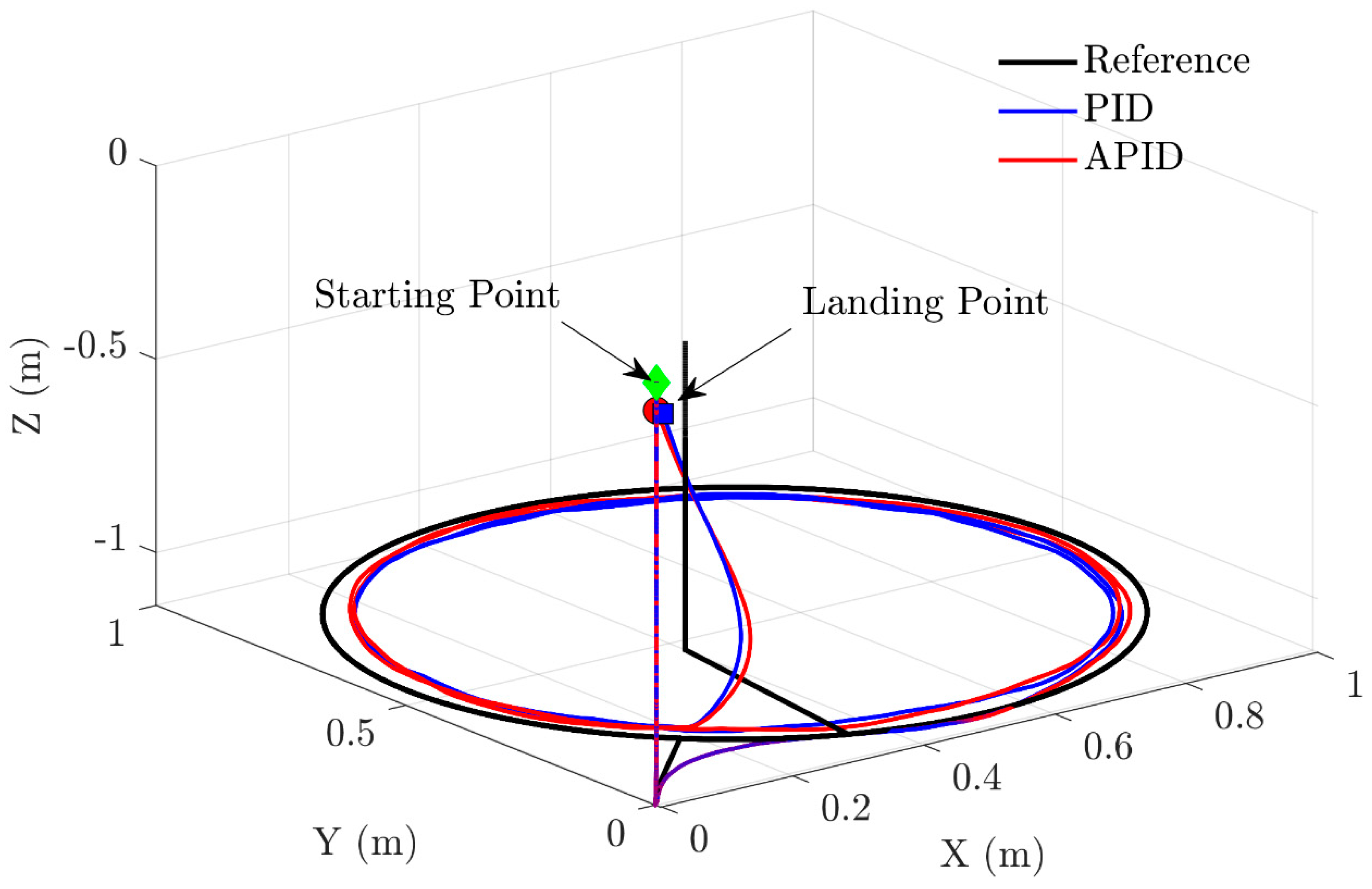
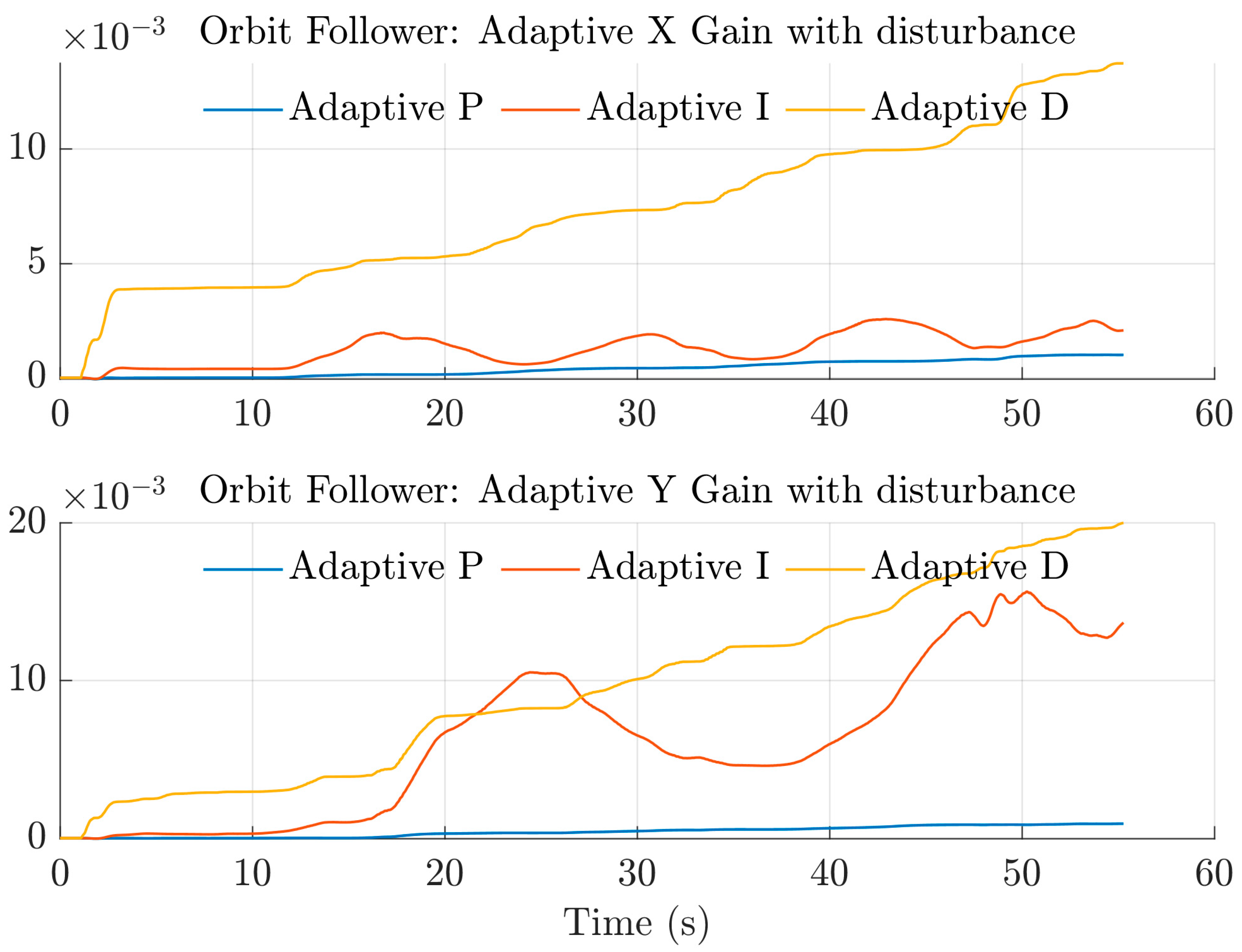
4.1.2. Orbit Follower

Orbit follower simulation begins by typing ‘parrotMinidroneOrbitFollowerStart’ in MATLAB command windows to open project model. For this orbit simulation, the orbit radius is fixed as 0.5 m in clockwise orbit direction with 1.1 m altitude. The drone is set to orbit twice. The yaw reference signal is held at zero, while the pitch and roll reference are produces by the virtual controller of x and y, respectively.

Figure 9 and Figure 10 show the transient response along the x and y axes, and the trajectory in Cartesian coordinates. These figures depict that the drone is capable of completing two orbits by employing either the PID or APID control schemes. However, from Table 3, the proposed APID controller scheme has improved over the PID controller by 5.5% and 7.4% for x and y, respectively.

Figure 11 and Figure 12 illustrate the response of the system along the x and y axes, as well as the trajectory represented in Cartesian coordinates, while the aerodynamic force is being applied. Figure 11 indicates that both the PID and APID control schemes enabled the drone to follow the track 15 s before the aerodynamic force was introduced into the system. However, after the force was introduced, the flight was affected, causing the drone to deviate slightly from the track. Nonetheless, the controller was able to steer the drone back on course. Additionally, Figure 12 provides a clear visualization of the drone following the orbit while overcoming the aerodynamic forces. According to the information presented in

Table 4. Orbit Tracking error performance index using ISE.

	Dimension	PID	APID
Orbit	$X$	0.8348	0.7885
	$Y$	0.7841	0.7257
Orbit (Wind Gust)	$X$	0.8774	0.8575
	$Y$	0.9577	0.9079

, we can make the assertion that the APID control scheme demonstrates greater robustness than PID, with an improvement of approximately 3% to 5%.

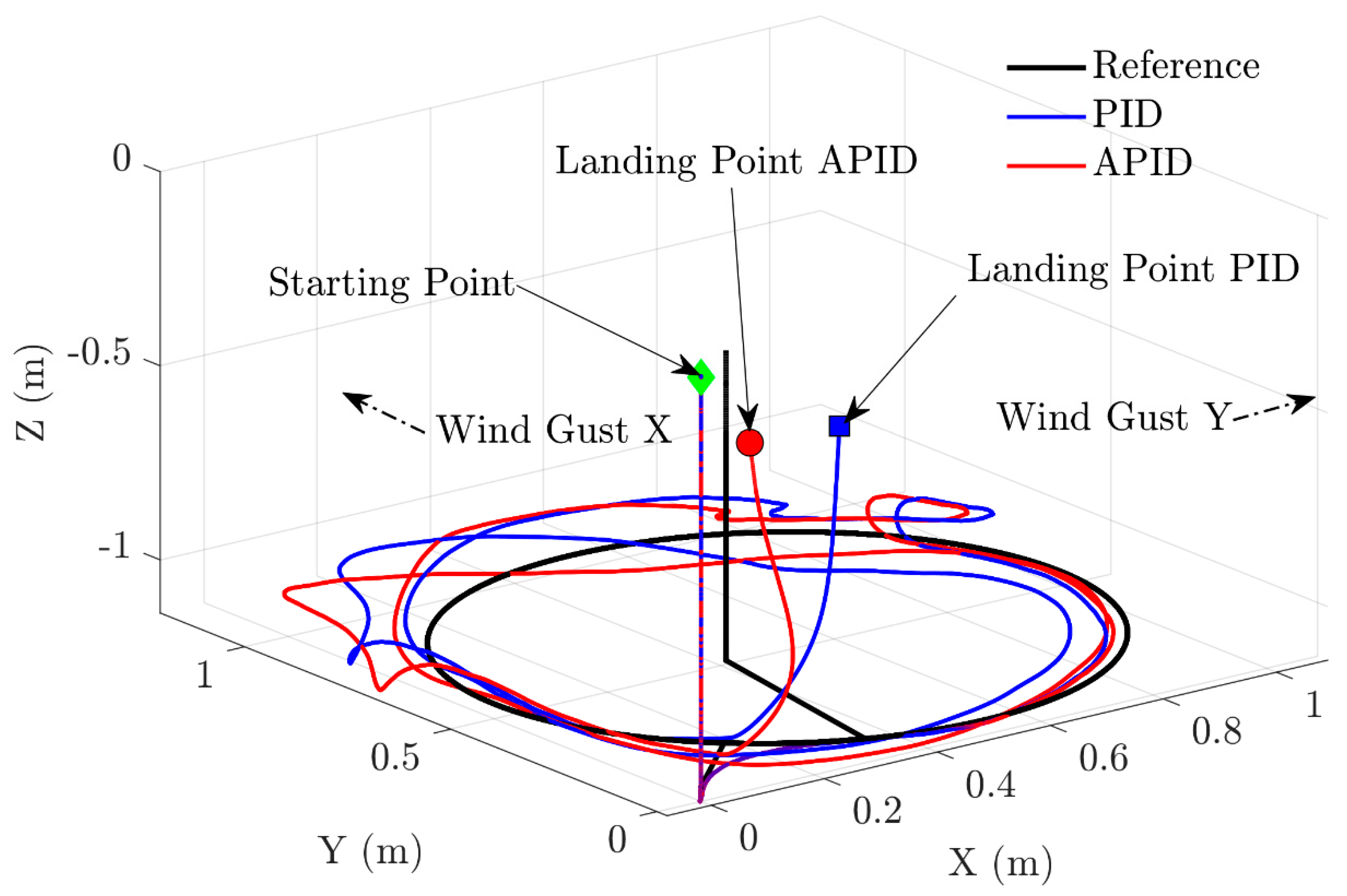
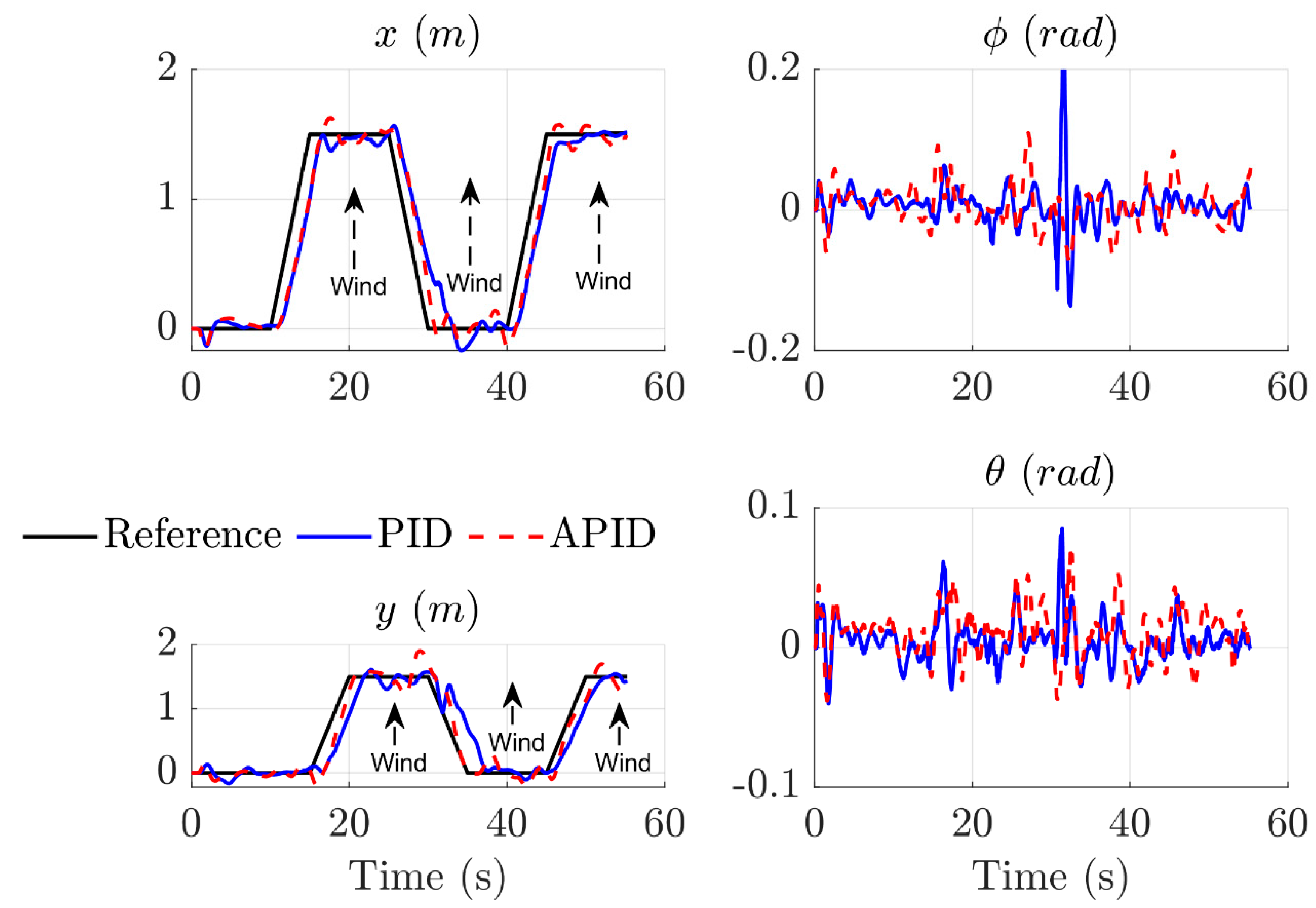
4.2. Experimental Results

Figure 13 depicts the hardware architecture of the Parrot Mambo Minidrone used in this experiment. The drone is equipped with two clockwise and two counterclockwise motors, an ultrasonic sensor, an optical flow sensor, and an MPU6050 3-axis gyroscope and accelerometer, all of which are controlled by an ARM9 microcontroller. The drone is powered by a 550 mAh 1S Lithium-Polymer (LiPo) battery, which allows for up to 9 min of flight time. Figure 14 illustrates the six-stage design and implementation flow for algorithm deployment, which includes:

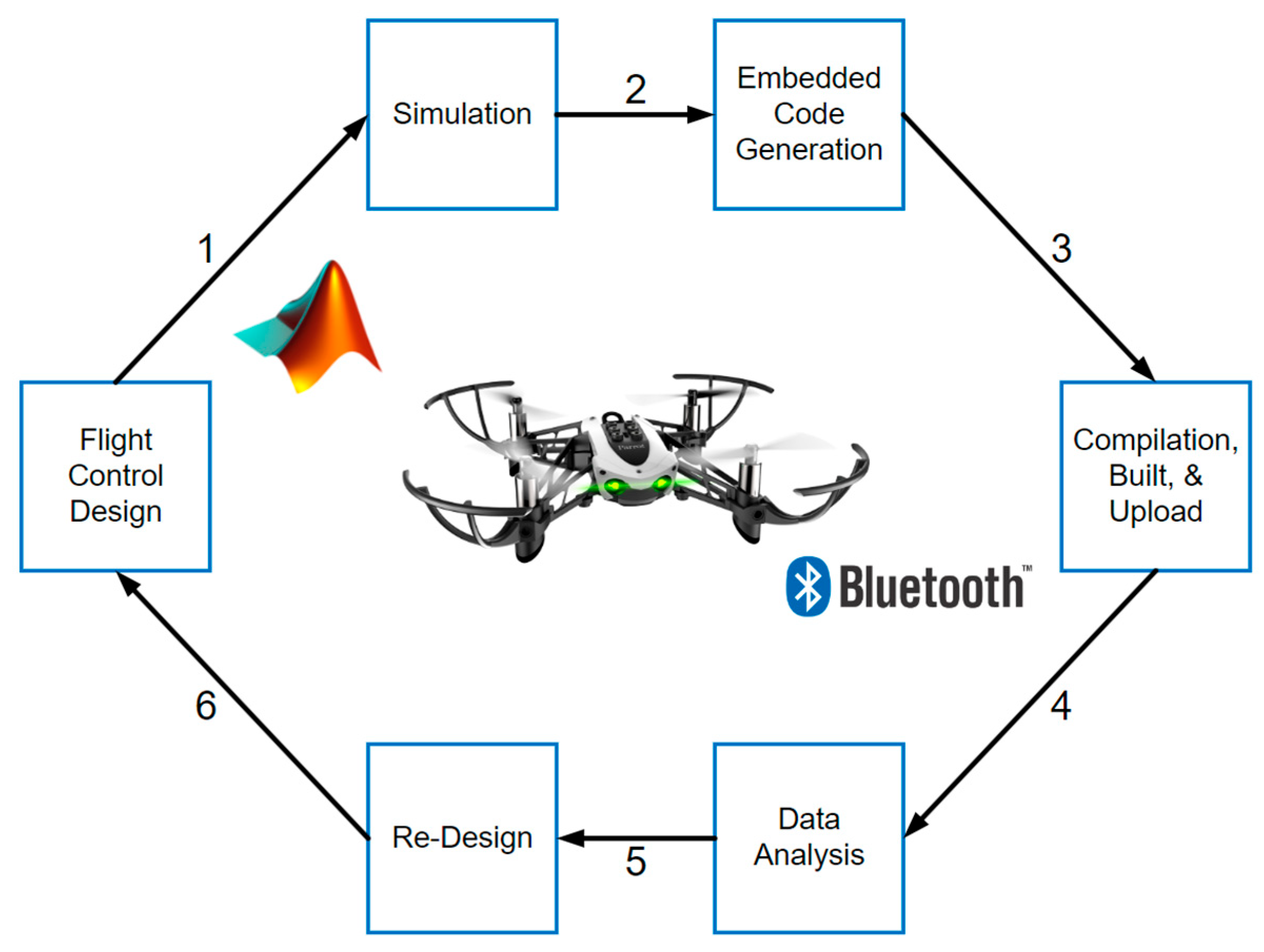
• Design of flight control: For this part, the control algorithms that will be implemented on the drone are designed using control theory principles to ensure the drone’s stability and safety while performing the desired flight maneuvers.
• Simulation: The flight control algorithms are tested in a MATLAB SIMULINK environment to identify potential issues and optimize the algorithms before deploying them on the actual Parrot Mambo Minidrone.
• Embedded Code Generation: After the flight control algorithms are validated in the simulation environment, the code that will be embedded into the drone’s flight control system is generated by MATLAB.
• Compilation, Built, and Upload: The generated code is compiled and built into the final firmware, which is uploaded wirelessly via Bluetooth onto the drone’s flight control system.
• Data Analysis: Once the drone is flying, data is collected from onboard sensors to ensure it behaves as expected. The data is downloaded from the internal storage of the drone’s flight control system and analyzed to identify potential issues and refine the control algorithms for improvement.
• Redesign: The control algorithms will be modified based on the data analysis to achieve desired performance. The design, simulation, and testing cycle is repeated to ensure the drone is safe, stable, and performs the desired flight maneuvers.

Figure 13. Parrot Mambo Minidrone Architecture.

Figure 13. Parrot Mambo Minidrone Architecture.

Figure 14. Design and implementation flow of algorithms deployment.

Figure 14. Design and implementation flow of algorithms deployment.

Figure 15 displays the layout and test field. To enhance optical flow sensitivity for height approximation, masking tape is applied on the floor black surface to establish visual differences. Parrot Minidrone is used to initiate its movement in a forward direction, and a blower is positioned 2 m away from its path. To produce wind gusts during this experiment, the Dong Cheng (DQF32) blower is utilized. It pulsates every 15 s randomly for approximately 1 s, generating an estimated gust volume of 1.6 m³/min (at Level 1 setting). The Parrot Minidrone will start in forward direction and the gust is set 2 m from the path. Table 5 displays the ISE performance index obtained upon the experiment completion, which is used to assess the controller performance. In this testing, the following hypotheses are made:

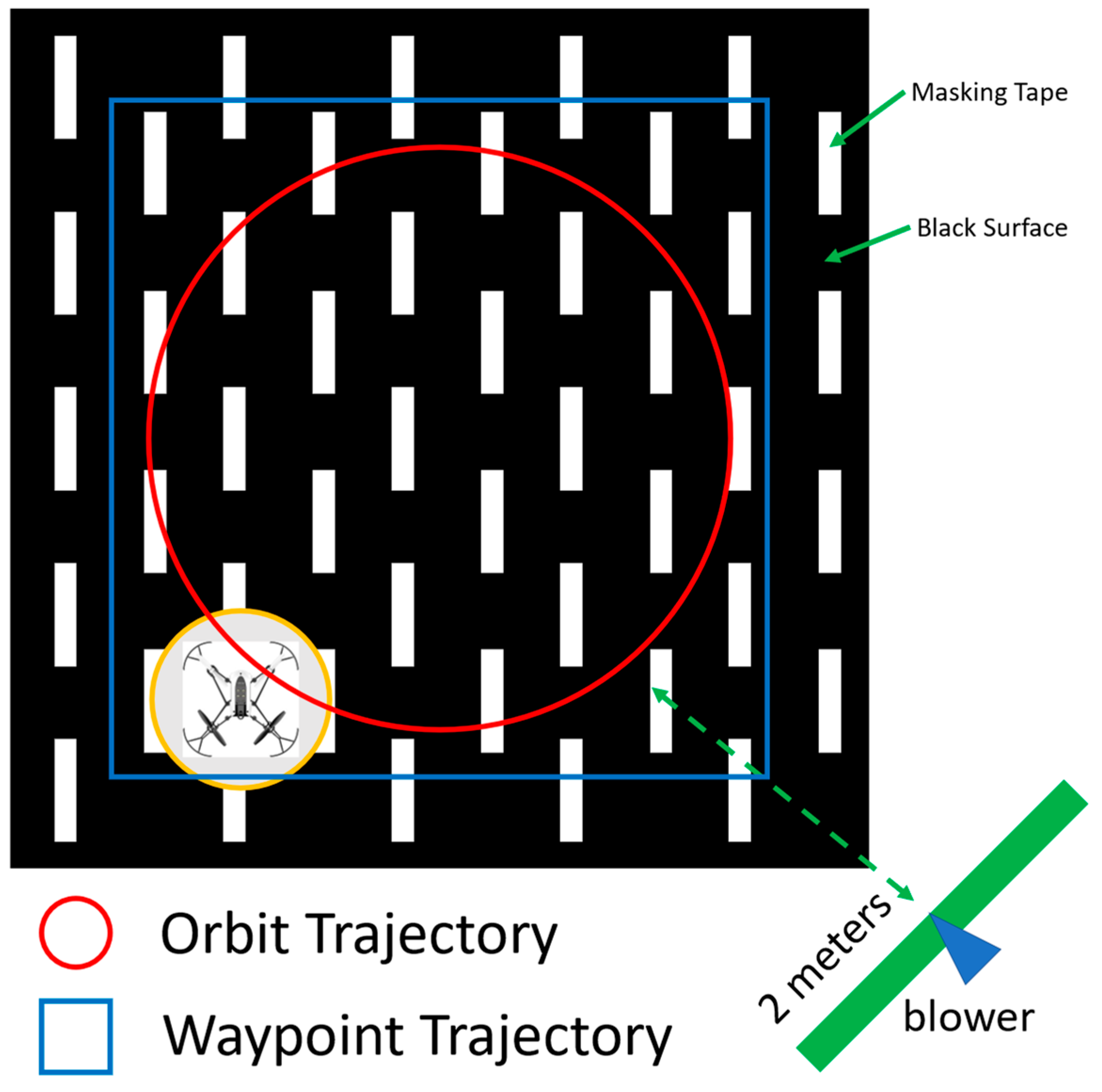
• Testing is performed in an air-conditioned hall.
• Parrot Mambo Minidrone form is presumed to be in a decent state.
• Propellers are assumed to also be in decent state, devoid of any dents.
• Motors are presumed to be in a decent state.
• Execution starting point remains the same.
• Lighting state is deemed to be in the range of fair to good.
• Wind gusts are arbitrarily produced.

Figure 15. Experiment setup and blower position.

Figure 15. Experiment setup and blower position.

Table 5. Error performance index using ISE during experiment with external disturbances.

	Dimension	PID	APID
Waypoint	X	2.9155	2.1500
	Y	4.1389	2.2719
Orbit	X	0.7560	0.7061
	Y	0.8278	0.6142

Table 5. Error performance index using ISE during experiment with external disturbances.

	Dimension	PID	APID
Waypoint	X	2.9155	2.1500
	Y	4.1389	2.2719
Orbit	X	0.7560	0.7061
	Y	0.8278	0.6142

4.2.1. Waypoint Follower

Figure 16 and Figure 17 depict the behavior of the drone in response to wind gust, showcasing the transient response along the x and y axes, as well as the trajectory in the xy coordinate system. Both the PID and APID control schemes are employed in this study, and these figures demonstrate their effectiveness in maintaining the drone’s trajectory. It is clear from the visual data that both controllers are capable of keeping the drone on track.

Further analysis, as presented in Table 5, reveals that the APID controller outperforms the PID controller by 26.2% and 45.1% in the x and y axes, respectively. These findings strongly suggest that the suggested APID control strategy is significantly more resistant towards external disruptions when compared to a standard PID controller. Considering these results, it can be concluded that the implementation of the APID controller can significantly enhance the overall stability and robustness of the drone system.

4.2.2. Orbit Follower

The impact of a wind gust during orbit following is a critical issue that affects the stability and performance of drone systems. In this context, Figure 18 and Figure 19 provide a visual representation of the transient response of the drone system along the x and y axes, as well as the trajectory in the xy coordinate system. These figures demonstrate that both the PID and APID controllers can maintain the drone’s trajectory in the presence of external disturbances.

To gain further insights, Table 5 presents a detailed comparison between the performance of the PID and APID control schemes. The results reveal that the APID control scheme exhibits a 6.6% improvement in the x-axis and a 25.8% improvement in the y-axis compared to the PID controller. These findings strongly suggest that the suggested APID control strategy is more frugal and efficient in mitigating the effects of external disturbances, thereby enhancing the overall stability and performance of the drone system during orbit following. It can be concluded that the suggested APID control scheme will significantly improve the resilience and stability of drone systems, particularly when dealing with challenging environmental conditions.

Figure 20 and Figure 21 show the adaptation of gain P, I, and D for both the Orbit and Waypoint followers, respectively, recorded during the experiment with external disturbances. From these figures, the adaptive gain P tends to converge at a specific point. It is clearly shown that while overcoming wind gusts, the adaptive gain I and adaptive gain D try to converge and stabilize over time.

5. Conclusions

This research work presents the real-time execution of position controllers deploying the APID method, as compared to the standard PID approach, for a Parrot Mambo Minidrone. A second order sliding mode control with adaptive mechanism is employed to modify the conventional parameters of the altitude controller. The success of this approach is evaluated through simulation and experimentation involving a waypoint follower and an orbit follower, with wind gusts acting as external disturbances. When the parameters that seemed optimal in simulations do not produce the desired outcomes in actual trials, the experiment has to be repeated with the parameters changed. The discrepancies might be caused by a number of factors, such as unaccounted environmental variables or limitations on how accurately the simulation can represent the intricate interactions of the system. These discrepancies can lead to unforeseen consequences or problems, such as the activation of a blower, which further complicate the experiment and require additional modifications to achieve the desired results. Finally in the experiment, it was found that the APID control scheme exhibited an improvement of more than 5% when compared to the PID controller. This is as determined by the integral square error. This observation suggests that the suggested APID control strategy is significantly more frugal against external interruptions such as wind gusts. Overall, these results highlight the potential benefits of the APID approach for the development of high-performance control systems for drones.