Abstract
Transonic buffet is a phenomenon of large self-excited shock oscillations caused by shock wave-boundary layer interaction, which is one of the common flow instability problems in aeronautical engineering. This phenomenon involves unsteady flow, which makes optimal design more difficult. In this paper, aerodynamic shape optimization design is combined with reinforcement learning to address the problem of transonic buffet. Using the deep deterministic policy gradient (DDPG) algorithm, a reinforcement learning-based design framework for airfoil shape optimization was constructed to achieve effective suppression of transonic buffet. The aerodynamic characteristics of the airfoil were calculated by the computational fluid dynamics (CFD) method. After optimization, the buffet onset angles of attack of the airfoils NACA0012 and RAE2822 were improved by 2° and 1.2° respectively, and the lift-drag ratios improved by 83.5% and 30% respectively. Summarizing and verifying the optimization results, three general conclusions can be drawn to improve the buffet performance: (1) narrowing of the leading edge of the airfoil; (2) situating the maximum thickness position at approximately 0.4 times the chord length; (3) increasing the thickness of the trailing edge within a certain range. This paper established a reinforcement learning-based unsteady optimal design method that enables the optimization of unsteady problems, including buffet.
1. Introduction
During the transonic flight of a vehicle, the phenomenon of self-excited shock oscillation caused by shock wave-boundary layer interaction at a certain combination of Mach numbers and angle of attack is called transonic buffet. This phenomenon involves unsteady flows, and there is still a lack of a unified explanation for its mechanism. Early researchers explained the occurrence mechanism of transonic buffet by constructing a feedback model of shock–Kutta wave interaction [1]. In addition, Crouch et al. [2,3]. drew the conclusion that such instability could lead to shock oscillations and dramatic lift fluctuations from the perspective of the global instability of the flow. Despite the possibility of encountering buffet, transonic flight has higher flight efficiency, therefore, most modern high-speed aircraft still use transonic speed as the cruise flight state. However, the pulsating load caused by transonic buffet can cause aircraft control deterioration, structural fatigue, and even flight accidents. The research on transonic buffet of vehicles has been difficult and has therefore become a hot spot in the field of aviation.
The early suppression and the elimination of the adverse effects of transonic buffet are usually conducted by two methods: control [4,5,6,7] and aerodynamic shape optimization [8]. Control is further divided into active control and passive control. There are two common passive control methods: (1) from the structural point of view, increasing structural damping to suppress transonic buffet or installing vibration isolators to protect the internal instruments of the vehicle; (2) changing the flow characteristics of the fluid on the wing surface, such as trailing edge slotting. The streamwise slot is a simple passive control [4,5] that can retard the expansion of flow separation caused by normal shock, but it is not effective in controlling the shock of periodic self-excited oscillations. The active control method is mainly to suppress the transonic buffet by improving the flow stability, such as installing a fluidic vortex generator (FVG) and a trailing edge deflector (TED) to control the flow in the trailing edge region. Yun [9] designed a shock control bump with a specific shape to achieve effective control of buffet. Gao et al. [10] established an unsteady flow model with oscillatory shock and a moving boundary. The model-based feedback control of buffet by trailing edge flap was designed by using pole configuration and the linear quadratic method respectively, which effectively controls the buffet. The open-loop, closed-loop, and machine learning adaptive control for buffet was also realized.
Although control measures are effective in controlling buffet, they often require additional structure and weight. In contrast, the aerodynamic shape optimization method can consider the transonic buffet constraint from the perspective of airfoil design, which can effectively achieve buffet suppression and also expand the flight envelope at the design stage. In addition, this method is carried out at the early stage of the vehicle design, which can reduce the design cost. Therefore, the aerodynamic shape optimization design is an ideal approach for the suppression of transonic buffet of a vehicle.
Thanks to the rapid development of computer technology, the accuracy and efficiency of CFD technology have been significantly improved. With the efficient CFD technology and optimization algorithm, the efficiency of aerodynamic shape optimization design has been greatly improved. It has gradually become a hot spot for research in various disciplines. At present, the aerodynamic shape optimization can be roughly divided into three categories according to different optimization methods: gradient optimization; global optimization based on the surrogate model; aerodynamic shape optimization based on machine learning.
Gradient optimization refers to identification of the optimal point by finding the partial derivatives of the objective function with respect to the design variables to determine the search direction. The gradient of the objective function can be derived by the direct method or the adjoint equation method [11]. Compared with the direct method, the efficiency of the adjoint method depends only on the number of objective functions, which validates its computational advantages. Jameson [12] first proposed the adjoint method based on Euler’s equation for transonic aerodynamic shape optimization of a vehicle. In terms of unsteady aerodynamic optimization, Nadarajah and Jameson [13] used this method to perform unsteady aerodynamic optimization of a helicopter rotor with drag reduction as the optimization objective, and achieved a 46% reduction in drag. Lee et al. [14] carried out flapping airfoils optimization based on the unsteady discrete adjoint approach. Although the adjoint gradient-based optimization method has fast convergence and high optimization efficiency, it is a local optimization algorithm, and the optimization falls into a local optimum. The global optimization algorithm can find the global optimal solution. However, in the process of aerodynamic shape optimization, the number of CFD calls of the global optimization algorithm is much larger than that of the gradient optimization algorithm, which also requires high computational cost. In order to improve the optimization efficiency, it is meaningful to use mathematical means to replace the large number of CFD numerical calculations in the optimization process by surrogate models. Sun [15] established a surrogate model based on artificial neural network to realize the optimization of aircraft aerodynamic performance. Wu [16] used a non-intrusive polynomial method and Kriging model to construct a stochastic surrogate model with random aerodynamic characteristics, and adaptively updated it based on historical optimization data to carry out optimization design. The model dimensionality is reduced based on the idea of transformation and decomposition. Later, with the booming development of machine learning, in order to further improve the efficiency of optimization, researchers began to apply it to aerodynamic shape optimization design. Li [17] used the data-driven approach to optimize the aerodynamic shape for buffet-onset constraint. Hu [18] used an artificial intelligence method based on deep neural networks to improve efficiency. In addition, Viquerat et al. [19]. used deep reinforcement learning to perform direct shape optimization and applied it to the field of aerodynamics, that is, the optimal design of the aerodynamic shape of a vehicle. Runze [20] used a deep reinforcement learning approach based on a surrogate model to achieve the optimal design of drag reduction for a supercritical airfoil in a steady state. Therefore, the introduction of machine learning made the optimization framework more efficient.
Most of the previous aerodynamic shape optimizations were performance optimizations in a steady state, where a surrogate model between lift-drag and shape parameters was constructed by CFD. In contrast, transonic buffet optimization involves an unsteady flow problem where it is difficult to build a traditional surrogate model. The reinforcement learning derived from machine learning, has a powerful inductive learning capability, and has great potential for application in the field of flow field modeling and aerodynamic optimization [21,22,23,24].
This paper studies from the perspective of aerodynamic shape optimization, which is able to obtain the desired aerodynamic performance by adjusting the aerodynamic shape of a vehicle (e.g., airfoil) without adding additional structures or devices. Based on reinforcement learning, a framework is constructed for the aerodynamic shape optimization design of a vehicle using the deep deterministic policy gradient (DDPG) algorithm. The class shape transformation parametric method is performed to represent the airfoil shape efficiently and accurately with a small number of parameters. The aerodynamic performance is calculated by CFD approach based on the Reynolds average Navier–Stokes. Using this framework, it is possible to achieve the optimal design of the aerodynamic shape of a vehicle in an unsteady state.
2. Numerical Setup
2.1. Shape Parameterization Method and Simulation Method
The class shape transformation (CST) parameterization method has strong fitting ability [25]. Figure 1 shows CST parameterization fitting results of NACA0012 airfoil. In this study, the CST is used to achieve the parameterization of the airfoil shape. The geometric coordinates of the shape can be directly represented by the CST equation with the following expression:
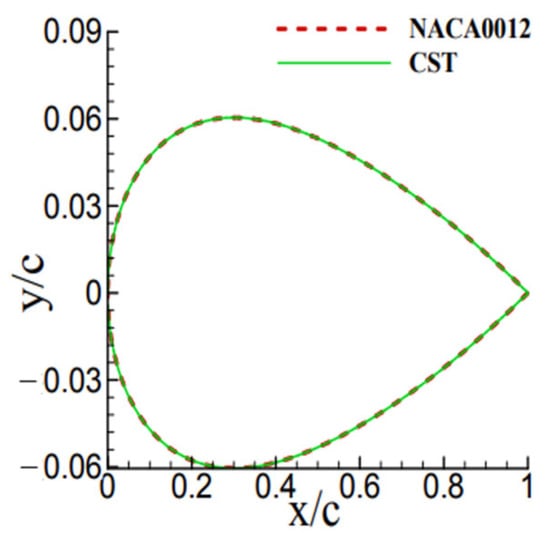
Figure 1.
Comparison between NACA0012 airfoil and CST parameterized fitted result.
In the above Formula (1), is a class function:
is a type function and meets the following requirements:
where, is the Bernstein polynomial, and is the undetermined coefficient solved by the least square method by substituting the shape data of the airfoil. In Equation (1), is the thickness of the trailing edge of the airfoil. For the conventional airfoil with a thicker leading edge and a thinner trailing edge, and are taken as 0.5 and 1.0.
The numerical simulation method used in this study is the unsteady Reynolds average Navier–Stokes (URANS). The URANS equation based on the turbulence model is capable of analyzing the transonic aerodynamic characteristics, including transonic buffet, which is a commonly used numerical simulation method for complex turbulent flows in engineering.
Based on the continuous fluid hypothesis, URANS equations are used to represent the fluid motion laws. The transonic buffet is numerically simulated by using the two-dimensional URANS equation, which can be expressed in the integral form of Equation (2):
where, represents a control unit. The equation is for two-dimensional flow. is a surface; represents its boundary; is the normal unit vector outside the boundary; is the control volume area; is the side length. is the vector of conservative variables; is the fluid density; is the velocity vector; is the total energy per unit area. and represent inviscid flux and viscous flux respectively.
The N-S equation is applied directly to the dissected unstructured grid cell, and then the integral equation is transformed into a discrete set of equations by solving the inviscid and viscous flux terms, where the unknown quantity is the flow parameter at the center of the grid cell. Equation (2) can be discretized as:
is the area of the i-th grid cell and denotes the residual value of the i-th grid cell. The second-order backward differencing of the derivative part of the left-hand side is shown below:
where denotes the length of the real time step, and denotes the number of the real time steps. The derivative of the conservation variable with respect to the pseudo-time is introduced at the left end of the above equation:
Due to the stochastic nature of turbulent motion and the nonlinearity of the N-S equation, the Reynolds averaging equation is not closed, and so an empirical turbulence model is often introduced to close it. In this study, the Spalart–Allmaras (S–A) turbulence model is used [26]. Based on the eddy viscosity assumption, the S–A model working variables are solved by the transport equation:
In addition, for the mesh deformation problem caused by the change of the airfoil in the optimization process, this paper adopts the radial-basis functions (RBFs) dynamic mesh method [27]. This method has high computational efficiency, good adaptability to large scale deformation problems, and the quality of the computational mesh after deformation can be effectively guaranteed.
2.2. Simulation Method Validation
To verify the accuracy of the numerical simulation method proposed in this paper, the buffet onset boundaries of two airfoils, NACA0012 and RAE2822, were calculated and compared with results from previous studies [28,29]. As shown in Figure 2, a computational grid was established for the RAE2822 airfoil. Figure 3a shows the transonic buffet onset boundaries for NACA0012 and compares them with the results of the wind tunnel test by Doerffer et al. [28]. in 2011; Figure 3b shows the calculations for supercritical airfoil RAE2822 and compares them with the results from Tian’s study [29]. The results of the simulation method are in close agreement with those of the references, which establishes the methodological basis for subsequent research on transonic buffet optimization design on reinforcement learning.
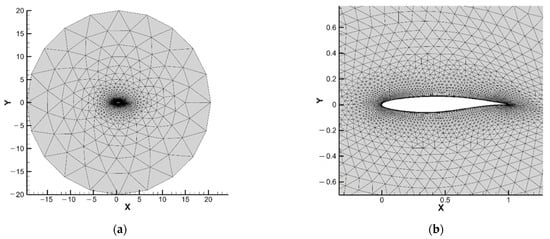
Figure 2.
The CFD computational grid of the RAE2822 airfoil. (a) The global grid of RAE2822 airfoil; (b) the near-wall grid.
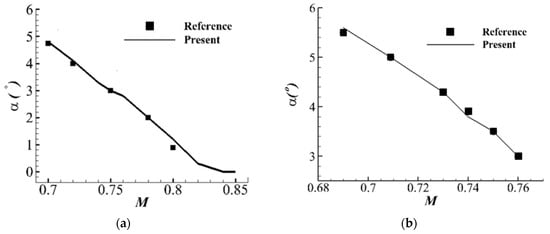
Figure 3.
Calculation of the transonic buffet onset boundary by the simulation method. (a) The comparison of calculated results of NACA0012 with the wind tunnel test result of Doerffer [28] (b) The comparison of calculated results of RAE2822 with the reference result of Tian [29].
3. Reinforcement Learning-Based Design Framework for Aerodynamic Optimization
3.1. DDPG Algorithm
Reinforcement learning can be categorized into two types at the model level: model-based and model-free. In the model-based approach, an agent learns a model that describes how the environment works based on its observations and uses this model to plan actions. However, in most applications, the model is unknown. A way to find the optimal policy without modeling the environment is model-free reinforcement learning. The DDPG is a model-free approach to reinforcement learning, which is a mathematical model that does not rely on the environment, usually with actions as inputs and states as outputs. The DDPG algorithm [30] contains several networks and related concepts, the mathematical definitions of which are given below.
Deterministic action policy : in the DDPG algorithm, the action of the agent at each step is calculated by Equation (6), where denotes the state:
Actor network : the deterministic action policy is approximated by applying a fully connected neural network, and the approximated network is called the actor network. The actor network consists of two parts: the online actor network and the target actor network. The online actor network updates the network parameters and selects an action based on the current state , which is used to interact with the environment and generate the next state and reward . The target actor network selects the optimal next action based on the next state .
Action policy distribution : this is the distribution function of the set of states produced by an agent under a certain action policy .
Value function: this is the value expectation obtained by taking action under state according to deterministic action policy , based on the definition of Bellman equation as shown in Equation (7):
Critic network: as can be seen from Equation (7), the value function is a recursive function, and in order to avoid recursively computing the value , the DDPG algorithm approximates the value function using a fully connected neural network, which is named the critic network .
In the DDPG algorithm, the actor network is used to represent the deterministic policy in reinforcement learning, and the input and output are the state and the deterministic action . The critic network is used to represent the action value function , and is used to solve the Bellman equation. The actor network is used to update the policy and the critic network is used to approximate the value function. The objective function is the expectation of discounted cumulative rewards, as shown in the following equation:
The optimal deterministic policy is the policy that maximizes the objective function :
The gradient of the objective function with respect to the actor network is equivalent to the expected gradient of with respect to . Therefore, the derivative of can be derived based on the chain derivative rule. The method for updating the actor network is obtained as shown in Equation (9):
In the above equation, denotes the reward obtained after choosing an action according to policy in state . And . With the deterministic policy , Equation (9) can be deformed as
The objective function which uses the gradient ascent algorithm in Equation (9) above is optimally designed. To reach the goal of increasing the cumulative reward expectation, the agent is made to update the actor network along the direction of increasing .
The critic network in the DDPG algorithm, on the other hand, is updated based on the deep Q-learning (DQN) approach [31], and the critic network gradient is shown as follows:
where the target value is and denote the target critic network and the target actor network, respectively. The goal of the DDPG algorithm training is to maximize the target function while minimizing the loss of the critic network . Similarly, the critic network is divided into the online critic network and the target critic network. The former updates the network parameters and calculates the Q-value of the current state-action pair ; while the latter is responsible for calculating the .
3.2. Reinforcement Learning-Based Optimization Framework
The framework of reinforcement learning contains five elements: agent, state, environment, reward, and action. Among them, the agent is the ontology of reinforcement learning and acts as the decision maker or learner in the process. The environment refers to everything in the reinforcement learning except the agent, which mainly consists of the state set. In this framework, the environment refers to the flow field. The state is loaded with the data of the environment. The action refers to the action made by the agent. After making an action, the agent obtains the reward signal from the environment and learns how to maximize this reward. Figure 4 shows the block diagram of the reinforcement learning process, where the algorithm first initializes the grid parameters and then interacts with the environment. During each interaction, the agent outputs an action based on the state observed from the environment, after which the environment moves to the next state and provides feedback on the reward. The agent judges whether the network parameters converge at the end of each round; if they do not, they are optimized using the interaction data; and if they do, the reinforcement learning optimization is ended.
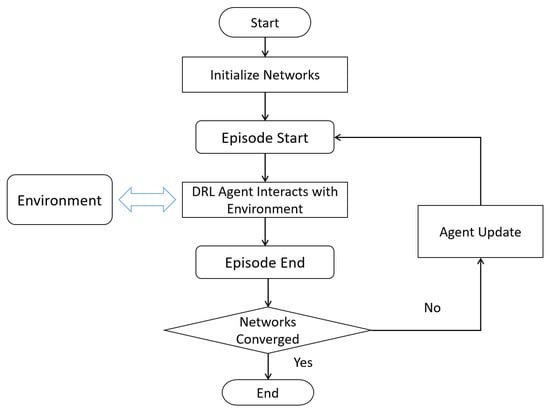
Figure 4.
Reinforcement learning process block diagram.
In this paper, the reinforcement learning framework is divided into the following modules: (1) empirical cache pool; (2) fully connected neural network framework; (3) reinforcement learning algorithm; (4) main function. The empirical cache pool realizes the data caching and sampling extraction of the interaction between the flow field (environment) and the optimization system. The fully-connected neural network framework module implements the fully-connected neural network framework construction. Set the activation function. The reinforcement learning algorithm module inherits the above two modules and sets up the optimizer to realize sampling from the experience cache pool. It then calculates the difference between the output of the actor and critic networks and the target value, and optimizes the two groups of networks and the saving and loading of the network model. The relevant hyperparameters are set in the main function, and the flow simulation executable is called. After one round, the data is read into the experience cache pool, and the loss function is defined according to the optimization target. The neural network is optimized, and the optimization process reward changes are recorded, while the neural network parameters are saved after the convergence condition is satisfied. The actor network has three layers; the input is the state and the output is the action; the intermediate layer has an input dimension. The critic network also has three layers; the input is the state and action, and the output is the reward; the middle layer input dimension is 256, while the output dimension is 128.
3.3. Optimization Framework Validation
The proposed optimization framework in airfoil optimization is verified through a comparative study. The airfoil steady drag reduction optimization is performed for the RAE2822 airfoil using the reinforcement learning-based aerodynamic shape optimization framework, with reference to the study on aerodynamic shape optimization conducted by Wu et al. [16,32].
In the study of Wu et al. [32], the optimized design of drag reduction airfoil for the RAE2822 airfoil was carried out in steady state, and the optimized state was selected as Ma = 0.734, Re = 6.5 × 106, α = 2.8°. The optimized mathematical model is shown in Equation (10):
The lift coefficient, airfoil area and pitch moment coefficient constraints with drag coefficient reduction are set as the goal. The optimization state is consistent with that in the reference, and the optimization results in this section are given in Table 1 for comparison with the results of Wu et al. [32]. Compared with the airfoil drag reduction rate of 42% of the reference, the optimized framework achieves a stronger one of about 46% from 0.0193 to 0.0105. Figure 5a shows the results of optimization; (b) shows the pressure coefficient distribution on the airfoil surface before and after the optimization. Figure 6 shows the comparison of flow field before and after the drag reduction optimization. After optimization, the airfoil shock intensity is significantly weakened, and the distribution of pressure coefficients on the upper surface is similar to the literature results [32], with two shocks, the first of which is close to the leading edge position of the airfoil, and the drag force is reduced.

Table 1.
Comparison of the optimization results of the proposed framework with the reference results.
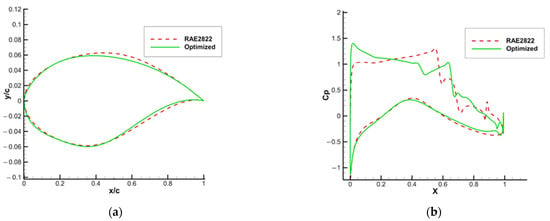
Figure 5.
Optimization results of RAE2822 airfoil drag reduction at Ma = 0.734, α = 2.8°, Re = 6.5 × 106. (a) The comparison of the airfoil before and after optimization. (b) The pressure coefficient distribution before and after optimization.
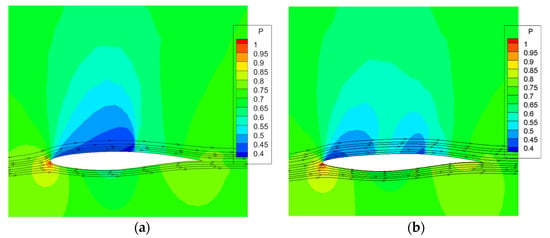
Figure 6.
Comparison of the flow field diagram before and after RAE2822 airfoil drag reduction optimization at Ma = 0.734, α = 2.8°, Re = 6.5 × 106. (a) The pre-optimized. (b) The post-optimized.
4. Reinforcement Learning-Based Optimization for Transonic Buffet
The variance of the lift coefficient is chosen as the buffet optimization design index. The transonic buffet of the aircraft involves the unsteady flow of the fluid, and the determination of the design index is the prerequisite for buffet optimization. Successfully characterizing the strength of the buffet and refining the optimization index determine the success of the optimization. Thomas and Dowell et al. [33]. used the amplitude of lift coefficient pulsation generated by the airfoil as the optimization objective, and its practical effect is to achieve buffet suppression by suppressing the lift pulsation under forced motion. In addition, Kenway and Martins [34] used the separation zone on the wing surface as an indicator to assess the buffet strength. However, since buffet occurs in an unsteady state, this makes the area of the separation very difficult to solve, coupled with the increase in the angle of attack, while the gradual expansion of the separation zone contradicts the existence of exit boundary of the buffet. Xu et al. [35] used the buffet load as a design index and constructed a surrogate model to carry out the optimal design of the aerodynamic shape of the vehicle. In this work, the following points were considered.
- (1)
- By considering the airfoil as a stationary rigid body, the original problem is simplified to optimize the elimination of the pulsation load generated by the flow instability on the airfoil surface.
- (2)
- Since the pulsation of the lift coefficient is often the strongest among all the aerodynamic indices when the flow instability buffet occurs, the goal of the optimized design is to suppress it.
- (3)
- The design index is extracted from the indicators characterizing the strength of the lift coefficient pulsation, while the variance of the lift coefficient within a certain period of time is selected as the design index.
- (4)
- Optimization is carried out in the state of strong lift pulsation, and different design states are selected for different airfoil types.
- (5)
- The research on aerodynamic shape optimization design is based on reinforcement learning.
The constructed mathematical model for transonic buffet optimization is given by Equation (11). is the variance of the lift coefficient, which is used to characterize the buffet strength, and ; is the number of sampling points of the lift coefficient; and denote the mean values of lift coefficient and drag coefficient, respectively; is the maximum thickness of the airfoil:
Figure 7 shows the research framework of the reinforcement learning-based transonic buffet optimization design.
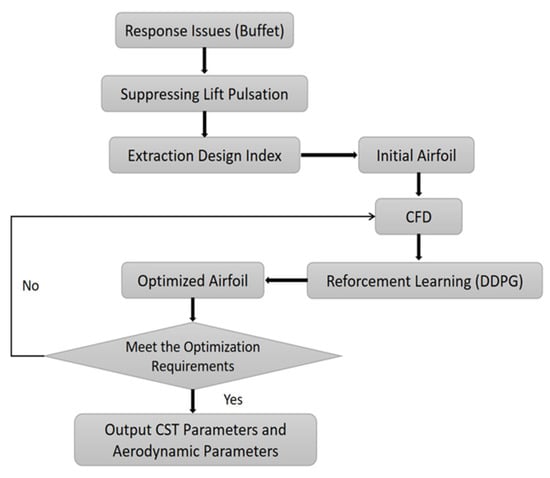
Figure 7.
Framework for the reinforcement learning based transonic buffet optimization design.
4.1. NACA0012 Airfoil Buffet Optimization
The reinforcement learning reward is set according to Equation (11). For the base airfoil NACA0012, the state Ma = 0.7, α = 5.5°, and Re = 3 × 106 has intense transonic buffet, and so it is selected as the optimized state. The reinforcement learning reward is set as follows:
is the variance of lift coefficient, which is the target, to ensure that the optimized airfoil can play a significant role in suppressing buffet. is the difference between the time-averaged values of the lift coefficients before and after optimization, which is one of the constraints to guarantee that the lift performance of the optimized airfoil. In addition, is the drag constraint to ensure that the drag performance of the optimized airfoil will not deteriorate. is the maximum thickness of the airfoil, and its geometry shape is constrained by setting this objective. ω is the weighting factor of the objective and each constraint. denote the time-averaged values of the lift coefficient and drag coefficient of the initial airfoil NACA0012, respectively, and is the maximum thickness of the airfoil NACA0012.
As shown in Figure 8, while the leading edge of the optimized airfoil is obviously narrower, the maximum thickness position is shifted back from 0.3 times of the original chord length to about 0.4 times of that. However, the maximum thickness remains meanwhile unchanged, the thickness of the trailing edge is slightly increased, and the leading edge of the airfoil narrows. As shown in Figure 9, the optimized airfoil has a higher lift coefficient and lower drag coefficient, which improves the aerodynamic performance compared to the initial airfoil. As shown in Figure 10, the buffet is completely suppressed in the optimized state and the buffet onset boundary is raised. No buffet occurs between 4° and 6.1°, and only a slight buffet occurs at 6.3°. Figure 10b shows the comparison of buffet onset boundaries before and after transonic buffet optimization at different Mach numbers.
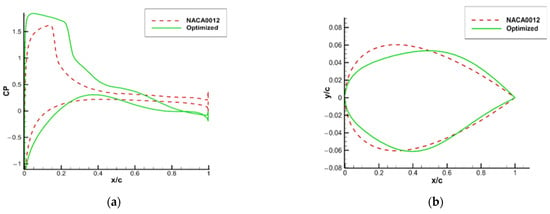
Figure 8.
NACA0012 airfoil transonic buffet optimization results at Ma = 0.7, Re = 3 × 106. (a) The airfoil surface pressure coefficient distribution before and after optimization at (b) The comparison of airfoil before and after optimization.
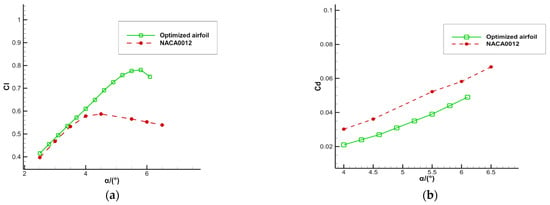
Figure 9.
Comparison of aerodynamic performance of NACA0012 airfoil before and after optimization at Ma = 0.7, Re = 3 × 106. (a) The comparison of lift coefficients before and after optimization. (b) The comparison of drag coefficients before and after optimization.
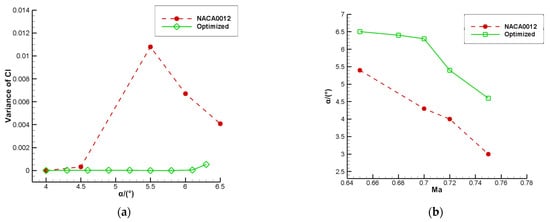
Figure 10.
The buffet performance of NACA0012 optimization results. (a) The buffet strength at different angles of attack before and after optimization. (b) The comparison of buffet onset boundaries before and after optimization at different Mach numbers.
Figure 11 shows the flow field diagrams near the airfoil before and after the optimization of NACA0012. Figure 11a–d displays the flow field diagrams at four different moments within one buffeting cycle. With the change of time, the shock on the airfoil surface and the separation zone near the trailing edge also change periodically. At moment , the shock is the closest to the leading edge and the flow separation near the trailing edge is the most intense. Figure 11e shows the flow field diagram of the optimized airfoil. The optimized airfoil surface flow is stable, and the shock range is expanded compared with the initial airfoil. Because of the narrowing leading edge, the shock position appears to be shifted back, which results in a suction peak at the leading edge of the optimized airfoil and a significant improvement in the aerodynamic performance. Additionally, the flow near the trailing edge is stable, and no flow separation occurs. The buffet is significantly suppressed due to the suppression of the interaction between the shock and the separation zone.
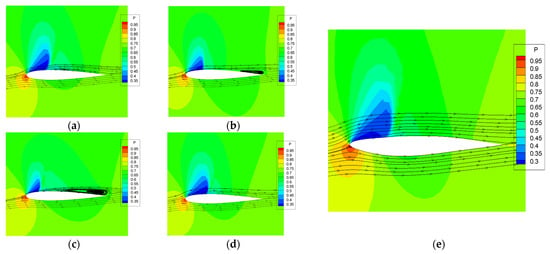
Figure 11.
Distribution of streamlines near the airfoil before and after optimization. (a)–(d) The streamline distributions of the NACA0012 airfoil at moments respectively. (e) The streamline distribution of the airfoil after optimization.
4.2. RAE2822 Airfoil Buffet Optimization
In this section, the transonic buffet optimization is performed for the RAE2822 airfoil. For the optimization of NACA0012, not only the buffet performance but also its steady aerodynamic performance is improved. However, as a typical symmetric airfoil, NACA0012 has poor aerodynamic performance itself in the transonic state, and the optimization can often achieve a large performance improvement. The RAE2822 airfoil, on the other hand, is a supercritical airfoil with superior performance at transonic velocities, and its performance is further improved by the buffet optimization, which proves the advantages of the method.
Set the reinforcement learning reward. Similar to NACA0012, the state with intense buffet is selected as the optimization state, for RAE2822 that is, Ma = 0.75, Re = 1.2 × 107, and α = 4.0° [29]. The specific reward settings are as follows:
In the above equation, the lift coefficient variance is selected as the optimization objective. Similar to the reward setting in the optimization of NACA0012, the lift, drag, and airfoil maximum thickness constraints are set. is the time-averaged value of the lift coefficient after optimization; are the time-averaged value of the lift coefficient, the time-averaged value of the drag coefficient, and the maximum thickness of the airfoil of the initial RAE2822, respectively. The airfoil area is measured after NACA0012 buffet optimization, and a slight reduction is found. Therefore, in the optimization for RAE2822, the airfoil area constraint is added so that the optimized airfoil area is not lower than the initial one (). In addition, the RAE2822 airfoil itself has good lift-drag characteristics. Based on the NACA0012, the weighting factors are adjusted, and , , , and are appropriately reduced to further focus the optimization on the buffet suppression.
The optimized airfoil buffet is suppressed with the lift coefficient increased and the drag coefficient reduced. Figure 12 shows the results of the airfoil optimization. Similar to NACA0012, the optimized airfoil shows a narrowing leading edge and a thickening of the trailing edge, with the maximum thickness position appearing at about 0.4 times the chord length. As shown in Figure 13 and Figure 14, the optimized airfoil has improved buffet performance and aerodynamic performance. In the optimized state (Ma = 0.75, α = 4.0°, Re = 1.2 × 107), the optimized airfoil completely eliminates the buffet and improves the buffet onset boundary, slight buffet occurs at the angle of attack α = 4.2°, and the buffet onset angle of attack boundary is improved by about 1.2°. Figure 13b shows the buffet optimization result of the RAE2822 airfoil. The optimized airfoil improves the buffet boundary not only in the optimized state, but also in other states.
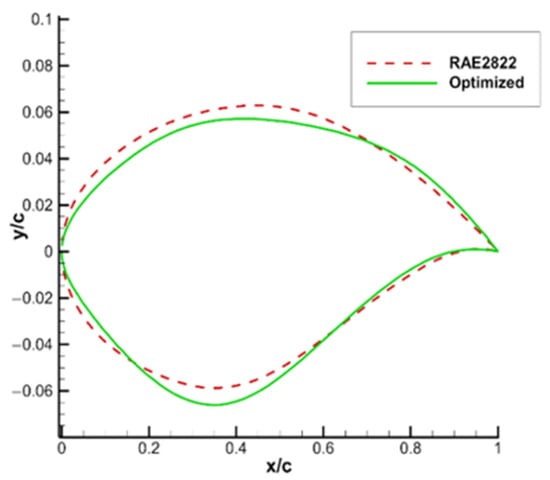
Figure 12.
The comparison of RAE2822 airfoil before and after optimization.
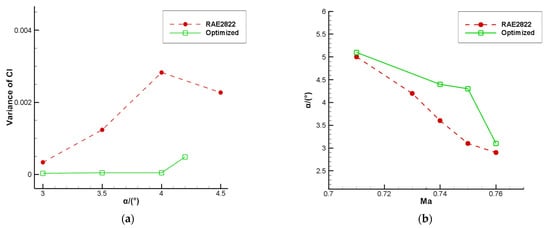
Figure 13.
RAE2822 airfoil transonic results with Ma = 0.75, Re = 1.2 × 107. (a) The comparison of the airfoil before and after optimization. (b) The comparison of buffet onset boundaries before and after optimization at different Mach numbers.
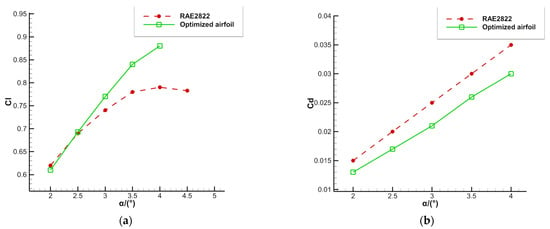
Figure 14.
Comparison of the lift coefficients and drag coefficients before and after optimization at Ma = 0.75 and Re = 1.2 × 107. (a) The comparison of lift coefficients before and after optimization. (b) The comparison of drag coefficients before and after optimization.
As shown in Figure 15a–d, in one buffet cycle, the RAE2822 airfoil upper surface shock is closer to the leading edge at , and the flow separation at the trailing edge is more drastic. After the optimization, the leading edge of the airfoil becomes narrower; the shock is shifted back. Two shock waves appear on the upper surface, and the flow stability increases. In addition, the thickness of the trailing edge is increased, so that the flow separation is limited, and the buffet is eliminated. Before optimization, the strength and area of the shock wave expend when buffet occurs. When buffet is suppressed, there is no flow separation behind the shock foot. This is consistent with the findings of Zhang et al. [36].
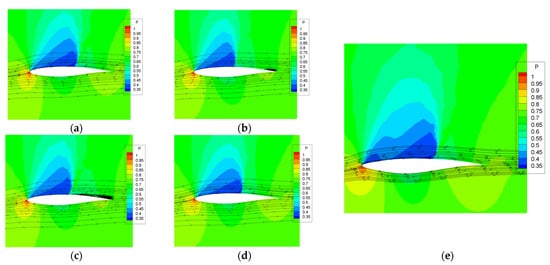
Figure 15.
Distribution of streamlines near the airfoil before and after optimization. (a)–(d) The streamline distributions of the RAE2822 airfoil at moments respectively. (e) The streamline distribution of the airfoil after optimization.
4.3. The Relationship between Buffet and Airfoil Geometric Characteristics
The optimized design results of the buffet for two different airfoils, NACA0012 and REA2822, show that the unsteady aerodynamic shape optimization design method can effectively suppress transonic buffet and significantly improve transonic flow stability. Based on the final optimization results of NACA0012 and REA2822 airfoils, three conclusions can be drawn.
- (1)
- The thickness of the leading edge has an influence on the transonic buffet. A narrower leading edge thickness is beneficial to improve the transonic buffet performance, suppress buffet, and improve the flow stability of the airfoil surface.
- (2)
- The position of the maximum thickness has an influence on the transonic buffet. In the optimization results of the above two airfoils, the maximum thickness position of the airfoil changes, and it appears near to 0.4 times the chord length.
- (3)
- The trailing edge thickness has an influence on transonic buffet. Both the symmetric airfoil NACA0012 and the supercritical airfoil RAE2822 can suppress buffet by increasing the trailing edge thickness of the airfoil in the optimization process of the design for transonic buffet. The flow stability can be increased by appropriately increasing the trailing edge thickness to suppressed the buffet.
The relationship was investigated between buffet and airfoil geometry characteristics. Although there is consistency in the optimization results of buffet for two airfoils, the conclusions presented above are still specific to these configurations and their generality needs to be further verified. Therefore, this paper further investigated the relationship between buffet and airfoil geometrical characteristics. The effect of airfoil leading edge thickness, trailing edge thickness, and maximum thickness position on the buffet performance was investigated in turn by the control variable method. First, the leading edge thickness and trailing edge thickness of the airfoil are quantified as follows:
As shown in the Figure 16, is the maximum thickness position, and and are the area of the front and back sections of the airfoil respectively.
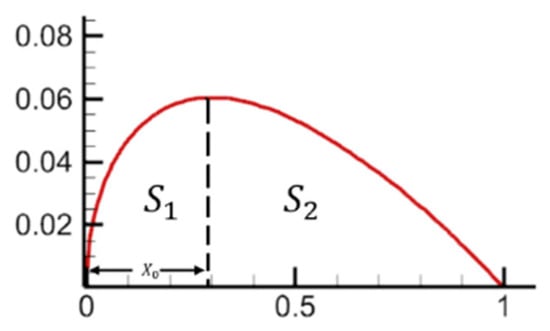
Figure 16.
Schematic diagram for calculating the thickness of the leading and trailing edge of the airfoil.
Airfoil samples are generated by varying the CST parameters of the airfoil. The NACA0012 airfoil is selected as the initial airfoil, and different airfoil samples are generated by changing the leading edge thickness, trailing edge thickness and maximum thickness position of the airfoil, and the buffet performance of these samples is computed. Using the above definition we obtain, the leading edge thickness , trailing edge thickness , and the maximum thickness position for the NACA0012 airfoil.
Figure 17, Figure 18 and Figure 19 show the buffet onset boundaries for different airfoil leading edge thicknesses, trailing edge thickness, and maximum thickness positions at Ma = 0.7 and Re = 3 × 106. The airfoil samples are kept as symmetric, and only the upper boundary is given in the figure. When the leading edge thickness of the airfoil decreases, the buffet performance is improved, and the angle of attack for the onset of transonic buffet increases. A certain degree of trailing edge thickness increase can also improve the buffet onset boundary, but beyond that range, it does not contribute to the improvement of buffet performance. When the maximum thickness position of the airfoil , the angle of attack for the onset of buffet increases with the backward shift of the maximum thickness position; and when , the angle of attack decreases with the backward shift. Therefore, when the maximum thickness position is located near to 0.4 times the chord length, the buffet onset angle of attack of the airfoil reaches its peak and the buffet performance is optimal. This is consistent with the results of the above reinforcement learning-based airfoil buffet optimization.
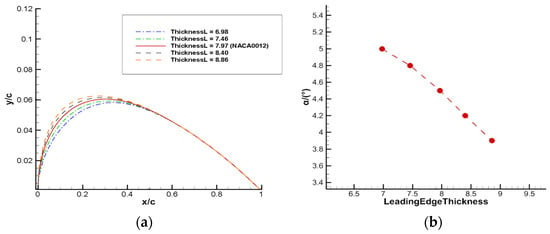
Figure 17.
Influence of airfoil leading edge thickness on buffet onset boundary. (a) Airfoil shapes corresponding to different leading edge thickness. (b) The buffet onset boundary for airfoils with different leading edge thickness.
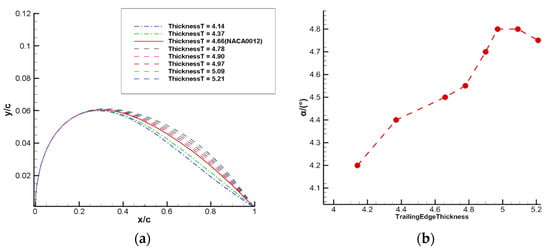
Figure 18.
Influence of airfoil trailing edge thickness on buffet onset boundary. (a) Airfoil shapes corresponding to different trailing edge thickness. (b) The buffet onset boundary for airfoils with different trailing edge thickness.
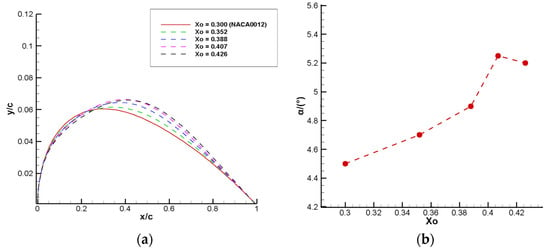
Figure 19.
Influence of the maximum thickness position of the airfoil on the buffet onset boundary. (a) Airfoil shapes corresponding to different maximum thickness positions. (b) The buffet onset boundary for airfoils with different maximum thickness positions.
5. Conclusions and Discussion
The transonic buffet performance of an airfoil is an important aerodynamic index for the lift-drag ratio and is also a hot spot and a difficult area of research in the aviation industry. This paper studied a deep reinforcement learning based approach and constructed a reinforcement learning framework using the DDPG algorithm. The airfoil was parameterized by the CST parameterization method and a CFD program constructed based on the URANS equation for airfoil aerodynamic performance calculation. The buffet optimization design study was carried out for the symmetric airfoil NACA0012 and the supercritical airfoil RAE2822. With the lift coefficient pulsation strength as the key design index, a suitable design state was selected. Through the reinforcement learning based airfoil transonic buffet optimization design study, the buffet optimization of the airfoil was completed without a priori knowledge, and the buffet performance was significantly improved.
In the transonic buffet optimization design study for NACA0012, the optimized airfoil shows a large improvement in buffet performance. Compared with the initial airfoil, there is a 2° increase in the buffet onset angle of attack, and the buffet intensity is significantly lower than that of the initial airfoil. In addition, the steady aerodynamic performance of the airfoil such as lift and drag was also significantly improved. Under the optimized state of Ma = 0.7, α = 5.5° and Re = 3 × 106, the lift coefficient of the airfoil was increased from 0.561 to 0.776, an increase of 38.3%, and the drag coefficient reduction was 33.1%. Meanwhile, in the buffet optimization for RAE2822, the optimized airfoil buffet onset boundary was improved by 1.2°. The steady aerodynamic performance was also improved, with the lift coefficient increasing by 13.9%, from 0.79 in the initial airfoil to 0.88, and the drag coefficient decreasing from 0.035 to 0.030, a reduction of 14.3%.
The results of the airfoil buffet optimization show that there is a connection between the airfoil geometric characteristics and transonic buffet. The airfoil maximum thickness position, leading edge thickness, and trailing edge thickness all affect the fluid flow stability on the airfoil surface. This leads to three general conclusions below related to the airfoil transonic buffet optimization. First, when the airfoil leading edge becomes narrower, the shock moves back and the flow separation near the trailing edge is suppressed. Therefore, the flow stability increases and the buffet is suppressed. Second, when the airfoil trailing edge is thickened within a certain range, the flow separation near the trailing edge is also suppressed, and the buffet performance is improved, however, when the trailing edge thickness 5, the buffet performance decreases. Third, the maximum thickness position also affects the buffet performance, and when it is near 0.4 times the chord length, the buffet onset angle of attack is the largest, and the buffet performance is the best.
Compared with the traditional buffet control method [37], this study constructively combines buffet optimization with reinforcement learning shape optimization design. Unlike most studies on reinforcement learning based aerodynamic shape optimization design, which focus on the optimization of steady aerodynamic performance such as lift-drag in a steady state, this paper is aimed at the study of transonic buffet in an unsteady state. At the same time, the optimization framework built in this paper, which has the advantages of high transferability and efficiency, can be used for other aerodynamic optimizations of aircraft. In addition, reinforcement learning is computationally superior to the global optimization algorithms. For general aerodynamic shape optimization problems, global optimization algorithms often require hundreds or thousands of CFD calls, and the computational cost increases dramatically when high-dimensional problems are involved. In contrast, reinforcement learning has a strong learning induction capability, and so the number of CFD calls in the optimization process is fewer. Therefore, the efficiency of traditional global optimization algorithms is much lower than that of reinforcement learning, which limits their application in many engineering fields. Although the use of surrogate models can significantly improve the optimization efficiency [38,39,40,41], it is difficult to build surrogate models on unsteady flow problems, including buffet. The flow field possesses dynamic and complex characteristics. Reinforcement learning has the ability to adjust optimization strategies based on changes in the environment. When applied to aerodynamic shape optimization, it enables adaptive behavior within the flow field. Furthermore, reinforcement learning does not require prior knowledge of the mathematical model of the problem, making it easier to construct an optimization framework.
There is room for improvement. In the buffet optimization process, the buffet criterion mainly relies on CFD calculation, which makes the optimization process more computationally expensive. The optimization process can be further accelerated through the automatic extraction and judgment of transonic buffet features in a data-driven framework. In addition, the flow field information is not fully utilized. The optimization efficiency can be improved by using the buffet flow field characteristics as the optimization variables, extracting the design index from the flow field, and realizing the accurate regulation of the flow field. In recent years, dynamic mode decomposition (DMD) [42] has been widely used to extract the coherent structure of complex flows and to construct a reduced-order model of flow field evolution [43]. During the numerical simulation process, DMD can accelerate the convergence of the flow field [44,45] and reduce the CFD computational costs. Moreover, neural networks have the ability to learn complex nonlinear relationships, process and analyze large amounts of data, and extract buffet features from the flow field. Therefore, it can also improve the optimization efficiency. Our next step is to develop efficient convergence methods to accelerate buffet numerical simulations, which are of great engineering importance, to improve the optimization efficiency of reinforcement learning-based aerodynamic shape optimization design.
Author Contributions
Conceptualization, H.C.; software, K.R.; validation, J.W.; formal analysis, C.G.; data curation, K.R.; writing—original draft preparation, H.C.; writing—review and editing, C.G. and W.Z.; supervision, C.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Aviation Science Foundation of China, grant number No. 2019ZH053003. This research was also funded by Fundamental Research Funds for the Central Universities, grant number No. D5000210592.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, B.H.K.; Murty, H.; Jiang, H. Role of Kutta waves on oscillatory shock motion on an airfoil. AIAA J. 1994, 32, 789–796. [Google Scholar] [CrossRef]
- Crouch, J.D.; Garbaruk, A.; Magidov, D. Predicting the onset of flow unsteadiness based on global instability. J. Comput. Phys. 2007, 224, 924–940. [Google Scholar] [CrossRef]
- Crouch, J.D.; Garbaruk, A.; Magidov, D.; Travin, A. Origin of transonic buffet on aerofoils. J. Fluid Mech. 2009, 628, 357–369. [Google Scholar] [CrossRef]
- Raghunathan, S.; Mabey, D.G. Passive shock-wave/boundary-layer control on a wall-mounted model. AIAA J. 1987, 25, 275–278. [Google Scholar] [CrossRef]
- Smith, A.; Babinsky, H.; Fulker, J.; Ashill, P.R. Shock wave/boundary-layer interaction control using streamwise slots in transonic flows. J. Aircr. 2004, 41, 540–546. [Google Scholar] [CrossRef]
- Dandois, J.; Lepage, A.; Dor, J.-B.; Molton, P.; Ternoy, F.; Geeraert, A.; Brunet, V.; Coustols, É. Open and closed-loop control of transonic buffet on 3D turbulent wings using fluidic devices. Comptes Rendus Mec. 2014, 342, 425–436. [Google Scholar] [CrossRef]
- Gao, C.; Zhang, W.; Kou, J.; Liu, Y.; Ye, Z. Active control of transonic buffet flow. J. Fluid Mech. 2017, 824, 312–351. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M.; Martins, J.R.R.A.; Shu, C. Efficient aerodynamic shape optimization with deep-learning-based geometric filtering. AIAA J. 2020, 58, 4243–4259. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, P.; Peng, J. Using shock control bump to improve transonic buffet boundary of airfoil. Acta Aeronaut. Sin. 2011, 32, 1421–1428. [Google Scholar]
- Gao, C.; Zhang, W.; Ye, Z. Reduction of transonic buffet onset for a wing with activated elasticity. Aerosp. Sci. Technol. 2018, 77, 670–676. [Google Scholar] [CrossRef]
- Carpentieri, G.; Koren, B.; van Tooren, M.J.L. Adjoint-based aerodynamic shape optimization on unstructured meshes. J. Comput. Phys. 2007, 224, 267–287. [Google Scholar] [CrossRef]
- Jameson, A. Aerodynamic design via control theory. J. Sci. Comput. 1988, 3, 233–260. [Google Scholar] [CrossRef]
- Nadarajah, S.K.; Jameson, A. Optimum shape design for steady flows with time-accurate continuous and discrete adjoint method. AIAA J. 2007, 45, 1478–1491. [Google Scholar] [CrossRef]
- Lee, B.J.; Liou, M.-S. Unsteady Adjoint Approach for Design Optimization of Flapping Airfoils. AIAA J. 2012, 50, 2460–2475. [Google Scholar] [CrossRef]
- Sun, G.; Wang, S. A review of the artificial neural network surrogate modeling in aerodynamic design. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 5863–5872. [Google Scholar] [CrossRef]
- Wu, X. Research on Uncertainty and High-Dimensional Problems in Aerodynamic Shape Optimization Design. Ph.D. Thesis, Northwestern Polytechnic University, Xi’An, China, 2018. [Google Scholar]
- Li, J.; He, S.; Zhang, M.; Martins, J.R.R.A.; Khoo, B.C. Physics-Based Data-Driven Buffet-Onset Constraint for Aerodynamic Shape Optimization. AIAA J. 2022, 60, 4775–4788. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, J.; Xiang, Y.; Wang, W. Neural Networks-Based Aerodynamic Data Modeling: A Comprehensive Review. IEEE Access 2020, 8, 90805–90823. [Google Scholar] [CrossRef]
- Viquerat, J.; Rabault, J.; Kuhnle, A.; Ghraieb, H.; Larcher, A.; Hachem, E. Direct shape optimization through deep reinforcement learning. J. Comput. Phys. 2021, 428, 110080. [Google Scholar] [CrossRef]
- Li, R.; Zhang, Y.; Chen, H. Learning the Aerodynamic Design of Supercritical Airfoils Through Deep Reinforcement Learning. AIAA J. 2021, 59, 3988–4001. [Google Scholar] [CrossRef]
- Li, J.; Du, X.; Martins, J.R. Machine learning in aerodynamic shape optimization. Prog. Aerosp. Sci. 2022, 134, 100849. [Google Scholar] [CrossRef]
- Hui, X.; Wang, H.; Li, W.; Bai, J.; Qin, F.; He, G. Multi-object aerodynamic design optimization using deep reinforcement learning. AIP Adv. 2021, 11, 085311. [Google Scholar] [CrossRef]
- Gron, A. Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems, 1st ed.; O’Reilly Media Inc.: Beijing, China, 2017; pp. 352–376. [Google Scholar]
- Li, J.; Zhang, M.; Tay, C.M.J.; Liu, N.; Cui, Y.; Chew, S.C.; Khoo, B.C. Low-Reynolds-number airfoil design optimization using deep-learning-based tailored airfoil modes. Aerosp. Sci. Technol. 2022, 121, 107309. [Google Scholar] [CrossRef]
- Kulfan, B.M. Universal Parametric Geometry Representation Method. J. Aircr. 2008, 45, 142–158. [Google Scholar] [CrossRef]
- Bueno-Orovio, A.; Castro, C.; Palacios, F.; Zuazua, E. Continuous Adjoint Approach for the Spalart-Allmaras Model in Aerodynamic Optimization. AIAA J. 2012, 50, 631–646. [Google Scholar] [CrossRef]
- Zhang, W.; Gao, C.; Ye, Z. Research progress on mesh deformation method in computational aeroelasticity. Acta Aeronaut. Astronaut. Sin. 2014, 35, 303–319. [Google Scholar]
- Doerffer, P.; Hirsch, C.; Dussauge, J.P.; Babinsky, H.; Barakos, G.N. (Eds.) Steady Effects of Shock Wave Induced Separation; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Tian, Y.; Gao, S.; Liu, P.; Wang, J. Transonic buffet control research with two types of shock control bump based on RAE2822 airfoil. Chin. J. Aeronaut. 2017, 30, 1681–1696. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: London, UK, 1998; pp. 131–133. [Google Scholar]
- Wu, X.; Zhang, W.; Peng, X.; Wang, Z. Benchmark aerodynamic shape optimization with the POD-based CST airfoil parametric method. Aerosp. Sci. Technol. 2019, 84, 632–640. [Google Scholar] [CrossRef]
- Thomas, J.; Dowell, E. Discrete adjoint method for aeroelastic design optimization. In Proceedings of the 15th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Atlanta, GA, USA, 16–20 June 2014; p. 2298. [Google Scholar]
- Kenway, G.K.W.; Martins, J. Buffet-Onset Constraint Formulation for Aerodynamic Shape Optimization. AIAA J. 2017, 55, 1930–1947. [Google Scholar] [CrossRef]
- Xu, Z.; Saleh, J.H.; Yang, V. Optimization of Supercritical Airfoil Design with Buffet Effect. AIAA J. 2019, 57, 4343–4353. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, C.; Zhou, F.; Yang, D.; Zhang, W. Study on flow noise characteristic of transonic deep buffeting over an airfoil. Phys. Fluids 2023, 35, 046109. [Google Scholar] [CrossRef]
- Yao, W.; Zhang, H.; Jiang, D.; Gui, M.; Zhao, Z.; Chen, Z. The transformation mechanisms of vortex structures on vortex-induced vibration of an elastically mounted sphere by Lorentz force. Ocean Eng. 2023, 280, 114436. [Google Scholar] [CrossRef]
- Han, Z.H. Kriging surrogate model and its application to design optimization: A review of recent progress. Acta Aeronaut. Astronaut. Sin. 2016, 37, 3197–3225. [Google Scholar]
- Liu, H.; Ong, Y.-S.; Cai, J. A survey of adaptive sampling for global metamodeling in support of simulation-based complex engineering design. Struct. Multidiscip. Optim. 2018, 57, 393–416. [Google Scholar] [CrossRef]
- Liu, J.; Song, W.-P.; Han, Z.-H.; Zhang, Y. Efficient aerodynamic shape optimization of transonic wings using a parallel infilling strategy and surrogate models. Struct. Multidiscip. Optim. 2017, 55, 925–943. [Google Scholar] [CrossRef]
- Mackman, T.J.; Allen, C.B.; Ghoreyshi, M.; Badcock, K.J. Comparison of adaptive sampling methods for generation of surrogate aero-dynamic models. AIAA J. 2013, 51, 797–808. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Kou, J.; Le Clainche, S.; Zhang, W. A reduced-order model for compressible flows with buffeting condition using higher order dynamic mode decomposition with a mode selection criterion. Phys. Fluids 2018, 30, 016103. [Google Scholar] [CrossRef]
- He, G.; Wang, J.; Pan, C. Initial growth of a disturbance in a boundary layer influenced by a circular cylinder wake. J. Fluid Mech. 2013, 718, 116–130. [Google Scholar] [CrossRef]
- Kou, J.; Zhang, W.; Liu, Y.; Li, X. The lowest Reynolds number of vortex-induced vibrations. Phys. Fluids 2017, 29, 041701. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).