Abstract
With the increasing requirements for aerodynamic performance, aerodynamic configuration design of aircraft based on traditional design experience has gradually failed to meet the needs of the future. Therefore, the new concept aerodynamic shape design will be the development trend for future aircraft, but the current new concept aerodynamic shape design is still based on the designer’s understanding of the existing flow physics. One novel technology that can be useful is topology design. Compared with traditional design, topology design not only has more undetermined parameters, but also its topology variables have a greater impact on the design goals. In this perspective, we propose the concept of Artificial Intelligent Topology Design (AITD) for aerodynamic configuration design based on topology design and artificial intelligence technology and discuss its potential in the application of the new concept of aerodynamic configuration design.
1. Introduction
In the development of aircraft, aerodynamic configuration design is very important, which directly affects the flight performance and flight quality of aircraft and has a decisive impact on flight safety, flight efficiency, and the economy of aircraft. At the same time, the aerodynamic configuration design of the aircraft is also the basis for the aircraft structure and system design. It can be said that the aerodynamic configuration design is the top priority of the aircraft design. The breakthrough and progress of the aerodynamic configuration design have played a strong role in promoting the continuous development of the aircraft and its design technology. Especially with the development of aerospace technology, faster flight speeds, longer flight distances, higher flight altitudes, and a larger flight field have become the goals of aerospace scientists and technicians. The development of hypersonic vehicles has become a research hotspot and a technical difficulty in the field of aerospace technology, and the aerodynamic configuration design of wide-speed range vehicles has been one of the core research issues at present. At the current design level, it is very difficult to meet the aerodynamic performance requirements of multiple speeds at the same time with a fixed configuration.
The traditional aerodynamic configuration has been developed for decades, and its potential to improve the aerodynamic performance of aircraft is increasingly limited. To further improve the aerodynamic performance of aircraft, relevant research institutions have conducted some research on the new concept of aerodynamic aircraft configuration.
1.1. Deficiency
At present, the new concept configuration is basically designed by designers based on their existing design experience and the laws of flow physics. Experience-based design is a double-edged sword. Its advantage is to constantly improve the design ideas within the existing design framework to ensure the reliability of the design results. Its disadvantage is that it cannot jump out of the existing design ideas to get some creative design results.
1.2. Solution
This perspective aims to reverse the design idea, that is, jump out of the existing design experience, no longer rely on the existing flow physics to design the aerodynamic configuration, but directly explore the new concept configuration of aircraft, and then obtain some new flow physics according to the design results. Therefore, the idea of aerodynamic intelligent topology design (AITD) is proposed in this perspective, which is expected to be a new technology to find new concept configurations of aircraft in the future.
2. Aerodynamic Intelligent Topology Design (AITD) Method
The AITD method is mainly composed of two parts. The first part is the aerodynamic shape topology parameterization method, and the second part is the artificial intelligence technology. The topological parameterization method of aerodynamic configuration is inspired by topology optimization design, which is widely used in structural design. The following is an overview of structural topology optimization technology and artificial intelligence technology.
2.1. Topology Design
According to different design variables, there are three methods for aerodynamic layout design: size design, shape design, and topology design. The relationship between them and each design stage is shown in Figure 1. The first method is to optimize the configuration parameters based on the existing configuration to obtain the optimal size parameters. This optimization method is convenient to operate, and the calculation process is simple, but the existing configuration is required, and then the appropriate parameters are selected. The second method is shape design, which further designs the optimal shape for the preliminary design. The process is accompanied by size optimization. This method can design a relatively optimal aerodynamic configuration, but it is not necessarily the optimal solution. The third method is the most design-oriented topology.
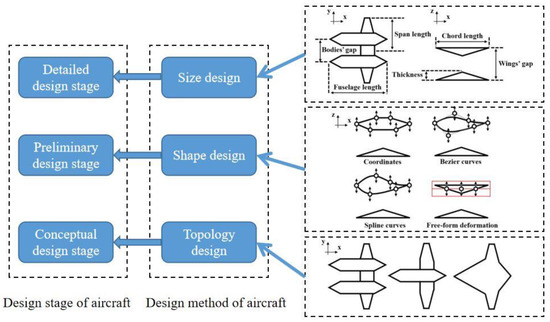
Figure 1.
Relationship between optimization methods and design stages [1].
Topology is a mathematical concept that mainly studies the topological relationships of elements in topological space after a series of transformations. Topology design does not require a preliminary design in advance. Only a design area needs to be given, and the structure, including topological relationships, shape, and size, can be designed according to the constraints. Topology design is a higher-level design method than size design and shape design. Topology design, when compared to size and shape design, not only has more undetermined parameters, but its topology variables have a greater impact on the design goals, resulting in greater economic benefits. It is more attractive to engineering designers and has become a research hotspot in the current design field.
Topology optimization methods have been widely used in the field of solid structure optimization. At present, the commonly used topology optimization design methods include the homogenization method [2], the variable density method [3], the level set method [4,5], the evolutionary structure optimization (ESO) method [6], etc.
There is also some related research in the field of fluid optimization.
In the internal flow field, Borrvall et al. [7] introduced the topology optimization method into the field of fluid optimization. Based on the assumption of plane flow, they combined the Stokes equation describing low Re (Reynolds number) flow with Darcy’s theorem, assumed the optimization design domain as a porous medium model, and introduced the variable density method in topology optimization to link the unit density with the reciprocal of the unit permeability through interpolation functions. Thus, the relationship between the unit density and the flow resistance is established, and the description of the fluid-solid properties of the unit is realized. With the goal of minimizing the energy loss in the flow process as the optimization goal, the Stokes flow problem in the two-dimensional pipe is optimized through the gradient optimization algorithm.
For the external flow, Payot et al. [8] proposed an aerodynamic shape optimization method, which can deal with topological design changes and detailed surface control. The method of material distribution or volume of solid is used to accurately reproduce the circular arcs. Final test cases include geometric fitting of arbitrary shapes, as well as drag minimization of topologies in supersonic flow, demonstrating that the parameterization can investigate single and multi-body aerodynamic design problems. The optimization design case of NACA0012 is shown in Figure 2.
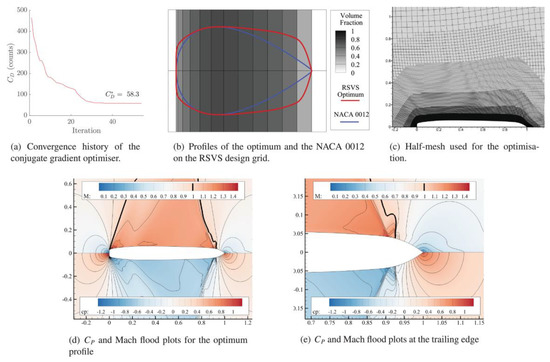
Figure 2.
Optimization of the ADODG Case one using ten active design variables [8].
Ban and Yamazaki [1] developed a black-box function aerodynamic topology optimization algorithm based on machine learning technology (FANTOM). In the FANTOM method, an effective global optimization method is adopted for discontinuous optimization problems in infeasible regions, and an efficient global optimization method based on clustering/classification methods and exploration strategies is adopted for topology optimization problems. The effectiveness of the method is proved in the inviscid drag minimization problem under two-dimensional supersonic flow conditions, and the optimal topology of the Busemann biplane is provided. The case of Busemann’s double wings is shown in Figure 3.
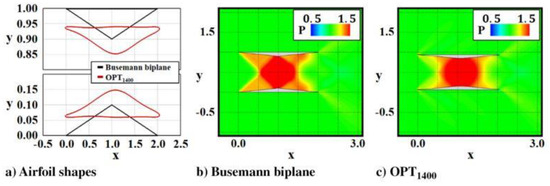
Figure 3.
Comparison between the Busemann biplane and the final optimal airfoils [1].
Sheikh et al. [9] proposed a design-by-morphing (DbM) method to create a search space for topology optimization of two-dimensional airfoils. This method is not constrained by geometric parameters or designer experience, thus allowing a radical and large search space with only a few parameters. DbM is applied to a two-dimensional airfoil example to maximize the lift-to-drag ratio and the stall angle tolerance. The results show that the optimized airfoil has a significant improvement over the existing reference shape. Figure 4 shows nine representative optimal airfoil shapes on the Pareto front in ascending order of maximum lift-drag ratio. In addition, the authors of [10] further applied the combination of DbM and Bayesian optimization to optimize the three-dimensional airfoil of a hydrodynamic turbine, a vertical-axis wind turbine, and a wind turbine tube. The optimization calculation is shown in Figure 5.
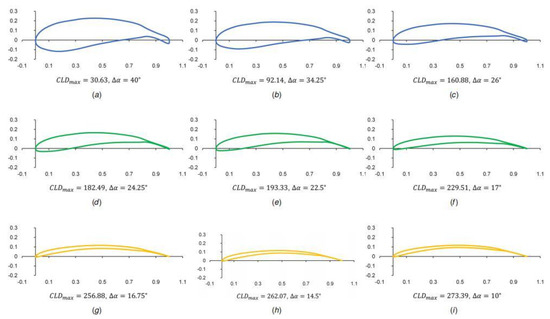
Figure 4.
Nine representative Pareto-optimal airfoil shapes (a–c) are in cluster 1, (d–f) are in cluster 2, and (g–i) are in cluster 3 [9].
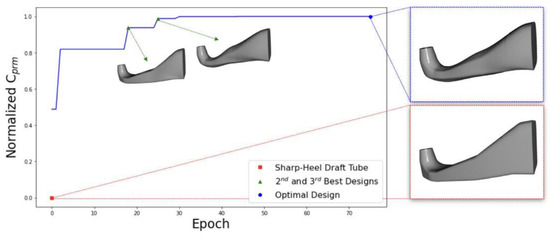
Figure 5.
Optimization progress [10].
At present, the research on the external flow is basically aimed at the two-dimensional shape, and there is no research on the topological design of the overall aerodynamic layout of the aircraft. Although there are great challenges in topology parameterization, this technology is worthy of further research.
2.2. Artificial Intelligence
Artificial intelligence technology is becoming rapidly popular and may be the leading technology in the future. With the arrival of the era of big data and the improvement of computer performance, machine learning algorithms represented by deep learning have achieved great success in the applications of computer vision, natural language processing, autonomous vehicles, and other fields. AI is divided into strong AI and weak AI. Strong artificial intelligence is defined as the need for self-awareness and the ability to make decisions on problems as human beings when encountering problems. However, it is very difficult to achieve this situation, so there has been little progress in the research on strong artificial intelligence. Weak AI has no consciousness of thinking and can only work according to the program prepared by the programmer. Compared with strong AI, it has developed rapidly in the past 60 years. Now, the development of AI is mainly focused on weak AI.
In 2006, Hinton et al. [11] proposed deep learning. The organic integration of AI technology and big data has led to a new direction in machine learning, and the development of AI technology has ushered in another peak. In deep learning, unsupervised learning, feature extraction, and optimization are used to improve the overall optimization results. In addition, deep learning adopts a layer-by-layer training mechanism, and the units are connected locally, which reduces the number of weight parameters and improves the training efficiency. At present, the commonly used deep learning network models include convolutional neural networks, recurrent neural networks, and autoencoders; the commonly used algorithms are the RBM algorithm and the deep belief network. Deep learning is not simply mechanical memory but comes from a deep understanding of knowledge and deep-thinking construction.
In addition, due to the limitations of deep learning itself, artificial intelligence technologies such as reinforcement learning and transfer learning have been developed. Artificial intelligence technology has been applied in the fields of aerodynamic coefficient estimation [12,13,14,15] and aerodynamic optimization of aircraft design [16]. Li et al. [17] made a comprehensive summary of relevant research work. The perfect combination of reinforcement learning and aerodynamic optimization design can be used to learn from the experience of designers during the optimization process, while transfer learning can be used as a means of reusing experience to accelerate the efficiency of the target design. However, the problem is also obvious; that is, whether it is reinforcement learning or transfer learning, it is ultimately the use of existing design experience, unable to jump out of the limitations of design experience. Therefore, this paper takes aerodynamic topology design as a technology to break through design experience. As an auxiliary technology, artificial intelligence technology can solve the problem of massive computing caused by high dimensions and precision.
3. Discussion
In this perspective, the aerodynamic topology design of aircraft is divided into two categories:
- Aerodynamic topology design of continuous configurations;
- Aerodynamic topology design of discrete configurations.
In the following, some classic aerodynamic configurations designed by existing human designers based on their design experience and understanding of the laws of flow physics are used as cases to classify accordingly, making the concept of this paper more intuitive. Here, we take supersonic flow as an example [18].
3.1. Aerodynamic Topology Design of Continuous Configurations
Eggers and Syvertson [19] proposed a configuration called “flat-top” based on the momentum principle when studying the hypersonic aerodynamic configuration with a high lift-drag ratio. The upper part of the configuration is flat, making full use of the beneficial interference of the lower surface fuselage and wing, that is, the fuselage acts as the main shock generator and the wing acts as the capture surface and bearing surface of the high-pressure flow field behind the wave, so as to obtain high lift and a high lift-to-drag ratio at α (small angles of attack). The further developed configuration enhances the beneficial interference effect by using a downfolded wingtip, as shown in Figure 6.
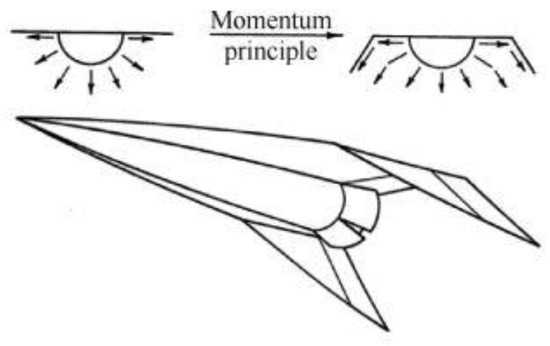
Figure 6.
Modified “flat-top” configuration.
Lv et al. [20] proposed a design principle called passive waverider, whose idea is to “ride” some components on the shock wave generated by other components to obtain high lift. Its essence is similar to the wedge interference wing and “flat-top” configuration, and it is also a beneficial supersonic interference configuration. The typical shape designed by this method is shown in Figure 7. The vertical stabilizer is placed in the belly of the aircraft as a shock generator, and the high-pressure flow field behind the wave acts on the lower surface of the wing to generate high lift.
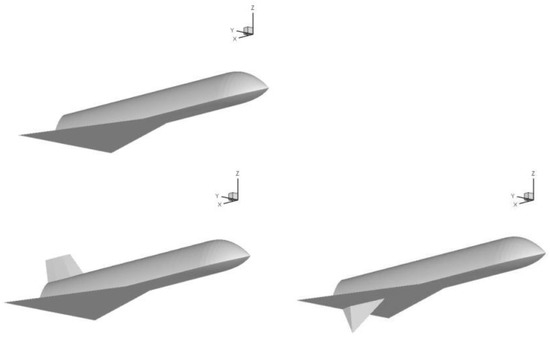
Figure 7.
The original and modified configurations of hypersonic vehicles [20].
The pressure on the afterbody is obviously different between the two configurations. The lower surface of case two rides on the shock wave produced by the oblique wedge, and the pressure rises immediately after passing through the shock wave. Although the modification on the wedge induces an area of low pressure, it does not affect the augment of the lift coefficient.
Liu et al. [21] developed the design method for the double sweep waverider configuration. By properly designing the shape, the waverider can not only maintain high performance at hypersonic speed but also have advantages in longitudinal stability and vortex effect enhancement at low speed, which has developed a new way for the development of hypersonic aircraft in a wide speed range, as shown in Figure 8.
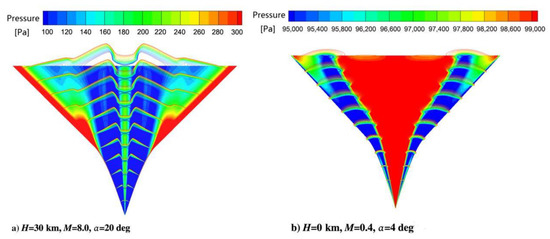
Figure 8.
Pressure distribution on the upper surface of the double-swept waverider [21].
The above three aerodynamic configurations can be classified as the aerodynamic topology design of the continuous configurations mentioned in this perspective, that is, the continuous change of the profile and the generation of topology based on the existing baseline configuration.
3.2. Aerodynamic Topology Design of Discrete Configurations
Yamazaki and Kusunose [22] studied the twin-body/biplane-wing configuration with a cruise Ma (Mach number) of 1.7. The results show that the shock wave drag can be effectively reduced by the combination of supersonic twin-wing and twin-body as shown in Figure 9.
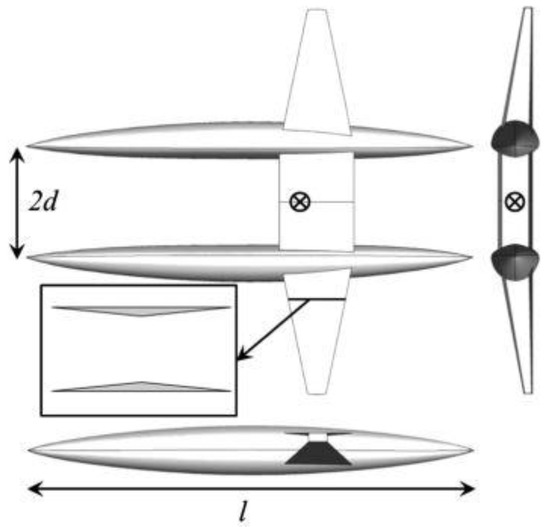
Figure 9.
Trihedral figure of proposed twin-body/biplane-wing configuration [22].
After the two oblique shock waves generated at the leading edge of the wings intersect, they respectively propagate to the throat of the wings and interfere with the expansion wave generated here, so as to weaken the shock wave strength and reduce the shock wave drag. Pressure contours are as shown in Figure 10.
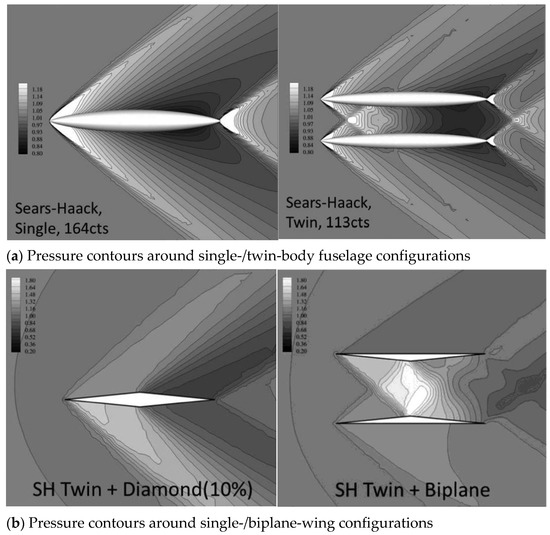
Figure 10.
Pressure contours [22].
In the face of a series of contradictory performance requirements of hypersonic aircraft for high lift-to-drag ratio, high lift, large volume, etc., Cui et al. [23] studied the principle of hypersonic beneficial interference and proposed a high-pressure capture wing aerodynamic configuration similar to half-ring wings and umbrella wings. The CFD results show that the lift and lift-to-drag ratios of the aircraft can be improved by using high-pressure capture wings, as shown in Figure 11.
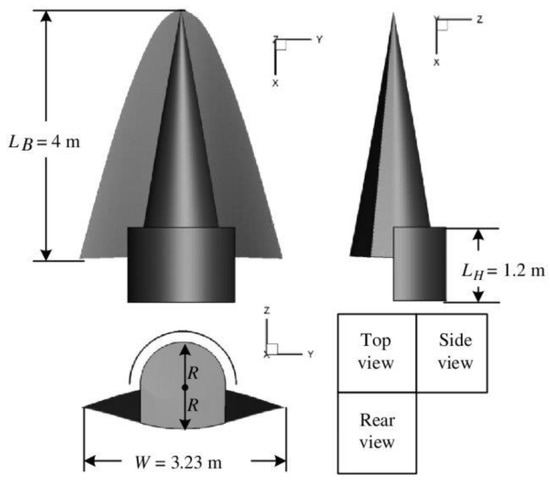
Figure 11.
Three-view of a waverider-HCW combination configuration [23].
The above two kinds of aerodynamic configurations can be classified as aerodynamic topology design of the discrete configuration mentioned in this perspective, that is, discrete shape change, and topological structure generation based on the existing baseline configuration.
3.3. Outlook
Faced with increasingly complex flight environments and high standard aerodynamic performance requirements, new concept aerodynamic configuration designs of aircraft will be the trend in the development of future aircraft. It is not enough to give full play to the subjective initiative under the existing design experience. Using Aerodynamic Artificial Topology Design (AITD) technology in a broader design space can help overcome existing experience limitations and obtain an aerodynamic configuration that exceeds our existing cognition. Especially for hypersonic wide-speed range aircraft, which is currently a research hotspot, this technology is expected to find a new configuration with better performance than the traditional configuration to meet the aerodynamic performance requirements at multiple speeds. As an advanced technology, artificial intelligence technology can provide assistance for aerodynamic configuration design. However, it is worth noting that it is unrealistic to independently design a new concept aircraft beyond the current cognition by relying on artificial intelligence itself to jump out of the existing design experience.
Some existing new concept aircraft, such as those with high-pressure capturing wing configurations, have a very typical topology structure, which uses aerodynamic interference to improve the lift-drag ratio of the aircraft. Of course, this was designed by the designer based on the principle of aerodynamic interference. Are there any more configurations that we cannot design with our existing knowledge but that exist objectively and may even bring new flow mechanisms? These are worthy of further study.
Some challenges:
- -
- The CFD solver with fidelity levels equivalent to those of the RANS-based CFD solver seems to be the only one that can be utilized in this field because RANS simulates based on mesh. Low-fidelity solvers such as XFOIL and AVL would not be sufficient;
- -
- The optimum solution might not have a smooth surface since the geometry resolution is based on the mesh resolution. The lower the mesh resolution, the poorer the mesh/geometry quality of the optimum solution, which might make topology optimization fail to generate sharp edges (such as a trailing edge);
- -
- Following the previous point, the definition of geometric constraints could be a challenge in order to keep the optimum solution manufacturable;
- -
- In supporting the topology optimization, the existing artificial intelligence might need some improvements to learn with a small number of samples. The computational cost becomes expensive as the number of evaluations with the RANS CFD solver increases. Meanwhile, typical AI requires a considerable number of samples to improve model accuracy.
Possible solutions:
- (1)
- The contradiction between the high-precision calculation data and the number of samples will produce a large number of samples in the design process, so it will produce a very large amount of calculation. This can be solved in two aspects: one is to reduce the number of samples generated, and the other is to select a calculation method with appropriate accuracy according to specific problems or use artificial intelligence technology to conduct multi precision data fusion;
- (2)
- Reduce the number of samples generated. In the design process, appropriate geometric constraints need to be imposed. Topological design cannot generate strange geometric shapes in the design space at will. If artificial constraints are completely discarded, a large number of useless geometric shapes will be generated. Therefore, it can be solved by the semi-empirical method. Only some specific parts can be relaxed for geometric constraints, and some sharp edges can be modified according to the actual needs of the project (such as a certain leading-edge radius due to hypersonic flight), or the number of discrete topology structures can be constrained;
- (3)
- Select the calculation method with appropriate accuracy according to the specific problem or conduct multi-precision data fusion with the aid of artificial intelligence technology. For topology design in details (such as a drag reduction structure on a shark skin surface), high-precision calculation methods must be used. At the macrolevel, appropriate calculation methods that reflect the overall aerodynamic law without requiring high accuracy can be chosen for the aerodynamic configuration design of aircraft. Or use artificial intelligence technology for multi-precision data fusion to reduce dependence on high-precision data.
Author Contributions
Conceptualization, P.L.; methodology, P.L.; software, P.L.; validation, P.L., W.S., P.D., F.F. and Y.Z.; formal analysis, P.L.; investigation, P.L.; resources, P.L.; data curation, P.L.; writing—original draft preparation, P.L.; writing—review and editing, P.L., W.S., P.D., F.F. and Y.Z.; visualization, P.L.; supervision, Y.Z.; project administration, F.F.; funding acquisition, F.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 12172345).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ban, N.; Yamazaki, W. Black-Box Function Aerodynamic Topology Optimization Algorithm via Machine Learning Technologies. AIAA J. 2021, 59, 5174–5185. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Bendsøe, M.P. Optimal shape design as a material distribution problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Wang, M.Y.; Wang, X.; Guo, D. A level set method for structural topology optimization. Comput. Methods Appl. Mech. Eng. 2003, 192, 227–246. [Google Scholar] [CrossRef]
- Karrman, A.M.B.; Allaire, G. Structural optimization using sensitivity analysis and a level-set method, in Scilab and Matlab. Techn. Rep. Ec. Polytech. 2009, 194, 1–13. [Google Scholar]
- Xie, Y.M.; Steven, G.P. A simple evolutionary procedure for structural optimization. Comput. Struct. 1993, 49, 885–896. [Google Scholar] [CrossRef]
- Borrvall, T.; Petersson, J. Topology optimization of fluids in Stokes flow. Int. J. Numer. Methods Fluids 2003, 41, 77–107. [Google Scholar] [CrossRef]
- Payot, A.D.J.; Rendall, T.C.S.; Allen, C.B. Restricted snakes volume of solid (RSVS): A parameterisation method for topology optimisation of external aerodynamics. Comput. Fluids 2019, 182, 60–84. [Google Scholar] [CrossRef]
- Sheikh, H.M.; Lee, S.; Wang, J.; Marcus, P.S. Airfoil optimization using design-by-morphing. arXiv 2022, arXiv:2207.11448. [Google Scholar]
- Sheikh, H.M.; Callan, T.A.; Hennessy, K.J.; Marcus, P.S. Optimization of the shape of a hydrokinetic turbine’s draft tube and hub assembly using Design-by-Morphing with Bayesian optimization. Comput. Methods Appl. Mech. Eng. 2022, 401, 115654. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Tumse, S.; Bilgili, M.; Sahin, B. Estimation of aerodynamic coefficients of a non-slender delta wing under ground effect using artificial intelligence techniques. Neural Comput. Appl. 2022, 34, 10823–10844. [Google Scholar] [CrossRef]
- Tumse, S.; Karasu, I.; Sahin, B. Experimental Investigation of Ground Effect on the Vortical Flow Structure of a 40° Swept Delta Wing. J. Aerosp. Eng. 2022, 35, 04022055. [Google Scholar] [CrossRef]
- Karasu, I.; Tumse, S.; Tasci, M.O.; Sahin, B.; Akilli, H. Near-surface particle image velocimetry measurements over a yawed slender delta wing. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2021, 235, 2466–2478. [Google Scholar] [CrossRef]
- Liao, P.; Yao, L.; Bai, G.; Zhao, H. Prediction of hybrid airfoil leading edge pressure distribution based on deep learning. J. Aerosp. Power 2019, 34, 1751–1758. [Google Scholar]
- Liao, P.; Song, W.; Du, P.; Zhao, H. Multi-fidelity convolutional neural network surrogate model for aerodynamic optimization based on transfer learning. Phys. Fluids 2021, 33, 127121. [Google Scholar] [CrossRef]
- Li, J.; Du, X.; Martins, J.R. Machine Learning in Aerodynamic Shape Optimization. Prog. Aerosp. Sci. 2022, 134, 100849. [Google Scholar] [CrossRef]
- Liu, R.; Bai, P. Concept of aerodynamic configuration based on supersonic favorable interference principle: Review. Acta Aeronaut. Astronaut. Sin. 2020, 41, 23784. [Google Scholar]
- Eggers, A.J.; Syvertson, C.A. Aircraft Configurations Developing High Lift-Drag Ratios at High Supersonic Speeds; NACA: Washington, DC, USA, 1956. [Google Scholar]
- Lv, Y.; Jiang, C.; Gao, Z.; Lee, C. Passive Waverider Method and Its Validation. In Proceedings of the AIAA SPACE 2014 Conference and Exposition, San Diego, CA, USA, 4–7 August 2014; p. 4346. [Google Scholar]
- Liu, C.; Bai, P.; Tian, J.; Liu, Q. Nonlinearity Analysis of Increase in Lift of Double Swept Waverider. AIAA J. 2020, 58, 304–314. [Google Scholar] [CrossRef]
- Yamazaki, W.; Kusunose, K. Biplane-wing/twin-body-fuselage configuration for innovative supersonic transport. J. Aircr. 2014, 51, 1942–1952. [Google Scholar] [CrossRef]
- Cui, K.; Li, G.L.; Xiao, Y.; Xu, Y.Z. High-pressure capturing wing configurations. AIAA J. 2017, 55, 1909–1919. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).