A Simulation Framework for Aircraft Take-Off Considering Ground Effect Aerodynamics in Conceptual Design
Abstract
1. Introduction
1.1. Overview of the Research
1.2. State of the Art of Take-Off Simulation Methods
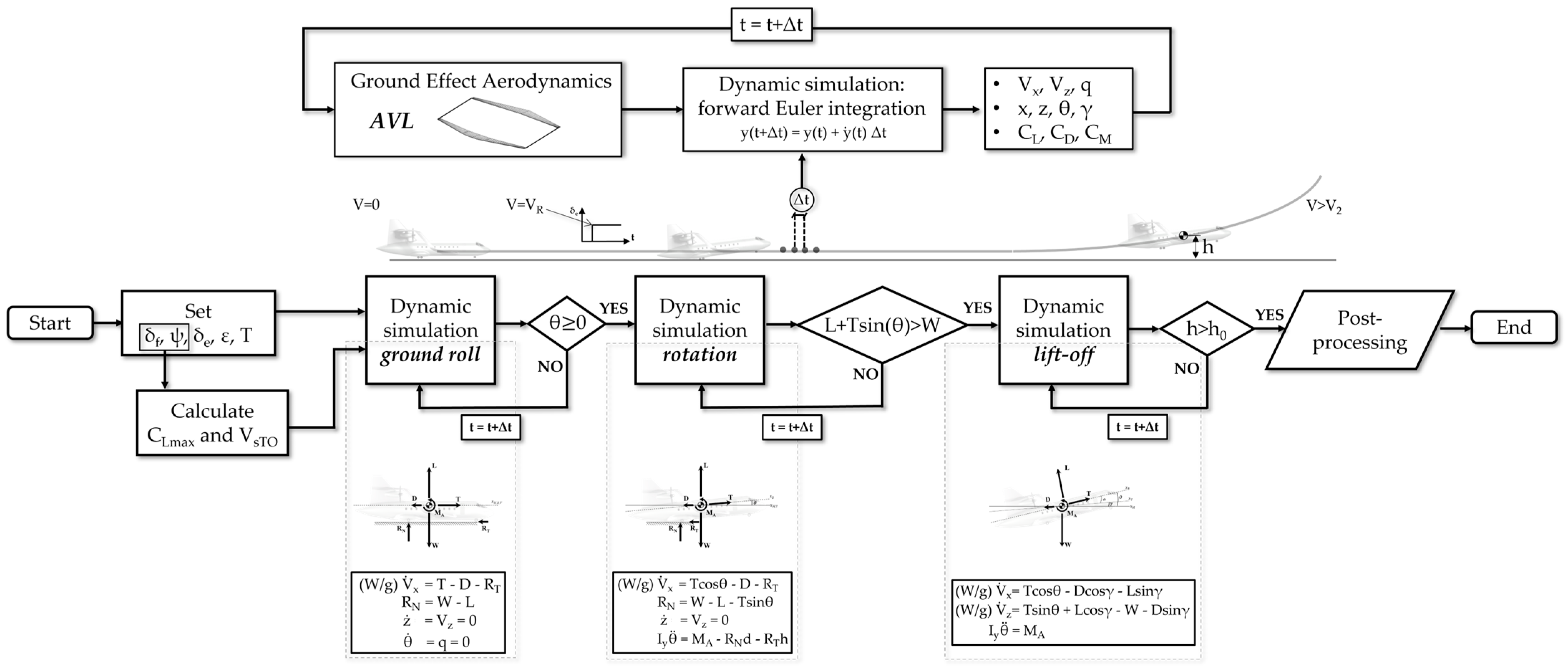
2. Mathematical Model of the Take-Off Manoeuvre
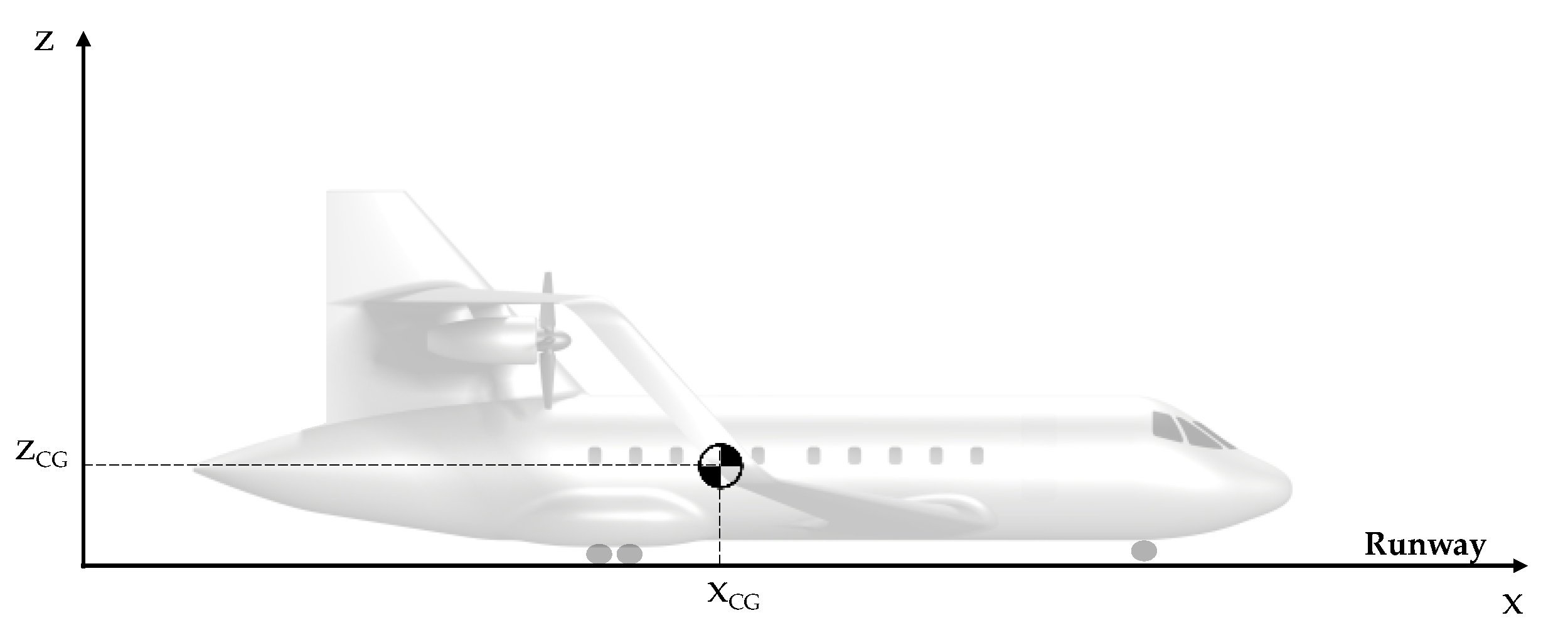
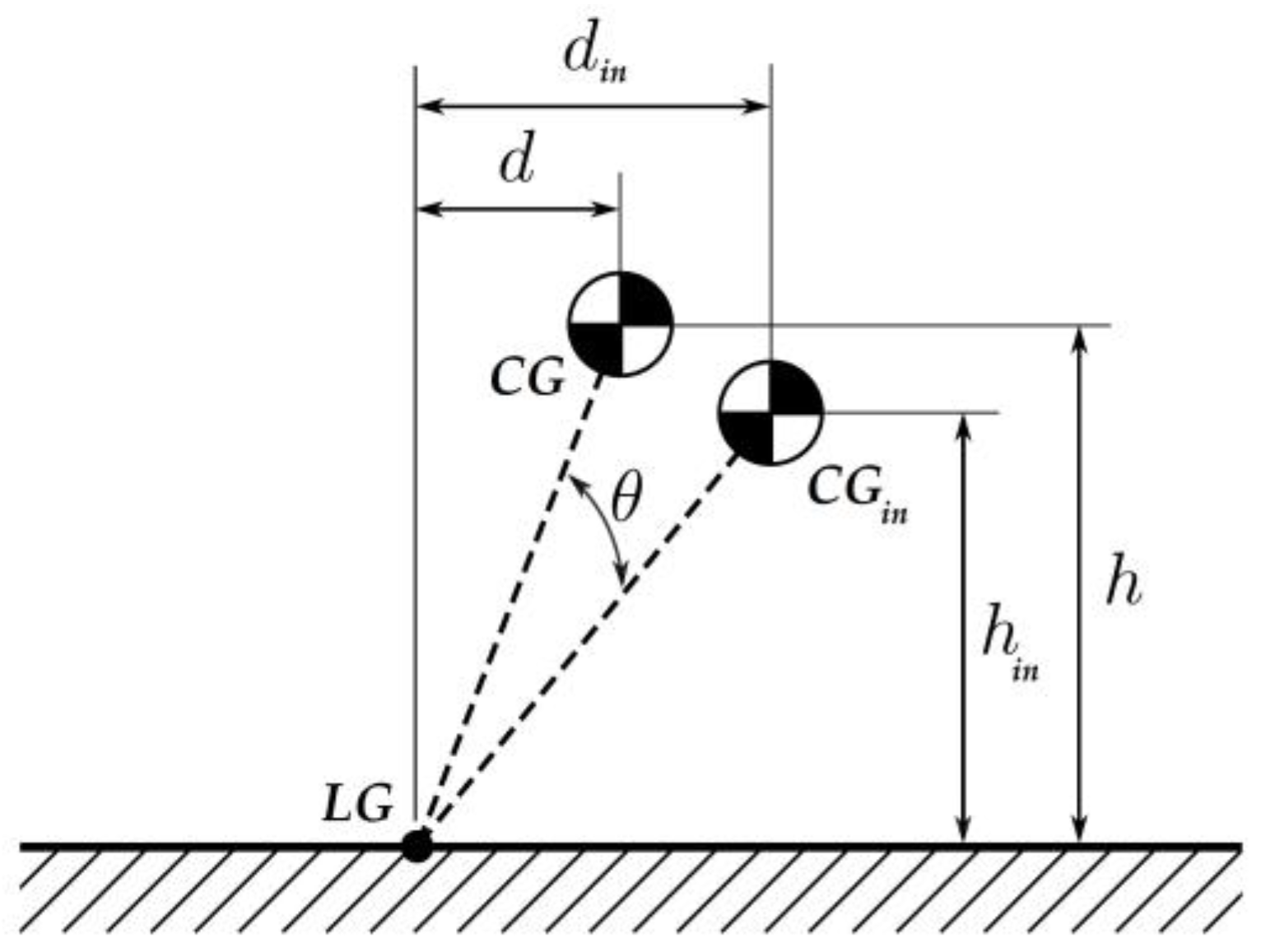
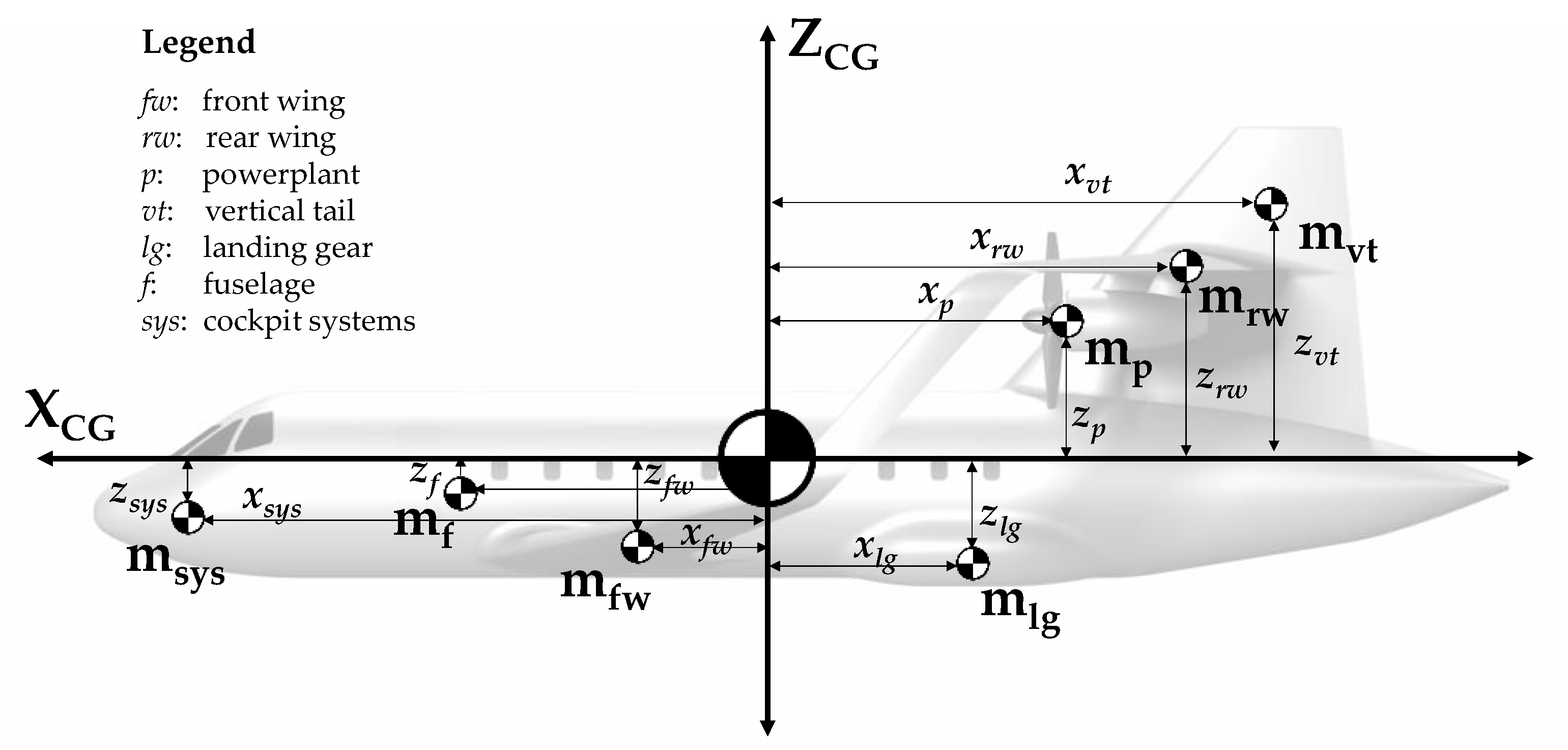
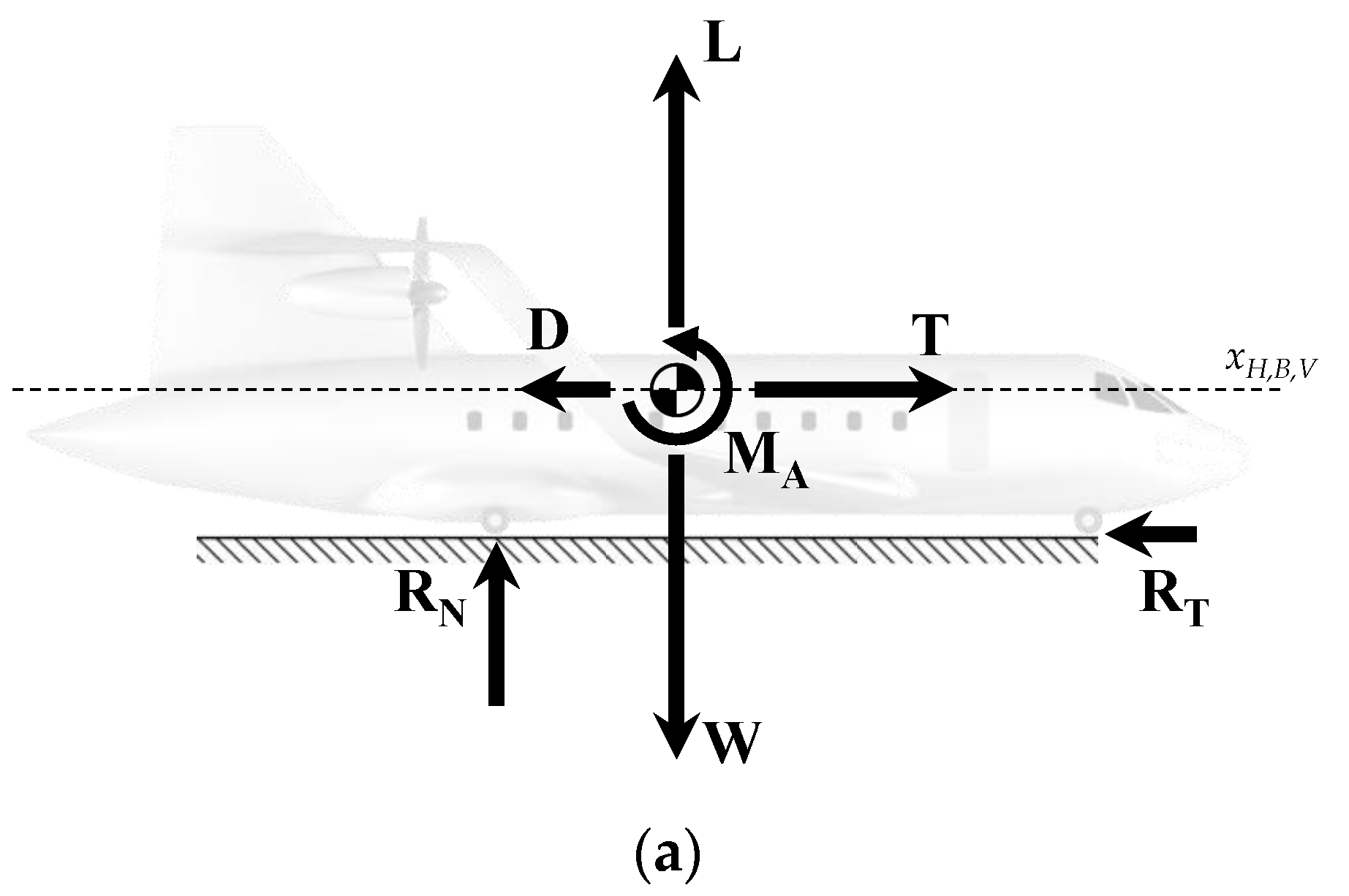
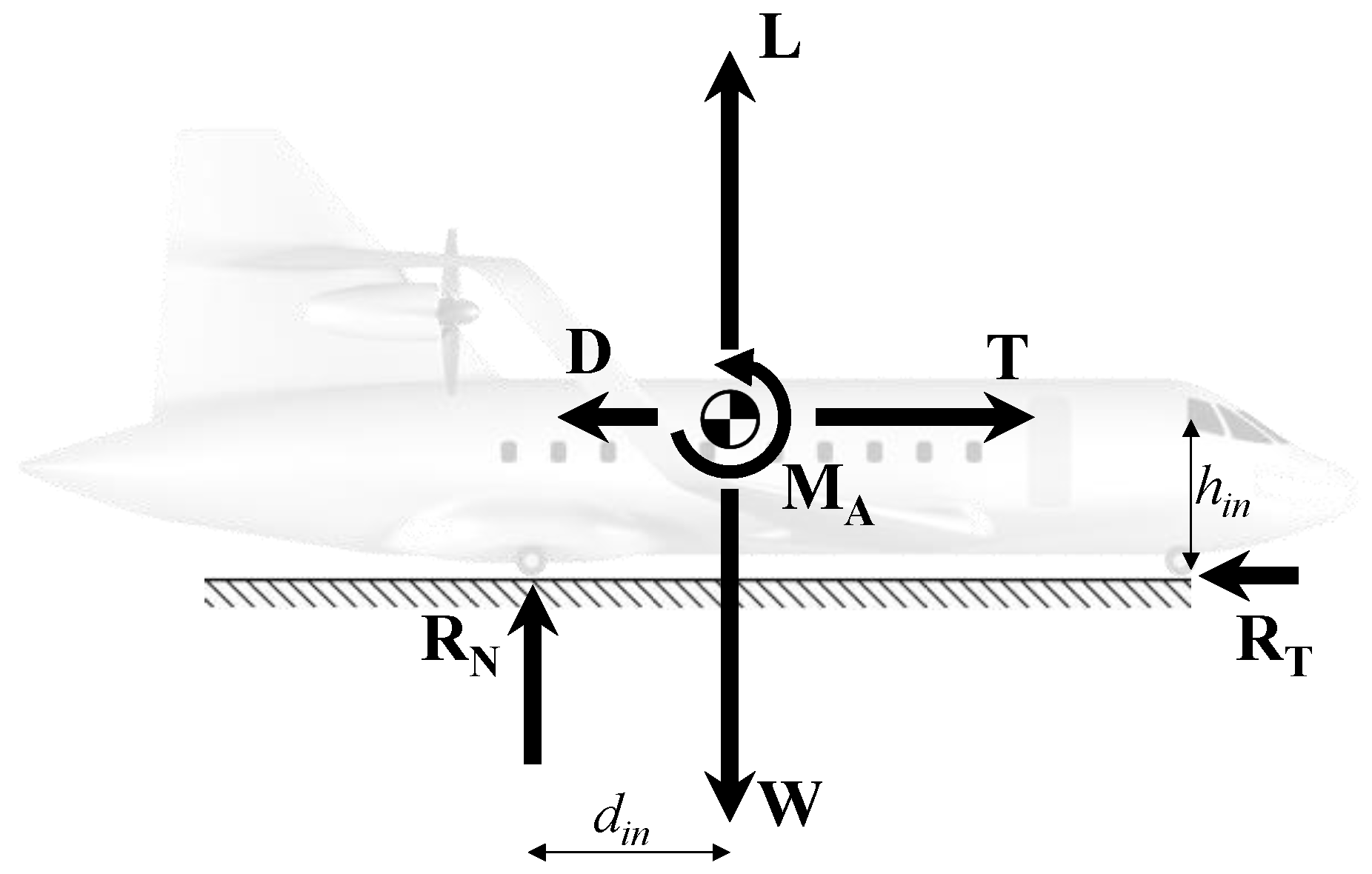
2.1. Equations of Motion
2.2. Aerodynamic Model
2.3. Thrust Model
2.4. Simulation Technique
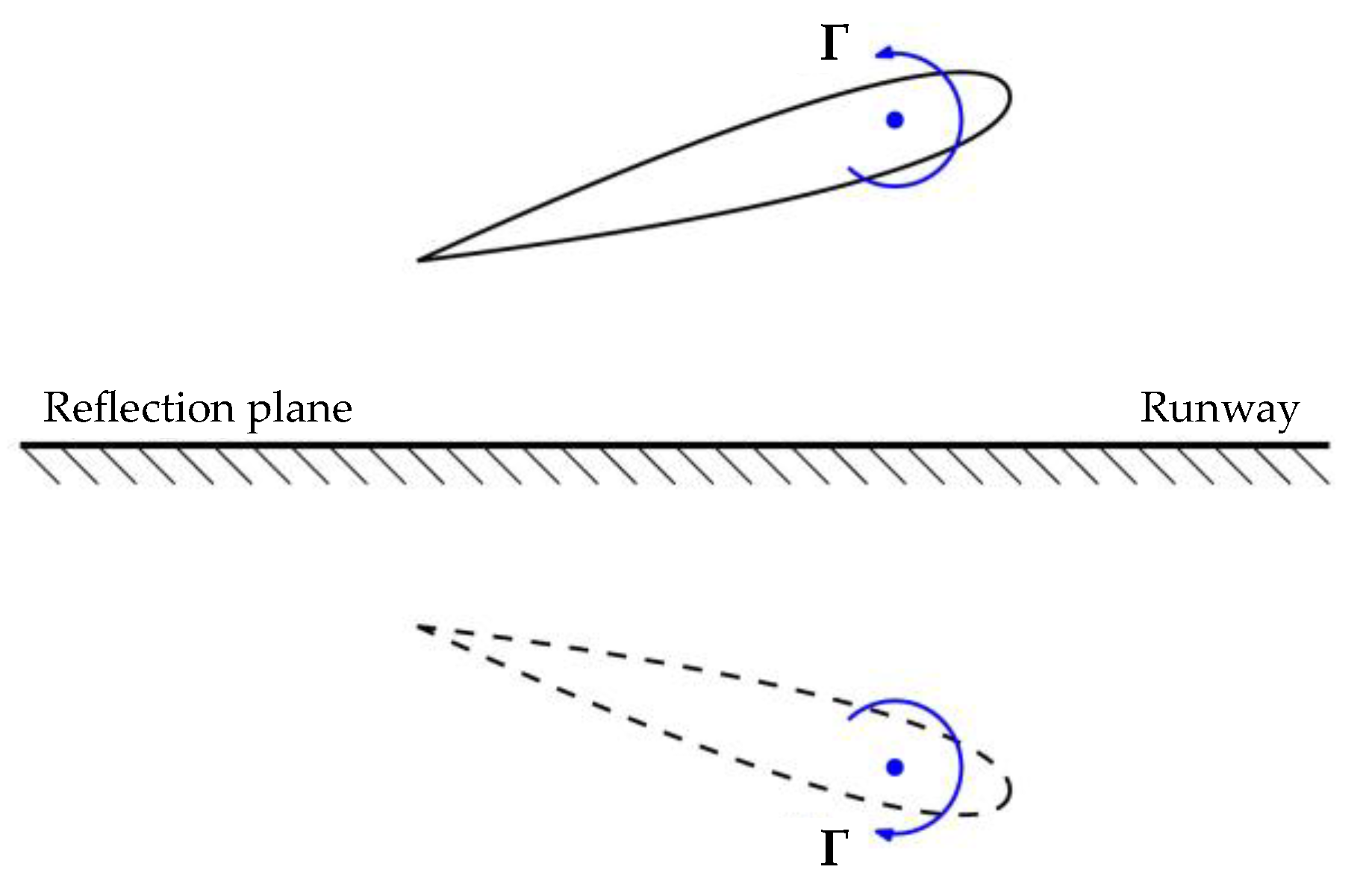
3. Ground Effect Aerodynamics
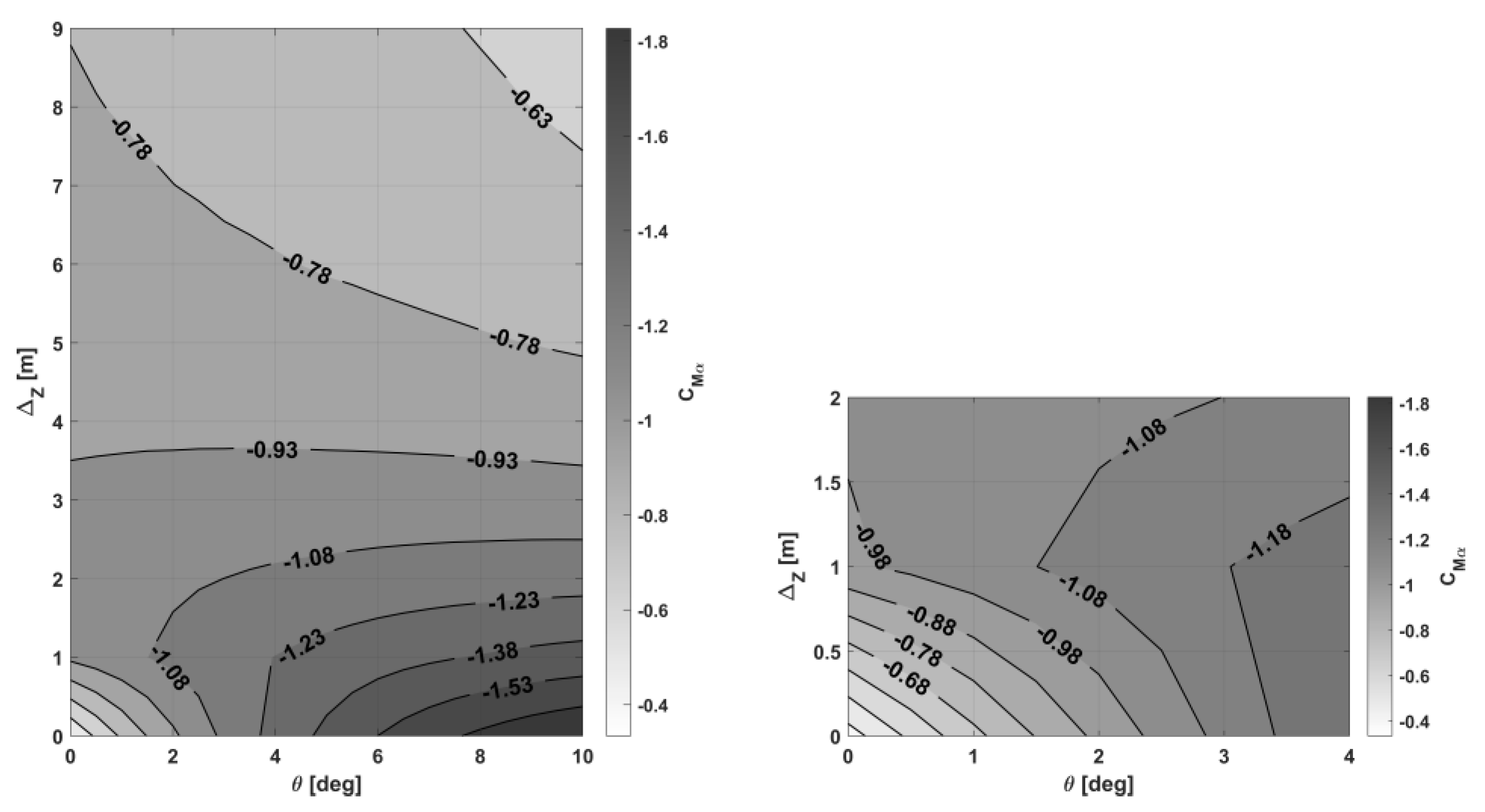
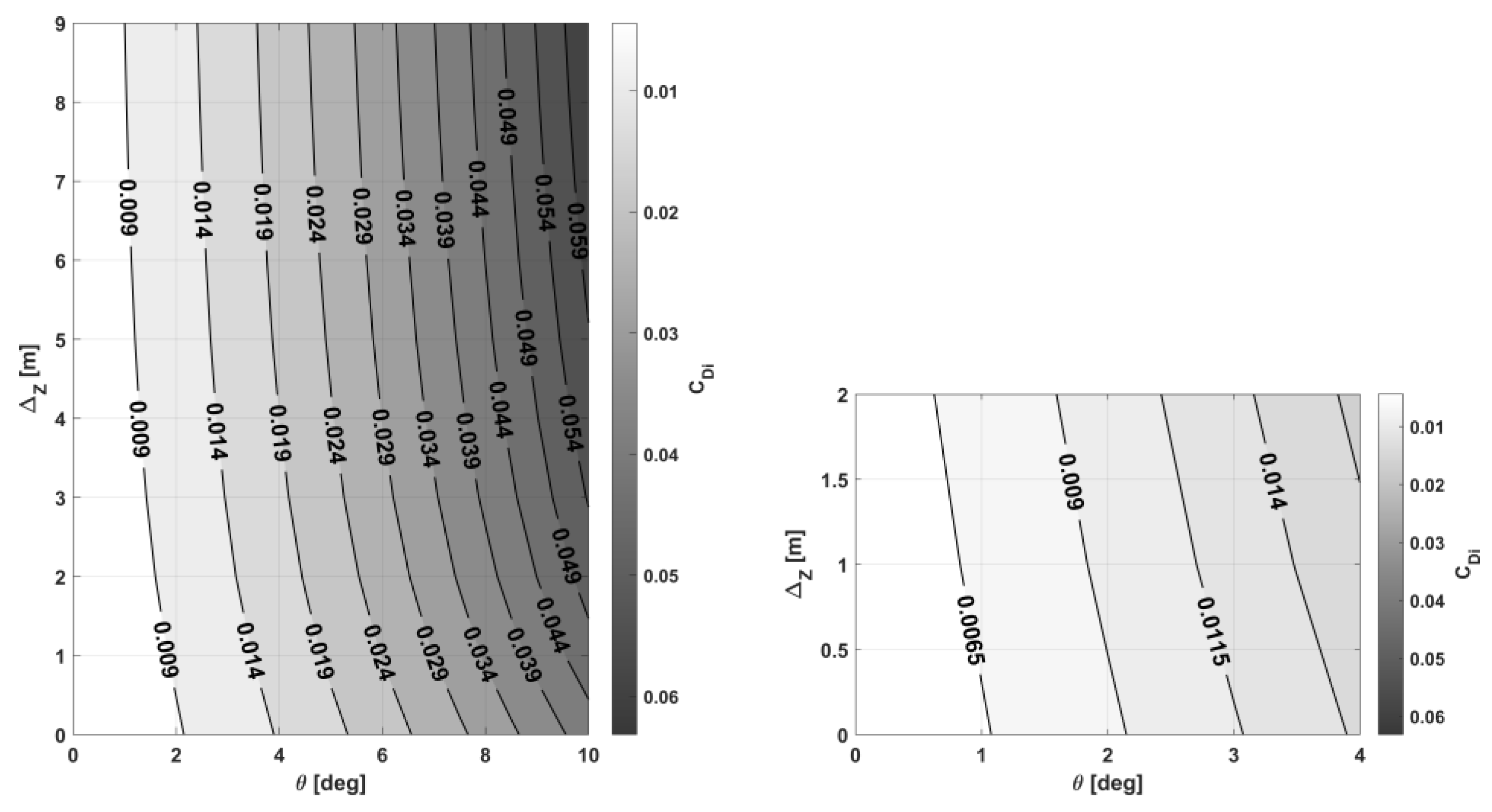
3.1. Evaluation of Aerodynamic Performance
3.2. Test-Case Configurations
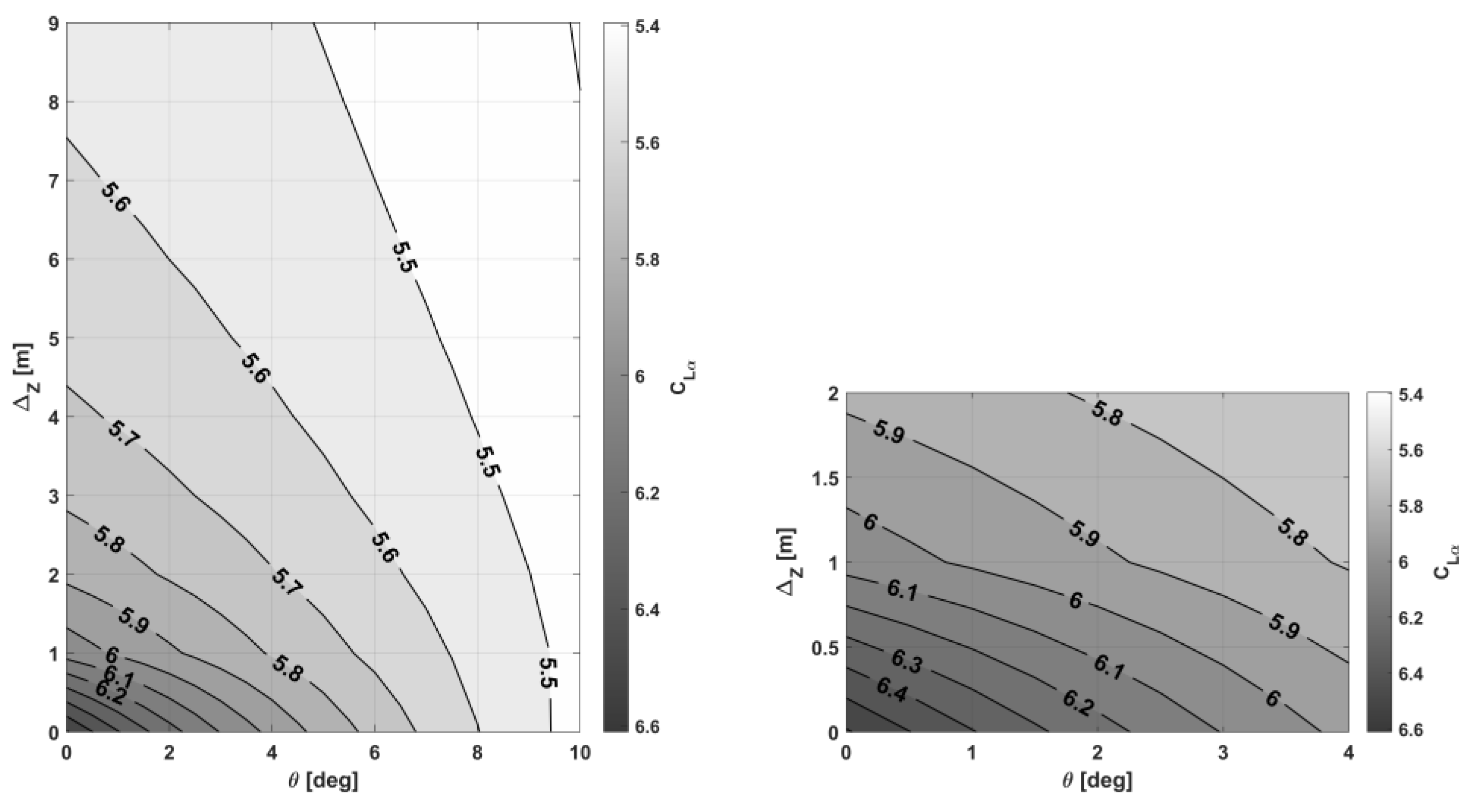
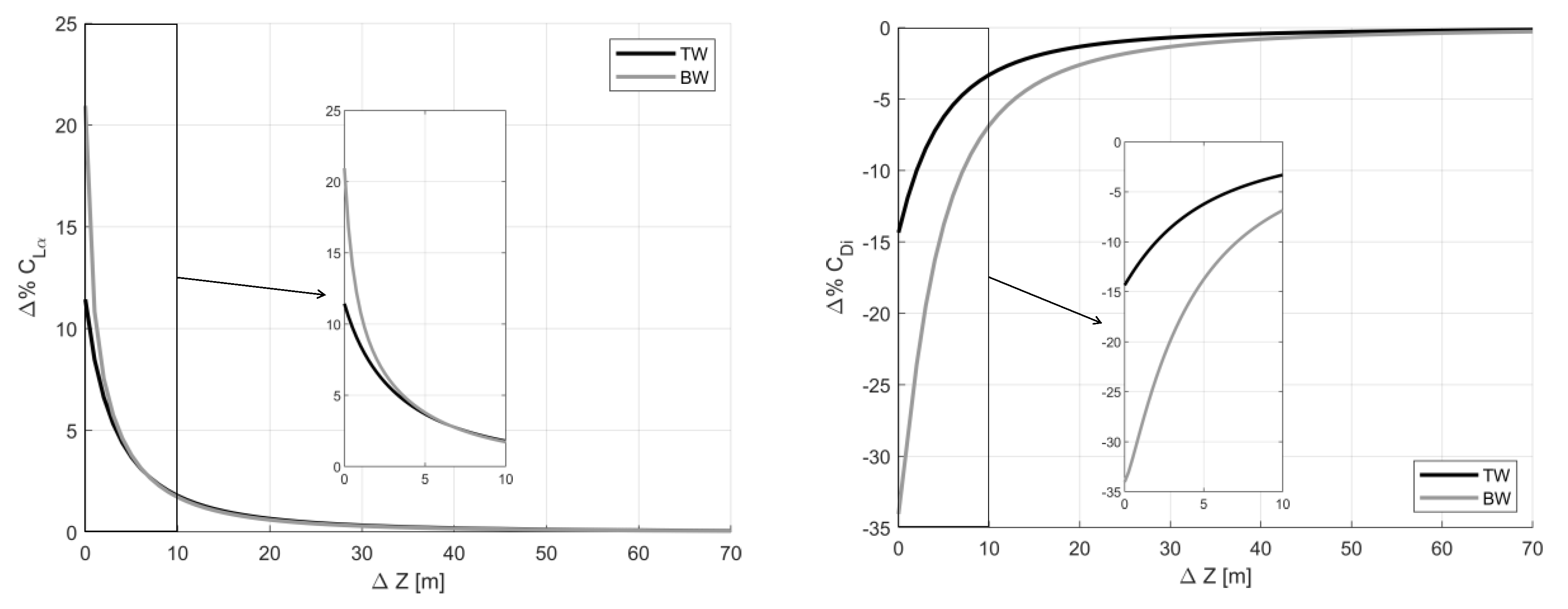
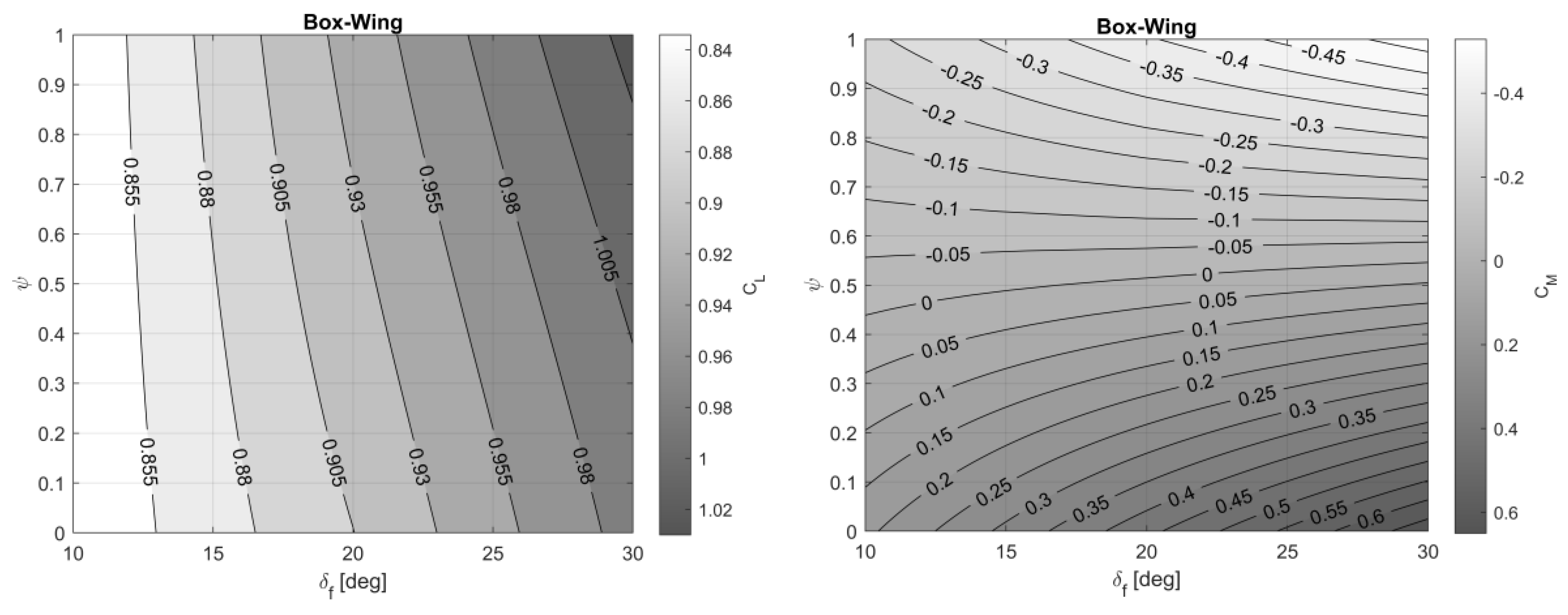
3.3. Analysis of the Impact of Ground Effect on Aerodynamic Performance
4. Simulations Results
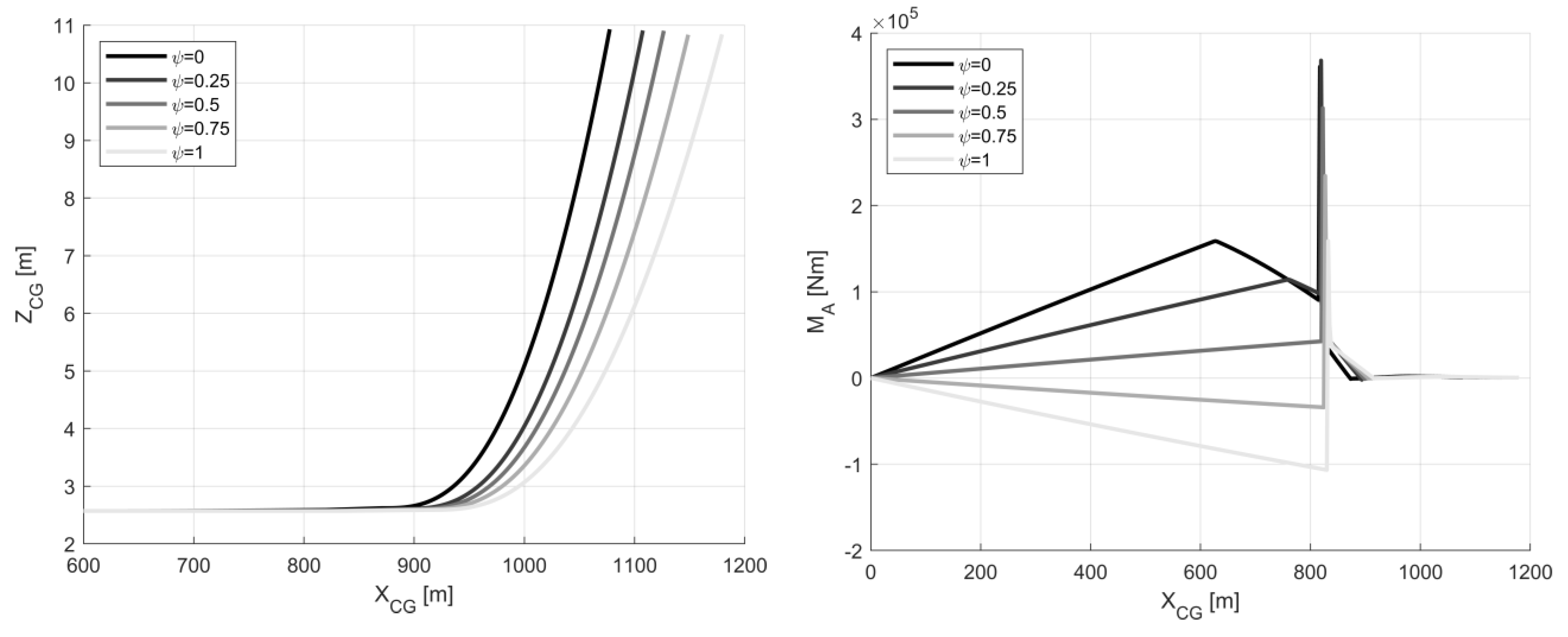
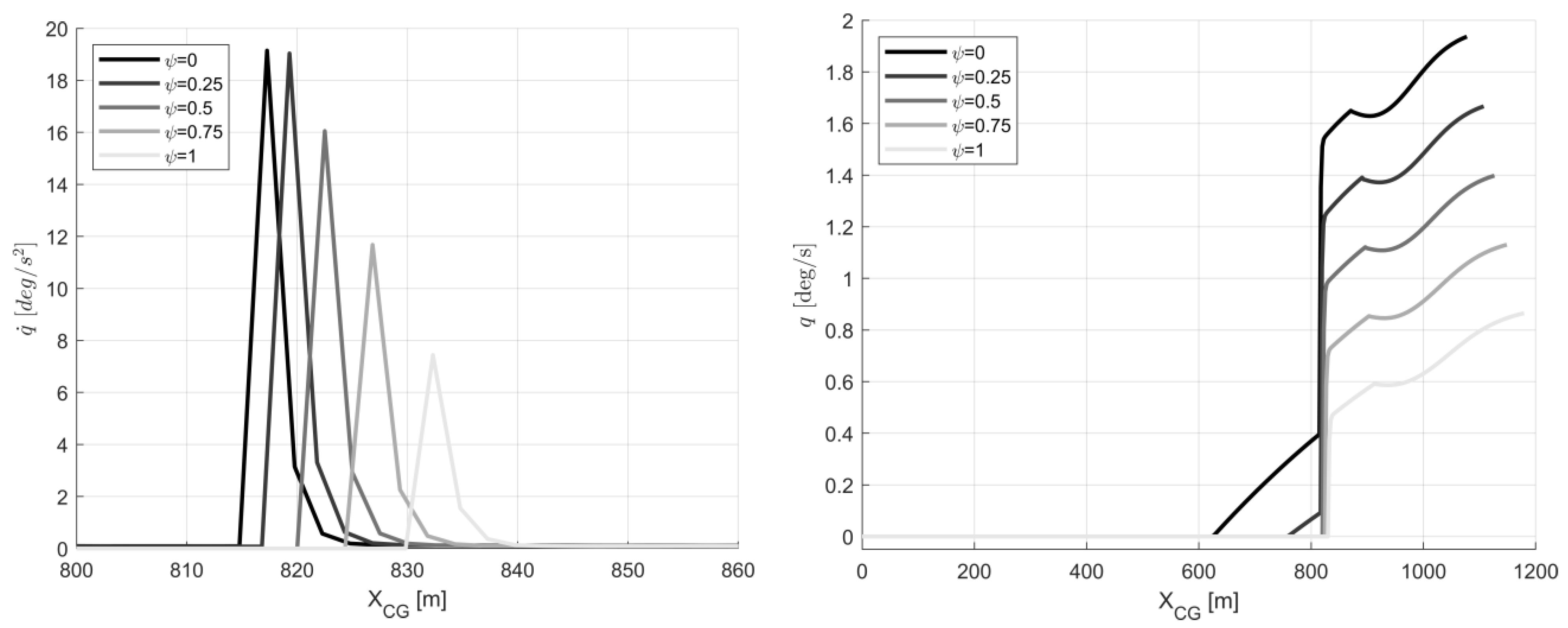
4.1. Box-Wing Aircraft Aeromechanics Features during Take-Off
4.2. Tube-and-Wing Aircraft Aeromechanics Features during Take-Off
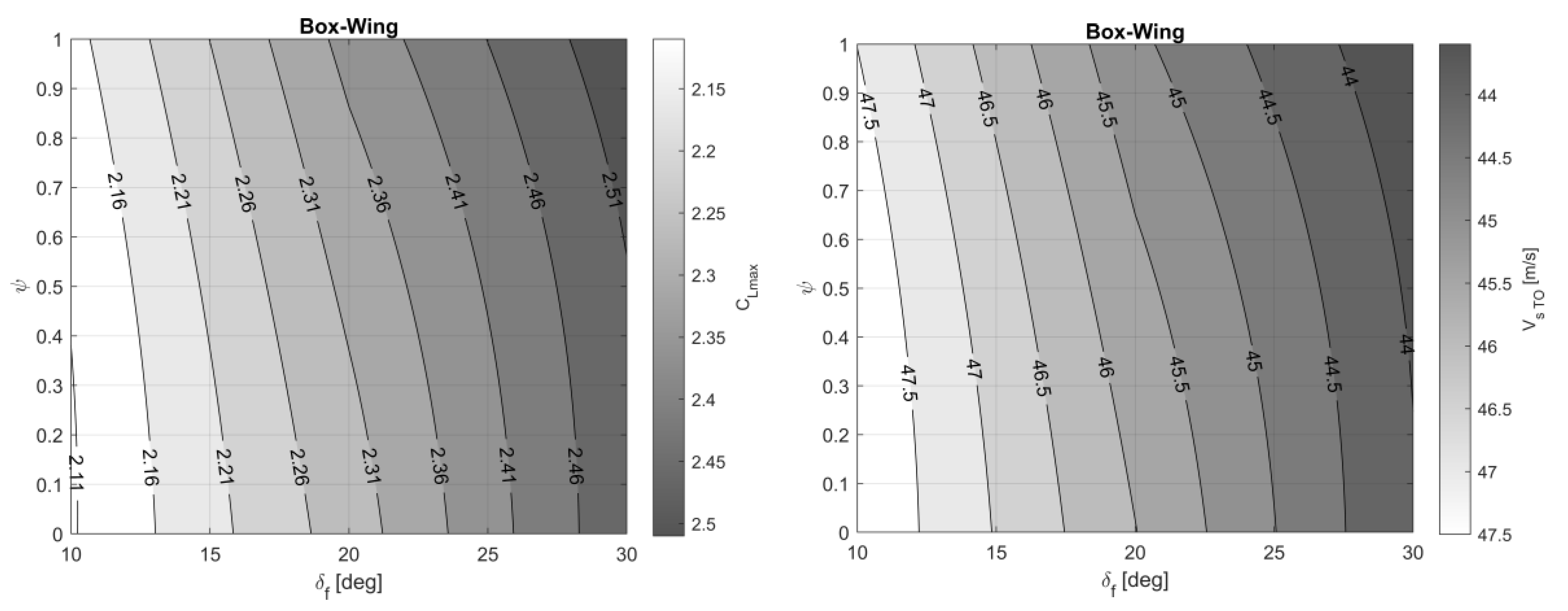
5. Optimization Results
5.1. Optimization Procedure
5.2. Comparison of Box-Wing and Tube-and-Wing Optima Take-Off Performance
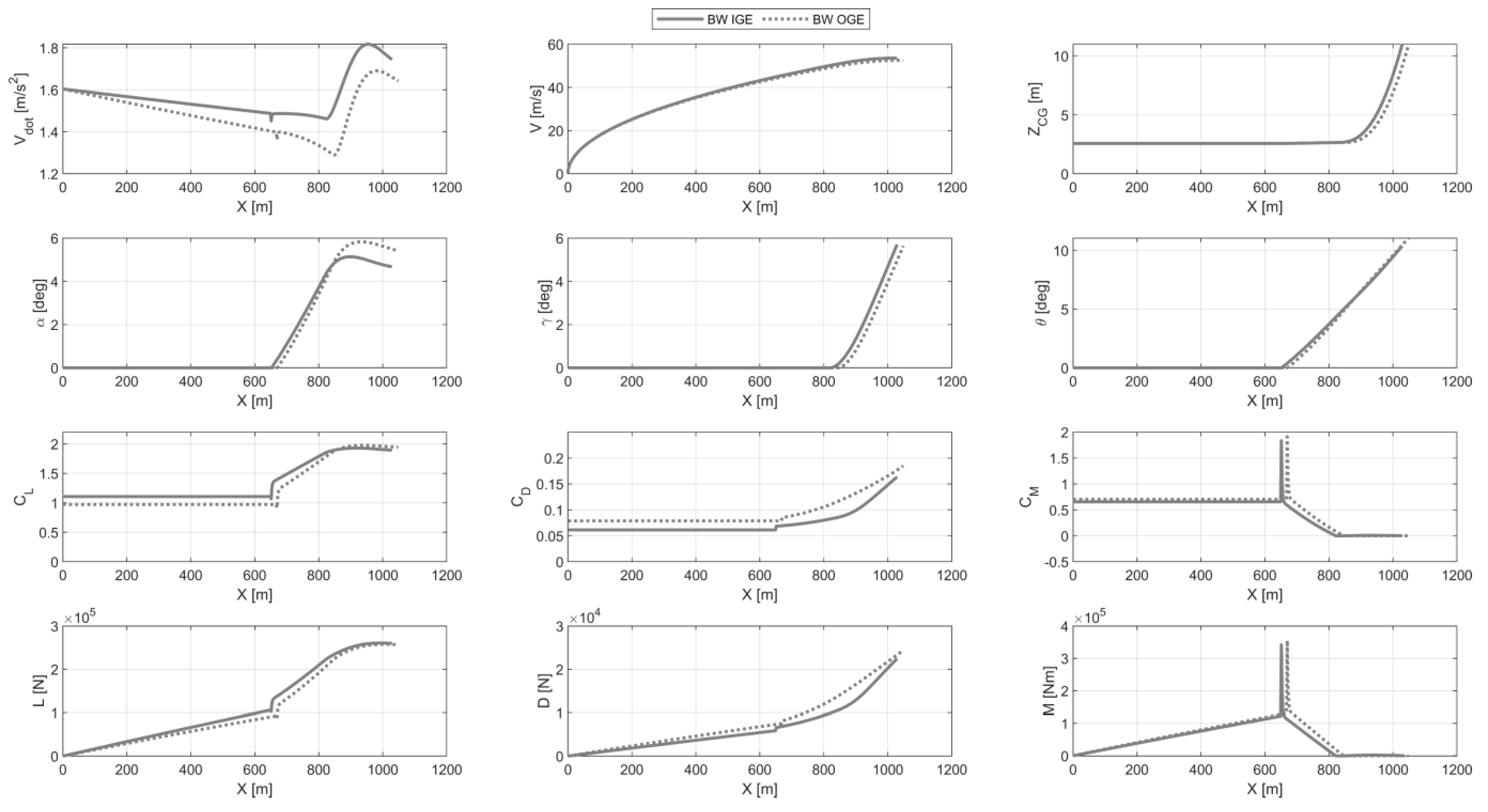
5.3. Comparison of Performance In-Ground-Effect and Out-of-Ground-Effect
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| List of Symbols | ||
| AR | wing aspect ratio | - |
| b | reference wingspan | m |
| c | mean aerodynamic chord | m |
| CD0 | parasite drag coefficient | - |
| CD f | fuselage parasitic drag coefficient | - |
| CD lg | landing gear parasitic drag coefficient | - |
| CD wb | wing-body parasitic drag coefficient | - |
| CDi | induced drag coefficient | - |
| CL | lift coefficient | - |
| CLα | lift coefficient derivative w.r.t. α | - |
| CLmax | maximum lift coefficient | - |
| CM | pitching moment coefficient | - |
| CMα | pitching moment coefficient derivative w.r.t. α | - |
| CMq | pitching moment coefficient derivative w.r.t. q | - |
| Cmδe | pitching moment coefficient derivative w.r.t. δe | - |
| D | aerodynamic drag | N |
| d | horizontal distance between LG and CG | m |
| df | fuselage diameter | m |
| dp | propeller diameter | ft |
| fw | subscript for front wing | - |
| g | gravity acceleration | m/s2 |
| h | vertical distance between LG and CG | m |
| hLG | landing gear length | m |
| Iy | longitudinal moment of inertia | kg m2 |
| L | lift | N |
| L/S | wing loading | N/m2 |
| lb | design variables lower boundary vector | - |
| lf | fuselage length | m |
| m | mass | kg |
| MA | aerodynamic pitching moment | Nm |
| MR | ground reaction moment | Nm |
| Ne | number of engines | - |
| Pi | installed power | MW |
| q | pitch angular speed | deg/s |
| RN | ground normal reaction | N |
| RT | ground tangential reaction | N |
| rw | subscript for rear wing/tail | - |
| S | reference wing surface | m2 |
| T | thrust | N |
| t | time | s |
| ub | design variables upper boundary vector | - |
| V | aircraft speed | m/s |
| VR | rotation speed | m/s |
| VRe | real rotation speed | m/s |
| Vs TO | take-off stall speed | m/s |
| Vx | horizontal speed | m/s |
| Vz | vertical speed | m/s |
| W | aircraft weight | N |
| W/S | aircraft wing loading | kgf/m2 |
| x | longitudinal position | m |
| XTO | runway length | m |
| z | vertical position | m |
| α | angle of attack | rad |
| γ | trajectory slope | rad |
| ε | elevator gain | - |
| δer | rear elevator deflection | rad |
| δe | elevator deflection | rad |
| δf | main flap deflection | rad |
| δfr | rear flap deflection | rad |
| Δt | time step | s |
| θ | pitch angle | rad |
| λ | by-pass ratio | - |
| μ | friction coefficient | - |
| ξ | vector of optimization variables | - |
| ρ | air density | kg/m3 |
| ψ | flap gain | - |
| List of Abbreviations | ||
| AVL | Athena Vortex Lattice | |
| BW | Box-Wing | |
| CG | Centre of Gravity | |
| HE | Hybrid Electric | |
| IGE | In Ground Effect | |
| LG | Landing Gear | |
| MTOW | Maximum Take-Off Weight | |
| NP | Neutral Point | |
| OGE | Out of Ground Effect | |
| SQP | Sequential Quadratic Programming | |
| TW | Tube-and-Wing | |
| VLM | Vortex Lattice Method | |
Appendix A
References
- Neufeld, D.; Chung, J.; Behdinian, K. Aircraft conceptual design optimization considering fidelity uncertainties. J. Aircr. 2011, 48, 1602–1612. [Google Scholar] [CrossRef]
- Torenbeek, E. Advanced Aircraft Design: Conceptual Design, Analysis and Optimization of Subsonic Civil Airplanes; John Wiley & Sons: Hoboken, NJ, USA, 2013; ISBN 9781118568101. [Google Scholar] [CrossRef]
- Kundu, A.K.; Price, M.A.; Riordan, D. Conceptual Aircraft Design: An Industrial Approach; John Wiley & Sons: Hoboken, NJ, USA, 2019; ISBN 978-1-119-50028-5. [Google Scholar]
- van Gent, I.; Aigner, B.; Beijer, B.; Jepsen, J.; La Rocca, G. Knowledge architecture supporting the next generation of MDO in the AGILE paradigm. Prog. Aerosp. Sci. 2020, 119, 100642. [Google Scholar] [CrossRef]
- Orefice, F.; Della Vecchia, P.; Ciliberti, D.; Nicolosi, F. Aircraft Conceptual Design Including Powertrain System Architecture and Distributed Propulsion. In Proceedings of the 2019 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), Indianapolis, IN, USA, 22–24 August 2019; pp. 1–20. [Google Scholar] [CrossRef]
- Fioriti, M.; Boggero, L.; Prakasha, P.S.; Mirzoyan, A.; Aigner, B.; Anisimov, K. Multidisciplinary aircraft integration within a collaborative and distributed design framework using the AGILE paradigm. Prog. Aerosp. Sci. 2020, 119, 100648. [Google Scholar] [CrossRef]
- Sanchez, F.; Liscouët-Hanke, S.; Tfaily, A. Improving aircraft conceptual design through parametric CAD modellers—A case study for thermal analysis of aircraft systems. Comput. Ind. 2021, 130, 103467. [Google Scholar] [CrossRef]
- Smith, H.; Sziroczák, D.; Abbe, G.; Okonkwo, P. The GENUS aircraft conceptual design environment. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 2932–2947. [Google Scholar] [CrossRef]
- Lee, D.S.; Fahey, D.W.; Forster, P.M.; Newton, P.J.; Wit, R.C.; Lim, L.L.; Owen, B.; Sausen, R. Aviation and global climate change in the 21st century. Atmos. Environ. 2009, 43, 3520–3537. [Google Scholar] [CrossRef]
- Lee, D.S.; Pitari, G.; Grewe, V.; Gierens, K.; Penner, J.E.; Petzold, A.; Prather, M.J.; Schumann, U.; Bais, A.; Berntsen, T.; et al. Transport impacts on atmosphere and climate: Aviation. Atmos. Environ. 2010, 44, 4678–4734. [Google Scholar] [CrossRef]
- Grewe, V.; Dahlmann, K.; Flink, J.; Frömming, C.; Ghosh, R.; Gierens, K.; Heller, R.; Hendricks, J.; Jöckel, P.; Kaufmann, S.; et al. Mitigating the Climate Impact from Aviation: Achievements and Results of the DLR WeCare Project. Aerospace 2017, 4, 34. [Google Scholar] [CrossRef]
- Lai, Y.Y.; Christley, E.; Kulanovic, A.; Teng, C.C.; Björklund, A.; Nordensvärd, J.; Karakaya, E.; Urban, F. Analysing the opportunities and challenges for mitigating the climate impact of aviation: A narrative review. Renew. Sustain. Energy Rev. 2022, 156, 111972. [Google Scholar] [CrossRef]
- Bravo-Mosquera, P.; Catalano, F.; Zingg, D.W. Unconventional aircraft for civil aviation: A review of concepts and design methodologies. Prog. Aerosp. Sci. 2022, 131, 100813. [Google Scholar] [CrossRef]
- Abu Salem, K.; Cipolla, V.; Palaia, G.; Binante, V.; Zanetti, D. A physics-based multidisciplinary approach for the preliminary design and performance analysis of a medium range aircraft with box-wing architecture. Aerospace 2021, 8, 292. [Google Scholar] [CrossRef]
- Bravo-Mosquera, P.D.; Cerón-Muñoz, H.D.; Catalano, F.M. Design, aerodynamic analysis and optimization of a next-generation commercial airliner. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 609. [Google Scholar] [CrossRef]
- Cipolla, V.; Abu Salem, K.; Picchi Scardaoni, M.; Binante, V. Preliminary design and performance analysis of a box-wing transport aircraft. In Proceedings of the AIAA Scitech Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Hosseini, S.; Ali Vaziri-Zanjani, M.; Reza Ovesy, H. Conceptual design and analysis of an affordable truss-braced wing regional jet aircraft. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2020, 0954410020923060. [Google Scholar] [CrossRef]
- Harrison, N.A.; Gatlin, G.M.; Viken, S.A.; Beyar, M.; Dickey, E.D.; Hoffman, K.; Reichenbach, E.Y. Development of an efficient M = 0.80 transonic truss-braced wing aircraft. In Proceedings of the AIAA Scitech Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Karpuk, S.; Liu, Y.; Elham, A. Multi-Fidelity Design Optimization of a Long-Range Blended Wing Body Aircraft with New Airframe Technologies. Aerospace 2020, 7, 87. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, M.; Chen, Y.; Sang, W.; Tan, Z.; Li, D.; Zhang, B. Assessment on critical technologies for conceptual design of blended-wing-body civil aircraft. Chin. J. Aeronaut. 2019, 32, 1797–1827. [Google Scholar] [CrossRef]
- Zhu, W.; Yu, X.; Wang, Y. Layout Optimization for Blended Wing Body Aircraft Structure. Int. J. Aeronauical Space Sci. 2019, 20, 879–890. [Google Scholar] [CrossRef]
- Zhu, W.; Fan, Z.; Yu, X. Structural mass prediction in conceptual design of blended-wing-body aircraft. Chin. J. Aeronaut. 2019, 32, 2455–2465. [Google Scholar] [CrossRef]
- Brelje, B.; Martins, J. Electric, hybrid, and turboelectric fixed-wing aircraft: A review of concepts, models, and design approaches. Prog. Aerosp. Sci. 2018, 104, 1–19. [Google Scholar] [CrossRef]
- Ye, X.I.E.; Savvarisal, A.; Tsourdos, A.; Zhang, D.; Jason, G.U. Review of hybrid electric powered aircraft, its conceptual design and energy management methodologies. Chin. J. Aeronaut. 2021, 34, 432–450. [Google Scholar] [CrossRef]
- Sahoo, S.; Zhao, X.; Kyprianidis, K. A Review of Concepts, Benefits, and Challenges for Future Electrical Propulsion-Based Aircraft. Aerospace 2020, 7, 44. [Google Scholar] [CrossRef]
- Gnadt, A.; Speth, R.; Sabnis, J.; Barrett, S. Technical and environmental assessment of all-electric 180-passenger commercial aircraft. Prog. Aerosp. Sci. 2019, 105, 1–30. [Google Scholar] [CrossRef]
- Pornet, C.; Isikveren, A. Conceptual design of hybrid-electric transport aircraft. Prog. Aerosp. Sci. 2015, 79, 114–135. [Google Scholar] [CrossRef]
- de Vries, R.; Brown, M.; Vos, R. Preliminary Sizing Method for Hybrid-Electric Distributed-Propulsion Aircraft. J. Aircr. 2019, 56, 2172–2188. [Google Scholar] [CrossRef]
- Marciello, V.; Orefice, F.; Nicolosi, F.; Ciliberti, D.; Della Vecchia, P. Design of hybrid-electric aircraft with fault-tolerance considerations. Chin. J. Aeronaut. 2023, 36, 160–178. [Google Scholar] [CrossRef]
- Hoelzen, J.; Liu, Y.; Bensmann, B.; Winnefeld, C.; Elham, A.; Friedrichs, J.; Hanke-Rauschenbach, R. Conceptual Design of Operation Strategies for Hybrid Electric Aircraft. Energies 2018, 11, 217. [Google Scholar] [CrossRef]
- Khandelwal, B.; Karakurt, A.; Sekaran, P.R.; Sethi, V.; Singh, R. Hydrogen powered aircraft: The future of air transport. Prog. Aerosp. Sci. 2013, 60, 45–59. [Google Scholar] [CrossRef]
- Baroutaji, A.; Wilberforce, T.; Ramadan, M.; Olabi, A.G. Comprehensive investigation on hydrogen and fuel cell technology in the aviation and aerospace sectors. Renew. Sustain. Energy Rev. 2019, 106, 31–40. [Google Scholar] [CrossRef]
- Palladino, V.; Bartoli, N.; Pommier-Budinger, V.; Benard, E.; Schmollgruber, P.; Jordan, A. Optimization of a hydrogen-based hybrid propulsion system under aircraft performance constraints. Chin. J. Aeronaut. 2023. [Google Scholar] [CrossRef]
- Rao, A.G.; Yin, F.; Werij, H. Energy transition in aviation: The role of cryogenic fuels. Aerospace 2020, 7, 181. [Google Scholar] [CrossRef]
- Ciampa, P.D.; Nagel, B. AGILE Paradigm: The next generation collaborative MDO for the development of aeronautical systems. Prog. Aerosp. Sci. 2020, 119, 100643. [Google Scholar] [CrossRef]
- La Rocca, G.; Van Tooren, M.J. Knowledge-based engineering approach to support aircraft multidisciplinary design and optimization. J. Aircr. 2009, 46, 1875–1885. [Google Scholar] [CrossRef]
- Feng, H.; Luo, M.; Liu, H.; Wu, Z. A knowledge-based and extensible aircraft conceptual design environment. Chin. J. Aeronaut. 2011, 24, 709–719. [Google Scholar] [CrossRef]
- Lefebvre, T.; Bartoli, N.; Dubreuil, S.; Panzeri, M.; Lombardi, R.; D’Ippolito, R.; Della Vecchia, P.; Nicolosi, F.; Ciampa, P.D. Methodological enhancements in MDO process investigated in the AGILE European project. In Proceedings of the 18th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Varriale, C.; Raju Kulkarni, A.; La Rocca, G.; Voskuijl, M. A hybrid, configuration- agnostic approach to aircraft control surface sizing. In Proceedings of the 25th International Congress of the Italian Association of Aeronautics and Astronautics AIDAA, Rome, Italy, 9–12 September 2019; ISBN 1259560074. [Google Scholar]
- Raymer, P. Aircraft Design: A Conceptual Approach; AIAA Education Series; American Institute of Aeronautics and Astronautics, Inc.: Washington DC, USA, 1992; ISBN 0-930403-51-7. [Google Scholar]
- Sun, J.; Hoekstra, J.M.; Ellerbroek, J. OpenAP: An Open-Source Aircraft Performance Model for Air Transportation Studies and Simulations. Aerospace 2020, 7, 104. [Google Scholar] [CrossRef]
- Lin, R.; Afjeh, A. An Extensible, Interchangeable and Sharable Database Model for Improving Multidisciplinary Aircraft Design. In Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, USA, 4–6 September 2002; p. 5613. [Google Scholar] [CrossRef]
- Filippone, A. Advanced Aircraft Flight Performance; Cambridge University Press: Cambridge, UK, 2012; ISBN 978-1139161893. [Google Scholar]
- Casarosa, C. Meccanica del Volo; Pisa University Press: Pisa, Italy, 2013; ISBN 978-8867410163. [Google Scholar]
- Palaia, G. Design and Performance Assessment Methodologies for Box-Wing Hybrid-Electric Aircraft from Urban to Regional Transport Applications. Ph.D. Thesis, University of Pisa, Pisa, Italy, 2022. Available online: https://etd.adm.unipi.it/theses/available/etd-11092022-150110/ (accessed on 5 April 2023).
- Ohme, P. A Model-based approach to aircraft takeoff and landing performance assessment. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Chicago, IL, USA, 10–13 August 2009. [Google Scholar] [CrossRef]
- Lymperopoulos, I.; Lygeros, J.; Lecchini, A. Model based aircraft trajectory prediction during takeoff. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar] [CrossRef]
- Kim, M.; Kim, J. Improved method of analysing takeoff/landing performance of turboprop aircraft through modeling and simulation. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Montreal, QC, Canada, 6–9 August 2001. [Google Scholar] [CrossRef]
- Erturk, S.A.; Gomec, F.S. The analyses of aircraft performance during takeoff and landing with aerodynamic interference effects and the 6-DOF model. In Proceedings of the AIAA Aviation Forum, Virtual Event, 15–19 June 2020. [Google Scholar] [CrossRef]
- Riboldi, C.E.D.; Cacciola, S.; Ceffa, L. Studying and Optimizing the Take-Off Performance of Three-Surface Aircraft. Aerospace 2022, 9, 139. [Google Scholar] [CrossRef]
- Nöding, M.; Schuermann, M.; Bertsch, L.; Koch, M.; Plohr, M.; Jaron, R.; Berton, J.J. Simulation of Landing and Take-Off Noise for Supersonic Transport Aircraft at a Conceptual Design Fidelity Level. Aerospace 2022, 9, 9. [Google Scholar] [CrossRef]
- De Marco, A.; Trifari, V.; Nicolosi, F.; Ruocco, M. A Simulation-Based Performance Analysis Tool for Aircraft Design Workflows. Aerospace 2020, 7, 155. [Google Scholar] [CrossRef]
- Nicolosi, F.; De Marco, A.; Attanasio, L.; Della Vecchia, P. Development of a Java-based framework for aircraft preliminary design and optimization. J. Aerosp. Inf. Syst. 2016, 13, 234–242. [Google Scholar] [CrossRef]
- De Marco, A.; Di Stasio, M.; Della Vecchia, P.; Trifari, V.; Nicolosi, F. Automatic modeling of aircraft external geometries for preliminary design workflows. Aerosp. Sci. Technol. 2020, 98, 105667. [Google Scholar] [CrossRef]
- Hurt, H.H. Aerodynamics for Naval Aviators; FAA Handbooks Series; Federal Aviation Administration; Aviation Supplies & Academics: Washington, DC, USA, 1992; ISBN 978-1508489481. [Google Scholar]
- Federal Aviation Administration. FAR 25, Airworthiness Standards: Transport Category Airplanes; Federal Aviation Administration: Washington, DC, USA, 1980.
- Drela, M.; Youngren, H. AVL 3.36 User Primer; Online Software Manual; 2017; Available online: https://perma.cc/R35R-W29F (accessed on 5 April 2023).
- Sun, J.; Hoekstra, J.M.; Ellerbroek, J. Aircraft drag polar estimation based on a stochastic hierarchical model. In Proceedings of the 8th SESAR Innovation Days, Salzburg, Austria, 3–7 December 2018. [Google Scholar]
- Abu Salem, K. Development of Design Tools and Methods for Box-Wing Airplanes and Application of the PrandtlPlane Concept to a Short-Medium Range Aircraft. Ph.D. Thesis, University of Pisa, Pisa, Italy, 2021. Available online: https://etd.adm.unipi.it/theses/available/etd-05312021-171241/ (accessed on 2 April 2023).
- Abu Salem, K.; Palaia, G.; Cipolla, V.; Binante, V.; Zanetti, D.; Chiarelli, M. Tools and methodologies for box-wing aircraft conceptual aerodynamic design and aeromechanic analysis. Mech. Ind. 2021, 22, 39. [Google Scholar] [CrossRef]
- Cui, E.; Zhang, X. Ground Effect Aerodynamics. Encycl. Aerosp. Eng. 2010, 1, 245–256. [Google Scholar] [CrossRef]
- Phillips, W.F.; Hunsaker, D.F. Lifting-line predictions for induced drag and lift in ground effect. J. Aircr. 2013, 50, 1226–1233. [Google Scholar] [CrossRef]
- Lee, J.; Han, C.S.; Bae, C.H. Influence of wing configurations on aerodynamic characteristics of wings in ground effect. J. Aircr. 2010, 47, 1030–1040. [Google Scholar] [CrossRef]
- Qu, Q.; Lu, Z.; Guo, H.; Liu, P.; Agarwal, R.K. Numerical investigation of the aerodynamics of a delta wing in ground effect. J. Aircr. 2015, 52, 329–340. [Google Scholar] [CrossRef]
- Jamei, S.; Maimun, A.; Mansor, S.; Azwadi, N.; Priyanto, A. Numerical investigation on aerodynamic characteristics of a compound wing-in-ground effect. J. Aircr. 2012, 49, 1297–1305. [Google Scholar] [CrossRef]
- Hooker, S. A review of current technical knowledge necessary to develop large scale wing-in-surface effect craft. In Proceedings of the AIAA Advanced Marine Vehicles Conference, Arlington, VA, USA, 5–7 June 1989. p. 1497. [CrossRef]
- Fischenberg, D.; Mönnich, W.; Krag, B.; Jategaonkar, R.V. Aspects of C-160 simulator model determination and validation on and close to the ground. In Proceedings of the AIAA Flight Simulation Technologies Conference, Scottsdale, AZ, USA, 1–3 August 1994; pp. 22–31. [Google Scholar] [CrossRef]
- Hess, J.L.; Smith, A.O. Calculation of potential flow about arbitrary bodies. Prog. Aerosp. Sci. 1967, 8, 1–138. [Google Scholar] [CrossRef]
- Wieselsberger, C. Wing resistance near the ground. In NACA Technical Memorandum; TM-77; 1922. Available online: https://ntrs.nasa.gov/citations/19930081293 (accessed on 5 April 2023).
- Pistolesi, E. Ground effect-theory and practice. In NACA Technical Memorandum; TM-828; 1937. Available online: https://ntrs.nasa.gov/citations/19930094588 (accessed on 5 April 2023).
- Fink, M.P.; Lastinger, J.L. Aerodynamic Characteristics of Low-Aspect-Ratio Wings in Close Proximity to the Ground, NASA Technical Note; D-926; 1961. Available online: https://ntrs.nasa.gov/citations/19980231058 (accessed on 5 April 2023).
- Carter, A.W. Effects of Ground Proximity on the Longitudinal Aerodynamic Characteristics of an Unswept Aspect-Ratio-10 Wing. NASA Technical Note; D-5662; 1970. Available online: https://ntrs.nasa.gov/citations/19700009363 (accessed on 5 April 2023).
- Palaia, G.; Abu Salem, K. Mission Performance Analysis of Hybrid-Electric Regional Aircraft. Aerospace 2023, 10, 246. [Google Scholar] [CrossRef]
- Palaia, G.; Zanetti, D.; Abu Salem, K.; Cipolla, V.; Binante, V. THEA-CODE: A design tool for the conceptual design of hybrid electric aircraft with conventional or unconventional airframe configurations. Mech. Ind. 2021, 22, 19. [Google Scholar] [CrossRef]
- Della Vecchia, P.; Nicolosi, F. Aerodynamic guidelines in the design and optimization of new regional turboprop aircraft. Aerosp. Sci. Technol. 2014, 38, 88–104. [Google Scholar] [CrossRef]
- ATR. ATR 42-600 Aircraft. Available online: https://www.atr-aircraft.com/our-aircraft/atr-42-600/ (accessed on 5 April 2023).
- Eisenhut, D.; Moebs, N.; Windels, E.; Bergmann, D.; Geiß, I.; Reis, R.; Strohmayer, A. Aircraft Requirements for Sustainable Regional Aviation. Aerospace 2021, 8, 61. [Google Scholar] [CrossRef]
- Fletcher, R. Practical Methods of Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2013; ISBN 978-1-118-72318-0. [Google Scholar]
- Gill, P.E.; Murray, W.; Saunders, M.A. SNOPT: An SQP Algorithm for Large-Scale Constrained Optimization. SIAM Rev. 2005, 47, 99–131. [Google Scholar] [CrossRef]
- Martins, J.R.; Ning, A. Engineering Design Optimization; Cambridge University Press: Cambridge, UK, 2021; ISBN 978-1108833417. [Google Scholar]
- Zanetti, D. Studio Preliminare della Dinamica Libera e delle Qualita’ di volo Della Configurazione PrandtlPlane. (transl. “PRELIMINARY Study of the Flight Dynamics and Handling Qualities of the PrandtlPlane Configuration”). Master’s Thesis, University of Pisa, Pisa, Italy, 2014. Available online: https://etd.adm.unipi.it/theses/available/etd-09172014-114441/ (accessed on 5 April 2023).




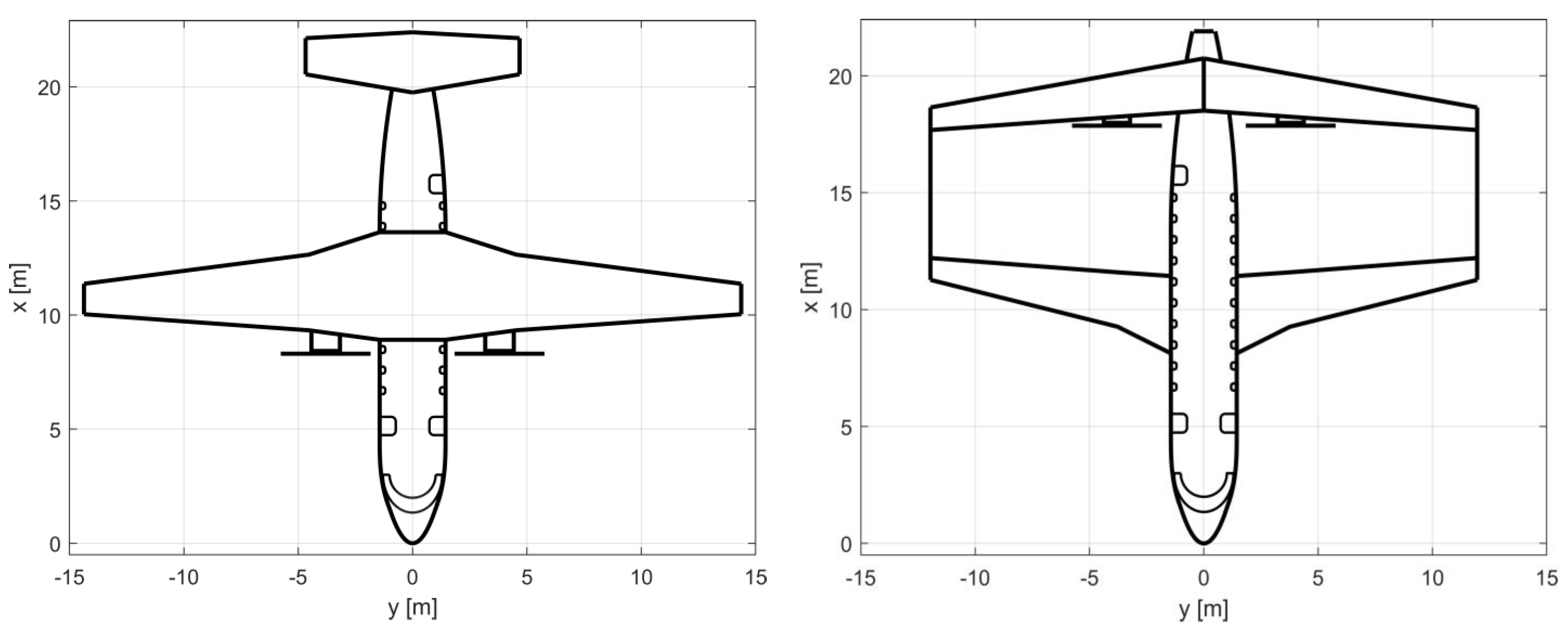




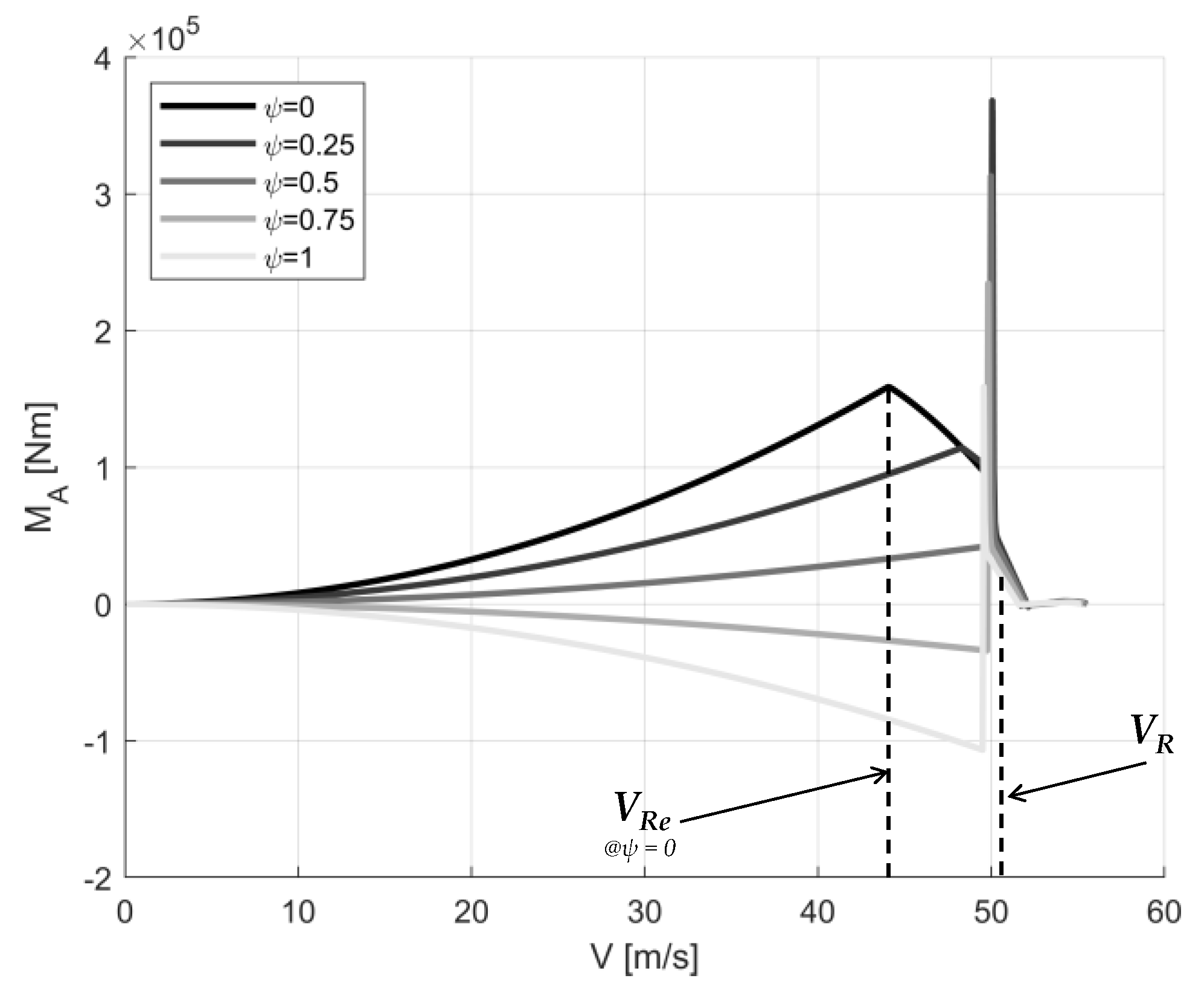
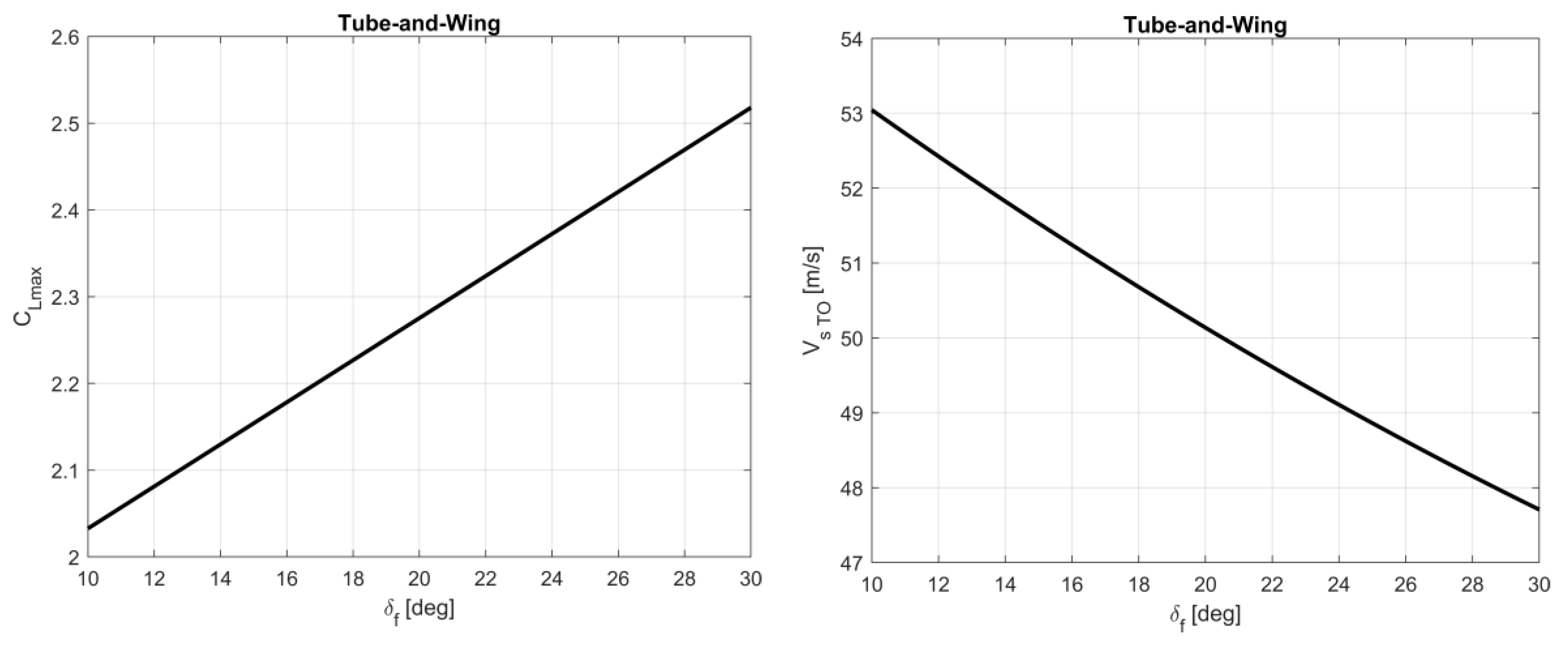
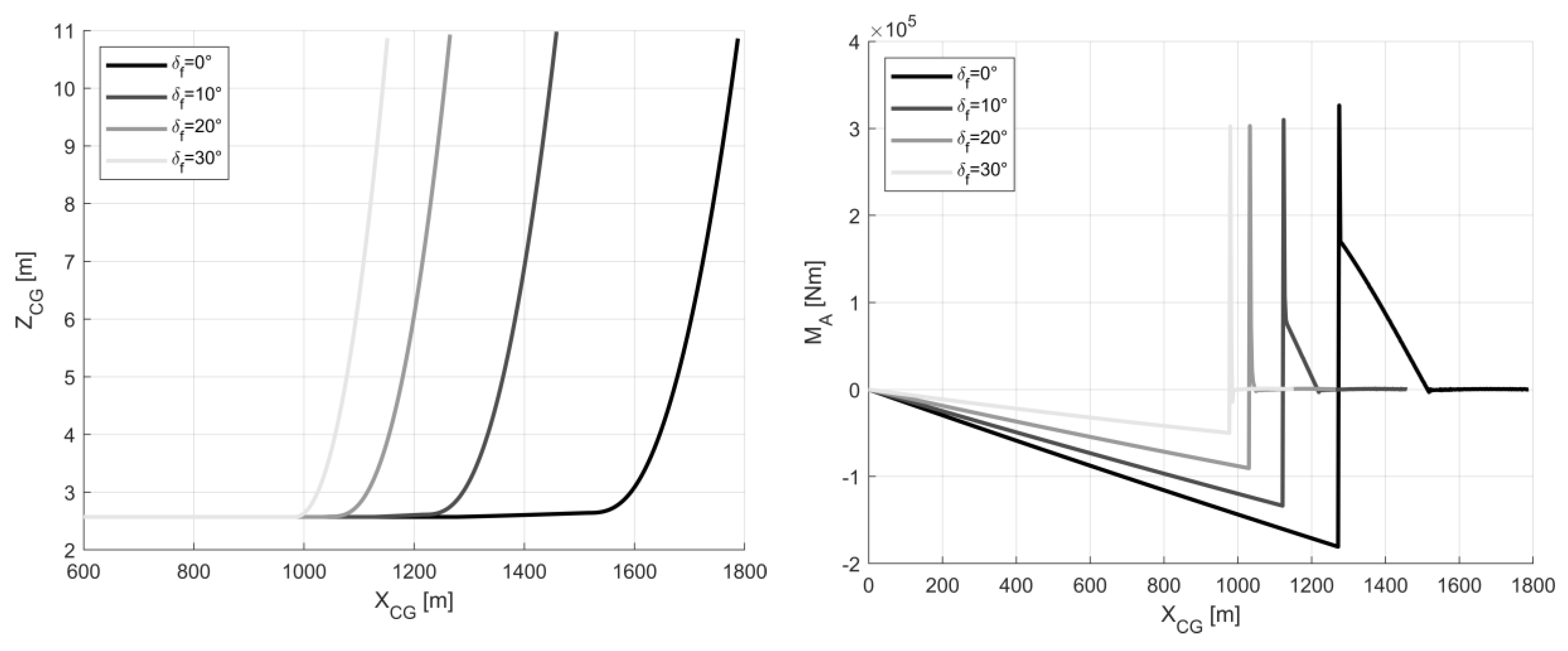
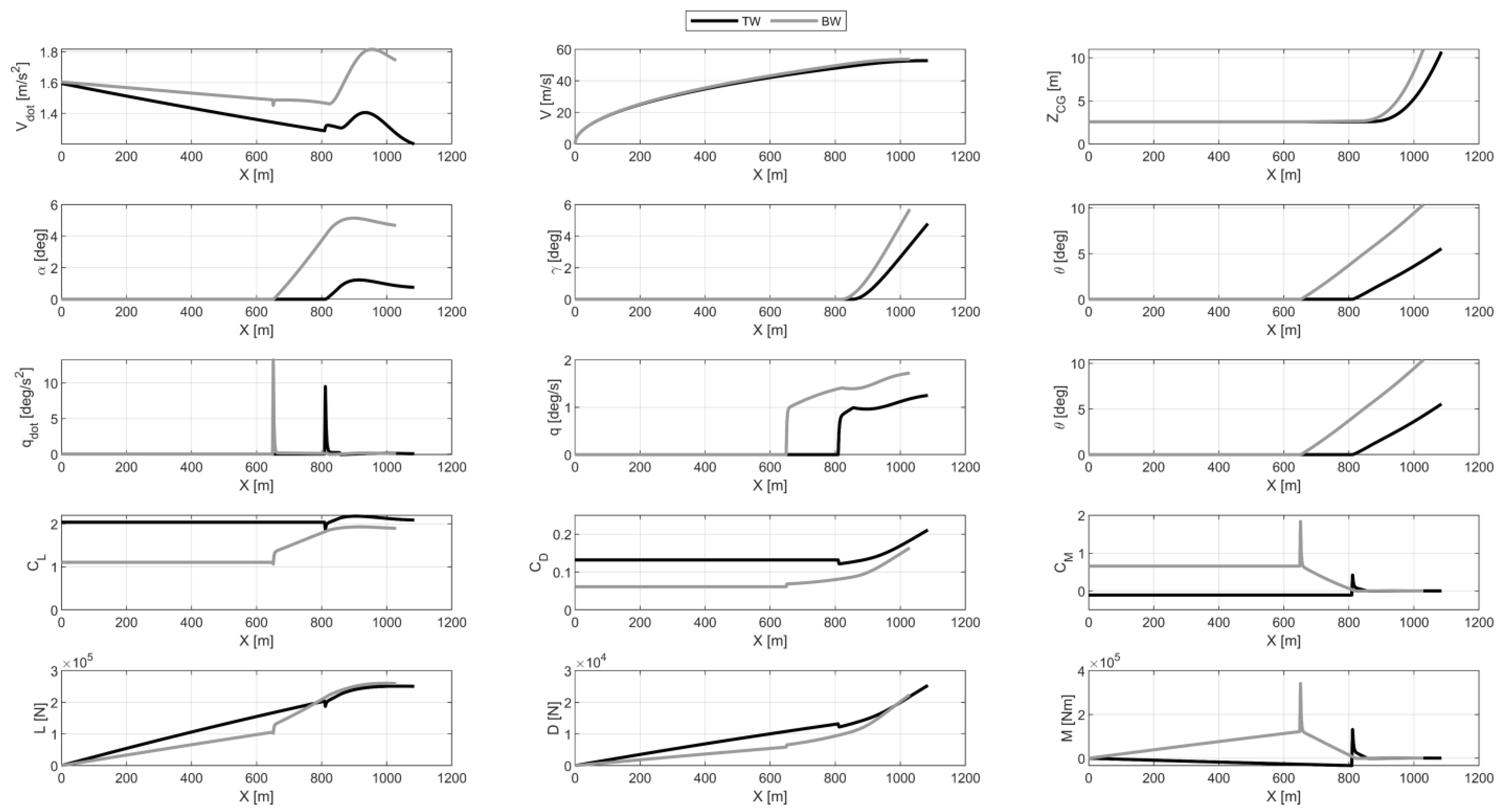

| HE Tube-and-Wing | HE Box-Wing | |
|---|---|---|
| MTOW | 22,935 kg | 22,921 kg |
| S | 70.6 m2 | 78.1 m2 |
| Sfw | 70.6 m2 | 39.8 m2 |
| Srw | 19.8 m2 | 38.2 m2 |
| b | 28.7 m | 23.9 m |
| bfw | 28.7 m | |
| brw | 9.4 m | |
| ARfw | 9.7 | 11.4 |
| ARrw | 4.4 | 14.9 |
| W/S | 325 kg/m2 | 294 kg/m2 |
| (L/S)fw @cruise | 316 kg/m2 | 385 kg/m2 |
| (L/S)rw @cruise | 33 kg/m2 | 195 kg/m2 |
| lf | 21.9 m | |
| df | 2.88 m | |
| hLG | 0.65 m | |
| dp | 3.93 m | |
| Pi | 5.70 MW | 5.73 MW |
| Configuration | Boundaries | Design Variables | ||||
|---|---|---|---|---|---|---|
| TW | 10° | - | 10° | - | 1.03 | |
| 30° | - | 25° | - | 1.2 | ||
| BW | 10° | 0 | 10° | −1 | 1.03 | |
| 30° | 1 | 25° | 0 | 1.2 | ||
| Configuration | Optima Design Variables | Objective Function | ||||
|---|---|---|---|---|---|---|
| TW | 30° | - | 14° | - | 1.06 | 1085 m |
| BW | 30° | 0 | 25° | −1 | 1.04 | 1029 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abu Salem, K.; Palaia, G.; Chiarelli, M.R.; Bianchi, M. A Simulation Framework for Aircraft Take-Off Considering Ground Effect Aerodynamics in Conceptual Design. Aerospace 2023, 10, 459. https://doi.org/10.3390/aerospace10050459
Abu Salem K, Palaia G, Chiarelli MR, Bianchi M. A Simulation Framework for Aircraft Take-Off Considering Ground Effect Aerodynamics in Conceptual Design. Aerospace. 2023; 10(5):459. https://doi.org/10.3390/aerospace10050459
Chicago/Turabian StyleAbu Salem, Karim, Giuseppe Palaia, Mario R. Chiarelli, and Mario Bianchi. 2023. "A Simulation Framework for Aircraft Take-Off Considering Ground Effect Aerodynamics in Conceptual Design" Aerospace 10, no. 5: 459. https://doi.org/10.3390/aerospace10050459
APA StyleAbu Salem, K., Palaia, G., Chiarelli, M. R., & Bianchi, M. (2023). A Simulation Framework for Aircraft Take-Off Considering Ground Effect Aerodynamics in Conceptual Design. Aerospace, 10(5), 459. https://doi.org/10.3390/aerospace10050459







