Abstract
Air cycle systems (ACSs) are primarily used in aircraft environmental control systems (ECSs) to provide a suitable cabin temperature and pressure environment for passengers and avionics. It comprises heat exchangers, compressors, turbines, water separators, and various other components that are interconnected to form an information-transmission network. Traditional research on ACSs has focused primarily on their thermal performance. This study abstracted ACSs into network graphs based on their information-transmission characteristics, determined the weight of each information-transmission route using the fuel weight penalty method, calculated and compared the order degree of different ACSs using the structure entropy method, and measured the importance of each component using centrality for the first time. The results showed that the order degree of the ACSs gradually increased with an increase in the number of wheels in the air cycle machine (ACM), and ACSs with high-pressure water separation had a higher order degree under wet conditions than under dry conditions. Moreover, based on the centrality of each vertex in the graphs, the ACM and secondary heat exchanger in the ACS were fundamentally important and should be focused on during the system design. The methodology proposed in this study provides a theoretical basis for the evaluation of the ACS organizational structure and the design performance of components.
1. Introduction
The environmental control system (ECS) is an important part of an aircraft, given that it controls the pressure, temperature, humidity, and other parameters of the cabin air when an aircraft flies in harsh environments. It guarantees the safety of passengers and the normal operation of avionics in the cabin [1]. Currently, air cycle systems (ACSs) are primarily used in ECSs [2]. Based on the utilization mode of the turbine (T) output power in the air cycle machine (ACM), ACSs can be divided into two-wheel types (applicable to the B737, MD-80, etc.), three-wheel types (applicable to the B747, A320, etc.), and four-wheel types (applicable to the B777, A380, etc.) to meet the environmental control requirements of different aircraft under complex flight conditions [3,4,5,6,7,8,9]. The traditional design of an ACS has focused primarily on its thermal performance, such as its cooling capacity and water separation capacity. By changing the parameters of various components in the system to achieve the overall system design objectives, many researchers have conducted thermodynamic modeling and analysis of various ACSs [10,11,12,13,14,15,16,17]. With an increasing number of wheels in such systems, they have become more complex, although their thermal performance has gradually improved [18].
An ACS comprises heat exchangers, compressors, turbines, water separators, and various other components that are interconnected to form an information-transmission network. The application of information entropy to ACS evaluation from an information-flow perspective is both interesting and meaningful. The information entropy theory—which is widely used in signal complexity measurements—was proposed by Shannon [19] and can be used to evaluate the order degree or complexity of systems [20]. This theory has been applied to the complexity evaluation of static networks in many fields, such as urban ecosystems, transportation networks, microbiological distribution, and stock markets [21,22,23,24,25,26,27]. Yan et al. proposed the structure entropy method (SEM) based on the information entropy theory, which could be used to evaluate the order degree of e-commerce systems from the timeliness and accuracy of the information-transmission perspective [28]. Wang et al. used this method to evaluate systems with network structures quantitatively and to evaluate the order degree of the organization of a power regulatory institution [29]. In terms of thermal systems, Yang et al. conducted research on an environmental control and life support system with a hierarchical structure inside a spacecraft—using the SEM to calculate the order degree of the system—and evaluated its complexity quantitatively [30]. Yang et al. conducted structure entropy analysis on a series/parallel two-wheel ACS and integrated/split four-wheel ACS with traditional engine bleed air and compared the order degree of each system [20,31].
However, Yang’s research on ACSs did not analyze the dry and wet conditions under which they operated or compare systems with a different number of wheels. This study considers the electrically-driven ACS the research object, regards each component of the system as a vertex and the information-transmission path as an edge based on graph theory, and constructs directed graphs for two-, three-, and four-wheel ACSs, and the analysis object is further improved. The fuel weight penalty method is used to calculate the additional value of the takeoff weight caused by each route and is applied as a weight on the edge of the graph for the first time in ACS studies, reflecting the relationship between ACSs thermodynamic performance and information-transmission. The weighted directed graphs are used to calculate the order degree of each system using the SEM. Moreover, the components represented by each vertex in the graphs have different degrees of importance in the system. This study uses the centrality algorithm in graph theory to evaluate the importance of each component for the first time in ACS studies. Moreover, this study uses SEM to evaluate the order degree of the ACS network from an information-flow perspective, extending the traditional thermodynamic analysis to the field of information and improving the algorithm in comparison to previous studies. The results of this research can explain the system-level architecture optimization brought about by the development of ACS and serve as a basis for future research on new ACSs.
2. Methodology
2.1. Graph and Network Structure
2.1.1. Path and Degree
In graph theory, a graph is a structure comprising several vertices and edges typically used to describe a specific relationship between certain things. The vertices represent the things, and the edges connecting the two vertices represent the relationship between the corresponding things. Depending on whether the edges have directivity, graphs can be divided into directed or undirected graphs [32], as shown in Figure 1.

Figure 1.
Undirected and directed graphs.
Vertices and edges constitute the basic elements of a graph, and the concepts of degree and path can be extended accordingly. The degree of a single vertex refers to the number of edges associated with that vertex. The degree of a directed graph can be divided into indegree and outdegree based on whether the vertex is at the start or end of an edge. A path refers to a sequence of vertices from one to another. The path length is the sum of the lengths of all edges on the path, the shortest path being the shortest of all feasible paths, which may not be unique. If the weight of each edge in the graph is set to represent the distance, cost, or time from one vertex to another, the path length becomes the sum of the weights of all the edges on the path.
For ACSs, there are heat and mass transfer phenomena such as the fresh air flow, ram airflow, and water spray, and these can be attributed to information transmission between components from another perspective while actual mass or heat exchange occurs. Therefore the system can be abstracted as a directed graph by taking the components to be vertices and the information transmissions to be edges.
2.1.2. Centrality
Degree, closeness, and betweenness centrality in graph theory can be used to evaluate the importance of each component in a system. Degree centrality describes the degree to which a vertex can be associated with all other vertices in a graph, representing the level of connectivity between a component and other components. The greater the number of other vertices it connects to, the higher the degree of centrality [33]. For a directed graph, indegree centrality and outdegree centrality are directly added when calculating the degree centrality of a vertex in this study. The normalized formula can be expressed as shown in Equation (1), where N denotes the total number of vertices in the graph and Din(i) and Dout(i) denote the indegree and outdegree of point i, respectively.
Closeness centrality can be used to describe whether a vertex can efficiently transmit information through the graph. It can be determined by calculating the reciprocal of the sum of distances from a single vertex to other vertices, which measures whether a component is in a central position in the system based on its distance from other components. It can also be further divided into inbound and outbound closeness centrality, which are directly added—consequently, the normalized formula proposed by Wasserman and Faust [34] is used in this study, as expressed in Equation (2), where Bin(i) and Bout(i) denote the number of inbound and outbound reachable vertices, respectively, Lji denotes the distance from the vertices corresponding to Bin(i) to vertex i, and Lik denotes the distance from vertex i to the vertex corresponding to Bout(i).
Betweenness centrality can be used to measure the number of times a vertex appears in the shortest path between any two vertices, thus characterizing its importance in the perspective of controlling information transmission [35], measuring centrality by whether a component is in a critical position for information flow in the system. The calculation of betweenness centrality needs to consider any two vertices besides itself, which involves all possible combinations (N − 1) (N − 2). The formula can be expressed as shown in Equation (3), where denotes the number of shortest paths from vertex s to t that do not include vertex i, and denotes the number of paths passing through vertex i among .
Equations (1)–(3) can characterize the centrality of components in ACS from different perspectives and, to some extent, reflect the importance of each component in the entire system.
2.2. Structure Entropy Method
The information transmission between each vertex in a graph has a certain efficiency and accuracy, which can be evaluated using the SEM [28,29]. Based on the information entropy theory, structure entropy relates the shortest path between two vertices and the degree of a single vertex in a graph to the efficiency and accuracy of information transmission, respectively, calculates the timeliness and quality of the network structure, and finally obtains the total order degree of the system.
The information entropy of data can reflect its uncertainty; therefore, it must be calculated using its realization probability. The microscopic state of the system and its realization probability must be determined using the SEM to calculate its structure entropy.
2.2.1. Timeliness
Timeliness entropy reflects the uncertainty of the information-transmission efficiency. Defining the timeliness microstate to be the shortest path between two vertices Lij, the total number of timeliness microstates of the system can be calculated by summing all the lengths of the shortest paths, as expressed in Equation (4).
When information transmission occurs between any two vertices in the system, the realization probability can be expressed as follows:
Therefore, the uncertainty of the information-transmission efficiency between two vertices can be calculated using the timeliness entropy, as expressed in Equation (6), where the base value a of the logarithm is 2.
The total timeliness entropy of the system can be obtained by summing the timeliness entropy of any two vertices, as expressed in Equation (7), which represents the uncertainty in the information-transmission efficiency of the entire system.
The maximum timeliness entropy that the system can theoretically reach can be defined based on the total number of timeliness microstates of the system as follows:
Finally, the timeliness of the system can be defined by Equation (9), which has a theoretical value range of [0,1). The larger the value, the higher the information-transmission efficiency of the system.
2.2.2. Quality
Quality entropy reflects the uncertainty of the information-transmission accuracy. The quality microstate can be defined as the sum of the indegree and outdegree of a single vertex, and the total number of quality microstates of the system can be calculated as follows:
When a vertex receives information transmitted from another vertex, the realization probability can be expressed as follows:
Therefore, the uncertainty of the accuracy of a single vertex receiving information can be calculated using the quality entropy:
The total quality entropy of the system can then be obtained by summing the quality entropy of all the vertices, as expressed in Equation (13), which represents the uncertainty of the information-transmission accuracy of the entire system.
The maximum quality entropy that the system can theoretically reach can be defined based on the total number of quality microstates of the system as follows:
Finally, the quality of the system can be defined using Equation (15), which has a theoretical value range of [0,1). The larger the value, the higher the information-transmission accuracy of the system.
2.2.3. Total Order Degree
The total order degree of the system can be obtained by linearly adding timeliness and quality, as expressed in Equation (16). The order degree is a comprehensive evaluation index that integrates the efficiency and accuracy of system information transmission. The weights of timeliness (α) and of quality (β) can be adjusted to reflect the different degrees of concern for the two indices in different systems; this paper defines α = β = 0.5.
3. Aircraft Environmental Control System
3.1. Architectures of Different ACSs
In this study, electrically-driven two-, three-, and four-wheel ACSs were considered. There are simple and bootstrap types among two-wheel ACSs and low-pressure and high-pressure water separation types based on the bootstrap type; three-wheel ACSs can be divided into low-pressure and high-pressure water separation types; and existing four-wheel systems are generally high-pressure water separation ACSs, the integrated and split types of which were considered.
3.1.1. Two-Wheel System
The simple- and bootstrap-type two-wheel ACSs are shown in Figure 2. The system first inhales the environmental air as fresh air, which first increases the pressure through the electric compressor (EC), then flows through the primary heat exchanger (HX1) and secondary heat exchanger (HX2) successively, finally supplying the cabin after expansion and cooling in the ACM T. Conversely, the ram air is also inhaled from the environmental air as the system cold source, pumped by the ACM fan (F), before flowing through HX2 and HX1 successively. By comparison, the ACM of the bootstrap system replaces the F with a compressor (C) placed between HX1 and HX2 in the fresh air route to increase the system pressure so that the T can generate greater output power and an associated drop in temperature.

Figure 2.
Two-wheel air cycle system (ACS); (a) Simple type; (b) Bootstrap type.
The outlet temperature of the T in the bootstrap system is usually low—consequently, if the moisture content of the fresh air is high, free water will be separated. A water separator (WS) can be used for water separation to form a low-pressure water separation system, as shown in Figure 3a. If a reheater (RH) and a condenser (COND) are added to cool the fresh air and separate the water in a high-pressure state before flowing through the T, then a WS can be used for water separation, forming a high-pressure water separation system with a better water separation effect, as shown in Figure 3b. Since the separated free water is still in a high-pressure state, it can be sprayed onto the cold side of HX2 and used as the cold source in the system, together with ram air. Under dry conditions, the environmental air is completely dry, or the moisture content is low, and there is no free water separated in the WS and no spray.

Figure 3.
Two-wheel air cycle system (ACS) with water separation; (a) Low-pressure water separation; (b) High-pressure water separation.
3.1.2. Three-Wheel System
Compared with the two-wheel system, the three-wheel system has one more F in the ACM, and the output power of the T is supplied to the C and F. Thus, the ACS can inhale ram air through the F at a low flight speed, ensuring that the system has a sufficient flow rate on the cold side. Similar to the two-wheel system, the three-wheel system can be divided into low-pressure and high-pressure water separation systems, as shown in Figure 4.


Figure 4.
Three-wheel air cycle system (ACS) with water separation; (a) Low-pressure water separation; (b) High-pressure water separation.
3.1.3. Four-Wheel System
Compared with the three-wheel system, the four-wheel system adds a new secondary turbine (T2) in the ACM, which can reduce the energy loss when fresh air flows through the primary turbine (T1), reducing the possibility of the free water freezing and blocking the COND. The existing four-wheel system is generally a high-pressure water separation system, as shown in Figure 5a. However, the disadvantage of the four-wheel system is that the F, C, T1, and T2 are coaxial in the ACM, the power and speed of the four wheels being different, making the mechanical structure designed for realizing coaxial rotation more complex. Consequently, the system can be improved via the split type [31]—in which the ACM can be split such that T1 and T2 output power to the C and F, respectively, eliminating the redundancy of the structure, as shown in Figure 5b.
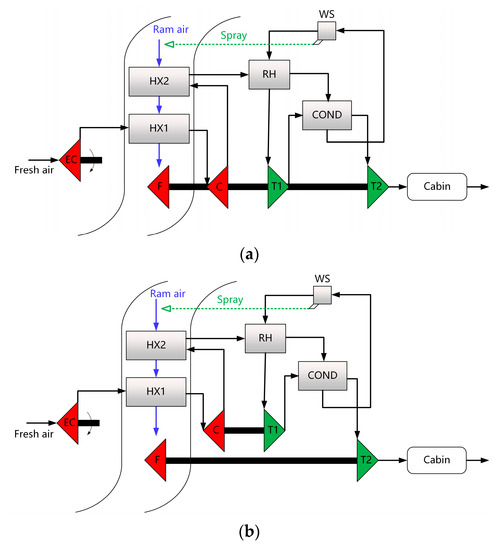
Figure 5.
Four-wheel high-pressure water separation air cycle system (ACS); (a) Integrated-type; (b) Split-type.
3.2. Network Graph
Each ACS, as described in Section 3.1, can be abstracted as a directed graph, the ACM being regarded as one component and the information transmitted between different vertices along each route. These routes can be divided into three types: fresh air, ram air, and spray, as shown in Figure 6. Moreover, for high-pressure water separation systems, there is a spray route under wet conditions but not under dry conditions.
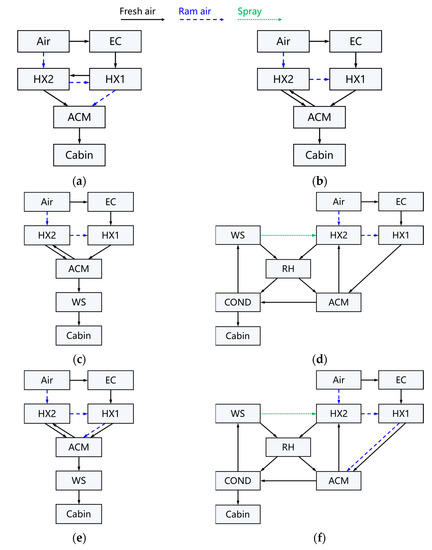
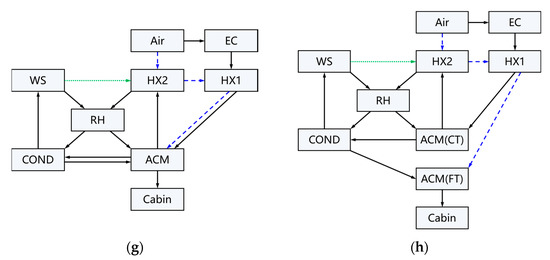
Figure 6.
Graph of different air cycle systems (ACSs); (a) Two-wheel simple ACS; (b) Two-wheel bootstrap ACS; (c) Two-wheel bootstrap ACS with low-pressure water separation; (d) Two-wheel bootstrap ACS with high-pressure water separation; (e) Three-wheel ACS with low-pressure water separation; (f) Three-wheel ACS with high-pressure water separation; (g) Integrated four-wheel ACS with high-pressure water separation; (h) Split four-wheel ACS with high-pressure water separation.
3.3. Fuel Weight Penalty
The importance of each route in the graph is different. When an aircraft is equipped with an ACS, extra energy is consumed to transport a system of a certain weight, overcome aerodynamic drag, etc. All the extra energy consumed can be generalized to the fuel consumption of the aircraft [36,37,38]. The aerodynamic drag caused by air inhalation and shaft power extraction are considered in this calculation, and the fuel weight penalty method [39] can be used to determine the weight of each route.
3.3.1. Ram Air Route
ACSs need to inhale air from the outside environment as ram air on the cold side of the system. The extra aerodynamic drag caused by inhalation requires more fuel consumption to increase engine thrust. The fuel weight penalty for this can be calculated using Equations (17) and (18), where D denotes the aerodynamic drag, K denotes the lift-drag ratio, g denotes gravity acceleration, Ce denotes the specific fuel consumption for thrust, τ0 denotes the flight time, qm denotes the mass flow of air, and v denotes the flight speed.
3.3.2. Spray Route
Under wet conditions, the free water separated by the WS in high-pressure water separation systems is sprayed onto the HX2, which reduces the temperature of the ram air, making it possible to achieve the same heat exchange capacity of HX1 and HX2 with less ram air. The reduced ram air flow rate can also be compensated for using the fuel weight penalty method, which can be calculated based on Equations (17) and (18).
3.3.3. Fresh Air Route
Electrically-driven ACSs also need to inhale fresh air from the outside environment. Similar to ram air, they generate a fuel weight penalty caused by aerodynamic drag, which can be calculated based on Equations (17) and (18).
Additionally, the EC power consumption is provided by the shaft power extracted from the engine, which causes the engine thrust to decrease, requiring additional fuel. The corresponding fuel weight penalty can be calculated using Equation (19), where P denotes the extracted shaft power, qf,P denotes the additional fuel consumption for extracting the unit shaft power—which can be calculated based on engine parameters such as the fuel combustion heat and engine compressor pressure ratio.
The total fuel weight penalty for the fresh air route can be calculated by adding the above two parts of the penalty.
3.3.4. Calculation Condition
This calculation uses the takeoff status of the A320 aircraft as an example, the takeoff parameters of which are shown in Table 1.

Table 1.
Takeoff parameters of the A320.
The extracted shaft power (P) and aerodynamic drag (D) required by Equations (17)–(19) can be calculated based on the thermal state of each point in the ACS. The parameters of all components of each system are listed in Table 2. Only the compressor pressure ratio or turbine efficiency is adjusted to make the overall refrigeration capacity of all systems consistent (29.97 kW) so as to calculate the power consumption of the EC, water separation capacity, and other parameters and further calculate the weight of each route under dry and wet conditions.

Table 2.
Parameters of components.
3.3.5. Route Weight Setting
Larger weights represent a greater resistance to information transmission to the edges of a graph. If the fuel weight penalty of a route is large, it means that the information transmission of that route is more important and that we should be more concerned about this route. Consequently, its weight should be smaller than other routes so that the information is transmitted primarily along this route. Additionally, owing to the large differences in the fuel weight penalties of each route, the weight can be defined by taking the logarithm of mi, with 10 being added to the numerator to ensure that the minimum route weight is 1. The formula can be expressed as follows:
4. Results and Discussion
4.1. Route Weight
The thermal performance of the ACSs was calculated based on Table 2, the route weights of each system being calculated based on Equations (17)–(20), the results of which are listed in Table 3.

Table 3.
Route weight.
Due to the different thermal states of the WS in each system, their water separation capacities differ; as such, the weights of the spray routes differ. Consequently, the enthalpy method [40] was used in this study to calculate the ACSs, the enthalpy of fresh air under dry conditions being lower than that under wet conditions. The power consumption of the EC is lower, so the fuel weight penalty of fresh air is lower, and the weight of the ram air route is lower.
4.2. Order Degree
4.2.1. Two-Wheel Simple and Bootstrap ACS
A comparison between the two-wheel simple and bootstrap ACSs is shown in Figure 7. Compared with the simple-type ACS, the bootstrap-type ACS has one more C in the fresh air route; the route becomes longer, and thus timeliness decreases. There is no obvious change in the quality of the two systems; consequently, the overall order degree of the simple type is higher. Although the order degree of the bootstrap type is lower, a water separation system could be developed, which has advantages in dealing with high-humidity takeoff environments.
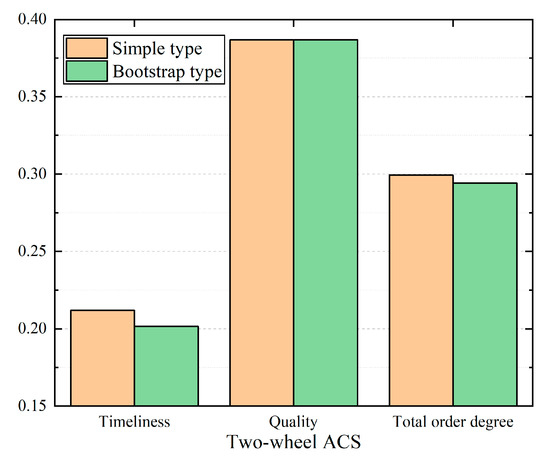
Figure 7.
Comparison of the two-wheel simple and bootstrap air cycle systems (ACSs).
4.2.2. Different Number of Wheels
A comparison of the two-, three-, and four-wheel high-pressure water separation systems is shown in Figure 8. With an increase in the number of wheels, the communication paths between the components increase, and timeliness decreases. However, if there are other vertices also connected to the vertex ACM, the degree of the ACM increases, and the degree distribution of the graph becomes more concentrated, leading to an increase in quality. In general, the overall order degree of the system gradually increases with an increase in the number of wheels, the system structure gradually being optimized. The results also show that the development of the ACS from a simple two-wheel ACS to a more complex four-wheel ACS improves not only its thermal performance but also the order degree of information transmission.

Figure 8.
Comparison of air cycle systems (ACSs) with differing wheel numbers.
4.2.3. Dry and Wet Condition
A comparison of the two-, three-, and four-wheel systems under dry and wet conditions is shown in Figure 9. Compared to the dry conditions, wet conditions have an additional spray route from the WS to the HX2, the weight of the ram air route being higher. Some new connectable component pairs appear under wet conditions; therefore, the number of timeliness microstates increases, reducing the information-transmission efficiency. However, the degrees of the HX2 and WS increase and the degree distribution of the graph becomes more concentrated, therefore, increasing the quality. All the systems are of lower timeliness but higher in quality and overall order degree under wet conditions.
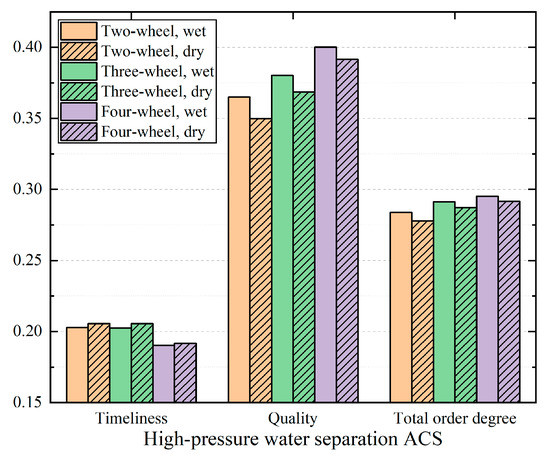
Figure 9.
Comparison of dry and wet conditions.
4.2.4. High-Pressure and Low-Pressure Water Separation
A comparison of the high- and low-pressure water separation systems of the two- and three-wheel ACSs is shown in Figure 10. The high-pressure water separation system is more complex than the low-pressure system, and the fresh air route is longer as one RH and one COND are added, and there is a spray route from the WS to the HX2. In general, the high-pressure system has lower timeliness, higher quality, and a lower overall order degree. Using the three-wheel system as an example, the water separation capacity of the low-pressure system is 17.23 g/kg dry air, and that of the high-pressure system is 20.77 g/kg dry air. It is evident that the high-pressure system achieves better water separation performance despite sacrificing the order degree.
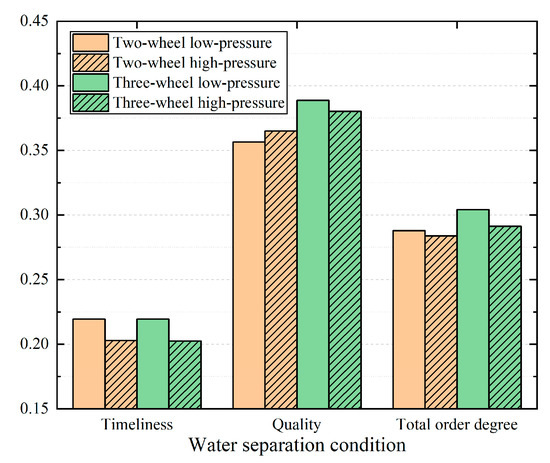
Figure 10.
Comparison of high-pressure and low-pressure water separation air cycle systems (ACSs).
4.2.5. Integrated and Split Four-Wheel ACS
A comparison of the integrated and split four-wheel systems is shown in Figure 11. The split system eliminates the redundancy of shaft power transmission in the integrated system by splitting the original ACM into two new ACMs, which is convenient for practical engineering design. The split system has a higher timeliness; however, the degree distribution of the graph becomes scattered, and the quality decreases considerably, resulting in a decrease in the overall order degree. However, the split system is not as effective as the integrated system in terms of organization and component layout.

Figure 11.
Comparison of integrated and split four-wheel air cycle systems (ACSs).
4.3. Component Centrality
To highlight the centrality of components, consider the integrated four-wheel high-pressure water separation system, as summarized in Table 4. It is evident that the value of the ACM is highest in all three centrality types, as it is in the middle of the fresh air and ram air routes, and it is connected by many other components. The ACM can be considered to perform the function of thermal-power conversion, playing an important role in system information transmission; consequently, its performance needs to be definitively considered in the system design. Additionally, the centrality of the HX1 and HX2 is high, and the heat exchange efficiency of these components should be considered a priority in system design.

Table 4.
Component centrality of the four-wheel high-pressure water separation ACS.
The most central components determined by the three centralities of each system are listed in Table 5. In each system, the ACM has many connected components and is usually located centrally; therefore, the frequency of its appearance in the table is high. In two-wheel systems, there are relatively fewer components connected with the ACM; therefore, the HX2 is the most central component in some two-wheel systems; it also has non-negligible importance.

Table 5.
The component with the highest centrality of each system.
Additionally, it is evident that the centrality of the ACM increases with an increase in the number of wheels in the high-pressure water separation system, implying that the importance of the ACM in information transmission gradually increases, which supports the conclusion drawn from the analysis of Figure 8 in Section 4.2, that an increase in the number of wheels makes the degree distribution more concentrated. Conversely, the centrality of the ACM decreases owing to splitting in the split four-wheel system, the HX2 having the highest degree of centrality and betweenness centrality.
5. Conclusions
ACSs were abstracted as a graph structure in this study, and the fuel weight penalty method was used to determine the weight of each information-transmission route. The SEM was used to calculate and compare the order degree of different ACSs, and the importance of components was evaluated using the centrality algorithm in graph theory. The following conclusions could be drawn from this study:
- With the increase in the number of wheels in the high-pressure water separation system, the fresh air route lengthened, and the degree distribution grew more concentrated, resulting in a decrease in timeliness, an increase in quality, and total order degree. Although the system structure gradually becomes more complex, its thermodynamic efficiency and order degree have been improved.
- In the case of free water spray from the WS to the HX2 under wet conditions, the system had lower timeliness and higher quality than that under dry conditions, enabling the system to obtain a higher order degree after the addition of a spray route while achieving better cooling effects of the ram air.
- Compared with low-pressure water separation systems, high-pressure systems exhibited higher timeliness, lower quality, and order degree but improved water separation performance.
- The ACM is one of the most central components of each system, playing a key role in information transmission, with the HX2 also exhibiting a high centrality in some systems. The performance of these two important components should be prioritized during the system design process.
It should be noted that the order degree calculated using the SEM cannot directly explain the advantages or disadvantages of the system in terms of thermal performance, which also needs to be determined by combining its actual cooling capacity and water separation capacity. However, this study establishes a connection between the existing thermodynamic analysis and information transmission in ACSs and provides a methodology for evaluating the structural arrangement and component importance of the ACS design from an information theory perspective. Future studies could focus on the optimization of the ACS structure or component performance based on the adjustment of the weights of routes in the graphs.
Author Contributions
Conceptualization and methodology, J.L., C.Y., and H.Y.; validation, J.L.; resources, C.Y.; writing—original draft preparation, J.L.; writing—review and editing, H.Y.; supervision, C.Y.; project administration, C.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| a | Base value of logarithm in information entropy |
| A1 | Total number of timeliness microstates |
| A2 | Total number of quality microstates |
| Bin | Number of inbound reachable vertexes |
| Bout | Number of outbound reachable vertexes |
| CB | Betweenness centrality |
| CC | Closeness centrality |
| CD | Degree centrality |
| Ce | Specific fuel consumption for thrust, kg/(N·s) |
| D | Aerodynamic drag, N |
| Din | Indegree |
| Dout | Outdegree |
| g | Gravity acceleration, m/s2 |
| H1 | Timeliness entropy |
| H1max | Theoretical maximum timeliness entropy |
| H2 | Quality entropy |
| H2max | Theoretical maximum quality entropy |
| K | Lift-drag ratio |
| L | Length of path |
| m | Fuel weight penalty, kg |
| mf,D | Fuel weight penalty caused by drag, kg |
| mf,P | Fuel weight penalty caused by shaft power extraction from the engine, kg |
| p1 | Realization probability of timeliness microstate |
| p2 | Realization probability of quality microstate |
| P | Shaft power extraction from an engine, W |
| qm | Flowrate of fresh air, kg/s |
| qf,P | Additional fuel consumption for extracting unit shaft power, kg/(W·s) |
| R | Total order degree |
| R1 | Timeliness |
| R2 | Quality |
| v | Flight speed, m/s |
| wt | Route weight |
| Greek letters | |
| α | Weight of timeliness |
| β | Weight of quality |
| σ | Number of shortest paths |
| τ0 | Flight time, s |
| Abbreviations | |
| ACM | Air cycle machine |
| ACS | Air cycle system |
| C | Compressor |
| COND | Condenser |
| EC | Electric compressor |
| ECS | Environmental control system |
| F | Fan |
| HX1 | Primary heat exchanger |
| HX2 | Secondary heat exchanger |
| RH | Reheater |
| SEM | Structure entropy method |
| T | Turbine |
| WS | Water separator |
References
- Cao, Q.; Liu, Y.; Liu, W.; Lin, C.H.; Wei, D.; Baughcum, S.; Norris, S.; Shen, X.; Long, Z.; Chen, Q. Experimental study of particle deposition in the environmental control systems of commercial airliners. Build. Environ. 2016, 96, 62–71. [Google Scholar] [CrossRef]
- Linnett, K.; Crabtree, R. What’s Next in Commercial Aircraft Environmental Control Systems? SAE International: Warrendale, PA, USA, 1993. [Google Scholar]
- Brasseur, A.; Leppert, W.; Pradille, A. Inside the 747-8 New Environmental Control System. Aero-Magazine 2012, 1, 19–25. [Google Scholar]
- Hunt, E.H. Commercial Airliner Environmental Control System Engineering Aspects of Cabin Air Quality. In Proceedings of the Aerospace Medical Association Annual Meeting, Anaheim, CA, USA, 7–11 May 1995. [Google Scholar]
- Weiguo, Z. Cabin Environment and Air Quality in Civil Transport Aircraft; Cranfield University: Cranfield, UK, 2012. [Google Scholar]
- Sinnett, M. 787 No-bleed systems: Saving fuel and enhancing operational efficiencies. Aero Q. 2007, 18, 6–11. [Google Scholar]
- Zandstra, R.S.S. Bleed Air versus Electric Power Off-takes from a Turbofan Gas Turbine over the Flight Cycle. In Proceedings of the 7th AIAA Aviation Technology, Integration and Operations Conferences, Belfast, Northern Ireland, 18–20 September 2012. [Google Scholar]
- Warner, J.L. Environmental control system condensing cycle. U.S. Patent 5086622-A, 11 February 1992. [Google Scholar]
- Yang, H.; Yang, C. Derivation and comparison of thermodynamic characteristics of endoreversible aircraft environmental control systems. Appl. Therm. Eng. 2020, 180, 115811. [Google Scholar] [CrossRef]
- Alebrahim, A.; Bejan, A. Entropy Generation Minimization in a Ram-Air Cross-Flow Heat Exchanger. Int. J. Thermodyn. 1999, 2, 145–157. [Google Scholar]
- Conceição, S.T.; Zaparoli, E.L.; Turcio, W.H.L. Thermodynamic Study of Aircraft Air Conditioning Air Cycle Machine: 3-wheel×4-wheel. In SAE Brasil 2007 Congress and Exhibit; SAE International: Warrendale, PA, USA, 2007. [Google Scholar]
- Figliola, R.S.; Tipton, R.; Li, H. Exergy Approach to Decision-Based Design of Integrated Aircraft Thermal Systems. J. Aircr. 2003, 40, 49–55. [Google Scholar] [CrossRef]
- Ordóñez, J.C.; Bejan, A. Entropy generation minimization in parallel-plates counterflow heat exchangers. Int. J. Energy Res. 2000, 24, 843–864. [Google Scholar] [CrossRef]
- Vargas, J.V.C.; Bejan, A. Thermodynamic optimization of finned crossflow heat exchangers for aircraft environmental control systems. Int. J. Heat Fluid Flow 2001, 22, 657–665. [Google Scholar] [CrossRef]
- Vargas, J.V.C.; Bejan, A. Integrative thermodynamic optimization of the environmental control system of an aircraft. Int. J. Heat Mass Transfer 2001, 44, 3907–3917. [Google Scholar] [CrossRef]
- Li, Y.; Hu, H.; Sun, H.; Wu, C. Dynamic simulation model for three-wheel air-cycle refrigeration systems in civil aircrafts. Int. J. Refrig. 2023, 145, 353–365. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, S.; Sheng, C.; Xie, H.; Luo, G.; Hou, Y. Study on coupling performance of turbo-cooler in aircraft environmental control system. Energy 2021, 224, 120029. [Google Scholar] [CrossRef]
- DeFrancesco, G.L. Condensing Cycle Air Conditioning System. In International Conference On Environmental Systems; SAE International: Warrendale, PA, USA, 1993. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Yang, H.; Yang, C.; Zhang, X.; Yuan, X. Influences of Different Architectures on the Thermodynamic Performance and Network Structure of Aircraft Environmental Control System. Entropy 2021, 23, 855. [Google Scholar] [CrossRef]
- Zhu, J.; Wei, D. Analysis of stock market based on visibility graph and structure entropy. Phys. A 2021, 576, 126036. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Z.; Li, W. Analyses of urban ecosystem based on information entropy. Ecol. Modell. 2006, 197, 1–12. [Google Scholar] [CrossRef]
- Zareie, A.; Sheikhahmadi, A.; Fatemi, A. Influential nodes ranking in complex networks: An entropy-based approach. Chaos Solitons Fractals 2017, 104, 485–494. [Google Scholar] [CrossRef]
- Wang, B.; Tan, F.; Zhu, J.; Wei, D. A new structure entropy of complex networks based on nonextensive statistical mechanics and similarity of nodes. Math. Biosci. Eng. 2021, 18, 3718–3732. [Google Scholar] [CrossRef]
- Tan, F.; Wang, B.; Wei, D. A new structural entropy measurement of networks based on the nonextensive statistical mechanics and hub repulsion. Math. Biosci. Eng. 2021, 18, 9253–9263. [Google Scholar] [CrossRef]
- Fu, Z.; Cong, J.; Wang, L.; Shi, L.; Guo, W. A novel evolutionary analysis model for social collaborative design ecosystem based on information entropy. Adv. Eng. Inf. 2023, 55, 101871. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, M. A betweenness structural entropy of complex networks. Chaos Solitons Fractals 2022, 161, 112264. [Google Scholar] [CrossRef]
- Yan, Z.; Qiu, W.; Chen, Z. Evaluation of system order degree as viewed from entropy. Syst. Eng. Theory Pract. 1997, 17, 45–48. (In Chinese) [Google Scholar]
- Wang, Z.X.; He, L.Y.; Li, D.D. Assessment of the degree of order in the organisational structure of electricity regulatory institution in China based on shannon entropy. Energy Policy 2019, 132, 429–439. [Google Scholar] [CrossRef]
- Yang, K.; Yang, C.; Yang, H.; Zhou, C. Complexity Evaluation of an Environmental Control and Life-Support System Based on Directed and Undirected Structural Entropy Methods. Entropy 2021, 23, 1173. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Yang, C. Thermodynamic Characteristics and Order Degree of Air Cycle System. Int. J. Refrig. 2020, 118, 61–71. [Google Scholar] [CrossRef]
- Chartrand, G.; Zhang, P. Introduction to Graph Theory; Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Bonacich, P. Factoring and weighting approaches to status scores and clique identification. J. Math. Sociol. 1972, 2, 113–120. [Google Scholar] [CrossRef]
- Wasserman, S.; Faust, K. Social Network Analysis: Methods and Applications; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Freeman, L.C. A Set of Measures of Centrality Based on Betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Dollmayer, J.; Bundschuh, N.; Carl, U.B. Fuel mass penalty due to generators and fuel cells as energy source of the all-electric aircraft. Aerosp. Sci. Technol. 2006, 10, 686–694. [Google Scholar] [CrossRef]
- Rong, A.; Liping, P.; Xinying, J.; Bin, Q.; Yong, S. Analysis and comparison of potential power and thermal management systems for high-speed aircraft with an optimization method. Energy Built Environ. 2021, 2, 13–20. [Google Scholar] [CrossRef]
- He, X.; Kang, Y.; Hui, Y. Modeling and Analysis of Different Architecture for Civil Aircraft Hydraulic System. J. Phys. Conf. Ser. 2021, 2068, 012028. [Google Scholar] [CrossRef]
- Committee, A.A.E.S. Aircraft Fuel Weight Penalty Due to Air Conditioning; SAE International: Warrendale, PA, USA, 2011. [Google Scholar]
- Yang, H.; Yang, C. Analysis of a novel pressurized dehumidification air conditioning system for urban underground space. Build. Environ. 2021, 206, 108400. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).