Prediction of Aircraft Surface Noise in Supersonic Cruise State
Abstract
1. Introduction
2. Non-Linear Acoustics Solver and Its Numerical Solution
3. Method Verification
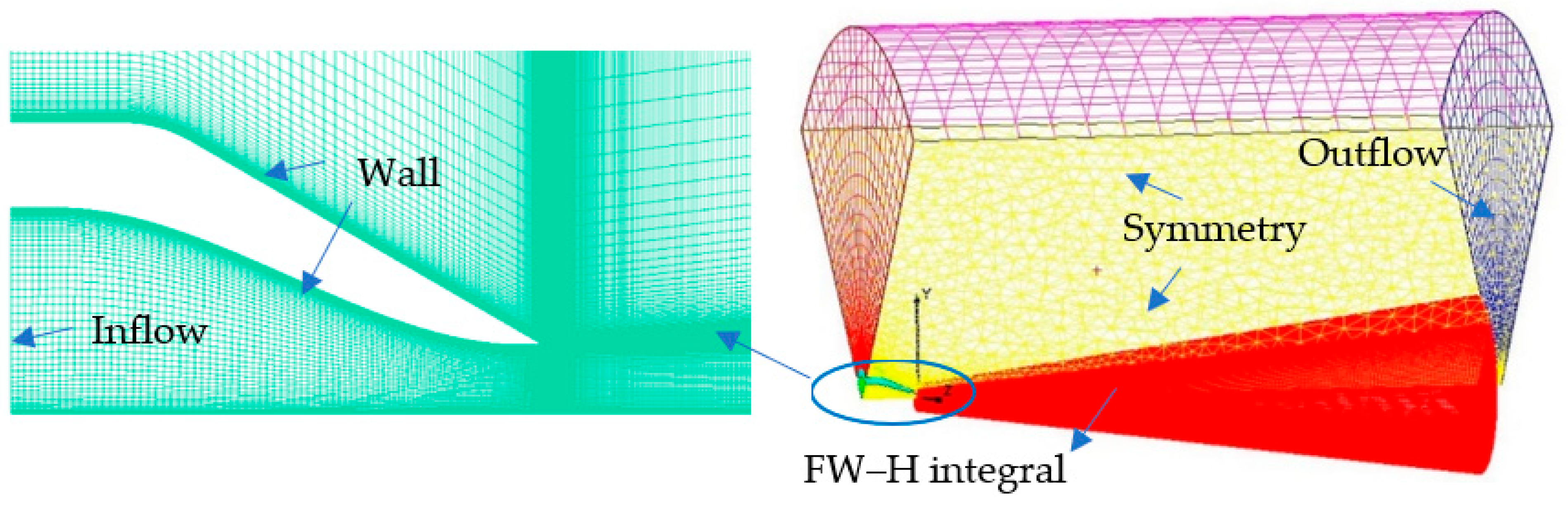
3.1. Verification of Near-Wall Noise Calculation
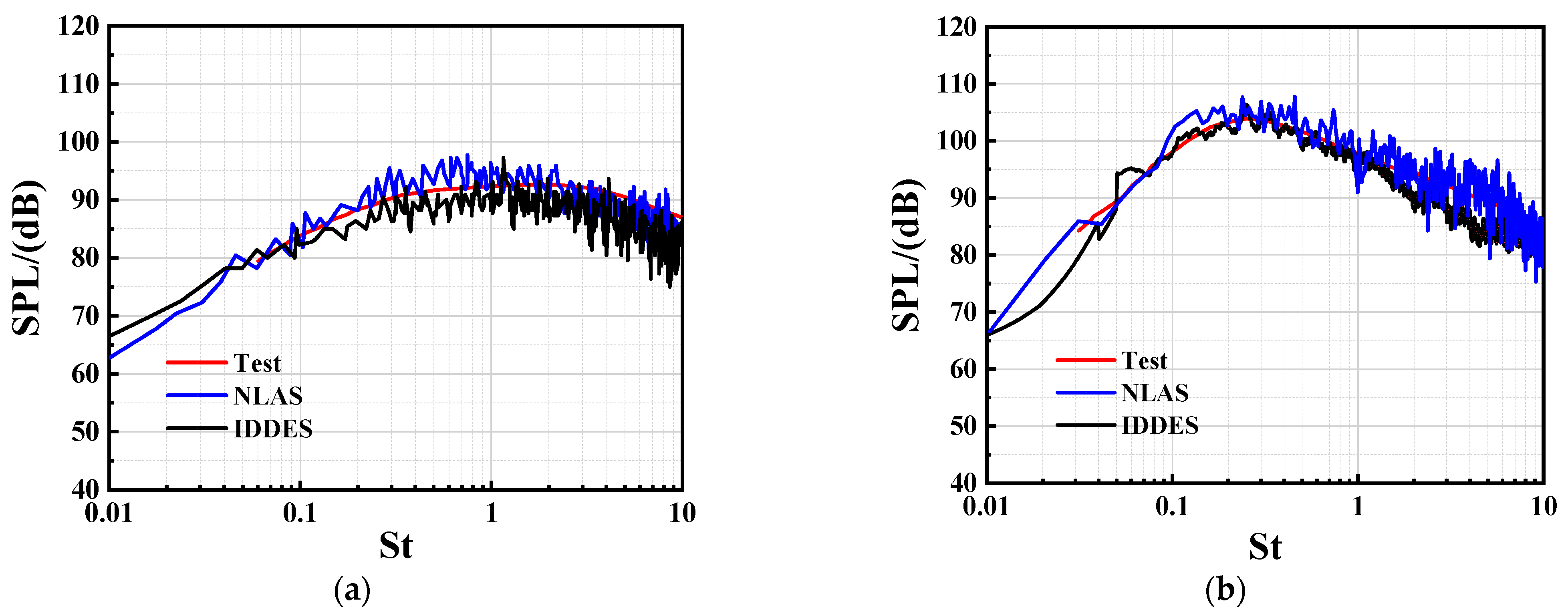
3.2. Verification of Jet Noise Calculation
4. Calculation of Aircraft Surface Noise in Cruise State
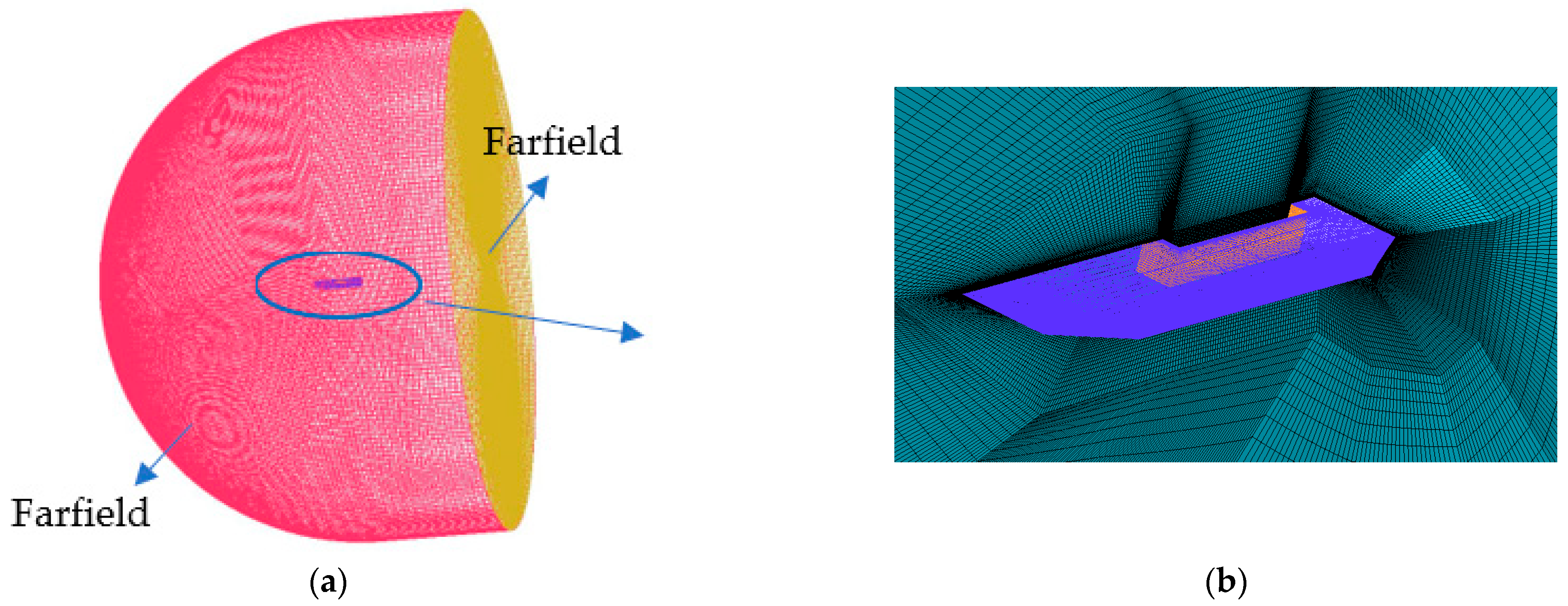
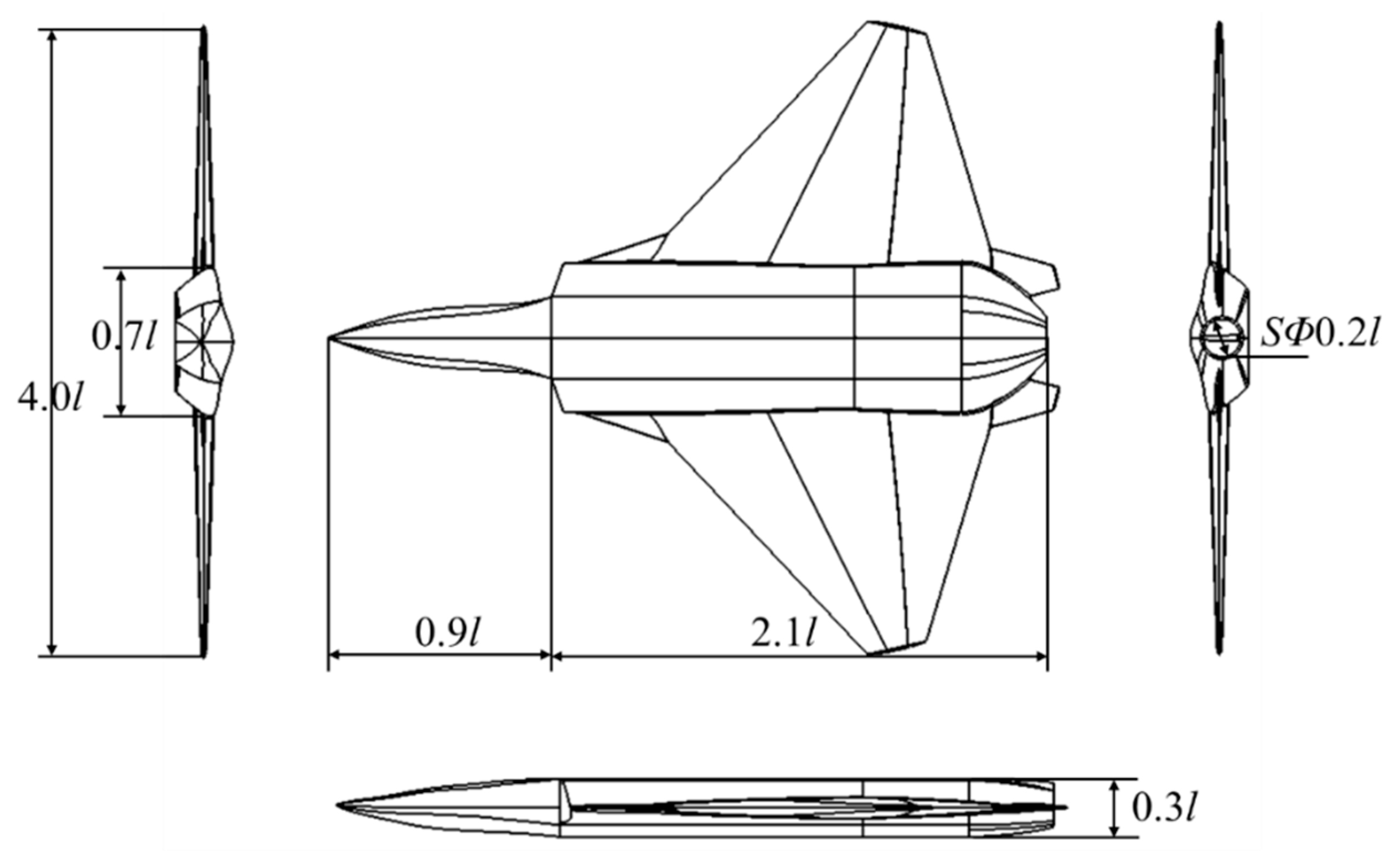
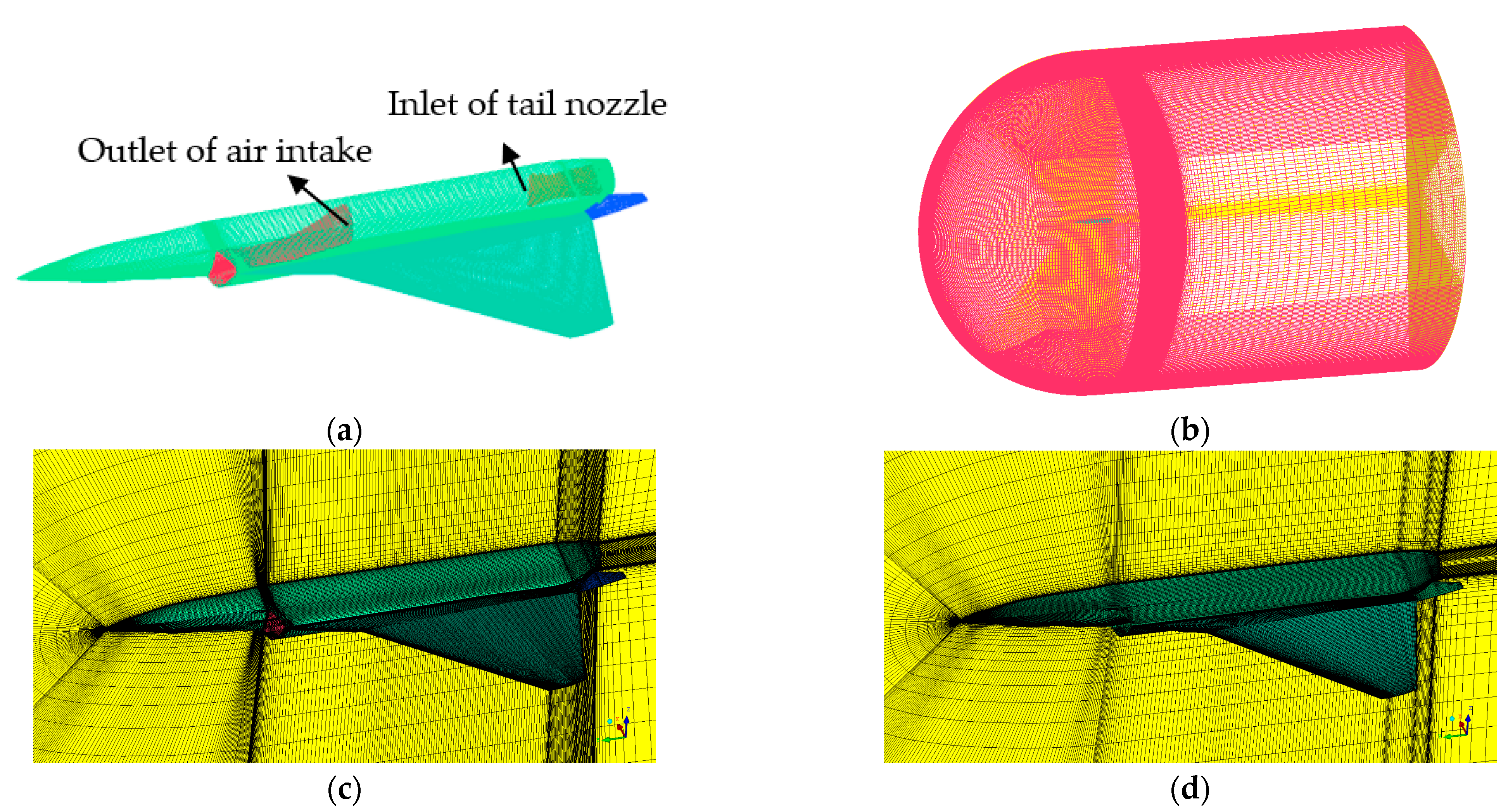
4.1. Geometry and Mesh Model
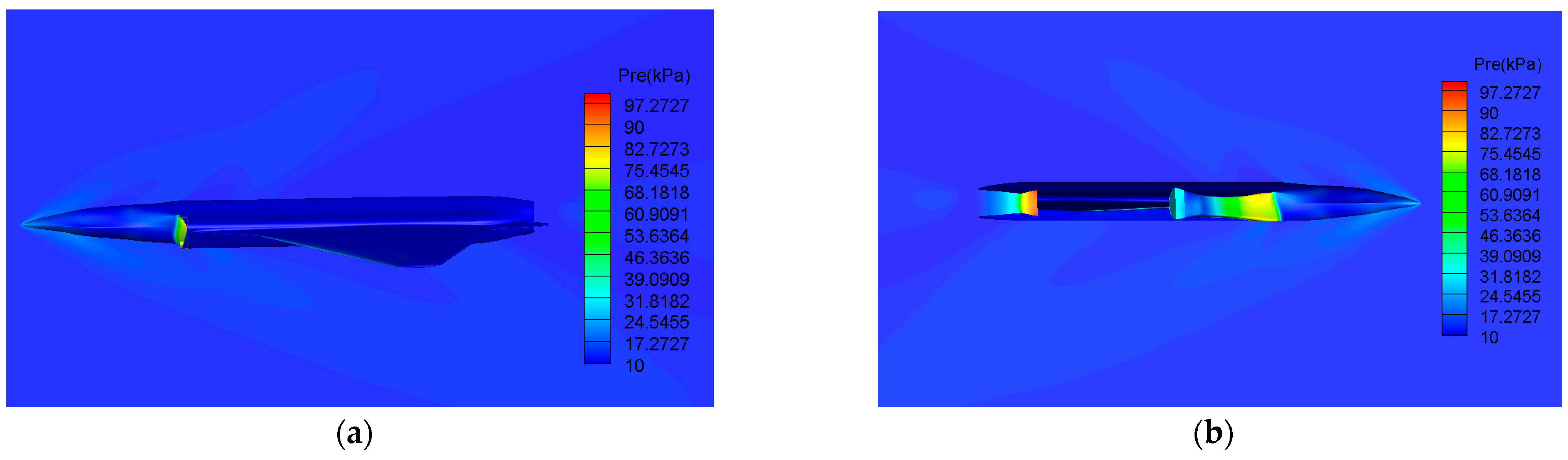
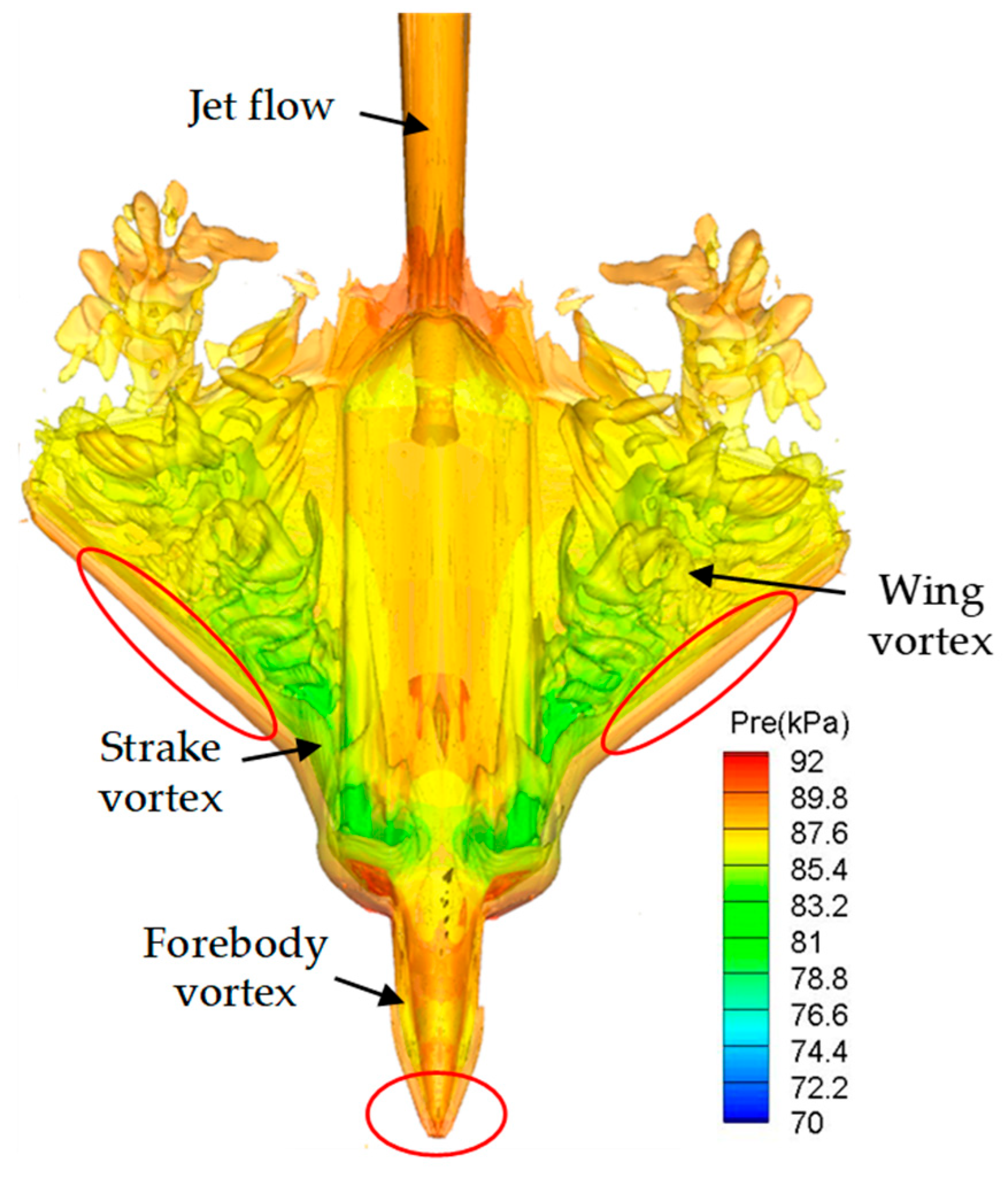
4.2. Numerical Results and Discussion
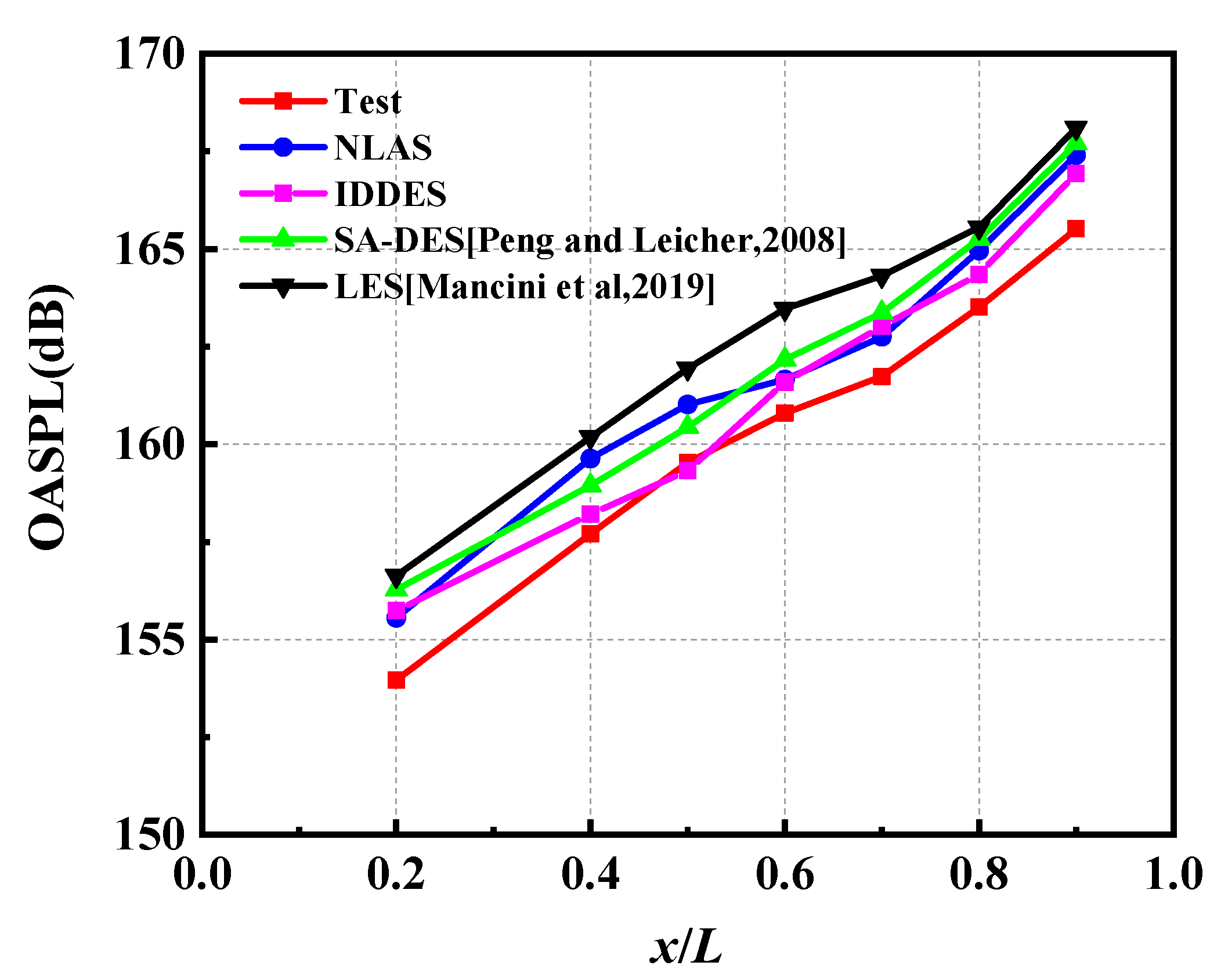
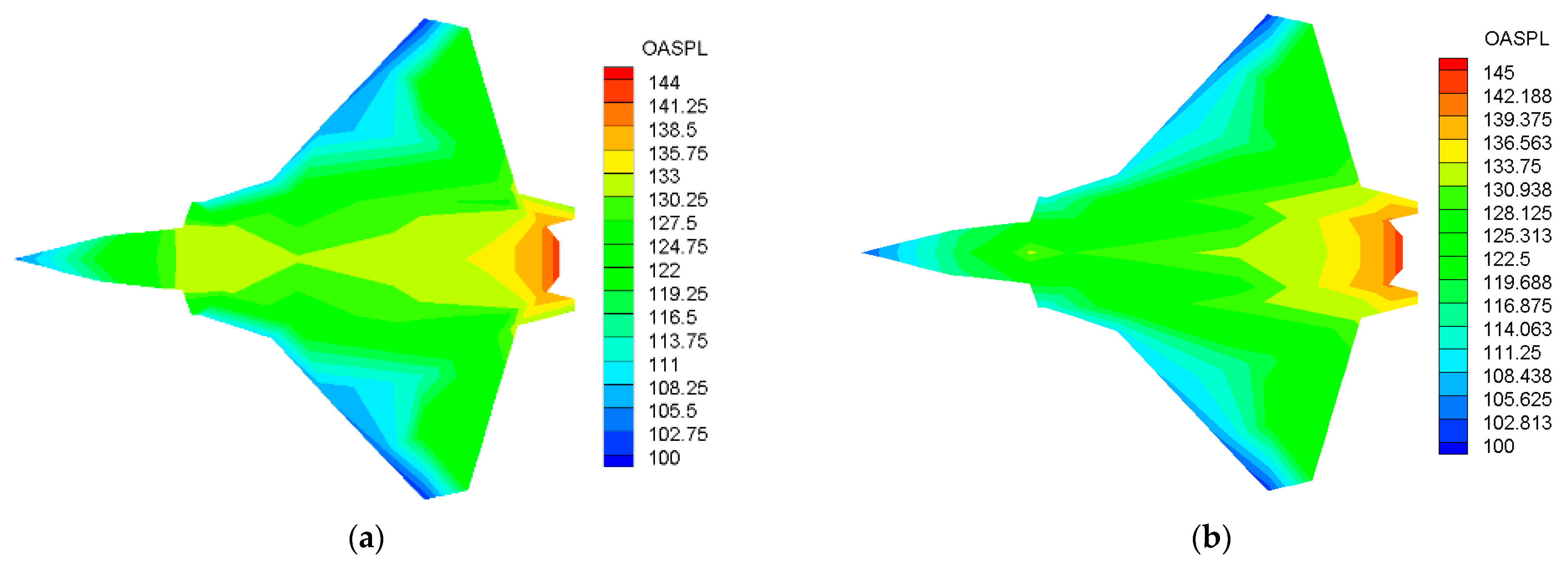
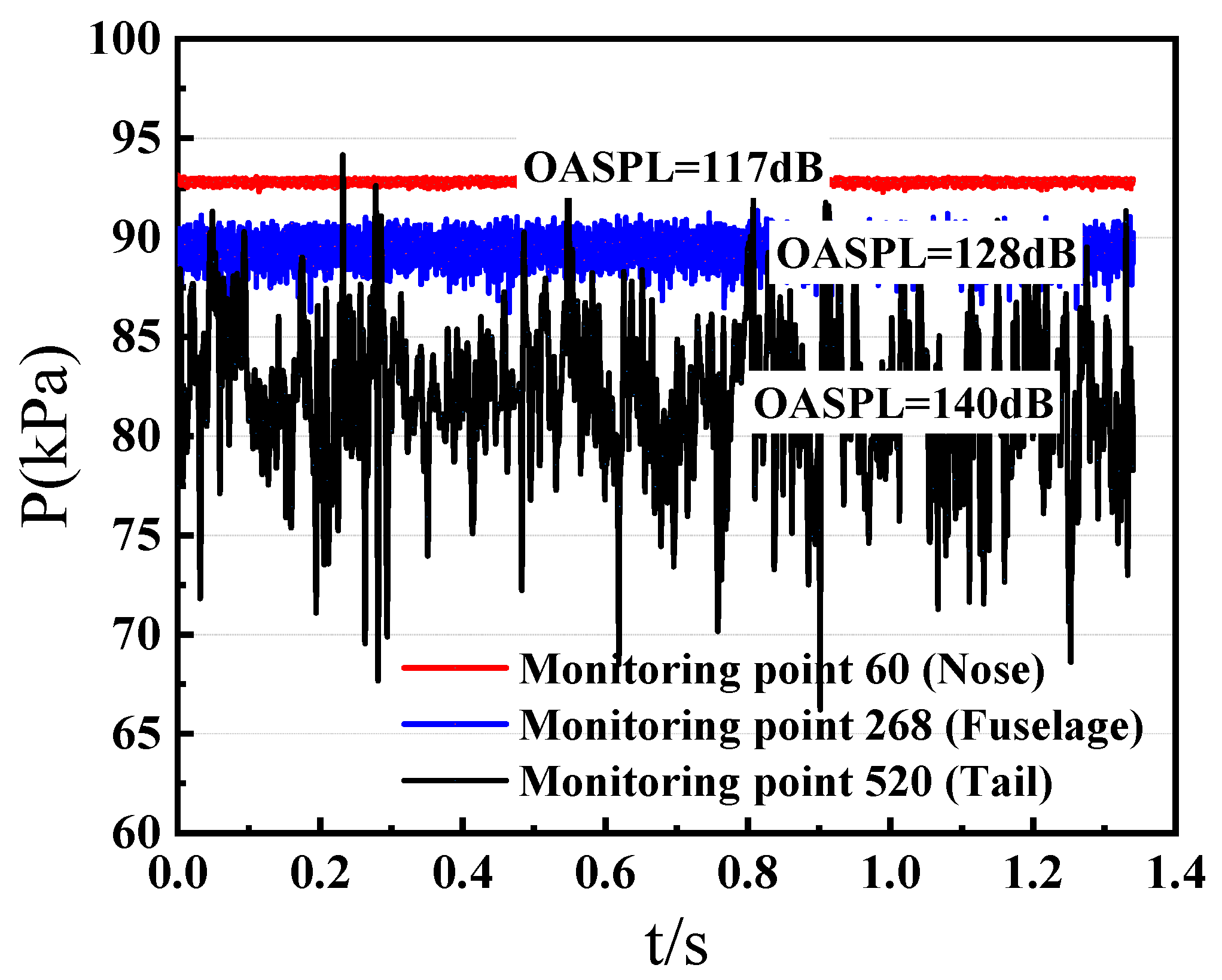
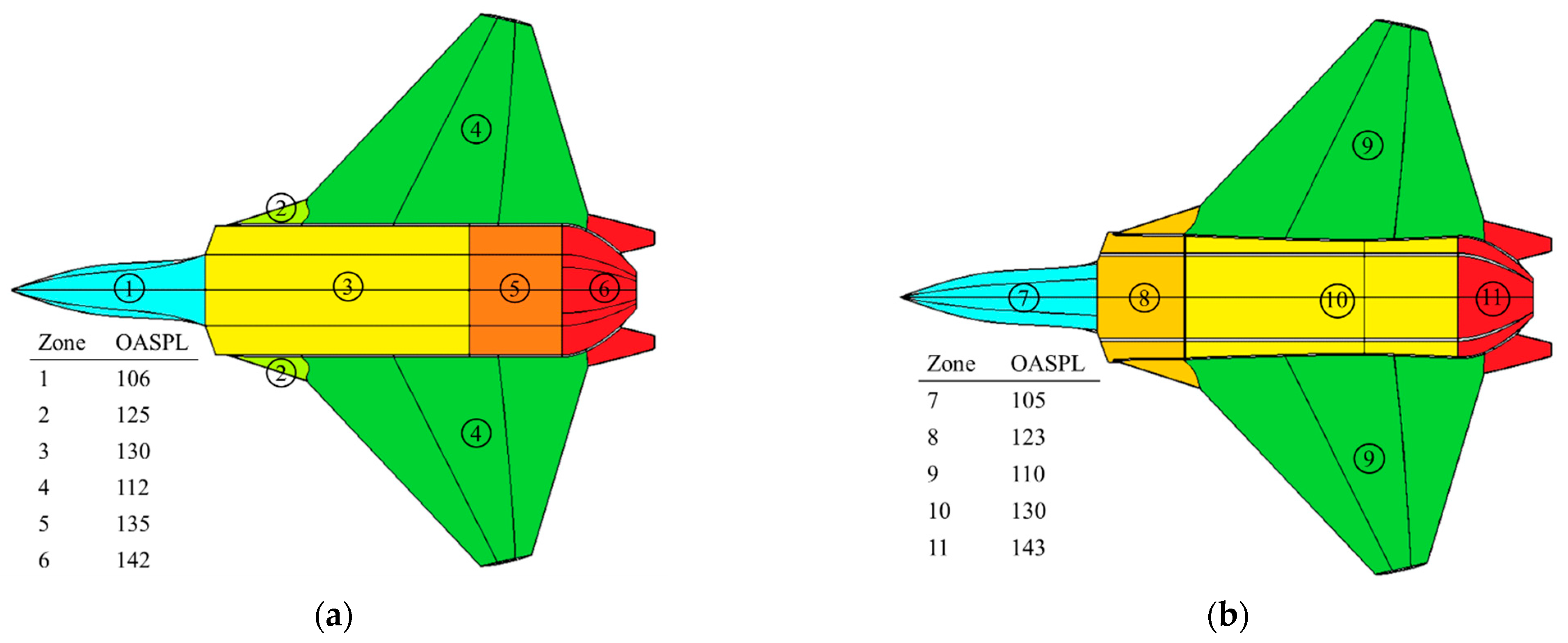
4.2.1. OASPL on Aircraft Surface
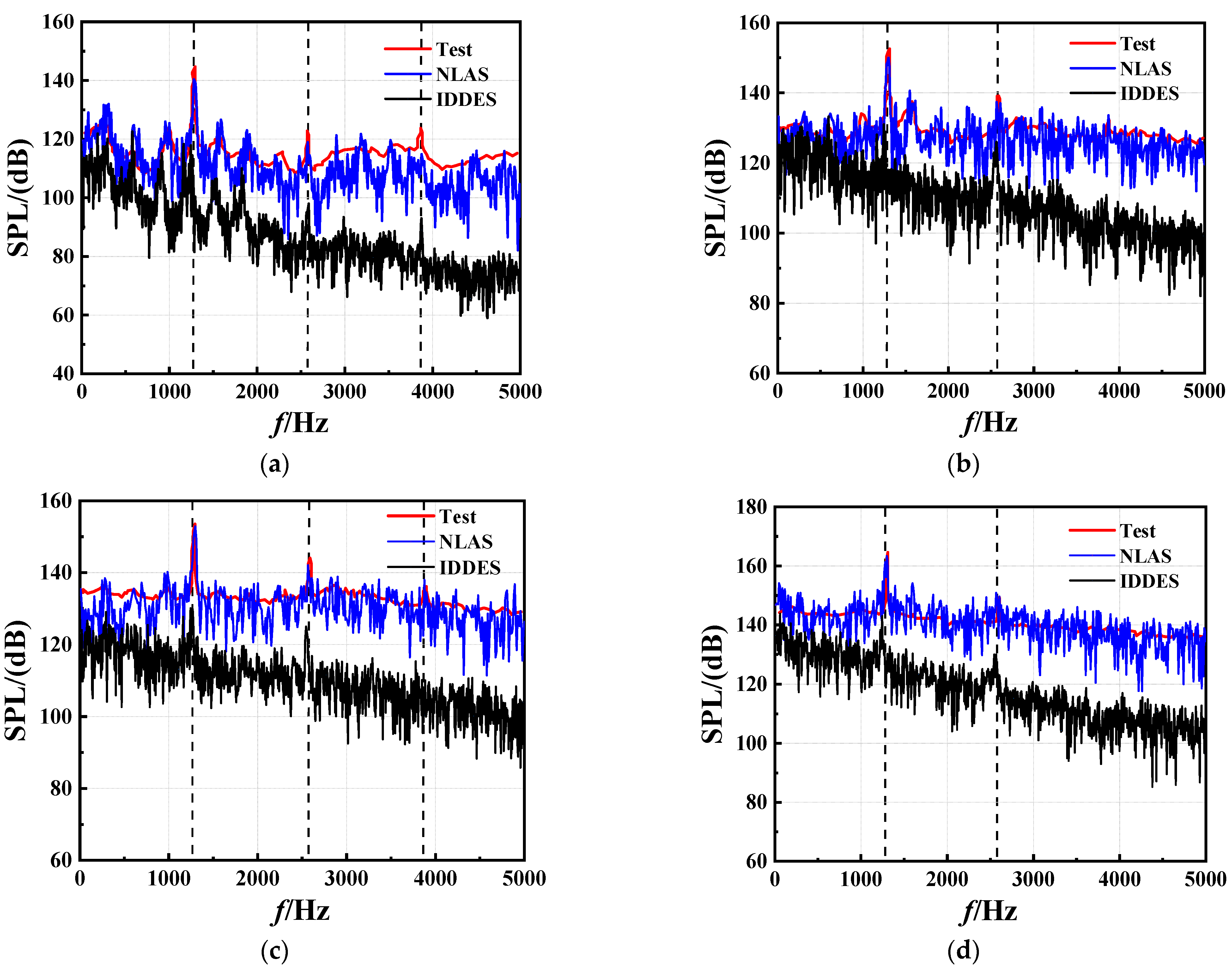
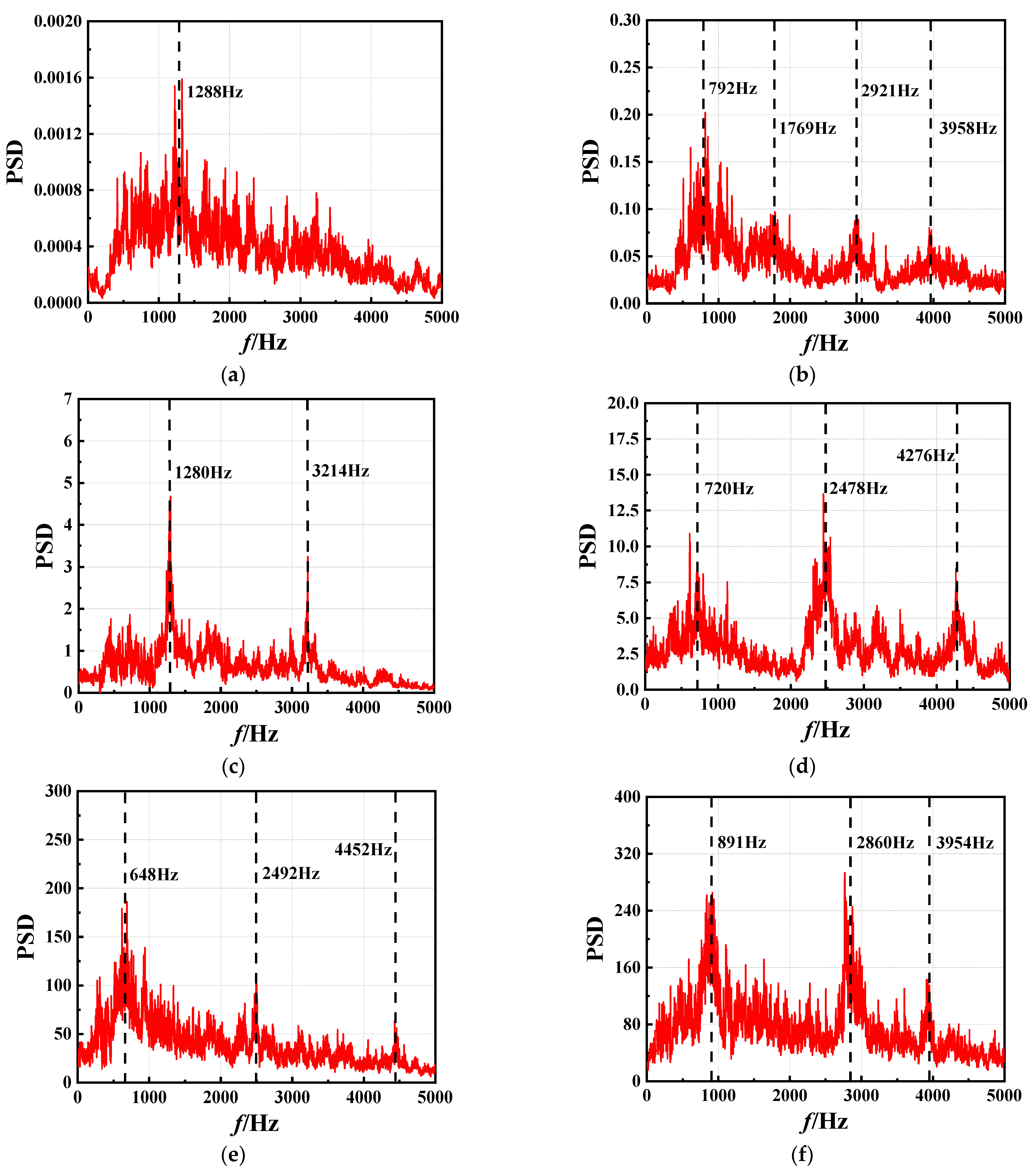
4.2.2. Power Spectral Density of Pressure Fluctuation
4.3. Calculation with Empirical Formulas
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Filippone, A. Aircraft noise prediction. Prog. Aerosp. Sci. 2014, 68, 27–63. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Zhang, D. Control strategies for aircraft airframe noise reduction. Chin. J. Aeronaut. 2013, 26, 249–260. [Google Scholar] [CrossRef]
- Thawre, M.; Pandey, K.; Dubey, A.; Verma, K.; Peshwe, D.; Paretkar, R.; Jagannathan, N.; Manjunatha, C. Fatigue life of a carbon fiber composite T-joint under a standard fighter aircraft spectrum load sequence. Compos. Struct. 2015, 127, 260–266. [Google Scholar] [CrossRef]
- Khorrami, M.; Lockard, D.; Humphreys, W.; Choudhari, M.; Van de Ven, T. Preliminary analysis of acoustic measurements from the NASA-Gulfstream airframe noise flight test. In Proceedings of the 14th AIAA/CEAS Aeroacoustics Conference (29th AIAA Aeroacoustics Conference), Vancouver, BC, Canada, 5–7 May 2008. [Google Scholar] [CrossRef]
- Stoker, R.; Gutierrez, R.; Larssen, J.; Underbrink, J.; Gatlin, G.; Spells, C. High Reynolds number aeroacoustics testing in NASA’s national transonic facility (NTF). In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; p. 838. [Google Scholar]
- Blacodon, D. Analysis of the Airframe Noise of an A320/A321 with a Parametric Method. J. Aircr. 2007, 44, 26–34. [Google Scholar] [CrossRef]
- Scarselli, G.; Amoroso, F.; Lecce, L.; Janssens, K.; Vecchio, A. Numerical simulation, experimental comparison with noise measurments and sound synthesis of airframe noise. In Proceedings of the 13th AIAA/CEAS Aeroacoustics Conference (28th AIAA Aeroacoustics Conference), Rome, Italy, 21–23 May 2007; p. 3460. [Google Scholar] [CrossRef]
- Sanders, M.P.J.; Koenjer, C.F.J.; Botero-Bolivar, L.; dos Santos, F.L.; Venner, C.H.; de Santana, L.D. Trailing-Edge Noise Comparability in Open, Closed, and Hybrid Wind Tunnel Test Sections. AIAA J. 2022, 60, 4053–4067. [Google Scholar] [CrossRef]
- Kuo, C.W.; Veltin, J.; McLaughlin, D.K. Acoustic measurements of models of military style supersonic nozzle jets. Chin. J. Aeronaut. 2014, 27, 23–33. [Google Scholar] [CrossRef]
- Chen, B.; Yang, X.; Chen, G.; Tang, X.; Ding, J.; Weng, P. Numerical study on the flow and noise control mechanism of wavy cylinder. Phys. Fluids 2022, 34, 036108. [Google Scholar] [CrossRef]
- Yu, P.; Peng, J.; Bai, J.; Han, X.; Song, X. Aeroacoustic and aerodynamic optimization of propeller blades. Chin. J. Aeronaut. 2020, 33, 826–839. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, S.; Chen, R.; Zhou, S.; Zhao, Y. Numerical study on aerodynamic drag and noise of circular cylinders with a porous plate. Aerosp. Sci. Technol. 2022, 123, 107460. [Google Scholar] [CrossRef]
- Tao, J.; Sun, G. An artificial neural network approach for aerodynamic performance retention in airframe noise reduction design of a 3D swept wing model. Chin. J. Aeronaut. 2016, 29, 1213–1225. [Google Scholar] [CrossRef]
- Incheol, L.E.E.; Zhang, Y.; Dakai, L.I.N. A model-scale test on noise from single-stream nozzle exhaust geometries in static conditions. Chin. J. Aeronaut. 2018, 31, 2206–2220. [Google Scholar] [CrossRef]
- Bu, Y.; Song, W.; Han, Z.; Zhang, Y.; Zhang, L. Aerodynamic/aeroacoustic variable-fidelity optimization of helicopter rotor based on hierarchical Kriging model. Chin. J. Aeronaut. 2020, 33, 476–492. [Google Scholar] [CrossRef]
- Cavalieri, A.V.G.; Jordan, P.; Colonius, T.; Gervais, Y. Axisymmetric superdirectivity in subsonic jets. J. Fluid Mech. 2012, 704, 388–420. [Google Scholar] [CrossRef]
- Reba, R.; Narayanan, S.; Colonius, T. Wave-packet models for large-scale mixing noise. Int. J. Aeroacoust. 2010, 9, 533–557. [Google Scholar] [CrossRef]
- Abalakin, I.; Dervieux, A.; Kozubskaya, T. High accuracy finite volume method for solving nonlinear aeroacoustics problems on unstructured meshes. Chin. J. Aeronaut. 2006, 19, 97–104. [Google Scholar] [CrossRef]
- Legendre, C.; Ficat-Andrieu, V.; Poulos, A.; Kitano, Y.; Nakashima, Y.; Kobayashi, W.; Minorikawa, G. A machine learning-based methodology for computational aeroacoustics predictions of multi-propeller drones. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Washington, DC, USA, 11–13 August 2021; Institute of Noise Control Engineering: Reston, VA, USA; Volume 263, pp. 3467–3478. [Google Scholar]
- Pham, N.K.; Nguyen, P.K.; Duong, N.T. Computational Simulation of Aerodynamic Noise Generation on High-Lift Configuration. J. Aeronaut. Astronaut. Aviat. 2022, 54, 393–403. [Google Scholar] [CrossRef]
- Lockard, D.; Choudhari, M. Noise radiation from a leading-edge slat. In Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference), Miami, FL, USA, 11–13 May 2009; p. 3101. [Google Scholar] [CrossRef]
- König, D.; Koh, S.; Schröder, W.; Meinke, M. Slat noise source identification. In Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference), Miami, FL, USA, 11–13 May 2009; p. 3100. [Google Scholar] [CrossRef]
- Ricciardi, T.R.; Wolf, W.R.; Moffitt, N.J.; Kreitzman, J.R.; Bent, P. Numerical noise prediction and source identification of a realistic landing gear. J. Sound Vib. 2021, 496, 115933. [Google Scholar] [CrossRef]
- Redonnet, S.; Ben Khelil, S.; Bulté, J.; Cunha, G. Numerical characterization of landing gear aeroacoustics using advanced simulation and analysis techniques. J. Sound Vib. 2017, 403, 214–233. [Google Scholar] [CrossRef]
- Prasad, C.; Hromisin, S. Coupled LES-experimental noise source imaging and fluid-thermodynamic mode decomposition of supersonic jets with fluid inserts. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1000. [Google Scholar]
- Shen, W.; Patel, T.K.; Miller, S.A. Extraction of large-scale coherent structures from large eddy simulation of supersonic jets for shock-associated noise prediction. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0742. [Google Scholar]
- Yen, J.; Kimbrell, A.; Connor, C. Study of WICS data using an emerging lower-order CAA method. In Proceedings of the US Air Force T&E Days 2010, Nashville, TN, USA, 2–4 February 2010; p. 1742. [Google Scholar] [CrossRef]
- Rodriquez, G.; Velez, C.; Ilie, M. Numerical studies of high-speed cavity flows using LES, DDES and IDDES. In Proceedings of the 51st AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]
- André, B.; Castelain, T.; Bailly, C. Shock oscillations in a supersonic jet exhibiting antisymmetrical screech. AIAA J. 2012, 50, 2017–2020. [Google Scholar] [CrossRef]
- Yao, C.; Zhang, G.H.; Liu, Z.S. Forced shock oscillation control in supersonic intake using fluid–structure interaction. AIAA J. 2017, 55, 2580–2596. [Google Scholar] [CrossRef]
- Batten, P.; Ribaldone, E.; Casella, M.; Chakravarthy, S. Towards a generalized non-Linear acoustics solver. In Proceedings of the 10th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10–12 May 2004. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Diffusion by a random velocity field. Phys. Fluids 1969, 13, 22–31. [Google Scholar] [CrossRef]
- Smirnov, A.; Shi, S.; Celik, I. Random flow generation technique for large eddy simulations and particle-dynamics modeling. J. Fluid. Engin. 2001, 123, 359–371. [Google Scholar] [CrossRef]
- Batten, P.; Goldberg, U.; Chakravarthy, S. Reconstructed sub-grid methods for acoustics predictions at all Reynolds numbers. In Proceedings of the 8th AIAA/CEAS Aeroacoustics Conference, Breckenridge, CO, USA, 17–19 June 2002. [Google Scholar] [CrossRef]
- Henshaw, M.J. M219 cavity case. In Verification and Validation Data for Computational Unsteady Aerodynamics; Techology Report RTO-TR-26, AC/323(AVT)TP/19; QinetiQ: Farnborough, UK, 2002; pp. 453–472. [Google Scholar]
- Peng, S.H.; Leicher, S. DES and Hybrid RANS-LES Modelling of Unsteady Pressure Oscillations and Flow Features in a Rectangular Cavity. Advances in Hybrid RANS-LES Modelling; Springer: Berlin/Heidelberg, Germany, 2008; pp. 132–141. [Google Scholar]
- Mancini, S.; Kolb, A.; Gonzalez-Martino, I.; Casalino, D. Very-large eddy simulations of the m219 cavity at high-subsonic and supersonic conditions. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 5–7 January 2019; p. 1833. [Google Scholar] [CrossRef]
- Bridges, J.; Brown, C. Validation of the small hot jet acoustic rig for aeroacoustic research. In Proceedings of the 11th AIAA/CEAS Aeroacoustics Conference, Monterey, CA, USA, 23–25 May 2005; p. 2846. [Google Scholar] [CrossRef]
- Ungar, E.E.; Wilby, J.F.; Bliss, D.B.; Pinkel, B.; Galaitsis, A. A Guide for Estimation of Aeroacoustic Loads on Flight Vehicle Surfaces; Bolt Beranek and Newman Inc.: Cambridge, MA, USA, 1977. [Google Scholar]
- Coe, C.F.; Chyu, W.J. Pressure-Fluctuation Inputs and Response of Panels Underlying Attached and Separated Supersonic Turbulent Boundary Layers; NASA-TM-X-62189; NASA: Washington, DC, USA, 1972.
- Lowson, M.V. Prediction of Boundary Layer Pressure Fluctuations; Wyle Labs Inc.: Huntsville, AL, USA, 1968. [Google Scholar]
- Lew, H.G.; Laganelli, A.L. Fluctuating Pressure Loads for Hypersonic Vehicle Structures. Phase 1; Techquest Inc.: Huntsville, AL, USA, 1991. [Google Scholar]
- Laganelli, A.L. Prediction of the Pressure Fluctuations Associated with Maneuvering Reentry Weapons; Flight Dynamics Laboratory, Air Force Wright Aeronautical Laboratories, United States Air Force: Dayton, OH, USA, 1984.
- Wiley, D.R.; Seidl, M.G. Aerodynamic Noise Tests on X-20 Scale Models. Volume 2. Summary and Analysis Report; Boeing Aerospace Co.: Seattle, WA, USA, 1965. [Google Scholar]






| Point | Longitudinal x/L | Vertical y/D |
|---|---|---|
| 1 | 0.2 | |
| 2 | 0.4 | |
| 3 | 0.5 | |
| 4 | 0.6 | |
| 5 | 0.7 | |
| 6 | 0.8 | |
| 7 | 0.9 | |
| 8 | 0.143 | |
| 9 | 0.286 | |
| 10 | 0.429 | |
| 11 | 0.571 | |
| 12 | 0.714 | |
| 13 | 0.857 |
| Number of CPU Cores | Time Step | Number of Grid Cells | Calculation Time | Advantages | Disadvantages | |
|---|---|---|---|---|---|---|
| IDDES | 64 | 2.5 × 10−6 s | 7.5 million | 25 days | High accuracy of subsonic calculation. Unsteady state conditions can be calculated. | Low accuracy of supersonic calculation. Low efficiency. |
| NLAS | 64 | 5 × 10−6 s | 3.2 million | 6 days | High accuracy of subsonic and supersonic calculations. High efficiency, suitable for engineering applications. | Calculating based on the RANS equation and dynamic unsteady conditions cannot be done. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Dang, H.; Li, B. Prediction of Aircraft Surface Noise in Supersonic Cruise State. Aerospace 2023, 10, 439. https://doi.org/10.3390/aerospace10050439
Zhang X, Dang H, Li B. Prediction of Aircraft Surface Noise in Supersonic Cruise State. Aerospace. 2023; 10(5):439. https://doi.org/10.3390/aerospace10050439
Chicago/Turabian StyleZhang, Xiaoguang, Huixue Dang, and Bin Li. 2023. "Prediction of Aircraft Surface Noise in Supersonic Cruise State" Aerospace 10, no. 5: 439. https://doi.org/10.3390/aerospace10050439
APA StyleZhang, X., Dang, H., & Li, B. (2023). Prediction of Aircraft Surface Noise in Supersonic Cruise State. Aerospace, 10(5), 439. https://doi.org/10.3390/aerospace10050439






