Evaluation of Air Combat Control Ability Based on Eye Movement Indicators and Combination Weighting GRA-TOPSIS
Abstract
1. Introduction
2. Literature
3. Air Combat Control Ability Evaluation Indicator Modeling
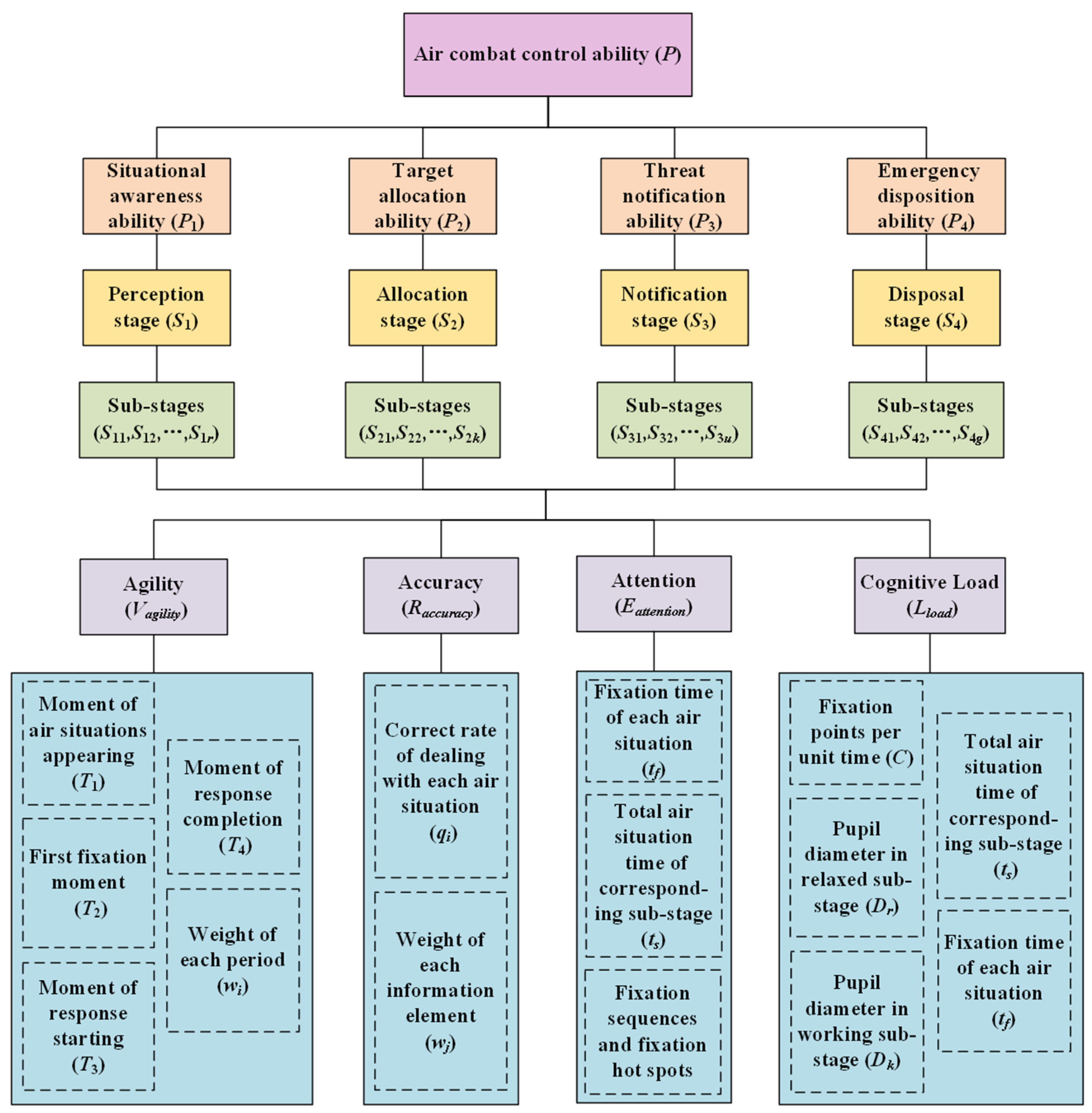
3.1. Indicator System
3.2. Indicator Model
4. Air Combat Control Ability Assessment Method
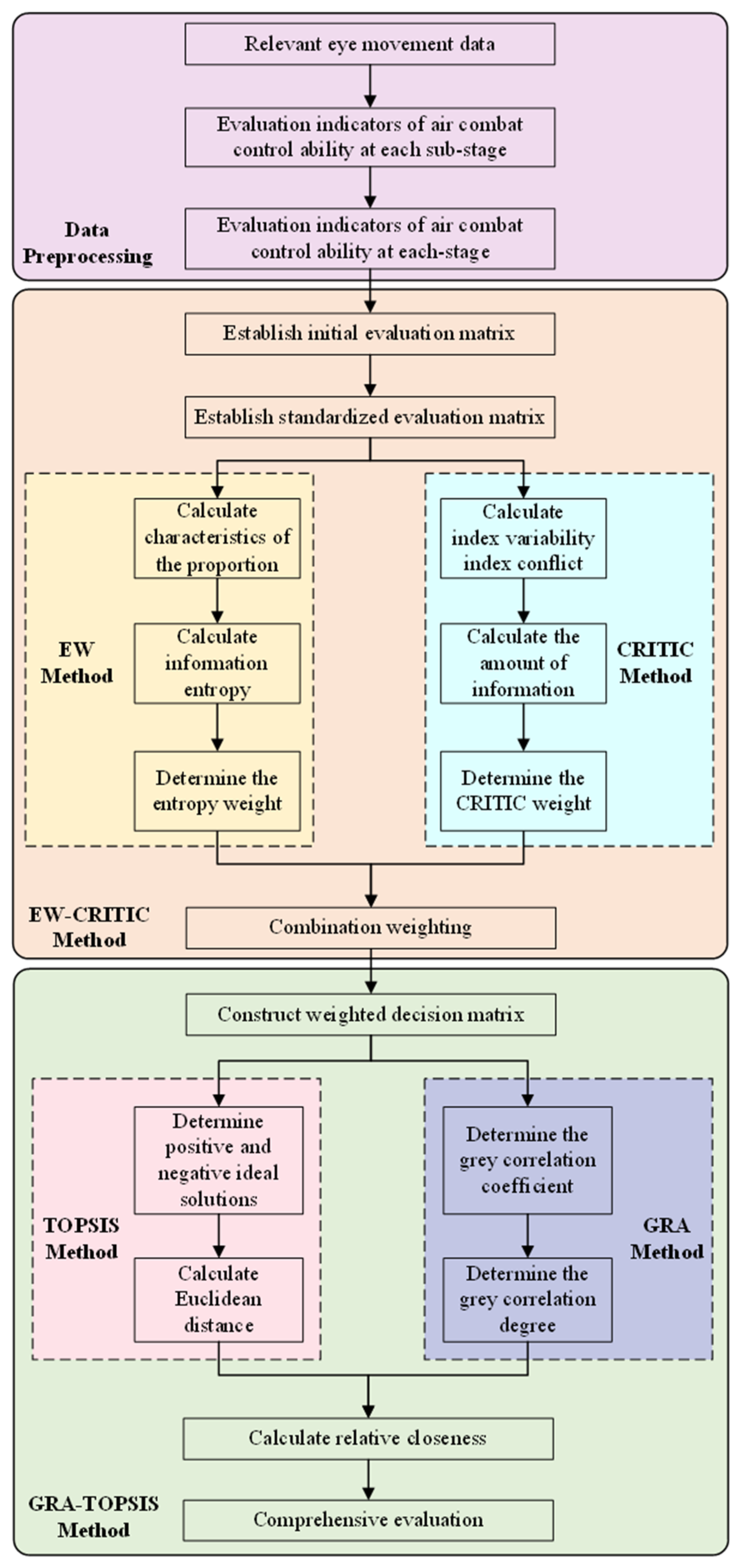
4.1. EW-CRITIC Combination Weighting
4.2. GRA-TOPSIS
5. Case Analysis of Air Combat Control Ability Evaluation
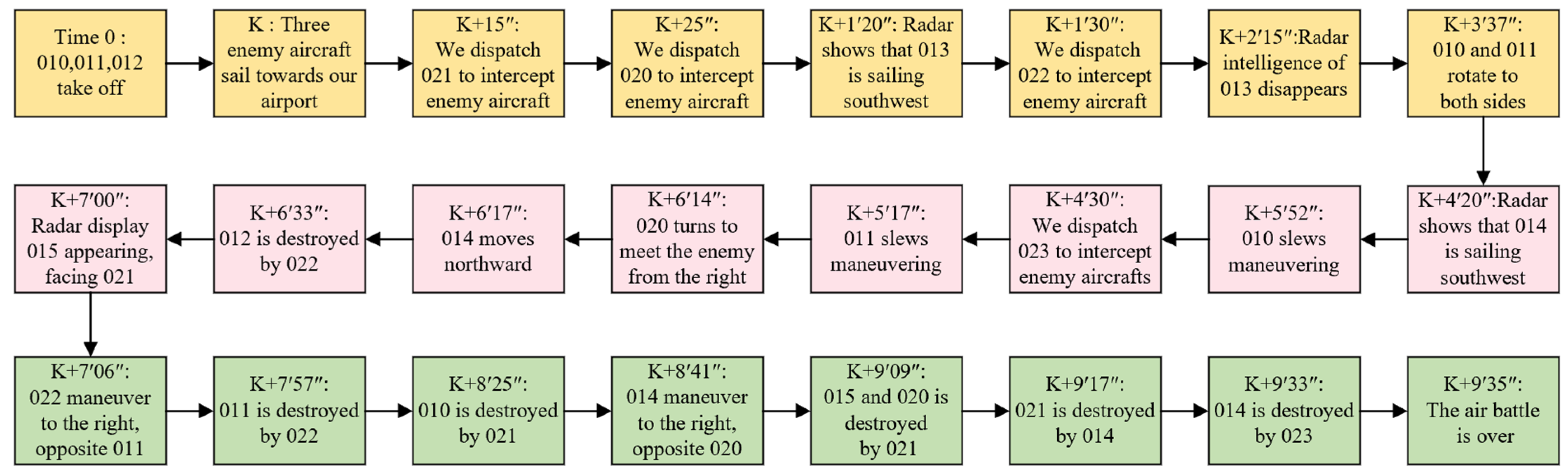
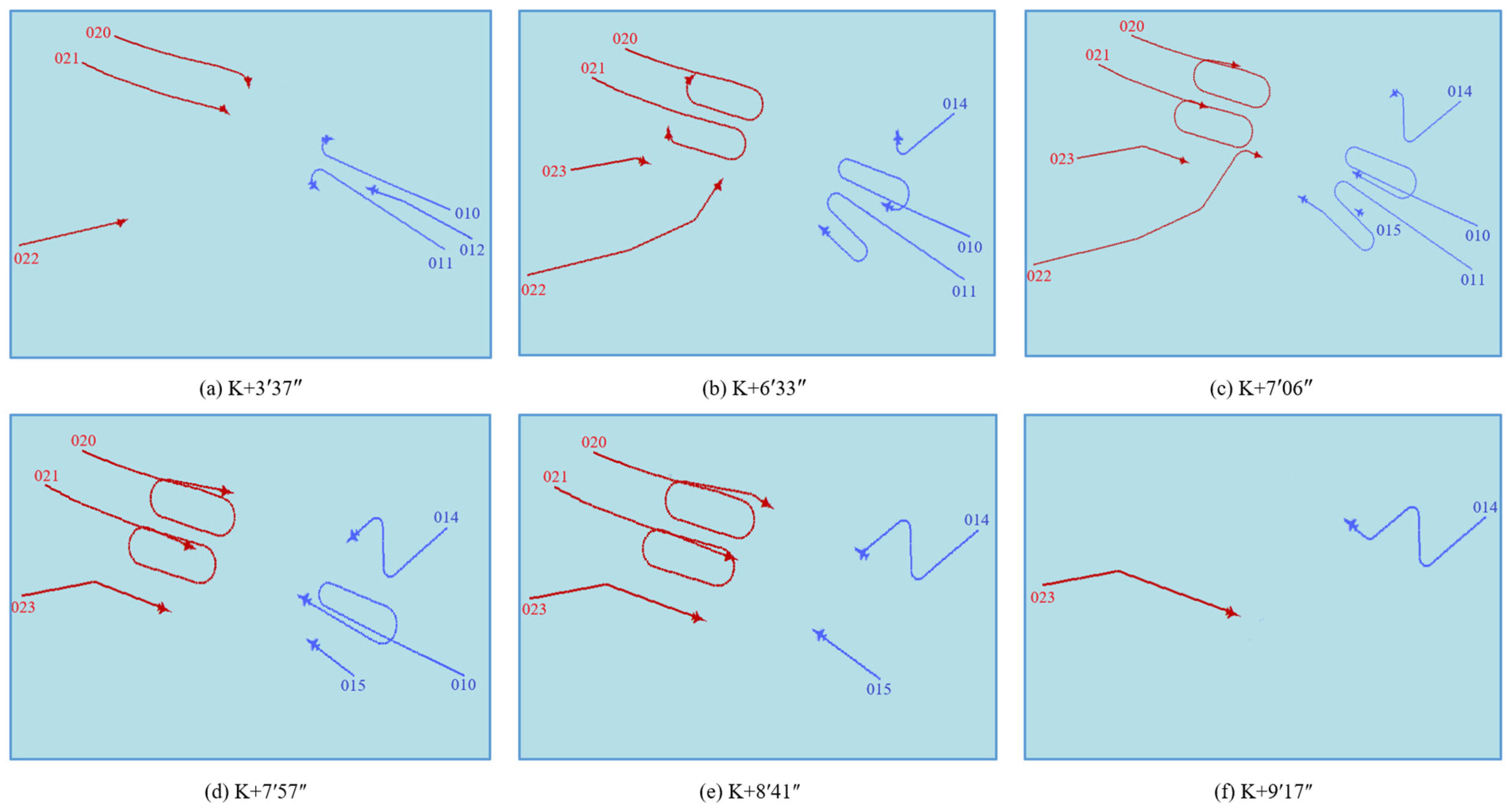
5.1. Experimental Design
5.2. Instance Calculation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fowley, J.W. Undergraduate Air Battle Manager Training: Prepared to Achieve Combat Mission Ready; Air Command and Staff College, Distance Learning, Air University Maxwell AFB United States: Montgomery, AL, USA, 2016. [Google Scholar]
- Luppo, A.; Rudnenko, V. Competence assessment of air traffic control personnel. Proceedings Natl. Aviat. Univ. 2012, 2, 47–50. [Google Scholar] [CrossRef]
- Picano, J.J.; Roland, R.R.; Williams, T.J.; Bartone, P.T. Assessment of elite operational personnel. In Handbook of Military Psychology; Springer: Berlin/Heidelberg, Germany, 2017; pp. 277–289. [Google Scholar]
- Majaranta, P.; Bulling, A. Eye Tracking and Eye-Based Human-Computer Interaction; Advances in Physiological Computing; Springer: Berlin/Heidelberg, Germany, 2014; pp. 39–65. [Google Scholar]
- Brunyé, T.T.; Drew, T.; Weaver, D.L.; Elmore, J.G. A review of eye-tracking for understanding and improving diagnostic interpretation. Cogn. Res. Princ. Implic. 2019, 4, 7. [Google Scholar] [CrossRef] [PubMed]
- Moore, L.J.; Vine, S.J.; Smith, A.N.; Smith, S.J.; Wilson, M.R. Quiet eye training improves small arms maritime marksmanship. Mil. Psychol. 2014, 26, 355–365. [Google Scholar] [CrossRef]
- Wetzel, P.A.; Anderson, G.M.; Barelka, B.A. Instructor use of eye position based feedback for pilot training. Hum. Factors Ergon. Soc. 1998, 2, 59. [Google Scholar] [CrossRef]
- Dubois, E.; Blättler, C.; Camachon, C.; Hurter, C. Eye movements data processing for ab initio military pilot training. In Proceedings of the International Conference on Intelligent Decision Technologies, Algarve, Portugal, 21–23 June 2017; pp. 125–135. [Google Scholar]
- Babu, M.D.; Jeevitha Shree, D.V.; Prabhakar, G.; Saluja, K.P.S.; Pashilkar, A.; Biswas, P. Estimating pilots’ cognitive load from ocular parameters through simulation and in-flight studies. J. Eye Mov. Res. 2019, 12. [Google Scholar] [CrossRef]
- Li, W.-C.; Jakubowski, J.; Braithwaite, G.; Jingyi, Z. Did you see what your trainee pilot is seeing? Integrated eye tracker in the simulator to improve instructors’ monitoring performance. In Eye-Tracking in Aviation, Proceedings of the 1st International Workshop (ETA-VI 2020), ISAE-SUPAERO, Toulouse, France, 17 March 2020; Université de Toulouse; Institute of Cartography and Geoinformation (IKG), ETH Zurich: Zurich, Switzerland, 2020; pp. 39–46. [Google Scholar]
- Van Gompel, R.P. Eye Movements: A Window on Mind and Brain; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Zhao, Y.; Zhang, C.; Wang, Y.; Lin, H. Shear-related roughness classification and strength model of natural rock joint based on fuzzy comprehensive evaluation. Int. J. Rock Mech. Min. Sci. 2021, 137, 104550. [Google Scholar] [CrossRef]
- Mardani, A.; Zavadskas, E.K.; Govindan, K.; Senin, A.A.; Jusoh, A. VIKOR technique: A systematic review of the state of the art literature on methodologies and applications. Sustainability 2016, 8, 37. [Google Scholar] [CrossRef]
- Llamazares, B. An analysis of the generalized TODIM method. Eur. J. Oper. Res. 2018, 269, 1041–1049. [Google Scholar] [CrossRef]
- Jana, C.; Pal, M. A dynamical hybrid method to design decision making process based on GRA approach for multiple attributes problem. Eng. Appl. Artif. Intell. 2021, 100, 104203. [Google Scholar] [CrossRef]
- Papathanasiou, J.; Ploskas, N. Topsis. In Multiple Criteria Decision Aid; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–30. [Google Scholar]
- Vavrek, R. Evaluation of the Impact of Selected Weighting Methods on the Results of the TOPSIS Technique. Int. J. Inf. Technol. Decis. Mak. 2019, 18, 1821–1843. [Google Scholar] [CrossRef]
- Liu, S.; Yang, Y.; Cao, Y.; Xie, N. A summary on the research of GRA models. Grey Syst. Theory Appl. 2013, 3, 7–15. [Google Scholar] [CrossRef]
- Liu, D.; Qi, X.; Fu, Q.; Li, M.; Zhu, W.; Zhang, L.; Faiz, M.A.; Khan, M.I.; Li, T.; Cui, S. A resilience evaluation method for a combined regional agricultural water and soil resource system based on Weighted Mahalanobis distance and a Gray-TOPSIS model. J. Clean. Prod. 2019, 229, 667–679. [Google Scholar] [CrossRef]
- Podvezko, V. Application of AHP technique. J. Bus. Econ. Manag. 2009, 10, 181–189. [Google Scholar] [CrossRef]
- Xiang, C.; Yin, L. Study on the rural ecotourism resource evaluation system. Environ. Technol. Innov. 2020, 20, 101131. [Google Scholar] [CrossRef]
- Dalkey, N.C. Delphi. In An Introduction to Technological Forecasting; Routledge: London, UK, 2018; pp. 25–30. [Google Scholar]
- Faber, D.S.; Korn, H. Applicability of the coefficient of variation method for analyzing synaptic plasticity. Biophys. J. 1991, 60, 1288–1294. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of entropy weight method in decision-making. Math. Probl. Engine-Ering 2020, 2020, 1–5. [Google Scholar] [CrossRef]
- Dwivedi, A.; Kumar, A.; Goel, V. Selection of nanoparticles for battery thermal management system using integrated multiple criteria decision-making approach. Int. J. Energy Res. 2022, 46, 22558–22584. [Google Scholar] [CrossRef]
- Chen, Z.S.; Zhang, X.; Rodríguez, R.M.; Pedrycz, W.; Martínez, L.; Miroslaw, J.S. Expertise-structure and risk-appetite-integrated two-tiered collective opinion generation framework for large-scale group decision making. IEEE Trans. Fuzzy Syst. 2022, 30, 5496–5510. [Google Scholar] [CrossRef]
- Cheng, K.; Liu, S. Does Urbanization Promote the Urban–Rural Equalization of Basic Public Services? Evidence from Prefectural Cities in China. Evid. Prefect. Cities China 2023, 1–15. [Google Scholar] [CrossRef]
- Gong, H.; Wang, X.; Wang, Z.; Liu, Z.; Li, Q.; Zhang, Y. How Did the Built Environment Affect Urban Vibrancy? A Big Data Approach to Post-Disaster Revitalization Assessment. Int. J. Environ. Res. Public Health 2022, 19, 12178. [Google Scholar] [CrossRef]
- Chen, Z.S.; Yang, L.L.; Chin, K.S.; Yang, Y.; Pedrycz, W.; Chang, J.P.; Luis, M.; Mirosław, J.S. Sustainable building material selection: An integrated multi-criteria large group decision making framework. Appl. Soft Comput. 2021, 113, 107903. [Google Scholar] [CrossRef]
- Weng, X.; Yang, S. Private-Sector Partner Selection for Public-Private Partnership Projects Based on Improved CRI-TIC-EMW Weight and GRA-VIKOR Method. Discret. Dyn. Nat. Soc. 2022, 1–10. [Google Scholar] [CrossRef]
- Rostamzadeh, R.; Ghorabaee, M.K.; Govindan, K.; Esmaeili, A.; Nobar, H.B.K. Evaluation of sustainable supply chain risk management using an integrated fuzzy TOPSIS-CRITIC approach. J. Clean. Prod. 2018, 175, 651–669. [Google Scholar] [CrossRef]
- Babatunde, M.; Ighravwe, D. A CRITIC-TOPSIS framework for hybrid renewable energy systems evaluation under techno-economic requirements. J. Proj. Manag. 2019, 4, 109–126. [Google Scholar] [CrossRef]
- Chen, Z.S.; Zhang, X.; Govindan, K.; Wang, X.J. Third-party reverse logistics provider selection: A computational semantic a-nalysis-based multi-perspective multi-attributedecision-making approach. Expert Syst. Appl. 2021, 166, 114051. [Google Scholar] [CrossRef]
- Lu, H.; Zhao, Y.; Zhou, X.; Wei, Z. Selection of agricultural machinery based on improved CRITIC-entropy weight and GRA-TOPSIS method. Processes 2022, 10, 266. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, X.; Zhu, B.; He, K.; Wang, P. Measuring the maturity of carbon market in China: An entropy-based TOPSIS approach. J. Clean. Prod. 2019, 229, 94–103. [Google Scholar] [CrossRef]
- Sakthivel, G.; Ilangkumaran, M.; Nagarajan, G.; Priyadharshini, G.V.; Kumar, S.D.; Kumar, S.S.; Suresh, K.S.; Selvan, G.T.; Thilakavel, T. Multi-criteria decision modelling approach for biodiesel blend selection based on GRA–TOPSIS analysis. Int. J. Ambient. Energy 2014, 35, 139–154. [Google Scholar] [CrossRef]
- Chen, Z.-S.; Yang, Y.; Wang, X.-J.; Chin, K.-S.; Tsui, K.-L. Fostering linguistic decision-making under uncertainty: A proportional in-terval type-2 hesitant fuzzy TOPSIS approach based on Hamacher aggregation operators and andness optimization models. Inf. Sci. 2019, 500, 229–258. [Google Scholar] [CrossRef]
- Tian, J.; Wang, B.; Guo, R.; Wang, Z.; Cao, K.; Wang, X. Adversarial Attacks and Defenses for Deep-Learning-Based Unmanned Aerial Vehicles. IEEE Internet Things J. 2022, 9, 22399–22409. [Google Scholar] [CrossRef]
- Sweller, J. Cognitive load during problem-solving: Effects on learning. CognitiveScience 1988, 12, 257–285. [Google Scholar] [CrossRef]
- Privitera, C.M.; Stark, L.W. Algorithms for defining visual regions of interest: Comparison with eye fixations. Trans. Pattern Anal. Mach. Intell. 2000, 22, 970–982. [Google Scholar] [CrossRef]
- Henderson, J.M.; Ferreira, F. Effects of foveal processing difficulty on the perceptual span in reading: Implications for attention and eye movement control. J. Exp. Psychol. Learn. Mem. Cogn. 1990, 16, 417. [Google Scholar] [CrossRef]
- Hess, E.H.; Polt, J.M. Pupil size in relation to mental activity during simple problem solving. Science 1964, 143, 1190–1192. [Google Scholar] [CrossRef]
- Xue, Y.F.; Li, Z.W. Research on online learning cognitive load quantitative model based on eye-tracking technology. Mod. Educ. Technol. 2019, 29, 59–65. [Google Scholar]
- Kumar, R.; Singh, S.; Bilga, P.S.; Jatin; Singh, J.; Singh, S.; Scutaru, M.-L. Revealing the benefits of entropy weights method for multi-objective optimization in machining operations: A critical review. J. Mater. Res. Technol. 2021, 10, 1471–1492. [Google Scholar] [CrossRef]
- Žižović, M.; Miljković, B.; Marinković, D. Objective methods for determining criteria weight coefficients: A modification of the CRITIC method. Decis. Mak. Appl. Manag. Eng. 2020, 3, 149–161. [Google Scholar] [CrossRef]
- Yin, J.; Du, X.; Yuan, H.; Ji, M.; Yang, X.; Tian, S.; Wang, Q.; Liang, Y. TOPSIS Power Quality Comprehensive Assessment Based on A Combination Weighting Method. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22–25 October 2021; pp. 1303–1307. [Google Scholar]
- Wang, J.; Wang, Y. Analysis on Influencing Factors of Financial Risk in China Media Industry Based on Entropy-critic Method and XGBoost. Acad. J. Bus. Manag. 2022, 4, 102–106. [Google Scholar]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of-the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Wei, G.W. GRA method for multiple attribute decision making with incomplete weight information in intuitionistic fuzzy setting. Knowl. Based Syst. 2010, 23, 243–247. [Google Scholar] [CrossRef]
- Kirubakaran, B.; Ilangkumaran, M. Selection of optimum maintenance strategy based on FAHP integrated with GRA–TOPSIS. Ann. Oper. Res. 2016, 245, 285–313. [Google Scholar] [CrossRef]
- Bishop, R.; Rutyna, M. Eye Tracking Innovation for Aviation Research. J. New Bus. Ideas Trends 2021, 19, 1–7. [Google Scholar]
- Thibeault, M.; Jesteen, M.; Beitman, A. Improved Accuracy Test Method for Mobile Eye Tracking in Usability Scenarios. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting, Seattle, DC, USA, 28 October–1 November 2019; Volume 63, pp. 2226–2230. [Google Scholar]
- Steindorf, L.; Rummel, J. Do your eyes give you away? A validation study of eye-movement measures was used as indicators for mindless reading. Behav. Res. Methods 2020, 52, 162–176. [Google Scholar] [CrossRef]
- Joseph, A.W.; Murugesh, R. Potential eye tracking metrics and indicators to measure cognitive load in human-computer interaction research. J. Sci. Res. 2020, 64, 168–175. [Google Scholar] [CrossRef]
- Greef, T.; Lafeber, H.; Oostendorp, H.; Jasper, L. Eye movement as indicators of mental workload to trigger adaptive automation. In Proceedings of the International Conference on Foundations of Augmented Cognition, San Diego, CA, USA, 19–24 July 2009; pp. 219–228. [Google Scholar]
- Meghanathan, R.N.; van Leeuwen, C.; Nikolaev, A.R. Fixation duration surpasses pupil size as a measure of memory load in free viewing. Front. Hum. Neurosci. 2015, 8, 1063. [Google Scholar] [CrossRef]
- DeAngelus, M.; Pelz, J.B. Top-down control of eye movements: Yarbus revisited. Vis. Cogn. 2009, 17, 790–811. [Google Scholar] [CrossRef]
- Kramer, A.F. Physiological metrics of mental workload: A review of recent progress. Mult. Task Perform. 2020, 279–328. [Google Scholar]




| Methods | Merits | Defects |
|---|---|---|
| FCE | 1. Be able to make a more scientific, reasonable, and practical quantitative evaluation of the data with fuzzy information 2. The evaluation result is a vector rather than a point value and contains rich information 3. Make qualitative problems quantitative and improve the accuracy and feasibility of evaluation | 1. Complex calculation process 2. Strong subjectivity 3. Only consider the main factors and ignore the secondary factors so that the evaluation results are not comprehensive 4. When there are many indicators, the weight vector W does not match the fuzzy matrix R, which is easy to cause failure |
| VIKOR | 1. Considering the maximization of group utility and the minimization of individual regret at the same time, it has high-ranking stability and reliability 2. A compromise scheme with priority can be obtained so that there may be more than one optimal scheme | 1. Susceptible to subjective influence 2. The weight coefficient and value of the criterion are required to be determined, which is difficult to achieve in actual decision-making |
| TODIM | 1. Simple calculation process 2. Based on prospect theory, widely used | 1. Susceptible to subjective influence 2. It cannot evaluate the situation where the effect value is an interval value |
| GRA | 1. Accurately analyze the trend of the data curve as a scaling curve to measure the shape similarity 2. It is also applicable to the number of samples and the regularity of samples 3. Easy computational and convenient method 4. The quantitative results are consistent with the qualitative analysis results 5. Reduce the loss caused by information asymmetry | 1. Strong subjectivity 2. It is difficult to determine the optimal value of some indicators 3. It is necessary to determine the optimal value of each index |
| TOPSIS | 1. Scientific and objective evaluation process 2. There are no strict restrictions on data distribution, sample size, and indicators 3. Simple calculation process 4. It can well depict the comprehensive impact of multiple impact indicators 5. Wide application range | 1. The data of each indicator is required, and the selection of quantitative indicators will be difficult 2. It cannot determine the appropriate number of indicators to describe the impact of indicators |
| Methods | Merits | Defects |
|---|---|---|
| AHP | 1. Systematic analysis method 2. Simple and practical decision-making method 3. Less quantitative data information required | 1. Cannot provide new solutions for decision-making 2. Susceptible to subjective influence 3. When there are too many indicators, the data statistics are extensive, and the weight is difficult to determine 4. The exact solution of eigenvalues and eigenvectors is relatively complex |
| DARE | 1. The calculation process is simple and convenient 2. Make full use of all indicators | 1. The scope of application is small, and it is only applicable to problems with obvious comparable relations among the evaluation objects 2. Susceptible to subjective influence |
| Delphi | 1. Convenient evaluation process 2. It is conducive to independent thinking and judgment of experts | 1. Strong subjectivity 2. The investigation took quite a long time 3. The investigation conclusion may be close to the median or arithmetic mean |
| CV | 1. The calculation process is simple and convenient 2. Can effectively distinguish various indicators | 1. There are certain errors in the calculation results 2. The premise of use is that each indicator is of equal importance, and there are specific requirements for the selection of indicators |
| PCA | 1. No parameter limit 2. It can eliminate the relevant impact between evaluation indicators 3. Reduce the workload of indicator selection | 1. Eigenvalue decomposition has some limitations, such as the transformation matrix must be a square matrix 2. When the sign of the factor load of the principal component is positive or negative, the meaning of the comprehensive evaluation function is not clear |
| CRITIC | 1. Comprehensively consider the contrast strength and conflict of indicators 2. Simple and convenient calculation process | 1. Requirement of specific normalization formulations and relatively more evident modeling mechanism 2. The dispersion between indicator data is not considered |
| EW | 1. The deviation caused by human factors is avoided 2. The precision is high, which can better explain the results obtained 3. Unbiased, simple, and reliable 4. Modular and user-friendly 5. Produces more divergent coefficient values, hence can better resolve the inherent conflict between the criteria | 1. Too sensitive to abnormal data 2. Neglecting the importance of indicators, sometimes the determined indicator weights will be far from the expected results |
| Author | Problem | Weighting Method | Model | Reference |
|---|---|---|---|---|
| Dwivedi | Select suitable nanoparticles to remit the thermal issues in energy storage systems | AHP EW-CRITIC | GRA-TOPSIS | [27] |
| Cheng | Measure the equilibrium level of urban and rural basic public services | EW-CRITIC | TOPSIS | [29] |
| Gong | Evaluate the urban post-disaster vitality recovery | EW-CRITIC | OLS | [30] |
| Weng | Select private sector partners for public-private partnership projects | EW-CRITIC | GRA-VIKOR | [32] |
| Rostamzadeh | The risk assessment of a sustainable supply chain | CRITIC | TOPSIS | [33] |
| Babatundea Ighravweb | Evaluate the renewable energy system | CRITIC | TOPSIS | [34] |
| Lu | The process of agricultural machinery selection | EW-CRITIC | GRA-TOPSIS | [36] |
| Liu | Measure the maturity of China’s carbon market | EW | TOPSIS | [37] |
| Sakthivel | Evaluate the best fuel ratio | FAHP | GRA—TOPSIS | [38] |
| Sub-Stage | Indicator | Meaning | Unit |
|---|---|---|---|
| Perception Sub-stages (S1r) | V1ragility | The agility of perceiving critical aerial situations | piece·s−1 |
| m1 | The incident of ABMs’ situational awareness | piece | |
| t1rtotal, t1ra, t1rb, t1rc | The total perception time of air combat control, the discovery time, reaction time, and perception time to the critical aerial situations | s | |
| T1r1, T1r2, T1r3, T1r4 | The moment of critical aerial situations appearing, the first fixation moment of critical aerial situations, the moment of perception starting, and the moment of perception completing | s | |
| w1ra, w1rb, w1rc | The weight of each period | % | |
| Allocation Sub-stages (S2k) | V2kagility | The agility in assigning targets | piece·s−1 |
| m2 | The incident of ABMs assigning targets | piece | |
| t2ktotal, t2ka, t2kb, t2kc | The total time to assign targets, and the detection time, reaction time, and allocation time to the targets | s | |
| T2k1, T2k2, T2k3, T2k4 | The moment of the targets appearing, the first fixation moment of the targets, the moment of allocation starting, and the moment of allocation completing | s | |
| w2ka, w2kb, w2kc | The weight of each period | % | |
| Notification Sub-stages (S3u) | V3uagility | The agility of threat notification | piece·s−1 |
| m3 | The incident of ABMs reporting the threats | piece | |
| t3utotal, t3ua, t3ub, t3uc | The total time to report the threats, the detection time, reaction time, and notification time for the threats | s | |
| T3u1, T3u2, T3u3, T3u4 | The moment of the threats appearing, the first fixation moment of the threats, the moment of notification starting, and the moment of notification completing | s | |
| w3ua, w3ub, w3uc | The weight of each period | % | |
| Disposal Sub-stages (S4g) | V4gagility | The agility of flying emergency disposition | piece·s−1 |
| m4 | The incident of ABMs dealing with flying emergencies | piece | |
| t4gtotal, t4ga, t4gb, t4gc | The total time to deal with the flying emergencies, the discovery time, reaction time, and disposal time for the flying emergencies | s | |
| T4g1, T4g2, T4g3, T4g4 | The moment of appearance of the flying emergencies, the first fixation moment of flying emergencies, the moment of disposition starting, and the moment of disposition completing | s | |
| w4ga, w4gb, w4gc | The weight of each period | % |
| Sub-Stage | Indicator | Meaning | Unit |
|---|---|---|---|
| Perception Sub-stages (S1r) | R1raccuracy | The accuracy of perceiving critical aerial situations | % |
| q1r1, q1r2, …, q1rn | The correct rate of each information element when the ABMs perceive the critical aerial situations | % | |
| w1r1, w1r2, …, w1rn | The weight of each information element | % | |
| Allocation Sub-stages (S2k) | R2kaccuracy | The accuracy of assigning targets | % |
| q2k1, q2k2, …, q2kn | The correct rate of each allocation scheme when the ABMs assign targets | % | |
| w2k1, w2k2, …, w2kn | The weight of each allocation scheme | % | |
| Notification Sub-stages (S3u) | R3uaccuracy | The accuracy of threat notification | % |
| q3u1, q3u2, …, q3un | The correct rate of each information element when the ABMs report the threats | % | |
| w3u1, w3u2, …, w3un | The weight of each information element | % | |
| Disposal Sub-stages (S4g) | R4gaccuracy | The accuracy of flying emergency disposition | % |
| q4g1, q4g2, …, q4gn | The correct rate of each information element when the ABMs dispose of flying emergencies | % | |
| w4g1, w4g2, …, w4gn | The weight of each information element | % |
| Sub-Stage | Indicator | Meaning | Unit |
|---|---|---|---|
| Perception Sub-stages (S1r) | E1rattention | The attention to perceiving critical aerial situations | % |
| t1rfixation, t1rsum | The fixation time on the critical aerial situations, the total time of the critical aerial situations appearing | s | |
| T1r5, T1r6 | The appearance moment and the end moment of critical aerial situations | s | |
| Allocation Sub-stages (S2k) | E2kattention | The attention to assigning targets | % |
| t2kfixation, t2ksum | The fixation time on the targets, the total allocated time | s | |
| T2k5, T2k6 | The first fixation moment and completion moment of assigning targets | s | |
| Notification Sub-stages (S3u) | E3uattention | The attention to threat notification | % |
| t3ufixation, t3usum | The fixation time on threats, total notification time | s | |
| T3u5, T3u6 | The start moment and the end moment of threat notification | s | |
| Disposal Sub-stages (S4g) | E4gattention | The attention to flying emergency disposition | % |
| t4gfixation, t4gsum | The fixation time and total disposal time on the flying emergencies | s | |
| T4g5, T4g6 | The appearance moment of the flying emergencies, the completion moment of disposing of flying emergencies | s |
| Sub-Stage | Indicator | Meaning | Unit |
|---|---|---|---|
| Perception Sub-stages (S1r) | L1rload | The cognitive load from critical aerial situations | each·s−1·mm |
| t1rfixation, t1rsum | The fixation time on the critical aerial situations, the total time of the critical aerial situations appearing | s | |
| C1r | The fixation points per unit of time | each·s−1 | |
| D1rpupil-work, Dpupil-relax | The pupil diameter of the left eye in the working and relaxed state | mm | |
| Allocation Sub-stages (S2k) | L2kload | The cognitive load from assigning targets | each·s−1·mm |
| t2kfixation, t2ksum | The fixation time on the targets, the total allocated time | s | |
| C2k | The fixation points per unit of time | each·s−1 | |
| D2kpupil-work, Dpupil-relax | The pupil diameter of the left eye in the working and relaxed state | mm | |
| Notification Sub-stages (S3u) | L3uload | The cognitive load from threat notification | each·s−1·mm |
| t3ufixation, t3usum | The fixation time on threats, the total notification time | s | |
| C3u | The fixation points per unit of time | each·s−1 | |
| D3upupil-work, Dpupil-relax | The pupil diameter of the left eye in the working and relaxed state | mm | |
| Disposal Sub-stages (S4g) | L4gload | The cognitive load from flying emergency disposition | each·s−1·mm |
| t4gfixation, t4gsum | The fixation time and total disposal time on the flying emergencies | s | |
| C4g | The fixation points per unit of time | each·s−1 | |
| D4gpupil-work, Dpupil-relax | The pupil diameter of the left eye in the working and relaxed state | mm |
| Subject | Age | Education | Years of Service | Amount of Tasks Executed |
|---|---|---|---|---|
| X1 | 33 | bachelor | 10 | 19 |
| X2 | 30 | bachelor | 7 | 9 |
| X3 | 28 | bachelor | 5 | 7 |
| X4 | 29 | master | 6 | 17 |
| X5 | 29 | bachelor | 6 | 7 |
| X6 | 35 | bachelor | 12 | 10 |
| X7 | 31 | bachelor | 8 | 11 |
| X8 | 34 | master | 11 | 21 |
| X9 | 30 | master | 7 | 13 |
| X10 | 26 | bachelor | 3 | 8 |
| Serial Number | Indicator | Meaning | Unit |
|---|---|---|---|
| 1 | Fixation time | The duration between the first and last sample makes up a fixation point. It is shown that the subject’s visual focus stays on the observed object for at least 100–200 ms. | s |
| 2 | Pupil diameter | The pupil refers to the circular hole with a 2.5–4 mm diameter in the center of the eye’s iris. The changes in pupil diameter can reflect the subjects’ fatigue degree and cognitive load. | mm |
| 3 | Fixation hotspot | Each part of the interface is marked with different colors representing the heat to show the attention distribution of the subjects. Generally, the darker the color is, the higher the attention is. | none |
| 4 | Fixation sequence | It is a sign to measure the attention distribution of the subjects. Generally, the larger the radius of the fixation point is, the longer the fixation time is. | none |
| 5 | First fixation moment | The fixation moment of the first fixation point in the area of interest can be used as an essential indicator to measure perception speed. | s |
| 6 | Fixation points per unit of time | During a period, the ratio of the total number of fixation points in the area of interest to the total time can be used to measure the cognitive load of the subjects. | each |
| Attention | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 |
|---|---|---|---|---|---|---|---|---|---|---|
| E11attention | 0.432 | 0.461 | 0.207 | 0.490 | 0.146 | 0.882 | 0.294 | 0.350 | 0.325 | 0.454 |
| E12attention | 0.851 | 0.468 | 0.260 | 0.327 | 0.101 | 0.166 | 0.250 | 0.050 | 0.122 | 0.023 |
| E13attention | 0.005 | 0.344 | 0.031 | 0.041 | 0.033 | 0.006 | 0.179 | 0.052 | 0.096 | 0.023 |
| E14attention | 0.081 | 0.139 | 0 | 0.026 | 0.040 | 0.014 | 0.175 | 0.010 | 0.022 | 0.029 |
| E15attention | 0.048 | 0.324 | 0.181 | 0.215 | 0 | 0.106 | 0.093 | 0.175 | 0.279 | 0.207 |
| E16attention | 0.013 | 0.110 | 0 | 0.165 | 0.120 | 0.018 | 0.005 | 0.091 | 0.066 | 0.105 |
| E17attention | 0.077 | 0.537 | 0 | 0.357 | 0.063 | 0.018 | 0.256 | 0.291 | 0 | 0.123 |
| E21attention | 0.157 | 0.578 | 0.742 | 0.192 | 0.231 | 0.053 | 0.595 | 0.189 | 0.326 | 0.123 |
| E22attention | 0.070 | 0.541 | 0 | 0.115 | 0.255 | 0.179 | 0.522 | 0.457 | 0.426 | 0.122 |
| E23attention | 0.455 | 0.434 | 0.272 | 0.094 | 0.195 | 0.064 | 0.445 | 0.223 | 0.354 | 0.106 |
| E24attention | 0.289 | 0.403 | 0.233 | 0.104 | 0 | 0.127 | 0 | 0.832 | 0.537 | 0 |
| E25attention | 0.053 | 0 | 0.318 | 0.424 | 0 | 0.182 | 0 | 0.343 | 0.604 | 0 |
| E31attention | 0.118 | 0.369 | 0.225 | 0.262 | 0.304 | 0.083 | 0.284 | 0.247 | 0.111 | 0.061 |
| E32attention | 0.111 | 0 | 0.185 | 0.325 | 0.190 | 0.049 | 0 | 0.187 | 0.200 | 0.042 |
| E33attention | 0.207 | 0.385 | 0.163 | 0.073 | 0.082 | 0 | 0.482 | 0.222 | 0.192 | 0 |
| E34attention | 0 | 0.011 | 0.170 | 0.175 | 0.295 | 0.084 | 0.153 | 0.066 | 0.068 | 0.020 |
| E35attention | 0.052 | 0 | 0.288 | 0.428 | 0 | 0 | 0.250 | 0.206 | 0.317 | 0.011 |
| E36attention | 0.205 | 0.772 | 0.189 | 0.694 | 0.266 | 0.020 | 0.363 | 0.233 | 0.257 | 0 |
| E41attention | 0.185 | 0.625 | 0.397 | 0.198 | 0.419 | 0.416 | 0.519 | 0.502 | 0.413 | 0.320 |
| E42attention | 0.002 | 0.380 | 0.002 | 0.143 | 0 | 0.068 | 0.057 | 0 | 0 | 0.008 |
| E43attention | 0.290 | 0.358 | 0.337 | 0.059 | 0.283 | 0.206 | 0.410 | 0.276 | 0.153 | 0.240 |
| E44attention | 0.310 | 0 | 0.072 | 0.423 | 0 | 0.010 | 0.354 | 0.307 | 0.415 | 0.020 |
| Indicator | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 |
|---|---|---|---|---|---|---|---|---|---|---|
| V1guide | 0.367 | 0.056 | 0.053 | 0.459 | 1 | 0.054 | 0 | 0.482 | 0.350 | 0.192 |
| V2guide | 0.572 | 0.322 | 0.515 | 1 | 0.067 | 0.460 | 0.128 | 0.622 | 0.597 | 0 |
| V3guide | 0.585 | 0.028 | 0.537 | 0.212 | 0 | 0.428 | 0.691 | 1 | 0.491 | 0.152 |
| V4guide | 0.740 | 0.510 | 1 | 0.599 | 0 | 0.526 | 0.447 | 0.252 | 0.069 | 0.293 |
| R1accuracy | 0.467 | 1 | 0 | 0.464 | 0.224 | 0.901 | 0.812 | 0.583 | 0.693 | 0.676 |
| R2accuracy | 0.619 | 0.264 | 0.520 | 0 | 0.627 | 1 | 0.144 | 0.778 | 0.349 | 0 |
| R3accuracy | 0.881 | 0.163 | 0.387 | 0.185 | 0 | 0.396 | 0.401 | 0.828 | 1 | 0.494 |
| R4accuracy | 1 | 0.372 | 0.512 | 0.377 | 0 | 0.761 | 0.898 | 0.825 | 0.464 | 0.835 |
| E1attention | 0.557 | 1 | 0.037 | 0.533 | 0 | 0.245 | 0.412 | 0.200 | 0.128 | 0.144 |
| E2attention | 0.291 | 0.582 | 0.617 | 0.423 | 0.106 | 0.189 | 0.395 | 0.837 | 1 | 0 |
| E3attention | 0.289 | 0.608 | 0.639 | 1 | 0.472 | 0.047 | 0.777 | 0.568 | 0.619 | 0 |
| E4attention | 0.520 | 0.969 | 0.491 | 1 | 0 | 0.150 | 0.911 | 0.643 | 0.782 | 0.003 |
| L1load | 0.527 | 0.214 | 0.342 | 0.612 | 0.891 | 0 | 0.817 | 1 | 0.987 | 0.703 |
| L2load | 0.812 | 0.128 | 0 | 0.916 | 0.593 | 1 | 0.239 | 0.472 | 0.053 | 0.996 |
| L3load | 0.874 | 0.303 | 0 | 0.383 | 0.320 | 1 | 0.571 | 0.928 | 0.671 | 0.999 |
| L4load | 1 | 0 | 0.360 | 0.986 | 0.636 | 0.997 | 0.475 | 0.904 | 0.852 | 0.981 |
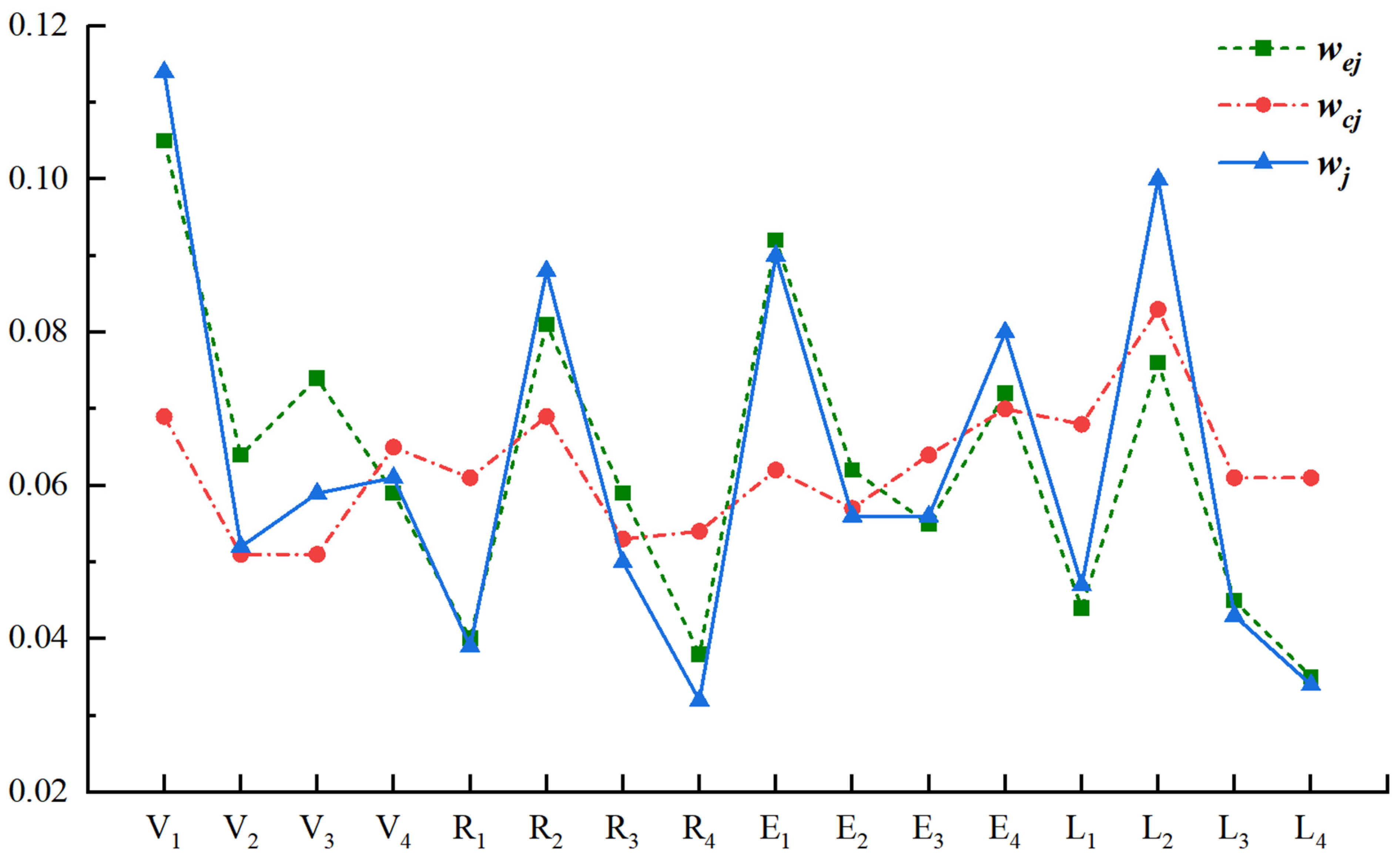
| Weight | V1agility | V2agility | V3agility | V4agility | R1accuracy | R2accuracy | R3accuracy | R4accuracy |
|---|---|---|---|---|---|---|---|---|
| wej | 0.105 | 0.064 | 0.074 | 0.059 | 0.040 | 0.081 | 0.059 | 0.038 |
| wcj | 0.069 | 0.051 | 0.051 | 0.065 | 0.061 | 0.069 | 0.053 | 0.054 |
| wj | 0.114 | 0.052 | 0.059 | 0.061 | 0.039 | 0.088 | 0.050 | 0.032 |
| Weight | E1attention | E2attention | E3attention | E4attention | L1load | L2load | L3load | L4load |
| wej | 0.092 | 0.062 | 0.055 | 0.072 | 0.044 | 0.076 | 0.045 | 0.035 |
| wcj | 0.062 | 0.057 | 0.064 | 0.070 | 0.068 | 0.083 | 0.061 | 0.061 |
| wj | 0.090 | 0.056 | 0.056 | 0.080 | 0.047 | 0.100 | 0.043 | 0.034 |
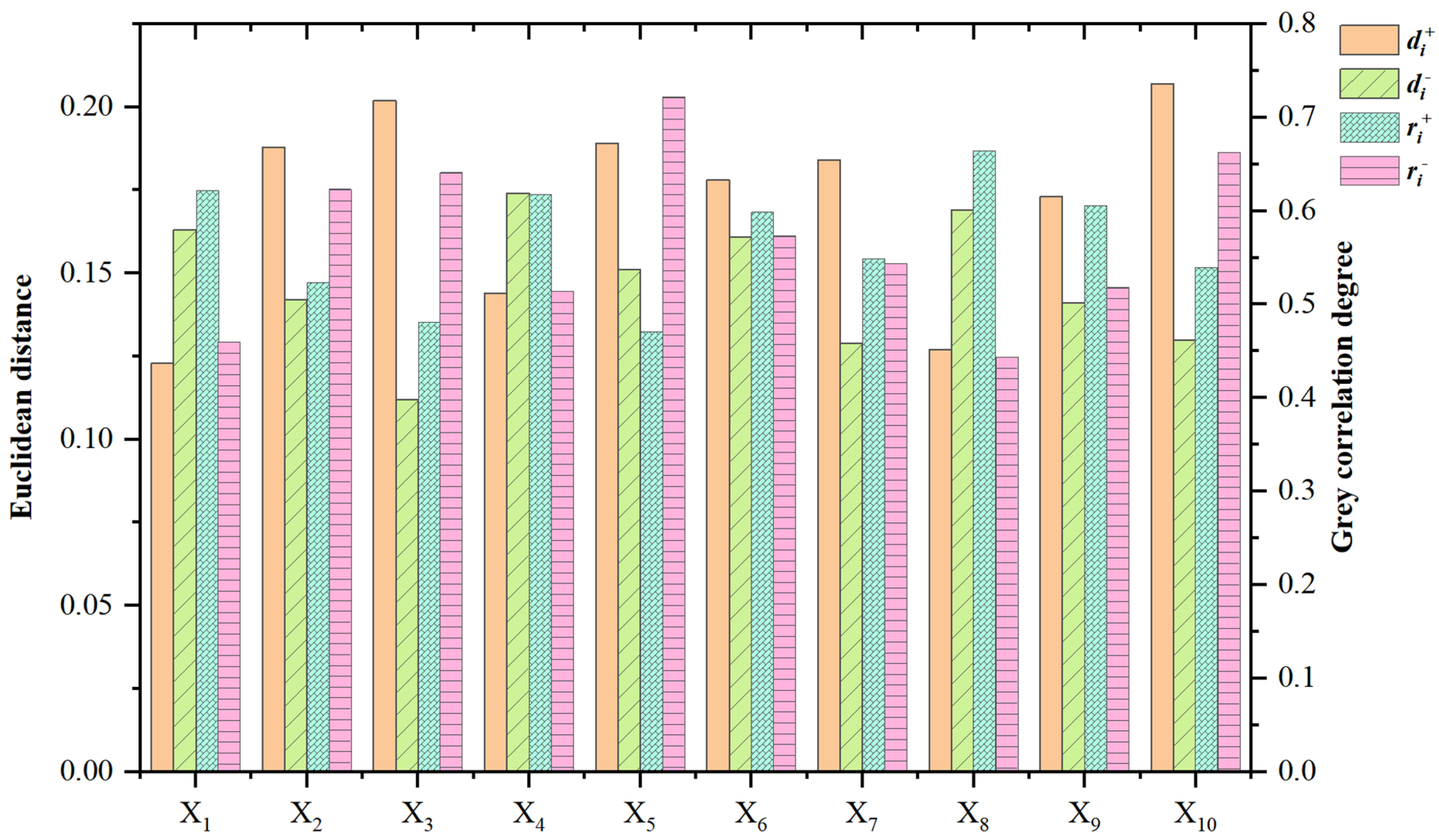
| Subject | Euclidean Distance | Grey Correlation Degree | Relative Closeness Ti | Comprehensive Ranking | ||
|---|---|---|---|---|---|---|
| di+ | di− | ri+ | ri− | |||
| X1 | 0.123 | 0.163 | 0.622 | 0.460 | 0.603 | 2 |
| X2 | 0.188 | 0.142 | 0.524 | 0.623 | 0.475 | 7 |
| X3 | 0.202 | 0.112 | 0.481 | 0.641 | 0.423 | 10 |
| X4 | 0.144 | 0.174 | 0.618 | 0.514 | 0.578 | 3 |
| X5 | 0.189 | 0.151 | 0.471 | 0.722 | 0.451 | 8 |
| X6 | 0.178 | 0.161 | 0.599 | 0.573 | 0.524 | 5 |
| X7 | 0.184 | 0.129 | 0.549 | 0.544 | 0.488 | 6 |
| X8 | 0.127 | 0.169 | 0.665 | 0.444 | 0.616 | 1 |
| X9 | 0.173 | 0.141 | 0.606 | 0.518 | 0.526 | 4 |
| X10 | 0.207 | 0.130 | 0.540 | 0.663 | 0.448 | 9 |
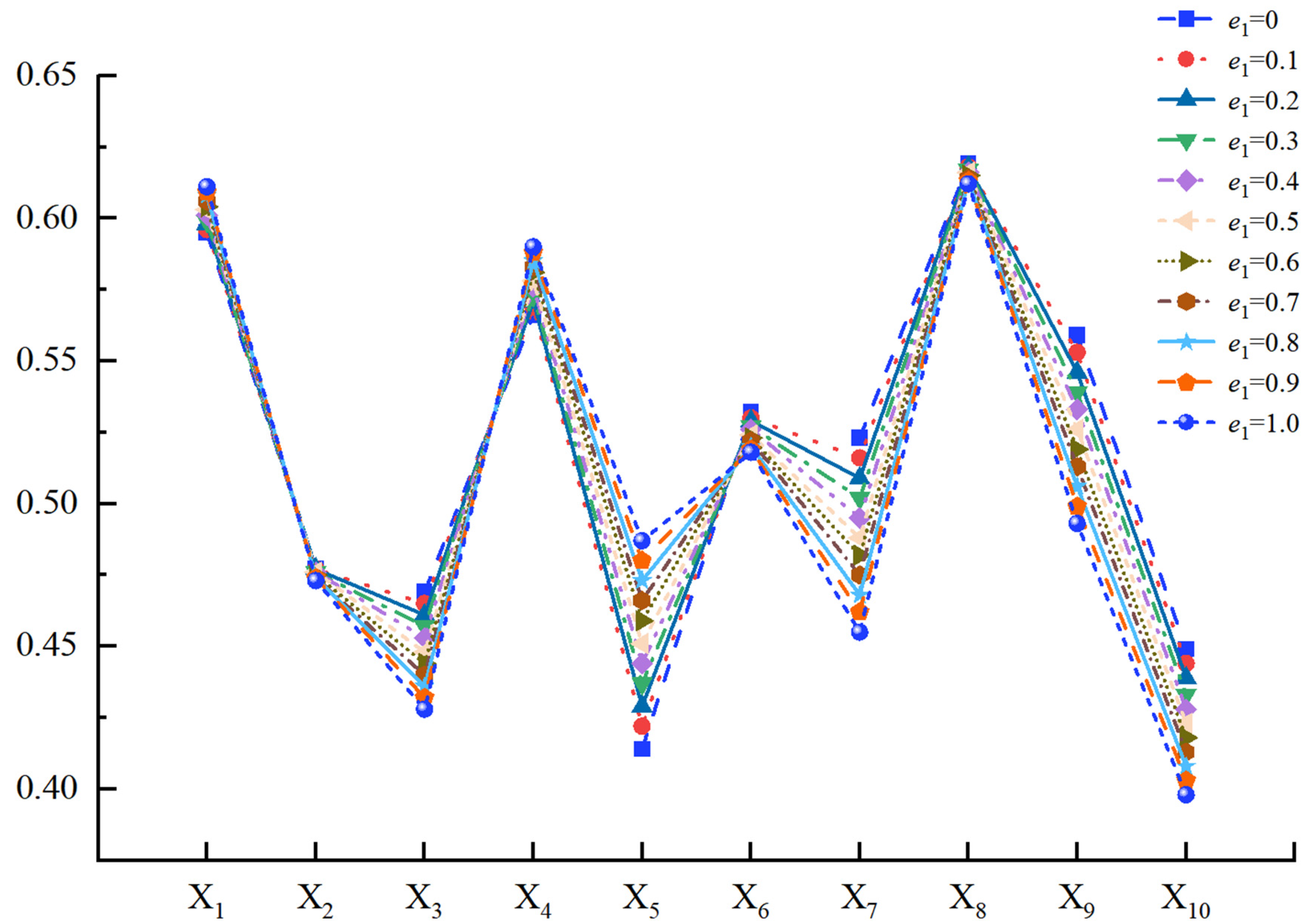
| No. | e1 | Tscore | Rank | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | |||
| 1 | 0 | 0.595 | 0.477 | 0.469 | 0.566 | 0.414 | 0.532 | 0.523 | 0.619 | 0.559 | 0.449 | X8 > X1 > X4 > X9 > X6 > X7 > X2 > X3 > X10 > X5 |
| 2 | 0.1 | 0.596 | 0.477 | 0.465 | 0.569 | 0.422 | 0.530 | 0.516 | 0.618 | 0.553 | 0.444 | X8 > X1 > X4 > X9 > X6 > X7 > X2 > X3 > X10 > X5 |
| 3 | 0.2 | 0.598 | 0.477 | 0.461 | 0.571 | 0.429 | 0.529 | 0.509 | 0.618 | 0.546 | 0.439 | X8 > X1 > X4 > X9 > X6 > X7 > X2 > X3 > X10 > X5 |
| 4 | 0.3 | 0.599 | 0.476 | 0.457 | 0.573 | 0.437 | 0.527 | 0.502 | 0.617 | 0.539 | 0.433 | X8 > X1 > X4 > X9 > X6 > X7 > X2 > X3 > X5 > X10 |
| 5 | 0.4 | 0.601 | 0.476 | 0.453 | 0.576 | 0.444 | 0.526 | 0.495 | 0.616 | 0.533 | 0.428 | X8 > X1 > X4 > X9 > X6 > X7 > X2 > X3 > X5 > X10 |
| 6 | 0.5 | 0.603 | 0.476 | 0.448 | 0.578 | 0.451 | 0.524 | 0.488 | 0.616 | 0.526 | 0.423 | X8 > X1 > X4 > X9 > X6 > X7 > X2 > X5 > X3 > X10 |
| 7 | 0.6 | 0.604 | 0.475 | 0.444 | 0.581 | 0.459 | 0.523 | 0.482 | 0.615 | 0.519 | 0.418 | X8 > X1 > X4 > X6 > X9 > X7 > X2 > X5 > X3 > X10 |
| 8 | 0.7 | 0.606 | 0.474 | 0.44 | 0.583 | 0.466 | 0.522 | 0.475 | 0.614 | 0.513 | 0.413 | X8 > X1 > X4 > X6 > X9 > X7 > X2 > X5 > X3 > X10 |
| 9 | 0.8 | 0.608 | 0.474 | 0.436 | 0.585 | 0.473 | 0.520 | 0.468 | 0.613 | 0.506 | 0.408 | X8 > X1 > X4 > X6 > X9 > X2 > X5 > X7 > X3 > X10 |
| 10 | 0.9 | 0.609 | 0.474 | 0.432 | 0.588 | 0.480 | 0.519 | 0.462 | 0.613 | 0.499 | 0.403 | X8 > X1 > X4 > X6 > X9 > X5 > X2 > X7 > X3 > X10 |
| 11 | 1.0 | 0.611 | 0.473 | 0.428 | 0.590 | 0.487 | 0.518 | 0.455 | 0.612 | 0.493 | 0.398 | X8 > X1 > X4 > X6 > X9 > X5 > X2 > X7 > X3 > X10 |
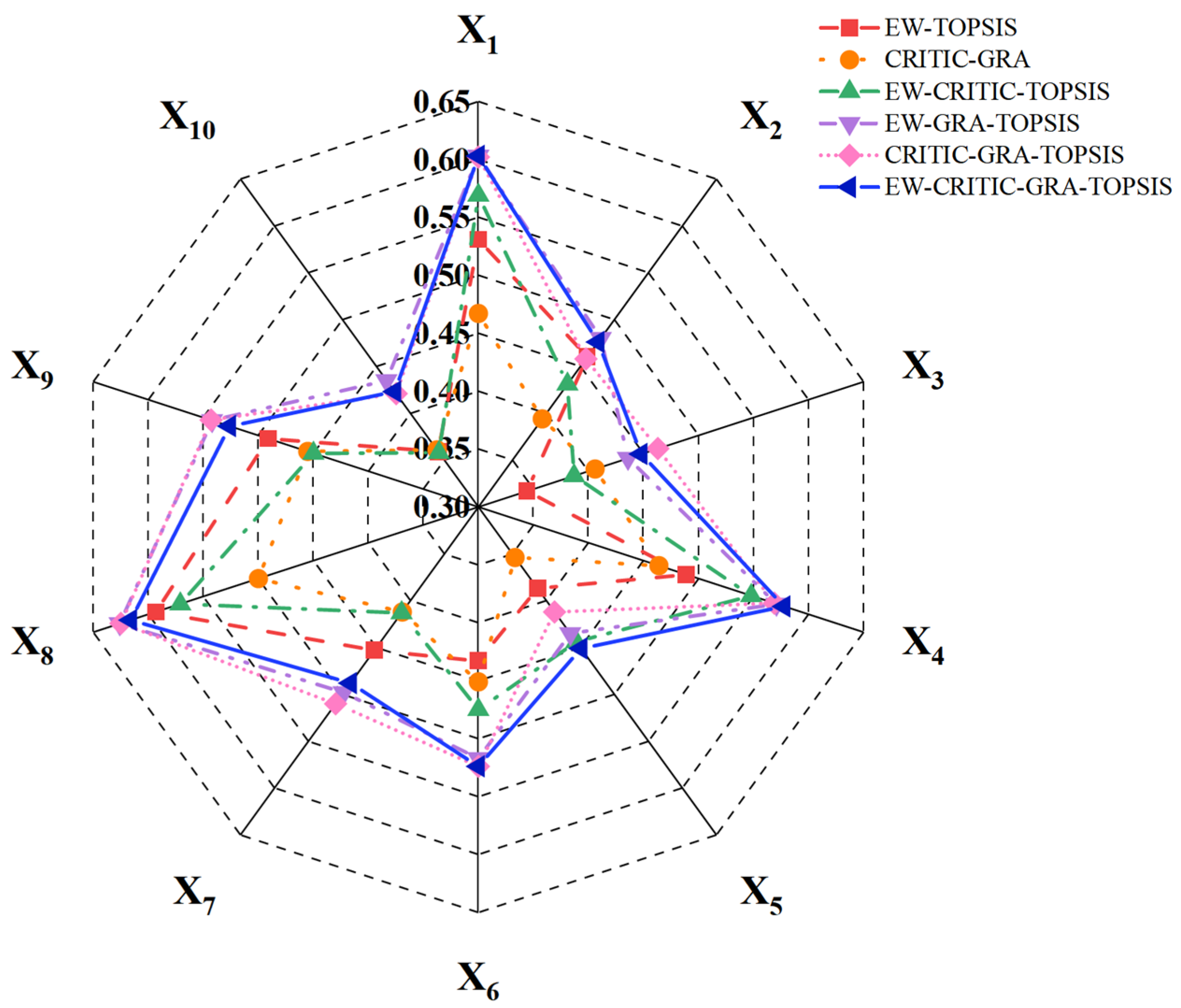
| No. | Subjects | EW-TOPSIS | CRITIC- GRA | EW-CRITIC -TOPSIS | EW-GRA- TOPSIS | CRITIC -GRA- TOPSIS | EW-CRITIC -GRA- TOPSIS | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Analysis Results | Rank | Analysis Results | Rank | Analysis Results | Rank | Analysis Results | Rank | Analysis Results | Rank | Analysis Results | Rank | ||
| 1 | X1 | 0.531 | 2 | 0.467 | 2 | 0.569 | 2 | 0.603 | 2 | 0.602 | 2 | 0.603 | 2 |
| 2 | X2 | 0.460 | 5 | 0.394 | 8 | 0.431 | 7 | 0.480 | 7 | 0.458 | 8 | 0.476 | 7 |
| 3 | X3 | 0.344 | 10 | 0.406 | 7 | 0.387 | 9 | 0.436 | 8 | 0.463 | 7 | 0.448 | 9 |
| 4 | X4 | 0.489 | 4 | 0.464 | 3 | 0.548 | 3 | 0.571 | 3 | 0.569 | 3 | 0.578 | 3 |
| 5 | X5 | 0.387 | 8 | 0.354 | 10 | 0.444 | 6 | 0.435 | 10 | 0.412 | 10 | 0.451 | 8 |
| 6 | X6 | 0.433 | 7 | 0.451 | 5 | 0.475 | 4 | 0.517 | 5 | 0.524 | 5 | 0.524 | 5 |
| 7 | X7 | 0.453 | 6 | 0.412 | 6 | 0.413 | 8 | 0.498 | 6 | 0.510 | 6 | 0.488 | 6 |
| 8 | X8 | 0.593 | 1 | 0.500 | 1 | 0.571 | 1 | 0.626 | 1 | 0.625 | 1 | 0.616 | 1 |
| 9 | X9 | 0.491 | 3 | 0.455 | 4 | 0.450 | 5 | 0.542 | 4 | 0.543 | 4 | 0.526 | 4 |
| 10 | X10 | 0.359 | 9 | 0.361 | 9 | 0.358 | 10 | 0.435 | 9 | 0.421 | 9 | 0.423 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, C.; Song, M.; Tian, J.; Xue, R. Evaluation of Air Combat Control Ability Based on Eye Movement Indicators and Combination Weighting GRA-TOPSIS. Aerospace 2023, 10, 437. https://doi.org/10.3390/aerospace10050437
Tian C, Song M, Tian J, Xue R. Evaluation of Air Combat Control Ability Based on Eye Movement Indicators and Combination Weighting GRA-TOPSIS. Aerospace. 2023; 10(5):437. https://doi.org/10.3390/aerospace10050437
Chicago/Turabian StyleTian, Chenzhi, Min Song, Jiwei Tian, and Ruijun Xue. 2023. "Evaluation of Air Combat Control Ability Based on Eye Movement Indicators and Combination Weighting GRA-TOPSIS" Aerospace 10, no. 5: 437. https://doi.org/10.3390/aerospace10050437
APA StyleTian, C., Song, M., Tian, J., & Xue, R. (2023). Evaluation of Air Combat Control Ability Based on Eye Movement Indicators and Combination Weighting GRA-TOPSIS. Aerospace, 10(5), 437. https://doi.org/10.3390/aerospace10050437






