Abstract
The article aims at reviewing the drop regions (DR) of the launch vehicles (LV) separating parts (SP) and methods of their determination. The DRs include sea and land areas; going beyond them is associated with a number of environmental, economic, and political factors. Their combination dictates the need to ensure the safety of the people, transport, infrastructure, and environment from the negative impact of LV SPs and fuel residues. The Monte Carlo method is mostly used to determine the impact areas. It enables an estimation of the probability of the SPs of LVs falling in certain areas, constituting the DRs. These points are varied according to a set of different initial parameters. The methods of controlling the impact areas are contingently divided into engineering (based on a change in the design appearance of the LV), mathematical (which includes the changes in or optimization of the LV’s trajectory or its SP), and “soft landing” (implying the return of the LV’s to the spaceport or to a certain prepared area). The present analysis can be used as a starting point when choosing a method for determining and controlling the projected LVs and the SPs’ area of impact.
1. Introduction
At present, there are many requirements for multistage LVs. Among them, the two main points can be distinguished: the first one is to solve the main task of LVs—to place a payload into the Earth’s orbit or a point in outer space; the second one is the necessity of providing the falling SPs of LVs into definite zones on the surface of the planet, called DRs.
The DR is the area on the land’s surface, where the points of impact of the LVs’ SPs are situated. In these predetermined areas, it is forbidden to build any structures or for people to be present, especially on the day of launch. These areas are strictly regulated by the Resolutions of the Government of the Russian Federation [1,2] and can be referred to as exclusion zones.
At the initial stage of rocket–space technology development, DRs were selected on the condition of their passage over the territory of the country at a significant distance from densely populated regions or over oceans. Each LV’s flight route required the allocation of DRs for the SPs, which were obviously overestimated [3]. This was due to the issues associated with determining the size of the DRs. The main reason for this is in various disturbances, which affect the LV during its movement in the active part of the trajectory. It created a certain deviation of the real rocket motion-control parameters from the previously calculated ones. The disturbing factors included errors in the LV motion-control program, influence of atmospheric parameters, and deviations from the nominal operation of the propulsion system, etc.
All this led to the fact that the SP of the LV on the passive part of the trajectory, or during CD, moved along a ballistic trajectory that differed from the initial one. In addition to the previously listed disturbing factors, there was another one caused by the presence of GFRs in the individual stages of loading the vehicles. Their odd movement in the fuel tanks could have been the reason for the oscillatory motion of the SPs [4]. Consequently, the actual area of the DR also differs from the calculated one.
According to the studies based on the methods of PJSC Energia, the GFR is about 1–3% of the initial fuel mass [5]. Some methods of calculation of liquid propellant rocket engines suggest that GFRs should make up approximately 2–5% of the total fuel volume [6]. Sometimes, this amounts to hundreds of kilograms.
Many components of liquid rocket fuel, such as asymmetrical dimethylhydrazine and nitrogen tetroxide, are extremely toxic and can contaminate the environment for a long time, if spilled. Soil and plants are capable of accumulating large amounts of toxins, which always leads to adverse environmental consequences [7,8]. Additionally, the possible purification methods that exist and are used at present are often unable to completely safeguard the environment or prove to be too expensive to be used [9]. The subsequent cleanup of the DRs from the SPs of the LVs and fuel is associated with additional economic and labor costs. The process of searching for the SPs of LVs; selecting environmental components, such as soil, water, and plant samples for future analysis; and measuring the gamma-radiation power in the impact areas of DR №981 is sufficiently described in [10]. All these procedures are costly both in terms of time and economic resources, since they involve the use of people, vehicles, helicopters, and other special equipment. In addition, if the DRs differ from the calculated ones, these costs will only increase.
The existing DRs in the European Union (EU), Japan, India, and the United States of America (USA) are located in the waters of the world ocean, which reduces the number of emerging environmental problems and the allocation of exclusion zones [11]. On the other hand, there are countries with space programs that require DRs to be located on dry land. Esrange, a rocket site in Sweden, can be used as an example. According to the article [12], the size of the DR there is approximately 5600 km2. Any activity that is not related to the rocket–space industry is forbidden in this area. In addition, the airspace area of 6100 km2 is restricted for any flights. For larger spaceports, the dimensions of these zones increase several times. Based on the information from the open sources, Figure 1 shows the approximate sizes and coordinates of the LVs’ DRs for the SPs from the main spaceports in the world.
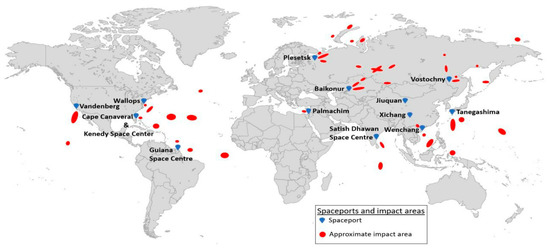
Figure 1.
Spaceports and DRs.
However, in addition to the obvious adverse effects on nature and infrastructures, there is another important factor in Russia and Kazakhstan—a political one. Since some exclusion zones are partially located on the territory of neighboring countries, going beyond them can lead to political conflicts. Thus, their size is strictly stipulated. For example, in the lease agreement for the Baikonur complex, there is a clause that takes into account the allocation of land, exclusively for DRs [13].
It should also be noted that, at present, the state of the space industry’s development (near-Earth space) is heavily contaminated in certain areas by used satellites, etc. According to a study [14], space debris weighing about 500 kg fell to the Earth every 9 days, and over 5 tones—every 215 days. Not all of the debris burns up in the atmosphere. Therefore, posing an already existing high risk for the planet, infrastructure, and population, the problem of determining and reducing DRs requires a specific solution.
By taking into account all the above-mentioned factors, it is possible to consider the urgency of the tasks to clearly define the DRs and to work out ways to reduce them. This requires a certain basic understanding of the historical background. The purpose of this work is to discuss the previously used, present, and future methods of calculating DRs, reducing their size, or completely eliminating them.
2. DRs and Methods for Their Determination
For many people, the rocket industry is associated with harmful effects on the environment. This problem is especially true for LVs with a liquid-propellant rocket engine because of some special properties of these types of vehicles. Partially, it is connected with the fact that GFRs are allocated during the design stage. Additionally, during the CD, some of the GFRs remain in the fuel lines and tanks of SPs. In addition, rockets with a liquid-propulsion system often undergo several stages. Thus, these fuel residues can lead to fires and explosions in the areas where the SPs land. Fuel leaks, caused by the heavy impact of SPs on the ground, can contaminate plants, soil, and water sources. These factors require the isolation of large areas of land for dropping the lighter parts of the LVs. However, this helps to protect both the environment and public health, since DRs are usually located in uninhabited, remote areas, or even in the ocean.
All these problems concern the space agencies around the world. However, in order to have a specific DR, or exclusion zone, it must be calculated in advance. For this purpose, engineers and mathematicians from all over the world have been working on various methods for determining DRs for many years.
2.1. A Brief History of the Methods’ Development for Determining DRs
Sounding rockets were among the first ones that required the calculation of specific DRs. A study of promising methods for analyzing the dispersion of sounding rockets was conducted by R. Ammons et al. in 1970 [15]. Most of them envisaged an analytical approach to solving the problem. The authors provided a brief description of the topics discussed, which included a model of DR displacement due to the Earth’s rotation, ballistic wind-error estimation, etc.
Some of the first computational practices assumed that the DRs would be circular in shape. A preliminary risk assessment of the Black Brant XII sounding rocket can be cited as an example of a historical method for DR calculation [16]. The authors noted that the probability of ground impact and the expected extent of damage were used as fall dispersion functions.
Thus, dispersion can be defined as the statistical deviation of the real drop point from the calculated one. In addition, the probability of falling into a particular point from the predicted location was assumed to be constant in all directions. The authors also estimated that the specified area was circular in shape, which can be clearly seen in Figure 2.
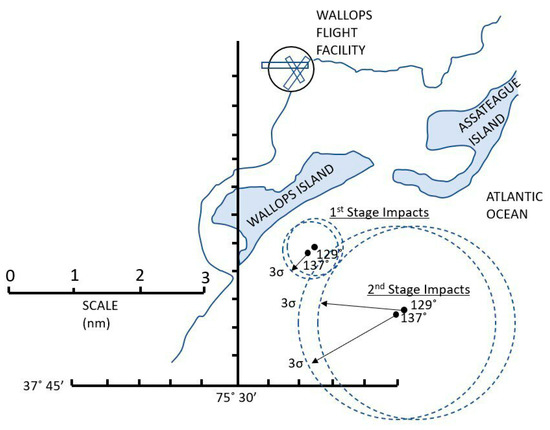
Figure 2.
Black Brant XII first- and second-stage DR calculations [16].
The variance was calculated theoretically; therefore, the study used three-sigma errors in elements such as thrust mismatch, displacement, momentum, launch angle, and drag forecast for flight modeling. The three-sigma variance value were then determined from the “square root of the sum of the squares” of the deviations from the planned drop. This process had to be performed for all four stages of the Black Brant XII sounding rocket. The authors assumed that the results could be used as a reference. Additionally, in order to transfer them to other missions, it is necessary to apply linear scaling, in proportion to the ratio of apogee heights between the reference and new missions.
Although this method was accurate enough for its time, it is outdated at present. Modern computational techniques allow for many more complex calculations to be completed at a much quicker rate and with better precision. Consequently, rapid simulations of rocket flights over 6 degrees of freedom can be performed on many modern computers, including personal ones. In addition, the increasing volume of sea, air traffic, and densely populated areas, as well as stricter public safety regulations, require more thorough methods for estimating DRs. As a result, complex modeling techniques with thousands of computational operations are required to analyze the dispersion of the LVs’ SPs.
The most popular method for determining a DR, which allows acceptable results to be achieved, is the Monte Carlo simulation, since it meets all the above-mentioned requirements. In order to calculate the planned dispersion area, the flight simulation is counted hundreds of times. Each calculation has several variables that change with the selected probability distribution in each simulation [17]. Figure 3 shows the results of implementing the Monte Carlo method for a calculation with 10,000 design points. The 1σ, 2σ, and 3σ ellipses characterize root-mean-square deviations and obey the three-sigma rule. According to this, the probability of the falling point to be within the 3σ ellipse is 99%, within the 2σ ellipse—95%, and 68%—for the 1σ ellipse.
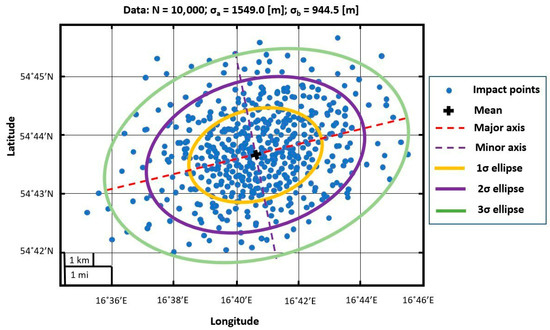
Figure 3.
Calculation results performed by the Monte Carlo method [17].
One of the first references of the Monte Carlo method’s application in the rocket industry can be found in an article by T. Moch (1966) [18]. The author points out that there are problems in identifying the boundaries for determining the flights and DRs. Therefore, a method using covariance error matrices was proposed. In order to find the DRs, functions depending on various parameters (velocity, mass of the LV, trajectory, etc.) were calculated. The obtained data were then used to determine the boundaries of the DRs using the Monte Carlo method.
2.2. Methods for the Risk Assessment of the LVs’ SPs
With the introduction of methods for adequate DR prediction, the issue concerning human and infrastructure safety from the risks associated with the activities of space agencies has become crucial for each country. Additionally, if these risks fall outside the acceptable limits, it is impossible to obtain launch clearance. The support for these ideas can be found in article [19]. The authors considered the possible risks to the population and infrastructure from the launch of LVs and their SPs. They also proposed a mathematical approach for determining the parameters of the SP fragments, their lethality, and possible damage to buildings.
The further development of these ideas can be found in the work of R. Beyma from the ASA Goddard Space Flight Center, who described the flight safety concept and methodology in 1986 [20]. The author mentioned that populated areas are always protected from high risks by the maximum levels of security applied to them. These safety factors are usually expressed in probabilistic terms. The latter includes probability criteria such as criteria such as land impact, ship impact and aircraft collision, the estimated damage, and the affected area. Each of these factors has a strictly defined value that must not be exceeded. The author also described methods for calculating each of the criteria mentioned above.
A more modern methodology for determining risk factors is presented in the work of F. Capristan and J. Alonso [21]. The authors presented a new calculation system, which makes it possible to determine risk factors, such as the impact of stationary and exploding SPs, toxic gas distribution, the consequences of explosions, and out-of-state errors, etc., for the infrastructure and population. The system developed was verified by comparing the calculated data obtained with the actual SP distribution on the ground areas in the United States.
Australian scientists together with the Defense Science and Technology Organization of Australia presented range safety template toolkits [22]. Such templates are a set of parameters, selected for specific missions and having the possibility to vary within certain limits. The authors offered a model of their own safety template, the parameters for which were developed based on the flight data from a suborbital two-stage sounding rocket. The template generation process included several stages—obtaining information about the spacecraft and its mission, modeling the spacecraft’s behavior, estimations, generalizing the results, and creating the template. Formed on the obtained data, a model with 6 degrees of freedom was developed, considering various error or failure options, and simulated using the Monte Carlo method to obtain a set of impact points the DRs were compiled from. The authors noted that the accuracy of their method was much higher than that of the traditional approaches. Moreover, it allowed them to estimate not only the DRs, but also the entire trajectory, considering the possible failures.
However, the proposed calculation method already presented disadvantages at that time. For example, M. Sanchez and P. Shome, in their paper [23], noted that the calculation method proposed by T. Mokh did not work well for large LVs. This was due to the fact that many LVs’ functional dependencies of this class could only be expressed in terms of nonlinear functions, which made it very difficult to obtain an adequate result. In addition, the authors noted that the method was difficult to apply to a CD. In turn, this causes the DR dimensions to be too large. As a result, the authors proposed their method based on the estimation of the covariance matrix, which is further imposed by the Green’s transition matrix. Then, the obtained result was projected to the plane that the boundaries of the DR sizes were determined from. To confirm the results of the calculations, the authors also conducted a Monte Carlo method calculation, which allowed them to set the coordinates of the impact points for 500 LVs’ SPs. According to the article’s results, all these points lie within the set DRs.
2.3. Monte Carlo Method and Alternative Options
In the modern world, the Monte Carlo method is frequently used. Its effectiveness has been confirmed by a recent study by P. D. Wilde based on the calculation of sounding rocket dispersion [24]. It was noted that the Monte Carlo simulation involves nonlinear combinations of various input parameter perturbations’ combinations, which include thrust and launch angles, thrust offset, etc. The author cited a number of different examples that demonstrated the dependence of scattering regions on numerous parameters and their uncertainties. For example, the shape of the obtained DR would be different for the same rocket, even if only the nominal altitude was changed in the calculation.
However, the Monte Carlo method has a number of drawbacks. First, it requires hundreds of calculations for satisfactory results to be achieved. Consequently, the more calculations are performed, the more accurately the DR is determined. In the study [25], the authors emphasized this point. They stated that, when dealing with uncommon events with probabilities below 10−2, 500 Monte Carlo simulations are obviously not appropriate but can be employed for events with probabilities higher than 0.1. In order to obviate this, the authors proposed a method called IS. This term is used to define a group of Monte Carlo techniques where a target distribution’s mathematical expectation is approximated by a weighted average of random draws from a different distribution. In this approach, rare events occur more frequently than in the Monte Carlo simulation, which makes the DR estimation more accurate. The authors applied both methods to the algorithm and compared the results. As a result, they concluded that significantly fewer calculations were required to achieve acceptable IS results. For example, 500 iterations were sufficient to achieve the same overall view of the scattering area as the 105 iterations using the Monte Carlo method, which is best demonstrated in Figure 4. Thus, it involves some changes in the probability density function in order to resample the system inputs and achieve adequate results.
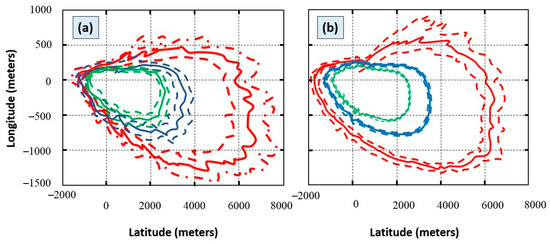
Figure 4.
The launch safety zone estimated with 500 importance sampling simulations. The solid line represents mean deviation and the dashed line represents the standard deviation (95% = green, 99% = blue, and 99.99% = red). (a) The 500 importance sampling and (b) 105 Monte Carlo simulations. (Compiled from [25]).
The second problem is that the Monte Carlo method has difficulty in estimating the probability of a very rare event. Therefore, it is practically impossible to calculate the likelihood of an SP falling at a distance much greater than a given safety limit for a particular type of calculation. In the article [26], the authors described algorithms for parametric and nonparametric ISs in the presence of an uncertain input distribution that solved this problem. The source contained information about existing IS adaptive methods and provides a brief description of them. The authors then proposed their method, which was a complementary approach of classical cross-entropy and nonparametric adaptive IS. This method has been tested on various problems, one of which was the LV DR’s estimation. In the results section, the authors concluded that the proposed method was much more efficient than the direct probabilistic estimation using IS and did not lead to an increase in the relative error, while reducing the number of computational iterations.
Another way to fix this issue was proposed in the article [27]. The authors claimed that, in order to reduce the overall numerical cost of simulations such as the Monte Carlo method, a Gaussian process based on active learning methods could be used. They proposed a methodology that enabled the quantification of the sensitivity of the failure probability estimator to uncertainties, which allowed for controlling the whole error associated with the failure probability estimate. Thus, it provided an accuracy criterion for the assessment. This resulted in the development of a variance-based active Gaussian process learning procedure, which improved a major source of uncertainty during the learning phase and integrated a stopping criterion based on the total variance of the probability of the failure estimation. The developed approach was applied for both a Monte Carlo-based as well as an IS-based method, resulting in the improvement in the estimation of rare-event probabilities.
A major study by J. Morio, described in the book [28], included a section devoted to the problem of determining LVs’ SP drop areas using various calculation methods. The problem included the determination of the initial parameters, such as the separation altitude, velocity fluctuations, trajectory, separation angle azimuth, LV mass, and weather fluctuations. These data were first used for the crude Monte Carlo method, which showed satisfactory results for this kind of problem.
As a benchmark, 108 iterations of the crude Monte Carlo method were calculated. All further results were compared with those obtained at this stage. The author then moved on to more specific calculation methods and described them in detail. First of all, the effectiveness of the adaptive technique was evaluated. The source noted a high relative error of the final results; however, the efficiency remained quite high.
Then, the possibility of using the IS method, discussed above, was considered. The author also noted its high efficiency, while reducing the number of iterations required for the calculation. As a result, it also decreased the resources spent both in terms of time and machinery.
The subsequent method considered was directional sampling. The maximum efficiency when using this method can be achieved only by increasing the number of iterations, which leads to a sharp decrease in the relative error, but increases the calculation time. However, the adaptive directional sampling method shows much more adequate data, since it is more adapted to this kind of problem. Nevertheless, both of these methods are outmatched by IS and its variations.
Then, the effectiveness of using first- and second-order reliability methods was discussed. These calculation methods proved to be ineffective in the problem under consideration, since the obtained drop points did not correspond to the previously determined ones, and only one basic error was used in the described algorithms. Thus, some of the described methods can be applied to determine the DRs, together with or instead of the crude Monte Carlo method. The choice of the particular method of calculation depends on the availability of computational power and allowable errors.
L. Brevault et al. in [29] described a system of reliability assessments in the presence of aleatoric (constant with increasing data) and epistemic (decreasing with increasing data) uncertainties in determining the DRs of LVs’ SPs. The authors proposed a sequential approach in order to determine the probability bounds based on a Subset Simulation and Kriging model to reduce the number of calls to the computationally costly limit state function. The methodology includes two recurring steps—combining interval and probabilistic analysis models and an improved Kriging model. The resulting system makes it possible to obtain accurate data precisely in the area of interest, specifically in the applicability to the DRs—near the boundary of the estimated impact area. As a result, the authors compared the developed methodology with the Monte Carlo simulation, highlighting the disadvantages and advantages of their system. The main difference was that it could obtain more accurate data in the boundary area, while the Monte Carlo method could not. This is best demonstrated in Figure 5.
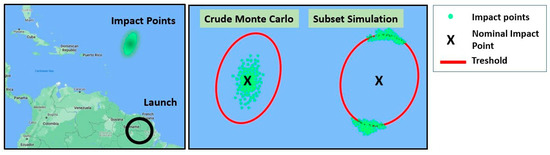
Figure 5.
Calculation results by the crude Monte Carlo method and subset simulation. (Compiled from [28]).
The source [30] presents the sequential Monte Carlo Square algorithm, describing the basic principles of its function and applicability. The proposed algorithm was adapted for the rare-events analysis to be sampled from the target distribution. The two sets of the particles were defined as: one for the parameter space and another for the state space. It was further used to produce the unbiased estimates of the calculated probabilities. In particular, the authors considered the possibility of its use to calculate a specific problem related to the determined DRs for the LVs’ SPs. It concluded by assessing the probability of the distance to the impact estimated point exceeding 0.72 km. The meteorological data, mass, and angle between the vertical axis and velocity vector direction of the LVs’ SPs were used as varying parameters. As a result, a conclusion was attained, according to which the influence of the initial parameters on the definition of rare events should be taken into account. In addition, it is necessary to consider the probability of rare-events occurrence in order to achieve the maximum efficiency of calculations aimed at identifying the impact areas and determining their specific boundaries.
Another method for DR calculations is described in source [31]. Based on this, the decreasing effectiveness of the DR’s size for aerospace systems is mentioned in source [32]. The authors described an end-to-end optimization of branching trajectories, according to the Pontryagin maximum principle. The term “branch” is used to define a trajectory. The main branch represents an exit trajectory; the side branches correspond to the trajectories of passive separable parts. The problem solved in the paper is to the optimize a branching main trajectory with cones of lateral branches. The paper explained the choice to use the L. Pontryagin method and presented its main advantages.
Thus, the authors applied a perturbation model, calculated the planned optimal trajectory, the boundary of the scattering ellipse, and provided a verification methodology. The result provided the developed methodology’s application to the example of the Pontryagin maximum principle for the Proton LV trajectories. The example took into account the limitations on the DRs of SPs and atmospheric conditions. As a result, the authors presented graphs for the optimum pitch angle as a function of time and the optimum Proton exit trajectory, the optimum branching trajectories with optimum and common impact points. In addition, the paper provided a comparison of the developed method and Monte Carlo simulations for calculating DR ellipses. The authors stated that the method under discussion allowed reducing the number of operations up to 105–107 times in comparison with the Monte Carlo simulation to achieve satisfactory results. The described method’s implementation is presented in the source [33]. The difference between the Monte Carlo simulation and the discussed method is shown in Figure 6.
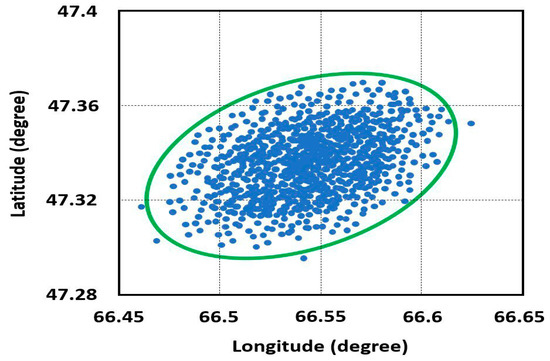
Figure 6.
Calculation results by the crude Monte Carlo method (+) and Pontryagin maximum principle (blue line). (Compiled from [31]).
Another method for DR calculations is described in the article [34]. The authors presented a mathematical description of the DRs for LVs’ SPs with their drop points’ random distributions. The discussed methods covered the situation with non-destructive SPs and their destruction into fragments. The main idea was that, by determining the DRs for destructible SPs, the scattering ellipses for each element must be taken into account when determining the total DR ellipses’ limits. Thus, the dispersion ellipses envelopes needed to be calculated. For this purpose, the authors described two methods. The first involved the use of polygons. In this case, a small polygon was circumscribed to each scattering ellipse. Then, all the small polygons were added into the large one, which then included all of them. Subsequently, its dimensions were gradually reduced to achieve the smallest possible area bounded by the large polygon. The final result created the smallest possible total scattering ellipse, which was the DR.
The second method was similar to the first one in many aspects. The main difference was that, instead, the polygons’ smaller scattering ellipses were added to a larger one. At each step of the approximation, its size decreased, while all the smaller scattering ellipses remained within their boundaries. The final result also provided the smallest total DR. Although this method is quite simple and provides adequate results, it is not as precise as the other discussed approaches.
In the article [35], the authors argued that in order to improve the accuracy of the calculation methods for the DRs of the LVs’ SPs, certain factors should be taken into account. First of all, the actual atmospheric parameters should be applied to all calculations. This will make it possible to correct the initial calculations if there is any discrepancy with the pre-calculated results for the day of launch. Second, the authors suggested focusing on the SPs’ breakdown, which should also improve the accuracy of the calculated dispersion ellipses.
The necessary confirmation of taking into account the operational atmospheric parameters can be found in article [36]. S. Yeliseykin and co-authors pointed to the need for the accurate determination of DRs in modern times and focused on a number of problems. In particular, the authors discussed the need of paying attention to the geography of the DRs and the seasonal, often local, atmospheric parameters. According to the authors, the absence of these data led to large systematic deviations of the calculated impact points from the real ones. For large SPs, the difference was about 10 km, whereas for the small SPs, it could be up to 30 km. Side-to-side deviations are usually several times smaller and accounted for by estimating the variations in the parameters of the standard atmosphere. This method shows satisfactory results applicable to large-sized SPs; however, for small ones, it does not allow for considering the joint effect of seasonal systematic and random variations in atmospheric parameters. According to the authors, this was the reason for periodic exits of the SPs’ impact points from the DRs. In order to avoid this, a switch from the standard atmospheric model to local, or operational, meteorological conditions was proposed. This allowed reducing the scattering ellipse area by more than half.
In addition, there are studies aimed at a statistical analysis of the real impact points of LVs’ SP distributions. As an example, article [37] can be cited. V. Klyushnikov et al. proposed an approach to estimating the separation parameters of the Soyuz rocket’s side blocks based on the coordinates of their actual impact points. The paper considered the possibility of introducing a full mathematical model of motion as applied to the drop point dispersion of the LVs’ SPs and described the necessity of switching to a simplified mathematical model. The authors chose the angles of deviation of the velocity vector of the SPs’ CMs relative to the velocity vector of the central-block CMs as parameters determining the SPs’ flight. As a result of the calculations, scattering ellipses images for all four units of the Soyuz rocket were obtained, which agreed well with the experimental data.
Closely related ideas can be found in article [38] by I. Agapov and A. Dvurechenskiy. The authors considered the peculiarities of the Soyuz-2 LV side-blocks’ scattering ellipse and offered a way to rationalize the search for the LVs’ SPs. The statistical data used by authors are provided in Figure 7.
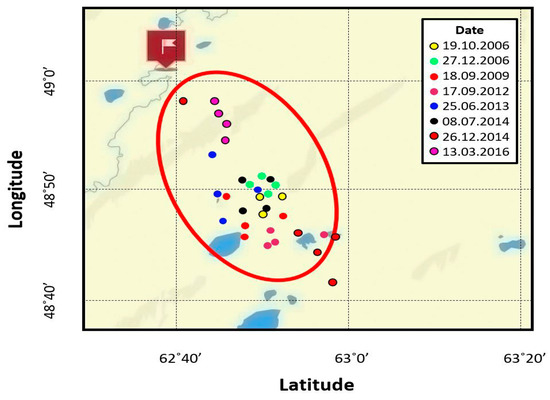
Figure 7.
Drop region #120 and separated parts’ impact points. (Compiled from [38]).
The authors conclude that each of the four side blocks had its own motion characteristics, which affected its position in the DR. Presumably, this was due to the difference in their position in space and the different impact of the reactive forces during separation. The analysis performed by the authors allowed us to conclude that it was necessary to take into account the statistical data on past launches both in the development of new rocket launches and in further improvements to the methods of searching for the LVs’ SPs. If applied, this approach can significantly decrease the time required to find the SPs.
The method of assessing the failure of SPs in the example of the Soyuz LV second stage is presented in the article by A. Karchin [39]. The author proposed a methodology for identifying the fracture of the SPs during CD. As the input data, it was proposed to use the atmospheric parameters along the launch route, the motion parameters of the LVs’ SPs, the aerothermodynamic parameters of the hull loading on the CD, the design parameters, and the materials used. Based on the available data, the author developed a mathematical model and calculation scheme for the Soyuz LVs block “A” loading. As a result, it was possible to obtain the values of the breakdown altitude and develop a proposal for the evaluation of structural fragments’ mass-geometric parameters, which, as the author explained, can be used as the initial data for ballistic calculations. It was also noted in the article that the experimental data proved to be trustworthy when compared with the real results. Thus, the considered methodology can be used for a more accurate DR calculation.
A further development of the above-mentioned ideas was presented by the same author in article [40]. The work under consideration was aimed at performing a simulation of the Soyuz LV “A” block fracture at the CD, taking into account the methods considered earlier. As a result, the fracture heights and mass-geometric characteristics of the structural fragments were presented. They were compared with the real characteristics of the block “A” structural elements, which were provided by the search teams. Based on the obtained results, it is possible to conclude that the methods considered by the author are sufficient and appropriate.
The need to take into account the fracture factor in the calculated mathematical models was also discussed by S. Pirogov and co-authors [41]. The authors argued that the exclusion of this element from the calculations led to a discrepancy between the DR calculated characteristics and real values. The aerodynamic heating of the hull shell was previously believed to be the main reason for the destruction of the LVs’ SPs, which did not allow for taking into consideration significant factors, such as the number of the forces that determine the hull stress–strain state. Because of this, it was impossible to calculate the heights of the SP fractures, and, accordingly, to assess the mass-dimensional and aerodynamic characteristics of the fractured elements. The authors distinguished several typical elements of the LVs’ SPs and their typical forms, based on the data for the rocket elements found in the DR. Moreover, the necessity of determining aerodynamic characteristics both at supersonic and subsonic speeds was noted, which was connected with different heights of the separation and destruction of the LVs’ SPs. This led to an increased influence of the wind at certain sections of the trajectory. On the basis of these data, the paper presented the calculation results of the Soyuz rocket’s SP typical structural fragments’ aerodynamic parameters, which were used in the simulation of the “A” block elements’ scattering ellipses.
The majority of the considered methods relied on the traditional assumption that the calculated CD trajectory was close to ballistic. That is, the influence of the aerodynamic lift force normal to the LVs’ SP trajectory on the motion of the CM was neglected. To justify this assumption, an allowance was taken into account. It stated that, during the rapid periodic character of the SP angular motion relative to the CM in dense layers of the atmosphere, the averaged lift force for a period was equal to zero [4]. In article [42], A. Golikov and co-authors presented the result comparison of determining the DRs for two initial trajectory conditions. In the first case, a low (40 km) separation point at a high initial velocity head was considered. In the second case, the described point was located at an altitude of 90 km, and the velocity head was much lower. The distribution of the other parameters used for the calculation was also described in the article. The results obtained by the authors are summarized as follows—in the first calculation case, the SPs perform rapid oscillations around the CM, and the resulting trajectory is close to ballistic. Thus, the calculated point of impact corresponds to that obtained using the above-mentioned assumption. In the second calculated case, however, there were no such serious oscillations, and the SPs glided almost to the maximum calculated longitudinal range. From this, it can be concluded that, when the SPs detach at high-velocity pressures, the estimated point of impact differs little from the traditional point of impact. However, when the SPs begin moving in thin atmospheric layers, a qualitatively new ring-type structure emerges.
The confirmation of the research described above can be found in an operations review aimed at the Ares I-X rocket’s safe flight, the test version of Ares I LV. Since a successful launch of a real Ares I-X LV rocket required a large amount of test data, during the launch of Ares I-X and during the evaluation of the results obtained, it became possible to evaluate the nominal flight path, the DR of the LV’s SPs, the acoustic effects, and much more. The detailed information about the conducted procedures is presented in source [43]; this paper focused on the operations related to the DR of LVs’ SPs.
The Monte Carlo method described earlier was used to determine the drop points and to compose the DRs. The latter was formed by a set of drop points corresponding to the LVs’ different parts. These included the first-stage simulators, the nose cap, the forward skirt extension, and the upper-stage simulator. In addition, the fact that the SP could be positioned differently during travel along the CD was taken into account. In particular, the first stage could be positioned in a forward, sideways, or rearward manner, toward the velocity vector. Depending on this, the maximum angle of attack and dynamic pressure varied. As a result, the authors provided data for the DR calculations for the first stage of the Ares I-X rocket, presented in Figure 8.
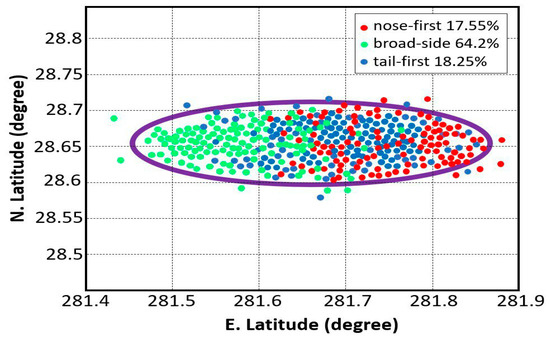
Figure 8.
Drop region for Ares I-X during the first stage with consideration of different separated parts’ orientations during descent. (Compiled from [43]).
The authors noted that the data obtained were used to prepare the DRs on real terrain. This included the notification of naval vessels and air transport machines concerning the route that passed through the specified area. In addition, the rescue ships of the SPs were located near the impact areas in advance, which allowed the simplification of and reduction in the operation cost for the return of the LVs’ SPs.
The calculated LV’s trajectory was updated on the day of the launch, paying attention to the operational data on the state of the atmosphere, which influenced the DR’s parameters. In addition, based on the test launch results, it was also possible to obtain specific coordinates for the LVs’ SPs’ impact points, which were superimposed on the first and second estimated DRs. In spite of the fact that the indicated ellipses had certain differences in size and shape, the real impact points were in agreement with each other. This indicated the effectiveness of the Monte Carlo method in calculating and determining the DRs in the present day.
3. Ways of Controlling and Changing the SPs’ DRs
To date, we discussed the existing methods of determining the size of LVs’ SPs’ DRs. Nevertheless, little has been said about the specific methods for their control and reduction. In this section, the main ones will be described, presenting their advantages and disadvantages.
3.1. Methods to Reduce the Technogenic Impact of the LVs on the DR
Most of the current methods are aimed at reducing or completely avoiding the DR, and they will be discussed further. However, we found it important to note that there are techniques focusing on reducing the technogenic impact of LVs’ SPs on DRs, rather than on getting rid of them altogether. We discuss some of them in the present section.
For example, in paper [44], the authors discussed opening a new route; hence, we considered the new DR for the LVs at a 51.6° inclination from the Vostochny spaceport. The paper discussed various limiting factors that must be considered when selecting DRs for the new launch route. These included inaccessibility to ordinary transport, a difficult terrain, hydrometeorological conditions, especially protected areas, offshore mineral deposits, heavy ship traffic, and the buoyancy of SPs. All these factors together narrowed down the total area of territories available for isolation.
Another example can be found in articles [11,45], which discuss the concept of mitigating the harmful effects of the space industry on the DR’s environment. The authors proposed the use of certain basic methodologies in determining the DRs. First of all, they argued that the optimal areas should be chosen based on their resistance to man-made impacts and the minimum cost of soil rehabilitation work. This includes criteria relating to fire safety, coverage of fertile land, vegetation cover, and the economic costs of ecosystem restorations. Secondly, the authors assumed that the SPs’ descent should be controlled in a passive trajectory, as a result of which the final drop point does not leave the calculated area.
3.2. Engineering and Mathematical Ways to Reduce DRs
One of the first sources describing the previously used methods for rescuing SPs was presented as early as 1951 by the US Department of Defense. An expanded and improved version was completed in 1978 [46]. This article made use of this edition of the book.
Since most of the US’s LVs’ SPs fall into the world ocean, the authors paid great attention to parachute systems. They made it possible to slow down the SPs’ descent in the CD, which not only resulted in a smaller DRs by reducing the speed of the SPs, but also allowed the SPs to be preserved and recovered by ships. The book considers the methods of attachment, development (using different materials), and application of parachute rescue systems to components, such as boosters (from Space Shuttle), inhabited compartments, different LV stages of different weights and configurations, drones, etc. The authors noted the possibility of using parachutes not only as means of escape, but also the controlled deceleration of rocket design elements. The use of less traditional ball and vane retarders was considered, too. Although parachute systems lead to an increased mass, their use was absolutely justified by their ease of use and construction, fairly high reliability, and relative cheapness. The book also discusses ways of constructing spacecrafts to simplify their return. However, they are relatively outdated at present and were not considered in this article. It is worth noting that the use of parachute systems allows us not only to reduce the DR’s size, but often completely eliminate them.
An example of the parachute system’s real application can be found in study [47]. The authors described various operations aimed at optimizing the characteristics and simplifying the design of the Space Shuttle booster escape system. It was noted that the results obtained were aimed at changing the actual design and contributed to cheaper launch costs and the return of the LVs’ SPs.
A similar technology was also investigated by Russian scientists. Its detailed description is presented in article [48]. The authors concluded that the most promising and easy-to-implement method is to capture SPs in flight by helicopters (or aircrafts). The method developed by the researchers was as follows: after the separation of the stage, the LV is stabilized; then, the parachute system opens, which controls the SP’s descent. In the process, it is seized by a helicopter with a special rotor device, which allows for stabilizing the SP’s position in space. The LV’s SP is then taken to a prepared site, and from it to the launch site. After the required operations, it can be used again. Eight years of research have shown that this technology can be applied to already existing LV, requires minimal time and material costs, and also makes it possible to reduce the reusable LV’s operation cost by 30%. The method is demonstrated in Figure 9a.
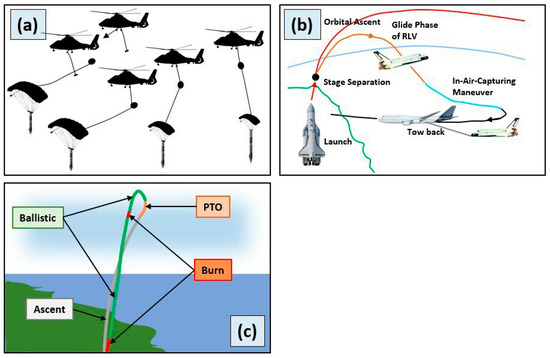
Figure 9.
Various techniques for controlling the DR. (Compiled from [11,48,49]). (a) SP stabilization with a parachute and capture with a helicopter. (b) Schematic display of in-air-capturing of reusable stages by an aircraft. (c) Soft-landing method trajectory by an example of trajectory reference for CALLISTO.
A recent study by Dutch engineers has shown the effectiveness of the above-mentioned technology in the modern world as well [50]. The article discusses the possibility of using a parachute and parafoil (parachute wing) for the stabilization and deceleration of the advanced Ariane-6 LV SP. The general capture procedure differs little from that discussed earlier; so, it will not be described again. The authors concluded that the system they developed was easy to implement in Ariane-6 LV without the need for major design changes. This would help to reduce the vehicle’s re-launch cost by 15%. Further areas of research include the possibility of parachute and parafoil mass reductions, improving the layout to reduce the occupied volume, etc.
A mathematical approach to the problem of using parachute systems was presented by Indian researchers in article [51]. The authors noted the effectiveness of such systems for the safe return of the LVs’ SPs. The article presented an analysis of 25 possible options for the layout of the parachute braking system and braking engines. The researchers sought how to minimize both the speed at which contact with the landing pad (located on the salvage ship) occurred and the structure’s total mass. Based on the set limitations, they presented several promising layout options and a mathematical justification for their effectiveness.
The combination of parachute systems and ships, on which the reusable stage of the LV landed, found wide application in the world. Therefore, the problem of developing navigation systems for precise landing on a specific site in the sea aroused the interest of scientists. An example is study [52]; the authors offered a unique of reusable LV navigation system. It is based on the fact that, in the near-infrared range, the reflectivity of laser radiation from the ship’s deck was four-times higher than the reflectivity from the sea. The system developed by the authors made it possible to estimate the inclination of the descent trajectory, height, and speed of the LVs’ SPs relative to the deck of the ship or the sea with a very high accuracy. The simulation results, in turn, demonstrate the ability of the navigation system to clearly identify the ship’s surface, the sea, and the parameters mentioned above. As a form of verification, an experiment was also conducted using a reduced model of the ship and the LV SPs, the results of which confirmed the theoretical calculations’ validity.
There are many inventions aimed at reducing the number of DRs. Among them, there is a way to reduce the DRs of spent rocket units by connecting them in parallel [53]. According to the idea proposed by the authors, the side blocks of the Soyuz LV’s first stage are equipped with a flexible mechanical tether and a parachute system. After the separation from the second stage, the SP launches a parachute, stabilizes, and gradually descends into a predetermined DR. A feature of the invention is the ability to eliminate several DRs (in the described case—four) and transition to just one, which greatly simplified the task of finding the SPs and clearing them from areas.
The other invention also reduces the DR’s size but operates using a completely different principle. The patent [54] describes a way of minimizing the DR for the LV’s SP and a device designed for its implementation. The general idea of the invention is to burn the SPs at the CD. The authors noted that, if the SPs are composed of polymeric composite materials, an autonomous combustion system can be implanted in their design. When the SP reaches the required section of the trajectory, it receives the command to release heat, which leads to the SP’s combustion. This method makes it possible to not only reduce the DR by minimizing the components falling to the ground, but to also reduce the costs of searching and cleaning the DR from the LV’s SPs. The developed invention is reflected in the article, which additionally provides calculations to determine the required masses of the combustion system’s components and the values of heights required to start the process of removing the SPs [55]. In addition, the study conducted a mathematical justification for the considered method’s effectiveness.
Another interesting idea that allowed for reducing the DR’s size was proposed by B. Titov and S. Rynkov in [56]. The authors developed a proposal that resulted in a deliberate separation of the spent rocket bodies. Based on the simulation results, the article described the dependence of the ejected payload mass on the DR’d size and provided an overall assessment of the developed approach’s effectiveness. According to the conclusions, the application of the structural partitioning made it possible to achieve an increase in the payload mass by 8% and to reduce the DR’s size by 15 km. It was possible to achieve an even greater reduction in the DR’s size; but, the mass of the payload to be launched decreased.
A study conducted by German engineers [57] suggested the possibility to reduce the DR’s size by controlling the position of the LVs’ SPs during a flight. The task for the researchers was to optimize the DR of the SHEFEX II sounding rocket (an experimental rocket based on the VS-40), and was further complicated by the fact that the missile lacked in-flight-positioning devices. In particular, there was no provision for the deflection of the propulsion system from its nominal position, and there were no aerodynamic rudders. Therefore, the DR’s size and coordinates could only be controlled by setting the necessary launch parameters, the direction of the second stage, and its launch time.
The authors emphasized that the shape of the calculated DR for standard launch conditions using the Monte Carlo method for 106 iterations resulted in an ellipse of approximately 90 times 110 km. However, the use of the algorithm for the adaptive positioning of the second stage in flight, presented in the article, made it possible to reduce the DR’s size by 78%. This was achieved by taking into account all the deviations obtained during the atmospheric flight phase and hardware corrections of them during the second-stage launch. The Monte Carlo re-calculation showed an area of approximately 25 times 70 km, which indicated the effectiveness of the methods used.
An interesting approach is described in article [58]. The paper presents the effectiveness of spin motion in the reduction in a two-stage solid-propellant sounding rocket flight dispersion due to thrust misalignment. One of the most interesting findings states that, by counting the fins during the first stage at 0.5, the rocket started spinning at the beginning of the flight and the resulting DR of the payload-release was halved. Although this approach was only tested on a meteorological rocket, it could be speculated that, to a certain extent, it might be applicable to LVs of smaller size.
The approach proposed by V. Arsenyev et al. in [59] is also of interest. The study examined the possibility of changing the pitch angle in order to reduce the DR of the LV’s SPs. Considering the initial parameters of the LV’s launch, the SPs’ detachment, and the operational parameters of the atmosphere, the model made it possible to calculate a trajectory that was optimal in DR terms. The main drawback of this method was the need to change the trajectory that was optimal in terms of the payload to be launched. This could be disadvantageous from an economic perspective; but, it could be justified by reducing the cost of finding the SPs and cleaning the area from debris and toxic fuel components.
In order to achieve a reduction in the LV’s SPs’ negative environmental impact, it is necessary to exhaust the remaining toxic fuel components in the LV’s tanks and fuel lines and, at the same time, to reduce the DR’s size. An approach for the realization of a system that solves both problems was proposed by V. Trushlyakov and V. Kudentsov in article [60]. The authors proposed an active onboard descent system and developed an algorithm of operation. The control commands were generated and implemented with the help of the operating built-in system using GFRs. As a result of mathematical modeling with a Rus-M LV, the authors managed to change the launch azimuth by 2.5° to the direct takeoff azimuth. The possibility of controlling the LV’s SPs at the CD can also be used to reduce the DR’s size.
The procedure of the GFR with its subsequent combustion gasification required a certain theoretical basis, which was provided in article [61]. In the study, the authors showed the applicability of the system to various fuel pairs and substantiated its efficiency. Although the methods described in the article did not lead to a direct DR reduction, they were very important for ensuring the safety of the DR for the LV’s SPs.
A detailed description of the active onboard descent system developed by the authors is presented in article [62]. The researchers considered, in detail, the algorithms of operation, the design, and the possibility of the system’s implementation for the LV. The GFR was gasified and used in maneuvers aimed at increasing the accuracy of SPs falling in the DR. Although the system may result in a 5% increase in the overall structural mass, the increased maneuverability of the SPs on the CD and the reduced cost of the DR’s subsequent cleanup offset were disadvantages, to a certain extent.
An additional value of the system was the reduction in the technogenic impact on the DR, since the probability of rocket fuel components’ explosions or leakages was significantly reduced. The development of these advantages, together with some new ideas, is presented in article [63]. As a result, the authors managed to draw attention to the problem of the negative technogenic impact of the LV’s SPs on the DR by real examples and proposed ways to solve it, simultaneously reducing the DR’s size.
The methodology proposed by M. Sippel and colleagues [64] is also of great interest. In 2001, the researchers noticed that the creation and use of multistage reusable LVs required suitable ways of returning the reusable stages. Since the authors considered the addition of fuel to restart the engine as rather dangerous and difficult to implement, they proposed their own approach to solve this problem. It consisted of capturing reusable SPs directly in flight by heavy cargo planes (Airbus A-340 or B-747).
After the reusable-stage separation, the CD began, where the SPs gradually descended and entered the planning phase. At this stage, a prepared cargo plane was already waiting for it. It approached from below, gradually equalizing its speed with the SPs, and, at the required distance, captured the reusable stages with a special harpoon. The authors noted that this method required the installation of equipment on the aircraft and had little effect on the SPs’ design. Additionally, the gripping process, while seemingly difficult to perform and implement, has a time frame of up to two minutes, which is quite sufficient for successful SP gripping. After attaching the stage to the aircraft, the latter takes it to the spaceport and detaches it nearby. Then, the SPs glides to a prearranged site, where they are picked up. Then, all the necessary procedures for the evaluation and refitting of the parts for re-launch are conducted. When evaluating the results, the authors concluded that this made it possible to increase the mass of the payload to be launched by 15–25% or reduce the dimensions of the reusable stage without losses in the payload to be launched. The discussed technique is shown in Figure 9b.
The idea of in-air-capturing has been recently discussed in further detail [65]. Overall, the capture and return procedure remains the same. It is worth noting that the patented system pays more attention to an aerodynamically controlled capturing device that is used to establish a mechanical connection between the returning SPs and cargo aircraft (A340–600 as a reference). An interesting aspect is that, at present, the method allows multiple attempts to capture the SPs. A vast array of aerodynamic calculations, which proves the feasibility of the discussed method, and a detailed investigation of the formation flight provide further knowledge of the in-air-capturing method, which is described in [66].
It is reasonable to assume that, for the return of the stage by such a method, it should be designed accordingly. The authors expressed ideas about the design of the first stage in article [67], where they noted the main variants of its shape and size. In addition, the study compared the effectiveness of various boosters and fuel pairs, and presented the main indicators (mass, ejection payloads, etc.) of the calculated first-stage designs. The authors concluded that the most effective replacement for the solid-propellant booster would be the first stage with a liquid rocket engine, fuel pair kerosene, and liquid hydrogen, and the possibility of its reuse.
Based on the previous research, the various layout options for the design based on the promising (at that time) Ariane-5 LV are presented in article [68]. The authors considered the possible layouts of the mentioned first-stage LVs in several variants—a single booster, two boosters, and two connected boosters (similar to a catamaran). Different layout options also imply the use of different engines, which include RD-0120, RD-180, and RS-76. The authors compared the efficiencies of each of the proposed layout options, estimated the mass of cargo launched into geostationary orbit, the total structure mass, and many other parameters. The design features required for the booster’s return to the launch site and reuse were also reviewed. The results make it possible to draw a conclusion about the advantages and disadvantages of each of the proposed variants of the Ariane 5 LV’s first stage. Thus, according to the authors, the symmetric configuration of multiple-use boosters using a fuel pair of kerosene and liquid oxygen should be considered as the most effective and promising methods. Additionally, it was noted that the use of reusable engines could replace solid-fuel boosters with a high degree of probability.
A modern comparison of different return options that mostly focuses on horizontal landing, vertical landing, and the in-air-capture method is presented in [69]. The authors pay a lot of attention to the description of the up- and downsides of the above-mentioned methods. They also provide an in-depth comparison of the mechanical and economical aspects of some of the most promising ones.
The very concept of reusability implies a departure from traditional methods of LVs splitting into stages and assembling. Korean researchers, in article [70], proposed their own method of breaking a LV into stages by adding the SPs’ descent phase to the standard approach and combining it with the trajectory optimization process. By considering an example of a missile with an optimal layout, the authors showed the consistency of their study.
The above-mentioned studies were discussed in detail in article [71]. The authors evaluated various methods of returning the reusable first stage, which can be divided into two groups—methods of SP capturing in flight and the independent return to the launch site. The first group of methods has already been discussed, while the second one requires some explanation. The authors stated that, after separation, the first stage reaches the maximum altitude of 160 km, re-enters the atmosphere, turns, and reaches conditions suitable for the ignition of air-breathing engines. Then, it begins a powered flight towards the landing site. The article compared parameters, such as the structure’s total mass, aerodynamics of takeoff and descent, return trajectory, etc. On the basis of the results, the authors concluded that the methods based on capturing SPs in flight were more effective. This is justified by the fact that such methods allow for returning to the reusable stage without a significant increase in the mass of the structure and, in addition, increasing the payload mass.
However, for a successful SPs landing, certain means of navigation are required. A modern navigation system for the reusable stages of the LV using analytical dynamics, based on a different approach, was discussed in [72]. The described program performs separate calculations for the longitudinal and transverse planes at the reusable stage, which allows one to rapidly generate control commands. The main difference from the existing methods is the concept of a “virtual target”, where the spacecraft is moving. In addition, the new system helps to reduce the time and resource costs of calculating the optimal descent trajectory.
3.3. Soft-Landing Techniques
There are also other ways to return the SPs to the spaceport. In particular, they are the so-called “soft-landing” methods. When they are used, the rocket block lands on its own without significant damage, which allows it to be used in the future. In addition to this obvious advantage, the soft-landing methods make it possible to remove the necessity of singling out the DR for the returnable stage completely. For example, the patent [73] describes a method for returning the rocket to the reusable first stage. It is based on the re-ignition of first-stage engines and landing thrusters immediately after the separation of the stage and turning around in the pitching plane. After the aerodynamic deceleration, the steering engines are activated at the desired altitude and the stage approaches the landing point with practically zero speed.
The described method also finds application in other sources. For example, in article [49], the German Center of Aviation and Astronautics, together with the French National Center for Space Research, offered a model for reusable first-stage demonstrations, CALLISTO. The authors noted that the main difference between Blue Origin New Shepard and Space-X Grasshopper was precisely the making of a non-vertical flight with the performance of an aerodynamic maneuver. The article discusses the design, aerodynamic, and aerothermal characteristics of the rocket. Particular attention is paid to the possibility of the stage reusability and study of the aspect under consideration. A more in-depth explanation of how CALLISTO’s deployment system operates and how it is affected by the influence of aerodynamics, exhaust plume, and vehicle’s attitude is discussed in article [74]. The reference trajectory for CALLISTO, which is similar to the one used by most LVs utilizing the soft-landing method, is provided in Figure 9c.
The previously mentioned Blue Origin New Shepard is discussed in detail in the source [75]. The main difference from CALLISTO is that the stage does not perform the same aerodynamic maneuver, but lands from a vertical position. The effectiveness of this system was demonstrated in 2015, when the rocket passed the Carman line and returned to Earth using the vertical-landing method. Additionally, already in 2016, the same stage was used again, which confirmed the reusability of the rocket under consideration.
The advances of SpaceX cannot be overlooked when it comes to the discussion of reusable launch vehicles, which utilize the soft-landing technique. This technology has been applied to Falcon 9 and Falcon Heavy LV, which are partially reusable. It is worth noting that, in the early days, SpaceX attempted to recover the first stages using parachutes; however, the SPs collapsed under aerodynamic stress during re-entry. As a result, the company decided to switch the parachutes for retro-propulsion—a basis for the soft-landing technique. However, in order to test this technique, a prototype was required. Thus, in 2011, the Grasshopper project was announced. It was a 32-meter-tall vehicle that performed eight low-altitude hover-landing test flights between 2012 and 2013, which formed the basis for a larger prototype of the Falcon 9 Reusable Development vehicle. Both these machines laid a foundation for the developments of reusable Falcon 9 and Falcon Heavy. In order to return safely, SPs follow a specific program. After separation, the returning part performs a flip maneuver with cold-gas thrusters; then, engines are lit again in order to move the trajectory toward a landing site. During the descent, the engines are lit one more time in order to slow the stage down and the grid fins are used to steer the lift produced by the first stage. Finally, the engines are lit for the last time in order to slow the returning stage down and enough to perform a precision landing on the prepared position. An in-depth discussion on the advances and development history of SpaceX’ LV can be found in [76].
The increase in popularity of the soft-landing methods opened new research possibilities. As a result, the EU decided to make launcher reusability the state-of-the-art method in Europe. This led to the creation of the Retro Propulsion-Assisted Landing Technologies Project, or RETALT. Its main goal was to study and develop critical technologies for launch recoveries based on retro-propulsion, which led to the creation of RETALT1 and RETALT2 LV concepts. The first LV is supposed to be partially reusable, while the second one should be completely reusable. As part of the research, the characterization of the LV was conducted both in test facilities and programmed simulations; new structural concepts and mechanisms for landing are also being developed. The authors noted that RETALT1 has 50 tons of fuel allocated to it for the return phase, which would allow the reusable stage either to return to a launch site or land on a ship in the ocean, depending on the main engine cut-off conditions [77]. A large number of experiments involving different possible configurations of RETALT’ aerodynamic control surfaces was conducted using both wind tunnels and simplified modeling. The authors came to the conclusion that using them to control the return stage could be challenging. However, it might lead to beneficial results at an angle of attack close to zero [78].
A detailed comparison of the economic, design, and ideological aspects of in air-capturing, SP self-return, as well as soft-landing methods discussed above can be found in articles [79,80,81]. The authors summarize the already-known information and, based on it, draw a conclusion about the most effective and promising methods for the return of LVs’ SPs. It was noted that the economic benefit was not always the main indicator for the choice of the reusable stage design method. In particular, SPs’ seizure by airplanes or helicopters allows one to achieve the best amounts of cargo that can be launched; but, this is not always justified from the economic side.
From a mathematical point of view, with regard to soft-landing methods, the question of the returned SPs’ trajectory optimizations is of interest. The researchers from China were interested in this problem and presented their results for trajectory optimizations with minimized fuel consumption [82]. A reduction in fuel consumption can increase the mass of the payload to be launched and reduce the cost of the LV. The paper presented this principle and described the basic algorithms of the software package, the purpose of which was to optimize the LV’s fuel consumption with a repeated boost-phase activation. The results obtained for three different calculation cases allow us to conclude that the software package can be adapted to the required tasks.
For vertical LV landing, the problem of the reusable stage return trajectory optimizing is often considered. An example of a study on this topic can be found in the source [83]. The authors proposed an approach to automatically determine the trajectory parameters, their classification, and determination of optimal algorithms using a cluster analysis. It was based on an automatic parameter estimation, selection of constraints using the k-means method, and selection of suitable ways of solving the resulting equations. The method proposed by the authors confirmed its effectiveness in a number of experiments, and also simplified the task of optimizing the return trajectory itself by automating the determination of the required calculation parameters.
However, the effectiveness of the vertical-landing method itself was also criticized. In article [84], the authors considered the possibility of optimizing the LV’s SP’s trajectory by changing it. The main difference from the already-familiar trajectory was the transfer of the propulsion unit re-ignition point from the vertical to the horizontal plane and the addition of a wind model to the problem of the LV’s reusable stage motion calculation. The authors performed trajectory optimization using the Particle Swarm Optimization algorithm and the Polynomial Guidance Law, which greatly simplified the calculations. Then, they verified the theoretical assumptions with two numerical experiments, the convergence of which indicated the effectiveness of the method proposed in the article. In addition to reducing the aerodynamic loads on the LVs, it was also possible to significantly increase the accuracy of the landing, which is an obvious advantage.
4. Discussion
The analysis of the literature shows the existence of various methods of both determining and controlling the DRs of LVs’ SPs. The existing methods of determining the DRs are summarized in Table 1. For ease of navigation, the “method” column also includes references to the cited articles.

Table 1.
Methods for determining the drop regions.
According to the information presented, the Monte Carlo method and its different variations are the best among the methods for the impact regions’ determination both in the number of applications and overall efficiency. This is due to the sufficient accuracy of the results and the ability to vary the parameters rapidly and precisely, depending on the task at hand. However, it has a number of drawbacks. First of all, the increase in accuracy diminishes with an increase in calculation iterations, especially after approximately 106 iterations. Secondly, this method is not suitable for finding impact points that are far out of 3σ ellipse borders, which might result in the underestimation of the DR’s size.
These drawbacks led to the creation of other techniques, which proved their effectiveness in particular cases. For instance, the Pontryagin maximum principle can be utilized in DR calculations to significantly decrease the number of required iterations; but, the resulting impact area is slightly larger than the one calculated by the Monte Carlo method. On the other hand, the techniques provided by the reliability analysis in the presence of aleatory and epistemic uncertainties can be adapted for this sort of analysis. The resulting calculation provides a lot of data on the area close to the DR boundary, but is not sufficient at its center, and the computational costs are quite high. This leads to the conclusion that the choice of the most suitable technique for DR calculations depends on the task at hand only, while the Monte Carlo method can be an overall good starting point.
The methods for DR control and change are described in Table 2.

Table 2.
Ways of controlling and changing the DRs for SPs.
The methods of controlling the DR differ in different countries around the world. Accordingly, the literature review shows that the use of parachute rescue systems is dominant in countries with a DR located on water. This is caused by the possibility of using small-sized parachutes capable of reducing the speed of LVs’ SPs so that they are not destroyed from their contact with water. However, such methods are not effective in countries where the prevailing number of DRs are located on land, because the dimensions and weight of the parachute systems constantly increases. Depending on the SPs’ size, it is possible to utilize helicopters to capture them mid-air, while they are slowed down by parachutes. However, the maximum carrying capacity of a rescue helicopter can be a limiting factor.
Because of this, methods of burning SPs in flight, trajectory optimization in order to reduce the DR, the use of GFRs to increase the chance of the LVs’ SPs hitting the DR, etc., are being developed and applied. The techniques aimed at identifying the optimal DRs from ecological, economic, and geographical points of view, if they cannot be sufficiently reduced, are of importance, too.
The “soft-landing” methods are of great interest. They are based on the multiple use of the LVs’ SPs, in particular, at the first stage. It should be noted that their application requires detailed calculations, an elaboration of the design, and is associated with a large number of costly experiments. However, such methods make it possible to eliminate DRs, exclude the allocation of land to them, and significantly reduce the percentage of accidents. This, in turn, leads to a reduction in the cost of subsequent land cleanups and possibly negative environmental consequences.
As a result, it is difficult to recommend a specific method as an ultimate best choice. Each of them has a number of significant positive and negative outcomes. Choosing the most appropriate one depends on a number of factors, such as the LV’s size, SP’s size, whether the DR is located on water or land, the land area, etc. When all these factors are known and accounted for, the appropriate technique can be implemented.
5. Conclusions
This study allowed us to draw a conclusion about the most frequently used methods for determining and controlling the impact areas of LVs’ SPs. Among the methods for determining the impact areas, the most effective was the Monte Carlo method and its various modifications.
The methods for DR control and change can be divided into three groups:
- Engineering, aimed at constructive changes in the LV’s appearance. This includes adding cables for the connection of the LVs’ SPs, using parachute rescue systems, etc.;
- Mathematical, based on a detailed elaboration or modification of LV trajectories and control programs;
- The “soft-landing” method, designed to eliminate DRs. These include various techniques for returning the SR to the spaceport without being destroyed.
Even before the DR is chosen, it is important to access the risk of SPs falling in a specific area. Then, the choice of the most effective method for controlling the DR depends on the specific requirements of the LV; the conducted study can be used as a reference when choosing and setting tasks for eliminating and controlling the DRs for LVs’ SPs.
The future research can be aimed at providing an good example for DRs controlling a rocket with a specific set of parameters, such as launch coordinates, launch atmospheric parameters, land- and water-resource availability for impact points, etc.
Author Contributions
Y.K.: project administration, supervision, funding acquisition, writing—review and editing, visualization. R.L.: writing—original draft preparation, visualization. R.P.: conceptualization, writing—review and editing. E.T.: writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
The research was performed within the state assignment of the Ministry of Science and Higher Education of the Russian Federation (project № FENU-2021-0014).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| DR(s) | Drop region(s) |
| LV(s) | Launch vehicle(s) |
| SP(s) | Separating part(s) |
| GFR(s) | Guaranteed fuel reserves |
| CD | Coasting descent |
| IS | Importance sampling |
| CM | Center of mass |
References
- On the Order and Conditions of the Occasional Use of the Areas of Impact of Separating Parts of Launch Vehicles: Russian Federation Government Resolution of May 31, 1995 No. 536. Available online: http://ips.pravo.gov.ru/?doc_itself=&nd=102035835&page=1&rdk=2#I0 (accessed on 1 February 2023).
- On Amendments and Additions to the Resolution of the Government of the Russian Federation of May 31, 1995 No. 536: Russian Federation Government Resolution of March 24, 1998 No. 350. Available online: http://ips.pravo.gov.ru/?docbody=&prevDoc=102035835&backlink=1&&nd=102052198/ (accessed on 1 February 2023).
- Trushlyakov, V.I.; Shalay, V.V.; Shatrov, Y.T. Reduction of the Technogenic Impact of Launch Vehicles with Liquid Toxic Fuel Components on Environment; Omsk State Technical University: Omsk, Russia, 2004; p. 219. (In Russian) [Google Scholar]
- Kuzmak, G.E. Dynamics of Uncontrolled Movement of Aircraft during Atmospheric Entry; Nauka: Moscow, Russia, 1970; p. 347. (In Russian) [Google Scholar]
- Gavrelyuk, O.P. Guaranteed fuel load for space launch vehicles. Space Engineering and Technology. Kosm. Tekhnika I Tekhnologii 2015, 3, 100–106. (In Russian) [Google Scholar]
- Dobrovolskiy, M.V. Liquid rocket engines. Design Basics: Textbook for Higher Educational Institutions; Bauman Moscow State Technical University: Moscow, Russia, 2016; p. 461. (In Russian) [Google Scholar]
- Ulyanovskiy, N.V.; Kosyakov, D.S.; Bogolitsyn, K.G.; Kozhevnikov, A.Y.; Falev, D.I. Assessment of rocket fuel contamination of impact sites of spent parts of launch vehicles in the north part of the Russian Federation. Ecol. Ind. Russ. 2013, 3, 63–66. (In Russian) [Google Scholar]
- Klimova, E.G.; Morokov, Y.N.; Rivin, G.S.; Borodulin, A.I.; Desyatkov, B.M.; Kotlyarova, S.S.; Zykov, S.V.; Ignatov, R.Y.; Rubinstein, K.G. Mathematical estimation of pollution of the ground surface by rocket fuel as a result of separable parts of launch vehicles’ falling. Atmos. Ocean. Opt. 2005, 18, 525–529. (In Russian) [Google Scholar]
- Novikov, V.K.; Novikov, S.V.; Tatarinov, V.V. Possible Directions for Reducing the Influence of the Rocket and Space Industry on the Environment. In Proceedings of the AIP Conference Proceedings, Moscow, Russia, 28 January–1 February 2019; AIP Publishing LLC: Melville, NY, USA, 2019; Volume 2171, p. 100003. [Google Scholar]
- Starostina, O.I. Safety ensurance and the results of environmental monitoring in the area of impact of the first stage of the «Soyuz-2.1 A» launch vehicle No. 981 (Amur Region) during the first launch from the Vostochny cosmodrome. In Proceedings of the 2017 Priority Tasks of Safety and Environmental Support of “Soyuz” type Launch Vehicles’ Launches of Russian Scientific-Practical Conference, Barnaul, Russia, 2017; Institute of Water and Environmental Problems of the Siberian Branch of the Russian Academy of Sciences: Barnaul, Russia, 2017; pp. 154–164. (In Russian). [Google Scholar]
- Trushlyakov, V.I.; Urbansky, V.A.; Yudintsev, V.V. Reducing Environmental Damage after Emergency Engine Cutoff of the Launch Vehicle. J. Spacecr. Rocket. 2021, 58, 3. [Google Scholar] [CrossRef]
- Abrahamsson, M.; Florin, G.; Lockowandt, C. Esrange Space Center–A European Rocket and Balloon Launch and Operation Site North of the Arctic Circle. In Proceedings of the 2018 SpaceOps Conference, Marseille, France, 28 May–1 June 2018; p. 2701. [Google Scholar]
- Lease Agreement of the Complex “Baikonur” between the Government of the Russian Federation and the Government of the Republic of Kazakhstan. 1994. Available online: https://www.mid.ru/ru/foreign_policy/international_safety/1585161/?ysclid=l6tionl7q6576350931 (accessed on 1 February 2023).
- Pardini, C.; Anselmo, L. Uncontrolled Re-Entries of Spacecraft and Rocket Bodies: A Statistical Overview over the Last Decade. J. Space Saf. Eng. 2019, 6, 30–47. [Google Scholar] [CrossRef]
- Ammons, R.; Hoult, C.; Sollow, P. Recent Advances in the Theory of Sounding Rocket Dispersion Analysis. In Proceedings of the 7th Conference on Sounding Rockets, Balloons and Related Space Systems, Ocean City, MD, USA, 28–30 October 1986. [Google Scholar] [CrossRef]
- Underwood, B.E. Preliminary Risk Assessment for the Black Brant XII. In Proceedings of the 7th Conference on Sounding Rockets, Balloons and Related Space Systems, Ocean City, MD, USA, 28–30 October 1986. [Google Scholar] [CrossRef]
- Noga, T.; Michałów, M.; Ptasiński, G. Comparison of Dispersion Calculation Methods for Sounding Rockets. J. Space Saf. Eng. 2021, 8, 288–296. [Google Scholar] [CrossRef]
- Moch, T.K. Determination of Launch Vehicle Trajectory Dispersions. J. Spacecr. Rocket. 1966, 3, 1682–1685. [Google Scholar] [CrossRef]
- Backer, J.B.; Collins, J.D.; Haber, J.M. Launch Risk Analysis. J. Spacecr. Rocket. 1977, 14, 733–738. [Google Scholar] [CrossRef]
- Beyma, R.J. Sounding rocket and balloon flight safety philosophy and methodologies. In Proceedings of the AIAA 7th Conference on Sounding Rockets, Balloons and Related Space Systems, Ocean City, MD, USA, 28–30 October 1986. [Google Scholar] [CrossRef]
- Capristan, F.M.; Alonso, J.J. Range Safety Assessment Tool (RSAT): An Analysis Environment for Safety Assessment of Launch and Reentry Vehicles. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 14 January 2014. [Google Scholar]
- Tisato, J.; Vuletich, I.; Brett, M.; Williams, W.; Wilson, S. Improved Range Safety Analysis for Space Vehicles Using Range Safety Template Toolkit. In Proceedings of the 5th IAASS Conference, Versailles, France, 17–19 October 2011. [Google Scholar]
- Sanchez, M.A.; Shome, P.L. An Accurate Range Safety Predictive Analysis Procedure for Launch Vehicles. In Proceedings of the AIAA Guidance, Navigation and Control Conference, Portland, OR, USA, 20–22 August 1990; pp. 902–910. [Google Scholar]
- Wilde, P.D. Range Safety Requirements and Methods for Sounding Rocket Launches. J. Space Saf. Eng. 2018, 5, 14–21. [Google Scholar] [CrossRef]
- Morio, J.; Pastel, R. Sampling Technique for Launcher Impact Safety Zone Estimation. Acta Astronaut. 2010, 66, 736–741. [Google Scholar] [CrossRef]
- Morio, J.; Balesdent, M. Estimation of a Launch Vehicle Stage Fallout Zone with Parametric and Non-Parametric Importance Sampling Algorithms in Presence of Uncertain Input Distributions. Aerosp. Sci. Technol. 2016, 52, 95–101. [Google Scholar] [CrossRef]
- Menz, M.; Dubreuil, S.; Morio, J.; Gogu, C.; Bartoli, N.; Chiron, M. Variance Based Sensitivity Analysis for Monte Carlo and Importance Sampling Reliability Assessment with Gaussian Processes. Struct. Saf. 2021, 93, 102116. [Google Scholar] [CrossRef]
- Morio, J.; Balesdent, M. Estimation of Rare Event Probabilities in Complex Aerospace and Other Systems: A Practical Approach; Elsevier Science & Technology: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Brevault, L.; Lacaze, S.; Balesdent, M.; Missoum, S. Reliability Analysis in the Presence of Aleatory and Epistemic Uncertainties, Application to the Prediction of a Launch Vehicle Fallout Zone. J. Mech. Des. 2016, 138, 111401. [Google Scholar] [CrossRef]
- Vergé, C.; Morio, J.; Moral, P.D. An Island Particle Algorithm for Rare Event Analysis. Reliab. Eng. Syst. Saf. 2016, 149, 63–75. [Google Scholar] [CrossRef]
- Filatyev, A.S.; Yanova, O.V. Through Optimization of Branching Injection Trajectories by the Pontryagin Maximum Principle Using Stochasticmodels. Acta Astronaut. 2011, 68, 1042–1050. [Google Scholar] [CrossRef]
- Filatyev, A.S.; Yanova, O.V. Optimization of Space System Launching with Limitations on Fall Zones for Spent Components. In Proceedings of the ICAS, Congress, 21st, Melbourne, Australia, 13–18 September 1998. [Google Scholar]
- Filatyev, A.S.; Buzuluk, V.; Yanova, O.; Ryabukha, N.; Petrov, A. Advanced Aviation Technology for Reusable Launch Vehicle Improvement. Acta Astronaut. 2014, 100, 11–21. [Google Scholar] [CrossRef]
- Averkiyev, N.F.; Bulekbayev, D.A.; Kubasov, I.Y. Calculation of dispersion ellipses’ envelopes of the impact points of the launch vehicles’ separable parts. Tr. Voyenno-Kosm. Akad. Im. A.F. Mozhayskogo 2012, 634, 5–9. (In Russian) [Google Scholar]
- Bulekbaev, D.A.; Bogachev, S.A.; Kubasov, I.Y.; Poluarshinov, A.M. Method of determining the characteristics of the impact areas of separable parts of launch vehicles, while taking into account the destruction of separable parts and operational data on the state of the atmosphere. Tr. Voyenno-Kosm. Akad. Im. A.F. Mozhayskogo 2013, 635, 14–17. (In Russian) [Google Scholar]
- Yeliseykin, S.A.; Podrezov, V.A.; Poluarshinov, A.M.; Shirshov, N.V. Problematic issues of calculation of impact areas of launch vehicles’ separable parts. Tr. Voyenno-Kosm. Akad. Im. A.F. Mozhayskogo 2016, 655, 107–113. (In Russian) [Google Scholar]
- Klyushnikov, V.Y.U.; Averkiyev, N.F.; Bogachev, S.A.; Bulekbaev, D.A.; Kubasov, I.Y.; Slatov, V.L. Separation parameter estimation of the “Soyuz”-type booster strap-on tanks on the basis of their actual impact point coordinates. Dual Technologies, Translator; Otsenka parametrov otdeleniya bokovykh blokov RN tipa “Soyuz” po koordinatam tochek ikh padeniya. Dvoynyye Tekhnologii 2015, 4, 11–15. [Google Scholar]
- Agapov, I.V.; Dvurechenskiy, A.I. Peculiarities of dispersal of the side blocks of the “Soyuz”-type carrier rocket during launches into a sun-synchronous orbit. In Proceedings of the 2017 Priority Tasks of Safety and Environmental Support of “Soyuz”-type Launch Vehicles’ Launches of Russian Scientific-Practical Conference, Barnaul, Russia, 2017; Institute of Water and Environmental Problems of the Siberian Branch of the Russian Academy of Sciences: Barnaul, Russia, 2017; pp. 180–187. (In Russian). [Google Scholar]
- Karchin, A.Y. Estimation of destruction parameters of block «A» of of the «Soyuz» series launch vehicles on the passive part of the trajectory. Tr. Voyenno-Kosm. Akad. Im. A.F. Mozhayskogo 2013, 640, 95–107. (In Russian) [Google Scholar]
- Karchin, A.Y. Estimation of destruction parameters of block «A» of the «Soyuz» series launch vehicles on the passive part of the trajectory in the problem of ballistic substantiation of the areas of impact of the separable parts of space rockets. Armament Econ. 2014, 4, 47–53. (In Russian) [Google Scholar]
- Pirogov, S.Y.; Karchin, A.Y.; Belyanin, D.G.; Apevalov, A.V. Methodology of determination of aerodynamic characteristics of launch vehicles separable parts’ elements. Izv. Tul’skogo Gos. Univ. Tekhnicheskiye Nauk. 2018, 7, 368–375. (In Russian) [Google Scholar]
- Golikov, A.A.; Demeshkina, V.V.; Leutin, A.P.; Filatyev, A.S. Peculiarities of Unguided Reentry of Space Transportation System Parts. Dokl. Phys. 2010, 55, 597–601. [Google Scholar] [CrossRef]
- Starr, B.R.; Gowan, J.W., Jr.; Thompson, B.G.; Tarpley, A.W. Ares IX Range Safety Analyses Overview. In Proceedings of the 58th JANNAF Propulsion Meeting, Arlington, VA, USA, 18–22 April 2011. [Google Scholar]
- Golikov, V.A.; Churakova, E.U.; Mikhailova, E.V.; Dvurechensky, G.A. Analysis of the Characteristics of Booster Rockets Drop Zones. In Proceedings of the AIP Conference Proceedings, Krasnoyarsk, Russia, 29–30 April 2021; AIP Publishing: Melville, NY, USA, 2021; Volume 2402, p. 020023. [Google Scholar] [CrossRef]
- Suimenbayev, B.T.; Trushlyakov, V.I.; Yermoldina, G.T.; Suimenbayeva, Z.B.; Bapyshev, A.M. Development of a Measures Complex to Reduce the Technogenic Impact of Launches of the Promising Irtysh Launch Vehicle in the Impact Areas of the Baikonur Cosmodrome. J. Phys. Conf. Ser. 2019, 1260, 112025. [Google Scholar] [CrossRef]
- Ewing, E.G.; Bixby, H.W.; Knacke, T.W. Recovery System Design Guide; Irvin Industries Inc.: Gardena CA, USA, 1978. [Google Scholar]
- Bacchus, D.L.; Kross, D.A.; Moog, R.D. Aerodynamic Challenges of SRB Recovery. In NASA Conference Publication, NASA. Johnson Space Center Space Shuttle Tech.; NASA: Washington, DC, USA, 1985. [Google Scholar]
- Antonenko, S.V.; Belavskiy, S.A. Mid-Air Retrieval Technology for Returning of Reusable Launch Vehicles’ Boosters. Prog. Propuls. Phys. 2009, 1, 481–494. [Google Scholar]
- Dumont, E.; Ecker, T.; Chavagnac, C.; Witte, L.; Windelberg, J.; Klevanski, J.; Giagkozoglou, S. CALLISTO-Reusable VTVL Launcher First Stage Demonstrator. In Proceedings of the Space Spropulsion Conference, Sevilla, Spain, 14–18 May 2018. [Google Scholar]
- Dek, C.; Overkamp, J.L.; Toeter, A.; Hoppenbrouwer, T.; Slimmens, J.; van Zijl, J.; Areso Rossi, P.; Machado, R.; Hereijgers, S.; Kilic, V.; et al. A Recovery System for the Key Components of the First Stage of a Heavy Launch Vehicle. Aerosp. Sci. Technol. 2020, 100, 105778. [Google Scholar] [CrossRef]
- Priyadarshi, P.; Joseph, L.; Saroha, K. Optimal Two-Stage Parachute and Retro Motor Sizing for Launch Vehicle Stage Recovery. Sadhana-Acad. Proc. Eng. Sci. 2020, 45, 241. [Google Scholar] [CrossRef]
- Zeng, T.; Wang, H.; Wei, W.; Cheng, H.; Zheng, C.L.; Feng, X.Y.; Shan, W. Four-Channel LIDAR Relative Navigation System for Rocket First Stage Recovery at Sea. Comput. Commun. 2021, 175, 123–141. [Google Scholar] [CrossRef]
- Mekhonoshin, Y.G.; Chizhukhin, V.N. Method for Reducing Drop Areas of Spent First Stage Rocket Carrier Rocket Units. Rus. Patent 2572014 C1, 12 December 2015. [Google Scholar]
- Trushlyakov, V.I.; Davydovich, D.Y.; Iordan, Y.V.; Lempert, D.B. Method and Device for Minimizing Exclusion Zones for the Separating Parts of Launch Vehicles. Rus. Patent RU 2700150 C1, 12 September 2019. [Google Scholar]
- Trushlyakov, V.; Zharikov, K.; Davydovich, D. Combustion Possibility Assessment for Separating Launch-Vehicle Components during Atmospheric Phase of Descent Trajectory. Acta Astronaut. 2019, 159, 540–546. [Google Scholar] [CrossRef]
- Titov, B.A.; Rynkov, S.A. Impact area decreasing for “Soyuz”-type carrier rocket’s spent blocks with their structure deliberately divided into parts. Bull. Samara State Aerosp. Univ. Named After Acad. S.P. Korolev (Natl. Res. Univ.) 2007, 1, 90–97. (In Russian) [Google Scholar]
- Scheurpflug, F.; Kallenbach, A.; Cremaschi, F. Sounding Rocket Dispersion Reduction Impact by Second Stage Pointing Control. J. Spacecr. Rocket. 2012, 49, 1159–1162. [Google Scholar] [CrossRef]
- Le, V.D.T.; Nguyen, A.T.; Nguyen, L.H.; Dang, N.T.; Tran, N.D.; Han, J.-H. Effectiveness Analysis of Spin Motion in Reducing Dispersion of Sounding Rocket Flight Due to Thrust Misalignment. Int. J. Aeronaut. Space Sci. 2021, 22, 1194–1208. [Google Scholar] [CrossRef]
- Arsenyev, V.N.; Kazakov, R.R.; Fadeyev, A.S. Ensuring the fall of the spent parts of the launch vehicle to specified areas during launches from new launch pads. Proc. Mosc. Aviat. Inst. 2012, 58, 10. (In Russian) [Google Scholar]
- Trushlyakov, V.I.; Kudentsov, V.Y. Using an active onboard descent system to change the rocket stage impact region. In 2013 Problems of Development, Manufacture and Operation of Rocket and Space Technology and Aerospace Engineering Training of VIII Russian Scientific Conference; Omsk State Technical University: Omsk, Russia, 2013; pp. 179–183. (In Russian) [Google Scholar]
- Trushlyakov, V.I.; Zharikov, K.I. The Issue of Ensuring the Safe Explosion of the Spent Orbital Stages of a Launch Vehicle with Propulsion Rocket Engine. MATEC Web Conf. 2016, 92, 01031. [Google Scholar] [CrossRef]
- Trushlyakov, V.; Shatrov, Y. Improving of Technical Characteristics of Launch Vehicles with Liquid Rocket Engines Using Active Onboard De-Orbiting Systems. Acta Astronaut. 2017, 138, 19–27. [Google Scholar] [CrossRef]
- Trushlyakov, V.; Shatrov, Y.; Sujmenbaev, B.; Baranov, D. The Designing of Launch Vehicles with Liquid Propulsion Engines Ensuring Fire, Explosion and Environmental Safety Requirements of Worked-off Stages. Acta Astronaut. 2017, 131, 96–101. [Google Scholar] [CrossRef]
- Sippel, M.; Klevanski, J.; Kauffmann, J. Innovative Method for Return to the Launch Site of Reusable Winged Stages. In Proceedings of the 52nd International Astronautical Congress, Paris, France, 1–5 October 2001; pp. 1–5. [Google Scholar]
- Stappert, S.; Singh, S.; Sippel, M. Developing an Innovative and High-Performance Method for Recovering Reusable Launcher Stages: The in-Air-Capturing Method. In Proceedings of the Deutscher Luft- und Raumfahrtkongress, Dresden, Germany, 27–29 September 2022. [Google Scholar]
- Singh, S.; Stappert, S.; Bussler, L.; Sippel, M.; Kucukosman, Y.C.; Buckingham, S. Full-Scale Simulation and Analysis of Formation Flight during in-Air-Capturing of a Winged Reusable Launch Vehicle. J. Space Saf. Eng. 2022, 9, 541–552. [Google Scholar] [CrossRef]
- Sippel, M.; Atanassov, U.; Kauffmann, J.; Klevanski, J.; Schmid, V. Reusable Hydro-Carbon Booster Stages as a Replacement for Large Solid Rocket Motors (Special Publication). In Proceedings of the 4th International Conference on Green Propellants for Space Propulsion 2001 ESTEC, Noordwijk, The Netherlands, 20–22 June 2001. [Google Scholar]
- Sippel, M.; Atanassov, U.; Klevanski, J.; Schmid, V. First-Stage Design Variations of Partially Reusable Launch Vehicles. J. Spacecr. Rocket. 2002, 39, 571–579. [Google Scholar] [CrossRef]
- Sippel, M.; Stappert, S.; Simioana, M. Technical Report on Different RLV Return Modes’ Performances (EC Project Number 821953); European Commission: Brussels, Belgium, 2020; Available online: https://elib.dlr.de/137735/ (accessed on 1 February 2023).
- Jo, B.U.; Ahn, J. Optimal Staging of Reusable Launch Vehicles Considering Velocity Losses. Aerosp. Sci. Technol. 2021, 109, 106431. [Google Scholar] [CrossRef]
- Bussler, L.; Sippel, M. Comparison of Return Options for Reusable First Stages. In Proceedings of the 21st AIAA International Space Planes and Hypersonics Technologies Conference, Xiamen, China, 6–9 March 2017. [Google Scholar]
- Ma, L.; Wang, K.; Xu, Z.; Shao, Z.; Song, Z. Trajectory Optimization for Powered Descent and Landing of Reusable Rockets with Restartable Engines. In Proceedings of the International Astronautical Congress, IAC, Bremen, Germany, 1–5 October 2018. [Google Scholar]
- Degtyar, V.G.; Danilkin, V.A.; Telitsyn, Y.S. Method of a Reusable First Stage Rocket Returning to the Launch Site. Rus. Patent 2309089 C1, 27 October 2007. [Google Scholar]
- Schneider, A.; Desmariaux, J.; Klevanski, J.; Schröder, S.; Witte, L. Deployment Dynamics Analysis of CALLISTO’s Approach and Landing System. CEAS Space J. 2023, 15, 343–356. [Google Scholar] [CrossRef]
- Wagner, E.B. Research Flights on Blue Origin’s New Shepard. Gravit. Space Res. 2021, 9, 62–67. [Google Scholar] [CrossRef]
- Seedhouse, E. SpaceX: Starship to Mars—The First 20 Years; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- De Zaiacomo, G.; Blanco Arnao, G.; Bunt, R.; Bonetti, D. Mission Engineering for the RETALT VTVL Launcher. CEAS Space J. 2022, 14, 533–549. [Google Scholar] [CrossRef]
- Marwege, A.; Hantz, C.; Kirchheck, D.; Klevanski, J.; Gülhan, A.; Charbonnier, D.; Vos, J. Wind Tunnel Experiments of Interstage Segments Used for Aerodynamic Control of Retro-Propulsion Assisted Landing Vehicles. CEAS Space J. 2022, 14, 447–471. [Google Scholar] [CrossRef]
- Stappert, S.; Wilken, J.; Bussler, L.; Sippel, M. A Systematic Assessment and Comparison of Reusable First Stage Return Options. In Proceedings of the 70th International Astronautical Congress, Washington, DC, USA, 21 October 2019. [Google Scholar]
- Sippel, M.; Stappert, S.; Bussler, L.; Dumont, E. Systematic Assessment of Reusable First-Stage Return Options. In Proceedings of the 68th International Astronautical Congress (IAC) 2017, Adelaide, Australia, 25–29 September 2017. [Google Scholar]
- Wilken, J.; Stappert, S.; Bussler, L.; Sippel, M.; Dumont, E. Future European reusable booster stages: Evaluation of vthl and vtvl return methods. In Proceedings of the 69th International Astronautical Congress (IAC), Bremen, Germany, 1–5 October 2018. [Google Scholar]
- Zhou, H.; Wang, X.; Cui, N. Glide Guidance for Reusable Launch Vehicles Using Analytical Dynamics. Aerosp. Sci. Technol. 2020, 98, 105678. [Google Scholar] [CrossRef]
- Zhao, J.; He, X.; Li, H.; Lu, L. An Adaptive Optimization Algorithm Based on Clustering Analysis for Return Multi-Flight-Phase of VTVL Reusable Launch Vehicle. Acta Astronaut. 2021, 183, 112–125. [Google Scholar] [CrossRef]
- Cheng, G.; Jing, W.; Gao, C. Recovery Trajectory Planning for the Reusable Launch Vehicle. Aerosp. Sci. Technol. 2021, 117, 106965. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).