Two-Way Coupled Aero-Structural Optimization of Stable Flying Wings

Abstract

An aero-structural algorithm to optimize a flying wing in cruise conditions for preliminary design is developed using two-way interaction between the structure and aerodynamics. A particle swarm routine is employed to solve the multi-objective optimization, aiming to reduce the weight of the structure and the aerodynamic drag at the design point. Different shapes are evaluated during the optimization process until the algorithm reaches the optimal wing aspect ratio, taper ratio, angle of incidence, twist angle, swept angle, and airfoil shape, where a six-parameters method is employed to allow reflex airfoils. A main isotropic I-beam models the wing structure. An extended vortex lattice model is employed to model the aerodynamics, along with a high-order panel method with fully coupled viscous interaction. The finite element method is used to solve the flying-wing structure under static loads. An algorithm is developed to iterate between the deflection of the wing and its impact on the aerodynamics until convergence is reached. Different constraints are implemented into the objective function to fulfil the structural criteria and the longitudinal static stability. A comparison against a baseline optimization is carried out, achieving higher efficiency and promising results in elliptical lift distribution, and a high static margin, without the use of non-constant twist. The results suggest that combining both reflex airfoils and sweep with washout is the optimal solution to reduce the drag and weight, keeping the longitudinal static stability criteria for tailless aircraft in the lower end of the transonic regime.

1. Introduction

Different projects from Airbus [1], Boeing, and NASA [2], indicate that flying wings are one of the most promising concepts for the future of commercial aviation, mainly due to their significant aerodynamic efficiency, which is about 20 percent higher than conventional aircraft [3], and, hence, fuel savings and much lower pollution [4]. Moreover, flying wings have other advantages [5], including greater internal volume, aerodynamics and structural efficiency, noise reduction, and a significant improvement in cost per seat-mile [2].

This work aims to develop and test an algorithm to optimize the drag and weight of a tailless aircraft to assist the preliminary design process and employ it in a study case to evaluate insights. A Multidisciplinary Design Optimization (MDO) is employed to optimize the flying-wing geometry and its main I-shaped beam, while longitudinal static stability is assured. Hence, the structure of the wing is simplified to a main beam [6], and the aerodynamic shape is the flying-wing itself. These two simplified approaches are enough, given that the article studies the preliminary design approach. The study case focuses on the lower end of the transonic regime, about Mach number $M=0.85$.

The wing geometry is parameterized essentially by the aspect ratio, tip to chord ratio, wing incidence, aerodynamic twist angle, sweep angle, and airfoil shape distribution. Throughout the optimization, each candidate wing is assessed using the Athena Vortex Lattice (AVL) method, given its low computational cost compared to other more robust methods, such as Computational Fluid Dynamics (CFD) [7]. Since inviscid potential methods have shown similar results only for the lift coefficient in comparison against CFD [8], AVL is employed for lift and stability analysis. However, the AVL is based on an extended Vortex Lattice Method (VLM) which considers the induced drag only, and, therefore, XFOIL (a panel-based algorithm coupled with an integral boundary layer formulation) is employed to estimate the skin and pressure drag, namely the parasitic drag.

The airfoil parameterization method selection aims at a low number of parameters to reduce the computational cost and enable generation of reflex airfoils, which improves the stability of tailless aircraft [2,9,10]. Although other optimizations of tailless aircraft have employed Bezier curves [11], a six parameters method [12] is implemented. The longitudinal stability of tailless aircraft can be obtained using a reflex airfoil or by using sweep and twist wings [9], but, due to modified pressure distribution over a reflex airfoil, the produced lift is less, compared to conventional airfoil, and the drag higher [13]. Hence, this work assesses what method of fulfilling stability in flying wings is more suitable.

The forces from AVL and XFOIL are the inputs for the structural module, where a Finite Element Analysis (FEA) is carried out. The von Mises stress with a safety factor is compared against the tensile yield strength of the beam material, which must be assumed isotropic. The aerodynamic module is fed into a two-way coupling by the vertical beam displacement as a dihedral distribution until it converges. Moreover, a penalty function is applied when the structural criterion is not fulfilled or when the longitudinal static stability criteria are not accomplished. The Particle Swarm Optimization (PSO) is employed to solve the constraint of the multi-objective, MDO, problem due to the fact it has been reported to be faster than other algorithms, such as generic algorithms or sine–cosine optimizers [14,15].

Recent studies have assessed wing optimization using XFOIL, CFD and non-linear lifting line methods without stability constraints [16]. Similarly, a stability-constrained aerodynamic optimization of flying wings has been assessed [10]. However, in both studies, the structural analysis was restricted to keeping a root bending moment constraint, which does not allow interaction between aerodynamics and structural deflection. Moreover, the assumption implicit in the approaches was that two wings with the same root bending moment have the same weight. Other works have evaluated a fully coupled aero-structural optimization using FEA and CFD [7], having a high computational cost, without considering stability constraints, and applied to conventional aircraft.

This research seeks to expand and contribute in different ways. First, it develops a two-way coupled aero-structural optimization algorithm to optimize the preliminary design of tailless aircraft. Based on this algorithm, conclusions about the feasibility of the finite element analysis are reached in terms of computational cost as the structural constraint, instead of using a root moment restriction. Finally, the optimal wing geometry of a tailless aircraft is studied and compared against the literature results, including how the aerodynamics and structures impact the different wing parameters.

Moreover, a study case is carried out to compare the results of the algorithm developed against a baseline optimization in the literature [9]. Other studies have stated that an elliptical lift distribution is achieved by non-constant twist (a piecewise function) [10,17] and that a positive static margin for tailless aircraft is hard to achieve, sometimes requiring the sacrifice of the elliptic lift distribution [2,10,11]. In contrast, the optimal aircraft found in the study case has a considerably high static margin and an almost elliptical lift distribution with a constant geometric twist -linear-.

2. Aerodynamic Modeling

During the optimization process, each candidate flying wing is analyzed under a static condition at the design point, usually cruise condition. First, the lift force is estimated by AVL, which is employed to find the equilibrium angle at which lift is equal to the weight and there is a zero total moment about the gravity center. Inviscid potential methods have shown similar results in comparison against CFD [8], especially for lift coefficient before stall. However, AVL methodology cannot estimate the parasitic drag and so XFOIL is employed to estimate it. Hence, each candidate wing geometry, including aerodynamic and geometric twist, is evaluated in AVL and XFOIL.

2.1. Airfoil Parameterization

There is a large set of airfoil parameterization methods. However, the best trade-off between low computational cost and the design space size must be considered. For instance, although the four digits NACA parameterization is able to produce a wide range of airfoil shapes with high aerodynamic efficiency with just three parameters [14], it is unable to produce reflex airfoils. Another standard parameterization that can produce reflex airfoils is the Bezier curve parameterization [11], which employs 12 parameters.

It is known that reflex airfoils can improve the stability of tailless aircraft [2,9,10], hence a six parameter method, [12] able to produce reflex airfoils, was selected, as seen in Figure 1. The Equations (1) and (2) are employed to get the airfoil coordinates, where $\theta \in [0,2\pi ]$.

$$X\left(\theta \right)=0.5+0.5\frac{{\left|cos\theta \right|}^B}{cos\theta }$$

(1)

$$Y\left(\theta \right)=\frac{T}{2}\frac{{\left|sin\theta \right|}^B}{sin\theta }(1-X^P)+Csin\left(X^E\pi \right)+Rsin\left(X2\pi \right)$$

(2)

2.2. AVL

AVL is based on VLM, which calculates lift curve slope, induced drag and lift distribution for the given wing. The modeling is performed by some elements that produce lift, called horseshoe vortices, distributed along span and chord. The airflow effect on the wing is estimated mainly using the Biot–Savart Law, the Kutta–Joukovsky theorem, the Hermann von Helmholtz theory, and the Prandtl lifting-line theory.

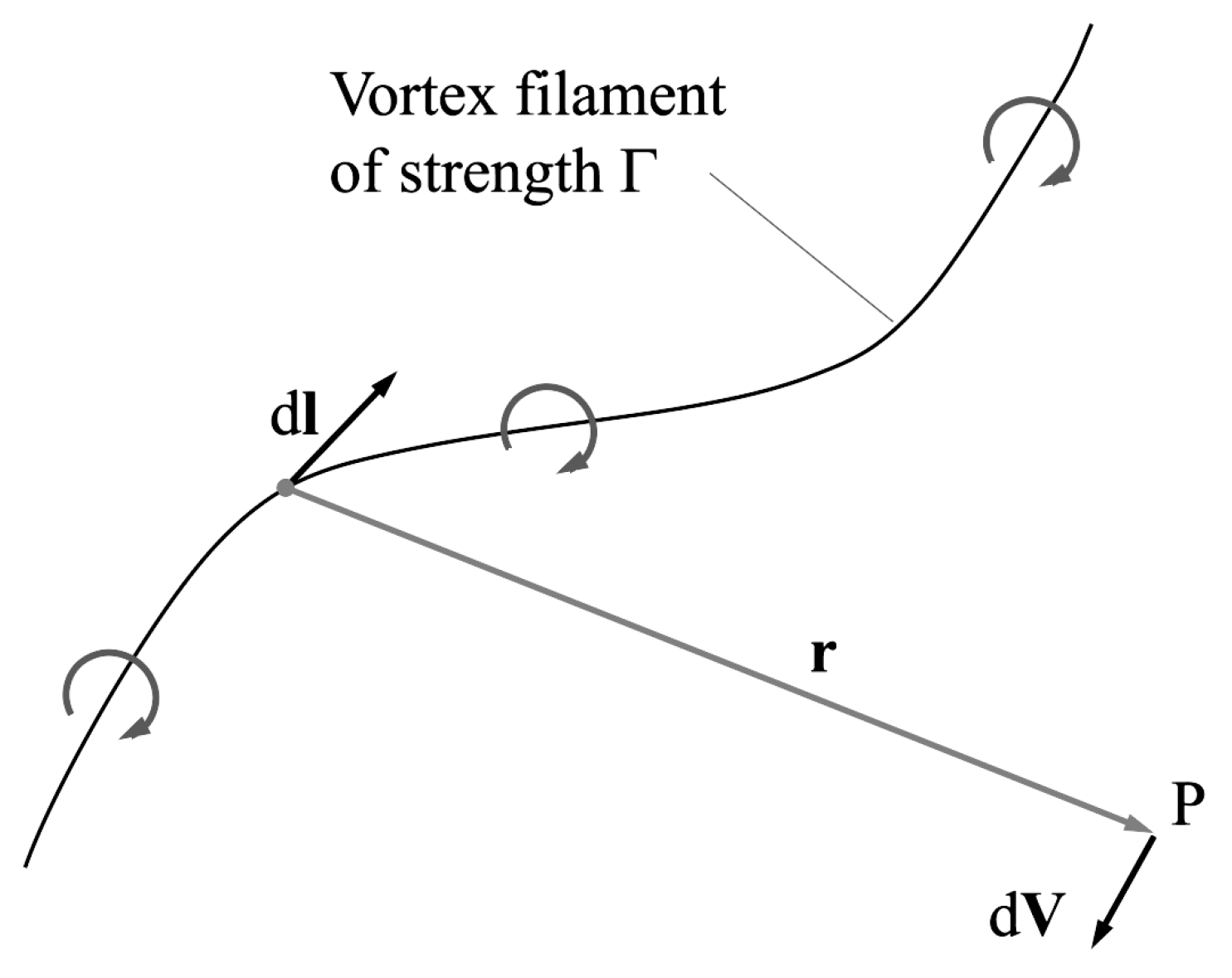
A vortex filament $dl$ induces a flow field in the surrounding space (Figure 2), estimated by the Biot–Savart Law (Equation (3)) [18], being Γ the strength of the vortex. This strength or circulation produces lift according to the Kutta–Joukovsky theorem (Equation (4)).

$$V_i=\frac{\Gamma }{4\pi }\int \frac{dl\times r}{{\left|r\right|}^3}$$

(3)

$$L={\rho }_{\infty }{V}_{\infty }\Gamma$$

(4)

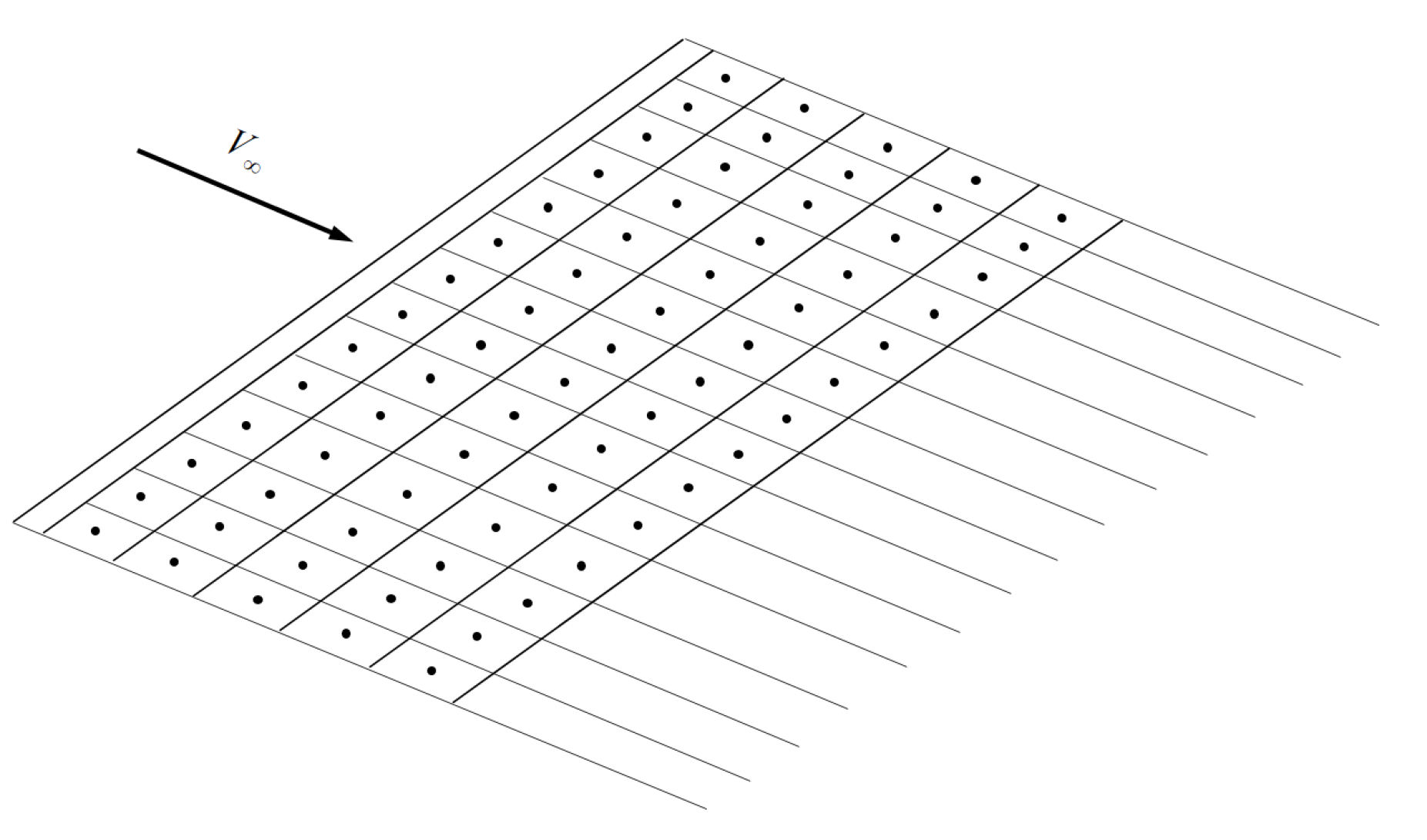
The Hermann von Helmholtz theory establishes that the vortex filament must be closed and its circulation constant. The closed vortex is modeled by four vortex filaments using the Prandtl lifting-line theory. Finally, the wing is divided into panels and a horseshoe vortex is located at each panel. A sample is shown in Figure 3. The total force is obtained by the sum of each panel contribution.

Since the flow is potential (linear aerodynamic), the main limitations of the methodology are the stall prediction, compressibility impact, and the fact that only induced drag can be estimated. To complete the aircraft drag, XFOIL is employed to account for the skin and pressure friction. The compressibility impact is taken into account by the subsonic Prandtl–Glauert Equation (5); the same equation is employed to correct the drag.

$$C_{l_M}=\frac{C_l}{\sqrt{1-M^2}}$$

(5)

2.3. XFOIL

XFOIL is a computational implementation of the panel method coupled to an integral boundary layer formulation and a $e^n$ laminar to turbulent transition technique [19]. This tool allows predicting $C_l$ and $C_d$ at small angles of attack, preferably before stall. In case of divergence, a recursion within the code is applied, increasing the nodes over the top and bottom surfaces of the airfoil. The initial setup is defined with 150 maximum iterations and 200 nodes over the airfoil surface, and a smoothing step, to avoid any high variation of the coordinates, is also applied.

Compressibility Correction

The Karman–Tsien correction [20,21] is employed to consider the Mach effect. The drag coefficient correction is shown in Equation (6), which is also valid for the lift coefficient.

$$c_{d_M}=\frac{c_d}{\sqrt{1-M^2}+\frac{{\displaystyle c_d{M}^2}}{{\displaystyle 2+2\sqrt{1-M^2}}}}$$

(6)

2.4. Reynolds Corrections

Despite the recursivity implemented, some airfoils occasionally do not converge. In these cases, the same airfoil is simulated at a higher Reynolds number, which usually helps in convergence, and some corrections are implemented to take this into account. The first is a drag correction [22] through Equation (7). On the other hand, the lift slope is not highly affected by the Reynolds number, but the stall angle is. The Equation (8) is employed to estimate this impact [23].

$$c_{d_{Re}}=c_d{\left(\frac{R{e}_{ref}}{Re}\right)}^{0.2}$$

(7)

$${\alpha }_{stall}={\alpha }_{stal{l}_{ref}}{\left(\frac{Re}{R{e}_{ref}}\right)}^{0.4}$$

(8)

3. Structural Modeling

The flying-wing structure is modeled by an I-shaped main beam centered at the wing’s quarter chord, as shown in Figure 4. The beam is located by considering the wing incidence and the equilibrium angle at the design point, which means the I beam is straight at the flight condition. The beam has two parameters, the height of the beam at the tip and at the root. These values are estimated from the wing geometry at these stations in order to keep the beam within the boundaries of the airfoil, and the sections between tip and root are linearly interpolated. The other beam parameters are estimated from the beam height using the relations employed in [6], Equations (9)–(11).

$$a=0.9012\times h$$

(9)

$$t=0.0494\times h$$

(10)

$$w=0.5\times h$$

(11)

Mesh and Boundary Conditions

The mesh for the FEA is composed of tetrahedral elements and is described by a quadratic element order, where each element has ten nodes, each at its corners and edge centers. The maximum mesh edge length is restricted to $0.25h_t$, and the mesh growth rate is set to $1.1$. Moreover, the mesh is further refined at the root (see Figure 5), where the stress increases rapidly. In the first lateral web and flange faces, the target edge size is calculated as $h_r/15$, and $0.25t_r$ on the clamped face.

The beam is centered at the quarter chord, where the aerodynamic forces are assumed. The clamped beam has the first face fixed, and the lift and drag forces are applied along the beam according to the load distribution from the aerodynamic method.

4. Optimization Algorithm

This optimization problem aims to reduce the total drag coefficient $C_D$ and the weight of the aircraft structure by decreasing the beam mass K while fulfilling the target lift at the equilibrium angle, the structural constraint via the yield strength, and the longitudinal static stability criteria, namely a zero pitch moment at the gravity center and the negative slope of the moment coefficient against the angle of attack. The routines have penalty functions to make the candidates move away from the zones where the constraints are not accomplished. Penalties are applied when structural safety is not fulfilled and when the slope of the moment coefficient against the angle of attack is not negative.

The optimization space is generated from 18 variables: the wing aspect ratio, the tip to root chord ratio, the angle of incidence, the geometric twist angle, the sweep angle, the airfoil parameters B, T, P, C, E, R for tip and root, and the position of the airfoil transition. The latter parameter refers to the place, in percentage, at which the airfoil changes from the root to the tip shape. The problem is as follows.

$$\begin{array}{cc}\mathrm{minimize}\hfill & C_{D}K=f(AR,\lambda ,i_w,{\alpha }_{twist},{\Lambda }_{sweep},foi{l}_r,foi{l}_t,x_{foil})\hfill \\ \mathrm{subject}\mathrm{to}\hfill & {\sigma }_{von}{\gamma }_f\le {\sigma }_{yield}\hfill \\ \hfill & C_{m,\alpha }<0\hfill \\ \hfill & C_m\left(x_{cg}\right)=0\hfill \\ \hfill & L\left({\alpha }_{eq}\right)=W\hfill \end{array}$$

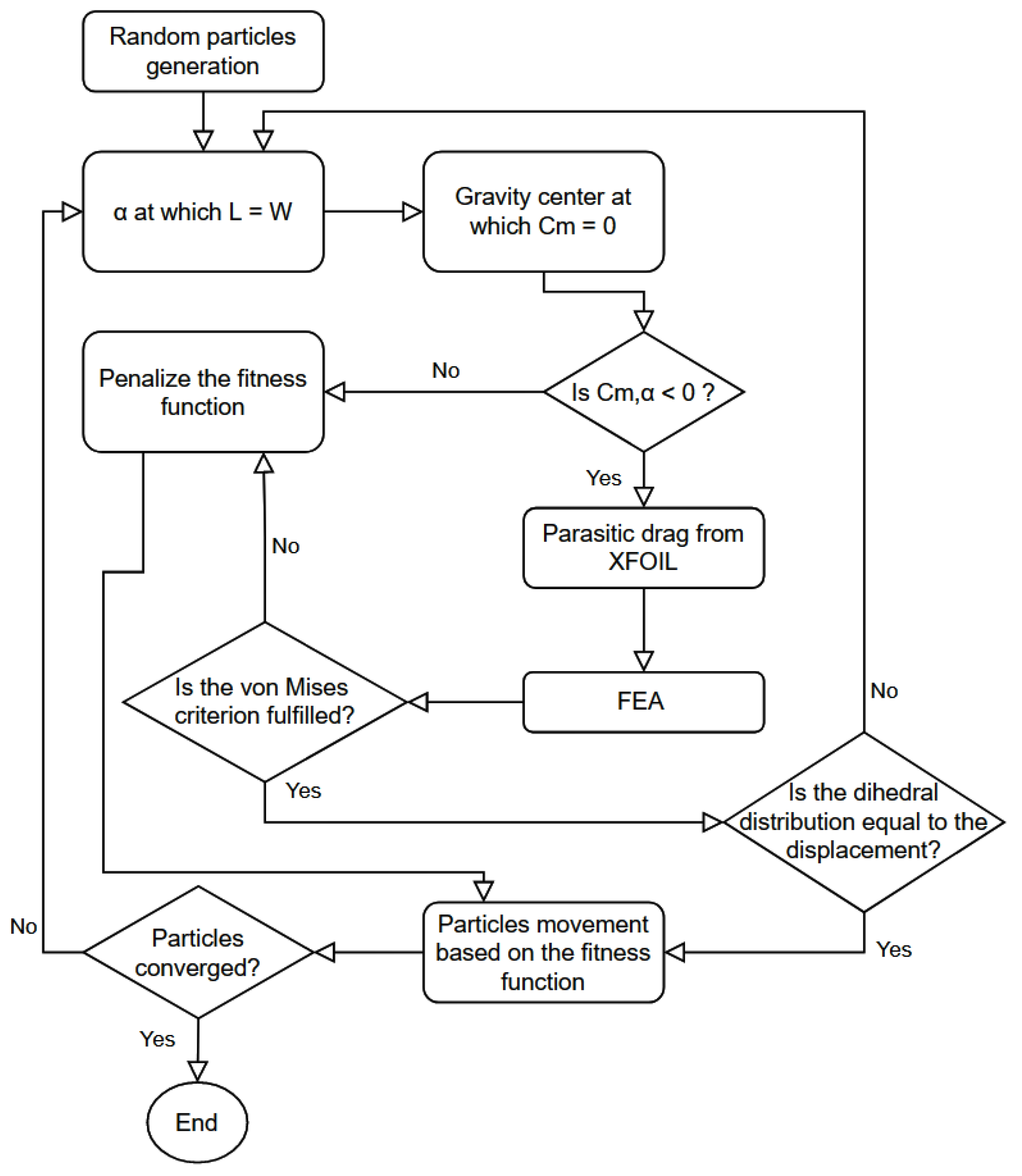
The objective function, where the aerodynamic and structural algorithms run, is optimized by a particle swarm algorithm, where a first random set of solutions is created, and then they move through the design space, being attracted to the best solution found by any particle and the best solution of their own particle history until they converge.

Figure 6 shows the general scheme of the optimization. Once the first candidate generation is created, each flying-wing is analyzed in AVL, where the angle at which the lift is equal to the weight is found, and recursion to find the gravity center position, to make the pitching moment zero, is employed. Next, the slope of the moment coefficient against the angle of attack is evaluated, and if its value is negative, the skin and pressure drag are estimated from XFOIL and added to the induced drag by AVL and, then, the structural model runs. Next, the beam is generated and analyzed via the finite element method, as described in the structural modeling section, where the structural safety is evaluated. If the structural constraint is fulfilled, the displacement in the vertical axis is employed as a dihedral angle distribution for AVL in a recursive algorithm until the structural loads and displacements converge with the aerodynamic forces and constraints with dihedral angle distribution. The displacement in the drag direction is neglected. Finally, the beam mass and the total drag coefficient turn into the fitness value for the optimization algorithm, with a penalty if any constraint is not fulfilled. This routine runs until the particle swarm ends.

The optimization algorithm searches the optimum within lower and upper boundaries for each design variable. These limits are: $AR\in [4,15]$, $\lambda \in [0.2,0.7]$, $i_w\in [-3,6]$, ${\alpha }_{twist}\in [-5,5]$, $x_{foil}\in [0.1,0.9]$, ${\Lambda }_{sweep}\in [5,45]$, $B\in [1.8,2.2]$, $T\in [0.08,1.13]$, $P\in [1,2]$, $C\in [0.02,0.06]$, $E\in [0.9,1.25]$, $R\in [-0.04,0.04]$. The boundaries for the airfoil parameters are the same for root and tip.

5. Case Study

To evaluate the algorithm and results, a case study was carried out. The same aerodynamic requirements and flight conditions (ISA 45000 ft) from another work [9], were employed for the optimization, as siin in

Table 1. Data and constraints for the optimization.

${\mathit{\gamma }}_{\mathit{f}}$	${\mathit{\rho }}_{\mathit{m}}\left[\frac{\mathbf{kg}}{{\mathbf{m}}^3}\right]$	${\mathit{\sigma }}_{\mathbf{yield}}$ [Pa]	YM [Pa]	$\mathit{\nu }$	W [N]	${\mathit{\rho }}_{\mathit{\infty }}\left[\frac{\mathbf{kg}}{{\mathbf{m}}^3}\right]$	V${}_{\mathit{\infty }}\left[\frac{\mathbf{m}}{\mathbf{s}}\right]$	M	S $\left[{\mathbf{m}}^2\right]$	$\mathit{\mu }$ [Pa·s]
2.5	2860	$614\times {10}^6$	$70\times {10}^9$	0.32	369270	0.23716	250.667	0.85	934	$1.432\times {10}^{-5}$

. In addition, the aluminum alloy 7055-T77 was assumed for the main beam [24] and a structural safety factor of $2.5$, regarding the load factor allowed for this kind of aircraft in the Federal Acquisition Regulation part 25.

5.1. Results

The optimum values for the study case are shown in

Table 2. Optimum variables for the case study.

AR	$\mathit{\lambda }$	i_w [° ]	${\mathit{\alpha }}_{\mathit{twist}}$ [° ]	${\mathit{\Lambda }}_{\mathit{sweep}}$ [° ]	x${}_{\mathit{foil}}$	B${}_{\mathit{r}}$	T${}_{\mathit{r}}$	P${}_{\mathit{r}}$
13.66	0.355	6	$-2.86$	27	0.85	1.8	0.102	1.055
C${}_{\mathit{r}}$	E${}_{\mathit{r}}$	R${}_{\mathit{r}}$	B${}_{\mathit{t}}$	T${}_{\mathit{t}}$	P${}_{\mathit{t}}$	C${}_{\mathit{t}}$	E${}_{\mathit{t}}$	R${}_{\mathit{t}}$
0.06	0.943	0.04	2.2	0.097	1.372	0.04	0.937	0.04

. These values achieved a minimum of 46.467, where the total drag coefficient was $C_D=0.00947$, and the beam mass was $K=4907$ kg. The optimal wing with the beam is shown in Figure 7.

The computational cost would vary drastically for different numbers of sections, FEA mesh parameters, and the size of the model. In this case study, a set up with a single Intel Core i7 8th generation and 32 GB of RAM was employed. For this set up, a single wing aerodynamic evaluation lasted about 3 s. When the stability criteria were met and the structural module ran, the wing evaluation lasted about 40 s, without considering the recursivity between the structural deflection and the updated wing geometry, which would depend on how much the wing was deflected.

The total PSO cost with 700 initial particles and 30 iterations was about 68 processor hours. The total time would be drastically decreased if a parallel strategy was applied. Many of the 700 initial particles did not fulfil the stability requirements, hence they ran in about 3 s. The high number of initial particles is required to have enough candidates that meet the stability criteria, to evolve in the subsequent iterations to the global optimal. Other similar studies have reported computing time for each function evaluation in the order of 10 min [25,26]. Higher order models have reported a single function evaluation cost for aero-structural wing optimization of around 1 h [27].

5.1.1. Wing Geometry

The optimum wing aspect ratio was $13.66$, in comparison to the value of 6 estimated in the baseline study [9], a study that did not consider structural modeling. However, other studies have shown optimal values of about 12 for metallic structures [28], where a multi-objective optimization was carried out to minimize fuel consumption and weight using CFD. This value also coincides with the aspect ratio of the blended wing body for subsonic transport of Boeing [2]. Hence the aspect ratio is a variable highly influenced by the interaction between the aerodynamic and structural optimizations.

The taper ratio of $0.355$ was in agreement with the results of optimizing a wing without twist using lifting line theory and using an airfoil with lift slope of $2\pi$, a study which showed an optimum value of about $0.35$ without structural considerations [29], and which had different optimization criteria and more restricted variables of wing aspect ratio and taper ratio. This value was similar to the baseline study results, where a taper ratio of $0.302$ was employed for the inboard wing and $0.5$ for the outboard wing. It suggests that the optimal root-to-tip ratio is not highly influenced by the structures but by the aerodynamics. The wing incidence reached the upper limit of 6° with a geometric twist of $-2.86$°. Other studies have dealt with non-constant geometric twist [10,17], and the baseline estimated an optimum twist of $-4$°.

The sweep angle at the quarter chord obtained for the study case was 27°, in comparison to the 30° of the outboard wing and $60$° for the inboard wing of the baseline study. The neutral point of the aircraft is altered primarily by changing the sweep of the wing [10], and, then, this angle is highly affected by the aerodynamics. Moreover, the Mach number normal to the leading edge of the wing is reduced by sweep [17]. The Mach was reduced to 0.757 in our case study (Equation (12)), eliminating the shock wave and the corresponding drag [10]. On the other hand, the effective bending moment is not necessarily aligned with the wing, and the torsional and bending component increases with the sweep [10]. Other tailless aircraft reported different sweeps for leading and trailing edges with a mean sweep of $31.5$° [17], which was also in agreement with the optimal range between 20° and 40° found in [30] for tailless aircraft. These results suggest that the sweep angle was mainly influenced by the aerodynamics but with a restriction by the structures.

$$M_{2D}=M_{3D}\cos {\Lambda }_{sweep}=0.757$$

(12)

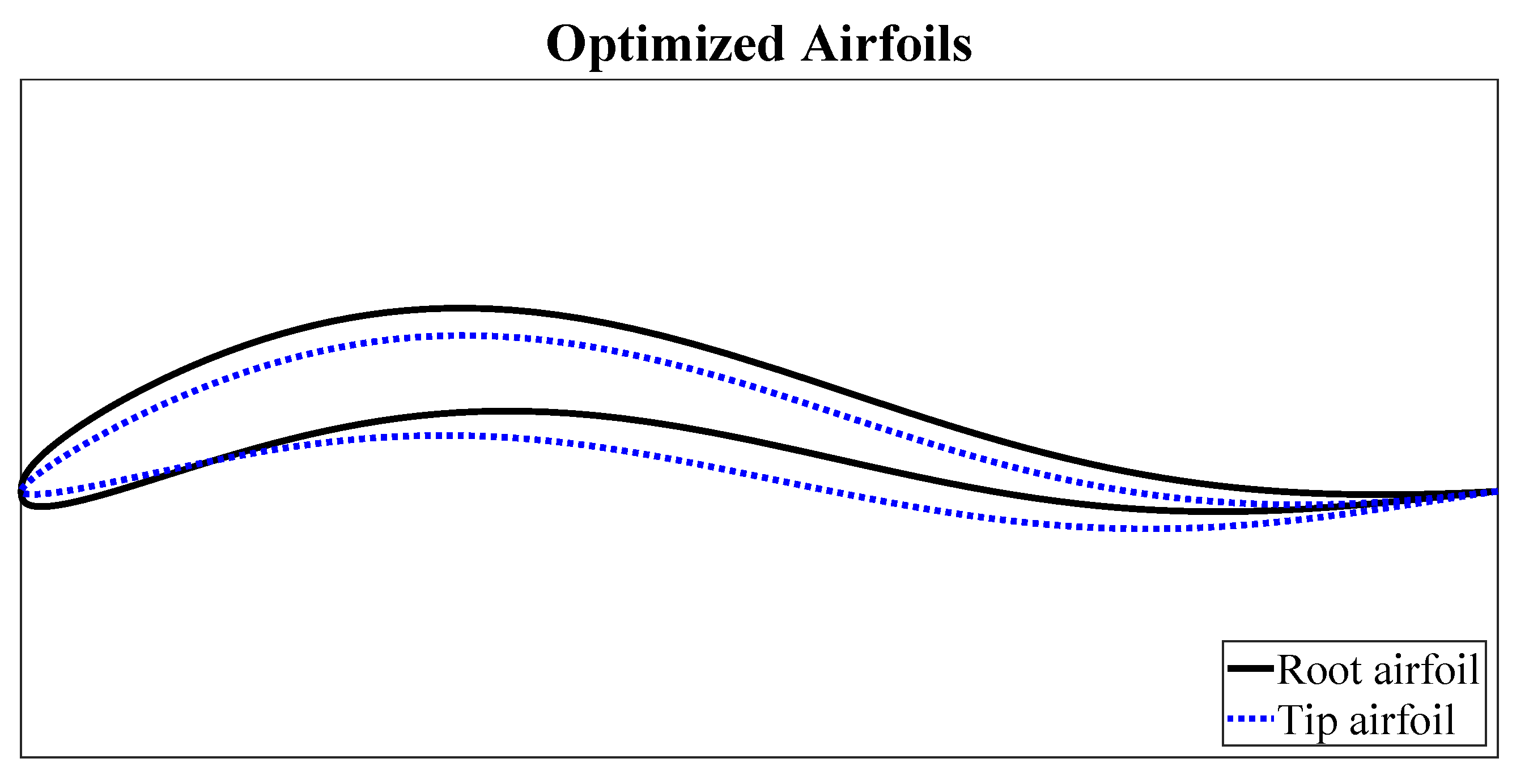
The aerodynamic twist is defined by three stations along the wing, the root, tip, and the transition section, which varied from 10% to 90%. The optimal value was obtained at 85%. The latter means that the wing has two different airfoils along the span-wise direction. The root and tip airfoil are defined by six parameters each, shown in Table 2, and the shapes are shown in Figure 8.

5.1.2. Airfoil Distribution

It is known that in order to accommodate passengers, cargo, and landing gear, the tailless aircraft requires inboard airfoils of a large thickness-to-chord ratio, about 17% [11]. However, these considerations are out of the scope of this work, and part of future work. The thickness distribution is only affected by aerodynamics and structures. The airfoil’s thickness increases towards the wing’s root to better withstand the larger bending moments. The latter means that the larger the thickness, the higher the beam, so more inertia can be used. This behavior is present in other similar studies [31].

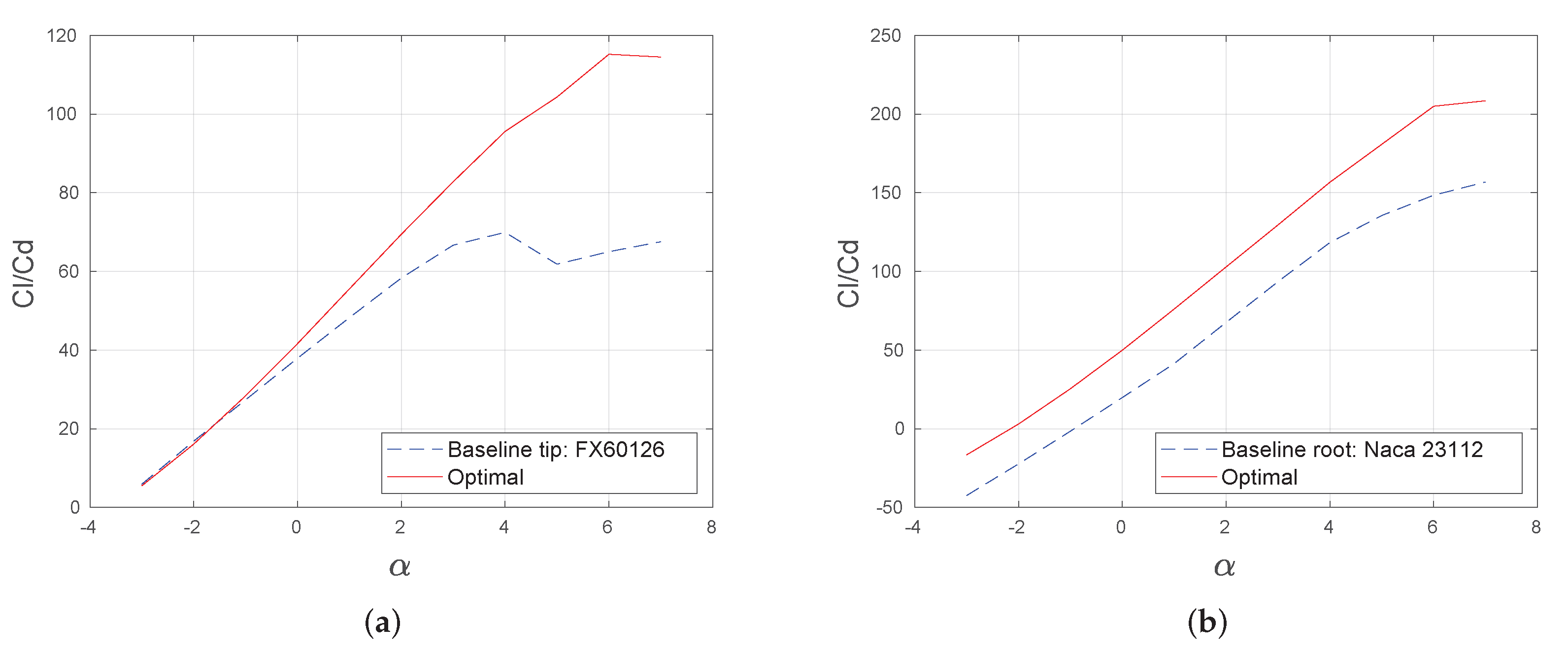
The baseline study employed the Wortmann FX 60-126 airfoil for the outboard wing with a maximum thickness of 12.6% and camber of 3.6%, and the NACA 23112 for the inboard wing with a maximum thickness of 12% and camber of 1.2%. The airfoils were optimized at 10.2% of maximum thickness and 6% of maximum camber at root and 9.7% of maximum thickness and 4% of maximum camber at the tip. The main differences were that the thickness of the baseline study was higher because of the constraints of volume, and the camber of the optimized airfoils was higher. Lower thickness of airfoils also reduces the effective Mach number, a similar effect to the sweep angle [32], reducing shock waves and drag. The thickness values did not reach the boundaries. On the other hand, the camber for the tip airfoil reached the upper limit.

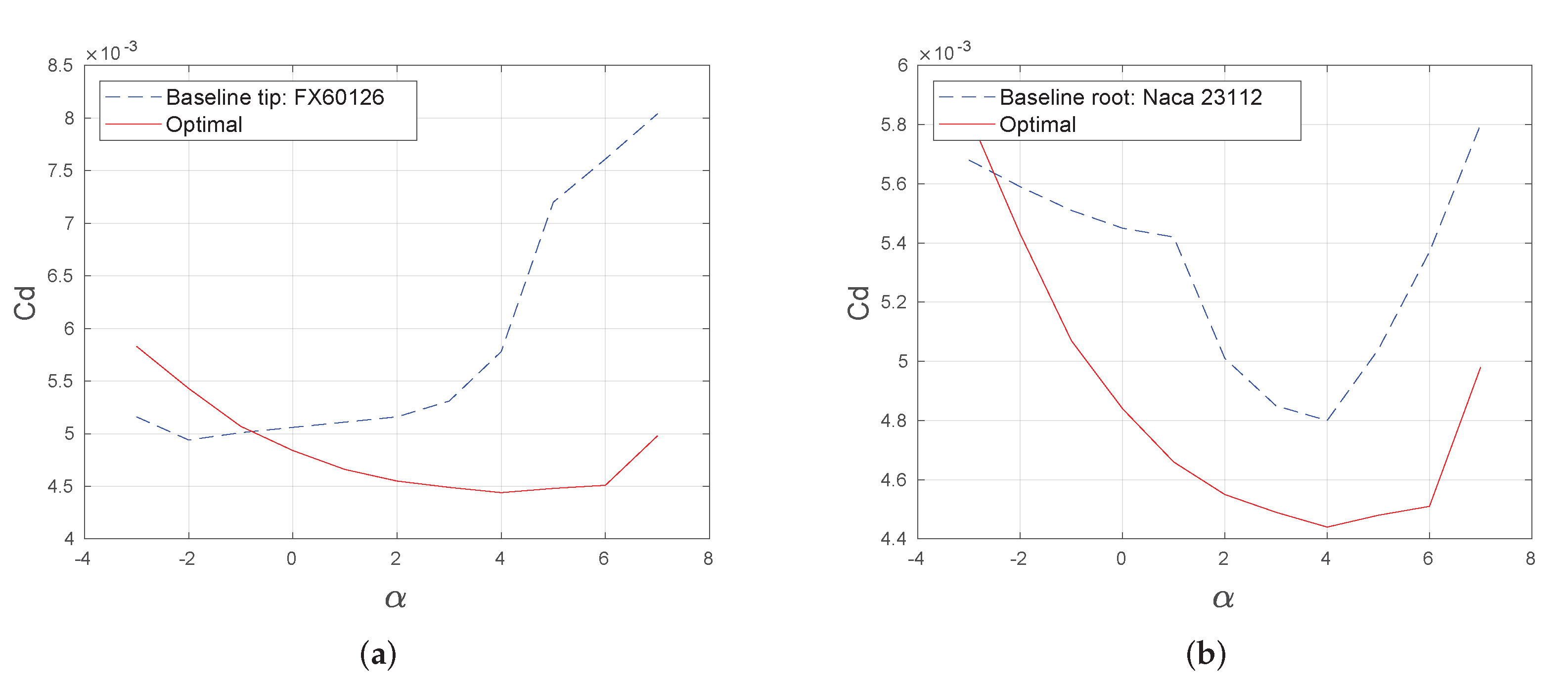
The airfoil and angle of attack distribution achieved remarkable aerodynamic characteristics compared to the baseline results, as summarized in

Table 3. Comparison of aerodynamics between baseline and optimization.

	CL/CD	C${}_{\mathbf{Dp}}$	C${}_{\mathbf{Di}}$	e
Baseline	25	0.009	Not available	0.987
Optimization	54.97	0.0044	0.00507	0.985

. The lift-to-drag ratio and the drag plots are also shown in Figure 9 and Figure 10. The parasitic drag was about the induced drag, which suggests that the optimization aimed to design the aircraft in such a way that the cruise condition was near the velocity of minimum drag, where induced and parasitic drag are equal. The parasitic drag of the optimized aircraft was about half of the baseline, while the span efficiency e was almost equal. However, the aspect ratio of the optimized wing was greater, which made the induced drag considerably lower. Regarding the lift-to-chord ratio, the proposed aero-structural optimization achieved more than twice the baseline aerodynamic efficiency. 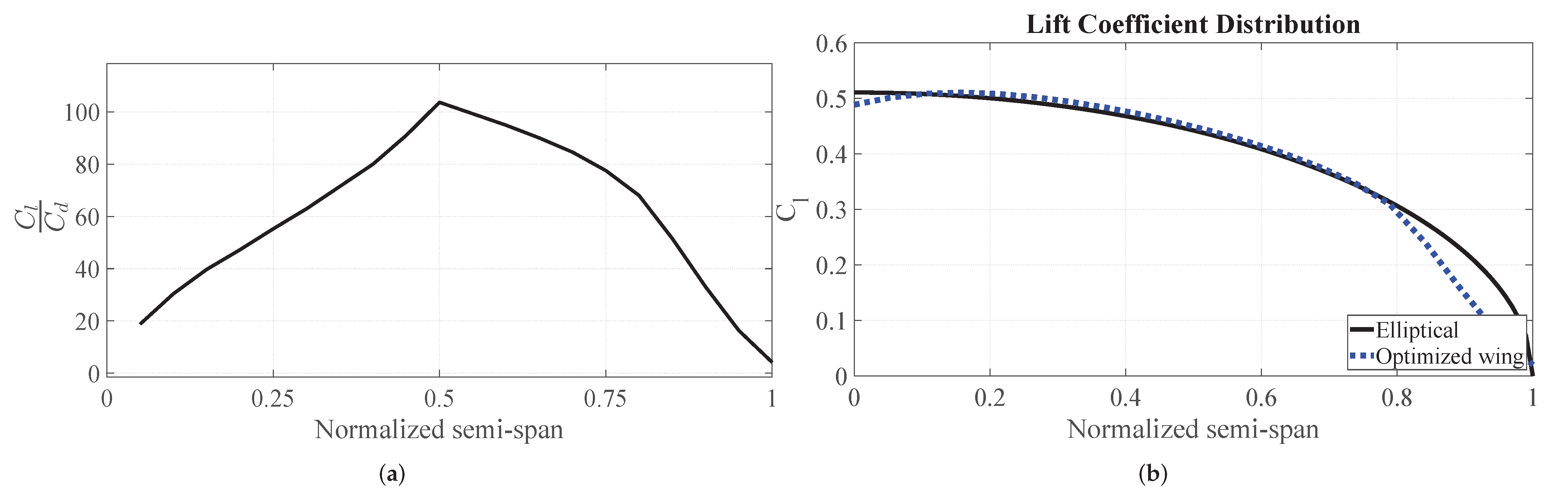This distribution is shown in Figure 11a, where the peak was in the middle of the semi-span. One reason is that the airfoils (shape and twist) towards the tip have a meaningful stability impact, and the airfoils towards the root have a more significant impact on structure (a higher thickness is required for the beam), being the middle where the airfoil shape is influenced mainly by the aerodynamic efficiency.

The reflex values for both airfoils reached the lower boundary, which was different from other studies where the reflex increased towards the tip, reducing the local lift and, thus, minimizing the induced drag [31]. This objective of minimizing induced drag was made by the geometric twist. The lift coefficient distribution of the optimized wing was almost the same elliptical distribution because it was the optimal distribution in induced drag, as seen in Figure 11. The tendency change near the 80% of the semi-span was due to the change in the airfoil. These results suggest that the twist is the best way to get the optimal induced drag distribution, and the parasitic drag should be minimized by the airfoil shape itself in terms of camber and thickness.

5.1.3. Wing Structure

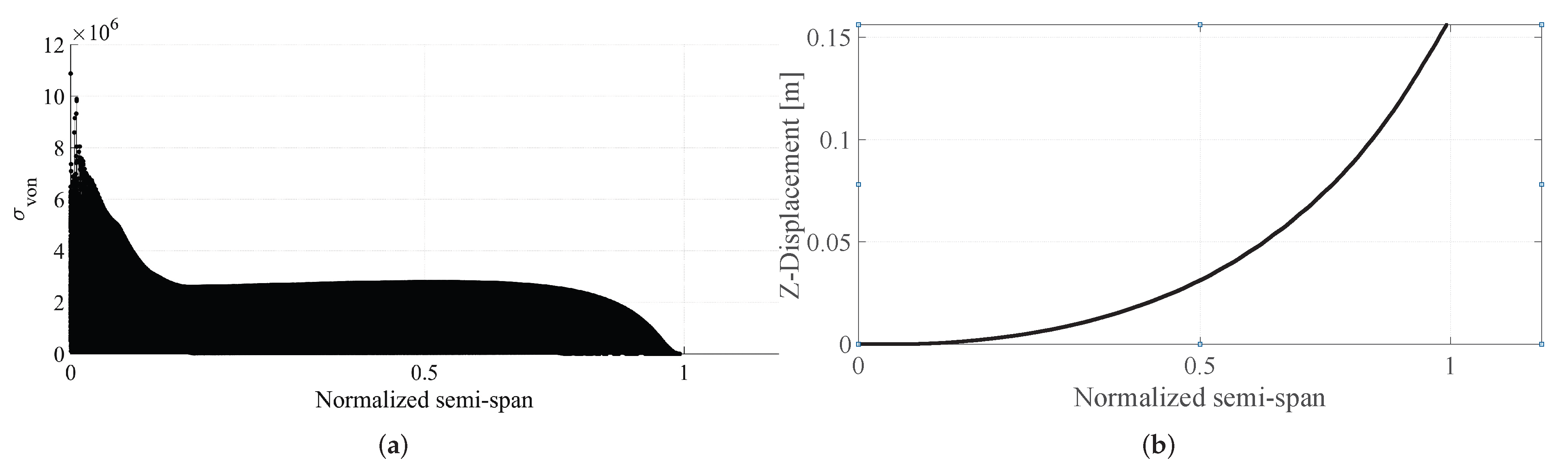
The structural constraint was fulfilled by the optimal, where the ${\sigma }_{von}{\gamma }_f=27.19$ MPa and the ${\sigma }_{yield}=614$ MPa. The mesh had $258.263$ nodes. The von Mises distribution along the semi-span is shown in Figure 12a and the vertical displacement in Figure 12b. The heat map of the von Mises stress at the clamped root is shown in Figure 13. The maximum von Mises stress was at the top-left of the clamped face where the compressive stress caused by drag added to the compressive stress by lift and at the bottom-right where the tension from lift added to the tension of drag. In other locations, the compressive and tension stress had destructive interference.

5.1.4. Wing Stability

The stability criteria in the optimization routine involve the zero pitching moment by moving the gravity center, and then checking the negative sign of the slope of the total moment about this gravity center against the angle of attack. The gravity center of the optimal was at 89.30% of the root chord, which was 10.90 m. The neutral point was at 12.35 m, with a static margin of 16.30%, related to the mean aerodynamic chord of 8.895 m. The static margin for tailless aircraft is usually small or negative, requiring a fly-by-wire control system [2,10,11]. Different studies suggest that a minimum static margin for tailless aircraft is 2% to 8% [33], and an optimal between 15% to 30% [34].

The slope of the moment coefficient at the gravity center against the angle of attack was $C_{M\alpha }=-0.98$, which was negative as expected. This condition is achieved in tailless aircraft by adding reflex to the airfoil or by twisting down the wing tips on a swept wing [34]. The latter approach allows the wingtips to serve as a horizontal tail, but it imposes a significant induced drag penalty. This is the reason that some designs allow significant negative static margins to preserve a near-elliptic span load [2].

However, the current design achieved a remarkable static margin with an almost elliptic lift coefficient distribution, where the only discrepancy occurred at 85% of the semi-span, due to the change in the airfoil. This change is shown in Figure 11b and reflected in the moment coefficient distribution in Figure 14. Moreover, the abrupt increment on the moment distribution occurred towards the tip, where the moment was further behind, and then it had a greater effect on the stability.

Hence, a little deviation from the elliptic distribution is the penalty to achieve longitudinal static stability and a high static margin. The washout also helps to increase the portion of the lift that is generated on the inner part of the wing, reducing the load reactions in the beam root [34]. Although the washout is beneficial for structures and stability, it did not reach the lower boundary within the optimization, suggesting that a low deviation from elliptic distribution is more important to the objective function, which is low drag and weight.

On the other hand, there is no consensus on which method to fulfil the static–stability requirement of tailless aircraft has the lower impact on performance, reflex airfoils, or swept and washout. The upper surfaces of reflex airfoils show high velocities in the first third of the chord, decreasing as the flow reaches the trailing edge [13]. This slow flow raises the pressure by Bernoulli’s principle, which causes loss of lift and increasing drag due to separation.

One study concludes that the airfoil shape is the best option for the subsonic regime and the lower end of the transonic regime [10]. As the flow is usually considered transonic between Mach 0.8 and 1.2, the case study would be in the lower end of the transonic regime, but the optimal was found by a combination of reflex and swept–washout. These results suggest that combining reflex airfoils and swept wing with washout is the best way to achieve an optimal and stable tailless aircraft.

6. Future Work

The algorithm developed is useful for preliminary design. However, it can be extended to account for other constraints and to optimize other desired values. Considering the passengers, cargo, and fuel, the airfoil thickness at the root would increase. Moreover, other structural components can be incorporated for optimization, such as a secondary spar and ribs, or a compound beam.

The distribution of different variables could be optimized with more stations along the semi-span, such as a non-constant twist [10], non-linear chord transition, more airfoil stations, and by allowing compound wings to have different sweep angles.

Other parameters can be added into the objective function with new constraints, such as take-off runway, lateral and dynamic stability, and dihedral angle. Moreover, more accurate aerodynamic models can be incorporated, depending on the computing power availability, such as FlightStream [35] or Reynolds-averaged Navier–Stokes (RANS) solvers, which would allow for incorporating stall constraints in the optimization.

7. Conclusions

The two-way coupled aero-structural optimization carried out by the constrained PSO proved to be a feasible solution in preliminary aircraft design. The Vortex Lattice Method, together with XFOIL, showed satisfactory results with a low computational cost. Similarly, the finite element method applied to the wing structure was fast enough for the optimization, due to the mesh developed, where smaller elements are located only near the root, where the stress increases rapidly.

Despite the recursivity employed, it is known that AVL and XFOIL have convergence issues with airfoils with high camber or thickness, or thick airfoils. A penalty function was applied where these issues emerged. However, it restricted the airfoil design space. A CFD solver could be used instead, but it requires higher computing power and reduces the design space dimension to avoid prohibitive computing times.

A transonic case study was conducted for specific flight conditions, structural material, and aircraft weight and area. The optimization results were analyzed and compared against a baseline optimization of a tailless aircraft. The span efficiency e of the optimized aircraft was almost the same as the original baseline study, but with a considerably higher wing aspect ratio, the induced drag was lower. Moreover, the parasitic drag of the optimized wing was about half of the baseline, mainly because well-established airfoils were employed in the baseline optimization, and the current algorithm created its own airfoil shapes from a six-parameters method. This airfoil parameterization proved to be versatile enough for optimization of tailless aircraft in comparison to other studies that employed the high cost Bezier parameterization [11].

In addition, the induced and parasitic drag were about the same value, which suggests that the entire optimization pushes the design in such a way that the operating point is the minimum drag velocity, where induced and parasitic are equal. Finally, the lift-to-drag ratio achieved by the algorithm was more than twice the baseline, even considering that the baseline study did not consider structural constraints.

The optimized wing aspect ratio was 13.66, which coincides with other studies that suggest 12 for metallic structures. The taper ratio was 0.355, which is almost the same optimal value estimated by lifting line theory. The latter indicates that structures do not highly influence the taper ratio.

The optimal wing had a washout of $-2.86$°, which, along the sweep, works as a tail for stability purposes. The sweep angle was 27°, similar to the baseline optimization of 30º and within the optimal range reported to be 20–40° for tailless aircraft. This sweep reduced the effective Mach number on each airfoil, which helps to eliminate shock waves and corresponding drag. However, the bending and torsional moment increase by sweep, the sweep angle being one of most influencing variables, together with airfoil thickness and wing aspect ratio.

The way tailless aircraft achieve longitudinal stability is by reflex airfoils and by sweep angle and twisting down the tips. However, there is no consensus on which method has the lower impact on performance. Other studies have stated that for subsonic, and the lower end of the transonic, regime, the best way to achieve stability is by the airfoil shape. Nevertheless, the study carried out shows that the optimal way to stabilize a tailless aircraft in the lower end of the transonic regime is the use of both techniques, reflex airfoils and swept–washout. It suggests that an extensive study should be carried out to conclude if this conclusion is also valid for subsonic aircraft. Hence, the use of an airfoil parameterization able to produce reflex airfoils is crucial to achieving low drag and a stable tailless aircraft.

The lift-to-drag ratio distribution along the semi-span showed a maximum at the middle. The latter is probably because the airfoil shape towards the root is highly influenced by the structures requiring a thicker airfoil to allocate a bigger beam, while the airfoil shape towards the tip is influenced more by the stability constraint to have a higher positive moment. The middle zone is where the airfoil is shaped with more freedom to achieve higher aerodynamic efficiency. The impact of the stability constraint in the airfoil shape towards the tip is confirmed by the moment coefficient distribution along the semi-span, where there was an abrupt increase of 85% to the tip, caused by the change in the airfoil shape.

Despite the fact that other studies have employed a non-constant twist to achieve an elliptical lift distribution for tailless aircraft, the current study achieved a distribution that follows almost exactly the elliptical one until 85% of the semi-span, where it deviates and where the moment increases because the airfoil changes. Hence, a little penalty on the performance is imposed to achieve stability. In addition, the reached static margin of $16.3\%$ of the MAC was considerably high, whereas other studies have reported difficulties in having a positive static margin on tailless aircraft or that, even to reach an elliptical lift distribution a high negative static margin is required [2,10,11].

According to the results, to reduce the computational cost of future studies, the wing aspect ratio, sweep angle and taper ratio can be fixed by the optimal values suggested in the literature, especially the taper ratio, which reached the same lifting line theory optimal of 0.355, showing null impact on the structure.