Abstract
To study the influence of the tilt-back design of a vertical tail on its aerodynamic stealth characteristics, an optimization method based on a quantitative weight coefficient and a two-particle search algorithm is presented. When the aerodynamic performance of the vertical tail is optimized separately, the reduction in the drag index is obvious, and the optimal solution appears at the boundary of the backward-tilt range. The optimal solution of separate stealth optimization is different from that of separate aerodynamic optimization within the given range of tilt back. The two-particle search algorithm can provide an optimal solution for comprehensive performance optimization under different weight coefficient distributions, where the fitness index, aerodynamic index, and radar cross-section index are all significantly reduced. The presented optimization method is effective for optimizing the aerodynamic stealth performance of the vertical tail.
1. Introduction
The vertical tail is an important aerodynamic component of aircraft with conventional aerodynamic configurations, such as fighter and attack planes. In order to ensure sufficient heading stability when flying at high altitudes and high speeds, the vertical tail has to occupy a large size, which has a negative impact on the aircraft’s lateral stealth performance [1,2,3]. How to optimize the aerodynamic stealth characteristics of the vertical tail without using the lateral tilt design has gained more interest.
Reasonable tail design affects aircraft performance and flight safety [4], where Reynolds-Averaged Navier–Stokes (RANS) solvers are used to obtain the aerodynamic results under additional flow conditions. The height of the vertical tail, the top surface, the tilt-back angle and the airfoil are considered. The flow field in the vertical tail of the scaled model aircraft under high angle-of-attack flight conditions is simulated [5,6]. In order to optimize the aerodynamic performance of an aircraft wing, detailed steps including the modeling plan, material selection, mesh generation and boundary conditions are presented [7,8]. The problem to be optimized is described, Cowell’s method is used to evaluate the maximum descent time, and the genetic algorithm is used to determine the global optimal solution during the optimization process [9]. The computational fluid dynamics (CFD) method based on the RANS equation is established, and the grids of airfoil surface and flow field space are generated [10,11]. Considering the radar cross-section (RCS) and infrared radiation characteristics, the intake and exhaust system of tailless aircraft is comprehensively designed [12], where unstructured grid technology is used to deal with flow field space. The configuration of a bistatic radar station is introduced, where the azimuth range of the transmitting antenna is 0°~360°, with an accuracy of 0.1° and a speed of 3°/s [13], while the range of required azimuth angles can vary for different observation targets. The vertical tail design with backward tilt can improve the aerodynamic drag characteristics, and the influence on its radar cross-section is worth exploring.
With minimum resistance and maximum durability as the optimization objectives, an optimization method based on particle swarm optimization and the pattern search algorithm is established [14]. The physical optics (PO) method is used to solve the facet RCS of the target [15,16,17]. A mixed element surface model is presented, which is beneficial for reducing its bistatic RCS performance. The physical theory of diffraction (PTD) is adopted to solve the edge contribution [18,19,20]. Different particle swarm optimization algorithms are introduced and compared with other evolutionary algorithms [21,22]. The introduction of multiple archiving operators enables particle swarm optimization to provide support for aircraft aerodynamic optimization [23,24,25]. The improved simulated annealing (SA) algorithm can provide technical support for the shape optimization of the vertical tail by adopting multi-objective indicators [26,27], where the search operators and transformation operations need to be formulated according to specific cases [28,29,30,31]. CFD and shooting and bouncing ray techniques are combined to achieve a comprehensive effect of low resistance and low RCS performance [32,33,34,35], where reasonable frameworks and algorithms can provide solutions for specific models. When pursuing the minimum aerodynamic drag, it is a question worth considering whether the design of vertical tail tilt back can achieve satisfactory results in terms of stealth index.
Obviously, the optimization of the aerodynamic stealth performance of the vertical tail is a multi-objective problem. As shown in the literature, common heuristic search algorithms can obtain satisfactory global optimal solutions. A simulated annealing algorithm is a string structure algorithm based on an iterative solution strategy. Particle Swarm Optimization is a parallel algorithm based on the observation of animal cluster activities. When the total number of searches (determined by the population size and the number of iterations) is determined, how to obtain the global optimal solution that meets the requirements has always been a direct exploration problem. Considering the reduction in aerodynamic drag caused by the design of vertical tail tilt back and the possible change of stealth performance, a comprehensive evaluation index based on quantitative weight coefficient is introduced, which can be used for separate aerodynamic optimization, separate radar stealth optimization, or comprehensive optimization of aerodynamic stealth. In order to determine the global optimal solution in the optimization process, a two-particle search (TPS) algorithm is conceived, where some operators of particle swarm optimization and an improved SA algorithm are used for reference. This research is of engineering value for the aerodynamic stealth design and optimization of the vertical tail.
2. Optimization Method
The diagram of aerodynamic stealth performance optimization of the vertical tail is shown in Figure 1, where the initial line indicates the top leading-edge position of the initial model of the vertical tail. Xt0 represents the distance from the top leading edge of the vertical tail initial model to the yz plane, noting that the symmetry plane of the vertical tail lies in the xz plane. Xt determines the back-tilt design of the updated vertical tail model. α represents the azimuth angle between the target and the radar station, and β represents the elevation angle. D represents the aerodynamic drag of the vertical tail in the flow field. Frh represents radar wave frequency and horizontal polarization.
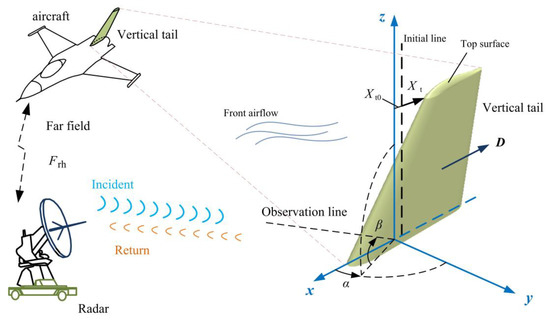
Figure 1.
Schematic of aero-stealth optimization for the backward-tilt vertical tail.
2.1. Quantitative Weight Coefficient
The comprehensive evaluation index of aerodynamic stealth of the vertical tail is determined as follows:
where Ec is a comprehensive evaluation index. Cqw represents the quantitative weight coefficient, and the additional numerical subscripts are used to distinguish different parameters. Dr is the reference value of aerodynamic resistance. σ represents the RCS mean within the given observation range, and σr represents a reference RCS value, noting that the unit of RCS here is m2. The conversion relationship between different units of RCS can be expressed in the following form:
When the occurrence of vertical tail individuals reaches the minimum in terms of comprehensive performance:
where Fn is the fitness function corresponding to the best individual. m is the individual of the vertical tail model. In the optimization process, some design parameters of the vertical tail are always constant, and then the equality constraints can be expressed as:
where Ct is the chord length of the vertical tail top airfoil. Cb is the chord length of the bottom airfoil. Hts is the height of the top surface. Hvm is the height of the main part of the vertical tail. M represents an individual, and subscripts i and j are used to distinguish different individuals. The inequality constraint can be expressed as follows:
where L represents the aerodynamic lift of the individual model. L0 is the limit value of the aerodynamic lift. During the optimization process, the lift of different individuals should not be less than the reference lift.
Generally, the sum of quantitative weight coefficients can be specified as follows:
When the aerodynamic characteristics of the vertical tail need to be optimized separately, the fitness function can be simplified as:
where Fs stands for the fitness function in the case of individual optimization, and additional numerical subscripts are used to distinguish different situations. At this time, Cqw2 = 0; thus, there are the following expressions:
For the optimization of a single performance, concise optimization goals can save computational time. When optimizing the target RCS separately:
where αm is a limit value of azimuth. During the optimization process, the bottom end face of the vertical tail is fixed in the current coordinate system.
2.2. Two-Particle Search Algorithm
This algorithm contains two search particles with a clear division of labor, where one particle (recorded as particle 1) is always responsible for the global search, and the other particle (particle 2) is responsible for searching near the current global optimum. For the particle responsible for the global search, its speed can be updated as follows:
where Xr is the value range of Xt, Ng is the number of iterations, and Rn represents a random number generated by a true random operator, where the additional numeric subscripts are used to distinguish different situations. vn represents the minimum search speed:
where Cn is a coefficient of the minimum search speed. Xm and Xn represent the maximum and minimum values of Xt, respectively. The search speed of another particle can be expressed as:
where Otr is the true random operator. The position of particle 1 can be updated to:
where Nc represents the current number of iterations. The current optimal solution can be updated as follows:
where F(m) is the fitness function. X* is the optimal solution when the fitness function is the smallest. Xg is the current global optimal solution. On this basis, the position of particle 2 can be updated as:
Therefore, the current optimal solution can be generated as follows:
As the search process continues, particle 1 can provide potential excellent individuals for particle 2 within a given number of iterations, while particle 2 will seek the optimal solution near these excellent individuals.
The presented search algorithm is verified, as shown in Figure 2, where the improved SA algorithm is used to obtain comparative data. For the SA method, the initialization temperature is set to 300 °C, and the final judgment temperature is 0.01 °C. The temperature drop rate is equal to 0.51, and the solution space size is equal to 5. The optimal solution obtained by this SA method is 2.4432 m, where the RCS indicator is −26.8021 dBm2. It can be seen that the change rule of the RCS index with Xt displayed by the search algorithm is obvious. For the TPS method, the number of iterations is set to 30, where Cn = 0.5, p1 stands for particle 1, and p2 refers to particle 2. The optimal solution determined by TPS is 2.4322 m, where the RCS indicator is −26.8048 dBm2. These results show that the presented TPS algorithm is able to assist in optimizing the performance index of the vertical tail.
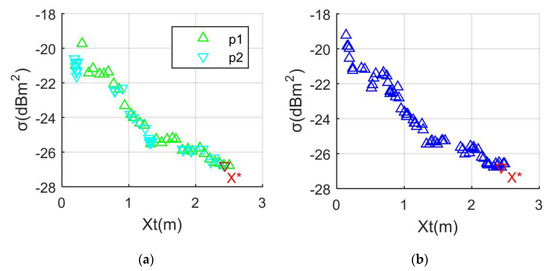
Figure 2.
Verification of the search algorithm. αm = 60°, Frh = 6 GHz, β = 0°: (a) TPS results; (b) SA results.
2.3. Aerodynamic Calculation
The CFD method based on the RANS equation is established to solve the flow field of the vertical tail, where the governing equation can be expressed as follows:
where t is time, V is volume, W refers to the conservation variable, Fc stands for the convection flux, Fv represents the viscous flux, and S is area. The standard k-ε two-equation model is adopted as the turbulence solver. Density, pressure, momentum, energy, and turbulent flow energy are all discretized by the second-order upwind scheme. The far-field fluid pressure is set at 101,325 Pa, and the temperature is 300 K. The incoming flow velocity is in the negative direction along the x-axis. For the dynamic boundary of the flow field, the derivative of pressure along the normal direction of the wall is zero:
where pw is the fluid pressure on the surface of the object, ρ1 is the fluid density of adjacent units, ρw is the fluid density on the surface of the object, and p1 is the fluid pressure of adjacent units. For thermodynamic boundary conditions, the derivative of temperature along the normal direction of the wall is zero:
where T represents temperature, indicating that the wall surface is an adiabatic wall.
The presented CFD method is verified, as shown in Figure 3, where V∞ refers to the incoming flow velocity, and Ps stands for the static pressure. The reference data come from the calculation results based on the renormalization group (RNG) turbulence model. It can be seen that the static pressure data obtained by the two methods are similar in change amplitude, curve shape, and overall trend. These results show that the CFD presented here is feasible for solving the flow field of the vertical tail.
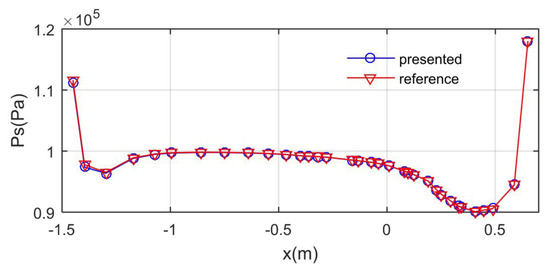
Figure 3.
Verification of the CFD method: Xt = 0.1 m; vertical tail wall section y > 0 m; z = 1.5 m; V∞ = 125.8 m/s.
2.4. RCS Assessment
The vertical tail side panel, the top surface, and the area near the leading edge are all surface features; thus, PO is used to calculate the scattering contribution of the facet. Considering the diffraction contribution of the leading edge, trailing edge, and end face edge, PTD is used to calculate edge diffraction. For areas with edge characteristics, the surface current can be expressed as:
where JS represents the surface current, JPTD means the current corresponding to PTD, and JPO is the current corresponding to PO. Therefore, the radar cross-section of the target can be expressed as follows:
where σt represents the total RCS of the target, subscript F refers to the facet contribution, and E means the edge contribution. NE is the number of edges, and NF represents the number of facets. The calculation method of the radar cross-section is verified, as shown in Figure 4, where the reference data come from the calculation results of PO + MOM (Method of Moment). It can be seen that the two data curves are similar in peak value, mean level, curve shape, and overall trend. These results show that the RCS calculation method presented is able to analyze the electromagnetic scattering characteristics of the vertical tail.
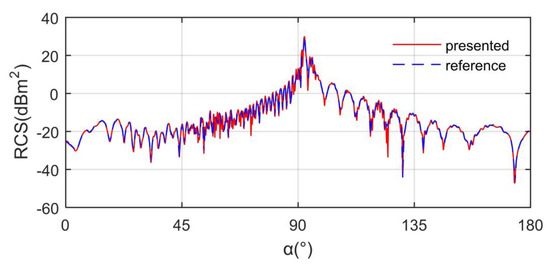
Figure 4.
Verification of the RCS calculation: Xt = 0.1 m; Frh = 6 GHz; β = 0°.
3. Model Establishment
The model of the vertical tail is established, as shown in Figure 5, where the symmetry plane of the vertical tail is always in the xz plane when in the optimization process. In addition, the configuration line of the top surface remains unchanged. The airfoil with a vertical tail section adopts a customized symmetrical airfoil. The data of the end face and height of the vertical tail model are shown in Table 1.
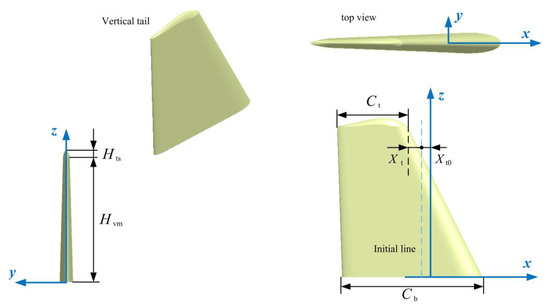
Figure 5.
Model of the vertical tail.

Table 1.
Parameters of the vertical tail.
The external flow field is a cuboid with a length of 55 m, a width of 60 m, and a height of 60 m, as seen in Figure 6, where the front-end face is 20 m away from the yz plane. The upper and lower end faces of the external flow field boundary are symmetric about the xy plane. The internal flow field is located in the front of the space center of the external flow field.
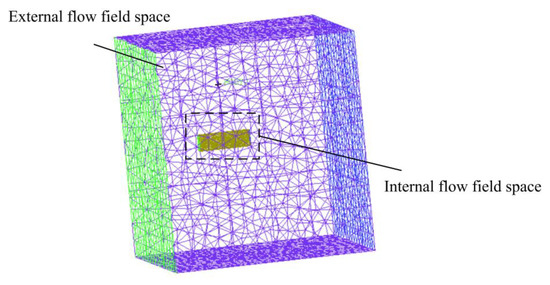
Figure 6.
Construction of the external flow field area.
The internal flow field is a narrow cuboid with a length of 14 m, a width of 2.7 m, and a height of 4.3 m, as shown in Figure 7, where the front-end face is 5 m from the yz plane. The top plane of the internal flow field is 3.75 m from the xy plane. In addition, the center of the internal flow field is located in the xz plane.
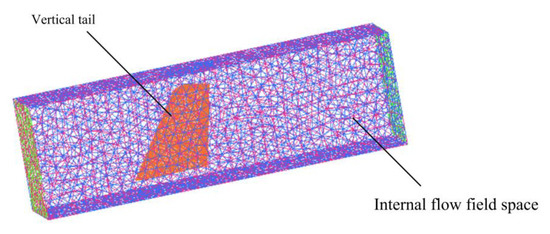
Figure 7.
Construction of the internal flow field area.
The wall surface of the vertical tail, the internal flow field space and the external flow field space have been processed through high-precision unstructured grid technology. The grid size of different areas of the vertical tail is shown in Table 2, where the minimum grid size for wall areas is determined based on the global minimum size. The mesh quality of the bottom profile, leading edge, trailing edge, and top surface edge of the vertical tail has been improved. The global minimum size is adopted to improve the mesh generation quality of small geometric features in the whole flow field space.

Table 2.
Grid size of the vertical tail model.
4. Results and Discussion
Figure 8 shows that in the current observation section, there is an obvious high-pressure zone near the leading edge of the vertical tail, which is shown in red, where the static pressure can reach 115,975.86 Pa. Under current observation conditions, the Reynolds number of the test case is 17.1 million. The static pressure color changes from red to orange and then to green when viewed from the front edge point along the vertical tail wall to the side. Near the midpoint of the vertical tail side panel, the static pressure is reduced to 98,012.945 Pa. When the observation point continues to move near the tail vertex, the static pressure data recovers to 109,239.77 Pa. Based on flow field calculation results, the aerodynamic moment around the positive direction of the z-axis is −146.4263 N∙m. These results show that the CFD method established here is feasible to analyze the flow field characteristics of this vertical tail under current conditions.
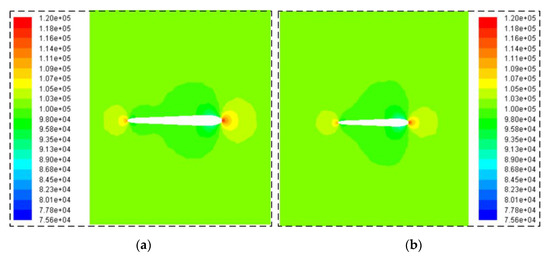
Figure 8.
Flow field analysis: Xt = 0.1 m; V∞ = 125.8 m/s; static pressure (Pa); (a) Section z = 0.5 m; (b) Section z = 2.5 m.
4.1. Separate Aerodynamic Optimization
When only the aerodynamic optimization of the vertical tail is needed, the quantitative weight coefficient of the stealth index cannot be considered, that is, Cqw2 = 0. Figure 9 shows that the aerodynamic resistance index increases slightly with the increase in Xt and then keeps decreasing continuously, within the given range. When Xt = 0.3736 m, the aerodynamic drag of the vertical tail reaches 1171 N. As Xt increases to 1.098 m, the D value decreases to 994.2 N. The optimal solution obtained from TPS is 2.5 m, and the aerodynamic drag of the vertical tail is 772.902 N. Due to the local search ability of particle 2, the overall Fs1n–Gen curve shows a gradual downward trend, where Fs1n represents the minimum value of Fs1 within the current iteration number, and Gen represents the number of iterations. After 12 iterations of the TPS algorithm, Fs1n is greatly reduced to 892.7 N. As a whole, the aerodynamic drag index after optimization is reduced by 366.098 N, while the reduction in Fs1n is also satisfactory.
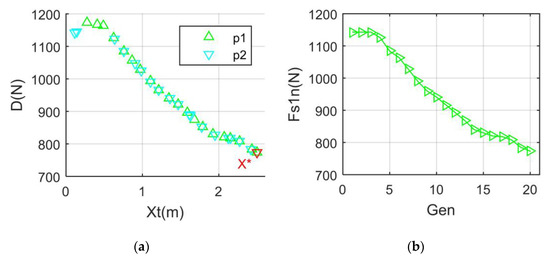
Figure 9.
Aerodynamic optimization: Xn = 0 m; V∞ = 125.8 m/s; (a) Drag index; (b) Min Fs1.
Figure 10 shows that the backward-tilt design can significantly change the flow field characteristics near the wall of the upper half of the vertical tail. At the same height, the static pressure at the leading edge is higher than that at the side. In the transition area between the leading edge and the side, a narrow light blue low-pressure area appears. Considering the wall static pressure at the bottom, it can be found that the static pressure near the leading-edge point is as high as 116,376.05 Pa, while the static pressure at the side at the close height is 99,171.32 Pa. Due to a large amount of backward inclination of the vertical tail, the downward component of the leading-edge pressure increases, noting that the aerodynamic force of the vertical tail along the negative z-axis is −610.475 N. Because the centers of the facets on the top of the trailing edge are far away from the z-axis, the contribution of aerodynamic torque on these panel surfaces is significant, where the aerodynamic moment of the vertical tail around the z-axis positive direction is 352.0966 N.m. It can be seen that under existing conditions, optimizing aerodynamic resistance indicators alone can achieve sufficient reductions, while there will be certain losses in lift and aerodynamic torque. Therefore, in order to obtain comprehensive and excellent aerodynamic individuals, it is feasible to incorporate more aerodynamic indicators into the target performance. The streamlines of particles at the top of the vertical tail well fit the wall of the top surface and pull out a long track to the rear. For the main part of the vertical tail, due to the back-tilt design and wingtip effect, the streamline passing through the leading edge first slightly deflects upward and then flows backward. In addition, the streamline length of the bottom particle is significantly longer than that of the middle particle.
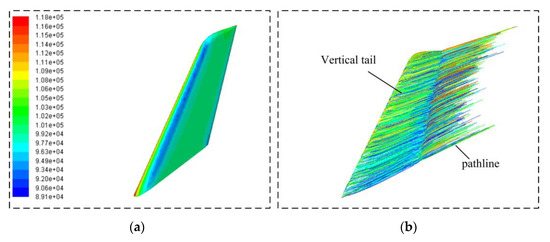
Figure 10.
Aerodynamic analysis: Xt = 2.5 m; V∞ = 125.8 m/s; (a) Static pressure (Pa); (b) Path line.
4.2. Separate Stealth Optimization
Figure 11 shows that the RCS index of the vertical tail has obtained an obvious reduction effect after optimization. Similarly, when conducting independent stealth optimization, the quantitative weight coefficient related to aerodynamics is ignored, i.e., Cqw1 = 0. It can be seen that the RCS index decreases with the increase in Xt on the whole, while there are many local fluctuations. When Xt = 0.1729 m, the RCS of the vertical tail is −21.49 dBm2 because the surface near the leading edge and side panel of the vertical tail provides more scattering contributions. As Xt increases to 1.303 m, the RCS index of the vertical tail decreases to −26.22 dBm2 after several fluctuations. It can be found that the optimal solution determined by the TPS algorithm is 2.3258 m, and the RCS index at this time is as low as –28.2899 dBm2. Obviously, this optimal solution is different from that of the aerodynamic optimization alone. In the whole optimization process, the performance of the minimum fitness is also satisfactory, where Fs2n represents the minimum value of Fs2 within the current iteration number. After 21 iterations, Fs2n is reduced to −25.51 dBm2, noting that the reduction in Fs2n in the whole optimization process reaches 6.8 dBm2. The performance of RCS indicators under different individuals is shown in Table 3. It can be seen that the RCS at the maximum value of Xt is significantly different from that at the optimal solution. These results show that the TPS method is beneficial for optimizing the electromagnetic scattering characteristics of the vertical tail.
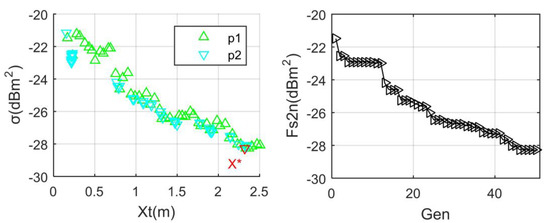
Figure 11.
Stealth optimization: Xn = 0 m; αm = 50°; Frh = 6 GHz; β = 0°.

Table 3.
RCS of the vertical tail.
Figure 12 shows that the optimized vertical tail has a significant reduction in RCS mean and peak values. When α = 16°, the surface near the leading edge of the vertical tail is a red strong scattering source. More orange and a little light red are distributed on the side of the vertical tail. The top surface is mainly orange, yellow, and a small amount of light blue. Near the bottom leading edge, the scattering feature changes from bright red to orange as the viewing area moves from the leading edge to the front-side surface. In the middle part of the bottom end face, the surface features are mainly orange, yellow, and a little green. Near the rear edge of the vertical tail, the surface features are mainly yellow, with a small amount of orange and a little cyan. When Xt = 0.28 m, the RCS curve has several peaks exceeding −14.43 dBm2, where the RCS mean is −21.25 dBm2. For the case of Xt = 0.6916 m, the peak value of the RCS curve is as high as –10.6472 dBm2 appearing at α = 50° because the front-side transition region provides many scattering contributions. The RCS mean of the curve with Xt = 0.1.129 m is –24.85 dBm2, while the peak performance of this curve is not prominent compared with the other three curves. Under most azimuths within the observation range, the RCS value of the X* curve is significantly lower than that of the other three curves. When α = 39.75°, the RCS of the curve with X* is −37.08 dBm2, while that of the curve with Xt = 0.28 m is −19.4 dBm2. These results show that the presented TPS algorithm is effective for optimizing the RCS index of the vertical tail.
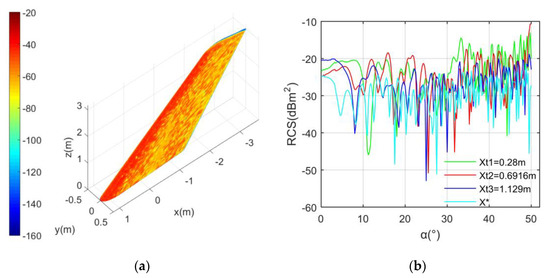
Figure 12.
RCS analysis of the vertical tail: RCS unit: dBm2; Frh = 6 GHz; β = 0°; (a) Surface scattering, M(X*), α = 16°; (b) RCS curve.
4.3. Aero-Stealth Optimization
When Cqw1 > Cqw2, the comprehensive evaluation index takes more account of the impact of the aerodynamic performance index. Figure 13 shows that the comprehensive evaluation index generally shows a decreasing trend with local fluctuations as Xt increases. When Xt = 1.118 m, the value of Ec decreased from the original high level to 1.512. As Xt continues to decrease to 1.976 m, Ec further decreases to 1.161. It can be found that the optimal solution determined by TPS is Xt = 2.4374 m, and the comprehensive evaluation index is 0.9856, noting that Ec = 1 when Xt = 2.5 m. Because of the quantitative weight Cqw1 = 0.7, the optimization solution of the comprehensive evaluation is more inclined to the result of independent aerodynamic optimization. As the number of iterations increases to 16, the value of Fn decreases from 2.102 to 1.284. When Gen = 29, the value of Fn is reduced to 0.9915. On the whole, Fn shows a stepwise decline with the increase in Gen. These results show that the presented TPS method is effective for optimizing the aero-stealth comprehensive index of the vertical tail.
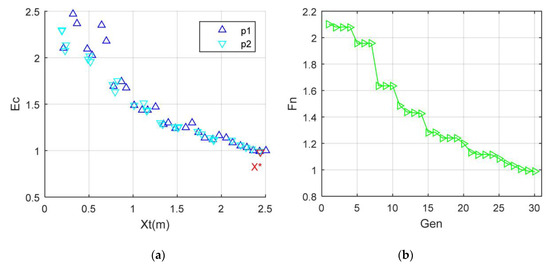
Figure 13.
Aero-stealth optimization: Cqw1 = 0.7; Cqw2 = 0.3; αm = 50°; Frh = 6 GHz; β = 0°; Xm = 2.5 m; V∞ = 125.8 m/s; (a) Comprehensive evaluation index; (b) Fn results.
Compared with the air velocity near the leading edge, the velocity of the front-side transition zone is significantly improved, as shown in Figure 14. Considering the velocity characteristics of the flow field near the bottom end face, a particle velocity vector near the leading edge is green and the velocity is 107.8173 m/s, while the velocity vector of a particle in the front-side transition zone is orange and the velocity is 135.9183 m/s.
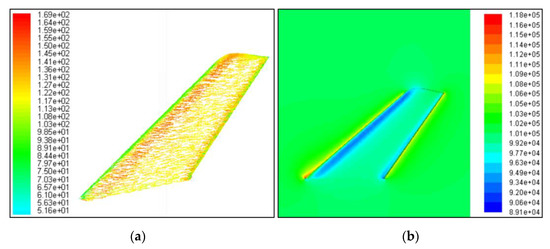
Figure 14.
Flow field analysis: Xt = 2.5 m; V∞ = 125.8 m/s; (a) Vector display, velocity (m/s); (b) Section y = 0, static pressure (Pa).
Near the bottom end face, the velocity of a particle in the middle of the side is 110.1591 m/s. Considering the top surface of the vertical tail, the velocity vector of some particles is green, and the velocity range is [96.1086, 107.8173] m/s. It can be found that there are obvious high- and low-pressure areas near the bottom leading edge, where the red area with high pressure of 117,809.75 Pa appears above the leading edge, while the low-pressure area with low pressure of 92,512.32 Pa appears below the bottom end face. From the bottom up along the leading edge, the static pressure near the leading-edge changes from red to yellow and then to cyan. Near the arc of the top surface, there are green (about 101,630.02 Pa) and cyan low-pressure areas.
4.4. Stealth-Aerodynamic Optimization
Since Cqw1 < Cqw2, the comprehensive evaluation index of the vertical tail is more affected by the stealth performance. Figure 15 shows that the initial size of Ec is obviously higher than that of the aero-stealth optimization. When Xt = 0.3256 m, the value of Ec is as high as 3.518. Because of the scattering contribution of the vertical tail leading edge and the front-to-side surface, the conversion of stealth performance makes the initial Ec level higher. As Xt increases to 0.8003 m, the value of Ec rapidly decreases to 1.913. It can be found that the optimal solution determined by TPS is X* = 2.3145 m, and the comprehensive evaluation index at this time is 0.9555. Because of different quantitative weight distributions, the optimal solution here is different from that of the previous aero-stealth optimization example. Between Xt = 0.65 m and Xt = 0.82 m, the reduction in the comprehensive evaluation index is obvious. Near the optimal solution, some feasible solutions with a low comprehensive evaluation index exist, including Xt = 2.235 m and Xt = 2.374 m. Due to the impact of multiple fluctuations in the RCS–Xt curve, Ec-Xt data features also exhibit many minimum values. As the number of iterations increases to 11, the value of Fn decreases rapidly to 1.597. When Gen = 24, the value of Fn is as low as 0.9862. It can be noted that the overall performance of the Fn–Gen curve is satisfactory under current conditions. Compared with the case where the aerodynamic weight coefficient is greater than the stealth weight coefficient, the initial level of the fitness indicator here is still slightly higher. When the number of iterations increases from 6 to 7, the fitness index decreases dramatically because at this time, two particles in the search algorithm have accumulated a certain number of initial samples and updated the individuals with the current minimum fitness, which significantly reduces the fitness of particle 2.
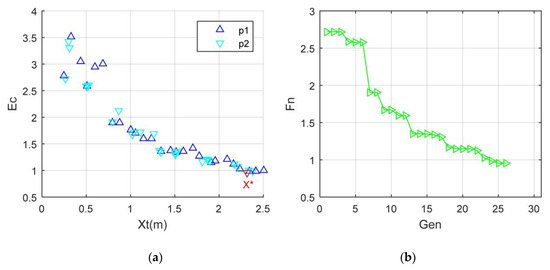
Figure 15.
Stealth-aerodynamic optimization: Cqw1 = 0.37; Cqw2 = 0.63; αm = 50°; Frh = 6 GHz; β = 0°; Xm = 2.5 m; V∞ = 125.8 m/s; (a) Ec results; (b) Fn results.
Figure 16 shows that under the given observation conditions, the scattering characteristics of the side panel of the vertical tail have changed significantly after optimization. For the case at Xt = 0.3256 m, the front edge of the vertical tail shows a large amount of red and a small amount of dark red. On the top surface, orange, yellow (about −75 dBm2), and a small amount of light blue (about −122 dBm2) are obvious. There is a lot of red and light red (about −50 dBm2) on the side of the vertical tail, and there is a small amount of orange and yellow between the red and light red. For the case at X*, the original small amount of dark red area on the leading-edge changes to red due to the increase in the design amount of vertical tail tilt back. Under current conditions, some panels near the leading edge are more likely to deflect some incident waves in non-threatening directions. Orange, yellow and a few blue (about −130 dBm2) features are distributed on the top surface of the vertical tail. On the side of the vertical tail, the original large number of red and light red areas have been significantly reduced, while the orange area has been greatly increased. These results show that stealth-aerodynamic optimization directly changes the scattering characteristics of the vertical tail surface.
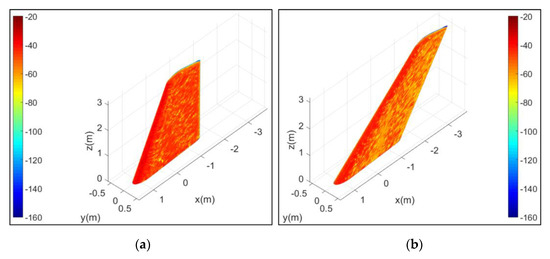
Figure 16.
Surface scattering analysis: RCS unit: dBm2; α = 25°; Frh = 6 GHz; β = 0°; (a) Case at Xt = 0.3256 m; (b) Case at X*.
Figure 17 shows that the RCS performance of the vertical tail in the given range after comprehensive optimization is satisfactory. When Xt = 0.3256 m, the RCS curve has several peaks exceeding −16.18 dBm2, where the RCS mean is −21.1199 dBm2. At this time, the aerodynamic resistance of the vertical tail is 1174.896 N. With Xt increasing to 0.8003 m, the peak value of the RCS curve is significantly weakened, and the average RCS is reduced to −24.6751 dBm2, where the drag index is 1073.162 N. For the case at Xt = 1.777 m, the RCS mean is −26.8057 dBm2, where the aerodynamic resistance of the vertical tail is 854.895 N. At α = 40.75°, the RCS of the X* curve is −40.43 dBm2, and that of the X* curve is −16.07 dBm2 because the scattering characteristics of the front-to-side transition surface of the vertical tail are weakened. Compared with the other three RCS curves, the curve of X* has a smaller local peak and a lower mean level. The RCS mean of the X* curve is −28.6256 dBm2, where the drag index is 800.8665 N. It can be seen that the aerodynamic performance index and stealth performance index of the optimized vertical tail have been improved. These results show that different quantitative weight coefficients can still be combined with the established TPS algorithm to realize the stealth-aerodynamic optimization of the vertical tail.
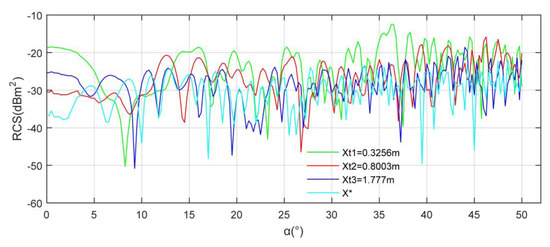
Figure 17.
RCS Analysis: αm = 50°; Frh = 6 GHz; β = 0°; Xm = 2.5 m.
5. Conclusions
Based on the quantitative weight coefficient and two-particle search algorithm, the optimization method of aerodynamic stealth performance of the vertical tail is established. Through the discussion of the aerodynamic analysis of the vertical tail, electromagnetic scattering results, and aerodynamic stealth optimization, the following conclusions can be drawn in this paper:
- (1)
- When only the weight coefficient of the aerodynamic performance index is considered, the two-particle search algorithm can provide a satisfactory optimal solution, while under the given conditions, the reduction in aerodynamic drag can reach 398.098 N;
- (2)
- In the same backward-tilt range, the optimal solution of separate stealth optimization is different from that of separate aerodynamic optimization, where the reduction in target performance is 6.7999 dBm2 when optimizing the stealth index alone;
- (3)
- When the weight coefficient of the aerodynamic index is greater than that of the stealth index, the two-particle algorithm can provide a satisfactory optimal solution for the aero-stealth optimization, where the comprehensive performance index and fitness index have been significantly reduced;
- (4)
- Considering the weight coefficient of the stealth index is greater than that of the aerodynamic index, the initial level of comprehensive performance indicators has changed significantly while the reduction effect is satisfactory, where the aerodynamic index has been reduced by 374.0295 N, and the RCS peak and mean indicator have been significantly reduced.
Author Contributions
Conceptualization and methodology, Z.Z. and J.H.; formal analysis and validation, Z.Z.; investigation and visualization, Z.Z. and J.H.; writing—original draft preparation, Z.Z.; writing—review and editing, Z.Z. and J.H.; funding acquisition, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the Project funded by the China Postdoctoral Science Foundation (Grant Nos. BX20200035, 2020M680005).
Data Availability Statement
Not applicable.
Acknowledgments
Thanks to Jun Huang for guiding the research in this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nicolosi, F.; Ciliberti, D.; Della Vecchia, P.; Corcione, S.; Cusati, V. A comprehensive review of vertical tail design. Aircr. Eng. Aerosp. Technol. 2017, 8, 547–557. [Google Scholar] [CrossRef]
- Liang, H.S. Stealth technology for radar onboard next generation fighter. Mod. Radar 2018, 40, 11–14. [Google Scholar]
- Moëns, F. A Fast Aerodynamic Model for Aircraft Multidisciplinary Design and Optimization Process. Aerospace 2023, 10, 7. [Google Scholar] [CrossRef]
- Ciliberti, D.; Della Vecchia, P.; Nicolosi, F.; De Marco, A. Aircraft directional stability and vertical tail design: A review of semi-empirical methods. Prog. Aerosp. Sci. 2017, 95, 140–172. [Google Scholar] [CrossRef]
- Dong, Y.; Chen, Y.; Peng, J. Development and prospect of variable swept wing. Flight Dyn. 2014, 32, 97–100. [Google Scholar]
- Lee, B.H.K. Vertical tail buffeting of fighter aircraft. Prog. Aerosp. Sci. 2000, 36, 193–279. [Google Scholar] [CrossRef]
- Azeez, A.A.; Gadala, M.; Al Khudhiri, N.; Dol, S.S. Aerodynamics optimization of RC plane winglet. In Proceedings of the 2019 8th International Conference on Modeling Simulation and Applied Optimization (ICMSAO), Manama, Bahrain, 15–17 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Zhang, Y.; Xu, S.; Wan, Y. Performance improvement of centrifugal compressors for fuel cell vehicles using the aerodynamic optimization and data mining methods. Int. J. Hydrog. Energy 2020, 45, 11276–11286. [Google Scholar] [CrossRef]
- D’Amato, E.; Notaro, I.; Panico, G.; Blasi, L.; Mattei, M.; Nocerino, A. Trajectory Planning and Tracking for a Re-Entry Capsule with a Deployable Aero-Brake. Aerospace 2022, 9, 841. [Google Scholar] [CrossRef]
- Hassanpour, M.; Azadani, L.N. Aerodynamic optimization of the configuration of a pair of vertical axis wind turbines. Energy Convers. Manag. 2021, 238, 114069. [Google Scholar] [CrossRef]
- Mader, C.A.; Kenway, G.K.W.; Yildirim, A.; Martins, J.R. ADflow: An open-source computational fluid dynamics solver for aerodynamic and multidisciplinary optimization. J. Aerosp. Inf. Syst. 2020, 17, 508–527. [Google Scholar] [CrossRef]
- Zhou, Z.; Huang, J. Mixed design of radar/infrared stealth for advanced fighter intake and exhaust system. Aerosp. Sci. Technol. 2021, 110, 106490. [Google Scholar] [CrossRef]
- Pisanu, T.; Muntoni, G.; Schirru, L.; Ortu, P.; Urru, E.; Montisci, G. Recent Advances of the BIRALET System about Space Debris Detection. Aerospace 2021, 8, 86. [Google Scholar] [CrossRef]
- Bashir, M.; Longtin-Martel, S.; Botez, R.M.; Wong, T. Aerodynamic design optimization of a morphing leading edge and trailing edge airfoil–application on the uas-s45. Appl. Sci. 2021, 11, 1664. [Google Scholar] [CrossRef]
- Zhou, Z.; Huang, J. Auto Sweptback Wing Based on Low Scattering Demand for an Unmanned Aerial Vehicle in Phase Flight. Aerospace 2022, 9, 757. [Google Scholar] [CrossRef]
- Sharma, A.; Ghosh, S.; Srivastava, K.V. A polarization-insensitive band-notched absorber for radar cross section reduction. IEEE Antennas Wirel. Propag. Lett. 2020, 20, 259–263. [Google Scholar] [CrossRef]
- Peršić, J.; Marković, I.; Petrović, I. Extrinsic 6dof calibration of a radar–lidar–camera system enhanced by radar cross section estimates evaluation. Robot. Auton. Syst. 2019, 114, 217–230. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Y.; Wu, T.; Cao, J.; Chen, Z.; Guan, J. Broadband radar cross section reduction by in-plane integration of scattering metasurfaces and magnetic absorbing materials. Results Phys. 2019, 12, 1964–1970. [Google Scholar] [CrossRef]
- Rahman, S.U.; Cao, Q.; Akram, M.R.; Amin, F.; Wang, Y. Multifunctional polarization converting metasurface and its application to reduce the radar cross-section of an isolated MIMO antenna. J. Phys. D Appl. Phys. 2020, 53, 305001. [Google Scholar] [CrossRef]
- Zhou, Z.; Huang, J. Numerical investigations on radar cross-section of helicopter rotor with varying blade pitch. Aerosp. Sci. Technol. 2022, 123, 107452. [Google Scholar] [CrossRef]
- Pervaiz, S.; Ul-Qayyum, Z.; Bangyal, W.H.; Gao, L.; Ahmad, J. A systematic literature review on particle swarm optimization techniques for medical diseases detection. Comput. Math. Methods Med. 2021, 2021, 5990999. [Google Scholar] [CrossRef]
- Jahandideh-Tehrani, M.; Bozorg-Haddad, O.; Loáiciga, H.A. Application of particle swarm optimization to water management: An introduction and overview. Environ. Monit. Assess. 2020, 192, 181. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Yang, Y.; Wang, Z.; Zhang, S.; Sun, X.; Feng, W. Design and Shape Monitoring of a Morphing Wing Trailing Edge. Aerospace 2023, 10, 127. [Google Scholar] [CrossRef]
- Xia, X.; Gui, L.; Yu, F.; Wu, H.; Wei, B.; Zhang, Y.-L.; Zhan, Z.-H. Triple archives particle swarm optimization. IEEE Trans. Cybern. 2019, 50, 4862–4875. [Google Scholar] [CrossRef] [PubMed]
- Shan, X.; Wang, Y.; Ji, Z. Energy efficiency optimization for discrete workshop based on parametric knowledge pigeon swarm algorithm. J. Syst. Simul. 2017, 29, 2140. [Google Scholar]
- Fathollahi-Fard, A.M.; Govindan, K.; Hajiaghaei-Keshteli, M.; Ahmadi, A. A green home health care supply chain: New modified simulated annealing algorithms. J. Clean. Prod. 2019, 240, 118200. [Google Scholar] [CrossRef]
- Yang, Q.; Deng, M.; Peng, Y. Urban UAV Path Planning Based on improved Beetle search algorithm. J. Syst. Simul. 2022, 8, 192760–192776. [Google Scholar] [CrossRef]
- Cai, Z.; Gao, Z. Design of a variable sweep wing driving mechanism and CFD simulation. J. Mach. Des. 2018, 35, 17–22. [Google Scholar]
- Zhou, Z.; Huang, J. Y-type quadrotor radar cross-section analysis. Aircr. Eng. Aerosp. Technol. 2022; ahead-of-print. [Google Scholar] [CrossRef]
- Su, F. 3D Path Planning of UAVs Based on Improved Bat Algorithm. Radio Engineering. 2022. Available online: https://kns.cnki.net/kcms/detail/13.1097.TN.20221028.0954.010.html (accessed on 28 October 2022).
- Al-Qassar, A.A.; Abdulkareem, A.I.; Humaidi, A.J.; Ibraheem, I.K.; Azar, A.T.; Hameed, A.H. Grey-wolf optimization better enhances the dynamic performance of roll motion for tail-sitter VTOL aircraft guided and controlled by STSMC. J. Eng. Sci. Technol. 2021, 16, 1932–1950. [Google Scholar]
- Taj, Z.U.D.; Bilal, A.; Awais, M.; Salamat, S.; Abbas, M.; Maqsood, A. Design Exploration and Optimization of Aerodynamics and Radar Cross Section for a Fighter Aircraft. Aerosp. Sci. Technol. 2023, 133, 108114. [Google Scholar] [CrossRef]
- Saheby, E.B.; Hays, A.P.; Xing, S. Aerodynamic design and evaluation of an open-nose supersonic drone. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 236, 3387–3410. [Google Scholar] [CrossRef]
- Klimczyk, W.; Sieradzki, A. RANS-Based Aeroacoustic Global Sensitivity Study and Optimization of UAV Propellers. Aerospace 2023, 10, 306. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.G.; Zhang, L. Deployment of SMP Miura-ori sheet and its application: Aerodynamic drag and RCS reduction. Chin. J. Aeronaut. 2022, 35, 121–131. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).