Abstract
Launching satellites into the Earth’s orbit is a critical area of research, and very demanding satellite services increase exponentially as modern society takes shape. At the same time, the costs of developing and launching satellite missions with shorter development times increase the requirements of novel approaches in the several engineering areas required to build, test, launch, and operate satellites in the Earth’s orbit, as well as in orbits around other celestial bodies. One area with the potential to save launching costs is that of the structural integrity of satellites, particularly in the launching phase where the largest vibrations due to the rocket motion and subsequent stresses could impact the survival ability of the satellite. To address this problem, two important areas of engineering join together to provide novel, complete, and competitive solutions: topology optimisation methods and additive manufacturing. On one side, topology optimisation methods are mathematical methods that allow iteratively optimising structures (usually by decreasing mass) while improving some structural properties depending on the application (load capacity, for instance), through the maximisation or minimisation of a uni- or multi-objective function and multiple types of algorithms. This area has been widely active in general for the last 30 years and has two main core types of algorithms: continuum methods that modify continuous parameters such as density, and discrete methods that work by adding and deleting material elements in a meshing context. On the other side, additive manufacturing techniques are more recent manufacturing processes aimed at revolutionising manufacturing and supply chains. The main exponents of additive manufacturing are Selective Laser Melting (SLM) (3D printing) as well as Electron Beam Melting (EBM). Recent trends show that topology-optimised structures built with novel materials through additive manufacturing processes may provide cheaper state-of-the-art structures that are fully optimised to better perform in the outer-space environment, particularly as part of the structure subsystem of novel satellite systems. This work aims to present an extended review of the main methods of structural topology optimisation as well as additive manufacture in the aerospace field, with a particular focus on satellite structures, which may set the arena for the development of future satellite structures in the next five to ten years.
Keywords:
structural topology optimisation; continuum topology; density methods; aerospace satellite structure; additive manufacture; homogenisation; SIMP; level-set methods; evolutionary structural optimisation ESO; BESO; SBESO; topological derivative; phase-field method; metaheuristics; genetic algorithm; machine learning; review For the goal is not the last, but the best.
Aristotle
1. Introduction
As modern society evolves into a globally interconnected entity, providing high-quality real-time solutions to most human problems, the required infrastructure to support current and future trends grows exponentially in terms of both technological challenges as well as costs. The aerospace industry is no exception. Although the hunger for scientific knowledge drives human beings to explore beyond Earth into the depths of the solar system through physically visiting our cosmic neighbourhood, the rush to attend to the necessities of ever-increasing humankind with ever-demanding and reliable global services [], boosts the industry related to the design, development, test, launch, operation, and disposal of satellite technologies in Earth’s orbit.
In this sense, the satellite industry holds much pressure to evolve, providing systems which are more optimised, efficient, less expensive, and more sustainable for the planet, as our resources are limited []. In this sense, much of the current research is devoted to tackling one or more of the aforementioned aspects, and it is expected to increase exponentially in the following decades [].
A key aspect is to reduce launch costs, as nowadays, launching a satellite to Low Earth Orbit (LEO) costs between EUR 20,000 and EUR 100,000 per kilogram of mass []; such a cost increases drastically to reach the GeoStationary Orbit (GEO). Although such costs are considered affordable for large aerospace companies and large space agencies of developed countries, it is clear that they hinder the development of satellite technologies for small companies, start-ups, and educational entities, as well as for underdeveloped countries.
Although the obvious tactic to bring down such costs is in the research of cheaper and more efficient rocket designs and better fuels, a possible solution within the reach of satellite manufacturers and sponsors is the mass reduction in the satellite [].
In this sense, probably the most effective way to reduce the mass of a satellite is in the structural subsystem that makes up the satellite itself. However, such an action could have an immediate effect on the overall capability of the satellite to withstand mechanical loads present during the launch phase, which are the most critical during the life-cycle of the satellite []. Thus, structural optimisation must be wisely applied to a wide variety of situations that arise during both the launch and service life of the satellite. Thus, optimisation techniques become crucial in the aerospace sector.
According to Arora et al. [], general optimisation is a mathematical process that involves a structured approach to identifying the best possible solution among a set of alternatives, taking into account specific objectives and constraints. The process encompasses several key stages. Initially, the optimisation problem is clearly defined, specifying the objectives to be minimised or maximised, as well as any restrictions that must be honoured. Decision variables, which can be adjusted to attain optimal results, are identified, along with their allowable ranges. To do so, a mathematical objective function is formulated to quantify the system’s performance in relation to such decision variables. A starting point is established by providing initial values for decision variables. The optimisation algorithm then iterates, refining the solution through adjustments while adhering to constraints. The process continues until a stopping criterion is met, which corresponds to either a predefined number of iterations or a satisfactory level of improvement.
In particular, structural optimisation following Rotwell et al. [] entails a systematic process aimed at achieving the best configuration for a structure while adhering to specific goals and constraints. This process encompasses several key steps. First, the problem is defined by setting clear objectives and identifying constraints, such as stress limits or material properties. Mathematical modelling is then used to represent the structure’s behaviour through methods like finite element analysis (FEA), breaking it down into elements and nodes to simulate its response to external forces. Design variables, such as geometry and material properties, are determined, and an objective function is formulated to measure the structure’s performance against optimisation goals. Constraints are established to ensure the design meets specified criteria.
Structural optimisation encompasses three distinct categories: size optimisation, shape optimisation, and topology optimisation (TO) []. According to [], size optimisation focuses on finding the most suitable values for parameters such as cross-sectional dimensions, thicknesses, and other geometric attributes of structural elements. Shape optimisation, on the other hand, involves modifying the geometric arrangement, specifically the boundary conditions of the governing equations. Shape optimisation can be either non-parametric (free-form) or parametric []. In the context of non-parametric shape optimisation, the design domain encompasses the surface nodes (referred to as design nodes) within the finite element model. At each design node, displacement vectors are assigned, and the optimisation process entails adjusting scalar displacements along these vectors, which are treated as implicit parameters in this free-form optimisation approach. In contrast, parametric shape optimisation is closely related to the Computer-Aided Design (CAD) geometry of the structure, directly modifying the selected shape parameters. Lastly, TO generates concepts for material layout by either altering the quantity and properties of structural elements or changing the number of holes within a structure [].
Choosing an appropriate optimisation algorithm for satellite structural optimisation is crucial, ranging from gradient-based techniques to evolutionary algorithms. Then, the algorithm is implemented, code is written to modify design variables and evaluate the objective function, and the process iterates, refining the design while considering constraints. Convergence criteria determine when the optimisation stops. The final design’s performance is evaluated through simulations, ensuring it meets goals and constraints [].
Upon achieving a satisfactory design, it should be implemented practically, involving manufacturing components according to the optimised specifications []. Testing the physical structure validates its real-world performance, confirming that the optimised design translates effectively into practical benefits []. Throughout this process, sensitivity analysis, robustness, manufacturability, and trade-offs between objectives are taken into account.
However, structural optimisation often yields very intricate designs and patterns, which in most cases are almost impossible to manufacture with traditional manufacturing processes [,,]. This fact has hindered the physical realisation of structurally optimised components in the last three decades. However, the recent development and trends in the field of additive manufacturing (AM) have posed it as a promissory option to manufacture and test structures coming from TO processes [].
In this sense, the aerospace industry finds strong appeal in both AM and TO due to their transformative capabilities, addressing key industry challenges. AM, also known as 3D printing, interest by offering weight reduction capabilities, while critically preserving structural integrity. Its ability to fabricate intricate and complex geometries not achievable through traditional methods aligns well with aerospace’s need for aerodynamic and structurally optimised components. Moreover, AM enables cost-effective customisation, rapid prototyping for iterative design, and reduced lead times through on-demand production, promoting agility in responding to challenging changes in the industry [].
TO’s ability to generate innovative designs aligns with aerospace’s pursuit of improved strength, stiffness, and other vital parameters. Its optimisation output can be tailored to manufacturing constraints, ensuring feasibility, particularly when coupled with AM techniques. With aerospace manufacturing’s cost constraints and resource considerations, TO provides an avenue for optimising resource utilisation and achieving cost-effective, sustainable manufacturing [].
Moreover, TO methods establish technical ways in which material used to sustain a determined load within a design space can be decreased without endangering the overall capability to sustain such a mechanical load [].
TO methods perform optimisation in a semi-automatic way, reducing design time and naturally reducing material waste as only the required amount of material needed is maintained in the final design. Thus, when coupled with manufacturing techniques like AM, such capabilities can be brought to the real world, where the material is scarce, valuable, and usually costly []. These two technologies enable individuals to have access to prime manufacturing capabilities without the need to invest high amounts of capital. This characteristic is highly desirable for countries that lack a highly developed aerospace industry as it fosters the beginning of serious research efforts and development with minimal spending of resources.
AM’s ability to minimise material waste, create complex multi-purpose optimised designs, and enable on-demand production makes it an environmentally friendly manufacturing method. By reducing material waste and its associated energy consumption, AM plays a role in conserving resources and contributing to a more sustainable approach to production [].
Furthermore, TO embraces multidisciplinary design considerations, a fundamental of aerospace systems. By optimising interconnected components, it contributes to system-level improvements and performance enhancements. Ultimately, the aerospace industry’s engagement with both AM and TO underscores a shared commitment to innovation, efficiency, sustainability, and the advancement of aerospace technology to meet the stringent demands of modern applications [].
This paper intends to present a comprehensive review of different TO techniques applied to satellite structures, along with a brief review of AM processes, particularly those that have been applied to manufacture satellite-optimised components. The final goal of this review is to gather in one place the state-of-the-art in TO methods and AM processes applied to satellite structural optimisation up to date. Thus, it is aimed at aiding professionals and researchers in the field as well as fostering this promissory area of knowledge in the following decade.
This work is organised as follows: Section 2 puts an emphasis on TO methods, providing a brief description of every method without disregarding their general acceptance within the scientific community. A brief overview of AM as a means to manufacture TO solutions is expressed in Section 3, including general mechanical requirements needed for taking into account the TO process for AM processes. On the other side, examples of the real applicability of TO on the topic of satellite structures and sub-structures are presented in Section 4 and Section 5, including AM processes if applicable. Finally, a discussion about the gathered information as well as brief final remarks is presented in Section 6.
2. Topology Optimisation Methods
Within the realm of structural mechanics, there exist diverse methods for optimising mechanical designs. In contrast to size optimisation and shape optimisation, TO stands apart. It does not require a nearly optimal starting design to properly work and has the capability to generate optimal solutions when conventional design strategies prove ineffective []. This might happen due to complex inter-relationships between design parameters and structural responses []. Applying TO can result in much greater savings of material than size optimisation or shape optimisation [,,,].
TO addresses the question—how can we strategically distribute a specified amount of material within a predefined design space to achieve optimal structural performance, considering defined loads and constraints?
The answer is characterised by its broad applicability, encompassing scenarios involving singular or multiple materials with isotropic or anisotropic behaviour. It extends to both two-dimensional and three-dimensional spaces and involves considerations related to weight, displacement, and stress restrictions, combined with multiple loads of diverse physical nature. Moreover, it encompasses a range of physical phenomena, including mechanical aspects such as stiffness, natural frequency, buckling, and impact, as well as thermo-mechanical and fluid interaction effects. These varied conditions have led to the emergence of a multitude of methods aiming to address as many combinations as possible. The underlying objective of these methods is to provide optimal solutions while maintaining efficiency and computational affordability.
To study the methods available, we categorise them as follows.
- Continuum approaches, which are based on the modification of continuous parameters such as mass density.
- Discrete approaches, which are based on the elimination or addition of material elements in a meshing context.
- Diverse approaches, containing TO continuum and discrete approaches that are used to solve specific problems such as multi-scale TO and multi-physics TO or that try to give a novel dimension to TO problems by integrating machine learning techniques.
The proposed classification can be observed in Table 1, where the Metaheuristic Algorithms and Metaheuristic Hybrid Algorithms have their own sub-classification, which can be found in Table 2 and Table 3, respectively.

Table 1.
Topology optimisation approaches.

Table 2.
Topology optimisation approaches—subclassification within Metaheuristic Algorithms in Table 1.

Table 3.
Topology optimisation approaches—subclassification within Metaheuristic Hybrid Algorithms in Table 1.
In what follows, we revise the most prominent exponents of each of these categories.
2.1. Topology Optimisation Continuum Approaches
2.1.1. Beginnings
The first formal paper to address the problem is probably proposed by Michell back in 1904 []. In this paper, he derived optimal criteria for the minimum weight layout of 2D truss structures.
Then, after some decades, the first general theory of TO was given by Prager and Rozvany in 1977 [] in the form of their “optimal layout theory”. In this work, the optimisation analysis is obtained analytically for grid-type structures.
Exact analytical solutions for TO problems are very difficult to obtain. Even today, there are very few papers that address the problem from such a point of view; the reader might find a thorough way to address the derivation of analytical solutions for TO problems in the recompilation of lectures given at the International Centre for Mechanical Sciences (CISM) [].
2.1.2. Homogenisation Method
The transition from truss structures to continuum structures undergoing TO began with the seminal paper of Bendsøe and Kikuchi in 1988 []. Originally, TO was perceived as a challenge involving discrete 0-1 variables, implying a binary design configuration. This particular configuration, often associated with structural compliance, is recognised as being ill-conditioned in nature [,,]. To tackle this issue, Bendsøe and Kikuchi introduced a solution. They proposed re-framing the problem by introducing intricate porous microstructures at a smaller separate scale. This is performed using the homogenisation theory, thereby transforming the problem into one that is mathematically well-defined.
The homogenisation method aims to optimise through density variables that are associated with a specific microstructure model at a separate lower scale. TO is achieved by iteratively modifying the corresponding size variables of each unit cell. It is a difficult method to implement due to mathematical complications, particularly in 3D extensions of method []. This paper meant the birth of practical (numerical) TO methods [,,,], and since their first appearance, their use has been extensive. This surge in numerical investigations coincided with revolutionary advances in computing capabilities and the progress made in numerical simulation techniques [].
The original paper of Bendsøe and Kikuchi meant the birth of practical (numerical) TO methods. Since its introduction, the concept of continuum TO has evolved in various ways, giving rise to a wide array of methods that have emerged and progressed over time.
2.1.3. Solid Isotropic Material with Penalty Method
To circumvent the mathematical complications inherent to homogenisation theory, Bendsøe [] proposed Solid Isotropic Material with Penalty (SIMP) in 1989, another density-based method with a simplified material assumption. By penalising exponentially the isotropic material density in terms of element density variables, it is possible to manipulate structural properties related to density (like structural stiffness). The design domain is discretised by using elastic linear isotropic continuum finite elements (FE), and then the finite element method (FEM) is used to obtain the structural response; analytical sensitivities are then calculated with an adjoint method (numerically solved via the Method of Moving Asymptotes (MMA) []). A filter is then applied to smooth sensitivities []. The process occurs in a loop until the required volume constraint is satisfied. The name (SIMP) was first suggested by Zhou and Rozvany in 1991 []. For its simple conceptualisation and numerical implementation, SIMP is one of the most popular and widespread TO methods [,,,].
Until today, SIMP has maintained its status and continues to develop. Recent advances include SIMP combined with phase-field method [], multi-material TO [,,,,,,,], anisotropic material behaviour [,], dynamic performance and fatigue TO [,,,,], large elastic deformation TO [], additive manufacturing (AM) constrained TO [,,,,,], subtractive manufacture (SM) constrained TO [], and casting constrained TO []. Some approaches lead to self-weight TO [], nonlinear load cases [,], stress constrained TO [], surface corrosion TO [], buckling considerations [,], non-linear heat conduction [], thermal dissipation [].
Some interesting applications include flexoelectric structures (nano-structures) [] and shape-memory alloys []. Recent approaches use Iso-Geometric Analysis (IGA) [,]. Others eliminate mesh of the design [].
2.1.4. Topology Derivative
Another approach that emerged in the 1990s is the utilisation of topology derivatives in the fields of topology and shape optimisation, pioneered by Eschenauer [] in 1994 through the introduction of the bubble-method. The fundamental concept underlying topology derivatives involves predicting the impact of introducing an infinitesimally small hole at any location within the design domain. The predictive information obtained is then employed to create holes. Topology derivative is used in conjunction with a shape optimisation method acting as the mechanism to place new holes that are then manipulated by the latter method. A more recent development is brought by Amstutz [], demonstrates that for some choices of material properties, the topology gradients used in minimising compliance correspond to the standard density gradients as used in the SIMP scheme []. Amstutz’s research highlighted that both methods yield equivalent outcomes under certain conditions (when the penalisation exponent is set to , specifically in the context of 2D elastic problems with a Poisson’s ratio of ). An additional aspect is that deriving topology derivatives demands the application of intricate mathematical concepts, as emphasised by Sokołowski and Zochowski [], a point later reiterated in []; this feature has the effect of prevent widespread of the method and practical applications, instead, one can find the topology derivative method implicit within level-set methods [,,,,,].
2.1.5. Level-Set Method
Methods up to now track changes in topology in an explicit way. level-set Method (LSM) is a TO method that defines boundary design implicitly. When dealing with the problem of TO, the groundwork for the LSM is initially laid out by Osher and Sethian [,]. This foundational mathematical framework subsequently found practical utility by Sethian [], Wang [,], Allaire [], and Jouve [].
LSM is originally developed to model moving boundaries. Initially, LSM is primarily employed to depict the progression of interfaces in scenarios like multi-phase flows and image segmentation. However, the application of LSM to TO commenced in the year 2000 with Sethian’s work and has advanced rapidly since then.
The core principle of the LSM involves expressing the interface (the demarcation between material and void within a design space) as the level set of a continuous function. Defining the interface enables the explicit formulation of objectives and restrictions pertaining to the interface while also facilitating the description of boundary conditions at that interface. Normally, the outcomes obtained through the utilisation of LSM are heavily reliant on the initial solution guess [,]. A notable limitation of this approach is its tendency to experience sub-optimal convergence rates, often requiring a substantial number of iterations during the optimisation process [].
A comprehensive examination of the utilisation of LSM in TO is provided by van Dijk in a detailed review [], whereas a more recent review by Gibou [] shows the capacities of this method, which has not stopped evolving.
Recent works on LSM are: LSM combined with BESO [], multi-material approaches [,], multi-component TO [], micro-architectured materials [], reliability-based TO [,,,,], dynamic TO [,], buckling [], design-dependent loads [], heat conduction TO [], AM constrained TO [,,,], SM constrained TO [], parallel LSM proposals [,,,], and Iso-Geometric Analysis (IGA) with LSM [,,].
Additionally, a level-set band approach has been introduced with the aim of enhancing the smoothness of objective and constraint functions. This method integrates the benefits of both the level-set method (LSM) and density-based techniques by introducing a single parameter, referred to as the ’level-set band’, to seamlessly merge the strengths of both methods [].
2.1.6. Phase-Field Method
The phase-field method for TO is initially developed as a means to depict the surface dynamics of phase-transition phenomena, particularly in scenarios involving transitions between solid and liquid states [,]. These methods have found application in various simulations of surface dynamics, particularly in materials science. They have been employed for tasks such as modelling diffusion, multi-phase flow, crack propagation, solidification, and phase transitions []. The phase-field method for TO is first introduced by Bourdin in 2003 [,] and then subsequently extended by Wang [].
Phase-field TO employs a penalty approach to approximate the perimeter of the interface. Through the selection of a very small positive penalty parameter, it becomes possible to achieve a penalty as a well-defined interface zone that separates solid regions from voids []. In contrast to LSM, the equations governing phase transition are solved across the entire design domain without any pre-existing knowledge regarding the whereabouts of the phase interface. However, there exist some problems; for example, the correct selection of the parameters is an important factor in ensuring the convergence behaviour of the numerical solution (affecting the number of iterations needed to obtain a solution). Unfortunately, the selection of parameters is case dependent and requires a set of tests []. Additionally, there is a high computational cost of solving the underlying fourth order Cahn–Hilliard Equation []. These are some of the reasons that have prevented the spread of the method. Despite not being a popular method, advances can be further studied in [,,,,].
2.2. Topology Optimisation Discrete Approaches
In TO discrete approaches, the treatment of individuals is twofold: one option consists of treating every finite element (FE) of a unique design as an individual of a population; then, least fit individuals of that population are removed as the optimisation process advances. This approach is common in Evolutionary Structural Optimisation methods. Specifics of formulation and implementation vary depending on each method. On the other side, the second option is to treat a design space (and its TO solution) as an individual; then, one wants to generate a large number of solutions (population) and apply some technique to generate the best individual. This approach is typical of genetic algorithms, for instance. We shall explore both approaches in what follows.
2.2.1. Evolutionary Structural Optimisation Methods
Evolutionary Structural Optimisation (ESO) is a discrete approach to the TO problem. Although in density approaches the discrete design space is relaxed, offering a continuous space design, in discrete methods, the design space is not relaxed and thus the design variable is completely discrete (0,1). The most prominent family of discrete methods is the ESO method, the first one being proposed by Xie and Steven in 1993 [,], which is grounded in the straightforward notion that a structure progresses towards an optimal state by progressively eliminating material experiencing low stress levels, while adhering to specified material volume criteria. However, achieving effective solutions can prove challenging under certain circumstances. In order to address its initial shortcomings, this method has undergone modifications throughout the years. First changes were aimed at enabling the restoration of removed elements, particularly those adjacent to heavily stressed components.
Originally, ESO could only remove low-stress elements, preventing finding optimal solutions. To improve ESO capabilities, bi-directional approaches allow previously eliminated individuals to reappear as part of the design. Early versions of the Bi-Directional ESO (BESO) method were developed by Querin [,] and Yang []. However, these methods relied heavily on heuristic concepts and lacked strong theoretical foundations. Additionally, they were susceptible to issues such as mesh dependency and the emergence of undesirable chequerboard patterns []. An improved BESO method was delivered by Huang and Xie [,], and, almost at the end of the decade a soft-kill BESO (SBESO) [] version of their method was proposed.
In SBESO, standard adjoint gradient analysis is incorporated, introducing a higher level of theoretical rigour to the approach. Additionally, filtering techniques similar to those employed in density-based methods are integrated to stabilise the algorithm and mitigate issues like chequerboard patterns. Various benchmark examples for BESO and SBESO are fully reported in the book by Huang and Xie []. For the final SBESO version, the design domain is discretised through a finite element mesh, and initial property values are assigned to construct an initial design. Subsequently, a finite element analysis is conducted and nodal sensitivity numbers are computed using an adequate compliance equation. Notably, these sensitivity numbers are directly derived from nodal values to avoid the need for elemental calculations. The implementation includes a mesh independence filter step that refines the sensitivity values by considering neighbouring nodes and employing linear weight factors within a specified radius. Furthermore, the process involves averaging the current sensitivity numbers with historical data to ensure continuity and readiness for the subsequent iteration. The determination of the target volume for upcoming iterations is based on an evolutionary volume ratio concept, wherein the structure’s volume undergoes adjustment until a predefined constraint is met. The optimisation process dynamically modifies the design configuration by introducing or removing elements according to specific conditions tied to sensitivity thresholds. Importantly, the iteration cycle, encompassing steps 2 to 6, persists until the prescribed constraint volume is attained and optimisation objectives are successfully achieved, all while maintaining convergence through a pre-established threshold.
A multitude of recent works were also found: LSM with BESO [], phase-field method with BESO [], nonlinear structures under dynamic loads [], non-linear reliability TO [], buckling TO [], fatigue considerations [], crashworthiness TO with BESO [], frequency optimisation [,], BESO with casting constraints [], and BESO with AM constraints [,,,,,]. Other interesting works are the Iso-Geometric Analysis (IGA) approach with BESO [], a meshless BESO technique [], and a parallel framework for BESO [].
2.2.2. Moving Morphable Voids Method
On 2014, Guo proposed Moving Morphable Components (MMC) []. In this method, a set of MMC are utilised as fundamental elements for TO. The process involves enhancing the arrangement, positioning, and configuration of these components to achieve an optimal structural layout; its ability to significantly decrease the quantity of design variables required in the problem definition makes this method appealing. This reduction proves advantageous in cutting down the required computational time for numerical optimisation procedures.
Based on Guo’s work, Zhang proposed Moving Morphable Voids (MMV) in 2017 [], where a set of MMV are adopted as basic building blocks for TO. This method decreases the number of design variables, the number of degrees of freedom involved in the FEA solution process, and it can also be further extended to 3D optimisation. Examples of use can be further explored in [,,,], whereas explicit use of Iso-Geometric Analysis (IGA) has also been explored [,,,].
2.2.3. Metaheuristic Topology Optimisation Methods
Although SIMP is a method exclusively centred around gradients, involving calculating derivatives of objective functions, metaheuristic algorithms prioritise sensitivity numbers by evaluating their magnitudes. As a result, this enables a more adaptable objective function and simplifies the implementation process, leading to significant advancements in the utilisation of TO within engineering disciplines []. In what follows, we shall revise some advancements in the application of metaheuristic algorithms to TO.
Genetic Algorithms
Over the past thirty years, efforts have been devoted to applying genetic algorithms (GAs) to address challenges in structural optimisation problems [,,]. GAs function by working with a population of potential solutions, as opposed to enhancing a singular solution. Because of this characteristic, a typical structural optimisation problem tackled with GAs has to contend with a significantly larger set of design variables compared to conventional mathematical programming methods. As a result, there is a notable drawback in terms of computational burden []. Research integrating GAs into structural optimisation has focused on relatively small problem sizes. The implementation of GAs in TO has been found utilising different approaches: we can find pure GAs applied to solve the TO problem for simple compliance optimisation [,,]. In this type of approach, the entire design space is considered as a component of the chromosome of a single individual; the idea is to generate hundreds or thousands of designs which evolve towards the optimal solution. For a structure to effectively withstand a mechanical load, it must possess a strong level of connectivity.
However, ensuring adequate structural connectivity through the use of GAs is challenging due to their inherently stochastic nature. This presents a significant limitation when applying GAs to TO, and finding a viable solution to this issue proves to be exceedingly difficult. Jackiela [,] suggests altering solid elements that lack connectivity to the seed elements in order to be emptied; ref. [,] suggests enhancing connectivity by incorporating a chromosome mask to selectively filter out chromosome segments originating from disconnected positions; Wang [,] suggests the incorporation of image processing techniques. Those approaches failed to effectively reduce randomly disconnected topologies, or are excessively cumbersome. However according to Li and other scholars, GAs might have better probabilities to converge towards global solutions [,,,,,].
For some successful applications of TO using GAs, it is appropriate to review the work in [,,].
Other Metaheuristic Approaches
Other metaheuristic techniques have been applied without hybridising. Such are the cases of artificial immune algorithms [,,], ant colonies [,,,], particle swarms [,,], simulated annealing [,,,], harmony search [,,,], and differential evolution [,].
There exist a plethora of other proposals aiming to apply metaheuristic approaches with TO, but they have not experienced further development. We observed a multi-objective TO based on bacterial chemotaxis [], a joint firefly and particle swarm optimisation (PSO) algorithm [], a symbiotic organisms search algorithm [], an improved electro-search algorithm [], a plasma generation optimisation [], a binary bat algorithm [], an enhanced binary GA along with morphological reconstruction [], a semi-definite programming-based approach combined with a GA [], as well as a ground structure approach based on curved elements []. A constant in metaheuristic methods is the large quantity of iterations needed to converge which makes them difficult to extend to 3D design spaces where the computational burden increases considerably.
There is another approach in which the idea is to combine established TO algorithms with metaheuristic algorithms. Such is the case of Garcia and Silva, [] who combined SIMP with simulated annealing, or Xue [] who combined SIMP with a GA. In this sense of hybridisation, there is a tendency to combine ESO and BESO methods with other metaheuristic algorithms. This is mainly due to the discrete nature of ESO algorithms, which makes hybridisation a relatively straightforward process.
Far from the approaches used in the application of pure metaheuristics, hybrid approaches do not work over populations of individual solutions; instead, they try to assist the base algorithm to improve individual solutions. Such is the case of Liu [,]; the proposed approach treats each element within a structural domain as an individual member of a genetic algorithm (GA) population, in contrast to creating multiple entire structural designs to compose the population. In this method, the traditional ESO sensitivity number is employed as a fitness function, and a natural selection process is employed to eliminate less-fit elements, mimicking the elimination of less-fit individuals in traditional GA design problems. Cui [] presents a work following Liu’s ideas. A similar work is presented by Zuo [] to generate a genetic version of BESO. Yhunzhen [] applies Zuo’s work to architectural design optimisation. Other works hybridising BESO with GAs might be consulted [,]. In a similar way, it is possible to find works hybridising BESO with other metaheuristics; such is the case of swarm optimisation algorithm [], simulated annealing [], and harmony search [].
2.3. Diverse Approaches
Multi-scale, multi-physics, and machine learning applied to TO constitute a series of problems that may be solved by applying TO techniques that use either continuum, discrete, or combined approaches. These novel approaches have seen important development in the last 10 to 20 years, positively expanding the realm of methods and techniques available to solve a multitude of TO problems.
2.3.1. Multi-Scale Topology Optimisation Methods
Over the past three decades, TO methods have predominantly focused on the macro-scale aspects of design. However, there has been a growing interest in the development of optimisation methods that can enhance the overall performance of structures by incorporating the concept of multi-scale structural TO.
Multi-scale TO offers a novel way to optimise structures. Taking into account that the structure itself may be composed of small unit cells with a certain degree of porosity, this characteristic gives multi-scale methods the ability to obtain comparably lighter structures than using full-scale TO methods.
Features of multi-scale, such as high level of porosity, may appear when using full-scale TO methods, small details on the mesoscale (ranging from 0.1 to 10 mm) may appear if the FE mesh is fine enough to capture such details. As a result, structures that resemble grid-like patterns filling the overall macro-scale structure are obtained. Such a full-scale approach is computationally intensive as the resources needed to solve 3D problems increase with mesh density. As an option to alleviate the problem, multi-scale approaches work in two or more levels (sometimes based on homogenisation theory) of optimisation; in one level, a unit cell is proposed to fill the design volume delimited by the macro optimisation level that resembles the usual solution obtained in full-scale approaches. The main difference is that lighter structures can be obtained. Periodic patterns using TO may be imposed by subdividing the design volume and then assigning a repetitive pattern on each subdomain. Such an approach allows the obtaining of Lattice structures, and if the density (size) of unit cells is allowed to change along the design, we are then speaking of functionally graded materials.
Multi-scale structures offer the potential to attain exceptional performance characteristics, all while possessing inherent qualities of being lightweight and versatile. However, the actual advantages of these innovative multi-scale structures must be verified through numerical simulations and experimental validations as investigation research matures. Multi-scale topology approaches have been extensively reviewed by Wu et al. [].
Many full-scale TO methods can be used to obtain multi-scale lattice structures and functionally graded materials; notable examples are:
- Multi-Scale Topology Optimisation with Homogenisation [,,,,]
- Multi-Scale Topology Optimisation with SIMP [,,,,,,,,,,,,,,]
- Lattice Structure Topology Optimisation with SIMP [,,,,,]
- Multi-Scale Topology Optimisation with Level-Set Methods [,]
- Lattice Structure Topology Optimisation with Level-Set Methods [,,,]
- Functionally Graded Material Topology Optimisation with Level-Set Methods []
- Multi-scale Topology Optimisation with BESO [,,,,,,,]
- Lattice Structure Topology Optimisation with BESO [,,].
2.3.2. Multi-Physics Topology Optimisation Approaches
TO is usually applied to mechanical problems were elasticity is the most relevant phenomenon at hand. However, there are problems where the interaction of multiple physical phenomena needs to be accounted for; such problems are categorised as “multi-physics” [].
It is possible, in general, to find TO applied to problems where thermal boundary conditions impose temperature gradients, yielding thermo-mechanical stresses acting on the structure. It is possible to find in the literature implementations that are either uni-objective or multi-objective, and that provide options on how to tackle the problem at hand. Coupled thermo-mechanical TO has found application on heat dissipation structure design [,,,,].
TO has also found application in electromagnetic actuators, the work in [] considers the coupled interaction between structural and electromagnetic phenomena, whereas the research in [] considers thermal and electromagnetic interaction, both employing multi-objective TO.
Furthermore, other less-studied multi-physics TO problems include fluid–structure interaction, which is usually relevant in aeronautics for the design and optimisation of airfoils, wings, and compressor blades. Relevant applications for the purpose of this paper are found in selected works where interaction between molecular atmosphere and satellite structure is relevant to optimise orbit lifetime [,,]. As interaction occurs in the surface of the structures, only shape optimisation is needed to solve the problem.
Finally, layout optimisation deserves to be mentioned, although it does not necessarily refer to TO. Layout optimisation refers to the optimisation of the relative position of objects inside the satellite with the intention of adjusting the satellite centre of mass. Such an optimisation might be of great help to improve stability characteristics in orbit. However, its integration with structural TO might prove useful for structure redesign in the late development stages. Satellite layout optimisation can be found in [,,,,].
2.3.3. Machine Learning Applied to Topology Optimisation
Research in this area has focused on data-driven TO, which means using a traditional TO method to gather a database of possible solutions for a problem [,,]. Then, aiming to improve the process of obtaining optimal structures, different machine learning techniques are applied, like supervised, unsupervised, as well as reinforcement learning. These techniques serve several purposes, including speeding up the design iteration [,,,,,,].
Apart from data-driven TO, some works try to achieve non-iterative optimisation [,,,,,,,,,,,,,,,,,], or intend to replace the typical FEM process, creating meta-models [,,,,,,,,,,,,,,,,,,]. Other approaches try to reduce the dimensionality of the design space [,,].
Such approaches have effectively accelerated the optimisation process and decreased computational burden. Despite the progress in this field, there remain challenges in many studies. These include addressing the low resolution of generated designs, enhancing the performance of machine learning methods, adapting the methodologies to different design domains (three-dimensional spaces), grappling with the costs associated with gathering data and managing the high computational burden of both FEA and the machine learning approach [].
3. Additive Manufacture in the Context of Satellite Structures
Typically, topology-optimal solutions are given in disregard of standard manufacturing techniques. As a result, intricate and organic designs with notably lower weight are achieved. Thus, it is challenging or even infeasible to fabricate such designs using traditional manufacturing methods [,,]. In this sense, the following question arises: is it possible to manufacture optimal solutions given by TO methods?
TO methods can be used for components produced through additive or subtractive methods, as well as by other techniques like casting. Subtractive Manufacturing (SM) refers to processes that create objects by removing material from a solid block or billet of material [,]. The material removal process involves removing material from a workpiece, conducted manually through methods like drilling, turning, and milling, as well as using Computerised Numerical Control (CNC) automation [].
This approach ensures high-dimensional accuracy, enabling the attainment of tight tolerances and exceptional surface finishes. Particularly suited for mass production, CNC machining is adept at efficiently manufacturing large volumes of uniform components []. However, this method generates material waste in the form of machining chips, scraps, and swarf. The fundamental traditional methods include milling, which involves using rotary cutters to shape complex 3D forms; turning, a technique where a workpiece rotates and a non-rotating cutting tool is used; drilling, employing specialised drill bits to create holes; grinding, using abrasive wheels to achieve precise surface finishes; and sawing, which employs thin blades to divide workpieces into desired configurations []. Nevertheless, SM has certain factors to consider when applied to the manufacture of TO solutions, such as tool accessibility, mould removal, significant time consumption, and the need for skilled operators to create holes, shapes, cylindrical forms, and mill surfaces. These factors limit the applicability of TO methods [,,,].
On the other side, AM is defined in the standard ISO 52900:2016 as the process of joining materials to make parts from 3D model data, usually layer upon layer, as opposed to subtractive and formative manufacturing methodologies [,]. The categorisation of AM processes is highly complex due to their wide range of applications and diverse operational methods. This makes the task of defining boundaries between processes and categories extremely challenging. However, Kumar in 2021 [] presented a classification that, unlike the one provided by the American Society for Testing and Materials (ASTM) in 2012 [] and the categorisation of the standard ISO 52900:2016 [], encompasses most of the current AM processes.
- Material bed process: This category encompasses techniques where the material is first laid down in bulk to create a bed, upon which the actual fabrication process takes place layer-by-layer. Some common examples of this category include:
- Binder Jetting 3D Printing (BJ3DP) [,,,,].
- Ceramic Laser Fusion (CLF) [,,].
- Stereolithography (SLA) [,,,,].
- Electron Beam Melting (EBM) [,,,,].
- Selective Laser Melting (SLM) [,,,,,].
- High-Speed Sintering (HSS) [,].
- Selective Laser Sintering (SLS) [,,,,].
- Digital Light Processing (DLP) [,,,,].
- Material deposition process: This process involves transferring material from a feed source to a substrate in order to fabricate a part directly, as opposed to forming an intermediate bed. This category is divided into the following categories:
- Solid deposition.
- −
- Fused Filament Fabrication (FFF) [,,,,,].
- −
- Direct Metal Deposition (DMD) [,,].
- −
- Direct Energy Deposition (DED) [,,].
- −
- Wire and Arc Additive Manufacturing (WAAM) [,,,,,].
- −
- Plasma Arc Additive Manufacturing (PAM) [,].
- −
- Cold Spray [,,,,,].
- Liquid deposition.
- −
- Ink Jet Printing (IJP) [,,].
- −
- Photopolymer Jetting (PJ) [,].
- −
- Metal Jetting [,,].
- −
- Rapid Freeze Prototyping (RFP) [,,,,].
- Slurry deposition.
- −
- Thermoplastic 3D Printing (T3DP) [,,,].
- −
- 3D Gel Printing (3DGP) [,,,].
- Motionless material process: Refers to AM techniques where the material feedstock remains static and does not require active conveying or deposition to construct each layer. In processes like Two-Photon Polymerisation (2PP) and Continuous Liquid Interface Production (CLIP), the photopolymer resin is already present in a vat or container. These motionless material techniques eliminate the motion requirements of powder beds, material extrusion, or droplet jetting.
AM enables the construction of intricate TO for complex shapes that would not be feasible using subtractive techniques. Examples of design-driven AM in manufacturing are presented later in Section 3.2.
It is worth mentioning that there are other manufacturing techniques that allow TO solutions to be manufactured such as casting [,,,,,] and extrusion [,,,,,]. However, these techniques have specific requirements that require considerable changes in the topology-optimal layout resulting in a structure that is sub-optimal. AM and SM processes have been demonstrated to be less intrusive and allow the manufacture of shapes closer to the optimal TO solution at hand.
3.1. General Considerations about Additive Manufacture for Topology Optimisation-Generated Solutions
There are numerous considerations about using AM to manufacture the optimal solutions generated by TO, which become especially important in the aerospace field, where high safety levels and high reliability are expected and required.
For instance, implementing length scale limitations in TO is essential to prevent the creation of impractical geometric attributes like small openings, fragile walls, or tiny joints []. Employing density filtering is a valuable method for restricting the minimum length scale [,,]. Since AM involves a sequential layer-by-layer construction process, horizontal overhangs require the use of support structures during the building process (although these supports can be subsequently removed [,,]). Additionally, unprocessed enclosed materials in cavities lead to local high temperatures, the reason for which they have to be removed [,,].
Moreover, due to the presence of substantial thermal gradients present in various AM techniques during the progressive solidification of layers, notable residual stresses can emerge [,,]. These stresses often result in distortions such as part warping and other geometric deviations.
Additionally, formed parts generally suffer from relatively low repeatability [,]. It has been noted that parts manufactured show anisotropy [,,]. Potential solutions exist to tackle this issue. Some options include optimising AM process parameters like build orientation [,], incorporating secondary processes such as laser re-melting [], or integrating true anisotropic material models into TO []. The goal is to achieve superior performance in additively manufactured structures. These and other limitations related to AM need to be considered when designing through TO.
Despite all the mentioned considerations affecting the manufacturing process, the aerospace industry within the AM market is expected to reach USD 1.4 billion by 2027, according to reports from SmarTech Publishing [] (https://www.smartechanalysis.com accessed on 1 October 2023).
3.2. Additive Manufacture Applied to the Satellite Industry
Around 2016, the National Aeronautics and Space Administration (NASA) estimated a minimal cost of USD 10,000 to put a pound (USD 22,000 per kilogram) of payload in Low Earth Orbit (LEO) [,]. With the costs involved in launching one kilogram of mass into LEO, there is a strong focus within the space industry on reducing the weight of satellites [].
The primary goal of TO applied to the aerospace industry in the context of satellite structures is to create tools that enhance the efficiency of structural mechanical design, aiming to reduce weight while optimising mechanical capabilities [].
In the realm of TO, AM offers benefits beyond creating lightweight optimised parts. It holds the potential to enhance component functionality, increase complexity, consolidate multiple parts into a single unit for efficient use of space, and thereby reduce manufacturing and assembly efforts [], improving mechanical properties by reducing or eliminating joints. Additionally, it has the capacity to significantly reduce manufacturing waste [].
In conventional aerospace and satellite component manufacturing, the fly-to-buy ratio typically ranges from 10:1 to 25:1. However, AM has the potential to substantially reduce this ratio to as low as 1.5:1 [,,]. A lower fly-to-buy ratio directly correlates to reduced material waste [], leading to cost savings. This reduction in waste is particularly crucial given the expensive materials commonly used in the aerospace and satellite industry, such as titanium alloys.
AM techniques have been effectively employed in the space sector for nearly two decades. In this sense, AM techniques for the fabrication of spacecraft parts and satellite structures have been successfully used by scholars [,,,,,,] and space contractors [,]. AM technology has also been used to manufacture functional engines suitable for small spacecraft [,]. In Section 4 and Section 5 of this manuscript, a summary of formal research applying TO methods to space applications is presented.
According to Gaudenzi and Ritz [,], the space industry predominantly employs AM methods for manufacturing space components []. Two prevalent methods are SLM and EBM, both of which use lasers or electron beams to melt powders []. Another technique, known as DMD [], involves injecting powders into a molten pool. In the case of plastics, common techniques include FFF [], SLS [], and SLA [].
According to the ESA Harmonisation Roadmap on AM for Space Applications [], the technical areas within satellite platforms that exhibit the greatest interest in TO are:
- Primary structure, structural components, and mechanisms.
- Propulsion systems, valves, filters, pipes, injectors, combustion chambers, nozzles, tanks, and multi-functional integrated components.
- Thermal systems, involving advanced thermo-optical surfaces, pre-cooling channels and piping, multi-functional integrated components, re-entry thermal protection, and gradient-sized meshes for cryogenic coolers.
- Electronics encompassing waveguides, micro-batteries, structurally embedded wiring, and intricate metallic components.
The development and testing of materials have enabled the implementation of AM in the aerospace field [,]. The review [] highlights various materials used in aerospace applications, mainly alloys, superalloys, and refractory materials. The low weight, low cost, and high strength of aluminium alloys, as well as their ease of use in manufacturing processes, allow their use in aerospace applications; however, their low melting temperature and poor corrosion resistance limit their use in this field []. Titanium alloys are widely used in aircraft due to their high temperature stability and specific corrosion resistance, as well as their compatibility with carbon fibre and polymer matrix composites [,]. Nickel and iron-based superalloys find application in the production of high-pressure turbine blades and discs []. This is because of their excellent mechanical attributes, which perform effectively under extremely high temperatures and pressures, even in corrosive surroundings. Copper alloys are frequently employed in heat exchangers intended for high-heat flux conditions where both strength and thermal conductivity are essential, particularly for cooling systems in high-pressure propellant or oxidizer environments. Refractory materials like niobium, tantalum, and tungsten are utilized in aerospace applications, particularly in situations characterized by extreme temperature conditions. Table 4 shows common materials used in the aerospace field.

Table 4.
Popular commercial materials available for AM [].
3.3. General Mechanical Requirements for Satellite Structures
In general, a TO method that is able to generate optimum solutions for real space application necessities is able to handle mechanical requirements derived from the specification of the structure under study.In this sense, the following question arises: which characteristics should a TO algorithm have to enable satellite TO? According to ECSS standard [], general mechanical requirements are as follows.
Artificial satellites must operate in an environment completely different from the terrestrial environment. Outer space is fundamentally empty (material outgas concerns arise). It must also be considered that the launch environment of a spacecraft is characterised by the imposition of high loads of a mechanical nature.
It is expected that every structure mounted on the launcher complies with minimal mechanical requirements, including both satellites and their payloads:
- Strength: the structure must endure the designated maximum loads without failure; it is imperative that any permanent deformations that might compromise the mission’s objectives are strictly controlled.
- Local yielding: in cases of metal structures or components, localised yielding may occur, as long as it does not induce overall permanent deformation, instability, or fatigue-related structural failure.
- Buckling: the stability (i.e., no buckling) of the structure must be verified under the prescribed design loads.
- Stiffness: stiffness requirements under specified loads and boundary conditions must be identified (stiffness is often quantified in terms of a minimum natural frequency requirement), thus preventing deformations that breach specified thresholds, gaps at joints, and dynamic interaction with other subsystems.
- Dynamic behaviour: the natural frequencies of the structure must fall within designated ranges to prevent dynamic resonance with significant excitation frequencies (e.g., fundamental frequencies of launch vehicles). Avoiding mechanical resonance is a must when TO is applied to satellite structures.
General mechanical requirements in the context of TO for satellites implies that the algorithm selected is fundamentally able to find a new material disposition, effectively reducing structure mass at the same time that stiffness is maximised (allowing enough safety factor to withstand launch-induced loads without experiencing permanent deformation). These optimisation objectives may be assessed either in a uni-objective or multi-objective sense.
All TO methods presented in Section 2 have been demonstrated to solve these problems at least in a uni-objective sense.
4. Cases of Study on Satellite Structures by Topology Optimisation Continuum Approaches
The scientific literature does not feature all the methods presented in Section 2 as effectively applied to obtain optimal solutions in the context of satellite structures. Thus, in this section, we only report an overview of study cases of different TO methods available for this purpose. Whenever the research includes the implementation of some AM technique to further create physical prototypes of optimised components, it is also covered.
Methods that lack any practical application in satellite structures TO are not listed in what follows.
4.1. Homogenisation Method
As discussed earlier, the homogenisation method has seen limited adoption for TO. This limitation is reflected in the minimal examples found in the literature documenting the use of homogenisation for the TO of satellite structures or components, whereas the fundamentals of the method remain strong, overcoming mathematical and computational barrier is vital for applying homogenisation more broadly in satellite TO. With the popularisation of multi-scale methods, we hope to see a surge in homogenisation practical applications. In this section, we present a case of study where the homogenisation method is applied to satellite development.
Small Satellite Structural Optimisation Using Genetic Algorithm Approach
A sandwich structure consists of two facesheets bonded to a lightweight core. This structure is commonly used in a variety of applications but in recent years it has been used in aerospace research and applications [,,,,,,]. Composite skin efficiently carries bending and membrane loads while the core transfers shear, also bringing support to the skin, aiding against buckling.
The challenge in the design of a honeycomb lies in modelling the mechanical behaviour of sandwich structures to enable optimisation. It is a complex task because composite materials are anisotropic and heterogeneous. An efficient modelling is needed to strike a balance between accuracy and computational feasibility. The proposed methodology for the implementation of optimisation is as follows:
- An unspecified mathematical homogenisation technique is presented to derive equivalent properties for the sandwich structure.
- There are derived relationships between the sandwich geometries and equivalent elastic module, shear rigidity, and plate rigidity.
- The equivalences enabled feasible analysis of the sandwich properties and optimisation of its design.
The model provides sandwich panel tension and compression stiffness as a function of facing the sheet module, Poisson’s ratio, and geometry. The equations offer useful approximations of the stiffness behaviours providing good initial estimates before costly 3D simulations. Further work is identified to capture additional failure mechanisms and improve upon the accuracy relative to 3D FEA. It is worth mentioning that this work is the closest found in the literature, along with method [], regarding the application of the homogenisation.
4.2. Solid Isotropic Material Interpolation Method
In what follows, we present cases of study where the SIMP method is applied to satellite development.
The work in [] presents a combination of TO and AM to design, analyse, manufacture, and qualify a lightweight satellite bracket. Lightweight aerospace structures can significantly improve performance and reduce emission but their design optimisation and manufacturing is challenging.
4.2.1. Design Optimisation and Validation for Additive Manufacturing: A Satellite Bracket Application
The goal of the paper is to reduce the mass of an existing satellite bracket subjected to mechanical and thermal loads during launch while maintaining structural integrity. Manufacturing constraints like printability, surface finish, overhang angles, and assembly interfaces need consideration in the design process. The methodology applied is as follows:
- Stress and size constraints involving a minimum member size were performed using the SIMP method through the software Altair OptiStruct® to obtain an initial optimised bracket configuration minimising compliance.
- SIMP expressed material properties as a power law function of density to interpolate between solid and void.
- The design is subjected to progressive FEA simulations under different loads to virtually validate its performance.
- The AlSi10Mg alloy is used in SLM to fabricate the final design.
Hence, TO is performed using the SIMP approach, taking into account minimum member size and stress constraints. This leads to a 25% reduction in mass, equivalent to 1.2 kg, compared to the initial bracket design intended for CNC manufacturing. Consequently, this reduction results in a decrease in launch costs, including fuel expenses, amounting to USD 15,600. Additionally, the lowered fuel demand contributes to a reduction in the environmental footprint of the launch process.
4.2.2. Topology Design of a Nanosatellite Structure with Optimal Frequency Responses Filled by Non-Uniform Lattices
A nanosatellite main structure filled with non-uniform lattices to improve stiffness and reduce mass is proposed in []. Nanosatellite structures require high stiffness and low weight. Lattice filling enables lightweight designs but controlling spatial lattice distribution for optimal performance.
The goal is to reduce nanosatellite box mass while retaining and improving stiffness to meet frequency requirements. Factors such as load paths, local weak points, vibration modes, and interfaces are considered in the lattice design. The steps followed by [] are:
- A nanosatellite box with uniform lattice panels is vibration tested to obtain target frequency response data in three orthogonal axes.
- An equivalent FE model of the box is created and density-based TO is performed using the SIMP method to maximise frequency under mass constraints.
- TO result is interpreted to design variable density lattices tailored to the load paths.
As a general result, the mass of the optimised design is reduced by 50.32% compared to the initial design, whereas the fundamental frequency increased by 1.19% with the new tailored lattice design.
4.2.3. Topology Optimisation and Modal Analysis of Nanosatellite Structure
Designing nanosatellite structures requires balancing strength, low mass, accessibility, and dynamic performance. Ref. [] presents the structural design, analysis, and optimisation of a nanosatellite structure.
The structure must withstand inertia, vibration, thermal, and mechanical loads during launch while being lightweight. The fundamental frequency needed to be sufficiently high to avoid resonance and dynamic issues. Additionally, the mass of the design is constrained to 800 g, which is 8% of the total satellite mass. Considerations made by [] are:
- A vertical partitioned conceptual nanosatellite structure is designed based on requirements.
- FE modelling and analysis are performed to evaluate strength under accelerations of 11 g’s longitudinal and 6 g’s lateral launch loads.
- TO is applied through ANSYS® to reduce mass while restricting maximum displacement and stress as constraints.
- Modal analysis determined the natural frequencies and mode shapes of the optimised structure.
This study yielded that TO obtains a 12% reduction in mass from 912 g to 800 g, whereas the total deformation is reduced from 0.262 mm before optimisation to 0.045 mm after optimisation.
4.2.4. Optimisation Design of the Spaceborne Connecting Structure for a Lightweight Space Camera
An optimisation method for the spaceborne connecting structure considering the camera line of sight (LOS) drift is presented in [], where a variable density TO method is utilised. The objective of the article is to optimise the optomechanical structure of the camera so that it achieves a high lightweight ratio considering the camera drift. The following key steps are taken in []:
- A FE model of the chamber and the initial structure is established using Hypermesh® software.
- The elastic modulus of each element is introduced using the SIMP method, whereas the optimisation model is solved by MMA.
- Parametric models were created and solved to ensure that the overall shape and dimensions of the topology remained consistent.
- A sensitivity analysis is conducted by employing a design of experiment approach to assess how size parameters impact the performance of the camera.
- Engineering analysis (static and dynamic) and performance comparison are realised.
The outcome is that the relative linear displacements and angular displacements between mirrors are within 10 µm and 10”, respectively, and the lightweight ratio of the connecting structures reached 54%. The optimised connecting structures have a higher lightweight ratio. Moreover, the relative linear displacement along the X-axis and the relative angular displacement in the Y direction for the optimised spaceborne connecting structure are 35% and 42% smaller compared with the traditional structure.
4.2.5. Optimum Design of the Support Structure of the CMG Based on CAE
A Control Moment Gyroscope (CMG) generates a torque for attitude control of manned satellites, a flywheel that rotates at a constant speed, supporting connecting rods and motors. that drive the cardan shafts. A rotating flywheel has angular momentum with a vector, of which the direction is changed by the movement of the gimbal and generates a torque due to the gyroscopic effect. Authors of the article [] propose the design of the support structure for a CMG, as well as a TO, frequency calculations and vibration tests.
The objective for this TO is to maximise the support stiffness. The authors’ methodology consists of:
- Study of facets of the support structure of the CMG with the ANSYS® FEM software package.
- The 3D models of the CMG are established based on the optimisation.
- Vibration tests to validate the optimised design.
In the vibration test, the peak response to the centre of the high-speed flywheel linked with the gimbal is shown in Table 5.

Table 5.
Peak results in evaluated point [].
4.2.6. Multi-Scale Design and Optimisation for Solid-Lattice Hybrid Structures and Their Application to Aerospace Vehicle Components
In the article [], authors propose a two-step structural optimisation method that integrates the SIMP topology method and lattice-based optimisation, then carrying out the optimisation of two aerospace structures, one of which is a satellite launch support.
The main objective of the method is to obtain manufacturable solid-lattice hybrid structures with better performance while meeting all design requirements. A two-step procedure is realised to design and optimise solid-lattice hybrid structures by the combination of TO and lattice-based optimisation. In this review, we focus on the optimisation process of a payload adaptor structure designed for satellite (see Figure 1).
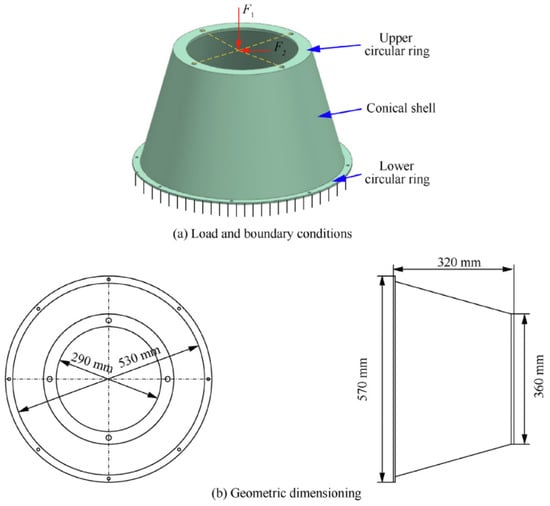
Figure 1.
A payload adaptor structure with load and boundary conditions [].
The authors propose a general methodology for applying the optimisation method as follows:
- Create a solid model and define design domain.
- Establish finite mesh model and impose boundary conditions.
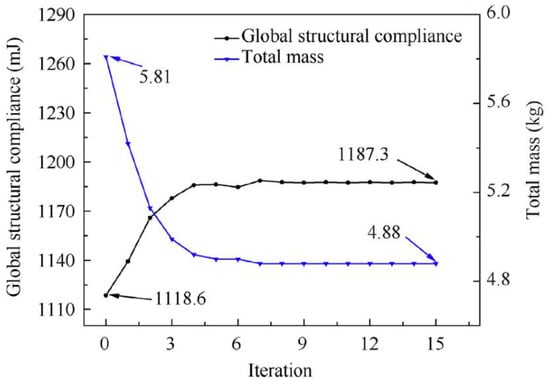 Figure 2. Iteration curves of objective function and mass constraint [].
Figure 2. Iteration curves of objective function and mass constraint [].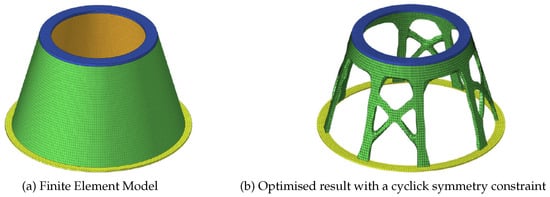 Figure 3. TO of the payload adaptor structure [].
Figure 3. TO of the payload adaptor structure [].- Reconstruct and lattice infill.
- Perform size optimisation and verify its convergence.
This study yields that the maximum deformation is 20.3% lower than the solid design and 55.5% lower than the lattice design as Figure 4 shows, whereas the solid-lattice hybrid design has the highest first-order modal frequency 14.8% and 49.8% higher to the solid design and lattice design, respectively.

Figure 4.
Global deformation and von Mises stress distribution of optimised solid-lattice hybrid payload adaptor structure [].
4.2.7. An Aerospace Bracket Designed by Thermo-Elastic Topology Optimisation and Manufactured by Additive Manufacturing
The lightweight and high-performance structures are critical for aerospace applications. The paper [] presents a combination of TO and SLM to design and manufacture a lightweight aerospace bracket. The goal of this work is to minimise the mass of an aerospace bracket subjected to mechanical loads and thermal stresses while maintaining its structural integrity (see Figure 5). The phases of the methodology followed by the authors are:
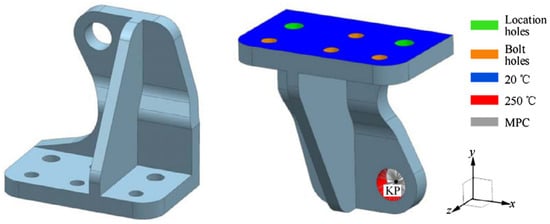
Figure 5.
Original design of the aerospace bracket [].
- A thermo-elastic TO formulation is proposed to minimise compliance under displacement, volume, and thermal load constraints.
- The Rational Approximation of Material Properties (RAMP) scheme is used for material interpolation. RAMP expressed the Young’s modulus, thermal stress coefficient, and thermal conductivity of the density variables.
- Sensitivity analysis is derived for the coupled thermo-elastic response and RAMP material properties.
 Table 6. Parameters in Figure 6.
Table 6. Parameters in Figure 6.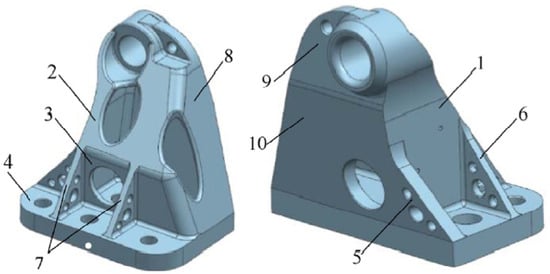 Figure 6. Reconstructed aerospace bracket []. Number parts can be consulted in Table 6.
Figure 6. Reconstructed aerospace bracket []. Number parts can be consulted in Table 6.
The results of this work can be summarised as follows:
- An 18.3% reduction in bracket mass is achieved while satisfying all stiffness, strength, and displacement constraints.
- Mechanical testing validates the performance of the additively manufactured bracket under extreme loads (see Figure 7).
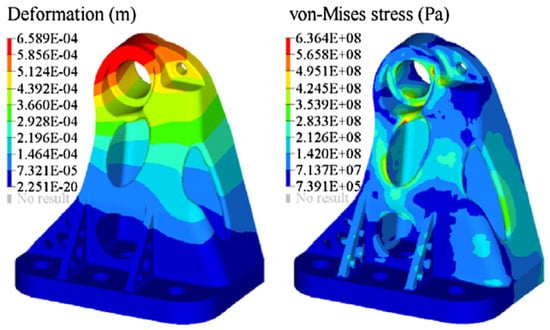 Figure 7. Final analysis [].
Figure 7. Final analysis []. - The paper demonstrates an effective integrated approach combining TO (RAMP method) and AM for aerospace applications.
4.3. Level-Set Methods
LSM are interesting for their ability to provide crisp boundaries, while also aiding in reducing the need for applying shape optimisation to TO solutions. However, as previously mentioned, the initial guess solution continues to be a problem; also, users need a fairly competent knowledge of the method and the problem at hand to perform TO effectively. These limitations are reflected in the minimal examples found in the literature documenting the use of LSM for the TO of satellite structures or components. In this section, we present a case study where LSM is applied to satellite development.
A Level- Set-Based Topology Optimisation Approach for Thermally Radiating Structures
Ref. [] presents a level-set-based TO approach for maximising the heat power radiated by a structure. The goal in this paper is to design thermally efficient radiating components, subject to a volume fraction constraint.
The authors consider a 2D problem of optimising a thin plate (see Figure 8) to maximise heat power radiated from a fixed radiating surface on one edge. An edge segment on the structural boundary is subjected to a Dirichlet boundary condition, whereas the radiating surface is defined as a fixed subdomain. Their general methodology is as follows:
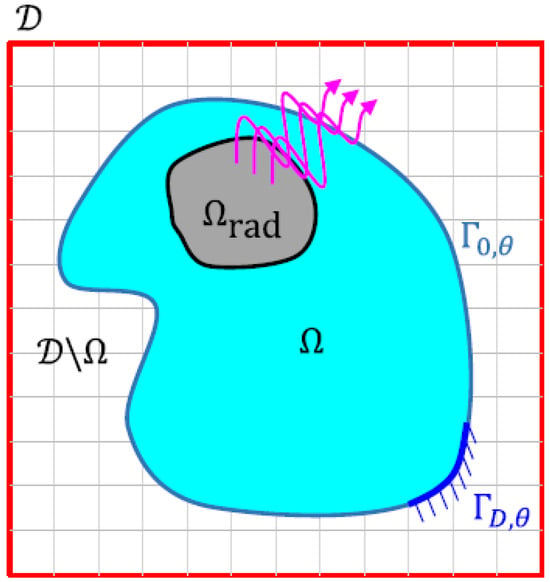
Figure 8.
Domains and boundaries for the thermal radiation problem in a 2D structural context [].
- To define the level-set function to implicitly represent structural boundaries.
- To construct augmented Lagrangian with volume constraint.
- To derive shape sensitivity Lagrangian using adjoint method.
- To solve state equations for and adjoint state q*.
- To construct velocity field from the shape sensitivity analysis.
- To solve the Hamilton–Jacobi equation to evolve the level set based on .
- To re-initialise periodically as signed distance function.
- To iterate steps (iii) to (vii) until convergence.
- To extract final structure shape .
- To validate the approach on a 2D aluminium plate with dimensions of 100 cm × 100 cm × 1 cm.
The main outcome converges locally optimal solutions (see Figure 9) for the 2D plate problem. The solution improves heat power radiated compared to baseline designs, showing that maximal thermal compliance is insufficient for this problem.
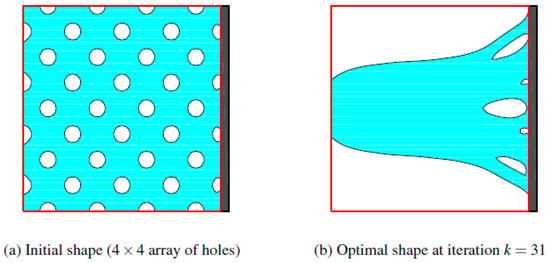
Figure 9.
The initial and optimal shapes for the optimisation problem with an initial configuration consisting of a 4 × 4 array of holes [].
4.4. Other Topology Optimisation Applications on Satellite Secondary Structures
It is possible to find published papers that feature the utilisation of optimisation tools integrated within finite element analysis (FEA) software to execute the optimisation process. Although this approach simplifies the optimisation procedure, it can also hinder objective comparisons due to the lack of transparency regarding algorithm specifics, parameters, and code implementation; although this practice streamlines optimisation, it often falls short of providing comprehensive insights necessary for detailed evaluation and comparative analysis. However, they are briefly mentioned in what follows.
Other applications of the SIMP method in the aerospace field within satellite structures can be found in.
In [], a mounting for a telescope is optimised using TO techniques to minimise mass while meeting constraints related to space environment like temperature, thermal conduction, and vibration resistance.
Article [] applied lattice TO to the main structure of a CubeSat, obtaining a structure that is 50% lighter, 20% stiffer, and consolidating 125 parts into only 25, while using Inconel 718 and 3D metal printing technology. Reportedly, the lighter assembly translated to USD 8000 to USD 10,000 in launch cost savings.
In [], authors describe the process of designing an optical bench for integrating instruments like mid-wavelength infrared (MWIR) imagers. The optical bench’s design process involves TO to ensure mechanical stability and thermal performance. The optimised version increases the net power emission by 36.5%. Verification methods, including vibration testing, confirm the suitability of AM-produced structures for spacecraft use.
The authors of [] apply TO to redesign and reduce the weight of a satellite’s secondary structure. A launcher connector is a mechanical device that supports the satellite inside the rocket fairing, and the authors accomplish TO without compromising mechanical performance. The optimised design is built via laser beam melting. Authors achieve a weight reduction of 57%, satisfying the first and second modal requirements; this is performed using specialised software that allows TO.
In paper [], TO using ANSYS® software is applied to maximise the kinetic energy of reaction wheels. They achieved a 15.8% increase in specific energy by introducing holes/spokes compared to a solid disk.
Similarly, in [], a reaction wheel is optimised using ANSYS®, resulting in a 16% increase in kinetic energy.
On the other hand, ref. [] also uses ANSYS® for performing TO; however, the problem addressed is reducing the mass of a star tracker bracket, achieving a 50% reduction in its mass.
The authors of [] reduce the vibration effects in the primary supporting structure of a microsatellite, performing a single objective TO (SIMP method is applied) in the software OptiStruct®.
In [], the redesign of a satellite panel using TO principles is used to enable manufacturability by laser powder bed fusion.
In [,], TO is applied for optimising the brackets of a structure that will be manufactured using AM.
Finally, there are three Master’s theses that perform TO to CubeSat structures [,,].
5. Cases of Study on Satellite Structures by Topology Optimisation Discrete Approaches
It should be noted that only a few of the techniques outlined in Section 2 have been employed to achieve optimal solutions in the field of satellite structures, according to existing scientific literature. In this regard, this section provides a concise overview of diverse case studies involving various TO methods for this specific purpose, of which metaheuristic methods are outstanding. Additionally, instances where the research incorporates the utilisation of AM techniques to produce tangible prototypes of optimised components are addressed.
5.1. Metaheuristic Methods
In the following cases of study where metaheuristic methods are applied to satellites, it is noted that metaheuristic approaches show a wide variability when talking about topology optimisation, and as the objective functions allow more flexibility, one can often see a mix of size, shape, and topology optimisation in the same problem.
5.1.1. Parallel Optimal Design of Satellite Bus Structures Using Particle Swarm Optimisation
The work [] presents an optimisation approach for satellite bus structures using particle swarm optimisation (PSO) in a grid-computing environment. The authors develop a framework to leverage grid computing to distribute the FEA.
The optimisation goal is to minimise the mass of a satellite adaptor-ring component through design optimisation. The adaptor ring model had 32 geometric design variables including dimensions, rib shapes, stiffener angles, and thicknesses. Constraints were placed on the first natural frequency (>18 Hz), and a maximum stress of less than 430 MPa, in order to ensure design feasibility. The steps followed are:
- The use of the PSO algorithm is suitable for problems with expensive function evaluations that can be easily parallelised.
- The use of a grid-computing framework to distribute simulation jobs for automatic mesh generation in FEA.
- The use of MSC Patran® 2004 and MSC Nastran® 2004 (commercial software) for meshing and analysis.
- The PSO algorithm module coordinated job submission and gathered results from the grid resources.
- Optimisation is performed in two stages: an initial optimisation execution, and then, a reinforcement is added to address constraint violations. Then, a second optimisation is performed.
The results of [] can be summarised as follows:
- Optimisation of a 32-variable adaptor-ring model, reducing its mass 54% from 26.2 kg to 12.4 kg.
- Performed optimisation in two stages:
- Optimised to 13.6 kg mass before violating constraints.
- Reinforced model and re-optimised to satisfy constraints mentioned above.
- A 60-node grid is leveraged to complete 1266 minutes of computations.
- Sensitivity analyses were conducted to study the impact of parameters on the optimised design.
5.1.2. Structural Optimisation Design of Shock Isolation Ring for Satellite–Rocket Separation
Authors of [] present the structural optimisation design of a shock isolation ring used between satellites and rockets. The harsh shock loads during separation can damage sensitive onboard electronics. Shock isolation rings are layered metal structures that attenuate shock waves through reflection and refraction. They convert shock energy into elastic strain energy.
The goal is to minimise the mass of the shock isolation ring structure with six variables: number of layers, number of blocks per layer, layer thickness, block height, outer radius, and inner radius. On the other side, the optimisation of the shock isolation ring structure has three key constraints: shock isolation ratio minimum of 30%, a minimum stiffness of N/m, and a safety factor of 1.25. The TO process is conducted under aluminium yield strength. To do so, the following methodology has been implemented:
- A shock response spectrum synthesis to obtain a transient time domain shock load is used.
- A FE model of the shock isolation ring structure in Catia®, Abaqus® and Matlab®.
- An objective function is defined by designing the variables and constraints mentioned above; mass minimisation is intended.
- Response surface models for shock isolation ratio and strength based on FEA at sample points are built.
- Adaptive simulated annealing algorithm to solve the mixed discrete-continuous optimisation problem is used.
- Computed sensitivities of objectives and constraints to design variables at the optimal design.
The main result is a reduced mass by 33.5% from 0.119 Kg to 0.089 Kg, and the maximum value of the impact response spectrum of the structure is attenuated by 80% while maintaining a safety factor greater than one.
5.1.3. Small Satellite Structural Optimisation Using Genetic Algorithm Approach
In paper [], authors present a case of study where they apply GAs for structural optimisation of small satellites using a GA in isogrid structures. Isogrid structures are commonly employed in satellite applications because of their superior stiffness-to-weight ratio when compared to solid sheets [,,]. The pattern increases stiffness through an array of equilateral triangle cutouts.
The key design challenge is determining the optimal geometry parameters such as rib web width for an isogrid structure that minimises mass while still meeting stiffness requirements.
A GA is proposed as an efficient search method for finding the optimal isogrid geometry. In the GA, the rib–web width parameter is encoded as a gene in a chromosome representation of the design. An initial population of designs is randomly generated across the web–width design space. The fitness of each individual is evaluated through FEA simulations, assessing objectives like mass and constraints like stiffness. High-fitness designs were selected and underwent crossover and mutation to produce the next generation of designs. GA parameters like population size, generation count, and operator probabilities are tuned to ensure an efficient search for this specific problem.
The GA is found to converge much faster than traditional gradient-based optimisation methods. Through the evolutionary process, the optimal rib–web width is determined to be 506.73 mm for the design constraints and objectives, demonstrating the effectiveness of the GA method for isogrid optimisation to achieve mass reduction.
5.1.4. The Topology Optimisation of Electronic Parts Mounted on Microsatellite
In small satellites, PCB design is fundamental to meeting mass and size constraints. In [], authors propose a multi-objective TO using a GA in the patterns design of PCBs with a numerical application of the power board of a microsatellite.
In PCB design, trial-and-error processes are often required during component placement to preserve key connections, despite auto-routing tools. The goal is to meet mass, size, and height specifications. A system that automates the entire pattern design and facilitates routing in component positioning is built so as to later optimise the PCB by using a GA.
The points described below are repeated until the established design criteria are met:
- Apply auto-positioning method: Components are placed on the board from upper left to right with an established distance between parts for a given pattern. In case a component crosses the right edge of the board, it is placed on the left edge below previously placed parts.
- Placement is evaluated with an autorouting function.
- The design variables are obtained from the evolutionary computation by MOGA with 70 generations to evolve. The established objective functions are to minimise board area and maximise autorouting rate.
A total of 3500 individuals were evaluated and 66 Pareto solutions were obtained. The routing rate is 89.5% and the board area is 2250 , whereas a 35.7% smaller board was obtained.
5.1.5. An Engineering Method for Complex Structural Optimisation Involving Both Size and Topology Design Variables
In the paper by Huang et al. [], the authors introduce a simultaneous optimisation approach that addresses both the topology and size of structures comprising bars, beams, plates, or various combinations thereof. They utilise a genetic algorithm (GA) for optimising discrete variables and a dual method for continuous variables. One of the numerical examples provided pertains to the structural optimisation of a microsatellite.
The problem description pertains to the practical application of the developed method. The boundary condition is defined as the connection interface between the entire satellite structure and the launch vehicle, specifically at the lower section of the main body. All the stiffeners utilised in this context feature solid rectangular cross-sections. The design problem involves optimising the thickness of eight plates and the configuration of the stiffeners within these plates. In this specific application, the objective is to minimise the structural mass of the empirical model, which is 1.183 Kg. Additionally, it is necessary to ensure that both the first and second modes of transverse bending vibration are greater than 25 Hz, and the first mode of longitudinal vibration exceeds 50 Hz. The following methodological phases were undertaken:
- The structural and sensitivity analysis of the initial design is carried out.
- The first-level problem is approximated by a Branched Multi-Point Approximation (BMA) function.
- Optimisation of discrete variables through a GA; if the problem is not convergent, it is repeated from the structural analysis.
- The second-level problem for the optimisation of continuous variables is approached and solved by means of the dual method for the calculation of the individual amplitude.
After optimisation, the mass is reduced by 31.69% compared to the empirical design. The first- and second-order transverse bending vibrations are 28.64 Hz and 28.95 Hz, respectively, whereas the first-order longitudinal vibration is 51.52 Hz.
5.2. Other Topology Optimisation Applications on Satellite Secondary Structures
We finish this section by briefly presenting three papers that perform TO for stiffness optimisation subject to weight minimisation while utilising a metaheuristic technique in the process.
Another example of an application of GA in a satellite context is given in []. The authors applied a GA to minimise the mass of a carbon fibre framework for a space camera. The optimised framework is 15.6 kg, 18.4% of the total camera mass. The manufactured framework passed the mechanical environment testing validation manufacture technique and stiffness optimisation procedure.
In [], authors present a redesign of a star tracker housing using TO and building it by AM, specifically by the Laser Powder Bed Fusion technique. The optimisation objective is set to maximise stiffness, subject to constraints on target volume (20% of design space), minimum member thickness (4 mm), and maximisation of natural frequency. Compared to the original bracket, the optimised design achieved a 36% reduction in weight.
In article [], the authors focus on the optimisation of a rotor for microsatellite reaction wheels based on a bio-inspired algorithm. As part of their results, this rotor reaches 7500 RPM, and with a diameter of 282 mm and an energy density of 4661 , a moment of inertia ratio of 0.7584 is achieved.
6. Discussion and Conclusions
In order to better grasp the information presented in Section 2, Section 3, Section 4 and Section 5, we highlight some relevant points of each section in a summarising way.
6.1. Topology Optimisation Methods
In Section 2, we offer a concise overview of several TO methods existing in the scientific literature, regardless of their overall acceptance. It is important to recognise that each method has numerous variations due to approximately three decades of development. Over the past ten years, there has been a notable surge in new approaches within the realms of metaheuristics and machine learning applied to TO. Interestingly, several of these methodologies continue to address the traditional stiffness optimisation problem. It is our hope that researchers will consistently expand their proposed techniques to tackle the wide array of TO challenges at hand. Some points to be addressed in future research in the field of TO stand out:
- Homogenisation methods are difficult to use, especially when implemented for 3D TO problems. Nonetheless, multi-scale approaches make use of them.
- SIMP methods require selecting an appropriate penalisation factor.
- LSMs are sensitive to initial solution guesses.
- Topological derivative methods are mathematically complicated.
- The BESO method is sensitive to ER-selected value.
- MVV is an interesting alternative approach but requires more development.
- Metaheuristic approaches lack consistent development. There is a large variety of methods and implementations but very few of them have seen active development. Additionally, a large number of function evaluations are required in metaheuristic approaches. Nonetheless, metaheuristic approaches allow flexible objective functions that allow the combination of discrete and continuous design variables.
- Machine learning approaches do not scale well to three-dimensional design space. An important number of implementations requires large amounts of previously optimised cases to work. Additionally, very few approaches are “physics informed”, nonetheless they are very promising and will see important development in the years to come.
6.2. Additive Manufacture Processes
In Section 3, we bring to the reader’s attention that AM emerges as a natural choice for producing optimal solutions through TO. This approach offers several benefits that align well with modern engineering practices, such as weight reduction, minimised waste, and decreased reliance on post-processing procedures, among others. Despite its merits, it is important to recognise that AM does have limitations and complexities that must be addressed before applying it to stringent real-world applications, especially within industries like aerospace, and in particular, satellite engineering. The anisotropy introduced in materials due to AM necessitates additional consideration during the optimisation process to ensure that the final design does not suffer from undesirable effects like reduced stiffness.
Furthermore, addressing thermal gradients inherent in AM’s production processes is crucial. This involves using simulation tools to assess potential residual stress, along with effectively managing porosity. Many of these considerations are intrinsically tied to the specifics of the AM process being used and the associated equipment.
The following points to be addressed in future research stand out:
- Length scale is necessary to eliminate tiny (not manufacturable) features.
- Thermal gradients, residual stresses, and anisotropy need to be addressed when TO solutions are intended to be manufactured.
- Requirements for supporting structures must be met in the AM fabrication process.
- Adequate control in machine parameters must be met to ensure repeatability.
6.3. Cases of Study for TO Methods Applied to Satellite Structures
In Section 4 and Section 5, we provide brief explanations of TO methods applied to satellite structures. A diverse distribution of applications across various TO techniques is observed, with a considerable number of them reaching the manufacturing stage. For such instances, AM is employed for fabrication. It is evident that each application shows optimised weight and safety margins appropriate for their intended use, which is sometimes demonstrated by applying verification techniques designed to validate satellite structures. Some applications are then successfully integrated into operational service.
The authors report a substantial reduction in mass in all revised works. According to the articles reviewed in this paper, mass reductions ranging from 8% to 55% have been observed in satellite structure components where TO has been applied, with a trend in the majority of the studies towards a 50% mass reduction. This wide variation is primarily attributed to differences in the studied satellite components as well as in the safety margins allowed. A relevant work that demonstrates the clear potential of the combination of TO and AM is presented in Section 4.2.1, where the application of TO resulted in cost savings of USD 15,600 just by decreasing slightly more than one kilogram of mass from a satellite component, the main reason for cost savings is mass reduction as launch costs are directly related to the total mass of the satellite as mentioned in Section 3.2. It is noteworthy that reporting monetary savings is unusual in the majority of papers.
Despite success, authors report challenges present in the development and fabrication of satellite structures, of which the following stand out:
- There is little support from FEA available software for the implementation of customised TO algorithms.
- FEA’s available software for TO tools does not report implemented algorithms and/or parameters to the final user, hindering the possibility of proper comparisons between scholars.
- There is a need for support structures in metal AM processes such as SLM to print overhangs and bridges. This adds mass and requires post-processing to remove supports.
- Achieving the necessary surface finishes for satellite components can pose a challenge due to the roughness resulting from AM. Typically, extra finishing processes are needed.
- Lack of design standards for AM satellite components, especially for structural parts and mechanisms. Current international regulations have not been aimed at encompassing all the AM methods [,]. Moreover, in the absence of robust AM regulations, the oversight of international regulations within the aerospace field has received even less attention and the few standards that do exist for certain methods [] (refs. [,,,,] under development are focused on administrative or other non-pertinent issues that are not related to AM. Even though NASA has published some standards such as Laser Powder Bed Fusion methods [,] and general requirements [].
- It is essential to recognise and certify novel AM alloys and methods for diverse satellite uses, as material characteristics may differ among various AM machines and methods.
Within the domain of TO methods, each approach discussed in Section 2 possesses the capability to conduct basic optimisation tasks for aerospace structures, even when considering satellite applications. Each method has demonstrated, at various stages, the capacity to optimise stiffness under a weight constraint. Furthermore, they can integrate localised displacement restrictions into the optimisation process. Similarly, all of these methods have exhibited the ability to maximise natural frequencies (except, perhaps, MMV). These key abilities have been showcased, at very least, from a single-objective standpoint.
The following question arises: why is there a limited range of TO methods being applied to satellite structures? Mathematical complexity is among the factors, particularly for techniques like topology derivative methods, phase change methods, and possibly for homogenisation (which has seen a resurgence with the emergence of multi-scale TO approaches).
Research underscores the fact that SIMP stands out as a highly favoured TO algorithm. Its popularity partially strives in the fact that it has been incorporated into several commercial software packages, facilitating its convenient and straightforward utilisation. This attribute is a distinctive advantage, unlike other algorithms that require a considerable understanding of the method’s intricacies to be implemented within computational code. Moreover, the implementation of TO algorithms necessitates obtaining pertinent data from structural responses, typically derived through FEA. This often leads to the need for coupling TO and FEA codes, demanding additional time and effort to grasp, and effectively employing both techniques. Thankfully, there is an abundance of educational codes available that are suitable for modelling simple 2D and 3D problems. To serve this purpose, for a comprehensive review on educational codes on TO containing readable code, readers can refer to the work by Wang et al. [].
6.4. Addressing Natural Frequency as Part of the TO Problem
Most of the works reviewed make use of the first natural vibration mode of the structure as a criterion for successful optimisation. They usually compare such a vibration mode with the expected frequency vibration induced by the launching vehicle. The reviewed works don’t usually centre their attention on how to determine the expected value of the vibration frequency, and they tend to rely on other works or, alternatively, they make use of technical specifications.
A tendency in reviewed works in Section 4 is applying TO and checking that the optimal solution complies with being greater than the lower bound, adequately selected beforehand [,,,,,,,,]. There are works in which such an optimal solution has been manufactured using AM; then, a standardised vibration test is carried in order to experimentally check that the structure is able to withstand mechanical loads. However, just checking that the optimal design complies with such a lower bound in frequency does not mean that the first vibration mode is optimised. Thus, in order to take vibration modes into account, works like [] propose a multi-objective approach by formulating frequency as part of the objective function to optimise. In such a work, authors demonstrate that a multi-objective approach gives comparably better results than the uni-objective approach, inviting authors to continue exploring ways of performing satellite TO. In such a fashion, a work that deviates slightly from the typical approximation performs by using shock response spectrum and its corresponding structural response to carry out satellite TO; works like [] use this approach effectively.
6.5. Multi-Scale Approaches on Satellite TO
A number of papers applying multi-scale TO were reviewed in Section 4 [,]. The results show that this is an area in active development, showing promising advantages such as an additional mass reduction with respect to standard TO. Multi-scale topology-optimised designs require numerical validation, model fabrication, and mechanical tests to check the structural properties of resulting optimised structures. They also impose their own challenges in the fabrication process: small features in the mesoscale require high precision to allow manufacturing and overhangs require support themselves, reducing the need for support structures. Applications of multi-scale methods in satellite structures are still lacking, and it is expected to see more developments all around the aerospace industry.
6.6. Multi-Physics Approaches to Satellite TO
TO applied to satellite structures is usually centred around decreasing mass while optimising mechanical properties in order to ensure structural integrity, and whereas this is of main concern from the structural point of view, characteristics like heat dissipation and thermal stresses might be of interest from a thermal management point of view. Characteristics like conductivity and low resonant frequency might be of interest from an electromagnetic point of view, especially in electromagnetic radiating devices.
Although structural integrity is always the main concern, combining structural and thermal requirements into TO might help in the development of multi-purpose structures, as well as for the benefit of the design of heat-dissipating structures. In a similar way, considering optimising material electromagnetic characteristics might be of interest. For instance, in the design of satellite communication systems, antennas that might be integrated as part of the structure of the satellite or deployed in orbit.
Reviewed works that somehow combine structural and thermal phenomena are, for instance, the work in [], which considers maximising heat power radiated by optimised radiating structures. Furthermore, the work [] considers a thermo-elastic formulation in a uni-objective approach, leaving thermal stresses out of the objective function but present in the final results.
Works performing electromagnetic considerations on the TO process were not extensively reviewed as they fall out of the scope of this work. However, the reader might refer to [,,,,,,].
The works herein reviewed, in general, fail to integrate multiple physics phenomena in a multi-objective approach that integrates thermal and mechanical properties in the objective function. We expect to see more development in the area of multi-physics TO in the near future.
6.7. Final Remarks
In this work, we intend to provide a comprehensive review of diverse TO techniques, categorising them into two broad classes: continuous and discrete approaches. The continuous methods examined include the homogenisation method, SIMP, topology derivative, LSM, and phase-field and multi-scale TO. Analysed discrete approaches encompass ESO and its variants like BESO and SBESO, MMV, metaheuristic algorithms, and machine learning techniques applied to TO. Both classes of methods have shown to be promising for optimising satellite structural components. This literature review has sought to synthesise recent research on the application of structural TO techniques for the design of satellite structures. Enabling the potential of AM processes to physically realise geometrically complex TO solutions has been discussed. In addition, we discussed different works in which TO techniques were used to optimise satellite components in order to achieve the desired mass reduction. Finally, we offered a brief discussion, highlighting important considerations, each of which constitutes a challenge on their own.
Author Contributions
Conceptualization, A.B.H.-P. and J.J.H.-G.; methodology, A.B.H.-P.; validation, A.B.H.-P. and J.J.H.-G.; formal analysis, A.B.H.-P., A.d.J.P.-S. and F.R.-L.; investigation, A.B.H.-P., A.d.J.P.-S. and F.R.-L.; resources, J.J.H.-G. and M.F.M.-R.; data curation, A.B.H.-P. and J.J.H.-G.; writing—original draft preparation, A.B.H.-P., A.d.J.P.-S., F.R.-L. and J.J.H.-G.; writing—review and editing, A.B.H.-P., J.J.H.-G. and M.F.M.-R. supervision, J.J.H.-G. and M.F.M.-R.; project administration, J.J.H.-G. and M.F.M.-R.; funding acquisition, J.J.H.-G. and M.F.M.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Secretaría de Investigación y Posgrado, Instituto Politécnico Nacional project numbers 20231067, 20230476, 20232774, and 20230593, as well as Project CONAHCYT 7051. The APC was funded by Secretaría de Investigación y Posgrado, Instituto Politécnico Nacional project 20231067.
Data Availability Statement
No data were generated and is not available for this research, as this is a Review paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 2PP | Two-Photon Polymerisation |
| 3DGP | 3D Gel Printing |
| AM | Additive Manufacture |
| ASTM | American Society for Testing and Materials |
| BESO | Bi-Directional ESO |
| BJ3DP | Binder Jetting 3D Printing |
| BMA | Branched Multi-Point Approximation |
| EBM | Electron Beam Melting |
| ESO | Evolutionary Structural Optimisation |
| CAD | Computer-Aided Design |
| CISM | Centre for Mechanical Sciences |
| CLF | Ceramic Laser Fusion |
| CLIP | Continuous Liquid Interface Production |
| CNC | Computerised Numerical Control |
| CMG | Control Moment Gyroscope |
| DED | Direct Energy Deposition |
| DLP | Digital Light Processing |
| DMD | Direct Metal Deposition |
| FE | Finite Element |
| FEA | Finite Element Analysis |
| FEM | Finite Element Method |
| FFF | Fused Filament Fabrication |
| GAs | Genetic Algorithms |
| GEO | GeoStationary Orbit |
| HSS | High-Speed Sintering |
| IGA | Iso-Geometric Analysis |
| IJP | Ink Jet Printing |
| LEO | Low Earth Orbit |
| LOS | Line of Sight |
| LSM | Level-Set Method |
| MMA | Method of Moving Asymptotes |
| MMC | Moving Morphable Components |
| MMV | Moving Morphable Voids |
| NASA | National Aeronautics and Space Administration |
| PAM | Plasma Arc Additive Manufacturing |
| PJ | Photopolymer Jetting |
| PSO | Particle Swarm Optimisation |
| RAMP | Rational Approximation of Material Properties |
| RFP | Rapid Freeze Prototyping |
| SIMP | Solid Isotropic Material with Penalty |
| SLA | Stereolithography |
| SLM | Selective Laser Melting |
| SLS | Selective Laser Sintering |
| SM | Subtractive Manufacture |
| T3DP | Thermoplastic 3D Printing |
| TO | Topology Optimisation |
| WAAM | Wire and Arc Additive Manufacturing |
References
- Salazar, V.K. Emerging Trends in the Satellite Industry. Master’s Thesis, MIT, Cambridge, MA, USA, 2012. [Google Scholar]
- Gaudenzi, P.; Atek, S.; Cardini, V.; Eugeni, M.; Nisi, G.G.; Lampani, L.; Pasquali, M.; Pollice, L. Revisiting the configuration of small satellites structures in the framework of 3D Additive Manufacturing. Acta Astronaut. 2018, 146, 249–258. [Google Scholar] [CrossRef]
- Gasman, L. Additive aerospace considered as a business. In Additive Manufacturing for the Aerospace Industry; Elsevier: Amsterdam, The Netherlands, 2019; pp. 327–340. [Google Scholar] [CrossRef]
- EOS GmbH. Certified for Universal Success: Additive Manufacturing of Satellite Components; EOS GmbH: Munich, Germany, 2018. [Google Scholar]
- Zhu, J.; Zhou, H.; Wang, C.; Zhou, L.; Yuan, S.; Zhang, W. A review of topology optimization for additive manufacturing: Status and challenges. Chin. J. Aeronaut. 2021, 34, 91–110. [Google Scholar] [CrossRef]
- Cappelletti, C.; Battistini, S.; Malphrus, B. CubeSat Handbook: From Mission Design to Operations; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Arora, R.K. Optimization: Algorithms and Applications; Chapman and Hall/CRC: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Rothwell, A. Optimization Methods in Structural Design; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Engineering Online Library; Springer: Berlin/Heidelberg, Germany, 2003; pp. xiv, 370. [Google Scholar] [CrossRef]
- Christensen, P.W.; Klarbring, A. An Introduction to Structural Optimization; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar] [CrossRef]
- Samareh, J.A. Survey of shape parameterization techniques for high-fidelity multidisciplinary shape optimization. AIAA J. 2001, 39, 877–884. [Google Scholar] [CrossRef]
- Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; Leary, M.; Berto, F.; du Plessis, A. Metal additive manufacturing in aerospace: A review. Mater. Des. 2021, 209, 110008. [Google Scholar] [CrossRef]
- Zhu, L.; Li, N.; Childs, P. Light-weighting in aerospace component and system design. Propuls. Power Res. 2018, 7, 103–119. [Google Scholar] [CrossRef]
- Orme, M.E.; Gschweit, M.; Ferrari, M.; Vernon, R.; Madera, I.J.; Yancey, R.; Mouriaux, F. Additive Manufacturing of Lightweight, Optimized, Metallic Components Suitable for Space Flight. J. Spacecr. Rocket. 2017, 54, 1050–1059. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, W.; Quan, D.; Shi, G.; Tang, L.; Hou, Y.; Breitkopf, P.; Zhu, J.; Gao, T. From Topology Optimization Design to Additive Manufacturing: Today’s Success and Tomorrow’s Roadmap. Arch. Comput. Methods Eng. 2020, 27, 805–830. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology optimization approaches. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Wu, J.; Sigmund, O.; Groen, J.P. Topology optimization of multi-scale structures: A review. Struct. Multidiscip. Optim. 2021, 63, 1455–1480. [Google Scholar] [CrossRef]
- Kokare, S.; Oliveira, J.; Godina, R. Life cycle assessment of additive manufacturing processes: A review. J. Manuf. Syst. 2023, 68, 536–559. [Google Scholar] [CrossRef]
- Vlah, D.; Žavbi, R.; Vukašinović, N. Evaluation of topology optimization and generative design tools as support for conceptual design. In Proceedings of the Design Society: DESIGN Conference, Cavtat, Croatia, 18–21 May 2020; Volume 1, pp. 451–460. [Google Scholar] [CrossRef]
- Rozvany, G.I.N. Aims, scope, methods, history and unified terminology of computer-aided topology optimization in structural mechanics. Struct. Multidiscip. Optim. 2001, 21, 90–108. [Google Scholar] [CrossRef]
- Saitou, K.; Izui, K.; Nishiwaki, S.; Papalambros, P. A Survey of Structural Optimization in Mechanical Product Development. J. Comput. Inf. Sci. Eng. 2005, 5, 214–226. [Google Scholar] [CrossRef]
- Deaton, J.D.; Grandhi, R.V. A survey of structural and multidisciplinary continuum topology optimization: Post 2000. Struct. Multidiscip. Optim. 2013, 49, 1–38. [Google Scholar] [CrossRef]
- Michell, A.G.M. LVIII. The limits of economy of material in frame-structures. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1904, 8, 589–597. [Google Scholar] [CrossRef]
- Prager, W.; Rozvany, G. Optimization of structural geometry. In Dynamical Systems; Academic Press: Cambridge, MA, USA, 1977; pp. 265–293. [Google Scholar] [CrossRef]
- Rozvany, G. Structural Topology Optimization (STO); Springer: Vienna, Austria, 2014; Volume 549, pp. 1–14. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Kohn, R.V.; Strang, G. Optimal design and relaxation of variational problems, I. Commun. Pure Appl. Math. 1986, 39, 113–137. [Google Scholar] [CrossRef]
- Kohn, R.V.; Strang, G. Optimal design and relaxation of variational problems, II. Commun. Pure Appl. Math. 1986, 39, 139–182. [Google Scholar] [CrossRef]
- Kohn, R.V.; Strang, G. Optimal design and relaxation of variational problems, III. Commun. Pure Appl. Math. 1986, 39, 353–377. [Google Scholar] [CrossRef]
- Zhu, J.H.; Zhang, W.H.; Xia, L. Topology Optimization in Aircraft and Aerospace Structures Design. Arch. Comput. Methods Eng. 2015, 23, 595–622. [Google Scholar] [CrossRef]
- Rozvany, G.I.N. A critical review of established methods of structural topology optimization. Struct. Multidiscip. Optim. 2009, 37, 217–237. [Google Scholar] [CrossRef]
- Xia, L.; Xia, Q.; Huang, X.; Xie, Y.M. Bi-directional Evolutionary Structural Optimization on Advanced Structures and Materials: A Comprehensive Review. Arch. Comput. Methods Eng. 2018, 25, 437–478. [Google Scholar] [CrossRef]
- Bendsøe, M.P. Optimal shape design as a material distribution problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Svanberg, K. The method of moving asymptotes—A new method for structural optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Bourdin, B. Filters in topology optimization. Int. J. Numer. Methods Eng. 2001, 50, 2143–2158. [Google Scholar] [CrossRef]
- Zhou, M.; Rozvany, G. The COC algorithm, Part II: Topological, geometrical and generalized shape optimization. Comput. Methods Appl. Mech. Eng. 1991, 89, 309–336. [Google Scholar] [CrossRef]
- Li, P.; Wu, Y.; Yvonnet, J. A SIMP-phase field topology optimization framework to maximize quasi-brittle fracture resistance of 2D and 3D composites. Theor. Appl. Fract. Mech. 2021, 114, 102919. [Google Scholar] [CrossRef]
- Zuo, W.; Saitou, K. Multi-material topology optimization using ordered SIMP interpolation. Struct. Multidiscip. Optim. 2017, 55, 477–491. [Google Scholar] [CrossRef]
- Huang, X.; Li, W. A new multi-material topology optimization algorithm and selection of candidate materials. Comput. Methods Appl. Mech. Eng. 2021, 386, 114114. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Zou, B.; Li, Q.; Ma, Y. Stress constrained multi-material topology optimization with the ordered SIMP method. Comput. Methods Appl. Mech. Eng. 2021, 373, 113453. [Google Scholar] [CrossRef]
- da Silveira, O.A.A.; Palma, L.F. Some considerations on multi-material topology optimization using ordered SIMP. Struct. Multidiscip. Optim. 2022, 65, 261. [Google Scholar] [CrossRef]
- Yi, B.; Yoon, G.H.; Zheng, R.; Liu, L.; Li, D.; Peng, X. A unified material interpolation for topology optimization of multi-materials. Comput. Struct. 2023, 282, 107041. [Google Scholar] [CrossRef]
- Chandrasekhar, A.; Suresh, K. Multi-Material Topology Optimization Using Neural Networks. CAD Comput. Aided Des. 2021, 136, 103017. [Google Scholar] [CrossRef]
- Agrawal, G.; Gupta, A.; Chowdhury, R.; Chakrabarti, A. Robust topology optimization of negative Poisson’s ratio metamaterials under material uncertainty. Finite Elem. Anal. Des. 2022, 198, 103649. [Google Scholar] [CrossRef]
- Duan, Z.; Liu, Y.; Fan, J.; Long, K.; Xu, B.; Zhu, J.; Yan, J. Concurrent multi-material and multi-scale design optimization of fiber-reinforced composite material and structures for minimum structural compliance. Compos. Struct. 2023, 311, 116796. [Google Scholar] [CrossRef]
- Bohrer, R.; Pamwar, M.; Sangha, B.; Kim, I.Y. Modified Multi-Material Topology Optimization Considering Isotropic and Anisotropic Materials Mixture; SAE Technical Papers: Warrendale, PA, USA, 2021. [Google Scholar] [CrossRef]
- Jantos, D.R.; Hackl, K.; Junker, P. Topology optimization with anisotropic materials, including a filter to smooth fiber pathways. Struct. Multidiscip. Optim. 2020, 61, 2135–2154. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, D.; Wang, R.; Zhao, H. Dynamic Topology Optimization of Long-Span Continuum Structures. Shock Vib. 2021, 2021, 4421298. [Google Scholar] [CrossRef]
- Resmy, V.; Rajasekaran, C. Stiffness maximization of concrete structures using topology optimization in static and dynamic problems. J. Struct. Eng. 2021, 48, 51–60. [Google Scholar]
- Zhao, T.; Zhang, Y.; Ou, Y.; Ding, W.; Cheng, F. Fail-safe topology optimization considering fatigue. Struct. Multidiscip. Optim. 2023, 66, 132. [Google Scholar] [CrossRef]
- Burri, S.; Legay, A. Static reinforcement and vibration reduction of structures using topology optimization. Mech. Ind. 2023, 24, 2023003. [Google Scholar] [CrossRef]
- Chen, Z.; Long, K.; Wen, P.; Nouman, S. Fatigue-resistance topology optimization of continuum structure by penalizing the cumulative fatigue damage. Adv. Eng. Softw. 2020, 150, 102924. [Google Scholar] [CrossRef]
- Huang, J.; Xu, S.; Ma, Y.; Liu, J. A topology optimization method for hyperelastic porous structures subject to large deformation. Int. J. Mech. Mater. Des. 2022, 18, 289–308. [Google Scholar] [CrossRef]
- McConaha, M.; Venugopal, V.; Anand, S. Design Tool for Topology Optimization of Self Supporting Variable Density Lattice Structures for Additive Manufacturing. J. Manuf. Sci. Eng. Trans. ASME 2021, 143, 4049507. [Google Scholar] [CrossRef]
- Kazemi, H.S.; Tavakkoli, S.M. A new algorithm for design of support structures in additive manufacturing by using topology optimization. Struct. Eng. Mech. 2023, 86, 93–107. [Google Scholar] [CrossRef]
- Qiu, Z.; Li, Q.; Luo, Y.; Liu, S. Concurrent topology and fiber orientation optimization method for fiber-reinforced composites based on composite additive manufacturing. Comput. Methods Appl. Mech. Eng. 2022, 395, 114962. [Google Scholar] [CrossRef]
- Zhang, K.; Cheng, G. Three-dimensional high resolution topology optimization considering additive manufacturing constraints. Addit. Manuf. 2020, 35, 101224. [Google Scholar] [CrossRef]
- Costa, G.; Montemurro, M.; Pailhès, J. Minimum length scale control in a NURBS-based SIMP method. Comput. Methods Appl. Mech. Eng. 2019, 354, 963–989. [Google Scholar] [CrossRef]
- Ntintakis, I.; Stavroulakis, G.E. Infill Microstructures for Additive Manufacturing. Appl. Sci. 2022, 12, 7386. [Google Scholar] [CrossRef]
- Lee, H.Y.; Zhu, M.; Guest, J.K. Topology optimization considering multi-axis machining constraints using projection methods. Comput. Methods Appl. Mech. Eng. 2022, 390, 114464. [Google Scholar] [CrossRef]
- Xu, B.; Han, Y.S.; Zhao, L.; Xie, Y.M. Topology optimization of continuum structures for natural frequencies considering casting constraints. Eng. Optim. 2019, 51, 941–960. [Google Scholar] [CrossRef]
- Zhang, S.; Li, H.; Huang, Y. An improved multi-objective topology optimization model based on SIMP method for continuum structures including self-weight. Struct. Multidiscip. Optim. 2021, 63, 211–230. [Google Scholar] [CrossRef]
- Ramamoorthy, R. Topology Optimization of Vehicle Components for Nonlinear Load Cases. In Lecture Notes in Mechanical Engineering; Springer Nature: Singapore, 2023; pp. 309–318. [Google Scholar] [CrossRef]
- Zhang, Y.; Qin, Y.; Gu, J.; Jiao, Q.; Wang, F.; Guo, Z.; Zhang, H.; Wang, J.; Mi, C.; Zheng, H. Topology optimization of unsymmetrical complex plate and shell structures bearing multicondition overload. J. Mech. Sci. Technol. 2021, 35, 3497–3506. [Google Scholar] [CrossRef]
- Kale, V.; Aage, N.; Secanell, M. Stress constrained topology optimization of energy storage flywheels using a specific energy formulation. J. Energy Storage 2023, 61, 106733. [Google Scholar] [CrossRef]
- Li, R.; Liu, S. Topology Optimization Method of Structures with Surface Corrosion Considered. Acta Mech. Solida Sin. 2023, 36, 241–253. [Google Scholar] [CrossRef]
- Gan, N.; Wang, Q. Topology optimization design of porous infill structure with thermo-mechanical buckling criteria. Int. J. Mech. Mater. Des. 2022, 18, 267–288. [Google Scholar] [CrossRef]
- Gan, N.; Wang, Q. Topology optimization design for buckling analysis related to the size effect. Math. Mech. Solids 2022, 27, 1301–1318. [Google Scholar] [CrossRef]
- Zhuang, C.; Xiong, Z.; DIng, H. Temperature-constrained topology optimization of nonlinear heat conduction problems. J. Comput. Des. Eng. 2021, 8, 1059–1081. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, H.; Wang, F.; Zhang, T.; Li, X. Topology optimization of non-Fourier heat conduction problems considering global thermal dissipation energy minimization. Struct. Multidiscip. Optim. 2021, 64, 1385–1399. [Google Scholar] [CrossRef]
- Zhuang, X.; Thai, T.Q.; Rabczuk, T. Topology optimization of nonlinear flexoelectric structures. J. Mech. Phys. Solids 2023, 171, 105117. [Google Scholar] [CrossRef]
- Hou, J.; Wei, C.; Wang, J.; Gu, X.; Zhu, J.; Zhang, W. Topology optimization for energy dissipation structures based on shape memory alloys. Struct. Multidiscip. Optim. 2023, 66, 55. [Google Scholar] [CrossRef]
- Gao, J.; Gao, L.; Xiao, M. Density-Based ITO Method. Eng. Appl. Comput. Methods 2022, 7, 17–49. [Google Scholar] [CrossRef]
- Li, B.; Duan, Y.; Yang, H.; Lou, Y.; Müller, W.H. Isogeometric topology optimization of strain gradient materials. Comput. Methods Appl. Mech. Eng. 2022, 397, 115135. [Google Scholar] [CrossRef]
- Ullah, Z.; Ullah, B.; Khan, W.; ul Islam, S. Proportional topology optimisation with maximum entropy-based meshless method for minimum compliance and stress constrained problems. Eng. Comput. 2022, 38, 5541–5561. [Google Scholar] [CrossRef]
- Eschenauer, H.; Kobelev, V.; Schumacher, A. Bubble method for topology and shape optimization of structures. Struct. Optim. 1994, 8, 42–51. [Google Scholar] [CrossRef]
- Amstutz, S. Connections between topological sensitivity analysis and material interpolation schemes in topology optimization. Struct. Multidiscip. Optim. 2011, 43, 755–765. [Google Scholar] [CrossRef]
- Sokołowski, J.; Zochowski, A. On the Topological Derivative in Shape Optimization. Siam J. Control Optim. 1999, 37, 1251–1272. [Google Scholar] [CrossRef]
- Novotny, A.; Feijóo, R.; Taroco, E.; Padra, C. Topological sensitivity analysis. Comput. Methods Appl. Mech. Eng. 2003, 192, 803–829. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, K.; Wang, M.Y. A new approach for simultaneous shape and topology optimization based on dynamic implicit surface function. Control Cybern. 2005, 34, 255–282. [Google Scholar]
- Céa, J.; Garreau, S.; Guillaume, P.; Masmoudi, M. The shape and topological optimization connection. Comput. Methods Appl. Mech. Eng. 2000, 188, 713–726. [Google Scholar] [CrossRef]
- Burger, M.; Hackl, B.; Wolfgang, R. Incorporating Topological Derivatives into Level Set Methods. J. Comput. Phys. 2004, 194, 344–362. [Google Scholar] [CrossRef]
- He, L.; Kao, C.Y.; Osher, S. Incorporating topological derivatives into shape derivatives based level set methods. J. Comput. Phys. 2007, 225, 891–909. [Google Scholar] [CrossRef]
- Sokolowski, J.; Zochowski, A. Topological Derivatives of Shape Functionals for Elasticity Systems. Mech. Struct. Mach. 2007, 29, 331–349. [Google Scholar] [CrossRef]
- Osher, S.J.; Sethian, J.A. Fronts propagating with curvature dependent speed: Algorithms based on Hamilton–Jacobi formulations. Final report. J. Comput. Phys. 1987, 79, 12–49. [Google Scholar] [CrossRef]
- Sethian, J.A. Level set methods and fast marching methods: Evolving interfaces in computational geometry, fluid mechanics, computer vision, and materials science, by J.A. Sethian. In Robotica; Cambridge University Press: Cambridge, UK, 2000; Volume 18, pp. 89–92. [Google Scholar] [CrossRef]
- Sethian, J.; Wiegmann, A. Structural Boundary Design via Level Set and Immersed Interface Methods. J. Comput. Phys. 2000, 163, 489–528. [Google Scholar] [CrossRef]
- Wang, M.Y.; Wang, X.; Guo, D. A level set method for structural topology optimization. Comput. Methods Appl. Mech. Eng. 2003, 192, 227–246. [Google Scholar] [CrossRef]
- Wang, X.; Wang, M.; Guo, D. Structural shape and topology optimization in a level-set-based framework of region representation. Struct. Multidiscip. Optim. 2004, 27, 1–19. [Google Scholar] [CrossRef]
- Allaire, G.; Jouve, F.; Toader, A.M. Structural optimization using sensitivity analysis and a level-set method. J. Comput. Phys. 2004, 194, 363–393. [Google Scholar] [CrossRef]
- Allaire, G.; Jouve, F.; Toader, A.M. A level-set method for shape optimization. Comptes Rendus Math. 2002, 334, 1125–1130. [Google Scholar] [CrossRef]
- van Dijk, N.; Langelaar, M.; Keulen, F. Explicit level-set-based topology optimization using an exact Heaviside function and consistent sensitivity analysis. Int. J. Numer. Methods Eng. 2012, 91, 67–97. [Google Scholar] [CrossRef]
- van Dijk, N.; Maute, K.; Langelaar, M.; Keulen, F. Level-set methods for structural topology optimization: A review. Struct. Multidiscip. Optim. 2013, 48, 437–472. [Google Scholar] [CrossRef]
- Gibou, F.; Fedkiw, R.; Osher, S. A review of level-set methods and some recent applications. J. Comput. Phys. 2018, 353, 82–109. [Google Scholar] [CrossRef]
- Xia, Q.; Shi, T. Generalized hole nucleation through BESO for the level set based topology optimization of multi-material structures. Comput. Methods Appl. Mech. Eng. 2019, 355, 216–233. [Google Scholar] [CrossRef]
- Noda, M.; Noguchi, Y.; Yamada, T. Extended level set method: A multiphase representation with perfect symmetric property, and its application to multi-material topology optimization. Comput. Methods Appl. Mech. Eng. 2022, 393, 114742. [Google Scholar] [CrossRef]
- Tan, Y.; Zhu, S. A discontinuous Galerkin level set method using distributed shape gradient and topological derivatives for multi-material structural topology optimization. Struct. Multidiscip. Optim. 2023, 66, 170. [Google Scholar] [CrossRef]
- Sheng, Z.; Hu, Q.; Xie, Y. Concurrent topology optimization of multiple components sharing partial design domain based on distance regularized parameterized level set method. Int. J. Numer. Methods Eng. 2023, 124, 3352–3386. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, Z.; Sha, W.; Zhang, Y.; Xiao, M.; Gao, L.; Liao, W.H. Level set-based topological design of multiphase micro-architectured materials using alternating active-phase method. Mater. Des. 2023, 225, 111448. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.; Li, Z.; Hu, J.; Han, B. Non-probabilistic reliability-based topology optimization (NRBTO) scheme for continuum structures based on the strength constraint parameterized level set method and interval mathematics. Thin-Walled Struct. 2023, 188, 110856. [Google Scholar] [CrossRef]
- Li, Z.; Wang, L.; Lv, T. A level set driven concurrent reliability-based topology optimization (LS-CRBTO) strategy considering hybrid uncertainty inputs and damage defects updating. Comput. Methods Appl. Mech. Eng. 2023, 405, 115872. [Google Scholar] [CrossRef]
- Wang, L.; Li, Z.; Ni, B.; Gu, K. Non-probabilistic Reliability-based Topology Optimization (NRBTO) Scheme for Continuum Structures Based on the parameterized Level-Set method and Interval Mathematics. Comput. Methods Appl. Mech. Eng. 2021, 373, 113477. [Google Scholar] [CrossRef]
- Li, Z.; Wang, L.; Luo, Z. A feature-driven robust topology optimization strategy considering movable non-design domain and complex uncertainty. Comput. Methods Appl. Mech. Eng. 2022, 401, 115658. [Google Scholar] [CrossRef]
- Pozzi, M.; Bonaccorsi, G.; Kim, H.A.; Braghin, F. Robust structural optimization in presence of manufacturing uncertainties through a boundary-perturbation method. Struct. Multidiscip. Optim. 2023, 66, 120. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Z.; Li, B.; Xie, M.; Hong, J.; Zheng, S. Topology optimization of high frequency vibration problems using the EFEM-based approach. Thin-Walled Struct. 2021, 160, 107324. [Google Scholar] [CrossRef]
- Wang, L.; Li, Z.; Gu, K. An interval-oriented dynamic robust topology optimization (DRTO) approach for continuum structures based on the parametric Level-Set method (PLSM) and the equivalent static loads method (ESLM). Struct. Multidiscip. Optim. 2022, 65, 150. [Google Scholar] [CrossRef]
- Townsend, S.; Kim, H.A. A level set topology optimization method for the buckling of shell structures. Struct. Multidiscip. Optim. 2019, 60, 1783–1800. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhao, M. Topology optimization under design-dependent loads with the parameterized level-set method based on radial-basis functions. Comput. Methods Appl. Mech. Eng. 2020, 369, 113235. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, L.; Li, Z.; Du, J. On the global optimum for heat conduction. Int. J. Heat Mass Transf. 2022, 198, 123381. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, Y.; Ma, Y.; Qureshi, A.; Ahmad, R. A Topology Optimization Method for Hybrid Subtractive—Additive Remanufacturing. Int. J. Precis. Eng. Manuf.-Green Technol. 2020, 7, 939–953. [Google Scholar] [CrossRef]
- Barrera, J.L.; Geiss, M.J.; Maute, K. Minimum feature size control in level set topology optimization via density fields. Struct. Multidiscip. Optim. 2022, 65, 94. [Google Scholar] [CrossRef]
- Miki, T. Self-support topology optimization considering distortion for metal additive manufacturing. Comput. Methods Appl. Mech. Eng. 2023, 404, 115821. [Google Scholar] [CrossRef]
- Yamada, T.; Noguchi, Y. Topology optimization with a closed cavity exclusion constraint for additive manufacturing based on the fictitious physical model approach. Addit. Manuf. 2022, 52, 102630. [Google Scholar] [CrossRef]
- Morris, N.; Butscher, A.; Iorio, F. A subtractive manufacturing constraint for level set topology optimization. Struct. Multidiscip. Optim. 2020, 61, 1573–1588. [Google Scholar] [CrossRef]
- Lin, H.; Liu, H.; Wei, P. A parallel parameterized level set topology optimization framework for large-scale structures with unstructured meshes. Comput. Methods Appl. Mech. Eng. 2022, 397, 115112. [Google Scholar] [CrossRef]
- Liu, H.; Wei, P.; Wang, M.Y. CPU parallel-based adaptive parameterized level set method for large-scale structural topology optimization. Struct. Multidiscip. Optim. 2022, 65, 30. [Google Scholar] [CrossRef]
- Li, H.; Yamada, T.; Jolivet, P.; Furuta, K.; Kondoh, T.; Izui, K.; Nishiwaki, S. Full-scale 3D structural topology optimization using adaptive mesh refinement based on the level-set method. Finite Elem. Anal. Des. 2021, 194, 103561. [Google Scholar] [CrossRef]
- Li, H.; Yu, M.; Jolivet, P.; Alexandersen, J.; Kondoh, T.; Hu, T.; Furuta, K.; Izui, K.; Nishiwaki, S. Reaction–diffusion equation driven topology optimization of high-resolution and feature-rich structures using unstructured meshes. Adv. Eng. Softw. 2023, 180, 103457. [Google Scholar] [CrossRef]
- Gao, J.; Xiao, M.; Zhou, M.; Gao, L. Isogeometric topology and shape optimization for composite structures using level-sets and adaptive Gauss quadrature. Compos. Struct. 2022, 285, 115263. [Google Scholar] [CrossRef]
- Jahangiry, H.A.; Gholhaki, M.; Naderpour, H.; Tavakkoli, S.M. Isogeometric Level Set-Based Topology Optimization for Geometrically Nonlinear Plane Stress Problems. CAD Comput. Aided Des. 2022, 151, 103358. [Google Scholar] [CrossRef]
- Aminzadeh, M.; Tavakkoli, S.M. A parameter space approach for isogeometrical level set topology optimization. Int. J. Numer. Methods Eng. 2022, 123, 3485–3506. [Google Scholar] [CrossRef]
- Wei, P.; Wang, W.; Yang, Y.; Wang, M.Y. Level set band method: A combination of density-based and level set methods for the topology optimization of continuums. Front. Mech. Eng. 2020, 15, 390–405. [Google Scholar] [CrossRef]
- Chen, L.Q. Phase-Field Models for Microstructure Evolution. Annu. Rev. Mater. Res. 2002, 32, 113–140. [Google Scholar] [CrossRef]
- McFadden, G. Phase-field models of solidification. In Recent Advances in Numerical Methods for Partial Differential Equations and Applications; American Mathematical Society: Providence, RI, USA, 2002; Volume 306. [Google Scholar] [CrossRef]
- Bourdin, B.; Chambolle, A. Design-dependent loads in topology optimization. ESAIM Control Optim. Calc. Var. 2003, 9, 19–48. [Google Scholar] [CrossRef]
- Bourdin, B.; Chambolle, A. The Phase-Field Method in Optimal Design. In Proceedings of the IUTAM Symposium on Topological Design Optimization of Structures, Machines and Materials; Bendsøe, M.P., Olhoff, N., Sigmund, O., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 207–215. [Google Scholar] [CrossRef]
- Wang, M.; Zhou, S. Phase Field: A Variational Method for Structural Topology Optimization. Cmes-Comput. Model. Eng. Sci. 2004, 6, 547–566. [Google Scholar] [CrossRef]
- Blank, L.; Garcke, H.; Sarbu, L.; Srisupattarawanit, T.; Styles, V.; Voigt, A. Phase-field Approaches to Structural Topology Optimization. Constrained Optim. Optim. Control Partial. Differ. Equ. 2012, 160, 245–256. [Google Scholar] [CrossRef]
- Marino, M.; Auricchio, F.; Reali, A.; Rocca, E.; Stefanelli, U. Mixed variational formulations for structural topology optimization based on the phase-field approach. Struct. Multidiscip. Optim. 2021, 64, 2627–2652. [Google Scholar] [CrossRef]
- Auricchio, F.; Bonetti, E.; Carraturo, M.; Hömberg, D.; Reali, A.; Rocca, E. A phase-field-based graded-material topology optimization with stress constraint. Math. Model. Methods Appl. Sci. 2020, 30, 1461–1483. [Google Scholar] [CrossRef]
- Almi, S.; Stefanelli, U. Topology optimization for incremental elastoplasticity. SIAM J. Control. Optim. 2021, 59, 339–364. [Google Scholar] [CrossRef]
- Almi, S.; Stefanelli, U. Topology optimization for quasistatic elastoplasticity. Esaim: COCV 2022, 28, 47. [Google Scholar] [CrossRef]
- Xie, Y.; Steven, G. A simple evolutionary procedure for structural optimization. Comput. Struct. 1993, 49, 885–896. [Google Scholar] [CrossRef]
- Xie, Y.M.; Steven, G.P. Evolutionary Structural Optimization; Springer: London, UK, 1997. [Google Scholar] [CrossRef]
- Querin, O.; Steven, G.; Xie, Y. Evolutionary structural optimisation (ESO) using a bidirectional algorithm. Eng. Comput. 1998, 15, 1031–1048. [Google Scholar] [CrossRef]
- Querin, O.; Young, V.; Steven, G.; Xie, Y. Computational efficiency and validation of bi-directional evolutionary structural optimisation. Comput. Methods Appl. Mech. Eng. 2000, 189, 559–573. [Google Scholar] [CrossRef]
- Yang, X.Y.; Xie, Y.M.; Steven, G.P.; Querin, O.M. Bidirectional Evolutionary Method for Stiffness Optimization. AIAA J. 1999, 37, 1483–1488. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.M.; Burry, M.C. A New Algorithm for Bi-Directional Evolutionary Structural Optimization. JSME Int. J. Ser. C 2006, 49, 1091–1099. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y. Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method. Finite Elem. Anal. Des. 2007, 43, 1039–1049. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.M. Bi-directional evolutionary topology optimization of continuum structures with one or multiple materials. Comput. Mech. 2008, 43, 393–401. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.M. Evolutionary Topology Optimization of Continuum Structures; John Wiley & Sons, Ltd.: Chichester, UK, 2010. [Google Scholar] [CrossRef]
- Xia, Q.; Shi, T.; Xia, L. Stable hole nucleation in level set based topology optimization by using the material removal scheme of BESO. Comput. Methods Appl. Mech. Eng. 2019, 343, 438–452. [Google Scholar] [CrossRef]
- Gao, J.; Song, B.; Mao, Z. Combination of the phase field method and BESO method for topology optimization. Struct. Multidiscip. Optim. 2020, 61, 225–237. [Google Scholar] [CrossRef]
- Shobeiri, V. Bidirectional evolutionary structural optimization for nonlinear structures under dynamic loads. Int. J. Numer. Methods Eng. 2020, 121, 888–903. [Google Scholar] [CrossRef]
- Habashneh, M.; Rad, M.M.; Fischer, S. Bi-directional Evolutionary, Reliability-based, Geometrically Nonlinear, Elasto-Plastic Topology Optimization, of 3D Structures. Acta Polytech. Hung. 2023, 20, 169–186. [Google Scholar] [CrossRef]
- Xu, T.; Lin, X.; Xie, Y.M. Bi-directional evolutionary structural optimization with buckling constraints. Struct. Multidiscip. Optim. 2023, 66, 67. [Google Scholar] [CrossRef]
- Nabaki, K.; Shen, J.; Huang, X. Evolutionary topology optimization of continuum structures considering fatigue failure. Mater. Des. 2019, 166, 107586. [Google Scholar] [CrossRef]
- Bahramian, N.; Khalkhali, A. Crashworthiness topology optimization of thin-walled square tubes, using modified Bidirectional Evolutionary Structural Optimization approach. Thin-Walled Struct. 2020, 147, 106524. [Google Scholar] [CrossRef]
- Teimouri, M.; Asgari, M. Multi-objective BESO topology optimization for stiffness and frequency of continuum structures. Struct. Eng. Mech. 2019, 72, 181–190. [Google Scholar] [CrossRef]
- Brecher, C.; Zhao, G.; Fey, M. Topology optimization for vibrating structures with the BESO method. Vibroeng. Procedia 2019, 23, 1–6. [Google Scholar] [CrossRef]
- Han, Y.S.; Xu, B.; Zhao, L.; Xie, Y.M. Topology optimization of continuum structures under hybrid additive-subtractive manufacturing constraints. Struct. Multidiscip. Optim. 2019, 60, 2571–2595. [Google Scholar] [CrossRef]
- Xiong, Y.; Yao, S.; Zhao, Z.L.; Xie, Y.M. A new approach to eliminating enclosed voids in topology optimization for additive manufacturing. Addit. Manuf. 2020, 32, 101006. [Google Scholar] [CrossRef]
- Cao, S.; Wang, H.; Lu, X.; Tong, J.; Sheng, Z. Topology optimization considering porosity defects in metal additive manufacturing. Appl. Sci. 2021, 11, 5578. [Google Scholar] [CrossRef]
- Xu, B.; Han, Y.; Zhao, L.; Xie, Y.M. Topological optimization of continuum structures for additive manufacturing considering thin feature and support structure constraints. Eng. Optim. 2021, 53, 2122–2143. [Google Scholar] [CrossRef]
- Qiu, W.; Jin, S.; Xia, L.; Shi, T. Length scale control schemes for bi-directional evolutionary structural optimization method. Int. J. Numer. Methods Eng. 2022, 123, 755–773. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Weng, Z.; Jiang, X.; Wang, R.; Ren, H.; Zheng, F. Space Node Topology Optimization Design Considering Anisotropy of Additive Manufacturing. Appl. Sci. 2022, 12, 9396. [Google Scholar] [CrossRef]
- Yin, L.; Zhang, F.; Deng, X.; Wu, P.; Zeng, H.; Liu, M. Isogeometric Bi-Directional Evolutionary Structural Optimization. IEEE Access 2019, 7, 91134–91145. [Google Scholar] [CrossRef]
- Gonçalves, D.; Lopes, J.; Campilho, R.; Belinha, J. An evolutionary structural optimization algorithm for the analysis of light automobile parts using a meshless technique. Eng. Comput. 2022, 39, 2081–2107. [Google Scholar] [CrossRef]
- Xiong, Y.; Zhao, Z.L.; Lu, H.; Shen, W.; Xie, Y.M. Parallel BESO framework for solving high-resolution topology optimisation problems. Adv. Eng. Softw. 2023, 176, 103389. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, W.; Zhong, W. Doing Topology Optimization Explicitly and Geometrically—A New Moving Morphable Components Based Framework. J. Appl. Mech. 2014, 81, 081009. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, J.; Zhu, X.; Zhou, J.; Xue, D.; Lei, X.; Guo, X. Explicit three dimensional topology optimization via Moving Morphable Void (MMV) approach. Comput. Methods Appl. Mech. Eng. 2017, 322, 590–614. [Google Scholar] [CrossRef]
- Xue, R.Y.; Du, Z.L.; Guo, X. Topology optimization of hyperelastic structures via moving morphable void (mmv) approach. Jisuan Lixue Xuebao/Chin. J. Comput. Mech. 2019, 36, 441–447. [Google Scholar] [CrossRef]
- Guo, G.; Zhao, Y.; Zuo, W. Explicit and efficient topology optimization for three-dimensional structures considering geometrical nonlinearity. Adv. Eng. Softw. 2022, 173, 103238. [Google Scholar] [CrossRef]
- Fang, L.; Wang, X.; Zhou, H. Topology optimization of thermoelastic structures using MMV method. Appl. Math. Model. 2022, 103, 604–618. [Google Scholar] [CrossRef]
- Fang, L.; Meng, Z.; Zhou, H.; Wang, X.; Guo, X. Topology optimization of piezoelectric actuators using moving morphable void method. Struct. Multidiscip. Optim. 2023, 66, 32. [Google Scholar] [CrossRef]
- Zhang, W.; Li, D.; Kang, P.; Guo, X.; Youn, S.K. Explicit topology optimization using IGA-based moving morphable void (MMV) approach. Comput. Methods Appl. Mech. Eng. 2020, 360, 112685. [Google Scholar] [CrossRef]
- Zhang, W.; Jiang, S.; Liu, C.; Li, D.; Kang, P.; Youn, S.K.; Guo, X. Stress-related topology optimization of shell structures using IGA/TSA-based Moving Morphable Void (MMV) approach. Comput. Methods Appl. Mech. Eng. 2020, 366, 113036. [Google Scholar] [CrossRef]
- Du, B.; Zhao, Y.; Yao, W.; Wang, X.; Huo, S. Multiresolution isogeometric topology optimisation using moving morphable voids. CMES-Comput. Model. Eng. Sci. 2020, 122, 1119–1140. [Google Scholar] [CrossRef]
- Gai, Y.; Zhu, X.; Zhang, Y.J.; Hou, W.; Hu, P. Correction to: Explicit isogeometric topology optimization based on moving morphable voids with closed B-spline boundary curves. Struct. Multidiscip. Optim. 2020, 61, 2217–2218. [Google Scholar] [CrossRef]
- Munk, D.J.; Vio, G.A.; Steven, G.P. Topology and shape optimization methods using evolutionary algorithms: A review. Struct. Multidiscip. Optim. 2015, 52, 613–631. [Google Scholar] [CrossRef]
- Goldberg, D.; Samtani, M.P. Engineering optimization via genetic algorithm, in will. In Electronic Computation, Proceedings of the 9th Conference on Electronic Computation, Birmingham, UK, 23–26 February 1986; Will, K.M., Ed.; American Society of Civil Engineers: New York, NY, USA, 1986. [Google Scholar]
- Hajela, P. Stochastic search in structural optimization: Genetic algorithms and simulated annealing. In Structural Optimization: Status And Promise; Kamat, M.P., Ed.; AIAA: San Diego, CA, USA, 1993; pp. 611–635. [Google Scholar]
- Jenkins, W. On the application of natural algorithms to structural design optimization. Eng. Struct. 1997, 19, 302–308. [Google Scholar] [CrossRef]
- Kane.; Schoenauerg, M. Topological Optimum Design using Genetic. Control Cybern. 1996, 25, 1059–1088. [Google Scholar]
- Jakiela, M.J.; Chapman, C.; Duda, J.; Adewuya, A.; Saitou, K. Continuum structural topology design with genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 339–356. [Google Scholar] [CrossRef]
- Ryoo, J.; Hajela, P. Handling variable string lengths in GA-based structural topology optimization. Struct. Multidiscip. Optim. 2004, 26, 318–325. [Google Scholar] [CrossRef]
- Wang, S.; Tai, K. Structural topology design optimization using Genetic Algorithms with a bit-array representation. Comput. Methods Appl. Mech. Eng. 2005, 194, 3749–3770. [Google Scholar] [CrossRef]
- Chapman, C.D.; Saitou, K.; Jakiela, M.J. Genetic Algorithms As an Approach to Configuration and Topology Design. In Proceedings of the ASME 1993 Design Technical Conferences, Albuquerque, NM, USA, 19–22 September 1993; pp. 485–498. [Google Scholar]
- Chapman, C.D.; Jakiela, M.J. Genetic algorithm-based structural topology design with compliance and topology simplification considerations. J. Mech. Des. 1996, 118, 89–98. [Google Scholar] [CrossRef]
- Fanjoy, D.W.; Crossley, W.A. Topology Design of Planar Cross-Sections with a Genetic Algorithm: Part 1–Overcoming the Obstacles. Eng. Optim. 2002, 34, 1–22. [Google Scholar] [CrossRef]
- Fanjoy, D.W.; Crossley, W.A. Topology Design of Planar Cross-Sections with a Genetic Algorithm: Part 2–Bending, Torsion and Combined Loading Applications. Eng. Optim. 2002, 34, 49–64. [Google Scholar] [CrossRef]
- Wang, S.; Tai, K.; Wang, M. An enhanced genetic algorithm for structural topology optimization. Int. J. Numer. Methods Eng. 2006, 65, 18–44. [Google Scholar] [CrossRef]
- Li, Q.; Liu, D.; Fang, J.; Tam, C. Multi-level optimal design of buildings with active control under winds using genetic algorithms. J. Wind. Eng. Ind. Aerodyn. 2000, 86, 65–86. [Google Scholar] [CrossRef]
- Li, Q.S.; Liu, D.K.; Leung, A.Y.T.; Zhang, N.; Luo, Q.Z. A multilevel genetic algorithm for the optimum design of structural control systems. Int. J. Numer. Methods Eng. 2002, 55, 817–834. [Google Scholar] [CrossRef]
- Li, Q.; Liu, D.; Tang, J.; Zhang, N.; Tam, C. Combinatorial optimal design of number and positions of actuators in actively controlled structures using genetic algorithms. J. Sound Vib. 2004, 270, 611–624. [Google Scholar] [CrossRef]
- Liu, D.; Yang, Y.; Li, Q. Optimum positioning of actuators in tall buildings using genetic algorithm. Comput. Struct. 2003, 81, 2823–2827. [Google Scholar] [CrossRef]
- Balamurugan, R.; Ramakrishnan, C.; Singh, N. Performance evaluation of a two stage adaptive genetic algorithm (TSAGA) in structural topology optimization. Appl. Soft Comput. 2008, 8, 1607–1624. [Google Scholar] [CrossRef]
- Madeira, J.F.A.; Pina, H.; Rodrigues, H.C. GA topology optimization using random keys for tree encoding of structures. Struct. Multidiscip. Optim. 2009, 40, 227–240. [Google Scholar] [CrossRef]
- Guest, J.; Genut, L.C.S. Reducing dimensionality in topology optimization using adaptive design variable fields. Int. J. Numer. Methods Eng. 2010, 81, 1019–1045. [Google Scholar] [CrossRef]
- Bureerat, S.; Limtragool, J. Performance enhancement of evolutionary search for structural topology optimisation. Finite Elem. Anal. Des. 2006, 42, 547–566. [Google Scholar] [CrossRef]
- Luh, G.C.; Chueh, C.H. Multi-modal topological optimization of structure using immune algorithm. Comput. Methods Appl. Mech. Eng. 2004, 193, 4035–4055. [Google Scholar] [CrossRef]
- Wu, C.Y.; Ku, C.C. Stress-enhanced clonal selection algorithm for structural topology optimization. Int. J. Numer. Methods Eng. 2012, 89, 957–974. [Google Scholar] [CrossRef]
- Ding, Y.; Chen, L.; Hao, K. Bio-Inspired Optimization Algorithms. In Proceedings of the Studies in Systems, Decision and Control; 2018. [Google Scholar] [CrossRef]
- Kaveh, A.; Hassani, B.; Shojaee, S.; Tavakkoli, S. Structural topology optimization using ant colony methodology. Eng. Struct. 2008, 30, 2559–2565. [Google Scholar] [CrossRef]
- Luh, G.C.; Lin, C.Y. Structural topology optimization using ant colony optimization algorithm. Appl. Soft Comput. 2009, 9, 1343–1353. [Google Scholar] [CrossRef]
- Wu, C.Y.; Zhang, C.B.; Wang, C.J. Topology optimization of structures using ant colony optimization. In Proceedings of the First ACM/SIGEVO Summit on Genetic and Evolutionary Computation, Shanghai, China, 12–14 June 2009; pp. 601–608. [Google Scholar] [CrossRef]
- Shobeiri, V. The optimal design of structures using ACO and EFG. Eng. Comput. 2016, 32, 645–653. [Google Scholar] [CrossRef]
- Luh, G.C.; Lin, C.Y.; Lin, Y.S. A binary particle swarm optimization for continuum structural topology optimization. Appl. Soft Comput. 2011, 11, 2833–2844. [Google Scholar] [CrossRef]
- Lu, J.; Chen, Y. Particle Swarm Optimization (PSO) Based Topology Optimization of Part Design with Fuzzy Parameter Tuning. Comput.-Aided Des. Appl. 2013, 11, 62–68. [Google Scholar] [CrossRef]
- Di Cesare, N.; Domaszewski, M. A new hybrid topology optimization method based on I-PR-PSO and ESO. Application to continuum structural mechanics. Comput. Struct. 2019, 212, 311–326. [Google Scholar] [CrossRef]
- Shim, P.Y.; Manoochehri, S. Generating optimal configurations in structural design using simulated annealing. Int. J. Numer. Methods Eng. 1997, 40, 1053–1069. [Google Scholar] [CrossRef]
- Bureerat, S.; Limtragool, J. Structural topology optimisation using simulated annealing with multiresolution design variables. Finite Elem. Anal. Des. 2008, 44, 738–747. [Google Scholar] [CrossRef]
- Najafabadi, H.R.; Goto, T.G.; Martins, T.C.; Barari, A.; Tsuzuki, M.S.G. Multi-objective Topology Optimization Using Simulated Annealing Method. In Proceedings of the 19th International Conference on Geometry and Graphics (ICGG 2020), São Paulo, Brazil, 9–13 August 2020; Springer: Cham, Switzerland, 2021; pp. 343–353. [Google Scholar]
- Goto, T.; Najafabadi, H.R.; Falheiro, M.; Martins, T.C.; Barari, A.; Tsuzuki, M.S. Topological Optimization and Simulated Annealing. IFAC-PapersOnLine 2021, 54, 205–210. [Google Scholar] [CrossRef]
- Lee, K.S.; Geem, Z.W. A new structural optimization method based on the harmony search algorithm. Comput. Struct. 2004, 82, 781–798. [Google Scholar] [CrossRef]
- Lee, S.M.; Han, S.Y. Topology optimization scheme for dynamic stiffness problems using harmony search method. Int. J. Precis. Eng. Manuf. 2016, 17, 1187–1194. [Google Scholar] [CrossRef]
- Lee, S.M.; Han, S.Y. Topology optimization based on the harmony search method. J. Mech. Sci. Technol. 2017, 31, 2875–2882. [Google Scholar] [CrossRef]
- Lee, D.; Shon, S.; Lee, S.; Ha, J. Size and Topology Optimization of Truss Structures Using Quantum-Based HS Algorithm. Buildings 2023, 13, 1436. [Google Scholar] [CrossRef]
- Wu, C.Y.; Tseng, K.Y. Stress-based binary differential evolution for topology optimization of structures. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2010, 224, 443–457. [Google Scholar] [CrossRef]
- Wu, C.Y.; Tseng, K.Y. Topology optimization of structures using modified binary differential evolution. Struct. Multidiscip. Optim. 2010, 42, 939–953. [Google Scholar] [CrossRef]
- Leon, J.; Guzman, M. Tuning parameters using bio-inspired multiobjective optimization algorithm for topology optimization based on bacterial chemotaxis. In Proceedings of the 4th International Conference on Engineering Optimization, Lisbon, Portugal, 8–11 September 2014; pp. 427–432. [Google Scholar]
- Gholizadeh, S.; Barati, H. Topology optimization of nonlinear single layer domes by a new metaheuristic. Steel Compos. Struct. 2014, 16, 681–701. [Google Scholar] [CrossRef]
- Prayogo, D.; Harsono, K.; Prasetyo, K.E.; Wong, F.T.; Tjandra, D. Size, Topology, and Shape Optimization of Truss Structures using Symbiotic Organisms Search. In Proceedings of the 2019 International Conference on Advanced Mechatronics, Intelligent Manufacture and Industrial Automation, Batu, Indonesia, 9–10 October 2019; pp. 197–201. [Google Scholar] [CrossRef]
- Bigham, A.; Gholizadeh, S. Topology optimization of nonlinear single-layer domes by an improved electro-search algorithm and its performance analysis using statistical tests. Struct. Multidiscip. Optim. 2020, 62, 1821–1848. [Google Scholar] [CrossRef]
- Kaveh, A.; Hosseini, S.M.; Zaerreza, A. Size, Layout, and Topology Optimization of Skeletal Structures Using Plasma Generation Optimization. Iran. J. Sci. Technol.-Trans. Civ. Eng. 2021, 45, 513–543. [Google Scholar] [CrossRef]
- Jaafer, A.A.; Al-Bazoon, M.; Dawood, A.O. Structural topology design optimization using the binary bat algorithm. Appl. Sci. 2020, 10, 1481. [Google Scholar] [CrossRef]
- Ruzbehi, S.; Hahn, I. Two-level Topology Optimization based on a Metaheuristic Method and Morphological Reconstruction. In Proceedings of the 47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–5. [Google Scholar]
- Wang, X.; Zhang, Q.; Qin, X.; Sun, Y. Discrete topology and sizing optimization of frame structures with compliance constraints: A semidefinite programming-based approach. Adv. Struct. Eng. 2021, 24, 2242–2254. [Google Scholar] [CrossRef]
- Mokhtari, M.; Varedi-Koulaei, S.M.; Zhu, J.; Hao, G. Topology optimization of the compliant mechanisms considering curved beam elements using metaheuristic algorithms. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 7197–7208. [Google Scholar] [CrossRef]
- Garcia-Lopez, N.; Sanchez-Silva, M.; Medaglia, A.; Chateauneuf, A. A hybrid topology optimization methodology combining simulated annealing and SIMP. Comput. Struct. 2011, 89, 1512–1522. [Google Scholar] [CrossRef]
- Xue, H.; Yu, H.; Zhang, X.; Quan, Q. A novel method for structural lightweight design with topology optimization. Energies 2021, 14, 4367. [Google Scholar] [CrossRef]
- Liu, X.; Yi, W.J.; Li, Q.; Shen, P.S. Genetic evolutionary structural optimization. J. Constr. Steel Res. 2008, 64, 305–311. [Google Scholar] [CrossRef]
- Liu, X.; Yi, W.J. Michell-like 2D layouts generated by genetic ESO. Struct. Multidiscip. Optim. 2010, 42, 111–123. [Google Scholar] [CrossRef]
- Cui, N.; Huang, S.; Ding, X. An Improved Strategy for Genetic Evolutionary Structural Optimization. Adv. Civ. Eng. 2020, 2020, 1–9. [Google Scholar] [CrossRef]
- Zuo, Z.H.; Xie, Y.M.; Huang, X. Combining genetic algorithms with BESO for topology optimization. Struct. Multidiscip. Optim. 2008, 38, 511–523. [Google Scholar] [CrossRef]
- He, Y.; Cai, K.; Zhao, Z.L.; Xie, Y.M. Stochastic approaches to generating diverse and competitive structural designs in topology optimization. Finite Elem. Anal. Des. 2020, 173, 103399. [Google Scholar] [CrossRef]
- Wu, B.N.; Xia, L.J. Research on bi-directional evolutionary structural optimization method based on improved genetic algorithm. Chuan Bo Li Xue/J. Ship Mech. 2021, 25, 193–201. [Google Scholar]
- Feng, S.; Wu, X.; Han, Q.; Qi, J.; Zhang, X. Novel multi-objective topology optimization method for stiffness and stress of continuum structures. Adv. Mech. Eng. 2022, 14, 16878132221145794. [Google Scholar] [CrossRef]
- Bao, D.W.; Yan, X.; Snooks, R.; Xie, Y. Swarmbeso: Multi-agent and evolutionary computational design based on the principles of structural performance. In Proceedings of the 26th International Conference of the Association for Computer-Aided Architectural Design Research in Asia, Hong Kong, China, 29 March–1 April 2021; pp. 241–250. [Google Scholar]
- Chen, L.; Zhang, H.; Wang, W.; Zhang, Q. Topology Optimization Based on SA-BESO. Appl. Sci. 2023, 13, 4566. [Google Scholar] [CrossRef]
- Radman, A. Combination of BESO and harmony search for topology optimization of microstructures for materials. Appl. Math. Model. 2021, 90, 650–661. [Google Scholar] [CrossRef]
- Murphy, R.; Imediegwu, C.; Hewson, R.; Santer, M. Multiscale structural optimization with concurrent coupling between scales. Struct. Multidiscip. Optim. 2021, 63, 1721–1741. [Google Scholar] [CrossRef]
- Thillaithevan, D.; Bruce, P.; Santer, M. Robust multiscale optimization accounting for spatially-varying material uncertainties. Struct. Multidiscip. Optim. 2022, 65, 40. [Google Scholar] [CrossRef]
- Al Ali, M.; Shimoda, M. Investigation of concurrent multiscale topology optimization for designing lightweight macrostructure with high thermal conductivity. Int. J. Therm. Sci. 2022, 179, 107653. [Google Scholar] [CrossRef]
- Al Ali, M.; Shimoda, M. On concurrent multiscale topology optimization for porous structures under hygro-thermo-elastic multiphysics with considering evaporation. Int. J. Numer. Methods Eng. 2023, 124, 3219–3249. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, T.; Xu, S.; Liu, J. Multiscale topology optimization for solid-lattice-void solid–lattice–void hybrid structures through an ordered multi-phase interpolation. CAD Comput. Aided Des. 2023, 154, 103424. [Google Scholar] [CrossRef]
- Meng, Z.; Guo, L.; Li, Q. Uncertainty-oriented multi-scale topology optimization of coupled thermo-mechanical continuum structures. Compos. Struct. 2023, 315, 116940. [Google Scholar] [CrossRef]
- An, R.; Ge, X.; Wang, M. Design and Microscale Fabrication of Negative Poisson’s Ratio Lattice Structure Based on Multi-Scale Topology Optimization. Machines 2023, 11, 519. [Google Scholar] [CrossRef]
- Mejías, G.; Zegard, T. Simultaneous discrete and continuum multiresolution topology optimization. Struct. Multidiscip. Optim. 2023, 66, 137. [Google Scholar] [CrossRef]
- Hu, J.; Luo, Y.; Liu, S. Three-scale concurrent topology optimization for the design of the hierarchical cellular structure. Struct. Multidiscip. Optim. 2022, 65, 143. [Google Scholar] [CrossRef]
- Patel, D.; Bielecki, D.; Rai, R.; Dargush, G. Improving connectivity and accelerating multiscale topology optimization using deep neural network techniques. Struct. Multidiscip. Optim. 2022, 65, 126. [Google Scholar] [CrossRef]
- Ali, M.A.; Shimoda, M. Toward multiphysics multiscale concurrent topology optimization for lightweight structures with high heat conductivity and high stiffness using MATLAB. Struct. Multidiscip. Optim. 2022, 65, 207. [Google Scholar] [CrossRef]
- Montemurro, M.; Bertolino, G.; Roiné, T. A general multi-scale topology optimisation method for lightweight lattice structures obtained through additive manufacturing technology. Compos. Struct. 2021, 258, 113360. [Google Scholar] [CrossRef]
- Christoff, B.G.; Almeida, J.H.S., Jr.; Cardoso, E.L.; Tita, V. A multiscale topology optimisation framework for hollow spheres as cellular materials. Eng. Struct. 2023, 284, 115990. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, R.; Chu, X.; Liu, H. Multiscale Design of Graded Stochastic Cellular Structures for the Heat Transfer Problem. Appl. Sci. 2023, 13, 4409. [Google Scholar] [CrossRef]
- Gao, J.; Luo, Z.; Xia, L.; Gao, L. Concurrent topology optimization of multiscale composite structures in Matlab. Struct. Multidiscip. Optim. 2019, 60, 2621–2651. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, M.; Li, H.; Gao, L.; Chu, S. Multiscale concurrent topology optimization for cellular structures with multiple microstructures based on ordered SIMP interpolation. Comput. Mater. Sci. 2018, 155, 74–91. [Google Scholar] [CrossRef]
- Gu, X.; He, S.; Dong, Y.; Song, T. An improved ordered SIMP approach for multiscale concurrent topology optimization with multiple microstructures. Compos. Struct. 2022, 287, 115363. [Google Scholar] [CrossRef]
- Yan, J.; Sui, Q.; Fan, Z.; Duan, Z. Multi-Material and Multiscale Topology Design Optimization of Thermoelastic Lattice Structures. CMES-Comput. Model. Eng. Sci. 2022, 130, 967–986. [Google Scholar] [CrossRef]
- Yi, B.; Zhou, Y.; Yoon, G.H.; Saitou, K. Topology optimization of functionally-graded lattice structures with buckling constraints. Comput. Methods Appl. Mech. Eng. 2019, 354, 593–619. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, Y.; Fan, S.; Yang, N.; Wu, N. Design and optimization of graded lattice structures with load path-oriented reinforcement. Mater. Des. 2023, 227, 111776. [Google Scholar] [CrossRef]
- Wang, C.; Gu, X.; Zhu, J.; Zhou, H.; Li, S.; Zhang, W. Concurrent design of hierarchical structures with three-dimensional parameterized lattice microstructures for additive manufacturing. Struct. Multidiscip. Optim. 2020, 61, 869–894. [Google Scholar] [CrossRef]
- Hu, J.; Luo, Y.; Liu, S. Two-scale concurrent topology optimization method of hierarchical structures with self-connected multiple lattice-material domains. Compos. Struct. 2021, 272, 114224. [Google Scholar] [CrossRef]
- Chen, X.; Li, C.; Bai, Y. Topology optimization of sandwich structures with solid-porous hybrid infill under geometric constraints. Comput. Methods Appl. Mech. Eng. 2021, 382, 113856. [Google Scholar] [CrossRef]
- Nakagawa, M.; Noguchi, Y.; Matsushima, K.; Yamada, T. Level set-based multiscale topology optimization for a thermal cloak design problem using the homogenization method. Int. J. Heat Mass Transf. 2023, 207, 123964. [Google Scholar] [CrossRef]
- Murai, N.; Noguchi, Y.; Matsushima, K.; Yamada, T. Multiscale topology optimization of electromagnetic metamaterials using a high-contrast homogenization method. Comput. Methods Appl. Mech. Eng. 2023, 403, 115728. [Google Scholar] [CrossRef]
- Liu, X.; Gao, L.; Xiao, M. Multiscale concurrent topology optimization of hierarchal multi-morphology lattice structures. Comput. Methods Appl. Mech. Eng. 2023, 415, 116209. [Google Scholar] [CrossRef]
- Xu, Y.; Ma, Z.; Huang, Q. Multi-constrained topology optimization of prefabricated joints in large-span latticed structures. Structures 2023, 56, 104809. [Google Scholar] [CrossRef]
- Jansen, M.; Pierard, O. A hybrid density/level set formulation for topology optimization of functionally graded lattice structures. Comput. Struct. 2020, 231, 106205. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Ding, Z.; Gao, L.; Xiao, M.; Liao, W.H. A multiscale topological design method of geometrically asymmetric porous sandwich structures for minimizing dynamic compliance. Mater. Des. 2022, 214, 110404. [Google Scholar] [CrossRef]
- Banh, T.T.; Nam, L.G.; Lee, D. A smooth boundary scheme-based topology optimization for functionally graded structures with discontinuities. Steel Compos. Struct. 2023, 48, 73–88. [Google Scholar] [CrossRef]
- Al Ali, M.; Shimoda, M.; Benaissa, B.; Kobayashi, M. Concurrent Multiscale Hybrid Topology Optimization for Light Weight Porous Soft Robotic Hand with High Cellular Stiffness. In Lecture Notes in Civil Engineering (LNCE); Springer International Publishing: Cham, Switzerland, 2023; Volume 317, pp. 265–278. [Google Scholar] [CrossRef]
- Qiao, H.; Wang, S.; Zhao, T.; Tang, H. Topology optimization for lightweight cellular material and structure simultaneously by combining SIMP with BESO. J. Mech. Sci. Technol. 2019, 33, 729–739. [Google Scholar] [CrossRef]
- Da, D.; Cui, X.; Long, K.; Cai, Y.; Li, G. Multiscale concurrent topology optimization of structures and microscopic multi-phase materials for thermal conductivity. Eng. Comput. 2019, 36, 126–146. [Google Scholar] [CrossRef]
- Yan, X.; Xu, Q.; Huang, D.; Zhong, Y.; Huang, X. Concurrent topology design of structures and materials with optimal material orientation. Compos. Struct. 2019, 220, 473–480. [Google Scholar] [CrossRef]
- Yan, X.; Xu, Q.; He, J.; Huang, D.; Huang, X. Integrated design of structure and anisotropic material based on the BESO method. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Suzhou, China, 29–31 March 2019; Volume 531. [Google Scholar] [CrossRef]
- Yan, X.; Xu, Q.; Hua, H.; Huang, D.; Huang, X. Concurrent topology optimization of structures and orientation of anisotropic materials. Eng. Optim. 2020, 52, 1598–1611. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, B.; Xie, Y.M.; Wu, X.; Zhou, S. FFT-based Inverse Homogenization for Cellular Material Design. Int. J. Mech. Sci. 2022, 231, 107572. [Google Scholar] [CrossRef]
- Cai, J.; Huang, L.; Wu, H.; Yin, L. Concurrent topology optimization of multiscale structure under uncertain dynamic loads. Int. J. Mech. Sci. 2023, 251, 108355. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Wei, P.; Wang, W. Parameterized level-set based topology optimization method considering symmetry and pattern repetition constraints. Comput. Methods Appl. Mech. Eng. 2018, 340, 1079–1101. [Google Scholar] [CrossRef]
- Maute, K. Topology optimization of coupled multi-physics problems. CISM Int. Cent. Mech. Sci. Courses Lect. 2014, 549, 421–437. [Google Scholar] [CrossRef]
- Meng, Q.; Xu, B.; Huang, C.; Wang, G. Lightweight topology optimization of thermal structures under compliance, stress and temperature constraints. J. Therm. Stress. 2021, 44, 1121–1149. [Google Scholar] [CrossRef]
- Das, S.; Sutradhar, A. Multi-physics topology optimization of functionally graded controllable porous structures: Application to heat dissipating problems. Mater. Des. 2020, 193, 108775. [Google Scholar] [CrossRef]
- Thurier, P.; Lesieutre, G.; Frecker, M.; Adair, J. A two-material topology optimization method for structures under steady thermo-mechanical loading. J. Intell. Mater. Syst. Struct. 2019, 30, 1717–1726. [Google Scholar] [CrossRef]
- Tang, T.; Xia, S.; Rop, P.; De Wispelaere, S.; Subramanian, R.; Koos, B. Multi-physics topology optimization for thermal-flow problems applied to additively manufactured heat exchangers. In Proceedings of the ASME Turbo Expo, 2021: Turbomachinery Technical Conference and Exposition, Online, 7–11 June 2021; Available online: https://asmedigitalcollection.asme.org/GT/proceedings-abstract/GT2021/84935/V02DT36A019/1119851 (accessed on 1 August 2023).
- Akhtar, H.; Terry, H.; Ioannou, P.; Mills, L.; Samanthula, S.; Wise, A. Additive manufactured heatsinks for power electronics assemblies–multi physics topology optimisation. In Proceedings of the International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Online, 3–7 May 2021; pp. 1–9. Available online: https://ieeexplore.ieee.org/document/9472374/authors#authors (accessed on 1 August 2023).
- Nomura, T.; Sato, K.; Nishiwaki, S.; Yoshimura, M. Multi-disciplinary multi-objective topology optimization of electromagnetics and structural mechanics (for case of optimal dielectric resonator antenna designs). Nihon Kikai Gakkai Ronbunshu A Hen/Trans. Jpn. Mech. Eng. Part A 2007, 73, 1111–1119. [Google Scholar] [CrossRef][Green Version]
- Park, S.; Yoo, J. Structural optimization of a multi-physics problem considering thermal and magnetic effects. IEEE Trans. Magn. 2012, 48, 3883–3886. [Google Scholar] [CrossRef]
- Walsh, J.; Berthoud, L.; Allen, C. Drag reduction through shape optimisation for satellites in Very Low Earth Orbit. Acta Astronaut. 2021, 179, 105–121. [Google Scholar] [CrossRef]
- Hild, F.; Traub, C.; Pfeiffer, M.; Beyer, J.; Fasoulas, S. Optimisation of satellite geometries in Very Low Earth Orbits for drag minimisation and lifetime extension. Acta Astronaut. 2022, 201, 340–352. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, J.; Tian, P.; Liang, T.; Li, Z.; Wen, D. Aerodynamic drag analysis and reduction strategy for satellites in Very Low Earth Orbit. Aerosp. Sci. Technol. 2023, 132, 108077. [Google Scholar] [CrossRef]
- Chen, X.; Liu, S.; Sheng, T.; Zhao, Y.; Yao, W. The satellite layout optimization design approach for minimizing the residual magnetic flux density of micro- and nano-satellites. Acta Astronaut. 2019, 163, 299–306. [Google Scholar] [CrossRef]
- Fakoor, M.; Mohammad Zadeh, P.; Momeni Eskandari, H. Developing an optimal layout design of a satellite system by considering natural frequency and attitude control constraints. Aerosp. Sci. Technol. 2017, 71, 172–188. [Google Scholar] [CrossRef]
- Fakoor, M.; Taghinezhad, M. Layout and configuration design for a satellite with variable mass using hybrid optimization method. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 230, 360–377. [Google Scholar] [CrossRef]
- Huo, J.Z.; Teng, H.F. Optimal layout design of a satellite module using a coevolutionary method with heuristic rules. J. Aerosp. Eng. 2009, 22, 101–111. [Google Scholar] [CrossRef]
- Sun, Z.G.; Teng, H.F. Optimal layout design of a satellite module. Eng. Optim. 2003, 35, 513–529. [Google Scholar] [CrossRef]
- Wang, D.; Xiang, C.; Pan, Y.; Chen, A.; Zhou, X.; Zhang, Y. A deep convolutional neural network for topology optimization with perceptible generalization ability. Eng. Optim. 2022, 54, 973–988. [Google Scholar] [CrossRef]
- Xiang, C.; Wang, D.; Pan, Y.; Chen, A.; Zhou, X.; Zhang, Y. Accelerated topology optimization design of 3D structures based on deep learning. Struct. Multidiscip. Optim. 2022, 65, 99. [Google Scholar] [CrossRef]
- Shin, J.; Kim, C. Bi-directional evolutionary 3D topology optimization with a deep neural network. J. Mech. Sci. Technol. 2022, 36, 3509–3519. [Google Scholar] [CrossRef]
- Banga, S.; Gehani, H.; Bhilare, S.; Patel, S.; Kara, L. 3D Topology Optimization using Convolutional Neural Networks. arXiv 2018, arXiv:1808.07440. [Google Scholar] [CrossRef]
- Sosnovik, I.; Oseledets, I. Neural networks for topology optimization. Russ. J. Numer. Anal. Math. 2019, 34, 215–223. [Google Scholar] [CrossRef]
- Bi, S.; Zhang, J.; Zhang, G. Scalable Deep-Learning-Accelerated Topology Optimization for Additively Manufactured Materials. arXiv 2020, arXiv:2011.14177. [Google Scholar] [CrossRef]
- Kallioras, N.; Lagaros, N. DL-SCALE: A novel deep learning-based model order upscaling scheme for solving topology optimization problems. Neural Comput. Appl. 2021, 33, 7125–7144. [Google Scholar] [CrossRef]
- Lagaros, N.; Kallioras, N.; Kazakis, G. Accelerated topology optimization by means of deep learning. Struct. Multidiscip. Optim. 2020, 62, 1185–1212. [Google Scholar] [CrossRef]
- Sun, H.; Ma, L. Structural Topology Optimization by Combining BESO with Reinforcement Learning. J. Harbin Inst. Technol. (New Ser.) 2021, 28, 85–96. [Google Scholar] [CrossRef]
- Wang, L.; Shi, D.; Zhang, B.; Li, G.; Helal, W.M.; Qi, M. Deep learning driven real time topology optimization based on improved convolutional block attention (Cba-U-Net) model. Eng. Anal. Bound. Elem. 2023, 147, 112–124. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Koric, S.; Sobh, N.A. Topology optimization of 2D structures with nonlinearities using deep learning. Comput. Struct. 2020, 237, 106283. [Google Scholar] [CrossRef]
- Almasri, W.; Bettebghor, D.; Ababsa, F.; Danglade, F. Shape related constraints aware generation of Mechanical Designs through Deep Convolutional GAN. arXiv 2020, arXiv:2010.11833. [Google Scholar]
- Cang, R.; Yao, H.; Ren, Y. One-shot generation of near-optimal topology through theory-driven machine learning. Comput.-Aided Des. 2019, 109, 12–21. [Google Scholar] [CrossRef]
- Keshavarzzadeh, V.; Alirezaei, M.; Tasdizen, T.; Kirby, R.M. Image-Based Multiresolution Topology Optimization Using Deep Disjunctive Normal Shape Model. Comput.-Aided Des. 2021, 130, 102947. [Google Scholar] [CrossRef]
- Kollmann, H.T.; Abueidda, D.W.; Koric, S.; Guleryuz, E.; Sobh, N.A. Deep learning for topology optimization of 2D metamaterials. Mater. Des. 2020, 196, 109098. [Google Scholar] [CrossRef]
- Lew, A.J.; Buehler, M.J. Encoding and exploring latent design space of optimal material structures via a VAE-LSTM model. Forces Mech. 2021, 5, 100054. [Google Scholar] [CrossRef]
- Li, B.; Huang, C.; Li, X.; Zheng, S.; Hong, J. Non-iterative structural topology optimization using deep learning. Comput.-Aided Des. 2019, 115, 172–180. [Google Scholar] [CrossRef]
- Rade, J.; Balu, A.; Herron, E.; Pathak, J.; Ranade, R.; Sarkar, S.; Krishnamurthy, A. Algorithmically-consistent deep learning frameworks for structural topology optimization. Eng. Appl. Artif. Intell. 2021, 106, 104483. [Google Scholar] [CrossRef]
- Rawat, S.; Shen, M. A novel topology design approach using an integrated deep learning network architecture. arXiv 2018, arXiv:1808.02334. [Google Scholar]
- Rawat, S.; Shen, M.H. Application of Adversarial Networks for 3D Structural Topology Optimization. In Proceedings of the WCX SAE World Congress Experience, SAE International, Detroit, Mi, USA, 9–11 April 2019. [Google Scholar] [CrossRef]
- Rawat, S.; Shen, M.H.H. A Novel Topology Optimization Approach using Conditional Deep Learning. arXiv 2019, arXiv:1901.04859. [Google Scholar]
- Sharpe, C.; Seepersad, C. Topology DesignWith Conditional Generative Adversarial Networks. In Proceedings of the ASME 2019 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Anaheim, CA, USA, 18–21 August 2019. [Google Scholar] [CrossRef]
- Yu, Y.; Hur, T.; Jung, J.; Jang, I.G. Deep learning for determining a near-optimal topological design without any iteration. Struct. Multidiscip. Optim. 2018, 59, 787–799. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, J.; Yuan, Z.; Xu, S.; Zou, B.; Li, L.; Ma, Y. A novel lattice structure topology optimization method with extreme anisotropic lattice properties. J. Comput. Des. Eng. 2021, 8, 1367–1390. [Google Scholar] [CrossRef]
- Nie, Z.; Lin, T.; Jiang, H.; Kara, L.B. TopologyGAN: Topology Optimization Using Generative Adversarial Networks Based on Physical Fields Over the Initial Domain. arXiv 2020, arXiv:2003.04685. [Google Scholar] [CrossRef]
- Qiu, C.; Du, S.; Yang, J. A deep learning approach for efficient topology optimization based on the element removal strategy. Mater. Des. 2021, 212, 110179. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Zhou, W.; Chen, X.; Yao, W.; Zhao, Y. TONR: An exploration for a novel way combining neural network with topology optimization. Comput. Methods Appl. Mech. Eng. 2021, 386, 114083. [Google Scholar] [CrossRef]
- Asanuma, J.; Doi, S.; Igarashi, H. Transfer Learning Through Deep Learning: Application to Topology Optimization of Electric Motor. IEEE Trans. Magn. 2020, 56, 1–4. [Google Scholar] [CrossRef]
- Aulig, N.; Olhofer, M. Topology optimization by predicting sensitivities based on local state features. In Proceedings of the 5th Eur. Conf. Comput. Mech. (ECCM V), Barcelona, Spain, 20–25 July 2014. [Google Scholar]
- Chi, H.; Zhang, Y.; Tang, T.L.E.; Mirabella, L.; Dalloro, L.; Song, L.; Paulino, G.H. Universal machine learning for topology optimization. Comput. Methods Appl. Mech. Eng. 2021, 375, 112739. [Google Scholar] [CrossRef]
- Deng, H.; To, A.C. Topology optimization based on deep representation learning (DRL) for compliance and stress-constrained design. Comput. Mech. 2020, 66, 449–469. [Google Scholar] [CrossRef]
- Deng, C.; Qin, C.; Lu, W. Deep-Learning-Enabled Simulated Annealing for Topology Optimization. arXiv 2020, arXiv:2002.01927. [Google Scholar]
- Doi, S.; Sasaki, H.; Igarashi, H. Multi-Objective Topology Optimization of Rotating Machines Using Deep Learning. IEEE Trans. Magn. 2019, 55, 1–5. [Google Scholar] [CrossRef]
- Kim, C.; Lee, J.; Yoo, J. Machine learning-combined topology optimization for functionary graded composite structure design. Comput. Methods Appl. Mech. Eng. 2021, 387, 114158. [Google Scholar] [CrossRef]
- Keshavarzzadeh, V.; Kirby, R.M.; Narayan, A. Stress-based topology optimization under uncertainty via simulation-based Gaussian process. Comput. Methods Appl. Mech. Eng. 2020, 365, 112992. [Google Scholar] [CrossRef]
- Lee, S.; Kim, H.; Lieu, Q.X.; Lee, J. CNN-based image recognition for topology optimization. Knowl.-Based Syst. 2020, 198, 105887. [Google Scholar] [CrossRef]
- Li, H.; Kafka, O.; Gao, J.; Yu, C.; Nie, Y.; Zhang, L.; Tajdari, M.; Tang, S.; Guo, X.; Li, G.; et al. Clustering discretization methods for generation of material performance databases in machine learning and design optimization. Comput. Mech. 2019, 64, 281–305. [Google Scholar] [CrossRef]
- Sasaki, H.; Igarashi, H. Topology Optimization Accelerated by Deep Learning. IEEE Trans. Magn. 2019, 55, 7401305. [Google Scholar] [CrossRef]
- Patel, J.; Choi, S.K. Classification approach for reliability-based topology optimization using probabilistic neural networks. Struct. Multidiscip. Optim. 2010, 45, 529–543. [Google Scholar] [CrossRef]
- Qian, C.; Ye, W. Accelerating gradient-based topology optimization design with dual-model neural networks. arXiv 2020, arXiv:2009.06245. [Google Scholar] [CrossRef]
- Sasaki, H.; Igarashi, H. Topology optimization of IPM motor with aid of deep learning. Int. J. Appl. Electromagn. Mech. 2018, 59, 1–10. [Google Scholar] [CrossRef]
- Takahashi, Y.; Suzuki, Y.; Todoroki, A. Convolutional Neural Network-based Topology Optimization (CNN-TO) by Estimating Sensitivity of Compliance from Material Distribution. arXiv 2019, arXiv:2001.00635. [Google Scholar]
- White, D.A.; Arrighi, W.J.; Kudo, J.; Watts, S.E. Multiscale topology optimization using neural network surrogate models. Comput. Methods Appl. Mech. Eng. 2019, 346, 1118–1135. [Google Scholar] [CrossRef]
- Xia, M.; Yang, S.; Ho, S.L. A New Topology Optimization Methodology Based on Constraint Maximum-Weight Connected Graph Theorem. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Zheng, L.; Kumar, S.; Kochmann, D.M. Data-driven topology optimization of spinodoid metamaterials with seamlessly tunable anisotropy. Comput. Methods Appl. Mech. Eng. 2021, 383, 113894. [Google Scholar] [CrossRef]
- Zhou, Y.; Saitou, K. Topology optimization of composite structures with data-driven resin filling time manufacturing constraint. Struct. Multidiscip. Optim. 2017, 55, 2073–2086. [Google Scholar] [CrossRef]
- Ulu, E.; Zhang, R.; Kara, L.B. A data-driven investigation and estimation of optimal topologies under variable loading configurations. Comput. Methods Biomech. Biomed. Eng. Vis. 2016, 4, 61–72. [Google Scholar] [CrossRef]
- Guo, T.; Lohan, D.J.; Cang, R.; Ren, M.Y.; Allison, J.T. An Indirect Design Representation for Topology Optimization Using Variational Autoencoder and Style Transfer. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Li, M.; Cheng, Z.; Jia, G.; Shi, Z. Dimension reduction and surrogate based topology optimization of periodic structures. Compos. Struct. 2019, 229, 111385. [Google Scholar] [CrossRef]
- Shin, S.; Shin, D.; Kang, N. Topology optimization via machine learning and deep learning: A review. J. Comput. Des. Eng. 2023, 10, 1736–1766. [Google Scholar] [CrossRef]
- Sathish, K.; Senthil Kumar, S.; Magal, R.T.; Selvaraj, V.; Narasimharaj, V.; Karthikeyan, R.; Sabarinathan, G.; Tiwari, M.; Kassa, A.E. A Comparative Study on Subtractive Manufacturing and Additive Manufacturing. Adv. Mater. Sci. Eng. 2022, 2022, 6892641. [Google Scholar] [CrossRef]
- Jayawardane, H.; Davies, I.; Gamage, J.; John, M.; Biswas, W. Sustainability perspectives—A review of additive and subtractive manufacturing. Sustain. Manuf. Serv. Econ. 2023, 2, 100015. [Google Scholar] [CrossRef]
- Kumar, V.; Isanaka, B.R.; Gupta, S.; Kushvaha, V. Future Trends and Technologies in Additive and Substractive Manufacturing. In Additive and Subtractive Manufacturing of Composites; Mavinkere Rangappa, S., Gupta, M.K., Siengchin, S., Song, Q., Eds.; Springer: Singapore, 2021; pp. 227–247. [Google Scholar] [CrossRef]
- Orme, M.; Mouriaux, F.; Gschweitl, M.; Vernon, R.; Ferrari, M.; Madera, I.; Yancey, R. A demonstration of additive manufacturing as an enabling technology for rapid satellite design and fabrication. In Proceedings of the International SAMPE Technical Conference, The Society for the Advancement of Material and Process Engineering (SAMPE®), Long Beach, CA, USA, 23–26 May 2016. [Google Scholar]
- Lim, J.; Le, K.Q.; Lu, Q.; Wong, C. An Overview of 3-D Printing in Manufacturing, Aerospace, and Automotive Industries. IEEE Potentials 2016, 35, 18–22. [Google Scholar] [CrossRef]
- Rahman, M.; Saleh, T.; Jahan, M.; McGarry, C.; Chaudhari, A.; Huang, R.; Tauhiduzzaman, M.; Ahmed, A.; Mahmud, A.; Bhuiyan, M. Review of Intelligence for Additive and Subtractive Manufacturing: Current Status and Future Prospects. Micromachines 2023, 14, 508. [Google Scholar] [CrossRef] [PubMed]
- ISO/ASTM 52900:2021(E); Additive Manufacturing—General Principles—Fundamentals and Vocabulary. ISO/ASTM: Geneva, Switzerland, 2021.
- Krolikowski, M.A.; Krawczyk, M.B. Does Metal Additive Manufacturing in Industry 4.0 Reinforce the Role of Substractive Machining? In Advances in Manufacturing II, VOL 1-Solutions for Industry 4.0, Lecture Notes in Mechanical Engineering, Proceedings of the 6th International Scientific-Technical Conference on Advances in Manufacturing II (MANUFACTURING), Poznan, Poland, 19–22 May 2019; Trojanowska, J., Ciszak, O., Machado, J., Pavlenko, I., Eds.; Springer International Publishing: New York, NY, USA, 2019; pp. 150–164. [Google Scholar] [CrossRef]
- ASTM F2792-12a; Standard Terminology for Additive Manufacturing Technologies, (Withdrawn 2015). ISO/ASTM: West Conshohocken, PA, USA, 2012.
- Mostafaei, A.; Elliott, A.M.; Barnes, J.E.; Li, F.; Tan, W.; Cramer, C.L.; Nandwana, P.; Chmielus, M. Binder jet 3D printing—Process parameters, materials, properties, modeling, and challenges. Prog. Mater. Sci. 2021, 119, 100707. [Google Scholar] [CrossRef]
- Chen, L.; Chen, W.; Fu, Z.; Ding, G.; Chen, Z.; Zhu, D. Binder Jet 3D Printing of 316L Stainless Steel: Orthogonal Printing and Sintering Process Optimization. Adv. Eng. Mater. 2023, 25, 2200641. [Google Scholar] [CrossRef]
- Chen, W.; Chen, Z.; Chen, L.; Zhu, D.; Fu, Z. Optimization of Printing Parameters to Achieve High-Density 316L Stainless Steel Manufactured by Binder Jet 3D Printing. J. Mater. Eng. Perform. 2023, 32, 3602–3616. [Google Scholar] [CrossRef]
- Le Néel, T.A.; Mognol, P.; Hascoët, J.Y. A review on additive manufacturing of sand molds by binder jetting and selective laser sintering. Rapid Prototyp. J. 2018, 24, 1325–1336. [Google Scholar] [CrossRef]
- Del Giudice, L.; Vassiliou, M.; Marelli, S. Global sensitivity analysis of sand-based binder jet 3D printed material. In Current Perspectives and New Directions in Mechanics, Modelling and Design of Structural Systems, Proceedings of the 8th International Conference on Structural Engineering, Mechanics and Computation, Kapstadt, Südafrika, 5–7 September 2022; pp. 368–373. [Google Scholar] [CrossRef]
- Tang, H.; Yen, H.; Chiu, M.; Jou, J. The characteristics and applications of Ceramic Laser Fusion and Ceramic Laser Sintering. In Proceedings of the 19th Annual International Solid Freeform Fabrication Symposium (SFF 2008), Austin, TX, USA, 4–6 August 2008; pp. 206–215. [Google Scholar]
- Tang, H.H.; Yen, H.C. Ceramic parts fabricated by ceramic laser fusion. Mater. Trans. 2004, 45, 2744–2751. [Google Scholar] [CrossRef]
- Yen, H.; Chiu, M.; Huang, P. A new layer casting system for ceramic laser rapid prototyping apparatus. In Proceedings of the 19th Annual International Solid Freeform Fabrication Symposium, SFF 2008; 2008; pp. 254–265. [Google Scholar]
- Huang, J.; Qin, Q.; Wang, J. A review of stereolithography: Processes and systems. Processes 2020, 8, 1138. [Google Scholar] [CrossRef]
- Kafle, A.; Luis, E.; Silwal, R.; Pan, H.M.; Shrestha, P.L.; Bastola, A.K. 3d/4d printing of polymers: Fused deposition modelling (fdm), selective laser sintering (sls), and stereolithography (sla). Polymers 2021, 13, 3101. [Google Scholar] [CrossRef]
- Halloran, J.W. Ceramic Stereolithography: Additive Manufacturing for Ceramics by Photopolymerization. Annu. Rev. Mater. Res. 2016, 46, 19–40. [Google Scholar] [CrossRef]
- Bove, A.; Calignano, F.; Galati, M.; Iuliano, L. Photopolymerization of Ceramic Resins by Stereolithography Process: A Review. Appl. Sci. 2022, 12, 3591. [Google Scholar] [CrossRef]
- Ge, Q.; Li, Z.; Wang, Z.; Kowsari, K.; Zhang, W.; He, X.; Zhou, J.; Fang, N.X. Projection micro stereolithography based 3D printing and its applications. Int. J. Extrem. Manuf. 2020, 2, 022004. [Google Scholar] [CrossRef]
- Murr, L.E.; Gaytan, S.M.; Ramirez, D.A.; Martinez, E.; Hernandez, J.; Amato, K.N.; Shindo, P.W.; Medina, F.R.; Wicker, R.B. Metal Fabrication by Additive Manufacturing Using Laser and Electron Beam Melting Technologies. J. Mater. Sci. Technol. 2012, 28, 1–14. [Google Scholar] [CrossRef]
- Uçak, N.; Çiçek, A.; Aslantas, K. Machinability of 3D printed metallic materials fabricated by selective laser melting and electron beam melting: A review. J. Manuf. Process. 2022, 80, 414–457. [Google Scholar] [CrossRef]
- Lin, B.c.; Chen, W. Mechanical properties of TiAl fabricated by electron beam melting—A review. China Foundry 2021, 18, 307–316. [Google Scholar] [CrossRef]
- Zafar, M.Q.; Wu, C.C.; Zhao, H.; Wang, J.; Hu, X. Finite element framework for electron beam melting process simulation. Int. J. Adv. Manuf. Technol. 2020, 109, 2095–2112. [Google Scholar] [CrossRef]
- Zhang, L.; Han, X.; Lv, T.; Zhao, H. Topological optimization design for SM system of large aperture telescope. Hongwai Jiguang Gongcheng/Infrared Laser Eng. 2018, 47, 818008. [Google Scholar] [CrossRef]
- Gokuldoss, P.K.; Kolla, S.; Eckert, J. Additive manufacturing processes: Selective laser melting, electron beam melting and binder jetting-selection guidelines. Materials 2017, 10, 672. [Google Scholar] [CrossRef]
- Song, B.; Zhao, X.; Li, S.; Han, C.; Wei, Q.; Wen, S.; Liu, J.; Shi, Y. Differences in microstructure and properties between selective laser melting and traditional manufacturing for fabrication of metal parts: A review. Front. Mech. Eng. 2015, 10, 111–125. [Google Scholar] [CrossRef]
- Gao, B.; Zhao, H.; Peng, L.; Sun, Z. A Review of Research Progress in Selective Laser Melting (SLM). Micromachines 2023, 14, 57. [Google Scholar] [CrossRef] [PubMed]
- Zhou, R.; Liu, H.; Wang, H. Modeling and simulation of metal selective laser melting process: A critical review. Int. J. Adv. Manuf. Technol. 2022, 121, 5693–5706. [Google Scholar] [CrossRef]
- Ao, X.; Liu, J.; Xia, H.; He, Q.; Ren, C. A Review of Meso-micro Modeling and Simulation Methods of Selective Laser Melting Process. Jixie Gongcheng Xuebao/J. Mech. Eng. 2022, 58, 239–257. [Google Scholar] [CrossRef]
- Sefene, E.M. State-of-the-art of selective laser melting process: A comprehensive review. J. Manuf. Syst. 2022, 63, 250–274. [Google Scholar] [CrossRef]
- Ellis, A.; Noble, C.J.; Hartley, L.; Lestrange, C.; Hopkinson, N.; Majewski, C. Materials for high speed sintering. J. Mater. Res. 2014, 29, 2080–2085. [Google Scholar] [CrossRef]
- Jerman, E.; Wiedenmann, F.; Eichberger, M.; Reichert, A.; Stawarczyk, B. Effect of high-speed sintering on the flexural strength of hydrothermal and thermo-mechanically aged zirconia materials. Dent. Mater. 2020, 36, 1144–1150. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Sharma, V.; Sachdeva, A. Progress in selective laser sintering using metallic powders: A review. Mater. Sci. Technol. 2016, 32, 760–772. [Google Scholar] [CrossRef]
- Lupone, F.; Padovano, E.; Casamento, F.; Badini, C. Process phenomena and material properties in selective laser sintering of polymers: A review. Materials 2022, 15, 183. [Google Scholar] [CrossRef] [PubMed]
- Han, W.; Kong, L.; Xu, M. Advances in selective laser sintering of polymers. Int. J. Extrem. Manuf. 2022, 4, 042002. [Google Scholar] [CrossRef]
- Volpato, N.; Childs, T.; Stewart, T.; Watson, P. Indirect selective laser sintering of metal parts with overhung features. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2001, 215, 873–876. [Google Scholar] [CrossRef]
- Li, Z.; Gan, X.; Fei, G.; Xia, H. Progress on Selective Laser Sintering of Polymers and Polymer Composites. Gaofenzi Cailiao Kexue Yu Gongcheng/Polym. Mater. Sci. Eng. 2017, 33, 170–174. [Google Scholar] [CrossRef]
- Mamatha, S.; Biswas, P.; Johnson, R. Digital light processing of ceramics: An overview on process, materials and challenges. Prog. Addit. Manuf. 2022, 8, 1083–1102. [Google Scholar] [CrossRef]
- Zhao, Z.; Tian, X.; Song, X. Engineering materials with light: Recent progress in digital light processing based 3D printing. J. Mater. Chem. C 2020, 8, 13896–13917. [Google Scholar] [CrossRef]
- Chaudhary, R.; Fabbri, P.; Leoni, E.; Mazzanti, F.; Akbari, R.; Antonini, C. Additive manufacturing by digital light processing: A review. Prog. Addit. Manuf. 2023, 8, 331–351. [Google Scholar] [CrossRef]
- Ge, Q.; Jian, B.; Li, H. Shaping soft materials via digital light processing-based 3D printing: A review. Forces Mech. 2022, 6, 100074. [Google Scholar] [CrossRef]
- Fang, H.B.; Chen, J.M. 3D printing based on digital light processing technology. Beijing Gongye Daxue Xuebao/J. Beijing Univ. Technol. 2015, 41, 1775–1782. [Google Scholar] [CrossRef]
- Singh, S.; Singh, G.; Prakash, C.; Ramakrishna, S. Current status and future directions of fused filament fabrication. J. Manuf. Process. 2020, 55, 288–306. [Google Scholar] [CrossRef]
- Dey, A.; Eagle, I.N.R.; Yodo, N. A review on filament materials for fused filament fabrication. J. Manuf. Mater. Process. 2021, 5, 69. [Google Scholar] [CrossRef]
- Gao, X.; Qi, S.; Kuang, X.; Su, Y.; Li, J.; Wang, D. Fused filament fabrication of polymer materials: A review of interlayer bond. Addit. Manuf. 2021, 37, 101658. [Google Scholar] [CrossRef]
- Brenken, B.; Barocio, E.; Favaloro, A.; Kunc, V.; Pipes, R.B. Fused filament fabrication of fiber-reinforced polymers: A review. Addit. Manuf. 2018, 21, 1–16. [Google Scholar] [CrossRef]
- Tao, Y.; Kong, F.; Li, Z.; Zhang, J.; Zhao, X.; Yin, Q.; Xing, D.; Li, P. A review on voids of 3D printed parts by fused filament fabrication. J. Mater. Res. Technol. 2021, 15, 4860–4879. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, R.; Singh, T.; Batish, A. Fused filament fabrication: A comprehensive review. J. Thermoplast. Compos. Mater. 2023, 36, 794–814. [Google Scholar] [CrossRef]
- Niu, X.; Singh, S.; Garg, A.; Singh, H.; Panda, B.; Peng, X.; Zhang, Q. Review of materials used in laser-aided additive manufacturing processes to produce metallic products. Front. Mech. Eng. 2019, 14, 282–298. [Google Scholar] [CrossRef]
- Gu, D.; Meiners, W.; Wissenbach, K.; Poprawe, R. Laser additive manufacturing of metallic components: Materials, processes and mechanisms. Int. Mater. Rev. 2012, 57, 133–164. [Google Scholar] [CrossRef]
- Kovalev, O.; Zaitsev, A.; Novichenko, D.; Smurov, I. Theoretical and experimental investigation of gas flows, powder transport and heating in coaxial laser direct metal deposition (DMD) process. J. Therm. Spray Technol. 2011, 20, 465–478. [Google Scholar] [CrossRef]
- Lalegani Dezaki, M.; Serjouei, A.; Zolfagharian, A.; Fotouhi, M.; Moradi, M.; Ariffin, M.; Bodaghi, M. A review on additive/subtractive hybrid manufacturing of directed energy deposition (DED) process. Adv. Powder Mater. 2022, 1, 100054. [Google Scholar] [CrossRef]
- Tepylo, N.; Huang, X.; Patnaik, P.C. Laser-Based Additive Manufacturing Technologies for Aerospace Applications. Adv. Eng. Mater. 2019, 21. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Charalampous, P.; Kostavelis, I.; Tzetzis, D.; Tzovaras, D. Impact of metal additive manufacturing parameters on the powder bed fusion and direct energy deposition processes: A comprehensive review. Prog. Addit. Manuf. 2021, 6, 349–365. [Google Scholar] [CrossRef]
- Treutler, K.; Wesling, V. The current state of research of wire arc additive manufacturing (Waam): A review. Appl. Sci. 2021, 11, 8619. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Y.; Ge, Y.; Hou, Z.; Chen, S. Wire and arc additive manufacturing of metal components: A review of recent research developments. Int. J. Adv. Manuf. Technol. 2020, 111, 149–198. [Google Scholar] [CrossRef]
- Derekar, K. A review of wire arc additive manufacturing and advances in wire arc additive manufacturing of aluminium. Mater. Sci. Technol. 2018, 34, 895–916. [Google Scholar] [CrossRef]
- Wu, B.; Pan, Z.; Ding, D.; Cuiuri, D.; Li, H.; Xu, J.; Norrish, J. A review of the wire arc additive manufacturing of metals: Properties, defects and quality improvement. J. Manuf. Process. 2018, 35, 127–139. [Google Scholar] [CrossRef]
- Tomar, B.; Shiva, S.; Nath, T. A review on wire arc additive manufacturing: Processing parameters, defects, quality improvement and recent advances. Mater. Today Commun. 2022, 31, 103739. [Google Scholar] [CrossRef]
- Omiyale, B.; Olugbade, T.; Abioye, T.; Farayibi, P. Wire arc additive manufacturing of aluminium alloys for aerospace and automotive applications: A review. Mater. Sci. Technol. 2022, 38, 391–408. [Google Scholar] [CrossRef]
- Lin, J.; Lv, Y.; Liu, Y.; Sun, Z.; Wang, K.; Li, Z.; Wu, Y.; Xu, B. Microstructural evolution and mechanical property of Ti-6Al-4V wall deposited by continuous plasma arc additive manufacturing without post heat treatment. J. Mech. Behav. Biomed. Mater. 2017, 69, 19–29. [Google Scholar] [CrossRef] [PubMed]
- Bai, X.; Colegrove, P.; Ding, J.; Zhou, X.; Diao, C.; Bridgeman, P.; roman Hönnige, J.; Zhang, H.; Williams, S. Numerical analysis of heat transfer and fluid flow in multilayer deposition of PAW-based wire and arc additive manufacturing. Int. J. Heat Mass Transf. 2018, 124, 504–516. [Google Scholar] [CrossRef]
- Prashar, G.; Vasudev, H. A comprehensive review on sustainable cold spray additive manufacturing: State of the art, challenges and future challenges. J. Clean. Prod. 2021, 310, 127606. [Google Scholar] [CrossRef]
- Assadi, H.; Kreye, H.; Gärtner, F.; Klassen, T. Cold spraying—A materials perspective. Acta Mater. 2016, 116, 382–407. [Google Scholar] [CrossRef]
- Bagherifard, S.; Monti, S.; Zuccoli, M.V.; Riccio, M.; Kondás, J.; Guagliano, M. Cold spray deposition for additive manufacturing of freeform structural components compared to selective laser melting. Mater. Sci. Eng. A 2018, 721, 339–350. [Google Scholar] [CrossRef]
- Yin, S.; Cavaliere, P.; Aldwell, B.; Jenkins, R.; Liao, H.; Li, W.; Lupoi, R. Cold spray additive manufacturing and repair: Fundamentals and applications. Addit. Manuf. 2018, 21, 628–650. [Google Scholar] [CrossRef]
- Huang, C.; Wu, H.; Xie, Y.; Li, W.; Verdy, C.; Planche, M.P.; Liao, H.; Montavon, G. Advanced brass-based composites via cold-spray additive-manufacturing and its potential in component repairing. Surf. Coat. Technol. 2019, 371, 211–223. [Google Scholar] [CrossRef]
- Benenati, G.; Lupoi, R. Development of a Deposition Strategy in Cold Spray for Additive Manufacturing to Minimize Residual Stresses. Procedia CIRP 2016, 55, 101–108. [Google Scholar] [CrossRef]
- Stringer, J.; Althagathi, T.M.; Tse, C.C.; Ta, V.D.; Shephard, J.D.; Esenturk, E.; Connaughton, C.; Wasley, T.J.; Li, J.; Kay, R.W.; et al. Integration of additive manufacturing and inkjet printed electronics: A potential route to parts with embedded multifunctionality. Manuf. Rev. 2016, 3, 12. [Google Scholar] [CrossRef]
- Pan, Z.; Wang, Y.; Huang, H.; Ling, Z.; Dai, Y.; Ke, S. Recent development on preparation of ceramic inks in ink-jet printing. Ceram. Int. 2015, 41, 12515–12528. [Google Scholar] [CrossRef]
- Loffredo, F.; Mauro, A.D.G.D.; Burrasca, G.; La Ferrara, V.; Quercia, L.; Massera, E.; Di Francia, G.; Sala, D.D. Ink-jet printing technique in polymer/carbon black sensing device fabrication. Sens. Actuators B Chem. 2009, 143, 421–429. [Google Scholar] [CrossRef]
- Gothait, H.; Even, R.; Danai, D. Photopolymer jetting technology in rapid prototyping. In Proceedings of the 1st International Conference on Advanced Research in Virtual and Rapid Prototyping, Leiria, Portugal, 1–4 October 2003. [Google Scholar]
- Harr, M.; Moy, P.; Yu, J. Mechanical Properties of Transparent Laminates Fabricated Using Multi-Material Photopolymer Jetting. In Dynamic Behavior of Materials, Volume 1; Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Cham, Switzerland, 2020; pp. 47–51. [Google Scholar] [CrossRef]
- Priest, J.; Jacobs, E.; Smith Jr., C.; DuBois, P.; Holt, B.; Hammerschlag, B. Liquid metal-jetting technology: Application issues for hybrid technology. Int. J. Microcircuits Electron. Packag. 1994, 17, 219–227. [Google Scholar]
- Godin, R. Metal jetting solders on. Mater. World 1997, 5, 451–453. [Google Scholar]
- Aboulkhair, N.T.; Bosio, F.; Gilani, N.; Phutela, C.; Hague, R.J.; Tuck, C.J. Additive Manufacturing Processes for Metals; Elsevier: Amsterdam, The Netherlands, 2022; pp. 201–258. [Google Scholar] [CrossRef]
- Leu, M.; Zhang, W.; Sui, G. Experimental and analytical study of ice part fabrication with Rapid Freeze Prototyping. CIRP Ann.-Manuf. Technol. 2000, 49, 147–150. [Google Scholar] [CrossRef]
- Sui, G.; Leu, M.C. Investigation of layer thickness and surface roughness in rapid freeze prototyping. J. Manuf. Sci. Eng. 2003, 125, 556–563. [Google Scholar] [CrossRef]
- Liu, Q.; Leu, M.C.; Richards, V.L.; Schmitt, S.M. Dimensional accuracy and surface roughness of rapid freeze prototyping ice patterns and investment casting metal parts. Int. J. Adv. Manuf. Technol. 2004, 24, 485–495. [Google Scholar] [CrossRef]
- Sui, G.; Leu, M.C. Thermal analysis of ice walls built by rapid freeze prototyping. J. Manuf. Sci. Eng. 2003, 125, 824–834. [Google Scholar] [CrossRef]
- Bryant, F.D.; Leu, M.C. Modeling and experimental results of concentration with support material in rapid freeze prototyping. Rapid Prototyp. J. 2009, 15, 317–324. [Google Scholar] [CrossRef]
- Hartel, A.; Scheithauer, U.; Schwarzer, E.; Weingarten, S.; Slawik, T.; Richter, H.J.; Moritz, T. Additive manufacturing of metallic and ceramic multimaterial components using thermoplastic 3D printing (T3DP); [Additive Herstellung mehrkomponentiger metallischer und keramischer Bauteile mittels Thermoplastischen 3D-Druckes (T3DP)]. Keram. Z. 2016, 68, 43–47. [Google Scholar] [CrossRef]
- Özden, I.; Iveković, A.; Kocjan, A. Additive manufacturing of ceramics from thermoplastic feedstocks. Open Ceramics 2021, 6. Cited by: 6; All Open Access, Gold Open Access. [Google Scholar] [CrossRef]
- Scheithauer, U.; Schwarzer, E.; Haertel, A.; Richter, H.; Moritz, T.; Michaelis, A. Processing of Thermoplastic Suspensions for Additive Manufacturing of Ceramic-and Metal-Ceramic-Composites by Thermoplastic 3D-Printing (T3DP); The American Ceramic Society: Westerville, OH, USA, 2016; Volume 258, pp. 19–30. [Google Scholar] [CrossRef]
- Scheithauer, U.; Weingarten, S.; Johne, R.; Schwarzer, E.; Abel, J.; Richter, H.J.; Moritz, T.; Michaelis, A. Ceramic-Based 4D Components: Additive manufacturing (AM) of ceramic-based functionally graded materials (FGM) by thermoplastic 3D printing (T3DP). Materials 2017, 10, 1368. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.; Shao, H.; Lin, T.; Zheng, H. 3D gel-printing—An additive manufacturing method for producing complex shape parts. Mater. Des. 2016, 101, 80–87. [Google Scholar] [CrossRef]
- Shao, H.; Zhao, D.; Lin, T.; He, J.; Wu, J. 3D gel-printing of zirconia ceramic parts. Ceram. Int. 2017, 43, 13938–13942. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, Z.; Chen, C.; Yang, W. Additive manufacturing of WC-20Co components by 3D gel-printing. Int. J. Refract. Met. Hard Mater. 2018, 70, 215–223. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, X.; Guo, Z.; Volinsky, A.A. 3D gel-printing of Sr ferrite parts. Ceram. Int. 2018, 44, 22370–22377. [Google Scholar] [CrossRef]
- Zhu, J.H.; Gu, X.J.; Zhang, W.H.; Beckers, P. Structural design of aircraft skin stretch-forming die using topology optimization. J. Comput. Appl. Math. 2013, 246, 278–288. [Google Scholar] [CrossRef]
- Wang, Y.; Kang, Z. Structural shape and topology optimization of cast parts using level set method. Int. J. Numer. Methods Eng. 2017, 111, 1252–1273. [Google Scholar] [CrossRef]
- Harzheim, L.; Graf, G. A review of optimization of cast parts using topology optimization: I-Topology optimization without manufacturing constraints. Struct. Multidiscip. Optim. 2005, 30, 491–497. [Google Scholar] [CrossRef]
- Harzheim, L.; Graf, G. A review of optimization of cast parts using topology optimization: III-Topology optimization with manufacturing constraints. Struct. Multidiscip. Optim. 2006, 31, 388–399. [Google Scholar] [CrossRef]
- Gersborg, A.R.; Andreasen, C.S. An explicit parameterization for casting constraints in gradient driven topology optimization. Struct. Multidiscip. Optim. 2011, 44, 875–881. [Google Scholar] [CrossRef]
- Xia, Q.; Shi, T.; Wang, M.Y.; Liu, S. A level set based method for the optimization of cast part. Struct. Multidiscip. Optim. 2010, 41, 735–747. [Google Scholar] [CrossRef]
- Kim, Y.Y.; Kim, T.S. Topology optimization of beam cross sections. Int. J. Solids Struct. 1999, 37, 477–493. [Google Scholar] [CrossRef]
- Liu, S.; An, X.; Jia, H. Topology optimization of beam cross-section considering warping deformation. Struct. Multidiscip. Optim. 2008, 35, 403–411. [Google Scholar] [CrossRef]
- Li, H.; Li, P.; Gao, L.; Zhang, L.; Wu, T. A level set method for topological shape optimization of 3D structures with extrusion constraints. Comput. Methods Appl. Mech. Eng. 2015, 283, 615–635. [Google Scholar] [CrossRef]
- Ishii, K.; Aomura, S. Topology optimization for the extruded three dimensional structure with constant cross section. JSME Int.J. Ser. A Solid Mech. Mater. Eng. 2004, 47, 198–206. [Google Scholar] [CrossRef][Green Version]
- Zuberi, R.H.; Zhengxing, Z.; Kai, L. Topological optimization of beam cross section by employing extrusion constraint. AIP Conf. Proc. 2010, 1233, 964–969. [Google Scholar] [CrossRef]
- Vatanabe, S.L.; Lippi, T.N.; Lima, C.R.d.; Paulino, G.H.; Silva, E.C. Topology optimization with manufacturing constraints: A unified projection-based approach. Adv. Eng. Softw. 2016, 100, 97–112. [Google Scholar] [CrossRef]
- Mani, M.; Witherell, P.; Jee, H. Design Rules for Additive Manufacturing: A Categorization. In Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Cleveland, OH, USA, 6–9 August 2017; p. V001T02A035. [Google Scholar] [CrossRef]
- Guest, J.K.; Prévost, J.H.; Belytschko, T. Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int. J. Numer. Methods Eng. 2004, 61, 238–254. [Google Scholar] [CrossRef]
- Sigmund, O. Morphology-based black and white filters for topology optimization. Struct. Multidiscip. Optim. 2007, 33, 401–424. [Google Scholar] [CrossRef]
- Wang, F.; Lazarov, B.; Sigmund, O. On projection methods, convergence and robust formulations in topology optimization. Struct. Multidiscip. Optim. 2011, 43, 767–784. [Google Scholar] [CrossRef]
- Gaynor Andrew, G.J. Topology optimization considering overhang constraints: Eliminating sacrificial support material in additive manufacturing through design. Struct. Multidiscip. Optim. 2016, 54, 1157–1172. [Google Scholar] [CrossRef]
- Mass, Y.; Amir, O. Topology optimization for additive manufacturing: Accounting for overhang limitations using a virtual skeleton. Addit. Manuf. 2017, 18, 58–73. [Google Scholar] [CrossRef]
- Ibhadode, O.; Zhang, Z.; Bonakdar, A.; Toyserkani, E. A Post-Topology Optimization Process for Overhang Elimination in Additive Manufacturing: Design Workflow and Experimental Investigation. Int. J. Adv. Manuf. Technol. 2023, preprint. [Google Scholar] [CrossRef]
- Liu, S.; Li, Q.; Chen, W.; Tong, L.; Cheng, G. An identification method for enclosed voids restriction in manufacturability design for additive manufacturing structures. Front. Mech. Eng. 2015, 10, 126–137. [Google Scholar] [CrossRef]
- Luo, Y.; Sigmund, O.; Li, Q.; Liu, S. Additive manufacturing oriented topology optimization of structures with self-supported enclosed voids. Comput. Methods Appl. Mech. Eng. 2020, 372, 113385. [Google Scholar] [CrossRef]
- Shiomi, M.; Osakada, K.; Nakamura, K.; Yamashita, T.; Abe, F. Residual Stress within Metallic Model Made by Selective Laser Melting Process. CIRP Ann. 2004, 53, 195–198. [Google Scholar] [CrossRef]
- Önder, S.; Saklakoğlu, N.; Sever, A. Selective laser melting of Ti6Al4V alloy: Effect of post-processing on fatigue life, residual stress, microstructure, microhardness and surface roughness. Mater. Charact. 2023, 196, 112571. [Google Scholar] [CrossRef]
- Kumar, V.P.; Jebaraj, A.V. Comprehensive review on residual stress control strategies in laser-based powder bed fusion process—Challenges and opportunities. Lasers Manuf. Mater. Process. 2023, 10, 400–442. [Google Scholar] [CrossRef]
- Mukherjee, T.; Elmer, J.; Wei, H.; Lienert, T.; Zhang, W.; Kou, S.; DebRoy, T. Control of grain structure, phases, and defects in additive manufacturing of high-performance metallic components. Prog. Mater. Sci. 2023, 138, 101153. [Google Scholar] [CrossRef]
- Kok, Y.; Tan, X.; Wang, P.; Nai, M.; Loh, N.; Liu, E.; Tor, S. Anisotropy and heterogeneity of microstructure and mechanical properties in metal additive manufacturing: A critical review. Mater. Des. 2018, 139, 565–586. [Google Scholar] [CrossRef]
- Simonelli, M.; Tse, Y.; Tuck, C. Effect of the build orientation on the mechanical properties and fracture modes of SLM Ti-6Al-4V. Mater. Sci. Eng. A 2014, 616, 1–11. [Google Scholar] [CrossRef]
- Popovich, V.; Borisov, E.; Popovich, A.; Sufiiarov, V.; Masaylo, D.; Alzina, L. Functionally graded Inconel 718 processed by additive manufacturing: Crystallographic texture, anisotropy of microstructure and mechanical properties. Mater. Des. 2017, 114, 441–449. [Google Scholar] [CrossRef]
- Yadollahi, A.; Shamsaei, N.; Thompson, S.M.; Elwany, A.; Bian, L. Effects of building orientation and heat treatment on fatigue behavior of selective laser melted 17-4 PH stainless steel. Int. J. Fatigue 2017, 94, 218–235. [Google Scholar] [CrossRef]
- Yasa, E.; Kruth, J.P.; Deckers, J. Manufacturing by combining Selective Laser Melting and Selective Laser Erosion/laser re-melting. CIRP Ann. 2011, 60, 263–266. [Google Scholar] [CrossRef]
- Yang, K.K.; Zhu, J.; Wang, C.; Jia, D.; Song, L.; Zhang, W. Experimental validation of 3D printed material behaviors and their influence on the structural topology design. Comput. Mech. 2018, 61, 581–598. [Google Scholar] [CrossRef]
- FlightCenter, N.S. Advanced Space Transportation Program: Paving the Highway to Space. 2016. Available online: https://archive.ph/Yq9EA (accessed on 1 August 2023).
- Haddad, D. Tools, processes and examples of Space Structures Optimisation. In Proceedings of the 1st European Conference on Materials and Structures in Aerospace (EUCOMAS), VDIBERICHTE, Berlin, Germany, 26–27 May 2008; Volume 2028, pp. 347–354. [Google Scholar]
- Fetisov, K.; Maksimov, P. Topology optimization and laser additive manufacturing in design process of efficiency lightweight aerospace parts. J. Phys. Conf. Ser. 2018, 1015, 052006. [Google Scholar] [CrossRef]
- Kobryn, P.A.; Ontko, N.R.; Perkins, L.P.; Tiley, J.S. Additive Manufacturing of Aerospace Alloys for Aircraft Structures. 2006. Available online: https://www.semanticscholar.org/paper/Additive-Manufacturing-of-Aerospace-Alloys-for-Kobryn-Ontko/6f5d50d21042beb12ce613d7ddb14254064055cf (accessed on 1 August 2023).
- Huang, R.; Riddle, M.; Graziano, D.; Warren, J.; Das, S.; Nimbalkar, S.; Cresko, J.; Masanet, E. Energy and emissions saving potential of additive manufacturing: The case of lightweight aircraft components. J. Clean. Prod. 2016, 135, 1559–1570. [Google Scholar] [CrossRef]
- Sahini, D.; Ghose, J.; Jha, S.K.; Behera, A.; Mandal, A. Optimization and Simulation of Additive Manufacturing Processes: Challenges and Opportunities—A Review. In Additive Manufacturing Applications for Metals and Composites; IGI Global: Hershey, PA, USA, 2020; pp. 187–209. [Google Scholar] [CrossRef]
- Quincieu, J.; Robinson, C.; Stucker, B.; Mosher, T. Case study: Selective laser sintering of the USUSat II small satellite structure. Assem. Autom. 2005, 25, 267–272. [Google Scholar] [CrossRef]
- Espalin, D.; Muse, D.; Macdonald, E.; Wicker, R. 3D Printing multifunctionality: Structures with electronics. Int. J. Adv. Manuf. Technol. 2014, 72, 963–978. [Google Scholar] [CrossRef]
- Obilanade, D.; Kingston, J. Spacecraft designers’ guide to using additive manufacturing processes for large metallic spacecraft structures. In Proceedings of the International Astronautical Congress, IAC, Adelaide, Australia, 25–29 September 2017; Volume 13, pp. 8280–8304. [Google Scholar]
- Cismilianu, A.M.; Munteanu, C.E.; Oncescu, I.C.; Bibire, R.P.; Stoenescu, V.; Pricop, M.V.; Rey, E.; Eyrignoux, S. End-to-end process of hollow spacecraft structures with high frequency and low mass obtained with in-house structural optimization tool and additive manufacturing. INCAS Bull. 2017, 9, 13–20. [Google Scholar] [CrossRef]
- Willner, R.; Lender, S.; Ihl, A.; Wilsnack, C.; Gruber, S.; Brandão, A.; Pambaguian, L.; Riede, M.; López, E.; Brueckner, F.; et al. Potential and challenges of additive manufacturing for topology optimized spacecraft structures. J. Laser Appl. 2020, 32, 032012. [Google Scholar] [CrossRef]
- Blachowicz, T.; Ehrmann, G.; Ehrmann, A. Metal additive manufacturing for satellites and rockets. Appl. Sci. 2021, 11, 12036. [Google Scholar] [CrossRef]
- Boschetto, A.; Bottini, L.; Macera, L.; Vatanparast, S. Additive Manufacturing for Lightweighting Satellite Platform. Appl. Sci. 2023, 13, 2809. [Google Scholar] [CrossRef]
- Rawal, S.; Brantley, J.; Karabudak, N. Additive manufacturing of Ti-6Al-4V alloy components for spacecraft applications. In Proceedings of the 2013 6th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 12–14 June 2013; pp. 5–11. [Google Scholar] [CrossRef]
- Lockheed Martin. Design Evolution: Lockheed Martin is using 3-D Printed Parts for U.S. Military Satellites. 2017. Available online: https://news.lockheedmartin.com/2017-04-04-Design-Evolution-Lockheed-Martin-is-using-3-D-Printed-Parts-for-U-S-Military-Satellites (accessed on 1 August 2023).
- Krassenstein, B. Aerojet Rocketdyne 3D Prints an Entire Engine in Just Three Parts. 2014. Available online: https://3dprint.com/7355/3d-printed-engine/ (accessed on 1 August 2023).
- Spacex. SpaceX’s New SuperDraco Thrusters on Dragon V2 Feature Advanced 3D Printed Engine Chamber. 2014. Available online: https://3dprint.com/4740/spacex-dragon-2-3d-print/ (accessed on 1 August 2023).
- Ritz, D.; Misuri, T.; Raiji, H.; Pace, G.; Valentini, D.; Hadavandi, R.; Pasini, A. Additive manufacturing techniques applied to the space industry. In Proceedings of the International Astronautical Congress, IAC, October 2018; Volume 2018. [Google Scholar]
- Tian, X.; Zhao, Z.; Wang, H.; Liu, X.; Song, X. Progresses on the additive manufacturing of functionally graded metallic materials. J. Alloys Compd. 2023, 960, 170687. [Google Scholar] [CrossRef]
- Bankapalli, N.K.; Gupta, V.; Saxena, P.; Bajpai, A.; Lahoda, C.; Polte, J. Filament fabrication and subsequent additive manufacturing, debinding, and sintering for extrusion-based metal additive manufacturing and their applications: A review. Compos. Part B Eng. 2023, 264, 110915. [Google Scholar] [CrossRef]
- Williams, J.; Revington, P. Novel use of an aerospace selective laser sintering machine for rapid prototyping of an orbital blowout fracture. Int. J. Oral Maxillofac. Surg. 2010, 39, 182–184. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Davim, J. (Eds.) Additive Manufacturing: Applications and Innovations, 1st ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Gumpinger, J.; Pambaguian, L.; Bonvoisin, B.; Makaya, A.; Pigliaru, L.; Gerard, R. Harmonisation Roadmap on Additive Manufacturing for Space Applications. 2021. Available online: https://technology.esa.int/page/harmonisation (accessed on 1 August 2023).
- Gradl, P. Principles of Directed Energy Deposition for Aerospace Applications. Seminar for WM Keck Center for 3D Innovation; NASA Technical Reports Server: Cleveland, OH, USA, 2021. [CrossRef]
- Gradl, P.; Mireles, O.R.; Katsarelis, C.; Smith, T.M.; Sowards, J.; Park, A.; Chen, P.; Tinker, D.C.; Protz, C.; Teasley, T.; et al. Advancement of extreme environment additively manufactured alloys for next generation space propulsion applications. Acta Astronaut. 2023, 211, 483–497. [Google Scholar] [CrossRef]
- Debroy, T.; Wei, H.; Zuback, J.; Mukherjee, T.; Elmer, J.; Milewski, J.; Beese, A.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components–Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Williams, J.C.; Boyer, R.R. Opportunities and issues in the application of titanium alloys for aerospace components. Metals 2020, 10, 705. [Google Scholar] [CrossRef]
- Akca, E.; Gürsel, A. A review on superalloys and IN718 nickel-based INCONEL superalloy. Period. Eng. Nat. Sci. 2015, 3. [Google Scholar] [CrossRef]
- ECSS. ECSS-E-ST-32C Rev.1–Structural General Requirements; Technical Report; ECSS: Cologne, Germany, 2008. [Google Scholar]
- Kodiyalam, S.; Nagendra, S.; DeStefano. Composite sandwich structure optimization with application to satellite components. AIAA J. 1996, 34, 614–621. [Google Scholar] [CrossRef]
- Gohar, S.; Hussain, G.; Ali, A.; Ahmad, H. Mechanical performance of honeycomb sandwich structures built by FDM printing technique. J. Thermoplast. Compos. Mater. 2023, 36, 182–200. [Google Scholar] [CrossRef]
- Aborehab, A.; Kamel, M.; Nemnem, A.F.; Kassem, M. Finite element model updating of a satellite honeycomb sandwich plate in structural dynamics. Int. J. Space Struct. 2021, 36, 105–116. [Google Scholar] [CrossRef]
- Ganilova, O.A.; Cartmell, M.P.; Kiley, A. Experimental investigation of the thermoelastic performance of an aerospace aluminium honeycomb composite panel. Compos. Struct. 2021, 257, 113159. [Google Scholar] [CrossRef]
- Luo, H.; Fu, J.; Wang, H.; Li, Y. Research on modeling method of honeycomb plate and its application on solar wing. IOP Conf. Ser. Mater. Sci. Eng. 2019, 563, 052020. [Google Scholar] [CrossRef]
- Yan, L.; Xu, H.; Deng, Y. 3D digital mockup for honeycomb sandwich panels of satellites. In Proceedings of the 2018 IEEE 4th Information Technology and Mechatronics Engineering Conference, ITOEC 2018, Chongqing, China, 14–16 December 2018; pp. 1956–1959. [Google Scholar] [CrossRef]
- Zheng, K.; Liao, W.; Qin, Y. Analysis and research of honeycomb sandwich structure for microsatellite based on equivalent theory. Key Eng. Mater. 2010, 426-427, 472–476. [Google Scholar] [CrossRef]
- Chen, C.; Jin, P.; Wang, D. The satellite structure topology optimization based on homogenization method and its size sensitivity analysis. Acta Mech. Solida Sin. 2005, 18, 173–180. [Google Scholar]
- Gökdağ, I.; İzgü, O.; Dağkolu, A.; Tanrıkulu, A.A.; Acar, E. Design optimization and validation for additive manufacturing: A satellite bracket application. Struct. Multidiscip. Optim. 2022, 65, 237. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, B.; Huang, S.; Dou, W.; Xin, S.; Yan, J. DMA2022-Topological Design of a Nanosatellite Structure with Optimal Frequency Responses Filled by Non-Uniform Lattices. Chin. J. Mech. Eng. 2023. preprint. [Google Scholar] [CrossRef]
- Vinay Kumar, K.; Sesha Sai CharanTej, K.; Jana, N.K.; Sharma, D.; Esakki, B. Topology Optimization and Modal Analysis of Nanosatellite Structure. In Lecture Notes in Mechanical Engineering; Springer: Singapore, 2020; pp. 17–29. [Google Scholar] [CrossRef]
- Shao, M.; Zhang, L.; Jia, X. Optimization Design of the Spaceborne Connecting Structure for a Lightweight Space Camera. Appl. Sci. 2020, 10, 8249. [Google Scholar] [CrossRef]
- Gao, Y.X.; Yang, D.; Liu, Z.J. Optimum Design of the Support Structure of the CMG Based on CAE. In Applied Mechanics and Materials, Proceedings of the International Conference on Frontiers of Mechanical Engineering and Materials Engineering (MEME 2012), Pts 1 and 2, Hong Kong, China, 27–29 July 2012; Sung, W., Kao, J., Chen, R., Eds.; Trans Tech Publications Ltd.: Hong Kong, China, 2012; Volume 184–185, pp. 364–367. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, J.; Wu, M.; Hou, J.; Zhou, H.; Meng, L.; Li, C.; Zhang, W. Multi-scale design and optimization for solid-lattice hybrid structures and their application to aerospace vehicle components. Chin. J. Aeronaut. 2021, 34, 386–398. [Google Scholar] [CrossRef]
- Shi, G.; Guan, C.; Quan, D.; Wu, D.; Tang, L.; Gao, T. An aerospace bracket designed by thermo-elastic topology optimization and manufactured by additive manufacturing. Chin. J. Aeronaut. 2020, 33, 1252–1259. [Google Scholar] [CrossRef]
- Cohen, B.S.; March, A.I.; Willcox, K.E.; Miller, D.W. A level set-based topology optimization approach for thermally radiating structures. Struct. Multidiscip. Optim. 2022, 65, 167. [Google Scholar] [CrossRef]
- Manil, P.; Jan, Y.; Nunio, F.; Lomello, F.; Arhancet, A.; Lacroix, M.; Bachet, D.; Lapresle, J. Structural optimization, additive manufacturing and vibration testing of titanium alloy supports based on the space detector SVOM-MXT. In Proceedings of the SPIE-The International Society for Optical Engineering, Online, 6–10 April 2020; Volume 11451. [Google Scholar] [CrossRef]
- nTopology Inc. Air Force Optimizes CubeSat Bus Using Architected Materials. 2021. Available online: http://web.archive.org/web/20080207010024/http://www.808multimedia.com/winnt/kernel.htm (accessed on 1 November 2023).
- Schimmerohn, M.; Bierdel, M.; Gulde, M.; Sholes, D.; Pfaff, A.; Pielok, M.; Hoschke, K.; Horch, C.; Schäfer, F. Additive manufactured structures for the 12U nanosatellite ERNST. In Proceedings of the 32nd Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 4 August 2018. [Google Scholar]
- Berrocal, L.; Fernández, R.; González, S.; Periñán, A.; Tudela, S.; Vilanova, J.; Rubio, L.; Martín Márquez, J.M.; Guerrero, J.; Lasagni, F. Topology optimization and additive manufacturing for aerospace components. Prog. Addit. Manuf. 2019, 4, 83–95. [Google Scholar] [CrossRef]
- Lottes, L.M.; Kaiser, N.; Goossens, N.; Oelze, H.W.; Braxmaier, C. TOMARES: Topology optimization of an additive manufactured reaction flywheel designed for an Earth-observation satellite. CEAS Space J. 2021, 13, 521–532. [Google Scholar] [CrossRef]
- Yongxin, G.; Lihua, Z.; Zhijia, L.; Yimin, G.; Lingxi, M. Optimization Design of Star Tracker Bracket of Small Satellite for 3D Printing. In Proceedings of the 2019 5th International Conference on Control, Automation Furthermore, Robotics (ICCAR), Beijing, China, 19–22 April 2019; pp. 808–811. [Google Scholar] [CrossRef]
- Tan, L.; Li, L.; Gu, S.; Wang, D. Multi-objective topology optimization to reduce vibration of micro-satellite primary supporting structure. J. Vibroeng. 2017, 19, 831–843. [Google Scholar] [CrossRef]
- Caiazzo, F.; Alfieri, V.; Fabbricatore, A.; Argenio, P. Topological optimization and additive manufacturing of a metal functional panel for multi-mission modular satellite platform. In Proceedings of the 2022 IEEE 9th International Workshop on Metrology for AeroSpace, MetroAeroSpace 2022, Pisa, Italy, 27–29 June 2022; pp. 509–513. [Google Scholar] [CrossRef]
- Lee, H.Y.; Carroll, J.D.; Guest, J.K. Topology optimization for additively manufactured self-supporting axisymmetric structures. In Proceedings of the ASME Design Engineering Technical Conference, Online, 17–19 August 2021; Volume 3A-2021. [Google Scholar] [CrossRef]
- Orme, M.; Madera, I.; Gschweitl, M.; Ferrari, M. Topology Optimization for Additive Manufacturing as an Enabler for Light Weight Flight Hardware. Designs 2018, 2, 51. [Google Scholar] [CrossRef]
- Carvalho, S. Design Optimization for Additive Manufacturing of a 1U CubeSat’s Mechanical System. Master’s Thesis, Instituto Superior Técnico, Universidade de Lisboa, Lisbon, Portugal, 2019. [Google Scholar]
- Dell’Acqua, M. Optimization and Additive Manufacturing of a Single-Piece 1u Cubesat Primary Structure. Master’s Thesis, Politecnico Di Milano: School of Industrial and Information Engineering, Master of Science in Space Engineering, Milan, Italy, 2020. [Google Scholar]
- Esteves, M.C.G. Design Optimization for AM of MECSE CubeSat’s Mechanical System. Master’s Thesis, Universidade da Beira Interior, Covilhã, Portugal, 2018. [Google Scholar]
- Yoon, Y.H.; Moon, J.K.; Lee, E.S.; Kim, S.J.; Kim, J.H. Parallel optimal design of satellite bus structures using particle swarm optimization. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, AIAA, Honolulu, HI, USA, 23–26 April 2007; p. 1. [Google Scholar]
- Zhu, L.; Li, X.; Hu, D.; Zhou, Z. Structural Optimization Design of Shock Isolation Ring for Satellite Rocket Separation. Yuhang Xuebao/J. Astronaut. 2022, 43, 946–956. [Google Scholar] [CrossRef]
- Boudjemai, A.; Bouanane, M.H.; Merad, L.; Mohammed, A.M.S. Small satellite structural optimisation using genetic algorithm approach. In Proceedings of the 2007 3rd International Conference on Recent Advances in Space Technologies, Istanbul, Turkey, 14–16 June 2007; Volume 1, pp. 398–406. [Google Scholar] [CrossRef]
- Stevens, C.L. Design, Analysis, Fabrication, and Testing of a Nanosatellite Structure. Master’s Thesis, Faculty of the Virginia Polytechnic Institute, Blacksburg, VA, USA, 2002. Aerospace Engineer. [Google Scholar]
- Fortescue, P.; Swinerd, G.; Stark, J. Spacecraft Systems Engineering, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Dawood, S.D.S.; b. Inayatullah, O.; b. Samin, R. Computational study of the effect of using open isogrids on the natural frequencies of a small satellite structure. Acta Astronaut. 2015, 106, 120–138. [Google Scholar] [CrossRef]
- Nakamura H, M.T. The topology optimization of electronic parts mounted on micro satellite. In Proceedings of the 4th International Conference on Engineering Optimization, ENGOPT 2014, Lisbon, Portugal, 8–11 September 2014. [Google Scholar]
- Hai, H.; Haichao, A.; Haibo, M.; Chen, S. An engineering method for complex structural optimization involving both size and topology design variables. Int. J. Numer. Methods Eng. 2019, 117, 291–315. [Google Scholar] [CrossRef]
- Yahg, S.; Sha, W.; Chen, C.Z.; Zhang, X.X.; Ren, J.Y. Design and optimization of carbon fiber framework for space camera. Guangxue Jingmi Gongcheng/Opt. Precis. Eng. 2017, 25, 697–705. [Google Scholar] [CrossRef]
- Vogel, D.; Geismayr, L.; Langer, M.; Leslabay, P.; Schlick, G. Combining additive manufacturing and biomimetics for the optimization of satellite structures. In Proceedings of the International Astronautical Congress, IAC, Bremen, Germany, 1–5 October 2018; Volume 2018. [Google Scholar]
- Kaiser, N.; Nils, G.; Ane, J.; Laraudogoitia, I.; Psarras, S.; Stavros, T. Advanced manufacturing concept of a bio-inspired reaction wheel rotor for small- and medium-sized constellation satellites. CEAS Space J. 2023, 1, 1–4. [Google Scholar] [CrossRef]
- ISO/ASTM 52942:2020; Additive Manufacturing—Qualification Principles—Qualifying Machine Operators of Laser Metal Powder Bed Fusion Machines and Equipment Used in Aerospace Applications. Technical Report; ISO/ASTM: Geneva, Switzerland, 2020.
- ISO/ASTM 52926-1; Additive Manufacturing of Metals—Qualification Principles—Part 1: General Qualification of Operators. ISO/ASTM: Geneva, Switzerland, 2023; Under development.
- ISO/ASTM 52926-2; Additive Manufacturing of Metals—Qualification Principles—Part 2: Qualification of Operators for PBF-LB. ISO/ASTM: Geneva, Switzerland, 2023; Under development.
- ISO/ASTM 52926-3; Additive Manufacturing of Metals—Qualification Principles—Part 3: Qualification of Operators for PBF-EB. ISO/ASTM: Geneva, Switzerland, 2023; Under development.
- ISO/ASTM 52926-4; Additive Manufacturing of Metals—Qualification Principles—Part 4: Qualification of Operators for DED-LB. ISO/ASTM: Geneva, Switzerland, 2023; Under development.
- ISO/ASTM 52926-5; Additive Manufacturing of Metals—Qualification Principles—Part 5: Qualification of Operators for DED-Arc. ISO/ASTM: Geneva, Switzerland, 2023; Under development.
- MSFC-STD-3716; Standard for Additively Manufactured Spaceflight Hardware by Laser Powder Bed Fusion in Metals. NASA Marshall Space Flight Center: Huntsville, AL, USA, 2017.
- MSFC-SPEC-3717; Specification for Control and Qualification of Laser Powder Bed Fusion Metallurgical Processes. NASA Marshall Space Flight Center: Huntsville, AL, USA, 2017.
- NASA-STD-6030; Additive Manufacturing Requirements for Spaceflight Systems. NASA Office of the Chief Engineer: Washington, DC, USA, 2021.
- Wang, C.; Zhao, Z.; Zhou, M.; Sigmund, O.; Zhang, X. A comprehensive review of educational articles on structural and multidisciplinary optimization. Struct. Multidiscip. Optim. 2021, 64, 2827–2880. [Google Scholar] [CrossRef]
- Liu, S.; Wang, q.; Gao, R. A topology optimization method for design of small GPR antennas. Struct. Multidiscip. Optim. 2014, 50, 1165–1174. [Google Scholar] [CrossRef]
- Zhou, S.; Li, W.; Li, Q. Level-set based topology optimization for electromagnetic dipole antenna design. J. Comput. Phys. 2010, 229, 6915–6930. [Google Scholar] [CrossRef]
- Erentok, A.; Sigmund, O. Topology Optimization of Sub-Wavelength Antennas. IEEE Trans. Antennas Propag. 2011, 59, 58–69. [Google Scholar] [CrossRef]
- Hassan, E.; Wadbro, E.; Berggren, M. Topology Optimization of Metallic Antennas. IEEE Trans. Antennas Propag. 2014, 62, 2488–2500. [Google Scholar] [CrossRef]
- Zhu, S.H.; Yang, X.S.; Wang, J.; Wang, B.Z. Miniaturization of patch antenna based on hybrid topology optimization. Int. J. Microw. Comput.-Aided Eng. 2020, 30, e22308. [Google Scholar] [CrossRef]
- Herscovici, N.; Osorio, M.; Peixeiro, C. Miniaturization of rectangular microstrip patches using genetic algorithms. IEEE Antennas Wirel. Propag. Lett. 2002, 1, 94–97. [Google Scholar] [CrossRef]
- Ouedraogo, R.O.; Rothwell, E.J.; Diaz, A.; Chen, S.Y.; Temme, A.; Fuchi, K. In Situ Optimization of Metamaterial-Inspired Loop Antennas. IEEE Antennas Wirel. Propag. Lett. 2010, 9, 75–78. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).