The Optimization of a Model for Predicting the Remaining Useful Life and Fault Diagnosis of Landing Gear
Abstract
:1. Introduction
2. Problem Statement
2.1. Effects of Missing Data on the Prediction Model
2.2. Challenges to Identifying Different Fault Causes through Vibration Signals
3. Methodology
3.1. Basics of PHM Methodology
- First step: data acquisition;
- Second step: data preprocessing;
- Third step: feature extraction;
- Fourth step: feature selection;
- Last step: constructing a health assessment model, a fault diagnosis model, and an RUL model.
3.2. Hyperparameter Optimization
3.2.1. Optimization of the RUL Model
| Algorithm 1: Random Search Optimization |
| function RandomSearch(model, hyperparameter_space, iterations): |
| best_score = 0 |
| for i = 1 to iterations do: |
| sampled_hyperparameters = SampleFrom(hyperparameter_space) |
| current_model = TrainModel(model, sampled_hyperparameters) |
| current_score = Evaluate(current_model) |
| if current_score > best_score: |
| best_score = current_score |
| best_hyperparameters = sampled_hyperparameters |
| return best_hyperparameters |
3.2.2. Optimization of the Fault Diagnosis Model
| Algorithm 2: Bayesian Optimization |
| Function BayesianOptimization(model, hyperparameter_space, evaluations): |
| Initialize an empty dataset D to store hyperparameters and their respective scores for i = 1 to evaluations do: surrogate_model = Fit(D) next_hyperparameters = SelectNext(surrogate_model, hyperparameter_space) new_score = Evaluate(model, next_hyperparameters) new_data_point = (next_hyperparameters, new_score) Add new_data_point to D best_hyperparameters = hyperparameters in D with the highest score return best_hyperparameters |
4. Results and Discussion
4.1. Health Indicator Model
4.2. RUL Prediction Model
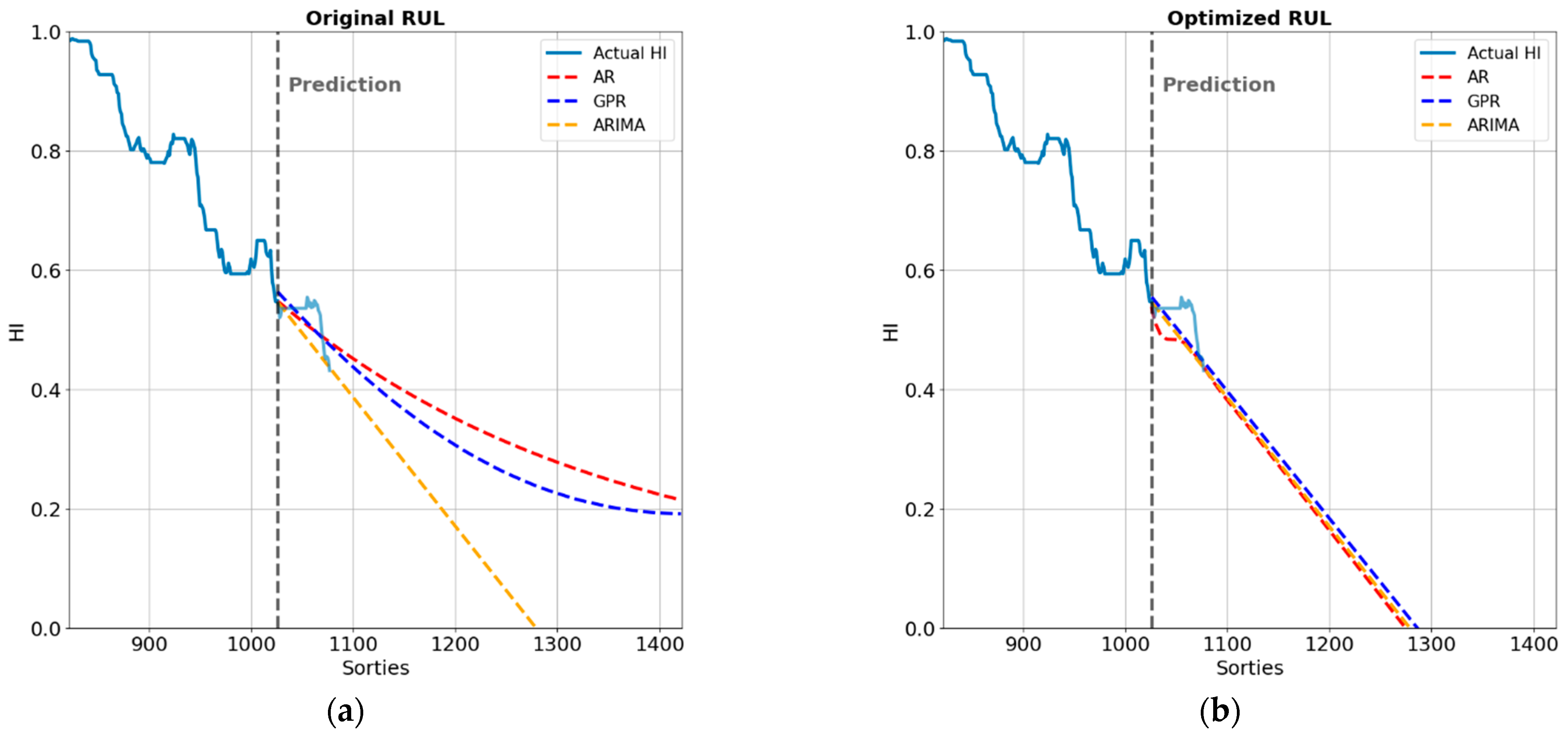
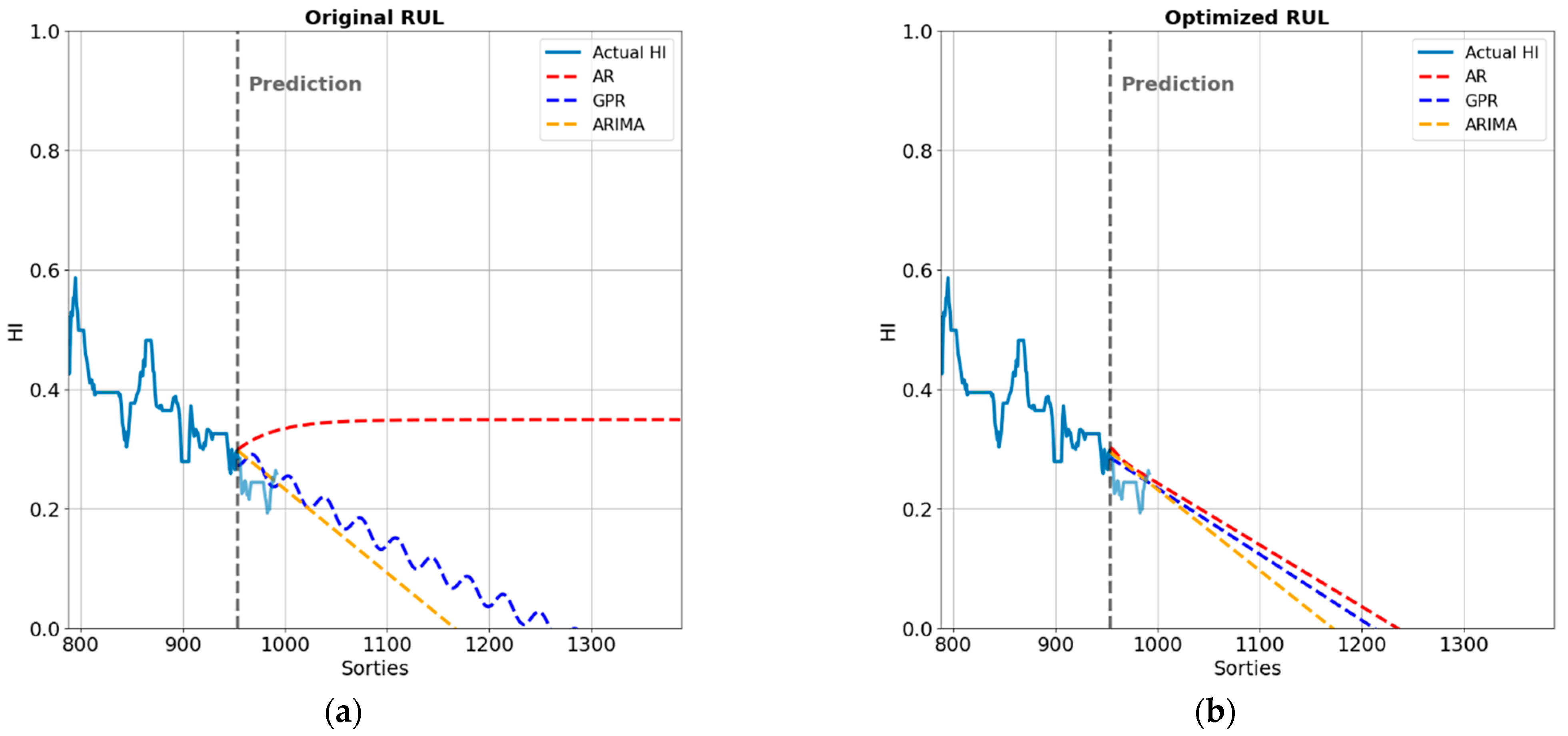
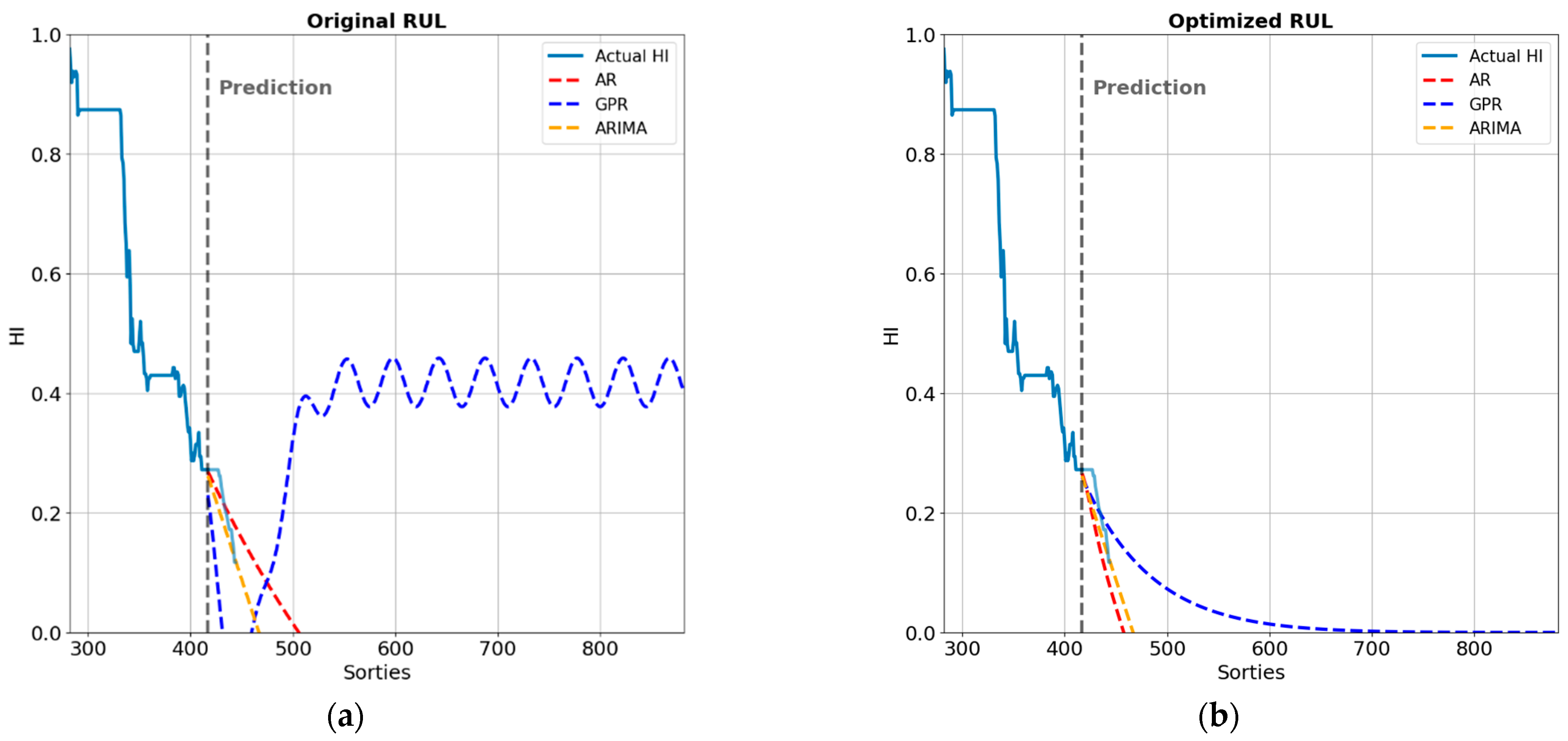
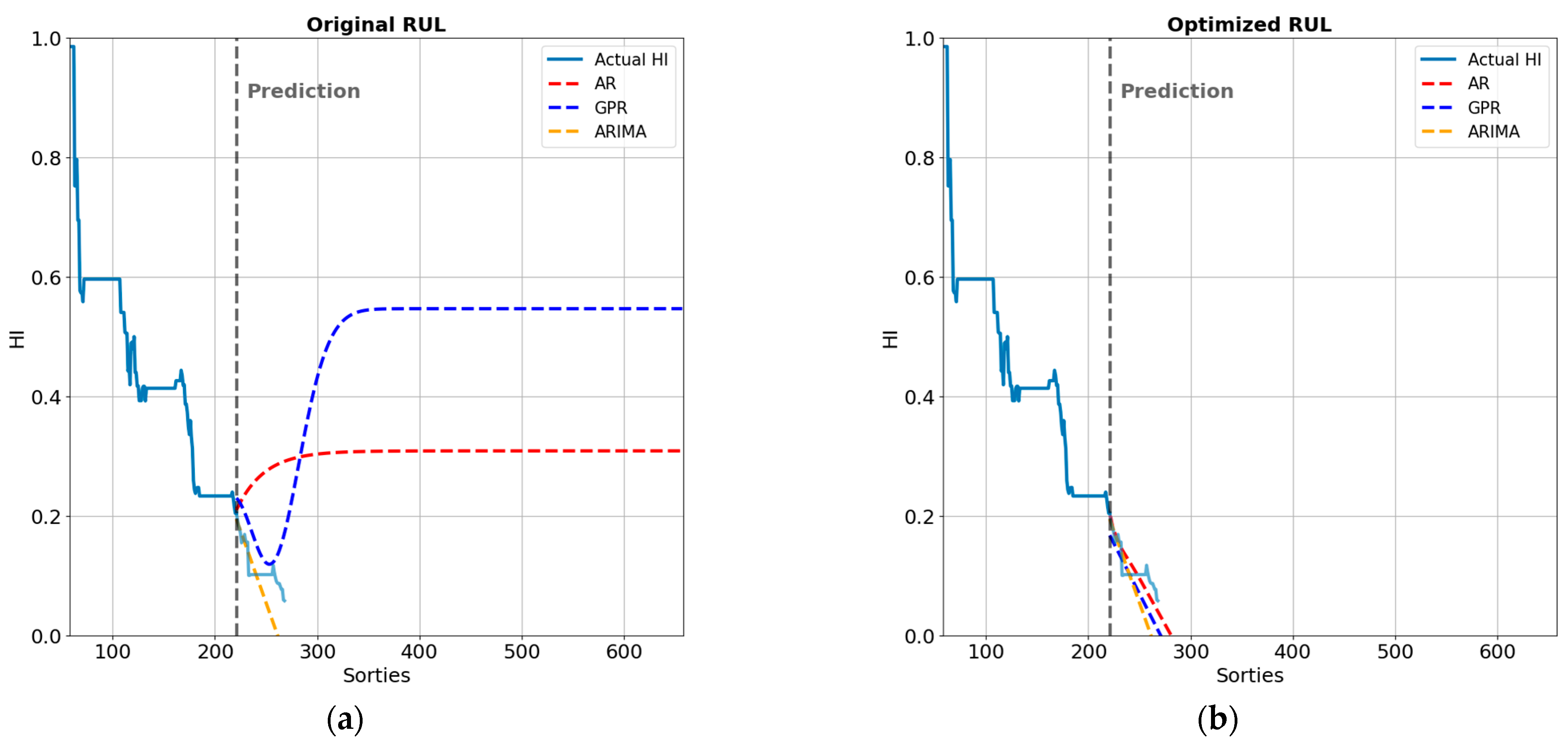
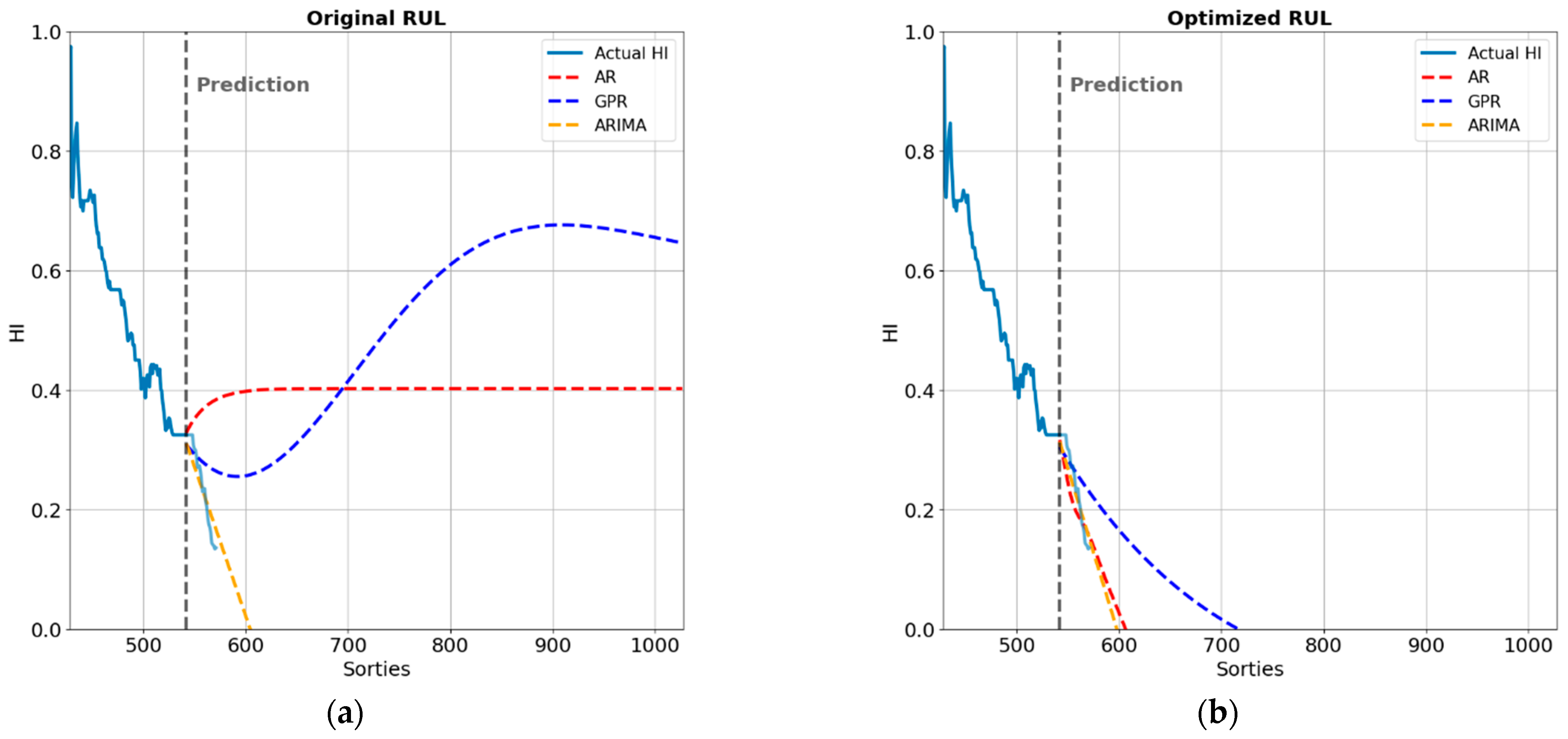
4.3. Optimization of the RUL Prediction Model
4.4. Optimization of the Fault Diagnosis Model
4.5. Applications of RUL Prediction Model and the Fault Diagnosis Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lernbeiss, R.; Plöchl, M. Simulation Model of an Aircraft Landing Gear Considering Elastic Properties of the Shock Absorber. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2007, 221, 77–86. [Google Scholar] [CrossRef]
- Currey, N.S. Aircraft Landing Gear Design: Principles and Practices; AIAA Education Series; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 1988; Available online: https://arc.aiaa.org/doi/book/10.2514/4.861468 (accessed on 25 October 2023).
- Czaban, M. Aircraft Corrosion—Review of Corrosion Processes and Its Effects in Selected Cases. Fatigue Aircr. Struct. 2018, 2018, 5–20. [Google Scholar] [CrossRef]
- Haider, S. Overview of prognostics and health management for landing gear maintenance. In Proceedings of the 2019 Annual Reliability and Maintainability Symposium (RAMS), Orlando, FL, USA, 28–31 January 2019; IEEE: New York, NY, USA, 2019; pp. 1–7. [Google Scholar]
- Lee, J.; Pater, I.; Boekweit, S.; Mitici, M. Remaining-Useful-Life prognostics for opportunistic grouping of maintenance of landing gear brakes for a fleet of aircraft. In Proceedings of the 7th European Conference of the Prognostics and Health Management Society, Turin, Italy, 6–8 July 2022. [Google Scholar]
- Lin, L.; Tong, C.; Guo, F.; Fu, S.; Lv, Y.; He, W. A Self-Attention Integrated Learning Model for Landing Gear Performance Prediction. Sensors 2023, 23, 6219. [Google Scholar] [CrossRef] [PubMed]
- Hsu, T.H.; Chang, Y.J.; Hsu, H.K.; Chen, T.T.; Hwang, P.W. Predicting the Remaining Useful Life of Landing Gear with Prognostics and Health Management (PHM). Aerospace 2022, 9, 462. [Google Scholar] [CrossRef]
- Allison, P.D. Missing data. In The Sage Handbook of Quantitative Methods in Psychology; Millsap, R.E., Maydeu-Olivares, A., Eds.; Sage Publications Ltd.: London, UK, 2009; pp. 72–89. [Google Scholar] [CrossRef]
- Smeulers, J.P.M.; Zeelen, R.; Bos, A. PROMIS—A Generic PHM Methodology Applied to Aircraft Subsystems. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 9–16 March 2002; Volume 6, p. 6. [Google Scholar]
- DoD Instruction. Operation of the Defense Acquisition System. DoD Instruction 5000.2. 12 May 2003. Available online: https://acqnotes.com/acqnote/acquisitions/dodi-5000 (accessed on 3 June 2016).
- Sodemann, A.; Li, Y.; Lee, J.; Lancaster, R.; Rucker, M.; Carnagie, J.; Inman, A. Data-driven surge map modeling for centrifugal air compressors. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Chicago, IL, USA, 5–10 November 2006. [Google Scholar]
- Sun, B.; Zeng, S.; Kang, R.; Pecht, M.G. Benefits and challenges of system prognostics. IEEE Trans. Reliab. 2012, 61, 323–335. [Google Scholar] [CrossRef]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Wang, D.; Tsui, K.L.; Miao, Q. Prognostics and health management: A review of vibration based bearing and gear health indicators. IEEE Access 2017, 6, 665–676. [Google Scholar] [CrossRef]
- Nguyen, K.T.P.; Medjaher, K.; Tran, D.T. A review of artificial intelligence methods for engineering prognostics and health management with implementation guidelines. Artif. Intell. Rev. 2023, 56, 3659–3709. [Google Scholar] [CrossRef]
- Li, P.; Jia, X.; Feng, J.; Davari, H.; Qiao, G.; Hwang, Y.; Lee, J. Prognosability Study of Ball Screw Degradation Using Systematic Methodology. Mech. Syst. Signal Process. 2018, 109, 45–57. [Google Scholar] [CrossRef]
- Watt, J.; Borhani, R.; Katsaggelos, A. Machine Learning Refined: Foundations, Algorithms, and Applications; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar] [CrossRef]
- Yule, G.U. Why do we sometimes get nonsense-correlations between time series? A study in sampling and the nature of time series. J. R. Stat. Soc. 1926, 89, 1–64. [Google Scholar] [CrossRef]
- Fattah, J.; Ezzine, L.; Aman, Z.; El Moussami, H.; Lachhab, A. Forecasting of demand using ARIMA model. Int. J. Eng. Bus. Manag. 2018, 10, 1847979018808673. [Google Scholar] [CrossRef]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Chen, H.; Peng, Y.; Yang, Q.; Yan, L. Fault Diagnosis of Uninterruptible Power System Based on Gaussian Mixed Model and XGBoost. In Proceedings of the 2020 15th International Conference on Computer Science & Education (ICCSE), Delft, The Netherlands, 18–22 August 2020; pp. 627–634. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Zhu, P.; Liu, W.; Sun, Y.; Chai, W.; Guo, P. Wind Turbine Generator Bearing Early Fault Warning Based on Feature Fusion and XGBoost. In Proceedings of the 10th Renewable Power Generation Conference (RPG 2021), Online Conference, 14–15 October 2021; pp. 633–640. [Google Scholar] [CrossRef]
- Frazier, P.I. A tutorial on Bayesian optimization. arXiv 2018, arXiv:1807.02811. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Parameters of AR, ARIMA Used in the Statsmodels Package. Available online: https://www.statsmodels.org/devel/generated/statsmodels.tsa.arima.model.ARIMA.html (accessed on 20 August 2023).
- Parameters of GPR Used in the Scikit-Learn Package. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.gaussian_process.GaussianProcessRegressor.html (accessed on 20 August 2023).
- Bergstra, J.; Yamins, D.; Cox, D. Making a Science of Model Search: Hyperparameter Optimization in Hundreds of Dimensions for Vision Architectures. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 115–123. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 4. [Google Scholar]
- Fu, Y.; Liu, Y.; Gao, Z. Multiple actuator fault classification in wind turbine systems using multi-linear principal component analysis techniques. In Proceedings of the 2019 25th International Conference on Automation and Computing (ICAC), Lancaster, UK, 5–7 September 2019; IEEE: New York, NY, USA, 2019; pp. 1–6. [Google Scholar]
- Cleveland, W.S. Robust Locally Weighted Regression and Smoothing Scat-terplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Jain, A. Mastering XGBoost Parameter Tuning: A Complete Guide with Python Codes. 2023. Available online: https://www.analyticsvidhya.com/blog/2016/03/complete-guide-parameter-tuning-xgboost-with-codes-python/ (accessed on 25 October 2023).
- Vabalas, A.; Gowen, E.; Poliakoff, E.; Casson, A.J. Machine learning algorithm validation with a limited sample size. PLoS ONE 2019, 14, e0224365. [Google Scholar] [CrossRef] [PubMed]

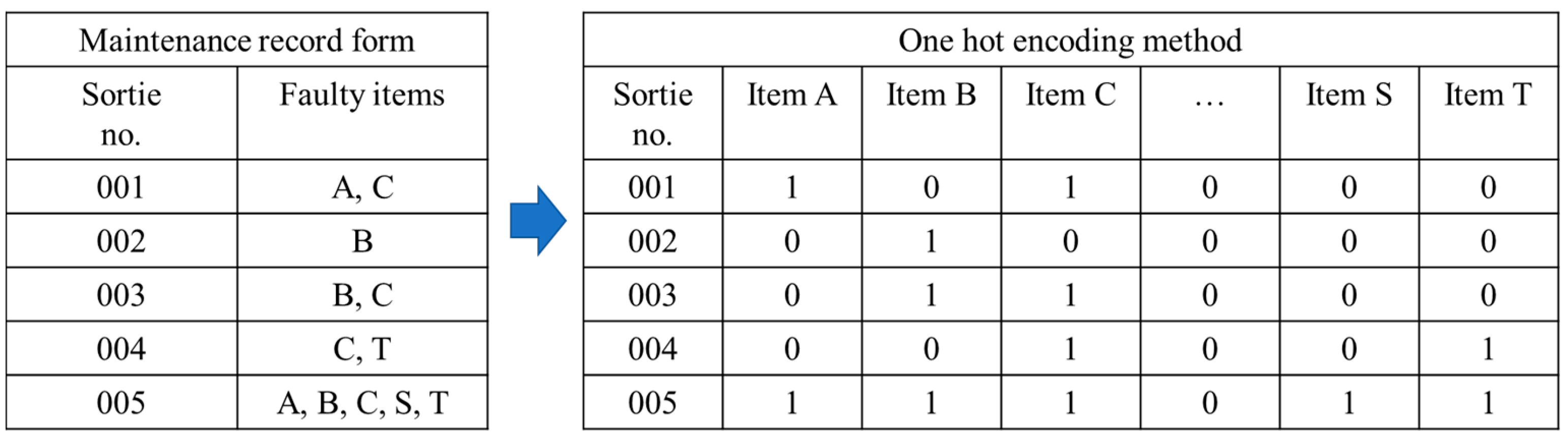

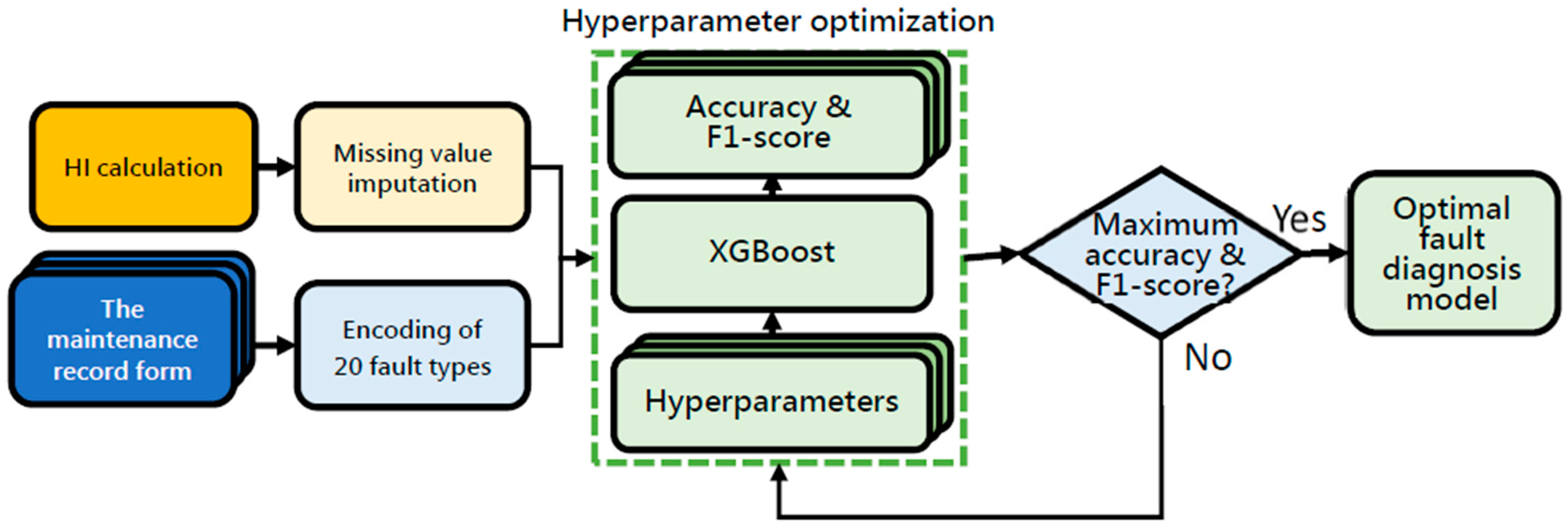
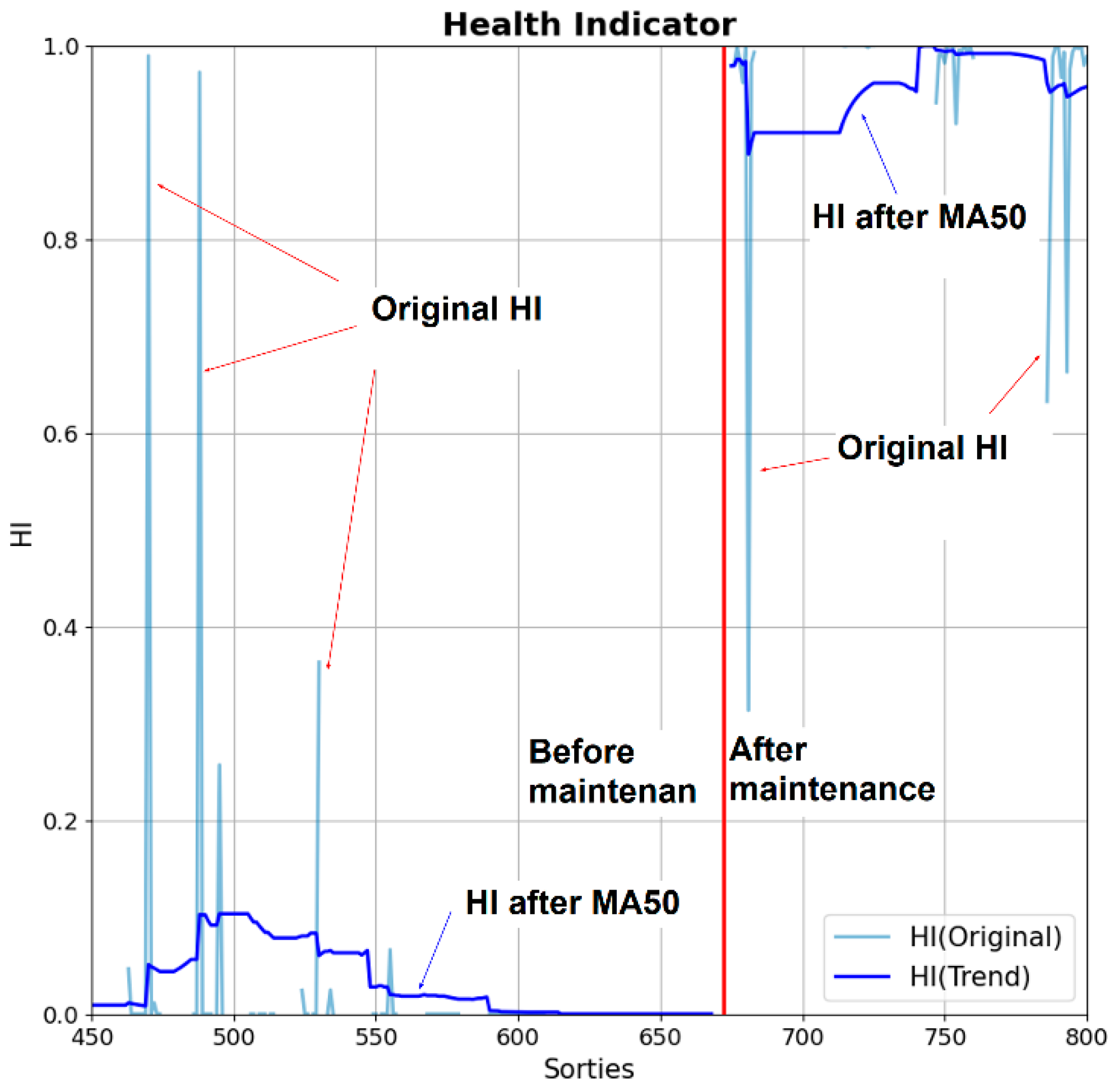
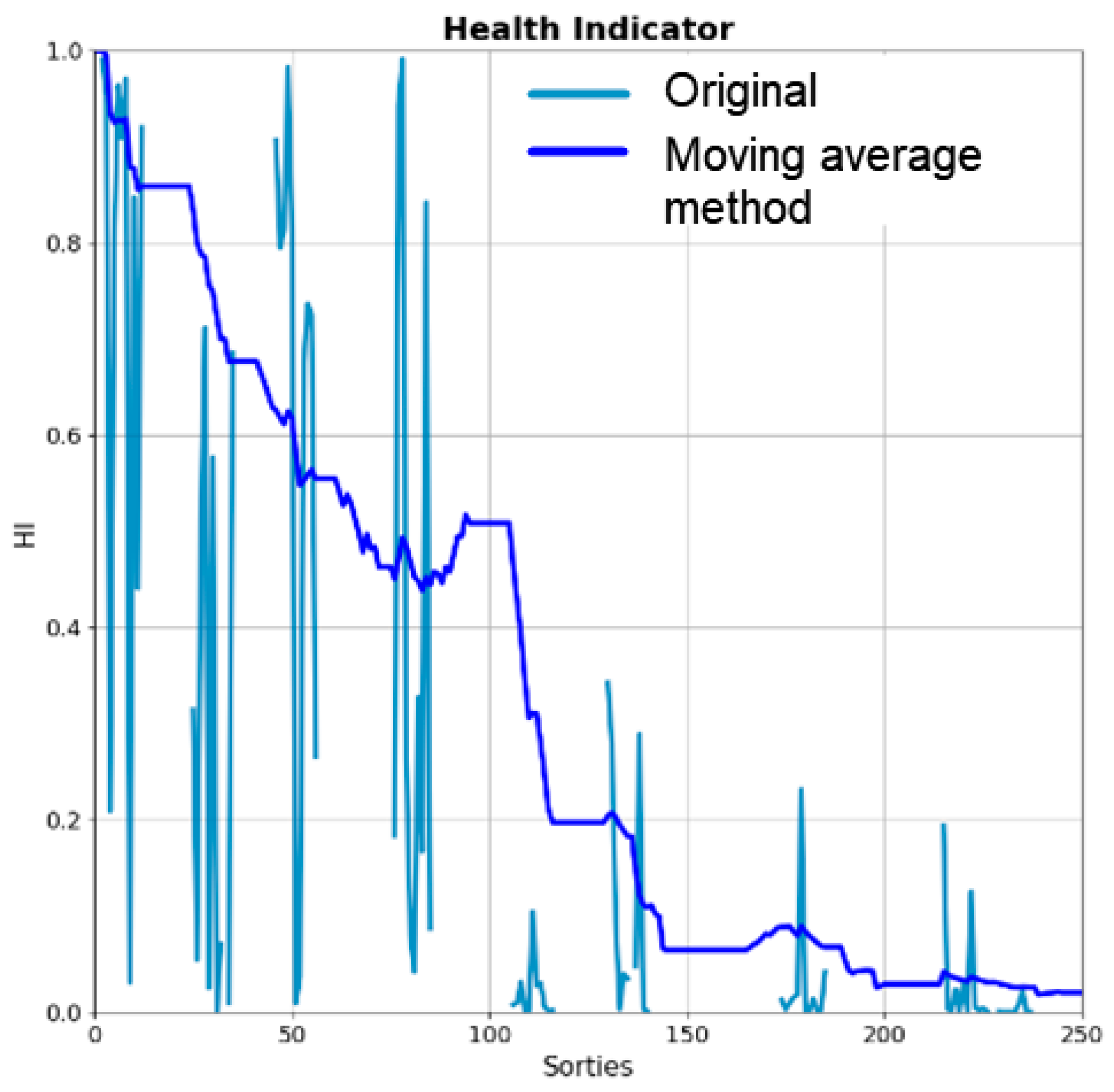




| Item No. | Malfunctioning Item | Number of Data |
|---|---|---|
| A | Rose wheel/tire | 224 |
| B | Left main wheel/tire | 947 |
| C | Right main wheel/tire | 899 |
| D | Main wheel/tire | 57 |
| E | Main wheel hub | 106 |
| F | Nose wheel hub | 77 |
| G | Nose landing gear drag brace | 25 |
| H | Left landing gear drag brace | 25 |
| I | Right landing gear drag brace | 41 |
| J | Left landing gear brake | 69 |
| K | Right landing gear brake | 61 |
| L | Nose landing gear retract actuator | 22 |
| M | Left landing gear retract actuator | 24 |
| N | Right landing gear retract actuator | 27 |
| O | Nose landing gear shock strut | 37 |
| P | Left landing gear shock strut | 37 |
| Q | Right landing gear shock strut | 40 |
| R | Steering actuator | 27 |
| S | Steering control valve | 5 |
| T | Brake control valve | 26 |
| Total | 2776 |
| No | Hyperparameter | Search Range | Description |
|---|---|---|---|
| 1 | P | Integer (0–10) | Number of previous time steps. |
| No | Hyperparameter | Search Range | Description |
|---|---|---|---|
| 1 | P | Integer (0–10) | Number of previous time steps. |
| 2 | D | Integer (0–5) | Number of times differencing. |
| 3 | Q | Integer (0–10) | Number of previous forecast errors. |
| No | Hyperparameter | Search Range | Description |
|---|---|---|---|
| 1 | Kernel | Categorical (‘kernel_rbf’, ‘kernel_rq’, ‘kernel_expsine’, ‘kernel_matern’, ‘kernel_dotproduct’) | Kernel specifying the covariance function of the Gaussian process. |
| 2 | Alpha | Integer ( , , , , ,) | Value added to the diagonal of the kernel matrix during fitting. |
| 3 | n_restarts_optimizer | Integer (0, 1, 2, 3) | Number of restarts of the optimizer for finding the kernel parameters that maximize the log-marginal likelihood. |
| No | Hyperparameter | Search Range | Description |
|---|---|---|---|
| 1 | n_estimators | Integer (100–10,000) | Number of boosting rounds. |
| 2 | max_depth | Integer (100–10,000) | Maximum tree depth for base learners. |
| 3 | learning_rate | Real number (0.01–0.5) | Boosting learning rate. |
| 4 | Booster | Categorical (‘gbtree’, ‘dart’) | Specify which booster to use: gbtree, gblinear, or dart. |
| 5 | Gamma | Real number (0–1000) | Minimum loss reduction required to make a further partition on a leaf node of the tree. |
| 6 | min_child_weight | Real number (1–100) | Minimum sum of instance weight (hessian) needed in a child. |
| 7 | Subsample | Real number (0.5–1) | Subsample ratio of the training instance. |
| 8 | colsample_bytree | Real number (0.5–1) | Subsample ratio of columns when constructing each tree. |
| 9 | reg_alpha | Real number (0–1) | L1 regularization term on weights. |
| 10 | reg_lambda | Real number (0–1) | L2 regularization term on weights. |
| Airplane Number | Optimization | Actual HI of Latest Flight | Predicted HI of Latest Flight | RMSE | Error Range |
|---|---|---|---|---|---|
| Airplane #1 | Before | 0.379 | 0.391 | 0.013 | [−0.017, 0.026] |
| After | 0.379 | 0.358 | 0.022 | [0.000, 0.047] | |
| Airplane #2 | Before | 0.718 | 0.712 | 0.026 | [−0.081, 0.010] |
| After | 0.718 | 0.685 | 0.030 | [−0.045, 0.048] | |
| Airplane #3 | Before | 0.431 | 0.479 | 0.027 | [−0.048, 0.050] |
| After | 0.431 | 0.436 | 0.050 | [−0.005, 0.071] | |
| Airplane #4 | Before | 0.259 | 0.331 | 0.082 | [−0.133, 0.014] |
| After | 0.259 | 0.251 | 0.040 | [−0.071, 0.012] | |
| Airplane #5 | Before | 0.117 | 0.176 | 0.028 | [−0.062, 0.039] |
| After | 0.117 | 0.077 | 0.056 | [−0.007, 0.081] | |
| Airplane #6 | Before | 0.058 | 0.291 | 0.157 | [−0.233, −0.006] |
| After | 0.058 | 0.040 | 0.022 | [−0.043, 0.043] | |
| Airplane #7 | Before | 0.136 | 0.384 | 0.145 | [−0.249, −0.003] |
| After | 0.136 | 0.155 | 0.040 | [−0.027, 0.063] | |
| Average | Before | 0.0682 | |||
| After | 0.0371 |
| Airplane Number | Optimization | Actual HI of Latest Flight | Predicted HI of Latest Flight | RMSE | Error Range |
|---|---|---|---|---|---|
| Airplane #1 | Before | 0.379 | 0.340 | 0.038 | [0.005, 0.065] |
| After | 0.379 | 0.342 | 0.036 | [0.004, 0.064] | |
| Airplane #2 | Before | 0.718 | 0.677 | 0.024 | [−0.050, 0.044] |
| After | 0.718 | 0.677 | 0.024 | [−0.050, 0.044] | |
| Airplane #3 | Before | 0.431 | 0.436 | 0.043 | [−0.022, 0.081] |
| After | 0.431 | 0.435 | 0.044 | [−0.021, 0.081] | |
| Airplane #4 | Before | 0.259 | 0.244 | 0.038 | [−0.066, 0.019] |
| After | 0.259 | 0.243 | 0.037 | [−0.064, 0.020] | |
| Airplane #5 | Before | 0.117 | 0.120 | 0.037 | [−0.008, 0.063] |
| After | 0.117 | 0.120 | 0.037 | [−0.008, 0.063] | |
| Airplane #6 | Before | 0.058 | −0.032 | 0.054 | [−0.037, 0.100] |
| After | 0.058 | −0.032 | 0.054 | [−0.036, 0.100] | |
| Airplane #7 | Before | 0.136 | 0.167 | 0.027 | [−0.044, 0.043] |
| After | 0.136 | 0.151 | 0.025 | [−0.030, 0.045] | |
| Average | Before | 0.0372 | |||
| After | 0.0367 |
| Airplane Number | Optimization | Actual HI of Latest Flight | Predicted HI of Latest Flight | RMSE | Error Range |
|---|---|---|---|---|---|
| Airplane #1 | Before | 0.379 | 0.704 | 0.163 | [−0.325, −0.002] |
| After | 0.379 | 0.314 | 0.063 | [0.024, 0.094] | |
| Airplane #2 | Before | 0.718 | 0.771 | 0.068 | [−0.136, −0.043] |
| After | 0.718 | 0.707 | 0.027 | [−0.080, 0.014] | |
| Airplane #3 | Before | 0.431 | 0.474 | 0.027 | [−0.043, 0.050] |
| After | 0.431 | 0.446 | 0.037 | [−0.030, 0.071] | |
| Airplane #4 | Before | 0.259 | 0.238 | 0.039 | [−0.073, 0.027] |
| After | 0.259 | 0.243 | 0.032 | [−0.060, 0.020] | |
| Airplane #5 | Before | 0.117 | −0.107 | 0.206 | [0.043, 0.268] |
| After | 0.117 | 0.173 | 0.031 | [−0.058, 0.049] | |
| Airplane #6 | Before | 0.058 | 0.171 | 0.051 | [−0.113, −0.005] |
| After | 0.058 | 0.009 | 0.037 | [−0.027, 0.071] | |
| Airplane #7 | Before | 0.136 | 0.264 | 0.068 | [−0.131, 0.029] |
| After | 0.058 | 0.009 | 0.037 | [−0.027, 0.071] | |
| Average | Before | 0.0888 | |||
| After | 0.0398 |
| Item | Malfunctioning Item | Accuracy | Precision Rate | Recall Rate | F1 Score |
|---|---|---|---|---|---|
| A | Nose wheel/tire | 99.96% | 100.00% | 96.88% | 98.41% |
| B | Left main wheel/tire | 99.73% | 100.00% | 95.56% | 97.73% |
| C | Right main wheel/tire | 99.80% | 100.00% | 96.44% | 98.19% |
| D | Main wheel/tire | 99.97% | 100.00% | 91.23% | 95.41% |
| E | Main wheel hub | 99.95% | 100.00% | 92.45% | 96.08% |
| F | Nose wheel hub | 99.97% | 100.00% | 93.51% | 96.64% |
| G | Nose landing gear drag brace | 99.99% | 100.00% | 96.00% | 97.96% |
| H | Left landing gear drag brace | 100.0% | 100.00% | 100.00% | 100.00% |
| I | Right landing gear drag brace | 100.0% | 100.00% | 100.00% | 100.00% |
| J | Left landing gear brake | 99.98% | 100.00% | 95.45% | 97.67% |
| K | Right landing gear brake | 99.98% | 100.00% | 95.08% | 97.48% |
| L | Nose landing gear retract actuator | 100.00% | 100.00% | 100.00% | 100.00% |
| M | Left landing gear retract actuator | 100.00% | 100.00% | 100.00% | 100.00% |
| N | Right landing gear retract actuator | 99.99% | 100.00% | 96.30% | 98.11% |
| O | Nose landing gear shock strut | 99.99% | 100.00% | 97.30% | 98.63% |
| P | Left landing gear shock strut | 100.00% | 100.00% | 100.00% | 100.00% |
| Q | Right landing gear shock strut | 99.99% | 100.00% | 97.50% | 98.73% |
| R | Steering actuator | 100.00% | 100.00% | 100.00% | 100.00% |
| S | Steering control valve | 100.00% | 100.00% | 100.00% | 100.00% |
| T | Brake control valve | 99.99% | 100.00% | 92.31% | 96.00% |
| Average | 99.96% | 100.00% | 96.80% | 98.35% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.-J.; Hsu, H.-K.; Hsu, T.-H.; Chen, T.-T.; Hwang, P.-W. The Optimization of a Model for Predicting the Remaining Useful Life and Fault Diagnosis of Landing Gear. Aerospace 2023, 10, 963. https://doi.org/10.3390/aerospace10110963
Chang Y-J, Hsu H-K, Hsu T-H, Chen T-T, Hwang P-W. The Optimization of a Model for Predicting the Remaining Useful Life and Fault Diagnosis of Landing Gear. Aerospace. 2023; 10(11):963. https://doi.org/10.3390/aerospace10110963
Chicago/Turabian StyleChang, Yuan-Jen, He-Kai Hsu, Tzu-Hsuan Hsu, Tsung-Ti Chen, and Po-Wen Hwang. 2023. "The Optimization of a Model for Predicting the Remaining Useful Life and Fault Diagnosis of Landing Gear" Aerospace 10, no. 11: 963. https://doi.org/10.3390/aerospace10110963
APA StyleChang, Y.-J., Hsu, H.-K., Hsu, T.-H., Chen, T.-T., & Hwang, P.-W. (2023). The Optimization of a Model for Predicting the Remaining Useful Life and Fault Diagnosis of Landing Gear. Aerospace, 10(11), 963. https://doi.org/10.3390/aerospace10110963






